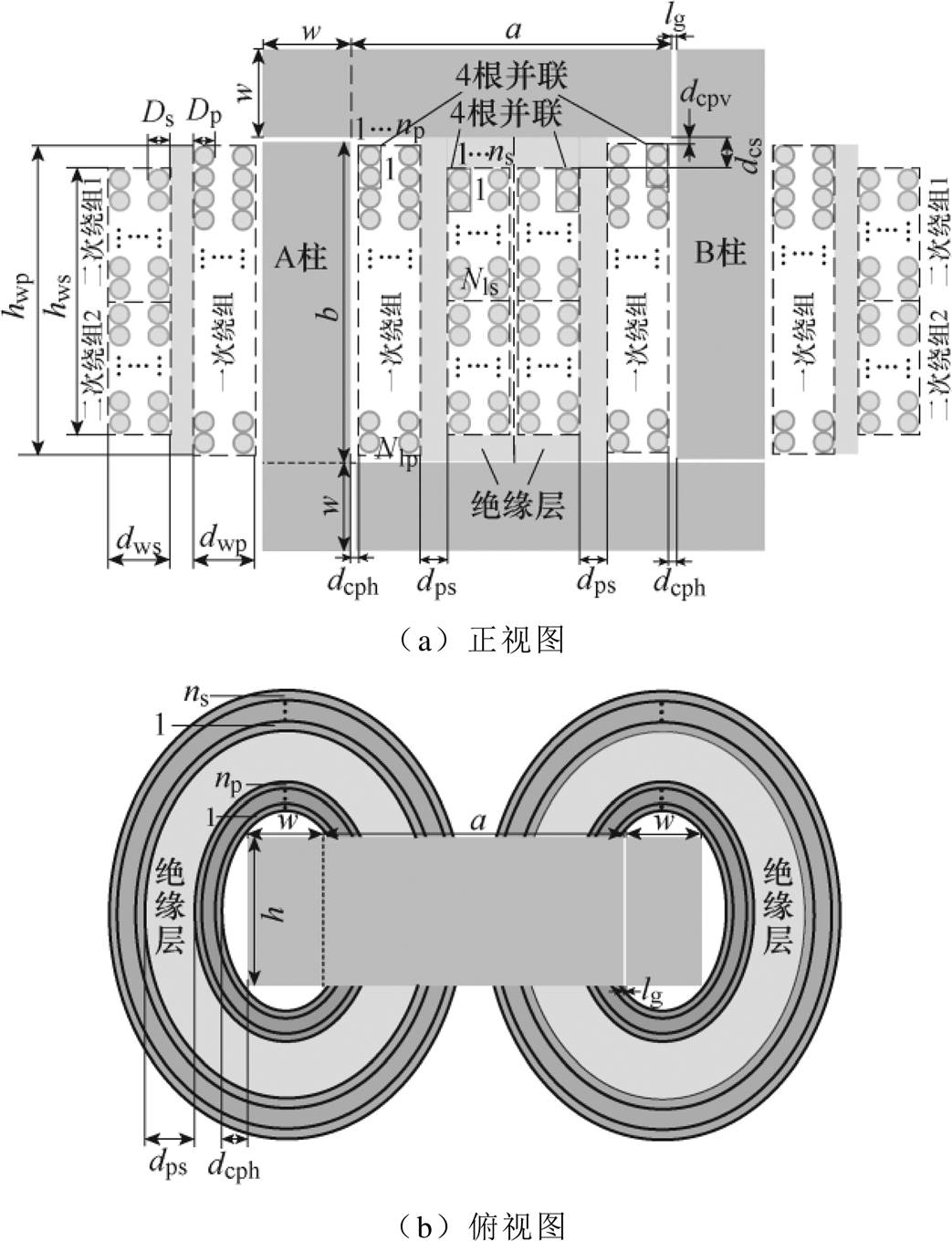
图1 MFT的结构
Fig.1 Structure of MFT
摘要 应用于光伏并网系统的中压绝缘大功率中频变压器（MFT）不仅要求其高低压侧绕组之间需要满足较大的绝缘间距，而且其内部也需要浇注隔热的绝缘材料。然而，这会导致MFT出现电磁干扰现象严重、散热困难等问题。针对这些问题，该文提出一种全面考虑铁心尺寸、绕组线径和绕组排布结构的MFT优化设计方法。该方法通过面积乘积（AP）法确定铁心体积，再通过自由变量扫描对MFT进行损耗最小化设计。基于有限元仿真软件，验证了该优化设计方法可使变压器漏电感减小及周围的电磁干扰区域缩小。最后，通过该优化设计方法设计一台200kW/ 30kHz的MFT，并制作了样机。通过理论和实验的对比，验证了优化设计方法的有效性和准确性。
关键词：大功率中频变压器 绝缘 面积乘积法 损耗建模 优化设计 电磁干扰 有限元仿真
由于光伏发电逐渐形成大规模集中开发和中高压接入电网的局面，对电气设备的体积和质量也有一定的限制[1-4]，使得中压大功率电力电子变压器受到了广泛关注。相比于传统低频变压器，大功率电力电子变压器中工作频率大多在1～50kHz的中频范围，因此具有更小的体积和质量[5-9]。受目前开关器件耐压水平的限制，电力电子变压器的隔离和升压一般通过多个模块化大功率DC-DC变换器级联实现[10]，在低压侧并联，高压侧串联。
中频变压器（Medium Frequency Transformer, MFT）作为DC-DC变换器的核心器件之一，由于自身结构的紧凑性，以及中频和中压的结合，使其设计具有较大的挑战性。首先，频率的升高虽然可以实现更高的功率密度，但也会导致MFT的绕组损耗和铁心损耗增大[11-13]，从而增大了散热难度且限制了效率的提高。其次，中压带来的绝缘需求也会产生两个问题：①高压侧绕组和低压侧绕组之间需要保持较大的绝缘间距，这使得MFT会产生更多的高频漏磁，从而对DC-DC变换器中的其他电路产生电磁干扰[14]，影响稳定性；②MFT内部浇注隔热的绝缘材料，这导致变压器的散热难度进一步增大。所以在设计MFT时，不仅需要满足功率密度的需求，而且也需要最小化损耗来尽可能地降低温升，同时也要兼顾MFT电磁干扰的影响。
一般选择低损耗密度的铁心材料（如铁氧体、纳米晶）可以降低铁心损耗。通过降低绕组交流电阻和直流电阻的比值（称为交流电阻因子），可以降低绕组的交流损耗[15]。交流电阻因子主要受趋肤效应和邻近效应的影响[16]。绕组选择利兹线或者铜箔可以有效地降低趋肤效应的影响[17]；改变绕组排布（绕组层数）和铁心尺寸可以降低绕组周围的磁场强度，从而降低邻近效应的影响。故为了最小化MFT损耗，需要考虑铁心材料、铁心尺寸、绕组材料、绕组尺寸和绕组排布等关键参数。
由于铁心磁导率不是无穷大，故实际MFT会存在漏磁通。一方面，漏磁通形成的漏感可被LLC谐振变换器、隔离型DC-DC变换器等用作能量传递元件[18-20]。LLC谐振变换器因具有全负载范围内实现软开关的特性而被广泛使用。LLC谐振变换器使用漏感作为谐振电感时，漏感越小使得LLC谐振变换器的谐振电容电压应力越小；另一方面，因为模块化DC-DC变换器的功率密度较高，MFT的高频漏磁通产生的电磁干扰可能会在周围电路上产生感应电压和电流，同时产生额外损耗，从而降低电路稳定性和变换器的效率。因此，在设计MFT时应尽量减少漏磁通或对其进行屏蔽。
MFT的优化设计方法已有较多研究。面积乘积（Area Product, AP）法作为常用的MFT设计方法，能够快速地通过解析公式对MFT进行设计[21-22]。但因为AP法对铁心的设计多是根据其计算得到的面积乘积的值选择合适的商用铁心，这使得MFT的损耗并不一定能达到最小。文献[23]介绍了通过遗传算法来兼顾损耗和漏感的MFT多目标优化设计，并设计了一台3.52kW/20kHz的MFT。但自由变量仅仅考虑了绕组的排布参数，这也会导致损耗不能达到最小。文献[24]介绍了在考虑温度、磁通密度、介电强度以及外部尺寸的限制条件下，通过自由参数扫描选出以功率密度和损耗为设计目标的最优方案，并设计了一台166kW/20kHz的MFT。然而，绕组尺寸从标准尺寸列表中选择，同样会限制损耗的最小化设计。文献[25]介绍了通过自由参数扫描，找到满足效率、隔离、散热和漏感要求的最高功率密度MFT，设计了一台1MW/5kHz的具有较高绝缘性能的MFT。但没有考虑损耗的最小化设计以及绝缘带来的电磁干扰问题。文献[26]介绍了通过自由参数扫描法选出兼顾损耗、漏感和质量的MFT最优设计方案，设计了一台300kW/5kHz的高绝缘性能的MFT，同样也没有对电磁干扰问题进行研究。
为了实现中压绝缘大功率MFT的损耗最小化设计，同时兼顾电磁干扰问题。本文提出了一种全面考虑铁心尺寸、绕组线径和绕组排布结构的MFT优化设计方法。该方法使用AP法设计铁心体积，建立铁心和绕组损耗模型并通过自由参数扫描使MFT损耗达到最小。对所述的MFT损耗最小化方法进一步分析，证明其也会带来漏感的降低以及电磁干扰区域的缩小。随后，基于Ansys Maxwell有限元仿真软件，对上述分析的正确性进行验证。最后，根据提出的MFT优化设计方法设计并制作了一台35kV绝缘、200kW/30kHz的MFT样机，对所提优化设计方法的有效性和准确性进行验证。
本文研究的MFT应用于35kV光伏并网系统DC-DC变换器中，变换器为LLC谐振变换器，MFT结构和LLC谐振变换器电路拓扑分别如图1、图2所示。铁心选用铁氧体材料，由多个磁块拼接而成，气隙设置在铁心的拼接处。绕组由一个一次绕组（低压侧）和两个相同的二次绕组（高压侧）组成。一次和二次绕组每匝均使用4根相同的导线并联。绕组采用双柱绕制结构，一次与二次绕组均分成相同的两部分，分别绕制在铁心的A柱和B柱上。为了满足高压绕组与低压绕组、铁心之间35kV的绝缘要求，需要留出足够的绝缘间距用来填充绝缘材料。
图1 MFT的结构
Fig.1 Structure of MFT
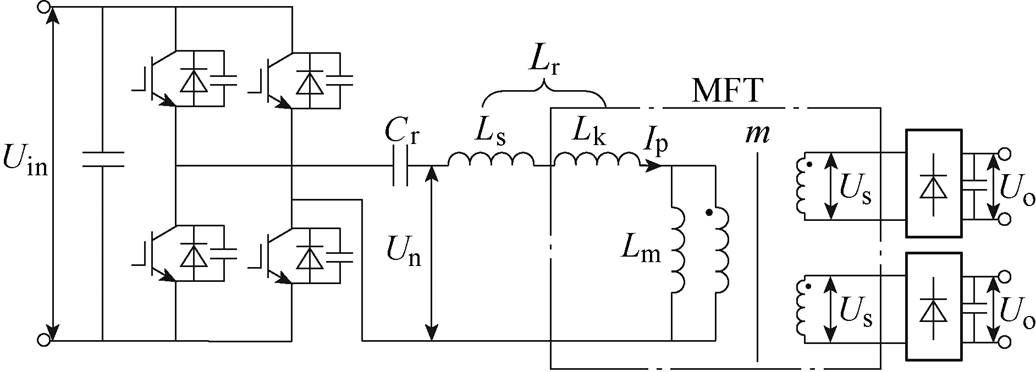
图2 LLC谐振变换器电路拓扑
Fig.2 LLC resonant converter circuit topology
图1中，a、b分别为铁心窗口的宽度和高度；w、h分别为铁心柱截面的宽度和厚度；lg为气隙的厚度；np、ns分别为一次和二次绕组的层数；Nlp、Nls分别为一次和二次绕组每层的匝数；Dp、Ds分别为一次和二次绕组的每根导线外直径（包含绝缘层）；dcph、dcpv分别为一次绕组到铁心柱和铁轭的距离；hwp和hws分别为一次和二次绕组的高度；dwp和dws分别为一次和二次绕组的宽度；dps为一次和二次绕组间的绝缘间距；dcs为二次绕组和铁心的绝缘间距。图2中，Uin为LLC谐振变换器的输入电压；Uo为LLC谐振变换器的输出电压；Cr为谐振电容；Lr为谐振电感，由外接电感Ls和MFT的漏感Lk组成；Lm为励磁电感；Un为Lr和Lm上的电压之和；Us为变换器的输出电压。
基于应用场合相关电气参数，35kV绝缘MFT的设计要求见表1。
表1 35kV MFT的绝缘设计要求
Tab.1 Design requirements of 35kV insulated MFT
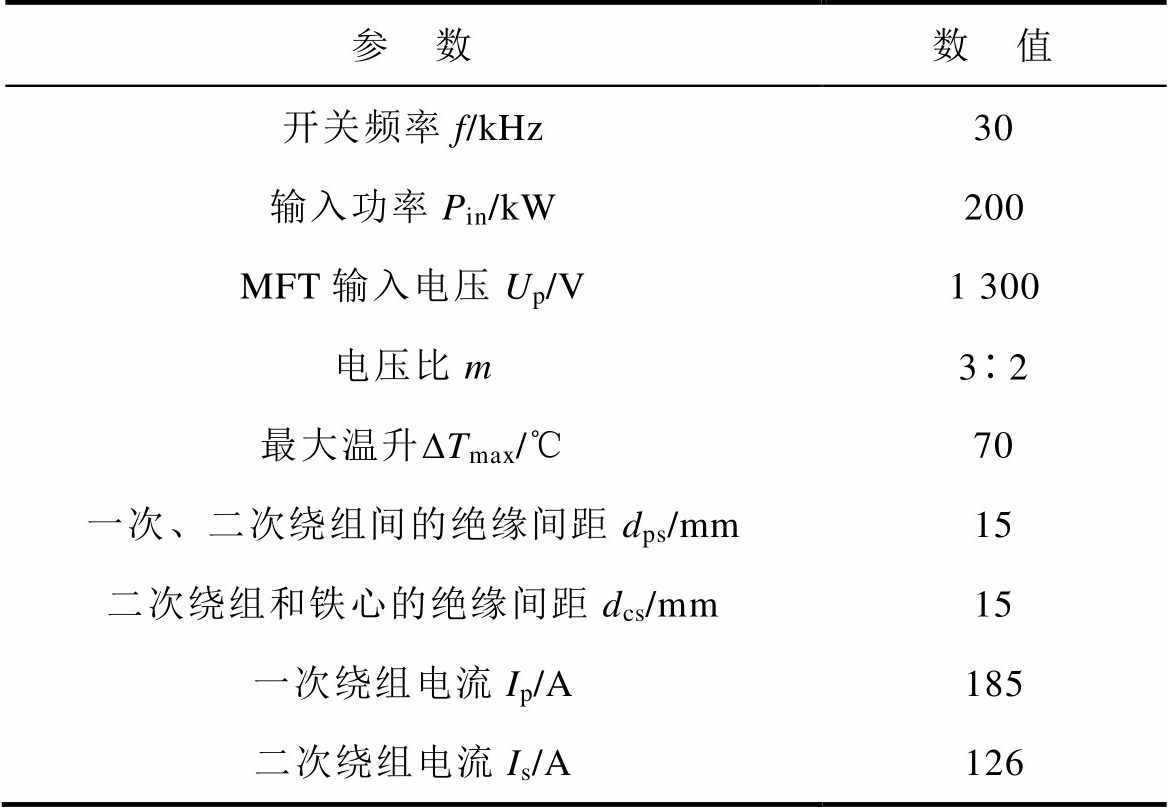
参 数数 值 开关频率f/kHz30 输入功率Pin/kW200 MFT输入电压Up/V1 300 电压比m32 最大温升DTmax/℃70 一次、二次绕组间的绝缘间距dps/mm15 二次绕组和铁心的绝缘间距dcs/mm15 一次绕组电流Ip/A185 二次绕组电流Is/A126
首先对MFT的铁心体积进行设计。根据文献[21]可知，MFT的铁心体积和AP值之间存在的约束关系为
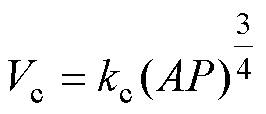（1）
式中，Vc为铁心体积；kc为一个常系数，与铁心类型有关。可以看出，在铁心材料确定后，保持AP的值不变，即可保证铁心体积不变。
为了能够满足温升限制，本文引用AP法中的面积乘积的计算公式设计铁心体积[22]，如式（2）所示。其中，初始的最大磁通密度Bm根据铁心类型与其损耗曲线选择合适的值。
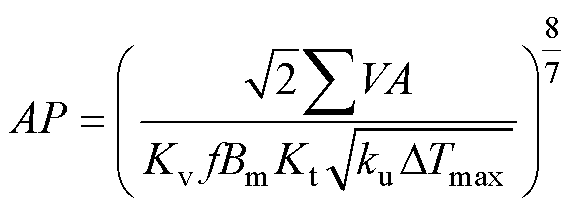（2）
式中，AP为铁心的窗口面积Aw和铁心柱的截面积Ae的乘积，根据图1所示的变压器铁心结构，AP值由窗口长度a、窗口高度b、铁心柱截面宽度w、铁心柱截面厚度h决定，为保证AP不变，应保证4个变量乘积与等式右边相等；
为MFT的输入和输出功率之和；Kv为电压波形因数，方波时Kv=4，正弦波时Kv=4.44；Kt为一个常系数，Kt=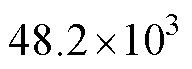
；ku为窗口利用率，其数值为铁心窗口中总的绕组有效截面积和窗口面积的比值。
在确定铁心体积之后，继续对铁心损耗和绕组损耗进行建模，并分析MFT关键的自由变量。
在电力电子变压器中，电压波形大多为矩形波。为了保证模型的精度，本文引用改进的通用斯坦梅兹公式（Improved Generalized Steinmetz Equation, IGSE）[27]，该公式可较为准确地计算任意非正弦激励下的铁心损耗，即
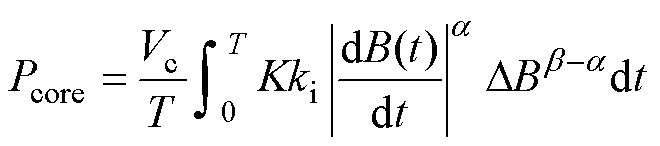（3）
其中
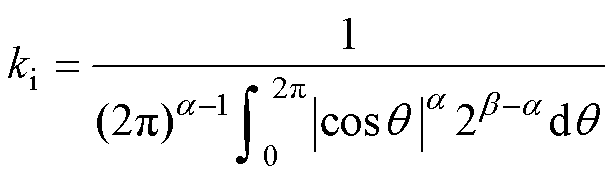（4）
式中，K、a、b为常系数，可以从铁心的损耗曲线或数据手册中得到；T为电压周期；dB(t)/dt为磁通密度B随时间t的变化率；DB为B的峰峰值，本文中，DB=2Bm。
根据法拉第电磁感应定律，Bm可以表示为
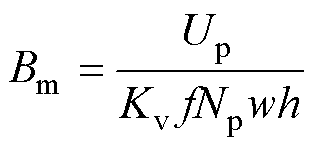（5）
式中，Np为一次绕组的匝数。因铁心体积不变可知，铁心损耗主要由Np、w和h决定。
在中高频下，绕组因邻近效应和趋肤效应而产生交流损耗，可采用Dowell模型对交流损耗进行计算[15]。
首先计算绕组的直流电阻，MFT的绕组选用利兹线制作，由于利兹线内部结构导致其截面的实际导流面积和整体面积有较大的差异，二者分别影响绕组损耗模型的精度与其在铁心窗口中的排布。所以为了同时满足绕组损耗建模精度和绕组在铁心窗口中的精确排布，建立参数：利兹线可用面积在整体面积中的占比为Kw，计算式如式（6）所示。本文根据开关频率，选择单股利兹线径为ds=0.15mm，然后根据利兹线实际制作工艺，确定Kw-avg（即不同利兹线股数对应的Kw平均值）为0.55。
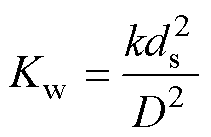（6）
式中，k为利兹线股数；D为利兹线截面直径。
由于本文中采用的绕组骨架结构为椭圆形，为了方便绕组的平均匝长建模且满足精度，本文将椭圆形结构简化为矩形结构，绕组匝长的简化模型如图3所示。
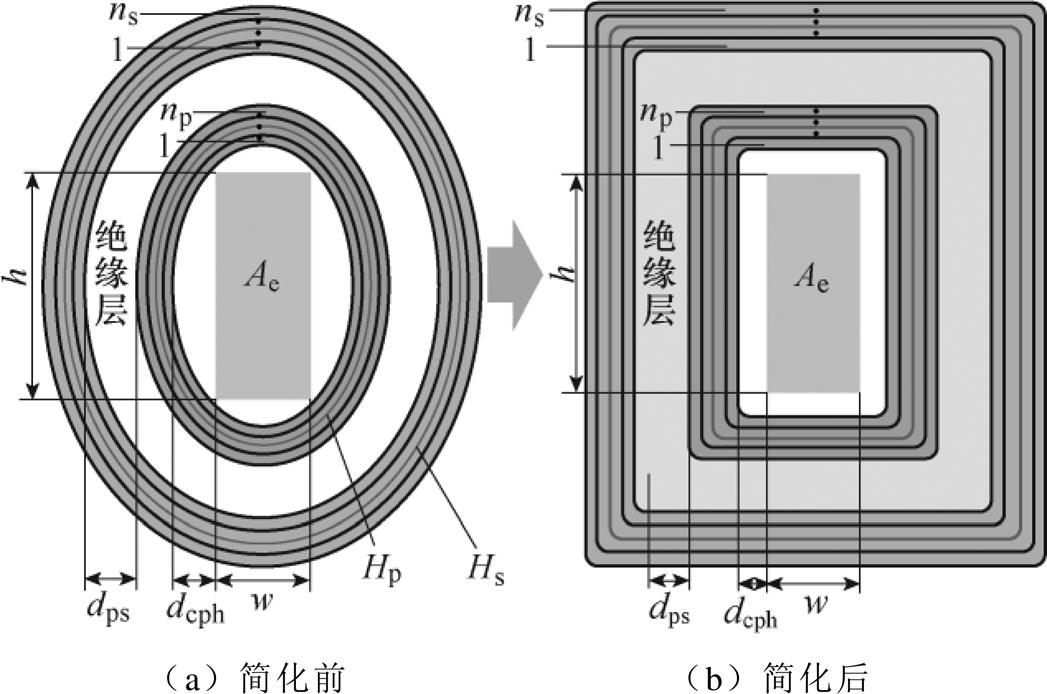
图3 绕组匝长的简化模型
Fig.3 Simplified model of winding turn length
针对特定的磁心，首先测量其相应的椭圆结构实际平均匝长。随后保持相同的绝缘距离，对如图3b所示的矩形结构进行理论平均匝长建模，与椭圆结构实际平均匝长作比得到平均匝长系数，基于此就可以建立椭圆形骨架的平均匝长模型。一次和二次绕组的平均匝长模型分别为
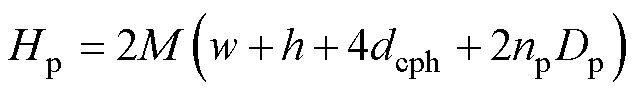（7）
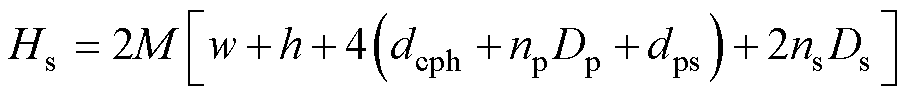（8）
式中，M为矩形结构的平均匝长转化为椭圆形结构的平均匝长系数；Hp、Hs分别为一次、二次绕组的平均匝长。
由于两个二次绕组完全相同，故为了方便二次绕组损耗建模，假设A、B铁心柱上的两个二次绕组串联，等效为一个绕组。等效二次绕组的每层匝数为2Nls，层数不变为ns，总绕组匝数为2Ns。
根据图1的MFT结构，一次与等效二次绕组的直流电阻Rdcp和Rdcs分别为
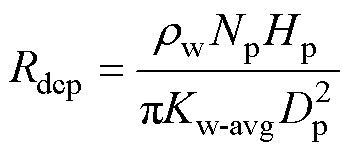（9）
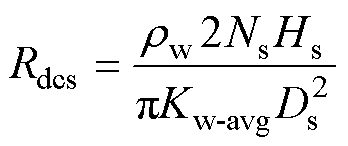（10）
式中，rw为导线的电阻率。
将直流电阻乘以Dowell模型求得的交流电阻因子FRi，即可得到绕组交流电阻[28-29]。在本文研究的MFT结构中，一次绕组需远离气隙以减小气隙效应带来的损耗，故上下端和铁轭之间需留出一定的间距；二次绕组因绝缘要求高，上下端和铁轭之间也需留出较大的绝缘间距。这导致一次、二次绕组实际的孔隙率x 都较低，使得Dowell模型的计算误差变大。为了提高该结构下的交流电阻计算精度，本文引入文献[30]的校正因子FRi，该校正因子主要是通过校正绕组高度的方式来校正，表达式为
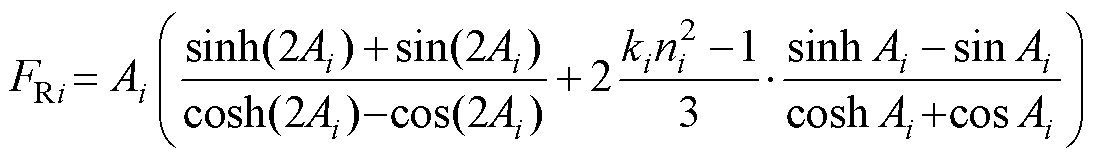i=p, s （11）
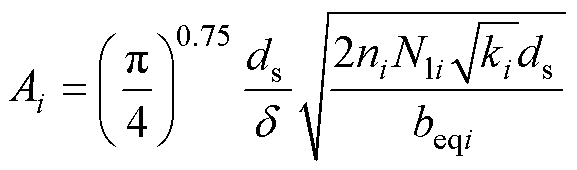i=p, s （12）
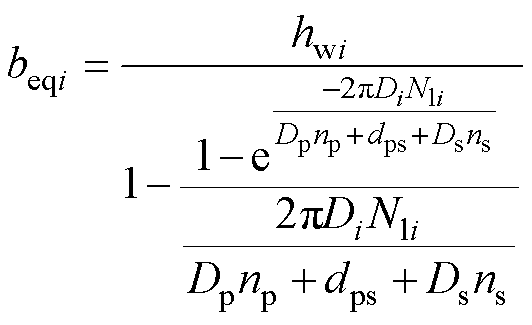i=p, s （13）
式中，FRi为交流电阻和直流电阻的比值；Ai为标准化后的单股线径和趋肤深度的比值；d 为趋肤深度；Nli为每层绕组的匝数（等效二次绕组按2Nls计算）；ki为单根利兹线股数；beqi为修正后的i绕组高度。
对于任意电流波形的绕组交流损耗计算，首先需要将电流进行傅里叶分解，然后将电流直流分量下的绕组损耗和各次谐波下的绕组交流损耗相加，本文所研究MFT应用于LLC谐振变换器，其中工作电流为正弦波，因此其绕组损耗可只考虑基波下的交流损耗，得到一次绕组损耗Pwindingp与二次绕组损耗Pwindings表达式分别为
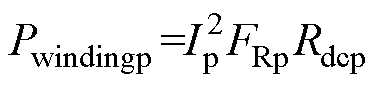（14）
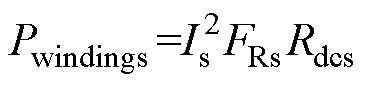（15）
在第1节对铁心体积、铁心损耗和绕组损耗模型的分析基础上，本节对参数如表1所示的MFT进行优化设计。
根据损耗模型的分析，可知铁心损耗与绕组损耗可由以下8个变量结合求得，因此将其作为优化关键变量，分别是关于铁心尺寸的3个变量：铁心柱截面两个尺寸w、h和铁心窗口高度b；关于绕组的5个变量：一次绕组匝数Np，一次、二次绕组的利兹线的直径Dp和Ds，一次、二次绕组的层数np和ns。其中，w、h、Np既影响铁心损耗也影响绕组损耗，b、Dp、Ds、np、ns只影响绕组损耗。
MFT的优化设计流程如图4所示。整个优化设计流程分为三大步。
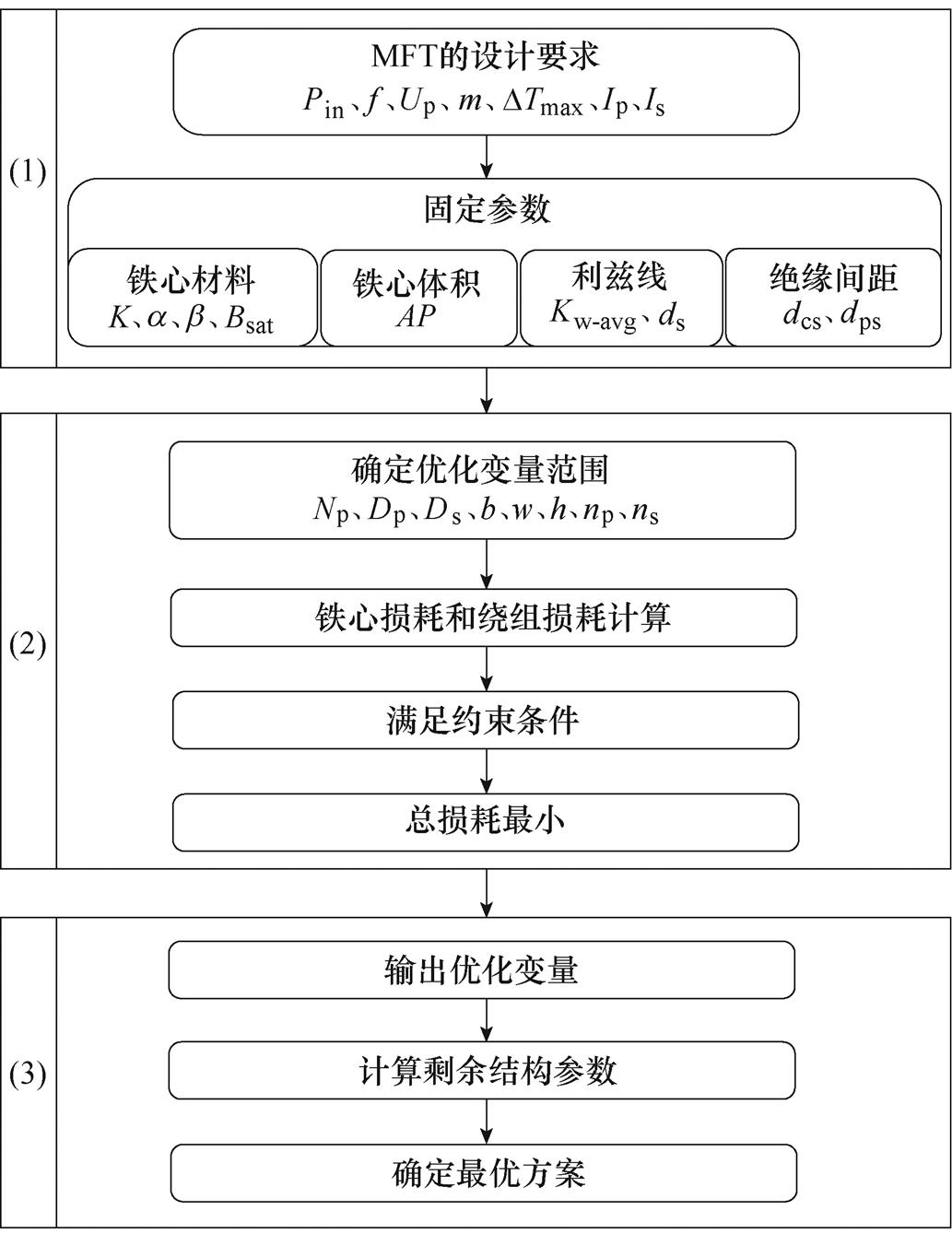
图4 MFT的优化设计方法流程
Fig.4 Flow chart of optimal design method of MFT
（1）先根据设计要求确定铁心材料、绕组材料和绝缘间距等相关固定参数，然后根据式（1）确定MFT的AP值。其中，本文选用的铁心材料为锰锌铁氧体材料。
（2）首先确定优化变量的设计范围，然后基于Matlab软件，扫描给定变量取值范围内的所有设计的总损耗值Ptot，总损耗Ptot为
（16）
再从所有设计点中找出满足约束条件的设计点，约束条件包括铁心AP值的限制和Bm的限制：Bm不得超过铁心柱中最大饱和磁通密度Bsat的50%；窗口预留绝缘距离与制作工艺误差裕度的限制，窗口需要给二次绕组预留2dcs的绝缘距离和不小于dps的工艺误差裕度，为一次绕组预留不小于dps的工艺误差裕度；窗口长度a裕值，除绕组所占距离之外，窗口还需预留15mm及以上，具体为
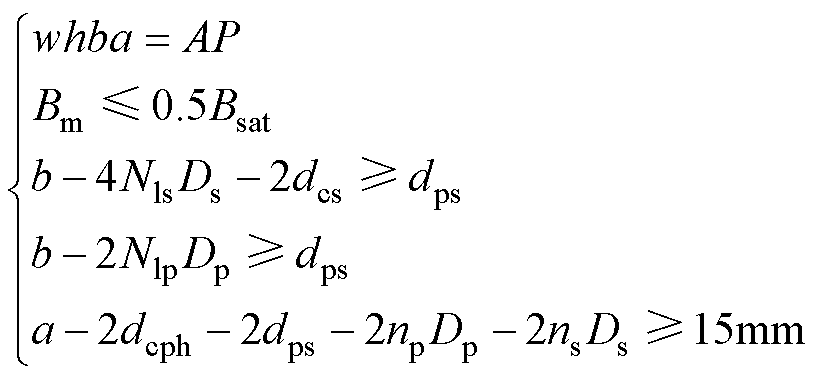（17）
式中，Bsat为铁心柱中最大饱和磁通密度。随后对比得出损耗最小值。
（3）首先输出总损耗最小对应的最优变量解集，然后计算变压器剩余的结构参数，最后确定最优设计方案。
优化变量的取值范围首先针对Np进行选取，选取一个较宽的取值范围，以获得较大的数据集。根据Np取值范围与Bm的取值，划定铁心柱截面的取值范围，即w与h的取值范围。Dp、Ds的取值范围按载流量1～8A/mm2选取，同时基于Np范围与Dp和Ds范围确定窗口高度b的范围。
随后，本文进一步分析了变量np、ns对损耗的影响程度以定性分析优化设计方法后MFT特点。在分析过程中，基于损耗模型与约束条件，分别改变np与ns，并将其余7个变量固定，计算损耗（包括铁心损耗、绕组损耗和总损耗），观察变化趋势；重复上述步骤。因样本量繁杂，趋势接近，难以全部展示，故选择一组具有代表性的数据进行展示，不同优化变量和MFT损耗的关系如图5所示。图中，主要分析满足约束条件的点（灰色区域覆盖），故不满足约束条件的点对应损耗被设置为0。变量np、ns只能取整数。
从图5中可以看出，np从1层增大到2层，绕组损耗增大了24.1%；ns从2层增大到3层，绕组损耗增大了36.4%。这是因为np和ns的增大会较大程度地加重邻近效应，从而导致绕组交流损耗较大幅地增加，且随着绕组层数的增大，绕组损耗的增加幅度越大。故在优化设计MFT时会尽可能减少绕组层数。层数的减少意味着每层绕组匝数的上升，因此会提高窗口高度b，并且由于AP值恒定的限制，窗口长度a具有减小趋势。
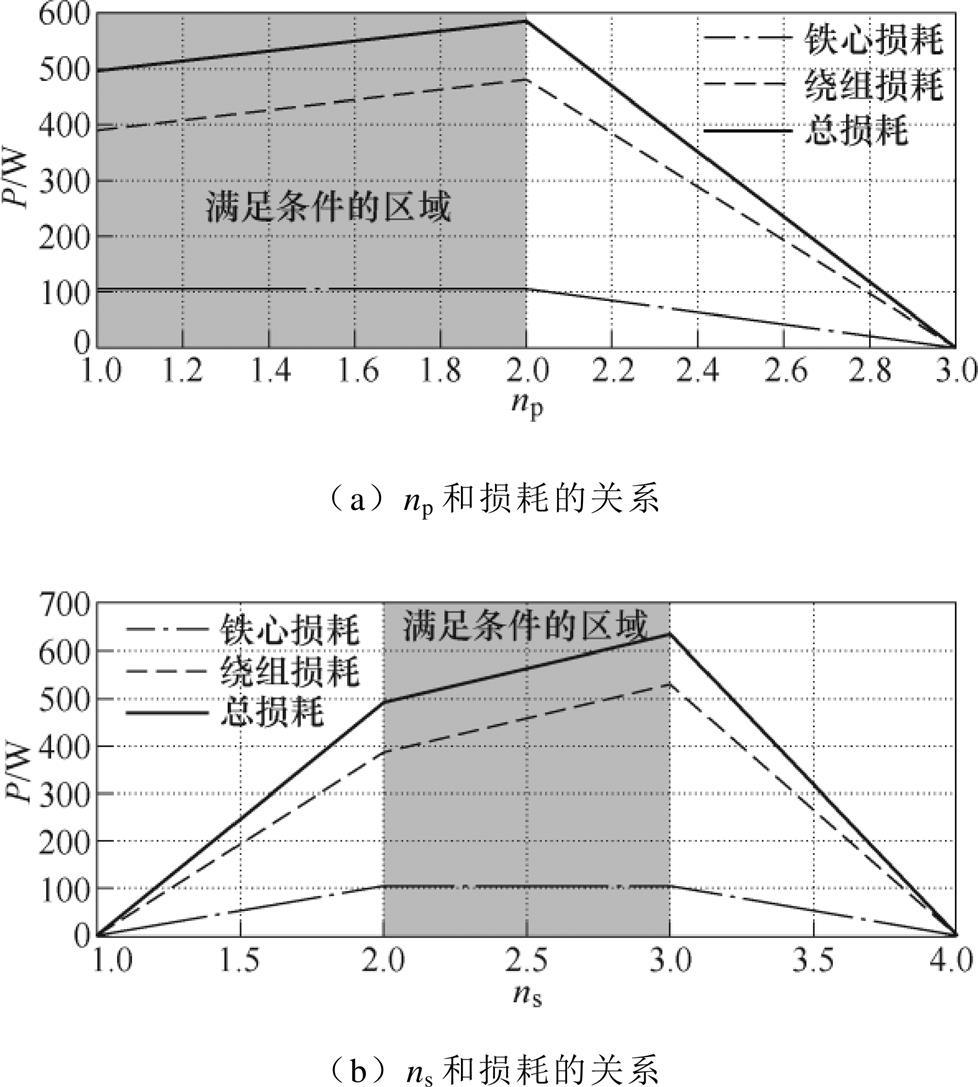
图5 不同优化变量和MFT损耗的关系
Fig.5 The relationship between different optimization variables and the loss of the MFT
因此，本文的损耗最小化设计方案中绕组具有较小的ni，铁心具有较高的窗口，呈现“瘦高型”。优化变量的取值范围见表2，铁心的厚度h方向采用多个截面为方形的铁氧体磁块进行拼接，s为拼接的数量。
表2 优化变量取值范围
Tab.2 Range of optimization variables
优化变量取值范围 w/mm[20, 40] s[1, 4] b/mm[150, 300] Np[3, 36] Dp/mm[4, 11] Ds/mm[4, 12] np[1, 2] ns[1, 3]
根据图4的优化设计流程，选择优化设计中最小MFT总损耗的设计结果方案，见表3。VMFT为MFT的体积；hMFT为MFT的效率；g 为MFT的功率密度。
表3 MFT的优化设计结果
Tab.3 Optimal design results of MFT
参 数数 值 结构a/mm117 b/mm220 w/mm40 h(s=2)/mm80 Np21
（续）
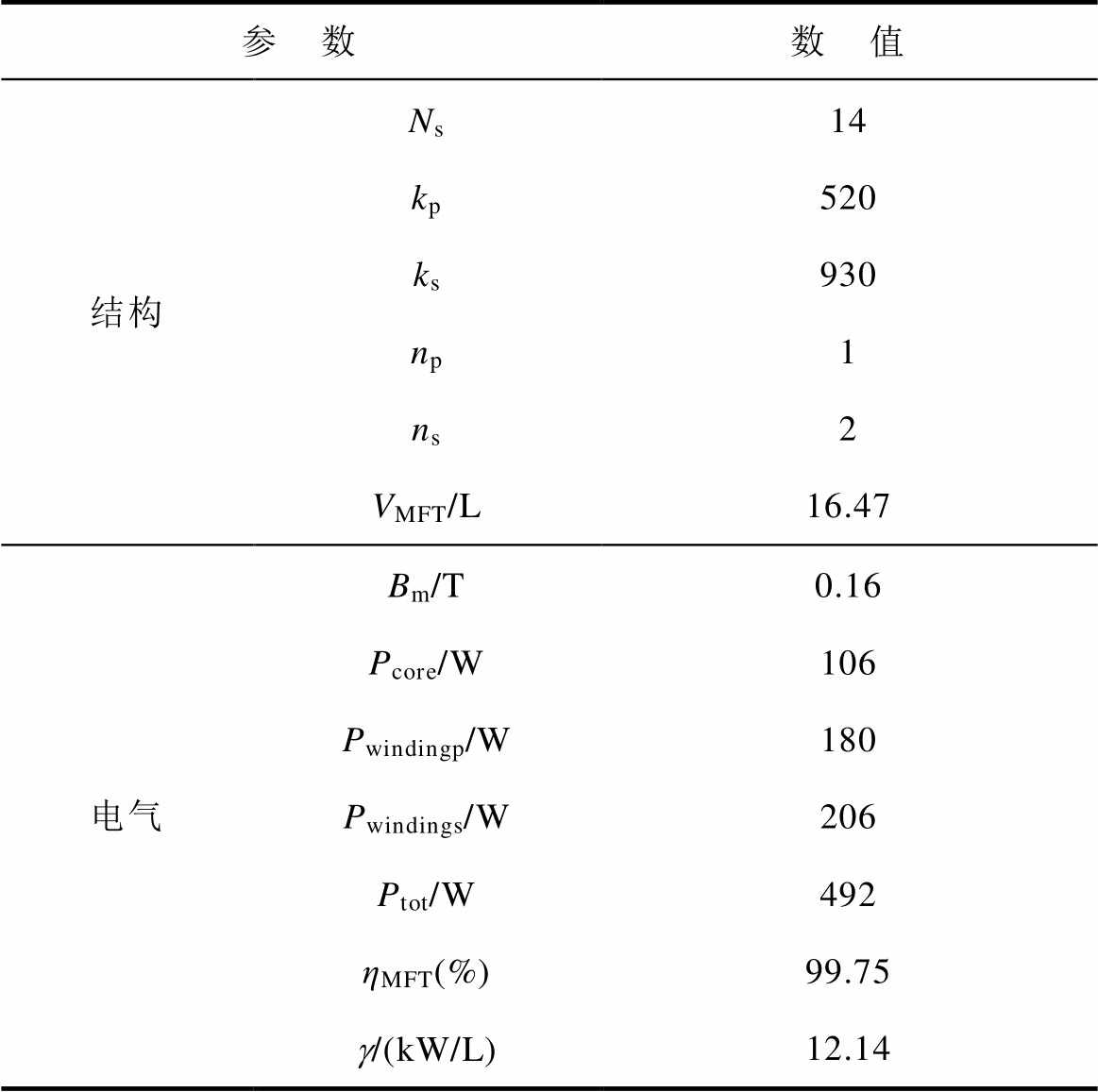
参 数数 值 结构Ns14 kp520 ks930 np1 ns2 VMFT/L16.47 电气Bm/T0.16 Pcore/W106 Pwindingp/W180 Pwindings/W206 Ptot/W492 ηMFT(%)99.75 g/(kW/L)12.14
本节主要研究了优化设计的MFT漏感和电磁干扰问题。漏感和电磁干扰主要由变压器的漏磁能量所致。漏磁能量一般由两部分组成[6]：一部分储存在绕组导体中，这部分漏磁大小会影响绕组的邻近效应强度，进而影响绕组的交流损耗，穿过导体的漏磁磁场强度越大，绕组交流损耗越大；另一部分储存在绝缘区域（包括空气），铁心窗口截面及绕组中的磁动势分布如图6所示。由安培环路定律以及图6可知，变压器的绕组层数n越大，最外层绕组的磁动势（Magnetomotive Force, MMF）越大，进而导致穿过该层和该层以外的绕组的漏磁磁场强度越大；铁心窗口高度b越小，则减小了窗口中磁通的磁路长度，导致穿过绕组导体和一次、二次绕组之间绝缘区域的漏磁磁场强度更大。故可以得知，增大b和减小n会带来穿过绕组导体和一次、二次绕组之间绝缘区域的漏磁磁场强度减小，进而带来漏感和变压器周围电磁干扰强度的降低。通过第2节分析可知，MFT的优化设计会带来b的增大和n的减小，并减小交流损耗，因此也可预见，MFT的优化设计方法不仅会降低交流损耗，也会使穿过绕组的漏磁磁场强度减小，从而减小漏感与电磁干扰。
为了验证本文优化设计的MFT在损耗达到最小化的同时也带来了漏感和电磁干扰现象的改善，本文引用文献[18]中的AP法对MFT进行设计，然后将AP法设计和本文所提优化方法设计的MFT在漏感和电磁干扰方面进行对比。
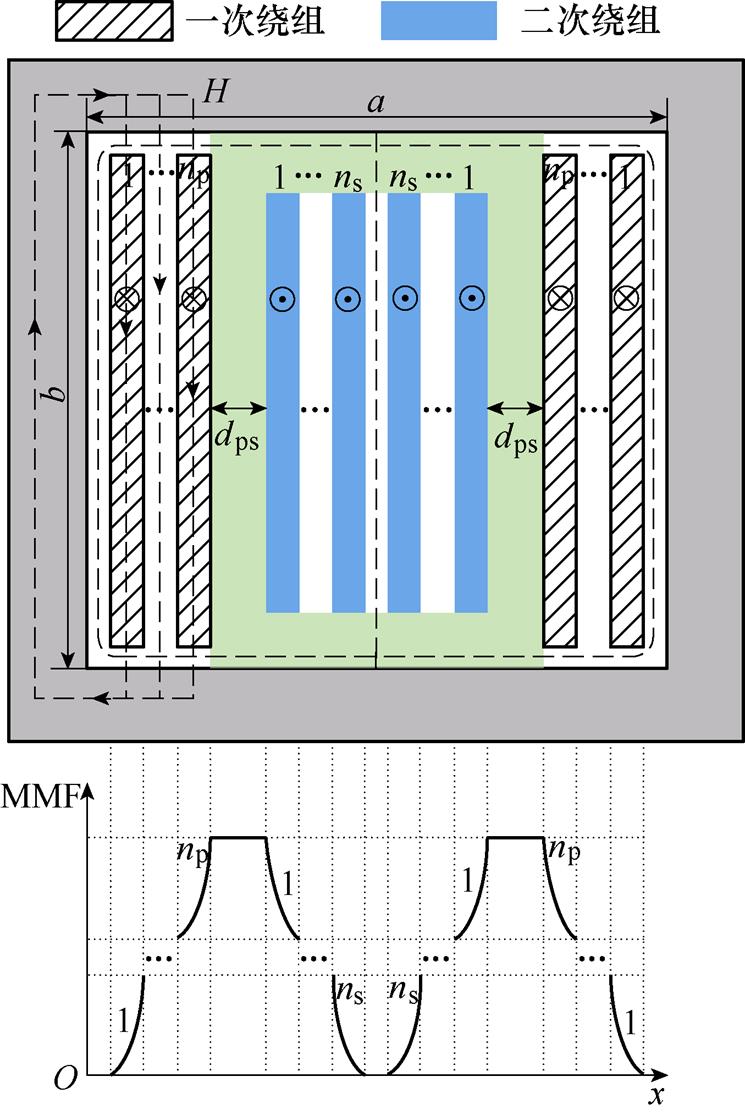
图6 铁心窗口截面及绕组中的磁动势分布
Fig.6 The core window section and MMF distribution in winding
表4为AP法设计的MFT参数，对比表4可以看出，本文的优化设计方法设计的MFT在绕组损耗上有较大程度的降低。
表4 AP法设计的MFT结构及电气参数
Tab.4 MFT structure and electrical parameters designed by APmethod
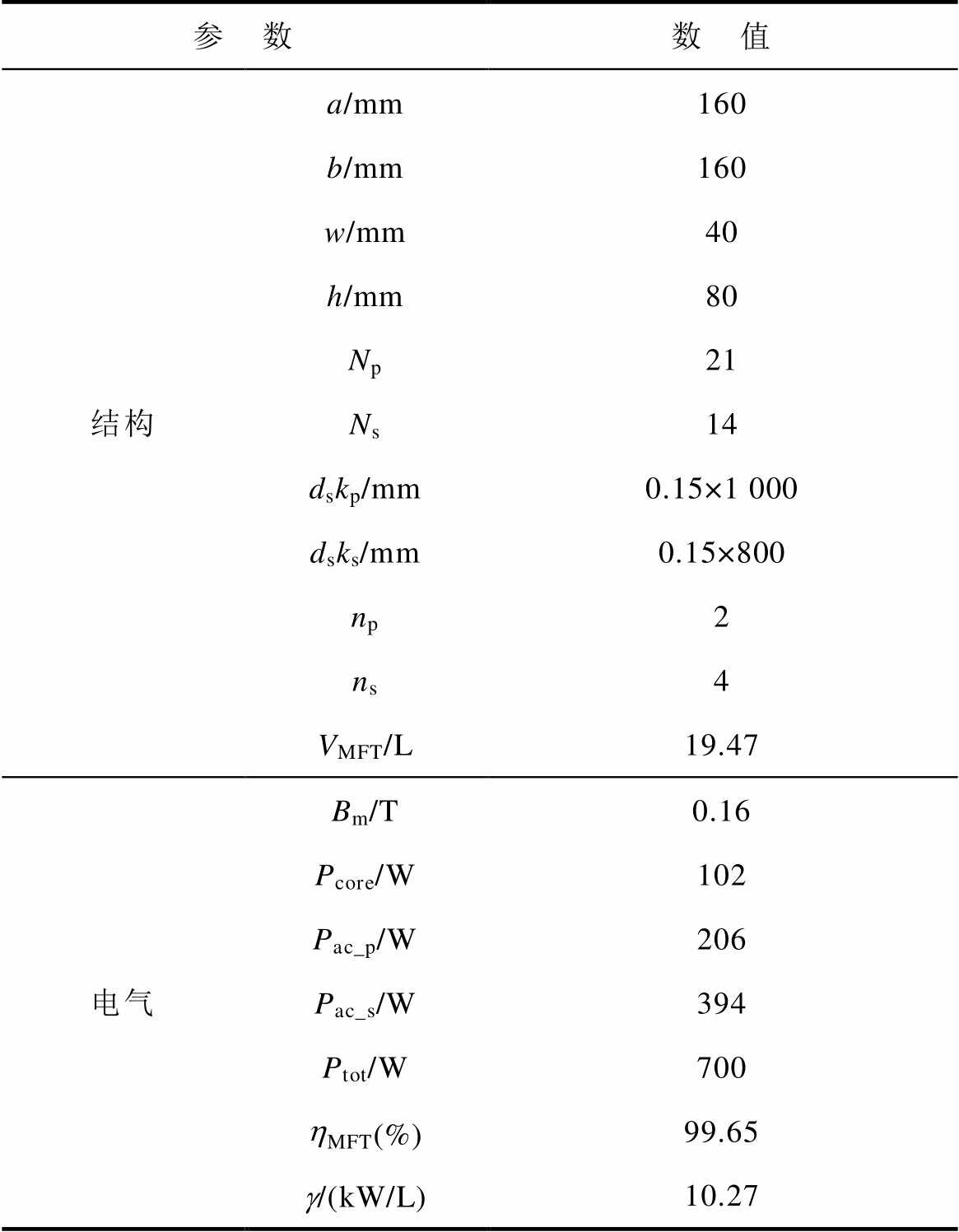
参 数数 值 结构a/mm160 b/mm160 w/mm40 h/mm80 Np21 Ns14 dskp/mm0.15×1 000 dsks/mm0.15×800 np2 ns4 VMFT/L19.47 电气Bm/T0.16 Pcore/W102 Pac_p/W206 Pac_s/W394 Ptot/W700 hMFT(%)99.65 g/(kW/L)10.27
利用Ansys Maxwell有限元仿真软件对表3和表4的MFT励磁电感Lm和漏感Lk进行仿真对比，结果见表5。
表5 AP法和本文优化方法设计的MFT的Lm和Lk仿真
Tab.5 The simulated values of Lm and Lk of MFT designed by AP method and the optimial method in this paper
电感参数AP法本文优化方法 Lm/mH295.13295.76 Lk/mH28.4715.90
从表5中可以看出，本文所提优化设计方法设计的MFT漏感比AP法的设计小了将近一半，证明了上述理论分析的正确性。同时两台变压器Lm的仿真值基本相同，因为气隙长度和绕组匝数相同。
然后对漏磁引起的电磁干扰现象进行研究，因漏磁场的分布难以用数学模型准确计算得到，为此也采用有限元仿真方法进行研究，通过观察变压器周围的漏磁场磁感应强度B和磁场强度H云图可较为直观地观察并对比电磁干扰的强度，但不易定量分析。为准确量化对比电磁干扰的强度，采用如下方法：通过在MFT外侧放置铝板，改变铝板到MFT二次绕组的距离d，观察铝板因漏磁场带来的涡流效应导致的损耗情况，漏磁场越强，则电磁干扰越强，涡流效应越明显，带来的损耗也越大，从而侧面定量反映MFT在此处的电磁干扰强弱。图7为在Ansys Maxwell软件中描述两台MFT外侧电磁干扰现象的简化仿真模型。
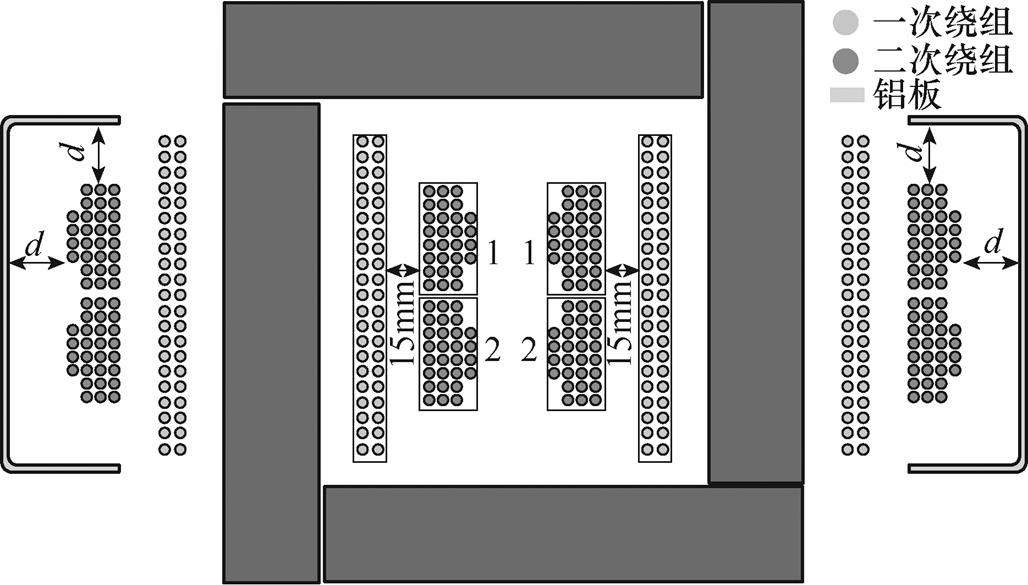
图7 MFT周围电磁干扰现象研究的简化模型
Fig.7 Simplified model for study of electromagnetic interference phenomena around MFT
图8展示了当d=50mm时，两台MFT外侧漏磁场磁感应强度B的分布，选用铝板为参照物。可以直观地看出，基于本文所提优化方法设计的MFT，铝板周围的B更小。从而说明本文所提优化方法设计的MFT对外侧的电磁干扰影响更小一些。
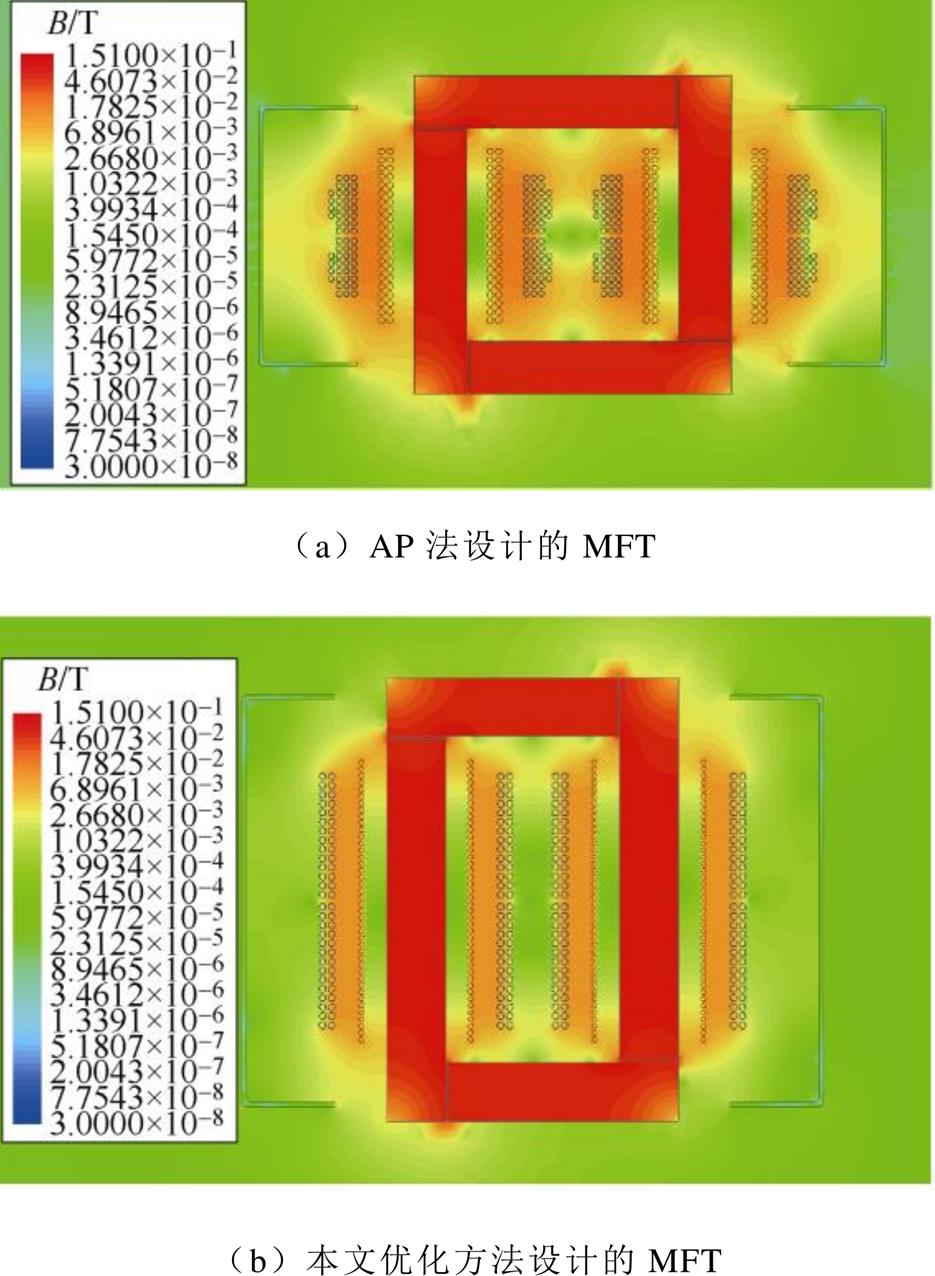
图8 d=50mm时，MFT周围B的分布
Fig.8 The distribution of B around the MFT when d=50mm
图9展示了两台MFT外侧的铝板损耗（两个MFT外侧的铝板损耗以AP法设计的MFT外侧铝板长度为基准，参照实际厚度，在保持相同电阻的情况下，进行了数据折算），以定量分析MFT对外电磁干扰的影响，随着铝板位置变化而变化的曲线。从图中可以看出，随着d的增大，铝板损耗越小，同时损耗的变化率也越来越小。当d为5～25mm的时候，基于AP法设计的MFT外侧铝板损耗可达优化设计后MFT外侧铝板损耗6～10倍，可知这段区域内基于AP法设计的MFT对外电磁干扰强度远超优化设计后的MFT对外电磁干扰强度。当d＞120mm时，基于AP法设计的MFT外侧铝板损耗接近0且损耗变化率趋于平稳，说明铝板在该范围内受电磁干扰的影响较小，可判定该范围属于电磁干扰较弱区域；反之，在0＜d＜120mm范围内属于电磁干扰较强区域。同理，基于本文优化方法设计的MFT，在0＜d＜80mm范围内属于电磁干扰较强区域。通过对比说明了相对于AP法的设计，本文所提优化方法设计的MFT的外侧电磁干扰区域也得到了较大程度的改善。
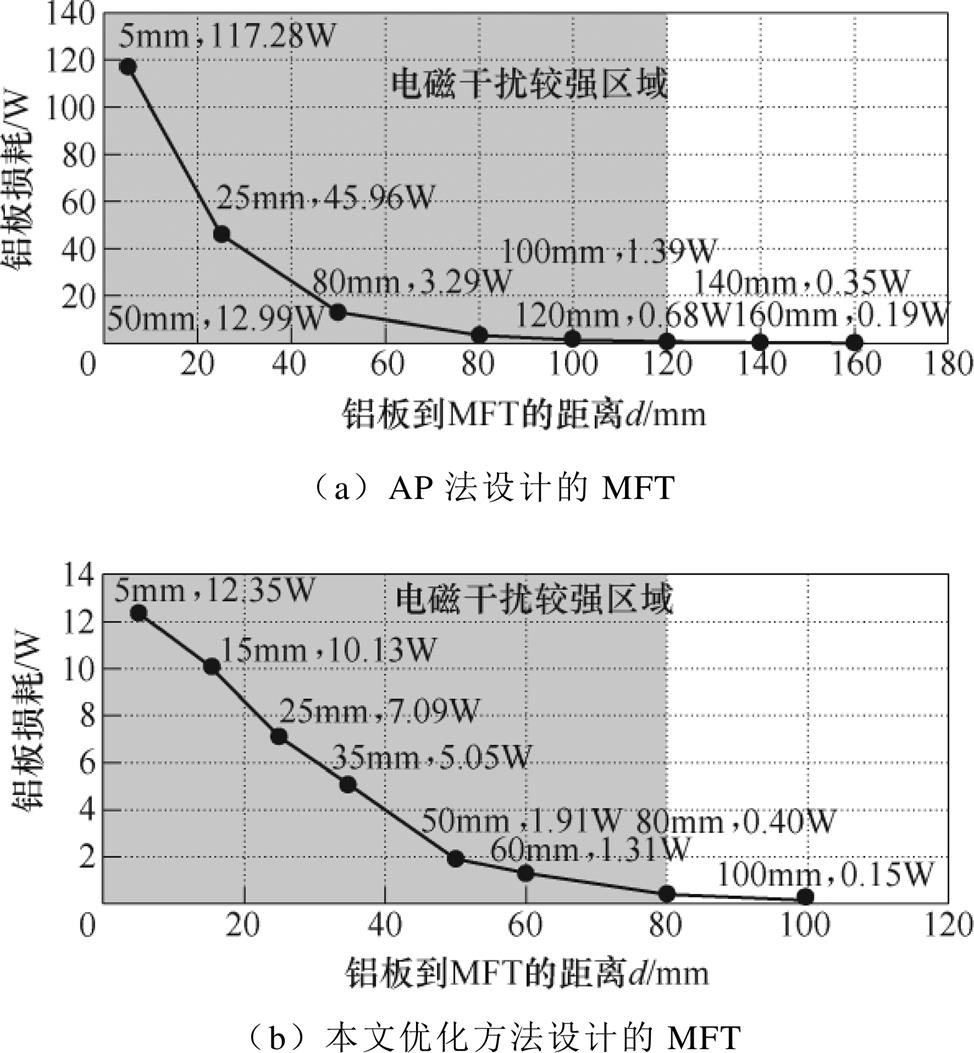
图9 两台MFT的电磁干扰强弱区域分布对比
Fig.9 Comparison of regional distribution of electromagnetic interference between two MFTs
为了验证本文所提优化设计方法的准确性，根据表3的设计结果，设计了一台200kW/30kHz的MFT样机，如图10所示，该样机预留了绝缘间距，暂未填充绝缘材料。其LLC谐振变换器实验平台如图11所示。
图10 优化设计的MFT样机
Fig.10 The MFT prototype after optimal design
首先对变压器样机的Lm和Lk大小进行测量。通过阻抗分析仪WK6500B对MFT样机的Lm和Lk的测试结果见表6，与表5对比可得，测量值和仿真值结果近似。误差产生的原因为变压器样机的气隙尺寸与仿真中的设定值不能保证完全一致，导致励磁电感无法完全一致；因实际利兹线与变压器骨架带来的偏差，实际的一次、二次绕组间的绝缘间距与仿真中的设定值不能保证完全一致，导致漏感的偏离，但该误差的偏差在可接受范围内。
图11 LLC谐振变换器实验平台
Fig.11 LLC resonant converter experiment platform
表6 Lm和Lk的测试值
Tab.6 Tested values of Lm and Lk
参 数测试值 Lm/mH284.65 Lk/mH14.07
为了验证本文优化设计的MFT的工作性能，本文从轻载到满载分别测试了9个功率点的工作状态。MFT的工作环境为：测试场地为密闭室内，室温约为28℃且室内无风，MFT的一端放置三联装风扇进行风冷散热，在风扇对侧放置热成像仪进行温升测量，如图11所示。LLC谐振变换器的输入电压恒定为1 300V。图12展示了100kW和200kW下的谐振电流Ip、谐振电感两端电压加上励磁电感两端电压之和Un的实验波形。从Ip的正弦波形中可以得出，LLC谐振变换器工作在谐振点附近。
使用功率分析仪YOKOGAWA WT3000E分别对LLC谐振变换器中9个功率点的效率进行了测量。为了验证优化设计方法的准确性，本文根据实际电压和电流值对各个功率点下的效率进行了理论计算。
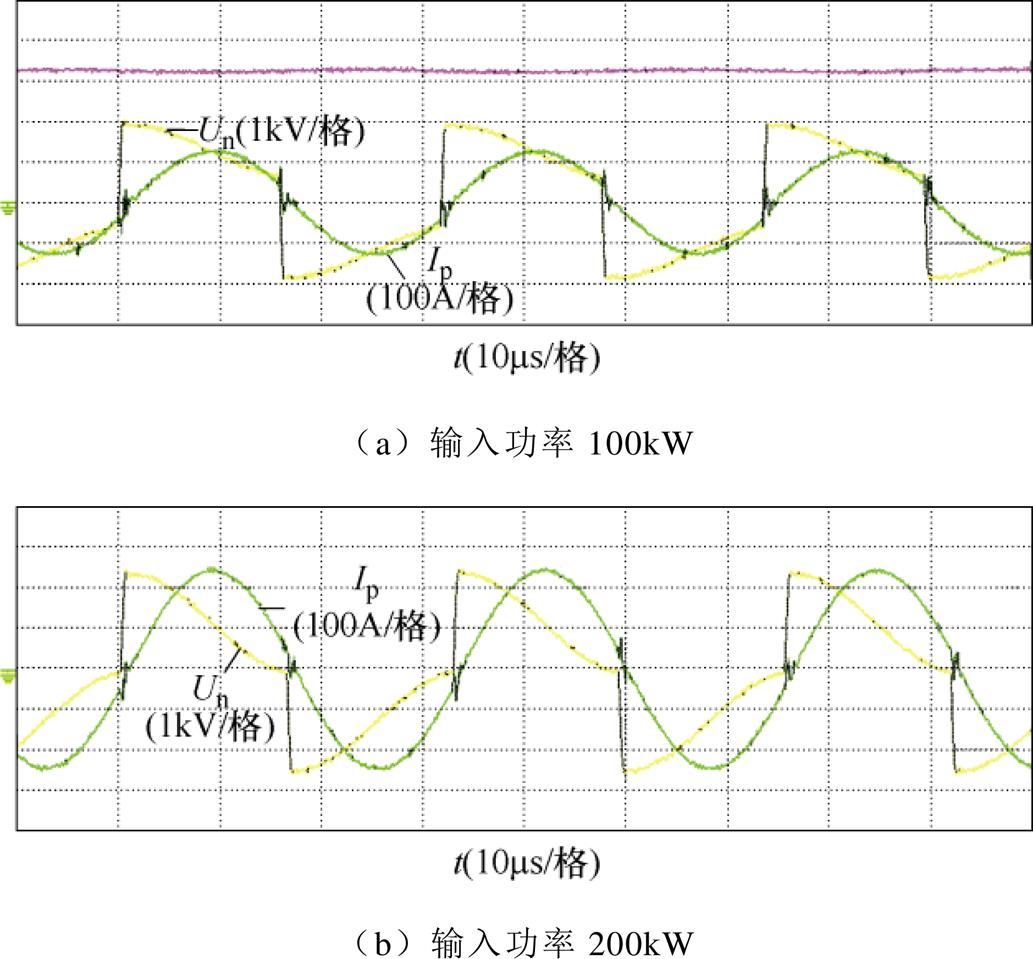
图12 Ip和Un的实验波形
Fig.12 Experimental waveforms of Ip and Un
理论计算主要考虑了逆变侧开关管的通态损耗和关断损耗、谐振电容的损耗、MFT总损耗、外接谐振电感损耗和整流二极管通态损耗。
其中，开关管的通态损耗为
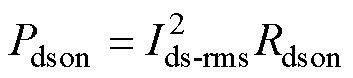（18）
式中，Ids-rms为流过开关管的电流有效值；Rdson为开关管的通态电阻。
开关管的关断损耗为
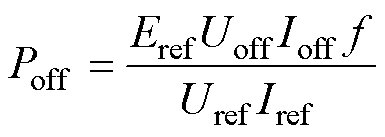（19）
式中，Uref、Iref和Eref分别为开关管Datasheet中给的参考关断电压、关断电流和关断时损失的能量；Uoff和Ioff分别为实际的关断电压和关断电流。
根据电容的等效串联电阻（Equivalent Series Resistance, ESR），谐振电容的损耗为
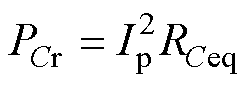（20）
式中，RCeq为电容的等效串联电阻。
整流二极管的通态损耗为
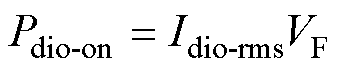（21）
式中，Idio-rms为流过二极管的电流有效值；VF为二极管的通态压降。外接电感的损耗建模方法与MFT一致。损耗计算中电压电流参数均由实验测得。
LLC谐振变换器效率的实测值和理论值的对比如图13所示，可以看出，效率的实测值和理论值近似，在测试过程中，因主功率电路结构设计问题，开关管和二极管的壳温极难测量。因而在开关管和二极管通态损耗中，Rdson和VF采用典型值计算，实际中Rdson和VF则具有正温度变换特性，产生些许误差，因此理论效率变换斜率稍小于实测效率，但误差在可接受范围内。实测值和理论值相当接近，证明了MFT理论模型的准确性。其中，最高实测效率点达到99.18%，满载时的实测效率为98.59%。当满载（200kW）时，LLC谐振变换器各部分的损耗分布理论值对比如图14所示，可以看出，损耗主要集中在逆变侧开关管的通态损耗和整流二极管的通态损耗。
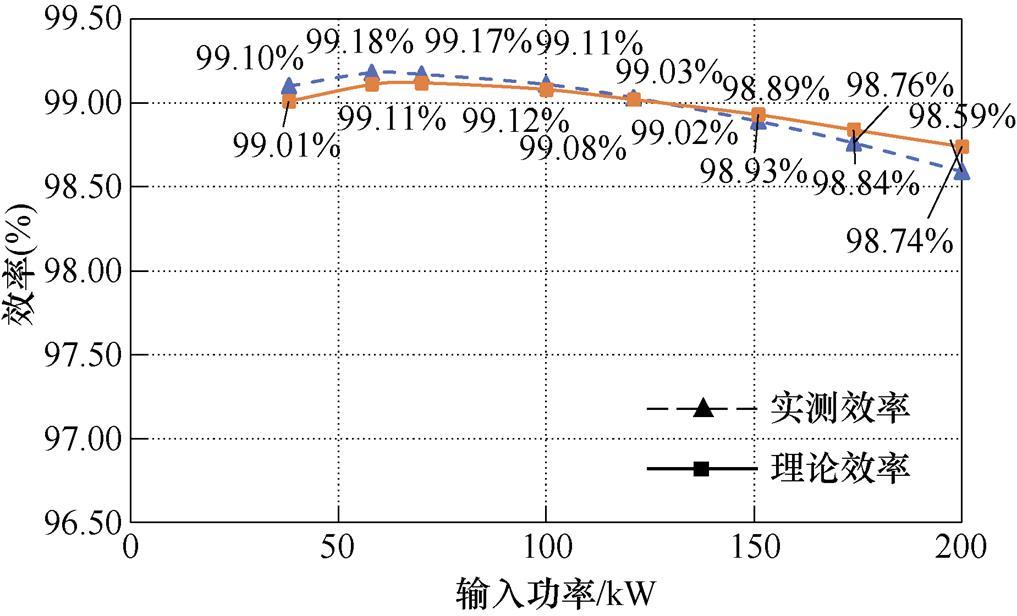
图13 LLC谐振变换器的效率实测值和理论值对比
Fig.13 Comparison of the measured efficiency and theoretical efficiency of the LLC resonant converter
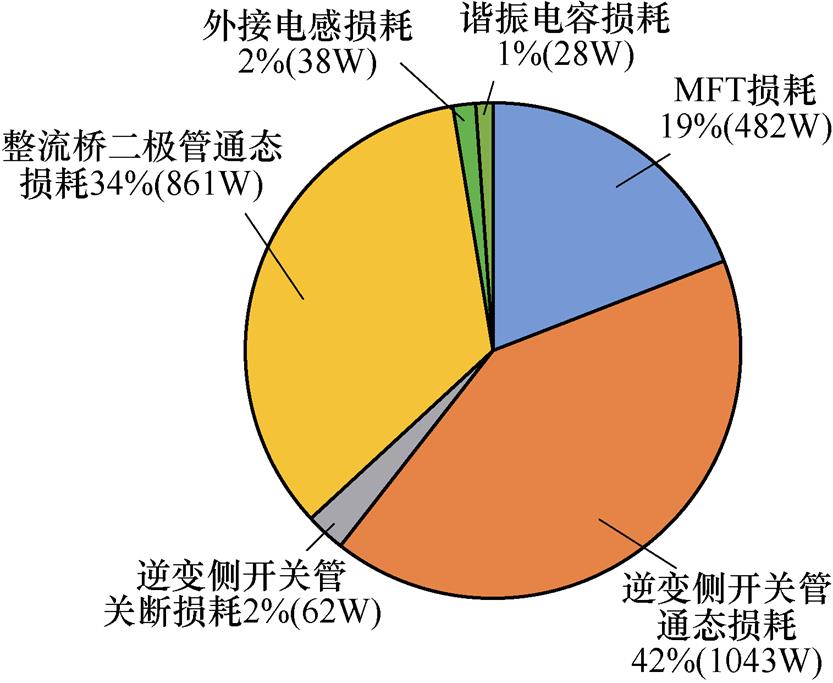
图14 Pin=200kW时，LLC谐振变换器的主要损耗分布
Fig.14 The loss distribution of the LLC resonant converter when Pin=200kW
损耗最小化设计带来直观优点是较低的温升。本文使用FLIR热成像仪对满载（200kW）下的MFT进行了温升测量。在此条件下，工作了40min后温度基本稳定，热成像结果如图15所示。由于外侧的二次绕组受风冷散热影响较大，故测得二次绕组温升较低；而内侧的一次绕组风扇难以吹到，同时热成像位置在风扇对侧，故测得一次绕组温升较高。目前，整个MFT的最高温为79.6℃，最大温升为51℃左右，为后续考虑绝缘材料的MFT温升裕留了足够大的空间。
图15 Pin=200kW时，MFT的热成像
Fig.15 Thermal image of the MFT when Pin=200kW
本文讨论了AP法设计铁心体积的解析模型以及铁心损耗和绕组损耗的解析模型，进一步讨论了绕组层数和损耗之间的关系，提出了一种MFT损耗最小化的优化设计方法，为MFT的设计提供了参考思路。
通过有限元仿真软件，证明了本文的MFT设计方法可以减小损耗的同时减小漏感与电磁干扰的影响。同时研究了变压器周围电磁干扰的强弱情况，为外围电路的放置位置提供参考。
最后，通过铁心和绕组的定制化，制作了一台应用于LLC谐振变换器的35kV绝缘、200kW、30kHz的MFT样机。通过理论和实际的效率对比，验证了本文方法的有效性和准确性。LLC谐振变换器的最高实测效率可达99.18%。同时变压器也未出现散热问题，在没有考虑加入绝缘材料的条件下，变压器的实测温升远低于设计要求，为后面继续研究加入绝缘材料的MFT裕留足够的温升空间。
参考文献
[1] 卢斯煜, 周保荣, 饶宏, 等. 高比例光伏发电并网条件下中国远景电源结构探讨[J]. 中国电机工程学报, 2018, 38(增刊1): 39-44.
Lu Siyu, Zhou Baorong, Rao Hong, et al. Research of the prospect of China power generation structure with high proportion of photovoltaic generation[J]. Pro- ceedings of the CSEE, 2018, 38(S1): 39-44.
[2] 丁明, 王伟胜, 王秀丽, 等. 大规模光伏发电对电力系统影响综述[J]. 中国电机工程学报, 2014, 34(1): 1-14.
Ding Ming, Wang Weisheng, Wang Xiuli, et al. A review on the effect of large-scale PV generation on power systems[J]. Proceedings of the CSEE, 2014, 34(1): 1-14.
[3] Zhu Rongwu, Andresen M, Langwasser M, et al. Smart transformer/large flexible transformer[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4): 264-274.
[4] Bahmani M A, Thiringer T, Rabiei A, et al. Com- parative study of a multi-MW high-power density DC transformer with an optimized high-frequency magnetics in all-DC off shore wind farm[J]. IEEE Transactions on Power Delivery, 2016, 31(2): 857- 866.
[5] She Xu, Huang A Q, Burgos R. Review of solid-state transformer technologies and their application in power distribution systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2013, 1(3): 186-198.
[6] 高范强, 李子欣, 李耀华, 等. 面向交直流混合配电应用的10kV-3MV·A四端口电力电子变压器[J]. 电工技术学报, 2021, 36(16): 3331-3341.
Gao Fanqiang, Li Zixin, Li Yaohua, et al. 10kV- 3MV·A four-port power electronic transformer for AC-DC hybrid power distribution applications[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3331-3341.
[7] 胡钰杰, 李子欣, 罗龙, 等. 基于串联谐振间接矩阵型电力电子变压器高频电流特性分析及开关频率设计[J]. 电工技术学报, 2022, 37(6): 1442-1454
Hu Yujie, Li Zixin, Luo Long, et al. Characteristic analysis of high-frequency-kink current of series resonant indirect matrix type power electronics transformer and switching frequency design[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1442-1454.
[8] 杨景刚, 张珂, 陈武, 等. 大功率中频变压器研究综述[J]. 电源学报, 2020, 18(1): 4-17.
Yang Jinggang, Zhang Ke, Chen Wu, et al. Review on researches of high-power medium-frequency trans- former[J]. Journal of Power Supply, 2020, 18(1): 4-17.
[9] 王迎迎, 程红. 应用于功率变换器的多绕组高频变压器模型[J]. 电工技术学报, 2021, 36(19): 4140- 4147.
Wang Yingying, Cheng Hong. Dual multi-winding high-frequency transformer equivalent circuit for power converter applications[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4140-4147.
[10] 张航, 李耀华, 高范强, 等. 级联H桥型电力电子变压器隔离级高频电流波动抑制策略[J]. 电力系统自动化, 2020, 44(7): 130-138.
Zhang Hang, Li Yaohua, Gao Fanqiang, et al. High- frequency current fluctuation suppression strategy for isolation stage of cascaded H-bridge based power electronic transformer[J]. Automation of Electric Power Systems, 2020, 44(7): 130-138.
[11] Zheng Jialin, Zhao Zhengming, Shi Bochen, et al. A discrete state event driven simulation based losses analysis for multi-terminal megawatt power electronic transformer[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4): 275-284.
[12] 赵争菡, 汪友华, 凌跃胜, 等. 大容量高频变压器绕组损耗的计算与分析[J]. 电工技术学报, 2014, 29(5): 261-264, 270.
Zhao Zhenghan, Wang Youhua, Ling Yuesheng, et al. Calculation and analysis of loss in high-capacity high- frequency transformers[J]. Transactions of China Elec- trotechnical Society, 2014, 29(5): 261-264, 270.
[13] 张重远, 王增超, 张欣, 等. 基于改进矢量匹配法的变压器铁芯频变涡流模型[J]. 高电压技术, 2015, 41(5): 1618-1623.
Zhang Zhongyuan, Wang Zengchao, Zhang Xin, et al. Transformer core modeling for frequency dependent eddy current based on modified vector fitting[J]. High Voltage Engineering, 2015, 41(5): 1618-1623.
[14] 李子欣, 高范强, 赵聪, 等. 电力电子变压器技术研究综述[J]. 中国电机工程学报, 2018, 38(5): 1274-1289.
Li Zixin, Gao Fanqiang, Zhao Cong, et al. Research review of power electronic transformer technolo- gies[J]. Proceedings of the CSEE, 2018, 38(5): 1274- 1289.
[15] Dowell P L. Effects of eddy currents in transformer windings[J]. Proceedings of the Institution of Electrical Engineers, 1966, 113(8): 1387-1394.
[16] Ferreira J A. Improved analytical modeling of con- ductive losses in magnetic components[J]. IEEE Transactions on Power Electronics, 1994, 9(1): 127- 131.
[17] Agheb E, Høidalen H K. Medium frequency high power transformers, state of art and challenges[C]// 2012 International Conference on Renewable Energy Research and Applications (ICRERA), Nagasaki, 2012: 1-6.
[18] 杨东江, 段彬, 丁文龙, 等. 一种带辅助双向开关单元的宽输入电压范围LLC谐振变换器[J]. 电工技术学报, 2020, 35(4): 775-785.
Yang Dongjiang, Duan Bin, Ding Wenlong, et al. An improved LLC resonant converter with auxiliary bi-directional switch for wide-input-voltage range applications[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 775-785.
[19] 刘瑞欣, 王议锋, 韩富强, 等. 应用于宽输入电压范围的两模式切换型软开关谐振直流变换器[J]. 电工技术学报, 2020, 35(22): 4739-4749.
Liu Ruixin, Wang Yifeng, Han Fuqiang, et al. A two- mode soft-switching resonant DC-DC converter for wide input voltage range applications[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4739-4749.
[20] 刘硕, 苏建徽, 赖纪东, 等. LLC谐振变换器PO模式增益公式与模式边界条件分析[J]. 电力系统自动化, 2020, 44(6): 164-170.
Liu Shuo, Su Jianhui, Lai Jidong, et al. Analysis on gain formula and mode boundary condition for LLC resonant converter in PO mode[J]. Automation of Electric Power Systems, 2020, 44(6): 164-170.
[21] Hurley W G, Wölfle W H. Transformers and indu- ctors for power electronics, theory, design and applications[M]. Chichester: John Wiley & Sons, 2013.
[22] Yu Xiong, Su Jianhui, Lai Jidong, et al. Analytical optimization of nonsaturated thermally limited high- frequency transformer/inductor design considering discreteness of design variables[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 6231-6250.
[23] 曹小鹏, 陈武, 宁光富, 等. 基于多目标遗传算法的大功率高频变压器优化设计[J]. 中国电机工程学报, 2018, 38(5): 1348-1355.
Cao Xiaopeng, Chen Wu, Ning Guangfu, et al. Optimization design of high-power high-frequency transformer based on multi-objective genetic algo- rithm[J]. Proceedings of the CSEE, 2018, 38(5): 1348-1355.
[24] Leibl M, Ortiz G, Kolar J W. Design and experimental analysis of a medium-frequency transformer for solid- state transformer applications[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(1): 110-123.
[25] Bahmani M A, Thiringer T, Kharezy M. Design metho- dology and optimization of a medium-frequency transformer for high-power DC-DC applications[J]. IEEE Transactions on Industry Applications, 2016, 52(5): 4225-4233.
[26] 律方成, 郭云翔, 李鹏. 大功率中频变压器多目标参数优化设计[J]. 高电压技术, 2017, 43(1): 210- 217.
Lü Fangcheng, Guo Yunxiang, Li Peng. Optimization design for multiple target parameters of high power medium frequency transformer[J]. High Voltage Engineering, 2017, 43(1): 210-217.
[27] Venkatachalam K, Sullivan C R, Abdallah T, et al. Accurate prediction of ferrite core loss with non- sinusoidal waveforms using only Steinmetz para- meters[C]//IEEE Workshop on Computers in Power Electronics, Mayaguez, 2002: 36-41.
[28] Kazimierczuk M K. High-frequency magnetic com- ponents[M]. Chichester: John Wiley & Sons, 2014: 338-351.
[29] Wojda R P, Kazimierczuk M K. Winding resistance of Litz-wire and multi-strand inductors[J]. IET Power Electronics, 2012, 5(2): 257-268.
[30] Mogorovic M, Dujic D. Medium frequency trans- former leakage inductance modeling and experimental verification[C]//2017 IEEE Energy Conversion Con- gress and Exposition (ECCE), Cincinnati, 2017: 419-424.
An Optimal Design Method for Medium-Voltage Insulated High-Power Medium-Frequency Transformer
Abstract The medium-voltage insulated high-power medium-frequency transformer (MFT) used in photovoltaic grid-connected systems not only requires a large insulation distance between the high and low voltage side windings, but also needs to be poured with thermal-protective insulating materials inside. However, it can lead to problems such as serious electromagnetic interference and difficult heat dissipation in the MFT. Therefore, this paper proposes an MFT optimal design method that fully considers the core size, winding wire diameter and winding arrangement structure. In this method, the core volume is determined by the area product (AP) method, and then the loss of the MFT is minimized by free variable scanning. Based on the finite element simulation software, it is verified that the optimized design method will also reduce the electromagnetic interference area around the transformer. Finally, a 200kW/30kHz MFT was designed through the optimized design method, and a prototype was made. The comparison between theory and experiment verifies the optimized design method.
keywords：High-power medium-frequency transformer, insulation, area product method, loss modeling, optimal design, electromagnetic interference, finite element simulation
DOI: 10.19595/j.cnki.1000-6753.tces.211799
中图分类号：TM432
国家自然科学基金面上项目（52077051）、合肥综合性国家科学中心能源研究院项目（19KZS207, 21KZS203）和高等学校学科创新引智计划项目（BP0719039）资助。
收稿日期 2021-11-04
改稿日期 2022-02-11
王佳宁 男，1985年生，副教授，研究方向为电力设备的封装和可靠性测试、电力电子转换器的集成、宽带隙电力设备的应用、电磁建模。E-mail: 16002530@163.com
胡嘉汶 男，1997年生，硕士研究生，研究方向为多相LLC谐振变换器设计与大功率中频变压器的优化设计。E-mail: hjw970604@qq.com（通信作者）
（编辑 陈 诚）