图1 阻抗分析仪测量三端元件的电路原理
Fig.1 Schematic diagram of measuring three-terminal components with impedance analyzer
摘要 功率MOSFET器件栅极分离电容C-V特性（CGS-VG、CGD-VG）的准确测量对于器件的建模及栅氧可靠性的评估十分重要。阻抗分析仪是测量CGS-VG、CGD-VG的关键设备。在利用阻抗分析仪测量三端器件的某个参数时，需对非测量的第三端进行屏蔽以消除其引入的并联阻抗误差。而功率MOSFET器件在栅压超过阈值电压时呈导通态，影响测量电路拓扑，进而引入其他测量误差。该文针对阻抗分析仪测量功率MOSFET器件的CGS-VG、CGD-VG进行详细的误差分析，揭示测量误差产生的原因；建立测量的等效电路，给出测量误差的解析表达式；结合实验和数值分析量化误差分析，验证了等效电路模型的有效性；最后，提出三种可实现C-V特性准确测量的调控方法并予以实验验证。结果表明，测量误差发生在器件导通后，此时器件漏源极间由电容态转变为低阻态，屏蔽端的寄生电感（L5）与自动平衡电桥的等效输入阻抗（L3）分流，引入误差。当L3和L5满足一定的匹配关系时，可实现不同频率下的准确测量。
关键词：功率MOSFET器件 阻抗分析仪 栅极分离电容C-V特性 等效电路模型 误差分析
随着电力电子技术的发展，功率半导体器件的应用领域日益扩大[1-3]。其中，功率MOSFET器件凭借其快速开关特性而广泛应用于高频开关电路 中[4-7]。由于功率MOSFET器件的极间电容在器件的开关过程中充放电，因此其必然会影响器件的开关性能[8]。随着偏置电压的变化，器件的衬底层发生积累或耗尽，引起功率MOSFET器件极间电容的变化。然而，MOSFET器件的数据手册中仅给出极间电容与漏极电压的非线性关系，未给出其与栅极电压的关系。器件的极间电容中与栅压相关的为栅极电容。此外，在考核器件的栅氧可靠性时，MOSFET器件栅极分离电容的C-V特性（CGS-VG/ CGD-VG）用于分析栅极不同位置的退化程度及退化机理[9]。因此量化功率MOSFET器件栅极分离电容的C-V特性十分重要。
获得功率MOSFET器件栅极分离电容C-V特性的方式有两种：一种是通过半导体物理仿真软件进行有限元仿真，提取栅极分离电容的C-V特性并通过电路仿真或者实验进行验证，该方法需要知道准确的器件结构参数，而其通常难以获得；另一种是直接通过实验进行测量，此时需保证实验测量的准确性。传统测量元件阻抗特性的设备为LCR表或者阻抗分析仪，很多学者在测量功率MOSFET器件栅极分离电容的C-V特性上做过大量的研究，研究内容主要集中在两方面。
一方面，利用栅极分离电容C-V特性的测量结果来指导器件建模，以提高模型的准确度。1991年美国斯克内克塔迪的R. S. Scott等针对极间电容与栅压的非线性特性建立LTspice模型，并与阻抗分析仪测量得到的CGS-VG、CGD-VG进行对比，验证模型的准确性[10]。2005年，飞利浦研究实验室的R. Elferich等基于对器件的测量和有限元仿真对功率MOSFET进行精确的建模，其中阻抗分析仪测试栅极电容特性时，栅压（VG）的测量范围很小，为-10～0V[11]。2008年，法国南希大学的S. RaËl等对栅极传输电容CGD进行建模，并与LCR表的测量结果进行对比，测量频率为10kHz[12]。
另一方面，器件栅极分离电容C-V特性测量的误差分析及测量方式的改进。针对误差分析，1991年，香港科技大学的P. C. Chan等指出，使用LCR表测量两端以上器件的寄生电容时存在误差，误差主要来源于衬底或阱区的电阻，电阻越小测量结果越准确，且测量频率为100kHz。但其没有分析屏蔽端阻抗以及器件导通时的测量误差问题[13]。2000年，飞利浦半导体的P. Habus等提到由于仪器测量拓扑的不稳定性，在沟道导通，即VG大于阈值电压（VTH）时，栅极分离电容的C-V测试结果无效[9]。2003年，安捷伦公司的Y. Okawa等分析了超薄栅介质下由于测量系统的寄生电容引起的负电容效应[14]。
针对测量方式的改进，JEDEC[15]和IEC[16]均标准化了带电容桥的功率器件极间电容测量方式，但未提供实际的测量拓扑。同时标准中指出，为避免寄生元件引入测量误差，测量频率最好低于2MHz[15]。2001年，诺维萨德大学的S. Mileusnic等利用LCR表测量器件栅极分离电容的C-V特性时，为避免非线性特性，测量频率选择100kHz[17]。2009年，日本京都大学的T. Funaki等提出了一种配合阻抗分析仪使用的、能够同时施加栅极和漏极电压的C-V特性测量电路。该电路可以测量器件在正常开关下的C-V特性，测量频率为100kHz。但测量电路较为复杂[8]。2017年，法国诺曼底大学的N. Moultif等在1MHz下测试了高温反偏（High Temperature Reverse Bias, HTRB）实验前后的CGS-VG特性，以评估HTRB对栅氧可靠性的影响[18]。2018年三菱电机的Y. Mukunoki等认为CGD的数值太小导致LCR表测量不准确，因此提出通过米勒平台的栅极电流计算CGD的方法[19]。
传统的LCR表或者阻抗分析仪测量元件阻抗特性的原理均为自动平衡电桥法，由于二者区别仅在于测量阻抗范围和频率范围的不同，后文统一用阻抗分析仪来表示。上述研究表明，功率MOSFET器件栅极分离电容C-V特性的准确测量对于器件的建模及栅氧可靠性的评估十分重要。而阻抗分析仪测量功率MOSFET器件栅极分离电容C-V特性时存在各种误差，且测量频率各有不同。受限于仪器本身可测量的频率范围，并且考虑到器件的开关频率等，可能会存在多个测量频率，然而不同频率下测量结果的正确性有待考量。这是因为阻抗分析仪测量三端器件时会引入一定的测量误差，特别地，对于功率MOSFET器件，在VG＞VTH时器件为通态，此时测量电路拓扑发生变化，必然会引入额外的测量误差。已有文献中，部分认为在器件导通时阻抗分析仪的测量结果无效，部分忽略了这个问题，认为测量结果正确。因此，有必要对阻抗分析仪测量功率MOSFET器件栅极分离电容的C-V特性进行系统的误差分析与评估，探索能够实现准确测量的方法，进一步提高器件建模及栅氧可靠性评估的准确性。
本文首先分析了阻抗分析仪测量功率MOSFET器件栅极分离电容C-V特性的原理与误差产生的原因。其次，建立了考虑寄生参数影响的阻抗分析仪测量功率MOSFET器件栅极分离电容C-V特性的等效电路模型，定性分析了各部分引入的误差并给出了误差测量的表达式。然后，结合实验量化了误差分析并验证了等效电路模型的有效性。最后，针对阻抗分析仪准确测量栅极分离电容C-V特性提出一些建议。
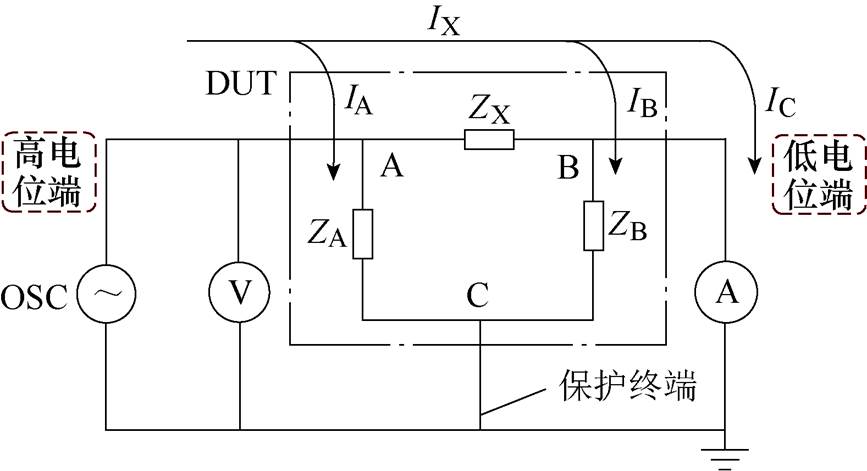
当被测元件为三端元件，被测量为其两端间的阻抗参数时，需通过保护技术消除第三端可能引入的并联阻抗测量误差。图1为阻抗分析仪测量三端元件的电路原理[20]。
图1中的高电位端和低电位端分别代表阻抗分析仪的高、低电位测量终端。自动平衡电桥的低电位端简化为电流表的形式，电流表的内阻即为自动平衡电桥电路的等效输入阻抗。DUT为被测元件，OSC为测量用交流小信号，ZX、ZA、ZB分别为三端元件被测阻抗、第三端与测量端A间的阻抗、第三端与测量端B间的阻抗。IX、IA、IB、IC分别为实际流过ZX的电流、流过ZA的电流、流过ZB的电流、流过电流表的电流（即测量得到的流过ZX的电流）。保护终端为自动平衡电桥中的虚位点，与大地电气隔离，但从电路上分析，保护终端的电位十分接近于零电位[18]，因此在电路原理中可将保护终端等效为接地。
图1 阻抗分析仪测量三端元件的电路原理
Fig.1 Schematic diagram of measuring three-terminal components with impedance analyzer
由图1可见，通过将被测器件的第三端与保护终端相连，流过ZA的电流IA将不会回流到电流表中。同时，由于电流表的内阻非常小，流过ZB的电流IB也很小。因此，实际电流表测量到的电流IC与流过ZX的电流IX基本一致，测量误差很小。然而，若ZB小到与电流表的内阻相当时，IB的值必然增大，导致电流表测量到的电流小于IX，测量误差增大。此外，进行第三端屏蔽时，若第三端与保护终端连接的引线的阻抗较大，IA将通过ZA流至ZB，最终计入实测电流IC，导致测量结果出现误差。
根据1.1节分析可得，阻抗分析仪测量三端元件时，保护终端的寄生阻抗带来的影响不可忽略。此外，对于功率MOSFET，在VG＞VTH时，器件导通，此时DS间的电容将被低导通电阻（Ron）旁路，导致图1中的ZB突变到一个很小的值，这必将引入其他的测量误差。因此，有必要建立考虑寄生参数影响的测量电路模型来分析各部分参数对测量结果的影响。
以测量CGS-VG为例，图2为考虑寄生参数后的阻抗分析仪测量功率MOSFET CGS-VG的等效电路模型。图中，DC为施加栅极偏置的阻抗分析仪内置直流源，G、S、D分别代表被测器件的栅极、源极和漏极，ZGS、ZGD、ZDS分别为被测器件栅源极、栅漏极、漏源极间的寄生阻抗，ZGS为被测阻抗。Z1和Z3分别为被测器件的G、S连接到阻抗分析仪及测量夹具的高、低电位端引入的寄生阻抗，Z5为第三端D连接到测量系统保护终端引入的寄生阻抗。
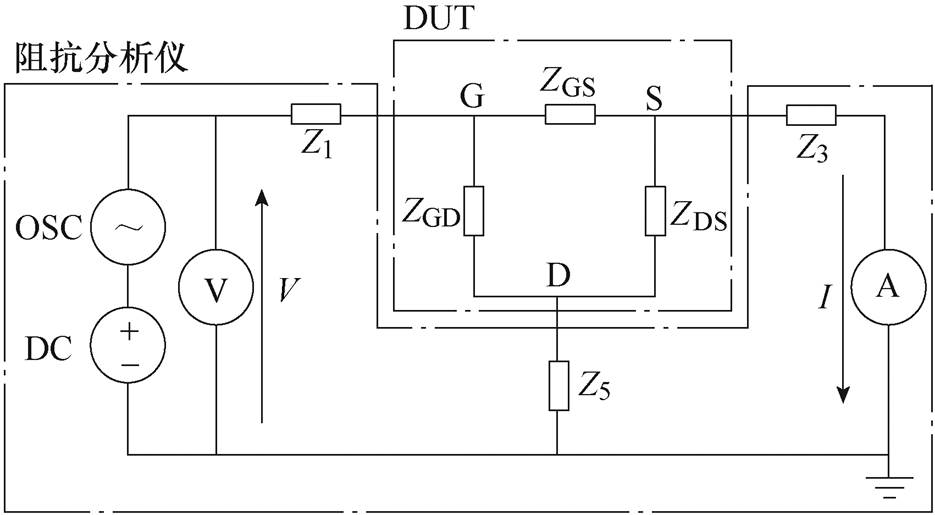
图2 阻抗分析仪测量功率MOSFET器件栅极分离电容C-V特性的等效电路
Fig.2 Equivalent circuit model of impedance analyzer to measure split C-V characteristics of power MOSFET device
求解图2的等效电路模型，可得实际测量阻抗ZGS(meas)表达式为
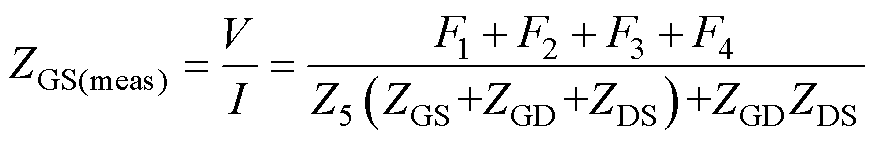（1）
其中
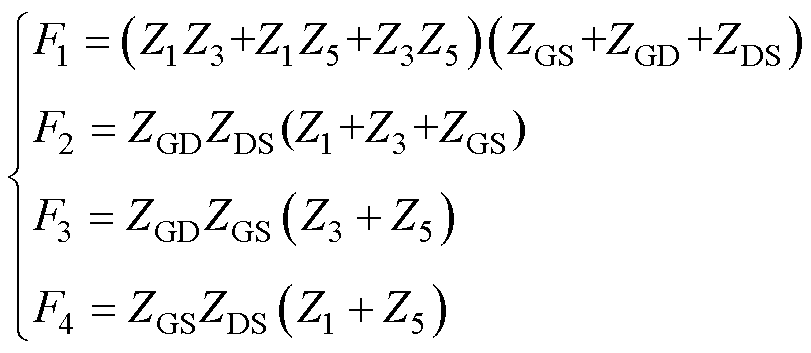（2）
由式（1）、式（2）可见，测量ZGS时，由于串联阻抗Z1、Z3、Z5及并联分流阻抗ZGD、ZDS的引入，导致实际测量所得ZGS(meas)≠ZGS。对于确定的被测器件，其极间阻抗的值均为确定量，即ZGS、ZGD、ZDS不可改变。因此图2中引入测量误差的量为Z1、Z3、Z5。显然，理想情况下Z1=Z3=Z5=0时，ZGS(meas)=ZGS，即图1所示电路。但实际测量电路中，Z1、Z3、Z5均不为0，因此必然会存在测量误差。
由于连接引入的Z1、Z3、Z5阻抗中的寄生电阻部分都较小，因此对于Z1、Z3、Z5，仅考虑其寄生电感的值，不计寄生电阻。考虑半导体材料的损耗特性，对于被测器件三端间的寄生阻抗ZGS、ZGD、ZDS，均采用电容和电阻并联的模型。对于功率MOSFET，阻抗分析仪进行栅极分离电容C-V特性测量时，器件导通前后测量等效电路的拓扑不同，因此需分别对导通前（VG＜VTH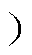
和导通后（VG＞VTH）两个阶段分别建模。两个阶段的差异在DS间的状态：在器件导通前DS间呈电容与电阻并联；导通后DS间为器件的导通电阻。根据以上原则将图2转化为器件导通前后参数化的等效电路，分别如图3、图4所示。图中的点画线框的部分代表器件导通前后等效电路模型拓扑改变的位置。
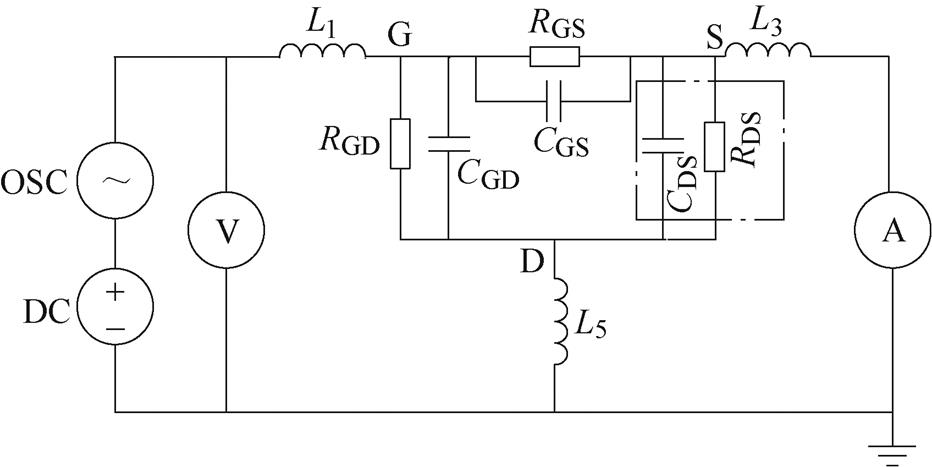
图3 VG＜VTH时，参数化的等效电路
Fig.3 Parametric equivalent circuit model (VG＜VTH)
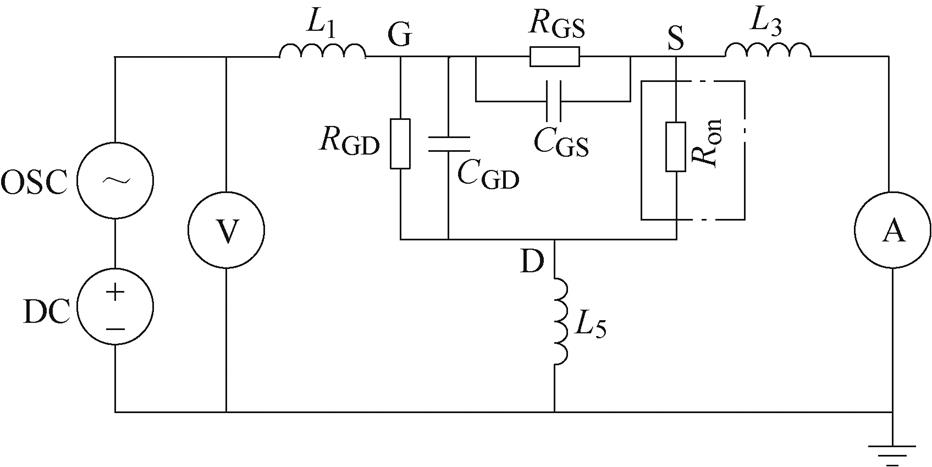
图4 VG＞VTH时，参数化的等效电路
Fig.4 Parametric equivalent circuit model (VG＞VTH)
对比图1和图3、图4可得，在器件导通前GD和DS间的阻抗都足够大，即图1中的ZA和ZB均足够大，电流表测到的电流基本为实际流过器件的电流，此时寄生电感L1、L3、L5影响应较小。器件导通后，GD间阻抗无变化，由于L1主要受GD间阻抗的影响，故器件导通后L1的影响仍较小；但DS间呈现低阻态，即图1中的ZB很小，此时L3、L5的影响将不可忽略，可等效为L5和Ron串联后与L3并联分流，进而影响实际流过电流表的电流，引起测量误差。根据图3或图4中参数化的等效电路模型，结合式（1）、式（2）得到被测阻抗的测量值ZGS(meas)，通过傅里叶分析方法从频域分析角度可求得被测电容CGS的测量值CGS(meas)及并联电阻的测量值RGS(meas)，表达式为
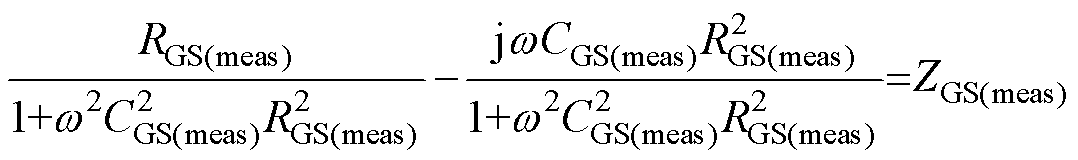（3）
由于ZGS(meas)的表达式较为复杂，根据式（1）～式（3）无法直接判断各部分参数引起的误差大小。因此下文将结合实验测量和数值分析量化各部分的测量误差。
以功率SiC MOSFET为例进行实验，验证上述等效电路模型的有效性并量化各个部分的误差。选取某商用SiC MOSFET为测量样本，封装形式为TO-247-3，待测量为CGS-VG和CGD-VG。对于TO封装的SiC MOSFET器件，可使用阻抗分析仪适配的夹具测量其栅极分离电容的C-V特性。以测量CGS-VG为例，测量的实验平台如图5所示，器件的栅极（G）、源极（S）分别与阻抗分析仪夹具输出的高、低电位端相连，第三端漏极（D）与夹具上的保护终端相连。根据JEDEC标准规定，测量频率低于2MHz。不同频率下SiC MOSFET栅极电容的C-V特性如图6所示。图6a～图6c分别展示了使用阻抗分析仪不同测量频率下CGS-VG、CGD-VG和栅极输入电容CISS-VG的测量结果。CISS的测试中，器件的DS短接，不涉及第三端屏蔽，该结果的展示仅为说明栅极分离电容CGS、CGD和栅极输入电容CISS间的关系。需说明的是，经测量，被测器件的VTH= 2.6V，Ron=80mW。
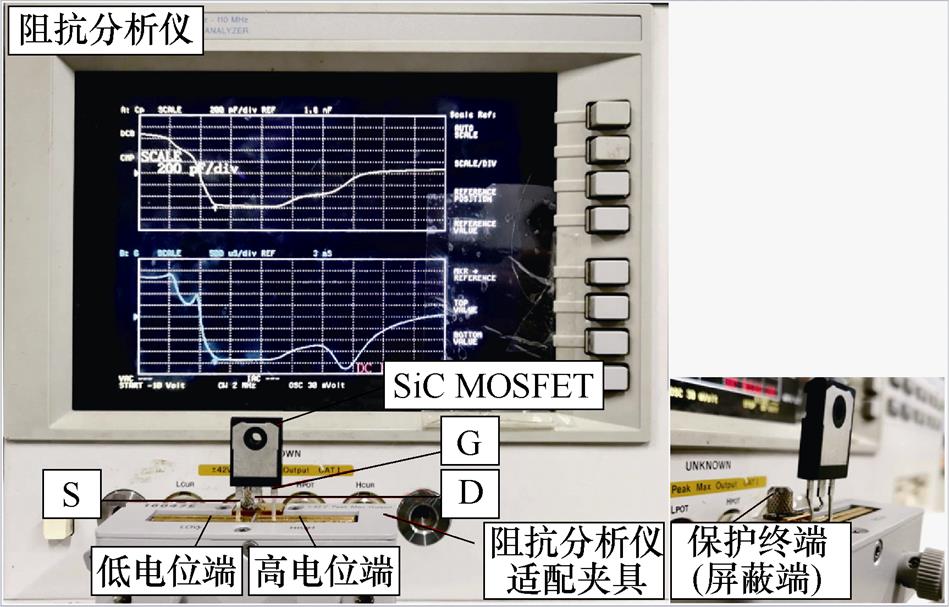
图5 阻抗分析仪测量功率MOSFET CGS-VG实验平台
Fig.5 Experimental platform of impedance analyzer to measure CGS-VG characteristics of power MOSFET
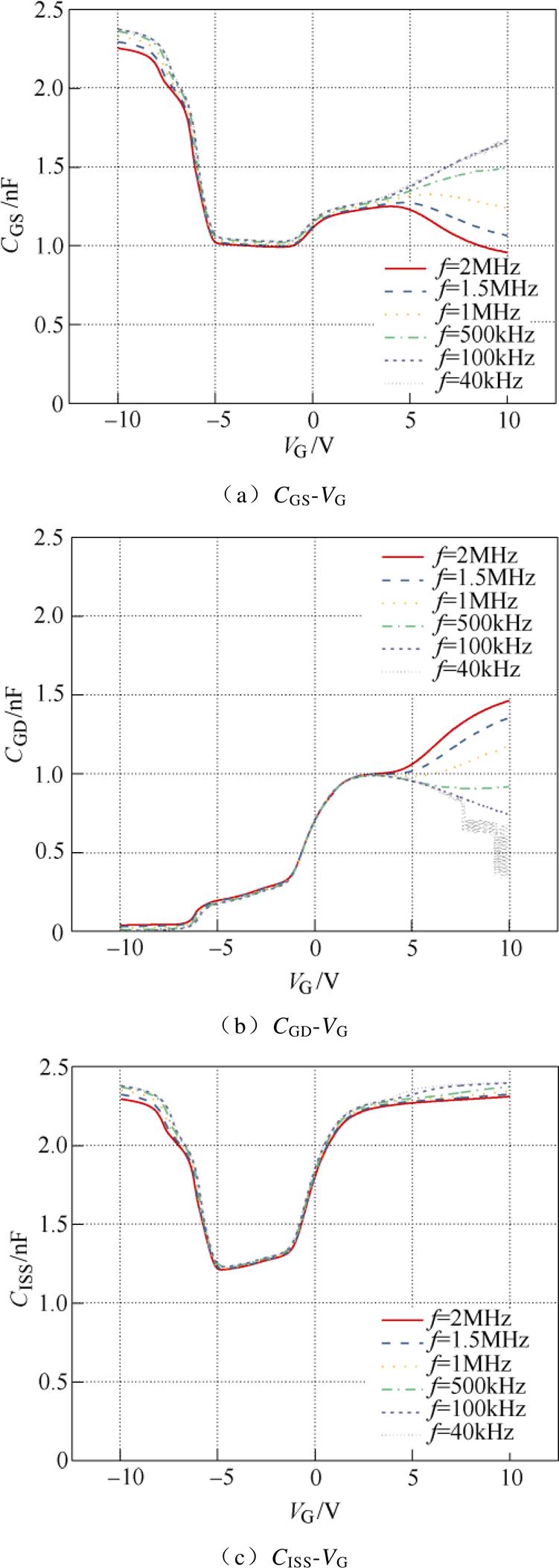
图6 不同频率下SiC MOSFET栅极电容的C-V特性
Fig.6 Split C-V characteristics of SiC MOSFET at different frequencies
对于CISS，图6c的测量结果与理论一致，即随VG增大，高低频下CISS在VG＞VTH时总会增大到饱和态，与低栅压下，沟道积累时的电容一致。这是由于在VG＞VTH时，器件的漏极和源极均能够给沟道区提供自由电子[21]。然而，图6a、图6b中，不同测量频率下CGS、CGD的测量结果局部存在较大分散性。大约以VTH为分界线，在VG＜VTH时，不同频率下的测量结果几乎重合，仅在VG=-10V附近测量存在较小分散性；而在VG＞VTH时，不同频率下测量结果分散性很大，且随频率的增大，CGS的测量值逐渐减小，CGD的测量值逐渐增大，二者的和恒为CISS。考虑到SiC MOSFET的栅极SiC/SiO2界面处存在较高的界面态密度，在不同测量频率下界面态电荷的充放电状态不同，可能会导致电容的变化。图6a、图6b中，对于VG＞VTH时不同频率下CGS、CGD出现的分散性，无法确定其是由测量误差还是由界面电荷引起，也无法判断测量结果的正确性。这是因为在VG＞VTH阶段，器件DS间状态发生改变，引起测量电路的拓扑改变，加之界面电荷的影响，此时电路中并不是单一变量。因此首先有必要对该测量结果中阻抗分析仪引入的测量误差进行分析。
定义ZGS和CGS的测量误差系数分别为
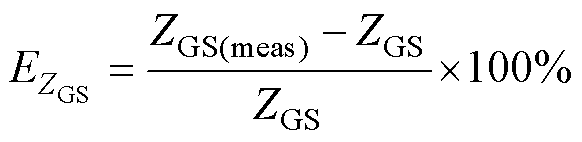（4）
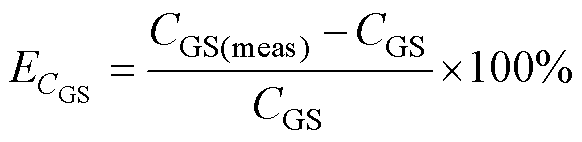（5）
同上，以CGS-VG为例进行分析。显然，图6栅极分离电容的测量结果中，测量频率为40kHz和100kHz时的测量结果几乎完全重合。但当测量频率低于100kHz时，器件导通后的测量结果明显有毛刺或者不规则振荡，可见频率太低时仪器的测量精度会降低，这一点在文献[13]中也有提及。基于此，后文的误差分析取测量频率范围为100kHz～2MHz。为便于分析，本文取测量中固定栅压下的一个点进行分析，由于测量差异在VG＞VTH阶段出现，本文取VG=VTH（临界点）处对应的电路参数对图3、图4的等效电路模型进行量化。若认为此时器件尚未导通，则对应图3的等效电路模型，模型中的参数分别为CGS=1.3nF, RGS=2kW，CGD=1nF, RGD=2kW, CDS=400pF, RDS=2kW。其中，CDS的值与VG无关，因此其参照了器件的数据手册中漏极电压VD与栅极电压VG均为0时对应的值；若此时器件已经导通，则对应图4的等效电路模型，模型中的参数除DS间变为Ron=80mW 外，其他参数不变。为验证第1节图3、图4等效电路模型的有效性，下文均分器件导通前（VG＜VTH）和导通后（VG＞VTH）两个阶段对测量误差进行分析。
2.2.1 L1引入的误差分析
根据器件导通前后对应的图3、图4等效电路模型，在器件导通前后GD间电路拓扑不变，故L1引入的误差应较小。在L3=L5=10nH的条件下，取L1=0～100nH，图7a、图7b分别展示了器件导通前后L1的误差分析结果。
由图7a可得，VG＜VTH时，测量电容随L1及测量频率的增大均略微增大。在L1=100nH，f =2MHz时，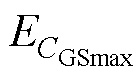
＜4%，可见，在器件未导通时L1对测量结果的影响很小。
由图7b可得，VG＞VTH时，在固定频率下，随L1的变化，测量电容变化很小；而在固定的L1下，测量电容随频率的增大而减小，L1=0nH，f =2MHz时，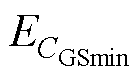
≈-10%。此外，从图中可得，L1=0与L1≠0的测量误差基本相同，这说明不同频率下测量结果的差异与L1基本无关。频率的变化也会影响L3和L5对应的阻抗，这可能是引起图7b中测量电容变化的根本原因，该结论将在下文具体分析。因此，器件导通后，L1对测量结果的影响也较小。以上验证了等效电路模型和分析的有效性。
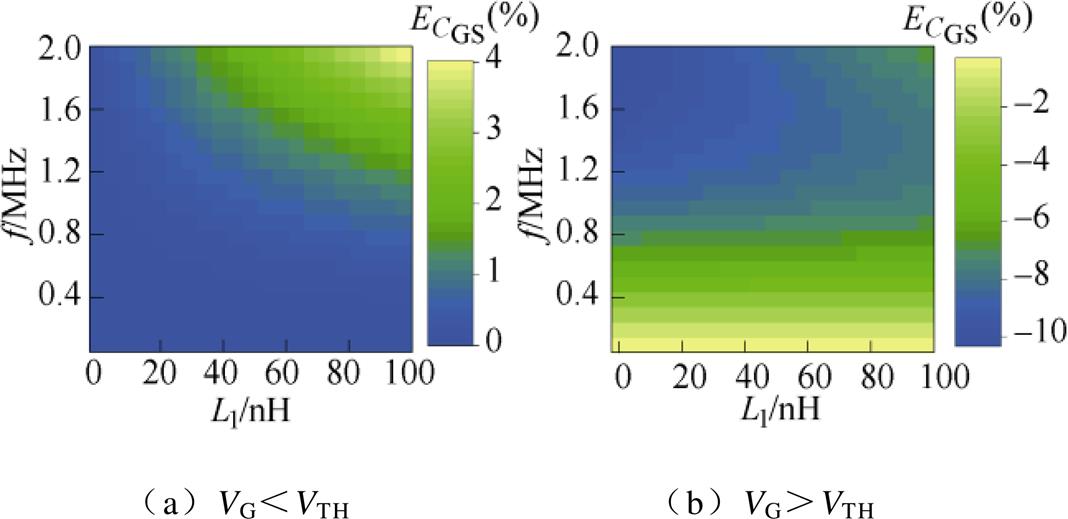
图7 L1引入的误差
Fig.7 Error introduced by L1
2.2.2 L3引入的误差分析
根据器件导通前后对应的图3、图4等效电路模型，改变器件导通前后DS间电路拓扑，故器件导通后L3引入的误差会发生变化。类似地，控制L1=L5=10nH，取L3=0～100nH，在VG=VTH的等效电路模型下分析导通前后L3引入的误差，结果分别如图8所示。
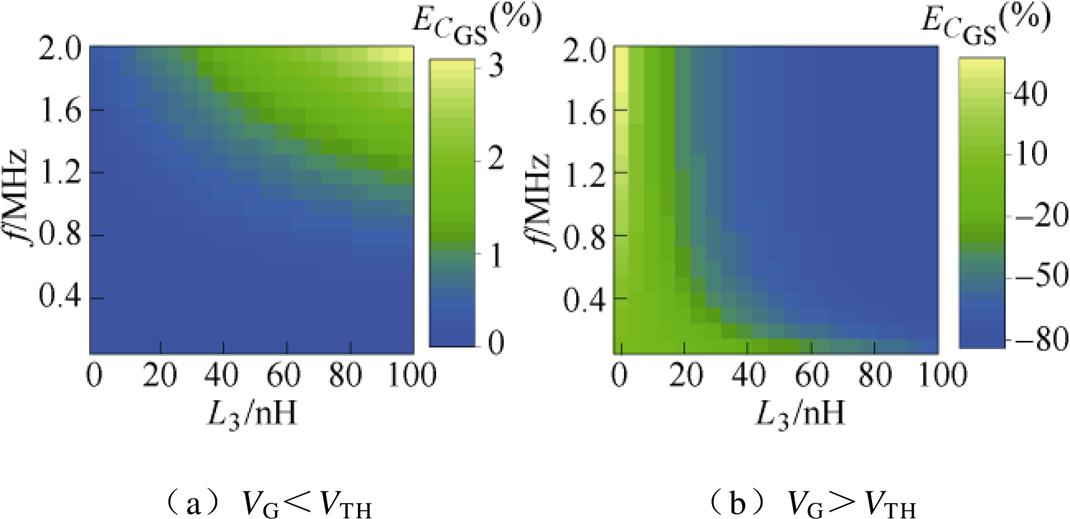
图8 L3引入的误差
Fig.8 Error introduced by L3
由图8a可得，VG＜VTH时，测量电容随L3以及测量频率的增大均略微增大。在L3=100nH，f =2MHz时，
＜3%，可见，在器件导通前L3对测量结果的影响很小。
由图8b可得，VG＞VTH时，在固定的测量频率下，测量电容随L3的增大而减小；在固定的L3取值下，测量电容随测量频率的变化非单调，且存在一定的分散性。提取图8b中几个频点下的结果转换成二维图如图9所示。
由图9可得，随L3的变化，100kHz下的测量结果最稳定。且L5=10nH的前提下，大约在L3=10nH时测量结果最准确。由器件导通后图4的等效电路模型可得，器件导通后DS间呈低阻态，电路可等效为L5和Ron串联后再与L3并联分流，实际测得的电流即流过L3的电流与L5相关，因此测量结果最准确时L3的取值显然依赖于L5的大小。由器件导通后的分析结果可见，L3引入的误差增大，验证了等效电路模型和分析的有效性。
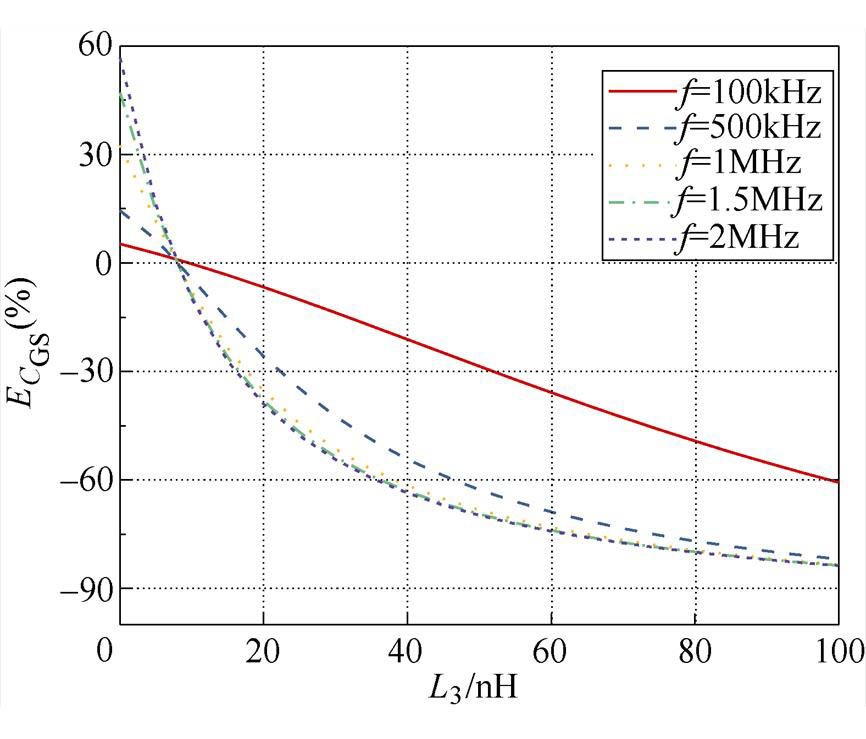
图9 VG＞VTH，不同频率下L3引入的误差
Fig.9 Error introduced by L3 at different frequencies (VG＞VTH)
2.2.3 L5引入的误差分析
根据器件导通前后对应的图3、图4等效电路模型，在器件导通前寄生参数的影响应都较小。器件导通后由于DS间呈低导通电阻，L3和L5将直接影响实际流过电流表的电流，此时L5的误差不可忽略。对于测量系统中的阻抗分析仪及其适配的夹具，在Z1和Z3的部分不存在人为引入的其他电路元件，因此测量系统本身引入的Z1、Z3寄生阻抗值很小。在此，假定阻抗分析仪及夹具测量器件的C-V特性时引入的L1=L3=10nH。考虑到实际的电路连接，屏蔽端阻抗L5的值可能较大，因此取L5=10～200nH进行误差分析。图10a、图10b分别展示了器件导通前后L5的误差分析结果。
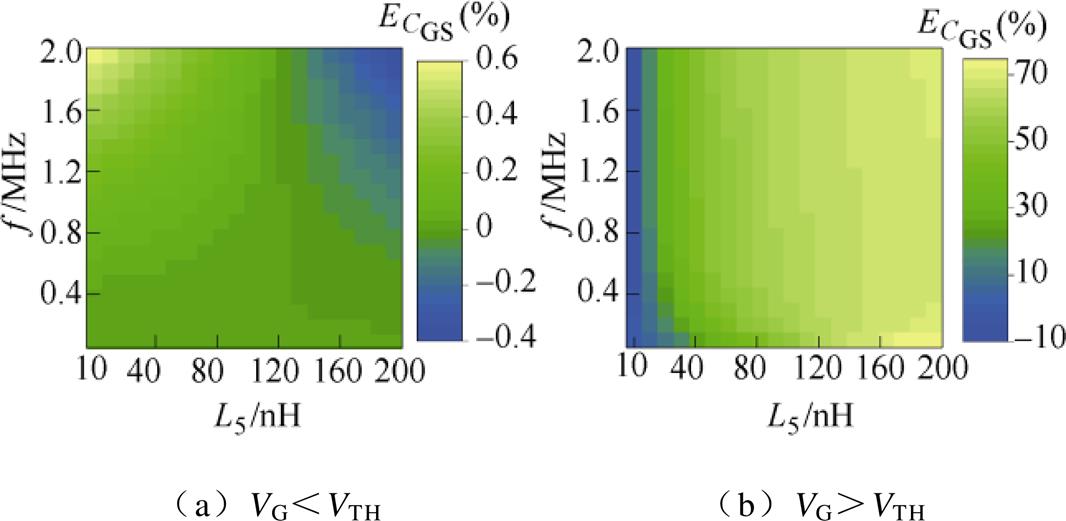
图10 L5引入的误差
Fig.10 Error introduced by L5
由图10a可得，VG＜VTH时，测量电容随L5的增大而减小，随测量频率的增大而增大。在L5= 10nH，f =2MHz时，＜0.6%。屏蔽端阻抗L5的主要作用为屏蔽掉通过L1和ZGD的电流，避免该
电流通过ZDS回流到电流表中，影响测量电流。在器件导通前，由于DS间呈电容和电阻的并联，ZDS很大，因此L5及频率的影响很小。以上分析表明，对于本文的被测器件，在器件导通前保护终端引入的寄生电感L5在200nH以内时对测量结果的影响误差均很小，可忽略不计。
由图10b可得，VG＞VTH时，在固定的测量频率下，测量电容随L5的增大而增大，且在L5最小时对应的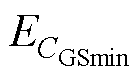＜0。该结果表明，在器件导通后，保护终端引线的寄生电感并不是越小越好。为得到准确的测量结果（
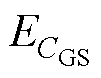=0），需要L5满足一定的条件。此外，不同测量频率下使得测量结果最准确的L5的值不同。从图10b中可见，在不同L5的取值下，测量结果随测量频率的变化并非线性关系。为确定在不同的测量频率下保护终端寄生电感的最佳取值，将图10b转换为不同频率下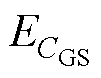随L5变化的二维平面图，VG＞VTH，不同频率下L5引入的误差如图11所示。为使展示效果更为清晰，图11中仅展示了5个频点下的误差分析曲线，但足以反映分析结果。
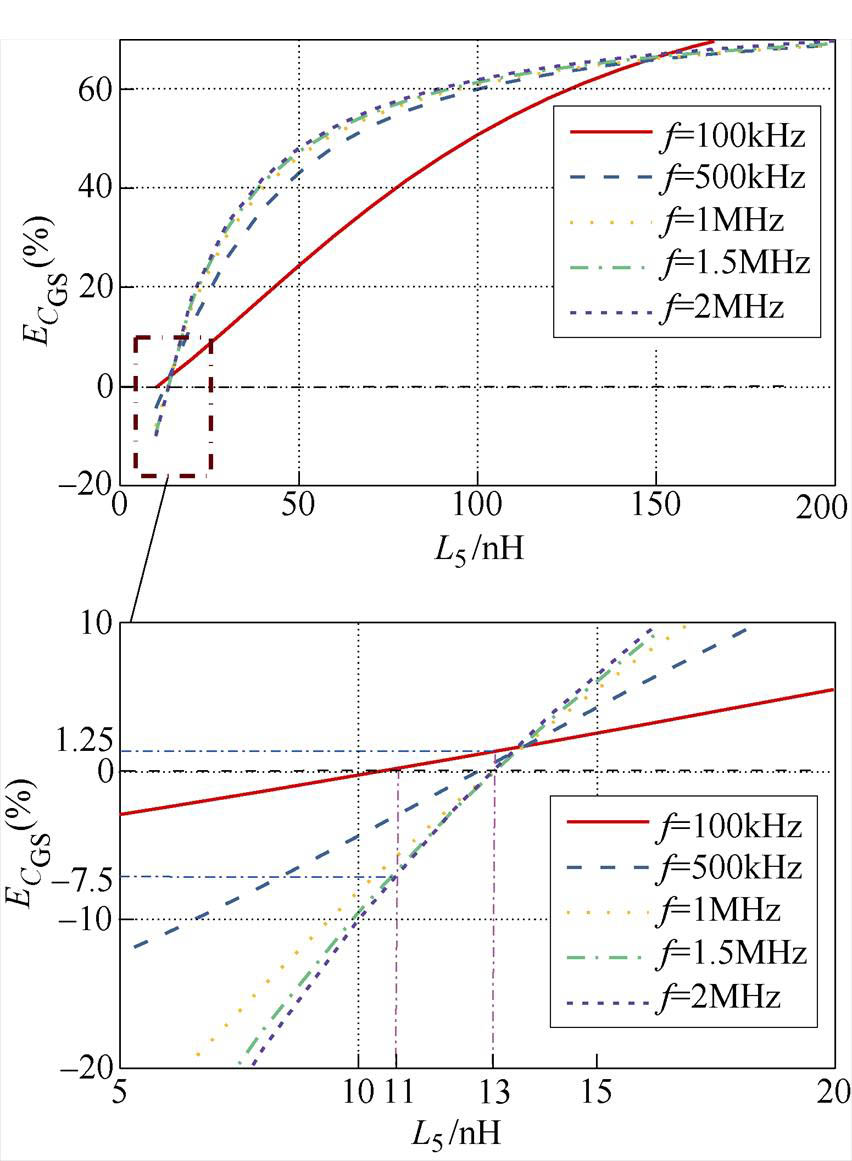
图11 VG＞VTH，不同频率下L5引入的误差
Fig.11 Error introduced by L5 at different frequencies (VG＞VTH)
图11表明，对于本文所测量的SiC MOSFET，器件导通后，大约在L5＜14nH时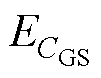，随测量频率的增大而减小，且频率越低该规律越明显；当14nH＜L5＜150nH时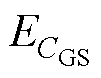，随测量频率的增大而增大，同理，频率越低时该规律越明显。对比图6a，器件导通后，测量电容随频率的增大而减小，因此图10的计算结果中L5＜14nH阶段与实际测量结果一致。
进一步地，随测量频率的增大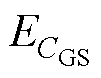，=0时对应的L5的最佳取值（下文记为L5(opti)）单调增大。在所分析的测量点VG=VTH处，随测量频率的增大，L5(opti)变化较小。取频率的两个极端值分析，规定f =100kHz时L5(opti)表示为L5(opti)_100kHz，可得L5(opti)_100kHz=11nH，同理L5(opti)_2MHz=13nH。此外，不同频率下测量结果对L5的灵敏度也不同，随测量频率的增大，测量结果对L5的灵敏度也增大。显然，随频率的增大，L5对应的阻抗增大，导致引入的测量误差增大。规定取L5=L5(opti)_2MHz时，100kHz下的测量误差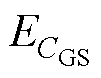表示为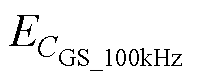
，同理，L5=L5(opti)_100kHz时，2MHz下的测量误差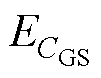表示为
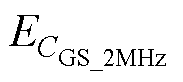。可得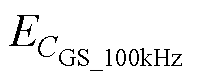= 1.25%，而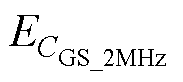=-7.5%。综上分析，在假设L3= 10nH的前提下，可认为阻抗分析仪及夹具本身屏蔽端引入的寄生电感L5＜14nH，且测量频率越低，误差越小且越稳定。由于在VG=VTH处为临界点，在此栅压下不同频率的测量结果基本重合，即测量结果应位于图10中的交点附近，此时100kHz测量结果略偏大，最大可近似为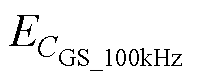=1.25%。可见即使100kHz下测量误差也非常小，并且100kHz下的测量误差随L5的波动最稳定。综上，在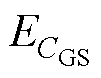＜1.25%的情况下，可认为100kHz下的测量结果是准确的。
假定上述分析成立，取测量结果分散性最大的点（VG=10V）进一步分析导通状态下的误差。以f = 100kHz的测量结果为基准，VG=10V时，CGS= 1.67nF, RGS=2kW，CGD=0.73nF, RGD=2kW，此时器件已经导通，因此按照图4的等效电路模型进行分析，DS间取Ron=80mW。误差分析结果如图12所示。
由图12可得，在VG=10V处，随测量频率的增大，仍呈现L5(opti)单调增大的规律。此时，L5(opti)_100kHz= 11nH，L5(opti)_2MHz=22.5nH。其中VG=10V时与VG=VTH分析点处所得的L5(opti)_100kHz相同。且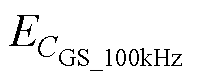= 4.5%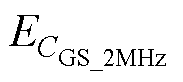，=-20%。该结果与图6a的测量结果一致，即VG越大，不同频率下测量结果的分散性越大，且高频下测得的电容偏小。可见，在不同栅压下，100kHz时L5(opti)基本稳定在11nH，且与阻抗分析仪测量时保护终端寄生电感的预估值（L3=10nH的情况下，L5＜14nH）较为接近。故可认为100kHz下测量结果准确，2MHz下的测量误差最大，为-20%。数值分析结果与实验结果的一致性很好地证明了等效电路模型的有效性。
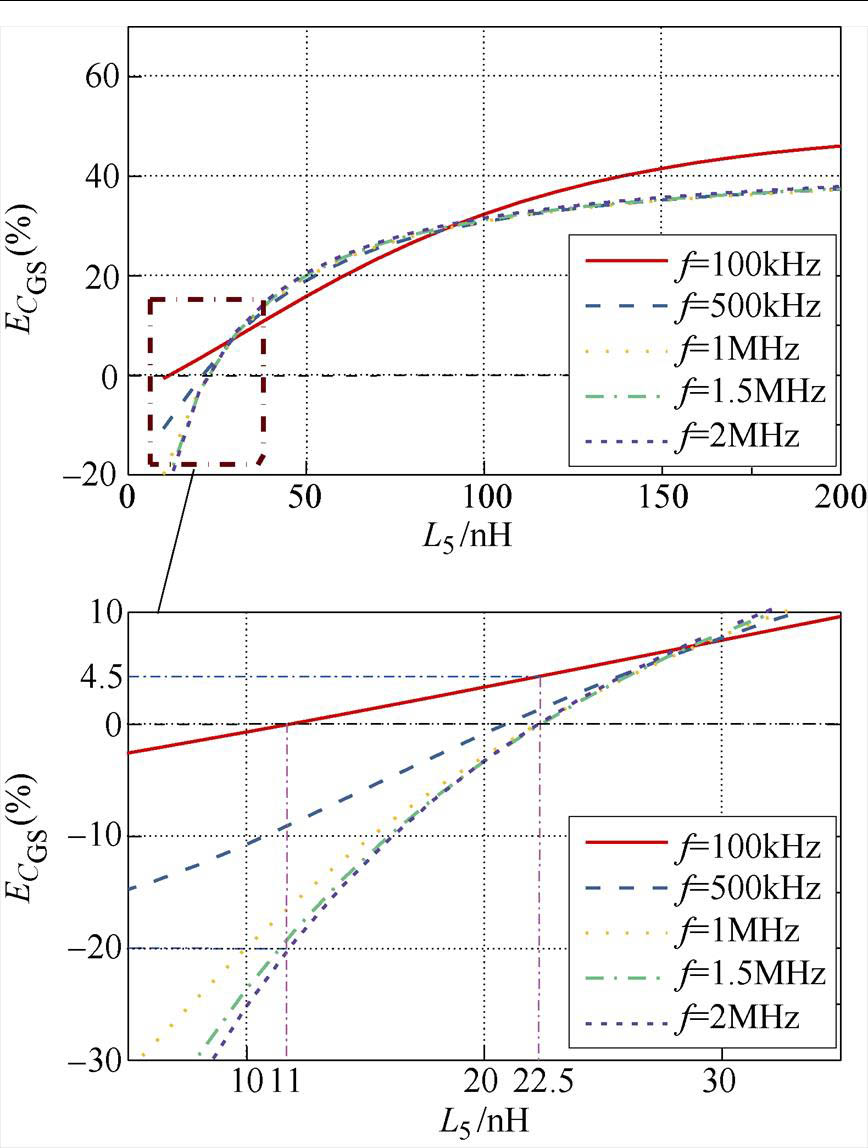
图12 VG＞VTH，不同频率下L5引入的误差（分析点为VG=10V）
Fig.12 Error introduced by L5 at different frequencies (VG＞VTH, analysis at VG=10V)
需注意的是，上述分析均以L3=10nH为前提。显然，器件导通后L3和L5共同影响不同频率下的测量结果。二者间的关系以及如何通过二者的有效匹配实现最准确的测量将在第3节中进行讨论。
2.2.4 导通电阻的误差分析
上述分析表明阻抗分析仪测量功率MOSFET器件栅极分离电容C-V特性时，测量误差主要发生在器件导通后，主要原因是器件导通后DS间的低阻态引起的屏蔽端寄生电感L5与自动平衡电桥的等效输入阻抗L3的分流。显然，器件导通后，导通电阻的值必然会影响测量结果。假定L3=L5=10nH，分析导通电阻对测量结果的影响，结果如图13所示。
由图13可得，在固定频率下，导通电阻Ron越大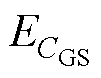，越接近0，测量结果越准确。且固定导通电阻下，测量频率越大误差越大。该结果进一步验证了等效电路模型及误差分析的有效性，即导通电阻越大，屏蔽端阻抗的分流越小，此时电流表测得的电流越大，越接近于真实值。测量频率的增大导致屏蔽端阻抗的增大，进而增大了测量误差。
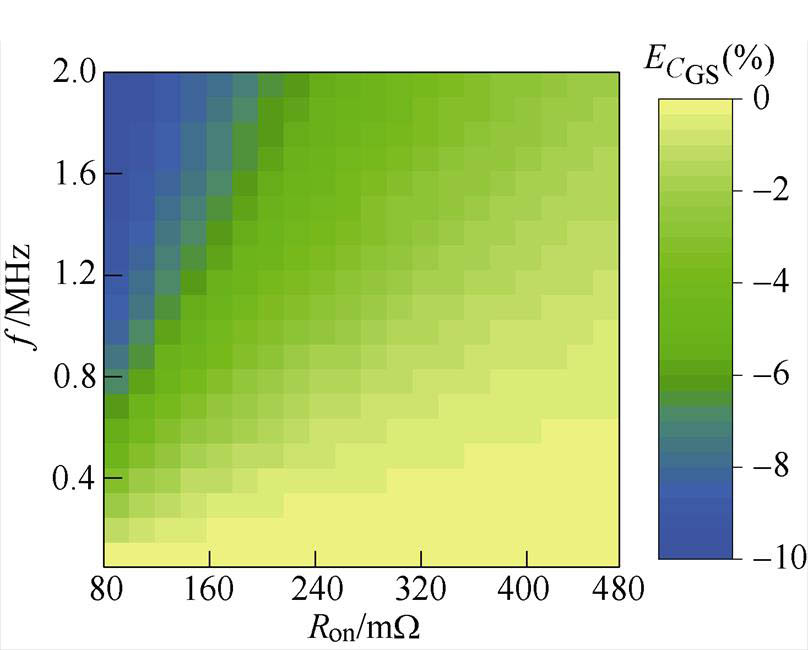
图13 VG＞VTH，导通电阻引入的误差
Fig.13 Error introduced by Ron (VG＞VTH)
对于确定的被测系统，被测器件的导通电阻Ron确定，自动平衡电桥的等效输入阻抗L3一般也确定。因此根据第2节对测量等效电路模型的数值分析可得，阻抗分析仪测量功率MOSFET的栅极分离电容C-V特性时，测量误差主要来源是器件导通后屏蔽端寄生阻抗L5的影响，且其引入误差与测量频率密切相关，因此主要通过实验验证这部分引入的误差。同上，以测量CGS-VG为例，通过实验中在器件的D端串联不同大小的电感来研究L5对测量结果的影响，串联的电感用LS来表示。在测量频率为1MHz和100kHz下测量的CGS-VG结果如图14所示。
由图14可得，不同测量频率下，屏蔽端串联的寄生电感在0～63.4nH变化时，仅影响VG＞VTH段的电容测量结果，VG＜VTH的测量结果完全重合，验证了测量误差出现在器件导通后，且与屏蔽端寄生电感有关；VG＞VTH时，测量所得电容随屏蔽端寄生电感的增大而增大，且f =100kHz时测量结果的分散性较f =1MHz时小，这与图10b的数值分析结果一致，验证了误差分析的有效性。
器件导通后，屏蔽端的寄生电感将起到两方面的作用：一是屏蔽掉流过L1和ZGD的电流，这部分与器件是否导通无关，图10a的分析证明了L5在200nH以内时这部分的影响很小，可忽略不计；二是器件导通后，DS间呈现低阻态，此时被测电流会通过DS间的低阻流向屏蔽端，导致流过电流表的电流减小，即L5与L3间存在并联分流的关系。因此需要L3和L5的匹配以实现准确测量。
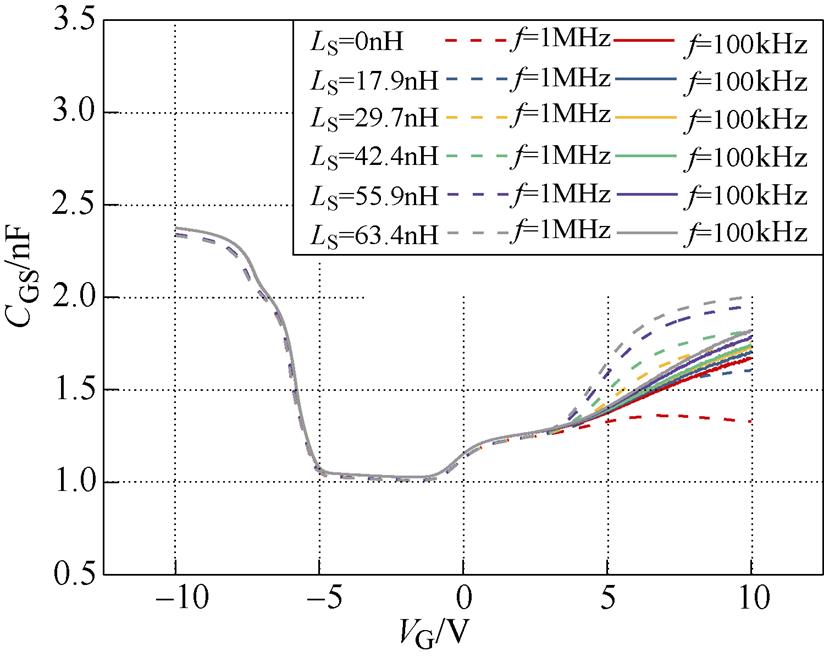
图14 不同频率下，不同屏蔽端寄生电感的测量结果
Fig.14 Measurement results of different L5 under different frequency
第2节的分析结果表明，L5(opti)随测量频率的变化而变化。此外，由于器件导通后L5与L3的分流直接影响了测量结果，因此L5(opti)与L3相关。在Ron=80mW时，取L3=5nH, 10nH, 15nH分别计算不同频率下的L5(opti)及测量误差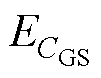。图15和表1分别展示了L5(opti)和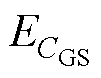的结果。
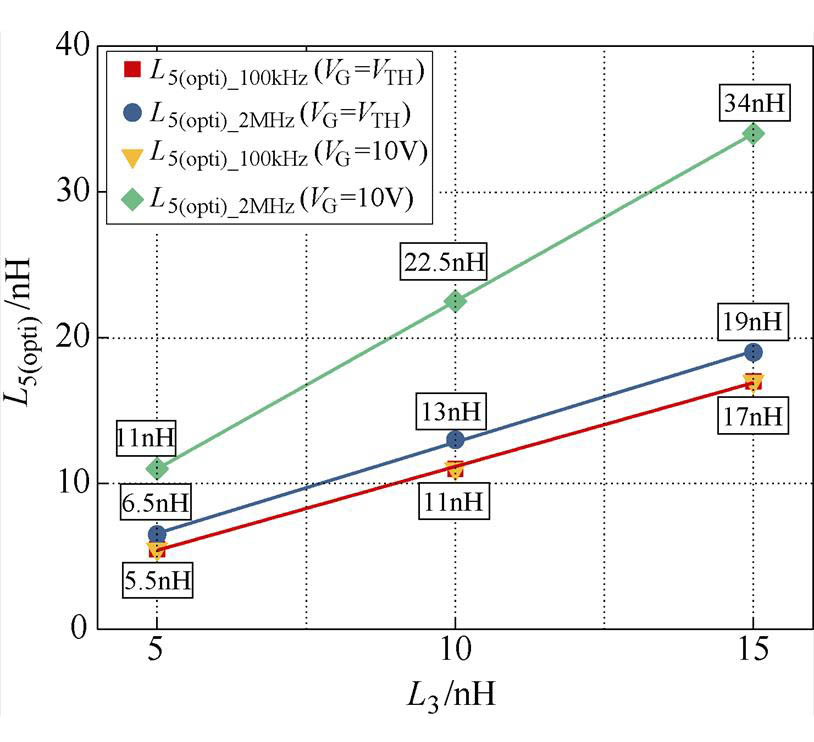
图15 VG＞VTH，不同L3下L5(opti)
Fig.15 L5(opti) under different L3 (VG＞VTH)
由图15可得，100kHz下VG=10V与VG=VTH时的L5(opti)相等，且随L3的增大而增大，验证了100kHz下测量结果的稳定性。低频100kHz测量时寄生阻抗小，随VG的变化L5(opti)基本稳定在一个确定的值，且该值仅与L3相关。2MHz下VG=10V时的L5(opti)大于VG=VTH的值，这是由于在器件导通后，器件的CGS和CGD随着VG的变化而改变，并且随着VG的增大，CGS和CGD的差值也增大，导致在高频下测量时L5(opti)随VG的增大而增大，同时L5(opti)也随L3的增大而增大。
表1 VG＞VTH，不同L3下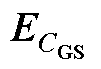
Tab.1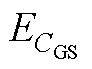 
under different L3 (VG＞VTH)
L3/nHVG/V(%)(%) 52.6(VTH)1— 10—-18 102.6(VTH)1.25— 10—-20 152.6(VTH)2— 10—-19
由表1可得，以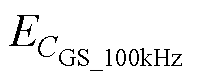来评估100kHz下VG= VTH时的测量误差（此时100kHz的误差最大），该测量误差随L3的增大而增大，L3=15nH时最大误差仅为2%。VG=10V时，显然，100kHz下的测量结果最准确；以
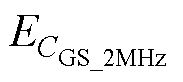来评估VG=10V时2MHz下的测量误差（此时2MHz的测量误差最大），其随L3的增大几乎不变，但误差本身较大，约为20%。因此，随VG的变化，100kHz下的测量结果较为准确。
综上分析，针对阻抗分析仪准确测量功率MOSFET器件栅极分离电容的C-V特性提出以下三点调控方法，并通过本文中利用阻抗分析仪适配的夹具测量功率MOSFET的CGS-VG实验进行验证。
1）低频测量不做补偿
若使用阻抗分析仪及其适配的夹具进行测量，测量系统本身引入的L3和L5值较小，此时测量频率越低，测量结果越准确。然而受仪器精度限制，测量频率小于100kHz时，波形存在不规则振荡，因此实际测量频率为100kHz时，测量误差最小。经本文分析，若阻抗分析仪及测量夹具本身引入的寄生电感满足L3＜15nH、L5＜19nH，100kHz下的测量结果误差均小于2%，即在2%的误差允许范围内可认为100kHz的测量结果较为准确。
图14的结果侧面反映了本方案的有效性。图中，在屏蔽端串联的寄生电感LS=0nH的情况下测量系统中的寄生参数仅为阻抗分析仪及其适配的夹具引入的部分，而测量系统本身引入的L3、L5值均很小。故认为100kHz下的测量误差最小，测量结果最准确。
2）低频测量做补偿
针对被测元器件的不同封装形式、不同测量方式（比如探针台测试芯片等），需要引入其他的测量引线或者自主设计适配的夹具，此时L3、L5均可改变。由图15可得，在较低频率如100kHz下测量时，L5(opti)仅与L3相关，且二者呈近似线性关系，表达式可写为
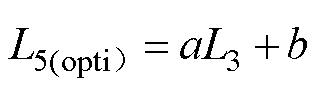（6）
式中，a、b分别为L5(opti)与L3线性关系中的斜率和截距。
在100kHz下测量时，按式（6）对L5和L3进行补偿，可以得到最准确的测量结果。对于本文的测量系统，100kHz测量时对应的a=1.15、b=-0.33。
由于本文实验利用阻抗分析仪适配的夹具进行测量，夹具本身引入的L3、L5的准确值无法获知，为验证低频测量补偿方案的有效性，只能通过在器件的源极与漏极分别补偿不同值的L3和L5来使补偿后100kHz的测量值与未补偿时的结果一致，实验结果如图16所示。
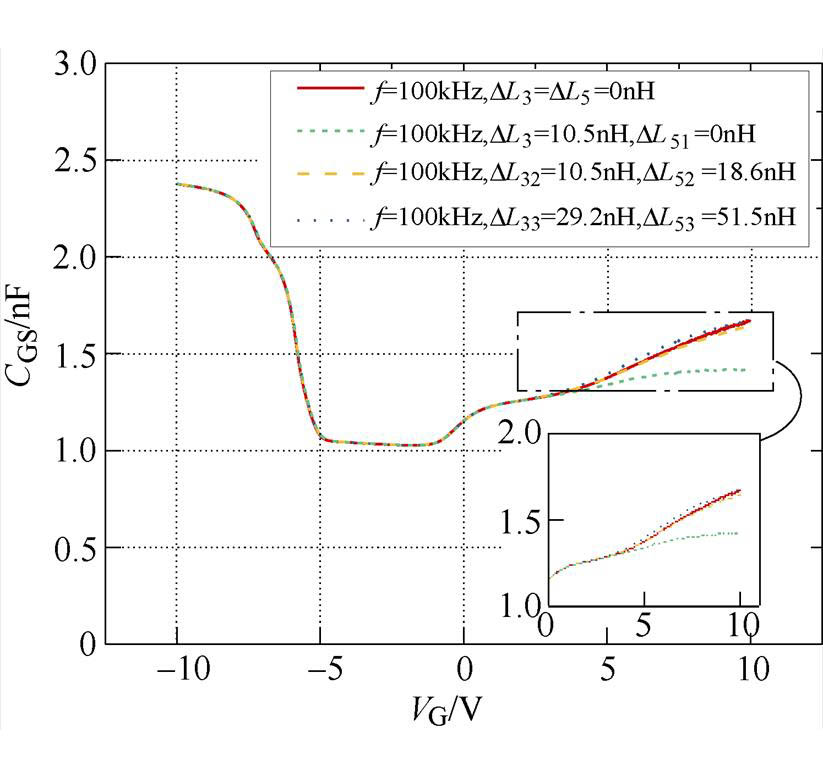
图16 100kHz下做补偿的实验结果
Fig.16 Experimental results of compensation under 100kHz
对比图16中L3补偿10.5nH时，L5不补偿和补偿28.6nH两种情况，显然当L5不补偿时，器件导通后的测量误差很大，此时L5再补偿28.6nH，测量结果准确，证明了补偿可行性；此外，DL32=10.5nH、DL52=28.6nH和DL33=27.5nH、DL53=51.5nH两组补偿参数下均与未补偿时100kHz下的测量结果相同，即测量结果准确。且满足如下方程
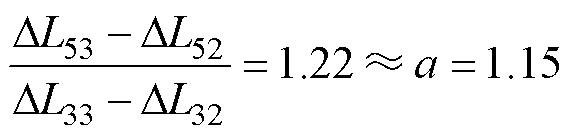（7）
式（7）证明了在误差允许范围内，补偿参数符合式（6）所提出的补偿关系式，定量验证了低频测量做补偿的有效性。
3）高频测量做补偿
根据JEDEC标准规定，测量频率小于2MHz。受限于测量仪器的频率范围或考虑到其他测量频率的要求，有时需在100kHz～2MHz间的频点进行测量。经本文分析，通过L5(opti)和L3间的匹配可实现不同频率下的准确测量。
由图15可得，较高频率下L5(opti)不仅与L3相关，而且与VG有关。高频下L5(opti)与L3仍呈近似线性关系，计及VG影响时，VG越大，随L3的增大，L5(opti)增大的速率越快，但仍呈线性关系。高频下VG=VTH时L5(opti)与L3的线性关系与100kHz时基本平行，即斜率一致。故高频下L5(opti)和L3的关系可表示为
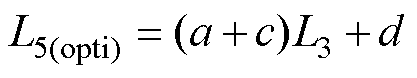（8）
式中，a与式（6）中的a相同，表示了VG=VTH时L5(opti)与L3需满足的线性关系；c为VG＞VTH时VG对L5(opti)的影响；d为考虑VG影响后L5(opti)与L3线性关系中的截距。
需注意的是，式（8）仅代表固定频率、固定VG时的补偿方案，若固定L3、不同VG下进行其他频率的准确测量，需通过图4的等效电路模型求解对应的补偿参数。对于本文的测量系统，2MHz、VG=10V下的c=1.15、d=-0.5。
此调控方法的验证方式同2），实验结果如图17所示。
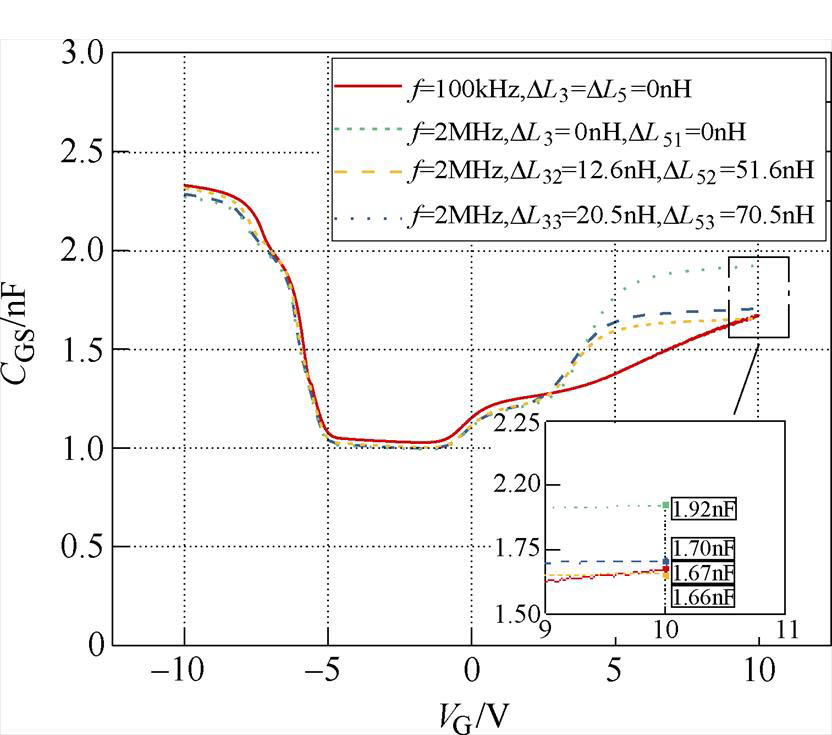
图17 2MHz做补偿的实验结果
Fig.17 Experimental results of compensation under 2MHz
同上分析，对比图17中L5补偿51.6nH，L3不补偿和补偿12.6nH两种情况，显然当L3不补偿时，2MHz下VG=10V时测量误差达到了15%，此时L3再补偿12.6nH，测量误差减小到1.8%，认为测量准确，证明了高频补偿可行性；此外，DL32=12.6nH、DL52=51.6nH和DL33=20.5nH、DL53=70.5nH两组补偿参数下均实现了VG=10V时2MHz与未补偿时100kHz下测量结果几乎相同，即测量准确，且满足
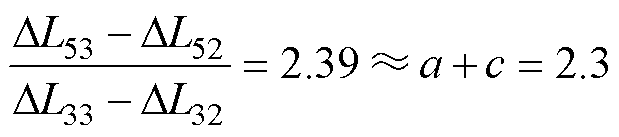（9）
式（9）证明了在误差允许范围内，补偿参数符合式（8）所提出的补偿关系式，定量验证了高频测量做补偿的有效性。
本文重点研究了阻抗分析仪测量功率MOSFET器件栅极分离电容C-V特性的误差问题，建立了测量的等效电路模型，揭示了引入误差的原因，结合实验数值分析了各部分寄生参数引入的误差大小，验证了模型的有效性并针对测量准确性提出一些建议。主要结论如下：
1）阻抗分析仪测量功率MOSFET器件栅极分离电容的C-V特性时，器件导通后DS间由电容电阻的并联转变为低导通电阻，引起电路拓扑的改变，因此引入了测量误差。
2）屏蔽端的寄生电感是引入功率MOSFET器件栅极分离电容C-V特性测量误差的主要参数。在器件导通后，其与自动平衡电桥的等效输入阻抗分流进而影响了测量结果。
3）提出了自动平衡电桥的等效输入阻抗和屏蔽端寄生电感在一定范围内时低频测量不补偿的方法，及不同频率下二者按一定关系匹配补偿的方法来实现功率MOSFET器件栅极分离电容的C-V特性的准确测量。本文所提调控方法对使用阻抗分析仪适配夹具或自制夹具测量功率器件栅极C-V特性均具有重要的指导意义。
参考文献
[1] 盛况, 任娜, 徐弘毅. 碳化硅功率器件技术综述与展望[J]. 中国电机工程学报, 2020, 40(6): 1741- 1753.
Sheng Kuang, Ren Na, Xu Hongyi. A recent review on silicon carbide power devices technologies[J]. Proceedings of the CSEE, 2020, 40(6): 1741-1753.
[2] 高晖胜, 訾鹏, 黄林彬, 等. 能量约束下电力电子并网装备的最优频率控制[J]. 电力系统自动化, 2020, 44(17): 9-18.
Gao Huisheng, Zi Peng, Huang Linbin, et al. Optimal frequency control of grid-connected power electronic devices with energy constraints[J]. Automation of Electric Power Systems, 2020, 44(17): 9-18.
[3] 顼佳宇, 李学宝, 崔翔, 等. 高压大功率IGBT器件封装用有机硅凝胶的制备工艺及耐电性[J]. 电工技术学报, 2021, 36(2): 352-361.
Xu Jiayu, Li Xuebao, Cui Xiang, et al. Preparation process and breakdown properties of silicone gel used for the encapsulation of IGBT power modules[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 352-361.
[4] 周林, 李寒江, 解宝, 等. SiC MOSFET的Saber建模及其在光伏并网逆变器中的应用和分析[J]. 电工技术学报, 2019, 34(20): 4251-4263.
Zhou Lin, Li Hanjiang, Xie Bao, et al. Saber modeling of SiC MOSFET and its application and analysis in photovoltaic grid-connected inverter[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4251-4263.
[5] 陈杰, 邓二平, 赵子轩, 等. 不同老化试验方法下SiC MOSFET失效机理分析[J]. 电工技术学报, 2020, 35(24): 5105-5114.
Chen Jie, Deng Erping, Zhao Zixuan, et al. Failure mechanism analysis of SiC MOSFET under different aging test methods[J]. Transactions of China Electro- technical Society, 2020, 35(24): 5105-5114.
[6] 王莉娜, 马浩博, 袁恺, 等. SiC MOSFET半桥电路开关瞬态过电流、过电压建模与影响因素分析[J]. 电工技术学报, 2020, 35(17): 3652-3665.
Wang Lina, Ma Haobo, Yuan Kai, et al. Modeling and influencing factor analysis of SiC MOSFET half- bridge circuit switching transient overcurrent and overvoltage[J]. Transactions of China Electro- technical Society, 2020, 35(17): 3652-3665.
[7] 张建忠, 吴海富, 张雅倩, 等. 一种SiC MOSFET谐振门极驱动电路[J]. 电工技术学报, 2020, 35(16): 3453-3459.
Zhang Jianzhong, Wu Haifu, Zhang Yaqian, et al. A resonant gate driver for SiC MOSFET[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(16): 3453-3459.
[8] Funaki T, Phankong N, Kimoto T, et al. Measuring terminal capacitance and its voltage dependency for high-voltage power devices[J]. IEEE Transactions on Power Electronics, 2009, 24(6): 1486-1493.
[9] Habas P, Mileusnic S, Zivanov T. Characterization of power VDMOSFETs by split C-V measurements[C]// International Conference on Microelectronics, Nis, Yugoslavia, 2000: 339-342.
[10] Scott R S, Franz G A, Johnson J L. An accurate model for power DMOSFETs including interelectrode capacitances[J]. IEEE Transactions on Power Elec- tronics, 1991, 6(2): 192-198.
[11] Elferich R, Lopez T, Koper N. Accurate behavioural modelling of power MOSFETs based on device measurements and FE-simulations[C]//European Con- ference on Power Electronics and Applications, Dresden, Germany, 2005: 9.
[12] RaËl S, Davat B. A physics-based modeling of interelectrode MOS capacitances of power MOSFET and IGBT[J]. IEEE Transactions on Power Elec- tronics, 2008, 23(5): 2585-2594.
[13] Lin W W, Chan P C. On the measurement of parasitic capacitances of device with more than two external terminals using an LCR meter[J]. IEEE Transactions on Electron Devices, 1991, 38(11): 2573-2575.
[14] Okawa Y, Norimatsu H, Suto H, et al. The negative capacitance effect on the C-V measurement of ultra thin gate dielectrics induced by the stray capacitance of the measurement system[C]//International Con- ference on Microelectronic Test Structures, Monterey, CA, USA, 2003: 197-202.
[15] JESD6 Measurement of small values of transistor capacitance[S]. VA, USA, 1967.
[16] IEC 60747 Semiconductor devices[S]. Geneva, Switzerland, 2006.
[17] Mileusnic S, Zivanov M, Habas P. MOS transistors characterization by split C-V method[C]//Inter- national Semiconductor Conference, Sinaia, Romania, 2001: 503-506.
[18] Moultif N, Joubert E, Masmoudi M, et al. Charac- terization of HTRB stress effects on SiC MOSFETs using photon emission spectral signatures[J]. Micro- electronics Reliability, 2017, 76/77: 243-248.
[19] Mukunoki Y, Nakamura Y, Konno K, et al. Modeling of a silicon-carbide MOSFET with focus on internal stray capacitances and inductances, and its veri- fication[J]. IEEE Transactions on Industry Appli- cations, 2018, 54(3): 2588-2597.
[20] Keysight Technologies. Impedance analyzer handbook 6th[EB/OL]. https://www.keysight.com/ca/en/assets/ 7018-06840/application-notes/5950-3000.pdf?success=true.
[21] Hu Chenming. Modern semiconductor devices for integrated circuits[M]. Upper Saddle River, NJ: Prentice Hall, 2011.
Error Analysis and Regulation Method of Impedance Analyzer in Measuring Split C-V Characteristics of Power MOSFET Device
Abstract The accurate measurement of the split C-V characteristics (CGS-VG and CGD-VG) of power MOSFET devices is very important for device modeling and gate oxide reliability evaluation. Impedance analyzer is the key equipment to measure the CGS-VG and CGD-VG. When using the impedance analyzer to measure a parameter of a three-terminal device, it is necessary to shield the non-measured third terminal to eliminate the introduced parallel impedance error. However, the power MOSFET device turns on when the gate voltage exceeds the threshold voltage, which affects the measurement circuit topology and introduces other measurement errors. In this paper, a detailed error analysis of the CGS-VG and CGD-VG measured by the impedance analyzer was carried out, and the reason of measurement error was revealed. The equivalent circuit model of the measurement was established, and the analytical expression of the measurement error was given. The error analysis was quantified and the effectiveness of the equivalent circuit model was verified by combining experiment and numerical analysis. Finally, three control methods that can achieve accurate measurement of C-V characteristics were proposed and verified by experiments. The results show that the measurement error occurs after the device turns on. The drain and source of the device transition from capacitance to low resistance. The parasitic inductance of the guarding (L5) is shunted from the equivalent input impedance of the automatic balance bridge (L3), which introduces errors. An accurate measurement under different frequencies can be achieved when L3 and L5satisfya certain matching relationship.
keywords：Power MOSFET device, impedance analyzer, split C-V characteristics, equivalent circuit model, error analysis
DOI: 10.19595/j.cnki.1000-6753.tces.210661
中图分类号：TN386
收稿日期 2021-05-10
改稿日期 2021-07-27
国家重点研发计划资助项目（2018YFB0905703）。
蔡雨萌 女，1996年生，博士研究生，研究方向为高压大功率电力电子器件封装与可靠性测试。E-mail: caiyumeng@ncepu.edu.cn
赵志斌 男，1977年生，教授，博士生导师，研究方向为电磁场数值计算、高压大功率电力电子器件封装与测试。E-mail: zhibinzhao@126.com（通信作者）
（编辑 陈 诚）