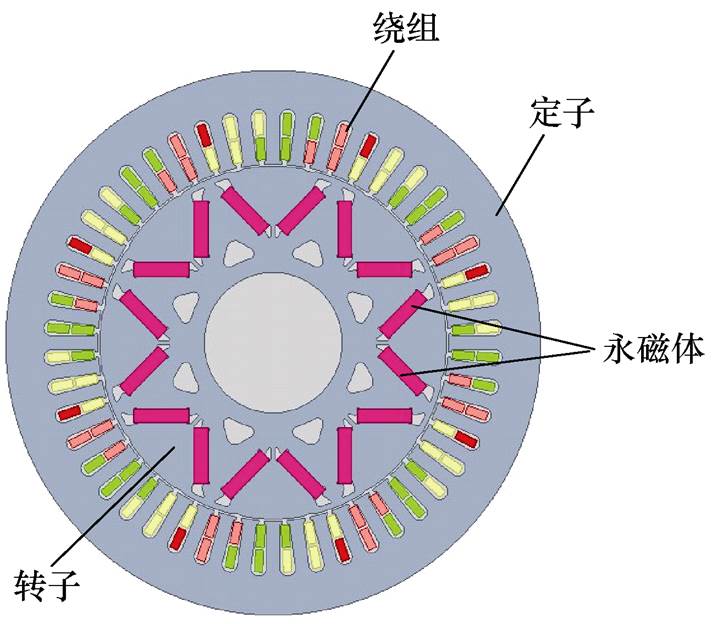
图1 V型内置式永磁电机拓扑结构
Fig.1 Topology of the V-shape IPM motor
摘要 为了提高计算精度,提出了一种可考虑磁桥不均匀饱和的内置式永磁同步电机(IPMSM)改进等效磁网络(EMN)模型。在分析不均匀饱和现象产生机理的基础上,将极间磁桥划分为四个子区域,根据每个子区域的几何结构及其磁力线走向搭建相应的多段非线性磁导单元,以考虑磁桥不均匀饱和及饱和偏移现象。以一台20kW车用IPMSM为例,利用所提出的模型对电机的空载、负载磁场及空载反电动势进行计算,并将计算结果与传统EMN模型、有限元分析及实验结果进行对比。结果表明,相比于传统EMN模型,所提出的改进EMN模型对气隙磁通密度和空载反电动势的计算精度可提高4%以上。最后,分析所提出模型的适用性,结果表明,当磁桥内磁通密度最大值与最小值的比大于约1.3时,磁桥不均匀饱和现象严重,需通过所提出的改进EMN模型来准确计算电机的电磁特性。
关键词:内置式永磁同步电机 等效磁网络法 磁桥不均匀饱和 有限元分析
内置式永磁(Interior Permanent Magnet, IPM)电机凭借其高转矩密度、宽恒功率运行区、低永磁体涡流损耗等特点,在混合动力汽车和纯电动汽车领域得到了广泛的应用[1-3]。精确的磁场计算是预测电机性能和判断其设计合理性的前提。目前,常用的电机磁场分析方法包括解析法、等效磁网络(Equivalent Magnetic Network, EMN)法和有限元分析(Finite Element Analysis, FEA)法。
由于IPM电机的转子结构复杂,其边界条件难以确定,因此很难直接采用基于麦克斯韦方程的解析法计算此类电机的磁场分布。采用FEA法虽可以精确地获得电机磁场分布,但由于IPM电机转子结构的多样性以及软件对网格数量的要求,导致该方法计算时间较长,不利于电机的初始设计[4]。EMN法由于具有计算速度较快且精度适中的特点,近年来受到众多学者的关注[5-15]。
文献[6]针对磁通切换永磁电机建立一种考虑电机负载时定子轭部与齿部之间漏磁的EMN模型。文献[7-8]分别建立了磁通反向直线旋转永磁电机和轴向磁通永磁同步电机的三维EMN模型,通过与FEA对比,三维EMN模型在保证计算精度的情况下,计算速度显著提升。文献[9-10]分别针对车载双永磁游标电机和表贴式永磁同步电机建立了EMN模型,两者都采用了一种菱形网格单元来进行局部建模以提高模型的计算精度。在IPM电机领域,文献[11]提出了一种U型IPM电机的动态EMN模型。文献[12]针对三层三段IPM电机提出了一种考虑转子交叉耦合效应的EMN模型。文献[13]针对非对称转子IPM电机建立了一种考虑磁桥端部漏磁的EMN模型。文献[14]针对IPM电机提出了一种结合了精确保角映射的EMN模型。文献[15]针对IPM电机提出了一种EMN模型,该模型采用十字形磁导对气隙进行建模来提高计算精度。然而,上述IPM电机的EMN模型虽能较为准确地计算出电机空载时气隙磁通密度幅值处的波形,但由于模型在极间磁桥区域的磁导建模较为简单,无法准确考虑到磁桥区域存在的不均匀饱和现象,导致计算出的磁桥正对气隙区域的磁通密度波形与实际情况存在误差;在IPM电机负载情况下,不均匀饱和现象会更加严重,同时还会伴随着磁桥饱和偏移的发生,这会进一步加大计算误差。
针对该问题,本文提出一种考虑磁桥不均匀饱和以及饱和偏移的改进磁网络模型。通过分析不均匀饱和现象产生的原因,将极间磁桥划分为四个子区域,并对各自区域建立多段十字形磁导以考虑交叉耦合的影响。为了验证该模型,本文以一台20kW车用V型IPM电机为例,通过所提出的模型对电机的空载磁场、负载磁场及空载反电动势进行计算,并将计算结果与传统EMN模型、FEA及实验结果进行对比。此外,本文通过改变电机的磁桥结构,还对该模型的适用性进行分析。
以V型IPM电机为例,本文将转子中包含异性磁极间漏磁通的区域统称为极间磁桥区域,图1所示为V型IPM电机的拓扑结构。电机额定负载下的有限元仿真结果及磁桥区域划分如图2所示,根据极间磁桥区域的几何结构及磁通密度分布情况,将极间磁桥划分为4个子区域,可以看出,不均匀饱和现象主要存在于区域2和3。

图1 V型内置式永磁电机拓扑结构
Fig.1 Topology of the V-shape IPM motor
为了考虑磁桥的不均匀饱和,本文对极间磁桥区域提出如图3所示的EMN建模方法。对于区域1,由于其饱和程度通常较低,磁通密度分布较为均匀,故将此区域磁导等效为一段圆弧形的磁导。对于区域2,其磁通密度分布主要受几何结构的影响,越接近区域3的位置,磁通路径越窄,进而磁通密度越大。同时,根据磁力线走向可以看出,该区域还存在一部分直接进入气隙的磁力线。出于对以上两种情况的考虑,本文将区域2分为多个近似梯形的磁导单元,并在每个单元中建立十字形磁导,在考虑该区域几何结构变化的同时也为磁通提供了流入气隙路径。

图2 内置式永磁同步电机磁通密度云图及磁桥区域划分
Fig.2 Flux density distribution and division of bridge of IPMSM
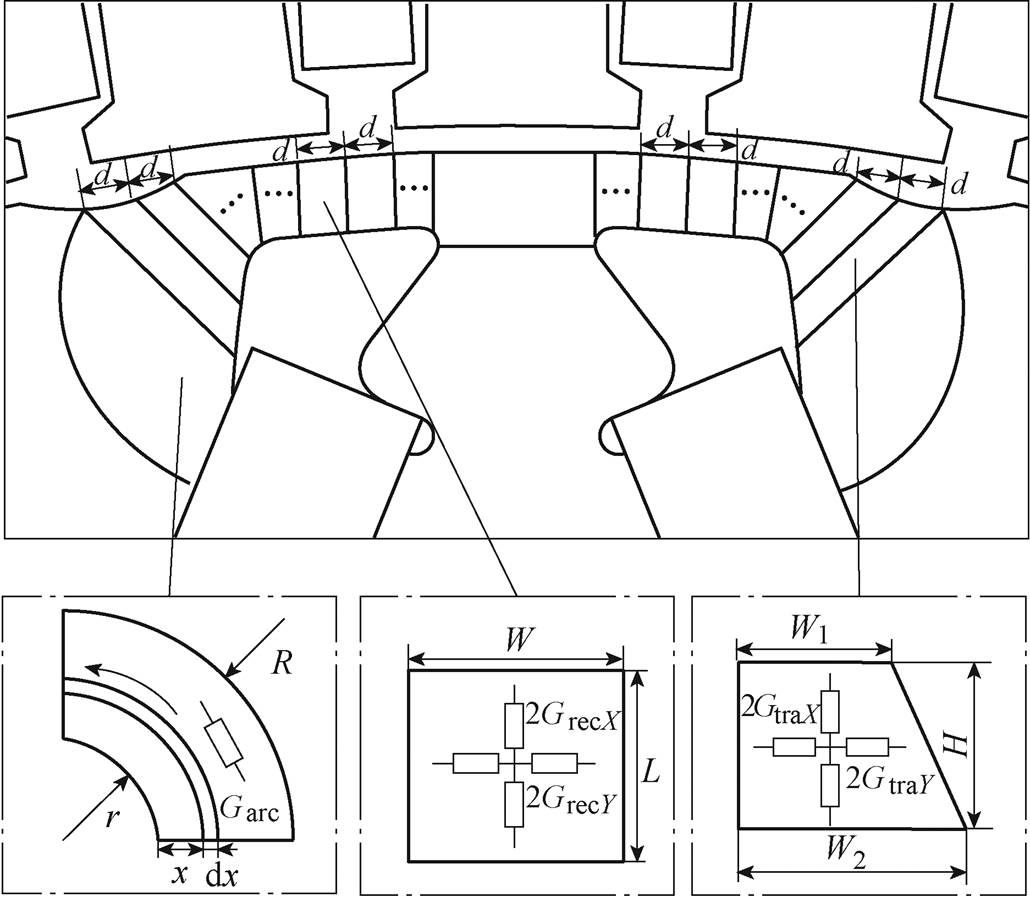
图3 极间磁桥区域的磁导模型
Fig.3 Model of bridge permeance
区域2的磁通密度分布呈现出一种递增的变化趋势,并在与区域3的交界处达到最大值。同时根据磁力线走向可以看出,在区域3中,同样存在大量进入气隙的磁力线,导致等宽的磁桥内部磁通密度也在不断变化,故区域3仍然存在较为明显的不均匀饱和现象。本文将区域3分为多个矩形磁导单元,并在每个单元中建立十字形磁导,为从该区域进入气隙的磁通提供了流通路径。对于区域4,由于其磁通密度分布较为均匀,故将此区域简化为一个矩形磁导单元,并建立十字形磁导。
对于图3所示的磁网络模型,建立的十字形磁导的数目越多,气隙磁通密度的计算结果越精确。但磁导数目增加的同时也会导致计算量的增加,并且当磁导数目增加到一定值后,气隙磁通密度的计算精度将不会产生明显的提升。经过多次尝试,本文最终将极间磁桥区域的磁导单元数目确定为15个。需要注意的是,为了方便后续转子EMN模型和气隙EMN模型的组合,需要保证图3中磁导单元的宽度d尽可能相同。
图3中所用到的矩形磁导 、圆弧形磁导
、圆弧形磁导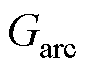 及梯形磁导
及梯形磁导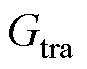 分别为
分别为
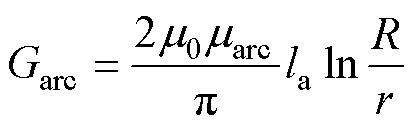 (1)
(1)
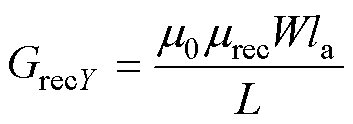 (2)
(2)
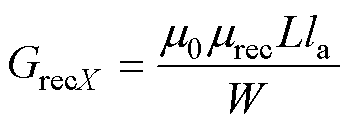 (3)
(3)
 (4)
(4)
 (5)
(5)
式中,m0为真空磁导率;marc为圆弧形磁导的相对磁导率;R和r分别为圆弧形磁导对应磁通路径的外半径和内半径;mrec为矩形磁导的相对磁导率;la为电机轴向长度;L和W分别为矩形磁导对应磁通路径的长度和宽度;mtra为梯形磁导的相对磁导率;W1、W2和H分别为梯形磁导对应磁通路径的上底、下底长度和高度。
定子等效磁网络模型如图4所示。其中,包含齿部磁导、轭部磁导、槽漏磁导及电枢绕组等效磁动势源。考虑到定子齿尖局部饱和,在每个齿的齿顶部位加入了两个非线性磁导。图4中,磁导的值可以通过式(2)进行计算,由分布绕组产生的磁动势可表示为与轭部磁导相串联的磁动势源,其值为
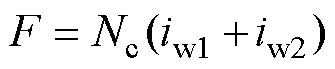 (6)
(6)
式中,Nc为槽内每个线圈的匝数;iw1和iw2为槽内电枢绕组所通的电流。
气隙区域的EMC模型由两种磁导组成,分别是气隙磁导和槽口磁导。气隙区域可以被划分为多层矩形磁导单元,并在每个单元中建立十字形磁导,如图5a所示。文献[15]中提出,气隙磁导单元层数的增加对气隙磁通密度计算精度的改善较为有限。因此,综合考虑模型计算精度与计算时间,本文气隙磁导单元的层数选为1。槽口区域可以近似等效为两段圆弧型磁导单元,如图5b所示。图5中所有的气隙磁导值可由式(1)~式(3)计算得到。
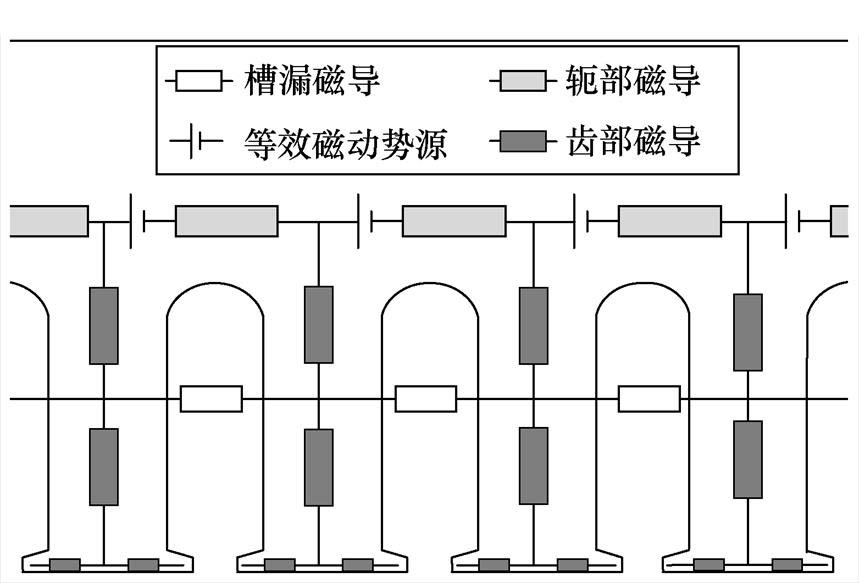
图4 定子等效磁网络模型
Fig.4 EMN model of the stator

图5 气隙等效磁网络模型
Fig.5 EMN model of air gap
转子除极间磁桥区域外的等效磁路模型如图6所示,包含永磁体磁导、转子磁导以及永磁体等效磁通源。转子磁导为非线性磁导,磁导单元结构大致可以等效为矩形或梯形,并通过式(2)~式(5)对转子磁导进行计算。永磁体磁导GPM及等效磁通源 分别为
分别为
 (7)
(7)
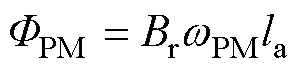 (8)
(8)
式中,mPM为永磁材料相对磁导率;wPM和hPM分别为永磁体的宽度和厚度;Br为永磁体剩磁。
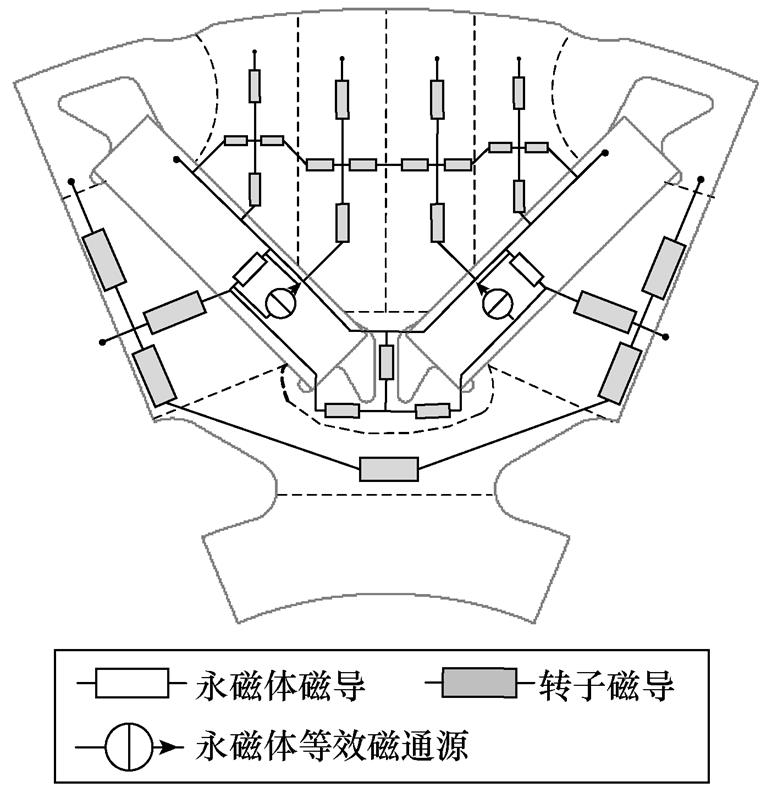
图6 转子除极间磁桥区域外的等效磁路模型
Fig.6 EMN model of rotor except the magnetic bridge between poles
考虑不均匀饱和前后的极间磁桥区域EMN模型如图7所示。两种模型都包含有永磁体漏磁导和磁桥磁导。改进EMN模型中可连接气隙磁导的节点明显多于传统EMN模型。即考虑不均匀饱和的EMN模型所提供的流入气隙磁通路径更多,更能反映电机在极间磁桥区域的实际磁通走向,进而可提高计算精度。图7中所有的磁导都可以通过式(1)~式(5)得到。
非线性磁导相对磁导率需要通过迭代求得。首先,根据转子位置确定完整的EMN模型,并设置非线性磁导相对磁导率为mk,通过mk计算出每条支路的磁导。与电路中的节点电压方程类似,EMN模型的节点磁动势矩阵F为
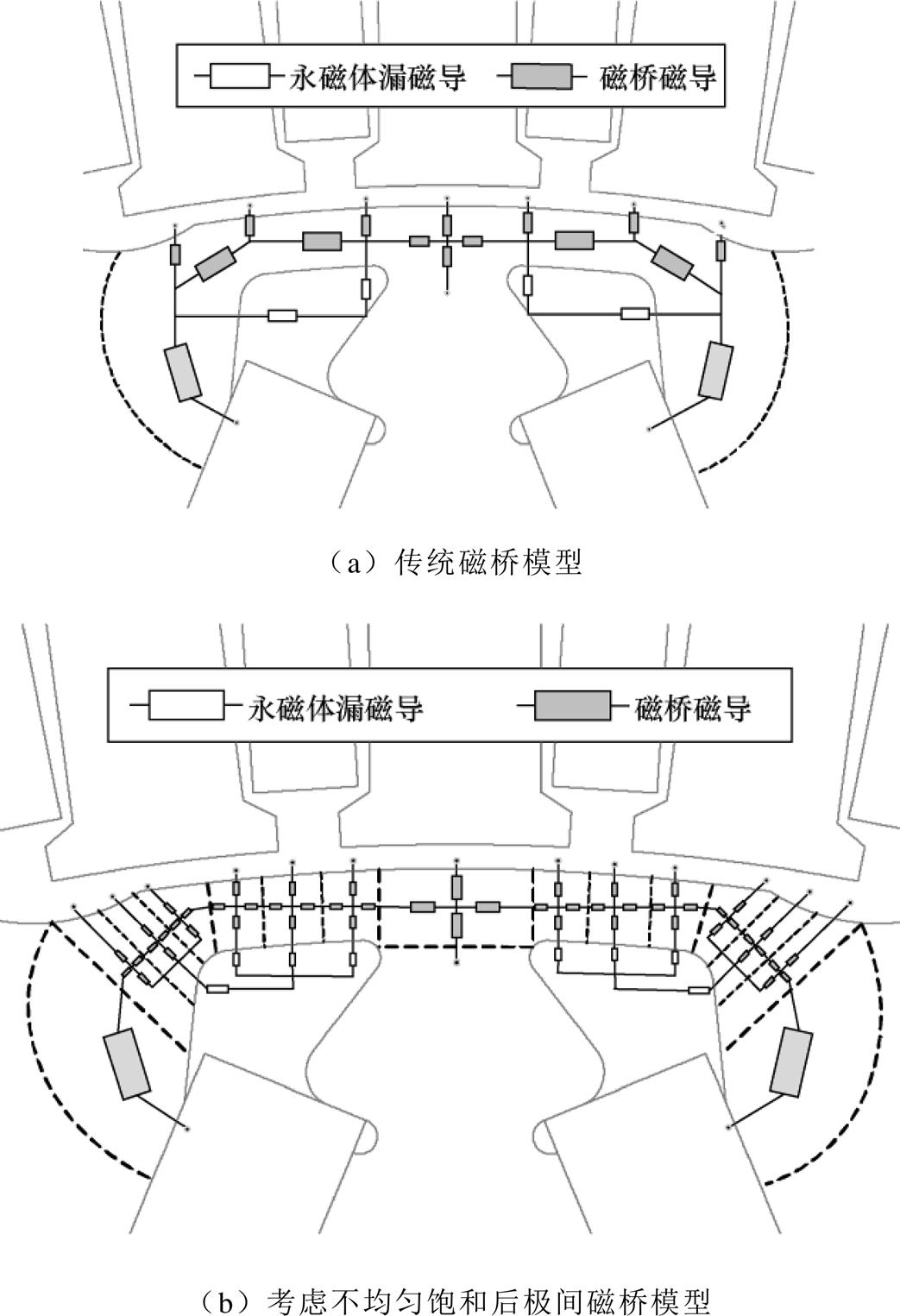
图7 极间磁桥区域等效磁路模型
Fig.7 EMN model of the magnetic bridge between poles
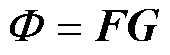 (9)
(9)
 (10)
(10)
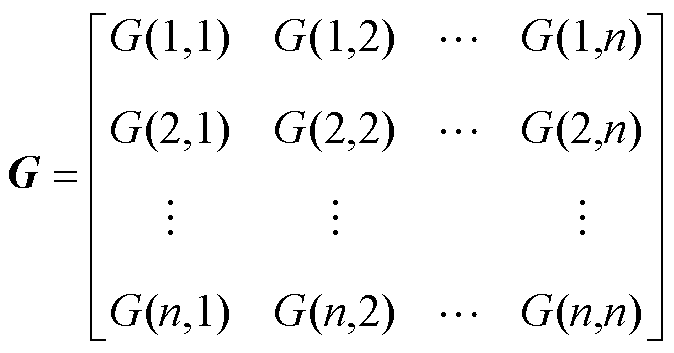 (11)
(11)
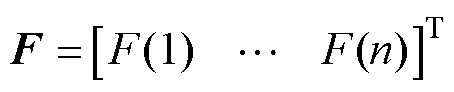 (12)
(12)
式中,n为节点数;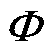 为磁通矩阵;
为磁通矩阵; 为磁通源注入节点i的磁通;F为节点磁动势矩阵;F(i)为节点i的磁动势;G为磁导矩阵;G(i, j)为节点i与节点j之间的磁导。
为磁通源注入节点i的磁通;F为节点磁动势矩阵;F(i)为节点i的磁动势;G为磁导矩阵;G(i, j)为节点i与节点j之间的磁导。
其中,磁导矩阵G具有以下特性
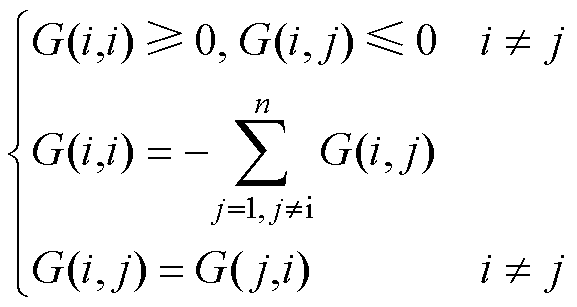 (13)
(13)
在求得节点磁动势矩阵F后,各支路磁导所对应的磁通密度Be为
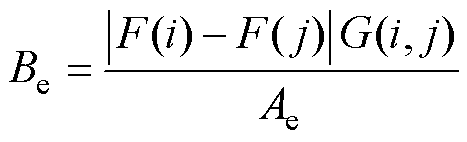 (14)
(14)
式中,Ae为i与j两节点之间磁通经过的截面积。
计算得到的Be后,在查找铁磁材料的B-H曲线后便可以得到相对磁导率mk+1。为了加快迭代循环的计算速度,磁导率更新迭代公式[16]为
 (15)
(15)
式中,p1=0.95;p2=0.05;mup为更新后的相对磁导率。
迭代过程的终止条件是磁导率收敛到设定的误差范围内,该条件可以表示为
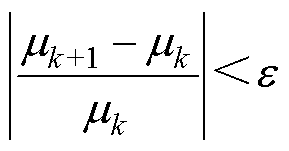 (16)
(16)
式中,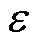 为设定的误差范围。
为设定的误差范围。
当某个转子位置的循环结束后,调整节点连接顺序,更换新的转子位置重新进行循环,直到完成所有位置的计算。非线性磁导求解流程如图8所示。
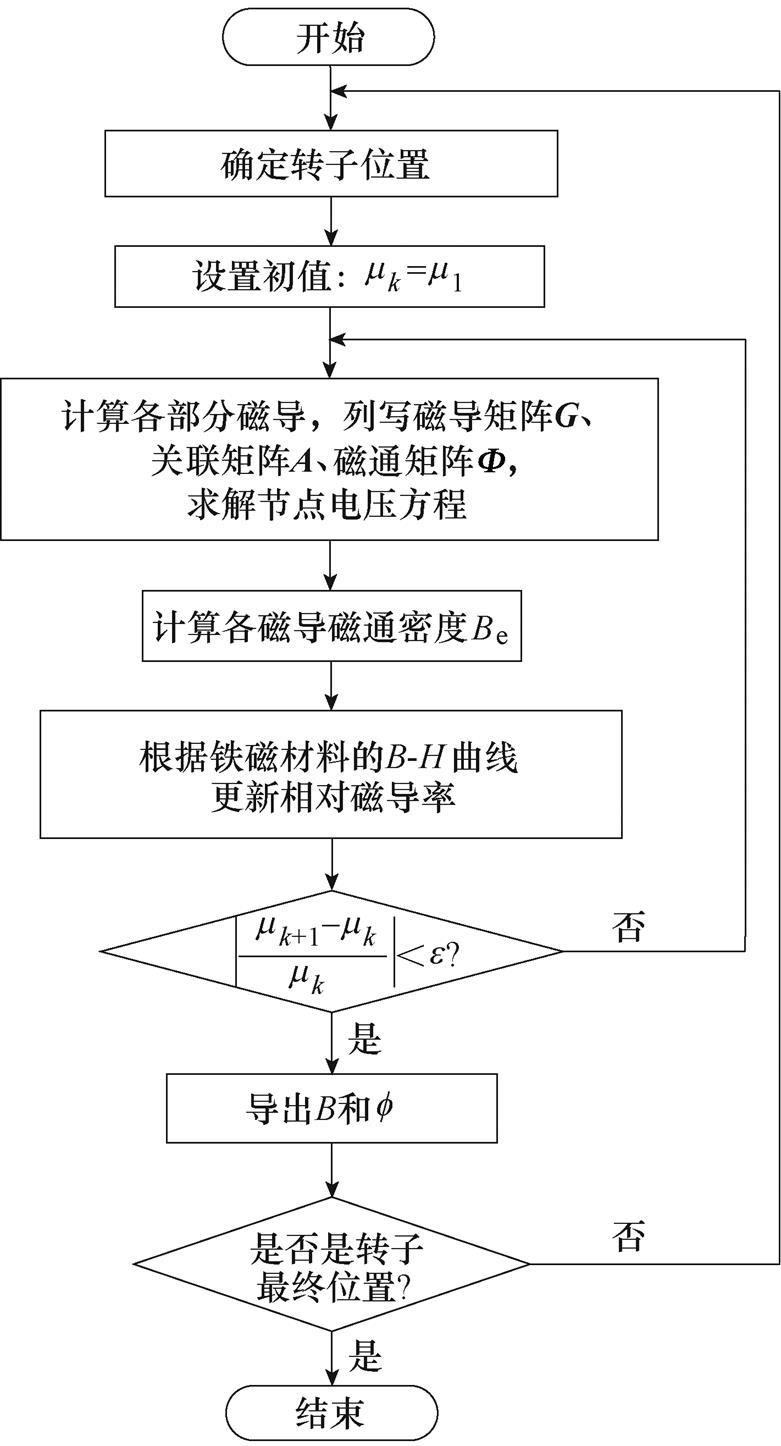
图8 非线性磁导求解流程
Fig.8 Flow chart of nonlinear permeability solution
为了验证所提出模型的有效性,本文分别用考虑磁桥不均匀饱和前后的两种EMN模型对一台V型IPM电机进行了计算,并将结果与FEA及实验结果进行对比。其中,样机结构及测试平台如图9所示,电机主要参数见表1。为了区分两种模型的计算结果,本文将改进EMN模型表示为EMN1,传统EMN模型表示为EMN2。

图9 样机图片及实验平台
Fig.9 Prototype and experimental platform
表1 内置式永磁同步电机参数
Tab.1 IPM machine parameters
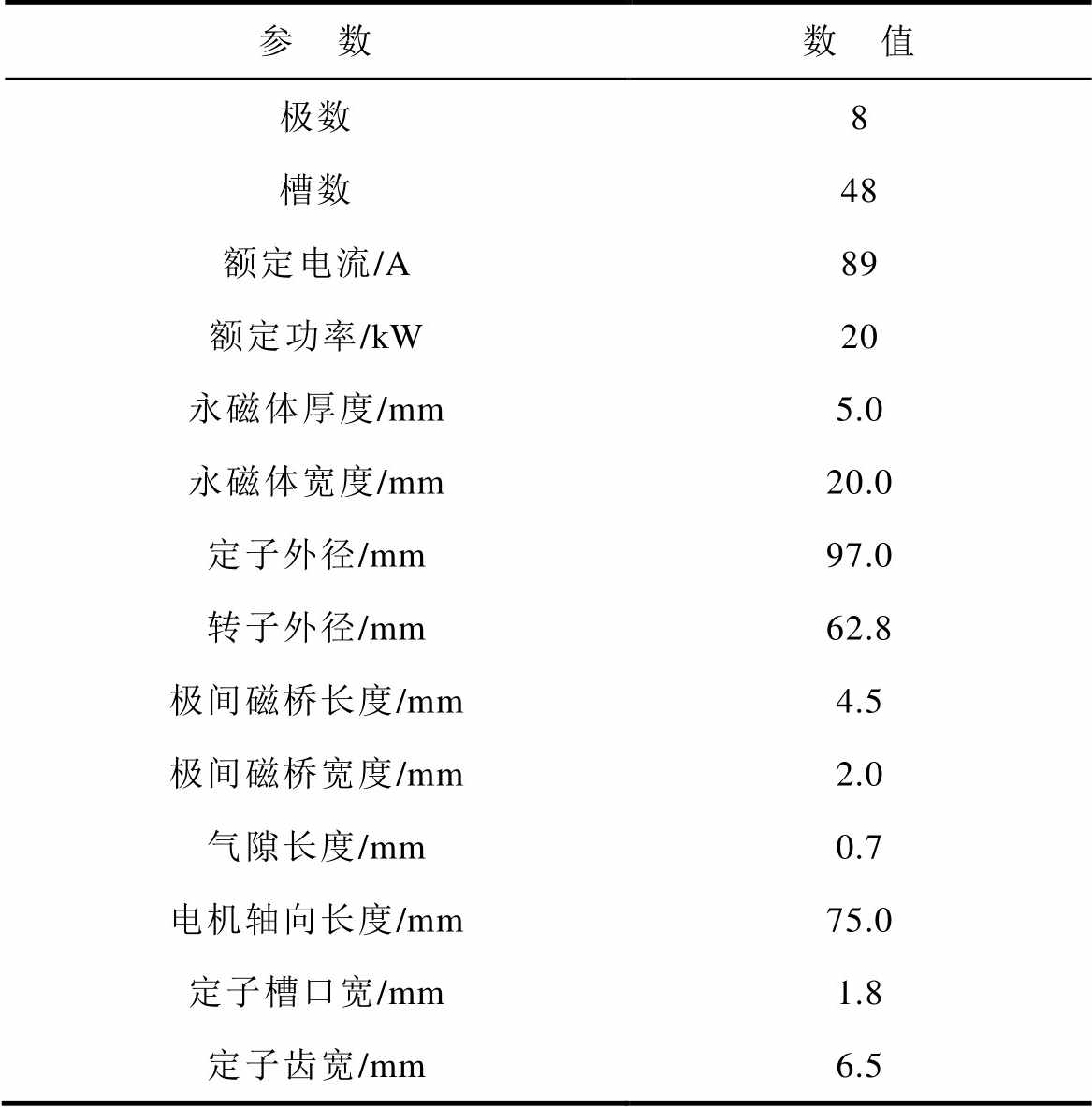
参 数数 值 极数8 槽数48 额定电流/A89 额定功率/kW20 永磁体厚度/mm5.0 永磁体宽度/mm20.0 定子外径/mm97.0 转子外径/mm62.8 极间磁桥长度/mm4.5 极间磁桥宽度/mm2.0 气隙长度/mm0.7 电机轴向长度/mm75.0 定子槽口宽/mm1.8 定子齿宽/mm6.5
不同定、转子相对位置时空载气隙磁通密度波形如图10所示,图中,位置1表示转子d轴正对于定子齿中央;位置2表示转子d轴正对于定子槽中央。可以看出,EMN2模型在气隙磁通密度波形幅值处的计算结果与FEA结果吻合较好,而在点画线范围内极间磁桥正对的气隙磁通密度波形与FEA结果存在明显偏差。对于EMN1模型而言,整体气隙磁通密度波形与FEA结果吻合良好。为了对比磁网络结果与FEA结果间的差别,对气隙磁通密度进行误差分析,有
 (17)
(17)
式中,BEMNi为EMN模型第i个磁导处的气隙磁通密度;BFEAi为与EMN模型第i个磁导相同周向位置处的FEA计算磁通密度;n为EMN模型中的气隙磁导单元数目。

图10 不同转子位置时空载气隙磁通密度波形
Fig.10 No-load air gap flux density waveforms at different rotor positions
通过计算得到,位置1处EMN1、EMN2计算结果与FEA结果的误差分别为2.14%和6.64%;位置2处EMN1、EMN2计算结果与FEA结果的误差分别为3.36%和8.09%。可以看出,EMN1模型计算结果具有更高的精度,尤其对于图10中点画线范围内的气隙磁通密度过零处,波形计算结果得到了明显的改善,这表明改进EMN模型可有效考虑磁桥不均匀饱和的影响。
图11所示为电机负载情况下,不同电流相位时的气隙磁通密度的计算值,此时电流有效值为89A。通过计算得到,当相位为0°时,EMN1、EMN2计算结果与FEA结果的误差分别为5.54%和10.71%;相位为45°时,EMN1、EMN2计算结果与FEA结果的误差分别为5.31%和10.18%。可以看出,负载时受磁桥不均匀饱和以及磁桥饱和偏移的影响,EMN2模型的计算结果与FEA结果误差更为显著,但EMN1模型的计算结果仍与FEA结果吻合性较好,尤其对于图11中点画线范围内的极间磁桥区域正对的气隙磁通密度处,波形计算结果得到了明显的改善,这表明改进EMN模型可有效考虑电机在负载情况下磁桥不均匀饱和以及饱和偏移的影响。
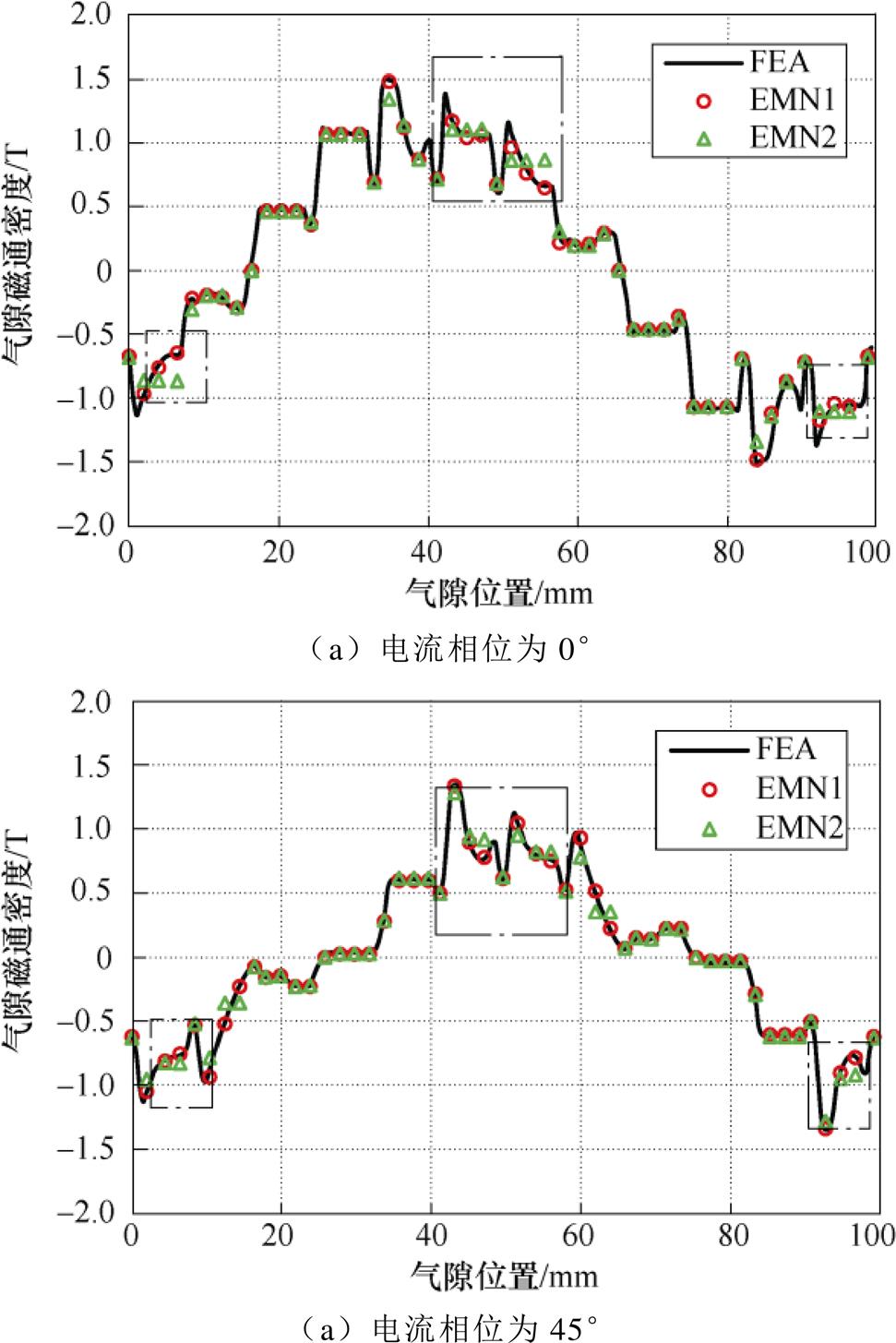
图11 不同电流相位下的气隙磁通密度波形
Fig.11 Load air gap flux density waveforms of different phase angle
此外,与空载气隙磁通密度计算结果相比,在负载情况下受磁桥饱和偏移的影响,改进EMN模型的计算精度有所下降,可以通过适当增加磁桥中磁导单元的数目来提高负载情况下的计算精度。
在得到电机的空载气隙磁通密度波形后,电机的磁链 可以计算为
可以计算为
 (18)
(18)
式中,N为该相绕组的匝数;R为气隙处半径; 为转子的位置角;
为转子的位置角;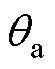 为一个线圈的节距角。
为一个线圈的节距角。
计算得到该电机的磁链波形如图12所示。通过磁链波形,可以计算得到IPM电机的空载反电动势,即
 (19)
(19)

图12 磁链波形对比
Fig.12 Fluxlinkagewaveforms
图13所示为两种EMN模型计算的空载反电动势波形与有限元及实验的对比结果,其中空载反电动势的实测波形如图14所示。通过计算得到EMN1、EMN2计算结果与实验结果的误差分别为5.23%和10.35%,该结果进一步表明了改进EMN模型拥有更高计算精度。
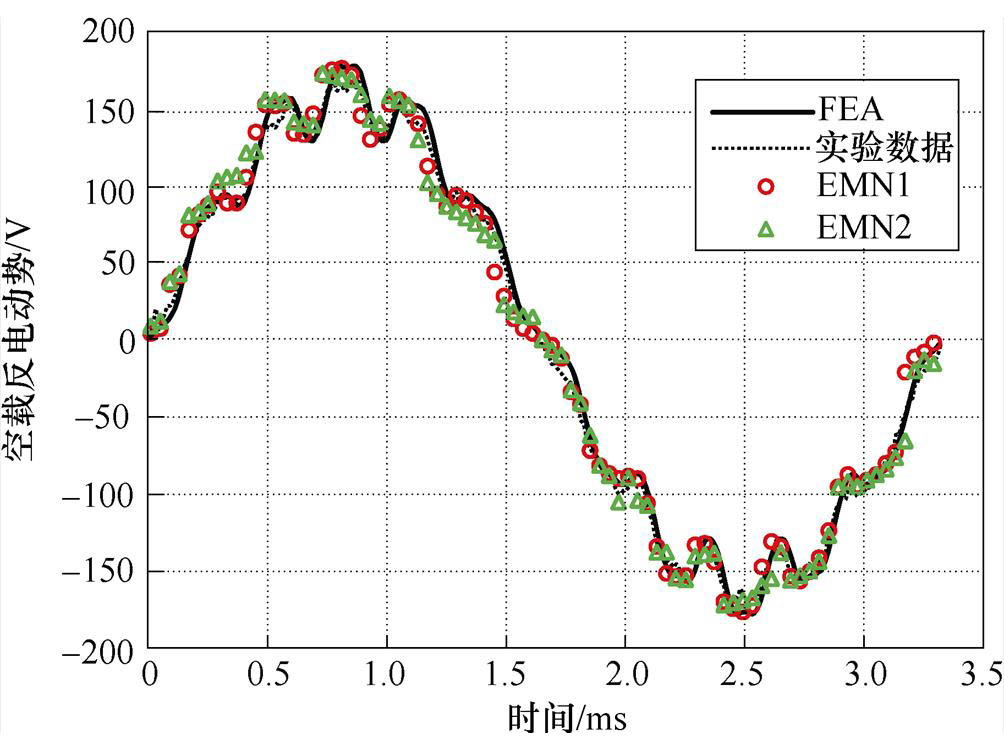
图13 空载反电动势波形对比
Fig.13 No-load back EMF waveforms

图14 空载反电动势测试结果
Fig.14 Test no-load back EMF
为了总结所提出模型的适用条件,本文对不同磁桥尺寸下的电机气隙磁通密度进行了分析,如图15所示。保证磁桥长度为4.5mm不变,只改变磁桥宽度时两种EMN模型的空载气隙磁通密度的计算结果如图15a所示,图中,2mm、2.5mm和3mm为磁桥的宽度。保证磁桥宽度为2mm不变,只改变磁桥长度时两种EMN模型的空载气隙磁通密度的计算结果如图15b所示,图中,3mm、4.5mm和6mm为磁桥的长度。通过式(17)计算得到不同磁桥尺寸下两种模型对气隙磁通密度的计算结果与FEA结果的误差见表2。
由表2可以看出,不同磁桥尺寸对两种模型的计算精度有一定影响,即磁桥尺寸的改变引起了磁桥内部不均匀饱和程度的改变。为了验证模型的适用性,本文以IPM电机极间磁桥内部磁通密度最大值与最小值的比值来表示该磁桥的不均匀饱和程度。图16所示为不同磁桥尺寸下磁桥内部的磁通密度变化曲线,以长为4.5mm,宽为2mm的磁桥为例,图16中横坐标对应的磁桥位置如图17所示。不同磁桥尺寸下磁桥内部磁通密度的比值见表2。

图15 不同磁桥尺寸下电机的气隙磁通密度波形
Fig.15 Air gap magnetic density waveforms of motors with different bridge sizes
表2 不同磁桥尺寸两种模型计算误差对比
Tab.2 Calculation errors of two models at different bridge sizes
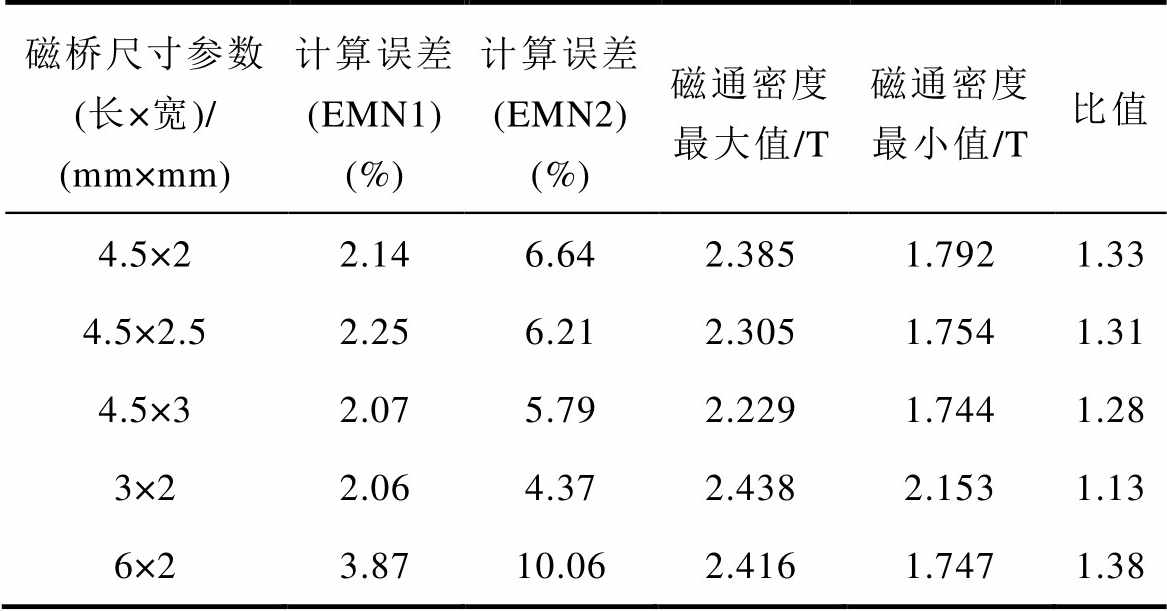
磁桥尺寸参数 (长×宽)/ (mm×mm)计算误差(EMN1) (%)计算误差(EMN2) (%)磁通密度最大值/T磁通密度最小值/T比值 4.5×22.146.642.3851.7921.33 4.5×2.52.256.212.3051.7541.31 4.5×32.075.792.2291.7441.28 3×22.064.372.4382.1531.13 6×23.8710.062.4161.7471.38

图16 不同磁桥尺寸下磁桥内部的磁通密度变化
Fig.16 Variation curve of magnetic density inside bridge with different sizes

图17 图16中横坐标所对应的磁桥位置
Fig.17 The bridge position corresponding to the abscissa in Fig.16
通过计算,当磁桥内磁通密度最大值与最小值的比小于约1.30时,两种模型的计算误差都可以控制在6%以内,此时采用拥有较少磁导数目的传统EMN模型更为适合;当磁桥内磁通密度最大值与最小值的比大于约1.30时,磁桥不均匀饱和现象严重,传统EMN模型的计算误差较大,需要通过所提出的改进EMN模型来准确计算电机磁场分布。
本文针对IPM电机提出了一种能够考虑磁桥不均匀饱和的建模方法。用该方法建立的车用IPM电机EMN模型能够考虑电机转子中存在的极间磁桥不均匀饱和现象以及负载时的饱和偏移现象。
为了验证该方法,本文以一台20kW车用V型IPM电机为例,通过所提模型对电机的空载磁场、负载磁场及空载反电动势进行了计算,并将计算结果与传统EMN模型、有限元分析及实验结果进行了对比。通过误差分析的结果表明,相较于传统的EMN模型,改进EMN模型对气隙磁通密度波形的计算精度可提高4%以上,对空载反电动势的计算精度可提高5%以上。
最后,本文还对所提出模型的适用性进行了分析,结果表明,对于磁桥内磁通密度最大值与最小值的比小于约1.30的IPM电机,本文所提出模型计算精度与传统EMN模型相当,此时采用拥有较少磁导数目的传统EMN模型更为适合;当磁桥内磁通密度最大值与最小值的比大于约1.30时,磁桥不均匀饱和现象严重,需要通过所提出的改进EMN模型来准确计算电机磁场分布。
参考文献
[1] 唐任远. 现代永磁电机理论与设计[M]. 北京: 机械工业出版社, 2006.
[2] 马伟明, 王东, 程思为, 等. 高性能电机系统的共性基础科学问题与技术发展前沿[J]. 中国电机工程学报, 2016, 36(8): 2025-2035.
Ma Weiming, Wang Dong, Cheng Siwei, et al. Com- mon basic scientific problems and development of leading-edge technology of high performance motor system[J]. Proceedings of The CSEE, 2016, 36(8): 2025-2035.
[3] 樊英, 谭超. 内置式交替极永磁同步电机性能及机理研究[J]. 电工技术学报, 2018, 33(11): 2414-2422.
Fan Ying, Tan Chao. Analysis of electromagnetic performance and principles in inserted consequent- pole permanent magnet synchronous machines[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2414-2422.
[4] Wu Shuang, Shi Tingna, Guo Liyan, et al. Accurate analytical method for magnetic field calculation of interior PM motors[J]. IEEE Transactions on Energy Conversion, 2020, 36(1): 325-337.
[5] Yang Shuo, Salim A, Sami H, et al. Introduction to mesh based generated lumped parameter models for electromagnetic problems[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(2): 152-162.
[6] 张淦, 花为, 程明, 等. 磁通切换型永磁电机非线性磁网络分析[J]. 电工技术学报, 2015, 30(2): 34-42.
Zhang Gan, Hua Wei, Cheng Ming, et al. Analysis of nonlinear magnetic network models for flux- switching permanent magnet machines[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(2): 34-42.
[7] 郭凯凯, 郭有光. 磁通反向直线旋转永磁电机三维非线性等效磁路模型分析[J]. 电工技术学报, 2020, 35(20): 4278-4286.
Guo Kaikai, Guo Youguang. 3D Nonlinear equivalent magnetic circuit model analysis of a flux reversal linear rotary permanent magnet machine[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(20): 4278-4286.
[8] He Mingjie, Li Weiye, Peng Jun, et al. Multi-layer quasi three-dimensional equivalent model of axial- flux permanent magnet synchronous machine[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(1): 3-12.
[9] Cao Donghui, Zhao Wenxiang, Ji Jinghua, et al. A generalized equivalent magnetic network modeling method for vehicular dual-permanent-magnet vernier machines[J]. IEEE Transactions on Energy Conversion, 2019, 34(4): 1950-1962.
[10] Cao Donghui, Zhao Wenxiang, Ji Jinghua, et al. Parametric equivalent magnetic network modeling approach for multiobjective optimization of PM machine[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(8): 6619-6629.
[11] 陈威, 吴桂初, 方攸同. 基于绕组分布函数理论和动态磁网络的两种内置式永磁牵引电机解析建模方法[J]. 电工技术学报, 2020, 35(增刊2): 377-386.
Chen Wei, Wu Guichu, Fang Youtong. Two analytical models based on winding function theory and dynamic reluctance mesh for interior permanent magnet traction machines[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 377-386.
[12] Zhu Li, Jiang Shuzhong, Zhu Ziqiang, et al. Analytical modeling of multi-segment and multilayer interior permanent magnet machines[C]//2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, 2014: 28-33.
[13] Xu Gaohong, Liu Guohai, Jiang Shan, et al. Analysis of a hybrid rotor permanent magnet motor based on equivalent magnetic network[J]. IEEE Transactions on Magnetics, 2018, 54(4): 1-9.
[14] Li Zhaokai, Huang Xiaoyan, Wu Lijian, et al. Open- circuit field prediction of interior permanent-magnet motor using hybrid field model accounting for saturation[J]. IEEE Transactions on Magnetics, 2019, 55(7): 1-7.
[15] Liu Guohai, Wang Yong, Chen Qian, et al. Design and analysis of a new equivalent magnetic network model for IPM machines[J]. IEEE Transactions on Magnetics, 2020, 56(6): 1-12.
[16] Tong Wenming, Wang Shuai, Dai Shanhong, et al. A quasi-three-dimensional magnetic equivalent circuit model of a double-sided axial flux permanent magnet machine considering local saturation[J]. IEEE Transa- ctions on Energy Conversion, 2018, 33(4): 2163- 2173.
Equivalent Magnetic Network Model for Interior Permanent Magnet Machines Considering Non-Uniform Saturation of Magnetic Bridges
Abstract In order to improve the calculation accuracy, an improved equivalent magnetic network (EMN) model is proposed for interior permanent magnet synchronous motors (IPMSM) considering the non-uniform saturation of the magnetic bridge. By analyzing the causes of uneven saturation phenomenon, the magnetic bridge is divided into four regions. According to the geometric structure and flux distribution of each region, the nonlinear permeance unit is used to consider the non-uniform saturation and the saturation shift of the magnetic bridge. Then, taking a 20kW IPMSM as an example, the proposed model is used to analyze the no-load and load magnetic fields and no-load back electromotive force (EMF), and the calculated results are compared with the traditional EMN model, finite element analysis (FEA) and experimental results. It is shown that the proposed model can improve the calculation accuracy by more than 4% compared with the traditional EMN model. Finally, the applicability of the proposed model is analyzed. The results show that when the ratio of the maximum to minimum magnetic density in the magnetic bridge is greater than about 1.3, it is necessary to consider the non-uniform saturation of the magnetic bridge by the proposed model.
keywords:Interior permanent magnet synchronous motor, equivalent magnetic network, non- uniform saturation of bridge, finite element analysis
DOI: 10.19595/j.cnki.1000-6753.tces.210491
中图分类号:TM351
辽宁省“兴辽英才计划”(XLYC2007107)、国家重点研发计划(2016YFB0300503)和辽宁省百千万人才工程资助项目。
收稿日期 2021-04-13
改稿日期 2021-06-25
佟文明 男,1984 年生,博士,教授,博士生导师,研究方向为特种电机及其控制与电机多物理场仿真分析。E-mail: twm822@126.com(通信作者)
姚颖聪 男,1997年生,硕士研究生,研究方向为基于集总参数法的内置式永磁同步电机电磁和热研究。E-mail: 463440276@qq.com
(编辑 崔文静)