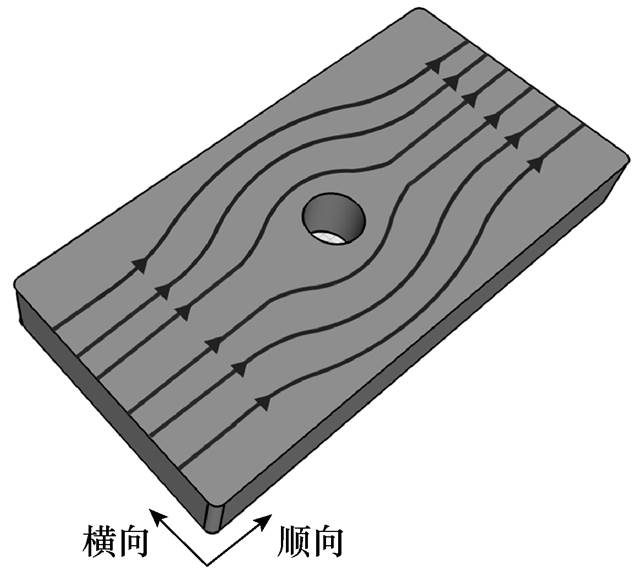
图1 设置工艺孔后的磁通流线示意图
Fig.1 The schematic diagram of magnetic flux flow line with a technological hole
摘要 变压器的工艺堆叠孔会增加铁心损耗,导致变压器局部温升,甚至影响变压器正常运行。为了研究工艺孔对变压器铁心损耗及其性能的影响,该文对硅钢材料的双向交变磁特性与损耗特性进行测量与分析,结合Steinmetz损耗计算公式对带工艺孔的铁心模型进行二维磁场解析计算,提出由不同形状、尺寸工艺孔造成铁心损耗增长的理论计算方法,基于有限元法对变压器铁心常用的取向硅钢片进行二维瞬态磁场仿真计算,对比分析了不同类型工艺孔对变压器铁心损耗的影响。构建带工艺孔的硅钢样片损耗测试平台,定量测试铁心材料由工艺孔造成的损耗以及局部温升,验证理论计算方法的有效性与准确性。仿真及实验结果表明,提出的变压器工艺孔铁心损耗增长的计算方法具有较高的计算精度和工程适用性。
关键词:干式变压器 工艺堆叠孔 铁心损耗
在变压器铁心装叠过程中,通常在硅钢叠片上设置工艺孔。基于自动化装备的工艺孔叠片可提高叠制效率,但会增加铁心损耗并影响变压器运行性能。对于工艺孔式的叠片方法,其广泛适用于容量5 000kV·A以内的变压器中,为满足铁心装叠要求,需在铁心柱及铁轭处均匀设置工艺孔[1]。研究表明,工艺孔所引起的损耗增量正比于孔数[2],一台设置双孔的SJL3-320/10变压器,其损耗可增加5.8%。因此,准确计算铁心工艺孔所引起的损耗变化对分析变压器运行性能至关重要。
而铁心损耗的准确计算是变压器设计中的难点,尤其当铁心设置工艺孔后。由于冷轧硅钢的磁导率远高于空气,当磁通经过工艺孔附近时,会沿磁阻最小的路径流动,即原本均匀分布的磁通流线会在工艺孔周围发生绕行,造成工艺孔边缘顺向磁通密度增加,此时,磁力线发生弯曲,在硅钢叠片的垂直轧制方向上产生横向磁通分量,使得工艺孔铁心的损耗分析计算变得更加困难[3]。
现有的铁心损耗计算方法大致可归为三类:基于铁心磁化物理现象的磁滞模型法[4-7]、基于铁损可分离假设的损耗分离法[8-10]以及Steinmetz经验公式法[11-12]。用于铁心损耗计算的Preisach和Jiles- Atherton模型具有一定的统计规律和理论基础,但模型识别参数较多,且与有限元结合过程复杂,难以在工程实践中应用;损耗分离法基于畴壁运动机理将损耗分离成多个部分[13],相较于磁滞模型法,损耗分离法简化了铁损的分析过程,但仍涉及较多辨识参数,因此较少在工程中使用。而Steinmetz损耗公式利用频率与磁通密度计算损耗密度,其公式简单,涉及参数较少,被广泛应用于工程计算[12, 14-15]。
国内外学者已采用多种方法分析工艺孔影响。较早的研究给出了铁损基于实验数据的经验定性关系[2, 16]。随后有研究基于有限元仿真分析了圆形工艺孔尺寸对损耗的定性影响[17]。近年来,大量研究关注工艺孔尺寸、形状、位置以及切割方法对孔周围局部磁通与磁畴结构的损伤影响[3, 18-20]。而目前,对于不同形状、尺寸的工艺孔造成的铁心损耗增长,并没有一套准确的理论计算方法,且不同形状和尺寸的工艺孔对铁心性能的影响也有待研究。综合考虑形状与尺寸参数对工艺孔铁心损耗的影响,可为工程实践中变压器铁心的精细化设计提供参考。
本文基于Steinmetz损耗公式,在考虑并测量硅钢铁心材料实际磁化与损耗特性的同时,对铁心二维电磁场进行解析计算,提出了一种考虑工艺孔形状和尺寸参数的铁心损耗增长计算方法,给出了更具普适性和精确性的理论计算公式,并通过有限元仿真和相关实验对比分析了不同形状、不同尺寸的工艺孔对变压器铁心性能的影响,验证了理论计算方法的精确性,本文所提方法可为带工艺孔铁心的损耗计算提供理论指导与技术支撑。
硅钢片设置工艺孔后,磁通流线发生弯曲,造成轧制方向(Rolling Direction, RD)上的顺向磁通密度和垂直轧制方向(Transverse Direction, TD)上的横向磁通分量增加,如图1所示。因此,为准确计算工艺孔铁心轧制方向与垂直轧制方向的铁心损耗,本文采用二维单片磁特性测试系统[21-23],对硅钢片铁心材料的双向磁特性展开实验,如图2所示,该测试系统由测量装置、传感系统、差分放大电路、功率放大器、Labview控制系统、阻抗匹配电路构成。

图1 设置工艺孔后的磁通流线示意图
Fig.1 The schematic diagram of magnetic flux flow line with a technological hole
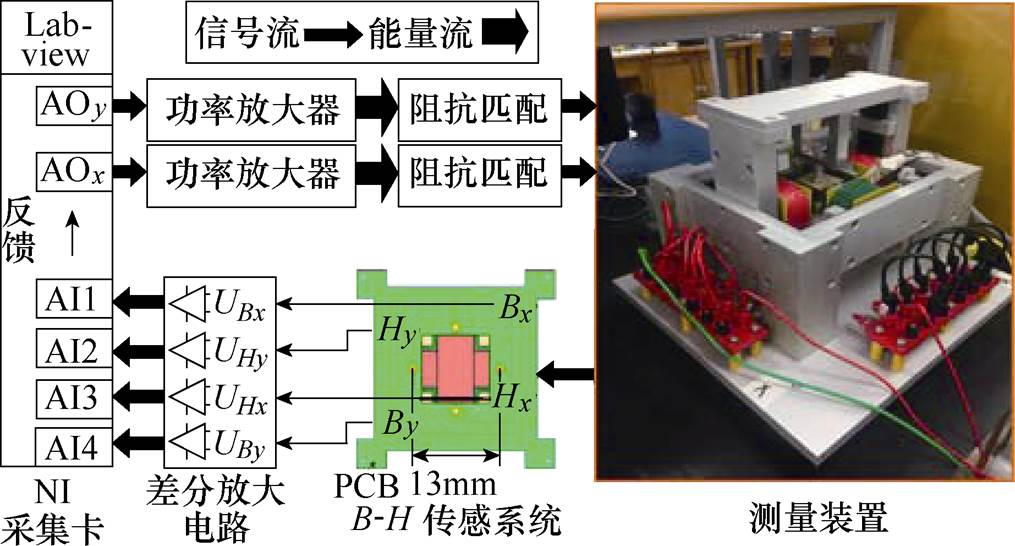
图2 二维磁特性测试系统
Fig.2 The 2-D magnetic properties testing system
图3a给出了B30P120硅钢片在50Hz频率和不同磁感应强度下沿轧制方向和垂直轧制方向的磁滞回线(内嵌对应的磁化曲线),图3b给出了磁感应强度峰值Bm为0.1~1.8T时,频率分别为50Hz、75Hz、100Hz条件下硅钢铁心材料沿轧制方向和垂直轧制方向的损耗曲线。结果表明,硅钢铁心材料在轧制方向具有更高的磁导率,双向铁心损耗随着频率和磁感应强度的增加而增加,其中垂直轧制方向的损耗明显高于轧制方向,具有明显的各向异性。此外,从数值结果来看,在相同的磁感应强度下,本文所用取向钢片在垂直轧制方向的损耗值约为轧制方向损耗的3倍。
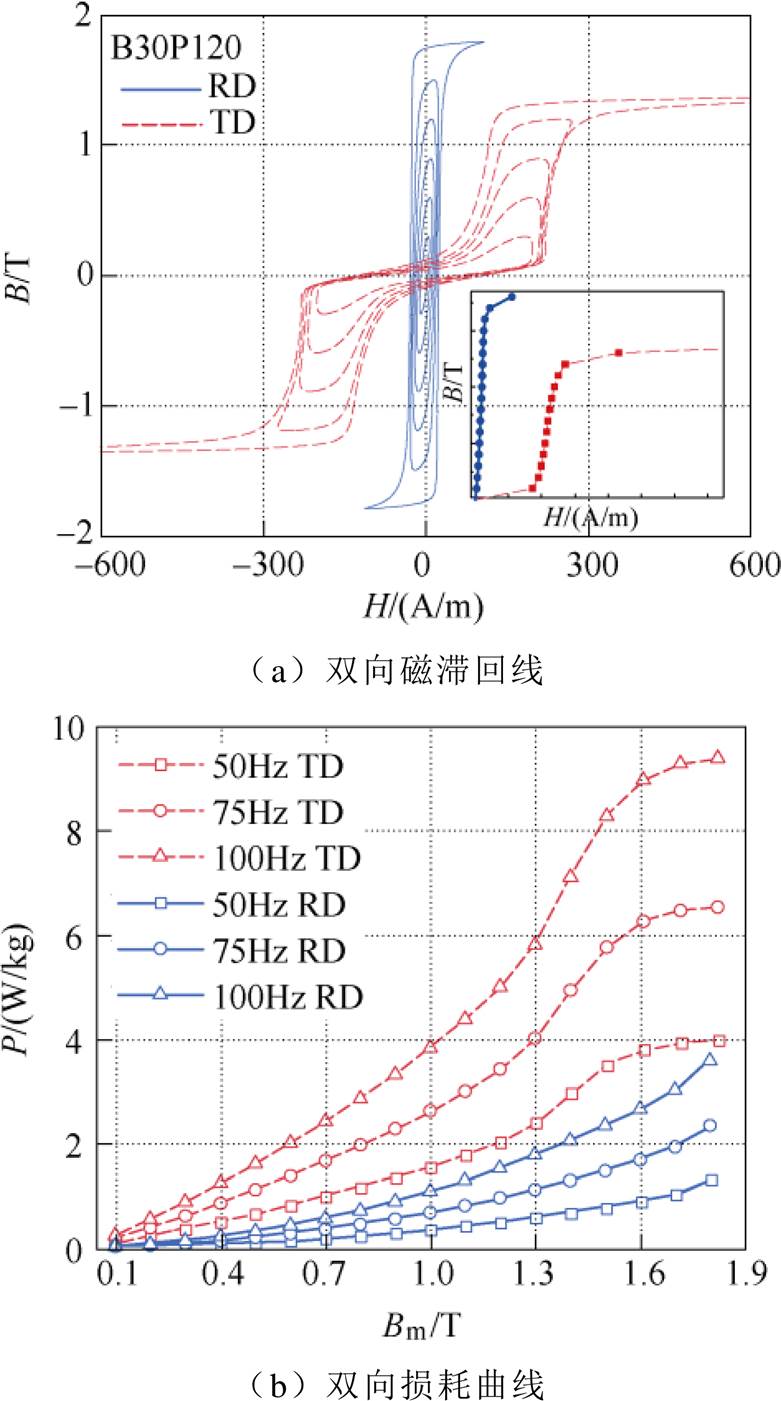
图3 样片轧制与垂直轧制方向磁滞回线和损耗曲线
Fig.3 Hysteresis loops and loss of sample along rolling direction and transverse direction
基于上述实验测试结果,对变压器铁心叠片设置工艺孔后,由顺向磁通与横向磁通增加所导致的损耗增长进行计算分析和研究。
Steinmetz损耗计算公式OSE(original Steinmetz equation)可表示[11]为
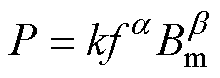 (1)
(1)
式中,P为铁心损耗;Bm为磁通密度峰值;f为励磁电压频率;k、a、b 分别为Steinmetz系数、频率系数和磁通密度系数。系数与变压器铁心材料磁特性有关,一般由厂商提供。本文为提高计算精度,基于1.1节中的实际测量结果进行曲线拟合,得到OSE中系数分别为:轧制方向k=0.142, a=1.218, b= 2.005;垂直轧制方向k=0.426 3,a=1.321, b=1.998。
而对于变压器而言,工艺孔对铁心的影响为铁心损耗,主要包括磁滞损耗和涡流损耗两部分。正弦激励下的磁滞损耗为
 (2)
(2)
式中,Ph为磁滞损耗;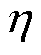 为磁滞损耗系数。即磁滞损耗与
为磁滞损耗系数。即磁滞损耗与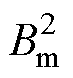 成正比。
成正比。
根据楞次定律,正弦激励下的铁心涡流损耗可计算[10]为
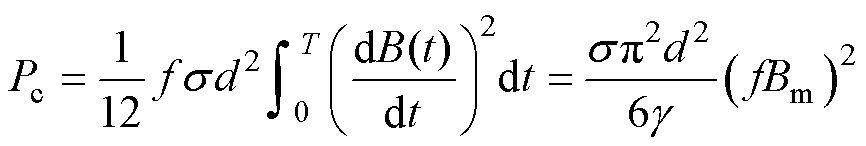 (3)
(3)
式中,Pc为涡流损耗; 为铁心硅钢片电导率;d为硅钢片厚度;
为铁心硅钢片电导率;d为硅钢片厚度; 为铁心密度;T为激励周期。由式(3)可知,涡流损耗也与
为铁心密度;T为激励周期。由式(3)可知,涡流损耗也与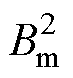 成正比,即与磁滞损耗一致。基于1.1节中实测数据的拟合结果可知,铁心材料B30P120的铁损P与
成正比,即与磁滞损耗一致。基于1.1节中实测数据的拟合结果可知,铁心材料B30P120的铁损P与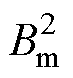 成正比,其垂直轧制方向损耗约为轧制方向3倍。上述结果将作为后续铁心损耗计算的依据。
成正比,其垂直轧制方向损耗约为轧制方向3倍。上述结果将作为后续铁心损耗计算的依据。
考虑到铁心硅钢片的厚度远小于宽度,忽略涡流与趋肤效应的影响,可认为磁通沿各级叠片的分布均匀,将三维场简化成二维场进行分析。
当变压器硅钢铁心受工艺孔影响时,原本相对均匀的磁通流线和磁感应强度发生重新分布,造成工艺孔附近的磁感应强度集中和磁通流线的弯曲。因此,损耗的增加主要来自两个方面:一部分由工艺孔局部轧制方向的顺向磁通密度增加引起;另一部分由磁通弯曲所产生的垂直轧制方向的横向磁通密度分量引起。
工艺孔局部区域示意图如图4所示。设无孔时均匀分布的磁感应强度峰值为B0,定义工艺孔曲率
半径为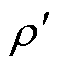 ,工艺孔极角为
,工艺孔极角为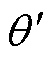 ,由文献[24]可知,通过求解磁通流线方程,可近似给出如图4所示的工艺孔局部区域的磁感应强度分布为
,由文献[24]可知,通过求解磁通流线方程,可近似给出如图4所示的工艺孔局部区域的磁感应强度分布为
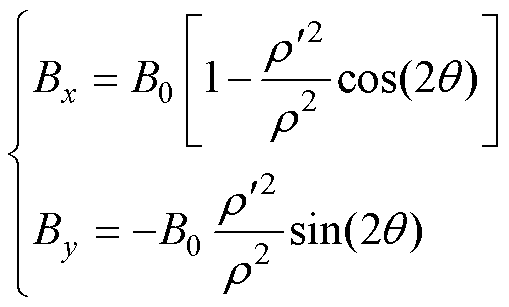
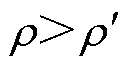 (4)
(4)
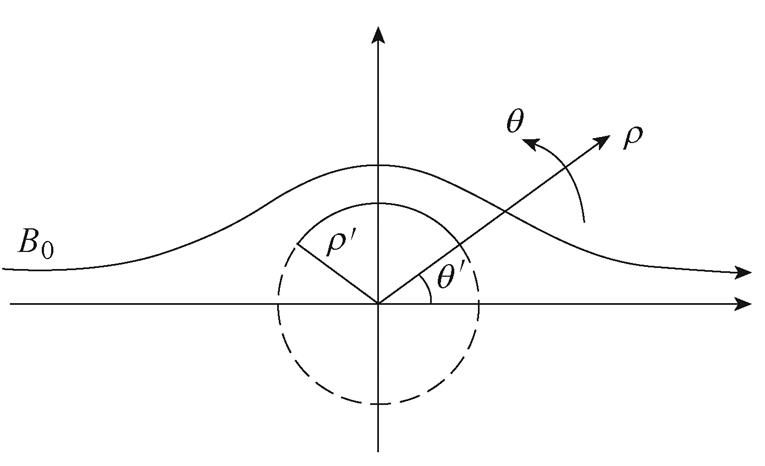
图4 工艺孔局部区域示意图
Fig.4 Schematic diagram of technological hole local area
式中,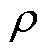 、
、 为局部区域内位置坐标。当
为局部区域内位置坐标。当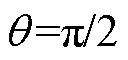 时,有
时,有
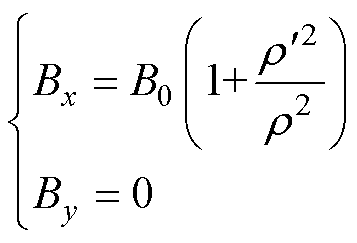 (5)
(5)
即随着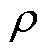 的增大,Bx迅速减小。假设工艺孔上下区域宽度为
的增大,Bx迅速减小。假设工艺孔上下区域宽度为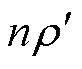 ,可计算Bx的平均值为
,可计算Bx的平均值为
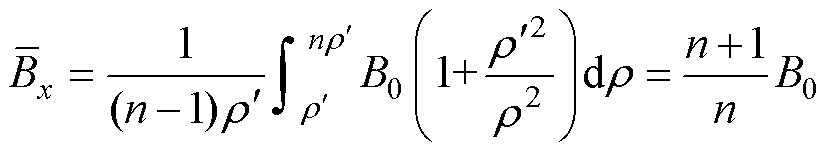
 (6)
(6)
式中,n为工艺孔上下区域宽度与其曲率半径的比值。工艺孔周围产生的横向磁通密度分量为By,也可按照平均值考虑。由文献[17]可知,工艺孔周围磁通密度的分布在几何上满足对称关系。因此,可求得 方向上的几何平均位置为
方向上的几何平均位置为
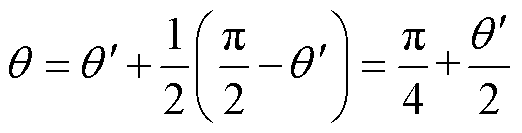
代入式(4)得
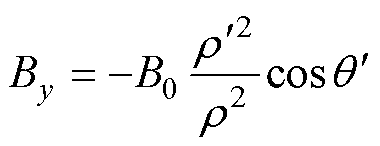
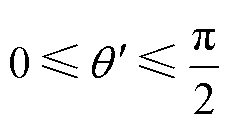 (7)
(7)
对于工艺孔周围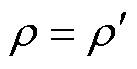 到
到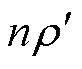 的区域,可计算区域内By平均值为
的区域,可计算区域内By平均值为
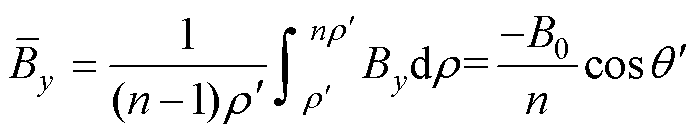 (8)
(8)
上述局部区域磁感应强度平均值的计算结果将代入式(1)中,以进一步计算和分析铁心损耗。
单片铁心及其局部工艺孔如图5所示,图中,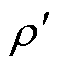 为工艺孔曲率半径,
为工艺孔曲率半径,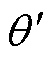 为工艺孔极角,定义铁心柱外接圆半径为R,铁心柱片宽为h,工艺孔相对大小为
为工艺孔极角,定义铁心柱外接圆半径为R,铁心柱片宽为h,工艺孔相对大小为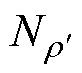 ,则对于单片铁心,铁心柱片宽为
,则对于单片铁心,铁心柱片宽为
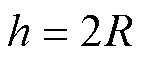
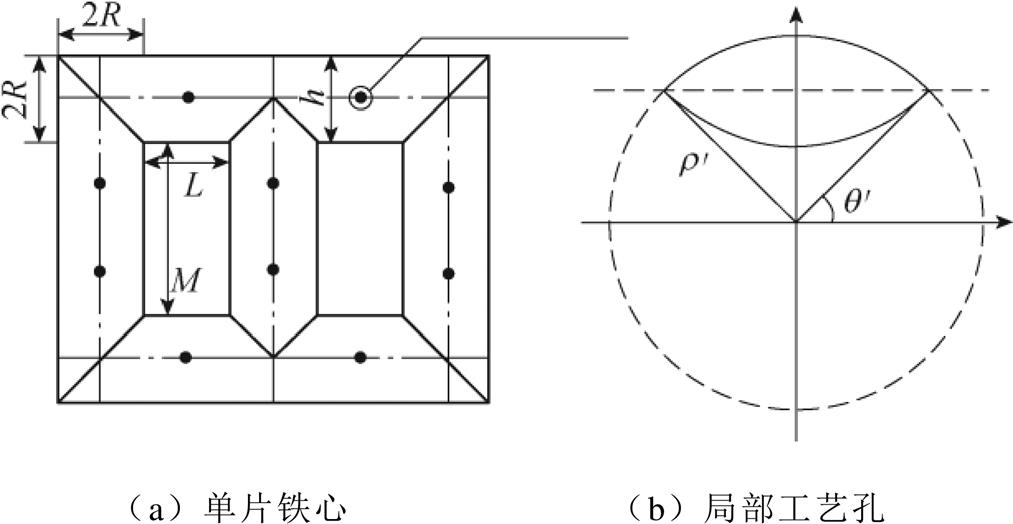
图5 单片铁心及其局部工艺孔示意图
Fig.5 The schematic diagram of core sheet and localized technological hole
工艺孔相对大小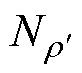 为
为
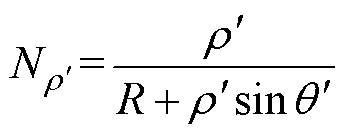 (9)
(9)
当工艺孔极角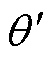 =0时,该工艺孔为圆形孔。
=0时,该工艺孔为圆形孔。
由文献[3]可知,铁心设置工艺孔后会产生局部损伤区域,对铁心的影响只发生在该区域内,如图6所示阴影区域为顺向磁通密度增加所影响的损伤区域,计算时,只考虑该区域内的损耗增量。因此,将n=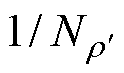 代入式(6)中,可计算图6所示工艺孔损伤区域内的顺向磁感应强度Bx的平均值为
代入式(6)中,可计算图6所示工艺孔损伤区域内的顺向磁感应强度Bx的平均值为
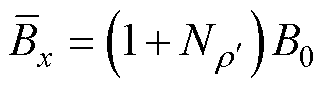 (10)
(10)
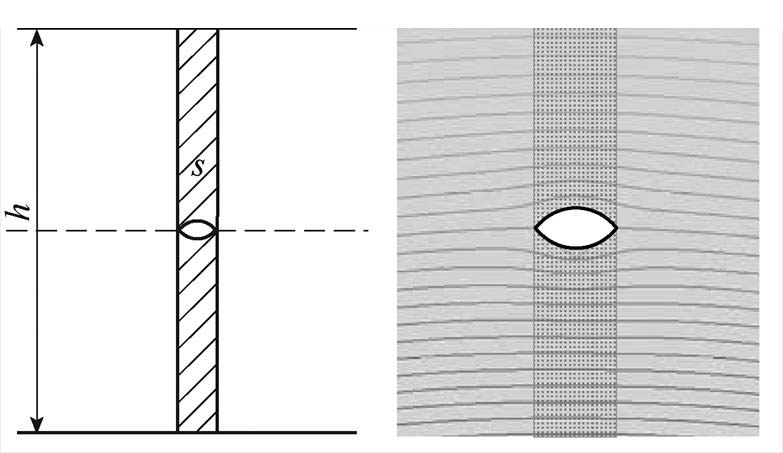
图6 顺向磁通密度影响的工艺孔损伤区域
Fig.6 The deteriorating area around the hole affected by the forward magnetic density
由于铁心损耗与磁感应强度幅值的二次方成正比,顺向磁感应强度的增加,将导致局部损耗增加。
设无孔时损耗密度为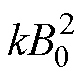 ,则由顺向磁感应强度增加所引起的平均损耗增长率可计算为
,则由顺向磁感应强度增加所引起的平均损耗增长率可计算为
 (11)
(11)
式中,k1为比例常数;s为顺向磁通密度影响的损伤区域面积;S为铁心单片总面积。
对图6所示的工艺孔损伤区域,可计算其面积为
 (12)
(12)
对于图5a所示三相三柱变压器铁心,设其铁心外接圆半径为R,窗高M=aR,窗宽L=bR,其中a、b为常数,则单片的面积为
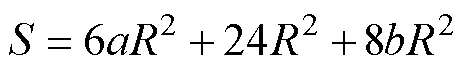 (13)
(13)
对于单片铁心,由于工艺孔面积远小于单片和工艺孔损伤区域面积,可忽略不计,故每个损伤区域的面积占铁心面积的百分比为
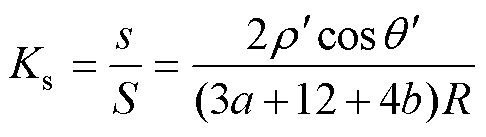 (14)
(14)
将式(14)代入式(11)中,得到单片铁心每个损伤区域内由于顺向磁通密度增加所引起的平均损耗增长率为
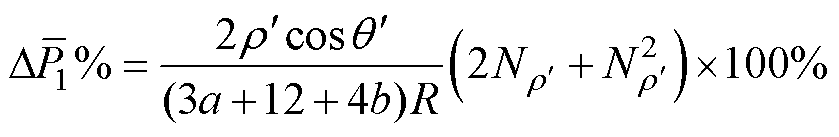 (15)
(15)
横向磁通密度影响的工艺孔损伤区域如图7所示。同理,可计算横向磁通密度分量所引起的平均损耗增长率。如图7所示阴影区域为
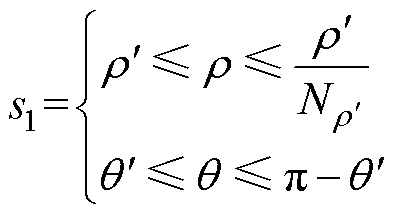
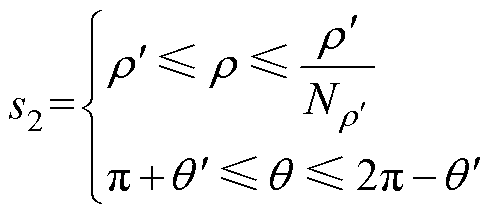
式中,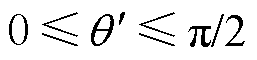 ,
,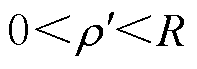 ,为垂直轧制方向的横向磁通密度分量所影响的损伤区域。将n=
,为垂直轧制方向的横向磁通密度分量所影响的损伤区域。将n=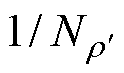 代入式(8)中,可计算图7所示工艺孔损伤区域内垂直轧制方向的横向磁通密度分量By的平均值为
代入式(8)中,可计算图7所示工艺孔损伤区域内垂直轧制方向的横向磁通密度分量By的平均值为
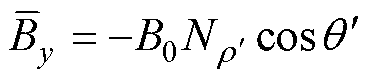 (16)
(16)
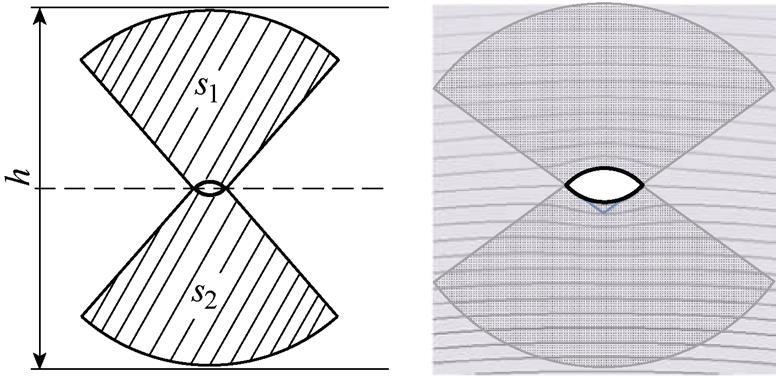
图7 横向磁通密度影响的工艺孔损伤区域
Fig.7 The deteriorating area around the hole affected by the transverse magnetic density
而取向钢片的损耗呈各向异性,垂直轧制方向的损耗是轧制方向的数倍,由第1.1节中双向磁特性测量结果及其分析可知,所研究的铁心材料,两个方向的损耗约为3倍关系,因此横向磁通密度分量的存在会导致局部损耗成倍增加。则由横向磁感应强度分量所引起的平均损耗增长率可计算为

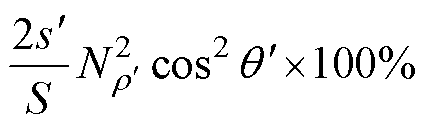 (17)
(17)
式中,k为比例常数;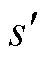 为横向磁通密度影响的损伤区域面积。
为横向磁通密度影响的损伤区域面积。
对于图7所示工艺孔损伤区域,可计算其面积为
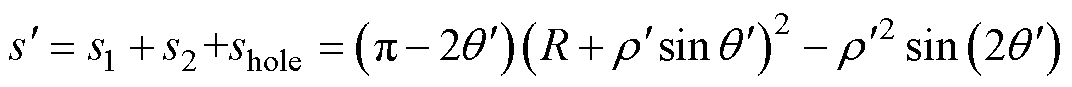 (18)
(18)
由式(18)可知,当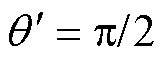 时,面积
时,面积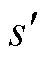 =0;当
=0;当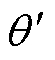 =0时,工艺孔损伤区域为圆形,面积
=0时,工艺孔损伤区域为圆形,面积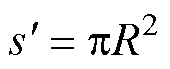 。
。
由于工艺孔面积远小于铁心单片和工艺孔损伤区域面积,可忽略不计,故每个损伤区域面积占铁心面积的百分比为
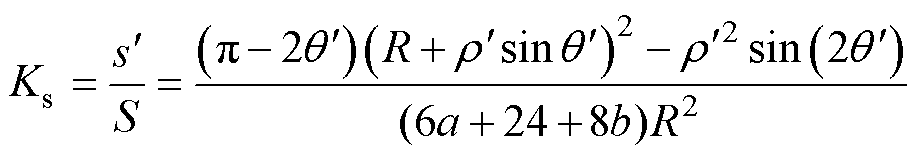 (19)
(19)
将式(19)代入式(17)中,得到单片铁心每个工艺孔损伤区域内由于横向磁通密度分量引起的平均损耗增长率为
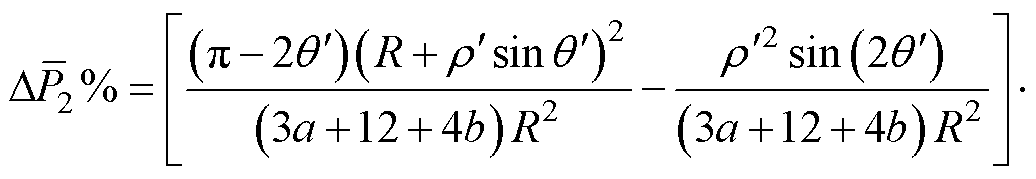
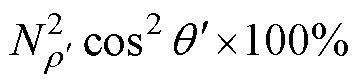 (20)
(20)
综上可知,变压器铁心工艺孔引起的损耗增长率为
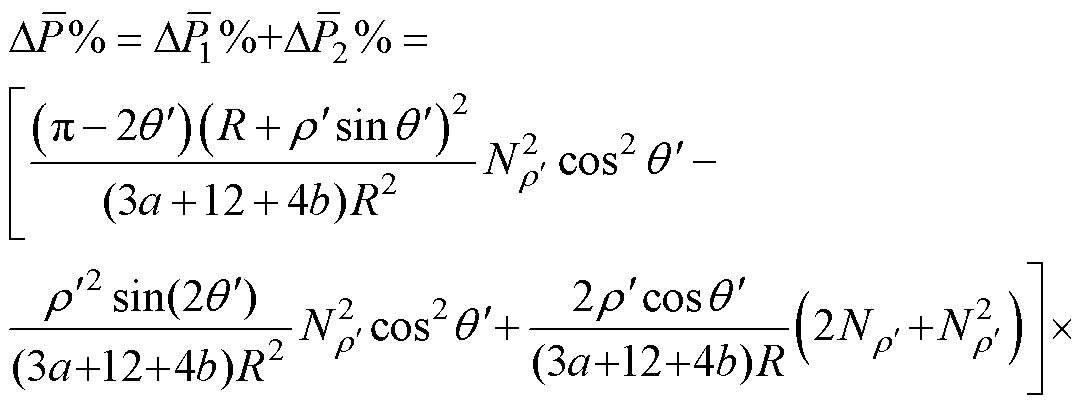
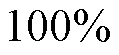 (21)
(21)
工程实际中R
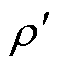 ,即
,即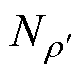
 1,则式(21)可近似为
1,则式(21)可近似为
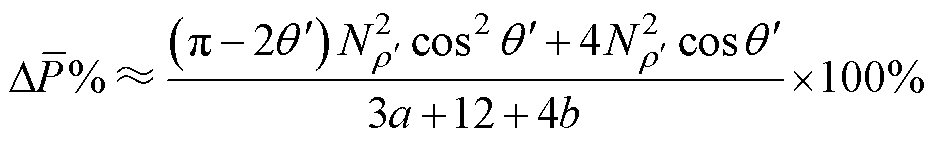 (22)
(22)
当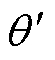 =0时,工艺孔为圆形孔,其所引起的损耗增长率为
=0时,工艺孔为圆形孔,其所引起的损耗增长率为
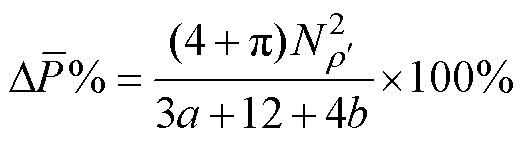 (23)
(23)
即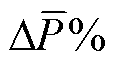 与
与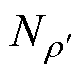 呈二次方关系,该结果与文献[2]中的实验测量结果一致;当
呈二次方关系,该结果与文献[2]中的实验测量结果一致;当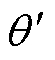 =
=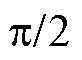 时,铁心无工艺孔,引起的损耗增长率为0。
时,铁心无工艺孔,引起的损耗增长率为0。
对于一台铁心窗高M=4R,窗宽L=2R的三相干式变压器,由式(22)可得其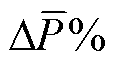 随
随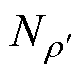 和
和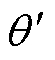 的变化关系,如图8所示,为方便后续的仿真与实验验证,选取其中
的变化关系,如图8所示,为方便后续的仿真与实验验证,选取其中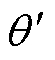 =0,
=0, 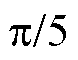 ,
, 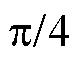 ,
, 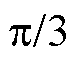 四条截面曲线,如图9所示。
四条截面曲线,如图9所示。
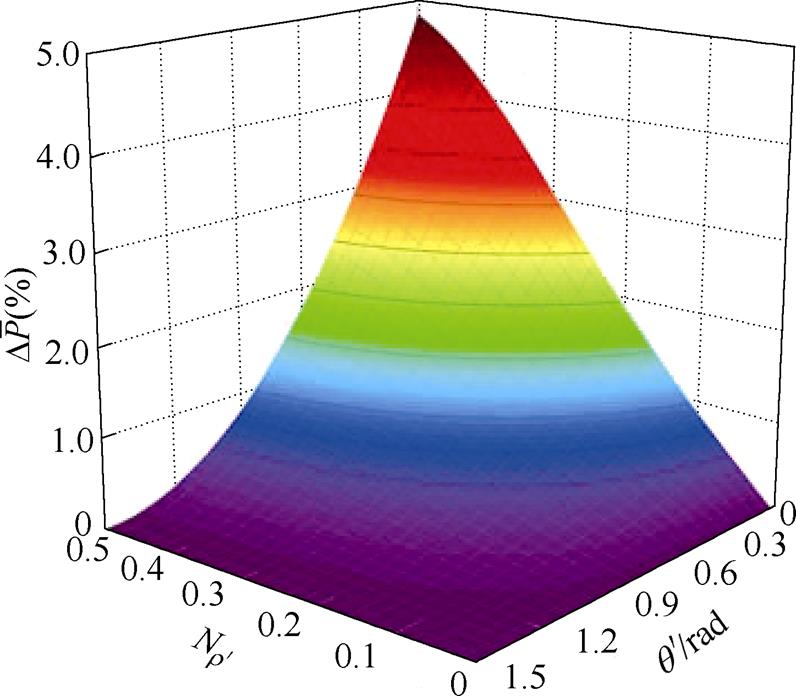
图8 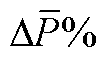 随
随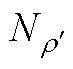 和
和 的变化关系
的变化关系
Fig.8 The relationship between 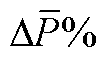 and
and 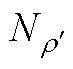 and
and 
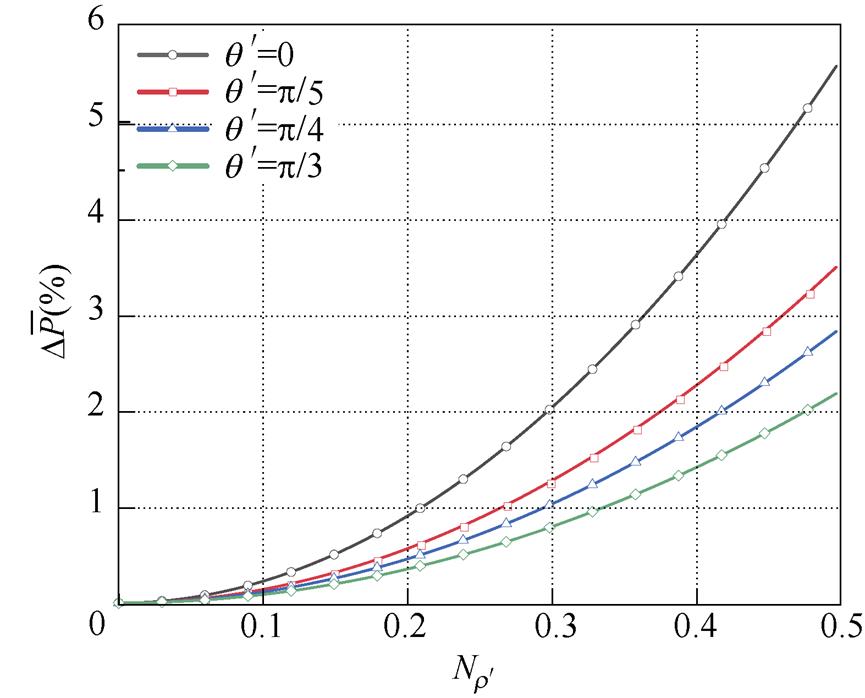
图9 各类工艺孔铁心损耗增长率理论值曲线
Fig.9 Theoretical value curves of core loss growth rate for various technological holes
为进一步验证理论计算结果的可行性与准确性,利用有限元计算方法分析实际工艺孔对铁心性能的影响,并基于瞬态电磁场求解器模拟变压器空载实验,研究设置工艺孔前后铁心的性能变化规律,并验证理论计算方法的准确性与合理性。
本文以一台标准的三相干式变压器为例,如图10a所示。低压侧绕阻为箔绕结构,铁心材料为B30P120取向硅钢片,忽略机座、垫块、树脂等对磁场分布影响微小的部件。选取其中的铁心硅钢单片作为研究对象,建立如图10b所示的单片铁心二维仿真模型。为充分考虑铁心导磁性能的非线性以及各向异性所引起的附加损耗,仿真中将第1.1节中硅钢材料B30P120的磁特性测量结果作为有限元的输入数据。铁心模型具体参数见表1。
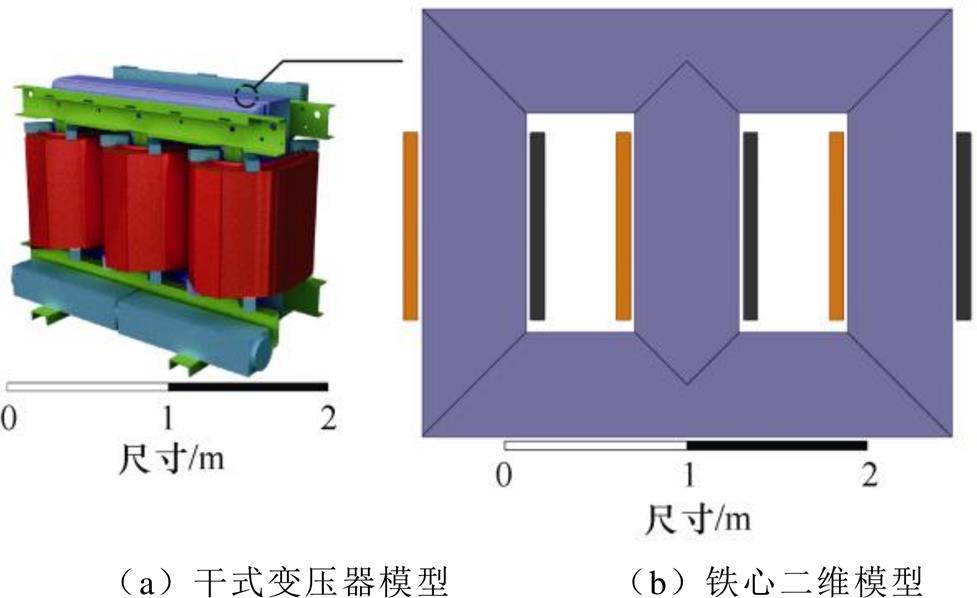
图10 干式变压器及其铁心磁场计算模型
Fig.10 Magnetic field calculation model of dry-type transformer and the core
表1 铁心模型参数(B30P120)
Tab.1 The model parameters of core (B30P120)
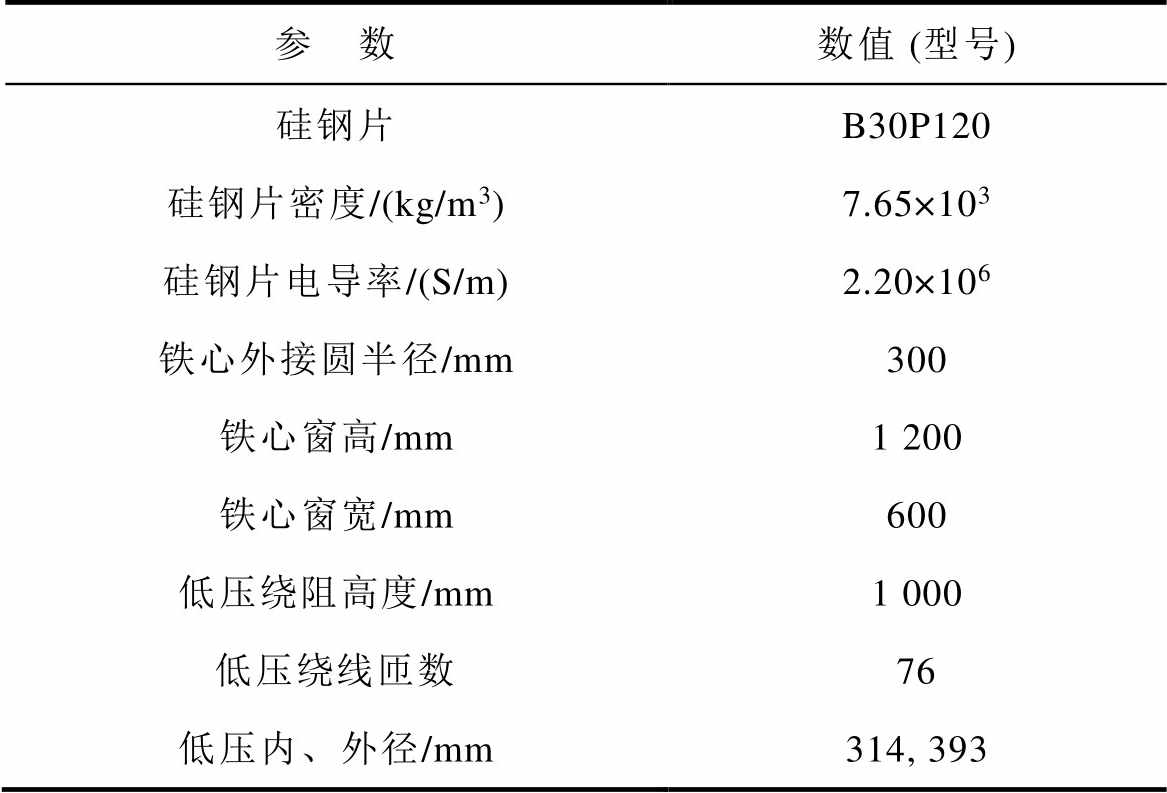
参 数数值 (型号) 硅钢片B30P120 硅钢片密度/(kg/m3)7.65×103 硅钢片电导率/(S/m)2.20×106 铁心外接圆半径/mm300 铁心窗高/mm1 200 铁心窗宽/mm600 低压绕阻高度/mm1 000 低压绕线匝数76 低压内、外径/mm314, 393
采用二维时步有限元方法,其磁场方程计算式为
 (24)
(24)
式中,A为矢量磁位;J为励磁电流密度,基于矢量磁位可计算铁心中磁感应强度。瞬态场的铁心损耗可由 模型计算[15]为
模型计算[15]为
 (25)
(25)
式中,Pe为附加损耗;kh、kc和ke为相应的各项损耗系数,由输入的损耗曲线拟合得到。
选用瞬态电磁场求解器模拟变压器空载运行,仿真过程中高压侧开路,在低压侧施加400V电压激励,得出低压三相励磁电流平均值为6A。仿真总时间为0.1s,每个周期为20ms,时间步长项设置为0.5ms,由仿真结果可知,运行到0.08s时,变压器基本达到稳态,且在0.096s时刻中间相达到最大磁场分布,计算中保存了0.08~0.1s内的场数据以便后期进行数值计算。
图11为0.096s时刻下,各类工艺孔附近的磁通流线分布,其中工艺孔类型分别为无孔(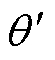 =
=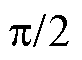 ),圆形孔(
),圆形孔(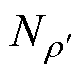 =0.05,
=0.05,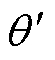 =0),纺锤孔1(
=0),纺锤孔1(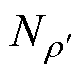 =0.05,
=0.05,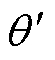 =
=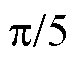 ),纺锤孔2(
),纺锤孔2(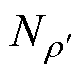 =0.05,
=0.05,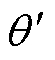 =
=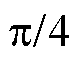 ),纺锤孔3(
),纺锤孔3(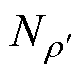 =0.05,
=0.05,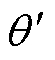 =
=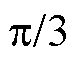 )。
)。
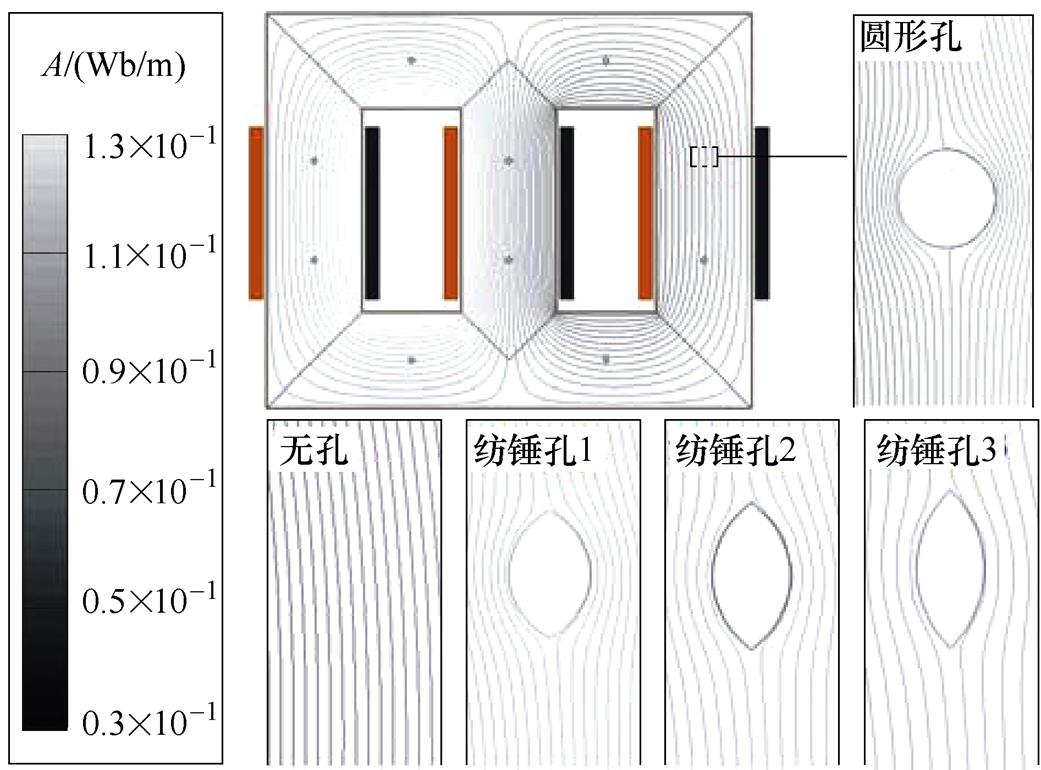
图11 各类工艺孔附近的磁通流线
Fig.11 The core magnetic flux flow lines distribution around various technological holes
图11表明,铁心未设置工艺孔时,变压器铁心柱处的磁通呈均匀分布,整体磁通沿取向方向通过,形成完整的闭合回路。而当铁心设置各类工艺孔后,铁心磁力线在工艺孔附近呈不均匀分布,在工艺孔左右部分,其顺向磁通密度明显集中,而原本均匀分布的取向磁通流线在工艺孔周围发生明显的绕行,产生横向磁通分量。对比可知,顺向磁通与横向磁通分量的局部增长现象,圆形孔最为明显,纺锤孔1、纺锤孔2、纺锤孔3三种类型孔依此减弱。上述影响发生在规定的工艺孔损伤区域内,该区域以外的铁心部分未受工艺孔的影响。
图12为变压器铁心模型运行至0.096s时刻下,各类工艺孔附近的磁感应强度分布。
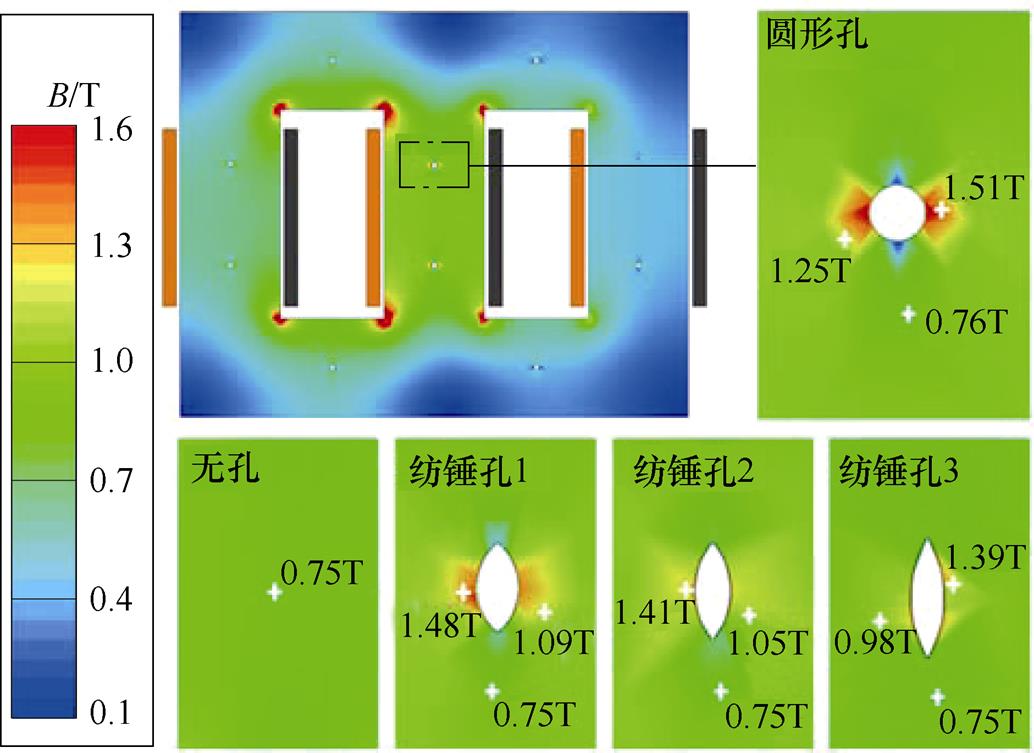
图12 各类工艺孔附近的磁感应强度分布
Fig.12 The core magnetic induction intensity distribution around various technological holes
图12表明,铁心无孔时,变压器铁心柱处磁感应强度分布均匀。当铁心设置各类工艺孔后,工艺孔附近的磁感应强度出现局部增大,且集中于工艺孔左右两侧,其数值随着与工艺孔边缘距离的增加而减小,由对比可知,此局部增大现象,圆形孔最为明显,纺锤孔1、2、3依此递减。
图13为变压器铁心模型运行至0.096s时刻时,各类工艺孔附近的损耗分布。仿真结果表明,未设置工艺孔时,变压器铁心柱处损耗呈均匀分布。当设置各类工艺孔后,工艺孔附近的损耗密度发生局部增大,相比正常区域,传统圆形工艺孔附近的局部最大损耗增加了330%,而对于新型纺锤孔3而言,仅增加了90%,由此可知,该局部增大现象在纺锤孔附近明显改善,新型纺锤孔相比传统圆形孔,具备更好的性能。
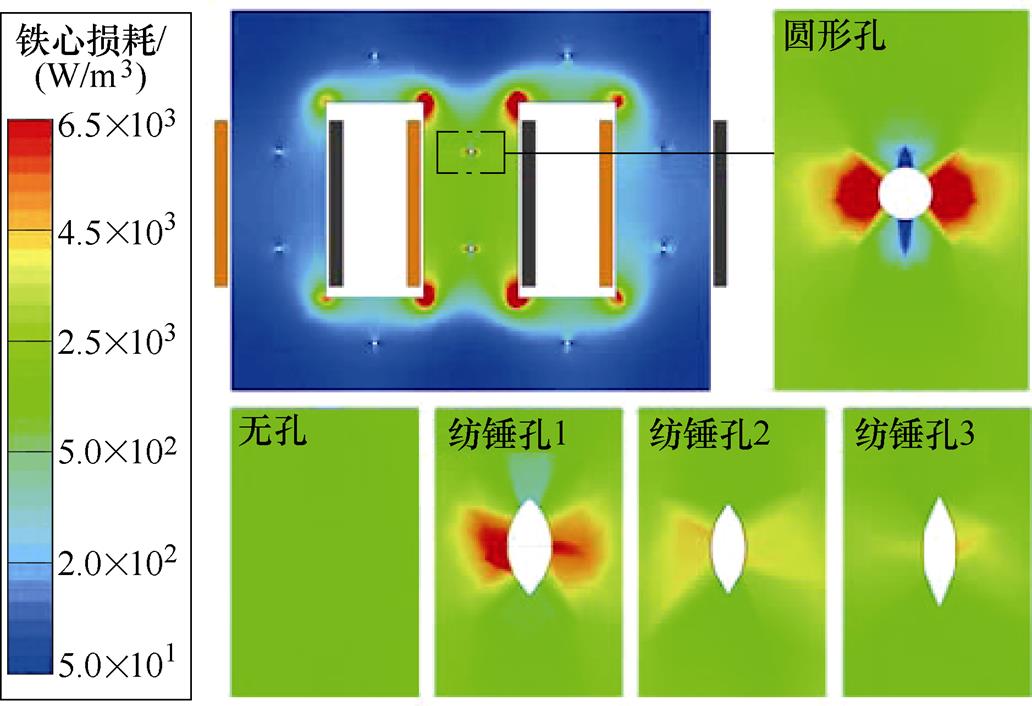
图13 各类工艺孔附近的损耗分布
Fig.13 The core loss distribution around various technological holes
为验证理论与仿真结果的一致性,分别对比分析了磁通密度分布和损耗增长结果。
由理论分析可知,当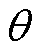 =
=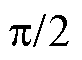 时,磁感应强度分布可由式(5)计算,选取仿真模型中各类工艺孔相同位置(
时,磁感应强度分布可由式(5)计算,选取仿真模型中各类工艺孔相同位置(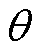 =
=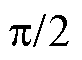 ),通过程序处理后得到该区域所有网格点的磁感应强度数据,理论与仿真值分布结果对比如图14所示,坐标横轴为网格点与工艺孔边缘距离,对比可知,当
),通过程序处理后得到该区域所有网格点的磁感应强度数据,理论与仿真值分布结果对比如图14所示,坐标横轴为网格点与工艺孔边缘距离,对比可知,当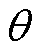 =
=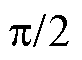 时,磁感应强度在各工艺孔边缘处达到最大,其数值为正常区域的2倍。理论与仿真值的分布均满足上述规律,具备一致性。
时,磁感应强度在各工艺孔边缘处达到最大,其数值为正常区域的2倍。理论与仿真值的分布均满足上述规律,具备一致性。
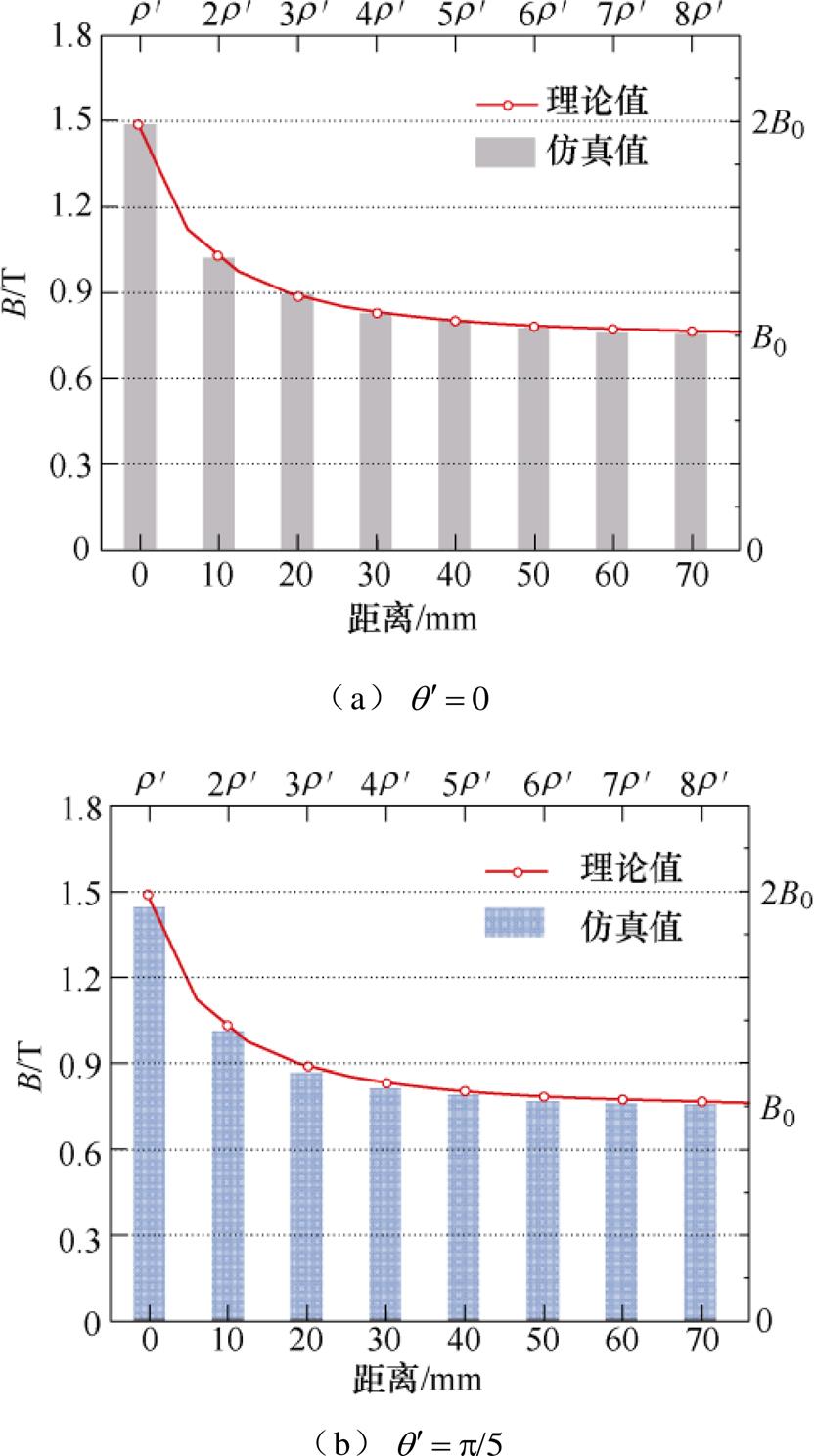
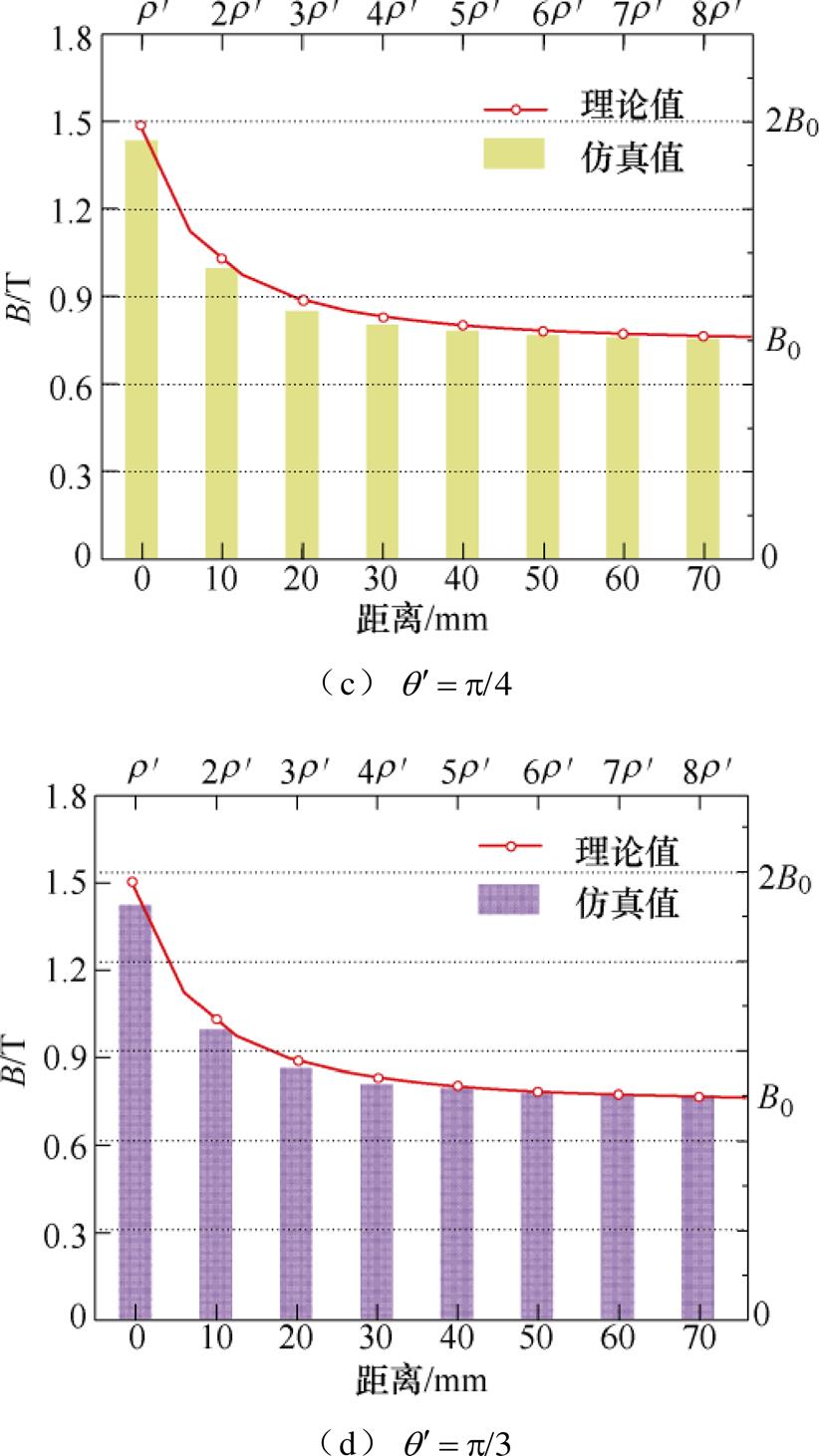
图14 磁感应强度分布理论与仿真值对比结果
Fig.14 Comparison result of magnetic induction intensity distribution theory and simulation
由理论分析可知,工艺孔所影响的局部损伤区域大小Ks可由式(19)计算得到,Ks与工艺孔相对大小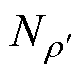 、极角
、极角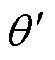 之间的变化关系如图15所示,选取其中
之间的变化关系如图15所示,选取其中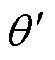 =0,
=0, 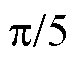 ,
, 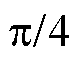 ,
, 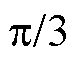 四条截面曲线如图16所示,计算结果表明,Ks随着工艺孔相对大小
四条截面曲线如图16所示,计算结果表明,Ks随着工艺孔相对大小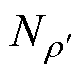 的增加而增加,且当R
的增加而增加,且当R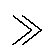
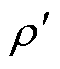 ,即
,即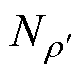
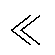 1时,圆形孔Ks值最大,纺锤孔1、2、3依此递减,这与仿真中各类工艺孔附近磁通密度、损耗的分布规律一致。
1时,圆形孔Ks值最大,纺锤孔1、2、3依此递减,这与仿真中各类工艺孔附近磁通密度、损耗的分布规律一致。
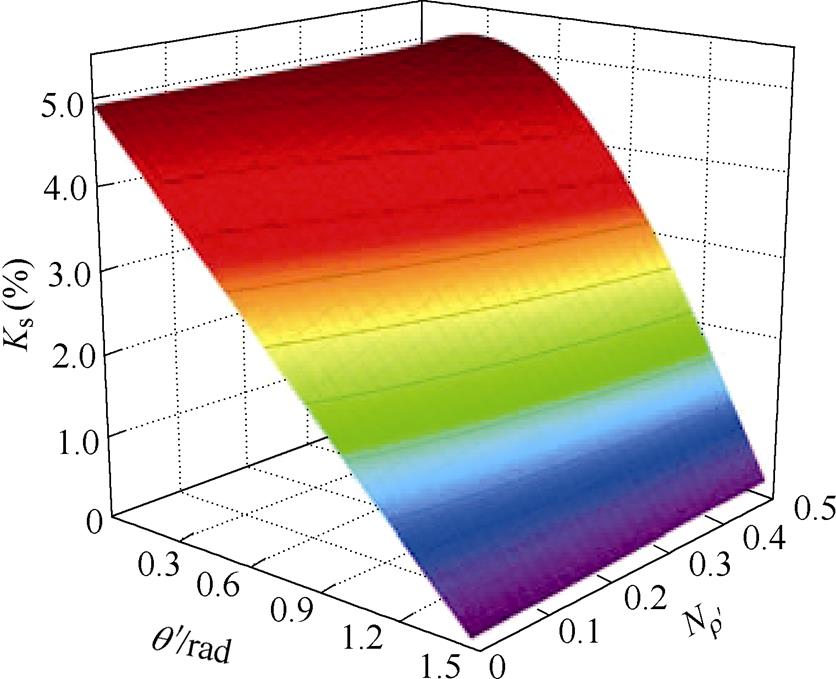
图15 Ks随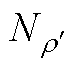 和
和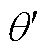 的变化关系
的变化关系
Fig.15 The relationship between Ksand 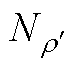 and
and 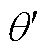
由理论分析可知,铁心模型中对不同类型工艺孔的损耗增长率理论值可由式(22)计算得到。通过仿真计算后处理可分别得到各类工艺孔铁心(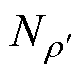 = 0.05)不同时刻的总铁心损耗P,其随时间变化的曲线如图17所示,选取其稳态运行一个周期的数据,通过式(26)可分别计算得到各类工艺单孔所引起的损耗增长率,理论与仿真对比结果如图18所示。
= 0.05)不同时刻的总铁心损耗P,其随时间变化的曲线如图17所示,选取其稳态运行一个周期的数据,通过式(26)可分别计算得到各类工艺单孔所引起的损耗增长率,理论与仿真对比结果如图18所示。
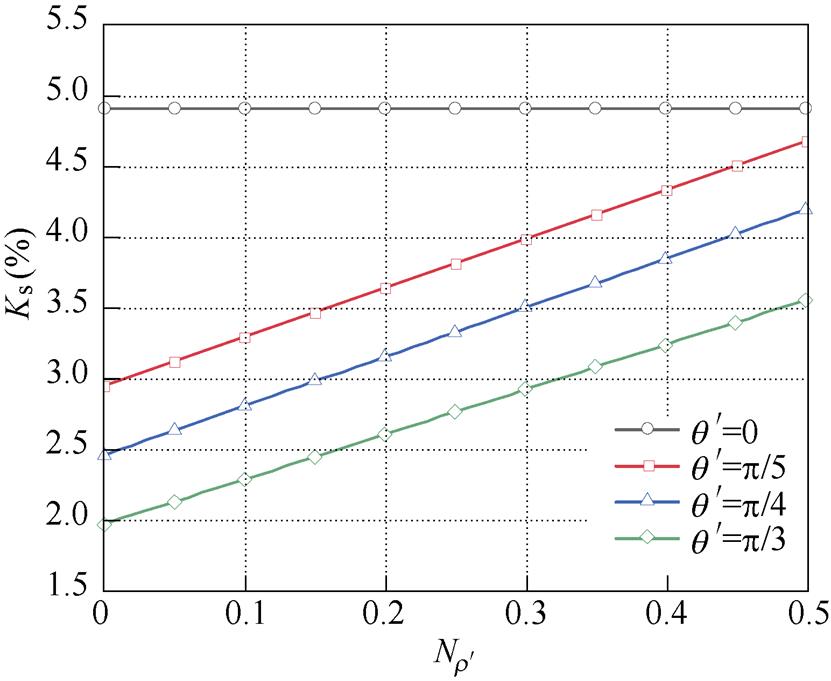
图16 各类工艺孔损伤区域的面积占比曲线
Fig.16 The ratio curves of the deteriorating area with various technological holes
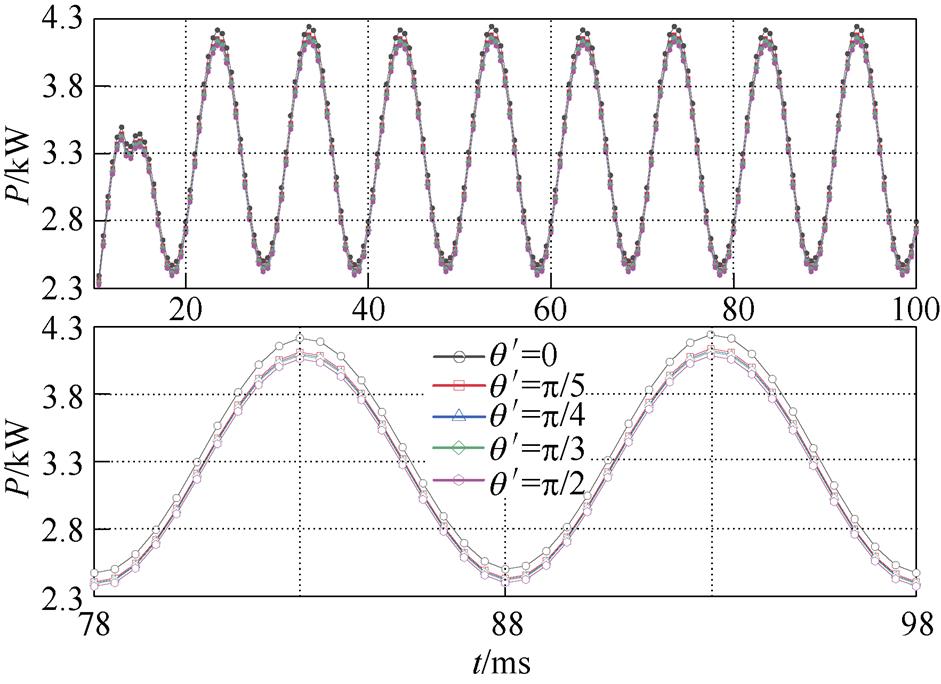
图17 各类工艺孔铁心随时间变化的损耗曲线
Fig.17 Core loss of various holes cores with time
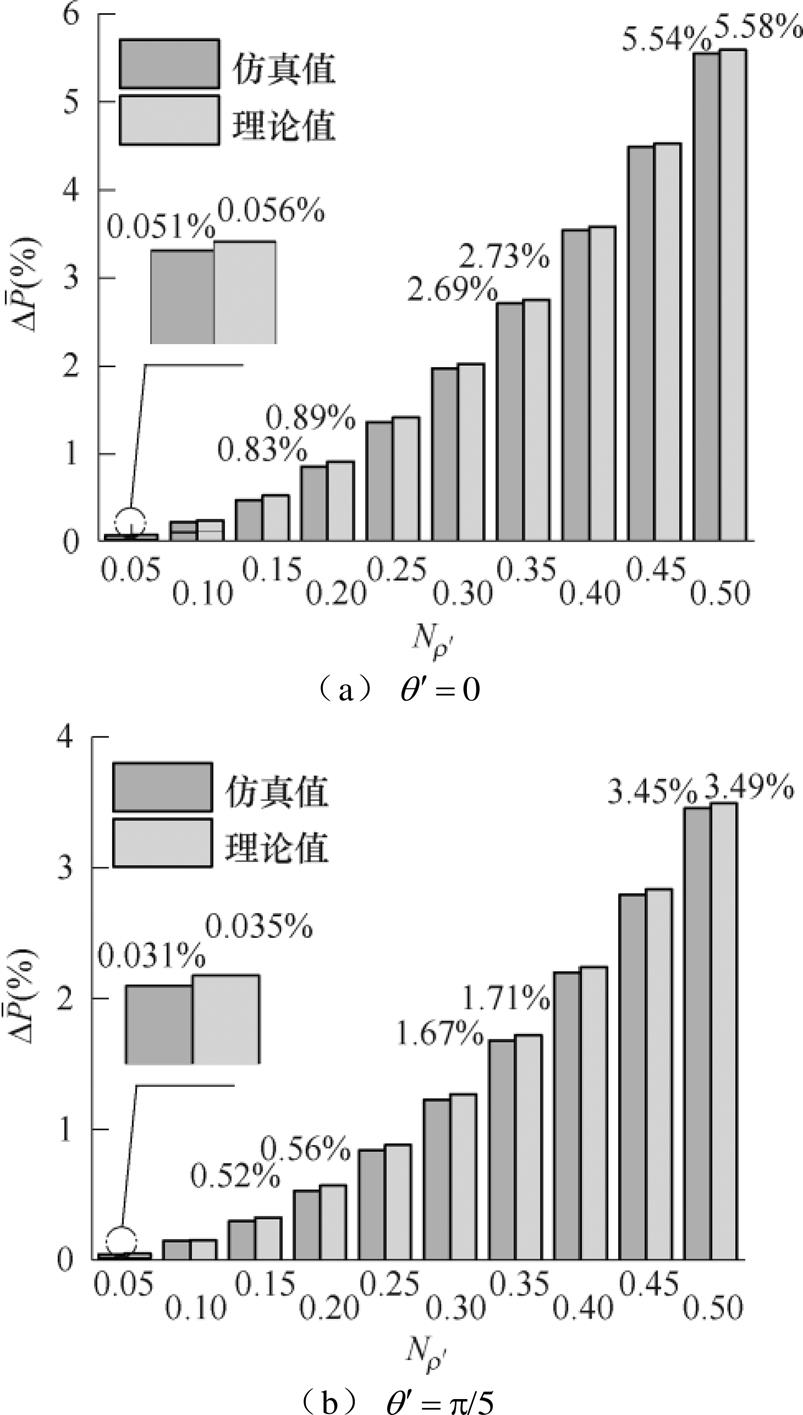
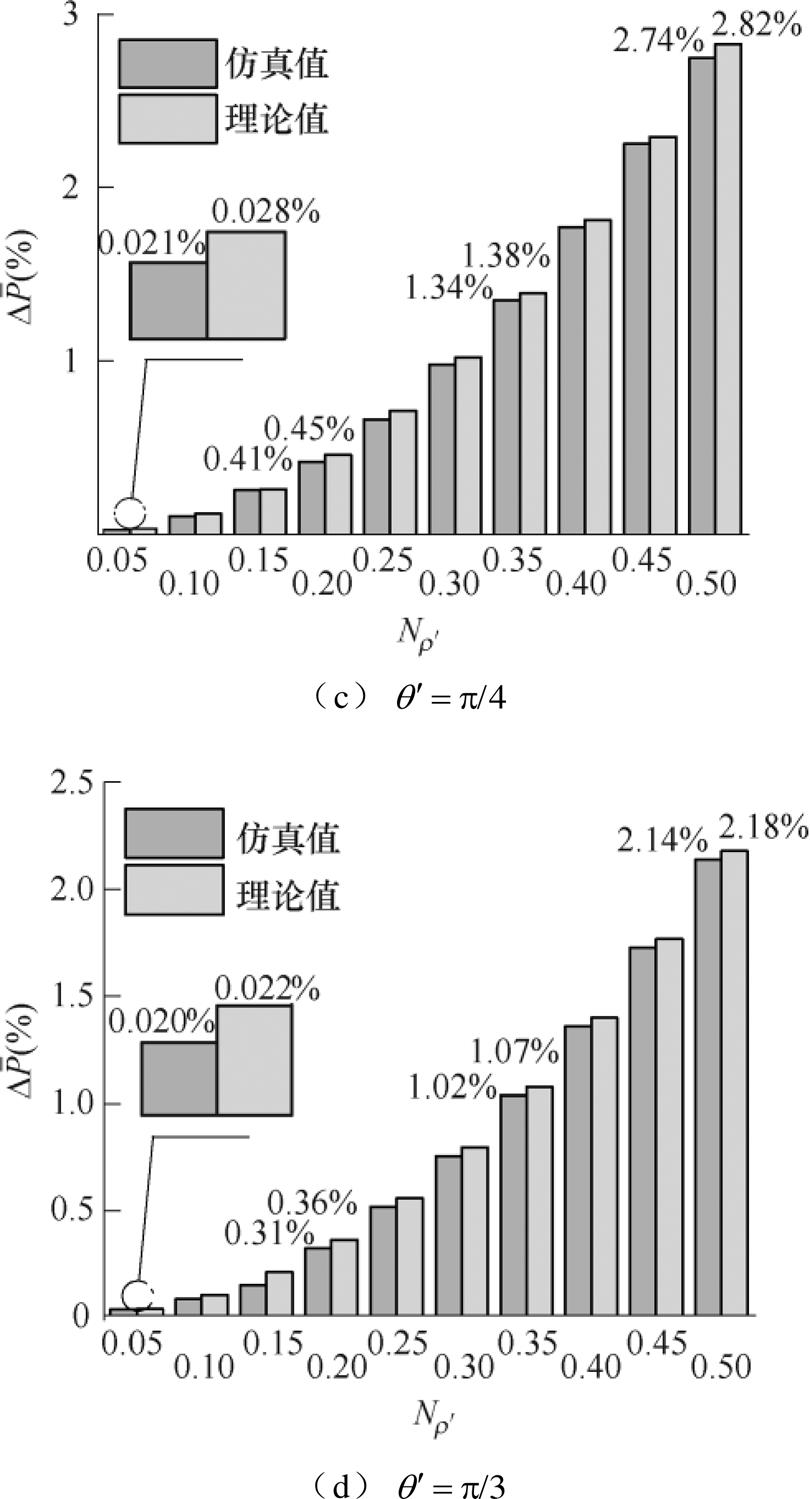
图18 各类工艺孔铁心损耗增长率理论与仿真对比结果
Fig.18 Theoretical and simulation comparison results of core loss growth rate for various technological holes
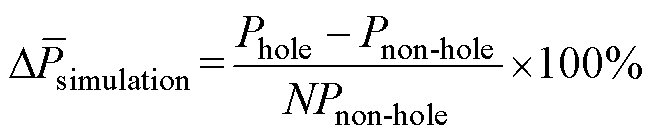 (26)
(26)
式中,N为工艺孔个数;Phole为带工艺孔铁心损耗;Pnon-hole为无孔铁心损耗。
通过对理论结果与仿真结果进行对比分析可知,两种结果基本一致,其平均误差在8%以内,验证了本文所提理论计算方法的准确性与可靠性。
为进一步验证工艺孔所引起的铁心损耗增长率计算方法的正确性,并依据仿真结果分析工艺孔对铁心温升的影响,搭建了基于IEC 60404-2标准的爱泼斯坦方圈测试系统,对设置各类型工艺孔的取向硅钢片B30P120的铁心损耗进行测量,并通过热成像仪与多路K型热电偶测量各类型工艺孔铁心空载运行时的温度分布。
采用的爱泼斯坦方圈测试系统与实验原理如图19所示,标准方圈匝数为700 700,利用高性能NI数据采集卡进行一次电流及二次电压值的多通道同步数据采集,并通过Labview程序对数据进行处理分析。实验利用法拉第电磁感应定律、安培环路定律和坡印亭定理计算测量数据得到相应的磁感应强度B、磁场强度H以及损耗P分别为
700,利用高性能NI数据采集卡进行一次电流及二次电压值的多通道同步数据采集,并通过Labview程序对数据进行处理分析。实验利用法拉第电磁感应定律、安培环路定律和坡印亭定理计算测量数据得到相应的磁感应强度B、磁场强度H以及损耗P分别为
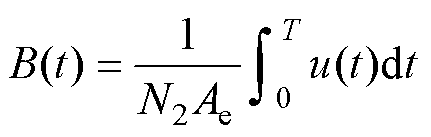 (27)
(27)
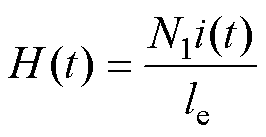 (28)
(28)
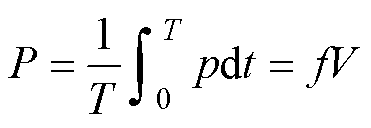
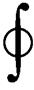
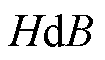 (29)
(29)
式中,N1、N2分别为一、二次绕阻匝数;Ae为有效磁路截面积;le为有效磁路长度;u(t)为二次电压;i(t)为一次电流;P为总铁心损耗;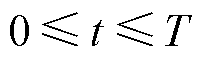 。
。
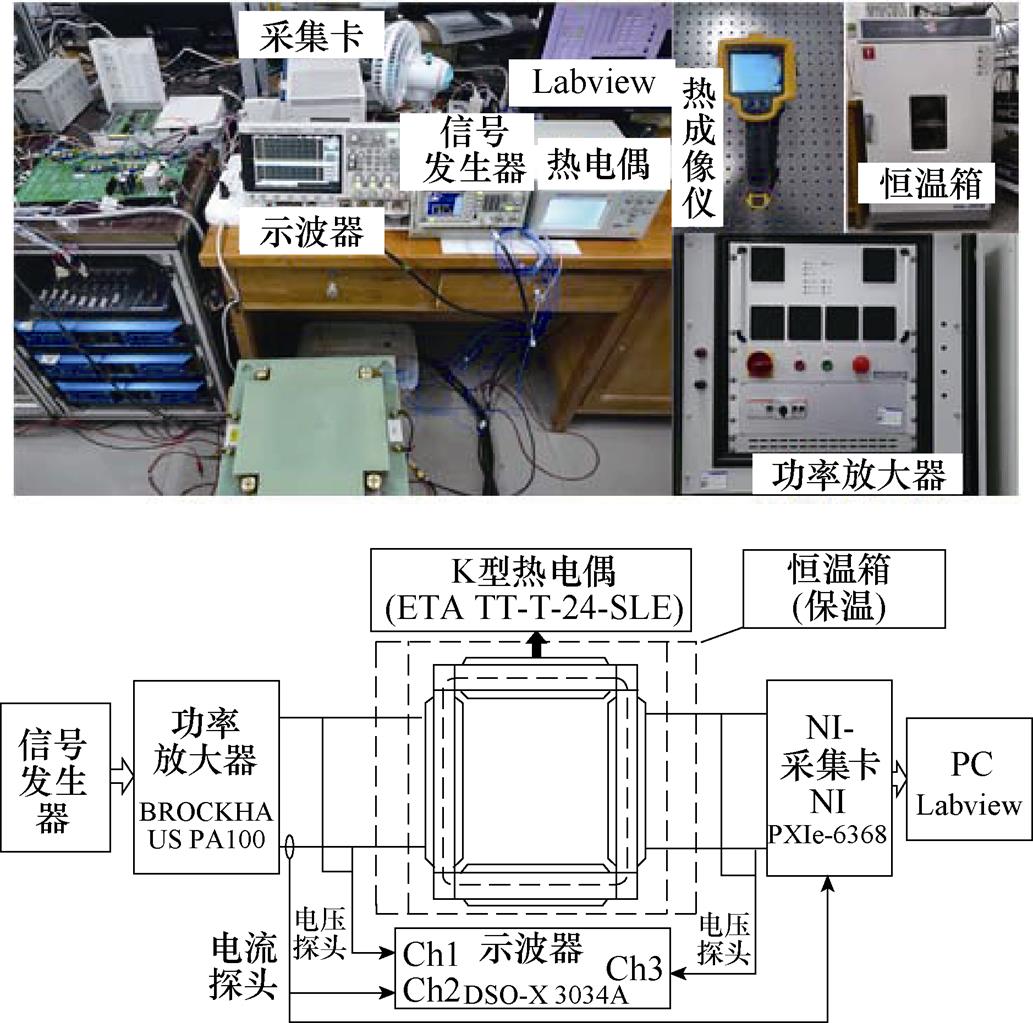
图19 爱泼斯坦方圈测试系统
Fig.19 Epstein frame experimental testing system
根据上述实验原理与系统,测量设置了各类型工艺孔的取向硅钢片B30P120的铁心损耗,为了降低单孔测量实验误差,并保证各工艺孔间无相互影响,需确定硅钢样片上工艺孔间距的合理范围。为此,本文采用局部磁特性测试系统[25],对工艺孔周围局部磁特性分布进行测试,测试过程如图20a所示,图中,移动型B-H传感安装在一台XYZ三轴精密定位装置上,其沿各个方向的位移精度为1mm,通过定位装置的控制能够实现B-H传感的精确移动。针对本文所用带工艺孔取向硅钢样片,测试了极角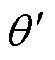 =0,相对大小
=0,相对大小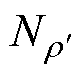 分别为0.05、0.16、0.23、0.30。工艺孔周围的损耗分布,如图20b所示。结果表明,工艺孔附近区域损耗增长显著,其最远影响距离为10mm,因此,当孔间距大于20mm时,两孔之间无相互影响。基于上述结果,本文在每单一样片上均匀设置如图21所示间距为30mm的8个工艺孔,每组32片,共计256个工艺孔。实验中控制磁通密度峰值Bm在0.1~1.8T,间隔0.1T,频率设置为50Hz。同时配备多路K型热电偶温度测试仪、Fluke Ti25红外热成像仪、WGL-230B恒温箱等实验器材,利用多路K型热电偶对样品各位置温度进行定量测试,并通过热成像定性分析工艺孔附近的温度分布。
分别为0.05、0.16、0.23、0.30。工艺孔周围的损耗分布,如图20b所示。结果表明,工艺孔附近区域损耗增长显著,其最远影响距离为10mm,因此,当孔间距大于20mm时,两孔之间无相互影响。基于上述结果,本文在每单一样片上均匀设置如图21所示间距为30mm的8个工艺孔,每组32片,共计256个工艺孔。实验中控制磁通密度峰值Bm在0.1~1.8T,间隔0.1T,频率设置为50Hz。同时配备多路K型热电偶温度测试仪、Fluke Ti25红外热成像仪、WGL-230B恒温箱等实验器材,利用多路K型热电偶对样品各位置温度进行定量测试,并通过热成像定性分析工艺孔附近的温度分布。
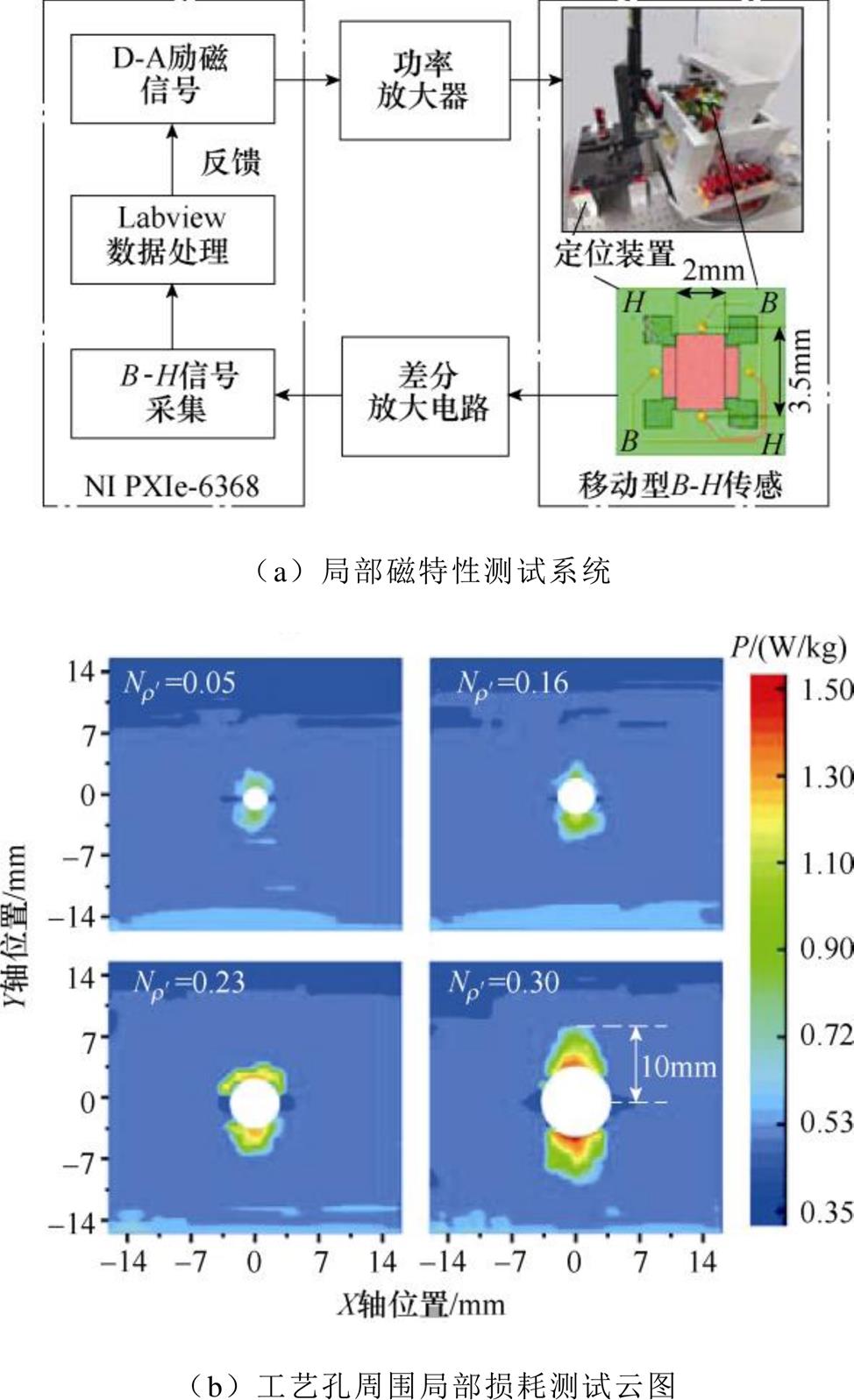
图20 局部磁特性测试系统与损耗测试结果
Fig.20 Local testing system and distributions of loss
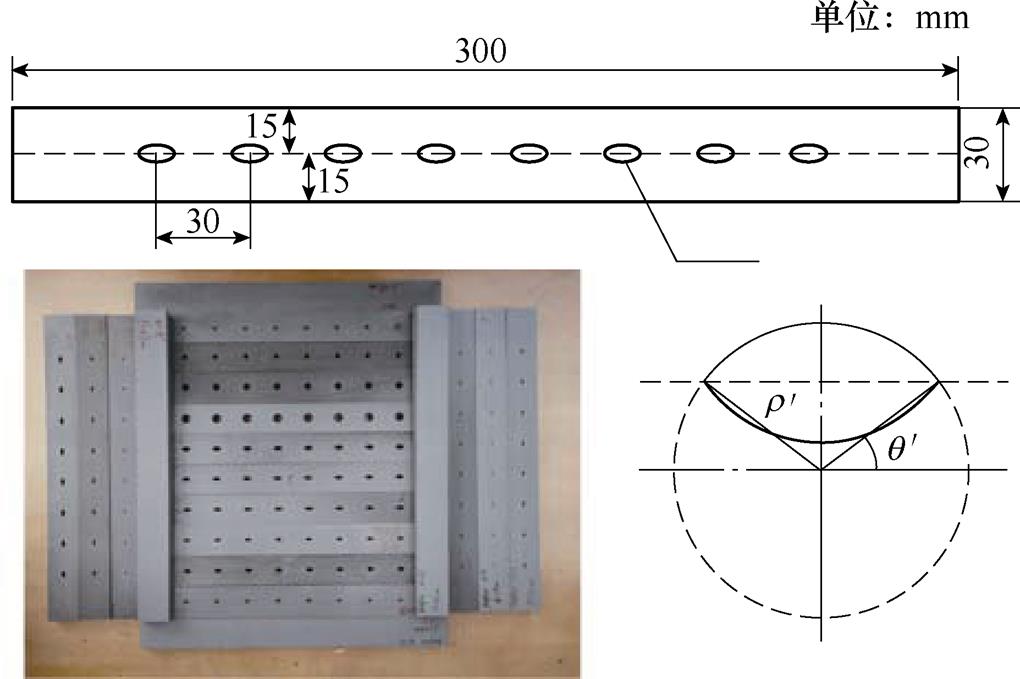
图21 方圈实验样片结构
Fig.21 Sample structure of frame experimental test
4.2.1 铁心局部温升的测试结果
为降低外部环境对实验温升的影响,本文将铁心样片置于恒温箱中进行空载实验,选取工艺孔局部区域内不同位置分析其温升规律,热电偶埋设位置如图22所示,测温点为上下距离孔心5mm、7mm、9mm、11mm处。同时通过红外热成像仪,观测工艺孔局部温度的分布结果。经过3h运行,样片各测温点在1h内的温升变化小于1℃,此时认为实验处于稳态运行。
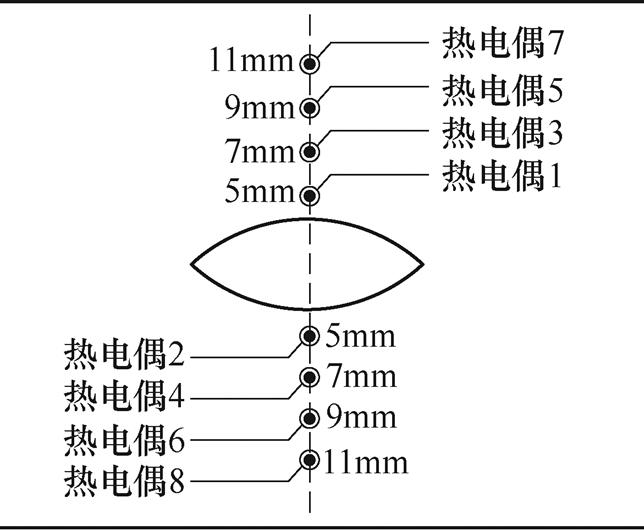
图22 热电偶埋设位置
Fig.22 Thermocouple buried positions
图23为样片不同位置的热电偶测温结果,坐标横轴为热电偶与孔心距离,在工艺孔上下5mm位置处,温升达到28.5℃,距离工艺孔越远,温升逐渐降低。图24为不同类型工艺孔局部的红外热成像仪测试结果,在靠近工艺孔的局部区域存在明显温升,该区域以外的铁心部分基本未受工艺孔的影响,此局部区域范围与理论和仿真中结果基本吻合。
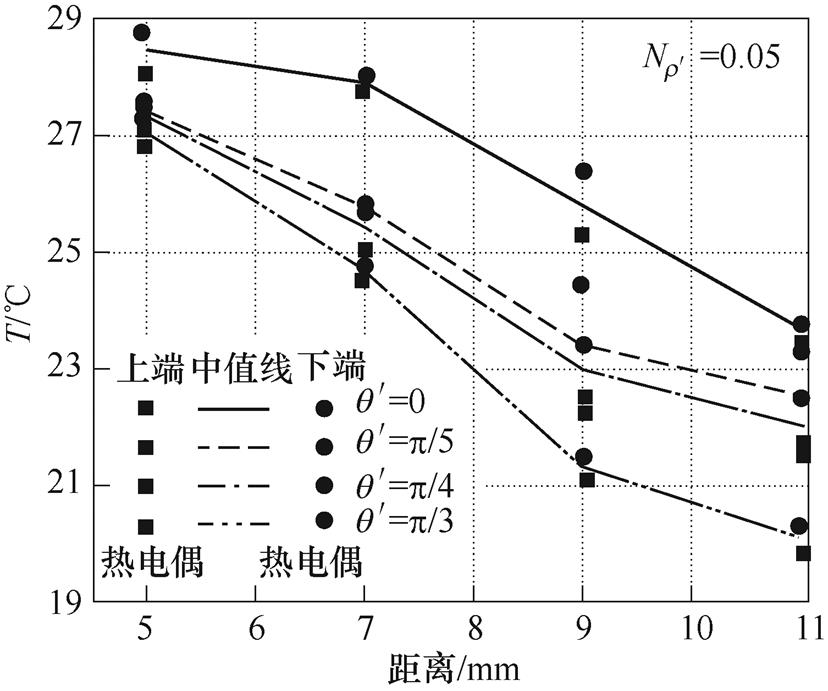
图23 热电偶温升测试结果
Fig.23 Thermocouple temperature rise test results
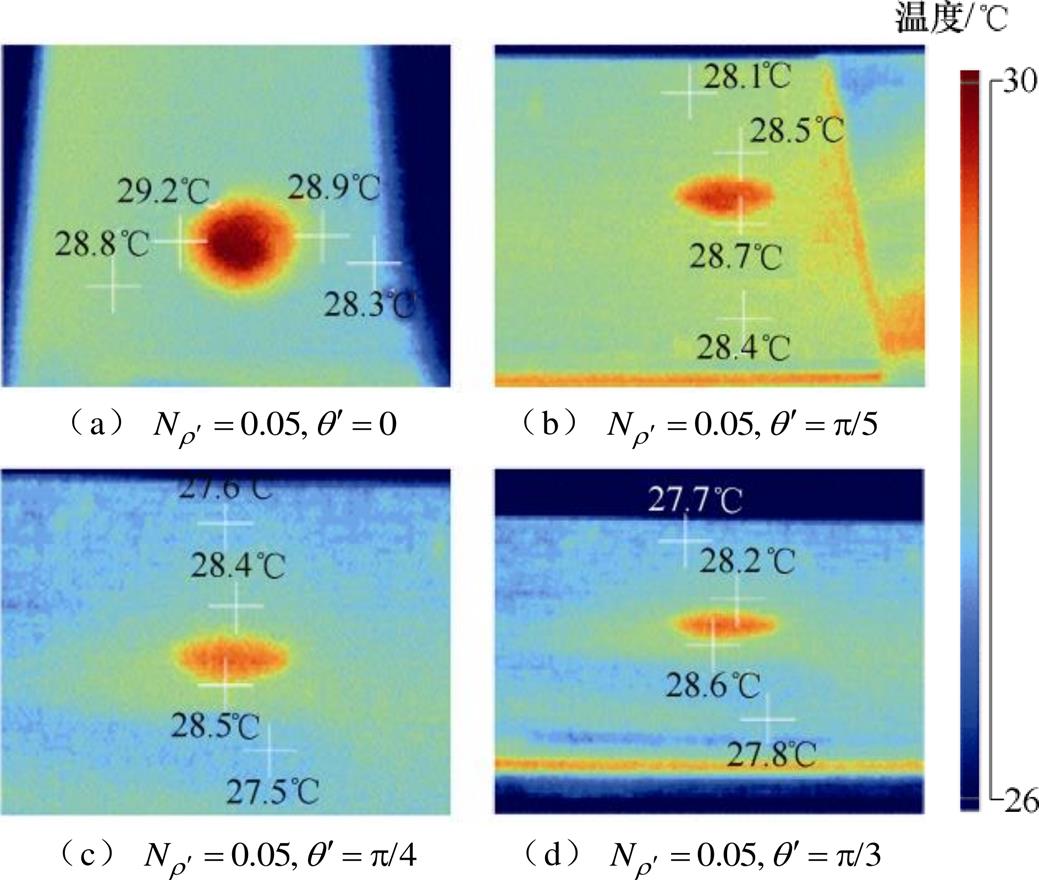
图24 红外线温升测试结果
Fig.24 Infrared temperature rise test results
4.2.2 工艺孔铁心损耗理论与实验结果对比
为验证理论与实验结果的一致性,采用本文提出的工艺孔铁心损耗计算方法,通过式(11)、式(17)可分别计算得到各类工艺孔所引起的损耗增长率理论值。基于第4.1节中的测试方法,可分别测量得到各类型工艺孔样片的铁心损耗如图25所示,通过
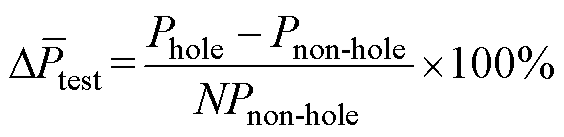 (30)
(30)
分别计算得到各类工艺孔所引起的损耗增长率实验值。理论与实验结果对比如图26所示。
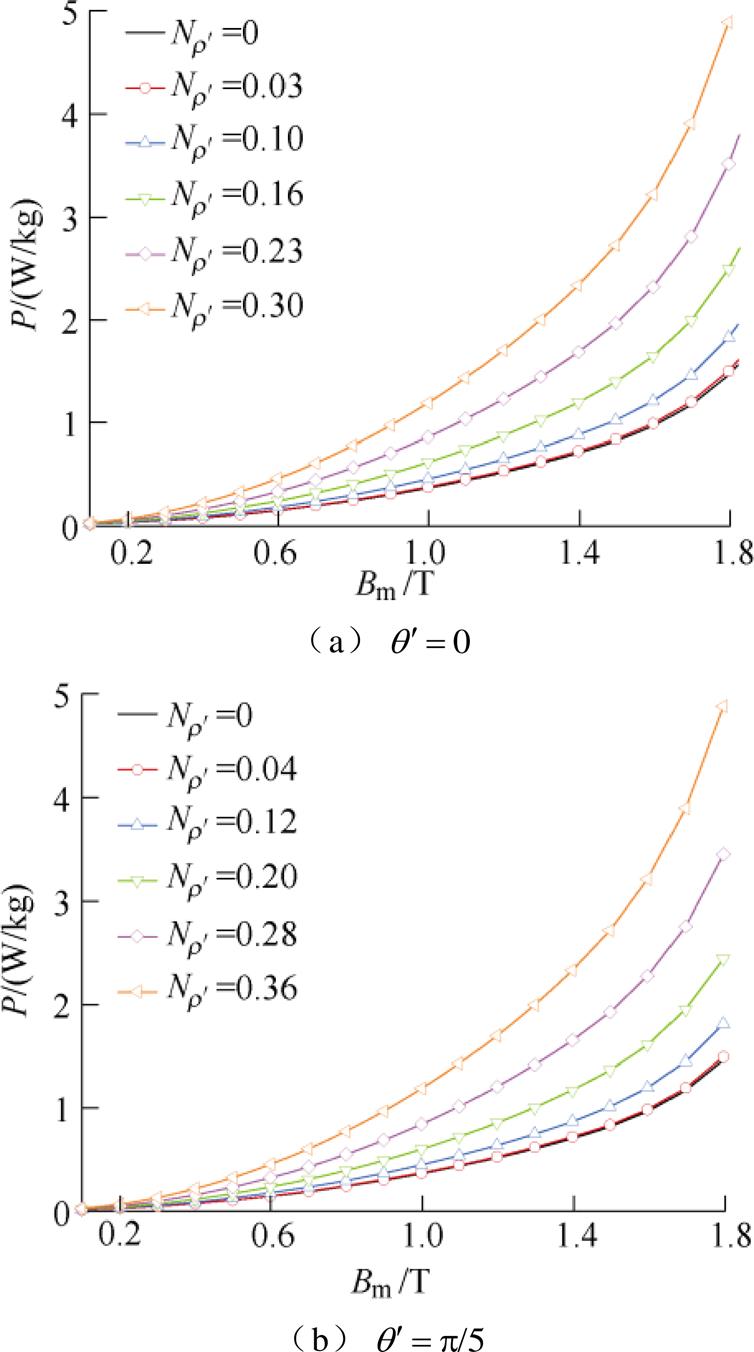

图25 各类工艺孔铁心随磁通密度变化的损耗曲线
Fig.25 The loss curves of various technological hole cores with magnetic flux density
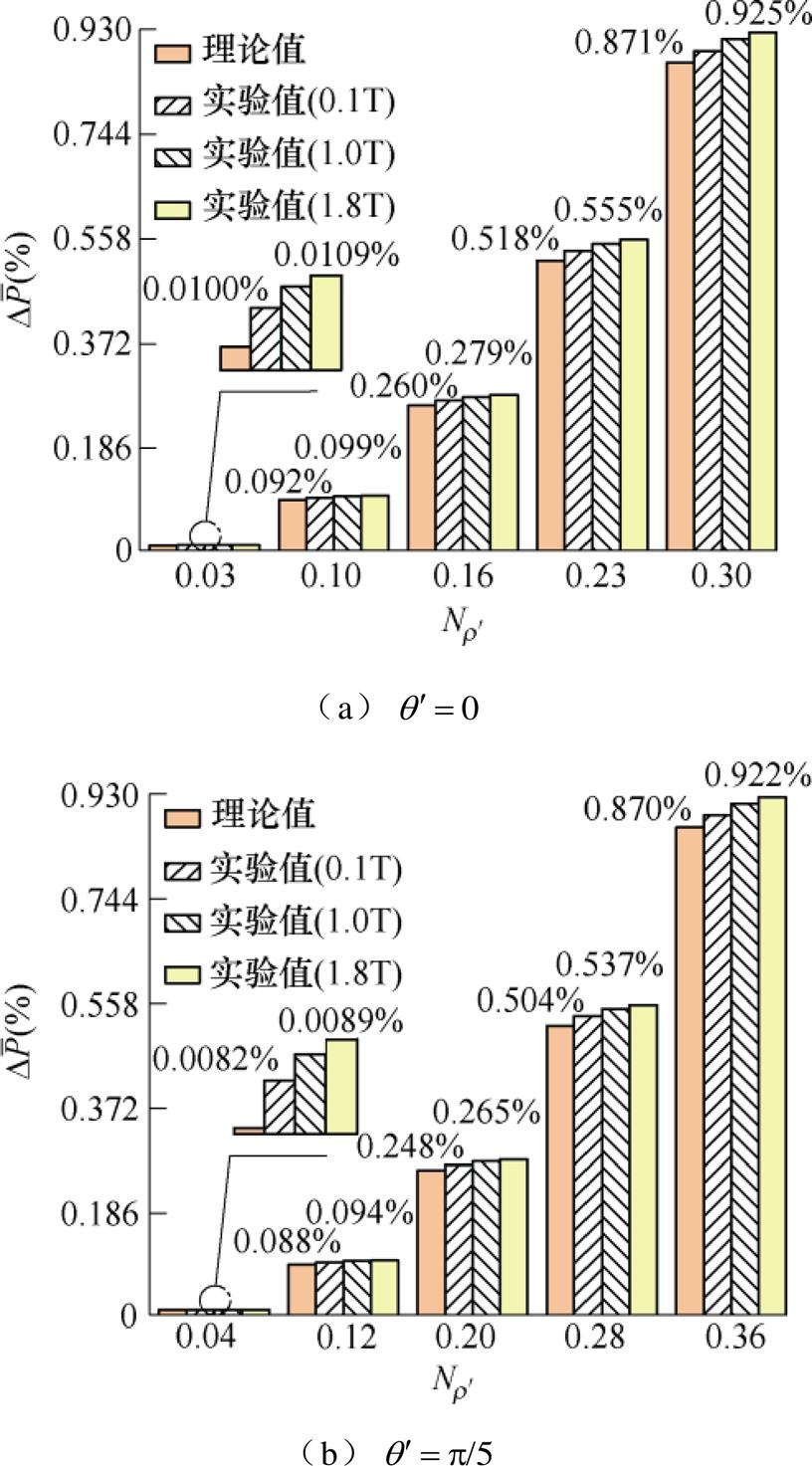

图26 各类工艺孔铁心损耗增长率理论与实验对比结果
Fig.26 Theoretical and experimental comparison results of core loss growth rate for various technological holes
对比可知,铁心损耗增长率计算值与实验测量值基本一致,为确定本文所提方法的可行性与准确性,对理论与实验对比结果进行误差分析,如图27所示。分析结果表明,当磁通密度峰值Bm为0.1~1.6T时,理论与实验误差在5%以内,仅当Bm>1.7T时,误差为6%~8%,而变压器在实际运行时,为防止过励磁故障,通常铁心中磁通密度低于饱和磁通密度,故本文所提方法具有工程适用性,具备可行性与准确性。

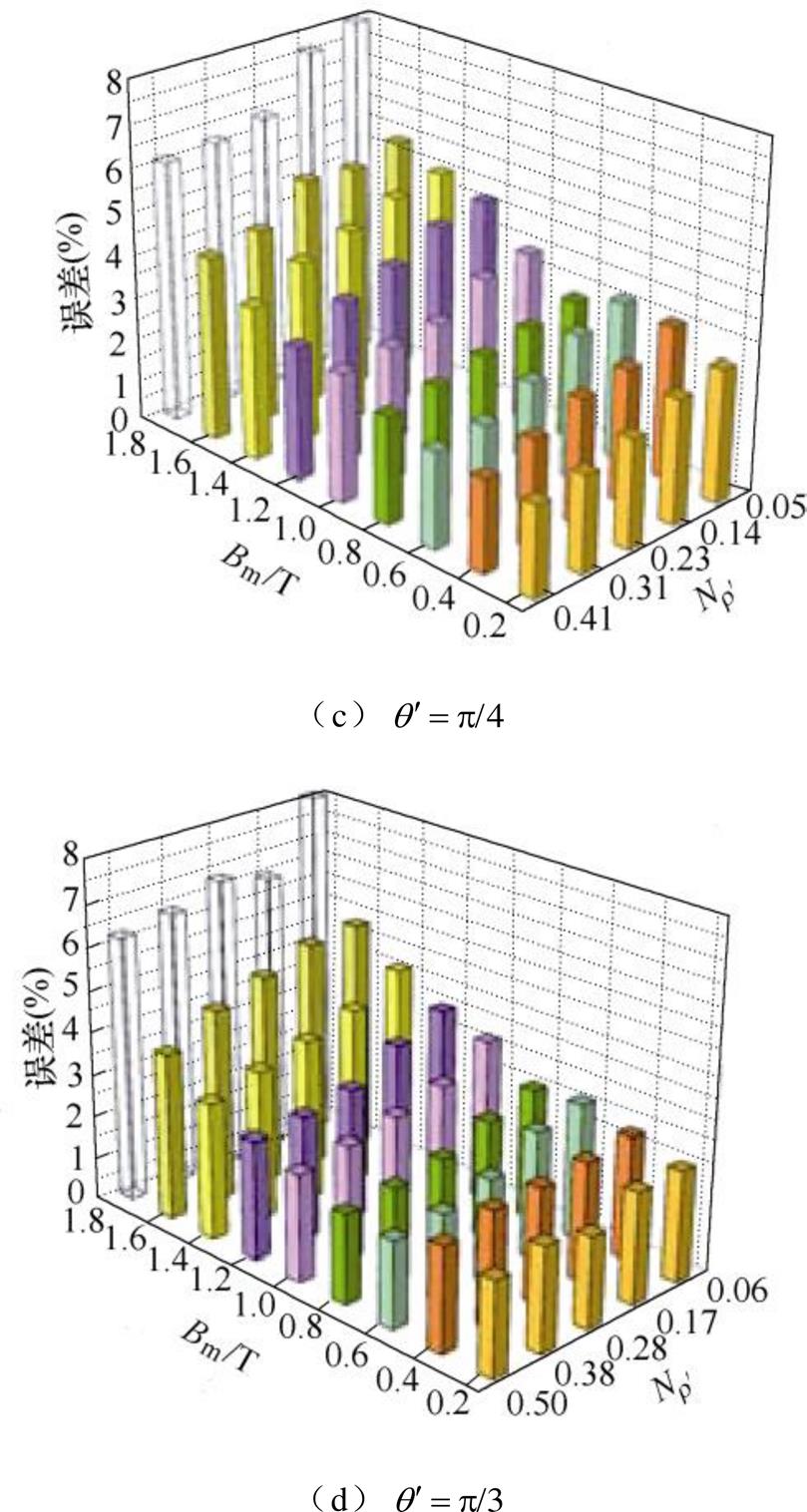
图27 理论与实验结果误差分析
Fig.27 Error analysis of theoretical and experimental results
上述误差的来源可能包含以下部分:
(1)实验理论所存在的近似性以及所用实验装置的局限性,造成一定的测量误差。
(2)涡流引起的误差,尽管保证了对比实验的单一变量,且叠片之间有绝缘涂层,但依然无法避免由于工艺孔的存在所造成的层间额外涡流损耗,从而导致损耗测量值略大于理论值。且该涡流损耗将随着磁通密度的增加而增加,这与误差分析结果一致。
(3)由工艺孔引起的局部过热,也会影响损耗测量值。
本文基于Steinmetz损耗公式,通过对铁心二维电磁场进行解析计算,提出一种考虑工艺孔影响的变压器铁心损耗增长计算公式,通过有限元仿真分析和模型实验验证了其可行性;并对比分析了不同形状、不同尺寸的工艺孔对变压器铁心损耗的影响规律。本文研究方法可为变压器设计过程中铁心损耗的准确计算提供技术方案,具体结论如下:
1)提出了干式变压器铁心设置各类工艺孔后损耗增长率的计算方法,该方法可以准确计算铁心单片由不同极角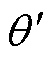 、不同相对大小
、不同相对大小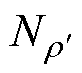 工艺孔所引起的损耗增长率。且该增长率与
工艺孔所引起的损耗增长率。且该增长率与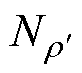 的二次方成正比。
的二次方成正比。
2)当工艺孔相对大小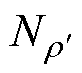
 1时,对于相同的
1时,对于相同的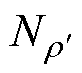 ,圆形工艺孔对铁心性能的影响最大,随着工艺孔极角
,圆形工艺孔对铁心性能的影响最大,随着工艺孔极角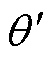 的增加,工艺孔对铁心性能的影响将减小。
的增加,工艺孔对铁心性能的影响将减小。
3)工艺孔对变压器铁心的影响,只发生在各自规定的工艺孔损伤区域内,且该影响区域的范围将随着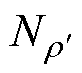 的增加而增加,在
的增加而增加,在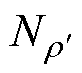
 1时,将随着
1时,将随着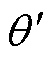 的增加而减小。
的增加而减小。
4)工艺孔会造成铁心的局部过热,距离工艺孔越近,温升越大,该温升影响只发生在规定的损伤区域内。
参考文献
[1] 宋悠全, 李高龙, 姚秋华, 等. 叠片工艺孔对变压器铁心性能影响分析[J]. 变压器, 2019, 56(8): 14-18.
Song Youquan, Li Gaolong, Yao Qiuhua, et al. Influence analysis of auxiliary hole on performance of transfomer core[J]. Transformer, 2019, 56(8): 14-18.
[2] 鲁殿国. 变压器铁心的制造对损耗的影响[J]. 变压器, 1980, 5(9): 25-27.
Lu Dianguo. Influence of transformer core manufa- cturing on loss[J]. Transformer, 1980, 5(9): 25-27.
[3] Gunes T, Derebasi N, Erdonmez C. Localized flux density distribution around a hole in non-oriented electrical steels[J]. IEEE Transactions on Magnetics, 2015, 51(1): 1-4.
[4] 赵小军, 刘小娜, 肖帆, 等. 基于Preisach模型的取向硅钢片直流偏磁磁滞及损耗特性模拟[J]. 电工技术学报, 2020, 35(9): 1849-1857.
Zhao Xiaojun, Liu Xiaona, Xiao Fan, et al. Hysteretic and loss modeling of silicon steel sheet under the DC biased magnetization based on the Preisach model[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1849-1857.
[5] 赵志刚, 马习纹, 姬俊安, 等. 谐波激励条件下铁心动态Energetic建模与验证[J]. 电工技术学报, 2020, 32(20): 4241-4250.
Zhao Zhigang, Ma Xiwen, Ji Jun'an, et al. Dynamic energetic modeling and verification of core under harmonic excitation[J]. Transactions of China Elec- trotechnical Society, 2020, 32(20): 4241-4250.
[6] 陈龙, 易琼洋, 贲彤, 等. 全局优化算法在Preisach磁滞模型参数辨识问题中的应用与性能对比[J]. 电工技术学报, 2021, 36(12): 2585-2593, 2606.
Chen Long, Yi Qiongyang, Ben Tong, et al. Appli- cation and performance comparison of global optimi- zation algorithms in the parameter identification problems of the Preisach hysteresis model[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(12): 2585-2593, 2606.
[7] 迟青光, 张艳丽, 陈吉超, 等. 非晶合金铁心损耗与磁致伸缩特性测量与模拟[J]. 电工技术学报, 2021, 36(18): 3876-3883.
Chi Qingguang, Zhang Yanli, Chen Jichao, et al. Measurement and modeling of loss and mag- netostrictive properties for the amorphous alloy core[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3876-3883.
[8] 赵志刚, 徐曼, 胡鑫剑. 基于改进损耗分离模型的铁磁材料损耗特性研究[J]. 电工技术学报, 2021, 36(13): 2782-2790.
Zhao Zhigang, Xu Man, Hu Xinjian. Research on magnetic losses characteristics of ferromagnetic materials based on improvement loss separation model[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2782-2790.
[9] Bertotti G. General properties of power losses in soft ferromagnetic materials[J]. IEEE Transactions on Magnetics, 1988, 24(1): 621-630.
[10] 刘刚, 孙立鹏, 王雪刚, 等. 正弦及谐波激励下的铁心损耗计算方法改进及仿真应用[J]. 电工技术学报, 2018, 33(21): 4909-4918.
Liu Gang, Sun Lipeng, Wang Xuegang, et al. Improvement of core loss calculation method and simulation application under sinusoidal and harmonic excitations[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4909-4918.
[11] Steinmetz C. On the law of hysteresis[J]. Transactions of the American Institute of Electrical Engineers, 1892, 9(1): 1-64.
[12] 康丽, 张艳丽, 唐伟, 等. 基于变系数Steinmetz公式的直流偏磁下铁心损耗计算[J]. 电工技术学报, 2019, 34(1): 1-6.
Kang Li, Zhang Yanli, Tang Wei, et al. Calculation of core loss under DC bias based on the variable coefficient Steinmetz formula[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 1-6.
[13] Krings A, Soulard J. Overview and comparison of iron loss models for electrical machines[J]. Journal of Electrical Engineering, 2010, 10(3): 162-169.
[14] Roshen W A. A practical, accurate and very general core loss model for nonsinusoidal waveforms[J]. IEEE Transactions on Power Electronics, 2007, 22(1): 30-40.
[15] 律方成,郭云翔. 非正弦激励下中频变压器铁损计算方法对比分析[J]. 高电压技术, 2017, 43(3): 808-813.
Lü Fangcheng, Guo Yunxiang. Comparative analysis of core loss calculation methods for medium fre- quency transformer under nonsinusoidal excitation[J]. High Voltage Engineering, 2017, 43(3): 808-813.
[16] Valkovic Z. Additional losses in three-phase trans- former cores[J]. Journal of Magnetism and Magnetic Materials, 1984, 41(1-3): 424-426.
[17] teNyenhuis G, Girgis R S, Mechler G F. Other factors contributing to the core loss performance of power and distribution transformers[J]. IEEE Transactions on Power Delivery, 2001, 16(4): 648-653.
[18] Erdonmez C, Derebasi N, Gunes T. Influence of hole geometry on magnetic flux density distribution in lasercut non-oriented electrical steels at power fre- quencies[J]. Journal of Superconductivity and Novel Magnetism, 2017, 30(11): 3309-3313.
[19] Derebasi N, Erdonmez C. Influence of hole size and cutting method on localised flux density distribution around a hole in non-oriented electrical steels[J]. Journal of Superconductivity and Novel Magnetism, 2017, 30(6): 1643-1648.
[20] Gunes T, Schäfer R, Derebasi N. Quantitative analysis of magnetic field distribution around circular non- magnetic region in grain-oriented Fe-3%Si steel[J]. IEEE Transactions on Magnetics, 2018, 54(2): 1-8.
[21] Li Yongjian, Cheng Hao, Lin Zhiwei, et al. A modi- fied characterization method for core loss calculation under rotational magnetization[J]. IEEE Transactions on Magnetics, 2021, 57(2): 1-6.
[22] Yang Ming, Li Yongjian, Yang Qingxin, et al. Design of novel high-frequency 2-D magnetic properties tester for nanocrystalline alloy[J]. IEEE Transactions on Applied Superconductivity, 2020, 30(4): 1-5.
[23] 张长庚, 杨庆新, 李永建. 电工软磁材料旋转磁滞损耗测量及建模[J]. 电工技术学报, 2017, 32(11): 208-216.
Zhang Changgeng, Yang Qingxin, Li Yongjian. Measurement and modeling of rotational hysteresis loss of electric soft magnetic material[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 208- 216.
[24] 鲁殿国. 电工钢片冲孔对铁心损耗的影响[J]. 变压器, 1991, 2(2): 34-37.
Lu Dianguo. Influence of punching of electrical steel sheet on core loss[J]. Transformer, 1991, 2(2): 34- 37.
[25] Li Yongjian, Fu Yu, Dou Yu, et al. Magnetic properties measurement and analysis of electrical steel sheet under cutting influence[J]. AIP Advances, 2021, 11(2): 025115.
Calculation and Analysis of Transformer Core Loss Due to Technological Hole
Abstract The loss and local temperature of the transformer core will be increased due to the presence of technological stacking holes, and even the performance of the transformer will be deteriorated. To study the influence of technological holes on transformer core loss and performance, the alternating magnetic properties of silicon steel materials are measured and the two-dimensional magnetic field of the holed core model is analyzed based on the Steinmetz formula. The theoretical calculation method of core loss caused by the hole with different shapes and sizes is proposed. Based on the finite element method, the two-dimensional transient magnetic field simulations of the grain-oriented steel sheets commonly used in transformer core are carried out, and the influence of technological holes with different types on transformer core loss is compared and analyzed. The magnetic properties testing system for silicon steel samples with the holes is established. The core loss and local temperature rise caused by the holes are quantitatively measured to verify the theoretical calculation method. The simulation and experimental results show that the calculation method of the core loss rise caused by the technological holes has high accuracy and engineering applicability.
keywords:Dry-type transformer, technological stacking hole, core loss
DOI: 10.19595/j.cnki.1000-6753.tces.210123
中图分类号:TM412
窦润田 男,1994年生,博士研究生,研究方向为无线电能传输技术、工程电磁场与磁技术、电磁场数值计算。E-mail: drt9428@163.com
张 献 男,1983年生,教授,博士生导师,研究方向为无线电能传输技术、工程电磁场与磁技术。E-mail: zhangxian@hebut.edu.cn(通信0000作者)
收稿日期 2021-01-22
改稿日期 2021-11-04
国家自然科学基金项目(51977147, 51777055)、优秀青年科学基金项目(52122701)和河北省自然科学基金创新群体项目(E2020202142)资助。
(编辑 崔文静)