0 引言
我国配电网遵循“闭环设计,开环运行”的原则[1]。当配电网线路长时间高负荷运行或设备计划检修时,需对负荷进行转供,目前广泛采用“先通后断”的方式,即合环转供电[2-3]。合环转供电可在供电不间断的情况下,实现负荷转移,满足电力用户对供电可靠性的要求[4-5]。但合环过程中可能会产生较大的稳态环流及冲击电流,导致继电保护误动、电力设备过载,造成合环失败[6]。因此,合环稳态电流与冲击电流计算是进行合环分析的基础,而配电网合环模型则是进行合环电流计算的关键。
现有的合环稳态电流分析模型基本围绕稳态环流计算展开。文献[7]在计算合环前联络开关两侧的电压和稳态环流时直接忽略负荷的作用,仅保留合环环路中的阻抗,形成简化的合环模型,算出的合环稳态电流可能会有较大误差。文献[8]将馈线上的负荷处理为一个集中负荷,接在馈线的首端或末端,形成四种合环分析模型,然后考虑合环电流最严重的情形,进行保守的合环风险判断。文献[9]考虑了三种特殊的负荷分布情形,即均匀分布、递增分布、递减分布,分析了不同负荷分布情形下的合环稳态电流。文献[8-9]分析了负荷分布对合环前联络开关两侧电压的影响,而在稳态环流的计算模型中,没有考虑负荷的分流作用。
对于合环冲击电流,文献[10]建立复频域下的戴维南等效电路,得到合环支路的电流表达式,再通过拉普拉斯反变换,得到时域下的全电流表达式。文献[11]建立时域下的戴维南等效电路,利用三要素公式得到合环支路以及非合环支路全电流表达式,进而求得各支路的冲击电流。文献[12]建立时域下戴维南等效电路的微分方程,得到最严重情况下的冲击电流,即用稳态电流幅值乘以冲击系数。文献[10-12]求解冲击电流时所用的分析模型都是忽略负荷阻抗的简化戴维南等效电路,而事实上冲击电流的衰减时间常数,不仅与合环环路的阻抗有关,还受负荷阻抗的影响。文献[13]提出了一种基于最佳频率法求解合环过程中衰减时间常数的方法,但所述求解方法比较繁琐,需对合环前后最佳频率下的网络进行潮流计算。
馈线负荷具有随机特性,随时间有较大的波动性[14-17],一般难以获取馈线每个负荷的实时数据,处理起来相对困难,故现有的合环模型基本都忽略负荷。随着实时同步测量技术的发展,通过微型同步相量测量装置(micro-Phasor Measurement Unit,μPMU)可实时获取配电网节点相量数据,μPMU 以其优异性能在配电网具有广阔的应用前景[18-21]。
本文考虑负荷对合环稳态与暂态过程的影响,基于馈线首末端少量μPMU 的实时量测信息对负荷进行等效处理,提出计及负荷等值阻抗的合环转供电分析模型。同时,基于最佳频率法[13],结合本文所提的合环分析模型,给出了求解合环冲击电流的一种有效方法,以提高冲击电流计算的准确性,避免繁琐的潮流计算过程,最后通过算例验证了本文所提模型及方法的有效性。
1 配电网合环模型
图1 是典型的合环示意图,图中S1、S2 分别为馈线a、b 的出线开关,S 为联络开关,Sai、Sbj(i,j=1,2,···,n)分别为馈线a、b 所带负荷。当母线1发生故障或检修时,就需要母线2 转带母线1 的负荷。具体操作流程是:先闭合联络开关,再断开S1,将馈线a 的负荷转移到馈线b,以此来保证不间断供电,这种闭合联络开关的方式就是合环转供电操作[22]。

图1 典型合环示意图
Fig.1 Schematic diagram of a typical loop closing
1.1 馈线负荷处理
配电网馈线负荷众多,往往成梳状结构[23]。随着经济的发展,城市配电网负荷快速增长[24]。当配电网馈线所带负荷较重时,由于负荷越大所对应的负荷阻抗越小,合环时其分流作用不可忽视,故建立合环电流分析模型时需将负荷阻抗考虑在内。但如果建立每个馈线负荷的负荷模型,则工作量很大,不利于合环电流的分析计算。采用等效负荷模型[25]可以将一段馈线之间的所有负荷等效为一个负荷,能在简化计算的同时反映原有的负荷特性,提高合环模型的准确度。
图2 是一段简单梳状馈线示意图,UA、UB 分别为馈线首末端节点A、B 的电压,θA、θB 为两个电压的相角,PA+jQA、PB+jQB 分别为馈线首末端的功率,Pi+jQi 为节点i 处的负荷功率,Lij 为节点i 和节点j 之间的线路长度,馈线AB 的总长为L,馈线单位长度(km)的阻抗z=r+jx。

图2 简单梳状馈线示意图
Fig.2 Schematic diagram of simple comb feeder
图 3 是经过负荷等效后的示意图,其中PK+jQK 为等效负荷节点K 的功率,IK∠θIK 为流过等效负荷的电流相量,IA∠θIA 为节点A 流向节点K 的电流相量,IB∠θIB 为节点K 流向节点B 的电流相量,L1、L2 分别为等效负荷节点距离节点A、B 的长度。

图3 馈线AB 的等效负荷
Fig.3 Equivalent load of feeder AB
负荷等效过程实际上是根据节点A、B 的电压相量和功率推导出等效负荷的大小和位置。随着μPMU 在配电网的发展,实时获取配电网节点电压相量成为可能,而要实现馈线AB 的负荷等效,仅需在节点A、B 两处配置μPMU 即可。
负荷等效的原则是:由节点A 电压降落公式得到的等效负荷节点电压UK和由节点B 电压降落公式得到的等效负荷节点电压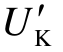 相等。其中
相等。其中

这里可以通过迭代法求出L1 和L2 的值,给定一个误差函数![]() 和迭代步长ΔL,通过不断修正L1 的长度可以使得误差函数满足给定精度ε,从而确定等效负荷的位置K,计算流程如图4 所示。
和迭代步长ΔL,通过不断修正L1 的长度可以使得误差函数满足给定精度ε,从而确定等效负荷的位置K,计算流程如图4 所示。

图4 求解L1、L2 的流程
Fig.4 Flow chart for solving L1 and L2
由图3 可得

式中,![]() 分别为节点A、B 功率的共轭值;
分别为节点A、B 功率的共轭值;![]()
![]() 分别为节点A、B 电压相量的共轭值;
分别为节点A、B 电压相量的共轭值;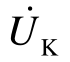 为等效负荷节点K 的电压。
为等效负荷节点K 的电压。
可以求出等效负荷功率SK,即
式中, 为等效负荷电流相量的共轭值。
为等效负荷电流相量的共轭值。
以上是梳状馈线的等效负荷求解过程。如果馈线AB 间带有分支馈线,相当于在分支节点处接入一个大小与分支馈线首端功率相等的负荷,同样可以根据梳状馈线的方法进行负荷等效。
负荷等效过程是在保证节点A、B 的电压和功率不变的前提下进行的,所以等效负荷在节点A、B 产生的效果与实际负荷分布产生的效果是等效的,不影响合环电流的计算。等效负荷的大小和位置可以反映馈线中负荷的实际分布情况,如果等效负荷较大且靠近源端,则该段馈线负荷较重且分布偏向源端;反之,馈线负荷较轻且分布偏向末端。当所分析的配电网是负荷密集的大型城市配电网时,负荷对合环的影响不能忽视,等效负荷就比较适用。
1.2 计及负荷等值阻抗的合环模型
在求得等效负荷参数后,由功率公式可得到等效负荷的阻抗ZK=RK+jXK,即

也可直接根据欧姆定律求得,即

该负荷等值阻抗是基于实时量测信息等效,能反映馈线实时负荷分布情况,由此得到馈线AB 的等效电路,如图5 所示。图5 中,R1+jX1 为馈线L1段的阻抗,R2+jX2 为馈线L2 段的阻抗。

图5 馈线AB 的等效电路
Fig.5 Equivalent circuit of feeder AB
基于上述方法,将馈线上的负荷处理为一个等效负荷,并用其等值阻抗代替,将10kV 以上的电源和阻抗折算到10kV 侧,得到计及负荷等值阻抗的合环模型如图6 所示。

图6 计及负荷等值阻抗的合环模型
Fig.6 Loop closing model considering load equivalent impedance
图6 中, 、
、 为10kV 以上电压源折算到10kV 侧的电压,
为10kV 以上电压源折算到10kV 侧的电压, 、
、 为10kV 母线电压,
为10kV 母线电压, 、
、 为联络开关S 两侧电压。Za0为10kV 母线以上等效到10kV 侧的阻抗,Zka 为a 侧等效负荷所对应的阻抗,Zal1 为母线1 其他馈线总负荷的等值阻抗,Zal2为a 侧馈线末端负荷 San的等值阻抗,Z a1为a 侧馈线L1 段的阻抗,Za2为a 侧馈线L2 段的阻抗;b侧的相关阻抗参数与a 侧类似。
为联络开关S 两侧电压。Za0为10kV 母线以上等效到10kV 侧的阻抗,Zka 为a 侧等效负荷所对应的阻抗,Zal1 为母线1 其他馈线总负荷的等值阻抗,Zal2为a 侧馈线末端负荷 San的等值阻抗,Z a1为a 侧馈线L1 段的阻抗,Za2为a 侧馈线L2 段的阻抗;b侧的相关阻抗参数与a 侧类似。
2 合环稳态电流分析
2.1 稳态环流计算
根据图6 中的合环模型,可以求出其ab 端口的戴维南等效电路,如图7 所示。

图7 戴维南等效电路
Fig.7 Thevenin equivalent circuit
图7 中,![]() 为合环前联络开关两侧相电压
为合环前联络开关两侧相电压![]() 之差,即
之差,即
等值阻抗Zeq 的计算需要将负荷等值阻抗计算在内,具体计算公式为

式中,Zeqa 为联络开关a 侧等值阻抗;Zeqb 为联络开关b 侧等值阻抗。当联络开关S 闭合且达到稳态时,可求出稳态环流 ,即
,即

2.2 稳态馈线电流计算
在联络开关闭合且到达稳态后,流过联络开关的电流 保持恒定。根据替代定理,支路ab 可以等效为一个电流相量为
保持恒定。根据替代定理,支路ab 可以等效为一个电流相量为 的电流源,合环后的稳态等效电路如图8 所示。
的电流源,合环后的稳态等效电路如图8 所示。
图8 中,合环后流过馈线开关的稳态电流  和
和 可通过叠加原理来求解。将合环后的网络分解为两个网络,如图9 所示。其中
可通过叠加原理来求解。将合环后的网络分解为两个网络,如图9 所示。其中 、
、 为图9a 中流过两侧馈线开关的电流,
为图9a 中流过两侧馈线开关的电流, 、
、 为图9b 中流过两侧馈线开关的电流。
为图9b 中流过两侧馈线开关的电流。

图8 合环后稳态等效电路
Fig.8 Steady-state equivalent circuit after closing loop

图9 利用叠加原理求解合环后馈线电流
Fig.9 Using superposition principle to solve the feeder current after closing loop
![]() 为合环前馈线电流
为合环前馈线电流![]() 与合环后稳态环流
与合环后稳态环流![]() 的叠加,即
的叠加,即

式中, 、
、 可以由μPMU 测量得到;
可以由μPMU 测量得到;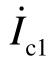 、
、 可以由图9b 求得,即
可以由图9b 求得,即

3 合环冲击电流分析
3.1 合环支路冲击电流计算
求解合环过程中的冲击电流,需要对图7 中戴维南等效电路进行暂态分析,将![]() 写成Emsin(ω t+α)的形式,将Zeq写成Req+jωLeq的形式,列写微分方程为
写成Emsin(ω t+α)的形式,将Zeq写成Req+jωLeq的形式,列写微分方程为

式中,Em、ω、α 分别为戴维南等效电压源的幅值、角频率和初相角;Req、Leq 分别为戴维南等效电阻和电感;ic 为合环支路ab 的全电流。假设在t=0 时刻合上联络开关,求解式(13)中的周期分量与非周期分量,相加可得ic 为
式中,ip、iap 分别为ic 的周期分量和非周期分量;Ic为周期分量有效值;φ 为戴维南等效电路的阻抗角;C 为非周期分量初始值;Ta 为衰减时间常数。![]() (ω t+α -φ)对应的相量就是式(10)中求出的
(ω t+α -φ)对应的相量就是式(10)中求出的 ,由换路定则可知
,由换路定则可知![]() 。
。
对于衰减时间常数Ta 的计算,现有文献的方法大都是在工频下进行求解[10-12],即先求出合环点处的戴维南等值阻抗Zeq=Req+jωLeq(ω 为工频下的角频率),则Ta=Leq/Req,该方法多适用于各支路R/X相差不大的网络,且对于网状电力网络的计算精度不是很高。
最佳频率法能在各支路R/X 相差较大的情况下仍保持Ta 有较高精确度,在网状电力网络几种求解Ta 的方法中作为推荐方法[26],当要处理的网络是大型城市电网时,使用最佳频率法能有更高的精确性。最佳频率法求解Ta 的基本思路是:对于合环后某个时刻,取一个特定的频率,即最佳频率fc,将合环网络中所有额定频率fn 下的阻抗转换为fc 下的阻抗,求出最佳频率下的戴维南等值阻抗Zeq(fc)=Req(fc)+jXeq(fc),则衰减时间常数Ta 为

求解冲击电流时,对于50Hz 的电网,最佳频率fc 通常取20Hz[26]。本文求解Ta 的方法是先对负荷进行等效处理,得到等效负荷参数后换算成相应的等值阻抗,然后求解Ta,具体求解步骤如下:
(1)按前述方法进行负荷处理,得到计及负荷等值阻抗的合环模型,如图6 所示。
(2)将图6 中所有额定频率下的阻抗转换成最佳频率下的阻抗。
(3)利用式(9)计算最佳频率下的戴维南等值阻抗Zeq(fc)。
(4)根据式(15)计算衰减时间常数Ta。
求解合环电流最大瞬时值 icmax,只需调用Matlab 中的max 函数,即可快速求出式(14)中的最大值。对应于50Hz 的频率,周期为0.02s,实际合环操作中,控制具体的合闸时刻较为困难,而不同的合闸时刻对应不同的非周期分量初值C,所以关注最严重情况下的合环电流最大值,即合环冲击电流。通过对合环过程的暂态分析[27],如果假定t=0时刻是最严重的合闸时刻,则有α -φ=-π/2,由此得出最严重情况下合环支路ab 的全电流表达式为
利用max 函数求得式(16)的最大值与最大值出现的精确时刻,该最大值即为支路ab 的合环冲击电流icim。
假定上述求得的最大值时刻为tc,则支路ab 合环电流最大有效值计算公式为
3.2 馈线冲击电流计算
对于流过馈线开关的冲击电流,应用叠加原理求解。将ic1 的全电流与合环前馈线a 的全电流相加,即可得到合环后馈线a 的全电流ia 表达式;将合环前馈线b 的全电流减去ic2 的全电流,即可得到合环后馈线b 的全电流ib 表达式。假设在t=0 时刻合上联络开关,有

式中,Ia0、θa 分别为合环前馈线a 电流的有效值和初相角;Ib0、θb 分别为合环前馈线b 电流的有效值和初相角;Ic1、θc1 分别为 分布到馈线a 首端电流
分布到馈线a 首端电流 的有效值和初相角;Ic2、θc2 分别为
的有效值和初相角;Ic2、θc2 分别为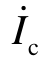 分布到馈线b 首端的电流 I˙c2的有效值和初相角;C1、C2 分别为ia、ib 非周期分量初始值,
分布到馈线b 首端的电流 I˙c2的有效值和初相角;C1、C2 分别为ia、ib 非周期分量初始值,![]() ,
,![]() 。式(18)中前两项之和对应的相量实际上就是合环后馈线a 的电流相量
。式(18)中前两项之和对应的相量实际上就是合环后馈线a 的电流相量 。式(19)中前两项之和对应的相量为合环后馈线b 的电流相量
。式(19)中前两项之和对应的相量为合环后馈线b 的电流相量 。
。
假定t=0 时刻是最严重的合闸时刻,考虑最严重情况下的馈线合环冲击电流。显然,当合环支路中流过最严重情况下的环流ic 时,即式(16)中的表达式,有最严重的馈线合环冲击电流。此时,式(18)中相量 最严重情况下初相角
最严重情况下初相角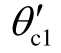 应取-π/2,
应取-π/2,![]() 。合环前馈线a 电流相量最严重情况下的初相角
。合环前馈线a 电流相量最严重情况下的初相角![]() ,则可得馈线a 最严重情况下的全电流表达式为
,则可得馈线a 最严重情况下的全电流表达式为

同理,可求出馈线b 最严重情况下的全电流为

调用Matlab 里的max 函数,可以求出式(20)和式(21)t=0 时刻后的最大绝对值(馈线b 绝对值最大时ib 为负值),即最严重情况下馈线a、b 的合环冲击电流。这里如果直接用稳态电流幅值乘冲击系数来求解最严重情况下馈线a 的合环冲击电流可能会产生较大误差,因为式(20)中非周期分量初始值可能与馈线a 合环后稳态电流幅值相差较大,馈线b 也是如此。
将式(20)中的前两项相加得到
式中,Ia 为馈线a 合环后稳态电流有效值;θk 为式(20)中前两项相加后电流的初相角,当θa-θc1 较大时,θk 会偏离-π/2 较大角度,如图10 所示,此时不满足合环电流最大瞬时值发生在t=0.01s 左右的条件。

图10 式(20)与式(22)中的电流相量图
Fig.10 The current phasor diagram in equations(20) and (22)
通过max 函数找出式(22)最大值出现的精确时刻,设最大值时刻为ta,则馈线a 合环电流最大有效值计算公式为

同理,馈线b 合环电流最大有效值为
式中,tb 为馈线b 电流出现最大负值的时刻;Ib 为合环后馈线b 稳态电流有效值。通常,合环后一侧馈线电流会增大,而另一侧减小,但当环流很大时,可能会造成一侧潮流反向,导致两侧电流都增大。若馈线b 合环后稳态电流小于合环前稳态电流,可不计算馈线b 的冲击电流与合环电流最大有效值。
4 算例验证
以图11 中某具体合环网络为例,进行合环电流分析,并与PSCAD 的仿真结果进行对比。网络参数如下:T1、L11、T3 折算到 10kV 侧的阻抗为(0.023 2+j0.453 7)Ω,T2、L12、T4 折算到10kV 侧的阻抗为(0.023 2+j0.376 7)Ω,图11 中的馈线均采用YJV22 型电缆,阻抗为(0.097 8+j0.091 1)Ω/km,每段馈线的长度已标注在图11 中,负荷的分布情况如图11 所示,功率单位为MV·A,母线上所接的功率为其他馈线的功率之和。合环前母线1 的线电压相量为10.60∠-30.34° kV,母线2 的线电压相量为10.46∠-35.87° kV。

图11 某具体的合环网络
Fig.11 A specific loop closing network
在进行PSCAD 建模时,负荷用相应的负荷阻抗表示。在本算例中,仿真时长设置为2s,通过对合环暂态过程的分析,当合环支路ab 的周期电流分量取幅值时,为最严重合闸时刻,其中一个最严重合闸时刻为0.998 2s,控制联络开关在0.998 2s 闭合。进行合环电流计算,首先,对两侧馈线的负荷进行等效处理,按照图4 所示的流程分别计算出两侧馈线L1和L2的值,其中,a 侧馈线L1初值取2km,b 侧馈线L1 初值取3.5km,并计算出两侧馈线的等效负荷功率。根据程序运行结果和计算结果,将两侧馈线的等效负荷参数记录在表1 中。
表1 两侧馈线的等效负荷参数
Tab.1 Equivalent load parameters of feeders on both sides

然后利用本文所提的合环模型进行合环电流的计算,并和其他方法对比。合环稳态电流计算值与仿真实测值的对比见表2,其中均匀分布模型、递增分布模型、递减分布模型均为考虑负荷阻抗时的计算结果。
表2 合环稳态电流的计算结果及对比
Tab.2 Calculation results and comparison of loop closing steady-state current

为了比较使用最佳频率法求解的冲击电流值与现有文献中采用工频求解衰减时间常数所得冲击电流值的精确性,在各种不同负荷处理形式下,分别利用现有文献中工频求解衰减时间常数的方法和最佳频率法求解冲击电流,并将计算结果分别记录在表3 和表4 中。这里计算的合环冲击电流与合环电流最大有效值均是最严重情况下的值。在本算例中,由于馈线b 合环后的稳态电流减小,故无需对馈线b 进行冲击电流计算。
表3 工频下合环冲击电流计算结果及对比
Tab.3 Calculation results and comparison of loop closing surge current at power frequency

表4 最佳频率下合环冲击电流计算结果及对比
Tab.4 Calculation results and comparison of loop closing surge current at the optimal frequency

(续)

由表2~表4 的数据分析可得出如下结论:
(1)各方法计算出来的稳态电流以及冲击电流值,基本上为负误差,这在实际运用中需要加以注意,为保证安全合环,可以将计算结果乘以一个稍大于1 的安全系数来避免出现负误差。对于利用本文模型与方法的计算结果而言,稳态电流以及冲击电流icim、iaim 可以乘以1.005 来避免出现负误差,而合环电流最大有效值Icim、Iaim 的计算结果,可以乘以1.05 来避免出现负误差。
(2)由表3 和表4 的误差对比可知,对于同一负荷处理形式而言,与现有文献中工频求解衰减时间常数得出的冲击电流值相比,最佳频率法求解的冲击电流误差更小(忽略负荷阻抗时,两者计算结果相同),采用基于本文合环模型的最佳频率法求解冲击电流,与仿真值最接近,验证了本文最佳频率法求解冲击电流方法的有效性。
(3)由表2 和表4 的误差数据可知,采用本文的合环模型及计算方法,稳态电流及冲击电流icim、iaim 的误差绝对值在0.3%以内,合环电流最大有效值Icim、Iaim 的误差绝对值在3%以内;忽略负荷阻抗的稳态电流及冲击电流icim、iaim 的误差绝对值多在2%以上,最高超过4%,合环电流最大有效值Icim、Iaim 的误差绝对值最大接近5%;其他考虑负荷分布模型的稳态电流及冲击电流icim、iaim 的误差绝对值多在1%~2%之间,合环电流最大有效值Icim、Iaim 的误差绝对值多在3%~4%之间。验证了本文所提合环模型的有效性。
5 结论
针对现有配电网合环模型在负荷处理上存在的不足,本文考虑了馈线负荷对合环稳态与暂态过程的影响,基于馈线首末端少量μPMU 的实时量测信息,利用等效负荷模型将馈线上的负荷等效为一个集中负荷,再用等效负荷相应的等值阻抗代替,提出了计及负荷等值阻抗的配电网合环分析模型。在该模型的基础上,进行合环稳态电流及冲击电流的计算。在稳态电流的求解过程中,对叠加定理的应用原理进行了详细分析。对于合环冲击电流,重点研究了最严重合闸时刻下的计算方法,同时,根据本文的合环模型,提出了一种基于最佳频率法求解冲击电流的有效方法,可以提高冲击电流计算的准确性,且不需要进行复杂的潮流计算过程。算例分析结果表明,采用本文合环模型及方法计算合环电流准确性较高,验证了本文所提模型及计算方法的有效性。
新型电力系统背景下,随着分布式电源、电动汽车等大量接入配电网,需要进一步研究考虑分布式电源出力不确定性以及电动汽车充电随机性的配电网合环分析模型。
[1]刘健,孙泉,张小庆,等.配电网合环分析与合环条件判断[J].电力系统自动化,2014,38(11):130-135.
Liu Jian,Sun Quan,Zhang Xiaoqing,et al.Analysis on and criteria for loop closing operation for distribution grids[J].Automation of Electric Power Systems,2014,38(11):130-135.
[2]周念成,兰雪珂,莫复雪,等.计及线路接头温升约束的受端电网转供优化模型[J].电工技术学报,2021,36(15):3237-3249.
Zhou Niancheng,Lan Xueke,Mo Fuxue,et al.A power transfer optimization model of receiving-end power systems considering line joint temperature rise constraints[J].Transactions of China Electrotechnical Society,2021,36(15):3237-3249.
[3]肖白,赵龙安,张宇,等.城市中压配电网合环操作分析与决策[J].电力系统保护与控制,2014,42(16):133-138.
Xiao Bai,Zhao Longan,Zhang Yu,et al.Analysis and decision of loop closing operation in urban midvoltage distribution network[J].Power System Protection and Control,2014,42(16):133-138.
[4]吴振辉,彭晓涛,沈阳武,等.一种配电网环型供电模型及其合环运行方式的研究[J].中国电机工程学报,2013,33(10):57-63.
Wu Zhenhui,Peng Xiaotao,Shen Yangwu,et al.Study on a loop power supply model and its loop-close operation mode for distribution network[J].Proceedings of the CSEE,2013,33(10):57-63.
[5]章坚民,相炜,罗刚,等.配电网30°相角差线路不停电转供的解决方案及关键分析[J].电力系统自动化,2018,42(1):74-81.
Zhang Jianmin,Xiang Wei,Luo Gang,et al.Solution and its key issue analysis for load transfer without power interruption of distribution lines with 30° phase angle difference[J].Automation of Electric Power Systems,2018,42(1):74-81.
[6]周念成,谷飞强,雷超,等.考虑合环电流约束的主动配电网转供优化模型[J].电工技术学报,2020,35(15):3281-3291.
Zhou Niancheng,Gu Feiqiang,Lei Chao,et al.A Power transfer optimization model of active distribution networks in consideration of loop closing current constraints[J].Transactions of China Electrotechnical Society,2020,35(15):3281-3291.
[7]付轲,蔡泽祥,邱建,等.10kV 电网电磁合环操作安全性评估方法[J].电力系统及其自动化学报,2010,22(4):71-76.
Fu Ke,Cai Zexiang,Qiu Jian,et al.Safety assessment methods of loop closing operation in 10 kV distribution network[J].Proceedings of the CSUEPSA,2010,22(4):71-76.
[8]李晓明.配电网络合环模型与算法研究[D].天津:天津大学,2007.
[9]张荣安,彭显刚,翁奕珊,等.考虑馈线负荷分布的10kV 配电线路合环电流计算[J].广东电力,2014,27(7):111-115.
Zhang Rongan,Peng Xiangang,Weng Yishan,et al.Calculation on loop current of 10 kV distribution line considering feeder load distribution[J].Guangdong Electric Power,2014,27(7):111-115.
[10]陈霄,王磊,李扬.配电网络合环冲击电流的分析[J].电力自动化设备,2005,25(4):40-42.
Chen Xiao,Wang Lei,Li Yang.Analysis of surge current due to closing loop in distribution grid[J].Electric Power Automation Equipment,2005,25(4):40-42.
[11]吴艳娟,王皓月,杨理.配电网合环冲击电流精确算法[J].电力系统及其自动化学报,2020,32(4):123-129.
Wu Yanjuan,Wang Haoyue,Yang Li.Accurate algorithm for closing-loop surge current in distribution network[J].Proceedings of the CSUEPSA,2020,32(4):123-129.
[12]葛少云,李晓明.基于戴维南等值的配电网合环冲击电流计算[J].电力系统及其自动化学报,2007,19(6):124-127.
Ge Shaoyun,Li Xiaoming.Study on surge current due to closing loop in distribution network based on Thevenin's equivalent[J].Proceedings of the CSUEPSA,2007,19(6):124-127.
[13]甘国晓,王主丁,李瑞,等.配电网合环冲击电流计算方法及其简化计算公式[J].电力系统自动化,2014,38(20):115-120.
Gan Guoxiao,Wang Zhuding,Li Rui,et al.Methods and simplified formulas for calculating surge currents from loop closing in distribution network[J].Automation of Electric Power Systems,2014,38(20):115-120.
[14]臧天磊,何正友,叶德意,等.计及负荷变化的配电网故障恢复区间数灰色关联决策[J].电力系统保护与控制,2013,41(3):38-43.
Zang Tianlei,He Zhengyou,Ye Deyi,et al.Distribution network service restoration based on interval number grey relation decision-making considering load change[J].Power System Protection and Control,2013,41(3):38-43.
[15]张帅,杨晶显,刘继春,等.基于多尺度时序建模与估计的电力负荷数据恢复[J].电工技术学报,2020,35(13):2736-2746.
Zhang Shuai,Yang Jingxian,Liu Jichun,et al.Power load recovery based on multi-scale time-series modeling and estimation[J].Transactions of China Electrotechnical Society,2020,35(13):2736-2746.
[16]雷怡琴,孙兆龙,叶志浩,等.电力系统负荷非侵入式监测方法研究[J].电工技术学报,2021,36(11):2288-2297.
Lei Yiqin,Sun Zhaolong,Ye Zhihao,et al.Research on non-invasive load monitoring method in power system[J].Transactions of China Electrotechnical Society,2021,36(11):2288-2297.
[17]Giacomuzzi S,Langwasser M,De Carne G,et al.Smart transformer-based medium voltage grid support by means of active power control[J].CES Transactions on Electrical Machines and Systems,2020,4(4):285-294.
[18]Cui Mingjian,Wang Jianhui,Florita A R,et al.Generalized graph Laplacian based anomaly detection for spatiotemporal MicroPMU data[J].IEEE Transactions on Power Systems,2019,34(5):3960-3963.
[19]邢晓东,石访,张恒旭,等.基于同步相量的有源配电网自适应故障区段定位方法[J].电工技术学报,2020,35(23):4920-4930.
Xing Xiaodong,Shi Fang,Zhang Hengxu,et al.Adaptive section location method for active distribution network based on synchronized phasor measurement[J].Transactions of China Electrotechnical Society,2020,35(23):4920-4930.
[20]张健磊,高湛军,陈明,等.考虑复故障的有源配电网故障定位方法[J].电工技术学报,2021,36(11):2265-2276.
Zhang Jianlei,Gao Zhanjun,Chen Ming,et al.Fault location method for active distribution networks considering combination faults[J].Transactions of China Electrotechnical Society,2021,36(11):2265-2276.
[21]刘安迪,李妍,谢伟,等.基于多源数据多时间断面的配电网线路参数估计方法[J].电力系统自动化,2021,45(2):46-54.
Liu Andi,Li Yan,Xie Wei,et al.Estimation method of line parameters in distribution network based on multi-source data and multi-time sections[J].Automation of Electric Power Systems,2021,45(2):46-54.
[22]邹俊雄.20kV 配电网闭环运行特性优化与保护控制策略研究[D].广州:华南理工大学,2016.
[23]叶清华,唐国庆,王磊,等.配电网合环操作环流分析系统的开发和应用[J].电力系统自动化,2002,26(22):66-69.
Ye Qinghua,Tang Guoqing,Wang Lei,et al.Development and application of the analysis system for closed loop operation of distribution network[J].Automation of Electric Power Systems,2002,26(22):66-69.
[24]Lin Zhe,Hu Zechun,Song Yonghua.Distribution network expansion planning considering N-1 criterion[J].IEEE Transactions on Power Systems,2019,34(3):2476-2478.
[25]刘健,毕鹏翔,董海鹏.复杂配电网简化分析与优化[M].北京:中国电力出版社,2002.
[26]Short-circuit currents in three-phase a.c.systems-Part 0:Calculation of currents:IEC 60909-0 [S].2001.
[27]何仰赞,温增银.电力系统分析[M].武汉:华中科技大学出版社,2002.