考虑气动系统的高速受电弓分层控制
杨 鹏1 张 静2 金 伟1 刘志刚1
(1. 西南交通大学电气工程学院 成都 611756 2. 西南交通大学机械工程学院 成都 610031)
摘要 针对气动系统动态特性影响受电弓主动控制精度的难题,提出一种计及响应时间延迟的分层控制策略。上层控制器采用混合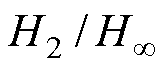 鲁棒控制策略。根据设定的受电弓运行状态的3个性能指标,构建多目标状态反馈控制律。通过求解线性矩阵不等式,得出主动控制力;下层控制器基于内模控制(IMC)理论,采用遗传算法,建立气动系统的一阶等效简化模型,设计仅与单一参数相关的内模-比例积分微分(PID)控制器。加快对上层控制器输出控制值的跟踪速率。通过列车不同运行速度下的仿真计算,验证了分层控制器的有效性和鲁棒性。仿真结果表明,下层控制器能够有效减少响应时间,明显改善气动系统的响应延迟。相比于传统单层控制,分层控制的接触力标准差下降率提高10%左右,有效抑制了弓网耦合振动,提高了高速弓网受流质量。
鲁棒控制策略。根据设定的受电弓运行状态的3个性能指标,构建多目标状态反馈控制律。通过求解线性矩阵不等式,得出主动控制力;下层控制器基于内模控制(IMC)理论,采用遗传算法,建立气动系统的一阶等效简化模型,设计仅与单一参数相关的内模-比例积分微分(PID)控制器。加快对上层控制器输出控制值的跟踪速率。通过列车不同运行速度下的仿真计算,验证了分层控制器的有效性和鲁棒性。仿真结果表明,下层控制器能够有效减少响应时间,明显改善气动系统的响应延迟。相比于传统单层控制,分层控制的接触力标准差下降率提高10%左右,有效抑制了弓网耦合振动,提高了高速弓网受流质量。
关键词:气动系统 响应时间 分层控制 混合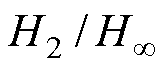 鲁棒控制 内模-比例积分微分(PID)控制
鲁棒控制 内模-比例积分微分(PID)控制
0 引言
随着高速列车运行速度的不断提升,弓网的垂向振动、纵向冲击、横向摆动及耦合振动等问题越发显著[1]。列车的动力来源于弓网滑动接触过程传递的电能,稳定的弓网受流是保证高速列车正常运行的重要条件,弓网系统如图1所示。
弓网系统的接触波动不仅增加弓网间接触磨损、离线燃弧等问题[2],也使得列车运行时的受流质量急剧恶化[3-5]。因此,有效降低弓网间的耦合振动,提高弓网受流质量,是当下亟须解决的问题之一。
目前,弓网受流质量的优劣主要采用弓网接触力波动程度表征[6]。为降低接触力波动,文献[7-9]提出对受电弓采取参数优化的方法,但能降低的接触力标准差极为有限。另外,文献[10-11]开展接触网吊弦、悬挂方式等结构优化方面的研究,建议对既有线路改造,但是改造工程耗资巨大。受电弓主动控制能够解决优化设计存在的局限性问题,文献[12-13]以接触力的偏差和控制器的能量约束等信息,建立多个控制目标,分别采用模糊控制和PID控制策略,并通过弓网模型验证了控制器的有效性。但是,上述研究皆仅选取弓网接触力作为反馈信号,且接触力信号获取过程中常存在过多噪声干扰。文献[14]提出了一种阻抗控制器,选取受电弓框架的位移量为反馈信息,并与PID控制策略比较。在抑制接触力波动的问题上,所提方法的控制效果更加明显。文献[15]以受电弓各结构的位移和速度为反馈控制量,设计了一种基于Backstepping方法的控制器,减小接触力实际值与参考值之间的偏差。文献[16]针对模型的不确定性和难以准确建模等问题,提出了一种模糊自适应终端滑模控制方法。在模型建模存在误差的情况下,仍能够保证良好的控制效果。文献[17]基于扩展状态变量下的受电弓非线性模型,采用微分几何理论进行线性化处理,并增设干扰观测器来提高控制系统的精确度。但在高速运行下,部分反馈量因传感器灵敏度难以达到控制器的要求而造成数据缺失,影响到控制系统的有效性。因此,文献[18]在采用二阶滑模控制策略的基础上,采用代数可观测性理论,根据受电弓上、下框架的位移测量值估计接触力,避免了直接对接触力信号的采集。文献[19]考虑到电磁干扰下的数据丢失问题,利用鲁棒卡尔曼滤波器对受电弓状态进行估计。但是,控制过程中出现时滞情况也会对控制效果造成一定影响。在此基础上,文献[20]采用最优控制策略,解决作动器输入延迟和接触力时变问题,该方法不仅能够调整状态和控制指标的相对权重,而且构建的稳定性判据兼顾系统稳定性。
综上所述,现有高速受电弓控制策略方面的研究主要是根据受电弓控制器计算主动控制力大小,并直接施加于受电弓模型。虽然部分文献中考虑了控制器造成的通信时滞和作动器输入时滞问题,但并未涉及高速受电弓气动系统动态特性的影响。在受电弓实际控制过程中,气动系统达到期望压强的响应时间远大于通信时滞和输入时滞此类纯时滞情况,较长的响应时间将会严重影响控制器精度。因此,在研究受电弓主动控制策略时,考虑气动系统的动态特性,以减少响应时间的影响具有重要理论意义和工程实用价值。
本文为有效降低气动系统响应时滞的影响,获得更高的弓网接触力波动控制精度,提出了一种高速受电弓分层控制策略。在设计合适的受电弓主动控制算法的基础上,增设下层气动系统控制器。根据混合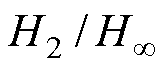 鲁棒控制理论和内模控制(Internal Model Control-PID, IMC-PID)理论,构造受电弓分层控制器。同时,考虑到列车运行时的关键影响因素,确定了3个性能指标,上层控制算法能够根据性能指标计算出减缓波动所需的控制抬升力。针对下层控制器构造等效内模模型时,采用遗传算法,完成等效模型参数寻优,以减小简化模型与气动系统模型之间的误差。最后,将分层控制器应用于非线性弓网模型上,针对不同运行时速工况,验证控制器的有效性。
鲁棒控制理论和内模控制(Internal Model Control-PID, IMC-PID)理论,构造受电弓分层控制器。同时,考虑到列车运行时的关键影响因素,确定了3个性能指标,上层控制算法能够根据性能指标计算出减缓波动所需的控制抬升力。针对下层控制器构造等效内模模型时,采用遗传算法,完成等效模型参数寻优,以减小简化模型与气动系统模型之间的误差。最后,将分层控制器应用于非线性弓网模型上,针对不同运行时速工况,验证控制器的有效性。
1 弓网及气压驱动系统模型
1.1 弓网系统模型
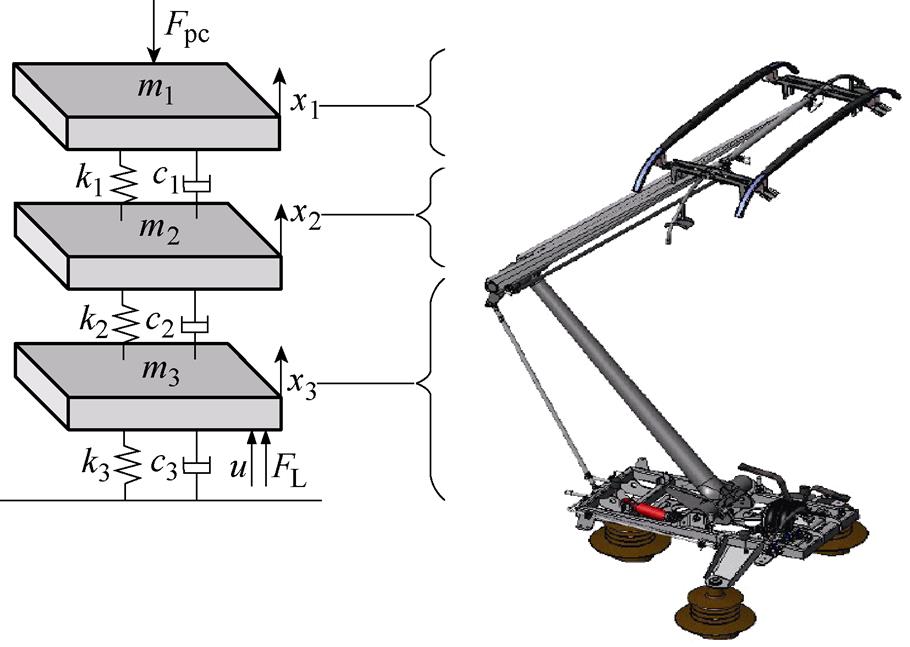
为更好表述受电弓的动态特性,在高速受电弓主动控制研究中,受电弓多是采用归算质量模 型[21]。本文选取受电弓三质量块模型,质量块之间通过等效弹簧刚度和阻尼建立连接关系。受电弓三质量块模型如图2所示。
受电弓三质量块的运动学方程为
式中,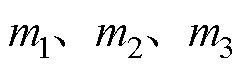 分别为受电弓弓头、上框架和下框架的等效质量;
分别为受电弓弓头、上框架和下框架的等效质量;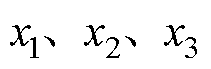 ,
,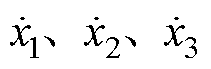 ,
,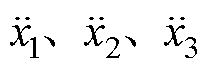 分别为受电弓弓头、上框架和下框架垂直方向上的位移、速度和加速度;
分别为受电弓弓头、上框架和下框架垂直方向上的位移、速度和加速度;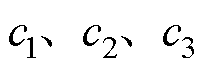 和
和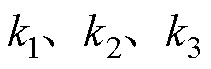 分别对应弓头与上框架之间、上下框架之间、下框架与底座之间的等效阻尼和等效刚度;
分别对应弓头与上框架之间、上下框架之间、下框架与底座之间的等效阻尼和等效刚度;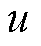 和
和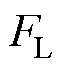 分别为垂直方向上的主动控制力和静态抬升力;
分别为垂直方向上的主动控制力和静态抬升力;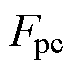 为垂直方向上的弓网接触力。
为垂直方向上的弓网接触力。
接触网结构较为复杂,包括接触线、承力索、定位器和吊线等装置。为建立更精确的模型,本文采用文献[22]中建立的接触网系统模型。使用有限元方法,完成接触网的建模。接触网有限元模型动力学方程为
式中,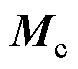 、
、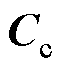 和
和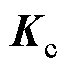 分别为接触网有限元各部分所组成的集中质量、等效刚度和等效阻尼矩阵;
分别为接触网有限元各部分所组成的集中质量、等效刚度和等效阻尼矩阵;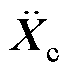 、
、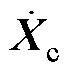 和
和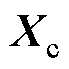 分别为接触网有限元划分节点加速度、速度和位移矩阵;
分别为接触网有限元划分节点加速度、速度和位移矩阵; 为接触网所受外力矩阵。
为接触网所受外力矩阵。
联合式(1)和式(2),取三质量块位移矩阵为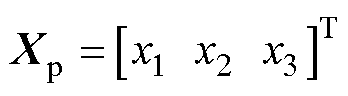 ,可建立弓网耦合方程,即
,可建立弓网耦合方程,即
其中

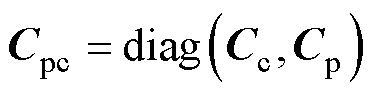
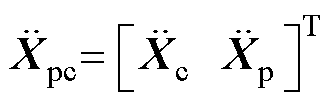
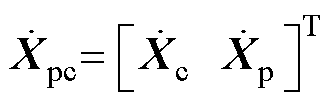
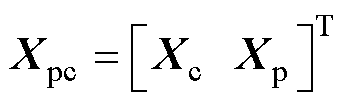
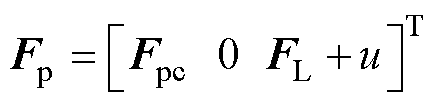
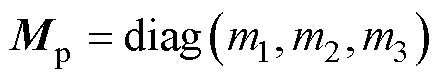
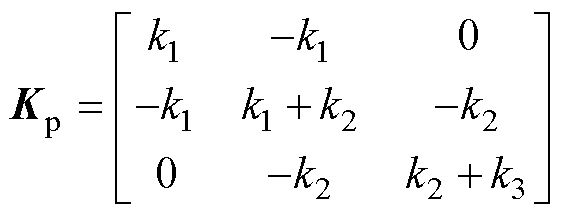
1.2 受电弓气动系统模型
在受电弓主动控制中,受电弓控制器的输出值以电信号传递给气动系统,受电弓气动系统原理如图3所示。
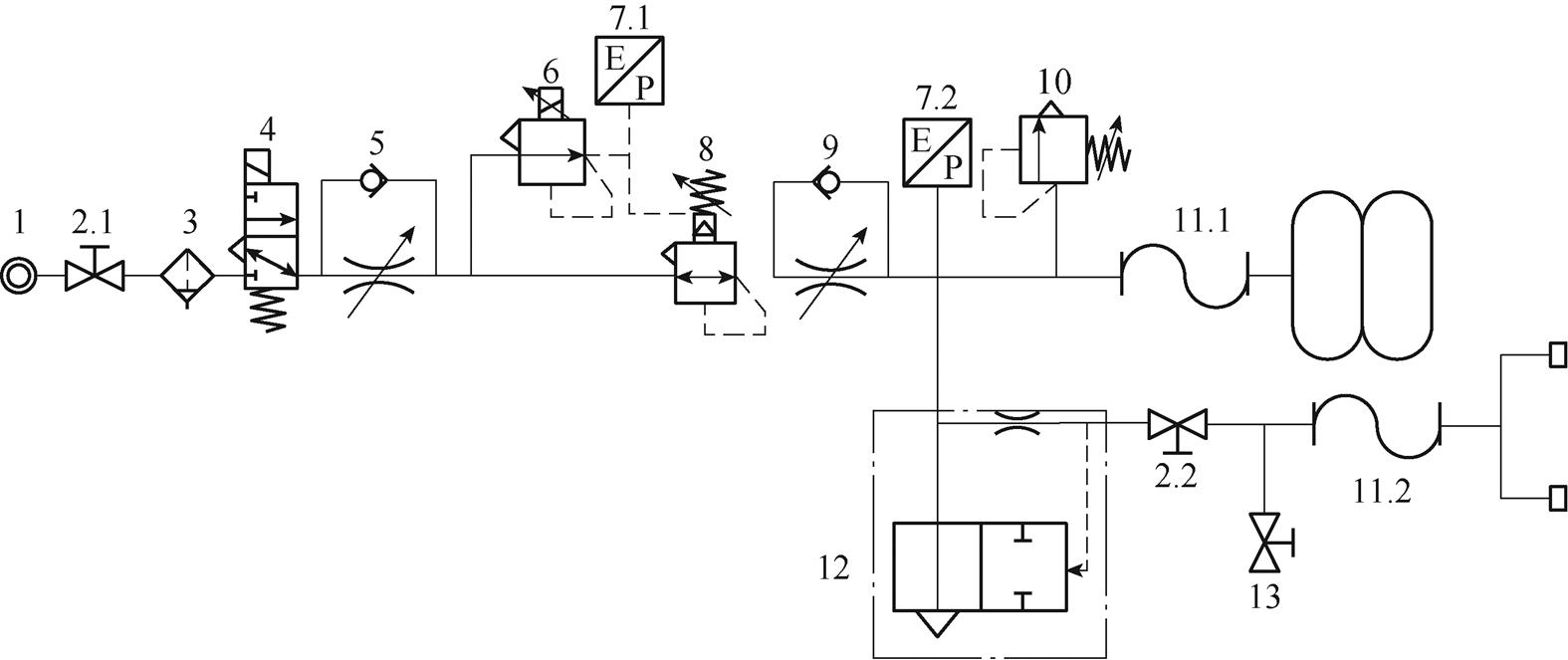
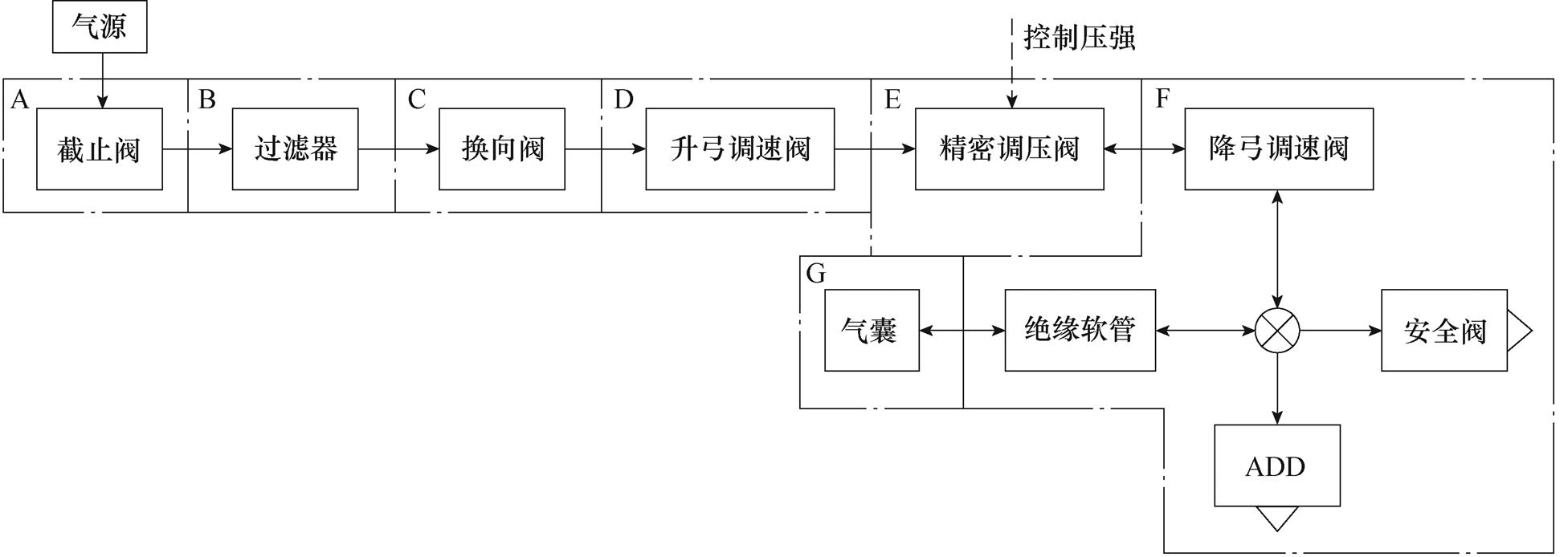
在气动系统工作时,两位三通电磁换向阀开启,使绝对压力为0.8MPa的气源装置向气动系统提供气压。当气体到达气控先导式精密调压阀后,根据控制器传递的控制信号,将气源压强转变为控制压强,并经过降弓调速阀、绝缘软管等输送至气囊内,完成气囊内部压力的调节,进而实现弓网接触力的控制。而对于较高的气压值,安全阀会根据设定值进行溢流动作,保护整个系统安全运作。同时,为减少气源的输出压力对气控先导式精密调压阀的冲击,所调压阀输入压力范围为0.005~0.8MPa。根据文献[23],假设气动系统内部恒温,根据气体流量和器件之间的压强差关系,建立气动系统的数学模型。针对各器件的功能,对整个系统进行虚拟容器划分,气动系统模型如图4所示。图中,ADD支路为受电弓气压驱动系统,为保证受电弓在特殊情况下能快速自动降落而设计的。电气比例阀根据控制回路产生的脉冲宽度调制(Pulse Width Modu- lation, PWM)电信号,由电磁阀控制产生控制压强。该过程对整个气动系统运行时的影响较小,可将电气比例阀视为理想元件,忽略控制器到气动系统之间信号转变过程造成的延迟影响。
1—气源 2—截止阀 3—过滤器 4—两位三通电磁换向阀 5—升弓调速阀 6—电气比例阀 7—压力传感器 8—气控先导式精密调压阀 9—降弓调速阀 10—安全阀 11—绝缘软管 12—快速排气阀 13—试验阀
Fig.3 Principle of pneumatic system of pantograph
2 受电弓分层
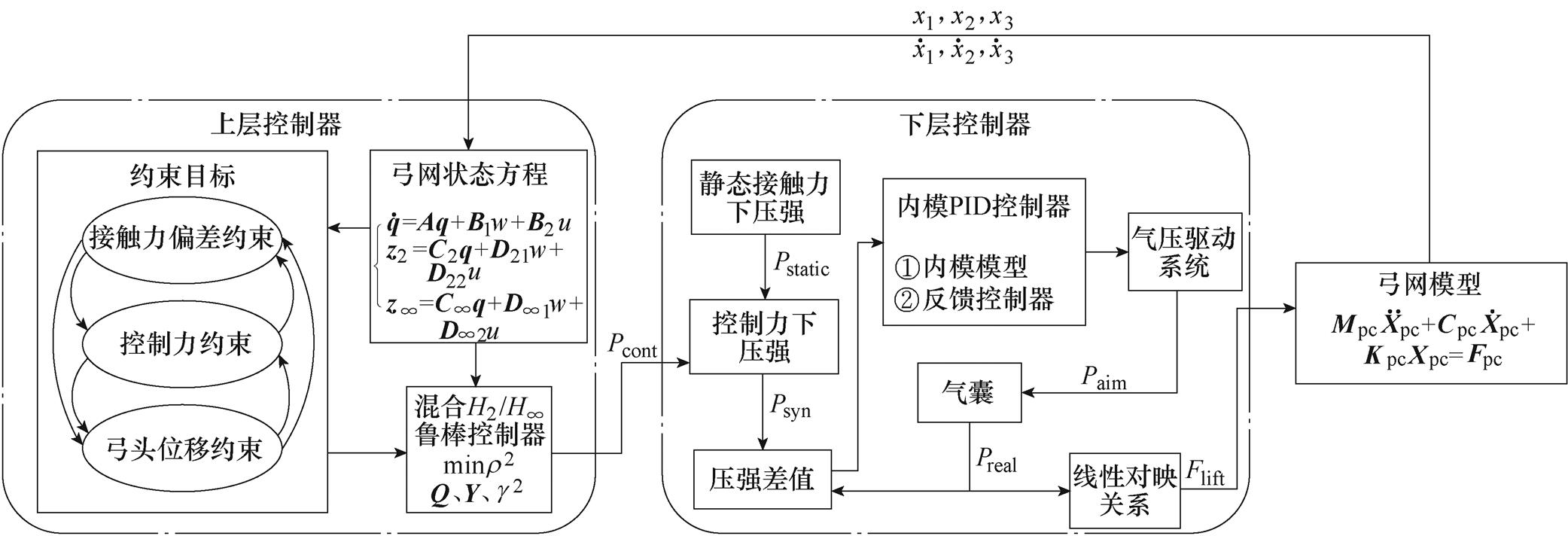
根据分层控制策略[24-25],本文将高速受电弓主动控制分为上层受电弓控制和下层气动系统响应控制两部分。上层控制器采用混合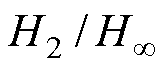 鲁棒控制方法,通过对弓网模型相关量的采集,计算出所需控制抬升力,并转换为相应压强值传输到气动系统。而基于IMC-PID控制策略的下层控制器根据气囊输出压强与控制压强之间的差值进行气动系统的响应时间调节,使输出压强能够有效跟踪上层控制器的控制目标。受电弓分层控制系统结构如图5所示。
鲁棒控制方法,通过对弓网模型相关量的采集,计算出所需控制抬升力,并转换为相应压强值传输到气动系统。而基于IMC-PID控制策略的下层控制器根据气囊输出压强与控制压强之间的差值进行气动系统的响应时间调节,使输出压强能够有效跟踪上层控制器的控制目标。受电弓分层控制系统结构如图5所示。
2.1 上层控制器设计
在设计上层控制器时,除了考虑弓网接触力波动外,还分析了主动控制力和弓头位移等因素的影响。因此,控制目标包含的具体性能指标选定为:
(1)弓网接触力的波动体现在接触力参考值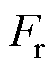 与实时接触力
与实时接触力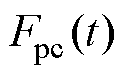 的差值上。为有效降低波动,
的差值上。为有效降低波动,
应尽可能减小两者之间的差值 ,即
,即
(2)在气动系统运行中,通过改变气囊内部的压强实现受电弓的控制。由于安全阀的存在,当气囊处的气压超过设定的最高值时,部分气压将从安全阀的排气口处溢出,使气动系统的输出压力保持在额定值以下。同时,气囊压力也不能过低,导致受电弓的抬升力不足。因此在设计上层控制器时需要限制主动控制力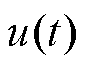 的输出大小,设输出控制力最值为
的输出大小,设输出控制力最值为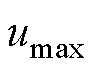 ,控制力比
,控制力比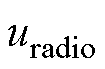 为
为
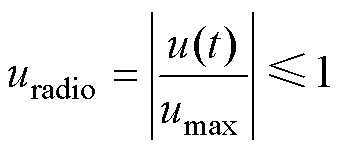 (5)
(5)
(3)弓网滑动接触过程中,弓头抬升量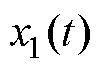 过大将会加快接触网的磨损程度,不利于接触网的正常工作。需要将其限定在一定范围内,设定抬升量最大值为
过大将会加快接触网的磨损程度,不利于接触网的正常工作。需要将其限定在一定范围内,设定抬升量最大值为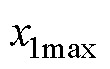 ,弓头抬升量比
,弓头抬升量比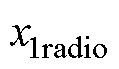 为
为
由于接触网有限元模型的复杂性,需要对模型进行简化,将接触网有限元模型等效为面向控制的静态刚度系数模型。目前,弓网间耦合关系主要通过罚函数关系建立[26],弓网之间的接触力为
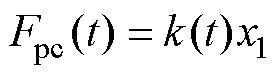 (7)
(7)
式中,x1为受电弓弓头的位移;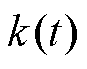 为接触网刚度系数。针对上述3个受电弓性能指标,为权衡各控制指标之间的关系,采用基于混合
为接触网刚度系数。针对上述3个受电弓性能指标,为权衡各控制指标之间的关系,采用基于混合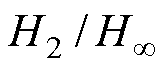 鲁棒策略的多目标控制算法,构建了合理的反馈控制率,完成上层控制器的设计。
鲁棒策略的多目标控制算法,构建了合理的反馈控制率,完成上层控制器的设计。
在设计控制器时,首先考虑降低弓网接触力波动的要求,实时接触力与接触力参考值的差值 是评价接触力波动控制效果的主要指标。同时,为了兼顾弓网系统实际情况和稳定性的要求,气压系统只能提供有限的主动力,其值应限制在一定范围内;而在弓网接触滑动过程中,弓头抬升量是影响弓网系统正常工作的主要因素,需要保证其在安全范围内。因此,控制器的设计原则为在弓头抬升量和控制器作动力约束输出指标不超过相应范围的条件下,最小化接触力差值输出性能指标。为保证在多个性能指标下得到合理的反馈控制率,将弓头抬升量和控制器作动力定义为
是评价接触力波动控制效果的主要指标。同时,为了兼顾弓网系统实际情况和稳定性的要求,气压系统只能提供有限的主动力,其值应限制在一定范围内;而在弓网接触滑动过程中,弓头抬升量是影响弓网系统正常工作的主要因素,需要保证其在安全范围内。因此,控制器的设计原则为在弓头抬升量和控制器作动力约束输出指标不超过相应范围的条件下,最小化接触力差值输出性能指标。为保证在多个性能指标下得到合理的反馈控制率,将弓头抬升量和控制器作动力定义为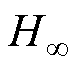 约束输出指标,在此条件下优化接触力差值
约束输出指标,在此条件下优化接触力差值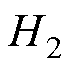 性能输出指标。综上,取
性能输出指标。综上,取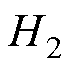 性能输出和
性能输出和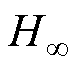 归一化约束输出分别为
归一化约束输出分别为
则弓网模型的状态空间方程可描述为状态变量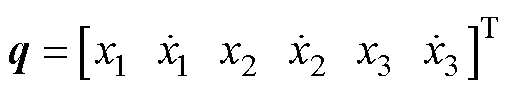 ,即
,即
 (9)
(9)
式中,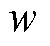 和
和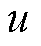 分别为外界扰动和主动控制力;
分别为外界扰动和主动控制力;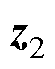 和
和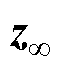 为控制输出目标,其余系数矩阵表达式为
为控制输出目标,其余系数矩阵表达式为
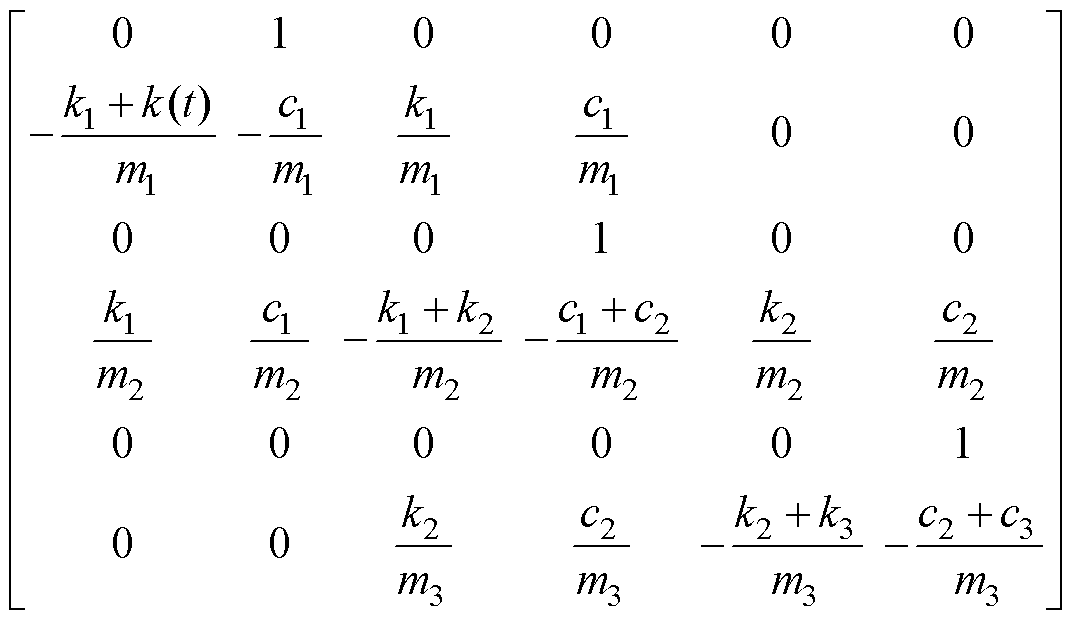

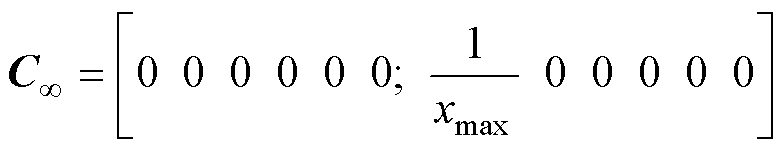
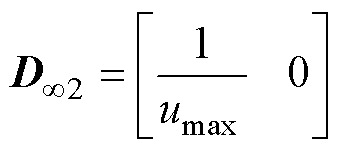
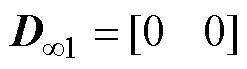
根据文献[27]的混合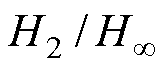 鲁棒多目标策略的状态反馈律为
鲁棒多目标策略的状态反馈律为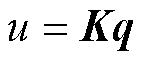 ,被控对象式(9)的状态反馈控制器设计如下。
,被控对象式(9)的状态反馈控制器设计如下。
(1)闭环系统内部稳定。
(2)闭环系统既要满足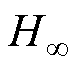 范数的约束要求,还要保证
范数的约束要求,还要保证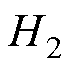 范数的性能指标达到最优化。
范数的性能指标达到最优化。
针对闭环系统的约束条件,控制器的矩阵不等式满足条件如下,其中“*”表示矩阵对称位置变量的转置。
(1)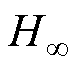 性能:对于参数
性能:对于参数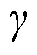 ,存在正定矩阵
,存在正定矩阵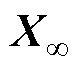 满足
满足
(2)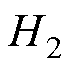 性能:对于参数
性能:对于参数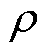 ,存在正定矩阵
,存在正定矩阵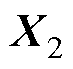 满足
满足
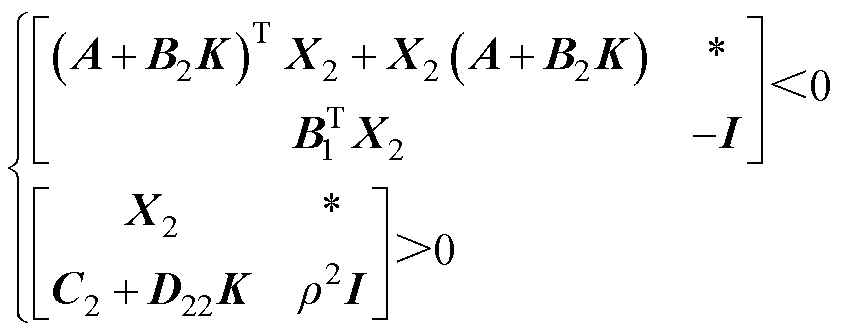 (11)
(11)
为解决混合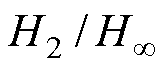 鲁棒的多目标控制问题,需要联合求解矩阵不等式(10)和式(11)。而采用线性矩阵不等式(Linear Matrix Inequality, LMI)方法,难以完成对非线性不等式(10)和式(11)的求解,且高速列车的控制器实时性要求较高。为提高控制器的计算速度且能满足控制器性能要求,将两个矩阵不等式中的Lyapunov矩阵设定为同一个矩阵,即
鲁棒的多目标控制问题,需要联合求解矩阵不等式(10)和式(11)。而采用线性矩阵不等式(Linear Matrix Inequality, LMI)方法,难以完成对非线性不等式(10)和式(11)的求解,且高速列车的控制器实时性要求较高。为提高控制器的计算速度且能满足控制器性能要求,将两个矩阵不等式中的Lyapunov矩阵设定为同一个矩阵,即
可将非线性矩阵不等式转变为求解线性凸约束问题,具体推导证明过程参考文献[28]。给参数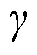 取值后,取
取值后,取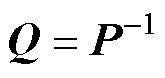 和
和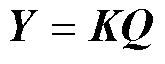 ,存在正定矩阵
,存在正定矩阵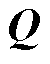 和向量
和向量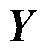 满足
满足
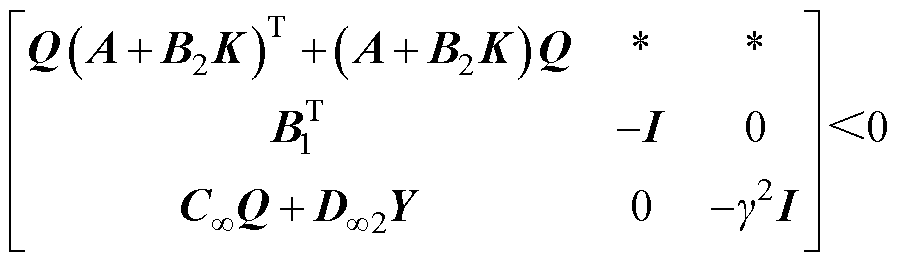 (13)
(13)
联立式(13)和式(14),当存在可行解时,可得增益矩阵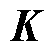 的最优解为
的最优解为
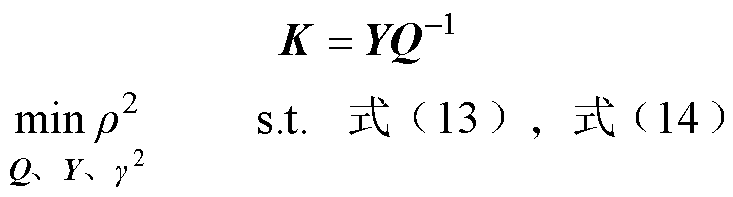 (15)
(15)
根据已构建的混合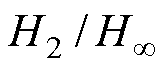 鲁棒多目标控制器的状态反馈律,可得受电弓的主动控制力为
鲁棒多目标控制器的状态反馈律,可得受电弓的主动控制力为
结合静态抬升力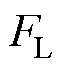 ,则上层控制器输出的控制抬升力表示为
,则上层控制器输出的控制抬升力表示为
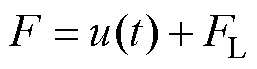 (17)
(17)
2.2 下层控制器设计
针对气动系统响应时间过长的问题,采用结构简单且适应性强的PID控制器。但考虑到PID控制器的整定参数过多,为保证良好的控制性能,需经过大量的调试,这一过程极大地增加了控制器设计的复杂程度。因此,本文将内模理论应用到PID控制器设计中[29],对气动系统采用IMC-PID控制策略。该方法将PID多参数调试难题简化为单一参数整定问题。通过对滤波常数的整定,完成PID参数的调节,从而实现响应时间的控制。内模控制结构及其等效形式如图6所示。
图6中,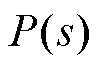 和
和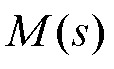 分别为被控对象(气动系统)及其内模模型,
分别为被控对象(气动系统)及其内模模型,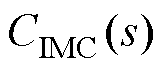 为内模控制器,
为内模控制器,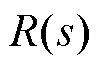 和
和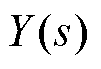 为整个气动控制系统的输入和输出,而点画线部分构成反馈控制器
为整个气动控制系统的输入和输出,而点画线部分构成反馈控制器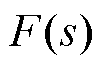 为
为
由于气压驱动系统的结构复杂,难以获取整个系统的内模模型传递函数。因此,在考虑到控制器通信过程的时滞时间基础上,将气动系统模型化简为一阶时滞模型[30]为
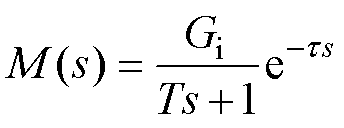 (19)
(19)
式中,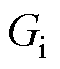 、
、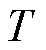 和
和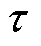 分别为增益值、响应时间常数和时滞时间。在设计内模控制器时,需对内模模型求逆,即
分别为增益值、响应时间常数和时滞时间。在设计内模控制器时,需对内模模型求逆,即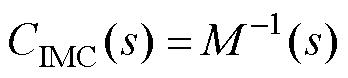 。但由于模型时滞项的存在而难以求解,故将简化后的内模模型分解为
。但由于模型时滞项的存在而难以求解,故将简化后的内模模型分解为
式中,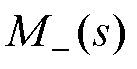 为模型的可逆部分;
为模型的可逆部分;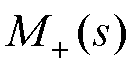 为包含模型的时滞项。模型分解能够解决存在时滞项而无法求逆的问题,但简化后的内模模型难以保证与实际系统之间完全重合,必然存在一定的模型误差。为防止对整个闭环系统造成不稳定的影响,通过在内模控制器上增设低通滤波器来增强系统的稳定性和鲁棒性。本文采用的低通滤波器为
为包含模型的时滞项。模型分解能够解决存在时滞项而无法求逆的问题,但简化后的内模模型难以保证与实际系统之间完全重合,必然存在一定的模型误差。为防止对整个闭环系统造成不稳定的影响,通过在内模控制器上增设低通滤波器来增强系统的稳定性和鲁棒性。本文采用的低通滤波器为
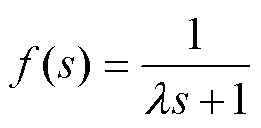 (21)
(21)
式中,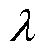 为滤波时间常数。故内模控制器可表示为
为滤波时间常数。故内模控制器可表示为
将引入低通滤波器后的内模控制器和简化的内模模型代入式(18),可得到系统的反馈控制器为
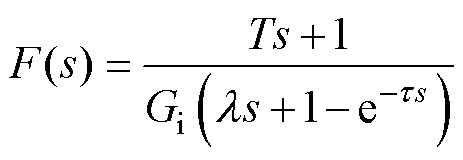 (23)
(23)
为方便控制器参数的整定,可将式(23)转换为
式中,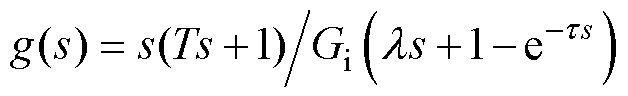 。
。
相比于响应时间,气压驱动系统的纯时滞时间较短。为保证气动系统的稳定性,在IMC-PID控制器中不考虑微分环节,故忽略二阶以上高阶项。将式(24)用麦克劳林公式展开,内模控制器转变为所需的PI控制器,具体表达式为
通过调节参数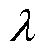 ,实现IMC-PID控制器的整定,而
,实现IMC-PID控制器的整定,而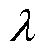 的取值大小与控制器的性能和稳定性相关联。
的取值大小与控制器的性能和稳定性相关联。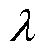 较小时,控制器的稳定性良好,但响应速度变慢;
较小时,控制器的稳定性良好,但响应速度变慢;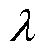 较大时,响应速度会有明显提升,但鲁棒性能有所降低,因此,应当合理选取
较大时,响应速度会有明显提升,但鲁棒性能有所降低,因此,应当合理选取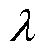 。
。
3 仿真分析
3.1 气动系统响应控制仿真
为验证下层控制器对缩短气动系统响应时间的效果,建立气动系统模型,参数见表1。
表1 气动系统元件参数
Tab.1 Parameters of pneumatic system components

参 数数 值 气源压强/MPa0.8 气路管道直径/mm9 调速阀中节流阀有效面积/mm28 调速阀中单向阀有效面积/mm212.3 调压阀主阀芯有效面积/mm210 快速排气阀有效面积/mm228 单位长绝缘软管有效面积/mm243 气囊有效截面积/mm234 640
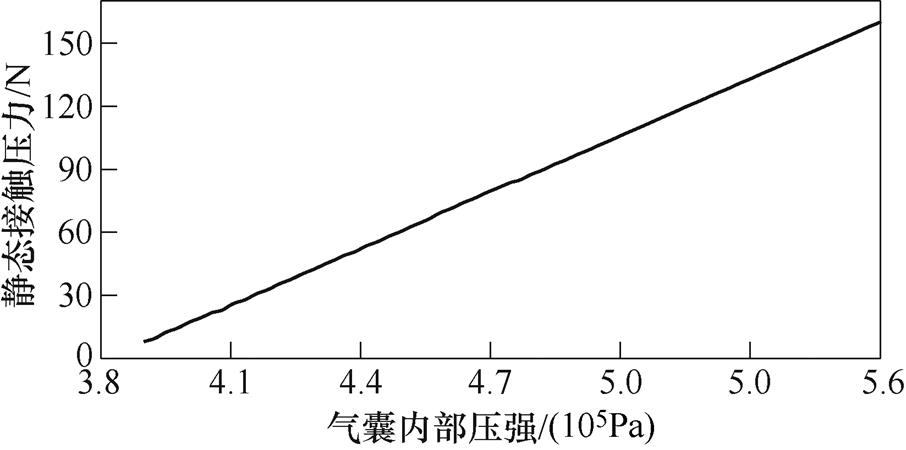
在安全阀设定的安全压力值下,通过对模型进行仿真,受电弓气囊压强与静态接触压力之间近似呈一定线性关系,其关系如图7所示。在文献[31]中通过对气压驱动系统的试验数据采集拟合,气囊压强对应静态接触压力间的大致线性关系进一步验证了仿真结论的可靠性。
而列车在未运行状态下,抬升力与接触压力互为相互作用力,故上层控制器计算的控制抬升力值可根据线性关系转换为相应压强值。对于输入输出信号皆为压强的气动系统,取增益值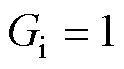 ;根据控制器通信过程存在的延时特性,取纯时滞时间
;根据控制器通信过程存在的延时特性,取纯时滞时间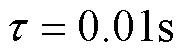 。为使简化模型能够与气压驱动系统模型尽可能重合,采用遗传算法寻优,获取响应时间常数
。为使简化模型能够与气压驱动系统模型尽可能重合,采用遗传算法寻优,获取响应时间常数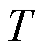 的值。经过20次迭代寻优后,得到响应时间常数最优值
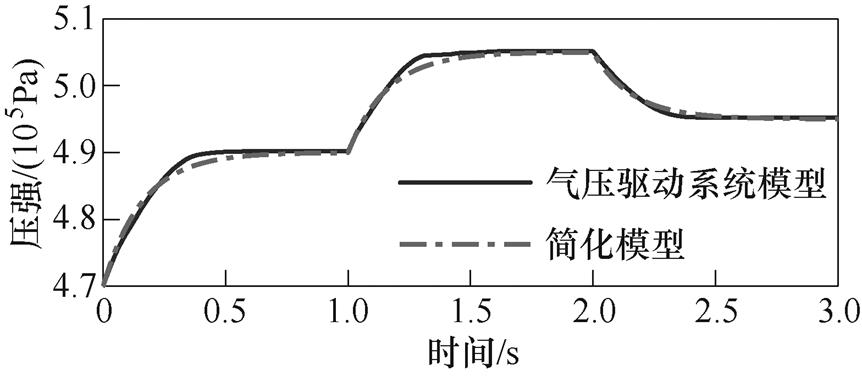
的值。经过20次迭代寻优后,得到响应时间常数最优值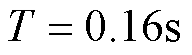 。故式(19)简化模型可表示为
。故式(19)简化模型可表示为
根据文献[32]可知,对于含有纯时滞的系统,滤波时间常数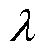 的取值可为时滞时间
的取值可为时滞时间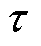 的倍数。在综合考虑控制器各指标性能的情况下,本文取控制参数值
的倍数。在综合考虑控制器各指标性能的情况下,本文取控制参数值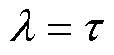 。结合式(25)可得参数值
。结合式(25)可得参数值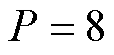 ,
,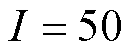 。采用相同阶跃信号,可得IMC-PID控制的输出曲线,如图9所示。
。采用相同阶跃信号,可得IMC-PID控制的输出曲线,如图9所示。
仿真结果表明,当控制信号改变时,相比于无控制状态下的输出曲线,采用IMC-PID控制的气动系统到达控制目标的响应时间明显缩短,显著加快了气动系统内部的响应速度,且调节过程中几乎无超调量产生,也不会对系统的稳定性造成过多的影响,有效改善了输出压强滞后问题。
3.2 弓网控制仿真分析
为了验证分层控制策略在受电弓主动控制中的有效性,与本文设计的混合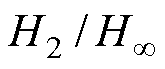 鲁棒多目标控制器在仅有受电弓控制下的单层控制效果对比。受电弓采用DSA380受电弓,接触网采用京津线的接触网模型,具体参数分别见表2和表3。
鲁棒多目标控制器在仅有受电弓控制下的单层控制效果对比。受电弓采用DSA380受电弓,接触网采用京津线的接触网模型,具体参数分别见表2和表3。
表2 DSA380受电弓质量块模型参数
Tab.2 DSA380 pantograph mass model parameters

参 数数 值 m1, m2, m3/kg7.12, 6, 5.8 c1, c2, c3/(N·s/m)0,0,70 k1, k2, k3/(N/m)9 430, 14 100, 0.1
表3 京津线接触网结构参数
Tab.3 Catenary structure parameters of Beijing-Tianjin line

参 数数 值 跨距/m48 结构高度/m1.6 承力索张力/kN21 接触线张力/kN27 承力索线密度/(kg/m)1.068 接触线线密度/(kg/m)1.083 预弛度(%)0.05 拉出值/m±0.2 吊弦间距/m5/9.5/9.5/9.5/9.5/5
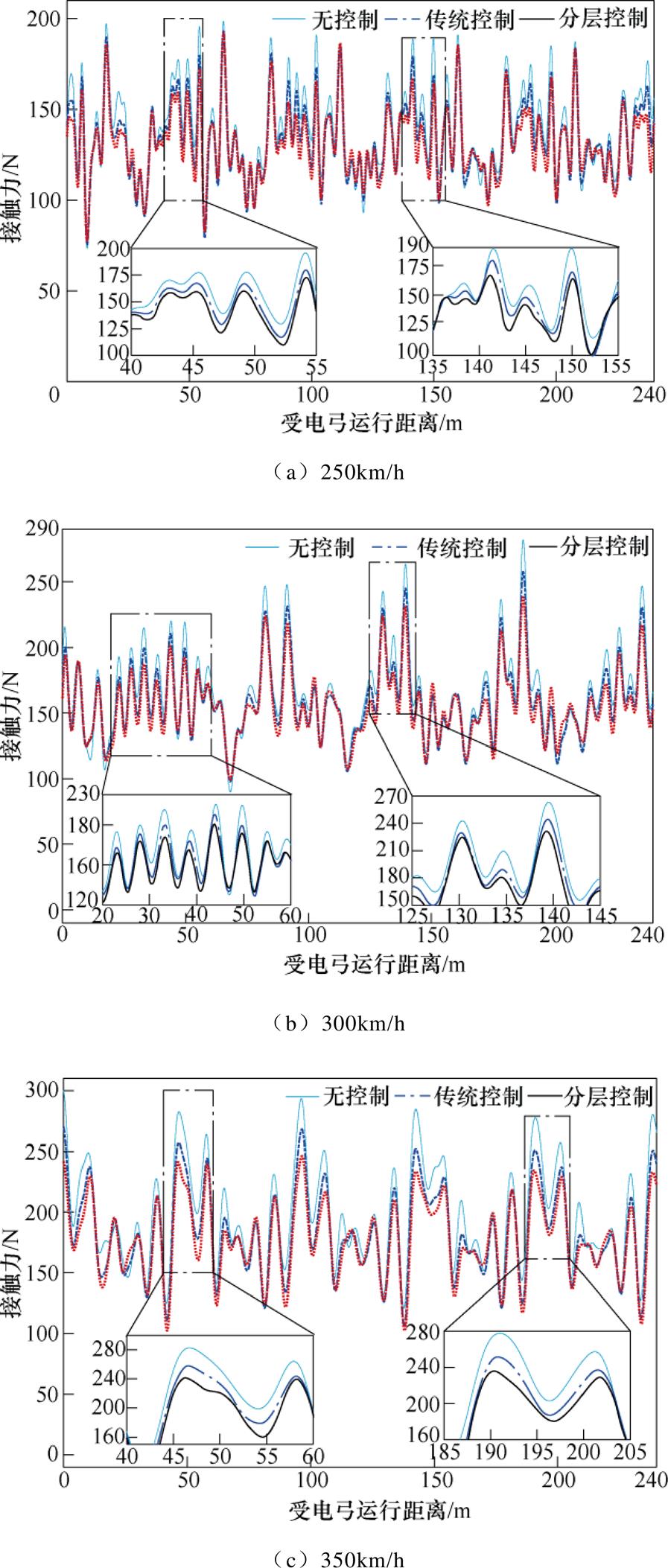
为验证受电弓主动控制器的普适性,分别在250km/h、300km/h和350km/h 3个运行工况下,对接触网5跨内的受电弓控制效果进行了仿真证明。比较无控制、传统单层控制策略和分层控制策略的控制效果,弓网接触力控制结果如图10所示。对于不同控制方法的弓网接触力标准差的计算值,具体结果见表4。
表4 不同控制策略的弓网接触压力标准差
Tab.4 Standard deviation of pantograph catenary contact pressure with different control strategies
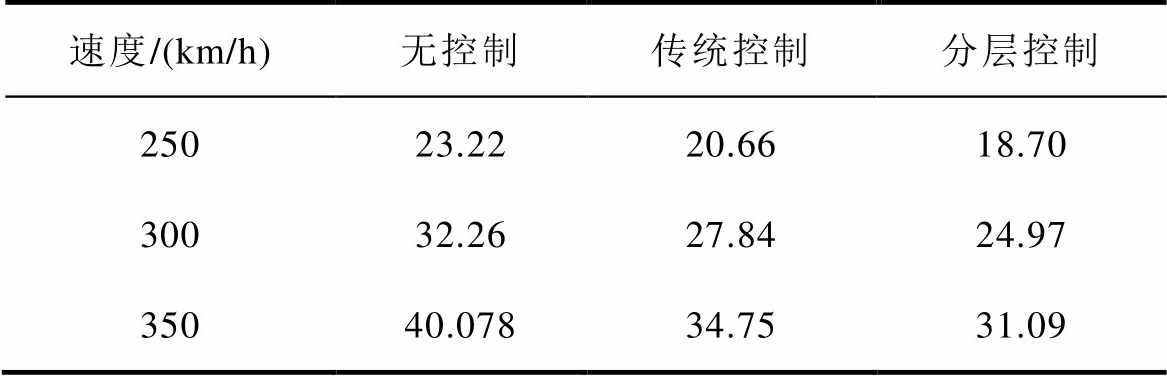
速度/(km/h)无控制传统控制分层控制 25023.2220.6618.70 30032.2627.8424.97 35040.07834.7531.09
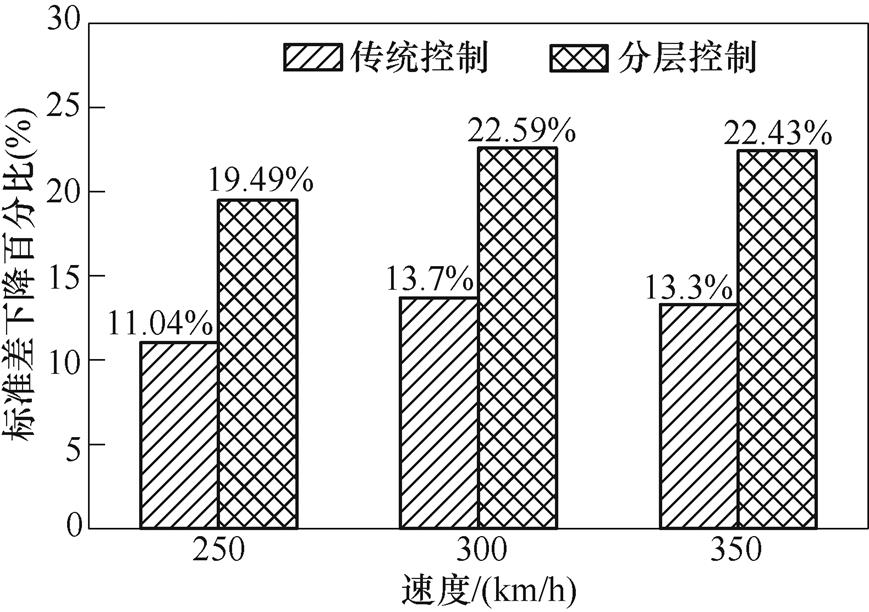
由图10可知,根据本文提出的控制策略所设计的传统控制器和分层控制器,都降低了弓网接触力的标准差。由表4可知,传统单层控制策略虽然能降低接触力波动,但控制效果并不明显,这是因为气动系统自身的响应时间过长,导致气囊压强变化难以跟踪单层控制器计算出的目标控制值。而在采用分层控制策略后,下层控制器的作用使响应时间明显减少,加快了气动系统的响应速度。图11为各速度的接触力标准差下降百分比。
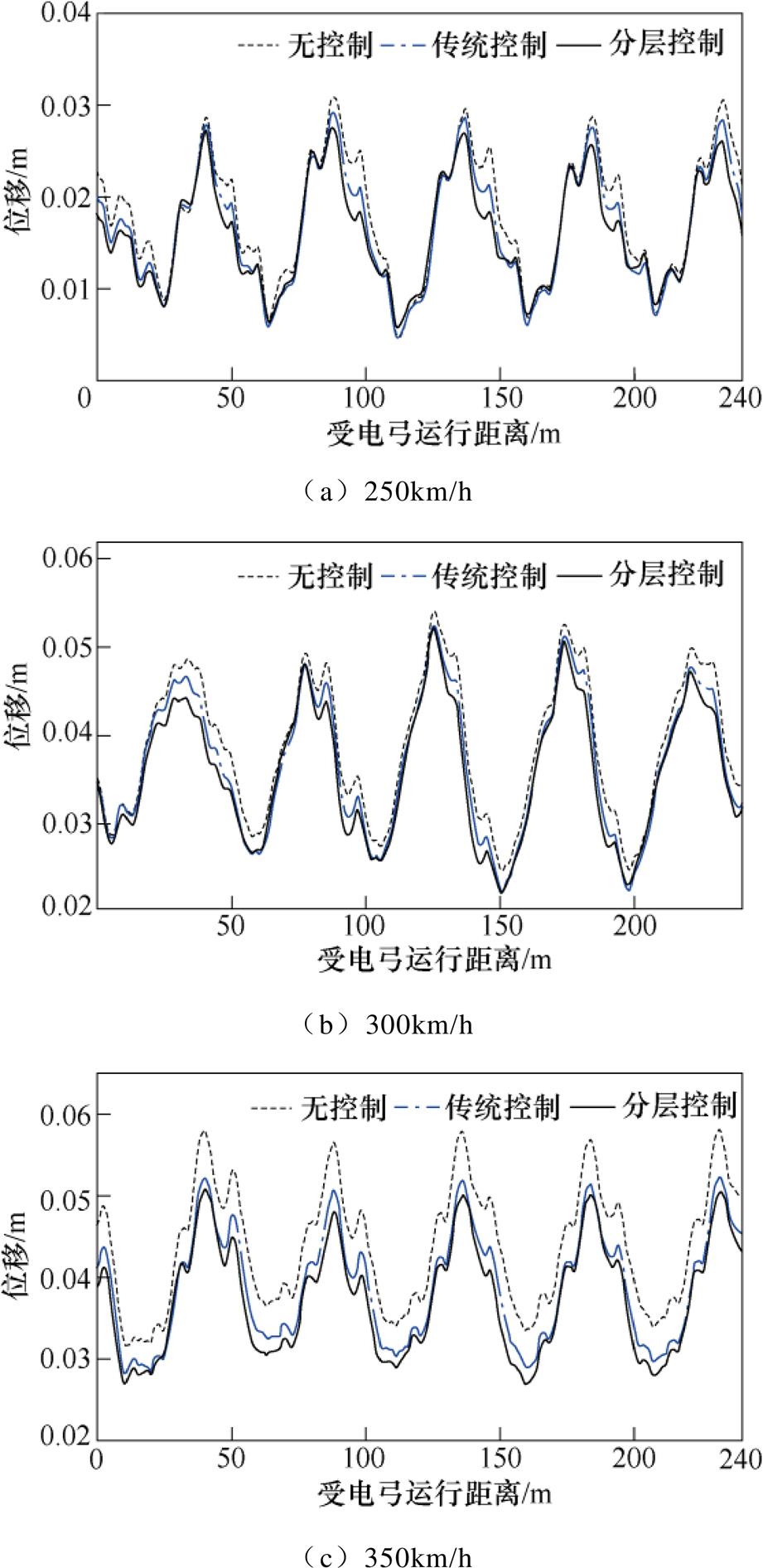
由图11可知,针对不同运行时速工况,在考虑了气动系统的动态特性影响后,相比传统单层控制的效果,受电弓分层控制的接触力标准差下降百分比提高10%左右,表明了分层控制方法在解决弓网耦合振动问题上具有明显优越性。针对弓网接触的弓头位移指标,具体仿真结果如图12所示。
两种控制策略对弓头位移均有一定程度减小。但分层控制下的控制量变化实时性更快,对弓头位移的约束效果优于传统控制策略。因此,弓头位移的仿真结果进一步证明了受电弓分层控制策略的有效性。
4 结论
本文针对受电弓气动系统中存在的响应时间较长的难题,在传统单层受电弓控制的基础上引入气动系统控制器,提出了一种基于分层结构的受电弓主动控制策略。在考虑气动系统动态响应影响的情况下,通过非线性弓网模型仿真计算,验证了分层控制策略降低接触力波动的有效性,可得到以下结论:
1)受电弓控制采用混合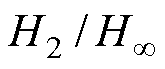 鲁棒控制策略,以求解线性矩阵不等式的形式,得到反馈控制参数的解。该策略克服了以往控制中仅以单一接触力优化为控制目标的缺陷,在考虑多目标约束的基础上,设计出状态反馈控制律。此策略不仅能改善接触力波动,还减小了弓头位移的振动幅度,从而降低滑板与接触线之间的磨损。
鲁棒控制策略,以求解线性矩阵不等式的形式,得到反馈控制参数的解。该策略克服了以往控制中仅以单一接触力优化为控制目标的缺陷,在考虑多目标约束的基础上,设计出状态反馈控制律。此策略不仅能改善接触力波动,还减小了弓头位移的振动幅度,从而降低滑板与接触线之间的磨损。
2)气动系统控制采用内模理论,根据简化后的气动系统模型,设计了内模控制器,并利用麦克劳林展开公式得到了仅与单一参数相关的PID控制器。在IMC-PID控制下,气动系统的响应时间明显缩短,大幅提升了对控制目标值的跟踪速率。
3)根据分层控制思想,引入混合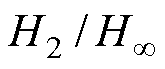 鲁棒控制和内模控制策略。与传统单层控制策略相比,分层控制策略不仅考虑了受电弓主动控制时的弓网接触力波动、主动控制力和弓头位移多个因素,并提高了控制器在响应时滞影响下的控制效果,进一步降低了弓网接触力的标准差。
鲁棒控制和内模控制策略。与传统单层控制策略相比,分层控制策略不仅考虑了受电弓主动控制时的弓网接触力波动、主动控制力和弓头位移多个因素,并提高了控制器在响应时滞影响下的控制效果,进一步降低了弓网接触力的标准差。
参考文献
[1] 张静, 刘志刚, 鲁小兵, 等. 高速弓网空气动力学研究进展[J]. 铁道学报, 2015, 37(1): 7-15.
Zhang Jing, Liu Zhigang, Lu Xiaobing, et al. Study on aerodynamics development of high-speed pantograph and catenary[J]. Journal of the China Railway Society, 2015, 37(1): 7-15.
[2] 陈忠华, 唐俊, 时光, 等. 弓网强电流滑动电接触摩擦振动分析与建模[J]. 电工技术学报, 2020, 35(18): 3869-3877.
Chen Zhonghua, Tang Jun, Shi Guang, et al. Analysis and modeling of high current sliding electrical contact friction dynamics in pantograph-catenary system[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3869-3877.
[3] Lee J H, Kim Y G, Paik J S, et al. Performance evaluation and design optimization using differential evolutionary algorithm of the pantograph for the high-speed train[J]. Journal of Mechanical Science and Technology, 2012, 26(10): 3253-3260.
[4] 刘方林. 电气化铁路动态弓网接触电阻研究[J]. 电气技术, 2018, 19(9): 69-72.
Liu Fanglin. Study on dynamic contact resistance between pantograph and catenary in electrified rail- way[J]. Electrical Engineering, 2018, 19(9): 69-72.
[5] 陈忠华, 吴迪, 回立川, 等. 波动载荷下弓网滑动电接触失效研究[J]. 电工技术学报, 2019, 34(21): 4492-4500.
Chen Zhonghua, Wu Di, Hui Lichuan, et al. Research on failure of pantograph-catenary sliding electrical contact under fluctuation load[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4492- 4500.
[6] Wang Hongrui, Liu Zhigang, Song Yang, et al. Dete- ction of contact wire irregularities using a quadratic time-frequency representation of the pantograph- catenary contact force[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 65(6): 1385- 1397.
[7] Kim J W, Yu S N. Design variable optimization for pantograph system of high-speed train using robust design technique[J]. International Journal of Precision Engineering and Manufacturing, 2013, 14(2): 267- 273.
[8] 周宁. 350km/h及以上弓网动态行为研究[D]. 成都: 西南交通大学, 2013.
[9] 吴孟臻, 刘洋, 许向红. 高速弓网系统动力学参数敏度分析及优化[J]. 力学学报, 2021, 53(1): 75-83.
Wu Mengzhen, Liu Yang, Xu Xianghong. Sensitivity analysis and optimization on parameters of high speed pantograph-catenary system[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(1): 75-83.
[10] 蒋先国, 古晓东, 邓洪, 等. 基于微动理论的整体吊弦损伤机理及优化研究[J]. 铁道学报, 2019, 41(6): 40-45.
Jiang Xianguo, Gu Xiaodong, Deng Hong, et al. Research on damage mechanism and optimization of integral dropper string based on fretting theory[J]. Journal of the China Railway Society, 2019, 41(6): 40-45.
[11] Zhang Weihua, Zhou Ning, Li Ruiping, et al. Panto- graph and catenary system with double pantographs for high-speed trains at 350 km/h or higher[J]. Journal of Modern Transportation, 2011, 19(1): 7-11.
[12] 时光, 刘健辰, 陈忠华, 等. 基于DE-EDA多目标优化的受电弓模糊控制[J]. 计算机工程与应用, 2016, 52(1): 229-232, 253.
Shi Guang, Liu Jianchen, Chen Zhonghua, et al. Control of pantograph based on DE-EDA multi- objective optimization[J]. Computer Engineering and Applications, 2016, 52(1): 229-232, 253.
[13] Cristina S R, Jimenez J O, Carnicero A. Active control strategy on a catenary-pantograph validated model[J]. Vehicle System Dynamics, 2013, 51(4): 554-569.
[14] Yoshitaka Y, Mitsuru I. Advanced active control of contact force between pantograph and catenary for high-speed trains[J]. Quarterly Report of RTRI, 2012, 53(1): 28-33.
[15] Zhu Bing, Ren Zhiling, Xie Wenjing, et al. Active nonlinear partial-state feedback control of contacting force for a pantograph-catenary system[J]. ISA Transa- ctions, 2019, 91(1): 78-89.
[16] 时光, 陈忠华, 郭凤仪, 等. 基于最优载荷的受电弓自适应终端滑模控制[J]. 电工技术学报, 2017, 32(4): 140-146, 153.
Shi Guang, Chen Zhonghua, Guo Fengyi, et al. Adaptive terminal sliding mode control of pantograph based on optimal load[J]. Transactions of China Elec- trotechnical Society, 2017, 32(4): 140-146, 153.
[17] 时光, 陈忠华, 郭凤仪, 等. 弓网接触力反馈线性化控制[J]. 控制理论与应用, 2016, 33(1): 85-91.
Shi Guang, Chen Zhonghua, Guo Fengyi, et al. Feedback linearization control of load between panto- graph and catenary[J]. Control Theory and Appli- cations, 2016, 33(1): 85-91.
[18] Pisano A, Usai E. Contact force estimation and regulation in active pantographs: an algebraic obser- vability approach[J]. Asian Journal of Control, 2011, 13(6): 761-772.
[19] 张静, 宋宝林, 谢松霖, 等. 基于状态估计的高速受电弓鲁棒预测控制[J]. 电工技术学报, 2021, 36(5): 1075-1083.
Zhang Jing, Song Baolin, Xie Songlin. Robust predictive control of high-speed pantograph based on state estimation[J]. Transactions of China Electro- technical Society, 2021, 36(5): 1075-1083.
[20] Lin Yuchen, Shieh N C, Liu V T. Optimal control for rail vehicle pantograph systems with actuator delays[J]. IET Control Theory and Applications, 2015, 9(13): 1917-1926.
[21] Lu Xiaobing, Liu Zhigang, Song Yang, et al. Estimator- based multi-objective robust control strategy for an active pantograph in high-speed railways[J]. Pro- ceedings of the Institution of Mechanical Engineers Part F-Journal of Rail and Rapid Transit, 2018, 232(4): 1064-1077.
[22] Song Yang, Liu Zhigang, Wang Hongrui, et al. Nonlinear modelling of high-speed catenary based on analytical expressions of cable and truss elements[J]. Vehicle System Dynamics, 2015, 53(10): 1455-1479.
[23] 任辉文. 气压驱动系统特性对受电弓动力学的影响[D]. 长沙: 湖南大学, 2019.
[24] 黄文龙, 胡海涛, 陈俊宇, 等. 枢纽型牵引变电所再生制动能量利用系统能量管理及控制策略[J]. 电工技术学报, 2021, 36(3): 588-598.
Huang Wenlong, Hu Haitao, Chen Junyu, et al. Energy management and control strategy of regener- ative braking energy utilization system in hub traction substation[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 588-598.
[25] 郭伟, 赵洪山. 基于事件触发机制的直流微电网多混合储能系统分层协调控制方法[J]. 电工技术学报, 2020, 35(5): 1140-1151.
Guo Wei, Zhao Hongshan. Coordinated control method of multiple hybrid energy storage system in DC microgrid based on event-triggered mechanism[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1140-1151.
[26] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003.
[27] 杨京, 王彤, 毕经天, 等. 含直驱风电机组的电力系统次同步振荡鲁棒阻尼控制[J]. 电力系统自动化, 2020, 44(3): 56-65.
Yang Jing, Wang Tong, Bi Jingtian, et al. Robust damping control of subsynchronous oscillation in power system with direct-drive wind turbines[J]. Automation of Electric Power Systems, 2020, 44(3): 56-65.
[28] 邹洲. 基于遗传算法的主动悬架多目标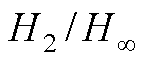 鲁棒控制[D]. 武汉: 武汉理工大学, 2010.
鲁棒控制[D]. 武汉: 武汉理工大学, 2010.
[29] 周天豪, 杨智, 祝长生, 等. 电磁轴承高速电机转子系统的内模-PID控制[J]. 电工技术学报, 2020, 35(16): 3414-3425.
Zhou Tianhao, Yang Zhi, Zhu Changsheng, et al. Internal model control-PID control of an active magnetic bearing high-speed motor rotor system[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3414-3425.
[30] Jin Qibing, Liu Qi. IMC-PID design based on model matching approach and closed-loop shaping[J]. ISA Transaction, 2014, 53(2): 462-473.
[31] 苗海涛. 基于空气弹簧高速受电弓的气压伺服主动控制研究[D]. 成都: 西南交通大学, 2009.
[32] 寇发荣, 李冬, 许家楠, 等. 车辆电动静液压主动悬架内模PID控制研究[J]. 液压与气动, 2018(6): 1-7.
Kou Farong, Li Dong, Xu Jianan, et al. Study on internal model PID control of vehicle active suspen- sion with electro-hydrostatic actuator[J]. Chinese Hydraulics and Pneumatics, 2018(6): 1-7.
Hierarchical Control of High-Speed Pantograph Considering Pneumatic System
Yang Peng1 Zhang Jing2 Jin Wei1 Liu Zhigang1
(1. School of Electrical Engineering Southwest Jiaotong University Chengdu 611756 China 2. School of Mechanical Engineering Southwest Jiaotong University Chengdu 610031 China)
Abstract In view of the problem that the dynamic characteristics of the pneumatic system affect the active control accuracy of pantograph, a hierarchical control strategy taking into account the response time delay was proposed. The upper controller adopted hybrid 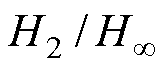 robust control strategy. According to the set three performance indexes of the pantograph operation state, a multi-objective state feedback control law was constructed. The active control force was obtained by solving linear matrix inequality. For the lower controller, based on internal model control (IMC) theory, the first-order equivalent simplified model of the pneumatic system was established by genetic algorithm, and an internal model -proportional integral derivative (PID) controller related to a single parameter was designed. The tracking rate of the output control value of the upper controller was accelerated. The simulation calculation under different train speeds verified the effectiveness and robustness of the hierarchical controller. The simulation results show that the lower controller can effectively reduce the response time and significantly improve the response delay of the pneumatic system. Compared with the traditional single control, the reduction rate of the standard deviation of the contact force of the hierarchical control is increased by about 10%, which effectively suppresses the pantograph-catenary coupled vibration and improves the current collection quality of the high-speed pantograph-catenary.
robust control strategy. According to the set three performance indexes of the pantograph operation state, a multi-objective state feedback control law was constructed. The active control force was obtained by solving linear matrix inequality. For the lower controller, based on internal model control (IMC) theory, the first-order equivalent simplified model of the pneumatic system was established by genetic algorithm, and an internal model -proportional integral derivative (PID) controller related to a single parameter was designed. The tracking rate of the output control value of the upper controller was accelerated. The simulation calculation under different train speeds verified the effectiveness and robustness of the hierarchical controller. The simulation results show that the lower controller can effectively reduce the response time and significantly improve the response delay of the pneumatic system. Compared with the traditional single control, the reduction rate of the standard deviation of the contact force of the hierarchical control is increased by about 10%, which effectively suppresses the pantograph-catenary coupled vibration and improves the current collection quality of the high-speed pantograph-catenary.
keywords:Pneumatic system, response time, hierarchical control, hybrid 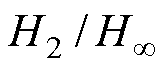 robust control, internal model-proportional integral derivative (PID) control
robust control, internal model-proportional integral derivative (PID) control
DOI: 10.19595/j.cnki.1000-6753.tces.210546
中图分类号:TM571
作者简介
杨 鹏 男,1996年生,硕士,研究方向为受电弓主动控制。E-mail: 18234136381@163.com
张静 女,1979年生,副教授,硕士生导师,研究方向为高速弓网动力学特性、参数优化及匹配及控制技术、外骨骼机器人优化设计及控制技术。E-mail: sdzj2006@126.com(通信作者)
收稿日期 2021-04-19
改稿日期 2021-08-25
国家自然科学基金资助项目(U1734202, 51405401)。
(编辑 陈 诚)
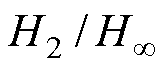 鲁棒控制策略。根据设定的受电弓运行状态的3个性能指标,构建多目标状态反馈控制律。通过求解线性矩阵不等式,得出主动控制力;下层控制器基于内模控制(IMC)理论,采用遗传算法,建立气动系统的一阶等效简化模型,设计仅与单一参数相关的内模-比例积分微分(PID)控制器。加快对上层控制器输出控制值的跟踪速率。通过列车不同运行速度下的仿真计算,验证了分层控制器的有效性和鲁棒性。仿真结果表明,下层控制器能够有效减少响应时间,明显改善气动系统的响应延迟。相比于传统单层控制,分层控制的接触力标准差下降率提高10%左右,有效抑制了弓网耦合振动,提高了高速弓网受流质量。
鲁棒控制策略。根据设定的受电弓运行状态的3个性能指标,构建多目标状态反馈控制律。通过求解线性矩阵不等式,得出主动控制力;下层控制器基于内模控制(IMC)理论,采用遗传算法,建立气动系统的一阶等效简化模型,设计仅与单一参数相关的内模-比例积分微分(PID)控制器。加快对上层控制器输出控制值的跟踪速率。通过列车不同运行速度下的仿真计算,验证了分层控制器的有效性和鲁棒性。仿真结果表明,下层控制器能够有效减少响应时间,明显改善气动系统的响应延迟。相比于传统单层控制,分层控制的接触力标准差下降率提高10%左右,有效抑制了弓网耦合振动,提高了高速弓网受流质量。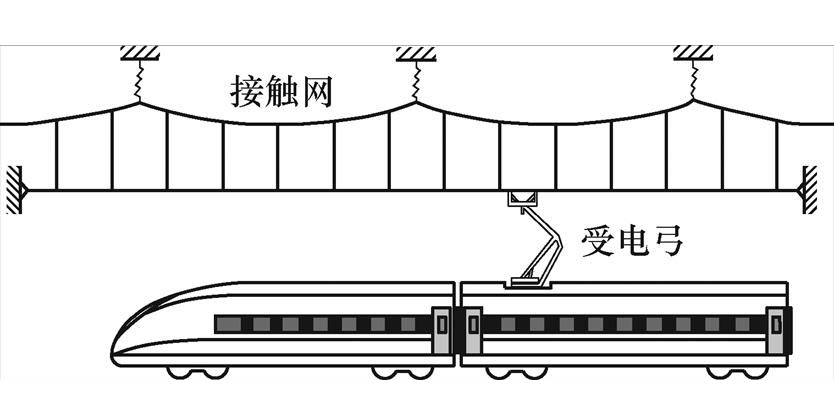
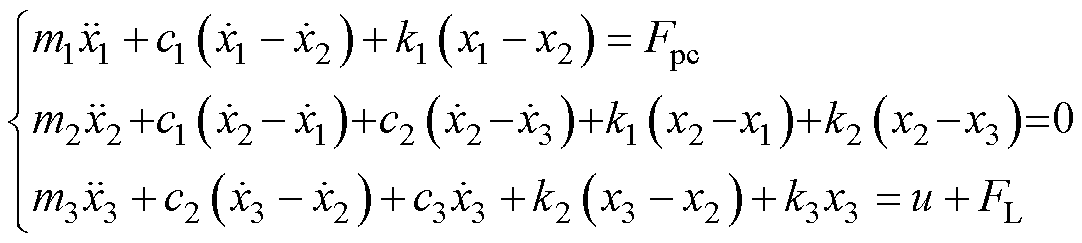 (1)
(1)
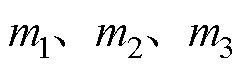 分别为受电弓弓头、上框架和下框架的等效质量;
分别为受电弓弓头、上框架和下框架的等效质量;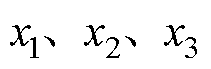 ,
,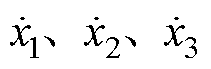 ,
,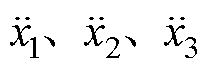 分别为受电弓弓头、上框架和下框架垂直方向上的位移、速度和加速度;
分别为受电弓弓头、上框架和下框架垂直方向上的位移、速度和加速度;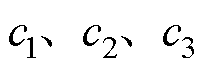 和
和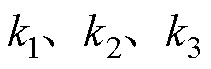 分别对应弓头与上框架之间、上下框架之间、下框架与底座之间的等效阻尼和等效刚度;
分别对应弓头与上框架之间、上下框架之间、下框架与底座之间的等效阻尼和等效刚度;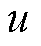 和
和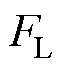 分别为垂直方向上的主动控制力和静态抬升力;
分别为垂直方向上的主动控制力和静态抬升力;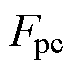 为垂直方向上的弓网接触力。
为垂直方向上的弓网接触力。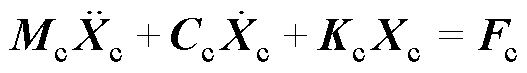 (2)
(2)
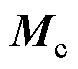 、
、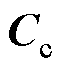 和
和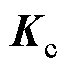 分别为接触网有限元各部分所组成的集中质量、等效刚度和等效阻尼矩阵;
分别为接触网有限元各部分所组成的集中质量、等效刚度和等效阻尼矩阵;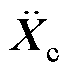 、
、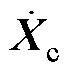 和
和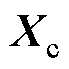 分别为接触网有限元划分节点加速度、速度和位移矩阵;
分别为接触网有限元划分节点加速度、速度和位移矩阵; 为接触网所受外力矩阵。
为接触网所受外力矩阵。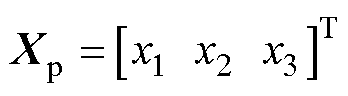 ,可建立弓网耦合方程,即
,可建立弓网耦合方程,即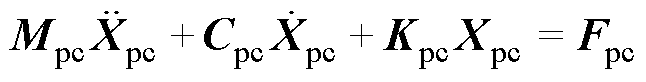 (3)
(3)

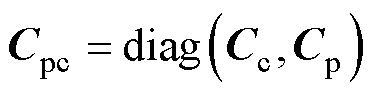
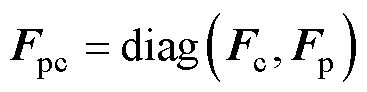

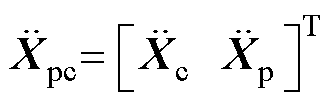
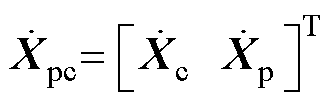
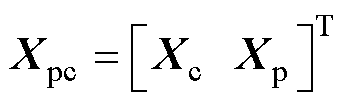
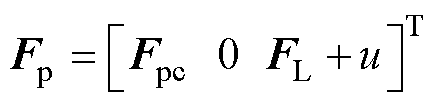
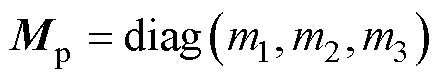
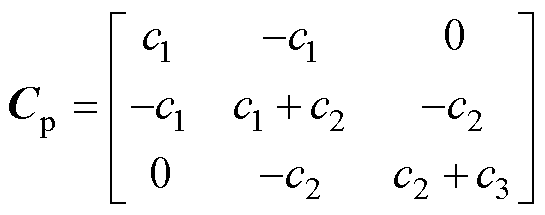
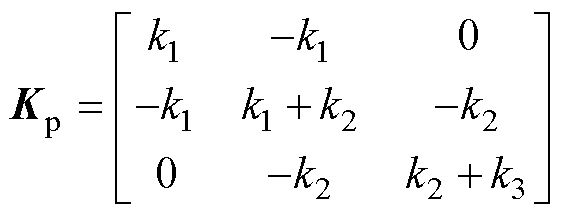
 与实时接触力
与实时接触力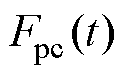 的差值上。为有效降低波动,
的差值上。为有效降低波动, ,即
,即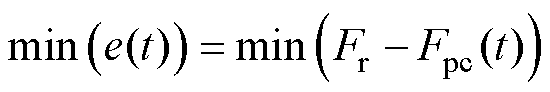 (4)
(4)
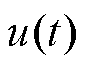 的输出大小,设输出控制力最值为
的输出大小,设输出控制力最值为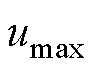 ,控制力比
,控制力比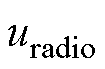 为
为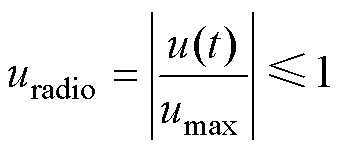 (5)
(5)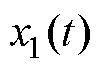 过大将会加快接触网的磨损程度,不利于接触网的正常工作。需要将其限定在一定范围内,设定抬升量最大值为
过大将会加快接触网的磨损程度,不利于接触网的正常工作。需要将其限定在一定范围内,设定抬升量最大值为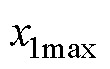 ,弓头抬升量比
,弓头抬升量比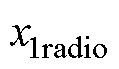 为
为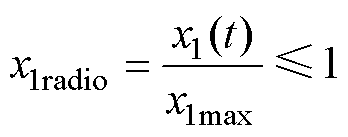 (6)
(6)
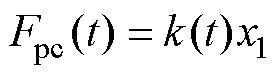 (7)
(7)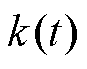 为接触网刚度系数。针对上述3个受电弓性能指标,为权衡各控制指标之间的关系,采用基于混合
为接触网刚度系数。针对上述3个受电弓性能指标,为权衡各控制指标之间的关系,采用基于混合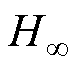 约束输出指标,在此条件下优化接触力差值
约束输出指标,在此条件下优化接触力差值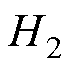 性能输出指标。综上,取
性能输出指标。综上,取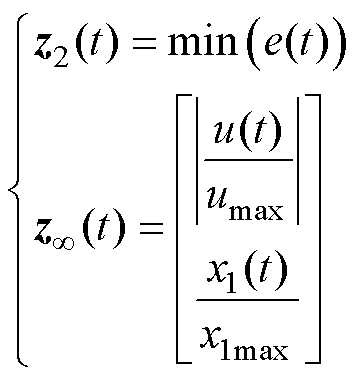 (8)
(8)
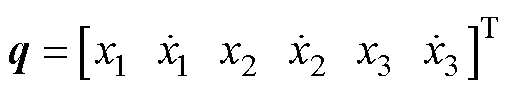 ,即
,即 (9)
(9)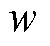 和
和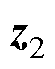 和
和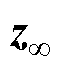 为控制输出目标,其余系数矩阵表达式为
为控制输出目标,其余系数矩阵表达式为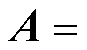
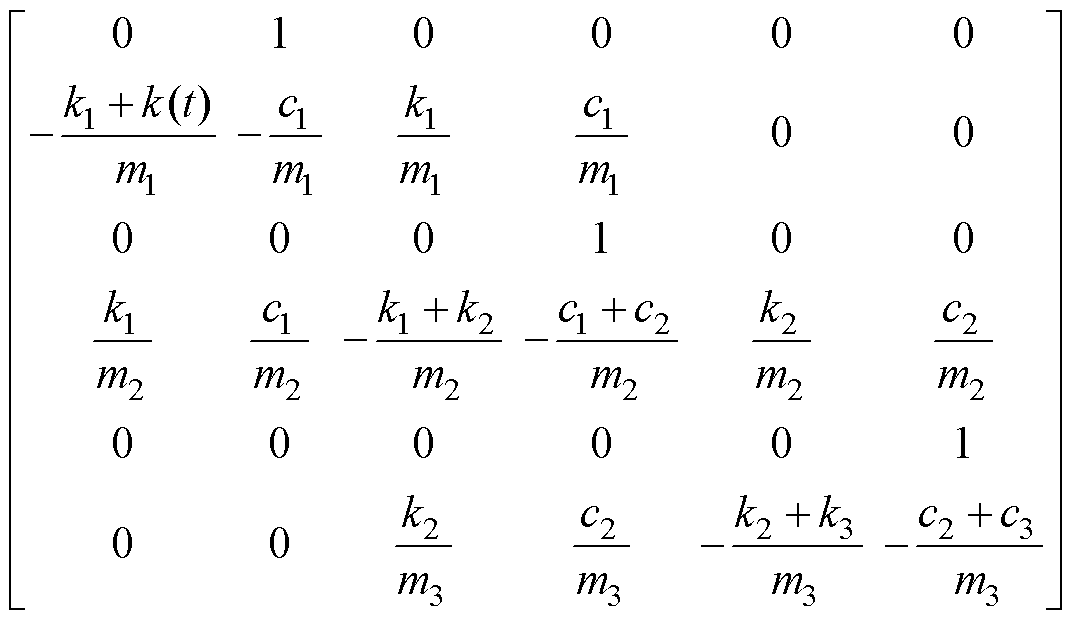

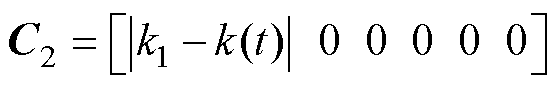
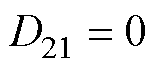
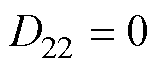
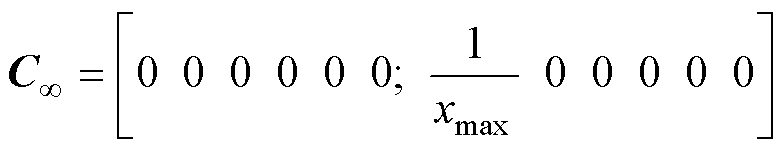
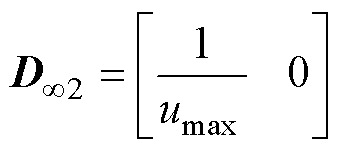
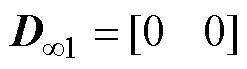
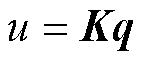 ,被控对象式(9)的状态反馈控制器设计如下。
,被控对象式(9)的状态反馈控制器设计如下。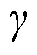 ,存在正定矩阵
,存在正定矩阵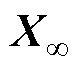 满足
满足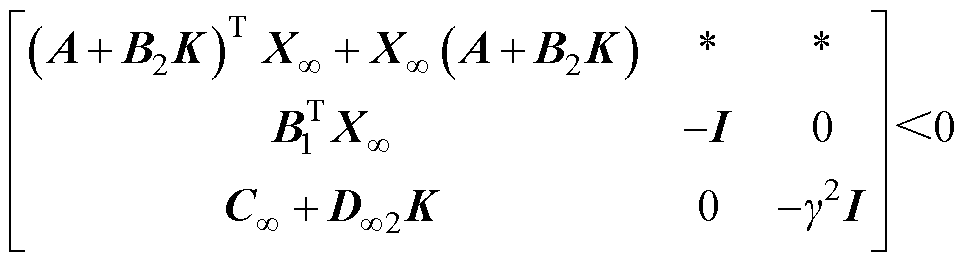 (10)
(10)
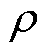 ,存在正定矩阵
,存在正定矩阵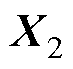 满足
满足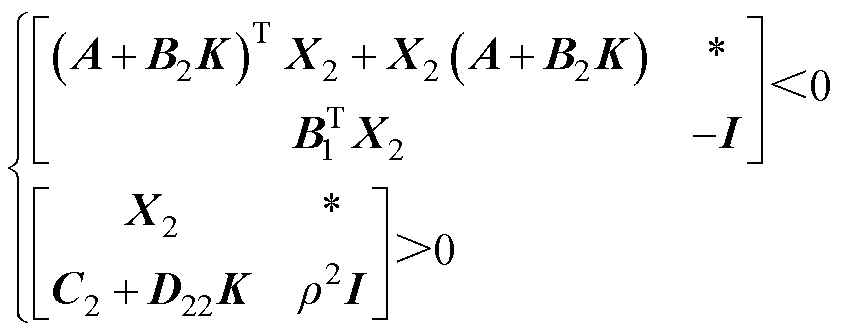 (11)
(11)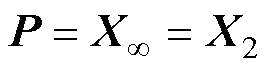 (12)
(12)
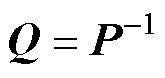 和
和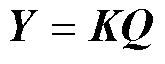 ,存在正定矩阵
,存在正定矩阵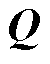 和向量
和向量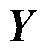 满足
满足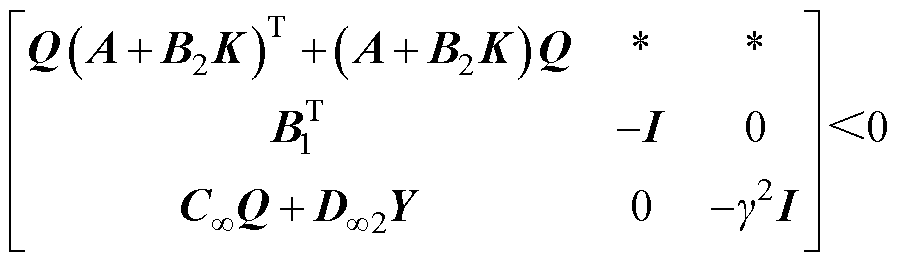 (13)
(13)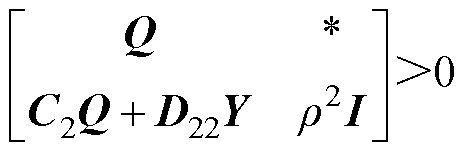 (14)
(14)
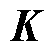 的最优解为
的最优解为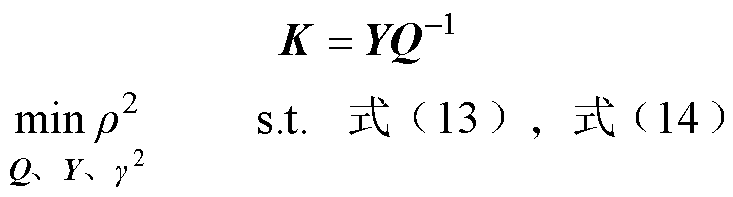 (15)
(15)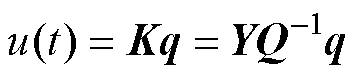 (16)
(16)
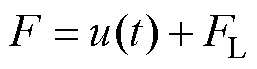 (17)
(17)
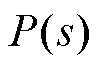 和
和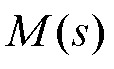 分别为被控对象(气动系统)及其内模模型,
分别为被控对象(气动系统)及其内模模型,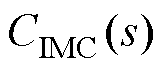 为内模控制器,
为内模控制器,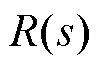 和
和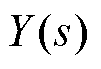 为整个气动控制系统的输入和输出,而点画线部分构成反馈控制器
为整个气动控制系统的输入和输出,而点画线部分构成反馈控制器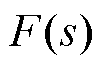 为
为 (18)
(18)
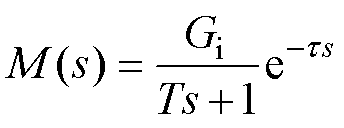 (19)
(19)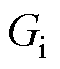 、
、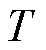 和
和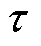 分别为增益值、响应时间常数和时滞时间。在设计内模控制器时,需对内模模型求逆,即
分别为增益值、响应时间常数和时滞时间。在设计内模控制器时,需对内模模型求逆,即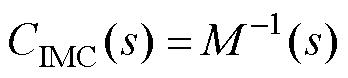 。但由于模型时滞项的存在而难以求解,故将简化后的内模模型分解为
。但由于模型时滞项的存在而难以求解,故将简化后的内模模型分解为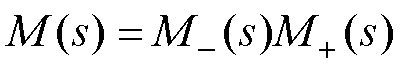 (20)
(20)
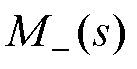 为模型的可逆部分;
为模型的可逆部分;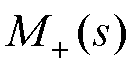 为包含模型的时滞项。模型分解能够解决存在时滞项而无法求逆的问题,但简化后的内模模型难以保证与实际系统之间完全重合,必然存在一定的模型误差。为防止对整个闭环系统造成不稳定的影响,通过在内模控制器上增设低通滤波器来增强系统的稳定性和鲁棒性。本文采用的低通滤波器为
为包含模型的时滞项。模型分解能够解决存在时滞项而无法求逆的问题,但简化后的内模模型难以保证与实际系统之间完全重合,必然存在一定的模型误差。为防止对整个闭环系统造成不稳定的影响,通过在内模控制器上增设低通滤波器来增强系统的稳定性和鲁棒性。本文采用的低通滤波器为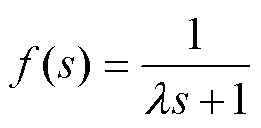 (21)
(21)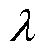 为滤波时间常数。故内模控制器可表示为
为滤波时间常数。故内模控制器可表示为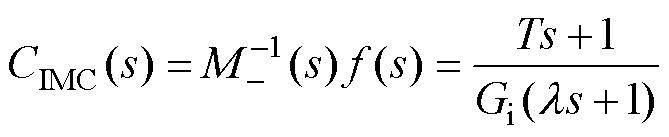 (22)
(22)
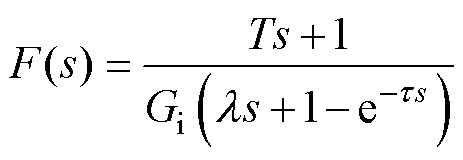 (23)
(23)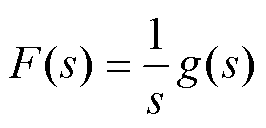 (24)
(24)
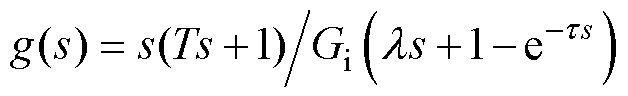 。
。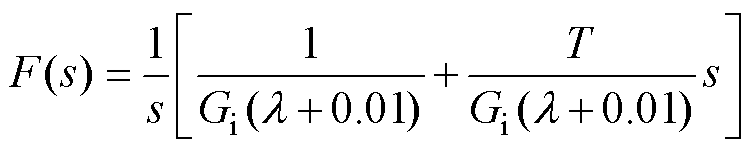 (25)
(25)

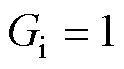 ;根据控制器通信过程存在的延时特性,取纯时滞时间
;根据控制器通信过程存在的延时特性,取纯时滞时间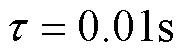 。为使简化模型能够与气压驱动系统模型尽可能重合,采用遗传算法寻优,获取响应时间常数
。为使简化模型能够与气压驱动系统模型尽可能重合,采用遗传算法寻优,获取响应时间常数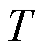 的值。经过20次迭代寻优后,得到响应时间常数最优值
的值。经过20次迭代寻优后,得到响应时间常数最优值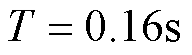 。故式(19)简化模型可表示为
。故式(19)简化模型可表示为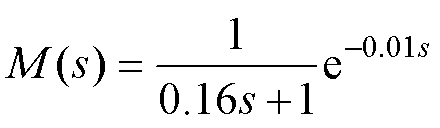 (26)
(26)
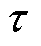 的倍数。在综合考虑控制器各指标性能的情况下,本文取控制参数值
的倍数。在综合考虑控制器各指标性能的情况下,本文取控制参数值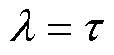 。结合式(25)可得参数值
。结合式(25)可得参数值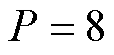 ,
,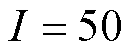 。采用相同阶跃信号,可得IMC-PID控制的输出曲线,如图9所示。
。采用相同阶跃信号,可得IMC-PID控制的输出曲线,如图9所示。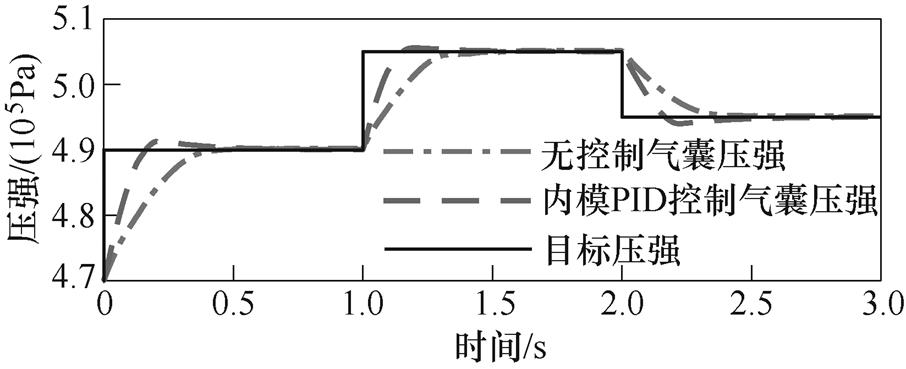
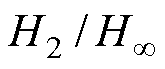 鲁棒多目标控制器在仅有受电弓控制下的单层控制效果对比。受电弓采用DSA380受电弓,接触网采用京津线的接触网模型,具体参数分别见表2和表3。
鲁棒多目标控制器在仅有受电弓控制下的单层控制效果对比。受电弓采用DSA380受电弓,接触网采用京津线的接触网模型,具体参数分别见表2和表3。


 鲁棒控制[D]. 武汉: 武汉理工大学, 2010.
鲁棒控制[D]. 武汉: 武汉理工大学, 2010.