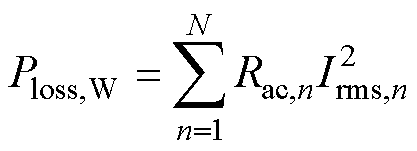 (1)
(1)
摘要 绕组损耗测量是目前大功率高频变压器(HFT)建模与设计中的难点,高精度的绕组损耗测量方法是校验绕组损耗理论研究正确性、提高建模与仿真精度的重要手段。目前广泛采用的短路阻抗测量方法的精度随测量频率的升高而降低,并不适用于HFT。借助辅助绕组(AW)提供额外测量节点是提高绕组损耗测量精度的有效措施。首先建立包含AW杂散参数的等效电路模型,基于该模型的分析结果表明,AW与被测绕组(WUT)之间漏感及耦合电容决定了绕组损耗测量频率范围及精度。提出一种考虑耦合电容的绕组电阻测量校正方法,降低耦合电容的影响,保证了高频下的测量精度。采用利兹线绕组中单股线作为AW以及AW与WUT之间的漏感被降至极低水平,扩展了测量频率范围,同时降低了工程实践难度。通过对一台100kV·A HFT样机绕组参数的测量,验证了电路模型和校正方法的有效性,并实现了1MHz频率下绕组交流电阻的有效测量。
关键词:高频变压器 绕组损耗 辅助绕组 误差分析
在智能电网快速发展背景下,电力电子变压器(Power Electronic Transformer, PET)成为构建新一代交直流配电网的关键设备[1-3],其中高频变压器(High-Frequency Transformer, HFT)是实现电气隔离、电压转换的核心部件。提高工作频率是降低变压器体积和质量的有效手段,为提高系统功率密度、降低造价提供了可能[4]。随着变压器工作频率的提高,受趋肤效应及邻近效应等高频效应的影响,绕组截面内电流分布趋于不均匀,甚至出现反向电流,绕组损耗随之增加[5-6]。在大功率HFT设计中,采用利兹线绕组是减小高频效应影响的有效方法[5, 7-8],众多学者对利兹线绕组损耗进行了大量的建模研 究[8-10]。然而实际利兹线绕组的非理想换位、绕组高度小于窗口高度、窗口内磁场非一维分布等情况给绕组损耗建模计算带来了巨大的挑战,导致计算值偏离实际值。有限元仿真计算是求解利兹线绕组损耗的另一重要方法[11-12],然而受限于计算机处理能力,目前三维有限元分析仅能解决小规模利兹线绕组的高频损耗计算问题[12],远不能处理实际大功率HFT中的利兹线绕组。考虑到HFT绕组损耗建模与仿真研究的实际困难,可靠的绕组损耗测量方法是校验理论研究正确性、提高建模与仿真精度的重要手段。
使用阻抗分析仪等仪器测量变压器短路阻抗是绕组损耗测量的常用方法[8-10]。文献[8]中使用阻抗分析仪在0~40kHz频率范围对几种绕组损耗模型的精度进行了验证,被测绕组(Winding Under Test, WUT)为单个空心线圈,未考虑二次绕组电流对绕组交流电阻的影响,而在HFT实际工况中二次绕组电流产生的磁场将影响绕组截面内的电流分布,从而影响绕组交流电阻。
为了解决传统参数测量方法不能分离各绕组杂散参数、测量精度差等问题,多位研究学者提出基于辅助绕组(Auxiliary Winding, AW)的绕组参数测量方法:通过在变压器中增加AW,引入额外测量节点以增加测量维度[13-15]。
文献[14]从分离绕组损耗和磁心损耗的角度,提出基于AW的电感绕组损耗测量方法,由于未进行定量分析,未说明该方法的频率和绕组参数测量应用范围。文献[15]从分离多个绕组漏感的角度,提出基于对称耦合AW的漏阻抗测量方法,该方法要求AW与变压器中两个绕组的耦合系数相同,在大功率HFT工程应用中难以实现。文献[14-15]中忽略了高频下基于AW实现绕组损耗或电阻高精度测量的关键因素:AW与WUT之间的漏感及耦合电容,导致只能达到与传统短路阻抗测量方法类似的测量效果,限制了该方法的频率测量范围及测量精度。
本文从扩展绕组损耗测量频率范围、提高测量精度的角度,首先建立了包含AW杂散参数的等效电路模型,对基于AW的绕组损耗测量方法进行了理论推导,定量分析了AW与WUT之间漏感及耦合电容对绕组损耗测量精度的影响。提出考虑耦合电容的绕组电阻测量校正方法,进一步扩展了频率测量范围,保证了高频下的测量精度。采用利兹线绕组中单股线作为AW,有效地降低了测量系统漏感,从而提升了频率测量范围。分别采用基于AW的损耗直接测量方法和基于AW的阻抗测量方法,对一台100kV·A HFT样机的绕组损耗和电阻进行测量。
双有源桥(Dual Active Bridge, DAB)变换器[3]和串联谐振变换器[16]是实现大功率DC-DC隔离变换的两种主要电路,分别对应两种典型的HFT绕组电流波形:梯形波和正弦波。梯形波电流中除了基波分量外,还包含3次、5次及更高次的谐波电流,梯形波电流及其各次谐波如图1所示。梯形波电流下绕组损耗Ploss,W由式(1)确定[8],由各次谐波下的损耗叠加得到。
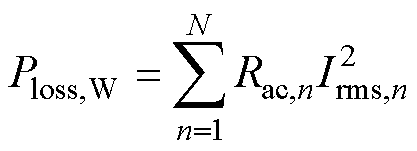 (1)
(1)
式中,Rac,n为n次谐波下的交流电阻;Irms,n为n次电流谐波有效值。
变压器绕组损耗主要有短路阻抗测量和交流功率测量两种测量方式,如图2所示。短路阻抗测量方式如图2a所示,使用阻抗分析仪测得绕组电流基波频率及主要谐波频率下的短路阻抗,再通过式(1)计算间接得到实际电流波形下的绕组损耗。对于交流功率测量方式,短路损耗测量如图2b所示,使用功率分析仪测量变压器在实际电流激励下的有功损耗。
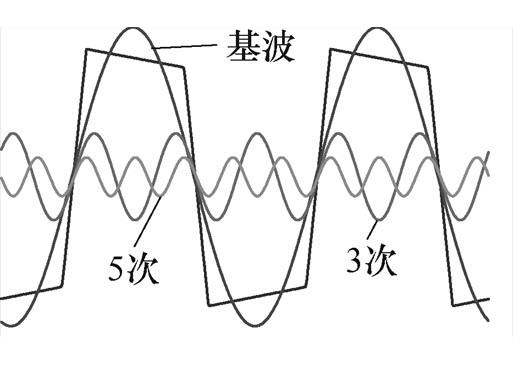
图1 梯形波电流及其各次谐波
Fig.1 Trapezoidal wave currents and their harmonics
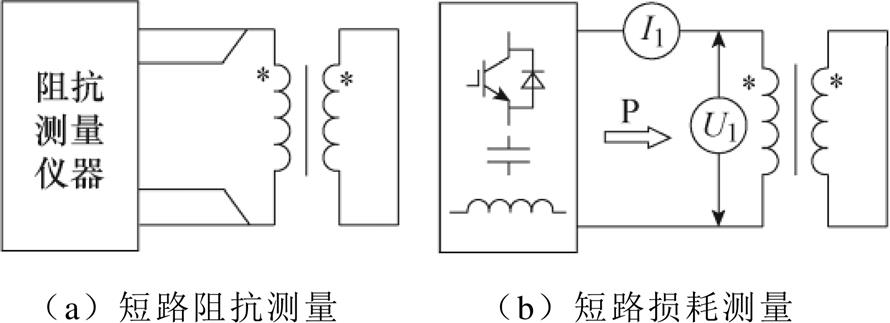
图2 传统绕组损耗测量方法
Fig.2 Traditional measurement methods of winding loss
传统绕组损耗测量方法的误差随测量频率升高而增大的主要原因是被测交流电压主要由感性分量组成,而可以提取绕组损耗信息的阻性分量只占极小部分。
为了实现交流电压信号中阻性分量与感性分量的分离,可在变压器中设置与WUT紧密耦合的AW,从而提取主磁通和漏磁通的感应电压。图3为基于AW的变压器绕组损耗测量电路,一次和二次绕组分别为BA和DC,其中绕组BA为WUT,绕组ba为相应的AW,绕组ba的b端悬空,a端与WUT的对应端短接。
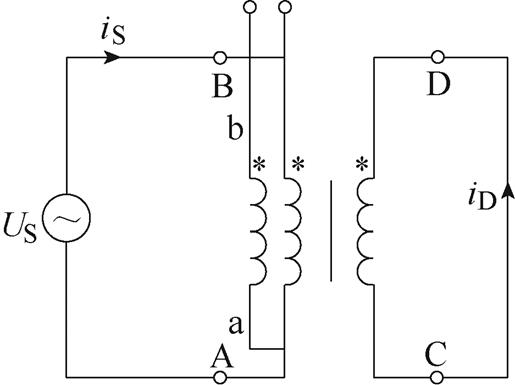
图3 基于AW的绕组损耗测量电路
Fig.3 Winding loss measurement circuit based on AW
本文中变压器参数及电压、电流值均为归算至一次侧后的数值。绕组BA、绕组DC、绕组ba自感分别为LB、LD、Lb,交流电阻分别为rB、rD、rb,定义绕组BA、DC之间的互感为MDB,绕组ba与绕组BA及DC的互感分别为MBb、MDb。
由于基于AW的测量方法要求AW与WUT之间紧密耦合,故考虑绕组ba与绕组BA之间在端口Bb处的等效耦合电容为Ceq,通过该耦合电容流过绕组ba的电流为ib。借助相量表示方法,测量角频率为w 时,绕组BA、DC、ba的电压可分别表示为
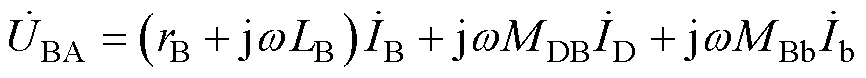 (2)
(2)
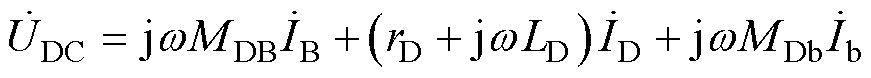 (3)
(3)
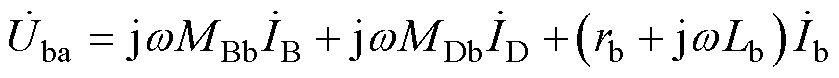 (4)
(4)
为了清楚地表示绕组BA、DC、ba三者之间的耦合关系,将各绕组的自感和互感做如下分解:绕组BA总漏感L1=LB-MDB,L1产生的漏磁链可分为匝链绕组ba的部分和只匝链其自身的部分,分别对应漏感L4和L3,则L3=LB-MBb,L4=MBb-MDB;类似地,绕组DC总漏感L2=LD-MDB,L2产生的漏磁链分为匝链绕组ba的部分和只匝链其自身的部分,分别对应漏感L5和L6,则L5=MDb-MDB,L6=LD-MDb。从绕组ba所有磁链中除去单独匝链绕组BA、单独匝链绕组DC及共同匝链两者的磁链,剩下部分即为只匝链自身的部分,对应绕组ba的漏感L7,故L7=Lb-L4-L5-MDB。
使用漏感L3~L7和互感MDB表示式(2)~式(4)中的自感LB、LD、Lb及互感MBb、MDb,则绕组BA、DC、ba的电压表达式可改写为
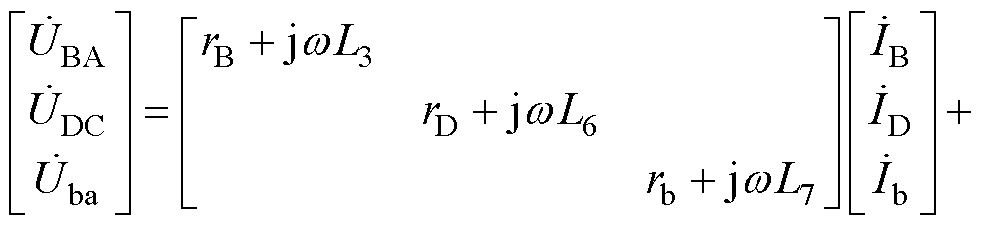
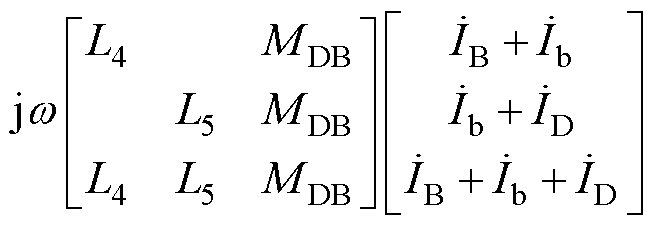 (5)
(5)
根据式(5),在变压器T型等效电路的基础上,包含AW的变压器等效电路如图4所示。
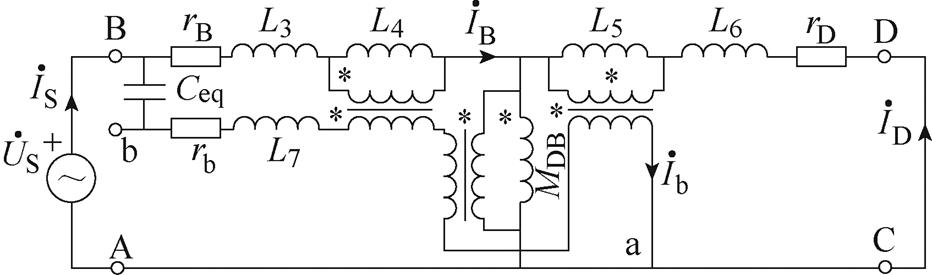
图4 包含AW的变压器等效电路
Fig.4 Transformer equivalent circuit including AW
首先忽略绕组ba与绕组BA之间的耦合电容Ceq,即令ib=0。根据式(5),端口Bb的电压差为
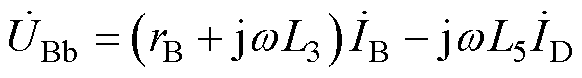 (6)
(6)
在变压器T型等效电路中一般使用与互感并联的等效电阻表示变压器磁心损耗[14-15]。在基于AW的绕组损耗测量中,该等效电阻位于绕组AB和绕组ab的共同支路上,等效电阻不会影响电压差uBb的表达式,实现绕组损耗测量与磁心损耗测量的解耦,故在本文中忽略磁心损耗的影响。
相对于基于AW的电感器件绕组损耗测量方 法[13-14],当AW应用于变压器绕组损耗测量时,由于漏感L5的存在,二次绕组电流iD将耦合至电压差uBb中。根据式(6),只有当电流iD的相位与绕组BA电流iB的相位相同、相反或iD=0时,电流iD才不会改变电压差uBb的阻性分量,否则电流iD将成为绕组损耗测量的系统误差来源之一。若使绕组DC开路即iD=0,受励磁电感的阻碍,激励电流iB将难以注入绕组BA中。如图3所示,将除WUT外的绕组短接,使WUT电流与其他绕组电流处于反相状态是便于实现且符合变压器绕组实际工况的测量状态。
根据变压器短路状态可得
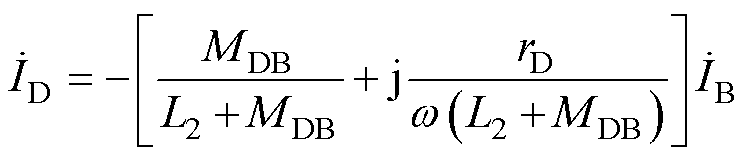 (7)
(7)
将式(7)代入式(6)可得
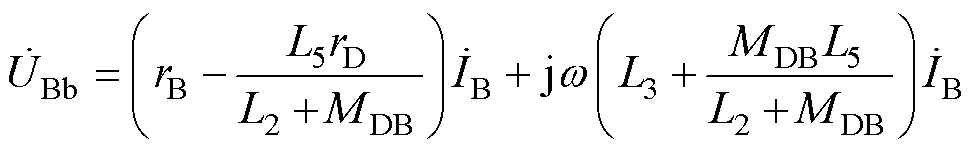 (8)
(8)
对HFT存在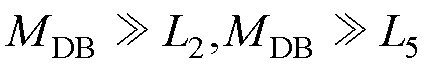 ,式(8)简化为
,式(8)简化为
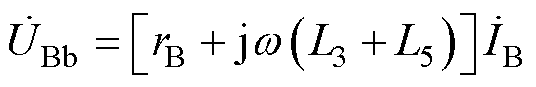 (9)
(9)
依据式(9),端口Bb电压与绕组BA电流产生的交流有功功率即为频率w 下绕组BA产生的损耗。由于不同频率电压和电流信号间的平均有功功率为0,从而式(9)也可用于非正弦实际工作电流激励下的损耗测量,测量结果包含基波及各次谐波引起的绕组损耗,故将该方法称为基于AW的损耗直接测量方法。对于绕组DC,可基于相同的方法测量其损耗,从而实现多个绕组损耗的分离。
式(9)中端口Bb电压仅与绕组BA电流线性相关,故可定义该电压电流的比值为绕组BA的虚拟阻抗ZAW=rB+jw(L3+L5),该阻抗值的实部即为绕组BA在频率w 下的交流电阻rB。为了区别于传统短路阻抗测量方法,将该方法称为基于AW的阻抗测量方法。
2.3.1 品质因数
对于基于AW的损耗直接测量方法,其交流有功功率测量误差E可表示[17]为
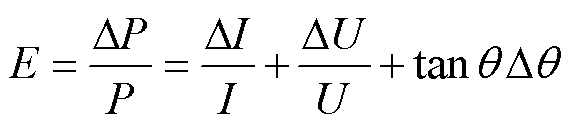 (10)
(10)
式中,DU、DI、Dq 分别为电压幅值U、电流幅值I及电压电流相位差q 的误差量;U和I的幅值测量误差线性叠加至测量误差E中,而相位q 的测量误差Dq 将被放大tanq 倍。
对式(9)计算有功功率测量误差E时,电压、电流相位差q 即为虚拟阻抗ZAW的阻抗角qAW,tanq 即为ZAW的虚部与实部之比,定义为品质因数QAW。
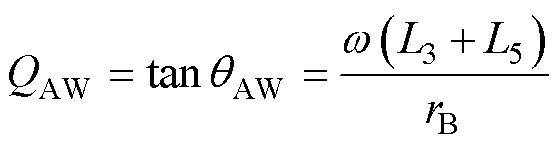 (11)
(11)
随着测试频率的提高,QAW也随之增大,表明绕组损耗的测量误差也随之增大,为了扩大有效测量频率范围,需尽可能减小漏感L3和L5,即增大AW与WUT之间的耦合程度。对于特定频率下绕组损耗测量结果,可通过该频率下的品质因数QAW和电压电流传感器的相位误差评估测量误差。
2.3.2 耦合电容
当测试频率w 足够高时,耦合电容Ceq的存在倾向于降低品质因数QAW的测量结果,同时通过电容Ceq注入的电流ib在绕组ba漏阻抗上的压降将影响端口Bb电压差的测量,从而降低虚拟阻抗ZAW的测量精度。
根据图4所示等效电路,当考虑耦合电容Ceq时,端口Bb电压可表示为
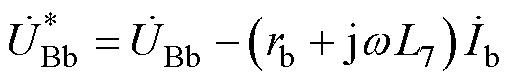 (12)
(12)
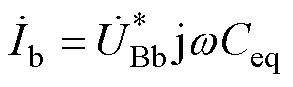 (13)
(13)
图4中,由外部激励US注入变压器的总电流iS等于绕组BA电流iB与绕组ba电流ib之和,故图4中实际测得的虚拟阻抗值为
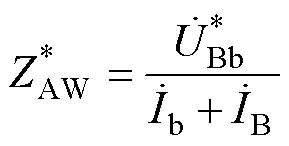 (14)
(14)
联立式(9)和式(12)~式(14),可得
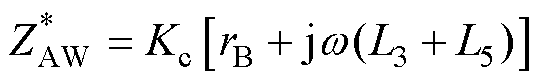 (15)
(15)
其中
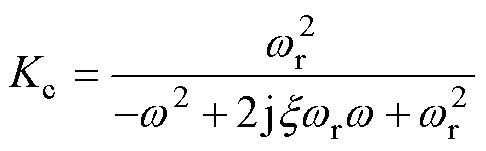 (16)
(16)
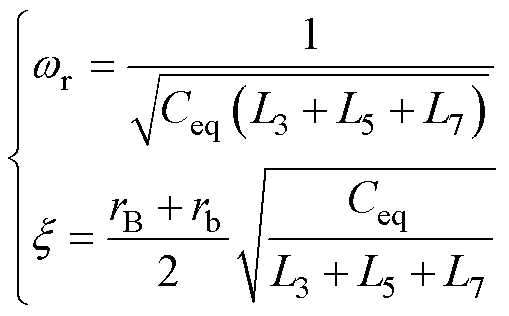 (17)
(17)
根据式(15),当考虑耦合电容Ceq时,实际测量阻抗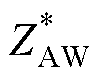 为ZAW的Kc倍,系数Kc即谐振频率为wr、阻尼比为x 的二阶系统在频率w 下的稳态增益。根据二阶系统频率响应特性,当测试频率w 远低于谐振频率wr时,Kc约为1;当测试频率w 逐渐接近谐振频率wr时,Kc趋于-j/(2x),导致实测阻抗
为ZAW的Kc倍,系数Kc即谐振频率为wr、阻尼比为x 的二阶系统在频率w 下的稳态增益。根据二阶系统频率响应特性,当测试频率w 远低于谐振频率wr时,Kc约为1;当测试频率w 逐渐接近谐振频率wr时,Kc趋于-j/(2x),导致实测阻抗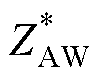 的实部偏离绕组BA阻值rB,故wr定义了基于AW的阻抗测量方法的频率上限。
的实部偏离绕组BA阻值rB,故wr定义了基于AW的阻抗测量方法的频率上限。
系数Kc与多个绕组杂散参数有关,难以直接计算Kc的准确值,但可通过测量端口Bb处阻抗ZBb的频率特性间接计算Kc。对于图4所示的等效电路,将激励源连接至B端和b端之间,A端悬空,此时端口Bb之间的等效电路模型如图5所示,频率w 下阻抗ZBb表示为
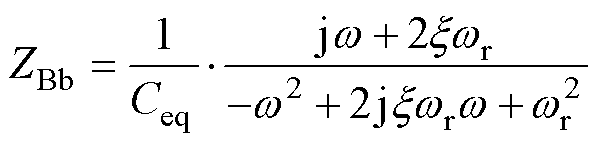 (18)
(18)
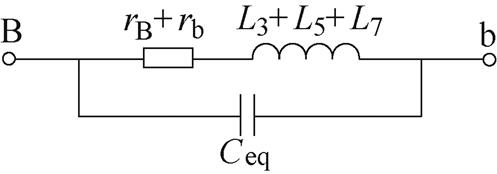
图5 端口Bb之间的等效电路模型
Fig.5 Equivalent circuit model between port B and b
由于端口Bb之间的阻抗ZBb和系数Kc表示的二阶系统有着相同的谐振频率wr和阻尼比x,故通过测量阻抗ZBb的幅频和相频特性即可确定Kc的特征参数,从而确定测量频率w 下Kc的具体数值。当测量频率w 接近谐振频率wr时,可通过式(19)校正电容Ceq导致的测量误差,从而扩展基于AW的阻抗测量方法的适用频率范围,提高高频测量精度。
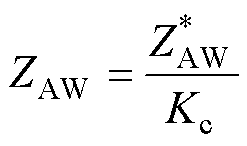 (19)
(19)
根据式(11),为了提高绕组损耗的测量精度,需要尽量降低AW与WUT之间的漏感,即增大两者之间的耦合程度,使WUT电流产生的磁通都能匝链AW。本文比较了三种AW形式:AW1、AW2、AW3,三种形式的辅助绕组如图6所示,图中,AW1与WUT并行,AW2连续缠绕WUT,AW3为WUT中随机选取的单股线且与WUT中其他股线相互绝缘。三种AW均在同一端与WUT短接,AW另一端与WUT的对应端均无直接电气联系。
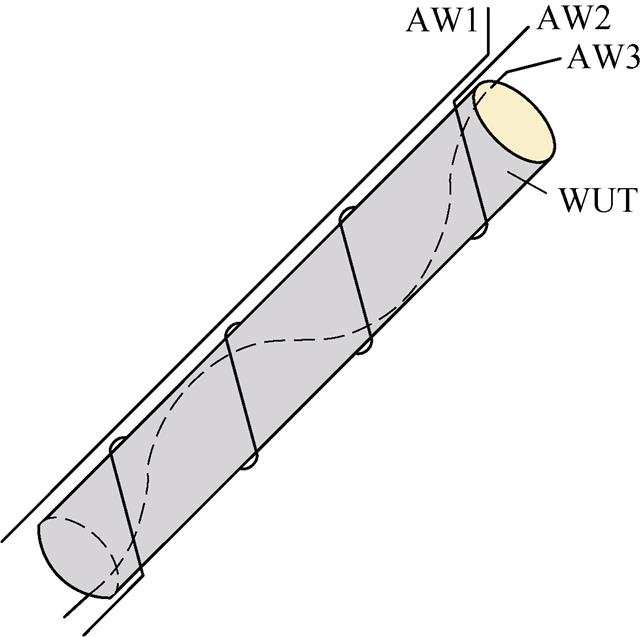
图6 三种形式的辅助绕组
Fig.6 Three forms of auxiliary winding
为了降低测量电路杂散参数对阻抗测量结果的影响,4端对阻抗测量方法中将电压测量支路与激励电流支路分离[18],与图3所示的测量方式一致,故可用于虚拟阻抗的测量,4端对阻抗测量平台及测量原理如图7所示。图7中,HCUR-LCUR为激励电流支路,使得20mA激励电流流经WUT,HPOT-LPOT测量WUT与AW之间的电压差,测得的阻抗即为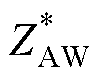 。为了提高nH级别漏感的测量精度及测量结果可重复性,设计了图7中所示的阻抗测试夹具[18]。
。为了提高nH级别漏感的测量精度及测量结果可重复性,设计了图7中所示的阻抗测试夹具[18]。
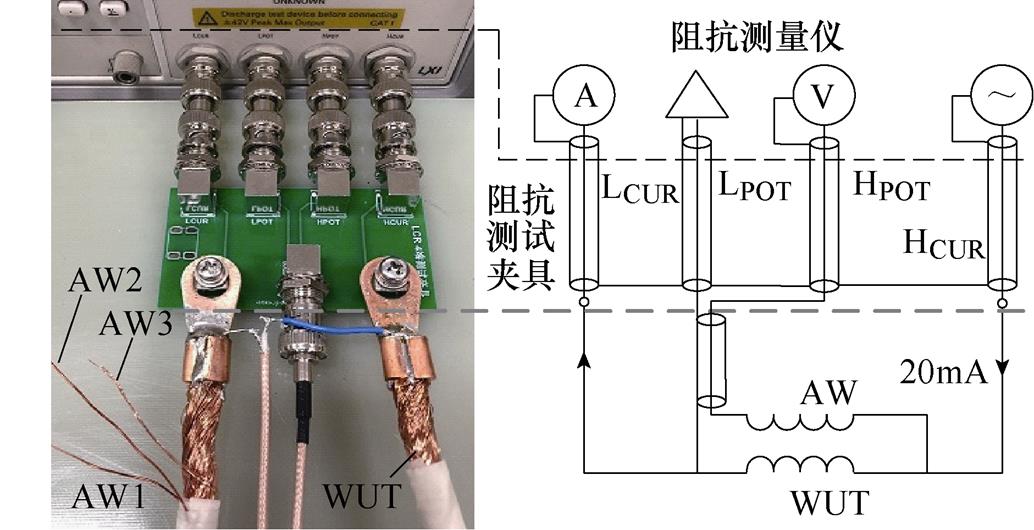
图7 4端对阻抗测量平台及测量原理
Fig.7 Four-terminal impedance measuring platform and measuring principle
图7中,WUT为单股直径为0.2mm、股数为640的利兹线绕组,长度为1m,WUT与AW1、AW2、AW3之间的漏感测试结果如图8所示,其中包括四组随机选择AW3的测量结果。容易看出,AW3与WUT之间漏感远小于AW1、AW2,即采用利兹线中单股线作为AW的方式能够实现更高频率下的绕组损耗测量,提高测量精度。
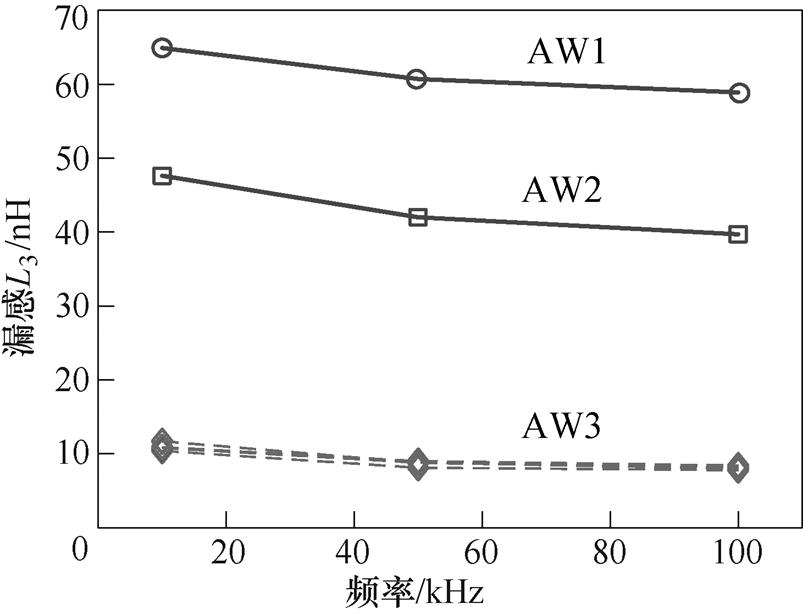
图8 辅助绕组漏感测量结果
Fig.8 Leakage inductance measuring results of auxiliary winding
设计了一台HFT样机用于绕组损耗及交流电阻测量,其绕组参数见表1。HFT样机一次、二次绕组的有效截面积均为20mm2,绕组电流密度设计为3A/mm2,绕组额定电流为60A,绕组额定电压设计为1 700V,在10kHz工作频率下纳米晶磁心磁通密度约为0.5T。HFT样机的一次绕组与二次绕组之间保持15mm间距,约为AC 10kV工作电压下使用环氧树脂作为绝缘介质所需的间距,且满足75kV冲击电压要求。HFT样机一次绕组和二次绕组均设置AW3形式的辅助绕组,为了便于AW连接示波器和阻抗测量夹具,将AW测量节点通过同轴连接器引出,设置AW的HFT样机如图9所示。
表1 HFT样机绕组参数
Tab.1 Winding parameters of HFT prototype
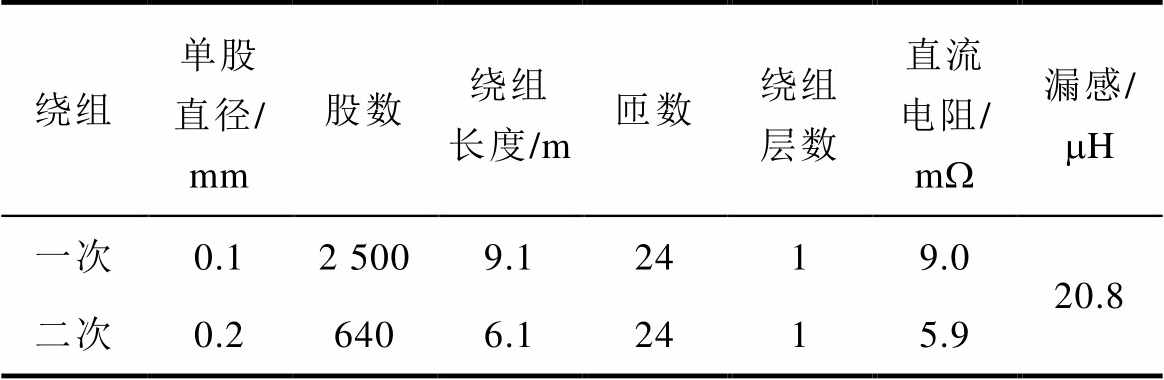
绕组单股直径/ mm股数绕组长度/m匝数绕组层数直流电阻/ mW漏感/mH 一次0.12 5009.12419.020.8 二次0.26406.12415.9
同时测量HFT样机的一次及二次绕组损耗,实验平台如图10所示,将HFT样机一次电流iB、二次电流iD、一次绕组BA与对应AW的电压差信号uBb、二次绕组DC与对应AW的电压差信号uDd依次接入示波器。图10中,使用中点钳位型三电平半桥逆变器作为电压激励源,将HFT样机一次绕组A端连接至逆变输出,一次绕组B端连接三电平半桥直流母线电容中点,同时将逆变器直流母线电容中点接地,有效降低逆变器共模噪声对AW与WUT间电压差信号的影响。

图9 设置AW的HFT样机
Fig.9 A HFT prototype with AW
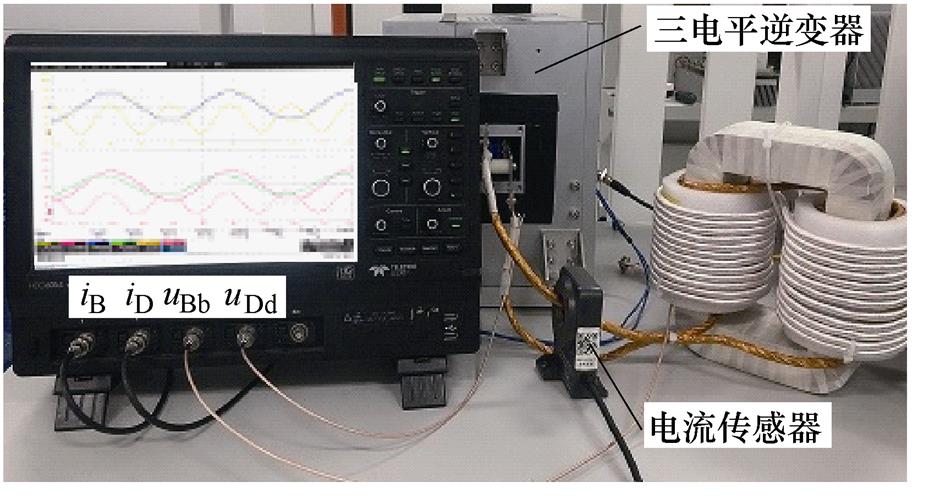
图10 HFT绕组损耗测量平台
Fig.10 Measurement platform of HFT winding loss
设置三电平逆变器调制频率为测量频率,保持三电平逆变器输出正电平和负电平脉冲宽度均为30°,该角度约为DAB变换器额定工况下的移相角度,从而获得与DAB变换器中相同形状的梯形波绕组电流,电流幅值通过逆变器直流母线电压调节。
在10kHz梯形波电流激励下,绕组电流及辅助绕组电压信号波形如图11a所示,在示波器内分别计算P1=iBuBb及P2=iDuDd,P1和P2即为包含漏感无功的绕组瞬时损耗功率,其平均值分别为一次和二次绕组在该激励电流下的损耗。由于WUT与AW之间的漏感足够低,在电流激励下该漏感带来的无功功率也足够小,故瞬时功率P1和P2波形几乎没有小于0的部分。
正弦激励电流可通过LC串联谐振实现,具体方法为:在逆变器输出端与HFT样机一次绕组A端之间串联电容,调整电容容值使得电容与绕组漏感的谐振频率约等于电压源频率。在10kHz及50kHz正弦电流激励下,绕组电流及辅助绕组电压信号波形分别如图11b和图11c所示,激励电流有效值为额定电流60A。表2中给出不同电流激励下测量得到的绕组损耗和等效电阻值。
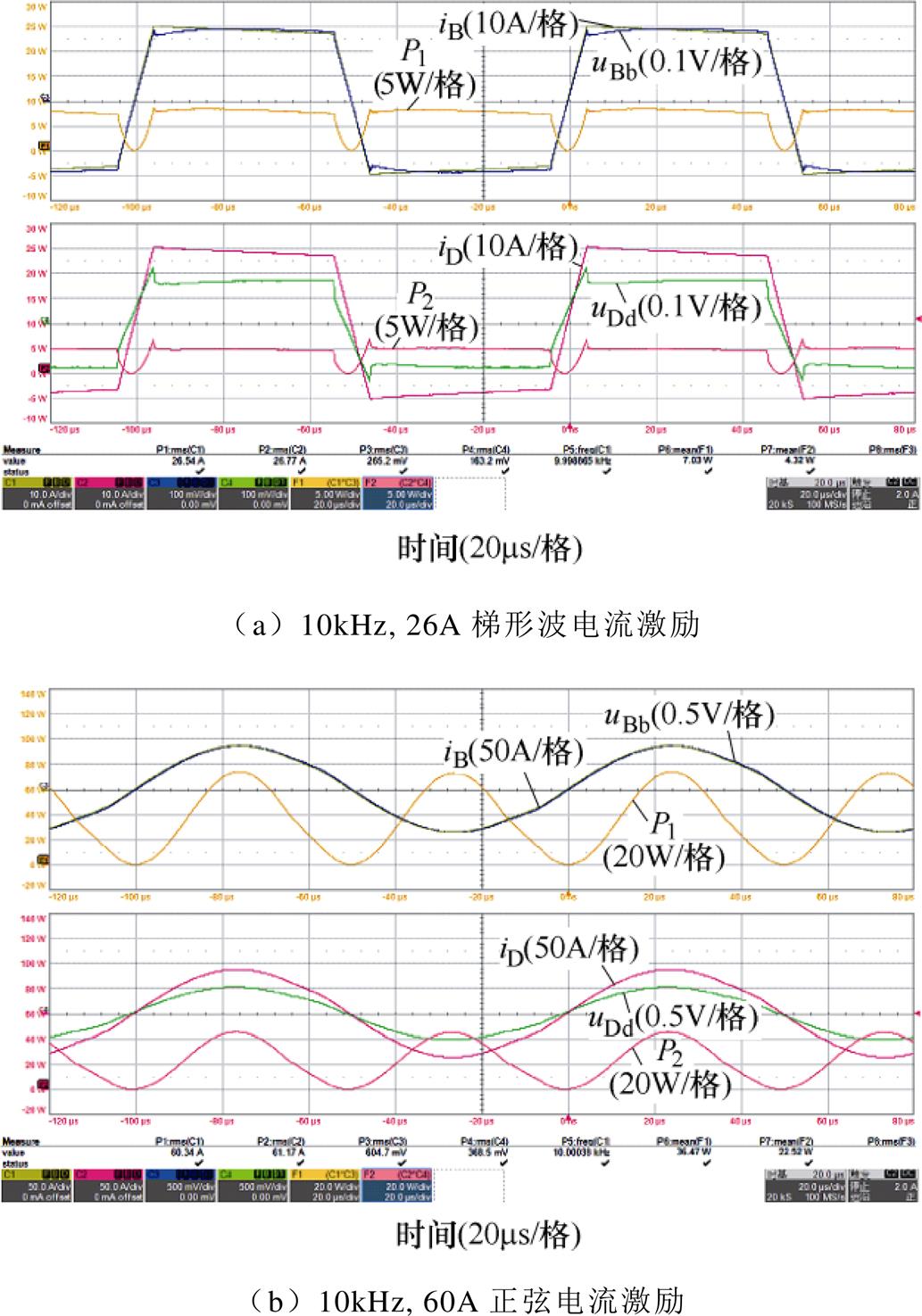
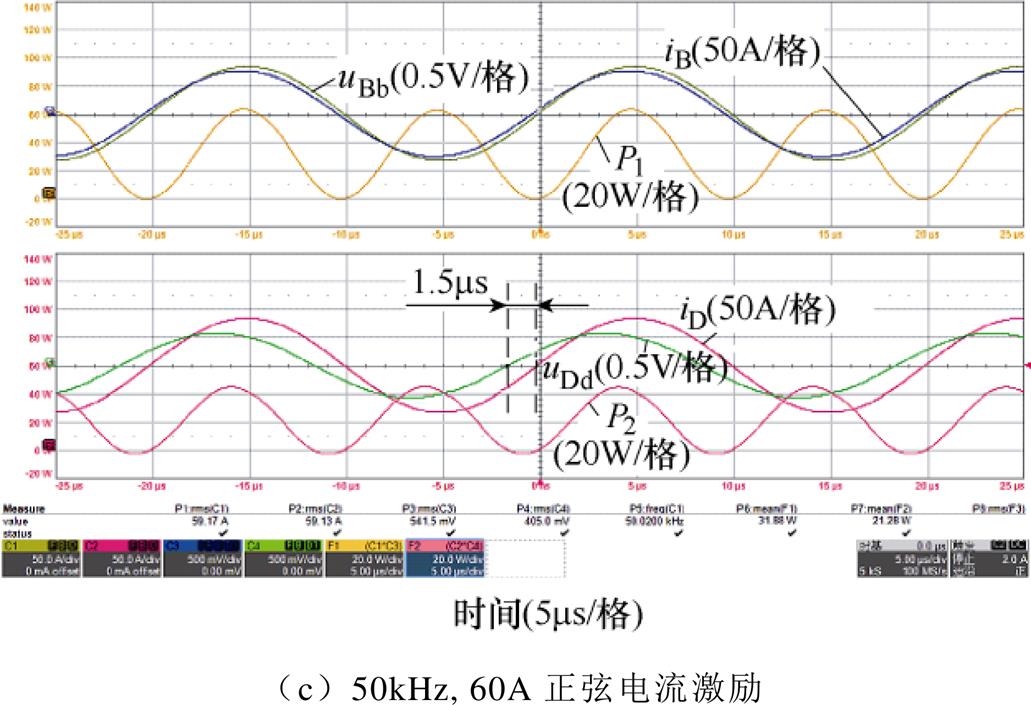
图11 不同激励电流下绕组损耗测量波形
Fig.11 Waveforms of winding loss measurement under different excitation currents
如图11b和图11c所示,10kHz频率下电压差信号与激励电流几乎完全同相位,当激励频率提高至50kHz时,漏感带来的感性电压分量随之增大,电压信号略微超前激励电流。对于HFT样机的二次绕组,在50kHz激励频率下,uDd超前iD 1.5ms,即qAW=27°,QAW=tanqAW=0.51。图10所示的实验平台中直接使用同轴线缆测量辅助绕组电压信号,在50kHz下幅值和相位误差可忽略不计,电流传感器为来自HIOKI的CT6863[19],其额定电流为200A,-3dB带宽约为500kHz。在50kHz 60A电流激励下,电流传感器CT6863的幅值测量最大误差可估计为±(2%×60/200+0.02%)=±0.62%,相位测量最大误差可估计为±(0.5+50×0.1)°=±0.096rad。根据误差计算表达式(10),50kHz 60A激励电流下,HFT样机二次绕组的损耗测量最大误差Emax=0.0062+0.51×0.096=5.5%。
表2 不同激励电流下的绕组损耗测量结果
Tab.2 Winding loss measurement results under different excitation currents

绕组电流激励损耗/W等效电阻/mW 一次10kHz 26A梯形7.09.8 10kHz 60A正弦36.59.7 50kHz 60A正弦31.99.1 二次10kHz 26A梯形4.36.0 10kHz 60A正弦22.56.0 50kHz 60A正弦21.36.1
根据表2,一次及二次绕组在50kHz频率下的等效交流电阻分别为9.1mW和6.1mW,该HFT样机绕组漏感为20.8mH,对于图2b所示的测量方法,等效电感品质因数约为430,约为QAW的840倍,该方法的最大误差也约为AW方法的840倍。若使用相同的电流传感器,仅考虑传感器相位误差,传统测量方法已不能获得可信的绕组损耗。
受激励源工作频率及电流传感器带宽的限制,基于AW的绕组损耗直接测量方法可在数十kHz范围内获得可靠的测量结果,而基于AW的阻抗测量方法可将测量频率扩展至数百kHz。
为了定量分析高频下耦合电容Ceq对虚拟阻抗ZAW的测量影响,首先使用阻抗分析仪测量了HFT样机一次及二次绕组阻抗ZBb的幅频及相频特性曲线。根据阻抗ZBb的频率特性曲线,采用式(18)所示的阻抗模型进行参数拟合,拟合结果见表3。对于样机一次绕组,阻抗ZBb频率特性的测量曲线和拟合曲线如图12所示,在10kHz~3MHz频率范围内,拟合曲线与测量曲线基本吻合,表明图5所示的等效电路模型能够在该频率范围内描述实际绕组特性。
表3 阻抗ZBb的拟合参数
Tab.3 Fitting parameters of impedance ZBb
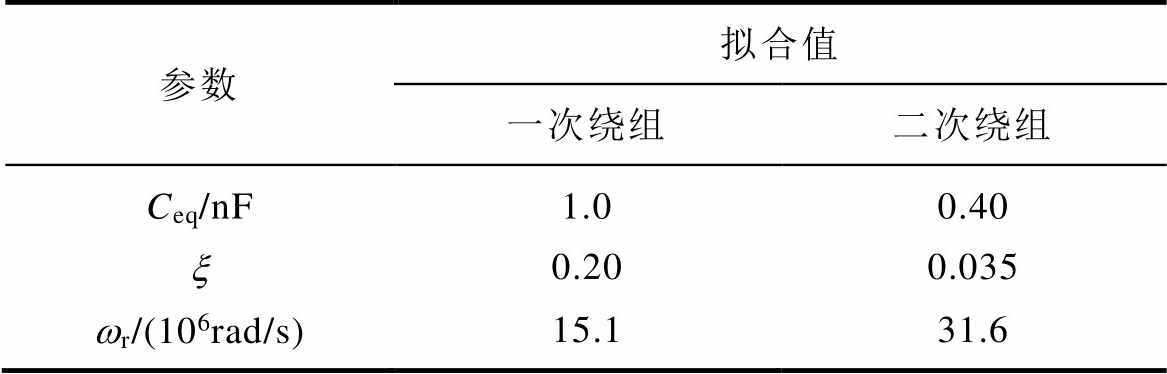
参数拟合值 一次绕组二次绕组 Ceq/nF1.00.40 x0.200.035 wr/(106rad/s)15.131.6
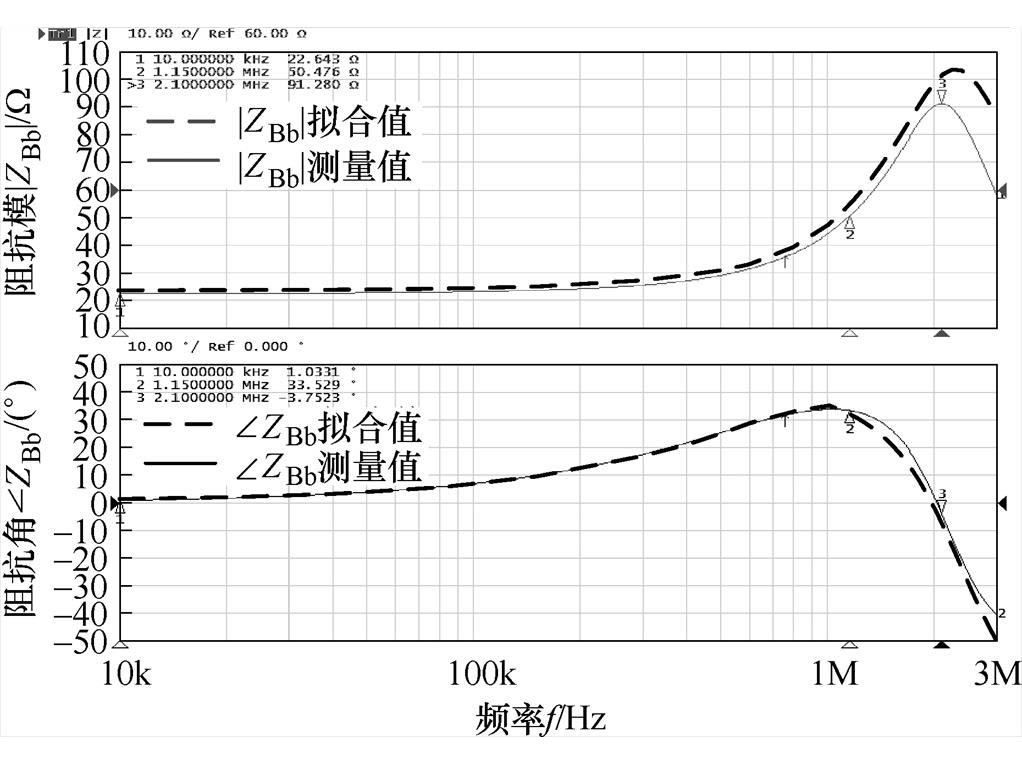
图12 阻抗ZBb的幅频及相频特性曲线
Fig.12 Amplitude-frequency and phase-frequency curves of ZBb
采用图7中的测量方法及测量平台,在10kHz~1MHz频率范围内,对HFT样机的一次、二次绕组的虚拟阻抗值进行测量,需要注意的是,实际测量得到的阻抗值为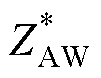 。采用表3中的拟合参数,根据式(18)和式(19)对阻抗
。采用表3中的拟合参数,根据式(18)和式(19)对阻抗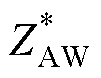 进行校正计算,得到阻抗ZAW。通过对比阻抗值
进行校正计算,得到阻抗ZAW。通过对比阻抗值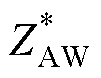 和校正后阻抗值ZAW的实部,即可分析不同频率下耦合电容Ceq对绕组交流电阻测量结果的影响,绕组交流电阻校正前后对比如图13所示。
和校正后阻抗值ZAW的实部,即可分析不同频率下耦合电容Ceq对绕组交流电阻测量结果的影响,绕组交流电阻校正前后对比如图13所示。
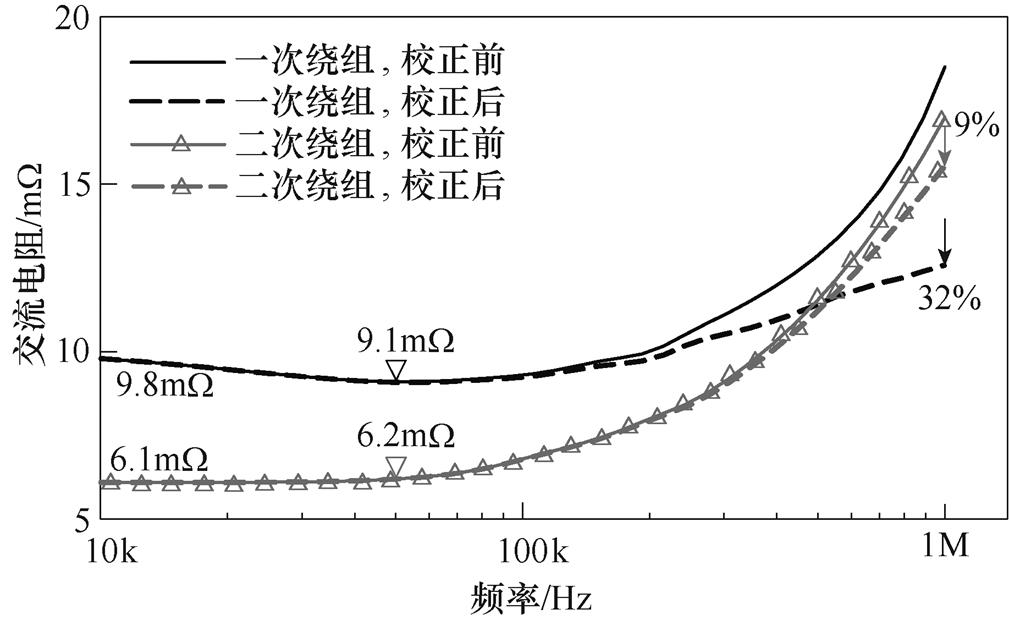
图13 绕组交流电阻校正前后对比
Fig.13 Comparison of winding AC resistance with and without correction
在低频下,耦合电容Ceq对绕组交流电阻测量影响较小,随着频率升高,若不考虑Ceq,交流电阻测量值将逐渐偏离实际值。对于HFT样机的一次绕组,其绕组长度大于二次绕组长度,且单股直径小于二次绕组股径,即一次绕组与AW的耦合更为紧密,故一次绕组与AW之间的等效耦合电容相对较大,进而导致一次绕组电阻未校正测量值的误差也更大。在1MHz频率处,经系数Kc校正后,一次及二次绕组电阻测量值分别减小了32%和9%。
在高频下,绕组交流电阻的准确测量不仅需要考虑耦合电容的影响,也决定于阻抗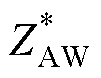 的测量精度。与有功测量误差类似,对于阻抗测量仪器,当被测器件品质因数Q>10时,其阻性分量测量误差显著增大,测量误差可表示为QE,其中E为由仪器自身、测试夹具及被测器件阻抗值决定的基础误差[12]。在10kHz~1MHz频率范围内,HFT样机一次及二次绕组阻抗
的测量精度。与有功测量误差类似,对于阻抗测量仪器,当被测器件品质因数Q>10时,其阻性分量测量误差显著增大,测量误差可表示为QE,其中E为由仪器自身、测试夹具及被测器件阻抗值决定的基础误差[12]。在10kHz~1MHz频率范围内,HFT样机一次及二次绕组阻抗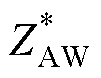 对应品质因数
对应品质因数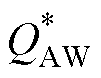 的测量结果如图14所示,其中1MHz频率点下品质因数分别为0.86和3.3,故在该频率下
的测量结果如图14所示,其中1MHz频率点下品质因数分别为0.86和3.3,故在该频率下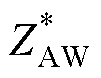 测量值依然有着较高的精度,表明从利兹线中选取单股线作为AW的方法可有效扩展AW测量方法的频率范围。
测量值依然有着较高的精度,表明从利兹线中选取单股线作为AW的方法可有效扩展AW测量方法的频率范围。
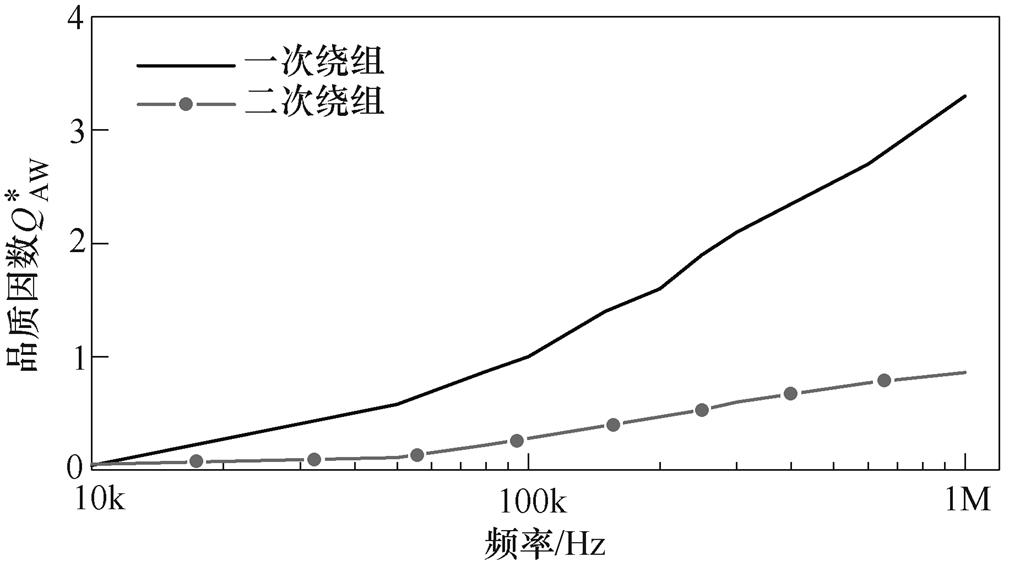
图14 品质因数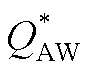 测量结果
测量结果
Fig.14 Measuring results of quality factor 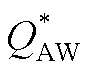
变压器中增加AW提供额外测量节点是提高绕组损耗测量精度的有效措施,根据等效电路分析模型,AW与WUT之间的漏感及耦合电容大小决定了AW方法的测量精度和适用频率范围。本文中100kV·A HFT样机的绕组损耗和电阻测量过程为AW方法的工程应用提供了有益参考。提高AW方法测量精度并扩展测量频率范围的要点可概括为:
1)尽可能减小AW与WUT之间的漏感,采用利兹线绕组中单股线作为AW是减小漏感的有效方法,同时降低了工程实施难度。
2)AW与WUT之间的谐振频率决定了测量频率上限,当测量频率接近谐振频率时,采用本文提出的校正方法可有效提高测量精度。
参考文献
[1] 涂春鸣, 黄红, 兰征, 等. 微电网中电力电子变压器与储能的协调控制策略[J]. 电工技术学报, 2019, 34(12): 2627-2636.
Tu Chunming, Huang Hong, Lan Zheng, et al. Coor- dinated control strategy of power electronic trans- former and energy storage in microgrid[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(12): 2627-2636.
[2] 兰征, 涂春鸣, 姜飞. 基于虚拟电机技术的直流微电网与主电网柔性互联策略[J]. 电工技术学报, 2019, 34(8): 1739-1749.
Lan Zheng, Tu Chunming, Jiang Fei. The flexible interconnection strategy between DC microgrid and AC grid based on virtual electric machinery tech- nology[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1739-1749.
[3] 周兵凯, 杨晓峰, 张智, 等. 能量路由器中双有源桥直流变换器多目标优化控制策略[J]. 电工技术学报, 2020, 35(14): 3030-3040.
Zhou Bingkai, Yang Xiaofeng, Zhang Zhi, et al. Multi-objective optimization control strategy of dual-active-bridge DC-DC converter in electric energy router application[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 3030-3040.
[4] 李子欣, 高范强, 徐飞, 等. 中压配电网用10kVAC- 750VDC/1MVA电力电子变压器功率密度影响因素研究[J]. 电工电能新技术, 2016, 35(6): 1-6.
Li Zixin, Gao Fanqiang, Xu Fei, et al. Power density analysis of 10kVAC-750VDC/1MVA power electronictransformer/solid-state transformer for medium voltage distribution grid[J]. Advanced Technology of Elec- trical Engineering and Energy, 2016, 35(6): 1-6.
[5] Leibl M, Ortiz G, Kolar J W. Design and experimental analysis of a medium-frequency transformer for solid-state transformer applications[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2017, 5(1): 110-123.
[6] Guillod T, Huber J, Krismer F, et al. Litz wire losses: effects of twisting imperfections[C]//2017 IEEE 18th Workshop on Control and Modeling for Power Electronics (COMPEL), Stanford, USA, 2017: 1-8.
[7] Marko, Mogorovic, Drazen, et al. 100kW, 10kHz medium-frequency transformer design optimization and experimental verification[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1696-1708.
[8] 张珂, 曹小鹏, 乔光尧, 等. 高频变压器绕组损耗解析计算分析[J]. 中国电机工程学报, 2019, 39(18): 5536-5546.
Zhang Ke, Cao Xiaopeng, Qiao Guangyao, et al. Analysis of winding loss calculation methods for high frequency transformers[J]. Proceedings of the CSEE, 2019, 39(18): 5536-5546.
[9] Ehrlich S, Rossmanith H, Sauer M, et al. Fast numerical power loss calculation for high frequency litz wires[J]. IEEE Transactions on Power Electronics, 2020, 36(2): 2018-2032.
[10] Chen Bin, Li Lin. Semi-empirical model for precise analysis of copper losses in high-frequency trans- formers[J]. IEEE Access, 2018, 6: 3655-3667.
[11] Andreas R, Eberhard B, Christopher J, et al. Calcu- lation of power losses in litz wire systems by coupling FEM and PEEC method[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6442-6449.
[12] Zhang R Y, White J K, Kassakian J G, et al. Realistic litz wire characterization using fast numerical simu- lations[C]//2014 IEEE Applied Power Electronics Conference and Exposition, Fort Worth, USA, 2014: 738-745.
[13] Javidi N F, Nymand M. A new method for measuring winding AC resistance of high efficiency power inductors[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10736-10747.
[14] 叶建盈, 陈为, 郑荣进, 等. 磁元件绕组损耗的直接测量法[J]. 中国电机工程学报, 2018, 38(5): 1369- 1374.
Ye Jianying, Chen Wei, Zheng Rongjin, et al. The direct measurement method of magnetic winding losses[J]. Proceedings of the CSEE, 2018, 38(5): 1369-1374.
[15] 王瑞田, 肖飞, 赵治华, 等. 基于辅助绕组的中频变压器绕组交流电阻测量方法[J]. 电工技术学报, 2019, 34(2): 245-254.
Wang Ruitian, Xiao Fei, Zhao Zhihua, et al. Investigation on measurement method of transformer winding AC resistance by using auxiliary winding[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 245-254.
[16] 刘建强, 赵楠, 孙帮成, 等. 基于LLC谐振变换器的电力电子牵引变压器控制策略研究[J]. 电工技术学报, 2019, 34(16): 3333-3344.
Liu Jianqiang, Zhao Nan, Sun Bangcheng, et al. Research on control strategy of power electronic traction transformer based on LLC resonant con- verter[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3333-3344.
[17] Lim M H F, Wyk J D V. Errors in electrical core loss measurement for extremely small samples applicable to integrated converters[C]//IEEE Applied Power Electronics Conference & Exposition, Washington, USA, 2009: 1022-1026.
[18] Keysight Technologles. Impedance measurement handbook[EB/OL]. Santa Clara, USA: Keysight Tech- nologies, 2016, https://www.keysight.com/cn/zh/assets/7018-06840/application-notes/5950-3000.pdf.
[19] HIOKI. CT6862, CT6863, CT6862-10, CT6863-10, CT6862-05, CT6863-05 AC/DC CURRENT SENSOR Instruction Manual[EB/OL]. Nagano, Japan: HIOKI E.E CORPORATION, 2018. https://www.hioki.cn/ userscenter/intellectual/download.php?id=1449.
A Measurement Method of Winding Loss for High-Frequency Transformer Based on Auxiliary Winding
Abstract The measurement of winding loss is a difficult issue in the modeling and design of high-power high-frequency transformers (HFT), and a high precision winding loss measurement method is an important tool for verifying the correctness of winding loss theory and improving the accuracy of modeling and simulation. The accuracy of short-circuit impedance measurement method widely used at present decreases with the increase of measurement frequency, so it is not suitable for HFT. Creating additional measurement nodes by aiding auxiliary windings (AW) is an effective measure to improve the measurement accuracy of winding loss. An equivalent circuit model including stray parameters of AW was established, and the analysis results show that the leakage inductance and coupling capacitance between AW and winding under test (WUT) greatly affect the frequency range and accuracy of winding loss measurement. A correction method of winding resistance measurement considering coupling capacitance was proposed, which extended the measurement range of frequency and kept the measurement accuracy under high frequency. A single strand in Litz wire winding was used as AW, the leakage between AW and WUT was thus reduced to a very low level, and the engineering practice of winding loss measurement was simplified. By measuring the winding parameters of a 100kVA HFT prototype, the circuit model and the correction method were verified, and the effective measurement of the winding AC resistance at 1MHz was realized.
keywords:High-frequency transformer, winding loss, auxiliary winding, error analysis
DOI: 10.19595/j.cnki.1000-6753.tces.210528
中图分类号:TM433
汪 涛 男,1981年生,硕士,研究方向为柔性直流输电及柔性交流输电。E-mail: wangtao@nrec.com
骆仁松 男,1992年生,硕士,研究方向为大功率电力电子变换器的设计与优化。E-mail: luors@nrec.com(通信作者)
收稿日期 2021-04-16
改稿日期 2021-06-22
国家电网公司科技资助项目(5500-202040326A-0-0-00)。
(编辑 陈 诚)