图1 微电网系统结构示意图
Fig.1 Structure of microgrid system
摘要 该文提出一种具有高电能质量且无需远程通信线的微电网平滑切换控制策略。微电网主要由多台并联分布式发电单元和一台预同步单元构成,针对分布式发电单元中的接口逆变器提出一种统一并网电流控制结构,具有如下优点:①无需孤岛检测便能实现逆变器并网运行状态电流控制模式和孤岛运行状态电压控制模式的自动切换,以确保负载供电质量;②所提统一并网电流控制结构能有效抑制并网电流与电容电压中的谐波;③当电网频率发生波动时,逆变器仍能按照指令值输出相应的有功及无功功率,并且在并网运行状态无需锁相环或锁频环即可实现与电网同步。此外,所提出的预同步单元能够在不依赖远程通信线的情况下实现微电网电压与电网电压的预同步控制,减小孤岛运行状态转为并网运行状态时的冲击电流。最后,对控制参数进行优化设计,并通过实验验证所提控制策略的有效性和可行性。
关键词:无缝切换 并网模式 孤岛模式 预同步 电能质量
近年来,伴随着微电网的快速发展,逆变器作为微电网中重要的电力电子变换器,其控制方法对微电网系统的稳定运行具有重要意义[1-2]。一个稳定的微电网系统不仅要求其能够在并网(Grid-Connected, GC)模式和孤岛(Stand-Alone, SA)模式下稳定运行,而且其需要保证能够在两种模式间实现无缝切换,从而确保系统内关键负载的供电质量。
目前,多逆变器协调控制策略主要分为集中控制和分布控制两类。其中集中控制需要中央控制器和远程通信线,当微电网系统规模较大,分布式发电(Distributed Generation, DG)单元分布较分散时,远程通信线会大幅增加建设成本并降低系统的可靠性,因此无通信线的分布控制是目前研究的重点。
分布控制主要包括主从控制与对等控制。对于主从控制中主逆变器在并网模式与孤岛模式间的无缝切换策略,学者们已经做了诸多研究。文献[3]提出了一种应用于光伏-电池储能的控制策略,其将电流控制与电压控制相结合,使得系统可以在电网故障时平滑地切换到孤岛模式运行。但是在两种不同的控制器间切换可能会使切换受到励磁涌流和畸变电压的影响。鉴于此,文献[4]提出一种基于观测器的无传感电容电流控制策略,在并网模式下,并网电流外环与孤岛控制结构相结合,形成了一个利于模式切换的复合控制结构。然而,电容电压的参考值选取依赖于孤岛检测,在检测时间内的供电质量无法得到保证。对此,一种间接电流控制策略成为研究热点,即在并网模式下,并网电流环作用将逆变器控制为一个电流源;而在孤岛模式中,其会自动饱和切换为电压控制[5]。但是这种方法对主逆变器可靠性要求高,整个系统额定功率大且其中远距离设备供电电压质量较差。对等控制作为另一种无需通信的控制方法[6-9],同样存在诸多问题。例如,当电网发生波动时,并网电流和电容电压中均会存在谐波扰动,此时系统内的供电质量必然会受到一定程度的影响。
当电网恢复后,首先应对并网开关两侧的电压进行预同步控制。现有预同步控制策略大多依赖远程通信线获取电网电压信息,逆变器据此来调节自身输出电压使其与电网电压一致。但实际上,DG单元通常分布较为分散,这大大增加了微电网系统的建设成本与难度。
基于上述分析,本文提出了一种无通信高电能质量的微电网平滑切换控制策略,微电网包括分布式发电单元以及预同步单元。该策略可以在不同模式下稳定运行,并且具有以下优点:
(1)针对分布式发电单元的接口逆变器,提出一种统一并网电流控制结构,其d轴与q轴分别采用比例积分(Proportional Integral, PI)控制器和比例(Proportional, P)控制器。在并网模式下,PI控制器调节并网电流d轴分量igd使其追随其参考值,在q轴上建立逆变器角频率w 与并网电流q轴分量igq间的下垂关系,因此无需锁相环(Phase-Locked- Loop, PLL)或锁频环(Frequency-Locked-Loop, FLL),从而简化了控制算法。
(2)实现平滑切换,确保不同状态切换时的负载供电质量,且该策略适用于并联逆变器。当孤岛发生后,并网电流环中d轴的积分控制器将自动饱和,从而由PI控制变为P控制,在电容电压d轴分量vCd与并网电流d轴分量igd间建立起下垂关系。在孤岛模式时,该电流下垂控制可以实现并联逆变器间的功率均分。此外,在并网电流与电容电压环中均添加了重复控制(Repetitive Control, RC)器,用于抑制电流与电压中的谐波扰动。
(3)所提预同步单元位于公共连接点(Point of Common Coupling, PCC)附近,该单元可以方便地检测到并网开关两侧的电压,从而根据两侧电压差调节自身输出功率,进而影响系统内其他逆变器的输出电压,实现预同步控制。因此,无需用于调节DG输出电压的反馈控制以及相关的远程通信线路。
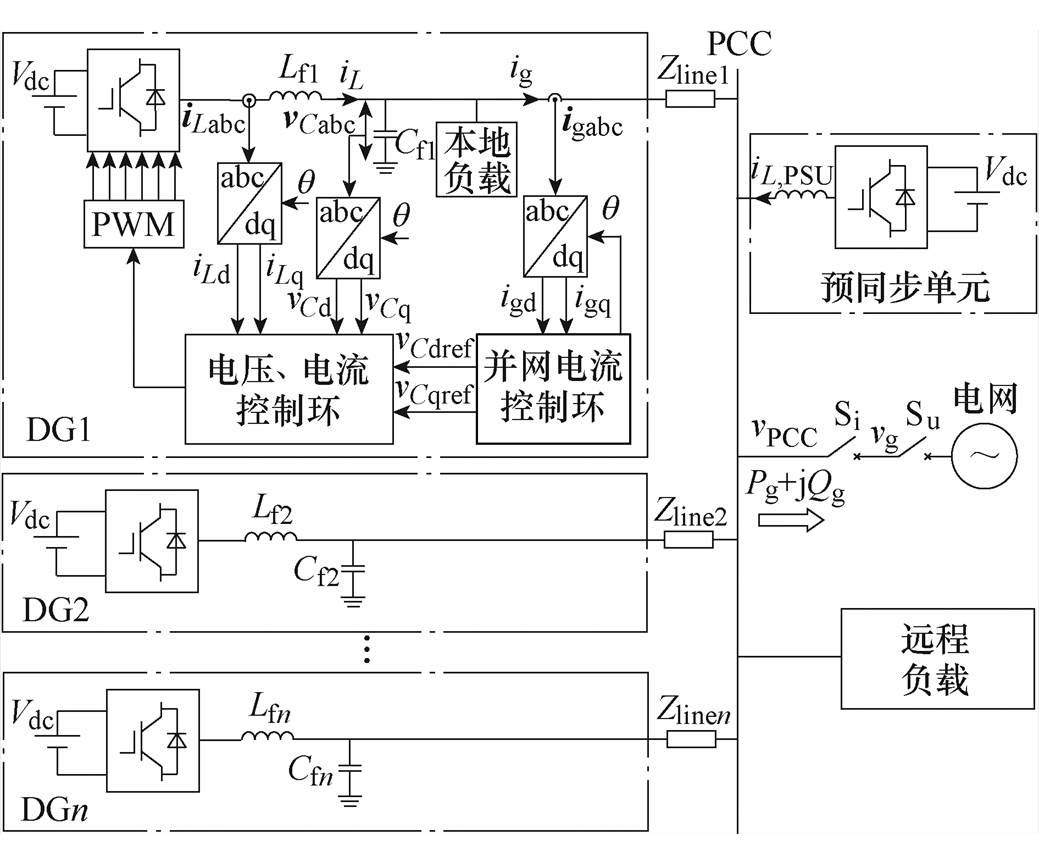
图1给出了微电网系统结构示意图,图中,包含n个并联的DG单元、预同步单元、线路阻抗、本地及远程负载。图中,Zlinen为各台逆变器与PCC之间的线路阻抗,Vdc为直流母线电压,Lfn和Cfn共同组成LC滤波器。在所提控制策略中,采样LC滤波器电感电流iLabc、电容电压vCabc、并网电流igabc用于控制,通过Park变换将abc坐标系下的模型变换至dq坐标系中。dq坐标系中,iLd、iLq为电感电流,vCd、vCq为电容电压,igd、igq为并网电流,q 为Park变换的相位,下标ref表示给定的参考值。同时采样微电网PCC电压vPCC以及并网保护开关Si、网侧电压vg用于实现预同步控制,iL,PSU为预同步单元的输出电流,其同样作用于预同步控制。

图1 微电网系统结构示意图
Fig.1 Structure of microgrid system
当电网正常运行时,并网保护开关Si和断路器Su均保持闭合,微电网运行在并网模式下,假设此时微电网向电网注入功率Pg+jQg;当电网发生故障时,断路器Su会立即断开,同时形成一个孤岛状态,系统在检测到该孤岛后,并网保护开关Si随即断开;当电网故障解除时,断路器Su立即闭合;当并网保护开关两侧电压同步后,Si随即闭合。
分布式发电单元接口逆变器的控制结构框图如图2所示,由并网电流环、电容电压环和电感电流内环组成。
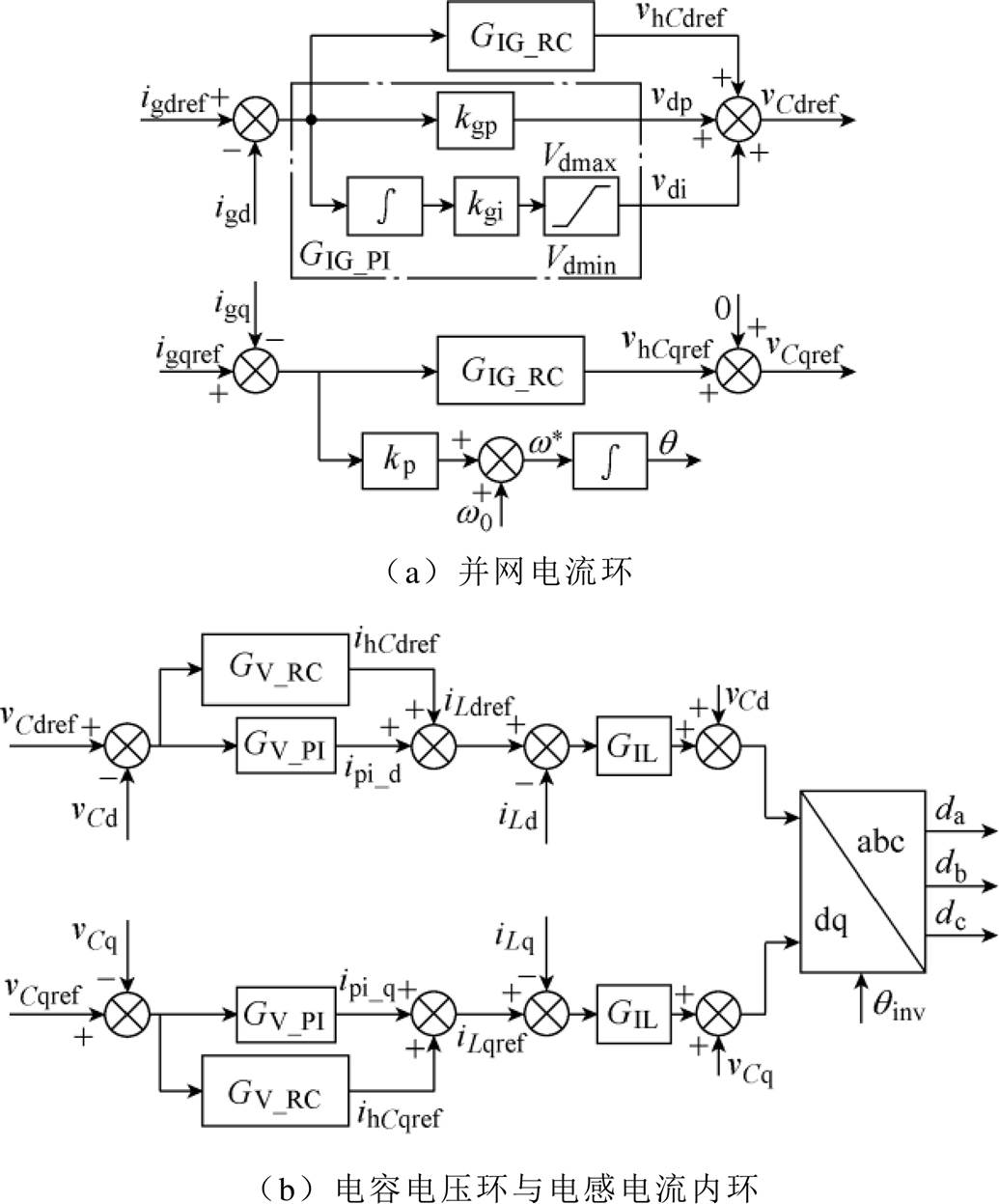
图2 逆变器控制结构框图
Fig.2 Control structure block of inverter
1.2.1 并网电流环
并网电流环的d轴由PI控制器GIG_PI和RC控制器GIG_RC构成,其中,kgp为PI控制器的比例系数。在并网状态下,限幅器不限制积分器的输出,PI控制器GIG_PI使并网电流igd跟随其指令值igdref。当故障时,并网电流立刻减为0,PI控制器GIG_PI中的积分控制器输出将持续增大至限幅器上限值,从而使得积分控制器失效,此时PI控制器GIG_PI转变为P控制器。
RC控制器GIG_RC抑制并网电流谐波,其内部结构示意图如图3所示。内模中的Q(z)为辅助补偿器,可将系统的开环极点置于单位圆内,从而稳定闭环系统。Gf (z)为另一个补偿器,用于补偿系统的幅值和相位。
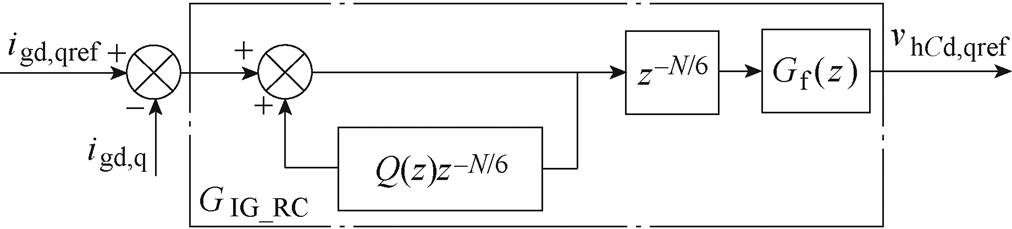
图3 RC控制器GIG_RC结构示意图
Fig.3 Structure of RC controller GIG_RC
并网电流环的q轴构建了一个w-igq的下垂控制结构,使逆变器电压相位自动与电网电压相位同步,从而省略了锁相环。
1.2.2 电容电压环
电容电压环基于dq坐标变换,d轴与q轴结构完全对称。PI控制器GV_PI的作用是实现零稳态误差,使得电容电压vCdq跟随指令值vCd,qref。并网电流环中的输出vhCd,qref作为电容电压环中RC控制器GV_RC的参考值,使得电容电压vCdq中的谐波分量跟随其变化。
1.2.3 电感电流内环
电感电流内环的作用是增加系统的阻尼,增强系统的快速性,GIL为P控制器。
执行预同步操作的预同步单元内部控制结构如4所示。
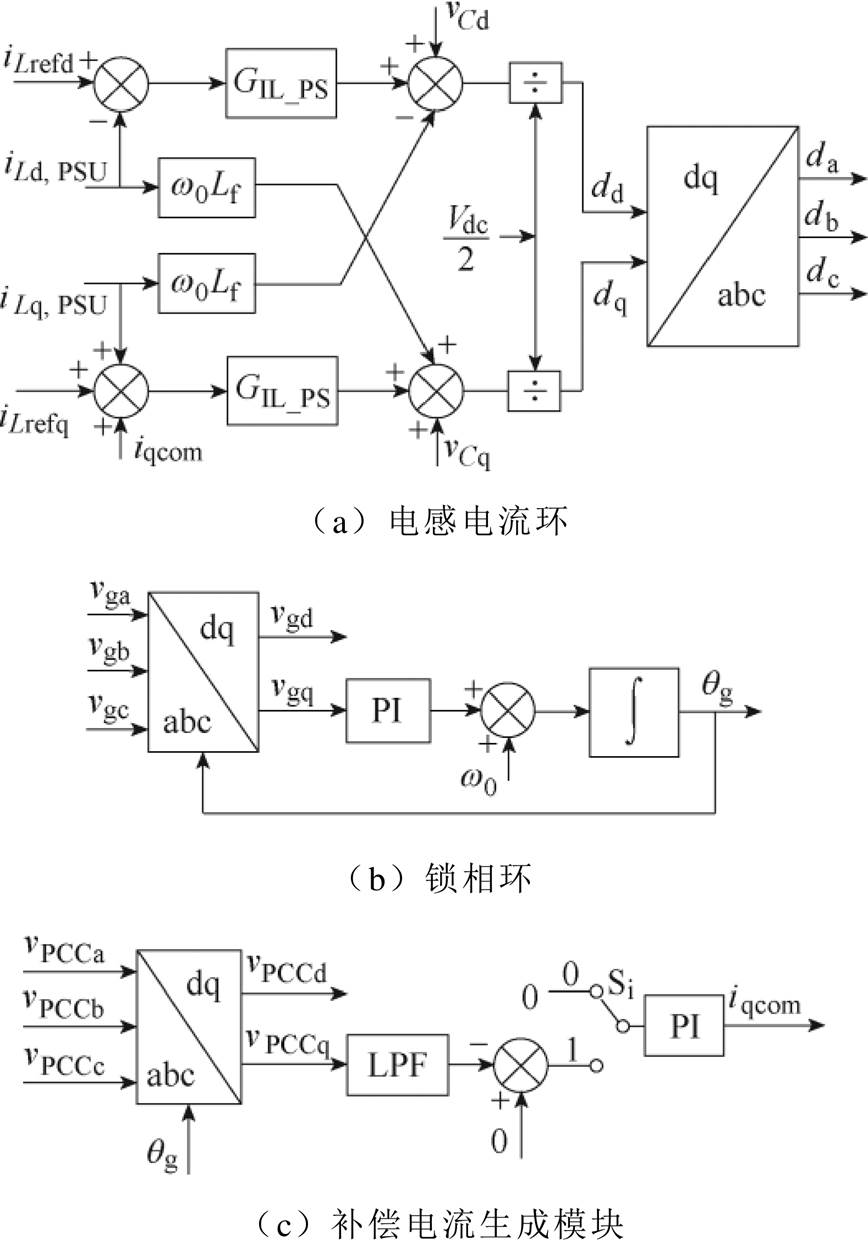
图4 预同步单元控制结构
Fig.4 Control block of pre-synchronization unit
预同步单元直接与PCC连接,便于测量并网保护开关Si两侧的电压vPCC和vg。如图4c所示,将锁相环检测出的电网电压vg的相位qg用于PCC电压的坐标变换。PCC电压的q轴分量vPCCq经低通滤波器滤波后,由PI控制器调节,以产生图4a中的q轴补偿电流参考iqcom。
在预同步过程中,该单元输出额外的无功功率以调节其他逆变器的频率,并且实现并网保护开关Si两侧的电压vPCC和vg的相位同步。
基于该控制结构的接口逆变器运行原理分为以下四个模式具体介绍:并网运行模式、并网转孤岛运行模式、孤岛运行模式和孤岛转并网运行模式。
当系统运行在并网运行模式下,逆变器被控制为电流源。在该模式下,d轴的PI调节器GIG_PI控制d轴并网电流分量igd跟随其参考值igdref,可使并网逆变器与电网角频率保持同步,具体分析如下:
假设电网角频率wg约为额定角频率w0,根据图2结构,可得逆变器电容电压与电网电压间的相位差d 为
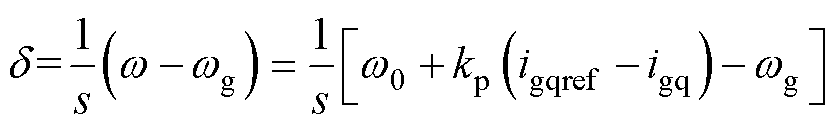
 (1)
(1)
并网逆变器的简化模型如图5所示,图中,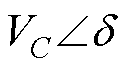 为逆变器电容电压,
为逆变器电容电压,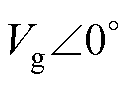 为电网电压,
为电网电压,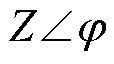 =R+jX为线路阻抗。
=R+jX为线路阻抗。
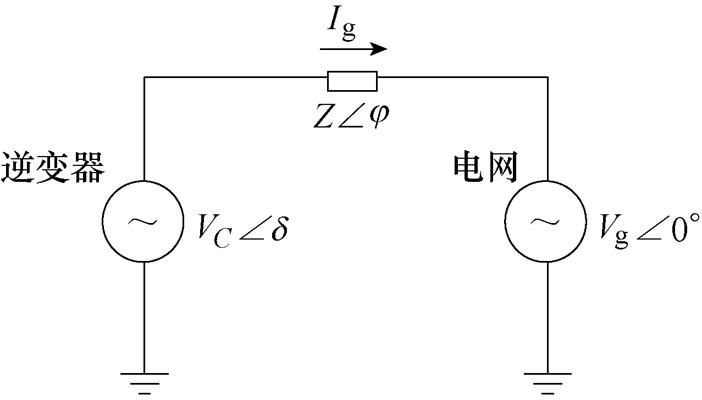
图5 并网逆变器简化模型
Fig.5 Simplified model of grid-connected inverter
根据图5所示,可得并网电流Ig为
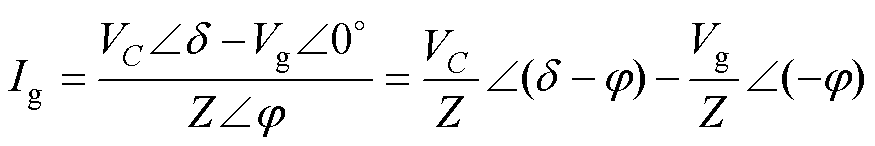 (2)
(2)
逆变器向电网注入的有功和无功功率分别为
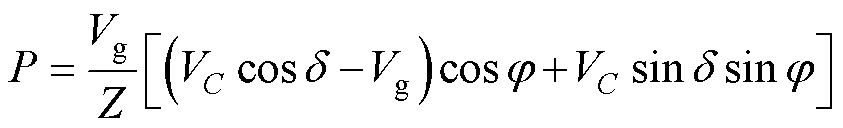 (3)
(3)
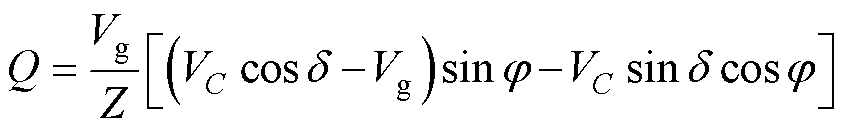 (4)
(4)
在低压微电网中, ,从而
,从而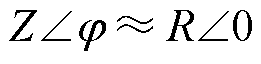 。由于d 通常很小,所以式(3)与式(4)可简化为
。由于d 通常很小,所以式(3)与式(4)可简化为
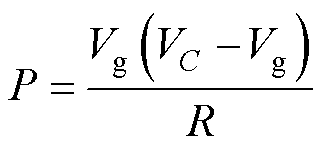 (5)
(5)
 (6)
(6)
由于电容电压d轴分量vCd的幅值通常远大于q轴分量vCq的幅值,所以逆变器向电网注入的有功与无功功率亦可表示为
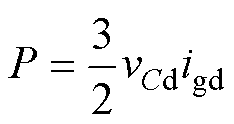 (7)
(7)
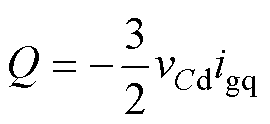 (8)
(8)
结合式(6)与式(8)可知,并网电流q轴分量igq与电压相位差d 成正比。同时,结合图2中构建的w-igq的下垂关系,即可确保逆变器与电网相位的同步,即
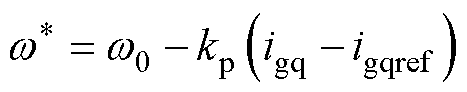 (9)
(9)
假设逆变器角频率w(忽略w 与其参考值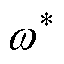 之差)大于电网角频率wg,那么相位差d 随即增大,由于正比关系的存在,igq也会增大。当igq增大时,由于下垂关系的存在,w 随即减小,最后与wg相等,逆变器实现与电网相位的同步。因此,基于该结构控制的逆变器可以在没有锁相环的条件下并网运行。
之差)大于电网角频率wg,那么相位差d 随即增大,由于正比关系的存在,igq也会增大。当igq增大时,由于下垂关系的存在,w 随即减小,最后与wg相等,逆变器实现与电网相位的同步。因此,基于该结构控制的逆变器可以在没有锁相环的条件下并网运行。
当电网正常工作时,由于逆变器角频率w 等于或近似等于额定角频率w0,因此根据式(10),电网电流q轴分量igq会跟随其参考值igqref 变化,最终相等。
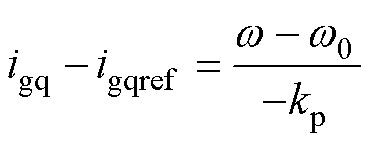 (10)
(10)
当电网电压失真时,并网电流环与电容电压环中的重复控制器同时作用,抑制电流与电压中的各次谐波分量。
当故障时,断路器Su会立刻断开,并建立孤岛,微电网向电网注入的有功功率和无功功率均降为0,DG的输出功率保持恒定。此时,远程负载的有功功率及无功功率增加,从而导致PCC处电压幅值增加,频率下降。根据文献[10]中的分析,在低压微电网中,并网电流d轴分量igd下降,q轴分量igq增加。因此,如图2所示,并网电流环中的d轴PI控制器GIG_PI的输入大于零,并且积分控制器的输出一直增加到上限值后,积分器失效,P控制器继续工作,并且在并网电流d轴分量igd和电容电压d轴分量vCd之间建立起下垂关系。
当系统检测到孤岛后,并网保护开关Si断开。此时,逆变器在并网电流环路中采用P调节器,分别在d轴和q轴上建立vCd-igd,w-igq下垂控制。有功与无功功率都可以在逆变器间做到大致均分。如果并网电流q轴分量igq在逆变器间没有做到均分,则根据式(9),每个逆变器的角频率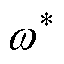 都不相同,从而导致逆变器电容电压与PCC处电压间相位差发生变化,igq也将随相位差的变化而变化,最终各台逆变器的角频率
都不相同,从而导致逆变器电容电压与PCC处电压间相位差发生变化,igq也将随相位差的变化而变化,最终各台逆变器的角频率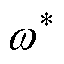 相等,igq实现均分。
相等,igq实现均分。
各台逆变器并网电流d轴分量igd是否相等取决于各自的线路阻抗Zlinen,如果各台逆变器线路阻抗相等,则igd可以实现均分;如果各台逆变器的线路阻抗不相等,vCd-igd下垂关系示意图如图6所示,vCd-igd的下垂关系也有助于均分igd。

图6 vCd-igd下垂关系示意图
Fig.6 Diagram of vCd-igd droop relationship
当逆变器运行在孤岛状态时,并网电流环中的RC控制器GIG_RC失效,电容电压环中的RC控制器GV_RC继续作用,用来抑制此时由非线性负载引起的电容电压谐波。
当电网故障恢复后,断路器Su随即闭合,当执行完预同步操作,即PCC处的电压vPCC与电网电压vg同步后,并网保护开关Si闭合。
预同步单元通过检测电网电压vg判断电网是否运行正常,如果运行正常,图4c补偿电流生成模块中的开关将由0切换到1。根据派克变换公式,该模块中的变换可表示为
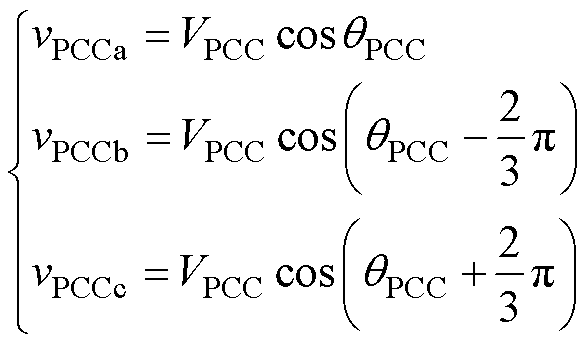 (11)
(11)
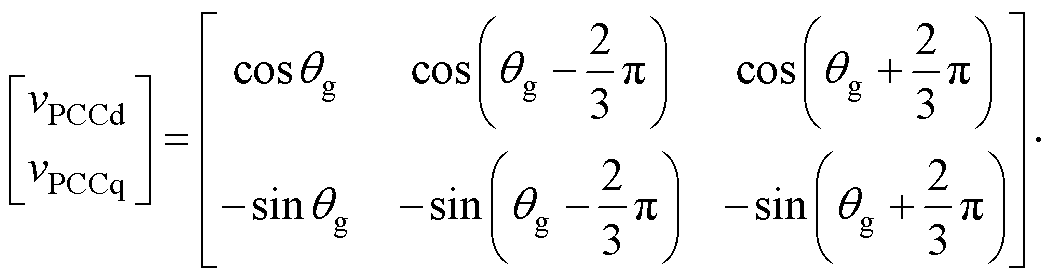
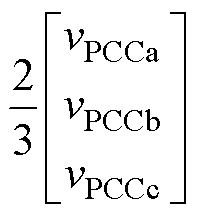 (12)
(12)
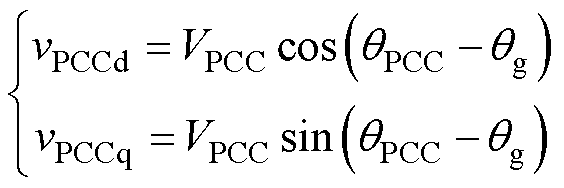 (13)
(13)
式中,使用电网电压相位qg作为派克变换中的变换角。
PCC处电压q轴分量vPCCq与0作差后经PI控制输出q轴补偿电流参考值iqcom,如图4a所示,PI控制器GIL_PSU控制预同步单元实际输出电流q轴分量iLq,PSU跟随其指令值iLrefq+iqcom变化。
由于w-igq存在下垂关系,单个逆变器的角频率将随其输出无功功率的变化而变化。逆变器输出电压的相位发生变化,PCC处电压也会发生变化。由于图4c中PI控制器GIL_PSU的作用,预同步单元的输出电流q轴分量iLq,PSU改变,使得qPCC与qg趋于相等,最终完成qPCC和qg的同步,从而实现无需远程通信线的相位预同步。
最后,并网保护开关Si闭合,微电网与电网重新连接。一段时间后,并网电流环中d轴积分控制器后的限幅器去饱和,PI调节器GIG_PI再次发挥作用,激活并网电流环中的重复控制器GIG_RC。并且,在并网保护开关Si闭合后,预同步单元中的补偿电流iqcom置零。
正如第2节所述,假设微电网向电网注入功率,当逆变器从并网模式向孤岛模式过渡时,并网电流环中积分控制器的输出会持续增加至上限值;若电网向微电网注入功率,则积分控制器的输出会持续减小至下限值。限幅器上限值应大于额定电容电压幅值,下限值应小于额定电容电压幅值。同时,根据标准IEEE 1547-2018[10],电压允许运行范围是0.88~1.1Vnom,其中Vnom是额定电容电压幅值。因此为了确保电容电压始终满足规定,限幅器幅值亦应遵循以下原则
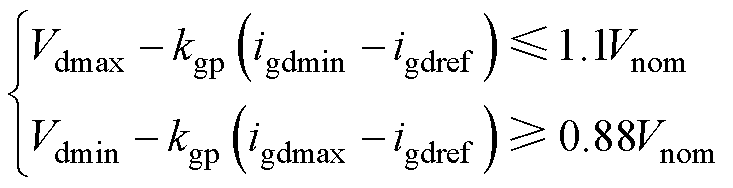 (14)
(14)
电容电压环的作用是调节电容电压,其内部的电感电流内环用于改善系统动态性能并增加阻尼。根据文献[11],电压环控制器控制目标的传递函数如式(15)所示,主电路参数见表1,控制框图如图7所示。图中,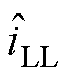 为小信号模型下的本地负载电流。
为小信号模型下的本地负载电流。
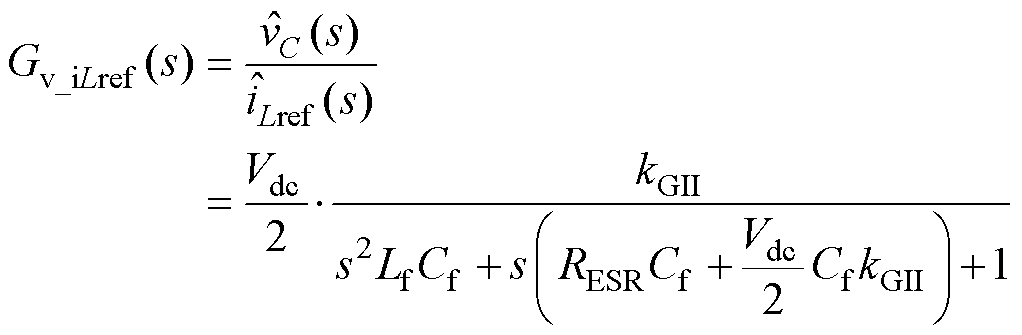 (15)
(15)
表1 主电路参数
Tab.1 The main circuit parameters
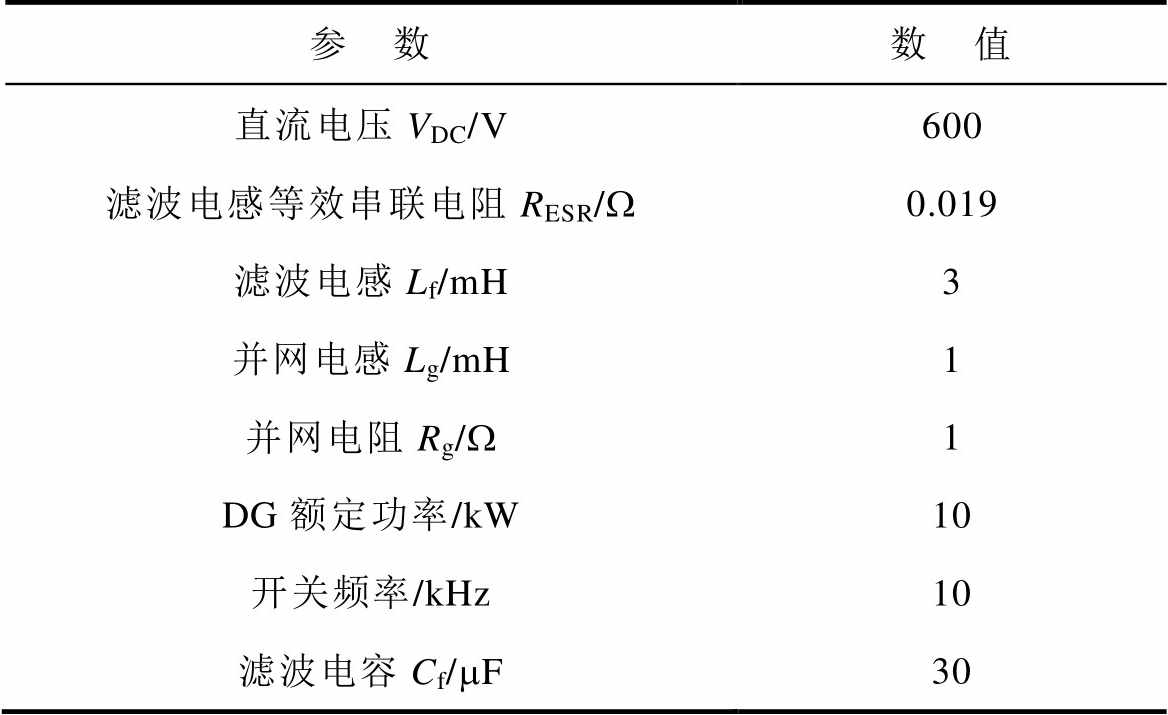
参 数数 值 直流电压VDC/V600 滤波电感等效串联电阻RESR/W0.019 滤波电感Lf/mH3 并网电感Lg/mH1 并网电阻Rg/W1 DG额定功率/kW10 开关频率/kHz10 滤波电容Cf/mF30
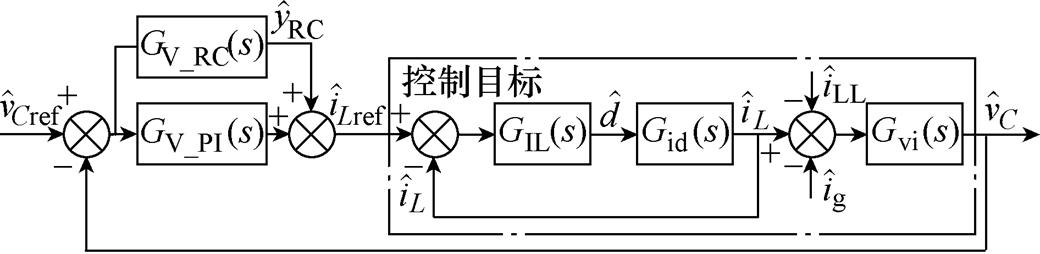
图7 电容电压环控制目标
Fig.7 Control objective of capacitor voltage controller
电感电流内环中GIL(s)的比例系数kGII根据二阶系统的最佳阻尼系数z 进行设计,取kGII=0.0707。电容电压环中的PI控制器GV_PI参数设计在参考文献[11]中已做详细说明,在此不再赘述。
由于电容电压环与并网电流环中RC控制器的结构相同,且RC控制器通常在离散域中设计,参照图3,GV_RC的z域传递函数为
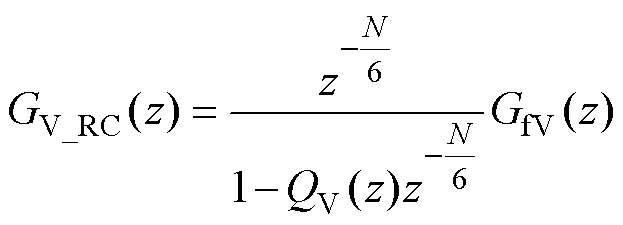 (16)
(16)
周期采样数N=fs/f =104/50=200,辅助补偿器QV(z)=0.98,补偿器GfV(z)=KrVzkSV(z)通常根据零相移跟踪理论进行设计,用来补偿系统的幅值与相位,其中,KrV用于补偿幅值,通常取(0, 1)间的常数;zk为相位补偿环节,其用于补偿RC控制内模中的延迟环节产生的相位滞后;SV(z)为滤波器,通常设计成一个二阶低通滤波器,提高系统抗干扰能力。关于RC控制器参数设计文献众多,在此不再赘述[12-16]。从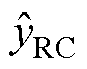 到
到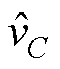 的传递函数可以视为电容电压环RC控制器的控制目标,其传递函数如式(17)所示,等效控制框图如图8所示。
的传递函数可以视为电容电压环RC控制器的控制目标,其传递函数如式(17)所示,等效控制框图如图8所示。
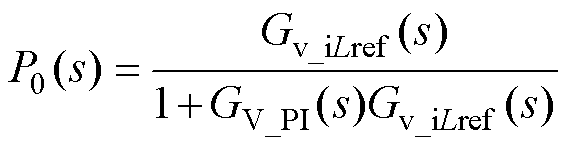 (17)
(17)
补偿前后离散域中等效控制目标的Bode图如图9所示。H1(z)与H2(z)的表达式分别为
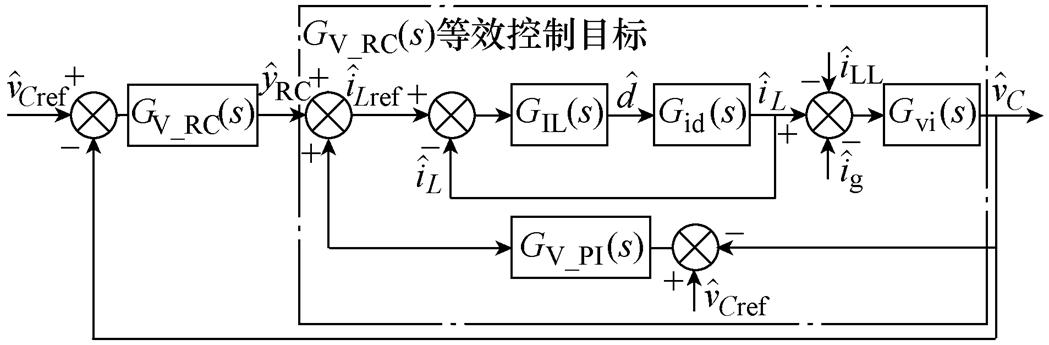
图8 GV_RC等效控制框图
Fig.8 Equivalent control object of GV_RC
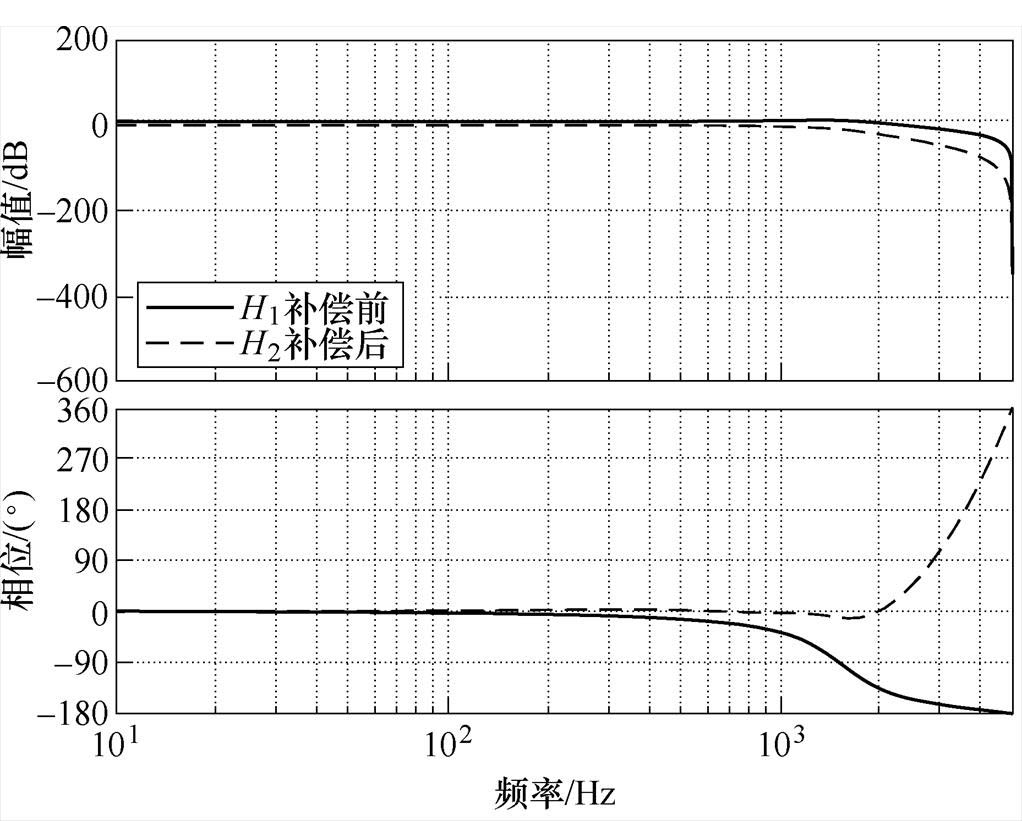
图9 GV_RC补偿前后控制目标Bode图
Fig.9 Bode plot of the control objective of GV_RC before and after compensation
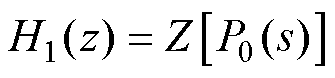 (18)
(18)
 (19)
(19)
式中,Z[x]为x的离散域表达式;GV_RC的补偿器GfV(s)中,取KrV=0.45,相位补偿设为二阶;二阶低通滤波器SV(z)的截止频率为800×2πrad/s,阻尼比为0.707。
因为并网电流环路的带宽比电容电压环路的带宽要高得多,所以在设计并网电流环中的控制器时,可以将电容电压环视为理想环路,其闭环传递函数的增益在全频段都是相同的。
并网电流环的控制目标如图10所示。可以简化为
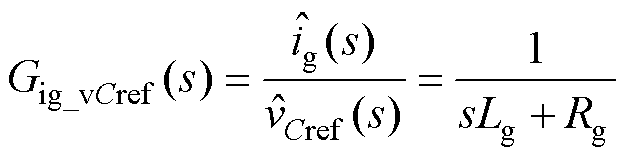 (20)
(20)
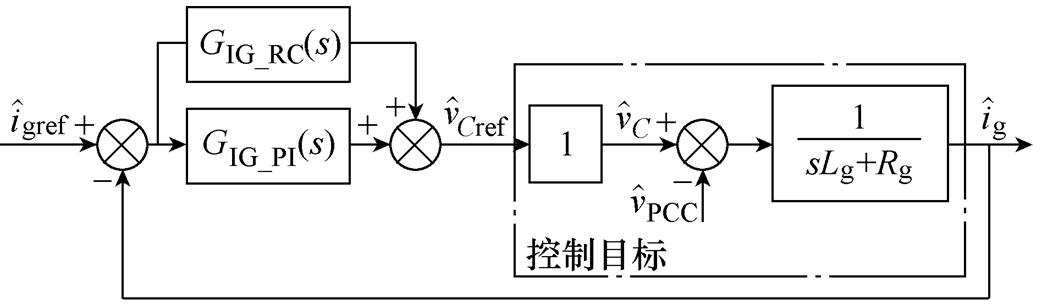
图10 并网电流环控制目标
Fig.10 Control objective of grid current controller
并网电流环的环路增益与实际电压环路和理想电压环路的Bode曲线如图11所示。在频率低于300Hz时,两条曲线几乎重合。因此,简化电压环是合理的。
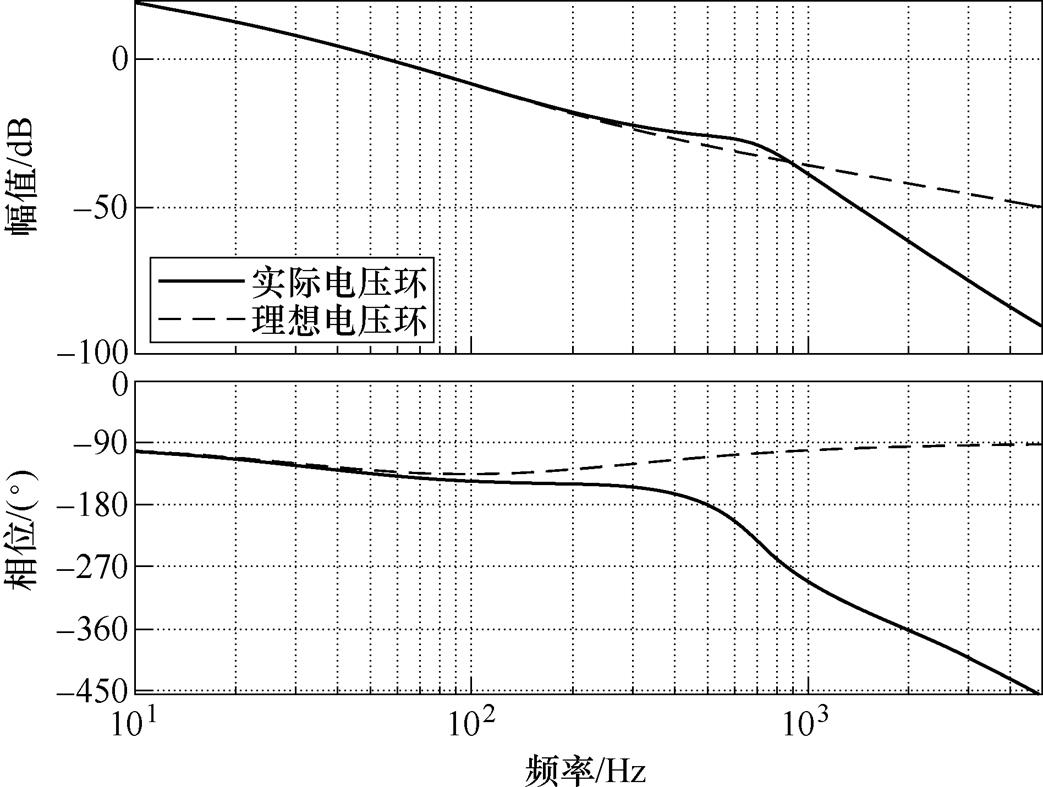
图11 并网电流环的环路增益与实际电压环路和理想电压环路的Bode曲线
Fig.11 Bode plot of the loop gain of grid current loop with ideal and actual voltage loop
PI控制器GIG_PI的参数设计同样在文献[11]中已做过详细说明,不再赘述。RC控制器GIG_RC的传递函数与电压环中的GV_RC类似。其中周期采样数N=200,QIG(z)=0.98,GfIG(z)=KrIGzkSIG(z)。GIG_RC的等效控制目标如图12所示,离散域中补偿前后等效控制目标的Bode图如图13所示。
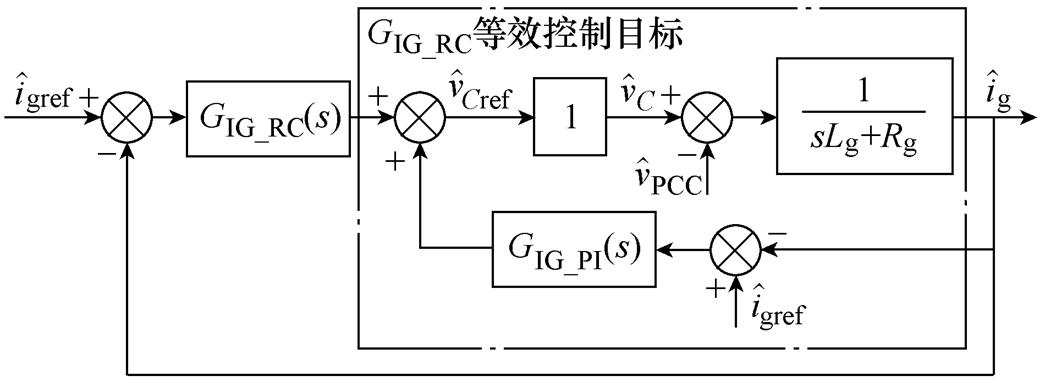
图12 GIG_RC等效控制目标
Fig.12 Equivalent control object of GIG_RC
在补偿项GfIG(z)中,超前拍数k=4,KrIG=0.5,二阶低通滤波器SIG(z)的截止频率为650×2πrad/s,阻尼比为0.707。
为了改善动态性能,预同步单元仅用一个电感电流环控制,其小信号模型可以描述为
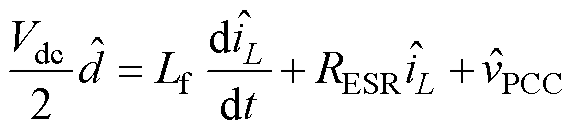 (21)
(21)
式中,Vdc为直流电压;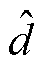 为小信号占空比;RESR为滤波电感Lf的等效串联电阻;
为小信号占空比;RESR为滤波电感Lf的等效串联电阻;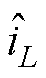 和
和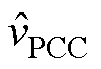 分别为电感电流和PCC电压的小信号。
分别为电感电流和PCC电压的小信号。
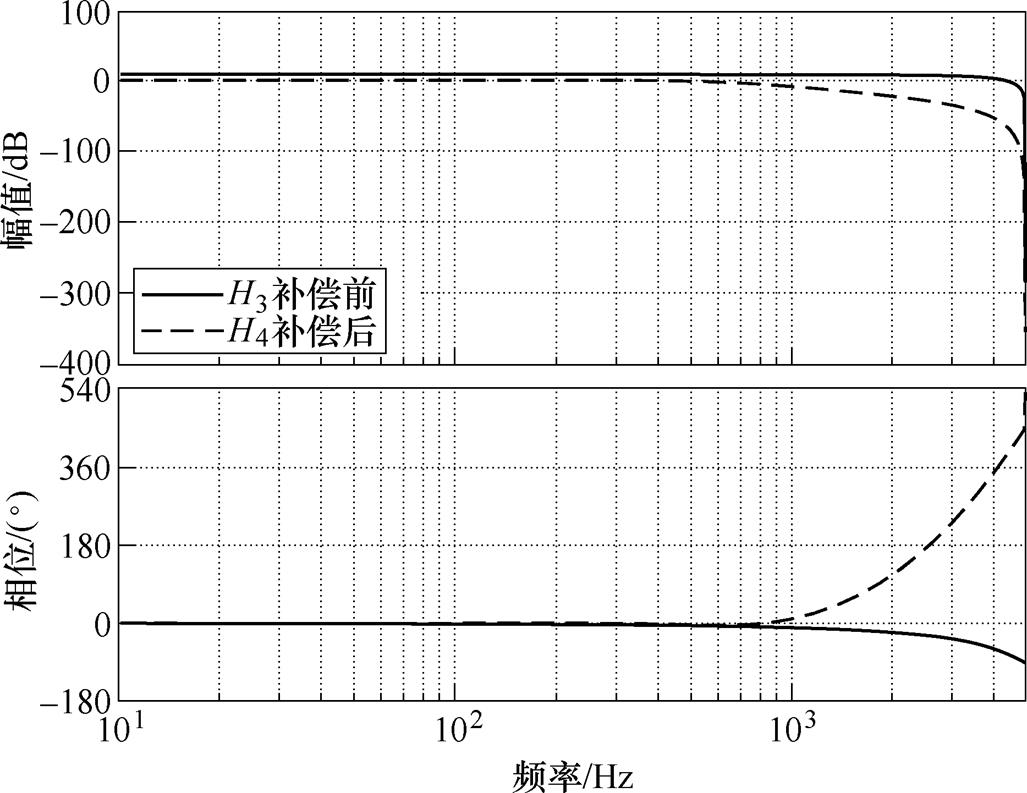
图13 GIG_RC补偿前后控制目标Bode图
Fig.13 Bode plot of the control objective of GIG_RC before and after compensation
忽略PCC电压的动态,控制电流的小信号模型可以表示为
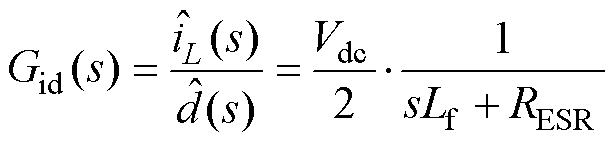 (22)
(22)
电感电流环环路增益Bode图如图14所示,相位裕度为41.9°,穿越频率为1 200Hz。
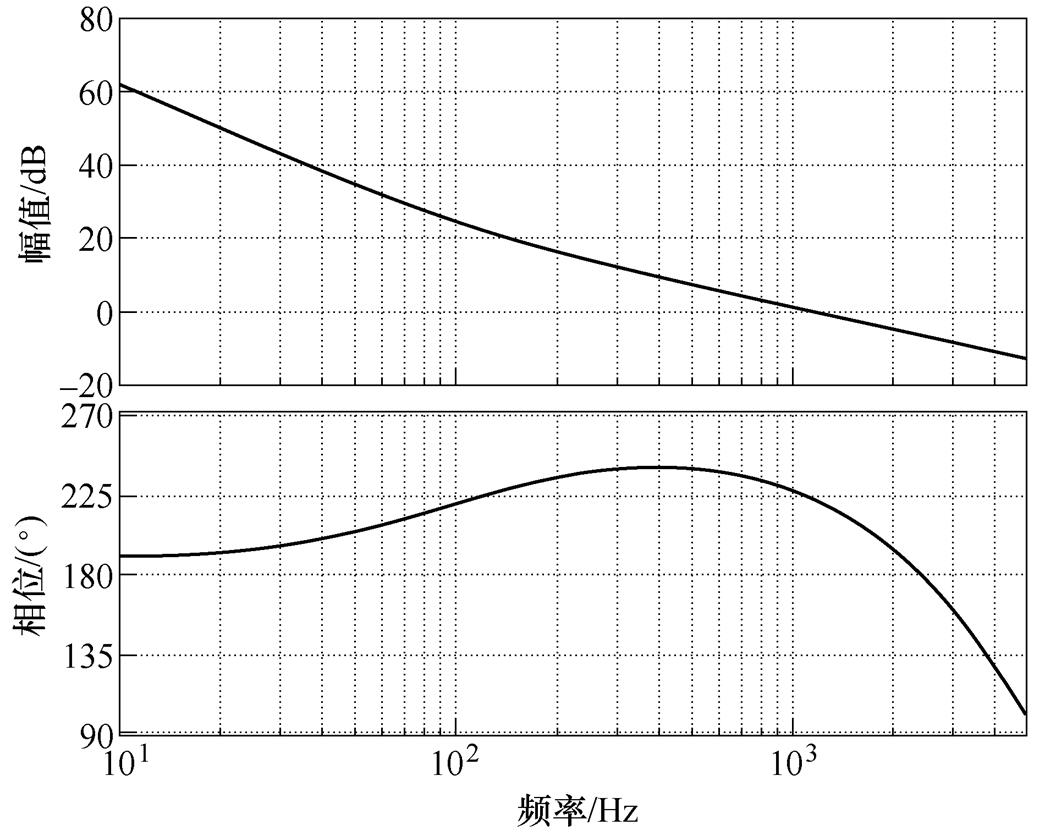
图14 电感电流环环路增益Bode图
Fig.14 Bode plot of the loop gain of inductor current control loop
为了验证所提控制策略的有效性,搭建了如图15所示的实验平台,实验参数见表2。
(1)逆变器1的并网电流d轴和q轴分量参考值igdref、igqref分别为6A和0A,在t1时刻,igdref变为9A,在t2时刻igqref变为-3A。逆变器1的A相电网电流t1与t2时刻实验波形如图16所示,并网电流d轴与q轴分量均可准确跟随其参考值,从而验证了基于该控制策略的逆变器可以在没有锁相环或锁频环的情况下与电网保持同步。
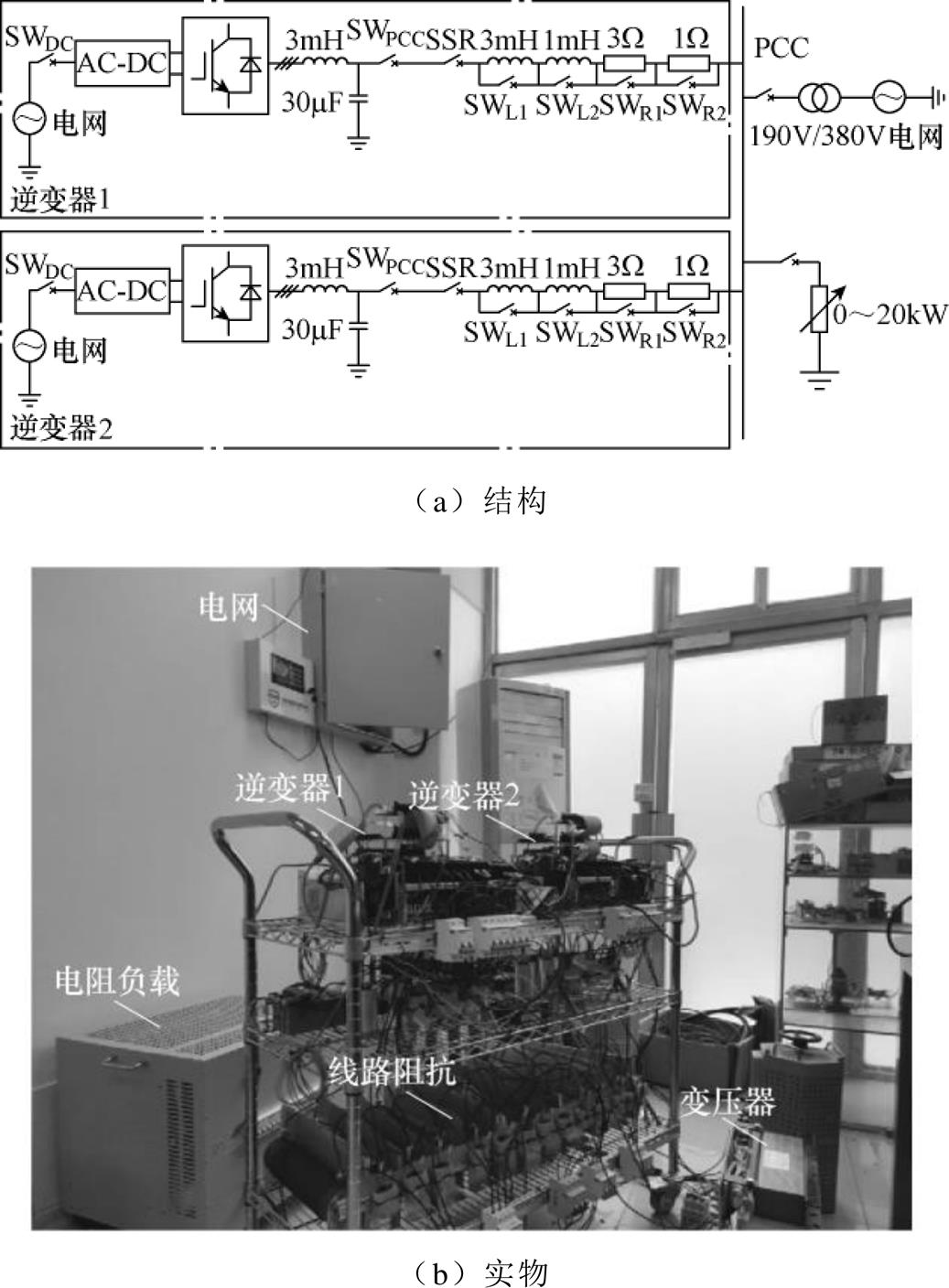
图15 实验平台
Fig.15 Experimental platform
表2 实验参数
Tab.2 The experimental parameters
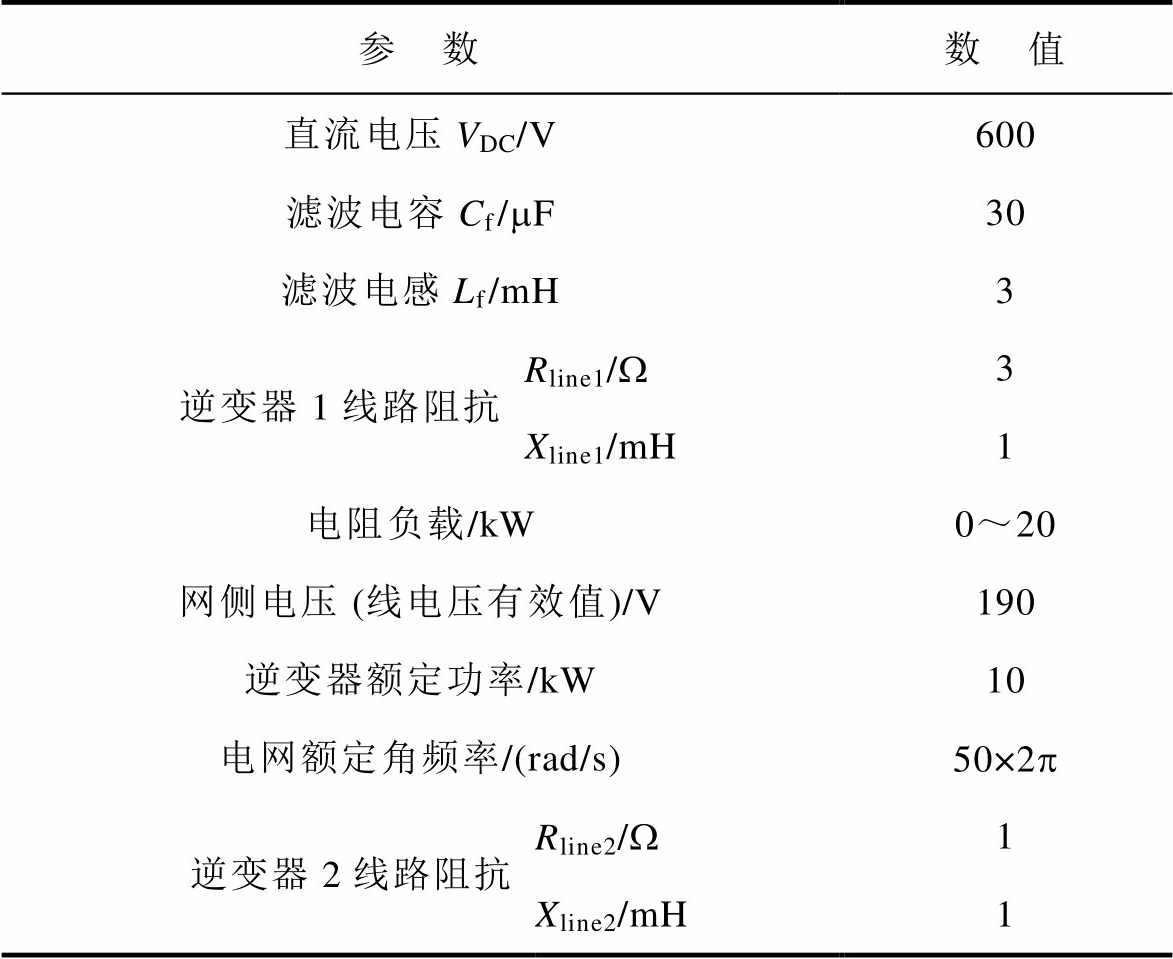
参 数数 值 直流电压VDC/V600 滤波电容Cf/mF30 滤波电感Lf/mH3 逆变器1线路阻抗Rline1/W3 Xline1/mH1 电阻负载/kW0~20 网侧电压 (线电压有效值)/V190 逆变器额定功率/kW10 电网额定角频率/(rad/s)50×2p 逆变器2线路阻抗Rline2/W1 Xline2/mH1
(2)验证基于该控制策略的并联逆变器可以实现从并网到孤岛模式的无缝切换,并可以实现孤岛模式下各逆变器间的功率均分。
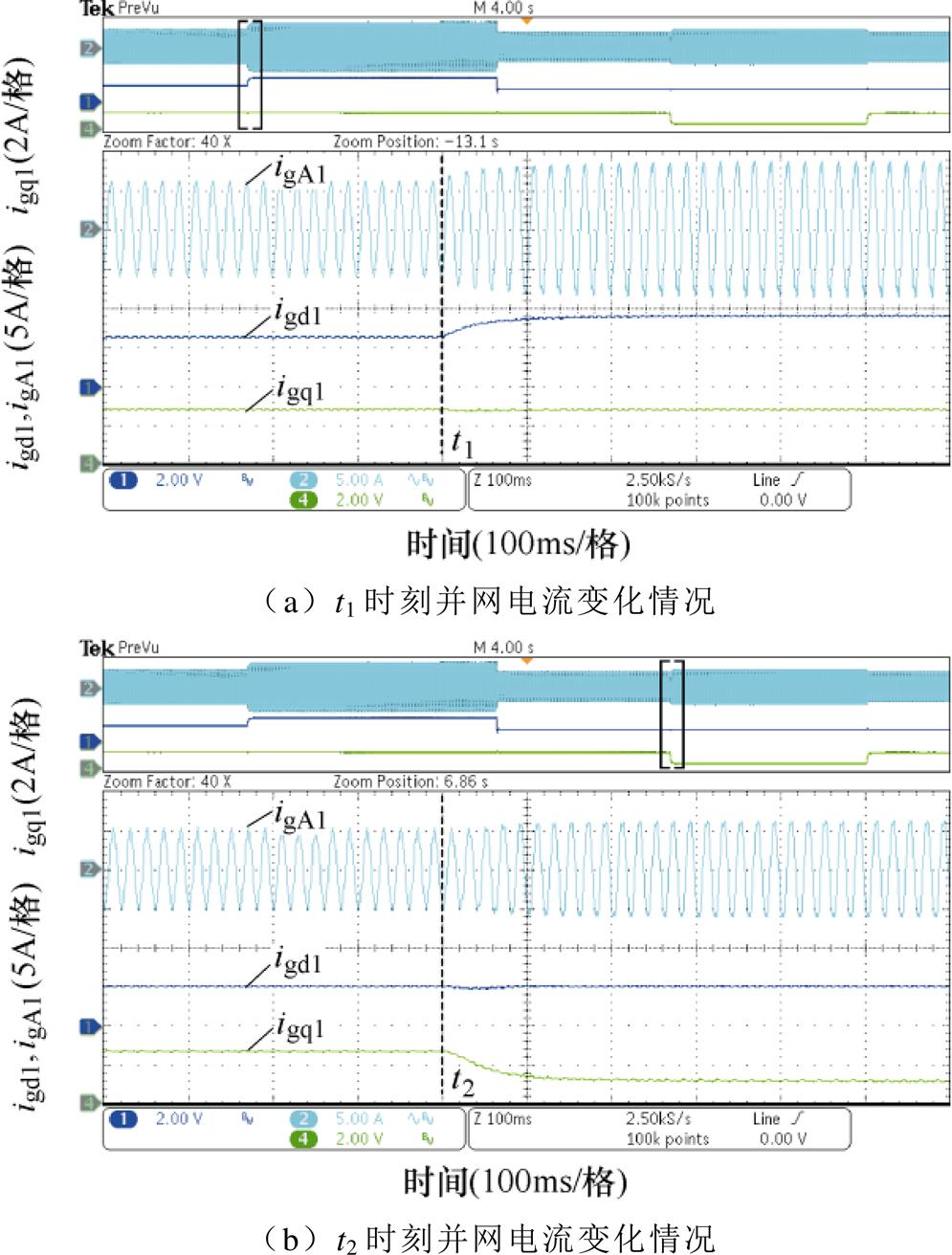
图16 逆变器1的A相电网电流实验波形
Fig.16 Experimental waveforms of phase A grid current of inverter 1
首先微电网运行在并网模式,t1时刻电网故障,形成孤岛,t2时刻孤岛被检测到。并网模式转孤岛模式如图17a所示,孤岛没有被检测到时,电容电压的质量良好,本地关键负载的电压质量可以得到保证。
孤岛模式下,两台并联的逆变器基于vCd-igd,w-igq下垂控制以提供电压支撑,无功功率准确均分,有功功率在两个逆变器间大致均分,孤岛模式时负载发生突变如图17b所示,逆变器1和2的并网电流略有差别。
(3)验证所提策略可以在并网模式下有效抑制并网电流中的谐波分量,在孤岛模式下抑制电容电压中的谐波分量。
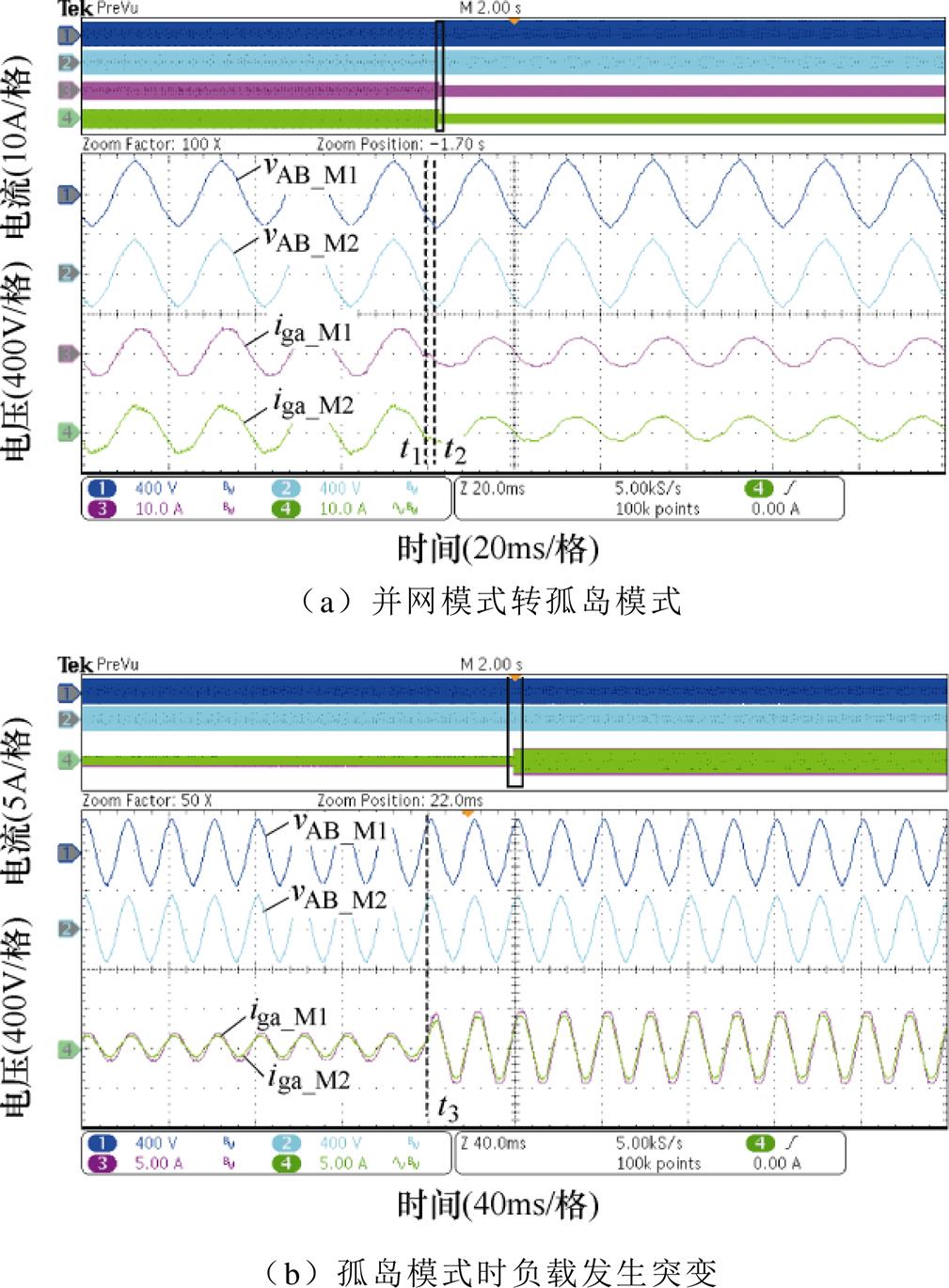
图17 逆变器1和2电容电压与并网电流实验波形
Fig.17 Experimental waveforms of capacitor voltage and grid current of inverter 1 and 2
并网电流和电容电压谐波抑制实验波形如图18所示,图18a中,带下垂控制的逆变器的并网电流失真,总谐波畸变率(Total Harmonic Distortion, THD)为8.38%。但是,基于所提控制策略逆变器的并网电流近似为纯正弦波,THD=4.18%,如图18b所示。类似地,孤岛模式时基于下垂控制的逆变器电容电压THD=5.87%,而基于所提控制策略的THD= 3.81%,谐波受到了明显抑制。
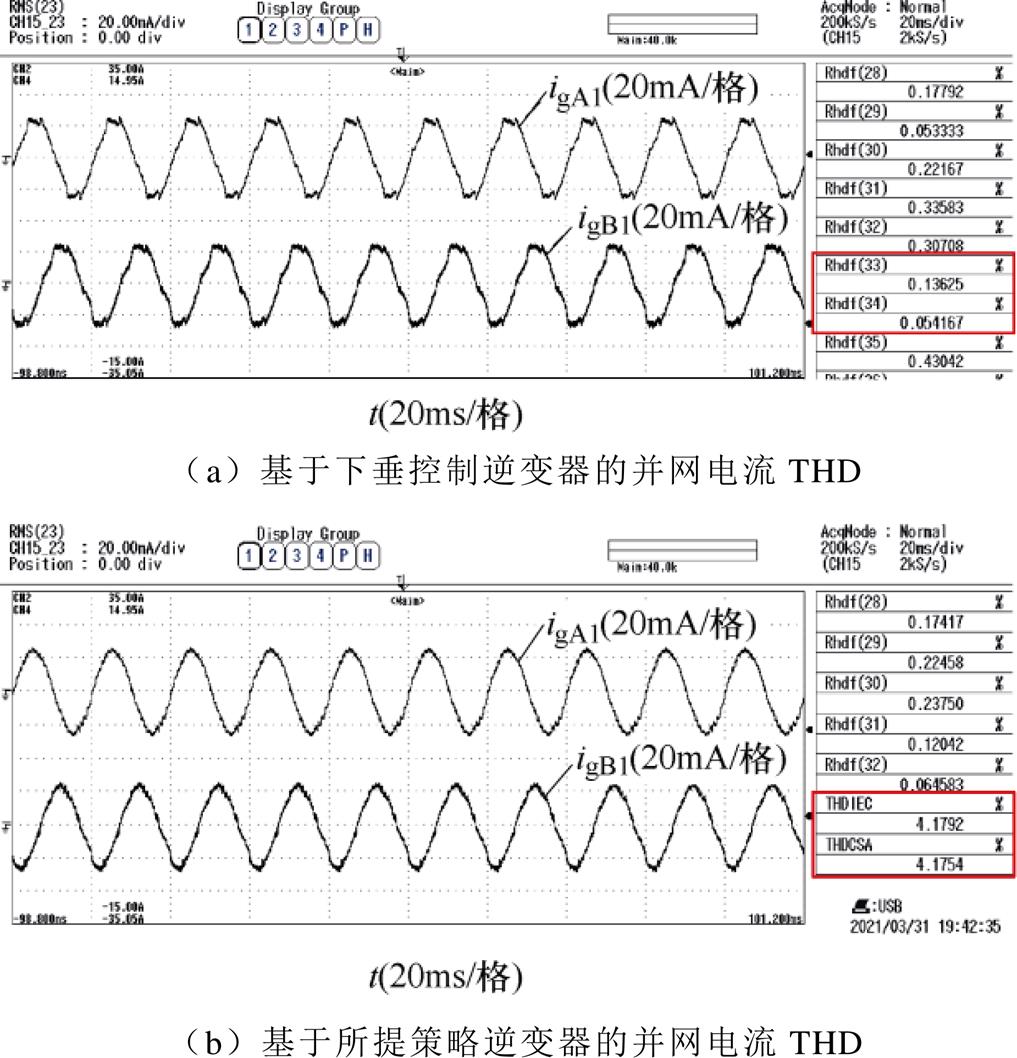
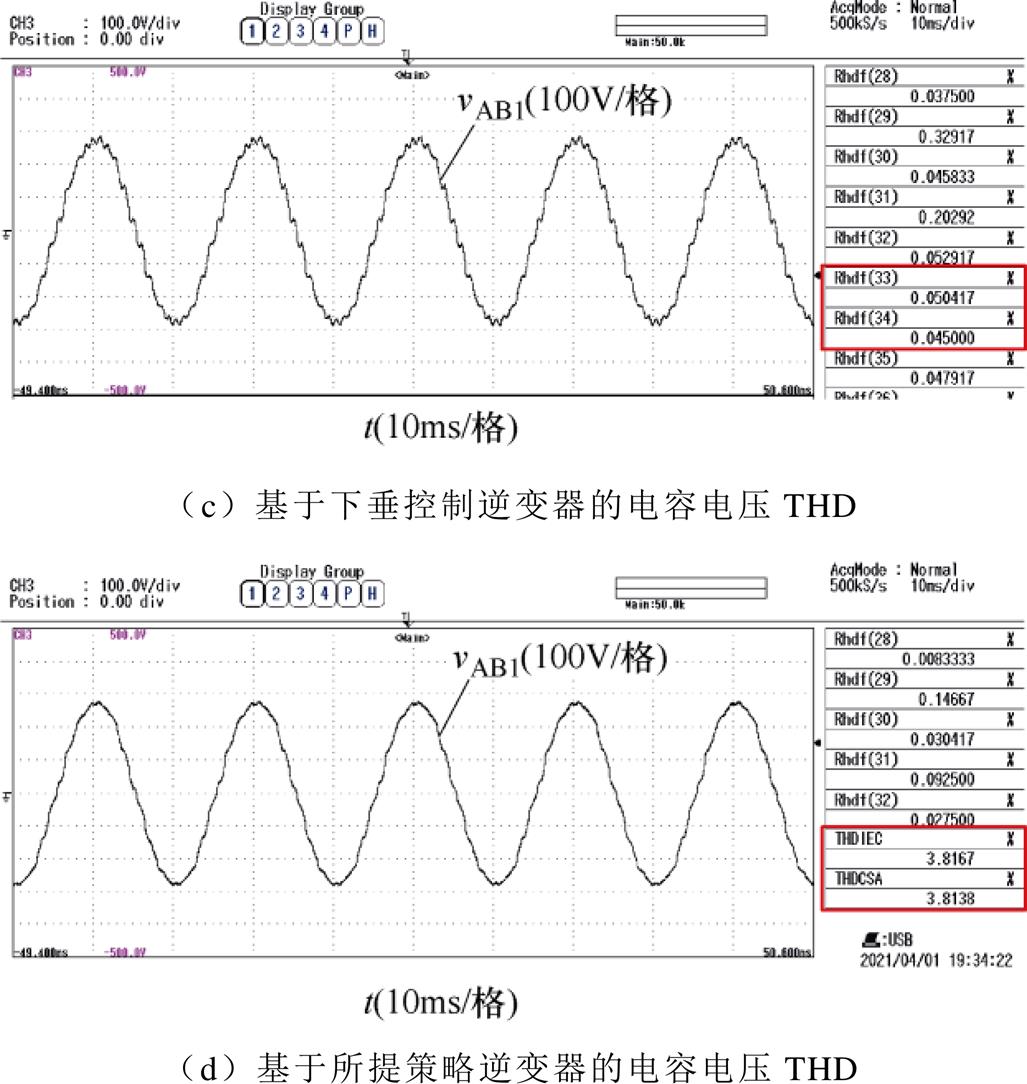
图18 并网电流和电容电压谐波抑制实验波形
Fig.18 Experimental waveforms of grid current and capacitor voltage harmonic suppression
(4)验证微电网由孤岛切换到并网模式时预同步单元的功能。由于设备有限,所以将逆变器1设置为预同步单元,逆变器2基于所提控制策略进行控制。当电网解除故障后,预同步单元检测到其功能恢复,PCC处的电压和电网电压波形与相位如图19a和图19b所示。电压波形与相位差均逐步减小,预同步功能实现。
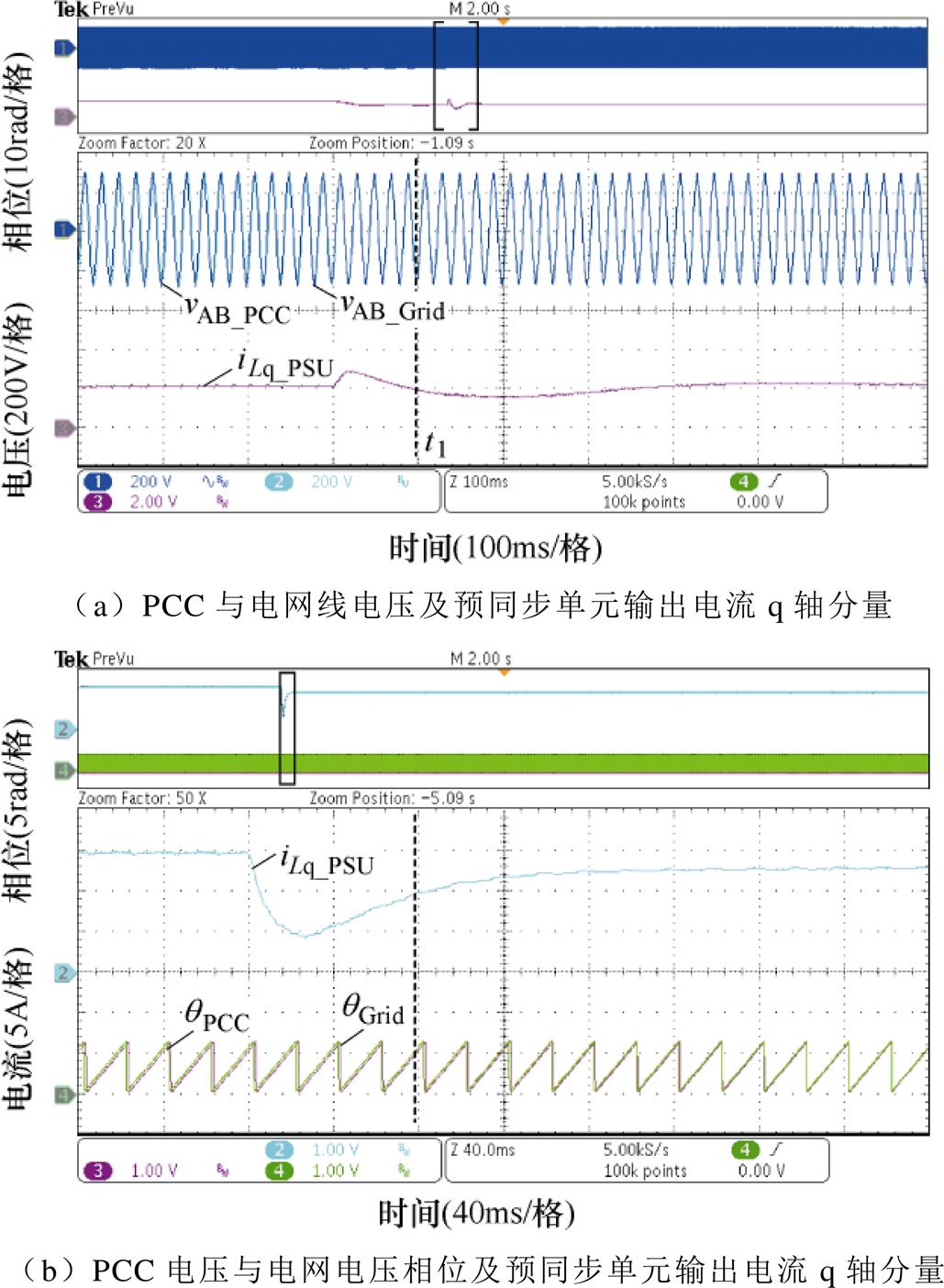
图19 预同步单元实验波形
Fig.19 Experimental waveforms of pre-synchronization unit
本文提出了一种具有高电能质量且无需远程通信线的微电网平滑切换控制策略。基于该控制策略的接口逆变器,在并网模式下无需PLL或FLL即可稳定运行,且利用并网电流环中的限幅器可以实现从并网到孤岛模式的无缝切换。同时,通过添加RC控制器,有效抑制了并网电流与电容电压中的谐波分量,保证了电能质量。此外,策略中设计的预同步单元,使得微电网系统实现了无需远程通信线的并网相位预同步。最后,通过实验样机进一步验证。实验结果表明,所提策略可以实现微电网中并联逆变器在并网模式与孤岛模式间的平滑切换,且能够保证关键负载的供电质量。
参考文献
[1] 隋峥. 基于虚拟同步机的微网逆变器稳定性和控制技术研究[D]. 济南: 山东大学, 2020.
[2] 丁小俊. 分布式微网稳定性和运行控制研究[D]. 武汉: 华中科技大学, 2019.
[3] Kumar S, Singh B. Seamless operation and control of single phase hybrid PV-BES-utility synchronized system[J]. IEEE Transactions on Industry Appli- cations, 2019, 55(2): 1072-1082.
[4] Huang Shusyuan, Konishi Y, Yang Zongzhen, et al. Observer-based capacitor current sensorless control applied to seamless transfer single-phase inverter System[J]. IEEE Transactions on Power Electronics, 2019, 34(3): 2819-2828.
[5] Prabowo Y, Kwon M, Park S, et al. Improved indirect current control for utility-interactive inverter system with critical load[C]//2016 3rd Conference on Power Engineering and Renewable Energy (ICPERE), Yogyakarta, 2016: 1-5.
[6] Eskandari M, Li Li. Microgrid operation improvement by adaptive virtual impedance[J]. IET Renewable Power Generation, 2018, 13(2): 296-307.
[7] Alam F, Ashfaq M, Zaidi S S, et al. Robust droop control design for a hybrid AC/DC microgrid[C]// 2016 UKACC 11th International Conference on Control (CONTROL), Belfast, 2016: 1-6.
[8] Zhao Xiaojun, Dong Jie, Zhang Chunjiang, et al. Modeling and stability analysis of autonomous microgrid composed of inverters based on improved droop control[C]//2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC- ECCE Asia), Hefei, 2016: 1720-1724.
[9] Trinh Q, Lee H. An enhanced grid current com- pensator for grid-connected distributed generation under nonlinear loads and grid voltage distortions[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 6528-6537.
[10] IEEE 1547-2018 IEEE standard for interconnection and interoperability of distributed energy resources with associated electric power systems interfaces[S]. New York, 2018.
[11] Meng Xin, Liu Zeng, Zheng Haoyang, et al. A universal controller under different operating states for parallel inverters with seamless transfer capa- bility[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9794-9812.
[12] 江法洋, 郑丽君, 宋建成, 等. LCL型并网逆变器重复双闭环控制方法[J]. 中国电机工程学报, 2017, 37(10): 2944-2954.
Jiang fayang, Zheng Lijun, Song Jiancheng, et al. Repetitive-based dual closed-loop control approach for grid-connected inverters with LCL filters[J]. Proceedings of the CSEE, 2017, 37(10): 2944-2954.
[13] 张学广, 马彦, 李瑞, 等. 两相静止坐标系下并网逆变器的重复控制策略[J]. 电工技术学报, 2016, 31(9): 85-91.
Zhang Xueguang, Ma Yan, Li Rui, et al. Repetitive control strategy for grid-connected converters in stationary frame[J]. Transactions of China Electro- technical Society, 2016, 31(9): 85-91.
[14] 赵强松, 陈莎莎, 周晓宇, 等. 用于并网逆变器谐波抑制的重复-比例复合控制器分析与设计[J]. 电工技术学报, 2019, 34(24): 5189-5198.
Zhao qiangsong, Chen Shasha, Zhou Xiaoyu, et al. Analysis and design of combination controller based on repetitive control and proportional control for harmonics suppression of grid-tied inverters[J]. Transactions of China Electrotechnical Society, 2019, 34 (24): 5189-5198.
[15] 谭翠兰, 邢彦一, 陈启宏, 等. 三相四桥臂并网逆变器重复控制积分抗饱和策略[J]. 电工技术学报, 2019, 34(17): 3631-3639.
Tan Cuilan, Xing Yanyi, Chen Qihong, et al. Anti- windup strategy of repetitive controller for three- phase four-leg grid-tied inverter[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3631- 3639.
[16] 张旗, 蔡逢煌, 黄丽梅, 等. 单相程控电流源PI+重复控制[J]. 电工技术学报, 2019, 34(增刊1): 163-170.
Zhang Qi, Cai Fenghuang, Huang Limei, et al. PI+ repetitive control applied to single-phase program- mable standard power source[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 163- 170.
An Enhanced Power Quality and Smooth Transition Control Strategy for a Microgrid without Remote Pre-Synchronization Communication
Abstract The paper proposes a smooth transition control strategy for microgrids with high power quality and no need for remote communication lines. The microgrid is mainly composed of multiple parallel distributed power generation units and a pre-synchronization unit. A unified grid-connected current control structure is proposed for the interface inverter in the distributed power generation unit, which has the following advantages: ① Without island detection, the inverter can automatically switch between the current control state of the grid-connected mode and the voltage control state of the stand-alone mode to ensure the load power supply quality; ② The proposed unified grid-connected current control structure can effectively suppress the harmonics in grid-connected current and capacitor voltage; ③ When the grid frequency fluctuates, the inverter can still output the corresponding active and reactive power according to the command value, and can synchronize with the grid without a phase-locked-loop or a frequency-locked-loop in the grid-connected operation state. In addition, the proposed pre-synchronization unit can realize the pre-synchronization control of the microgrid voltage and the grid voltage without relying on the remote communication lines. It also reduces the inrush current when the stand-alone operation state changes to the grid-connected operation state. Finally, the control parameters are optimized, and the effectiveness and feasibility of the proposed control strategy are verified through experiments.
keywords:Seamless transition, grid-connected mode, stand-alone mode, pre-synchronization, power quality
DOI: 10.19595/j.cnki.1000-6753.tces.210575
中图分类号:TM464
郭慧珠 女,1998年生,硕士研究生,研究方向为逆变器控制。E-mail: guohuizhu1998@qq.com
孟 鑫 男,1992年生,博士,助理研究员,研究方向为新能源发电、变换器建模及控制。E-mail: mengxin_pe@163.com(通信作者)
收稿日期 2021-04-23
改稿日期 2021-09-16
四川大学博士后交叉学科创新启动基金和四川大学专职博士后研发基金资助项目。
(编辑 陈 诚)