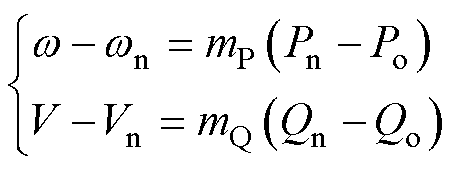 (1)
(1)
式中,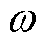 为IIDG的运行实时角频率;
为IIDG的运行实时角频率;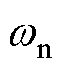 为IIDG的额定角频率,即电网的额定频率;
为IIDG的额定角频率,即电网的额定频率;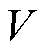 为IIDG的输出电压;
为IIDG的输出电压;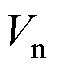 为IIDG的额定输出电压;
为IIDG的额定输出电压;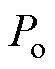 为IIDG输出有功功率;
为IIDG输出有功功率;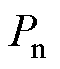 为IIDG额定输出有功功率;
为IIDG额定输出有功功率;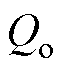 为IIDG输出无功功率;
为IIDG输出无功功率;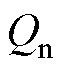 为IIDG额定输出无功功率;
为IIDG额定输出无功功率;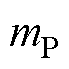 、
、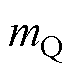 为下垂控制系数。
为下垂控制系数。
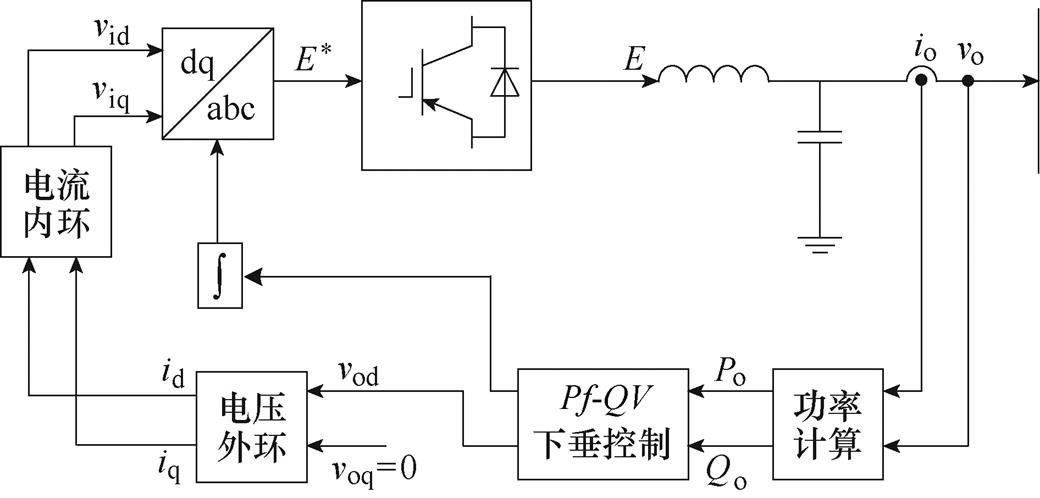
图1 逆变器控制系统
Fig.1 Control systems of the inverters
摘要 逆变型分布式电源(IIDG)是可再生能源在配电网中的重要应用方式,其稳定运行依赖于控制策略及其所接入的配电网系统。在配电网发生暂态事件时,IIDG暂态响应复杂,易出现输出功率、功角等波动或振荡。该文以IIDG控制系统及其接入电网的数学模型为基础,分析功角特性曲线,以功角曲线簇提出其暂态稳定性判据。对影响IIDG暂态稳定性的并网参数、额定功率进行系统性分析,比较不同参数对暂态稳定性的影响。通过刻画暂态过程,提出了暂稳迭代判定法,迭代计算暂态事件下IIDG的功角变化并对其暂态稳定性进行判断。在PSCAD/EMTDC中建立仿真算例,验证了IIDG暂态稳定性机理,并通过改变并网的网络参数,证明了暂稳迭代判定法的有效性与准确性。
关键词:逆变型分布式电源 暂态稳定机理 暂态稳定性计算 功角曲线 下垂控制
分布式发电是新能源应用的典型方式之一,具有灵活、环保与高效等优点[1]。随着分布式发电不断分散并网,其在配电网中的渗透率逐渐提高,电网故障、电压波动等暂态稳定事件的影响亟待解决。分布式电源(Distributed Generators, DG)的稳定运行与其自身特性、控制策略以及电网参数密切相关,并网运行时配电网的大扰动会对分布式电源控制产生较大干扰,影响分布式电源的运行稳定[2-3]。
DG并网运行的基本功能是以配电网为支撑,根据控制策略的输出响应,向就地负荷提供稳定可靠的电能。DG的暂态过程主要是在受到配电网大扰动后所表现出的电压、频率与功角特征,这些大扰动包括不同类型故障、负荷突变、运行方式切换等,其中短路故障对稳定性的影响最为严重。DG暂态失稳指DG在受到暂态事件的影响后,出现功率、频率周期性振荡的现象[4]。一旦DG失去稳定,系统的电压、频率将会不断波动,DG与配电网电源难以保持同步运行[5-6];在最严重的情况下,还可能导致DG与配电网的崩溃。因此,DG并网运行的暂态稳定已成为其大规模分散接入亟需解决的关键问题。
分布式电源接口模式与控制方式多样,逆变型分布式电源(Inverter Interfaced Distributed Generators, IIDG)是可再生能源发电的主要类型之一。直流电源或高频电源经逆变型接口可同步并网,IIDG具备运行和控制的灵活性,因此在配电网中得到了大量应用。但IIDG受控制策略影响较大,且IIDG缺乏惯性,在大扰动下将快速、大幅度地波动,因此IIDG并网时的暂态稳定性呈现一定的复杂性[7-8]。为了IIDG并网暂态稳定性问题,本文针对典型控制策略,研究典型结构下的IIDG暂态稳定性机理。分析IIDG的暂态稳定运行机理,判别它在不同暂态事件下的稳定能力是高渗透率可再生能源消纳与稳定运行的关键技术。
目前,仿真分析法是IIDG暂态稳定性研究的最主要方法之一[9-12]。通过建立IIDG及其接入配电网的数学模型,针对暂态事件仿真计算,根据仿真结果分析IIDG的暂态稳定特征。文献[9]建立了电压源型逆变器(Voltage Source Converter, VSC)的代数微分方程模型,并利用模型对IIDG的功角、电压暂态稳定性进行研究,提出了IIDG的暂态过程特征。文献[10-11]对多个采用P-f和Q-V三环下垂控制的IIDG进行了建模,分析了在电机起动、电机故障与电网故障三种情况下IIDG的电压、功率以及频率的动态变化。文献[12]基于Matlab/Simulink建立了包含IIDG、同步型DG以及电动机负荷的微电网模型,仿真分析微电网故障后孤岛运行的场景,通过仿真对比了不同逆变器控制策略对于临界故障消除时间(Critical Clearing Time, CCT)的影响。仿真分析法可详细计算暂态过程,较为简便地判断IIDG并网运行的暂态稳定性,但其结果一方面依赖仿真模型精度;另一方面无法给出暂态稳定机理与稳定评估方法。
为了研究IIDG在大干扰下的暂态稳定机理,评估IIDG的暂态稳定能力,需要对IIDG的暂态行为进行深入分析。目前,针对IIDG大干扰暂态稳定性机理与评估方法的研究较少,文献[13]将使用下垂控制的IIDG的模型与同步电机经典二阶模型进行了对比,并直接采用数值模拟仿真的方法对IIDG的暂态稳定性进行了评估。该文献提出的方法缺少对IIDG暂态稳定机理的描述,判稳条件复杂。文献[14-15]借鉴传统电力系统暂态稳定分析的方法,在计及逆变器的电流限流特性下,对VSC并网场景下电网电压波动后VSC的功角曲线进行了分析。该文献提出的虚拟功角概念值得借鉴,研究方法具有较好的参考价值,但所提方法主要针对IIDG连接线路电压跌落时的暂态特性,不适用于具体故障下暂稳分析,且文献假设逆变器出口电压保持恒定不变,不能充分反映IIDG的故障特征。文献[16]针对含IIDG的微电网,在计及孤岛运行的条件下分析了不同IIDG之间的暂态协同作用,依照可调节能力对各IIDG的暂态稳定调节能力进行了分类,然而该研究方法不能反映每台IIDG的稳定性。此外,李雅普诺夫法也被广泛用在暂态稳定性的分析中,文献[17]建立二次李函数,对孤岛微电网中的IIDG的暂态稳定机理进行分析,提出了针对暂态稳定的微电网故障切除稳定域。文献[18]推导了IIDG的能量函数,通过李雅普诺夫法判断IIDG的稳定性,但该文献未考虑IIDG的电压波动,因此其所建立的IIDG能量函数存在较大误差。
本文以IIDG的并网暂态运行为研究对象,重点考虑功角稳定,深入分析配电网发生短路故障后IIDG的暂态稳定性,提出IIDG的暂态稳定机理。综合功角失稳的特点,建立IIDG的暂稳迭代判定法。所提方法为含分布式电源的配电网暂态稳定性研究提供了借鉴与参考。
IIDG运行特性复杂,控制方式、输出阻抗、并网结构等因素均影响其暂态特性。为了深入研究IIDG的暂态稳定能力,应对IIDG控制系统及其接入的配电网系统进行建模与分析。
IIDG控制系统通常采用三环控制器[19],如图1所示。三环控制器包含下垂控制器与电压电流双闭环控制器。下垂控制的方程为
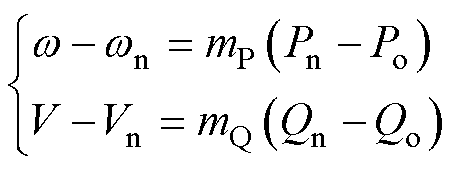 (1)
(1)
式中,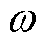 为IIDG的运行实时角频率;
为IIDG的运行实时角频率;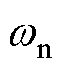 为IIDG的额定角频率,即电网的额定频率;
为IIDG的额定角频率,即电网的额定频率;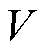 为IIDG的输出电压;
为IIDG的输出电压;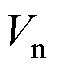 为IIDG的额定输出电压;
为IIDG的额定输出电压;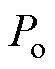 为IIDG输出有功功率;
为IIDG输出有功功率;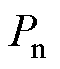 为IIDG额定输出有功功率;
为IIDG额定输出有功功率;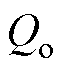 为IIDG输出无功功率;
为IIDG输出无功功率;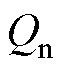 为IIDG额定输出无功功率;
为IIDG额定输出无功功率;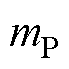 、
、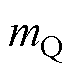 为下垂控制系数。
为下垂控制系数。

图1 逆变器控制系统
Fig.1 Control systems of the inverters
IIDG的暂态稳定性主要表现为功角失稳,属于大时间尺度下的稳定性问题。下垂控制器与IIDG的输出特性相关,当IIDG的输出特性因暂态事件而发生改变时,下垂控制可能无法稳定地控制电压、频率参考值,从而表现出暂态失稳。电压外环、电流内环的控制时间尺度相对较短,对功角稳定影响较小,因此可简化电压外环、电流内环的控制过程。电压外环与电流内环的控制过程存在一定延时,可认为其在暂态过程中呈现低通效果。IIDG的输出功率分量可在dq轴上灵活控制,通常为了充分利用新能源,IIDG运行于单位功率因数,因此电压外环的q轴输入电压Vq=0,此时可最大化IIDG的有功输出[20]。
IIDG接入的配电网就地负荷大小、并网线路阻抗以及暂态事件的类型均会影响到暂态过程。研究IIDG暂态稳定能力,需要对IIDG接入电网进行建模分析。
如图2所示为含IIDG的配电网系统典型连接方式,S1为环网运行开关,S2、S3为线路开关,P1、P2、P3为输送功率。在过去的配电网中,环网开环运行的实例较多,随着配电网的发展,为了增加配电网的运行可靠性,环网运行成为趋势,本文选择环网运行的配电网作为研究对象。

图2 IIDG并网形式
Fig.2 Operation structure for IIDG
逆变电源通常与负荷之间电气距离近[21],不需要通过远距离的电缆进行电能的交换,因此,可忽略IIDG与负荷之间的线路阻抗。而公共电网与逆变电源、负荷之间通常采用馈线连接,且距离较远,因此阻抗不可忽视。可将图2所示环形电网等效为如图3所示的电网等效结构与暂态等效。
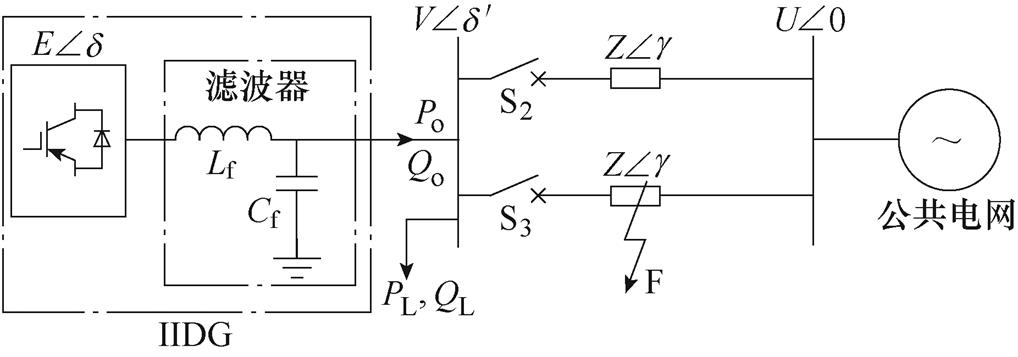
图3 电网等效结构与暂态等效
Fig.3 Equivalent structure and transient events
如图3所示,IIDG通过并网滤波器与负荷、公共电网相连,公共电网通过两条线路与逆变器及负荷连接。为了便于分析,假设与公共电网连接的两根馈线电缆阻抗相等,均为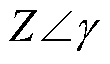 ,
,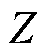 为馈线电缆阻抗幅值,
为馈线电缆阻抗幅值,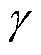 为馈线电缆阻抗角。逆变电源在并网滤波器前的电压为
为馈线电缆阻抗角。逆变电源在并网滤波器前的电压为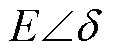 ,
,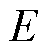 为IIDG的内电动势,
为IIDG的内电动势,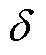 为逆变电源滤波器前端相较于公共电网的相位差,在并网滤波器之后的输出电压为
为逆变电源滤波器前端相较于公共电网的相位差,在并网滤波器之后的输出电压为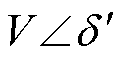 ,
,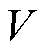 为IIDG出口处电压幅值,
为IIDG出口处电压幅值,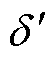 为IIDG出口处与公共电网的相位差。公共电网电压为
为IIDG出口处与公共电网的相位差。公共电网电压为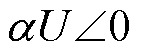 ,U为公共电网在正常运行状态下的电压。当电网内出现暂态事件时,电网电压会出现波动,为了体现电网在不同状态下的波动状况,加入电网电压暂态系数
,U为公共电网在正常运行状态下的电压。当电网内出现暂态事件时,电网电压会出现波动,为了体现电网在不同状态下的波动状况,加入电网电压暂态系数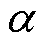 ,
,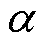 [22]满足
[22]满足
 (2)
(2)
在正常运行时,电网并无电压波动,因此取a=1,在暂态事件发生后,电网电压波动,此时a不再取值1,若暂态事件是短路故障,则通常a<1;当暂态事件切除时,电压会逐渐恢复,但由于系统出现拓扑变化,电压通常无法恢复至额定值。负荷是一压控负荷,它的功率大小与逆变器输出电压幅值线性相关,它的有功功率PL、无功功率QL满足
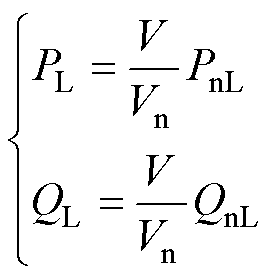 (3)
(3)
式中,Vn为IIDG额定电压;PnL、QnL分别为负荷额定有功功率、无功功率。
馈线短路故障是配电网中最为常见且对系统稳定运行影响最严重的一类暂态事件,短路故障如图3中F所示。当某一条馈线发生故障后,配电网中的继电保护装置将会切除故障线路,系统拓扑发生改变,这些因素将会影响IIDG的暂态稳定,影响稳定系统运行。
IDG暂态过程较为复杂,对IIDG的暂态稳定性进行判断需要分析IIDG的暂态稳定机理。
根据1.2节的含IIDG的配电网数学模型,IIDG输出的有功功率与无功功率分别为
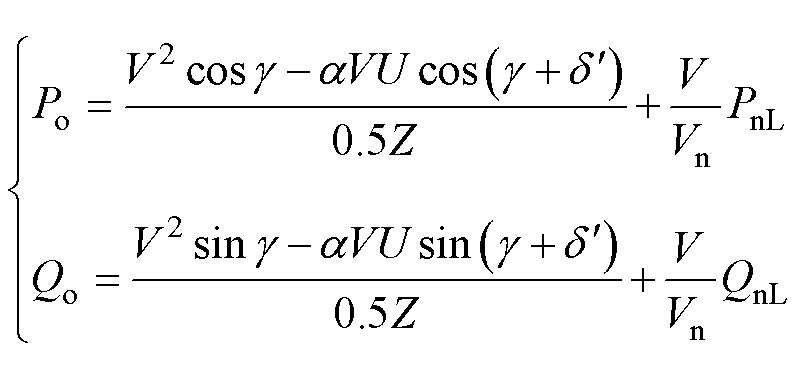 (4)
(4)
为方便分析,将IIDG内电动势与公共电网电压之间的相位差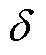 称为内功角,将IIDG输出电压与公共电网电压之间的相位差
称为内功角,将IIDG输出电压与公共电网电压之间的相位差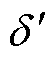 称为外功角,简称功角。
称为外功角,简称功角。
根据式(4),IIDG的有功功率,对某一电压V,以外功角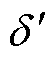 为自变量,则可得到一条正弦状的功角曲线。改变输出电压V,可得到一簇正弦状的功角曲线,如图4所示。这一簇功角曲线的幅值、极小值与极大值均随运行电压的增大而增大。
为自变量,则可得到一条正弦状的功角曲线。改变输出电压V,可得到一簇正弦状的功角曲线,如图4所示。这一簇功角曲线的幅值、极小值与极大值均随运行电压的增大而增大。
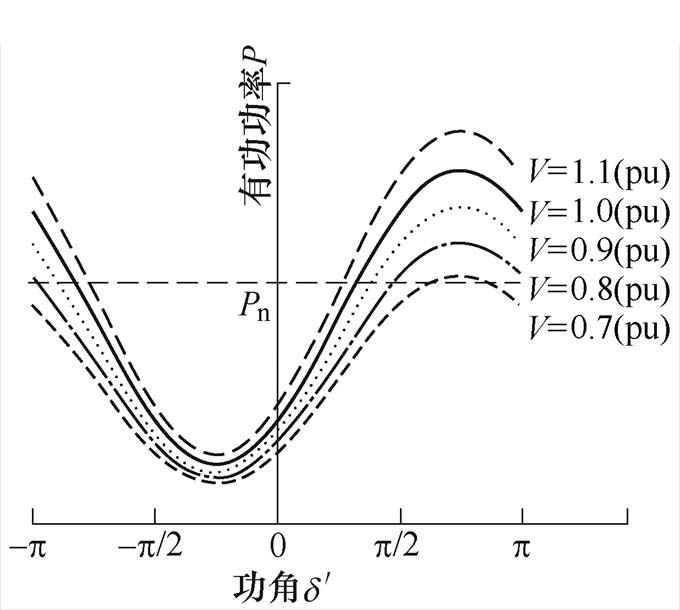
图4 IIDG功角曲线簇
Fig.4 Clusters of power angle curves of IIDGs
配电网发生暂态事件后,IIDG会脱离原本的稳定运行状态,在下垂控制的影响下,功角将会根据电压的变化在功角曲线簇之间不断变化[23-24]。当暂态事件严重且长时间存在,IIDG将会出现功率波动,甚至脱离电网。
若IIDG的输出功率与额定功率不相等,其输出功率与功角将会在下垂控制的作用下沿着功角曲线,向额定功率恢复。
IIDG的暂态过程可分为三个阶段:故障前、故障中与故障切除后。图5所示为IIDG暂态运行轨迹。故障前,IIDG工作在额定状态,此时功角曲线如图5中实线所示。故障后,电压下降,IIDG的功角曲线随之降低,如图5中细点线所示。此时,IIDG的输出有功功率将会下降,低于额定值。根据式(1)有
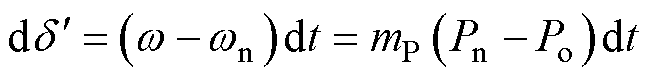 (5)
(5)
根据式(5),当IIDG的输出有功功率小于额定值时,下垂控制将会使IIDG的工作频率增加,从而使得功角逐渐增加。如图5所示,IIDG将会沿着故障后的曲线不断向前变化。
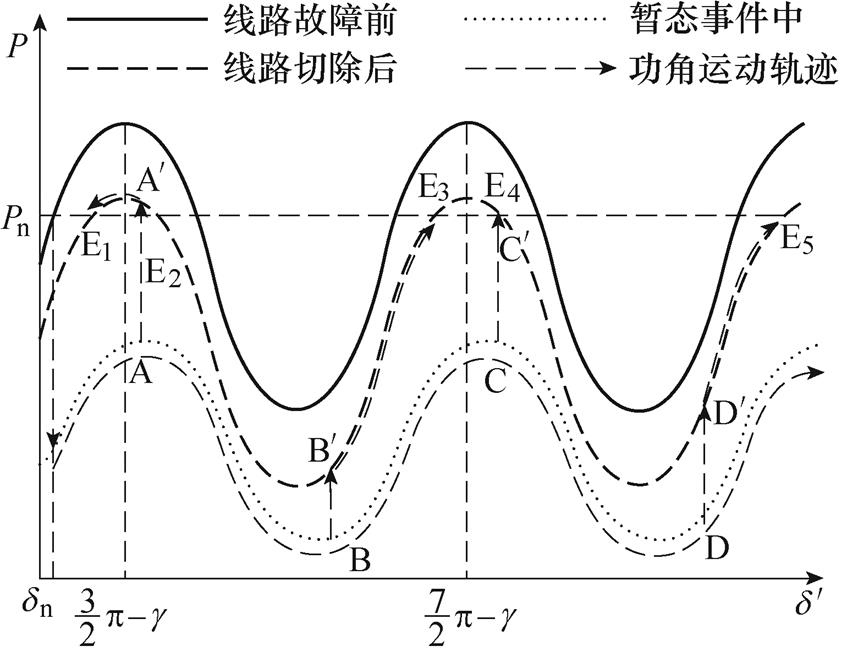
图5 IIDG功角轨迹
Fig.5 Locus of power angle of IIDG
如图5所示,虚线为故障线路切除后的功角曲线。其中,E1~E5为线路切除后功角曲线与额定有功功率的交点,称为功率平衡点。根据下垂控制方程可知,IIDG工作在E1~E5时有功功率与额定功率相等,功角不会再发生变化,将会维持稳定。
若在A点切除故障,IIDG的有功功率将会迅速变化至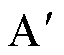 ,此时IIDG的有功功率将大于额定功率。根据式(5),功角将会逐渐减小,从而使得IIDG的工作点沿着虚线向功角减小的方向运动,当工作点在E1时,IIDG的输出功率等于额定功率,工作点将不再移动,IIDG将稳定在E1。
,此时IIDG的有功功率将大于额定功率。根据式(5),功角将会逐渐减小,从而使得IIDG的工作点沿着虚线向功角减小的方向运动,当工作点在E1时,IIDG的输出功率等于额定功率,工作点将不再移动,IIDG将稳定在E1。
若故障在B或D切除,切除后的IIDG功率将小于额定功率,此时IIDG的工作点将会沿着虚线向功角增大的方向移动,直到达到下一个功率平衡点,达到稳定。
若故障在C切除,切除后的IIDG工作点恰好在E4,此时IIDG的输出有功功率等于额定有功功率,功角不会移动,IIDG达到稳定。
因此,当故障切除后IIDG的功角曲线上存在功率平衡点时,IIDG将会沿着故障切除后功角曲线移动至功率平衡点,然后保持稳定运行。若故障切除后功角曲线无功率平衡点,即故障切除后功角曲线整体在额定功率下方,则IIDG的功角将在下垂控制的作用下沿着功角曲线不断变化,输出功率将会出现周期性振荡,IIDG暂态失稳。
由于故障切除后,电压在下垂控制的作用下逐渐恢复,功角曲线也随着电压的变化而不断变化。IIDG的输出功率与功角在故障切除后沿着一簇功角曲线移动,IIDG在每条功角曲线上的移动轨迹组合起来将形成一段变化轨迹,称功角轨迹。因此,可得IIDG暂态稳定判据:故障切除后其功角轨迹中是否存在功率平衡点。用数学准则表达则为
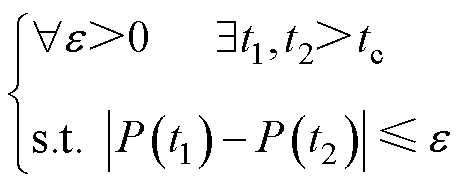
式中,tc为故障切除时间;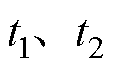 为故障切除之后的不同时间;P(t)为t时刻IIDG的输出功率。当功角轨迹中存在功率平衡点,则IIDG暂态稳定,且该功角轨迹将收敛于功率平衡点;若功角轨迹中不存在功率平衡点,则功角轨迹不收敛,IIDG暂态不稳定,该功角轨迹将出现周期性振荡。
为故障切除之后的不同时间;P(t)为t时刻IIDG的输出功率。当功角轨迹中存在功率平衡点,则IIDG暂态稳定,且该功角轨迹将收敛于功率平衡点;若功角轨迹中不存在功率平衡点,则功角轨迹不收敛,IIDG暂态不稳定,该功角轨迹将出现周期性振荡。
IIDG控制复杂,所连电网、负荷等参数众多,它的暂态稳定性受到多方面因素影响。为了更全面地研究IIDG的暂态稳定性,需要分析影响暂态稳定性的因素。
当故障线路被切除时,电网只有单条线路与IIDG和负荷相连,因此IIDG的输出功率为
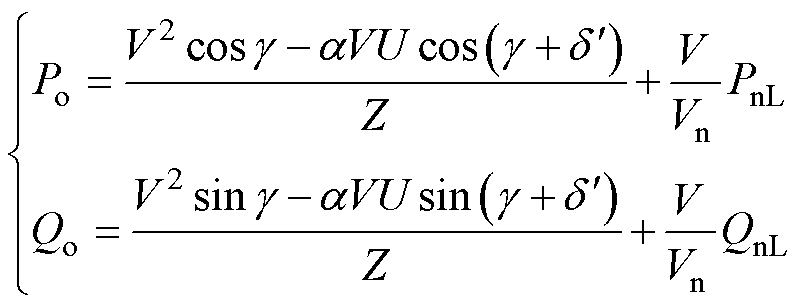 (6)
(6)
结合2.2节与式(6)的分析可知,IIDG在故障切除后的功角曲线与电压值、馈线阻抗值、负荷大小相关;此外额定功率直接影响了IIDG的稳定性判据。
2.3.1 网络参数
当故障发生时,电压瞬间下降至一个较低的值,当故障切除后,电压逐渐恢复。根据图4可知,对故障切除后的每一个时刻,IIDG的功角曲线随着输出电压的不断变化而改变。
配电网参数决定着功角曲线的特征,图6为四种不同网络参数下IIDG的功角曲线。Line1组的电压为a,电缆阻抗为b,本地负荷为c;Line2组的电压为0.5a,电缆阻抗为b,本地负荷为c;Line3组的电压为a,电缆阻抗为2b,本地负荷为c;Line4组的电压为a,电缆阻抗为b,本地负荷为0.5c。网络参数对有功功角曲线的影响见表1。
根据表1可知,输出电压、本地负荷与暂态稳定性成正相关,馈线阻抗与暂态稳定性成负相关。
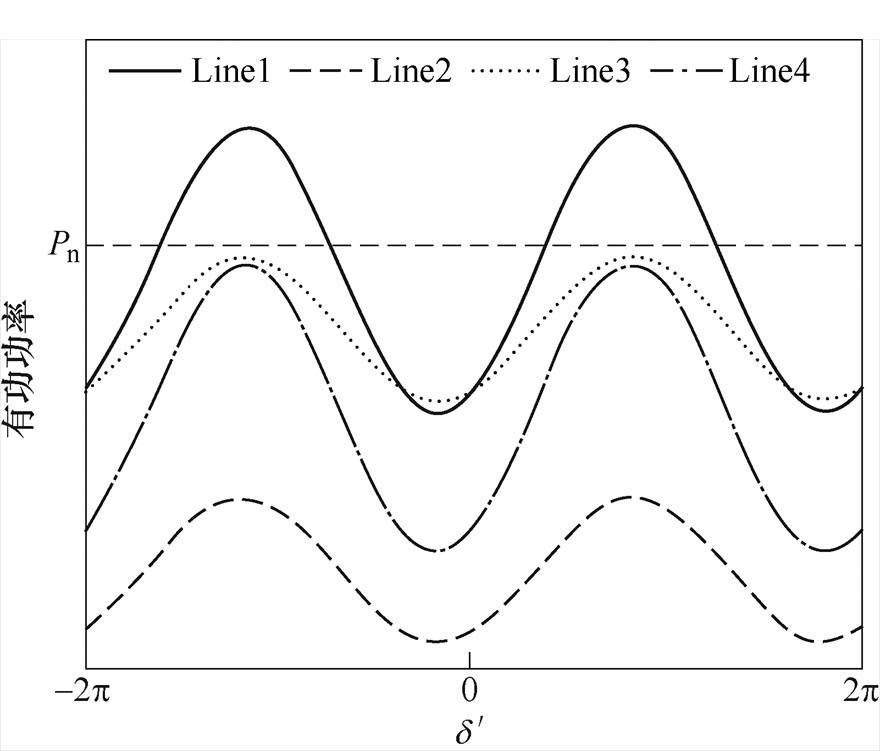
图6 不同网络参数下功角曲线
Fig.6 Power curves in different network parameters
表1 网络参数对功角曲线的影响
Tab.1 Influence on active power curves with different network parameters
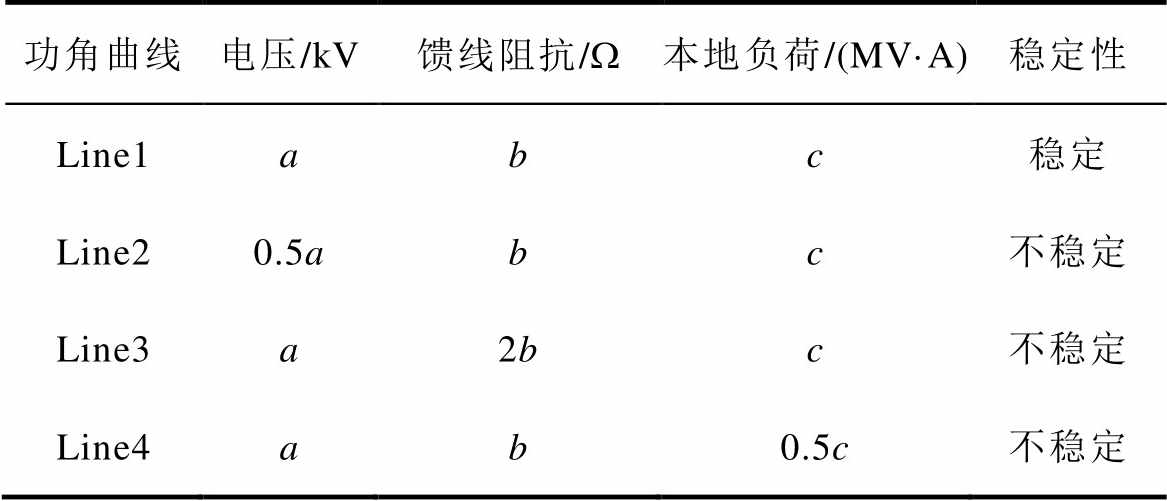
功角曲线电压/kV馈线阻抗/W本地负荷/(MV·A)稳定性 Line1abc稳定 Line20.5abc不稳定 Line3a2bc不稳定 Line4ab0.5c不稳定
注:当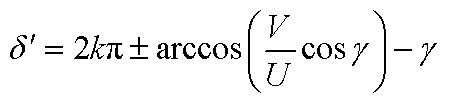 时,A与C的有功功角曲线相交。
时,A与C的有功功角曲线相交。
2.3.2 额定功率
根据2.2节的分析,IIDG额定功率是其暂态稳定性关键影响因素之一,当额定值较大时,可能会导致故障恢复后IIDG无法达到额定功率,从而出现失稳。图7所示为不同额定功率下IIDG功角变化轨迹。
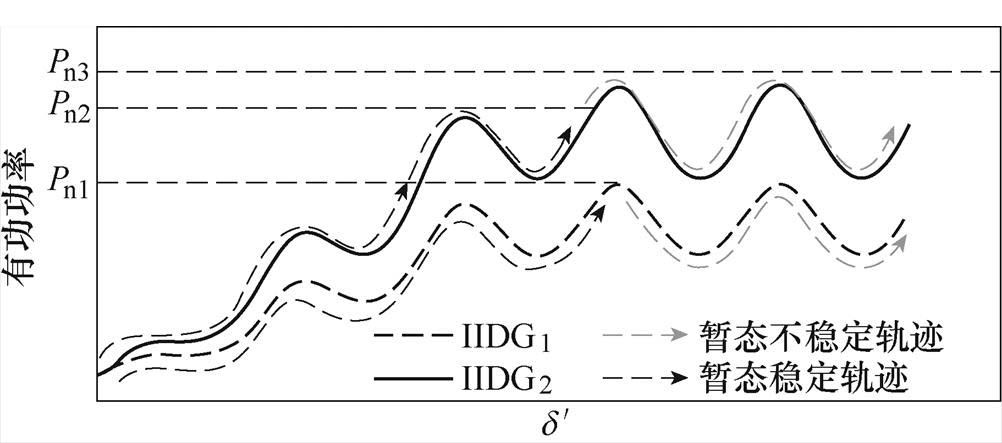
图7 不同额定功率下功角轨迹
Fig.7 Power angle variation traces with different rated active power
图7中实线为不同IIDG对应的两条功角轨迹,IIDG2比IIDG1有功功率值更大。当IIDG的额定功率为Pn1时,无论是哪条轨迹都能够达到功率平衡点,实现暂态稳定。当额定功率为Pn2时,由于IIDG1与额定功率值无交点,暂态不稳定;IIDG2与额定功率值有交点,暂态稳定。当额定功率值为Pn3时,IIDG1与IIDG2与额定功率均无交点,因此均暂态不稳定。
2.3.3 下垂参数
IIDG的控制参数极大地影响着其暂态之后的功角变化[25]。根据式(5),有功下垂因子mP决定着功角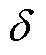 的变化速率,结合功角轨迹平衡点的数学表达与式(6)可知
的变化速率,结合功角轨迹平衡点的数学表达与式(6)可知
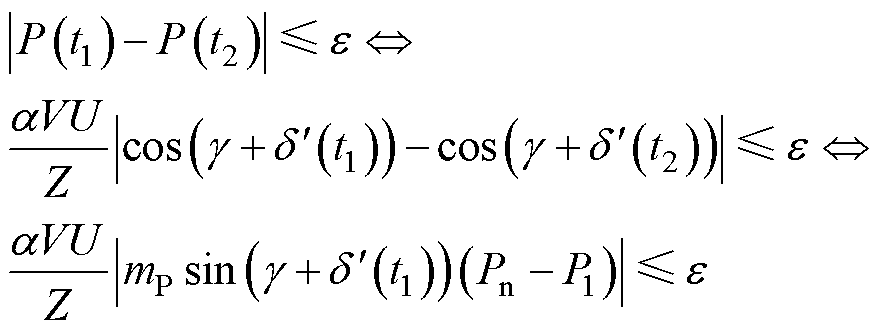 (7)
(7)
可以看出,当mP较大时,不等式左边大,满足功角轨迹稳定的平衡点少,因此IIDG暂态稳定性较差。
根据式(1)无功方程部分,可以看出,V的变化幅度与mQ相关。mQ越大,V的变化幅度越大,当IIDG外部出现暂态事件而电压下降时,IIDG的电压越容易恢复到额定值。因此,mQ越大,IIDG的稳定性越强。
在故障切除后,IIDG恢复过程的电压、电流以及配电网电压如图8所示。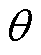 为d轴与电网电压
为d轴与电网电压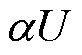 的夹角,
的夹角,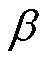 为d轴与IIDG输出电流
为d轴与IIDG输出电流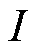 的夹角。由IIDG的三环控制可知,IIDG在控制过程中,一直保持电压V的q轴分量Vq=0,因此可认为V的方向即d轴方向。
的夹角。由IIDG的三环控制可知,IIDG在控制过程中,一直保持电压V的q轴分量Vq=0,因此可认为V的方向即d轴方向。
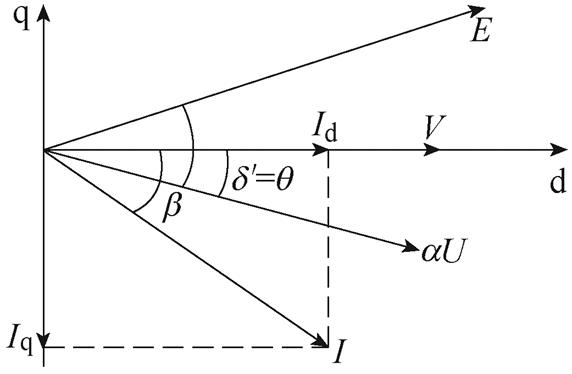
图8 IIDG相量图
Fig.8 Phasor diagram of IIDG
控制系统对IIDG内电动势角度进行控制,在暂态过程中,IIDG的电压以及其角度、输出功率可表示为
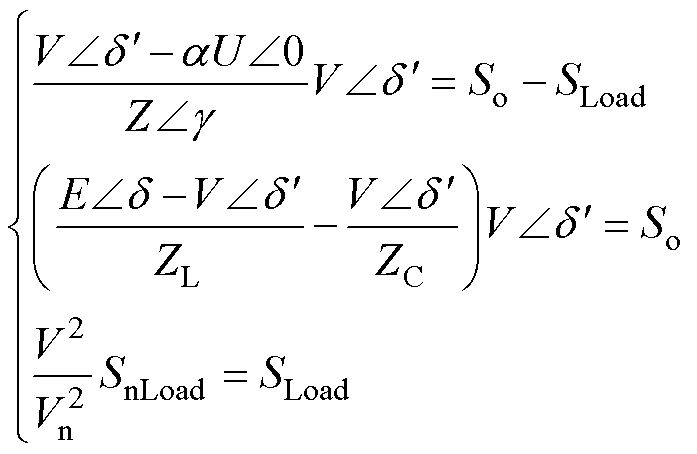 (8)
(8)
式中,So为IIDG的输出视在功率;SLoad为本地负荷消耗的视在功率;SnLoad为本地负荷额定消耗的视在功率;ZL为滤波电抗;ZC为滤波容抗。在故障切除后的每个时刻,系统中的潮流满足式(8)。
在暂态事件切除后,IIDG的输出电压与功率将会持续变化,其变化的数学解析式较为复杂,难以直观地反映IIDG的稳定性,因此,本文对IIDG的输出功率、电压等进行迭代计算。记迭代计算的时间步长为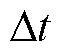 。
。
在暂态事件切除的一瞬间,IIDG的输出电压为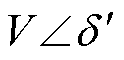 ,暂态切除时,IIDG的功角与电压还来不及发生变化,记此刻功角与电压为
,暂态切除时,IIDG的功角与电压还来不及发生变化,记此刻功角与电压为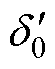 与
与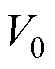 。
。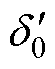 的计算公式为
的计算公式为
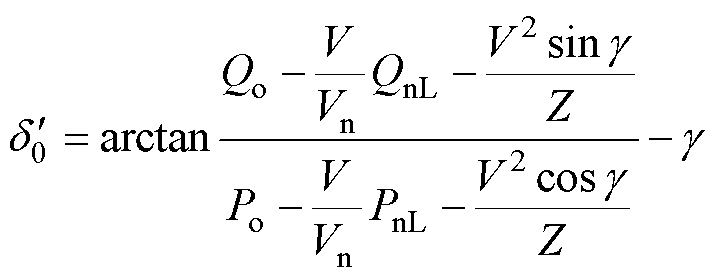 (9)
(9)
由于暂态事件切除后,电网的拓扑发生变化,此刻IIDG的功角曲线将从故障中的功角曲线变化为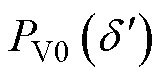 ,IIDG的功率输出也将变为
,IIDG的功率输出也将变为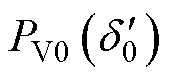 。由式(8)可对IIDG的内功角与内电动势进行计算,记作
。由式(8)可对IIDG的内功角与内电动势进行计算,记作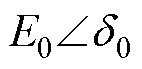 ,可假设IIDG的内电动势不变[26]。
,可假设IIDG的内电动势不变[26]。
此时,IIDG的输出功率与额定功率不相等,根据式(4),IIDG的输出电压、功角等将会在下垂控制器的作用下开始变化。则t时刻后,IIDG的下垂控制器输出的电压信号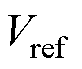 与角频率信号
与角频率信号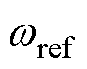 分别为
分别为
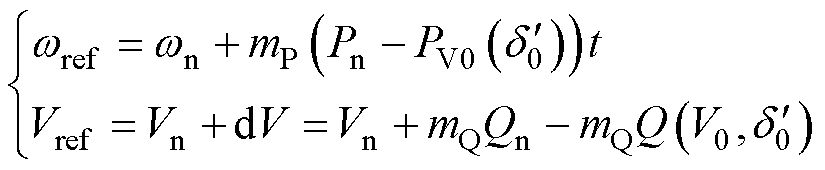 (10)
(10)
式中,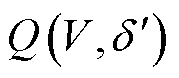 为IIDG在功角为
为IIDG在功角为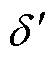 、电压为V时的无功输出,它满足
、电压为V时的无功输出,它满足
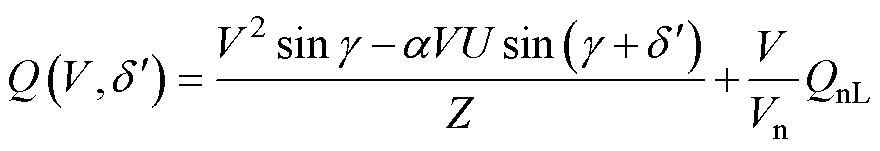 (11)
(11)
根据式(5),在经过一个步长的迭代时间后,内功角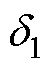 为
为
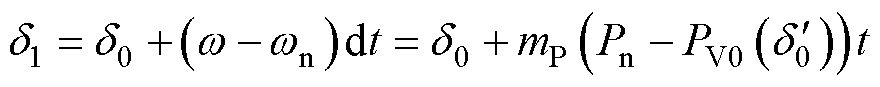 (12)
(12)
电压信号经过电压外环控制器、电流内环控制器、坐标变换与脉冲宽度调制(Pulse Width Modu- lation, PWM)后至逆变电路,并最终输出电压。将上述过程等效为二阶低通滤波器,可得到逆变器输出电压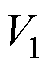 为
为
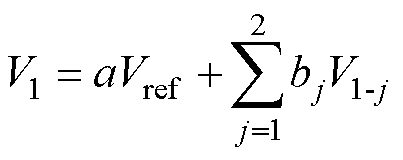 (13)
(13)
输出电压满足
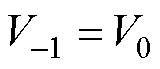 (14)
(14)
由式(8),可对此刻功角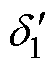 进行计算。此时,由于功角与电压发生改变,IIDG的功角曲线变为
进行计算。此时,由于功角与电压发生改变,IIDG的功角曲线变为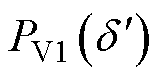 ,输出功率变为
,输出功率变为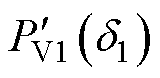 、
、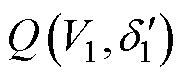 。同理,下一刻IIDG的功角与电压仍可按下垂控制方程进行推导。最终,可得到暂态事件发生后IIDG的功角与电压随时间变化的递推公式为
。同理,下一刻IIDG的功角与电压仍可按下垂控制方程进行推导。最终,可得到暂态事件发生后IIDG的功角与电压随时间变化的递推公式为
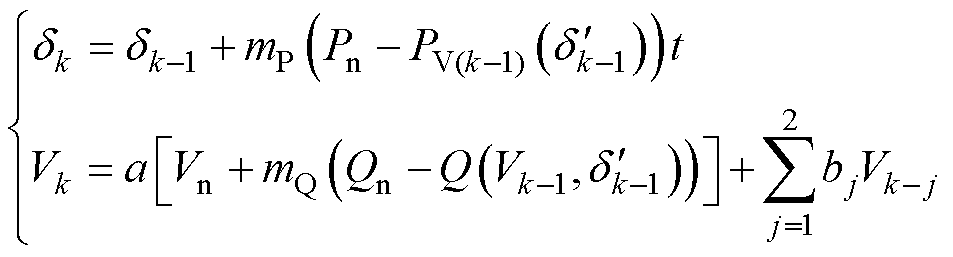 (15)
(15)
将得到的功角与电压代入式(8),可得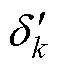 。
。
按照递推公式可得功角与电压的数列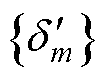 、
、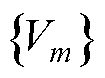 ,其中m为IIDG暂态稳定性计算的迭代次数。根据2.2节所推导的IIDG暂态稳定判据可知,若存在功率平衡点,则系统是暂态稳定的,否则是暂态不稳定。为此,可对功角、电压的数列在故障切除后是否存在稳定点进行判断。
,其中m为IIDG暂态稳定性计算的迭代次数。根据2.2节所推导的IIDG暂态稳定判据可知,若存在功率平衡点,则系统是暂态稳定的,否则是暂态不稳定。为此,可对功角、电压的数列在故障切除后是否存在稳定点进行判断。
若IIDG在暂态事件后存在功率平衡点,则功率、电压与功角均将稳定在某个值的邻域;若IIDG暂态不稳定,则IIDG不存在功率平衡点,根据式(5)可知,IIDG功角将向同一方向不断变化,功角的数列将无法收敛。因此,当得到了功角与电压的数列后,可利用功角数列的收敛性对IIDG的暂态稳定性进行判断:
对某一极小值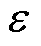 ,
,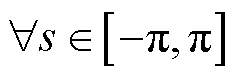 ,
,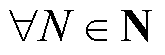 ,若均
,若均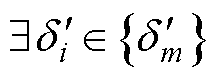 且
且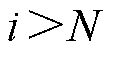 ,s.t.
,s.t.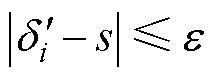 ,则可认为IIDG在故障后的功角在
,则可认为IIDG在故障后的功角在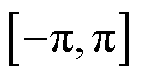 的区间内不停变化,且遍历该区间,因而IIDG在振荡,即IIDG在故障后不满足暂态稳定性准则。在迭代计算中,需要对IIDG是否满足稳定性准则进行判断。
的区间内不停变化,且遍历该区间,因而IIDG在振荡,即IIDG在故障后不满足暂态稳定性准则。在迭代计算中,需要对IIDG是否满足稳定性准则进行判断。
规定一个迭代的最大时间tmax,当时间达到tmax后则迭代结束,进行稳定性判断。在实际计算中,为了在离散化的数列实现对连续量收敛的判断,可以借鉴Cauchy收敛准则的方法,进行稳定性判断。
(1)取稳定时功角波动极小值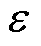 ,如
,如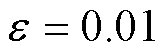 。
。
(2)取出在迭代过程中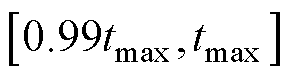 内的所有点,判断是否满足
内的所有点,判断是否满足
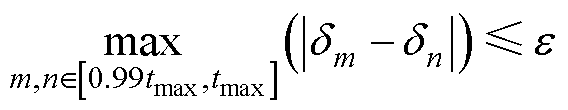 (16)
(16)
若满足式(16),则说明功角趋于稳定,IIDG暂态稳定;若不满足式(16),则说明功角仍在大幅度振荡,IIDG暂态不稳定。
IIDG暂态稳定性的迭代计算流程如图9所示。迭代算法对IIDG暂态稳定性的判断准确性与迭代步长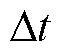 成反比,与迭代最大时间tmax成正比。
成反比,与迭代最大时间tmax成正比。
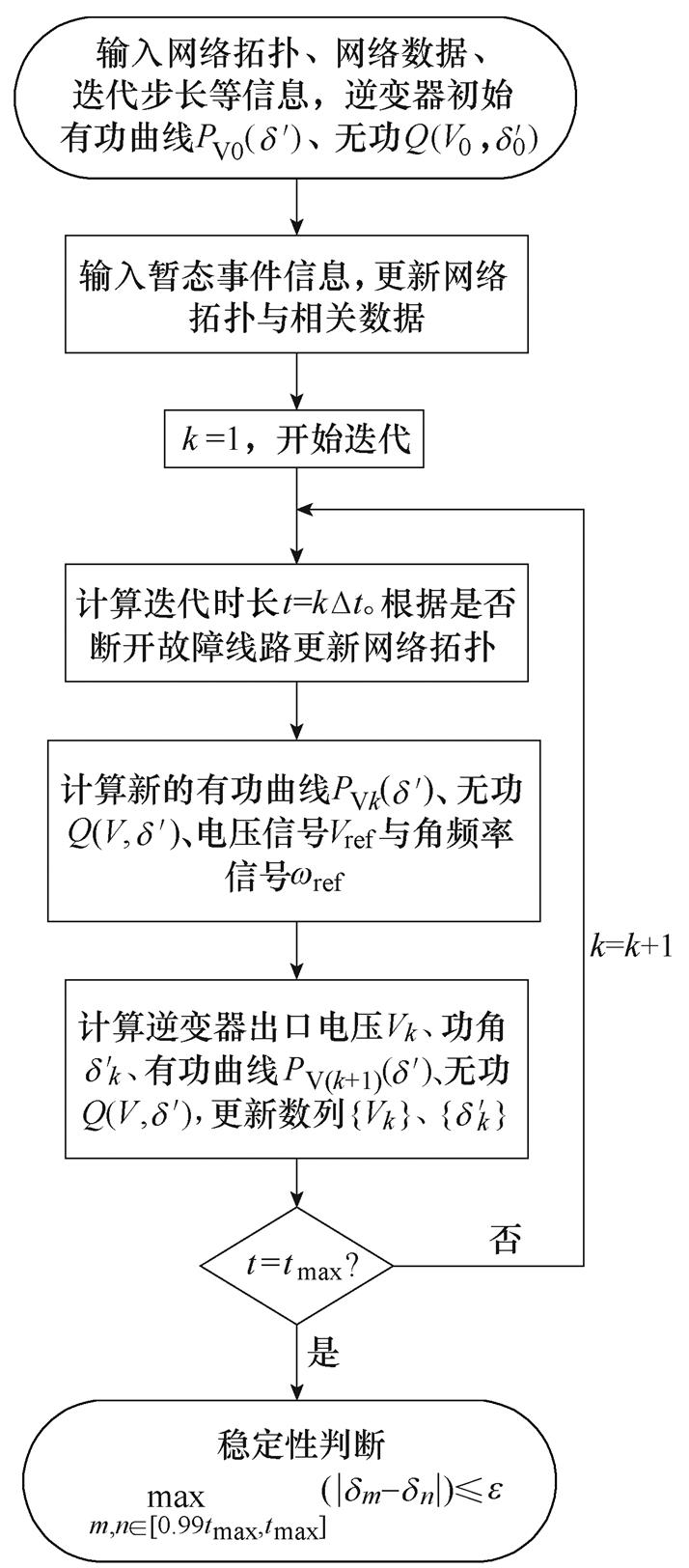
图9 IIDG暂稳迭代判定法
Fig.9 Computations of the transient stability of IIDGs
为了验证IIDG暂稳迭代判定法的有效性,明确IIDG的控制参数对IIDG暂态稳定性的影响,利用PSCAD/EMTDC建立算例,并进行仿真分析。
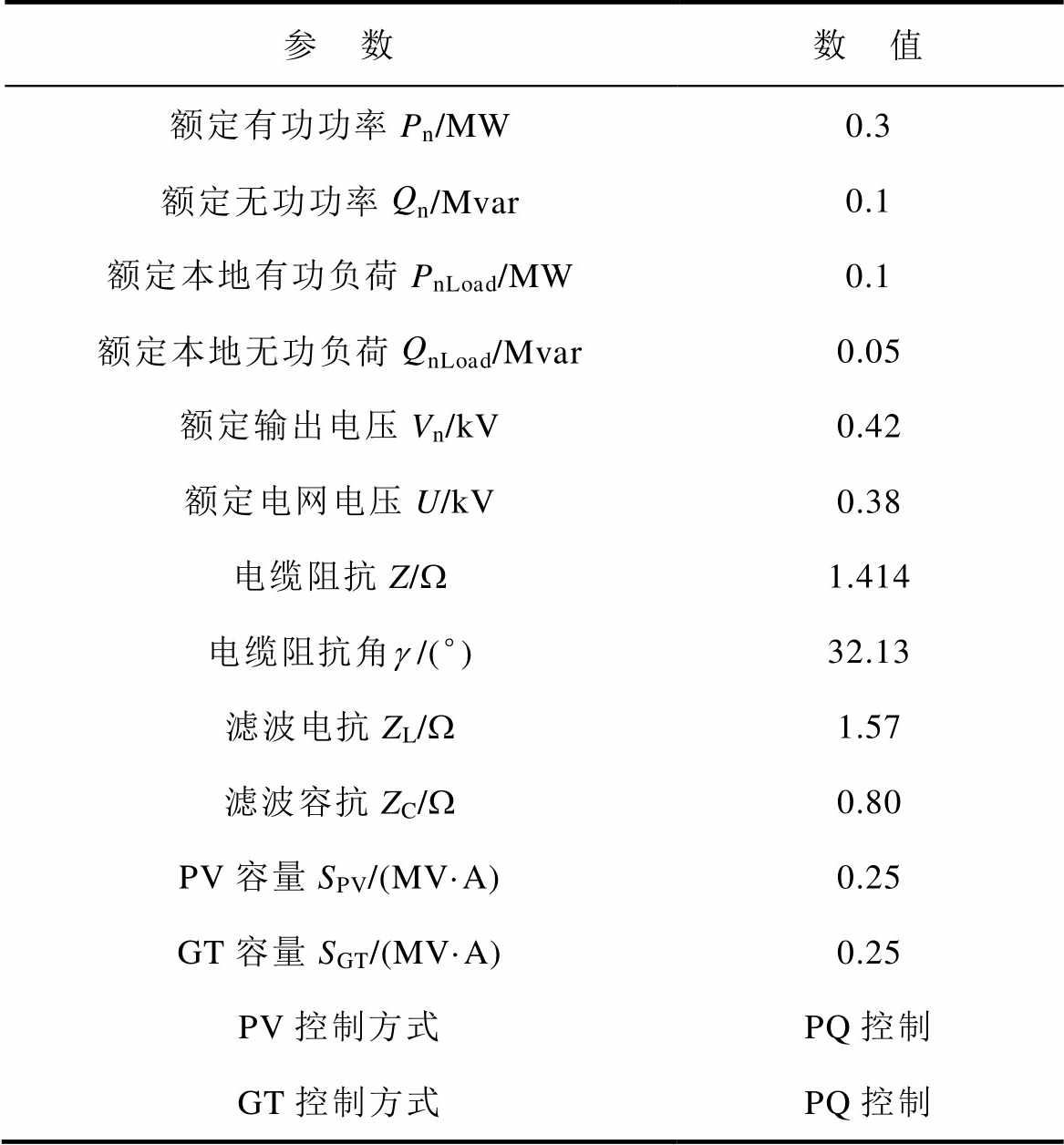
IIDG采用三环控制器控制电压、功率,仿真算例与图2所示系统相同,其中电网侧接入的分布式电源包括光伏发电单元(Photovoltaic Unit, PV)与燃气轮机(Gas Turbine, GT),算例参数来自广西三里一中微电网群,见表2[27]。
表2 仿真算例的系统参数
Tab.2 Parameters of the simulation cases
参 数数 值 额定有功功率Pn/MW0.3 额定无功功率Qn/Mvar0.1 额定本地有功负荷PnLoad/MW0.1 额定本地无功负荷QnLoad/Mvar0.05 额定输出电压Vn/kV0.42 额定电网电压U/kV0.38 电缆阻抗Z/W1.414 电缆阻抗角g/(°)32.13 滤波电抗ZL/W1.57 滤波容抗ZC/W0.80 PV容量SPV/(MV·A)0.25 GT容量SGT/(MV·A)0.25 PV控制方式PQ控制 GT控制方式PQ控制
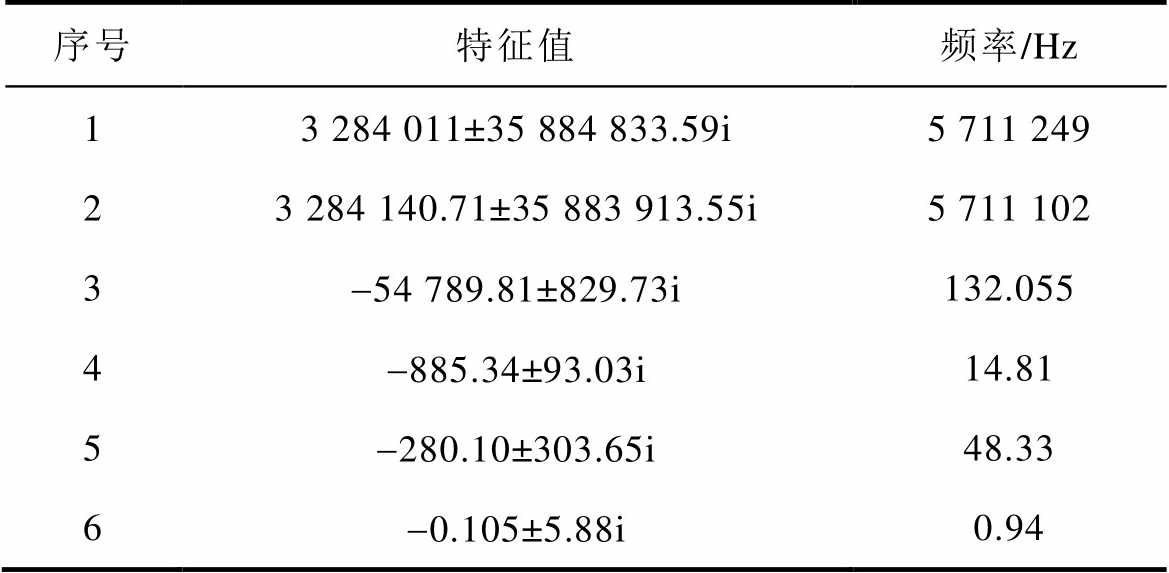
根据系统参数,参考文献[28]的计算方法可以得出系统特征值见表3,可以看出,此时系统的6对共轭特征值都有负的实部,系统静态稳定。因此后续系统的失稳可以推断为暂态事件引发。
表3 系统特征值
Tab.3 Eigenvalues of the system
序号特征值频率/Hz 13 284 011±35 884 833.59i5 711 249 23 284 140.71±35 883 913.55i5 711 102 3-54 789.81±829.73i132.055 4-885.34±93.03i14.81 5-280.10±303.65i48.33 6-0.105±5.88i0.94
三相接地短路是最严重的故障类型,对系统的稳定运行威胁最大,为反映IIDG的暂态稳定能力,算例中的暂态事件为馈线发生三相接地短路。当发生故障时,故障越严重,IIDG越可能出现失稳,因此选择在5s时三相短路低阻接地故障发生,过渡电阻选为0.15W。为了能观察到1~2个完整周期的振荡,故障持续1s后切除,故障状态时电网电压暂态参数a 取值0.8,故障切除后a 取值0.9。
为了验证暂稳判断迭代法的有效性与准确性,本文将暂稳迭代判定法计算的结果与PSCAD/EMTDC上的仿真结果进行对比。暂稳迭代判定法与PSCAD/ EMTDC仿真的计算时长见表3。
图10所示为系统按照表2数据进行的仿真实验得到的电压波形、功角波形、有功功率波形与无功功率波形,其中实线为PSCAD/EMTDC仿真得到的结果,虚线为提出的暂稳迭代判定法计算得到的结果。从PSCAD/EMTDC的仿真结果中可以看出,在以表2的数据参数进行仿真时,系统在5s前是处于稳定运行状态,IIDG工作在额定值;在5s,故障发生,电压瞬间跌落,有功功率、无功功率显著下降,功率无法外送。在有功功率急剧下降的情况下,下垂控制增加IIDG角频率,导致IIDG的功角增加。在6s时,故障切除,系统的电压回升,有功功率、无功功率在下垂控制作用下逐渐恢复,功角的变化速率变缓。但由于有功功率无法恢复至额定值,功角开始发生振荡,并使得IIDG的电压与功率均出现振荡。从暂稳迭代判定法计算结果可以看出,暂稳迭代判定法准确地预测了IIDG的暂态不稳定,并在IIDG进入稳定的振荡后,较好地模拟了IIDG发生振荡时的振荡幅度与频率。但暂稳迭代判定法在故障刚发生时与仿真有一定差异,其原因是暂稳迭代判定法采用低通滤波器的方式等效了IIDG的电压内环与电流内环,因此在系统出现瞬间大幅度变化时,暂稳迭代判定法与实际系统的动态响应有差距,这也导致IIDG稳定振荡时算法计算出的IIDG的振荡相位有差距。但暂稳迭代判定法对IIDG的暂态稳定性判断是准确的。
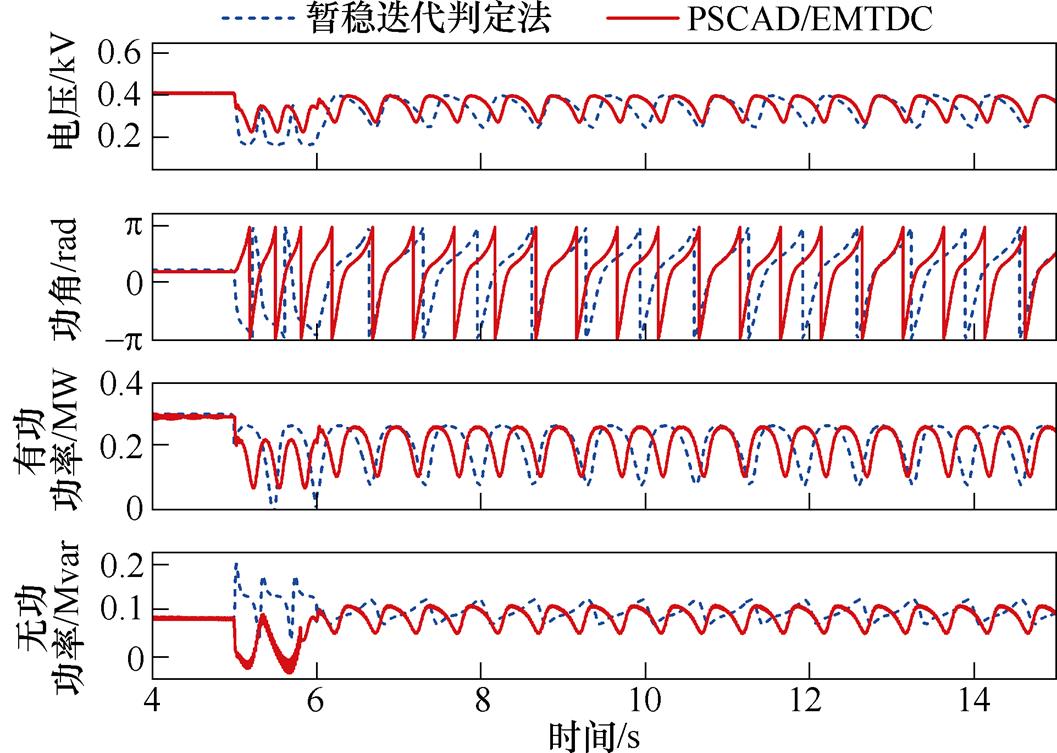
图10 仿真与迭代算法对比(Pn=0.3MW)
Fig.10 Compare between simulations on PSCAD/EMTDC and proposed computation method (Pn=0.3MW)
仿真过程中,PV与GT的功率变化如图11所示。在故障之后,由于电压的不稳定,PV与GT的功率均产生了周期性波动。可推断由于IIDG的暂态不稳定,影响了电网内其他发电设备的正常运行。
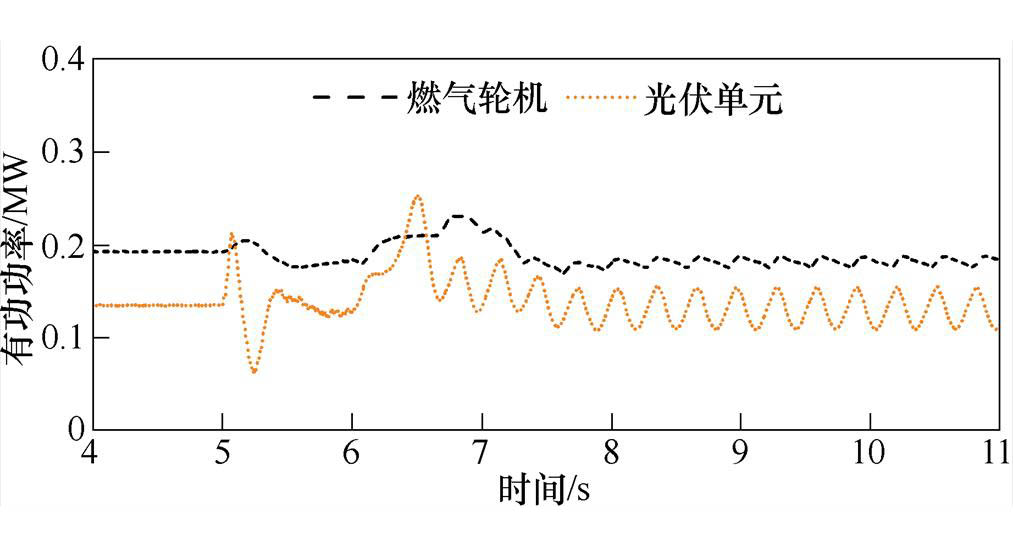
图11 PV与GT功率变化(Pn=0.3MW)
Fig.11 Power change of PV and GT (Pn=0.3MW)
为了进一步验证暂稳迭代判定法的准确性,将IIDG的额定有功功率降低至0.2MW,使其在暂态过程中保持稳定。降低了额定有功功率后的暂稳迭代判定法与PSCAD/EMTDC仿真结果对比如图12所示。
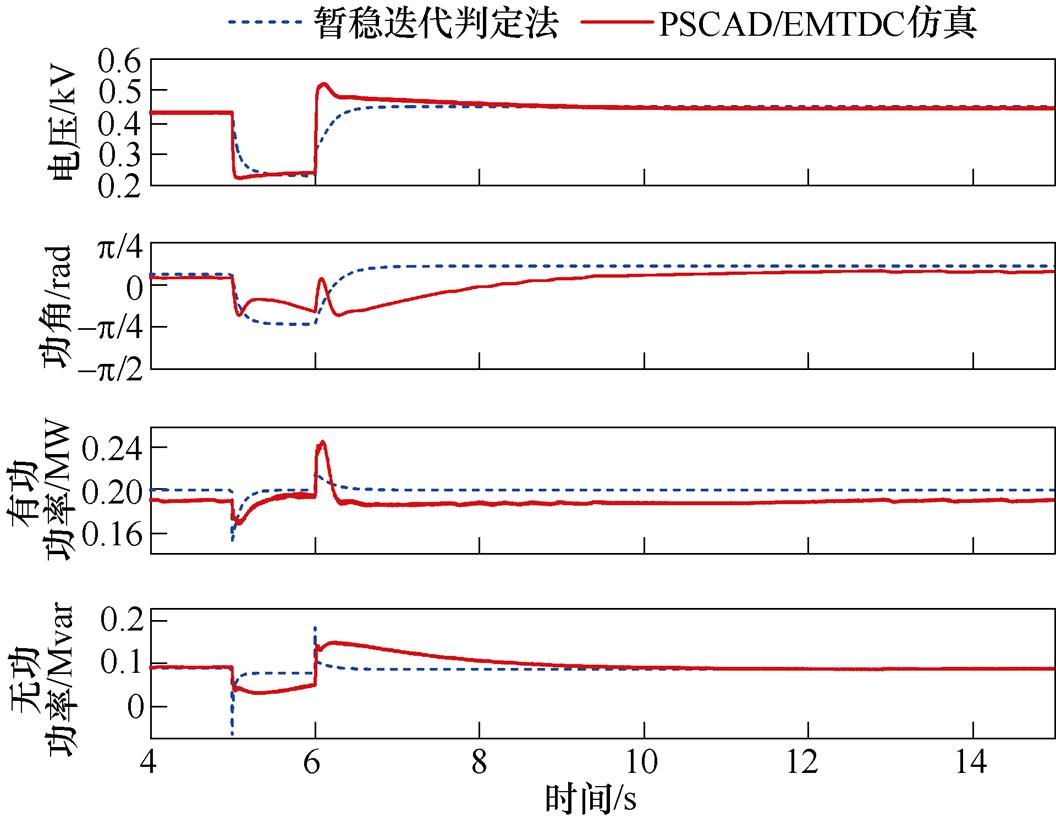
图12 仿真与迭代算法对比(Pn=0.2MW)
Fig.12 Compare between simulations on PSCAD/EMTDC and proposed computation method (Pn=0.2MW)
图12中,IIDG在暂态发生前、故障阶段、故障切除后,均出现明显的振荡。从与仿真的对比可以看出,暂态迭代算法能够准确地判断IIDG是否暂态稳定,并计算出IIDG在稳定后的稳定值。
仿真过程中PV与GT的功率变化如图13所示。相对于图11中的功率变化,在IIDG额定功率取为0.2MW时,PV与GT的功率输出非常稳定,并未在暂态事件之后受到较大影响。
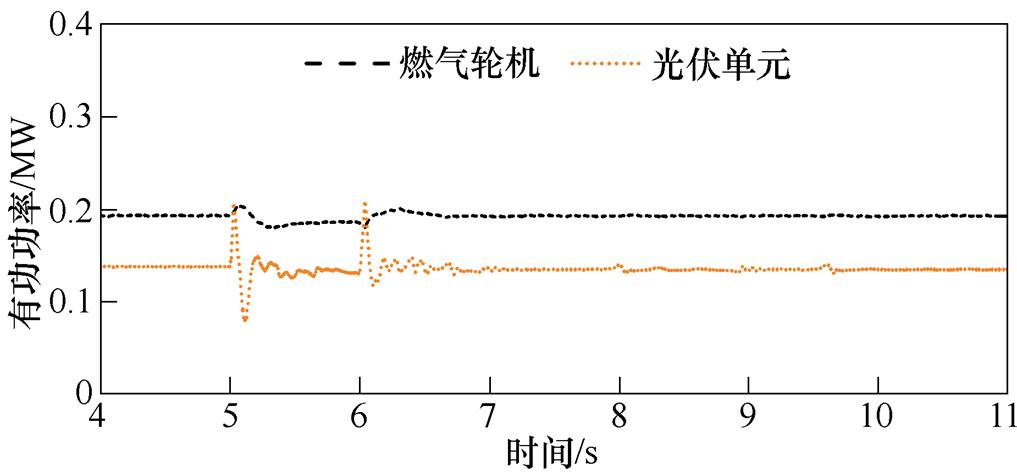
图13 PV与GT功率变化(Pn=0.2MW)
Fig.13 Power change of PV and GT (Pn=0.2MW)
为了验证IIDG与其他电源耦合时,暂稳迭代判定法依然能够适用,仿真了PV在出现阳光遮蔽时的有功突变,将PV的有功功率从0.15MW降低至0.1MW,此时IIDG的功率变化如图14所示。
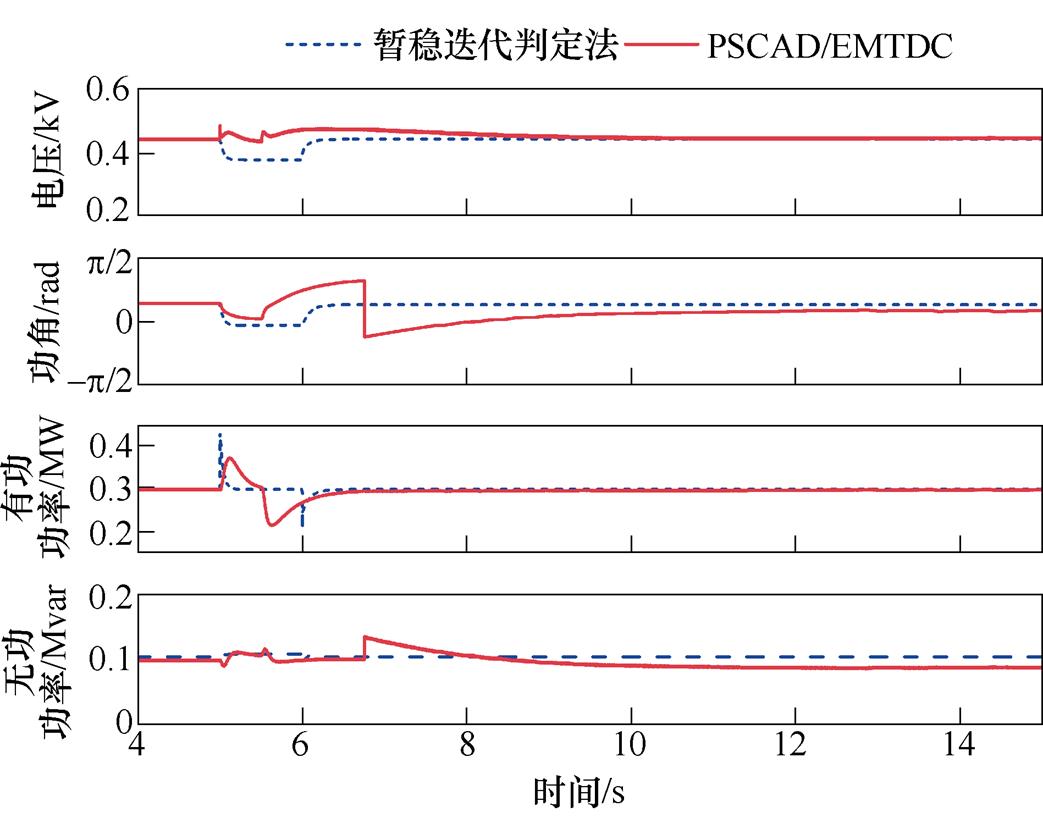
图14 PV功率突变时PSCAD/EMTDC仿真与迭代算法对比(Pn=0.3MW)
Fig.14 Simulation results with PSCAD/EMTDC and iterative computation method when PV output changes (Pn=0.3MW)
图14中,IIDG在PV的功率发生突变后,均未出现明显的功率、电压振荡,因为PV与IIDG之间虽然存在耦合,但是PV的功率波动并未造成IIDG外部运行环境发生大扰动,因此IIDG仍然保持稳定运行。
PSCAD/EMTDC仿真耗时与暂稳迭代判定法的对比见表4,可以看出,在相同性能的计算机上,暂稳迭代判定法的计算耗时相较于电磁仿真具有极大的优势。
为了检验不同网络参数对IIDG暂态稳定性的影响,本文利用提出的暂稳迭代判定法对2.3节所分析的电压、电缆阻抗、本地负荷以及额定功率值与暂态稳定性的影响进行定量研究。
表4 PSCAD/EMTDC仿真与迭代算法耗时对比
Tab.4 Time consumption between simulations with PSCAD/EMTDC and iterative computation method (单位: s)

算例耗时 Pn=0.2MWPn=0.3MW PSCAD/EMTDC32.231.4 暂稳迭代判定法0.2480.225
根据2.3节的分析,以电压、电缆阻抗与本地负荷大小作为变量,分别在不同的额定功率下进行IIDG暂态稳定性的计算。采用PSCAD/EMTDC仿真得到的结果与采用暂稳迭代判定法得到的暂态稳定性结果见表5~表7,两种方法得到的功角轨迹线如图15与图16所示。除了额定功率与相应改变的网络参数外,IIDG系统中的其余参数仍与表2所列保持一致。当IIDG暂态不稳定时,记录IIDG在故障切除后有功功率达到的最大值Pmax;当IIDG暂态稳定时,记录IIDG最终稳定后的功角值dS。表中的功角值dS已约化至-p ~p 之间。
表5 电压对暂态稳定性的影响
Tab.5 The influence of voltage on transient stability
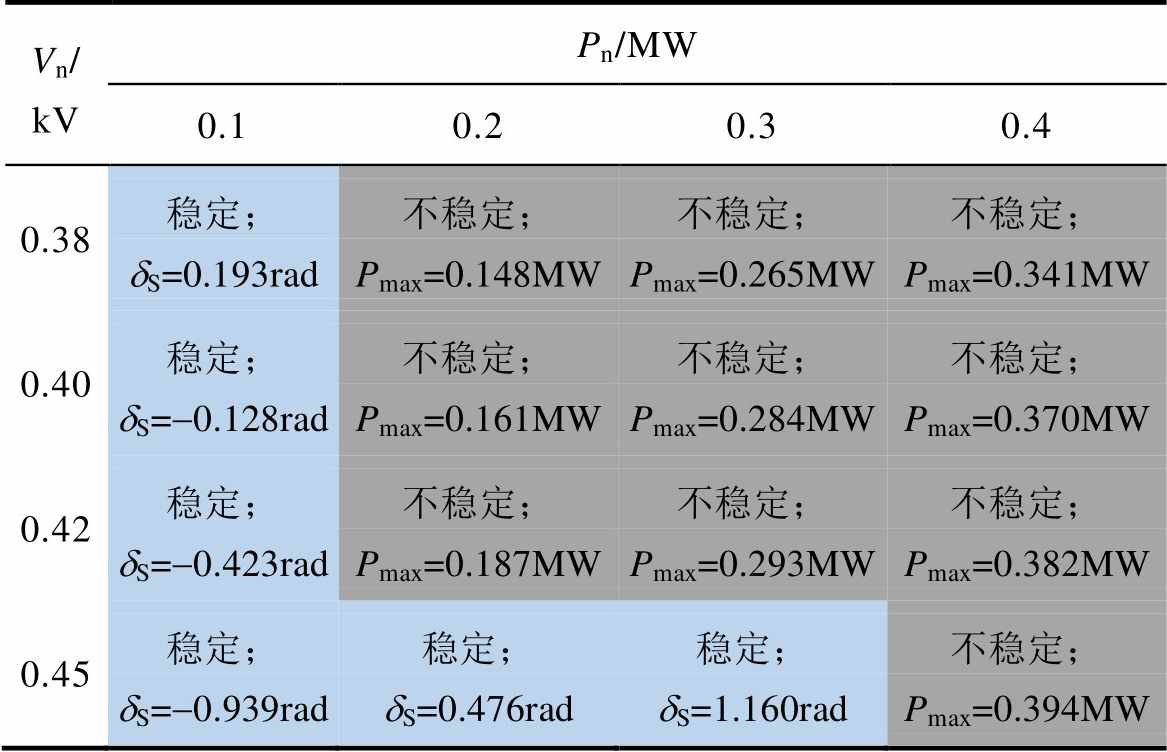
Vn/ kVPn/MW 0.10.20.30.4 0.38稳定;dS=0.193rad不稳定;Pmax=0.148MW不稳定;Pmax=0.265MW不稳定;Pmax=0.341MW 0.40稳定;dS=-0.128rad不稳定;Pmax=0.161MW不稳定;Pmax=0.284MW不稳定;Pmax=0.370MW 0.42稳定;dS=-0.423rad不稳定;Pmax=0.187MW不稳定;Pmax=0.293MW不稳定;Pmax=0.382MW 0.45稳定;dS=-0.939rad稳定;dS=0.476rad稳定;dS=1.160rad不稳定;Pmax=0.394MW
表6 电缆阻抗对暂态稳定性的影响
Tab.6 The influence of cable impedances on transient stability

Z/WPn/MW 0.10.20.30.4 0.707稳定;dS=-0.070rad稳定;dS=0.797rad稳定;dS=0.633rad稳定;dS=0.507rad 1.414稳定;dS=-0.128rad不稳定;Pmax=0.156MW不稳定;Pmax=0.293MW不稳定;Pmax=0.366MW 2.828稳定;dS=-0.236rad不稳定;Pmax=0.143MW不稳定;Pmax=0.240MW不稳定;Pmax=0.348MW 5.656不稳定;Pmax=0.092MW不稳定;Pmax=0.131W不稳定;Pmax=0.233MW不稳定;Pmax=0.338MW
表7 本地负荷对暂态稳定性的影响
Tab.7 The influence of local loads on transient stability
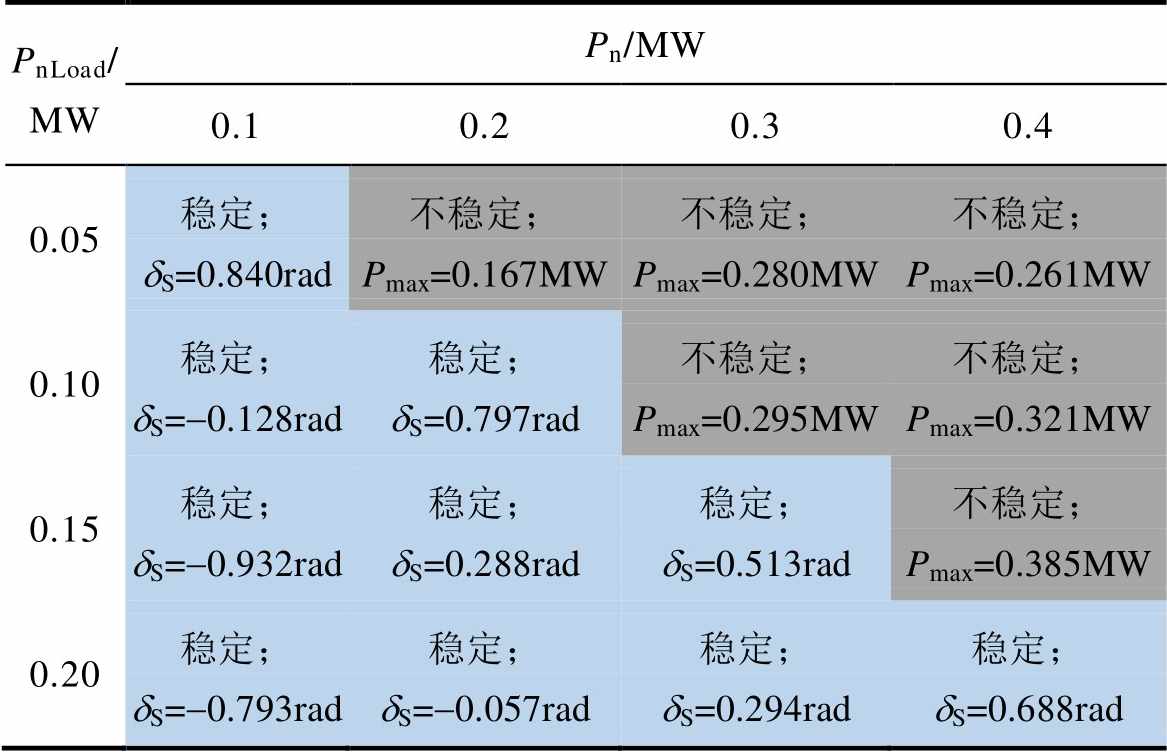
PnLoad/ MWPn/MW 0.10.20.30.4 0.05稳定;dS=0.840rad不稳定;Pmax=0.167MW不稳定;Pmax=0.280MW不稳定;Pmax=0.261MW 0.10稳定;dS=-0.128rad稳定;dS=0.797rad不稳定;Pmax=0.295MW不稳定;Pmax=0.321MW 0.15稳定;dS=-0.932rad稳定;dS=0.288rad稳定;dS=0.513rad不稳定;Pmax=0.385MW 0.20稳定;dS=-0.793rad稳定;dS=-0.057rad稳定;dS=0.294rad稳定;dS=0.688rad
表5显示了在不同电压与不同额定功率下IIDG的暂态稳定性。从表中可以看出,当电压越高时,IIDG越稳定。表6显示了在不同电缆阻抗与不同额定功率下IIDG的暂态稳定性,从表中可以看出,当电缆阻抗越大时,IIDG越不稳定。表7显示了在不同本地负荷大小与额定功率下IIDG的暂态稳定性,从表中可以看出,当本地负荷越大时,IIDG越稳定。此外,结合表5~表7可以推断,当IIDG的额定有功功率越大时,IIDG越容易失去稳定性。以上结论与2.3节分析相符。
图15~图17分别对应表5~表7的仿真结果。由图15~图17可知,在暂态稳定状态下,功角轨迹波动幅度较小,在暂态事件前后功角与有功功率的稳定值只发生小幅度改变。
图15展示了不同电压等级与额定功率时,功角轨迹的变化,由图15a、图15e、图15i、图15m、图15n可知,在暂态事件发生前,功角轨迹稳定;暂态事件发生时,功角增大,同时有功功率上升;在暂态事件切除后,功角下降,有功功率逐渐恢复到额定值。此五种场景中,暂态事件发生时,功角轨迹未出现大幅度变化,说明在短路过程中的功角曲线与额定功率有相位点,使得IIDG在短路过程中仍能保持输出稳定,因此,IIDG在此五种场景中的暂态事件前、事件中、事件后均存在稳定点。图15o中,IIDG在暂态事件前与事件后均保持稳定,但是在暂态事件过程中暂态轨迹出现了较大幅度的波动,说明在暂态事件过程中功角曲线与额定功率并无相交点,因此IIDG沿着短路过程中的暂态轨迹线发生波动。在此场景中,IIDG虽然在暂态事件中出现了大幅度波动,但暂态事件后仍能保持稳定。其余子图中,IIDG均暂态不稳定,说明在此部分场景中IIDG在暂态事件后的功角曲线与额定功率无交点。

图15 不同电压等级与额定功率的功角轨迹
Fig.15 Power angle variation traces with different voltages and rated active power
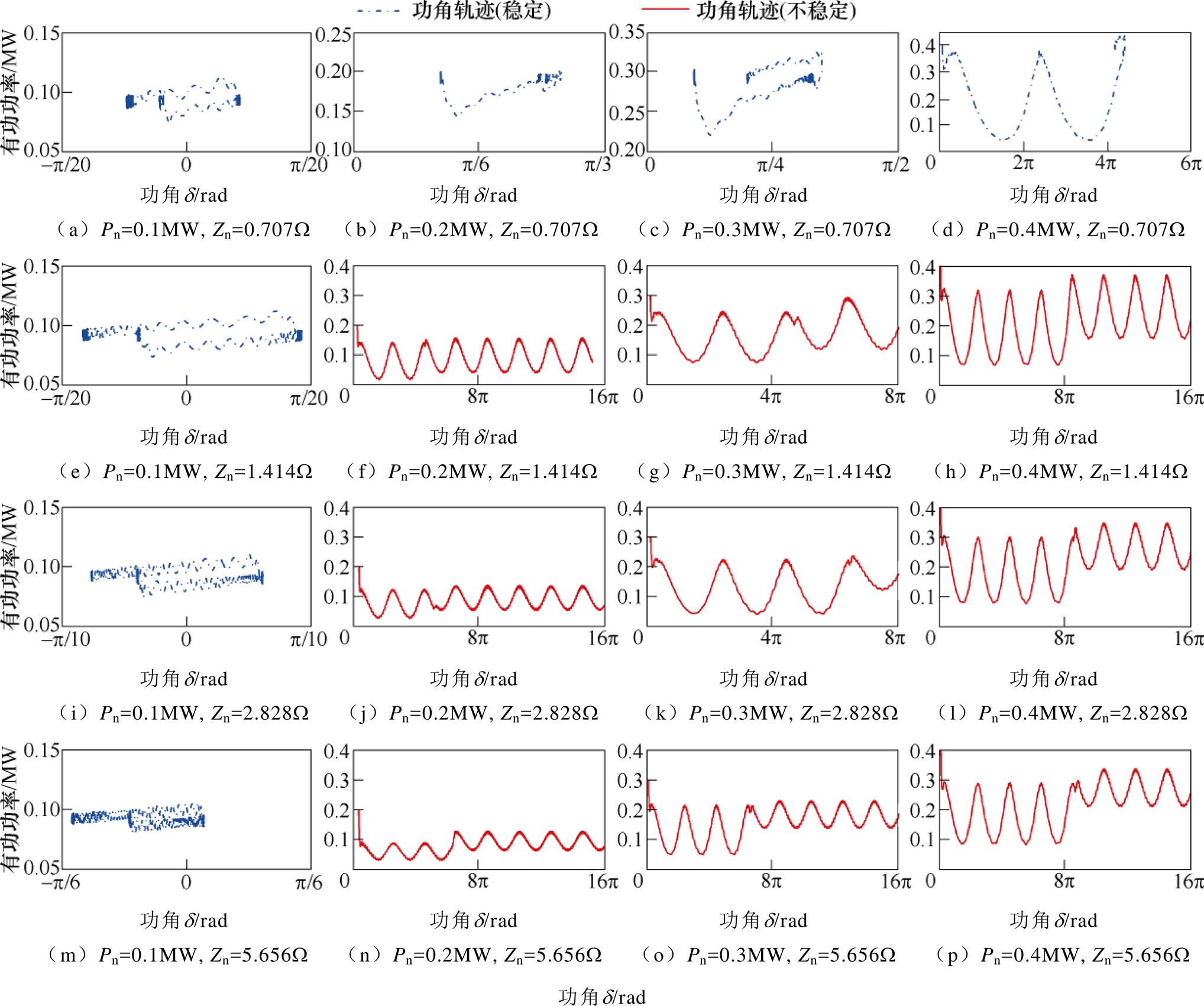
图16 不同电缆阻抗与额定功率的功角轨迹
Fig.16 Power angle variation traces with different cable impedances and rated active power

图17 不同本地负荷与额定功率的功角轨迹
Fig.17 Power angle variation traces with different local loads and rated active power
值得注意的是,本次仿真每组实验仿真时长均为10s,然而部分仿真中功角在10s内变化幅度较小,如图15j所示,部分仿真中功角在10s内变化幅度较大,如图15d、图15h、图15l、图15p所示,部分仿真中功角变化范围太大,则统一选取了一定的范围值。由式(5)可知,造成这种差异的原因是IIDG的功角变化速率与功角曲线与额定功率差值相关。因此,根据功角变化速率也可推断出功角曲线的大小。由图15~图17中暂态不稳定的场景可知,IIDG在暂态事件中与暂态事件后的功角轨迹幅值及峰值有明显差异,说明IIDG的功角曲线在事件切除后增大。图15~图17中,所有暂态不稳定的场景里IIDG的功角轨迹均未与额定功率相交,验证了IIDG暂态稳定判据的正确性。
由图15可知,当电压增大时,IIDG的暂态稳定性增加。保持额定功率不变纵向对比图15中的各组功角轨迹,可知当IIDG暂态不稳定时,IIDG的功角曲线随电压的增大而增大,当增大到一定值时,IIDG暂态稳定。保持电压不变横向比较图15中各组功角轨迹,可知当IIDG暂态不稳定时,额定功率越大,功角变化速率越快,IIDG输出波动频率也越大;减小IIDG的额定功率后,IIDG达到稳定。
由图16可知,当电缆阻抗增加时,IIDG的暂态稳定性减小。保持额定功率不变纵向对比图16中的各组功角轨迹,可知当IIDG暂态稳定时,增大电缆阻抗将导致IIDG暂态不稳定,且电缆阻抗值越大,IIDG功角曲线越小,功角波动速率越大。由图17可知,当本地负荷增加时,IIDG的暂态稳定性增加。保持额定功率不变纵向对比图17中的各组功角轨迹,可知当IIDG暂态不稳定时,增加IIDG的本地负荷将使IIDG暂态稳定。
本文研究逆变型分布式电源在短路故障、负载投切等暂态事件下的暂态稳定性机理,并提出逆变型分布式电源暂态稳定性判定方法。通过对并网逆变型分布式电源的控制系统与并网电路进行研究,建立了并网逆变型分布式电源功角稳定判据,基于功角曲线簇,提出了逆变型分布式电源并网运行的暂态稳定性机理。分析暂态过程中电气量变化规律,提出了迭代计算并网逆变型分布式电源功角的暂稳判定方法。通过理论分析与仿真计算,本文针对逆变型分布式电源暂态稳定性的研究结论如下:
1)暂态事件下逆变型分布式电源的功角曲线与其额定功率直线存在交点,则其暂态稳定;否则该暂态事件下系统暂态不稳定。
2)逆变型分布式电源额定功率及所接入配电网网络参数对暂态稳定性的影响较大。IIDG暂态稳定性与其输出电压及本地负荷大小正相关,与馈线阻抗及其额定功率负相关。
3)暂稳迭代判定法通过迭代计算暂态事件下IIDG功角轨迹,对功角的振荡进行判断,以此判定IIDG的暂态稳定性。仿真算例验证了暂稳迭代判定法的有效性与准确性,判断结果准确度高。
逆变性分布式电源暂态稳定性对配电网的可靠、稳定运行十分重要,本文提出的暂态稳定性机理与暂稳迭代判定方法,较好地解决了IIDG并网暂态稳定性判定的问题,提高了逆变型分布式电源暂态运行分析与判断能力,为进一步提高配电网新能源渗透率奠定了基础,同时可为含多类型分布式电源配电网暂态稳定的研究提供参考。
参考文献
[1] 倪萌, 王蓓蓓, 朱红, 等. 能源互联背景下面向高弹性的多元融合配电网双层分布式优化调度方法研究[J]. 电工技术学报, 2022, 37(1): 208-219.
Ni Meng, Wang Beibei, Zhu Hong, et al. Study of two-layer distributed optimal scheduling strategy for highly elastic multi-resource fusion distribution network in energy interconnection environment[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 208-219.
[2] 杨珺, 侯俊浩, 刘亚威, 等. 分布式协同控制方法及在电力系统中的应用综述[J]. 电工技术学报, 2021, 36(19): 4035-4049.
Yang Jun, Hou Junhao, Liu Yawei, et al. Distributed cooperative control method and application in power system[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4035-4049.
[3] 马麟, 刘建鹏. 考虑时序特性和环境效益的多目标多类型分布式电源规划[J]. 电力系统保护与控制, 2016, 44(19): 32-40.
Ma Lin, Liu Jianpeng. Multi-objective planning of multi-type distributed generation considering timing characteristics and environmental benefits[J]. Power System Protection and Control, 2016, 44(19): 32-40.
[4] Katiraei F, Iravani M R, Lehn P W. Micro-grid autonomous operation during and subsequent to islanding process[J]. IEEE Transactions on Power Delivery, 2005, 20(1): 248-257.
[5] 刘子文, 苗世洪, 范志华, 等. 基于自适应下垂特性的孤立直流微电网功率精确分配与电压无偏差控制策略[J]. 电工技术学报, 2019, 34(4): 795-806.
Liu Ziwen, Miao Shihong, Fan Zhihua, et al. Accurate power allocation and zero steady-state error voltage control of the islanding DC microgird based on adaptive droop characteristics[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 795-806.
[6] 陈海焱, 段献忠, 陈金富. 分布式发电对配网静态电压稳定性的影响[J]. 电网技术, 2006, 30(19): 27-30.
Chen Haiyan, Duan Xianzhong, Chen Jinfu. Impacts of distributed generation on steady state voltage stability of distribution system[J]. Power System Technology, 2006, 30(19): 27-30.
[7] 帅智康, 邹福筱, 涂春鸣. 微网暂态稳定性研究[J]. 电力系统自动化, 2015, 39(16): 151-159.
Shuai Zhikang, Zou Fuxiao, Tu Chunming. Review on transient stability of microgrid[J]. Automation of Electric Power Systems, 2015, 39(16): 151-159.
[8] Majumder R. Some aspects of stability in micro- grids[J]. IEEE Transactions on Power Systems, 2013, 28(3): 3243-3252.
[9] Ortega A, Milano F. Generalized model of VSC-based energy storage systems for transient stability analysis[J]. IEEE Transactions on Power Systems, 2016, 31(5): 3369-3380.
[10] 刘津铭, 陈燕东, 伍文华, 等. 孤岛微电网序阻抗建模与高频振荡抑制[J]. 电工技术学报, 2020, 35(7): 1538-1552.
Liu Jinming, Chen Yandong, Wu Wenhua, et al. Sequence impedance modeling and high-frequency oscillation suppression method for island microgrid[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1538-1552.
[11] 刘彦呈, 庄绪州, 张勤进, 等. 基于虚拟频率的直流微电网下垂控制策略[J]. 电工技术学报, 2021, 36(8): 1693-1702.
Liu Yancheng, Zhuang Xuzhou, Zhang Qinjin, et al. A virtual current-frequency droop control in DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1693-1702.
[12] Alaboudy A H K, Zeineldin H H, Kirtley J. Microgrid stability characterization subsequent to fault-triggered islanding incidents[J]. IEEE Transactions on Power Delivery, 2012, 27(2): 658-669.
[13] Omagari Y, Funaki T. Numerical study of transient stability criteria for an inverter-based distributed generator[C]//2012 3rd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aalborg, Denmark, 2012: 865-871.
[14] 黄林彬, 章雷其, 辛焕海, 等. 下垂控制逆变器的虚拟功角稳定机理分析[J]. 电力系统自动化, 2016, 40(12): 117-124.
Huang Linbin, Zhang Leiqi, Xin Huanhai, et al. Mechanism analysis of virtual power angle stability in droop-controlled inverters[J]. Automation of Electric Power Systems, 2016, 40(12): 117-124.
[15] Xin Huanhai, Huang Linbin, Zhang Leiqi, et al. Synchronous instability mechanism of Pf droop- controlled voltage source converter caused by current saturation[J]. IEEE Transactions on Power Systems, 2016, 31(6): 5206-5207.
[16] Ibrahim H M, El Moursi M S, Huang P H. Adaptive roles of islanded microgrid components for voltage and frequency transient responses enhancement[J]. IEEE Transactions on Industrial Informatics, 2015, 11(6): 1298-1312.
[17] Nguyen D H, Tran H N, Narikiyo T, et al. A Lyapunov approach for transient stability analysis of droop inverter-based mesh microgrids using line- based model[C]//IEEE Control Technology and Applications (CCTA), Hawaii, America, 2017: 1655- 1660.
[18] Hart P, Lesieutre B. Energy function for a grid-tied, droop-controlled inverter[C]//IEEE North American Power Symposium (NAPS), Pullman, America, 2014: 1-6.
[19] Quan Xiangjun, Wu Zaijun, Dou Xiaobo, et al. Load current decoupling based LQ control for three-phase inverter[J]. IEEE Transactions on Power Electronics, 2017, 33(6): 1670-1676.
[20] Ghosh S, Rahman S, Pipattanasomporn M. Distri- bution voltage regulation through active power curtailment with PV inverters and solar generation forecasts[J]. IEEE Transactions on Sustainable Energy, 2017, 8(1): 13-22.
[21] Wang Zhaoyu, Wang Jianhui, Chen Bokan, et al. MPC-based voltage/var optimization for distribution circuits with distributed generators and exponential load models[J]. IEEE Transactions on Smart Grid, 2014, 5(5): 2412-2420.
[22] 吴丽, 郑昕, 朱小红, 等. 三相四线制系统中计及零序电流特性的分布式电源逆变器有功和无功功率控制[J]. 电力系统保护与控制, 2019, 47(22): 126-133.
Wu Li, Zheng Xin, Zhu Xiaohong, et al. Active and reactive power control with zero sequence current characteristics for distributed generation inverters in three-phase four-wire system[J]. Power System Protection and Control, 2019, 47(22): 126-133.
[23] 任振宇, 张师, 田超华, 等. 基于轨迹灵敏度的风火打捆系统暂态稳定预防控制[J]. 电气技术, 2016, 17(6): 5-8.
Ren Zhenyu, Zhang Shi, Tian Chaohua, et al. Preventive control of improving wind-thermal bundled system transient stability based on trajectory sensiti- vity[J]. Electrical Engineering, 2016, 17(6): 5-8.
[24] Potamianakis E G, Vournas C D. Short-term voltage instability: effects on synchronous and induction machines[J]. IEEE Transactions on Power Systems, 2006, 21(2): 791-798.
[25] Barklund E, Pogaku N, Prodanovic M, et al. Energy management in autonomous microgrid using stability- constrained droop control of inverters[J]. IEEE Transactions on Power Electronics, 2008, 23(5): 2346-2352.
[26] 杨道培, 丁志刚, 曹炜. 基于下垂控制的直流微电网小扰动稳定性分析[J]. 电气技术, 2015, 16(7): 20-26.
Yang Daopei, Ding Zhigang, Cao Wei. Small signal stability analysis of dc micro-grid based on droop control[J]. Electrical Engineering, 2015, 16(7): 20-26.
[27] Soultanis N L, Papathanasiou S A, Hatziargyriou N D. A stability algorithm for the dynamic analysis of inverter dominated unbalanced LV microgrids[J]. IEEE Transactions on Power Systems, 2007, 22(1): 294-304.
[28] Iyer S V, Belur M N, Chandorkar M C. A generalized computational method to determine stability of a multi-inverter microgrid[J]. IEEE Transactions on Power Electronics, 2010, 25(9): 2420-2432.
Transient Stability Mechanism and Judgment for Inverter Interfaced Distributed Generators Connected with Public Grids
Abstract The inverter interfaced distributed generator (IIDG) connected with the distributed grid is an important application of renewable energy. The stable operation of the IIDG depends on its control system and the connected grid. The transient response of the IIDG is complex, and it is prone to fluctuations or oscillations in output power and power angle when a transient evert occurs. This paper analyzes the controller and the structure of the connected grid to build the active power curves of the IIDG. The transient stability criteria are also proposed by analyzing the active power curve cluster. The influence of the network parameters and nominal power on the transient stability is also analyzed. A transient stability iteration algorithm is proposed by establishing the transient process of the IIDG, which can calculate the power angle variation. Study cases built in PSCAD/EMTDC verify the proposed mechanism, and show that the transient stability iteration algorithm is effective and feasible.
keywords:Inverter interfaced distributed generators, transient stability mechanism, transient stability computation, power angle curve, droop control
DOI: 10.19595/j.cnki.1000-6753.tces.201391
中图分类号:TM773
余墨多 男,1993年生,博士研究生,研究方向为微电网稳定性及控制。E-mail: m18817519493@163.com
黄文焘 男,1989年生,博士,副教授,研究方向为配电网控制及保护。E-mail: hwt8989@sjtu.edu.cn(通信作者)
收稿日期 2020-10-23
改稿日期 2021-03-03
教育部科学技术研究项目(113023A)、国家重点研发计划(2017YFB0903202)和上海市青年科技英才扬帆计划(17YF1410200)资助。
(编辑 崔文静)