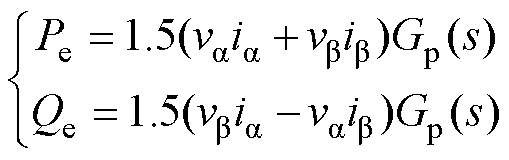（1）
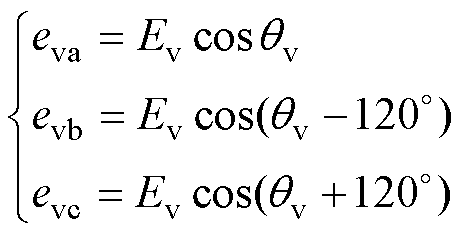（2）
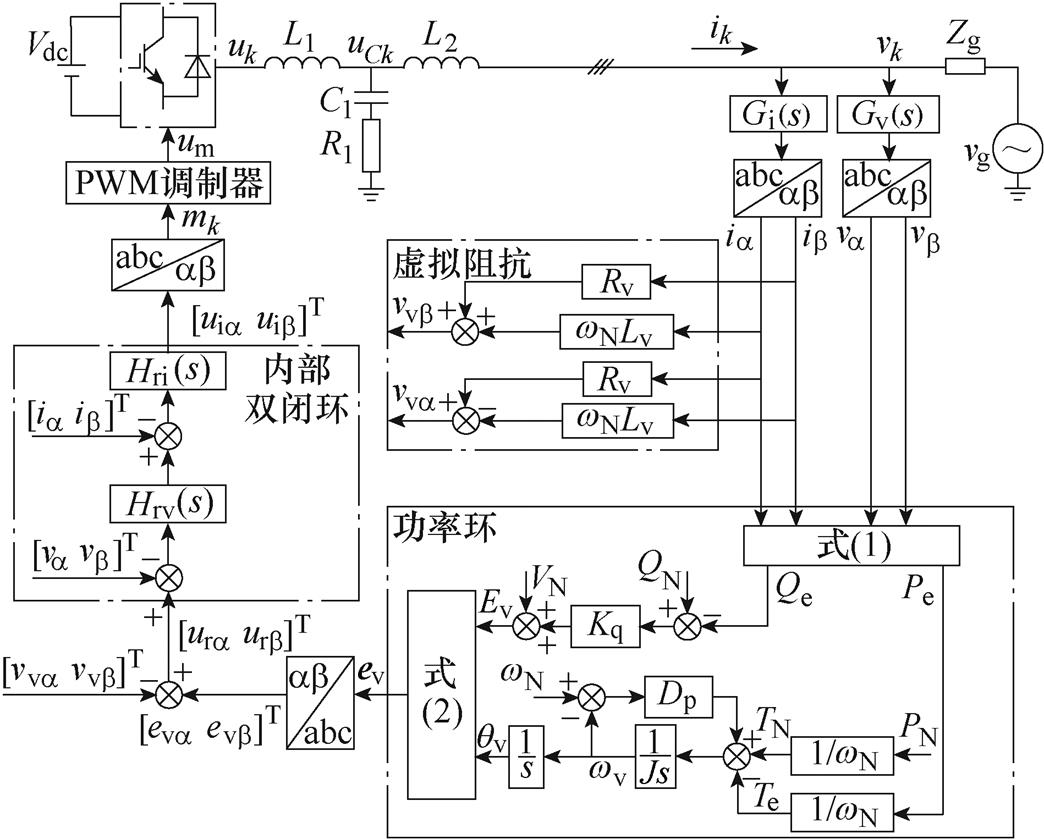
图1 VSG-VCI并网系统结构
Fig.1 Configuration of the grid-connected VSG-VCI
摘要 针对虚拟同步机（VSG）的同步频率谐振（SFR）现象，鉴于多输入多输出功率耦合模型的不足，通过建立可描述VSG宽频域动态特性的单输入单输出序阻抗模型，提出一种基于序导纳和序阻抗的SFR分析方法，并对单环和多环控制VSG的SFR现象进行对比研究。基于序导纳的极点分布，有效研究SFR与VSG功率环控制参数、虚拟阻抗、内环控制及电网阻抗之间的关系；基于序阻抗的频率特性曲线，对比内环控制引入前后SFR的阻尼特性，从“负阻尼”的角度揭示单环和多环控制VSG的SFR谐振机理；搭建基于RT-Box的实验平台，验证VSG在不同控制方案及不同电网阻抗下的SFR现象，指明VSG控制的优化设计方向。
关键词：虚拟同步机 同步频率谐振 序阻抗 负阻尼 内环控制
作为一种模拟同步发电机外特性的并网逆变器控制技术，虚拟同步机（Virtual Synchronous Gener- ator, VSG）不仅可为系统提供电压和频率支撑[1-2]，还可改善高渗透率新能源发电并网系统的稳定性[3]。此外，虚拟惯性和阻尼的加入，给系统动态特性和稳态性能的提高增加了更多的自由度[4]。目前有关VSG功率振荡现象的研究大多忽略了电感磁链的动态过程[5]，其惯性和阻尼参数的选取依靠功率环简化的二阶模型。这种忽略多建立在VSG的整体响应带宽远小于系统同步频率的前提下[6]，此时虚拟惯性系数较大，电感磁链的动态变化量较小。然而，在新能源渗透率较大的新型电网中，要求VSG的响应速度能够满足源载快速变化的要求，若VSG功率控制参数设计不当，则会激发其电磁动态过程，引起同步频率谐振（Synchronous Frequency Resonance, SFR）问题。
根据内部电压电流双闭环控制存在与否，可将VSG分为只含功率环的单环控制VSG以及含功率环和内部双闭环的多环控制VSG两种。目前有关SFR问题的研究仅局限于单环控制VSG，研究内容涉及SFR建模、谐振机理分析与谐振抑制[7-10]。其中，文献[7]通过分析电磁动态，建立了考虑功率耦合时VSG功率闭环控制的传递函数，揭示了SFR的谐振机理及其与功率控制参数之间的关系。文献[8]通过VSG功率闭环控制传递函数，指出线路阻抗在dq坐标系下的频移是导致功率产生SFR的原因，并提出了一种相位-幅值交互调节方法来抑制SFR。文献[9]针对阻感比较小时，VSG控制在同步频率处相位裕度不足的特点，提出了一种相位补偿加前馈补偿的控制方法来改善SFR。文献[10]针对传统虚拟电阻所引起的功率耦合加强的副作用，提出了一种暂态虚拟电阻方法来抑制SFR。对于多环控制VSG，文献[6]指出功率环、虚拟阻抗、内环控制和电磁动态之间均存在相互作用，鉴于多环控制VSG技术的普遍应用，尚需对多环控制VSG的SFR现象进行研究，揭示虚拟阻抗和内环控制对SFR的影响。
此外，已有研究表明，功率耦合会恶化SFR[7-8]，因此，SFR的建模分析需考虑VSG的功率耦合现象。然而，当考虑功率耦合时，现有的SFR分析模型均为基于功率闭环传递函数的多输入多输出或等效的单输入单输出模型，模型较为复杂，且难以应用于VSG的宽频域稳定性分析。对VSG控制并网逆变器来说，其稳定性问题可能产生于多个频率段[7, 11-13]，因此，有必要将对SFR的研究统一于VSG其他稳定性问题的研究模型中，建立可描述VSG控制并网逆变器宽频域动态特性的稳定性分析模型。
序阻抗作为一种描述系统端口特性的模型，被广泛应用在逆变器并网系统的小信号交互稳定性研究中[14]。在VSG控制逆变器并网系统的稳定性分析中，序阻抗也得到了有效应用[15]。但现有的VSG序阻抗模型应用局限于分析弱电网下VSG控制逆变器并网系统的交互稳定性。鉴于SFR与线路阻尼密切相关，而序阻抗能反映VSG的宽频域阻尼特性。因此，本文旨在将SFR的建模分析统一于序阻抗模型中，通过序阻抗模型揭示SFR的谐振机理。
具体来说，本文以基于VSG的电压控制型逆变器（VSG-based Voltage Controlled Inverter, VSG- VCI）为研究对象，综合考虑有功-频率、无功-电压控制、虚拟阻抗、内环控制和电磁动态，采用谐波线性化方法，详细建立单环和多环控制型VSG-VCI的序阻抗模型；提出通过序导纳的极点分布对SFR现象进行分析的方法，并站在序阻抗“负阻尼”的角度，阐明SFR的产生及抑制原理；对比单环和多环控制型VSG-VCI功率谐振的异同，全面研究SFR与VSG功率控制参数、虚拟阻抗及电网阻抗之间的关系，并进行实验验证。
图1所示为本文所研究的VSG-VCI并网系统结构，包含功率环、虚拟阻抗和内部电压电流双闭环，是一个多环控制系统。主电路中，Vdc为恒定的直流母线电压；L1、C1、L2组成LCL滤波器，R1为其阻尼电阻；vk和ik分别为系统采样电压和电流，Gv(s)和Gi(s)分别为电压和电流采样函数；uk和uCk分别为逆变桥输出电压和电容支路电压；vg和Zg分别为电网电压及其线路阻抗，Zg=Rg+jwLg。VSG功率环中，PN、QN为有功、无功功率给定；Pe、Qe为经式（1）计算得到的有功、无功功率，Gp(s)为功率滤波器；VN、wN为电压、角频率给定值；J为虚拟惯量；Dp为有功阻尼系数；Kq为无功下垂系数；θv为有功环输出的相位；Ev为无功环输出的电压幅值，它们通过式（2）为内环提供参考电压ev。Lv和Rv分别为虚拟电感和虚拟电阻。VSG内环控制中，Hrv(s)和Hri(s)分别为ab 坐标系下的电压和电流控制器。多环控制型VSG-VCI的PWM信号取自内环控制的输出电压[uia uib]T；而单环控制型VSG-VCI不含内环控制，其PWM信号取自内环输入电压[ura urb]T。为了全面认识VSG的SFR现象，本文将分别对单环和多环控制型VSG-VCI进行SFR分析。此外，k=a, b, c，代表a、b、c三相。
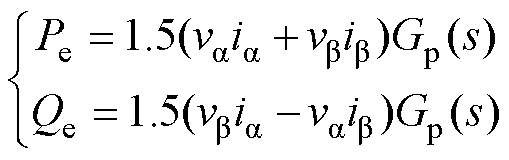（1）
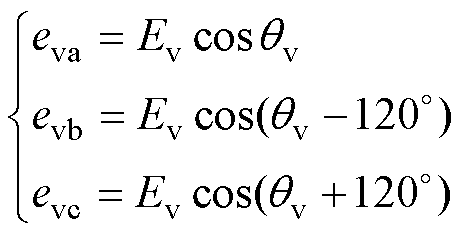（2）
图1 VSG-VCI并网系统结构
Fig.1 Configuration of the grid-connected VSG-VCI
根据图1所示的给定功率与输出功率之间的响应过程，可以得到如图2所示的功率闭环控制框图。图中，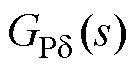
和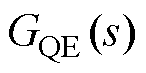
为功率环的传递函数[7]；
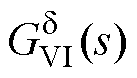和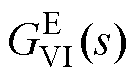
为内环控制的传递函数[6]（单环控制型VSG-VCI的
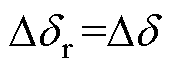, DEr=DE）；
、
、
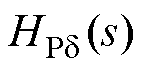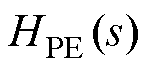和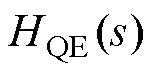
为描述VSG基于线路阻抗进行功率传输的小信号模型，包含了电磁动态过程，其表达式如式（3）所示，其中，an、bn和cn（n=1, 2, 3, 4）为与系统稳定工作点相关的常量[7]。
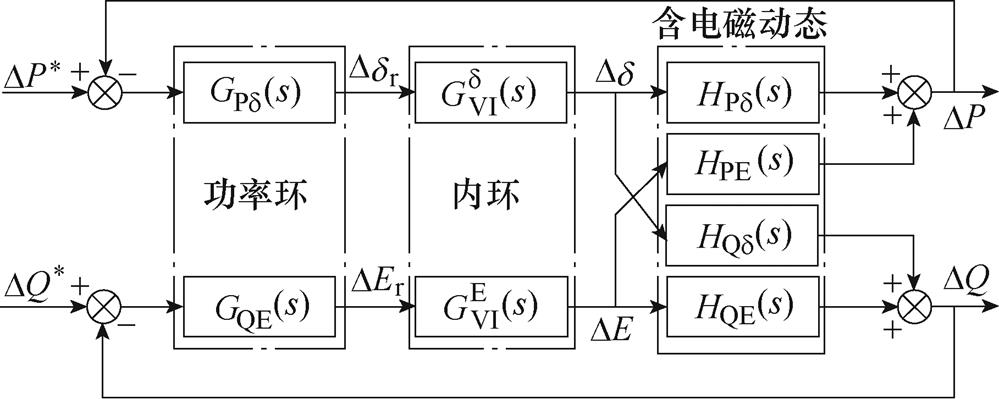
图2 VSG-VCI功率闭环控制框图
Fig.2 Closed-loop power control scheme of the VSG-VCI
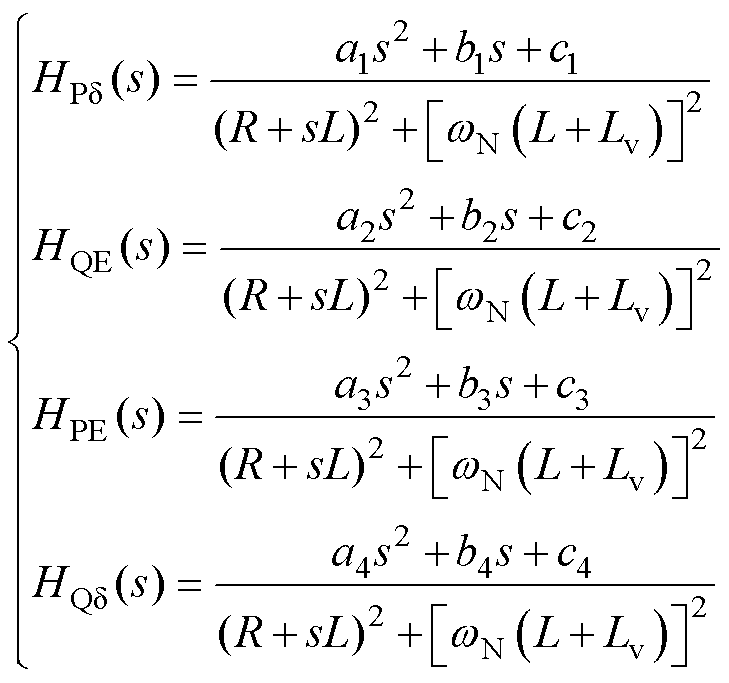（3）
式中，R和L+Lv为VSG输出电动势ev与电网电压vg之间的等效线路电阻和电感，对单环控制型VSG- VCI来说，R=Rv+Rg，L=L1+L2+Lg；对多环控制型VSG-VCI来说，R=Rv+Rg，L=Lg。因此，单环控制型VSG-VCI的电磁动态不仅与电网阻抗Zg有关，还关系到滤波总电感L1+L2；而多环控制型VSG- VCI的电磁动态只与电网阻抗Zg有关。式（3）中的小信号模型具有共同的共轭极点，即
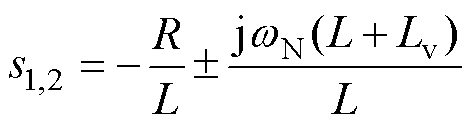（4）
可见该极点的实部与系统总的阻感比密切相关。若系统总电阻R太小，对Lv=0mH的VSG-VCI来说，s1,2≈±jwN，表明功率在同步频率wN处存在谐振点，本文称该共轭极点为SFR极点；对Lv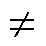
0mH的VSG-VCI来说，s1,2≈±jwN(L+Lv)/L，可见虚拟电感Lv将改变VSG的功率谐振频率；当Lv＞0mH时，VSG并网功率会产生超同步谐振，本文称该共轭极点为超SFR极点。
根据图2所示的功率闭环控制框图，功率环、内环控制、电磁动态之间存在相互作用，影响式（4）所描述的功率谐振状态。现有的基于功率闭环传递函数的SFR分析需分别推导图2中各环节的表达式，较为复杂。此外，功率耦合作用使得SFR分析模型需以多输入多输出或等效为单输入单输出的形式表达，这为SFR的分析带来不便[7]。因此，本文提出通过单输入单输出序阻抗模型，从VSG-VCI并网端口特性的角度对SFR问题进行研究。
首先，由图1可得逆变器的主电路平均模型为
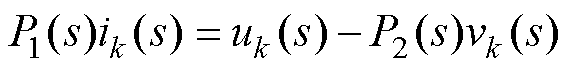（5）
其中
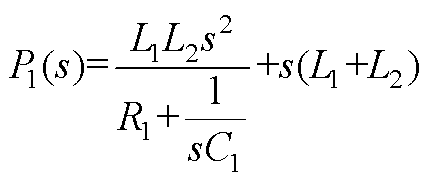
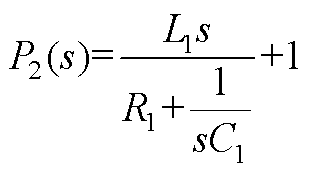
式中，P1(s)和P2(s)分别为与LCL滤波相关的传递函数；uk(s)=mkGd(s)，Gd(s)为数字控制延迟，Gd(s)=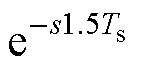 
，Ts为开关周期。
根据谐波线性化建模过程[14]，在vk中注入小信号电压扰动，则A相输出电压和电流可表示为
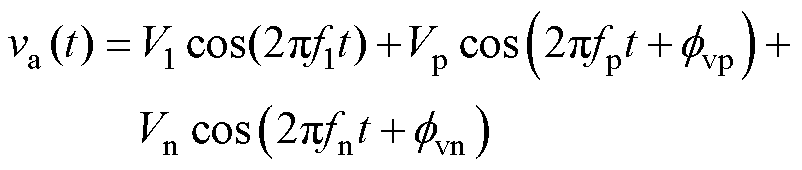（6）
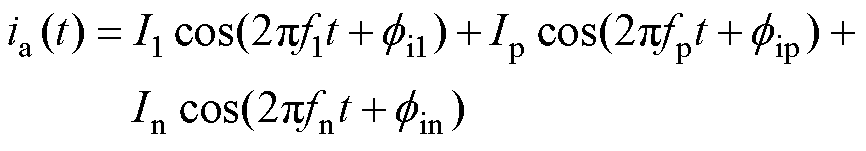（7）
式中，V1、f1分别为基波电压的幅值、频率；Vp、fp、fvp分别为正序电压扰动的幅值、频率、相位；Vn、fn、fvn分别为负序电压扰动的幅值、频率、相位；I1、fi1分别为逆变器输出基波电流的幅值、相位；Ip、fip分别为输出正序电流谐波的幅值、相位；In、fin分别为输出负序电流谐波的幅值、相位。
式（6）和式（7）对应的频域信号经Clarke变换后可表示为
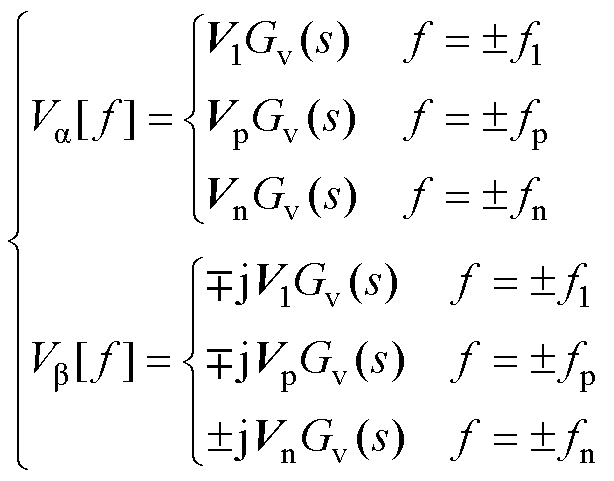（8）
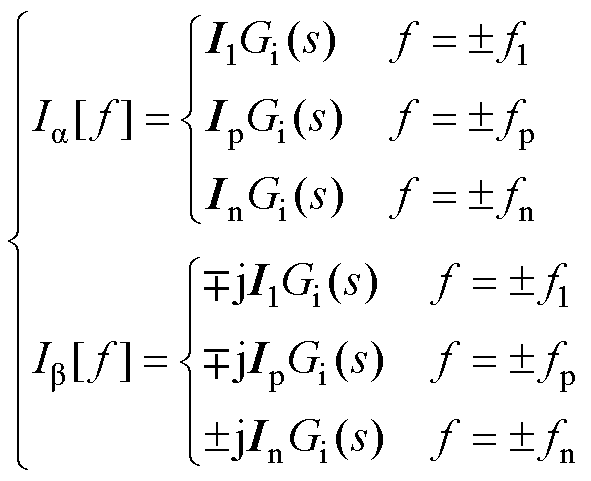（9）
式中，V1=(V1/2)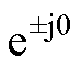
；Vp=(Vp/2)
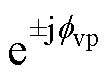；Vn=(Vn/2)
；I1=(I1/2)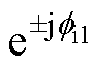
；Ip=(Ip/2)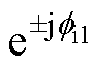；In=(In/2)
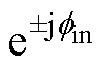。这里认为功率因数约为1，则fi1≈0，I1=PN/(1.5V1)。
将式（8）和式（9）代入图1所示的功率环，忽略二阶小信号扰动项和正负序电压扰动在耦合频率处的响应，定义K1(s)=-0.75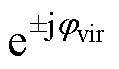
V1M(s∓jw1)Gp(s∓jw1)/wN，K2(s)=∓0.75j
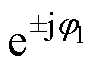Gp(s∓jw1)Kq，其中，w1=2p f1，j1= arcsin[PewNL/(EV1)]，jvir=j1+p/2，M(s)=1/(Js2+Dps)。可得功率环输出a 轴电压eva 中扰动信号的频域表达式为
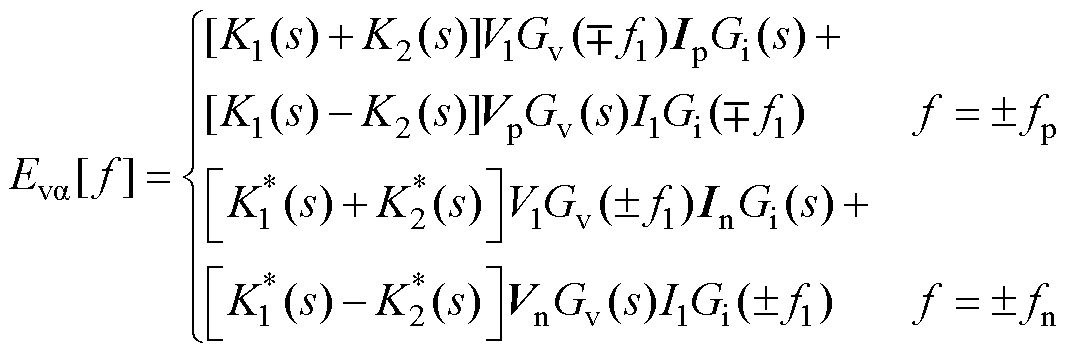（10）
式中，“*”为其对应复数的共轭。
将式（9）和式（10）代入图1中的虚拟阻抗控制，可得内环输入a 轴电压ura 的频域表达式为
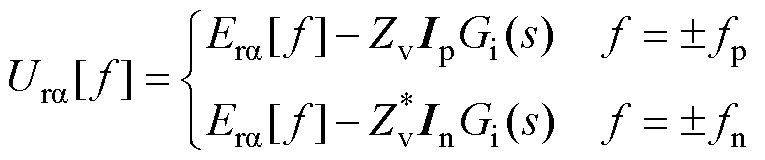（11）
式中，Zv=Rv±jwNLv。
将式（8）、式（9）和式（11）代入内环控制，可得内环输出a 轴电压uia 的频域表达式为
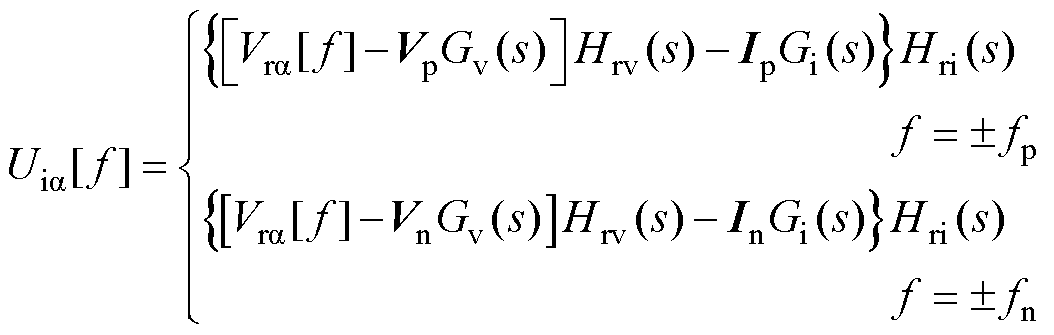（12）
对单环控制型VSG-VCI来说，频域下调制信号满足Ma[ f]=Ura[ f]，将其代入到主电路表达式（5），计算可得正序阻抗Zsp(s)和负序阻抗Zsn(s)的表达式如式（13）所示。对多环控制型VSG-VCI来说，频域下满足Ma[ f]=Uia[ f]，将其代入到主电路表达式（5），计算可得正序阻抗Zmp(s)和负序阻抗Zmn(s)的表达式如式（14）所示。
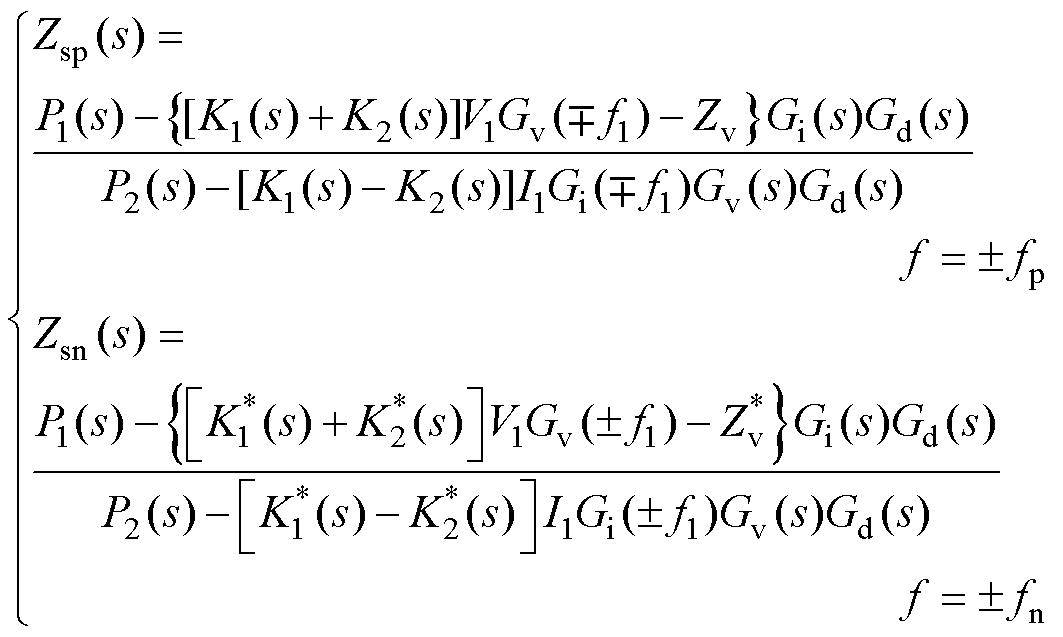（13）
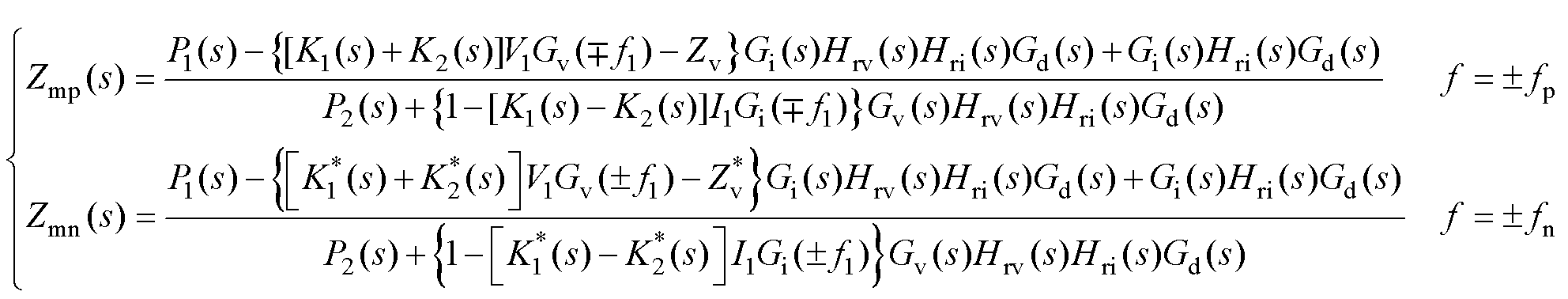（14）
VSG-VCI的系统参数见表1。本文借助Plecs软件通过阻抗扫描的方式对所建立的序阻抗模型进行分析验证。图3和图4分别为单环和多环控制型VSG- VCI的序阻抗模型及其仿真测量结果，可见本文建立的序阻抗模型与仿真得到的结果相吻合，证明了该建模的准确性。
表1 VSG-VCI的系统参数
Tab.1 Parameters of the studied VSG-VCI
参 数数 值 Vdc/V700 V1, VN/V311 w1, wN/(rad/s)314 fs/kHz10 Lv/mH5 PN/kW5 QN/kvar0 Kq0.001 Gp(s)1/(10-3s+1) Hrv(s)0.5+50s(s2+)-1 L1/mH2.2 C1/mF10 L2/mH2.2 R1/W3.5 Rv/W0.3 J/(kg·m2)0.03 Dp5 Gv(s), Gi(s)1/(10-4s+1) Hri(s)8+1 000s(s2+)-1
此外，从整体模型来看，单环控制型VSG-VCI的输出阻抗在低频段呈感性，而多环控制型VSG- VCI的输出阻抗在低频段呈阻感特性，表明内环控制的引入改变了VSG-VCI的阻抗特性。
3.1.1 SFR与序导纳之间的关系
根据序阻抗的建模过程，可以看到序阻抗中包含了VSG-VCI的控制环路及主电路信息。在并网模式下，注入固定电压扰动，引起的电流响应实际也代表了相应的功率响应，因此，电流与电压之比，即序导纳（序阻抗的倒数）可以代表整个系统的闭环行为，其零极点特性与功率闭环特性密切相关。
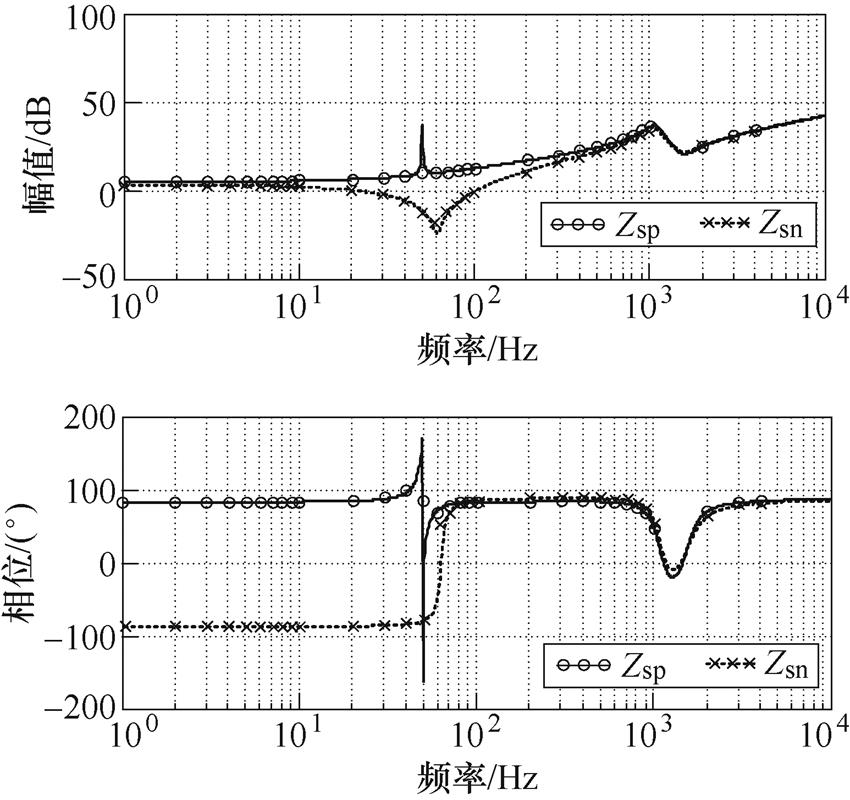
图3 单环控制型VSG-VCI序阻抗模型验证
Fig.3 Verification of sequence-impedances of the single-loop VSG-VCI
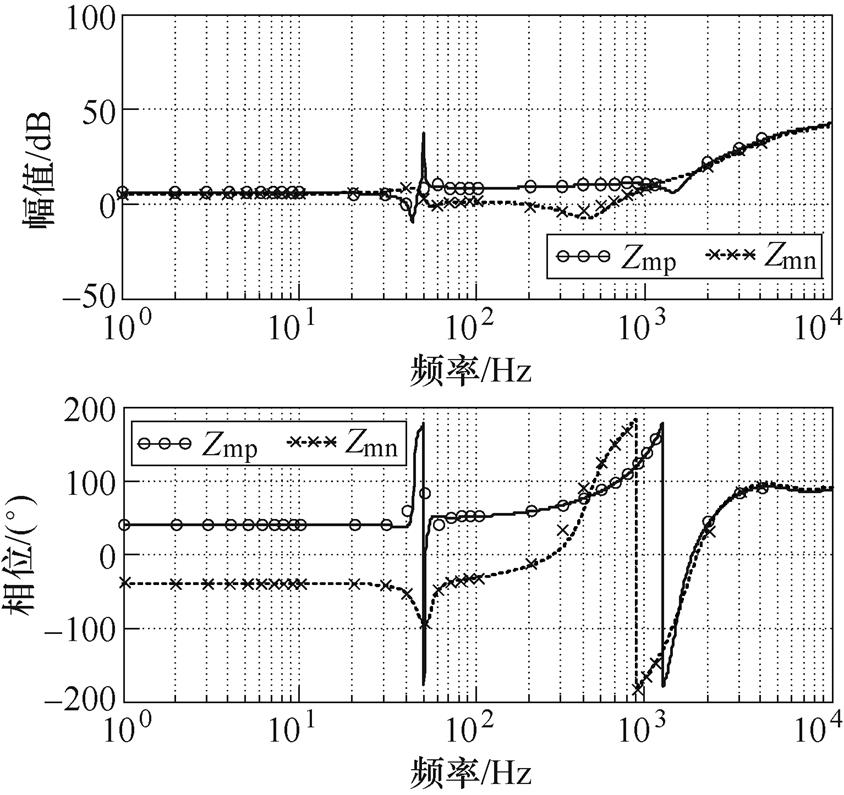
图4 多环控制型VSG-VCI序阻抗模型验证
Fig.4 Verification of sequence-impedances of the multi-loop VSG-VCI
图5和图6分别为理想电网下（Zg=0时），单环和多环控制型VSG-VCI序导纳的零极点。其中，单环控制型VSG-VCI的Lv=0mH、Rv=0.3W，多环控制型VSG-VCI的Lv=5mH、Rv=0.3W，其他参数与表1保持一致。如图5和图6所示，VSG-VCI输出序导纳的零极点主要分布在三个频率段：与LCL滤波和数字控制延时相关的高频段（kHz）、与控制环参数相关的中频段（50～100Hz）和基频段（50Hz）。
图5 单环控制型VSG-VCI序导纳的零极点
Fig.5 Pole-zero of sequence-admittances of the single-loop VSG-VCI
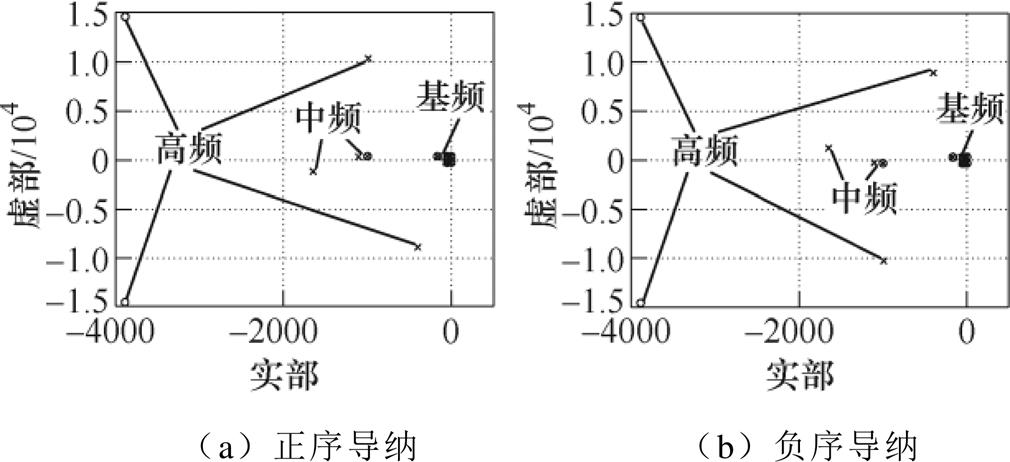
图6 多环控制型VSG-VCI序导纳的零极点
Fig.6 Pole-zero of sequence-admittances of the multi-loop VSG-VCI
此外，图5所示的序导纳中还存在一对特殊的共轭极点，它们的频率远小于基频。考虑到并网功率与电压、电流、序阻抗之间存在50Hz频移，所以，这对共轭极点可反映VSG并网功率在(10.3+50)Hz处的稳定性。然而，由式（4）可知，当Lv=0mH时，由电磁动态引发的功率谐振频率为50Hz，其与(10.3+50)Hz存在一定的偏差，这是因为前者未将控制环的交互影响考虑在内。因此，通过虚线所指出的极点可以分析SFR现象，图中，该SFR极点实部小于0，表明0.3W 的虚拟电阻可完全抑制SFR；反之，当SFR极点移动到右半平面时，表明SFR问题产生。
不同于图5、图6所示的序导纳模型不存在SFR极点。说明加入内环控制后，理想电网下多环控制型VSG-VCI并网系统中滤波线路动态不会引发SFR。这是因为内环的反馈控制信号为滤波后的电压和电流，在双闭环可以良好地跟踪功率环输出的情况下，滤波总电感L1+L2所引起的线路动态被抵消。当Zg=0时，式（3）中各传递函数的分母只包含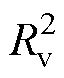
+(wNLv)2项，不存在SFR极点。只有当Zg≠0时，才会产生式（4）所示的SFR或超SFR极点。
以上是对理想电网下单环和多环控制型VSG- VCI输出序导纳的零极点分析，只涵盖了VSG等效内电动势与并网点之间的等效线路动态。当考虑电网阻抗Zg的动态时，需根据式（15）所示的等效序阻抗Zevp(s)和Zevn(s)来进行SFR分析。其中，Zvp(s)和Zvn(s)分别为单环或多环控制型VSG-VCI的正序和负序阻抗。
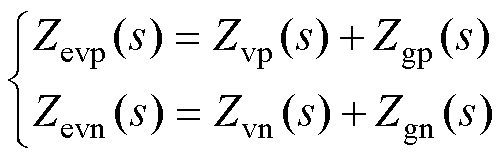（15）
由图5可得，SFR极点在正负序导纳中互为共轭极点。因此，只需根据正序（或负序）导纳即可分析SFR与系统运行参数之间的关系。
3.1.2 单环控制型VSG-VCI的SFR谐振特性分析
单环控制型VSG-VCI的电磁动态同时与滤波电路和电网阻抗动态有关，因此，通过正序导纳Ysp(s)= 1/Zsp(s)和正序等效导纳Yevp(s)=1/[Zsp(s)+Zgp(s)]分别对理想电网和实际电网下VSG的SFR进行分析，研究虚拟阻抗、功率控制和电网阻抗对单环控制VSG功率谐振现象的影响。
图7所示为理想电网下，当J=0.03kg·m2、Dp=5、Kq=0.001时，Ysp的SFR极点随虚拟电阻Rv（通过Rv的变化来改变式（4）中的阻感比R/L）、虚拟电感Lv变化的分布情况。由图7a可知，随Rv减小，极点向右半平面移动，说明VSG-VCI并网系统稳定性降低，在所选的Rv取值范围内，当Rv＜0.1W 时，SFR极点位于右半平面，表明系统失稳，根据极点频率进一步可知，失稳系统的并网功率存在55.7Hz左右的谐振。由图7b可知，因电磁动态引发的功率谐振频率会随Lv增大而增大，这与式（4）所示的功率谐振结论一致。比如，当Lv=4mH时，由图可知，功率谐振频率约为100Hz，而根据式（4）计算可得功率谐振频率为50(L1+L2+Lv)/(L1+L2)≈100Hz，两者相符，表明基于序导纳模型进行SFR现象分析的准确性。
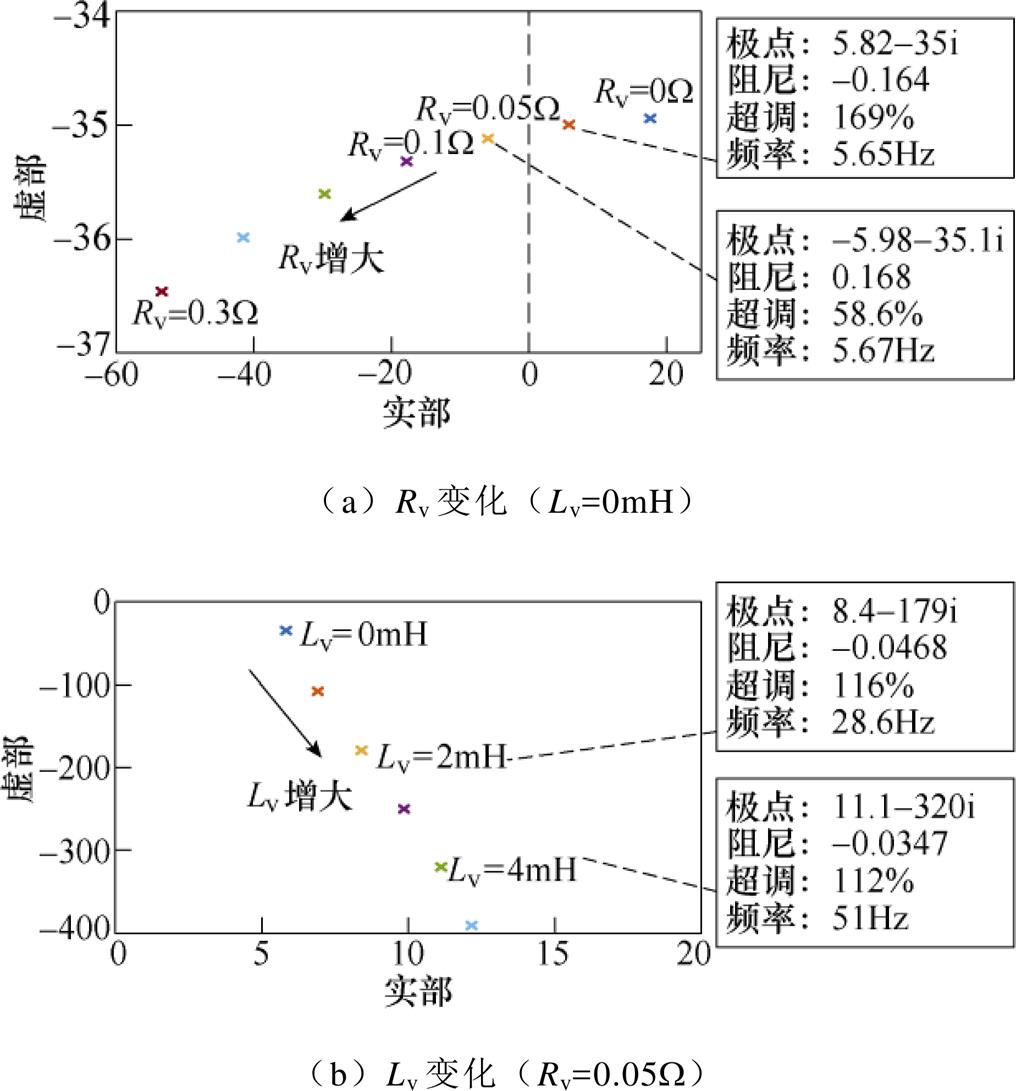
图7 Ysp的SFR极点随虚拟阻抗Zv变化的分布
Fig.7 Map of the SFR poles of Ysp with varied Zv
图7显示，理想电网下，当J=0.03kg·m2、Dp=5、Kq=0.001且Lv=0mH、Rv=0.1W 时，单环控制型VSG- VCI的SFR可被有效抑制。若改变功率环的控制参数，基于序导纳SFR极点分布的分析结果表明（见附图1）：即使Rv=0.1W 的虚拟电阻可提供抑制SFR的阻尼，J太小（如J＜0.02kg·m2）或Kq太大（如Kq＞0.001）均会导致极点移到右半平面，产生SFR问题，证明了功率环与电磁动态会发生相互作用，从而影响SFR阻尼；而有功阻尼系数Dp对SFR的影响较小，当Dp发生大范围变化时，VSG-VCI并网系统的稳定性保持不变。
进一步地，考虑电网阻抗Zg的动态，当J= 0.03kg·m2、Dp=5、Kq=0.001时，基于序导纳SFR极点分布的分析结果表明（见附图2）：只要单环控制型VSG-VCI本身的控制参数设计得当（即理想电网下VSG-VCI不存在SFR问题），那么电网电感Lg变化不会影响SFR，即SFR问题与电网强度无关；而电网电阻Rg可有效阻尼SFR，且其阻尼效果近似于Rv，因此，当并网线路阻尼不足时，可通过虚拟电阻的方式来削弱电磁动态引发的功率谐振。
3.1.3 多环控制型VSG-VCI的SFR谐振特性分析
多环控制型VSG-VCI的电磁动态与滤波电路无关（即与L1+L2无关），仅与电网阻抗Zg有关。因此，通过正序等效导纳Yevp(s)=1/[Zmp(s)+Zgp(s)]对实际电网下VSG的SFR进行分析，研究电网阻抗、虚拟阻抗和功率控制对多环控制VSG功率谐振现象的影响。
图8所示为当J=0.03kg·m2、Dp=5、Kq=0.001时，SFR相关极点随电网电感Lg和电网电阻Rg变化的分布，此外，图中虚拟电阻Rv和虚拟电感Lv分别为0W 和4mH，因Lv＞0mH，由式（4）可知，与电磁动态有关的极点频率大于50Hz，为超SFR极点。由图8a可见，超SFR极点与Lg之间呈非线性关系。在图8所示的Lg变化范围内，虽然系统总的等效电阻R=Rg+Rv=0W，但只有当Lg取值为3～6mH时，Yevp(s)才存在右半平面极点，且极点频率约为50Hz，说明VSG-VCI并网系统存在100Hz左右的功率谐振。当Lg=4mH时，由图8b可见，将Rg增加到0.2W，超SFR极点移动到左半平面，且Rg越大，超SFR极点离虚轴越远，说明增加电网线路的阻性成分有助于抑制该功率谐振。
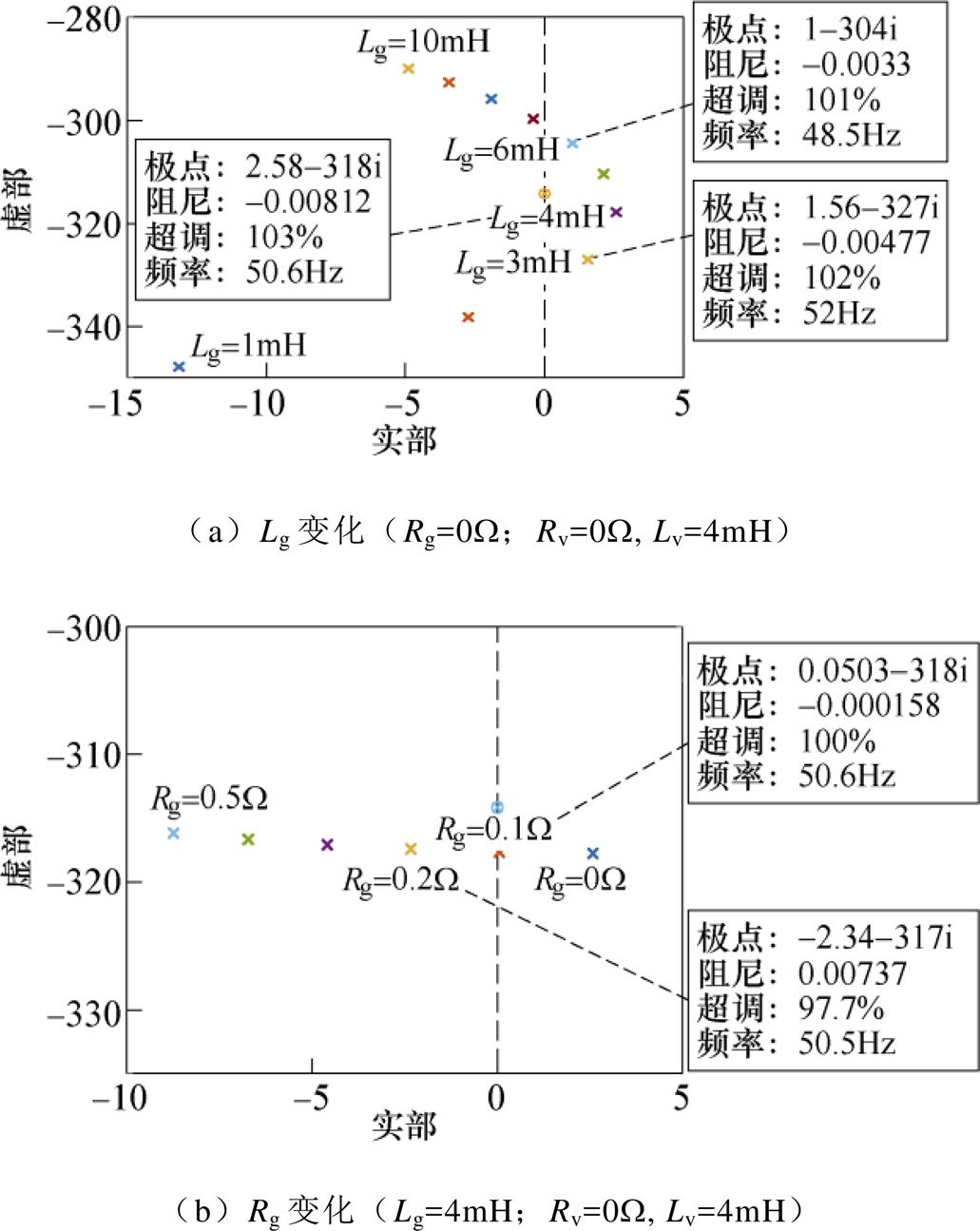
图8 Yevp的超SFR极点随电网阻抗Zg变化的分布
Fig.8 Map of the super-SFR poles of Yevp with varied Zg
图8显示，当J=0.03kg·m2、Dp=5、Kq=0.001时，若保持R=0W 且Lv=4mH不变，只有当Lg取值为3～6mH时，电磁动态才会引起100Hz附近的功率谐振。然而，若保持R=0W 且Lg=6mH不变，基于序导纳超SFR极点分布的分析结果表明（见附图3a），只有当Lv取值为4～7mH时，超SFR极点位于右半平面，系统产生100Hz左右的功率谐振。由此可得，对多环控制型VSG-VCI来说，当Lg≈Lv时，VSG-VCI并网功率易产生100Hz附近的超SFR现象。此外，若保持Rg=0W 且Lg=Lv=4mH不变，改变Rv，基于序导纳超SFR极点分布的分析结果表明（见附图3b），当Rv≥0.2W 时，超SFR极点位于左半平面，将其与图8b对比可知，Rv与Rg的阻尼效果近似相同，表明当多环控制型VSG-VCI在近似纯感性的电网中运行时，可通过虚拟电阻来有效抑制超SFR。
进一步地，当Lv=4mH、Lg=3mH且R=0W 时，若改变功率环的控制参数，基于序导纳超SFR极点分布的分析结果表明（见附图4），减小Kq有助于抑制超SFR，而J和Dp变化对超SFR的影响较小，这与单环控制型VSG-VCI的功率谐振特性有所不同（见附图1）。究其原因，单环控制VSG功率谐振频率约为50Hz，而图8显示多环控制VSG易产生100Hz左右的功率谐振，后者的功率谐振频率远超出有功环控制参数的作用范围。
根据以上对SFR现象的分析结果可知，等效线路阻尼与SFR有直接的关系，而VSG功率环控制会影响阻尼效果，进而产生恶化或抑制SFR的作用。本节将通过对序阻抗“负阻尼”特性的研究，更清晰直观地揭示VSG-VCI的同步频率谐振机理。由于单环和多环控制型VSG-VCI的SFR现象均与电网阻抗Zg的动态有关，下面将通过分析不同电网阻抗下等效序阻抗的频率特性，对比单环和多环控制VSG之间SFR“负阻尼”特性的差异。
图9所示为单环控制型VSG-VCI并网等效序阻抗Zevp(s)=Zsp(s)+Zgp(s)随Zg变化的频率特性曲线。图中，灰色阴影区相位大于90°，代表负阻尼区。图9a所示为当Rg=0W、Rv=0.1W 时，Zevp(s)随Lg变化的频率特性曲线，可见在低频范围内，阻抗均具有正阻尼特性，虽然其相位随Lg增加而增加，但仍小于90°。图9b所示为当Lg=0mH、Rv=0W 时，Zevp(s)随Rg变化的频率特性曲线，由图可知，当Rg=0.05W时，序阻抗存在低频负阻尼区，表明其低频电阻分量为负，VSG-VCI并网存在SFR问题；随Rg增加，序阻抗在低频段由负阻尼区向正阻尼区转移，表明低频电阻分量由负变正，SFR得以抑制。因此，单环控制型VSG-VCI的SFR“负阻尼”以低频负电阻的形式存在，会导致VSG-VCI并网功率产生50Hz左右的谐振（Lv=0mH），该图对SFR的分析结果与附图2一致。
图10所示为当Rv=0W、Lv=4mH时，多环控制型VSG-VCI的并网等效序阻抗Zevp(s)=Zmp(s)+Zgp(s)随电网阻抗Zg变化的频率特性曲线。图中，相位大于90°或小于-90°的灰色阴影区，代表负阻尼区。如图10所示，Zevp(s)在50Hz附近存在谐振峰，若在谐振频率处相位变化超过180°，则代表系统阻尼
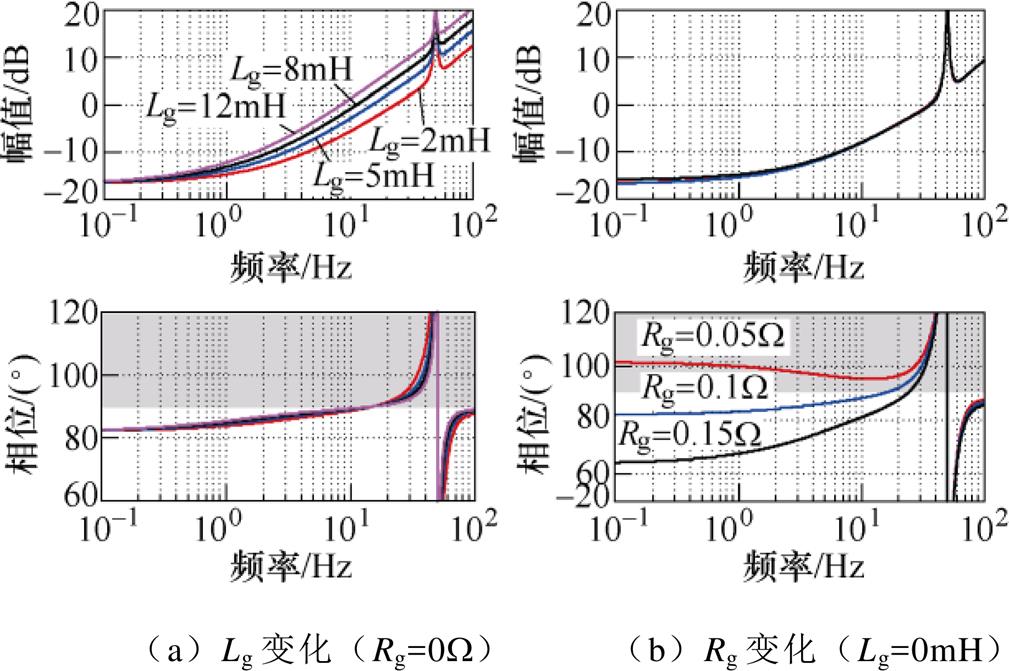
图9 单环控制型VSG-VCI的Zevp随Zg变化的频率特性
Fig.9 Bode plots of Zevp of the single-loop VSG-VCI with varied Zg
不足，即具有“负阻尼”特性，从而引发系统产生100Hz左右的功率谐振。由图10a可得，当Lg处于4mH左右（包括3mH, 4mH, 5mH, 6mH）时，相位发生超出180°或近似180°的跳变，表明系统存在谐振问题，且谐振频率随Lg增大而减小。如图10b所示，电网电阻Rg可为谐振峰提供有效的阻尼，且Rg越大，阻尼效果越好。因此，多环控制型VSG-VCI的SFR“负阻尼”以谐振峰的形式存在，会导致VSG- VCI并网功率产生100Hz左右的谐振，当电网电感与虚拟电感相差较大时，功率谐振频率wN(Lg+Lv)/ Lg离100Hz较远，对应序阻抗离50Hz较远，序阻抗呈正电阻特性，表明系统阻尼充分。该图对SFR的分析结果与图8一致。
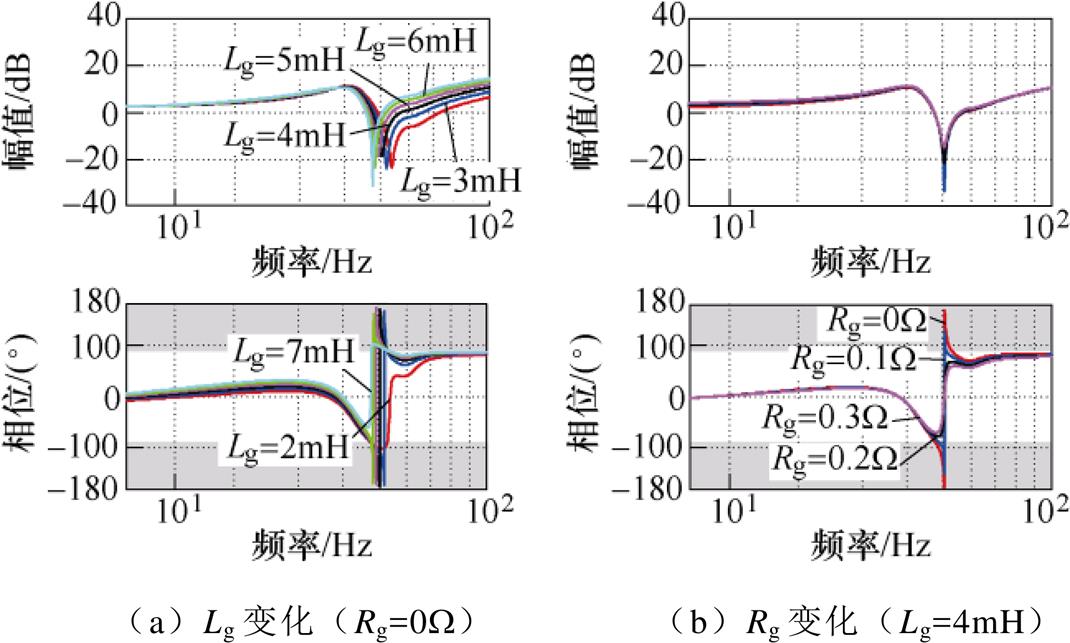
图10 多环控制型VSG-VCI的Zevp随Zg变化的频率特性
Fig.10 Bode plots of Zevp of the multi-loop VSG-VCI with varied Zg
本文通过一台5kW的并网逆变器对SFR现象进行实验验证，采用基于RT-Box的硬件在环实验平台如图11所示，即通过图中的RT-Box运行并网逆变器的主电路部分，控制部分采用芯片TMS320F28335。其中，RT-Box中运行的主电路来源于Plecs软件中搭建的三相并网逆变器功率电路模型（见图1），主电路的离散时间为10ms，开关频率和控制电路的采样频率均为10kHz，其他实验系统参数与表1保持一致。
图11 基于RT-Box的硬件在环实验平台
Fig.11 Hardware-in-loop experimental platform based on the RT-Box
实验通过采集逆变器并网有功功率Pe的波形来监测功率谐振现象，将在RT-Box中实时计算得到的Pe传送至模拟输出口，进而通过转接板和刺刀螺母连接器（BNC）接口的传输线将功率数据传输到示波器中进行观测分析。
图12所示为理想电网下，单环控制型VSG-VCI有功功率Pe随控制环参数变化的实验波形。由图12a可见，当虚拟电阻Rv=0.05W 时，Pe发生谐振，且由放大波形可知谐振周期为20ms，表明Pe的谐振频率为50Hz，系统存在SFR问题（图12所示波形是因实验平台模拟输出限幅所致，不影响SFR分析结果）；当Rv增加到0.1W 后，SFR现象消失，系统输出稳定的有功功率波形。当Rv=0.05W 时，若将虚拟电感Lv的值由0mH改变为4mH，如图12b所示，Pe的谐振周期减小到约10ms，表明Pe的谐振频率约为100Hz，这与图7阐明的现象相符。当Rv=0.1W、Lv=0mH时，由图12c和图12e可知，减小惯性系数J或增加无功下垂系数Kq会影响VSG-VCI并网功率的稳定性，即使0.1W 的虚拟电阻可提供抑制SFR的阻尼（见图12a），但当J减小到0.01或Kq增加到0.002时，Pe波形再次出现SFR现象。由图12d可见，有功阻尼系数Dp的大范围变化不会影响系统的稳定性。实验结果验证了理论分析的准确性。
实际电网中，同理可以通过实验验证电网阻抗Zg变化对SFR现象的影响，这里不再赘述。
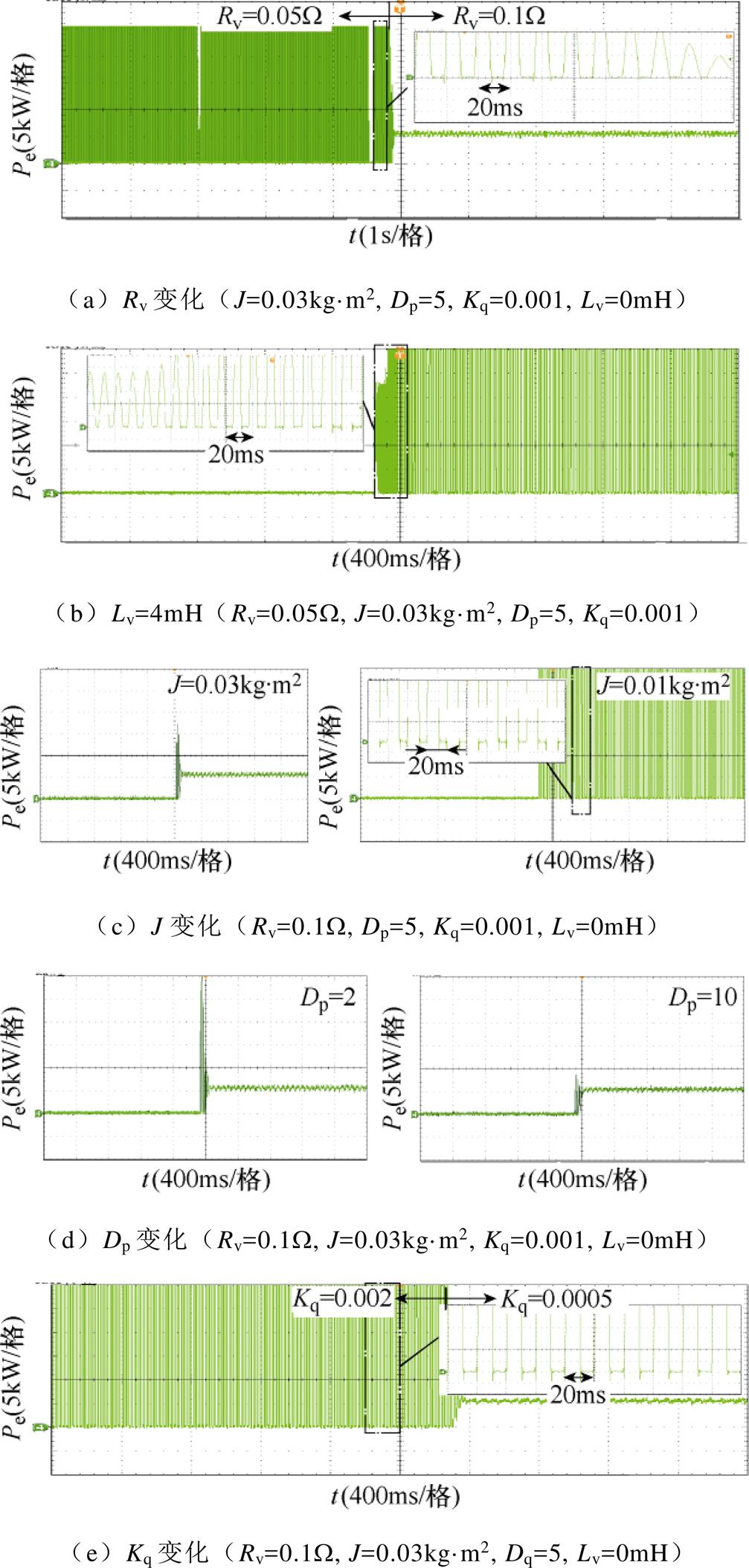
图12 理想电网下，单环控制型VSG-VCI随控制参数变化的有功功率
Fig.12 Active power waveforms of the single-loop VSG-VCI with varied control parameters in ideal grid
保持功率环控制参数J=0.03、Dp=5、Kq=0.001不变，图13所示为当Rv=0W、Lv=4mH时，多环控制型VSG-VCI的有功功率Pe随电网阻抗Zg变化的实验波形；图14所示为当Rg=0W、Lg=6mH时，多环控制型VSG-VCI的有功功率Pe随虚拟阻抗Zv变化的实验波形。
当Rg=0W 时，由图13可知，当Lg为2mH和7mH时，即使系统阻尼R=Rv+Rg=0W，Pe波形仍可保持稳定；当Lg为3～6mH时，由放大的功率波形可见，Pe存在100Hz的谐振。此外，由图13d可知，加入0.3W 的电网电阻Rg可抑制功率谐振。实验结果验证了图8所示的理论分析。
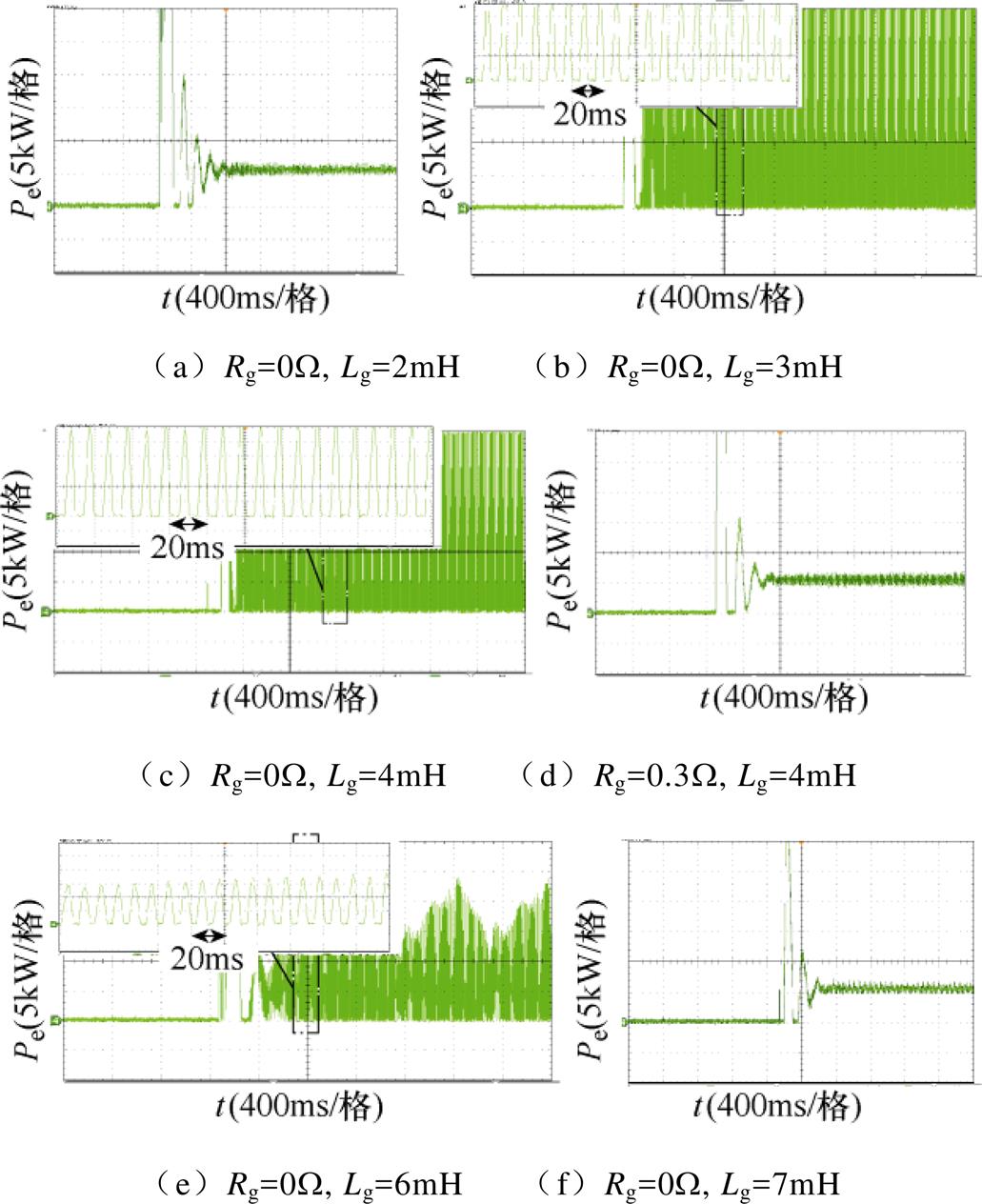
图13 多环控制型VSG-VCI随Zg变化的有功波形
Fig.13 Active power waveforms of the multi-loop VSG-VCI with varied Zg
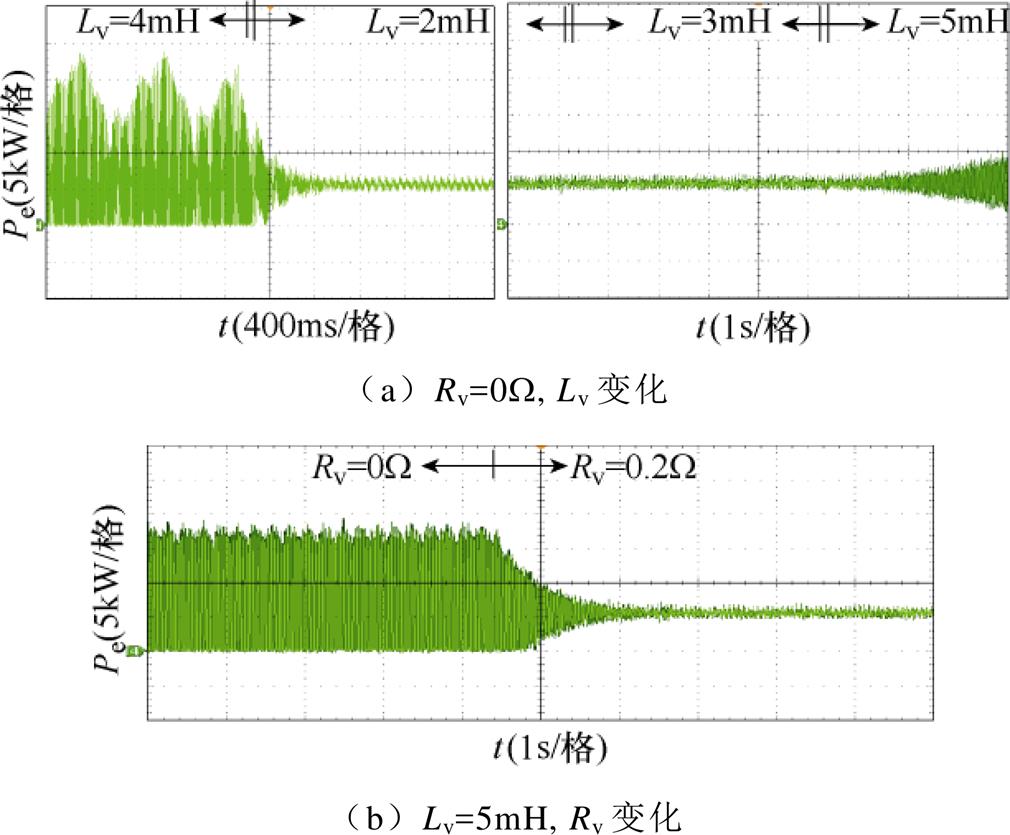
图14 多环控制型VSG-VCI随Zv变化的有功波形
Fig.14 Active power waveforms of the multi-loop VSG-VCI with varied Zv
由图14a可见，当Lv=2mH和Lv=3mH时，Pe波形稳定在5kW；当Lv=4mH和Lv=5mH时，功率失稳，加入0.2W 的虚拟电阻Rv可使功率波形重新恢复稳定。实验结果验证了附图3所示的理论分析。此外，结合图13的实验结果可证明，对多环控制型VSG-VCI并网系统来说，只有当Lg和Lv的值接近时，系统才容易产生因电磁动态引发的功率谐振现象，且谐振频率约为100Hz。
同理可以通过实验验证功率环控制参数变化对超SFR现象的影响，这里不再赘述。
针对VSG电磁动态引发的SFR问题，为了对其进行有效的建模分析且将其统一于VSG宽频域稳定性的研究中，本文提出了基于单输入单输出序阻抗模型的SFR分析方法，并全面对比研究了单环和多环控制VSG的SFR特性与功率环控制参数、虚拟阻抗、电网阻抗之间的关系。研究表明：
1）虚拟阻抗和内环控制的引入会极大地改变SFR表现形式。单环控制VSG的功率谐振频率会随Lv的增大而增大，而多环控制VSG的功率谐振频率均在100Hz附近。这是因为内环控制的引入改变了VSG-VCI的输出阻抗特性，引发了50Hz附近的谐振峰，从而改变了系统的负阻尼特性。
2）单环控制VSG的SFR与滤波线路动态密切相关，在VSG-VCI自身设计参数合理、阻尼充分的情况下，电网阻抗变化不会影响SFR；而多环控制VSG的SFR与滤波线路动态无关、与电网阻抗动态密切相关，但是只有当虚拟电感与电网电感值接近时，系统才会出现100Hz附近的功率谐振。
3）虚拟电阻Rv与电网电阻Rg都可有效阻尼SFR，且同样阻值下它们的阻尼效果近似相同。因此，在近似纯感性的电网中，可通过引入虚拟电阻Rv的方式有效抑制SFR。
附 录
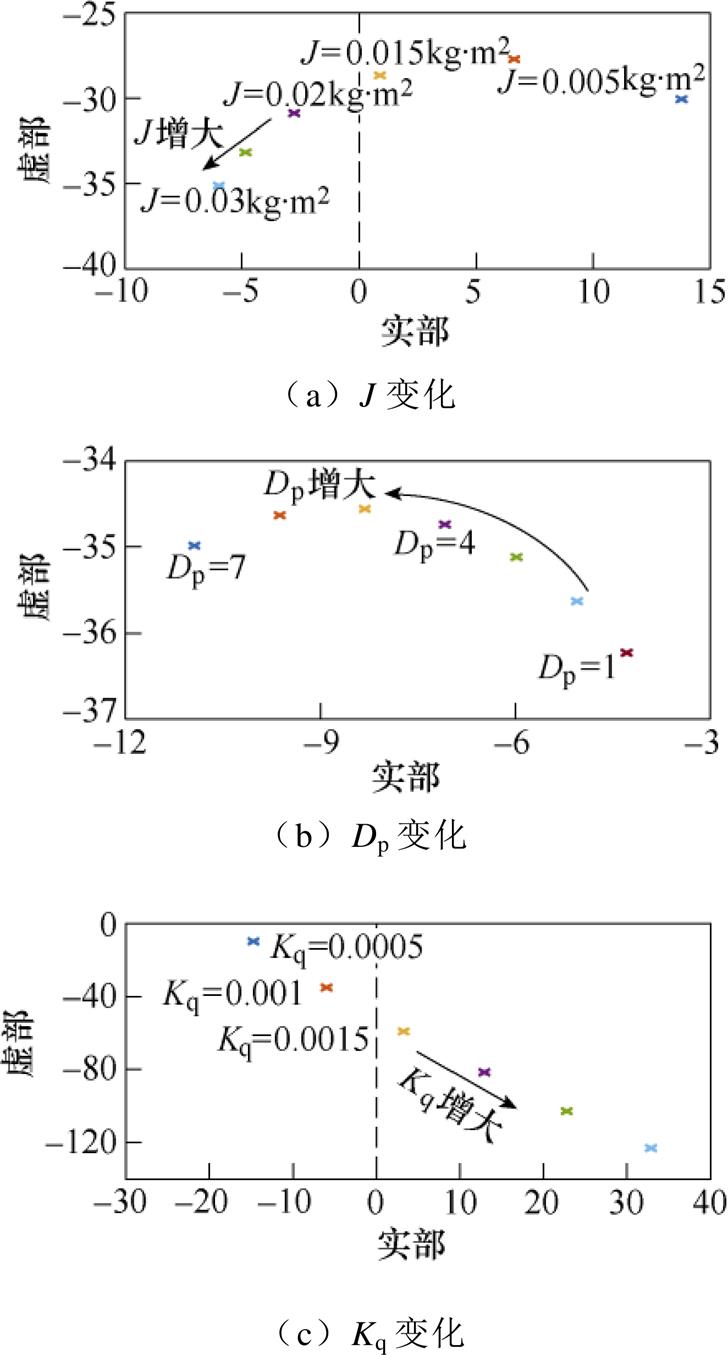
附图1 Ysp的SFR极点随功率环控制参数变化的分布
App.Fig.1 Map of the SFR poles of Ysp with varied power control parameters
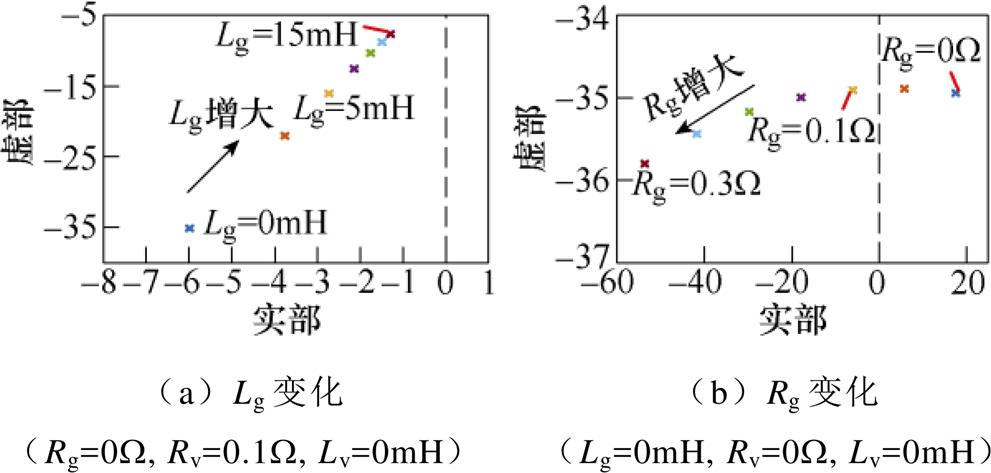
附图2 Yevp的SFR极点随电网阻抗Zg变化的分布
App.Fig.2 Map of the SFR poles of Yevp with varied Zg
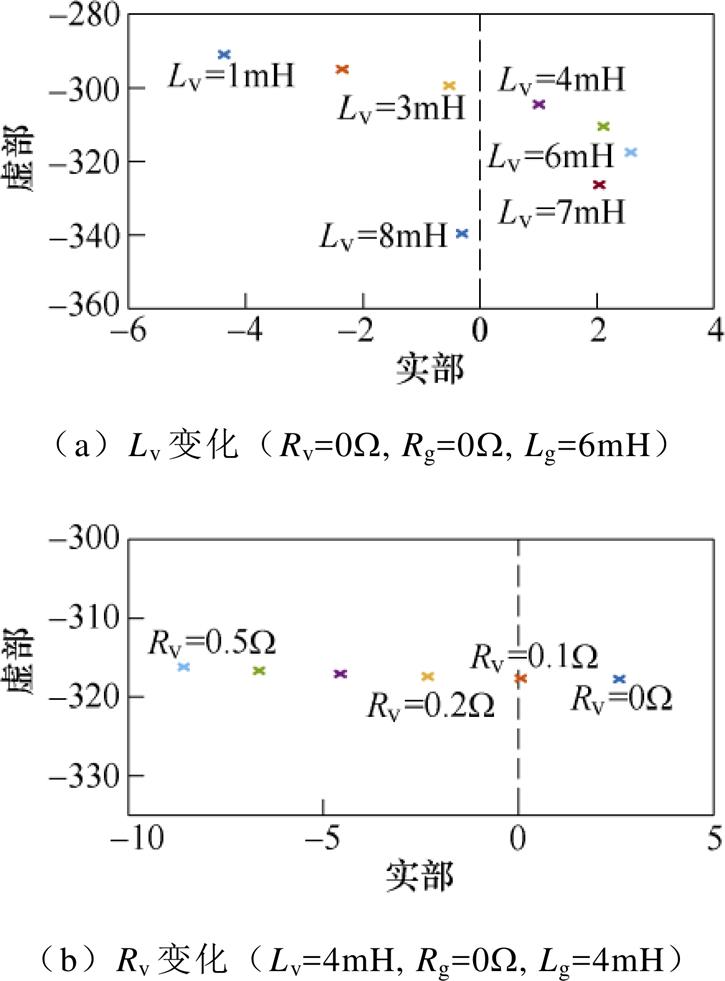
附图3 Yevp的超SFR极点随虚拟阻抗Zv变化的分布
App.Fig.3 Map of the super-SFR poles of Yevp with varied Zv
附图4 Yevp的超SFR极点随功率环控制参数变化的分布
App.Fig.4 Map of the super-SFR poles of Yevp with varied power control parameters
参考文献
[1] 姜静雅, 王玮, 吴学智, 等. 基于自适应无功功率补偿的虚拟同步机功率解耦策略[J]. 电工技术学报, 2020, 35(13): 2747-2756.
Jiang Jingya, Wang Wei, Wu Xuezhi, et al. Power decoupling strategy in virtual synchronous generator based on adaptive reactive power compensation[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2747-2756.
[2] 章艳, 高晗, 张萌. 不同虚拟同步机控制下双馈风机系统频率响应差异研究[J]. 电工技术学报, 2020, 35(13): 2889-2900.
Zhang Yan, Gao Han, Zhang Meng. Research on frequency response difference of DFIG system controlled by different virtual synchronous generator controls[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2889-2900.
[3] 张琛, 蔡旭, 李征. 具有自主电网同步与弱网稳定运行能力的双馈风电机组控制方法[J]. 中国电机工程学报, 2017, 37(2): 476-485.
Zhang Chen, Cai Xu, Li Zheng. Control of DFIG- based wind turbines with the capability of automatic grid-synchronization and stable operation under weak grid condition[J]. Proceedings of the CSEE, 2017, 37(2): 476-485.
[4] Liu Jia, Miura Y, Ise T. Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverter-based distributed gener- ators[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3600-3611.
[5] 颜湘武, 贾焦心, 王德胜, 等. 基于P/w“导纳”的并联虚拟同步机功频响应建模与分析[J]. 电工技术学报, 2020, 35(15): 3191-3202.
Yan Xiangwu, Jia Jiaoxin, Wang Desheng, et al. Modeling and analysis of active power-frequency response of parallel VSGs using a P/w “Admittance”[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3191-3202.
[6] Chen Junru, O'Donnell T. Parameter constraints for virtual synchronous generator considering stability[J]. IEEE Transactions on Power Systems, 2019, 34(3): 2479-2481.
[7] 李武华, 王金华, 杨贺雅, 等. 虚拟同步发电机的功率动态耦合机理及同步频率谐振抑制策略[J]. 中国电机工程学报, 2017, 37(2): 381-390.
Li Wuhua, Wang Jinhua, Yang Heya, et al. Power dynamic coupling mechanism and resonance suppression of synchronous frequency for virtual synchronous generators[J]. Proceedings of the CSEE, 2017, 37(2): 381-390.
[8] Yang Dongsheng, Wu Heng, Wang Xiongfei, et al. Suppression of synchronous resonance for VSGs[J]. The Journal of Engineering, 2017, 13(1): 2574- 2579.
[9] Li Xin, Hu Yaowei, Shao Yuting, et al. Mechanism analysis and suppression strategies of power oscilla- tion for virtual synchronous generator[C]//IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 2017: 4955-4960.
[10] 张行, 张兴, 李明, 等. 基于暂态虚拟电阻VSG同步频率谐振抑制策略[J]. 电力电子技术, 2019, 53(3): 68-70, 81.
Zhang Hang, Zhang Xing, Li Ming, et al. Synchronous frequency resonance suppression strategy for virtual synchronous generators based on transient virtual resistance[J]. Power Electronics, 2019, 53(3): 68-70, 81.
[11] 涂春鸣, 谢伟杰, 肖凡, 等. 控制延时对虚拟同步机全局稳定性的影响分析[J]. 电网技术, 2020, 44(8): 3021-3028.
Tu Chunming, Xie Weijie, Xiao Fan, et al. Analysis of influence of control delay on stability of virtual synchronous machine[J]. Power System Technology, 2020, 44(8): 3021-3028.
[12] 李辉, 王坤, 胡玉, 等. 双馈风电系统虚拟同步控制的阻抗建模及稳定性分析[J]. 中国电机工程学报, 2019, 39(12): 3434-3442.
Li Hui, Wang Kun, Hu Yu, et al. Impedance modeling and stability analysis of virtual synchronous control based on doubly-fed wind generation systems[J]. Proceedings of the CSEE, 2019, 39(12): 3434-3442.
[13] 涂春鸣, 谢伟杰, 肖凡, 等. 多虚拟同步发电机并联系统控制参数对稳定性的影响分析[J]. 电力系统自动化, 2020, 44(15): 77-86.
Tu Chunming, Xie Weijie, Xiao Fan, et al. Influence analysis of control parameters of parallel system with multiple virtual synchronous generators on stability[J]. Automation of Electric Power Systems, 2020, 44(15): 77-86.
[14] Cespedes M, Sun Jian. Adaptive control of grid- connected inverters based on online grid impedance measurements[J]. IEEE Transactions on Sustainable Energy, 2014, 5(2): 516-523.
[15] Wu Wenhua, Chen Yandong, Zhou Leming, et al. Sequence impedance modeling and stability com- parative analysis of voltage-controlled VSGs and current-controlled VSGs[J]. IEEE Transactions on Industrial Electronics, 2019, 66(8): 6460-6472.
Synchronous Frequency Resonance in Virtual Synchronous Generator Based on Sequence-Impedance
Abstract As for the synchronous frequency resonance (SFR) phenomenon existing in virtual synchronous generator (VSG), considering the shortcomings of multi-input multi-output power coupling SFR analysis models, a sequence-admittance and sequence-impedance based SFR analysis method is proposed by modeling the single-input single-output sequence impedance model that can describe the wide-frequency dynamics of the VSG, and the SFR phenomena of single-loop and multi-loop VSG are comparatively studied. Based on the pole distribution map of sequence admittance, the relationships between SFR and the VSG power control loop parameters, virtual impedance, inner-loop control and grid impedance are effectively studied. Based on the Bode diagrams of sequence-impedance, the damping characteristics of SFR with and without the inner-loop control are compared, and then the resonance mechanism of SFR in single-loop and multi-loop VSG is revealed from the perspective of negative damping. By building the experimental platform based on the RT-Box, the SFR phenomena of VSG under different control schemes and grid impedances are verified, indicating the optimal design direction of VSG control.
keywords：Virtual synchronous generator, synchronous frequency resonance, sequence-impedance, negative damping, inner-loop control
DOI: 10.19595/j.cnki.1000-6753.tces.210697
中图分类号：TM464
于彦雪 女，1991年生，博士研究生，研究方向为弱电网下并网逆变器建模及稳定性研究。E-mail: yuyanxueppkz@163.com
李浩昱 男，1974年生，教授，博士生导师，研究方向为微网环境变换器协调控制技术、极端环境电能变换与控制。E-mail: lihy@hit.edu.cn（通信作者）
收稿日期 2021-05-18
改稿日期 2021-12-10
黑龙江电力公司科技资助项目（522437200038）。
（编辑 陈 诚）