 1。Uab、Ucd分别为变压器一次和二次电压;S1~S4为一次侧功率开关管,Q1~Q4为二次侧功率开关管。
1。Uab、Ucd分别为变压器一次和二次电压;S1~S4为一次侧功率开关管,Q1~Q4为二次侧功率开关管。摘要 为了同时减小双有源桥(DAB)DC-DC变换器的电流应力和提高动态响应速度,该文在建立三重移相下六种模式的传输功率、电流应力等工作特性模型的基础上,提出一种基于三重移相的结合电流应力优化与虚拟电压补偿的控制方法。该方法由电流应力最优移相角模型和虚拟电压补偿方法构成,通过KKT条件获取电流应力最优的移相角模型,结合虚拟电压补偿方案估算传输功率值以提高负载突变及输入电压扰动时的动态响应速度。该方法在保证电流应力优化的同时,能够实现快速的动态响应,并且参数易于调节,可移植性好。最后,搭建了一台小功率样机进行三种方案的对比实验,验证了该文控制方法的正确性及优越性。
关键词:双有源桥DC-DC变换器 三重移相 电流应力 动态性能 虚拟电压补偿
双有源桥(Dual Active Brige, DAB)变换器由于具有高功率密度、易实现软开关、双向能量流动、电气隔离等优点,是DC-DC变换器的研究热点[1-6]。当前DAB变换器的研究主要集中在DAB的控制方法、电流应力和动态性能优化等方面。
文献[7]提出的单移相(Single Phase Shift, SPS)控制方法具有控制自由度少、容易实现等优点,但当输入、输出电压不匹配时[8-9],存在DAB变换器电流应力大、变换效率低、可靠性差等不足。为了解决这一问题,文献[10]提出了一种双移相(Dual Phase Shift, DPS)加SPS的优化控制策略,通过建立最优的控制轨迹,确保变换器工作于最小电流状态,但该策略的实现相对复杂。文献[11]基于DPS推导其模式下电流应力最小的控制模型,并提出实现方案,能显著降低电流应力。文献[12]在SPS的基础上,通过增加一次侧H桥的移相角,建立了扩展移相(Extend Phase Shift, EPS)控制下的电流应力优化目标函数并求解最优移相量,但所得最优移相量仅为局部最优解并非全局最优解。文献[13]提出基于EPS控制的电流应力优化策略,具有显著的电流应力优化效果,但其仅给出了一种工作模式分析,不能保证变换器性能最优。文献[14]在EPS基础上,通过增加二次侧H桥的移相角构成三重移相(Triple Phase Shift, TPS),该控制策略存在三个控制自由度,能够实现变换器真正意义上的最优控制,获得最优的电流应力优化效果。
为了提高DAB变换器的动态性能,文献[15]采用负载电流前馈控制,提高系统在负载波动时的动态性能,但是当变换器参数发生变化时,前馈控制的效果不明显。文献[16]通过模型预测控制算法提高变换器的动态响应,但系统的建模及分析较为复杂,可移植性差。文献[17]提出的直接功率控制策略,通过结合移相模型及PI控制器能够显著提高动态响应速度,但仅针对单移相进行分析,存在电流应力较大的不足。文献[18]在直接功率基础上提出了虚拟功率控制策略,该控制策略可推广至DPS、EPS及TPS控制方案中,但控制器参数范围对电路硬件参数准确性依赖大。文献[19]提出了一种DAB自然切换面(Natural Switching Surfaces, NSS)方法,通过弧形切换面推导出了变换器的非线性控制律,该方法具有克服负载瞬态、跟踪输出电压基准变化的优点,但存在控制复杂、实现困难等不足。上述控制策略均只以提高动态响应为单一目标进行研究,不适用于需同时具备良好的稳态特性和动态响应场合。
为使变换器同时具有较高的动态与稳态性能,文献[20]基于EPS控制求得电流最优解并构建环内直接功率环,在减小电流应力的同时提高变换器动态性能,但引入的效率参数降低了控制灵活度。文献[21]提出一种EPS控制下结合动态矩阵控制的电流应力优化策略,实现了电流应力与动态性能的同时优化,但该策略将DAB电路近似为线性系统且存在模型复杂等不足。文献[22]在TPS控制下求得电流应力最优表达式并结合PI控制器构建环路,实现电流应力与动态性能的同时优化,但未考虑全部工作模式,因此求出的电流应力优化解并非全局最优。
本文基于三重移相提出了一种适用于DAB变换器的结合电流应力优化与虚拟电压补偿的优化控制方法(Combining current Stress Optimization and Virtual Voltage Compensation control scheme based on Triple Phase Shift, CSO-VVC-TPS),同时提高变换器的动态响应速度和减小电流应力。首先,全面分析推导TPS各个模态下的输出功率和电流应力特性,建立数学模型,并根据KKT(karush-kuhn- tucker)条件求解电流应力最优的移相角组合;其次,结合虚拟电压补偿方案,通过快速改变传输功率值,提高变换器的动态性能;最后,通过仿真及实验对所提控制方法进行验证。
双有源桥DC-DC变换器电路拓扑如图1所示。图中,Ui、Uo分别为输入、输出电压;C1、C2为直流侧支撑电容;Lk、iLk分别为辅助电感、电感电流;变压器匝比为n 1。Uab、Ucd分别为变压器一次和二次电压;S1~S4为一次侧功率开关管,Q1~Q4为二次侧功率开关管。
1。Uab、Ucd分别为变压器一次和二次电压;S1~S4为一次侧功率开关管,Q1~Q4为二次侧功率开关管。
DAB变换器在TPS控制下,从一次侧向二次侧能量流动的一个开关周期内各个模态工作模式及原理波形如图2所示。DAB变换器在TPS控制下有A、B、C、D、E、F六种工作模式,其中,D1、D2、D0分别为开关管S1和S4、Q1和Q4、S1和Q1之间的移相角占空比,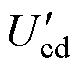 为Ucd折算到一次侧的等效电压;Ts、Th分别为一个和1/2个开关周期。
为Ucd折算到一次侧的等效电压;Ts、Th分别为一个和1/2个开关周期。
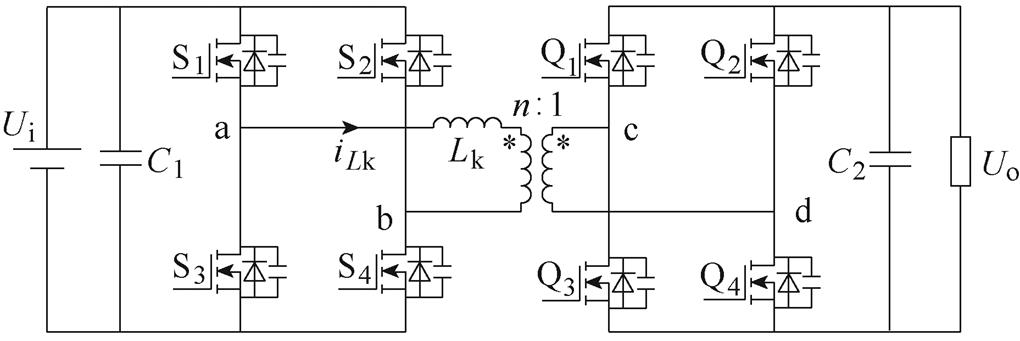
图1 双有源桥DC-DC变换器电路拓扑
Fig.1 Dual active bridge DC-DC converter circuit topology
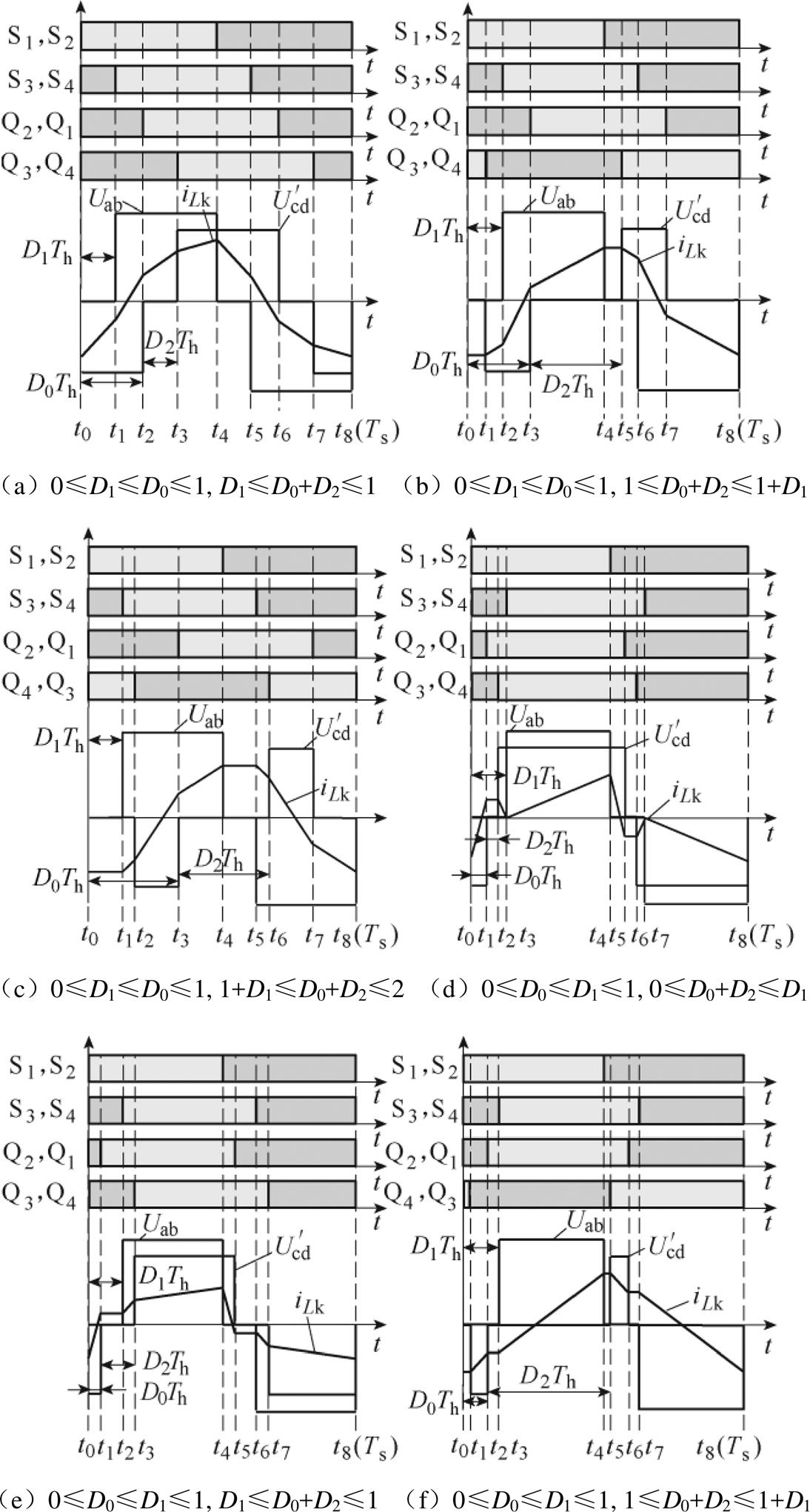
图2 TPS控制下的工作模式及原理波形
Fig.2 Operating modes and principle waveforms under TPS control
由于电感电流具有半波对称性,即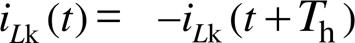 ,通过电感的电压、电流微分方程可计算半个周期内模式A、B、C、D、E、F的电感电流表达式,分别为
,通过电感的电压、电流微分方程可计算半个周期内模式A、B、C、D、E、F的电感电流表达式,分别为
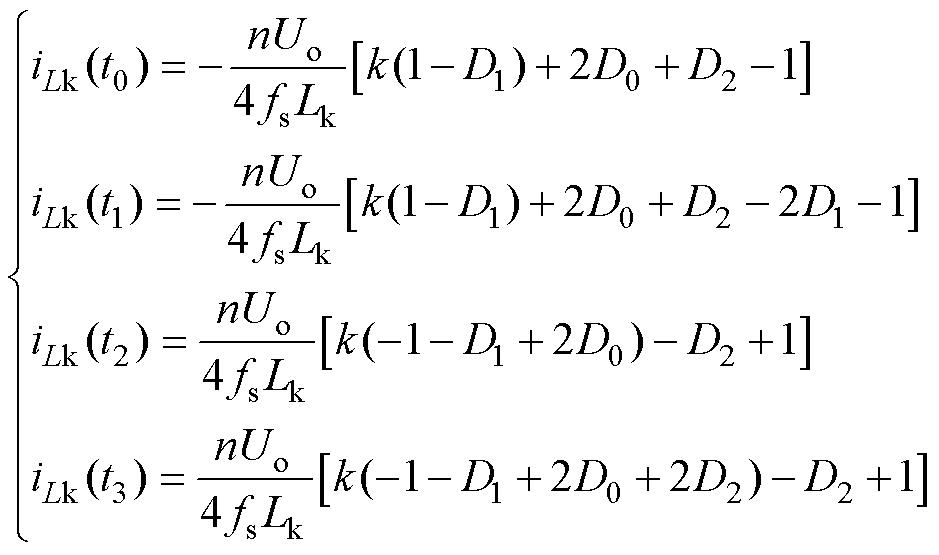 (1)
(1)
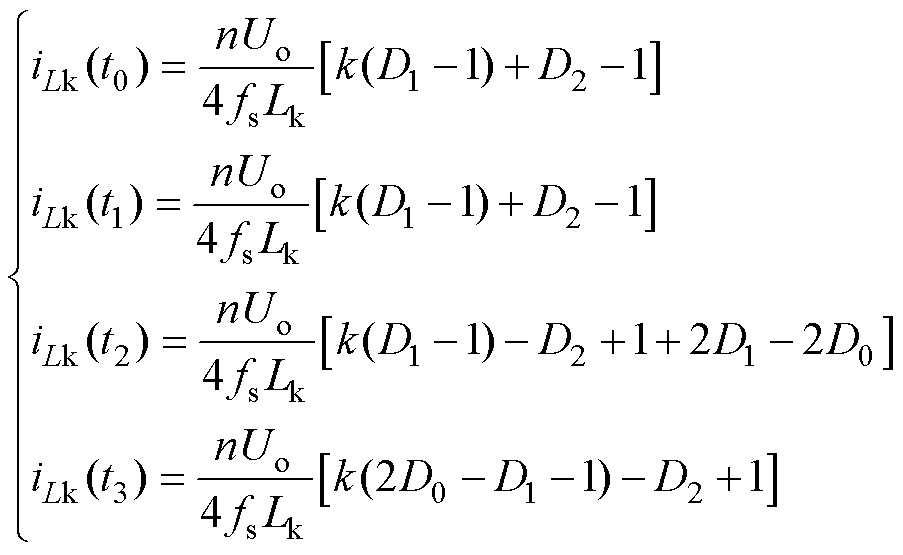 (2)
(2)
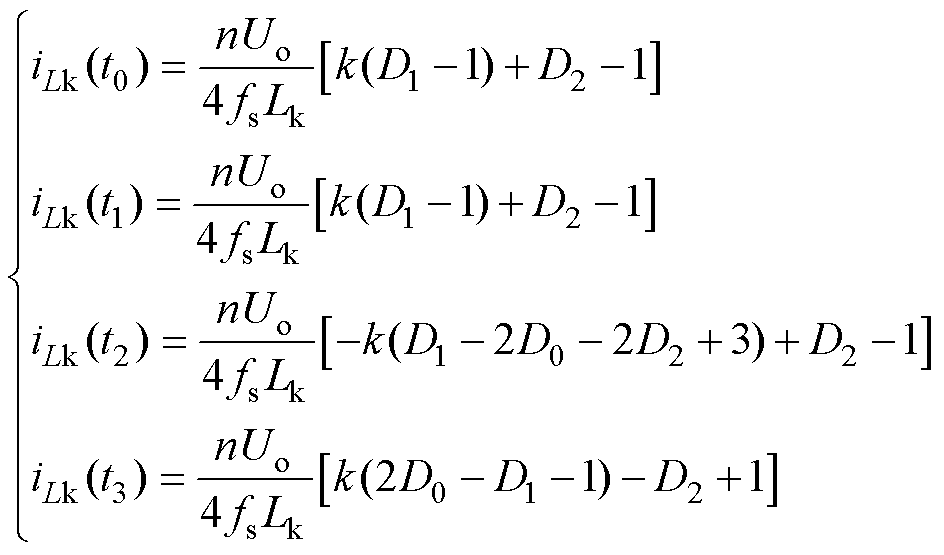 (3)
(3)
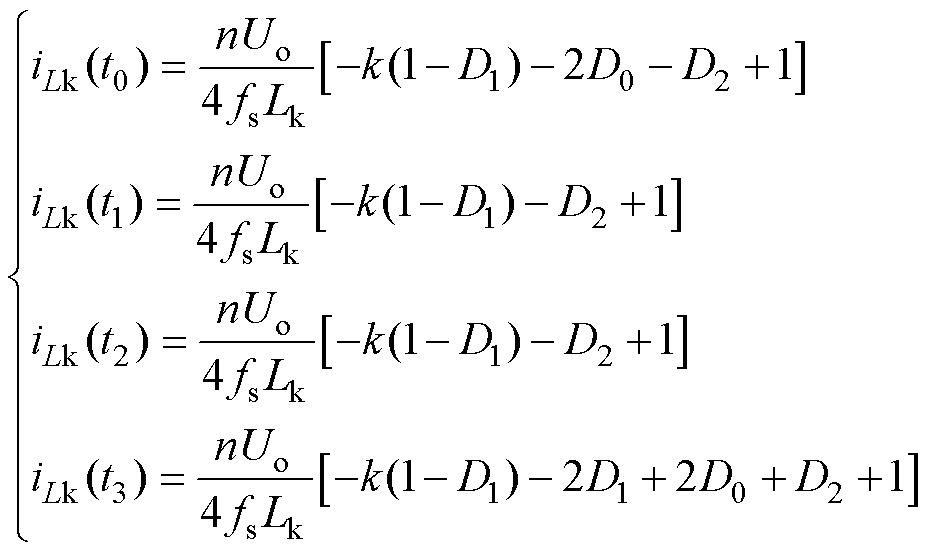 (4)
(4)
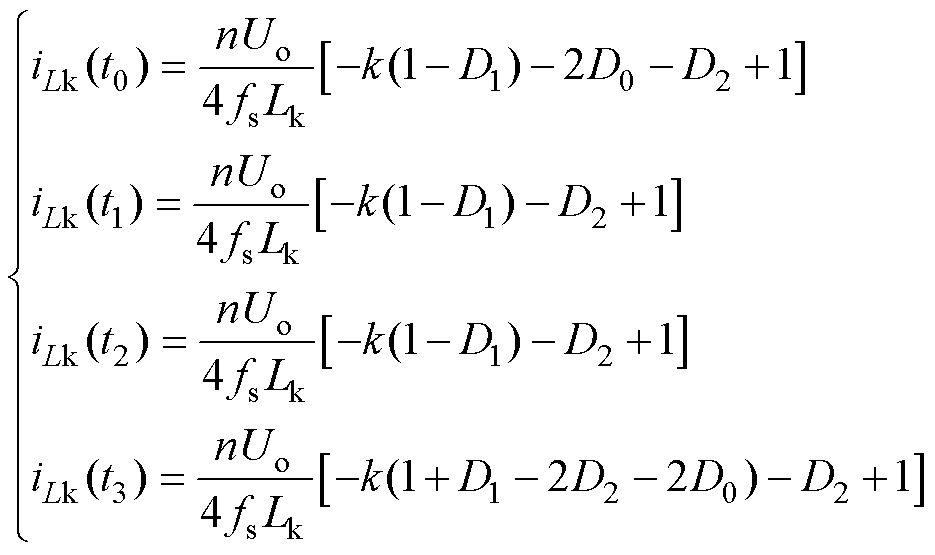 (5)
(5)
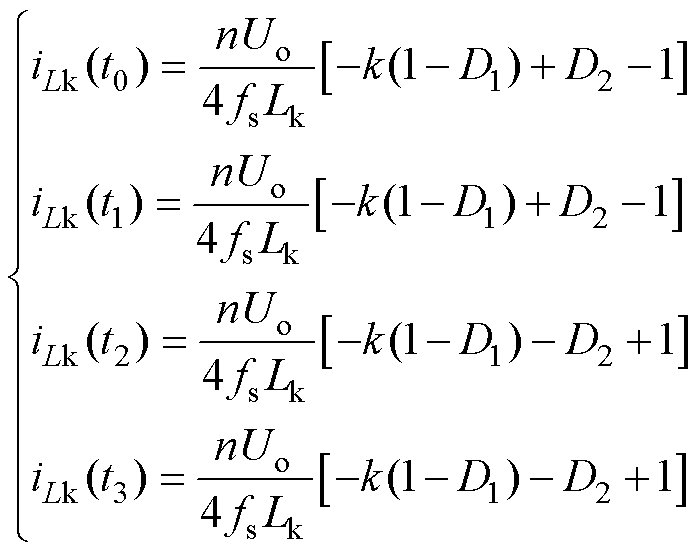 (6)
(6)
式中,k为电压比,k=Ui/(nUo);fs为开关频率,fs=1/Ts。DAB变换器的电流应力ip和平均传输功率P分别为
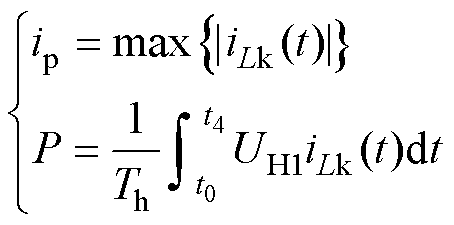 (7)
(7)
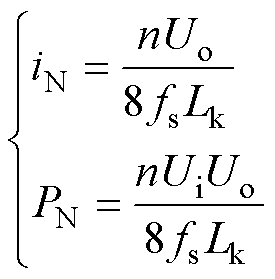 (8)
(8)
式中,iN为电流应力基准值;PN为传输功率基准值。
将式(1)~式(6)代入式(7),并根据式(8)给出的基准值,得到标幺化后的电流应力及传输功率分别见表1与表2。
表1 TPS控制下DAB变换器的标幺化电流应力
Tab.1 Standardized current stress of DAB under TPS modulation

模式标幺化电流应力 A、D、E B、C、F
表2 TPS调制下DAB变换器的标幺化传输功率
Tab.2 Standardized transmission power of DAB under TPS modulation

模式标幺化传输功率p A B C D E F
分别对表2六种模式下传输功率模型中的(D0, D1, D2)求偏导,并将驻点及移相角关系限制条件分别代入各模式的传输功率模型,可求得各模式下传输功率范围,见表3。表中,模式A的传输功率范围为0~1;模式B、E的功率传输范围为0~0.67;而模式C、D、F的功率传输范围为0~0.5。
表3 TPS控制下各模式传输功率范围
Tab.3 Transmission power range of each mode under TPS control

模式标幺化传输功率范围(pu) A B C D E F
将标幺化电流应力作为目标函数,标幺化传输功率及移相角关系作为等式约束和不等式约束条件,通过基因遗传算法[23](Genetic Algorithm, GA)求解各功率段时的最小电流应力,变化趋势如图3所示。
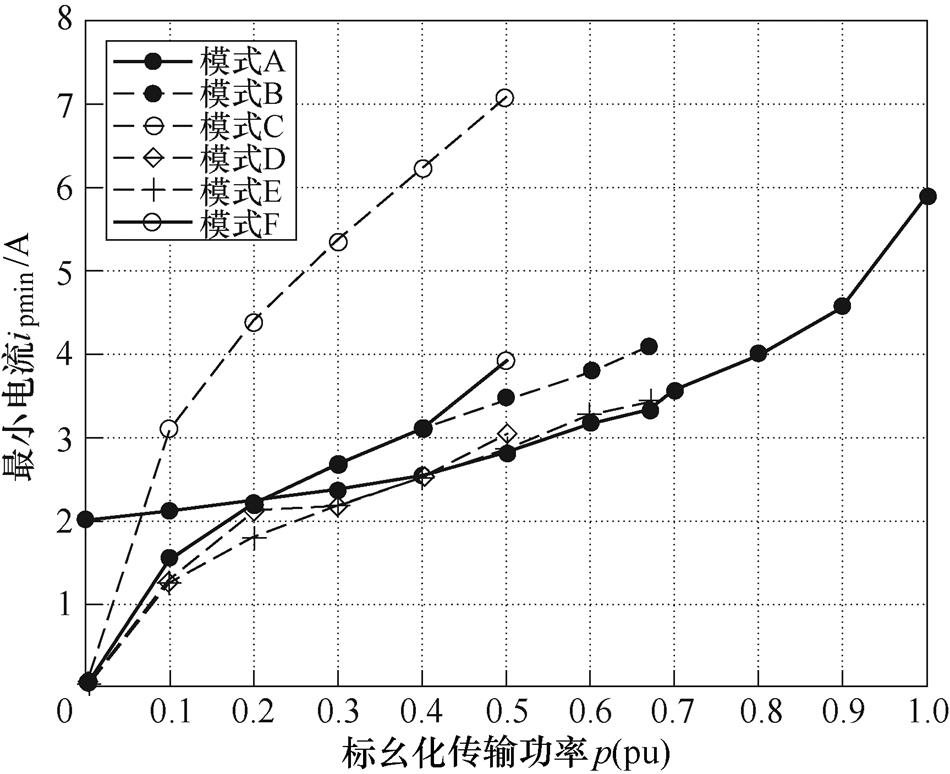
图3 k=3时六种模式下电流应力对比
Fig.3 Comparison of the current stress of the six modes when k=3
需要说明的是,GA只能根据约束条件近似寻优,并不能准确计算各功率点的最小电流应力,因此可以根据各模式电流应力的变化曲线分析电流应力最小的工作模式。模式A在中功率段电流应力较小,但在低、高功率段电流应力较大,而模式D、E的电流应力在中、低功率范围内相较于模式A、B、C、F更小。同时,由图2可知变换器工作在B、C、F模式时,一个开关周期内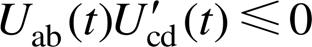 恒成立,即B、C、F工作模式在传输功率的过程中,需要先经过辅助电感Lk进行储能,所以在传输相同功率时,模式B、C、F存在更大的电感电流。因此,三重移相下,工作模式D、E下的电流应力优于工作模式A、B、C、F。
恒成立,即B、C、F工作模式在传输功率的过程中,需要先经过辅助电感Lk进行储能,所以在传输相同功率时,模式B、C、F存在更大的电感电流。因此,三重移相下,工作模式D、E下的电流应力优于工作模式A、B、C、F。
由第1节分析可知,工作模式D、E下的电流应力优于工作模式A、B、C、F,但模式D、E的功率传输范围不能组成全功率范围,由于模式A功率传输范围可以弥补缺失的功率区间,并仅在低、高功率段存在较大电流应力。因此,针对模式A、D、E寻优求得电流应力最小移相角组合(D0, D1, D2)的表达式。模式A、D、E的电流应力标幺值与传输功率标幺值分别为
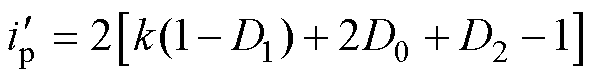 (9)
(9)
 (10)
(10)
以电流应力最小为目标,根据式(10)建立KKT目标函数,同时加入传输功率、移相角关系的等式约束及不等式约束限制条件,优化问题可以描述为
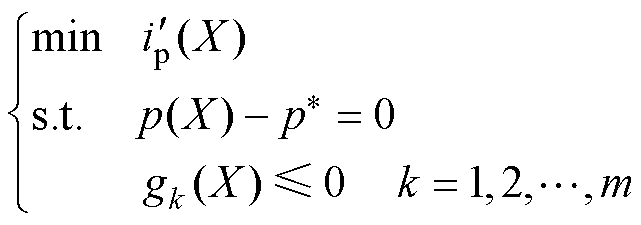 (11)
(11)
式中,X为关于D0、D1、D2的最优解集合;p*为期望传输功率标幺值;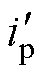 与
与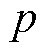 分别为标幺化电流应力及传输功率;
分别为标幺化电流应力及传输功率;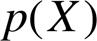 为功率模型组成的等式约束集合;
为功率模型组成的等式约束集合;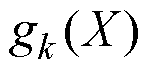 为由移相角关系形成的不等式约束集合。根据式(9)~式(11),电流应力优化的KKT条件基本形式可表示为
为由移相角关系形成的不等式约束集合。根据式(9)~式(11),电流应力优化的KKT条件基本形式可表示为
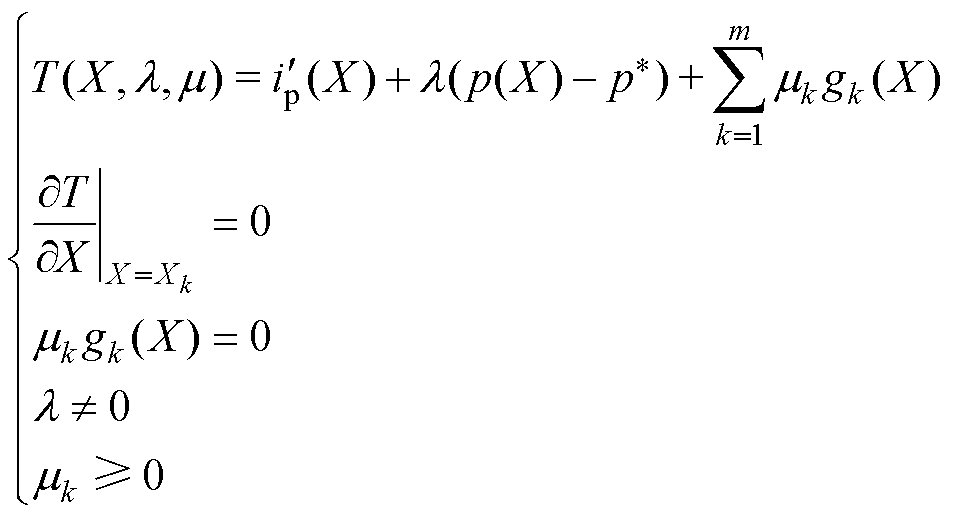 (12)
(12)
当DAB变换器工作在模态A时,根据式(12),可得电流应力最优的移相角表达式为
 (13)
(13)
将式(13)分别代入式(9)及模式A的限制条件0≤D1≤D0≤1,D1≤D0+D2≤1中,可得模式A的电流应力最小值与传输功率p的范围分别为
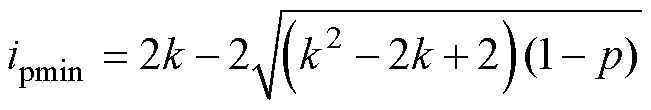 (14)
(14)
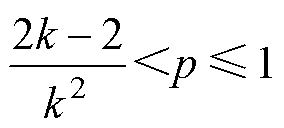 (15)
(15)
同理,当DAB变换器工作在模式E时,根据式(10)、式(12)可得
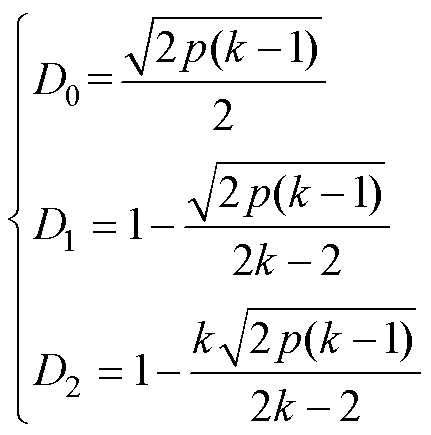 (16)
(16)
将式(16)分别代入式(9)及模式E的限制条件0≤D0≤D1≤1,D1≤D0+D2≤1中,可得模式E的电流应力最小值与传输功率p的范围分别为
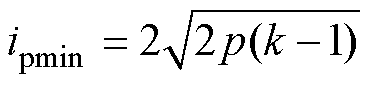 (17)
(17)
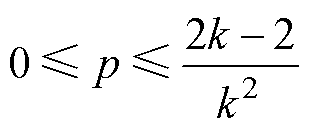 (18)
(18)
当DAB变换器工作在模式D时,无法求解,故DAB变换器工作在模式A、D、E时求得的最优电流应力表达式能够在全功率工作范围内减小电流应力。
表4给出了DAB变换器在传统SPS[14]控制方案、基于双重移相的电流应力优化[12](Current Stress Opti-mization with Double Phase Shift, CSO-DPS)控制方案及本文CSO-VVC-TPS方案在全功率范围内的电流应力最优解,并分别绘制出各方案的标幺化电流应力与电压比k、传输功率p的最优解三维图,如图4所示。图中,在全功率段,SPS方案的电流应力随着电压比k的增加而提高;CSO-VVC-TPS方案与CSO-DPS方案在高功率段的电流应力优化效果基本一致,但CSO-DPS方案在低功率段时存在初始电流应力,因此,CSO-VVC-TPS方案在整体上的电流应力优化效果最好。当k=3、p=0.26时,SPS方案、CSO-DPS方案及CSO-VVC-TPS方案的最优电流应力标幺值分别为4.28(pu)、2.31(pu)和2.1(pu)。
表4 各控制方案下的电流应力最优解
Tab.4 The optimal solution of current stress under SPS, CSO-DPS and CSO-VVC-TPS control scheme

控制方案传输功率p、电压比k电流应力 传统SPS CSO-DPS CSO-VVC-TPS
针对SPS方案、CSO-DPS方案及CSO-VVC- TPS方案,在输入电压75V、输出电压50V、负载50W 时,三种方案下电流应力仿真对比如图5所示。图中,SPS方案、CSO-DPS方案及CSO-VVC-TPS方案在系统达到稳态时的电流应力值分别为10.5A、6.1A和5.56A。根据式(8)及电路参数可得传输功率、电流应力基准值分别为187.5W和2.5A,因此,可进一步求出仿真条件下稳态时的传输功率标幺值为0.26(pu),则图5三种方案下的电流应力值经过标幺化计算后分别为4.2(pu)、2.44(pu)及2.22(pu)。通过与表4的电流应力标幺值表达式对比,仿真结果与理论分析基本一致,考虑到读取电流应力值存在一定误差,因此仿真结果与理论分析吻合。

图4 三种方案下标幺化电流应力最优解三维图
Fig.4 Three-dimensional diagram of the optimal solution of the unitized current stress under the three schemes

图5 三种方案下电流应力仿真对比
Fig.5 Comparison of current stress simulation diagrams under the three schemes
相比于传统SPS方案,CSO-DPS方案能够显著降低电流应力,但由于没有选择合适的工作模式,因此所得电流应力并非全局最优解。CSO-VVC-TPS方案通过对TPS控制下的工作模式进行合理分析,优选工作模式求得最优解,理论分析表明,该方案在低功率段能够进一步降低电流应力。
传统TPS控制优化方案通过PI算法控制桥间移相角D0,通过电流应力优化策略给定前后桥移相角D1、D2,进而实现输出电压的稳定。但电流应力优化策略中的D1、D2会与传输功率产生耦合现象,因此仅通过PI控制器输出D0,系统的动态性能较差。为了在减小电流应力的同时提高变换器的动态响应速度,本文引入虚拟电压量Uv来补偿功率损耗与开关管压降所引起的功率差,当输入电压、负载电阻在实际工作中发生变化时,传输功率立刻随之改变,并同步输出给电流应力优化表达式(13)、式(16),给定当前D0、D1、D2的最优值。
DAB变换器的传输功率P定义为
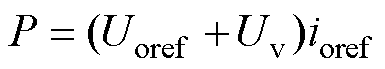 (19)
(19)
式中,Uoref为输出电压期望值;ioref为输出电流期望值;Uv为虚拟电压。同时,ioref定义为
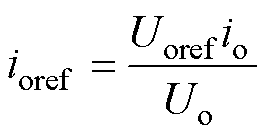 (20)
(20)
综合式(19)、式(20)可得
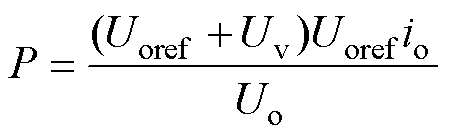 (21)
(21)
式中,Uo、io分别为输出电压及电流;Uv为PI控制器的输出值。对式(21)进行标幺化可得
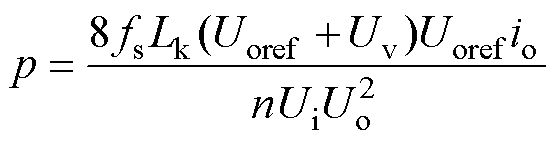 (22)
(22)
由于可通过Uv补偿变换器的开关频率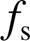 、电感
、电感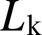 以及变压器匝比
以及变压器匝比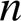 所造成的误差,故式(22)可简化为
所造成的误差,故式(22)可简化为
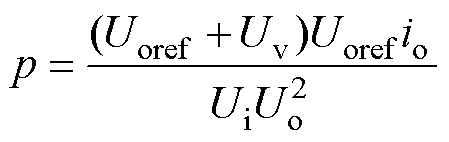 (23)
(23)
综上,本文提出的结合电流应力优化与虚拟电压补偿的TPS优化方案控制框图,如图6所示。
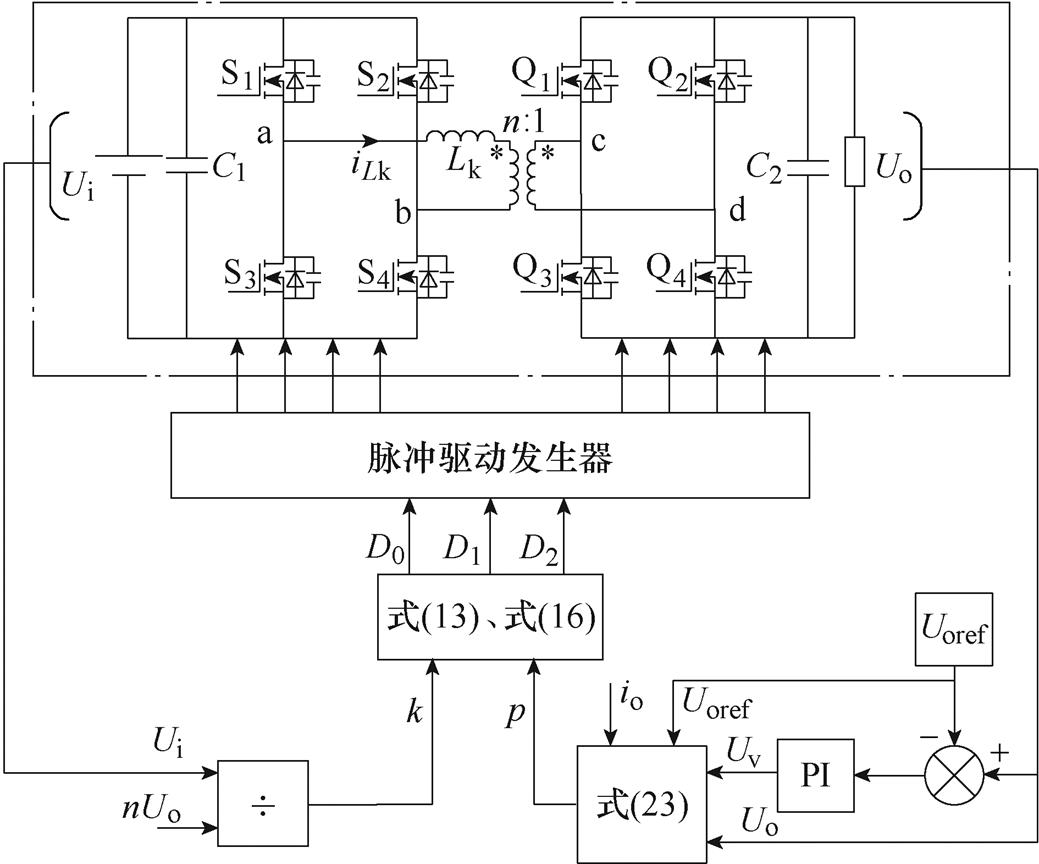
图6 TPS下结合电流应力优化与虚拟电压补偿的控制框图
Fig.6 Control block diagram combining current stress optimization and virtual voltage compensation under TPS
首先通过采样输出电压Uo与参考电压Uoref作差,通过PI控制器输出虚拟电压Uv,根据式(23)计算得到传输功率标幺值p,同时,Ui除以nUo得到电压比k,由p、k确定DAB变换器工作的功率区间,最后根据式(13)、式(16)计算出最优移相角,驱动对应的主电路开关管,同时优化电流应力及动态性能。通过引入虚拟电压量,当变换器负载突变或输入电压扰动时,控制器能够立刻计算出新的传输功率标幺值,并根据电流优化策略立刻计算出当前时刻的最优移相角,实现输出电压的快速 调节。
以TI公司的DSP芯片TMS320F28069为主控芯片搭建了DAB变换器的实验样机,如图7所示,主要电路参数见表5。

图7 实验样机
Fig.7 Experimental prototype diagram
表5 主要电路参数
Tab.5 Main circuit parameters
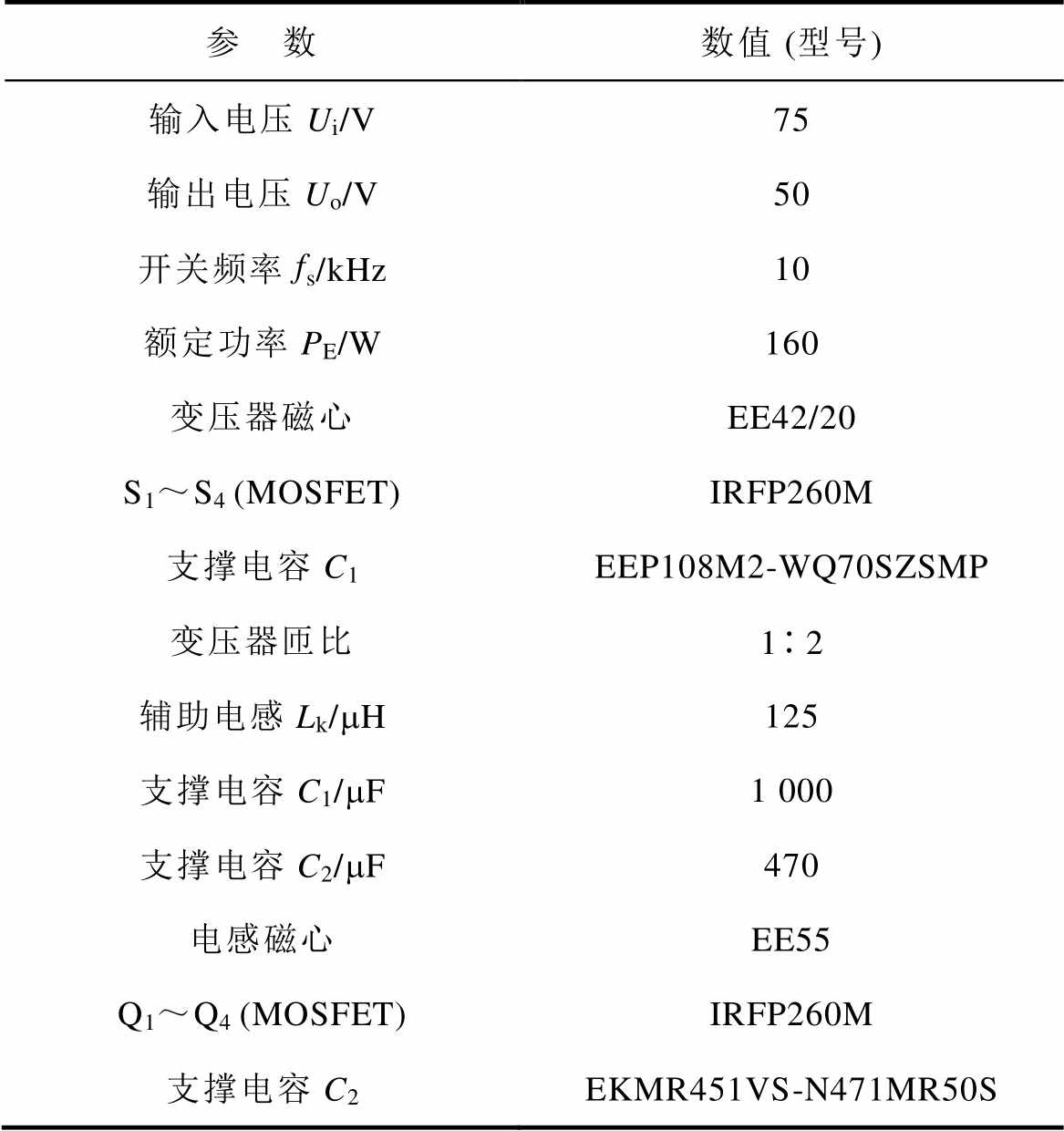
参 数数值 (型号) 输入电压Ui/V75 输出电压Uo/V50 开关频率fs/kHz10 额定功率PE/W160 变压器磁心EE42/20 S1~S4 (MOSFET)IRFP260M 支撑电容C1EEP108M2-WQ70SZSMP 变压器匝比12 辅助电感Lk/mH125 支撑电容C1/mF1 000 支撑电容C2/mF470 电感磁心EE55 Q1~Q4 (MOSFET)IRFP260M 支撑电容C2EKMR451VS-N471MR50S
为了验证本文所提CSO-VVC-TPS方案的有效性及优越性,在同等实验条件下将传统SPS方案与CSO-DPS方案[12]作为对比实验方案进行验证。
图8给出了在输入电压为75V,输出电压为50V,负载分别为50W、27W、15.6W 时三种方案达到稳态的一次电压Uab、二次侧折算电压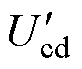 、电感电流iLk的波形。
、电感电流iLk的波形。
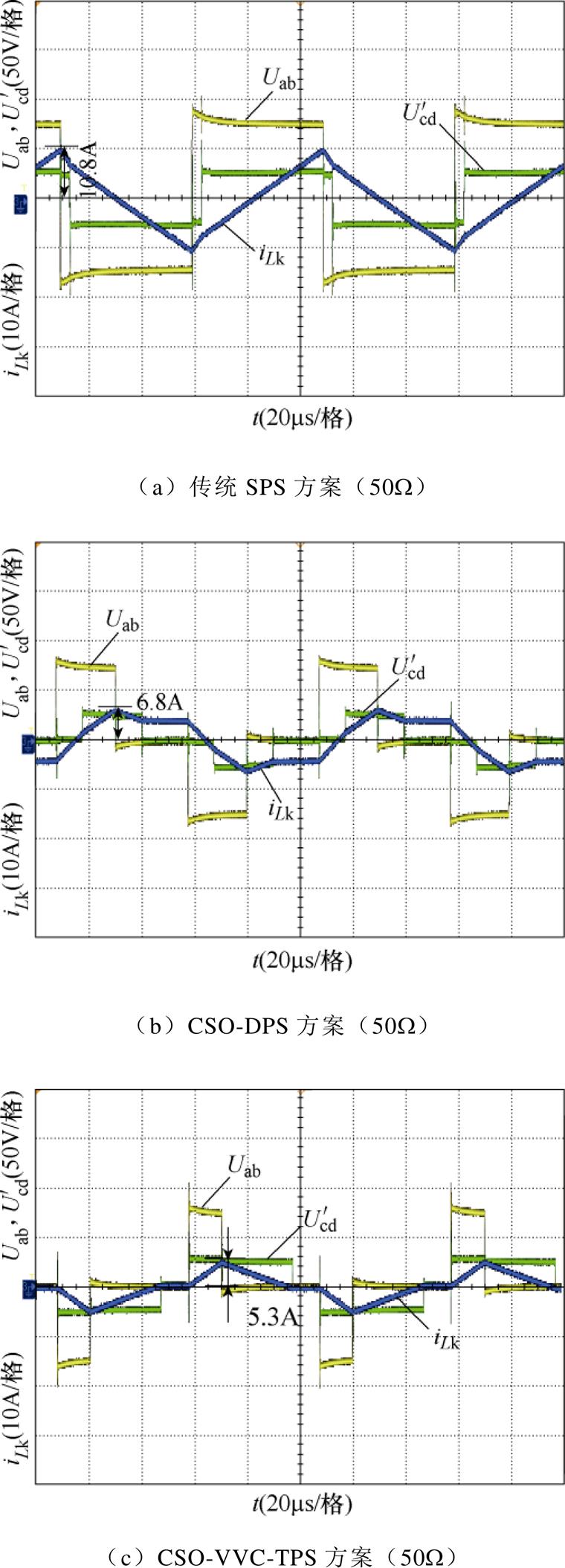
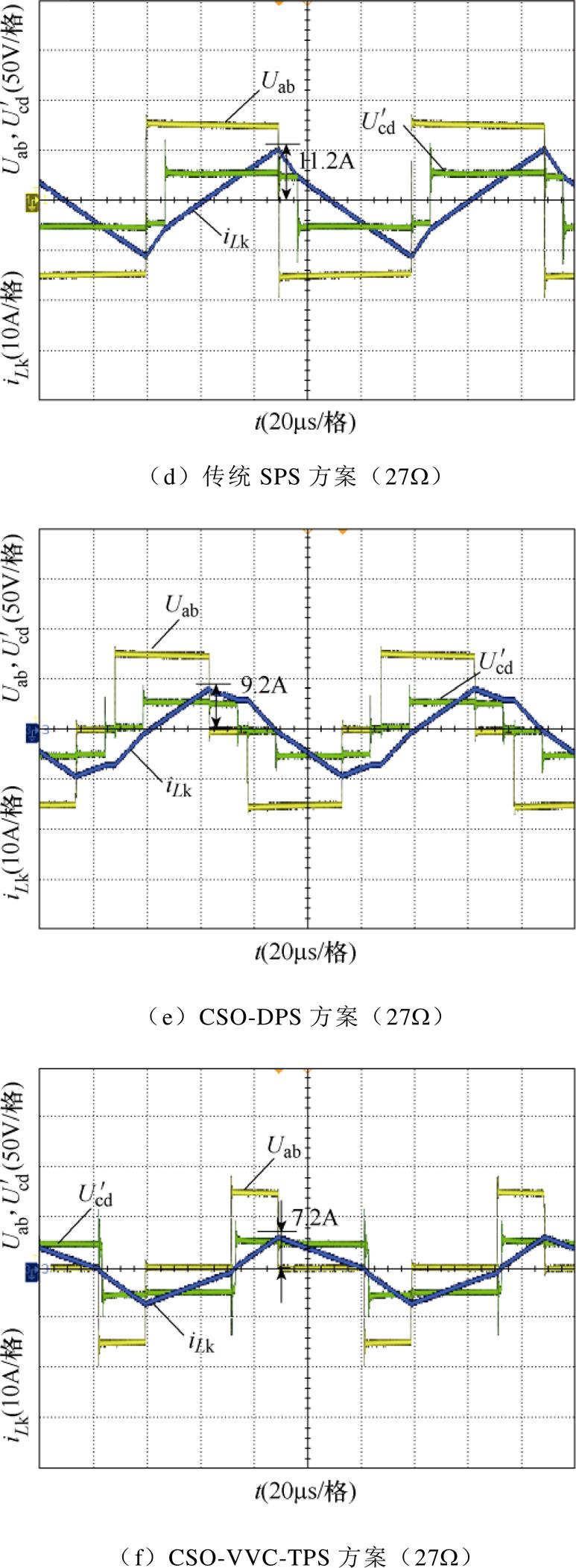
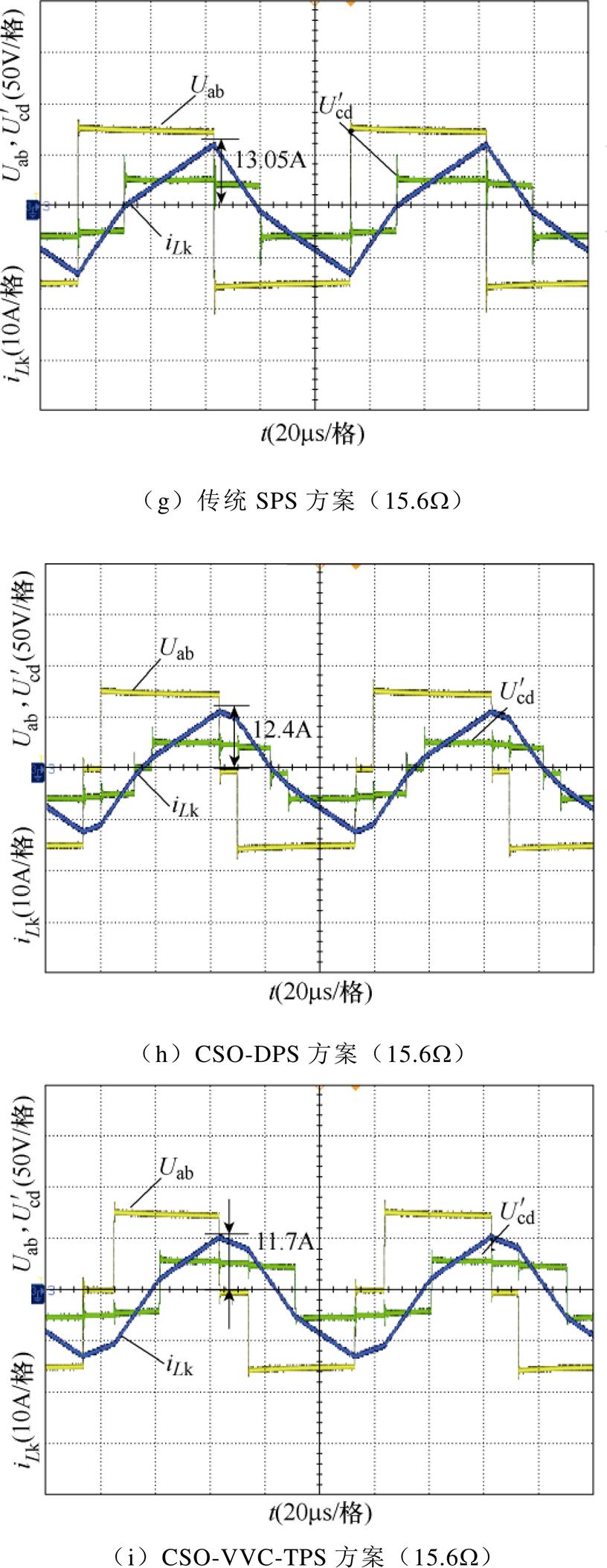
图8 电流应力实验波形
Fig.8 Waveforms diagram of current stress experiment
图8中,电压比k=3,当负载为50W 时,传统SPS方案的电流应力值约为10.8A,如图8a所示。CSO-DPS方案有效地减小了变换器的电流应力,其电流应力约为6.8A,如图8b所示,但是由于CSO- DPS方案仅考虑一种工作模态,因此还具有优化空间。本文的CSO-VVC-TPS方案基于三重移相,通过分析变换器的全部工作模态进行寻优,使得电流应力最小,约为5.3A,如图8c所示。当负载为27W 时,如图8d~图8f所示,传统SPS方案的电流应力值约为11.2A,CSO-DPS方案的电流应力值约为9.2A,而CSO-VVC-TPS方案的电流应力约为7.2A。当负载为15.6W 时,如图8g~图8i所示,传统SPS方案的电流应力值约为13.05A,CSO-DPS方案的电流应力值约为12.4A,而CSO-VVC-TPS方案的电流应力约为11.7A。同时,由图8a~图8c与图5a~图5c对比发现,实验结果与理论结果基本一致,证明了CSO-VVC-TPS方案的有效性及优越性。
当输出电压为50V,负载为50W 时,图9给出了输入电压从50V增长到100V时,变换器在三种控制方案下电流应力随输入电压变化的曲线。其中,本文的CSO-VVC-TPS方案电流应力值最小,尤其是电压比越大时,电流应力优化的效果越明显。当Ui=100V时,CSO-VVC-TPS方案的电流应力为6.55A,而此时SPS方案和CSO-DPS方案的电流应力值分别为15.4A和8.2A。
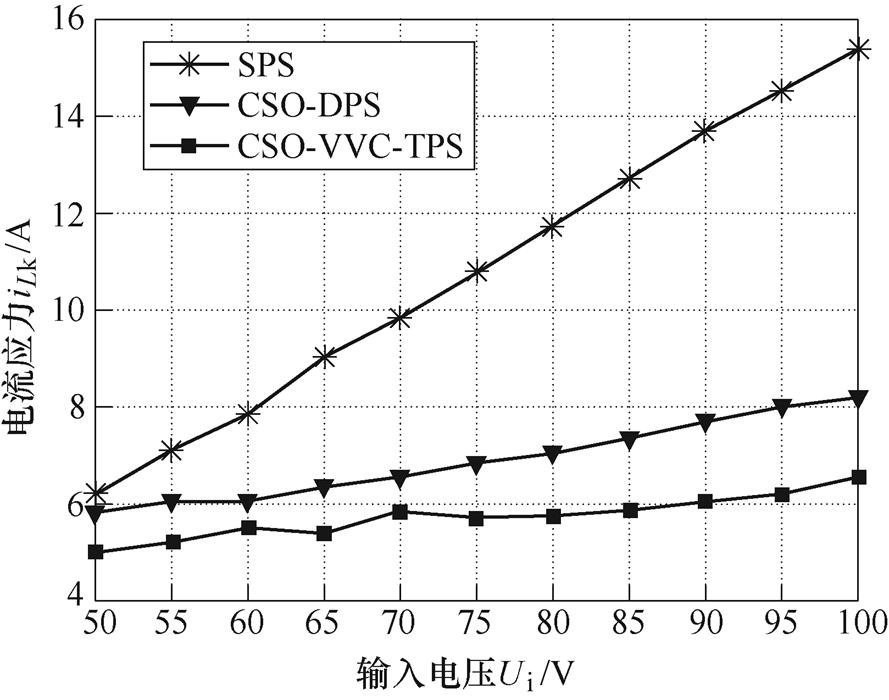
图9 电流应力随输入电压变化曲线
Fig.9 Current stress variation curves with input voltage
读取功率分析仪显示的输入、输出功率,计算此时的传输效率,效率实验曲线如图10所示。当功率为50W(50W)时,改变输入电压Ui,如图10a所示,当输入电压Ui=50V时,SPS方案传输效率为89.76%,CSO-DPS方案效率为90.46%,而CSO- VVC-TPS方案的传输效率为91.1%。当输入电压增大到100V时,SPS方案传输效率为63.24%,CSO- DPS方案效率为75.42%,而CSO-VVC-TPS方案的传输效率为90.3%。当功率为105W(23.81W),输入电压Ui=50V时,SPS方案传输效率为91.68%,CSO-DPS方案效率为91.64%,而CSO-VVC-TPS方案的传输效率为91.79%。当输入电压增大到100V时,SPS方案传输效率为78.36%,CSO-DPS方案效率为82.92%,而CSO-VVC-TPS方案的传输效率为91.34%。因此CSO-VVC-TPS方案能够在不同工况下进一步提高变换器的传输效率。
改变负载阻值,效率随功率变化的曲线如图10b所示。当功率为50W(50W)时,SPS方案传输效率为79.03%,CSO-DPS方案效率为87.8%,而CSO-VVC-TPS方案的传输效率为92.52%。当功率增大到105W(23.81W)时,SPS方案传输效率为88.25%,CSO-DPS方案效率为90.22%,而CSO- VVC-TPS方案的传输效率达到了93.79%。当功率增大到160W(15.6W)时,SPS方案传输效率为89.07%,CSO-DPS方案效率为89.65%,CSO-VVC- TPS方案的传输效率为89.66%。因此CSO-VVC- TPS方案在全功率范围内也能保证较高的传输效率。同时,需要说明的是,随着负载的增加,输出电流也会随之增大,由于DAB电路中的通态损耗与输出电流的二次方呈正相关,因此,通态损耗会随着负载的增加而增大,电路运行在重载功率段时,传输效率会降低。
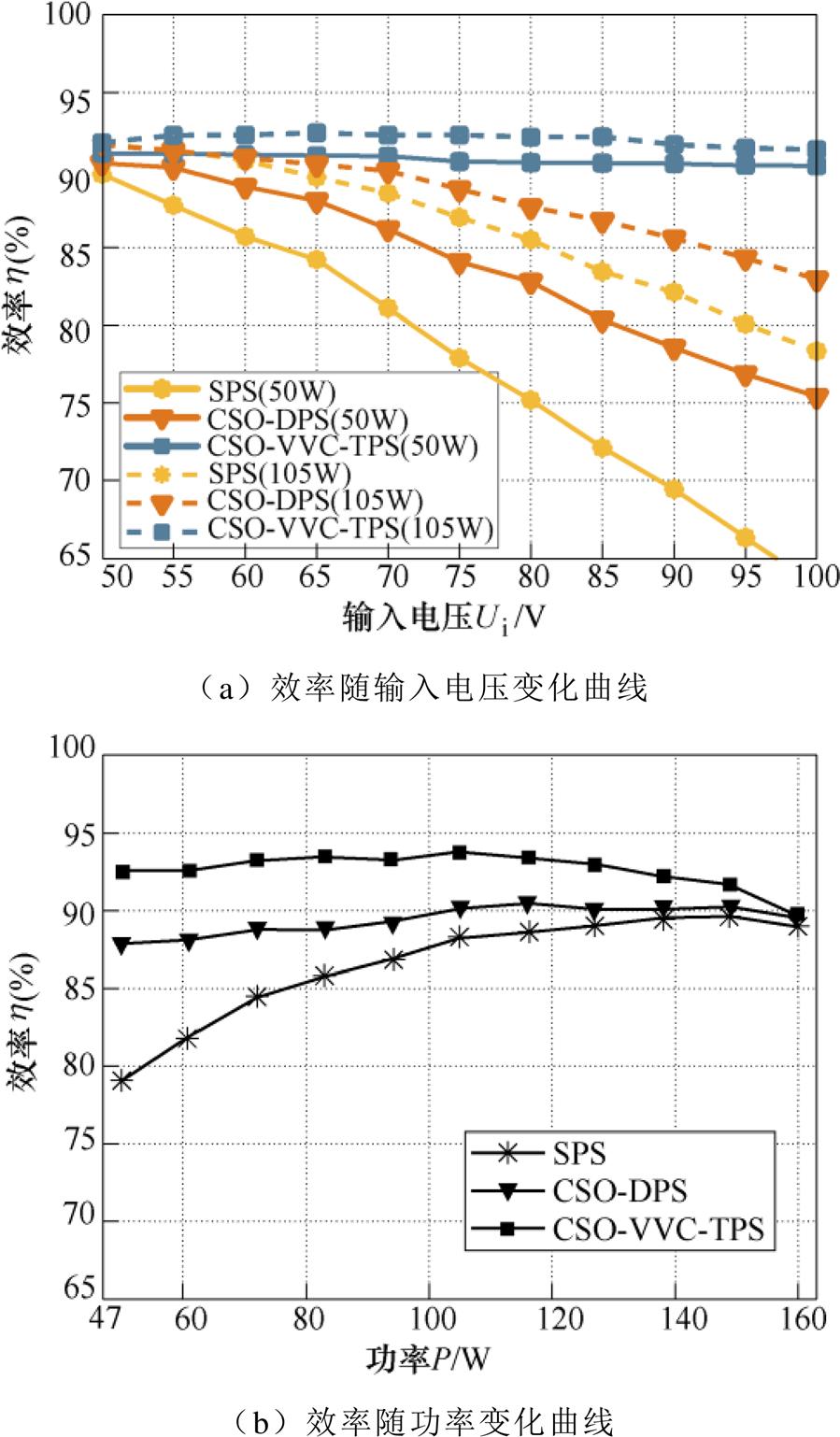
图10 效率实验曲线
Fig.10 Experimental curves of efficiency
当输入电压Ui=75V、输出电压Uo=50V时, DAB变换器在三种控制方案下动态性能的电压电流实验波形,如图11所示。
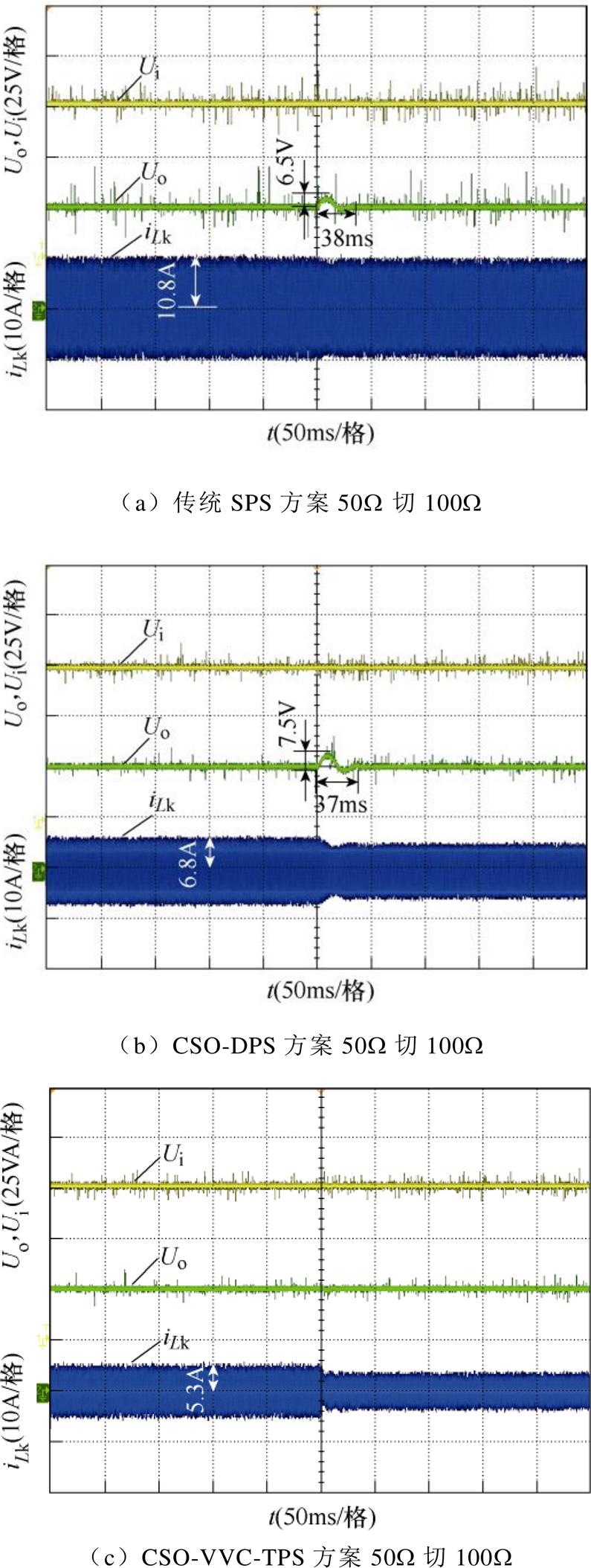
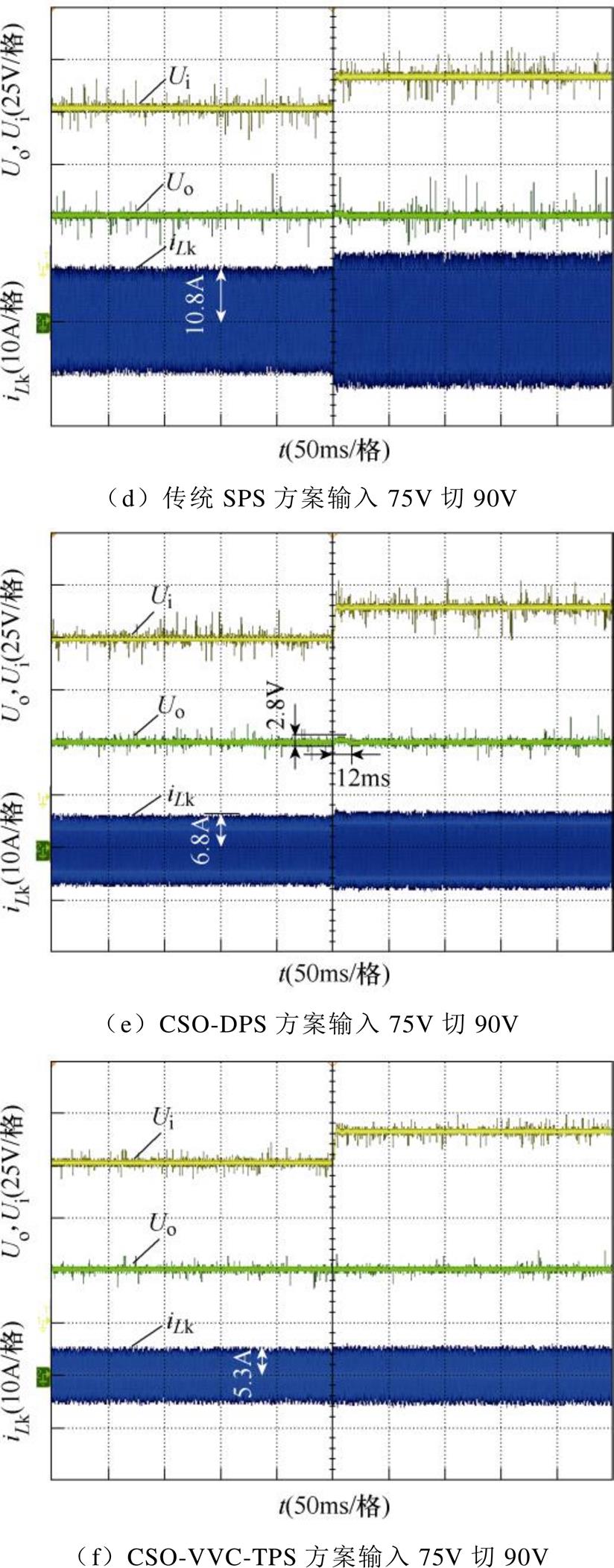
图11 三种方案动态性能电压电流实验波形
Fig.11 Dynamic performance voltage and current experimental waveforms of the three schemes
DAB变换器在三种控制方案下负载由50W 切至100W 时的电压电流波形如图11a~图11c所示。传统SPS方案切载时输出电压的动态响应时间约为38ms、输出电压波动约为6.5V;CSO-DPS方案的输出电压响应时间约为37ms、输出电压波动约为7.5V;本文的CSO-VVC-TPS方案在负载突变时,动态响应时间几乎为0、输出电压几乎没有变化。
当输入电压Ui=75V、负载为50W 时,DAB变换器在三种控制方案下输入电压由75V切至90V时的电压电流波形如图11d~图11f所示。传统SPS方案切换输入电压的动态响应时间约为13ms、输出电压的波动达到3.2V;CSO-DPS方案的输出电压响应时间约为12ms、输出电压波动约为2.8V;而本文的CSO-VVC-TPS方案的输出电压几乎没有变化,动态响应调节时间几乎为0。
因此,本文的CSO-VVC-TPS方案在负载突变、输入电压扰动时的动态性能均较为优异。
针对DAB变换器提出了一种结合电流应力优化与虚拟电压补偿的TPS优化控制方案,推导了变换器在三重移相下六种模态的工作特性模型并分析各模态的工作特性,根据KKT条件函数求得电流应力最优的移相量组合。同时,结合虚拟电压补偿方案,加快变换器的动态响应速度。最后,与传统单移相方案及双重移相电流应力优化方案进行实验对比。理论分析和实验表明:
1)结合电流应力优化与虚拟电压补偿的TPS优化控制方案,相较于传统电流应力优化方案,可以进一步减小变换器的电流应力,提高变换器的效率。
2)当输入电压发生扰动、负载发生变化时,所提出的控制方案在保证电流应力最优的同时,实现快速的动态响应且电压波动小,进一步提升系统的稳定性。
3)提出的控制方案具有较强的可移植性及适用性,可以结合如回流功率、电流有效值等其他目标进行方案优化。
参考文献
[1] 高国庆, 雷万钧, 袁晓杰, 等. 双有源全桥变换器全状态离散迭代建模与输出电压纹波分析[J]. 电工技术学报, 2021, 36(2): 330-340.
Gao Guoqing, Lei Wanjun, Yuan Xiaojie, et al. Full- state discrete-time model and the output-voltage- ripple analysis of the dual active bridge converter[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 330-340.
[2] 刘飞龙, 张涵, 孙孝峰, 等. 双有源桥四绕组变压器双向DC-DC变换器[J]. 电工技术学报, 2019, 34(20): 4272-4282.
Liu Feilong, Zhang Han, Sun Xiaofeng, et al. Improved dual active bridge bidirectional DC-DC converter with four-winding transformer structure[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4272-4282.
[3] 周兵凯, 杨晓峰, 张智, 等. 能量路由器中双有源桥直流变换器多目标优化控制策略[J]. 电工技术学报, 2020, 35(14): 3030-3040.
Zhou Bingkai, Yang Xiaofeng, Zhang Zhi, et al. Multi-objective optimization control strategy of dual- active-bridge DC-DC converter in electric energy router application[J]. Transactions of China Electro- technical Society, 2020, 35(14): 3030-3040.
[4] 安峰, 杨柯欣, 王嵩, 等. 基于模型前馈的双有源全桥DC-DC变换器电流应力优化方法[J]. 电工技术学报, 2019, 34(14): 2946-2956.
An Feng, Yang Kexin, Wang Song, et al. Current stress optimized scheme with model-based feedfor- ward for dual-active-bridge DC-DC converters[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2946-2956.
[5] 涂春鸣, 管亮, 肖凡, 等. 基于扩展移相控制下双有源桥移相角优化选取与分析[J]. 电工技术学报, 2020, 35(4): 850-861.
Tu Chunming, Guan Liang, Xiao Fan, et al. Parameter optimization selection and analysis of dual active bridge based on extended phase shift control[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 850-861.
[6] Zhang Jianjia, Shao Shuai, Li Yucen, et al. Arm voltage balancing control of modular multilevel resonant converter[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4): 303-308.
[7] Huang Jun, Wang Yue, Li Zhuoqiang, et al. Unified triple-phase-shift control to minimize current stress and achieve full soft-switching of isolated bidirectio- nal DC-DC converter[J]. IEEE Transactions on Indu- strial Electronics, 2016, 63(7): 4169-4179.
[8] Shi Haochen, Wen Huiqing, Hu Yihua, et al. Reactive power minimization in bidirectional DC-DC con- verters using a unified-phasor-based particle swarm optimization[J]. IEEE Transactions on Power Elec- tronics, 2018, 33(12): 10990-11006.
[9] Shi Haochen, Wen Huiqing, Chen Jie, et al. Minimum- reactive-power scheme of dual-active-bridge DC-DC converter with three-level modulated phase-shift control[J]. IEEE Transactions on Industry Appli- cations, 2017, 53(6): 5573-5586.
[10] 吴俊娟, 孟德越, 申彦峰, 等. 双重移相控制与传统移相控制相结合的双有源桥式DC-DC变换器优化控制策略[J]. 电工技术学报, 2016, 31(19): 97- 105.
Wu Junjuan, Meng Deyue, Shen Yanfeng, et al. Optimal control strategy of dual active bridge DC-DC converter with combined dual-phase-shift and traditional- phase-shift controls[J]. Transactions of China Electro- technical Society, 2016, 31(19): 97-105.
[11] 王玉斌, 王杉杉, 封波, 等. 基于双重移相控制的双有源DC-DC变换器的最优电流控制[J]. 电工技术学报, 2015, 30(14): 488-496.
Wang Yubin, Wang Shanshan, Feng Bo, et al. Optimal current control strategy of dual-active-bridge DC-DC converter based on dual-phase-shift control[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 488-496.
[12] 张勋, 王广柱, 王婷. 双向全桥DC-DC变换器基于电感电流应力的双重移相优化控制[J]. 电工技术学报, 2016, 31(22): 100-106.
Zhang Xun, Wang Guangzhu, Wang Ting. Optimized control based on current-stress of bi-directional full-bridge DC-DC converters with dual-phase- shifting control[J]. Transactions of China Electro- technical Society, 2016, 31(22): 100-106.
[13] Zhao Biao, Yu Qingguang, Sun Weixin. Extended- phase-shift control of isolated bidirectional DC-DC converter for power distribution in microgrid[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4667-4680.
[14] Hou Nie, Song Wensheng, Wu Mingyi. Minimum- current-stress scheme of dual active bridge DC-DC converter with unified-phase-shift control[J]. IEEE Transactions on Power Electronics, 2016, 31(12): 8552-8561.
[15] 侯聂, 宋文胜, 武明义. 双向全桥DC-DC变换器的负载电流前馈控制方法[J]. 中国电机工程学报, 2016, 36(9): 2478-2485.
Hou Nie, Song Wensheng, Wu Mingyi. A load current feedforward control scheme of dual active bridge DC/DC converters[J]. Proceedings of the CSEE, 2016, 36(9): 2478-2485.
[16] Chen Linglin, Gao Fei, Shen Ke, et al. Predictive control based DC microgrid stabilization with the dual active bridge converter[J]. IEEE Transactions on Industrial Electronics, 2020, 67(10): 8944-8956.
[17] 侯聂, 宋文胜, 武明义. 全桥隔离DC/DC变换器的直接功率控制方法[J]. 电力系统自动化, 2016, 40(17): 204-209.
Hou Nie, Song Wensheng, Wu Mingyi. Direct power control scheme of full-bridge isolated DC/DC con- verters[J]. Automation of Electric Power Systems, 2016, 40(17): 204-209.
[18] Song Wensheng, Hou Nie, Wu Mingyi. Virtual direct power control scheme of dual active bridge DC-DC converters for fast dynamic response[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(2): 1750-1759.
[19] Oggier G G, Ordonez M, Galvez J M, et al. Fast transient boundary control and steady-state operation of the dual active bridge converter using the natural switching surface[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 946-957.
[20] 郭华越, 张兴, 赵文广, 等. 扩展移相控制的双有源桥DC-DC变换器的优化控制策略[J]. 中国电机工程学报, 2019, 39(13): 3889-3899.
Guo Huayue, Zhang Xing, Zhao Wenguang, et al. Optimal control strategy of dual active bridge DC-DC converters with extended-phase-shift control[J]. Pro- ceedings of the CSEE, 2019, 39(13): 3889-3899.
[21] 杨向真, 陈曦, 杜燕, 等. 基于动态矩阵控制的双有源桥DC-DC变换器电流应力优化策略[J]. 电源学报, 2020, 92(6): 109-118.
Yang Xiangzhen, Chen Xi, Du Yan, et al. Optimal current stress control strategy for dual active bridge DC-DC converter based on dynamic matrix control[J]. Journal of Power Supply, 2020, 92(6): 109-118.
[22] 黄珺, 王跃, 李卓强, 等. 基于三重移相控制的双主动全桥直流变换器优化调制策略[J]. 中国电机工程学报, 2016, 36(6): 1658-1666.
Huang Jun, Wang Yue, Li Zhuoqiang, et al. Opti- mized modulation scheme of dual active bridge DC-DC converter based on triple-phase-shift con- trol[J]. Proceedings of the CSEE, 2016, 36(6): 1658- 1666.
[23] Meng Lexuan, Dragicevic T, Vasquez J C, et al. Tertiary and secondary control levels for efficiency optimization and system damping in droop controlled DC-DC converters[J]. IEEE Transactions on Smart Grid, 2015, 6(6): 2615-2626.
Triple-Phase-Shift Optimal Control of Dual-Active-Brige DC-DC Converter with Current Stress Optimization and Virtual Voltage Compensation
Abstract In order to simultaneously reduce the current stress and improve the dynamic characteristics of the dual-active-bridge (DAB) DC-DC converter, this paper establishes the operating characteristic model of transmitted power and current stress for six modes under triple phase shifting. Accordingly, a control scheme based on triple phase shifting combining current stress optimization and virtual voltage compensation is proposed. The scheme consists of the current stress optimal phase shift angle model and the virtual voltage compensation method. The KKT condition is used to obtain the current stress optimal phase shift angle model, and the virtual voltage compensation method is used to estimate the transmission power value to improve the dynamic characteristics when the load is suddenly changed and the input voltage is disturbed. The scheme can achieve fast dynamic response while ensuring current stress optimization, and the parameters are easily adjustable and portable. Finally, a small power prototype was built for the comparison experiment to verify the correctness and superiority of the proposed scheme.
keywords:Dual-active-brige DC-DC converter, triple phase shift, current stress, dynamic performance, virtual voltage compensation
DOI: 10.19595/j.cnki.1000-6753.tces.210576
中图分类号:TM46
蔡逢煌 男,1976年生,教授,硕士生导师,研究方向为电力电子变换技术。E-mail: caifenghuang@fzu.edu.cn
江加辉 男,1989年生,讲师,硕士生导师,研究方向为电力电子变换技术和新能源发电技术。E-mail: qdujiangjiahui@sina.com(通信作者)
收稿日期 2021-04-23
改稿日期 2021-08-13
山东省自然科学基金(ZR2019QEE004)和福州市科技计划(2019-G-44)资助项目。
(编辑 陈 诚)