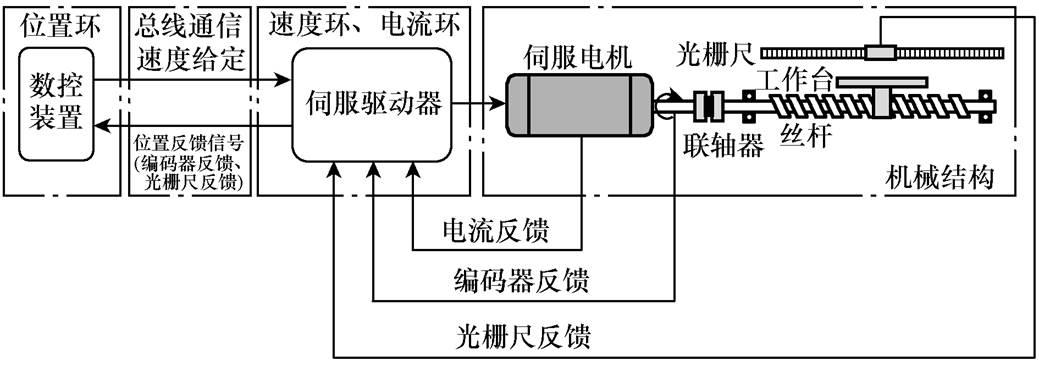
图1 进给系统控制结构框图
Fig.1 Control structure diagram of feed system
摘要 现代数控系统通常采用数控装置负责计算、伺服驱动器负责执行的结构理念，二者间的总线数据交互不可避免地存在通信延时，尤其在高速进给的应用场合中，为了避免由通信延时引起的超调及控制精度降低的问题，该文对全闭环数控系统时延问题展开研究。首先，基于双位置反馈控制架构，建立含通信延时的全闭环伺服驱动系统模型，采用频率根轨迹分析方法，分析通信延时对系统稳定性的影响，指出延时补偿的必要性。为了更好地对通信延时进行补偿，研究并设计Smith预估补偿器，分析Smith预估补偿器在应用中存在的模型失配问题，在此基础上，总结模型误差来源。最后，结合扰动观测器理论，设计基于扰动观测器的通信扰动观测补偿策略，解决模型失配问题在通信延时补偿中的影响，提高延时补偿方法的适用性和简易性。通过仿真验证所提算法的有效性。
关键词：伺服驱动系统 全闭环控制 通信延时补偿
装备制造业是我国经济和国防建设的战略产业，代表着国家经济实力和科技水平。作为先进机械制造的典型代表，数控机床的制造水平是衡量一个国家工业现代化程度的重要标志。在《国家中长期科学和技术发展规划纲要（2006—2020）》中明确指出，要实现高档数控机床的自主设计制造，将数字化和智能化设计作为装备制造业优先发展主题[1]。随着现代科技不断发展，制造业向精度更高、品种更多、周期更快的方向发展成为了必然选择，如何实现高速、高精控制，是未来的机遇与挑战。
目前，数控系统通常采用数控（Numerical Con- troller, NC）系统负责计算、伺服驱动器负责执行的结构理念，通常将位置环控制放在数控装置中执行，而伺服驱动器主要执行速度环和电流环控制。NC通过总线通信与各伺服轴进行数据交互，各轴伺服驱动器通过总线通信将位置反馈信号传送给NC，NC通过总线通信将转速指令信号发送给各轴伺服驱动器，由此完成位置、转速和电流的三闭环控制。由此可见，总线通信的存在不可避免地会在位置环控制环路中引入时间延时环节。通信延时的存在使得位置环增益裕度大大降低，也从根本上限制了数控机床“高速高精”的可能性。
降低延时环节对控制系统性能影响的方法可以分为硬件方法和软件方法。硬件方法是指通过优化系统硬件设计来降低延时环节，如采用较高传输频率的总线通信、采样延时较小的传感器、性能较好的主控芯片等。在数控机床领域，文献[2]提出了一种驱动一体技术来降低数控系统和伺服驱动器之间的通信延时，该技术有效地利用了多合一芯片的优势，利用片上数据共享取代了常规的总线通信，能够最大程度地降低通信延时对控制性能的影响。软件方法是指在系统硬件条件不变的情况下，采用算法降低通信延时对控制系统性能影响的方法[3-4]。根据算法设计方法的不同，可以将软件方法分为模型法和无模型法。
在模型法中，最为常用的方法为Smith预估补偿器法，该方法在已知系统模型的基础上对含延时系统响应进行预估，将预估后得到的延时导致的系统误差项补偿到控制器输出中，以此实现延时环节的补偿。从该方法的原理可以看出，Smith补偿法对延时项的补偿效果很大程度地受模型准确性的影响，当预估模型与实际系统匹配时，延时环节能够得到很好的补偿。但当系统模型存在误差时，补偿效果会明显恶化[5-6]。
为了解决Smith预估补偿器法存在系统参数鲁棒性较差的问题，很多学者提出了优化方案。文献[7]提出了改进方法，解决了Smith预估补偿器法抗扰性差的问题，但没有解决参数鲁棒性差的问题。文献[8]提出了在Smith预估补偿器的主反馈回路中串联一阶低通器环节的方法，用来解决参数扰动时补偿稳定性问题。文献[9]通过增加在线估算延时时间环节解决了延时时间不确定对Smith预估补偿器的影响。文献[10]通过引入扰动补偿方法提高了Smith预估补偿器抗扰性问题，能够实现系统输入响应和扰动响应的解耦，但该方法同时存在参数设置复杂的问题。在Smith预估补偿器法的基础上，文献[11-13]针对双摇摆系统提出了一种基于扰动观测器的延时补偿方法，该方法将延时环节导致的系统响应误差等效于系统扰动环节，通过设计扰动观测器实现延时环节的补偿。
无模型法主要有线性预测法、模糊控制、神经网络控制和专家控制等[14-21]。尽管这些方法能够实现算法鲁棒性和补偿性能的兼顾，但缺点也十分明显，例如，模糊控制不适用于高精度控制场合；神经网络控制需要较长的时间去训练；专家控制过度依赖于经验知识，缺乏自学习、自适应能力，因此很难应用到工业伺服系统中，仅在理论层面获得一定研究成果。
综上所述，高档数控机床高速高精的加工需求对位置增益裕度提出了极高的要求，然而主流的数控系统通常采用数控装置串联伺服驱动器的架构，二者间的总线数据交互不可避免地存在通信延时，极大地降低了位置环控制稳定性。
因此，为了避免由通信延时引起的超调及控制精度降低的问题，首先，本文基于双位置反馈控制架构，建立含通信延时的全闭环伺服驱动系统模型，分析通信延时对系统稳定性的影响，指出延时补偿的必要性。其次，为了更好地对通信延时进行补偿，研究并设计Smith预估补偿器，分析Smith预估补偿器在应用中存在的模型失配问题，在此基础上，分析模型误差来源。通过设计基于扰动观测器的通信扰动观测补偿策略，解决模型失配问题在通信延时补偿中的影响。最后，通过实验验证所研究方法的有效性。
为了更好地分析位置环控制通信延时对全闭环位置控制的影响，首先需要建立含通信延时的全闭环伺服驱动系统模型。结合现代数控机床数控系统结构，即数控装置、伺服驱动单元和机械传动系统三部分，可以得到含位置环通信延时的全闭环伺服轴位置控制结构框图，如图1所示。由图1可以看出，位置环控制在数控装置中执行，而伺服驱动器主要执行速度环和电流环控制，数控装置通过总线通信与各伺服轴进行数据交互，各轴伺服驱动器通过总线通信将位置反馈信号传送给数控装置，数控装置通过总线通信将转速指令信号发送给各轴伺服驱动器，由此完成位置、转速和电流的三闭环控制。
图1 进给系统控制结构框图
Fig.1 Control structure diagram of feed system
结合数控机床位置控制系统中通信延时产生的方式，可以得到含通信延时环节的数控机床全闭环位置控制系统框图如图2所示。
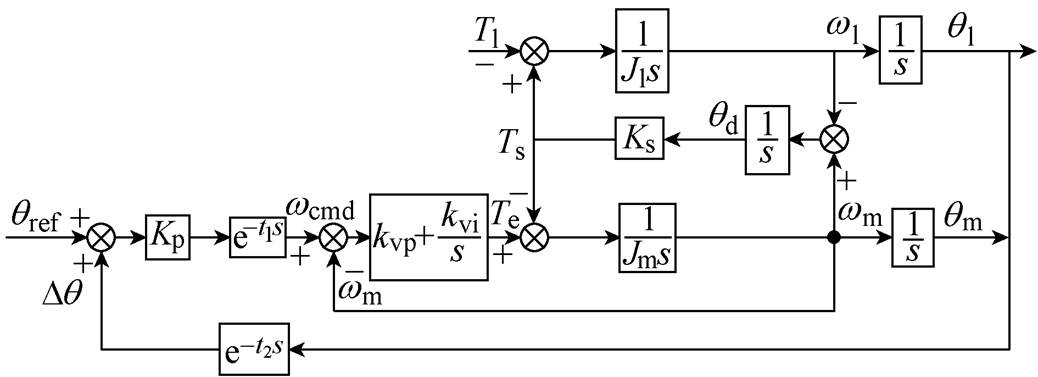
图2 含通信延时的双位置反馈控制系统框图
Fig.2 Full-closed loop servo drive system model with communication delay
为了方便分析，将图2系统模型进行简化，得到如图3所示的模型。
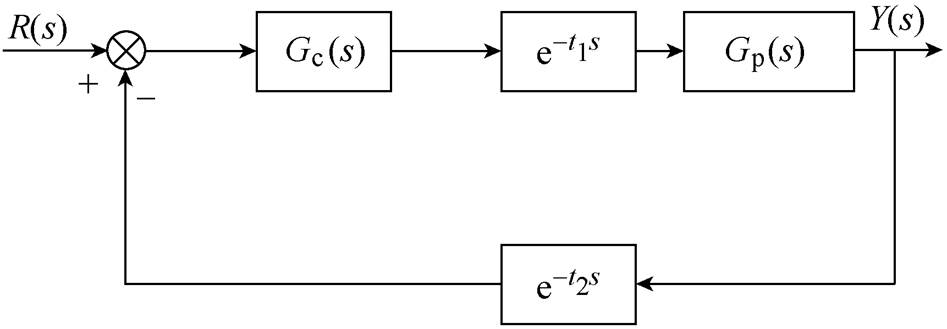
图3 含通信延时的全闭环伺服驱动系统简化模型
Fig.3 Simplified model of full-closed loop servo drive system with communication delay
图3中，t1、t2分别为前向通道和反向通道中的延时时间，Gc(s)为位置环控制传递函数，Gp(s)为包含速度环和机械负载模型的传递函数，分别表示[5]为
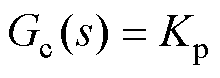（1）
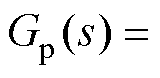
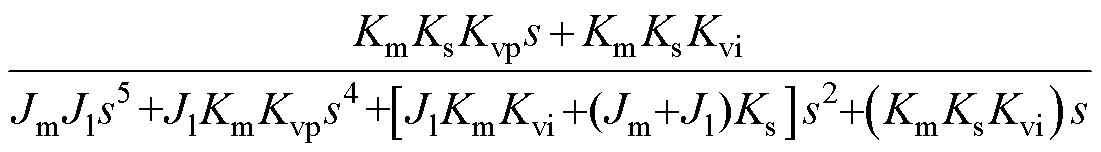（2）
式中，Jm、Jl分别为电机惯量和负载惯量；Ks为滚珠丝杆轴刚度系数；Km为电机力矩常数；Kp为位置环控制器增益系数；Kvp、Kvi分别为速度环PI控制器的比例环节和积分环节增益系数。
由式（1）、式（2）可得系统特征方程H(s)为
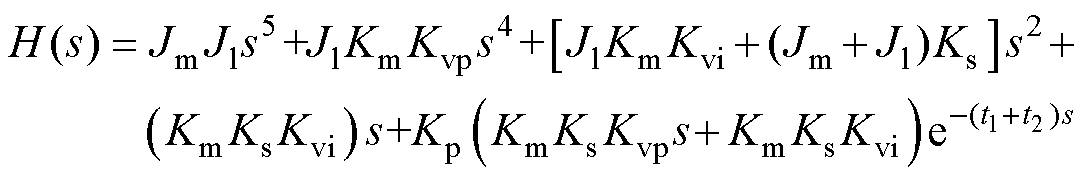（3）
为了分析式（3）所示的系统特征方程特性，需要对式中的延时项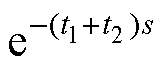
进行有理化近似。结合已有的延时项近似方法的优缺点及应用场景，这里选用Pade近似法对延时项进行近似，Pade近似的多项式表达式可以表示为
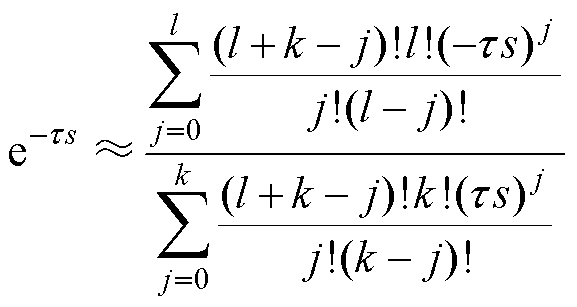（4）
式中，t 为延时项延时时间；k、j为Pade逼近系数。
为了对比Pade近似的有效性，选取一阶惯性环节近似进行对比，一阶惯性环节近似表达式为
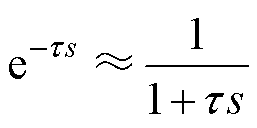（5）
图4为当延时时间为1ms时，不同阶次Pade近似和一阶惯性环节近似在时域和频率的对比波形。从仿真波形可以看出，Pade近似效果要明显好于一阶惯性环节。同时，随着Pade近似多项式阶次的增高，有理化近似的效果也越好，但高阶次会引起计算量增大的问题，这就限制了高阶次近似在实际工程中应用。考虑到伺服驱动系统位置环控制带宽相对较低的特性，因此在接下来的分析中选用一阶Pade近似来等效延时环节。
图4 Pade近似及一阶惯性环节近似对比
Fig.4 Comparison of Pade approximation and first-order inertial link approximation
接下来对含延时全闭环位置控制系统进行稳定性分析。结合图2，可以得到含延时全闭环位置控制系统的开环传递函数为
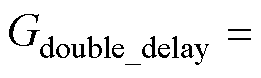
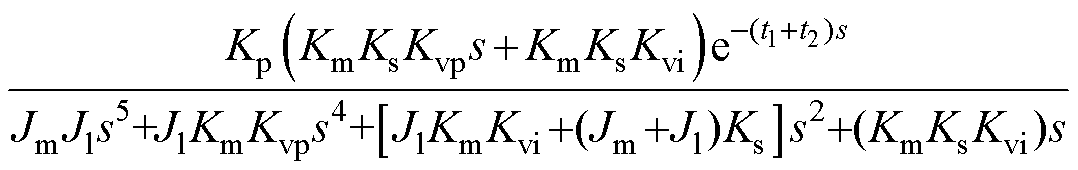（6）
为了使理论分析与实验相吻合，理论分析采用表1中数控机床镗床的系统参数。将表1中参数代入式（6），并在延时时间分别为1ms、2ms和3ms条件下绘制系统根轨迹图如图5所示。图5中，b 为相应根轨迹所对应的位置环控制器增益。
表1 系统参数
Tab.1 System parameters
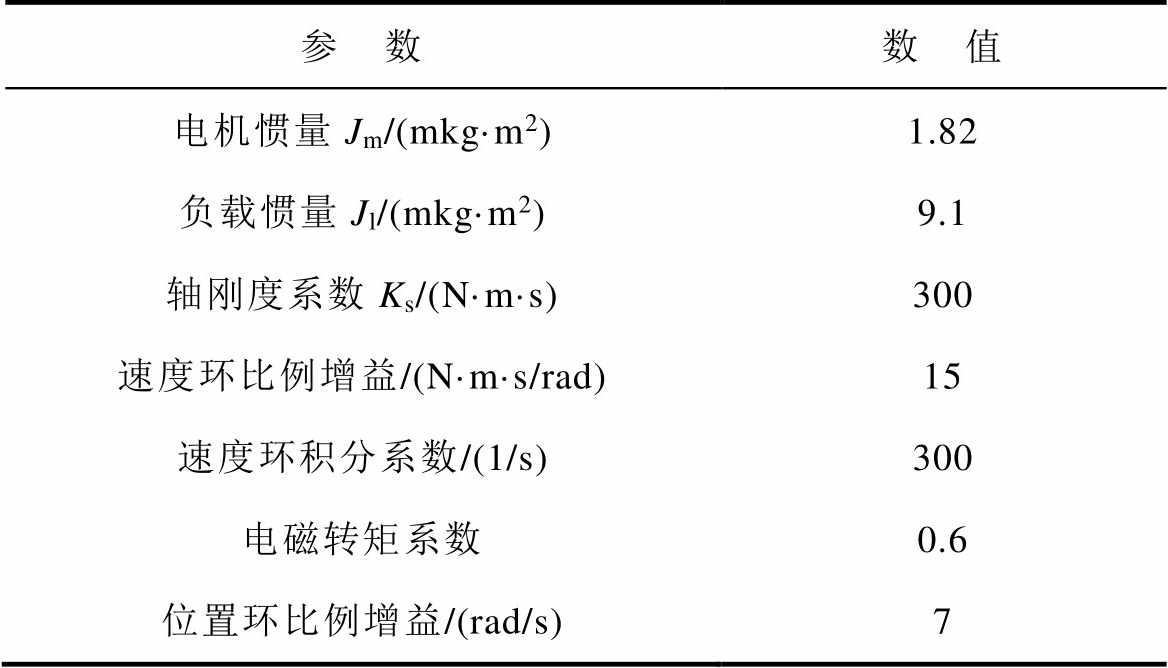
参 数数 值 电机惯量Jm/(mkg·m2)1.82 负载惯量Jl/(mkg·m2)9.1 轴刚度系数Ks/(N·m·s)300 速度环比例增益/(N·m·s/rad)15 速度环积分系数/(1/s)300 电磁转矩系数0.6 位置环比例增益/(rad/s)7
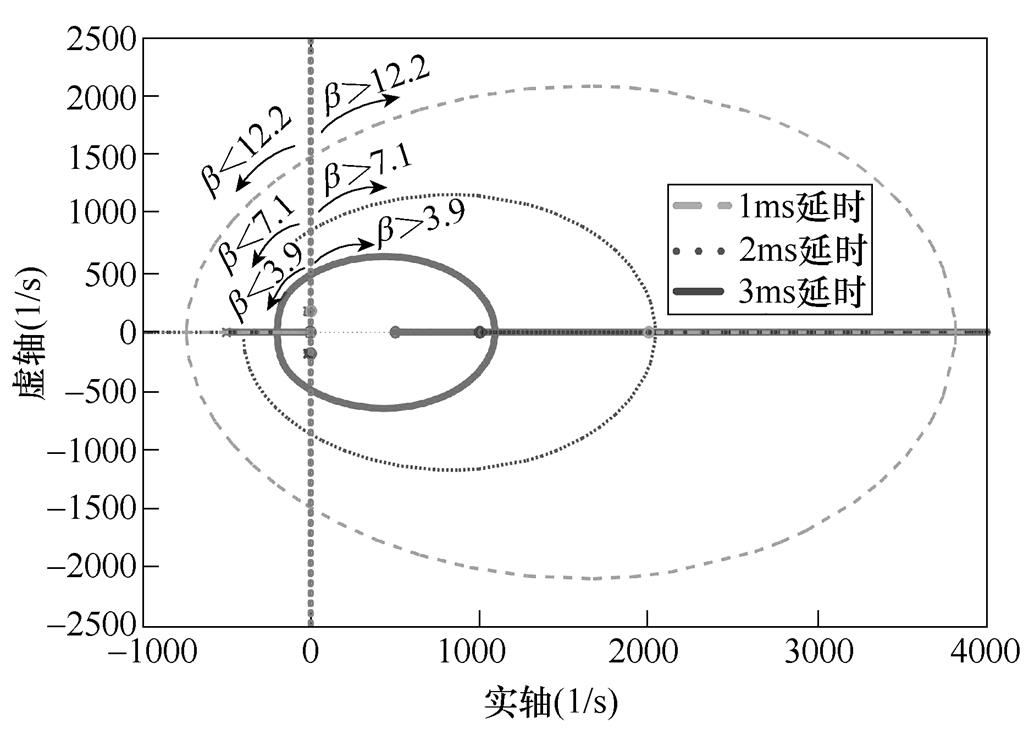
图5 不同延时时间的系统根轨迹图
Fig.5 System root locus diagrams with different delay times
由图5所示的不同延时时间时系统根轨迹图可以看出，延时时间的存在会对系统稳定性产生影响。具体地，延时时间越大，系统的稳定域越小，即稳定的位置环增益系数越小。由此可见，延时环节的存在会导致最大位置环增益的降低，限制位置环的带宽。
Smith预估补偿器经常被用于含延时环节的系统补偿中，其原理如图6所示。图中，Gc(s)、Gp(s)和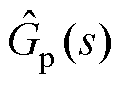
分别为控制器传递函数、系统传递函数和预估模型传递函数，tp为估计延时时间。
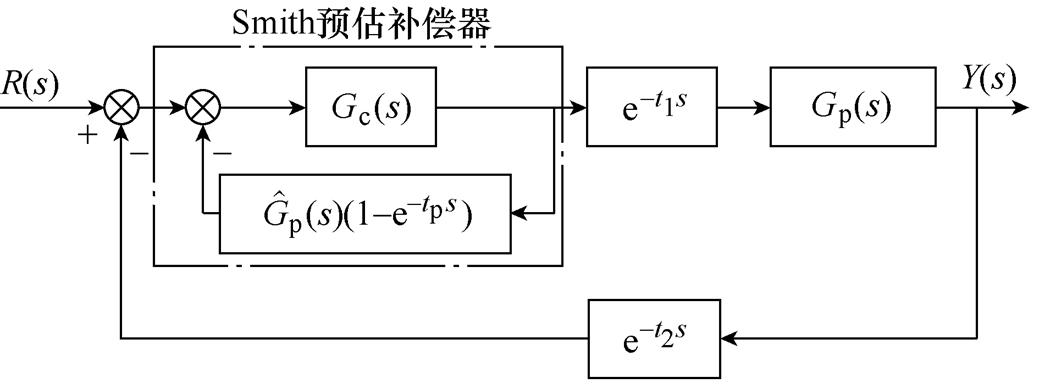
图6 Smith预估补偿器原理
Fig.6 Schematic of Smith predictor
由图6可知，原系统的闭环传递函数为
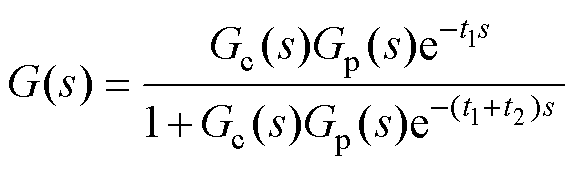（7）
加入Smith预估补偿器后，系统的闭环传递函数为
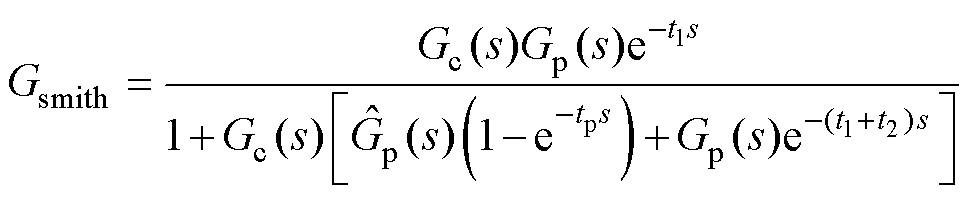（8）
由式（8）可知，当预估模型及预估延时时间与实际系统完全相同时，即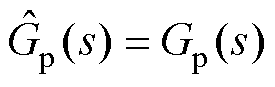
，
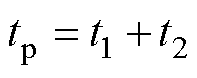时，系统闭环传递函数为
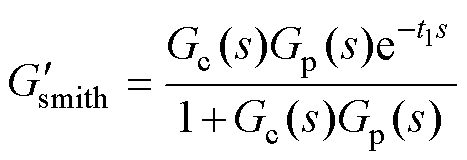（9）
通过式（7）和式（9）可以看出，当预估模型及延时时间均与实际系统参数相吻合时，Smith预估补偿方法能够得到很好的延时补偿效果，补偿后的系统特征方程并不含有延时项。
由Smith预估补偿器的原理可以搭建基于Smith预估补偿器的全闭环位置控制通信延时补偿方法原理如图7所示。
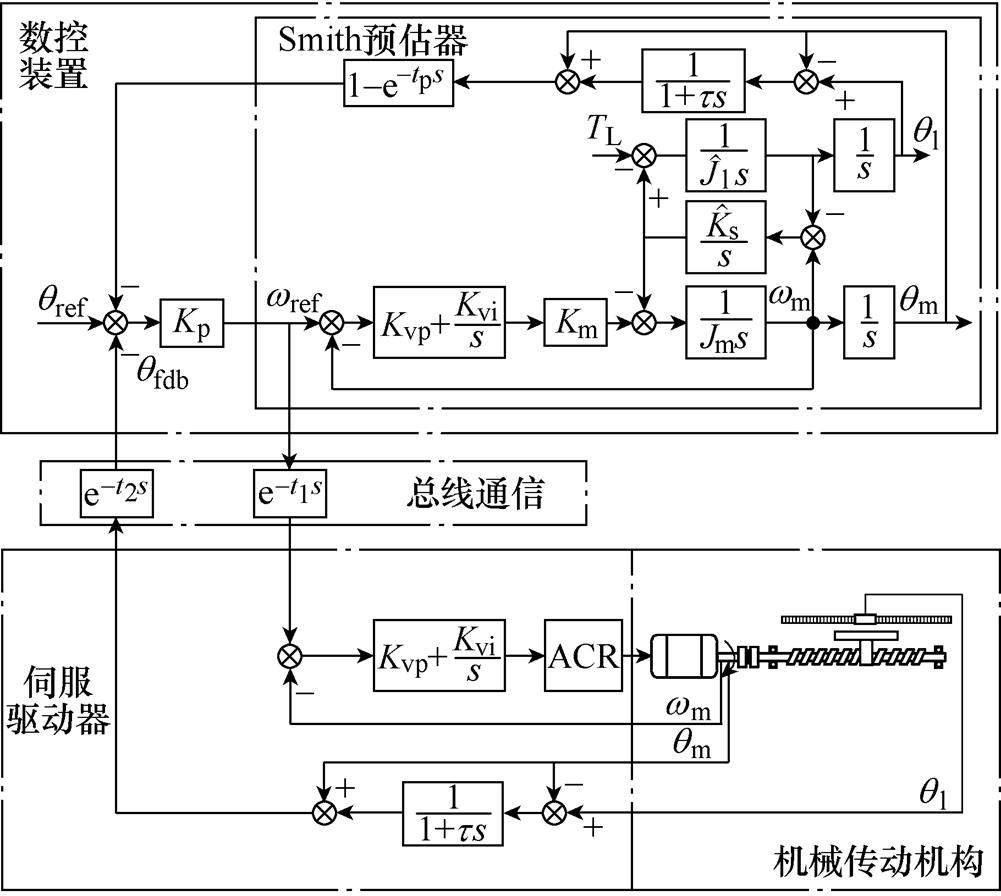
图7 基于Smith预估补偿器的全闭环位置控制通信延时补偿方法原理
Fig.7 Schematic diagram of communication delay compensation method for full closed loop position control based on Smith predictive compensator
在实际建模过程中，速度环比例增益及积分增益系数是已知的，电机转动惯量和电磁转矩系数可以通过电机参数获取，模型失配主要来源于三个位置，首先是负载转动惯量难以获得，尤其类似铣床进给机构这种大惯量、多惯量系统，即使通过惯量辨识算法进行辨识，仍然会存在较大的误差；其次是传动轴的轴刚度系数难以获取，且系数值会随着温度和使用时间产生变化，难以准确建模；最后是总线传输数据量可能不同，具体通信延时的时间难以准确获取。
为了验证模型失配对Smith预估补偿器的影响，参照图7及表1搭建仿真模型并进行仿真，仿真中位置环比例增益为Kp=1 500rad/s，延时时间为2ms，位置给定为直线进给定位响应，模型失配比例为50%，仿真结果如图8所示。由图8的仿真结果可以看出，在模型适配时，Smith预估补偿器能够对延时环节实现很好的补偿，补偿后位置响应超调量及调节时间明显降低。但当负载惯量、轴刚度系数和延时时间出现参数失配时，在一定情况下，补偿不仅没有提高系统的响应性能，还会引起末端位置振荡问题，恶化位置环控制效果。
综上所述，传统Smith预估补偿器在系统模型及延时时间模型可以准确获取的场合中能够实现很好的延时补偿效果。但在数控机床领域中，由于负载惯量和轴刚度系数受环境因素变化影响较大，参数本身无法准确获取，因而无法获得较好的通信延时补偿效果。
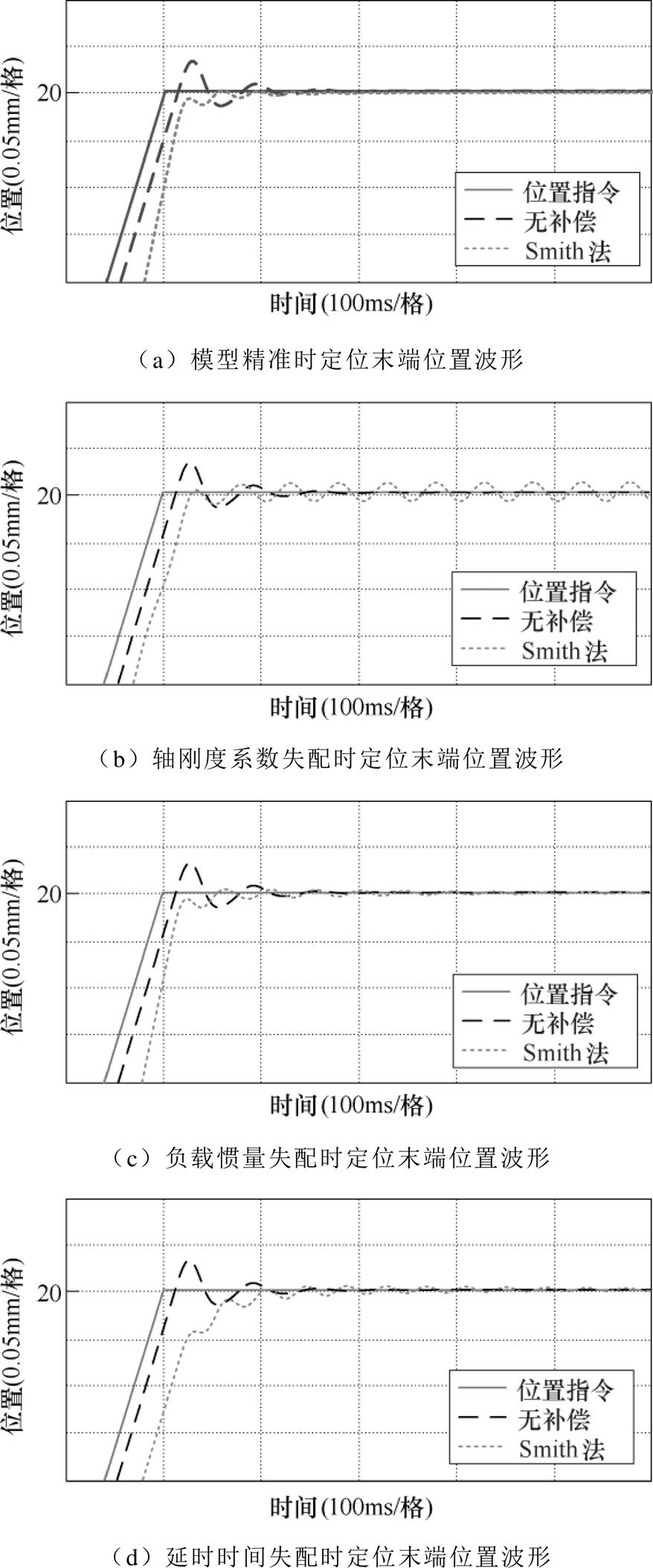
图8 Smith预估补偿器延时补偿效果分析
Fig.8 Analysis of delay compensation effect of Smith predictor
针对Smith预估补偿器存在的参数鲁棒性差的问题，本文采用通信扰动观测器（Communication Disturbance Observer, CDOB）对数控系统通信延时进行补偿。相比于Smith预估补偿器，CDOB将延时环节等效为系统扰动量，该方法对系统模型参数鲁棒性较高，同时参数设计较为明确。
图9a和图9b分别为包含输入延迟T1和输出延迟T2的时滞系统和含输入扰动的控制系统。
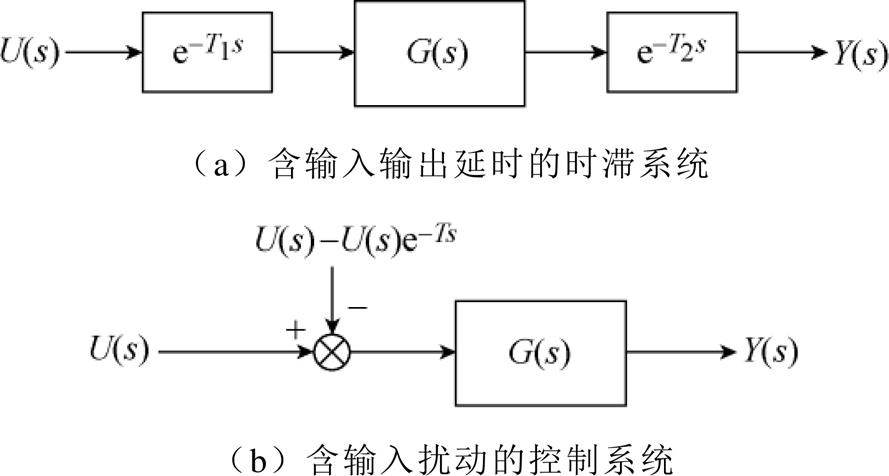
图9 时滞系统与含扰动系统框图
Fig.9 Block diagrams of time-delay systems and systems with disturbances
由图9可以看出，可以将具有延时环节的系统等效为网络扰动系统进行分析。CDOB可以在观测网络扰动的基础上对系统进行补偿，其中网络扰动估算原理和基于CDOB的延时补偿原理分别如图10、图11所示。
通过对扰动观测器极点位置的适当选取实现较好的观测效果进行补偿，其极点位置选取应参照扰动项的动态特性进行选取[20]。结合图9和图10，得到扰动项的表达式为
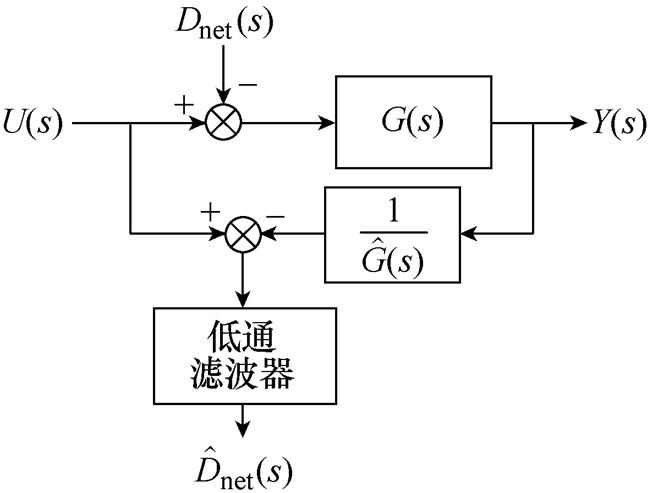
图10 网络扰动估算原理
Fig.10 Network disturbance estimation schematic
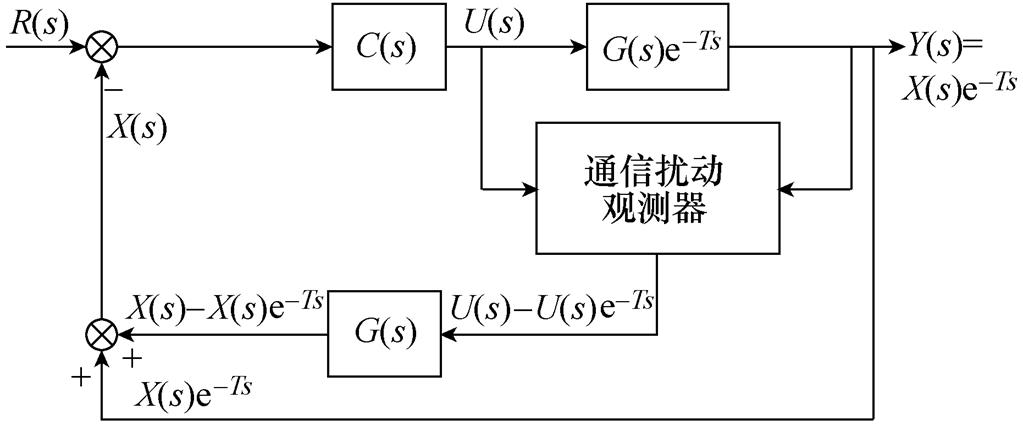
图11 CDOB延时补偿原理
Fig.11 CDOB delay compensation schematic
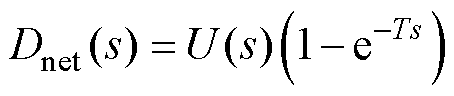（10）
式中，Dnet(s)为扰动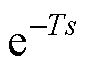项；
为延时项。
沿用含延时系统稳定性分析中所用的一阶Pade逼近法，将延时项进行有理近似，可得
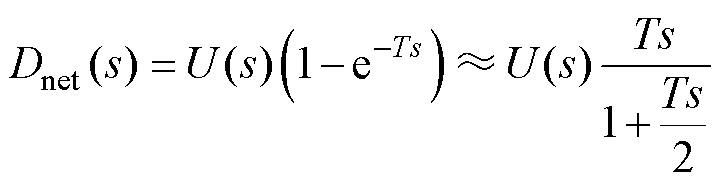（11）
将式（11）中的极点称为pnd，设CDOB低通滤波器形式如式（12）所示，极点位置称为pcdob。
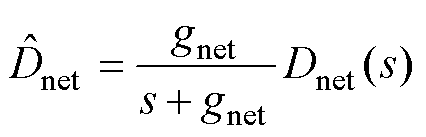（12）
式中，
为CDOB中低通滤波器的截止频率。
为了实现较好的跟随性，CDOB估计误差的收敛速度应快于扰动项的动态特性，故由控制原理可得，极点位置的选取条件如式（13）所示，CDOB极点实部应小于扰动项的极点实部位置。
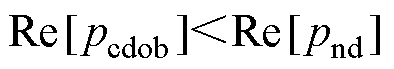（13）
将式（11）与式（13）结合，得到极点位置的选取准则为
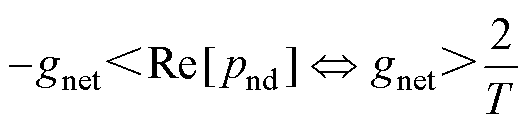（14）
CDOB极点配置示意图如图12所示。图12较为具体地描述了坐标系中极点配置法则。
由以上分析可得，采用CDOB延时补偿方法的双位置反馈的全闭环铣床原理如图13所示。
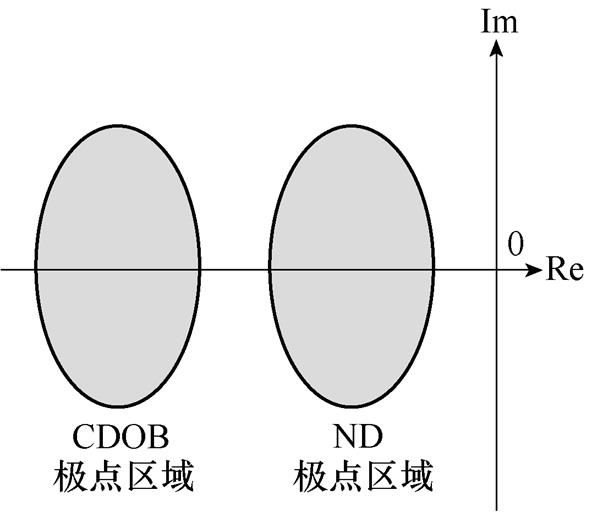
图12 CDOB极点配置示意图
Fig.12 Diagram of CDOB pole configuration
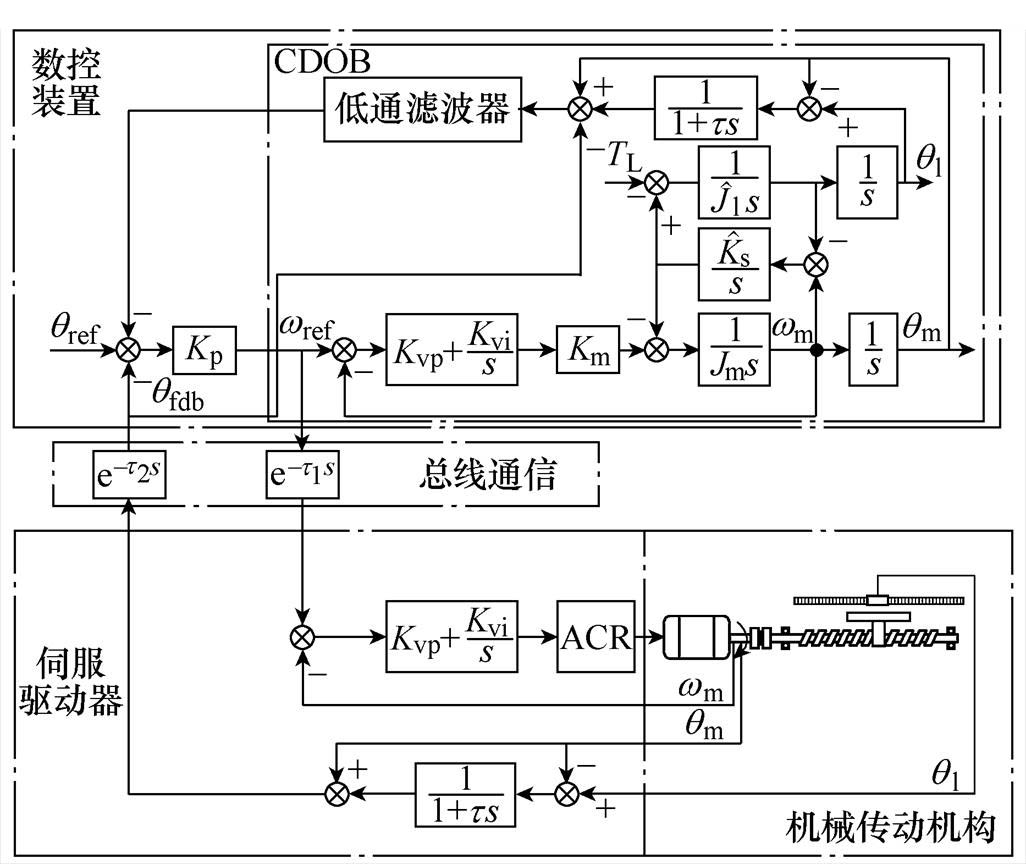
图13 基于双位置反馈控制的CDOB补偿原理
Fig.13 Schematic diagram of CDOB compensation based on dual position feedback control
在实际应用中，所设计的扰动观测器的极点位置需要根据实际系统的响应需求来进行选择，在观测器稳定的前提下，不同极点位置会使实际系统产生不同的响应特性。
为验证CDOB极点参数配置的有效性，在图13的基础上进行仿真验证，仿真中延时时间总计为4ms。经计算可知，在此系统中，CDOB的gnet值应大于500，因此取gnet分别取为600、300和100进行仿真，仿真结果如图14所示。由仿真结果可以看出，当极点位置靠近虚轴时，补偿效果明显变差，甚至会出现发散现象，影响系统稳定性。因此，在实际应用中，为满足CDOB的瞬态响应快于扰动项的动态特性，扰动观测器的极点位置要取得比延时等效的扰动环节的极点远，如此才能有比较好的补偿效果。
实验在广州数控三轴加工中心机床上进行，实验平台如图15所示，该机床采用GSK 25Mb-H系列数控系统，伺服驱动器为广州数控自研驱动器，末端位置传感器为高精度光栅尺。实验条件为Y轴位置定位，位置环比例增益为2 000rad/s，进给速度为10 000mm/min，数控系统与伺服驱动器间的通信周期设为2ms。
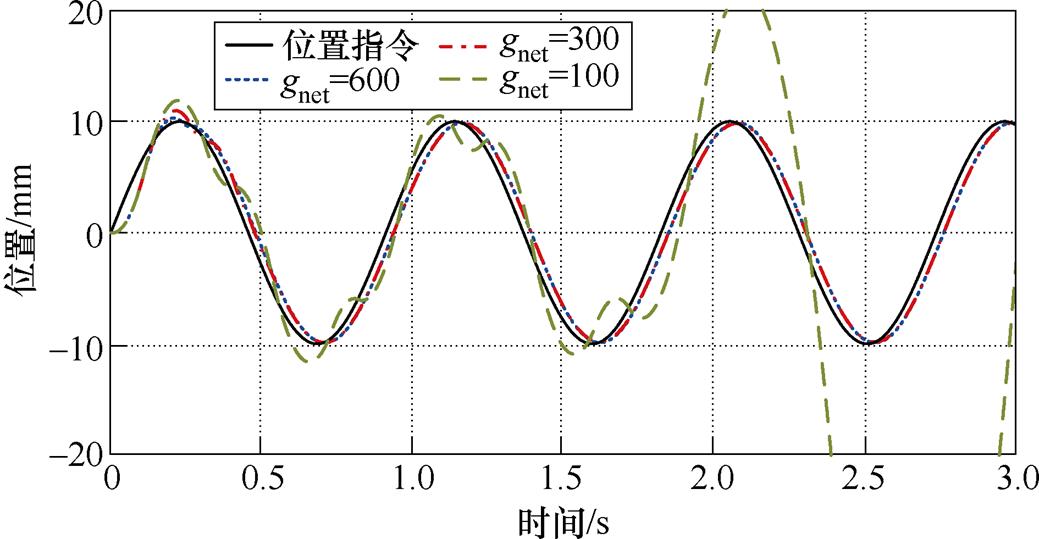
图14 不同极点配置下的延时补偿效果
Fig.14 Delay compensation effect under different pole configurations
图15 三轴加工中心数控机床
Fig.15 Three-axis machining center computerized numerical control machine
图16为未进行通信延时补偿时，全闭环位置控制模式（双位置反馈控制）下，位置定位实验波形。由图16可以看出，通信延时项的存在会导致轴端速度与末端速度出现自持振荡问题，轴端转速振荡的峰-峰值约为400mm/min，末端位置振荡的峰峰值约为610mm/min。直线末端位置也存在振荡，振荡幅值约为75mm。
图17、图18为采用Smith预估补偿器进行通信延时补偿后的位置定位实验波形，其中图17为Smith 预估器模型精确时的补偿结果，图18为Smith预估补偿器中轴刚度系数及负载惯量均存在50%失配时的补偿结果。
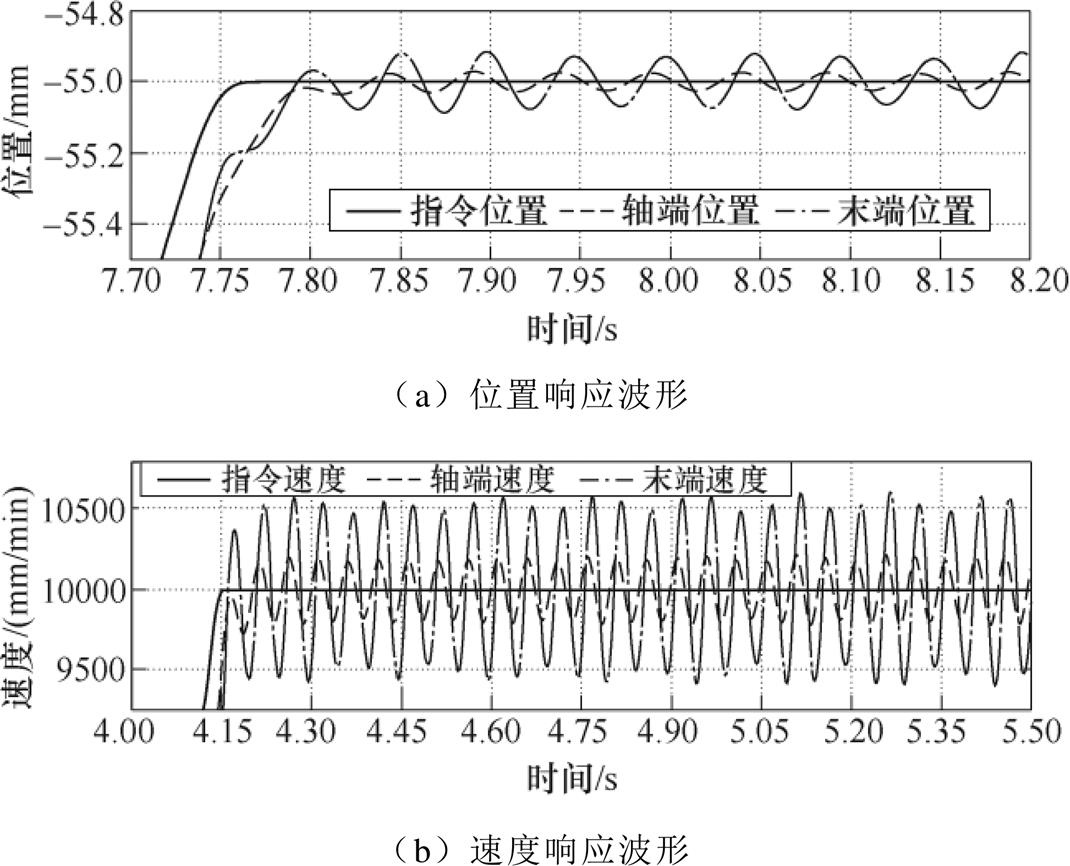
图16 未进行通信延时补偿时位置定位实验结果
Fig.16 Experimental results of position response without communication delay compensation
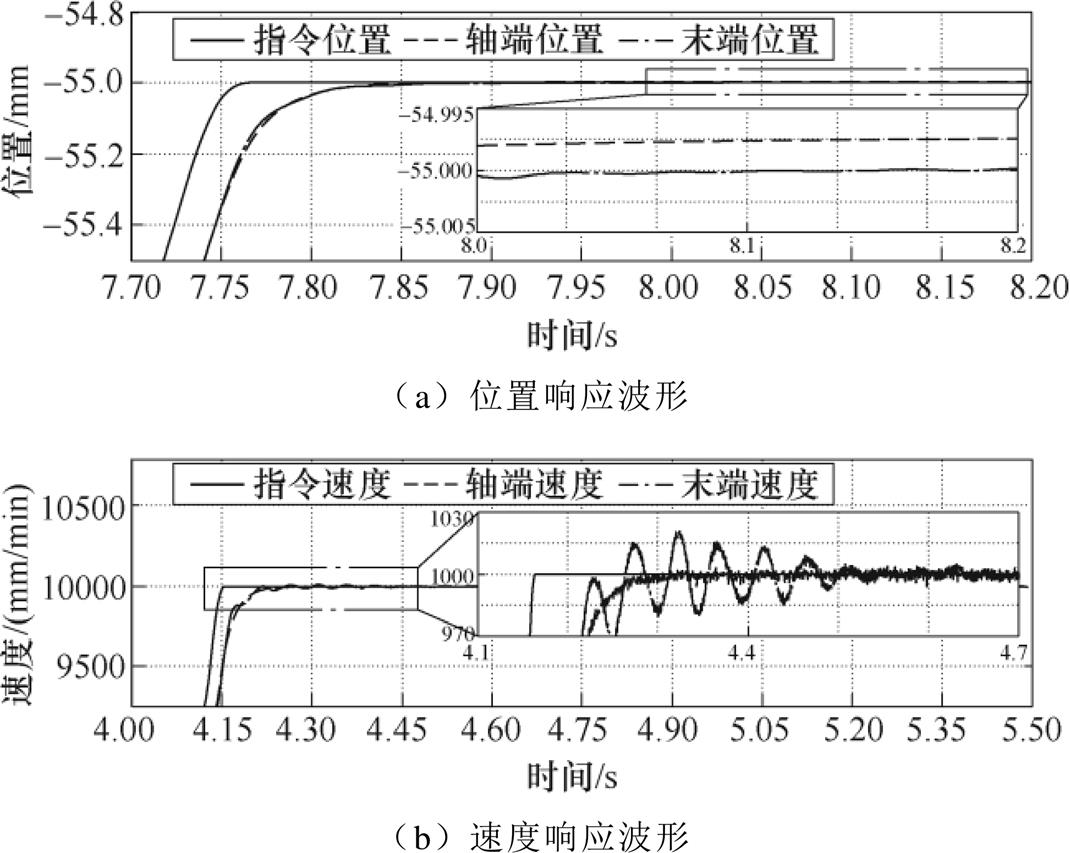
图17 模型精准时Smith预估补偿器延时补偿实验结果
Fig.17 Experimental results of position response using Smith predictor
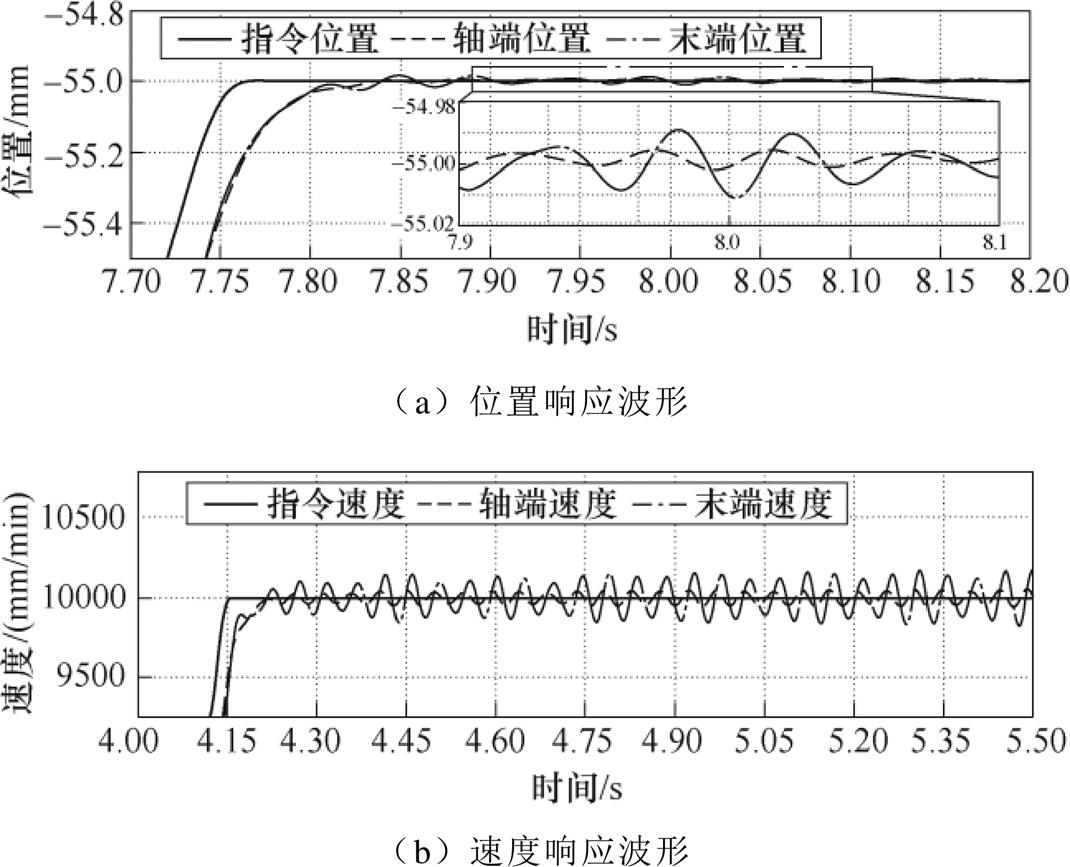
图18 存在模型失配时Smith预估补偿器延时补偿实验结果
Fig.18 Experimental results of position response using Smith predictor with model mismatch
从图17和图18的实验结果可以看出，采用Smith预估补偿器能够实现通信延时的补偿，达到提高位置控制系统的稳定性的目的，但当模型存在失配时，补偿效果会变差。图17中，轴端速度无振荡超调，末端速度有微小超调振荡并逐渐收敛，末端转速振荡的峰-峰值为56mm/min，直线末端定位误差幅值约为0.15mm。图18中，轴端速度与末端速度仍然会存在自持振荡问题，轴端转速振荡的峰-峰 值约为140mm/min，末端位置振荡的峰峰值约为420mm/min，同时，直线末端位置也存在振荡，振荡幅值约为2mm。
图19、图20为采用通信扰动观测器进行通信延时补偿后的位置定位实验波形，其中图19为CDOB模型精确时的补偿结果，图20为CDOB中轴刚度系数及负载惯量均存在50%失配时的补偿结果。
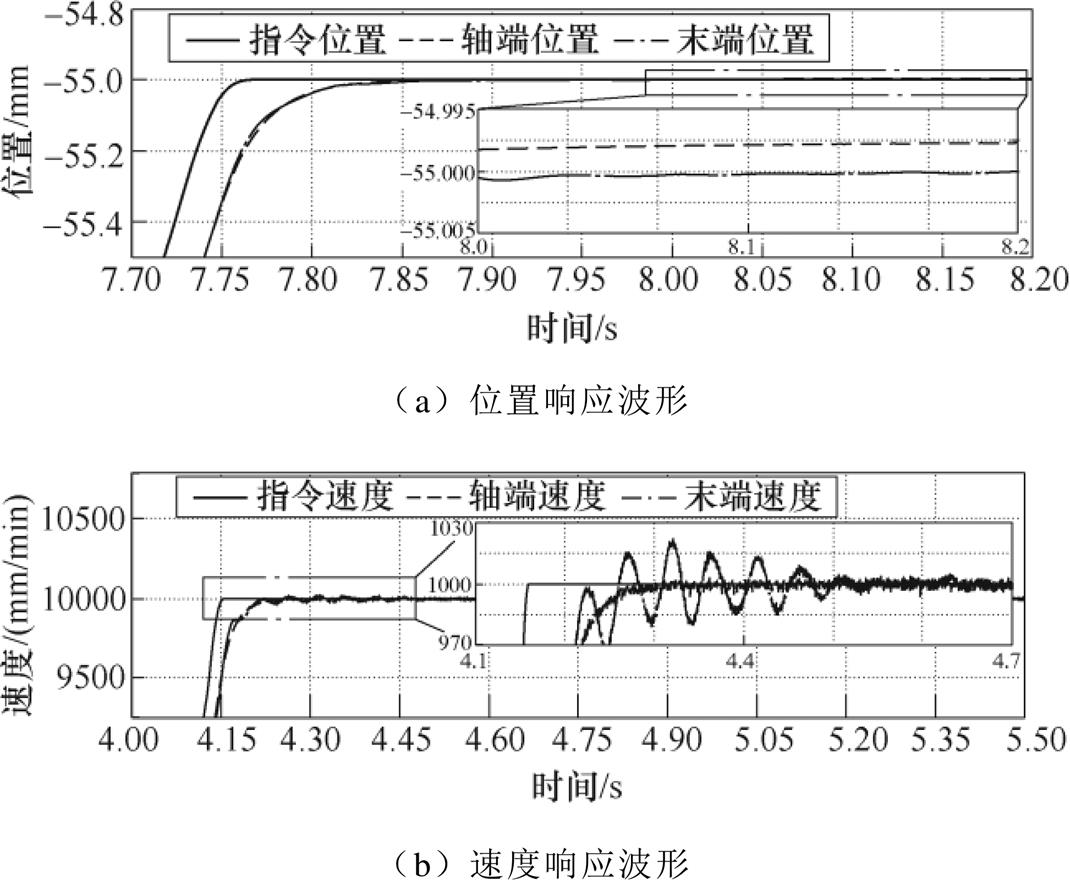
图19 模型精准时CDOB延时补偿实验结果
Fig.19 Experimental results of position response using CDOB
由图19和图20可以看出，在模型精确时，补偿后轴端速度无振荡超调，末端速度有微小超调振荡并逐渐收敛，末端转速振荡的峰-峰值为40mm/min，直线定位误差约为0.15mm。即使在模型存在失配时，CDOB也能获得很好的补偿效果，此时，轴端速度无振荡超调，末端速度有微小超调振荡并逐渐收敛，末端转速振荡的峰-峰值为50mm/min，直线定位误差约为0.2mm。
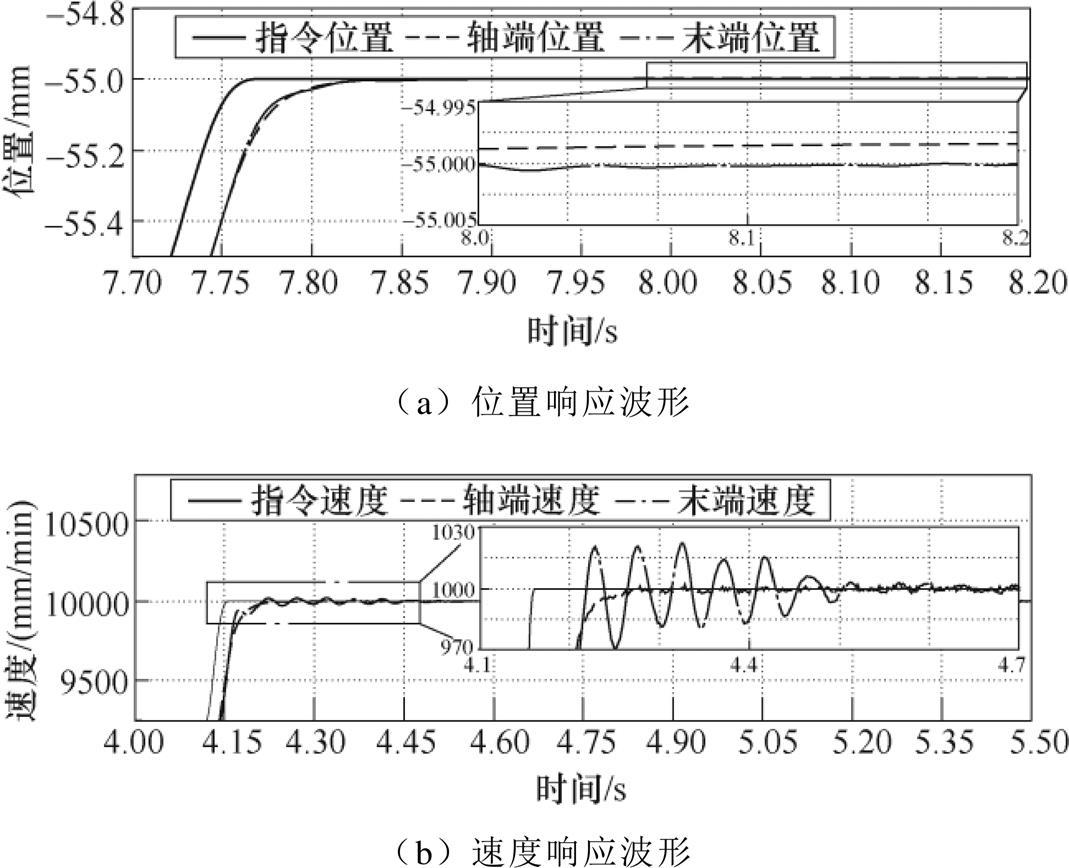
图20 存在模型失配时CDOB延时补偿实验
Fig.20 Experimental results of position response using CDOB with model mismatch
通过以上实验可以看出，在系统模型不存在失配问题时，Smith预估补偿器及通信扰动观测器均可以实现很好的通信延时补偿，补偿后，位置控制系统裕度明显提高。但当系统模型存在较为严重的失配问题时，Smith预估补偿器会存在补偿效果不佳的问题，相比之下，通信扰动观测器具有更好的参数鲁棒性。
本文对数控机床全闭环进给系统进行了研究，在采用双位置反馈控制的基础上，对实际数控系统中存在的通信延时进行分析和补偿。当延时项存在于系统的闭环环路中时，系统的特征方程中会存在延时项，而延时项的存在使得特征方程成为超越方程无法解析。对比了常见的有理近似方法，选取Pade变换进行近似，代入系统中绘制根轨迹，发现延时的存在降低了稳定根轨迹增益，影响了系统稳定性。采用Smith预估补偿器进行延时补偿。实际系统中的轴刚度系数、负载惯量及通信延时时间均难以准确获取，存在模型失配问题，而Smith预估补偿器对模型准确度较为敏感，模型失配时补偿效果恶化。结合系统扰动原理，将延时环节等效为系统扰动，设计了基于扰动观测器的通信延时补偿方法，解决了模型失配问题在通信延时补偿中的影响，从而提高算法的自适应性。
本文对数控机床全闭环进给系统进行了研究，在采用双位置反馈控制的基础上，针对典型数控系统架构中总线通信延时引起的位置控制超调及控制精度降低的问题，提出了基于扰动观测器的通信扰动观测补偿方法，消除了通信延时对位置环控制性能的影响。建立了含通信延时的全闭环伺服驱动系统模型，结合延时项有理近似方法，得出了系统的特征方程，利用根轨迹分析方法，分析了延时项对全闭环位置控制系统稳定性的影响。从常用的基于Smith预估补偿器的延时补偿方法出发，分析了实际系统中普遍存在的模型失配问题的影响。基于此，结合系统扰动原理，将延时环节等效为系统扰动，建立了基于扰动观测器的通信扰动观测器补偿方法，解决了模型失配问题在通信延时补偿中的影响，提高了延时补偿方法的适用性。
参考文献
[1] 苏光靖, 李红梅, 李争, 等. 永磁同步直线电机无模型电流控制[J]. 电工技术学报, 2021, 36(15): 3182-3190.
Su Guangjing, Li Hongmei, Li Zheng, et al. Research on model-free current control of permanent magnet synchronous linear motor[J]. Transaction of China Electrotechnical Society, 2021, 36(15): 3182-3190.
[2] 杨明, 曹佳, 徐殿国. 基于输入整形技术的交流伺服系统抖动抑制[J]. 电工技术学报, 2018, 33(21): 4979-4986.
Yang Ming, Cao Jia, Xu Dianguo. Suppression of vibration of AC servo system based on input shaping technique[J]. Transaction of China Electrotechnical Society, 2018, 33(21): 4979-4986.
[3] García P, Albertos P, Hägglund T. Control of unstable non-minimum-phase delayed systems[J]. Journal of Process Control, 2006, 16(10): 1099-1111.
[4] Najafi M, Hosseinnia S, Sheikholeslam F, et al. Closed-loop control of dead time systems via sequential sub-predictors[J]. International Journal of Control, 2013, 86(4): 599-609.
[5] 李洪乾, 韩松, 周忠强. 基于样本协方差矩阵特征特性的电网多重扰动定位方法[J]. 电工技术学报, 2021, 36(3): 646-655.
Li Hongqian, Han Song, Zhou Zhongqiang. Eigen characteristic of sample covariance matrix based multi- disturbance positioning method of power system[J]. Transaction of China Electrotechnical Society, 2021, 36(3): 646-655.
[6] 李争, 肖宇, 孙鹤旭, 等. 基于速度前瞻的双轴直线电机交叉耦合控制策略[J]. 电工技术学报, 2021, 36(5): 973-983.
Li Zheng, Xiao Yu, Sun Hexu, et al. Speed prospective based cross-coupling control strategy for dual-axis linear motor[J]. Transaction of China Electrotechnical Society, 2021, 36(5): 973-983.
[7] Watanabe K, Ito M. A process-model control for linear systems with delay[J]. IEEE Transactions on Automatic Control, 1981, 26(6): 1261-1269.
[8] 李雪, 于洋, 姜涛, 等. 基于稀疏增强动态解耦的电力系统振荡模式与模态辨识方法[J]. 电工技术学报, 2021, 36(13): 2832-2843.
Li Xue, Yu Yang, Jiang Tao, et al. Sparsity promoting dynamic mode decomposition based dominant modes and mode shapes estimation in bulk power grid[J]. Transaction of China Electrotechnical Society, 2021, 36(13): 2832-2843.
[9] Lai Chien-Liang, Pau-Lo Hsu. Design the remote control system with the time-delay estimator and the adaptive smith predictor[J]. IEEE Transactions on Industrial Informatics, 2009, 6(1): 73-80.
[10] Birs I, Muresan C, Nascu I, et al. A survey of recent advances in fractional order control for time delay systems[J]. IEEE Access, 2019, 7: 30951-30965.
[11] Natori K, Oboe R, Ohnishi K. Stability analysis and practical design procedure of time delayed control systems with communication disturbance observer[J]. IEEE Transactions on Industrial Informatics, 2008, 4(3): 185-197.
[12] Natori K, Tsuji T, Ohnishi K, et al. Time-delay compensation by communication disturbance observer for bilateral teleoperation under time-varying delay[J]. IEEE Transactions on Industrial Electronics, 2009, 57(3): 1050-1062.
[13] Bibian S, Jin H. Time delay compensation of digital control for DC switchmode power supplies using prediction techniques[J]. IEEE Transactions on Power Electronics, 2019, 15(5): 835-842.
[14] Yao Wenli, Yang Yongheng, Zhang Xiaobin, et al. Design and analysis of robust active damping for LCL filters using digital notch filters[J]. IEEE Transa- ctions on Power Electronics, 2016, 32(3): 2360- 2375.
[15] Lu Minghui, Wang Xiongfei, Loh P C, et al. Graphical evaluation of time-delay compensation techniques for digitally controlled converters[J]. IEEE Transactions on Power Electronics, 2017, 33(3): 2601-2614.
[16] Wang Jianguo, Yan Jiudun, Jiang Lin, et al. Delay- dependent stability of single-loop controlled grid- connected inverters with LCL filters[J]. IEEE Transa- ctions on Power Electronics, 2015, 31(1): 743-757.
[17] Khanesar M A, Kaynak O, Yin Shen, et al. Adaptive indirect fuzzy sliding mode controller for networked control systems subject to time-varying network- induced time delay[J]. IEEE Transactions on Fuzzy Systems, 2014, 23(1): 205-214.
[18] Khanesar M A, Kaynak O, Teshnehlab M. Direct model reference Takagi-Sugeno fuzzy control of SISO nonlinear systems[J]. IEEE Transactions on Fuzzy Systems, 2011, 19(5): 914-924.
[19] 王丽馨, 杨德友, 蔡国伟, 等. 自然激励下发电机有功参与因子提取及其在阻尼调制中的应用[J]. 电工技术学报, 2022, 37(5): 1194-1203.
Wang Lixin, Yang Deyou, Cai Guowei, et al. Extraction of participation factor with respect to generation active power under natural excitation and its application in damping modulation[J]. Transaction of China Electrotechnical Society, 2022, 37(5): 1194- 1203.
[20] Wu Bingfei, Lin Chun-Hsien. Adaptive neural predi- ctive control for permanent magnet synchronous motor systems with long delay time[J]. IEEE Access, 2019, 7: 108061-108069.
[21] Li Zhijun, Su Chunyi. Neural-adaptive control of single-master-multiple-slaves teleoperation for coor- dinated multiple mobile manipulators with time- varying communication delays and input uncer- tainties[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 24(9): 1400-1413.
Communication Delay Compensation Technology of Full-Closed Loop Position Control for Servo Drive System
Abstract The modernized numerical system usually adopts the concept that the computerized numerical control is responsible for computation and the servo driver is responsible for the execution. There is an inevitable communication delay between the two, especially in the high-speed feeding occasions. In order to avoid the overshot and control accuracy deterioration caused by communication delay, the delay issues in full-closed loop control are studied in detail. First, based on the dual-position feedback control structure, the servo driver system model integrating the communication delay is established, and the influence of communication delay on system stability is analyzed by the frequency root locus analysis method. For a better communication delay compensation, the Smith predictor is researched and designed accordingly, and its model mismatch problem is analyzed. Accordingly, the model error sources are summarized. Finally, the communication disturbance observation compensation strategy is designed combined with the disturbance observer theory, which solves the model mismatch problem in communication delay and improves the feasibility and simplicity of the delay compensation. The effectiveness of the proposed algorithm is verified by simulation.
keywords：Servo drive system, full-closed loop control, communication delay compensation
DOI: 10.19595/j.cnki.1000-6753.tces.201336
中图分类号：TM341
倪启南 男，1991年生，博士，研究方向为电力电子与电力传动。E-mail: niqn_hit@163.com
杨 明 男，1978年生，教授，博士生导师，研究方向为电力电子技术及应用、交流永磁伺服系统和智能控制应用。E-mail: yangming@hit.edu.cn（通信作者）
收稿日期 2020-10-09
改稿日期 2021-01-12
国家自然科学基金重大项目《高品质伺服电机系统关键科学问题》子课题《高品质伺服电机系统层级化理论与综合设计方法》（51991385）和国家科技重大专项（2012ZX04001051）资助。
（编辑 崔文静）