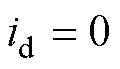 的矢量控制策略,其PMLSM在dq轴下对应的电压方程[12-15]为
的矢量控制策略,其PMLSM在dq轴下对应的电压方程[12-15]为摘要 由于永磁直线同步电机位置伺服系统易受参数扰动、外部干扰和端部效应的影响,该文提出一种定结构滑模控制器与扩展滑模扰动观测器相结合的复合式滑模位置控制方法。定结构滑模控制器通过加入限制条件,保证了系统状态都位于滑模面的同一侧,削弱了传统变结构滑模控制器由切换控制产生的抖振现象,提高了滑模滑动运动的品质。扩展滑模扰动观测器可以对定结构滑模控制器中无法精确测量的系统扰动项进行观测并补偿,从而消除了系统扰动项对定结构滑模控制器的影响。最后通过实验验证了该复合式滑模控制方法的有效性。实验结果表明,相比于传统的滑模控制,该复合式滑模控制方法可以实现更高的位置跟踪精度,不仅削弱了抖振现象,而且增强了位置跟踪系统的鲁棒性能。
关键词:永磁直线同步电机 扰动观测器 定结构滑模控制器 抖振 鲁棒性
随着精密运动控制技术的进步,永磁直线同步电机(Permanent Magnet Linear Synchronous Motor, PMLSM)的应用有逐渐增加的趋势[1-2]。与传统的“旋转电机+传动装置”驱动方式不同,永磁直线同步电机由于其结构上无需使用任何丝杠、齿条和滑轮等装置,采用直接驱动方式,具有刚度高、推力大和精度高等优点,因此在高精密仪器、运送传输设备和半导体芯片加工等领域逐渐崭露头角[3-5]。但是PMLSM由于无机械传动环节,使得外部干扰和本身参数变化不能得到缓冲,再加上它本身固有的端部效应,使得其相较于传统的旋转电机更难进行精确控制。因此,为消除这些干扰对系统造成的扰动,需要设计一个高性能的控制器来实现对PMLSM位置伺服系统的精确控制。
滑模控制(Sliding Mode Control, SMC)由于滑模面的设计与电机参数及负载扰动无关,使得它具有对负载扰动和电机自身参数变化不灵敏等优点,从而受到广泛的关注[6-7]。但是由于传统变结构滑模控制中切换控制项的不连续性,使得控制系统容易产生抖振现象,如果抖振现象过大,可能造成控制系统产生较大的误差,更严重时甚至会造成控制系统的损伤。为此,针对传统变结构滑模控制中存在的问题,文献[8]在传统指数趋近律的基础上,提出了一种新型变指数趋近律,该趋近律有效地解决了传统指数趋近律在削弱抖振和提高趋近速度方面存在的矛盾,提高了系统的响应速度和跟踪精度,但是切换项的增益不能在线实时更新,当系统扰动变化较大时,容易降低系统的跟踪性能。文献[9]采用两个滑模面相结合的方式来设计滑模控制器,以保证系统状态沿着两个滑模面的交点向平衡点移动,提高了滑模滑动运动的品质,并且为了抑制滑模控制器引起的抖振现象,该方法通过Elman神经网络来实时更新滑模切换项的增益,提高了系统的跟踪性能,但是Elman神经网络设计过程复杂、计算较难且不易分析。文献[10]通过对传统终端滑模控制进行改进,提出了一种具有非奇异性的改进型快速终端滑模控制方法,该方法可以显著地抑制传统终端滑模控制中存在的抖振现象,避免了奇异性对系统造成的影响,加快了系统的响应速度,并且为了实时估计系统扰动上界中存在的不确定性参数,将自适应控制引入到滑模控制器的设计当中,减小了扰动对系统造成的影响,提高了系统的抗扰动能力,但整体算法设计较复杂,且扰动项的上界存在未知性,其包含的状态变量较难定义。文献[11]通过对传统滑模面进行改进,提出了一种基于分数阶滑模面的滑模控制方法,该方法有效地抑制了系统状态在滑模面上向平衡点滑动过程中存在的抖振现象,提高了系统的跟踪性能,并且为了更好地避免系统扰动对系统造成的影响,该方法通过设计的自适应模糊观测器来观测并补偿系统的扰动项,但模糊规则的设定需要大量的实验经验,并且其观测器的设计过程也比较复杂。
为了实现对PMLSM位置伺服系统的精确控制,本文提出一种定结构滑模控制器(Fixed Structure Sliding Mode Controller, FSSMC)与扩展滑模扰动观测器(Extended Sliding Mode Disturbance Observer, ESMDO)相结合的复合式滑模位置控制(Composite Sliding Mode Position Control, CSMPC)方法。首先,针对传统变结构滑模控制本身固有的抖振现象,通过加入限制条件,提出一种定结构滑模控制方法来削弱传统变结构滑模控制本身固有的抖振现象,提高了滑模滑动运动的品质;然后,采用扩展滑模扰动观测器对定结构滑模控制器中无法精确测量的系统扰动项进行观测并补偿,来消除系统扰动项对定结构滑模控制器的影响;最后,通过实验对该复合式滑模位置控制方法的有效性进行验证。
本文采用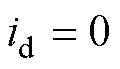 的矢量控制策略,其PMLSM在dq轴下对应的电压方程[12-15]为
的矢量控制策略,其PMLSM在dq轴下对应的电压方程[12-15]为
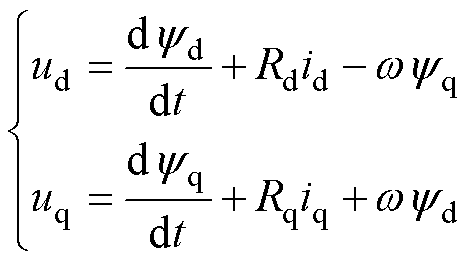 (1)
(1)
式中,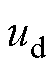 和
和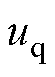 分别为
分别为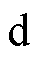 、
、 轴的电压;
轴的电压;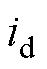 和
和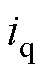 分别为
分别为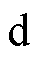 、
、 轴的电流;
轴的电流;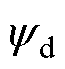 和
和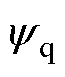 分别为
分别为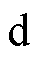 、
、 轴的磁链;
轴的磁链;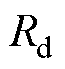 、
、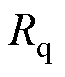 分别为
分别为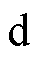 、
、 轴的电阻,
轴的电阻, ;
;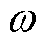 为电角速度。
为电角速度。
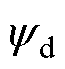 、
、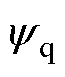 和
和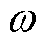 可分别表示为
可分别表示为
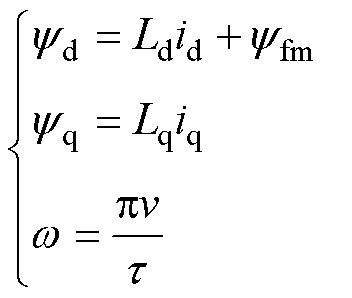 (2)
(2)
式中,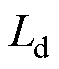 和
和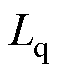 分别为
分别为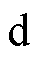 、
、 轴的电感;
轴的电感;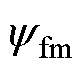 为永磁体磁链;
为永磁体磁链;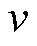 为动子线速度;
为动子线速度;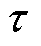 为极距。
为极距。
则将式(2)代入式(1)可得
 (3)
(3)
PMLSM的电磁功率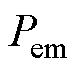 为
为
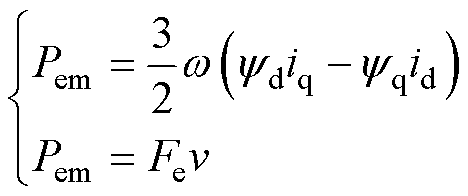 (4)
(4)
经过整理得PMLSM的电磁推力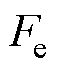 为
为
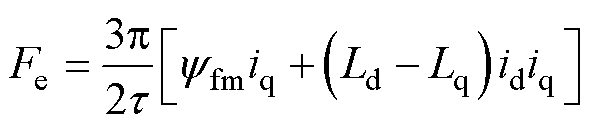 (5)
(5)
由于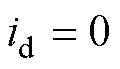 ,则此时电磁推力变为
,则此时电磁推力变为
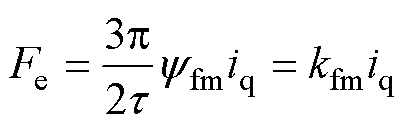 (6)
(6)
式中,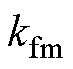 为电磁推力系数。并且对于式(6),当PMLSM的极对数为
为电磁推力系数。并且对于式(6),当PMLSM的极对数为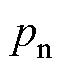 时,
时,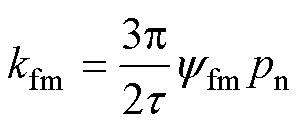 。
。
PMLSM的机械运动方程为
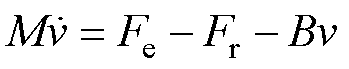 (7)
(7)
式中, 为负载扰动;
为负载扰动;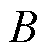 为粘滞摩擦因数;
为粘滞摩擦因数;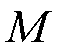 为动子总质量。
为动子总质量。
本文提出的定结构滑模控制方法通过加入限制条件,保证了系统状态都位于滑模面的同一侧,削弱了传统变结构滑模控制器由切换控制产生的抖振现象,提高了滑模滑动运动的品质,减小了系统的跟踪误差。
假设一个线性非时变系统为
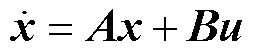 (8)
(8)
式中,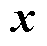 为
为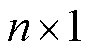 的状态向量;
的状态向量;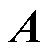 为
为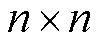 的系统矩阵;
的系统矩阵;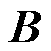 为输入
为输入 矩阵;
矩阵; 为输入
为输入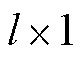 向量。
向量。
定义滑模面为
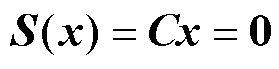 (9)
(9)
其中,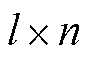 的常数矩阵C为
的常数矩阵C为
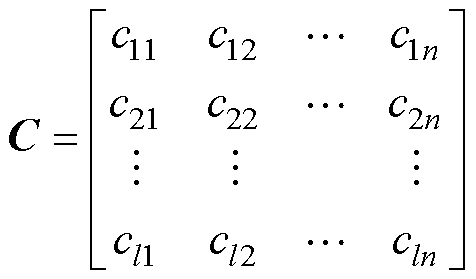
滑模面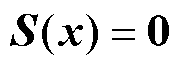 仅有一个渐进稳定的平衡点,即原点。设计希望系统的状态能够在较短的时间内抵达滑模面,并且沿着此滑模面渐进稳定于原点。因此,设计了以下两种控制方式:
仅有一个渐进稳定的平衡点,即原点。设计希望系统的状态能够在较短的时间内抵达滑模面,并且沿着此滑模面渐进稳定于原点。因此,设计了以下两种控制方式:
(1)顺滑控制:系统状态进入设计的滑模面后,能够沿着此滑模面渐进稳定于原点,此控制过程称为顺滑控制。
(2)迫近控制:当系统初始状态不在设计的滑模面上时,通过此控制方式能够使得系统状态在有限时间内进入此滑模面,此控制过程称为迫近控制。
对式(9)求导得
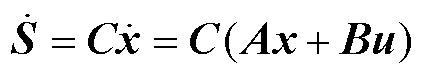 (10)
(10)
当系统状态进入滑模面时,满足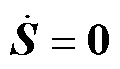 和
和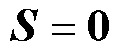 ,则由式(10)可得
,则由式(10)可得
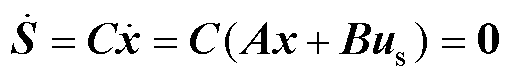 (11)
(11)
对式(11)进行化简可得顺滑控制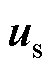 为
为
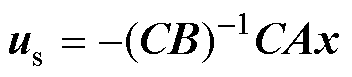 (12)
(12)
假设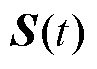 在
在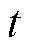 时刻可导,这里的
时刻可导,这里的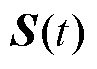 为在
为在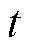 时刻的系统状态,则
时刻的系统状态,则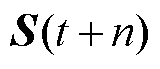 可由泰勒级数展开为
可由泰勒级数展开为
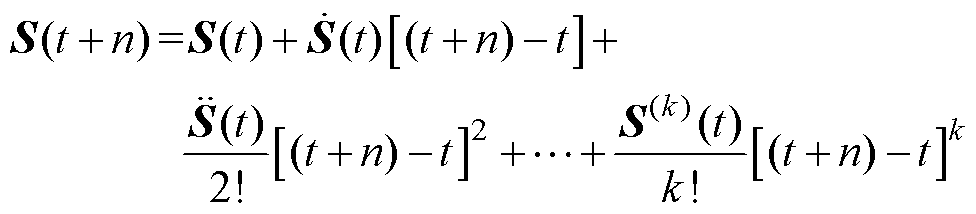 (13)
(13)
式中,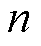 为一个很小的正常数;
为一个很小的正常数;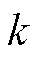 为一个趋于无穷大的正整数。由于
为一个趋于无穷大的正整数。由于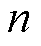 的值很小,从而式(13)等号右侧从第三项开始往后所有项的值都接近于零。因此,
的值很小,从而式(13)等号右侧从第三项开始往后所有项的值都接近于零。因此,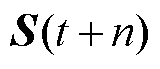 的值可以看成式(13)右侧前两项值的和,进而式(13)化简为
的值可以看成式(13)右侧前两项值的和,进而式(13)化简为
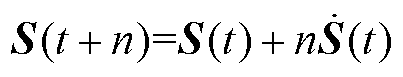 (14)
(14)
结合式(14),为了削弱系统的抖振现象,则需要保证系统状态都位于滑模面的同一侧,即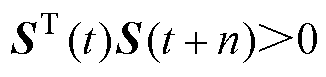 ,从而有式(15)成立。
,从而有式(15)成立。
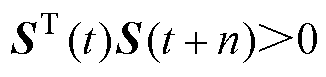
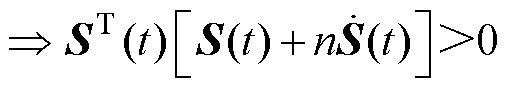
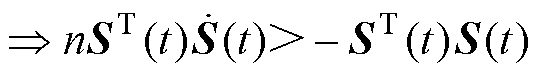 (15)
(15)
式(15)保证了在下一时刻的系统状态位于滑模面的同一侧。从式(15)可知,为了削弱系统的抖振现象,需要加入限制条件为
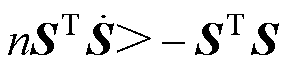 (16)
(16)
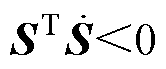 (17)
(17)
令迫近控制为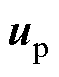 ,则可得
,则可得
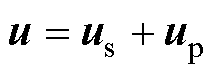 (18)
(18)
由式(10)、式(16)~式(18)可得
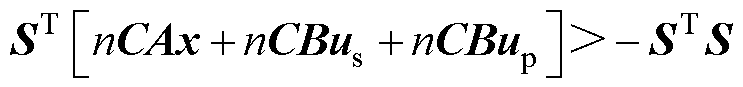 (19)
(19)
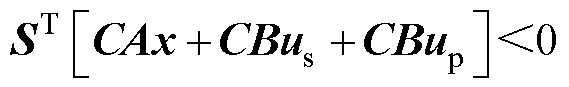 (20)
(20)
由式(19)和式(20)可知,存在一个正常数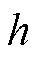 ,使得式(21)成立。
,使得式(21)成立。
 (21)
(21)
式中,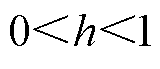 。
。
则根据式(12)和式(21)可得,迫近控制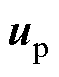 为
为
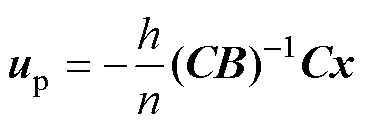 (22)
(22)
对式(7)进一步的化简可得
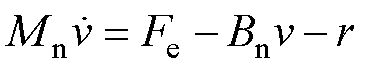 (23)
(23)
其中
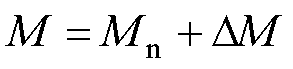
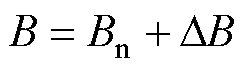
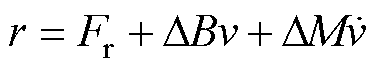
式中, 和
和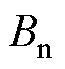 为PMLSM的额定参数;
为PMLSM的额定参数;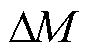 和
和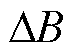 分别为参数
分别为参数 和
和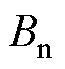 的变化量;
的变化量;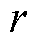 为总扰动项。
为总扰动项。
令PMLSM动子的给定位置为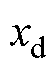 ,实际位置为
,实际位置为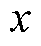 ;给定速度为
;给定速度为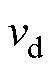 ,实际速度为
,实际速度为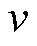 。则有式(24)~式(26)成立。
。则有式(24)~式(26)成立。
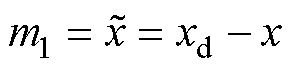 (24)
(24)
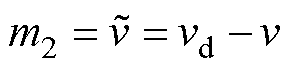 (25)
(25)
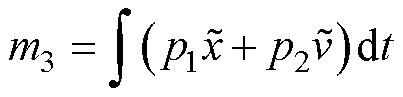 (26)
(26)
式中,m1~m3为状态变量;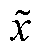 为位置误差;
为位置误差;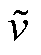 为速度误差;p1、p2为积分系数。
为速度误差;p1、p2为积分系数。
将式(23)代入式(25)可得
 (27)
(27)
对式(25)求导得
 (28)
(28)
对式(24)求导得
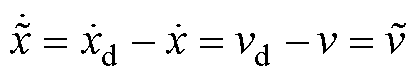 (29)
(29)
由式(26)、式(28)和式(29)可得
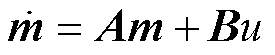 (30)
(30)
其中
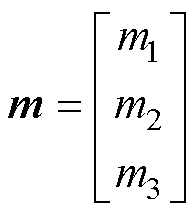
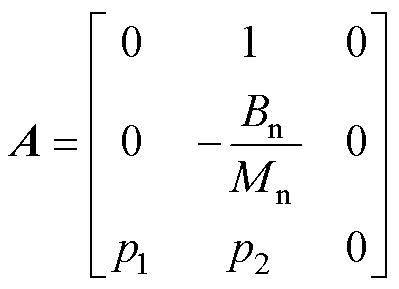
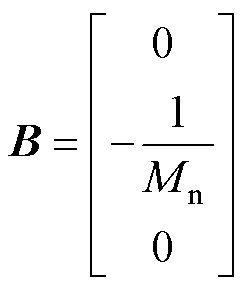
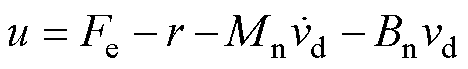
定义滑模面S为
 (31)
(31)
根据式(12)和式(30)可得,顺滑控制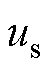 为
为
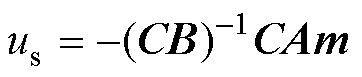
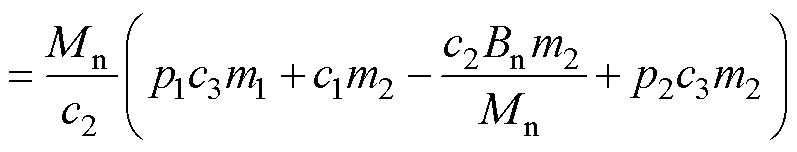 (32)
(32)
根据式(22)和式(30)可得,迫近控制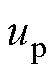 为
为
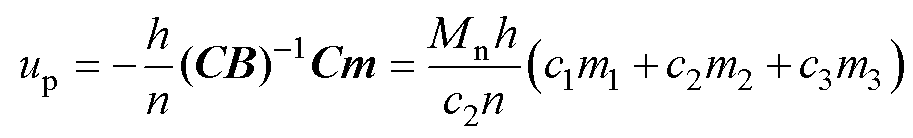 (33)
(33)
由式(18)、式(32)和式(33)可得到总的控制输入项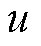 为
为
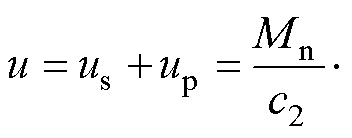
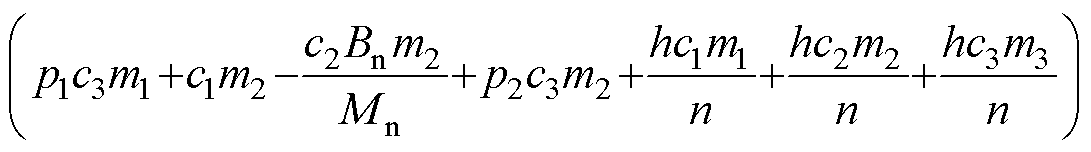 (34)
(34)
将式(31)、式(34)代入式(30)可得
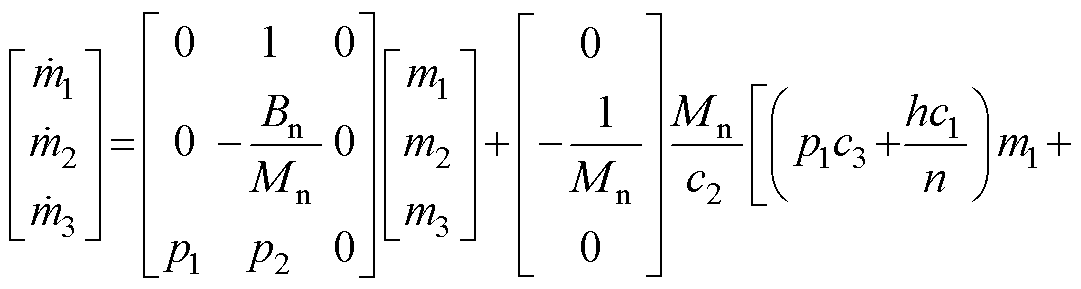
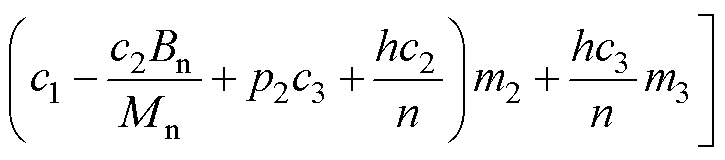
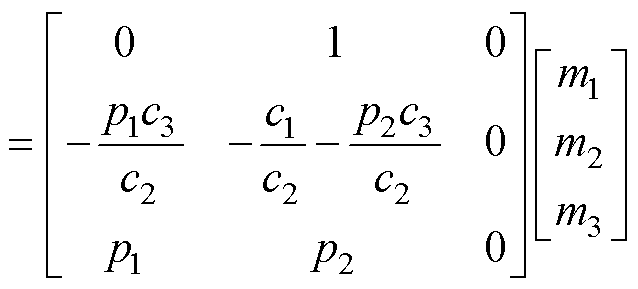 (35)
(35)
对式(35)求其极点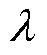 可得
可得
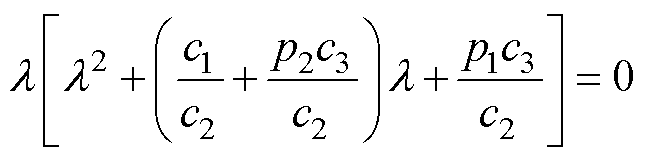 (36)
(36)
从式(36)中可以看出,系统的一个极点位于原点,而另外两个极点可通过比较系数法,将其配置于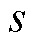 平面的左半平面来保证系统的稳定。基于CSMPC的PMLSM位置伺服系统框图如图1所示。
平面的左半平面来保证系统的稳定。基于CSMPC的PMLSM位置伺服系统框图如图1所示。
由于定结构滑模控制器总的控制输入项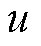 中存在一个无法精确测量的总扰动项
中存在一个无法精确测量的总扰动项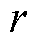 (见式(23)),因此需要设计一个扩展滑模扰动观测器对总扰动项进行观测并补偿。
(见式(23)),因此需要设计一个扩展滑模扰动观测器对总扰动项进行观测并补偿。
根据式(6)和式(23)可得

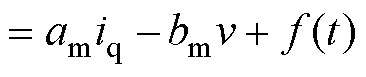 (37)
(37)
其中
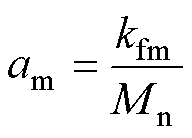
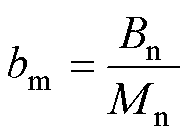
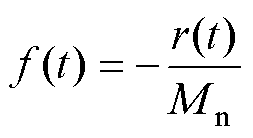
式中,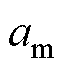 、
、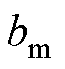 、
、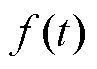 为扰动项。
为扰动项。
将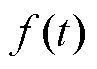 视为扩展状态,则可得
视为扩展状态,则可得
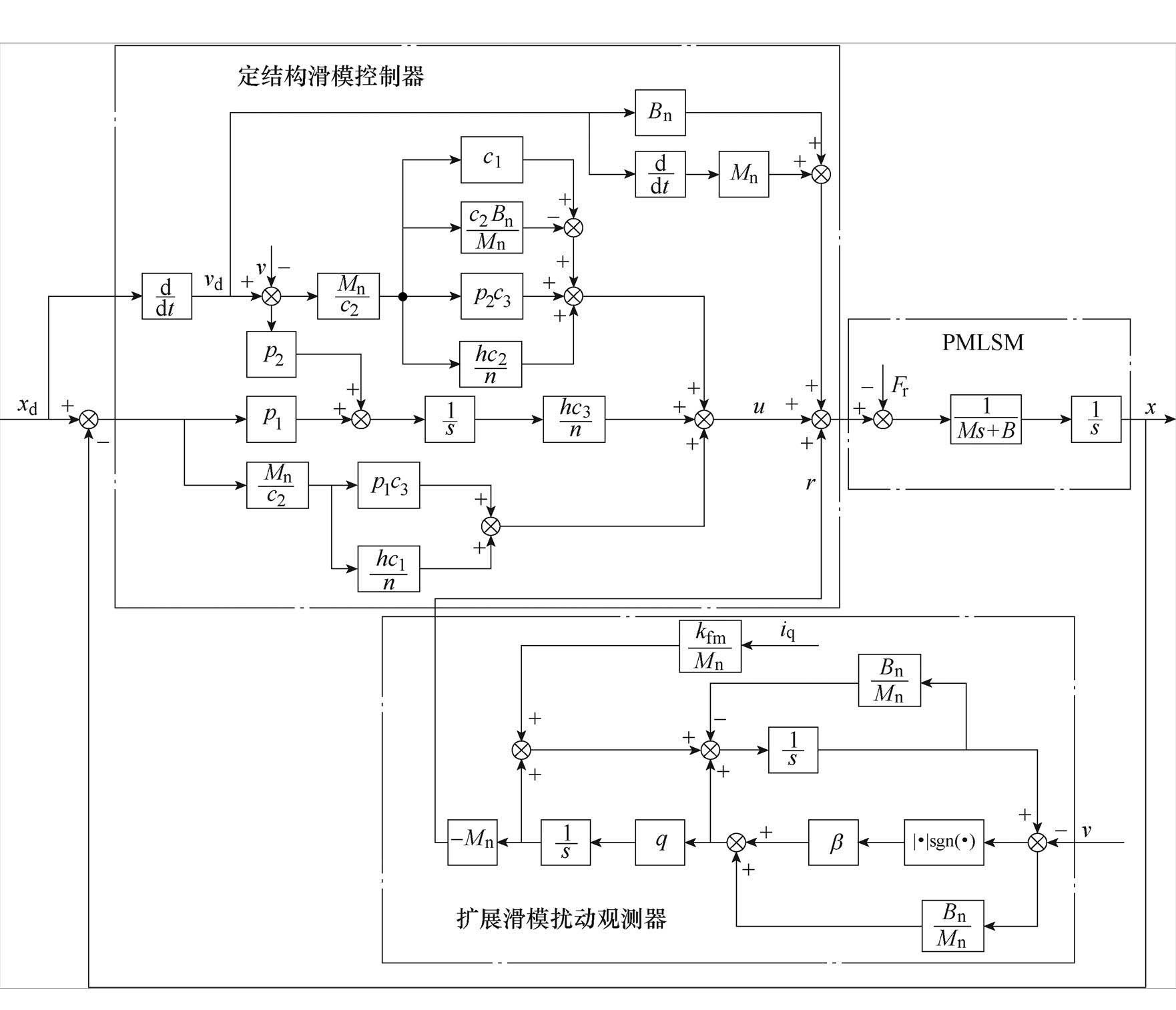
图1 基于CSMPC的PMLSM位置伺服系统框图
Fig.1 Block diagram of PMLSM position servo system based on CSMPC
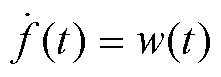 (38)
(38)
式中,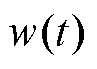 为
为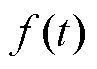 的变化率。
的变化率。
根据式(37)和式(38),可定义扩展滑模扰动观测器为
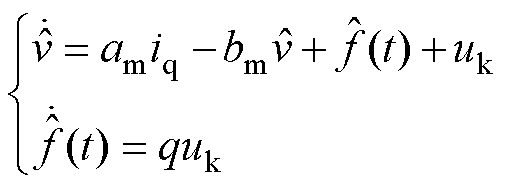 (39)
(39)
式中,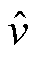 为速度估计值;
为速度估计值; 为扰动项估计值;
为扰动项估计值;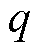 为滑动模态参数;
为滑动模态参数;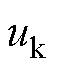 为滑模控制律。
为滑模控制律。
根据式(37)~式(39)可得
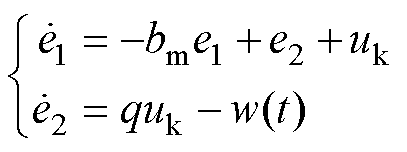 (40)
(40)
其中
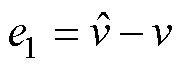
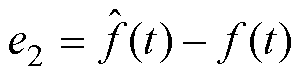
式中,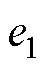 为速度估计误差;
为速度估计误差;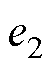 为扰动估计误差;
为扰动估计误差;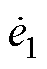 和
和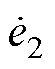 分别为
分别为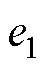 和
和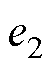 的变化率。
的变化率。
令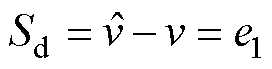 代表滑模面,并且设计滑模趋近律[16]为
代表滑模面,并且设计滑模趋近律[16]为
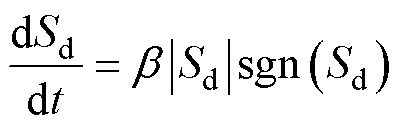 (41)
(41)
式中, 。
。
根据式(40)和式(41),可将扩展滑模扰动观测器的滑模控制律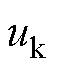 定义为
定义为
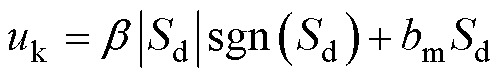 (42)
(42)
根据式(40)和式(42),为保证系统状态抵达滑模面,由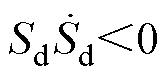 可得
可得
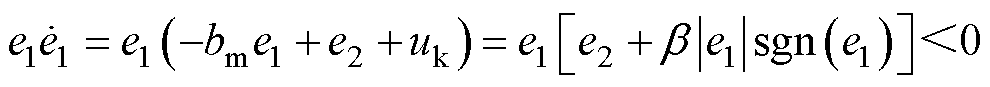 (43)
(43)
由式(43)可得
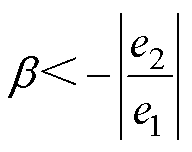 (44)
(44)
选择参数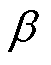 满足式(44)可保证系统状态在较短的时间内抵达滑模面,并维持在滑模面上。这就意味着
满足式(44)可保证系统状态在较短的时间内抵达滑模面,并维持在滑模面上。这就意味着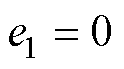 ,
,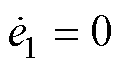 ,此时式(40)变为
,此时式(40)变为
 (45)
(45)
将式(45)进行变形得
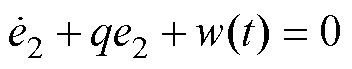 (46)
(46)
对式(46)进行求解得
 (47)
(47)
式中, 为一个常数;当
为一个常数;当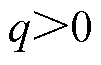 时
时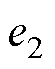 收敛于零。
收敛于零。
本文采用的运动控制平台由ICD05-030型PMLSM、工控机(内含控制卡)、光栅编码器、机柜(内含伺服驱动器)、限位开关和上位机组成,如图2所示。

图2 运动控制系统平台
Fig.2 Motion control system platform
图2中,PMLSM的参数为: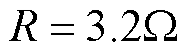 ,
,
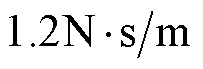 ,
,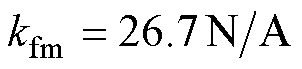 ,
,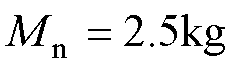 ,
,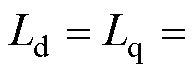
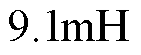 ,
,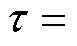
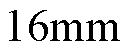 。SMC的参数为:
。SMC的参数为: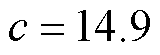 ,
,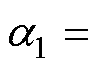
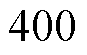 ,
,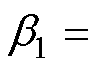
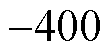 ,
,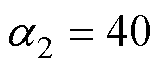 ,
,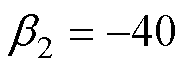 。CSMPC的参数为:
。CSMPC的参数为:
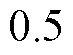 ,
,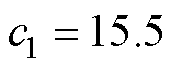 ,
,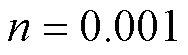 ,
,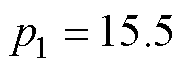 ,
,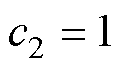 ,
, ,
,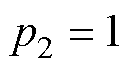 ,
,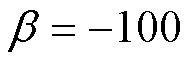 ,
,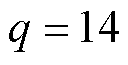 。
。
为验证CSMPC控制方法的有效性,本文分别采用SMC和CSMPC两种方法来对比分析PMLSM伺服系统的位置跟踪性能。进行了三项实验,分别为:①动子总质量 ,位置给定为
,位置给定为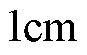 的阶跃位置信号;②动子总质量
的阶跃位置信号;②动子总质量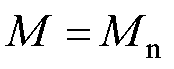 ,位置给定值为
,位置给定值为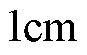 的阶跃信号,在
的阶跃信号,在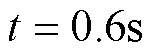 时突加
时突加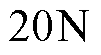 的恒定负载扰动;③动子总质量
的恒定负载扰动;③动子总质量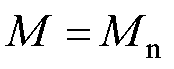 ,给定幅值为
,给定幅值为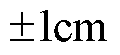 ,周期
,周期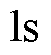 的梯形位置信号。
的梯形位置信号。
实验①:基于SMC和CSMPC的系统位置阶跃响应曲线分别如图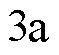 、图
、图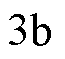 所示,扩展滑模扰动观测器的观测值如图
所示,扩展滑模扰动观测器的观测值如图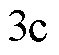 所示。对比图
所示。对比图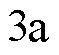 和图
和图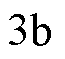 可知,当动子总质量为
可知,当动子总质量为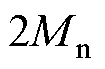 时,基于CSMPC的PMLSM伺服系统位置阶跃响应较平滑,响应速度较快,在
时,基于CSMPC的PMLSM伺服系统位置阶跃响应较平滑,响应速度较快,在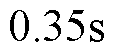 时达到稳态值;而基于传统SMC的PMLSM伺服系统位置阶跃响应则产生了一定的超调,经调整在
时达到稳态值;而基于传统SMC的PMLSM伺服系统位置阶跃响应则产生了一定的超调,经调整在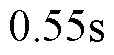 时才达到稳态值。当系统位置阶跃响应曲线达到稳态值后,对比两者的局部放大图可以看出,基于CSMPC的PMLSM位置伺服系统的稳态误差为
时才达到稳态值。当系统位置阶跃响应曲线达到稳态值后,对比两者的局部放大图可以看出,基于CSMPC的PMLSM位置伺服系统的稳态误差为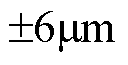 左右,而基于传统SMC的PMLSM位置伺服系统的稳态误差为
左右,而基于传统SMC的PMLSM位置伺服系统的稳态误差为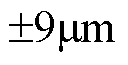 左右。并且从图
左右。并且从图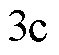 中可以看出,扩展滑模扰动观测器能够有效地估计出动子在运行过程中所受到的系统扰动。从而由以上可知:与传统SMC相比,基于CSMPC的PMLSM位置伺服系统的鲁棒性更强,且具有更好的位置跟踪精度。
中可以看出,扩展滑模扰动观测器能够有效地估计出动子在运行过程中所受到的系统扰动。从而由以上可知:与传统SMC相比,基于CSMPC的PMLSM位置伺服系统的鲁棒性更强,且具有更好的位置跟踪精度。
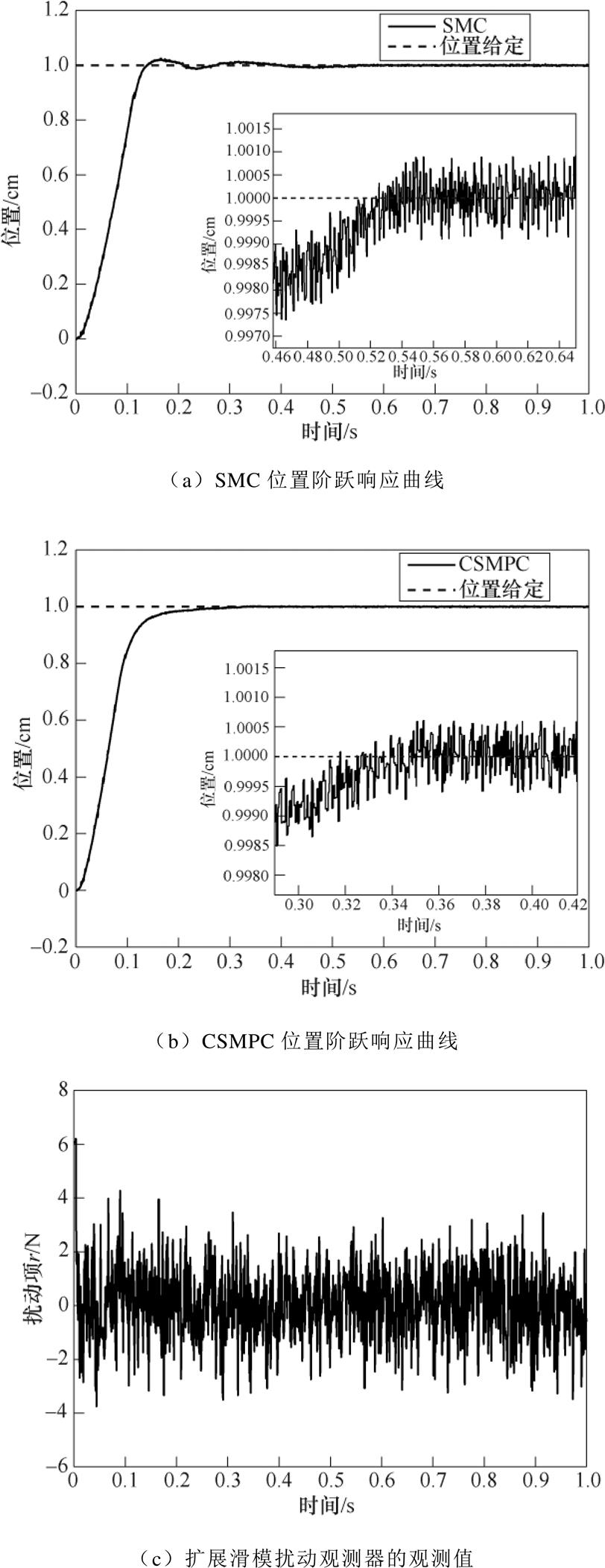
图3 电机参数变化下的两种控制器响应曲线(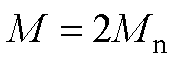 )
)
Fig.3 Response curves of two kinds of controllers with variable motor parameters (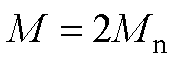 )
)
实验②:基于SMC和CSMPC的系统位置阶跃响应曲线分别如图 、图
、图 所示,位置误差曲线分别如图
所示,位置误差曲线分别如图 、图
、图 所示,扩展滑模扰动观测器的观测值如图
所示,扩展滑模扰动观测器的观测值如图 所示。对比图
所示。对比图 和图
和图 可知,与传统的SMC相比,基于CSMPC的PMLSM位置伺服系统响应速度更快、动态特性更好。从图
可知,与传统的SMC相比,基于CSMPC的PMLSM位置伺服系统响应速度更快、动态特性更好。从图 和图
和图 中可以看出,当在
中可以看出,当在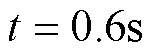 时加入
时加入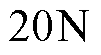 的恒定负载扰动后,基于CSMPC的PMLSM位置伺服系统最大跟踪误差为
的恒定负载扰动后,基于CSMPC的PMLSM位置伺服系统最大跟踪误差为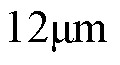 ,经调整在
,经调整在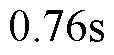 时稳定于
时稳定于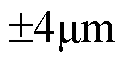 左右;而基于传统SMC的PMLSM位置伺服系统最大跟踪误差为
左右;而基于传统SMC的PMLSM位置伺服系统最大跟踪误差为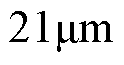 ,经调整在
,经调整在 时稳定于
时稳定于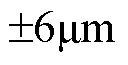 左右。并且从图
左右。并且从图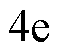 中可以看出,扩展滑模扰动观测器能够快速准确地估计出系统所受到的外部扰动,消除了系统扰动项对定结构滑模控制器的影响。从而由以上可知:基于CSMPC的PMLSM位置伺服系统具有更好的位置跟踪精度,且在受到扰动时表现出更强的鲁棒性。
中可以看出,扩展滑模扰动观测器能够快速准确地估计出系统所受到的外部扰动,消除了系统扰动项对定结构滑模控制器的影响。从而由以上可知:基于CSMPC的PMLSM位置伺服系统具有更好的位置跟踪精度,且在受到扰动时表现出更强的鲁棒性。
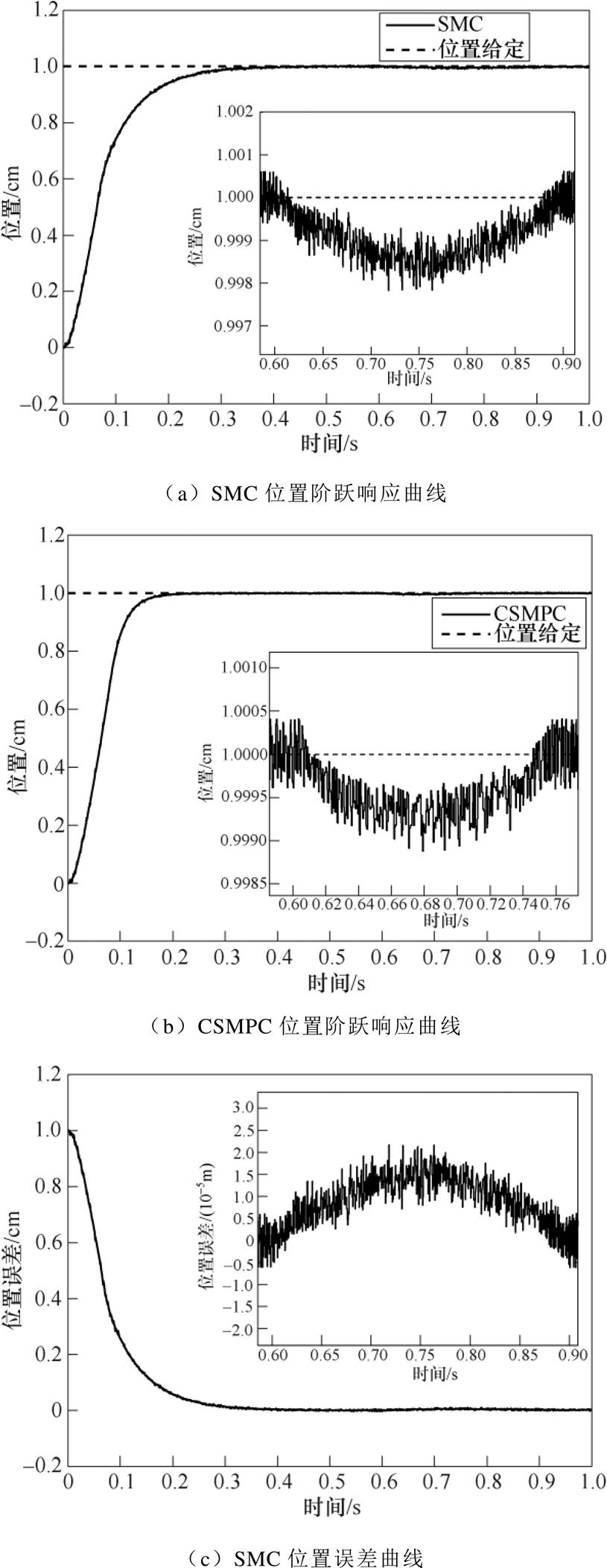
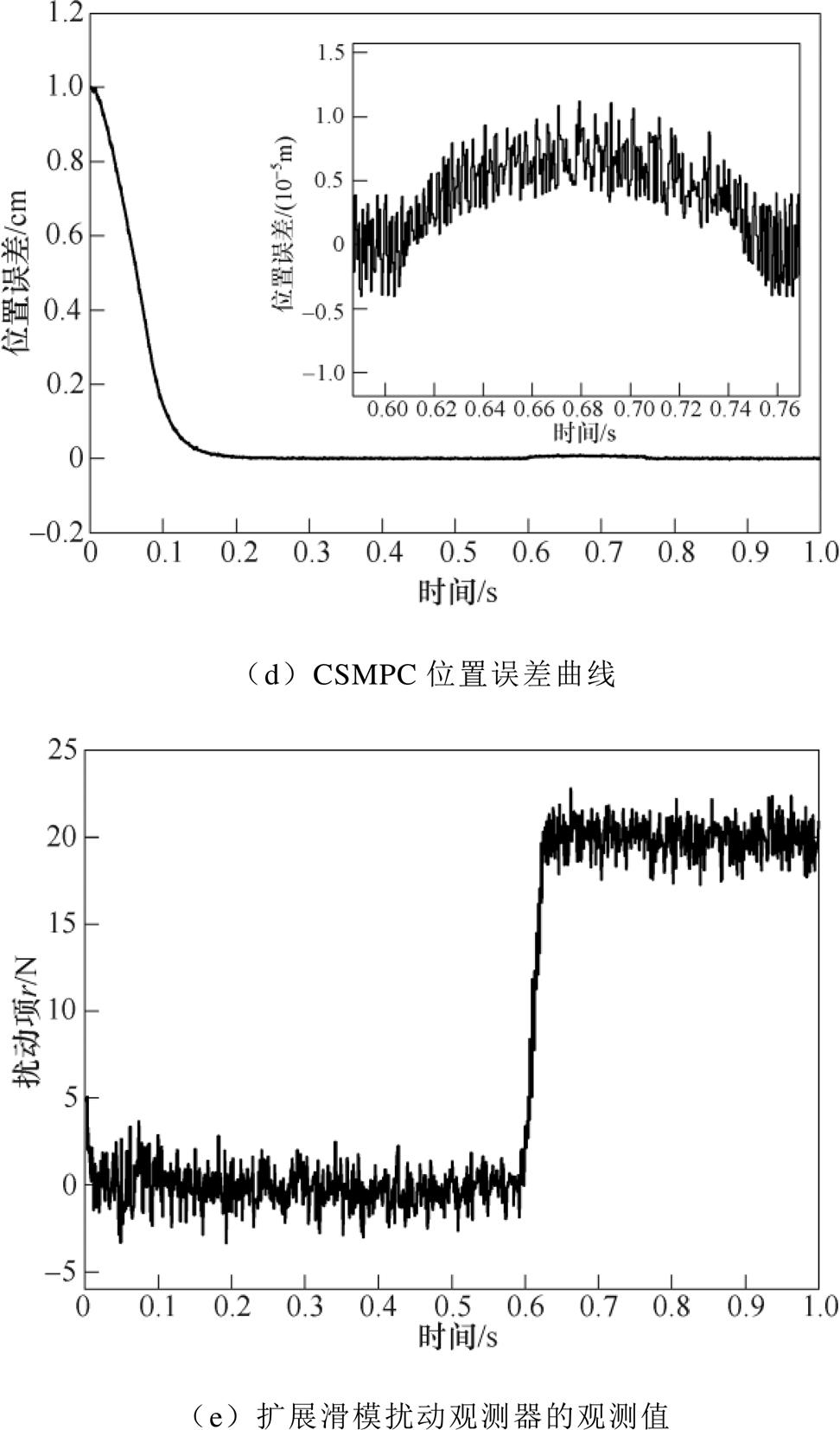
图4 恒定负载扰动下的两种控制器响应曲线(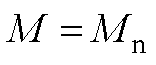 )
)
Fig.4 Response curves of two controllers under constant load disturbance (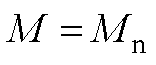 )
)
实验③:为了更好地验证CSMPC方法的有效性,进行了实验③,基于CSMPC的梯形位置响应曲线如图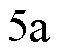 所示,位置误差曲线如图
所示,位置误差曲线如图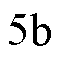 所示,扩展滑模扰动观测器在一个周期内的观测值如图
所示,扩展滑模扰动观测器在一个周期内的观测值如图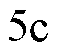 所示。从图中可以看出,扩展滑模扰动观测器能够有效地估计出系统所受到的扰动项,使得基于CSMPC的PMLSM位置伺服系统能够较好地跟踪梯形位置信号,其位置误差小于等于
所示。从图中可以看出,扩展滑模扰动观测器能够有效地估计出系统所受到的扰动项,使得基于CSMPC的PMLSM位置伺服系统能够较好地跟踪梯形位置信号,其位置误差小于等于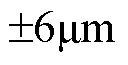 。
。

图5 梯形位置信号输入下CSMPC响应曲线(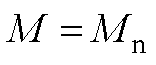 )
)
Fig.5 CSMPC response curve under trapezoidal position signal input (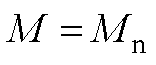 )
)
本文提出一种定结构滑模控制器与扩展滑模扰动观测器相结合的复合式滑模位置控制策略来抑制参数扰动、外部干扰和端部效应对永磁直线同步电机位置跟踪精度的影响。定结构滑模控制方法通过加入限制条件,削弱了传统变结构滑模控制器由切换控制产生的抖振现象,提高了滑模滑动运动的品质。并且采用扩展滑模扰动观测器对定结构滑模控制器中无法精确测量的系统扰动项进行观测并补偿,消除了系统扰动项对定结构滑模控制器的影响。实验表明,相比于传统的滑模控制方法,基于CSMPC的PMLSM位置伺服系统响应速度更快、位置跟踪精度更高,并且在受到扰动时表现出更强的鲁棒性。
参考文献
[1] 魏惠芳, 王丽梅. 永磁直线同步电机自适应模糊神经网络时变滑模控制[J]. 电工技术学报, 2022, 37(4): 861-869.
Wei Huifang, Wang Limei. Adaptive fuzzy neural network time-varying sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 861-869.
[2] 王明杰, 徐伟, 杨存祥, 等. 基于精确子域模型的永磁直线同步电机空载磁场解析计算[J]. 电工技术学报, 2020, 35(5): 943-953.
Wang Mingjie, Xu Wei, Yang Cunxiang, et al. Analytical calculation of no-load magnetic field in permanent magnet linear synchronous motors based on an accurate subdomain model[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 943- 953.
[3] 金鸿雁, 赵希梅, 原浩. 永磁直线同步电机动态边界层全局互补滑模控制[J]. 电工技术学报, 2020, 35(9): 718-723.
Jin Hongyan, Zhao Ximei, Yuan Hao. Dynamic boundary layer global complementary sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 718-723.
[4] 张康, 王丽梅. 基于反馈线性化的永磁直线同步电机自适应动态滑模控制[J]. 电工技术学报, 2021, 36(19): 4016-4024.
Zhang Kang, Wang Limei. Adaptive dynamic sliding mode control of permanent magnet linear synchronous motor based on feedback linearization[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(19): 4016-4024.
[5] 郭科宇, 李耀华, 史黎明, 等. 电枢分段供电永磁直线同步电机的非线性数学模型[J]. 电工技术学报, 2021, 36(6): 1126-1137.
Guo Keyu, Li Yaohua, Shi Liming, et al. Non-linear mathematic model of a segmented powered permanent magnet linear synchronous machine[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1126- 1137.
[6] 原浩, 赵希梅. 基于积分滑模的永磁直线同步电动机直接推力控制[J]. 电工技术学报, 2019, 34(3): 39-44.
Yuan Hao, Zhao Ximei. Direct thrust force control based on integral sliding mode for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 39-44.
[7] 金鸿雁, 赵希梅. 基于Sugeno型模糊神经网络和互补滑模控制器的双直线电机伺服系统同步控制[J]. 电工技术学报, 2019, 34(13): 2727-2733.
Jin Hongyan, Zhao Ximei. Dual linear motors servo system synchronization control based on Sugeno type fuzzy neural network and complementary sliding mode controller[J]. Transactions of China Electro- technical Society, 2019, 34(13): 2727-2733.
[8] 童克文, 张兴, 张昱, 等. 基于新型趋近律的永磁同步电动机滑模变结构控制[J]. 中国电机工程学报, 2008, 28(21): 102-106.
Tong Kewen, Zhang Xing, Zhang Yu, et al. Sliding mode variable structure control of permanent magnet synchronous machine based on a novel reaching law[J]. Proceedings of the CSEE, 2008, 28(21): 102- 106.
[9] 赵希梅, 金鸿雁. 基于Elman神经网络的永磁直线同步电机互补滑模控制[J]. 电工技术学报, 2018, 33(5): 974-979.
Zhao Ximei, Jin Hongyan. Complementary sliding mode control for permanent magnet linear syn- chronous motor based on Elman neural network[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 974-979.
[10] 付东学, 赵希梅. 永磁直线同步电机自适应非奇异快速终端滑模控制[J]. 电工技术学报, 2020, 35(4): 717-723.
Fu Dongxue, Zhao Ximei. Adaptive nonsingular fast terminal sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 717-723.
[11] Chen Syuan-Yi, Chiang Hsin-Han, Liu Tung-Sheng, et al. Precision motion control of permanent magnet linear synchronous motors using adaptive fuzzy fractional-order sliding-mode control[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(2): 741- 752.
[12] 武志涛, 杨永辉. 一种永磁直线电机驱动X-Y平台精密轮廓跟踪控制策略[J]. 电工技术学报, 2018, 33(17): 4037-4043.
Wu Zhitao, Yang Yonghui. A precise contour tracking control method for X-Y table driven by permanent magnet linear motors[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4037-4043.
[13] 张晓光. 永磁同步电机调速系统滑模变结构控制若干关键问题研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.
[14] Wang Mingyi, Yang Rui, Zhang Chengming, et al. Inner loop design for PMLSM drives with thrust ripple compensation and high-performance current control[J]. IEEE Transactions on Industrial Elec- tronics, 2018, 65(12): 9905-9915.
[15] Cui Fengrui, Sun Zhaolong, Xu Wei, et al. Com- parative analysis of bilateral permanent magnet linear synchronous motors with different structures[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(2): 142-150.
[16] Zhang Xiaoguang, Cheng Yu, Zhao Zhihao, et al. Robust model predictive direct speed control for SPMSM drives based on full parameter disturbances and load observer[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 8361-8373.
Fixed Structure Sliding Mode Position Tracking Control for Permanent Magnet Linear Synchronous Motor Based on Extended Sliding Mode Disturbance Observer
Abstract Since the permanent magnet linear synchronous motor position servo system is susceptible to parameter disturbance, external disturbance and end effect, this paper proposes a composite sliding mode position control method based on fixed structure sliding mode controller and extended sliding mode disturbance observer. By adding restriction conditions, the fixed structure sliding mode controller ensures that the system state is located on the same side of the sliding mode surface, which weakens the chattering caused by the switch control of the conventional variable structure sliding mode controller and improves the quality of the sliding mode sliding motion. The extended sliding mode disturbance observer can compensate the system disturbance items that cannot be accurately measured in the fixed structure sliding mode controller, thereby eliminating the influence of the system disturbance items. In the end, the experiment indicates that the composite sliding mode control method is effective. Compared with the conventional sliding mode control, the compound position of sliding mode control method with superior tracking accuracy can weaken the chattering phenomenon and strengthen the robustness of position tracking system.
keywords:Permanent magnet linear synchronous motor, disturbance observer, fixed structure sliding mode controller, chattering, robustness
DOI: 10.19595/j.cnki.1000-6753.tces.201504
中图分类号:TP273
武志涛 男,1981年生,博士,副教授,研究方向为直线电机控制。E-mail: aswzt@163.com
程万胜 男,1969年生,教授,博士生导师,研究方向为机器人应用系统研究与设计。E-mail: cws_hit@126.com(通信作者)
收稿日期 2020-11-14
改稿日期 2021-01-03
辽宁省教育厅科学研究项目(LJKZ0308)和特种电机与高压电器教育部重点实验室开放课题(KFKT202104)资助。
(编辑 崔文静)