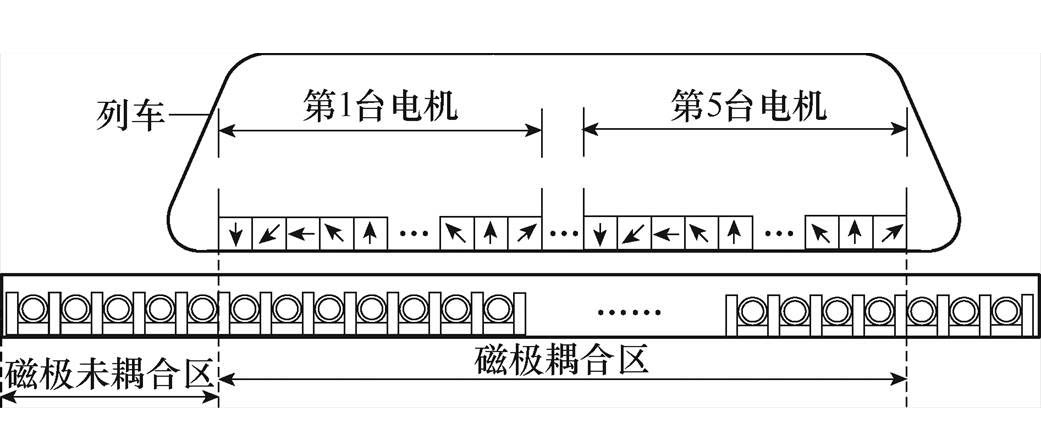
图1 中速磁悬浮列车及LS-PMLSM的结构
Fig.1 Medium-speed maglev train and the structure of LS-PMLSM
摘要 采用分段式长定子永磁直线同步电机牵引的中速磁悬浮列车在定子段换步时，相邻定子段绕组交链的永磁磁链的改变会导致牵引力损失，除此以外，在牵引过程中，馈电电缆长度的增加使得电机漏阻抗增大，在变流器供电容量的限制下，列车无法在试验线中完成全速度运行。该文首先建立含有定子段换步的长定子永磁直线同步电机数学模型，在此基础上，提出全速度运行的换步控制策略，以及适用于该电机的弱磁控制策略。该策略对q轴电流实时分配，保证在换步区间相邻定子段的q轴电流均跟随参考值；利用电机端电压计算得到d轴电流参考值，使电机在id=0控制和弱磁控制两种工况之间平滑切换。通过硬件在环实验，验证了采用所提策略可在线路长度和变流器容量限制下，实现列车全速度运行，并消除电机在定子段换步时的牵引力损失。
关键词：中速磁悬浮列车 长定子永磁直线同步电机 定子段换步 弱磁控制 硬件在环
轨道交通的大规模建设是城市快速发展的体现之一，相比于地铁和轻轨，磁悬浮交通克服了车辆与轨道之间的接触和磨损，可显著减少噪声污染和维修成本[1]。采用无铁心分段式长定子永磁直线同步电机（Long Stator Permanent Magnet Linear Syn- chronous Motor, LS-PMLSM）牵引的时速200km/h中速磁悬浮列车具有噪声低、牵引力波动小、转弯半径小、爬坡能力强等优点[2]，可在城市内以及其卫星城市之间等交通运输领域推广应用。
目前，我国磁悬浮交通的商业运营线的典型代表主要有采用常导长定子直线同步电机（Linear Synchronous Motor, LSM）牵引和电磁悬浮（Electro- magnetic Suspension, EMS）的上海高速磁浮线以及采用短定子直线感应电机（Linear Induction Motor, LIM）牵引和EMS技术的长沙磁浮快线[3]。中速磁悬浮列车采用LS-PMLSM牵引和“F”形电磁铁的EMS技术，不同于常导高速磁悬浮，其牵引系统和悬浮系统不存在直接的电气耦合，牵引电机为中置式，永磁励磁磁极安装在车底中部，与之耦合的无铁心长定子沿轨道铺设。为减小磁极与定子段非耦合区域的长度，提高运行效率和功率因数，长定子设置为分段式，并使用两台变流器通过馈电电缆为长定子交替供电。在列车换步时，正在驶离的定子段耦合的永磁磁链逐渐减小，则电机输出的牵引力逐渐减小，正在进入的定子段耦合的永磁磁链逐渐增大，输出的牵引力由零开始增大，变化速率与列车行驶速度有关。因此，在列车换步时，与电枢绕组耦合的永磁磁链的变化会导致电机牵引力降低和损失。除此以外，当列车正向牵引到不同定子段时，馈电电缆长度也在增大，即漏阻抗逐渐增大，这会提高对变流器供电容量的要求。在变流器容量的限制下，漏阻抗的增大会导致功率因数和效率降低，励磁磁极非耦合区的压降也会增大，逆变器输出能力达到上限时不能输出足够的电流以满足加速度的需要，进而导致列车无法在线路长度的限制下完成全速度运行。
目前，对LS-PMLSM牵引的中速磁悬浮列车控制策略研究较少，由于电机本体以及磁悬浮列车的特殊性，现有的旋转永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）以及高速磁悬浮列车牵引用的常导LSM的控制策略无法直接运用到LS-PMLSM上。上海高速磁浮运营线同样采用分段式长定子，在正线上采用三步法，车站和维修基地内采用两步法。其中，两步法在换步过程中存在电枢电流为零的时期，这会造成牵引力损失。三步法通过三套变流器轮流给两侧电枢绕组供电，不会造成牵引力损失，但是增加了变流站数量，建造成本较高[4]。针对中速磁悬浮列车的换步策略，文献[5]提出了牵引力损失最小的策略，但该策略未在全速工况下实现，并且未考虑换步时永磁磁链的变化造成两个变流器输出电压的动态变化过程。文献[6-7]分析了用于弹射的有铁心LS-PMLSM电感和磁链在动子出入定子段过程中的变化规律，并提出了定子段间电流同步跟踪策略。文献[8]对电机长定子的每个定子段设置了独立的控制环节，当永磁磁极运动到某一定子段时，对该定子段的电压和电流进行控制，控制系统较为复杂。
磁悬浮列车行驶在较高速度时反电动势较大，常导高速磁悬浮通过输出变压器增大供电电压，通过双端供电提供足够的电流以保证所需的牵引力[9-10]，但这种方式的牵引供电及控制系统复杂。而中速磁悬浮列车的牵引供电系统没有设置输出变压器，且采用单端供电的方式，列车的加速能力和最高速度受变流器容量的限制。若在不改变变流器容量的情况下进一步提高电机运行速度，可在较高速度时采用弱磁控制抵消一部分空载反电动势，以减小电机端电压，达到升速的目的[11]。在牵引系统中，弱磁控制可分为空间矢量脉宽调制（Space Vector Pulse Width Modulation, SVPWM）线性调制区和过调制区等不同策略，其中当SVPWM过调制时可实现对逆变器直流母线电压利用率的最大化，但此时电机电流谐波含量较多，造成牵引力波动较大[12]。在SVPWM线性调制区内的弱磁控制，电枢电流谐波特性较好，逆变器始终在正弦调制下。与旋转式PMSM弱磁控制不同的是，磁悬浮列车所受空气阻力随速度的增大而增大，为保证足够的加速度，d轴去磁电流负向增大的同时不能随之减小q轴电流，即在弱磁控制工况中，电流矢量幅值并不保持电流极限值不变。同时，去磁电流会在励磁磁极与定子段的非耦合区及馈电电缆处产生电压降落，且速度越高，漏感抗越大，去磁电流造成的电压降落越大，这有可能会造成电机端电压不降反升，达不到弱磁升速的效果。在PMSM中，常用的弱磁控制算法主要有梯度下降法、负直轴电流补偿法、公式计算法、单电流调节器法[13-16]等，需根据中速磁悬浮列车的特点，结合相应弱磁控制算法，提出适用于LS-PMLSM的弱磁控制策略。
本文首先分析了中速磁悬浮列车的牵引电机LS-PMLSM本体的牵引力、法向力和定子段换步时永磁磁链动态变化过程等电磁特性，得到了牵引电机的相关电气参数，并建立了dq旋转坐标系下考虑换步的LS-PMLSM数学模型。在此基础上，根据中速磁悬浮列车的牵引特点，提出了结合弱磁控制的定子段换步牵引控制策略。最后利用RT-Lab硬件在环实验平台验证了所提策略的有效性。实验结果表明，所提策略可使列车在换步时牵引力无损失，在变流器供电容量和试验线长度的限制下，实际速度可很好地跟随参考速度曲线，完成全速度运行。
中速磁悬浮列车采用中置式LS-PMLSM牵引，一节车厢共计5台电机。电机励磁磁极为安装在车厢底部的Halbach永磁体阵列，沿轨道铺设的长定子使用环氧树脂固定电枢绕组，不包含铁磁材料，列车及牵引电机的结构如图1所示。无铁心的长定子与电机励磁磁极不产生额外的法向力，有利于列车的悬浮控制。按照Halbach阵列排布的磁极使得永磁磁通密度集中在电机气隙侧，在磁极背侧的磁通密度近似为零，可减小励磁磁场对乘客的影响。
以单台LS-PMLSM为研究对象，建立有限元模型。在一个定子段内，产生牵引力的励磁磁极与定子段耦合区占比较小，非耦合区视为电机的漏阻感。当励磁磁极与定子段完全耦合时，单台LS-PMLSM的牵引力与法向力的力角特性曲线如图2所示。LS- PMLSM牵引力和法向力随电流矢量角度q 变化的曲线相位相差90°，则采用id=0控制时，单台电机可获得6kN的牵引力，而法向力为零。
图1 中速磁悬浮列车及LS-PMLSM的结构
Fig.1 Medium-speed maglev train and the structure of LS-PMLSM
图2 单台LS-PMLSM牵引力和法向力的力角特性
Fig.2 Force-angle characteristics of traction and normal force of single LS-PMLSM
当励磁磁极处在定子段换步位置，即励磁磁极与相邻两个定子段均存在耦合时，两个定子段电枢绕组交链的永磁磁链动态变化过程如图3所示。
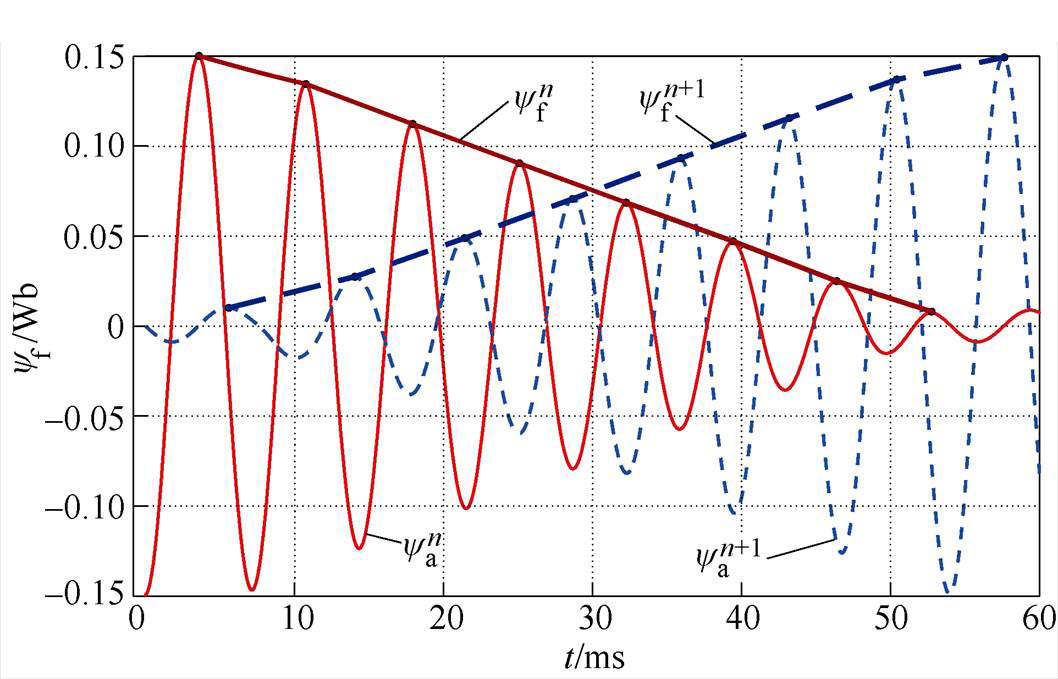
图3 单台电机换步时永磁磁链动态变化过程
Fig.3 Dynamic change process of permanent magnet flux linkage during the changeover of the single motor
图3给出了换步过程中相邻定子段的a相电枢绕组交链的单台电机永磁磁链动态变化过程，相永磁磁链的幅值经等幅值变换后即为dq坐标系下的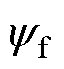
，可见第n段（设n为奇数）定子段的
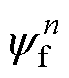呈线性减小趋势，第n+1段定子段的
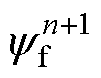呈线性增大趋势。因此，在换步过程中，相邻定子段耦合的磁链可看作是线性变化的，变化速率正比于当前列车行驶速度。单台LS-PMLSM的电气参数见表1。
表1 单台LS-PMLSM电气参数
Tab.1 Electrical parameters of single LS-PMLSM
参 数数 值 定子电阻Rs/(mW/m)0.45 d轴电感Ld/(mH/m)2.22 q轴电感Lq/(mH/m)2.22 永磁磁链yf/Wb0.144 95 极距t/m0.2
中速磁悬浮供电系统的牵引变电站由两套变流器单元构成，交替给定子段供电。牵引变电站由35kV电网经过移相变压器接入12脉波不控整流器，再使用5MV·A的三电平中点钳位（Neutral Point Clamped, NPC）逆变器通过馈电电缆给轨道电枢绕组供电，逆变器直流母线电压为3 500V，该牵引供电系统框图如图4所示。
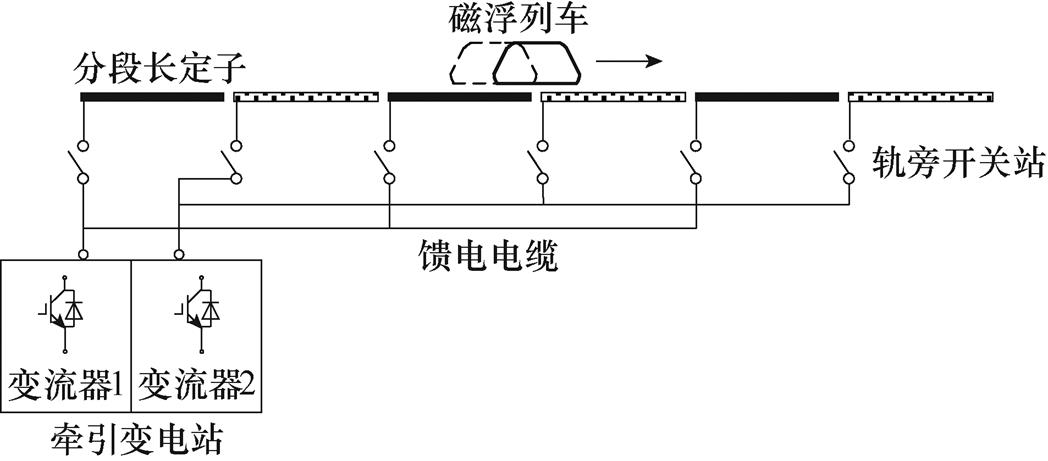
图4 中速磁悬浮列车牵引供电系统
Fig.4 Traction power supply system of medium-speed maglev train
图4中箭头所指方向为正向牵引方向，左起第一个定子段编号为1。牵引变电站内的变流器1给奇数段定子供电，变流器2给偶数段定子供电，通过轨旁开关站进行切换。两编组的中速磁悬浮列车包含10台电机，励磁磁极长度l共计27m，而定子段长度L为500m，除此以外还有长度不定的馈电电缆。电机有效出力部分是励磁磁极和定子段的耦合区域，定子段内的非耦合部分和馈电电缆是电枢绕组的漏阻感，可将逆变器输出端的整体视为一个电机。根据传统PMSM的dq坐标系下电压方程，建立含馈电电缆的LS-PMLSM数学模型，其等效电路如图5所示。ud、uq分别为d、q轴电压，id、iq分别为d、q轴电流。Rs、Ro分别为电机励磁磁极与定子段耦合区和非耦合区的电阻。Lds、Lqs为耦合区的电枢反应电感，LS-PMLSM为隐极机，d轴和q轴电感相等。Ldos、Lqos为励磁磁极与定子段非耦合区漏感，LS-PMLSM的永磁体上没有导磁材料，且永磁体磁导率和空气磁导率近似相等，因此可忽略电枢绕组电感值受电机励磁磁极位置的影响[17]。Rk和Ldk（Lqk）分别为馈电电缆电阻、电感。非耦合区和馈电电缆上的阻感与定子电阻Rs、电感Lds（Lqs）为串联关系，令R、Ld、Lq为逆变器输出端所接阻感之和，有
图5 含馈线的LS-PMLSM等效电路
Fig.5 Equivalent circuit of LS-PMLSM with feeder cable
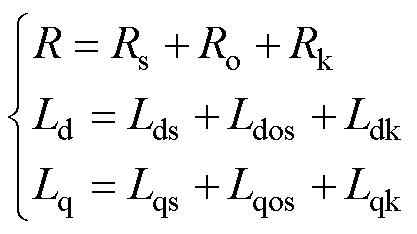（1）
直线电机电角速度we和速度v的关系为
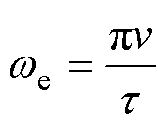（2）
当电机励磁磁极与定子段完全耦合时，根据LS-PMLSM等效电路可得到dq坐标系下的电压方程为
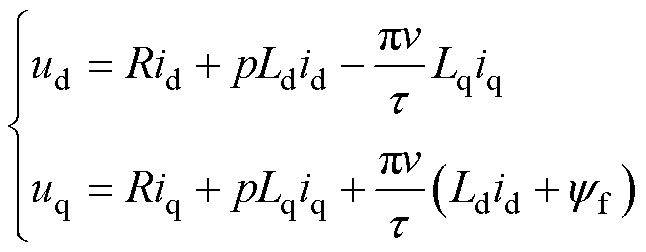（3）
式中，p为微分算子。LS-PMLSM牵引力Fe的方程为
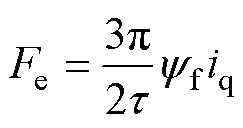（4）
式（3）和式（4）即为非换步区间LS-PMLSM的数学模型。电机励磁磁极和电枢侧均无铁心，可不考虑磁阻力，则在列车行驶过程中，空气阻力为主要部分，空气阻力FA与列车编组数N和行驶速度v有关，可表示[18]为
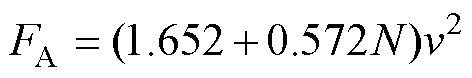（5）
中速磁悬浮列车的运动方程为
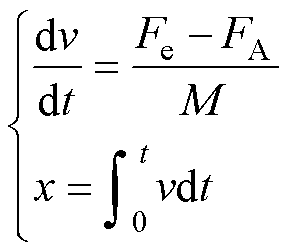（6）
式中，M为列车质量；x为电机位置。
当电机励磁磁极与第n段定子段完全耦合时，其永磁磁链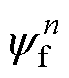为
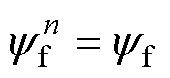（7）
当电机励磁磁极与第n段定子段不耦合时，有
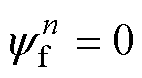（8）
列车在换步时，式（3）和式（4）中的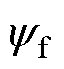是一个变值，相邻定子段的永磁磁链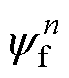和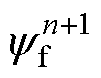分别线性减小和增大，励磁磁极逐渐驶离第n段定子段，逐渐进入第n+1段定子段，此时两定子段电枢绕组交链的永磁磁链分别为
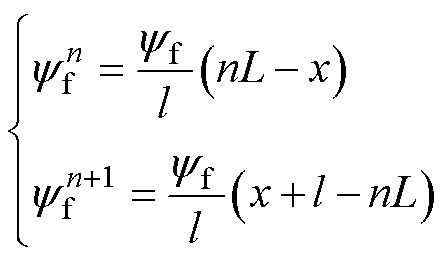（9）
式中，L为定子段长度；l为电机励磁磁极长度；n为定子段编号。当列车行驶到不同定子段上时，馈电电缆长度不同，漏阻抗也就不同，即式（3）中阻感值不定。中速磁悬浮线路定子段所连接的馈电电缆长度与定子段长度相等，则不同定子段上馈电电缆电感、电阻可分别表示为
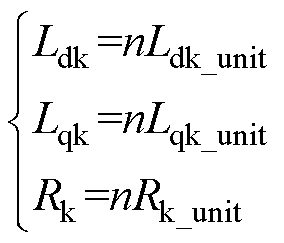（10）
式中，Ldk_unit（Lqk_unit）和Rk_unit分别为500m长度的馈电电缆的电感、电阻。换步时由变流器1和变流器2共同为长定子供电，则在换步时电机的数学模型为
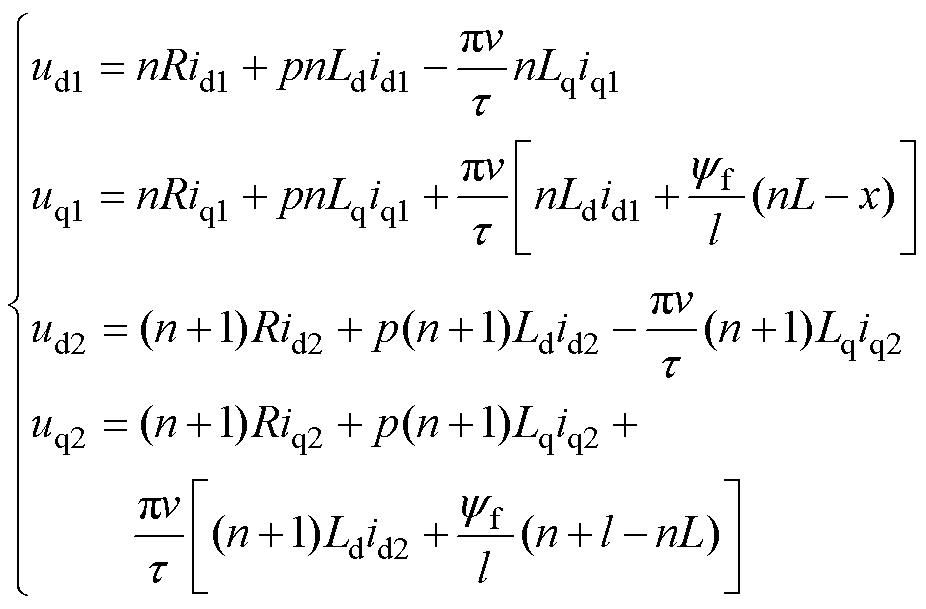（11）
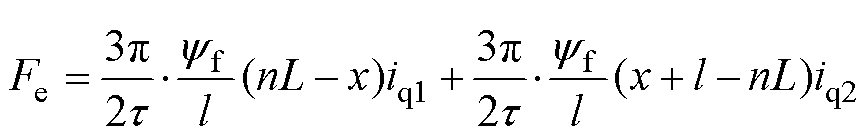（12）
式中，下标1、2分别为变流器1、2的输出电压和电流。
将式（3）、式（4）与式（11）、式（12）结合即为考虑换步的LS-PMLSM数学模型。
中速磁悬浮列车的牵引控制主要面临由馈电电缆长度逐渐增大导致的负载变大和换步时牵引力损失等问题。由于逆变器输出能力有限，采用id=0控制，当逆变器输出电压达到上限时，电流调节器饱和，逆变器无法输出足够的电流以保证加速度的需要。在换步区间需要保证相邻两段定子段电流准确跟随电流参考值，使得换步时电机牵引力不损失。
根据LS-PMLSM的数学模型和上述分析，本文采用SVPWM线性调制区内的弱磁控制策略。列车在较高速度下，电机端电压接近逆变器输出最大值时，通入去磁电流以抵消部分空载电动势，减小电机端电压，从而能够继续提高电机速度。采用弱磁控制时，id＜0，在牵引系统和悬浮系统具有强耦合的常导高速磁悬浮中，不常使用该方法。而在中速磁悬浮中，LS-PMLSM和EMS式电磁铁不存在直接的电气耦合，因此调节id不会直接影响悬浮系 统[19]。
由式（3）可知，ud、uq方程中存在关于电感的耦合项，且速度越高，耦合项所占比重越大，在较高速度时，感抗产生的电压降落远大于电阻造成的电压降落[20]，因此可重写ud、uq方程为
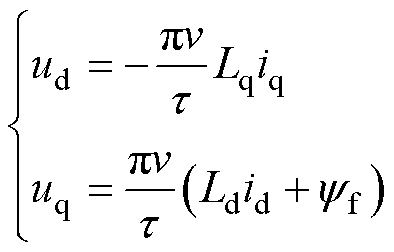（13）
电机端电压幅值，即逆变器输出电压幅值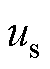
为
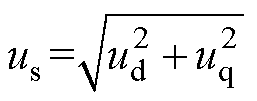（14）
联立式（13）和式（14）可得到idiq平面上电压圆的方程为
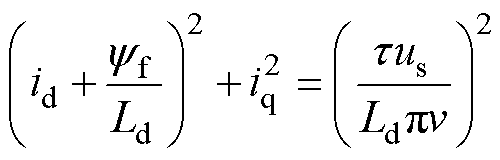（15）
将式（15）转化为
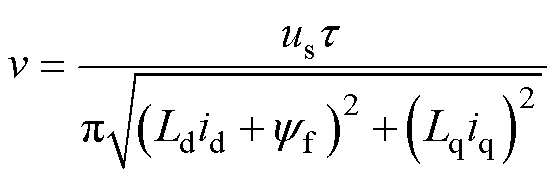（16）
通过式（16）可知，当逆变器输出电压幅值达到最大值usmax时，采用id=0控制电机无法升速，可通入负值的d轴去磁电流，降低空载反电动势，即采用弱磁控制提高电机速度。随着电机速度v增大，式（15）中电压圆的半径逐渐缩小，形成一系列随速度变化的关于逆变器输出电压的圆形轨迹，圆心坐标为（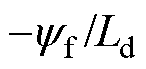
, 0）。逆变器输出电流幅值is为
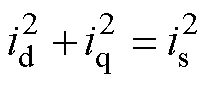（17）
式（17）是idiq平面上电流圆的方程。以列车正向牵引为例，即逆变器工作在第一和第二象限，将式（15）和式（17）的轨迹同时画在idiq平面上，逆变器输出电压和电流的轨迹如图6所示。
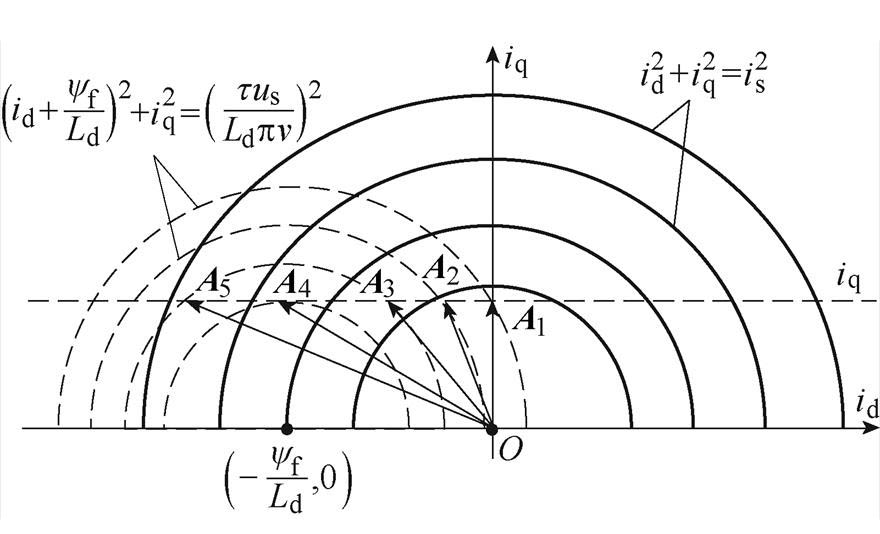
图6 逆变器输出电压和电流的轨迹
Fig.6 Trajectories of inverter output voltage and current
在电机达到某一速度时，此时电流矢量为图6中的A1，电枢电流完全为q轴分量。若此时电机端电压即将达到逆变器输出最大值，需通入d轴去磁电流实现弱磁升速，且为了抵抗列车空气阻力，在q轴电流不变情况下，逐渐负向增大d轴电流，电流矢量按照从A1～A5的顺序转动。这一过程中，d轴电流分量由零变负，电流矢量末端所经过的电压圆轨迹的半径先减小后增大，即电机端电压先减后增，所以在这种工况下，控制d轴去磁电流在一定范围内变化可使电机端电压降低，从而逆变器可以继续输出电流，使电机具备加速能力。
将上述分析应用在不同速度情况下，如图7所示给出了保持q轴电流不变并在弱磁控制时电机端电压幅值的变化情况。q轴电流设定为500A，可以发现，在0～200km/h速度范围内，通入逐渐负向增大的d轴去磁电流，电机端电压先减小后增大，说明只要保证d轴去磁电流不超过让端电压开始转折的值，就可以减小电机端电压。
在磁悬浮列车牵引中，一些工况需保持加速度不变，图8给出了在列车加速度设定为0.5m/s2时，不同速度下进入弱磁控制时电机端电压幅值的变化情况。可见，通入逐渐负向增大的d轴去磁电流后，电机端电压仍呈先减小后增大的变化趋势。
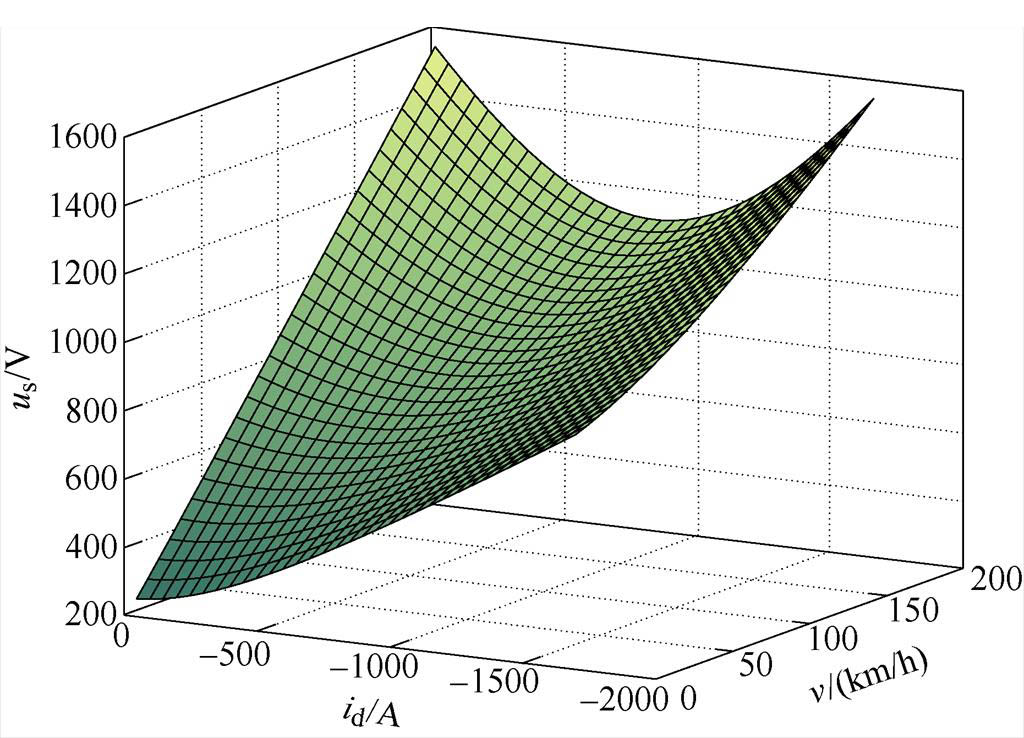
图7 q轴电流不变时电机的端电压
Fig.7 Terminal voltage of motor with constant iq
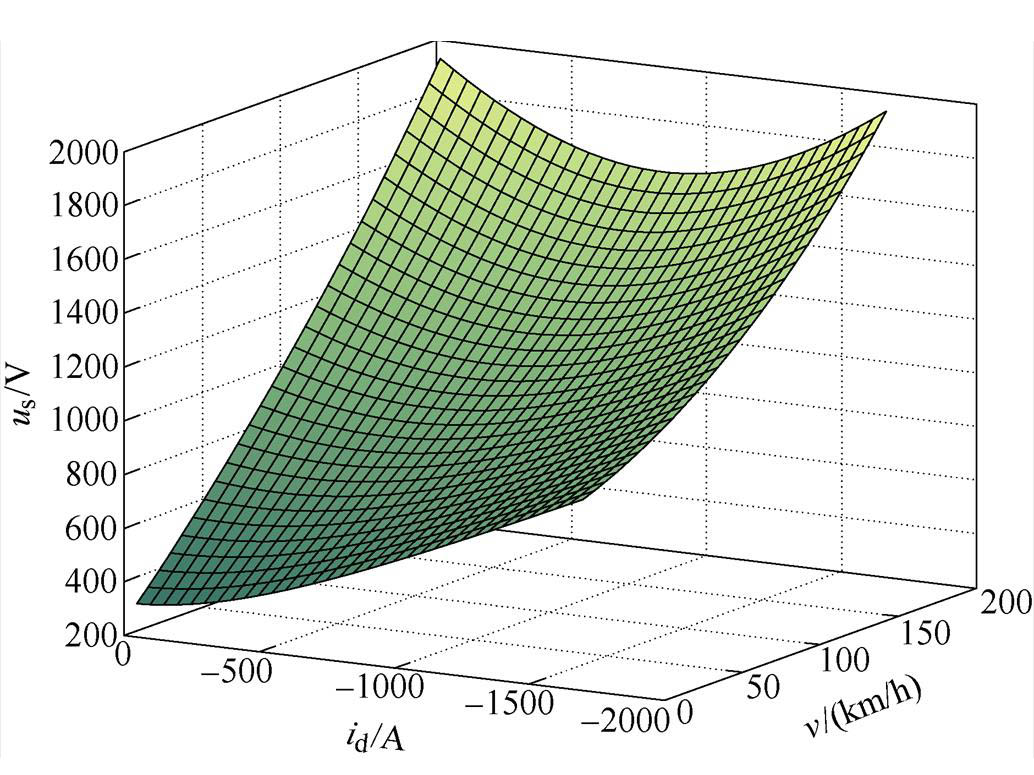
图8 加速度不变时电机的端电压
Fig.8 Terminal voltage of motor with constant acceleration
综上所述，对于含有馈电电缆的LS-PMLSM，可以通过弱磁控制减小电机端电压，进而使逆变器继续输出电流并使得电机升速。
根据上述分析，需当电机端电压即将达到逆变器输出电压最大值时，d轴电流由零变负，即进入弱磁工况。在SVPWM线性调制区，逆变器输出最大电压的幅值usmax与直流母线电压udc的关系为
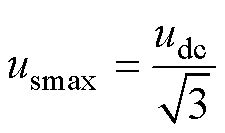（18）
当电机端电压us接近usmax后，逆变器开始输出去磁电流。因此，需采集两台逆变器的输出电压，并与该值实时比较，从而计算出d轴电流的参考值，弱磁控制策略框图如图9所示。
两台逆变器交替为长定子供电，选择输出电压的较大值作为电机端电压去进行运算。图9中的弱磁电流PI调节器输出上限为0，下限为d轴去磁电流最小设定值，需保证该值不小于让端电压开始转折的值。当电机端电压小于逆变器最大输出电压δ时，该PI调节器输出的d轴电流参考值为0，即id=0控制；当电机端电压超过该设定阈值时，PI调节器开始输出负的d轴电流作为参考值，即进入弱磁控制。采用这种弱磁控制策略可根据实时运行工况输出需要的去磁电流，不依赖电机参数，简单方便，易于工程实现。对于分段式LS-PMLSM，在弱磁控制时，相比于id=0控制多出一个自由度，还需考虑在定子段换步时d轴电流的分配。
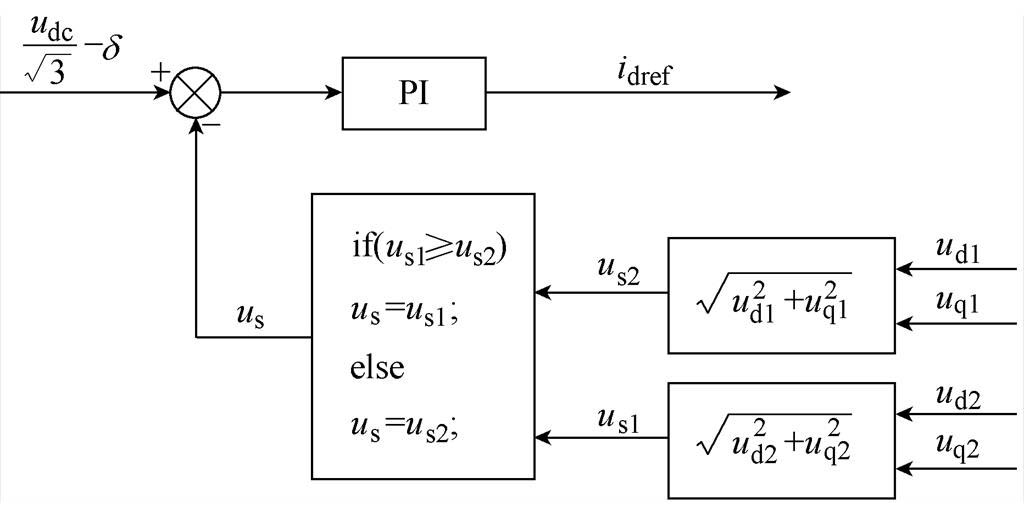
图9 弱磁控制策略框图
Fig.9 Block diagram of flux weakening control strategy
中速磁悬浮列车的LS-PMLSM采用基于励磁磁场定向的控制策略。定子段换步示意图如图10所示。在一个牵引供电分区内由两套变流器交替给定子段供电，分别控制奇数段和偶数段定子。当电机励磁磁极与定子段n完全耦合且车头距离换步点的距离大于Dx时，只有定子段n的轨旁开关站处于闭合状态，由变流器1供电，如图10a所示。为保证换步时牵引力不损失，当列车距离换步点为Dx时，提前闭合定子段n+1的轨旁开关站，变流器2开始起动供电，须保证车头达到换步点时，定子段n+1的电枢电流达到电流参考值，如图10b所示。在列车换步过程中，变流器1和变流器2同时工作，且定子段n和定子段n+1的电枢电流频率、幅值与相位均相同，如图10c所示。如图10d所示，当列车完全离开定子段n时，此时电机励磁磁极开始完全与定子段n+1耦合，控制定子段n的电流开始下降，当电流下降到0时，定子段n的轨旁开关站断开，开始仅由变流器2供电，标志一次换步完成，后续换步过程与上述同理。
（a）仅由变流器1供电
（b）变流器2起动供电
（c）变流器1、2同时供电
（d）开始仅由变流器2供电
图10 定子段换步示意图
Fig.10 Schematic diagram of stator segment changeover
中速磁悬浮列车牵引用LS-PMLSM的牵引控制策略框图如图11所示。
LS-PMLSM采用速度电流双闭环控制，q轴电流参考值由速度调节器和q轴电流前馈共同计算得出，q轴电流前馈值由阻力FA和列车加速度a计算得到，加速度a由变流器的输出能力决定，通过加速度a可得到速度参考曲线。定子段换步控制需根据电机的绝对位置x，并由q轴电流分配模块和d轴电流分配模块实现，分别通过4个电流PI调节器，加上电压前馈值得到d轴和q轴参考电压信号，去控制两台三电平NPC逆变器，然后对LS-PMLSM进行交替供电，其中d轴和q轴的电压前馈信号根据式（3）和式（11）计算得出。
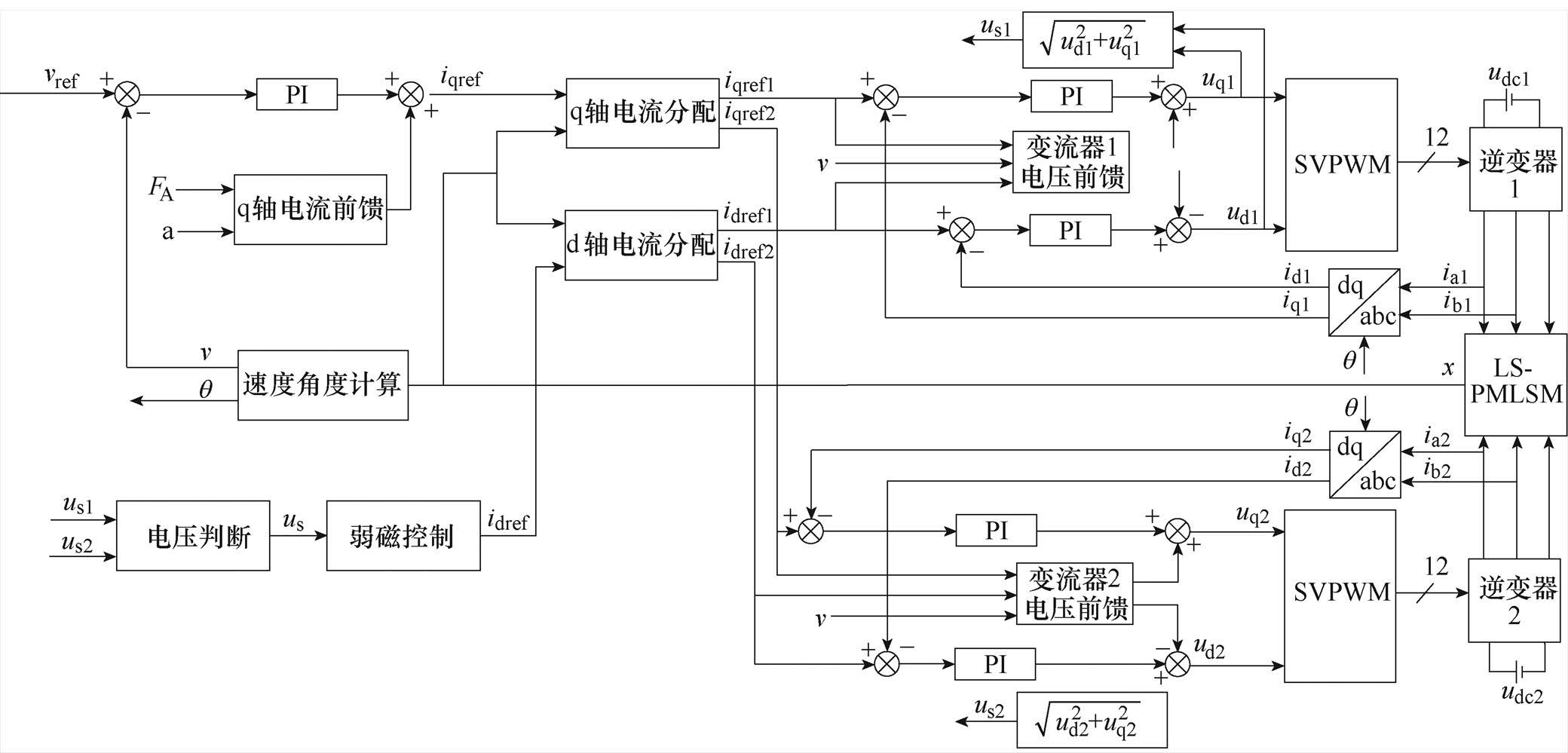
图11 LS-PMLSM牵引控制策略框图
Fig.11 Block diagram of traction control strategy for LS-PMLSM
在生成加速度曲线和弱磁控制时，需要采集逆变器输出电压us，在非换步时区间，通过比较两个逆变器输出电压us1和us2，选择较大的值进行相应运算。在换步过程中，定子段n耦合的永磁磁链在减小，定子段n+1耦合的磁链从零开始增大，因此空载反电动势减小，这会导致两台逆变器输出电压均降低，进而导致加速度和d轴电流参考值突变。由于换步时间较短，可在换步过程中，保持加速度和d轴电流参考值为开始换步前一拍的值不变。
根据本文所提出的LS-PMLSM牵引控制策略，在RT-Lab硬件在环平台进行实验验证，实验平台主要由RT-Lab仿真机和控制系统两部分组成。其中RT-Lab仿真机的CPU型号为OP5600，内部运行中速磁悬浮列车牵引变流器和LS-PMLSM本体模型，通过仿真机的OP5353数字量输入板卡、OP5330-3模拟量输出板卡以及通信模块与真实的控制系统进行数据交互。控制系统为基于PowerPC芯片、VxWorks操作系统的机箱，该机箱完成A-D采样、电机闭环控制和三电平NPC逆变器调制等功能。中速磁悬浮实验平台架构示意图和实物分别如图12和图13所示。
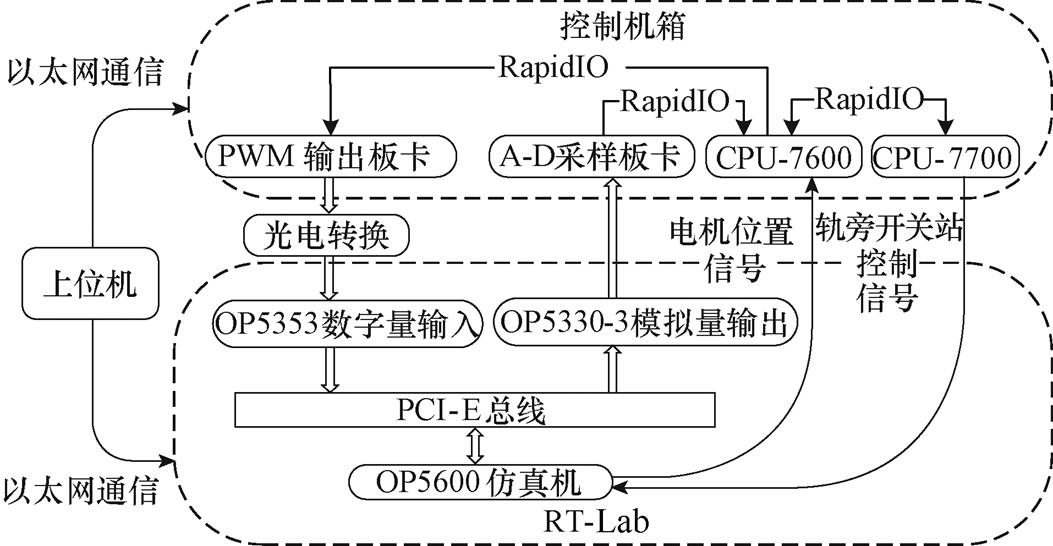
图12 中速磁悬浮实验平台架构示意图
Fig.12 Schematic diagram of medium-speed maglev experimental platform
图13 中速磁悬浮RT-Lab实验平台
Fig.13 Medium-speed maglev RT-Lab experimental platform
RT-Lab仿真机中模型参数采用实际的中速磁悬浮试验线数据，共计8个定子段，每个定子段长度L均为500m，有效位移为4km减去列车总长，两编组的列车共计10台牵引电机，列车长度为34m，质量M=44t，目标速度为200km/h，按照表1中所列电机参数进行实验，验证所提出的LS-PMLSM换步控制及弱磁控制策略。
在中速磁悬浮列车正向牵引过程中，每一定子段耦合的10台电机的永磁磁链变化波形如图14所示。图中给出了第1次和第6次换步过程中相邻定子段电枢绕组交链的永磁磁链动态变化过程局部放大图。正在离开的定子段上交链的永磁磁链由最大值线性减小为零，即将进入的定子段上交链的磁链由零线性增大为最大值1.449 5Wb。8个定子段共需进行7次换步，换步时永磁磁链的变化速率体现列车运行速度。
图14 带有换步的永磁磁链波形
Fig.14 Permanent magnet flux linkage waveforms with changeover
在到达换步点前，需要将下一定子段绕组中的q轴电流跟随上参考电流，以保证在换步时牵引力不损失。在实验中，设定当列车达到换步点前200m闭合下一个定子段的轨旁开关并让变流器开始供电；当列车完全驶离上一个定子段时，相应的变流器开始停止供电，直至输出电流为零，再关断轨旁开关。两台牵引变流器输出的q轴电流波形如图15所示。以第一个换步过程为例，在车头进入换步区间之前，逆变器2输出的iq2已上升到电流参考值iqref，使得在换步过程中，两台逆变器共同工作，均按照iqref为参考调节输出电流。即使定子段1和定子段2的永磁磁链在变化，仍可保证两个定子段的电机励磁磁极耦合部分出力总和不损失。q轴电流的变化趋势体现列车速度从零加速到目标速度再制动到零的全速度运行过程，在每一换步点均可实现平滑换步。
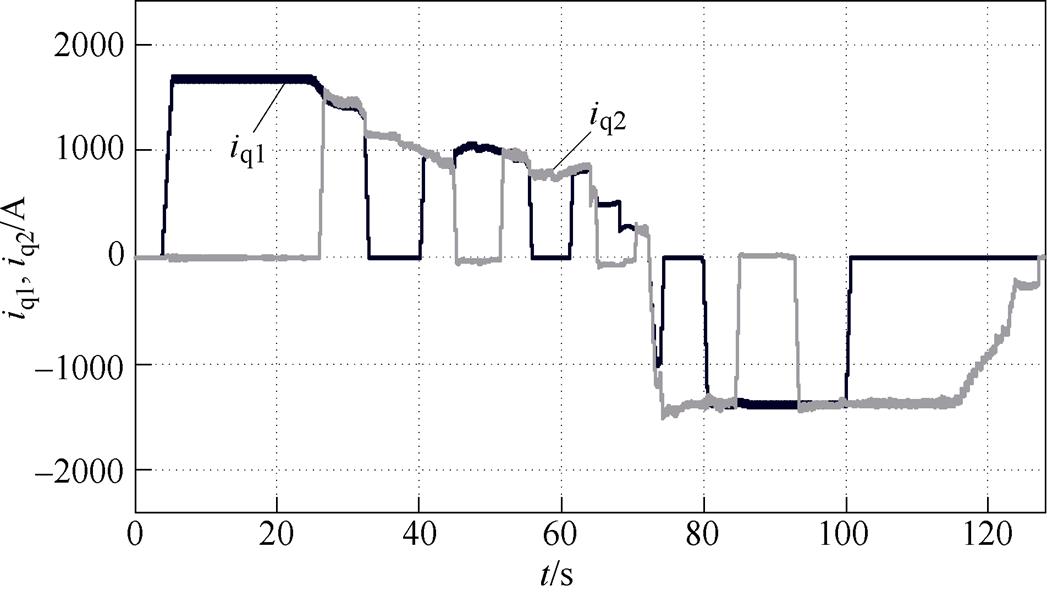
图15 q轴电流波形
Fig.15 Current waveforms of q-axis
当列车处在换步区间时，由两个逆变器同时供电，输出电流需保证同频同相且幅值相等。如图16所示为第一次换步时逆变器1和逆变器2输出的a相电流，可见二者基本一致。
图17分别为分段牵引力、分段牵引力之和与参考牵引力的比较，参考牵引力由q轴电流参考值计算得到。分段牵引力的变化趋势与永磁磁链变化趋势一致，励磁磁极与定子段耦合部分可输出牵引力，换步时第n段定子段输出牵引力减小，第n+1段定子段输出牵引力增大，将二者相加得到分段牵引力的合力Fe，可发现合力与参考牵引力Fe_ref吻合程度较高，说明所提换步策略在全速度范围内换步时列车牵引力几乎不损失，显著减小了换步时的牵引力波动，保证换步时加速度不突变，提高了运行效率。
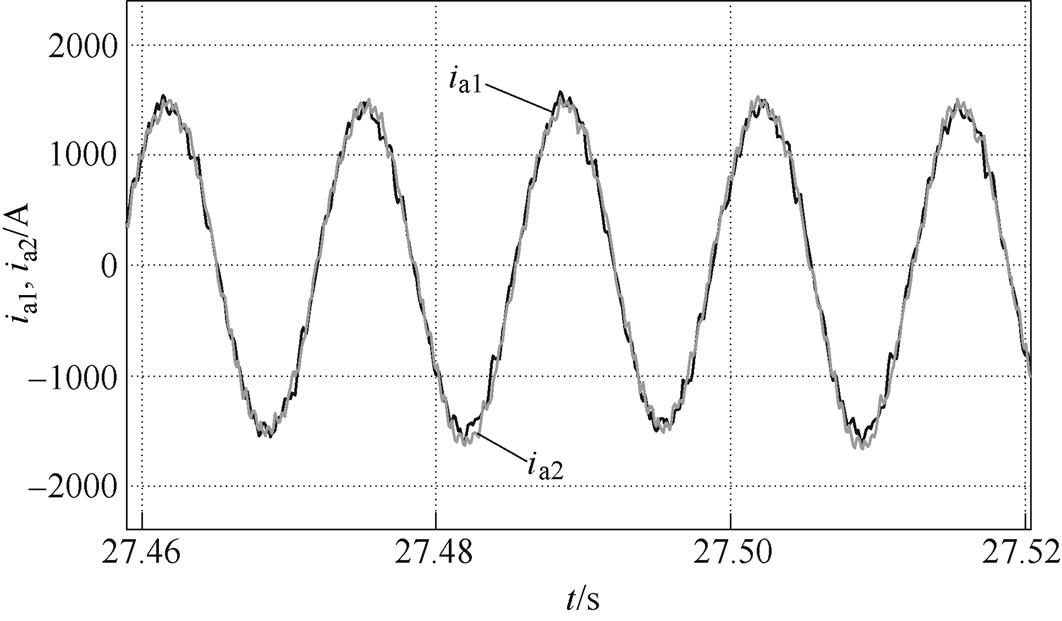
图16 两逆变器输出的a相电流波形
Fig.16 Current waveforms of a-phase output by two inverters
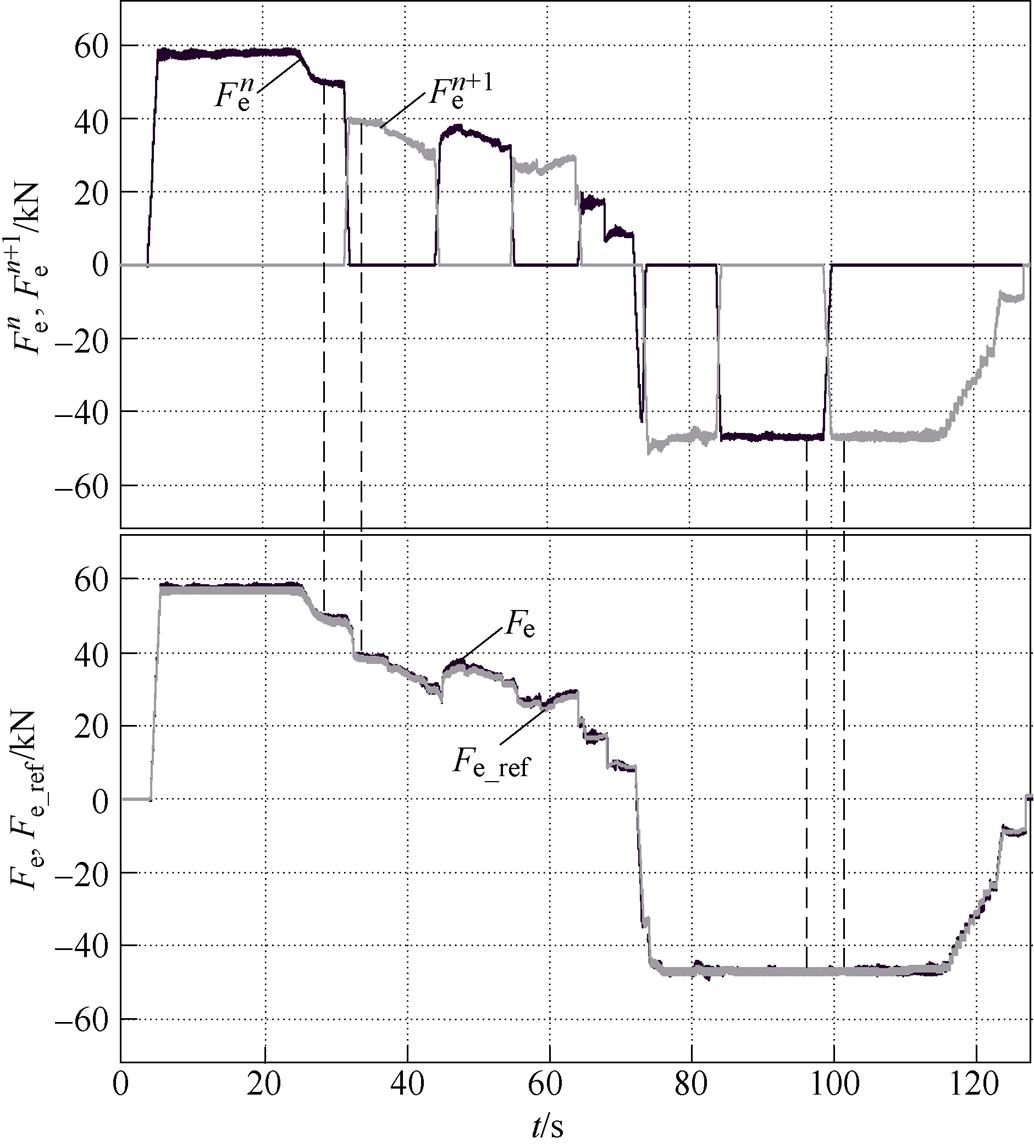
图17 分段牵引力及合力波形
Fig.17 Sectional traction and total force waveforms
在运行全程仅使用id=0控制策略时，两编组的中速磁悬浮列车的速度曲线和d轴电流波形如图18所示。可见，列车在4km的试验线范围内没有完成全速度运行。列车加速到200km/h所用时间为73.4s，平均加速度为0.76m/s2，d轴电流的波动因列车换步所致。
采用所提出的适用于LS-PMLSM的弱磁控制策略，列车实际速度与参考速度曲线以及不同定子段d轴电流波形如图19所示。实际速度与参考速度基本吻合，速度曲线平滑且达到了最大目标速度200km/h，牵引加速过程63.2s，制动过程54.4s，牵引过程平均加速度为0.88m/s2。相比于仅使用id=0控制，牵引时间缩短了10.2s，加速度提升了0.12m/s2。在牵引加速和最高速度阶段，d轴电流由零变负，表明电机进入了弱磁工况。在SVPWM线性调制区，逆变器能够输出的最大电压为2 020.73V，为避免电流调节器饱和，在实验中设置id=0控制和弱磁控制的切换点电压为1 600V，d轴电流参考值下限设定为-600A，列车运行过程中可根据电机端电压实时调整d轴去磁电流的参考值。实验结果表明，该弱磁控制策略适用于LS-PMLSM，可实现弱磁升速，实际速度能够准确跟踪参考速度。弱磁控制时，在换步区间采用与q轴电流相同的电流分配策略，保证运行模式的连续以及平滑过渡。
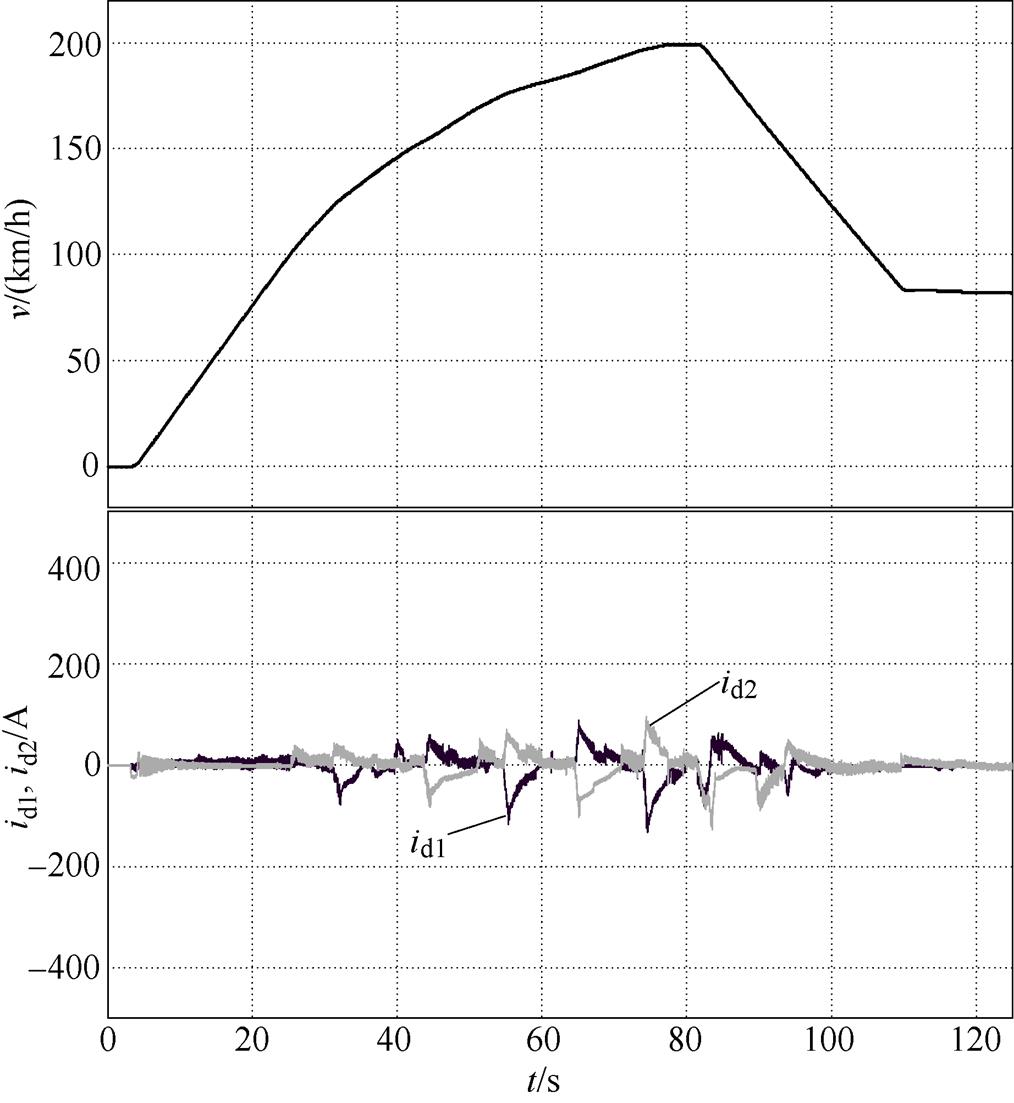
图18 id=0控制速度曲线与d轴电流波形
Fig.18 id=0 control speed curve and d-axis current waveforms
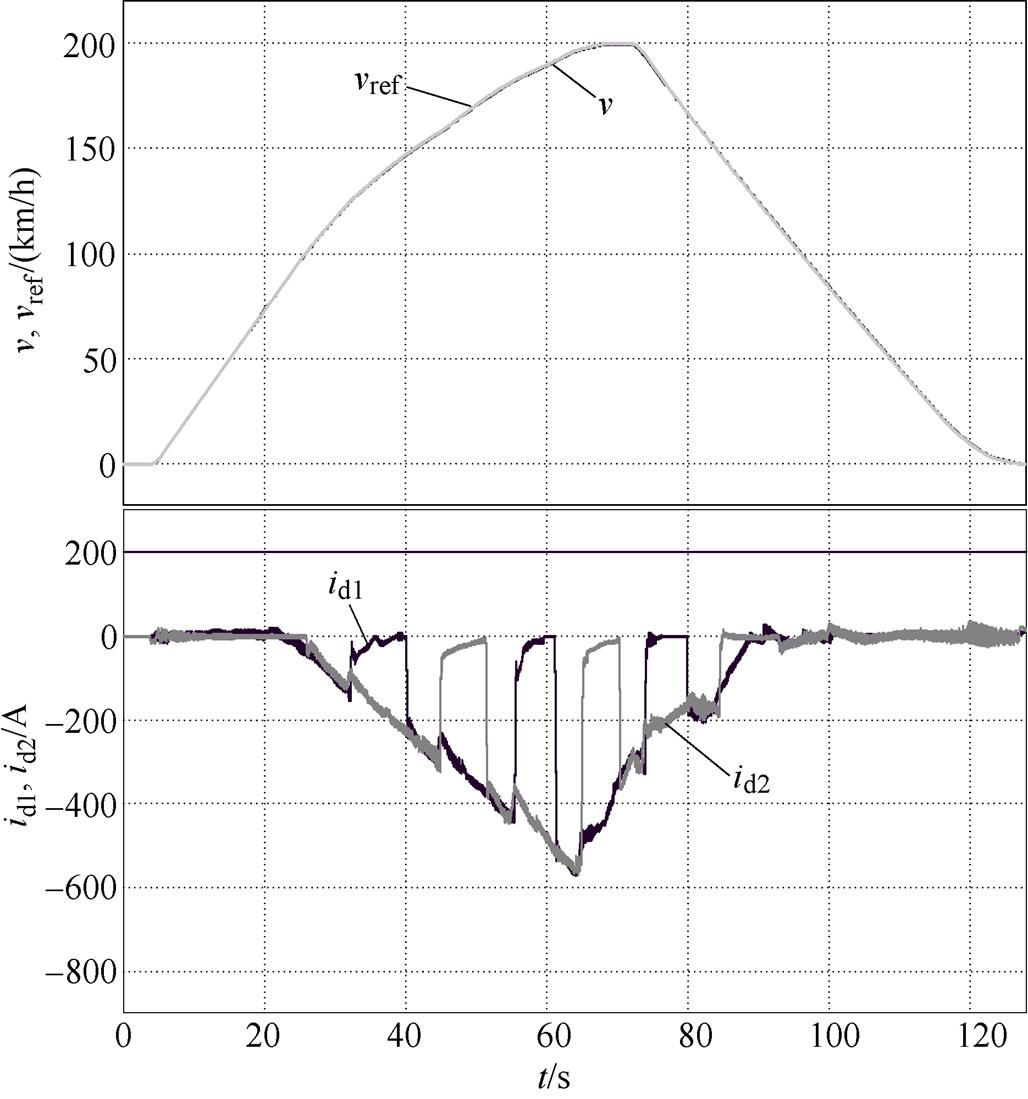
图19 弱磁控制速度曲线与d轴电流波形
Fig.19 Flux weakening control speed curves and d-axis current waveforms
图20为采用所提弱磁控制时列车的位移曲线，行驶距离为3 760m，处于最大有效行驶距离3 966m范围内。表明所提适用于LS-PMLSM的弱磁控制策略可使中速磁悬浮列车在规定行驶范围内，达到最大目标速度，实现全速度运行。
图20 列车位移曲线
Fig.20 The displacement curve of the train
本文对中速磁悬浮列车牵引用的LS-PMLSM控制策略进行研究，首先分析了牵引电机励磁磁极与定子段完全耦合时和换步时的电磁特性，得到了换步时永磁磁链的变化规律并提出了完备的电机数学模型。在此基础上，提出了定子段换步牵引控制策略，该策略可消除LS-PMLSM在不同工况下换步时牵引力的损失。针对列车在运行过程中，由馈电电缆长度变化引起的电机漏阻抗增大问题，提出一种适合于LS-PMLSM的弱磁控制策略，使得列车可在有限行驶范围内和变流器容量限制下，完成全速度运行。最后通过硬件在环实验，实现了中速磁悬浮列车的牵引力无损换步和全速度运行，验证了所提换步策略和LS-PMLSM弱磁控制策略的有效性。
参考文献
[1] 吴祥明. 磁悬浮列车[M]. 上海: 上海科学技术出版社, 2003.
[2] Wang Ke, Ge Qiongxuan, Shi Liming, et al. Develop- ment of ironless Halbach permanent magnet linear synchronous motor for traction of a novel maglev vehicle[C]//2017 11th International Symposium on Linear Drives for Industry Applications (LDIA), Osaka, 2017: 1-5.
[3] 吕刚. 直线电机在轨道交通中的应用与关键技术综述[J]. 中国电机工程学报, 2020, 40(17): 5665-5675.
Lü Gang. Review of the application and key tech- nology in the linear motor for the rail transit[J]. Proceedings of the CSEE, 2020, 40(17): 5665-5675.
[4] 王娟. 磁悬浮列车用长定子直线同步电机特性研究与故障分析[D]. 北京: 中国科学院电工研究所, 2004.
[5] Wang Ke, Deng Zhuoyuan, Shi Liming, et al. Traction control of multi-section long primary ironless linear synchronous motor for maglev vehicle[C]//2019 12th International Symposium on Linear Drives for Industry Applications (LDIA), Neuchatel, 2019: 1-4.
[6] 祝贺, 张今朝, 董睿, 等. 绕组分段永磁直线同步电机无传感器控制[J]. 电工技术学报, 2017, 32(21): 65-76.
Zhu He, Zhang Jinzhao, Dong Rui, et al. Sensorless control of winding segmented permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2017, 32(21): 65-76.
[7] 李立毅, 祝贺, 刘家曦, 等. 初级绕组分段永磁直线电机段间推力优化控制[J]. 电机与控制学报, 2014, 18(4): 79-87.
Li Liyi, Zhu He, Liu Jiaxi, et al. Optimal inter- segment thrust control applied in primary winding segmented PMLSM[J]. Electric Machines and Control, 2014, 18(4): 79-87.
[8] Suzuki K, Kim Y J, Dohmeki H. Driving method of permanent-magnet linear synchronous motor with the stationary discontinuous armature for long-distance transportation system[J]. IEEE Transactions on Industrial Electronics, 2012, 59(5): 2227-2235.
[9] 孙鹏琨, 葛琼璇, 王晓新, 等. 基于硬件在环实时仿真平台的高速磁悬浮列车牵引控制策略[J]. 电工技术学报, 2020, 35(16): 3426-3435.
Sun Pengkun, Ge Qiongxuan, Wang Xiaoxin, et al. Traction control strategy of high-speed maglev train based on hardware-in-the-loop real-time simulation platform[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3426-3435.
[10] 刘金鑫, 葛琼璇, 王晓新, 等. 高速磁浮牵引控制系统半实物实验研究[J]. 电工技术学报, 2015, 30(14): 497-503.
Liu Jinxin, Ge Qiongxuan, Wang Xiaoxin, et al. Hardware-in-loop research of traction-system for high-speed maglev[J]. Transactions of China Electro- technical Society, 2015, 30(14): 497-503.
[11] 张梓绥, 王琛琛, 游小杰, 等. 基于单Q轴电流调节器的永磁同步电机电流轨迹控制[J]. 电工技术学报, 2018, 33(24): 5779-5788.
Zhang Zisui, Wang Chenchen, You Xiaojie, et al. Current locus control of permanent magnet syn- chronous motor based on single Q-axis current regulator flux-weakening method[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5779- 5788.
[12] 王贺超, 夏长亮, 阎彦, 等. 基于谐振控制的表贴式永磁同步电机弱磁区电流谐波抑制[J]. 电工技术学报, 2014, 29(9): 83-91.
Wang Hechao, Xia ChangLiang, Yan Yan, et al. Current harmonic suppression in the flux-weakening control of surface permanent magnet synchronous motors using resonant controllers[J]. Transactions of China Electrotechnical Society, 2014, 29(9): 83-91.
[13] 盛义发, 喻寿益, 桂卫华, 等. 轨道车辆用永磁同步电机系统弱磁控制策略[J]. 中国电机工程学报, 2010, 30(9): 74-79.
Sheng Yifa, Yu Shouyi, Gui Weihua, et al. Field weakening operation control strategies of permanent magnet synchronous motor for railway vehicles[J]. Proceedings of the CSEE, 2010, 30(9): 74-79.
[14] Jang-Mok K, Seung-Ki S. Speed control of interior permanent magnet synchronous motor drive for the flux weakening operation[J]. IEEE Transactions on Industry Applications, 1997, 33(1): 43-48.
[15] Chi Song, Xu Longya, Zhang Zheng. Efficiency- optimized flux-weakening control of PMSM incorporating speed regulation[C]//2007 IEEE Power Electronics Specialists Conference, Orlando, 2007: 1627-1633.
[16] Morimoto S, Sanada M, Takeda Y. Effects and compensation of magnetic saturation in flux- weakening controlled permanent magnet synchronous motor drives[J]. IEEE Transactions on Industry Applications, 1994, 30(6): 1632-1637.
[17] 耿伟伟, 张卓然. 新型外转子Halbach永磁阵列定子无铁心电机设计与分析[J]. 电工技术学报, 2015, 30(14): 130-137.
Geng Weiwei, Zhang Zhuoran. Design and analysis of external rotor coreless permanent magnet motor with Halbach magnet array[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 130-137.
[18] 李峥. 中速磁浮列车牵引供电系统优化及特性仿真研究[D]. 北京: 中国科学院大学, 2018.
[19] Zhao Mutian, Zhang Ruihua, Du Yumei, et al. A subsection flux weakening scheme based on direct traction control for long primary permanent magnet linear synchronous motor[C]//2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, 2019: 1-5.
[20] 朱进权, 葛琼璇, 孙鹏琨, 等. 基于自抗扰的高速磁浮列车牵引控制策略[J]. 电工技术学报, 2020, 35(5): 1065-1074.
Zhu Jinquan, Ge Qiongxuan, Sun Pengkun, et al. Traction-system research of high-speed maglev based on active disturbance rejection control[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(5): 1065-1074.
Traction Control Strategy of Segmented Long Stator Permanent Magnet Linear Synchronous Motor for Medium-Speed Maglev Train
Abstract Medium-speed maglev train is driven by the segmented long stator permanent magnet linear synchronous motor (LS-PMLSM), the change of the permanent magnet flux linkage of the adjacent stator windings will lead to the loss of traction during a changeover. Besides, the increase of the length of the feeder cable in the traction process will increase the leakage impedance of the motor. Under the limitation of the converter’s power supply capacity, the train cannot run at full speed in the test line. In this paper, the mathematical model of LS-PMLSM with stator segment changeover is established. On this basis, the changeover strategy at full speed and the flux weakening control strategy suitable for the motor are proposed. The strategy allocates the q-axis current in real-time to ensure that the current of adjacent stator segments in a changeover period follows the reference value. The d-axis reference current is calculated by the motor terminal voltage, which can make the motor smoothly switch between id=0 and flux weakening control. Through the Hardware-in-the-Loop experiment, it is verified that the strategy can realize the full speed operation under the constraints of the line length and converter capacity, and eliminate the traction loss of the motor during the stator segment changeover.
keywords：Medium-speed maglev train, long stator permanent magnet linear synchronous motor, stator segment changeover, flux weakening control, hardware-in-the-loop
DOI: 10.19595/j.cnki.1000-6753.tces.201570
中图分类号：TM359.4
赵牧天 男，1995年生，博士研究生，研究方向为大功率变流器与直线电机牵引控制技术。E-mail: zhaomutian@mail.iee.ac.cn
葛琼璇 女，1967年生，研究员，博士生导师，研究方向为高压大功率变流器控制技术、高性能电机牵引控制技术。E-mail: gqx@mail.iee.ac.cn（通信作者）
收稿日期 2020-11-30
改稿日期 2021-02-03
国家重点研发计划高速磁浮交通系统关键技术研究课题资助项目（2016YFB1200602-19）。
（编辑 崔文静）