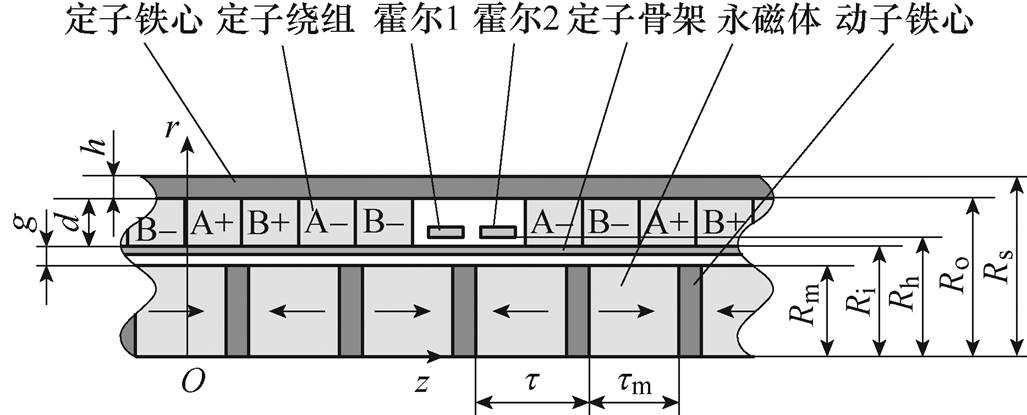
图1 两相无槽TPMSLM结构示意图
Fig.1 Construction of the two-phase slotless TPMSLM
摘要 由于具有价格低、对机械扰动不敏感的优势，线性霍尔传感器被应用于圆筒型永磁同步直线电机动子位置检测。但线性霍尔传感器位置辨识精度会受到磁场谐波的影响而下降。为提升霍尔传感器的位置检测精度，该文在考虑机械加工误差的情况下，进行直线电机的可靠性与鲁棒性优化设计。首先，建立直线电机位置辨识精度与电机推力的解析模型，基于解析模型分析设计变量与设计指标之间的影响关系。然后，使用神经网络建立直线电机设计指标的响应曲面模型，通过不同推力系数下Pareto最优前沿得到优化设计的概率约束条件。最后，使用可靠性与鲁棒性优化设计的方法，在略微削减推力系数与磁通密度峰值的情况下，大幅降低磁场谐波含量，将电机霍尔位置的检测精度从357mm提升至109mm。
关键词：直线电机 线性霍尔传感器 神经网络 可靠性与鲁棒性优化设计
直线电机由于可以省去传动机构直接提供直线运动，没有回程误差，被大量地应用于数控机床、工业自动化等领域。其中，圆筒型永磁同步直线电机（Tubular Permanent Magnet Synchronous Linear Motor, TPMSLM）具有结构简单、推力密度大，且不存在横向端部效应的优势，在直线驱动领域具有广泛的应用前景[1]。
永磁同步直线电机的矢量控制需要较为准确的动子位置反馈。线性光栅尺是常用的位置反馈传感器。光栅尺可以提供mm级的高精度的反馈位置信息。通过光栅细分技术，分辨率可以提升至纳米精度。但线性光栅尺存在安装体积大，对振动、灰尘、油污等环境干扰较为敏感等缺点，同时也存在价格昂贵的问题。
为了提升伺服系统的鲁棒性、降低系统成本，相继提出基于反电动势辨识的无传感算法[2]与基于高频信号注入的无传感算法[3]。但基于反电动势辨识的无传感算法位置精度会受到电机参数准确性的影响下降，并且在零速与低速情况下无法使用。而依赖于电机凸极性的高频信号注入无传感算法则由于直线电机存在端部效应，导致dq轴电感随动子位置变化，算法实现困难[4]。
因此，价格便宜、安装体积小、对环境扰动不敏感的线性霍尔传感器受到了越来越多的关注[5-8]。线性霍尔传感器的工作原理为霍尔效应，传感器输出电压与垂直于载流体的磁通密度成正比。使用霍尔传感器检测与动子位置相关的气隙磁通密度，进而可以求解得到电机动子位置。在霍尔传感器安装形式上，相距90°电角度的双霍尔传感器[6-7]和间距120°电角度的三霍尔传感器[5]最为常见。同时也有学者提出使用霍尔传感器阵列来提升位置检测精 度[9]。在实际应用中，由于传感器零漂、不同霍尔传感器之间放大系数的差异和磁场谐波等因素的影响，霍尔传感器的位置检测精度会下降[10]。传感器零漂和放大系数差异这两类干扰一般采用离线标定的方式进行补偿。磁场谐波干扰抑制的方法主要包括滤波算法与霍尔传感器安装位置优化。其中，滤波算法包括正交锁相环[7]、自适应陷波器[11]、同频率提取器[12]、卡尔曼滤波器[13]等方法。对于霍尔传感器安装位置优化的研究内容较少，文献[14]采用二维有限元方法定量分析了霍尔传感器轴向安装位置与磁场谐波含量之间的关系，并选择了可以忽略定子铁心影响的最小轴向距离作为最终的传感器安装位置。文献[15]采用有限元算法研究了TPMSLM中霍尔传感器径向安装位置与磁通密度谐波含量的关系，发现随着离轴距离增加，磁通密度幅值与谐波含量同时减小。以上文献只进行了霍尔传感器安装位置优化，并未考虑进行电机结构的优化设计，导致谐波含量减小程度受限。同时针对大批量电机制造场合，需要在考虑制造误差的情况下进行电机的可靠性鲁棒优化设计，以保证电机性能的一致性，减少生产制造过程中的次品率。
本文采用可靠性鲁棒优化设计（Reliability- Based Robust Design Optimization, RBRDO）的方法，在考虑加工制造误差的情况下，进行了霍尔传感器安装位置与电机结构的优化设计。首先，建立了电机位置辨识精度与电机推力的解析模型，基于解析模型分析了设计变量对设计指标的影响规律。然后，使用神经网络拟合的方法建立了TPMSLM的设计目标模型，通过多目标优化求解得到的Pareto最优前沿确定了RBRDO的概率约束条件。采用蒙特卡洛算法与遗传算法进行了TPMSLM的可靠性鲁棒优化设计。最后，通过优化前后样机性能对比验证了优化算法的有效性。
本文以两相无槽轴向充磁的TPMSLM为研究对象。电机包括定子与动子两部分。定子由定子铁心、定子绕组、定子骨架与两个相距90°电角度的霍尔传感器构成。其中，AB两相环形绕组以90°电角度的间隔依次排布并缠绕在由聚酰亚胺制成的定子骨架上。霍尔传感器通过胶棒固定在定子骨架中部。电机动子由永磁体和动子铁心构成。永磁体沿轴向充磁，其磁极性沿轴向交替变化并由动子铁心隔开。两相无槽TPMSLM结构示意图如图1所示。
图1 两相无槽TPMSLM结构示意图
Fig.1 Construction of the two-phase slotless TPMSLM
图1中，O为圆柱坐标系原点，Rs为电机半径，Ro为线圈绕组外径，Ri为线圈绕组内径，Rh为霍尔传感器安装位置，Rm为永磁体半径，h为定子铁心厚度，d为定子绕组线圈厚度，g为物理气隙厚度，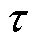
为电机极距，
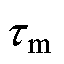为永磁体长度。
文献[16]基于标量磁位的原理解析计算了TPMSLM的磁通密度分布模型，在此直接引用其结论并做简要说明。该模型做出了以下假设：
（1）动子与定子铁心相对磁导率为无穷，同一铁心表面为等磁位面。
（2）忽略直线电机端部效应对于磁场分布造成的影响。
（3）永磁体的工作点为剩余磁通密度，即B=Br。
基于以上假设，通过求解标量磁位的拉普拉斯方程可以得到气隙中径向磁通密度分布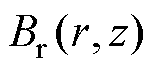
为
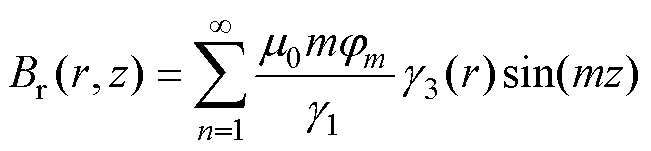（1）
其中
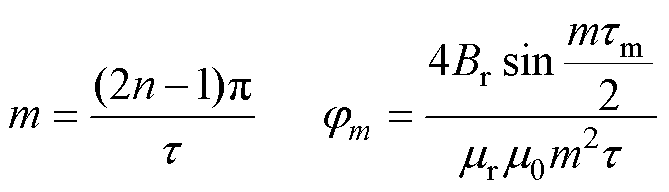
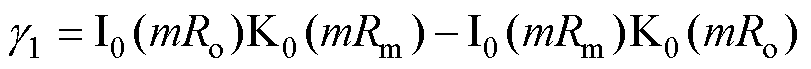
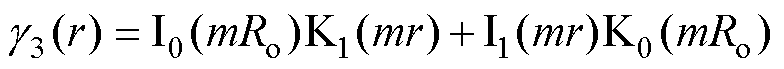
式中，r为圆柱坐标系半径；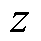
为距原点的轴向距离；
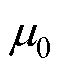为真空磁导率；
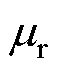为永磁体相对磁导率；
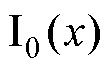与
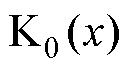为第一和第二类零阶变型贝塞尔函数；
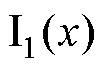与
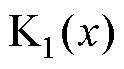为第一和第二类一阶变型贝塞尔函数。
为方便后续推导，定义定子坐标系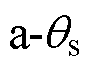
，动子坐标系
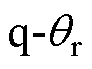，两坐标系之间距离为
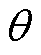，表示动子位置。TPMSLM坐标系定义示意图如图2所示。其中，
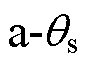坐标系a轴与A相绕组中心重合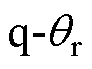，坐标系q轴与永磁体中心重合。可以得到两坐标系角度之间的换算关系为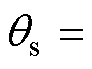
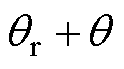。其中，所有角度定义为电机的电角度，与轴向距离的转换关系为
。
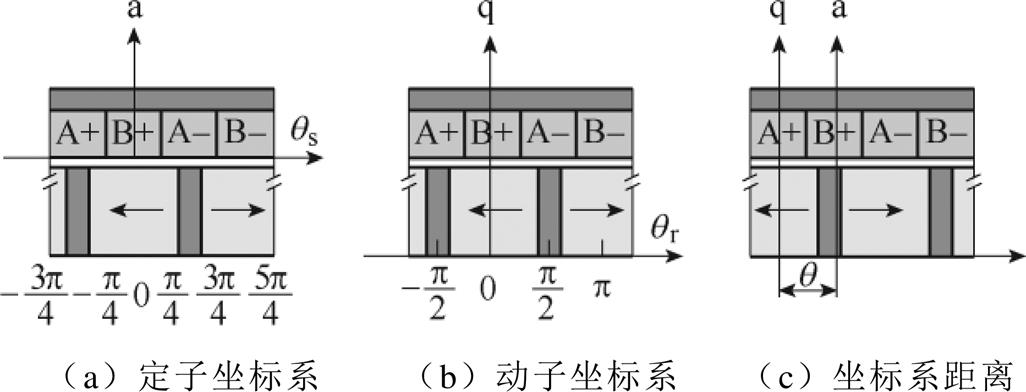
图2 TPMSLM坐标系定义示意图
Fig.2 The reference coordinate systems of TPMSLM
由1.1节中气隙径向磁通密度分布可以得到霍尔传感器1和霍尔传感器2安装位置处的磁通密度分别为
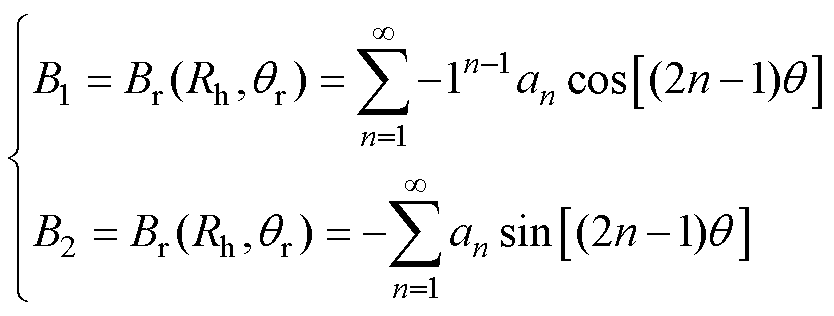（2）
式中，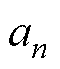
为2n-1次磁通密度谐波幅值，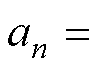
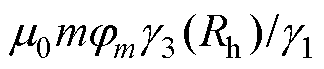。采样得到霍尔传感器1与霍尔传感器2处磁通密度后，可以由反正切函数计算得到电角度的估计值
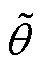为
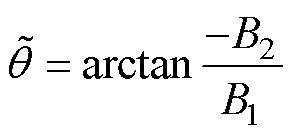（3）
由此，可以得到动子位置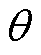的估计误差为
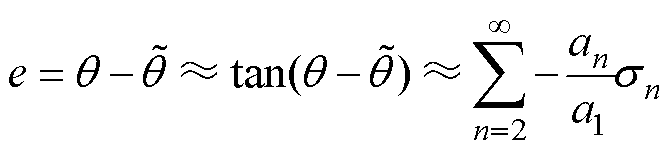（4）
其中
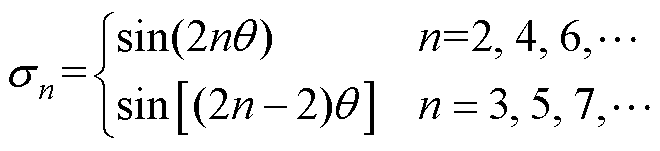
可以看到，动子位置估计误差为实际位置的正弦函数。且磁通密度的奇次谐波带来偶次谐波的位置估计误差。估计误差的最大值与谐波含量有关，可以得到位置估计误差的上界为
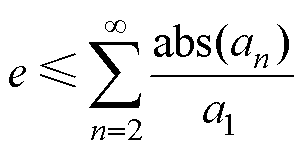（5）
由式（5）可知，位置估计误差上界为磁通密度谐波含量的绝对值累加，降低磁场谐波含量可以有效降低霍尔传感器的位置估计误差。为了保证动子位置辨识的精度，设立以下两项霍尔传感器安装位置处磁场评价标准：磁通密度峰值（Peak Flux Density, PFD）与总谐波畸变率（Total Harmonic Distortion, THD）。两项指标定义为
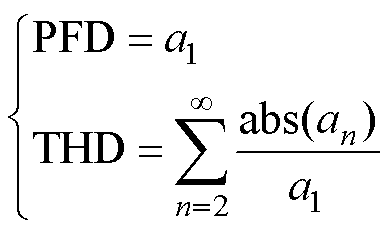（6）
式中，PFD为磁场基波幅值，决定了霍尔传感器采集信号的信噪比，PFD值越大，由测量噪声引起的位置估计误差越小；THD则决定了由磁场谐波带来的位置估计误差，THD越小，位置辨识越精确。
TPMSLM单位截面积的导体受到的洛伦兹力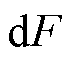
可以表示为
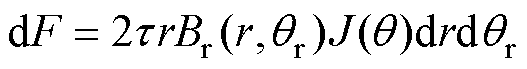（7）
式中，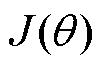
为电荷面密度分布函数，对于A相绕组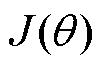，可以表示为
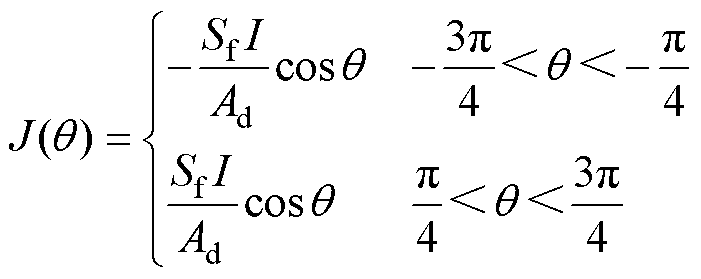
式中，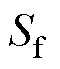
为槽满率；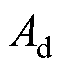
为单个导线的截面积；
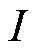为相电流的幅值。A相绕组所产生的电磁推力
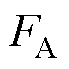可以由式（7）的积分得到，有
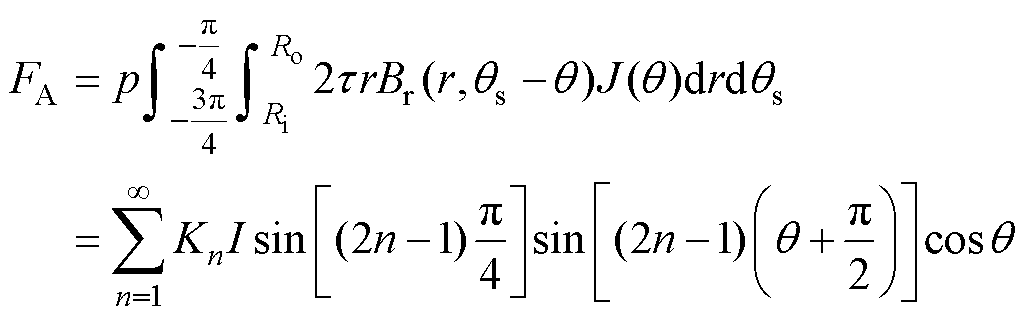（8）
其中
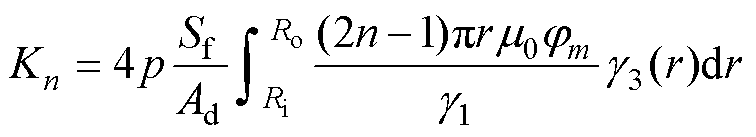
式中，p为A相绕组的虚槽数。
同理，可以得到B相绕组电磁推力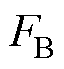
，两者相加可以得到电机的电磁推力为
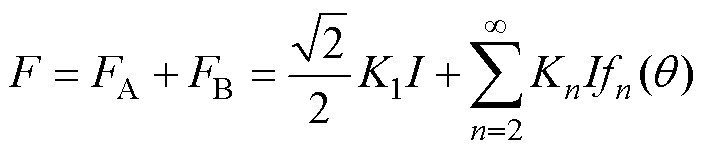（9）
其中
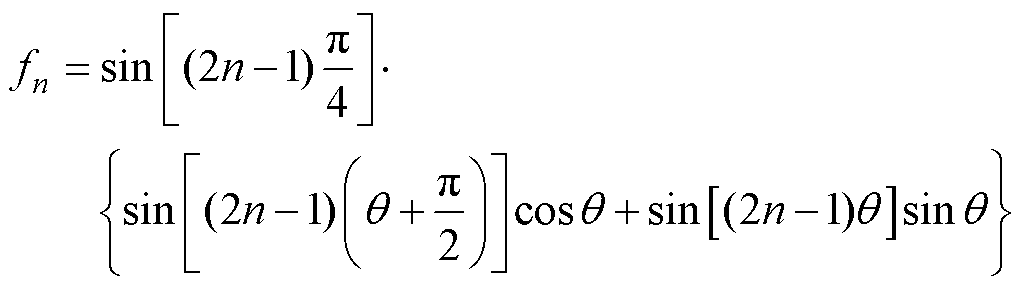
从式（9）可以看到，电磁推力由两部分组成：第一项为电磁推力的直流分量，由磁场基波产生，可以衡量电磁推力的大小；第二项为电磁推力的谐波分量，由磁场谐波产生，是造成直线电机推力波动的原因之一。定义TPMSLM的推力系数（Thrust Coefficient, TC）为
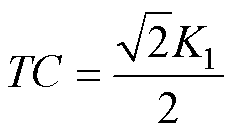（10）
易知，TC的物理含义为单位q轴电流所产生的电磁推力值。
从PFD、THD和TC的解析表达式可知，永磁体长度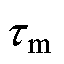、永磁体半径Rm、线圈厚度d与霍尔传感器安装位置Rh为重要影响变量。同时，在绕组线圈半径Ro与物理气隙长度g不变的情况下，可以得到Rm与d之间的关系为
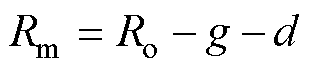（11）
因此，选择永磁体长度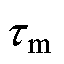、线圈厚度d与霍尔传感器安装位置Rh作为最终的设计变量。TPMLSM固定参数见表1，设计变量的取值范围与公差见表2。
表1 TPMLSM的固定参数
Tab.1 The fixed parameters of TPMLSM
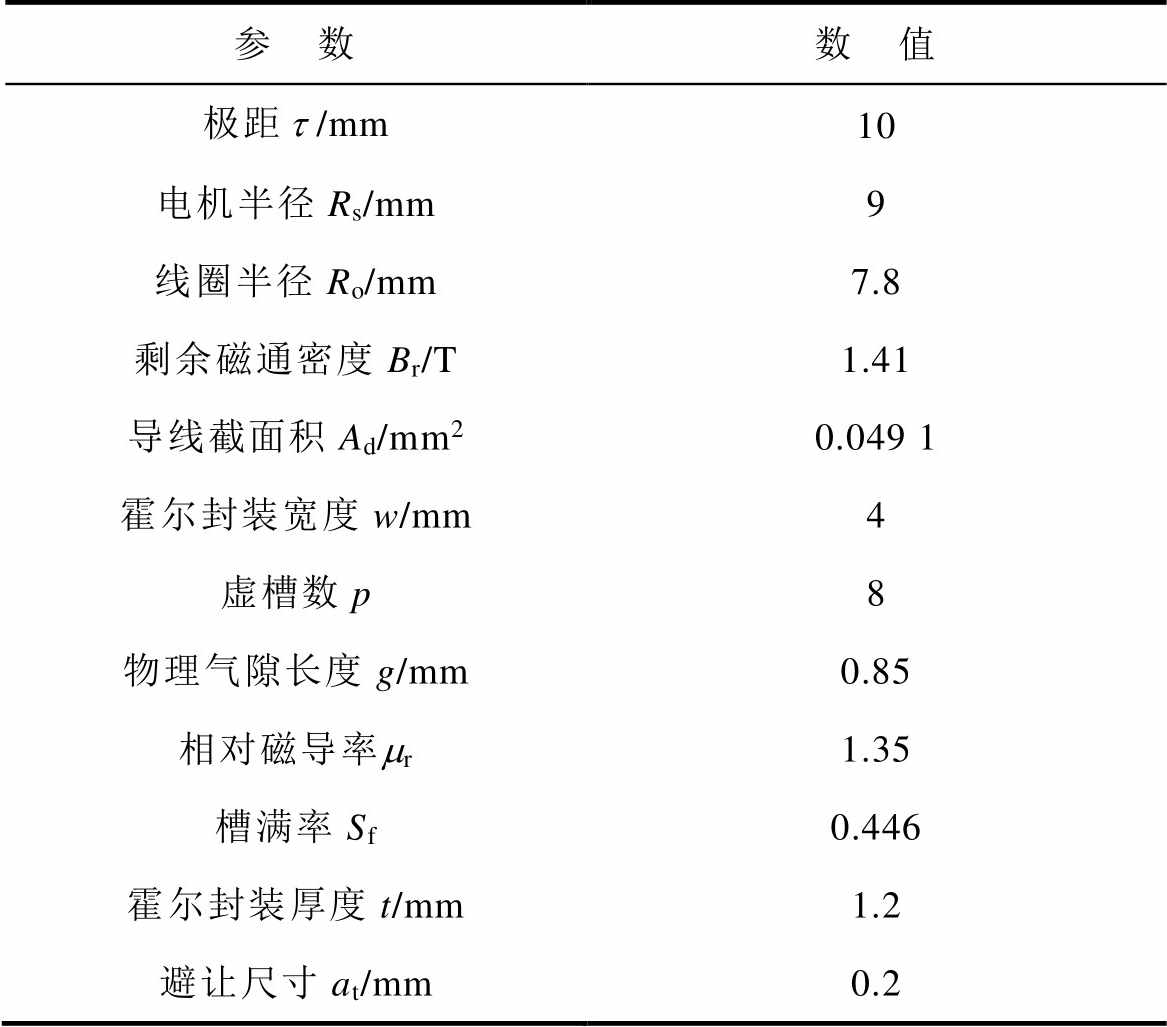
参 数数 值 极距/mm10 电机半径Rs/mm9 线圈半径Ro/mm7.8 剩余磁通密度Br/T1.41 导线截面积Ad/mm20.049 1 霍尔封装宽度w/mm4 虚槽数p8 物理气隙长度g/mm0.85 相对磁导率mr1.35 槽满率Sf0.446 霍尔封装厚度t/mm1.2 避让尺寸at/mm0.2
表2 TPMLSM设计变量取值范围与公差
Tab.2 The constraints and tolerances of design variables
参数取值范围公差 永磁体长度tm/mm4≤tm≤8±0.04 线圈厚度d/mm1.8≤d≤2.8±0.03 霍尔安装位置Rh/mm＞0±0.2
表2中，函数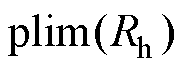
的定义为
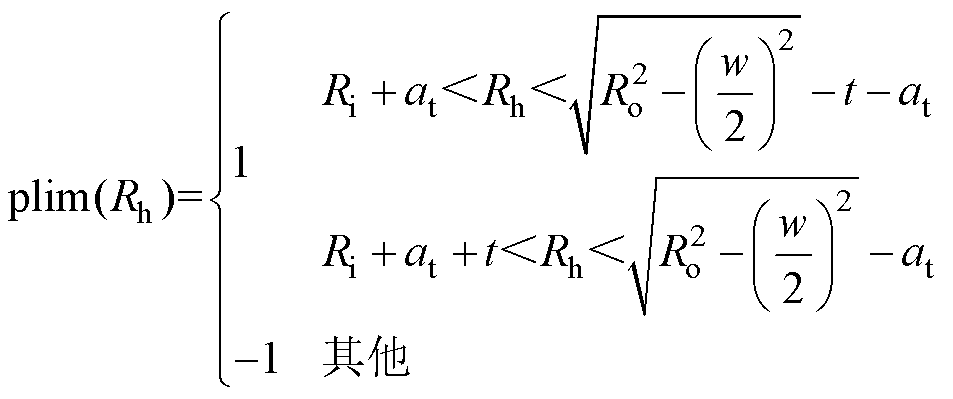（12）
式中，w为霍尔传感器封装宽度；t为霍尔传感器封装厚度；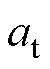
为考虑到安装可行性的避让尺寸，具体取值见表1。
采用第1节中的解析模型分析设计变量与设计指标的关系。在此，给出永磁体长度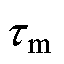、线圈厚度d与PFD、THD和TC之间的关系曲面，如图3所示。
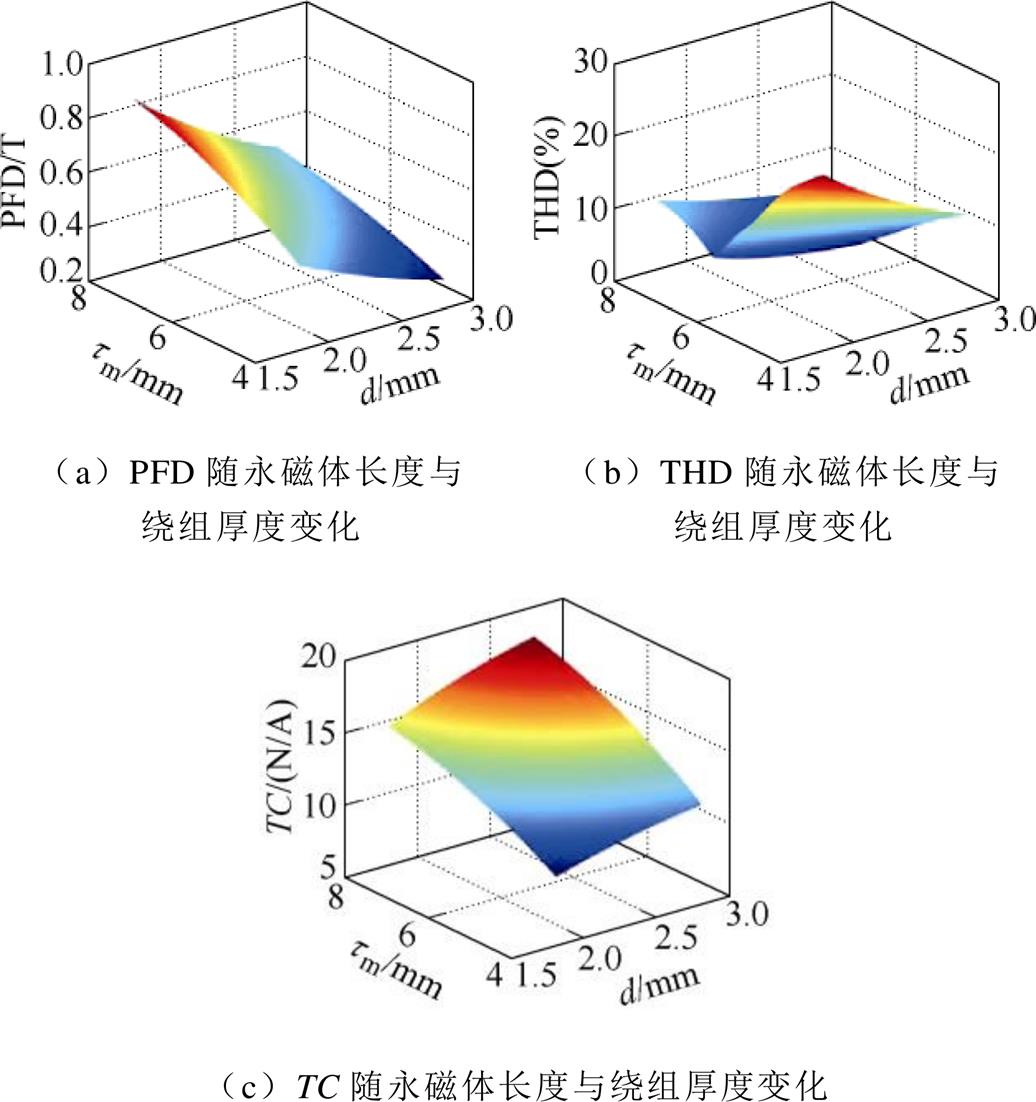
图3 设计指标与设计变量关系曲面
Fig.3 The relationships between design objectives and design variables
从图3中可以看到，PFD随永磁体长度增加而增大，随线圈厚度增大而减小。THD随线圈厚度增加而减小。同时在固定线圈厚度的情况下，存在一最优的永磁体长度使得THD取值最小。TC则随永磁体长度和线圈厚度增加而增大，但增大速率逐渐降低。可以看到，PFD、THD与TC之间最优取值为相互约束的关系，需要采用优化设计的方式寻找最优的设计参数配置。
解析法、有限元法是进行电机结构参数优化设计常用的建模方法。由于存在较多的假设条件，解析法所得到的电机模型精度有限。本文中解析模型忽略了永磁体实际工作点的变化，导致气隙磁通密度与推力系数的求解结果与实验值相比偏大，解析法与有限元法精度比较如图4所示。而基于有限元的电机模型计算结果较为准确，但是计算耗时较长，不适合用于优化过程中的迭代计算。为了平衡模型精度与计算复杂度，响应曲面法被应用于模型的求解。二次多项式响应曲面[17]和神经网络响应曲面[18]是常用的两种响应曲面构造方法。相较而言，二次响应曲面适合变量范围小、非线性程度弱的目标函数的拟合。神经网络响应曲面则适合拟合样本量大、非线性较强的函数。为了获得更优的拟合精度，本文采用神经网络曲面来拟合电机模型。
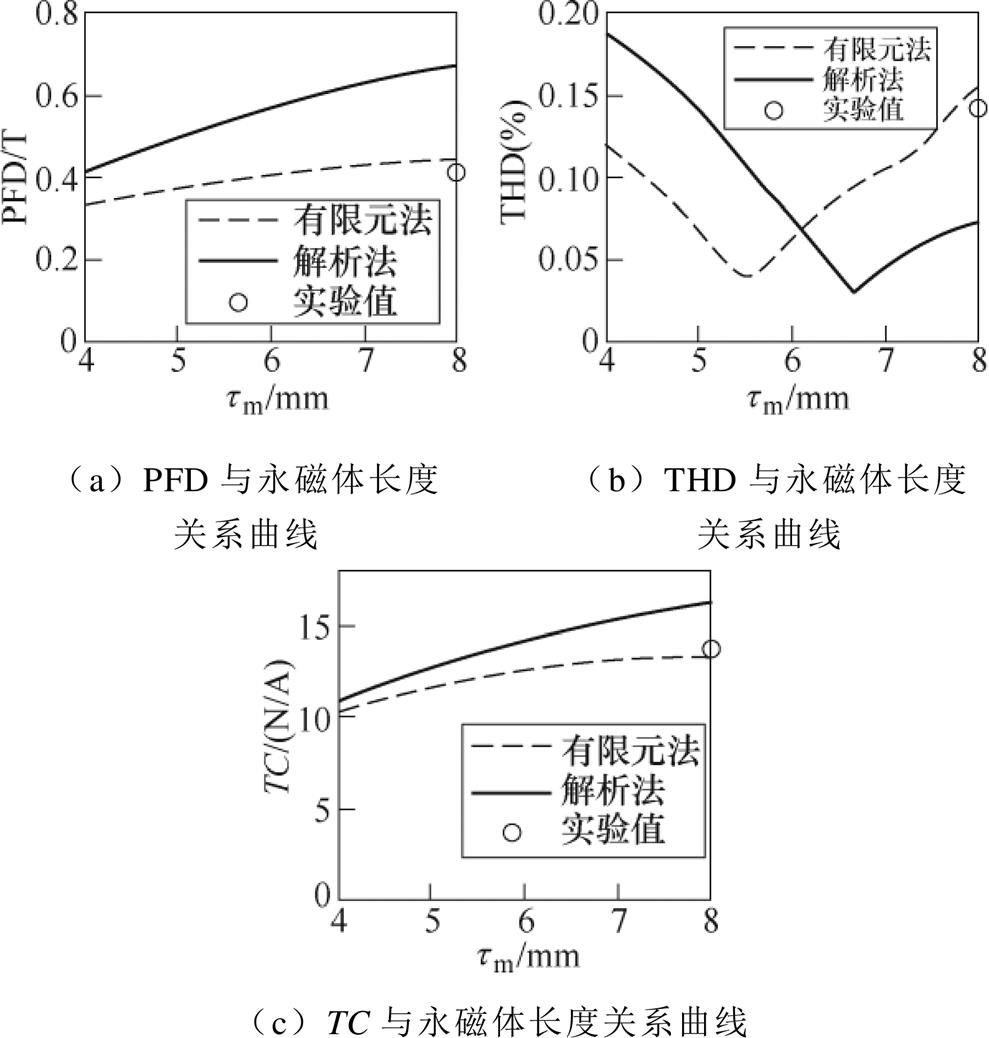
图4 解析法与有限元法精度比较
Fig.4 Results of analytical method and finite element method
本文所采用的神经网络模型如图5所示。其包括输入层、3层隐层和1层输出层，各隐层包含神经元数量为16、8、1。其中，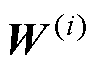
为各隐层的权重系数矩阵，
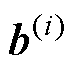为各隐层的偏置向量。输入层的输入向量为
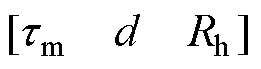，各隐层的输出向量为
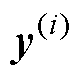，可以表示为
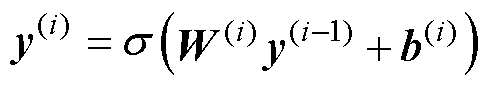。其中，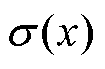
为激活函数，隐层1和隐层2采用sigmod函数为激活函数，隐层3采用线性函数为激活函数。各神经网络对应输出分别为PFD、THD与TC。使用经典的误差前馈算法进行网络的训练。
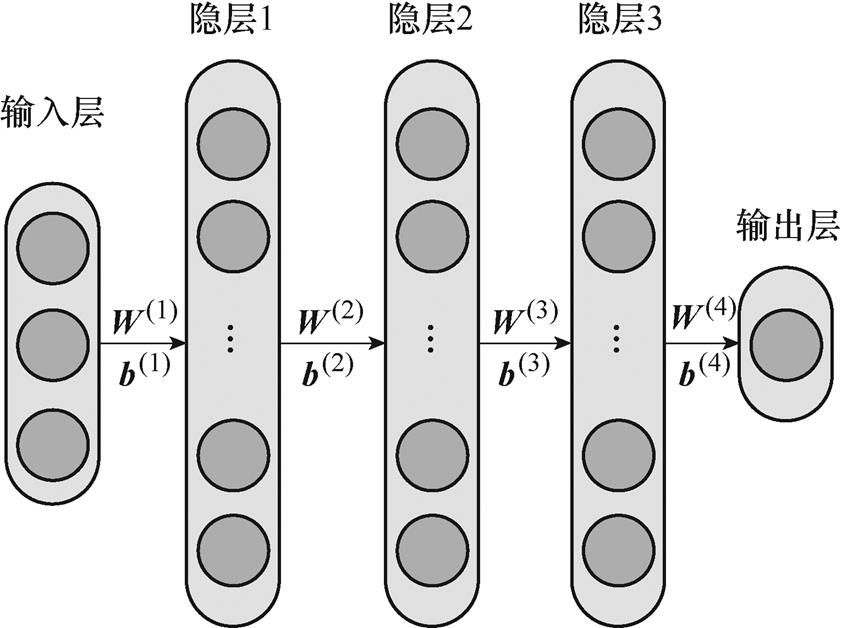
图5 神经网络结构
Fig.5 The construction of neural network
神经网络训练所用样本通过2D有限元仿真得到。仿真样本中各设计变量为等间隔分布，具体取值见表3。
表3 仿真样本中设计变量取值
Tab.3 Values of design variables in simulation samples
设计变量初值终值间隔 永磁体长度tm/mm480.5 线圈厚度d/mm1.82.80.2 霍尔安装位置Rh/mm7.8-d7.8d/5
各设计指标的拟合效果采用拟合优度R2进行评价。R2计算表达式为
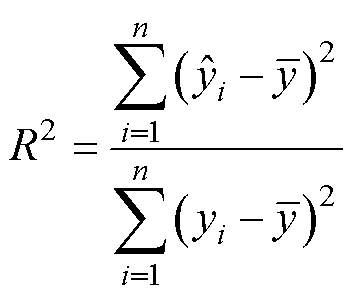（13）
式中，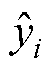
为预测值；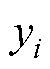
为实际值；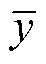
为实际值平均值。基于神经网络和二次多项式的响应曲面法的拟合优度对比结果见表4。
表4 不同方法的拟合优度
Tab.4 R2 of different fitting methods
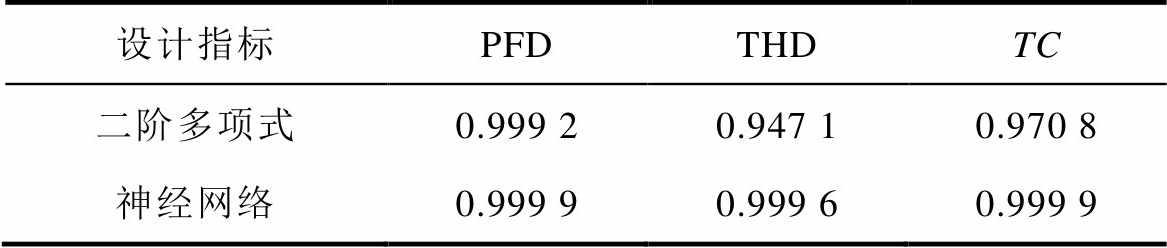
设计指标PFDTHDTC 二阶多项式0.999 20.947 10.970 8 神经网络0.999 90.999 60.999 9
可以看到，对于非线性较弱的PFD与TC值，二阶多项式与神经网络都表现出较好的拟合优度。对于非线性较强的THD值，神经网络的拟合优度明显优于二阶多项式方法。
RBRDO是考虑到设计对象在生产制造过程中加工装配误差的一种优化设计方法，其综合了可靠性优化设计（Reliability-Based Design Optimization, RBDO）和鲁棒性优化设计（Robust Design Opti- mization, RDO）两者的特点[19]。其中，RBDO可以保证设计指标的失效概率小于给定概率约束。鲁棒性由设计目标的前两阶统计矩：均值与方差来描述。RDO的优化目标为最小化包含均值与方差的价值函数，使实际设计目标均值与名义值尽可能接近的同时，保证方差尽可能小。因此，RBRDO方法可以表示为
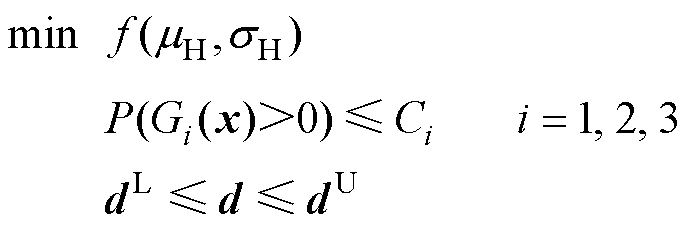（14）
式中，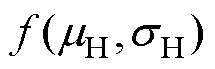
为价值函数；
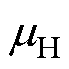与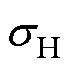
分别为设计指标的平均值与标准差；
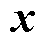为呈正态分布的随机变量，其均值为设计变量，标准差基于表2中给定的公差带宽通过
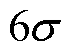的原则进行求取；
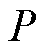为求取概率分布的算子；
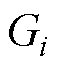为概率约束条件；
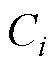为给定失效概率，本文中取值为0.01%；
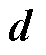为的均值，即设计变量值；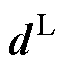
与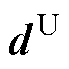
分别为设计变量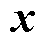的下、上界，具体取值见表2。
提升霍尔传感器位置检测精度的RBRDO方法为：在给定PFD、THD与TC的概率约束条件下，最小化电机THD的均值误差与标准差，以提升电机THD指标的一致性。因此价值函数的定义为
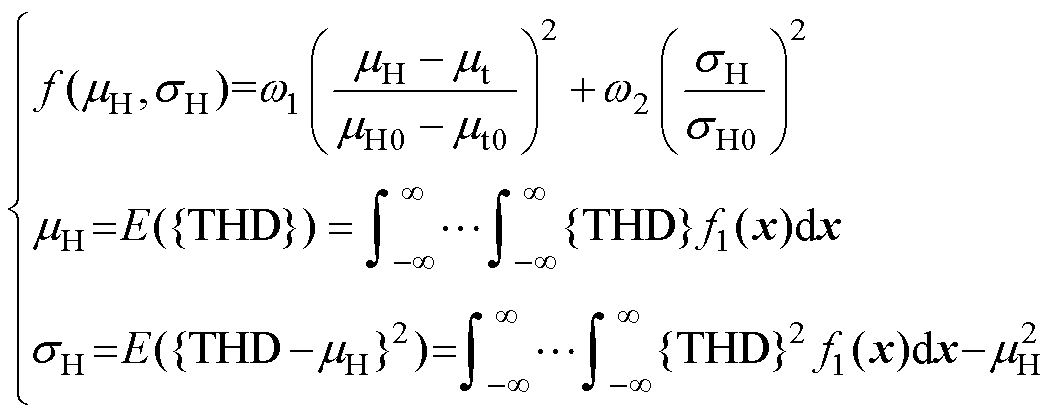（15）
式中，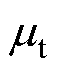
为THD的名义值；
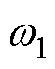与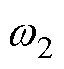
为人为决定的权重系数；
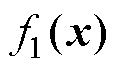为随机变量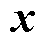的联合概率分布函数。同时采用初始的
、
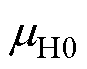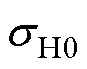与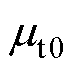
来归一化价值函数。
概率约束为PFD、THD、TC的失效概率约束，有
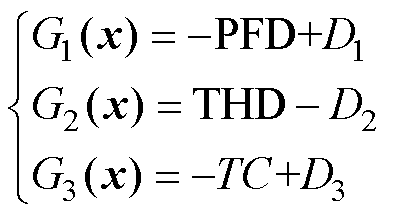（16）
式中，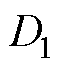
、
、
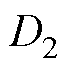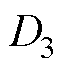为对应约束值，由设计者根据电机性能和应用场合需求进行决定。
满足概率约束条件的失效概率计算表达式为
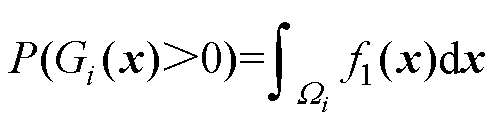（17）
式中，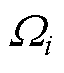
为积分区域，是满足
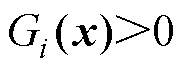这一约束条件的可行区间。式（15）、式（17）中，均值、方差与失效概率的计算方法包括泰勒展开、降维法、矩方法、蒙特卡洛法等[19]。为了获得更高的计算精度，本文采用蒙特卡洛法进行均值、方差与概率约束的计算。为了保证计算结果的可靠性，设计变量的采样次数为106次。
原有TPMSLM样机的设计变量取值为d0= [8.00mm 2.20mm 6.40mm]T，对应的设计指标名义值为 (0.445T, 15.5%,13.2N/A)。可以看到，霍尔传感器处谐波畸变较大。为了减少谐波畸变带来的位置误差估计影响，希望尽可能地降低THD的设计值。由于原始样机设计指标已是Pareto最优前沿上点，因此无法在不降低PFD与TC设计值的情况下减小THD的设计值。为此，需要适当减小PFD与TC的概率约束值，实现THD值的降低。通过多目标优化算法NSGA-Ⅱ[20]得到满足实际使用需求的不同TC设计值约束条件下的Pareto最优前沿，如图6所示。
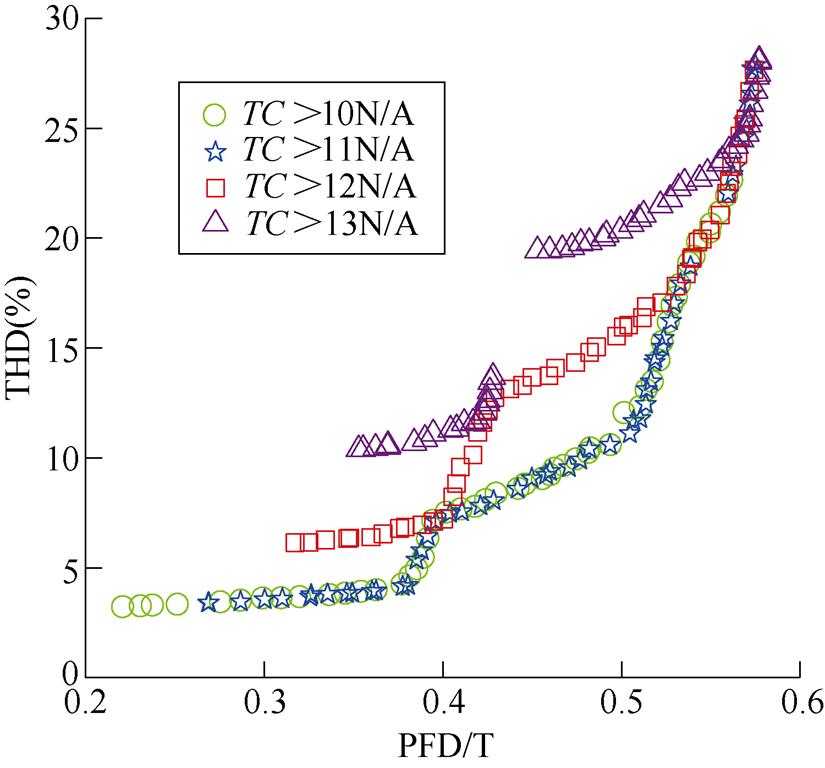
图6 不同TC值下约束下的Pareto最优前沿
Fig.6 Pareto-optimal fronts under different TC constraints
由图6可以看到，随着TC设计值降低，所得到的Pareto最优前沿向左下方移动，最小THD值不断减小。对于TC＞10N/A和TC＞11N/A这两种约束条件，其Pareto最优前沿几乎重合，即降低TC的设计值并不能进一步减小THD的最小值。因此，选择11N/A作为TC的概率约束值，同时将曲线上两拐点处的THD与PFD值作为最终的约束条件，即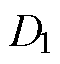
=0.36T，
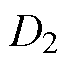=9.0%，
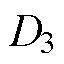=11N/A。
基于4.2节给定的约束条件，分别采用RDO与RBRDO进行优化设计，并采用遗传算法进行优化结果的求取。得到优化后对应的设计变量取值分别：d1= [5.48mm 1.96mm 7.33mm]T, d2=[5.51mm 1.91mm 7.33mm]T。优化前与优化后的性能指标见表5。
表5 优化前后性能对比
Tab.5 Performances before and after optimization
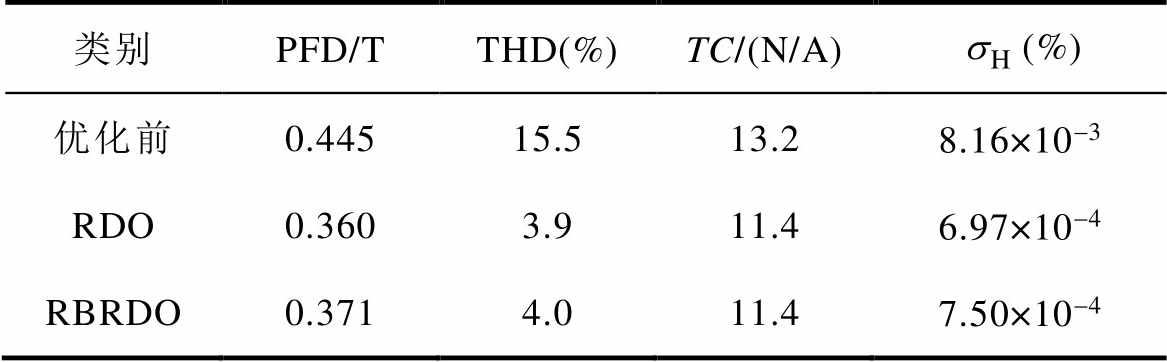
类别PFD/TTHD(%)TC/(N/A)(%) 优化前0.44515.513.28.16×10-3 RDO0.3603.911.46.97×10-4 RBRDO0.3714.011.47.50×10-4
可以看到，与优化前指标相比，RBRDO在TC下降13.6%，PFD值下降16.7%的情况下，将THD的设计值从15.5%优化至4.0%，THD设计值下降了74.2%。同时，其THD均方差由原来的8.16×10-3%下降至7.50×10-4%。这表明经过优化后，THD的分布更加集中，对参数变化的鲁棒性更强。相较于RDO，RBRDO的均方差略大，这是由于RBRDO需要满足可靠性概率约束条件，这使得其的可行解空间要小于RDO的可行解空间。THD的概率密度函数如图7所示，可以看到，经过优化后，THD的分布更加集中。
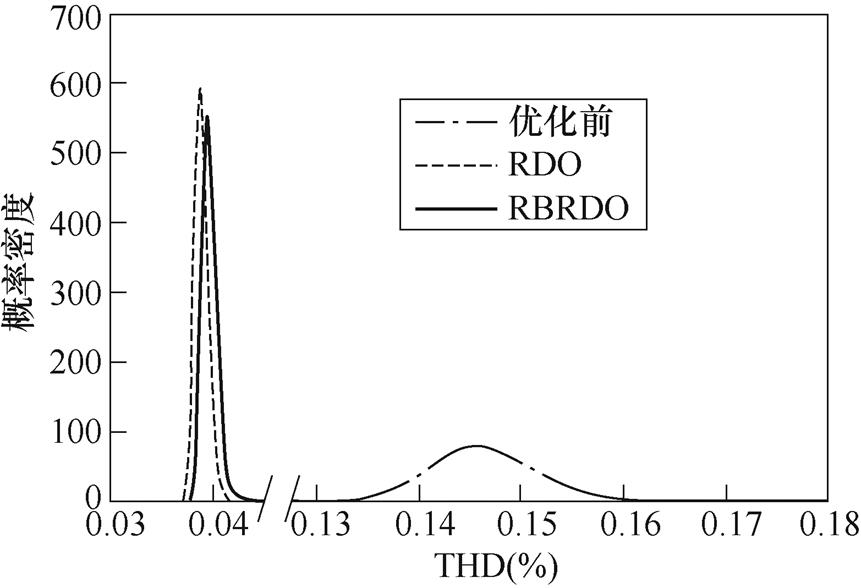
图7 THD的概率密度函数
Fig.7 The probability density of THD
实验设备如图8所示。实验平台如图8a所示，包括直线电机、电机控制板、光栅尺、上位机四个部分。其中，电机样机如图8b所示，优化前后电机永磁体长度分别8mm和5mm；驱动器母线电压为48V；霍尔传感器采用东芝公司生产的THS119霍尔传感器；控制器芯片为德州仪器公司的TMS320F28335，采用芯片自带的12位AD进行霍尔信号的采样；选用信和KA-500线性光栅尺作为位置反馈基准信号，光栅尺精度为1mm。实验平台前端的滑轮用于悬挂砝码，调节负载力的大小。采样数据通过串口传输至上位机中。
图8 实验设备
Fig.8 Experimental equipment
推力系数测量原理如下。直线电机空载匀速运动时，受力情况为
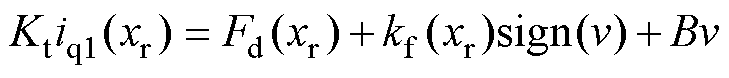（18）
式中，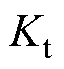
为电机推力系数；
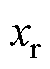为动子位置；
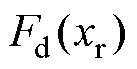为直线电机的端部力；
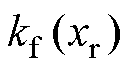为库伦摩擦力；
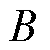为粘滞摩擦因数；
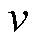为电机的运动速度；
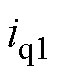为对应q轴驱动电流；
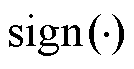为符号函数。由于本电机没有铁心，因此不存在齿槽力的作用。
当滑轮末端悬挂负载匀速运动时，电机受力变为
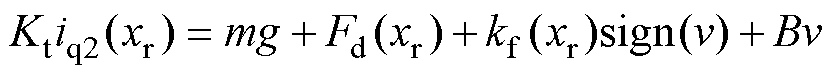（19）
式中，m为悬挂砝码质量，本实验选用1kg砝码提供电机负载力；g为重力加速度；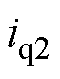
为对应q轴驱动电流。
在同一动子位置处，联立式（18）和式（19），可以得到推力系数的求解公式为
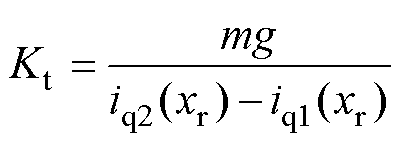（20）
优化前后电机空载和带下驱动电流波形如图9所示。在不同位置处，由式（20）计算可以得到电机推力系数，求取平均值可以得到优化前与优化后的TC值为13.4N/A和11.1N/A。
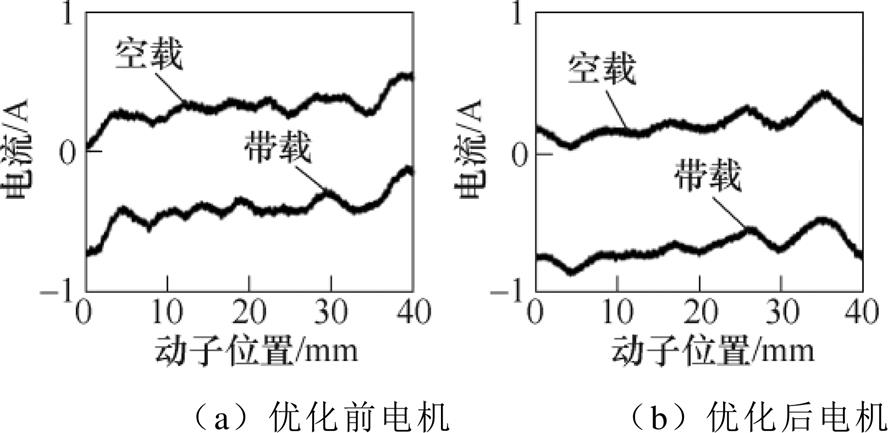
图9 不同负载下的驱动电流
Fig.9 Driving current under different loads
控制电机做匀速运动，得到原样机和优化样机霍尔传感器处磁通密度曲线与位置检测误差如图10所示。可以看到，优化前样机的磁通密度分布曲线更接近三角波，优化后电机磁通密度分布曲线与正弦波更为接近。同时，优化后样机的磁通密度幅值相较于优化前略微下降，但位置检测精度大幅提升。
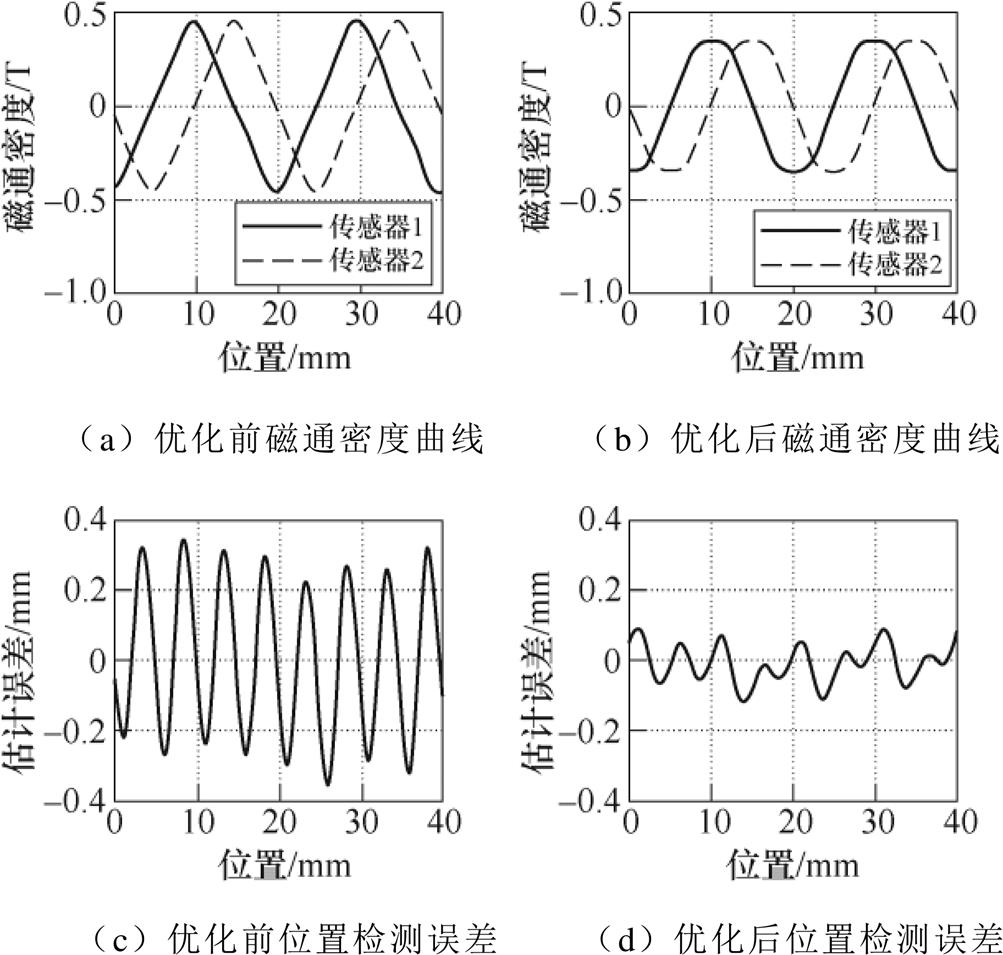
图10 磁通密度与位置检测误差曲线
Fig.10 Curves of flux density and position detection error
通过快速傅里叶变换，得到优化前后样机性能对比见表6。可以看到，相较于优化前，优化后PFD与TC值分别下降12.5%和17.1%。但THD的值从13.8%下降至5.1%，THD值下降63%，谐波含量显著降低。由霍尔传感器测量得到位置估计值最大误差从357mm下降至109mm。
表6 优化前后样机性能对比
Tab.6 Performances of prototypes before and after optimization
类别PFD/TTHD(%)TC/(N/A)Max(e)/mm 优化前0.41513.813.4357 优化后0.3635.111.1109
本文以TPMSLM霍尔传感器位置辨识精度的提升为目的，建立了PFD、THD与TC值的解析模型与响应曲面模型。并基于响应曲面进行了电机的可靠性与鲁棒性优化设计。该设计方法有如下特点：
1）采用神经网络拟合得到了设计指标的响应曲面模型。相较于传统的二次多项式算法，其对于非线性强的目标函数具有更好的拟合优度。
2）使用多目标优化算法进行了RBRDO概率约束值的选择。使得概率约束值的选取不依赖于经验试凑，约束选择更加科学合理。
3）在优化设计过程中，考虑了设计变量制造误差对设计指标产生的影响。在保证可靠性与鲁棒性的同时将降低磁通密度谐波含量，提升位置检测精度。
参考文献
[1] 许孝卓, 孙震, 汪旭东, 等. Halbach交替极永磁同步直线电机特性分析[J]. 电工技术学报, 2019, 34(9): 1825-1833.
Xu Xiaozhuo, Sun Zhen, Wang Xudong, et al. Characteristic of a novel permanent magnet linear synchronous motor with Halbach array consequent- pole[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1825-1833.
[2] Morimoto S, Kawamoto K, Sanada M, et al. Sensor- less control strategy for salient-pole PMSM based on extended EMF in rotating reference frame[J]. IEEE Transactions on Industry Applications, 2002, 38(4): 1054-1061.
[3] 吴春, 陈科, 南余荣, 等. 考虑交叉饱和效应的变角度方波电压注入永磁同步电机无位置传感器控制[J]. 电工技术学报, 2020, 35(22): 4678-4687.
Wu Chun, Chen Ke, Nan Yurong, et al. Variable angle square-wave voltage injection for sensorless control of PMSM considering cross-saturation effect[J]. Transactions of China Electrotechnical Society, 2020, 32(22): 4678-4687.
[4] 张春雷, 张辉, 叶佩青, 等. 两相圆筒型永磁同步直线电机无传感算法[J]. 电工技术学报, 2019, 32(23): 4901-4908.
Zhang Chunlei, Zhang Hui, Ye Peqing, et al. Research on sensorless algorithm of two-phase tubular permanent magnet synchronous linear motor[J]. Transactions of China Electrotechnical Society, 2019, 32(23): 4901-4908.
[5] Paul S, Chang J. A new approach to detect mover position in linear motors using magnetic sensors[J]. Sensors, 2015, 15(10): 26694-26708.
[6] Zhu Ziqiang, Shi Y, Howe D. Rotor position sensing in brushless AC motors with self-shielding magnets using linear hall sensors[J]. Journal of Applied Physics, 2006, 99(8): 308-313.
[7] 刘刚, 肖烨然, 宋欣达. 永磁同步电机用线性霍尔位置检测的误差补偿[J]. 电机与控制学报, 2014, 18(8): 36-42.
Liu Gang, Xiao Yeran, Song Xinda. Error com- pensation of rotor position detection for permanent magnetic synchronous motor based on linear hall sensors[J]. Electric Machines and Control, 2014, 18(8): 36-42.
[8] 严乐阳, 叶佩青, 张勇, 等. 圆筒型永磁直线同步电机用线性霍尔位置检测的误差补偿[J]. 电工技术学报, 2017, 32(5): 26-32.
Yan Leyang, Ye Peiqing, Zhang Yong, et al. Error compensation of linear hall based position detection for tubular permanent magnetic linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2017, 32(5): 26-32.
[9] Du Shengwu, Hu Jinchun, Zhu Yu, et al. A hall sensor-based position measurement with on-line model parameters computation for permanent magnet synchronous linear motor[J]. IEEE Sensors Journal, 2018, 18(13): 5245-5255.
[10] Reigosa D, Fernandez D, Gonzalez C, et al. Permanent magnet synchronous machine drive control using analog hall-effect sensors[J]. IEEE Transa- ctions on Industry Applications, 2018, 54(3): 2358- 2369.
[11] Jung S Y, Nam K. PMSM control based on edge-field hall sensor signals through ANF-PLL processing[J]. IEEE Transactions on Industrial Electronics, 2011, 58(11): 5121-5129.
[12] Song Xinda, Fang Jiancheng, Han Bangcheng. High- precision rotor position detection for high-speed surface PMSM drive based on linear hall-effect sensors[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 4720-4731.
[13] Yan Leyang, Ye Peiqing, Zhang Chunlei, et al. An improved position detection method for permanent magnet linear motor using linear hall sensors[C]// International Conference on Electrical Machines and Systems, Sydney,Australia, 2017: 1-4.
[14] Liu Xiao, Ye Yunyue, Zheng Zhuo, et al. Study of the linear hall-effect sensors mounting position for PMLSM[C]//IEEE Conference on Industrial Elec- tronics and Applications, Harbin, China, 2007: 1175-1178.
[15] Pan Songhan, Commins P A, Du Haiping. Tubular linear motor position detection by hall-effect sensors[C]//Australasian Universities Power Engineering Conference, Wollongong, 2015: 1-6.
[16] 赵镜红, 张晓锋, 张俊洪, 等. 圆筒永磁直线同步电机磁场和推力分析[J]. 电机与控制学报, 2010, 14(1): 12-17.
Zhao Jinghong, Zhang Xiaofeng, Zhang Junhong. Field and thrust analysis of tubular permanent magnet linear synchronous motor[J]. Electric Machines and Control, 2010, 14(1): 12-17.
[17] 刘国海, 王艳阳, 陈前. 非对称V型内置式永磁同步电机的多目标优化设计[J]. 电工技术学报, 2018, 33(增刊2): 385-393.
Liu Guohai, Wang Yanyang, Chen Qian. Multi- objective optimization of an asymmetric V-shaped interior permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 385-393.
[18] 杨阳, 赵吉文, 宋俊材, 等. 基于深度神经网络模型的无铁心永磁同步直线电机结构优化研究[J]. 中国电机工程学报, 2019, 39(20): 6085-94.
Yang Yang, Zhao Jiwen, Song Juncai, et al. Structural optimization of air-core permanent magnet syn- chronous linear motors based on deep neural network models[J]. Proceedings of the CSEE, 2019, 39(20): 6085-6094.
[19] Lee I, Choi K, Du Liu, et al. Dimension reduction method for reliability-based robust design optimi- zation[J]. Computers & Structures, 2008, 86(13-14): 1550-1562.
[20] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.
Design of Tubular Permanent Magnet Synchronous Linear Motor by Reliability-Based Robust Design Optimization
Abstract With the advantages of low cost and high robustness, linear hall sensors are utilized to detect the mover position of the tubular permanent magnet synchronous linear motor (TPMSLM). However, the position detection accuracy of linear hall sensor is affected by magnetic field harmonics. To reduce the harmonics, the TPMSLM was designed by reliability-based robust design optimization (RBRDO) considering the manufacturing tolerance. Firstly, a model of the position identification and thrust force analysis was established. The relationship between design variables and design objectives was analyzed. Then, the response surface model of design objectives was established by the neural network. The probability constraints were obtained by Pareto optimal front under different thrust coefficients. Finally, the total harmonic distortion is greatly reduced by RBRDO, while the thrust coefficient and the peak flux density are slightly reduced. And the position detection accuracy is improved from 357mm to 109mm.
keywords：Linear motor, linear hall sensor, neural network, reliability-based robust design optimization
DOI: 10.19595/j.cnki.1000-6753.tces.201339
中图分类号：TM351
张春雷 男，1994年生，博士研究生，研究方向为电机设计及其控制。E-mail: clzhang13@ 163.com
张 辉 女，1969年生，博士，副教授，研究方向为先进制造装备及其自动化。E-mail: wwjj@mail.tsinghua.edu.cn（通信作者）
收稿日期 2020-10-09
改稿日期 2021-03-22
国家自然科学基金资助项目（51875312）。
（编辑 崔文静）