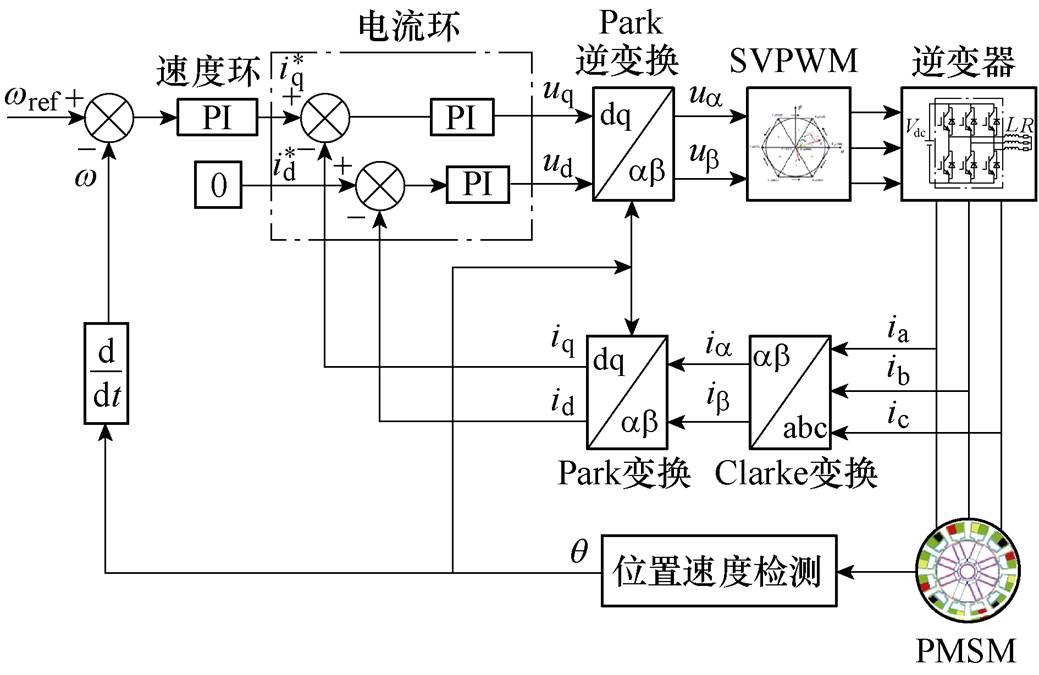
图1 永磁同步电机SVPWM控制模型
Fig.1 Simulation model of SVPWM for PMSM
摘要 该文以电动汽车后桥驱动用12槽-10极永磁同步电机及其控制系统为研究对象,基于周期谐波扩频调制技术,对常规空间矢量脉宽调制(SVPWM)技术所引入的边带谐波成分与高频声振响应进行抑制与优化研究。分析了边带电流谐波频谱与径向电磁力主要的阶次特征分布。建立了完整的谐波扩频功率谱解析模型,对锯齿波和正弦波两种典型的周期信号进行了理论解析,并分析了扩频宽度和调制因子对抑制效果的影响。通过样机及测控实验平台,对不同工况下的边带电流谐波和声振响应进行了验证。结果表明,周期谐波扩频调制能够有效抑制边带电流谐波,多转速工况下噪声响应的中心频带优化20dBA以上;锯齿波扩频调制的抑制效果优于正弦波扩频调制;正弦波扩频调制对扩频宽度的变化较为敏感。
关键词:永磁同步电机 空间矢量脉宽调制 边带电流谐波 谐波扩频调制 振动噪声抑制
当前,凭借高功率密度、高转速区间、较好的动态响应等优点,永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)已被广泛应用于各种工业环境。然而,在电动汽车电驱动系统应用当中,由于电机及电控系统所引入的电磁激励,对动力传动系统的可靠耐久性、整车层面的电磁干扰与NVH(noise, vibration, harshness)性能均具有重要的影响,受到了国内外学者及企业的广泛关注[1-3]。
通常,永磁同步电机由电压源型逆变器(Vector Source Inverter, VSI)驱动,为了实现良好的稳态与瞬态性能,以空间矢量脉宽调制(Space Vector Pulse-Width Modulation, SVPWM)策略为代表的调制技术被广泛搭载使用[4-6]。然而,常规SVPWM技术采用固定的载波频率,致使主控电路功率逆变器在运行过程中产生高频的边带电压和电流谐波成分,集中在载波频率及其整数倍范围内,进而导致电机系统产生受边带电磁激励力影响的高频机械振动与辐射噪声[7]。为了满足高功率输出,大多数VSI工作条件被设定于4 000~8 000Hz,而人耳的敏感频带位于5 000~10 000Hz,此类寄生效应所辐射的“啸叫”,会令驾乘人员感到反感不适[8];此外,边带谐波分量会增加定子铁心损耗、电枢铜耗以及永磁体涡流损耗,影响电机工作效率,因而亟待解决。
对于边带电压与电流谐波成分与声振响应的时间与空间特征分析,涉及到电机控制、电磁场、电机本体结构、声振响应的多物理场预测模型,诸多学者采用有限元数值计算与解析法进行了研究。文献[9]中,基于有限元数值计算方法,融合控制策略与VSI电路模型到气隙磁场分析中,运用模态叠加法,对定子轭部施加分布应力,准确预测电机壳体的声振响应。文献[10-12]中,采用双重傅里叶级数方法,对搭载SVPWM策略所输出的PWM信号进行分解,构建了定、转子坐标系下的边带电流谐波解析模型[10];运用麦克斯韦张量法对径向电磁力幅值、空间阶次与频率分布进行了完整解析[11-12],实现了从电磁谐波到机械响应之间的特征耦合与多物理场解析。此外,基于模态实验半解析声振预测模型,能够进一步提高电磁振动噪声的预测精度[13]。
以上特征分析与预测方法可为边带电流谐波及声振响应的抑制优化提供思路,其中,最为有效且常用的方法被称为谐波扩频调制(harmonic spread spectrum modulation),即基于帕斯维尔(Parseval)原理,信号在时域和频域内的能量保持不变,通过扩大谐波分布频谱范围,以达到降低谐波幅值的效果。根据所选信号种类,谐波扩频调制可以分为基于周期性信号和离散随机性信号两种方式。文献[14-15],对基于三角波和正弦波的两种周期性载波扩频调制效果进行了分析,初始的固定载波频率以确定的方式在截止频率的范围内进行波动,结果表明边带谐波成分得到了有效抑制优化。另外,基于离散随机信号的脉宽调制(Random Pulse Width Modulation, RPWM)技术应用最为广泛[16],离散的随机信号可以使载波频率随机化,从而使原本集中的边带谐波能量扩展至较宽的频域范围,且抑制效果要优于周期扩频调制[17];相比于周期性扩频调制,载波频率随机化会使逆变器开关损耗增加[18-19],且使系统鲁棒性降低。
综上,周期谐波扩频调制可以有效抑制边带谐波成分及声振响应,且对系统动态性能影响较小[20]。然而,目前的研究中仍然缺少关于不同周期信号与调制参数的理论解析与对比。因此,本文采用功率谱密度解析方法,提出了锯齿波与正弦波两种典型周期信号的扩频效果理论分析模型,分析讨论了不同调制参数对抑制效果的影响,并结合样机实验,对边带电流谐波与声振响应进行了多工况验证。
常规的SVPWM技术现已广泛用于PMSM、感应电机和开关磁阻电机中,与传统的PWM技术不同,SVPWM将VSI和电机视为整体,将定子电压矢量转换为dq轴空间矢量,通过计算空间电压矢量的作用时间,使其变换轨迹接近于圆形,进而趋近于理想的定子磁链圆,实现控制逆变器功率元件的开关模式,如图1所示[21-22]。SVPWM采用双闭环回路与PI调节控制,双反馈回路可以输出dq轴电压指令。因此,对于边带电压与电流谐波成分的解析,应首先建立等效谐波解析模型。

图1 永磁同步电机SVPWM控制模型
Fig.1 Simulation model of SVPWM for PMSM
常规的SVPWM过程可以等效为对称放置零矢量的常规采样PWM的结果,输出相电压可以被等效为“马鞍”调制波与三角载波频率调制的结果[23],如图2所示。考虑到两种不同类型的频率调制,在定子坐标系中A相电压UA谐波可由双重傅里叶级数解析,即
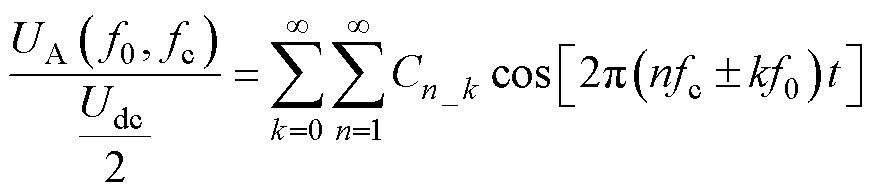 (1)
(1)
式中,Udc为直流母线电压;f0和fc分别为调制波与载波频率;Cn_k为在第n倍载波频段内的k次边带谐波的幅值。
以第一载波频段为例,即n=1,忽略高阶谐波成分,边带电压谐波可以近似表示为
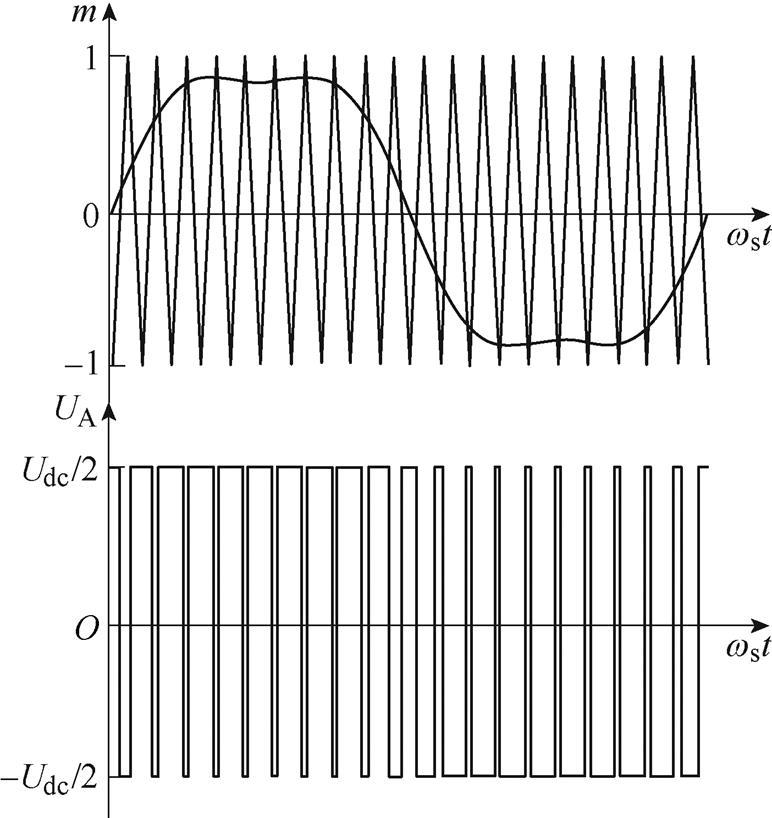
图2 SVPWM对称规则采样示意
Fig.2 Symmetrical regular sampled in SVPWM
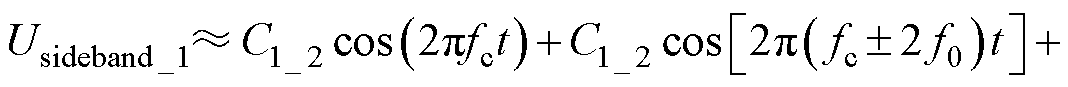
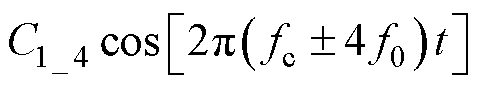 (2)
(2)
由式(2)可以看出,边带电压谐波中不包含3倍次谐波。此外,在边带电压谐波的幅值计算中,通常引入贝塞尔函数,忽略高次贝塞尔级数的幅值,第一载波频率内的谐波电压主要分布于0、2和4次。
边带电流谐波的解析式无法从谐波电压中直接推导,需要先通过Park变换将相电压谐波分量转化为转子坐标系中的dq轴分量,再由逆Park变换表示出定子坐标系的边带电流谐波解析式,有
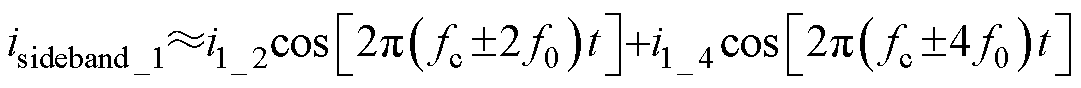 (3)
(3)
式中,i1_2和i1_4为边带电流谐波分量的幅值,与电机主要电磁参数相关,如dq轴的电感。
对于径向磁通永磁同步电机,作用于定子齿面的电磁激励是引起壳体振动及辐射噪声的主要原因。对于边带电磁振动及辐射噪声的分析,应首先确定边带电流谐波及其相关谐波磁场分量[24]。通常,气隙电磁力可以由Maxwell应力张量法来定义,即
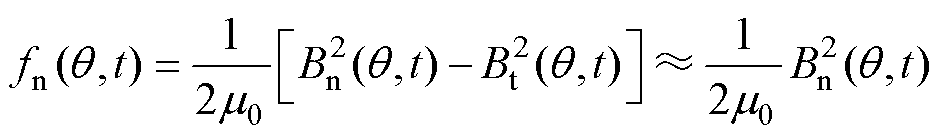 (4)
(4)
式中,m0为真空磁导率;Bn和Bt分别为气隙磁通密度的径向与切向分量,具有相同的时间与空间特征,而切向分量远小于径向分量,因此予以忽略。
忽略磁饱和效应并考虑磁场叠加原理,径向气隙磁通密度Bn又可以分解为定子电枢磁场Barm和转子永磁体磁场Bmag两部分,如式(5)所示。其中,为了解析边带谐波成分,定子电枢磁场可以被分解为基波磁场B0与谐波磁场Bh的叠加,即
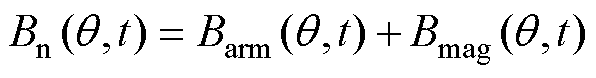 (5)
(5)
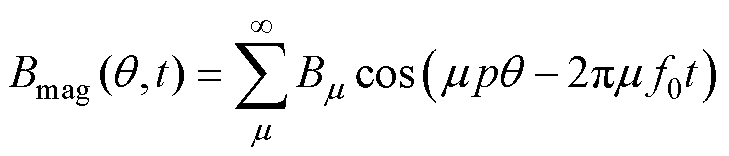 (6)
(6)
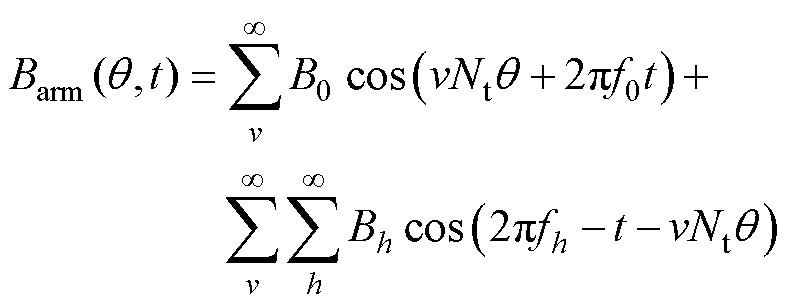 (7)
(7)
式中,m 为永磁体磁场阶次,考虑到永磁体基波磁场是振动噪声的主要贡献量,m 取值为1;v为电枢磁场谐波阶次,v=6k+1, k=0, ±1, ±2, ±3,…;q 为空间机械角度;fh为谐波电流频率,h=6k±1, k=1, 2, 3,…;Nt为单元电机,数值上为电机极对数p与槽数z的最大公约数。
将式(5)~式(7)代入式(4)中,可以得到径向电磁力密度的解析表达式,完整的解析式中有12项,分别表示受电枢基波磁场、谐波磁场、永磁体磁场及相互作用的分量[4, 9]。为了体现出边带电流谐波分量,简化后的径向电磁力解析式中只考虑永磁体基波磁场与定子电枢谐波磁场的相互作用,具体表示为
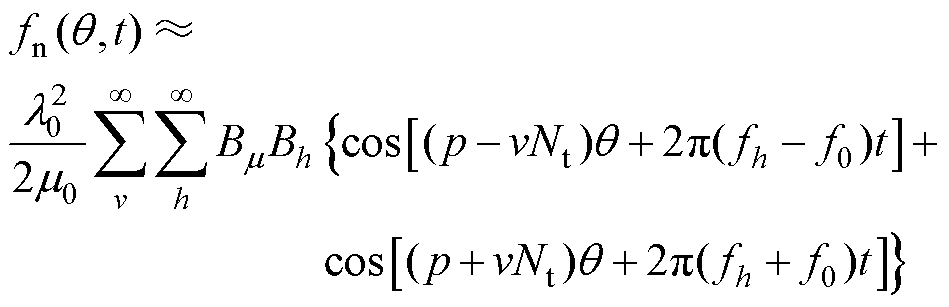 (8)
(8)
由式(8)可以看出,边带电磁分量与机械声振响应之间的多物理场解析模型可以通过时空特征的耦合关系建立。以时间频率特征为例,在声振响应中的频率特征为fh ± f0次,结合第一载波频率附近的边带电流谐波特征频率fc±2 f0和fc±4 f0,边带径向电磁力的主要阶次为fc± f0,fc±3 f0和fc±5 f0。
根据1.2节可以看出,由于常规SVPWM的载波频率被设定为固定值,令VSI输出具有明显频率阶次的边带谐波激励,从而导致电机产生边带声振响应。基于Parseval原理,可以将固定的载波频率在一定范围内进行变化,使原先集中的谐波能量被分散扩展到较宽的范围,从而达到边带谐波成分的抑制效果。
为了更好地分析周期扩频调制对边带电流谐波的抑制效果,本文以典型的锯齿波与正弦波周期信号为例,采用功率谱密度(Power Spectral Density, PSD)分析方法,对扩频调制后的信号幅值及频率分布进行了分析。在一个周期内的锯齿波与正弦波时域信号可以分别表示为
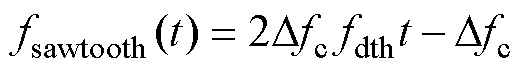
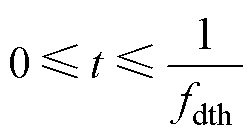 (9)
(9)
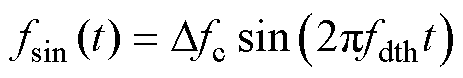 (10)
(10)
式中,D fc为周期信号的幅值,在扩频调制中间接代表了载波频率波动的范围;fdth为周期信号的频率,代表载波信号波动的快慢。基于上述两种周期信号的载波频率调制示意图如图3所示。
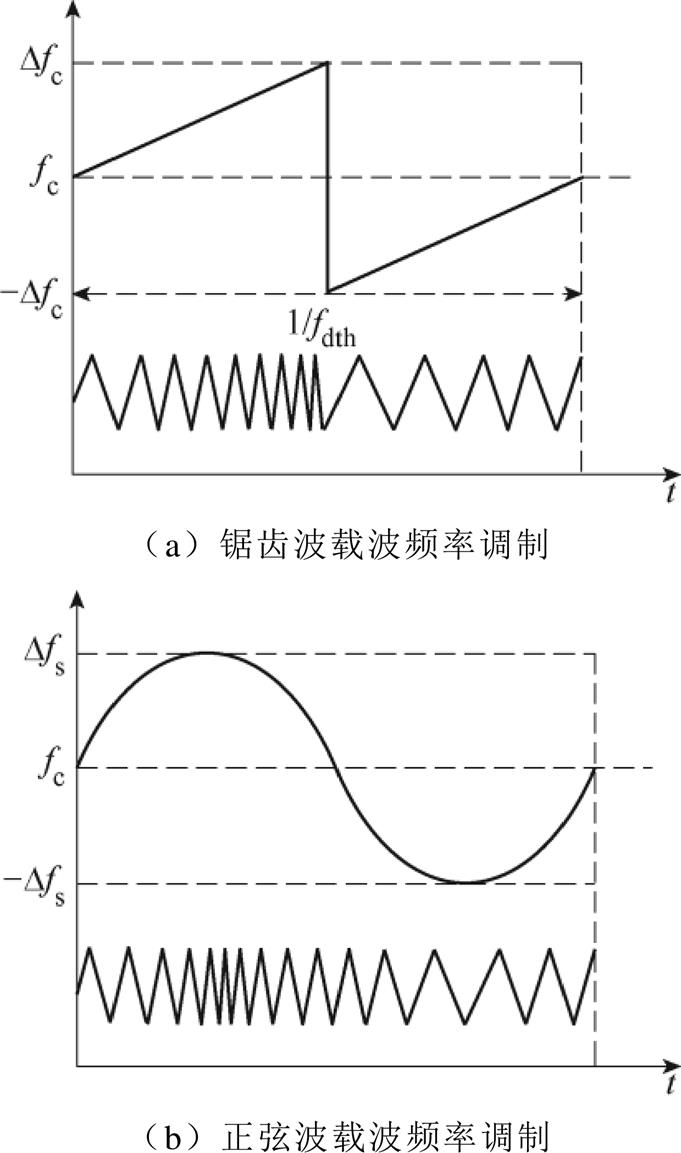
图3 两种周期信号载波频率调制与载波频率示意图
Fig.3 Diagram of two types of periodic carrier frequency modulations and the relatd carrier frequency
根据以上周期信号的时域信号,本文建立了完整的功率谱密度解析模型,以正弦波扩频调制信号为例,功率谱密度可以表示为
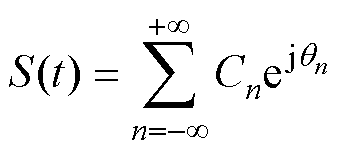 (11)
(11)
式中,Cn为n阶边带谐波的幅值;qn为n阶边带谐波的相位,实际为周期性载波频率调制信号瞬时频率在时间上的积分。
首先,需要将正弦波时域信号转化为关于g 的傅里叶级数,有
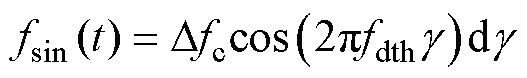 (12)
(12)
将式(12)代入式(11)中,则正弦波扩频调制的功率谱密度为
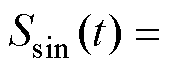
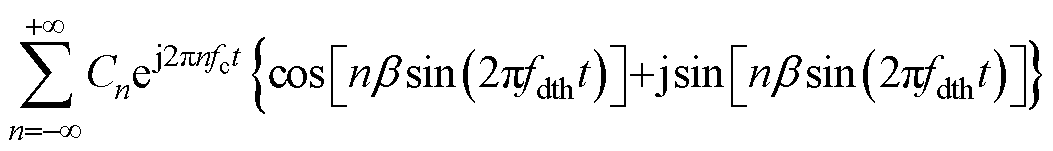 (13)
(13)
式中,b 为调制因子,在运算中被视为Dfc与fdth的比值,即
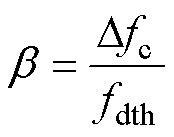 (14)
(14)
将式(13)中的sin与cos项使用雅克比(Jacobi)方程转换,正弦波功率谱密度函数中
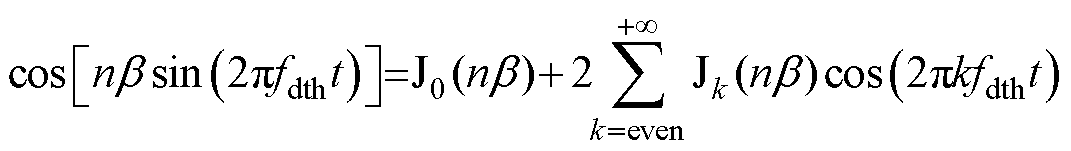 (15)
(15)
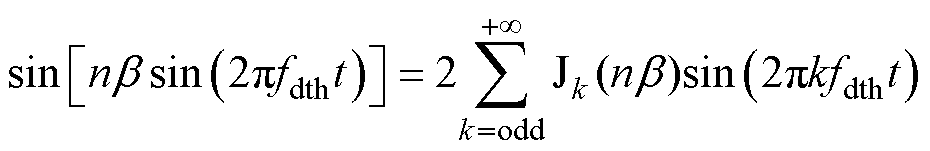 (16)
(16)
根据欧拉公式,将所有经过雅克比转化后的函数进行指数化化简,可以得出功率谱密度在时域范围内的定义函数。本文为了能够获得更直观的频率分布与调制因子之间的关系,提取功率谱密度函数中指数部分的频率分量,统一定义为
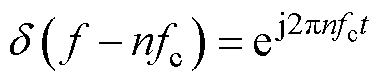 (17)
(17)
功率谱密度函数由原先的S(t)重构为S( f, b)的形式。此外,基于以上推导过程,锯齿波的功率谱密度解析过程在附录中给出,基于两种周期信号的功率谱密度解析结果为
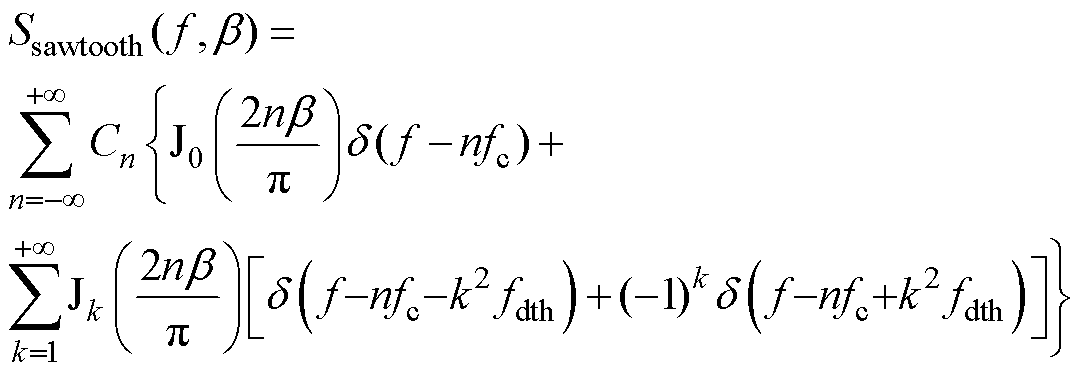 (18)
(18)
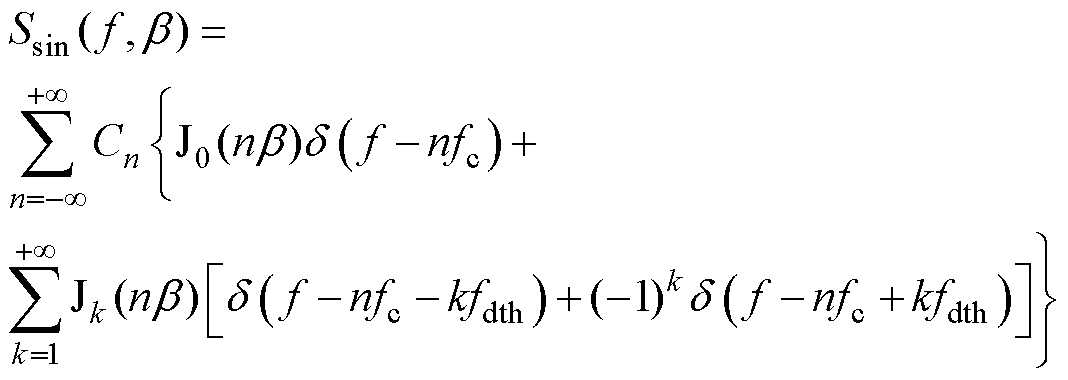 (19)
(19)
由式(18)和式(19)可以得出,锯齿波和正弦波扩频调制的功率谱密度频率分布与幅值特性,具体分析如下:
(1)经过周期扩频调制,边带电流谐波的幅值由解析式中的Jk(∙)项决定,Jk(∙)项可以用贝塞尔级数定义,锯齿波与正弦波扩频调制中的Jk(∙)最大值变化趋势如图4所示。本质上,Jk(x)随x值的增大而减小,从而使边带电流谐波抑制效果增加;在相同x值条件下,锯齿波扩频调制的抑制效果优于正弦波扩频调制。
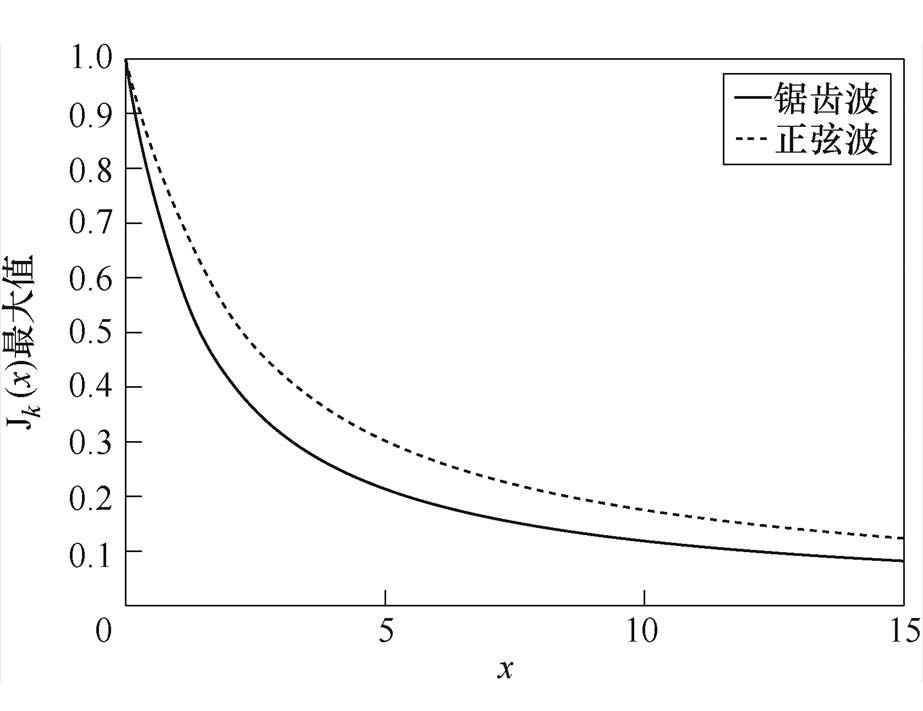
图4 Jk(x)最大值随x值的变化趋势
Fig.4 Trend of maximum Jk(x) with the value of x
(2)n和b 是影响两种周期扩频调制的共同因素。由于b 与D fc和fdth相关,对于不同调制参数对边带电流谐波的抑制效果仍需进一步讨论。此外,由图4还可以看出,当x足够大时,即nb 值足够大时,抑制效果不会显著增加,且趋于饱和。
(3)周期扩频调制后的边带谐波频率分布可以由d(∙)项定义。锯齿波扩频调制的频率特征以k2fdth二次项分布,而正弦波扩频调制的边带谐波频率特征以k fdth线性分布,这就使得正弦波扩频调制对调制参数的敏感程度要高于锯齿波。
由2.1节可以看出,由b 所决定的调制参数对边带电流谐波的抑制具有较大的影响。从功率谱密度解析模型中可以看出,随着b 值的增加,抑制效果随之增大,这意味着D fc和fdth分别对应不同的设定范围。首先,考虑到周期信号对于载波频率的波动过程,当fdth的取值较小时,载波频率的变化较为缓慢,从而在相对较长的时间范围内使抑制效果不明显;以极端情况fdth=0为例,此时载波频率将回归固定值,本质上周期扩频调制将失效。为了在每个扩频周期内获得相同的抑制效果,fdth的取值至少应该与PWM占空比信号的基频相等,即与电机电枢电流基频f0相等,即fdth=f0。
其次,b 的取值与D fc相关,这涉及到周期扩频调制中载波频率的波动范围,即频谱中的扩频宽度。由上述分析可以看出,随着扩频宽度的增加,b 的值将会增大,抑制效果也会随之增加。扩频宽度的定义为
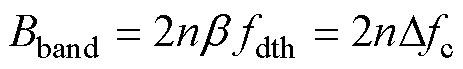 (20)
(20)
以第一载波频率为例,n=1,扩频宽度Bband为2倍的周期信号的幅值。由于随着b 取值的逐渐增大,抑制效果将趋于饱和,因此本文在实验验证中选取几组扩频宽度进行了对比,最大扩频宽度的选择将综合考虑边带电流谐波与声振响应的抑制效果。
为了验证常规SVPWM与所提出的两种周期扩频调制技术对边带电流谐波与声振响应的抑制效果,本文选用了一款电动汽车后桥驱动12槽/10极永磁同步样机,具体参数见表1,并建立了相应的样机实验平台,主要包括测试平台、电机测控系统与主控电路,如图5和图6所示。
表1 永磁同步电机样机参数
Tab.1 Parameters of the prototype PMSM
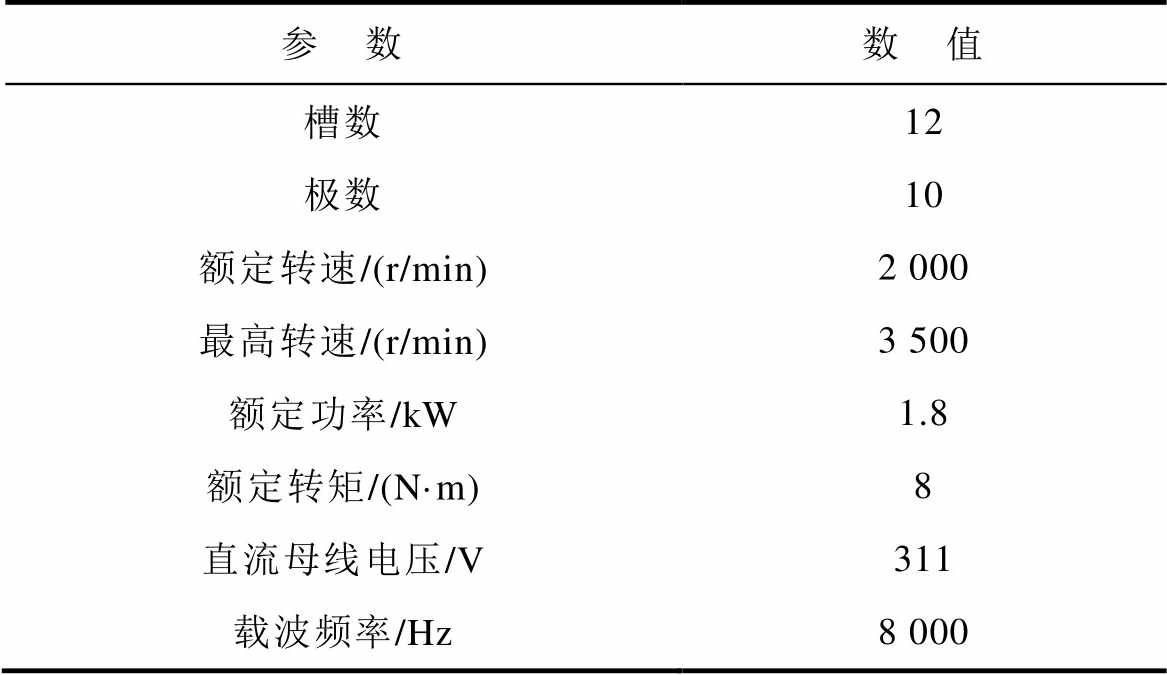
参 数数 值 槽数12 极数10 额定转速/(r/min)2 000 最高转速/(r/min)3 500 额定功率/kW1.8 额定转矩/(N·m)8 直流母线电压/V311 载波频率/Hz8 000

图5 实验与测试平台
Fig.5 Experimental setup and measurements
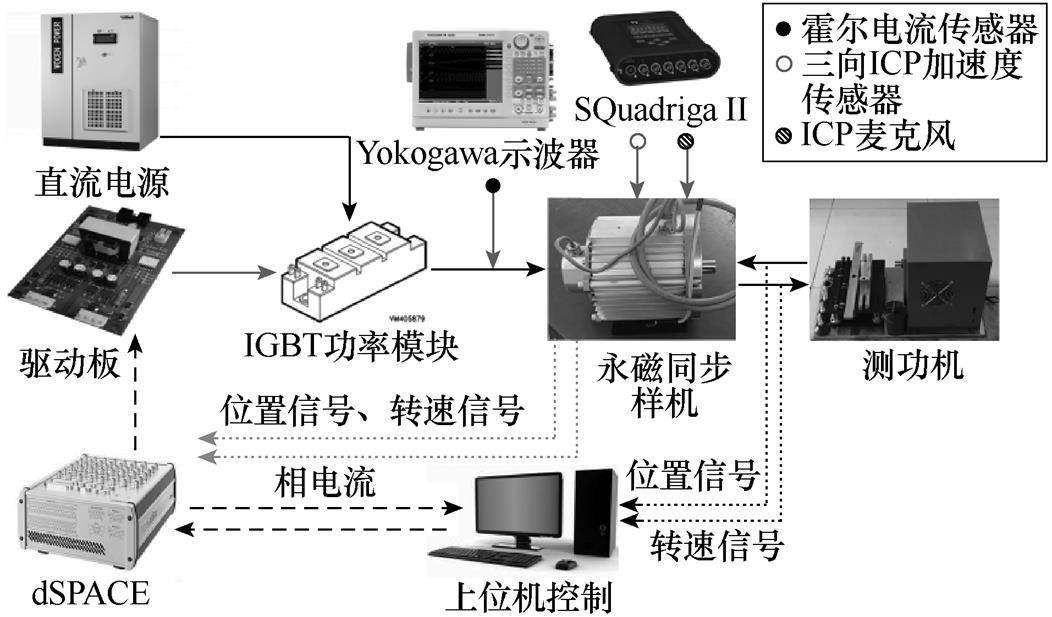
图6 实验平台布置原理
Fig.6 Principle of experimental platform
实验中的测试平台是基于20N·m磁粉测功机实现转矩加载;直流电源采用80kW·h电池模拟器输出311VDC-3kW,驱动电路与三相全桥功率模块选用Infineon-BSM-75GB120DN2。本文所提出的所有PWM策略均使用dSPACE1103半实物仿真平台及其实时监控上位机系统实现PWM信号发波、电流与位置信号的反馈、策略切换与参数实时更替。
在测量电机振动信号时,将三向压电式加速度传感器安装在电机壳体上,传感器灵敏度为42.32mV/g;辐射噪声信号采用ICP型麦克风进行采集;振动噪声信号,使用朗德SQuadriga II数据采集仪进行采集与运算。相电流信号使用霍尔电流传感器和Yokogawa示波器进行采集。
考虑到实际VSI的高功率输出,本文在实验测试中将载波频率设定为8 000Hz,这将导致边带电流谐波及其声振响应的频谱集中在8 000Hz及其整数倍范围。由于人耳对于12 000Hz以上的高频噪声不敏感,加之麦克风传感器的测量范围的限制,本文选择8 000Hz附近的频谱,即第一载波频率范围,进行了相应的分析。
为了清楚地验证边带电流谐波与声振响应,本文首先对样机在稳态工况1 000r/min和4N·m条件下的常规SVPWM和周期扩频调制技术进行了验证与比较。电机转动频率fr=16.67Hz,根据f0=pfr,电流基波频率f0=83.34Hz;在周期扩频调制验证中,调制参数中的调制因子设定为1,扩频宽度设定为2 000Hz。相电流波形与边带电流谐波如图7所示,其中边带电流频谱通过PSD计算方法进行了处理。
从实验数据中可以看出,常规SVPWM所产生的边带电流谐波在载波频率附近显示出明显的阶次分布,特征频率为7 667Hz ( fc-4 f0),7 833Hz ( fc-2 f0),8 167Hz ( fc+2 f0)和8 334Hz ( fc+4 f0);其中边带电流谐波的幅值峰值出现在fc±2 f0,幅值为-26.49dB/Hz;fc±4 f0处的幅值为-39.81dB/Hz。经过两种周期扩频调制后,边带电流谐波成分均被扩展到7 000~9 000Hz区间,原本的4个主要的特征阶次被有效抑制,现有特征阶次间隔f0;主要阶次的边带电流谐波的幅值被抑制到-40dB/Hz以下,正弦波扩频调制后的边带电流谐波在截止频率7 000Hz和9 000Hz附近大于-40dB/Hz,验证了功率谱密度解析模型的有效性。
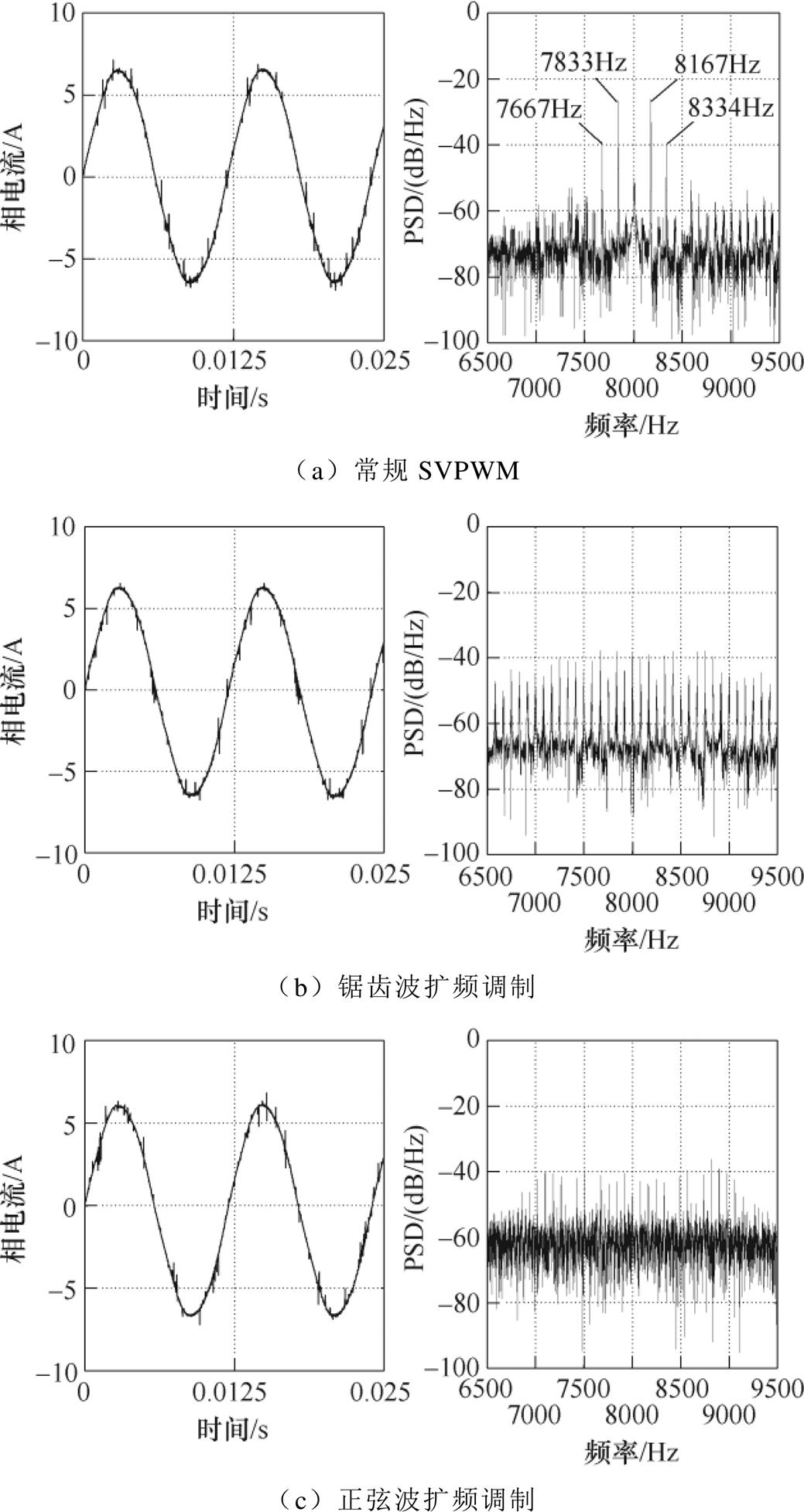
图7 常规SVPWM和周期扩频调制技术相电流波形与边带电流频谱分析
Fig.7 Phase current waves and sideband current harmonic components in conventional SVPWM and periodic spread sprectum modulations
边带声振响应的频谱如图8所示,其中,为了计算动态声压级,噪声数据经过了声压级A计权(SPL-A)处理。从常规SVPWM的声振频谱可以看出与边带电流谐波相似的阶次分布,特征频率分别为7 583Hz ( fc-5f0),7 750Hz ( fc-3f0),7 917Hz ( fc-f0),8 084Hz ( fc+f0),8 250Hz ( fc+3f0)和8 416Hz ( fc+5f0),验证了边带声振响应与边带电流谐波之间的相关性。以噪声数据结果为例,常规SVPWM边带噪声的峰值位于fc± f0处53.36dBA;经过两种周期扩频调制后,原中心频带的幅值下降至30dBA以下,锯齿波扩频调制抑制效果最优,低于23dBA;正弦波扩频调制低于25dBA,中心频带优化20dBA以上。
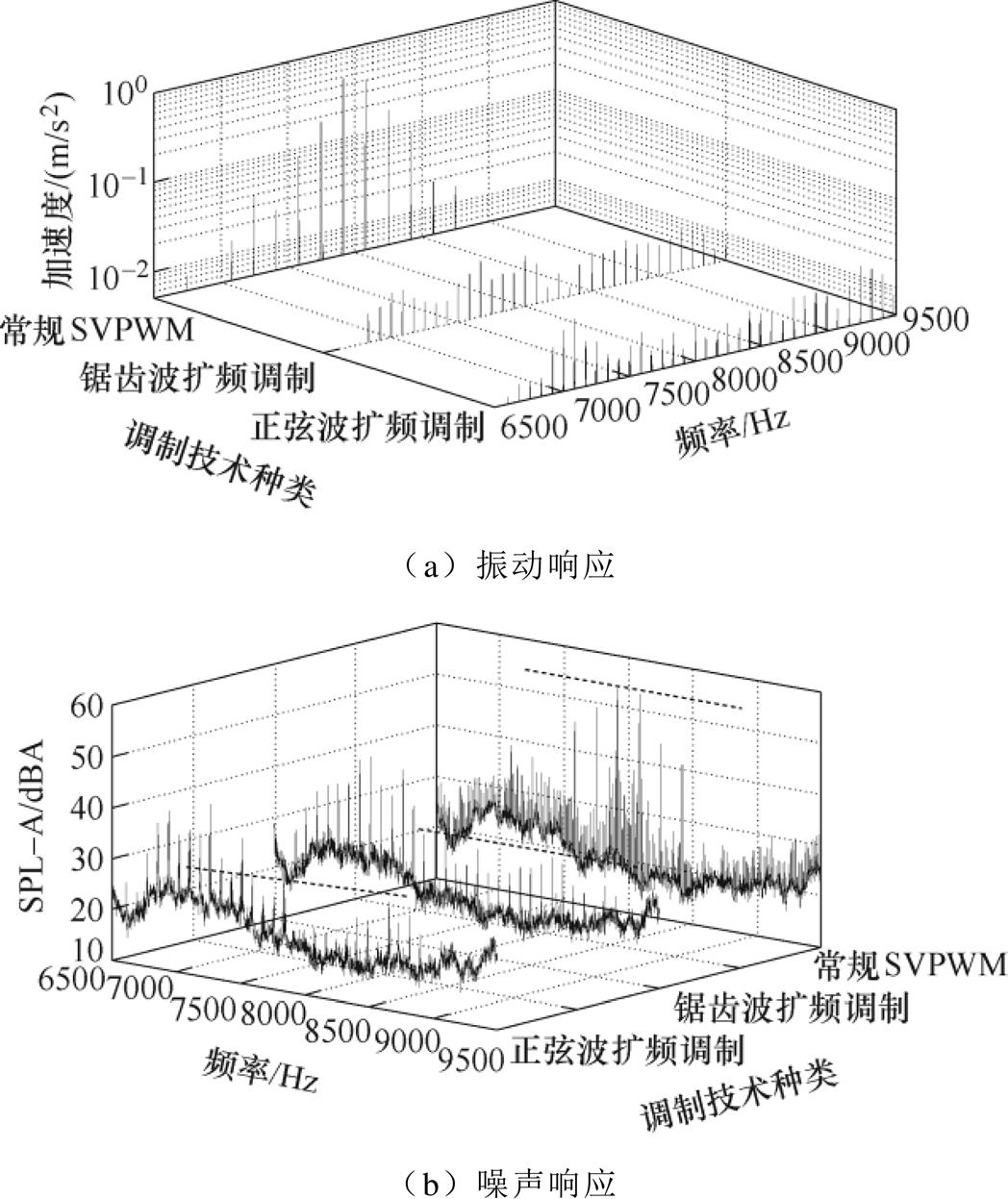
图8 常规SVPWM和周期扩频调制技术边带声振响应
Fig.8 Sideband vibro-acoustics in conventional SVPWM and periodic spread sprectum modulations
应用两种优化方法后,相电流功率谱密度数据中6 500~7 500Hz频段出现15~20dB/Hz的增长,造成了在所对应的频段范围的声振响应0.05m/s2和15dBA的增长。此外,在7 000~7 500Hz的区间内出现较大的噪声幅值,这是由于边带电磁激励力的频率与实验平台的共振频率重合,从而产生了额外的10dBA谐振噪声。即使如此,经过周期扩频调制后,边带声振响应依然呈现出较为显著的抑制效果。
为了完整评估周期扩频调制在不同工况下的抑制效果,本文在相同转矩模式下选取了500r/min、1 000r/min、1 500r/min和2 000r/min转速条件下的边带噪声峰值与中心频带峰值进行了比较,如图9所示。结果表明,受频率调制影响,边带噪声幅值受转速影响较大;周期频率调制在多工况下,均能呈现出较好的抑制效果。
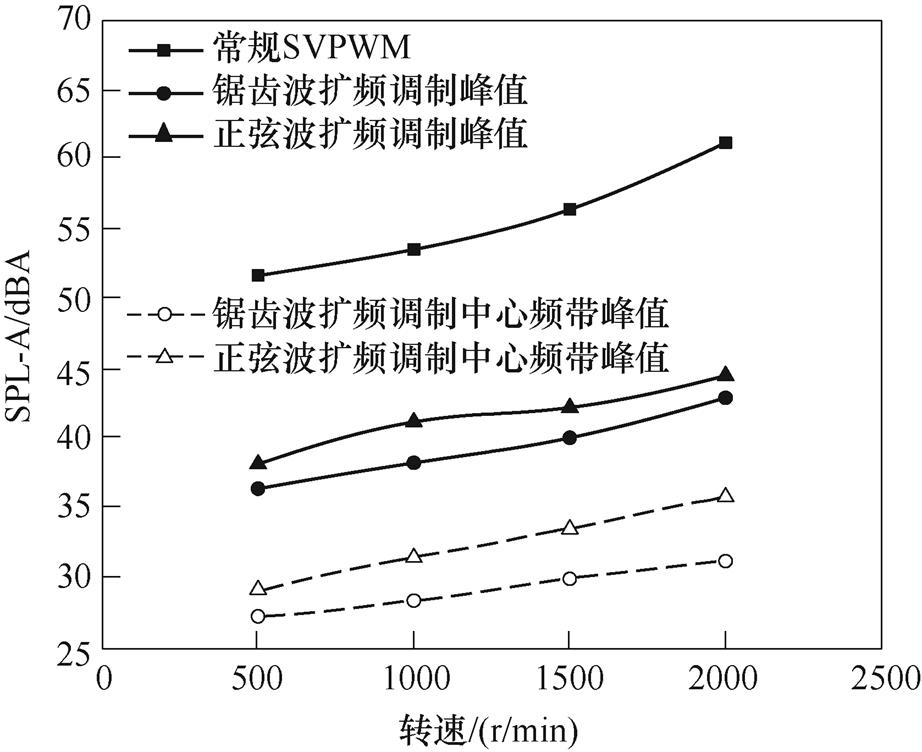
图9 不同转速工况下边带噪声响应抑制效果
Fig.9 The comparison of sideband acoustic responses with different rotation speeds
根据第2.1节的分析,调制参数对边带电流谐波的抑制具有较大影响。可以确定的是,调制因子与扩频宽度是相互独立的影响因素,抑制效果在fdth=f0时达到最佳;扩频宽度的增加会产生更优的抑制效果。考虑到噪声响应频谱较为嘈杂,而振动响应较为纯净且能清晰地反映出幅值变化,本文选取了边带振动响应频谱,对400Hz、800Hz、1 600Hz和2 000Hz四种不同扩频宽度进行了比较分析。
不同扩频宽度的边带振动响应如图10所示,随着扩频宽度的增加,锯齿波扩频调制的抑制效果优于正弦波频率调制;正弦波扩频调制对于扩频宽度较为敏感;扩频宽度在1 600~2 000Hz区间时,抑制效果达到了饱和。
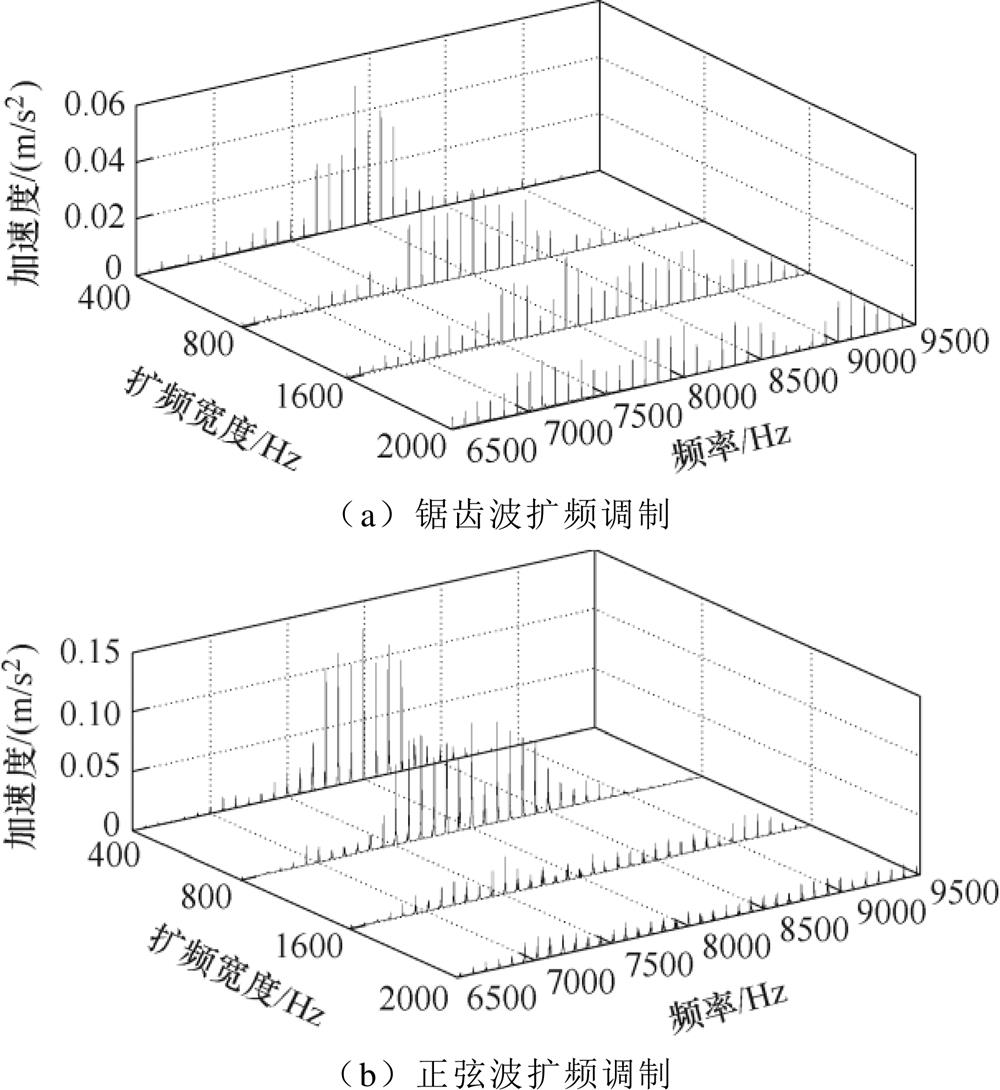
图10 不同扩频宽度的边带振动响应
Fig.10 The comparison of sideband vibration responses with different bandwidths
本文针对常规SVPWM所引入的边带电压与电流谐波成分与高频声振响应进行了抑制与优化研究,提出了两种典型的周期扩频调制策略与功率谱密度解析模型。结合不同工况下的样机实验验证,分析了调制参数对抑制效果的影响,所得出的结论如下:
1)基于典型的锯齿波和正弦波周期信号的功率谱解析模型,能够有效分析扩频调制后的频谱分布与抑制效果。
2)对不同转速工况下的实验结果表明,所提出的两种典型的周期扩频调制方法能够有效抑制边带电流谐波分量;在声振响应中也呈现出显著的优化效果,中心频带的噪声响应达到了20dBA以上。
3)所提出的周期扩频调制方法中,锯齿波扩频调制的抑制效果优于正弦波扩频调制;正弦波扩频调制受扩频宽度影响较为敏感,并且随着扩频宽度的持续增加,抑制效果逐渐趋于饱和。
4)所提出的功率谱解析模型与实验验证结果可以被拓展到基于其他周期信号的扩频调制技术,对于调制参数的选择仍需针对不同系统进行多目标优化。此外,本文为开发新型混合扩频调制策略,实现低声振电驱动系统提供了理论依据与实践参考。
附 录
锯齿波时域信号转化为关于g 的傅里叶级数为
 (A1)
(A1)
将式(A1)代入式(11)后可得
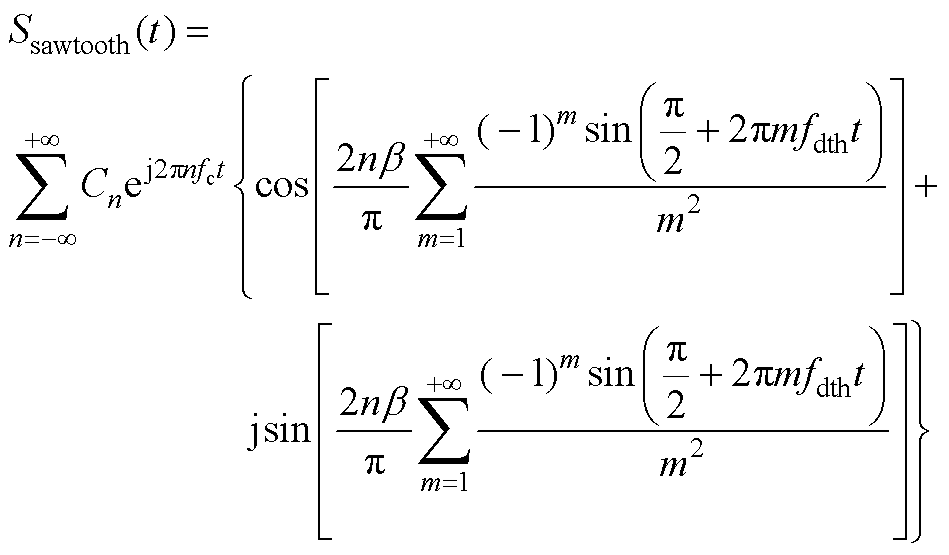 (A2)
(A2)
其中,sin与cos项可以使用雅克比(Jacobi)方程转换,有
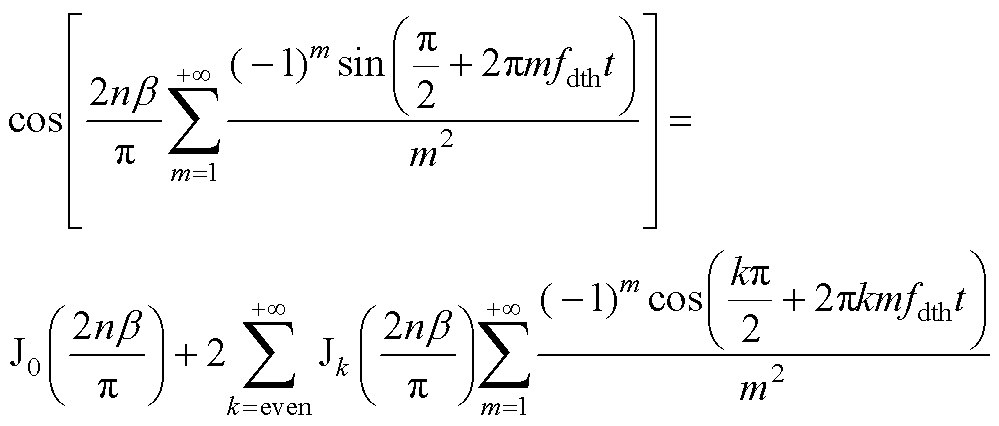 (A3)
(A3)
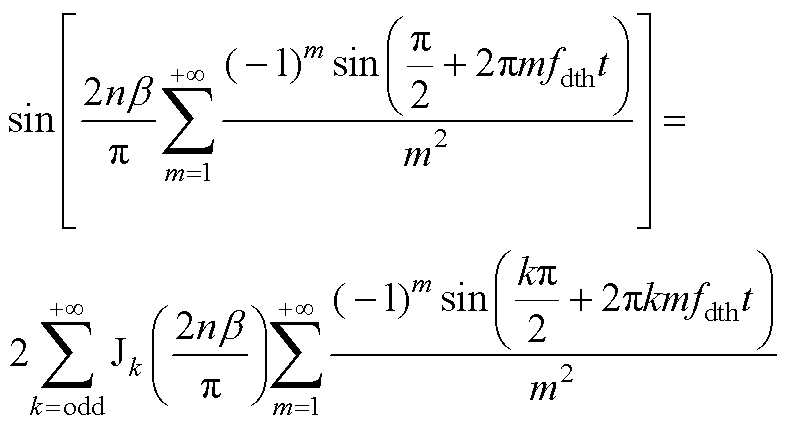 (A4)
(A4)
参考文献
[1] Deng Wenzhe, Zuo Shuguang. Electromagnetic vibration and noise of the permanent-magnet synchronous motors for electric vehicles: an overview[J]. IEEE Transactions on Transportation Electrification, 2019, 5(1): 59-70.
[2] Dong Qichao, Liu Xintian, Qi Hongzhong, et al. Vibro-acoustic prediction and evaluation of permanent magnet synchronous motors[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2020, 234(12): 2783- 2793.
[3] 邱子桢, 陈勇, 康洋, 等. 电动汽车驱动永磁同步电机声品质预测研究[J]. 噪声与振动控制, 2020, 40(2): 146-151.
Qiu Zizhen, Chen Yong, Kang Yang, et al. Sound quality prediction for permanent magnet synchronous motors used in electric vehicles[J]. Noise and Vibration Control, 2020, 40(2): 146-151.
[4] Deng Wenzhe, Zuo Shuguang. Comparative study of sideband electromagnetic force in internal and external rotor PMSMs with SVPWM technique[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 956-966.
[5] 吕康飞, 董新伟, 刘丽丽, 等. 考虑零序电流抑制的开绕组永磁同步电机断相故障下统一调制策略[J]. 电工技术学报, 2020, 35(11): 2387-2395.
Lü Kangfei, Dong Xinwei, Liu Lili, et al. The unified modulation scheme of open-end winding PMSM with common DC bus under the open-phase fault con- sidering the suppression of zero-sequence current[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2387-2395.
[6] 李晓华, 赵容健, 田晓彤, 等. 逆变器供电对电动汽车内置式永磁同步电机振动噪声特性影响研究[J]. 电工技术学报, 2020, 35(21): 4455-4464.
Li Xiaohua, Zhao Rongjian, Tian Xiaotong, et al. Study on vibration and noise characteristics of interior permanent magnet synchronous machine for electric vehicles by inverter[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4455-4464.
[7] 高瞻, 李耀华, 葛琼璇, 等. 适用于大功率三电平中点钳位整流器的SVPWM和DPWM策略研究[J].电工技术学报, 2020, 35(23): 4864-4876.
Gao Zhan, Li Yaohua, Ge Qiongxuan, et al. Research on SVPWM and DPWM strategies suitable for high power three-level neutral point clamped rectifier[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4864-4876.
[8] Fang Yuan, Zhang Tong. Sound quality of the acoustic noise radiated by PWM-fed electric power- train[J]. IEEE Transactions on Industrial Electronics, 2018, 65(6): 4534-4541.
[9] 陈勇, 胡世同, 邱子桢, 等. 新能源车用永磁同步电机辐射噪声预测研究[C]//2019中国汽车工程学会年会, 上海, 2019(4): 117-122.
[10] Liang Wenyi, Wang Jianfeng, Luk C K, et al. Analytical modeling of current harmonic components in PMSM drive with voltage-source inverter by SVPWM technique[J]. IEEE Transactions on Energy Conversion, 2014, 29(3): 673-680.
[11] Qiu Zizhen, Chen Yong, Liu Xu, et al. Analysis of the sideband current harmonics and vibro-acoustics in the PMSM with SVPWM[J]. IET Power Electronics, 2020, 13(5): 1033-1040.
[12] Liang Wenyi, Luk P C, Fei Weizhong. Analytical investigation of sideband electromagnetic vibration in integral-slot PMSM drive with SVPWM technique[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4785-4795.
[13] 左曙光, 刘晓璇, 于明湖, 等. 永磁同步电机电磁振动数值预测与分析[J]. 电工技术学报, 2017, 32(1): 159-167.
Zuo Shuguang, Liu Xiaoxuan, Yu Minghu, et al. Numerical prediction and analysis of electromagnetic vibration in permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2017, 32(1): 159-167.
[14] Xu Yongxiang, Yuan Qingbin, Zou Jibin, et al. Sinusoidal periodic carrier frequency modulation in reducing electromagnetic noise of permanent magnet synchronous motor[J]. IET Electric Power Appli- cations, 2013, 7(3): 223-230.
[15] Xu Yongxiang, Yuan Qingbing, Zou Jibin, et al. Influ- ence of periodic carrier frequency modulation on inverter loss of permanent magnet synchronous motor drive system[C]//International Conference on Electrical Machines and Systems, Hangzhou, China, 2014: 2101-2106.
[16] Zhang Wentao, Xu Yongxiang, Huang Yingliang, et al. Reduction of high-frequency vibration noise for dual-branch three-phase permanent magnet syn- chronous motors[J]. Chinese Journal of Electrical Engineering, 2020, 6(2): 42-51.
[17] Pindoriya R M, Rajpurohit B S, Kumar R. A novel application of harmonics spread spectrum technique for acoustic noise and vibration reduction of PMSM drive[J]. IEEE Access, 2020, 8: 103273-103284.
[18] 刘和平, 刘庆, 张威, 等. 电动汽车用感应电机削弱振动和噪声的随机PWM控制策略[J]. 电工技术学报, 2019, 34(7): 1488-1495.
Liu Heping, Liu Qing, Zhang Wei, et al. Random PWM technique for acoustic noise and vibration reduction in induction motors used by electric vehicles[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1488-1495.
[19] 原庆兵. 永磁同步电机系统的周期频率调制策略研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.
[20] Xu Yongxiang, Yuan Qingbin, Zou Jibin, et al. Periodic carrier frequency modulation in reducing low frequency electromagnetic interference of permanent magnet synchronous motor drive system[J]. IEEE Transactions on Magnetics, 2015, 51(11): 8109604.
[21] 陆原, 胡丙辉, 张军伟, 等. 基于SVPWM调制的三段式算法研究[J]. 电力系统保护与控制, 2016, 44(6): 68-75.
Lu Yuan, Hu Binghui, Zhang Junwei, et al. A three-segment algorithm research based on SVPWM modulation[J]. Power System Protection and Control, 2016, 44(6): 68-75.
[22] 高瞻, 葛琼璇, 李耀华, 等. 一种基于载波实现的三电平中点钳位变流器零矢量首发SVPWM方法[J].电工技术学报, 2020, 35(10): 2194-2205.
Gao Zhan, Ge Qiongxuan, Li Yaohua, et al. A carrier- based SVPWM begins with the zero voltage vector for three-level neutral point clamped converter[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2194-2205.
[23] Holmes D G. Pulse width modulation for power converters: principles and practice[M]. Piscataway: Wiley-IEEE Press, 2003.
[24] 林福, 左曙光, 毛钰, 等. 考虑电流谐波的永磁同步电机电磁振动和噪声半解析模型[J]. 电工技术学报, 2017, 32(9): 24-31.
Lin Fu, Zuo Shuguang, Mao Yu, et al. Semi-analytical model of vibration and noise for permanent magnet synchronous motor considering current harmonics[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 24-31.
Periodic Harmonic Spread Spectrum Modulation for High-Frequency Sideband Vibro-Acoustic Suppression in Permanent Magnet Synchronous Motor
Abstract In this paper, a 12-slot/10-pole permanent magnet synchronous motor and control system for the electric vehicle rear axle drive has been taken as the research object. Based on the periodic harmonic spread spectrum modulation technique, the sideband harmonic components and high-frequency vibro-acoustic response introduced by the conventional space vector pulse width modulation (SVPWM) technology are suppressed. The main frequency distribution and other characteristics are analyzed in sideband current harmonics and radial electromagnetic force. A comprehensive power spectrum analysis model of harmonic spread spectrum modulation has been established, where two typical periodic signals of sawtooth wave and sinusoidal wave are analyzed. The influence of bandwidth and modulation ratio on the suppression effect is also discussed. The related sideband current harmonics and vibro-acoustic responses are verified by the measurement and control experimental platform under different operational conditions. The results show that the periodic harmonic spread spectrum modulation can effectively suppress sideband harmonic components, and the central frequency band of noise responses is optimized by more than 20dBA. The sawtooth signal-based scheme exhibits better suppression effect than the sinusoidal signal-based scheme. Moreover, the sideband harmonics in the sinusoidal signal-based scheme are more sensitive to the bandwidth changes.
keywords:Permanent magnet synchronous motor, space vector pulse-width modulation, sideband current harmonics, harmonic spread spectrum modulation, vibro-acoustics control
DOI: 10.19595/j.cnki.1000-6753.tces.201525
中图分类号:TM341
邱子桢 男,1992年生,博士研究生,研究方向为电驱动系统振动与噪声控制。E-mail: qiuzizhen@catarc.ac.cn
陈 勇 男,1954年生,教授,博士生导师,研究方向为汽车动力传动系统CAE设计与分析。E-mail: chenyong1585811@163.com(通信作者)
收稿日期 2020-11-18
改稿日期 2021-03-08
宁波市科技计划项目(2019B10111)、国家留学基金项目(201906700001)和河北省研究生创新项目(CXZZBS2021033)资助。
(编辑 崔文静)