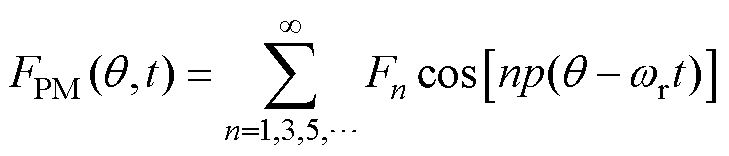 (1)
(1)
摘要 分析了永磁电机在空载和负载工况下高模数电磁力波对电机电磁振动的影响。首先通过麦克斯韦应力张量法推导了电机电磁力波的幅值、频率和模数特征。其次阐述了引起永磁电机低阶电磁振动源的高模数和低模数电磁力波特点并探讨了齿宽对两种电磁力的影响。然后计算和详细对比了电机空载和负载工况下两种电磁力波对低阶电磁振动的贡献,并用模态叠加法仿真电机的振动,对理论进行验证。最后在一台10极12槽永磁电机上进行空载电磁振动实验,与仿真计算结果吻合较好。研究表明,高模数电磁力波能引起较大的低阶电磁振动,但在分数槽电机中,其贡献程度随负载的增加而减弱。该文的研究将为永磁电机电磁振动的准确预测和减振提供 思路。
关键词:高模数电磁力波 低阶电磁振动 齿斩波效应 永磁同步电机
永磁电机因具有高效率、高功率密度、高可靠性等优点而广泛应用于国民经济的各个领域。在一些特殊的应用场合,如舰艇、电动汽车、高端家用电器等领域,振动噪声是高性能永磁电机的关键指标[1],日益受到关注。
目前,已有许多学者对永磁电机的电磁振动源进行分析。文献[2-3]采用解析法分析了永磁电机的电磁振动特性,认为电机中电磁力波的最小模数能引起较大的电磁振动,且最小模数为电机槽数和极数的最大公约数。文献[4]采用电磁和结构有限元法对六种不同齿槽配合的永磁电机电磁力波和电磁振动进行计算,结果表明电磁力波模数越小,引起的电磁振动越大。类似地,文献[5]对不同极槽配合下的电机电磁振动进行分析,并认为低阶电磁力波是引起低阶电磁振动的主源。文献[6]对10极12槽的分数槽永磁电机的空载、电枢反应及负载下的电磁力波进行了详细的解析和有限元计算,认为电机中模数2的电磁力波能引起显著的振动,并对模数2的电磁力波来源进行了细致的分析。
在永磁电机的电磁振动解析计算方面,学者P. Timar将电机定子等效为圆柱壳,提出了一种解析计算电机电磁振动的公式[7]。基于圆柱壳理论,文献[8]计算了一台6极9槽永磁电机的电磁振动。文献[9]简化电机定子为圆环结构,以电磁力源为激励源解析计算了电机电磁振动。基于机械静态平衡原理,文献[10]计算了圆壳型电机定子结构表面的位移。文献[11]以电磁力波为输入源,提出了一种基于模态叠加法的电机振动噪声分析方法。文献[12-13]分析了变频器引入的高频谐波电流对电机电磁振动的影响。
然而,在开槽定子结构的电机电磁振动分析过程中,将电机简化为圆环结构进行电磁振动计算会带来较大的误差,文献[14-16]已经注意到了定子开齿对电机电磁振动的影响。文献[14]运用有限元法分析了一台6极9槽永磁电机的电磁振动,结果发现模数6的电磁力波能引起3阶的电磁振动,但并未进一步分析原因。文献[15]采用齿调制效应揭示了10极12槽永磁电机模数10的电磁力波产生2阶电磁振动这一现象,并对电机空载工况进行了仿真分析和实验,认为模数10的电磁力波是2阶电磁振动的主要激振源,但未对负载工况下高模数电磁力波的影响进行分析。文献[16]针对整数槽永磁电机中突出的槽频振动,提出了齿斩波效应,空载工况下的仿真和实验结果表明,槽数模数电磁力波是0阶槽频振动的主源,但未对负载工况下的电机电磁振动进行分析。
在文献[14-16]的基础上,本文对负载工况下10极12槽永磁电机中引起低阶振动的高模数和低模数电磁力波进行详细分析,并探究了高模数和低模数电磁力波的来源。首先采用解析法计算了永磁电机中的电磁力波,分析了其特性。其次分析了引起低阶振动的低阶和高阶电磁力的特点及其与齿槽的关系。再次采用解析和有限元法分析了10极12槽永磁电机在空载和负载工况下产生低阶电磁振动的高模数和低模数电磁力波激励源。最后基于模态叠加法仿真分析了永磁电机的电磁振动,验证了齿斩波效应的正确性,并通过样机实验加以验证。基于本文采用齿斩波效应研究定子开齿对电机电磁振动特性的影响,不仅有利于从本质上认清低阶电磁振动源,还能为开齿永磁电机电磁振动的准确预测和减振提供思路。
文献[17]已经对永磁电机中永磁体产生的电磁力波进行了详细推导,这里只给出主要的计算结果。由永磁体产生的磁动势FPM为
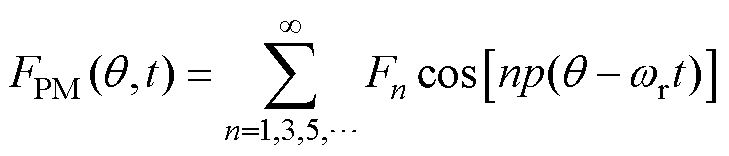 (1)
(1)
式中,p为电机极对数;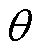 为转子空间位置角;
为转子空间位置角;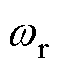 为转子机械角频率;Fn为n次谐波磁动势,n=1, 3, 5,…。
为转子机械角频率;Fn为n次谐波磁动势,n=1, 3, 5,…。
电机在三相对称绕组正弦电流激励下产生的磁动势FAr[18]为
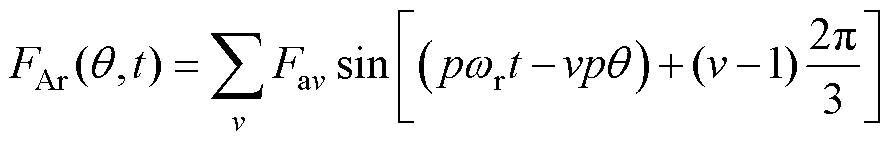 (2)
(2)
其中
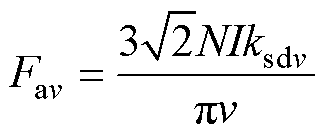
式中,Fav为v次谐波磁动势幅值,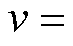
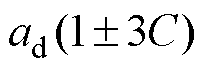 ,
,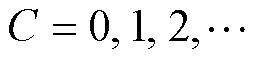 ,
,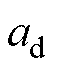 为单元电机数;N为绕组匝数;I为电流有效值;ksdv为v次谐波绕组系数。
为单元电机数;N为绕组匝数;I为电流有效值;ksdv为v次谐波绕组系数。
当考虑电机定子开槽对磁场的影响时,一般可用磁导函数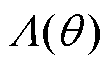 表示[17],即
表示[17],即
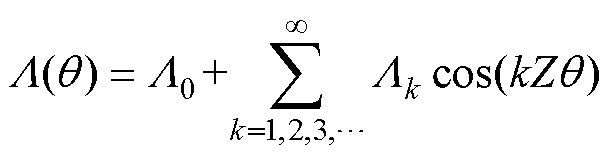 (3)
(3)
式中,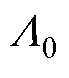 为平均磁导;
为平均磁导;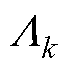 为k次谐波磁导;Z为电机定子槽数。
为k次谐波磁导;Z为电机定子槽数。
当考虑定子开槽影响后,电机的径向磁通密度Br即可表示为磁动势与气隙磁导相乘,即
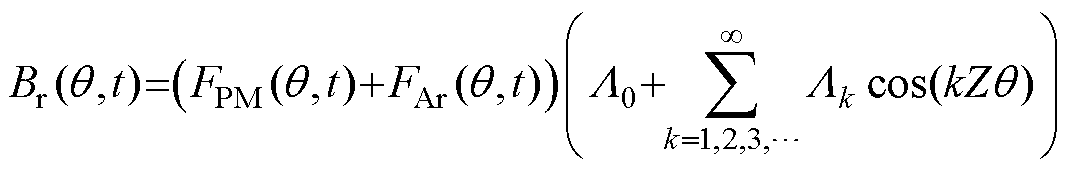
 (4)
(4)
式中,BPM和BAr分别为永磁体和电枢绕组产生的磁通密度。根据Maxwell应力张量法可求得气隙中的电磁力波,当忽略切向磁通密度时,表达式可写为
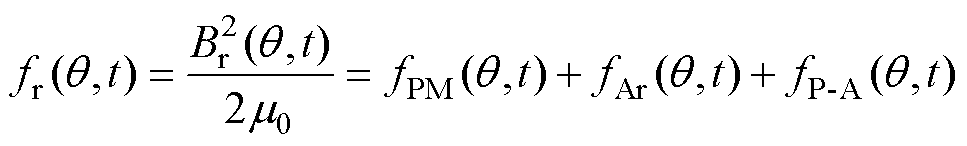 (5)
(5)
式中,m0为真空磁导率;fAr为绕组电枢反应磁场产生的电磁力波;fP-A为永磁体与绕组相互作用产生的电磁力波;fPM为永磁体产生的电磁力波,为便于分析,根据平均磁导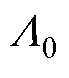 和谐波磁导
和谐波磁导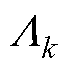 的作用情况,可将fPM表示为
的作用情况,可将fPM表示为
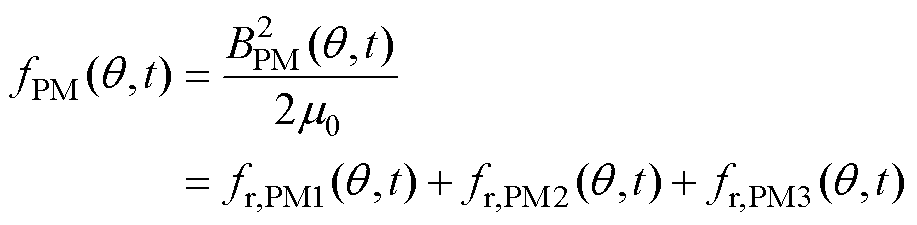 (6)
(6)
其中
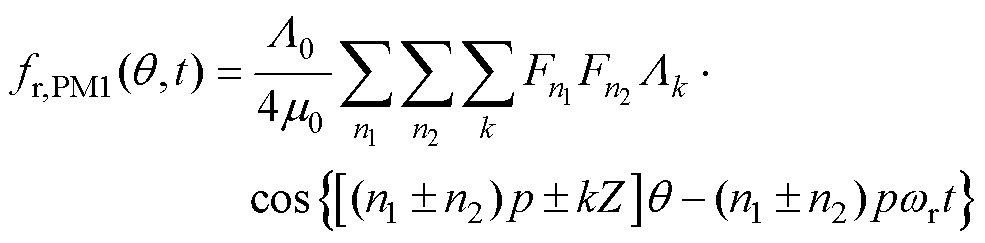 (7)
(7)
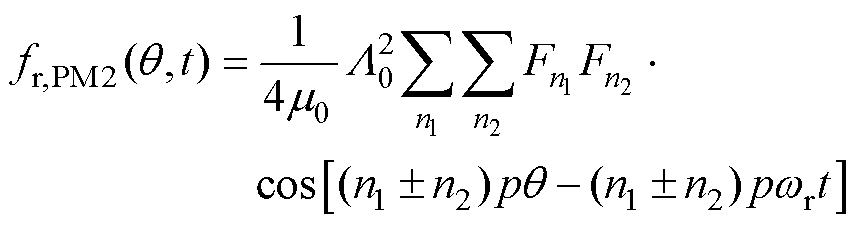 (8)
(8)
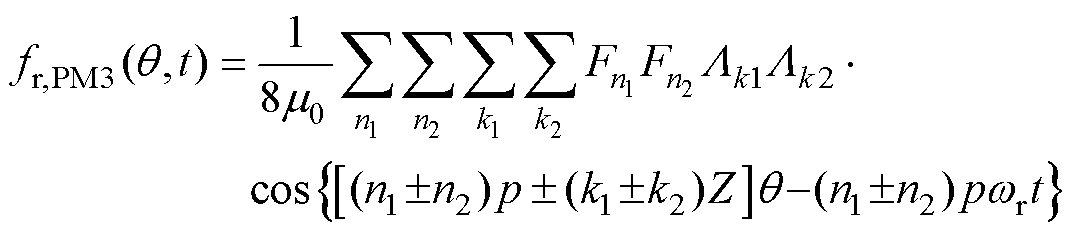 (9)
(9)
根据平均磁导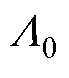 和谐波磁导
和谐波磁导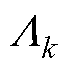 的作用情况,
的作用情况,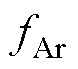 表达式可写为
表达式可写为
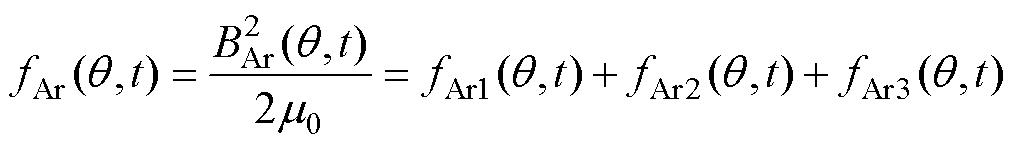 (10)
(10)
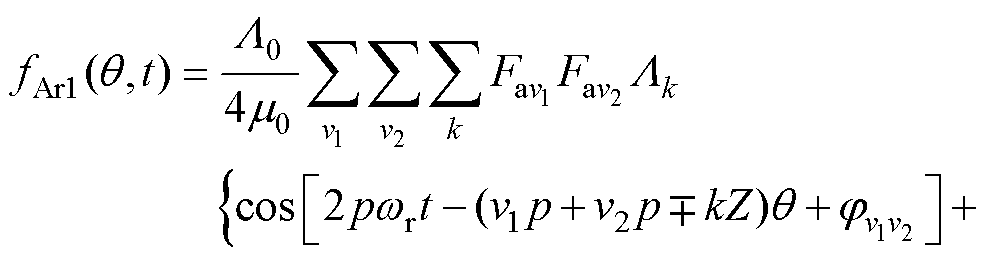
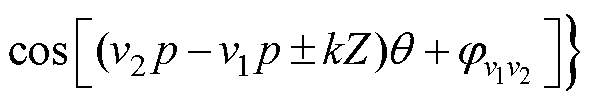 (11)
(11)
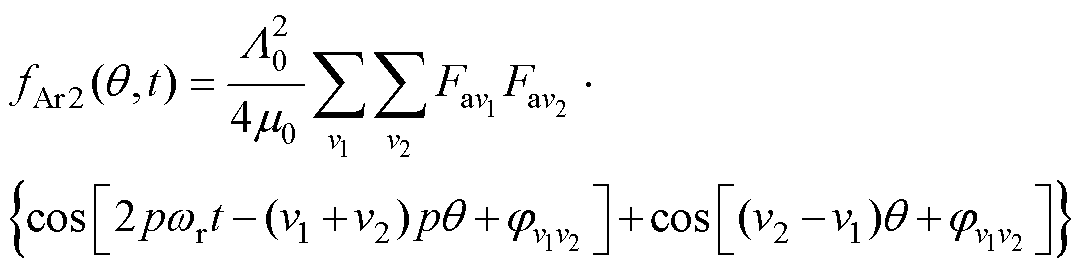 (12)
(12)
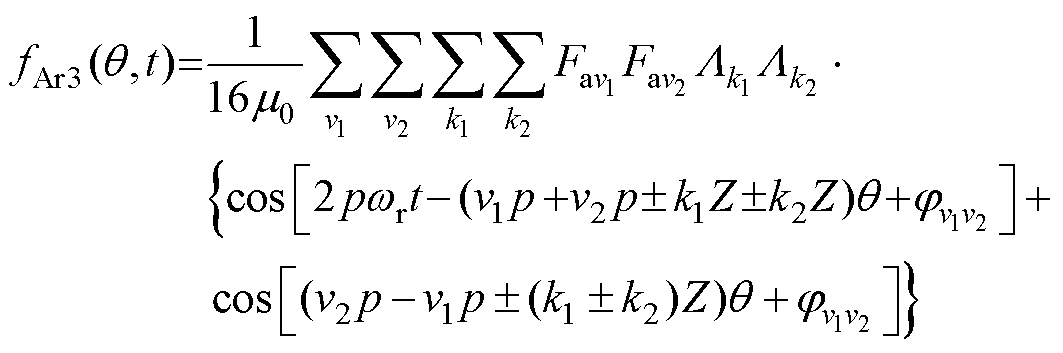 (13)
(13)
式中,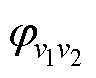 为
为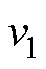 次谐波与
次谐波与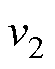 次谐波之间的夹角。
次谐波之间的夹角。
根据平均磁导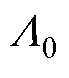 和谐波磁导
和谐波磁导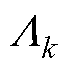 的作用情况,
的作用情况,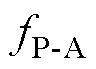 表达式可写为
表达式可写为
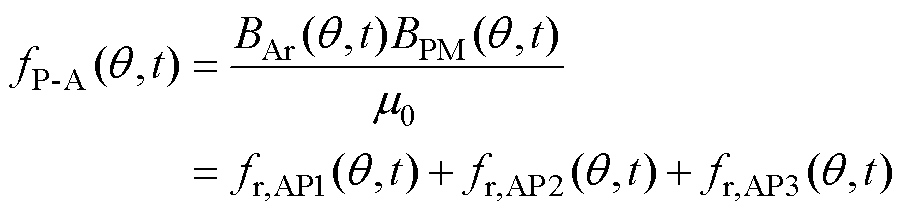 (14)
(14)
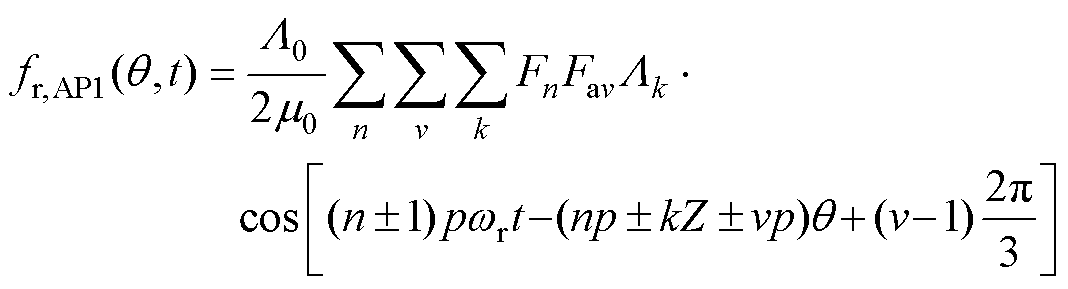 (15)
(15)
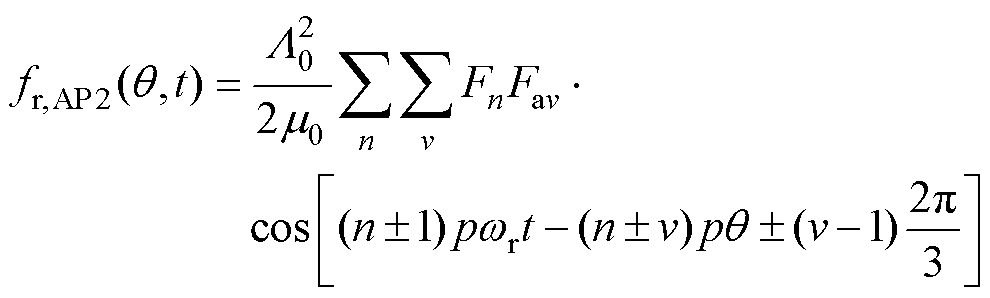 (16)
(16)
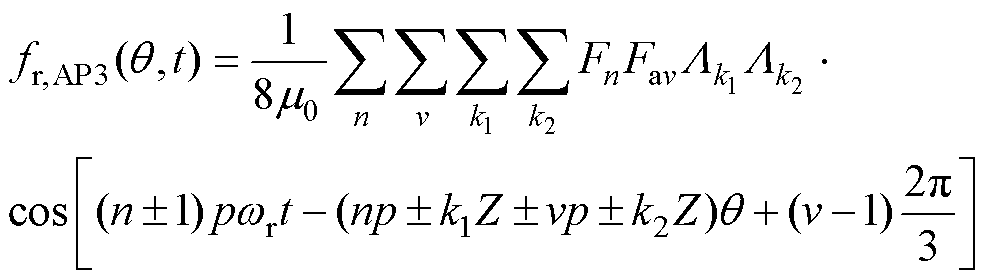 (17)
(17)
式(7)、式(11)、式(15)为平均磁导和谐波磁导相关的力波;式(8)、式(12)、式(16)为与平均磁导相关的力波,其幅值较大;式(9)、式(13)、式(17)为谐波磁导相关的力波,其幅值较小,本文将忽略此项影响。
文献[14-16]揭示了高模数电磁力波产生低阶振动的现象。本节将对比分析高模数力波与低模数力波对低阶电磁振动的贡献。作用在齿上的径向集中力通过齿的传递作用到电机定子轭部。在空载工况下,作用在第i个齿上的径向集中力Fr,i(t)可表示为
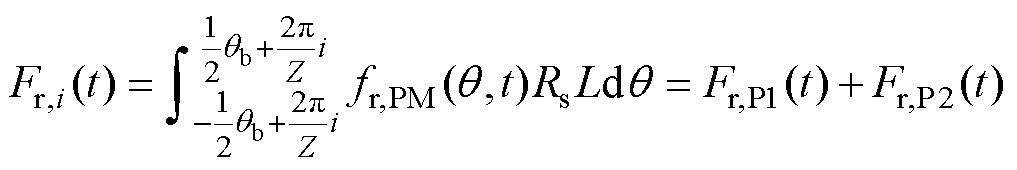 (18)
(18)
其中
(1)当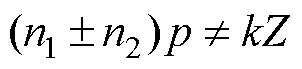 时
时
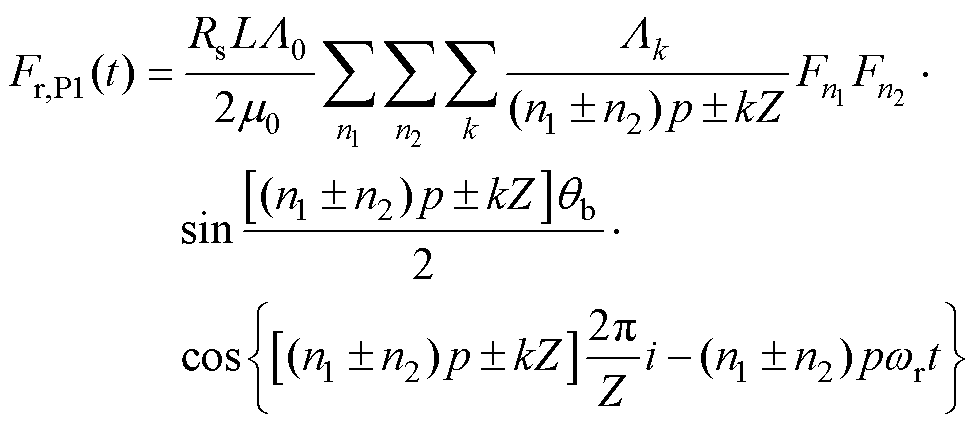 (19)
(19)
 (20)
(20)
(2)当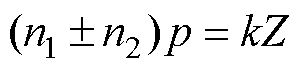 时
时
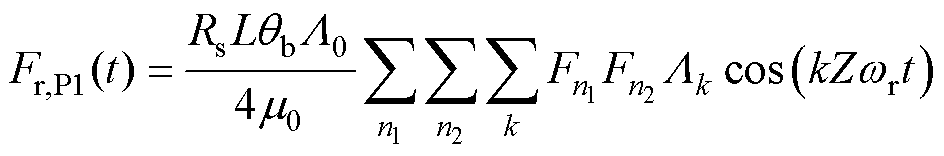 (21)
(21)
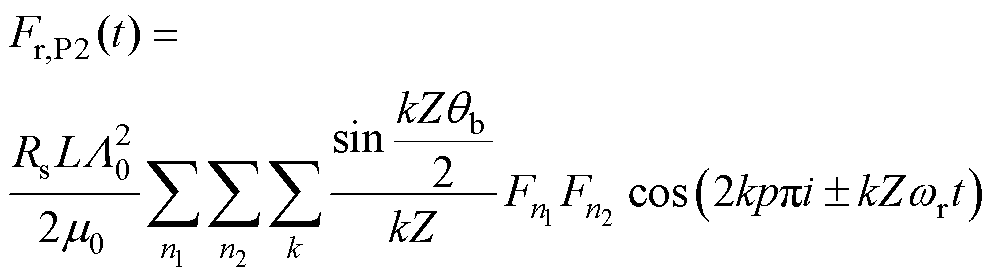 (22)
(22)
式中, 为齿宽;Rs为定子内径;L为铁心轴向长度。式(19)和式(21)表示的齿部径向集中力由式(7)电磁力波积分得到。式(20)和式(22)表示的齿部径向集中力由式(8)的高模数电磁力波积分得到。由式(19)可得,当
为齿宽;Rs为定子内径;L为铁心轴向长度。式(19)和式(21)表示的齿部径向集中力由式(7)电磁力波积分得到。式(20)和式(22)表示的齿部径向集中力由式(8)的高模数电磁力波积分得到。由式(19)可得,当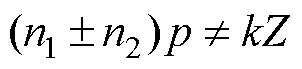 时,这些低模数的电磁力波将产生低阶的电机径向电磁振动。例如,在8极9槽、10极12槽、6极9槽和8极12槽电机中,对应的模数1、2、3和4的电磁力波将产生1、2、3和4阶的电磁振动。
时,这些低模数的电磁力波将产生低阶的电机径向电磁振动。例如,在8极9槽、10极12槽、6极9槽和8极12槽电机中,对应的模数1、2、3和4的电磁力波将产生1、2、3和4阶的电磁振动。
式(20)表示的齿部径向集中力由式(8)的高模数电磁力波积分得到。由于正弦函数的周期是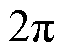 的整数倍,式(20)中增加了
的整数倍,式(20)中增加了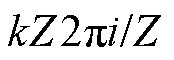 项。由式(20)可知,高模数的电磁力波也能产生电机的低阶振动。以10极12槽永磁电机为例,在极频(2倍电频率)下,极数模数为10的电磁力积分后作用在每个齿上的径向集中力如图1所示。从图1可以清楚地看到,模数为10的电磁力波经过定子齿积分后,得到的电机的阶数不是10阶,而是2阶。这意味着,在开槽电机中,电机的高模数电磁力波也能激发电机的低阶径向振动。这种高模数引起低阶电磁振动的现象称之为齿斩波效应[15-16]。
项。由式(20)可知,高模数的电磁力波也能产生电机的低阶振动。以10极12槽永磁电机为例,在极频(2倍电频率)下,极数模数为10的电磁力积分后作用在每个齿上的径向集中力如图1所示。从图1可以清楚地看到,模数为10的电磁力波经过定子齿积分后,得到的电机的阶数不是10阶,而是2阶。这意味着,在开槽电机中,电机的高模数电磁力波也能激发电机的低阶径向振动。这种高模数引起低阶电磁振动的现象称之为齿斩波效应[15-16]。
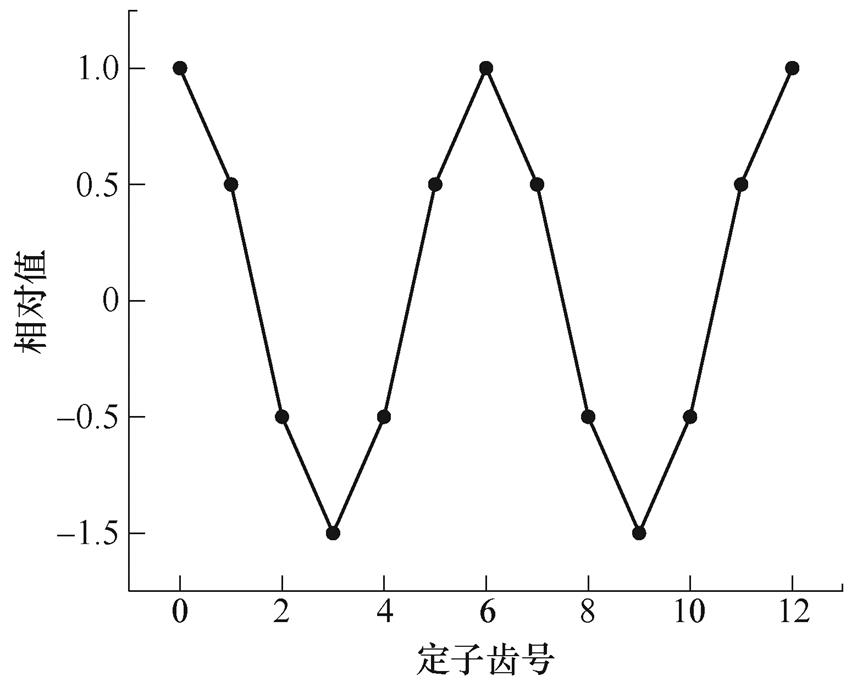
图1 作用在每个齿上的集中力
Fig.1 The concentrated force acting on the tooth
由于绕组电枢反应磁场较小,因此,负载工况时主要考虑永磁体产生的电磁力波fPM和永磁体与绕组相互作用产生的电磁力波fP-A。将电磁力波fP-A在一个齿上进行积分,可以得到
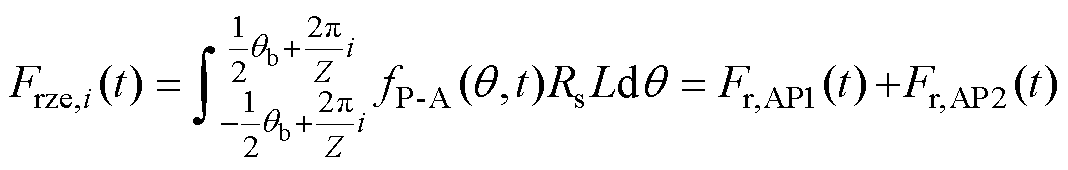 (23)
(23)
其中
(1)当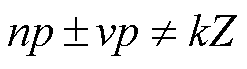 时
时
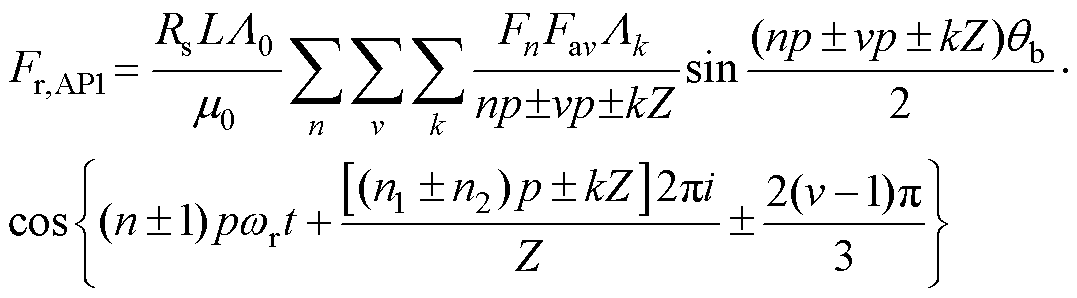 (24)
(24)
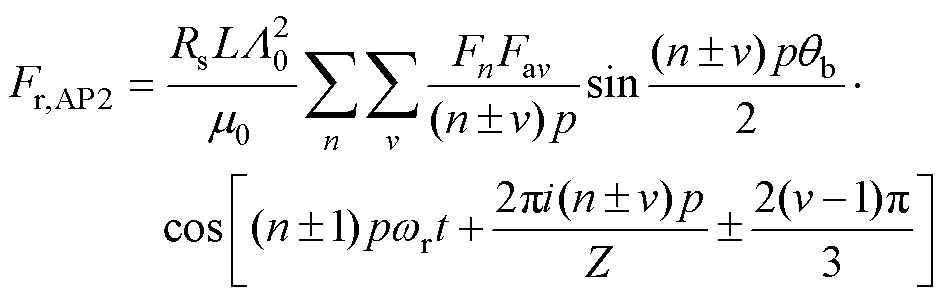 (25)
(25)
(2)当 时
时
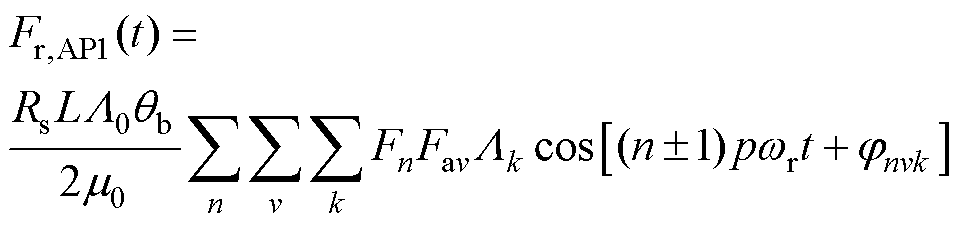 (26)
(26)
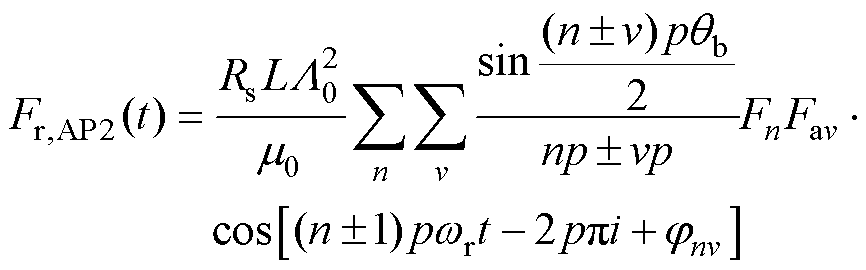 (27)
(27)
式中,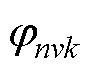 和
和 为不同谐波次数之间的夹角。在近极槽配合的永磁电机中,以10极12槽永磁电机为例,模数为极槽数最大公约数2的电磁力波能引起电机的2阶电磁振动,而模数为极数10的电磁力波也能引起电机的2阶电磁振动。为分析模数2与模数10电磁力波对2阶电磁振动的贡献,用模数2与模数10电磁力波积分后得到的齿部电磁力幅值之比进行衡量,其比值可写为
为不同谐波次数之间的夹角。在近极槽配合的永磁电机中,以10极12槽永磁电机为例,模数为极槽数最大公约数2的电磁力波能引起电机的2阶电磁振动,而模数为极数10的电磁力波也能引起电机的2阶电磁振动。为分析模数2与模数10电磁力波对2阶电磁振动的贡献,用模数2与模数10电磁力波积分后得到的齿部电磁力幅值之比进行衡量,其比值可写为
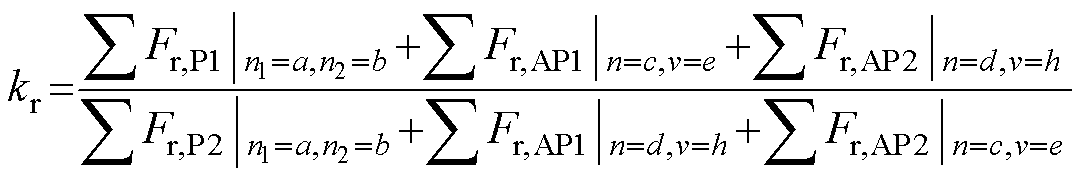 (28)
(28)
式中,a, b, c, d, e, h为系数,对应到各项式中的谐波次数。实际上,不同空间阶次的电磁力波同时也具有时间谐波特性,由于10极12槽永磁电机中2倍电频率的电磁振动较大[3, 15, 19],因此,对2倍电频率下的电磁力波阶次进行分析,即 ,
, 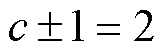 和
和 。根据该电机绕组系数谐波幅值特点,式(28)中各系数的取值见表1。对于在不同的负载电流激励下,幅值比值kr的变化规律如图2所示。由图2可知,比值随着槽宽占比b0的增加而增加。空载工况下,当槽宽占比为0.12时,比值kr=0.14,这意味着由低模数电磁力波积分得到的齿集中力远小于由高模数电磁力波积分得到的齿集中力。因此,在空载工况下,高模数电磁力波是引起低阶电磁振动的主源。在负载工况下,比值随着绕组电流(负载)增加而增加,这表明,当负载增加时,电机中模数2电磁力波在2阶电磁振动源的占比逐渐增加。在小负载工况下,模数10电磁力波能产生较大的2阶电磁振动,当负载增加到一定程度时,模数2电磁力将成为电磁振动的主源。
。根据该电机绕组系数谐波幅值特点,式(28)中各系数的取值见表1。对于在不同的负载电流激励下,幅值比值kr的变化规律如图2所示。由图2可知,比值随着槽宽占比b0的增加而增加。空载工况下,当槽宽占比为0.12时,比值kr=0.14,这意味着由低模数电磁力波积分得到的齿集中力远小于由高模数电磁力波积分得到的齿集中力。因此,在空载工况下,高模数电磁力波是引起低阶电磁振动的主源。在负载工况下,比值随着绕组电流(负载)增加而增加,这表明,当负载增加时,电机中模数2电磁力波在2阶电磁振动源的占比逐渐增加。在小负载工况下,模数10电磁力波能产生较大的2阶电磁振动,当负载增加到一定程度时,模数2电磁力将成为电磁振动的主源。
表1 谐波次数选择
Tab.1 The choice of harmonic number

系数谐波次数 a11335577 b13153759 c13—————— e55—————— d133————— h71317—————
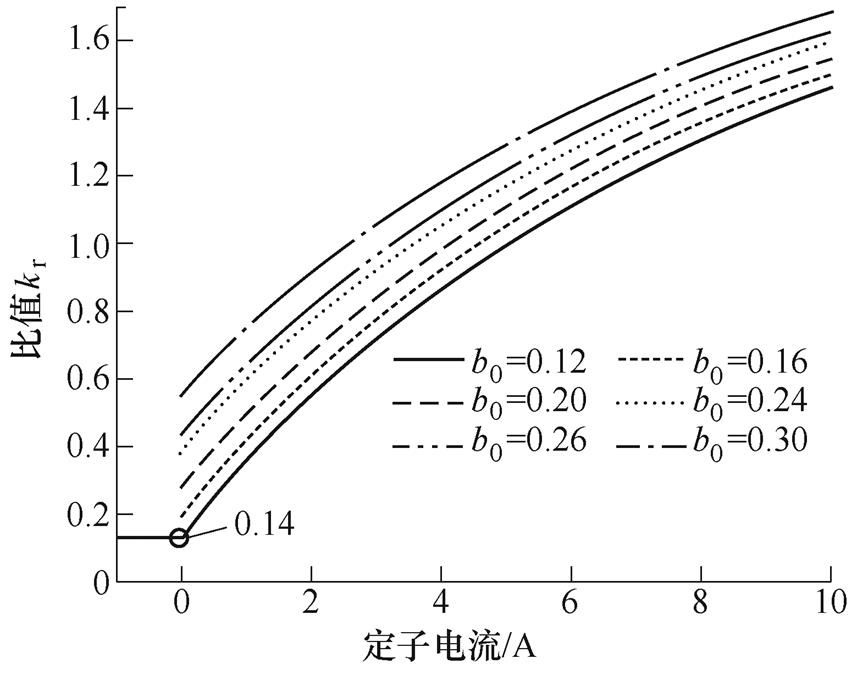
图2 比值kr随电流变化结果
Fig.2 Ratio kr varying with current
在多极数的整数槽电机中,电机中槽频0阶电磁振动最为突出[20-21],此时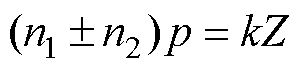 和
和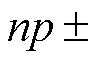
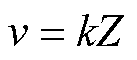 ,本文以6极36槽整数槽永磁电机为例,模数为0的电磁力波能引起电机的0阶电磁振动,而模数为槽数36的电磁力波也能引起电机的0阶电磁振动。为分析模数0与模数36电磁力波对0阶电磁振动的贡献,用模数0与模数36电磁力波积分后得到的齿部电磁力幅值之比进行分析,记为krr。因模数0主要为谐波磁导参与作用的电磁力波,而模数36为平均磁导参与作用的电磁力波,故比值可以写成
,本文以6极36槽整数槽永磁电机为例,模数为0的电磁力波能引起电机的0阶电磁振动,而模数为槽数36的电磁力波也能引起电机的0阶电磁振动。为分析模数0与模数36电磁力波对0阶电磁振动的贡献,用模数0与模数36电磁力波积分后得到的齿部电磁力幅值之比进行分析,记为krr。因模数0主要为谐波磁导参与作用的电磁力波,而模数36为平均磁导参与作用的电磁力波,故比值可以写成
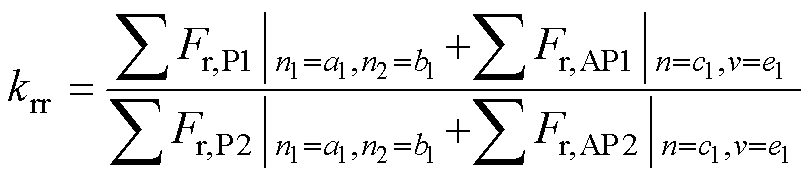 (29)
(29)
式中,a1, b1, c1, e1为系数,对应到各项中的谐波次数。考虑到整数槽永磁电机中槽频电磁振动较大,故对槽频下的电机电磁振动进行分析,即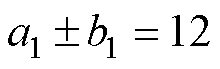 ,
,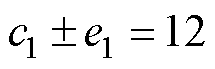 。根据绕组系数的谐波特点,式(29)中各系数的取值见表2。在不同的负载转矩和槽宽占比下,幅值比值krr的变化规律如图3所示。由图3可知,比值随着槽宽占比b0的增加而减小。这说明当槽宽占比增加时,模数0的电磁力密度对0阶电磁振动的贡献逐渐减小,而模数36的电磁力密度的贡献逐渐增加。而且,这种贡献并不会随着负载的增加而发生变化,即在不同的负载工况下,两者的比值基本保持不变。
。根据绕组系数的谐波特点,式(29)中各系数的取值见表2。在不同的负载转矩和槽宽占比下,幅值比值krr的变化规律如图3所示。由图3可知,比值随着槽宽占比b0的增加而减小。这说明当槽宽占比增加时,模数0的电磁力密度对0阶电磁振动的贡献逐渐减小,而模数36的电磁力密度的贡献逐渐增加。而且,这种贡献并不会随着负载的增加而发生变化,即在不同的负载工况下,两者的比值基本保持不变。
表2 谐波次数选择
Tab.2 The choice of harmonic number
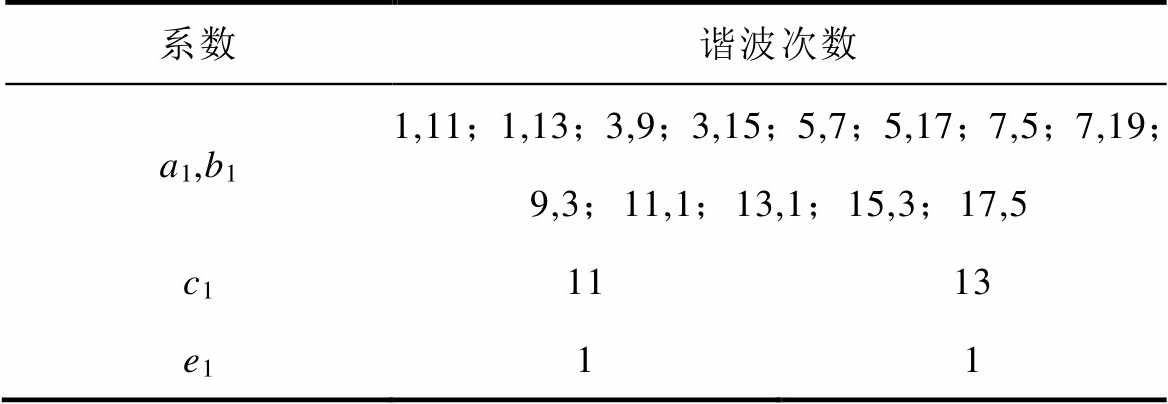
系数谐波次数 a1,b11,11;1,13;3,9;3,15;5,7;5,17;7,5;7,19;9,3;11,1;13,1;15,3;17,5 c11113 e111
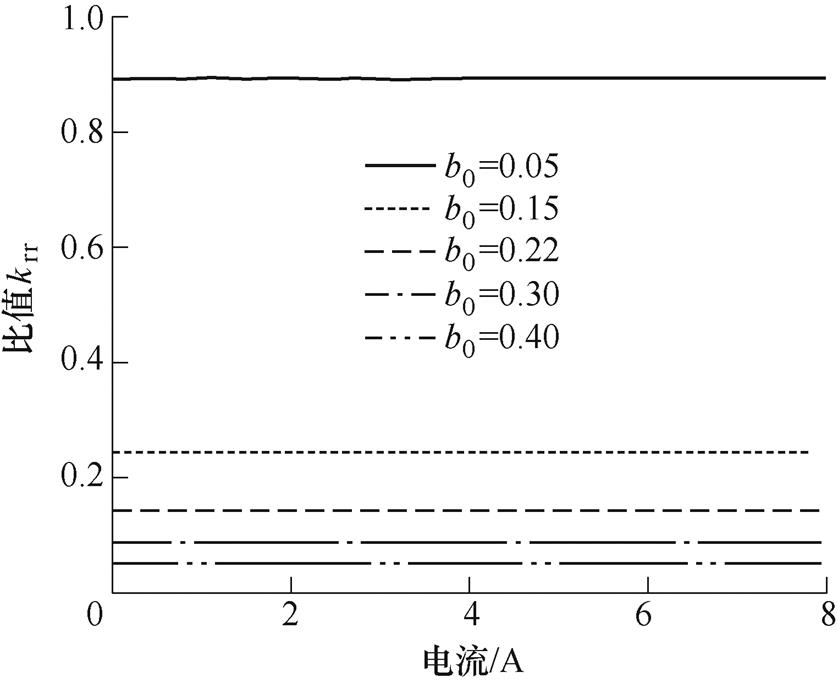
图3 比值krr随电流变化结果
Fig.3 Ratio krr varying with current
为验证理论分析的正确性,分别对一台10极12槽分数槽和6极36槽整数槽永磁电机进行仿真研究,样机结构如附图1所示,样机参数分别见附表1和附表2。
建立10极12槽永磁电机的有限元模型,采用瞬态场对其进行求解。图4为某一时刻电机在空载、绕组激励和负载下沿靠近定子一侧气隙单元圆周的径向磁通密度空间分布和谐波分析结果。
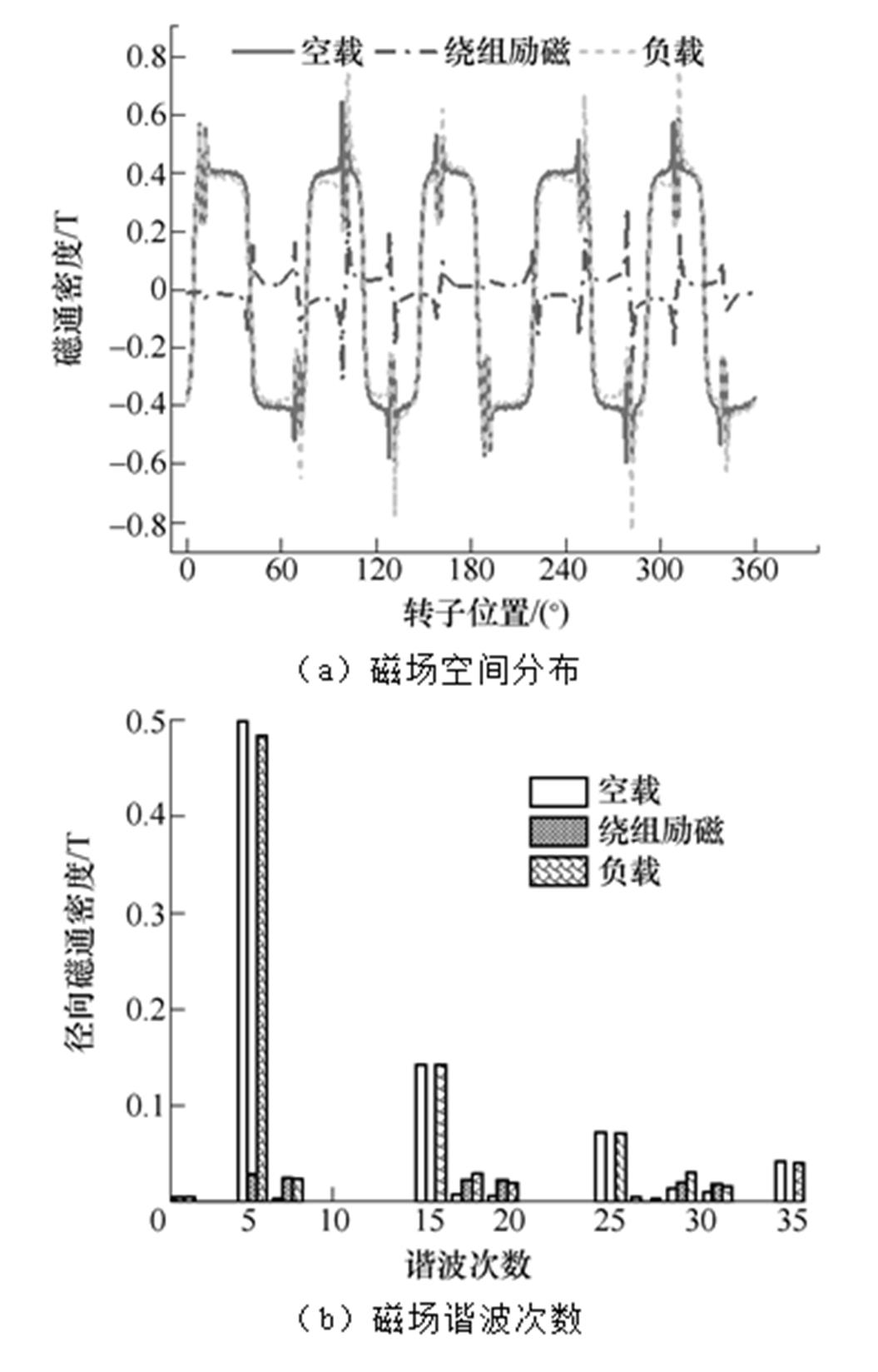
图4 磁场分布及其谐波分析结果
Fig.4 The air-gap flux distribution and its spectrum
由图4可知,空载工况下,永磁体产生的气隙磁场的幅值较大,除了5、15、25、35次等谐波分量外,还有与开槽有关的17、19、29、31次等谐波分量。绕组电流产生的电枢反应磁场幅值较小,其分量不仅有5次主波分量磁场,还有1、7、11次等谐波分量,各分量的幅值与绕组谐波系数有关。在负载工况(1N·m)时,与空载磁场相比,谐波含量更加丰富,而且各谐波幅值会因电枢反应而受影响。采用麦克斯韦应力张量法计算了气隙中的径向力波,结果如图5所示。

图5 10极12槽永磁电机径向力波分布
Fig.5 Radial force distribution of 10p/12s PM motor
由图5可知,电机在空载工况下力波主要是永磁体产生磁场间的相互作用,其空间模数主要为10、20、30、…。由绕组电流产生的径向力波谐波分量更为复杂,空间模数包括2、4、6、8、10等偶次谐波,但与永磁体产生力波相比,其幅值较小。在负载工况下,由于电枢反应磁场的影响,径向电磁力波分量更为丰富,由于永磁体和绕组电流的相互作用,谐波分量幅值会有较大的变化。由齿斩波效应可知,气隙中模数10的径向力波也能够引起电机2阶电磁振动,为了深层次地探究电磁力波特性,将从磁场源入手进行分析,2倍频电磁力磁场谐波源如图6所示。
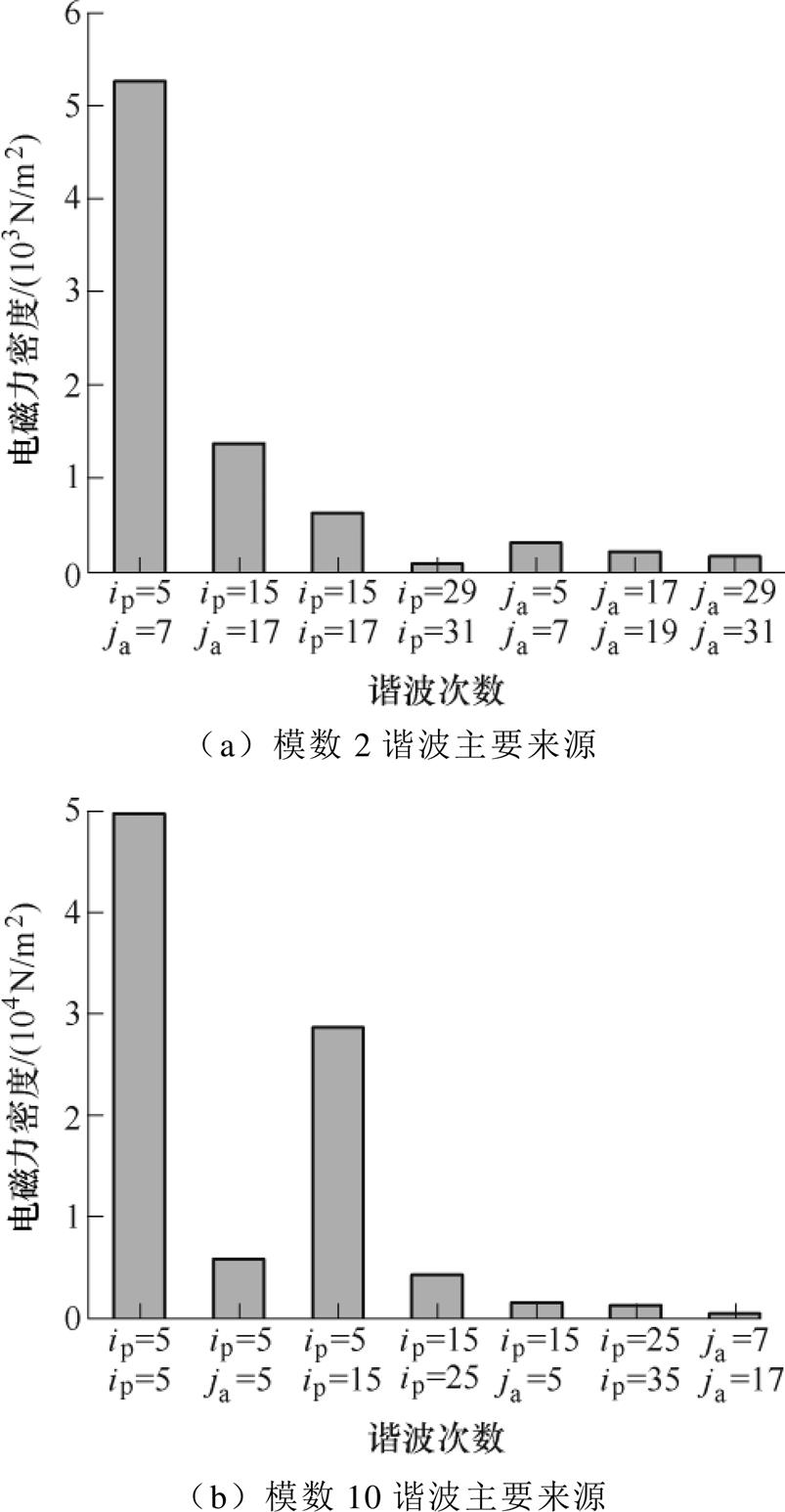
图6 10极12槽电机径向力波中磁场源分析
Fig.6 Analysis of magnetic field source in radial force of 10-pole 12-slot motor
图6中,ip为永磁体产生的磁场谐波次数,ja为绕组电流产生的磁场谐波次数。由图可得,对于最小的模数2电磁力波,其主要由永磁体产生的空间5次磁场(也是基波磁场)和电枢反应的7次谐波磁场相互作用产生。另外还包括永磁体产生的15次谐波磁场和电枢反应的17次谐波磁场作用以及电枢反应的5次和7次谐波磁场之间的相互作用产生的力波。对于幅值较大的模数10电磁力波,其主要由永磁体的空间5次磁场相互作用产生。此外,永磁体产生的空间5次磁场和15次谐波磁场以及15次谐波磁场和25次谐波磁场相互作用也会产生较大的模数10电磁力波。
对空载工况下电机气隙中径向电磁力进行二维快速傅里叶变换(Fast Fourier Transformation, FFT),可以得到电磁力的时间和空间分布结果,如图7所示。对于10极12槽永磁电机,在2倍电频率下,模数2和模数10的电磁力波幅值分别为785.6N/m2和15 280N/m2。样机中定子齿宽机械角度为26.4°,两种模数产生的齿集中力幅值分别为0.534N和3.475N。模数2与模数10产生的单齿集中力的幅值之比为0.534N/3.475N=0.153,与图2中解析计算值0.14较为接近,验证了齿斩波效应的有效性,这说明空载下电机的2阶电磁振动主要是由模数10的电磁力波激发的。由图6可知,空载2倍频时2阶电磁力源的主要磁场源为ip=15, ip=17和ip=29, ip=31。10阶电磁力源的主要谐波磁场源为ip=5, ip=5、ip=5, ip=15和ip=15, ip=25。
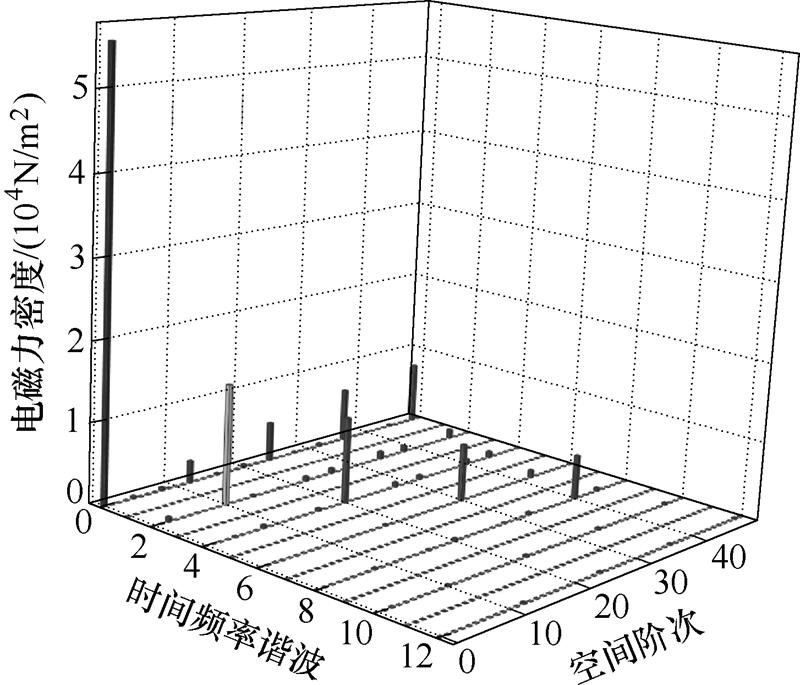
图7 空载工况电磁力密度二维FFT结果
Fig.7 Radial force harmonics of 2-D FFT under no-load
进一步地,图8给出了不同负载时模数2与模数10电磁力波产生的齿集中力比值。由图可得,比值随着负载的增加而增加,这表明模数2电磁力波产生齿集中力在2阶电磁振动中的比重逐渐增加。其原因主要是绕组产生的7次谐波磁场会随负载而增强。当负载转矩T与额定转矩Tn之比小于2/3时,比值kr<1,即模数2电磁力波对电磁振动的贡献将小于模数10电磁力波。当T/Tn=2/3时,比值kr=1,即模数2和模数10的电磁力波对2阶电磁振动的贡献相等。当T/Tn>2/3时,比值kr>1,即模数2电磁力波对电磁振动的贡献大于模数10电磁力波。
图9为6极36槽永磁电机在空载和负载下的磁场分析。由图可知,空载工况下,永磁体产生的气隙磁场主要为3、9、15、21等奇数次谐波分量。绕组电流产生的电枢反应磁场幅值较小,其分量不仅有3次主波分量磁场,还有15、21、33、39次等谐波分量,各分量的幅值与绕组谐波系数有关。负载工况T=2.5N·m时,气隙磁场空间谐波次数同空载工况。采用麦克斯韦应力张量法计算了气隙中的径向力波,结果如图10所示。
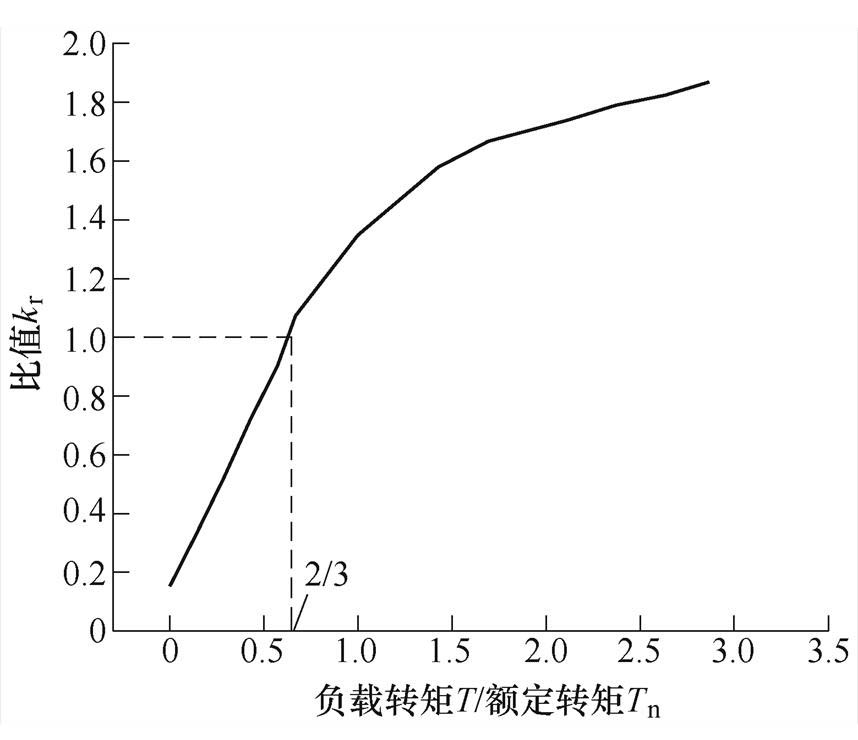
图8 比值kr随负载的变化
Fig.8 Ratio kr varying with different loads
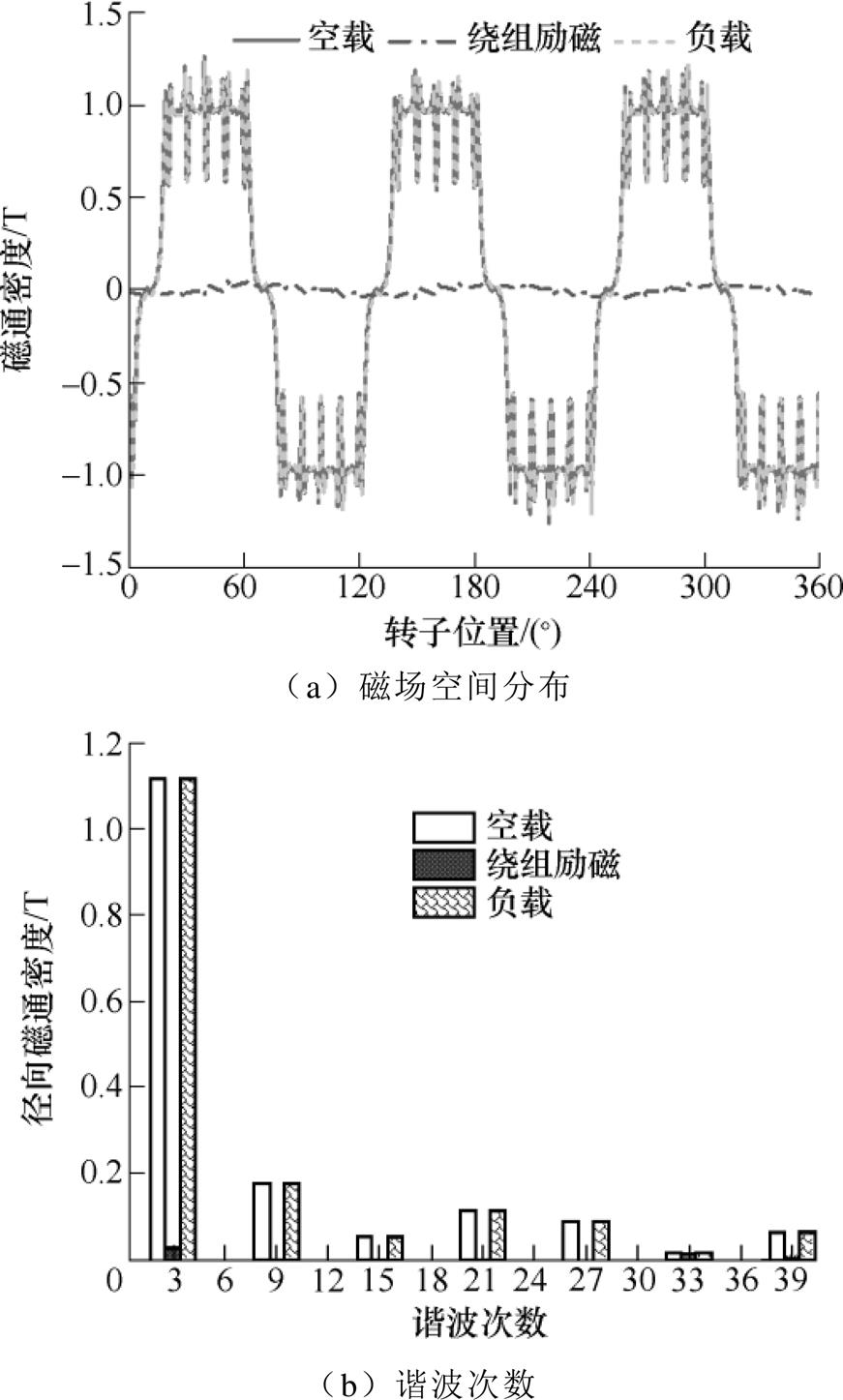
图9 气隙磁场分布
Fig.9 The air-gap flux distribution
由图10可知,电机在空载和负载工况下电磁力波空间模数主要为6、12、18、24等极数倍数谐波。相比于永磁体产生的电磁力波,绕组产生的电磁力波幅值较小。由齿斩波效应[16]可知,气隙中模数36的径向力波也能够引起电机0阶电磁振动,为了深层次地把握,将从磁场源入手对12倍频模数36和模数0的径向力波源进行分析,结果如图11所示。
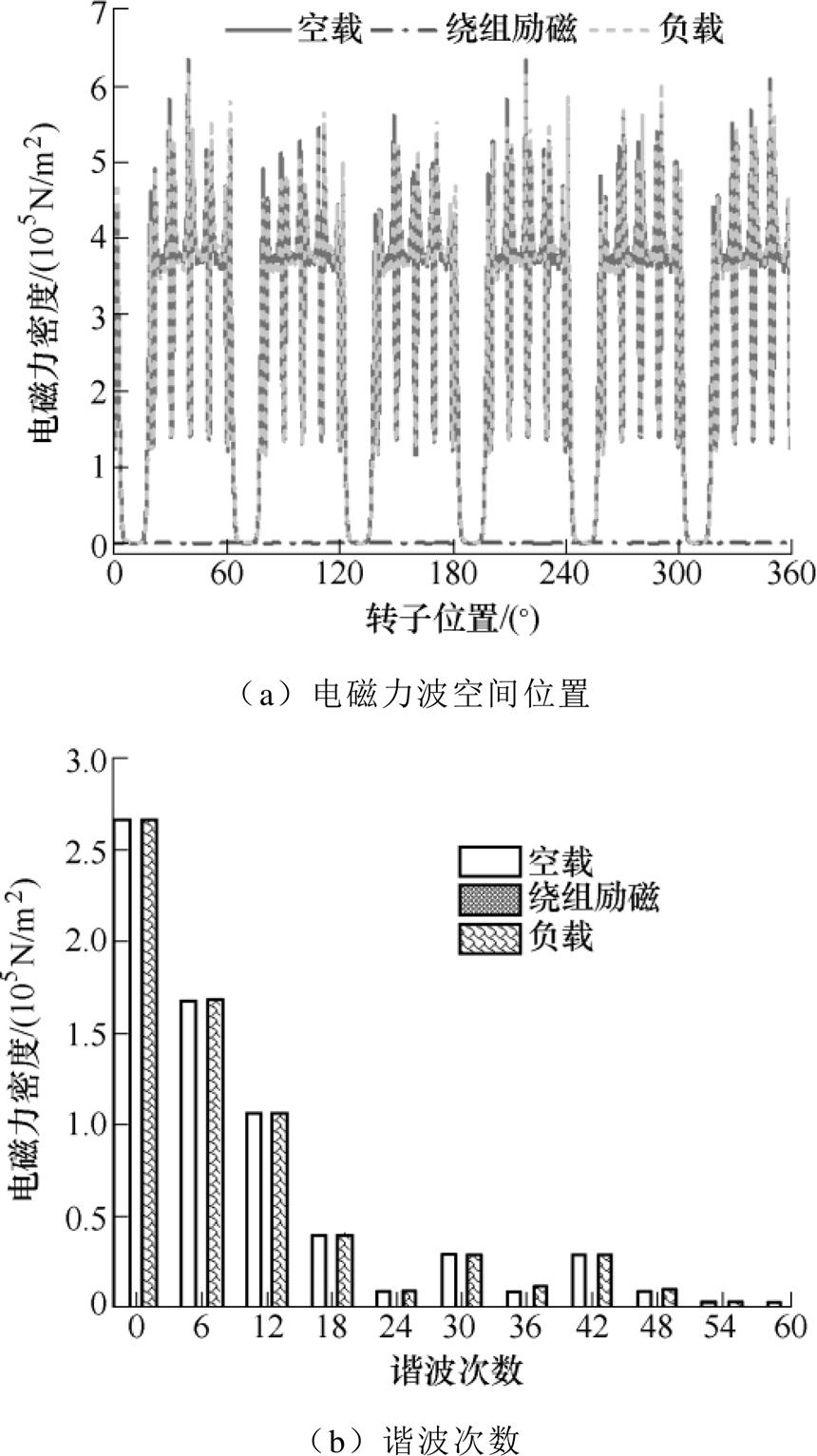
图10 径向电磁力波分布
Fig.10 The radial force distribution
由图11可得,对于模数36的电磁力波,其主要由永磁体产生的3次磁场(即基波磁场)和39次谐波磁场相互作用产生的,另外还包括永磁体产生的3次磁场和33次谐波磁场,9次谐波磁场和27次谐波磁场以及永磁体的3次磁场和绕组的33次谐波磁场相互作用产生的电磁力波。
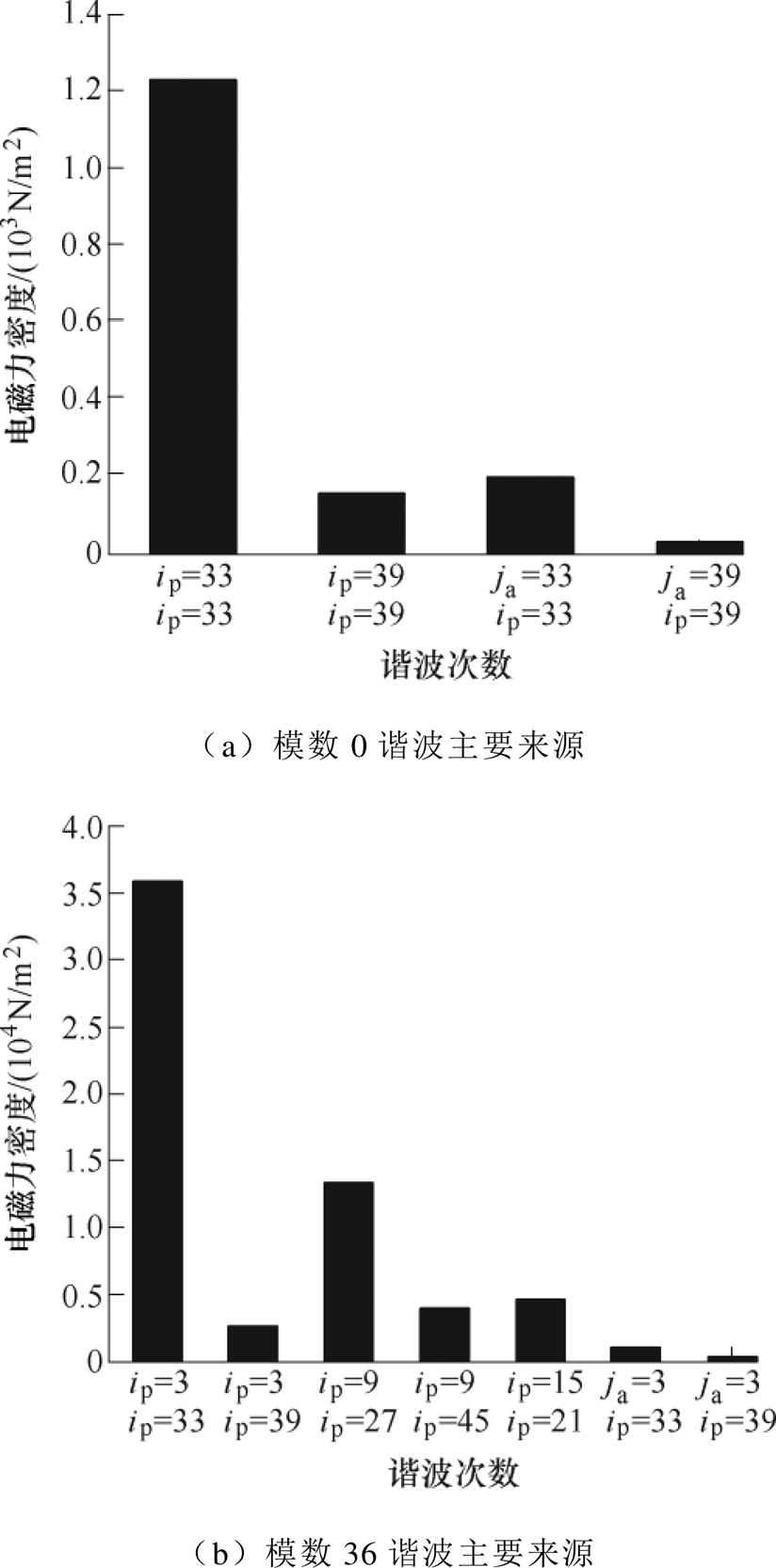
图11 6极36槽电机径向力波中磁场源分析
Fig.11 Analysis of magnetic field source in radial force of 6-pole 36-slot motor
图12给出了电机定子齿宽b0=0.22时,不同负载工况槽频下模数0与模数36电磁力波产生的齿集中力比值。由图可知,比值krr 1,这说明电机中模数36的电磁力密度为0阶电磁振动的主源,且随着负载的增加,比值基本保持不变,这表明模数36电磁力波产生齿集中力对0阶电磁振动的贡献不随负载变化。
1,这说明电机中模数36的电磁力密度为0阶电磁振动的主源,且随着负载的增加,比值基本保持不变,这表明模数36电磁力波产生齿集中力对0阶电磁振动的贡献不随负载变化。
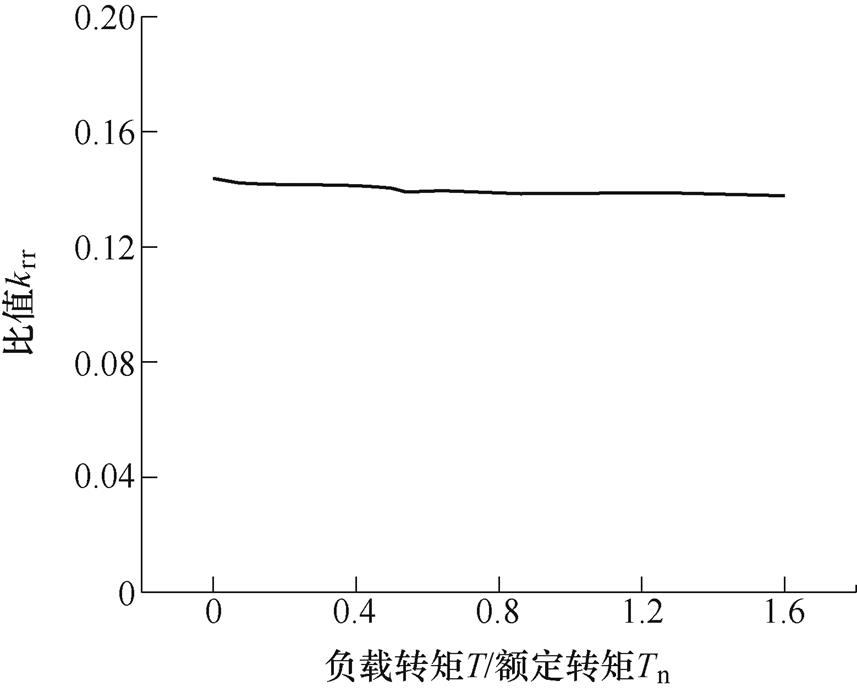
图12 比值krr随负载的变化
Fig.12 Ratio krr varying with different loads
采用谐响应分析对永磁电机的电磁振动进行仿真。主要步骤为将定子齿电磁力导入电机三维结构场进行振动计算,具体的仿真流程见文献[16],考虑到实际测试过程中,电机被弹性绳吊起悬挂在支架上,为了和实验保持一致,仿真时电机端面施加弹性约束条件。空载下10极12槽永磁电机在转速900r/min时定子机壳上一点的径向振动加速度结果如图13所示。
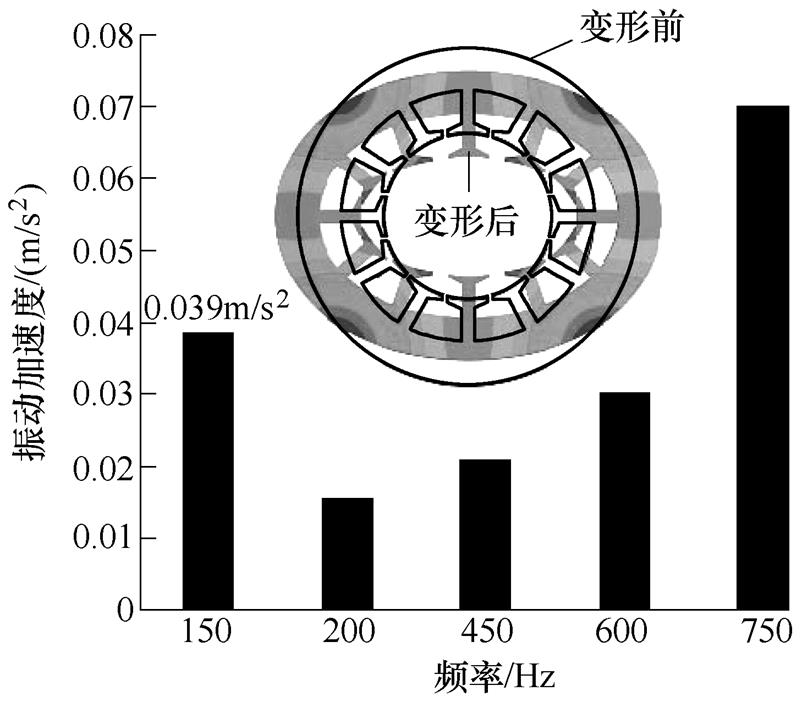
图13 电机在转速900r/min下的振动频谱
Fig.13 Vibration spectra of the motor at 900r/min
由图13可得,电机2倍电频率下的电机振型阶次为2,其振动幅值为0.039m/s2。为了对引起该2阶振动的源进行分析,将模数2的电磁力波和模数10的电磁力波分别加载到定子内齿上,如图14所示。图中,fr为力密度。图15给出这两种激励源下电机2倍电频率时的振动加速度。该图说明了不仅模数2的电磁力波可以引起2阶的电机定子振动,模数10的电磁力波也可以激发出2阶的定子振动,而且其引起的振动加速度幅值为0.041m/s2,远大于前者引起的加速度幅值0.005 58m/s2。
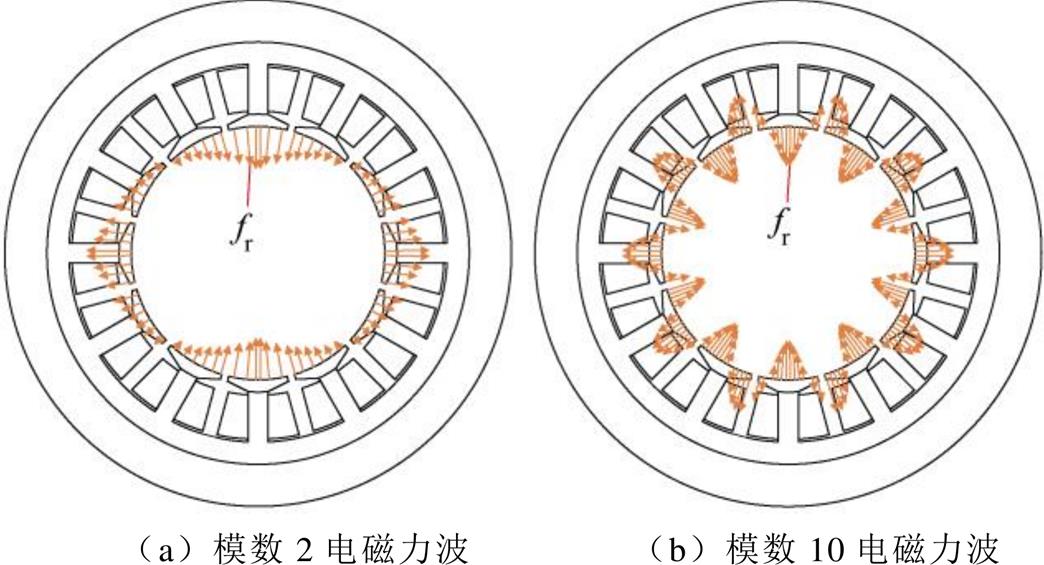
图14 电磁力波加载
Fig.14 The loaded radial force

图15 2倍电频率下电机径向振动
Fig.15 Radial vibration accelerations of the motor at twice the fundamental frequency
图16给出了10极12槽永磁电机不同负载工况模数2和模数10产生的振动加速度幅值比值,由图16可知,当负载增加时,由于负载电流的引入,模数2引起的电机振动加速度幅值占比逐渐增加。图17给出了6极36槽永磁电机3 000r/min时槽频频率下模数0和模数36产生的0阶电磁振动加速度幅值比值随负载的变化结果。由结果可知,槽频下0阶电磁振动主要是由槽数模数电磁力激发的,且其贡献基本上不随负载而变化。
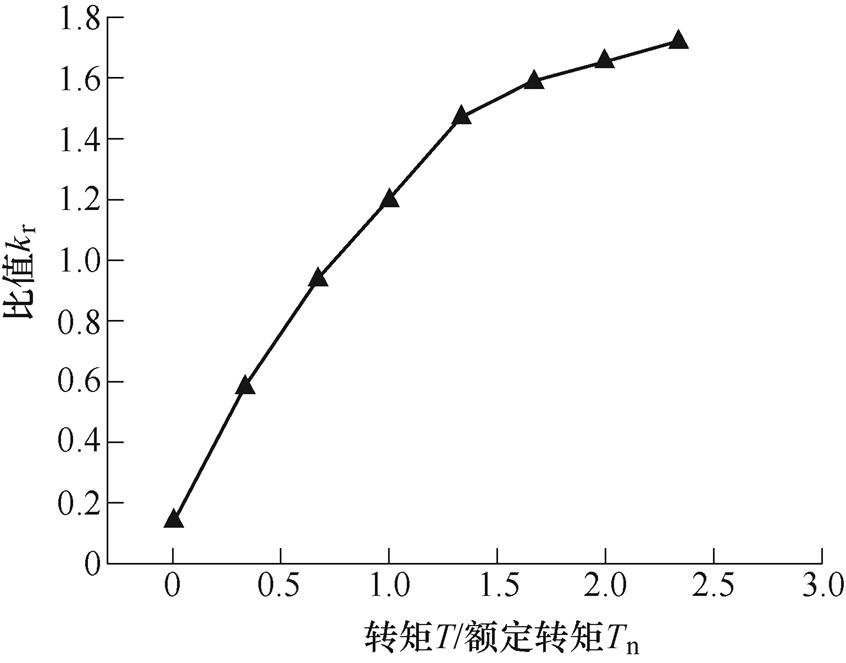
图16 不同负载下由模数2和模数10电磁力波引起的电磁振动加速度对比
Fig.16 The ratio of vibration caused by 2-order force to that caused by 10-order force under different loads
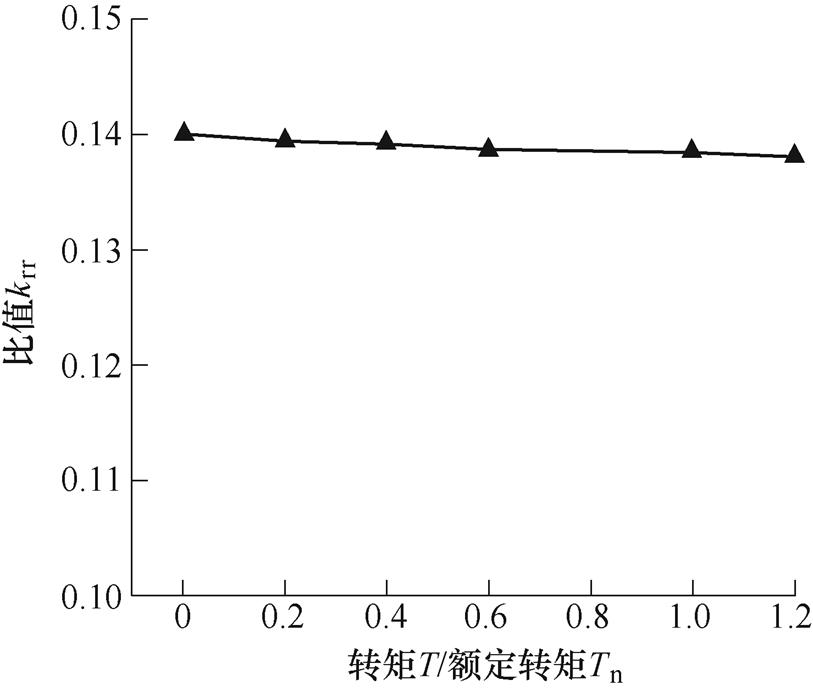
图17 不同负载下由模数0和模数36电磁力波引起的0阶电磁振动加速度对比
Fig.17 The ratio of vibration caused by 0-order force to that caused by 36-order force under different loads
本实验对10极12槽永磁电机空载工况进行了电机振动测试。为了避免外部设备对电机振动的干扰,用弹性绳将电机吊起,使其悬挂在半空中,并将弹性绳固定在实验架上,实验样机和测试平台如图18所示。

图18 振动测试实验装置
Fig.18 Vibration test rig
为了能够测量到电机的振型,本文采用多探头法,在定子机壳外圆一周均匀布置16个加速度传感器,将采集到的16路振动信号输入西门子数据采集系统,采用FFT可以获取电机机壳表面的振动幅值,对各探头之间的相位进行分析,可以得到实际电机运行时的振动变形。
空载下10极12槽永磁同步电机在900r/min时的振动加速度及振型如图19所示。图19a为机壳表面相邻4个探头A, B, C, D的时域振动波形(该波形已通过截止频率为250Hz的低通滤波器处理),相邻两个探头的振动信号之间的相位差为45°。图19b表明电机振动信号的频谱分量主要为电机的极数与转子频率乘积及其倍数分量。在2倍电频率(150Hz)下电机的实际测量振动值为0.042m/s2,而仿真值为0.039m/s2,两者误差为7%,在其他频率点下,实测振动值与仿真振动值变化趋势一致。电机在2倍电频率时的电机振型表现为2阶,如图19c所示,这与仿真结果是一致的。从电机振动幅值和振型来看,仿真和实验值基本一致,仿真与实验振动幅值的误差主要是忽略了转子质量以及端盖的影响。由于实验中测量的振动为电机中各种激振力源综合作用的总加速度,因此,只能通过比较电机振动的仿真值和实测值进行判断。从仿真与实验结果来看,电机空载运行下,永磁电机2倍电频率时的2阶振动源主要是由模数10的电磁力波贡献的。
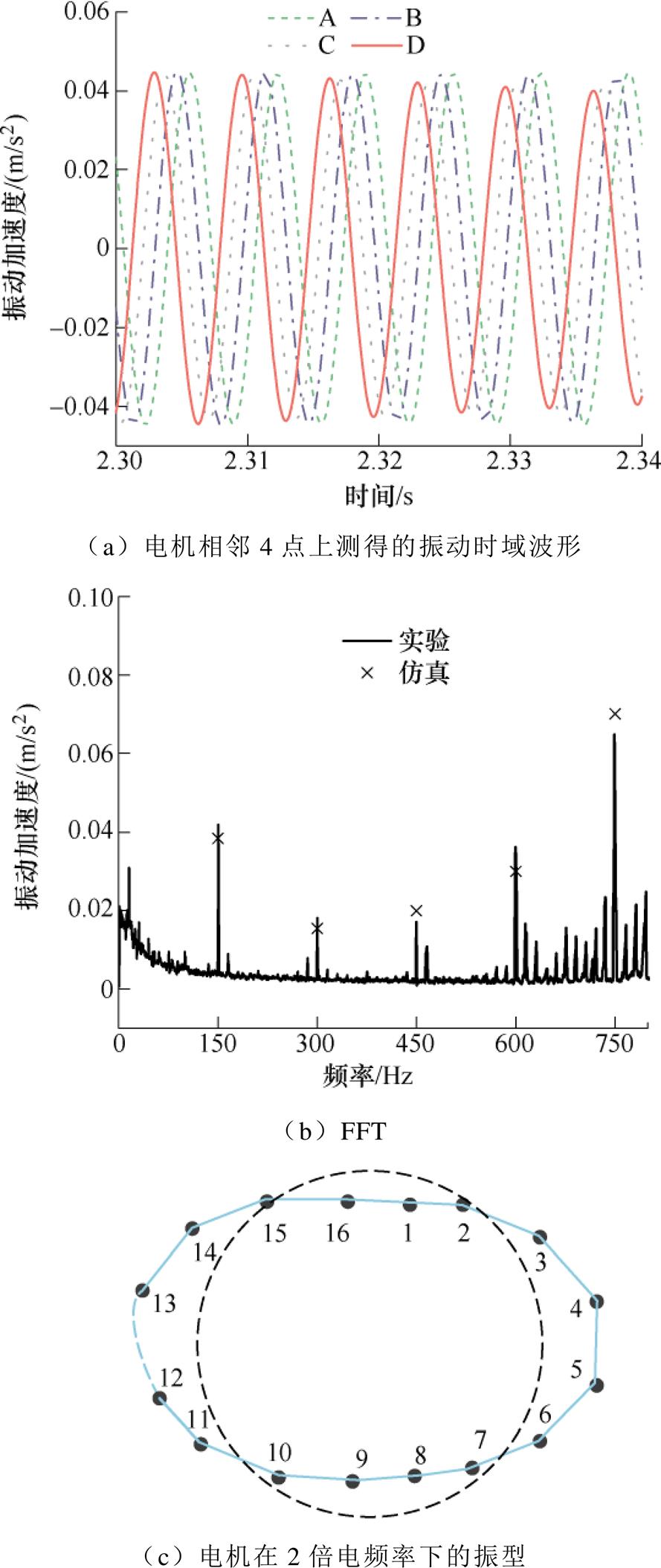
图19 10极12槽永磁电机900r/min下的振动加速度
Fig.19 Measured vibration acceleration of the 10-pole/12-slot motor at 900r/min
本文分析了高模数电磁力对开齿永磁电机低阶电磁振动的影响。从理论和仿真分析了高模数电磁力对永磁电机电磁振动的特点,讨论了电机在空载和负载工况下高模数电磁力对低阶电磁振动的贡献,并用样机空载实验进行了验证。本文可得到以下结论:
1)高阶电磁力波能引起低阶电磁振动。例如:在10极12槽分数槽永磁电机中,模数10电磁力波也能引起2阶电磁振动。在6极36槽整数槽永磁电机中,模数36电磁力波能引起0阶电磁振动。
2)解析和仿真结果表明,在分数槽永磁电机中,高模数电磁力波对低阶电磁振动的贡献与齿宽和负载程度有关。随着齿宽和负载增加,高模数电磁力波引起的低阶电磁振动占比逐渐减小。在负载增加时,电机低模数力波逐渐占主导作用,是电机低阶电磁振动的主源。在多极数的整数槽电机中,槽数模数电磁力波是0阶电磁振动的主源,其贡献与负载程度无关。
3)永磁电机中高模数电磁力波主要是由永磁体产生的磁场相互作用产生的,且其贡献与齿结构有关,因此在电机减振结构设计过程中,可从永磁体结构和定子齿结构入手展开优化工作。
附 录
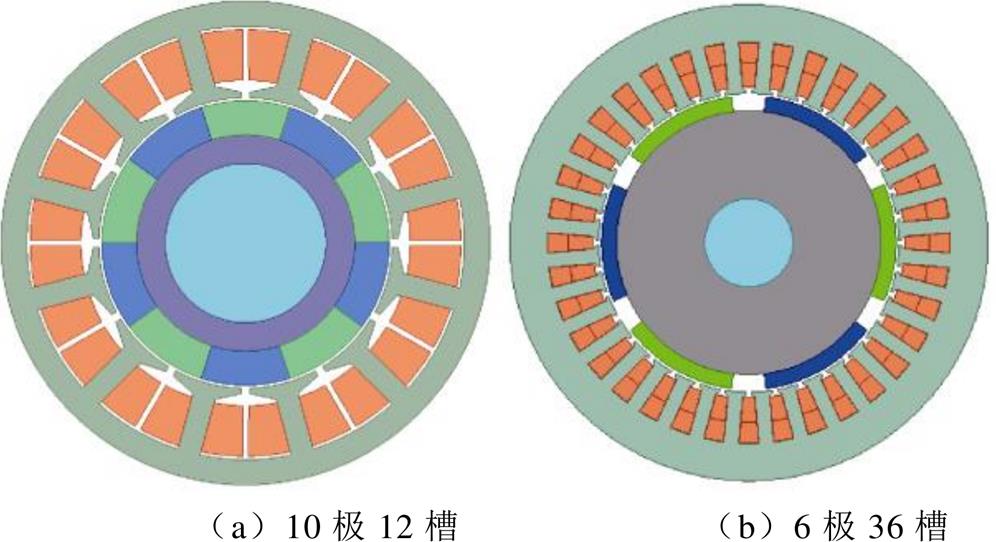
附图1 永磁电机结构框图
App.Fig.1 Structure model of PM motor
附表1 10极12槽永磁电机参数
App.Tab.1 Parameters of 10-pole/12-slot PM motor
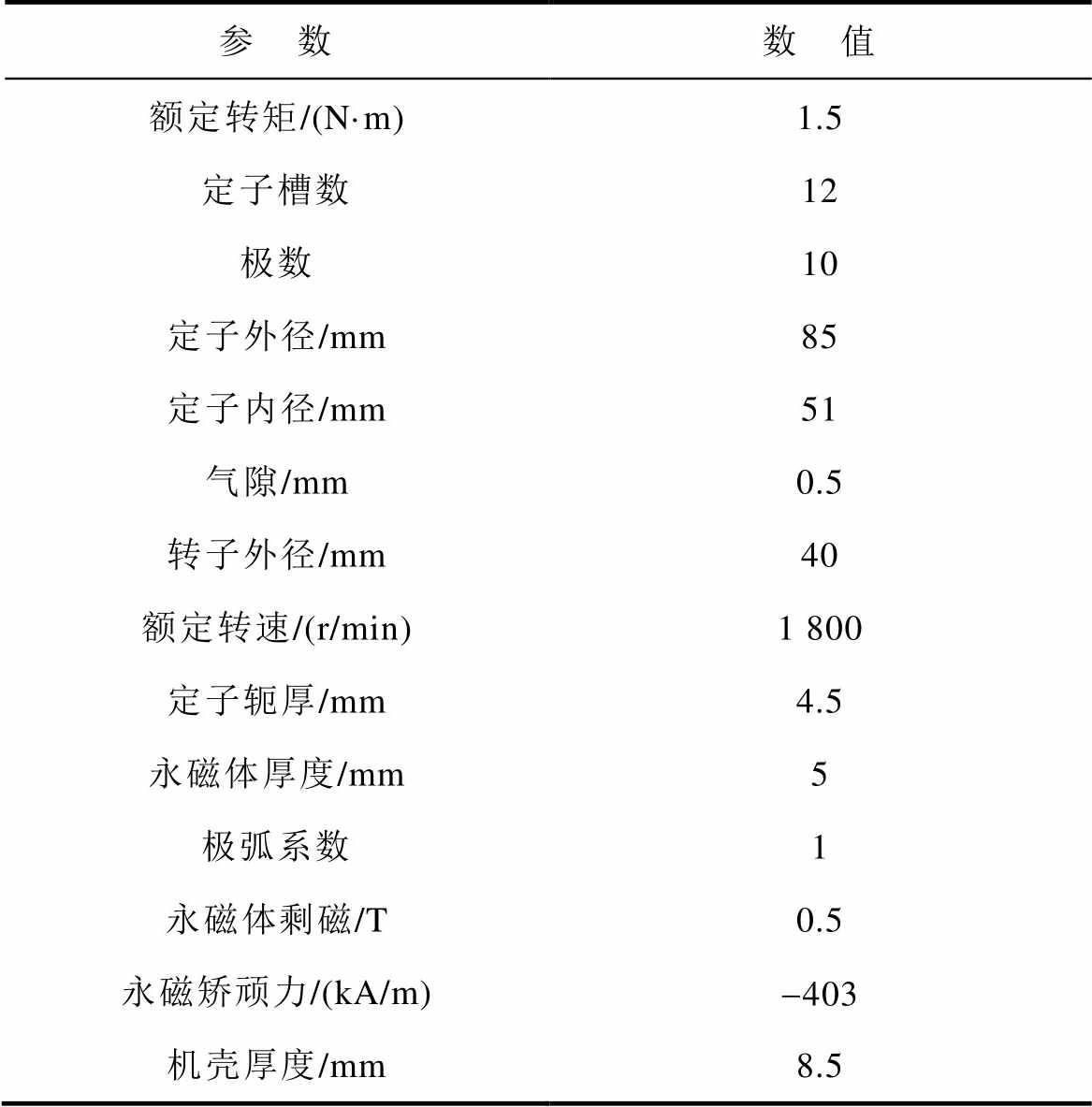
参 数数 值 额定转矩/(N·m)1.5 定子槽数12 极数10 定子外径/mm85 定子内径/mm51 气隙/mm0.5 转子外径/mm40 额定转速/(r/min)1 800 定子轭厚/mm4.5 永磁体厚度/mm5 极弧系数1 永磁体剩磁/T0.5 永磁矫顽力/(kA/m)-403 机壳厚度/mm8.5
附表2 6极36槽永磁电机参数
App.Tab.2 Parameters of 6-pole/36-slot PM motor

参 数数 值 额定转矩/(N·m)5 定子外径/mm130 定子内径/mm81.6 轭部厚度/mm10.2 定子长度/mm60
(续)

参 数数 值 机壳长度/mm130 槽口宽度/mm1.5 额定转速/(r/min)3 000 槽高/mm14 气隙长度/mm0.8 轴径/mm24 永磁体剩磁/T1.21 永磁体厚度/mm4 极弧系数0.76
参考文献
[1] 马伟明, 王东, 程思为, 等. 高性能电机系统的共性基础科学问题与技术发展前沿[J]. 中国电机工程学报, 2016, 36(8): 2025-2035.
Ma Weiming, Wang Dong, Cheng Siwei, et al. Common basic scientific problems and development of leading-edge technology of high performance motor system[J]. Proceedings of the CSEE, 2016, 36(8): 2025-2035.
[2] Yang Haodong, Chen Yangsheng. Influence of radial force harmonics with low mode number on electro- magnetic vibration of PMSM[J]. IEEE Transactions on Energy Conversions, 2014, 29(1): 38-45.
[3] 陈益广, 韩柏然, 沈勇环. 永磁同步推进电机电磁振动分析[J]. 电工技术学报, 2017, 32(23): 16-22.
Chen Yiguang, Han Boran, Shen Yonghuan. Electro- magnetic vibration analysis of permanent magnet synchronous propulsion motor[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 16-22.
[4] 杨浩东, 陈阳生, 邓志奇. 永磁同步电机常用齿槽配合的电磁振动[J]. 电工技术学报, 2011, 26(9): 24-30.
Yang Haodong, Chen Yangsheng, Deng Zhiqi. Electro- magnetic vibration of PM synchronous motors with different combinations of slot and pole number[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 24-30.
[5] Carraro E, Bianchi N, Zhang S, et al. Design and performance comparison of fractional slot con- centrated winding spoke type synchronous motors with different slot-pole combinations[J]. IEEE Transactions on Industry Applications, 2018, 54(3): 2276-2284.
[6] Zhu Z Q, Xia Z P, Wu Lijian, et al. Analytical modeling and finite-element computation of radial vibration force in fractional-slot permanent-magnet brushless machines[J]. IEEE Transactions on Industry Applications, 2010, 46(5): 1908-1918.
[7] Timar P, Fazekas A, Kiss J, et al. Noise and vibration of electrical machines[M]. New York: Elsevier, 1989: 69-89.
[8] 林福, 左曙光, 毛钰, 等. 考虑电流谐波的永磁同步电机电磁振动和噪声半解析模型[J]. 电工技术学报, 2017, 32(9): 24-31.
Lin Fu, Zuo Shuguang, Mao Yu, et al. Semi-analytical model of vibration and noise for permanent magnet synchronous motor considering current harmonics[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 24-31.
[9] Chen Yangsheng, Zhu Ziqiang, Howe D. Vibration of PM brushless machines having a fractional number of slots per pole[J]. IEEE Transaction on Magnetics, 2006, 42(10): 3395-3397.
[10] Islam R, Husain I. Analytical model for predicting noise and vibration in permanent-magnet synchronous motors[J]. IEEE Transactions on Industry Appli- cations, 2010, 46(6): 2346-2354.
[11] 李晓华, 黄苏融, 李良梓. 电动汽车用永磁同步电机振动噪声的计算与分析[J]. 电机与控制学报, 2013, 17(8): 37-42.
Li Xiaohua, Huang Surong, Li Liangzi. Calculation and analysis of vehicle vibration and noise of permanent magnet synchronous motor applied in electric vehicle[J]. Electric Machines and Control, 2013, 17(8): 37-42.
[12] 刘和平, 刘庆, 张威, 等. 电动汽车用感应电机削弱振动和噪声的随机PWM控制策略[J]. 电工技术学报, 2019, 34(7): 1488-1495.
Liu Heping, Liu Qing, Zhang Wei, et al. Random PWM technique for acoustic noise and vibration reduction in induction motors used by electric vehicles[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1488-1495.
[13] 李晓华, 赵容健, 田晓彤, 等. 逆变器供电对电动汽车内置式永磁同步电机振动噪声特性影响研究[J]. 电工技术学报, 2020, 35(21): 4455-4464.
Li Xiaohua, Zhao Rongjian, Tian Xiaotong, et al. Study on vibration and noise characteristics of interior permanent magnet synchronous machine for electric vehicles by inverter[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4455-4464.
[14] Liang Wenyi. The investigation of electromagnetic radial force and associated vibration in permanent magnet synchronous machines[D]. Bedfordshire: Cranfield University, 2017.
[15] Fang Haiyang, Li Dawei, Qu Ronghai, et al. Modu- lation effect of slotted structure on vibration response in electrical machines[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 2998-3007.
[16] Wang Shanming, Hong Jianfeng, Sun Yuguang, et al. Analysis of zeroth mode slot frequency vibration of integer slot permanent magnet synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2019, 67(4): 2954-2964.
[17] Huang Surong, Aydin M, Lipo T. Electromagnetic vibration and noise assessment for surface mounted PM machines[C]//Power Engineering Society Summer Meeting, Vancouver, Canada, 2001: 1417-1426.
[18] 杨浩东. 永磁同步电机电磁振动分析[D]. 杭州: 浙江大学, 2011.
[19] 杨浩东, 陈阳生. 分数槽永磁同步电机电磁振动的分析与抑制[J]. 中国电机工程学报, 2011, 31(24): 83-89.
Yang Haodong, Chen Yangsheng. Electromagnetic vibration analysis and suppression of permanent magnet synchronous motor with fractional slot combination[J]. Proceedings of the CSEE, 2011, 31(24): 83-89.
[20] 李晓华, 刘成健, 梅柏杉, 等. 电动汽车IPMSM宽范围调速振动噪声源分析[J]. 中国电机工程学报, 2018, 38(17): 5219-5227.
Li Xiaohua, Liu Chengjian, Mei Boshan, et al. Vibration and noise source analysis of IPMSM for electric vehicles in a wide-speed range[J]. Proceedings of the CSEE, 2018, 38(17): 5219-5227.
[21] Li Xiaohua, Huang Surong, Zhang Qi, et al. Electro- magnetic noise assessment for EV’s PM driving machines[C]//The 17th International Conference Elec- trical Machines and Systems, Hangzhou, 2014: 1552- 1555.
The Influence of High-Order Force on Electromagnetic Vibration of Permanent Magnet Synchronous Motors
Abstract The influences of electromagnetic force harmonics with high mode number on electromagnetic vibration of permanent magnet motor under no load and load condition is analyzed. First, the amplitude, frequency and order of the electromagnetic force of the motor are derived by the Maxwell stress tensor method. Then, the low- and high-order forces that cause low-mode vibration under no-load and load conditions are calculated, and the influence of tooth width on the forces is discussed. Next, the contributions of two kinds of electromagnetic forces to the low-order electromagnetic vibration is analyzed and compared in detail by the modal superposition method, and the analytical results are verified by the finite element method. Finally, the no-load electromagnetic vibration test is carried out on a 10-pole 12-slot permanent magnet motor, and the experimental results are consistent with the simulation results. The results show that the high-order force can cause large low-mode vibrations, but in fractional slot PM motors, its contribution decreases with the increase of load. This paper can provide an idea for the accurate vibration prediction and vibration reduction of the slotted permanent magnet motor.
keywords:High-order force, low-mode vibration, teeth chopping effect, permanent magnet synchronous motor
DOI: 10.19595/j.cnki.1000-6753.tces.201385
中图分类号:TM351
洪剑锋 男,1988年生,助理研究员,研究方向为低振动永磁电机的优化设计与控制。E-mail: hongjianfeng2009@126.com
王善铭 男,1972年生,研究员,博士生导师,研究方向为永磁电机的优化设计及其控制技术。E-mail: wangsm96@mail.tsinghua.edu.cn
收稿日期 2020-10-15
改稿日期 2021-04-10
国家自然科学基金资助项目(51677103, 52007091)。
(编辑 崔文静)