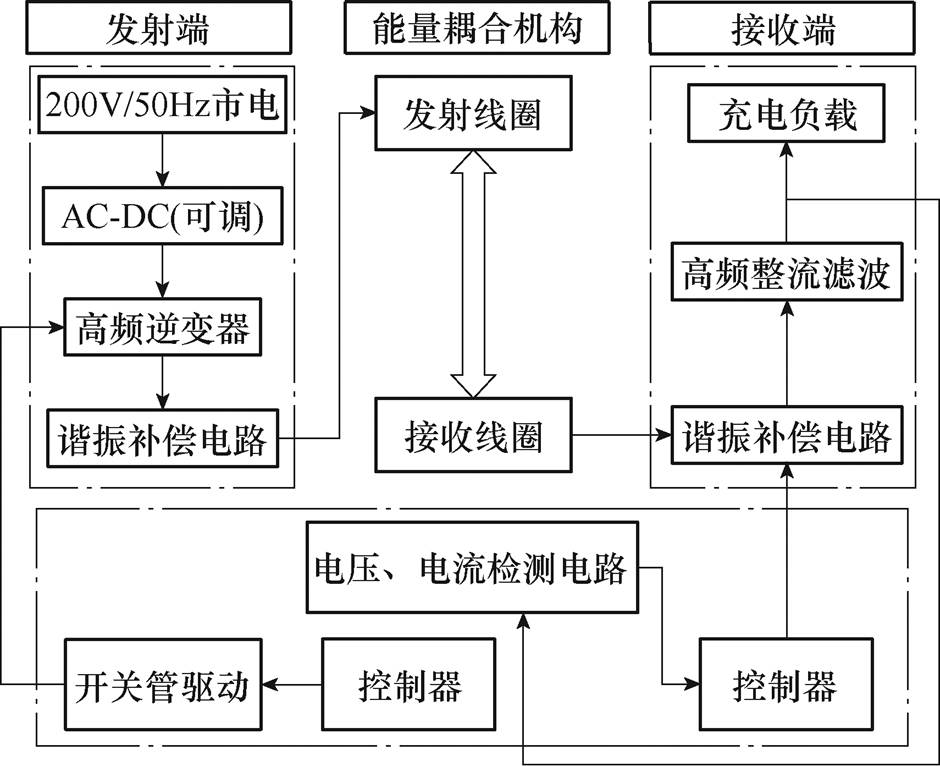
图1 无线充电系统结构示意图
Fig.1 Structure diagram of wireless charging system
摘要 为了减少混合谐振式无线充电系统的开关器件和无源元件数量，提高系统输出功率，同时简化原、副边的控制策略，提出一种基于LCL-LCL/S混合自切换谐振式无线充电系统，无需原、副边通信和增加任何无源元件，仅通过LCL结构的自投切操作更改拓扑网络来实现无线充电系统恒流恒压的切换。首先，依靠T型网络分析恒流或恒压输出与输入阻抗呈纯阻性的关系；然后，引入混合型补偿网络数学模型，分析实现系统输入电流和电压之间零相角（ZPA）与恒流或恒压输出特性的参数配置条件；接着，依据蓄电池充电曲线特征、谐振电流阈值、电压跳变阈值和耦合系数变化约束，进一步提出一种适用于混合谐振式拓扑网络参数优化的设计方法，在避免谐振网络参数经验选值的局限性导致参数不确定性问题的同时，也为参数选取提供了理论依 据；最后，搭建实验平台验证该方案的可行性与有效性。实验结果表明，优化谐振网络参数的无线充电系统具有较好的恒流恒压输出特性，系统最大传输效率为81%，完全满足恒流恒压无线充电需求。
关键词：磁耦合谐振式无线电能传输 LCL-LCL/S拓扑 参数优化设计 恒流恒压充电
无线电能传输可以避免用电设备直接接触电源，具有安全、可靠和经济等诸多优点。相比于传统的有线电能传输，避免了外露通电接点和频繁插拔的缺点，保障了电能传输的安全性与可靠性。因此无线电能传输的研究具有广阔的发展前景[1]。
常用的无线电能传输技术有磁耦合感应式和磁耦合谐振式等[2]。磁耦合感应式无线电能传输（Magnetically-Coupled Inductive Wireless Power Transfer, MCI-WPT）方式，能量传输效率低，传输距离为mm级，但电路设计简单，一般用于低成本微功率场合。磁耦合谐振式无线电能传输（Magnetically- Coupled Resonant Wireless Power Transfer, MCR- WPT）方式，能量传输功率可达几kW，具有传输功率大、传输效率高、传输距离远等特点。因此，MCR-WPT技术已经广泛应用于电动汽车、医疗装置、机器人充电以及轨道交通的供能等领域[3]。随着机器人技术的快速发展，机器人正在各领域中扮演着不可或缺的角色。电力行业的发展也不例外，电力巡检机器人具有安全、可靠和精准等优点，已日渐取代人工巡检的方式。然而机器人现有的充电方式都是接触式充电，其存在电火花、漏电和线路老化等弊端，严重威胁着电力系统的安全运行。将MCR-WPT技术应用于电力巡检机器人充电，可以有效解决此类弊端，具有重要的意义，也是目前的研究热点[4]。
由于机器人需要独立工作，其供电系统一般采用蓄电池或锂电池。由典型的蓄电池或锂电池充电曲线可知，充电过程可以分为恒流充电（Constant Current, CC）和恒压充电（Constant Voltage, CV）两个阶段[5]。将恒流恒压充电与无线电能传输技术相结合是实现电池安全、可靠充电的保障。
目前基于MCR-WPT的恒流恒压充电的实现方法大致可分为两类：一类为动态调节法；另一类为变静态补偿法[6]。动态调节法主要包括在原边或副边加入直流-直流（DC-DC）变换电路、移相控制、变频控制等方式。文献[7]在原、副边添加了DC-DC变换电路，系统利用接收端采样信息反馈控制DC-DC变换器，从而实现对负载的恒流恒压充电。文献[8]在恒定频率下，系统根据采样信息反馈控制逆变电路开关管驱动信号相位差，通过相位差的变化调节输出电压有效值，从而控制恒流恒压充电。文献[9]利用谐振电路在不同工作频率点表现出的不同特性，通过跳频控制来实现恒流恒压充电。这些控制方式虽然控制精度高、调节范围广，且大多数不占用充电设备有限空间，然而它们都需要原、副边之间通信，增加了系统控制的复杂度和成本，且进行跳频控制时，频率的变化会影响系统的稳定性，有时易引起频率分裂现象[10]。变静态补偿法主要包含混合补偿等方式。具有CC或CV输出特性的不同无源谐振网络进行组合，并使用开关进行状态切换以此实现系统的恒流恒压输出。文献[11]中提出一种基于LCCL-LCCL补偿网络的感应耦合电能传输系统，通过频率控制和开关切换的配合实现锂电池充电的恒流恒压切换。文献[12-16]中在副边电路增加电容或电感等无源元件，通过切换开关实现系统的恒流恒压输出。上述方法中系统所需添加的无源元件和开关数量众多，不但增加了系统成本，而且谐振网络参数都是依靠经验选值，没有考虑系统的负载特性，很难实现零相角（Zero Phase Angle, ZPA）特性，使得系统输出效率普遍偏低。
为克服上述问题，本文首先通过结合T型网络分析恒流型输出和恒压型输出的参数配置条件，并根据恒流型和恒压型参数配置特点，设计了一种新型的混合自切换谐振式无线充电系统，给出了实现恒流和恒压切换输出的条件；然后，根据负载特性和谐振网络特性对混合式自切换谐振拓扑网络的参数进行优化设计；最后，搭建了实验硬件平台，验证了参数选择的合理性和谐振拓扑网络的有效性。
无线充电系统结构示意图如图1所示，磁耦合谐振式无线充电系统主要包含原边电能变换装置和副边电能感应耦合装置两大组成部分。原边主要包含可调的AC-DC变换电路、高频逆变电路、谐振补偿电路和发射线圈等部分；副边主要包含接收线圈、谐振补偿电路、高频整流滤波电路、充电负载等部分。首先220V/50Hz市电经可调直流电源输出稳定的直流电压；然后经过高频逆变器输出高频交流电，高频交流电经发射线圈产生交变磁场，经线圈感应耦合与谐振补偿后，副边谐振补偿电路输出高频交流电；最后输出的高频交流电经整流滤波后给负载充电，同时电压、电流检测电路实时监测充电电压和电流的大小，并通过控制器控制开关切换，实现阶段式恒流恒压充电。
图1 无线充电系统结构示意图
Fig.1 Structure diagram of wireless charging system
T型网络[17]是分析LCL谐振网络的重要理论基础，其等效电路如图2所示。
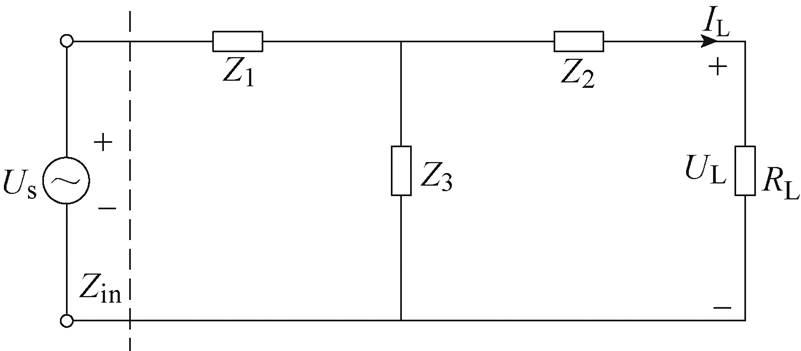
图2 T型网络拓扑
Fig.2 T-type network topology
图2中，Us为电源端恒定电压，Z1、Z2和Z3为谐振元件阻抗，RL为负载，UL为输出电压，IL为输出电流。
假设Z1Z2=a、Z1Z3=b、Z2Z3=g、Z1+Z2=A、Z1+Z3=B、Z2+Z3=C，由图2可得T型网络的输入阻抗Zin为
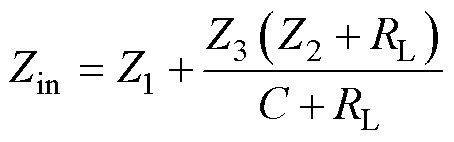（1）
简化式（1）输入阻抗Zin的方程，其实部与虚部方程分别为
（2）
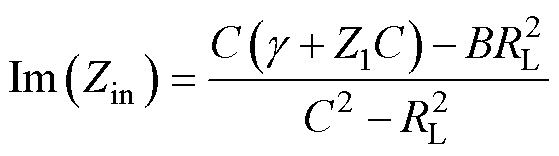（3）
由式（2）与式（3）可得，当B=0且C=0时，输入阻抗Zin虚部为零，呈纯阻型，且与负载电阻RL的大小无关。
基于二端口网络理论，假设T型网络输入为电压源，可以求出互导增益Giv、电压增益Gvv分别为
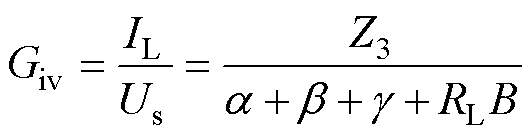（4）
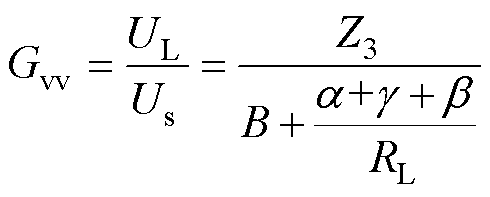（5）
根据式（4）互导增益方程可得，当B=0时，互导增益Giv与负载RL无关。简化式（4）可得
（6）
由式（6）可知，Us的大小不变时，其输出电流的大小可以通过改变a、b、g 的值来进行调节，系统可以实现恒流输出。
根据式（5）电压增益方程可得，当a+b+g=0时，电压增益Gvv与负载RL无关。假设Z1/Z3=a，简化式（5）可得
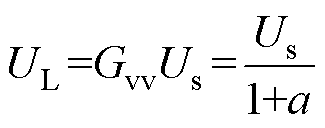（7）
由式（7）可知，Us的大小不变时，其输出电压的大小可以通过改变a的值来进行调节，系统可以实现恒压输出。
假设恒流型输出为事件Ⅰ，恒压型输出为事件Ⅱ，输入阻抗呈纯阻性为事件Ⅲ。基于上述对T型网络分析可知，事件Ⅲ所发生的条件是事件Ⅰ发生条件的子集；事件Ⅱ所发生的条件与事件Ⅲ发生的条件为互不相容事件。
基于第1节分析可知，单纯依靠T型网络所形成的谐振拓扑无法在原边输入阻抗呈纯阻性的前提下，实现副边的恒流恒压输出。因此，本文结合二阶和三阶网络的输出特性，提出一种混合自切换谐振式LCL-LCL/S的网络拓扑，如图3所示为其等效电路。
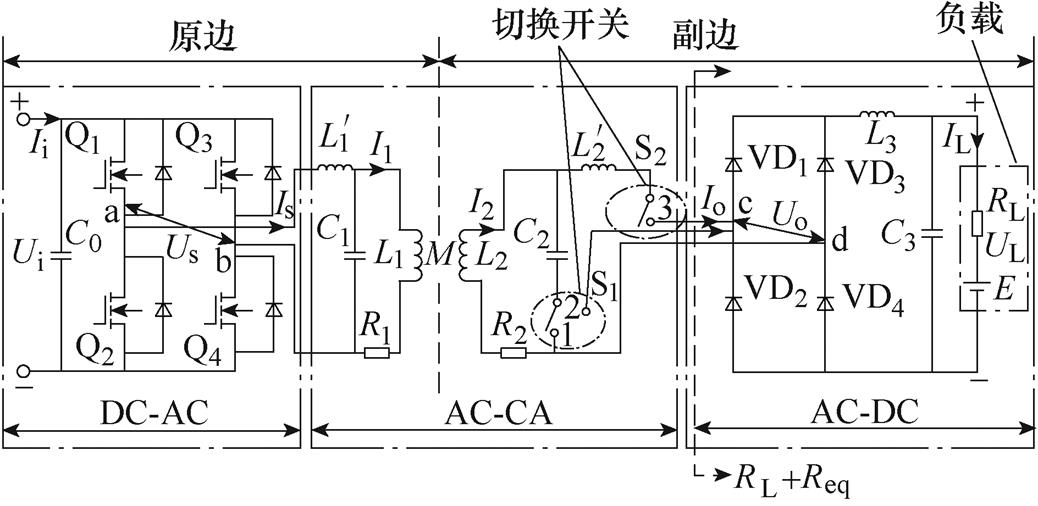
图3 LCL-LCL/S谐振网络拓扑
Fig.3 LCL-LCL/S resonant network topology
如图3所示，原边采用单相全桥高频逆变电路，其桥臂分别由Q1与Q4、Q2与Q3构成。Ui为原边输入电压，Ii为原边输入电流，Us与Is分别为逆变器输出的电压和电流。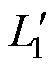
、C1、L1和R1构成发射端LCL谐振网络，M为发射线圈与接收线圈之间的互感；副边采用电感电容滤波的单相不可控高频整流电路，其桥臂分别由VD1与VD4、VD2与VD3构成。Uo与Io分别为整流电路的输入电压和电流。L2、C2、
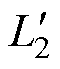与R2构成了接收端LCL谐振网络，L2、C2和R2构成接收端S谐振网络。L3和C3分别为滤波电感与滤波电容，RL和E相当于反电动势负载，即蓄电池充电负载。
逆变电路直流侧输入电压Ui与输出电压Us的关系[18]为
（8）
图3中，对于高频整流电路，当满足式（9）时，T为交流电源周期，此时整流器输入电压Uo、输入电流Io与系统输出电压UL、电流IL的关系[19]为
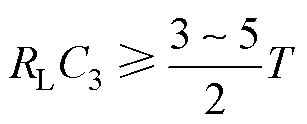（9）
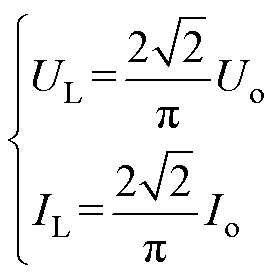（10）
当S1连接1触点，S2连接3触点时，副边谐振网络拓扑为LCL-LCL型，即恒流模式。假设逆变器移相角为π，则根据功率守恒定律计算所得整流器相关电路的等效电阻Req与蓄电池等效内阻RL的关系[20]为
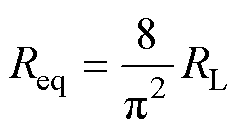（11）
因此，整流器及负载电路等效总电阻
为
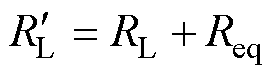（12）
依据以上分析，建立了LCL-LCL型谐振网络拓扑等效电路，如图4所示。
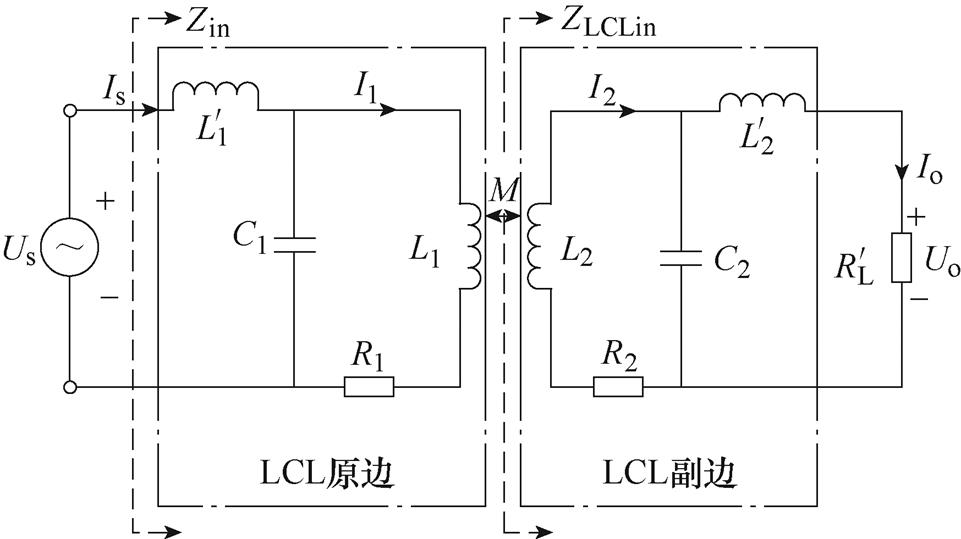
图4 LCL-LCL型系统等效电路拓扑
Fig.4 Equivalent circuit topology of LCL-LCL system
忽略线圈电阻的影响，假设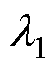
为原边两电感量之比，即
，
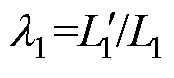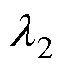为副边两电感量之比，即
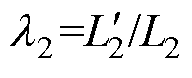；w 为LCL电路工作角频率，w0为系统谐振角频率；k为发射线圈与接收线圈间的耦合系数。
依据T型网络拓扑对副边谐振电路分析可知，当取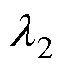=1，且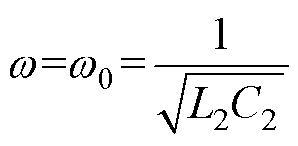
时，副边阻抗ZLCLin为
（13）
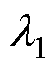当取=1，且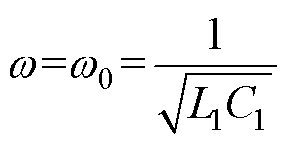
时，将副边阻抗等效至原边，可得系统原边输入阻抗Zin为
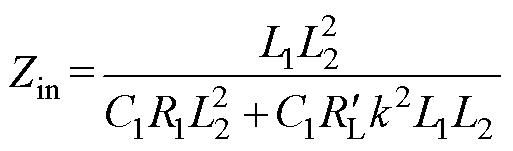（14）
由式（14）可知，LCL-LCL型系统输入阻抗Zin纯阻性，可以实现ZPA特性。
基于基尔霍夫电压定律，可得
（15）
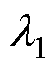当=1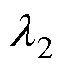，=1时，电感L1与电容C1、电感L2与电容C2满足
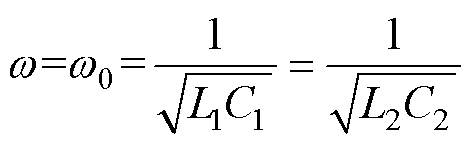（16）
将式（16）代入式（15）中，可得系统原边输出电流I1和副边输出电流Io分别为
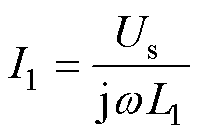（17）
（18）
由式（18）可知，当无线充电系统的谐振补偿拓扑为LCL-LCL型时，系统的输出电流与负载等效电阻的大小无关，为恒流型输出，即系统处于CC模式。
定义副边输出电流Io与逆变器输出电压Us之比为Giv，即系统的互导增益为
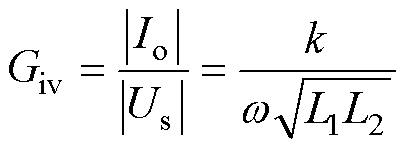（19）
由式（19）可知，CC模式时，系统的互导增益只与耦合系数、谐振频率以及电感参数有关。
当S1连接2触点，S2断开3触点时，副边谐振网络拓扑为LCL-S型，即恒压模式。同理，为整流器及负载电路的等效电阻，Us为逆变器输出电压，LCL-S型谐振网络拓扑等效电路如图5所示。
忽略线圈电阻的影响，对副边串联电路分析可知，副边阻抗ZSin为
（20）
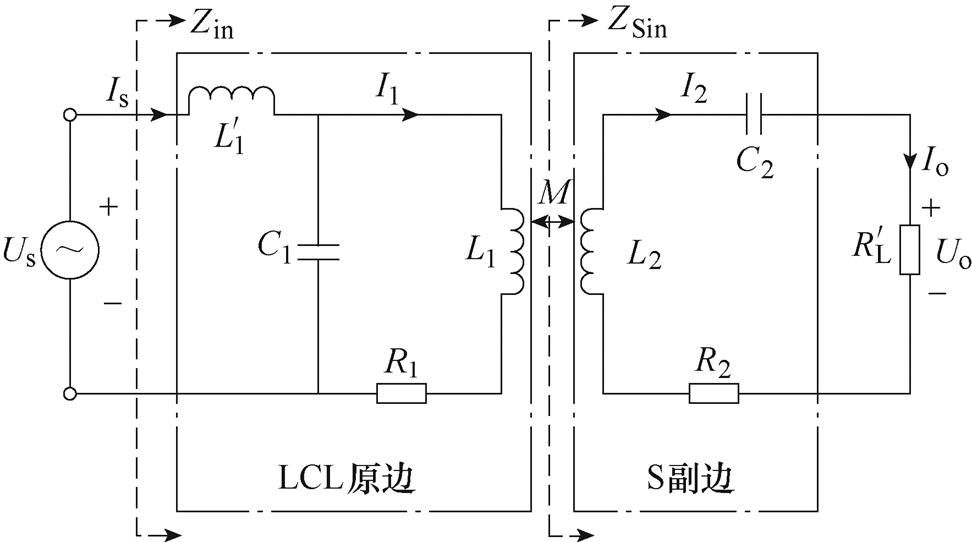
图5 LCL-S型系统等效电路
Fig.5 Equivalent circuit topology of LCL-S system
当取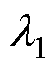=1，且
时，将副边阻抗ZSin等效至原边可得系统原边输入阻抗Zin为
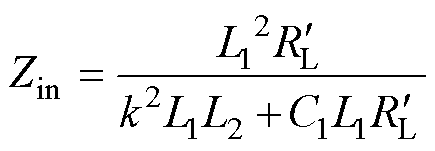（21）
由式（21）可知，LCL-S型系统输入阻抗Zin呈纯阻性，系统可以实现ZPA特性。
基于基尔霍夫电压定律，可得
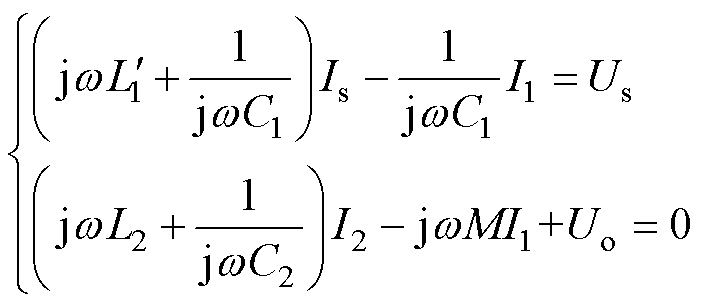（22）
将式（16）代入式（22），可得原边谐振电流I1和系统输出电压Uo分别为
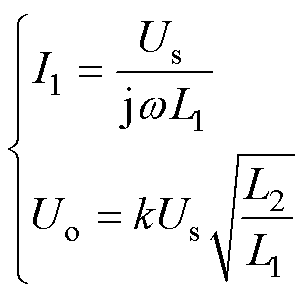（23）
由式（23）可知，无线充电系统的谐振补偿拓扑为LCL-S型时，系统的输出电压与负载等效电阻的大小无关，系统为恒压型输出，即系统处于CV模式。
定义系统输出电压Uo与逆变器输出电压Us之比为Gvv，即系统的电压增益为
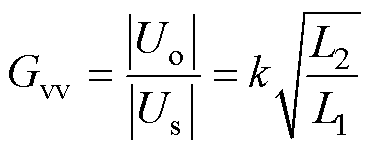（24）
由式（24）可知，CV模式时，系统的电压增益只与耦合系数和电感参数有关。
综上所述，当S1连接1触点，S2连接3触点时，系统谐振拓扑结构为LCL-LCL型，此时系统工作于CC模式；当S1连接2触点，S2断开3触点时，系统谐振拓扑结构为LCL-S型，此时系统工作于CV模式，且开关切换前后谐振频率相等。因此，通过监测负载端电压的大小来控制开关S1、S2的工作状态，可以实现LCL-LCL与LCL-S两种谐振拓扑结构的切换，从而在恒定频率下实现CC模式与CV模式的自切换。
通过对LCL-LCL/S两种谐振拓扑的分析可知，依靠副边LCL谐振网络的自切换即可实现恒流和恒压不同特性的输出，无需增加多余的无源元件和开关，进而可改善系统的输出特性，使得在实际应用中更为高效。然而，在实际选取谐振网络的电感和电容参数时，传统方法依靠经验选取，没有具体的理论依据，使得参数选取的不准确性会影响无线充电系统的传输功率和效率。因此，需要对谐振网络的参数进行设计与优化。
典型的蓄电池充电曲线如图6所示，从图中看出，电池充电过程主要包括恒流充电和恒压充电两个阶段。为了保证充电过程的安全可靠性，需要无线充电系统提供恒定的输出电流和电压。
图6 典型的蓄电池充电曲线
Fig.6 Typical battery charging curves
图6中，设Imax和Umax分别为CC模式下的最大充电电流及CV模式下的最大充电电压，即Imax= IL，Umax=UL；其中Ucc和Icv分别为CC模式下的充电电压及CV模式下的充电电流。
将式（8）、式（10）代入式（23）得原边直流电压Ui为
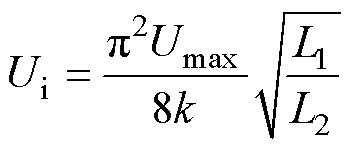（25）
将式（8）和式（10）代入式（18），并结合式（25）可得，副边线圈自感L2=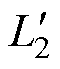的值为
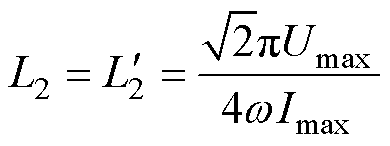（26）
由式（16）和式（26）可得电容C1及C2的值分别为
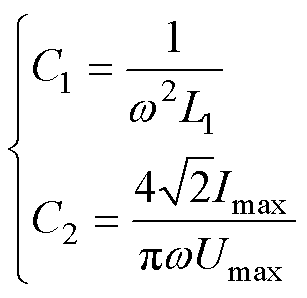（27）
式（25）～式（27）给出了混合自切换谐振式网络拓扑LCL-LCL/S的参数设计方法，按照该方法设计的谐振拓扑，能够实现对蓄电池的恒流恒压充电，且在整个充电过程中能实现原边的ZPA特性。
根据系统参数设计方法可知，副边线圈自感L2不受耦合系数的影响，而原边线圈自感L1与耦合系数成正比。因此在固定电感值下，当线圈间距离发生变化或线圈发生偏移时无法实现恒流恒压输出。为了保证参数选取的正确性与可行性，本文提出一种适用于混合式谐振网络拓扑参数优化的设计方法。
该方法依据典型的蓄电池充电曲线特性，对混合式谐振网络参数进行巧妙设计。
（1）恒流模式。在保持充电电流恒定的前提下，整流滤波后输出电流不小于最大充电电流Imax。
（2）恒压模式。在保持充电电压恒定的前提下，系统输出电压不小于最大充电电压Umax。
（3）阈值约束。为了保证充电网络的安全，防止过充、避免不充等情况，需要给谐振网络原边与副边的谐振电流设定安全阈值。
（4）跳变电压阈值约束。为了防止混合拓扑结构进行开关切换时引起的电压冲击，需要设定电压切换的阈值，保证平稳的切换。
（5）耦合系数变化约束。为了防止线圈间距发生变化或线圈发生偏移时导致系统无法实现恒压输出，需要设定约束范围，保证电压的变化率最小。
3.2.1 恒流模式
当系统进行恒流充电时，谐振网络拓扑会切换至LCL-LCL型。在系统发生谐振时，由式（19）可得，互导增益Giv与等效负载电阻无关，因此选择Giv作为CC模式下的约束条件。图6中，在恒流充电阶段，蓄电池最大充电电流为Imax，根据式（10）可得，整流器输入电流Io≈1.11Imax；假设逆变器最大移相角为p，由式（8）可知，逆变器输出电压Us≈0.9Ui。因此，LCL-LCL谐振网络的互导增益Giv存在最大值，即
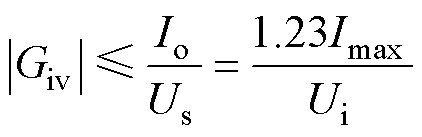（28）
综合式（19）和式（28）可得电感量参数L2约束为
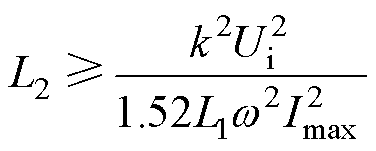（29）
3.2.2 恒压模式
当系统进行CV充电时，谐振网络拓扑会切换至LCL-S型。在系统发生谐振时，由式（24）可得，电压增益Gvv与负载电阻无关。图6中，在恒压充电阶段，蓄电池最大充电电压Umax，根据式（10）可得，整流器输入电压Uo≈1.11Umax。因此，LCL-S谐振网络的电压增益Gvv存在最小值，即
（30）
综合式（24）和式（30）可得，电感量参数L2约束为
（31）
3.2.3 原边谐振电流阈值
蓄电池充电时，在B或C点处，I1达到最大值，之后逐渐减小。因此必须保证谐振网络的原边谐振电流不大于其允许的最大值Ix1，由式（17）和式（23）可得
（32）
综合式（8）和式（32）可得，电感量参数L1的约束为
（33）
3.2.4 副边谐振电流阈值
系统运行在CC充电阶段时，副边感应电压ULCLin为
（34）
将式（8）、式（17）代入式（34），并结合式（13）可得CC模式下的副边谐振电流I2为
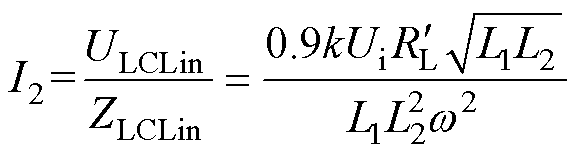（35）
同理，CC模式下副边谐振电流I2需要满足
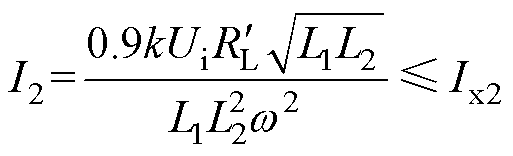（36）
同理可知，系统运行在CV充电阶段时，系统的互导增益Giv为
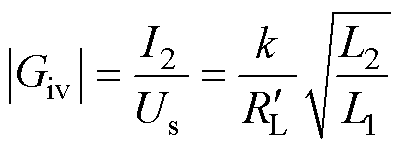（37）
将式（10）代入式（37）可得，CV模式下的副边谐振电流为
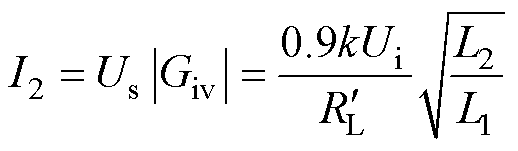（38）
则CV模式下的副边谐振电流I2需要满足
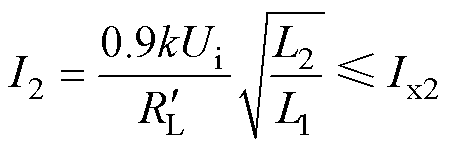（39）
综合式（36）和式（39）可得电感量参数的约束为
（40）
3.2.5 切换点电压跳变阈值
蓄电池从CC模式切换至CV模式时，会造成瞬间的跳变电压，在实际的蓄电池充电过程中，对电池的损伤较大，严重影响电池的使用寿命。因此，为了保证充电过程中充电电压的恒定，需要确保混合式谐振拓扑切换点处电压的一致性，即Uo(CC)= Uo(CV)。由式（18）与式（23）可得，CC模式下蓄电池等负载的充电电压Uo(CC)与CV模式下的充电电压Uo(CV)分别为
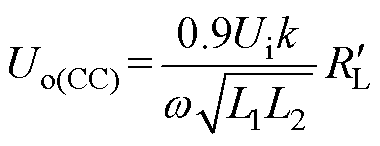（41）
（42）
由于蓄电池等效内阻随着充电电压的增大逐渐增大，因此需保证Uo(CC)≥Uo(CV)，即副边线圈自感量需满足
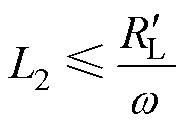（43）
3.2.6 耦合系数变化约束
实际无线充电过程中，线圈间距与偏移的变化会影响互感M，进而导致耦合系数k的变化，从而影响系统的功率和传输效率。两组垂直放置的平面圆形线圈，采用极坐标的方式对线圈进行建模并计算互感M为
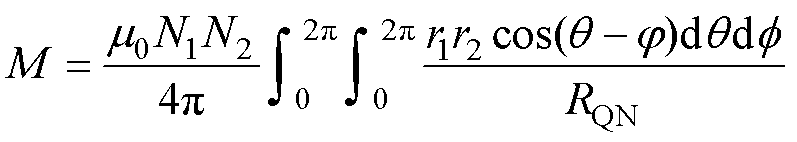（44）
其中
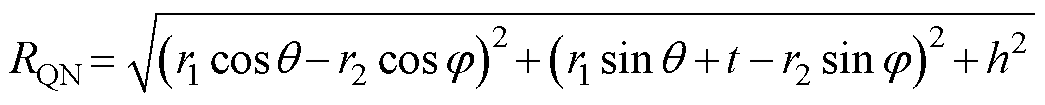
式中，q 和j 为极坐标下的参数；r1和r2分别为发射线圈和接收线圈外半径；h为线圈间距；N1和N2为线圈匝数。
在线圈无偏移的情况下，互感M为
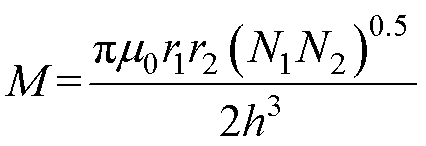（45）
线圈耦合系数k的大小与线圈半径r1、r2和匝数N1、N2成正比，与线圈间距h的三次方成反比。因此，线圈间距变化或线圈发生偏移时，耦合系数会发生变化。在实际充电过程中，耦合系数k在0.7～0.9之间变化[21-22]。代入式（25）得
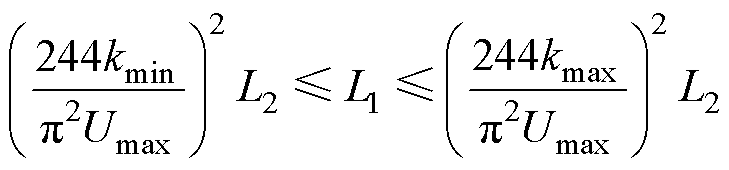（46）
综上可知，结合式（29）、式（31）、式（33）、式（40）、式（43）、式（46）可得，在不同条件下，谐振网络的电感参数约束范围见表1。
表1 电感参数约束范围
Tab.1 Constraint range of inductance parameters
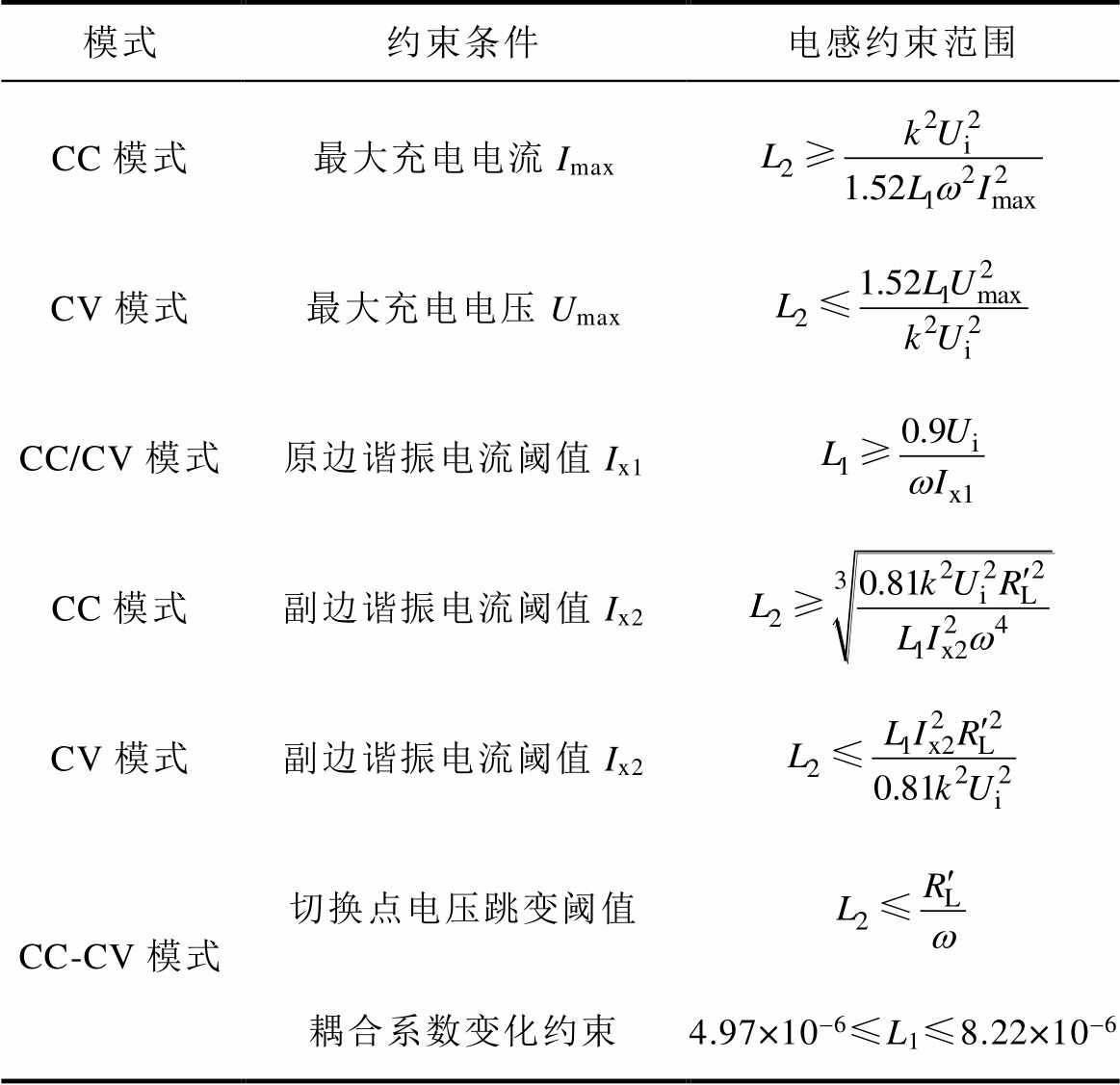
模式约束条件电感约束范围 CC模式最大充电电流Imax CV模式最大充电电压Umax CC/CV模式原边谐振电流阈值Ix1 CC模式副边谐振电流阈值Ix2 CV模式副边谐振电流阈值Ix2 CC-CV模式切换点电压跳变阈值 耦合系数变化约束4.97×10-6≤L1≤8.22×10-6
为了验证所设计的基于LCL-LCL/S混合自切换谐振式网络拓扑结构的合理性以及无线充电系统恒流恒压切换的可行性，以蓄电池作为充电负载，对提出的拓扑结构进行了实验验证，并对谐振网络参数优化方法进行了有效性验证。
4.1.1 蓄电池参数
以2节12V/40A·h蓄电池作为负载，最大充电电流为蓄电池额定容量的10%，即设置为4A；最大充电电压设置为24V。
表2 蓄电池参数
Tab.2 Battery parameters
参 数数 值 蓄电池容量Q/(A·h)40 蓄电池最大充电电压Umax/V24 蓄电池最大充电电流Imax/A4 切换时蓄电池等效电阻/W6
4.1.2 逆变网络及谐振网络相关参数
根据系统参数设计方法可知，由于参数间相互耦合，在设计谐振网络参数前，需要确定原边直流电压Ui、谐振频率w、耦合系数k等参数的值。同时为了保证充电过程的安全性，还需确定原、副边谐振电流的阈值。逆变网络及谐振网络相关参数见表3。
表3 逆变网络及谐振网络相关参数
Tab.3 Parameters of inverter network and resonant network
参 数数 值 原边直流电压Ui/V30.5 谐振频率f/kHz111 原边谐振电流阈值Ix1/A8 副边谐振电流阈值Ix2/A8 线圈间耦合系数k0.7
由图6可知，蓄电池充电过程中对应的4个点（A、B、C和D）分别对应不同的充电模式。A点为CC模式下的起始点，B点和C点为CC-CV模式切换点，D点为CV模式下的终止点。并且随着充电过程的进行，蓄电池等效电阻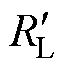
不断增大，且以谐振网络中副边线圈自感L2为因变量，原边线圈自感量L1为自变量。结合CC模式下最大充电电流，CV模式下最大充电电压，原、副边谐振电流阈值以及CC-CV切换点电压跳变阈值等诸多约束条件，可得到谐振网络参数的约束区域，如图7所示。
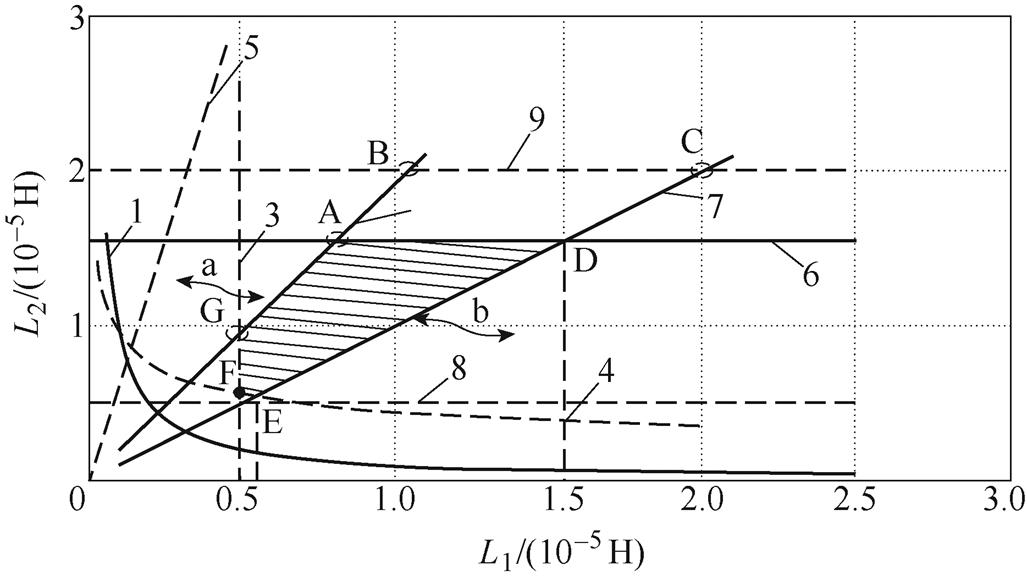
图7 电感量参数约束区域
Fig.7 Constraint region of inductance parameters
图7中，1号曲线为CC模式下限定最大充电电流时的副边线圈自感取值的下限；2号曲线为CV模式下限定最大充电电压时的副边线圈自感取值的上限；3号曲线为CC模式和CV模式下原边谐振电流阈值限定时的原边线圈自感取值的下限；4号和5号曲线为CC模式和CV模式下副边谐振电流阈值限定时的副边线圈自感取值的下限；6号曲线为CC-CV切换时电压跳变阈值限定时的上限；7号曲线为L1=L2条件限定时的下限；8号和9号曲线为线圈实际安装位置大小限定时的上、下限。
综合上述多个约束条件，可以得出发射线圈与接收线圈自感量的优化范围，即为五边形ADEFG构成的阴影部分。区域点坐标参数见表4。
表4 区域点坐标参数
Tab.4 Area point coordinate parameters
区域点L1/mHL2/mH A8.0715.5 B10.4120 C2020 D15.515.5 E5.445.44 F4.925.63 G4.929.45
从图7中看出，耦合系数k变化时，1号、2号、4号、5号曲线发生偏移，此时并不影响原、副边自感量的取值范围。根据表4数据得出原边线圈自感L1=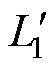
∈[4.92, 15.5]mH，其耦合系数约束区间为该区间的子集，系统可以实现稳定输出。
按照图3所示的电路结构搭建实验硬件平台，实验平台如图8所示。系统原边采用AC-DC电能变换功率为2 000W的可调直流电源，采用隔离变压器实现安全供电，电压调节范围0～400V；原边采用的主控制器选择Cortex M4内核的阿波罗STM32F429开发板，带有FPU和DSP指令集，拥有更多的资源和外设功能，STM32F429最高运行频率可达180MHz，功耗较低；逆变器采用IRFP460型第三代场效应晶体管构成全桥逆变电路，驱动芯片选用IR2110，它兼有光耦隔离、电磁隔离的优点。副边整流器采用RHRP3060型快恢复整流二极管构成的全桥整流电路，负载选用大功率管数控负载仪，兼容四大放电模式（恒流、恒功率、恒电阻、恒压）。实验平台详细参数见表5。
图8 混合自切换谐振无线充电系统实验平台
Fig.8 Experimental platform of hybrid self switching resonant wireless charging system
表5 实验参数
Tab.5 Experimental parameters
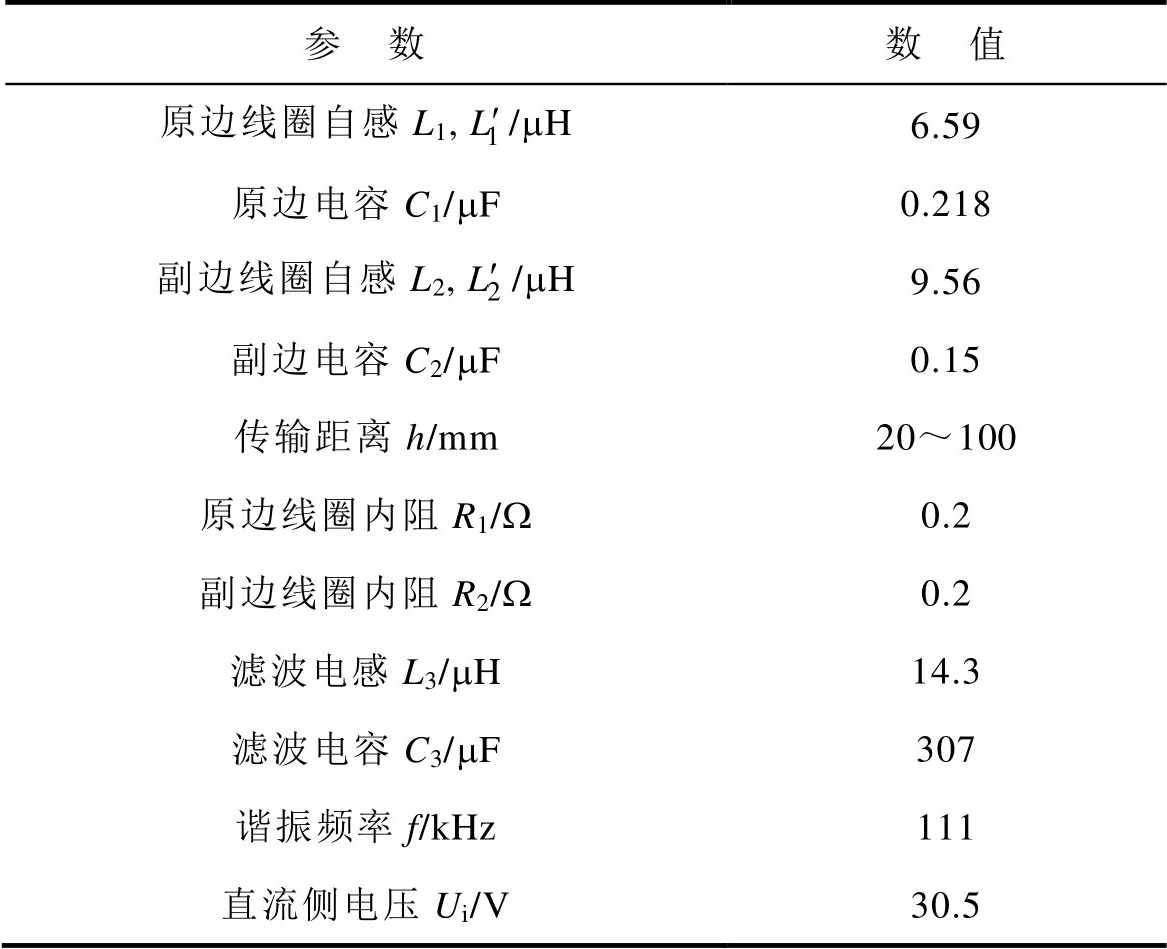
参 数数 值 原边线圈自感L1,/mH6.59 原边电容C1/mF0.218 副边线圈自感L2,/mH9.56 副边电容C2/mF0.15 传输距离h/mm20～100 原边线圈内阻R1/W0.2 副边线圈内阻R2/W0.2 滤波电感L3/mH14.3 滤波电容C3/mF307 谐振频率f/kHz111 直流侧电压Ui/V30.5
4.2.1 ZPA特性验证
当接收端切换为LCL或S型谐振补偿结构时，根据第2节所述，逆变电路的输出电压与电流波形零相位，即可实现ZPA特性，输入阻抗为纯阻性。由于大负载下更能测试ZPA特性，因此本次实验是在负载电阻RL分别为50W、100W 的条件下进行测试的。
图9和图10分别为不同拓扑结构、不同电阻下的测试结果。从图中可以看出，负载的变化对逆变器输出几乎没有影响，逆变电路工作在软开关模式下，系统实现了ZPA特性，验证了2.1节与2.2节理论分析计算的正确性。
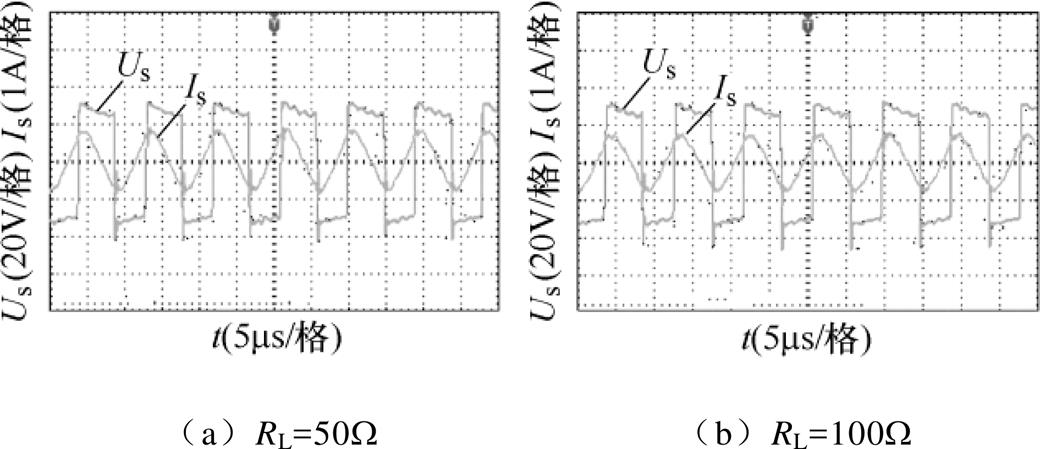
图9 LCL-LCL型-不同负载下逆变器输出电压、电流波形
Fig.9 LCL-LCL type-output voltage and current waveforms of inverter under different loads
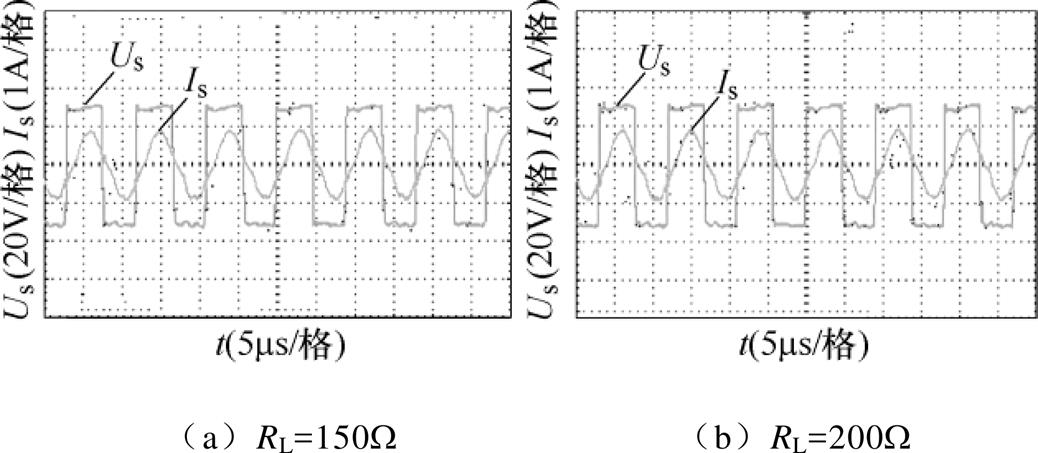
图10 LCL-S型-不同负载下逆变器输出电压、电流波形
Fig.10 LCL-S type-output voltage and current waveforms of inverter under different loads
4.2.2 恒流恒压特性验证
当接收测切换为LCL型谐振拓扑时，无线充电系统工作在恒流模式下。图11和图12分别为负载电阻6W 和8W 时的逆变器输出电压和电流波形以及负载侧充电电压和充电电流数值。
图11a中，负载充电电压的平均值为24V，充电电流的平均值为4A，系统的输出功率为96W，无线充电系统整体的传输效率为81%。
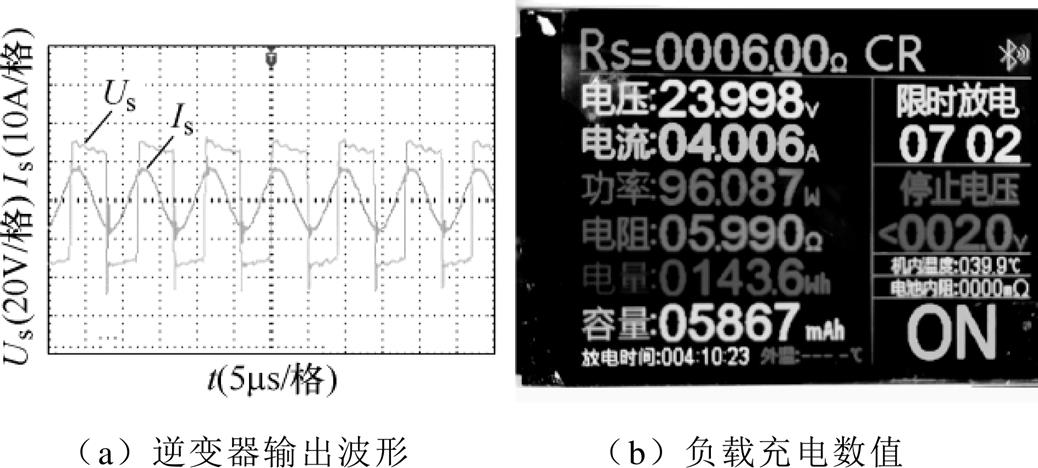
图11 负载电阻为6W
Fig.11 Load resistance is 6W
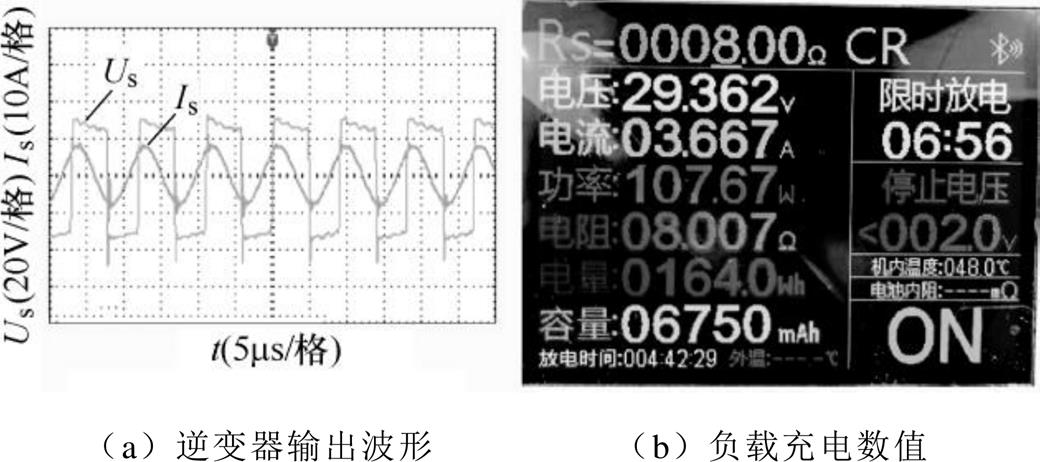
图12 负载电阻为8W
Fig.12 Load resistance is 8W
图12a中，负载充电电压的平均值为29.36V，充电电流的平均值为3.67A，系统的输出功率为107.75W，无线充电系统整体的传输效率为83%。可以看出，负载逐渐增大时，充电电流变化范围±0.34A，电流波动小，满足恒流的充电条件。
当接收测切换为S型谐振拓扑，无线充电系统工作在恒压模式。同恒流型测试条件一致，图13和图14分别为负载电阻为16W 和18W 时逆变器输出电压、电流波形及负载侧充电电压、电流波形。
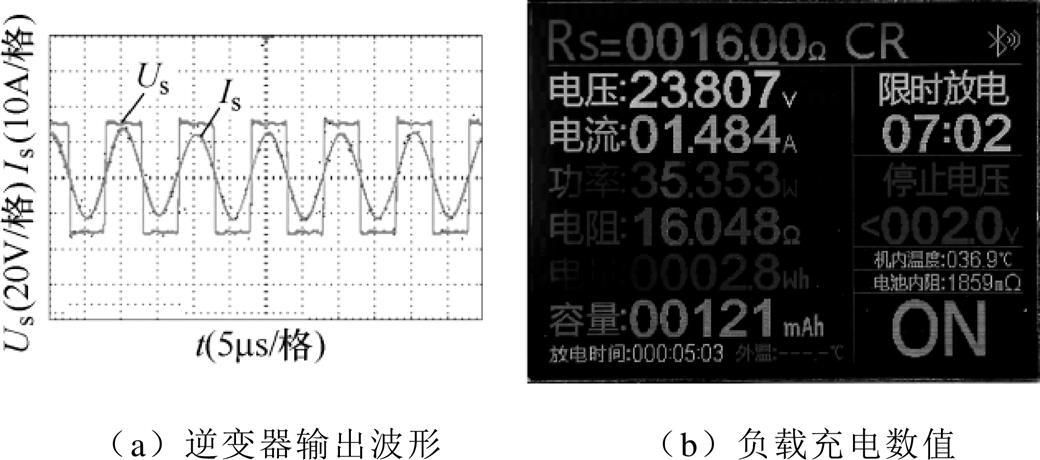
图13 负载电阻为16W
Fig.13 Load resistance is 16W
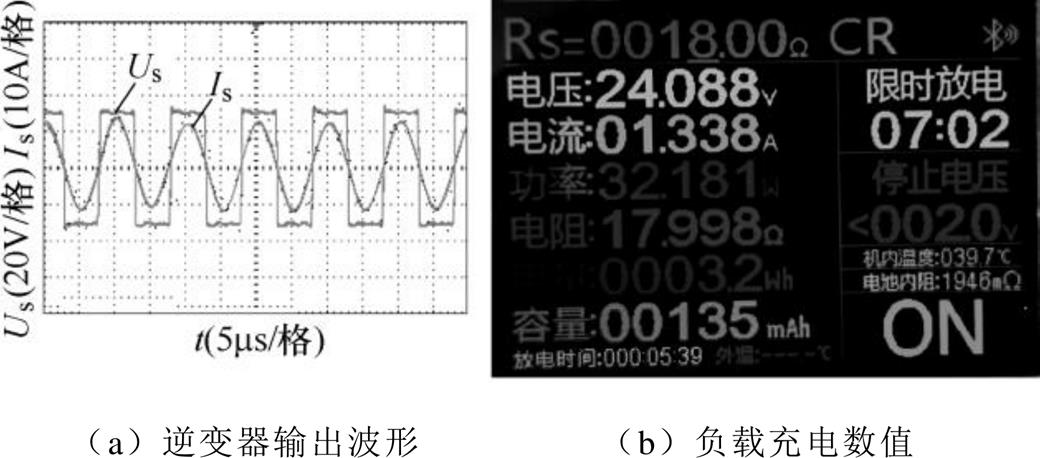
图14 负载电阻为18W
Fig.14 Load resistance is 18W
图13a负载充电电压的平均值为23.81V，电流的平均值为1.48A，系统的输出功率为35.24W，系统整体的传输效率为82%。
图14a中，负载充电电压的平均值为24.09V，充电电流的平均值为1.34A，系统的输出功率为34.28W，无线充电系统整体的传输效率为84%。可以看出，负载逐渐增大，充电电压的变化范围±0.28V，电压波动小，满足恒压的充电条件。
4.2.3 恒流−恒压切换特性验证
本次实验采用了电子负载模拟蓄电池充电过程中等效电阻的变化。在电池充电的第一阶段：恒流充电，电池的等效负载逐渐增大至6W，充电电流稳定至4A左右，电池电压逐渐增大至24V；电池充电的第二阶段：恒压充电，电池的等效负载由6W逐渐增大至57.6W，充电电压稳定在24V左右，电池充电电流逐渐减小至0.4A，至此电池充电过程 结束。
图15所示为开关S1和S2切换时逆变器和负载输出波形。从图中可以看出，开关切换前后逆变器输出电流Is略有下降，输出电压Us几乎保持不变，负载充电电压和充电电流在切换点处略有波动。
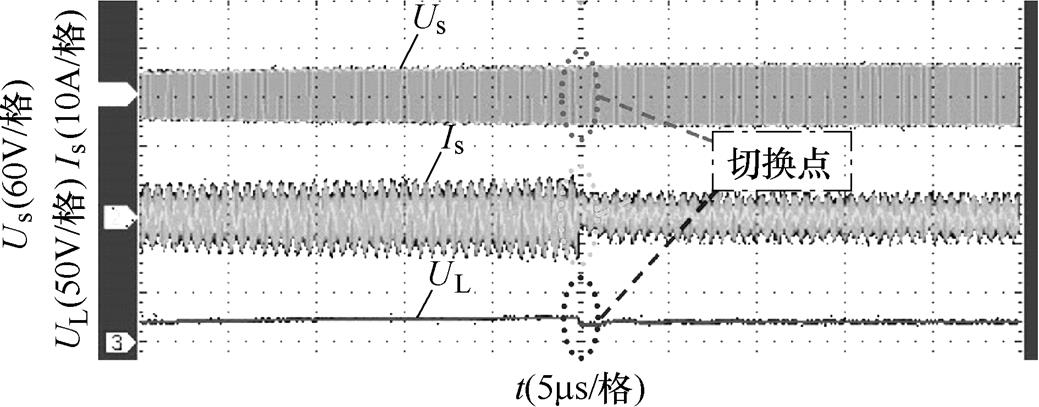
图15 开关切换时逆变器和负载输出波形
Fig.15 Output waveforms of inverter and load during switch switching
图16所示为电池等效负载为57.6W 时逆变器和负载输出波形和数值。从图中可以看出，逆变器输出电压保持不变，输出电流逐渐较小至一定值，负载充电电压维持在24V附近，充电电流减小至0.4A左右时，电池充电过程结束。
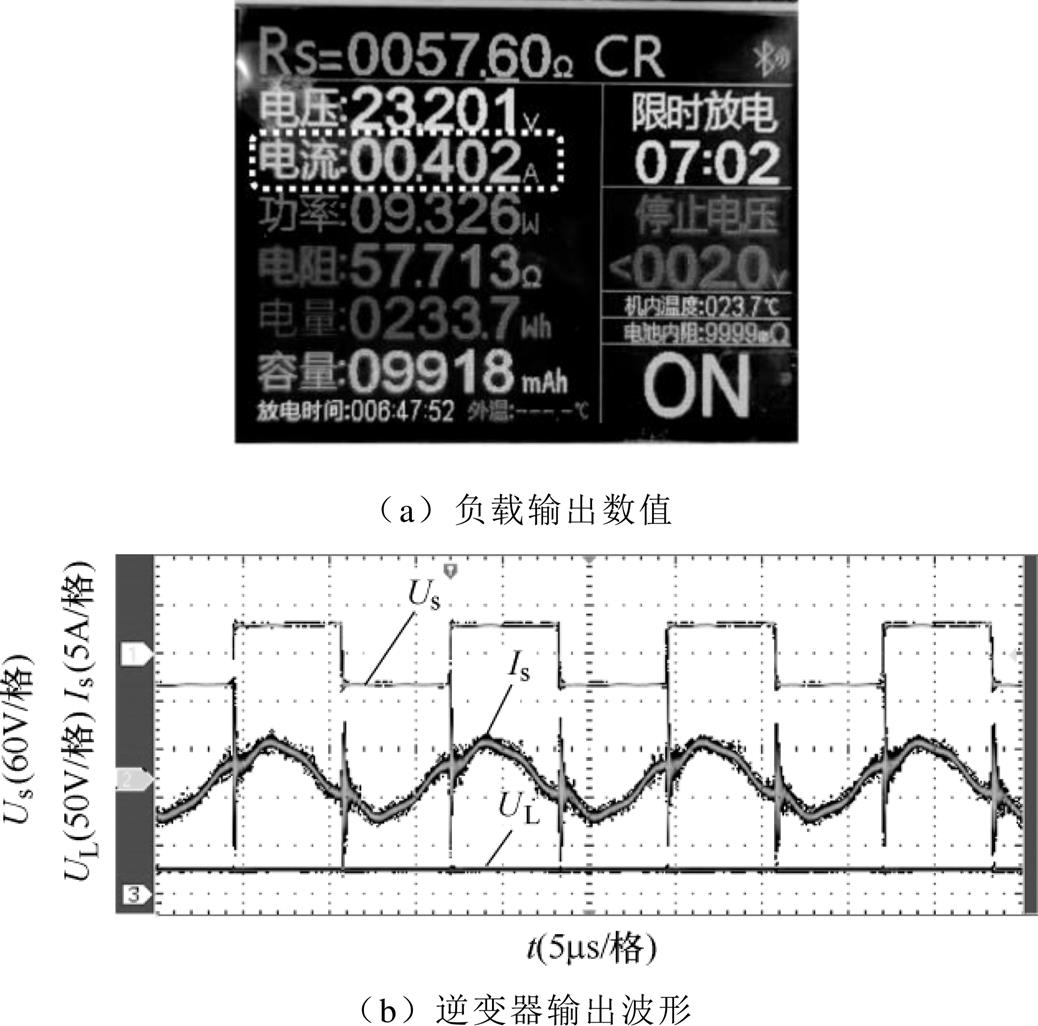
图16 充电完成时逆变器和负载输出波形和数值
Fig.16 Output waveforms and value of inverter and load when charging is completed
本次实验还模拟了恒流模式和恒压模式下，随着电池等效电阻的逐渐增加，系统充电电压和充电电流变化的趋势。恒流模式和恒压模式下系统的充电电压和电流变化趋势完全不同。图17所示为系统充电电压和电流随等效电子负载变化的曲线，从图中可以看出，本次实验搭建的平台完全满足蓄电池两段式充电的需求。在恒流模式下，电流从开始的4.01A下降至4A，电流变化率为0.25%，充电电流几乎保持稳定；在恒压模式下，电压从开始的23.7V上升至24.1V，电压变化率为1.68%，充电电压基本保持恒定。
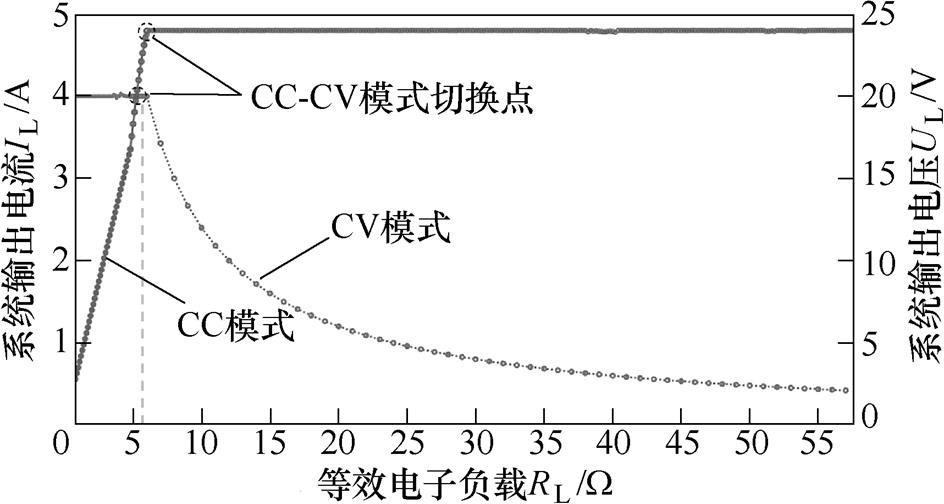
图17 系统充电电压和电流随等效电子负载变化曲线
Fig.17 Variation curves of system charging voltage and current with equivalent electronic load
图18为无线充电过程中随着负载变化的系统充电效率曲线，恒流充电时，系统的充电效率由开始的66%左右上升至81%左右；恒压充电时，系统的充电效率由开始的81%左右下降至63%左右完成充电，无线充电系统在工作区间内可以完成蓄电池正常充电。
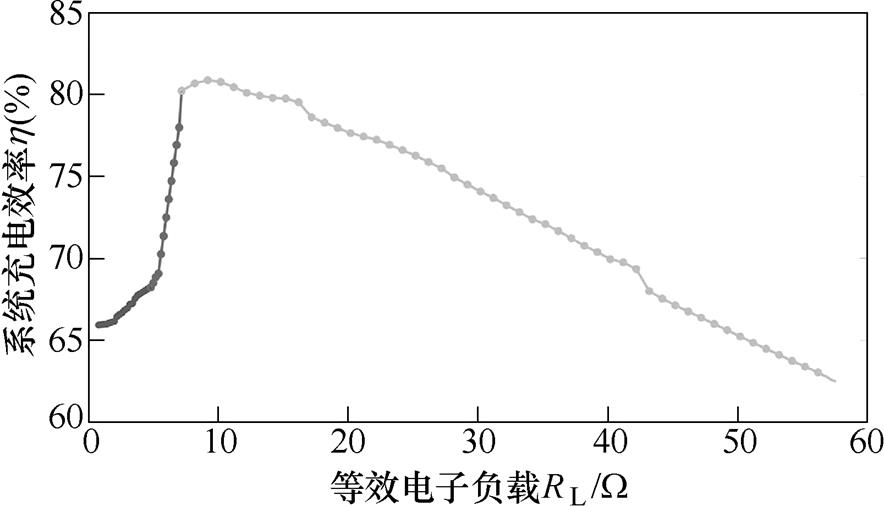
图18 系统充电效率随等效电子负载变化曲线
Fig.18 Variation curves of system charging efficiency with equivalent electronic load
针对传统变静态补偿设计方法中无源元件和开关数量过多、参数选择困难等问题，提出一种基于LCL-LCL/S混合自切换谐振式无线充电系统。结合典型蓄电池恒流/恒压充电曲线特征、谐振电流阈值、电压跳变阈值和耦合系数变化约束，又给出一种适用于混合式谐振拓扑网络参数的优化设计方法，为参数的选取提供了可行性分析，能够在中小功率且位置相对固定的场所下进行高效的无线充电。由实验结果可知，应用优化参数后的混合谐振拓扑网络，能够在很小的电压和电流波动范围内实现稳定恒流恒压切换输出。系统最大传输效率为81%且无需增加无源元件来实现CC-CV模式的切换。所提方案在无需原、副边之间通信的同时实现零无源切换，简化了控制系统，提高了系统传输效率，具有较好的工程应用价值。
参考文献
[1] 薛明, 杨庆新, 章鹏程，等. 无线电能传输技术应用研究现状与关键问题[J]. 电工技术学报, 2021, 36(8): 1547-1568.
Xue Ming, Yang Qingxin, Zhang Pengcheng, et al. Application status and key issues of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.
[2] 贾金亮, 闫晓强. 磁耦合谐振式无线电能传输特性研究动态[J]. 电工技术学报, 2020, 35(20): 4217- 4231.
Jia Jinliang, Yan Xiaoqiang. Research tends of magnetic coupling resonant wireless power transfer characteristics[J]. Transactions of China Electro- technical Society, 2020, 35(20): 4217-4231.
[3] 沈栋, 杜贵平, 丘东元, 等. 无线电能传输系统电磁兼容研究现况及发展趋势[J]. 电工技术学报, 2020, 35(13): 2855-2869.
Shen Dong, Du Guiping, Qiu Dongyuan, et al. Research status and development trend of electro- magnetic compatibility of wireless power trans- mission system[J]. Transactions of China Electro- technical Society, 2020, 35(13): 2855-2869.
[4] Wang Junhua, Hu Meilin, Cai Changsong. Optimi- zation design of wireless charging system for autonomous robots based on magnetic resonance coupling[J]. AIP Advances, 2018, 8(5): 2158-3226.
[5] 谭平安, 廖佳威, 谭廷玉, 等. 基于发射侧T/F变结构补偿网络的恒压/恒流无线充电系统[J]. 电工技术学报, 2021, 36(2): 248-257.
Tan Ping’an, Liao Jiawei, Tan Tingyu, et al. Constant voltage/constant current wireless charging system based on T/F variable structure compensation network of transmitter-side[J]. Transactions of China Electro- technical Society, 2021, 36(2): 248-257.
[6] 麦瑞坤, 陈阳, 张友源, 等. 基于变次级补偿参数的感应式无线充电系统研究[J]. 中国电机工程学报, 2017, 37(11): 3263-3269.
Mai Ruikun, Chen Yang, Zhang Youyuan, et al. Study on secondary compensation capacitor alteration based IPT charging system[J]. Proceedings of the CSEE, 2017, 37(11): 3263-3269.
[7] Li Hongchang, Li Jie, Wang Kangping, et al. A maximum efficiency point tracking control scheme for wireless power transfer systems using magnetic resonant coupling[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3998-4008.
[8] 孙跃, 陈宇, 唐春森, 等. 感应电能传输系统输出电压调压电路研究[J]. 电工技术学报, 2015, 30(增刊1): 226-230.
Sun Yue, Chen Yu, Tang Chunsen, et al. A voltage regulating circuit for secondary of inductive power transfer systems[J]. Transactions of China Electro- technical Society, 2015, 30(S1): 226-230.
[9] 蒋勇斌, 王跃, 刘军文, 等. 基于跳频控制策略的串联-串联谐振无线电能传输系统的参数优化设计方法[J]. 电工技术学报, 2017, 32(16): 163-174.
Jiang Yongbin, Wang Yue, Liu Junwen, et al. The optimal design methodology of series-series resonant tank parameters of wireless power transmission system based on leap frequency control strategy[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 163-174.
[10] Ahn D, Hong S. A study on magnetic field repeater in wireless power transfer[J]. IEEE Transactionson Industrial Electronics, 2013, 60(1): 360-371.
[11] 浦润琴, 唐忠, 王晓毅. 恒压恒流型无线充电系统负载识别特性研究[J]. 电气传动, 2020, 50(9): 122- 128.
Pu Runqin, Tang Zhong, Wang Xiaoyi. Research on load identification characteristics of constant voltage constant current wireless charging system[J]. Electric Drive, 2020, 50(9): 122-128.
[12] 麦瑞坤, 张友源, 陈阳, 等. 可配置充电电流的变结构无线充电系统研究[J]. 中国电机工程学报, 2018, 38(11): 3335-3343.
Mai Ruikun, Zhang Youyuan, Chen Yang, et al. Study on IPT charging systems with hybrid topology for configurable charge currents[J]. Proceedings of the CSEE, 2018, 38(11): 3335-3343.
[13] Chen Yafei, Zhang Hailong, Park S J, et al. A switching hybrid LCC-S compensation topology for constant current/voltage EV wireless charging[J]. IEEE Access, 2019, 7: 133924-133935.
[14] Chen Yang, Kou Zhihao, Zhang Youyuan, et al. Hybrid topology with configurable charge current and charge voltage output-based WPT charger for massive electric bicycles[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(3): 1581-1593.
[15] Mai Ruikun, Chen Yang, Li Yong, et al. Inductive powertransfer for massive electric bicycles charging based on hybrid topology switching with a single inverter[J]. IEEE Transactions on Power Electronics, 2017, 32(8): 5897-5906.
[16] 麦瑞坤, 陈阳, 刘野然. 基于变补偿参数的IPT恒流恒压电池充电研究[J]. 中国电机工程学报, 2016, 36(21): 5816-5821.
Mai Ruikun, Chen Yang, Liu Yeran. Compensation capacitor alteration based IPT battery charging application with constant current and constant voltage control[J]. Proceedings of the CSEE, 2016, 36(21): 5816-5821.
[17] 吴丽君, 李冠西, 张朱浩伯. 一种具有恒流恒压输出自切换特性的电动汽车无线电能传输系统拓扑[J]. 电工技术学报, 2020, 35(18): 3781-3790.
Wu Lijun, Li Guanxi, Zhang Zhuhaobo. A wireless power transfer system topology with automatic switching characteristics of constant current and con- stant voltage output for electric vehicle charging[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3781-3790.
[18] 薄强, 王丽芳, 张玉旺, 等. 应用于无线充电系统的SiC MOSFET关断特性分析[J]. 电力系统自动化, 2021, 45(15): 150-157.
Bo Qiang, Wang Lifang, Zhang Yuwang, et al. Analysis of turn off characteristics of SiC MOSFET applied to wireless charging system[J]. Transactions of Power System Automation, 2021, 45(15): 150-157.
[19] 陈飞彬, 麦瑞坤, 李勇. 基于调频控制的三线圈结构无线电能传输系统效率优化研究[J]. 电工技术学报, 2018, 33(增刊2): 313-320.
Chen Feibin, Mai Ruikun, Li Yong. Efficiency optimization of three-coil structure wireless power transfer system based on frequency-varied control[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 313-320.
[20] Liu Suqi, Tan Jianping. Using uniform magnetic field to obtain the constant output power and transfer efficiency for MCR-WPT[J]. Circuit World, 2019, 46(1): 42-47.
[21] Chen Yafei, Zhang Hailong, Park Sung-Jun. A comparative study of S-S and LCCL-S compensation topologies in inductive power transfer systems for electric vehicles[J]. Energies, 2019, 12(10): 1913- 1931.
[22] Zhao Jingying, Zhang Zhenyuan, Xing Yongqi. Design and implementation of double-sided LCL variable compensation topology of MCR-WPT system[J]. IEEJ Transactions on Electrical and Elec- tronic Engineering, 2020, 12(15): 1853-1862.
Hybrid Self-Switching Resonant Wireless Charging System Based on LCL-LCL/S
Abstract This paper aims to reduce the number of switching devices and passive components in a hybrid topology charging system, improve the output power of the system, and simplify the control strategy of the primary and secondary sides. A hybrid self-switching resonant wireless charging system based on LCL-LCL/S is proposed, which does not need primary and secondary side communication or any passive components. The constant current and constant voltage switching of the wireless charging system is realized only by changing the network topology through the automatic switching operation of the LCL structure. Firstly, a relationship between constant current or constant voltage output and input impedance was analyzed by a T-type network. Then, a mathematical model of the hybrid compensation network was introduced to analyze the parameter configuration conditions for realizing the zero-phase angle (ZPA) between the input current and voltage of the system and the constant current or constant voltage output characteristics. Next, according to the characteristics of the battery charging curve, resonant current threshold, voltage jump threshold, and coupling coefficient change constraints, a design method suitable for hybrid resonant topology network parameter optimization was proposed. This solution not only avoids the problem of parameter uncertainty caused by the limitation of empirical selection of resonant network parameters, but also provides a theoretical basis for parameter selection. Finally, an experimental platform was built to verify the feasibility and effectiveness of the solution. The experimental results show that the wireless charging system with optimized resonant network parameters possesses good constant current and constant voltage output characteristics. The maximum transmission efficiency of the system is 81%, which fully meets the requirements of constant current and constant voltage wireless charging.
keywords：Magnetically-coupled resonant wireless power transfer (MCR-WPT), LCL-LCL/S topology, parameter optimization design, constant current and constant voltage charging
DOI: 10.19595/j.cnki.1000-6753.tces.210591
中图分类号：TM724
郭 星 男，1996年生，硕士研究生，研究方向为无线电能传输。E-mail: guoxingxg@163.com
刘利强 男，1975年生，教授，硕士生导师，研究方向为电路理论及其应用。E-mail: llqiang@imut.edu.cn（通信作者）
收稿日期 2021-04-27
改稿日期 2021-08-04
国家自然科学基金（61763037, 61863029）和内蒙古自治区自然科学基金（2019LH6007, 2020MS05029）资助项目。
（编辑 陈 诚）