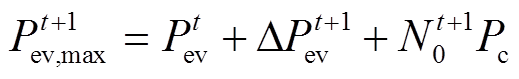 (1)
(1)摘要 针对电动汽车(EV)和风电、光伏等新能源发电大规模入网造成的功率波动、调度成本过高以及运行稳定性差等问题,该文提出一种基于电动汽车参与调峰定价策略的区域电网两阶段优化调度方案。首先,根据EV负荷运行特性进行分类,分别建立刚性、可调度、灵活型和智能换电四种EV负荷模型;其次,考虑EV参与调峰的各项成本,基于模糊层次分析法(FAHP),给出EV调峰定价策略;然后基于该策略对区域电网进行两阶段优化调度。在第一阶段以负荷峰谷差最小为目标,并在此目标下对EV调峰定价进行决策,以降低电力系统调峰容量调整区域电网负荷分布;在第二阶段依托第一阶段得到的调峰定价曲线,以EV用户充电费用最小为目标安排EV负荷。最后利用算例仿真验证了EV参与调峰的有效性、合理性以及该定价策略的经济性。
关键词:电动汽车 调峰定价策略 区域电网 模糊层次分析法 两阶段优化
随着“双碳目标”的提出及新能源大规模并网,电力系统发展面临巨大的挑战。目前我国多地供电形势紧张,电力系统等效负荷峰谷差在逐步增大,调峰压力也越来越大[1], 需在用电高峰期实行错峰用电。电动汽车(Electric Vehicles, EV)作为一种新型负荷,具有可调度性和灵活性,既能将EV负荷转移到系统低谷时期,实现削峰填谷,又能通过EV馈电增强系统调峰能力[2]。通过合理的激励引导EV充放电参与电力系统调峰具有重要意义,但是目前还没有成熟的EV参与调峰定价策略,相应的区域电网优化调度策略也有待进一步研究。
EV参与调峰主要与其可转移负荷特性相关联。文献[3]通过区域电网内EV与可控负荷的协调优化参与调度,并对参与调峰的系统进行两阶段优化;文献[4]研究了EV充放电与风电、火电机组的联合协调优化策略,但是未考虑EV参与调峰运行特性;文献[5]针对EV可调特性,对大规模风电接入的系统机组组合相关调度问题进行研究,但是未将其可转移特性运用到调峰优化。随着分布式电源的广泛应用,其接入电网时的功率波动及预测误差将成为研究热点。文献[6]通过引导EV充放电,调节由于风电、光伏接入而产生的系统功率波动,从而参与系统调峰,但是预测误差对系统功率波动的影响被理想化;文献[7]研究了EV的种类和运行特性,考虑到负荷需求响应与需求差异得到了基于长短期记忆网络的区域电网调度计划,但是未研究风机及常规负荷预测误差对EV运行的影响;文献[8]对可充放电的EV进行容量调度,研究了风电接入下灵活性EV参与系统优化的特性,但是未研究EV如何参与系统调峰和风电预测误差对系统功率的影响。以上研究均考虑了EV特性和参与调峰的可行性,忽略了分布式电源预测误差对机组、负荷功率平衡的影响,但并未深入研究EV参与调峰的灵活性价值。
近年来关于智能换电EV的研究也逐步发展起来。文献[9]引入换电站与换电EV,对电动公交车的行驶特性进行分析得到换电需求,对换电EV参与电网运行进行优化调度;文献[10]提出了EV惩罚机制,对换电EV及含风电微电网结合的联合系统进行优化调度;文献[11]考虑需求响应负荷曲线,将换电EV作为辅助负荷,计及车辆转移机制对微电网进行联合优化调度。上述智能换电EV的研究将为电动汽车参与系统调峰运行带来积极作用。
作为新型调峰辅助服务品种,EV负荷暂时还没有合理的充放电电价机制,参与调峰的主动性和积极性也受到限制。为了提高EV参与调峰的积极性,本文提出了一种基于EV参与调峰定价策略的区域电网两阶段优化调度方案。首先对EV负荷模型进行分类,考虑了可调度EV负荷、灵活性EV负荷和智能换电EV负荷。其次利用模糊层次分析法(Fuzzy Analytic Hierarchy Process, FAHP)给出基于成本的调峰定价模型。然后基于定价策略对区域电网进行两阶段优化调度:在第一阶段,考虑负荷峰谷差最小,得到各个EV负荷出力并在此目标下给出定价策略;在第二阶段,基于BP神经网络模拟训练,考虑风、光及负荷预测误差,以EV充电费用最小为目标,得到EV参与调峰的日内调度功率。最后通过算例对比本文所提定价策略与电力市场分时电价对EV充电费用的影响,验证了EV参与调峰的有效性与合理性以及该定价策略的经济性。
刚性EV负荷主要特性是充放电无序,无法对其进行调节[7]。不接受调度的电动私家车满足刚性EV运行特性,将其归为此类。刚性EV与常规负荷接入电网特性相似,为了便于研究,本文将刚性EV负荷视为常规负荷。
可调度EV负荷在并网过程中接受EV聚合商的调度,但是不能向电网馈电,充电过程会造成一定的EV电池损耗,一般在用电低谷期进行调度,且聚合商会额外收取充电桩的相关运营服务费用[12]。
根据可调度EV的相关数据对可调度容量上、下限进行预测,根据t时刻可调度EV的实际负荷量预测出可调度EV在下一时刻(t+1时刻)的负荷最大值和最小值[7]。
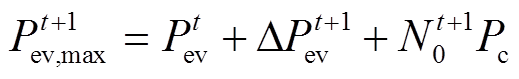 (1)
(1)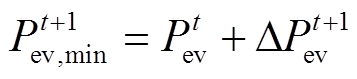 (2)
(2)
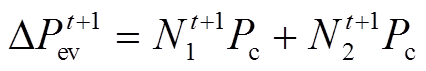 (3)
(3)
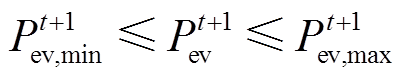 (4)
(4)式中,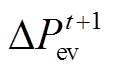 为在t+1时刻必须增加的可调度EV负荷;
为在t+1时刻必须增加的可调度EV负荷;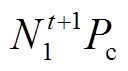 为t+1时刻增加的负荷;
为t+1时刻增加的负荷;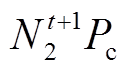 为t+1时刻减少的负荷;
为t+1时刻减少的负荷;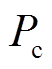 为可调度EV的充电功率;
为可调度EV的充电功率;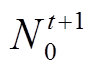 为满足条件
为满足条件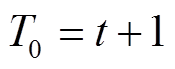 和
和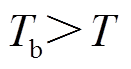 的可调度EV数量,
的可调度EV数量,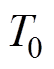 是EV停驶在充电桩的时间,
是EV停驶在充电桩的时间,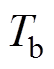 是EV入网时间,T为时间周期;
是EV入网时间,T为时间周期;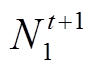 为满足条件
为满足条件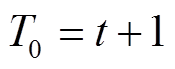 和
和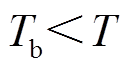 的可调度EV数量;
的可调度EV数量;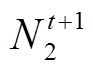 为满足条件
为满足条件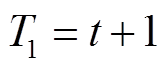 或
或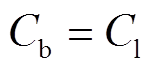 的可调度EV数量,
的可调度EV数量,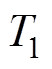 是EV离开充电桩时间,
是EV离开充电桩时间,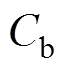 表示EV停驶荷电状态,
表示EV停驶荷电状态, 表示EV离网时用户期望荷电状态;
表示EV离网时用户期望荷电状态;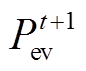 为EV在下一时刻的实际负荷量。
为EV在下一时刻的实际负荷量。
对于t+2时刻的EV负荷容量可以根据t时刻预测出的t+1时刻的最大负荷值和最小负荷值进行预测。将处于最大负荷和最小负荷时的所有EV做式(1)~式(4)相同的计算,可得到EV处于最大负荷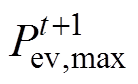 状态下,下一时刻的最大负荷
状态下,下一时刻的最大负荷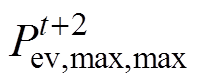 和最小负荷
和最小负荷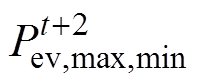 ;同理可得到EV处于最小负荷
;同理可得到EV处于最小负荷 状态下,下一时刻的最大负荷
状态下,下一时刻的最大负荷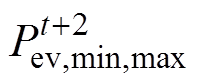 和最小负荷
和最小负荷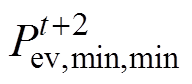 。下一时刻t+2可调度EV的最大负荷
。下一时刻t+2可调度EV的最大负荷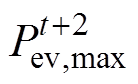 和最小负荷
和最小负荷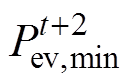 分别是
分别是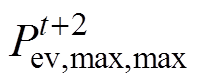 、
、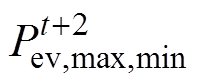 、
、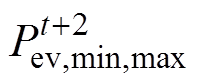 、
、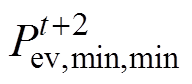 中的最大值和最小值。之后所有时刻的EV负荷容量都可以根据公式进行类推,可调度EV容量预测如图1所示。
中的最大值和最小值。之后所有时刻的EV负荷容量都可以根据公式进行类推,可调度EV容量预测如图1所示。
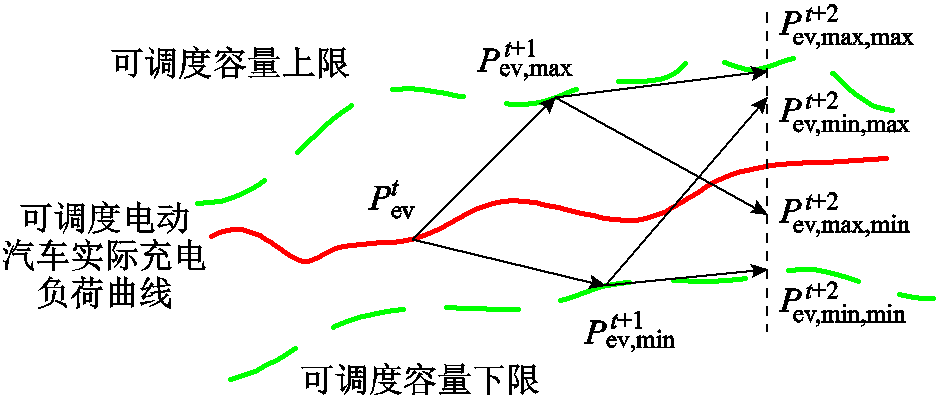
图1 可调度EV容量预测示意图
Fig.1 Schematic diagram of schedulable EV capacity prediction
灵活性EV负荷可以根据用电需求进行负荷转移,在高峰期减少区域电网负荷,同时可以作为电源向系统馈电,相对于可调度EV负荷,它的电池损耗更大。灵活性EV负荷要求运营商提供的充电桩要有向电网放电的能力,并且享受政府的补贴。
灵活性EV参与调度的时间节点图如图2所示。图中,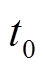 为EV在停止工作最后一次并网的时间,此时它的荷电状态为
为EV在停止工作最后一次并网的时间,此时它的荷电状态为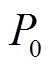 ;
;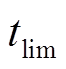 为灵活性EV可参与馈电调度的最大时间点;
为灵活性EV可参与馈电调度的最大时间点;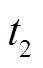 为用户期望离网的时间;
为用户期望离网的时间;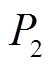 为在离网时用户期望的荷电状态值。
为在离网时用户期望的荷电状态值。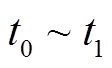 为EV的调度阶段,
为EV的调度阶段,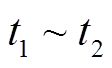 为未调度阶段,
为未调度阶段,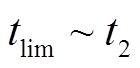 为EV放电结束之后的充电阶段,此时段电量需达到用户的荷电状态期望值。
为EV放电结束之后的充电阶段,此时段电量需达到用户的荷电状态期望值。
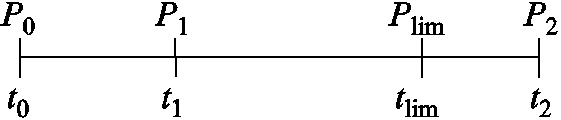
图2 灵活性EV充放电时间节点图
Fig.2 Node diagram of flexible EV charging and discharging time
由以上可得灵活性EV负荷的充放电表达式为
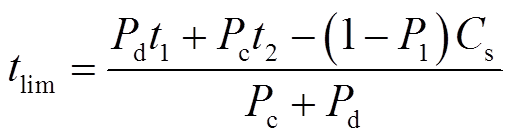 (5)
(5)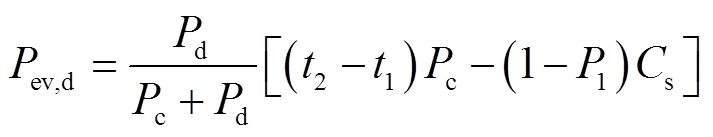 (6)
(6)
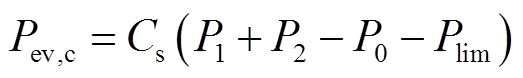 (7)
(7)
式中,Pc为灵活性EV充电功率;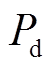 为灵活性EV的放电功率; Cs为电池容量;Pev,d为EV的放电容量;Pev,c为EV充电容量。
为灵活性EV的放电功率; Cs为电池容量;Pev,d为EV的放电容量;Pev,c为EV充电容量。
智能换电EV依托换电站对电池进行充电、为EV供给满状态电池、替换电量较低电池等。在满足用户对智能换电EV电量需求的情况下,换电站尽量在用电低谷期对电池充电。
在任意时刻t,根据换电站中电池荷电状态与充放电性质,可将电池状态分为四类[13]:①满负荷电状态(M状态);②正在充电状态(C状态);③正在放电状态(D状态);④等待充电状态(W状态)。电池状态转换示意图如图3所示,EV在换电站进行换电的过程可以描述成这四种状态的互相转换。
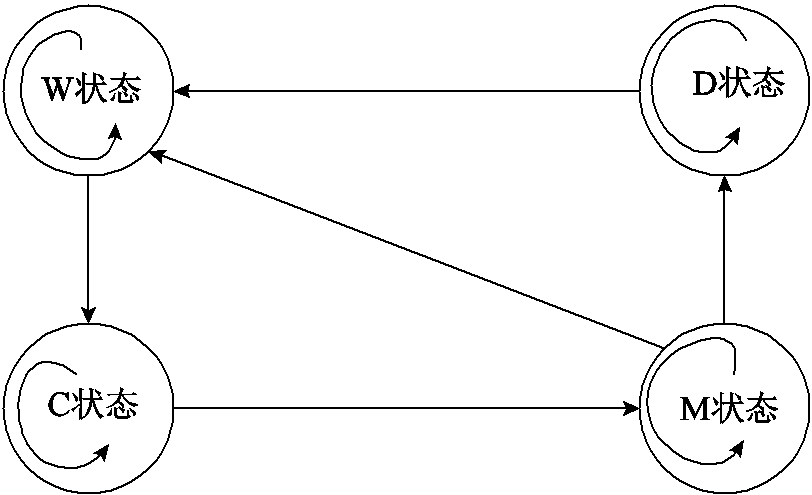
图3 电池状态转换示意图
Fig.3 Schematic diagram of battery state transition
四种状态的电池数量在初始时刻t分别为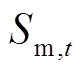 ,
,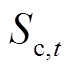 、
、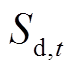 、
、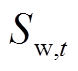 。t+1时刻处于M状态的电池数量
。t+1时刻处于M状态的电池数量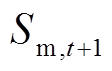 取决于在t时刻由M状态转移到W状态(M→W)、D状态(M→D)、M状态(M→M)和C状态转移到M状态(C→M)的电池数量。其他状态电池数量同理。
取决于在t时刻由M状态转移到W状态(M→W)、D状态(M→D)、M状态(M→M)和C状态转移到M状态(C→M)的电池数量。其他状态电池数量同理。
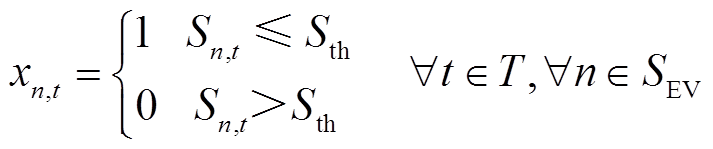 (8)
(8)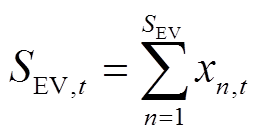 (9)
(9)
 (10)
(10)
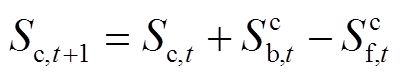 (11)
(11)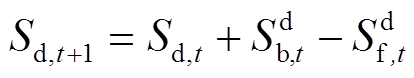 (12)
(12)
式中,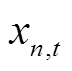 为换电需求,
为换电需求,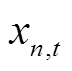 =0时表示不需要换电,
=0时表示不需要换电,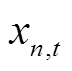 =1时表示需要换电;
=1时表示需要换电;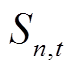 为EV在t时刻的荷电状态;
为EV在t时刻的荷电状态;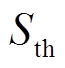 为EV的荷电状态阈值;
为EV的荷电状态阈值;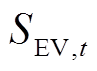 为t时刻EV换电需求量;
为t时刻EV换电需求量;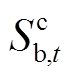 、
、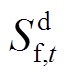 分别为t时刻开始充电和结束放电的电池数量;
分别为t时刻开始充电和结束放电的电池数量;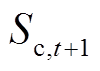 、
、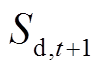 分别为t+1时刻处于C状态和D状态的电池数量。
分别为t+1时刻处于C状态和D状态的电池数量。
电池的充放电可视为连续过程,因此当假设电池充电所需要的时间为Tc,放电时间为Td时,t时刻由W状态转移到C状态的电池数量等于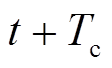 时刻由C状态转移到M状态的电池数量。同理可得到放电过程为
时刻由C状态转移到M状态的电池数量。同理可得到放电过程为
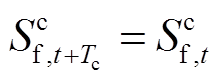 (13)
(13)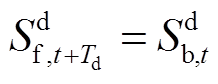 (14)
(14)
为简化过程,本文假设EV换电电池有效充放电区间SOC为[0.25, 0.95],并将SOC=0.25状态定义为空电池,SOC=0.95状态定义为满电池;空电池充满、满电池放空和充满EV置换的电池均需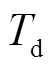 时间段;假设所有EV换电卸下的旧电池剩余SOC 均相同,则换电站的功率为
时间段;假设所有EV换电卸下的旧电池剩余SOC 均相同,则换电站的功率为
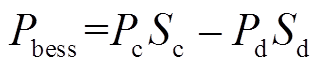 (15)
(15)式中,Pc、Pd分别为充电机的充、放电额定功率。
FAHP是一种将决策问题按照总目标以及评判准则进行求解权重系数的方法,此方法适用于不同的评估对象,但对于不同的决策因素以及目标函数,权重系数会发生改变[14]。该方法为本文量化需求关系、政府激励及竞争关系三种评价指标,以及选择最优权重系数提供了依据,增加了定价的准确性。
运行FAHP决策时大致可分为三个步骤:
(1)确定系统中各决策元素之间的因果关系,对同一层次的元素进行两两比较,根据目标函数及方案采用0.1~0.9标度法得到模糊判断矩阵。
(2)根据模糊判断矩阵求解得到各决策元素的权重。
(3)求解得到权重之后,利用相容性指标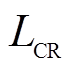 对模糊判断矩阵进行一致性检验。对于一致性检验结果,若LCR<0.1,认为模糊判断矩阵的一致性可以接受;若LCR>0.1,需重新构建模糊判断矩阵[15]。
对模糊判断矩阵进行一致性检验。对于一致性检验结果,若LCR<0.1,认为模糊判断矩阵的一致性可以接受;若LCR>0.1,需重新构建模糊判断矩阵[15]。
本文EV调峰定价策略选择的三个决策因素分别为需求关系、政府激励措施以及EV负荷和火电机组的竞争关系。基于FAHP可以确定三种决策元素在定价模型中的权重。在2.2节中将计及定价过程中的各项成本,代入本节得到的权重系数,最终得到EV的调峰定价模型。
2.2.1 EV参与调峰成本模型
定价之前需要明确区域电网的各项运营成本。EV投入运营主要与EV聚合商相关联,除了区域电网内部的火电机组成本外,EV聚合商还承担着向区域电网购电、充电桩与换电站的运行维护等相关责任。
1)火电机组燃料成本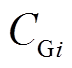
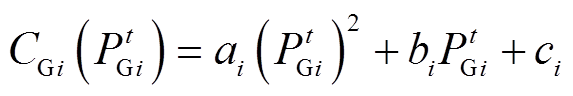 (16)
(16)式中,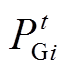 为机组i在t时刻的发电功率;
为机组i在t时刻的发电功率;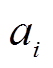 、
、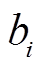 、
、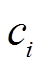 为机组i的燃料成本系数。
为机组i的燃料成本系数。
2)购电成本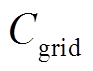
当区域电力系统内部能源不足时,会从外部电网购电,购电单价为电网分时电价。
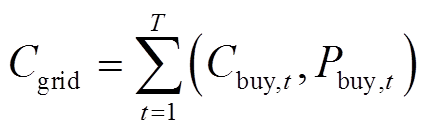 (17)
(17)式中,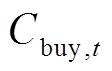 为分时购电单价;
为分时购电单价;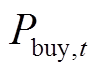 为区域电力系统在t时刻的购电功率。
为区域电力系统在t时刻的购电功率。
3)锂电池运行与维护成本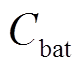
针对智能换电EV负荷,EV聚合商需要在换电站中准备足够的锂电池供电池更换。
锂电池运行寿命为
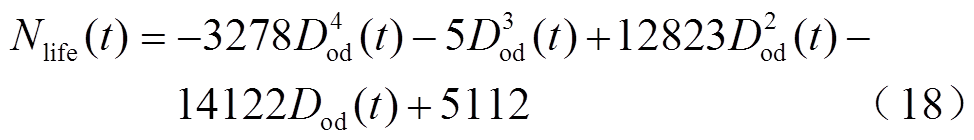
式中, Dod(t)为锂电池在t时刻的放电深度;Nlife (t)为锂电池在t时刻放电深度为Dod(t)下的循环寿命。
运行和维护成本为
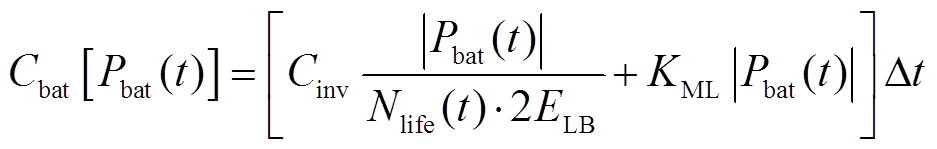 (19)
(19)式中,Cinv为锂电池初始投资;Pbat(t)为锂电池充放电功率;ELB为锂电池额定容量;KML为锂电池的维护成本系数。
4)场地建设成本Cs
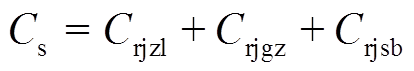 (20)
(20)式中,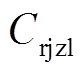 为日均场地租赁费用;
为日均场地租赁费用;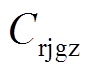 为聚合商日均服务费用;
为聚合商日均服务费用;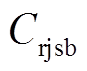 为日均设备成本。
为日均设备成本。
综上所述,在调峰阶段的运行成本为
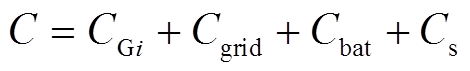 (21)
(21)2.2.2 EV参与调峰定价模型
在定价过程中,影响EV价格的因素很多,本文选取了较为典型的三个决策因素——政府激励措施、需求关系和EV负荷与火电机组竞争关系。
1)政府激励措施的影响——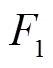
风电、光伏、火电机组等新能源参与调峰会减少环境污染,政府会给予一定的价格补偿[16]。火电机组的调峰成本由其边际成本决定,在EV参与调峰的区域电网内具有重要作用。根据火电机组调峰补偿,列写阶梯式价格补偿表达式为
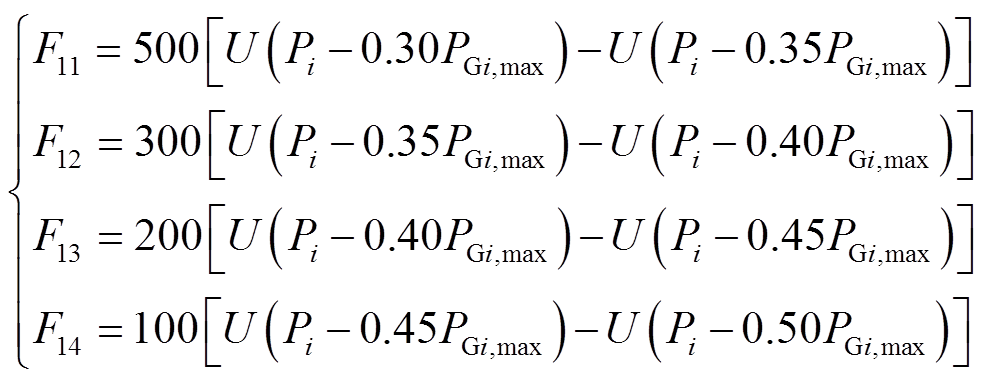 (22)
(22)式中,U为单位阶跃函数,当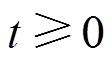 时,U=1,当
时,U=1,当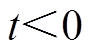 时,U=0;
时,U=0;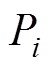 为火电机组i发电功率;
为火电机组i发电功率;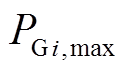 为火电机组i的最大容量。
为火电机组i的最大容量。
写成统一形式为
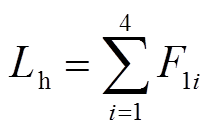 (23)
(23)式中,Lh为EV参与调峰的补偿价格。
2)需求关系的影响——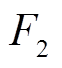
在电力市场机制下,供需与价格呈现负相关特性[17]。即当价格升高时,用户对负荷的需求量降低,反之亦然。用线性函数表征这一关系为
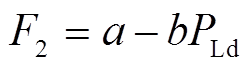 (24)
(24)式中,PLd为EV等效负荷量;a、b为电力市场逆需求函数参数,本文分别取值为a=12和b=0.06[18]。
3)EV负荷与火电机组竞争的影响——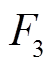
在调峰市场中,EV参与调峰的成本低于火电机组灵活性改造成本[19],因此EV负荷进行转移调峰与火电机组出力调峰之间存在不完全竞争关系,即当EV参与调峰发生负荷转移时,火电机组出力的竞争力就会小,呈现出“反竞争”的关系,可用函数关系式表达为
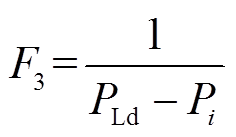 (25)
(25)将三个影响因素转换为权重系数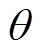 ,且需满足
,且需满足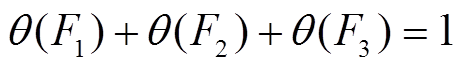 。基于FAHP决定这三种决策因子的权重系数,根据调峰定价目标利润率15%[20],可得到成本与定价的系数。模拟成本到实际价格的计算公式为
。基于FAHP决定这三种决策因子的权重系数,根据调峰定价目标利润率15%[20],可得到成本与定价的系数。模拟成本到实际价格的计算公式为
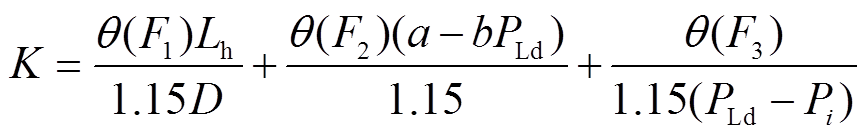 (26)
(26)
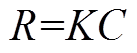 (27)
(27)式中,D为货币之间的换算系数,本文D=6.48;R为调峰的单位容量定价。
本节对EV参与调峰的区域电网进行两阶段优化,区域电网调度结构如图4所示。
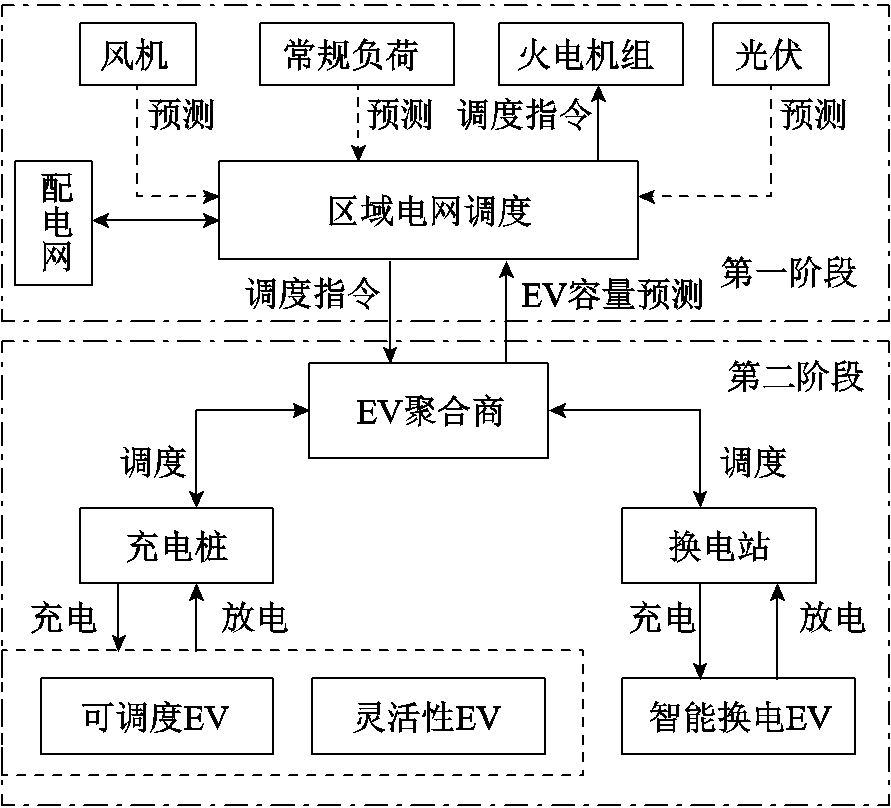
图4 区域电网调度模型
Fig.4 Regional power grid dispatching model
在第一阶段,区域电网调度中心可通过风机、光伏和常规负荷的预测值,以负荷峰谷差最小为目标,向火电机组发出调度指令,同时根据FAHP方法,考虑需求关系、政府激励及竞争关系对EV进行定价;在第二阶段,考虑新能源出力预测误差和常规负荷预测误差,根据第一阶段定价策略,以EV充电费用最小为目标,EV聚合商可根据充电桩和换电站采集EV的充放电需求,响应区域电网调度。
第一阶段,在已知风机功率、光伏功率、常规负荷和EV负荷日前预测数据的情况下,可建立混合整数规划模型。
3.1.1 目标函数
第一阶段将一天分为24个时间段,以1h为时间尺度,目标为负荷峰谷差最小,函数表达式为
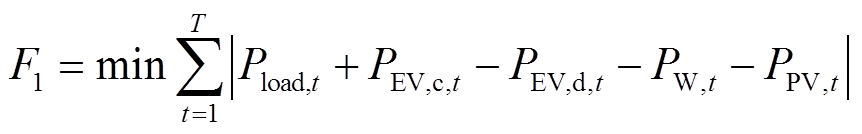 (28)
(28)式中,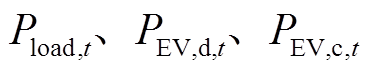 分别为t时刻常规负荷量、EV向电网放电功率和负荷功率(充电功率);
分别为t时刻常规负荷量、EV向电网放电功率和负荷功率(充电功率);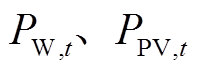 分别为t时刻的风机和光伏发电功率。
分别为t时刻的风机和光伏发电功率。
结合第1节中EV负荷模型,在该目标函数下可确定第一阶段参与调峰的EV负荷量;根据第2节关于定价策略与模型的分析,结合权重系数与相关参数,代入到式(26)可得到定价系数K;再计及成本代入式(27)得到定价R。
3.1.2 约束条件
1)区域电网功率平衡约束
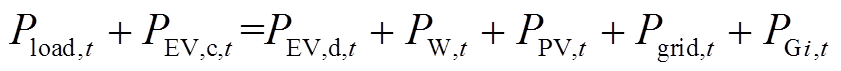 (29)
(29)式中,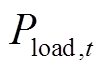 为常规负荷的负荷电量;
为常规负荷的负荷电量;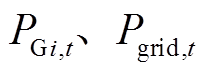 分别为t时刻火电机组及外部电网发电功率。
分别为t时刻火电机组及外部电网发电功率。
2)EV约束条件
(1)可调度EV约束条件
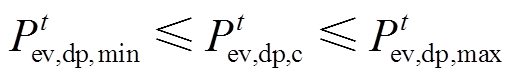 (30)
(30)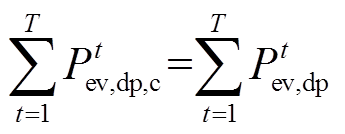 (31)
(31)
式中,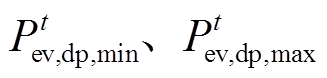 分别为可调度EV充电容量下、上限;
分别为可调度EV充电容量下、上限;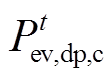 为可调度EV充电容量;
为可调度EV充电容量;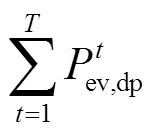 为可调度EV总负荷量。
为可调度EV总负荷量。
(2)灵活性EV约束条件
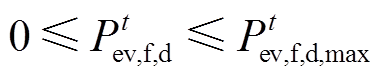 (32)
(32)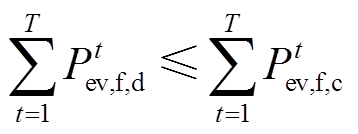 (33)
(33)
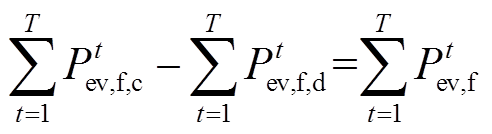 (34)
(34)
式中,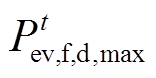 为t时刻灵活型EV的放电容量上限;
为t时刻灵活型EV的放电容量上限;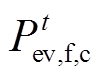 为t时刻灵活型EV的充电容量;
为t时刻灵活型EV的充电容量;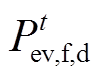 为t时刻灵活型EV放电容量;
为t时刻灵活型EV放电容量;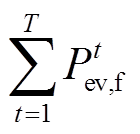 为灵活性EV总负荷量。
为灵活性EV总负荷量。
(3)智能换电EV约束条件
智能换电EV可通过换电站的充、放电机实现与区域电网的能量交互[13],其约束条件表示为
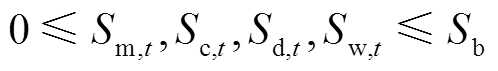 (35)
(35)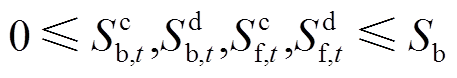 (36)
(36)
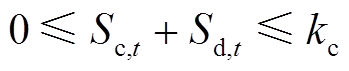 (37)
(37)
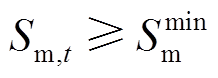 (38)
(38)式中,kc为充电机个数;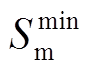 为满电量电池数量最小值。
为满电量电池数量最小值。
3)火电机组爬坡约束
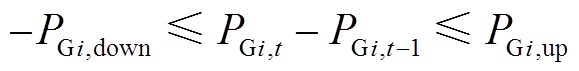 (39)
(39)式中,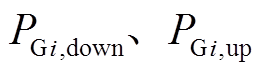 分别为火电机组最大向下和最大向上爬坡速率。
分别为火电机组最大向下和最大向上爬坡速率。
在第二阶段考虑分布式电源、负荷的预测误差,研究日内模拟调度和日内优化调度。
3.2.1 日内模拟/优化目标函数
日内阶段以EV充电费用最小为目标。根据日前EV定价以及EV可调度容量,建立目标函数为
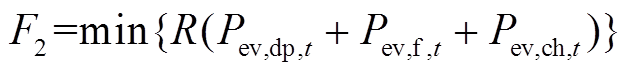 (40)
(40)式中,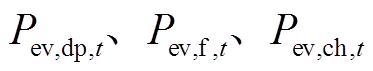 分别为参与调峰的可调度EV、灵活型EV和智能换电EV的负荷量。
分别为参与调峰的可调度EV、灵活型EV和智能换电EV的负荷量。
3.2.2 日内模拟调度
日内模拟调度阶段将一天分为96个时段,时间尺度为15min。在该阶段对风机、光伏、常规负荷的功率值增加扰动,模拟日内的实际数据,以第二阶段目标函数进行优化,得到模拟调度数据,代入BP神经网络中进行模拟训练,求解得到日内调度模型[21]。本文将日前预测阶段的风机功率、光伏功率、常规负荷功率作为输入数据,对第二阶段的目标函数进行求解,得到在此条件下各个单元调度的最优情况,并将可调度EV负荷量、智能换电EV负荷量、灵活性EV负荷充放电负荷量和火电机组功率作为输出样本。
考虑日内阶段风机、光伏等新能源发电功率,常规负荷日前预测的误差,在光伏和风机输出功率预测过程中,光伏和风机的输出功率在未达到装机容量时,输出功率的预测误差符合正态分布,即
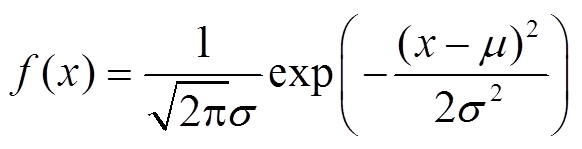 (41)
(41)随机变量x符合正态分布,记做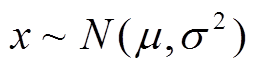 。
。
在训练神经网络模型过程中,新能源输出功率和常规负荷叠加正态分布,作为日前阶段预测误差模拟值[22]。
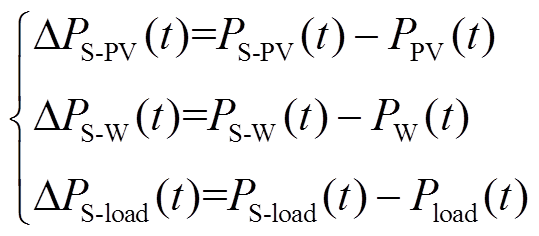 (42)
(42)式中,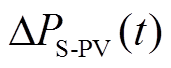 为t时刻预调度阶段模拟光伏功率与日前预测光伏功率差值;
为t时刻预调度阶段模拟光伏功率与日前预测光伏功率差值;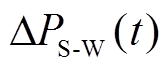 为t时刻预调度阶段模拟风机功率与日前预测风机功率差值;
为t时刻预调度阶段模拟风机功率与日前预测风机功率差值;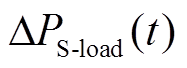 为t时刻预调度阶段模拟常规负荷功率与日前预测常规负荷功率差值。
为t时刻预调度阶段模拟常规负荷功率与日前预测常规负荷功率差值。
3.2.3 日内优化调度
将日内风机、光伏、常规负荷短期预测数据输入到日内调度模型中,得到日内调度数据,即可完成可调度EV、灵活EV、智能换电EV及火电机组的日内优化调度。同时,第一阶段已经得到EV负荷参与调峰的定价曲线,第二阶段可基于EV负荷模型,利用优化目标得到EV参与调峰负荷曲线,验证该调峰定价策略的经济性。
4.1.1 基本参数
本文采用改进的区域电网系统进行算例分析,该系统包含5台火电机组,基本参数见表1。16个80MW容量的风电场,1个50MW容量的光伏电站;电动汽车聚合商向大电网购电电价参考文献[11],即谷时段电价0.35元/(kW∙h) (0:00~7:00)、平时段电价0.68元/(kW∙h) (7:00~11:00, 16:00~19:00, 22:00~ 24:00)和峰时段电价1.18元/(kW∙h) (11:00~16:00, 19:00~22:00);智能换电站基本参数见表2,含有的锂电池参数见文献[22]。
表1 火电机组基本参数
Tab.1 Basic parameters of thermal power unit
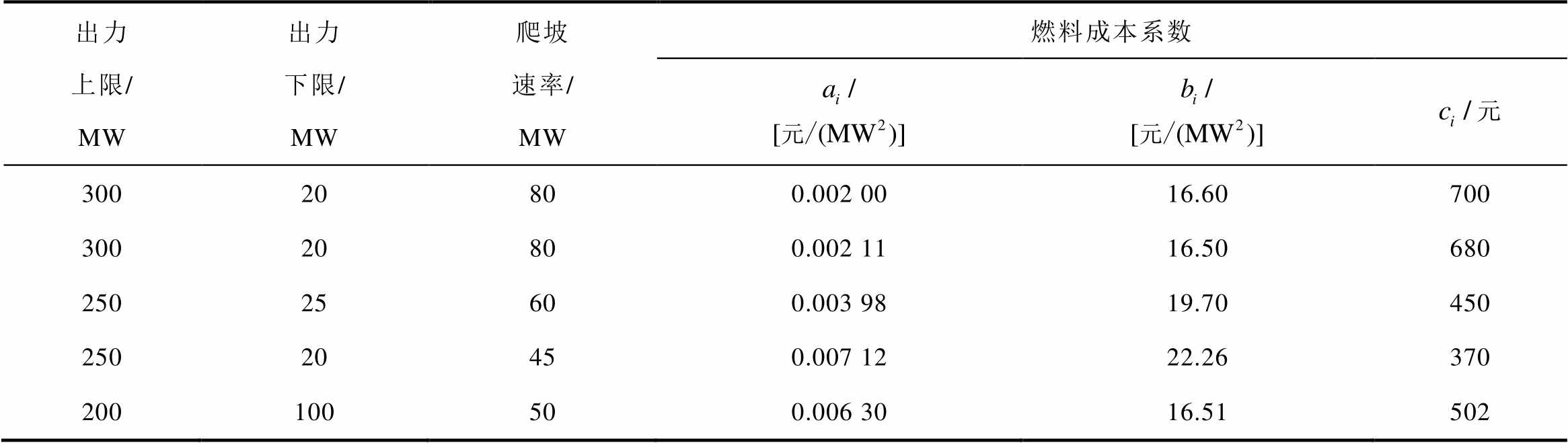
出力上限/MW出力下限/MW爬坡速率/MW燃料成本系数 30020800.002 0016.60700 30020800.002 1116.50680 25025600.003 9819.70450 25020450.007 1222.26370 200100500.006 3016.51502
表2 智能换电站基本参数
Tab.2 Basic parameters of smart switching station

参数数值 电池总数M1 000 充电机数量kc250 满电电池数量最小值100 电池放电容量/kW50 电池充电容量/kW50 电池放电所需时间/h1 电池容量/(kW∙h)50
4.1.2 定价模型权重系数确定
本文第2节给出了各决策因素之间的关系,根据文献[14]中专家调研及协商可以得到政府激励措施、需求关系以及EV负荷与火电机组竞争关系三种因素的权重见表3。
表3 定价模型各决策元素权重系数的确定
Tab.3 Determination of the weight coefficient of each decision element in the pricing model

系数 权重0.30.40.3
依据三个决策因素之间的相关性以及FAHP判断矩阵的构建原则,得到判断矩阵为
 (43)
(43)经过一致性检验得到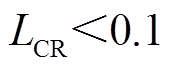 ,表明这一权重系数选择合理。
,表明这一权重系数选择合理。
4.1.3 EV负荷参数
为便于分析,本文设置区域电网中有EV共11000辆,分别为可调度EV5000辆,灵活性EV 5 000辆,智能换电EV 1 000辆,此时的电动汽车负荷量占区域电网总负荷约为14%。为了减少电池损耗,假设EV剩余电量20%~50%时充电,离网时间设置为7h,离网时期望负荷服从80%~100%的均匀分布[7]。
可调度EV、灵活性EV的充放电容量如图5所示,其中可调度EV无法向电网馈电,其放电容量为0;灵活性EV的放电电容量下限也为0。智能换电EV表征得到的换电站中锂电池数量和图6所示。
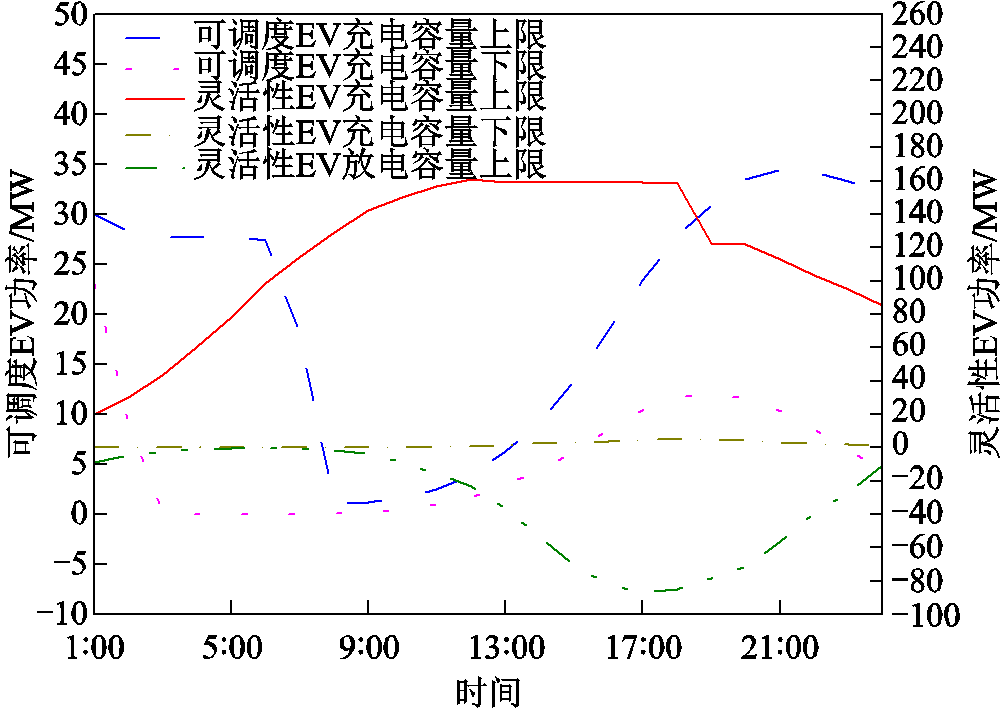
图5 可调度EV、灵活性EV充放电容量
Fig.5 Dispatchable EV, flexible EV capacity
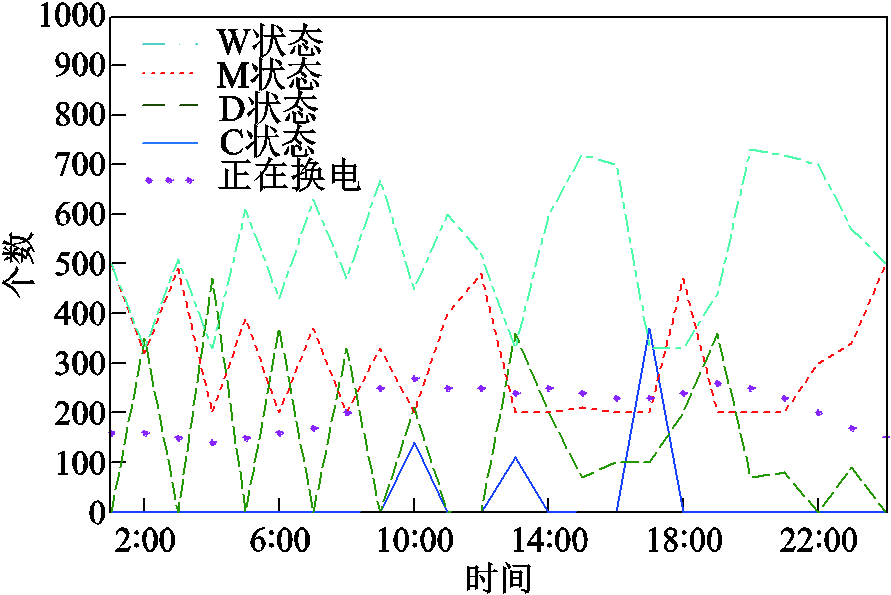
图6 换电站锂电池数量
Fig.6 Number of batteries in the replacement station
第一阶段火电机组的预测出力如图7所示。由图7可以看出火电机组出力跟随负荷峰谷变化,负荷较大时火电机组出力较大;反之亦然。
风电、光伏及常规负荷的日前预测及日内实际值如图8所示。由图8可知,风机、光伏和常规负荷的日前预测数据和日内实际值之间存在较大误差。目前常用的减少误差的手段是火电机组调峰,但是文献[19]指出EV参与调峰的成本远低于火电机组的灵活性改造,因此,本文研究在区域电网中通过调度EV进行调峰。
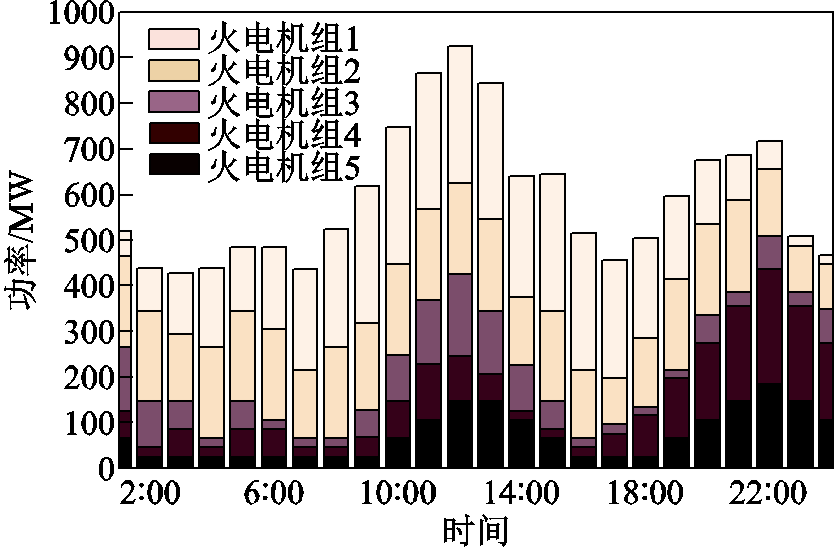
图7 火电机组日前预测出力
Fig.7 The output of the thermal power unit in the optimization stage is forecasted a few days ago
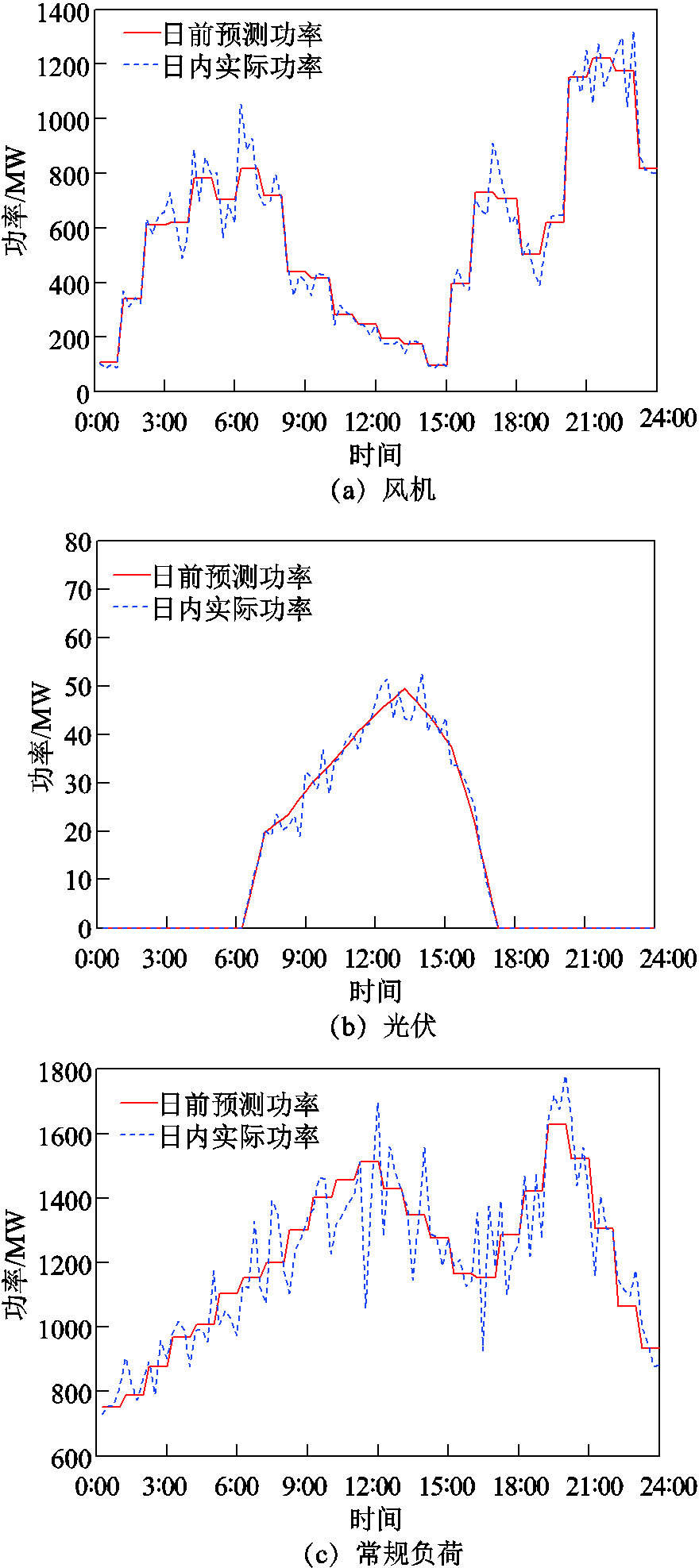
图8 风机、光伏及常规负荷的日前预测结果与日内实际值
Fig.8 Day-ahead forecast results and actual values of wind turbines, photovoltaics and conventional loads
图9是第一阶段EV参与调峰定价时的成本负荷转移示意图。
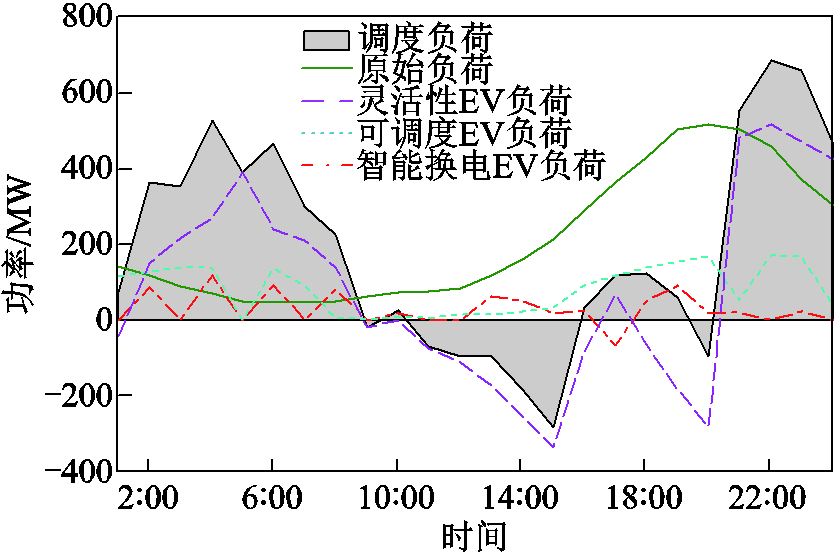
图9 第一阶段EV参与调峰定价的成本负荷
Fig.9 Cost transfer load of EV participating in peak shaving pricing in the first stage
由图9可知,在EV参与调峰之前,区域电网内负荷的峰、谷时期集中且单一。引入EV之后,在9:00~16:00和18:00~21:00,智能换电EV减少充电,并通过换电站对区域电网进行放电,可调度EV减少充电需求,灵活性EV通过充电桩向系统放电,这个时间段对应于用电高峰期。在16:00~18:00,下班高峰期EV的使用量增加,也有了充电需求,智能换电EV可在换电站进行换电,站内空闲的满电电池可通过换电站向区域电网放电,灵活性EV也可以在满足自身使用的前提下向区域电网放电;在22:00~24:00和0:00~9:00,可调度EV和智能换电EV在这个时间段可选择充电;灵活性EV此时可进行充电,满足第二天的出行需求,这个时间段对应于用电低谷。通过EV在峰、谷时期充放电时期转移或者充电需求的增减,可以实现区域电网的调峰。
由表3确定的权重系数及式(26)的定价模型,可以得到如图10所示的EV参与调峰的定价曲线,该定价是在24h内相对固定的价格。当到达用电高峰期时,即11:00~13:00和19:00~22:00时,相应的EV充电定价最高,为225~389元/(MW∙h),此时EV参与调峰,充电需求较少,充电费用最低;当到达用电低谷期,即0:00~7:00、16:00~18:00和23:00~24:00时,相应的EV充电定价最低,此时EV有较大的充电需求,相对来说充电费用也会较低。
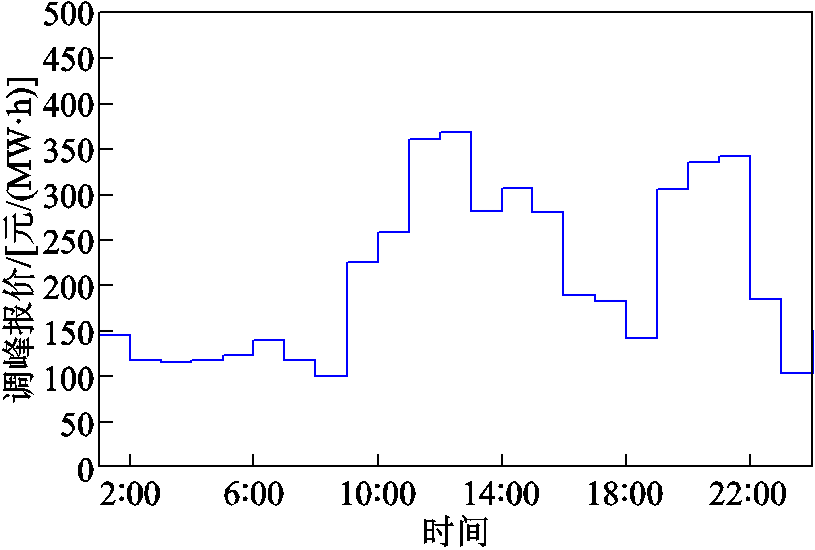
图10 EV调峰定价曲线
Fig.10 EV peak shaving quotation curve
由图9和图10可知,EV参与调峰时的转移负荷在11:00~13:00,19:00~21:00达到高峰,EV充电费用高,旨在降低可调度EV在用电高峰时期的充电功率,灵活性EV可在此时增大放电功率或减少充电功率,引导换电站使用备用电池向区域电网放电或减少充电需求;反之亦然。与一般分时电价不同,该定价曲线参考多种决策因素,考虑了国家政策、需求关系、竞争关系等因素,增加了峰谷时期充电费用的差值,更有利于调动EV用户在负荷低谷时充电、负荷高峰时放电或者减少充电的积极性。
4.3.1 日内模拟优化调度条件
在日内模拟优化调度阶段,在光伏、风机、常规负荷的基础上增加模拟误差,模拟误差服从正态分布,置信区间为95%,模拟运行得到的数据按照输入、输出样本输入BP神经网络,经过300次训练后得到日内调度模型,仿真环境为Intel(R) Core(TM) i7-10750H CPU@2.60GHz 2.59 GHz,利用MatlabR2014a软件进行计算,模型训练时间为8min,调用模型时间为0.002 13s,算法求解效率满足日内调度需求。
4.3.2 日内优化与日后验证
图11所示为第一阶段优化得到的外部电网注入功率。
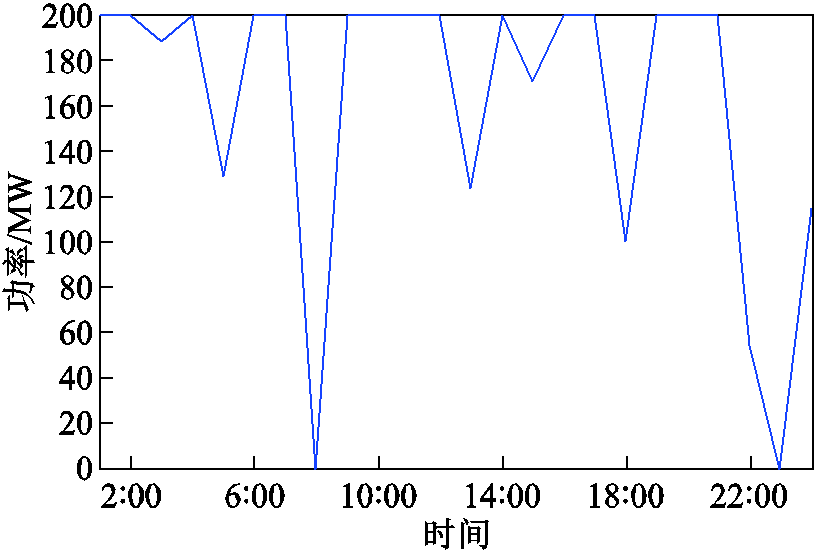
图11 外部电网注入功率
Fig.11 Power injected from external grid
图11表示配电网与区域电网交互功率,是日前阶段以峰谷差最小求解得到的,基于此电网外部注入功率,在第二阶段的日内优化考虑减少区域电网对配电网的影响,按照此既定功率运行。
图12是火电机组在日内优化调度阶段出力图。由图12可知,在EV参与调峰之后火电机组在用电高峰期的出力降低,减少火电机组在负荷高峰时的压力,增加火电机组在负荷低谷时的出力,有利于机组长期稳定运行。
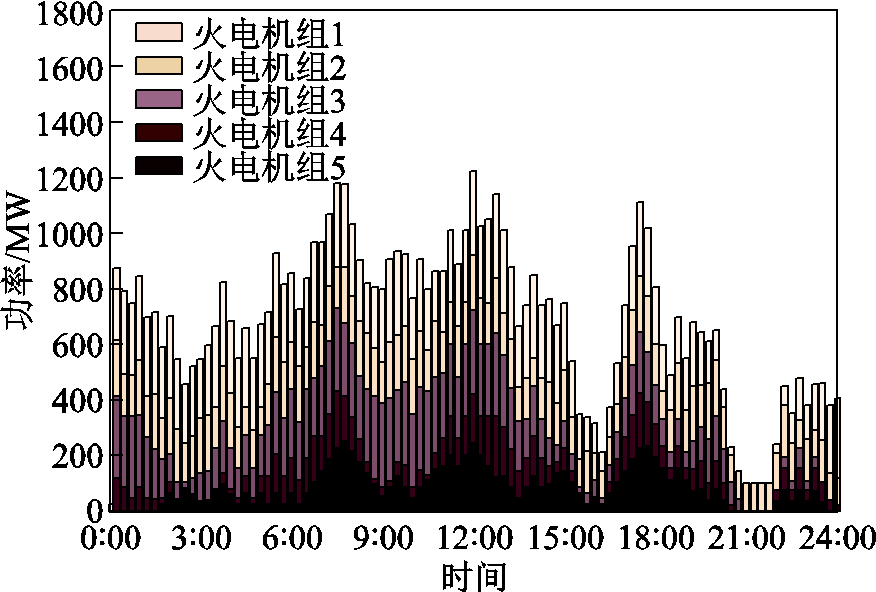
图12 火电机组日内调度阶段出力
Fig.12 The output of thermal power units in the dispatch phase during the day
日内阶段,考虑光伏、风机、常规负荷的实际波动,对区域电网进行日内优化调度,图13和图14所示分别为可调度EV、智能换电EV和灵活性EV参与调峰定价的日内调度、日后验证对比图。
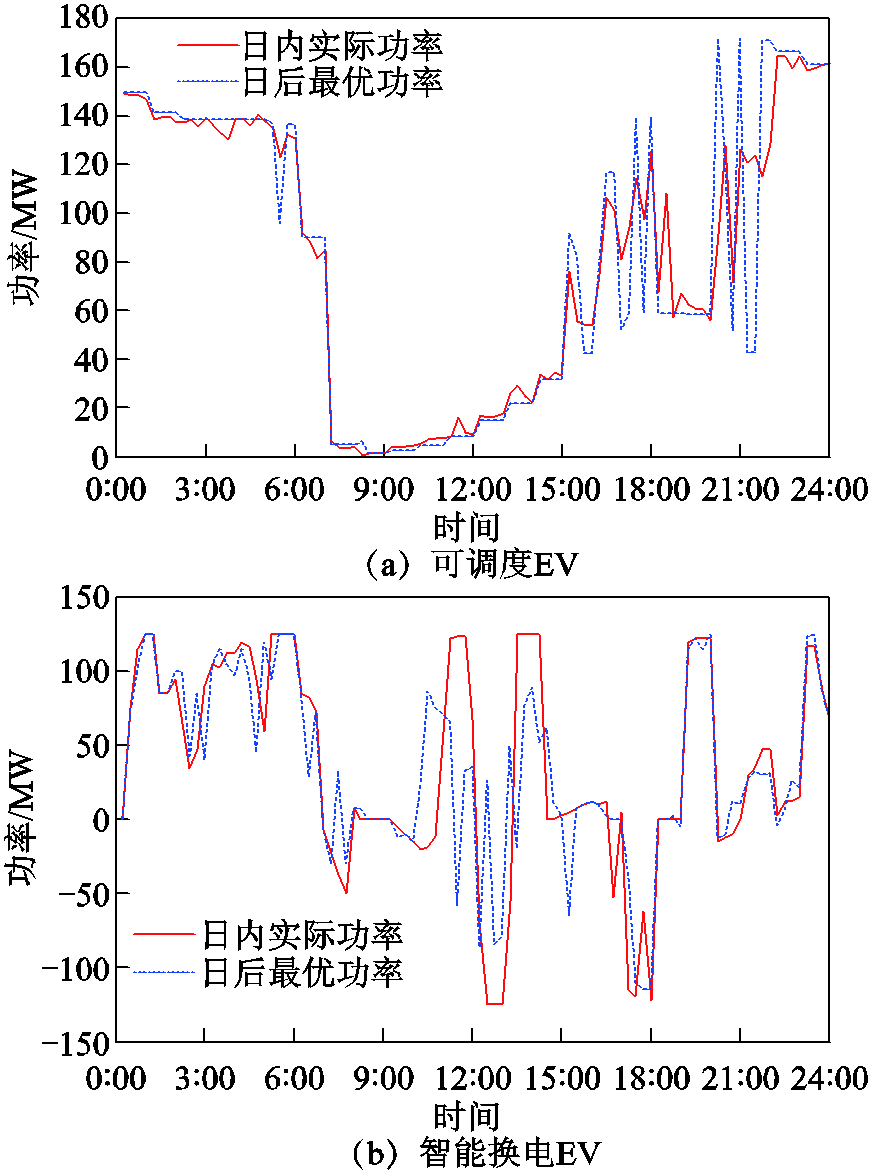
图13 可调度/智能换电EV日内调度与日后验证对比
Fig.13 Comparison of dispatchable /smart swapping EVs in the day and in the future
由图13可以看出,可调度EV负荷的日内调度功率与日后验证功率曲线大体一致,但是在17:00~18:00和20:00~22:00有较大偏差,这是因为可调度EV的可调度容量较大,在参与调度时允许出现较大误差。智能换电EV的日内调度功率与日后验证曲线基本一致,但在11:00~13:00有较大差别,这是因为换电站既需要满足电池满状态的数量要求,又需要在区域电网内用电高峰期时充当放电单元。由图14可知,灵活性EV的日内充放电调度功率和日后验证曲线基本一致,不仅平抑了充电过程中大部分时段的波动尖峰,还对放电功率进行了调整,在用电高低峰时期的充放电特征明显。
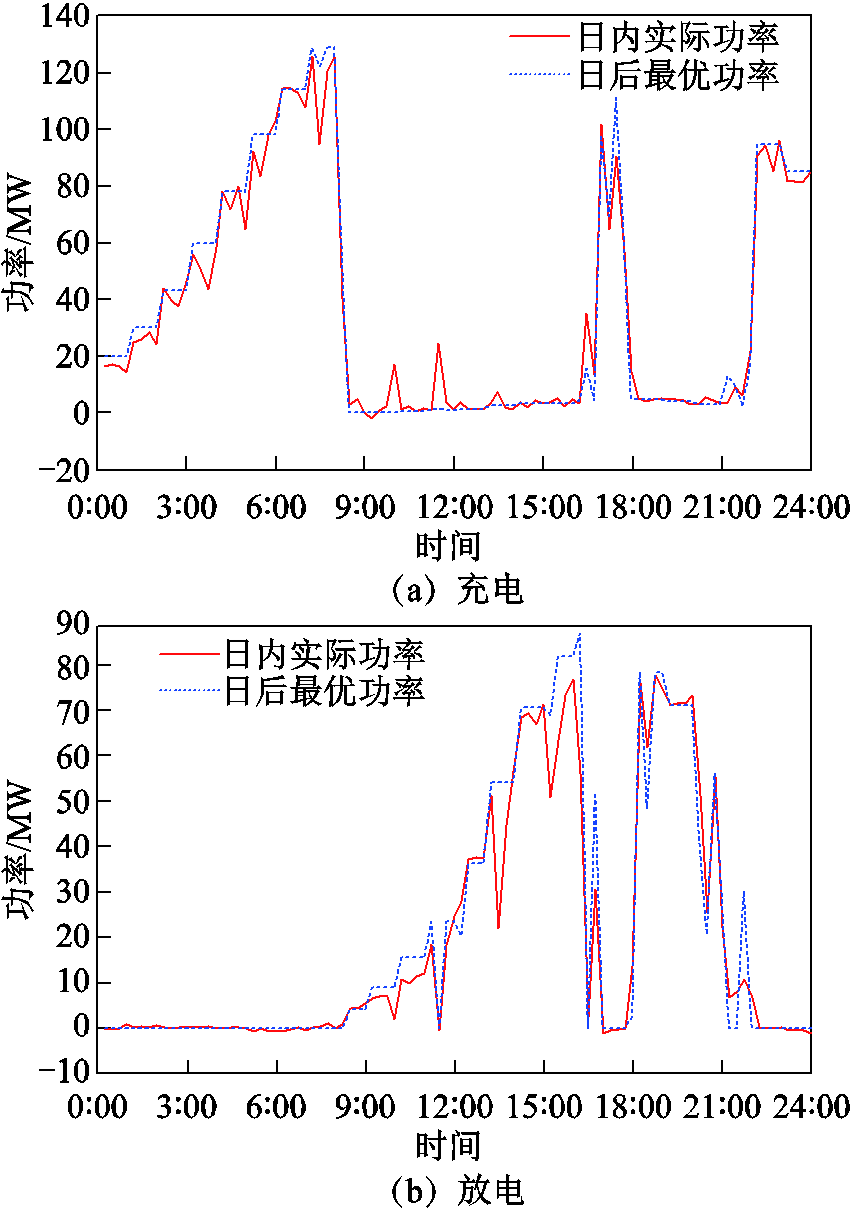
图14 灵活性EV日内调度与日后验证对比
Fig.14 Flexibility EV day and future comparison
日内调度与日后验证误差对比分析见表4。可以看出,可调度EV、灵活性EV与智能换电EV的日内调度和日后验证的方均根误差、相对误差最大值均在可接受范围内,说明日内调度策略具有有效性与合理性。
表4 日内调度与日后验证误差对比分析
Tab.4 Future verification and intra-day scheduling error analysis

误差可调度EV灵活性EV充电灵活性EV放电智能换电EV 方均根误差(%)6.505 46.998 46.810 89.025 3 相对误差最大值(%)11.081 212.097 213.458 413.600 0
文献[23]构建计及车入网参与辅助服务的EV充电计划经济调控模型,在用电高峰期时EV反向放电,利用峰谷价差获得调峰收益;在用电低谷期时EV充电,获得在低谷充电的额外补偿收益。将文献[23]调峰策略与本文调峰策略进行对比,可得到图15和图16所示第二阶段区域电网调度功率对比图。
由图15和图16可知,本文的调峰策略相比于文献[23]的调峰策略效果更好。以图16灵活性EV在不同调峰策略下的充放电调度功率对比为例,在用电低谷时采用本文调度策略的充电功率大,填谷效果更理想,且功率波动相比于文献[23]得到的功率波动更小;在用电高峰期时采用本文调度策略的放电功率大,削峰效果更明显,且功率平稳性更好。
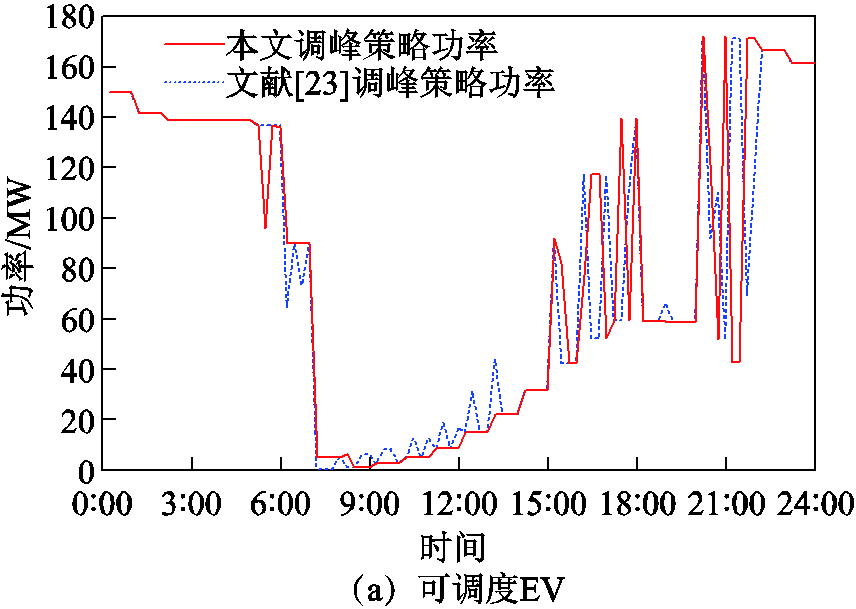
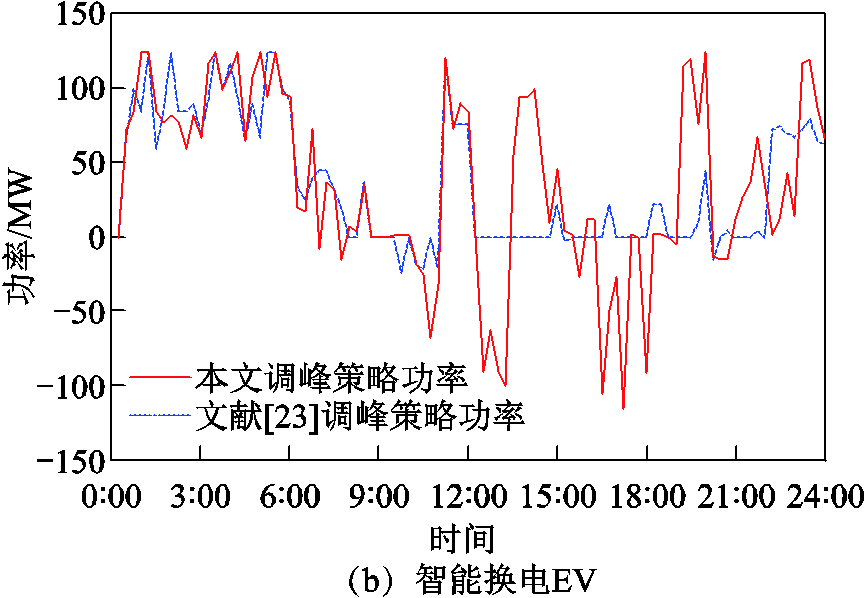
图15 可调度/智能换电EV在不同调峰策略下的对比
Fig.15 Comparison of dispatchable/smart swapping EVs under different peak shaving strategies
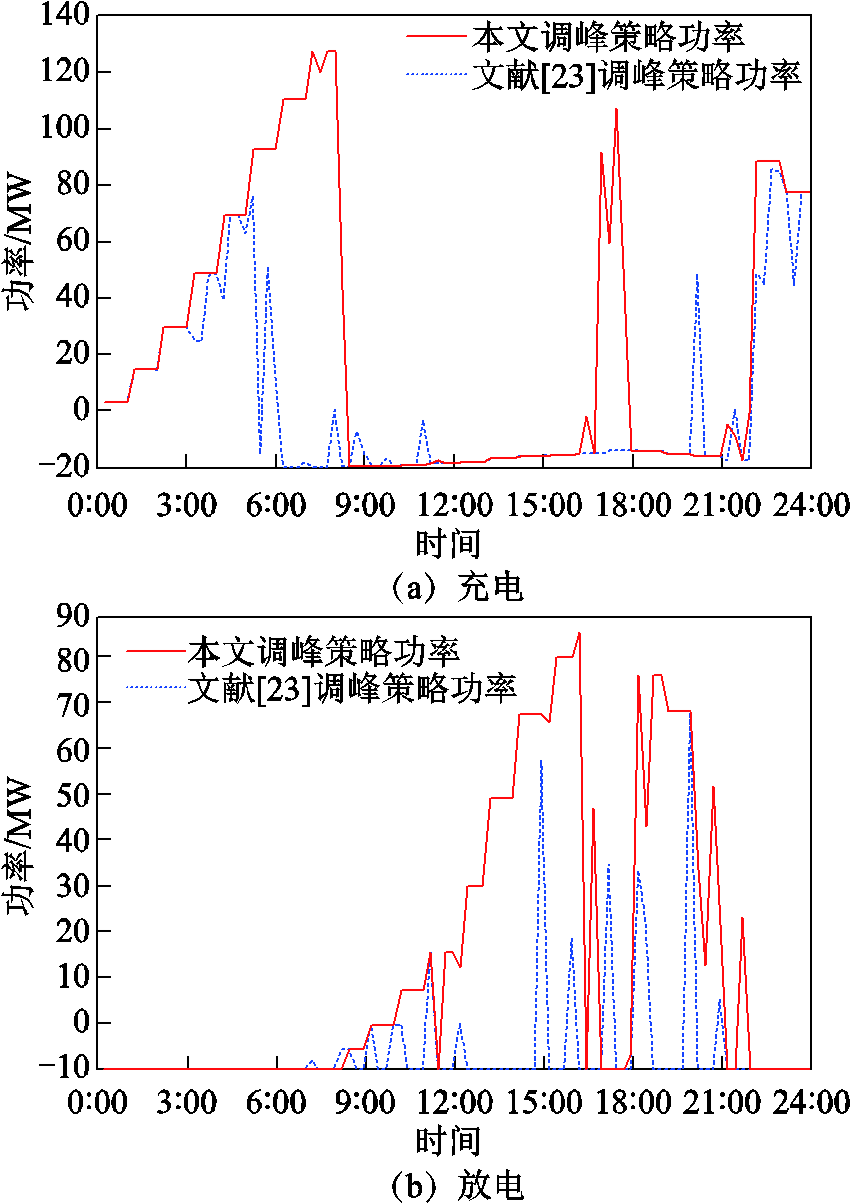
图16 灵活性EV在不同调峰策略下的对比
Fig.16 Comparison of flexible EV under different peak shaving strategies
表5所示是在日内调度与日后阶段对本文定价策略的验证。这里采用的分时电价视EV种类不同而有区别[24-25]:对于可调度EV的充电电价,峰时段(10:00~15:00,18:00~21:00)为265元/(MW∙h),平时段(7:00~10:00,15:00~18:00,21:00~23:00)为116元/(MW∙h),谷时段(23:00~7:00)为85元/(MW∙h);对于灵活性EV充电电价,峰时段为366元/(MW∙h),平时段为153元/(MW∙h),谷时段为71元/(MW∙h),放电电价为205元/(MW∙h);对于智能换电EV充放电电价与灵活性EV一致。
表5 电动汽车充电费用
Tab.5 Electric vehicle charging costs

电价策略调峰定价策略分时电价策略 充电费用/[元/(MW∙h)] 日内日后日内日后 200 447192 710223 871214 890
在日内调度与日后验证阶段采用本文给出的定价曲线时,充电费用分别为200 447元/(MW∙h)和192 710元/(MW∙h);采用电力市场分时电价时,充电费用分别为223 871元/(MW·h)、214 890元/(MW∙h)。可以看出,EV参与调峰的充电费用是最低的,且相比于现有的电力市场分时电价而言,充电费用也低,这可以在满足区域电网调峰要求的同时提高EV参与调峰的积极性。并且EV更环保,在未来将其成本降低后,在区域电网乃至整个微电网调峰市场也会有更广阔的前景。
本文针对当前新能源大规模入网引起的电网功率波动等问题,提出了一种基于电动汽车参与调峰定价策略的区域电网两阶段优化调度方案,得到如下结论:
1)本文将EV引入区域电网参与调峰,考虑预测误差及三种EV负荷实现日内调度并进行日后验证,相比于主流调度策略可以更有效地缓解区域电网的调峰压力,降低成本,减少负荷峰谷差,提高风电光伏的消纳水平。
2)本文将EV参与调峰与电力辅助服务市场结合,设计了基于各项成本和三个决策因素的定价模型。第一阶段以区域电网负荷峰谷差最小,第二阶段计及预测误差,以充电费用最小为目标进行调度与日后验证,可以提升EV参与调峰的积极性。
3)算例验证了本文所提出的EV参与调峰定价策略的有效性,EV参与调峰定价策略可以提高EV调峰积极性,改善区域电网的灵活性,同时也为可转移负荷参与调峰进行了有益的尝试。
本文针对EV参与调峰的相关问题提出了可行方案,将得到的定价曲线与电力市场分时电价进行对比研究,可以为我国电力辅助服务市场和区域电网日内调度提供参考。
参考文献
[1] 崔杨, 张家瑞, 仲悟之, 等. 计及电热转换的含储热光热电站与风电系统优化调度[J].中国电机工程学报, 2020, 40(20): 6482-6494.
Cui Yang, Zhang Jiarui, Zhong Wuzhi, et al. Optimal scheduling of concentrating solar power plant with thermal energy storage and wind farm considering electric-thermal conversion[J]. Proceedings of the CSEE, 2020, 40(20): 6482-6494.
[2] Fang Chen, Zhao Xiaojin, Xu Qin, et al. Aggregator-based demand response mechanism for electric vehicles participating in peak regulation in valley time of receiving-end power grid[J]. Global Energy Interconnection, 2020, 3(5): 453-463.
[3] 鞠立伟, 于超, 谭忠富. 计及需求响应的风电储能两阶段调度优化模型及求解算法[J]. 电网技术, 2015, 39(5): 1287-1293.
Ju Liwei, Yu Chao, Tan Zhongfu. A two-stage scheduling optimization model and corresponding solving algorithm for power grid containing wind farm and energy storage system considering demand response[J]. Power System Technology, 2015, 39(5): 1287-1293.
[4] 刘东奇, 王耀南, 袁小芳. 电动汽车充放电与风力/火力发电系统的协同优化运行[J]. 电工技术学报, 2017, 32(3): 18-26.
Liu Dongqi, Wang Yaonan, Yuan Xiaofang. Cooperative dispatch of large-scale electric vehicles with wind-thermal power generating system[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 18-26.
[5] 师景佳, 袁铁江, Saeed Ahmed Khan, 等. 计及电动汽车可调度能力的风/车协同参与机组组合策略[J]. 高电压技术, 2018, 44(10): 3433-3440.
Shi Jingjia, Yuan Tiejiang, Saeed Ahmed Khan, et al. Unit commitment strategy considering cooperated dispatch of electric vehicles based on scheduling capacity and wind power generation[J]. High Voltage Engineering, 2018, 44(10): 3433-3440.
[6] 姚一鸣,赵溶生,李春燕,等.面向电力系统灵活性的电动汽车控制策略[J/OL].电工技术学报: 1-12[2021-09-18].https://doi.org/10.19595/j.cnki.1000-6753.tces. 210515.
Yao Yiming, Zhao Rongsheng, Li Chunyan, et,al. Control strategy of electric vehicles oriented to power system flexibility[J/OL]. Transactions of China Electrotechnical Society: 1-12[2021-09-18].https:// doi.org/10.19595/j. cnki.1000-6753.tces.210515.
[7] 史文龙, 秦文萍, 王丽彬, 等. 计及电动汽车需求和分时电价差异的区域电网 LSTM 调度策略[J]. 中国电机工程学报, https://doi.org/10.13334/j. 0258- 8013. pcsee.202473.
Shi Wenlong, Qin Wenping, Wang Libin, et al. Regional power grid LSTM dispatch strategy considering the difference between electric vehicle demand and time-of-use electricity price[J]. Proceedings of the CSEE, https:// doi.org/10.13334/j. 0258-8013.pcsee.202473.
[8] Liu Yujun, Xu Qingshan, Zang Haixiang, et al. Research on the evaluation method of capacity on electric-vehicle energy storage system[J]. Proceedings-2014 IEEE International Workshop on Intelligent Energy Systems, 2014: 88-92.
[9] 刘灵恺, 雷霞, 李竹, 等. 电动汽车换电站可用电池组数动态调度策略[J].电工技术学报, 2017, 32(22): 242-250.
Liu Lingkai, Lei Xia, Li Zhu, et al. Dynamic scheduling strategy for available battery number of electric vehicle in battery-swap station[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 242-250.
[10] 崔杨, 刘柏岩, 仲悟之, 等. 考虑积压惩罚机制的含BSS微网联合系统优化调度策略[J]. 电网技术, 2020, 44(10): 3787-3793.
Cui Yang, Liu Baiyan, Zhong Wuzhi, et al. Optimal scheduling strategy for joint system with micro-grid containing BSS considering overstock punishment mechanism[J]. Power System Technology, 2020, 44(10): 3787-3793.
[11] 崔杨, 刘柏岩, 赵钰婷, 等. 计及车辆转移机制的含BSS微网联合系统优化调度策略[J]. 高电压技术, https://doi.org/10.13336/j.1003-6520.hve.20201633.
Cui Yang, Liu Baiyan, Zhao Yuting, et al. Optimal scheduling strategy for joint system with microgrid containing BSS considering vehicle transfer mechanism[J]. High Voltage Engineering, https://doi.org/ 10.13336/j.1003-6520.hve. 20201633.
[12] 许刚, 张丙旭, 张广超. 电动汽车集群并网的分布式鲁棒优化调度模型[J]. 电工技术学报, 2021, 36(3): 565-578.
Xu Gang, Zhang Bingxu, Zhang Guangchao. Distributed and robust optimal scheduling model for large-scale electric vehicles connected to grid[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 565-578.
[13] 张立静, 娄素华, 陈艳霞, 等. 基于电池租赁模式的电动汽车换电站电池容量优化[J].电网技术, 2016,40(6):1730-1735.
Zhang Lijing, Lou Suhua, Chen Yanxia, et al. Battery capacity optimization of electric vehicle swapping station based on leasing mode[J]. Power System Technology, 2016, 40(6): 1730-1735.
[14] 时珉, 许可, 王珏, 等. 基于灰色关联分析和GeoMAN模型的光伏发电功率短期预测[J]. 电工技术学报, 2021, 36(11): 2298-2305.
Shi Min, Xu Li, Wang Jue, et al. Short-term photovoltaic power forecast based on grey relational analysis and GeoMAN model[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2298-2305.
[15] 崔杨, 修志坚, 刘闯, 等. 计及需求响应与火-储深度调峰定价策略的电力系统双层优化调度[J]. 中国电机工程学报, 2021, 41(13): 4403-4414.
Cui Yang, Xiu Zhijian, Liu Chuang, et al. Dual level optimal dispatch of power system considering demand response and pricing strategy on deep peak regulation[J]. Proceedings of the CSEE, 2021, 41(13): 4403-4414.
[16] 王轶禹, 马世俊, 皮俊波, 等. 关于国调直调电厂“两个细则”的讨论[J].电力系统自动化, 2018, 42(16): 174-179, 186.
Wang Yiyu, Ma Shijun, Pi Junbo, et al. Key parameter design of smart grounding distribution systems[J]. Automation of Electric Power Systems, 2018, 42(16): 174-179, 186.
[17] 张文韬, 王秀丽, 吴雄, 等. 大规模风电接入下含大用户直购电的电力系统调度模型研究[J]. 中国电机工程学报, 2015, 35(12): 2927-2935.
Zhang Wentao, Wang Xiuli, Wu Xiong, et al. An analysis model of power system with large-scale wind power and transaction mode of direct power purchase by large consumers involved in system scheduling[J]. Proceedings of the CSEE, 2015, 35(12): 2927-2935.
[18] 宋艺航, 何楠, 张会娟, 等. 电力市场下发电企业碳排放定价模型[J].中国电力, 2013, 46(10): 151-154.
Song Yihang, He Nan, Zhang Huijuan, et al. Carbon pricing model for power generation enterprises in electricity markets[J]. Electric Power, 2013, 46(10): 151-154.
[19] 苏南. 电动汽车储能参与电网优化调度, 调峰成本远低于火电机组灵活性改造[N]. 中国能源报, 2021-01-13, https://finance.eastmoney.com/a/202101131773649198.html.
Sunan. Electric vehicle energy storage participates in the optimal dispatch of the power grid, and the cost of peak shaving is much lower than the flexible transformation of thermal power units[N]. China Energy News, 2021-01-13, https:// finance.eastmoney.com/a/202101131773649198.html.
[20] 罗桓桓, 王昊, 葛维春, 等. 考虑报价监管的动态调峰辅助服务市场竞价机制设计[J]. 电工技术学报, 2021, 36(9): 1935-1947, 1955.
Luo Huanhuan, Wang Hao, Ge Weichun, et al. Design of dynamic peak regulation ancillary service market bidding mechanism considering quotation supervision[J].Transactions of China Electrotechnical Society, 2021, 36(9): 1935-1947, 1955.
[21] 朱云杰, 秦文萍, 于浩, 等. 基于神经网络的微电网参与上层电网实时优化调度策略[J]. 电力建设, 2020, 41(10): 9-19.
Zhu Yunjie, Qin Wenping, Yu Hao, et al. Strategy based on neural network for microgrid participating in real-time optimal scheduling of upper grid[J]. Electric Power Construction, 2020, 41(10): 9-19.
[22] 于浩, 秦文萍, 魏斌, 等. 考虑预测误差的交直流混合微电网经济调度策略[J].电网技术, 2019, 43(11): 3987-3996.
Yu Hao, Qin Wenping, Wei Bin, et al. Economic dispatch of hybrid AC/DC microgrid considering prediction error[J]. Power System Technology, 2019, 43(11): 3987-3996.
[23] 周椿奇, 向月, 张新, 等. V2G辅助服务调节潜力与经济性分析: 以上海地区为例[J]. 电力自动化设备, 2021, 41(8):135-141.
Zhou Chunqi, Xiang Yue, Zhang Xin, et al. Potential regulation ability and economy analysis of auxiliary service by V2G: taking Shanghai area for an example[J]. Electric Power Automation Equipment, 2021, 41(8): 135-141.
[24] 尹琦琳, 秦文萍, 于浩, 等. 计及风电波动性和电动汽车随机性的电力现货市场交易模型[J]. 电力系统保护与控制, 2020, 48(11): 1-12.
Yin Qilin, Qin Wenping, Yu Hao, et al. Transaction model for electricity spot market considering the volatility of wind power and the randomness of electric vehicles[J]. Power System Protection and Control, 2020, 48(11): 1-12.
[25] 文雯. 《电动汽车与电网互动的商业前景——上海市需求响应试点案例》报告发布 需求响应破解电动汽车发展难题[J]. 环境经济, 2020(12):36-38.
Wen Wen. The report of “The Commercial Prospects of the Interaction of Electric Vehicles and Grids-Shanghai Demand Response Pilot Cases” is released. Demand response solves the problems of electric vehicle development[J]. Environmental Economy, 2020(12): 36-38.
Two-Stage Optimal Dispatching of Regional Power Grid Based on Electric Vehicles' Participation in Peak-Shaving Pricing Strategy
Abstract In response to problems such as power fluctuations, high dispatching cost and poor operation stability caused by the large-scale access of electric vehicles(EV), wind power, photovoltaics and other new energy power generation to the grid, this paper proposes a strategy,two-stage optimized dispatching plan for the regional power grid,based on the participation of EV in peak shaving. Firstly, classify according to the EV load operating characteristics, and establish four EV load models: rigid, schedulable, flexible, and smart swapping; secondly, considering the cost of EV participation in peak shaving, and giving EV peak shaving pricing strategy based on the Fuzzy Analytic Hierarchy Process (FAHP); then based on this strategy, a two-stage optimal dispatching of the regional power grid is carried out. In the first stage, the goal is to minimize the load peak-valley difference, and to make decisions on EV peak shaving pricing under this target, so as to reduce the peak shaving capacity of the power system and adjust the regional grid load distribution; in the second stage, relying on the peak shaving pricing curve obtained in the first stage, the EV load is arranged with the goal of minimizing the charging cost of EV users; finally, a simulation example is used to verify the effectiveness and rationality of EV participation in peak shaving and the economics of the pricing strategy.
keywords:Electric vehicles, peak shaving pricing strategy, regional power grid, fuzzy analytic hierarchy process, two-stage optimization
DOI:10.19595/j.cnki.1000-6753.tces.211274
中图分类号:TM724
国家自然科学基金(51777132)和山西省科技重大专项(20181102028)资助项目。
收稿日期 2021-08-13
改稿日期 2021-08-27
杨镜司 女,1997年生,硕士研究生,研究方向为交直流微电网能量管理及优化运行控制。E-mail:1638214845@qq.com
秦文萍 女,1972年生,教授,博士生导师,研究方向为电力系统可靠性分析、微电网运行与控制、新能源发电技术和微机保护。E-mail:qinwenping@tyut.edu.cn(通信作者)
(编辑 郭丽军)