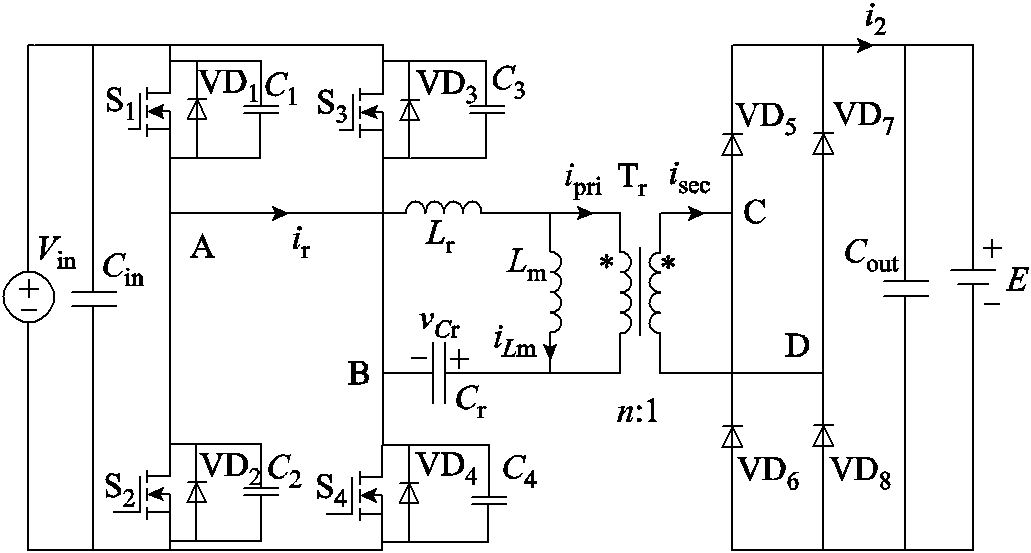
图1 全桥LLC谐振变换器拓扑
Fig.1 Full-bridge LLC resonant converter topology
摘要 LLC谐振变换器以其优异的性能被广泛应用于电动汽车直流充电领域。针对电动汽车宽输出电压范围、高转换效率的充电需求,该文对直流充电模块后级全桥LLC谐振变换器软开关运行的输出电压边界进行了分析。零电压开通(ZVS)上边界处,变压器励磁电感参与谐振,其二次侧等效峰值电压与负载电压相等,整流二极管临界导通;ZVS下边界处,谐振电流与谐振腔的输入电压同时过零,LLC谐振变换器运行于临界感性区间。该文利用时域分析法详细分析了变换器ZVS上下边界处的工作状态,计算出变换器软开关运行所允许的输出电压范围,揭示了变换器的软开关特性与工作频率、谐振参数之间的关系,为变换器的参数设计和变频控制提供了理论指导。最后,通过仿真和实验对理论分析进行了验证。
关键词:LLC谐振变换器 软开关运行 输出电压边界 零电压开通(ZVS) 电动汽车
近几年,电动汽车因其污染小、使用成本低[1]等特点逐渐成为了新能源汽车的主要发展方向。电动汽车充电装置作为其核心技术之一受到了广泛关注和研究。其中,大功率直流充电机由于能显著缩短充电时间[2]而成为研究的重点。
直流充电机的功率模块一般可由前级AC-DC和后级隔离型DC-DC变换器构成[3-4]。作为后级变换器的常用方案之一,LLC谐振变换器具有良好的调压特性,可通过变频调制、移相调制或混合控制方式[5-8]获得比较宽的电压增益范围。另外,LLC谐振变换器可实现一次侧开关器件的零电压开通(Zero Voltage Switching, ZVS)和二次侧整流二极管的自然换流[7, 9]。软开关的实现对提高变换器效率、功率密度和减小电磁噪声具有重要意义[8,10]。鉴于LLC谐振变换器的上述优点,其在电动汽车充电领域得到了广泛应用[11-13]。
在电动汽车的充电过程中,随着电池荷电状态(State of Charge, SOC)的改变,电池端电压也会发生较大改变。为了减小开关损耗和电磁干扰,在充电过程中应尽可能地使变换器始终运行在软开关状态下[8,10]。然而,LLC谐振变换器软开关运行状态下的调压范围有限[5],宽电压增益运行可能会导致变换器失去软开关特性。因此,为保证直流充电机的高效运行,本文对全桥LLC谐振变换器的软开关特性进行了研究。
针对LLC谐振变换器的软开关运行,文献[13]指出了软开关的成因是励磁电流在死区时间内为开关器件的寄生电容放电,在其开通前使漏源电压下降到0,并以此为依据对励磁电感和死区时间进行设计;文献[14]指出软开关实现的两个约束条件是谐振腔阻抗呈感性和励磁电流能够在死区时间内将开关器件的寄生电容端电压释放到零,并对其进行了补充,为ZVS边界添加了两个新的限制,但是并没有明确计算出边界工况对应的输出电压;文献[2]利用基波分析法对谐振变换器进行了分析,将谐振腔阻抗呈纯阻性时的工况作为变换器的ZVS边界,并按照此工况为充电机设计谐振参数,但其分析过程偏数学化,不能直观地反映变换器在边界处的工作模态;文献[15]分析了LLC谐振变换器带电池负载时,变换器工作在ZVS边界下谐振电容的电压上限,并根据该约束条件设计出谐振电容的取值,确保变换器在输出最大功率时不进入容性工作区。
针对电动汽车宽输出电压、高转换效率充电需求下直流充电功率模块后级全桥LLC谐振变换器的软开关运行问题,本文通过时域分析法对变换器在ZVS边界处的运行状态进行分析,分别计算出变换器ZVS上、下边界对应的输出电压,揭示了不同工况下变换器的软开关特性与工作频率、谐振参数之间的关系。最后,通过仿真和实验平台对理论分析进行了验证。
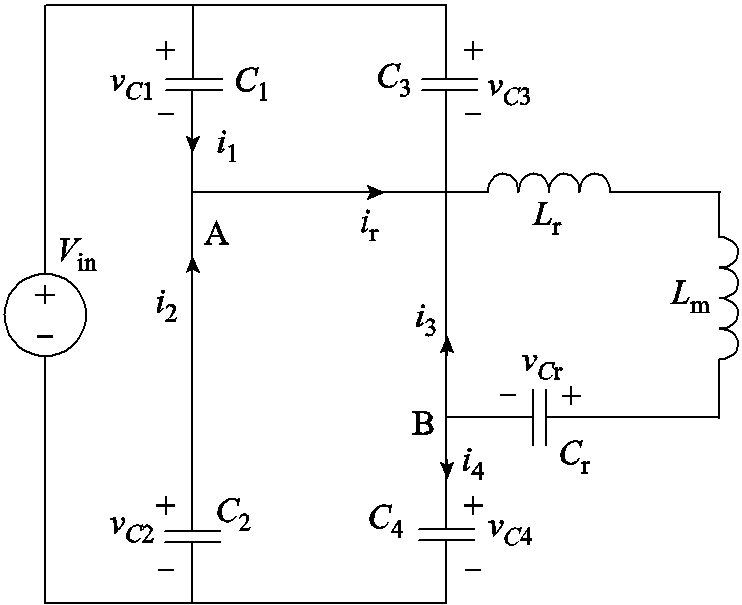
全桥LLC谐振变换器拓扑如图1所示。它由逆变全桥、LLC谐振腔、高频变压器、整流桥和输入输出电容构成。在充电过程中,由于短时间内电池端电压几乎不变,因此在理论分析中用恒压源E代替之。其中,VD1~VD4分别为开关管S1~S4的体二极管;C1~C4分别为开关管S1~S4的寄生电容;VD5~VD8为整流二极管;Lm为变压器励磁电感;Lr为变压器漏感;Cr为谐振电容;Vin为输入电压;ir为谐振电流;E为负载电压。

图1 全桥LLC谐振变换器拓扑
Fig.1 Full-bridge LLC resonant converter topology
定义开关频率为fs,开关周期为Ts;Lr、Cr串联谐振频率为fr,谐振周期为Tr;Lm、Lr、Cr串联谐振频率为fm,谐振周期为Tm,谐振角频率为ωm;定义励磁电感Lm与漏感Lr之比为λ,变压器的电压比为n:1。
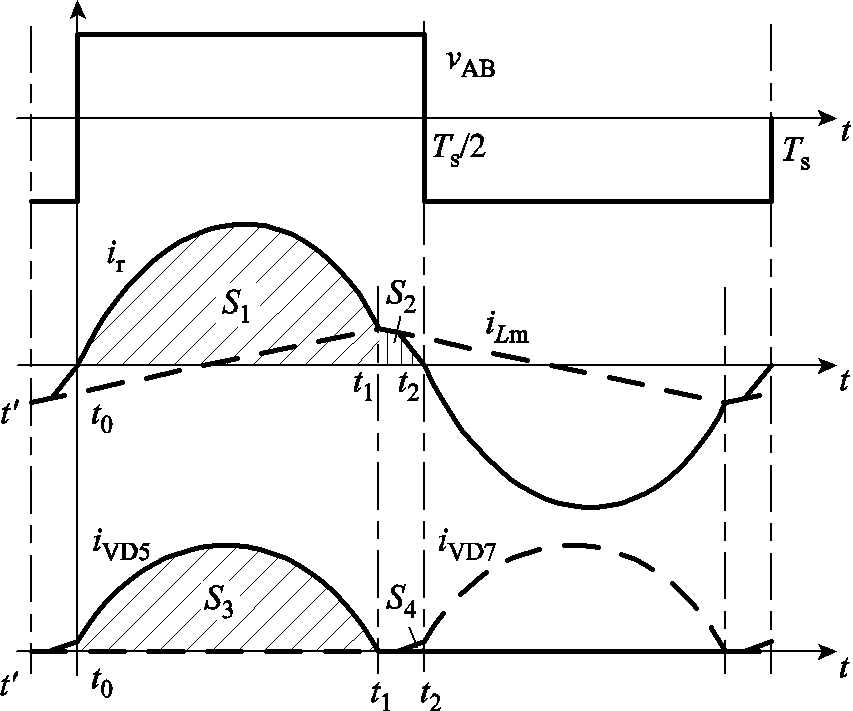
在满足控制要求的条件下,为了降低开关损耗,应使LLC谐振变换器运行在一次侧开关器件零电压开通、二次侧整流二极管自然换流的工作区域,开关频率须满足fm<fs<fr[16]。因此本文的理论分析仅针对fm<fs<fr的工况,并将电路中所有元件均视为理想元件。此工况下变换器工作波形如图2所示,其中,vAB为一次侧桥臂中点电压,iVD5和iVD7分别为流过二次侧整流二极管VD5和VD7的电流。在[t0, t1]时间段内,Lr和Cr串联谐振,而由于励磁电感被输出电压钳位,励磁电流iLm线性增加;在[t1, t2]时间段内,Lm、Lr和Cr串联谐振,二次侧整流二极管关断,但由于时间段[t1, t2]远小于[t0, t1]且Tm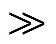 Tr,可认为此段时间内谐振电流ir保持不变。
Tr,可认为此段时间内谐振电流ir保持不变。
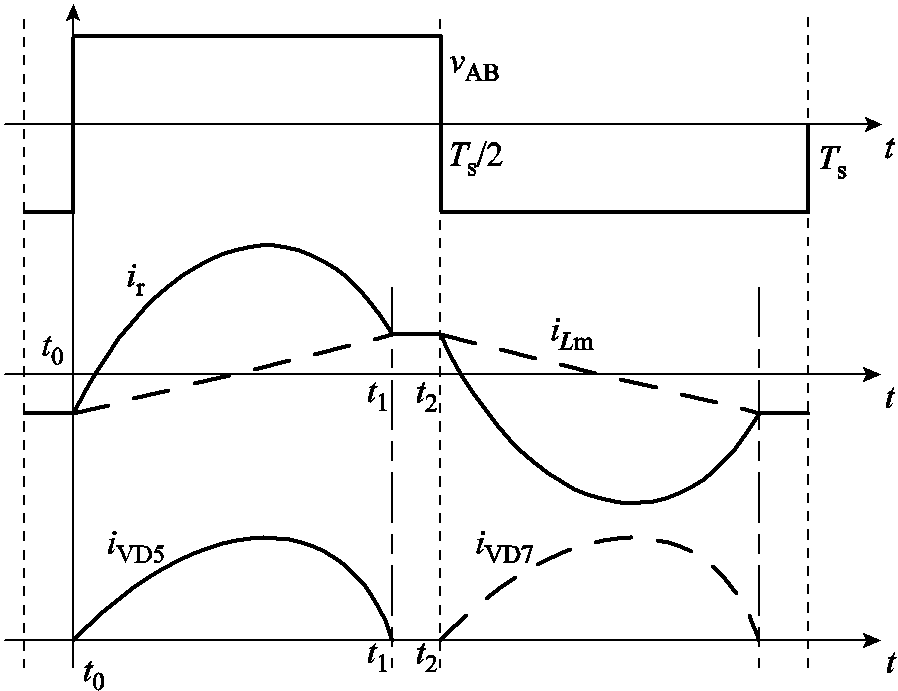
图2 软开关工况下全桥LLC谐振变换器工作波形
Fig.2 The waveforms of full bridge LLC resonant converter operating under soft switching condition
在ZVS上边界处,变换器输出软开关运行状态下的最大电压。此时负载电压E的一次侧等效电压nE与励磁电感电压vLm(t)的峰值恰好相等,二次侧整流二极管在整个开关周期内均反向截止,变换器始终处于Lm、Lr和Cr的串联谐振状态[14],输出功率为零[14, 17]。此时,变换器在稳态条件下的等效电路如图3所示。根据图3可得到微分方程组
图3 上边界处的等效电路
Fig.3 The equivalent circuit on the upper boundary
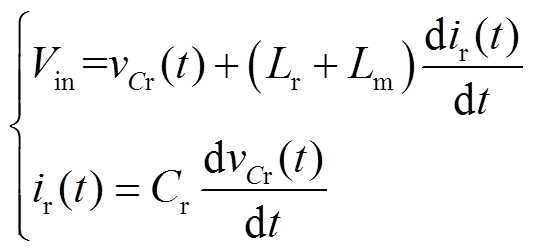 (1)
(1)开关频率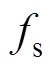 下,Lm、Lr和Cr串联谐振时的谐振电容电压vCr(t)、谐振电流ir(t)的波形如图4所示。
下,Lm、Lr和Cr串联谐振时的谐振电容电压vCr(t)、谐振电流ir(t)的波形如图4所示。
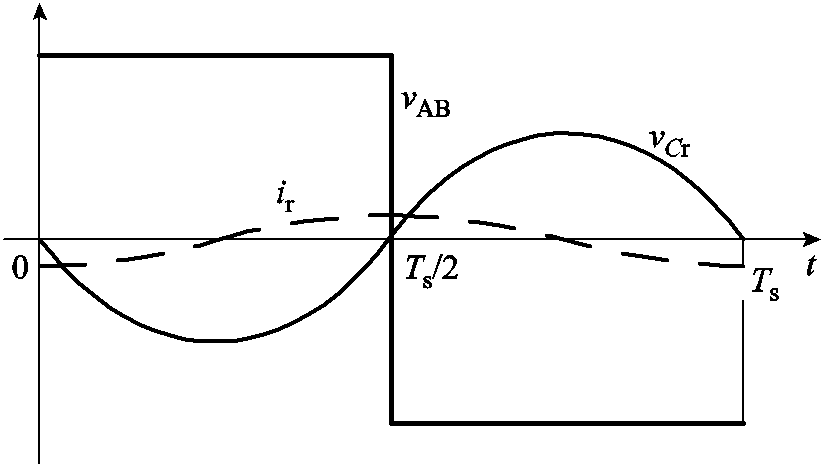
图4 上边界处电容电压vCr、谐振电流ir的稳态波形
Fig.4 Steady-state waveforms of the capacitor voltage and the resonant current on the upper boundary
根据式(1)和图4,可得vCr(t)和ir(t)的时域表达式为
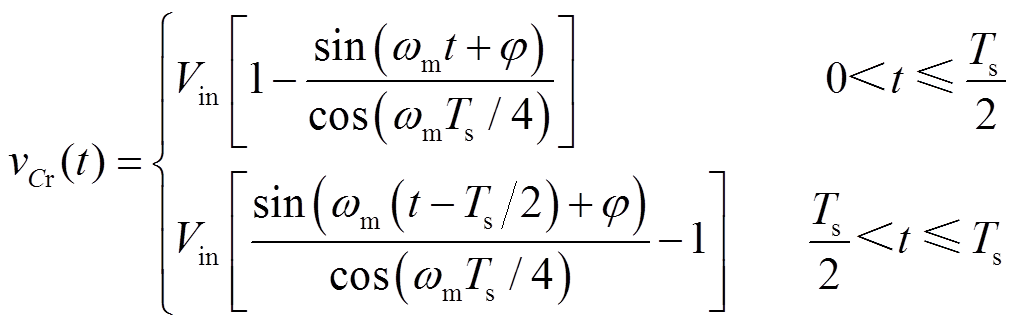 (2)
(2)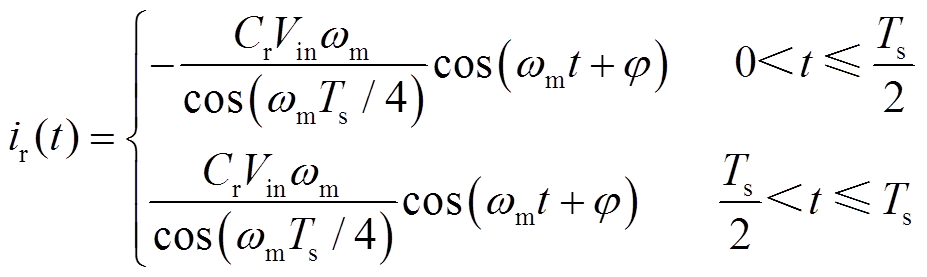 (3)
(3)
其中
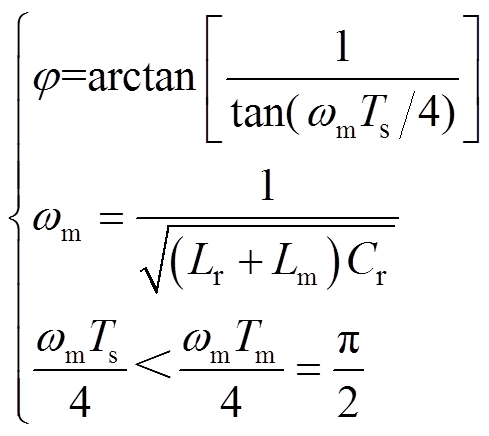 (4)
(4)则可得到vLm(t)的表达式为
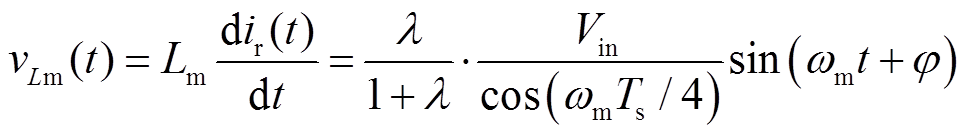 (5)
(5)
其中
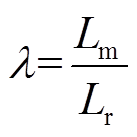 (6)
(6)在上边界处,二次侧整流二极管反向截止,根据基尔霍夫电压定律可以得到临界状态下整流二极管端电压的最大值Vdiode_max满足关系
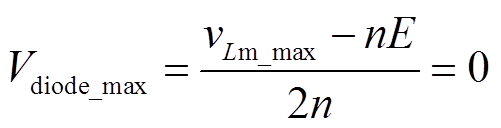 (7)
(7)
式中,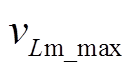 为
为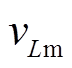 的最大值。
的最大值。
根据式(5)和式(7)可得到上边界输出电压Vupper(fs)为
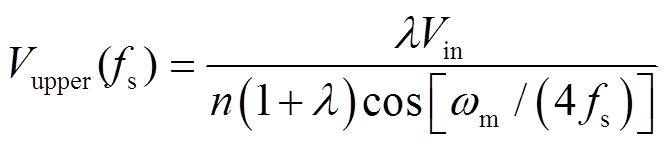 (8)
(8)当负载电压E达到或超过Vupper(fs)时,整流二极管反向截止,变换器输出功率为零,能量将不能正向传输。
在ZVS下边界处,变换器输出软开关运行状态下的最小电压。当负载电压E小于该边界电压时,谐振电流ir先于谐振腔输入电压vAB过零,变换器失去软开关特性,进入容性工作区。
与图2所示的理想工作状态不同的是,在下边界处,t1时刻Lm、Lr和Cr串联谐振,t2时刻前励磁电感被输出电压箝位,使本该在t2时刻导通的VD6、VD7桥臂提前导通续流,变换器进入Lr和Cr的串联谐振状态,谐振电流ir不再与励磁电流iLm相等,且ir在t2时刻过零。t1时刻变换器的等效电路如图5所示。
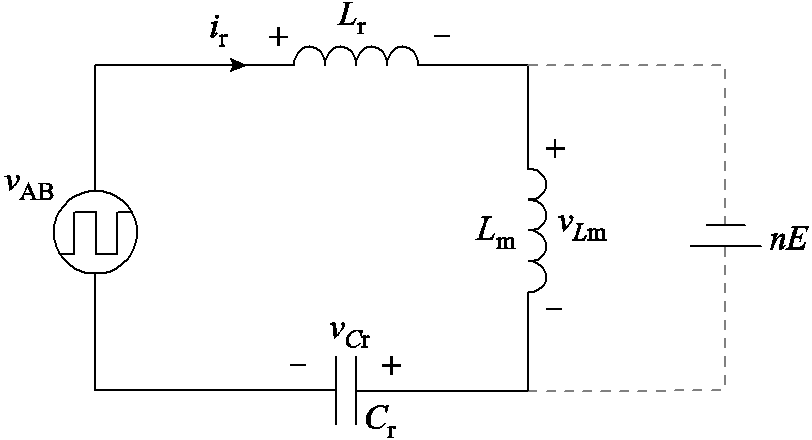
图5 t1时刻下边界的等效电路
Fig.5 The equivalent circuit on the lower boundary at t1
若使用时域分析法对下边界处的各模态列微分方程,则会因为Lm、Lr和Cr三元件串联谐振状态的存在而无法得到输出电压的解析解[2,10]。因此,在下边界输出电压的计算过程中,需要采取一定近似处理。故对时间段[t1, t2]内的电流做近似处理,将t2时刻的谐振电流ir近似为0;认为谐振电流ir和励磁电流iLm在[t1, t2]时间段内线性变化,并认为vLm在t1时刻约等于-nETr/Ts,忽略死区时间的影响。开关频率fs下的理想化波形如图6所示。
在t1时刻,根据图5和KVL,有
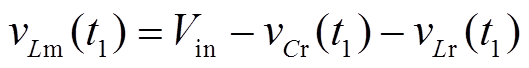 (9)
(9)其中
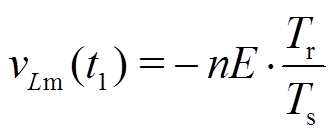 (10)
(10)
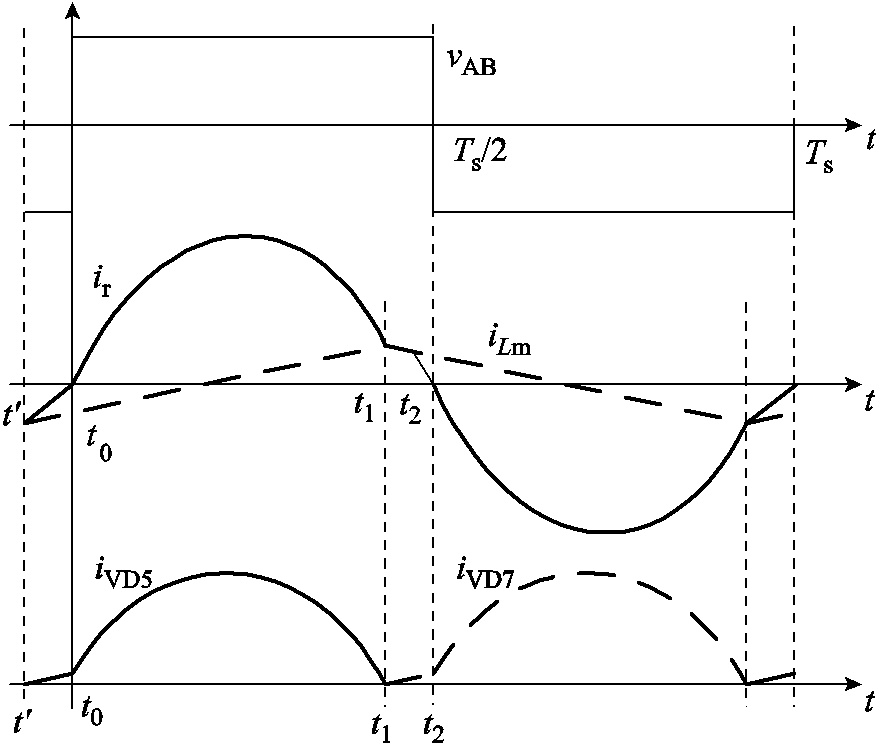
图6 下边界处的理想化波形
Fig.6 The ideal waveforms on the lower boundary
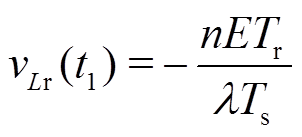 (11)
(11)稳态条件下,有
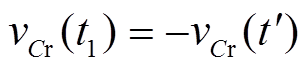 (12)
(12)
在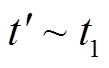 这段时间内,电容电压变化量约为
这段时间内,电容电压变化量约为
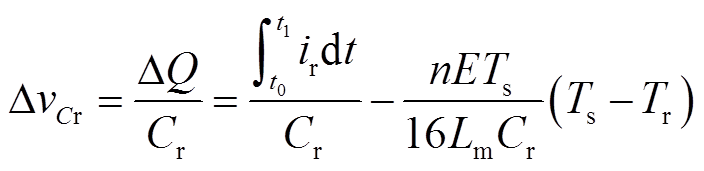 (13)
(13)故由式(12)和式(13),t1时刻的电容电压计算式为
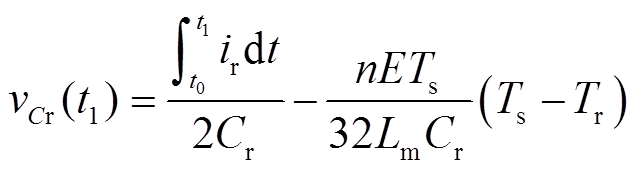 (14)
(14)
稳态条件下,根据功率守恒有
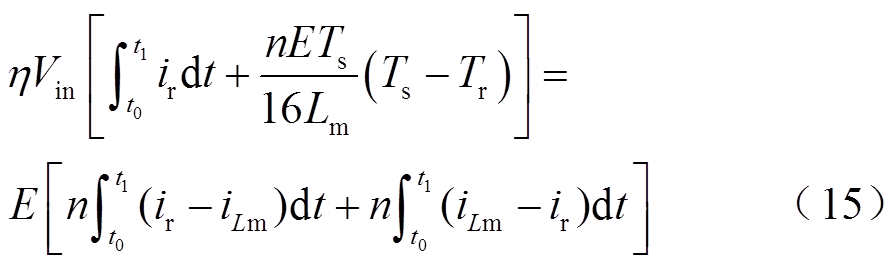
这里η为变换器效率,式(15)可进一步化简为
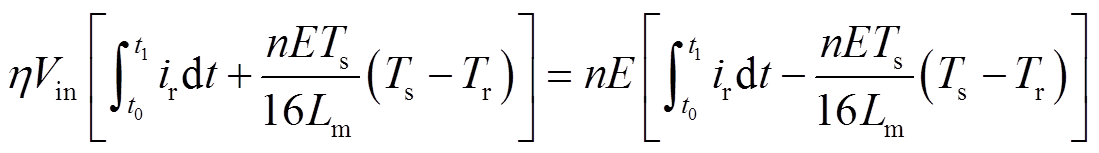 (16)
(16)
联立式(9)~式(11)、式(14)和式(16),得到关于nE的一元二次方程为
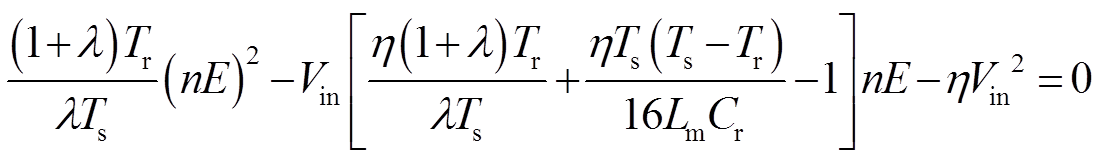 (17)
(17)其中
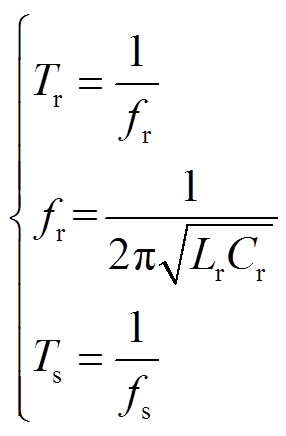 (18)
(18)
则式(17)可以写成
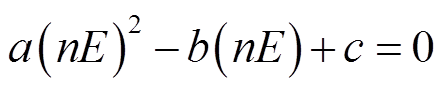 (19)
(19)其中
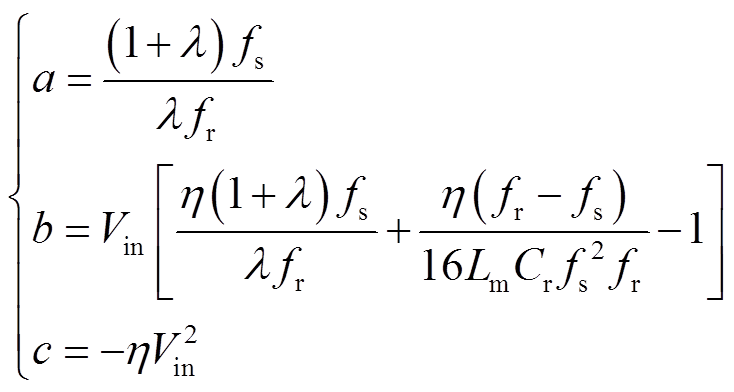 (20)
(20)
若完全忽略损耗,即认为η=1,则有
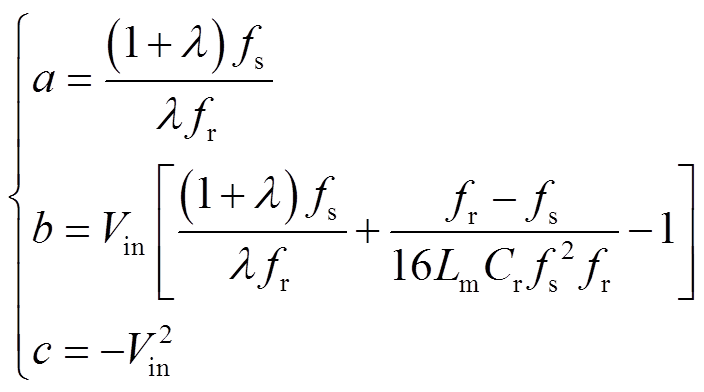 (21)
(21)求解式(19),可得变换器的ZVS下边界对应的输出电压vlower(fs)为
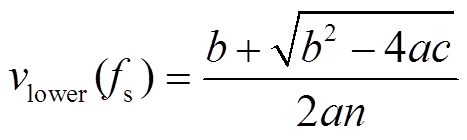 (22)
(22)
当负载电压E<Vlower(fs)时,变换器失去软开关特性,进入容性工作区。
本文基于Simulink搭建LLC谐振变换器仿真模型。仿真模型的主要参数见表1,其谐振频率fr为104.944 kHz,Lm、Lr、Cr串联谐振角频率ωm=246 177.4 rad/s。
表1 仿真模型的主要参数
Tab.1 Main parameters in simulation

参数数值 输入电压Vin/V48 谐振电容Cr/nF100 谐振电感Lr/μH23 励磁电感Lm/μH142 变压器电压比n1 二极管管压降/ V0.5
调整负载电压E使输出电流恰好减小到零,此时的E即为上边界输出电压Vupper(fs)。仿真中的 取80kHz,当输出电压E=57.6V时,变换器工作在上边界处。此时vCr(t)和ir(t)的仿真波形如图7所示,vCr(t)的峰值约为19V;当t=0时vCr(t)的值为0;ir(t)的峰值约为1.16A;当t=Ts/4时ir(t)的值为0;vCr(t)和ir(t)的周期与vAB相同,均为开关周期Ts。
取80kHz,当输出电压E=57.6V时,变换器工作在上边界处。此时vCr(t)和ir(t)的仿真波形如图7所示,vCr(t)的峰值约为19V;当t=0时vCr(t)的值为0;ir(t)的峰值约为1.16A;当t=Ts/4时ir(t)的值为0;vCr(t)和ir(t)的周期与vAB相同,均为开关周期Ts。
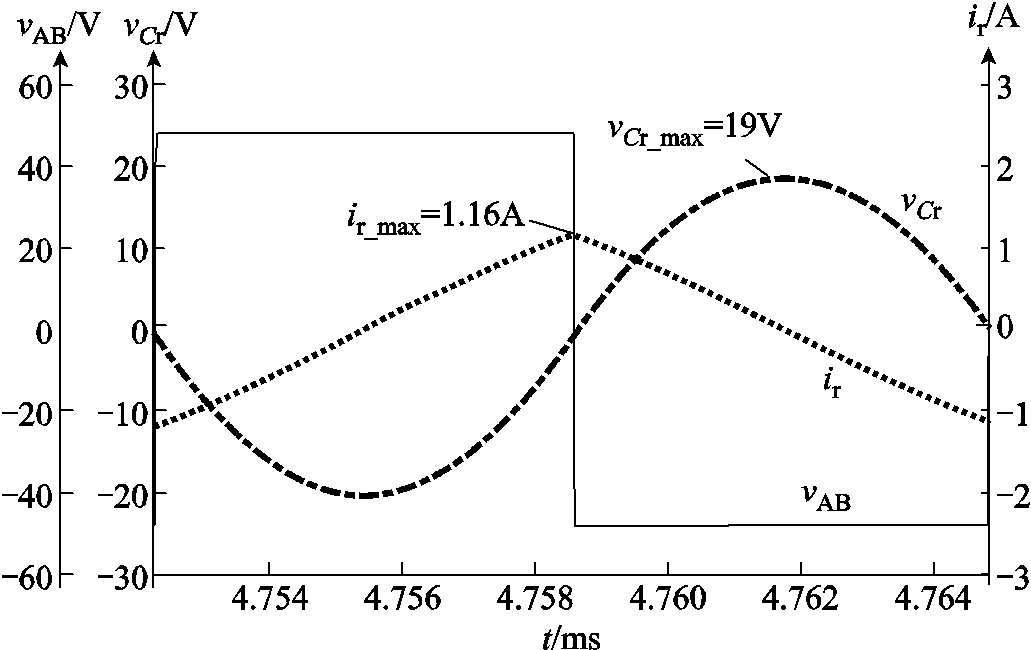
图7 上边界处vCr和ir的稳态波形(取fs=80kHz)
Fig.7 Steady-state waveforms of the capacitor voltage and the resonant current on the upper boundary (fs=80kHz)
根据式(8),当fs=80kHz时,Vupper(fs)的理论值为57.5V;根据式(2)和式(3),此时vCr(t)的峰值应为18.82V、周期为Ts,当t=0时,vCr(t)=0;ir(t)的峰值应为1.144A、周期为Ts,当t=Ts/4时,ir(t)=0。因此,上边界处仿真波形与理论分析一致。
当负载电压Vlower(fs) <E<Vupper(fs)时,变换器软开关运行,效率较高。随着E的减小,谐振电流峰值会逐渐增大,变换器的传输功率也逐渐增大。当E减小到Vlower(fs)时,变换器在软开关条件下的传输功率达到最大。
调整负载电压E使谐振电流在t2时刻恰好减小到零,此时的E即为下边界输出电压Vlower(fs)。仿真中的fs取80kHz,当输出电压E为52.7V时,变换器工作在下边界处。此时iLm(t)和ir(t)的仿真波形如图8所示,其中励磁电流iLm(t)的峰值约为1.1A,周期为Ts;谐振电流ir(t)在vAB反向时过零,下边界处仿真波形与理论分析一致。
本文基于试制的全桥LLC谐振变换器实验样机,验证理论分析的正确性。样机参数与仿真参数一致。实验平台如图9所示,其中,直流电压源作为直流输入,双向电源作为直流负载。
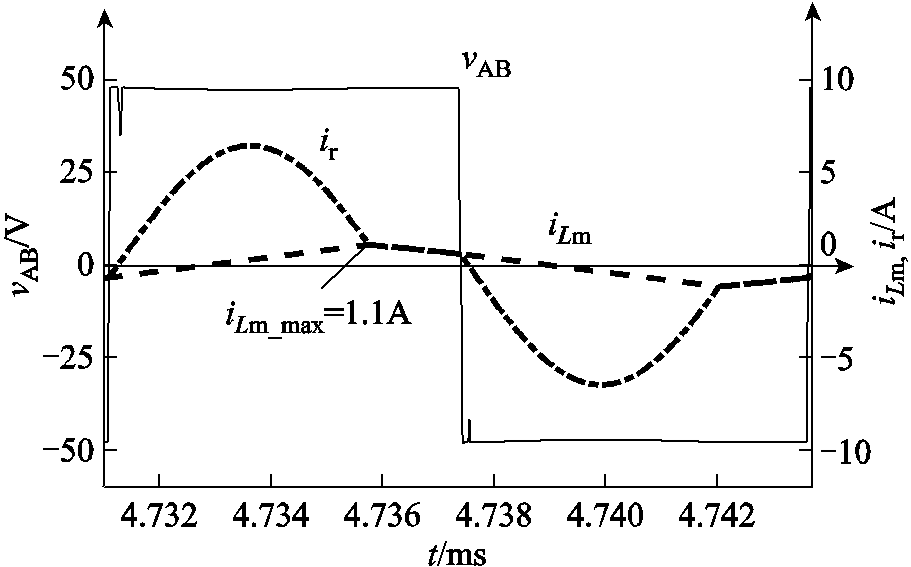
图8 下边界处iLm和ir波形(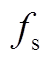 =80kHz)
=80kHz)
Fig.8 Waveforms of the resonant current ir and iLm on the lower boundary (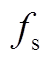 =80kHz)
=80kHz)

图9 实验平台
Fig.9 The photo of the experiment platform
调整负载电压E的大小,获取变换器在软开关边界处的工作波形。观察fs取80kHz时变换器上、下边界处的工作波形,分别如图10和图11所示。
从图10中可以看出,此时的vCr(t)的峰值约为19V,ir(t)的峰值约为1A,且二者的周期、相位均与理论和仿真一致。实验得到的80kHz处的上边界Vupper(fs)为57.5V,此时的谐振电流即将与励磁电流分离,二次侧整流二极管开始导通。实验结果与理论分析相符。
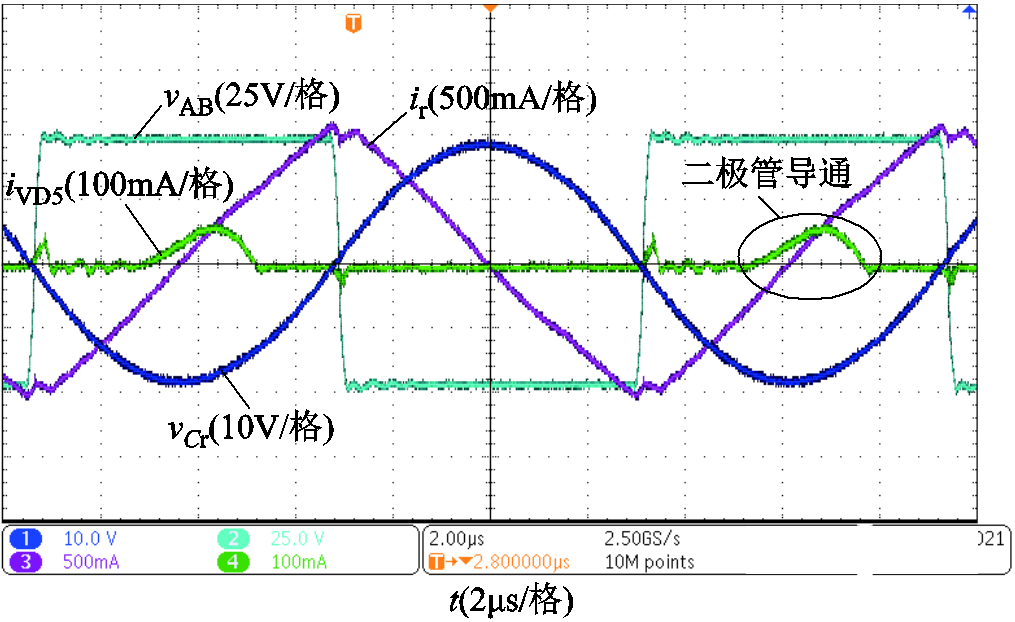
图10 上边界处vCr和ir的实验波形(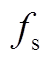 =80kHz)
=80kHz)
Fig.10 Experimental waveforms of the capacitor voltage and the resonant current on the upper boundary (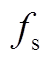 =80kHz)
=80kHz)
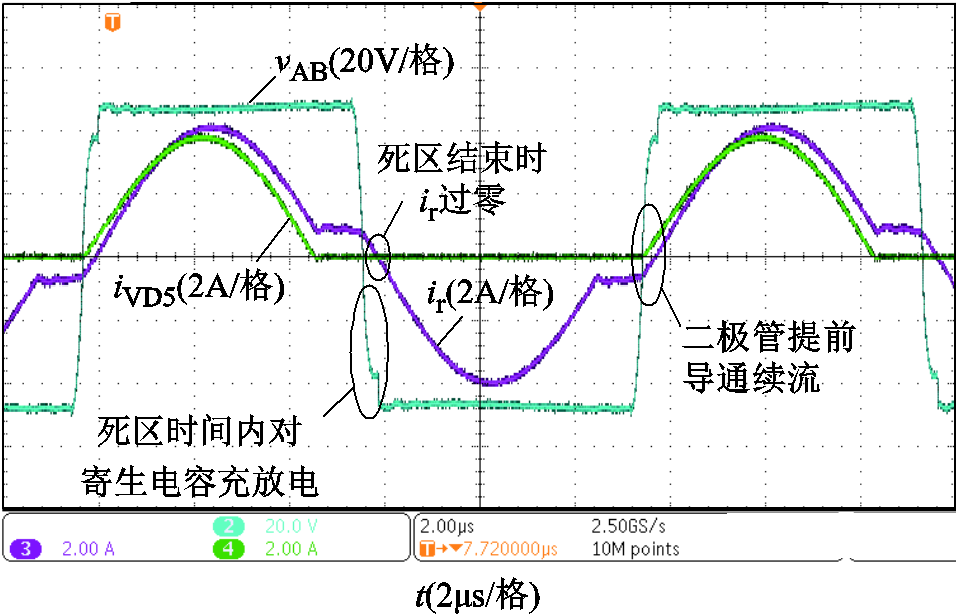
图11 下边界处vAB和ir实验波形(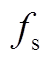 =85kHz)
=85kHz)
Fig.11 Experimental waveforms of the voltage vAB and the resonant current ir on the lower boundary (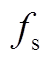 =85kHz)
=85kHz)
从图11中可以看出,下边界处,谐振电流在死区时间结束时过零,t2时刻开关管开通时寄生电容端电压接近0,此时变换器即将失去软开关特性。当负载电压E<Vlower(fs)时,死区时间内谐振电流无法使寄生电容充分放电,且谐振电流在过零后又反向为寄生电容充电,导致变换器失去软开关特性,在实际操作中应避免变换器进入此模态。实验得到的85kHz处的下边界数值为50V,与理论分析结果相吻合。
在仿真和实验中每隔5kHz获取一组数据,将不同开关频率下获取的边界输出电压与计算出的理论值相比较,分别如图12和图13所示。图12中的三条曲线几乎完全重合,图7、图10、图12能够证明上边界处理论分析的正确性。
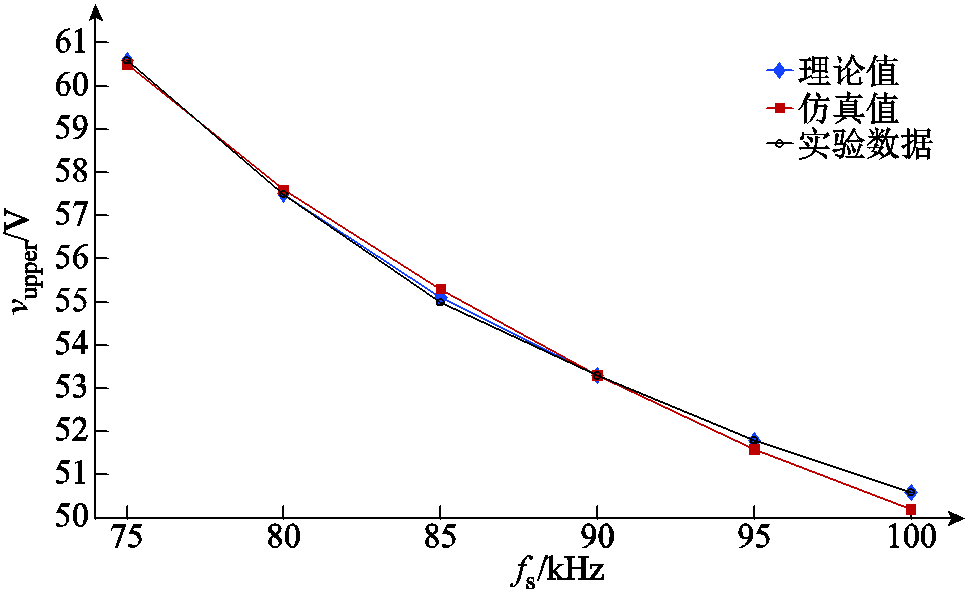
图12 上边界处输出电压理论值、仿真值与实验值
Fig.12 The theoretical, simulation and experimental value of the output voltage on the upper boundary
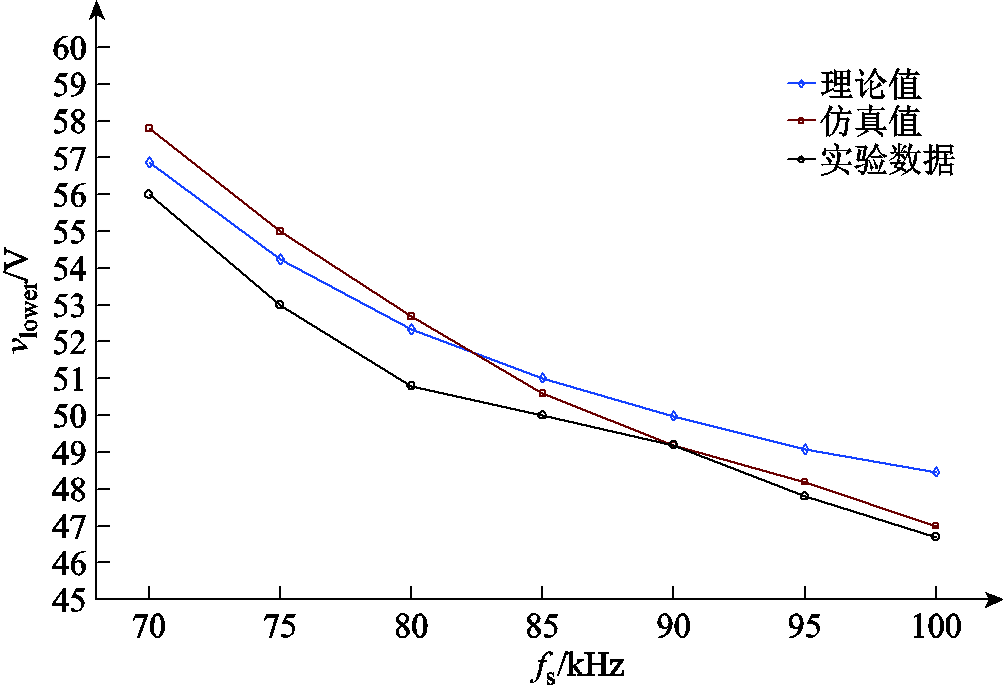
图13 下边界处输出电压理论值、仿真值与实验值
Fig.13 The theoretical, simulation and experimental value of the output voltage on the lower boundary
从图13中可以看出,下边界处的理论分具有一定精度。而理论分析产生误差的原因主要有:(1)分析过程中并未考虑损耗对输出电压的影响;(2)在式(13)、式(15)和式(16)的推导过程中,对t1~t2段的电流积分采用了近似计算;(3)当fs远小于fr时,t1~t2段的谐振电流不能再简单视作直线,vLm在t1时刻的值也不能近似为-nETr/Ts。仿真与实验结果能够证明下边界理论分析的正确性。
针对电动汽车直流充电功率模块宽输出电压范围、高转换效率的应用场合,本文利用时域分析法阐述了直流充电功率模块后级全桥LLC谐振变换器在ZVS区域边界处的工作状态,详细计算了变换器ZVS上、下边界对应的输出电压,确定了变换器ZVS运行所允许的输出电压范围,揭示了不同工况下变换器的软开关特性与工作频率、谐振参数之间的关系。在分析过程中,根据充电过程中电池端电压在短时间内基本不变这一特点,在等效电路中将电池等效为恒压源E。将变换器的软开关特性以输出电压范围的形式呈现,所得结果尤其适用于电池的充电场景,不仅可直观地判断LLC谐振变换器是否运行在软开关工况下,还可为变换器后续的参数设计和变频控制提供理论指导。
1. 对于参数已确定的LLC谐振变换器,在开关频率fs下(fm<fs<fr),当负载电压逐渐减小时,谐振电流峰值逐渐增大,死区时间内的谐振电流逐渐减小。
在实验中,开关频率fs取75kHz,仅改变负载电压E,且Vlower(fs)<E<Vupper(fs),记录变换器在不同负载电压下的谐振电流波形,如附图1所示。
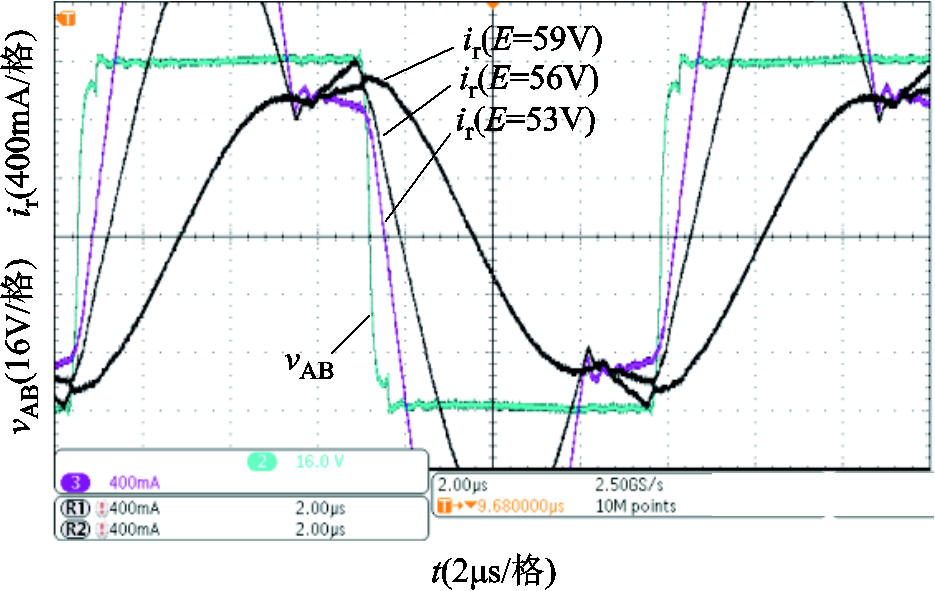
附图1 负载加重时谐振电流的变化过程
App.Fig.A1 The change process of resonant current when the load is heavier
因此,根据软开关的形成原因,空载(输出电流为0)时变换器最容易实现软开关,而重载时最难实现软开关,且空载时变换器一定能实现软开关,否则变换器在全负载范围内均不能实现软开关。因此,空载时变换器输出最大电压,对应上边界;重载时变换器输出软开关状态下的最小电压,对应下边界。
2. 式(15)和式(16)的具体推导过程
在半个开关周期内,谐振变换器的输入功率与谐振电流的积分成正比。在附图2中,S1+S2乘以Vin即为输入电压在半个开关周期内输出的有功功率;S3+S4乘以E即为负载在半个开关周期内吸收的有功功率。在计算过程中,将S2近似为直角三角形,且认为励磁电流峰值为nETs/(4Lm)。其中
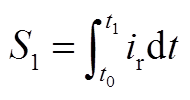 (A1)
(A1)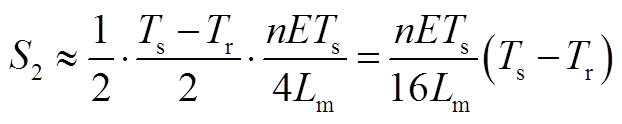 (A2)
(A2)
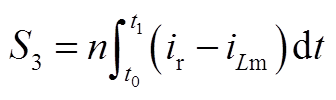 (A3)
(A3)
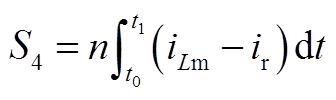 (A4)
(A4)记变换器的传输效率为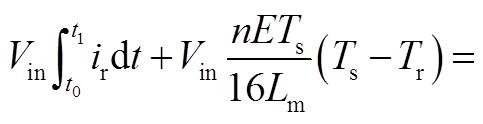
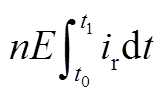 ,因此有
,因此有
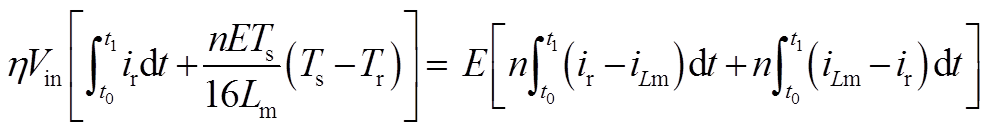 (A5)
(A5)
而
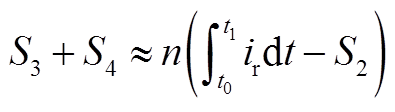 (A6)
(A6)故式(A5)即
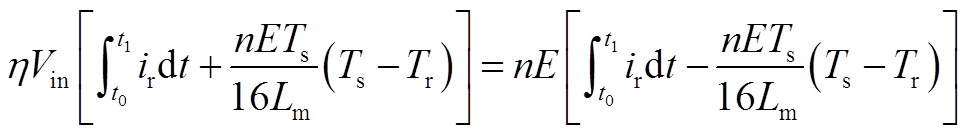 (A7)
(A7)
附图2 半个开关周期内变换器的功率传输情况
App.Fig.2 Power transmission of the converter in Ts/2
3. 通常可通过对比MOSFET栅源极电压与漏源极电压之间的关系来判断开关管是否工作在软开关状态。但通过观察谐振腔输入电压vAB在死区时间内的波形也可判断开关管是否为软开关,判断过程具体如下。
死区时间内变换器一次侧等效电路如附图3所示。在一次侧四个MOSFET均关断的情况下,vAB即为两下管寄生电容C2和C4的电压差。
附图3 死区时间内变换器一次侧的等效电路
App.Fig.3 Equivalent circuit of converter's primary side in dead time
若死区时间结束时vAB的值为+Vin,则C2两端电压vC2为Vin而C4两端电压vC4为0,此时对S4(以及S1)进行开通即为零电压开通。同理,若死区时间结束时vAB的值为-Vin,则C2两端电压vC2为0而C4两端电压vC4为Vin,此时对S2(以及S3)进行开通即为零电压开通。
4. 当负载电压E小于下边界Vlower时,变换器将失去软开关特性。65kHz下变换器失去软开关特性时的工作波形如附图4所示。
可以看出,当E小于下边界Vlower时,谐振电流在死区时间内几乎无法再为寄生电容放电,且谐振电流在过零后又反向为寄生电容充电。在开关管开通时,其漏源电压仍为Vin,桥臂中点电压vAB的边沿将产生过冲与振荡,变换器失去软开关特性。在实际工程中应避免变换器进入此模态。
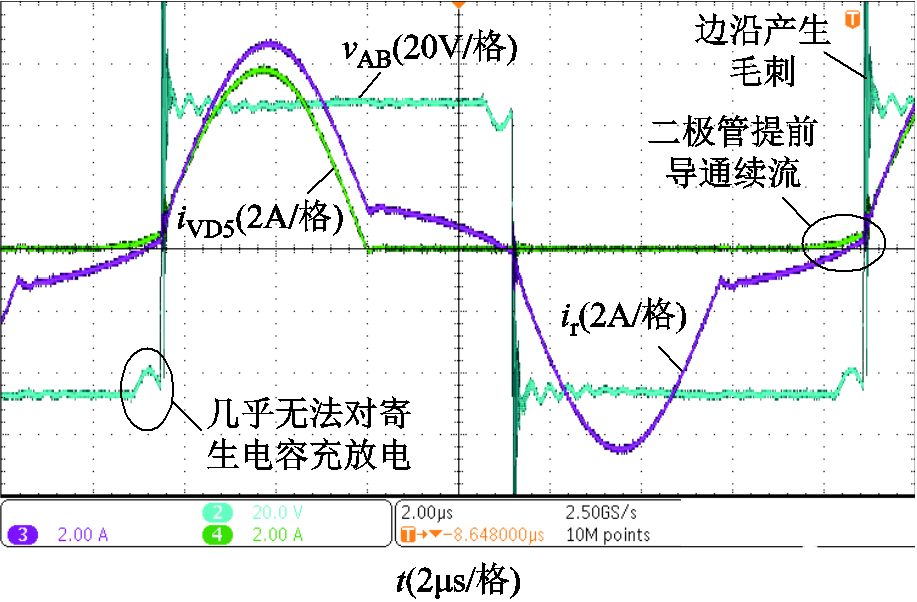
附图4 失去软开关特性时的工作波形(fs=65kHz)
App.Fig.4 The operating waveforms of the converter missing soft switching characteristics(fs=65kHz)
参考文献
[1] 郭康. 宽输出电压范围车载充电机的研究[D]. 哈尔滨:哈尔滨工业大学, 2018.
[2] 邓钧君. 用于电动汽车的车载充电机高效率谐振变换器研究[D]. 西安:西北工业大学, 2015.
[3] 张永泉. LLC变换器混合控制策略的计算机辅助设计研究[D]. 杭州:浙江大学, 2020.
[4] Wang Haoyu, Li Zhiqing. A PWM LLC type resonant converter adapted to wide output range in PEV charging applications[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 3791-3801.
[5] 陶文栋, 王玉斌, 张丰一, 等. 双向LLC谐振变换器的变频-移相控制方法[J]. 电工技术学报, 2018, 33(24): 5856-5863.
Tao Wendong, Wang Yubin, Zhang Fengyi,, et al. Pulse frequency modulation and phase shift combined control method for bidirectional LLC resonant converter[J]. Transactions of China Electro- technical Society, 2018, 33(24): 5856- 5863.
[6] Xiao Yudi, Mao Xingkui, Zhang Zhe, et al. New hybrid control for wide input full-bridge LLC resonant DC/DC converter[C]//2018 3rd International Conference on Intelligent Green Building and Smart Grid (IGBSG), IEEE, Yilan, China, 2018, DOI: 10.1109/IGBSG. 2018. 8393556.
[7] 吕正, 颜湘武, 孙磊. 基于变频-移相混合控制的L-LLC谐振双向DC-DC变换器[J]. 电工技术学报, 2017, 32(4): 12-24.
Lü Zheng, Yan Xiangwu, Sun Lei. A L-LLC resonant bidirectional DC-DC converter based on hybrid control of variable frequency and phase shift[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 12-24.
[8] 石林, 刘邦银, 段善旭. 一种基于Burst-PWM混合控制的LLC谐振变换器宽电压范围输出策略[J]. 电工技术学报, 2019, 34(22): 4772-4780.
Shi Lin, Liu Bangyin, Duan Shanxu. A burst-PWM hybrid control method for wide output voltage range of LLC converter[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4772-4780.
[9] 吕清松, 许宜申, 倪兆麟, 等. 基于半桥LLC谐振的AC-DC变换器研究与设计[J]. 电气技术, 2019, 20(10): 35-40.
Lv Qingsong, Xu Yishen, Ni Zhaolin, et al. Research and design half-bridge LLC resonant for AC-DC converter[J]. Electrical Engineering, 2019, 20(10): 35-40.
[10] 郭兵, 张一鸣, 张加林, 等. 基于直接移相角控制的移相全桥LLC变换器混合控制策略[J]. 电工技术学报, 2018, 33(19): 4583-4593.
Guo Bing, Zhang Yiming, Zhang Jialin, et al. Hybrid control strategy of phase-shifted full-bridge LLC converter based on digital direct phase-shift control[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4583-4593.
[11] 刘晓东, 董保成, 吴慧辉, 等. 基于并联变压器切换的LLC谐振变换器宽范围效率优化控制策略[J]. 电工技术学报, 2020, 35(14): 3018- 3029.
Liu Xiaodong, Dong Baocheng, Wu Huihui, et al. Wide range efficiency optimization control strategy for LLC resonant converter based on parallel transformer switching[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 3018-3029.
[12] 林辉品. 宽范围LLC谐振变换器的研究[D]. 杭州:浙江大学, 2019.
[13] 夏天. 双移相控制谐振变换器研究[D]. 南京:南京航空航天大学,2016.
[14] Ren Ren, Liu Bo, Jones E A , et al. Accurate ZVS boundary in high switching frequency LLC converter[C]// 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 2016, DOI: 10.1109/ECCE. 2016.7854813.
[15] Hu Sideng, Deng Junjun, Chris M, et al. Optimal design of line level control resonant converters in plug-in hybrid electric vehicle battery chargers[J]. Electrical Systems in Transportation, 2014, 4(1): 21-28.
[16] 向俊霖. 基于氮化镓晶体管的高频车载DC-DC变换器的研究[D]. 南京:南京航空航天大学, 2017.
[17] Rothmund D, Huber J E, Kolar J W. Operating behavior and design of the half-cycle discontinuous- conduction-mode series-resonant-converter with small DC link capacitors[C]// 2013 IEEE 14th Workshop on Control and Modeling for Power Electronics (COMPEL), IEEE,Salt Lake City, UT, USA, 2013: 1-9.
Analysis of Soft Switching Voltage Boundary of LLC Resonant Converter for EV DC Charging System
Abstract LLC resonant converter has been widely used in the field of DC charging for electric vehicles due to its excellent performance. Aiming at the charging requirements of electric vehicles with wide output voltage range and high efficiency, the output voltage boundary of the full bridge LLC resonant converter in DC charging module was analyzed in this paper. At the upper boundary of (zero voltage switching, ZVS), the magnetizing inductance of the transformer resonates, whose equivalent peak voltage of the secondary side is equal to the load voltage, and the rectifier diode conducts critically. And at the lower boundary of ZVS, the resonant current and the input voltage of the resonator cross zero at the same time, and the converter runs in the critical inductive region. In this paper, the working state at the ZVS upper and lower boundaries of the converter was analyzed in detail by the time-domain analysis method. The output voltage range of the converter operated in the soft switching state was calculated, and the relationship between the soft switching characteristics of the converter and the working frequency and resonance parameters was revealed, which could provide guidance for parameter design and frequency conversion control of the converter. Finally, the analytical method was verified by simulation and experiment platform.
keywords:LLC resonant converter, soft switch operation, output voltage boundary, zero voltage switching (ZVS), electric vehicles
DOI:10.19595/j.cnki.1000-6753.tces.211292
中图分类号:TM46
湖南省重点研发计划项目(2018GK2031)、汽车车身先进设计与制造国家重点实验室自主研究项目(71965005)、湖南省高层次人才聚集工程(项目编号2019RS1016)、国家111创新引智项目(B17016)和长沙市优秀创新青年项目(KQ2009037)资助。
收稿日期 2021-08-15
改稿日期 2021-08-27
丁 超 男,1996年生,硕士研究生,主要研究方向为LLC谐振变换器拓扑及其控制策略。E-mail:dingchao@hnu.edu.cn
李 勇 男,1982年生,教授,博士生导师,主要研究方向为能源电力系统稳定性分析与控制、电能变换系统与装备、电能质量分析与控制等。E-mail:yongli@hnu.edu.cn(通信作者)
(编辑 郭丽军)