图1 功率循环试验平台
Fig.1 Power cycling test platform
摘要 通过器件的功率循环试验可建立寿命模型，如最常用的CIPS08公式，用来预测实际工况下的寿命情况。其中结温波动和结温最大值对键合线寿命的影响最大，但是在功率循环试验中往往需要同时调节负载电流大小和开通时间来达到相同的结温波动和结温最大值。为了进一步评估负载电流和开通时间这两个参数对键合线寿命的贡献，尤其是负载电流的影响机制，该文对650V/20A的TO封装IGBT器件在相同的结温波动和结温最大值，但在不同的负载电流大小和开通时间的组合条件下进行了功率循环试验。结果表明，不同的负载电流和开通时间组合对器件寿命有不可忽略的影响，电流增大会显著降低IGBT器件中键合线的寿命。为了解释试验出现的现象并揭示其作用机制，该文建立TO封装IGBT器件的电-热-力多物理场有限元模型，考虑铝键合线和表面金属层的弹塑性特性，分析电流影响键合线应力大小的机理。同时引入金属疲劳寿命模型，得到的仿真寿命趋势与试验结果相吻合。该文研究可为IGBT器件的精确模型建立和键合线疲劳寿命预测提供指导意义。
关键词：TO封装IGBT 功率循环测试 负载电流 精确有限元模型 寿命预测
绝缘栅双极型晶体管（Insulated Gate Bipolar Transistor, IGBT）器件已全面应用到新能源发电、柔性直流输电、电力机车牵引和电动汽车等领域[1-2]，在这些应用中，IGBT器件通常工作在严苛的运行环境中，可靠性面临严重的挑战，其健康管理和可靠性评估越来越受到学术界和工业界的关注[3-5]。功率循环试验是考核IGBT器件封装长期可靠性最重要的测试，通过加速老化的方法提前暴露可能的薄弱点[6]。研究器件在功率循环试验下的失效机理和寿命对实际工况下的器件寿命预测有重要意义[7]。
在20世纪90年代，LESIT的研究项目通过大量的功率循环试验，确定了影响IGBT器件寿命最重要的两个因素为结温波动DTj和最大结温Tjmax，得到了标准IGBT器件的寿命模型[8]。目前的很多产品手册（datasheet）中也仅给出功率循环寿命与结温波动DTj和最高结温Tjmax的关系曲线[9]，如上所述的简化模型可以合理地预测器件寿命，但对于负载电流导致器件键合线失效的机理尚未可知。在功率循环试验中，一般使用负载电流和开通时间这两个变量来控制结温波动DTj和最高结温Tjmax。不同的负载电流和开通时间的组合可以达到同样的结温波动DTj和最高结温Tjmax，按照上述的寿命模型，这些组合的寿命预测是一样的，具有一定的准确性，但只是统计学原理的展现，并没有从导致失效的物理原理进行分析，缺乏说服力。
从器件的失效机理来看，IGBT器件的封装结构通常由多层不同材料组成，在功率循环过程中各层不同材料之间的热膨胀系数不匹配产生的循环热应力是造成器件老化失效的主要原因。在IGBT器件的失效模式中，键合线的脱落是最容易发生的[10]，占到IGBT器件失效的70%左右[11]。键合线在功率循环作用下受到热应力的反复作用，产生疲劳现象，出现裂纹，裂纹生长甚至出现分层、空洞或气泡，并最终导致键合线的脱落[12]。其中结温波动DTj和最高结温Tjmax对热应力的产生有直接影响，但是负载电流和开通时间对寿命的贡献机理并不明确，两者对器件中键合线疲劳失效的影响无法定义，目前并没有相关文献对此进行过类似研究。因此，有必要研究功率循环试验中负载电流对IGBT器件中键合线处的失效机理。
为了研究负载电流和开通时间对键合线寿命的影响，本文首先对Infineon的650V/20A TO封装IGBT模块进行功率循环试验，为了保证在试验中结温波动DTj和最高结温Tjmax相同的情况下改变负载电流，需要同时改变负载电流和开通时间的组合。在不同电流大小和开通时间下研究负载电流对其失效寿命的影响作用，并建立了器件的电-热-力多物理场有限元模型，揭示器件内部的温度分布和应力分布规律，分析不同的电流大小和开通时间组合对键合线产生的应力差异和作用机理，深入探究负载电流对键合线寿命的影响，同时引入金属疲劳模型对键合线部分进行了寿命预测。该研究结果可以为TO封装的IGBT器件的精确建模和键合线疲劳寿命预测提供指导意义。
功率循环试验采用的待测器件为Infineon的650V/20A TO封装IGBT模块，功率循环试验平台如图1所示，功率循环试验原理如图2所示，相关的物理变量定义如下：Iload为负载电流，用于加热待测器件至指定结温；Isense为测量电流，用于间接法测量待测器件的结温，一般为负载电流的1/1 000[13]；VCE为集电极-发射极的电压降，分为负载电流下的压降VCE(L)（用于表征器件的老化状态）和测量电流下的压降VCE(S)（用于计算器件结温）；Tj为虚拟结温，通过小电流下饱和压降法即VCE(T)法测得[14]。在单次功率循环过程中，各变量变化如图3所示，ton为开通时间，即被测器件通过负载电流加热到指定结温的时间；toff为关断时间，即被测器件切断加热电流后，通过外部水冷使器件结温下降的时间；tcycle为单次功率循环的周期，为开通时间ton和关断时间toff的和，即tcycle=ton+toff。
图1 功率循环试验平台
Fig.1 Power cycling test platform
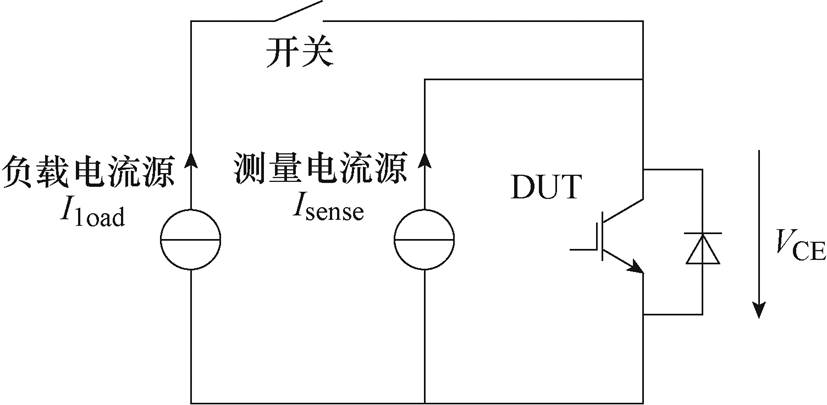
图2 功率循环试验原理
Fig.2 Schematic diagram of power cycling test
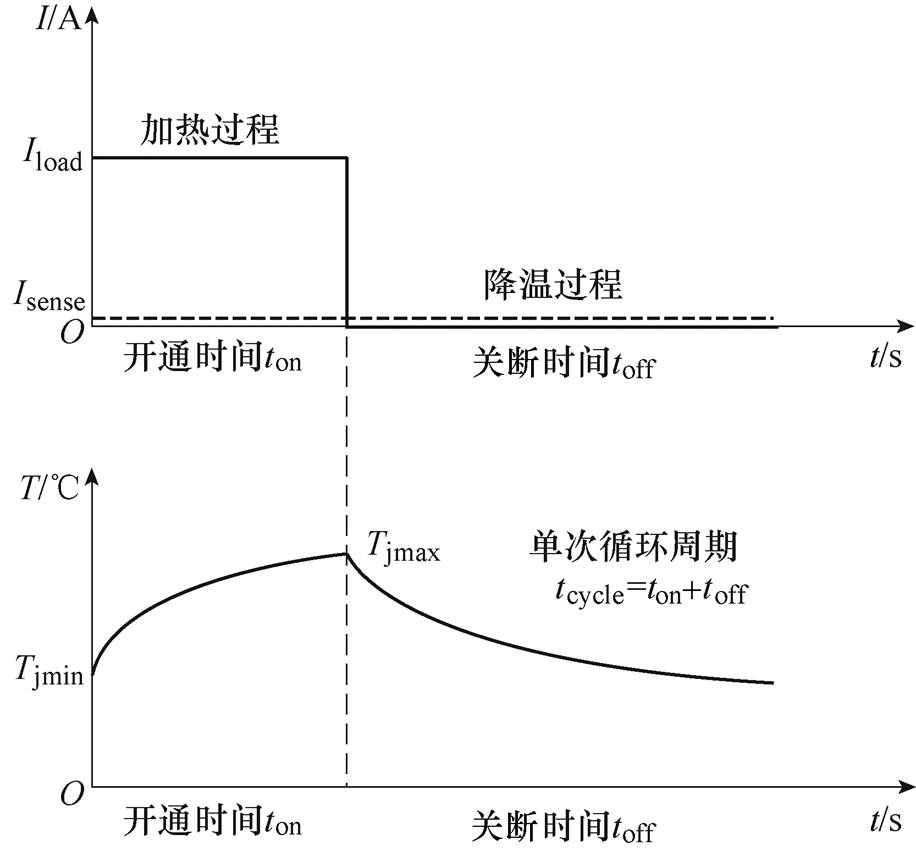
图3 单次循环变量变化
Fig.3 Variable variation diagram of single cycle
功率循环试验中各个物理变量的精确测量是试验成功的关键，每个功率循环周期均需要对被测器件在升温和降温过程中的物理变量进行测量，测量变量时序示意图如图4所示。测量点分别设置在负载电流开通瞬间的a和b点以及负载电流关断瞬间的c和d点，分别对应负载电流上升沿和下降沿的前后瞬间。其中a和b点是器件结温最低的状态，所以定义为冷却状态；而c和d点对应的状态则为器件结温最高的状态，定义为加热状态。在a和d点处测量电流Isense下的通态压降VCE(S)，可以通过VCE(T)法来计算最小和最大虚拟结温Tjmin和Tjmax，同时定义Tjm为被测器件在功率循环过程中的平均温度，即Tjm=(Tjmin+Tjmax)/2。b点处最低结温时负载电流下的通态压降VCE(cold)可以表征键合线的健康状态，记作VCE(L)。虽然通态压降VCE(L)还与温度相关，但是最低温度一般不随器件老化而升高，在整个功率循环的过程中几乎保持恒定。因此此处通态压降值仅受键合线健康状态的影响，当键合线发生老化，VCE(L)会增加。
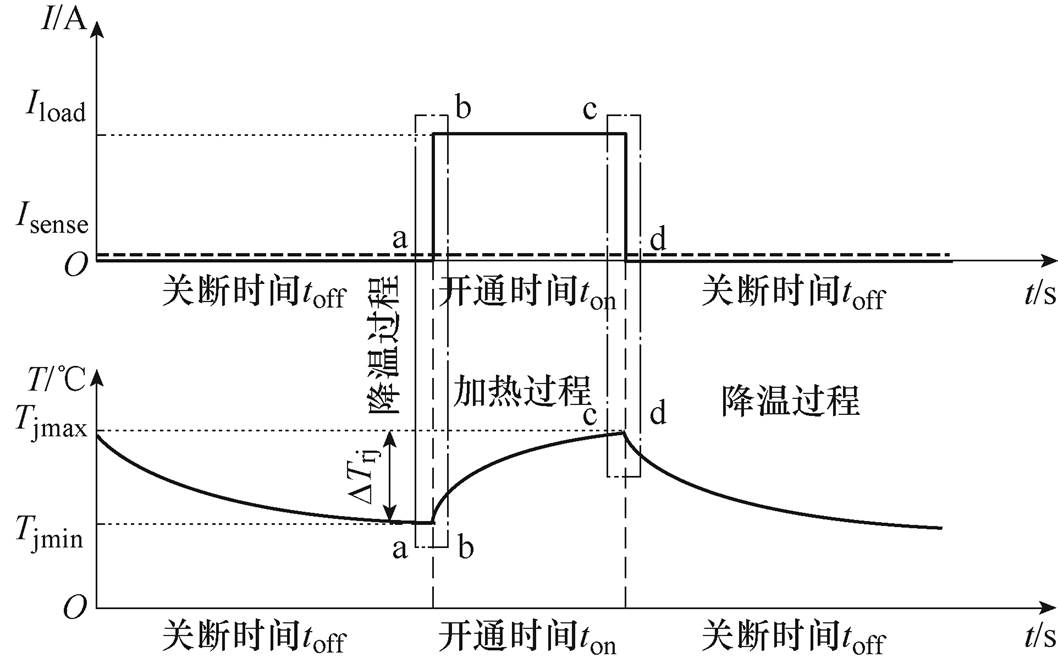
图4 测量变量时序示意图
Fig.4 Schematic diagram of parameters measured
为了研究不同电流大小和开通时间组合对IGBT器件失效机理的影响，必须采用控制变量法，设计试验时需保证两组对比试验中结温波动DTj和最高结温Tjmax相同。键合线的失效过程包括裂纹的形成、裂纹的扩展和裂纹的断裂失效。其中裂纹的形成以及裂纹的扩展过程在整个失效过程中占比很高，决定了器件的寿命。为了在试验中有效加速老化进程，缩短试验时间，采用了分步试验的方法。在试验开始初期，两个被测器件均使用相同的较大结温波动DTj和最高结温Tjmax，试验条件见表1中Test 1，形成初始裂纹。需要实时在线监测两个被测器件VCE(L)的变化，当两者的VCE(L)均提高5%时，认为形成同等程度的初始裂纹。此后，通过改变负载电流Iload和开通时间ton的组合保证相同的结温波动DTj和最高结温Tjmax，让键合线进入裂纹扩展阶段，见表1中Test 2。将被测器件1的开通时间从2s缩短至0.15s，负载电流保持43A不变；将被测器件2的开通时间ton保持2s不变，负载电流从43A降低至23A，直到器件彻底失效。
表1 试验条件
Tab.1 Test conditions
试验阶段结温波动DTj/K负载电流Iload/A开通时间ton/s DUT-1Test 1100432 Test 240430.15 DUT-2Test 1100432 Test 240232
在两种不同试验条件下，功率循环试验中被测器件的通态压降VCE(L)的变化趋势如图5所示，其中负载电流下的压降VCE(L)已做归一化处理。图中，试验阶段Test 1区域中，第一段平直曲线内通态压降的突然跃升是由水冷系统短暂失效导致，并非老化造成，因此在恢复水冷系统后通态压降的变化又回到正常值。试验阶段Test 1中，两个被测器件在相同的初始试验条件下达到相同的疲劳程度，即VCE(L)均上升到相同标准，此时认为器件的键合线处形成了初始裂纹。可以看到，器件间也存在一定的差异性，裂纹形成的时间不完全一样，这是器件个体差异导致的。改变试验条件后，从图5试验结果的第二段中可以看出，被测器件1在43A、0.15s功率循环电流作用下，失效周期为20 098次循环，然后VCE(L)迅速上升至失效；被测器件2在23A、2s功率循环电流下，失效周期为38 450次循环，然后VCE(L)迅速上升，器件失效。在此过程中，VCE(L)的上升表明键合线处的裂纹发生扩展，最终键合线发生脱落，器件失效。两个被测器件的失效模式均为键合线失效，在第二阶段试验裂纹扩展的过程中，被测器件1的失效寿命明显小于器件2，说明在相同的结温波动DTj和最高结温Tjmax时，负载电流的增大会显著加速器件老化，且会加快键合线裂纹扩展的失效速度。
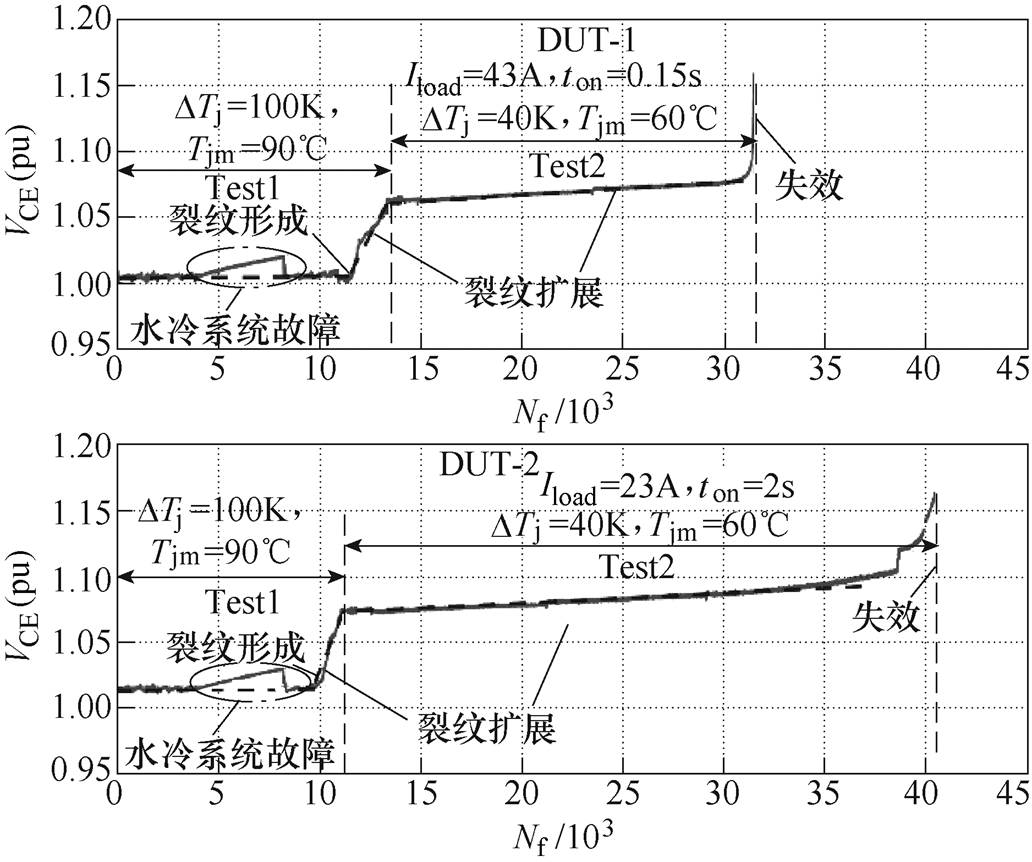
图5 功率循环试验结果
Fig.5 Results in power cycling test
键合线的失效主要是温度循环产生的热应力导致的，由于IGBT器件内部结构复杂，直接测量键合线的受力情况较为困难，使用三维有限元分析的方法可以解决模块内部热应力分布的难题。本文以TO封装的IGBT模块作为研究对象，建立三维的有限元模型如图6所示，分析该器件的电热力响应过程，器件模型的物理尺寸和材料参数见表2～表4。
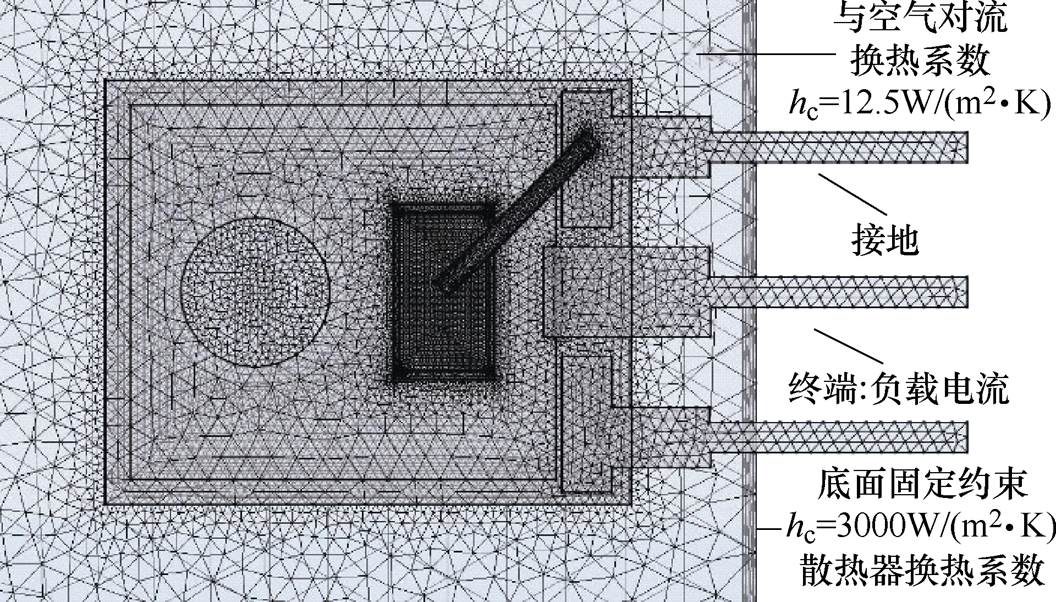
图6 TO模块的有限元模型
Fig.6 Finite element model of TO module
表2 TO模块物理尺寸
Tab.2 Geometry parameters of TO module
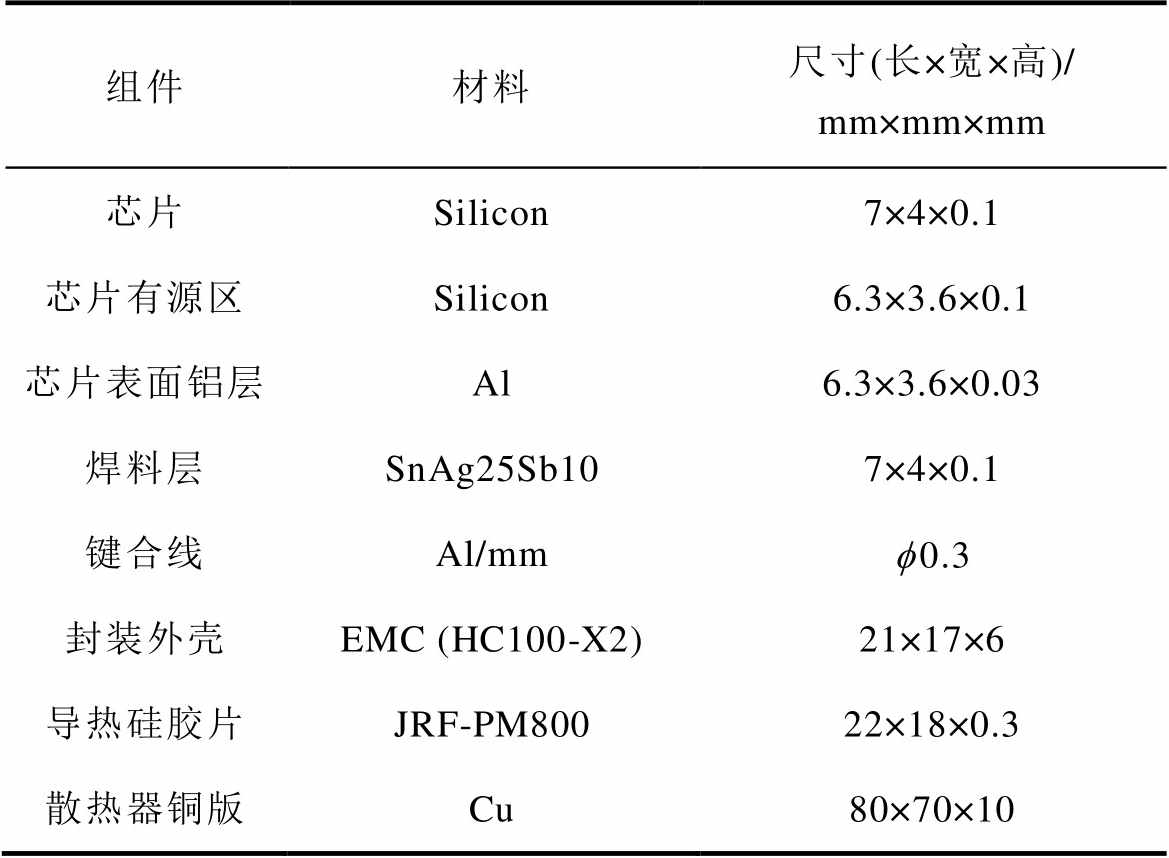
组件材料尺寸(长×宽×高)/mm×mm×mm 芯片Silicon7×4×0.1 芯片有源区Silicon6.3×3.6×0.1 芯片表面铝层Al6.3×3.6×0.03 焊料层SnAg25Sb107×4×0.1 键合线Al/mmf0.3 封装外壳EMC (HC100-X2)21×17×6 导热硅胶片JRF-PM80022×18×0.3 散热器铜版Cu80×70×10
表3 材料电热学参数
Tab.3 Thermal-electrical parameters of materials
材料导热系数/[W/(m·K)]热膨胀系数/(10-6/K)恒压热容/[J/(kg·K)]电导率/(S/m) 铜40017.53855.998×107 铝238239003.774×107 硅[15]1302.670020(导通) SnAg25Sb1055192197×107 EMC(HC100-X2)0.078201 20010-10 JRF-PM8008222 80010-10
表4 材料力学参数
Tab.4 Mechanical parameters of materials
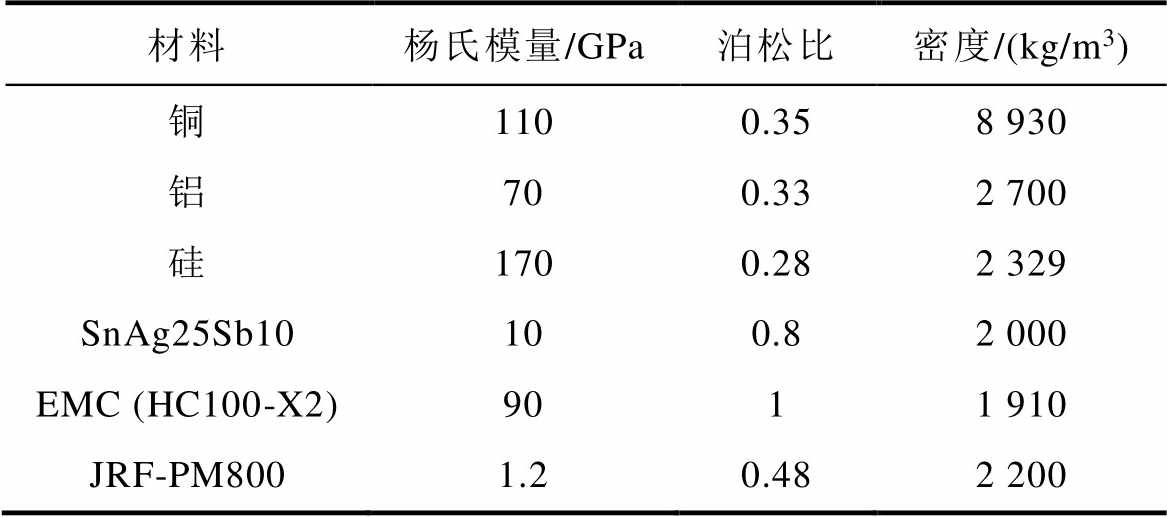
材料杨氏模量/GPa泊松比密度/(kg/m3) 铜1100.358 930 铝700.332 700 硅1700.282 329 SnAg25Sb10100.82 000 EMC (HC100-X2)9011 910 JRF-PM8001.20.482 200
为了有效地表征和反映器件键合线在循环热应力以及不同电流作用下的热应力分布情况，边界条件的设置参照试验条件。电学部分将集电极设置为电流源，发射极设置为接地，芯片有源区按照电阻处理；热学部分将散热器底面设置为对流换热模式，通过仿真得到的结温和试验测得的结温进行校准，确定对流传热系数为3 000W/(m2·K)，其余的表面设置为与空气的对流换热，对流传热系数为12.5W/(m2·K)，如图6所示；结构场中，由于IGBT模块是通过夹具固定在散热器上的，因此将底部的散热器进行固定约束。
为了讨论功率循环试验第二段中不同电流大小和开通时间组合对器件寿命的影响，设置两个对比条件，采用与试验类似的方法，通过同时改变负载电流Iload和开通时间ton来实现保持结温波动DTj和最高结温Tjmax不变，仿真条件设置见表5。仿真结果表明，在第4个开通冷却周期以后，功率循环达到准稳定状态，即每个周期的最高最低结温平均值相同，结温平均值的波动也相同，稳定后一个周期内的结温变化过程如图7所示。此时在第4个循环周期，开通0.15s之后最大结温在81℃左右，冷却1.85s之后结温降至42℃，结温波动在40℃左右。与本文第二段试验中结温波动为40℃、最大结温为80℃基本一致。
表5 仿真条件设置
Tab.5 simulation condition
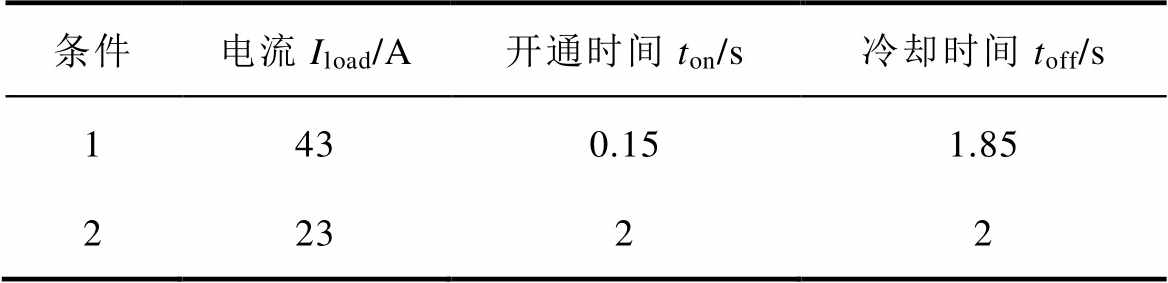
条件电流Iload/A开通时间ton/s冷却时间toff/s 1430.151.85 22322
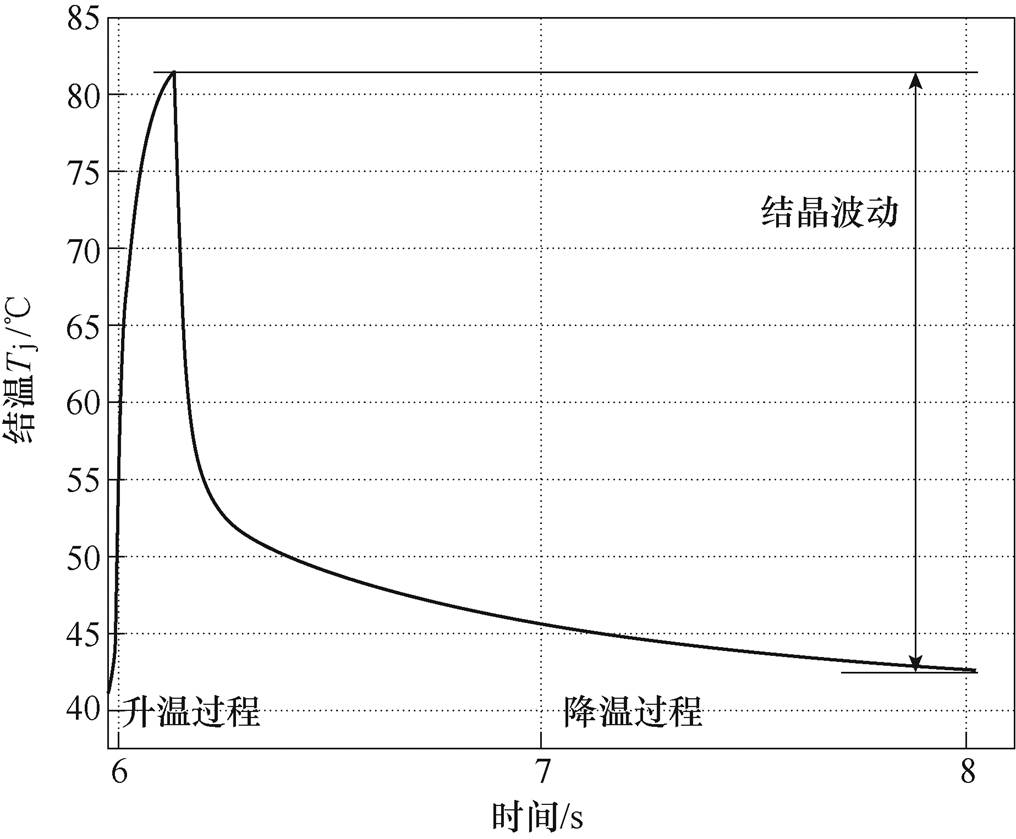
图7 温度波动的仿真结果
Fig.7 Simulation results of junction temperature swing
2.3.1 电热学特性
模型结构为电热力耦合，由于焦耳热的产生导致热膨胀，热膨胀的形变产生应力。根据传热学理论，热流在TO封装的IGBT模块内部的传递过程[16]可以描述为
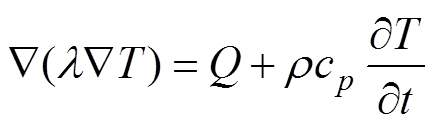（1）式中，l 为材料导热系数；r 为材料密度；cp为材料的比定压热容；Q为芯片的发热功率；T为模块内部温度分布；芯片的发热功率Q可以通过功率循环试验中测得芯片的VCE和负载电流Iload得到。
仿真条件1的热学仿真结果如图8所示，可以看出，芯片表面的温度分布存在温度梯度，中心的温度高于两侧。由于仿真条件1和2的负载电流大小不同，导致电流产生的焦耳热密度大小不同，进一步导致芯片表面存在不同的温度梯度，在功率循环瞬态仿真中，对比仿真条件1和2，提取芯片表面横向温度分布，提取路径如图8所示。
两种功率循环条件下的仿真结果见表6。根据图8中的温度提取路径，取仿真达到准稳定状态后，两个仿真条件下芯片平均温度均达到81℃左右，芯片表面温度梯度如图9所示。从图中可以看出，温度分布的趋势是一样的，但是存在一定程度上的差异：43A、0.15s电流的温度梯度比23A、2s更大。当选取相同的芯片平均温度Tj时，大电流43A和小开通时间0.15s产生的最高温度是96.06℃，小电流23A和大开通时间2s产生的最高温度是85.54℃，两者之间相差10℃（16%）之多。因此当在功率循环试验中选取相同的结温最大值和结温波动作为指标时，43A电流下的温度梯度比23A要大得多，43A负载电流在芯片中心所产生的最高温度也会更高。在高温环境时，由于铝材料的非线性特征，温度带来的热膨胀会更明显，与此同时产生的塑性应变也越明显。这时候只考虑平均温度的作用不再合适，最高温度的影响也需同时考虑。
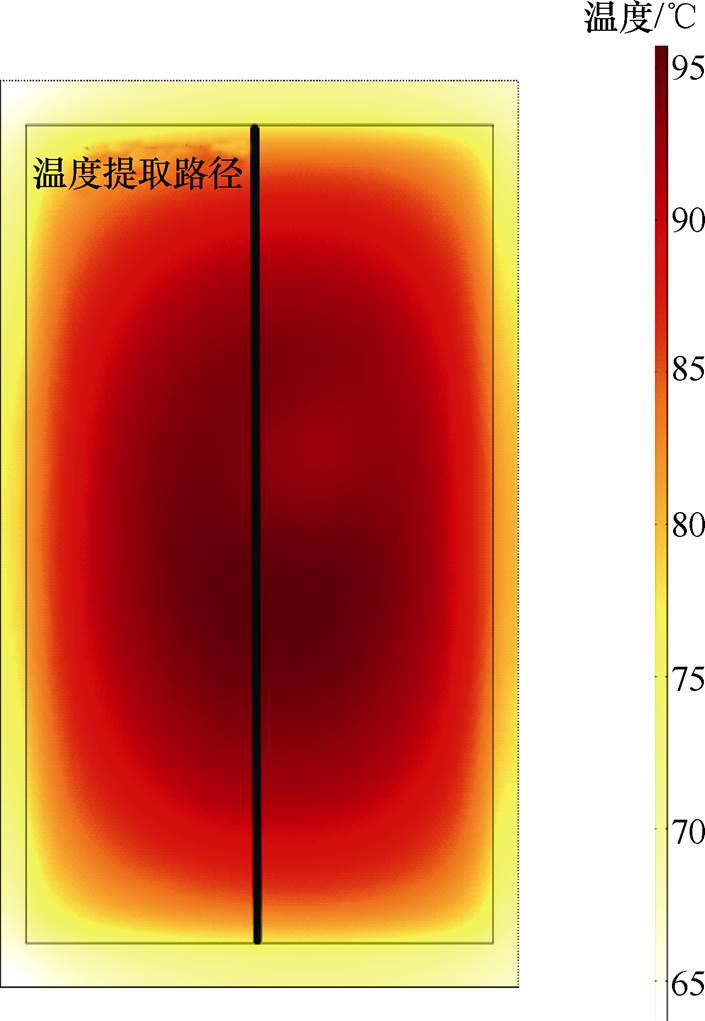
图8 芯片表面温度分布和温度提取路径
Fig.8 Temperature distribution and Extraction path of chip surface
表6 功率循环热学仿真结果
Tab.6 Thermal simulation results of power cycling
条件电流Iload/A开通时间ton/s结温波动DTj/℃芯片平均温度Tj/℃芯片最高温度Tmax/℃ 1430.1541.2381.2396.06 223241.8481.8485.54
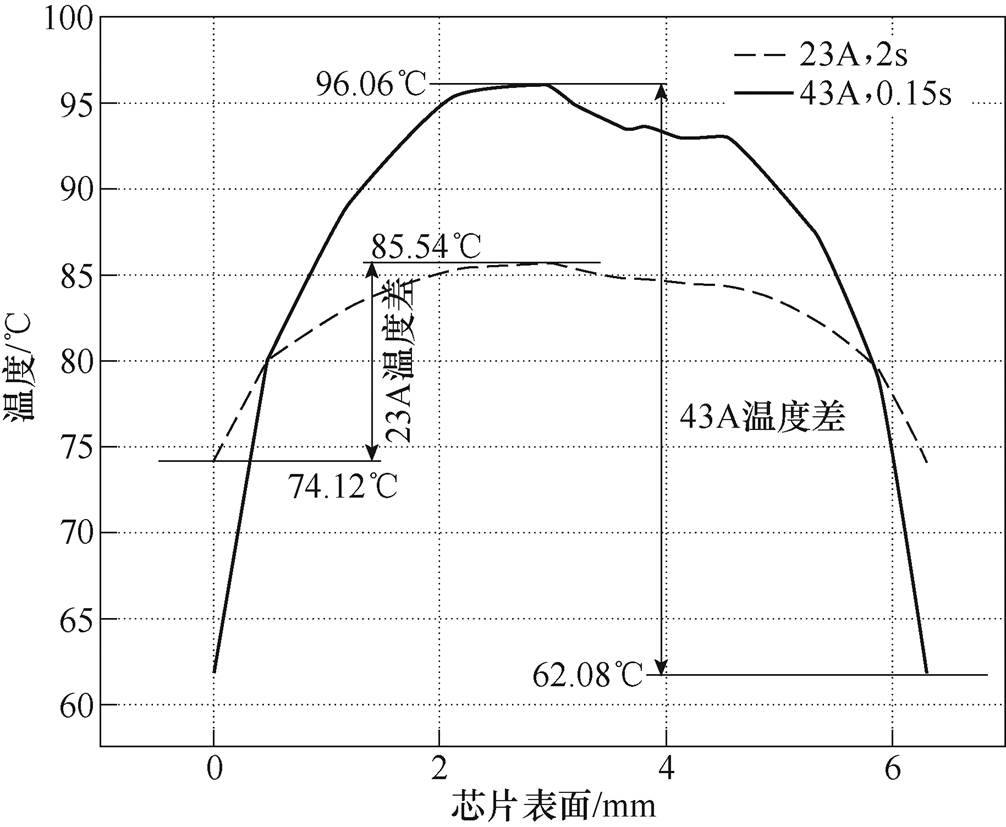
图9 芯片表面温度梯度
Fig.9 Temperature gradient of chip surface
2.3.2 力学特性
从功率循环试验的结果可知，器件失效发生在键合线处，所以在力学部分主要考察键合线的应力大小和分布情况。键合线应力分布如图10所示。应力最大的地方出现在键合线键角处，该点由于结构的固有原因导致应力集中，同时由于芯片表面存在上文描述的温度梯度，该点的温度明显高于周围区域，热膨胀程度明显，产生的应力也最大。在老化失效过程中，应力最大的地方贡献最大，为主要失效点，因此重点关注。
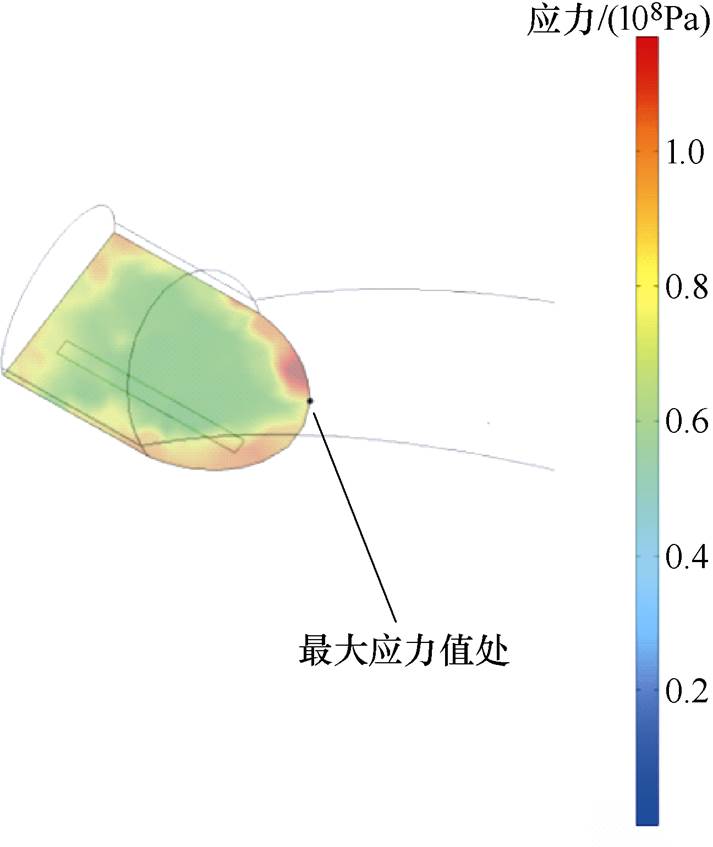
图10 键合线应力分布
Fig.10 Stress distribution of bonding wire
同时注意到，键合线和芯片上铝层的材料属性均为非线性，其中，弹塑性材料中的应力应变本构关系对仿真的准确性尤为重要。在使用线性的材料属性时，仿真计算变得简单且易于收敛；使用非线性的材料属性时，非线性的引入导致计算量增大且收敛性减弱。文献[17]指出，在器件温度循环时，温度的加载足够大，会使键合线发生塑性形变。所以在仿真中为了模拟实际情况，需要对键合线部分采用弹塑性材料的模型，其余部分为了计算速度采用弹性材料。
为了描述高温环境时的金属材料受力特点和疲劳特性，需要重点考察塑性形变部分[18]。在固体力学中，描述材料的本构关系有全量理论和增量理论，在弹塑性材料中，增量理论更容易被接受，其中基于Levy-Mises流动法则，同时考虑塑性变形中的弹性变形部分，可以得到应力应变本构方程为
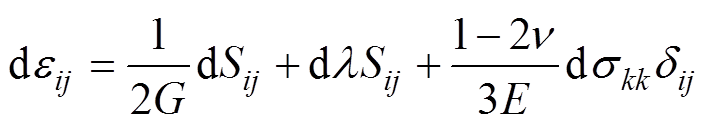（2）式中，eij为应变增量分量；Sij为应力增量分量；G为剪切模量；dl 为瞬时非负比例系数；n 为泊松比；E为杨氏模量；skk为该方向的应力；dij为克罗内尔符号。
文献[19]通过试验得到铝材料的精确应力应变本构关系，在仿真中直接使用这种关系会使仿真变得十分复杂，收敛性和计算速度都会下降。在仿真中通过分段线性的方式近似表达材料的应力应变关系。采用双线型模型表达弹塑性，在保证精确性的同时又兼顾了计算速度[20]，铝材料的双线型模型如图11所示，需要设置弹性范围内的杨氏模量为64.4GPa、双线型本构参数屈服强度为78.41MPa和塑性范围内的剪切模量0.62GPa。
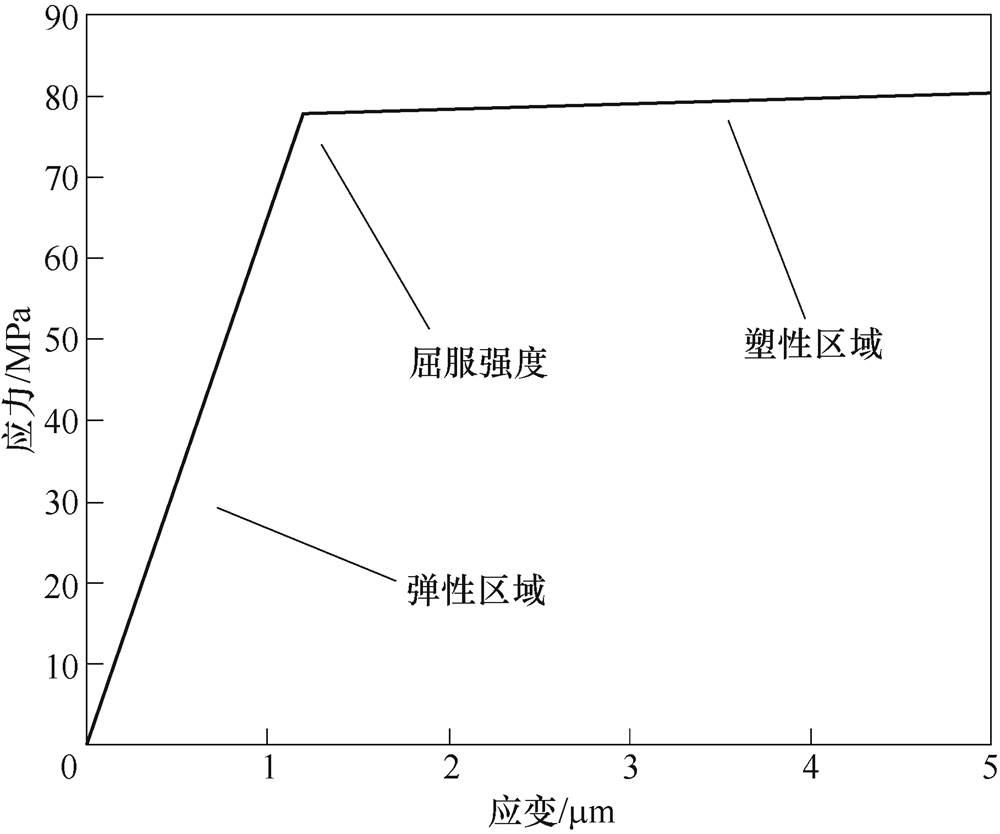
图11 铝材料的双线型模型
Fig.11 Bilinear model of aluminum
对比两种模型的仿真速度，在相同的边界条件下，双线型模型的计算时间为1 300s，常数模型的计算时间为65s。不同本构关系的仿真结果见表7，分别对比1、2和3、4，均可以得出，在芯片平均温度一样时，更大的负载电流会产生更大的应力。正是由于芯片温度梯度的存在，使得键合线键角处的应变应力不仅与芯片平均温度Tj相关，而且与温度梯度形成的最高温度有关。分别对比1、3和2、4，均可以得到在仿真条件相同时，双线型模型比常数本构关系的应力结果更大。对比2和4，在改变本构关系后最大应力上升了7.8%；对比1和3，在改变本构关系后最大应力上升了58.9%，远大于2和4之间的差距，即在更大的电流下芯片表面温度梯度更大，最高温度更大，所产生的热膨胀也越剧烈，同时由于金属材料进入塑性区域后的应力变化更明显，少量的温度升高就会带来明显的应力变化，同时所累积的塑性应变也更多。为了准确描述芯片最高温度对结构的影响，虽然会花费更多计算时间，但是用双线型模型替代常数模型是有必要的。
表7 不同本构关系的仿真结果
Tab.7 Simulation results of different constitutive relation
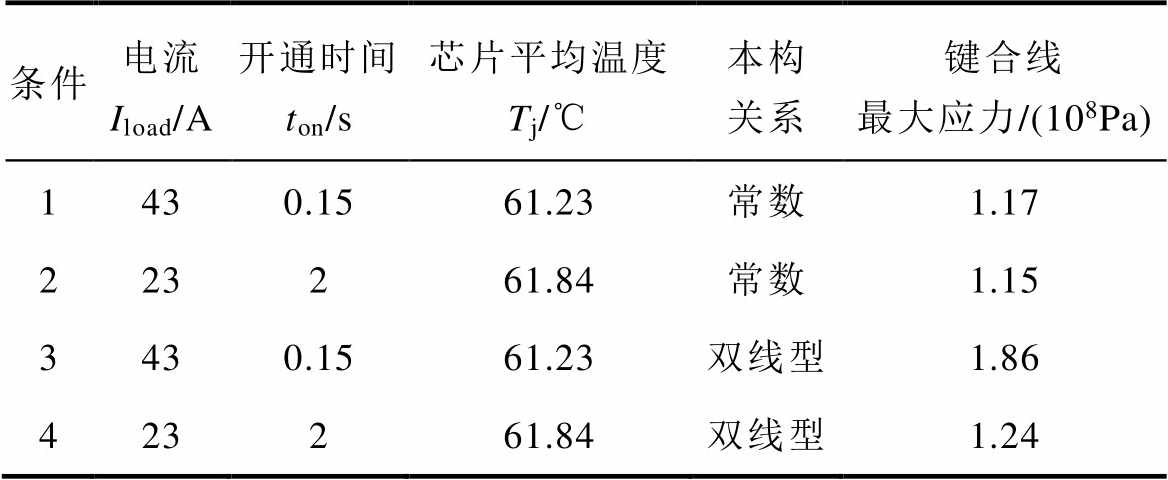
条件电流Iload/A开通时间ton/s芯片平均温度Tj/℃本构关系键合线最大应力/(108Pa) 1430.1561.23常数1.17 223261.84常数1.15 3430.1561.23双线型1.86 423261.84双线型1.24
2.4.1 疲劳寿命预测模型
为了更好地量化电流大小对器件寿命的影响，在得到器件的应力应变分布后，通过引入疲劳模型给出对应的失效周期。从失效的键合线来看，金属材料在高循环应力作用下会产生塑性应变[21]，塑性应变会导致金属永久变形或者出现断裂，进而发生疲劳失效，此种失效模式被称为“应变疲劳”。对于金属应变疲劳来说，最为经典的是Coffin-Mason模型。Coffin等[22]、S. S. Mason等[23]在20世纪50年代提出了经验性的低周循环应变寿命公式，使用材料的塑性应变作为参量。同时Morrow发现塑性应变不是唯一导致材料疲劳的变量，为了使寿命公式能反映实际工况，在Coffin-Mason公式中引入弹性形变的影响，同时运用了平均应力sm进行修正，得到
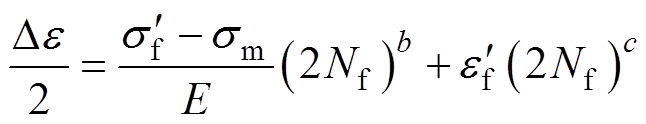（3）式中，De 为指应变范围；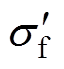
为疲劳强度系数；
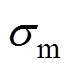为一个循环周期内的平均应力；Nf为失效循环次数；b为疲劳强度指数；
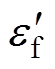为疲劳延性系数；c为疲劳延性指数。
对于特定的铝材料，文献[21]中提出了预测应变疲劳曲线的“通用斜率法”，得到通用表达式为
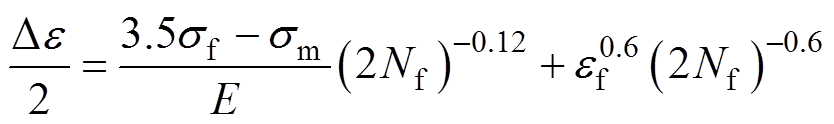（4）通过抗拉强度和断面收缩率来计算sf和ef[24]如式（5）、式（6）所示，并得到铝材料的疲劳寿命预测参数[25]见表8。
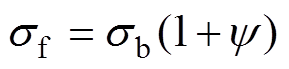（5）
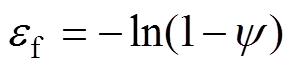（6）表8 铝材料疲劳寿命预测参数
Tab.8 Fatigue life prediction parameters of aluminum
材料抗拉强度sb/MPa断面吸收率y(%)断裂强度sf/MPa断裂延性er疲劳强度系数/MPa疲劳延性系数 铝5090952.30332.51.649
2.4.2 疲劳寿命仿真结果
在仿真中添加疲劳模型，选取键合线部分作为研究对象，取进入准稳态后一个周期的力学仿真结果代入到疲劳仿真中，对比两种功率循环仿真条件下的疲劳寿命，得到的循环失效周期见表9，同时得到键合线的疲劳寿命分布如图12所示。
表9 疲劳寿命仿真结果
Tab.9 Fatigue life prediction results
电流Iload/A开通时间ton/s失效循环次数Nf 430.1555 449 23279 382
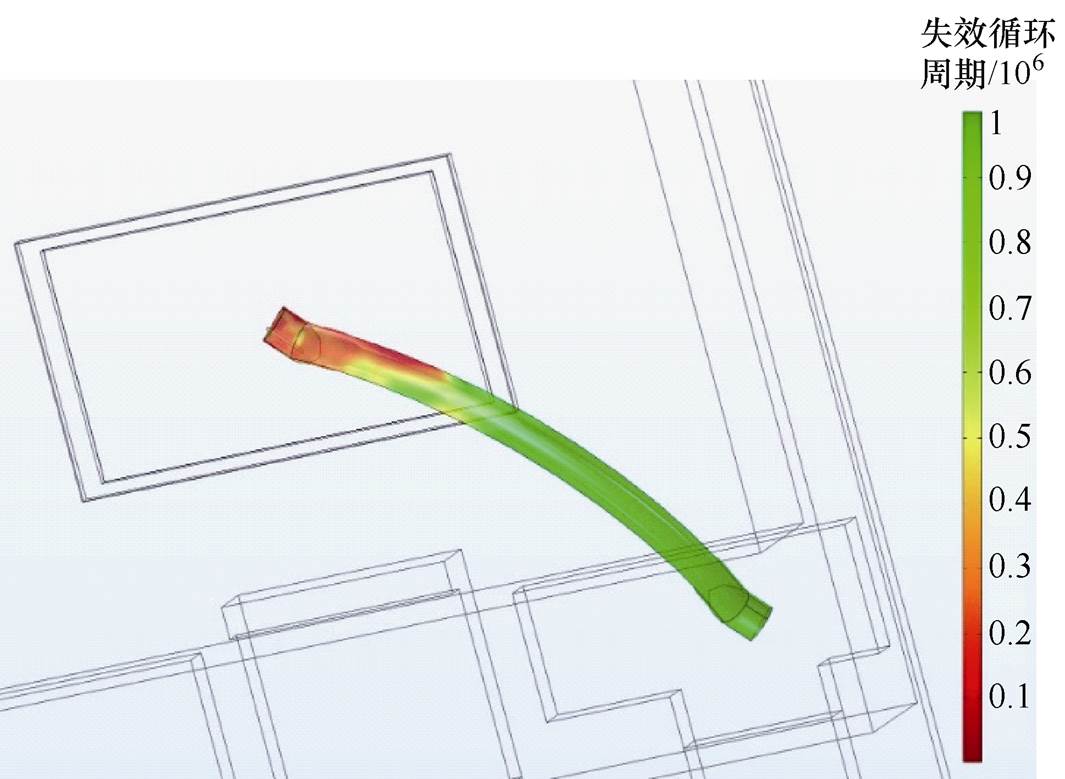
图12 键合线疲劳寿命分布
Fig.12 Fatigue life distribution of bonding wire
通过键合线疲劳寿命分布的仿真结果可以看出，键合线的寿命最小值出现在键角处，与应力最大值点对应，为器件的薄弱环节，最有可能首先发生失效。在表9的参数条件下，条件1（43A, 0.15s）的金属疲劳寿命是55 449；条件2（23A, 2s）的金属疲劳寿命是79 382，得到在功率循环条件下结温波动DTj和最高结温Tjmax相同时，由于键合线应变疲劳的作用，随着负载电流的增大，键合线的寿命有减小的趋势，与本文功率循环试验第二阶段的结果类似。通过电热分析可以看出，虽然器件在条件2下的焦耳热明显大于条件1，但是在大负载电流（条件1）作用下的器件芯片表面存在更大的温度梯度，即在相同的结温波动DTj和最高结温Tjmax时，芯片的最高温度与芯片平均温度Tj之间的差距更大。由于键合线的疲劳寿命主要受到应变作用的驱动，根据键合线金属材料的热膨胀特性，更高的温度可以得到更大的形变，在材料的弹性范围和塑性范围内，会产生更大的应变。在使用Coffin-Manson公式进行疲劳寿命预测时，更大的应变必然导致寿命减小。
本文通过功率循环试验和有限元仿真的方法研究了不同负载电流大小和开通时间组合对TO封装的IGBT器件失效机理的影响。试验中通过同时改变负载电流和开通时间（分别是43A，0.15s；23A，2s），保持结温波动DTj和最高结温Tjmax不变。本文得到的结论如下：
1）功率循环试验中，在相同最大结温波动DTj和最高结温Tjmax的条件下，存在多种负载电流和开通时间的组合。试验结果表明，负载电流越大，IGBT器件的键合线寿命越低。
2）TO模型的电热学仿真结果表明，在功率循环条件下，芯片表面存在温度梯度，即存在温度差。当负载电流增大，开通时间降低时，温度梯度会提高，即最高温度与平均温度的差距会增大；从力学和疲劳寿命模型可以看出，键合线的疲劳寿命分布与应力分布存在对应关系，键合线键脚区域是疲劳薄弱环节也是应力最大的区域。
3）功率循环试验中测得的结温波动DTj和最高结温Tjmax均为平均温度值，通过仿真结果可以看出，更大的负载电流会在芯片表面产生更大的温度梯度，出现比平均温度更高的温度从而提升最大应变应力，显著减小了键合线的疲劳寿命，与试验第二阶段的结果吻合，体现了负载电路对器件寿命的影响机制。
参考文献
[1] Choi U, Blaabjerg F, Munk-Nielsen S, et al. Con- dition monitoring of IGBT module for reliability improvement of power converters[J]. 2016 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Busan, 2016: 602- 607.
[2] Blaabjerg F, Chen Zhe, Kjaer S B. Power electronics as efficient interface in dispersed power generation systems[J]. IEEE Transactions on Power Electronics, 2004, 19(5): 1184-1194.
[3] GopiReddy L R, Tolbert L M, Ozpineci B. Power cycle testing of power switches: a literature survey[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2465-2473.
[4] 曾正, 欧开鸿, 吴义伯, 等. 车用双面散热功率模块的热-力协同设计[J]. 电工技术学报, 2020, 35(14): 3050-3064.
Zeng Zheng, Ou Kaihong, Wu Yibo, et al. Thermo- mechanical co-design of double sided cooling power module for electric vehicle application[J]. Transa- ctions of China Electrotechnical Society, 2020, 35 (14): 3050-3064.
[5] 吴理豪, 张波. 电动汽车静态无线充电技术研究综述(下篇)[J]. 电工技术学报, 2020, 35(8): 1662- 1678.
Wu Lihao, Zhang Bo. Overview of static wireless charging technology for electric vehicles: Part 2[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1662-1678.
[6] Smet V, Francois Forest, Jean-Jacques Huselstein, et al. Ageing and failure models of IGBT modules in high-temperature power cycling[J]. IEEE Transa- ctions on Industrial Electronics, 2011, 58(10): 4931- 4941.
[7] Held M, Jacob P, Nicoletti G, et al. Fast power cycling test of IGBT modules in traction app- lication[J]. Proceedings of Second International Conference on Power Electronics and Drive Systems, Singapore, 1997, 1: 425-430.
[8] Fuji Electric: Chapter 11 reliability of power module[EB/OL]. www.fujielectric.com, 2015.
[9] 邓二平, 陈杰, 赵雨山, 等. 90kW/3000A高压大功率IGBT器件功率循环测试装备研制[J]. 半导体技术, 2019, 44(3): 223-231.
Deng Erping, Chen Jie, Zhao Yushan, et al. Deve- lopment of 90kW/3000A power cycling equipment for high power and high voltage IGBT modules[J]. Semiconductor Technology, 2019, 44(3): 223-231.
[10] 邓二平, 张经纬, 李尧圣, 等. 焊接式IGBT模块与压接型IGBT器件可靠性差异分析[J]. 半导体技术, 2016, 41(11): 801-810, 815.
Deng Erping, Zhang Jingwei, Li Yaosheng, et al. Reliability difference analysis of wire-bond IGBT module and press-pack IGBT device[J]. Semicon- ductor Technology, 2016, 41(11): 801-810, 815.
[11] Wu Wuchen, Held M, Jacob P, et al. Investigation on the long term reliability of power IGBT modules[C]// Proceedings of International Symposium on Power Semiconductor Devices and IC's: ISPSD '95, Yokohama, Japan, 1995: 443-448.
[12] Hu Borong, Ortiz Gonzalez J, Li Ran, et al. Failure and reliability analysis of a SiC power module based on stress comparison to a Si device[J]. IEEE Transa- ctions on Device and Materials Reliability, 2017, 17(4): 727-737.
[13] Shabany Y. 传热学: 电力电子器件热管理[M]. 北京: 机械工业出版社, 2013.
[14] 赖伟, 陈民铀, 冉立, 等. 老化试验条件下的IGBT失效机理分析[J]. 中国电机工程学报, 2015, 35(20): 5293-5300.
Lai Wei, Chen Minyou, Ran Li, et al. Analysis of IGBT failure mechanism based on ageing experi- ments[J]. Proceedings of the CSEE, 2015, 35(20): 5293-5300.
[15] Chen Jie, Deng Erping, Xie Luhong, et al. Investig- ations on averaging mechanisms of virtual junction temperature determined by VCE (T) method for IGBTs[J]. IEEE Transactions on Electronic Devices, 2020, 67(3): 1106-1112.
[16] 贾英杰, 罗毅飞, 肖飞, 等. 一种符合欧姆定律的IGBT等效电阻模型[J]. 电工技术学报, 2020, 35(2): 310-317.
Jia Yingjie, Luo Yifei, Xiao Fei, et al. An equivalent electrical resistance model of IGBT suitable for Ohm’s law[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 310-317.
[17] Chidambaram N V. A numerical and experimental study of temperature cycle wire bond failure[C]// Proceedings 41st Electronic Components & Tech- nology Conference, Atlanta, GA, USA, 1991: 877- 882.
[18] Zahra S Hosseini, Mohsen Dadfarnia, Brian P Somerday, et al. On the theoretical modeling of fatigue crack growth[J]. Journal of the Mechanics and Physics of Solids, 2018, 121: 341-362.
[19] 张朝晖. ANSYS 12.0结构分析工程应用实例解析[M]. 3版. 北京: 机械工业出版社, 2010.
[20] 廖俊, 张毅刚. 焊接空心球节点荷载-位移曲线双线性模型研究[J]. 空间结构, 2010, 16(2): 31-38.
Liao Jun, Zhang Yigang. Study on bilinear model of load displacement curve of welded hollow spherical joints[J]. Spatial Structure, 2010, 16(2): 31-38.
[21] 王学梅, 张波, 吴海平. 基于失效物理的功率器件疲劳失效机理[J]. 电工技术学报, 2019, 34(4): 717- 727.
Wang Xuemei, Zhang Bo, Wu Haiping. A review of failure mechanism of power devices based on physics- of-failure[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 717-727.
[22] Coffin, Jr L F. A study of the effects of cyclic thermal stresses on a ductile metal[J]. Ryūmachi. [Rheumatism], 1953, 22(6): 419-606.
[23] Manson S S. Behavior of materials under conditions of thermal stress[J]. Technical Report Archive & Image Library, 1953, 7(s3-4): 661-665.
[24] Bathias C, Pineau A. Fatigue of materials and structures: fundamentals[M]. London: ISTE Ltd, 2010.
[25] 张经纬, 邓二平, 赵志斌, 等. 压接型IGBT器件单芯片子模组疲劳失效的仿真[J]. 电工技术学报, 2018, 33(18): 4277-4285.
Zhang Jingwei, Deng Erping, Zhao Zhibin, et al. Simulation study on fatigue failure of single IGBT chip module of press-pack IGBTs[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4277- 4285.
The Influence and Failure Mechanism Analysis of the Load Current on the IGBT Lifetime with Bond Wire Failure
Abstract Through the power cycle experiment of the device, a life model can be established. For example, the CIPS08 formula is often used to predict the life condition under actual working conditions. The maximum junction temperature and junction temperature fluctuation have the greatest impact on life. However, in the power cycling test, different combinations of load current and load pulse duration can achieve the same maximum junction temperature and junction temperature fluctuation. It reflects the strong coupling relationship of these four parameters. In order to further evaluate the contribution of load current and load pulse duration to the lifetime of bonding wire, in this paper, 650V/20A IGBT devices are tested under the combined conditions of the same maximum junction temperature and junction temperature fluctuation but different load current and load pulse duration. Meanwhile, the junction temperature and on-state voltage drop in each cycle are monitored in real time during the test. The results show that the load current has a significant effect on the lifetime of the IGBT device. Larger current will reduce the life of IGBT devices obviously. Furthermore, an electric-mechanical-thermal multi-physics finite element model of the TO package IGBT device is established, considering the elastic-plastic characteristics of the aluminum bonding wire and the surface metal layer. The mechanism of the current effect on the stress of the bonding wire is analyzed, and the fatigue model is introduced. Simulation results are consistent with the test results. This paper can provide guidance for the accurate modeling and the lifetime prediction of bonding wire in IGBT devices.
keywords：TO packaged IGBT, power cycling test, load current, accurate finite element model, lifetime prediction
DOI: 10.19595/j.cnki.1000-6753.tces.201056
中图分类号：TN322.8
国家自然科学基金资助项目（52007061）。
收稿日期 2020-08-19
改稿日期 2020-11-11
赵子轩 男，1996年生，硕士研究生，研究方向为IGBT器件老化失效机理和寿命评估。E-mail: 13520085253@163.com
邓二平 男，1989年生，博士，讲师，研究方向为高压大功率IGBT器件封装及可靠性。E-mail: dengerpinghit@163.com（通信作者）
（编辑 陈诚）