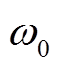不随等效电阻变化而变化的特点被广泛使用。本文以一个单发射，单接收串联谐振WPT系统为例进行研究。一种典型SS拓扑结构如图1所示，其中
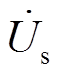为交流电压源，L1、L2和C1、C2分别为一次侧、二次侧谐振电感和电容，其共同构成整个系统的谐振网络，R1、R2为一次侧和二次侧线圈内阻，Req为系统等效电阻。线圈之间基于电磁感应方式电能传输，M为线圈之间的互感，耦合系数可用关系式
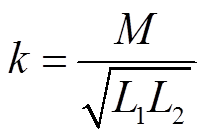表达。摘要 针对无线电能传输系统（WPT）中传输效率对耦合系数、负载变化敏感的特点，该文提出一种基于断续电流模式（DCM）有源阻抗匹配网络的最大效率跟踪方法。首先，分析不同DC-DC变换器输入阻抗表达式，证明了DCM模式Buck-Boost变换电路阻抗匹配的优越性。其次，给出了一种基于耦合系数辨识的最大效率跟踪控制策略，无需负载实时监测及进一步跟踪控制，即可在较大负载变化范围内使系统传输效率实现最大化并保持稳定；耦合系数变化时，系统也可根据发射接收侧电压电流信息实时辨识耦合系数并通过接收侧变换器占空比调节实现自适应最大效率跟踪。最后，利用实验验证了该方法的可行性和有效性，并且在动态响应、提高传输效率等方面有明显优势。
关键词：无线电能传输 最大效率跟踪 断续电流模式 阻抗匹配
磁耦合式无线电能传输（Wireless Power Transfer, WPT）技术基于电磁感应原理，实现从电源到负载无接触电能传输。相比传统有线电能传输方式，其具备安全、可靠及方便等特点，因此正受到越来越多的关注。如今，无线电能传输技术已经在国内外得到了非常广泛的研究，成功应用在电动汽车[1-4]、可植入式医疗设备[5]、无人机[6]、移动电子产品[7]和水下自主航行器[8]等多个领域。
在无线电能传输技术应用中，传输效率是评价系统性能最重要指标之一。在电动汽车等应用中，希望系统能工作在最大效率模式下，尽可能减小系统损耗，然而传输效率往往受限于耦合强度、参数特征及负载特性等因素，在系统运行期间跟踪最大效率相对困难[9]。很多文献已对此做了相关研究，其中阻抗匹配是效率跟踪最常用的方法。无源阻抗匹配使用电感、电容网络实现阻抗转换[10-13]，这些无源网络具有较强的调节能力，能有效减小系统中无功分量，且具有较高设计自由度，可结合各种智能算法动态跟踪阻抗，但同时也造成了诸如系统体积大、控制方式复杂及切换开关损耗高等问题。有源阻抗匹配方法使用DC-DC转换器实现大范围阻抗变换，以及变耦合系数情况下动态跟踪[14-16]。
在最大效率跟踪进一步研究中，学者们开始考虑输出电压控制。文献[17]将负载变化和输出控制结合在一起，分别在发射和接收侧增加DC-DC有源阻抗匹配网络，通过输出电压控制实现最大效率跟踪。由于输入功率和系统效率直接相关，假设输出电压恒定，最小输入功率点就是最大效率点。因此，文献[18-19]提出了一种跟踪最小输入电流实现最大效率跟踪的方法，然而控制方向事先未知，需采用试错法，导致系统可能在频繁变化下振荡。针对此问题，文献[20]提出了一种基于耦合系数动态辨识的最大效率跟踪方法，通过提前辨识耦合系数值，利用耦合系数和系统最优等效电阻线性关系式实现阻抗变化精确控制。但该方法需同时检测耦合系数和负载电阻，且发射/接收侧DC-DC变换器占空比相互牵制，导致负载响应时间较长。
本文提出了一种基于断续电流模式（Discontinous Current Mode, DCM）有源阻抗匹配网络的最大效率跟踪方法。通过建模分析，发现DCM模式下Buck-Boost变换器输入电阻独立于输入/输出电压及负载电阻，因此该方法无需负载实时检测，并简化了负载变化过程中进一步进行跟踪的过程，提高了负载响应速度。同时，也综合考虑了耦合系数和负载变化自适应性及输出可控性等几乎所有最大效率跟踪要求。
目前磁耦合式系统主要包括SS、SP、PS、PP四种基本拓扑结构，SS型系统因其固有谐振频率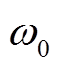不随等效电阻变化而变化的特点被广泛使用。本文以一个单发射，单接收串联谐振WPT系统为例进行研究。一种典型SS拓扑结构如图1所示，其中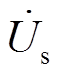为交流电压源，L1、L2和C1、C2分别为一次侧、二次侧谐振电感和电容，其共同构成整个系统的谐振网络，R1、R2为一次侧和二次侧线圈内阻，Req为系统等效电阻。线圈之间基于电磁感应方式电能传输，M为线圈之间的互感，耦合系数可用关系式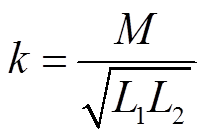表达。
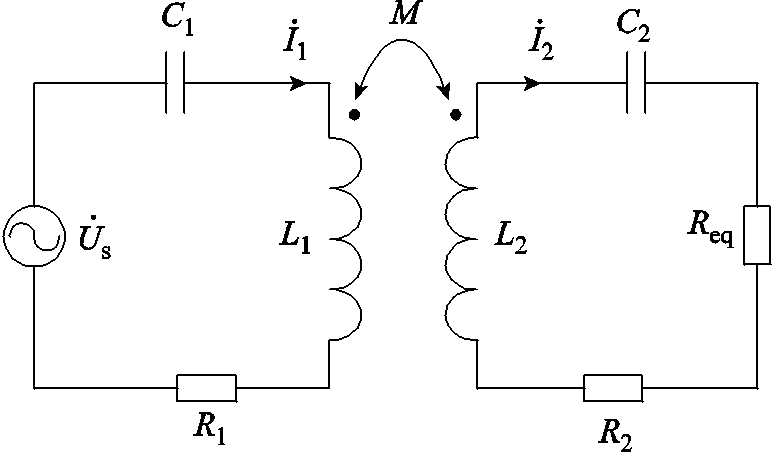
图1 典型的SS拓扑结构
Fig.1 Typical SS topology diagram
通过基尔霍夫电压方程可得到表达式为
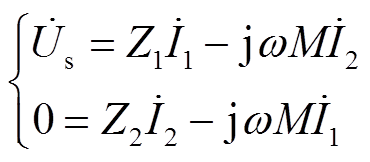（1）式中，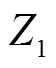
、
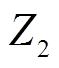分别为一次侧和二次侧等效阻抗，且满足
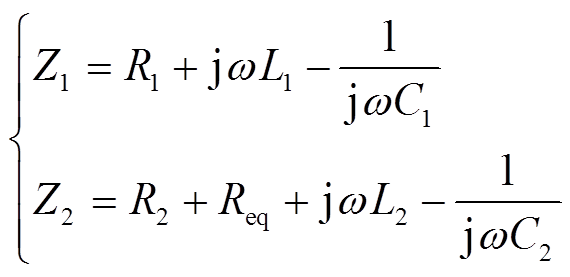（2）
根据式（1）和式（2），一次侧和二次侧谐振电流表达式为
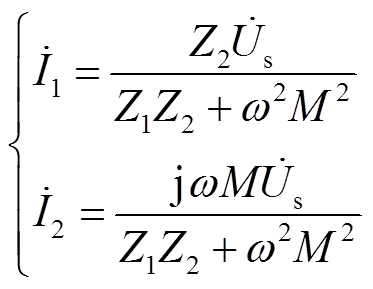（3）假设SS型WPT系统满足谐振状态，其谐振频率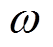
满足w=2pf，且其他参数满足L1=L2=L，C1=C2=C，R1=R2=R，则一次侧和二次侧等效阻抗为Z1=R，Z2=Rl+R，系统输入功率和输出功率表达式为
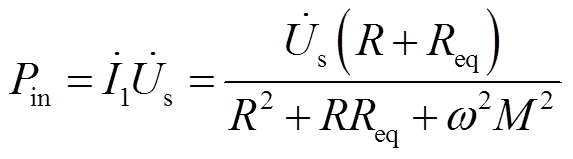（4）
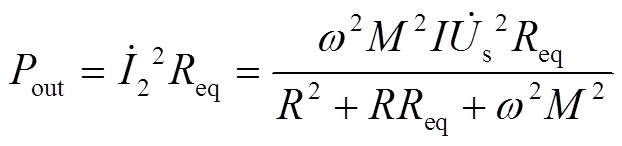（5）根据式（4）和式（5），WPT系统传输效率表达式为
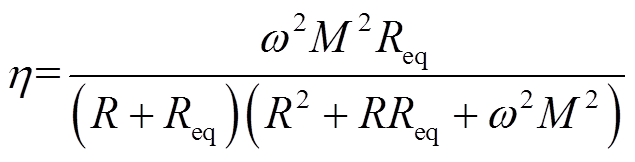（6）
在实际应用中，谐振频率w和线圈内阻R为固定参数，WPT系统传输效率和与等效电阻Req及线圈间耦合系数k密切相关。通过式（6）对等效电阻Req进行求导可得最大化传输效率对应的最优等效电阻为
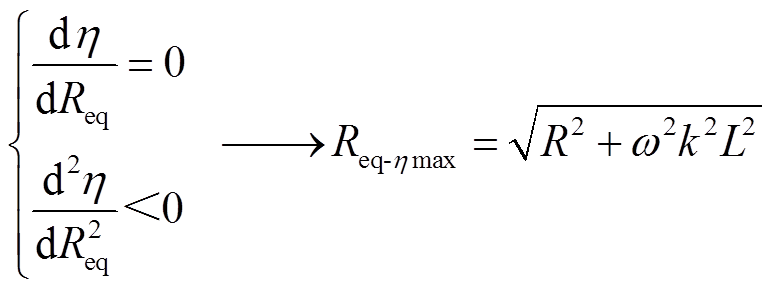（7）式中，k为两线圈的耦合系数。
在特定耦合系数条件下，存在最优等效电阻使系统传输效率最大化，当等效电阻偏离最优值或耦合系数发生变化时，会导致WPT系统传输效率下降。将式（7）代入式（6）可得特定耦合系数下WPT系统传输效率最大值为
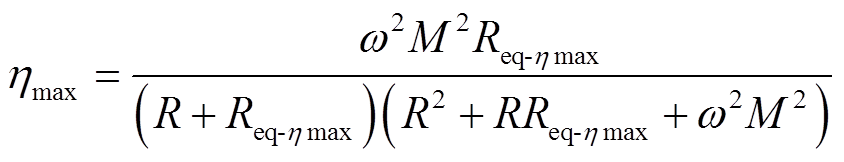（8）为选取合适的DC-DC变换器用于WPT系统阻抗匹配，本节讨论了Buck、Boost、Buck-Boost三种基本拓扑结构的DC-DC变换器在不同工作模式下输入/输出电压[21]及输入/负载电阻之间关系表达式，见表1。
参考表1，CCM模式下三种拓扑DC-DC变换器的输入电阻Rin都与负载电阻RL相关。DCM模式下，Buck和Boost变换器输入电阻与输入电压Uin和输出电压UL的比例相关；Buck-Boost变换器输入电阻则独立于输入/输出电压及负载电阻[22]，其公式推导过程具体见附录。本文通过在Matlab中建立三种变换器模型，得到不同负载电阻条件下变换器输入电阻变化情况如图2所示。
表1 DC-DC变换器关系表达式
Tab.1 DC-DC variator relation expression
拓扑模式输入/输出电压输入/负载电阻 BuckCCM DCM BoostCCM DCM Buck-BoostCCM DCM
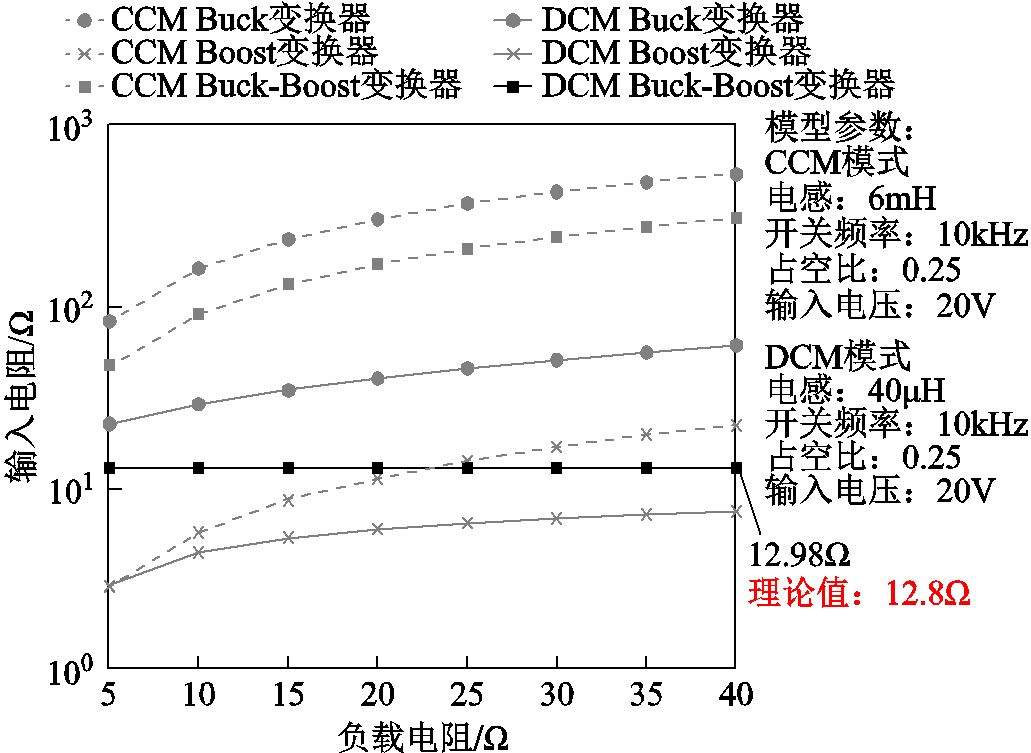
图2 变换器输入电阻变化情况
Fig.2 Change in converter input resistance
假设电感、开关频率、占空比确定，DCM模式下Buck-Boost变换器输入电阻将保持恒定，与理论值基本相同；其余变换器输入电阻与负载电阻呈正相关。此外，DCM工作模式下电感值大为减小，且具有开关管零电流开关、二极管无反向恢复时间等优点[23]。因此，相比其他拓扑结构DC-DC变换器，DCM模式Buck-Boost变换器更适合于WPT系统阻抗匹配。
通过上述讨论，本文提出在整流器与负载电阻之间加入DCM模式Buck-Boost阻抗匹配网络，如图3所示。其左侧为单发射单接收谐振线圈，VD1～VD4构成全桥整流，Cin为整流侧输出滤波电容，右侧为DCM模式Buck-Boost变换器。Rin为变换器输入电阻，Req为WPT系统等效电阻，其表达式为
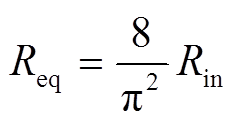（9）
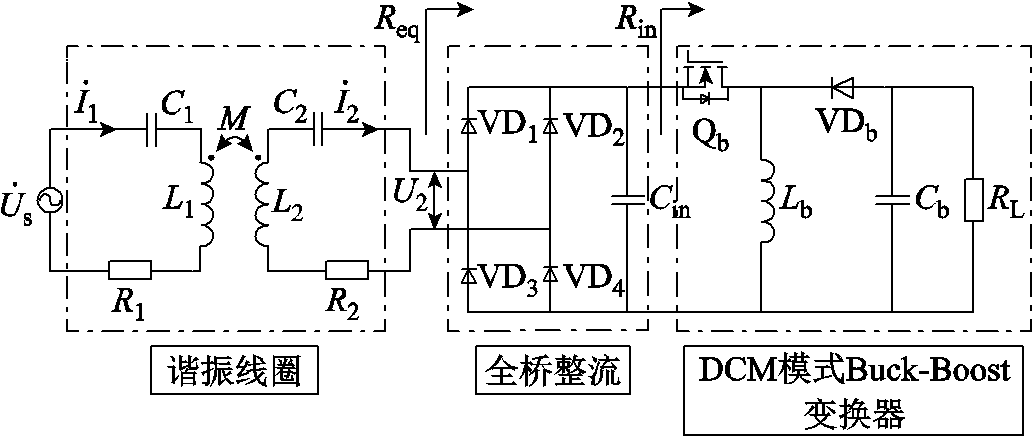
图3 WPT系统结构
Fig.3 WPT system structure diagram
输入电阻占空比调节如图4所示，改变开关管Qb占空比d2可在一定范围内调节输入电阻Rin及等效电阻Req。由式（7）可知，固定参数条件下系统存在唯一最优等效电阻Req-hmax，因此，通过控制和驱动电路对占空比d2进行寻优，可提升系统与负载的匹配程度，进而提高WPT系统传输效率。开关管占空比最优解可表示为
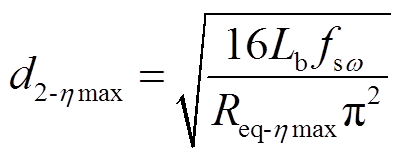（10）
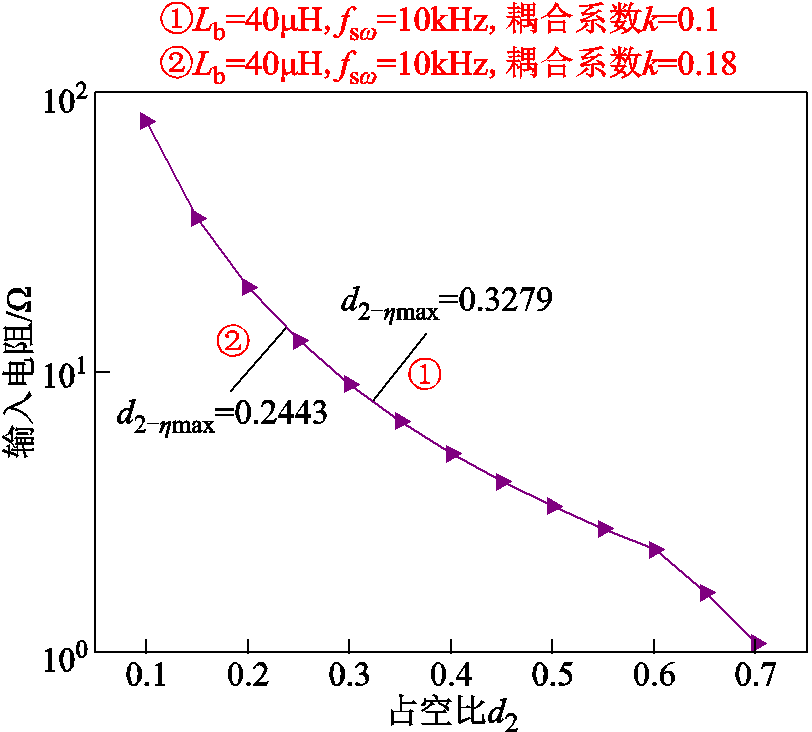
图4 输入电阻占空比调节
Fig.4 Input resistance duty cycle adjustment
根据图3在Matlab仿真软件中搭建了WPT系统模型，并得到不同负载电阻条件下系统传输效率变化情况如图5所示。仿真结果表明，因DCM模式Buck-Boost变换器输入电阻表达式与负载电阻无关，系统传输效率对负载变化有良好的的抗干扰性，可在较宽负载范围内保持最大化稳定输出。并在负载电阻RL=5 000W情况下，系统传输效率仍可维持在80%左右。
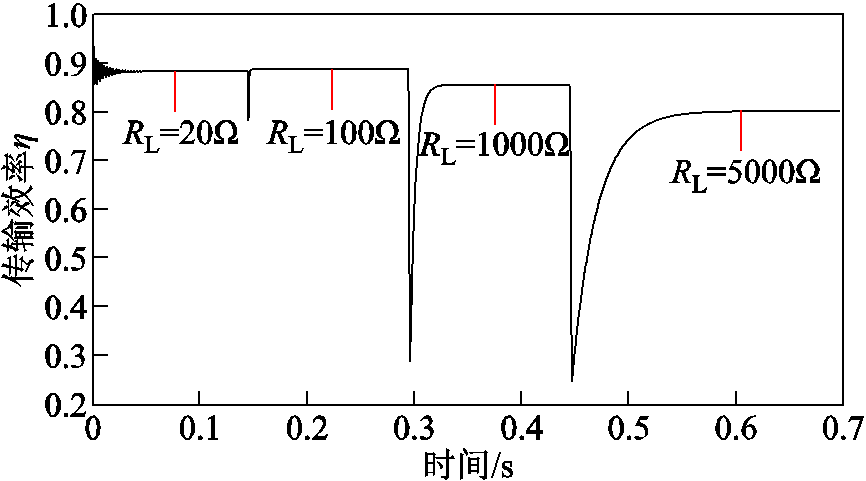
图5 系统传输效率变化情况
Fig.5 Change in system transmission efficiency
在某些特殊应用场合如电池充电过程中，需保持恒定输出电压维持稳定的输出功率，从而减小对电池的损伤。为保证系统输出电压值恒定在负载需要的电压范围内，一般需设置闭环控制单元使输出电压快速调整至设定值。
由表1可知，DC-DC变换器不仅可提升系统负载匹配程度，还可实现直流电能电压等级转换。CCM模式下Buck和Boost变换器输出电压范围有限，相比CCM模式，DCM模式变换器输出电压表达式更复杂。因此，本文在电源与逆变器之间加入CCM模式Buck-Boost变换电路，并采用数字PI控制作为控制器，构建的电压单环反馈控制框图如图6所示。控制器实时采集当前输出电压信息UL与设定输出值Vref相减，得到当前控制误差量Verr，误差量Verr经数字PI控制器运算处理后得到控制量Vcl，Vcl经上下限幅后得到当前控制量Vc，经与锯齿波Sw比较后获得占空比PWM脉冲，调整电路快速恢复至设定输出值。
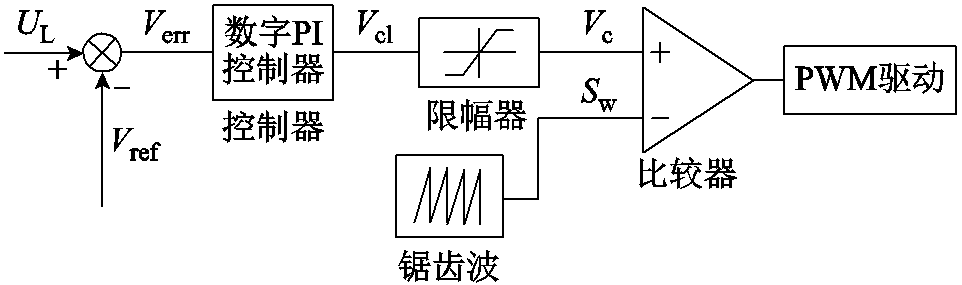
图6 电压单环反馈控制框图
Fig.6 Voltage single-loop feedback control block diagram
图7为WPT系统拓扑结构，VDC为直流电压源，Qa、La、VDa、Ca构成CCM模式Buck-Boost变换器，调节输出电压。Q1～Q4构成全桥逆变器，输出高频交流输出电压U1。U2为WPT系统等效电阻输入电压，Uin为DCM模式Buck-Boost变换器输入电压，Zref为二次侧反射阻抗，ZS为二次侧等效阻抗。图8为系统闭环控制结构框图，负载电压UL、变换器输入电压Uin及电流Iin通过无线通信反馈至发射侧控制器。发射侧控制器通过数字PI控制，改变开关管Qa占空比d1调节输出电压UL，并通过驱动电路脉宽调制信号S1～S4控制全桥逆变。最优等效电阻Req-hmax通过无线通信反馈至接收侧，并根据式（10）调整变换器占空比d2，跟踪最大传输效率。
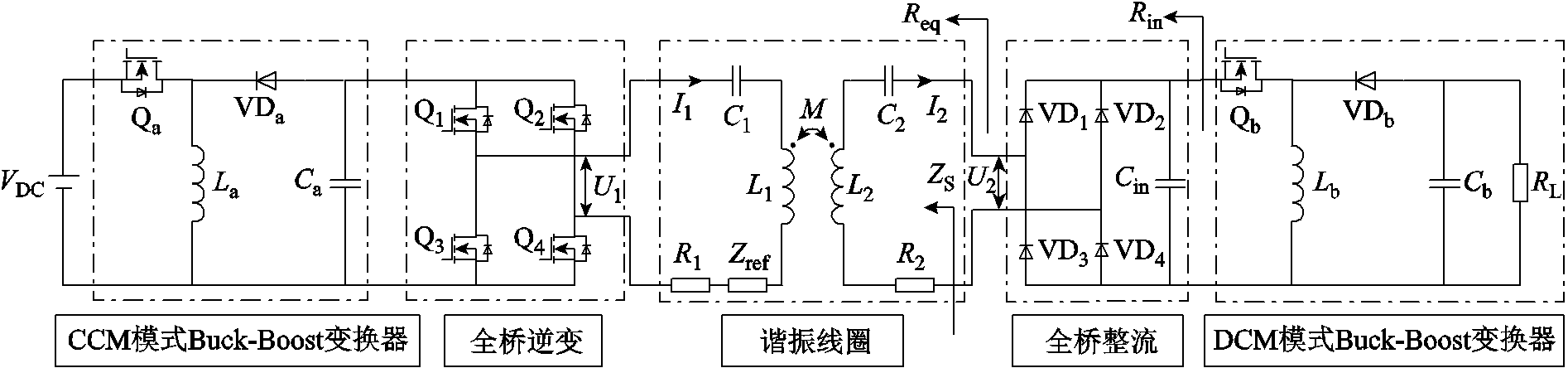
图7 WPT系统拓扑结构
Fig.7 WPT system topology structure
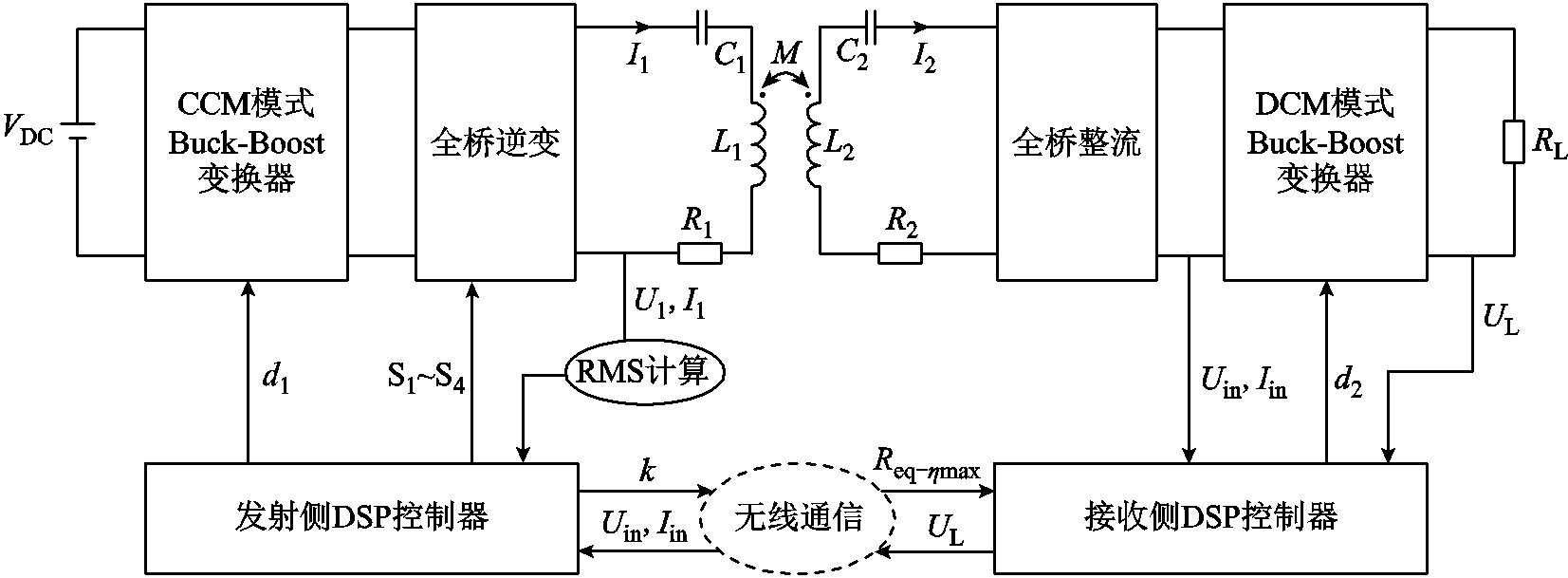
图8 闭环控制框图
Fig.8 Closed-loop control block diagram
由式（7）和式（10）可知，为实现最大效率跟踪控制，需要耦合系数k作为已知参数。而实际应用中两线圈耦合系数无法直接测量得到，在某些特定场合下，例如电动汽车充电过程，耦合系数可能随电动汽车移动而改变。因此，需实时辨识动态耦合系数。
本节将结合图7分析耦合系数辨识方法。假设系统中发射和接收线圈参数相同，线圈内阻R1=R2=R。
根据图7和式（9）可得到接收侧环路阻抗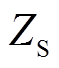
的表达式为
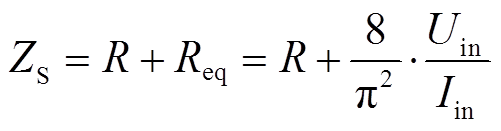（11）一次侧谐振电流表达式为
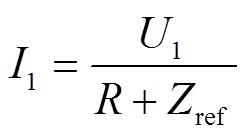（12）
式中，Zref为接收侧到发射侧反射阻抗，且满足Zref =w2k2L2/。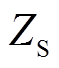
将式（11）代入式（12），则U1/I1表达式为
（13）耦合系数k表达式为
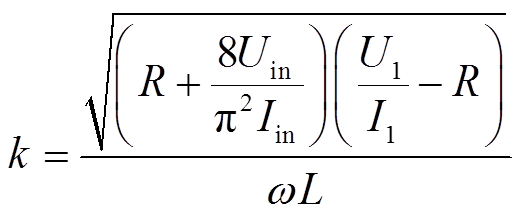（14）
根据式（14）估算实时耦合系数即可实现最大效率跟踪控制。第3.2小节将具体介绍基于实时耦合系数辨识的最大效率跟踪过程。
基于实时耦合系数辨识的最大效率跟踪控制框图如图9所示。接收侧控制器实时采集变换器输入电压、电流信息Uin、Iin，经无线通信模块反馈至发射侧。发射端结合式（14）和式（7）实时辨识耦合系数k及最优等效电阻Req-hmax，随后将结果发送至接收端。接收侧控制器根据式（10）计算DCM模式Buck-Boost变换器占空比最优解d2-hmax，并通过驱动电路调整实现最大效率跟踪。同时，接收端控制器反馈输出电压信息UL至发射侧。发射端控制器基于数字PI控制自适应调节CCM模式Buck-Boost变换器占空比的d1，恢复输出电压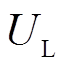
至设定值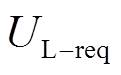
。
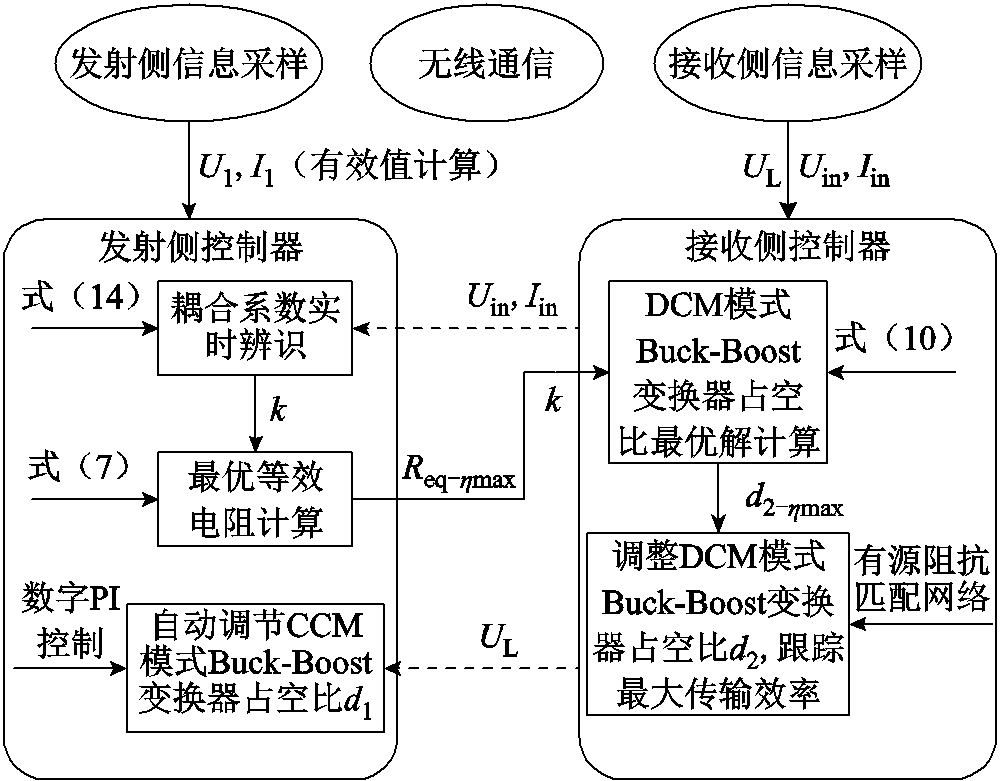
图9 最大效率跟踪控制框图
Fig.9 Maximum efficiency tracking control block diagram
接收侧控制流程如图10所示。负载电阻变化时，输出电压UL通过无线通信由接收侧传输至发射侧，并通过调节变换器占空比d1恢复输出电压至设定值。耦合系数k变化时，接收侧控制器根据发射端反馈信息（耦合系数k、最优等效电阻Req-hmax）调节变换器占空比d2满足式（10），跟踪最大效率点，并重复负载电阻变化过程调节电压输出至设定值。
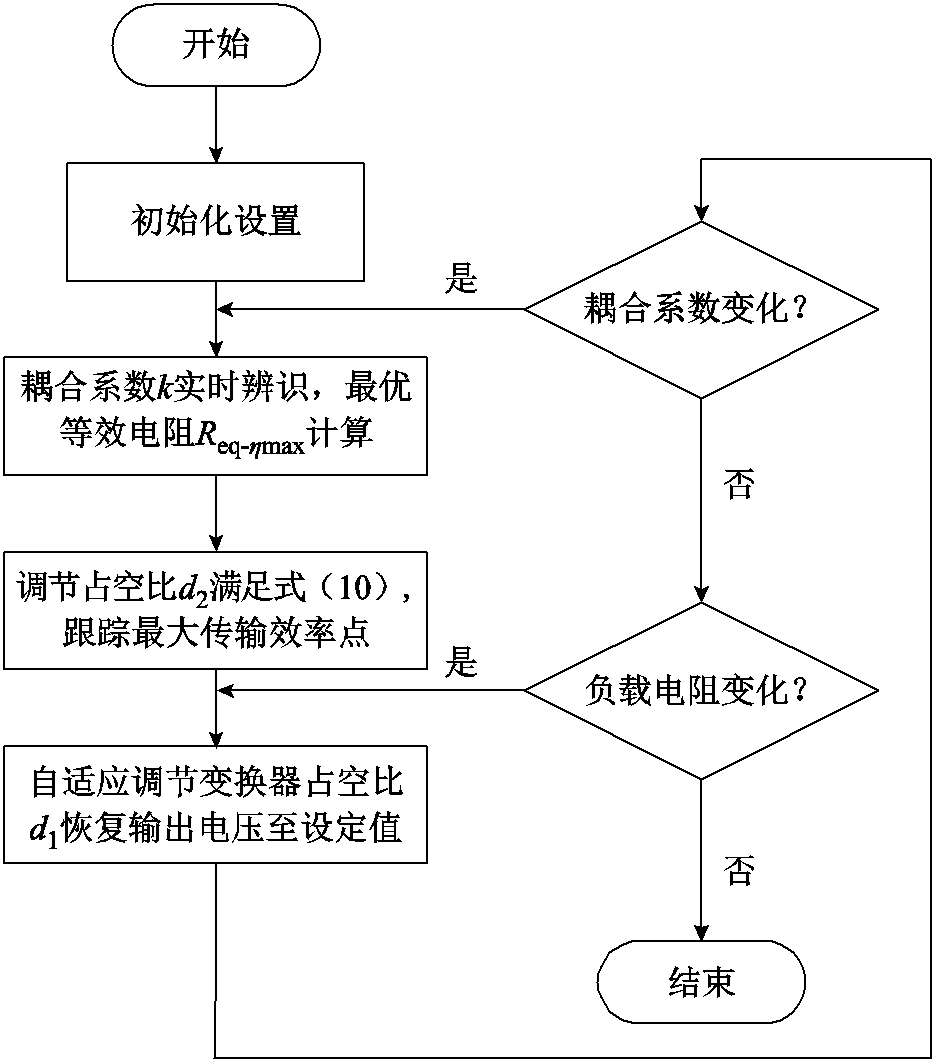
图10 接收侧控制流程
Fig.10 Receive-side control flow chart
为了验证本文所提最大效率跟踪方法的有效性，本文搭建了如图11所示的实验平台。SKT-600霍尔传感器（300kHz）采集一次侧谐振电压/电流及负载侧变换器输入电压/电流信息， AD637（60dB范围内）计算交流电压/电流有效值。发射侧和接收侧选用两个DSP控制器（TMS320F28335，150MHz）进行数据采集、分析和信号驱动。两个ARM芯片（STM32W108）用以实现无线通信。具体参数请见表2，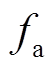
、
、f分别为CCM模式、DCM模式Buck-Boost变换器及全桥逆变开关频率。
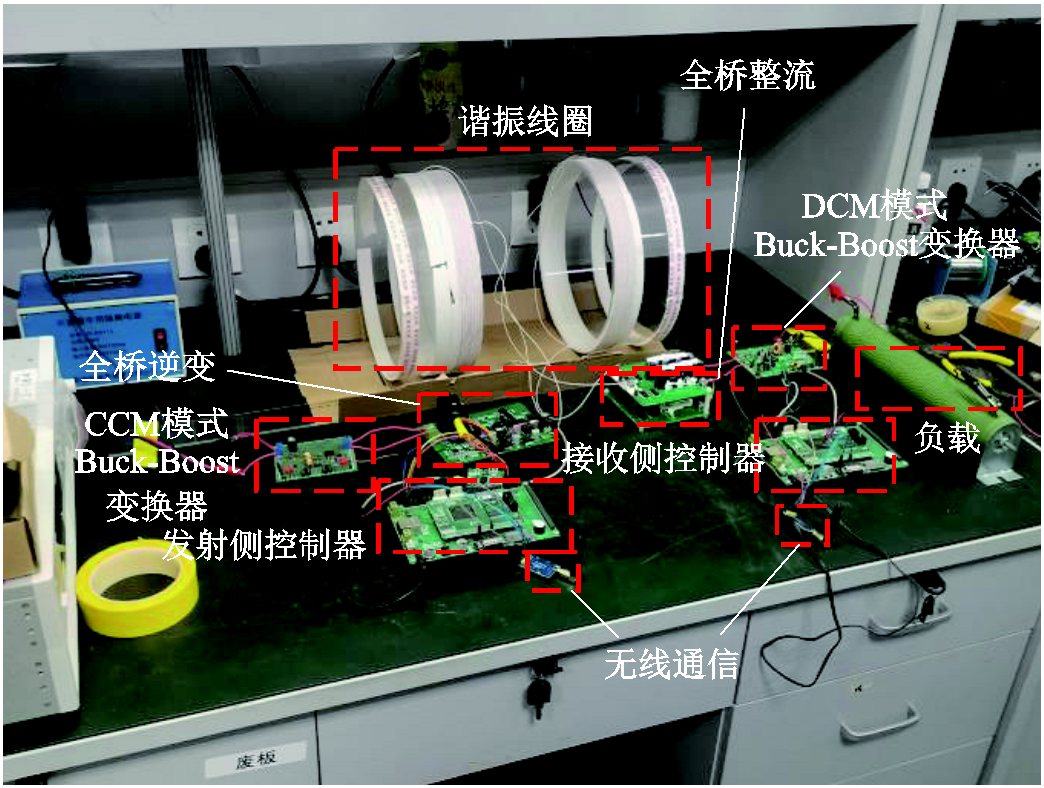
图11 WPT系统实验平台
Fig.11 WPT system experimental platform
表2 实验系统参数
Tab.2 Experimental system parameters
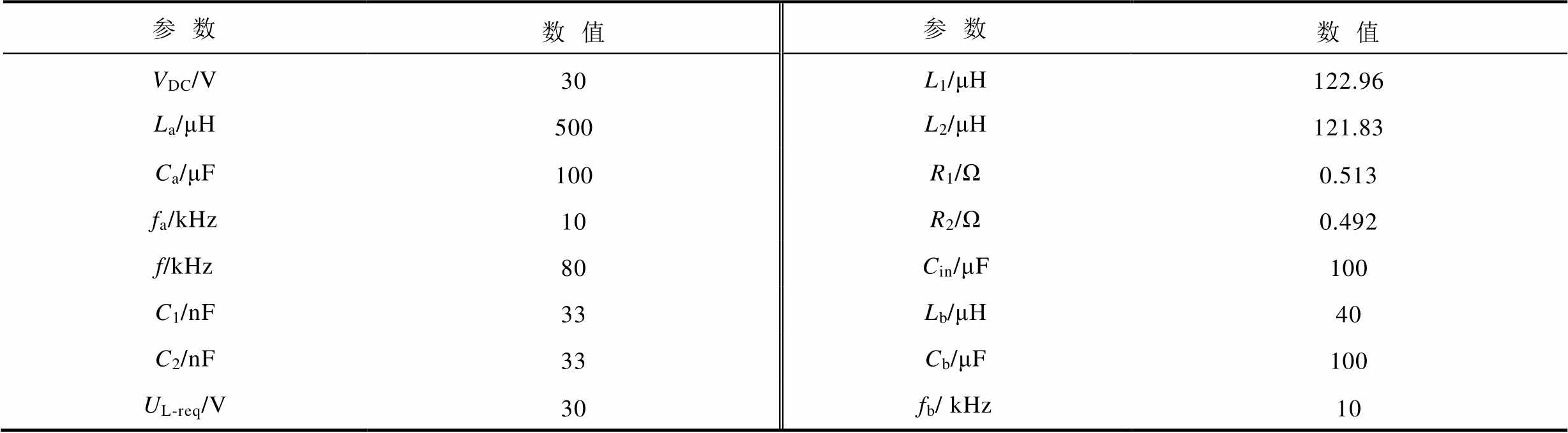
参数数值参数数值 VDC/V30L1/μH122.96 La/μH500L2/μH121.83 Ca/μF100R1/Ω0.513 fa/kHz10R2/Ω0.492 f/kHz80Cin/μF100 C1/nF33Lb/μH40 C2/nF33Cb/μF100 UL-req/V30fb/ kHz10
实验中，由于耦合系数变化需要，建立了如图11所示谐振线圈结构，一次和二次线圈之间距离在10cm和30cm范围内变化。如第3节所述，耦合系数通过采集电压电流U1、I1、Uin、Iin及其有效值计算和低通滤波进行估算，辨识结果见表3，由于实验中采样误差，实验精度略小于仿真值。发射和接收线圈距离与耦合系数k关系如图12所示。从表3和图12可以看出，耦合系数估算结果与目标值匹配良好，因此实验结果进一步验证了耦合系数辨识方法的可行性。
表3 耦合系数
辨识结果
Tab.3 Real-time identification results of the coupling coefficient k
目标值仿真实验 仿真值准确率(%)实验值准确率(%) 0.100.102 197.900.103 097.00 0.130.133 297.540.133 897.08 0.150.152 898.130.154 996.73 0.180.184 697.440.185 696.89
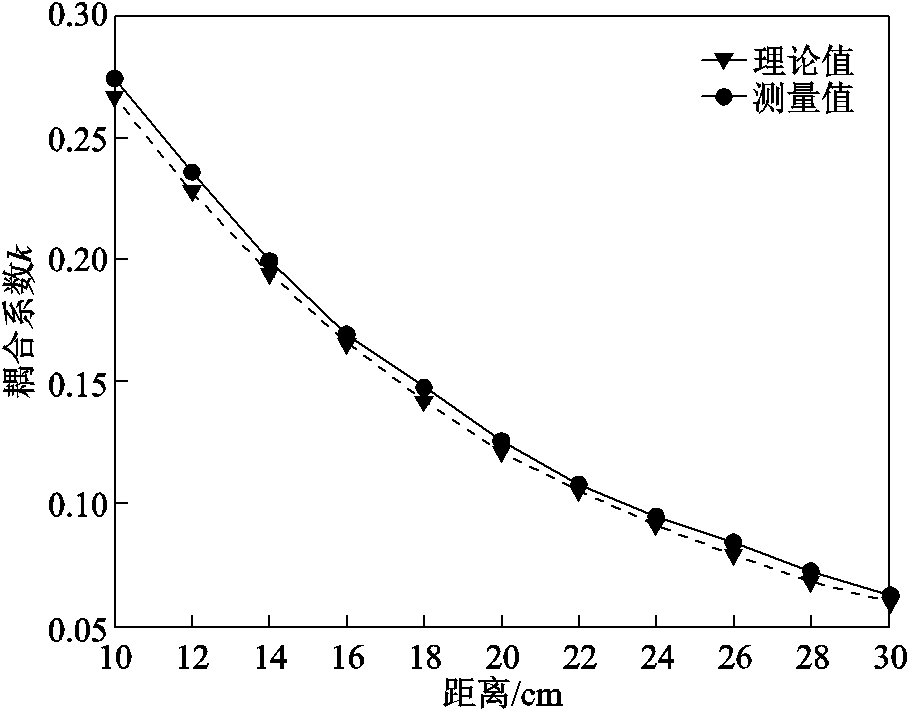
图12 线圈距离与耦合系数关系图
Fig.12 The coil distance and the coupling coefficient
图13a和图13b分别给出了耦合系数和负载电阻变化条件下加入DCM模式有源阻抗匹配网络前后的传输效率。由图13可知，匹配前随着负载和等效电阻逐渐偏离Req-hmax，传输效率出现一定程度下降，且越来越明显；加入阻抗匹配网络后等效电阻被修正到Req-hmax，效率在不同线圈距离和负载电阻下均获得提升。值得注意的是，由于实验过程中开关管器件额外损耗，实验值与计算值存在一定偏差，未能实现理想化最大效率跟踪。
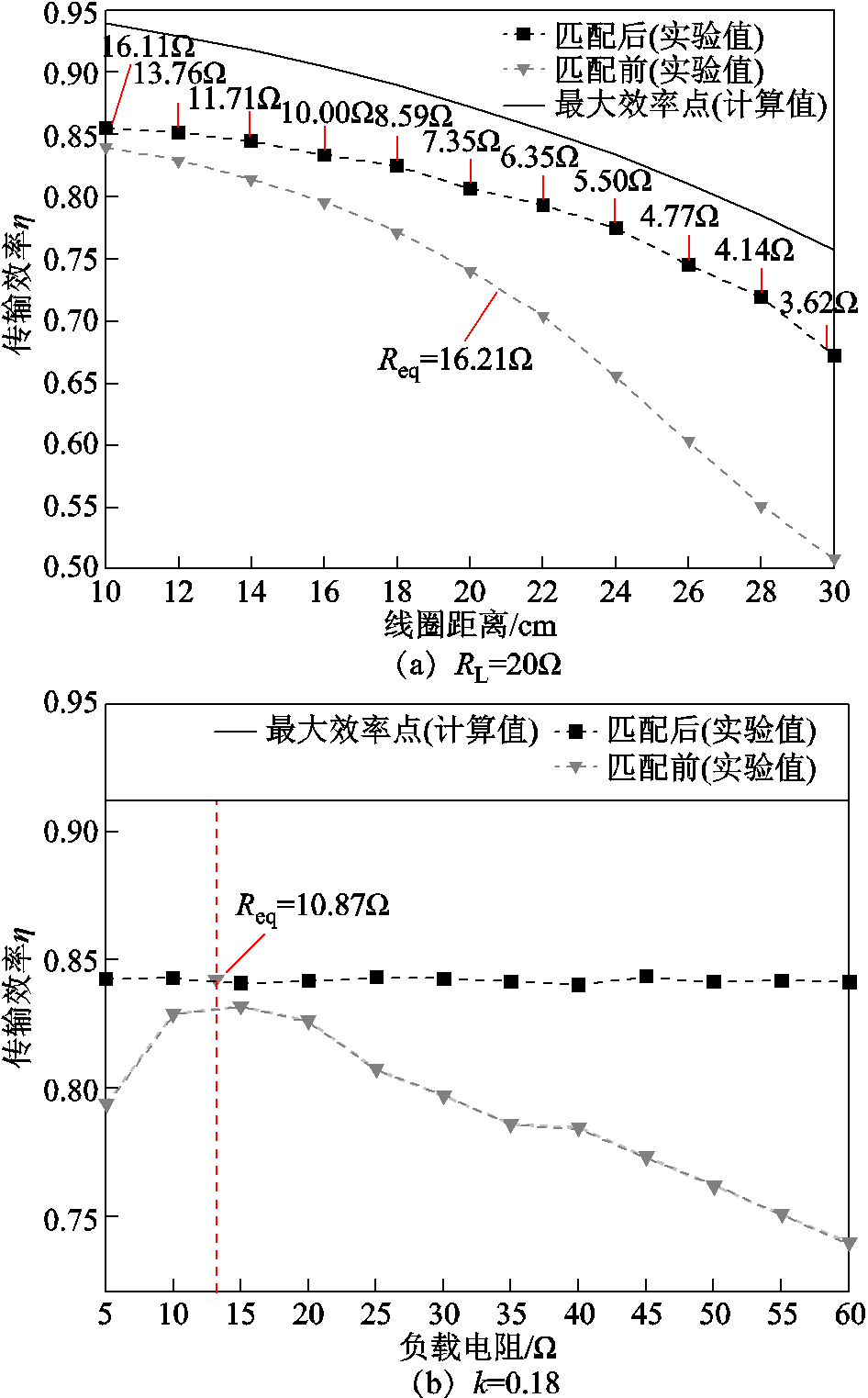
图13 WPT系统传输效率
Fig.13 WPT system transmission efficiency
4.3.1 控制策略验证
开环状态记录了三组参数（k=0.1,0.15,0.18）条件下，系统传输效率和变换器占空比d2关系曲线，如图14a所示。实验从t0时刻开始，负载电阻为20W。k=0.1条件下最佳等效电阻通过变换器占空比d2的控制在t1时刻达到。t2时刻，随着线圈之间距离变化，耦合系数k从0.1变化至0.15，因为变化点处系统等效电阻偏离最优值，传输效率快速下降。通过DCM模式Buck-Boost变换器跟踪控制（d2的调节），系统在t3时刻再次达到最优等效电阻，实现了更高的传输效率。耦合系数从0.15变化至0.18时，在t4和t5时刻重复之前过程。如图14所示，当线圈距离发生变化后，系统分别在t1、t3、t5达到最佳负载电阻。
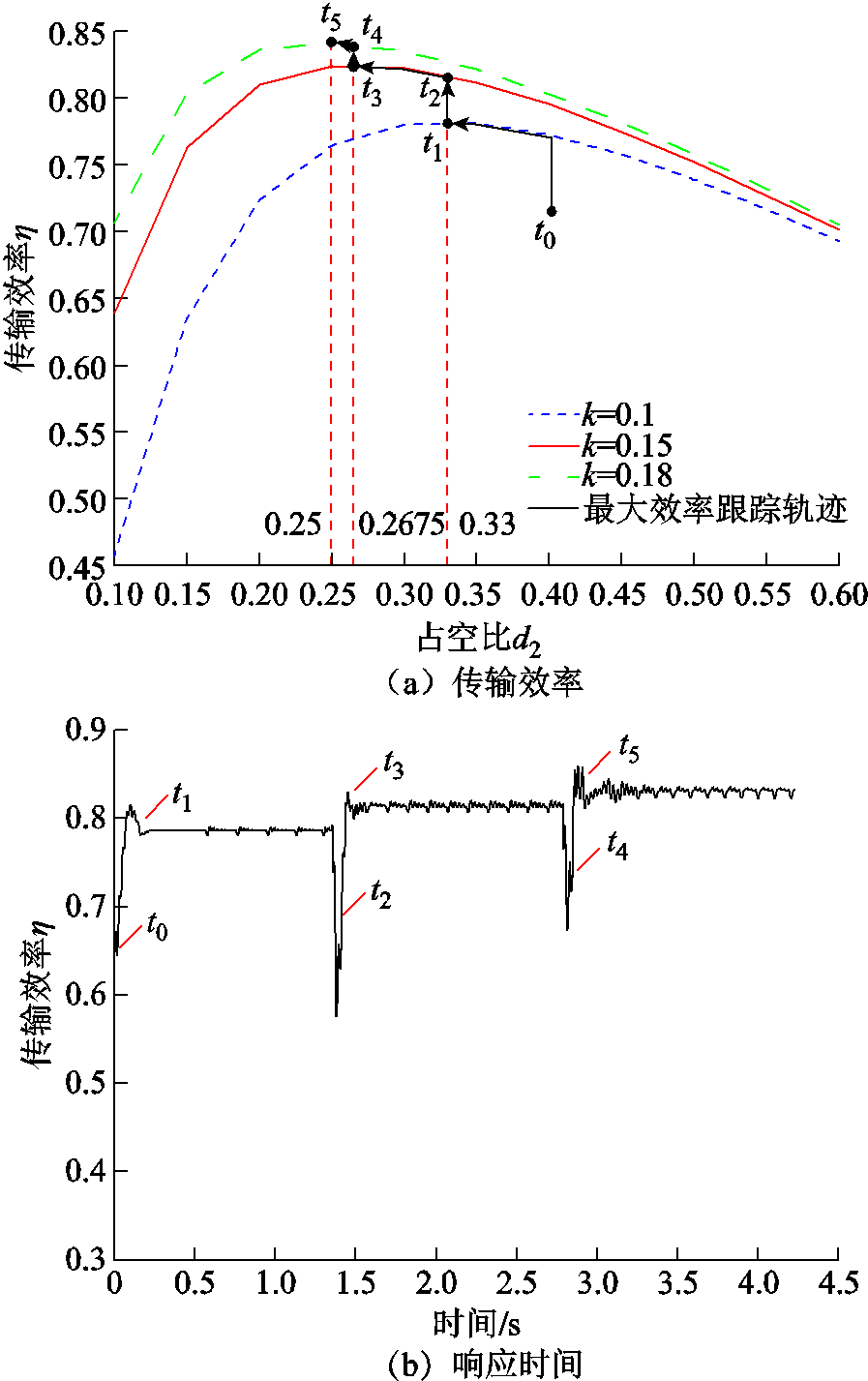
图14 耦合系数变化下最大效率跟踪过程
Fig.14 Maximum efficiency tracking process under changing coupling coefficient
同样在开环状态下记录了三组不同负载电阻（RL=20W, 30W, 40W）条件下，系统传输效率和变换器占空比d2关系曲线，如图15a所示。从图中可看出，因DCM模式Buck-Boost变换器输入电阻独立于输入/输出电压及负载电阻，三组曲线几乎一致，与之前理论分析相同。因此，负载电阻变化过程中只需控制输出电压至给定值即可。从t0时刻开始，耦合系数为0.18。RL=20W条件下最优等效电阻通过变换器d2控制在t1时刻达到。t2时刻，负载电阻从20W变化至30W，系统输出功率由45W降至30W，发射端通过接收端功率反馈信息实时调整发射功率，并对效率检测造成一定程度扰动。t3时刻系统恢复稳定状态，传输效率返回t1时刻最大值。同样，负载电阻从30W变化至40W，t4和t5时刻重复之前过程。如图15所示，系统t1时刻达到最优等效电阻，并一直保持至t5时刻。
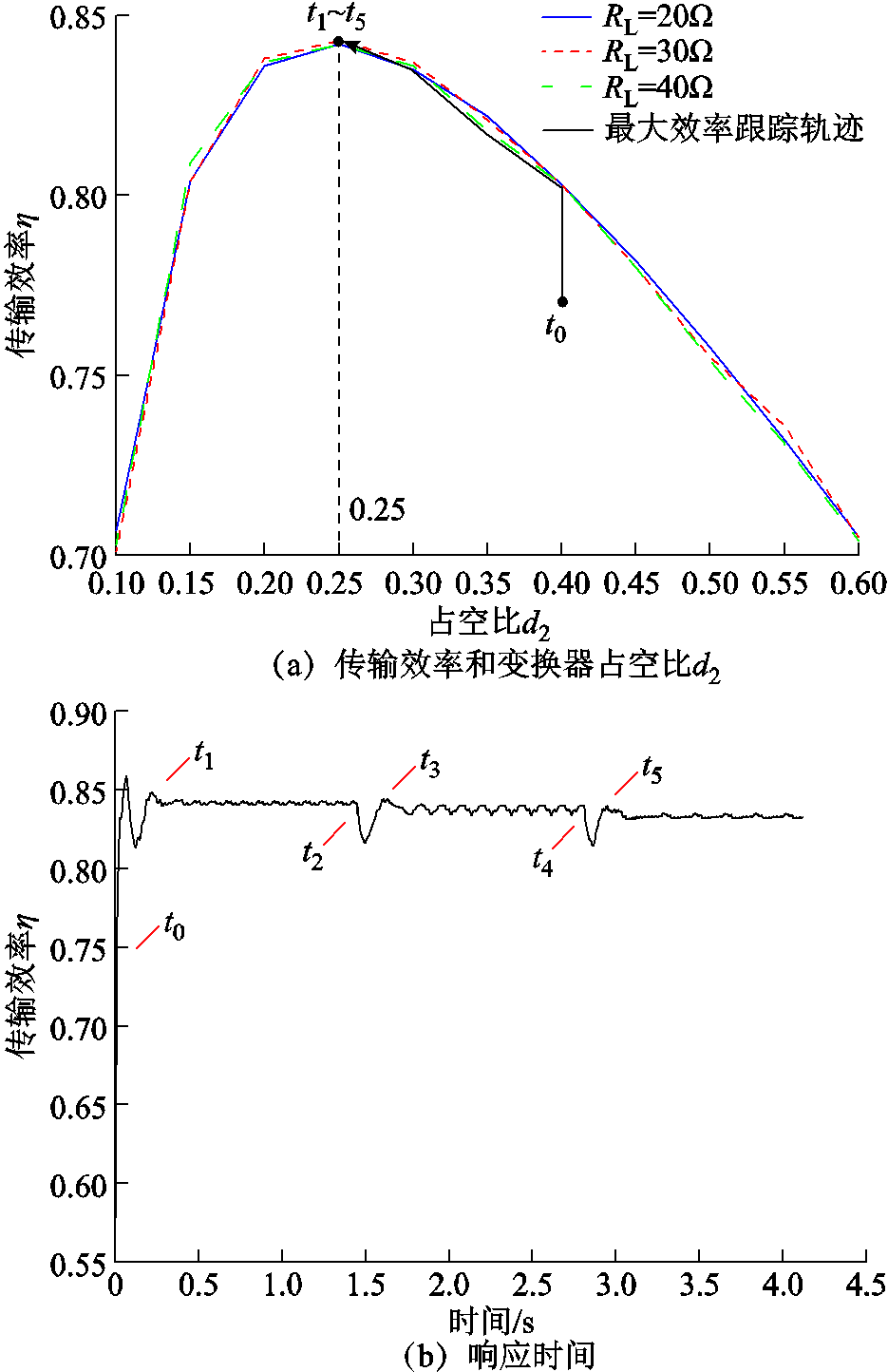
图15 负载电阻变化下最大效率跟踪过程
Fig.15 Maximum efficiency tracking process under load resistance changes
4.3.2 实验波形讨论
加入闭环控制后，测试了耦合系数和负载电阻变化情况下效率最大跟踪。图16和图17分别为线圈距离变化时和负载电阻变化时跟踪结果。通道1和通道2分别为输出电压UL和输出电流IL的波形，通道3和4分别为CCM模式和DCM模式Buck-Boost变换器占空比d1和d2的波形（0～1V电压表示占空比为0～100%）。
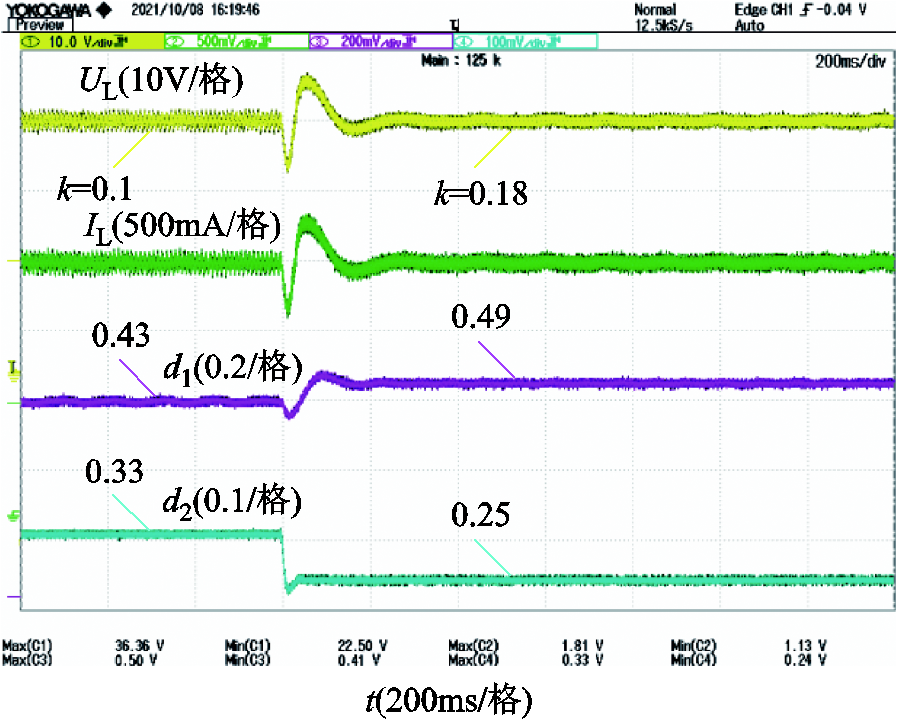
图16 线圈距离变化时系统输出波形
Fig.16 The system has an output waveforms when the coil distance changes
图17 负载电阻变化时系统输出波形
Fig.17 The system has an output waveforms when the load resistance changes
实验过程中手动调节发射和接收线圈之间的距离实现耦合系数变化，k=0.1变化至k=0.18的跟踪过程如图16所示。线圈距离发生变化时，发射侧控制器实时辨识耦合系数k，并计算最佳等效电阻Req-hmax传输至接收侧，接收侧控制器调节DCM模式变换器占空比至最优值d2-hmax跟踪最大效率值。与此同时，发射侧控制器基于接收侧输出电压反馈信息，自动调节CCM模式变换器占空比d1，使输出电压恢复至设定值UL-req=30V。整个过程大约需要180ms左右。
负载电阻RL从20Ω变化至30Ω再返回至20Ω跟踪过程如图17所示。根据上文所述，DCM模式Buck-Boost变换器输入电阻独立于负载电阻，因此，负载变化过程中占空比d2恒定（且满足d2=d2-hmax）。整个阶段只需调节CCM模式变换器占空比d1匹配输出电压。负载从20W变化至30W跟踪过程大约需要160ms左右，从30W至20W跟踪过程大约需要130ms左右。表4比较了几种最大效率跟踪方法在系统参数变化条件下负载响应时间。实验结果表明，相比其他WPT系统，本文所提方法具有更快的负载响应速度。
表4 WPT系统最大效率跟踪方法比较
Tab.4 Comparison of the maximum efficiency tracking method of the wpt system
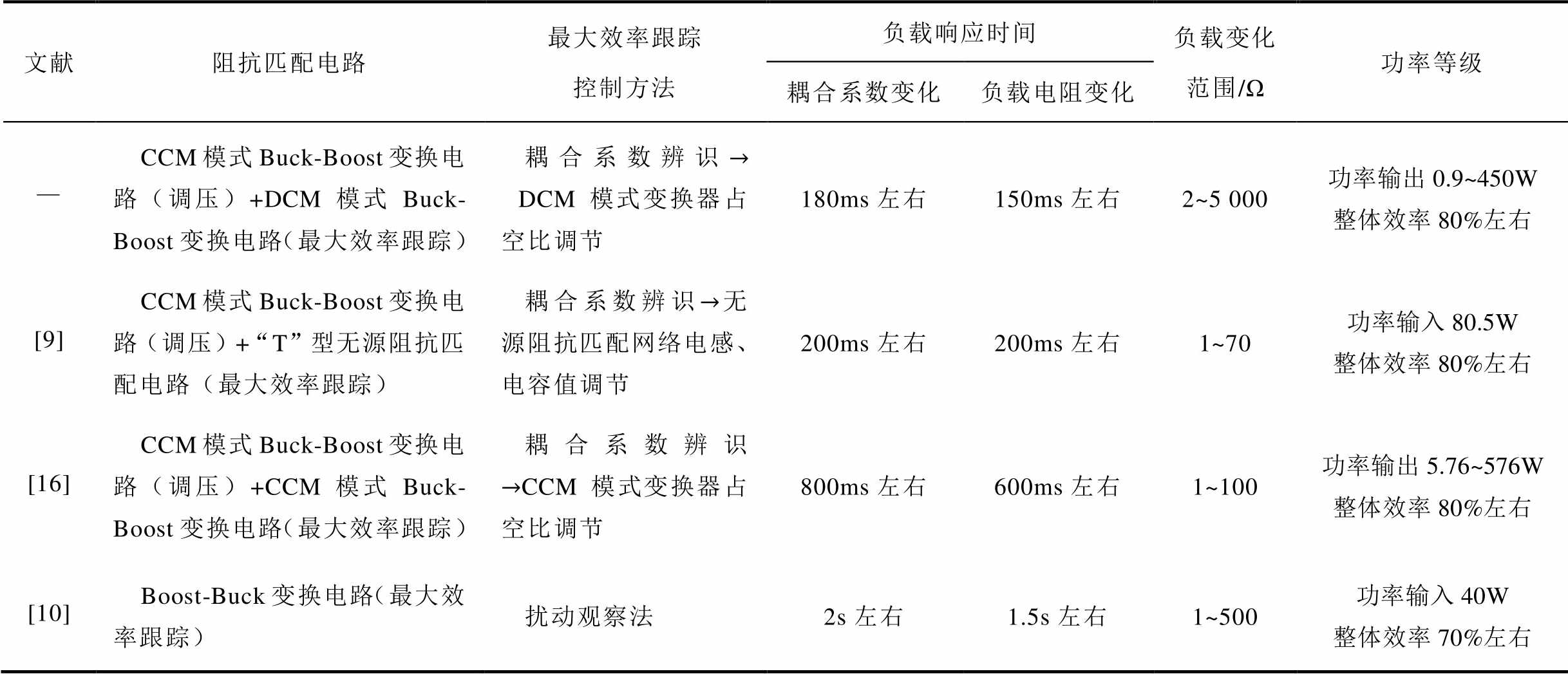
文献阻抗匹配电路最大效率跟踪控制方法负载响应时间负载变化范围/Ω功率等级 耦合系数变化负载电阻变化 —CCM模式Buck-Boost变换电路（调压）+DCM模式Buck-Boost变换电路（最大效率跟踪）耦合系数辨识DCM模式变换器占空比调节180ms左右150ms左右2～5 000功率输出0.9～450W整体效率80%左右 [9]CCM模式Buck-Boost变换电路（调压）+“T”型无源阻抗匹配电路（最大效率跟踪）耦合系数辨识无源阻抗匹配网络电感、电容值调节200ms左右200ms左右1～70功率输入80.5W整体效率80%左右 [16]CCM模式Buck-Boost变换电路（调压）+CCM模式Buck-Boost变换电路（最大效率跟踪）耦合系数辨识CCM模式变换器占空比调节800ms左右600ms左右1～100功率输出5.76～576W整体效率80%左右 [10]Boost-Buck变换电路（最大效率跟踪）扰动观察法2s左右1.5s左右1～500功率输入40W整体效率70%左右
图18为不同参数条件（耦合系数和负载电阻）下系统稳态工作波形。通道1和通道2分别为系统输出电压UL和输出电流IL波形，通道3和通道4分别为发射侧和接收侧Buck-Boost变换器Qa和Qb的驱动电压Ua和Ub。通道3和4的“Duty”值表示占空比d1和d2。由图18可知，三组参数的输出电压均恒定在设定值30V左右。比较图18a和图18b，在相同耦合系数k下，不同负载电阻的占空比d2相同；当负载电阻较大时，d1变小。比较图18a和图18c，负载电阻相同情况下，当耦合系数较大时，d1变大，d2变小。实验结果与理论研究保持一致。表5显示了最大效率跟踪结果，其中理想值由式（8）计算，并且耦合系数k越大，最大传输效率值越大。由于电力电子系统不是一个理想的系统，功率开关管和非理想电感、电容元件不可避免地给WPT系统带来额外功率损耗，因此实验结果略小于理想结果。
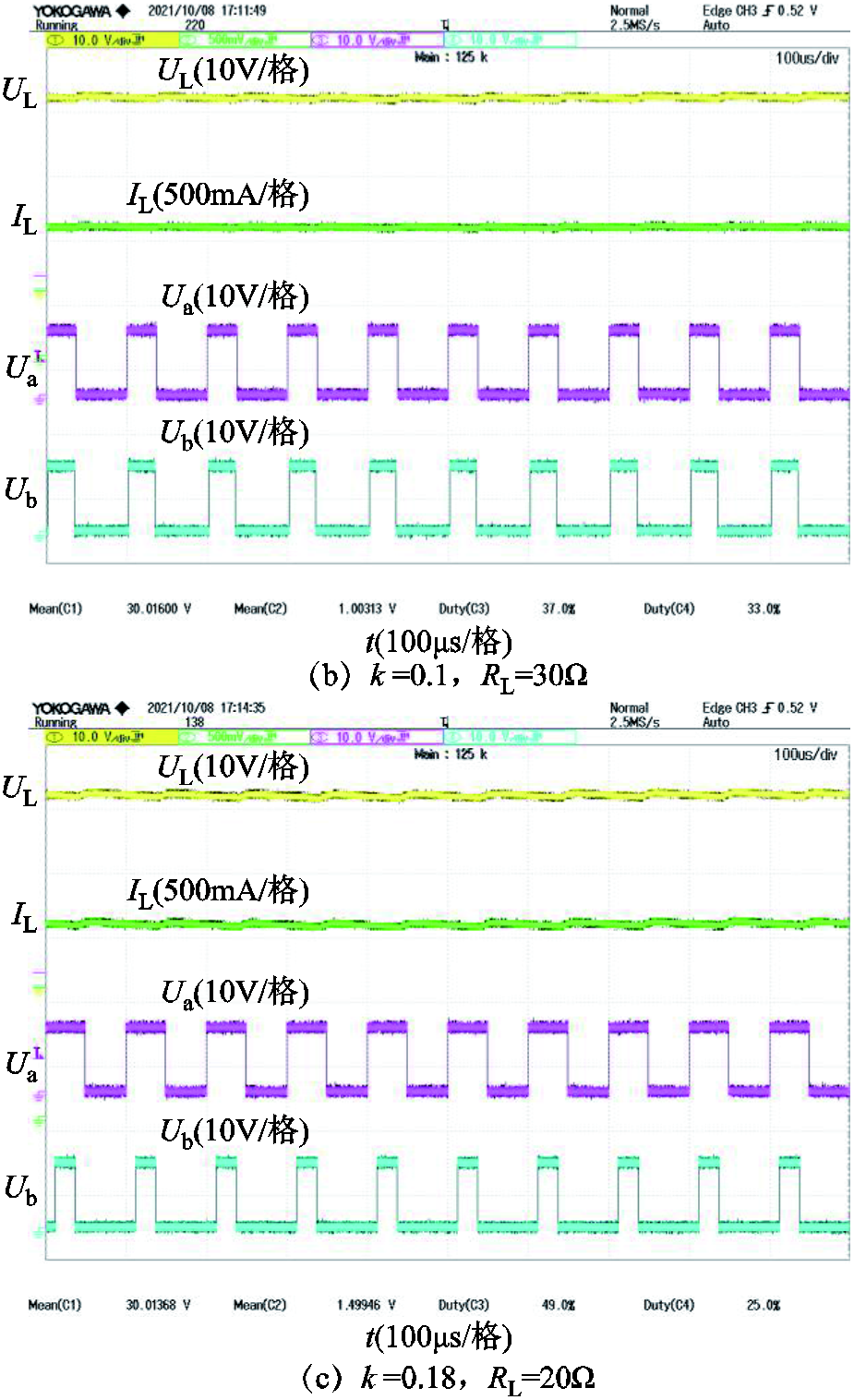
图18 系统稳态工作波形
Fig.18 The system has no perturbative state operating waveforms
表5 系统最大传输效率
Tab.5 Maximum system transmission efficiency
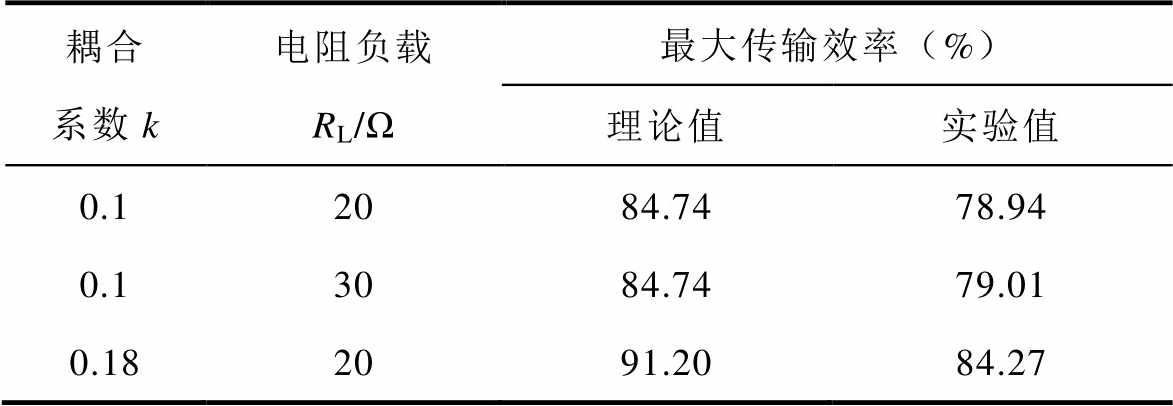
耦合系数k电阻负载RL/Ω最大传输效率（%） 理论值实验值 0.12084.7478.94 0.13084.7479.01 0.182091.2084.27
本文分析讨论了不同工作模式下三种DC-DC变换器输入/负载电阻转换能力。显然，DCM模式下Buck-Boost变换器输入电阻与负载电阻及输入电压无关，相比其他拓扑结构DC-DC变换器，其更适合于WPT系统阻抗匹配。因此，本文提出了一种基于DCM模式有源阻抗匹配网络的WPT最大效率跟踪方法。通过采集发射和接收侧电压电流信息实时辨识耦合系数，并通过无线通信模块反馈调节DCM模式变换器占空比匹配最优等效电阻，耦合系数识别精度达95%以上。实验结果表明，本文提出的最大效率跟踪控制方法能够实现精确的恒定输出电压控制，大幅提升了系统传输效率，并且相比其他WPT系统，本文所提方法具有更快的负载响应速度。
一种典型的Buck-Boost DC-DC转换电路如附图1所示。相比CCM模式，DCM模式下电感在周期结束时完全放电，电感器电流周期时间内突降为0，电流变化在一定程度上直接影响了输出电压和输入电阻。
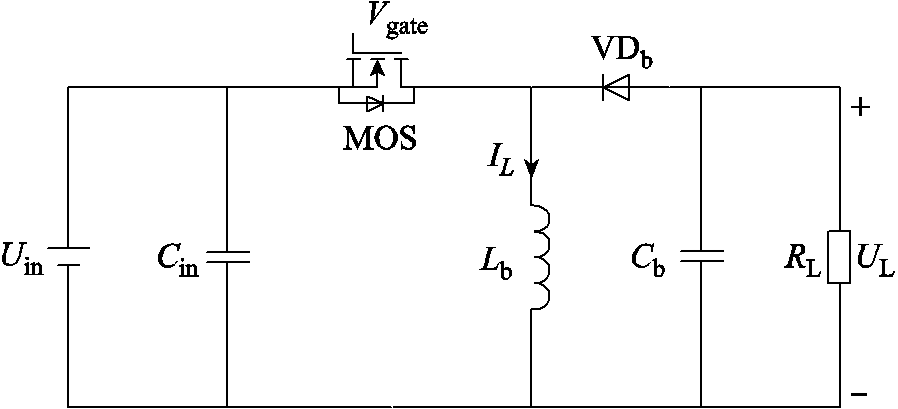
附图1 Buck-Boost变换器结构
App.Fig.1 Buck-Boost converter structure diagram
当变换器在DCM模式下运行时，电感器根据其时间间隔分为三种工作状态，如附图2所示：0～t1为导通状态，电感电流线性增加；t1～t2为关断状态，电感电流线性减小；t2～T为零状态，此时电感电流保持为0。这些时间段满足下列表达式
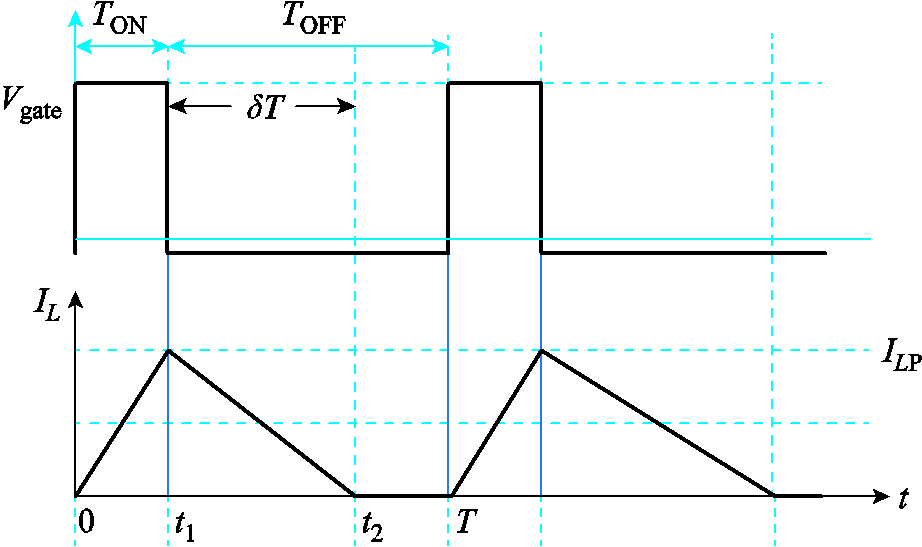
附图2 电感电流和栅极电压
App.Fig.2 Inductance current and gate voltage
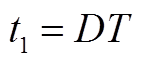（A1）
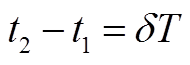（A2）
当变换器处于导通状态时，电流通过MOSFET管流向电感器，输入电压出现在电感器上。电感电流从0增加至峰值电流ILP，导通状态下电感电流变化为
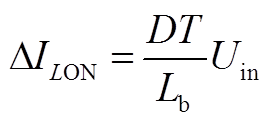（A3）当变换器处于关断状态时，电流从电感流向负载和二级管，当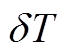
周期结束，电感电流降为0，输出电压出现在负载上。假设二极管电压降为0，则关断状态下电感电流变化为
（A4）
变换器处于稳态运行情况下电感电流总变化为0，根据式（A3）和式（A4），可得到
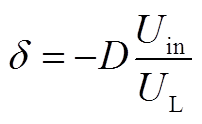（A5）当变换器处于零状态时，电感电流保持为0，且没有电流流向负载和二极管，变换器此时处于休眠状态。导通状态下，没有电流流向负载和二极管，输出电流等于二极管电流平均值；关断状态下，二极管电流等于电感电流值。因此，输出电流可表达为
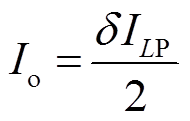（A6）
根据式（A3）、式（A5）以及式（A6），输出电压表达式为
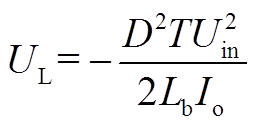（A7）相比CCM模式，DCM模式下变换器输出电压表达式更复杂。DCM模式下变换器输出功率表达式为
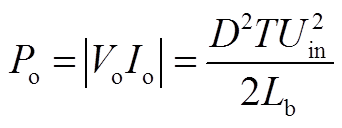（A8）
假设变换器传输过程中没有额外功率损耗，Pin=Po，其中，fsw为栅极电压Vgate的频率，fsw=1/T，则变换器输入阻抗表达式为
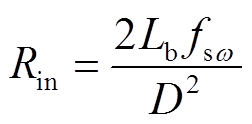（A9）参考文献
[1] 薛明, 杨庆新, 章鹏程, 等. 无线电能传输技术应用研究现状与关键问题[J]. 电工技术学报, 2021, 36(8): 1547-1568.
Xue Ming, Yang Qingxin, Zhang Pengcheng, et al. Application status and key issues of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.
[2] 吴理豪, 张波. 电动汽车静态无线充电技术研究综述（上篇）[J]. 电工技术学报, 2020, 35(6): 1153-1165.
Wu Lihao, Zhang Bo. Overview of static wireless charging technology for electric vehicles: part Ⅰ[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1153-1165.
[3] 吴理豪, 张波. 电动汽车静态无线充电技术研究综述（下篇）[J]. 电工技术学报, 2020, 35(8): 1662-1678.
Wu Lihao, Zhang Bo. Overview of static wireless charging technology for electric vehicles: part Ⅱ[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1662-1678.
[4] 吴丽君, 李冠西, 张朱浩伯, 等. 一种具有恒流恒压输出自切换特性的电动汽车无线电能传输系统拓扑[J].电工技术学报, 2020, 35(18): 3781-3790.
Wu Lijun, Li Guanxi, Zhang Zhuhaobo, et al. A wireless power transfer system topology with automatic switching characteristics of constant current and constant voltage output for electric vehicle charging[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3781-3790.
[5] Lyu H, Babakhani A. A 13.56-MHz-25-dBm-sensitivity inductive power receiver system-on-a-chip with a self-adaptive successive approximation resonance compensation front-end for ultra-low-power medical implants[J]. IEEE Transactions on Biomedical Circuits and Systems, 2021, 15(1): 80-90.
[6] Chittoor P K, Chokkalingam B, Mihet-Popa L. A review on UAV wireless charging: fundamentals, applications, charging techniques and standards[J]. IEEE Access, 2012, 9(2): 69235-69266.
[7] 谢文燕, 陈为. 全方向无线电能传输技术研究进展[J]. 电力系统自动化, 2020, 44(4): 202-215.
Xie Wenyan, Chen Wei. Progress in full-direction radio energy transmission technology[J]. Automation of Electric Power Systems, 2020, 44(4): 202-215.
[8] Yang Lei, Zhang Yuanqi, Li Xiaojie, et al. Analysis and design of four-plate capacitive wireless power transfer system for undersea applications[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(3): 202-211.
[9] 苏玉刚, 阳剑, 戴欣, 等.基于TensorFlow神经网络的MCR-WPT系统负载与互感识别方法[J]. 电力系统自动化, 2021, 45(18): 162-169.
Su Yugang, Yang Jian, Dai Xin, et al. Load and mutual recognition of MCR-WPT system based on TensorFlow neural network[J]. Automation of Electric Power Systems, 2021, 45(18): 162-169.
[10] Li Yang, Dong Weihao, Yang Qingxin, et al. Automatic impedance matching method with adaptive network based fuzzy inference system for WPT[J].IEEE Transactions on Industrial Informatics, 2020, 16(2): 1076-1085.
[11] Li Yang, Dong Weihao, Yang Qingxin, et al. An automatic impedance matching method based on the feedforward-backpropagation neural network for a WPT system[J]. IEEE Transactions on Industrial Electronics,2019, 66(5): 3963-3972.
[12] Liu Yuanyuan, Feng Hongwei. Maximum efficiency tracking control method for WPT system based on dynamic coupling coefficient identification and impedance matching network[J].IEEE Journal of Emerging and Selected Topics in Power Electronics,2020, 8(4): 3633-3643.
[13] 赵鱼名, 王智慧, 苏玉刚, 等. 基于T型CLC谐振网络的恒压型电场耦合电能传输系统负载自适应技术[J]. 电工技术学报, 2020, 35(1): 106-114.
Zhao Yuming, Wang Zhihui, Su Yugang, et al. Load adaptive technology of constant voltage electric-field coupled power transfer system based on T-CLC resonant network[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 106-114.
[14] Fu Minfan, Yin Fe, Zhu Xinen, et al. Analysis and tracking of optimal load in wireless power transfer systems[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3952-3963.
[15] Fu Minfan, Ma Chengbin, Zhu Xinen. A cascaded Boost-Buck converter for high-efficiency wireless power transfer systems[J]. IEEE Transactions on Industrial Informatics, 2014, 10(3): 1972-1980.
[16] Huang Y, Shinohara N, Mitani T. Theoretical analysis on DC-DC converter for impedance matching of a rectifying circuit in wireless power transfer[C]// 2015 IEEE International Symposium on Radio-Frequency Integration Technology, Sendai, 2015: 229-231.
[17] Li Hongchang, Li Jie, Wang Kangping, et al. A maximum efficiency point tracking control scheme for wireless power transfer systems using magnetic resonant coupling[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3998-4008.
[18] Zhong W X, Hui S Y R. Maximum energy efficiency tracking for wireless power transfer systems[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 4025-4034.
[19] Yeo T, Kwon D, Khang S, et al. Design of maximum efficiency tracking control scheme for closed-loop wireless power charging system employing series resonant tank[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 471-478.
[20] Dai Xin, Li Xiaofei, Li Yanling, et al. Maximum efficiency tracking for wireless power transfer systems with dynamic coupling coefficient estimation[J].IEEE Transactions on Power Electronics, 2018, 33(6): 5005-5015.
[21] SkvareninaT L. The power electronics hand-book[M]. Los Angeles: CRC Press, 2002.
[22] Huang Y, Shinohara N, Mitani T. Impedance matching in wireless power transfer[J]. IEEE Transactions on Microwave Theory and Techniques, 2017, 65(2): 582-590.
[23] 闫凯歌, 刘坤, 潘盈盈, 等. 电流断续模式Boost PFC峰值电流控制[J]. 控制与信息技术, 2019(1): 56-58, 78.
Yan Kaige, Liu Kun, Pan Yingying, et al. Peak current control in discontinuous conduction mode of Boost PFC[J]. Control and Information Technology, 2019(1): 56-58, 78.
Maximum Efficiency Tracking Study of Active Impedance Matching Network Discontinous Current Mode in Wireless Power Transfer System
Abstract Aiming at the characteristics that the transmission efficiency is sensitive to the coupling coefficient and load change in wireless power transfer (WPT) system, this paper proposes a maximum efficiency tracking method based on the intermittent current mode (DCM) active impedance matching network. First, We analyzed expressions of different DC-DC converter inputs impedance to demonstrate the superiority of impedance matching of the DCM mode Buck-Boost transform circuit.Secondly, a maximum efficiency tracking control strategy based on the coupling coefficient identification was given, which can maximize and stabilize the large load transmission efficiency without real-time load monitoring and further tracking control. When the coupling coefficient changes, the system could also identify the coupling coefficient in real time according to the transmit and receive side voltage and current information, and realize the adaptive maximum efficiency tracking through adjusting the receiver side converter duty cycle. Finally, the feasibility and effectiveness of the method are verified and has obvious advantages in dynamic response and improved transmission efficiency.
keywords：Wireless power transfer, maximum efficiency tracking, continuous current current mode，impedance matching
DOI:10.19595/j.cnki.1000-6753.tces.211179
中图分类号：TM724
上海自然科学基金资助项目（21ZR1425300）。
收稿日期 2021-08-01
改稿日期 2021-08-13
赵进国 男，1997年生，硕士研究生，研究方向为无线电能传输技术。E-mail：1767093975@qq.com
赵晋斌 男，1972年生，教授，博士生导师，研究方向为电力电子技术，无线电能传输技术等。E-mail：zhaojinbin@shiep.edu.cn（通信作者）
（编辑 郭丽军）