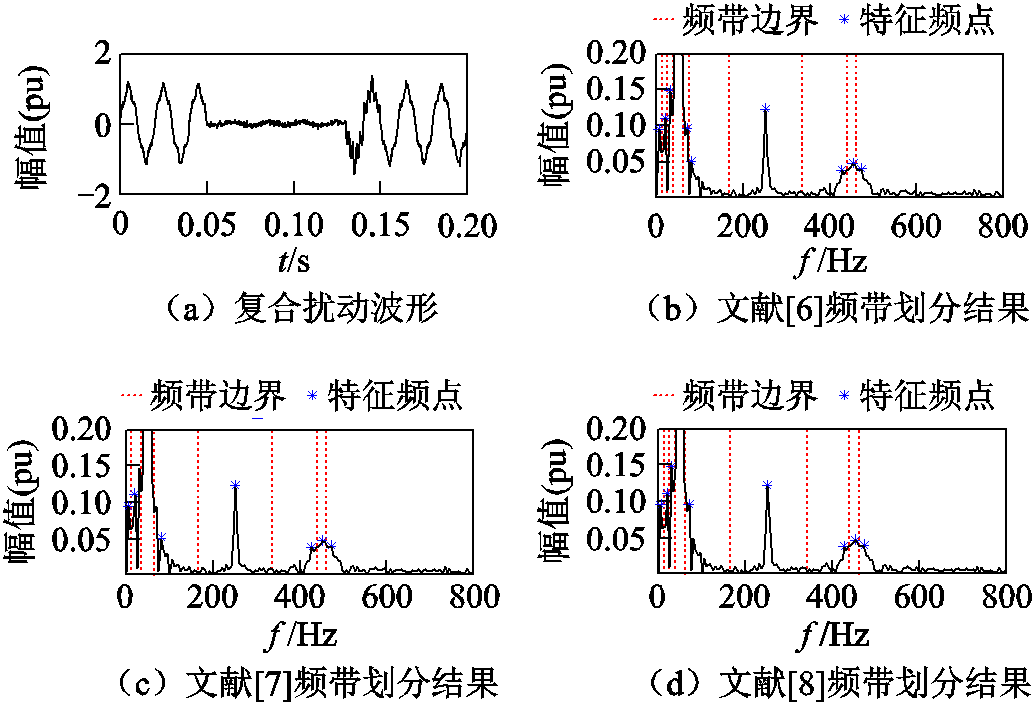
图1 复合扰动及其频带划分结果
Fig.1 Multiple PQ disturbance and its spectrum division results
摘要 针对电能质量复合扰动分类方法在分类数目和分类性能方面存在的不足，提出一种基于改进经验小波变换（MEWT）和极限梯度提升（XGBoost）的电能质量复合扰动分类方法。首先，对传统经验小波变换进行改进，使之适用于复合扰动特征提取；然后，根据基本扰动MEWT分析结果，从时频域多角度提取能够有效刻画不同扰动特性的特征序列；最后，基于问题转换策略构造以XGBoost为子分类器的多标签复合扰动分类模型，并通过特征选择与超参数优化相结合的模型训练方法进一步提升分类效果。实验结果表明，所提方法可实现48类扰动的有效辨识，较之传统多标签扰动分类方法在分类精度和噪声鲁棒性方面表现更优，且运算速度更快，适用于工程实践。
关键词：电能质量复合扰动 经验小波变换 尺度空间表示 多标签分类 极限梯度提升
近年来，随着大量非线性负载和分布式电源的广泛接入，电网中发生电能质量（Power Quality, PQ）扰动事件的概率大幅攀升，不同扰动间的交叉耦合也使得扰动类型日趋复杂，对电力系统的安全经济运行构成严重威胁[1]。面对监测装置所记录的海量扰动数据，实现复杂电能质量扰动的实时准确分类存储[2]是针对性分析和治理电能质量问题的关键前提，因而具有重要的研究意义。
经过多年研究积累，各种PQ扰动分类方法层出不穷，但大多数可归纳为特征提取和扰动分类两个步骤。作为典型的时变信号，时频分析方法被广泛应用于PQ扰动特征提取。短时傅里叶变换（Short Time Fourier Transform, STFT）[3]可联合时频域信息刻画信号特征，但其窗函数固定，仅适用于平稳信号分析；离散小波变换（Discrete Wavelet Transform, DWT）[4]虽然具有可变时频分辨率，但其分析效果受分解层数和小波基选取影响较大；S变换（S- Transform, ST）[5]兼具良好的抗噪性和时频分析性能，但其仍受制于海森堡测不准原理，且实时性差。
经验小波变换（Empirical Wavelet Transform, EWT）[6]是一种建立在小波变换理论框架之上的信号时频分析方法，其继承了小波变换的多尺度特点和经验模态分解的自适应性，在不依赖母小波选取的同时有效抑制了模态混叠现象，且运算量小，已被广泛应用于工程信号分析。文献[7]首次将EWT用于PQ信号分析，并基于横-纵双阈值频带划分方法实现了PQ信号的指标估计；文献[8-9]针对时变PQ扰动分析问题，分别提出了基于可变双阈值的广义EWT和基于分治策略的改进型EWT，但两者均未考虑噪声污染对特征频点选取产生的干扰，其分解结果中仍存在虚假分量；文献[10]对EWT的频带划分规则进行了调整，以提高其噪声污染下的谐波分析鲁棒性；文献[11]将文献[9]所提改进型EWT与多尺度排列熵相结合，用于单一扰动的特征提取，为PQ扰动分类提供了新的思路。由此可见，EWT已成为PQ信号分析的有效途径之一，但在处理复杂扰动信号时，其频带划分准确性仍有待提高。
在扰动分类阶段，现有研究大多采用直接多分类方法，但该策略仅适用于对单一扰动和少量复合扰动进行辨识。随着所考虑扰动类型的增加，分类器将面临维数灾难，分类效率及精度也将大打折扣。为此，文献[12]将多标签分类思想引入PQ扰动分类问题，其实现方法具体又可以分为算法改造策略和问题转换策略两类。文献[13-14]分别基于改造后的多标签径向基函数（Multi Label Radial Basis Function, MLRBF）神经网络和三层贝叶斯网络（Three-Layer Bayesian Network, TLBN）对PQ复合扰动进行辨识，该类算法可充分挖掘扰动标签间的关联性以提升分类效果，但通常需要付出巨大的运算成本代价；文献[15]采用二元关联（Binary Relevance, BR）方法将多标签问题转换为多个二分类子问题，算法的时间复杂度被明显降低，其分类精度在很大程度上依赖各子分类器的泛化性能。极限梯度提升（eXtreme Gradient Boosting, XGBoost）是梯度提升理论的一种全新高效系统实现方式[16]，采用解析法而非数值优化方法求取损失函数的最优解是其与传统梯度提升树（Gradient Boosting Decision Tree, GBDT）之间最显著的差异，与决策树（Decision Tree, DT）、支持向量机（Support Vector Machine, SVM）、随机森林（Random Forest, RF）等传统机器学习算法相比，具有不易过拟合、损失函数求解精度更高、支持稀疏数据处理等优势[17]。因此，本文选用XGBoost作为BR方法的子分类器。
为实现复杂PQ扰动的快速准确辨识，本文提出一种基于改进经验小波变换（Modified Empirical Wavelet Transform, MEWT）和XGBoost的PQ复合扰动分类方法。首先，充分考虑复合扰动时频特征和现有EWT技术存在的不足，提出一种基于尺度空间表示（Scale-Space Representation, SSR）和动态测度的MEWT分析方法；其次，基于扰动MEWT分析结果，设计了12维扰动分类特征；最后，将前向序列特征选择与贝叶斯超参数调优相结合，构造并训练BR-XGBoost多标签扰动分类模型对复合扰动进行分类。实验结果表明，本文方法在不同噪声背景和频率偏移情况下均表现良好，较之其他方法分类精度更高且实时性更优，工程应用前景广阔。
图1a为信噪比（Signal-to-Noise Ratio, SNR）为30dB的中断+谐波+振荡复合扰动，采用文献[7-9]方法对其进行分析，所得频带划分结果如图1所示。
图1 复合扰动及其频带划分结果
Fig.1 Multiple PQ disturbance and its spectrum division results
由图1可知，电压中断在基波频谱附近引起了明显的频谱泄露，噪声污染则使得原本光滑的暂态振荡频谱曲线变得崎岖，两者都严重干扰了特征频点的判断，导致上述方法在基波和暂态振荡频谱附近均不同程度地出现了频带“过切分”问题。这是因为无论是双阈值思想[7-8]还是分治策略[9]，两者都着眼于获取较高的特征频点频域分辨率，适用于谐波、间谐波类的PQ扰动分析。虽然其也在一定程度上抑制了频谱泄露对特征频点选取产生的干扰，但在处理复合PQ扰动时，频带错分现象依然严重。此外，上述方法在设计之初均未考虑噪声对暂态振荡频谱的污染，这些都增加了基于现有EWT技术对扰动特征提取的难度。
考虑到上述方法均直接依据原始Fourier谱来划分频带，且效果不太理想，因此，本文从谱线平滑角度出发对EWT的频带划分规则进行改进，提出一种适用于复合PQ扰动分析的MEWT方法。对于包含N个有限带宽固有模态（Band-Limited Intrinsic Mode Functions, BLIMFs）分量的离散时间信号f(t)，其MEWT变换主要包含以下三个步骤：
1）尺度空间表示：设f(t)的离散Fourier变换为F(w)，定义高斯核函数为
（1）式中，n为尺度因子。则F(w)的尺度空间表示的离散形式可定义为
（2）
式中，M为近似系数，当M=ceil(6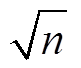
+1)时高斯核函数的离散近似误差可忽略不计[18]。SSR能够在保留频谱特征信息的同时，对局部干扰峰值进行平滑处理，可显著降低特征频点的判别难度。
2）动态测度：由SSR定义可知，干扰频点随着n增大将逐渐消失，但特征频点也会随之被淹没。为了获取更高的特征频点频域分辨率，同时考虑到较小尺度下的SSR中仍可能存在幅值较大的干扰极值点，本文采用动态测度对SSR中的极大值点进行去趋势评价。设xu为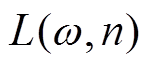
的中某一极大值点，若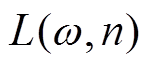中存在比xu更高的点，则xu的动态测度Dyn(xu)等于其到所有等高点路径中最小路径的动态测度，即
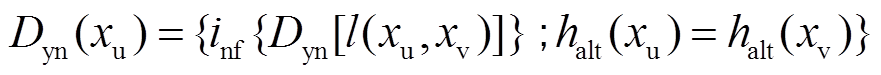（3）式中，l(xu, xv)为xu通向等高点xv的路径；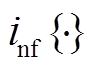
为下确界；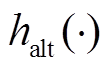
为高度。此时，若Dyn(xu)大于判别阈值Td，即可判定xu为特征频点。
3）经验小波分解：确定特征频点序列{Wn}N n=1后，取相邻两特征频点间的中点频率构造频带边界序列{wn}N n=0（其中w0=0、wN=p为频谱自身边界）。考虑到多数PQ扰动特征频点分布于低频区域，若依照现有的EWT频谱分割规则划分频带，那么特征频点WN所对应的最高频扰动分量将与大量高频噪声分量一同落入频带区间[wN-1，wN]，此时EWT分解结果中的最高频分量将不可避免地受到高频噪声污染。为此，本文在保留现有前N个频带边界{wn}N-1 n=0的基础上，依照式（4）对频带边界进行平移增补
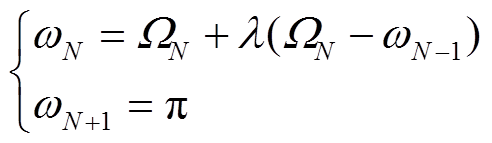（4）式中，l为平移系数。考虑到PQ扰动分量在频域关于谱峰具有对称性，令l=1可以在保留最高频扰动分量频谱信息的同时，使之完全落入带通区间为[wN-1,w N]的滤波器内，从而抑制高频噪声的干扰。此时，F(w)将被分割成N+1个连续区间{Ln}N+1 n=1，由此构造经验小波并实施经验小波变换，即可将各扰动分量及噪声分量从原始信号中的分离出来，有关经验小波变换的详细原理及实施过程可参见文献[6]。
由MEWT原理可知，尺度因子n和判别阈值Td是决定其频带划分效果和后续扰动特征提取的关键参数。因此，本节就MEWT的参数整定展开讨论。
1）尺度因子n的设定。不同于文献[18]在全尺度下对F(w)实施SSR，本文仅计算某一固定尺度下的尺度空间曲线，因而n的选取至关重要。经过大量随机参数仿真实验后，在30dB噪声下，以电压中断扰动f2(t)={1-0.95[e(4.35T)-e(2.75T)]}sin(wt)，谐波扰动f1(t)=sin(wt)+0.3sin(3wt)+0.06sin(5wt)+ 0.2sin(7wt)，以及暂态振荡扰动f3(t)=sin(wt)+0.2e-75(t-2T)[e (4T)-e (2T)]sin(9w (t-2T))为例，其中w=100p，T为工频周期，e(×)为阶跃函数。分别在尺度n=0.09、n=9和n=900下求取上述扰动频谱的SSR及其动态测度，结果如图2所示。图2的每幅子图中，左图为扰动频谱的尺度空间曲线，右图为SSR的极大值动态测度结果。
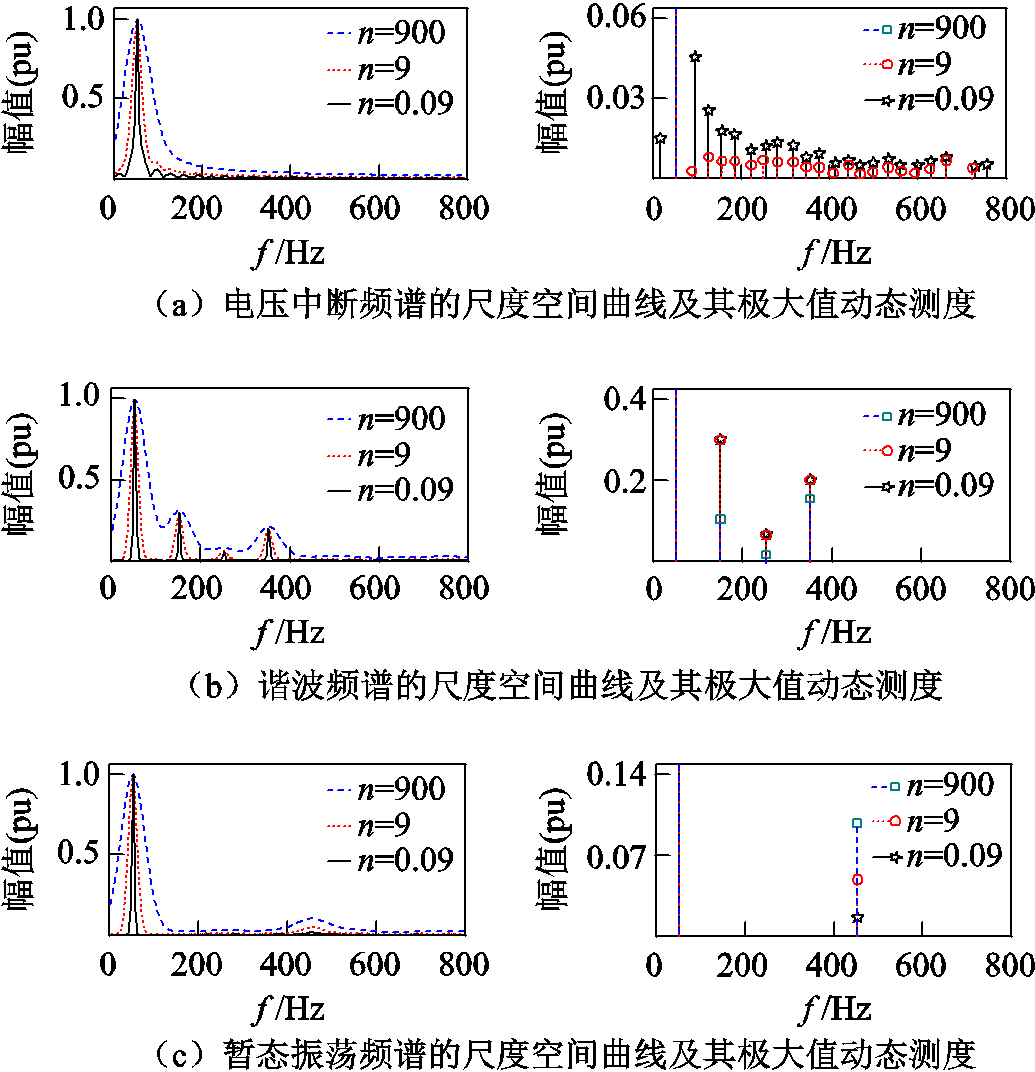
图2 不同尺度因子n下扰动频谱的SSR及其动态测度
Fig.2 SSR and its dynamic of disturbance spectrums with different n
由图2a可知，当n=900时，扰动频谱SSR中的无效峰值均已被平滑；当n降至9时，SSR中开始出现干扰频点，且幅值最高可达0.1(pu)，但其动态测度大小均低于0.01(pu)，充分展现了动态测度良好的去趋势评价效果；当n=0.09时，SSR已与原始频谱十分近似，此时干扰频点的动态测度也有所升高，不利于特征频点的准确判断。由图2b可知，当n取0.09、9时，各谐波特征频点的SSR幅值及其动态测度均与原始频谱相近，但随着n增大，各特征频点的SSR幅值虽几乎不变，但其动态测度却明显减小，5次谐波的动态测度仅为0.016(pu)，难以从中判定幅值较小的谐波分量所对应的特征频点。由图2c可知，随着n值增大，暂态振荡所对应特征频点的SSR幅值及其动态测度也随之增大，这一特性将有助于判定幅值较小的暂态振荡特征频点。综上所述，为了规避无效峰值的干扰，同时又能捕捉高频分量的特征信息，本文取n=9。
2）判别阈值Td的设定。由于动态测度反映的是特征频点的相对大小，因此设置固定判别阈值Td为
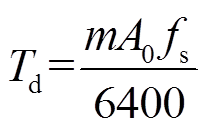（5）式中，m为阈值因子；A0为正常信号幅值；fs为采样频率。恰当的m可使Td大于干扰频点的动态测度且小于特征频点的动态测度。为提高特征频点的判别准确率，选取谐波、暂态振荡两类多频扰动和频谱泄漏最为严重的电压中断为研究对象，参照文献[19-20]在Matlab中生成扰动信号各500组，信号时长0.2s，fs取6.4kHz，SNR为30dB，记录n=9时电压中断、暂态振荡扰动的SSR动态测度的次大值，以及谐波扰动特征频点所对应的SSR动态测度的最小值，结果如图3所示。由图3可知，当n=9、m=5即Td=5时，MEWT的特征频点捕捉能力可取得满意效果。
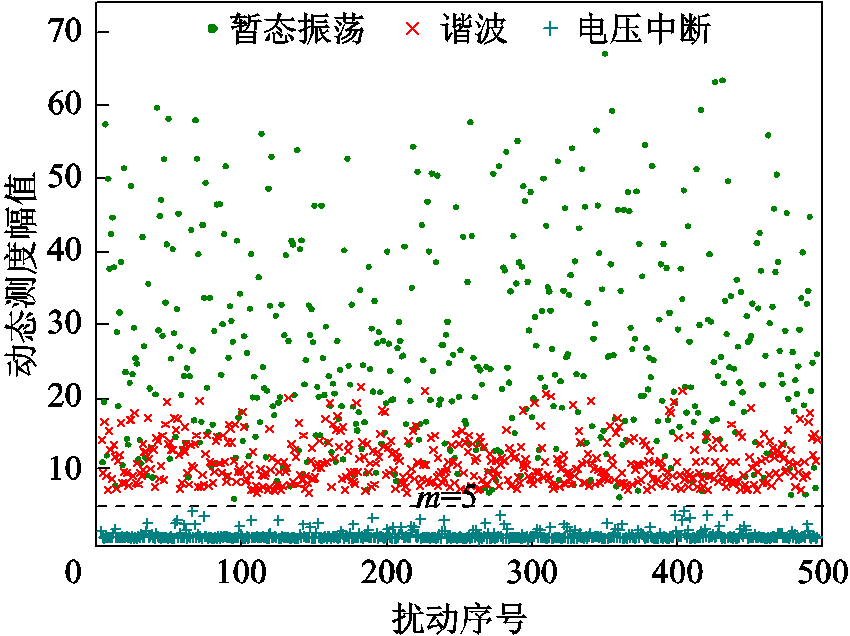
图3 n=9时不同扰动中主要频点的动态测度
Fig.3 Dynamic measures of main frequency points in different disturbances with n=9
PQ复合扰动通常由多个基本信号叠加而成，本文所研究的基本信号包括正常信号（C0），以及电压暂升（C1）、电压中断（C2）、电压暂降（C3）、谐波（C4）、暂态振荡（C5）、暂态脉冲（C6）、电压闪变（C7）扰动，同样参照文献[19-20]构建电能质量扰动基本信号模型见表1。在30dB信噪比下对基本信号进行MEWT分析，结果如图4所示。图4各子图中自上而下分别为原始信号、信号分解结果BLIMFn（n=1, 2,
, N+1）和MEWT频带划分结果。
表1 电能质量扰动基本信号模型
Tab.1 Basic signal models of power quality disturbances
标签信号模型参数范围 C0 C1 C2 C3 C4 C5 C6 C7
由图4可知，由于MEWT采用了频带平移增补策略，C0～C3和C6、C7单频信号被分解为低频分量BLIMF1和高频分量BLIMF2，低频分量几乎完全保留了基波信号的时域特征，高频分量中除噪声污染外，暂态脉冲分量及暂升、中断、暂降扰动的暂态过程也在其中得以体现。对于C4、C5多频扰动，MEWT可准确判定其特征频点，并将低频分量BLIMF1和高频分量BLIMFn（n≠1）从原始信号中依次分离出来，此处的低频分量同样为去噪后的近似基波信号，高频分量中则包含各次谐波、暂态振荡等扰动分量及噪声污染。
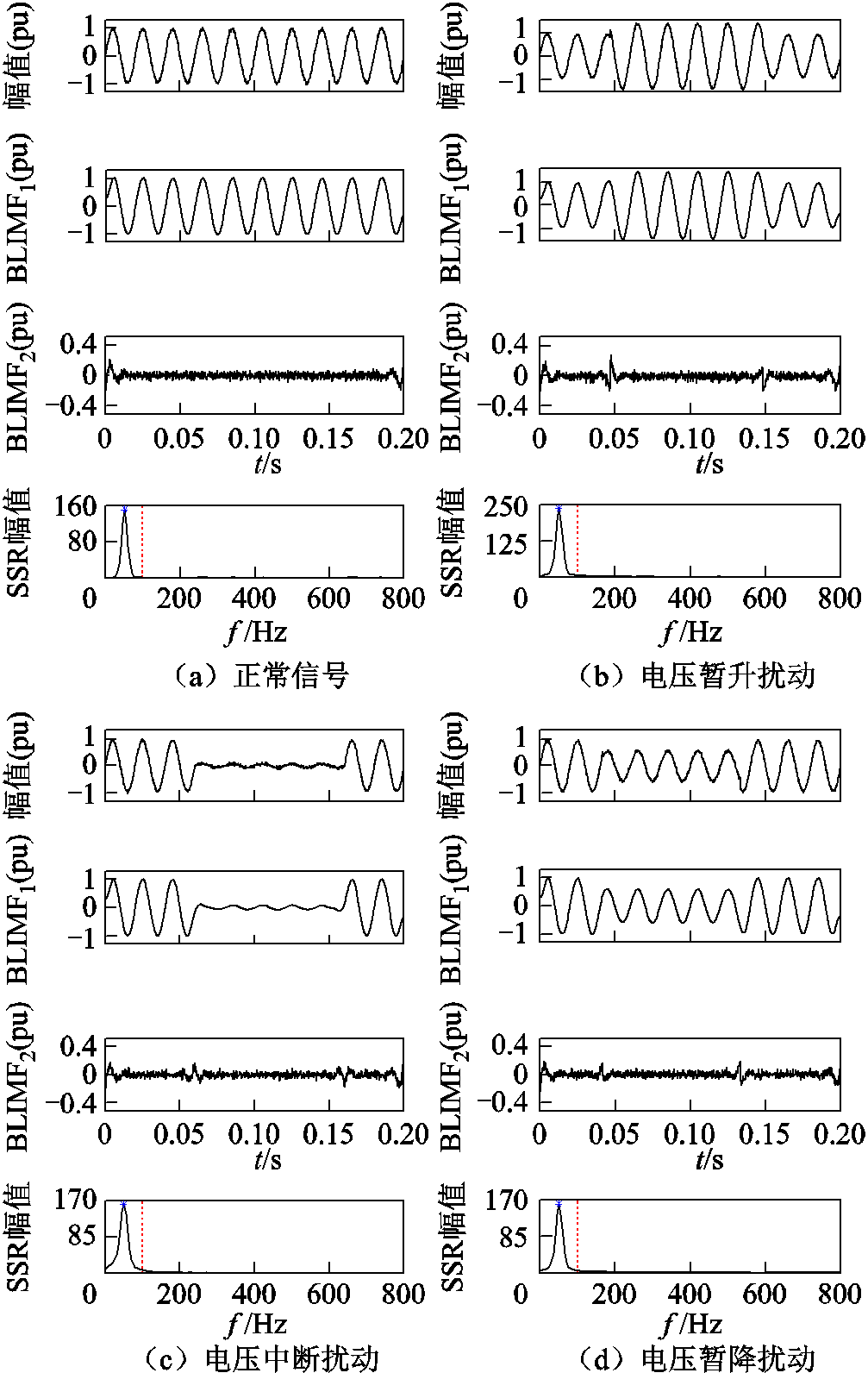
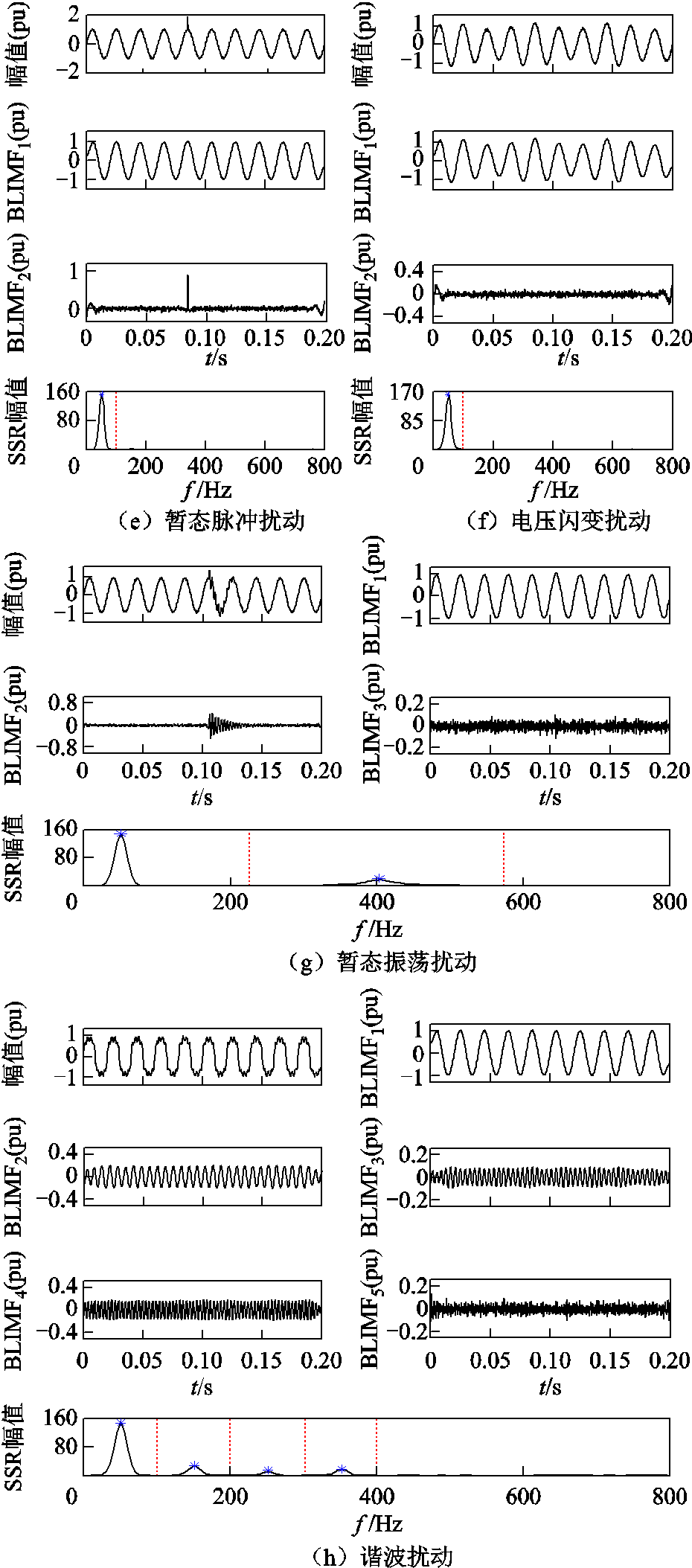
图4 PQ信号波形及MEWT分析结果
Fig.4 PQ signal waveforms and results of MEWT analysis
2.2.1 低频分量特征
鉴于MEWT所提取的低频分量BLIMF1能够有效保留PQ扰动中基频信号的原始特征，本文从BLIMF1中提取特征F1～F7。
1）令A(p)=|BLIMF1(p)|，p为采样点序号，p=1, 2, …, P（P为PQ信号总采样点数），基于双阈值策略[7]在A(p)中筛选极大值点，形成低频分量极值点包络序列Peak，其中横阈值T1=0，纵阈值T2=fsT/4。以图4d暂降扰动为例，其极值点包络序列如图5所示。由图5可知，Peak能够准确刻画PQ扰动中基波信号的幅值变化情况，因此，本文从Peak中提取特征F1～F3。定义特征F1、F2分别为有效上穿越次数和有效下穿越次数。若Peak向上或向下穿越阈值d1，且高于d1的持续长度大于一个极值点，即为一次有效上穿越；同理，若Peak向上或向下穿越阈值d2，且低于d2的持续长度大于一个极值点，即为一次有效下穿越。本文取d1=1.08、d2=0.92。此外，将Peak中极值点（首、末两元素也被视为极值点）所对应的序号从小到大依次记录于序列U中，计算Peak中相邻两极值点大小之差，可求得幅值波动序列S为
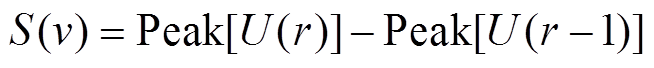（6）式中，r=2,3,…,R（R为Peak中极值点总数）；S(v)为第v次幅值波动大小，v=1,2,…,R-1。S(v)中大于阈值d3的元素数目即为特征F3，本文中d3=0.18。
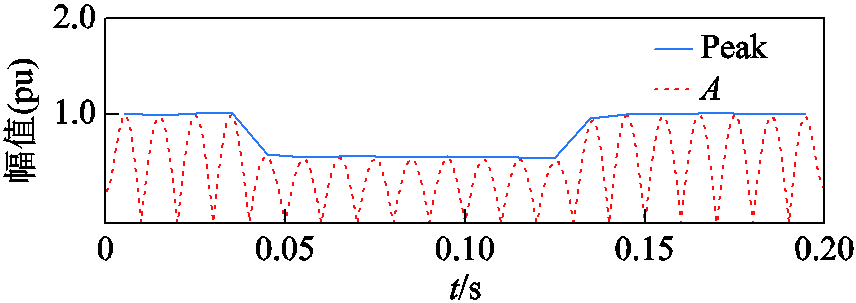
图5 BLIMF1极值点包络序列
Fig.5 Envelope sequence of extreme points in BLIMF1
2）采用长度为W的滑窗可以求取低频分量的有效值序列ARMS，其计算过程为
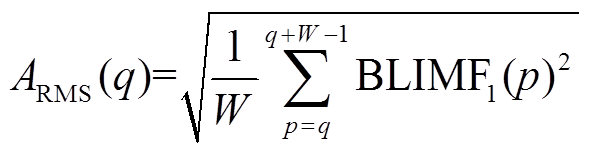（7）式中，W=fsT/2；q为有效值序列序号，q=1, 2,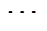, P-W+1。从ARMS中可以提取有效值特征F4～F7分别为ARMS的最大值、最小值、平均值及标准差。
结合各类基频信号的时域特性可知，F1～F3可将基频信号划分为正常信号、暂升、暂降（含中断）和其他扰动（闪变及含闪变的复合基频扰动）四大类，F4～F7则可在此基础上进一步对上述大类中的后两个类别进行细分，从而完成所有基频信号的准确划分。
2.2.2 SSR动态测度特征
对于谐波、暂态振荡等高频扰动，其特征主要体现在频域，且不受其他附加扰动影响，因此可从MEWT的SSR动态测度结果中提取特征F8、F9。
1）对于含谐波的PQ扰动，其谐波频率所对应的SSR动态测度明显大于其他不含谐波的扰动。考虑到实际电网可能存在频率偏移，定义F8为
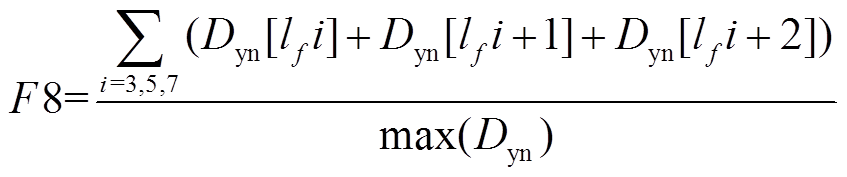（8）式中，i为所考虑谐波次数；lf为基频频点所在位置，lf=P/(fsT)。
2）暂态振荡也会使振荡频率所对应的SSR动态测度明显升高，因此定义F9为暂态振荡所处高频段400～1600Hz内SSR动态测度的最大值[20]。
2.2.3 高频分量特征
MEWT的变换结果中除低频分量外，还存在多条数量不等的高频分量，从中可提取特征F10～F12。
1）定义特征F10、F11分别为最高频分量BLIMFN+1的最大值和峭度，当PQ扰动中存在暂态脉冲时，上述特征数值将明显增大。
2）考虑到不同扰动在不同时频面上的能量分布各不相同，定义高频分量能量特征F12如式（9）所示，用于辅助判别各类扰动。
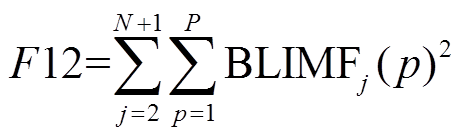（9）与传统基于Boosting思想的监督式树模型算法类似，XGBoost通过多轮迭代与残差拟合，将若干弱分类器集成为一个强分类器，具有良好的泛化性能和运算效率，其详细原理可参见文献[17]。需要指出的是，在XGBoost的梯度提升过程中，被选作分裂特征次数越多的特征重要度越高，因此，XGBoost可对所有输入特征的重要度进行排序。
鉴于本文在PQ扰动特征提取阶段已经充分考虑了所有扰动标签的扰动特性，因此，本文基于图6所示的框架构造并训练BR-XGBoost多标签扰动分类模型，将多标签分类问题分解为Q个单标签二分类问题（Q为标签数）。对于标签j，设训练集Dj={(Xi,yi)|1≤i≤n}（1≤j≤Q），其中i为样本序号，X为特征向量，变量yi∈{1,0}表示样本i是否属于标签j。基于Dj训练构造XGBoostj二分类模型，从而可以求得标签j的预测结果yj，再将多个二分类器组合成BR-XGBoost，即可输出多标签扰动分类结果Y=[y1 y2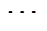 yQ]。
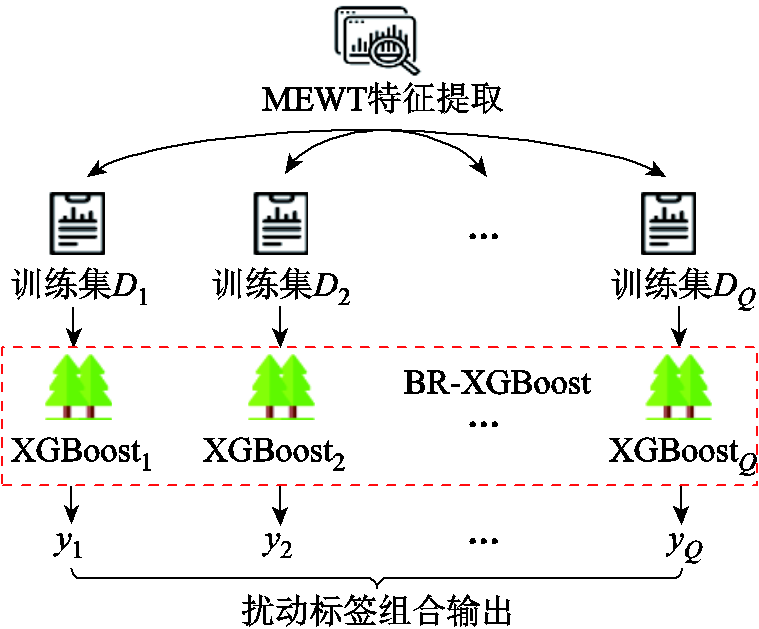
图6 BR-XGBoost多标签扰动分类模型训练框架
Fig.6 Training framework of multi label disturbance classification model based on BR-XGBoost
针对不同的分类问题，特征选择可有效去除特征集合中的冗余元素，从而起到提高模型泛化性能的效果。因此，本文基于前向序列选择方法[17]对每个XGBoostj进行特征选择。对于标签j，首先基于XGBoost获取全部特征的重要度排序，随后依次将排序靠前的特征加入特征子集（初始为空集），并在每次添加后计算特征子集的交叉验证分类准确率（Accuracy, ACC），若ACC提高则将该特征保留，反之剔除，遍历所有特征即可获取标签j的最优特征子集。
模型的表现除受到训练集影响外，很大程度上还取决于其内置参数即超参数的选取。为避免人工调参的复杂与不确定性，本文在Pycharm平台下调用分布式异步超参数优化模块（hyperopt）[21]，基于贝叶斯优化理论[17]，采用交叉验证方式，在确定各超参数范围的基础上对每个XGBoost进行调优，从而提升BR-XGBoost的模型精度。
综上，结合特征选择和超参数调优的XGBoostj扰动标签分类流程如图7所示。
为验证所提方法的有效性，本文依据IEEE 1159标准和文献[19-20, 22]，在Matlab中随机生成正常信号、7类基本扰动、17类双重扰动、17类三重扰动及6类四重扰动样本各1 000条，从中随机选取50%作为训练集，剩余用作测试集。PQ信号基频50Hz，采样频率6.4kHz，信号时长0.2s。XGBoost的学习目标选用“binary：logistic”，剩余参数均为默认值，BR-XGBoost及对比模型的构建与分析均在Python 3.8环境下实现。实验计算机配置为Intel i5-8500 C(PU)和16GB RAM。
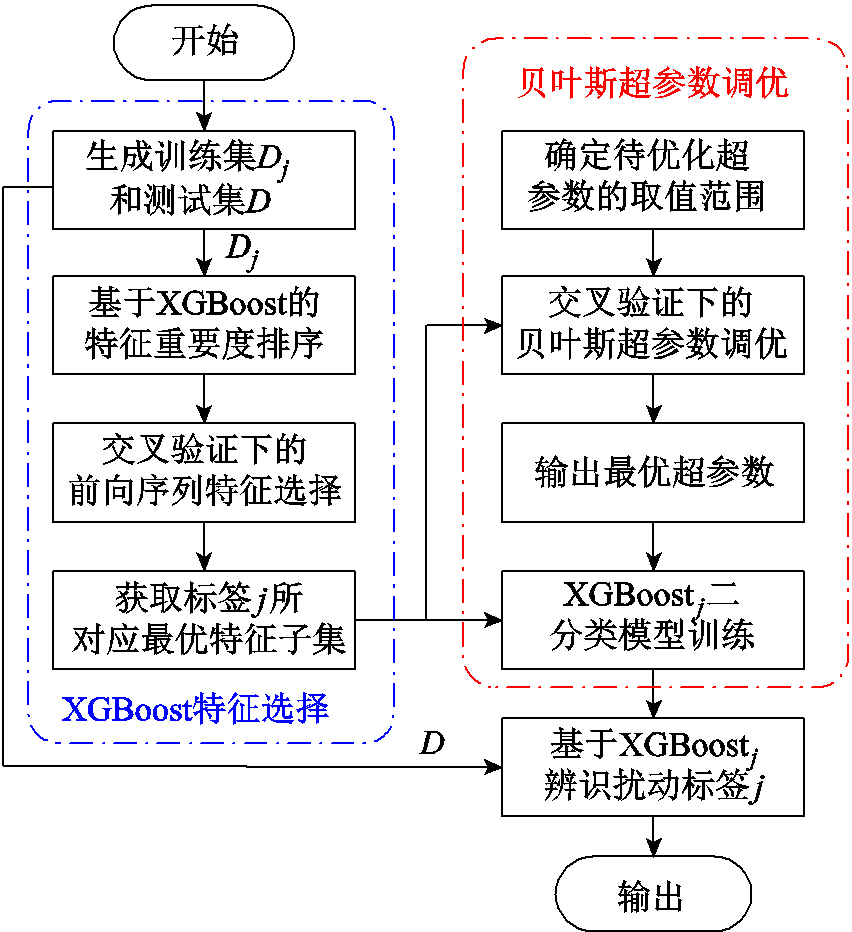
图7 基于XGBoostj的扰动标签分类流程
Fig.7 Flowchart of disturbance label classification based on XGBoostj
首先，在无噪训练集下基于XGBoost获取7类标签各自的特征相对重要度如图8所示。由图8可知，F1～F6的重要度主要分布于C1～C3、C7等基频扰动，而F8～F10则分别对于扰动C4～C6，具有最高的重要度，这些均与扰动特征的设计初衷及其各自所蕴含的物理意义相符，验证了所提特征的合理性。接着，基于不同标签所对应的特征重要度排序结果，在5折交叉验证下对不同标签进行前向序列特征选择。以标签C1为例，其交叉验证下的ACC指标随特征子集中特征加入的变化情况如图9所示。由图9可知，除F10、F8、F12和F2由于导致准确率下滑而被剔除外，XGBoost的交叉验证指标随有效特征的不断加入而逐渐提高。对不同标签重复上述操作，求得无噪环境下各类扰动所对应的最优特征子集见表2。进一步地，分别采用最优特征子集和全部12维特征对BR-XGBoost进行训练，求得各个XGBoost的平均交叉验证准确率分别为99.52%和99.37%，充分反映了特征选择对于分类器泛化性能的促进作用。
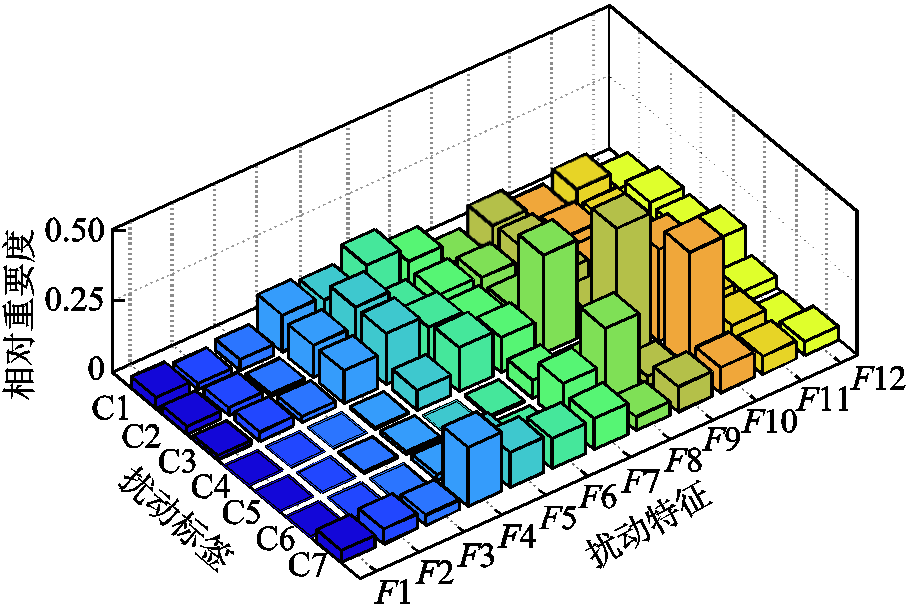
图8 不同标签所对应的扰动特征相对重要度
Fig.8 Relative importance of disturbance characteristics for different labels
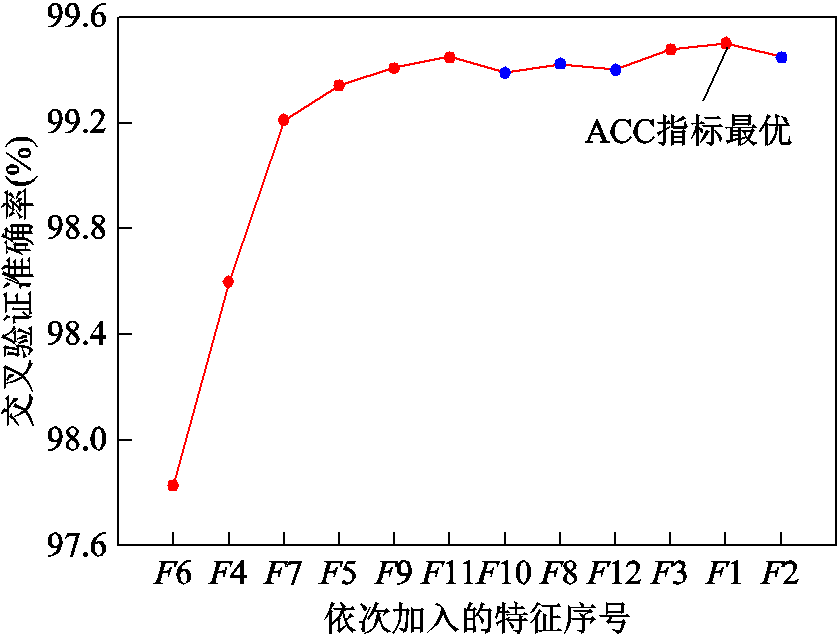
图9 标签C1的前向序列特征选择结果
Fig.9 Forward sequence feature selection results of C1
表2 不同标签所对应的最优特征子集
Tab.2 Optimal feature subsets for different labels
扰动标签最优特征子集 C1F6、F4、F7、F5、F9、F11、F3、F1 C2F5、F9、F4、F10、F7、F6、F8、F11、F2 C3F5、F6、F9、F4、F7、F10、F12、F8、F2 C4F8、F12 C5F9、F10、F11、F7、F6、F5 C6F10、F11 C7F4、F5、F7、F6、F10、F9、F2、F1、F3
基于贝叶斯优化理论，在经过特征选择后的无噪训练集下对每个XGBoost进行超参数调优，选取交叉验证指标ACC最高的一组超参数作为最终参数，所涉及的超参数名称、优化调整范围及以XGBoost1为例的超参数优化结果见表3。
表3 超参数优化调整范围
Tab.3 Optimal adjustment range of hyperparameters
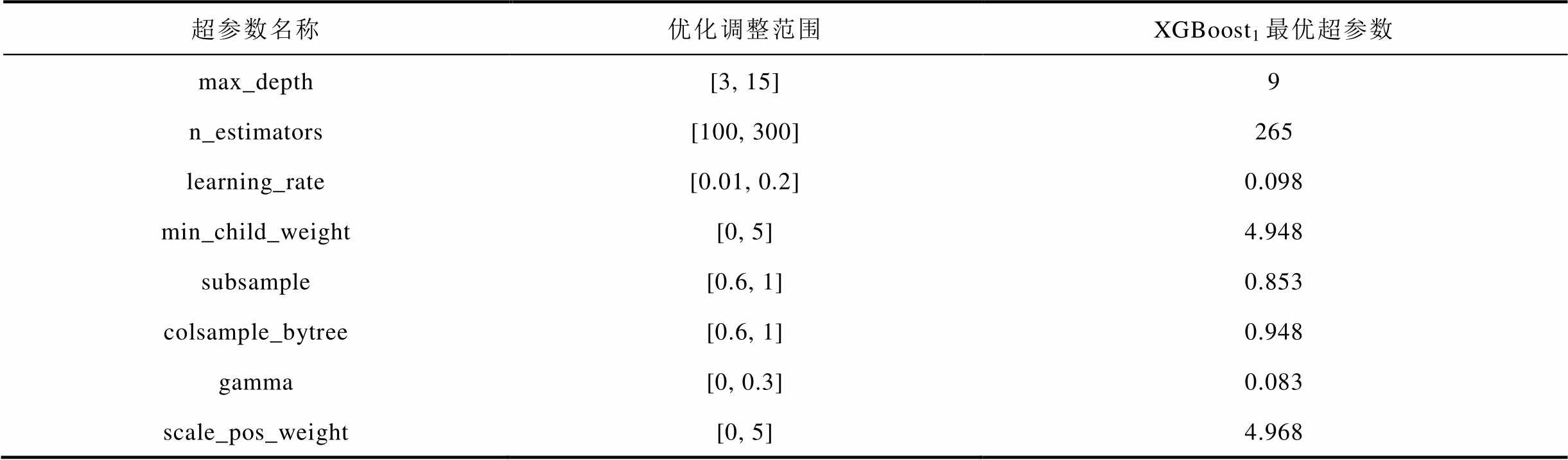
超参数名称优化调整范围XGBoost1最优超参数 max_depth[3, 15]9 n_estimators[100, 300]265 learning_rate[0.01, 0.2]0.098 min_child_weight[0, 5]4.948 subsample[0.6, 1]0.853 colsample_bytree[0.6, 1]0.948 gamma[0, 0.3]0.083 scale_pos_weight[0, 5]4.968
图10给出了无噪环境下超参数调优前后XGBoostj的交叉验证指标变化情况。从图10中可知，除标签C4、C6由于输入特征维数较低而导致模型泛化效果提升空间不足外，剩余标签的准确率指标均在参数调优后得到了进一步改善。
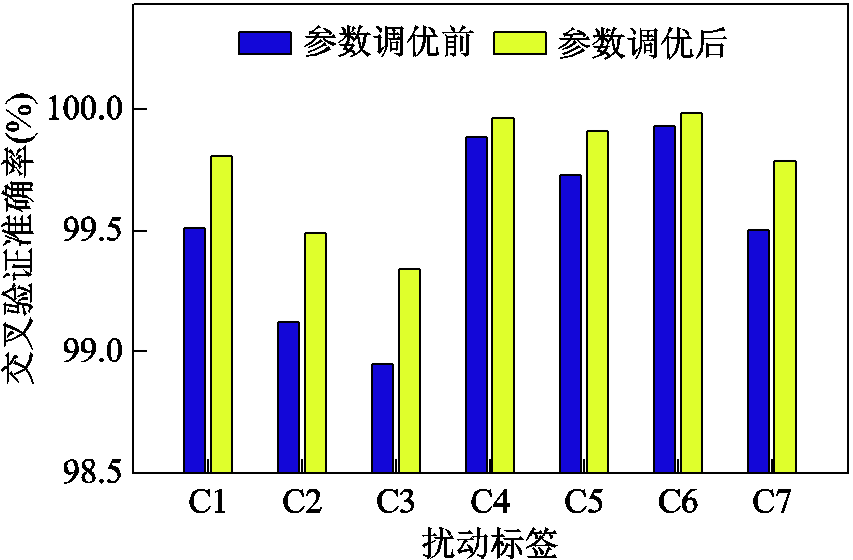
图10 超参数调优前后XGBoostj性能对比
Fig.10 Performance comparison of XGBoostj before and after hyperparameter optimization
噪声污染是PQ扰动分类在工程应用中所无法回避的重要问题。为验证所提方法的噪声鲁棒性，分别向扰动样本中添加信噪比为40dB、30dB和20dB的噪声，在不同噪声环境下均采用上述特征选择与超参数调优相结合的方法训练BR-XGBoost模型。最后基于测试集求得不同信噪比下PQ基本扰动、双重扰动、三重扰动和四重扰动的分类准确率分别见表4～表6。
表4 基本扰动分类结果
Tab.4 Classification results of basic disturbances
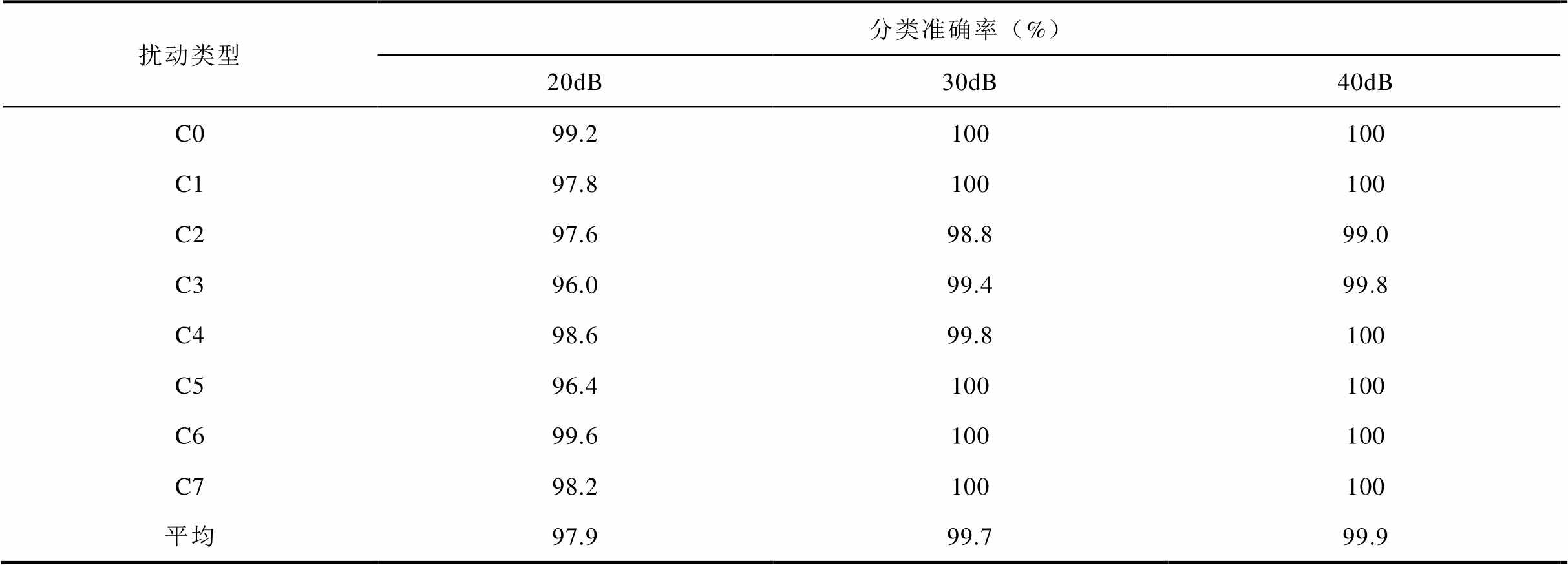
扰动类型分类准确率（%） 20dB30dB40dB C099.2100100 C197.8100100 C297.698.899.0 C396.099.499.8 C498.699.8100 C596.4100100 C699.6100100 C798.2100100 平均97.999.799.9
由表4～表6可知，扰动分类精度总体随扰动类型复杂度及背景噪声强度的提高而逐渐降低。具体而言，当SNR≥30dB时，各类型扰动的平均准确率仅出现了轻微下降，即便对于20dB信噪比下的四重PQ扰动，本文模型的平均准确率依然可以达到94.1%，充分说明了所提方法良好的分类效果与抗噪能力。
表5 双重扰动分类结果
Tab.5 Classification results of double disturbances
扰动类型分类准确率（%）扰动类型分类准确率（%） 20dB30dB40dB20dB30dB40dB C1C499.2100100C3C591.699.699.2 C1C594.610099.6C3C695.898.098.8 C1C698.299.6100C3C792.497.898.8 C1C795.497.898.2C4C594.699.699.8 C2C496.099.699.0C4C699.4100100 C2C592.899.299.4C4C798.099.8100 C2C695.699.299.2C5C796.699.8100 C2C796.899.099.0C6C797.498.699.2 C3C495.098.698.0平均95.899.299.3
表6 多重扰动分类结果
Tab.6 Classification results of multiple disturbances
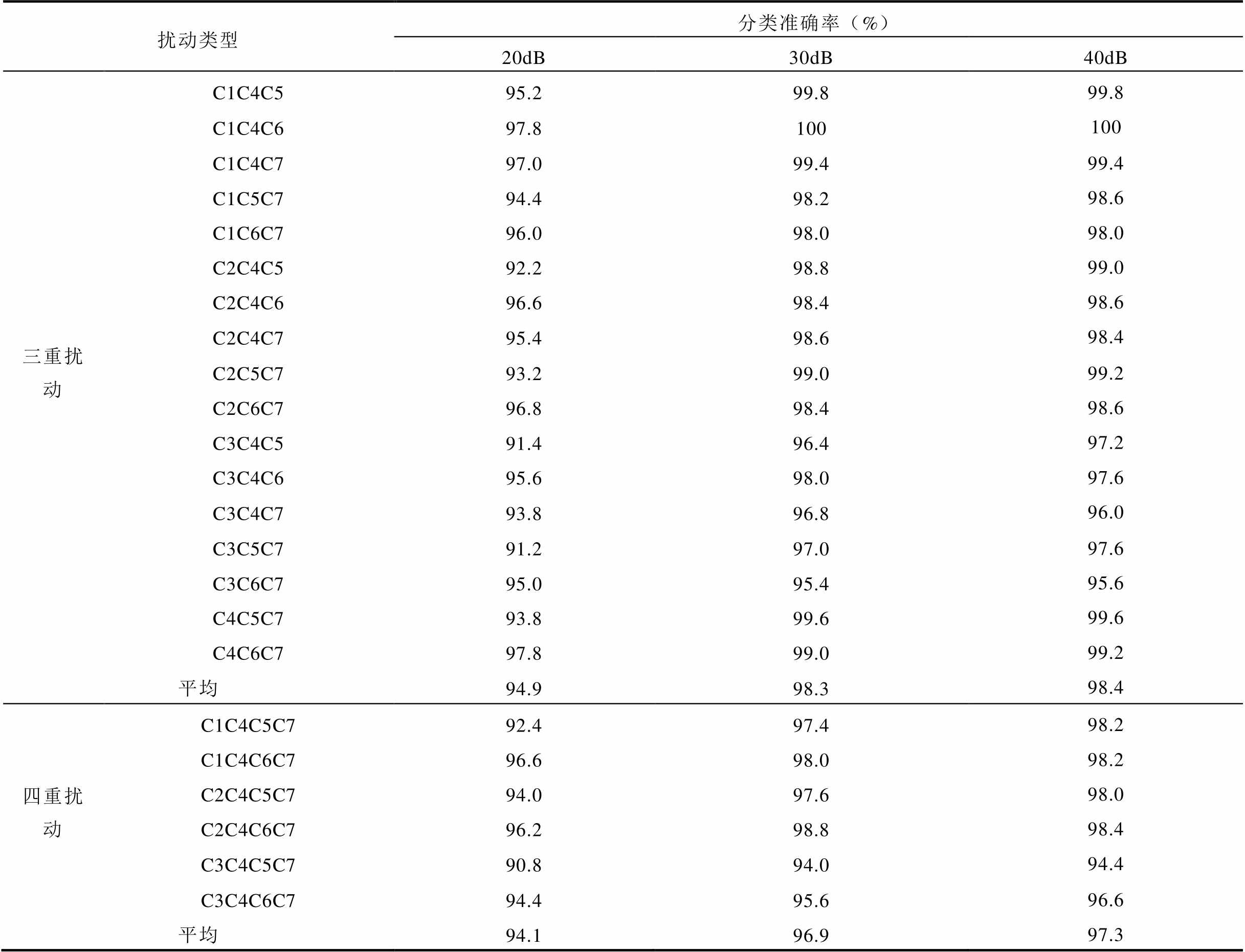
扰动类型分类准确率（%） 20dB30dB40dB 三重扰动C1C4C595.299.899.8 C1C4C697.8100100 C1C4C797.099.499.4 C1C5C794.498.298.6 C1C6C796.098.098.0 C2C4C592.298.899.0 C2C4C696.698.498.6 C2C4C795.498.698.4 C2C5C793.299.099.2 C2C6C796.898.498.6 C3C4C591.496.497.2 C3C4C695.698.097.6 C3C4C793.896.896.0 C3C5C791.297.097.6 C3C6C795.095.495.6 C4C5C793.899.699.6 C4C6C797.899.099.2 平均94.998.398.4 四重扰动C1C4C5C792.497.498.2 C1C4C6C796.698.098.2 C2C4C5C794.097.698.0 C2C4C6C796.298.898.4 C3C4C5C790.894.094.4 C3C4C6C794.495.696.6 平均94.196.997.3
为验证所设计模型训练方法的有效性，分别采用不同模型训练方法求得PQ复合扰动的平均测试准确率见表7。从中可知，在使用特征选择与超参数调优相结合的模型训练方法后，不同信噪比下的平均分类精度均有了不同程度的提高。
表7 扰动平均分类结果
Tab.7 Average classification results of disturbances
是否采用特征选择与参数调优平均分类准确率（%） 20dB30dB40dB 否94.397.898.2 是95.698.698.8
此外，考虑到实际电网中存在由基波频率偏移现象，本文基于所设计的模型训练方法，在30dB信噪比下对基波频率偏移时（49.5～50.5Hz，步长0.1Hz）所提方法的准确性进行测试，结果如图11所示。由图11可知，随着频率偏移量的增大，不同扰动的平均分类准确率总体呈现轻微下滑趋势，可见本文方法对于基波频率偏移具有良好的耐受性能。
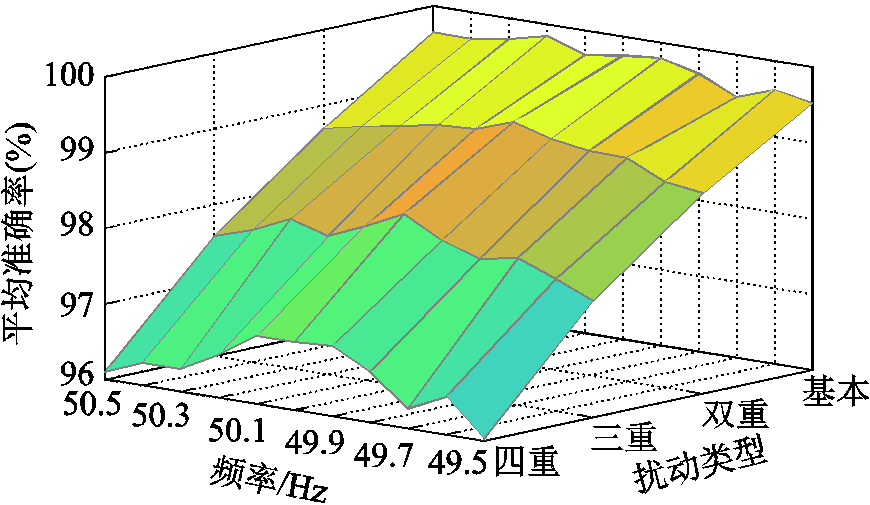
图11 基波频率偏移时的扰动分类结果
Fig.11 Disturbance classification results with fundamental frequency fluctuation
对于本文所采用的基于问题转换策略的多标签分类模型，其总体分类精度直接取决于各子分类器的性能。因此，分别选用C4.5决策树、Adaboost、RF及GBDT等传统树模型作为子分类器，基于4.2节中所述模型训练方法，在不同噪声环境下对扰动样本进行辨识，并将所得平均测试准确率与本文方法进行对比，结果如图12所示。
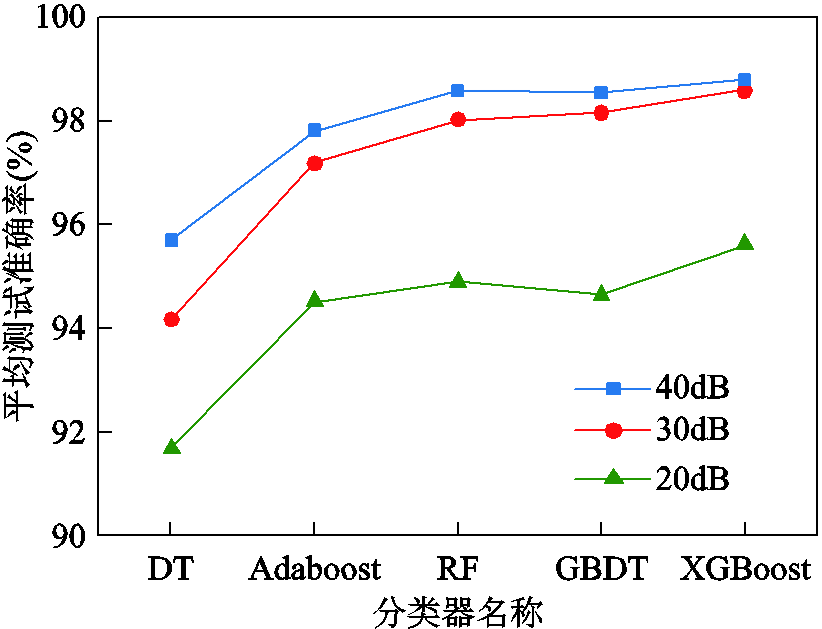
图12 不同分类器所得扰动分类结果
Fig.12 Disturbance classification results obtained by different classifiers
由图12可知，DT在所有分类器中分类效果最差，剩余模型由于采用了集成学习策略，因而准确率良好，其中以XGBoost最为突出。此外，分类效率也是衡量分类器性能的另一重要因素，测得30dB信噪比下DT、Adaboost、RF、GBDT的耗时分别为0.053s、3.075s、1.216s、0.178s，而XGBoost的耗时则为0.127s，逊于分类效果较差的DT但优于其他集成树模型，可见XGBoost在保证分类精度同时还兼具良好的分类效率。
为进一步说明所提方法的优越性，将本文方法与混合策略[23]、STFT-BRSVM[24]、DWT-MLRBF[25]、TQWT-BRRF[26]等现有复合扰动分类方法进行对比，结果见表8。从中可知，本文方法可依据少量特征对48类扰动进行辨识，且在30dB、40dB信噪比下均能取得最高准确率，仅在SNR=20dB时略低于文献[26]。考虑到文献[26]只计及了23类扰动，且不含闪变扰动，由此可见本文方法较之现有技术在可区分扰动种类及分类精度方面存在优势。
表8 PQ复合扰动分类方法性能对比
Tab.8 Comparison of classification methods for multiple PQ disturbances
分类方法特征维数扰动种类平均分类准确率（%） 20dB30dB40dB 混合策略[23]1148——88.7 STFT-BRSVM[24]837—91.393.4 DWT-MLRBF[25]1437—93.793.5 TQWT-BRRF[26]302396.598.198.7 本文方法124895.698.698.8
注：“—”表示对应文献中无相应结果。
此外，以上述文献共有的19类PQ扰动，总计19×500=9 500条测试信号为例，在30dB信噪比下对各类方法的分类处理时间进行分析，结果如图13所示。就特征提取耗时而言，相较于集总经验模态分解（混合策略）、STFT、DWT等传统时频分析方法，MEWT继承了EWT在计算复杂度方面的优势，与可调品质因子小波变换（Tunable Q-factor Wavelet Transform, TQWT）耗时相仿，但考虑到本文方法所需特征数目远少于文献[26]，故耗时最短。在分类器耗时方面，XGBoost由于引入了正则项以限制模型复杂度，同时还支持多线程并行计算，因此相比于其他分类器耗时更短。由此可见，较之现有复合扰动分类技术，本文方法具有良好的实时性。
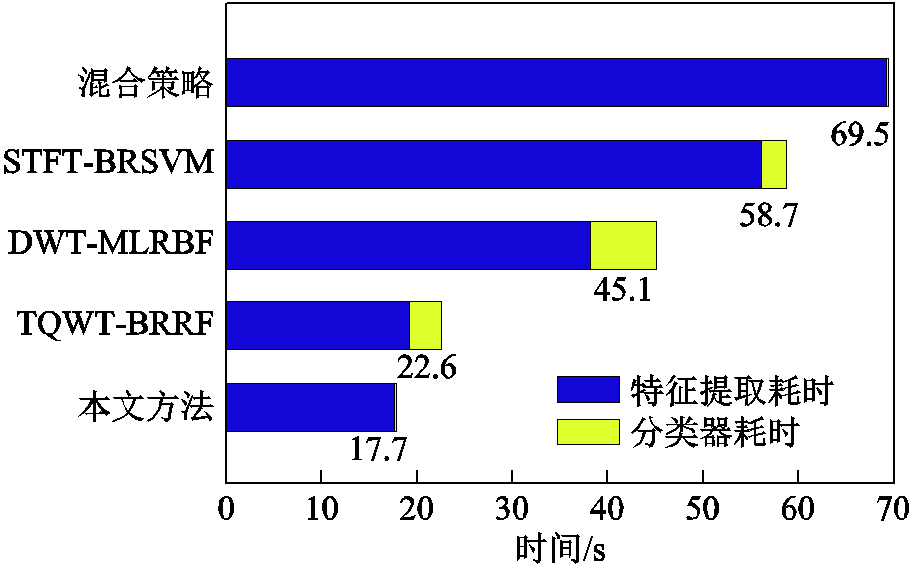
图13 不同方法分类处理时间对比
Fig.13 Comparison of classification processing time of different methods
以江苏电网某110kV变电站电能质量监测装置捕获的125组单相PQ扰动实测信号为研究对象，对本文方法应用于工程实践的可行性展开验证。每组实测信号的采样频率均为12.8kHz，信号时长0.2s，且都已经过归一化处理，其中两组典型实测信号波形及其MEWT时频谱如图14所示。由图14中可知，对于电压闪变，MEWT能够准确刻画其时域幅值特征，对于电压暂降+谐波复合扰动，MEWT则可对各模态进行有效分解，并从中提取暂降、谐波扰动的时频域特征，可见其对于实测信号同样具有良好的特征表达能力。
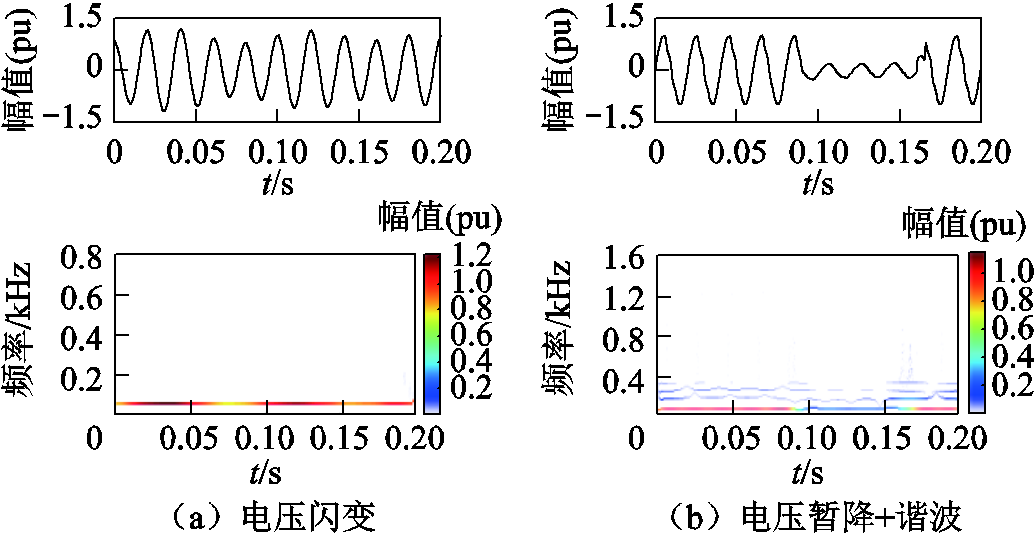
图14 典型实测信号波形及其MEWT分析结果
Fig.14 Waveform of typical measured signals and its analysis results of MEWT
取相同规格的仿真信号对BR-XGBoost进行训练，进而对实测信号的扰动类型进行辨识，测试结果见表9。进一步分析测试结果可知，由于对于凹陷幅值的定义相近，1组暂降扰动被标定为电压中断；1组闪变扰动由于幅值波动过大而被误判为暂降+闪变；1组暂升+振荡复合扰动由于振荡分量能量过低而导致标签丢失。由此可见，实测信号的不规则性导致本文方法的准确率较之仿真信号有所降低，但依然可以达到97.6%，表明了本文方法在工程实践应用中的有效性与准确性。
表9 实测信号分类结果
Tab.9 Classification results of measured signals
序号人工统计标签预测标签 1正常信号22组正常信号22组 2暂升13组暂升13组 3中断2组中断2组 4暂降36组暂降35组、中断1组 5谐波14组谐波14组 6脉冲5组脉冲5组 7闪变17组闪变16组、暂降+闪变1组 8暂升+振荡6组暂升+振荡5组、暂升1组 9暂降+谐波10组暂降+谐波10组
本文提出了一种基于MEWT和BR-XGBoost的PQ复合扰动多标签分类方法。首先，该方法针对传统EWT存在的频谱“过切分”现象，设计了一种结合SSR和动态测度的特征频点筛选机制，以提升EWT对于复杂PQ扰动的特征表达能力。其次，充分考虑扰动叠加前后扰动特征的变化规律，在MEWT时频分析结果基础上构造能够有效描述不同扰动特性的特征序列。此外，提出一种基于前向序列特征选择和贝叶斯超参数调优的模型训练方法，使BR-XGBoost的泛化性能得到进一步优化。实验结果表明，较之现有多标签扰动分类技术，本文方法在准确性、鲁棒性及实时性方面优势明显，可满足工程应用中海量PQ扰动事件的分类精度与效率需求。
现有研究暂未考虑高次谐波对扰动分类结果的影响，同时对所提方法在嵌入式系统中的应用讨论较少，后续工作将重点对上述问题展开分析。
参考文献
[1] 陶顺, 罗超, 肖湘宁, 等. 电流物理分量理论改进方法及其在电能质量评估中的应用[J]. 电工技术学报, 2019, 34(9): 1960-1970.
Tao Shun, Luo Chao, Xiao Xiangning, et al. A modified current physical components theory and its application in power quality assessment[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1960-1970.
[2] 王鹤, 李石强, 于华楠, 等. 基于分布式压缩感知和边缘计算的配电网电能质量数据压缩存储方法[J]. 电工技术学报, 2020, 35(21): 4553-4564.
Wang He, Li Shiqiang, Yu Huanan, et al. Compression acquisition method for power quality data of distribution network based on distributed compressed sensing and edge computing[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4553-4564.
[3] 黄建明, 李晓明. 结合短时傅里叶变换和谱峭度的电力系统谐波检测方法[J]. 电力系统保护与控制, 2017, 45(7): 43-50.
Huang Jianming, Li Xiaoming. Detection of harmonic in power system based on short-time Fourier transform and spectral kurtosis[J]. Power System Protection and Control, 2017, 45(7): 43-50.
[4] 肖贤贵, 李开成, 蔡得龙, 等. 一种电能质量扰动信号的联合去噪算法[J]. 电工技术学报, 2021, 36(21): 4418-4428.
Xiao Xiangui, Li Kaicheng, Cai Delong, et al. A combined de-noising method for power quality disturbances events[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4418-4428.
[5] 李建闽, 林海军, 梁成斌, 等. 基于双分辨率S变换和学习向量量化神经网络的电能质量扰动检测方法[J]. 电工技术学报, 2019, 34(16): 3453-3463.
Li Jianmin, Lin Haijun, Liang Chengbin, et al. Detection method of power quality disturbances based on double resolution S transform and learning vector quantization neural network[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3453-3463.
[6] Gilles J. Empirical wavelet transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010.
[7] Thirumala K, Umarikar A C, Jain T. Estimation of single-phase and three-phase power-quality indices using empirical wavelet transform[J]. IEEE Transactions on Power Delivery, 2015, 30(1): 445-454.
[8] Thirumala K, Shantanu S, Jain T, et al. Visualizing time-varying power quality indices using generalized empirical wavelet transform[J]. Electric Power Systems Research, 2017, 143: 99-109.
[9] Thirumala K, Umarikar A C, Jain T. An improved adaptive filtering approach for power quality analysis of time-varying waveforms[J]. Measurement, 2019, 131: 677-685.
[10] 吴建章, 梅飞, 陈畅, 等. 基于经验小波变换的电力系统谐波检测方法[J]. 电力系统保护与控制, 2020, 48(6): 136-143.
Wu Jianzhang, Mei Fei, Chen Chang, et al. Harmonic detection method in power system based on empirical wavelet transform[J]. Power System Protection and Control, 2020, 48(6): 136-143.
[11] 徐艳春, 樊士荣, 谭超, 等. 基于改进EWT-CMPE的高渗透率主动配电网电能质量扰动检测与分类[J]. 电网技术, 2020, 44(10): 3991-4000.
Xu Yanchun, Fan Shirong, Tan Chao, et al. Power quality disturbance detection and classification in high permeability active distribution network with improved EWT-CMPE[J]. Power System Technology, 2020, 44(10): 3991-4000.
[12] 周雒维, 管春, 卢伟国. 多标签分类法在电能质量复合扰动分类中的应用[J]. 中国电机工程学报, 2011, 31(4): 45-50.
Zhou Luowei, Guan Chun, Lu Weiguo. Application of multi-label classification method to catagorization of multiple power quality disturbances[J]. Proceedings of the CSEE, 2011, 31(4): 45-50.
[13] 管春, 周雒维, 卢伟国. 基于多标签RBF神经网络的电能质量复合扰动分类方法[J].电工技术学报, 2011, 26(8): 198-204.
Guan Chun, Zhou Luowei, Lu Weiguo. Recognition of multiple power quality disturbances using multi-label RBF neural networks[J].Transactions of China ElectrotechnicalSociety, 2011, 26(8): 198-204.
[14] Luo Yi, Li Kaicheng, Li Yuanzheng, et al. Three layer bayesian network for classification of complex power quality disturbances[J]. IEEE Transactions on Industrial Informatics, 2018, 14(9): 3997-4006.
[15] Lin W M, Wu C H, Lin C H, et al. Detection and classification of multiple power-quality disturbances with wavelet multiclass SVM[J]. IEEE Transactions on Power Delivery, 2008, 23(4): 2575-2582.
[16] 刘翊枫, 周国鹏, 刘昕, 等. 基于智能相似日识别及偏差校正的短期负荷预测方法[J]. 电力系统保护与控制, 2019, 47(12): 138-145.
Liu Yifeng, Zhou Guopeng, Liu Xin, et al. A short- term load forecasting method based on intelligent similar day recognition and deviation correction[J]. Power System Protection and Control, 2019, 47(12): 138-145.
[17] Guo Junqi, Yang Lan, Bie Rongfang, et al. An XGBoost-based physical fitness evaluation model using advanced feature selection and Bayesian hyper-parameter optimization for wearable running monitoring[J]. Computer Networks, 2019, 151(14): 166-180.
[18] Gilles J, Heal K. A parameter less scale-space approach to find meaningful modes in histograms -application to image and spectrum segmentation[J]. International Journal of Wavelets, Multiresolution & Information Processing, 2014, 12(6): 1450044.
[19] 黄南天, 彭华, 蔡国伟, 等. 电能质量复合扰动特征选择与最优决策树构建[J]. 中国电机工程学报, 2017, 37(3): 776-786.
Huang Nantian, Peng Hua, Cai Guowei, et al. Feature selection and optimal decision tree construction of complex power quality disturbances[J]. Proceedings of the CSEE, 2017, 37(3): 776-786.
[20] Juan José González de la Rosa, Muñoz A M, Gallego A, et al. Higher-order characterization of power quality transients and their classification using competitive layers[J]. Measurement, 2009, 42(3): 478-484.
[21] Bergstra J, Komer B, Eliasmith C, et al. Hyperopt: a Python library for model selection and hyperparameter optimization[J]. Computational Science & Discovery, 2015, 8: 1-24.
[22] Liu Zhigang, Cui Yan, Li Wenhui. A classification method for complex power quality disturbances using EEMD and rank wavelet SVM[J]. IEEE Transactions on Smart Grid, 2015, 6(4): 1678-1685.
[23] 张杨, 刘志刚. 一种基于时频域多特征量的电能质量混合扰动分类新方法[J]. 中国电机工程学报, 2012, 32(34): 83-90, 13.
Zhang Yang, Liu Zhigang. A new method for power quality mixed disturbance classification based on time-frequency domain multiple features[J]. Proceedings of the CSEE, 2012, 32(34): 83-90, 13.
[24] 黄建明, 瞿合祚, 李晓明. 基于短时傅里叶变换及其谱峭度的电能质量混合扰动分类[J]. 电网技术, 2016, 40(10): 3184-3191.
Huang Jianming, Qu Hezuo, Li Xiaoming. Classification for hybrid power quality disturbance based on STFT and its spectral kurtosis[J]. Power System Technology, 2016, 40(10): 3184-3191.
[25] 瞿合祚, 刘恒, 李晓明, 等. 一种电能质量多扰动分类中特征组合优化方法[J]. 电力自动化设备, 2017, 37(3): 146-152.
Qu Hezuo, Liu Heng, Li Xiaoming, et al. Feature combination optimization for multi-disturbance classification[J]. Electric Power Automation Equipment, 2017, 37(3): 146-152.
[26] 杨晓梅, 郭林明, 肖先勇, 等. 基于可调品质因子小波变换和随机森林特征选择算法的电能质量复合扰动分类[J]. 电网技术, 2020, 44(8): 3014-3020.
Yang Xiaomei, Guo Linming, Xiao Xianyong, et al. Classification of multiple power quality disturbances based on TQWT and random forest feature selection algorithm[J]. Power System Technology, 2020, 44(8): 3014-3020.
Recognition of Multiple Power Quality Disturbances Based on Modified Empirical Wavelet Transform and XGBoost
Abstract Aiming at the shortcomings of multiple power quality disturbances classification method in terms of classification number and classification performance, a recognition method of multiple power quality disturbances based on modified empirical wavelet transform (MEWT) and extreme gradient boosting (XGBoost) was proposed. Firstly, the traditional empirical wavelet transform was improved to make it suitable for feature extraction of multiple disturbances. Then, according to the MEWT analysis results of basic disturbances, feature sequences which can effectively depict different disturbance characteristics were extracted from time and frequency domain. Finally, a multi label classification model for multiple disturbances with XGBoost as sub classifier was constructed based on the problem transformation strategy, and the model training method combining feature selection and hyperparameter optimization was used to further improve the effect of classification. The experimental results show that the proposed method can effectively identify 48 types of disturbances. Compared with the traditional multi label disturbance classification method, the proposed method performs better in classification accuracy and noise robustness, and has faster operation speed, which is suitable for engineering practice.
keywords：Multiple power quality disturbances, empirical wavelet transform, scale-space representation, multi label classification, XGBoost
DOI:10.19595/j.cnki.1000-6753.tces.201363
中图分类号：TM76
江苏省重点研发计划（BE2020027）、国家电网公司科技（52199918000C）和国家重点研发计划（2018YFB0905000）资助项目。
收稿日期 2020-10-12
改稿日期 2021-03-21
吴建章 男，1996年生，博士研究生，研究方向为电能质量信号检测与分析。E-mail：wujianzhang@seu.edu.cn（通信作者）
梅 飞 男，1982年生，讲师，博士，研究方向为新能源发电技术、电气设备在线监测与故障诊断。E-mail：meifei@hhu.edu.cn
（编辑 赫蕾）