图1 园区综合能源商两级市场运营框图
Fig.1 Schematic diagram of the operation of park integrated energy supplier
摘要 随着能源市场化改革的有序推进，未来有望建成开放完善、充分竞争的综合能源市场体制。综合能源商作为重要市场主体，如何在综合能源市场体制中合理优化交易策略尚待开展研究。为此，该文计及能源批发与零售两级市场，构建一种具有前瞻性的园区综合能源商市场交易策略及协同优化方法。首先，分析综合能源批发市场及零售市场的运行机制，基于离散选择模型量化了零售价格对市场份额的影响，并构建远期收益函数；其次，计及用户综合需求响应，以综合能源商为领导者，以用户为跟随者，建立基于主从博弈的分布式协同优化模型；接着，论证了Stackelberg均衡解的存在性，并采用改进布谷鸟算法与二次规划相结合的方法进行分布式优化求解；最后，仿真验证了该文所提交易策略及优化模型的可行性与优越性，为未来园区综合能源商的市场交易决策提供指导。
关键词：园区综合能源商 批发与零售市场 离散选择模型 主从博弈
构建以能源互联网为支撑的现代能源体系是我国能源发展的重要战略目标。综合能源系统作为能源互联网的具体表现形式[1]，充分利用多能互补的优势，有效提升可再生能源消纳率，提高综合能源利用水平，是能源革命的必然选择。众多园区凭借坚实的用户基础及优越的自然社会资源，正在逐步转型为园区综合能源系统，为用户提供综合能源服务[2]。同时，随着新电力体制改革和天然气市场化改革的有序推进，未来有望逐步建成开放完善、充分竞争的综合能源市场体制[3]。在此市场环境下，园区综合能源商充分利用不同属性、不同时间尺度能源市场的互补特性，挖掘用户侧综合需求响应，降低购能成本，促进新能源消纳，已成为当前的研究热点。
目前，国内外学者已在园区综合能源商参与能源批发市场交易方面开展了大量研究。然而，现有研究多集中在电力批发市场方面。文献[4]计及中长期市场和现货市场，构建售电商参与多时间尺度市场的购电模型，并合理评估了购售电的潜在风险。文献[5]以市场运营主体为领导者，以售电公司和综合能源商为跟随者，提出一种考虑多从方均衡的主从博弈交易优化模型。文献[6]提出基于差价合约的售电商期货市场购电策略，并对合作联盟与非合作联盟模式进行深入探讨。文献[7]基于集中式和分布式批发市场构建分层综合能源市场和综合能源市场交易模型。文献[8]计及电/气/热多能源网络约束，建立多能源日前市场模型，提出基于需求响应的综合能源市场最优联合交易策略。上述研究多侧重于电力市场，没有充分计及不同能源属性、不同时间尺度市场的互补特性，同时对于用户侧需求响应潜力的挖掘较少，忽略了零售市场对用户用能需求的影响，可能带来投标量的偏差，增加风险成本。
此外，园区综合能源商参与零售市场交易方面也已开展了大量研究。文献[9]计及零售电价对用户电量及用户对售电公司选择的影响，提出多对多非合作双层博弈模型，以优化零售电价。文献[10]建立综合能源商之间的博弈竞价模型，并分析零售市场中用户的用能特性对其竞价策略的影响。文献[11]阐述了综合能源零售商与用户之间博弈互动的实现机理，设计出一种零售商与社区智能枢纽之间的双层博弈模型，但对能源零售商的建模较为粗糙。文献[12]考虑未来综合能源零售市场多能互补的特点，介绍了用户综合需求响应的概念，提出一种分布式序数势博弈的综合需求响应优化策略。上述文献虽在运营商零售价格制定方面提供了较好的思路，但仍存在不足之处：一方面，上述文献未考虑综合能源批发市场对零售价格的影响，忽略了潜在的收益空间；另一方面，多数文献没有合理计及零售价格对市场份额及未来收益期望的影响。
为应对上述问题，本文计及综合能源批发与零售两级市场，充分挖掘多类型多尺度能源市场的互补特性，合理量化零售价格对市场份额及综合需求响应的影响，提出一种基于主从博弈的园区综合能源商市场交易分布式协同优化模型。本文主要创新点：①基于离散选择（Multinational Logit, MNL）模型评估了零售价格对多能零售市场份额的影响，并以远期收益形式纳入考量；②计及综合需求响应，充分挖掘多类型多尺度能源市场的互补潜能，提出了一种基于主从博弈的综合能源商分布式协同优化模型；③论证了Stackelberg均衡解的存在性，并采用改进布谷鸟算法与二次规划相结合的方法进行分布式高效求解。
园区综合能源商两级市场运营模式如图1所示。在能量流上，园区综合能源商从上游发电商、供气商购买能源，经过园区热电联产机组、燃气锅炉等设备将电-气能源转换为电-气-热三种能源，供给下游终端用户。在业务流上，园区综合能源商作为中间环节，协同参与上游批发市场与下游零售市场，实现综合能源的购入-转换-售出。信息流作为数据传输通道，一方面依托5G等通信网络，将能量流的感知数据发送至上层业务流，以供各主体进行决策优化及电力市场交易业务开展；另一方面将业务流交易数据以指令形式下达至各级能源设备，以控制能量流协同运作。在整体运营中，园区综合能源商以业务流为主导，协同参与综合能源批发和零售市场，同时以业务流、信息流引导能量流，实现多能流供给平衡，以满足用户的用能需求。
图1 园区综合能源商两级市场运营框图
Fig.1 Schematic diagram of the operation of park integrated energy supplier
从能源属性上，批发市场分为电力和天然气两个市场。一般而言，天然气市场对电力市场的影响并不显著[13]。此外，由于电-气需求通常存在错峰现象，电力与天然气批发市场具有一定的互补性。从时间粒度上，批发市场又可大体分为现货市场和期货市场。
1）现货市场一般包括日前与实时市场，且以市场为导向制定价格，能够充分挖掘电-气商品属性，实现资源的合理配置，具有价格低、风险高的特点。综合能源商参与日前现货市场的购能成本Cr可表示为
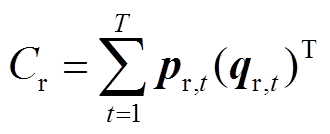（1）式中，pr,t为t时段现货市场能源价格向量，pr,t=[per,tpgr,t]，per,t、pgr,t分别为电、气价格；qr,t为t时段运营商的现货市场能源购买量向量，qr,t=[qer,tqgr,t]，qer,t、qgr,t分别为电、气购买量；T为时段数，取24。
2）期货市场的时间尺度较大，通常存在日/周/月/季/年多种形式，主要有金融和物理两种交割方式。相较于现阶段的中长期市场，期货市场更为成熟和规范。期货市场具有套期保值功能，可降低现货市场的价格波动，存在价格高、风险低的特点，能够反映真实的电力供需情况[14]。期货市场的交易形式主要有差价合约、期权合约、期货合约，其中以差价合约最为成熟。差价合约签订的能源量不涉及物理交割，合约另一方根据履约价格及签订能源量对运营商通过现货市场购买的能源成本进行多退少补，因此可等同认为签订能源量是运营商通过中长期合约购入[6]。运营商参与该市场的购能成本Cq可表示为
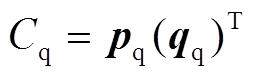（2）式中，pq为期货市场能源价格向量，pq=[pq,epq,g]，pq,e、pq,g分别为电、气差价合约履约价格；qq为运营商的电、气签订能源量向量。
此外，为响应国家政策，促进可再生能源技术的发展，园区综合能源商需考虑在绿色证书市场购买满足配额的绿色证书[4]。假定1MW·h电量产生1个绿色证书，则绿色证书购买成本Cl为
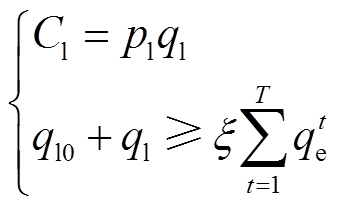（3）式中，ql0为综合能源商在批发市场中购买绿色能源所捆绑获得的绿色证书量，本文取0；ql为绿色证书的购买量；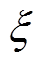
为可再生能源最低配额要求；
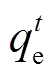为t时段的售电量；pl为绿色证书价格。
目前，我国电力现货市场试运行在广东等地已逐步开展[15]。为解决政府主导定价方式导致的天然气定价机制浑浊化等问题，天然气现货市场也将起步建设[16]。期货市场虽然在我国发展缓慢，但其作为现货市场架构较为完善状态下的高级伴随形式[14,16]，近年来已成为研究热点。本文立足于未来，充分考虑多类型多尺度市场之间的互补特性，在满足用户用能需求前提下，合理安排各市场交易量，有效地减小现货市场交易风险，降低整体市场交易成本，从而实现经济运行。
1.3.1 市场机制
随着能源互联网的发展和售电侧改革的推进，零售市场逐步开放与完善，未来有望形成电/气/热综合能源零售新业态。综合能源商凭借自身技术优势，通过提供综合能源服务、多样化能源套餐和APP自助服务等，抢占零售市场空间，稳固市场利润。用户根据自身偏好、能源零售价格及公司口碑等，自由选择零售代理商，并借助智能终端设备与代理商签订或续签次日的能源供应合同。此外，电网、气网、热网作为公共设施，负责各能源的输送，并根据输送容量收取过网费用，不再参与市场交易。
1.3.2 基于MNL模型的市场份额收益
完全竞争的零售市场中，各综合能源商的市场份额取决于零售价格、服务质量、用户粘性等因素，其中零售价格占据主导地位[17]。为合理解析零售价格对市场份额及远期收益的影响，本节采用MNL模型量化零售价格与市场份额的关系。
MNL模型是一种基于随机效用理论的市场选择行为分析方法[18]。它模拟了选择者与备选项之间的效用，并以效用最大的备选项作为选择者的决策，以此得到每个备选项被选中的概率。效用函数通常由固定项与随机项两部分构成，以本文为例，用户i选择综合能源商j的效用Uij为
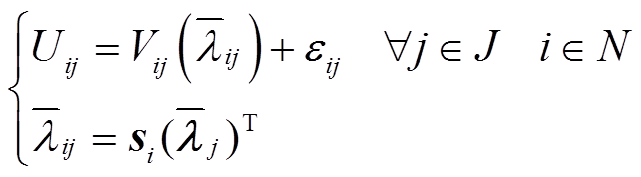（4）式中，Vij为可观测的固定效用，可通过层次分析法评估衡量[17]；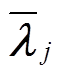
为关于零售价格矩阵lj（l=[lelhlg]，le、lh、lg分别为运营商的电、热、气实时零售价格列向量）的平均值向量，
=[
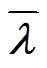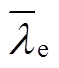
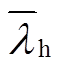
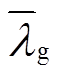]；si为用户i的价格敏感度系数向量，s=[seshsg]，se+sh+sg=1，se、sh、sg可通过用户i的各类能源历史支出在其总购能历史支出中的占比估值；εij为不可观测的随机扰动效用；J为综合能源商集合；N为用户集合。
由此，用户i选择综合能源商j的概率，即综合能源商j的市场份额可表示为
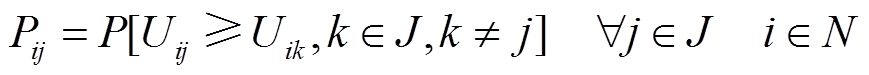（5）在完全竞争的零售市场中，各综合能源商之间具有相同且独立的地位，可认为随机变量εj之间相互独立且服从相同的分布[18]。为方便求解、提高应用，假定εj服从独立的极值分布，此时MNL模型转换为多项Logit模型，对应的市场份额为[19]
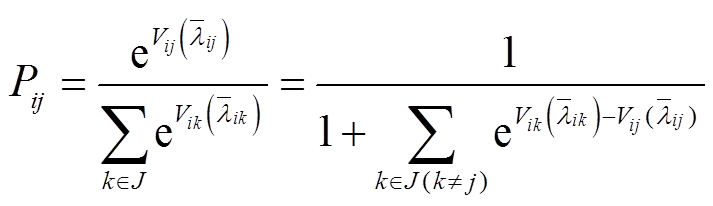（6）
当综合能源商j的零售价格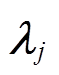
发生变化时，假定其他综合能源商k的零售价格
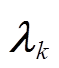不变，即Vik(
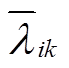)为常数，此时
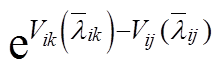为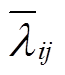
的函数。进一步可将式（6）转换为[1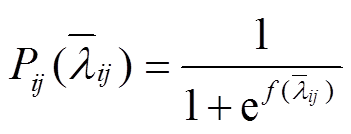7]
（7）式中，f(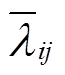
)可表示为关于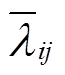的二次效用函数，即
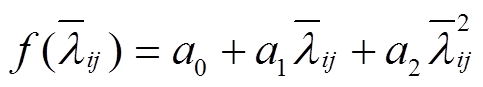（8）
进一步量化零售价格对综合能源商j未来收益的影响，本节以市场份额的潜在价值作为远期收益来衡量[18]，具体形式为
（9）式中，Bj为综合能源商j的未来收益，本文仅以园区综合能源商为分析对象，故简写为B；Pj0为当前市场份额；μ为单个用户的潜在价值，认为短期内近似不变，借助综合能源商历史盈利数据进行评估。
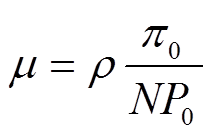（10）
式中，ρ为修正系数，体现综合能源商的主观因素，取值在1附近；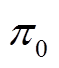
为综合能源商典型日收益。
日前现货市场价格预测具有不确定性，而差价合约的价格由多方撮合得到，为确定性参数。因此，园区综合能源商在日前优化阶段，需要合理计及日前现货市场价格不确定性的影响。本文拟采用分布鲁棒优化进行处理。该方法继承了随机规划和鲁棒优化的优点，通过寻找大量数据场景的最恶劣概率分布，得到风险折中的方案[20]。传统基于矩信息的分布鲁棒优化存在计算理论复杂、处理困难、数据挖掘深度不够的缺点；基于K-L散度、H距离等的分布鲁棒优化存在适用范围狭窄、非线性严重等问题。而基于Wasserstein距离的分布鲁棒优化易于处理，适用范围广泛，能够有效挖掘数据场景的价值[21]。本文采用基于Wasserstein距离的分布鲁棒优化进行不确定性处理。现货市场价格场景模糊集
的定义与其他相关说明详见附录。因此，风险成本R可表述为
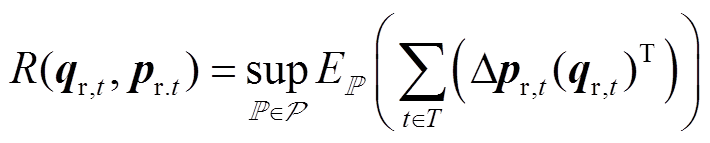（11）式中，pr,t为不确定参数；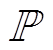
为实际节点价格的真实分布；
为价格场景分布模糊集；E为期望值；
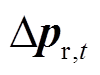为现货市场电/气预测价格的偏差向量。
综合能源商的收益函数主要包括批发市场购能成本、零售市场售能收益及远期收益，以其收益最大化为目标函数，即
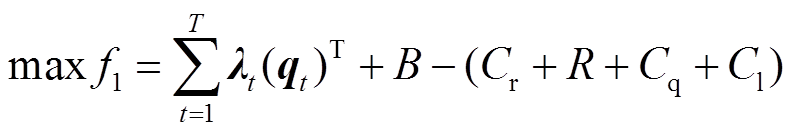（12）
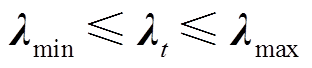（13）
式中，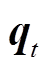
为综合能源商售能量向量，也是园区用户总购能量向量，
，
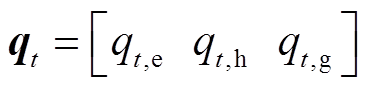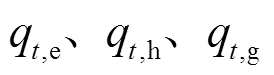分别为t时段的电、热、气售能量，
，
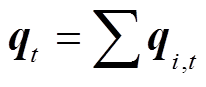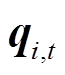为用户i的购能量向量，=[
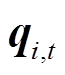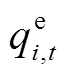
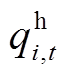
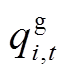]；lmax、 lmin分别为综合能源商制定电/热/气价格的上、下边界。
综合能源商在运行优化时，还需要考虑园区内能量转换装置的运行约束[22]和供需平衡约束。本文以能源集线器的形式进行构建，具体结构如图1所示，约束为
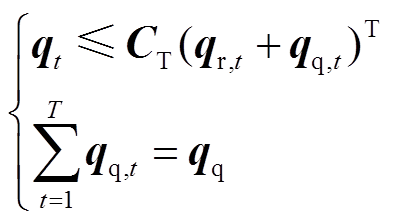（14）
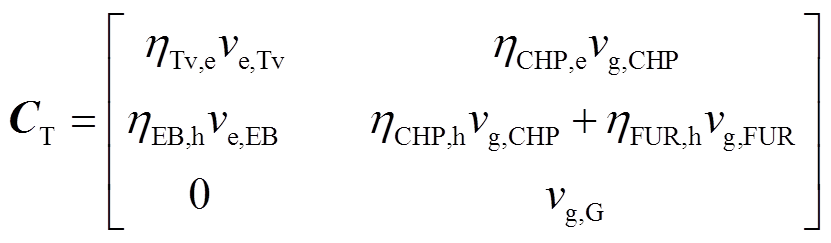（15）
式中，CT为3×2阶转换矩阵，表示能量集线器内部的能量转换关系，调度运行方式确定后CT为常值矩阵[22]；η为各设备能量转换效率；v为各设备能源调度系数；Tv、EB、CHP、FUR、G分别代表变压器、电热锅炉、热电联产、燃气炉、天然气管道。
用户侧装设有智能终端设备，以控制家用设备运行和零售市场交易。在综合能源商公布零售价格后，智能终端设备根据零售价格调整次日综合用能计划，并上报综合能源商。为合理计及用户满意度，本节采用线性递减边际收益的二次效用函数来表征用户i的用能满意度[9]，即
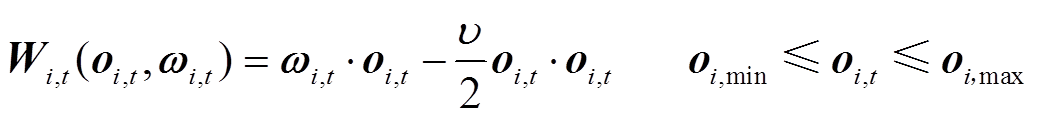（16）式中，符号“·”代表矩阵之间的点乘；Wi,t为用户i的用能满意度向量，Wi,t=[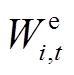
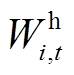
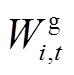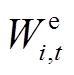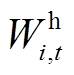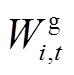]，、、分别为用户的用电、热、气满意度；oi,t为t时段用户i实际能源消耗量向量，oi,t=[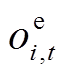
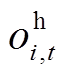
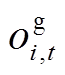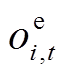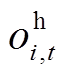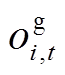]，、、分别为用电、热、气量；ωi,t为t时段用户i购买意愿因子向量，ωi,t=[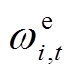
]；
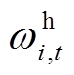
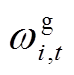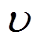为常系数，取值为1；oi,max、oi,min分别为用户i需求的上、下限。
用户i以最大化效用即满意度函数与用能成本之差为目标函数，表述为
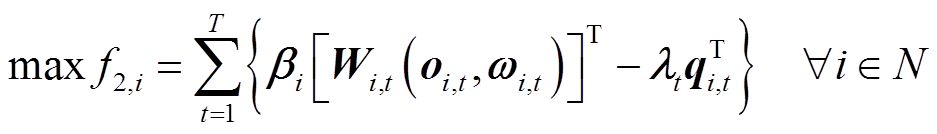（17）
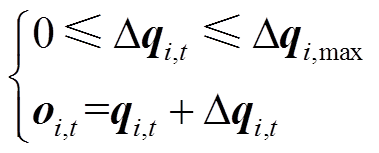（18）
式中，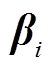
为偏好系数向量，=[
]，、、
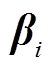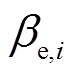
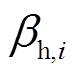
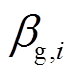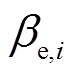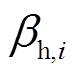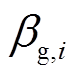通过用户历史用电、热、气量的比例进行估值，且有
+
+
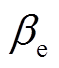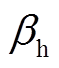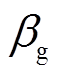=1；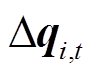
为用户i设备能源转换量[12]；
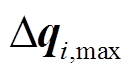为用户i的能源转换设备限制功率。
家用设备本质为能源耦合设备，考虑到转换效率和经济性，仅设有气转电、电转热、气转热三种。暂不考虑设备使用成本，能量转换公式为
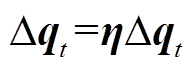（19）式中，η为3阶方阵，对角线元素为零，非对角线元素为相应耦合设备的能量转换效率系数。
为充分调动用户需求响应潜力，园区综合能源运营商采用实时能源价格形式与用户交易。由于用户用能行为与价格密切相关，园区综合能源运营商在制定价格时采用主从博弈形式[23]进行价格优化。其中，各用户作为跟随者，根据能源运营商公布的实时价格进行用能调整，最大化自身效用。而能源运营商作为价格主导者，将综合考虑上游批发市场及用户用能需求变动，动态调整电、热、气实时能源价格，实现利益最大化。通过多次博弈，双方最终达到Stackelberg均衡，即任何一方均不能通过单独改变自身策略来获取更多的效益[24]。
综上分析，主从博弈双层优化模型表述为以下问题。
1）综合能源商优化主问题
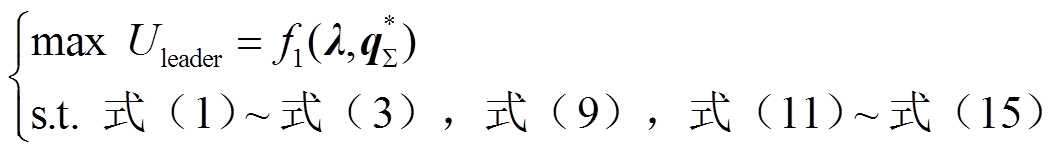（20）2）多用户优化从问题
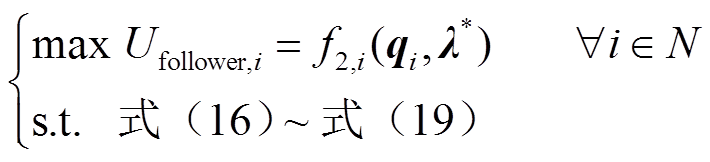（21）
式中，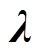
为主方的价格策略集；
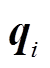为从方的需求策略集；
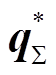和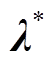
为给定策略集，其中
。
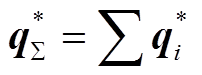定理：对于主从博弈，策略集、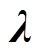
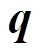的取值区间均为非空、有界、封闭的凸集，若同时满足以下条件，则可认为其存在Stackelberg均衡[24]：①Uleader是关于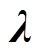、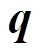的连续函数；②Ufollower是关于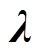、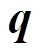的连续函数；③Ufollower是关于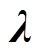、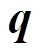的拟凸函数。
园区综合能源运营商的效益Uleader和用户的Ufollower分别利用式（12）和式（17）计算得到，其关于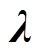、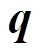的连续性是显而易见的，因此条件①、条件②得证。
对于条件③的证明：用户效用函数Ufollower的第一项为满意度函数，根据式（16），该项为凸函数；而Ufollower的第二项为线性成本函数，由此可知Ufollower在整体上是关于q的凸函数。凸函数一定为拟凸函数，即可证得Ufollower是关于q的拟凸函数。同理，Ufollower是关于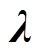的拟凸函数。
综上所述，本文的主从博弈存在Stackelberg均衡解。
传统集中式优化需要全局信息，存在用户隐私泄露的风险。此外，双层优化问题较为复杂，难以直接迭代优化。为此，本文主从博弈问题根据分布式协同优化框架，采用改进布谷鸟算法求解。布谷鸟算法采用Lévy飞行和局部随机移动机制实现最优解搜索，具有所需参数少、搜索速度快、易与其他算法融合等优点，但在迭代后期寻优速度较慢。因此，本文利用粒子群算法的全局概率特性，在布谷鸟算法更新种群过程中插入粒子群操作算子进行并行搜索，增大算法迭代后期跳出局部最优困境的概率，实现算法改进[25]。同时，为提高求解的速度和精度，用户模型作为二次规划问题嵌入并借助CPLEX求解。算法的具体改进和求解流程如图2所示，其中主从方策略不再发生变化时判定为达到均衡。
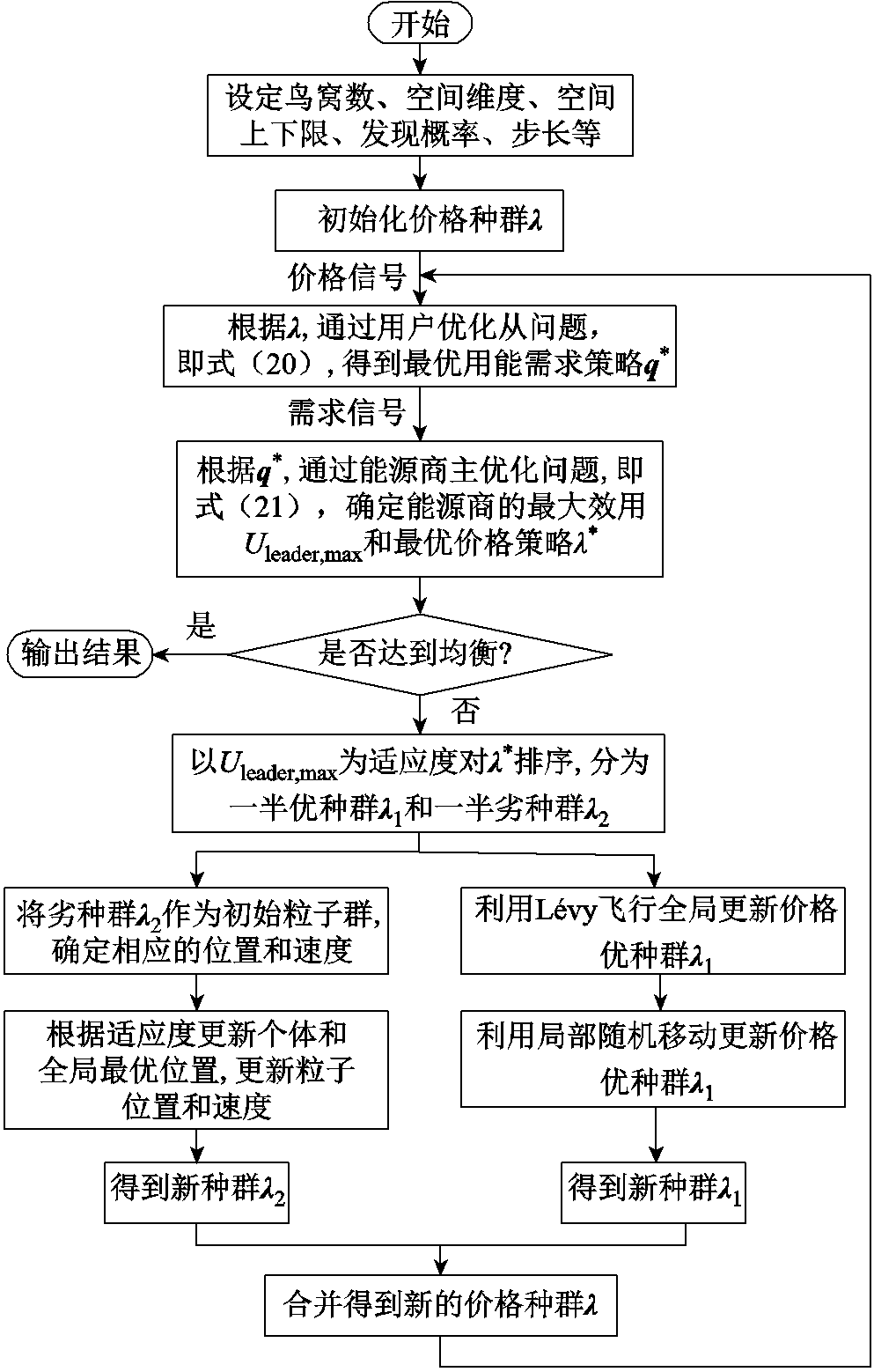
图2 算法求解流程
Fig.2 The algorithmic flow chart
本节以我国某典型园区综合能源系统[26-27]为例进行仿真分析。由于园区用户数较多且本文以综合能源商为主要分析角度，为简化处理，将所有用户视为同一类型。结合国内市场行情，园区典型日总能源负荷、零售参考价格[27-28]及现货市场节点预测电价与预测气价[29]曲线如附图1～附图3所示。综合能源商制定的实时零售价格限制在参考价格曲线的0.8～1.4倍内，而用户的能源需求在日能源负荷曲线的0.8～1.2倍内变化。其余参数设置见附表1和附表2。
首先，本节对主从博弈分布式优化方法的收敛性进行分析，结果如图3所示。可以看出，在内外层迭代20次左右即可达到收敛。此外，相较于原始的布谷鸟算法，改进布谷鸟算法具有更好的收敛效果。
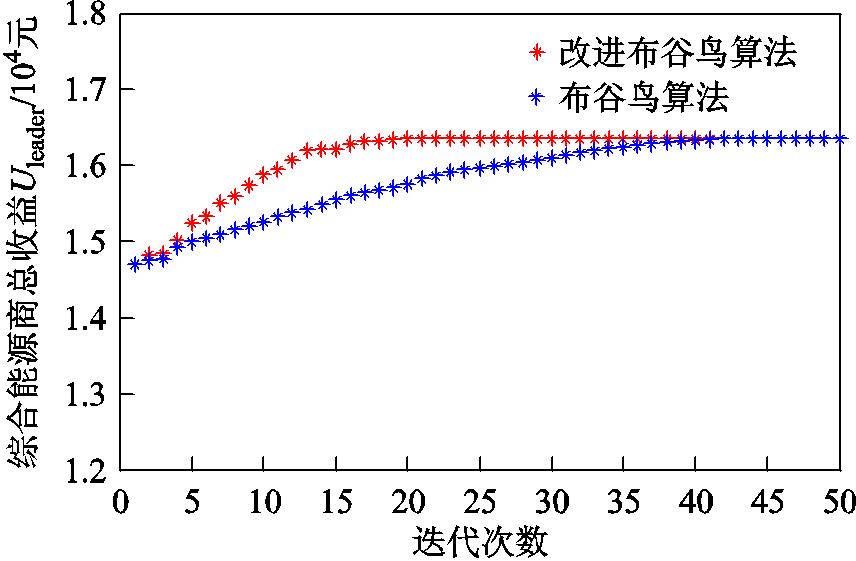
图3 综合能源商收敛曲线
Fig.3 Convergence curves of integrated energy supplier
其次，为更好地展示批发与零售市场协同优化对园区综合能源商交易策略的影响，本节设置如下三种市场交易策略进行对比分析。
方案1：本文所提计及批发与零售市场的交易策略。
方案2：仅计及批发市场的综合能源商交易策略，忽略用户侧综合需求响应，认为负荷固定。
方案3：仅计及零售市场的综合能源商交易策略，批发市场购能成本仅以中长期合约考虑。
各方案下综合能源商优化结果见表1。由表1可知，方案2下综合能源商购能成本相较于方案1增加了25%。究其原因，方案1考虑用户侧综合需求响应，将高峰时段负荷转移到低谷价格时段，从而减少购能成本。而方案2忽略了用户需求响应的影响，其负荷预测量与实际情况相差较大，导致购入过多能源产生亏损。方案3因其仅考虑中长期市场购电，忽略了综合能源批发市场的互补特性，导致其购能成本相较于方案1也增加了3.5%。此外，为增加整体收益，三种方案下的综合能源商均通过牺牲部分市场份额，不同程度地提高零售价格以换取当前利润，故表1中的远期收益均为负值。综上分析，能源互联与市场自由化的背景下，方案1计及综合能源批发与零售市场协同优化，既可充分挖掘不同时间尺度不同能源批发市场的互补潜力，协调风险与成本，又可同时兼顾用户零售市场环节，激发用户综合需求响应潜能，稳固零售市场份额，制定更全面、更贴合实际的交易策略，从而提高自身收益，促进长远发展。
表1 不同方案下综合能源商运营仿真结果
Tab.1 Operational optimization results of park integrated energy supplier under different modes
方案总成本/元当前收益/元远期收益/元市场份额（%）总效用/元实际收益/元 180 84921 955-5 593.262.2016 36221 955 2107 10026 440-6 206.161.9020 233-5 490 383 72018 710-5 257.862.3713 44018 710
最后，进一步分析方案1下综合能源商零售市场策略行为特点。综合能源商的最优零售价格曲线和用户负荷曲线分别如图4和图5所示。由图可知，电、热零售价格相较于参考价格，峰谷差值增大，且用户电、热总用量峰谷差值降低。例如，12:00～20:00时段高峰期电负荷需求明显下降，供电压力得到了较大缓解。这说明综合能源商合理计及用户负荷特点，通过调整实时零售价格，实现削峰填谷，缓解高峰期供能压力等，同时有利于延缓容量扩建，降低发电成本和配网投资成本。此外，天然气零售价格相较于参考价格整体上浮。究其原因：一方面用户侧天然气需求响应容量较小；另一方面天然气价格本身较低，综合能源商为谋求更大利润空间，在用户可接受范围内，倾向于制定较高的天然气零售价格。夜间热负荷需求明显下降且热价相应上涨，则是因为热负荷作为最直接的能源利用方式，用户侧有较多的转换为热能的耦合设备，用户的热能直接需求浮动性大，综合能源商为维持利润也倾向于制定较高的热价。因此，在方案1下，综合能源商能够同时兼顾自身收益和用户综合需求响应，制定出合理的零售价格。
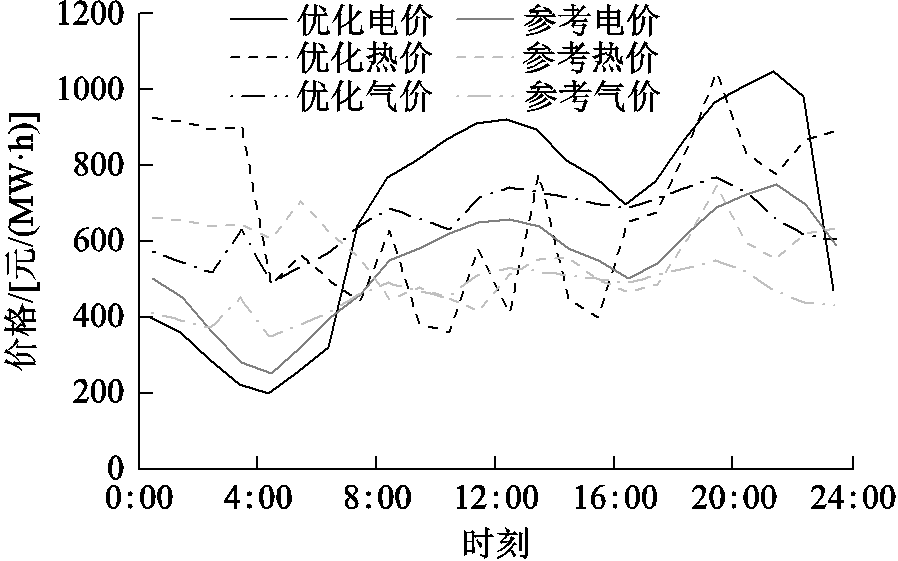
图4 综合能源商最优零售价格曲线
Fig.4 Optimal real-time price formulated by park integrated energy supplier
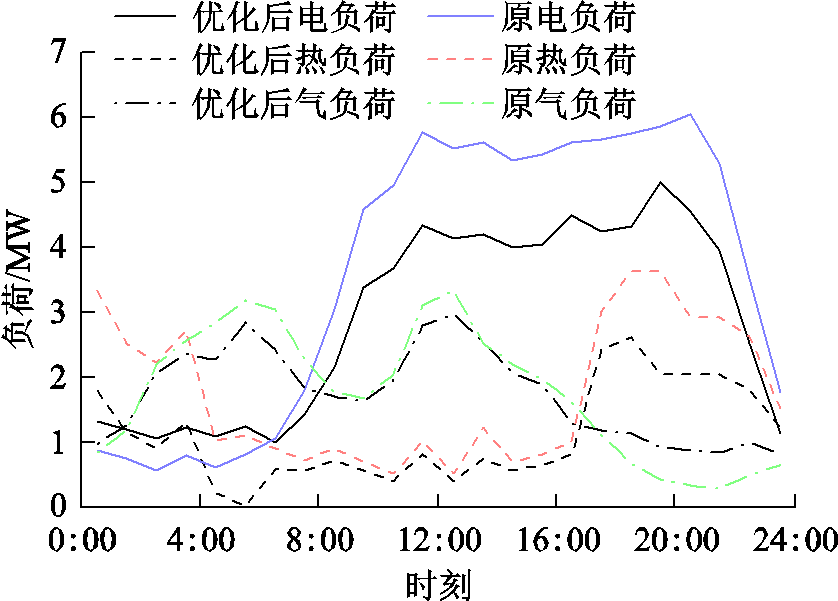
图5 优化前后园区日总能源负荷曲线
Fig.5 Simulated park energy daily load curve
为探究用户潜在价值μ对零售价格以及市场份额的影响，本节设置不同μ值进行仿真，得到了如图6所示综合能源零售价格平均值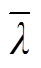
和市场份额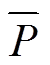
与μ的关系曲线。
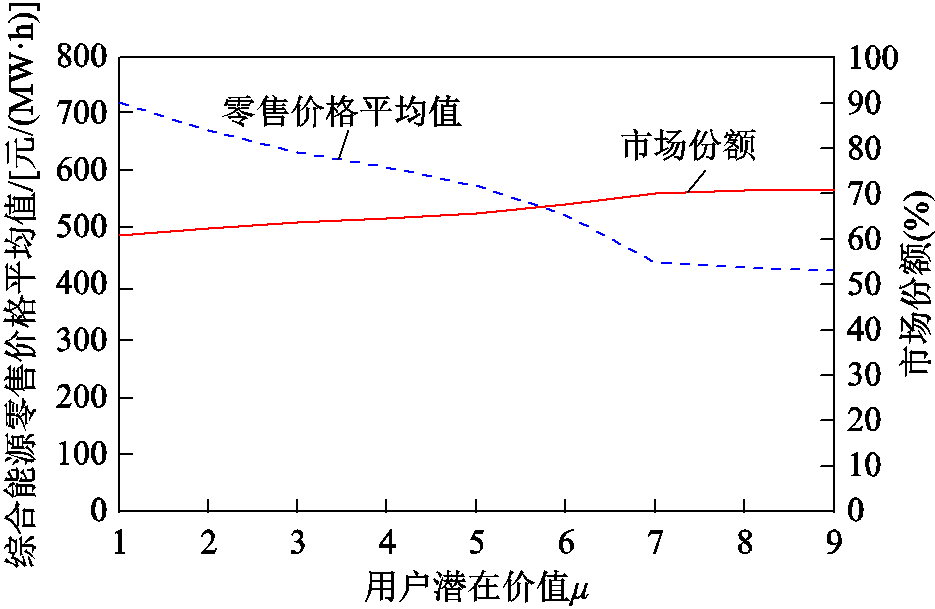
图6 用户潜在价值μ对零售价格和市场份额的影响
Fig.6 Effect of user potential value on retail price and market share
由图6可知，随着用户潜在价值μ的变大，零售价格平均值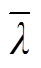减小，市场份额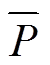增加。这是因为用户潜在价值较高时，市场份额所蕴含的价值较大，远期可观测收益较高，此时综合能源商倾向于以低零售价格来换取更高的市场份额。需要注意的是，当用户潜在价值μ增大到一定程度后，零售价格降低趋势放缓，并逐渐趋近于其边际价格，市场份额也将达到极限。因此，本文通过引入远期收益的方法，能够合理兼顾综合能源商当前收益与远期收益，引导其制定有利于长期良性发展的零售价格策略。
此外，用户潜在价值μ的评估至关重要。当μ取值过高时，综合能源商错判远期收益形势，导致当前收益受损；当μ取值过低时，综合能源商将侧重于当前收益形势，零售价格偏高，导致远期收益不佳。因此，综合能源商需要根据历史盈利数据准确量化用户潜在价值μ。同时，对于发展上升期的综合能源商，其用户群体基数较少，此时用户潜在价值μ可设置得较高，以低价策略吸引活跃用户，抢占市场份额。当综合能源商进入平稳期后，其市场份额趋于稳定，此时用户群体基数较大，用户潜在价值μ可适当调低，考虑通过增值服务提高用户粘性，培养忠实用户群体，适当提升零售价格，从而提高利润。
现货市场价格具有波动性，给综合能源商的购能行为带来一定的风险。为探究现货市场价格的波动对综合能源商批发市场交易策略的影响，本节设置不同的标准差来模拟不同波动幅度的现货市场价格场景。不同价格波动下综合能源商仿真结果见表2。
表2 不同价格波动下综合能源商仿真结果
Tab.2 Comparison of park integrated energy supplier’s simulation results under different price fluctuations
市场价格波动范围（%）购能总成本/元现货市场购能成本/元期货市场交易成本/元风险成本/元当前收益/元 077 82936 28341 546024 971 ±178 16535 98842 17731124 635 ±578 91435 89543 0191 05623 886 ±1079 62731 70147 9261 62123 173 ±2080 84925 71855 1312 53821 955 ±3083 72320 35463 3703 25119 077
由表2可知，在现货市场价格波动增大的情形下，综合能源商风险成本随之增大。为降低自身风险，综合能源商购能策略也随之变化。当现货市场价格波动较大时，综合能源商倾向于减少在现货市场的购能量，增加在期货市场的合约量，通过期货市场的套期保值功能实现对现货市场价格风险的中和。这体现了在优化模型中考虑现货市场价格波动风险的必要性，也展现了采用基于Wasserstein距离的分布鲁棒优化方法量化市场风险成本的可行性。
本文针对能源互联网背景下各类能源批发、零售市场的演变趋势与相关特点，立足未来，设计了一种包括用户多能零售市场、电力-天然气批发市场在内的两级市场协同交易策略，以此为基础构建园区综合能源运营商的市场运营优化模型。在搭建相应的仿真场景后，算例分析验证了模型的可行性与合理性。结果表明：一方面，上下游市场协同优化的园区综合能源运营模式更全面更实际，可准确把握用户需求变动和市场价格波动，从而同时调整购能组合方案与价格制定策略，挖掘联合市场潜力，合理考虑风险，提高收益；另一方面，综合能源商需要考虑能源零售价格制定策略对用户选择与市场份额的影响，在不同的发展阶段合理地兼顾当前收益和未来收益。
需要指出，本文仅侧重探讨了园区综合能源商的整体市场交易部分，受篇幅所限，对用户侧的经济型、多样性等问题未展开研究，这将是后续研究的重点之一。同时，能源集线器的优化调度、分布式发电和储能系统的加入等问题均对综合能源商的运营有直接影响，如何将其纳入考虑，也需进一步开展研究。
Wasserstein距离是场景缩减前后随机优化目标函数之间差值的上确界定义的场景集之间的距离[30]。表述为
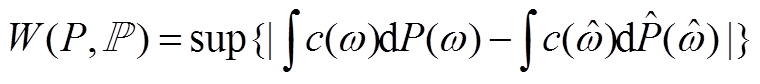（A1）式中，c为随机优化函数，在本文指现货市场购能成本；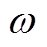
、
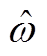为不确定参数，分别服从经验分布P和真实分布
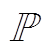，经验分布P根据现货市场价格历史数据获得，是对真实价格分布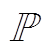的估计，满足
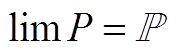，并以此构建价格场景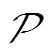模糊集
，模糊集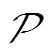应尽可能地包含真实分布，是一个在全概率分布空间
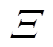中，以经验分布
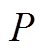为中心，以e(K)为半径的Wasserstein球[21]， e(K)具体为
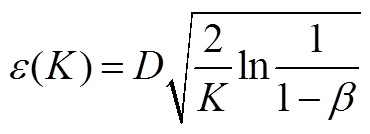（A2）
式中，b为置信水平；D为系数。
本文风险成本为价格预测偏差导致的购能成本波动，用各场景价格偏差与购能量乘积和的期望表示，即
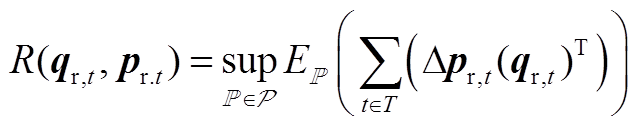（A3）式（A3）由Wasserstein距离进行概率分布的度量，根据对偶理论对其进一步简化处理，转换为
式中，ε为置信因子；к为对偶变量；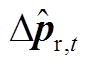
为价格预测偏差的历史经验数据，在本文中采用蒙特卡洛抽样模拟。
现引入辅助变量τ，对式（A4）进行等价变形为
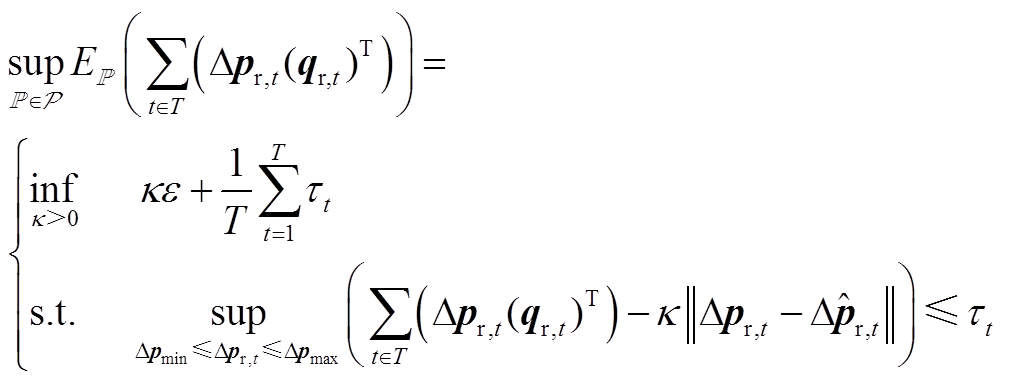（A5）式中，
为辅助变量；Δpmin、Δpmax分别为
中现货市场价格预测偏差量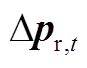
的上边界和下边界。
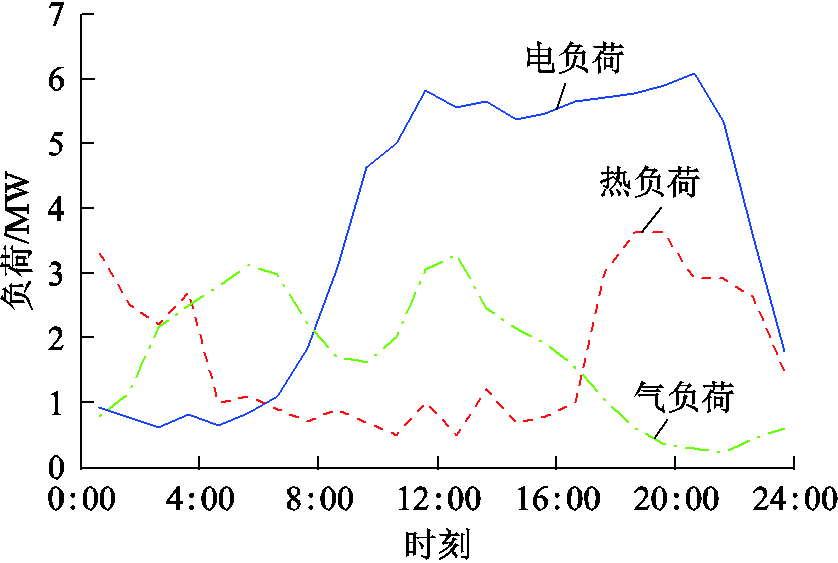
附图1 园区当日总能源负荷曲线
App.Fig.1 Total energy load curves of the park on the day
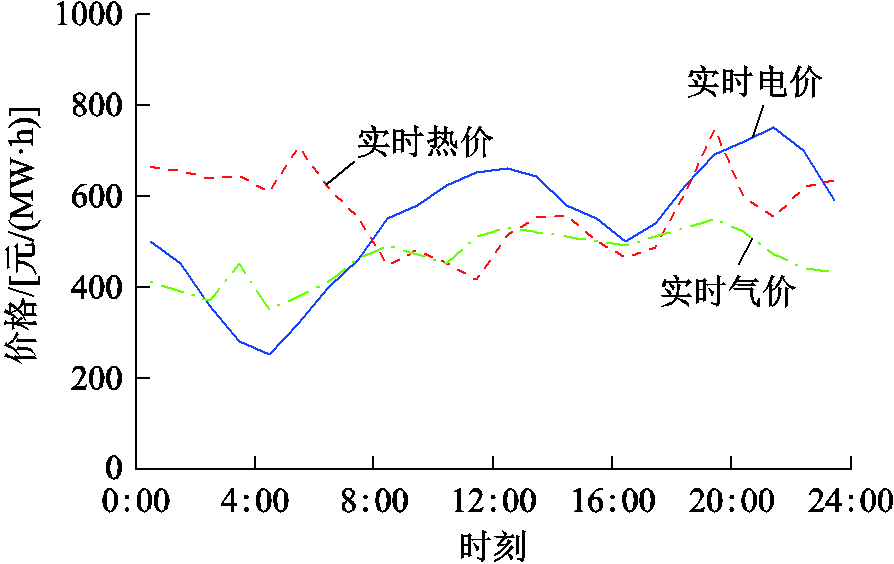
附图2 园区综合能源商参考实时能源价格曲线
App.Fig.2 Real-time energy reference price curves of integrated energy supplier in the park
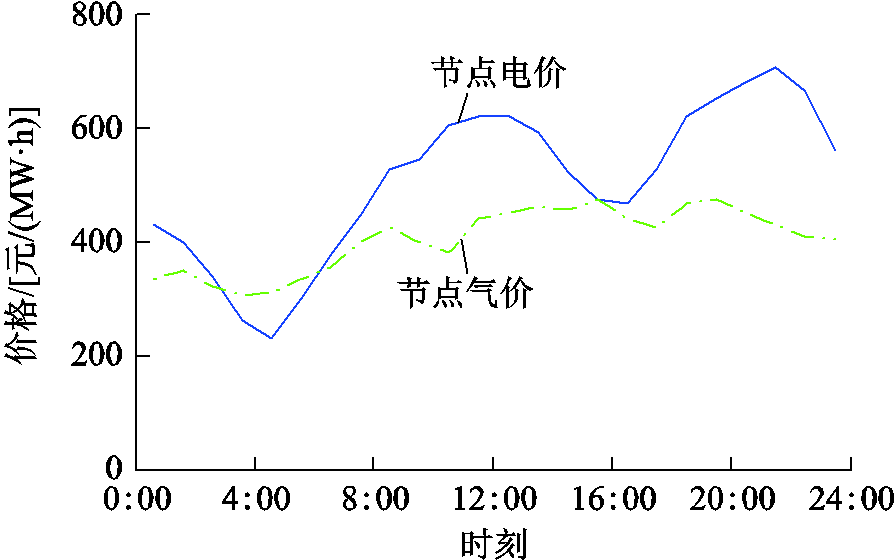
附图3 综合能源商预测的现货市场出清价格曲线
App.Fig.3 Spot market clearing price curves predicted by integrated energy supplier
附表1 综合能源商相关参数
App.Tab.1 Simulation parameters of integrated energy supplier
参数数值 置信因子ε0.975 差价合约价格pq/[元/(MW·h)][530440] 绿证价格pl/[元/(MW·h)]10 可再生能源配额ξ(%)15 总用户数N/万户10 调度系数ve,Tv0.7 ve,EB0.3 vg,CHP0.5 vg,FUR0.1 vg,G0.4 市场基础份额P0(%)65 市场份额函数多项式系数a0-2.232 6 a10.006 94 a20 单个用户潜在价值μ2 能量转换装置效率ηTv,e0.95 ηEB,h0.9 ηCHP,e0.5 ηCHP,h0.45 ηFUR,h0.95
附表2 用户相关参数
App.Tab.2 Simulation parameters of users
参数数值 偏好系数β[0.5 0.25 0.25] 敏感度系数s[0.5 0.25 0.25] 能源耦合设备效率ηge0.9 ηgh0.95 ηeh0.95
（续）
参数数值 ωt,e1:00～6:00rand[1, 4] 7:00～18:00rand[4, 8] 19:00～24:00rand[2, 4] ωt,h/ωt,g1:00～6:00rand[1, 2] 7:00～18:00rand[2, 4] 19:00～24:00rand[1, 2]
参考文献
[1] 张义志, 王小君, 和敬涵, 等. 考虑供热系统建模的综合能源系统最优能流计算方法[J]. 电工技术学报, 2019, 34(3): 562-570.
Zhang Yizhi, Wang Xiaojun, He Jinghan, et al. Optimal energy flow calculation method of integrated energy system considering thermal system modeling[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 562-570.
[2] 周长城, 马溪原, 郭祚刚, 等. 面向工程应用的用户级综合能源系统规划[J]. 电工技术学报, 2020, 35(13): 2843-2854.
Zhou Changcheng, Ma Xiyuan, Guo Zuogang, et al. User-level integrated energy system planning for engineering applications[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2843-2854.
[3] 谈金晶, 李扬. 多能源协同的交易模式研究综述[J].中国电机工程学报, 2019, 39(22): 6483-6497.
Tan Jinjing, Li Yang. Review on transaction mode in multi-energy collaborative market[J]. Proceedings of the CSEE, 2019, 39(22): 6483-6497.
[4] 罗舒瀚, 蒋传文, 王旭, 等. 新电改背景下售电公司的购售电策略及风险评估[J], 电网技术, 2019, 43(3): 944-953.
Luo Shuhan, Jiang Chuanwen, Wang Xu, et al. Power trading strategy and risk assessment of electricity retailing company under power system reform[J]. Power System Technology, 2019, 43(3): 944-953.
[5] 杨皓钦, 魏震波, 黄宇涵, 等. 跨区域现货市场下多主体购售能主从博弈模型[J]. 电网技术, 2019, 43(8): 2781-2791.
Yang Haoqin, Wei Zhengbo, Huang Yuhan, et al. Multi-agent purchase and sale master-slave game model in cross-regional spot market[J]. Power System Technology, 2019, 43(8): 2781-2791.
[6] 张晨, 韩新阳, 白翠粉, 等. 基于合作博弈的电力市场模式下售电商购电策略模型[J]. 中国电力, 2017, 50(6): 177-184.
Zhang Chen, Han Xinyang, Bai Cuifen, et al. Purchasing strategy model for power supplier based on the cooperative game theory in an open electricity market[J]. Electric Power, 2017, 50(6): 177-184.
[7] 赵天辉, 王建学, 陈洋. 面向综合能源交易的新型城镇分层市场架构和出清算法[J]. 电力系统自动化, 2021, 45(4): 73-80.
Zhao Tianhui, Wang Jianxue, Chen Yang. Hierarchical market structure and clearing algorithm for integrated energy trading of new-type towns[J]. Automation of Electric Power Systems, 2021, 45(4): 73-80.
[8] 刘珮云, 丁涛, 贺元康, 等. 基于综合需求响应的负荷聚合商最优市场交易策略[J]. 电力自动化设备, 2019, 39(8): 224-231.
Liu Peiyun, Ding Tao, He Yuankang, et al. Optimal trading strategy for load aggregator based on integrated demand response[J]. Electric Power Automation Equipment, 2019, 39(8): 224-231.
[9] Chai Bo, Chen Jiming, Yang Zaiyue, et al. Demand response management with multiple utility companies: a two-level game approach[J]. IEEE Transactions on Smart Grid, 2014, 5(2): 722-731.
[10] 李鹏, 马溪原, 郭祚刚, 等. 基于双层优化的综合能源服务商博弈策略[J]. 电网技术, 2021, 45(2): 460-469.
Li Peng, Ma Xiyuan, Guo Zuogang, et al. Research on game strategy of integrated energy service providers based on bi-level optimization[J]. Power System Technology, 2021, 45(2): 460-469.
[11] Wu Jie, Zhou Wenhui, Zhong Weifang, et al. Multi-energy demand response management in energy internet: a Stackelberg game approach[J]. Chinese Journal of Electronics, 2019, 28(3): 640-644.
[12] Bahrami S, Sheikhi A. From demand response in smart grid toward integrated demand response in smart energy Hub[J]. IEEE Transactions on Smart Grid, 2016, 7(2): 650-658.
[13] 聂光华. 中国天然气价格变动传导效应分析[J]. 天然气工业, 2012, 32(12): 114-117, 137.
Nie Guanghua. Analysis of the transmission effect of natural gas price fluctuation in China[J]. Natural Gas Industry, 2012, 32(12): 114-117, 137.
[14] 李晓龙. 基于市场微观结构理论的我国电力期货市场构建研究[D]. 北京: 华北电力大学(北京), 2019.
[15] 龙苏岩, 冯凯, 徐骏, 等. 电力现货市场下不平衡费用构成及分摊机制研究[J]. 电网技术, 2019, 43(8): 2649-2658.
Long Suyan, Feng Kai, Xu Jun, et al. Research on unbalanced cost composition and allocation mechanism in spot electricity market[J]. Power System Technology, 2019, 43(8): 2649-2658.
[16] 任姝艳, 黄国飞, 张倩. 中国天然气现货市场与期货市场关系研究[J]. 能源与节能, 2014(1): 4-5, 20.
Ren Shuyan, Huang Guofei, Zhang Qian. Research on the relationship between spot market and futures market of natural gas in China[J]. Energy and Energy Conservation, 2014(1): 4-5, 20.
[17] 罗琴. 市场环境下售电公司购售电策略研究[D]. 上海: 上海交通大学, 2014.
[18] 王灿, 王德, 朱玮, 等. 离散选择模型研究进展[J]. 地理科学进展, 2015, 34(10): 1275-1287.
Wang Can, Wang De, Zhu Wei, et al. Research progress of discrete choice models[J]. Progress in Geography, 2015, 34(10): 1275-1287.
[19] 刘勇, 王高. 离散选择模型在零售研究中的应用—基于MNL、MNP和Mixed Logit的比较[C]//中国高等院校市场学研究会2009年年会论文集, 北京, 2009: 351-364.
[20] 夏鹏, 刘文颖, 张尧翔, 等. 考虑风电高阶不确定性的分布式鲁棒优化调度模型[J]. 电工技术学报 2020, 35(1): 189-200.
Xia Peng, Liu Yingwen, Zhang Yaoxiang, et al. A distributionally robust optimization scheduling model considering higher-order uncertainty of wind power[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 189-200.
[21] 竺如洁, 韦化, 白晓清. 多源动态最优潮流的分布鲁棒优化方法[J]. 中国电机工程学报, 2020, 40(11): 3489-3498.
Zhu Rujie, Wei Hua, Bai Xiaoqian. Distributionally robust optimization of multi-energy dynamic optimal power flow[J]. Proceedings of the CSEE, 2020, 40(11): 3489-3498.
[22] 丛昊, 王旭, 蒋传文, 等. 基于联盟博弈的综合能源系统优化运行方法[J]. 电力系统自动化, 2018, 42(14): 14-22.
Cong Hao, Wang Xu, Jiang Chuanwen, et al. Coalition game based optimized operation method for integrated energy systems[J]. Automation of Electric Power Systems, 2018, 42(14): 14-22.
[23] 熊宇峰, 司杨, 郑天文, 等. 基于主从博弈的工业园区综合能源系统氢储能优化配置[J]. 电工技术学报, 2021, 36(3): 507-516.
Xiong Yufeng, Si Yang, Zheng Tianwen, et al. Optimal configuration of hydrogen storage in industrial park integrated energy system based on Stackelberg game[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 507-516.
[24] 周长城, 马溪原, 郭晓斌, 等. 基于主从博弈的工业园区综合能源系统互动优化运行方法[J]. 电力系统自动化, 2019, 43(7): 74-84.
Zhou Changcheng, Ma Xiyuan, Guo Xiaobin, et al. Leader-follower game based optimized operation method for interaction of integrated energy system in industrial park[J]. Automation of Electric Power Systems, 2019, 43(7): 74-84.
[25] 张艺瀛, 金志刚. 求解多峰优化问题的改进布谷鸟算法[J]. 哈尔滨工业大学学报, 2019, 51(11): 89-99.
Zhang Yiying, Jin Zhigang, An improved Cuckoo search for multimodal optimization problems[J]. Journal of Harbin Institute of Technology, 2019, 51(11): 89-99.
[26] 李宇泽, 齐峰, 朱英伟, 等. 多能互补综合能源电力系统的建设模式初探[J]. 电力科学与技术学报, 2019, 34(1): 3-10.
Li Hongze, Qi Feng, Zhu Yingwei, et al. A preliminary investigation on construction modes of a multi-energy complementary integrated energy system[J]. Journal of Electric Power Science and Technology, 2019, 34(1): 3-10.
[27] 高滢. 计及综合需求响应的电-气互联能源系统协同规划[D]. 杭州: 浙江大学, 2019.
[28] 刁涵彬, 李培强, 王继飞, 等. 考虑电/热储能互补协调的综合能源系统优化调度[J]. 电工技术学报, 2020, 35(21): 4532-4543.
Diao Hanbin, Li Peiqiang, Wang Jifei, et al. Optimal dispatch of integrated energy system considering complementary coordination of electric/thermal energy storage[J]. Transactions of China Electrote-chnical Society, 2020, 35(21): 4532-4543.
[29] 丛昊, 王旭, 蒋传文. 电力-天然气异步市场环境下的综合能源系统优化运行策略[J]. 电网技术, 2019, 43(9): 3110-3120.
Cong Hao, Wang Xu, Jiang Chuanwen. Strategies of optimal operation of integrated energy system in asynchronous market environment[J]. Power System Technology, 2019, 43(9): 3110-3120.
[30] 董骁翀, 孙英云, 蒲天骄, 等. 一种基于Wasserstein距离及有效性指标的最优场景约简方法[J]. 中国电机工程学报, 2019, 39(16): 4650-4658, 4968.
Dong Xiaochong, Sun Yingyun, Pu Tianjiao, et al. An optimal scenario reduction method based on Wasserstein distance and validity index[J]. Proceedings of the CSEE, 2019, 39(16): 4650-4658, 4968.
Purchase and Sale Strategies of Park Integrated Energy Suppliers in Wholesale and Retail Markets
Abstract With the orderly progress of energy market reform, an open and fully competitive integrated energy market is expected to be built in the future. As an important market entity, how to optimize the trading strategy in the integrated energy market is still to be carried out. Based on this, this paper constructs a market trading strategy and collaborative optimization method for park-level integrated energy supplier considering the wholesale and retail energy markets. First, this paper analyzes the operating mechanism of wholesale and retail market. Based on the discrete choice model, the effect of retail price on market share is quantified and the forward returns function is constructed. Second, considering the integrated demand response of users, a distributed collaborative optimization model based on the Stackelberg game is constructed. Then, the existence of Stackelberg equilibrium solution is proved and the distributed model is solved by Cuckoo algorithm embedded with quadratic programming. Finally, the simulation verifies the feasibility and superiority of the trading strategy and optimization model proposed in this paper, and provides guidance for integrated energy suppliers to make market trading decisions.
keywords：Park integrated energy supplier, wholesale and retail market, discrete choice model, Stackelberg game
DOI:10.19595/j.cnki.1000-6753.tces.201400
中图分类号：TM71
国家电网公司科技资助项目（5700-201999495A-0-0-00）。
收稿日期 2020-10-26
改稿日期 2020-12-22
陈 岑 男，1998年生，硕士研究生，研究方向为新能源微网规划调度。E-mail：1125544530@qq.com
武传涛 男，1995年生，博士研究生，研究方向为新能源微网规划调度。E-mail：chuantao_wu@hust.edu.cn（通信作者）
（编辑 赫蕾）