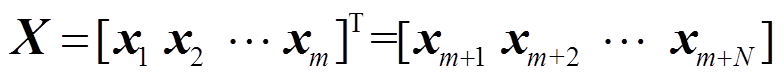 (1)
(1)摘要 准确、有效地辨识电力系统主导振荡模式、主导振荡模态和参与因子等低频振荡特征参数,对深入探究电力系统低频振荡诱因、提出科学合理的振荡抑制措施具有重要价值。为此,该文提出一种基于最优变量投影(OVP)的电力系统主导振荡模式、模态和参与因子综合辨识方法。该方法采用有限差分法(FDM)预处理电力系统的广域量测信息;借助处理后的广域量测信息构建含系统关键动态振荡信息的低阶状态矩阵,进而从低阶状态矩阵中提取电力系统的关键振荡特征信息;结合广域量测信息和关键振荡特征信息构建变量投影函数,通过OVP对其进行求解,以辨识振荡模式及其模态;引入累积能量权重从所辨识的振荡模式及模态中分离电力系统的主导振荡模式及模态,并根据分离的主导振荡模态实现参与因子的评估。最后,通过IEEE 68节点测试系统和中国南方电网公司算例对所提方法进行分析,验证了所提方法的准确性和有效性。
关键词:同步相量量测 最优变量投影 主导振荡模式 主导振荡模态 参与因子
区域电网互联规模不断扩大、高比例电力电子化设备投入使用、大规模可再生能源并网发电,使得电力系统低频振荡问题更加复杂,已成为限制区域间联络断面功率传输能力、威胁电网安全稳定运行的主要因素之一[1-2]。因此,准确辨识电力系统低频振荡的关键特征参数、深入分析电力系统低频振荡诱因、提出科学合理的低频振荡抑制措施,对提升含高比例可再生能源的电力系统动态稳定性具有重要的理论和工程研究价值[3]。
电力系统低频振荡的特征参数主要包括主导振荡模式和主导振荡模态。传统基于模型的特征值分析法(Eigenvalue Analysis, EA)虽然可以有效辨识系统所有关键特征参数,但该方法的辨识准确性依赖于所建模型精度和参数准确性。对实际电力系统而言,构建高精度、大规模的区域互联电力系统动态模型十分困难,且模型参数也随时间动态变化,所辨识出的结果不能真实反映系统当前运行状态下的动态稳定性。因此,特征值分析法常用于电力系统低频振荡的离线分析。
同步相量测量单元(Phasor Measurement Unit, PMU)在电力系统大规模应用,为基于广域量测信息的电力系统低频振荡特征参数辨识提供了新机遇[4-6]。为从电力系统的广域量测信息中辨识出系统的主导振荡模式,文献[7]于1990年首次将Prony算法应用到电力系统低频振荡的振荡模式识别中;文献[8]进一步引入差分正交匹配追踪算法(Difference Orthogonal Matching Pursuit, DOMP)提高Prony在主导振荡模式辨识中的抗噪能力;文献[9]借助多元经验模式分解(Multivariate Empirical Mode Decomposition,MEMD)追踪系统主导振荡模式的瞬变特性,且有效抑制了多振荡模式间的模式混频效应;文献[10]将连续小波变换(Continuous Wavelet Transform, CWT)与递归最小二乘相结合,实现了基于广域量测信息的电力系统低频振荡模式辨识;文献[11]引入自回归滑动平均模型(Auto-Regressive Moving-Average eXogenous, ARMAX)从电力系统的类噪声信号中辨识出系统的区域间振荡模式;文献[12]采用快速迭代随机子空间辨识方法(Fast iterative Stochastic Subspace Identification, FSSI)从电力系统的广域量测信息中准确、高效地辨识主导振荡模式的振荡频率与阻尼比。
在基于广域量测信息的主导振荡模态辨识方面,文献[13]在文献[8]的基础上首先引入奇异值分解(Singular Value Decomposition, SVD)来估计系统模型阶数,然后实现了与主导振荡模式强相关的主导振荡模态辨识;文献[14]在文献[10]的基础上,提出了基于多通道CWT的电力系统主导振荡模式及模态协同辨识方法;文献[15]在文献[11]基础上进一步实现了基于ARMAX的主导振荡模态辨识;文献[16]基于文献[12]的SSI辨识方法,提出了一种数据驱动的电力主导振荡模式及模态辨识方法;文献[17]采用多参考点复指数法(Poly-Reference Complex Exponential, PRCE)从电力系统广域量测信息中提取系统区域间主导振荡模式及对应的振荡模态。
在基于广域量测信息的参与因子辨识方面,文献[18]借助动态模态解耦(Dynamic Mode Decomposition, DMD)辨识系统主导振荡模式及其模态,并结合各振荡模式的能量权重,计算各发电机在主导振荡模式下的参与因子,实现了基于广域量测信息的参与因子辨识;文献[19]在采用库普曼模态分解(Koopman Mode Decomposition, KMD)辨识系统主导振荡模式基础上,进一步辨识出发电机及其励磁系统在各主导振荡模式下的参与因子,为电力系统低频振荡分析与抑制提供了丰富的信息。
上述分析方法虽在主导振荡模式、模态和参与因子辨识方面开展了深入研究,但受线性处理、复杂辨识过程等因素的影响,其辨识结果易丢失系统较为重要的动态振荡信息,且抗噪能力较弱,在较高噪声环境下辨识精度急剧降低,严重影响辨识结果的准确性。针对该问题,本文提出一种基于最优变量投影(Optimized Variable Projection, OVP)的电力系统主导振荡模式、模态和参与因子的综合辨识方法。该方法首先引入有限差分法(Finite Difference Method, FDM)对电力系统广域量测信息预处理;然后,根据预处理的广域量测信息构建可反映系统动态振荡信息的低阶状态矩阵;进一步,提取低阶状态矩阵的关键振荡信息,构建变量投影函数,借助OVP实现振荡模式及模态的准确辨识;在此基础上,根据各模式的累积能量权重筛选出主导振荡模式及模态,并根据主导振荡模态,计算出可表征各发电机振荡灵敏度的参与因子;最后通过IEEE 68节点测试系统和中国南方电网公司算例对所提方法进行分析和验证。
变量投影(Variable Projection, VP)最初是由苏黎世大学的G. H. Golub教授和V. Pereyra教授提出,以解决非线性最小二乘中的变量分离问题[20]。本节将VP应用于电力系统中,通过电力系统广域量测信息及其隐含的系统关键振荡信息构建变量投影函数,进而利用VP的非线性特性对变量投影函数进行求解,获取系统的振荡模式与振荡模态。该方法可有效避免量测信息因线性化处理而被滤除重要振荡信息的不足,且在处理非线性、时变信号时具有较高的辨识精度和抗噪能力,因而在化学工程、光谱分析等领域得到了广泛应用。采用VP辨识电力系统动态振荡信息的基本原理如下。
首先从PMU中获取电力系统广域量测信息X,即
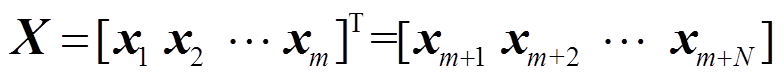 (1)
(1)式中,x1, x2, …, xmÎR1´N、xm+1, xm+2, …, xm+NÎR1´m为广域量测信息;m为量测通道;N为量测信息采样点数量。
定义含矩阵X关键振荡信息的特征值a=[a1a2… am]的非线性函数F(a)为
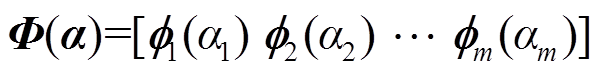 (2)
(2)式中,fi(ai)为含系统振荡信息的向量,fi(ai)=exp(aitj);tj为量测信息的第j个采样时间,j=1, 2,…, N。
根据F(a)重构量测信息矩阵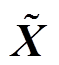 为
为
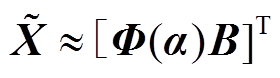 (3)
(3)
式中,B为系数矩阵。
借助最小二乘计算广域量测信息重构前后的残差矩阵r为
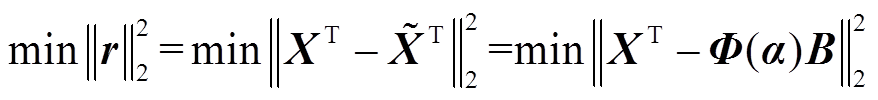 (4)
(4)由于含有关键振荡信息的a与低频振荡特征参数联系紧密,为通过a准确辨识出电力系统低频振荡特征参数,引入B=F†(a)XT将式(4)转换为式(5)所示的非线性最小二乘问题以获取a的最优解。
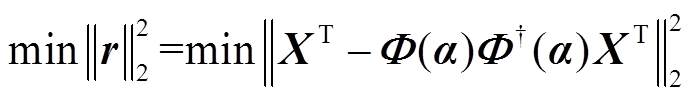 (5)
(5)
式(5)为基于矩阵X和a所构建的变量投影函数。参考文献[21],借助Levenberg-Marquardt原理提升变量投影函数的收敛速度,并通过迭代更新a来获取其最优解。Levenberg-Marquardt原理的核心为计算变量投影函数的Jacobi矩阵,表达式为
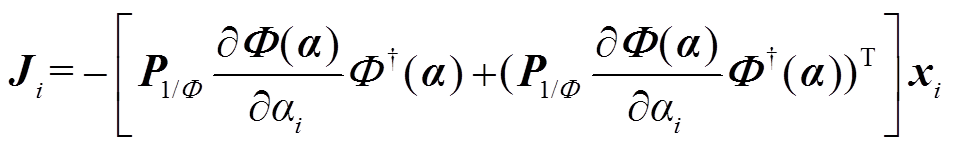 (6)
(6)式中,P1/F=I-PF,PF=F(a)F†(a),IÎRN´N为单位矩阵;xi为第i个量测通道的量测信息,xiÎR1´N。
求解变量投影函数得到a的最优解aovp=[a1,ovpa2,ovp… am,ovp]和优化B所得最优系数矩阵Bovp,其中,ai,ovp即为振荡模式对应的特征值li,并可根据Bovp计算系统的振荡模态。但在辨识过程中发现:VP对给定的a要求极为严格,若a不在合理的范围内,将极大地影响VP的收敛速度和辨识精度。
第1节基于VP实现了低频振荡信息的有效提取,而运用VP辨识电力系统低频振荡特征参数的关键在于如何获取较为合理的a来提高辨识精度并增强鲁棒性。为获取较为合理的a,本节引入OVP以实现电力系统主导振荡模式、模态与参与因子的综合辨识。
如前所述,采用VP辨识系统振荡模式及模态时,需预先提供合理的、含系统动态振荡信息的a。若所提供的a不在系统实际振荡特征参数的合理范围内,将会导致变量投影函数迭代不收敛。为此,本节首先从广域量测信息X中提取系统的关键动态振荡信息,进而为VP提供更为合适的初值。
首先,假设相邻时间点量测信息xm+j与xm+j+1间存在线性映射关系A,构建表达式为
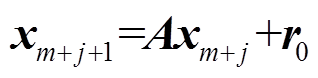 (7)
(7)式中,A为高阶复杂矩阵,蕴含量测信息的振荡特性,其特征值和特征向量与低频振荡特征参数具有强相关性;r0为残差向量。
忽略式(7)中残差矩阵r0,可得矩阵X的前N-1列X1=[xm+1xm+2 xm+N-1]与后N-1列X2=[xm+2xm+3
xm+N-1]与后N-1列X2=[xm+2xm+3 xm+N]所构建的矩阵存在如下关系:
xm+N]所构建的矩阵存在如下关系:
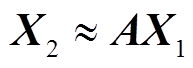 (8)
(8)为有效分离矩阵X1与X2含有的噪声信号或虚假振荡信息,采用FDM变换式(8)得
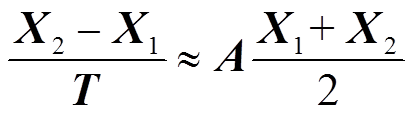 (9)
(9)
式中,(X1+X2)/2=Y1、(X2-X1)/T=Y2,Y1、Y2为变换后的量测信息;T为含n-1个量测时间间隔的矩阵,T=diag(t2-t1, , tn-tn-1)。
, tn-tn-1)。
借助SVD提取矩阵Y1含有的系统关键振荡信息,并将其代入式(9)得矩阵Y2为
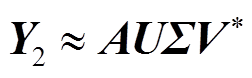 (10)
(10)式中,U、V为左、右奇异向量矩阵,二者为酉矩阵,满足U*U=V*V=I,且矩阵U和ΣV*分别包含系统的空间及时间振荡信息;Σ为奇异值矩阵; 表示复数的共轭转置。
表示复数的共轭转置。
为便于计算,引入低阶状态矩阵F近似描述高阶复杂矩阵A的关键振荡信息,即
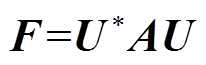 (11)
(11)则可得含有系统固有振荡信息低阶状态矩阵F的表达式为
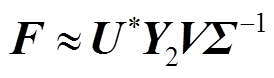 (12)
(12)
为获取系统的关键振荡信息,对F特征值分解为
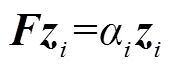 (13)
(13)式中,αi为式(2)中蕴含系统振荡信息的特征值;zi为αi的特征向量。
参考文献[22],引入F-范数,将由矩阵X和a构建的变量投影函数变换为
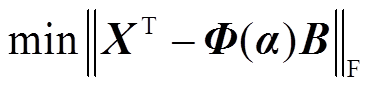 (14)
(14)采用VP计算式(14)中a的最优解aovp,即振荡模式对应的特征值li,则系统第i个振荡模式的振荡频率fi与阻尼比zi为
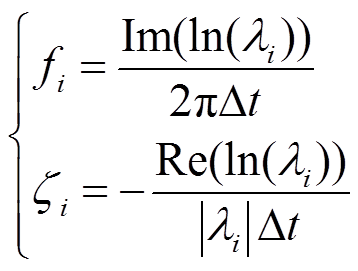 (15)
(15)
进一步由式(14)获取Bovp,计算与第i个振荡模式具有强相关性的振荡模态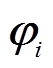 为
为
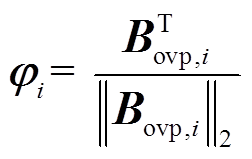 (16)
(16)式中,Bovp,i为Bovp的第i个行向量。
受限于故障时间、类型、地点及量测噪声等多重因素影响,根据式(15)辨识的振荡模式中可能含有虚假振荡模式和噪声振荡模式。为从含虚假振荡模式和噪声振荡模式的振荡模式辨识结果中准确地分离出电力系统主导振荡模式,本文首先根据式(17)计算各振荡模式的能量值Ei为
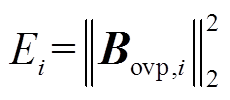 (17)
(17)将各振荡模式的能量值Ei按从大到小排序,计算排序后振荡模式的累积能量权重Es,k为
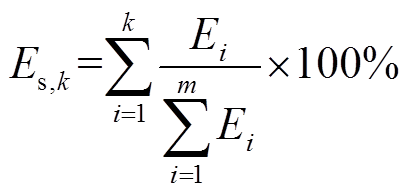 (18)
(18)
若前k个振荡模式的累积能量权重Es,k大于所设定的累积能量权重阈值E0,则可认为该k个振荡模式即为系统的主导振荡模式。由于振荡模式与振荡模态间的对应关系,根据式(16)可进一步从φi中有效筛选出主导振荡模式所对应的主导振荡模态。
上述过程实现了电力系统主导振荡模式及模态的有效辨识。显然,由上述过程可知:所提OVP方法首先引入FDM对广域量测信息进行预处理,提取含系统动态振荡信息的特征值以解决VP所面临的初值选取问题;然后,采用VP优化前述所计算特征值,进而辨识系统振荡模式及模态,并通过Es,k筛选出含系统关键振荡信息的主导振荡模式及模态。显然,该方法仅采用有限个主导振荡模式及模态即可有效表征出系统量测信息所隐含的关键振荡信息,进而为电网动态稳定在线监测与控制提供参考信息。
进一步,为给电网运行和研究人员提供更为丰富的动态振荡信息,本文借鉴文献[23]引入参与因子来评估主导振荡模式下各发电机参与振荡的程度,通过所计算的参与因子,使得主导振荡模式与各发电机间的相关程度得以定量表征和描述。根据前述所筛选出的主导振荡模式、振荡模态及能量值,可得参与因子的表达式为
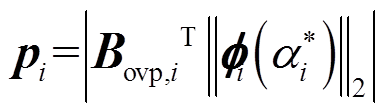 (19)
(19)式中,pi为振荡模式i中k台发电机的参与因子向量,pi=[pi1pi2…pik]T,pik值越大,表明第k台发电机在第i个振荡模式下的振荡参与度越高;反之,则越低。根据各发电机的振荡参与度大小可实现系统振荡源的准确定位,进而可针对参与度最高的前几台发电机上采取相关措施来抑制系统的低频振荡。
综上所示,本文所提基于OVP的电力系统主导振荡模式、模态与参与因子综合辨识方法计算流程如图1所示,具体步骤如下:
(1)从PMU装置中采集电力系统的状态量测信息,然后构建如式(1)所示的电力系统广域量测信息矩阵X。
(2)分别提取量测信息矩阵X的前N-1列构建矩阵X1和后N-1列构建矩阵X2,通过式(9)获取矩阵Y1和矩阵Y2。
(3)根据式(10)引入SVD分解矩阵Y1求得矩阵U、Σ、V。
(4)通过式(12)利用矩阵Y2以及分解Y1所得子矩阵U、Σ、V计算矩阵F。
(5)采用特征值分解,计算矩阵F的特征值αi,并将矩阵X和αi作为初值代入式(14)中。
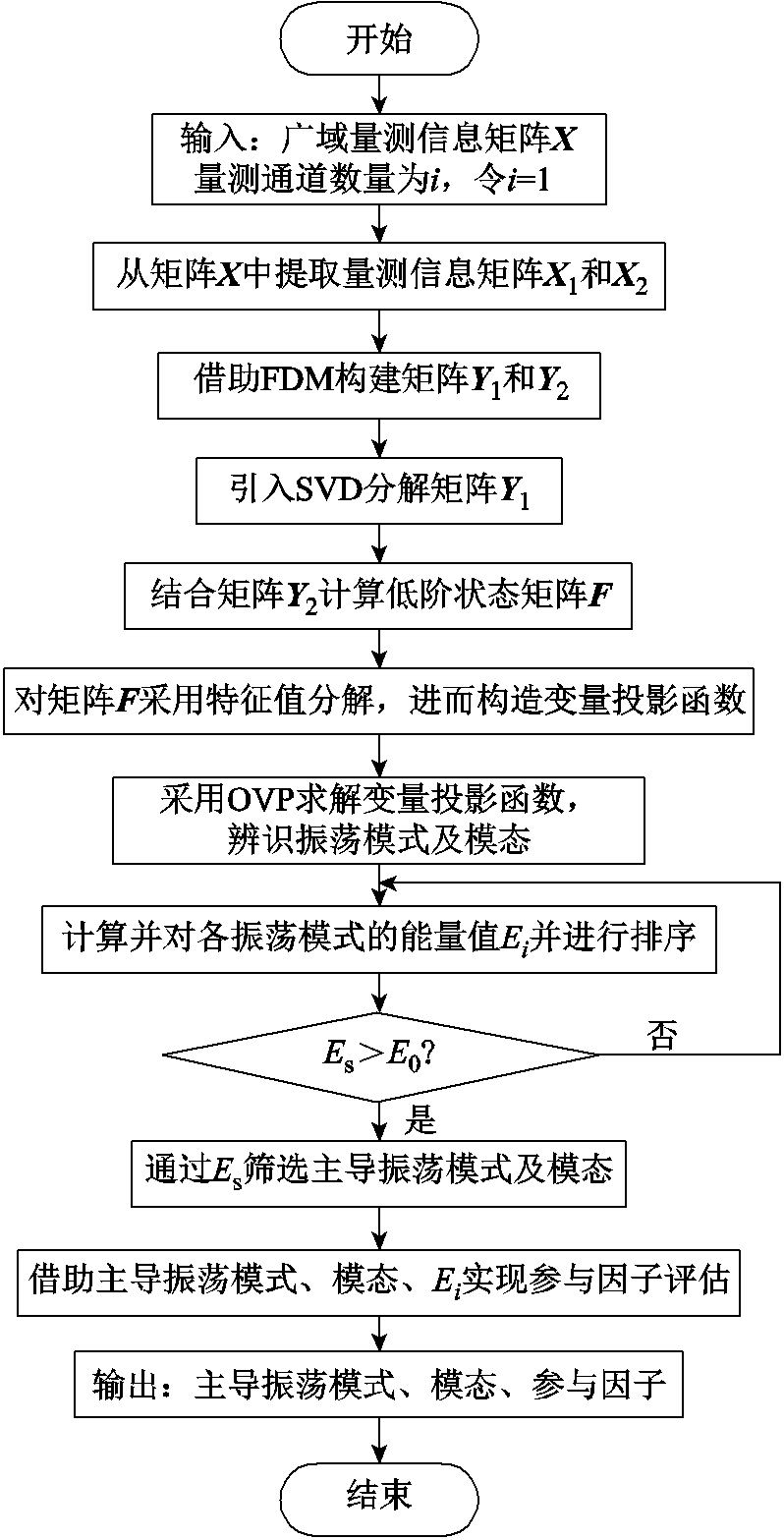
图1 本文方法辨识流程
Fig.1 Flowchart of the proposed method
(6)借助OVP求解式(14),并通过式(15)和式(16)计算系统的振荡模式和振荡模态。
(7)根据式(17)和式(18)计算各振荡模式的累积能量权重Es,k,筛选含系统关键振荡信息的主导振荡模式及模态。
(8)根据主导振荡模式、模态及能量值,通过式(19)计算各发电机或母线的参与因子。
针对所提基于OVP的电力系统主导振荡模式、模态及参与因子综合辨识方法,本节分别以IEEE 68节点测试系统和中国南方电网为例分析、验证所提方法的准确性和有效性。
IEEE 68节点测试系统如图2所示,该系统中发电机G1~G9、G10~G13、G14、G15、G16分别属于区域1~5,系统具体参数详见文献[24]。
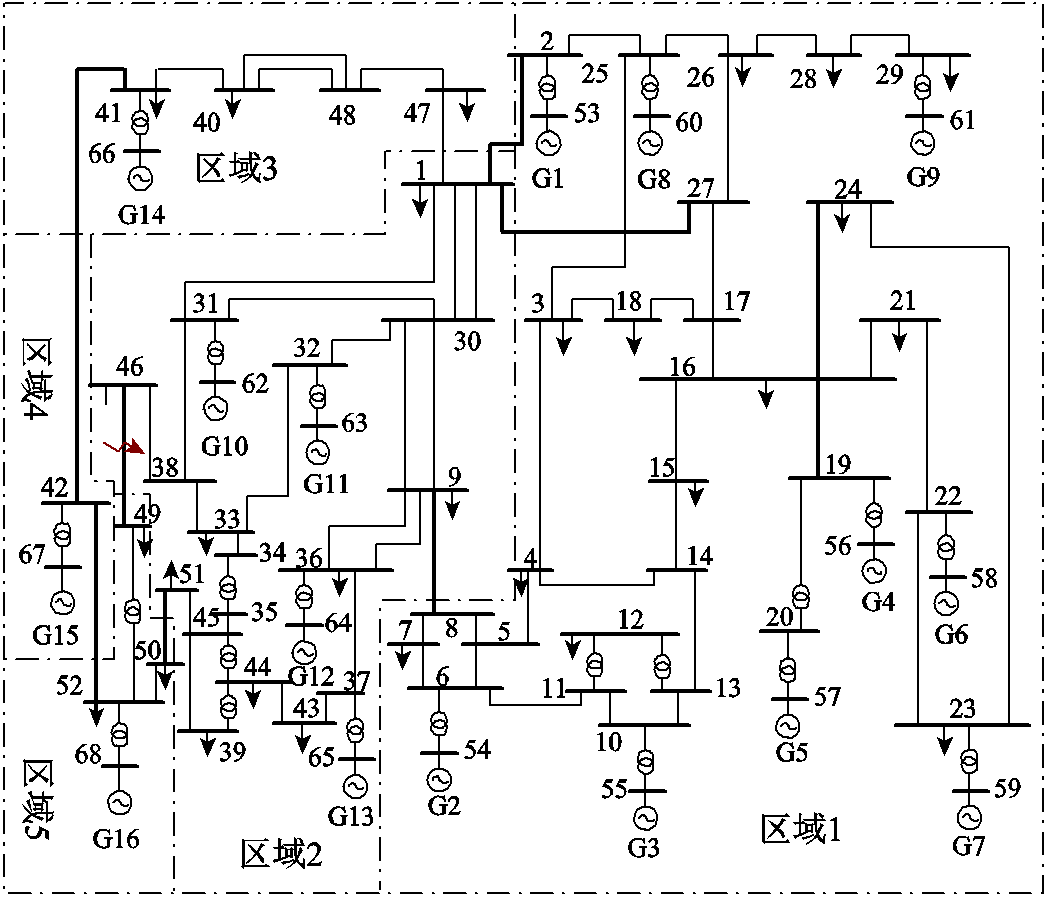
图2 IEEE 68节点测试系统
Fig.2 IEEE 68 bus test system
本节中,IEEE 68节点测试系统的故障设置如下:0.1s时支路46-49发生三相短路故障,0.16s后近节点49侧断路器跳开,0.18s后远节点46侧断路器跳开,采样频率为100Hz,仿真时间为1min。图3为发生故障后发电机相对转子角与角速度摇摆曲线,选取发电机转子角和角速度的前30s数据作为输入。

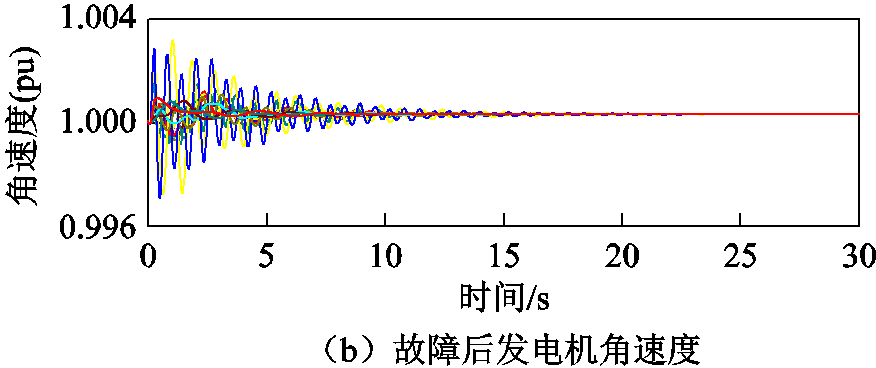
图3 发电机转子角与角速度摇摆曲线
Fig.3 Oscillation curves of rotor angles and speeds
3.1.1 无噪声环境下辨识结果分析
1)主导振荡模式辨识
首先,根据式(1)构建电力系统的广域量测信息矩阵X,提取矩阵X的前N-1列和后N-1列分别构建矩阵X1和X2,并由式(9)计算得矩阵Y1和Y2;根据式(10),引入SVD将矩阵Y1分解为子矩阵U、Σ、V;根据式(12)中矩阵Y2及U、Σ、V计算低阶状态矩阵F,并采用特征值分解得到F的特征值αi;将矩阵X和αi作为初值代入式(14)所示的变量投影函数中,并通过VP求解式(14),进而利用式(15)和式(16)辨识系统的振荡模式和振荡模态;由式(17)和式(18)计算各振荡模式的能量值Ei及累积能量权重Es,k,选取累积能量权重阈值E0=85%。若累积能量权重Es,k≥E0,则认为该k个振荡模式为含系统关键振荡信息的主导振荡模式。由于量测通道数为30个,所提方法共辨识出15组振荡模式,因机电振荡的振荡频率范围为0.2~2.5Hz,滤除三组非机电振荡频率范围的模式后,图4给出了所保留的12组模式的能量值Ei。
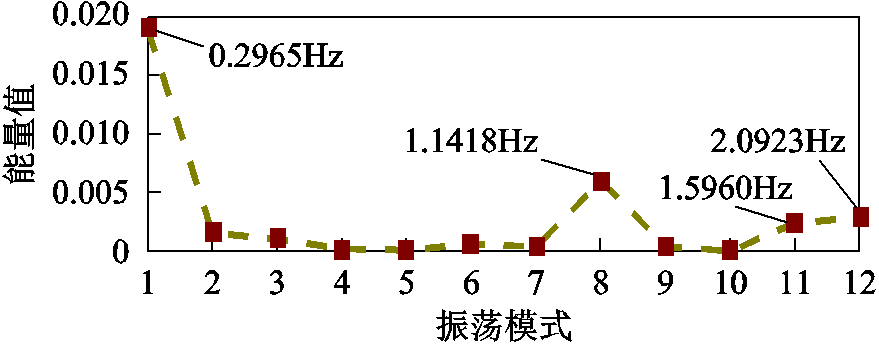
图4 OVP辨识各振荡模式的Ei
Fig.4 Eiof modes identified by OVP
显然,由图4结果可知:所辨识出的12组模式中,有四组模式的能量值明显大于其他模式,其能量值分别为0.019 0、0.006 0、0.002 4和0.002 9,且其累积能量权重Es,k=87.47%>E0=85%,故可认为这四组模式对系统振荡的影响程度最大,并将其视为系统的主导振荡模式。
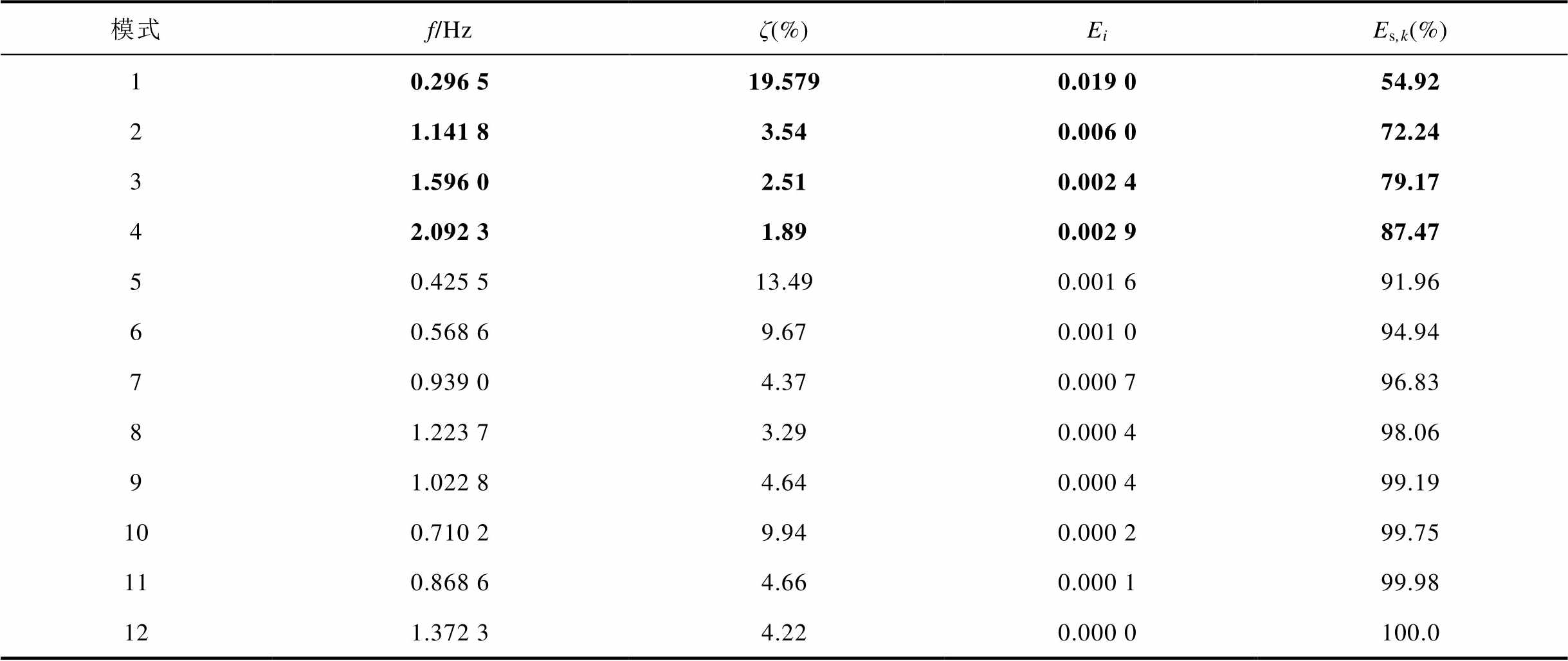
表1进一步详细给出了采用OVP辨识出的各振荡模式的能量值Ei及累积能量权重Es,k。显然,由表1计算结果可知:前四组模式所对应的累积能量权重Es,k足够大,可认为是此次故障下系统被激发出的四组主导振荡模式。
表1 OVP辨识的各振荡模式Ei和Es,k
Tab.1 Ei and Es,k of all modes identified by OVP
模式f/Hzζ(%)EiEs,k(%) 10.296 519.5790.019 054.92 21.141 83.540.006 072.24 31.596 02.510.002 479.17 42.092 31.890.002 987.47 50.425 513.490.001 691.96 60.568 69.670.001 094.94 70.939 04.370.000 796.83 81.223 73.290.000 498.06 91.022 84.640.000 499.19 100.710 29.940.000 299.75 110.868 64.660.000 199.98 121.372 34.220.000 0100.0
图5进一步给出了以图3b的发电机转速作为输入,采用FFT进行频谱分析的结果。由图5的频谱分析结果可知:系统故障后共激发出四组振荡模式,其振荡频率分别为0.268 6Hz、1.147 5Hz、1.599 1Hz和2.099 6Hz,该结果与图4和表1所提OVP的主导振荡频率辨识结果一致,有效验证了所提OVP方法辨识系统主导振荡频率的准确性。
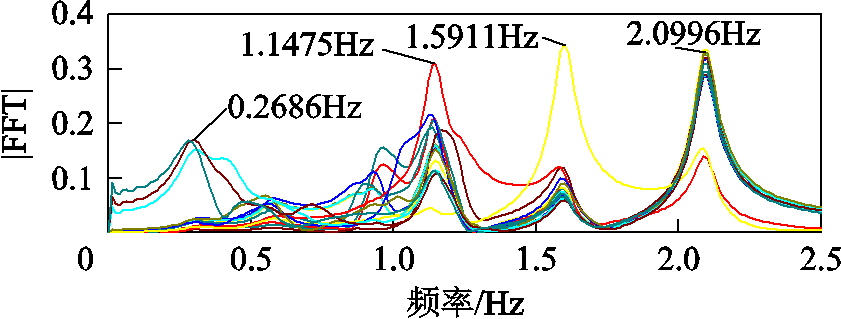
图5 FFT的频谱分析图
Fig.5 Spectrum analysis result of FFT
图6分别以振荡频率和阻尼比为横、纵坐标,对比了OVP、DMD、本征正交分解(Proper Orthogonal Decomposition,POD)、KMD和EA所辨识的主导振荡模式。由图6可知:DMD所辨识出模式1的阻尼比结果与EA相差较大;KMD所辨识出的四组主导振荡模式偏差均较大;POD振荡频率辨识结果较准,但其缺陷在于不能辨识系统的阻尼比;本文所提OVP与EA辨识结果近似重合,具有更高的辨识精度。
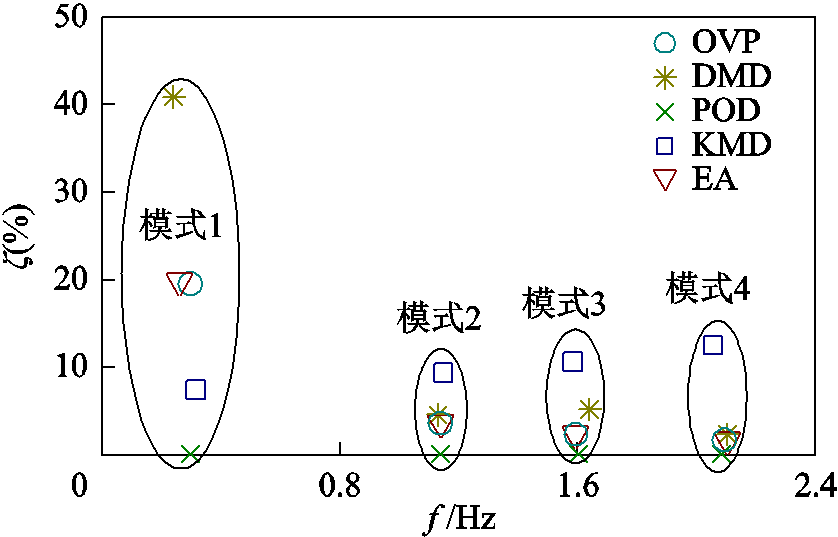
图6 不同方法辨识的主导振荡模式对比
Fig.6 Comparison of dominant modes estimated by different methods
表2详细给出了图6中OVP、DMD、POD、KMD和EA所辨识出的系统四组主导振荡模式的振荡频率和阻尼比。表3进一步以EA的辨识结果为基准,给出了OVP、DMD、POD和KMD的辨识误差。通过对比图6、表2和表3的辨识结果可知:所提OVP方法的主导振荡模式辨识结果与EA的辨识结果较为接近,均在合理范围内,而DMD和KMD的辨识误差较大,其计算精度严重不足,POD的辨识误差虽较小,但该方法不能辨识出振荡模式的阻尼比信息,因此所提OVP相对DMD、POD和KMD具有更高的辨识精度。
2)主导振荡模态辨识
在辨识出主导振荡模式后,本节进一步根据振荡模式与式(16)所辨识振荡模态间的对应关系,筛选出主导振荡模式所对应的振荡模态,结果如图7所示。
表2 不同方法辨识的主导振荡频率和阻尼比对比
Tab.2 Comparison of the dominant oscillation frequencies and damping ratiosestimated by different methods

模式参数数值 OVPDMDPODKMDEA 1f/Hz0.296 50.244 40.293 00.312 90.259 0 ζ(%)19.57940.893—7.352 419.986 2f/Hz1.141 81.125 01.135 31.148 61.140 7 ζ(%)3.541 64.501 2—9.425 23.509 5 3f/Hz1.596 01.637 61.599 11.583 41.591 8 ζ(%)2.514 85.281 2—10.72 02.519 1 4f/Hz2.092 32.103 22.087 42.051 32.098 3 ζ(%)1.890 12.493 5—12.53 61.896 1
表3 主导振荡模式误差分析
Tab.3 Estimation error comparisons of dominant modes
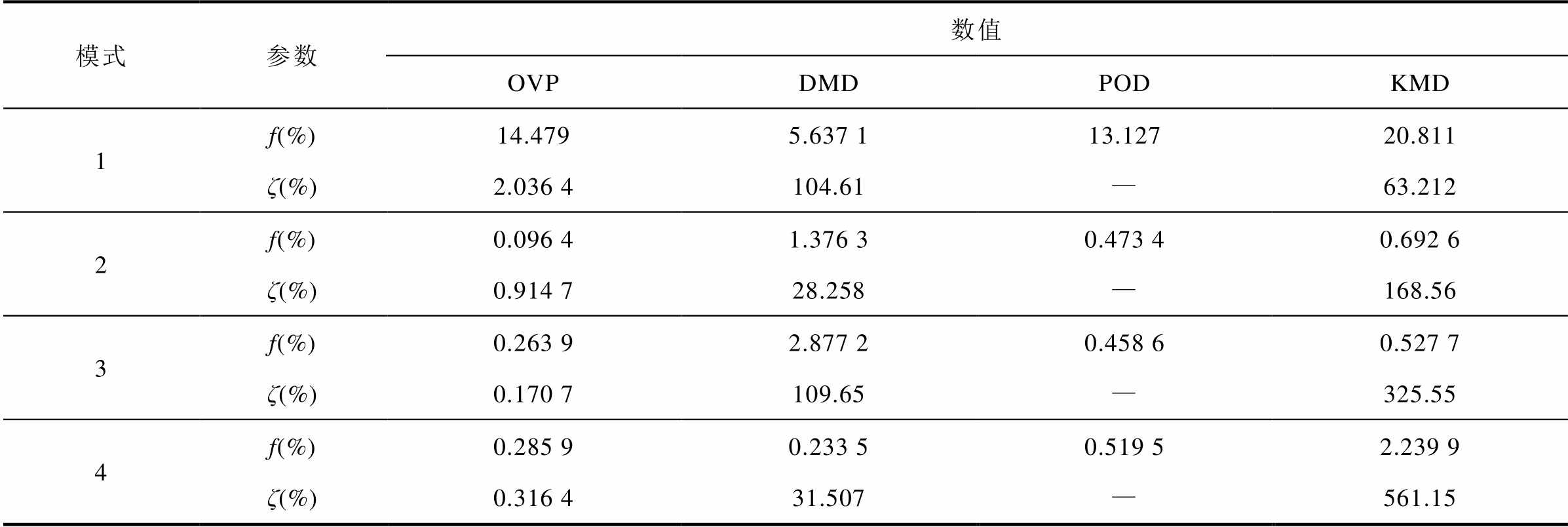
模式参数数值 OVPDMDPODKMD 1f(%)14.4795.637 113.12720.811 ζ(%)2.036 4104.61—63.212 2f(%)0.096 41.376 30.473 40.692 6 ζ(%)0.914 728.258—168.56 3f(%)0.263 92.877 20.458 60.527 7 ζ(%)0.170 7109.65—325.55 4f(%)0.285 90.233 50.519 52.239 9 ζ(%)0.316 431.507—561.15
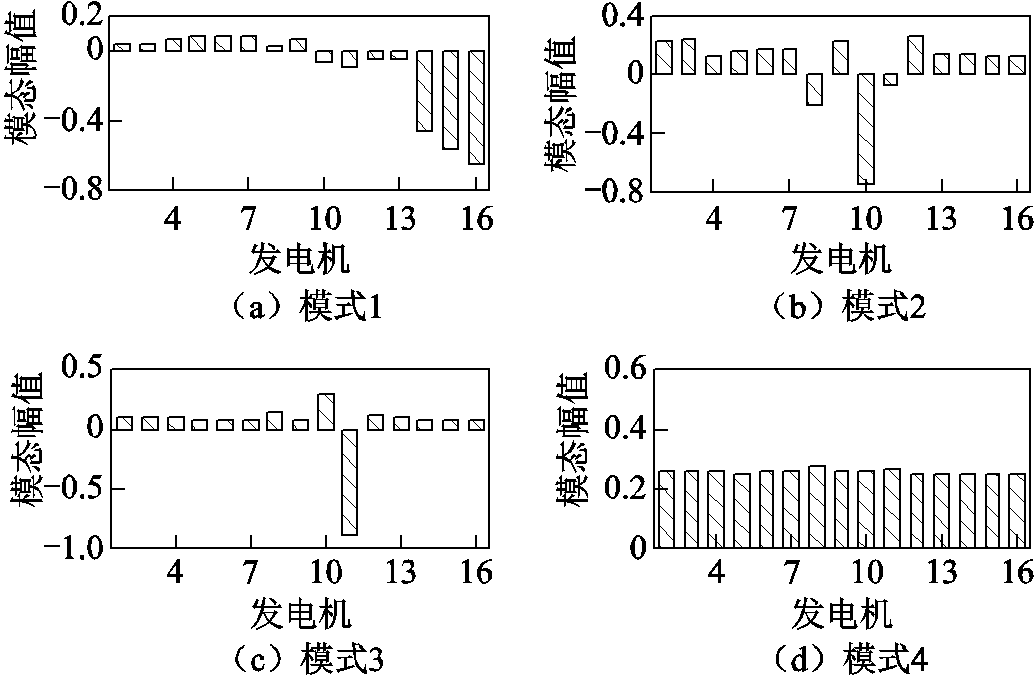
图7 OVP辨识的主导振荡模态
Fig.7 Results of dominant mode shapes estimated by OVP
由图7的主导振荡模态辨识结果可知:主导振荡模式1主要表现为位于区域1中的发电机G2~G9相对区域2~5中的发电机振荡;主导振荡模式2主要表现为发电机G8、G10、G11相对系统中其余发电机振荡;主导振荡模式3主要表现为位于区域2的发电机G11与系统中其他所有发电机相对振荡;主导振荡模式4主要表现为发电机G1与发电机G2~G16相对振荡。
为验证所提OVP方法辨识系统主导振荡模态的准确性,图8分别对比了所提OVP与DMD、POD、KMD和EA在上述四组主导振荡模式中的振荡模态辨识结果。
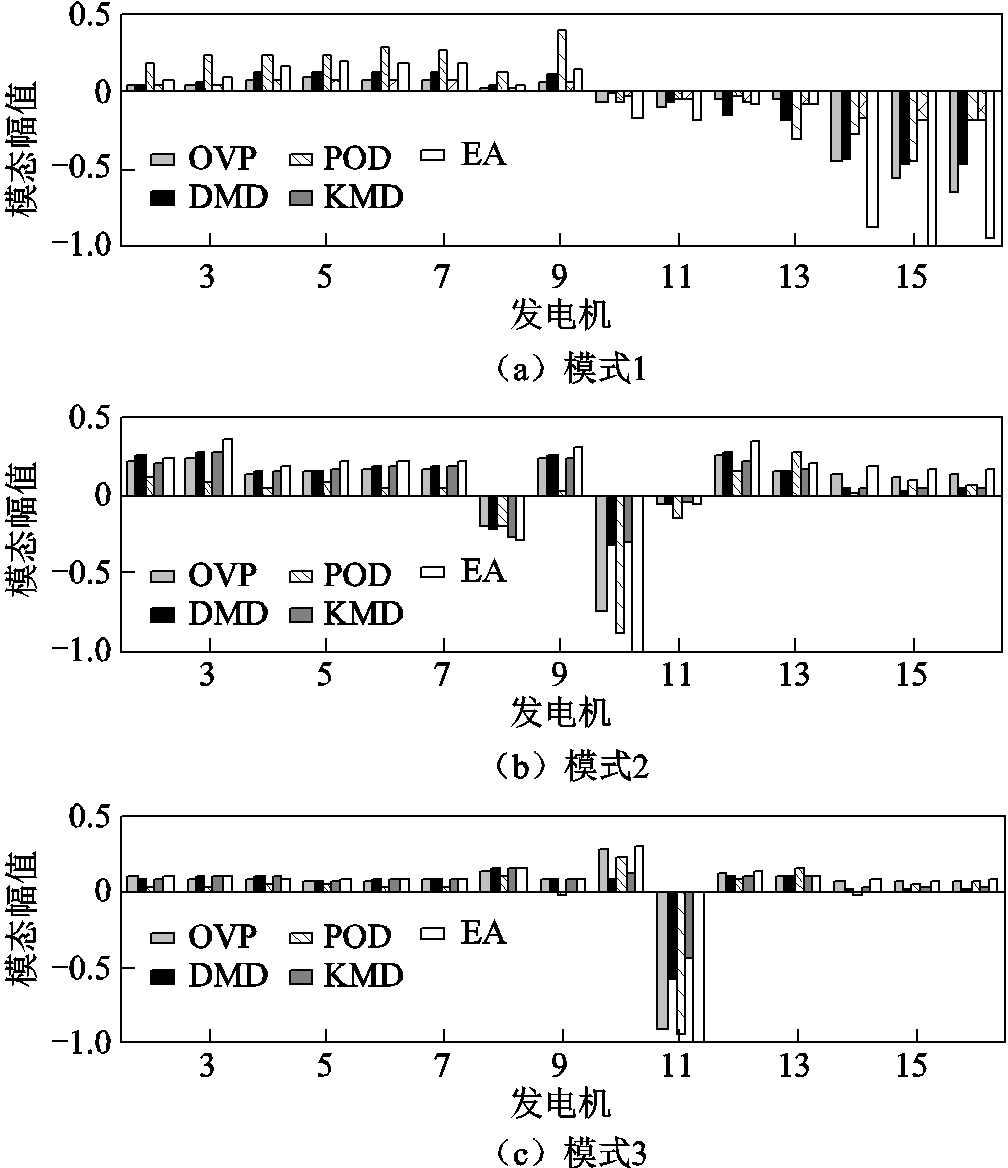
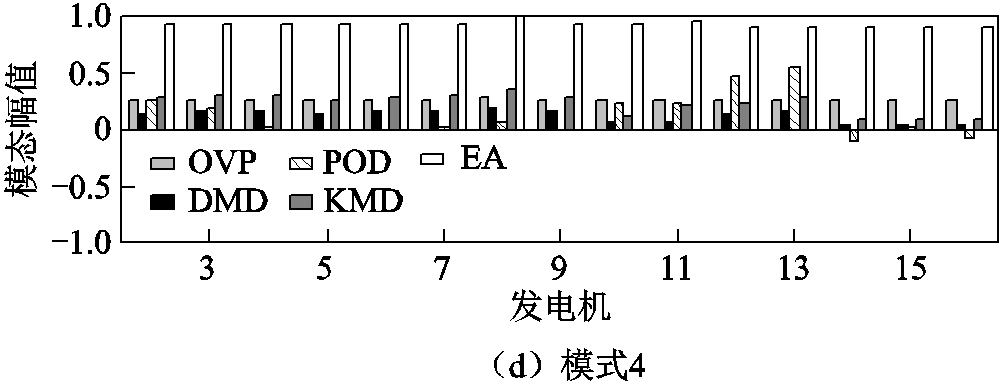
图8 不同方法辨识的主导振荡模态对比
Fig.8 Estimated dominant mode shapes compared with different methods
对比图8的主导振荡模态辨识结果可知:虽然OVP、DMD、KMD和EA所辨识出的主导振荡模态,因辨识原理不同导致辨识结果存在一定的偏差,但所揭示各主导振荡模式下各发电机间的相对振荡特性上是一致的;POD虽然在主导振荡模式1和2中所辨识的主导振荡模态结果与OVP、DMD、KMD及EA一致,但在主导振荡模式3和4的主导振荡模态辨识中与其他四种方法略有不同。通过对比图8中的主导振荡模态辨识结果可知:所提OVP方法可从电力系统广域量测信息中准确辨识出系统的主导振荡模态。
3)参与因子辨识
根据所辨识的主导振荡模式li、主导振荡模态φi及主导振荡模式的能量值Ei,本节进一步根据式(19)估计了该次故障下各发电机在四组主导振荡模式中的参与因子。图9分别对比了OVP、DMD、POD、KMD和EA所辨识出的参与因子。
根据图9的辨识结果,表4进一步详细给出了OVP、DMD、POD、KMD和EA所辨识出在各主导振荡模式中具有较高参与度的发电机。由表4中结果可知:虽然OVP与POD在主导振荡模式1和4中所辨识出的、具有较高参与度的发电机差异较大,与KMD在主导振荡模式2中的参与因子结果不同,但所提OVP方法与DMD、EA在四种主导振荡模式下辨识出的、具有较高参与度的发电机构成上一致,验证了所提方法可从电力系统的广域量测信息中准确辨识出各主导振荡模式中具有较高参与度的发电机。
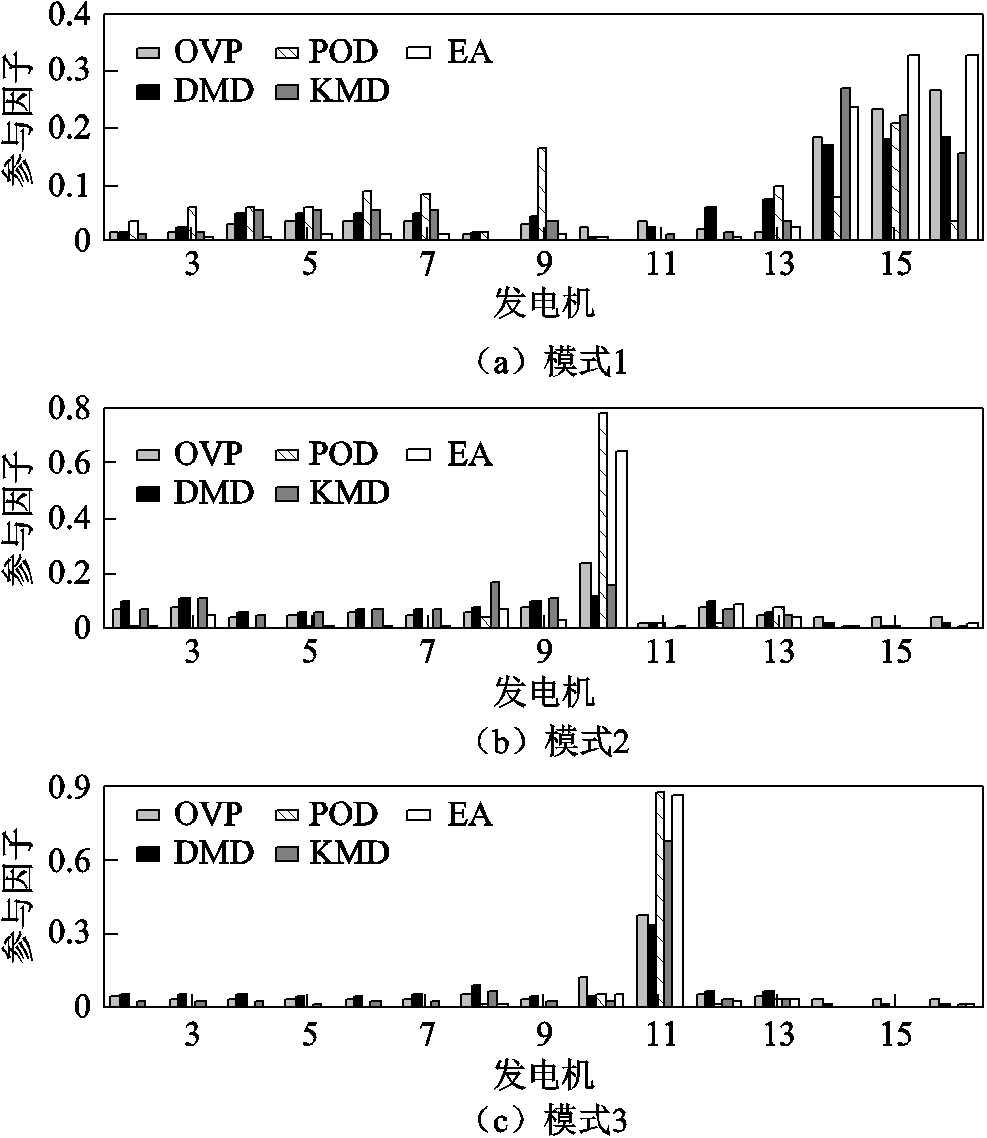
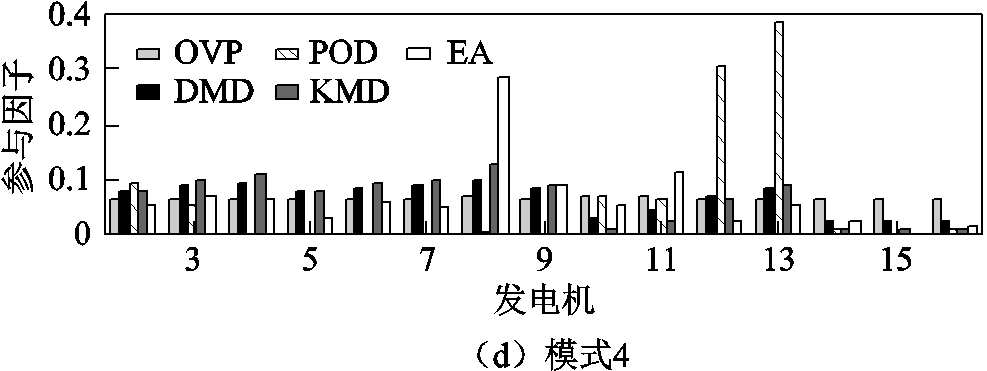
图9 不同方法辨识的参与因子对比
Fig.9 Estimated participation factors compared with different methods
表4 主振荡发电机对比
Tab.4 Comparisons of the estimated dominant generators

方法模式1模式2模式3模式4 OVPG14~G16G10G11G8 DMDG14~G16G10G11G8 PODG9、G15G10G11G12-G13 KMDG14~G16G8、G10G11G8 EAG14~G16G10G11G8
3.1.2 抗噪能力分析
为进一步验证所提方法的鲁棒性,本节分别在图3所示发电机转子角和转速信号中添加信噪比(Signal-to-Noise Ratio, SNR)为85dB、65dB、45dB、25dB的高斯白噪声,以测试所提方法的抗噪能力。
1)主导振荡模式辨识
表5分别给出了OVP、DMD、POD和KMD在不同信噪比下的主导振荡模式辨识结果,表6进一步以表2中OVP、DMD、POD和KMD的无噪声辨识结果为基准,给出各辨识算法在不同信噪比下的辨识结果相对误差。
表5 不同方法辨识的主导振荡模式对比(含噪声)
Tab.5 Comparison of dominant modes estimated by different methods(with noise)

SNR/dBOVPDMDPODKMD f/Hzζ(%)f/Hzζ(%)f/Hzζ(%)f/Hzζ(%) 850.3019.60.2886.00.29—0.318.10 1.143.481.1620.61.14—1.1523.3 1.602.521.6012.51.60—1.5815.6 2.091.902.098.822.09—2.0810.4
(续)

SNR/dBOVPDMDPODKMD f/Hzζ(%)f/Hzζ(%)f/Hzζ(%)f/Hzζ(%) 650.3019.60.4179.10.29—0.244.64 1.143.541.0755.51.14—1.1410.4 1.602.511.40—1.60—1.6614.4 2.091.891.99—2.09—2.0712.3 450.3019.70.43—0.29—0.337.71 1.143.55——1.14—1.155.95 1.602.53——1.60—1.657.13 2.091.90——2.09—2.187.82 250.3019.1——0.31—0.388.21 1.143.56——1.14—1.267.31 1.602.41——1.59—1.6210.9 2.091.84——2.09—2.025.80
表6 不同方法辨识的主导振荡模式误差对比(含噪声)
Tab.6 Error comparison of dominant modes estimated by different methods (with noise)
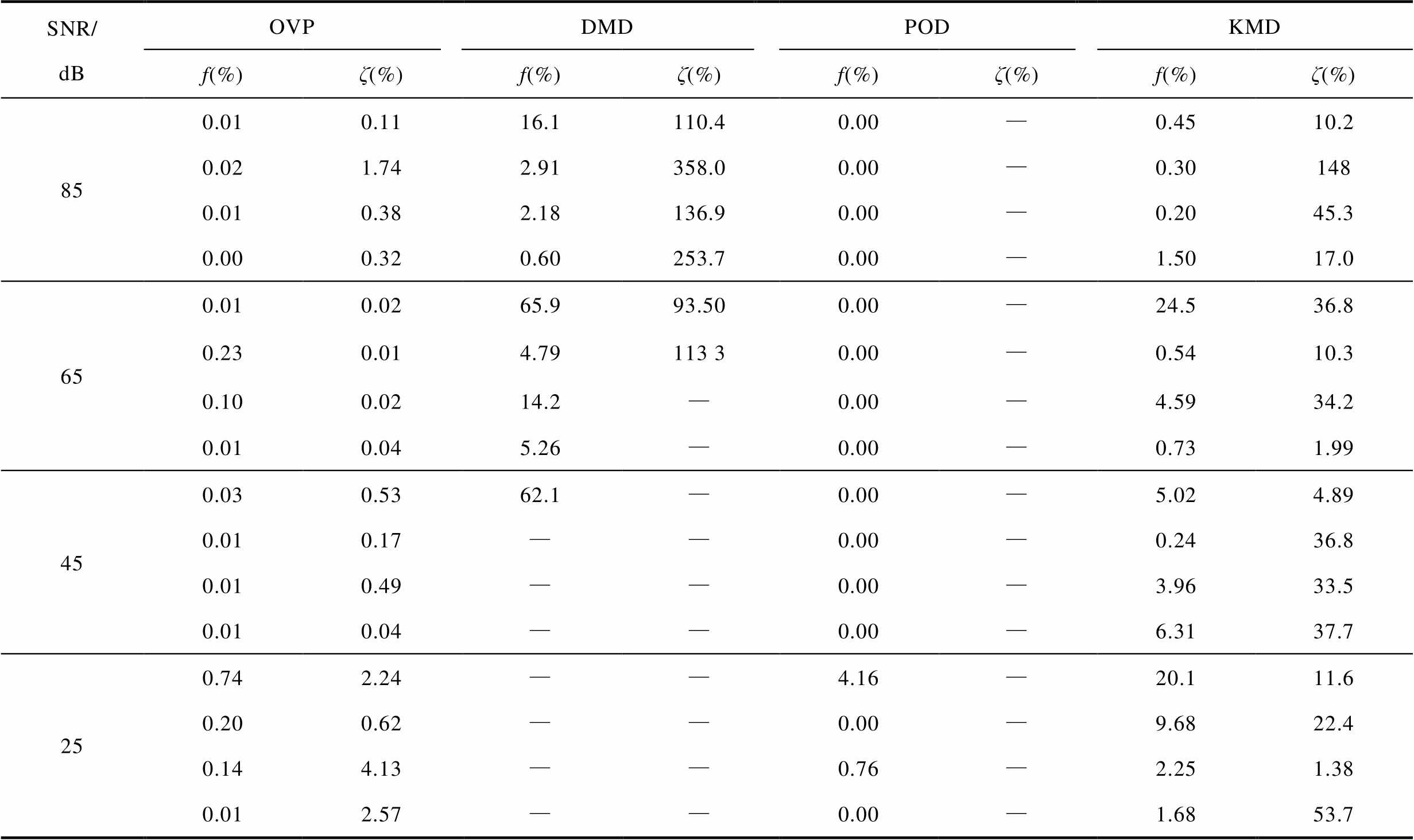
SNR/dBOVPDMDPODKMD f(%)ζ(%)f(%)ζ(%)f(%)ζ(%)f(%)ζ(%) 850.010.1116.1110.40.00—0.4510.2 0.021.742.91358.00.00—0.30148 0.010.382.18136.90.00—0.2045.3 0.000.320.60253.70.00—1.5017.0 650.010.0265.993.500.00—24.536.8 0.230.014.79113 30.00—0.5410.3 0.100.0214.2—0.00—4.5934.2 0.010.045.26—0.00—0.731.99 450.030.5362.1—0.00—5.024.89 0.010.17——0.00—0.2436.8 0.010.49——0.00—3.9633.5 0.010.04——0.00—6.3137.7 250.742.24——4.16—20.111.6 0.200.62——0.00—9.6822.4 0.144.13——0.76—2.251.38 0.012.57——0.00—1.6853.7
显然,由表5和表6的对比结果可知:OVP在SNR=85dB、65dB和45dB的主导振荡模式辨识结果与无噪声环境下的辨识结果大致相同,而SNR=25dB时的阻尼比误差最大,但仅为4.13%;DMD在SNR=65dB时的阻尼比误差就已达到90%,而在SNR=45dB时仅能辨识出系统主导振荡模式1的振荡频率,当SNR<45dB时,DMD则不能辨识出系统的主导振荡模式;POD虽然在SNR=85dB、65dB、45dB和25dB时均能准确辨识出系统的主导振荡频率,且误差较小,但不能给出主导振荡模式的阻尼比信息,辨识结果较为单一;KMD在SNR=85dB、65dB时,其主导振荡频率和阻尼比的辨识误差均在合理的范围内,但当SNR=45dB时,辨识误差已达到30%,SNR<45dB时,主导振荡模式辨识结果已与表2中KMD的无噪声辨识结果相差较大。表5和表6的对比结果表明:所提OVP方法在电力系统主导振荡模式辨识中具有较强的抗噪能力。
2)主导振荡模态辨识
前述分析对比了OVP、DMD、POD和KMD的主导振荡频率和阻尼比辨识结果,由于DMD在SNR=65dB时已不能较为精准地辨识出系统的主导振荡模式,因此本节在主导振荡模态辨识方面通过POD和KMD与所提OVP方法进行对比分析。
为测试所提OVP方法在主导振荡模态辨识中的抗噪能力,本节进一步在图10~图12中给出了OVP、POD和KMD在SNR=65dB、45dB和25dB 时的主导振荡模态辨识结果。通过图10~图12的对比结果可知:OVP在不同信噪比下所辨识主导振荡模态与无噪声环境的辨识结果一致,各发电机间的相对振荡趋势基本保持不变;POD在SNR=65dB和45dB时的主导振荡模态辨识结果与无噪声环境的辨识结果保持一致,但当SNR=25dB时,所辨识的主导振荡模式4的振荡模态与无噪声环境的辨识结果略有差异,而其他主导振荡模态与无噪声环境的辨识结果一致;KMD在SNR=65dB时所辨识主导振荡模态与无噪声环境的辨识结果差异较小,但当SNR<65dB时,所辨识出的四组主导振荡模态受噪声影响较大,其结果无法体现发电机间的相对振荡特性。图10~图12对比结果表明:所提OVP方法相对POD和KMD在振荡模态辨识中具有更强的抗噪能力。
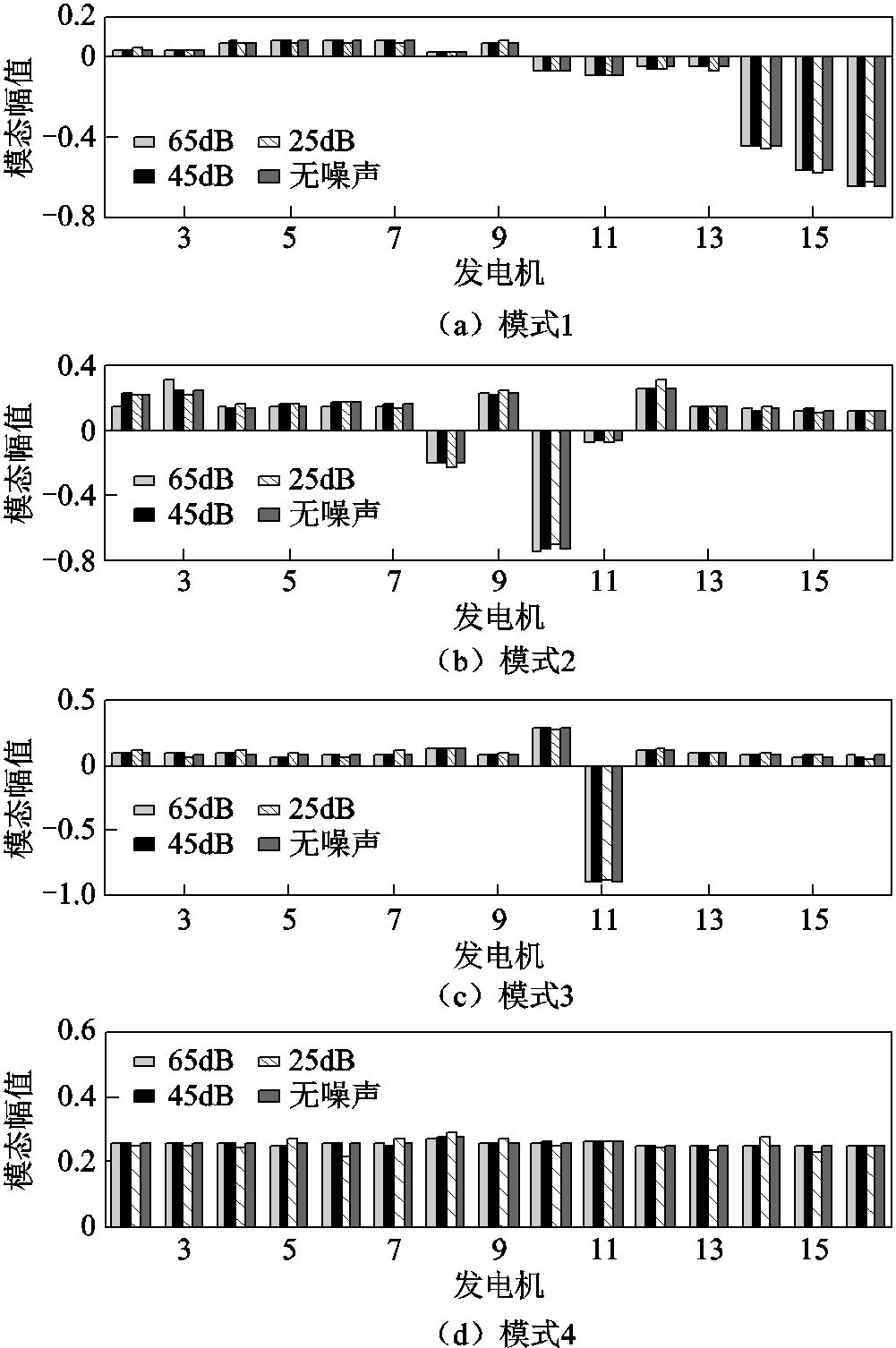
图10 OVP所辨识主导振荡模态对比
Fig.10 Estimated dominant mode shapes compared by OVP
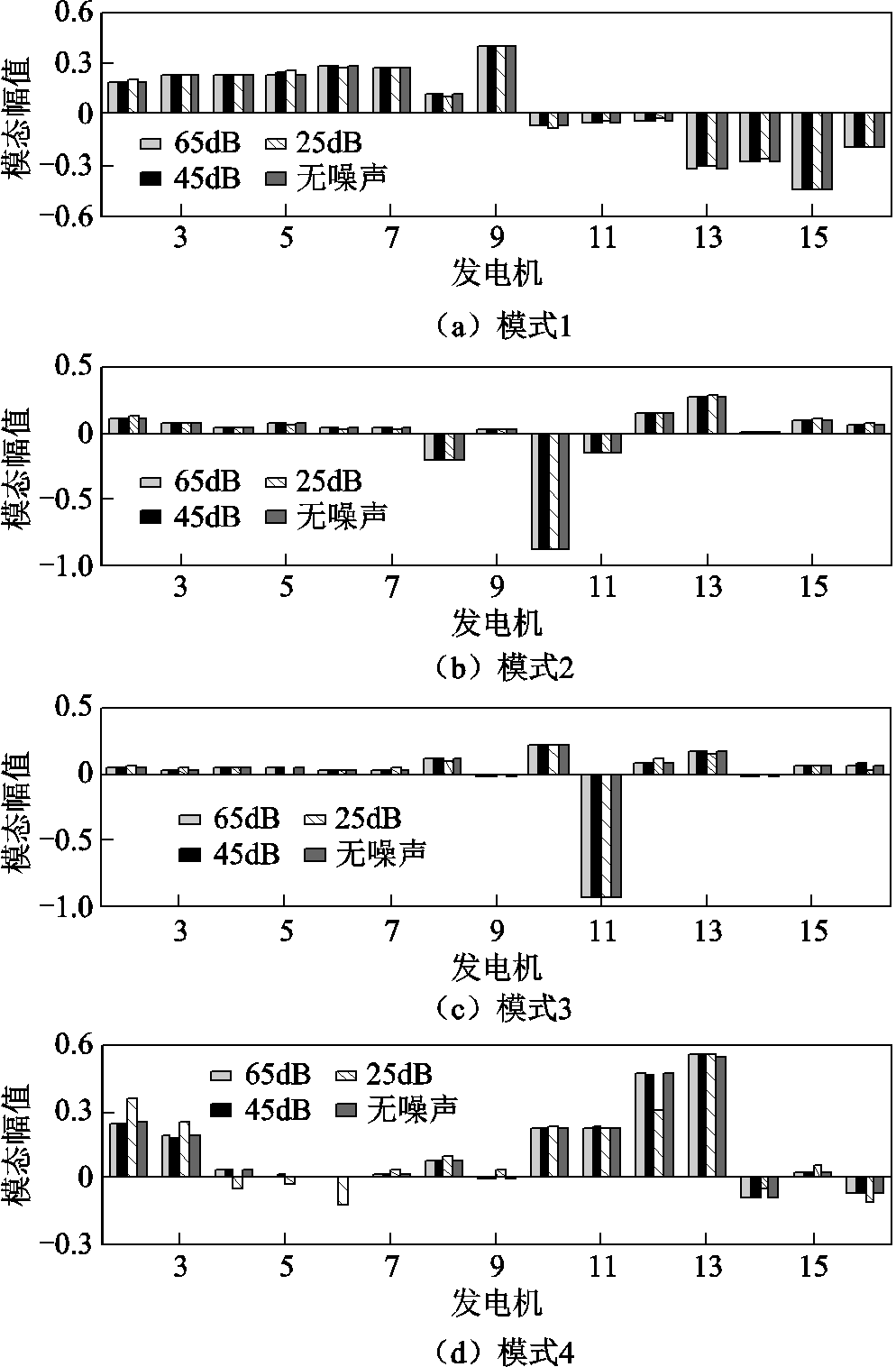
图11 POD所辨识主导振荡模态对比
Fig.11 Estimated dominant mode shapes compared by POD
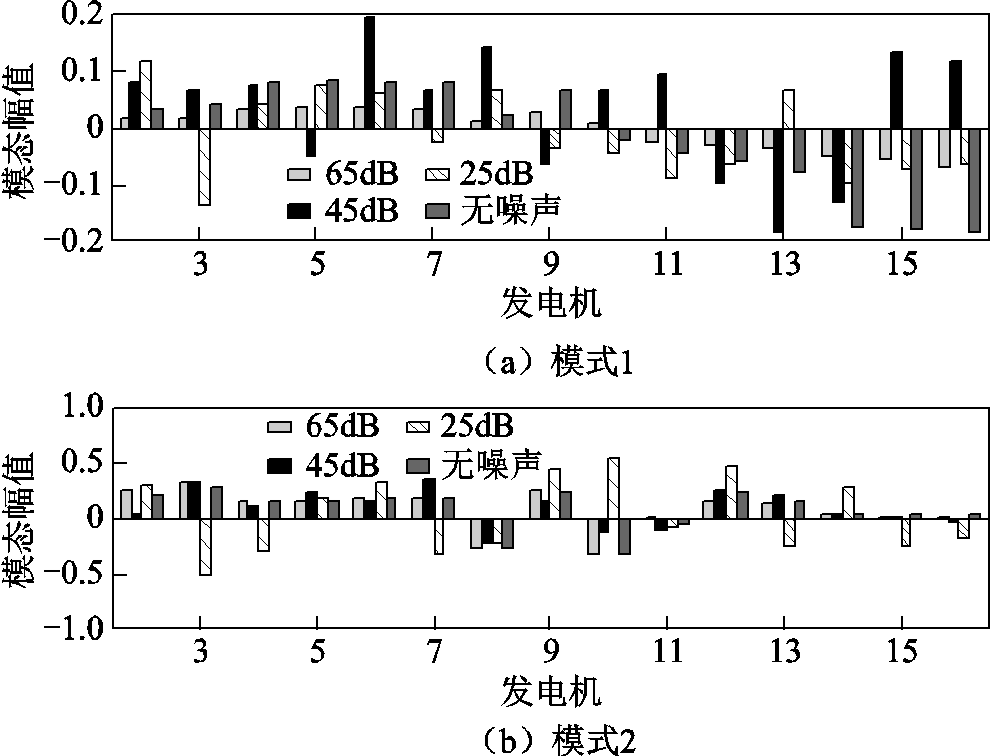
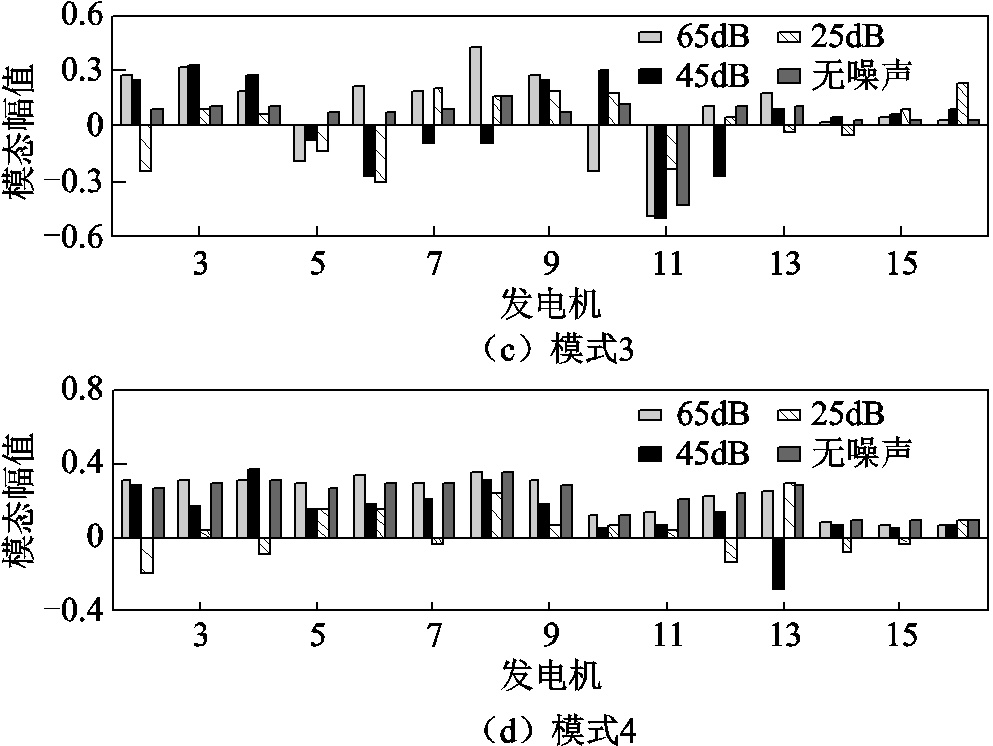
图12 KMD所辨识主导振荡模态对比
Fig.12 Estimated dominant mode shapes compared by KMD
3)参与因子辨识
上述分析验证了所提OVP方法在辨识电力系统主导振荡模式和主导振荡模态时的优势,为体现所提OVP方法的抗噪能力,下述分析给出了OVP、POD和KMD在不同信噪比下辨识的电力系统参与因子和各主导振荡模式系统的主振荡发电机群。
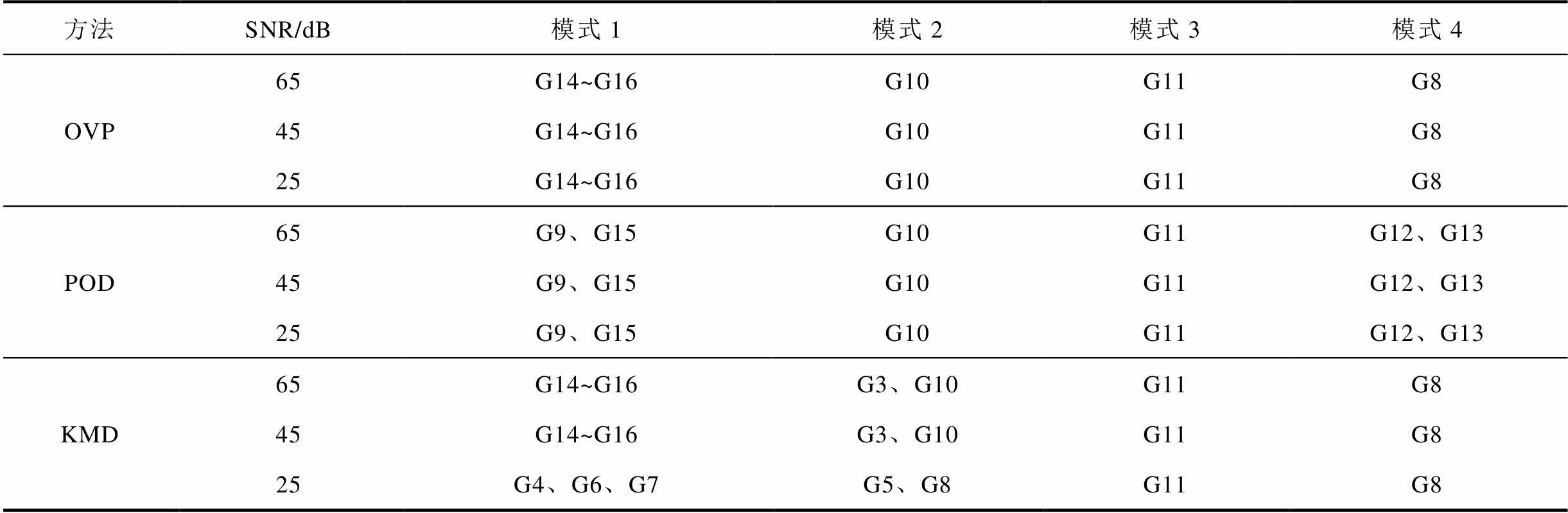
为进一步验证所提OVP方法在电力系统参与因子辨识中的抗噪能力,图13~图15分别给出了OVP、POD和KMD在SNR=65dB、45dB和25dB时的参与因子辨识结果,表7进一步以图13~图15的辨识结果为基准,给出了OVP、POD和KMD在SNR=65dB、45dB和25dB时辨识各主导振荡模式中具有较高参与度的发电机。
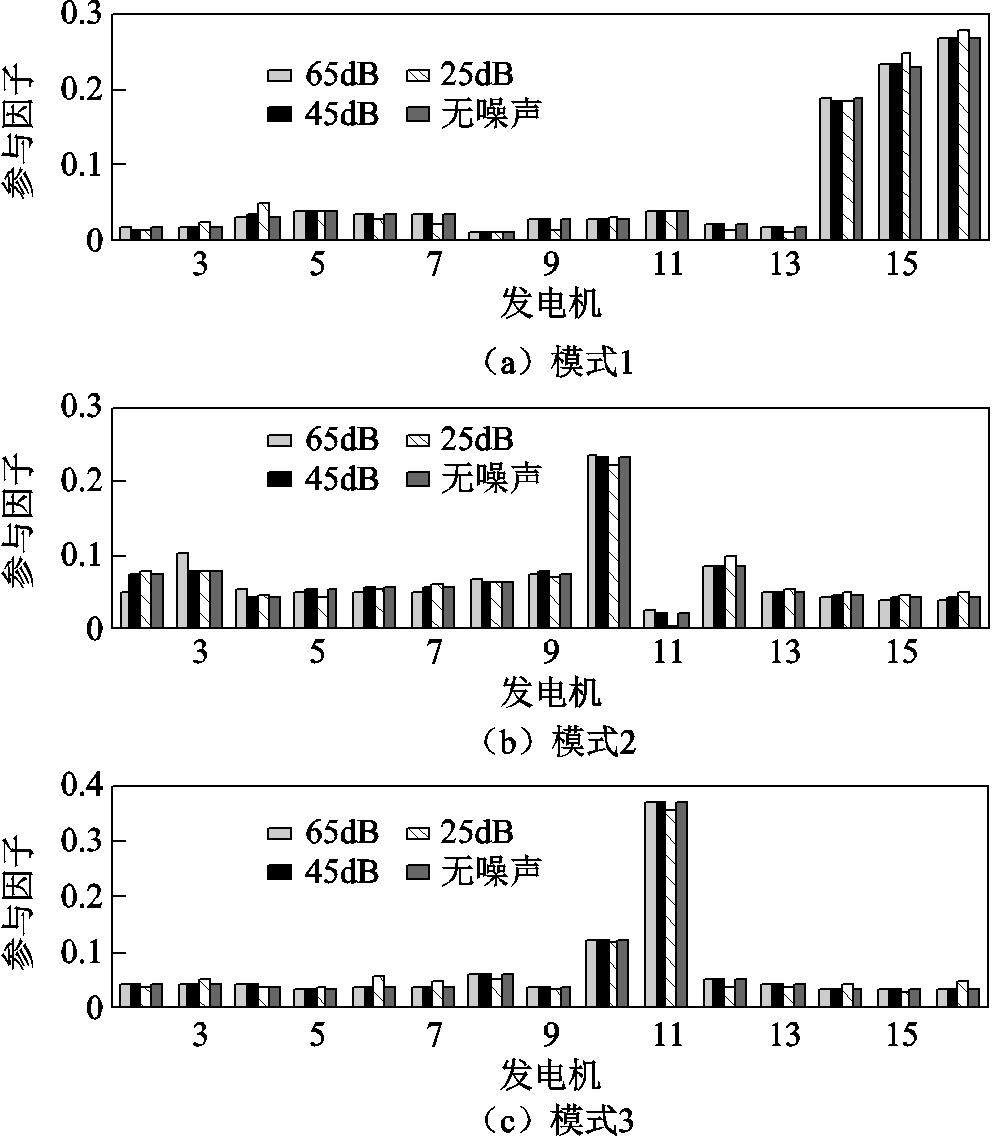

图13 OVP所辨识参与因子对比
Fig.13 Estimated participation factors compared by OVP
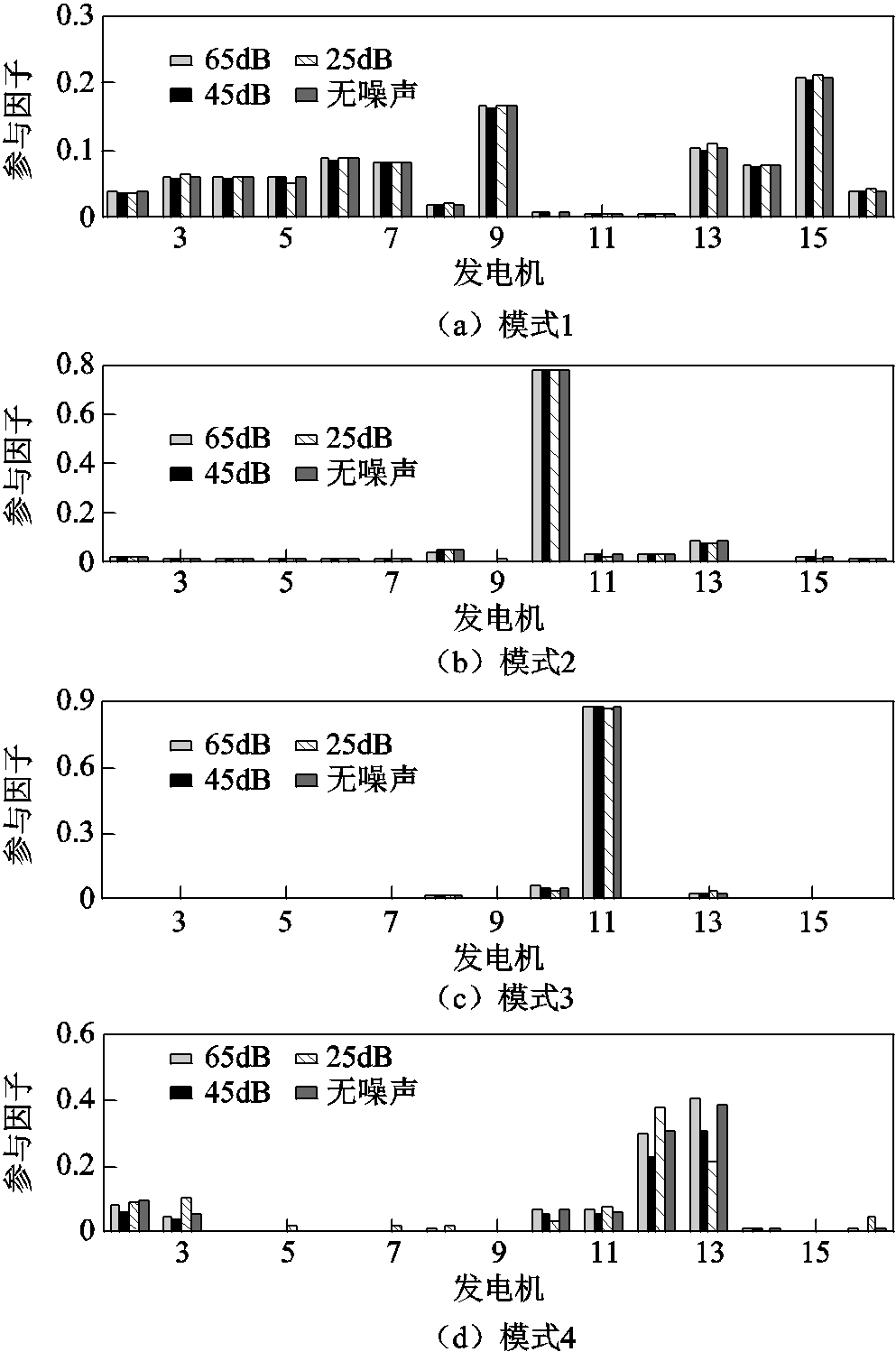
图14 POD所辨识参与因子对比
Fig.14 Estimated participation factors compared by POD
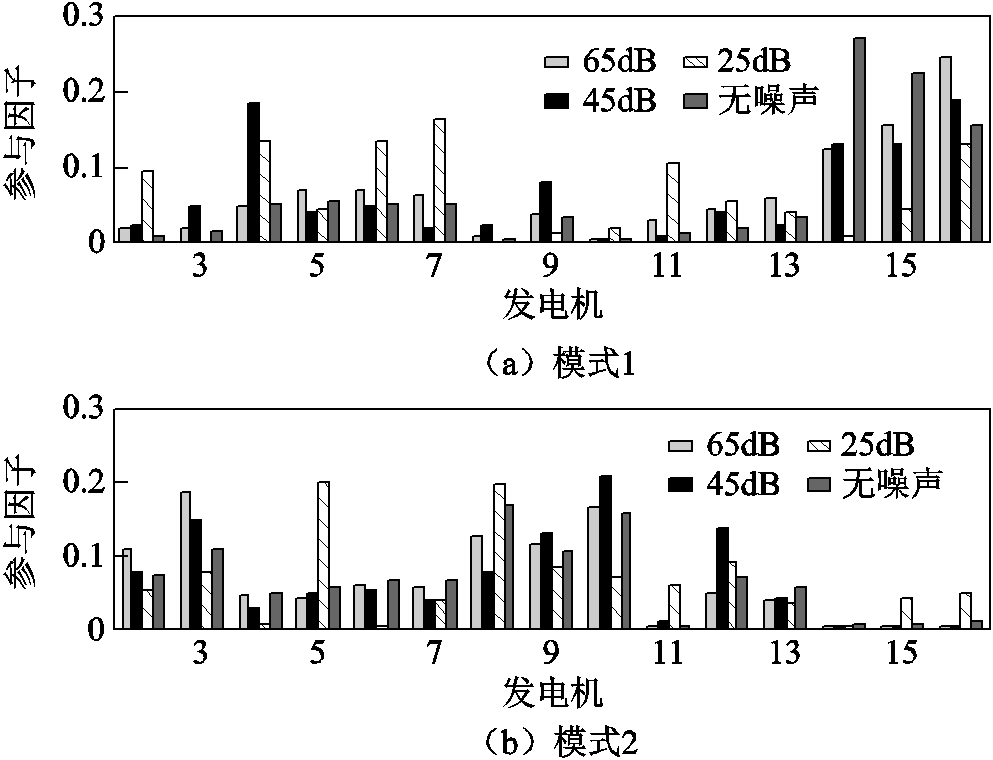
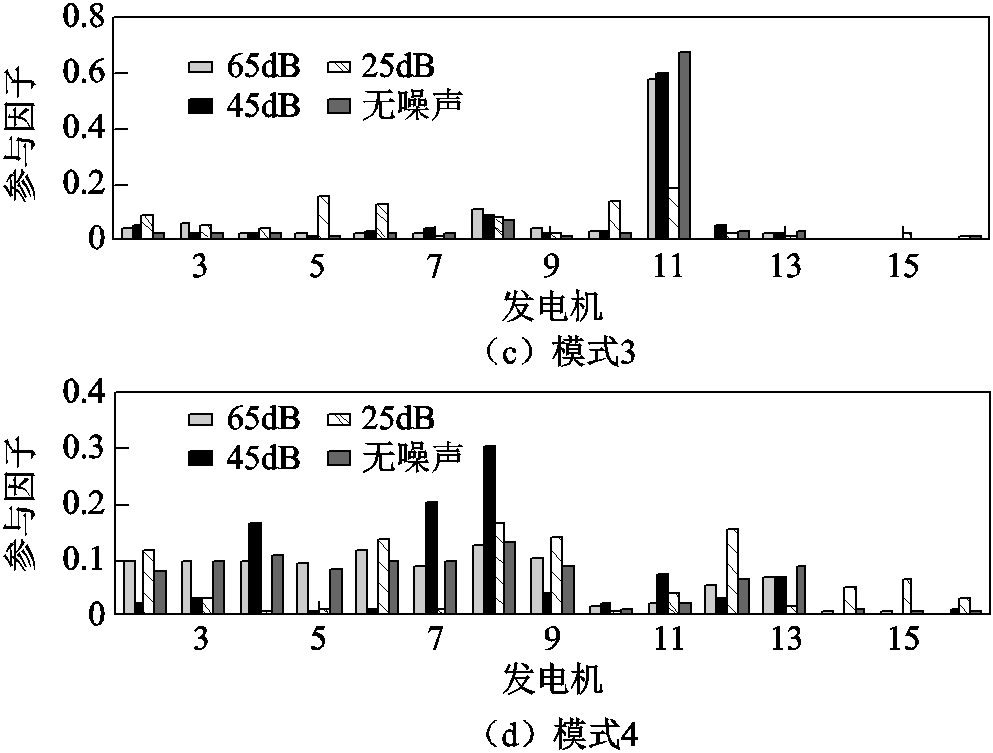
图15 KMD所辨识参与因子对比
Fig.15 Estimated participation factors compared by KMD
表7 不同方法辨识的主振荡发电机(含噪声)
Tab.7 Comparisons of the estimated dominant generators with different methods(with noise)
方法SNR/dB模式1模式2模式3模式4 OVP65G14~G16G10G11G8 45G14~G16G10G11G8 25G14~G16G10G11G8 POD65G9、G15G10G11G12、G13 45G9、G15G10G11G12、G13 25G9、G15G10G11G12、G13 KMD65G14~G16G3、G10G11G8 45G14~G16G3、G10G11G8 25G4、G6、G7G5、G8G11G8
对比图13~图15和表7结果可知:OVP和POD在不同信噪比下的参与因子辨识结果与无噪声环境的参与因子辨识结果相同;KMD在SNR=65dB和45dB时的参与因子辨识结果与无噪声环境下的辨识结果相同,而当SNR=25dB时,所辨识出的参与因子与无噪声环境下的辨识结果已有较为明显的差异。图13~图15和表7的对比结果表明:所提OVP方法在基于广域量测信息的参与因子辨识中具有较强的鲁棒性。
上述不同信噪比主导振荡模式、模态及参与因子的辨识结果对比,有效验证了OVP方法相对DMD、POD、KMD具有更高的辨识精度和更强的鲁棒性。
3.1节验证了所提方法的准确性与鲁棒性,本节进一步以中国南方电网公司为例,验证所提OVP方法辨识实际电网主导振荡模式、模态及参与因子的有效性和可行性。图16为某次故障下云南、贵州和广东六条母线的PMU实测频率,其中,LP位于云南;XR-I和XR-II位于贵州;SD、SZ和ZQ位于广东。
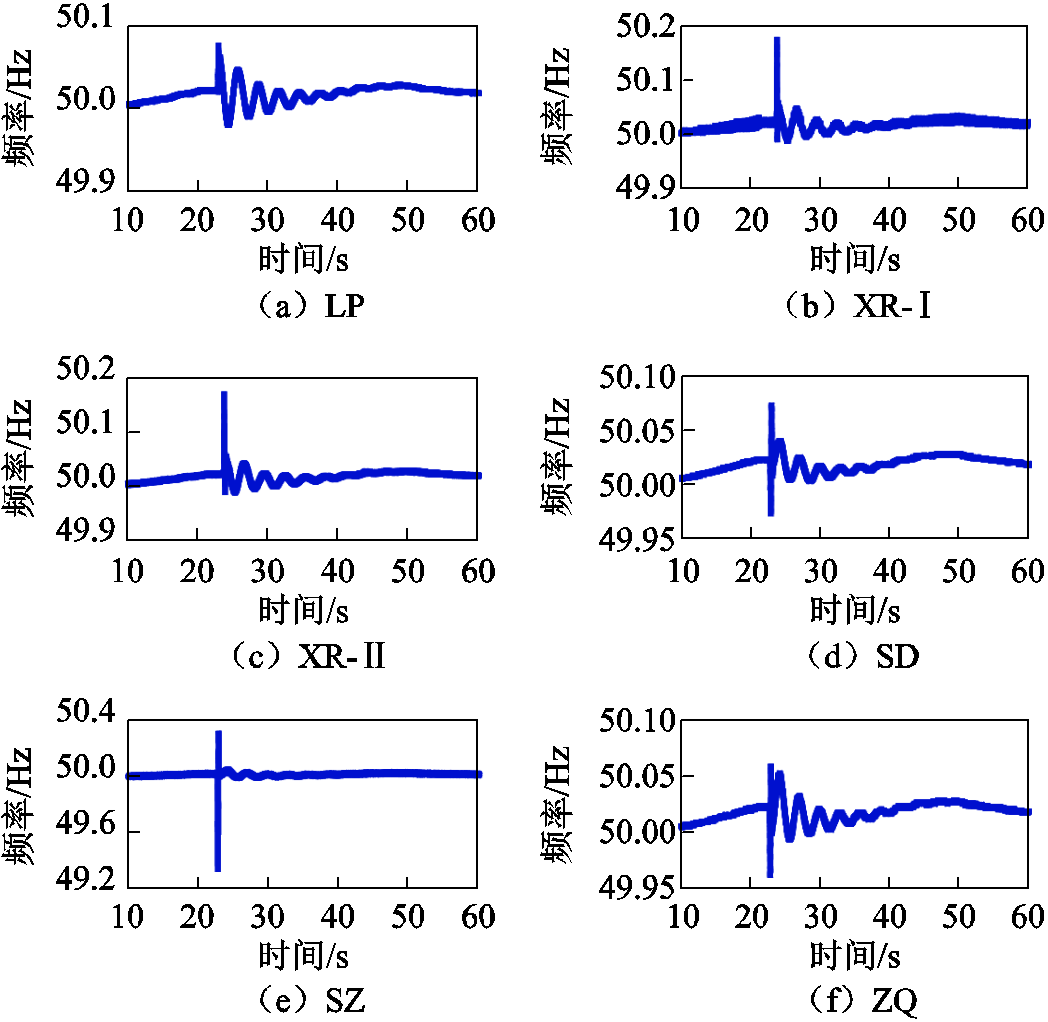
图16 PMU实测频率摇摆曲线
Fig.16 Field measurement frequencies collected from PMU
本节以PMU实测的10~60s的母线频率作为所提方法的输入。表8为OVP、DMD、POD和KMD方法从实测频率中辨识出的系统主导振荡模式。由表8中结果可知:OVP所辨识主导振荡模式1对应的振荡频率为0.443 5Hz,阻尼比为2.577 1%;主导振荡模式2对应的振荡频率为0.356 8Hz,阻尼比为2.148 5%。而通过DMD、POD和KMD所辨识结果与所提方法辨识结果大致相同。
表8 实测频率的主导振荡模式辨识结果
Tab.8 Dominant modes estimated from the field measurement frequencies

模式参数数值 OVPDMDPODKMD 1f/Hz0.443 50.408 20.354 00.421 9 ζ(%)2.577 12.155 9—7.027 0 2f/Hz0.356 80.332 70.341 80.322 5 ζ(%)2.148 53.479 8—8.518 7
图17和图18分别给出了OVP、DMD、POD和KMD方法在上述两种主导振荡模式下图16中6条母线的主导振荡模态及参与因子辨识结果。显然,由图17和图18可知:主导振荡模式1主要表现为位于云南的LP与位于贵州的XR-I、XR-II相对振荡,且相对位于广东的SD、SZ和ZQ具有较高的参与度,结果表明该主导振荡模式应为云贵振荡模式;主导振荡模式2主要表现为位于云南的LP与位于广东的SD、SZ、ZQ相对振荡,且相对位于贵州的XR-I、XR-II具有较高的参与度,即该振荡模式应为云广振荡模式。进一步,参考文献[25]可得:所提OVP方法的辨识结果与南方电网本次故障下的动态稳定分析结果一致,有效验证了所提OVP方法的准确性和有效性。
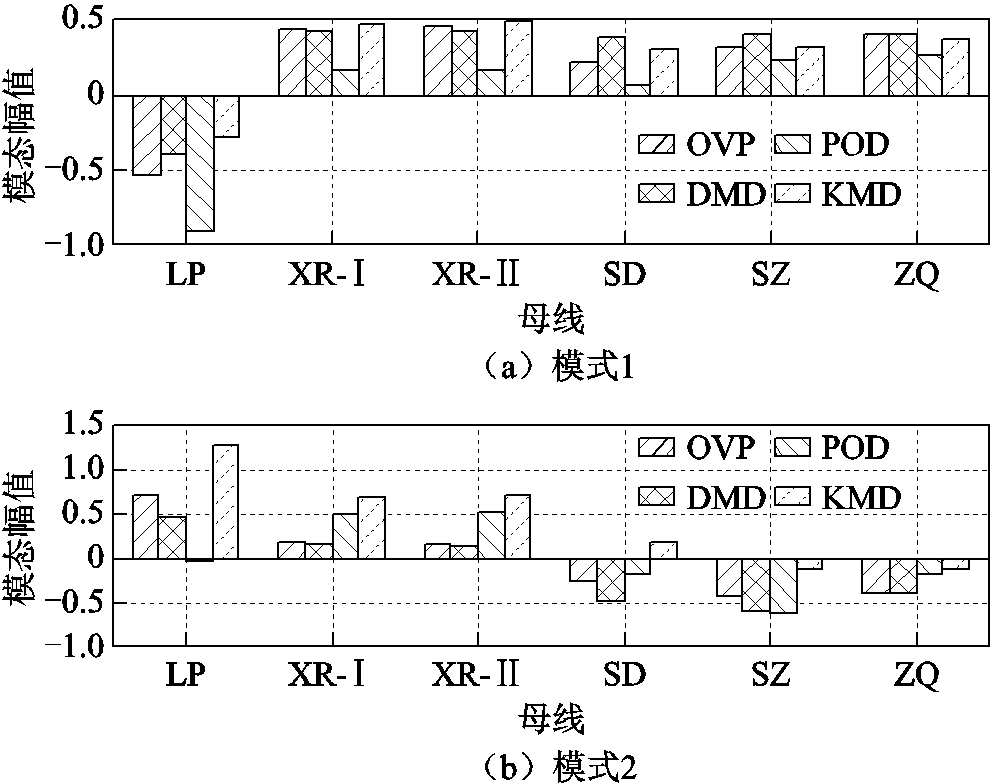
图17 主导振荡模态辨识结果
Fig.17 Dominant mode shapes estimated from the field measurement frequencies
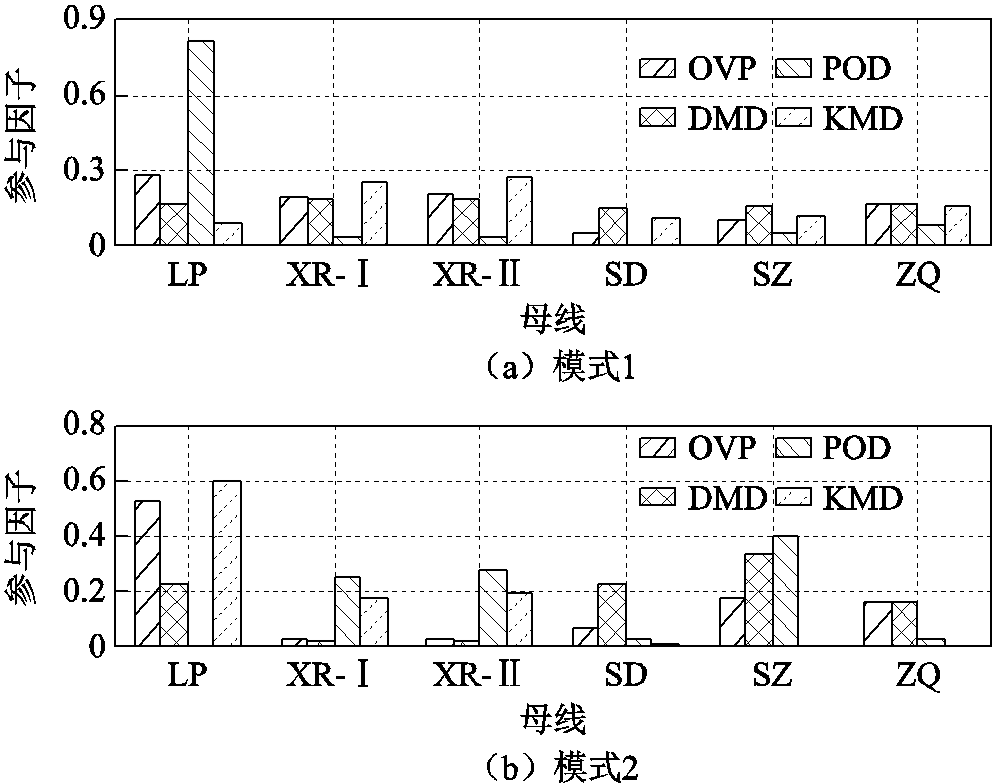
图18 参与因子辨识结果
Fig.18 Participation factors estimated from the field measurement frequencies
上述分析表明:所提OVP方法可从实际电力系统的广域量测信息中准确、有效地提取出系统主导振荡模式、模态及参与因子,实现电力系统动态稳定的综合评估,为电力系统动态稳定评估和控制提供了更为丰富的参考信息。
本文提出一种基于最优变量投影的电力系统主导振荡模式、模态与参与因子综合辨识方法,通过IEEE 68节点测试系统仿真数据和中国南方电网公司实测数据对所提方法进行分析、验证,相关结论如下:
1)所提最优变量投影方法无需建立电力系统的数学模型,仅通过广域量测信息即可实现电力系统主导振荡模式及模态的综合评估,相比传统特征值分析法所辨识出的结果更能反映电力系统实际的动态稳定性。
2)相比DMD、POD和KMD等辨识方法,所提方法在辨识电力系统低频振荡特征参数时具有更好的计算精度和抗噪能力,有利于定量综合评估电力系统的动态稳定,提高了电力系统低频振荡分析的准确性。
3)所提OVP可为电网调度运行人员的动态稳定实时监测与协调防御提供丰富的参考信息,在基于广域量测信息的电力系统动态稳定综合评估与预防控制中具有一定的应用前景。
参考文献
[1] 薛安成, 王嘉伟. 基于非光滑分岔的单机水电系统超低频频率振荡机理分析[J]. 电工技术学报, 2020, 35(7): 1489-1497.
Xue Ancheng, Wang Jiawei. Mechanism analysis of ultra-low frequency oscillation of single hydropower system based on non-smooth bifurcation[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1489-1497.
[2] 张民谣, 高云鹏, 吴聪, 等. 基于自适应变分模式分解的非稳态电压闪变包络参数检测[J]. 电工技术学报, 2021, 36(3): 599-608.
Zhang Minyao, Gao Yunpeng, Wu Cong, et al. Non-stationary voltage flicker envelope parameters detection based on adaptive variational mode decomposition[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 599-608.
[3] 刘一锋, 周小平, 洪乐荣, 等. 虚拟惯性控制的负荷变换器接入弱电网的序阻抗建模与稳定性分析[J]. 电工技术学报, 2021, 36(4): 843-856.
Liu Yifeng,Zhou Xiaoping,Hong Lerong,et al. Sequence impedance modeling and stability analysis of load converter with virtual inertia control connected to weak grid[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 843-856.
[4] 胡鹏, 艾欣, 肖仕武, 等. 静止无功发生器序阻抗建模及对次同步振荡影响因素的分析[J]. 电工技术学报, 2020, 35(17): 3703-3713.
Hu Peng, Ai Xin, Xiao Shiwu, et al. Sequence impedance of static var generator and analysis of influencing factors on subsynchronous oscillation[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3703-3713.
[5] 王迎晨, 杨少兵, 宋可荐, 等. 基于滑模结构无源控制的车网耦合系统低频振荡抑制方法[J]. 电工技术学报, 2020, 35(3): 553-563.
Wang Yingchen, Yang Shaobing, Song Kejian, et al. An approach based on SMS to suppress low-frequency oscillation in the EMUs and traction network coupling system using PBC[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 553-563.
[6] 崔屹峰, 李珍国, 贾清泉, 等. 基于参数辨识与状态估计的温控负荷响应能力动态评估[J]. 电力系统自动化, 2021, 45(1): 150-158.
Cui Yifeng, Li Zhenguo, Jia Qingquan, et al. Dynamic evaluation of response potential of thermostatically controlled load based on parameter identification and state estimation[J]. Automation of Electric Power Systems, 2021, 45(1): 150-158.
[7] Hauer J F, Demeure C J, Scharf L L. Initial results in Prony analysis of power system response signals[J]. IEEE Transactions on Power Systems, 1990, 5(1): 80-89.
[8] 孙英云, 游亚雄, 侯建兰, 等. 基于差分正交匹配追踪和Prony算法的低频振荡模态辨识[J]. 电力系统自动化, 2015, 39(10): 69-74, 167.
Sun Yingyun, You Yaxiong, Hou Jianlan, et al. Identification of low-frequency oscillation mode based on difference orthogonal matching pursuit and Prony algorithm[J]. Automation Electric Power Systems, 2015, 39(10): 69-74, 167.
[9] 苏安龙, 孙志鑫, 何晓洋, 等. 基于多元经验模式分解的电力系统低频振荡模式辨识[J]. 电力系统保护与控制, 2019, 47(22): 113-125.
Su Anlong, Sun Zhixin, He Xiaoyang, et al. Identification of low-frequency oscillation modes in power systems based on multiple empirical mode decomposition[J]. Power System Protection and Control, 2019, 47(22): 113-125.
[10] 李国庆, 王丹, 姜涛, 等. 基于递归连续小波变换的电力系统振荡模式辨识[J]. 电力自动化设备, 2016, 36(9): 8-16.
Li Guoqing, Wang Dan, Jiang Tao, et al. Power system oscillation mode identification based on recursive continuous wavelet transform[J]. Electric Power Automation Equipment, 2016, 36(9): 8-16.
[11] Liu Hesen, Zhu Lin, Pan Zhuohong, et al. ARMAX-based transfer function model identification using wide-area measurement for adaptive and coordinated damping control[J]. IEEE Transactions on Smart Grid, 2017, 8(3): 1105-1115.
[12] Jiang Tao, Li Xue, Yuan Haoyu, et al. Estimating electromechanical oscillation modes from synchrophasor measurements in bulk power grids using FSSI[J]. IET Generation, Transmission &Distribution, 2018, 12(10): 2347-2358.
[13] 张程, 金涛. 基于ISPM和SDM-Prony算法的电力系统低频振荡模式辨识[J]. 电网技术, 2016, 40(4): 1209-1216.
Zhang Cheng, Jin Tao. Identification of power system low frequency oscillations with ISPM and SDM-Prony[J]. Power System Technology, 2016, 40(4): 1209-1216.
[14] Li Xue, Cui Hantao, Jiang Tao, et al. Multichannel continuous wavelet transform approach to estimate electromechanical oscillation modes, mode shapes and coherent groups from synchrophasors in bulk power grid[J]. International Journal of Electrical Power & Energy Systems, 2018, 96: 222-237.
[15] Dosiek L, Pierre J W. Estimating electromechanical modes and mode shapes using the multichannel ARMAX model[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1950-1959.
[16] Yang Deyou, Cai Guowei, Chan K. Extracting inter-area oscillation modes using local measurements and data-driven stochastic subspace technique[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(5): 704-712.
[17] 谢剑, 王晓茹, 张鹏. 基于PRCE方法的低频振荡模式识别[J]. 中国电机工程学报, 2017, 37(11): 3129-3138.
Xie Jian, Wang Xiaoru, Zhang Peng. Identification of low-frequency oscillations based on PRCE algorithm[J]. Proceedings of the CSEE, 2017, 37(11): 3129-3138.
[18] Barocio E, Pal B C, Thornhill N F, et al. A dynamic mode decomposition framework for global power system oscillation analysis[J]. IEEE Transactions on Power Systems, 2015, 30(6): 2902-2912.
[19] Netto M, Susuko Y, Mili L. Date-driven participation factors for nonlinear systems based on Koopman mode decomposition[J]. IEEE Control Systems Letters, 2019, 3(1): 198-203.
[20] Golub G H, Pereyra V. Separable nonlinear least squares: the variable projection method and its applications[J]. Speech Communication, 2003, 45(1): 63-87.
[21] Borden A R, Lesieutre B C. Variable projection method for power system modal identification[J]. IEEE Transactions on Power Systems, 2014, 29(6): 2613-2620.
[22] Askham T, Kutz J N. Variable projection methods for an optimized dynamic mode decomposition[J]. SIAM Journal on Applied Dynamical Systems, 2018, 17(1): 380-416.
[23] Li Xue, Jiang Tao, Yuan Haoyu, et al. An eigensystem realization algorithm based data-driven approach for extracting electromechanical oscillation dynamic patterns from synchrophasor measurements in bulk power grids[J]. International Journal of Electrical Power & Energy Systems, 2020, 116: 105549.
[24] Rogers G. Power Systems Oscillations[M]. Norwell, MA: Kluwer, 2000.
[25] Jiang Tao, Yuan Haoyu, Li Guoqing, et al. Spatial-temporal decomposition approach for systematically tracking dominant modes, mode shapes and coherent groups in power systems[J]. IET Generation, Transmission & Distribution, 2017, 11(8): 1889-1900.
Estimating Dominant Oscillation Characteristics from Measurement Responses in Power Systems Utilizing Optimized Variable Projection
Abstract Estimating the accurate dynamic feature parameters of electromechanical oscillation, which include the dominant modes, mode shapes and participation factors, are very important for analyzing and damping the electromechanical oscillation in the bulk power grids. This paper develops a holistic assessment framework to estimate the dominant modes, mode shapes and participation factors from the synchrophasor measurements by using the optimized variable projection (OVP) in the power system. The synchrophasor measurements gathered from the PMUs is firstly preprocessed by finite difference method (FDM). Then, the preprocessed measurements are used to construct the low-order state matrix which contains the critical dynamic oscillation features of power systems. According to the constructed the low-order state matrix, the variable projection model is formulated, and the modes and mode shapes can be solved by optimized variable projection (OVP). For the estimated modes and mode shapes, cumulative energy weight of modes is developed to separate the dominant modes and their mode shapes of power systems from the estimated results. Further, the participation factors are estimated by using the separated dominant mode shapes. Finally, the proposed method is evaluated by the IEEE 68-bus test system as well as China Southern Power Grid. The results confirm that the proposed OVP based dynamic assessment approach performs great accuracy and effectiveness to estimate dominant modes and mode shapes from the synchrophasor measurements in bulk power grids.
Keywords:Synchrophasor measurements, optimized variable projection, dominant modes, dominant mode shapes, participation factors
DOI:10.19595/j.cnki.1000-6753.tces.201498
中图分类号:TM712
国家自然科学基金(51607034, 51877033, 52061635103)和国家重点研发计划(2016YFB0900903)资助项目。
收稿日期 2020-11-14
改稿日期 2021-03-02
李 雪 女,1986年生,博士,副教授,硕士生导师,研究方向为电力系统安全性与稳定性、电力系统高性能计算、电力市场。E-mail:xli@neepu.edu.cn
姜 涛 男,1983年生,博士,教授,博士生导师,研究方向为电力系统安全性和稳定性、可再生能源集成、综合能源系统。E-mail:t.jiang@aliyun. com(通信作者)
(编辑 赫蕾)