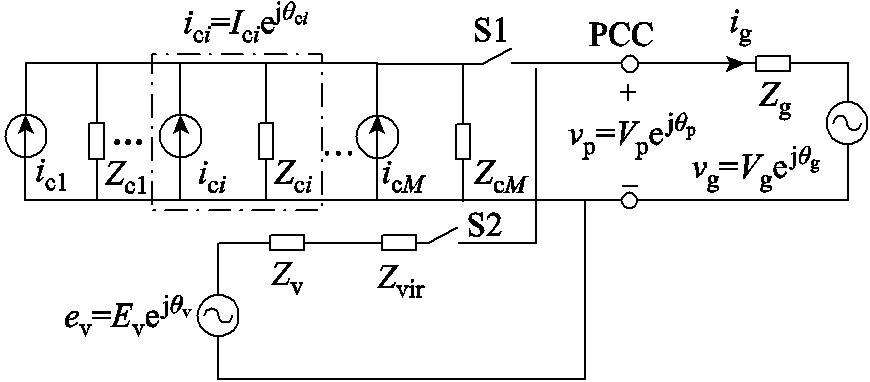
图1 HMG并网等效电路模型
Fig.1 Equivalent circuit of the grid-connected HMG
摘要 当多逆变器并联接入弱电网时,高电网阻抗与逆变器间的相互作用,易引发逆变器并网同步过程中的稳定性问题。针对弱电网下电流电压混合控制型微电网(HMG)逆变器的同步稳定性,通过建立准静态模型,分析锁相环(PLL)和虚拟同步机(VSG)在HMG系统中的同步机制,讨论PLL和VSG同步环间相互作用对电流(电压)控制型逆变器稳态工作点的影响,进而得到弱电网下HMG同步稳定性与电网阻抗、电网电压之间的关系。在此基础上,考虑弱电网下发生的电网电压跌落故障,对HMG同步稳定性与各逆变器稳态工作点、同步环参数之间的关系进行分析。实验结果验证了理论分析的正确性,为实际中HMG给定指令和同步参数的合理配置提供指导。
关键词:弱电网 混合控制型微电网 多逆变器 准静态模型 同步稳定性
微电网作为一种新的能源组织形式,既需要发挥资源整合优势与大电网友好互动,又需要促进新能源就地消纳向本地负荷独立供电[1-2]。逆变器作为微电网最后一级的能量变换接口,当其输入端连接光伏、风电等分布式发电单元时,常运行于电流控制模式[3];当其输入端连接储能单元时,常运行于电压控制模式为系统提供电压和频率支撑[4]。因此,多数微电网同时含有电压控制型逆变器(Voltage Controlled Inverters, VCIs)和电流控制型逆变器(Current Controlled Inverters, CCIs),这里称其为混合控制型微电网(Hybrid Microgrid, HMG)[5]。当HMG孤岛运行时,由VCI为系统提供电压和频率支撑;但当HMG并网时,通常由大电网为系统提供电压和频率支撑,CCIs和VCIs均采集公共耦合点(Point of Common Coupling, PCC)的电网同步信号,与电网进行功率交换[6-7]。因此,稳定的同步过程是HMG实现并网的第一步。
理想情况下,大电网能够为PCC提供足够的电压支持,各逆变器之间不存在耦合作用,多逆变器并联不影响各逆变器与电网的同步稳定运行[8]。但在传输线较长、变压器较多等弱电网环境下,电网的等效线路阻抗较大,各逆变器通过电网阻抗产生相互耦合,此时,逆变器与电网之间、逆变器与逆变器之间的相互作用易引发稳定性问题[3,6,8-10],包括小信号稳定性和同步稳定性问题。针对弱电网下多逆变器并网系统的稳定性,目前的研究多集中于分析小信号稳定性[9-10],而对因同步环稳态工作点设置不当或阻尼不足引发的同步稳定性问题尚未进行深入研究。不同于多CCI并网系统,HMG并网系统中VCI的输出阻抗较小,VCI与CCI并联运行时,HMG并网的等效输出阻抗也较小,基本不存在与弱电网产生相互作用引发的小信号稳定性问题[6]。此外,弱电网下高渗透率并网逆变器更易受电网故障影响而失去与电网的同步,引发同步稳定性中的暂态稳定性问题[11-13]。因此,随HMG系统应用的逐渐增多,对弱电网下HMG同步稳定性问题的研究显得尤为重要。
针对并网逆变器的同步稳定性,近期国内外学者在失同步机理、分析工具、改进方法等方面进行了相关研究[11,14]。文献[15]建立了基于PLL的CCI(PLL-based CCI, PLL-CCI)并网的准静态模型,分析了PLL-CCI与电网失同步的原因,并表明弱电网下PLL-CCI更易失去与电网的同步,进而失稳。进一步地,文献[16]通过相平面图研究了电网电压跌落故障下PLL-CCI的暂态稳定性,并提出了一种可实现一阶和二阶PLL灵活切换的自适应PLL方法来提高暂态稳定性。文献[17-18]研究发现,对一阶同步控制系统来说,只要稳态工作点存在,当发生电网故障或故障清除后,逆变器会通过自身的同步调节回到新的平衡点;而对于二阶同步控制系统来说,即使稳态工作点存在,逆变器也可能因自身同步动态无法达到新的平衡点,从而失去与电网的同步。文献[19]通过Lyapunov能量函数法研究了虚拟同步机(Virtual Synchronous Generator, VSG)的同步稳定性,并提出了通过调节给定参考功率来提高暂态稳定性的方法。
由此可见,对弱电网下单逆变器并网同步机制和同步稳定性的研究,目前已取得了一定的成果。相比之下,对弱电网下多逆变器并网系统,尤其是具备电压支撑能力的混合控制型微电网并网系统的同步机制及同步稳定性尚未进行深入研究。本文以多台PLL-CCI与单台基于VSG的VCI(VSG-based VCI, VSG-VCI)并联的HMG并网系统为研究对象,建立HMG系统中各同步环的准静态模型,并以此为基础,研究弱电网下HMG系统的同步稳定性与各逆变器稳态工作点以及同步环控制参数之间的关系。最后,搭建半实物实验平台进行理论验证。
HMG并网系统等效电路模型如图1所示,系统选用M台PLL-CCI和1台VSG-VCI并联的微电网结构。图1中,CCI等效为电流源ici并联其输出阻抗Zci,VCI等效为电压源ev串联其输出阻抗Zv和虚拟感抗Zvir=jωLvir(Lvir为虚拟电感),电网等效为电压源vg串联其线路阻抗Zg=Rg+jXg(Rg为线路电阻,Xg为线路感抗,且Xg=ωLg,Lg为线路电感)。

图1 HMG并网等效电路模型
Fig.1 Equivalent circuit of the grid-connected HMG
图1中,ici=Iciejθci,Ici为CCI的有功电流给定值,θci为PLL的锁相相位,下标“i”代表第i台CCI,i=1,…, M;ev=Evejθv,Ev为VSG无功环输出的电压幅值,θv为有功环输出的同步相位;vg=Vgejθg,Vg、θg分别为电网电压幅值和相位。PLL和VSG均采集PCC电压vp进行同步,vp=Vpe jθp,Vp、θp分别为PCC电压幅值和相位。S1和S2为并网控制开关,下面将分别研究仅S1闭合、仅S2闭合、S1和S2同时闭合这三种情况下PLL和VSG的同步机制。
当只有开关S1闭合时,HMG并网系统为多CCI并网系统。此时,PCC处的电压表达式为
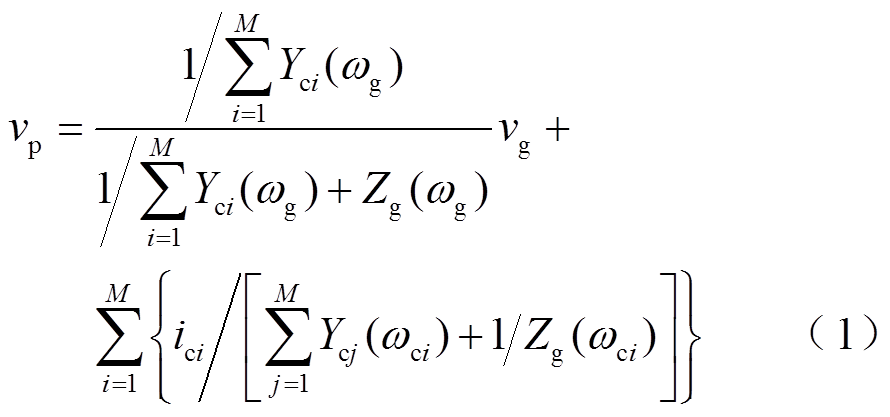
式中,Yci为第i台CCI的等效输出导纳,Yci=1/Zci;ωci为第i台CCI同步环输出角频率;ωg为电网角频率。稳态下满足ωci=ωg。定义式中的相关阻抗系数为
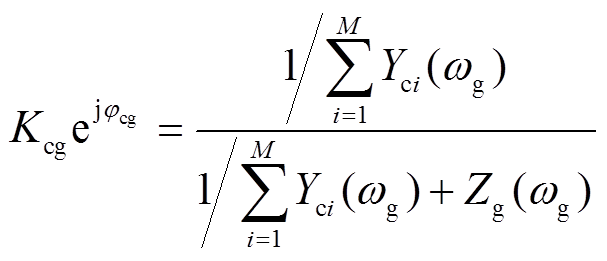 (2)
(2)
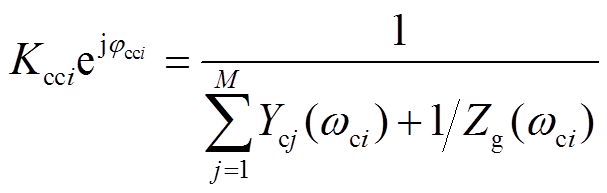 (3)
(3)则PCC电压可表示为
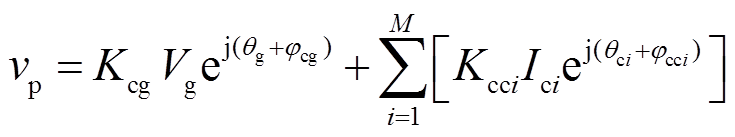 (4)
(4)
由式(4)可得,PLL的锁相电压vp除了受电网电压影响外,还受电网阻抗、各逆变器并网电流及其输出阻抗的影响。理想电网下(Zg=0),式(4)中系数Kcgejjcg=1且Kcci=0,此时,PLL的锁相电压vp=Vgejθg=vg,各CCI之间不存在耦合。实际电网中Zg≠0,各逆变器通过Zg产生耦合。
以第i台CCI为例,其锁相原理如图2所示。图中, 为给定角频率,并网时
为给定角频率,并网时 =ωg;Kp、Ki分别为PLL控制器的比例、积分系数;θci为PLL的锁相角。此外,vcq为由式(4)所示的PCC电压经Park变换后得到的q轴电压,Park变换的角度来自于PLL的输出θci。可见,其他M-1台CCI并网电流的大小和相位信息通过vp影响第i台CCI的锁相。
=ωg;Kp、Ki分别为PLL控制器的比例、积分系数;θci为PLL的锁相角。此外,vcq为由式(4)所示的PCC电压经Park变换后得到的q轴电压,Park变换的角度来自于PLL的输出θci。可见,其他M-1台CCI并网电流的大小和相位信息通过vp影响第i台CCI的锁相。
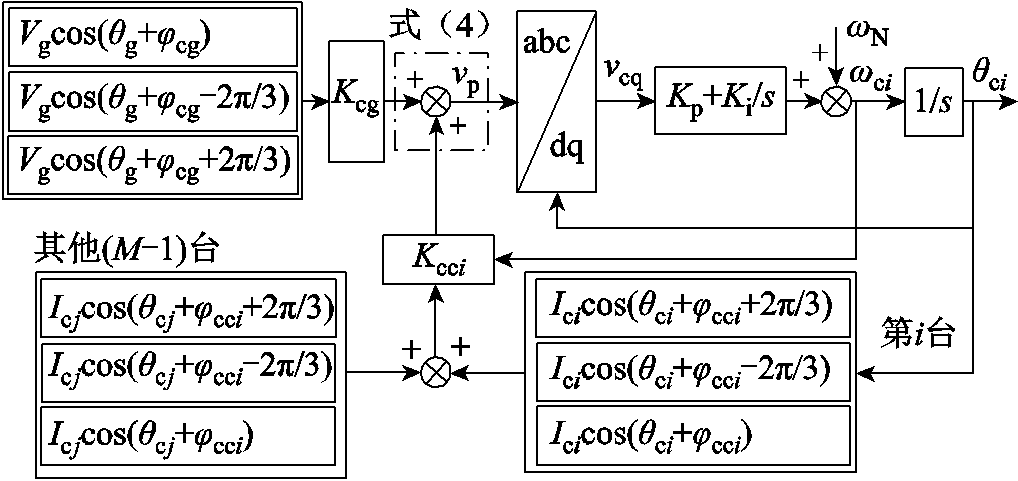
图2 多CCI并网系统中第i台CCI的PLL锁相示意图
Fig.2 Phase-locked mechanism of the PLL of the ith CCI in multi-CCI systems
根据Park变换公式,可得vcq为
 (5)
(5)基于式(5)和图2,可得图3所示的PLL准静态模型,可见PLL通过PI控制器(统称为同步器)调节其输出相位θci,使得误差信号Δ满足Δ=vcq=0。理想电网下,因Kcci=0,vcqi和vcqj所在的环路不存在,即各逆变器的运行电流不会影响PLL的同步过程。实际电网中,电网阻抗的存在不仅引入了第i台CCI的一阶自同步环路vcqi,还引入了并联CCI影响的二阶互同步环路vcqj(j=1,…,M,且j≠i)。若vcqj=0,即只有单台CCI并网时,根据文献[15],要保证PLL同步环存在稳态工作点,那么Ici取值存在上限。当CCI并联运行时,若保证系统平衡点存在,二阶同步环路vcqj将和vcqg共同限制Ici的取值。
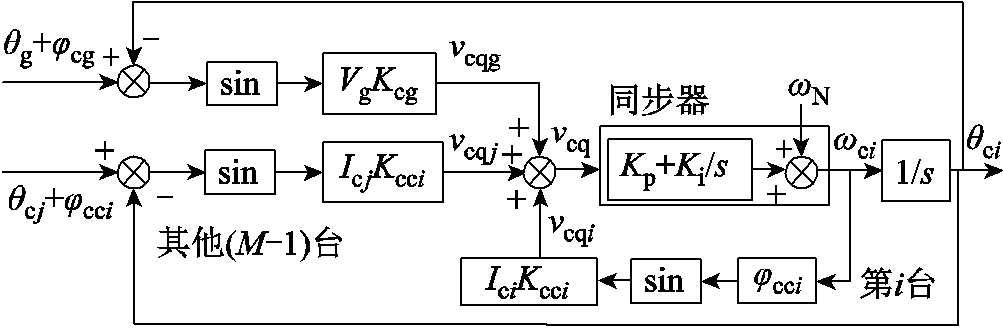
图3 多CCI并网系统中第i台CCI的PLL准静态模型
Fig.3 Quasi-static PLL model of the ith CCI in multi-CCI systems
当只有开关S2闭合时,HMG并网系统为单VCI并网系统。此时,PCC电压为
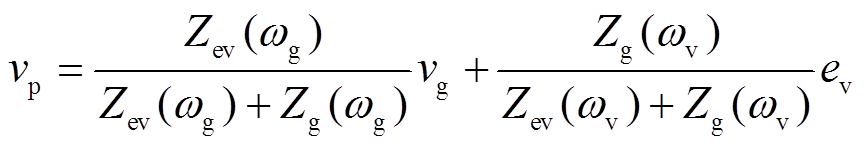 (6)
(6)式中,Zev为VSG-VCI总的等效输出阻抗,Zev=Zv+Zvir;ωv为VSG的输出角频率,稳态下满足ωv=ωg。定义式中的相关阻抗系数为
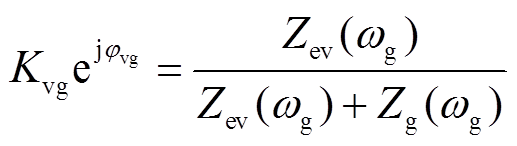 (7)
(7)
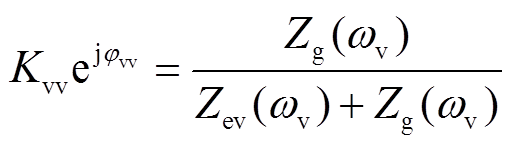 (8)
(8)则PCC电压可表示为
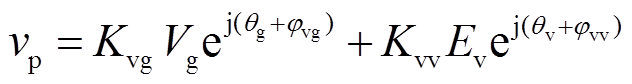 (9)
(9)
假设VSG反电动势ev与PCC电压vp之间的相位差为δv,因虚拟阻抗Zvir为纯感性,所以PCC有功和无功功率分别为
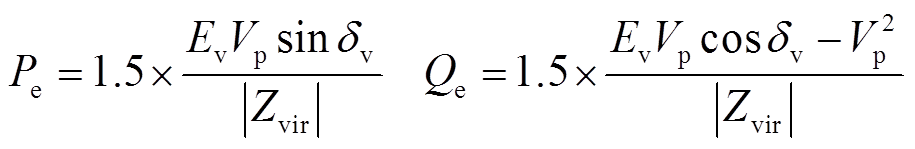 (10)
(10)可见,在有功和无功近似解耦的情况下,VSG的有功输出Pe与δv呈正相关,无功输出Qe与Ev呈正相关,即VSG-VCI通过有功控制与电网实现同步,因此无功环路的影响可被近似忽略,认为Ev≈Vg。类比PLL,根据PCC电压表达式(9),VSG的同步原理示意图如图4所示。图中,J为虚拟惯量,Dp为有功阻尼系数,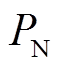 为有功功率给定,
为有功功率给定,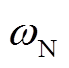 为给定角频率,并网时
为给定角频率,并网时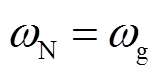 ,θv为VSG的同步输出角度。此外,vvq为由式(9)所示的PCC电压经Park变换后得到的q轴电压,Park变换的角度来自于VSG的输出θv。可见,θv同步信号vp同时受电网电压和其阻抗、逆变器自身并网电压及其等效总输出阻抗的影响;θv的同步过程受VSG有功环控制参数(统称为同步器)影响。
,θv为VSG的同步输出角度。此外,vvq为由式(9)所示的PCC电压经Park变换后得到的q轴电压,Park变换的角度来自于VSG的输出θv。可见,θv同步信号vp同时受电网电压和其阻抗、逆变器自身并网电压及其等效总输出阻抗的影响;θv的同步过程受VSG有功环控制参数(统称为同步器)影响。
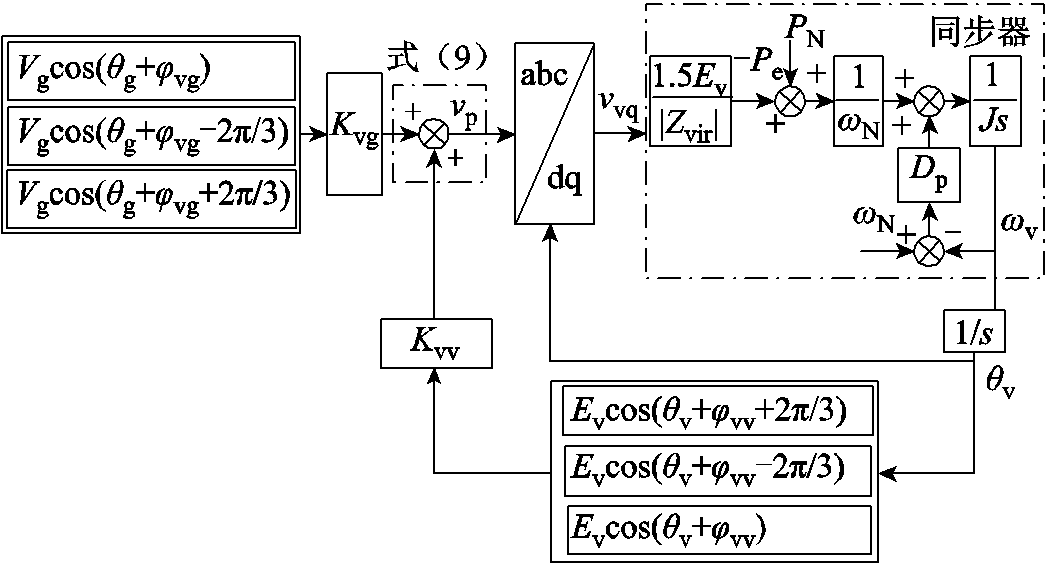
图4 单VCI并网系统中VSG同步原理示意图
Fig.4 Synchronization mechanism of the VSG in single VCI system
同理,可进一步得到图5所示的VSG有功同步环准静态模型,与PLL同步使Δ=vcq=0机制不同的是,VSG通过调节θv使得其误差信号Δ=PN-Pe=0,从而实现与电网同步进行功率传输的目的。此外,VSG同步环包含二阶电网同步环路vvqg和与VSG输出电压相关的一阶自同步环路vvqv,在它们的共同作用下,VSG完成同步。
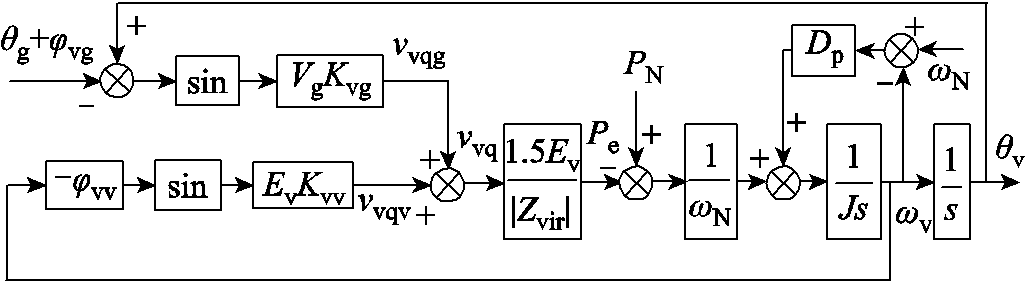
图5 单VCI并网系统中VSG的准静态模型
Fig.5 Quasi-static VSG model of single VCI system
当开关S1和S2同时闭合时,该系统为本文所研究的HMG并网系统。此时,PCC的电压为
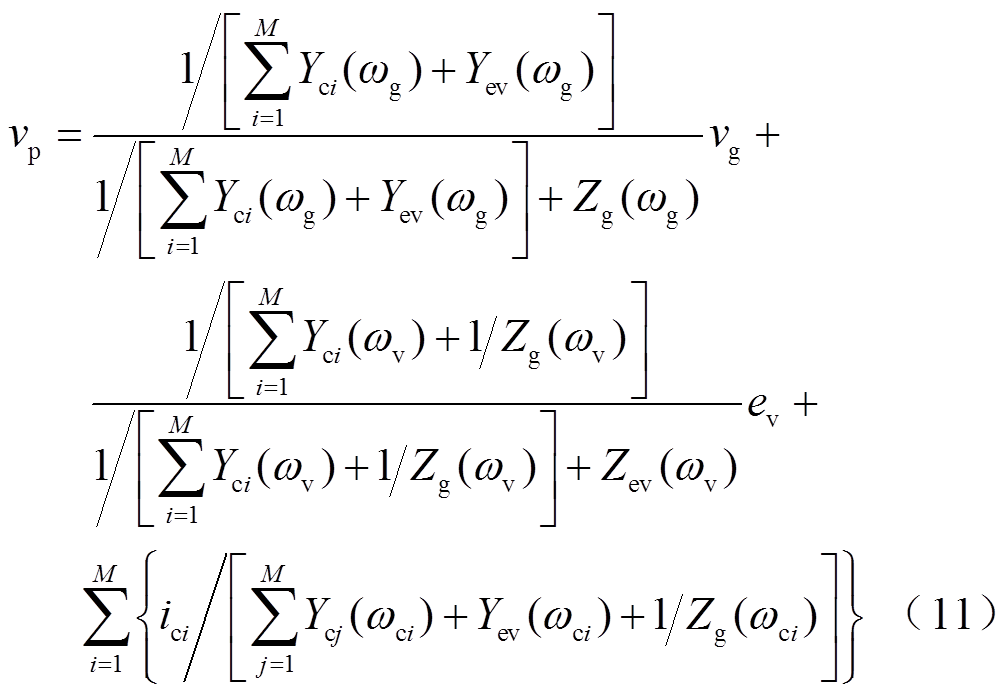
式中,Yev为VCI总的等效输出导纳,Yev=1/Zev。定义式中的相关阻抗系数为
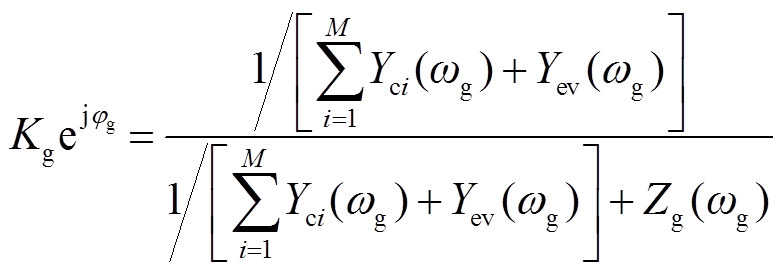 (12)
(12)
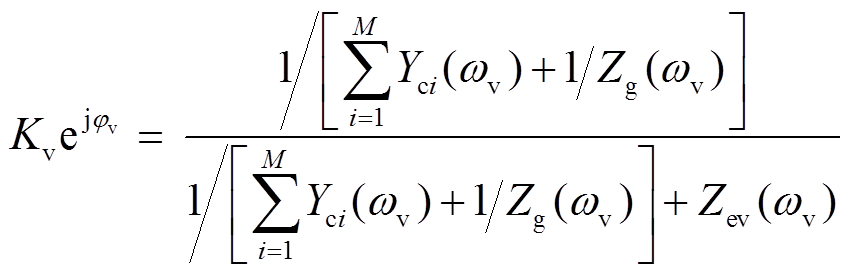 (13)
(13)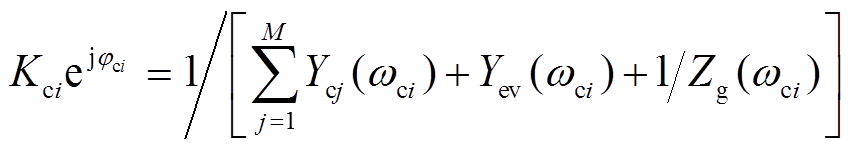 (14)
(14)
则PCC电压可表示为
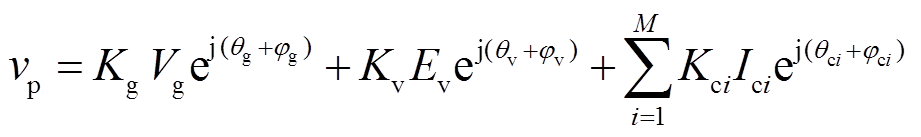 (15)
(15)由此可见,在HMG并网系统中,PCC电压vp同时受电网电压及其阻抗、每台CCI并网电流及其等效输出阻抗和VCI输出电压及其总等效输出阻抗的影响。根据1.1节和1.2节对PLL和VSG同步机制的认识,各逆变器通过PCC点产生耦合,该耦合作用使得各同步器的同步信号变得更加复杂,其必将对各逆变器的同步稳定性产生影响。
图6所示为HMG并网同步原理示意图,相应的准静态模型如图7所示,相比于图3,并联的VCI引入了额外的控制环路vvq;相比于图5,并联的M台CCI引入了M条额外的控制环路vcqi(i=1,…,M)。同样,PLL通过调节其锁相相位θci使q轴电压vq=0,VSG通过调节其同步相位θv使PN-1.5Evvq/ (ωNLvir)=0,从而各自实现与电网的同步。
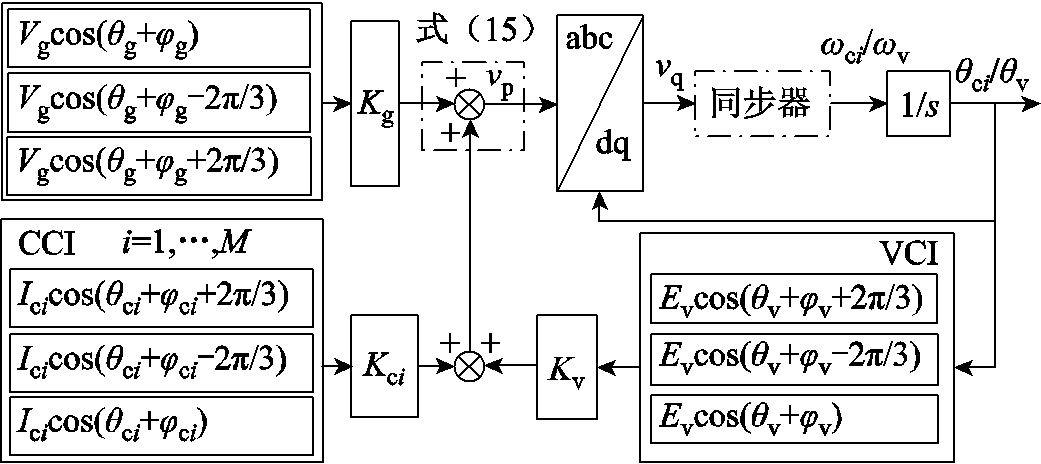
图6 HMG并网同步原理示意图
Fig.6 Synchronization mechanism of the HMG system
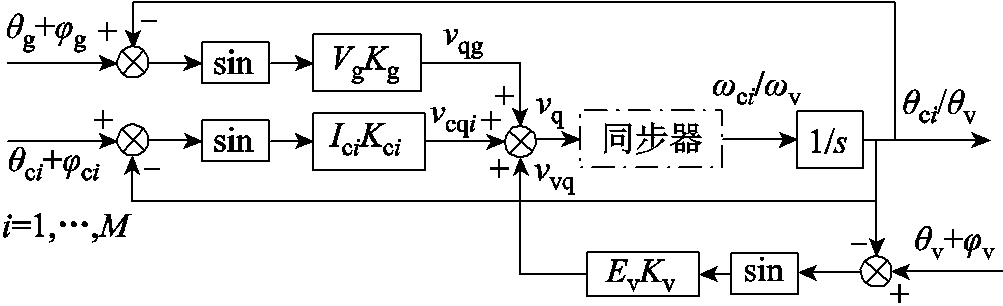
图7 HMG并网同步的准静态模型
Fig.7 Quasi-static synchronization model of the HMG
通过上述分析,在HMG系统中,同步环PLL和VSG间通过PCC电压vp产生耦合。如图7所示,该耦合导致各同步环中同步器的反馈信号vq同时受电网电压及其阻抗(Vg,θg,Zg)、CCI稳态工作点(Ici,θci,Zci)和VCI稳态工作点(Ev,θv,Zev)的影响,并作用于同步过程。接下来将通过对各逆变器稳态工作点的分析,得到HMG同步稳定性与各逆变器电流或功率给定值、电网阻抗、电网电压之间的关系。
本文所研究的HMG并网系统中,CCI无功电流给定为0,VCI的无功功率给定为0,以保证HMG并网的功率因数。HMG并网运行时,PLL-CCI通过控制PCC的并网电流跟随有功给定电流Ici、VSG-VCI通过控制PCC的电压间接控制其并网功率跟随给定功率PN,以此来进行功率传输。当满足内环对外环无误差跟随的条件时,稳态下,各逆变器的运行频率与电网频率相同,即ωci=ωN=ωg,ωv=ωN=ωg。在内环无误差的控制下,CCI的输出阻抗在ωg处幅值近似无穷大,从而保证工频输出电流尽可能流向电网;VCI的输出阻抗在ωg处幅值近似为0,以避免产生工频压降,即Zci(ωci)≈Zci(ωg)≈∞;Zv(ωv)≈Zv(ωg)≈0。
此外,为利用VSG的惯性和阻尼作用,避免逆变器内环控制动态、线路动态等带来的不利影响,通常VSG有功环带宽(几赫兹[20])远小于PLL的控制带宽(几十~百赫兹[12]);再者,逆变器的内环设计严格跟随外环给定,即内环控制带宽远高于外环PLL控制或VSG控制,其控制动态不会影响外环的同步效果。基于此,可作以下合理假设:①PLL控制和VSG控制之间是解耦的;②逆变器内部电压电流控制与外部PLL或VSG控制之间是解耦的。
接下来将分别分析不同开关状态下同步稳定性对Ici和PN取值的限制,即稳态工作点分析。
当只有开关S1闭合时,稳态下计算可得
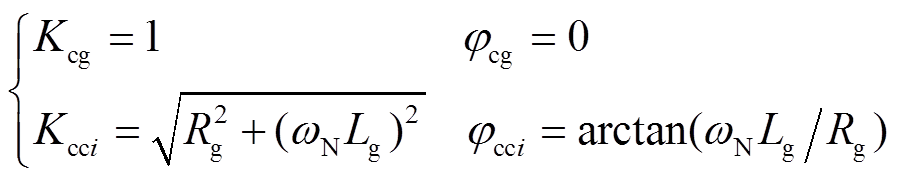 (16)
(16)将式(16)中的参数代入图3所示的准静态模型中,可得
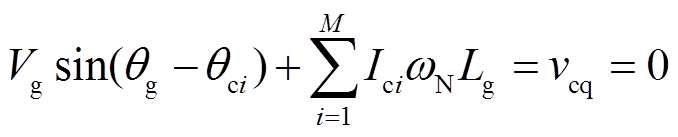 (17)
(17)
考虑到sin(θg-θci)的取值范围是[-1,1],为保证式(17)的平衡点存在,多CCI并网系统总的并网电流给定值需满足
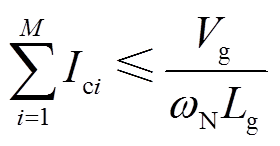 (18)
(18)可见,多CCI并联的总并网电流与单CCI并网电流的上限取值相同[15],其与电网电阻的大小无关,但会随电网电感增大、电网电压幅值跌落和电网频率抬升而减小。因此,弱电网和多CCI并联将降低单台CCI并网的最大运行电流。
当只有开关S2闭合时,稳态下计算可得
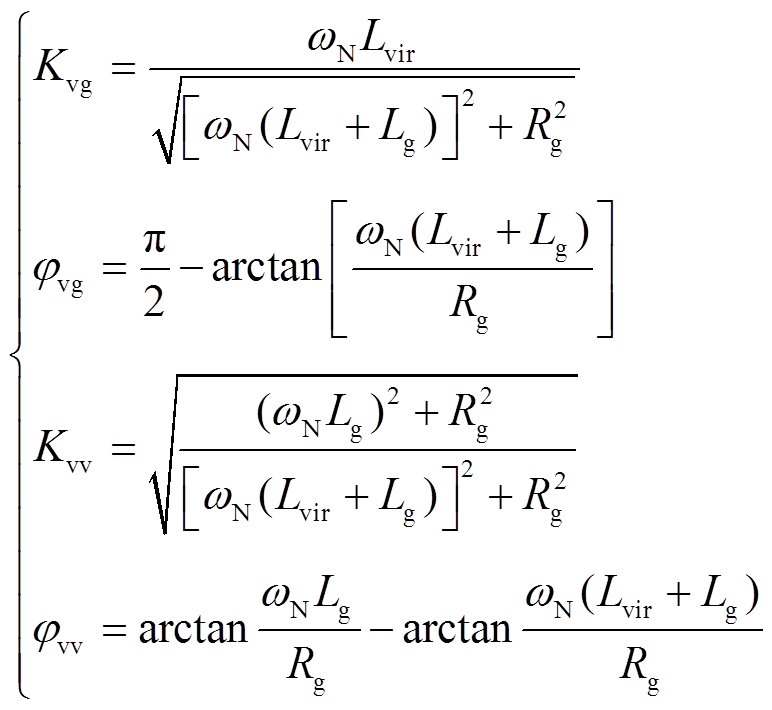 (19)
(19)将式(19)中的参数代入图5所示的准静态模型中,可得
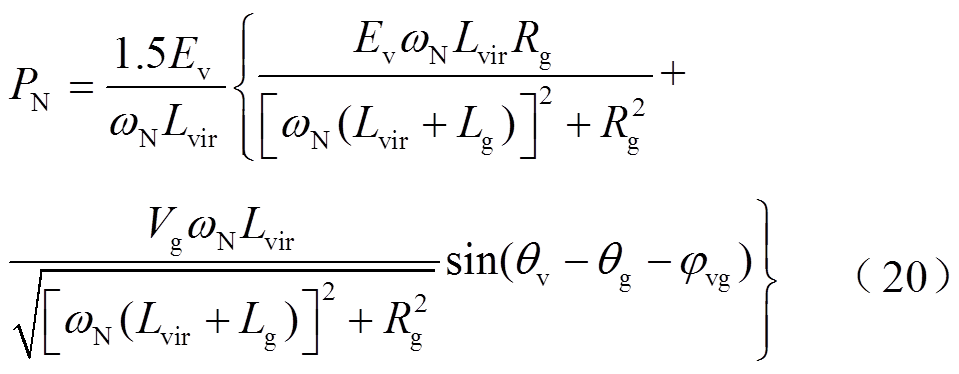
因sin(θv-θg-jvg)的取值范围为[-1,1],同样,要保证式(20)存在平衡点,要求VCI并网功率的给定值满足
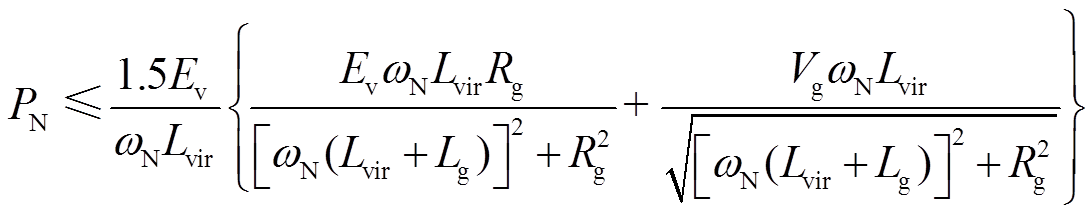 (21)
(21)由式(21)可得,对VCI来说,其并网功率的最大值既与电网电感有关,也与电网电阻有关。在以感性为主的弱电网环境下,即Rg≈0时,式(21)可表示为
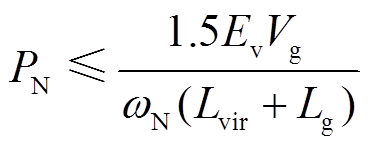 (22)
(22)
由式(22)可知,VSG-VCI的最大运行功率随虚拟电感增大、电网电感增大、电网电压幅值跌落和电网频率抬升而减小。这也意味着弱电网下,VSG-VCI的功率传输能力会受限。
为了进一步说明电网电阻的影响,基于式(21)和式(22),定义比值为
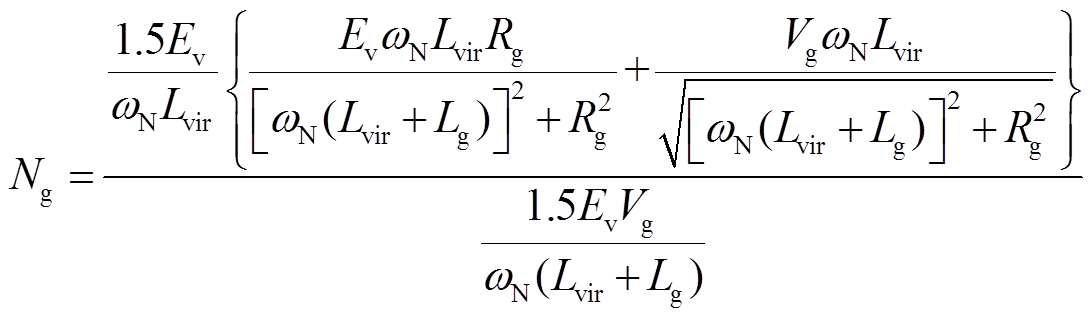 (23)
(23)当Ev=Vg=155V,ωN=314rad/s,Lvir=4mH时,可得Ng随Lg和Rg变化的曲线如图8所示。可以发现,适当的电网线路电阻有助于增大VSG的最大传输功率,但增大的程度有限,且存在最优电阻;若电网阻感比过大,可能会削弱VSG-VCI的最大功率传输能力。
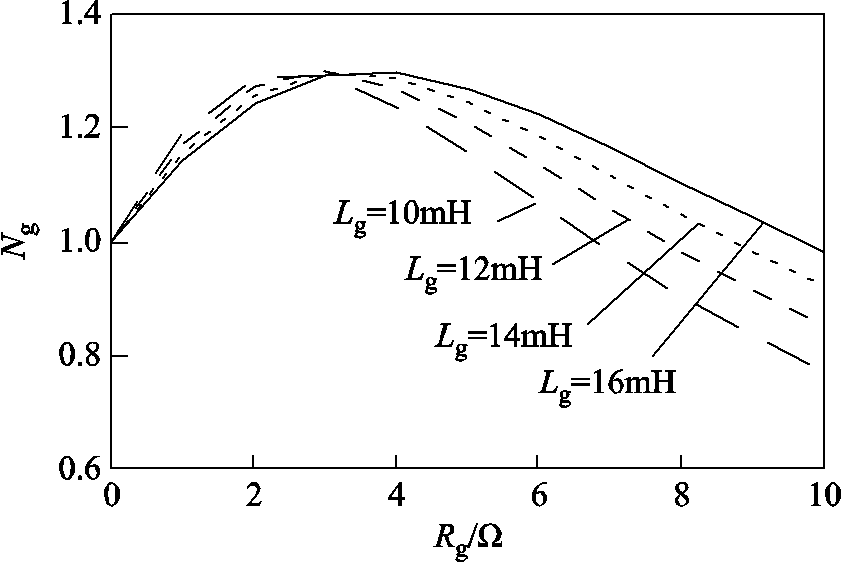
图8 Ng与电网阻抗之间的关系
Fig.8 Relationship of Ng with Zg
当开关S1和S2同时闭合时,稳态下,计算可得式(12)~式(14)中相关系数为
 (24)
(24)进而由式(24)推得
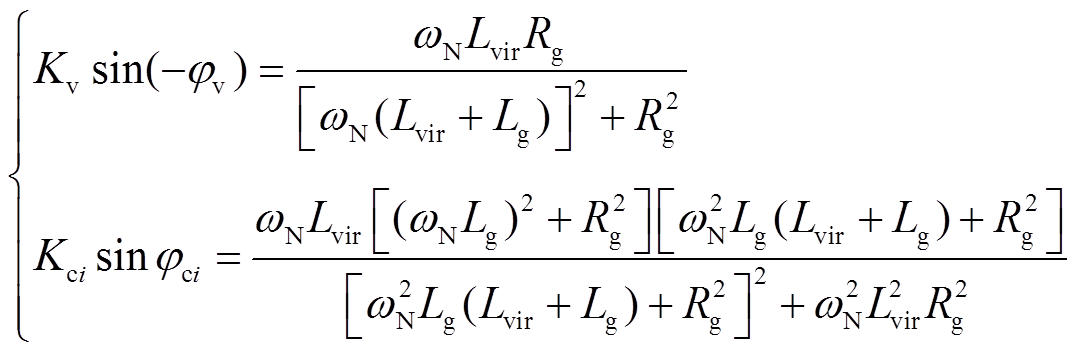 (25)
(25)
根据假设①,θv在PLL的同步过程中可近似视为恒定,此时,由图7可推导得到PLL-CCI并网电流满足
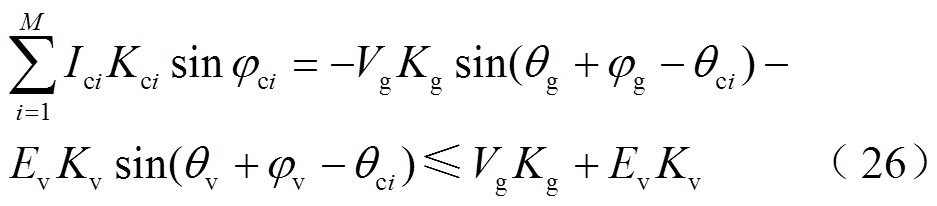
因此,HMG系统中,M台CCI总的并网电流取值变为
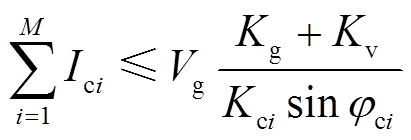 (27)
(27)
然而,对VSG-VCI来说,由于VSG的调节速度远小于PLL,所以PLL的输出相位θci不利于VSG达到其功率给定值,即图7中vcqi的引入使VSG同步必须满足PLL相位变化所带来的最差影响,这使VSG-VCI的有功给定最大值被限制为
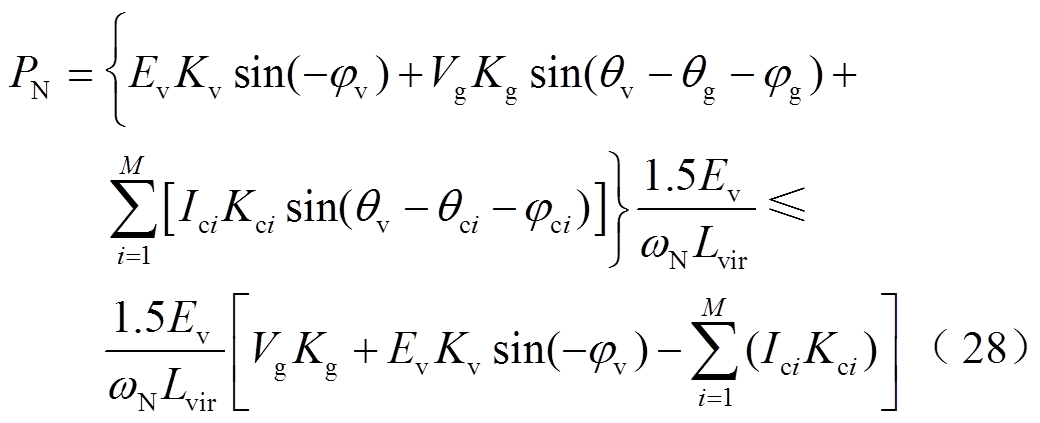
在以感性为主的弱电网环境下,即Rg≈0时,式(27)和式(28)可表示为
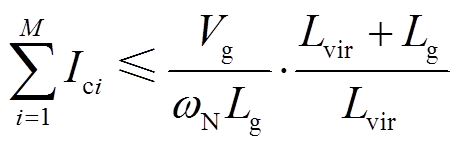 (29)
(29)
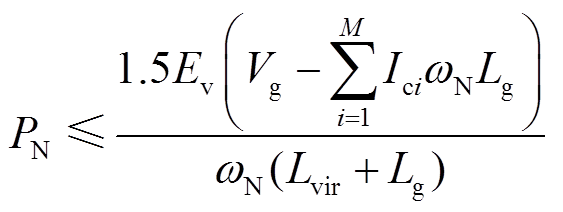 (30)
(30)对比式(18)和式(29)可以发现,并联VSG-VCI大大提高了弱电网下PLL-CCI的最大并网电流;而对比式(22)和式(30)可见,并联PLL-CCI减小了VSG-VCI的最大传输功率,且随着PLL-CCI并网电流Ici增大、电网电感增大,PLL-CCI对VSG-VCI功率传输能力的削弱加强。此外,当PLL-CCI总的并网电流大于Vg/(ωNLg)时,由式(30)计算可得PN最大值小于0。因此,在HMG系统中需合理设置各逆变器给定,以保证稳态工作点可达。
考虑电网电阻Rg,定义比值为
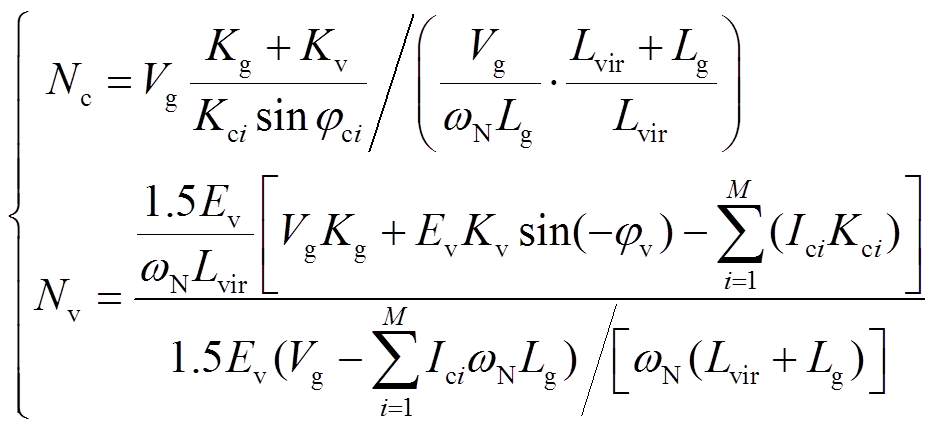 (31)
(31)图9给出了不同电网阻抗下Nc和Nv的值,可见:Rg的加入使得PLL-CCI的电流传输能力下降,但随着Lg增大,Rg对PLL-CCI电流传输能力的影响越小;而适当的Rg有助于增大VSG-VCI的最大传输功率,但是增大的程度有限,且存在最优电阻,这与单VSG并网情况相同。
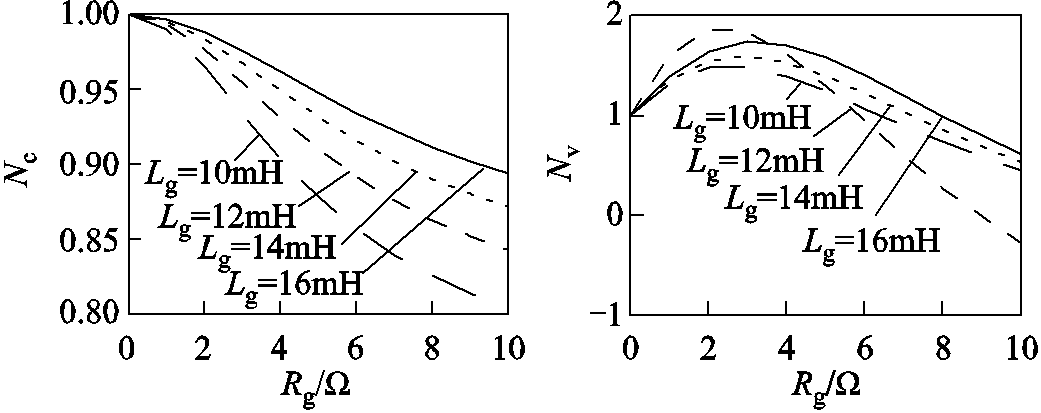
图9 Nc和Nv分别与电网阻抗之间的关系
Fig.9 Relationship of Nc and Nv with Zg
以上对稳态工作点的定量分析表明:①无论CCI和VCI以何种方式并入电网,CCI所能传输的最大并网电流及VCI所能传输的最大并网功率均会因电网电感增大、电网电压跌落和电网频率升高而下降;②在HMG并网系统中,VCI的并联接入极大地提高了CCI的最大并网电流(见式(29))。而VCI的最大并网功率却因并联CCI并网电流的增大而产生明显下降(见式(30)),但适当的电网电阻有助于提高VCI的最大并网功率(见图9)。
若CCI的给定电流和VCI的给定功率超过了本节计算得到的取值上限,那么相应的PLL和VSG将会因失去平衡点而产生同步稳定性问题。根据图7,各逆变器的同步稳定性还关系到同步器参数的选取。因此,接下来将针对弱电网下发生的电压跌落故障,通过定性分析同步器的动态调节过程,研究各同步器控制参数对同步稳定性的影响。
针对电网电压跌落故障,图10画出了相应的电压-相位差曲线[16-17],以分析二阶PLL和VSG同步器的调节过程。图10中,F(Vg)代表与电网电压相关的比例函数,对PLL来说F(Vg)=KgVg,对VSG来说F(Vg)=1.5EvVgKg/|Zvir|;δ代表相位差δc=θc-θg或δv=θv-θg,F0代表由逆变器给定信号决定的稳态工作点。曲线Ⅰ代表故障前逆变器的运行曲线,曲线Ⅱ、Ⅲ和Ⅳ为电网电压发生不同程度跌落时逆变器的运行曲线。这里假设PLL-CCI的给定电流和VSG-VCI的给定功率不随电网环境变化,即F0保持不变。如图10所示,故障前,逆变器稳定运行在a点,满足F(Vg)sinδ0=F0。电网电压跌落可分三种情况讨论。
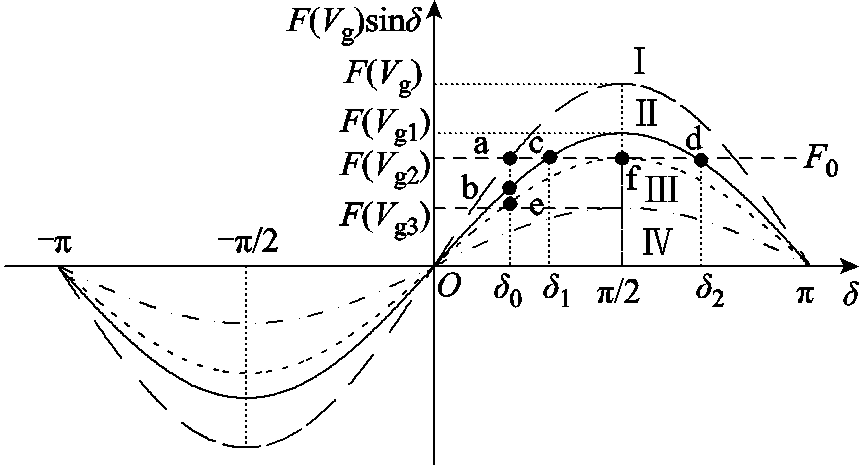
图10 电网电压跌落时PLL或VSG电压-相位差曲线
Fig.10 F(Vg)–δ curves of the PLL or VSG when the grid voltage sags
1)曲线Ⅱ:两个平衡点
如曲线Ⅱ所示,当电网电压幅值由Vg跌落到Vg1时,因F(Vg1)>F0,系统有两个平衡点c和d,其中c点为稳定运行点,d点为不稳定运行点。在电网电压跌落的瞬间,系统运行点由a点变为b点,因b点所代表的F(Vg1)sinδ0<F0(即误差信号Δ>0),所以同步环路的输出角频率ω(ω代表ωc或ωv)增大,δ增大,b点往c点方向移动,当到达稳态点c时,因ω>ωN,δ继续增大,而过了c点,因F(Vg1)sinδ>F0(即Δ<0),ω开始减小。最后,可能存在两种情况:
(1)在到达不稳定平衡点d之前,ω下降到ωN。因在c点和d点之间,F(Vg1)sinδ>F0(即Δ<0),ω减小到ωN后继续减小,使得δ往减小的方向移动,如此往复几个周期后,逆变器最终稳定运行在c点,满足F(Vg1)sinδ1=F0且ω=ωN。
(2)在到达不稳定平衡点d时,ω仍大于ωN。δ越过d点继续增大,一旦过了d点,F(Vg1)sinδ<F0(即Δ>0),ω又开始增大,δ继续增大,最终逆变器失去与电网的同步,无法稳定运行。
2)曲线Ⅲ:一个平衡点
曲线Ⅲ为只有一个平衡点f的情况,即F(Vg2)=F0。这也是曲线Ⅱ的一个特例(c点和d点合并为f点),若系统能稳定运行,在第一次到达稳态点f时,必须满足ω=ωN,而这个条件是不可能实现的。因为在故障点e处,ω=ωN,F(Vg2)sinδ0<F0(即Δ>0),所以ω开始增大,δ增大,e点向f点移动,当到达稳态点f时,F(Vg2)=F0,但因ω>ωN,δ继续增大,而过了点f,因F(Vg2)sinδ0<F0(即Δ>0),ω继续增大,也就是说ω会一直增大,因此逆变器并网失同步。
3)曲线Ⅳ:无平衡点
曲线Ⅳ代表的情况是无平衡点的情况,此时,系统始终无法达到给定信号,逆变器无法稳定运行。
由此可见,暂态过程的同步稳定性不仅与逆变器给定信号F0、电网电压F(Vg)有关;还取决于其同步器参数,且F(Vg)离F0越近,越易因同步器的二阶调节过程产生同步稳定性问题[19]。前者可参考第2节的稳态分析;后者对应暂态稳定性分析。接下来将通过相平面图,对电网电压跌落时暂态同步稳定性与PLL、VSG控制环参数之间的关系进行定性分析,具体对逆变器独立并入纯感性弱电网的情况进行分析。
对PLL-CCI独立并网系统来说,由图3可得
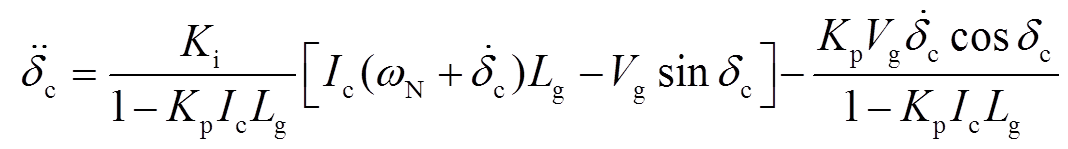 (32)
(32)式中,δc为PLL同步相位与PCC电压相位之差,δc=θc-θp。
由式(32)可见,PLL控制环路是一个二阶系统,其阻尼比可表示为[16]
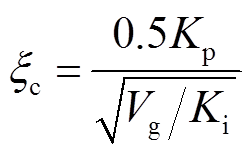 (33)
(33)以Lg=10mH,Ic=27A,电网电压跌落到0.6Vg(即Vg1=0.6Vg)为例分析暂态同步稳定性。其中Vg=155V,此时F0=IcXg=0.547Vg<F(Vg1)=Vg1,即系统有两个平衡点。根据式(32),图11给出了不同控制参数下PLL的相平面图。由图11可见,曲线Ⅰ、Ⅳ和曲线V代表的系统不能稳定运行,曲线Ⅱ和曲线Ⅲ代表的系统可以稳定运行。对比曲线Ⅰ、曲线Ⅱ和曲线V可得,减小Ki有助于提高系统的稳定性;对比曲线Ⅰ、曲线Ⅲ和曲线Ⅳ可得,增大Kp有助于提高系统的稳定性。而减小Ki、增大Kp都可增大系统的阻尼比ξc,这说明提高二阶PLL的阻尼比有助于暂态稳定性的改善。
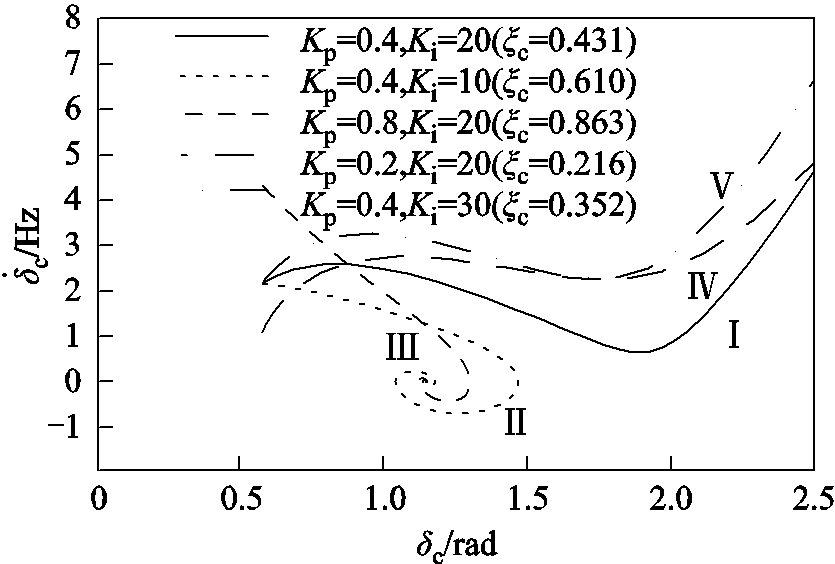
图11 电网电压从Vg跌落到0.6Vg时PLL的相平面图
Fig.11 Phase portraits of the PLL when the grid voltage drops from Vg to 0.6Vg
对VSG-VCI独立并网系统来说,由图5得
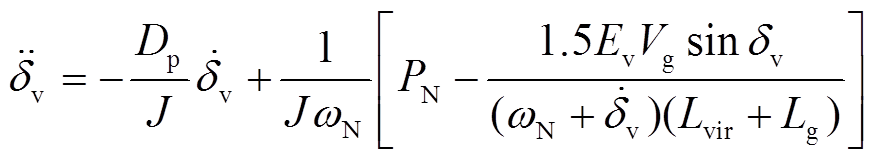 (34)
(34)式中,δv为VSG同步相位与PCC电压相位之差,δv=θv-θp。
可见VSG同样为二阶系统,其阻尼比为[18]
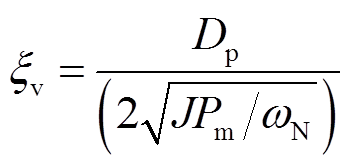 (35)
(35)式中,Pm=1.5EvVg/[ωN(Lvir+Lg)]。
以Lg=10mH,Lvir=4mH,PN=4850W,电网电压跌落到0.6Vg(即Vg1=0.6Vg)为例进行暂态同步稳定性分析。其中Vg=155V,此时F(Vg1)=Pm1=4 916W>F0=PN,即系统有两个平衡点。根据式(34),图12给出了不同控制参数下VSG的相平面图。
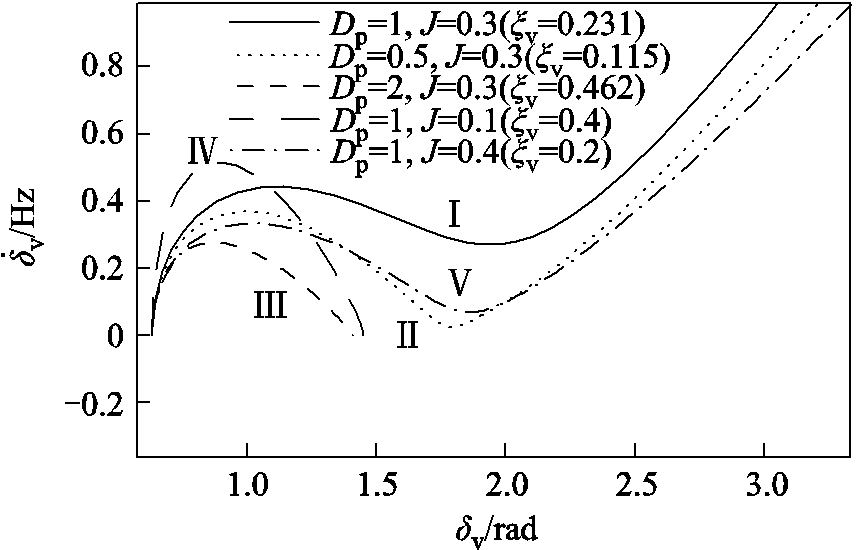
图12 电网电压从Vg跌落到0.6Vg时VSG的相平面图
Fig.12 Phase portraits of the VSG when the grid voltage drops from Vg to 0.6Vg
由图12可见,曲线Ⅰ、曲线Ⅱ和曲线Ⅴ代表的系统不可稳定运行,曲线Ⅲ和曲线Ⅳ代表的系统可稳定运行。对比曲线Ⅰ、曲线Ⅱ和曲线Ⅲ可得,增大Dp有助于提高系统的稳定性;对比曲线Ⅰ、曲线Ⅳ和曲线Ⅴ可得,减小J有助于提高系统的稳定性。而减小J、增大Dp都可增大系统的阻尼比ξv,同样地,这说明提高二阶VSG的阻尼比有助于其暂态稳定性的改善。
对于HMG并网系统来说,基于假设①,HMG同步的暂态过程取决于VSG的参数设计。当发生电网故障时,在VSG-VCI的支撑作用下,由式(29)可得PLL-CCI最大运行电流变大(即图8中F(Vg)远大于F0),其不易失稳,而VSG-VCI可能因系统阻尼不足或达不到给定功率产生暂态同步稳定性问题,对于前者,以上分析说明:可通过减小J、增大Dp来提高HMG系统的暂态同步稳定性。
针对VSG和PLL这种二阶同步环的暂态稳定性,文献[16]和文献[18]已得到了通过提高同步环阻尼比来改善暂态稳定性的结论。本文的研究重点在于HMG系统,通过定性分析发现,在VCI的支撑下,HMG的暂态稳定性主要取决于VSG的给定功率和控制参数选取。
本文通过半实物实验平台验证上述逆变器并网系统的同步稳定性分析结果,系统参数见表1,其中,当逆变器被控为PLL-CCI时内环采用电流环控制,当逆变器被控为VSG-VCI时内环采用电压电流双闭环控制,具体控制结构可参考文献[6]。
表1 HMG并网系统参数
Tab.1 System parameters of the grid-connected HMG

参数数值 CCI/VCI主电路参数直流母线电压Vdc/V400 机侧滤波器L1/mH2.8 网侧滤波器L2/mH1.4 滤波电容C1/µF9.4 滤波器阻尼电阻R1/Ω5 电网电感Lg/mH14或10 电网电阻Rg/Ω0或1 电网电压幅值Vg/V155 电网角频率ωg/(rad/s)314 CCI的控制环参数PLL控制器Kp, Ki1, 5 电流控制器Kpi, Kri10, 5 000 给定角频率/(rad/s)314 有功电流给定Idr/A可变 无功电流给定Iqr/A0 VCI的控制环参数VSG的虚拟惯量J/(kg•m2)0.03 VSG的有功阻尼系数Dp5 VSG的无功下垂系数Kq0.001 虚拟电感Lvir/mH4 电压控制器Kpv, Krv0.5, 100 电流控制器Kpvi, Krvi8, 1 000 给定角频率/(rad/s)314 给定电压155 有功功率给定可变 无功功率给定Qr/kvar0
图13所示为基于RT-Box的半实物实验平台,纯实物并网逆变器示于右下角,但本文研究的不稳定现象对电网和直流源冲击较大,易引起该实验系统保护动作,难以采集相关波形。因此,采用硬件在环半实物实验平台进行实验,即通过图13所示的RT-Box运行并网逆变器的主电路部分,控制部分采用芯片TMS320F28069,其中RT-Box中运行的主电路来源于Plecs软件中搭建的三相并网逆变器功率电路模型,主电路的离散时间为10µs,开关频率和控制电路的采样频率均为10kHz。

图13 实验平台
Fig.13 Experimental platform
实验将采集HMG系统中PLL-CCI和VSG-VCI在不同给定值下的稳态运行波形,以及在发生电网电压跌落时的暂态运行波形,示波器型号为TPS 2024和TPS 2024B。
稳态工作点缺失将导致逆变器并网系统产生同步稳定性问题。为验证HMG并网同步稳定性与各逆变器给定值、电网阻抗之间的关系,本文设计三个HMG并网实验案例。CaseⅠ:Lg=14mH时PLL-CCI和VSG-VCI分别独立并网;CaseⅡ:Lg=14mH时PLL-CCI和VSG-VCI并联并网;Case Ⅲ:Lg=14mH且Rg=1Ω时PLL-CCI和VSG-VCI并联并网。
4.1.1 CaseⅠ
两台PLL-CCI并网运行的电流波形如图14所示,实验中保持第2台CCI的给定电流Ic2=10A不变,改变第1台CCI的电流给定值Ic1。由式(18)可知,对CCI独立并网系统来说,同步稳定性要求CCI总的给定电流不大于35.3A。从图14可以发现,当Ic1由25A增大到26A时,总的给定电流Ic1+Ic2=36A>35.3A,导致第1台逆变器失稳,第2台逆变器因电网阻抗耦合和同步环间的相互作用也失去稳定性,进而使得总并网电流失稳。
将实验参数代入式(22)可得,VSG-VCI独立并网时,满足同步稳定性要求的给定功率最大值PNmax=6.4kW。从图15可以发现,当VCI的给定功率由6kW阶跃到6.5kW时,VCI失去与电网的同步,无法稳定运行。通过失稳的功率波形可以看出,功率上升到约6kW后跌落,如此循环,所以VCI是因并网功率无法达到给定功率而失稳。需要说明的是,图中功率通过采集RT-Box的模拟输出通道所得,其值限定在0~3.3V,因此,所采集到的功率波形最小值被限定在0kW,此波形不影响同步稳定性分析。
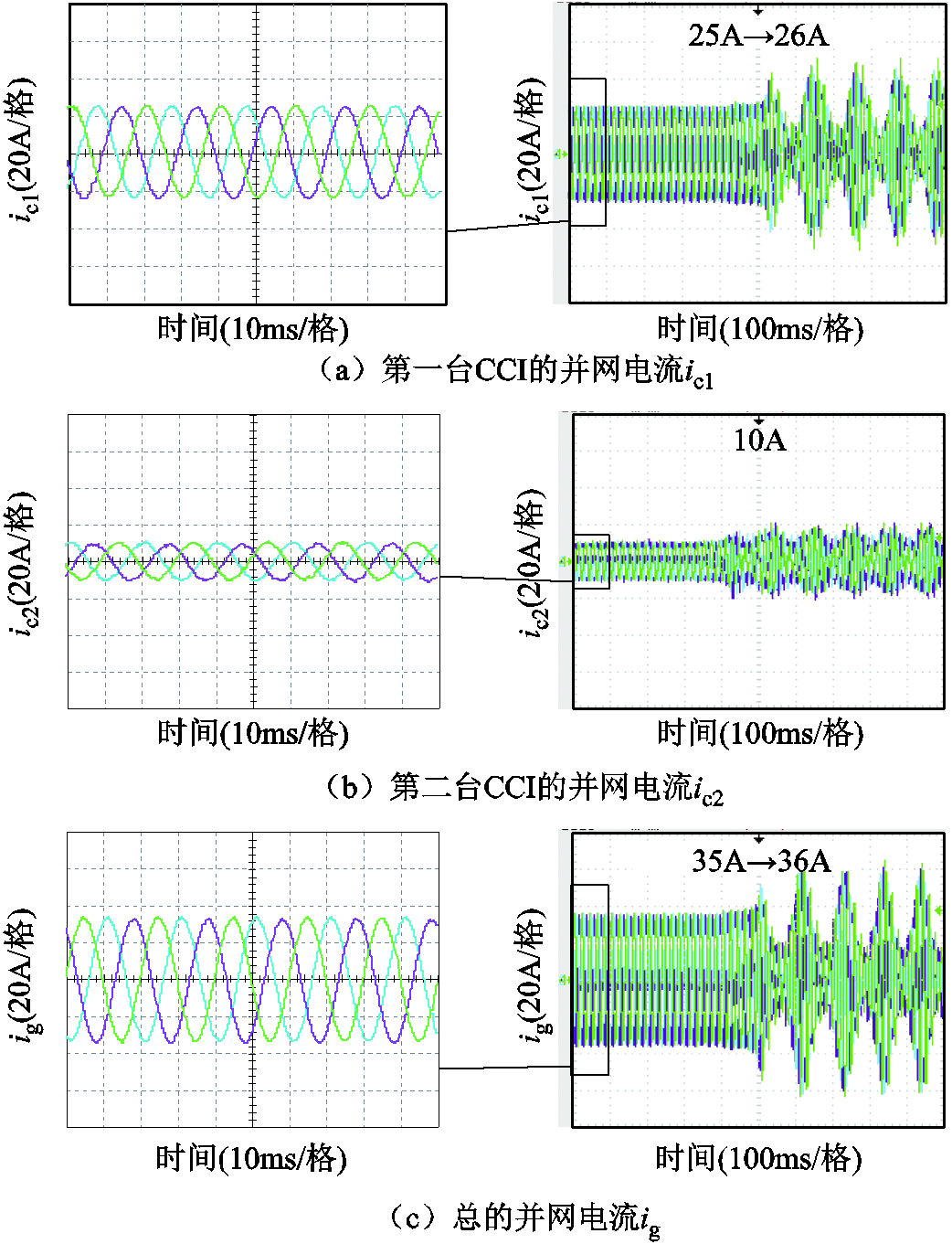
图14 两台PLL-CCI独立并网的电流波形
Fig.14 Waveforms of grid-connected currents in the two-paralleled grid-connected PLL-CCI system
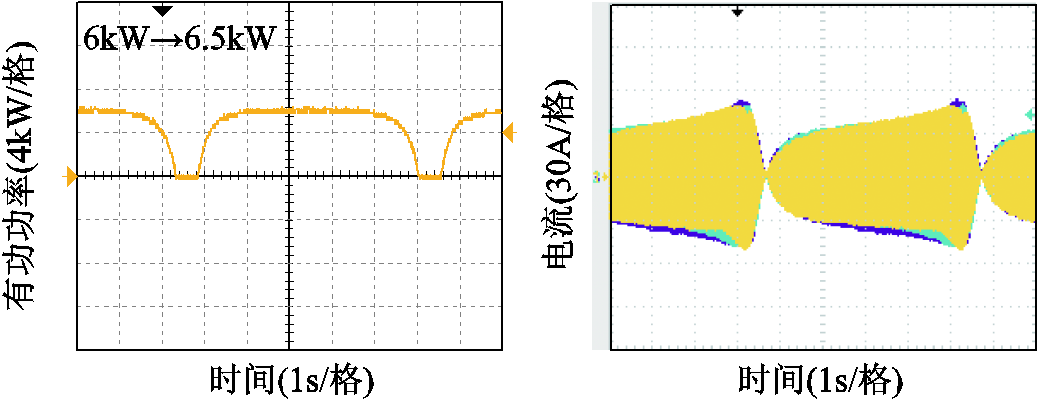
图15 单VSG-VCI独立并网的有功波形和电流波形
Fig.15 Waveforms of the active power and the grid-connected currents in the single grid-connected VSG-VCI system
4.1.2 CaseⅡ
当PLL-CCI和VSG-VCI并联运行时,在纯感性电网中,VSG-VCI的最大给定功率PNmax与PLL-CCI的并网电流Ic有关。若要满足同步稳定性要求,将实验参数代入式(30),当Ic=20A时,PNmax=2.8kW;当Ic=40A时,PNmax<0kW。
保持VSG-VCI的给定功率PN=2kW不变,当PLL-CCI的给定电流Ic由20A增大到40A时,由图16a可知,CCI并网电流一直保持稳定状态;而由图16b可知,当Ic=20A,VCI并网功率稳定,当Ic=40A,VCI并网功率波形失稳,且失稳时的最大功率小于0kW(为了显示VCI的失同步功率波形,采集时加入了一定的偏置)。可见,在HMG系统中,随CCI并网电流Ic增大,虽然CCI可满足式(29)的同步稳定性要求而保持稳定,但VCI会因Ic增大而无法满足式(30)的要求而导致系统失稳。图17中保持Ic=20A不变,当PN由2kW增大到3kW时,可以看出,虽然CCI的并网电流仍保持正弦,但VCI出现功率失稳现象,且VCI失稳时能达到的最大功率约为2.8kW,与理论值相符。
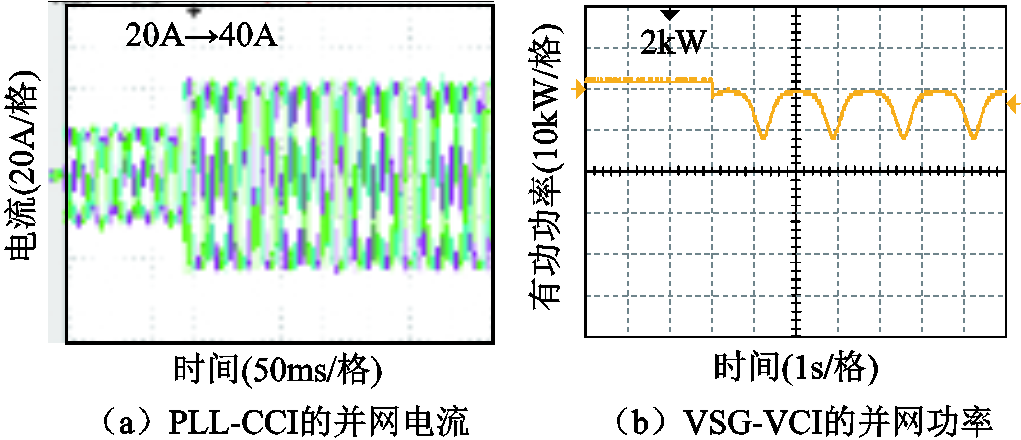
图16 PN=2kW时HMG并网的实验波形
Fig.16 Waveforms of the grid-connected HMG when PN=2kW
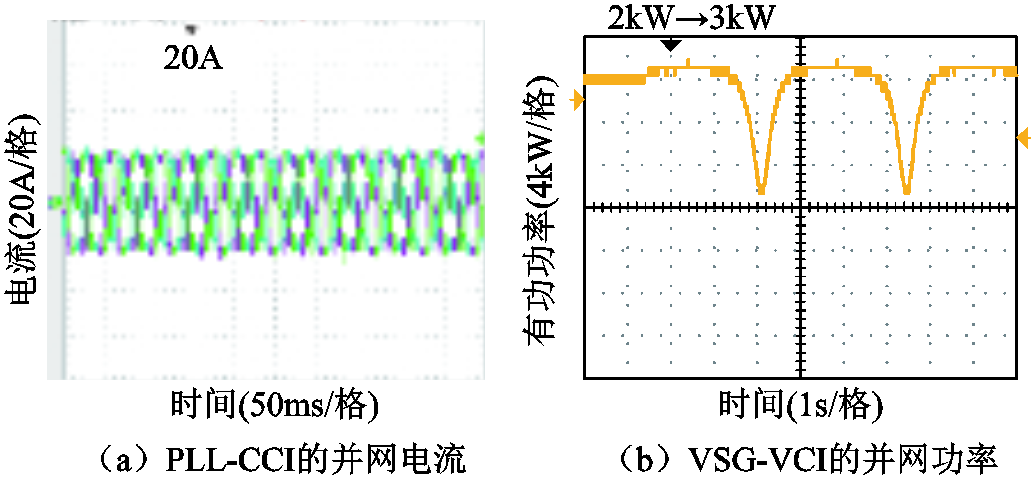
图17 Ic=20A时HMG并网的实验波形
Fig.17 Waveforms of the grid-connected HMG when Ic=20A
综合图16及图17可以发现,HMG并网系统中,无论是PLL-CCI的给定电流Ic发生变化,还是VSG-VCI的给定功率PN发生变化,Ic和PN必须满足式(30)才能保证HMG与电网的同步稳定运行。
4.1.3 Case III
在图17的实验中,加入电网电阻Rg=1Ω,由式(28)计算可得,VSG-VCI的最大并网功率PNmax由Rg=0Ω时的2.8kW增大到3.8kW。相应的VCI并网有功实验波形示于图18,可见加入电阻后,VCI在3kW的给定功率下可保证稳定功率传输。
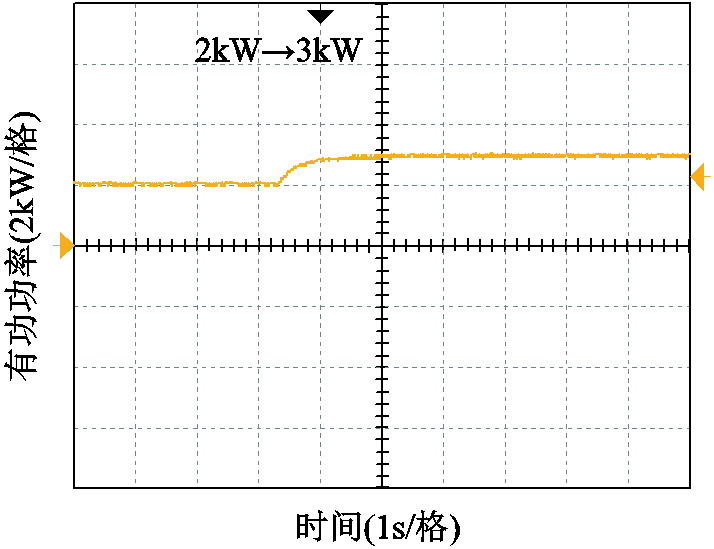
图18 Ic=20A,Rg=1Ω时HMG并网VCI的实验波形
Fig.18 Waveforms of the VCI in grid-connected HMG when Ic=20A and Rg=1Ω
当发生电网电压跌落故障时,通过对同步环二阶系统模型的定性分析发现,HMG系统的暂态同步稳定性取决于VSG-VCI的给定功率和控制参数。
图19所示为Lg=10mH,Ic=27A,PN=500W且电网电压跌落到0.6Vg时PLL-CCI的并网电流及VSG-VCI的并网功率波形,此时,PLL的控制参数Kp=0.2、Ki=20(代表图8所示的最差情况),VSG的控制参数Dp=5、J=0.03。如图19所示,在t1时刻发生电网电压跌落故障,故障后CCI仍输出稳定的正弦并网电流,而VCI出现功率失稳,且失稳的功率波形形状与图16和图17相似,说明故障后VCI是因给定功率过大失去稳态工作点而导致系统失稳。
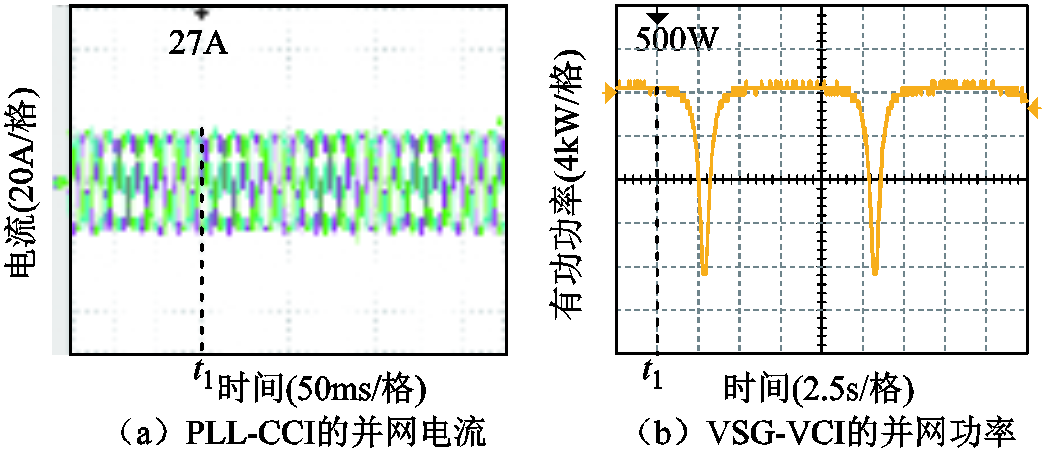
图19 电网电压跌落到0.6Vg时HMG的实验波形
Fig.19 Waveforms of the HMG when the grid voltage drops to 0.6Vg
图20所示为Lg=10mH,Ic=0A,PN=4.8kW且电网电压跌落到0.6Vg时VSG-VCI的并网功率波形,实验中保持PLL的控制参数Kp=0.2、Ki=20不变,改变VSG的有功控制参数Dp和J。由图20b可知,当Dp=1、J=0.3时,VCI因电网电压跌落而失稳,此时的失稳波形形状与图19不同,说明图中VCI失稳不是由稳态工作点缺失引起。通过图20c和图20d与图20b的对比可以发现,减小J和增大Dp之后,在电网电压跌落故障下VCI并网功率可稳定传输,说明图20b的失稳波形是因VSG阻尼不足导致。
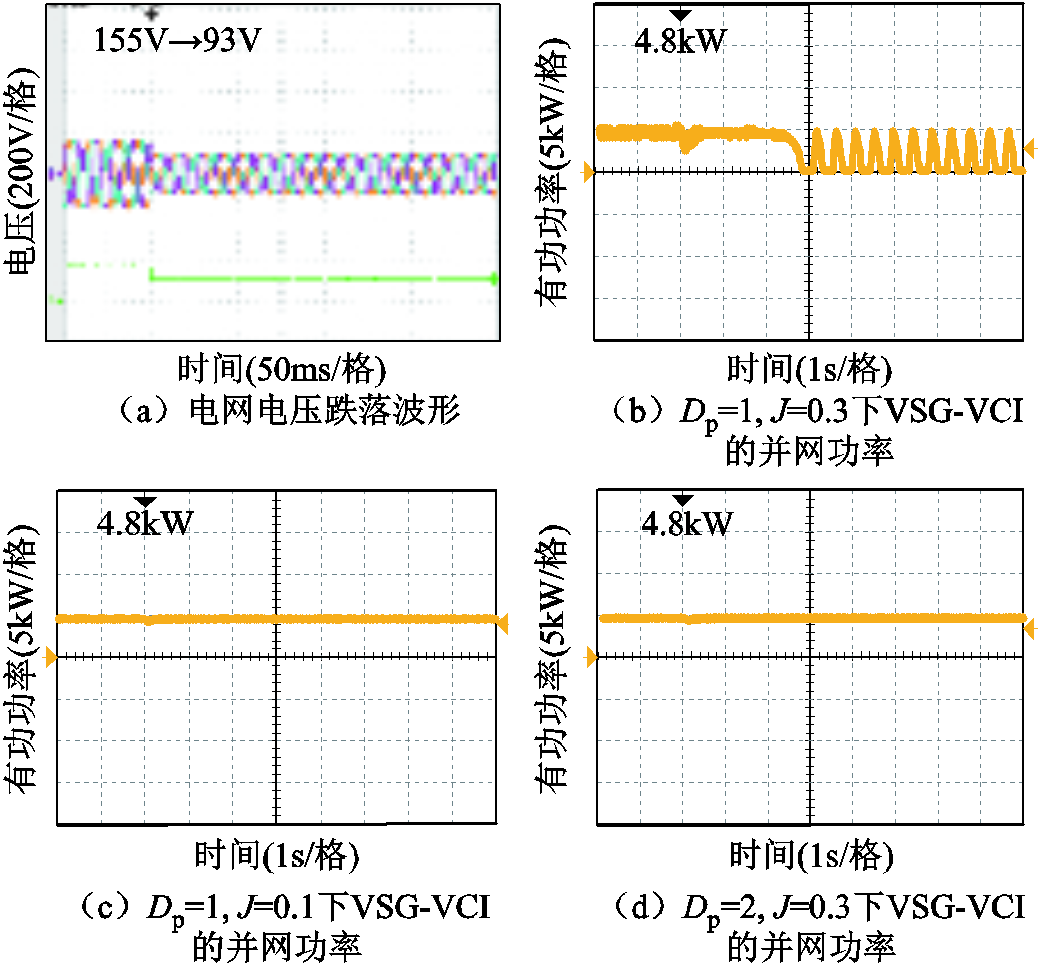
图20 电网电压跌落到0.6Vg时HMG系统中VSG-VCI的实验波形
Fig.20 Waveforms of the VSG-VCI in HMG when the grid voltage drops to 0.6Vg
本文以PLL-CCI和VSG-VCI并联的HMG并网系统为研究对象,建立准静态模型,揭示了系统中PLL和VSG的同步机制,并通过稳态工作点的定量分析和电网电压跌落时暂态同步过程的定性分析,对HMG并网的同步稳定性进行了具体研究。结果表明:
1)PLL-CCI的最大并网电流和VSG-VCI的最大并网功率均会随电网电压跌落、电网电感增大、电网频率升高而下降。
2)在HMG并网系统中,VSG的同步速度远低于PLL的锁相速度,所以VCI对CCI的功率传输能力具有支撑作用。并联的VCI能够显著提高CCI的最大并网电流,但VCI的最大传输功率会随CCI并网电流增大而产生明显下降。由此可知,VCI并网功率的运行范围决定了HMG系统的稳态工作点,需合理设置VCI的给定功率。否则,当电网发生故障时,HMG极易因VSG-VCI的平衡点缺失而失稳。
3)在HMG并网系统稳态工作点存在的情况下,HMG的暂态过程受VCI的影响,可通过减小VSG惯性系数J、增大阻尼系数Dp来提高HMG的暂态同步稳定性。
参考文献
[1] 杨新法, 苏剑, 吕志鹏, 等. 微电网技术综述[J]. 中国电机工程学报, 2014, 34(1): 57-70.
Yang Xinfa, Su Jian, Lü Zhipeng, et al. Overview on microgrid technology[J]. Proceedings of the CSEE, 2014, 34(1): 57-70.
[2] 刘津铭, 陈燕东, 伍文华, 等. 孤岛微电网序阻抗建模与高频振荡抑制[J]. 电工技术学报, 2020, 35(7): 1538-1552.
Liu Jinming, Chen Yandong, Wu Wenhua, et al. Sequence impedance modeling and high-frequency oscillation suppression method for island microgrid[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1538-1552.
[3] 杨苓, 陈燕东, 罗安, 等. 多机并联接入弱电网的改进型带阻滤波器高频振荡的抑制[J]. 电工技术学报, 2019, 34(10): 2079-2091.
Yang Ling, Chen Yandong, Luo An, et al. Suppression method of high-frequency oscillation by improved notch filter for multi-parallel inverters connected to weak grid[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2079-2091.
[4] Rocabert J, Luna A, Blaabjerg F, et al. Control of power converters in AC microgrids[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4734-4749.
[5] Guan Yajuan. Novel control strategies for parallel-connected inverters in AC microgrids[D]. Aalborg: Aalborg University, 2016.
[6] Yu Yanxue, Guerrero J, Zheng Xuemei, et al. Modeling and stability analysis of CCIs- and VCIs-based hybrid microgrids operating in grid-connected modes[C]//IEEE 2018 International Conference on Smart Energy Systems and Technologies (SEST), Sevilla, Spain, 2018: 1-6.
[7] 熊连松, 修连成, 王慧敏, 等. 储能系统抑制电网功率振荡的机理研究[J]. 电工技术学报, 2020, 34(20): 4373-4380.
Xiong Liansong, Xiu Liancheng, Wang Huimin, et al. Mechanism of energy storage system to suppress grid power oscillations[J]. Transactions of China Electrotechnical Society, 2020, 34(20): 4373-4380.
[8] Lu Minghui, Yang Yongheng, Johnson B, et al. An interaction-admittance model for multi-inverter grid-connected systems[J]. IEEE Transactions on Power Electronics, 2019, 34(8): 7542-7557.
[9] 谢志为, 陈燕东, 伍文华, 等. 弱电网下多逆变器并网系统的全局高频振荡抑制方法[J]. 电工技术学报, 2020, 35(4): 885-895.
Xie Zhiwei, Chen Yandong, Wu Wenhua, et al. A global high-frequency oscillation suppression method for multi-inverter grid-connected system in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 885-895.
[10] 秦本双, 徐永海, 袁敞, 等. 多VSG并网系统的P/ω导纳建模及功频振荡分析[J]. 中国电机工程学报, 2020, 40(9): 2932-2941.
Qin Benshuang, Xu Yonghai, Yuan Chang, et al. The P/ω admittance modeling and power-frequency oscillation analysis of multi-VSGs grid-connected systems[J]. Proceedings of the CSEE, 2020, 40(9): 2932-2941.
[11] Taul M G, Wang Xiongfei, Davari P, et al. An overview of assessment methods for synchronization stability of grid-connected converters under severe symmetrical grid faults[J]. IEEE Transactions on Power Electronics, 2019, 34(10): 9655-9670.
[12] 朱蜀, 刘开培, 秦亮, 等. 电力电子化电力系统暂态稳定性分析综述[J]. 中国电机工程学报, 2017, 37(14): 3948-3962.
Zhu Shu, Liu Kaipei, Qin Liang, et al. Analysis of transient stability of power electronics dominated power system: an overview[J]. Proceedings of the CSEE, 2017, 37(14): 3948-3962.
[13] 庄慧敏, 巨辉, 肖建. 高渗透率逆变型分布式发电对电力系统暂态稳定和电压稳定的影响[J]. 电力系统保护与控制, 2014, 42(17): 84-89.
Zhuang Huimin, Ju Hui, Xiao Jian. Impacts of inverter interfaced distributed generations with high penetration level on power system transient and voltage stability[J]. Power System Protection and Control, 2014, 42(17): 84-89.
[14] Wang Xiongfei, Taul M G, Wu Heng, et al. Grid-synchronization stability of converter-based resources-an overview[J]. IEEE Open Journal of Industry Applications, 2020, 1(1): 115-134.
[15] Dong Dong, Wen Bo, Boroyevich D, et al. Analysis of phase-locked loop low-frequency stability in three-phase grid-connected power converters considering impedance interactions[J]. IEEE Transactions on Industrial Electronics, 2015, 62(1): 310-321.
[16] Wu Heng, Wang Xiongfei. Design-oriented transient stability analysis of PLL-synchronized voltage-source converters[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 3573-3589.
[17] Wu Heng, Wang Xiongfei. Design-oriented transient stability analysis of grid-connected converters with power synchronization control[J]. IEEE Transactions on Industrial Electronics, 2019, 66(8): 6473-6482.
[18] Pan Donghua, Wang Xiongfei, Liu Fangcheng, et al. Transient stability of voltage-source converters with grid-forming control: a design-oriented study[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1019-1033.
[19] Shuai Zhikang, Shen Chao, Liu Xuan, et al.Transient angle stability of virtual synchronous generators using Lyapunov’s direct method[J]. IEEE Transactions Smart Grid, 2019, 10(4): 4648-4661.
[20] Chen Junru, O'Donnell T. Parameter constraints for virtual synchronous generator considering stability[J]. IEEE Transactions on Power Systems, 2019, 34(3): 2479-2481.
Synchronous Stability Research of Inverters in Hybrid Microgrid Based on the Quasi-Static Models under Weak Grid
Abstract When the multi-inverters are parallelly connected to the weak grid, interactions of the high grid impedance and inverters are easy to result in synchronization stability problems. To study the synchronization stability of the hybrid microgrid (HMG) consisting of current- and voltage-controlled inverters in weak grid, the quasi-static models were developed to analyze the synchronization mechanism of the phase locked loop (PLL) and virtual synchronous generator (VSG) in the HMG, and discuss the influences of interactions between the PLL and VSG on the steady-state operating points of inverters in the HMG. Thus, relationships of the synchronization stability with the grid impedance and grid voltage were derived in the HMG. Then, consider the grid voltage drop fault occurred in weak grid, relationships of the synchronization stability with the steady-state operating point and the synchronization loop parameters were analyzed in the HMG. The experimental results verified theoretical analyses. Researches in this paper can help the HMG to choose the running references and synchronization parameters reasonably.
keywords:Weak grid, hybrid microgrid, multi-inverter, quasi-static model, synchronization stability
DOI:10.19595/j.cnki.1000-6753.tces.201512
中图分类号:TM464
国网黑龙江公司科技项目“分布式能源高渗透接入对地区末端电网稳定性影响及抑制方法研究”资助(52243718000T)。
收稿日期 2020-11-14
改稿日期 2021-01-08
于彦雪 女,1991年生,博士研究生,研究方向为弱电网下并网逆变器建模及稳定性。E-mail:yuyanxueppkz@163.com
李浩昱 男,1974年生,教授,博士生导师,研究方向为微网环境变换器协调控制技术、极端环境电能变换与控制。E-mail:lihy@hit.edu.cn(通信作者)
(编辑 赫蕾)