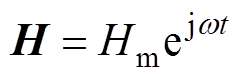 (1)
(1)摘要 超磁致伸缩材料TbDyFe合金具有温度敏感特性,该文测量变温条件下TbDyFe合金在不同频率f和磁通密度幅值Bm时的动态磁特性曲线,结果表明,当励磁磁场频率f和磁通密度幅值Bm一定时,随着环境温度的升高(从10℃增加到80℃),振幅磁导率逐步增加,动态磁滞回线横向变窄,所需磁场强度减少,磁能损耗也逐步减少。在此基础上,针对现有损耗计算模型无法对温度进行有效表征,而导致损耗计算结果误差较大的问题,提出一种变温条件下磁致伸缩材料的高频损耗计算模型,模型通过引入温度有关项对损耗系数进行修正;并且综合考虑高频磁滞特性和趋肤效应的影响,引入损耗附加磁通密度项及损耗附加频率项,从而建立可以有效考虑温度效应的改进损耗计算模型,通过多组测量值及计算值的对比结果验证了该模型的准确性和可行性。
关键词:TbDyFe合金 变温效应 高频动态磁滞特性 磁能损耗 磁导率幅值
超磁致伸缩材料TbDyFe合金被认为是制作大功率、高频磁致伸缩换能器核心驱动元件的理想材料,它具有能量密度高(约25kJ/m3)、响应速度快(ms级)、控制精度和位移分辨率高等优点,可广泛应用在超声清洗、超声加工、金属探伤、海底探测、脱硫和医疗器械等领域[1-3]。由于TbDyFe合金具有温度敏感特性[4-5],研究变温条件下TbDyFe合金的高频磁特性及损耗特性,为高频换能器的温控系统设计提供数据和理论支持,对于设计高频范围的磁致伸缩器件至关重要。
文献[6]指出在磁有序晶体中,温度的改变会引起磁有序状态和磁体内易磁化轴的变化,当材料处于磁化状态时,其磁矩方向受热运动影响很大,而呈现Brown转动的特点。文献[7]研究了温度对TbDyFe合金饱和磁化强度、磁致伸缩应变及杨氏模量的作用,证明了温度是磁特性研究不可忽略的因素,但是尚未就温度对损耗特性的影响进行测试分析。文献[8]通过对动态磁滞模型的研究发现,磁性材料中动态损耗的物理来源是平均再磁化速度,并基于磁通密度的加权时间导数提出了一种任意形状励磁电流下磁性材料的损耗计算方法。文献[9-11]基于TbDyFe合金的高频动态磁滞回线及损耗测试数据,探究了各项损耗系数随频率和磁通密度幅值的变化趋势,但忽略了温度对TbDyFe合金磁特性的作用。在此基础上,本文重点研究温度这一因素对TbDyFe合金高频磁能损耗的影响。
在经典的损耗分离模型中,损耗是关于磁化频率f和磁通密度幅值Bm的二元函数,在固定的磁化条件下,无论环境温度是多少,损耗模型的计算结果都不会发生变化,这与实验结果明显不符。
针对上述问题,本文搭建温度可控的高频磁特性测试系统,选用方形薄片样品来研究磁致伸缩材料的温度敏感特性。由于样品尺寸较小,且放在恒温箱中控制温度的变化,材料表面与内部的温差可以忽略不计,可看作是处于一个温度恒定且分布均匀的环境中,所以本实验中所给定的环境温度就是样品的工作温度。通过实验研究有限个均匀分布的温度条件下TbDyFe合金在不同频率f和磁通密度幅值Bm下的动态磁特性曲线,从中提取磁特性参数。建立一种基于Bertotti损耗分离理论,且面向工程应用的变温条件下材料的损耗计算模型。该模型基于损耗分离三项式引入温度有关项对损耗系数进行修正,并且综合考虑高频磁滞特性和趋肤效应的影响,引入了损耗附加磁通密度项及损耗附加频率项实现准确计算,根据实验结果进行计算,确定了损耗系数随磁化频率f、磁通密度幅值Bm、温度DT的变化规律,从而实现了考虑温度效应的改进损耗计算。通过对比多组损耗的实验测量值(频率范围为1~20kHz,磁通密度幅值范围为0.01~0.07T,温度范围为10~80℃)及模型计算值,验证了本文所提的变温条件下TbDyFe合金高频磁能损耗计算模型的准确性和可行性。
磁致伸缩材料在正弦励磁磁场下,由于存在阻碍磁矩运动的各种阻尼的作用,使磁通密度B的变化总是滞后于励磁磁场H一相位d。相位d 可以代表材料磁能损耗的大小,又称损耗角。将正弦励磁磁场和对应的磁感应强度用矢量表述为
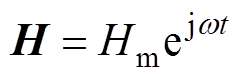 (1)
(1)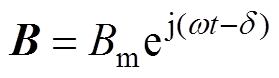 (2)
(2)
式中,Hm为磁场强度的峰值(A/m);w 为角频率(rad/s)。材料的磁导率是表征动态磁特性的参数,可表示为
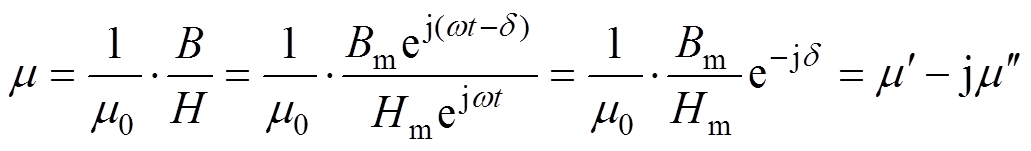 (3)
(3)其中
 (4)
(4)
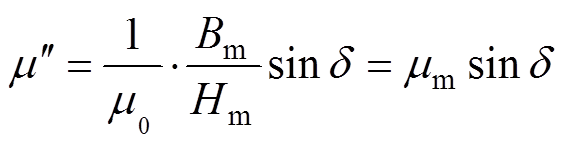 (5)
(5)式中,m0为真空磁导率;mm=Bm/(m0Hm)为材料的振幅磁导率; 为实部磁导率,描述了材料在动态磁化过程中的磁能储存量;
为实部磁导率,描述了材料在动态磁化过程中的磁能储存量;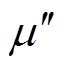 为虚部磁导率,描述了材料在励磁磁场中一个周期的磁能损耗量。
为虚部磁导率,描述了材料在励磁磁场中一个周期的磁能损耗量。
损耗因数tand 的物理意义是磁性材料在交变励磁磁场中每周期能量的损耗与能量的存储之比,用来描述软磁材料在磁化过程中磁能的损耗和存储性能。材料的损耗因数定义为磁导率虚部和实部之比,其倒数为品质因数Q,即
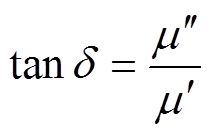 (6)
(6)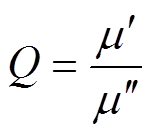 (7)
(7)
磁滞回线结构灵敏,容易受温度、应力等因素的影响,磁滞回线所包围的面积代表材料磁化一周的能量损耗。
基于Bertotti损耗分离法,TbDyFe合金的损耗可表示为磁滞损耗、涡流损耗及剩余损耗之和[12],其中磁滞损耗是当外加磁场增大时,磁畴发生畴壁位移及磁畴转动,去掉外磁场时,有一部分磁畴保持磁化方向不能恢复到初始位置,交变磁场激励时这部分磁畴会克服摩擦使磁心发热消耗能量,从而产生磁滞损耗;涡流损耗是由于铁磁材料的外加磁场发生变化时材料内部引起涡流而造成的能量损耗;剩余损耗是磁能损耗中除去磁滞损耗和涡流损耗以外的所有损耗的总称,它包括磁化弛豫效应或磁性滞后效应引起的损耗。损耗计算公式为
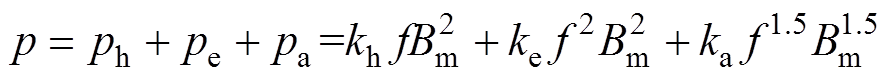 (8)
(8)式中,kh、ke和ka分别为磁滞损耗系数、涡流损耗系数和剩余损耗系数[13]。铁磁材料在外磁场作用下,磁畴发生畴壁位移及磁畴转动。当温度变化时,会破坏原子磁矩的有序排列。温度较低时,材料内原子热运动较小,磁场对磁畴磁矩的作用占绝对主导地位;当温度进一步升高,原子热运动剧烈,磁畴磁矩偏转更迅速。此外,温度的改变会引起磁有序状态和磁体内易磁化轴的变化,从分子学角度来说,分子的热运动会影响自发磁化区域中磁畴的状态,材料在励磁磁场中能量的损耗也有较大差异[7]。因此不能忽略温度对TbDyFe合金磁能损耗的影响。
在经典的损耗分离模型中,损耗系数固定,各项损耗的大小都只是关于磁化频率f和磁通密度幅值Bm的二元函数,当磁化条件不变时,无论环境温度是多少,损耗模型的计算结果都不会发生变化,这与实验结果明显不符。同时由于高频条件下TbDyFe合金受涡流趋肤效应和动态磁滞的影响显著,损耗系数不再恒定,此时传统的计算方法不再适用,必须对其进行改进[14-15]。为了能够体现温度变化对TbDyFe合金高频磁能损耗的影响,有必要研究损耗系数kh、ke和ka分别随DT、f、Bm的变化规律,故将磁滞、涡流和剩余损耗系数kh、ke和ka均看作是关于DT、f、Bm的三元函数,结合实验测试数据分析温度、频率和磁通密度幅值三个自由变量对损耗系数的影响权重,可将变系数高频磁能损耗计算模型改写为
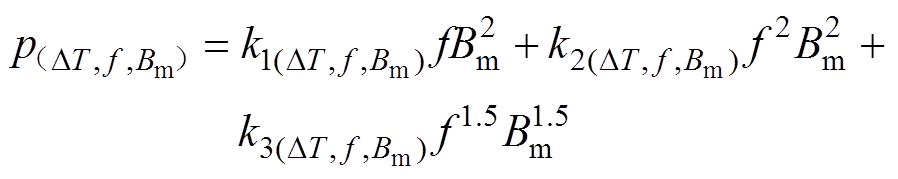 (9)
(9)式中,DT=Te-Tr,Te为外加温度,Tr为自旋再取向温度,对TbDyFe来说,Tr=0,本文中环境温度即为DT;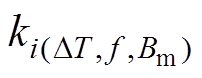 (i=1, 2, 3)分别为计及温度DT、频率f和磁通密度幅值Bm影响的磁滞损耗系数、涡流损耗系数和剩余损耗系数,可用泰勒级数将其展开成关于温度、频率以及磁通密度幅值的多项式,即
(i=1, 2, 3)分别为计及温度DT、频率f和磁通密度幅值Bm影响的磁滞损耗系数、涡流损耗系数和剩余损耗系数,可用泰勒级数将其展开成关于温度、频率以及磁通密度幅值的多项式,即
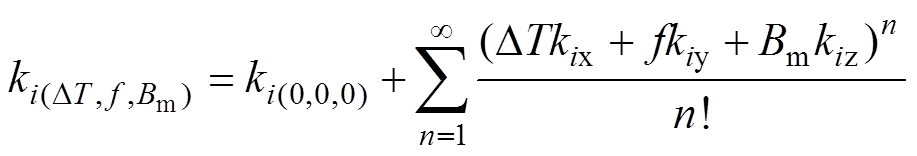 (10)
(10)式中,kix为当频率和磁通密度幅值为0时关于温度的偏导数;kiy为当温度和磁通密度幅值为0时关于频率的偏导数;kiz为当温度和频率为0时关于磁通密度幅值的偏导数。分别仅保留关于温度DT、频率f和磁通密度幅值Bm的线性部分,可得
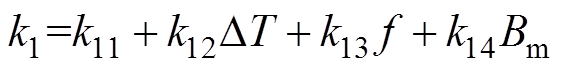 (11)
(11)
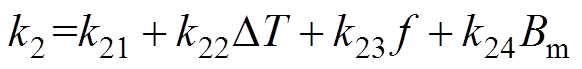 (12)
(12)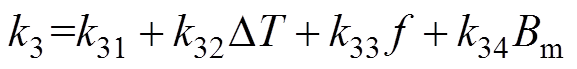 (13)
(13)
式中,k11~k34为材料的损耗相关参数,结合实验曲线,在边界给定的情况下,只需通过任意12组不同温度DT、频率f、磁通密度幅值Bm下材料的磁能损耗测试数据(本文的测试频率f范围为1~20kHz,磁通密度幅值Bm范围为0.01~0.07T,温度DT范围为10~80℃),即可获得一组齐次方程,求解齐次方程即可确定12个损耗相关参数。k11、k21、k31分别为磁滞、涡流和剩余损耗的原始损耗系数;k12、k22、k32分别为磁滞、涡流和剩余损耗体现温度敏感程度的线性项系数;k13、k23、k33分别为磁滞、涡流和剩余损耗中的损耗附加频率项系数;k14、k24、k34分别为磁滞、涡流和剩余损耗中的损耗附加磁通密度项系数。求解结果见表1。
表1 磁能损耗计算模型相关参数值
Tab.1 Parameter values of the magnetic energy loss calculation model

参数数值 k117.551 5 k123.410 7×10-3 k13-1.081 26×10-4 k14-9.344 6×101 k21-1.165 5×10-4 k225.54×10-6 k23-1.28×10-8 k24-9.349 4×10-4 k318.243 2×10-3 k32-2.258 2×10-4 k333.500 1×10-7 k344.966 7×10-1
基于变温条件下的高频动态磁滞回线测试数据,结合式(9)~式(13),整理化简可得材料的变系数高频磁能损耗表达式为
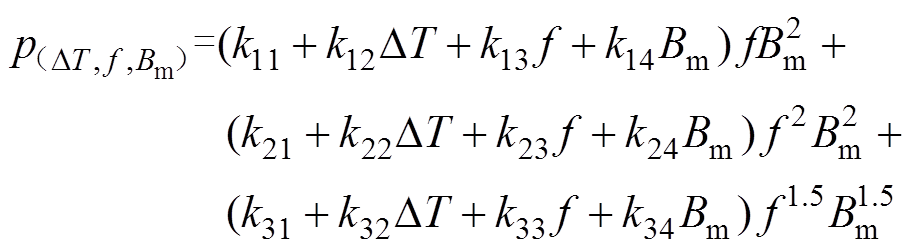 (14)
(14)式中,第一项是磁滞损耗;第二项是涡流损耗;第三项是剩余损耗。式(14)能清晰地体现各项损耗系数分别受磁化频率f、磁通密度幅值Bm和温度DT三个自由变量影响而变化的规律。并且由于固定边界条件下磁能损耗计算模型的12个损耗相关参数是确定的,因此只需给定温度DT、频率f、磁通密度幅值Bm的数值,即可通过式(14)预测算出在给定工作条件下磁致伸缩材料的高频磁能损耗数值,而不用依赖于过多的实验测试数据及相应的数据拟合方法和技术。
本文基于AMH-1M-S动态磁特性测试仪和调温箱搭建了温度可控的高频磁特性测试系统。实验中TbDyFe合金样品为正方形环状,被测样品的高频动态磁特性测试系统原理如图1所示。将样品的感应线圈和驱动线圈分别接入动态磁特性测试系统之后,再将样品通过恒温箱的外接通道放入到恒温箱内部,调节恒温箱温度实现变温控制,实验测试平台如图2所示。
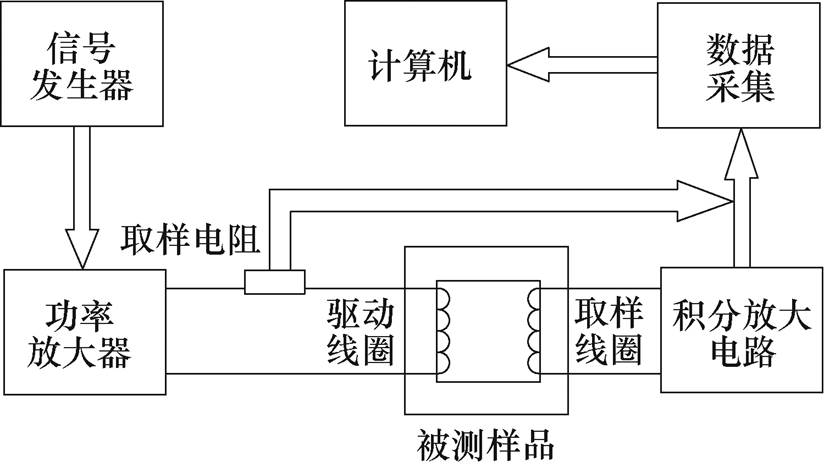
图1 动态磁特性测试系统原理
Fig.1 Principle of dynamic magnetic characteristic test system

图2 实验测试平台
Fig.2 Experiment platform
磁特性测试系统的工作原理为:信号发生器输出频率可调的正弦交变电流,经功率放大器后通过驱动线圈给被测样品提供同频率的正弦交变磁场,取样线圈与积分放大电路相连,积分放大电路与数据采集系统连接。被测样品中磁场强度的变化通过采样电阻上的电压得到,被测样品中磁通密度的变化则通过积分放大电路中电容电压来体现,经过积分放大电路的取样线圈数据和通过取样电阻的驱动线圈的数据,在计算机中进行数据处理,最终得到被测样品的动态磁滞回线。
以一个测试样品(外边长10mm,内边长4mm,厚度2mm的方形薄片样品)为例,驱动线圈选用20匝、线径为0.5mm的漆包线,取样线圈选用10匝、线径为0.15mm的漆包线。考虑到TbDyFe合金的高频磁能损耗与样品所处的温度DT、频率f、磁通密度幅值Bm密切相关,本文采用控制变量法分别在不同温度DT、频率f、磁通密度幅值Bm下进行大量测试。结合TbDyFe合金在水声和超声频段的具体应用场合,实验测试的频率范围为1~20kHz,磁通密度幅值范围为0.01~0.07T,温度变化范围为10~80℃。绘制出变温条件下TbDyFe合金在不同频率f和磁通密度幅值Bm下的动态磁特性曲线,从中提取磁特性参数,通过式(6)、式(7)可以求得损耗因数和品质因数的变化规律,利用高频磁能损耗模型式(14)预测材料的磁能损耗并与大量实验结果进行对比。
图3所示为TbDyFe合金在励磁磁场频率为10kHz,磁通密度幅值为0.06T时不同温度(10℃、20℃、40℃、60℃、80℃)下的动态磁滞回线。对比这五个磁滞回线发现:当磁通密度幅值一定时,随着温度增加,动态磁滞回线横向变窄,所需磁场强度减少,磁能损耗和矫顽力随之减少。由此可见,温度对材料内部磁畴壁移动和磁畴转动等行为有明显影响,这些影响通过材料的磁特性参数变化体现出来。
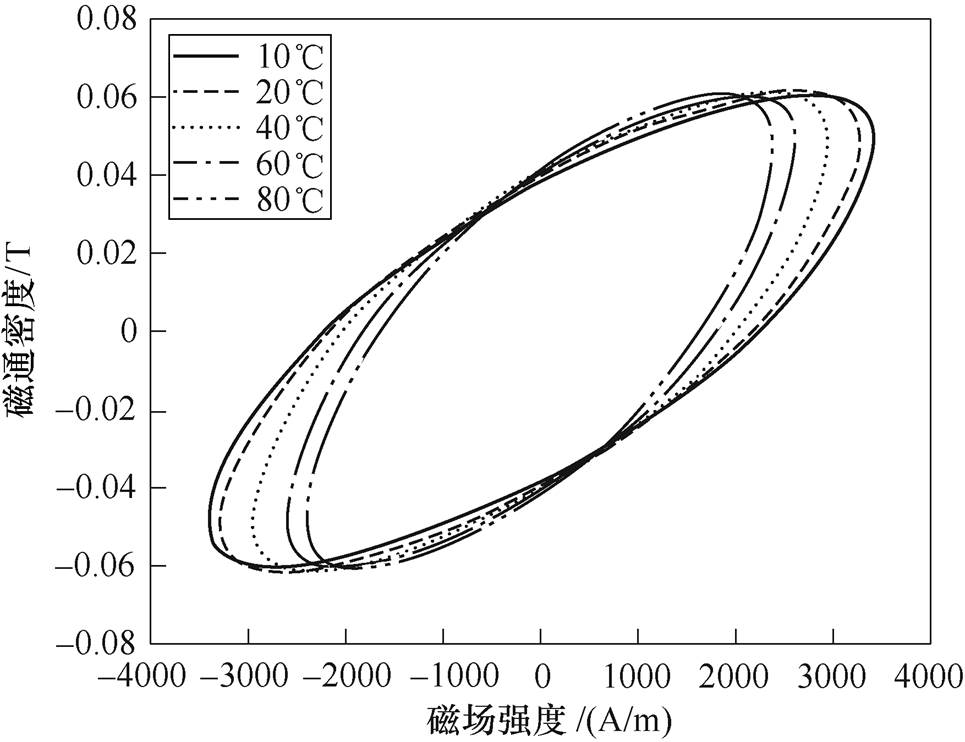
图3 不同温度下的动态磁滞回线(f=10kHz, Bm=0.06T)
Fig.3 Dynamic hysteresis loop at different temperatures (f=10kHz, Bm=0.06T)
材料的磁导率是表征电工材料动态磁特性的重要参数,图4所示为TbDyFe合金在励磁磁场频率为10kHz,磁通密度幅值为0.06T时,振幅磁导率及实、虚部磁导率随温度变化的曲线。可以发现,在温度从10℃变化到80℃的过程中,样品的振幅磁导率及实、虚部磁导率随温度的增加而逐步增大,该样品的振幅磁导率增大了46.04%(由10℃时的13.9增加至80℃时20.3)。在磁通密度幅值取定值时,振幅磁导率增大,说明随着温度的升高要在TbDyFe合金中建立同样大的磁通密度幅值Bm所需的磁场强度H减小,动态磁滞回线横向变窄,磁能损耗和矫顽力随之减少。
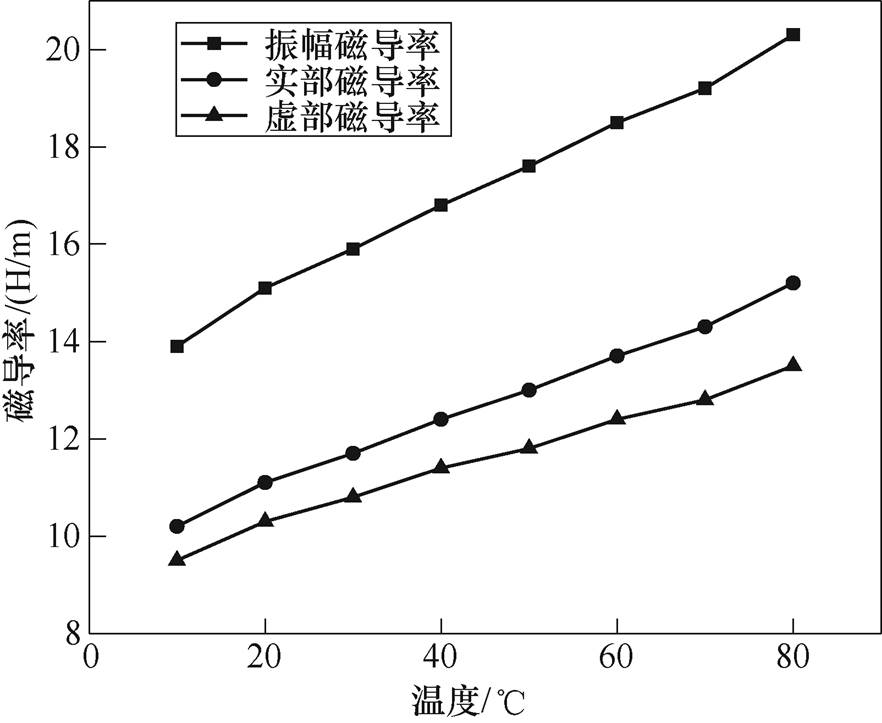
图4 振幅磁导率及实、虚部磁导率和温度的关系(f=10kHz, Bm=0.06T)
Fig.4 The relationship of permeability amplitude, the real and imaginary parts of the permeability vs. temperature(f=10kHz, Bm=0.06T)
TbDyFe合金的矫顽力代表着材料磁化过程中的不可逆的程度,图5所示为TbDyFe合金在励磁磁场频率为10kHz,磁通密度幅值为0.06T时,矫顽力随温度变化的曲线。可以发现,随着温度增加,矫顽力减少了24.9%(由10℃时的2 198.5A/m降至 80℃时的1 651.2A/m)。矫顽力减小,材料的不可逆磁化程度降低。
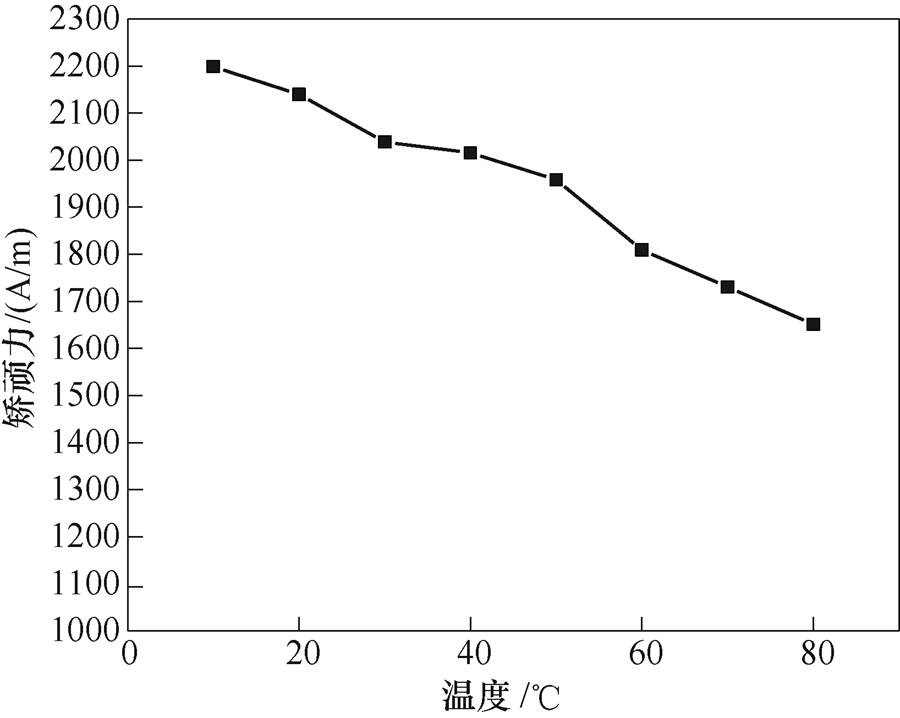
图5 矫顽力随温度的变化(f=10kHz, Bm=0.06T)
Fig.5 Change of coercivity with temperature (f=10kHz, Bm=0.06T)
图6所示为TbDyFe合金在励磁磁场频率为10kHz,磁通密度幅值为0.06T时,磁能损耗随温度变化的曲线。可以发现,随着温度增加,磁能损耗减少了20.67%(由10℃时的529.891W/kg降至80℃时的420.378W/kg)。
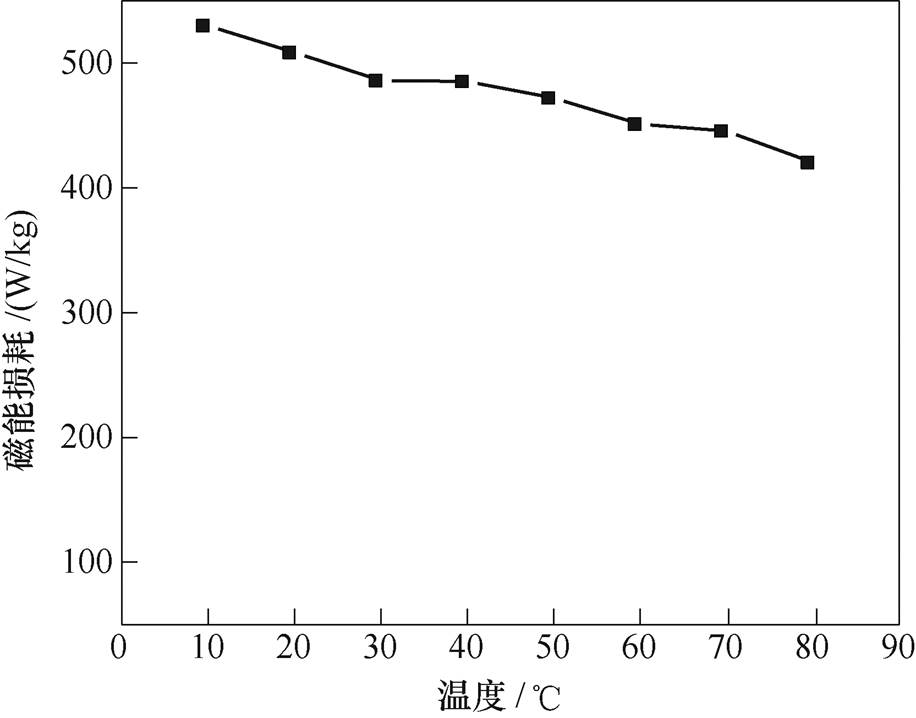
图6 磁能损耗随温度的变化(f=10kHz, Bm=0.06T)
Fig.6 Change of magnetic energy loss with temperature (f=10kHz, Bm=0.06T)
损耗因数和品质因数是衡量材料磁性的重要指标之一,用来描述软磁材料在磁化过程中磁能的存储和损耗性能,通过复数磁导率的实部和虚部计算得到。图7所示为TbDyFe合金在励磁磁场频率为10kHz,磁通密度幅值为0.06T时,损耗因数和品质因数随温度变化的曲线。可以发现,随着温度增加,损耗因数逐渐减小,品质因数逐渐增加。说明随温度的增加,该TbDyFe合金的高频磁能损耗逐渐减小。
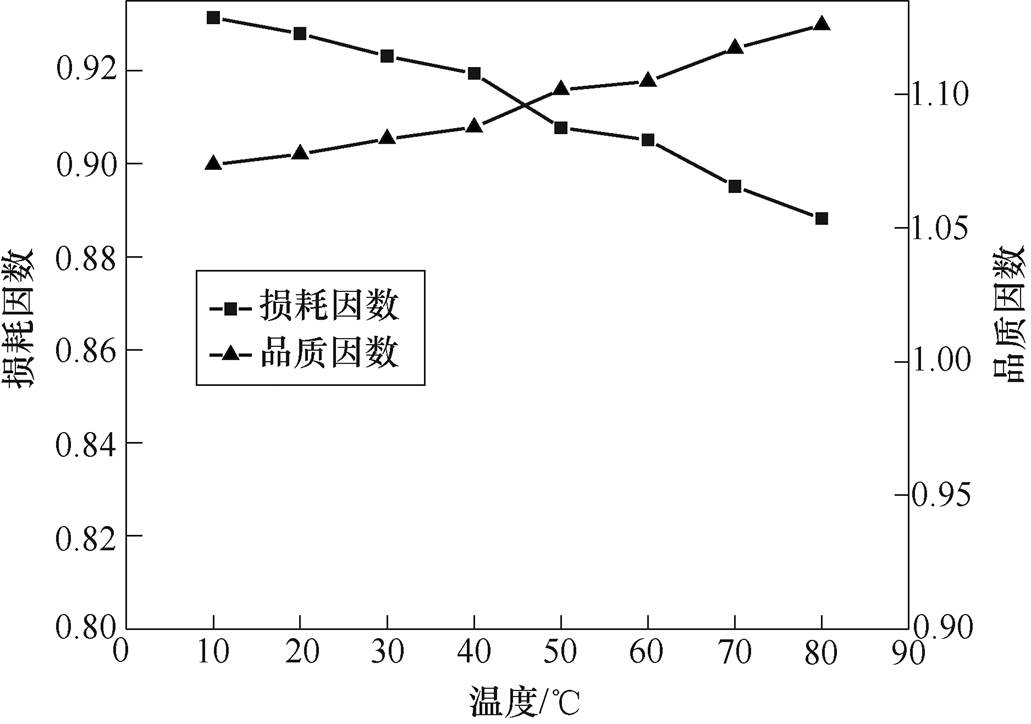
图7 损耗因数和品质因数随温度的变化(f=10kHz, Bm=0.06T)
Fig.7 Loss factor and quality factor change with temperature (f=10kHz, Bm=0.06T)
为了验证本文所建立的考虑温度效应的变系数高频磁能损耗计算模型的准确性与可行性,计算了给定工作条件下(温度DT、频率f、磁通密度幅值Bm的数值已知)磁致伸缩材料的高频磁能损耗数值,并与实验测量值进行对比分析,为了使对比结果更加清晰,本文采用控制变量法分别绘制了不同温度DT、频率f和磁通密度幅值Bm下的实验结果与模型计算结果对比,如图8~图10所示。
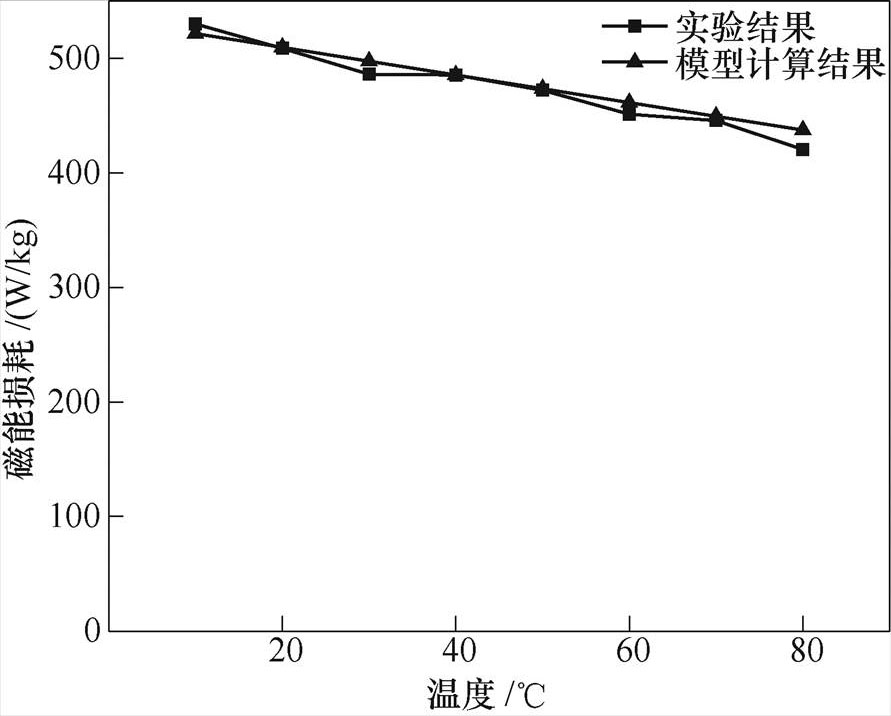
图8 不同温度下损耗实验结果与计算结果对比(f=10kHz, Bm=0.06T)
Fig.8 Comparison of loss experiment results and calculation results at different temperatures (f=10kHz, Bm=0.06T)
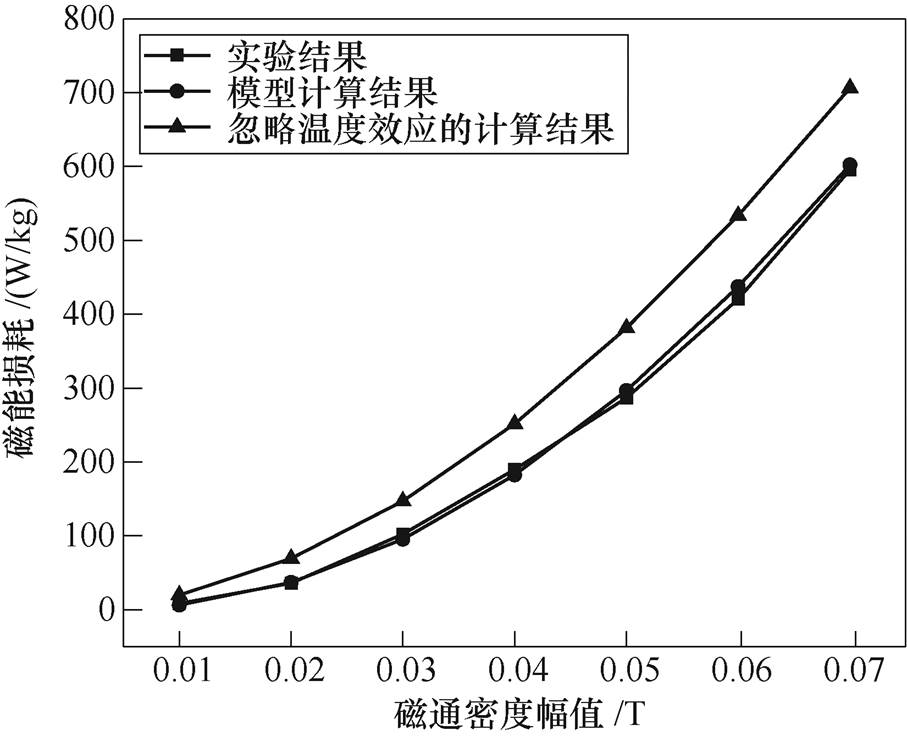
图9 不同磁密幅值下损耗实验结果与计算结果对比(f=10kHz, DT=80℃)
Fig.9 Comparison of loss experiment results and calculation results at different magnetic density amplitude(f=10kHz, DT=80℃)
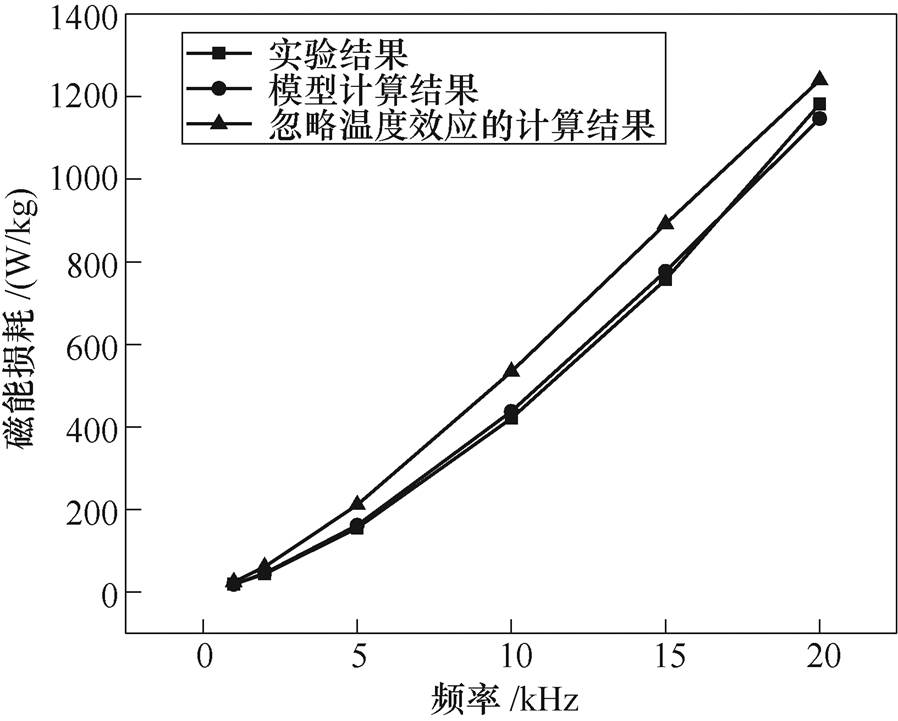
图10 不同频率下损耗实验结果与计算结果对比(Bm=0.06T, DT=80℃)
Fig.10 Comparison of loss experiment results and calculation results at different frequency (Bm=0.06T, DT=80℃)
图8所示为在频率f =10kHz、磁通密度幅值Bm= 0.06T时,不同温度DT下,磁能损耗实验结果和模型计算结果的对比。在温度DT为20℃、40℃、60℃、80℃时相对误差分别为0.18%、0.01%、2.26%、4.02%。可以发现,当频率f和磁通密度幅值Bm一定时,磁能损耗与温度大致呈线性相关(相对误 差=|实验结果-模型计算结果|/实验结果×100%)。
图9所示为在频率f=10kHz、温度DT=80℃时,不同磁通密度幅值Bm下,磁能损耗实验结果、模型计算结果以及忽略温度效应的计算结果的对比。在磁通密度幅值Bm为0.04T、0.06T、0.07T时,考虑温度效应的模型计算结果相对误差分别为4.03%、4.02%、1.07%;而不考虑温度效应的计算结果相对误差分别为32.46%、26.92%、18.57%。可以看出,忽略温度效应时的计算结果误差较大,因此不能忽略温度这一因素对磁能损耗的影响。
图10所示为在磁通密度幅值Bm=0.06T、温度DT=80℃时,不同频率f下,磁能损耗实验结果、模型计算结果以及忽略温度效应的计算结果的对比图。在频率f为1kHz、5kHz、10kHz、20kHz时,考虑温度效应的模型计算结果相对误差分别为1.66%、4.58%、4.02%、2.98%;而不考虑温度效应的计算结果相对误差分别为30.2%、36.36%、26.92%、49.42%。不难看出,忽略温度效应时的计算结果误差较大,温度会影响自发磁化区域中磁畴的状态及运动,所以材料在励磁磁场中能量的损耗受温度影响较大,不能忽略,否则会产生较大误差。
由图8~图10可以看出,考虑温度效应所建立的变温条件下的变系数高频磁能损耗计算模型,具有较高的精度,平均相对误差约为2.6%,验证了本文所提的变系数磁能损耗计算模型的准确性和可行性,但仍存在部分误差的可能因素为实验测试系统的准确度有限以及样品受振动、应力等因素的影响。
本文通过搭建温度可控的高频磁特性测试系统,测试并分析了不同温度条件下TbDyFe合金在不同励磁频率和磁通密度幅值下的动态磁特性,建立了考虑温度效应的变系数高频磁能损耗计算模型,主要结论如下:
1)当磁通密度幅值Bm≤0.07T、频率f≤20kHz时,随着环境温度从10℃增加到80℃,动态磁滞回线横向变窄,振幅磁导率逐步增加,矫顽力和磁能损耗逐步减少。
2)提出一种计及温度变化的磁致伸缩材料的高频磁能损耗计算模型。模型通过引入温度有关项对损耗系数进行修正;并且综合考虑了高频磁滞特性和趋肤效应的影响,引入了损耗附加磁通密度项及损耗附加频率项,从而建立了可以有效考虑温度效应的变系数高频磁能损耗计算模型。
本文的研究结果面向实际工程应用,可为磁致伸缩材料在实际工作中的高频损耗预测、温控系统设计及产品优化提供数据支持和理论支撑。
参考文献
[1] 刘素贞, 王淑娟, 张闯, 等. 钢板电磁超声表面波的仿真分析及缺陷定量检测[J]. 电工技术学报, 2020, 35(1): 97-105.
Liu Suzhen, Wang Shujuan, Zhang Chuang, et al. Simulation analysis and defect quantitative detection of electromagnetic ultrasonic surface wave of steel plate[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 97-105.
[2] 黄文美, 薛胤龙, 王莉, 等. 考虑动态损耗的超磁致伸缩换能器的多场耦合模型[J]. 电工技术学报, 2016, 31(7): 173-178.
Huang Wenmei, Xue Yinlong, Wang Li, et al. Multi- field coupling model of giant magnetostrictive trans- ducer considering dynamic loss[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 173-178.
[3] 周景涛, 何忠波, 刘国平, 等. 惯性式超磁致伸缩直线驱动器建模与实验[J]. 中国电机工程学报, 2020, 40(10): 3350-3359.
Zhou Jingtao, He Zhongbo, Liu Guoping, et al. Modeling and experiment of inertial giant magneto- strictive linear actuator[J]. Proceedings of the CSEE, 2020, 40(10): 3350-3359.
[4] 洪兴, 张洪平, 赵栋梁. 超磁致伸缩材料的温度性能研究进展[J]. 金属功能材料, 2007(4): 32-35.
Hong Xing, Zhang Hongping, Zhao Dongliang. Research progress on the temperature performance of giant magnetostrictive materials[J]. Functional Metal Materials, 2007(4): 32-35.
[5] 段娜娜, 徐伟杰, 李永建, 等. 一种考虑温度和压力影响的磁滞模型及其实验验证[J]. 电工技术学报, 2019, 34(13): 2686-2692.
Duan Nana, Xu Weijie, Li Yongjian, et al. A hysteresis model considering the effects of temper- ature and pressure and its experimental verification[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2686-2692.
[6] 冯端. 固体物理学大辞典[M]. 北京: 高等教育出版社, 1995.
[7] Zheng Xiaojiang, Sun Le. A nonlinear constitutive model of magneto-thermo-mechanical coupling for giant magnetostrictive materials[J]. Journal of Applied Physics, 2006, 100(6): 189.
[8] Albach M, Durbaum T, Brockmeyer A, et al. Calculating core losses in transformers for arbitrary magnetizing currents a comparison of different approaches[C]//Power Electronics Specialists Con- ference(PESC Record), Baveno, Italy, 1996: 1463-1468.
[9] 郜春艳, 黄文美, 刘卓锟, 等. Terfenol-D高频磁滞特性测试与分析[J]. 传感技术学报, 2018, 31(4): 518-522.
Gao Chunyan, Huang Wenmei, Liu Zhuokun, et al. Terfenol-D high-frequency hysteresis characteristics test and analysis[J]. Journal of Transducer Techno- logy, 2018, 31(4): 518-522.
[10] 翁玲, 常振, 孙英, 等. 不同磁致伸缩材料的高频磁能损耗分析与实验研究[J]. 电工技术学报, 2020, 35(10): 2079-2087.
Weng Ling, Chang Zhen, Sun Ying, et al. High- frequency magnetic energy loss analysis and experimental research of different magnetostrictive materials[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2079-2087.
[11] 黄文美, 吴晓晴, 李亚芳, 等. TbDyFe合金的高频动态磁特性及损耗特性分析[J]. 仪器仪表学报, 2020, 41(1): 215-222.
Huang Wenmei, Wu Xiaoqing, Li Yafang, et al. High frequency dynamic magnetic characteristics and loss characteristics analysis of TbDyFe alloy[J]. Journal of Instrumentation, 2020, 41(1): 215-222.
[12] Bertotti G. General properties of power losses in soft ferromagnetic materials[J]. IEEE Transactions on Magnetics, 2002, 24(1): 621-630.
[13] 赵志刚, 胡鑫剑. 考虑畸变磁通及局部磁滞回环影响的层叠铁心损耗有效算法及验证[J]. 中国电机工程学报, 2019, 39(24): 7436-7443, 7517.
Zhao Zhigang, Hu Xinjian. Effective algorithm and verification of laminated core loss considering the effects of distorted magnetic flux and local hysteresis loops[J]. Proceedings of the CSEE, 2019, 39(24): 7436-7443, 7517.
[14] 刘刚, 孙立鹏, 王雪刚. 正弦及谐波激励下的铁心损耗计算方法改进及仿真应用[J]. 电工技术学报, 2018, 33(21): 4909-4918.
Liu Gang, Sun Lipeng, Wang Xuegang. Improvement of core loss calculation method under sine and harmonic excitation and simulation application[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4909-4918.
[15] 迟青光, 张艳丽, 陈吉超, 等. 非晶合金铁心损耗与磁致伸缩特性测量与模拟[J]. 电工技术学报, 2021, 36(18): 3876-3883.
Chi Qingguang, Zhang Yanli, Chen Jichao, et al. Measurement and modeling of loss and magnetostrictive properties for the amorphous alloy core[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3876-3883.
Analysis of High Frequency Magnetic Properties and Loss Characteristics of TbDyFe Alloy under Variable Temperature
Abstract The giant magnetostrictive material TbDyFe alloy has temperature-sensitive characteristics. In this paper, the dynamic magnetic characteristic curves of TbDyFe alloy are measured under variable temperature conditions at different frequencies f and magnetic density amplitude Bm. When the frequency f and magnetic density amplitude Bm are fixed, with the increase of the ambient temperature (from 10℃ to 80℃), the amplitude permeability gradually increases, the dynamic hysteresis loop becomes narrower laterally, the required magnetic field strength decreases, and the magnetic energy loss gradually decreases. Since the existing loss calculation model cannot effectively characterize the temperature effect that leads to errors in the loss calculation results, a high-frequency loss calculation model for magnetostrictive materials under variable temperature conditions is proposed. The model corrects the loss coefficients by introducing temperature-related terms. Considering the influence of high-frequency hysteresis characteristics and skin effect, the loss additional magnetic flux density terms and loss additional frequency terms are introduced. Accordingly, an improved loss calculation model that can effectively consider the temperature effect is established. The comparison of measured and calculated results verifies the accuracy and feasibility of the model.
keywords:TbDyFe alloy, temperature effect, high-frequency dynamic hysteresis, magnetic energy loss, magnetic permeability amplitude
DOI: 10.19595/j.cnki.1000-6753.tces.201173
中图分类号:TM274
国家自然科学基金资助项目(51777053)。
收稿日期 2020-09-06
改稿日期 2020-10-23
黄文美 女,1969年生,博士,教授,研究方向为磁性材料与器件、电机电器及其控制。E-mail: huzwm@hebut.edu.cn(通信作者)
夏志玉 女,1995年生,硕士研究生,研究方向为磁性材料与器件、电机电器及其控制。E-mail: 3276337138@qq.com
(编辑 陈诚)