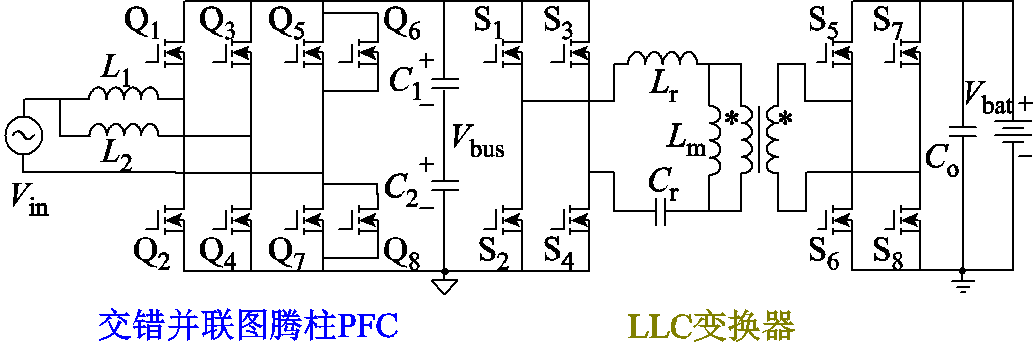
图1 两级式车载充电机拓扑
Fig.1 Topology of the two-stage on-board charger
摘要 图腾柱功率因数校正(PFC)被广泛应用于电动汽车充电机以提高充电效率。该文提出考虑零电压开通(ZVS)裕度和轻载频率限制的全范围ZVS控制模型,全电压范围内实现完全ZVS开通。分析了电流过零检测(ZCD)延迟对输入电流总谐波畸变率(THD)的影响,提出基于在线时间计算模型的ZCD延迟补偿方法,满载电流THD降低1.4%。针对两相交错相位误差,提出考虑开关周期变化量的相位误差补偿方法,提高交错精度,满载THD进一步降低0.5%。最后,搭建了一台3kW便携式充电机,验证所提控制策略的有效性,充电机前级图腾柱PFC最高效率为98.8%,整机最高充电效率为96.6%,满载THD为2.4%,相比补偿前降低1.9%。
关键词:便携式充电 临界电流模式 图腾柱功率因数校正 电流过零检测 交错并联
电动汽车因其高效的能源利用率而受到广泛关注[1-3],车载充电机作为电网与电动汽车动力电池的能量交互接口,成为电动汽车的核心零部件。与车载充电机相比,便携式充电机在出现故障时可以轻松更换,无需整车维修,售后维护成本显著降低,但要求质量轻、体积小、效率高,因此高效率和高功率密度是极其重要的指标[4]。
文献[5]提出了两级式SiC车载充电机拓扑架构,如图1所示,前级交错并联图腾柱功率因数校正(Power Factor Correction, PFC)变换器工作在连续电流模式(Continuous Current Mode, CCM),实现单位功率因数校正,后级全桥LLC谐振变换器作为电动汽车电池接口,实现高效率的高频隔离。

图1 两级式车载充电机拓扑
Fig.1 Topology of the two-stage on-board charger
CCM模式下图腾柱PFC工作在硬开关状态,器件开关损耗限制了开关频率的提升,从而导致PFC电感体积难以减小,限制了便携式充电机功率密度的提升。另一方面,高母线电压导致硬开关状态下CCM图腾柱PFC的开关损耗更大,充电机效率难以提高。临界导通模式(Critical Conduction Mode, CRM)图腾柱PFC具有零电压开关(Zero Voltage Switching, ZVS)能力,有助于提高开关频率,从而减小电感体积,提升充电机功率密度。
对于CRM图腾柱PFC,当Vin>0.5Vbus时,由于电感中存储的能量不足,无法自然实现ZVS[6]。为了保证全工频电压范围内实现ZVS,基本控制思路是延长同步整流(Synchronous Rectifier, SR)开关管的导通时间,使电感电流达到主开关管ZVS开通所需的负电流[7-8]。然而,文献[7]中ZVS只能在一个瞬间实现,开关管不能逐周期实现完全ZVS,因而产生部分开通损耗,导致效率降低。另外,轻载情况下,变换器开关频率将显著提高,严重影响轻载效率和控制的实现。文献[9]提出一种自适应控制方法,同时考虑了ZVS裕度和轻载频率限制,但控制比较复杂,且没有考虑零电流检测(Zero-Current-Detection, ZCD)延迟的影响。
CRM图腾柱PFC电感电流通常采用滞环电流控制[10-11]和变导通时间控制[12-13]两种控制方法。滞环电流控制可以在滞环内很好地调节电感电流峰值和谷值,但在高频应用中瞬时电流检测尤其具有挑战性。变导通时间控制通过ZCD获得电感电流过零信号,并通过实时计算的导通时间来实现开关管动作。该方法虽然避免了高频瞬时电流检测,但却对电流过零信号的准确检测有一定依赖,在实际应用中,ZCD电路、驱动电路及数字控制器中都存在信号传播延迟[14],实际ZCD存在延迟时间td,该延迟时间将导致SR延时导通时间过长,电感电流偏离正常轨迹,进而影响输入电流总谐波畸变率(Total Harmonic Distortion, THD)。
文献[14]提出了传统CRM Boost PFC的ZCD延迟补偿方法,根据数值关系,用两个电感电流过零点之间的时间差减去ZCD延迟时间。然而,图腾柱PFC软开关控制中,由于存在SR管延时导通时间tex,且tex与ZCD延迟td没有定量数值关系,因此该方法不适用于图腾柱PFC。
另外,CRM图腾柱PFC的另一个缺点是电流纹波大,导致更高的导通损耗及恶劣的差模噪声。采用两相交错并联技术,利用纹波消除效应,可以有效减小总输入电流纹波,同时减小滤波器体积[15-16]。然而,CRM图腾柱PFC的开关频率是时变的,导致精确的交错控制难以实现,文献[8]分析了移相时间为时钟周期整数倍所导致的离散相位误差对THD和差模噪声的影响,但没有考虑由于开关周期变化量所引起的交错相位误差。
针对便携式充电机前级CRM图腾柱PFC,本文提出考虑ZVS裕度和频率限制的全范围ZVS控制模型,在全电压范围内实现完全ZVS开通,轻载状态下限制最高开关频率,提高轻载效率;提出基于在线时间计算模型的ZCD延迟补偿方法,改善输入电流的THD。针对两相交错并联相位误差,提出考虑开关周期变化量的相位误差补偿方法,提高相位交错精度,进一步降低THD。最后,搭建了一台3kW充电机样机,验证了所提控制策略的有效性。
为了在全电压范围内完全实现ZVS开通并提高轻载效率,提出了综合考虑ZVS裕度和频率限制的在线时间计算ZVS控制模型,该模型适用于全输入电压和全负载范围的ZVS控制。
便携式充电机前级CRM图腾柱PFC电路如图2所示,Q1~Q4为高频开关管,Q5和Q6为工频管,Rs为ZCD检测电阻。
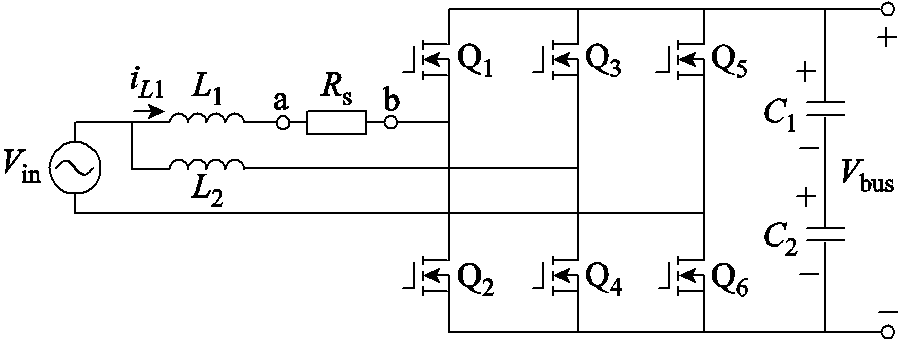
图2 交错并联CRM图腾柱PFC
Fig.2 Interleaved CRM totem pole PFC
图3所示的理论工作波形和状态平面轨迹说明了全范围ZVS CRM图腾柱PFC的基本工作原理,为简化分析,这里只讨论单路工作的基本原理。另外,本文所有的分析都是基于输入电压正半周期展开讨论,对负半周期的分析与正半周期相类似,唯一的区别是主开关管和SR管的角色互换。
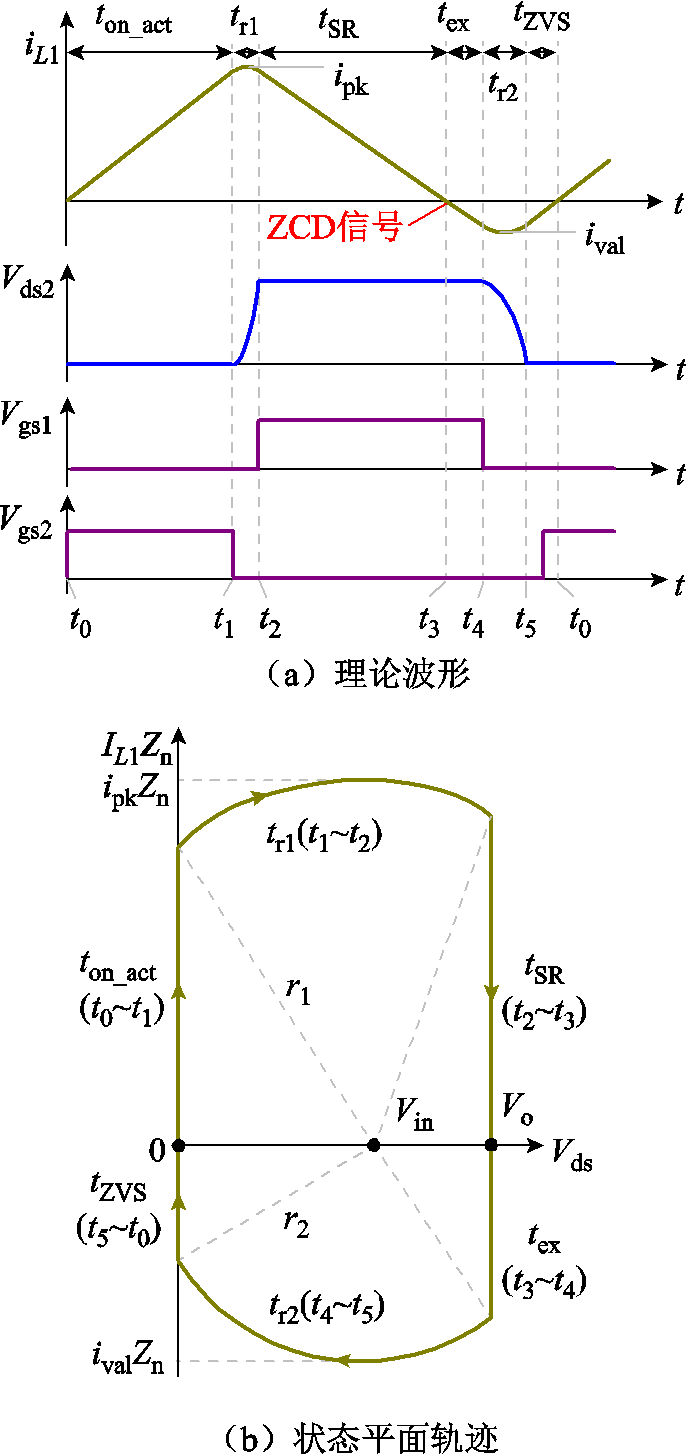
图3 理论波形和状态平面轨迹
Fig.3 Theore tical waveforms and state plan trajectory
阶段1[t0, t1]:对应主开关管导通时间ton_act,此阶段主开关管Q2导通,SR管Q1关断,电感电流从0线性上升。
阶段2[t1, t2]:对应谐振时间tr1,此时间间隔内开关管Q1和Q2均关断。电感L1与开关管结电容Coss谐振,Q2漏源极电压Vds2从0充电至Vbus,此阶段内电感电流峰值为ipk。
阶段3[t2, t3]:对应SR管开通时间tSR,在此时间间隔内,开关管Q1导通,Q2关断,电感电流iL1线性下降到0,产生ZCD信号。
阶段4[t3, t4]:对应SR管Q1延长导通时间tex,Q1仍然导通,Q2关断,电感电流iL1从0线性下降。
阶段5[t4, t5]:对应谐振时间tr2,在此时间间隔内Q1和Q2均关断。电感L1与开关管结电容Coss谐振,Vds2从Vbus放电到0,电感电流谷值为ival。
阶段6[t5, t0]:对应ZVS时间tZVS,此阶段内Vds2被钳位到零,Q2在tZVS时间内可以实现零电压开通。
根据单个开关周期内的工作原理分析,基于ZCD信号的开关管动作时刻如图4所示,以ZCD信号为DSP时基计数器置零点,需要分别实时计算SR开关管Q1的关断时刻tsr_off、开通时刻tsr_on、主开关管Q2的开通时刻tact_on及关断时刻tact_off。
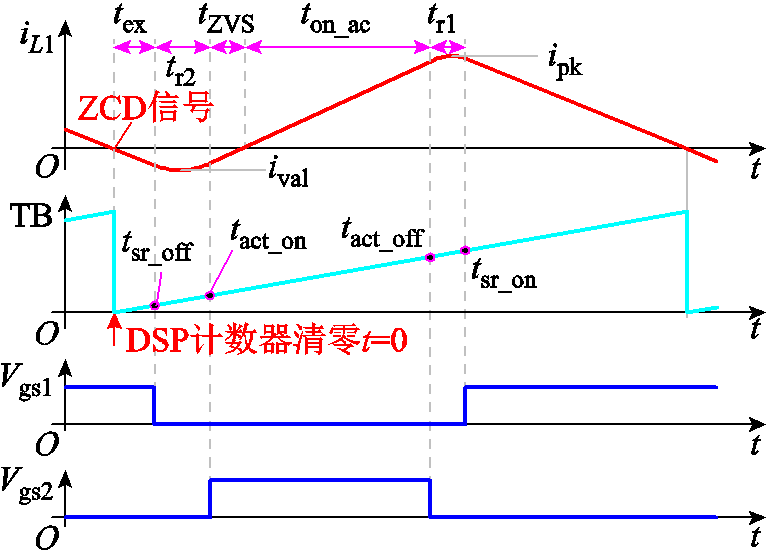
图4 基于ZCD信号的开关管动作时刻
Fig.4 MOSFET action moment based on ZCD single
正半周期内主开关管动作时刻可表示为
 (1)
(1)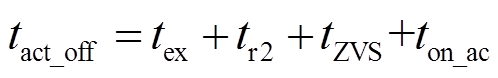 (2)
(2)
其中,主开关导通时间ton_ac包括恒定部分ton_c和变化的部分ton_var。
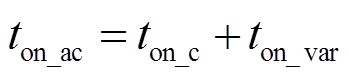 (3)
(3)SR管开通和关断时刻分别为
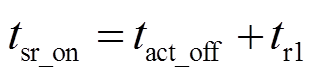 (4)
(4)
 (5)
(5)SR管驱动信号可由主开关管驱动在PWM模块中插入死区获得,死区时间分别为tr1和tr2。
图5给出了基于ZCD和在线时间计算的ZVS数字控制系统框图,控制系统包括两个环路,电压外环通过PI控制器调节母线电压并获得主开关管导通时间的恒定部分ton_c。电流内环以ZCD信号作为DSP定时器置零点,通过实时在线计算确定主开关管Q1开通关断时刻tact_on和tact_off,Q2的驱动信号由Q1的驱动在PWM模块中插入死区获得,死区时间分别为tr1和tr2。采用两路交错并联拓扑,从相定时器信号比主相滞后半个开关周期,因此高频开关管Q3和Q4的驱动信号分别比Q1和Q2滞后半个开关周期。另外,工频开关管Q5和Q6通过检测输入电压的极性来进行正负半周切换。
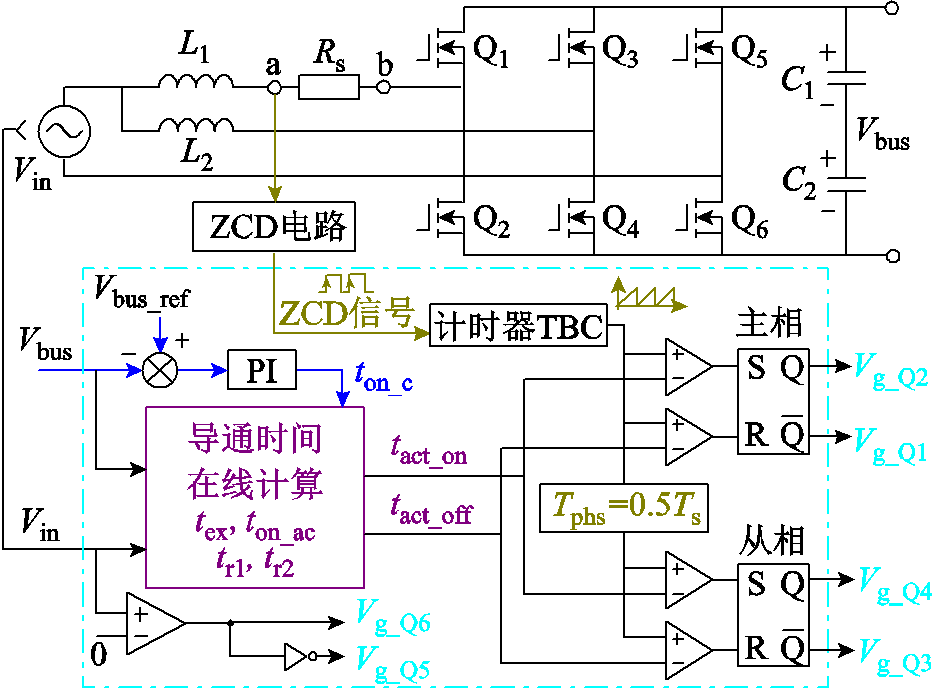
图5 数字控制框图
Fig.5 Digital control diagram
在传统CRM图腾柱PFC控制中,全输入电压范围内实现ZVS的条件为tZVS≥0,此时ZVS只能在一个瞬间实现,在实际应用中,tex随着Vin的变化而变化,无法保证在每个开关周期中完全实现ZVS。此外,轻载状态下,图腾柱PFC的开关频率将大大提高,过高的开关频率对轻载效率、控制器实现具有挑战性。因此本文将ZVS时间裕度和最高开关频率作为导通时间在线计算模型的约束条件,并由此确定SR管延长导通时间tex,谐振时间tr1、tr2,以及主开关的导通时间的变化部分ton_var。
由图3状态平面轨迹,ZVS时间tZVS和开关频率都与tr2阶段的谐振半径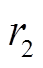 有关,
有关,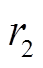 越大则tZVS越长,开关频率越低。因此,可以将谐振半径
越大则tZVS越长,开关频率越低。因此,可以将谐振半径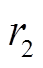 作为约束ZVS时间和最高开关频率的中间变量。
作为约束ZVS时间和最高开关频率的中间变量。
SR管延长导通时间tex与谐振半径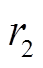 的关系为
的关系为
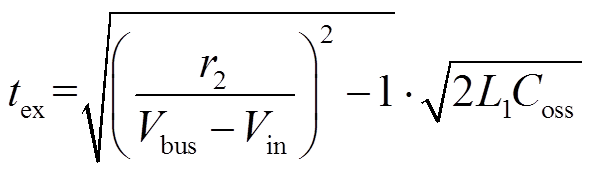 (6)
(6)电感电流谷值ival和谐振半径r2的关系为
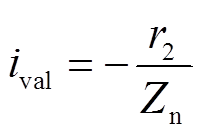 (7)
(7)
式中,Zn为特征阻抗,即
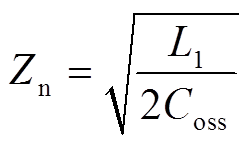 (8)
(8)电感峰值电流ipk由谷电流ival和电感的平均电流iavg决定,公式为
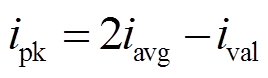 (9)
(9)
电感平均电流为
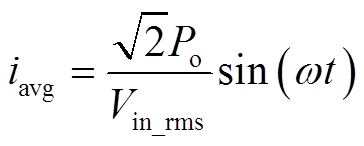 (10)
(10)式中,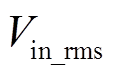 为
为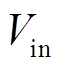 的有效值。
的有效值。
主开关管导通时间ton_ac时间段内电感电流线性上升,峰值电流ipk可用ton_ac表示为
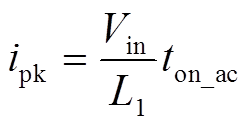 (11)
(11)由式(7)~式(11),可得
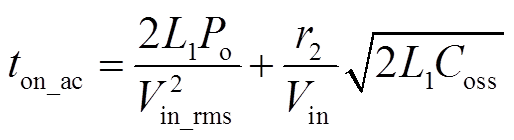 (12)
(12)
根据状态平面轨迹,ZVS时间裕度tZVS及谐振时间tr1、tr2可表示为
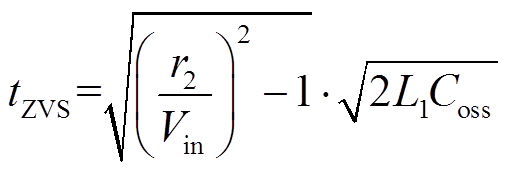 (13)
(13)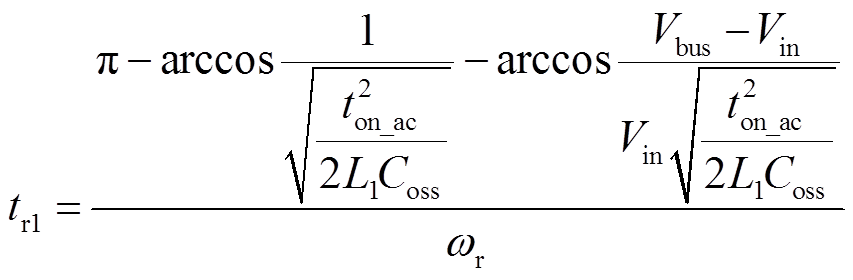 (14)
(14)
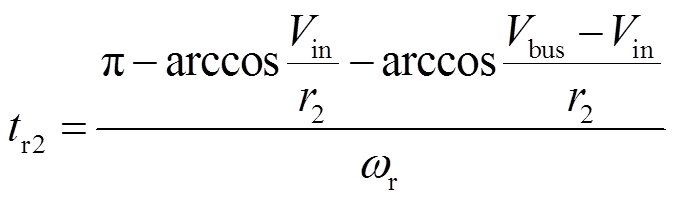 (15)
(15)
式中,ωr为谐振角速度,即
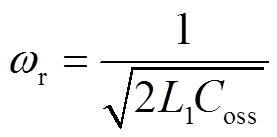 (16)
(16)(1)最小ZVS时间约束
根据最小的ZVS时间裕度要求,ZVS时间tZVS应不小于最小ZVS时间裕度tZVS_min,即
 (17)
(17)结合式(13)和式(17),可得满足ZVS最小时间裕度要求的谐振半径r2_ZVS约束为
 (18)
(18)
(2)最高开关频率约束
对于开关频率限制要求,应满足
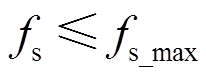 (19)
(19)为了简化开关周期Ts的计算,将电感电流近似为以ival为最小值、ipk为最大值的三角波。因此,开关周期Ts和开关频率fs可以表示为
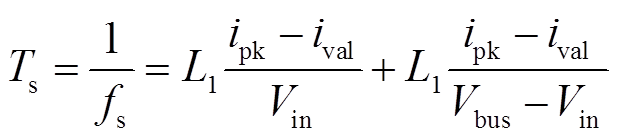 (20)
(20)
由式(7)~式(11),可得
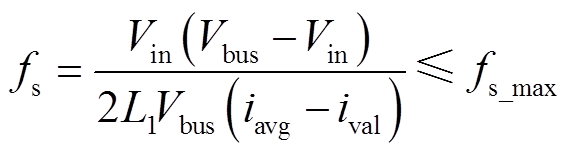 (21)
(21)由式(7)和式(21)可得满足最高开关频率约束的最小谐振半径为
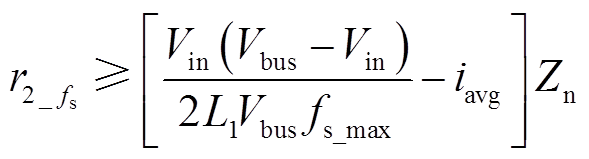 (22)
(22)
综上所述,为同时满足ZVS时间裕度和最大开关频率限制的要求,谐振半径r2应取两个约束条件下的更大值,由式(18)、式(22)可得
 (23)
(23)将式(23)代入式(6)、式(12)~式(15)可得同时满足ZVS裕度和最大开关频率限制的导通时间计算模型,通过实时计算即可获得各开关管精确的开通和关断时刻,从而实现全电压范围ZVS控制。
图6所示为ZCD信号检测电路,由高速比较器、RC滤波器和数字隔离器及DSP组成。ZCD电路通过检测电流采样电阻Rs两端的电压情况,获取电感电流过零点信息。
ZCD信号的检测与传输环节存在两部分延迟,第一部分为高速比较器、滤波器以及数字隔离器所产生的硬件延迟,该硬件延迟可以通过器件数据手册获得,如图6所示,高速比较器(ADCMP601)延迟时间约为3.5ns,RC滤波器延迟时间约为10ns,数字隔离器(ADUM1100)延迟时间约为12 ns;第二部分延迟为DSP信号处理延迟,ZCD电路对高dv/dt和di/dt噪声特别敏感,而错误的ZCD信号将导致开关误动作,导致过电流甚至损坏器件。为避免检测到错误的ZCD信号,通常在DSP中设置窗口保持时间,本文设置为90ns,因此产生DSP信号处理延迟。这两部分延迟时间共同组成ZCD延迟时间td,本文实际样机中td约为120ns。

图6 ZCD电路
Fig.6 ZCD circuit
ZCD延迟导致电感电流偏离理想运行轨迹,SR管关断时刻相比理想情况延迟td,电感电流谷值降低,由td引起的电感电流谷值变化量Δival为
 (24)
(24)为保持输出功率不变,外环PI控制器输出将会增加Δton_c以延长主开关管导通时间,且稳态下Δton_c为一个恒定值,Δton_c时间内对应电流变化量ΔiPI为
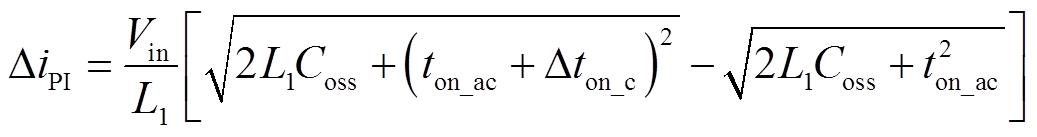 (25)
(25)
平均电流的变化量Δiavg可表示为
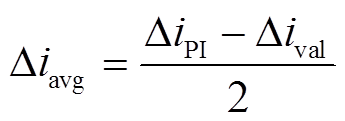 (26)
(26)Δival和ΔiPI随时间和输入电压的变化而变化,图7给出了由ZCD延迟导致的电感电流在半个工频周期内的变化曲线,可以看出,半个工频周期内电感平均电流变化量不为零,输入电流发生畸变。
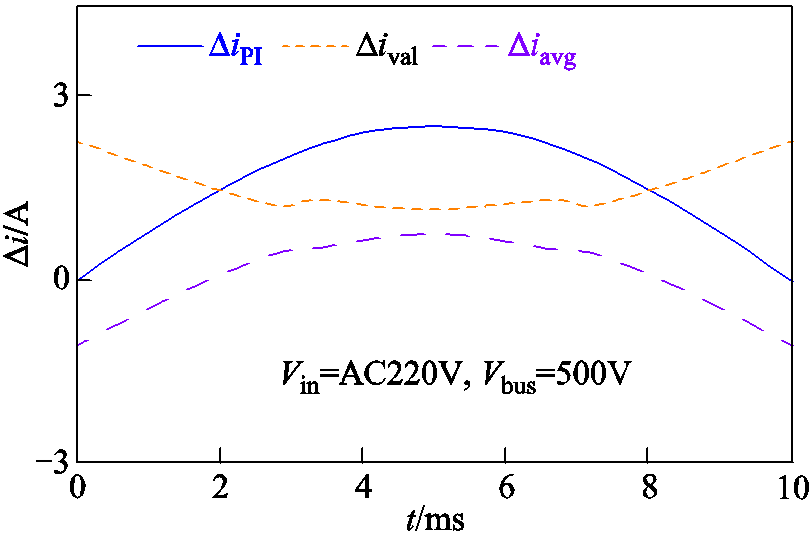
图7 ZCD延迟导致的电感电流变化
Fig.7 Inductor current change caused by ZCD delay
图8给出了满载条件下单路电感电流计算轮廓曲线,对比理想情况下的波形,可以看出,由于ZCD延迟时间td的影响,输入电压峰值处,电感电流峰值增加了2.3 A,输入电压过零点处,电感电流谷值下降2.1 A,电流纹波增大,产生额外的关断和导通损耗,且平均电流发生畸变,导致THD增大。

图8 理想情况与带延迟情况下的电感电流比较
Fig.8 Comparison of inductor currents between ideal case and the case with ZCD delay
为了补偿ZCD延迟,对所提CRM图腾柱PFC在线时间计算解析模型进行补偿。由于ZCD延迟增大了SR管的实际延长导通时间,因此可以在SR管原始延长导通时间tex的基础上减去ZCD延迟时间td,从而使总体延长导通时间保持不变。
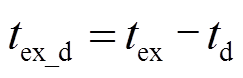 (27)
(27)根据所提在线时间计算解析模型,图9分别给出了满载、50%负载及30%负载下SR开关管延长导通时间tex,可以看出,tex随时间、负载等因素变化,且不能保证工频周期内tex一直大于td,当tex<td时,无法通过式(27)直接补偿。

图9 不同负载下SR开关管延长导通时间
Fig.9 Extended SR conduction time under different loads
当tex<td时,令tex=0,则此时SR管实际延长导通时间即为ZCD延迟时间td,由式(6)可得此时对应的谐振半径r2_d为
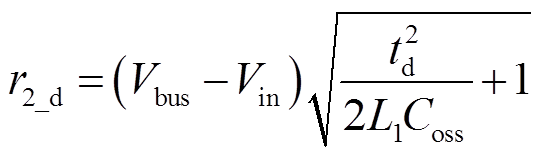 (28)
(28)将式(28)代入式(12)~式(15)即可求得主开关管导通时间tact_on,ZVS时间tZVS,以及谐振时间tr1、tr2,此时SR管延时导通时间tex=0。
综上所述,可将r2_d作为ZCD延迟补偿约束条件嵌入所提在线时间计算解析模型中,结合ZVS时间裕度约束以及最高频率限制约束,谐振半径r2取三个约束条件下的最大值
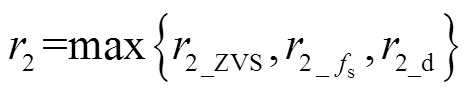 (29)
(29)此时原模型中的SR管延时导通时间tex修正为
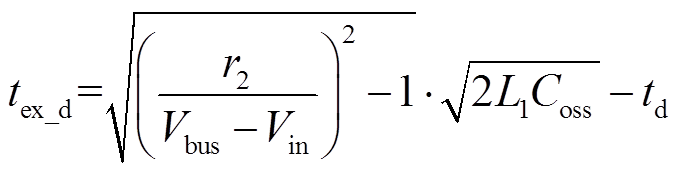 (30)
(30)
模型中主开关管导通时间tact_on、ZVS时间tZVS,以及谐振时间tr1、tr2计算模型仍然保持式(12)~式(15)不变。由式(30),当r2取r2_d时,tex_d自然为0。
将式(29)和式(30)代入所提在线时间计算解析模型中即可求得ZCD延迟补偿后的各阶段时间。
图10给出了ZCD延迟补偿后单路满载电感电流波形,可以看出,基于考虑ZCD延迟补偿的在线时间计算模型,电感电流平均值iavg保持理想情况不变,输入电流没有畸变。在tex>td区域,ZCD延迟td被完全补偿,电感电流纹波没有增加,在tex<td区域,电流纹波略有增大,但电感电流平均值仍保持不变。
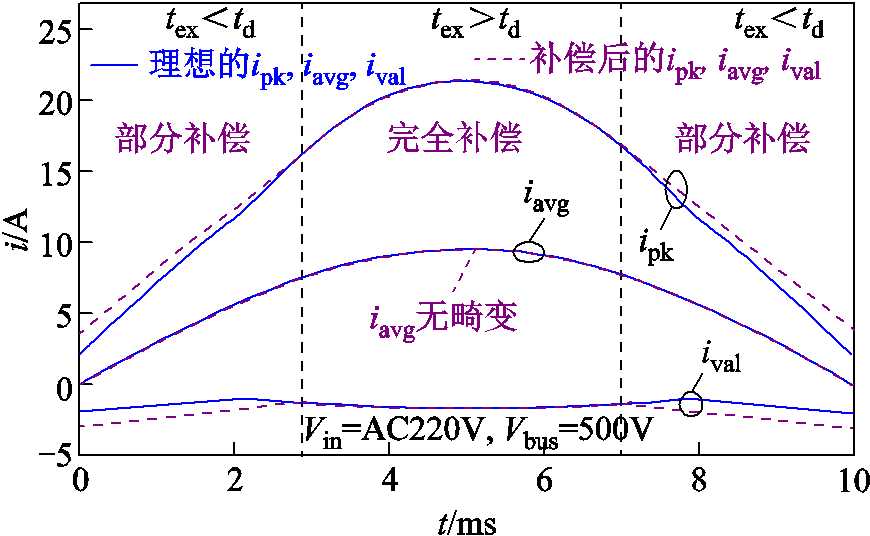
图10 延迟补偿后的满载电感电流波形
Fig.10 The full load inductor current waveforms after ZCD delay compensation
图11给出了ZCD延迟补偿前后输入电流THD计算结果对比,满载状态下补偿后的THD相比补偿前降低1.5%。
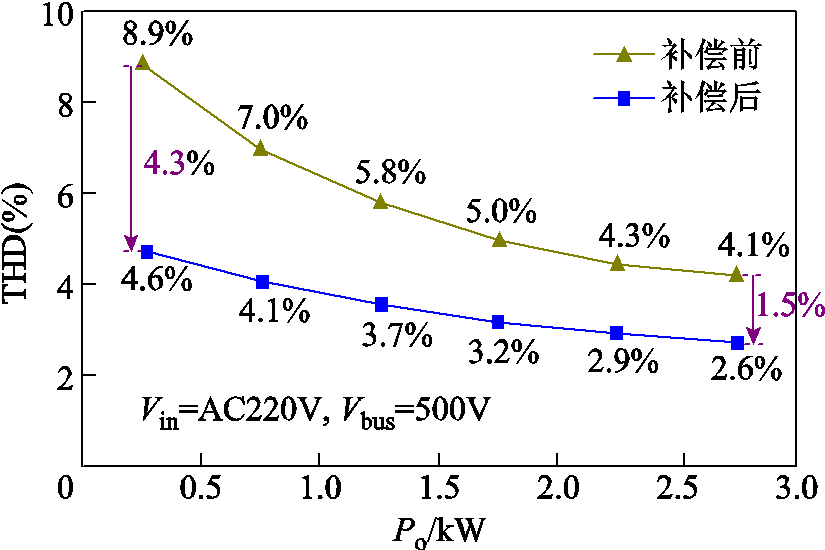
图11 ZCD延迟补偿前后输入电流THD计算结果对比
Fig.11 Comparison of the calculated THD before and after ZCD delay compensation
对于不同应用的实际系统,所提ZCD延迟补偿策略的模型是一致的,不受具体延迟时间数值影响。对于不同应用,ZCD电路硬件延迟部分可以根据实际硬件的数据手册获得,而DSP信号处理延迟时间保持为设定值不变,不随主控芯片的不同而变化,因此所提ZCD延时补偿控制策略具有通用性。
CRM模式下图腾柱PFC电流纹波大,限制了单路功率等级的提升。为满足便携式充电机功率需求,同时减小输入电流纹波,本文采用两路交错并联拓扑,控制框图如图5所示,采用开环控制方法,由主相ZCD信号触发时基计数器清零,从相计数器清零时刻比主相滞后0.5个开关周期,实现从相与主相的180°交错,典型波形如图12所示。
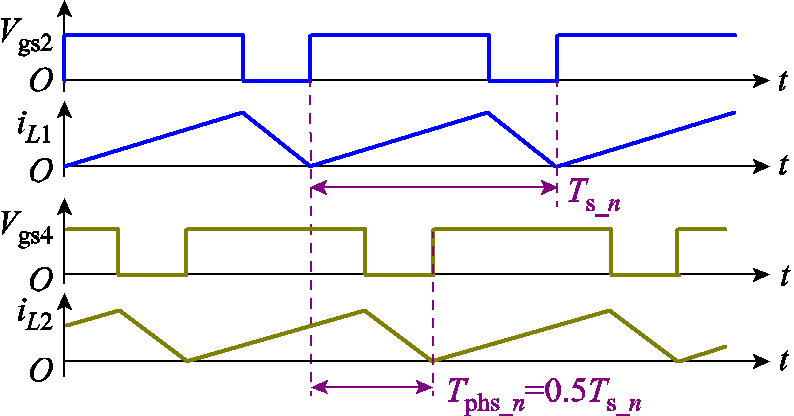
图12 两相交错并联典型波形
Fig.12 Typical waveforms of two-phase interleaving
如图12所示,为实现两相180°交错,理想状态下从相滞后主相时间为主相当前周期的一半,即
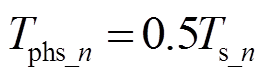 (31)
(31)然而,由于从相计数器清零时刻主相的当前开关周期还没有结束,因此此时采集的主相开关周期为前一个开关周期Ts_n-1,如图13所示。此时,从相滞后于主相的时间为
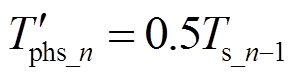 (32)
(32)
由于CRM图腾柱PFC的开关频率随时间变化,相邻两个开关周期时间不相等,因而导致了交错相位误差,如图13所示,两相交错角度偏离180°。
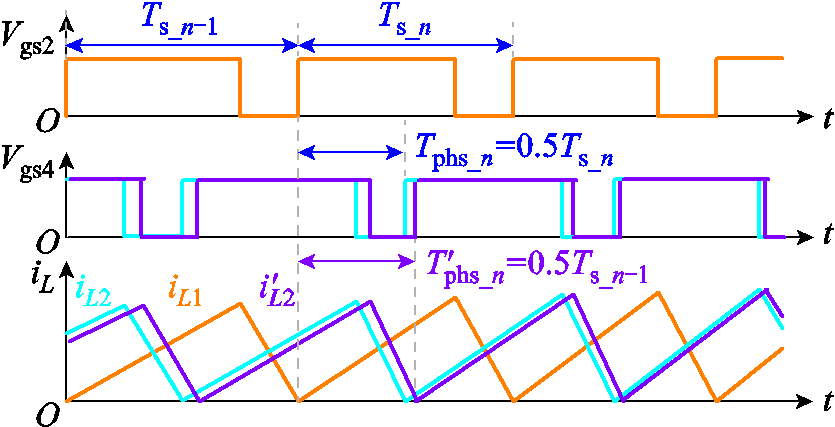
图13 交错相位误差的影响
Fig.13 Impact of interleaving phase error
根据所提在线时间计算模型,图14给出了半个工频周期内导通时间ton、关断时间toff以及开关周期Ts随时间变化的曲线,可以看出,开关周期随时间变化且越靠近交流电压过零点其变化率越大。
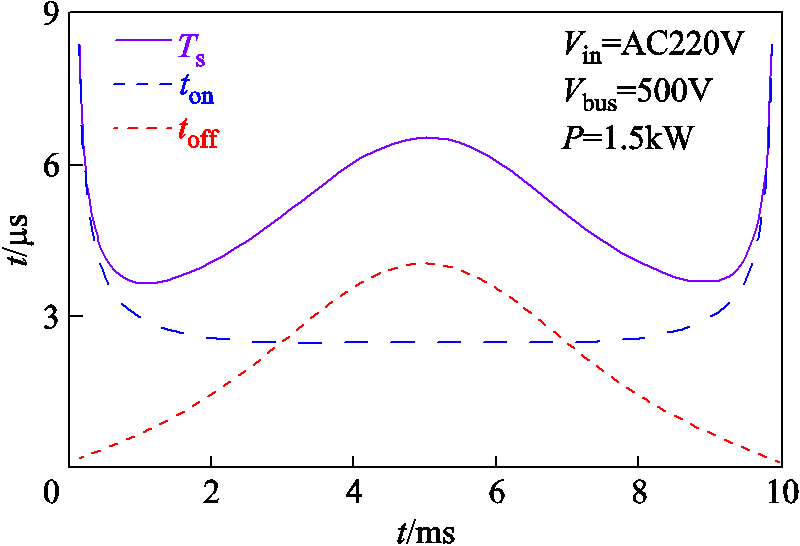
图14 半个工频周期器内开关周期曲线
Fig.14 Switching period curve within half line cycle
综合考虑效率和功率密度,便携式充电机前级CRM图腾柱PFC的工作频率设计为200~400kHz。选用TI公司DSP芯片(TMS320F280049C)实现所提数字控制算法,将DSP中ADC采样、PI计算、在线时间计算、PWM更新等控制环节串联执行,总数字控制周期约为12μs,考虑DSP的CPU利用率不高于80%,DSP中断周期设为15μs,即每2~4个开关周期执行一次控制中断。
图15为相邻开关周期和相邻控制周期下CRM图腾柱PFC开关周期变化率曲线,工频过零点死区时间设为200μs,相邻控制周期内最大变化率为8.8%,相邻开关周期内最大变化率为2.9%,该变化率将导致两相交错的角度偏离180°,电流纹波不能有效抵消,从而影响输入电流THD。
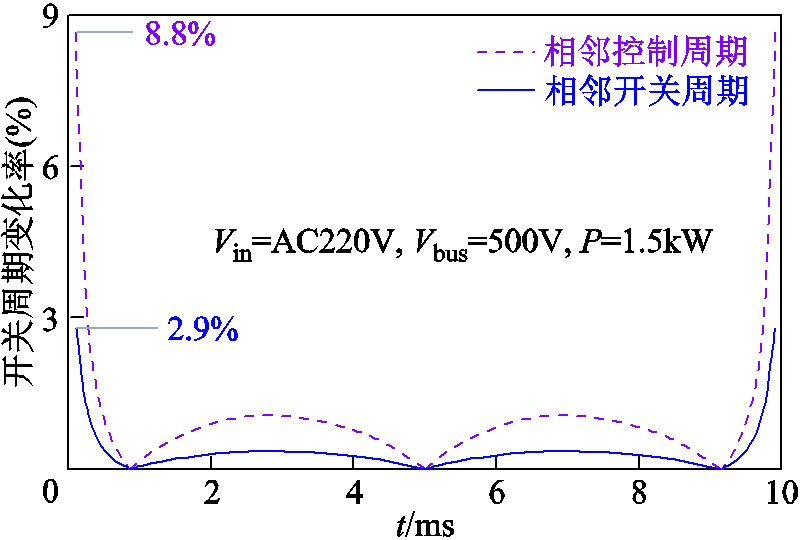
图15 半个工频周期器内开关周期的变化率
Fig.15 Change rate of switching period in half line cycle
虽然选用更高主频的主控芯片,提高控制频率,可以减小相位误差,但即使控制频率等于开关频率,过零点两侧的相位误差依然存在且不可忽略,而且更高主频的主控芯片必然导致成本显著增加。因此本文提出一种更通用的相位误差补偿方法。
交错相位误差补偿示意图如图16所示,相邻控制周期内检测到的开关周期变化量可以表示为
 (33)
(33)
图16 交错相位误差补偿
Fig.16 Interleaving phase error compensation
由于相邻开关周期的ΔTs变化极小,可以忽略,因此可以将ΔTs补偿到开关周期Ts中,即可获得补偿后的滞后时间
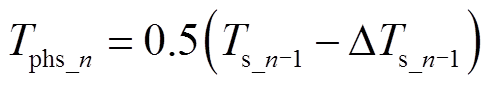 (34)
(34)如图16所示,将开关周期的变换量ΔTs补偿到交错控制的滞后时间Tphs中,即可消除开关周期变化率大的影响,提高交错精度,降低THD。
表1给出了不同主控芯片下相位误差补偿对比,开关周期测量时刻为输入电压工频周期15°时刻,输入电压AC220V,母线电压500V。由表1可以看出,中断周期由15μs增大为25μs时,补偿后的相位误差由0.6%增大为1.5%,补偿精度有所下降。但对于不同的主控芯片,相位误差补偿率均达到80%以上,因此本文所提相位误差补偿策略在不同主控芯片下具有通用性。
表1 不同主控芯片下的相位误差对比
Tab. 1 Phase error comparison under different MCUs

TMS320F280049中断周期15μsTMS320F28075中断周期20μsTMS320F28069中断周期25μs 补偿前补偿后补偿前补偿后补偿前补偿后 Ts_n-2/μs7.457.708.02 Ts_n-1/μs7.057.177.31 Ts_n/μs6.706.706.70 ΔTs_n-1/μs—0.40—0.53—0.71 Tphs_n/μs3.533.333.563.323.663.31 相位误差(%)5.20.66.30.99.31.5 补偿率(%)88.585.783.9
为了验证所提控制策略的有效性,本文搭建了一台3kW便携式充电机样机,如图17所示,采用CREE公司的SiC MOSFET(C3M0065090D)作为开关器件,充电机详细参数见表2。

图17 便携式充电机实验样机
Fig.17 Experimental prototype of portable charger
表2 便携式充电机电路参数
Tab.2 Circuit parameters of portable charger

参数数值 输出功率Po/kW3 输入电压Vin/VAC200~240 母线电压Vbus/V380~700 PFC电感L1,L2/μH37 母线电容Cbus/mF1.5 PFC开关频率fsw_PFC/kHz200~400 电池电压Vbat/V200~500 LLC谐振频率fr/kHz300 LLC开关频率fs_LLC/kHz290~400 励磁电感Lm/μH49.9 谐振电感Lr/μH12.8 谐振电容Cr/nF22
图18给出了充电机前级CRM图腾柱PFC的满载运行波形。由图中可以看出,输入电流被控制为良好的正弦波,功率因数PF达到0.998。
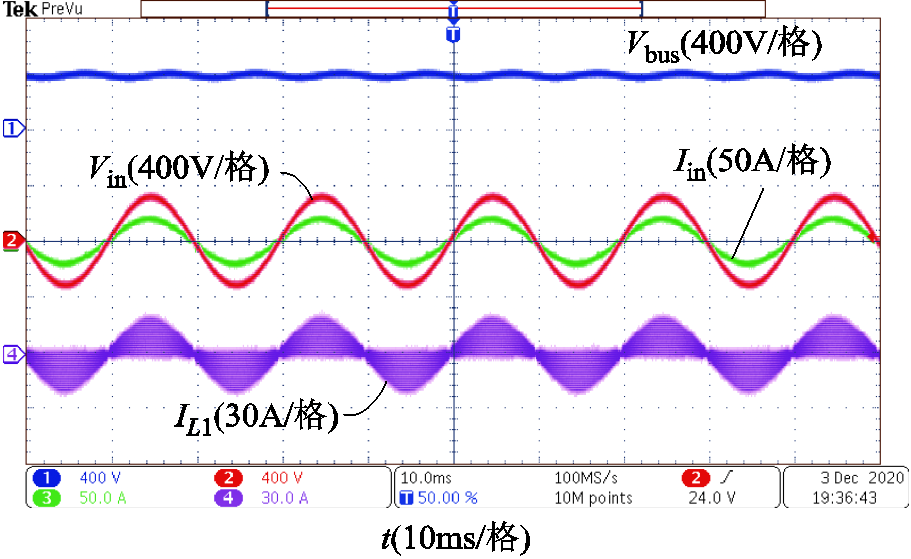
图18 CRM图腾柱PFC实验波形
Fig.18 Experimental waveforms of CRM totem-pole PFC
图19所示为未考虑ZVS裕度下的实验波形,主开关管开通时刻滞后于ZVS瞬间,开关管Q2开通时,Vds2不为零,只能实现部分ZVS。
图20给出了满载条件下考虑ZVS裕度的实验波形,设置最小ZVS开通时间裕度为30ns,软开关不再局限于一瞬间实现,可以看出全工频周期范围内开关管完全实现ZVS开通。

图19 无ZVS裕度实验波形
Fig.19 Experimental waveforms without ZVS margin

图20 考虑ZVS裕度的全范围软开关实现波形
Fig.20 Full range ZVS implementation waveforms with ZVS margin
图21给出了半载条件下最高开关频率限制实验波形,通过延长主管和SR管的导通时间,最高开关频率限制在400 kHz,避免了轻载下由于开关频率过高导致关断损耗过大,提高了轻载效率。
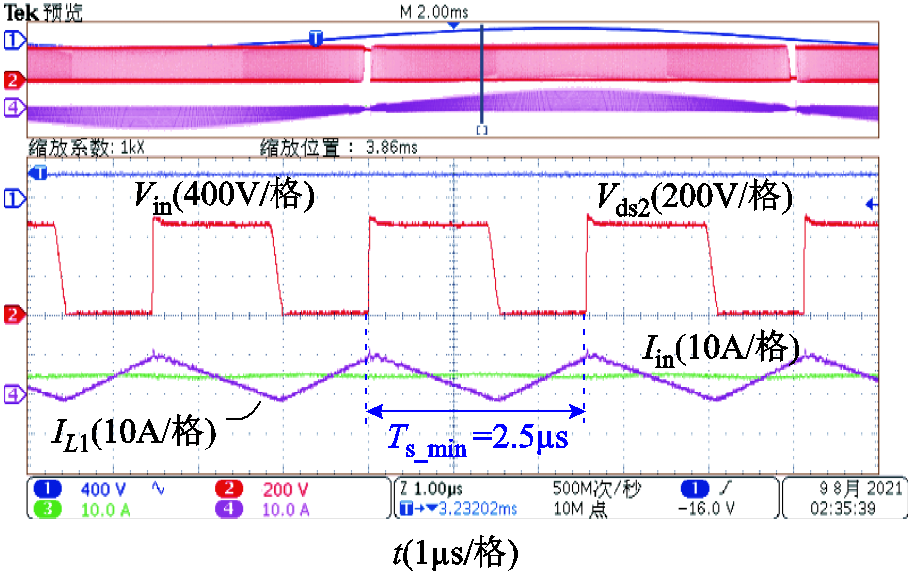
图21 半载最高频率限制400 kHz
Fig.21 Maximum frequency limit to 400 kHz at half load
图22给出了ZCD延迟补偿前后满载实验波形对比,输入电压AC220V,母线电压400V,补偿前输入电流存在明显畸变,电感电流峰值为23.1A。补偿后输入电流无畸变,电感电流峰值降低到20.8A,输入电流THD下降1.5%。
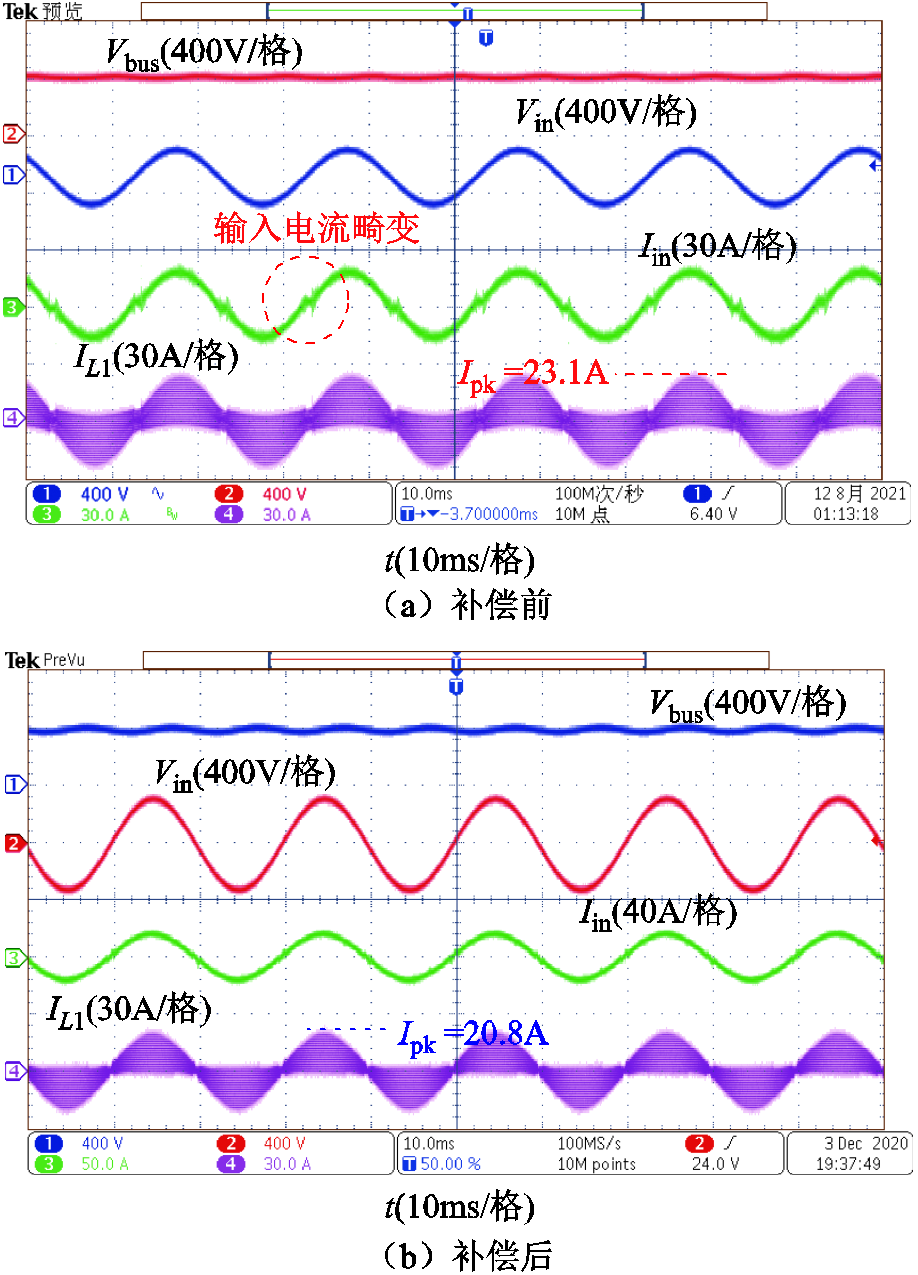
图22 ZCD延迟补偿前后实验波形对比
Fig.22 Comparison of experimental waveforms before and after ZCD delay compensation
图23给出了满载条件下交错相位误差补偿前后的实验波形。如图23a所示,无相位补偿条件下,从相滞后主相的时间Tphs大于主相周期的一半,两路交错相位误差为8.5%。如图23b所示,加入相位误差补偿后,相位误差降低到0.4%。
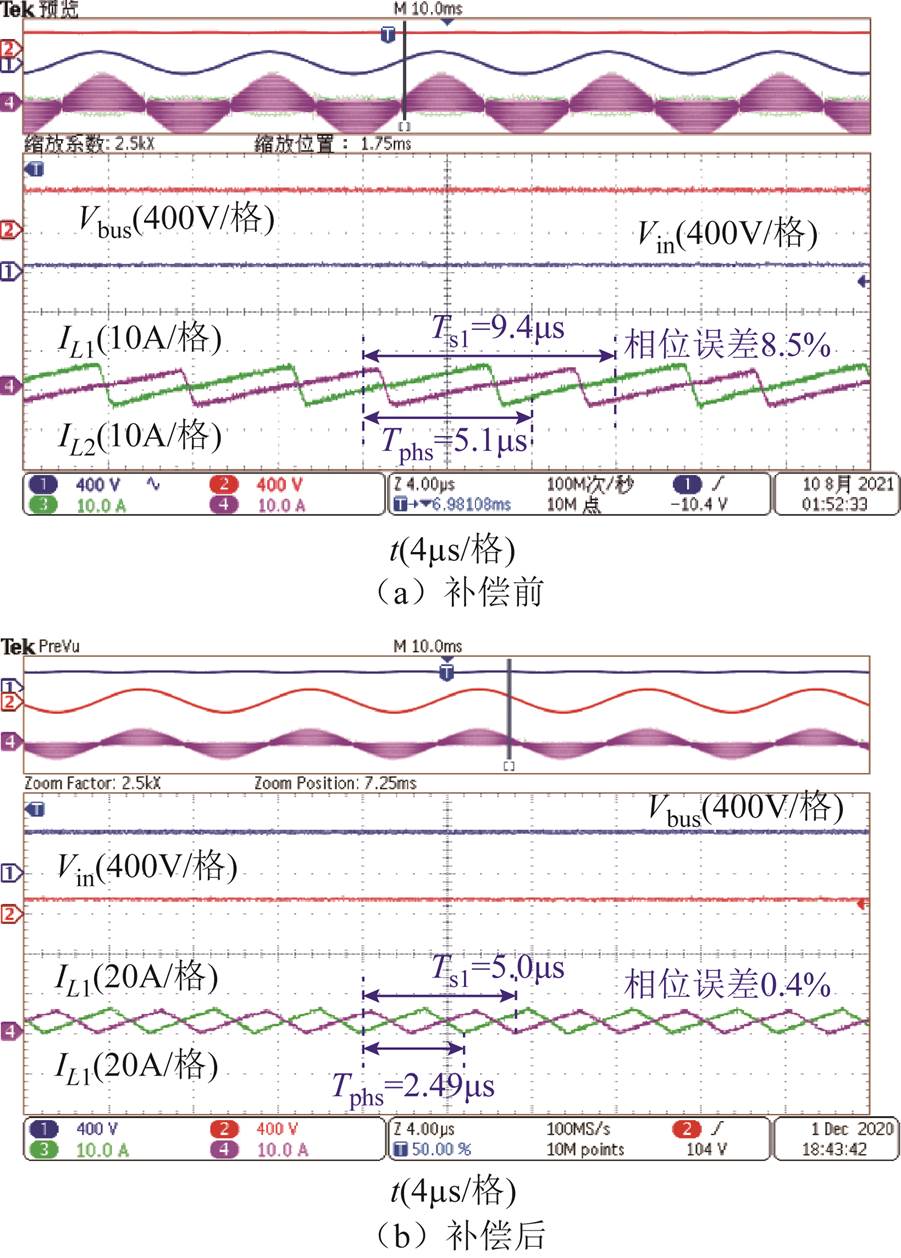
图23 交错相位误差补偿前后实验波形对比
Fig.23 Experimental waveforms comparison before and after interleaving phase error compensation
相位误差补偿前后输入电流波形对比如图24所示,补偿前由于存在相位误差,电流纹波不能有效抵消,输入电流过零点两侧存在较大电流纹波,补偿后两相交错180°,电流纹波有效抵消。
图25分别给出了三种情况下的输入电流THD对比,同时补偿情况下满载THD为2.4%,比无补偿时降低1.9%。500W负载下同时补偿时THD为4.3%,比无补偿时降低4.6%。
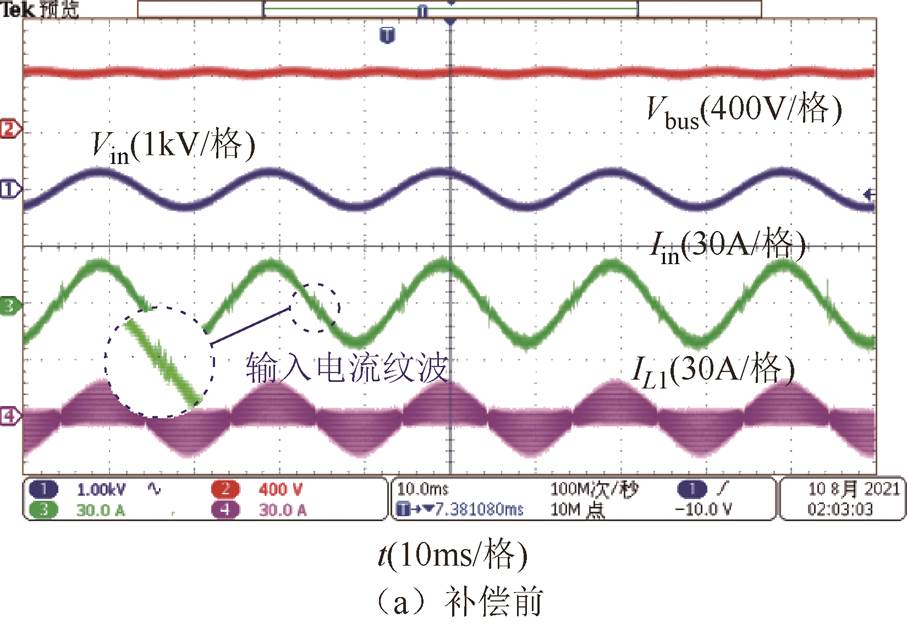
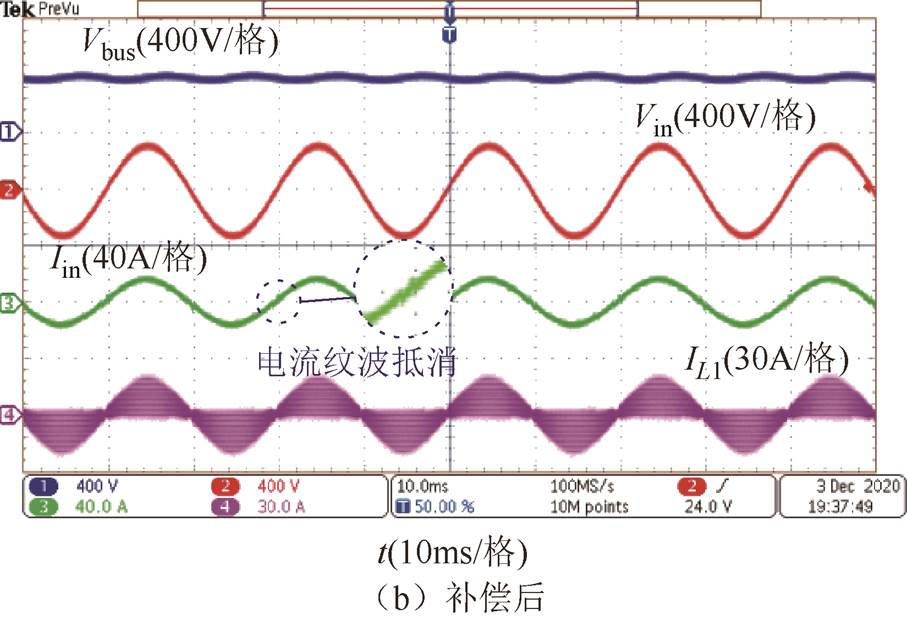
图24 交错相位补偿前后输入电流波形对比
Fig.24 Input current waveform comparison before and after interleaving phase error compensation
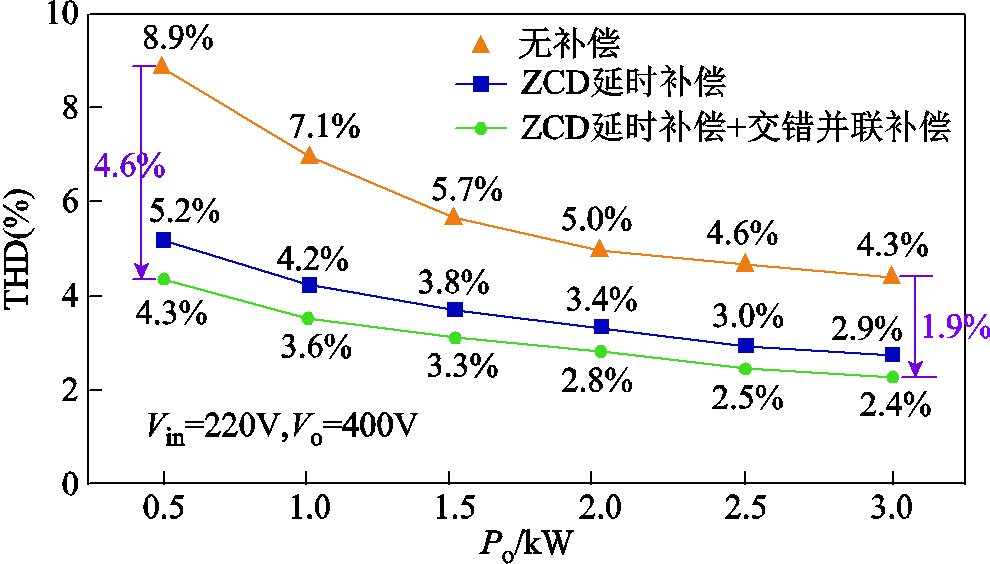
图25 输入电流THD测量结果对比
Fig.25 Comparison of measured input current THD
图26给出了充电机前级CRM图腾柱PFC效率曲线,400V母线电压下满载效率为98.6%,峰值效率为98.8%。轻载工作时,限制了最高工作频率,400 V母线电压,20%负载下的效率为98.2%。
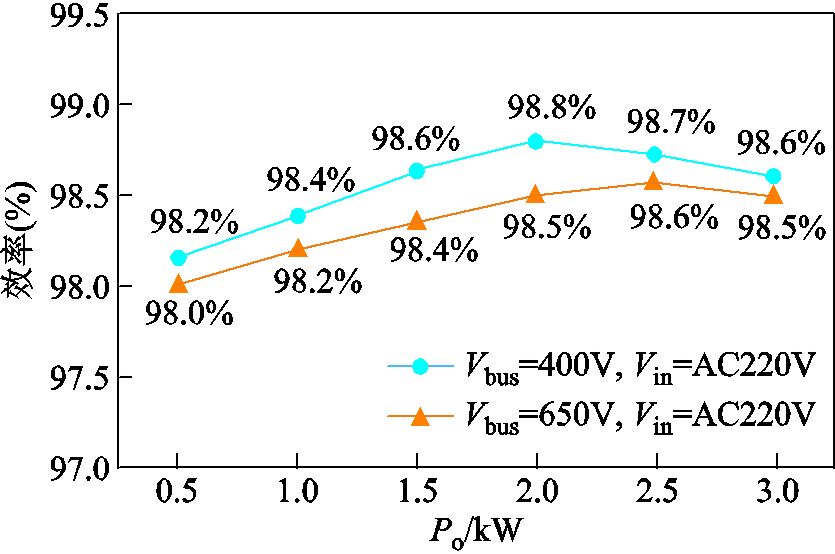
图26 CRM图腾柱PFC效率曲线
Fig.26 Efficiency curve of CRM totem-pole PFC
图27给出了便携式充电机后级LLC变换器满载实验波形,电池电压为350V,母线电压为500V,可以看出,LLC完全实现零电压开通。
图28给出了充电机整机充电效率曲线,350V电池电压下满载效率为96.2%,峰值效率为96.6%。
相比于文献[12]传统CRM Boost PFC变导通时间控制只能实现部分ZVS开通,本文所提在线时间计算控制模型实现了全电压范围ZVS开通;相比于文献[13]CRM图腾柱PFC控制模型未考虑轻载频率限制,本文在全范围ZVS控制的基础上增加了轻载频率约束,提高全负载范围充电效率;文献[14]ZCD延迟补偿方法仅适用于传统Boost PFC,本文提出适用于CRM图腾柱PFC的ZCD延迟补偿策略,在全范围ZVS控制的基础上,有效降低了输入电流THD。

图27 LLC实验波形
Fig.27 Experimental waveforms of LLC converter
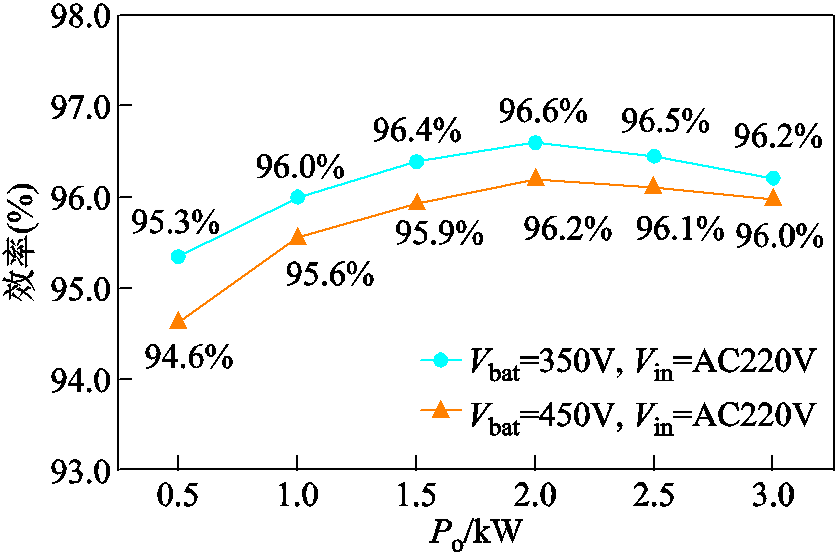
图28 便携式充电机整机效率
Fig.28 Charging efficiency of the portable charger
本文针对便携式充电机前级CRM图腾柱PFC,提出了综合考虑ZVS裕度和轻载频率限制的ZVS控制模型,全电压范围内实现完全ZVS开通,在轻载条件下限制了最高开关频率,提高了全负载范围的充电效率。分析了ZCD延迟对输入电流THD的影响,提出基于在线时间计算模型的ZCD延迟补偿方法,满载输入电流THD降低1.4%。分析了两相交错相位误差的影响,提出了考虑开关周期变化量的相位误差补偿方法,提高交错精度,满载THD进一步降低0.5%。最后,本文搭建了一台3kW便携式充电机实验样机,验证了所提全范围ZVS控制模型以及补偿控制方法的有效性,充电机前级图腾柱PFC最高效率为98.8%,整机最高充电效率为96.6%,满载THD为2.4%,比补偿前降低1.9%。
参考文献
[1] 银泽一, 王广柱, 程振兴. 基于模块化多电平变换器的插电式混合电动汽车系统充电控制策略[J]. 电工技术学报, 2020, 35(6): 1316-1326.
Yin Zeyi, Wang Guangzhu, Chen Zhenxing. Charge control strategy of plug-in hybrid electric vehicle system based on modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1316-1326.
[2] Khaligh A, D’Antonio M. Global trends in high-power on-board chargers for electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3306-3324.
[3] 张献, 白雪宁, 沙琳, 等. 电动汽车无线充电系统不同结构线圈间互操作性评价方法研究[J]. 电工技术学报, 2020, 35(19): 4150-4160.
Zhang Xian, Bai Xuening, Sha Ling, et al. Research on interoperability evaluation method of different coils in wireless charging system of electric vehicles[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4150-4160.
[4] Li Haoran, Wang Shengdong, Zhang Zhiliang, et al. Bidirectional synchronous rectification on-line calculation control for high voltage applications in SiC bidirectional LLC portable chargers[J]. IEEE Transactions on Power Electronics, 2021, 36(5): 5557-5568.
[5] Li Haoran, Zhang zhiliang, Wang Shengdong, et al. A 300kHz 6.6kW SiC bidirectional LLC Onboard charger[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2): 1435-1445.
[6] Marxgut C, Krismer F, Brotis D, et al. Ultraflat interleaved triangular current mode (TCM) single-phase PFC rectifier[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 873-882.
[7] Liu zhengyang, Li Bin, Lee F C, et al. High-efficiency high-density critical mode rectifier/inverter for WBG-device-based on-board charger[J]. IEEE Transactions on Industrial Electronics, 2017, 64(1): 9114-9123.
[8] Liu Zhengyang, Huang Zhengrong, Lee F C, et al. digital-based interleaving control for GaN-based MHz CRM totem-pole PFC[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(3): 808-814.
[9] Huang Qingyuan, Yu Ruiyang, Ma Qingxuan, et al. Predictive ZVS control with improved ZVS time margin and limited variable frequency range for a 99% efficient, 130-W/in3 MHz GaN totem-pole PFC rectifier[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 7079-7091.
[10] Yin Hao, Lang Tianchen, Li Xiang, et al. A hybrid boundary conduction modulation for a single-phase H-bridge inverter to alleviate zero-crossing distortion and enable reactive power capability[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 8311-8323.
[11] Fan Boran, Wang Qiong, Burgus Rolando, et al. Adaptive hysteresis current based ZVS modulation and voltage gain compensation for high-frequency three-phase converters[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 1143-1156.
[12] 周玉婷, 吴羽, 任小永, 等. 基于改进恒导通时间控制的临界连续导通模式Boost功率因数校正变换器[J]. 电工技术学报, 2021, 36(20): 4329-4338.
Zhou Yuting, Wu Yu, Ren Xiaoyong, et al. Improved constant on-time control of boundary conduction mode Boost power factor correction converter[J]. Transactions of China Electrotechnical Society, 2021, 36(20): 4329-4338.
[13] Sun Jingjing, Huang Xingxuan, Strain N N, et al. Inductor design and ZVS control for a GaN-based high efficiency CRM totem-pole PFC converter[C]//2019 IEEE Applied Power Electronics Conference and Exposition(APEC), Anaheim, 2019: 727-733.
[14] Ren Xiaoyong, Wu Yu, Guo Zhehui, et al. An online monitoring method of circuit parameters for variable on-time control in CRM Boost PFC converters[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1786-1797.
[15] 曹勇, 杨飞, 李春辉, 等. 不同耦合系数下的交错并联电流连续模式Boost功率因数校正变换器的传导电磁干扰[J]. 电工技术学报, 2019, 34(10): 2176-2186.
Cao Yong, Yang Fei, Li Chunhui, et al. Conducted electromagnetic interference of interleaved continuous current mode Boost power factor correction converter with different coupling coefficients[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2176-2186.
[16] 王议锋, 崔玉璐, 马小勇, 等. 一种交错并联双Buck全桥型双向并网逆变器[J]. 电工技术学报, 2019, 34(21): 4529-4539.
Wang Yifeng, Cui Yulu, Ma Xiaoyong, et al. An interleaved dual-Buck full-bridge type bidirectional grid-connected inverter[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4529-4539.
Compensation Control of Zero Current Detection Delay and Interleave Phase Error for CRM Totem-Pole Power Factor Correction in Portable Charging
Abstract Totem-pole power factor correction (PFC) is widely used in EV chargers to improve the charging efficiency. A full-range ZVS control model considering ZVS margin and light load frequency limitation is proposed in this paper, full ZVS operation is realized within full voltage range. The impact of zero-current-detection (ZCD) delay on the total harmonic distortion (THD) of input current is analyzed, and a ZCD delay compensation method based on the on-line time calculation model is proposed, the full load THD is reduced by 1.4%. For the phase error of two-phase interleaving, a phase error compensation method considering the change of switching period is proposed, which improves the interleaving accuracy and the full load THD is further reduced by 0.5%. Finally, a prototype of 3-kW portable charger is built to verify the effectiveness of the proposed control strategy. The maximum efficiency of the totem-pole PFC stage is 98.8%, and the maximum charging efficiency is 96.6%. The full load THD is 2.4%, which is 1.9% lower than that before compensation.
Keywords:Portable charging, critical conduction mode (CRM), totem-pole power factor correction (PFC), zero-current-detection (ZCD), interleave
DOI:10.19595/j.cnki.1000-6753.tces.211289
中图分类号:TM461
江苏省产业前瞻和关键核心技术基金资助项目(BE2019113)。
收稿日期 2021-08-15
改稿日期 2021-10-13
王生东 男,1989年生,博士研究生,研究方向为双向AC-DC变换技术、宽禁带器件高频功率变换技术。E-mail:wangsd@nuaa.edu.cn(通信作者)
李浩然 男,1991年生,博士,研究方向为双向DC-DC变换技术、高频功率变换技术。E-mail:haoranli@ahu.edu.cn
(编辑 郭丽军)