kV0.002 级多级励磁标准电压互感器设计与仿真分析kV0.002 级多级励磁标准电压互感器设计与仿真分析摘要 由于高压互感器绝缘设计较为困难，使得现有的标准电压互感器测量准确度难以得到有效的提升。该文以多级高低压混合励磁标准电压互感器电路为研究对象，结合多级励磁理论进行该电路在理想条件下的仿真分析。首先，根据该励磁方案建立其对应的等效电路；其次，根据该等效电路推导出互感器准确度计算公式；然后，结合实际需求，对
多级高低压混合励磁标准电压互感器进行理论参数计算，包括内阻抗与励磁阻抗参数计算；最后，根据上述的理论参数计算出该互感器的测量准确度，仿真结果表明该互感器结构的比差为-2.27×10−7%，角差为3.44×10−6%，该标准互感器足以满足准确度等级为0.002 级的要求，可尝试开发实物。
电压互感器是一种为测量仪表传送信号的变压器，在电力市场运行中主要用于电能计量，其准确度关系到电量交易的公平与公正[1]，而标准电压互感器通过对所测量的互感器校验分析确保了电量交易公平公正。标准电压互感器与常用的测量互感器类似，均包括单级互感器与双级互感器，但标准电压互感器准确度要高于测量互感器。目前单级互感器测量准确度在高电压环境下难以得到有效的提升[2]。相比于此，双级电压互感器由于其特定结构优势，通过补偿单级互感器的测量结构，使得测量准确度可以有效提升。现有的双级电压互感器包含高压励磁和低压励磁两种方式。在高压励磁方面，双级电压互感器国内外最高能达到10kV，准确度等级为0.001 级[3-4]；低压励磁可以降低高压互感器某一级励磁绕组与比例绕组的绝缘设计，对于110kV 的电压，其测量准确度等级可以达到0.002 级[5]。然而在更高电压等级下，电压互感器设计还未获得相近的准确度等级。
对于高电压等级电压互感器的设计，绝缘问题是其中问题关键之一[6]。许多学者考虑了该问题下准确度提高的可能性。彭时雄等提出一种特定的圆形铁心线圈绝缘结构，通过分段绕制高压一次绕组及设计补偿线路，使得在35kV 下能达到0.001 级[7]；Shao Haiming 等在励磁方面采用分离辅助互感器铁心为叠绕的环形铁心进行低压励磁的双级电压互感器结构，该结构可以有效地降低第一级互感器的绝缘要求，且在
达到0.001 级的测量准确度等级[8-10]。上述研究均采用低压励磁进行双级电压互感器设计，这表明低压励磁设计可以有效降低高压互感器的绝缘设计难度。
从单级电压互感器到双级电压互感器发展的历程看来，增加电压互感器级数可以对单级或双级电压互感器进行误差补偿。本文将低压励磁单级电压互感器与高压励磁双极电压互感器并联，得到图1所示的多级高低压混合励磁标准电压互感器。本文在文献[11]基础上，探索性地从理论计算出发，对图1 所示的多级高低压混合励磁电路原理进行讨论，并验证该电路在高电压环境下测量准确度的理论数值。最后给出多级励磁电压互感器测量准确度的理论计算方法，旨在验证多级励磁在高压互感器设计中改善测量准确度的可能性。论文先后通过铁心设计、绕组设计分别计算所需的内阻抗与励磁阻抗，结合该多级高低压混合励磁电路原理计算出图1 所示电路的准确度。
图1 多级高低压混合励磁标准电压互感器原理图
Fig.1 Schematic diagram of multi-stage high and low voltage hybrid excitation standard voltage transformer
图1 采用分离铁心C4 绕制辅助互感器绕组进行降压处理，并为第一级互感器铁心C1 低压励磁；将第一级互感器二次绕组绕在C1 铁心上，第二级互感器铁心C2 嵌入第一级互感器铁心C1 内部，并将第二级互感器一次绕组同时绕制在C1、C2 铁心上进行高压励磁；最后将第三级比例绕组同时绕制在C1、C2、C3 铁心上，进行比例降压处理。其中N1a 表示辅助互感器一次绕组匝数，N2a 表示辅助互感器二次绕组的匝数，N2e 表示第一级互感器二次绕组匝数，N1e 表示第二级互感器一次绕组的匝数，N1 表示比例绕组一次侧匝数，N2表示比例绕组二次侧匝数，P0 表示标准电压互感器高低压混合励磁部分，Pe 表示辅助互感器低压励磁供电部分，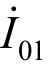
表示辅助互感器一次绕组励磁电流，
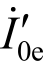表示辅助互感器二次绕组励磁电流，
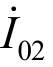表示第二级互感器一次绕组励磁电流，
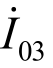表示第三级比例绕组一次侧励磁电流。
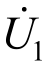表示标准互感器一次电压，
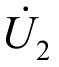表示标准互感器二次电压。
图1 给出了所研究的高低压混合励磁标准电压互感器原理图，本文在其基础上通过建立数学模型对
多级励磁标准电压互感器进行理论设计。该理论设计的环境如下：①假设该方案在实际设计中存在一种冷却散热技术，且能较好地抑制互感器温升问题，忽略绕组温升对其内阻的影响；②假设该互感器一次绕组相邻匝间均匀绕制，忽略泄漏电流对互感器测量准确度的影响[11]；③假设该方案在实际设计中存在较好的电磁场屏蔽方案，忽略电磁干扰对互感器测量准确度的影响。
在上述假设条件下，利用以下步骤得出其T 型等效电路：①分别抽取第一级互感器、第二级互感器、第三级互感器，以及辅助互感器各部分的内阻、漏抗和励磁阻抗；②分别将各级铁心二次绕组参数折算至其等效电路一次侧；③分别抽取各级互感器所包含的理想互感器部分，得到如图2 所示的等效电路。
图2 多级高低压混合励磁标准电压互感器等效电路
Fig.2 Multistage high and low voltage hybrid excitation standard voltage transformer equivalent circuit
图2 等效电路中，Z 1、 Z1e、Z1a 分别为第三级铁心一次绕组N1 的内阻抗、第二级铁心一次绕组N1e的内阻抗，以及辅助互感器一次绕组N1a 的内阻抗，
分别为辅助互感器折算至一次侧 N1a侧的二次绕组N2a 内阻抗、第一级互感器折算至一次侧的二次绕组的内阻抗及折算至一次侧的比例绕组N1 的二次侧内阻抗；
分别为比例绕组励磁阻抗、第二级铁心绕组的励磁阻抗、折算至第一级铁心绕组励磁阻抗、辅助互感器励磁阻抗。另外，图中的
分别为该多级励磁互感器一次侧接入电压、二次侧折算至一次侧的电压，
分别为辅助互感器励磁电压、折算至一次侧的第一级互感器二次绕组的励磁电压、第二级互感器励磁电压及第三级互感器励磁电压。
分别为辅助互感器励磁电流、折算至一次侧的第一级互感器励磁电流、第二级互感器励磁电流和第三级互感器励磁电流。
为了研究图1 所示的多级励磁电路，需要明确该电路的空载误差（本文条件下为励磁误差），而该误差计算需要结合图2 等效电路模型进行数学关系的推导。从图2 可以看出，第一级互感器由辅助互感器供电，故图1 在当前供电过程中将产生第一级互感器的空载误差、辅助互感器的供电误差[8]。
对于辅助互感器的供电过程，辅助互感器外接一次电压产生该互感器励磁电流，该励磁电流经一次绕组产生空载误差。由于该辅助互感器需给第一级互感器绕组供电，即第一级互感器将等效为辅助互感器的负载，进而第一级互感器的励磁电流为辅助互感器的负载电流。因此，第一级互感器励磁电流（辅助互感器中二次绕组外接的负载电流）将在辅助互感器一次绕组与二次绕组上产生误差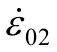 
。
当辅助互感器一次绕组外接其一次电压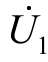
，由电压平衡关系得到
由于辅助互感器在当前一次电压下，其空载误差 ε˙01 来源于辅助互感器一次绕组，该绕组压降即为辅助互感器励磁产生的线损，由文献[12]得 ε˙01 为
当第一级互感器作为辅助互感器负载，由电压平衡关系得到
式中，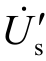
为折算至一次侧的第一级互感器绕组供电电压，考虑
，且
，即
等效为
由上述讨论可知，第一级互感器励磁电流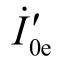
将在辅助互感器一次绕组与二次绕组产生绕组线损。由于这里内阻抗与励磁阻抗关系满足
由文献[12-13]得误差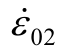
为
结合辅助互感器为第一级互感器供电过程及式（2）与式（5），得到辅助互感器误差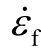
[8]为
对于第一级互感器，其励磁过程满足上述电压平衡关系式（4），由该式可知励磁电流将在
上产生压降，故其误差
为
式中， Z2e 为第一级互感器二次侧内阻抗； Zm1 为第一级互感器二次侧励磁阻抗。
由于第一级电压互感器经由辅助电压互感器进行低压励磁供电，故该部分结构的互感器误差由第一级互感器空载误差
和辅助互感器的误差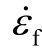
构成，满足
对于第二级互感器，其电压平衡关系为
对于第三级互感器，满足式（10）所示的电压平衡关系。
对于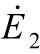
与
满足式（11）、式（12）电压关系。
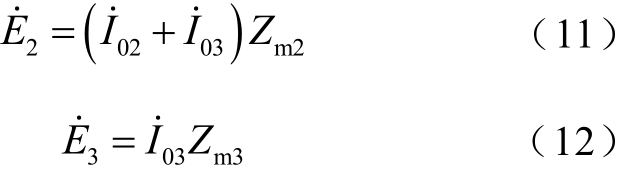
根据式（9）～式（12），结合文献[8]，整理得到式（13）与式（14），注意到式中
结合文献[11]中多级励磁电压互感器空载误差的定义及式（8）、式（13）与式（14），得出图2 等效电路空载误差为
式（15）代入数值，得到图2 等效电路空载误差为
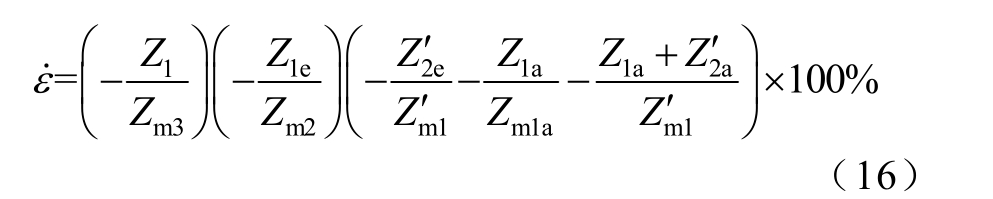
上述推导过程详细给出并联磁路多级励磁互感器空载误差（本文条件下为励磁误差）的计算数学关系模型。由式（16）可以看出，该等效电路测量准确度理论计算主要来源于绕组内阻抗，以及各级铁心励磁阻抗的数值。由等式右侧可知，该等效电路的空载误差等于各级互感器空载误差的乘积。这表明，对于实际高压互感器设计，该电路可作为提高互感器测量准确度的新方法。
1.2 节详细给出了图2 等效电路中测量准确度的理论计算模型，本节将参考多级励磁理论，结合图1 所示高低压混合励磁电路，计算
多级励磁标准电压互感器理论模型数值。
结合文献[11,14]进行互感器铁心设计，具体见附图1～附图3，在该铁心上进行绕制绕组得到图1结构所示的实际装置简图，如图3 所示。
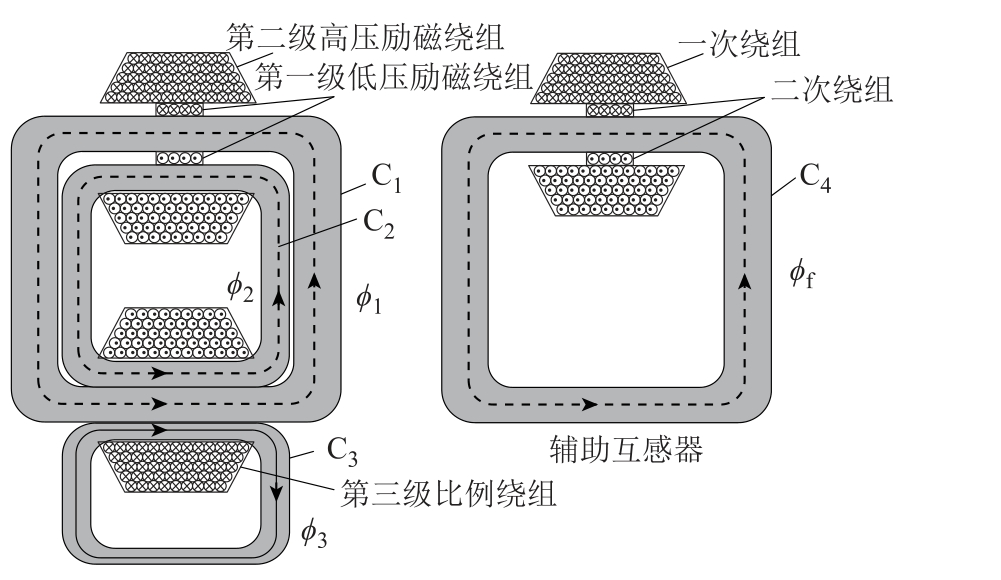
图3 多级高低压混合励磁绕组铁心简图
Fig.3 Schematic diagram of multistage high and low voltage hybrid excitation winding iron core
图3 中，各级铁心采用矩形结构，其中辅助互感器铁心与第一级铁心几何结构参数一致，且铁心界面为近似圆面，第二级铁心与第三级铁心几何结构近似，其铁心截面为矩阵。特别地，由于各级铁心一次绕组和二次绕组匝数差异较大，对一次绕组采用层式宝塔结构进行绕制，对于二次绕组采用单层式绕组结构。同时，由图3 结构简图可以看出，在实际互感器设计时，将辅助互感器一次绕组接入电源侧，通过其二次绕组外接第一级铁心二次绕组为其进行低压励磁供电，同时在高压侧并联第二级铁心绕组、第三级铁心绕组。结合图1，可以更加直观地了解该励磁结构中各级铁心之间的联系。
为了对图 2 等效电路测量准确度进行理论计算，依据图3 所示的互感器几何结构关系，将按照表1 设置互感器的参数。
表1 设计要求
Tab.1 Design Requirements
参数 数值 参数 数值(型号)额定一次电压U˙1/kV 500 3 铁心叠片系数 0.9额定二次电压U˙2/V 100 3 C1 材料 B30P105额定频率/Hz 50 C2 材料 1J85 N N N 150 000 C3 材料 1J85, ,匝数11e1a匝数2e,2a N N 1 500 C4 材料 B30P105匝数N2 30 一次绕组型号 0.1QZ 2 φ−绕组电阻率/( Ω⋅m) 8 1.7 10−×二次绕组型号 1.92QZ 2 φ−宝塔式结构层数 132
表1 中，互感器仿真环境为
，其一次绕组均相等且大于150 000 匝，保证了该互感器在低磁通环境下也可以得到较大的励磁阻抗[15]。该设计方案中采用宝钢取向硅钢B30P105 作为第一级和辅助互感器的铁心材料，采用1J85 坡莫合金作为第二级和第三级铁心的材料，进一步保证了该互感器的整机性能及运行稳定性[16-19]。在表1 参数设计的保障下，可计算出图2 所示高低压混合励磁等效电路中电路元件参数数值，分别包括各级铁心绕组内阻、绕组漏抗及各级铁心的励磁阻抗。
要计算图2 中所需的电路参数，首先需要明确该互感器一次绕组宝塔式结构的构成。该结构由绝缘骨架、内静电屏、宝塔层绕组、每层绕组的层间绝缘及外静电屏构成。该结构分成10 段，据此分别计算出每一段的轴向长度和径向高度[20]，结合这两个参数可以计算出绕组内阻及漏抗。
对于铁心绕组内阻计算，根据其计算定义式，需要明确电阻率、绕组长度及绕组截面积。该参数的计算主要取决于绕组长度的计算。二次绕组为单层式绕组结构，该部分绕组长度的计算为所有绕组匝数的周长之和。而一次绕组由多层组成，只需求出所有层的所有绕组的周长之和。这里通过求得各段的绕组直径即可求出周长，而绕组直径计算可以逐段累加求解[20]。
对于铁心绕组中漏抗计算，结合各段绕组的轴向长度和径向高度，假设各段绕组之间接触紧密，得到多个轴向长度与径向长度的基本四边形截面，根据文献[21-24]中漏抗的理论建模分析，分别计算出该绕组四边形截面下的各级铁心绕组的漏电抗。
对于各级铁心励磁阻抗的计算，当铁心材料提供励磁功率和铁损参数（也可用文献[25-26]计算铁损），结合文献[21, 27-28]先后计算各级铁心的体积与质量，利用励磁曲线及铁损参数，计算出各级铁心励磁所产生的励磁阻抗；当铁心材料提供铁心损耗角，可按照文献[12]的研究思路求出电压互感器角差及比差，通过所求得角差及比差推导出励磁阻抗。
利用上述思路与设计要求，通过Matlab 仿真得出图2 等效电路中各个阻抗元件数值，见表2。
表2 等效电路元件参数
Tab.2 Equivalent circuit element parameters
阻抗数值/kΩ 阻抗 数值/kΩ Z260+j653.6 Z2′ 0.24+j786.1 1a Z′ 36.62+j653.6 Z m 1 a 4.01×106+j4.65×106 2a Z′ 36.62+j0.64 Zm′1 4.01×106+j4.65×106 2e Z304.8+j399 Zm 2 1.45×105+j2.17×105 1e 1Z 301.28+j786.1 Zm3 8.11×104+j1.04×105
结合图2 及表2，总的看来，多级励磁电压互感器内阻抗均远小于励磁阻抗，说明了1.2 节仿真建立过程中简化的合理性，根据式（16）可预估到该互感器的测量准确度较高。如若采用单级电压互感器铁心结构，其测量准确度为内阻抗与励磁阻抗比值，结合表1 与表2 发现，无论采用哪种材料进行铁心励磁，该结构均不能得到一个高准确度角差与比差。而多级励磁绕组的存在，可以有效地对单级励磁电流进行分流，进而提高测量准确度，这就是提出多级励磁结构的原因。本文的多级励磁结构先后采用辅助互感器为第一级互感器低压励磁供电及第二级互感器高压励磁，可以极大地提高测量准确度。
2.1 节详细给出了图2 等效电路中内阻抗和励磁阻抗的求解方法及求解数值，利用该数值可通过式（16）计算该多级励磁电压互感器的测量准确度。然而在实际工程实验中，该测量准确度的理论公式是否可行，还需要结合该电路的仿真分析进行验证。
要利用图2 等效电路验证式（16）的准确性，需结合以下步骤搭建图4 多级高低压混合励磁电压互感器仿真模型：首先选择Simulink 中Inductor 模块作为图2 等效中的阻抗元件；然后选择AC Voltage Source 模块作为图2 等效电路中的一次侧电源电压，同时分别代入表2 阻抗元件参数及电源电压，利用Voltage Sensor 模块测量图2 等效电路一次与二次电压。由于该模块仅能测量电压数值，需要Fourier 模块对该电压进行傅里叶分解，分别选取一次电压和二次电压基波分量的幅值与相位，作为该互感器模型的输入输出端正弦电压的幅值与相位。为了导出仿真时段的所有测量结果进行不确定度分析，将数据输出模块Out1、Out2 接入“仿真比差”及“仿真角差”的模块的连接线上。
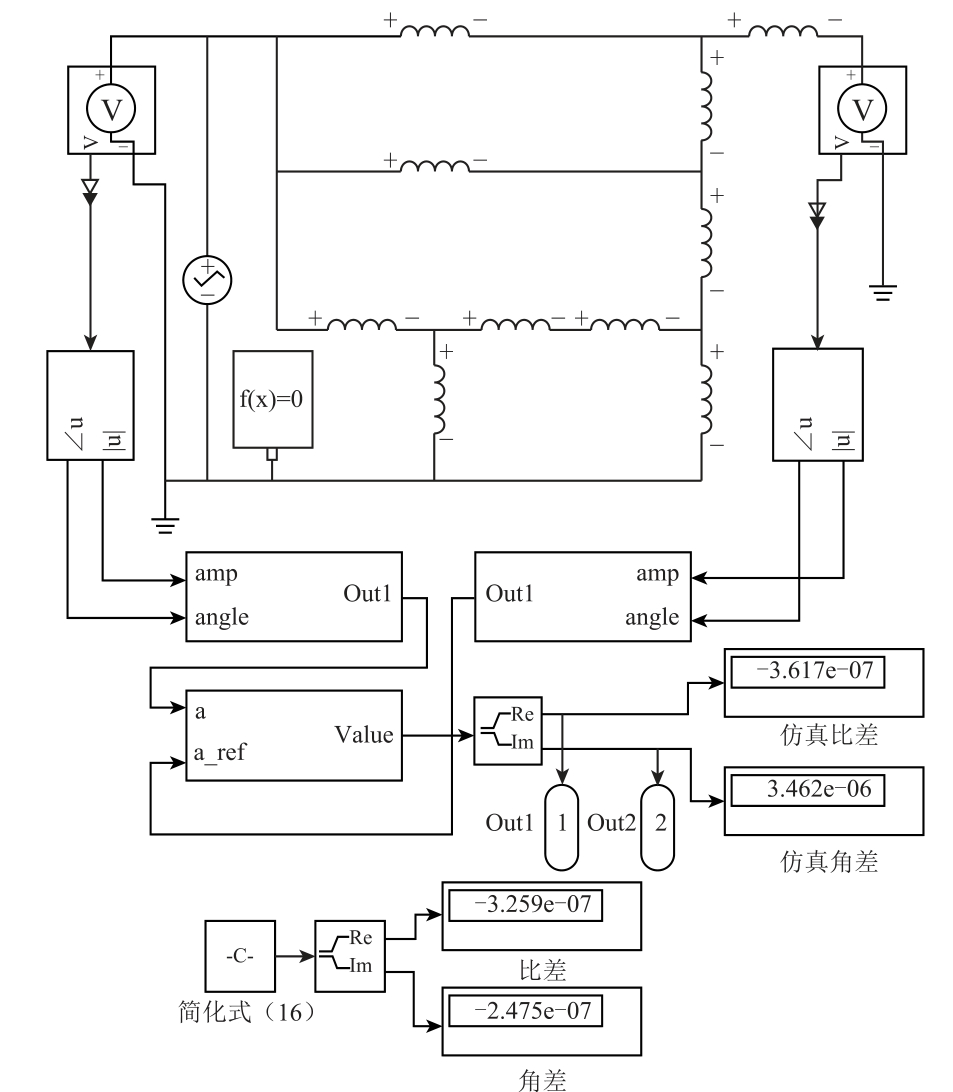
图4 多级高低压混合励磁电压互感器仿真模型
Fig.4 Schematic diagram of multistage high and low
voltage hybrid excitation winding iron core
仿真参数：图2 所示等效电路一次侧电源电压
，阻抗元件参见表2。
对于该电路仿真模型，采用式（17）对比验证式（16）的准确性。
式（17）计算数值显示在仿真电路图中的“仿真比差”与“仿真角差”模块，而式（16）理论计算数值显示在“比差”与“角差”模块。图4 中的“简化式（16）”模块数值为外部程序计算式（16）后通过函数传递至Simulink 界面中。
图4 中“比差”与“角差”模块以及“仿真比差”与“仿真角差”模块的结果显示，当U˙1 为该仿真电路激励时，该等效电路在仿真结束时刻下的仿真比差为-3.62×10−6%，角差为3.46×10−6%，所推导的式（16）比差为-3.26×10−7%，角差为-2.48×10−7%。由这一仿真结果可以看出，多级高低压混合励磁电压互感器在该电压等级下可以达到较高的测量准确度。虽然本文理论推导模型式（16）能得到较好的角差及比差，但该结果与仿真电路中计算的结果还是存在一定的差距。可能的误差来源如下：首先在理论推导过程中存在一定的简化，如式（2）、式（4）、式（5）等；其次在该等效电路的仿真中，这里的角差、比差实际上是通过傅里叶变换展开取其基波信号的幅值、相位来计算该等效电路的比差与角差，忽略了谐波对角差与比差的影响；另外，式（16）的计算结果为仅代入内阻抗与励磁阻抗所得，其表征该电路的整体特征，并不随仿真时间的变化而变化；而“仿真比差”与“仿真角差”模块的显示结果为某时刻一次、二次电压幅值与相位计算所得，该部分仅代表当前时刻下的电路特征。虽有不足，但就该等效电路及式（16）计算结果来看，其两两计算结果相差较小，该理论公式对于多级励磁标准电压互感器的理论设计具有一定的参考价值。
2.2 节给出“仿真比差”与“仿真角差”模块表示的含义，为了判断该电路的质量及价值，需对其进行不确定度分析。 通过图4 中Out1、Out2 模块导出“仿真比差”及“仿真角差”数值，绘制了数值随时间变化的关系如图5 所示。由图5 可看出，仿真模型是在0.02～1s 下进行的，其仿真比差总体分布在-2.27×10−7%附近。对于角差，其总体分布在3.44×10−6%附近，仿真比差及角差数值均存在几个较大的波动点，但总体均未超过20×10−6%。对于该仿真时间下的角差、比差数据，在本文条件下根据JJF1059.1—2012 技术规范及JJG314 规程得出仿真数据的比差的不确定度为2.27×10−8，角差的不确定度为1.86×10−8。
图4 模型给出了在
环境下的仿真结果，为了探究该仿真模型的适用性，本文在上述基础上分别研究了几个电压等级下的互感器测量角差及比差的数据，并通过各个电压下的仿真数据进行该互感器测量准确度的讨论，具体仿真的电压及仿真结果见表3。
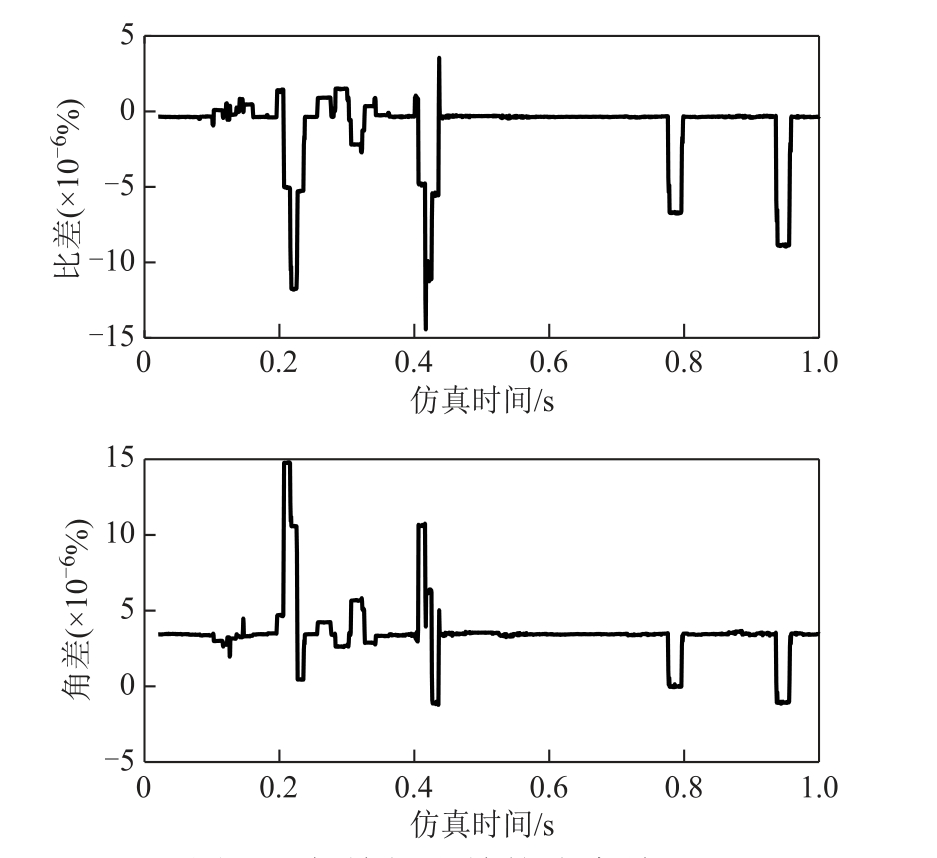
图5 角差与比差的仿真结果
Fig.5 Simulation results of angle difference and ratio difference
表3 不同电压等级下电路仿真结果
Tab.3 Circuit simulation results at different voltage levels
电压/kV 比差（%） 角差（%）60 -1.38×10-6 1.74×10-7 120 -6.40×10-7 -3.40×10-7 180 -4.42×10-7 -2.77×10-7 240 -3.39×10-7 -2.37×10-7 300 -3.26×10-7 -2.52×10-7
在表3 中，当仿真环境为60kV 时，该互感器的比差为-1.38×10-6%，这一结果相比于 180kV、240kV 及300kV，其比差有一定的增大。同时随着电压等级的不断提升，该互感器测量准确度的结果有趋向于稳定的趋势。结合图5 仿真结果也可以发现，当仿真环境的电压趋向于原始设计电压
时，其角差及比差接近图5 的仿真结果。根据互感器准确度定义，在空载情况下该等效电路的比差及角差的绝对值均不大于0.002%，所以该互感器满足0.002 级测量准确度水平。注意到引言部分提及的学者研究的互感器的准确度均是在校验下确定的，而本文中的准确度等级是在不包含补偿、不存在实际校验仪器，且在第1 节中三个假设环境下的理论结果，这仅从理论仿真的角度说明图1 电路提高测量准确度的可能性。
本文以多级高低压混合励磁电路为研究对象，通过铁心与绕组设计分别求出其理想条件下等效电路所需的内阻抗和励磁阻抗，结合理论公式及仿真电路交叉验证的思路证明了公式的可行性。鉴于上述结果，得出以下结论：
1）在表1 中的设计参数下，该标准电压互感器比差为-2.27×10−7%，角差为3.44×10−6%，且比差不确定度为2.27×10−8，角差不确定度为1.86×10−8，满足0.002 级互感器设计水平。
2）通过适用性研究发现，该多级励磁标准电压互感器在低电压等级下也能得到较好的比差与角差，且满足0.002 级互感器设计水平。
3）虽然本文是在理想情况下研究标准电压互感器的准确度等级，但其数值比0.002 级还要高出两个数量级。即使考虑其他误差源，满足0.002 级的可能性也很大。这对标准电压互感器的设计有一定参考意义，后续工作可根据标准电压互感器中的误差源进行开展。
附 录
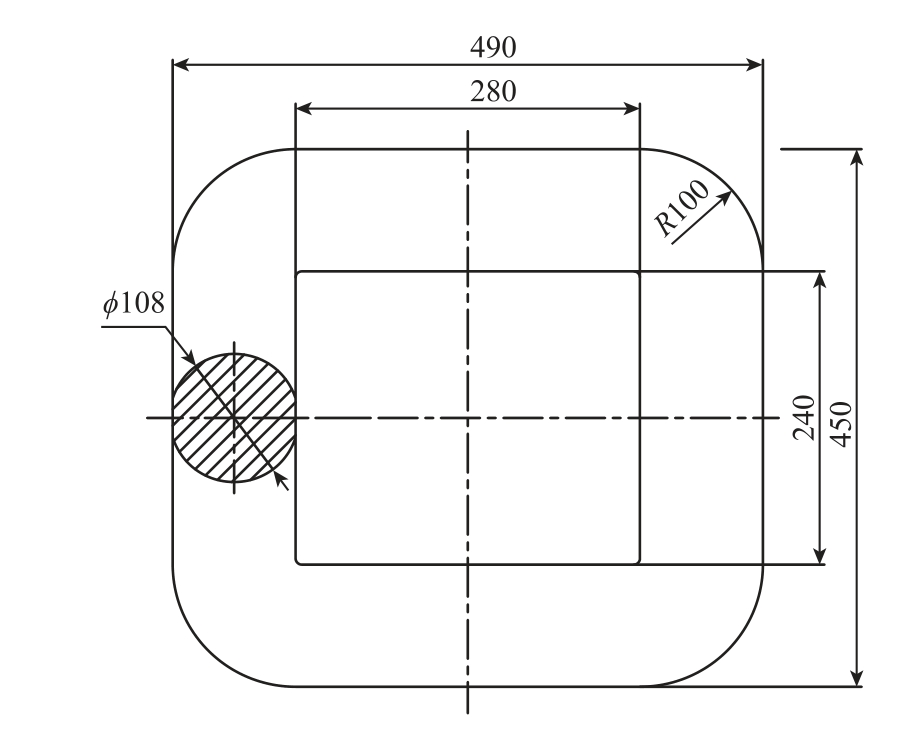
附图1 辅助互感器/第一级互感器铁心
App.Fig.1 Auxiliary transformer/first stage transformer core
附图2 第二级互感器铁心
App.Fig.2 The second stage transformer core
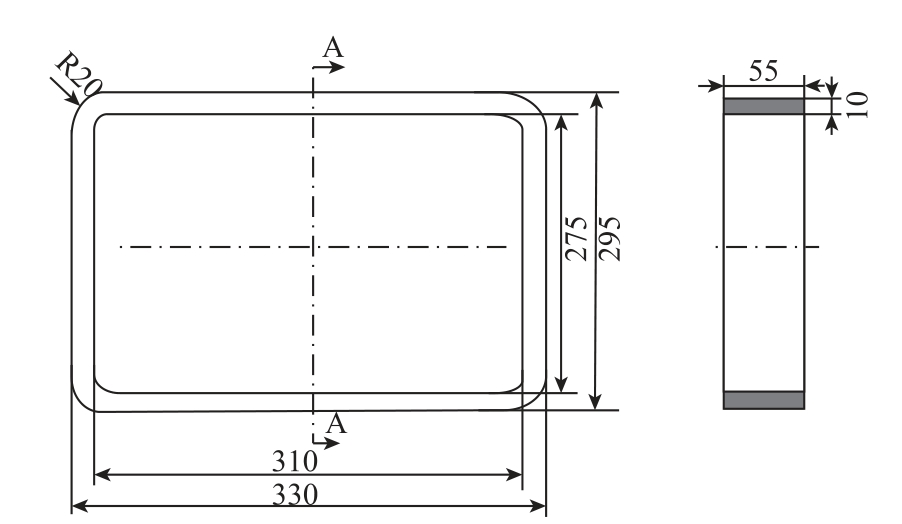
附图3 第三级互感器铁心
App.Fig.3 The third stage transformer core
[1] 刘涛. 电容式电压互感器校验及误差分析[D]. 济南: 山东大学, 2017.
[2] Slomovitz D. Electronic based high-voltage measuring transformers[J]. IEEE Transactions on Power Delivery, 2002,17(2): 359-361.
[3] Deacon T A, Hill J J. Two-stage inductive voltage dividers[J]. Proceedings of the Institution of Electrical Engineers, 1968, 115(6): 888-892.
[4] West J L, Miljanic P N. An improved two-stage current transformer[J]. IEEE Transactions on Instrumentation and Measurement, 1991, 40(3): 633-635.
[5] 潘滨. 220kV 多变比高精密双级电压比例标准的设计与生产[D]. 济南: 山东大学, 2018.
[6] 赵修明. 高压双级电压互感器的研究[J]. 电测与仪表, 1993, 30(2): 17-20.
Zhao Xiuming. Research on high voltage two-stage voltage transformers[J]. Electrical Measurement &Instrumentation, 1993, 30(2): 17-20.
[7] 彭时雄, 宋雨虹, 马玉祥. 35kV 0.001 级及
级双级电压互感器的研制[J]. 电力设备, 2005, 6(7): 10-16.
Peng Shixiong, Song Yuhong, Ma Yuxiang. R&D on two-stage potential transformers of 35kV with accuracy class of 0.001 and
with accuracy class of 0.002[J]. Electrical Equipment, 2005, 6(7):10-16.
[8] Shao Haiming, Lin Feipeng, Liang Bo, et al. The development of
two-stage voltage transformer with accuracy class 0.001[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(6): 1383-1389.
[9] Shao Haiming, Lin Feipeng, Liang Bo, et al. The development of a two-stage voltage transformer of
and class 0.001[C]//Precision Electromagnetic Measurements(CPEM 2014), Rio de Janeiro,Brazil, 2014: 774-775.
[10] Shao Haiming, Lin Feipeng, Liang Bo, et al. Voltage dependence measurement of a 110 kV LVETSVT[C]//Precision Electromagnetic Measurements(CPEM 2016), Ottawa, Canada, 2016: 1-2.
[11] Yin Xiaodong, Liu Hao, Lan Lei, et al. Precision
three-stage VT with double excitation[J].IET Science, Measurement & Technology, 2019,13(9): 1239-1244.
[12] 赵修明. 电压比例标准[M]. 太原: 山西科学技术出版社, 1993.
[13] 张荣伦, 王帅, 穆海宝, 等. 大型电力变压器损耗带电测试技术研究[J]. 电工技术学报, 2019, 34(4):683-692.
Zhang Ronglun, Wang Shuai, Mu Haibao, et al. The on-site method for the loss characteristic in power transformer[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 683-692.
[14] 卡罗尼尔·麦克莱曼. 变压器与电感器设计手册[M].北京: 中国电力出版社, 2014.
[15] Small G W, Budovsky I F, Gibbes A M, et al.Precision three-stage 1000 V/50 Hz inductive voltage divider[J]. IEEE Transactions on Instrumentation and Measurement, 2005, 54(2): 600-603.
[16] 毛卫平, 杨平. 电工钢的材料学原理[M]. 北京: 高等教育出版社, 2013.
[17] 仇圣桃, 付兵, 项利, 等. 高磁感取向硅钢生产技与工艺的研发进展及趋势[J]. 钢铁, 2013, 48(3): 1-7.
Chou Shengtao, Fu Bin, Xiang Li, et al. Recent research trends and developments of production process and technology for high magnetic induction grain-oriented silicon steel[J]. Iron & Steel, 2013,48(3): 1-7.
[18] 董晶, 卢凤喜. 变压器用取向硅钢片的现状及发展趋势预测[J]. 钢铁研究, 2005, 33(4): 59-61.
Dong Jing, Lu Fengxi. Present status and development trends of oriented silicon sheet used for transformer manufacturing[J]. Research on Iron and Steel, 200,335(4): 59-61.
[19] 程灵, 杨富尧, 马光, 等. 电力变压器用高磁感取向硅钢的发展及应用[J]. 材料导报, 2014, 28(6):115-118.
Cheng Ling, Yang Fuyao, Ma Guang, et al.Development and application of high magnetic induction grain-oriented silicon steel for power transformer[J]. Materials Reports, 2014, 28(6): 115-118.
[20] 雷民. 1000kV 串联式工频电压比例标准研究[D].武汉: 华中科技大学, 2009.
[21] 肖耀荣. 互感器原理与设计基础[M]. 沈阳: 辽宁科学技术出版社, 2003
[22] 赵修民. 环形铁心线圈漏抗的计算[J]. 变压器,1982(8): 2-4, 37.
Zhao Xiuming. Calculation of leakage reactance of ring core coil[J]. Transformer, 1982(8): 2-4, 37.
[23] 潘超, 米俭, 蔡国伟, 等. 交直流混杂环境下变压器漏电感参数分析方法[J]. 电机与控制学报, 2019,23(5):25-33.
Pan Chao, Mi Jian, Cai Guowei, et al. Analysis method of leakage inductance parameters under AC/DC hybrid environment in transformer[J]. Electric Machines and Control, 2019, 23(5): 25-33.
[24] 官瑞杨, 魏新劳, 王永红, 等. 铁心电抗器气隙边缘效应计算及影响因素[J]. 电机与控制学报, 2018,22(4):81-88.
Guan Ruiyang, Wei Xinlao, Wang Yonghong, et al.Calculation and influence factors of air-gap edge effect of iron-core reactor[J]. Electric Machines and Control, 2018, 22(4): 81-88.
[25] 刘刚, 孙立鹏, 王雪刚, 等. 正弦及谐波激励下的铁心损耗计算方法改进及仿真应用[J]. 电工技术学报, 2018, 33(21): 4909-4918.
Liu Gang, Sun Lipeng, Wang Xuegang, et al.Improvement of core loss calculation method and simulation application under sinusoidal and harmonic excitations[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4909-4918.
[26] 陈彬, 李琳, 赵志斌. 典型非正弦电压波激励下高频磁心损耗(英文)[J]. 电工技术学报, 2018, 33(8):1696-1704.
Chen Bin, Li Lin, Zhao Zhibin. Magnetic core losses under high-frequency typical non-sinusoidal voltage magnetization[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1696-1704(in English).
[27] 邹明继, 吴琦, 马璐瑶, 等. 三相三柱式配电变压器负载特性对其空载损耗在线检测的影响[J]. 电工技术学报, 2019, 34(增刊2): 493-500.
Zou Mingji, Wu Qi, Ma Luyao, et al. Influence of load characteristics of three-phase and three limbs distribution transformer on on-line detection of noload loss[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 493-500.
[28] 康丽, 张艳丽, 唐伟, 等. 基于变系数Steinmetz 公式的直流偏磁下铁心损耗计算[J]. 电工技术学报,2019, 34(增刊1): 1-6.
Kang Li, Zhang Yanli, Tang Wei, et al. Calculation of core loss under DC bias based on the variable coefficient Steinmetz formula[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 1-6.
Simulation Analysis and Design of 500
/kV Multistage Excitation Standard Voltage Transformer with Accuracy Class 0.002
Abstract Insulation design of high voltage transformers is too difficult to effectively improve the measurement accuracy of existing standard voltage transformers. In this paper, the circuit of standard voltage transformer with multistage voltage hybrid excitation, both high and low voltage are included,was studied through simulation analysis under ideal conditions combining with multistage excitation theory. Firstly, the equivalent circuit of high voltage transformer was established according to the excitation scheme; secondly, evaluation formula of measuring accuracy were derived according to the equivalent circuit. Then, in combination with the actual demands, the theoretical parameters of voltage transformer at
with multistage voltage hybrid excitation were calculated, including the calculation of the internal impedance and the calculation of the excitation impedance. Finally, according to the calculation results of the above theoretical parameters, the measurement accuracy simulation values of the transformer were given. The simulation results show that the ratio error of the transformer structure is -2.27×10−7% and the angle error is 3.44×10−6%, which meet the accuracy level requirements of 0.002 greatly. And it can be tried to develop physical objects with these parameters.
宋晓林 男，1973 年生，硕士，教授级高级工程师，研究方向为智能电能表、用电信息采集、数字化计量及智能电网等。E-mail：sxlgoodluck@163.com
汤晓君 男，1973 年生，博士，教授，研究方向为智能传感器技术，电力设备运行状态在线监测技术等。E-mail：xiaojun_tang@mail.xjtu.edu.cn（通信作者）