0 引言
随着新能源的不断接入、大功率远距离电能输送的迫切需求及现代电力电子技术与全控型功率器件的迅猛发展,直流输电系统的传输容量、电压等级、跨越距离都有了显著的提升,高压直流输电也成为大容量远距离输电的首选方式[1-2]。然而,直流系统阻尼小,导致直流故障电流上升速度快,过电流峰值高,对于保护的快速性要求很高,进而成为威胁系统安全稳定运行的一个巨大隐患。因此,亟需可靠经济的短路电流限制手段及设备,降低系统运行风险,保障其安全稳定运行[3-7]。
可变电感型限流器利用快速变化的电感值限制故障电流上升速度,是近些年来的热门研究方向,主要有开关投切[8-11]和磁饱和变化[12-15]两大类别。磁饱和型直流限流器利用铁磁材料磁化非线性特性,正常工作时铁心处于饱和状态,限流器对直流系统呈现小电感值,不影响系统稳定运行;故障时刻铁心退出饱和态,限流器对直流系统呈现大电感值,有效增大故障阻尼,大大降低了直流故障电流的上升速度。该方法采用铁磁材料作为能量传递媒介,设备耐受高压大电流能力强,整体性能及经济性佳,十分适合高压直流系统装设,是直流限流器相关研究的重要分支之一。
为了获得磁饱和型限流器的主要尺寸及电气参数,限流器设计计算是必不可少的一个步骤。目前磁饱和型限流器的设计计算方法主要分为如下几大类别:
(1)经验公式法:利用传统变压器设计公式,通过短路容量确定铁心边柱尺寸,电压确定绕组匝数,进而初步得到基本参数[15-16]。该方法设计速度快,但是精度不高,难以得到准确的尺寸与电气参数值。
(2)数值迭代法:基于有限元剖分解析[15]或磁链-电流公式[18-20]进行循环迭代计算,首先通过经验公式得到基本几何参数,然后设置约束条件迭代求解,获得精确尺寸及电气参数值。该方法精度高,但是比较耗费计算资源及时间,需要进一步优化算法求解过程。
(3)磁阻网络法:获得磁路不同部分的等效磁阻值,建立等效磁阻网络,求解磁路与电路方程,得到限流器电感及尺寸参数[14, 20-21]。该方法研究较为广泛,精度较高,计算速度快,其难点在于如何确定磁路不同区域的磁阻值,并且现有方法尚未考虑永磁偏磁型直流限流器的漏磁效应,对整体设计影响较大,需要进一步深入研究。
针对上述问题,本文结合上述设计计算方案的优缺点,提出一种基于高阶麦克劳林展开的磁通管区段拟合方法,充分考虑永磁体漏磁效应对磁饱和型直流限流器性能产生的影响,计算等效磁路的磁阻网络,得到计及永磁体漏磁效应的磁饱和型高压直流限流器设计计算方法,最后利用多组有限元仿真及等效实验验证了所述方案的有效性。
1 原理分析
图1 所示为典型永磁偏磁型高压直流限流器拓扑及等效电磁路[12]。
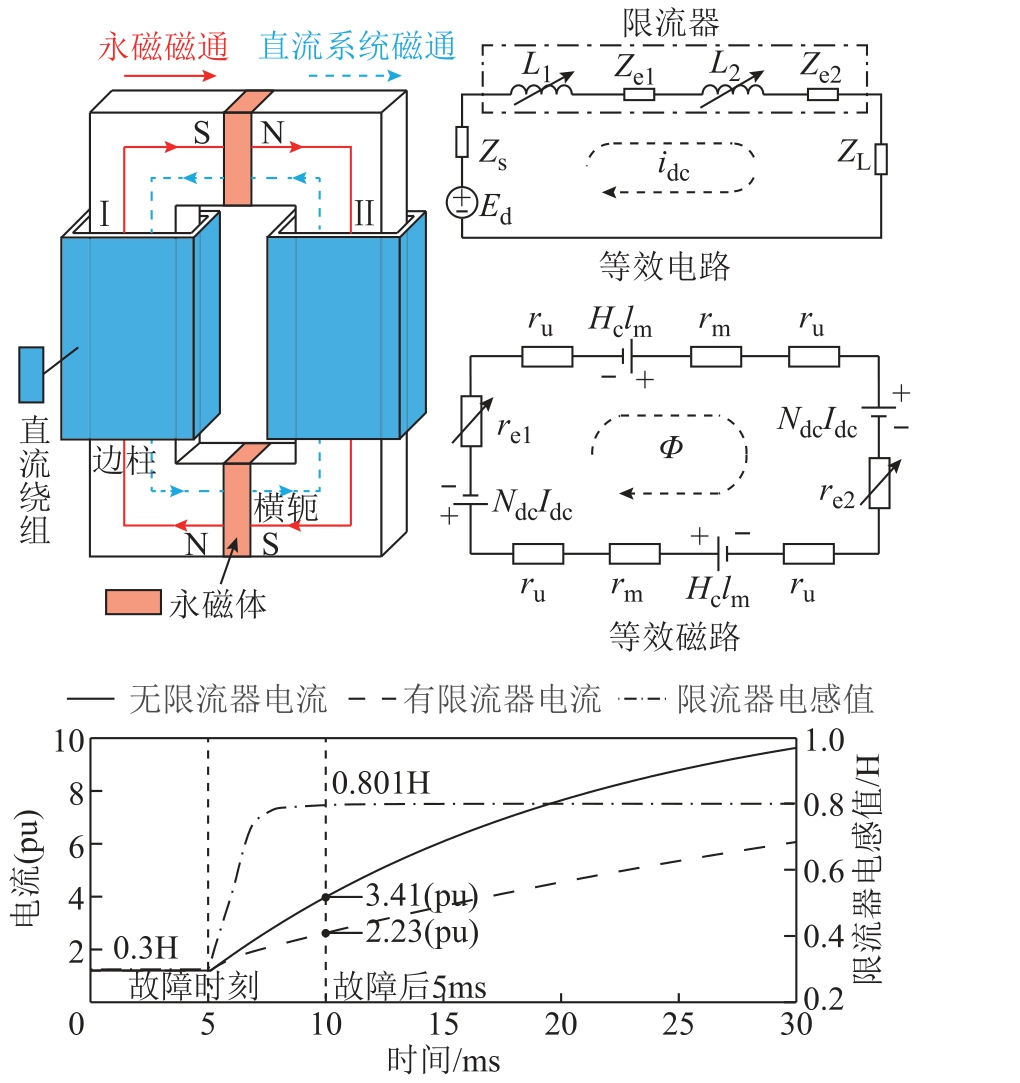
图1 永磁偏磁型直流限流器拓扑及等效电磁路图
Fig.1 Topology and equivalent circuits of PM biased saturated core FCL in HVDC system
该限流器由铁心、钕铁硼永磁体及直流绕组构成,直流绕组串联进入系统,产生的磁动势方向与永磁体相反。系统正常工作时电流较小,永磁体产生的磁动势远大于直流绕组产生的磁动势,使得双柱铁心饱和,直流绕组对外呈现小电感值,有效替代系统直流侧的平波电抗器;故障发生时刻,直流电流陡增,绕组产生的磁动势抵消大部分永磁体磁动势,此时双柱铁心退饱和,限流器电感值由初始临界饱和态的低电感值跃变为退饱和态的高电感值,变化时间约为2ms。在到达退饱和态高电感值后,铁心磁阻re 较永磁体磁阻rm 而言小很多,因此铁心持续退饱和时电感值维持不变,对外会持续呈现大电感的限流效果,如图1 所示。故障电流上升速度会显著降低,故障电流瞬时峰值也会较没有限流器时降低,此时故障电流产生的反向磁通增加速度也会降低。此外,铁心硅钢片临界饱和磁感应强度约为1.9T,达到反向饱和所需故障电流反向磁动势较大,铁心不会在短时间内进入反向饱和阶段。
考虑到目前直流系统配备的直流断路器动作时间在10ms 以内,由图1 所示的限流器故障态大电感持续时间大于20ms,铁心在此阶段始终未进入反向饱和状态。所述限流器与断路器配合工作,故障电流上升速度将显著放缓,断路器可以在故障初期5~10ms 内有效切断故障电流。因此,所述限流器在工作过程中不会因反向饱和而失去限流能力。
求解限流器等效电磁路,得到方程为
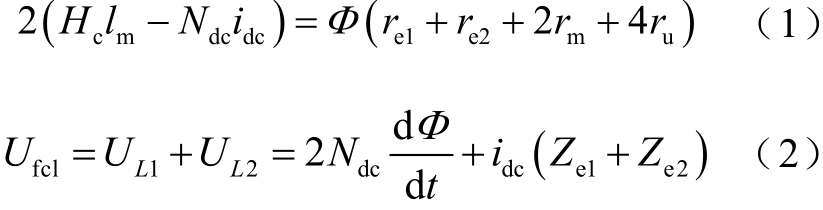
式中,Ndc 为直流绕组的匝数;Φ 为铁心磁通;re、ru 和rm 分别为边柱、铁轭和永磁体的磁阻,可以通过r=l/(μS)描述,其中l 为磁体长度、μ为磁体磁导率、S 是磁体截面积;U fcl 为限流器电压;UL1 、UL2为左、右绕组电压。
确定系统故障电流的变化范围,采用最大故障情况设计限流器尺寸参数并满足式(3),确定边柱铁心截面积等尺寸防止磁通过快反向。
式中,imax 为系统最大故障电流。
根据法拉第电磁感应定律及磁通连续性定律方程可得
将式(1)对时间t 求导可得

将式(5)代入式(4),可以求得限流器等效电感值为
不同于铁心深度饱和的磁饱和型交流限流器,永磁偏磁型高压直流限流器为了在正常工作时有一定电感值,双柱往往为临界饱和(非深度饱和),铁心存在一定磁导率。此时式(6)中两柱磁阻re1+re2 不会很大,而磁回路中永磁体磁阻2rm 将占总磁阻∑r 的较大部分,导致限流器工作电感值将在极大程度上取决于永磁体磁阻。现有计算方式往往将永磁体当作空气气隙计算其磁阻,未考虑其边缘漏磁效应,导致计算磁阻值偏高,与实际情况不符,因此需要进一步分析其漏磁特性,得到精确的设计计算方案。
2 磁通管区段拟合方法
为了解决上述设计计算不准确的问题,本文提出了一种基于漏磁磁通管区段拟合的方式,有效计及永磁体漏磁效应,重构磁阻网络,获得准确设计的计算值。限流器磁通管区段拟合方法如图2 所示。

图2 磁通管区段拟合方式
Fig.2 Configuration of the segment fitting strategy of the magnetic flux tube
根据磁通管计算原理,不同部分的磁导G 计算公式为
式中, 0μ 为空气磁导率, 0μ =4π ×10−7H/m;V 为所计算磁通管的体积;Lp 为该磁通管的等效长度。式(7)是磁导计算的通用公式,将不同磁通管部分的尺寸参数代入此式,即可得到所需部分的磁导值,进一步得到磁阻网络,计算结果准确可靠。
图2 中,l1、lm、lyoke1 和lyoke2 是不同磁通管部分的边界长度,θ1 和θ2 是A2 磁通管部分的边界圆心角度,r1 和r2 是其半径大小,W 是模型的厚度。利用磁通管分段方式,将永磁体漏磁区域分为A1~A4共4 个不同部分计算,分别如图2c~图2f 所示。根据这4 个部分的不同几何特征,采用上述磁通管计算式(7),确定其磁导计算方式,得到准确的限流器磁导矩阵。具体求解方案如下。
2.1 拱形磁通管A1
图3 所示为典型新月形磁通管计算模型图。由于图2 所示拱形磁通管A1 与新月形磁通管A3 部分的计算模型均可以此为基础,计算出此新月形磁通管通用模型后,改变不同的边界条件,代入通用模型公式即可得到A1 与A3 的磁导值。
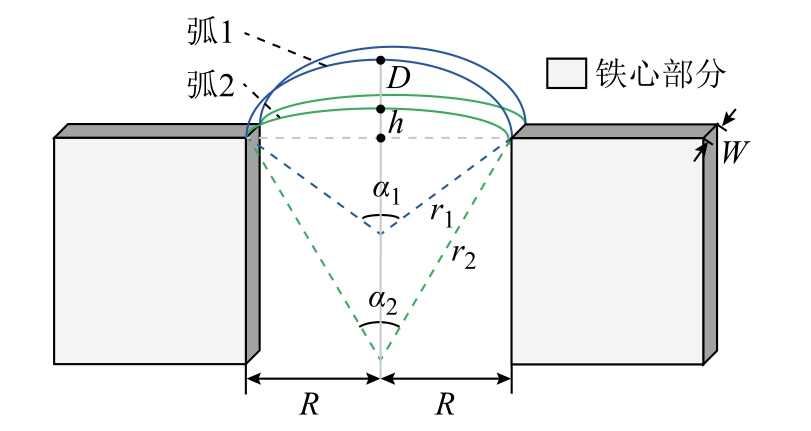
图3 典型新月形磁通管计算模型
Fig. 3 Typical flux distribution of crescent moon shape magnetic flux tube
图3 中,弧1、弧2 分别为新月形磁通管的上、下边界,其圆心在共同中轴线上。两弧共一弦,弦长为2R,半径分别为r1、r2,圆心角分别为α1、α2。由图3 可以看出,式(7)中的Lp 是弧1 与弧2 间的任意一条弧长,因此Lp 可以计算为

式(7)中的体积微元dV 可以由式(9)计算得到。
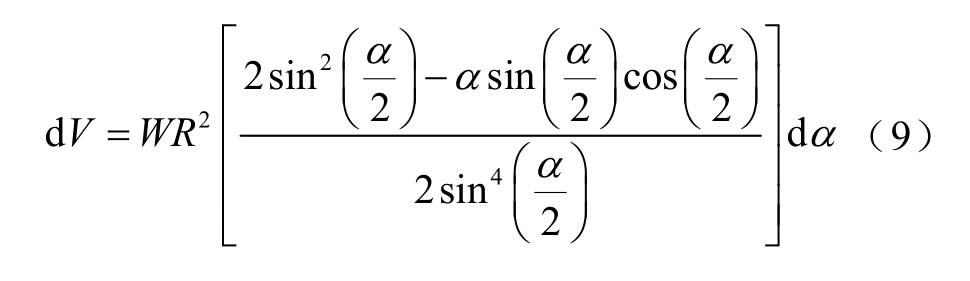
因此,将式(8)与式(9)代入式(7),可得该类磁通管磁导的计算式

对于拱形磁通管A1,将其边界条件α1=θ1,α2=0代入,可得其磁导为
2.2 半环形磁通管A2
磁通管A2 形状类似于半环形,如图2b 所示。按弦长方向进行磁通管积分,可以得到A2 部分的磁导值GA2 为

式中,l 为边界弧的半径r 在x 轴上的投影长度,即弦长的一半,其范围在0.5l1~0.5lm 之间,如图2d 和图2e 所示。由于式(12)中的![]() 项无法用α的初等函数简化表示,因此采用高阶麦克劳林展开方式,将
项无法用α的初等函数简化表示,因此采用高阶麦克劳林展开方式,将![]() 展开可得
展开可得

式中,o(α/2)为高阶无穷小项。
此外,由于图2 中α与l 的关系较为复杂,无法通过数学模型计算得到。因此本文采用Maxwell 仿真与Simulink 拟合结合的方式,首先搭建图2b 所示典型永磁体漏磁模型,有限元仿真得到A2 区域的漏磁磁力线分布云图,确定磁力线对应圆弧的半径、圆心角及半弦长,结合Simulink 曲线拟合工具箱,得到α与l 的关系。A2 部分参数Simulink 拟合结果如图4 所示。
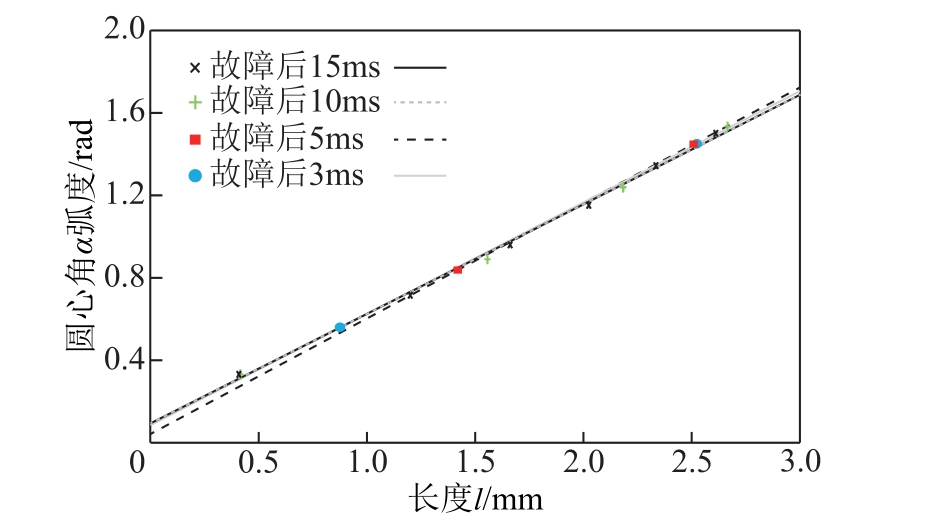
图4 A2 部分参数Simulink 曲线拟合结果
Fig.4 Curve fitting results of the A2 part
由图4 可知,A2 部分漏磁磁力线等效圆心角α与对应半弦长l 近似为线性关系,因此用式(14)描述其函数关系。
式中,m=531、n=0.093 5。将式(13)、式(14)代入式(12),可得GA2 磁导值为

2.3 新月形磁通管A3
如图3 所示,新月型磁通管A3 也是其计算模型的一种特殊情况。因此,将此新月形的边界条件,即α1=π、α2=θ2 代入式(11),可以得到此新月形磁通管A3 的磁导值GA3 为
2.4 拱桥形磁通管A4
作为最外层磁通管,拱桥形A4 的内外边界均为共圆心的半圆环,其计算模型如图5 所示。图中α为两边界磁力线的圆心角,r 为内部边界的半径,r+x为外部边界的半径。
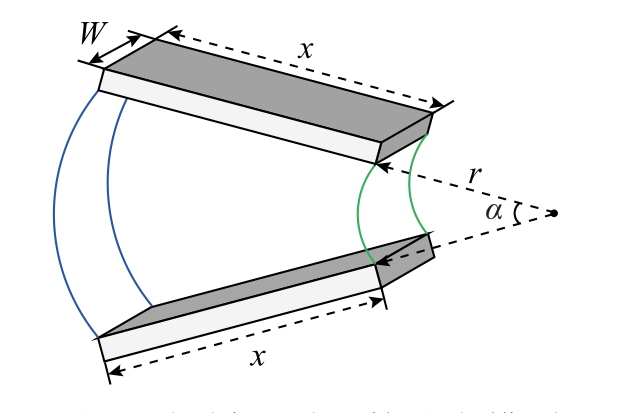
图5 拱桥形磁通管分布模型
Fig.5 Typical flux distribution of arch bridge shape magnetic flux tube
由图5 可知,式(7)中的磁通管等效长度 pL 以及体积微元dV 均可以由r、x、α表示为

因此,将式(17)代入式(7),可得到图5 所示拱桥形磁通管的通用磁导值计算公式为
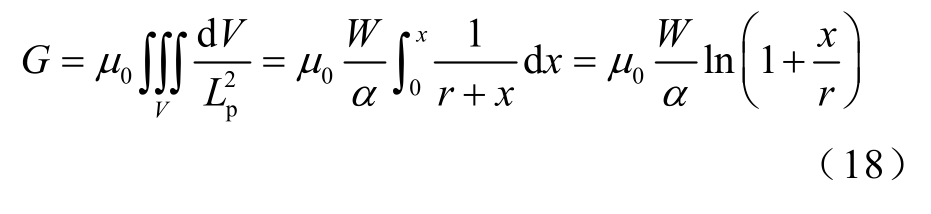
由图2f 可知,拱桥形磁通管A4 的边界条件为x=lyoke、r=lm/2、α=π,将其代入(18)中可得拱桥形磁通管A4 的磁导GA4 为
由于铁心结构原因,永磁体上下漏磁范围不同,此拱桥形磁通管也存在两个不同上界,即图2a 所示lyoke1 和lyoke2。将二者代入式(19),可得上下漏磁磁导GA4(1)和GA4(2)。
2.5 重构限流器磁阻网络
通过对上述不同部分磁导值GA1~GA4 的模型建构及计算,可以得到计及永磁体漏磁效应的限流器准确磁导值,将其代入图1 所示等效磁路中,可以得到考虑漏磁磁导的限流器等效磁路网络,如图6所示。其中磁导G 与磁阻r 的关系为
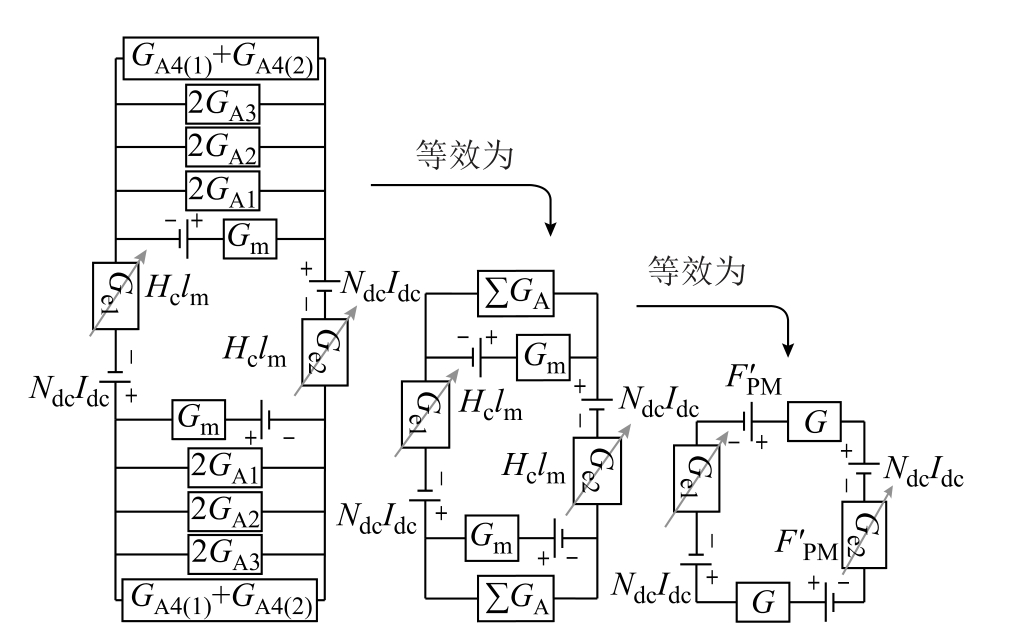
图6 等效磁导网络及简化流程
Fig.6 Equivalent magnetic circuit with leakage effect and simplification steps
相较图1 所示原始磁路,考虑漏磁效应的磁导网络将GA1~GA4 并联进永磁体磁导Gm 支路上,化简可得最终等效磁导G 以及等效磁动势 FPM′ 为
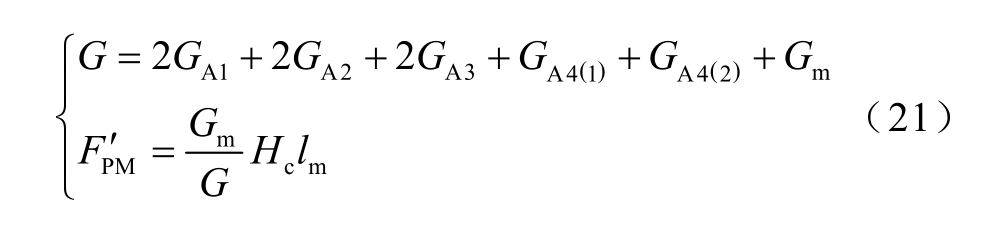
因此,最终可得准确限流电感计算值为

通过上述计算公式,可以得知这些磁导值仅取决于不同部分的尺寸参数与计算公式,与半径、圆心、匝数等间接计算参数解耦,因此计算精度及可靠性可以保证。
3 设计计算方案
依据上述计算方法,可以构建永磁偏磁型直流限流器以及相关电力设备(包括永磁预偏磁型功率电感、永磁型特种变压器等)的设计理论依据。设计流程如图7 所示。
为了简化设计流程,采取如下两个假设[22]:①所用磁性材料的磁化曲线为小斜面模型,如图8a 所示;②铁心的边柱截面积为正方形,厚度宽度均为W,其余尺寸如图8b 所示。
图7 永磁偏置型设备的设计流程
Fig.7 Design flow chart of the PM biased facilities

图8 模型设计参数
Fig.8 Parameters of the design model
由图 8a 可知,μm=Br/Hc、μu=Be/He、μs=(Bm-Be)/(Hm-He),其中μm、μu、μs 是永磁体、非饱和态铁心及饱和态铁心的磁导率。由图8b 可知,铁轭尺寸存在等式关系,即
根据变压器设计原则,得到铁心柱截面积计算式为
式中,K 为硅钢片系数,一般取5~6。将限流器饱和态电感值Ls 与非饱和态电感值Lu 代入式(22),可得磁阻间的等式关系,并依此求得铁心柱长度le的值。
此外,根据限流器磁路电路耦合方程,可以得到磁通、磁导、磁感应强度、电流、匝数、尺寸间的关系式为
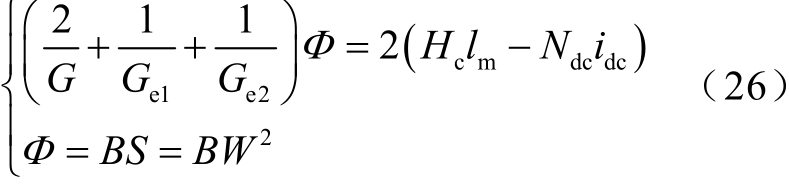
综上所述,首先根据式(23)~式(25)求得尺寸W、le 值,然后将正常及故障态的电流、磁感应强度等已知量代入式(11)、式(15)、式(16)、式(19)~式(22)、式(26),可以求得未知的lyoke1、lyoke2、lm、Ndc 值,进一步得到限流器全尺寸参数。对于永磁偏磁型电感设备,改变设备电压、电流、电感值、磁感应强度、磁导率、铁心参数等条件,可计算得到相应尺寸参数。
若设备磁结构发生变化,不再是两柱型永磁体中央镶嵌式结构,则本文方法需要进一步完善以适应结构变化。此时可将永磁及邻近铁心部分单独分块,各个分块形成一个类似图8b 铁轭部分的独立对称结构,再对各个模块进行磁导计算,最后通过对本体磁阻网络的分析,代入相应部分磁导值便可以计算得到装备的电感值。在已知电气及结构框架的前提下,也可以利用已知条件反推计算得到设备的具体尺寸参数。
4 仿真分析
为了验证上述方案的有效性,搭建了多组Ansoft 仿真模型,采用不同尺寸参数值及电压电流等级验证所述方案的有效性。仿真模型采用涡流场自适应剖分方法得到精密的剖分网格,导入瞬态场模型开展仿真分析,并采取0.1ms 计算步长,尽可能精细化求解有限元模型,使得其求解结果近似为实际准确值,尽可能减小有限元建模及计算带来的误差。同时,后续第5 节也开展了所述两柱式限流器的样机实验,将仿真、实验、计算所得结果均进行了对照,验证本文所述方法的正确性。
仿真平台为装备i7-8700k CPU、16GB RAM 的计算机,模型参数见表1。其中案例1~3 为小功率模型,改变不同永磁体及铁心尺寸验证所述方案有效性;案例4 为高压大功率模型,验证所述方案在HVDC 系统中的适用性;案例5 为三柱式铁心结构模型[14],验证本方案在不同磁结构下的有效性。对照分析将Ansoft 仿真作为准确解,以式(6)为代表的不考虑永磁漏磁效应的磁阻网络法作为传统方法对照组,验证本文新计算方法的有效性。
对于上述研究模型,存在如下给定的工作状态:圆心角θ1=32°=0.558 5(arc)、θ2=83°=1.448 6(arc),磁感应强度Bs=1.87T、Bu=1.3T,剩磁Br=1.425T,磁导率μs=30μ0、μu=7 000μ0、μm=1.163μ0,矫顽力Hc=975 000A/m,基础电感值L0=300mH。
表1 仿真模型参数
Tab.1 Parameters of the simulation models

案例 尺寸 电气参数 其他1 l1=1.752mm, lm=5mm,lyoke1=17.5mm, lyoke2=52.5mm,le=105 mm, W=35mm IN=1.2A,If=12A Ndc=716 m=531 n=0.093 5 2 l1=1.752mm, lm=5.5mm,lyoke1=17.5mm, lyoke2=52.5mm,le=105mm, W=35mm IN=1.2A,If=12A Ndc=731 m=531 n=0.093 5 3 l1=1.752mm, lm=6mm,lyoke1=17.5mm, lyoke2=52.5mm,le=105mm, W=35mm IN=1.2A,If=12A Ndc=741 m=531 n=0.093 5 4 l1=175.2mm, lm=500mm,lyoke1=1 750mm, lyoke2=5 250mm,le=10 500mm, W=3 500mm IN=1 200A,If=12 000A Ndc=71 m=0.095 12 n=0.078 37 5 l1=1.752mm, lmα=8mm,lmβ=3mm, lyoke1α=lyoke2α =15mm,lyoke1β=lyoke2β =51mm,Sα = 35mm×35mm, Sβ = 35 mm×45mm,le=105mm, lu1=72mm, W=35mm IN=1.2A,If=12A Ndc=1 080 m=531 n=0.093 5
以案例1 为例,图9 所示为模型的网格剖分及磁感应强度分布云图。由图9a 所示,有限元模型剖分网格细密,尤其是本文重点关注的永磁体及其邻近空气部分剖分精细,解析更为准确,因此可以将该有限元分析结果近似作为准确值进行参照对比,验证所述方案的有效性。正常工作时两柱呈现饱和态,故障发生后极短时间内双柱铁心退出饱和,与预期工作状态相吻合。图10 所示为永磁体附近的漏磁分布云图,其中lx 为铁心横轭由右到左的长度,ly 为铁心横轭自顶端朝空气方向的长度,其定义图示详见图9b。

图9 模型及剖分仿真结果(案例)
Fig.9 Simulation results (Case 1 for example)
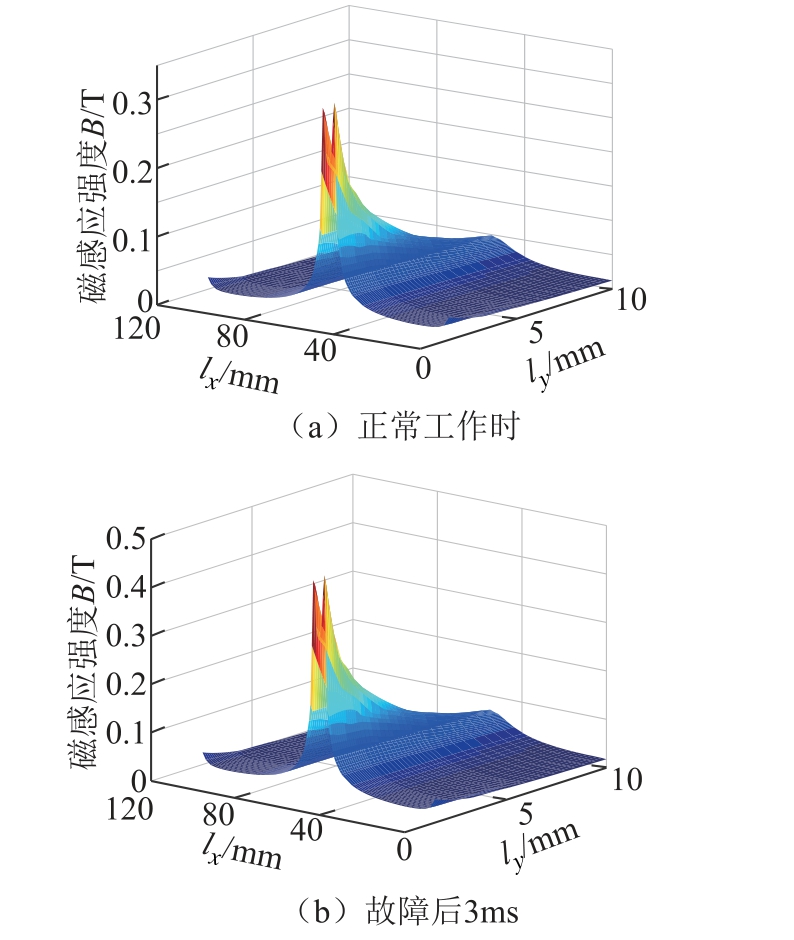
图10 永磁体附近漏磁分布
Fig.10 Flux density distribution of the vicinity of the magnet in the air
由图10 可得,永磁体中心附近空气漏磁效应较左右两侧边轭附近空气而言明显许多,且随着故障的发生,漏磁效应较正常工作时更为明显,空气处最大漏磁场强度增长了近2 倍。由此可见,在限流器工作过程中,漏磁效应是一个不可忽视的因素,需要在设计计算过程中加以考虑。
表2 所示为计算及仿真的对比情况。采用精确剖分的有限元仿真作为准确解,对比所述方法与不考虑漏磁效应传统方法的计算电感值,验证所述方法的准确性。传统方法由于不考虑永磁体上方漏磁效应,导致总磁阻偏高,因此计算电感值相较实际值偏低,存在20%左右的计算误差。相较传统方法而言,所述新方法考虑漏磁磁阻并重构磁阻网络,得到较为精确的计算电感值,不同模型的计算结果与有限元仿真的误差均在1.3%以内,验证了所述方法在不同场合下均有较好的精度与计算可靠性。
表2 仿真计算对比
Tab.2 Comparison between simulation and calculation
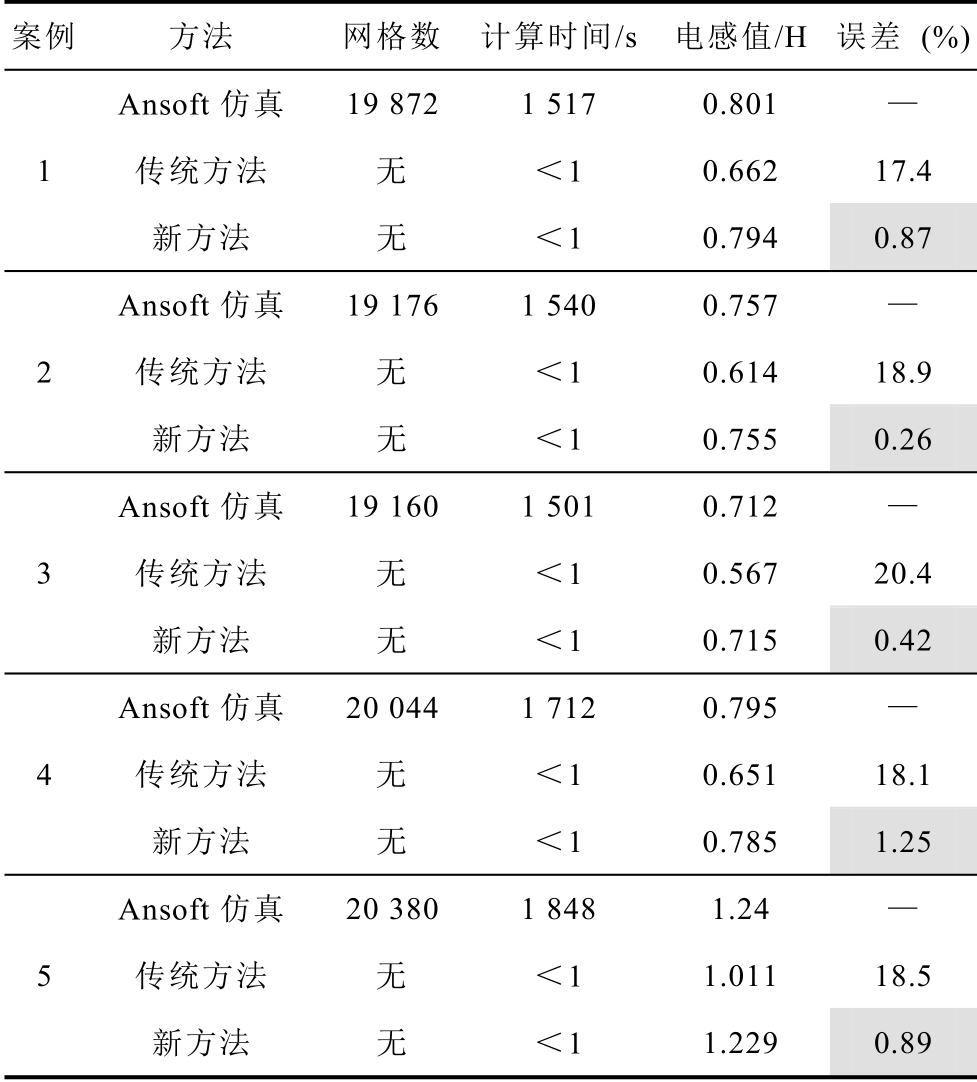
案例 方法 网格数 计算时间/s 电感值/H 误差 (%)Ansoft 仿真 19 872 1 517 0.801 —1传统方法 无 <1 0.662 17.4新方法 无 <1 0.794 0.87 Ansoft 仿真 19 176 1 540 0.757 —2传统方法 无 <1 0.614 18.9新方法 无 <1 0.755 0.26 Ansoft 仿真 19 160 1 501 0.712 —3传统方法 无 <1 0.567 20.4新方法 无 <1 0.715 0.42 Ansoft 仿真 20 044 1 712 0.795 —4传统方法 无 <1 0.651 18.1新方法 无 <1 0.785 1.25 Ansoft 仿真 20 380 1 848 1.24 —5传统方法 无 <1 1.011 18.5新方法 无 <1 1.229 0.89
为了验证本文所述方案在不同磁结构下的计算可行性,本文同时搭建了文献[14]所述的三柱式限流器结构并计算其电感值,其结构尺寸参数见表1 中案例5 所示,拓扑结构如图11 所示。永磁体分为上下三块,结构不对称,共同对左柱Ⅰ及上下两轭产生励磁磁动势。此时可将永磁体部分分割为三个区域,如图11 虚线框所示上下永磁体α 部分及中柱永磁体β 部分,并利用前述公式分别计算这三部分各自的永磁体磁导及空气漏磁导。考虑永磁体漏磁效应,并根据磁路网络分析,得到其电感值计算公式为
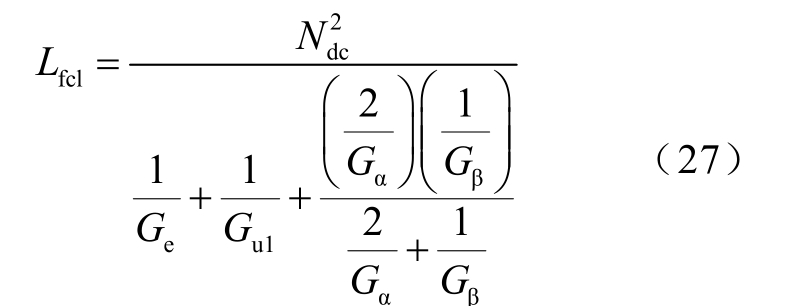
图11 三柱式限流器结构[14]
Fig.11 Three limb FCL topology in Ref[14]
式中,Ge、Gu1、Gα、Gβ 分别为左柱、上下轭、考虑漏磁的永磁体α及永磁体β各自部分的总磁导。最终可得到考虑永磁体漏磁效应的限流器电感计算值为1.229H,有限元仿真解为1.24H,二者误差为0.89%,验证了本方法在不同磁结构中的有效性。
此外,由于本方法基于数学解析原理,相较需要迭代计算的有限元方法而言节省了大量计算资源。得到限流器尺寸参数后,电感值的计算时间小于1s,较有限元法的数千秒而言速度快了多倍。此外,由于数值解析法得到的是限流器的理论公式解,可以依此进行限流器尺寸参数反演及参数优化工作,设计流程所需时间较前述数值迭代及有限元法而言耗时短,比较适合实际工程使用。
5 实验验证
基于上述工作原理,设计并搭建了小容量样机平台,验证所述方法的有效性,样机采用图1 所示两柱式结构拓扑。平台参数见表3。
表3 实验模型参数
Tab.3 Parameters of the experiment FCL model

模型参数 数值边柱 le=120mm Se=40×40mm2限流器永磁体 lm=6mm Sm=40×65mm2绕组 Ndc=185 Rfcl=0.5Ω性能参数 Bs=1.9T, Bu=1.3T Ln=20mH, Lf=55mH其他负载 R1=18Ω R2=2Ω电流 i0=1A if=7.6A
图12 所示为实验平台及等效电路。实验利用三相电压源配合三相不可控整流桥输出直流电流,通过投切电阻的方式模拟系统末端故障,正常工作时R1 与R2 均串入系统,故障发生时切掉大负载R1,模拟电流陡增效果。
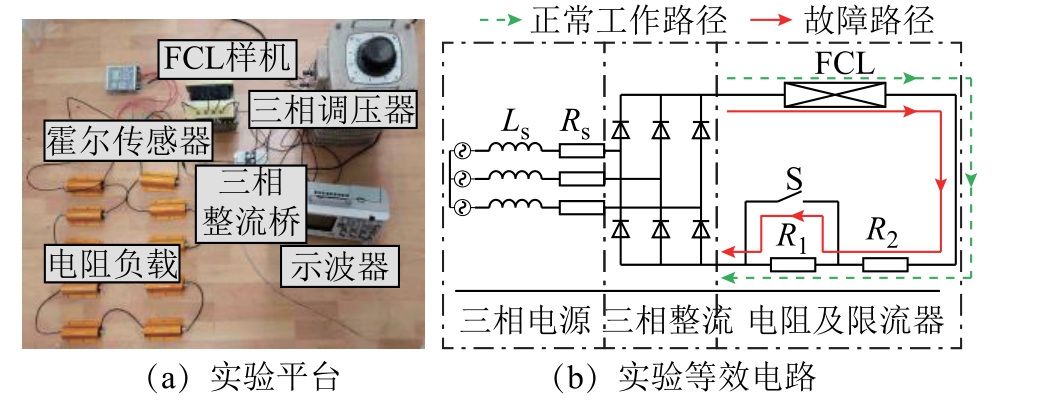
图12 实验平台及等效等效电路
Fig.12 Experimental diagram and equivalent circuit
实际直流系统中,直流侧往往会串入一个固定电抗实现滤除纹波、限制故障电流上升等作用。为了验证效果,本实验首先在直流侧输出端串入20mH 固定电抗,利用示波器录下正常及故障波形数据,然后将限流器替换固定电抗,进行对比仿真分析。实验等效电路如图12b 所示。
通过测量限流器上的电压电流及系统电流,并采用式(28)计算电感值。
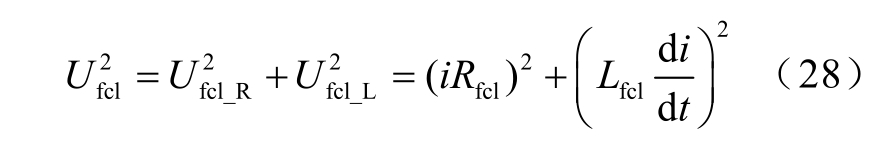
式中,Ufcl、Rfcl、Lfcl、i 分别为限流器两端测量电压值、限流器本体电阻值、限流器电感值和系统电流值。由式(28)计算可得限流器电感值为

5.1 正常工作状态
图13 所示为正常工作时限流器两端的电压及电流实验波形。由于实验采用三相不可控整流桥产生直流源,因此波形存在六脉频波动。系统电流波形实际是以单个电阻负载上的电压表示,由于负载为纯阻性,将电压除以单个负载阻值2Ω 即可得到实际系统电流。由于示波器同时测得限流器电压与负载电压,负极探头接在同一侧,两个探头测量电压方向相反,因此波形存在一正一负的情况。实际波形均为正值,图13 中实际系统电流值为1A。

图13 正常工作下限流器波形
Fig.13 Normal waveforms of FCL
因此,由式(29)及图13 数据可以算得,实验测量稳态时段内的限流器电感值为18.7mH。有限元仿真值为19.7mH,本文所述计算值为20.0mH。
5.2 故障限流状态
图14 所示为故障发生后时限流器两端的电压及电流实验波形。同样,由于示波器同时测得限流器电压与负载电压,负极探头接在同一侧,两个探头测量电压方向相反,因此波形存在一正一负的情况。实际系统电流应该是以x 轴镜像翻转波形,故障时刻由1A 上升至稳态7.5A。由于系统发生故障后系统工作状态发生剧变,导致纹波与扰动更加明显。由式(29)及图14 数据可以算得,实验测量稳态时段内的限流器电感值为55.3mH,有限元仿真值为53.8mH,本文所述计算值为53.3mH。
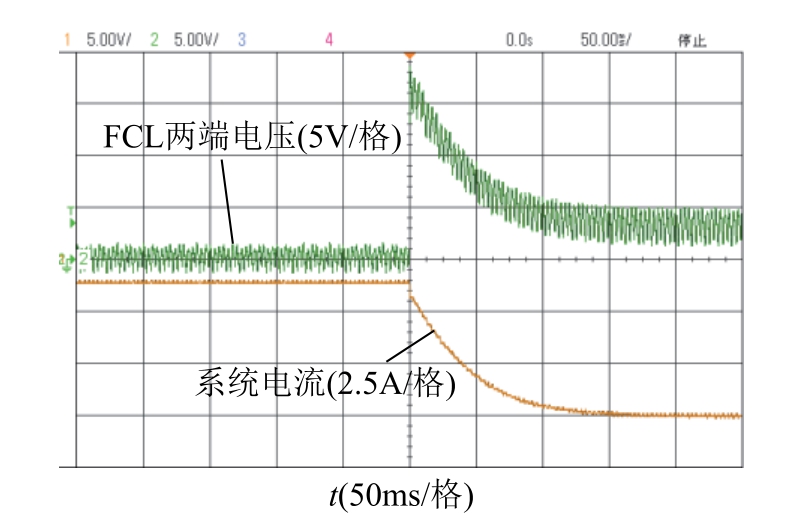
图14 故障发生后限流器波形
Fig.14 Fault waveforms of FCL
5.3 对比分析
限流器电感值结果对比见表4。正常工作时,计算值与仿真值、实验值间的误差分别为1.5%、6.9%,总体误差低于7%;故障发生后,计算值与仿真值、实验值间的误差分别为0.9%、3.6%,总体误差低于4%。在正常态与故障态,仿真、实验、计算三者吻合度均较好,验证了本文所述计算方法的有效性。
表4 限流器电感值结果对比
Tab.4 Results comparison of Lfcl
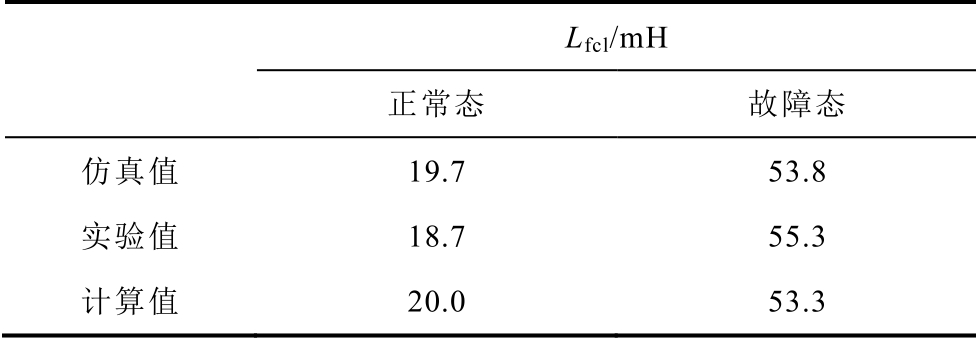
Lfcl/mH正常态 故障态仿真值 19.7 53.8实验值 18.7 55.3计算值 20.0 53.3
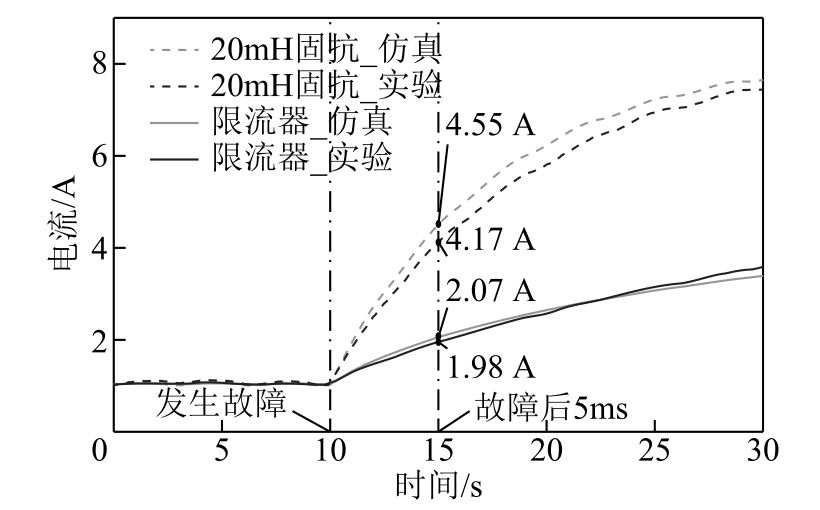
图15 限流效果对照
Fig.15 Fault limiting performance comparison
为了验证限流器的限流效果,将装设限流器前后的故障电流进行对比分析,由图15 可知,当系统仅有20mH 固定电抗时,电流在20ms 内上升至额定电流的近8 倍,需要限流手段限制故障电流上升速率。而将限流器替换固定电抗后,由于限流器正常电感值与20mH 电感接近,正常工作电流与串联固定电抗时基本吻合,对系统无影响;短路故障发生后,故障电流上升速度显著降低,5ms 内的故障电流由4.17A 降低至1.98A,限制率达52.5%。由此可知,所述限流器在故障发生时刻有效进入限流状态,可以显著降低故障电流上升速度,减少直流侧断路器所需开断能力。
由仿真与实验对比可知,20mH 固抗与限流器的仿真与实验波形基本吻合,限流器的仿真与实验波形的误差为4.3%,整体误差低于5%,验证了本文所述方案的有效性与准确性。
6 结论
针对现有永磁偏磁型直流限流器设计计算方法缺乏漏磁分析与计算,计算结果不准确,耗费计算资源多的问题,本文提出了一种计及永磁体漏磁效应的磁饱和型高压直流限流器设计计算方案,通过磁通管区段拟合方法,重构限流器等效磁路的磁阻网络,得到设计计算方案,最后利用多组有限元仿真及样机实验验证了所述方案的有效性。结论如下:
1)传统磁阻分析法未计及永磁体漏磁效应,导致永磁部分总磁阻偏低,最终设计计算结果不准确。本方法将永磁邻近部分空气漏磁进行分区段拟合,得到准确的磁阻网络。
2)多组有限元仿真与样机实验验证了所述方法的有效性,相较传统方法而言,本方法计算误差由20%左右降至1.3%以内,实验误差总体低于7%,验证了所述方案的有效性。本方案适用于不同设备容量等级及拓扑结构,设计计算效率高,可以广泛应用于永磁偏磁型铁心电感设备。
[1] 周光阳, 李妍, 何大瑞, 等. 含限流器的多端柔直系统故障保护策略[J]. 电工技术学报, 2020, 35(7):1432-1443.
Zhou Guangyang, Li Yan, He Darui, et al. Protection scheme for VSC-MTDC system with fault current limiter[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1432-1443.
[2] 赵成勇, 宋冰倩, 许建中. 柔性直流电网故障电流主动控制典型方案综述[J]. 电力系统自动化, 2020,44(5): 3-13.
Zhao Chengyong, Song Bingqian, Xu Jianzhong.Overview on typical schemes for active control of fault current in flexible DC grid[J]. Automation of Electric Power Systems, 2020, 44(5): 3-13.
[3] 范志华, 苗世洪, 刘子文, 等. 模块化多电平换流器子模块故障特性分析与解耦控制策略[J]. 电工技术学报, 2018, 33(16): 3707-3718.
Fan Zhihua, Miao Shihong, Liu Ziwen, et al. Modular multilevel converter sub-module fault characteristics analysis and decoupling control strategy[J].Transactions of China Electrotechnical Society, 2018,33(16): 3707-3718.
[4] 蔡洋, 郭文勇, 赵闯, 等. 模块化多电平换流器直流故障过电流精确计算与分析[J]. 电工技术学报,2021, 36(07): 1526-1536.
Cai Yang, Guo Wenyong, Zhao Chuang, et al. The accurate calculation and analysis of overcurrent under modular multilevel converter DC fault[J].Transactions of China Electrotechnical Society, 2021,36(7): 1526-1536.
[5] 郝鑫, 王盼宝, 孙红梅, 等. 直流故障限流器工作原理分析与特性研究[J]. 电网技术, 2019, 43(12):4414-4424.
Hao Xin, Wang Panbao, Sun Hongmei, et al. Principle and characteristic analysis of existing DC fault current limiters[J]. Power System Technology, 2019, 43(12):4414-4424.
[6] 王建华, 项彬, 杨騉, 等. 超导限流直流开断技术研究[J]. 电工技术学报, 2019, 34(20): 4196-4207.
Wang Jianhua, Xiang Bin, Yang Kun, et al.Superconducting fault current limiting DC current interrupting technology[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4196-4207.
[7] 涂春鸣, 李庆, 郭祺, 等. 桥式限流与动态电压恢复器融合设计及控制方法[J]. 电工技术学报, 2020,35(20): 4384-4396.
Tu Chunming, Li Qing, Guo Qi, et al. Fusion design and control method of bridge current limiter and dynamic voltage restorer[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4384-4396.
[8] 李承昱, 李帅, 赵成勇, 等. 适用于直流电网的限流混合式直流断路器[J]. 中国电机工程学报, 2017,37(24): 7154-7162.
Li Chengyu, Li Shuai, Zhao Chengyong, et al. A novel topology of current-limiting hybrid DC circuit breaker for DC grid[J]. Proceedings of the CSEE, 2017, 37(24):7154-7162.
[9] 刘清峰, 邱清泉, 张志丰, 等. 分裂电抗型超导限流器的交直流限流特性[J]. 高电压技术, 2018,44(2): 456-462.
Liu Qingfeng, Qiu Qingquan, Zhang Zhifeng, et al.AC/DC current limiting characteristics of the divisive reactance type superconducting fault current limiter[J].High Voltage Engineering, 2018, 44(2): 456-462.
[10] 张立晖, 石晶, 严思念, 等. 磁通约束型超导限流开关系统应用[J]. 电工技术学报, 2018, 33(22):5292-5299.
Zhang Lihui, Shi Jing, Yan Sinian, et al. System application of flux-coupling superconducting fault current limiting switch[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5292-5299.
[11] 唐诵, 贾冠龙, 张成浩, 等. 适用于直流电网的预限流型直流断路器拓扑[J]. 电力系统自动化, 2020,44(11): 152-162.
Tang Song, Jia Guanlong, Zhang Chenghao, et al.Topology of DC circuit breaker with pre-currentlimiting capability for DC grid[J]. Automation of Electric Power Systems, 2020, 44(11):152-162.
[12] Yuan Jiaxin, Zhou Hang, Gan Pengcheng, et al. A novel concept of fault current limiter based on saturable core in high voltage DC transmission system[J]. AIP Advances, 2018, 8(5): 056636.
[13] Li Botong, Jing Fangjie, Li Bin, et al. Study of the application of active saturated iron-core superconductive fault current limiters in the VSCHVDC system[J]. IEEE Transactions on Applied Superconductivity, 2018, 28(4): 1-6.
[14] Zhou Hang, Yuan Jiaxin, Chen Fan, et al. Performance investigation on a novel high inductance changing ratio MMC-based direct current system saturated core FCL[J]. IEEE Transactions on Power Delivery, 2020,35(3): 1502-1514.
[15] Dao V Q, Lee J, Kim C S, et al. Conceptual design of a saturated iron-core superconducting fault current limiter for a DC power system[J]. IEEE Transactions on Applied Superconductivity, 2020, 30(4): 1-5.
[16] Ahmadvand Mohammad, Khanabdal Saheb, Hagh Mehrdad Tarafdar. A novel three phase saturable-core fault current limiter structure[J]. IEEE Transactions on Power Delivery, 2019, 34(2): 410-419.
[17] 宋萌, 林哲侃, 罗运松, 等. 基于ANSYS 的饱和铁心型限流器建模与仿真[J]. 广东电力, 2019, 32(4):55-61.
Song Meng, Lin Zhekan, Luo Yunsong, et al.Modeling and simulation of saturated iron core fault current limiter based on Ansys[J]. Guangdong Electric Power, 2019, 32(4): 55-61.
[18] Vilhena Nuno, Arsenio Pedro, Murta-Pina Joao, et al.A methodology for modeling and simulation of saturated cores fault current limiters[J]. IEEE Transactions on Applied Superconductivity, 2015,25(3): 5600704.
[19] Eladawy Mohamed, Tarhuni Naser J, Metwally Ibrahim A. Transient dynamic analyses of presaturated core fault current limiters through flux and inductance versus current modelling[J]. IET Electric Power Applications, 2019, 13(9): 1263-1272.
[20] Li Bin, Wang Changqi, Hong Wei, et al. Modelling of the DC Inductive superconducting fault current limiter[J]. IEEE Transactions on Applied Superconductivity, 2020, 30(4): 1-5.
[21] 陈柏超, 魏亮亮, 雷洋, 等. 饱和铁心型桥式故障限流器的性能参数设计与实验[J]. 电工技术学报,2017, 32(13): 185-193.
Chen Baichao, Wei Liangliang, Lei Yang, et al.Performance parameter design and experiment of the bridge-type saturated core fault current limiter[J].Transactions of China Electrotechnical Society, 2017,32(13): 185-193.
[22] Yuan Jiaxin, Zhang Zhewei, Zhou Hang, et al.Optimized design method of permanent magnets saturated core fault current limiters for HVDC applications[J]. IEEE Transactions on Power Delivery,2021, 36(2): 721-730.