0 引言
太阳活动引起的地磁场剧烈变化称为磁暴。时变磁场在地面感应出的电场通过输电线、中性点接地变压器和大地构成的回路产生地磁感应电流(Geomagnetically Induction Current, GIC),其频率一般为 0.000 1~0.01Hz[1]。由其引起的变压器铁心半波饱和,会导致谐波、局部温升、无功损耗和振动、噪声增大等有害的干扰[2-8]。其中谐波和无功功率的波动会影响电力设备的安全稳定运行及整个系统的电压调控,因此危害最大[9]。近些年随着输电线路电压等级越来越高,导线电阻越来越小,变压器遭受的GIC 越来越大[10]。因此精确预测在地磁暴期间的变压器无功功率损耗就显得十分重要。
GIC 对不同类型变压器无功损耗影响大小以及两者之间的直接关系(以下简称为GIC-Q),国内外已有大量的研究[11-17]。目前普遍认为,单相变压器由于磁路结构的特点受GIC 影响导致的无功功率波动最大[18];虽然谐波电流受变压器励磁曲线影响,但在实际测得的GIC 数值范围内,基波无功功率与GIC 之间呈线性关系[19]。然而上述研究直接把GIC等效为直流电流,没有考虑GIC 的准直流特性,尤其是在GIC 由一个正峰值向一个负峰值变化的阶段,其变化率较大,此时GIC 的这种准直流特性不可忽略。文献[20]首次提出不考虑GIC 的准直流特性,可能会导致对GIC 风险评估的降低。因此IEEE在Std C57.163—2015 标准中,将一个地磁暴事件分割为多个小区间,每个区间对应一个直流电流,以此来考虑GIC 的准直流特性对温升计算的影响,但这种方法并没有涉及对铁心动态过程的分析。文献[21]认为对于含有三角形联结绕组的变压器,不考虑GIC 的准直流特性会影响其无功功率的计算精度,并通过理论计算与实测数据的对比,证明了结论的正确性。但其没有考虑实测GIC 数据的精度对计算结果的影响,也没有针对具体变压器进行分析。
因此本文通过搭建磁暴期间变压器铁心准直流零序等效电路模型,分析研究了GIC 的准直流特性对于无功损耗的影响,相比于将GIC 当作纯直流来研究,无功损耗的计算精度明显提高。通过使用不同步长的GIC 数据,对一台1 000kV 交流变压器和一台800kV 换流变压器进行了仿真计算,证明了若直接使用原始GIC 秒数据进行无功损耗计算会造成较大误差,必须对原始数据进行插值处理,并进一步总结了GIC 准直流特性对无功损耗的影响规律。最后通过改变变压器参数,确定了各参数对无功损耗影响的灵敏度大小。研究结论可为准确预测地磁暴期间变压器无功损耗及评估其遭受GIC 侵害大小提供理论依据。
1 静态无功功率理论计算
由于变压器铁心使用的硅钢片在饱和前后微分磁导率相差的非常大,因此可以用图1 所示的两条线性直线表示其 i- ϕ 关系,即忽略曲线在拐点附近的过渡过程。当不考虑GIC 的动态特性时,其在某一小时间段内可以完全等效为直流电流,因此GIC的静态无功功率理论推导可以当作是直流偏磁情况来处理。
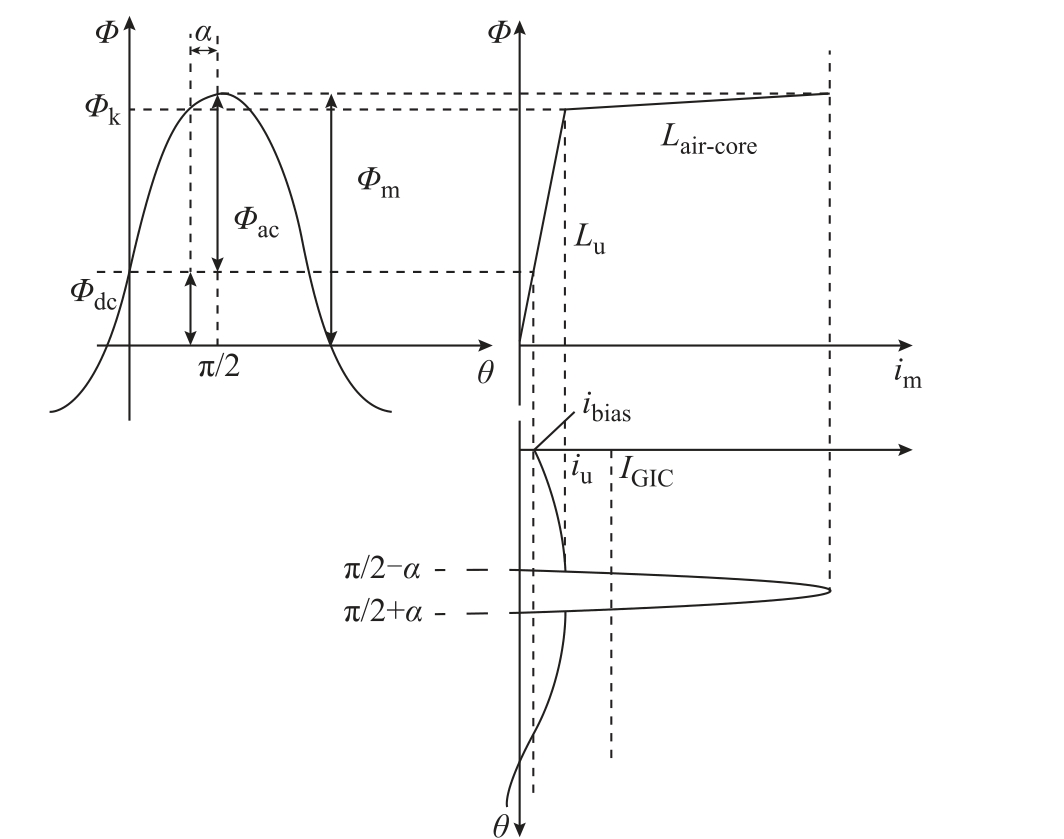
图1 直流偏磁时变压器铁心工作状态
Fig.1 Transformer core operating condition under dc bias
图1 中, Lair-core 、 Lu 分别为铁心饱和、非饱和微分电感,i bias 为直流磁通对应的直流电流分量,i u为额定励磁电流峰值。当GIC IGIC 流入变压器时,铁心中便会产生相应的直流磁通量dcΦ ,加上峰值为acΦ 的额定交流磁通量,此时铁心中总的磁通量最大值 mΦ 将会超过膝点磁通kΦ 使得铁心进入饱和状态。图中α 定义为过磁通角,直流电流越大该角数值越大,直流为零时,α ≈0 。图1 中各个磁通的关系如下。

式中,ω 为工频角频率。
由图1 可知在GIC 的作用下,一个周期内励磁电流的表达式为
式中
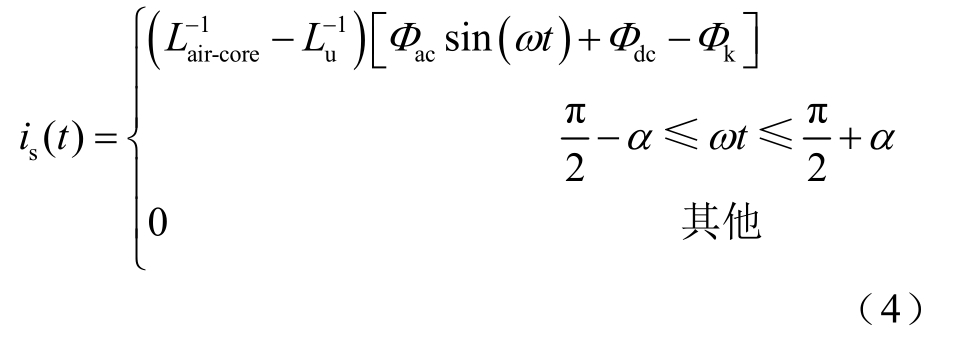
对励磁电流进行傅里叶分解,可得其直流含量I GIC和基频分量有效值 I 1的表达式分别为
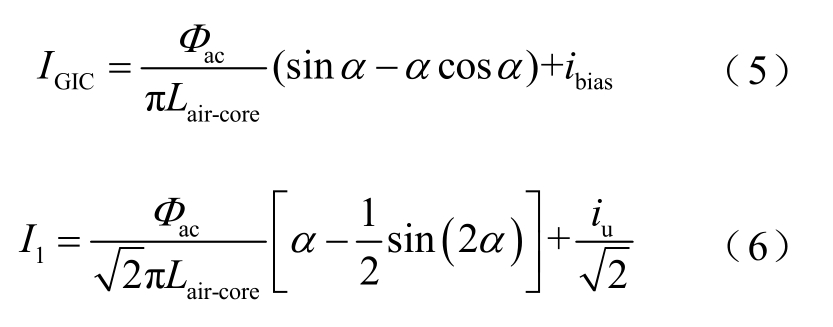
当变压器遭受直流侵害时铁心饱和,励磁电感迅速减小,此时单台变压器损耗的无功功率Q为正常时的无功损耗uQ 加上励磁电感消耗的无功mQ ,对应 I1 的两部分。假设变压器一次电压在GIC 入侵期间波形保持不变为额定基频电压,且与励磁电流的相位相差90°,即忽略铁心磁滞、涡流损耗。因此直流偏磁状态下,单台变压器的无功损耗为
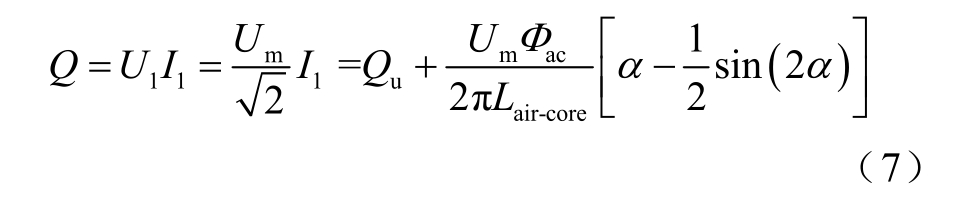
式中,U 1 、U m 分别为额定相电压的有效值和峰值。由式(7)结合式(5)和式(2)即可得到任意GIC I GIC下,单台变压器消耗的无功损耗。
2 GIC-Q 动态关系分析
在磁暴期间,假设A、B、C 三相系统的参数都是一样的,那么流经变压器每一相中的GIC 无论大小还是方向都是完全相同的,又因为其具有准直流特性,因此可以将GIC 看成是一组零序电流。直流输电工程一般为12 脉动结构,因此每一个单元包含一台阀侧为三角形联结的换流变压器,而交流变压器为了补偿系统无功损耗,一般也含有三角形联结的第三绕组。由于三角形联结绕组的存在,具有准直流特性的GIC 将会在三角形联结绕组中感应出循环电流,从而抵消铁心中的准直流磁通。因此在磁暴期间,流入变压器中的GIC,不是完全作用到铁心中并产生相应的无功损耗。图2 为变压器准直流零序等效电路,表示了在磁暴期间变压器铁心的动态特性。
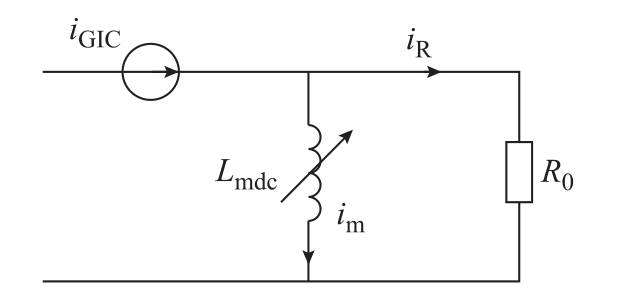
图2 变压器准直流零序电路
Fig.2 Transformer quasi-DC zero sequence circuit diagram
图 2 中 mi 为实际作用到铁心产生直流磁通的电流, 0R 为三角形联结绕组的零序等效电阻, Ri 为三角形联结绕组中的电流。因为GIC 的频率很低,因此变压器绕组漏电抗产生的电压降很小,可以忽略。变压器铁心的准直流特性用电感 Lm dc表示。由图1 可知直流磁通 Φd c的表达式为
式中,ω=2πf , f 为系统工频。当变压器铁心工作在线性区域时,即铁心磁通最大值 mΦ 小于膝点磁通kΦ ,直流电流与直流磁通的关系可由非饱和微分电感 uL 表示,所以此时准直流电感 Lmdc = uL 。当变压器铁心逐渐进入饱和状态时,即 mΦ > kΦ 时,实际作用到铁心的直流电流 mi 由两部分组成,即
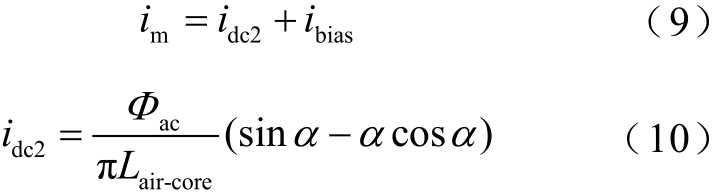
由定义可知,此时准直流电感 Lmdc 为

因此铁心饱和时的准直流电感 Lmdc 在数值上可以看成是电感 uL 和电感 Ldc2 的并联。
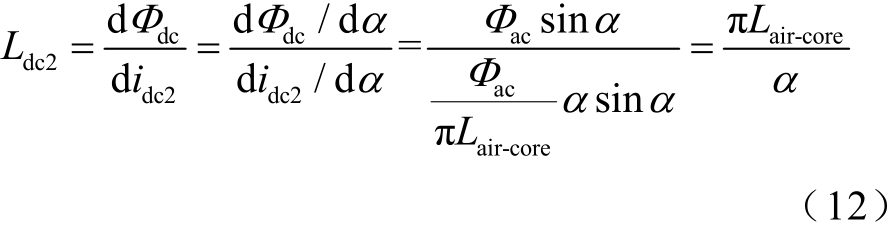
当变压器铁心在一个周期内全部处于饱和状态时,即![]() 时,此时铁心相当于一个数值为 Lair-core 的电感,因此 Lm dc= Lair-core。因为铁心完全处于饱和状态所需的直流电流远大于我国实测的GIC 最大值,因此在实际计算中可以不考虑此种情况。
时,此时铁心相当于一个数值为 Lair-core 的电感,因此 Lm dc= Lair-core。因为铁心完全处于饱和状态所需的直流电流远大于我国实测的GIC 最大值,因此在实际计算中可以不考虑此种情况。
综上所述准直流电感 Lmdc 的表达式为
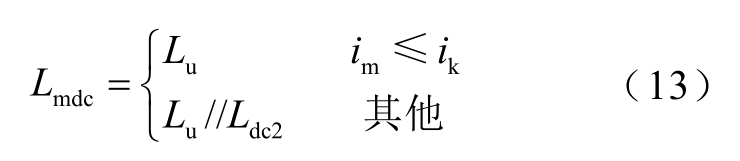
式中, ik 为变压器铁心达到膝点磁通所需的直流电流,其与 kΦ 的关系为
此时准直流电感 Lmdc 随电流 mi 变化关系如图3 所示。图3 中数值由表1 中交流变压器参数计算得到。

图3 准直流电感与直流电流关系
Fig.3 Diagram of relationship between quasi-DC inductance and DC current
表1 变压器参数
Tab.1 Transformer parameters

名称 交流变压器 换流变压器额定容量/(MV⋅A) 1 000/1 000/334 321.1/321.1额定电压/kV 1050 525//110 33 530 170.3/33绕组匝数 678/678/246 705/227膝点磁通/Wb 2.05 2.06额定磁通/Wb 1.954 6 1.75非饱和微分电感/H 0.850 2 0.849 8饱和微分电感/H 0.000 59 0.000 62零序电阻/Ω 0.19 0.2
根据图2 可以列出微分方程为
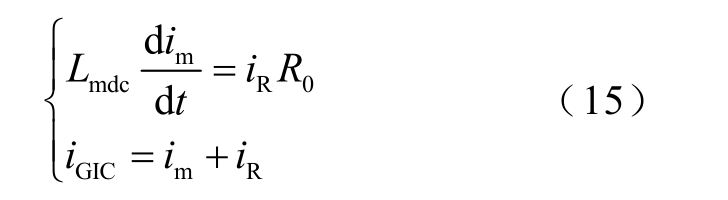
化简可得
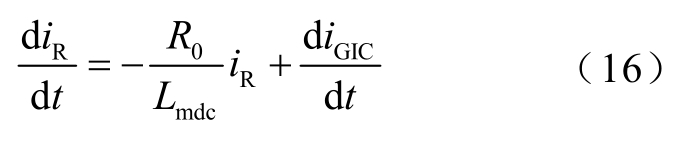
运用向后差分法,即可求得磁暴期间变压器三角形联结绕组中的电流 iR 以及实际作用于铁心的直流电流 mi ,进而计算出对应的无功损耗。
3 仿真计算
为了对比分析,本节分别针对1 000kV 交流变压器和800kV 换流变压器进行了仿真计算。两种变压器的参数见表1,其中交流变压器为三绕组自耦变压器,第三绕组为三角形联结,而换流变压器为双绕组结构,阀侧为三角形联结绕组。GIC 采用2004年11 月9 号广东岭澳核电站的实测秒数据,该电流的峰值为75A,是我国目前为止测量到的最大数值。为了提高计算效率,仿真时间只截取了包含GIC 峰值在内的5min 这一时段,如图4 所示。
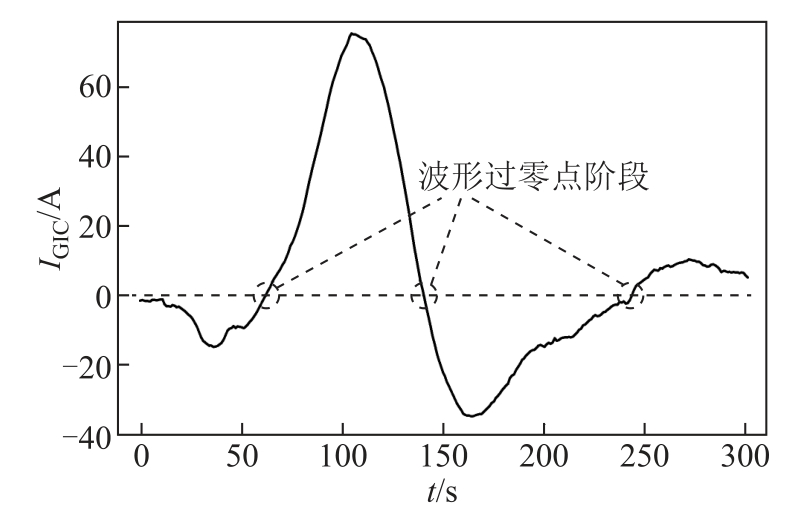
图4 实测GIC 数据
Fig.4 Measured GIC data
由于 ibias 与 IGIC 相比很小,uQ 与Q 相比也很小。因此式(5)和式(7)可化简为
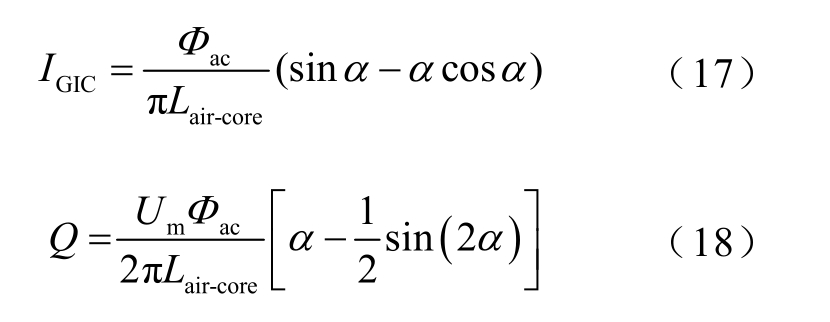
图5 为函数sinα −αcos α和α−0.5sin(2α )的关系图,由图可知当α <0.846rad,即48.5°时,函数α−0.5sin(2α ) ≈1.9(sinα −αcosα ),此时 I GIC和Q 的关系可以表示为
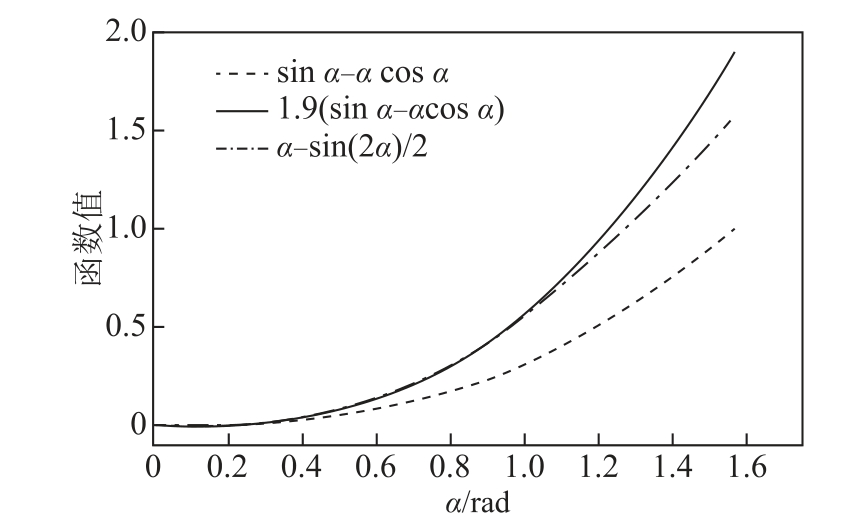
图5 函数关系图
Fig.5 Functional diagram
由于使得α >48.5°所对应的GIC 数值很大,实际情况中并不存在,因此可以认为在图4 所示的GIC 下,GIC 与无功损耗为线性关系。
图6 为不考虑GIC 准直流特性时,由式(2)、式(5)、式(7)计算得到的换流变压器无功损耗数值。通过对比图4 和图6,也验证了GIC 与无功损耗的线性关系。又因为在考虑GIC 准直流特性时,实际作用于铁心的直流电流 mi 为流入变压器中的实测GIC iGIC 减去三角形联结绕组中的电流 Ri 。因此三角形联结绕组中电流越大,变压器无功损耗受GIC 准直流特性影响变化量也越大。
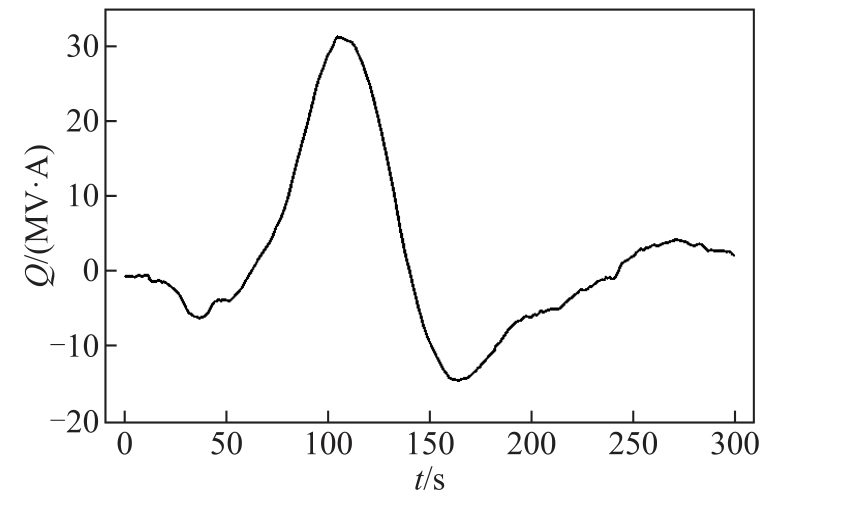
图6 不考虑GIC 准直流特性时换流变压器无功损耗
Fig.6 The reactive power loss of converter transformer with no quasi-DC characteristic
3.1 GIC 测量精度对仿真结果的影响
因为实测数据是每秒记录一次,为了避免GIC数据精度对计算结果造成影响,对GIC 秒数据进行线性插值,每两个数据点之间分别插入50 个和10个点,对应的仿真步长为0.02s 和0.1s。
图7 为分别使用步长为0.02s、1s、0.1s 的GIC数据计算的换流变压器无功损耗变化图(变化量为考虑GIC 准直流特性和将GIC 当作纯直流计算得到的无功损耗差值)。由图可知若直接使用GIC 秒数据计算,变压器的无功损耗与将GIC 当作纯直流计算相比变化较小,而使用经过插值处理的GIC 数据计算得到的无功变化却较大。从式(16)可以看出,准直流电感 mL 与 iGIC 变化率越大,三角形联结绕组中的电流 Ri 越大,无功损耗与不考虑GIC 准直流特性时相比变化就越大。而图3 则表明当作用于铁心的直流电流 mi 小于 ki 时电感 mL 最大,之后迅速减小,又因为变压器非饱和微分电感 uL 非常大,由式(14)计算出的 ik 只为0.365 A,因此若实测GIC数据采样间隔太大,如某一时刻GIC 为1A,1s 后测得GIC 为-2A,则计算时将不会考虑准直流电感为 uL 的情况,这会对无功计算造成较大的误差。
另外使用步长为0.02s 和0.1s 的GIC 数据计算得到的无功变化量基本一样,这说明使用步长为0.1s 的GIC 数据可以得到准确的计算结果,后续的计算都使用此数据。
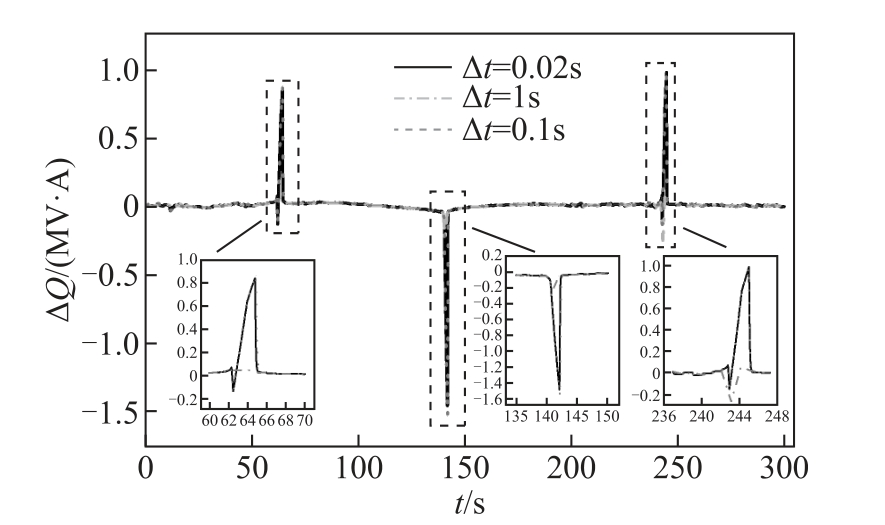
图7 换流变压器无功损耗变化量
Fig.7 Variation of reactive power loss in converter transformer
3.2 GIC 准直流特性对无功影响规律
通过对比图7 和图4 还可以看出,在GIC 流向发生转变所对应的波形过零点阶段,无功损耗发生了较大变化,而其余时段无功损耗与不考虑GIC 准直流特性时相比基本没有变化。这是因为在GIC 流向发生转变所对应的波形过零点阶段,准直流电感和GIC 变化率与其他时段相比都是最大的,所以在此阶段三角形联结绕组中电流激增,造成无功损耗较大的变化。另外当GIC 数值由正变负时,即流向变压器电流由流入变为流出,由于 iGIC 变化率为负,导致计算出的三角形联结绕组中的电流 iR 为负值,因此在这种情况下,实际作用于铁心的直流电流 mi大于流过变压器的GIC,造成无功损耗的增大。当GIC 流向由流出变压器变为流入时,结论则相反。
3.3 两种类型变压器差异分析
由于换流变压器和交流变压器的额定电压等级不一致,为了对比分析两者无功受GIC 准直流特性影响的大小,将交流变压器额定电压归算到换流变压器的额定电压,计算的无功变化量如图8 所示。对比图7 和图8 可知,两种变压器无功损耗有着相同的变化规律,都是在GIC 流向发生转变所对应的过零点阶段发生较大变化。但是交流变压器的无功变化却小于换流变压器的。这是因为换流变压器正常工作时,由于换流阀触发延迟角不平衡等原因,阀侧绕组中存在较小的直流电流,因此在设计换流变压器时会将其工作磁通设计得较低,所以其额定磁通比交流变压器小。而两者铁心硅钢片使用的型号分别为27ZH095 和27ZH100,非常接近。再加上都是单相四柱结构,所以其膝点磁通、非饱和微分电感、饱和微分电感相差不大。表1 列出了具体数值。因此结合式(16)就可以得出如下结论:在其余参数相同的情况下,额定磁通较低的换流变压器相比于交流变压器,无功损耗更容易遭受GIC 准直流特性影响。
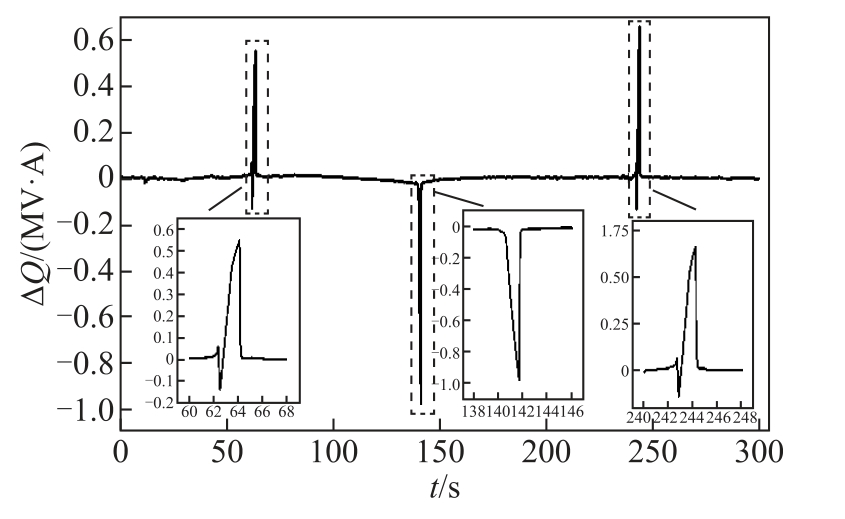
图8 交流变压器无功损耗变化量
Fig.8 Variation of reactive power loss in AC transformer
4 参数灵敏度分析
本节针对仿真参数对无功损耗的影响进行了灵敏度分析。由表1 和图7、图8 可知,变压器额定磁通越大其无功损耗受GIC 准直流特性影响就越小,且在额定磁通增加了11.6%的情况下(以表1 中换流变压器的参数为基准),无功损耗变化量的最大值减小了39 %。通过第3 节的分析可知,膝点磁通对变压器无功损耗的影响机理与额定磁通一样,因此两者的灵敏度分析一致。
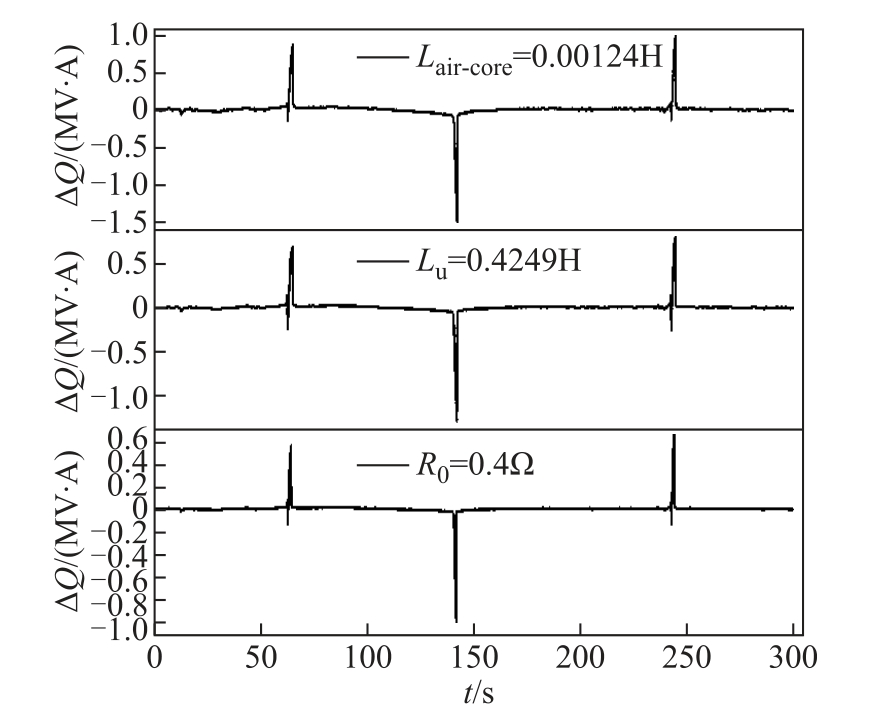
图9 仿真参数灵敏度分析图
Fig.9 Sensitivity analysis diagram of simulation parameters
图9 为饱和微分电感Lair-core 、非饱和微分电感Lu 、三角形联结绕组电阻R 0的灵敏度分析图,图中的变量均是以相应的换流变压器参数为比较对象。对比图7、图9 可知,当饱和微分电感变为原来的两倍时,无功损耗变化量数值基本不变。而非饱和微分电感越小,三角形联结绕组电阻值越大,无功损耗受GIC 准直流特性影响变化量越小。具体变化率为:非饱和微分电感减小为原来的一半,无功损耗变化量最大值减小了11.7%;三角形联结绕组电阻值增加为原来的两倍,无功损耗变化量最大值减小了32.75%。
综上所述变压器额定磁通和膝点磁通对其无功损耗受GIC 准直流特性影响最大,三角形联结绕组电阻和非饱和微分电感的影响依次减小,饱和微分电感对其几乎没有影响。
5 结论
本文建立了GIC-Q 之间的动态数学模型,研究了GIC 准直流特性对于含有三角形联结绕组的变压器无功损耗的影响。主要结论如下:
1)当考虑GIC 准直流特性时,对于含有三角形联结绕组的变压器而言,其无功损耗不仅与此刻的GIC 有关,还与上一时刻的GIC 有关。
2)GIC 准直流特性对于变压器无功损耗的影响主要发生在GIC 流向发生转变所对应的波形过零点阶段,其无功损耗的增减与GIC 的流向有关。
3)在其余参数相同的情况下,额定磁通较低的换流变压器相比于交流变压器,无功损耗更容易遭受GIC 准直流特性影响。
4)额定磁通越小、三角形联结绕组电阻越小、非饱和微分电感越大,变压器无功损耗受GIC 准直流特性影响越大,且这三个参数对无功损耗变化的影响程度依次减小。
[1] Albertson V D, Thorson J M, Miske S A, et al. The effects of geomagnetic storms on electric power system[J]. IEEE Transactions on Power Apparatus and System, 1974, PAS-93(4): 1031-1044.
[2] 赵小军, 刘小娜, 肖帆, 等. 基于 Preisach 模型的取向硅钢片直流偏磁磁滞及损耗特性模拟[J]. 电工技术学报, 2020, 35(9): 1849-1857.
Zhao Xiaojun, Liu Xiaola, Xiao Fan, et al. Simulation of DC magnetic bias hysteresis and loss characteristics of oriented silicon steel based on Preisach model[J].Transactions of China Electrotechnical Society, 2020,35(9): 1849-1857.
[3] Girgis R S, Vedante K B. Impact of GICs on power transformers: overheating is not the real issue[J].IEEE Electrification Magazine, 2015, 3(4): 8-12.
[4] Walling R A, Khan A N. Characteristics of transformer exciting-current during geomagnetic disturbances[J]. IEEE Transactions on Power Delivery,1991, 6(4): 1707-1714.
[5] 潘超, 王格万, 蔡国伟, 等. 交直流混杂模式下变压器励磁电流谐波与箱体损耗映射研究[J]. 电工技术学报, 2019, 34(13): 2830-2838.
Pan Chao, Wang Gewan, Cai Guowei, et al. Study on the mapping of transformer excitation current harmonics and enclosure loss in AC-DC hybrid mode[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2830-2838.
[6] 张鹏宁, 李琳, 程志光, 等. 并联电抗器与变压器模型铁心振动仿真与试验对比[J]. 电工技术学报,2018, 33(22): 5273-5281.
Zhang Pengning, Li Lin, Cheng Zhiguang, et al.Vibration simulation and test comparison of model cores of shunt reactor and transformer[J].Transactions of China Electrotechnical Society, 2018,33(22): 5273-5281.
[7] 杨晓辉, 王丰华, 段若晨, 等. 500kV 电力变压器直流偏磁耐受性能的仿真研究[J]. 电力系统保护与控制, 2014, 42(14): 60-66.
Yang Xiaohui, Wang Fenghua, Duan Ruocheng, et al.Simulation of DC magnetic bias tolerance of 500kV power transformer[J]. Power System Protection and Control, 2014, 42(14): 60-66.
[8] 李冰, 王泽忠, 刘恪, 等. 特高压变压器直流偏磁对绕组电流的影响[J]. 电工技术学报, 2020, 35(7):1422-1431.
Li Bing, Wang Zezhong, Liu Ke, et al. Influence of DC bias on winding current of UHV transformer[J].Transactions of China Electrotechnical Society, 2020,35(7): 1422-1431.
[9] 王梅义, 吴竞昌, 蒙定中. 大电网系统技术[M].2 版. 北京: 中国电力出版社, 1995.
[10] 刘连光, 王开让, 郭世晓, 等. 双电压等级电网GIC 的相互作用特征[J]. 中国科学·技术科学, 2015,45(12): 1311-1320.
Liu Lianguang, Wang Kairang, Guo Shixiao, et al.Characteristics of GIC interaction in a dual-voltagelevel power network[J]. Science·Technological Science, 2015, 45(12): 1311-1320.
[11] 王泽忠, 谭瑞娟, 李书连, 等. 基于动态电感-励磁电流曲线的特高压变压器空载直流偏磁计算[J].电工技术学报, 2017, 32(10): 154-161.
Wang Zezhong, Tan Ruijuan, Li Shulian, et al.Calculation of no-load DC bias of UHV Transformer based on dynamic inductance-excitation current curve[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 154-161.
[12] 王泽忠, 谭瑞娟, 刘连光, 等. 特高压变压器直流偏磁计算及无功功率特性分析[J]. 高压电器, 2017,53(2): 101-107.
Wang Zezhong, Tan Ruijuan, Liu Lianguang, et al. DC bias calculation and reactive power characteristic analysis of UHV transformer[J]. High Voltage Apparatus, 2017, 53(2): 101-107.
[13] 刘连光, 朱溪, 王泽忠, 等. 基于K 值法的单相四柱式特高压主体变的GIC-Q 损耗计算[J]. 高电压技术, 2017, 43(7): 2340-2348.
Liu Lianguang, Zhu Xi, Wang Zezhong, et al. GIC-Q loss calculation of single-phase four-column UHV transformer based on K-value method[J]. High Voltage Engineering, 2017, 43(7): 2340-2348.
[14] Dong Xuzhu, Liu Yilu, Kappenman J G. Comparative analysis of exciting current harmonics and reactive power consumption from GIC saturated transformers[C]//IEEE Power Engineering Society Winter Meeting,Columbus, OH, USA, 2001: 318-322.
[15] Marti L, Berge J, Varma R K. Determination of geomagnetically induced current flow in a transformer from reactive power absorption[J]. IEEE Transactions on Power Delivery, 2013, 28(3): 1280-1288.
[16] Price P R. Geomagnetically induced current effects on transformers[J]. IEEE Transactions on Power Delivery,2002, 17(4): 1002-1008.
[17] Rezaei-Zare A. Reactive power loss versus GIC characteristic of single-phase transformers[J]. IEEE Transactions on Power Delivery, 2015, 30(3): 1639-1640.
[18] 刘教民, 朱溪, 刘洪正, 等. 电力变压器的 GIC-Q损耗算法的研究综述[J]. 高电压技术, 2018, 44(7):2284-2291.
Liu Jiaomin, Zhu Xi, Liu Hongzheng, et al. A review of GIC-Q loss algorithms for power transformers[J].High Voltage Engineering, 2018, 44(7): 2284-2291.
[19] Mousavi S A, Bonmann D. Analysis of asymmetric magnetization current and reactive power demand of power transformers due to GIC[J]. Procedia Engineering, 2017, 202: 264-272.
[20] You Y, Fuchs E F, Lin D, et al. Reactive power demand of transformers with DC bias[J]. IEEE Industry Applications Magazine, 1996, 2(4): 45-52.
[21] Rezaei-Zare A. Behavior of single-phase transformers under geomagnetically induced current conditions[J]. IEEE Transactions on Power Delivery,2014, 29(2): 916-925.