0 引言
我国资源和负荷分布不均匀，能源利用不充分，远距离输电的格局已基本形成。文献[1-3]做出了关于“未来一体化大电网调控系统”的前瞻性研究，设计了大电网全局决策和监控框架。有功-无功协调调度是实现大电网智能调控、自动巡航的关键一环，是保证电网经济和安全运行的前提之一。
文献[4-6]基于网络特性，利用二阶锥松弛理论，实现配电网有功-无功的协调优化计算。然而，二阶锥松弛技术的计算速度无法达到较大电网的调度需求[7]。文献[8]分析了无功电压优化对新能源消纳的影响。文献[9]基于模型预测控制研究了配电网动态无功优化方法。文献[10]基于多目标优化算法研究了中压配电网中有功-无功的协调优化。文献[11]研究了考虑配网重构的多时间尺度无功优化。文献[12]研究了光伏并网系统的有功-无功控制问题。有功控制对象和无功控制对象通常分属于不同的地区和调度主体，部分控制目标之间存在冲突。在决策角度上，上述研究不能较好地解决有功-无功调度间的矛盾。
进而，实现有功-无功协调调度需要智能组织电力系统中的灵活调控资源，系统的灵活调控资源包含可调度常规能源、需求侧管理、储能和与其他互联市场的交易等[13]。但是，灵活多调控资源在最大化自身收益和优化区域调控指标间具有难以调和的矛盾，智能组织多种灵活调控资源是当前一大热点和难点。
多智能体技术是一类基于协同一致性原理，用于探索环境、解释未知、自主更新和协调冲突的有效技术。实现多智能体系统的“智能”可以运用强化学习方法。强化学习通常分为两类：①值迭代（value based）；②策略迭代（policy gradient）。文献[14-21]将值迭代类型的强化学习方法运用到电力系统中的优化调度、控制等领域。而受到Q 表存储和搜索的限制，智能体的状态空间和动作空间必须是离散的、低维的。上述研究均是采用将连续动作空间离散化的类似处理方法。在运用到有功-无功协调中时可能会损失一部分精度，且对训练过程中新出现的未知状态和动作适应性不强。
相比值迭代类的强化学习方法，采用策略迭代更加适用于解决电力系统有功-无功协调这类拥有连续、高维状态和动作空间的问题。由于该种算法直接由策略梯度更新神经网络参数，各智能体的动作选择差异会导致环境发生变化，影响了智能体在动作选择时的收敛性。所以，此类方法在电力系统中的应用较少。针对上述问题，本文在对各类算法和多智能体环境探索的基础上，提出适用于本文控制模型的改进多智能体深度确定策略梯度算法（Multi-Agent Deep Deterministic Policy Gradient,MADDPG）。在智能体更新时考虑其他智能体的动作选择，从而提高在多智能体环境中各智能体的训练效果。同时，搭建分层多智能体有功-无功协调调度框架；设计电力系统多智能体环境；构造状态空间、动作空间和智能体奖励函数表达。最后，通过算例仿真和对比分析，验证本文所提模型及算法的优势和有效性。
1 分层多智能体有功-无功协调框架
多智能体系统是分布式控制中的一种技术体现，分布式系统通常有四种组织形式[22]。分布式（distributed）的系统组织形式在通信成本、运行成本和可行性等方面具有一定优势。
基于此，将受控电网划分为不同的区域。统筹区域内灵活有功-无功调控资源，参考国际能源署（International Energy Agency, IEA）对灵活调控资源的定义，将区域中的有功-无功调控资源分为：常规机组智能体（Conventional Unit Agent, CUAgent）、电储能智能体（Electric Energy Storage Agent,EESAgent）、风/光电智能体（Wind-Solar Power Agent，WSAgent）、可投切电容器智能体（Switchable Shunt Capacitor Agent, SSCAgent）、有载调压变压器智能体（On-Load Tap Change Agent, OLTCAgent）和连续无功补偿智能体（Continuous Reactive Power Compensation Agent, CRPCAgent）。智能体组织关系如图1 所示。
图1 智能体组织关系示意图
Fig.1 Schematic diagram of organization of agents
全局主智能体（Global Master Agent, GMAgent）直接协调各区域智能体（Regional Agent, RAgent），RAgent 控制了区域中的各个智能体：常规机组智能体CUAgent、电储能智能体EESAgent、风/光电智能体WSAgent、无功补偿智能体（Q Compensation Agent, QCAgent)。其中，QCAgent 下设可投切电容智能体SSCAgent、连续无功补偿智能体CPRCAgent、有载调压变压器智能体OLTCAgent。全局主智能体GMAgent 监控全网状态，根据调度中的功率平衡需求确定调度方向，并将调度方向信息下发，调度方向的确定有利于提高各智能体的训练速度和输出正确的调度指令。区域智能体RAgent 接受GMAgent的信息，之后将采集到的本区域电力系统的状态信息经筛选和归一化处理后发送给下级各智能体。模型建立以省-地两层调度为基础。
1）常规机组智能体CUAgent 建模
CUAgent j 的运行成本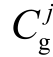
主要考虑发电成本
和辅助服务补偿
。辅助服务补偿包括响应自动发电控制（Automatic Generation Control, AGC）补偿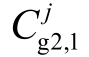
、启停调峰补偿
、深度调峰补偿
和冷/热备用补偿 
，如式（1）所示。
视常规机组发电成本为二次函数，则
式中，T 为调控周期；上标j 为CUAgent 的控制区域；
为常规机组数量；
为机组启停0-1 状态变量； 
为常规机组出力； a k、 bk 和 c k为发电机二次成本函数系数。
当电网中功率波动需要AGC 作用时，安装AGC装置的发电机需要动作，可能失去在电能量市场获利的机会，并对机组产生损耗，除了机组在爬坡过程付诸的成本
外，还需要按调节容量和调节电量获得补偿
，如式（3）～式（5）所示。
式中，
为机组k 爬坡成本系数，元/(MW·h)；
为参与AGC 服务的常规机组数量；
分别为机组k 的最大、最小出力；
、
分别为机组调节容量和调节电量的补偿价格系数，元/(MW·h)；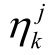
为第k 台机组AGC 投运率。
当电网中因为调峰要求需要启停机组，除了计算启停成本外，如果在停机后24h 内又因为调峰原因开启同一台机组，则按停机容量进行补偿[23]，如式（6）所示。
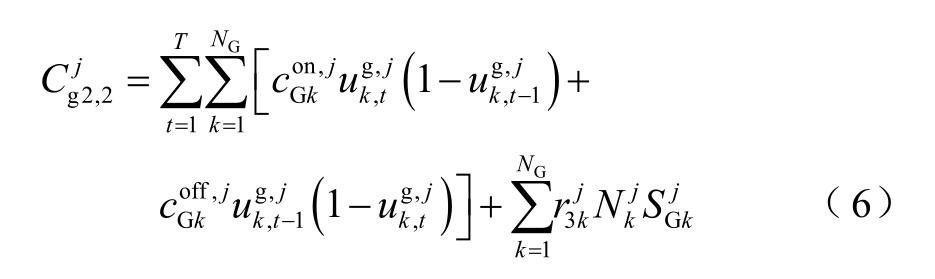
式中，
分别为机组k 的启、停成本；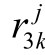
为机组k 的启停调峰补偿系数，元/MW；
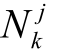为启停间隔在24h 内机组k 的启停次数；
为机组k 的总容量。
当机组运行在基本调峰需求基准以下时，称为深度调峰，按少发电量进行补偿[24]。
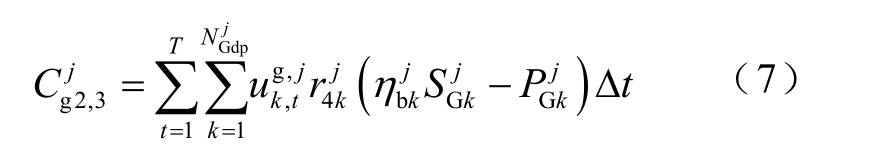
式中，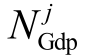
为参与深度调峰的机组数量；
为深度调峰机组k 的补偿系数，元/(MW·h)；
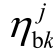为机组k的基本调峰系数（燃煤机组一般取0.55～0.60[25]）。
因电网调峰需求停机，在24h 内启机则按启停调峰进行补偿，若在24h 内继续保持停机，则按机组冷备用进行补偿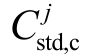
；若机组出力高于深度调峰基准，而又未达到机组计划出力，则按机组热备用进行补偿
，如式（8）所示。
式中，
为第k 台机组参与冷备用的次数；
为参与热备用的机组数量；
分别为第k 台机组参与冷备用和热备用的补偿价格系数，元/(MW·h)；
为第k 台机组参与第p 次冷备用的时间。
综上所述，常规机组智能体CUAgent j 的综合收益为
式中，
为机组k 的上网电价，元/(MW·h)。
2）电储能智能体EESAgent 建模
EESAgent j 的运行成本
主要考虑购电成本
和运维成本，如式（10）所示。
式中，上标j 为在EESAgent j 的控制范围内；
为电储能数量；
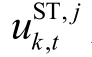为电储能k 的离网/并网0-1状态变量；
为第 k 个电储能向电网购电的价格，元/(MW·h)；
为电储能k 的单位运维成本，元/(MW·h)；
分别为电储能k 的充、放电功率。
电储能的收益
主要源于参与辅助服务，仿照常规机组的辅助服务补偿，电储能的收益按调节容量补偿
和调节电量补偿
获得。
式中，
分别为电储能k 的最大容量和最小容量；
别为电储能容量补偿系数和电量补偿系数，元/(MW·h)。
综上所述，电储能智能体EESAgent j 的综合收益为
3）风/光电智能体WSAgent 建模
风光电运行时没有燃料成本，其成本来源于运维成本
如式（13）所示。
式中，
分别为风/光电智能体WSAgent j在时间t 的实际出力；
分别为风电数量和光伏数量；
分别为风机和光伏离网/并网0-1 状态变量；
分别为第k 台风机光伏的运维成本补偿系数，元/(MW·h)。
WSAgent 除了向电网售电取得收益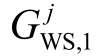
外，还会获得在深度调峰阶段被限电的补偿
，则WSAgent 的收益
为
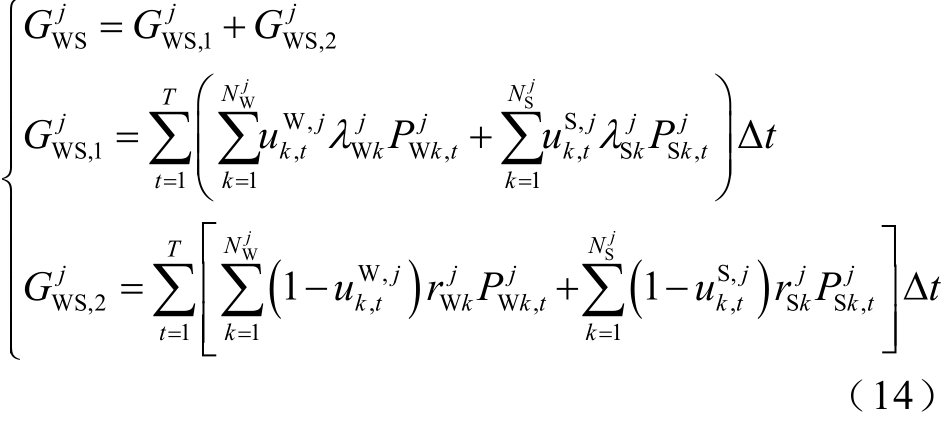
式中，
、
分别为第k 个风电和光伏的上网电价，元/(MW·h)；
、
分别为第k 个风电和光伏被限制出力后的补偿价格系数，元/(MW·h)。
综上所述，风/光电智能体WSAgent 的综合收益为
4）无功补偿智能体QCAgent 建模
区域无功调度任务由常规机组智能体CUAgent、可投切电容智能体SSCAgent、有载调压变压器智能体OLTCAgent 和连续无功补偿智能体CRPCAgent共同完成。SSCAgent、OLTCAgent 和CRPCAgent的无功补偿功能本质上是相同的，只在约束条件上稍有差别，且在运行过程中没有额外成本的产生。因此，只对这三种智能体设有“动作执行”的功能，而向上设置具有通信、决策、动作等完全功能的无功补偿智能体QCAgent。
SSCAgent、OLTCAgent 和 CRPCAgent 接收QCAgent 的无功控制指令是没有差别的，只受到网络拓扑的影响，根据奖励函数不同做出不同的动作，需要设计综合网损和节点电压偏差量的收益函数，并将OLTCAgent 的挡位调整的动作转换成注入无功功率的调整。控制区内电压与无功的关系由式（16）含灵敏度矩阵的线性方程组给出。
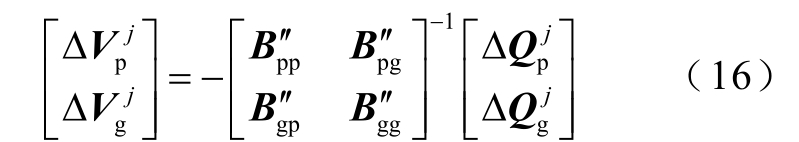
式中，
为中枢点母线[26]电压变化值；
为发电机节点电压变化值；
为中枢点母线无功功率变化值；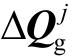
为发电机节点无功功率变化值；
为在B′ 中提取的中枢母线节点的节点导纳矩阵的虚部；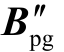
和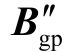
为发电机母线和中枢母线之间的互导纳；
为发电机母线的自导纳。
OLTCAgent 档位调整与无功/电压的关系为
式中， bii 和 bij 分别为节点i 的自导纳和支路ij 的互导纳。
QCAgent j 的运行成本CQCAgent 为
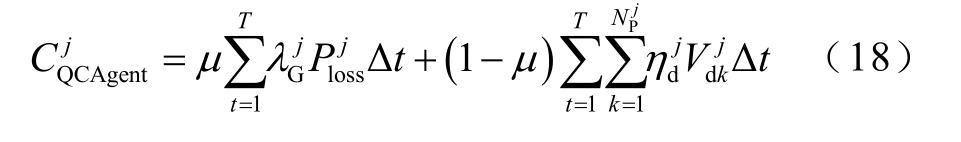
式中，
分别为区域j 的网损和中枢点母线电压偏差量；μ 为权重系数；
为中枢母线数量；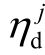
为电压偏移惩罚成本系数，元/pu。
的计算公式为
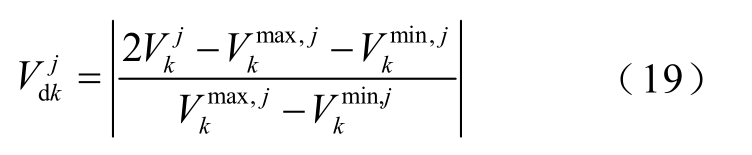
式中
分别为中枢母线k 的最大和最小电压幅值限制。
在CUAgent 与QCAgent 通信过程中，得到信息需要响应QCAgent 的无功控制指令时，由于受到发电机功率极限的限制，常规机组不得不放弃在电能量市场获利的机会，而为区域提供无功支撑。CUAgent 少获得的利润记为QCAgent 的调节成本，如式（20）所示。
式中，
为常规机组k 的有功-无功转换系数，表征受发电机功率极限图限制下的无功出力对应的有功功率。
式（9）、式（12）、式（15）和式（20）是对各智能体收益的数学表达，即为各智能体在训练中的目标函数。
2 深度强化学习算法设计
2.1 MADDPG 算法
多智能体深度确定策略梯度算法（MADDPG）是一种适用于多智能体系统的深度强化学习算法[27]，它最先由OpenAI 的研究人员提出[28]。
MADDPG 算法构建演员网络（Actor Network）和评论家网络（Critic Network）两个神经网络。演员网络将策略梯度和状态-行为值函数相结合，通过优化神经网络参数θ 来确定某状态下的最佳行为。评论家网络通过计算时间差分误差（temporal difference error）来评估演员网络产生的行为。每一个演员网络和评论家网络中又同时构建两个结构完全相同，但参数不同的神经网络，分别称为估值网络（evaluation network）和目标网络（target network）。估值网络的参数是随着训练而不断更新的，目标网络不进行训练，它的参数是一段时间前的估值网络的参数。MADDPG 算法中神经网络结构如图2所示。
图2 MADDPG 算法神经网络结构
Fig.2 Neural network structure of MADDPG algorithm
图2 中，s 和s_分别表示输入估值网络和目标网络的所有智能体的状态。MADDPG 算法实际上是一种部分观测的马尔科夫决策，它对状态集的要求并不严格，对分区智能体可以只对神经网络输入本区域内智能体的状态s，即观测o。a 和a_分别表示输入估值网络和目标网络的所有智能体的动作。
设有n 个智能体，n 个智能体是集中训练、分散执行。n 个智能体的权重参数集为
观测集为
；动作集为
策略集为
智能体i 奖励的期望值的策略梯度（下文简称为策略梯度）为
式中，
为集中式的状态-动作值函数，其输入是智能体i 对其他所有智能体在环境中作用的观测集x 和动作集a，输出是智能体i 的状态-动作值函数的值。为了改善使用依概率选择动作时收敛效率低的问题，MADDPG 算法推广到确定性策略选择上，设n 个智能体的连续确定策略为iθμ （简记为μi ），智能体i 的确定策略梯度为
式中，
表示经验回放缓存区（experience replay buffer），其作为智能体的知识库存储所有智能体的经验。
演员网络通过最大化状态-动作值函数 Q ( s , a)来更新网络参数，目标函数及参数更新规则分别为
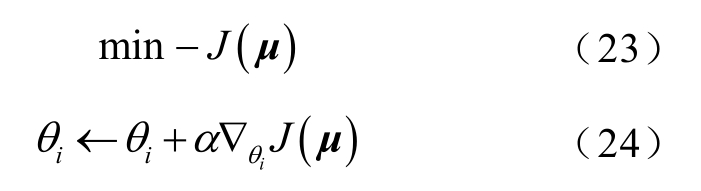
式中，α 为更新步长，即学习率。
评论家网络的损失函数为
其中
式中，
为具有延迟参数的策略集。
评论家网络通过最小化时间差分误差来更新网络参数，目标函数及参数更新规则分别为
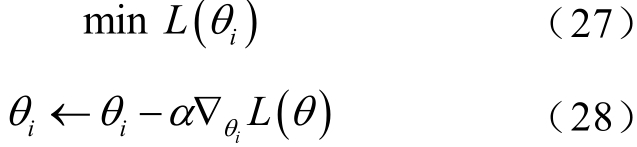
为了提高神经网络训练时的收敛速度和防止过拟合，每一次训练时，都从经验回放缓存区中随机采样一组记忆，输入到神经网络进行训练。
最后，即可通过式（29）所示的软更新策略，更新目标网络的参数。
式中，τ 为软替换（soft replacement）系数，且
分别为智能体i 的目标网络参数和估值网络参数。
2.2 状态-动作空间
对于电力系统的有功无功协调控制模型，状态空间的选取既要可以表征智能体执行某一动作iA后电力系统全面而真实的物理状态，又不能对神经网络的训练带来太多的计算负担。因此，本文将系统中每一个节点的电压相角、电压幅值、节点注入有功功率和无功功率作为电力系统的状态量输入进神经网络，如式（30）所示。
式中，V a 、 mV 、P bus 和 Qbus 分别为节点的电压相位、电压幅值、注入有功功率和注入无功功率的向量。
本文智能体的动作设计比较直观，均为各智能体的动作值。如CUAgent 的动作空间是其出力上下限的连续实数集。
2.3 奖励函数
奖励函数的正确设计是强化学习算法高效运作的必要条件。本文模型中奖励函数的设计有两个要点：①可以被准确量化并分布到智能体的每一动作；②奖励值必须来源于环境或与环境具有较强的关联。而仅按智能体实际收益设计CUAgent、WSAgent、EESAgent 的奖励函数与电力系统环境的耦合度依然不足，系统中平衡节点机组的有功出力容易越界，既不符合电力系统运行要求，又增加了智能体在不可行空间的探索次数。
由于CUAgent、WSAgent 和EESAgent 在环境中探索过于贪婪或保守，可能导致平衡节点机组出力越界。因此，需要附加智能体j 的过贪婪/过保守惩罚量PUNAgent j。智能体j 的综合奖励函数为
式中，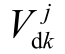
为GMAgent 控制区域j 内节点k 的电压偏差量；
为RAgent j 控制区域内的有功网损；R j 为CUAgent、EESAgent、WSAgent 等智能体的收益。
的计算式为
式中，rP 为越界惩罚系数；
为平衡节点机组的上网电价；
分别为平衡节点机组的出力下、上界；
为平衡节点机组出力；α j和β j分别为智能体j 的过贪婪和过保守惩罚系数，计算式为
式中，
为智能体j 的实际出力。
3 算例仿真
本文在某节点系统的基础上进行改进，从某电网SCADA 系统采集连续100 天真实节点有功、无功负荷数据（采样周期为15min），用以训练智能体的神经网络。设置5 个CUAgent（所在节点：1,2,3,6,8）；1 个WSAgent，含一个风电机组群（所在节点：5）和光伏机组群（所在节点：7）；1 个EESAgent（所在节点：4）；2 个SSCAgent（所在节点：9,10）；3 个OLTCAgent；2 个CRPCAgent（所在节点：11,12）。模型中的各参数按照其单位同比缩放。使用Python 编程，利用tensorflow 框架，搭建多智能体神经网络计算图（Graph）。
仿真测试硬件平台：Intel(R) Core(TM) i7-9700 CPU @ 3.00GHz；8GB 2666MHz RAM；GPU：NVIDIA GeForce GTX 1660 Ti；软件平台：Deepin 15.11（Linux 4.15）；Python 3.7.3；Tensorflow 1.14.0。
神经网络结构及超参数见表1。
表1 神经网络结构及超参数
Tab.1 Neural network structure and hyperparameters
评论家网络 演员网络学习率 0.000 1 0.001软替换系数 0.01 0.01隐层层数 5 5每层神经元个数 128 128隐层激活函数 线性整流函数 线性整流函数输出层激活函数 双曲正切函数 双曲正切函数训练集采样规模 1 024 1 024训练回合次数 300 300每回合训练次数 200 200经验回放元组规模 150 000 150 000
在神经网络训练过程中，使用Google 开发的深度学习可视化工具Tensorboard，采样并导出各个智能体评论家网络的状态-动作值函数Q(s,a)、估值网络与目标网络参数的时间差分误差∆Q(s,a;θ)来评估各智能体演员网络和评论家网络的训练效果，计算式为
为了便于归一化分析，状态-动作值函数Q(s, a)也取其时间差分ΔQ ( s , a ; t)，计算式为
训练结束时，各智能体状态-动作值函数时间差分值、神经网络参数的时间差分误差分别收敛于
数量级，智能体的动作选择趋于稳定，估值网络和目标网络参数更新也不再明显，验证了MADDPG 算法在本文所提模型与调度问题中运用的有效性。
4 对比分析
4.1 与传统有功-无功解耦调度模型对比
选取除训练集外的某电网SCADA 系统采集的1 天96 个时段的真实节点有功、无功负荷数据，用以对比分析本文所提有功-无功协调模型（下称：协调调度）与传统有功-无功解耦调度模型（下称：解耦调度）的调度效果。解耦调度以经济调度[29]与无功优化为基础，并用二阶锥松弛技术[4]处理非凸、非线性的潮流方程约束，目标函数是最大化智能体收益的总和。
比较分析CUAgent、WSAgent 在两种调度模型下的动作情况，以及系统非压控节点电压幅值变化、网损变化。协调调度和解耦调度对比分析效果如图3a～图3h 所示。系统总有功、无功负荷如图3i 所示。
如图3a、图3b 所示，采用协调调度的CUAgent相比采用解耦调度的CUAgent 在动作选择倾向上，有明显的不同。采用解耦调度的各CUAgent 基本跟随负荷的变化呈现同升同降的趋势，而采用协调调度的各CUAgent 在均衡各自收益下，不断维持最大化自身收益，并保证功率的实时平衡。CUAgent 2、4、5 的出力在96 时段中，出力基本持平，而将系统跟随负荷变化的调度任务交给性能更好的CUAgent 1、3。如图3c、图3d 所示，协调调度：96 时段总弃风207.53MW（3.65%）、总弃光171.89MW（9.6%）、总弃风/光新能源379.42MW（5.08%）；解耦调度：96 时段总弃风399.16MW（7.02%）、总弃光0MW（0%）、总弃风/光新能源399.16MW（5.34%）。尽管解耦调度中没有出现弃光的情况，但从风/光新能源消纳的总量上来看，协调调度较解耦调度提高风/光利用19.74MW（0.26%），说明协调调度是一种“协调统一、均衡收益”的策略，对电网调度机构、风电和光电等都较为公平与合理。如图3e、图3f 所示，采用协调调度控制，各非压控母线电压波动幅度更小，且没有节点电压越界，而采用解耦调度控制的节点电压波动更大，且节点7、9、10、11 的电压幅值，在部分时段越上界。如图3g 所示，协调调度中，系统96 时段总网损为417.99MW（1.28%），解耦调度中，系统 96 时段总网损为 441.18MW（1.35%），协调调度较解耦调度降低系统有功网损23.19MW（0.07%）。如图3h 所示，协调调度中，1～30 时段，风电大发，EESAgent 选择在此时段调用自身容量储备用以消纳风电；在50～62 时段，光伏大发时，EESAgent 无可用容量，只得选择弃风。解耦调度中，EESAgent 通过经济调度优化算法，选择在24～50 时段风电和光伏总和较大时，调用自身容量，减少风、光的弃用。
图3 协调调度与解耦调度效果对比图
Fig.3 Comparison of coordination and decoupling dispatching
以上对比分析说明，协调调度相比解耦调度，在均衡各智能体收益，协调电力系统不同控制主体间的利益矛盾，消纳风/光新能源，控制节点电压波动、优化系统网损方面具有一定的优势。
4.2 MADDPG 与其他强化学习算法对比
基于相同的电力系统环境配置，在策略迭代算法中选取DDPG 算法[30]，在值迭代算法中选取深度Q 网络（Deep Q-Network, DQN）和深度双Q 网络（Double DQN, DDQN）[31]算法，与本文MADDPG 算法在神经网络训练效率、智能体动作选择、电力系统网损和节点电压偏差方面进行比较。值迭代算法DQN 和DDQN 状态值的输入与MADDPG 算法保持一致，但其动作值的输入必须是离散的、有限的。为尽量保证与MADDPG 的可比性，将各智能体的连续动作区间均匀离散成 10 000 份，记为DQN-10 000 和DDQN-10 000。
将SCADA 系统每一个采样周期时采集到的电力系统节点有功、无功负荷作为一个训练集，共9 600 个训练集。在智能体神经网络训练的每一个回合中，随机采样一个场景进行训练，为了便于可视化说明，以下对比结果分析仅展示其中一个场景的训练效果。
系统中非压控母线的节点电压幅值在训练过程中的变化情况如图4 所示。
图4 MADDPG 与其他强化学习算法在训练过程中电压幅值的变化
Fig.4 Voltage amplitude changes during training of MADDPG and other reinforcement learning algorithm
MADDPG 和DDPG 分别在约160 和约260 训练回合后，结束神经网络训练。而DQN-10 000 和DDQN-10 000 无法在可接受的时间内收敛。MADDPG 算法的训练性能优于其他强化学习算法。MADDPG 算法中，所有节点电压均在设定的范围内，且逼近基准值1.0(pu)。而在DDPG 算法中，节点5、12 和13的电压幅值越上界，且其余节点电压逼近上界。在DQN-10 000 和DDQN-10 000 算法中，节点7、9 和11 电压越限明显。说明MADDPG 在控制节点电压幅值相比其他强化学习算法具有一定优势。
图5 所示为算法训练过程中CUAgent 动作选择变化。各智能体的输出层均采用双曲正切激活函数，可以保证除CUAgent1 外各智能体的动作输出不越界。为便于可视化分析，在DQN-10 000 和DDQN-10 000 算法中仅列出CUAgent1 的训练结果。
图5 中的两条点划线分别表示平衡节点机组智能体的出力上下界，分别为2.233(pu)和0.558(pu)。MADDPG 算法在第160 回合收敛，且平衡机组的出力保持在上、下界之间，而DDPG 算法中，在训练过程中，平衡节点最终收敛到越过下界的值0.556(pu)。DQN-10 000 和DDQN-10 000 算法中的CUAgent1均未在可接受的时间内选择到合适的动作值。
MADDPG 和其他强化学习算法训练过程中全网网损的变化如图6 所示。
DDPG 在神经网络训练时，没有考虑其他智能体的动作。虽然网损优化结果（3.53MW）优于MADDPG 算法（7.13MW），但网损的优化是由于平衡节点机组出力越下界和抬高节点电压以至于电压越界而实现的，总有一部分智能体在环境中占据优势，获得更多的收益，而另一部分智能体则处于劣势，导致某些电力系统的状态量超出规定限度。DQN-10 000 和DDQN-10 000 在训练中，全网的网损在10MW 附近变化，最终未能收敛。
在值迭代算法DQN-10 000 和DDQN-10 000 中，尽管将动作均匀离散成 10 000 份，但若想达到MADDPG 算法的动作选择精度，则需要将动作进一步细化。而从上述给出的DQN-10 000 和DDQN-10 000 仿真结果来看，进一步切分动作会使算法收敛性进一步劣化。尽管理论上DDQN 算法的适应性强于DQN 算法，但DDQN-10 000 和DQN-10 000整体上区别不大，可见基于值迭代的方法无法较好地适用于本文模型。
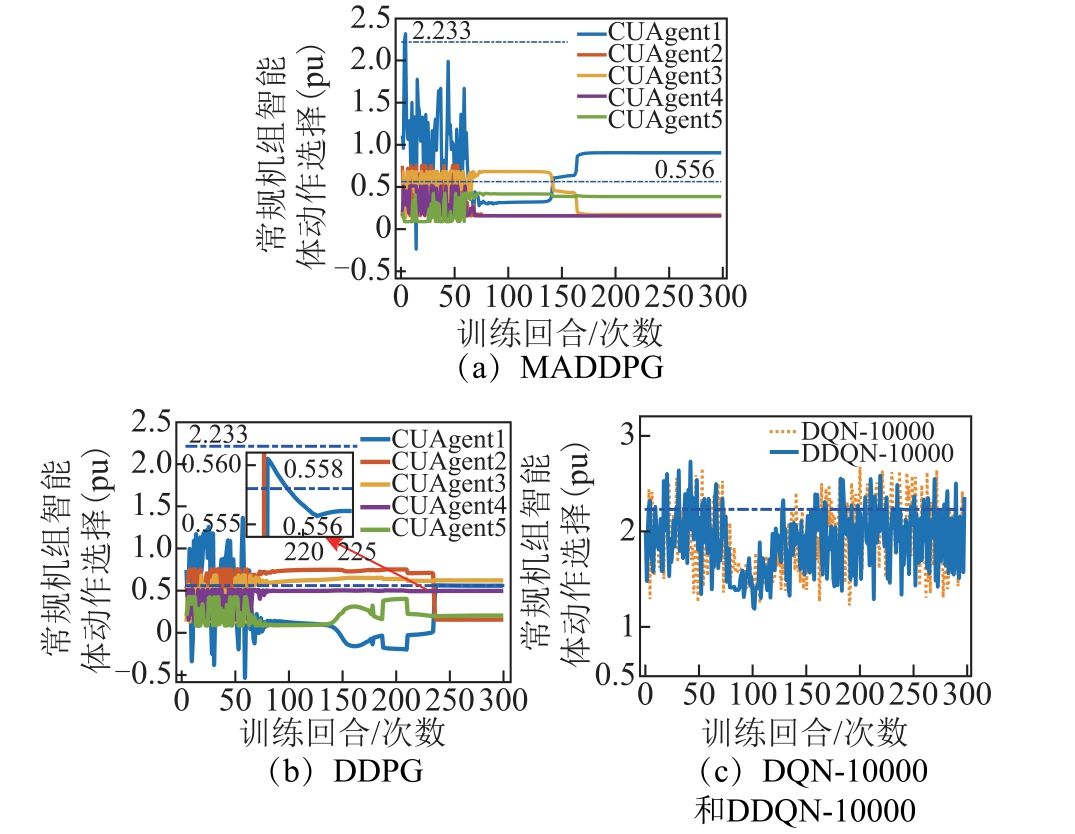
图5 MADDPG 与其他强化学习算法在训练过程中CUAgent 动作选择变化
Fig.5 Action choices of CUAgent during training of MADDPG and other reinforcement learning algorithm
图6 MADDPG 和其他强化学习算法在训练过程中网损的变化
Fig.6 Transmission losses changes during training of MADDPG and other reinforcement learning algorithm
综上所述，MADDPG 算法无论是在实现各智能体间收益的均衡、协调各智能体间矛盾、还是输出符合约束的电力调度指令上，都具有一定的优势。
4.3 计算性能对比
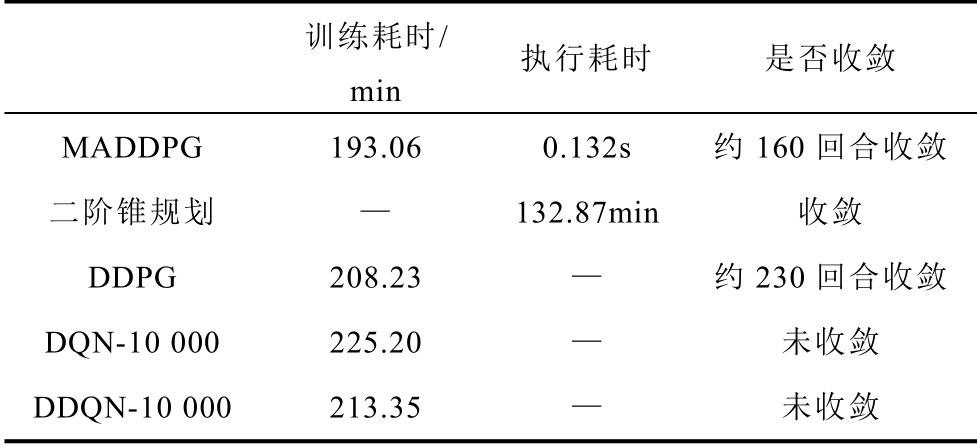
本文所提算法与对比分析中算法的计算性能对比见表2。
表2 不同算法的性能对比
Tab.2 Comparison of algorithms performance
训练耗时/min执行耗时 是否收敛MADDPG 193.06 0.132s 约160 回合收敛二阶锥规划 — 132.87min 收敛DDPG 208.23 — 约230 回合收敛DQN-10 000 225.20 — 未收敛DDQN-10 000 213.35 — 未收敛
现有有功-无功协调模型主要采用二阶锥规划法。虽然MADDPG 算法的耗时相比二阶锥规划法更长，但本文所提模型是一种“离线训练，在线执行”的框架，完成训练后的执行时间较短，为0.132s，而二阶锥规划算法的每一次优化都需要重新计算。同时，采用本文所提方法的优化效果要优于二阶锥规划方法。在强化学习类算法中，本文采用的MADDPG 相比DDPG、DQN 和DDQN 算法在优化效果和计算性能上均具有优势。
5 结论
1）本文将具有连续状态空间和连续动作空间的深度强化学习算法引入电力系统有功-无功协调调度领域，构建分层多智能体有功-无功协调调度框架，智能组织灵活多调控资源，使得多个控制主体在最大化自身收益的同时，优化区域内电压合格率、网损等指标，实现系统各个智能体收益的均衡和各个相冲突的控制目标的协调。
2）改进多智能体深度确定策略梯度算法，设计电力系统多智能体环境、状态函数、动作函数和奖励函数，在智能体更新时考虑其他智能体的动作选择，有效地解决电力系统环境在各智能体动作执行时的不稳定性，显著提高各智能体训练效果。
3）与传统调度模型相比，本文所提模型在均衡智能体收益，协调各智能体动作执行，提高风/光电消纳，维持节点电压稳定，优化网损等方面具有一定的优势。
4）本文对比了同属策略迭代类型的DDPG 算法和基于值迭代的DQN 算法和DDQN 算法。对比分析结果表明，本文所用MADDPG 算法在智能体的收敛性能、模型的求解效果和输出符合规定的调度指令方面具有一定的优势。
目前，本文针对调度计划的制定，设计了分层多智能体有功-无功协调调度模型，取得了一定的效果。未来，针对电力系统实时有功-无功协调控制，提高智能体的性能，结合数字仿真，将进一步研究投入数字仿真中的多智能体深度强化学习算法及有功-无功协调控制模型。
[1] 许洪强, 姚建国, 南贵林, 等. 未来电网调度控制系统应用功能的新特征[J]. 电力系统自动化, 2018,42(1): 1-7.
Xu Hongqiang, Yao Jianguo, Nan Guilin, et al. New features of application function for future dispatching and control systems[J]. Automation of Electric Power Systems, 2018, 42(1): 1-7.
[2] 郭建成, 南贵林, 许丹, 等. 大电网全局监控内涵与关键技术[J]. 电力系统自动化, 2018, 42(18): 1-8.
Guo Jiancheng, Nan Guilin, Xu Dan, et al.Connotation and key technology of global monitoring for large power grid[J]. Automation of Electric Power Systems, 2018, 42(18): 1-8.
[3] 许洪强, 姚建国, 於益军, 等. 支撑一体化大电网的调度控制系统架构及关键技术[J]. 电力系统自动化, 2018, 42(6): 1-8.
Xu Hongqiang, Yao Jianguo, Yu Yijun, et al.Architecture and key technologies of dispatch and control system supporting integrated bulk power grids[J]. Automation of Electric Power Systems, 2018,42(6): 1-8.
[4] 刘一兵, 吴文传, 张伯明, 等. 基于混合整数二阶锥规划的主动配电网有功–无功协调多时段优化运行[J]. 中国电机工程学报, 2014, 34(16): 2575-2583.
Liu Yibing, Wu Wenchuan, Zhang Boming, et al. A mixed integer second order cone programming based active and reactive power coordinated multi-period optimization for active distribution network[J].Proceedings of the CSEE, 2014, 34(16): 2575-2583.
[5] 任佳依. 有源配电系统有功无功协调优化研究[D].南京: 东南大学, 2017.
[6] 何婷. 主动配电网有功-无功电源的综合优化配置研究[D]. 广州: 华南理工大学, 2018.
[7] 陆文甜. 含连续/离散控制的多区域电力系统分布式优化调度方法研究[D]. 广州: 华南理工大学,2018.
[8] 颜湘武, 徐韵. 考虑网络动态重构含多异质可再生分布式电源参与调控的配电网多时空尺度无功优化[J]. 电工技术学报, 2019, 34(20): 4358-4372.
Yan Xiangwu, Xu Yun. Multiple time and space scale reactive power optimization for distribution network with multi-heterogeneous RDG participating in regulation and considering network dynamic reconfiguration[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4358-4372.
[9] 颜湘武, 徐韵, 李若瑾, 等. 基于模型预测控制含可再生分布式电源参与调控的配电网多时间尺度无功动态优化[J]. 电工技术学报, 2019, 34(10):2022-2037.
Yan Xiangwu, Xu Yun, Li Ruojin, et al. Multi-time scale reactive power optimization of distribution grid based on model predictive control and including RDG regulation[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2022-2037.
[10] 乐健, 王曹, 李星锐, 等. 中压配电网多目标分布式优化控制策略[J]. 电工技术学报, 2019, 34(23):4972-4981.
Le Jian, Wang Cao, Li Xingrui, et al. The multi-object distributed optimization control strategy of medium voltage distribution networks[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4972-4981.
[11] 颜湘武, 徐韵. 考虑网络动态重构含多异质可再生分布式电源参与调控的配电网多时空尺度无功优化[J]. 电工技术学报, 2019, 34(20): 4358-4372.
Yan Xiangwu, Xu Yun. Multiple time and space scale reactive power optimization for distribution network with multi-heterogeneous RDG participating in regulation and considering network dynamic reconfiguration[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4358-4372.
[12] 石宪, 薛毓强, 曾静岚. 基于有功-无功控制的光伏并网点电压调节方案[J]. 电气技术, 2019, 20(3): 50-56.
Shi Xian, Xue Yuqiang, Zeng Jinglan. Voltage regulation strategies based on power control for gridconnected photovoltaic at point of common coupling[J]. Electrical Engineering, 2019, 20(3): 50-56.
[13] International Energy Agency. Empowering variable renewables‐options for flexible electricity systems:(complete edition)[J]. International Energy, 2009(23):31-36.
[14] 张孝顺. 电力系统的迁移强化学习优化算法研究[D]. 广州: 华南理工大学, 2017.
[15] 张孝顺, 余涛. 互联电网AGC 功率动态分配的虚拟发电部落协同一致性算法[J]. 中国电机工程学报, 2015, 35(15): 3750-3759.
Zhang Xiaoshun, Yu Tao. Virtual generation tribe based collaborative consensus algorithm for dynamic generation dispatch of AGC in interconnected power grids[J]. Proceedings of the CSEE, 2015, 35(15):3750-3759.
[16] 刁浩然, 杨明, 陈芳, 等. 基于强化学习理论的地区电网无功电压优化控制方法[J]. 电工技术学报,2015, 30(12): 408-414.
Diao Haoran, Yang Ming, Chen Fang, et al. Reactive power and voltage optimization control approach of the regional power grid based on reinforcement learning theory[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 408-414.
[17] 余涛, 刘靖, 胡细兵. 基于分布式多步回溯Q(λ)学习的复杂电网最优潮流算法[J]. 电工技术学报,2012, 27(4): 185-192.
Yu Tao, Liu Jing, Hu Xibing. Optimal power flow for complex power grid using distributed multi-step backtrack Q(λ) learning[J]. Transactions of China Electrotechnical Society, 2012, 27(4): 185-192.
[18] 张孝顺, 余涛, 唐捷. 基于CEQ(λ)多智能体协同学习的互联电网性能标准控制指令动态分配优化算法[J]. 电工技术学报, 2016, 31(8): 125-133.
Zhang Xiaoshun, Yu Tao, Tang Jie. Dynamic optimal allocation algorithm for control performance standard order of interconnected power grids using synergetic learning of multi-agent CEQ(λ)[J]. Transactions of China Electrotechnical Society, 2016, 31(8): 125-133.
[19] 李宏仲, 王磊, 林冬, 等. 多主体参与可再生能源消纳的 Nash 博弈模型及其迁移强化学习求解[J].中国电机工程学报, 2019, 39(14): 4135-4150.
Li Hongzhong, Wang Lei, Lin Dong, et al. A nash game model of multi-agent participation in renewable energy consumption and the solving method via transfer reinforcement learning[J]. Proceedings of the CSEE, 2019, 39(14): 4135-4150.
[20] 席磊, 余璐, 付一木, 等. 基于探索感知思维深度强化学习的自动发电控制[J]. 中国电机工程学报,2019, 39(14): 4150-4162.
Xi Lei, Yu Lu, Fu Yimu, et al. Automatic generation control based on deep reinforcement learning with exploration awareness[J]. Proceedings of the CSEE,2019, 39(14): 4150-4162.
[21] 王怀智, 余涛, 唐捷. 基于多智能体相关均衡算法的自动发电控制[J]. 中国电机工程学报, 2014,34(4): 620-627.
Wang Huaizhi, Yu Tao, Tang Jie. Automatic generation control for interconnected power grids based on multi-agent correlated equilibrium learning system[J]. Proceedings of the CSEE, 2014, 34(4): 620-627.
[22] Kouveliotis-lysikatos I N, Koukoula D I, Hatziargyriou N D. A double-layered fully distributed voltage control method for active distribution networks[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 1465-1476.
[23] 梁琳. 电力市场环境下火电机组有偿与无偿调峰划分方法研究[D]. 北京: 华北电力大学, 2009.
[24] 薛晨, 任景, 张小东, 等. 含虚拟储能的新能源高渗透电网深度调峰备用决策模型[J]. 中国电力,2019, 52(11): 35-43.
Xue Chen, Ren Jing, Zhang Xiaodong, et al. A reserve decision model forhigh-proportional renew energy integrated power grid based on deep peak-shaving and virtual storage[J]. Electric Power, 2019, 52(11): 35-43.
[25] 邢振中, 冷杰, 张永兴, 等. 火力发电机组深度调峰研究[J]. 东北电力技术, 2014, 35(4): 18-23.
Xing Zhenzhong, Leng Jie, Zhang Yongxing, et al.Research on depth peak load cycling of thermal power generator units[J]. Northeast Electric Power Technology, 2014, 35(4): 18-23.
[26] 郭庆来, 孙宏斌, 张伯明, 等. 基于无功源控制空间聚类分析的无功电压分区[J]. 电力系统自动化,2005, 29(10): 36-40.
Guo Qinglai, Sun Hongbin, Zhang Boming, et al.Power network partitioning based on clustering analysis in Mvar control space[J]. Automation of Electric Power Systems, 2005, 29(10): 36-40.
[27] Peters J, Bagnell J A. Policy gradient methods[J].Encyclopedia of Machine Learning, 2010, 5(11): 774-776.
[28] Kim B, Park J, Park S, et al. Impedance learning for robotic contact tasks using natural actor-critic algorithm[J]. IEEE Transactions on Systems, Man,and Cybernetics, 2010, 40(2): 433-443.
[29] 陈启鑫, 康重庆, 夏清, 等. 低碳电力调度方式及其决策模型[J]. 电力系统自动化, 2010, 34(12): 18-23.
Chen Qixin, Kang Chongqing, Xia Qing, et al.Mechanism and modelling approach to low-carbon power dispatch[J]. Automation of Electric Power Systems, 2010, 34(12): 18-23.
[30] Lillicrap T P, Hunt J J, Pritzel A, et al. Continuous control with deep reinforcement learning[J].Computer Science, 2015, 8(6): A187.
[31] Duryea E, Ganger M, Hu W. Exploring deep reinforcement learning with multi Q-learning[J].Intelligent Control and Automation, 2016, 7(4): 129-144.