0 引言
近年来，为了解决能源危机和环保压力，智能配电网中分布式电源（Distribution Generator, DG）接入电网越来越多。DG 包括风力发电、太阳能光伏发电、小型燃气轮机等在改善系统电压水平，减少系统网损，增强系统可靠性等方面具有重要意义[1]。
然而，大量DG 的接入使系统面临诸多挑战。其中最常见的是对系统电压分布的影响和潮流的限制。此外，随着电力电子变换器接口的DG 大量并网，使得谐波成为制约DG 接入电网的一大重要因素[2-3]。文献[4]研究表明由于光伏模块输出功率的变化导致总谐波畸变率（Total Harmonic Distortion,THD）可达到20%，可能造成光伏逆变器停止工作。文献[5]指出，在高渗透率DG 接入配电网的情况下，由于逆变器与配电网构成谐振电路（并联或者串联谐振）可能导致逆变器THD 增大甚至停止工作。文献[6]从谐波畸变约束的角度考虑DG 最大准入功率的计算方法，但是该文中采用试探的方法对模型进行求解，所得结果可能并非最优解，且对于复杂模型难以有效应对。文献[7]以电网谐波电压总畸变率之和最小作为目标函数建立优化模型，但该目标函数无法反映系统各个节点谐波畸变水平，有可能由于个别节点谐波电压总畸变率过高而限制了DG 的准入功率。
传统上，对于分布式网络中的谐波分析仅仅是对谐波电压畸变水平的识别和治理，主要依靠频率扫描法[8]或者谐波潮流法[9]对谐波进行分析，进一步地设计滤波器来消除谐波的影响。这些方法主要进行确定性分析。然而，由于受环境（风速、光照等）因素的影响，DG 有较强的随机性和波动性，给电力系统基波潮流[10-11]和谐波潮流带来更多的不确定性[12-13]，使得传统确定性方法无法适应DG 接入的情况。
多目标优化问题即求解 Pareto 最优解和Pareto 最优前沿。处理多目标优化问题的有效方法有三大类：人工智能类算法[14]、将多目标按一定权重比例转化为单目标问题求解的加权法[15]、ε 约束法[16]。其中加权法本质上是将多目标问题转化为单目标问题，求得的解具有明显的偏向性；人工智能类算法具有依赖初始总群、收敛不稳定、容易早熟等缺点。针对ε 约束法不能保证所求解集均为Pareto最优解，文献[17]提出了扩展ε 约束法，扩展ε 约束法具有计算效率高、求解结果均为Pareto 有效解的优点。然而，扩展ε 约束法并没有反映各目标函数对产生Pareto 解集的重要性。文献[18]利用扩展ε 约束法结合CPLEX 软件对供应链多目标绩效优化问题进行求解。但是对于复杂非线性混合优化问题，传统商业软件CPLEX 难以有效应对。
针对上述问题，本文对不同类型DG（风电、光伏发电）有功出力的不确定性提出了基于点估计法的概率潮流计算方法。在此基础上，提出了一种评价全网谐波裕度-均衡度的指标，该指标既能反映电网各个节点的谐波电压总畸变率水平，也能综合体现全网谐波分布程度。进一步地，以DG 接入电网功率最大和电网谐波-裕度均衡度综合指标最小为目标函数，以DG 候选接入电网的位置以及准入功率为优化变量，在满足常规约束的情况下考虑系统谐波畸变水平，并以国标限值为约束条件建立优化模型。为了更好地求解该混合整型非线性规划问题，提出了一种基于权重的粒子群优化-扩展ε 约束法（Particle Swarm Optimization-ε-Constraint Method,PSO-AWCM）进行多目标优化计算，通过IEEE 33节点算例对本文所提方法进行验证。
1 DG 谐波源模型及概率潮流计算方法
1.1 DG 谐波源模型
DG 通过电力电子装置接口并网，通常将基于逆变器接口的DG 等效为谐波电流源[1,19-20]。参考文献[21]，简化的DG 模型可以表示为
式中，
为DG 在当前运行状态下第h 次谐波电流的频谱；
为节点i 处DG 总额定容量；V i 为节点电压；Ih, i 为DG 接入节点i 处向电网注入的h次谐波电流。
参考IEC61000-3-6[22]负载谐波电流求和的方法，可以将其扩展运用于同一节点多DG 谐波电流源求和，即
式中，N 为接入节点i 处的DG 个数；
为节点i处N 个DG 向电网注入的h 次谐波电流；指数β 表示不同频率下的聚合关系。具体地，当谐波次数h＜5时，β=1；当5≤h≤10 时，β=1.4；当h＞10 时，β=2。
1.2 基于2m+1 点估计法概率潮流计算方法
对于基波概率潮流，输入随机变量为DG 有功出力的变化，输出随机变量为各节点电压。有功网损映射函数为基波潮流计算方程，对于谐波概率潮流，输入随机变量为DG 注入的谐波电流，输出随机变量为各节点谐波电压和各支路谐波电流，映射函数为谐波潮流计算方程。基于2m+1 点估计基波/谐波概率潮流[13]计算方法如下：
（1）应用2m+1 点估计法，求取输入随机变量的三个估计值及三个估计值对应的概率值。
（2）将其中一个输入变量取估计值，其他取平均值
，采用映射函数计算输出随机变量值。
（3）对每一个随机变量执行步骤（2）。
（4）获取步骤（3）各估计值下求得输出随机变量大小，与步骤（1）中各估计值对应的概率值做乘法，并累加求和，即
得到输出随机变量的期望。
（5）获取步骤（3）各估计值下输出随机变量大小并取二次方，与步骤（1）中各估计值对应的概率值做乘法，并累加求和，即
（6）结合步骤（4）和步骤（5）得到输出随机变量的方差。
由此，通过以上步骤可以求得基波潮流下的各节点电压和网损分布，谐波潮流下各节点谐波电压和支路谐波电流分布。
2 考虑不确定性的谐波裕度-均衡度评估
DG 接入电网的同时会向网络中注入谐波，在靠近接入点的位置谐波畸变水平较大，当DG 接入功率增大到一定程度时，某些节点最先超过国标规定值。DG 接入电网，通过概率潮流计算后，如果节点谐波电压的CP95 值小于GB14549—1993 规定值，则说明该节点具有一定的谐波波动裕度。节点谐波电压裕度越大，其发生谐波超标的风险就越小。
木桶理论认为，是最短的木板决定了木桶的最大容量。为了在满足谐波不超标的基础上尽可能使DG 接入功率更多，应使电网各个节点谐波裕度分布尽可能均衡，避免由个别节点谐波电压裕度过小而限制DG 接入电网的功率。因此，本文提出了全网谐波裕度-均衡度综合评价指标。全网谐波裕度-均衡度综合评价指标由电网平均谐波裕度和电网整体谐波裕度-均衡度组成。
2.1 电网平均谐波裕度
本文通过基波概率潮流和谐波概率潮流计算后得到相应输出随机变量的概率分布，并以CP95 为真值，计算电网平均谐波裕度。电网平均谐波裕度可以反映电网整体谐波裕度水平的高低。
采用聚类算法计算均值，具体步骤如下：
（1）假设某电网所有节点的集合为S，共有N个节点，依照谐波裕度可分为K 类，并将这K 个集合命名为nK。其中，集合S1 有n1 个节点，集合S2有n2 个节点，依次类推，集合Sk 有nk 个节点。
（2）分别计算集合S1～Sk 的聚类中心CS1～CSk，然后依据每个集合所有节点的谐波裕度总和占电网所有节点的谐波裕度总和的比例分配权重AS1～ASk，计算公式为
式中， iλ 为节点i 的谐波裕度；S 为整个系统节点集合；Sj 为k 个集合中的第j 个子集。
（3）电网平均谐波裕度均值
的计算公式为
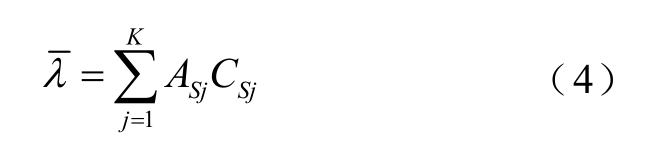
依据系统谐波裕度指标将电网节点自动聚类为从“裕度极大”至“裕度极小”的几类，对每一类节点单独赋予权重，使得计算结果更加精确。该指标反映了电网各个节点的谐波电压总畸变率水平，电网平均谐波裕度越大，表示电网谐波畸变水平越低。
2.2 电网整体谐波裕度均衡程度
单靠均值并不能体现聚类的每一类别内部的离散度。进一步，引入了离散度指标，即基尼系数。
基尼系数是一个0～1 之间的无量纲值，可以用一个数值从整体上反映数据分布的均匀程度。当基尼系数越大，则数据分布越不均衡；当基尼系数越小，则分布越均匀。基尼系数的计算公式为
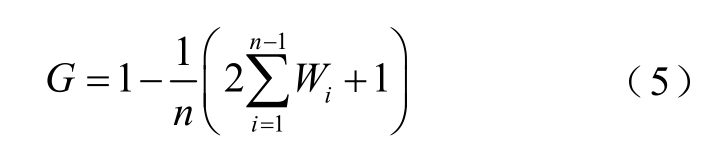
该公式的实质是利用定积分的定义，将对洛仑兹曲线的积分分成n 个等高梯形的面积之和。计算节点谐波电压裕度的基尼系数，各节点为单独个体，即一个节点为一组。将子集集合S1～Sk 的节点先按照谐波裕度数值从小到大进行排序，然后计算每个集合的基尼系数GS1～GSk。则电网谐波裕度基尼系数G 为
该指标反映全网谐波裕度分布均衡程度。电网谐波裕度基尼系数越大，则电网谐波风险越不均衡，电网谐波总畸变率超标风险越大；基尼系数G 越小，表示谐波裕度均衡度越好，电网谐波裕度分布越均衡，个别节点谐波越限风险越小。
2.3 电网整体谐波裕度均衡度综合评价指标
综合对电网平均谐波裕度式（4）和电网谐波裕度基尼系数式（6）进行分析，λ 的取值范围在[0，a%]，其中a%为国标规定的谐波限值；G 取值范围为[0,1]。为了将两个指标统一在同一数量级，分别对其进行归一化处理，即
可以采用基于层次分析 熵权法（AHP-EWM）确定两种指标的权重
和 PG ，AHP-EWM 具体见文献[17]。最终的电网整体谐波裕度-均衡度综合评价指标计算公式为
式中，
为电网整体平均谐波裕度指标的权重； PG为电网谐波裕度基尼系数评价指标的权重。
该指标综合了电网各个节点的谐波电压总畸变率水平和全网谐波分布均衡程度，电网整体谐波裕度-均衡度综合评价指标越小，电网各个节点的谐波电压总畸变率水平越小，全网谐波分布越均衡。
3 基于电网谐波裕度均衡度综合指标的DG 最大准入功率计算模型
3.1 目标函数
选取电网的谐波裕度-均衡度综合指标最小的同时系统接纳DG 有功出力最大作为优化目标，以DG 接入位置和接入功率作为优化变量，目标函数数学模型为M2，即
式中，PDG 为DG 接入系统准入功率；Vmar 为系统谐波裕度-均衡度综合指标。
3.2 约束条件
3.2.1 等式约束
等式约束中，基波潮流方程如式（10）所示，谐波潮流方程如式（11）所示。假设负荷水平给定，有
式中，Vi、Vj 分别为节点i、j 处电压；θij 为节点i、j 间相位差；PDGi、QDGi 分别为节点i 处的DG 有功和无功量；PDi、QDi 分别为节点i 处有功和无功负荷量；Yh 为h 次谐波节点导纳矩阵；Vh 为h 次谐波节点电压列向量；Ih 为h 次谐波注入电流列向量。
3.2.2 不等式约束
式中，
和
分别为节点电压上、下限值，在此分别取1.05(pu）和0.95(pu)；
分别为节点 i 处总谐波电压畸变率和总谐波电压畸变率限值，
取值根据GBT14549—1993 规定限值；
别为接入DG 后和未接入DG 前的网损。
4 基于PSOAWCM 多目标优化计算方法
为了更好地求解多目标优化问题，本文提出了基于权重的PSO-AWCM 多目标优化算法来求解本文所建立的模型。该方法考虑了目标函数在求解Pareto 解集的模型中的相对重要性，并与混合粒子群优化算法相结合，以设置不同的ε 约束值循环调用单目标的混合粒子群优化算法以求得模型的Pareto 最优解集。
4.1 扩展权重ε 约束法
扩展ε 约束法（ACM）多目标优化算法具体如下。
以DG 准入功率最大即 1f 作为主目标函数，以电网谐波裕度均衡度最小 f2 作为约束目标，基于扩展ε 约束法的多目标优化问题计算形式为
其中
式中，
与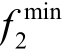
分别为在支付表中目标函数 f2的最大值和最小值；r1 为目标函数的跨度值；q 2 为第二个目标的间隔数； s2 为仅增约束条件引进的松弛变量。
然而，式（15）并没有反映目标函数 f1 、 f2 对产生Pareto 解集的重要性。为了反映各个目标函数对求解多目标优化Pareto 解集的影响，式（15）的目标函数可以写作
式中， wi 为第i 个目标函数的权重；p 为目标函数的数量（本文多目标优化模型中p=2）； is 为多目标优化问题约束条件的松弛变量；ir 为第i 个目标函数的跨度值，通过参数 ie 的迭代变化可以得到有效的Pareto 解集。值得注意的是，PSO-AWCM与将多目标按一定权重转化为单目标求解的传统方法相比，有本质不同，后者无法保证求得解的有效性。
4.2 基于PSO-AWCM 多目标计算方法
PSO-AWCM 的计算流程如下：
（1）计算支付表：按照字典顺序优化各个字母表得到支付表，以此来保障最终得到的解均为Pareto 最优解。
（2）计算第m 个目标函数跨度值：通过支付表第m 列中对应的目标函数m 的值，其中最大值和最小值表示目标函数的范围，通过该范围可以计算得到目标函数m 的跨度值。即
（3）转换目标函数：通过支付表得到所有目标函数rm 范围后，用 q2 −1 个网格点将目标函数 f2 的跨度值分割为 q2 个等间距。计算跨度的最小和最大值，对于 f2 有 q2 +1 个网格点。因此多目标优化最终转化为 q2 +1 个如式（17）的单目标优化问题以获得Pareto 最优解集。
（4）求解转换后的优化模型：式（16）的单目标优化问题可以用PSO 人工智能优化算法来求解。具体优化模型为
式中，X 为决策变量，即DG 接入位置及容量； iξ 为配电网系统中第i 个状态量； ξmax 为最大状态数；
为DG 接入容量。
4.3 最优解的选取
通过前文所述多目标数学规划方法可以得到Pareto 解集，然而决策者需要选择一个最佳折中的解来满足具有不同权重因子的各个目标函数。为了解决该问题，本文结合模糊决策理论，计算每个目标函数的线性隶属度函数，该函数反映了Pareto 最优解中各个目标函数的最大值与最小值间的相对距离。对于某个单独子目标函数，其值离最理想值越近，则隶属度函数值越大。
式中，
与
分别为第i 个目标函数在第k 个Pareto解集中的值和对应的隶属度函数。对于第k 个Pareto解集的总隶属度函数，将其归一化为
式中， iw 为第i 个目标函数的权重因子；m 为Pareto最优解集个数。
5 仿真算例与结果分析
5.1 算例说明
为了检验本文所提出的研究方法的有效性和优越性，本文利用改进的配电网IEEE 33 标准节点算例对所提方法进行验证。对于改进IEEE 33 节点标准算例，其拓扑结构如图1 所示。具体地，该配电网算例中含有33 个节点，37 条支路，基准电压为12.66kV，系统有功负荷为3 715kW，无功负荷为2300kvar，详细的支路参数与节点负荷数据可参考文献[24]。接入DG 的有功功率上限为2 000kW，由于DG 通常通过电压源换流器接入系统，可将无功控制在一定范围内，故在此只考虑有功功率。DG 待选安装节点为2, 3, 10, 17, 19, 20, 23, 27 和32。本文所研究的DG 主要包括风力发电和光伏发电。风机运行参数见文献[12]。风电向系统注入的谐波电流频谱参考文献[21]。
图1 IEEE 33 节点的拓扑系统
Fig.1 Topology of IEEE 33 distribution network system
5.2 DG 谐波频谱
对于风电系统来说，式（1）中谐波电流频谱
主要由风机的种类以及变换器控制方式等因素决定。风机的变换器尽管使用了PWM 控制技术，但是低次谐波（5 次、7 次等）仍然占主导。通过对大量数据的统计分析，各种风机发出的各次（主要是指非特征低次谐波）谐波电流含有率（即谐波电流频谱）与风机有功出力（运行点）的变化无关[23-24]，可近似为常数。而各次谐波电流幅值符合Weibull 分布[25]，即
式中，Ih 为第h 次谐波电流幅值；c 为Weibull 分布尺度参数；k 为Weibull 分布形状参数。对于低频段的谐波，k 取值相对较高（k≥3），此时谐波电流幅值分布近似正态分布。
对于光伏发电装置，其向电网等效注入的谐波与逆变器输出功率有关。文献[26]通过实测数据，拟合出其输出功率与发出谐波的关系，具体见表1。
表1 某光伏变换器发出的谐波值
Tab.1 Emission of harmonic of converter in PV system
发电水平(%额定功率)各次谐波电流（%基波）占有率3 5 7 11 13 15＜10% 16 20 7 7 6 4 10%～25% 5 16 1 2 1 1＞25% 0.7 1.3 0.7 0.9 0.4 0.7
表1 反映了光伏发电装置在不同发电水平下向电网注入各次谐波的水平，光伏发电装置渗透率越高，向电网注入的谐波水平越低。
为了简化研究，假设不同类型的DG 向电网注入谐波电流的相位相同，只考虑幅值的变化。
5.3 多目标优化算法对比
表2 为本文所提多目标优化方法支付表。如果忽略目标函数 1f 的约束，以 f2 为单目标函数，可得DG 最大消纳能力可达到1 592.58kW，此时对应的电网谐波裕度-均衡度综合指标为0.578。如果以 1f为单目标函数忽略目标函数 f2 ，则可以是电网谐波裕度-均衡度综合指标下降到0.485，但是此时对应的DG 最大消纳能力下降到1 070.22kW。也就是说，两个目标函数是相互矛盾的。最优解就是在多目标优化模的Pareto 解集中找到相对折中的解。
表2 计及谐波裕度-均衡度指标分布式电源接入问题支付表
Tab.2 Payoff table for distributed generator accessing scheme considering balance degree of harmonic margin
目标函数谐波裕度-均衡度最小( f1 )准入功率最大f2/kW谐波裕度-均衡度0.485 0.578准入功率 1 070.22 1 592.58
为了验证本文所提多目标优化算法 PSOAWCM 优越性，采用典型人工智能优化算法NGSAII[14]和ACM[17]算法进行对比。表3 中各个Pareto 解集的总隶属度函数的计算考虑了各个子函数的隶属度值和其权重，如式（20）。Pareto 解集中的最优解就是总隶属度函数值最大对应的解。改变权重因子，可以使决策者对最优解的选择具有偏向性。
根据表3，相对于传统ACM 算法与NGSA-II所求的结果，利用本文提出的PSO-AWCM 多目标优化算法求解本文提出的考虑谐波裕度-均衡度综合指标的分布式电源最大功率准入模型，所得Pareto 最优解的总隶属度函数值更大，根据上文提出的模糊决策理论，PSO-AWCM 求解出的Pareto 解为最优解。
表3 不同优化算法最优Pareto 解集对比
Tab.3 Comparison of the most preferred Pareto solution considering different weighting factor of object function
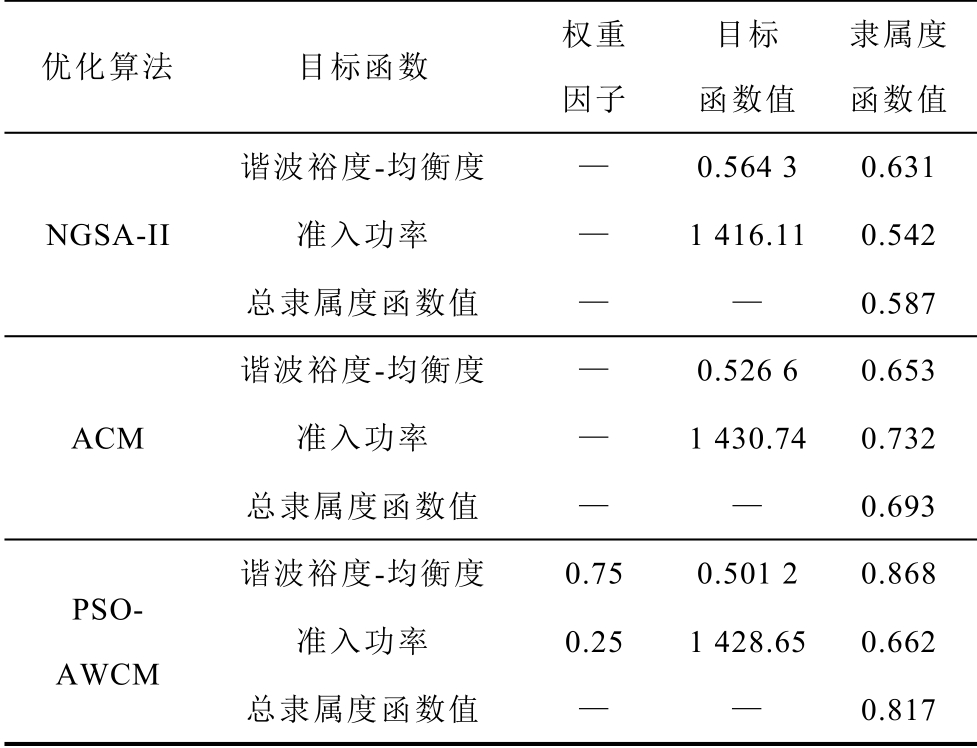
优化算法 目标函数权重因子目标函数值隶属度函数值谐波裕度-均衡度 — 0.564 3 0.631 NGSA-II 准入功率 — 1 416.110.542总隶属度函数值 — — 0.587谐波裕度-均衡度 — 0.526 6 0.653 ACM 准入功率 — 1 430.740.732总隶属度函数值 — — 0.693谐波裕度-均衡度 0.75 0.501 2 0.868 PSOAWCM准入功率 0.25 1 428.650.662总隶属度函数值 — — 0.817
表2 中第一行表示以子目标函数 1f 为单目标函数求解出的 f1 最小值和此时 f2 的值。将表3 中的最优解与表2 中第一行对比，可以发现单目标函数求得 1f 值略小于最优解中 1f 的值，然而最优解中对应的 f2 的值则明显大于单目标函数中对应的 f2 的值。表明了在牺牲DG 准入功率较少的情况下，电网谐波裕度均衡度更好，电网更加安全。
5.4 不同优化模型比较
为了验证本文所提出的电网整体谐波裕度-均衡度综合评价指标的优越性，作为对比，以系统谐波电压总谐波畸变率之和最小[8]以及系统接纳DG准入功率最大作为优化目标，标记为M1，本文所提优化模型见式（8），记作M2。对DG 进行接入位置和容量的确定。M1 数学模型为
式中，THDVi 为各个节点谐波电压总畸变率；THDtotal为系统谐波电压总畸变率；n 为系统节点数。优化算法中，取种群规模为100，迭代次数为30 次。在计算谐波裕度-均衡度综合评价指标过程中 λω 、 Gω分别取0.42 和0.58，所得结果见表4。
通过对表4 结果分析，相较于基于模型M1 所得接入方案，基于模型M2 所得接入方案最大接入容量更大、网损更小、电压水平更优。
1）在DG 准入容量方面：基于模型M2，最大接入容量为1 428.65kW，相较于基于模型M1 所得结果1 291.49kW，增加了10.62%，提升明显，而配电网的谐波电压总畸变率之和仅上升了2.98%。因此，采用谐波裕度-均衡度综合指标作为优化目标之一，可在通过均衡节点谐波电压分布水平，提高DG准入容量的同时，保证总的谐波畸变水平基本不变。在不同优化模型下各个节点谐波电压畸变率对比结果如图2 所示。
表4 结果对比分析
Tab.4 Analysis of comparison results
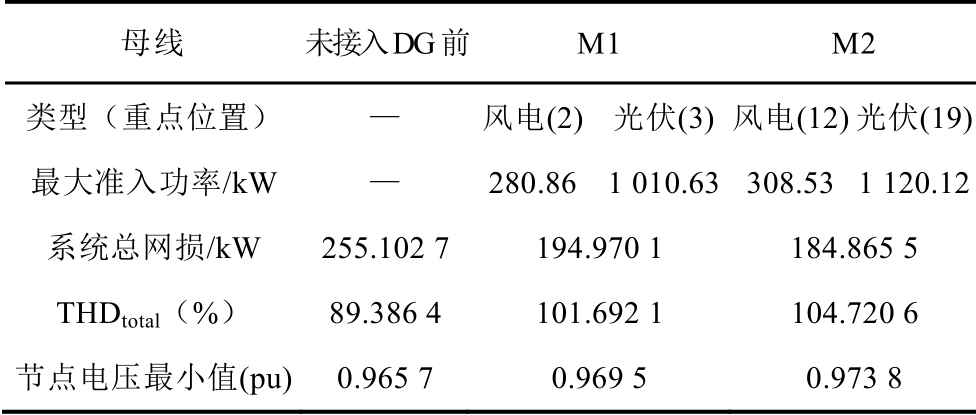
母线 未接入DG前M1 M2类型（重点位置）— 风电(2) 光伏(3) 风电(12)光伏(19)最大准入功率/kW— 280.86 1 010.63 308.53 1 120.12系统总网损/kW 255.102 7194.970 1 184.865 5 THDtotal（%） 89.386 4101.692 1 104.720 6节点电压最小值(pu) 0.965 7 0.969 5 0.973 8
图2 不同目标函数下的各节点谐波电压畸变率对比
Fig.2 THD comparison of each node harmonic voltage under different optimal model
2）在系统网损方面分析，模型M2 相较于模型M1 由194.970 1kW 降低到184.865 5kW。说明采用谐波裕度-均衡度综合指标作为优化目标之一能更好地降低网损。具体各支路有功损耗计算结果如图3 所示。
图3 不同优化模型下的有功损耗对比
Fig.3 Comparison of power loss under different optimal model
3）在系统各节点电压水平方面。基于模型M2，节点电压最小值由基于模型M1 的0.969 6(pu)上升到0.973 8(pu)，且如图4 所示，大部分节点的电压水平均不同程度地得到了提升。
图4 不同优化模型下各节点电压对比
Fig.4 Comparison of node voltage under different optimal model
6 结论
本文考虑了DG 出力不确定性和向系统注入谐波不确定性的情况，提出了一种电网整体谐波裕度-均衡度综合评价指标，并以此作为目标函数之一，建立 DG 最大准入容量优化模型，并提出 PSOAWCM 多目标优化计算方法对优化模型进行求解，基于改进的IEEE 33 节点配电网算例进行了仿真，验证了本文方法的有效性和优越性。得出以下结论：
1）以所提出的电网整体谐波裕度-均衡度综合评价指标作为目标函数之一，该指标既能反映电网各个节点的谐波电压总畸变率水平，也能综合体现全网谐波分布均衡程度。
2）以电网整体谐波裕度-均衡度综合评价指标为目标函数之一，可使得DG 接入时电网谐波分布更加均衡，从而避免了由于个别节点谐波水平过高而限制了DG 消纳能力的接入水平。
3）本文提出的PSO-AWCM 多目标优化计算方法以引入权重因子的方式考虑了各个子目标函数的相对重要性，使其能够更有效地进行多目标优化，并使决策者对最优解的选择具有偏向性和指向性。
本文仅以风电和光伏为例，研究了方法的有效性。为了使本文方法更符合实际生产需求，下一步工作考虑将更多类型的新能源接入电网问题。
[1] Rajkumar M, Mahadevan K, Kannan S, et al.Combined economic and emission dispatch with valve-point loading of thermal generators using modified NSGA-II[J]. Journal of Electrical Engineering& Technology, 2013, 8(3): 490-498.
[2] Chandana B, Elham M. Power quality studies in the presence of DG[J]. IEEE Transactions on Power Delivery, 2007, 18(7): 224-229.
[3] 钟清, 高新华, 余南华, 等. 谐波约束下的主动配电网分布式电源准入容量与接入方式[J]. 电力系统自动化, 2014, 38(24) :108-113.
Zhong Qing, Gao Xinhua, Yu Nanhua, et al.Accommodating capacity and mode of distributed generation under harmonic constraint in active distribution networks[J]. Automation of Electric Power System, 2014, 38(24):108-113.
[4] Filippo S, Paolo D L, Fab I O C, et al. Inverters for grid connection of photovoltaic systems and power quality: case studies[C]//3rd IEEE International Symposium on Power Electronics for Distributed Generation Systems(PEDG), Aswan, Egypt, 2012:564-569.
[5] Enslin J H R, Heskes P J M．Harmonic interaction between a large number of distributed power inverters and the distribution network[J]. IEEE Transactions on Power Electronics, 2004, 19(6): 1586-1593.
[6] 江南, 甘德强, 龚建荣. 考虑谐波影响的分布式电源准入功率计算[J].电力系统自动化, 2007, 31(3): 19-23.
Jiang Nan, Gan Deiqiang, Gong Jianrong. Computing the maximum penetrating level of distributed generators in distribution network by taking into account of harmonic constraints[J]. Automation of Electric Power System, 2007, 31(3): 19-23.
[7] 杭银丽. 分布式电源对电网谐波分布的影响及配置研究[D]. 南京: 南京理工大学, 2010.
[8] Jiang X, Gole A M. A frequency scanning method for the identification of harmonic instabilities in hvdc systems[J]. IEEE Transactions on Power Delivery,1995, 10(4): 1875-1881.
[9] Xia Daozhi, Heydt G T. Harmonic power flow studies to implementation and practical application[J]. IEEE Transactions on Power Apparatus and Systems, 1982,101(6): 1266-1270.
[10] 罗毅, 邵周策, 张磊, 等. 考虑风电不确定性和气网运行约束的鲁棒经济调度和备用配置[J]. 电工技术学报, 2018, 33(11): 2456-2467.
Luo Yi, Shao Zhouce, Zhang Lei, et al. Robust economic dispatch and reserve configuration considering wind uncertainty and gas network constraints[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2456-2467.
[11] 张建华, 曾博, 张玉莹, 等. 主动配电网规划关键问题与研究展望[J]. 电工技术学报, 2014, 29(2): 13-23.
Zhang Jianhua, Zeng Bo, Zhang Yuying, et al. Key issues and research prospects of active distribution network planning[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 13-23.
[12] 王守相, 张颖, 韩亮. 配电系统三相不确定谐波潮流的复仿射计算方法[J]. 电力系统自动化, 2015,39(7): 41-46.
Wang Shouxiang, Zhang Ying, Han Liang. A complex affine calculating method for three-phase uncertain harmonic power flow in distribution system[J].Automation of Electric Power System, 2015, 39(7):41-46.
[13] 余光正, 林涛, 徐遐龄, 等. 基于 2m+1 点估计法的考虑风力发电接入时电力系统谐波概率潮流算法[J]. 电网技术, 2015, 39(11): 3260-3265.
Yu Guangzheng, Lin Tao, Xu Xialing, et al. An algorithm based on 2m+1 point estimate method for harmonic probabilistic load flow calculation of power systems incorporating wind power[J]. Power System Technology, 2015, 39(11): 3260-3265.
[14] 彭春华, 孙惠娟. 基于非劣排序微分进化的多目标优化发电调度[J]. 中国电机工程学报, 2009, 29(34):71-76.
Peng Chunhua, Sun Huijuan. Multi-objective optimal power dispatch based on non-dominated sorting differential evolution[J]. Proceedings of the CSEE,2009, 29 (34): 71-76.
[15] 陈道君, 龚庆武, 张茂林, 等. 考虑能源环境效益的含风电场多目标优化调度[J]. 中国电机工程学报, 2011, 31(13): 10-17．
Chen Daojun, Gong Qingwu, Zhang Maolin, et al.Multi-objective optimal dispatch in wind power integrated system incorporating energy environmental efficiency[J]. Proceedings of the CSEE, 2011, 31(13):10-17.
[16] 杨柳青, 林舜江, 刘明波, 等. 考虑风电接入的大型电力系统多目标动态优化调度[J]. 电工技术学报, 2014, 29(10): 286-295.
Yang Liuqing, Lin Shunjiang, Liu Mingbo, et al.Multi-objective dynamic optimal dispatch for largescale power systems considering wind power penetration[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 286-295.
[17] George Mavrotas. Effective implementation of the econstraint method in multi-objective mathematical programming problems[J]. Applied Mathematics and Computation, 2009, 213(2): 455-465.
[18] 张卫华, 邱菀华. 基于供应链运作参考模型的供应链多目标绩效优化模型[J]. 计算机集成制造系统,2012, 18(9): 2052-2058.
Zhang Weihua, Qiu Wanhua. Multi-objective performance optimization model of supply chains based on SCOR[J]. Computer Integrated Manufacturing Systems, 2012, 18(9): 2052-2058
[19] 刘文学, 梁军等, 贠志皓, 等.考虑节能减排的多目标模糊机会约束[J]. 电工技术学报, 2016, 31(1):62-69.
Liu Wenxue, Liang Jun, Yun Zhihao, et al. Multiobjective fuzzy chance constrained dynamic economic dispatch considering energy saving and emission reduction[J]. Transactions of China Electro-technical Society, 2016, 31(1), 62-69.
[20] Sidrach-de-Cardona M, Carretero J. Analysis of the current total harmonic distortion for different singlephase inverters for grid-connected pv-systems[J].Solar Energy Materials & Solar Cells, 2005: 529-540.
[21] Wei Sun, Gareth P Harrison. Distribution network capacity assessment:incorporating harmonic distortion limits[C]//22nd IEEE Power Engineering Soeiety International Conference, San Diego, CA, USA, 2001:81-86.
[22] International Electrotechnical Commission (IEC). IEC/TR 61000-3-6 electromagnetic compatibility (EMC)-Part 3-6: limits-assessment of emission limits for the connection of distortinginstallations to MV, HV and EHV power systems[S]. 2008.
[23] Sokratis T T, Stavros A P. An investigation of the harmonic emissions of wind turbines[J]. IEEE Transactions on Energy Conversion, 2007, 22(1):150-158.
[24] Papathanassiou S A, Papadopoulos M P. Harmonic analysis in a power system with wind generation[J].IEEE Transaction on Power Delivery, 2006, 21(4):2006-2016.
[25] Luis S, Juan J M, Remus T. Deterministic and stochastic study of wind farm harmonic currents[J].IEEE Transaction on Energy Conversion, 2010, 25(4):1071-1080.
[26] 陈卫, 杨波, 张兆云, 等. 计及电动汽车充电站接入的配电网承载能力评估与优化[J]. 电工技术学报, 2014, 29(8): 27-35, 45.
Chen Wei, Yang Bo, Zhang Zhaoyun, et al.Distribution networks supportability evaluation and optimization considering electric vehicles charging stations[J]. Transactions of China Electrotechnical Society, 2014, 29(8): 27-35, 45.