0 引言
随着电力电子技术的发展，基于模块化多电平换流器（Modular Multilevel Converter, MMC）的柔性直流输电技术克服了传统基于晶闸管换流器直流输电的诸多缺陷，在功率控制、电能质量、供电可靠性方面具有明显优势[1-4]。但与常规直流输电相比，柔直输电系统阻尼低、惯性小、故障发展快，故障后电流在几毫秒内即可达到换流器耐受上限，对继电保护系统，尤其线路保护提出了巨大挑战[5-8]。
现有的直流输电线路保护可分两大类：
1）单元保护，主要利用线路两端电气量实现故障判别。如文献[9]基于Bergeron 分布参数模型构建纵联保护方案，解决了外部故障工况下电容放电催生的长延时问题，但该方法依赖大量的数据交换和严格的同步对时；文献[10]利用线路两端电流突变量计算夹角余弦值判断区内、外故障，耐受过渡电阻能力强且受线路分布电容电流的影响较小；文献[11]通过Prony 算法对电流进行频谱分析，利用两端的固有频率主频差构建直流线路纵联保护判据；文献[12]利用Hausdorff 距离表征并度量故障线路与非故障线路两侧同名行波与异名行波首波头的衰减特性差异，形成不依赖同步对时及边界元件的波形匹配式差动保护。上述文献在一定程度上减小了同步对时误差带来的不利影响，但依然需要传递大量非逻辑信号、存在通信延迟，因此现阶段纵联保护仍难以作为主保护用于柔直输电线路。
2）非单元式保护，主要利用单端电气量实现故障识别。实际柔直工程中，线路两端往往配置了限流电抗器限制电流的上升速度，为保护判断及断路器动作争取时间，同时也为边界保护应用于柔直系统中提供了基础[13-14]。目前直流线路主保护主要有行波保护和微分欠电压保护两种。其中，行波保护如ABB 和SIEMENS 公司的单端量行波保护，动作时间在几毫秒，满足速动性要求[15-16]，但存在高阻故障时保护灵敏度低的问题，两种保护方案都仅能耐受几十欧姆过渡电阻[17]。鉴于现有行波保护的不足，文献[18-21]基于限流电抗器等边界元件对高频信号的阻滞作用，利用区内外故障时高低频能量的不同构造单端量保护原理，不同程度地提升了现有行波保护的性能。但上述保护中频带的选取十分依赖线路边界元件的结构和参数，且保护定值一般通过仿真得到，给工程应用带来了困难。
针对以上问题与挑战，本文首先定量分析了首行波在线路上的色散效应及在边界处传播特性，揭示了区内外故障首行波弯曲程度的显著差异。在此基础上提出基于首行波曲率的直流输电线路单端量保护原理，并实现了数据窗的自适应选取。此外，根据双极柔性直流输电系统故障暂态特性，提出一种简单可靠的故障选极判据，并结合雷击干扰识别判据，形成了完整的柔直输电线路单端量保护方案。在PSCAD/EMTDC 中搭建模型进行了仿真，结果表明，保护方案能有效识别区内外故障并正确选极，耐受过渡电阻能力强。
1 首行波包含的故障信息
1.1 故障首行波解析方法
以双极柔性直流输电线路为例分析区内故障时首行波的传播特性，拓扑结构如图1 所示。其中，Ld c为限流电抗器；输电线路为架空线路，B11、B12与B21、B22 分别代表正负极线路首端与末端配置的直流保护；MMC1 与 MMC3 为正极换流器，MMC2 与MMC4 为负极换流器；f1 与f4 分别为线路正负极区内接地短路，f2 与f3 为限流电抗器和换流器之间故障，为区外故障。
图1 双极直流线路区内外故障拓扑结构
Fig.1 Internal and external faults of bipolar DC line
设故障点f1 与保护B11 之间的距离为l，发生故障时，保护B11 处电压首行波表达式为[22]
式中，i 为0 或1，分别代表零模和一模分量； γi( s)为直流线路传播系数； U ( s )=U i ( l ,s)为故障点所产生的电压行波； A ( s)= e -γi( s )l为线路的传递函数，其随频率变化，包含行波在线路上传播造成的波形畸变、衰减及延时信息。为方便计算，需对线路频变参数模型进行合理简化，将线路传递函数近似表示为[23]
式中，e− sl /v为行波线路传播延时，v 为行波波速度；(1−Ka )/(1+ sTa)描述行波沿线路传播过程中的衰减和色散作用引起的波形畸变；K a 为线路衰减比例系数，表示行波传播距离l 后幅值减小的比例； aT 为线路色散时间常数； ka 与 ta 分别为单位长度的衰减系数与色散时间常数；1+5tal 表征了行波传播距离l后波形相对于初始波形的畸变程度。
由于柔性直流线路中极分量存在耦合，且与零模波相比，线模行波色散程度小、稳定程度更高，因此采用线模行波作为分析对象。这样，故障点处产生的线模行波幅值可表示为[14]
式中，U dc 为线路额定电压； Zc1 与Zc0 分别为线路的线模与零模波阻抗；Rf 为故障点过渡电阻。初始行波可用阶跃信号表示，因此在复频域有
结合式（1）～式（4）得到保护B11 测得的行波复频域表达式为
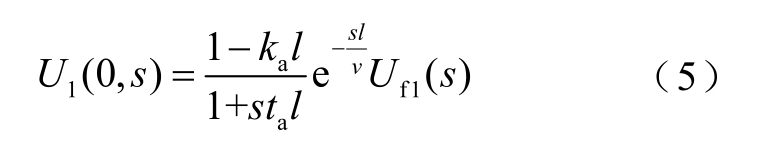
对区外故障f2，故障行波经限流电抗器到达保护B11 处。由于限流电抗器对高频分量的阻隔作用，行波波头将趋于平滑。文献[14]给出了用于分析故障行波在边界处情况的Peterson 等效电路，如图2 所示。
图2 区外故障时Peterson 等效电路
Fig.2 Peterson equivalent circuit for external fault
图2 中来自故障点的入射波用阶跃函数 ε(t)表示，实际的阶跃幅值已由式（3）给出； u1 、 i1 分别代表保护B11 处的一模电压、电流； Zm1 表示换流站1 的等效参数。转换为复频域求解可得
可用Matlab 等对式（5）、式（6）进行拉氏反变换求得各参数的时域表达式，从而得到B11 处的首行波解析式。
图3 所示为区外故障时B11 处行波解析计算结果与电磁暂态仿真结果的对比。在t=0ms 时刻发生故障，故障点f1 在线路中点，f2 位于限流电抗器和换流器之间。比较可见，解析计算结果与仿真结果有较高的一致性，首行波仿真值与理论值误差小于1.5%。故解析计算结果能准确描述故障首行波在线路及边界处的传播特性，从而为保护的设计与整定提供理论依据。本文重点分析故障首行波，图3 中f1 与f2 故障行波仿真值分别在1ms、1.4ms 左右的突变为故障首行波经线路边界或故障点反射回来的行波，故不考虑。
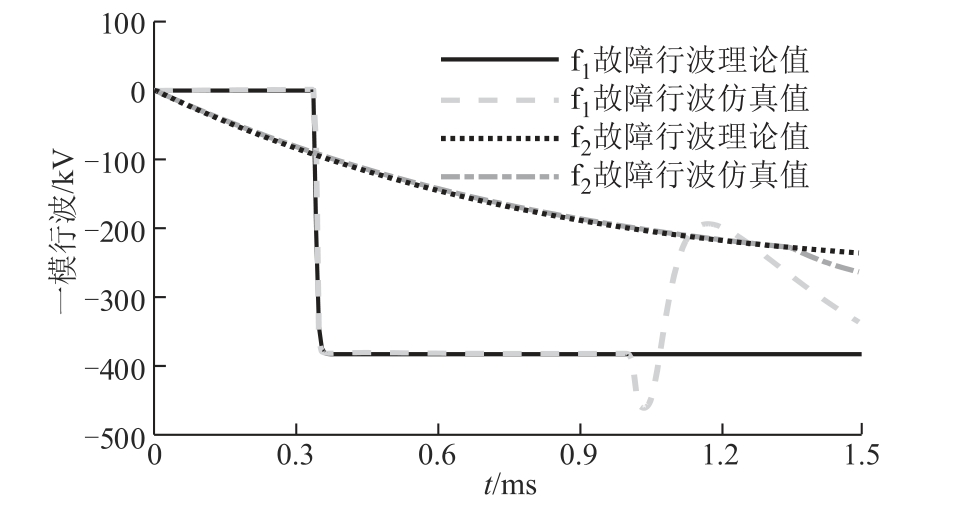
图3 区外故障时的初始行波
Fig.3 Initial traveling wave under external fault
1.2 行波曲率特征分析
由1.1 节分析可知，区内故障时，行波在线路上传播时会出现一定程度的色散现象，从而导致阶跃行波信号出现畸变；传播距离越长，色散现象越严重、畸变程度越大。区外故障时，行波经线路两端限流电抗器后，其波头的陡峭程度大大降低，行波畸变的程度远大于区内故障。由图3 不难看出，行波的畸变程度越大，直接表现为其弯曲程度越小。而曲率是描述曲线弯曲程度的理想参数，因此可利用行波曲率反映行波的畸变程度，从而准确识别区内、外故障。此外，由式（2）可知，区内故障时行波的畸变即弯曲程度仅与传播距离与线路参数有关，因此理论上该方法具有更强的抗过渡电阻能力。
曲率为曲线的几何属性，是针对曲线上某点的切线方向对弧长的转动率，通过微分定义并描述曲线偏离直线的程度[24]。在曲线C 上任意取两点M1与M2 ，两点之间的弧长为 ΔS ，如图4 所示。
图4 曲率定义
Fig.4 Definition of curvature
点M1 与点M2 切线的夹角分别为α 和 +α αΔ ，αΔ 则为点M1 到点M2 切线的转角。根据曲率的定义可得弧段
的平均曲率为
当 ΔS →0 时，平均曲率的极限即为点M1 处的曲率，记作K。
假设曲线的直角坐标方程为y =f ( t)，且其具有二阶导数。由于 y' =tanα，则有
又由弧长微分公式
得曲率为
同样以1.1 节故障情况为例，图5 给出了区内外故障时保护所检测到的首行波曲率曲线。结合图3 可知，区外故障时，首行波较为平滑，接近一条直线，其曲率为接近0 的数值；区内故障时，首行波曲率曲线存在最大值Kmax 且远大于区外故障，可据此设计故障识别判据。
图5 f1、f2 故障下首行波曲率曲线
Fig.5 Initial traveling wave curvatures of f1 and f2 faults
1.3 行波曲率影响因素分析
行波的波速度是频变的，故障行波中不同频率的分量在输电线路上的传播具有不同的波速度，其中高频分量较低频分量更快传播到线路首端[25]。故障距离越远，行波不同频率分量之间拉开的距离越大，导致保护测得的故障行波由上升到稳定的过程变长，畸变程度增大，即弯曲程度减小，不同故障距离的首行波如图6a 所示。因此，由曲率的定义不难得出，Kmax 将随故障距离的增加而减小，不同故障距离首行波曲率如图6b 所示。但是，由于线路两端限流电抗器的存在，行波经线路边界后趋于平滑，弯曲程度大大降低。因此即使在线路末端发生故障，K max与区外故障相比仍然存在较大差距。
图6 不同故障距离首行波及其曲率
Fig.6 Initial traveling wave and curvature at different fault locations
由式（2）、式（3）可知，过渡电阻的大小实际上只影响故障点处行波阶跃信号的幅值，而对于波速度的影响很小。因此过渡电阻的存在并不影响故障行波的畸变程度，即行波信号的弯曲程度基本不变，Kmax 仅存在微小变化，不同过渡电阻下的首行波及其曲率如图7 所示。双极短路故障线模行波曲率变化趋势与单极短路相同，不再赘述。
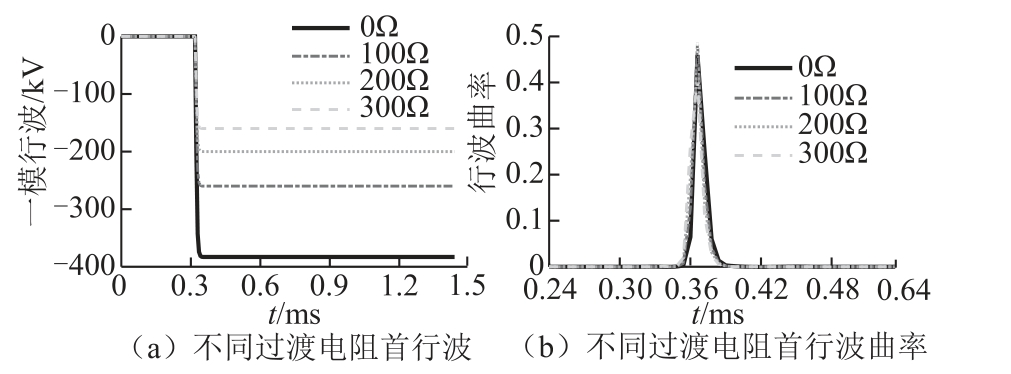
图7 不同过渡电阻下的首行波及其曲率
Fig.7 Initial traveling waves and curvatures under different fault resistance
2 基于首行波曲率的保护原理
2.1 故障识别判据
基于前述分析，设置故障识别判据为
式中，Kmax 为数据时窗内曲率最大值；Kset 为整定值； K0 为直流线路区外最严重故障时保护检测到的首行波曲率最大值；
为可靠系数。对于具有边界元件的直流线路，保护背侧限流电抗器和换流器之间发生金属性故障时为区外最严重的故障（如对保护B11 而言，f2 为最严重的区外故障）。由于区外故障与区内故障首行波曲率差别较大，因此可靠系数的选取具有较大裕度，本文取
1.1 节对行波在线路上的传递函数进行合理简化并给出了区内外故障时首行波解析式，结合1.2节中曲率计算方法即可对故障识别判据进行整定及灵敏度校验。式（9）中的一阶与二阶导数，可用数值微分代替，计算式为
式中，y =f (t)为电压线模行波； Δ t为采样间隔。
2.2 启动元件及数据窗选择
为快速检测故障，构建启动判据为
式中， u1 ( k) 为一模电压首行波信号；k 为采样点；Δu1 ( k)为两相邻采样点的差值；Δ s et为门槛值。区外发生高阻接地故障时，故障行波幅值较小且需经历线路边界到达保护安装处，此时行波信号的奇异性大大减弱，因此启动判据按躲过区外高阻接地（本文取200Ω）故障时采样点差值的最大值整定。
本文提出的保护方法需对行波到达时刻进行标定，采用小波变换模极大值法（Wavelet Transform Modulus Maximum, WTMM）对行波信号进行奇异性检测，行波到达时刻标定如图8 所示，其中t1 为行波数据中首个模极大值出现时刻即首行波到达时刻，t2 为首个干扰行波到达时刻， Δt 为首行波与干扰行波到达时间差。可以看到模极大值能够准确反映突变波头的时刻。
图8 行波到达时刻标定
Fig.8 Arrival time calibration for traveling wave
若相邻采样值的差值满足式（12），则启动直流线路保护算法，记录采样点k 对应的时刻为启动时刻，该时刻可能与行波到达时刻存在微小偏差，因此截取启动前0.1ms 与启动后0.5ms 的行波数据以确保首行波信号的完整性，基于这些数据，利用小波变换模极大值法检测行波到达时刻。行波到达时刻判据为
式中，W max 为保护检测到的行波信号模极大值；W set为行波到达时刻判据整定值（需躲过噪声影响）。
式中， nW 为正常运行时行波信号出现噪声干扰情况下（本文施加30db 白噪声）所出现的最大模极大值；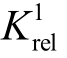
为可靠系数，取
本方法需提取故障首行波，若在曲率计算数据时窗内出现经故障点或线路对端反射回来的干扰行波，将对故障识别产生一定影响。为消除干扰行波影响，需灵活选取曲率计算的数据窗长。行波数据中首个模极大值出现时刻即为首行波到达时刻，记为t1，之后的模极大值所对应的均为干扰波到达时刻，记首个干扰行波到达时刻为t2，仅计算t1～ t2 时间段内的行波曲率。若未检测到干扰行波，则直接计算t1 后0.5ms 内首行波曲率，如图8 所示。综上所述，曲率计算数据窗长整定原则为
式中，T 为曲率计算数据时窗长度。与故障识别判据相同，可根据1.1 节区内外故障首行波表达式对启动判据进行整定。
2.3 故障选极判据
当双极柔性直流输电系统发生单极故障时，健全极仍能正常运行，因此快速选出故障极、保证非故障极的功率输送具有重要意义。
基于双极柔性直流输电系统故障暂态特性，提出一种简单可靠的故障选极判据。图9 给出了双极柔性直流输电系统发生单极接地短路时的故障电流通路，其中虚线表示子模块电容放电通路，粗实线为交流系统馈入短路点的电流通路。此时故障极电流将快速增大。由于站内接地，健全极无故障回路，因此其电流波动很小[26]。可见，线路发生单极接地短路时，短时窗内故障极电流的故障分量远大于健全极。
双极短路时，故障电流通过正极线路、正极换流器、负极换流器、负极线路形成闭合回路，此时正、负极电流大小几乎相同，故障分量也近似相等。
基于此，定义0.5ms 数据时窗内正、负极电流故障分量积分比值 pA 为
图9 双极柔直系统单极接地故障电流通路
Fig.9 Current path of pole-to-ground fault in bipolar flexible DC System
式中，t1 为首行波到达时刻；
与Δ in分别为正、负极电流故障分量。k 时刻的故障分量为
式中，k 为采样序列的序号；N 为0.5ms 数据窗长所对应的采样点个数，采样频率与故障识别判据相同。选极判据设置为
式中， Aset 为略大于1 的选极系数，考虑一定的裕度，取 Aset=1.3，使其能够有效区分不同类型的故障。
2.4 雷击干扰识别判据
雷电多为负极性，采用IEC 标准规定的标准1.2/50μs 负极性雷电波，用双指数的形式表示为
式中， Ig 为雷电流幅值；τ 1、 τ2分别为波头上升时间和半峰时间；对于标准雷电波，有
文献[27]提出，当输电线路遭受雷击时，其感应电流大部分在线模网络中流动，较少部分在地模网络中流动；而当输电线路发生双极短路时，地模电流基本为0。可利用此特点明显区分雷击干扰与区内双极短路。区内单极短路时，地模与线模中电流的分布与雷击时较为相似，但其模量能量的变化远不及雷击时强烈，线路故障的模量电流附加分量属于ms 级；而雷击引起的线模、地模附加分量属于μs 级。因此可通过判断μs 级数据窗内模量电流附加分量的幅值区分雷击与线路单极故障[27]。综上所述，设置雷击干扰识别判据为
式中，
与
分别为数据窗内地模、线模电流附加分量最大值； pset 与 qset 为相应的阈值，需躲过区内最严重故障即换流器出口金属性短路时所对应的数值，且需留有裕度。考虑到线模与零模波速度不同，线模电流与零模电流响应时刻可能存在微小差异，因此对于判据中p 的比较部分数据窗长度不能太小，结合线路长度并考虑一定的裕度，本文取线模首行波到达后0.3ms。经仿真测试，线路两端的雷电流波头上升时间在200～300μs 范围内，因此雷电干扰识别判据中q 的比较部分数据窗选为线模首行波到达后200μs。
2.5 保护流程
综合启动判据、故障识别判据、故障极选择判据和雷击干扰识别判据，基于首行波曲率的直流线路保护方案流程如图10 所示。
图10 保护方案流程
Fig.10 Flow chart of protection scheme
3 参数整定及仿真研究
3.1 参数整定
基于PSCAD/EMTDC 搭建如图1 所示的±500kV双极柔性直流输电系统模型，换流站为半桥MMC，整流侧采用定电压、无功功率控制，逆变侧采用定有功、无功功率控制；直流线路采用频变参数模型，线路结构见附录，线路长度为400km，线路两端限流电抗器Ldc 为200mH。保护采样频率为200kHz。根据2.1 节～2.4 节整定原则，对线路两端保护进行整定并列于表1。
表1 柔直系统保护整定值
Tab.1 Relay settings of flexible DC system
整定值保护Δ /kV Wset /kV Kset Aset pset qset/kA set B11 7.31 14.0 0.041 0.13 0.84 1.3 B12 7.26 13.1 0.040 0.13 0.87
3.2 仿真分析
以保护B11 为例，区内故障于直流线路每隔50km 由近至远设置正极接地故障；区外故障设置正向区外故障f3 和反向区外故障f2，过渡电阻分别考虑0Ω、200Ω、400Ω 及600Ω；故障时刻为1s。仿真结果见表2，其中
与
分别表示首行波及干扰行波模极大值变换结果，“—”表示由于无干扰行波或保护未启动而无计算结果。
仿真表明，区内故障时启动判据能正确动作，对于区外接地故障，过渡电阻超过200Ω 时，启动判据不动作。将各故障所对应的曲率计算结果绘制如图11 所示。由表2 及图11 不难看出，过渡电阻对Kmax 的影响很小，因此所提保护耐受过渡电阻能力强。经仿真验证，线路末端经800Ω 过渡电阻接地短路时，启动判据及故障识别判据仍能有效检测并识别区内故障。由图11 可知，过渡电阻相同时，故障距离越远，Kmax 会出现一定程度的下降，这是由于行波在线路上传播的色散造成的。但由于线路两端限流电抗器的存在，区内故障时Kmax 与区外故障相比存在较大差距。
表2 线路1 正极接地故障
Tab.2 Positive-pole grounded faults on line 1
故障位置/km过渡电阻/Ω计算结果1 W /kV 2 max W /kV Kmax pA max保护动作情况0 801 474 0.641 14.4 区内/正极50200 361 104 0.632 14.8 区内/正极400 236 44.4 0.629 16.6 区内/正极600 139 20.8 0.641 20.2 区内/正极0 761 — 0.467 14.0 区内/正极100200 356 — 0.467 13.9 区内/正极400 234 — 0.460 16.5 区内/正极600 174 — 0.452 19.5 区内/正极0 753 — 0.355 14.1 区内/正极150200 353 — 0.340 14.2 区内/正极400 232 — 0.338 13.9 区内/正极600 172 — 0.352 14.2 区内/正极
（续）
故障位置/km 200 250 300过渡电阻/Ω计算结果1 W /kV 2 max W /kV Kmax pA max保护动作情况0 747 — 0.302 13.4 区内/正极200 352 — 0.294 13.0 区内/正极400 230 — 0.289 12.9 区内/正极600 172 — 0.296 12.7 区内/正极0 740 — 0.249 10.4 区内/正极200 350 — 0.251 11.0 区内/正极400 228 — 0.253 10.6 区内/正极600 161 — 0.248 11.2 区内/正极0 732 — 0.197 9.8 区内/正极200 346 — 0.200 9.3 区内/正极400 226 — 0.201 9.9 区内/正极600 168 — 0.199 9.3 区内/正极0 728 2940.144 7.3 区内/正极350 200 343 2250.147 7.1 区内/正极400 224 1660.152 8.0 区内/正极600 167 1300.151 8.1 区内/正极0 90.4— 0.019 — 区外f2 200 — — — — 未启动400 — — — — 未启动600 — — — — 未启动0 86.2— 0.015 — 区外f3 200 — — — — 未启动400 — — — — 未启动600 — — — — 未启动
为验证区内负极及双极短路时故障识别与选极判据的有效性，在线路中点设置负极接地及双极短路故障，仿真结果见表3。观察表2 及表3 数据可知，故障位置及过渡电阻相同时，负极接地短路与正极接地短路故障识别判据结果相似，双极故障时其Kmax 较单极故障时稍大。此外，对于不同的故障类型，选极判据都能可靠识别。
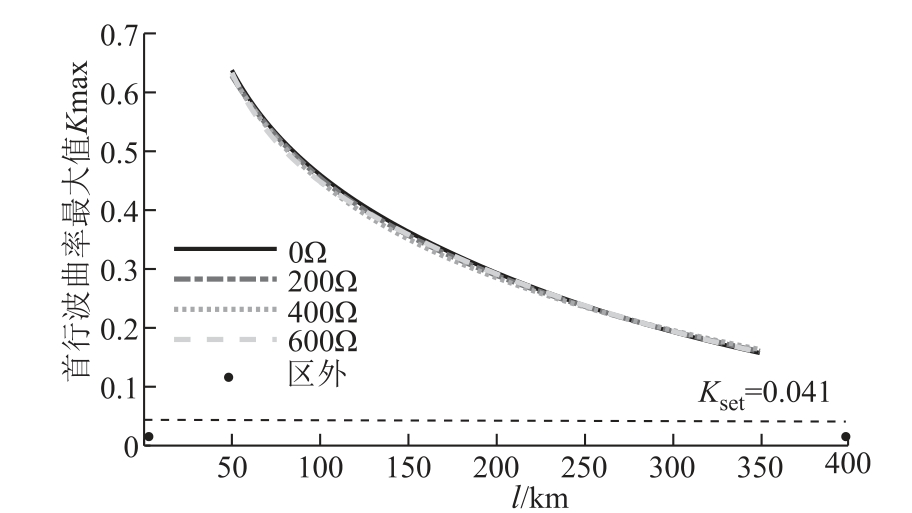
图11 曲率计算结果
Fig.11 Calculation results of curvature
表3 区内负极与双极短路故障
Tab.3 Negative-pole grounded and pole-to-pole faults on line1
故障类型过渡电阻/ΩW /kV 2 1 max计算结果 保护动作情况W /kV Kmax pA max 0 749 — 0.296 0.073 动作/负极负极接地200 350 — 0.302 0.069 动作/负极400 229 — 0.292 0.072 动作/负极600 173 — 0.197 0.082 动作/负极0 1 940 0.321 1.000 动作/双极双极短路200 1 124 0.330 1.000 动作/双极400 791 0.315 1.000 动作/双极600 523 0.326 1.000 动作/双极
3.3 与基于电压变化率的行波保护对比
目前常用的利用电压变化率(du /d t)判据进行线路区内外故障识别的保护中，du /d t 的大小与过渡电阻呈负相关且判据门槛值需躲过区外故障时可能出现的最大变化率，因此存在区内高阻故障时灵敏度不足的问题。文献[23]给出了基于电压变化率的行波保护解析、整定及灵敏度校验的具体方法。图12 给出了区内末端经不同过渡电阻接地短路时保护B11 的电压变化率情况。其中，Ksen_min 为保护需满足的最小灵敏度（此处取2）， ρ set为保护B11的整定值， 当区内故障的电压变化率满足
时，灵敏度满足要求[23]。
图12 线路末端接地故障时保护B11 电压变化率曲线
Fig.12 Curves of voltage change rate of B11 under fault at the end of DC line
对线路保护而言，末端故障为最轻微的区内故障，图12 中将线路末端经不同的过渡电阻接地时电压变化率的大小与整定值进行比较。不难看出，线路末端经400Ω 过渡电阻接地时保护出现灵敏度不足问题。本文方案利用首行波曲率构建区内外故障识别判据，由3.2 节仿真分析可知，与基于电压变化率的行波保护相比，其故障识别判据中Kmax 基本不受过渡电阻影响，在区内末端经800Ω 过渡电阻接地时依然有足够的灵敏度（高于3），因此具有更强的抗过渡电阻能力。
3.4 影响因素分析
工程实际中雷击输电线路时有发生，且雷电波与区内故障时的行波较为相似，可能导致保护误动。表4 给出了线路中点处发生雷击干扰或故障时，保护B11 雷击干扰识别判据的动作情况。不难看出，即使在雷电流较为微弱的情况下，该判据依然能够准确识别雷击干扰。
表4 雷击干扰识别判据动作结果
Tab.4 Results of lightning strike identification criterion
雷击干扰/故障参数值 判断结果p q/kA雷击干扰(Ig=5kA) 0.96 1.69 雷击雷击干扰(Ig=10kA) 0.94 3.20 雷击雷击干扰(Ig=15kA) 0.98 4.61 雷击单极接地 0.97 0.42 故障双极短路 0.008 0.86 故障
保护动作所需时间主要包括：①行波传输延时，对于400km 输电线路，由附录线路参数可求得线模行波波速度为2.95×108m/s，传输延时不大于1.36ms；②保护启动延时，经仿真测试约为3 个采样间隔，故该延时约0.015ms；③算法时间，含数据采集延伸至启动后0.5ms，小波变换等运算时间，参考现有硬件计算能力及速度[14]，算法时间约1ms。故本保护可在故障后2.5ms 左右出口。
此外，所提方案需准确捕捉故障行波，对采样频率要求较高，实际上，本文选取200kHz 的采样频率已留一定裕度。经仿真验证，采样频率为150kHz时，区内故障时保护依旧能可靠动作。当采样频率为100kHz 时，虽然波头波形的质量变差，计算得出曲率与高采样频率时存在一定差异，灵敏度也随之改变，但依然能够保证区内、外故障的正确识别。为确保可靠性，设置本方法的采样频率高于100kHz。考虑到目前柔直线路保护的采样频率一般为50～100kHz，实际工程中本方法对硬件水平要求略高。
4 结论
针对传统柔性直流输电线路单端量保护在高阻故障时的低灵敏度及拒动问题，在分析故障首行波传播特性的基础上，提出了一种基于首行波曲率的单端量保护原理，并得出以下结论：
1）线路的色散效应是故障首行波的弯曲程度变化的主要因素，因此首行波的曲率的大小与故障距离有直接关系，受过渡电阻影响较小，不受系统降压运行等工况影响。
2）所提保护方案能够可靠选极并通过数据窗长的自适应选择，避免反射波对保护判据的影响。
3）通过合理简化的线路频变参数模型，得到区内外故障首行波表达式，为保护的整定提供了理论依据。
仿真表明该保护方案的判据简单、动作速度快、可靠性高、耐受过渡电阻能力强。
本保护对采样频率要求较高，后续需进一步优化，保证在较低采样频率下依然具有优良性能，以更好地适应目前工程应用要求。
附 录
附图1 柔直线路模型
App.Fig.1 Flexible DC transmission line model
[1] 宋国兵, 王婷, 张晨浩, 等. 利用健全极MMC 注入特征信号的直流线路故障性质判别方法[J]. 电工技术学报, 2019, 34(5): 994-1003.
Song Guobing, Wang Ting, Zhang Chenhao, et al. DC line fault identification based on characteristic signal injection using the MMC of sound pole[J].Transaction of China Electronic technical Society,2019, 34(5): 994-1003.
[2] Sun Yuanxiang, Li Zhen, Zhang Zhenbin, Hybrid predictive control with simple linear control based circulating current suppression for modular multilevel converters[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 335-341.
[3] 张希鹏, 邰能灵, 郑晓冬, 等. 基于 WEMTR 的柔性直流输电线路故障测距[J]. 电工技术学报, 2019,34(3): 589-598.
Zhang Xipeng, Tai Nengling, Zheng Xiaodong, et al.Fault location in VSC-HVDC transmission lines based on WEMTR[J]. Transaction of China Electrotechnical Society, 2019, 34(3): 589-598.
[4] 贾科, 赵其娟, 王聪博, 等. 柔性直流配电系统线路保护与定值整定[J]. 电力系统自动化, 2019,43(19): 171-183.
Jia Ke, Zhao Qijuan, Wang Congbo, et al. Line protection and setting calculation for flexible DC distribution system[J]. Automation of Electric Power Systems, 2019, 43(19): 171-183.
[5] 王晓卫, 高杰, 吴磊, 等. 柔性直流配电网高阻接地故障检测方法[J]. 电工技术学报, 2019, 34(13):2806-2819.
Wang Xiaowei, Gao Jie, Wu Lei, et al. A high impedance fault detection method for flexible DC distribution network[J]. Transaction of China Electrotechnical Society, 2019, 34(13): 2806-2819.
[6] 李猛, 贾科, 张秋芳, 等. 基于全电流方向特征的柔性直流配电网纵联保护[J]. 电力系统自动化,2019, 43(23): 116-127, 130.
Li Meng, Jia Ke, Zhang Qiufang, et al. Directional pilot protection for flexible DC distribution network based on directional characteristics of instantaneous current[J]. Automation of Electric Power Systems,2019, 43(23): 116-127, 130.
[7] 周光阳, 李妍, 何大瑞, 等. 含限流器的多端柔直系统故障保护策略[J]. 电工技术学报, 2020, 35(7):1432-1443.
Zhou Guangyang, Li Yan, He Darui, et al. Protection scheme for VSC-MTDC System with fault current limiter[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1432-1443.
[8] 金涛, 苏见燊, 张明扬. 基于混合式断路器的直流电网保护方案研究[J]. 电机与控制学报, 2020,24(3): 106-113.
Jin Tao, Su Jianshen, Zhang Mingyang. Research on DC grid protection scheme based on hybrid circuit breaker[J]. Electric Machines and Control, 2020,24(3): 106-113.
[9] 高淑萍, 索南加乐, 宋国兵, 等. 高压直流输电线路电流差动保护新原理[J]. 电力系统自动化, 2010,34(17): 45-49.
Gao Shuping, Suonan Jiale, Song Guobing, et al. A new current differential protection principle for HVDC transmission lines[J]. Automation of Electric Power Systems, 2010, 34(17): 45-49.
[10] 周家培, 赵成勇, 李承昱, 等. 采用电流突变量夹角余弦的直流电网线路纵联保护方法[J]. 电力系统自动化, 2018, 42(14): 165-171.
Zhou Jiapei, Zhao Chengyong, Li Chengyu, et al. Pilot protection method for DC lines based on included angle cosine of fault current component[J].Automation of Electric Power System, 2018, 42(14):165-171.
[11] 宋国兵, 蔡新雷, 高淑萍, 等. 利用电流频率特性的VSC-HVDC 直流输电线路纵联保护[J]. 高电压技术, 2011, 37(8): 1989-1996.
Song Guobing, Cai Xinlei, Gao Shuping, et al. New pilot protection for VSC-HVDC transmission lines using natural frequency characteristic of current[J].High Voltage Engineering, 2011, 37(8): 1989-1996.
[12] 童宁, 范理想, 林湘宁, 等. 不依赖边界元件及同步对时的多端柔直电网波形匹配式差动保护原理[J].中国电机工程学报, 2019, 39(13): 3820-3833.
Tong Ning, Fan Lixiang, Lin Xiangning, et al.Waveform matching based protection strategy for VSC-MTDC independent on synchronization and boundary component[J]. Proceedings of the CSEE,2019, 39(13): 3820-3833.
[13] 李斌, 何佳伟, 冯亚东, 等. 多端柔性直流电网保护关键技术[J]. 电力系统自动化, 2016, 40(21): 2-12.
Li Bin, He Jiawei, Feng Yadong, et al. Key techniques for protection of multi-terminal flexible DC grid[J].Automation of Electric Power Systems, 2016, 40(21):2-12.
[14] 汤兰西, 董新洲, 施慎行, 等. 柔性直流电网线路超高速行波保护原理与实现[J]. 电网技术, 2018,42(10): 3176-3186.
Tang Lanxi, Dong Xinzhou, Shi Shenxing, et al.Principle and implementation of ultra-high-speed traveling wave based protection for transmission line of flexible HVDC grid[J]. Power System Technology,2018, 42(10): 3176-3186.
[15] 乔立华, 陶然, 宋国兵, 等. 直流线路边界特性保护综述[J]. 电力系统保护与控制, 2019, 47(19): 179-186.
Qiao Lihua, Tao Ran, Song Guobing, et al. A summary of the boundary characteristics used in DC system relay protection[J]. Power System Protection and Control, 2019, 47(19): 179-186.
[16] 宋国兵, 高淑萍, 蔡新雷, 等. 高压直流输电线路继电保护技术综述[J]. 电力系统自动化, 2012,36(22): 123-129.
Song Guobing, Gao Shuping, Cai Xinlei, et al. Survey of relay protection technology for HVDC transmission lines[J]. Automation of Electric Power Systems, 2012,36(22): 123-129.
[17] 董新洲, 汤兰西, 施慎行, 等. 柔性直流输电网线路保护配置方案[J]. 电网技术, 2018, 42(6): 1752-1759.
Dong Xinzhou, Tang Lanxi, Shi Shenxing, et al.Configuration scheme of transmission line protection for flexible HVDC grid[J]. Power System Technology,2018, 42(6): 1752-1759.
[18] 付华, 陈浩轩, 李秀菊, 等. 含边界元件的 MMCMTDC 直流侧单端量故障辨识方法[J]. 电工技术学报, 2021, 36(1): 215-226.
Fu Hua, Chen Haoxuan, Li Xiuju, et al. MMC-MTDC DC side single-ended quantity fault identification method with boundary elements[J]. Transaction of China Electrotechnical Society, 2021, 36(1): 215-226.
[19] 张保会, 孔飞, 张嵩, 等. 高压直流输电线路单端暂态量保护装置的技术开发[J]. 中国电机工程学报, 2013, 33(4): 179-185.
Zhang Baohui, Kong Fei, Zhang Song, et al. Technical development of non-unit protection devices based on transient signals for HVDC transmission lines[J].Proceedings of the CSEE, 2013, 33(4): 179-185.
[20] 陈仕龙, 束洪春, 万春红, 等. 一种特高压直流输电线路单端电压暂态保护原理[J]. 电力系统保护与控制, 2013, 41(3): 26-31.
Chen Shilong, Shu Hongchun, Wan Chunhong, et al.The principle of single-ended transient based voltage protection for UHVDC transmission line[J]. Power System Protection and Control, 2013, 41(3): 26-31.
[21] 束洪春, 田鑫萃, 张广斌, 等. ±800kV 直流输电线路的极波暂态量保护[J]. 中国电机工程学报,2011, 31(22): 96-104.
Shu Hongchun, Tian Xincui, Zhang Guangbin, et al.Protection for ±800 kV HVDC transmission lines using pole wave transients[J]. Proceedings of the CSEE, 2011, 31(22): 96-104.
[22] 彭楠, 杨智, 梁睿, 等. 一种半波长输电线路的分布式行波测距方法[J]. 电机与控制学报, 2019,23(8): 35-42.
Peng Nan, Yang Zhi, Liang Rui, et al. Distributed traveling wave fault location scheme for halfwavelength transmission lines[J]. Electric Machines and Control, 2019, 23(8): 35-42.
[23] 王艳婷, 范新凯, 张保会. 柔性直流电网行波保护解析分析与整定计算[J]. 中国电机工程学报, 2019,39(11): 3201-3212.
Wang Yanting, Fan Xinkai, Zhang Baohui. The analytical analysis and protection setting of traveling wave protection in VSC-HVDC grid[J]. Proceedings of the CSEE, 2019, 39(11): 3201-3212.
[24] 贾科, 王聪博, 毕天姝, 等. 考虑过渡电阻影响的柔性直流配电系统电流突变量保护[J]. 电网技术,2018, 42(10): 3187-3195.
Jia Ke, Wang Congbo, Bi Tianshu, et al. A DC current derivative protection with capability of resisting high resistance for flexible DC distribution system[J].Power System Technology, 2018, 42(10): 3187-3195.
[25] 张晨浩, 宋国兵, 董新洲. 一种应对高阻故障的单端自适应行波保护方法[J]. 中国电机工程学报,2020, 40(11): 3548-3556.
Zhang Chenhao, Song Guobing, Dong Xinzhou. A non-unit adaptive traveling wave protection method for high impedance faults[J]. Proceedings of the CSEE,2020, 40(11): 3548-3556.
[26] 陈继开, 孙川, 李国庆, 等. 双极 MMC-HVDC 系统直流故障特性研究[J]. 电工技术学报, 2017,32(10): 53-60, 68.
Chen Jikai, Sun Chuan, Li Guoqing, et al. Study in characteristics of DC fault in bipolar MMC-HVDC system[J]. Transaction of China Electrotechnical Society, 2017, 32(10): 53-60, 68.
[27] 顾垚彬, 宋国兵, 郭安祥, 等. 针对直流线路行波保护的雷击识别方法研究[J]. 中国电机工程学报,2018, 38(13): 3837-3845.
Gu Yaobin, Song Guobing, Guo Anxiang, et al. A lightning recognition method for DC line travlingwave protection of HVDC[J]. Proceedings of the CSEE, 2018, 38(13): 3837-3845.