0 引言
我国地域广阔,发电资源与用电负荷呈逆向分布,特高压直流输电以其输电容量大、输送距离远、线路走廊窄等优点,在中国具有广阔的应用前景[1-2]。特高压直流输电线路距离长,穿越地形及周边环境复杂,据统计,特高压直流输电线路故障约占整个直流输电系统故障的50%,而线路保护正确动作率却不高[3]。因此,亟需进一步研究特高压直流输电线路暂态保护。
目前国内外学者针对特高压直流输电线路保护已进行了一些研究。文献[4]利用区内、外故障时保护安装处高频暂态电压信号能量的不同区分直流输电线路区内、外故障。该保护方法没有深入考虑长距离直流输电线路对高频分量的衰减将大于物理边界的衰减,当直流线路末端故障时保护将拒动,不能保护直流线路全长。文献[4-5]利用小波变换技术提取高、低频电压信号小波能量,进而基于小波能量提出多套保护判据,能可靠保护直流线路全长。该方法保护判据较繁琐,若配合出错则会导致保护误动作;同时小波变换技术在理论上能处理非线性非平稳信号,但在实际算法实现中只能处理线性非平稳信号,应用在直流输电系统中存在一定适应性问题。文献[6-7]通过将故障后的突变量特征信息进行整合实现直流线路保护。该方法对直流线路通信通道要求较高,易受通信干扰。文献[8-9]利用叠加原理提取故障后的电流突变量作为保护所需电气量,但叠加原理只适用于线性系统,对于强非线性的特高压直流输电系统存在适应性问题。
针对以上缺陷,文中在分析特高压直流输电线路两端物理边界和直流输电线路特性的基础上,首先利用希尔伯特-黄变换(Hilbert-Huang Transform,HHT)对故障后暂态电压进行解析,提取暂态电压5~7kHz 高频带Hilbert 能量作为保护所需电气量;然后分析直流输电线路区内、外故障时,暂态电压5~7kHz 高频带Hilbert 能量幅值信息和波形信息,引入标准差来描述其特征,据此构造直流输电线路故障识别判据;最后利用正、负极标准差之比构造故障选极判据,实现故障极全线速动保护。通过在PSCAD 中搭建云广±800kV 双极直流输电系统模型提取故障信息,利用Matlab 实现保护算法,仿真结果证明原理有效性。
1 特高压直流输电系统物理边界及线路特性分析
本文参照文献[10]中云广特高压直流输电系统及各元件实际参数,搭建如图1 所示的±800kV 双极特高压直流输电模型。该模型由两端交流系统、换流变压器、整流器、平波电抗器、直流滤波器、直流输电线路和逆变器构成。如图1 所示。

图1 特高压直流输电系统
Fig.1 UHVDC transmission system diagram
图1 中,f1、f6 表示正、负极直流输电线路区内故障;f2、f3、f7、f8 表示直流线路区外故障,分别为正、负极整流侧出口故障和逆变侧出口故障;f4、f5表示整流侧交流母线三相故障、逆变侧交流母线三相故障。
1.1 希尔伯特-黄变换
直流输电系统是强非线性系统,输出电气量具有非线性,对其应用叠加原理提取突变量作为保护所需电气量的保护会存在适应性问题[11]。从保护的适应性角度出发,本文利用希尔伯特-黄算法对故障后暂态量进行预处理。
小波变换在实际算法实现中只能处理线性非平稳信号,而HHT 作为一种优秀的时频分析方法,能直接反映信号的时频本质[12],与傅里叶变换、小波理论和数学形态学等方法相比,更适合处理非线性非平稳信号,具有很强的自适应性,非常适合电力系统暂态信号的处理。
HHT 算法首先将原始信号X(t)经过经验模态分解(Empirical Mode Decomposition, EMD)为
式中,imfk 为k 个从高频到低频依次排列的固有模态函数分量;rn 为残余函数,是一个单调函数。
其次,将每个imf(t)分量分别进行Hilbert 变换得
式中,t 为时间。
得到解析信号为
进而可推出原始信号X(t)的另一种表达式为
式中,Re 表示取实部;ωk(t)为imfk 分量瞬时频率。
最后省略残余分量,得反映信号幅值随时间-频率分布的Hilbert 谱H(ω, t)为
定义Hilbert 瞬时能量为
式中,ω1、ω2 为角频率,ω=2πf;IE(t)为Hilbert 能量随时间变化的函数,能精确描述信号在某一频段内能量随时间的分布情况。
1.2 直流输电线路物理边界对Hilbert 能量波形形状的影响
基于文献[13]可知,当单独研究直流滤波器时,可得
式中,u2 为区外暂态电压;u 为u2 经直流滤波器传变至直流线路保护安装处的电压;Z1 为整流侧波阻抗;Z2 为直流滤波器阻抗。
当单独研究平波电抗器时,可得
式中,u2 为区外暂态电压;u 为u2 经直流滤波器传变至直流线路保护安装处的电压;Z3 为线路滤波阻抗;L 为平波电抗器的感抗。
本文基于文献[13]理论成果并利用电压信号作为保护所需电气量进行后续推导研究。
令原始信号为u(t),经EMD 分解后将等式两端对时间求偏导。因为rn 是一个单调函数或是一个常数,本文旨在分析物理边界与Hilbert 能量波形的关系,故省略rn 简化分析以突出本质特征,得到
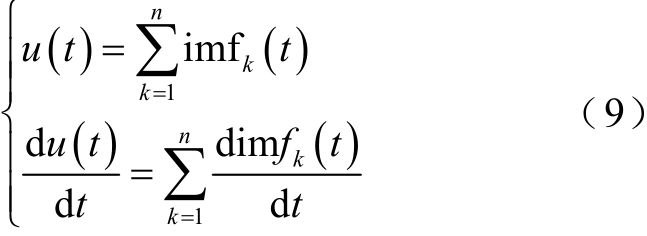
结合式(9)和imf 性质可得
对式(2)分析可知,Hilbert 变换实质为imfk(t)与1/(πt)卷积所得,将式(2)两端对时间求偏导,根据卷积微分性质得

结合式(3)、式(5)和式(6),并整理得

将式(12)两端对时间求偏导

将式(11)代入式(13)整理得
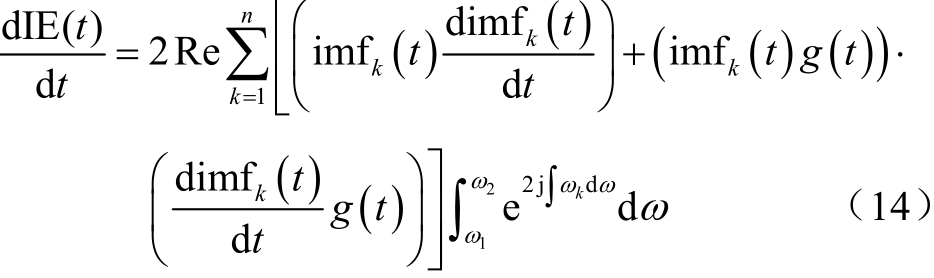
根据控制变量法的理念,将imf(t)分量视为定值(g(t)为时间的函数,为已知量且为正)。结合式(10)与式(14)并分析可知,随着电压变化率的增大(或减小),imf(t)变化率也增大(或减小),从而造成Hilbert 能量变化率增大(或减小),表达式为

为突出Hilbert 能量波形与电压波形的关系,进而将式(15)简化为
分析式(16)可知,单位时间内Hilbert 能量变化量与电压行波变化量呈正相关,即电压行波波形的平滑(陡峭)决定Hilbert 能量波形的平滑(陡峭)。
结合式(7)、式(8)和式(16)与前述结论可得,区外故障时直流滤波器和平波电抗器对Hilbert能量波形有平滑作用,且直流滤波器阻抗和平波电抗器感抗越大,平滑作用越明显。
1.3 直流输电线路物理边界对Hilbert 能量幅值的影响
特高压直流输电系统一般配备12/24/36 三调谐直流滤波器,与平波电抗器共同构成直流输电线路物理边界,如图2 所示。
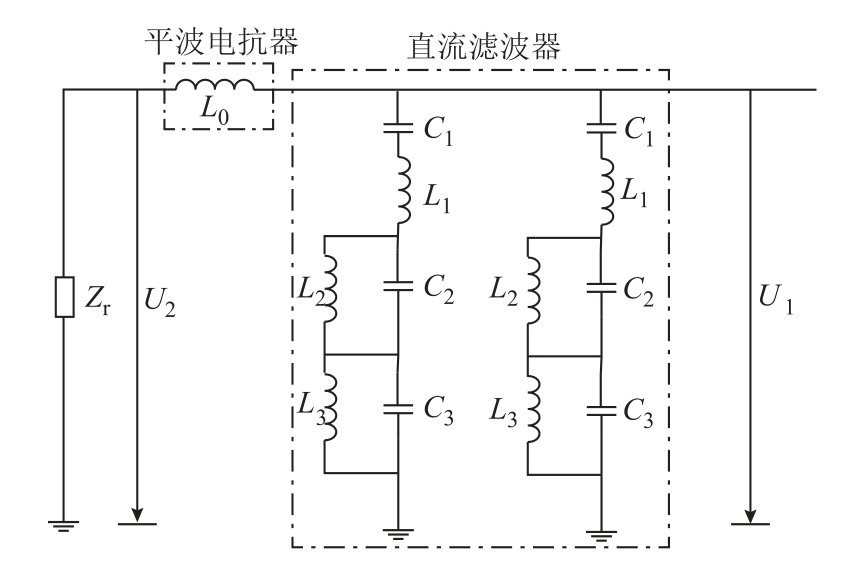
图2 直流输电线路物理边界
Fig.2 Physical boundary of DC transmission line
图2 中,U2 为区外暂态电压,U1 为U2 经线路物理边界传变至直流线路保护安装处的电压,Zr 为整流器等效内阻抗。平波电抗器、三调谐直流滤波器的阻抗分别如式(17)、式(18)所示。

定义线路物理边界元件的传递函数G(jω)为
根据式(19)可得直流线路物理边界元件幅频特性曲线,如图3 所示。

图3 物理边界元件幅频特性曲线
Fig.3 Physical boundary element amplitude-frequency characteristic curve
由图3 可得:直流分量及低频段0<f ≤100Hz,|G(jω)|≈1;100<f≤1.3kHz,|G(jω)|>1,尤其在800<f≤1kHz 频段,|G(jω)|≫1;在f>4.5kHz 的高频段,|G(jω)|≪1。可见直流输电线路物理边界对低频分量具有一定的增强作用,对高频分量具有强烈的衰减作用。基于以上分析得:直流输电线路区外故障时,直流线路保护安装处检测到的暂态高频分量较小,暂态低频分量较大。
1.4 特高压直流输电线路频率特性分析
实际直流输电线路为电导G=0 的均匀传输线。线路长度为x 的直流输电线路传输函数为
式中,j=0, 1,分别表示零模、线模分量;γj 为j 模传播系数,表达式为
式中,Rj、Lj 和Cj 分别为直流线路单位长度的j 模电阻值、电感值和电容值。
对双极特高压直流输电线路方程进行Clarke 相模变换,使其分解成两个独立的分量,即线模和零模分量[14]。零模传输函数的幅频特性与线模传输函数的幅频特性相似。本文提取线模分量进行分析说明特高压直流输电线路的频率特性。
由直流输电线路传输函数Aj(jω)的表达式可知,该函数为减函数,其幅值随频率的增大而降低,随线路长度的增加而减小。换言之,特高压直流输电系统双极运行时,特高压直流输电线路对各频率均有衰减作用,且频率越高、线路越长,衰减作用越强烈。特高压直流输电系统实际运行中,输电线路弧垂效应造成直流输电线路长度难以精确测量,如果实际工程中直流输电线路过长,线路对高频分量的衰减作用将超过线路物理边界元件对高频分量的衰减作用。由式(20)得到2 000km 直流输电线路线模传输函数和线路物理边界的幅频特性曲线对比图,如图4 所示。
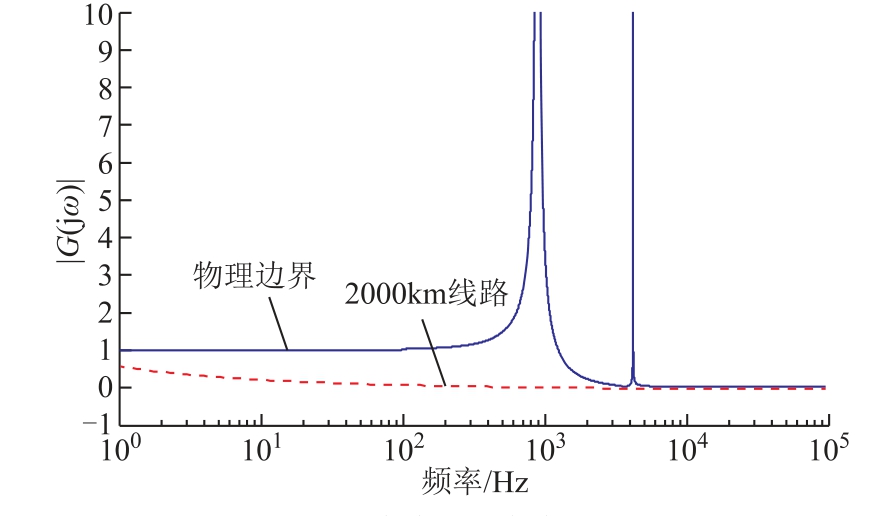
图4 全频段放大对比
Fig.4 Full-band magnification comparison chart
由图4 可知,直流长线路对大多数频段的衰减作用均大于直流线路物理边界元件的衰减作用。若仅利用行波暂态量幅值信息构造保护判据,不考虑长直流输电线路对各频率分量的强衰减作用,则在区分整流侧出口故障和直流输电线路末端故障时会出现选择性问题,造成保护拒动,不能实现直流线路全线保护[15]。因此,本文针对此问题展开后续研究。
2 基于Hilbert 能量幅值信息和波形信息的保护方案
2.1 启动判据
双极直流输电系统正常运行时,理论上保护安装处检测到的高频能量为零,实际上换流器相当于谐波电压源,在直流侧产生12k 次(k 为自然数)谐波,而直流输电线路物理边界元件对12k 次谐波具有滤除作用,故保护安装处检测到的高频能量几乎为零;故障发生时,保护安装处检测到的高频能量明显增大[16]。考虑发生故障后控制系统调节过程一般约为30ms,故时间窗长度不宜超过30ms;考虑雷电干扰影响,时间窗的长度不宜小于3ms。综合以上分析,时间窗长度选用5ms。本文用保护安装处5ms 前后暂态高频能量的比值作为保护启动判据,定义启动因子Q 为
式中,N 为5ms 时间窗内的采样个数;IE(k)为整流侧保护安装处检测到的暂态电压 5~7kHz 高频带Hilbert 瞬时能量的幅值;Kset1 为启动整定值,结合系统参数和仿真,选取Kset1=1.05。
2.2 区内、外故障分析与动作判据
直流输电线路故障时,暂态电气量中包含丰富的故障信息,现阶段基于暂态能量的行波保护仅利用行波暂态量幅值信息,没有充分利用暂态量中蕴含的其他故障信息,造成保护存在拒动问题。因此本文基于第1 节理论成果,综合Hilbert能量幅值信息和波形信息,构造直流输电线路保护判据。
结合上述分析与保护装置采样频率的局限,并兼顾数据量,本文选取5~7kHz 暂态高频带作为保护所需电气量展开研究。直流输电线路发生区内、外故障时,保护安装处检测到的暂态高频分量能量波形形状和能量幅值的高低明显不同,如图5 所示。
如图5 所示,直流输电线路区内、外故障时,5~7kHz 暂态高频带Hilbert 能量幅值和波形形状差异明显,可利用该特征构造区内、外故障识别判据。
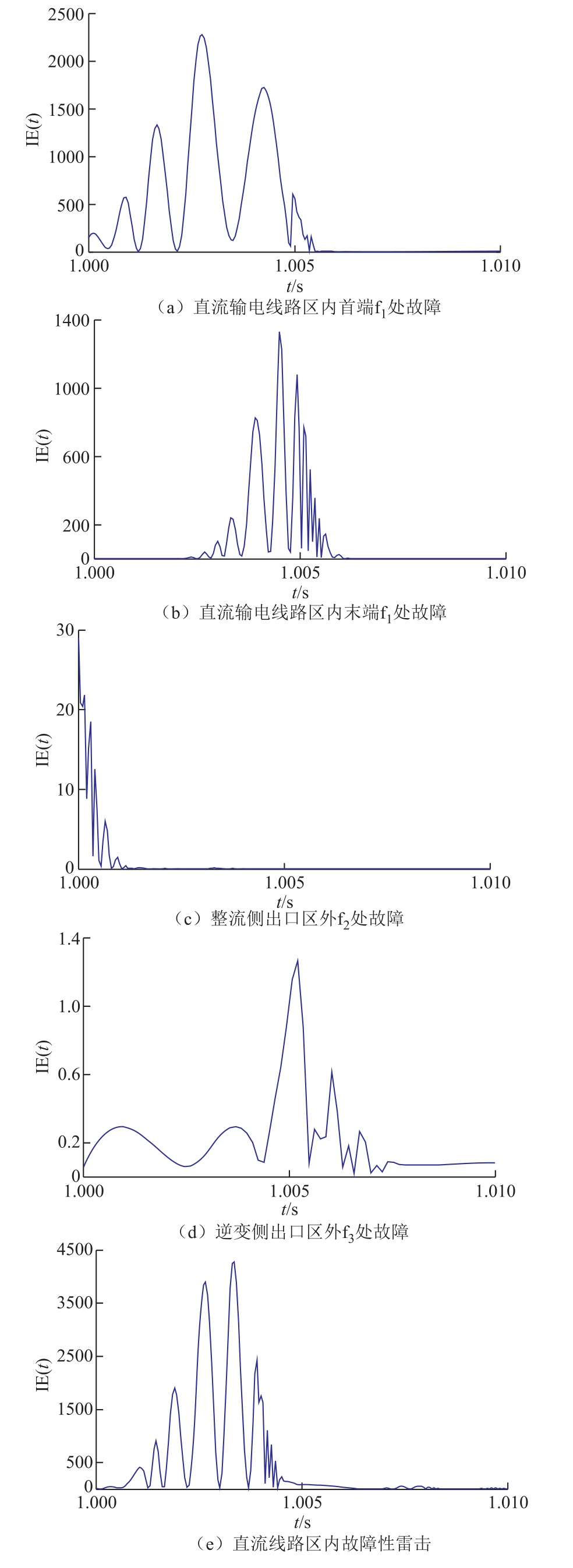
图5 暂态高频段Hilbert 瞬时能量的波形
Fig.5 Transient high-band Hilbert instantaneous energy waveforms
数理统计中,标准差能很好地反映数据总体的标志变动度,表达式为

式中,V 为标准差;N 为样本的数量;xi 为个体;r为样本的平均数。
本文以暂态电压5~7kHz 高频带Hilbert 能量作为判据所需电气量,利用标准差刻画5~7kHz 高频带Hilbert 能量波形的形状和能量幅值的高低,式(23)写为

式中,N 为5ms 时间窗内的采样个数;m 取1、2 表示正、负极,Vbm 为m 极Hilbert 瞬时能量的标准差;IE(k)为整流侧保护安装处检测到的暂态电压5~7kHz 高频带Hilbert 瞬时能量的幅值; 为5ms 时间窗口内暂态电压5~7kHz 高频带Hilbert 瞬时能量幅值的平均值。
为5ms 时间窗口内暂态电压5~7kHz 高频带Hilbert 瞬时能量幅值的平均值。
特高压直流输电系统具有强非线性,其整定值难以通过解析计算求取,目前实际工程中多采用仿真模拟结合经验值的方法确定整定值[17]。本文参照云广特高压直流输电系统及各元件实际参数,仿真模拟图1 所示不同故障情况,计算整流侧保护安装处的标准差,见表1。表中,Vb1、Vb2 分别为正、负极Hilbert 瞬时能量标准差。
对图5 和表1 进行分析可知:
(1)直流输电线路区内故障时,暂态电压Hilbert瞬时能量波形波动较剧烈(单位时间内变化量大),故障点距整流侧越近,暂态电压5~7kHz 高频带衰减越小,高频带Hilbert 能量幅值越大,标准差越大;故障点距整流侧越远,暂态电压5~7kHz 高频段衰减越大,高频段Hilbert 能量幅值越小,标准差越小。
表1 不同故障距离和过渡电阻的标准差特征
Tab.1 Standard deviation characteristics of different fault distances and transition resistances

故障类型 Vb1 Vb2直流输电线路首端区内故障(f1 在0km 处) 8.59 0.757直流输电线路末端区内故障(f1 在1 418km 处) 4.1250.388整流侧出口区外故障 1.8210.5801逆变侧出口区外故障 1.1310.472区内故障性雷击 5.9370.544区内非故障性雷击 17.121.17整流侧交流系统区外三相短路故障 0.4220.325逆变侧交流系统区外三相短路故障 0.2860.313
(2)整流侧出口区外故障时,暂态电压Hilbert瞬时能量波形相对平滑(单位时间内变化量小),物理边界元件对暂态电压高频分量具有衰减作用,5~7kHz 高频带Hilbert 能量幅值较小,标准差小于直流输电线路区内故障。
(3)逆变侧出口区外故障时,暂态电压Hilbert瞬时能量波形相对平滑,暂态电压高频分量经物理边界元件和直流长线路的双重衰减作用到达保护安装处,5~7kHz 高频带Hilbert 能量幅值很小,标准差小于直流输电线路区内故障。
(4)直流输电线路区内发生故障性雷击时,具有较大的高频分量,5~7kHz 高频带Hilbert 能量幅值与直流输电线路区内故障相当,暂态电压Hilbert瞬时能量波形与直流输电线路区内故障相似,标准差与直流输电线路区内故障相似;直流输电线路区内发生非故障性雷击时,5~7kHz 高频带Hilbert 能量幅值很大,暂态电压Hilbert 瞬时能量波形波动较剧烈,标准差很大。
根据以上分析及表1 数据,可构造故障识别判据表达式为
式中,Kset2、Kset3 为识别判据整定值,其值应考虑直流输电线路区内故障和故障性雷击时可能出现的最小、最大标准差,并能排除区外故障和非故障性雷击的干扰。
本文为保证判据的可靠性,适当调整判据整定值的裕度。选取Kset2=2.5,Kset3=10。动作判据满足式(25)时,判定为直流线路区内故障,保护动作;否则判为区外故障,保护不动作。
2.3 故障选极判据
双极直流输电线路之间存在耦合作用,单极故障时,健全极感应到暂态高频分量信号,但健全极感应到的暂态高频能量始终弱于故障极暂态高频能量。健全极Hilbert 能量波形较故障极平缓,因此健全极高频分量的Hilbert 瞬时能量标准差始终小于故障极的标准差,可利用正、负极Hilbert 瞬时能量标准差的差异构造故障选极判据。理想情况下,双极直流输电系统对称运行,当Vb1/Vb2>1 或Vb1/Vb2<1 时,即判定正极或负极故障;当Vb1/Vb2=1 时,则判为双极故障。然而,在工程运行需要时,双极直流输电系统将采用不对称运行方式,如某一极的冷却系统有问题,则需要降低该极能量供给,因此对于直流线路故障选极需要考虑一定的裕度,以保证选极判据具有一定的可靠性[18]。以双极Hilbert 瞬时能量标准差的比值为基础,构成如式(26)所示的故障选极判据。

2.4 保护逻辑
当整流侧保护安装处计算的启动因子 Q 大于启动整定值1.05 时,整流侧保护装置启动。当2.5<Vbm<10 时,判为区内故障;否则判为区外故障。若判为直流线路区内故障,则根据正、负极高频分量Hilbert 瞬时能量标准差的比值选择故障极,最终故障极保护动作。保护逻辑流程如图6 所示。

图6 保护逻辑流程
Fig.6 Protection logic flow chart
3 仿真验证
本文参照文献[10]中云广特高压直流输电系统和各元件实际参数,在PSCAD 中搭建如图1 所示的±800kV 双极直流输电模型提取故障信息,利用Matlab 实现保护算法。直流输电线路全长为1 418km,采用Frequency Dependent(Phase)Model Options 模型。部分相关参数见附录。
故障发生位置为图1 中的f1~f8。提取暂态电压5~7kHz 高频带Hilbert 能量作为保护判据所需电气量。本文选取采样频率为20kHz。
3.1 直流输电线路区内、外故障仿真分析
正极直流输电线路距整流侧600km 处发生非金属性接地故障,故障发生在t=1s 时刻,过渡电阻为200Ω,整流侧保护动作情况如图7 所示。
由图7 可知,正极直流线路区内发生故障后,正极暂态电压5~7kHz 高频能量增大,启动因子Q经0.7ms 延时,在t=1.000 7s 时大于启动整定值1.05,正极启动判据出口;区内、外故障识别判据经2.2ms延时,在t=1.002 2s 时,整流侧计算得到的标准差2.5<Vb1<10,判为直流线路区内故障;故障选极判据经2.2ms 延时,在t=1.002 2s 时,故障选极判据Vb1/Vb2>1.2。负极暂态电压5~7kHz 高频能量增大,但启动因子Q 小于启动整定值1.05,负极启动判据未出口,不进行后续计算。根据正、负极各判据动作情况,进而确定是正极直流输电线路区内故障,正极保护动作。


图7 正极直流线路区内f1 处故障
Fig.7 Fault at f1 in the positive DC line area
正极整流侧出口区外发生非金属性接地故障,故障发生在t=1s 时刻,过渡电阻为200Ω,整流侧保护动作情况如图8 所示。
由图8 可知,正极整流侧出口区外发生故障后,正极暂态电压5~7kHz 高频能量增大,启动因子Q经0.4ms 延时,在t=1.000 4s 时大于启动整定值1.05,正极启动判据出口;在故障发生后,整流侧计算得的标准差Vb1<2.5,判为直流线路区外故障。负极暂态电压5~7kHz 高频能量增大,但启动因子Q 小于启动整定值1.05,负极启动判据未出口,不进行后续计算。根据正、负极各判据动作情况,确定是直流输电线路区外故障,无论选极判据结果如何,保护都不动作。
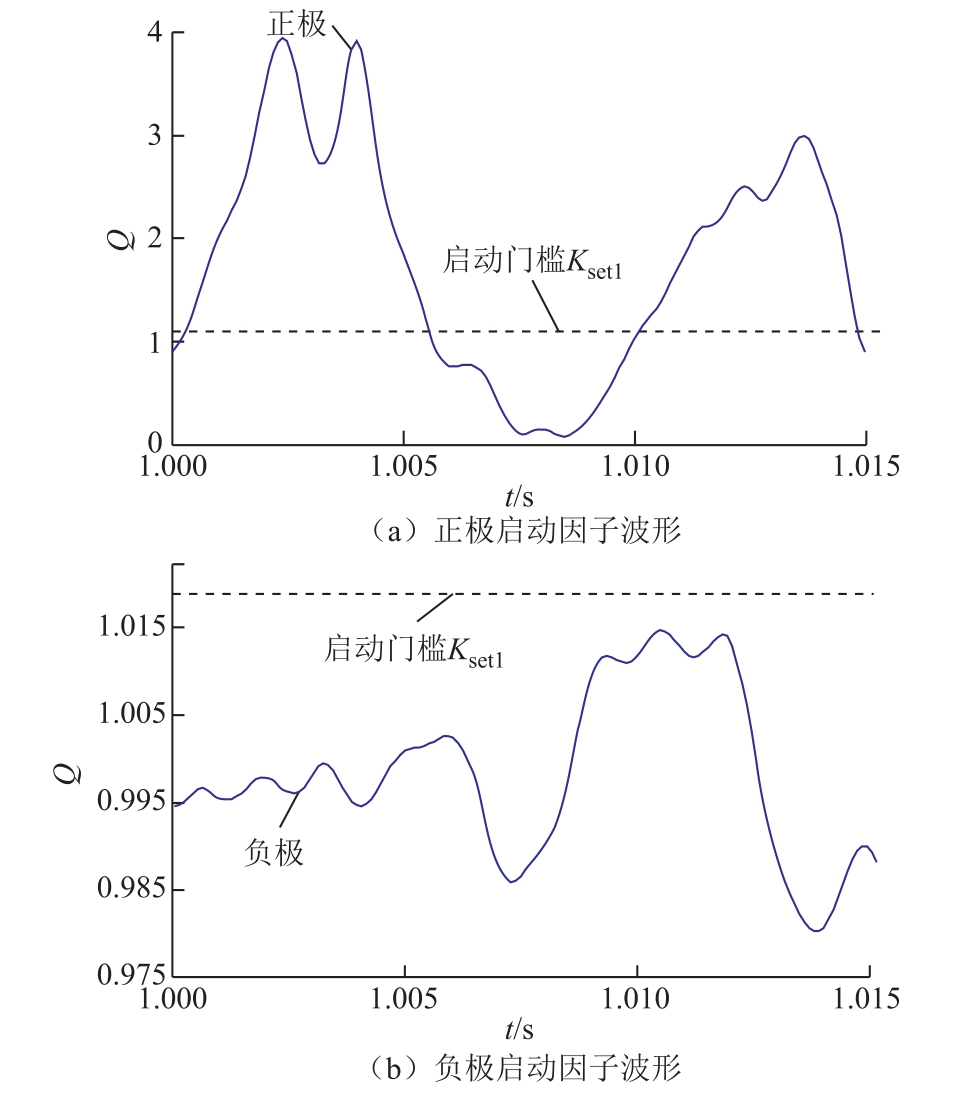
图8 正极整流侧出口区外f2 处故障
Fig.8 Fault at f2 outside the exit section of the positive rectifier side
正极逆变侧出口区外发生非金属性接地故障,故障发生在t=1s 时刻,过渡电阻为200Ω,整流侧保护动作情况如图9 所示。
由图9 可知,正极逆变侧出口区外发生故障后,正极暂态电压5~7kHz 高频能量增大,启动因子Q经3.5ms 延时,在t=1.003 5s 时大于启动整定值1.05,正极启动判据出口;在故障发生后,整流侧计算得的标准差Vb1<2.5,判为直流输电线路区外故障。负极暂态电压5~7kHz 高频能量增大,但启动因子Q 小于启动整定值1.05,负极启动判据未出口,不进行后续计算。根据正、负极各判据动作情况,确定是直流输电线路区外故障,无论选极判据结果如何,保护都不动作。


图9 正极逆变侧出口区外f3 处故障
Fig.9 Fault at the f3 outside the exit side of the positive inverter side
3.2 保护性能验证
为进一步验证保护方案的可靠性和灵敏性,将直流输电线路长度增长至2 000km,区内、外故障如图1 所示,分别考虑:不同故障距离经不同过渡电阻接地的情况、f1 处故障性雷击和f1 处非故障性雷击。仿真结果见表2。直流输电线路故障时电弧稳定,无需考虑大过渡电阻可能性[19],因此过渡电阻选取0Ω、100Ω 和300Ω 三种情况。若某一极线路启动判据未出口,则不计算标准差Vbm;当判为直流输电线路区外故障时,则不计算Vb1/Vb2。
表2 保护性能验证
Tab.2 Protection performance verification
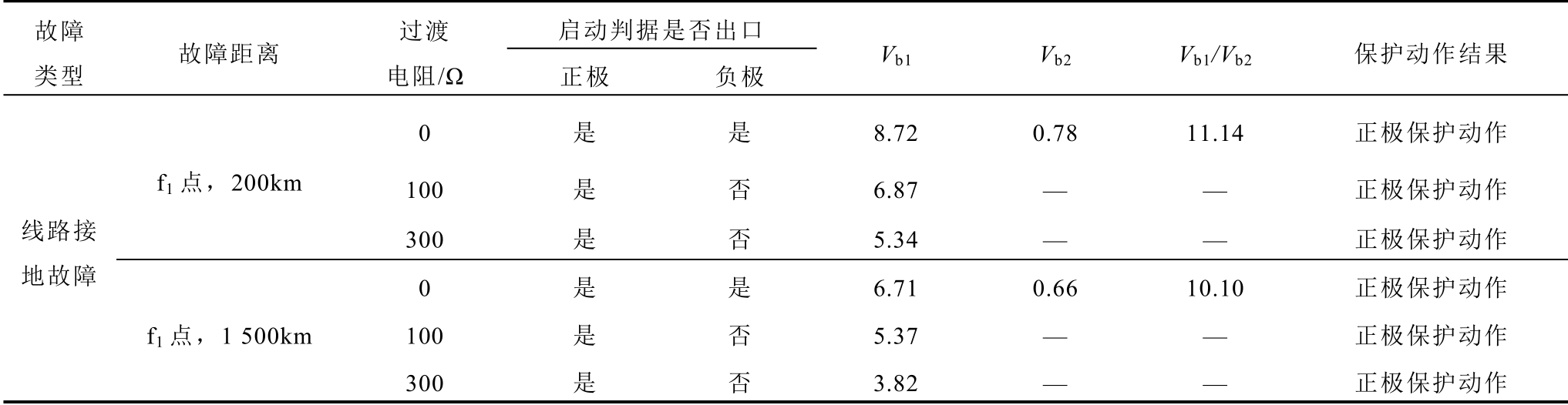
故障类型 故障距离 过渡电阻/Ω启动判据是否出口 Vb1 Vb2 Vb1/Vb2 保护动作结果正极 负极0 是 是 8.72 0.78 11.14 正极保护动作线路接地故障f1 点,200km 100 是 否 6.87 — — 正极保护动作300 是 否 5.34 — — 正极保护动作0 是 是 6.71 0.66 10.10 正极保护动作f1 点,1 500km 100 是 否 5.37 — — 正极保护动作300 是 否 3.82 — — 正极保护动作
(续)

故障类型 故障距离 过渡电阻/Ω启动判据是否出口 Vb1 Vb2 Vb1/Vb2 保护动作结果正极 负极0 是 是 5.41 0.61 8.84 正极保护动作f1 点,1 800km 100 是 是 4.49 0.36 12.43 正极保护动作300 是 否 2.82 — — 正极保护动作0 是 否 2.09 — — 保护不动作f2 点100 是 否 1.02 — — 保护不动作300 是 否 0.58 — — 保护不动作0 是 否 1.26 — — 保护不动作f3 点100 是 是 0.85 0.16 — 保护不动作300 是 否 0.55 — — 保护不动作0 是 是 0.43 0.36 — 保护不动作f4 点100 否 否 — — — 保护不动作300 否 否 — — — 保护不动作0 是 是 0.29 0.33 — 保护不动作f5 点100 否 否 — — — 保护不动作300 否 否 — — — 保护不动作0 否 是 — 8.72 — 负极保护动作f6 点,200km 100 是 是 0.46 6.83 0.07 负极保护动作300 是 是 0.36 5.37 0.07 负极保护动作0 否 是 — 6.63 — 负极保护动作f6 点,1 500km 100 是 是 0.41 5.33 0.08 负极保护动作300 是 是 0.28 3.83 0.07 负极保护动作0 是 是 0.62 5.39 0.12 负极保护动作f6 点,1 800km 100 否 是 — 4.40 — 负极保护动作300 是 是 0.39 2.89 0.13 负极保护动作0 否 是 — 2.07 — 保护不动作f7 点100 否 是 — 1.02 — 保护不动作300 否 是 — 0.59 — 保护不动作0 否 是 — 1.25 — 保护不动作f8 点100 是 是 0.15 0.85 — 保护不动作300 否 是 — 0.54 — 保护不动作故障性雷击非故障性雷击f1 点,200km — 是 是 8.36 0.54 15.35 正极保护动作f1 点,1 500km — 是 是 5.69 0.73 7.82 正极保护动作f1 点,1 800km — 是 是 6.53 0.51 12.90 正极保护动作f1 点,200km — 是 是 23.82 1.58 — 保护不动作f1 点,1 500km — 是 是 16.05 1.10 — 保护不动作f1 点,1 800km — 是 是 19.61 1.26 — 保护不动作
表2 中,“—”表示相应的启动判据未出口,而未进行后续计算。由表2 可知,在直流输电线路区内接地故障和区内故障性雷击情况下,保护能快速、可靠动作;在直流输电线路区外接地故障和非故障性雷击情况下,保护可靠不动作。本文所提保护方案不受故障距离的影响,对直流输电线路长度敏感性低,耐过渡电阻能力和抗雷击干扰能力强。
3.3 启动过程的影响
直流输电系统在启动及功率调整的过程中,可能会使启动判据误动作,但在启动和功率调整过程中,直流输电线路没有故障,即直流输电线路两端保护装置处检测不到故障行波,区内、外故障识别判据小于故障判别整定值。
正极直流输电线路距整流侧600km 处发生非金属性接地故障,过渡电阻为 10Ω,故障重启时间t=1.05s,整流侧保护动作情况如图10 所示。

图10 正极直流线路区内f1 处故障再启动
Fig.10 Fault restart at f1 in the positive DC line area
由图10 可知,故障重启过程中,启动因子Q 在启动整定值附近上下波动,但区内外故障识别判据Vb1 始终小于2.5,判为直流线路区外故障,保护未出口。负极启动因子Q 小于启动整定值1.05,负极启动判据未出口,不进行后续计算。根据正、负极各判据动作情况可知,直流输电系统在启动及负荷调整的过程中,启动判据可能会出口,但Vb1 和Vb2明显低于故障判别门槛值,保护可靠不动作。
3.4 直流滤波器组投退的影响
正极直流线路区内f1 处故障如图11 所示,在直流输电线路区内故障时,当线路两端各投入一组或无直流滤波器投入时,区内、外故障识别判据均在3ms 内满足整定值,即整流侧计算得的标准差2.5<Vb1<10,判为直流线路区内故障。

图11 正极直流线路区内f1 处故障
Fig.11 Fault at f1 in the positive DC line area
正极整流侧出口区外f2 处故障如图12 所示,在整流侧出口区外故障时,当线路两端各投入一组或无直流滤波器投入时,区内、外故障识别判据均不满足整定值,即整流侧计算得到的标准差Vb1<2.5,判为直流线路区外故障。

图12 正极整流侧出口区外f2 处故障
Fig.12 Fault at f2 outside the exit section of the positive rectifier side
综上分析可知,在直流滤波器组退出运行的情况下,该保护方法仍然有效。
4 结论
本文在分析特高压直流输电线路两端物理边界和直流输电线路特性的基础上,兼顾特高压直流输电线路保护的适应性,提出基于Hilbert 能量幅值信息和波形信息的特高压直流输电线路单端保护方法。该方法利用整流侧计算得到的暂态电压5~7kHz高频带Hilbert 能量标准差的特征识别直流线路区内、外故障,进一步利用正、负极标准差之比实现故障选极。经理论分析和仿真验证,该保护方法具有以下特点:
1)充分利用了暂态量中蕴含的幅值信息和波形信息,仅利用单一判据便可实现直流输电线路区内、外故障识别,同时无需考虑双端信息通信交互问题。
2)在直流输电线路区内接地故障和故障性雷击情况下,保护可靠动作;在直流输电线路区外故障和非故障性雷击情况下,保护可靠不动作,具有绝对选择性。另外,该保护受直流输电线路长度变化影响小,耐过渡电阻能力和抗雷击干扰能力强。
3)采用HHT 算法和不涉及叠加原理的暂态量,使该保护的适应性得到提高。
实际工程中,本文所提保护方案的整定值需仿真模拟并结合经验值确定,保护可靠性受到一定影响,因此保护整定值的确定是后续研究的重点。
附 录
物理边界参数:平波电抗器L0=0.15H;直流滤波器C1=1.2μF,L1=14.496mH,C2=3.361μF,L2=13.84mH,C3=4.355μF,L3=2.747mH。
直流输电线路参数:直流输电线路全长为1 418km,导线电阻R=0.046 33Ω/km,每极自电感L=0.001 81H/km,极间互电感M=0.000 99H/km,每极导体单位长度对地电容 C0=9.99×10-9F/km,每单位长度两极导体间的电容Cm=2.11×10-9F/km。
[1] 滕予非, 李小鹏, 林圣, 等. 特高压直流系统接地极线路阻抗监视系统适应性研究[J]. 电工技术学报, 2019, 34(19) : 4154-4161.
Teng Yufei, Li Xiaopeng, Lin Sheng, et al.Adaptability analysis of fault supervision systemfor long electrode line of UHVDC[J]. Transactions of China Electrotechnical Society, 2019, 34(19) : 4154-4161.
[2] 陈玉, 文明浩, 王祯, 等. 基于低频电气量的超高压交流线路出口故障快速保护[J]. 电工技术学报,2020, 35 (11): 2415-2426.
Chen Yu, Wen Minghao, Wang Yan, et al. A high speed protection scheme for outgoing line fault of HVAC transmission lines based on low frequency components[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2415-2426.
[3] 贾科, 赵其娟, 冯涛, 等. 柔性直流配电系统高频突变量距离保护[J]. 电工技术学报, 2020, 35(2): 383-394.
Jia Ke, Zhao Qijuan, Feng Tao, et al. High-frequency fault component distance protection for flexible DC distribution system[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 383-394.
[4] 束洪春, 刘可真, 朱盛强, 等. ±800kV 特高压直流输电线路单端电气量暂态保护[J]. 中国电机工程学报, 2010, 30(31): 108-117.
Shu Hongchun, Liu Kezhen, Zhu Shengqiang, et al.±800kV UHVDC transmission line protection based on single end electrical transient signal[J].Proceedings of the CSEE, 2010, 30(31): 108-117.
[5] 李振强, 鲁改凤, 吕艳萍. 基于小波变换的高压直流输电线路暂态电压行波保护[J]. 电力系统保护与控制, 2010, 38(13): 40-45.
Li Zhenqiang, Lu Jianfeng, Lü Yanping. A novel scheme of HVDC transmission line voltage traveling wave protection based on wavelet transform[J]. Power System Protection and Control, 2010, 38(13): 40-45.
[6] 齐国强, 王增平. 基于Hilbert-Huang 变换的HVDC突变量方向纵联保护方法[J]. 电力系统保护与控制, 2017, 45(20): 92-99.
Qi Guoqiang, Wang Zengping. Directional pilot protection method of fault component for HVDC transmission lines based on Hilbert-Huang transform[J]. Power System Protection and Control,2017, 45(20): 92-99.
[7] 高淑萍, 索南加乐, 宋国兵, 等. 利用电流突变特性的高压直流输电线路纵联保护新原理[J]. 电力系统自动化, 2011, 35(5): 52-56.
Gao Shuping, Sunan Jiale, Song Guobing, et al.Design and simulation of an improved control strategy for variable-speed pitch controlled wind turbine driven generator system[J]. Automation of Electric Power Systems, 2011, 35(5): 52-56.
[8] 邢鲁华, 陈青, 付兆远, 等. 基于电压和电流突变量的高压直流输电线路保护原理[J]. 电力系统自动化, 2012, 36(9): 61-66.
Xing Luhua, Chen Qing, Fu Zhaoyuan, et al.Protection principle for HVDC transmission lines based on fault component of voltage and current[J].Automation of Electric Power Systems, 2012, 36(9):61-66.
[9] 李振兴, 谭洪, 叶诗韵, 等. 应用ΔI 极性与信号处理的UHVDC 输电线路保护新方案[J]. 电力系统保护与控制, 2018, 46(15): 68-75.
Li Zhenxing, Tan Hong, Ye Shiyun, et al. A new scheme for UHVDC transmission line protection using ΔI polarity and signal processing[J]. Power System Protection and Control, 2018, 46(15): 68-75.
[10] 陈仕龙, 张杰, 毕贵红, 等. 一种基于高频量衰减特性的特高压直流输电线路故障测距方法[J]. 电力系统保护与控制, 2014, 42(10): 77-83.
Chen Shilong, Zhang Jie, Bi Guihong, et al. A fault location method based on high frequency attenuation characteristic of UHVDC transmission line[J]. Power System Protection and Control, 2014, 42(10): 77-83.
[11] 赵成勇, 赵强. HVDC 附近继电保护装置中工频故障分量元件的适用性分析[J]. 电网技术, 2010,34(3): 188-192.
Zhao Chengyong, Zhao Qiang. Analysis on applicability of fundamental frequency fault component element of protective relayings near to HVDC transmission line[J]. Power System Technology,2010, 34(3): 188-192.
[12] 段建东, 刘静, 陆海龙, 等. 基于行波瞬时频率的高压直流输电线路故障测距方法[J]. 中国电机工程学报, 2016, 36(7): 1842-1848.
Duan Jiandong, Liu Jing, Lu Hailong, et al. Fault location method based on traveling-wave instantaneous frequency for HVDC transmission lines[J].Proceedings of the CSEE, 2016, 36(7): 1842-1848.
[13] 娄二军. 基于PSCAD/EMTDC 的特高压直流输电线路保护的研究[D]. 广州: 华南理工大学, 2013.
[14] 王聪博, 贾科, 赵其娟, 等. 基于故障全电流相关性检验的柔性直流配电线路纵联保护[J]. 电工技术学报, 2020, 35(8): 1764-1775.
Wang Congbo, Jia Ke, Zhao Qijuan, et al. Pilot protection for flexible-DC distribution line based on correlation test of DC current[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1764-1775.
[15] 许小雪, 刘建锋, 江玉蓉. 基于多频带能量的高压直流输电线路单端暂态电流保护[J]. 电力系统保护与控制, 2016, 44(22): 32-39.
Xu Xiaoxue, Liu Jianfeng, Jiang Yurong. HVDC transmission line protection based on single-ended transient current using multiband energy[J]. Power System Protection and Control, 2016, 44(22): 32-39.
[16] 杨亚宇, 邰能灵, 刘剑, 等. 利用边界能量的高压直流线路纵联保护方案[J]. 中国电机工程学报,2015, 35(22): 5757-5767.
Yang Yayu, Tai Ningling, Liu Jian, et al. A pilot protection scheme for HVDC transmission lines based on boundary energy[J]. Proceedings of the CSEE,2015, 35(22): 5757-5767.
[17] 高本锋, 张学伟, 刘辛晔, 等. 高压直流输电保护定值整定流程的研究[J]. 电工技术学报, 2015,30(12): 400-407.
Gao Benfeng, Zhang Xuewei, Liu Xinyi, et al.Research of HVDC protection value setting process[J].Transactions of China Electrotechnical Society, 2015,30(12): 400-407.
[18] 戴志辉, 刘宁宁, 何永兴, 等. 基于直流滤波环节暂态能量比的高压直流线路纵联保护[J]. 电工技术学报, 2020, 35(9): 1985-1998.
Dai Zhihui, Liu Ningning, He Yongxing, et al. A pilot protection for HVDC transmission lines based on the ratio of DC filter link transient energy[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1985-1998.
[19] 王永进, 樊艳芳. 基于反行波与信号处理的特高压直流输电线路纵联保护方法[J]. 电力自动化设备,2020, 40(3): 114-121.
Wang Yongjin, Fan Yanfang. Longitudinal protection method based on reverse traveling wave and signal processing for UHVDC power transmission line[J].Electric Power Automation Equipment, 2020, 40(3):114-121.