0 引言
随着全球面临能源枯竭危机,新能源发展迫在眉睫,以光伏为代表的新型清洁能源正逐步得到发展。然而,光伏发电因其不确定性、随机性、波动性的特点,在大规模光伏并网中严重影响电网的正常运转,给电网的电能品质和稳定性带来严峻的挑战[1-2]。利用储能技术充/放电能够灵活调节功率不平衡的特点,平滑光伏出力波动,是有效降低光伏功率波动对电网的冲击、提高电网稳定性的重要手段[3-4],运用混合储能系统(Hybrid Energy Storage System, HESS)平滑光伏出力波动是众多研究的热点之一[5-6]。
在混合储能有功功率分配方面,文献[7-8]基于小波包分解提出了混合储能功率分配策略,通过小波包分解将功率信号分解为高、中、低频三部分,并进行功率重构得到最佳分配效果;文献[9]提出利用经验模态分解(Empirical Mode Decomposition,EMD)实现有功功率的分配,但EMD 分解过程中噪声较大,容易产生模态混叠现象;文献[10-11]提出了集合经验模态分解(Ensemble EMD, EEMD)实现有功功率的分解,借助时空滤波器得到高频和低频功率,但由于光伏功率信号具有不稳定性和非线性特征,时空滤波器滤波阶数不能准确确定,且EEMD 分解噪声大,使得功率信号提取不准确;文献[12]提出一种分层模型预测控制动态有功功率分配策略,得到了较好的分配效果。在光伏混合储能平滑出力波动控制策略方面,文献[13]考虑多种约束条件,通过确定一阶低通滤波截止频率,得到储能系统的充/放电补偿功率,实现了较好的平滑出力波动效果;文献[14]提出一种光伏最大功率跟踪工作点控制和混合储能系统协调平抑光伏并网功率波动策略;文献[15]利用模型预测控制提高光伏出力预测精度来获得最佳储能参考功率,降低了出力波动;文献[16-17]提出利用模糊控制算法平滑风电出力波动,得到了较好的平滑效果。但上述文献在平滑出力波动过程中只考虑了以波动动率为整体目标的单一评价指标,在降低波动率的同时,并未对有功功率波动曲线局部的光滑度作进一步分析。
针对上述问题,本文提出一种考虑光伏双评价指标的混合储能平滑出力波动控制策略。通过将集合经验模态分解过程中的异常信号再进行EMD 分解,去除伪分量得到最终的模态分量;基于灰色关联度对分解分量进行功率重构,得到超级电容和蓄电池各自的平滑出力波动指令;根据不同时间尺度以波动率和光滑度为平滑出力波动目标的双评价指标,以滑动平均滤波为充/放电功率指令,以蓄电池和超级电容器组成的混合储能电池组进行5min 时间尺度的平滑出力波动和以超级电容器组成的单一电池组进行1min 时间尺度的平顺光滑度,平顺光滑度跟随平滑出力波动,进行光伏平滑出力波动的协调控制;通过算例对EMD、EEMD、互补集合经验模态分解(Complementary EEMD, CEEMD)、自适应加噪的经验模态分解(Complete EEMD with Adaptive Noise, CEEMDAN)多种经验模态分解的充/放电功率进行对比及不同评价指标波动效果验证,结果表明所提策略有效。
1 考虑光伏双评价指标的混合储能平滑出力波动控制策略总体思路
考虑光伏双评价指标的混合储能平滑出力波动控制策略总体框图如图1 所示。由图1 可知,本文将总体思路分为四部分:第一部分根据光伏有功功率波动特性,根据不同时间尺度建立以波动率和光滑度为平滑出力波动目标的双评价指标;第二部分进行光伏混合储能的有功功率分配,主要包括基于MEEMD 有功功率信号分解和灰色关联度有功功率重构两个模块;第三部分对光伏混合储能的充/放电控制策略作进一步阐述,包括以滑动平均滤波得到充/放电目标参考功率,以蓄电池和超级电容器组成的混合储能电池组进行5min 时间尺度的出力波动的平滑,以超级电容器组成的单一电池组进行1min时间尺度的平顺光滑度的充/放电控制策略;第四部分为算例仿真部分,主要对比分析了MEEMD 与多种功率分解方法(EMD、EEMD、CEEMD、CEEMDAN、VMD、小波包)在充/放电频次和最大充/放电功率方面的优势,以及双重评价指标与单一评价指标相比在平滑出力波动效果的优势。

图1 考虑光伏双评价指标的混合储能平滑出力波动控制策略总体框图
Fig.1 Overall block diagram of a hybrid energy storage smoothing output fluctuation control strategy considering photovoltaic dual evaluation indicators
2 构建不同时间尺度平滑出力波动评价指标
本文以光伏有功功率波动率和光滑度为共同研究对象,组成5min 时间尺度以波动率为评价指标和1min 时间尺度以光滑度为评价指标的目标策略,根据时间尺度平滑不同储能系统的出力波动。国家电网光伏并网标准规定[18],光伏安全并网,光伏有功功率变化1 min 不超出装机容量的±10%,而更加平滑的功率曲线能够提高光伏并网稳定性。
2.1 建立5min 时间尺度平滑出力波动评价指标
光伏有功功率波动率的定义为:在一段时间T 内,光伏有功功率最大值减去最小值后与光伏电站额定功率的比值,光伏有功功率波动率表达式为[19-20]

其中

式中,r p v为光伏有功功率波动率; f pv(·)为计算光伏有功功率波动率的函数; Ppv-max 、 Ppv-min 分别为T 时段内光伏有功功率的最大值和最小值; Ppv-rated为光伏电站额定功率; Pp v(t ) 为t 时刻光伏有功功率; Δt为采样时间。
2.2 建立1min 时间尺度平顺光滑度评价指标
反映光伏有功功率光滑度的标准是噪声的大小,噪声越小,曲线光滑度越好;反之噪声越大,光滑度越差。本文采用多尺度排列熵方法对光伏有功功率的噪声大小进行分析,具体步骤如下。
(1)首先对光伏有功功率时间序列进行粗粒化,即
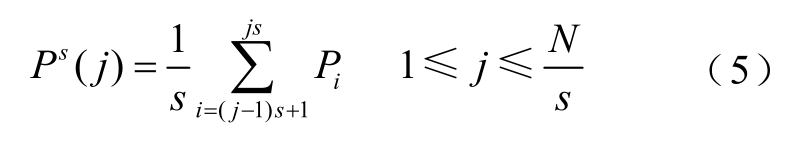
式中, P s( j) 为光伏有功功率多尺度时间序列;s 为尺度因子; iP 为长度为N 的光伏有功功率时间序列;![]()
(2)对光伏有功功率多尺度时间序列进行相空间重构,即

式中,P s为光伏有功功率多尺度时间序列重构矩阵;b 为嵌入维数;τ 为时间延迟;![]()
(3)对重构矩阵sP 的某一行时间重构序列 进行升序排列,得到
进行升序排列,得到
(4)令![]() 为该行各元素的初始位置,矩阵中的任一行均有 m! 种排列可能,计算每一行对应其出现的次数 hl 和概率
为该行各元素的初始位置,矩阵中的任一行均有 m! 种排列可能,计算每一行对应其出现的次数 hl 和概率![]()
(5)最终得到光伏有功功率的多尺度时间序列下的排列熵为
式中, 为光伏有功功率的多尺度排列熵值。
为光伏有功功率的多尺度排列熵值。
3 基于MEEMD 混合储能光伏有功功率分配
3.1 基于MEEMD 混合储能光伏有功功率分解
改进集合经验模态分解(MEEMD)能够有效解决经验模态分解(EMD)过程中产生的模态混叠现象和集合经验模态分解(EEMD)过程中计算量大、存在较多伪分量的问题[21]。光伏有功功率作为一种非线性、非平稳性的信号,采用MEEMD 进行分解,具体分解步骤如下。
(1)向光伏有功功率 Pp v(t )中加入两组均值为0的正、负白噪声 Pm ( t )和-Pm ( t),并进行EEMD 分解,得到第一阶IMF 分量,即
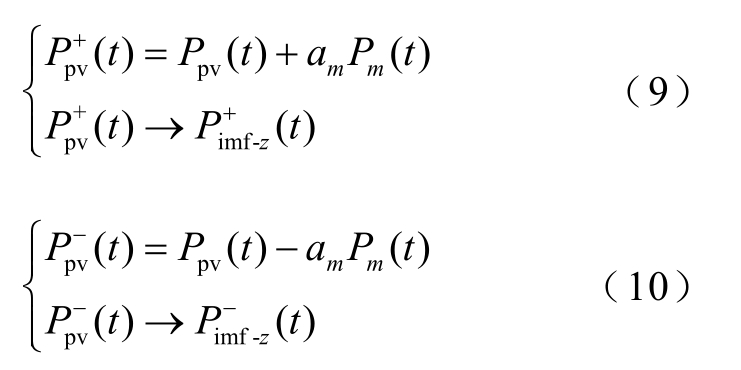
式中,P m ( t )为光伏有功功率添加的白噪声,m=1,2,3,…,Ne, N e为添加的白噪声的对数;a m为的白噪声幅值; Pimf- z(t )为第z 个IMF 分量。
(2)将得到的分量进行集成平均后,再进行多尺度排列熵分析,将异常信号定义为预分解IMF 分量,对预分解IMF 分量进行EMD 分解,得到

式中,P imf-x1( t )为异常IMF 分量 Pimf- z(t )经EMD 分解后的第一个IMF 分量; Pimf-g1(t )为剩余IMF 分量的叠加; Pimf-x k ( t )为 Pimf- z(t )经 EMD 分解后的第k 个IMF 分量; Pimf-g k(t )为相应剩余容量的叠加。
(3)分解完成后,得到最终的MEEMD 分解结果,即
式中, Pimf-u (t )为经MEEMD 分解后的各阶IMF 分量;t=1,2,3, …, u; Pr ( t )为余波分量。
3.2 基于灰色关联度分析光伏混合储能有功功率重构
由于光伏出力具有非线性和不确定的特征,采用时空滤波器构造的滤波阶次难以准确确定,可能存在功率混叠的情况,不能精确地提取光伏功率经经验模态分解后各分量的信号特征,而灰色关联度分析的优势是结构简单和计算量小,能够适用于光伏有功功率等非线性信号。光伏有功功率经MEEMD 分解去除伪分量后得到最终的各阶功率信号IMF 分量和余波分量,利用灰色关联分析对各阶功率信号IMF 分量和余波分量进行重构,得到高频和低频两部分,其中高频功率波动分量由超级电容平滑出力,低频功率波动分量由蓄电池平滑出力。考虑各分量之间的波动频率,采用灰色关联度分析各阶分量的关联度值,将关联度值相近的分量重构为高频组和低频组,灰色关联度分析步骤如下。
(1)确定各阶分量的目标序列和比较序列,计算目标序列和比较序列之间的灰色关联度为

式中,ξ P ( x)为关联系数;P mb- e ( x )为目标序列;P b j-f ( x)为比较序列;ρ 为灰色分辨系数,一般取值为0.5;![]()
(2)将求得的关联系数值代入关联度公式得到各比较序列与目标序列的关联度,即
式中, rhs 为关联度; ω( k)为权重。
(3)根据各序列的关联度值对IMF 各分量和余波分量进行重构,将比较序列与目标序列关联度相近的分为高频和低频分量,得到最终的高频和低频平滑出力功率指令,高频平滑出力功率指令为
式中, Ph igh(t ) 为高频平滑出力功率指令。
低频平滑出力功率指令为
式中, Plo w(t ) 为低频平滑出力功率指令。
光伏混合储能功率分配流程如图2 所示。
4 制定光伏双评价指标的混合储能控制策略
本文选用以蓄电池为代表的能量型储能和以超级电容为代表的功率型储能作为混合主储能[22-23],提出不同时间尺度的平滑出力波动策略,用蓄电池和超级电容器组成的混合储能电池组以5min 时间尺度对出力波动进行平滑,用超级电容器组成的单一电池组以1min 时间尺度进行光滑度平顺处理,平顺光滑度跟随平滑出力波动,得到不同时间尺度的储能系统优先级平滑出力波动策略。
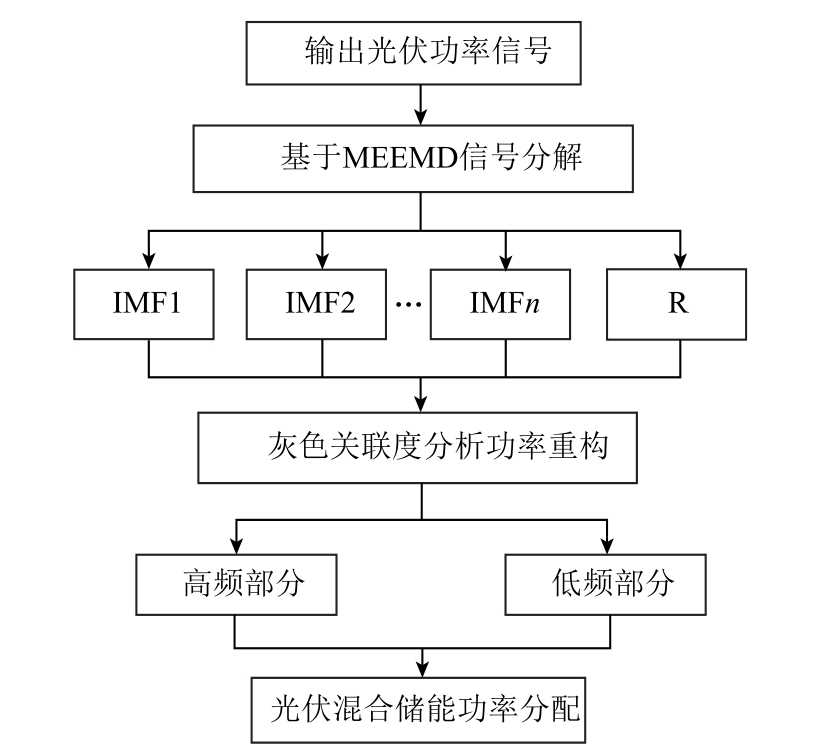
图2 光伏混合储能有功功率分配流程
Fig.2 Flow chart of active power distribution of photovoltaichybrid energy storage
4.1 选取混合储能充/放电目标参考功率
滑动平均滤波法(Moving Average Filter, MAF)是基于数据窗概念,在连续的采样数据队列中将每次采样得到的新数据放入队尾,并去掉原来队首的数据,将队列中的N 个数据进行算数平均,实现采样数据曲线的平滑,滑动平均滤波计算公式为
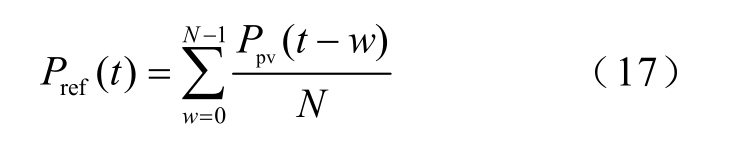
式中, Pr ef(t ) 为t 时刻滑动平均滤波目标参考功率;N 为数据窗口长度;w=0,1,2,…,N − 1。
超级电容的充/放电功率指令为
式中, Ps c(t ) 为t 时刻超级电容充/放电功率指令。Ps c( t ) 0> ,超级电容充电;P s c( t ) 0< ,超级电容放电。
蓄电池的充/放电功率指令为
式中, Pb ( t) 为t 时刻超级电容充/放电功率指令。Pb ( t ) 0> ,蓄电池充电; Pb ( t ) 0<,蓄电池放电。
4.2 制定不同时间尺度混合储能优先级控制策略
将光伏有功功率按时间单位分为5min 和1min,5min 可以反映光伏输出功率整体的波动趋势,1min可以反映光伏输出功率的光滑度。本文采用5min 以波动率为评价指标,使用超级电容和蓄电池为代表的混合储能电池组进行充/放电控制策略,采用1min 以光滑度为评价指标,使用超级电容器为代表的单一储能进行充/放电控制策略,实现不同时间尺度的储能系统优先级充/放电控制策略,控制策略具体如下。
(1)以光伏并网标准规定为目标,判断光伏有功功率是否满足并网标准,即

式中, Pc h(t ) 为1min 光伏有功功率变化值; Pm ax( t)为1min 最大有功功率值; Pm in(t ) 为1min 最小有功功率值;Cpv 为光伏总装机容量。
(2)光伏有功功率满足光伏并网标准内,蓄电池储能电池组处于停机状态,超级电容电池组进入工作状态,进行1min 时间尺度的平顺光滑度处理,表达式为

式中, Po ( t) 为光伏有功功率光滑度曲线;L 为光伏输出并网功率时间总长度。若![]() 超级电容充电;
超级电容充电;![]() ,超级电容放电。
,超级电容放电。
(3)光伏有功功率超出并网标准规定的上限值,进入平抑波动区域,蓄电池和超级电容电池组进入工作状态,以5min 时间尺度进行出力波动平滑处理,平顺光滑度跟随平滑出力波动,出力波动平滑处理后以1min 时间尺度进行光滑度平顺处理。主储能表达式为
式中,Ph ess( t) 为混合储能系统充放电功率。![]() ,混合储能充电;
,混合储能充电;![]() ,混合储能放电。
,混合储能放电。
(4)为防止储能系统在工作过程中可能存在过充过放的状态,需要对超级电容和蓄电池的SOC 进行约束,约束条件为

式中,SOC sc ( t )、SOC b (t )分别为超级电容和蓄电池在t 时刻的荷电状态;SOCsc-min( t )、SOCb-min (t )分别为超级电容和蓄电池在t 时刻的荷电状态最小允许范围;SOCsc-max ( t )、SOCb-max( t )分别为超级电容和蓄电池在t 时刻的荷电状态最大允许范围。
混合储能优先级充/放电控制策略流程如图 3所示。

图3 光伏混合储能优先级充/放电控制策略
Fig.3 Photovoltaic hybrid energy storage charge/discharge control strategy
5 算例分析
为验证本文所提方法的优势,通过与多种经验模态分解方法在充/放电功率频次和以波动率为单一评价指标的传统混合储能平滑出力波动效果进行比较,并以新疆某光伏电站某典型日数据为例,光伏有功功率数据如图4 所示,装机容量为20MW,采样间隔为5min,基于Matlab 进行算例分析。由超级电容和蓄电池组成的混合储能为主储能系统进行min级的出力波动平滑处理,额定功率/额定容量为2MW/20MW·h,由超级电容器为辅助储能进行s 级的光滑度平顺处理,额定功率/额定容量为0.4MW/4MW·h。
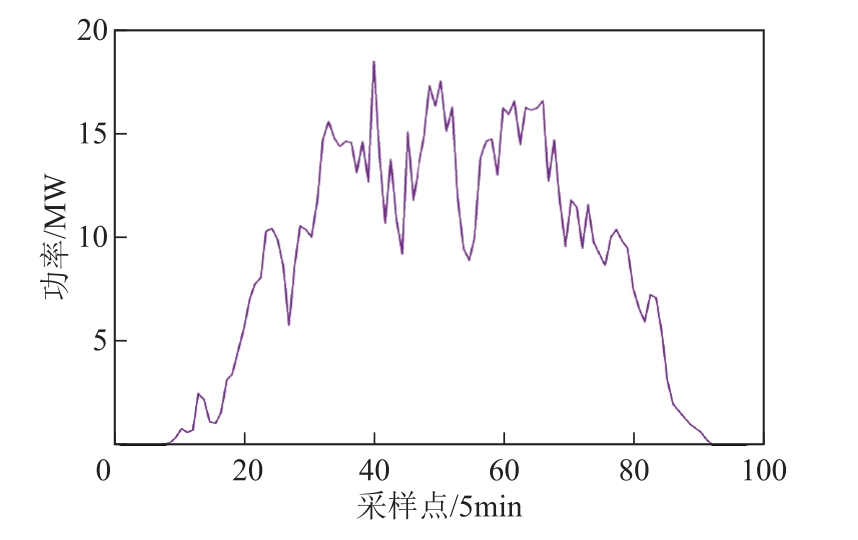
图4 光伏有功功率数据
Fig.4 Photovoltaic active power data
5.1 光伏混合储能有功功率分配分析
光伏有功功率作为一种非线性、非平稳性的信号,在信号分解过程中容易产生模态混叠现象并存在计算量大的问题,因此本文采用改进集合经验模态分解的方法(MEEMD)对光伏有功功率进行分解,光伏有功功率进行MEEMD 分解后的结果如图5所示。

图5 光伏有功功率MEEMD 分解
Fig.5 MEEMD decomposition of PV active power
由图5 可知,对光伏有功功率进行MEEMD分解后,共得到4 个IMF 分量和1 个余波分量R,由高频到低频分解较为清晰,而且在分解过程中分解较为准确,不会产生模态混叠现象,计算速度也有所提高。对MEEMD 分解后的各分量基于灰色关联度进行功率重构,功率重构结果如图 6所示。

图6 各分量灰色关联度分析
Fig.6 Grey relational degree of each component
由图6 可知,比较序列中关联度相近的分量有IMF1 和IMF2,关联度系数都大于0.2,另一组关联度相近的有IMF3、IMF4 和R,关联度系数都小于0.1。因此组成的高频分量为IMF1+IMF2,低频分量为IMF3+IMF4+R。
5.2 5min 时间尺度平滑出力波动分析
5.2.1 5min 时间尺度充/放电功率分析
基于MEEMD 对光伏有功功率重构后的高频部分和低频部分进行滑动平均滤波,分别得到超级电容平抑高频和蓄电池平抑低频的充/放电目标参考功率指令,如图7 所示。一般地,N 越大,曲线越平滑,出力波动的平滑效果越好,但相应的储能容量也会增加。以光伏有功功率变化1 min 时间尺度不超出装机容量的 ±10% 为目标,进行N 的选取。数据窗口的选取见表1,N 为10 时,光伏最大有功功率变化为1.97MW,符合并网标准。
5.2.2 多种经验模态分解充/放电功率对比
为体现基于MEEMD 信号分解的优势,本文通过多种经验模态分解方法与 MEEMD 分解进行对比,分别为经验模态分解(EMD)、集合经验模态分解(EEMD)、互补集合经验模态分解(CEEMD)自适应噪声集合经验模态分解(CEEMDAN),多种经验模态分解过程如附录附图1 所示,各分解分量排列熵值大小分布如附录附图2 所示。由附图1 和附图2 可知,MEEMD、EMD、EEMD、CEEMD CEEMDAN 分解分量的个数分别为5、6、8、8、8个,而且MEEMD 每个分解分量的排列熵值均未超过0.55,不需要进行二次分解,计算时间较短,而EMD、EEMD、CEEMD、CEEMDAN 都需要进行二、、次分解,计算时间较长,所以无论是分解分量个数还是计算时间,MEEMD 分解相较于多种经验模态分解,均具有较好的优越性。
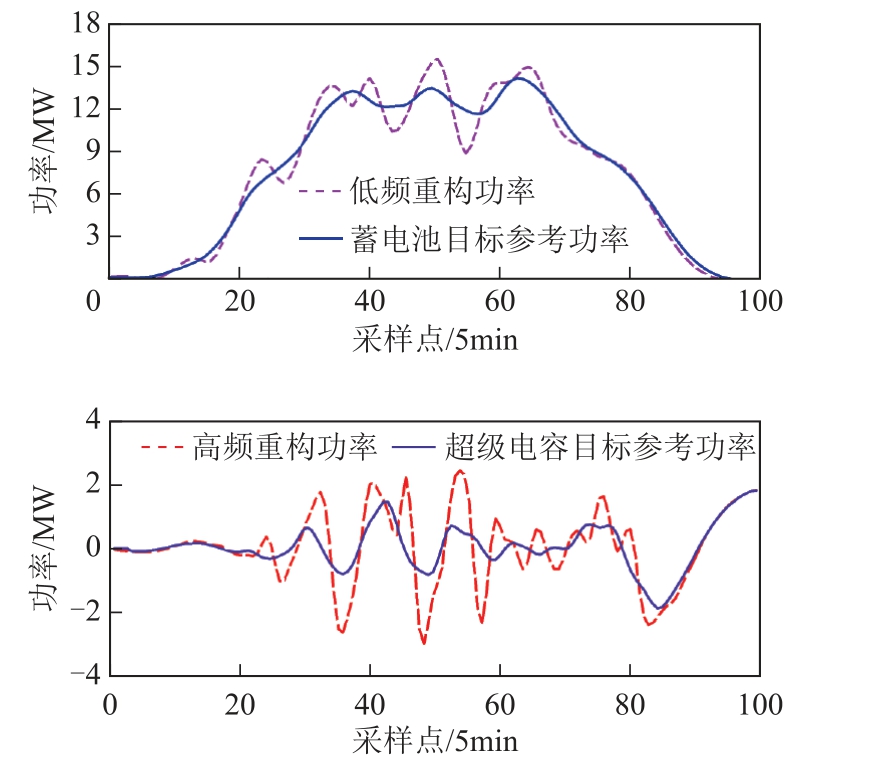
图7 高低频功率滑动平均滤波
Fig.7 Sliding average filtering of high and low frequency power
表1 数据窗口的选取Tab.1 Selection of data window

N 6 7 8 9 10最大功率变化/MW3.453.02 2.53 2.141.97
多种经验模态分解充/放电功率对比结果如图8所示。

图8 多种经验模态分解充/放电功率对比
Fig. 8 Comparison of charge/discharge power of variouempirical modes decomposition
由图8 可知,在主储能系统充/放电功率频次上,基于MEEMD 分解高频充/放电共计25 次,低频充/放电共计9 次;基于EMD 分解高频充/放电共计50次,低频充/放电共计18 次;基于EEMD 分解高频充/放电共计61 次,低频充/放电共计31 次;基于CEEMD 分解高频充/放电共计46 次,低频充/放电共计22 次;基于CEEMDAN 分解高频充/放电共计55 次,低频充/放电共计28 次;无论是高频超级电容还是低频蓄电池,基于MEEMD 分解的充/放电次数是最少的,其次是EMD、CEEMD、CEEMDAN 和EEMD,而充/放电次数的减少有利于延长储能系统使用寿命。在充/放电最大功率上,基于MEEMD 分解最大充/放电功率为1.99MW,最大充/放电功率也是最低的,其次为 EEMD(2.85MW)、EMD(2.96MW)、CEEMDAN(3.75MW)和 CEEMD(6.37MW)。
为了证明基于MEEMD 与其他经典算法相比在充放电功率上的优越性,本文分别对比了基于MEEMD 与小波包分解和变分模态分解(Variational Mode Decomposition, VMD)在充放电功率方面的优越性,充放电功率对比如图9 所示。

图9 MEEMD、VMD、小波包充/放电功率对比
Fig.9 Charging/discharging power comparison of MEEMD, VMD and wavelet packet
由图9 可知,虽然VMD 在高频充/放电的次数是最少的,为13 次,但在低频由超级电容器补偿的充/放电功率需要的储能容量较大,不利于经济性。而小波包分解在充/放电功率方面,无论是低频还是高频,其充/放电次数都要高于基于MEEMD 的充/放电功率,综合比较后,基于MEEMD 的充/放电功率要优于其他两种。
5.3 1min 时间尺度平顺光滑度分析
由超级电容作为单一电池组,主要跟随5min 时间尺度平滑出力波动后的1min 时间尺度平顺光滑度,超级电容电池组充/放电功率如图10 所示。

图10 辅助储能系统充/放电功率
Fig.10 Charge/discharge power of the auxiliary energy storage system
由图10 可知,超级电容、电池组在充/放电过程中其充/放电范围较为广泛,光伏出力时间段都为超级电容工作区间,是因为光伏有功功率在满足并网波动要求的同时,同样会对光伏有功功率的光滑度进行平滑。而且超级电容其充/放电频次较为频繁,总共进行了54 次,最大充/放电功率同样较小,最大充/放电功率仅有0.57MW,是因为采用超级电容器进行平滑光伏有功功率中波动比较小、且波动较为频繁的功率,符合超级电容本身容量小、快速充/放电的特性。
为体现提出的基于波动率和光滑度为双重评价指标进行平滑出力波动的优势,本文分别对以波动率为单一评价指标和以波动率、光滑度为双重评价指标的平滑出力波动效果进行多尺度排列熵值噪声对比分析,分析结果见表2。
表2 光滑度噪声分析
Tab.2 Smooth noise analysis

功率信号 排列熵值原始光伏功率波动 0.511 2单评价指标平滑出力波动 0.428 2双评价指标平滑出力波动 0.388 3
由表2 可知,双评价指标平滑出力波动信号相比于单评价指标平滑出力波动信号,排列熵值是最小的,为0.388 3。排列熵值越小,代表噪声越小,其光滑度越好,得到最终的平滑出力波动效果如图11 所示。
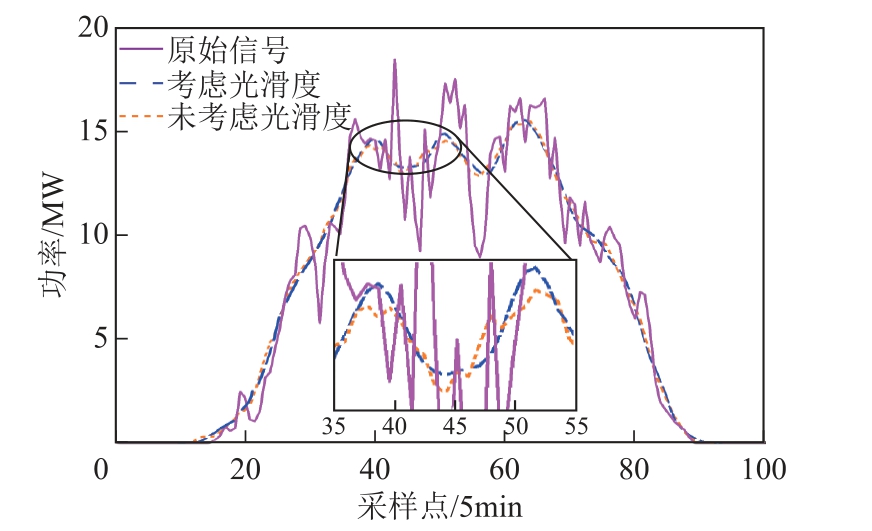
图11 光伏平滑出力波动效果
Fig.11 Photovoltaic smooth output fluctuation effect
由图11 可知,从整体评价来看,光伏有功功率波动发生了较大变化,波动率由原始有功功率的0.42 降低至平滑出力波动后的0.12,其1min 最大有功功率变化也缩小到1.97MW,满足并网要求。从局部评价来看,由局部放大图可以清晰表达,单一评价指标平滑出力波动后的有功功率存在小幅度的、较为频繁的功率波动,容易影响光伏并网的稳定性;加入光滑度评价指标后,曲线的光滑度得到了较大提升,在满足并网波动要求的同时,提高了并网稳定性。
6 结论
本文提出了一种考虑光伏双评价指标的混合储能平滑出力波动控制策略,基于该策略既减少了充/放电频次,延长了使用寿命,又实现了较好的平滑出力波动效果,主要内容如下:
1)根据光伏有功功率波动特性建立波动率和光滑度为平滑出力波动目标的双评价指标,基于MEEMD 信号分解和灰色关联度功率重构,得到了较好的高、低频功率分配效果。
2)采用5min 时间尺度平滑出力波动和1min时间尺度平顺光滑度相结合的形式,平顺光滑度跟随平滑出力波动进行优先级控制,最终波动率由 0.42 降低到0.12,光滑度噪声排列熵值由0.511 2 减小到0.388 3,达到了较好的平滑出力波动效果。
附 录

附图1 多种经验模态分解
App. Fig. 1 Multiple empirical modal decomposition

附图2 多种经验模态分解各分量排列熵值分布
App.Fig.2 Empirical mode decomposition entropy distribution of each component
[1] 李涛, 胡维昊, 李坚, 等. 基于深度强化学习算法的光伏-抽蓄互补系统智能调度[J]. 电工技术学报,2020, 35(13): 2757-2768.
Li Tao, Hu Weihao, Li Jian, et al. Intelligent economic dispatch for PV-PHS integrated system: a deep reinforcement learning-based approach[J]. Transactions of China Electrotechnical Society, 2020, 35(13):2757-2768.
[2] Zhang Xing, Wang Mingda, Zhao Tao, et al.Topological comparison and analysis of mediumvoltage and high-power direct-linked PV inverter[J].CES Transactions on Electrical Machines and Systems,2019, 3(4): 327-334.
[3] 李建林, 田立亭, 来小康. 能源互联网背景下的电力储能技术展望[J]. 电力系统自动化, 2015, 39(23): 15-22.
Li Jianlin, Tian Liting, Lai Xiaokang. Outlook of electrical energystorage technologies under energy internet background[J]. Automation of Electric Power Systems, 2015, 39(23): 15-22.
[4] 刁涵彬, 李培强, 王继飞, 等. 考虑电/热储能互补协调的综合能源系统优化调度[J]. 电工技术学报,2020, 35(21): 4532-4543.
Diao Hanbin, Li Peiqiang, Wang Jifei, et al. Optimal dispatch of integrated energy system considering complementary coordination of electric/thermal energy storage[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4532-4543.
[5] 颜湘武, 宋子君, 崔森, 等. 基于变功率点跟踪和超级电容器储能协调控制的双馈风电机组一次调频策略[J]. 电工技术学报, 2020, 35(3): 530-541.
Yan Xiangwu, Song Zijun, Cui Sen, et al. Primary frequency regulation strategy of doubly-fed wind turbine based on variable power point tracking and supercapacitor energy storage[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 530-541.
[6] 陈亚爱, 林演康, 王赛, 等. 基于滤波分配法的混合储能优化控制策略[J]. 电工技术学报, 2020,35(19): 4009-4018.
Chen Yaai, Lin Yankang, Wang Sai, et al. Optimal control strategy of hybrid energy storage based on filter allocation method[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4009-4018.
[7] 熊雄, 王江波, 杨仁刚. 基于小波包分解-概率模糊集特定策略下马尔可夫决策过程的微电网公共耦合点功率优化控制[J]. 电工技术学报, 2017, 32(22):189-197.
Xiong Xiong, Wang Jiangbo, Yang Rengang.Microgrid PCC power optimal control with Markov decision process using the specific policy of wavelet packet-probability fuzzy set[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 189-197.
[8] 吴振威, 蒋小平, 马会萌, 等. 用于混合储能平抑光伏波动的小波包–模糊控制[J]. 中国电机工程学报, 2014, 34(3): 317-324.
Wu Zhenwei, Jiang Xiaoping, Ma Huimeng, et al.Wave let pack-et-fuzzy control for the hybrid energy storage to control photovoltaic fluctuations[J].Proceedings of the CSEE, 2014, 34(3): 317-324.
[9] 田崇翼, 李珂, 严毅, 等. 基于经验模式分解的风电场多时间尺度复合储能控制策略[J]. 电网技术,2015, 39(8): 2167-2172.
Tian Chongyi, Li Ke, Yan Yi, et al. A multi-time scale control strategy of hybrid energy storage system in wind farm based on empirical mode decomposition[J].Power System Technology, 2015, 39(8): 2167-2172.
[10] 付菊霞, 陈洁, 滕扬新, 等. 基于集合经验模态分解的风电混合储能系统能量管理协调控制策略[J].电工技术学报, 2019, 34(10): 2038-2046.
Fu Juxia, Chen Jie, Teng Yangxin, et a1. Energy management coordination control strategy for wind power hybrid energy storage system based on EEMD[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2038-2046.
[11] 贾燕冰, 郑晋, 陈浩, 等. 基于集合经验模态分解的火-储联合调度调频储能容量优化配置[J]. 电网技术, 2018, 42(9): 2930-2937.
Jia Yanbing, Zheng Jin, Chen Hao, et a1. Capacity allocation optimization of energy storage in thermalstorage frequency regulation dispatch system based on EEMD[J]. Power System Technology, 2018, 42(9):2930-2937.
[12] Ye Lin, Zhang Cihang, Tang Yong, et al. Hierarchical model predictive control strategy based on dynamic active power dispatch for wind power cluster integration[J]. IEEE Transactions on Power Systems,2019, 34 (6): 4617-4629.
[13] 桑丙玉, 王德顺, 杨波, 等. 平滑新能源输出波动的储能优化配置方法[J]. 中国电机工程学报, 2014,34(22): 3700-3706.
Sang Bingyu, Wang Deshun, Yang Bo, et a1. Optimal allocation of energy storage system for smoothing the output fluctuations of new energy[J]. Proceedings of the CSEE, 2014, 34(22): 3700-3706.
[14] 马伟, 王玮, 吴学智, 等. 平抑光伏并网功率波动的混合储能系统优化调度策略[J]. 电力系统自动化, 2019, 43(3): 58-69.
Ma Wei, Wang Wei, Wu Xuezhi, et a1. Optimal dispatching strategy of hybrid energy storage system for smoothing power fluctuation caused by gridconnected photovoltaic[J]. Automation of Electric Power Systems, 2019, 43(3): 58-69.
[15] Lei Mingyu, Yang Zilong, Wang Yibo, et al. A MPC based ESS control method for PV power smoothing applications[J]. IEEE Transactions on Power Electronics, 2017, 33(3): 2136-2144.
[16] 刘春燕, 晁勤, 魏丽丽. 基于实证数据和模糊控制的多时间尺度风储耦合实时滚动平抑波动[J]. 电力自动化设备, 2015, 35(2): 35-41.
Liu Chunyan, Chao Qin, Wei Lili. Wind-storage coupling based on actual data and fuzzy control in multiple time scales for real-time rolling smoothing of fluctuation[J]. Electric Power Automation Equipment,2015, 35(2): 35-41.
[17] 李亚楠, 王倩, 宋文峰, 等. 混合储能系统平滑风电出力的变分模态分解-模糊控制策略[J]. 电力系统保护与控制, 2019, 47(7): 58-65.
Li Yanan, Wang Qian, Song Wenfeng, et a1.Variational mode decomposition and fuzzy control strategy of hybrid energy storage for smoothing wind power outputs[J]. Power System Protection and Control, 2019, 47(7): 58-65.
[18] 国家电网公司. Q/GDW 1617—2015 光伏电站接入电网技术规定[S]. 北京: 中国电力出版社, 2016.
[19] Li Xiangjun, Hui Dong, Lai Xiaokang. Battery energy storage sta tion(BESS)-based smoothing control of photovoltaic(PV) and wind power generation fluctuations[J]. IEEE Transactions on Sustainable Energy, 2013, 4(2): 464-473.
[20] 李相俊, 张晶琼, 何宇婷, 等. 基于自适应动态规划的储能系统优化控制方法[J]. 电网技术, 2016,40(5): 1355-1362.
Li Xiangjun, Zhang Jingqiong, He Yuting, et a1.Optimal control method of energy storage system based on adaptive dynamic programming[J]. Power System Technology, 2016, 40(5): 1355-1362.
[21] 郑近德, 程军圣, 杨宇. 改进的EEMD 算法及其应用研究[J]. 振动与冲击, 2013, 32(21): 21-26, 46.
Zheng Jinde, Cheng Junsheng, Yang Yu. Modified EEMD algorithm and its applications[J]. Journal of Vibration and Shock, 2013, 32(21): 21-26, 46.
[22] 吴鸣, 李振伟, 孙丽敬. 一种混合储能变换器的模型预测整体控制方法[J]. 电力系统保护与控制,2020, 48(21): 84-91.
Wu Ming, Li Zhenwei, Sun Lijing. A model predictive overall control method for a hybrid energy storage converter[J]. Power System Protection and Control,2020, 48(21): 84-91.
[23] Yang P, Nehorai A. Joint optimization of hybrid energy storage and generation capacity with renewable energy[J]. IEEE Transactions on Smart Grid, 2014, 5(4): 1566-1574.