0 引言
近年来，以风电为代表的新能源装机容量极大提高，截至2019 年年底我国风电累计装机容量达2.1 亿kW[1]，部分地区电网中风电装机占比已达23%[2]。但是风电出力的随机性使得风电场无法精确跟踪发电计划，导致电源侧功率波动加剧，严重威胁电网频率安全[3-6]。
储能作为解决风电并网问题的有效手段[7-10]，受国家政策支持[11-13]，在辅助风电场跟踪发电计划[14-15]、改善电网频率波动[16-18]等方面均有突出表现。文献[19]从提高风电预测精度入手，基于超短期风电功率预测提出了储能系统跟踪发电计划的控制策略。文献[20-21]提出利用大规模储能参与一次调频，并通过仿真验证了储能参与调频能显著提高频率稳定性。文献[21]提出利用大规模储能参与一次调频，通过电网幅频特性函数验证了储能参与调频能显著提高频率稳定性。文献[22]基于模型预测控制提出了风储联合参与调频的控制策略，实现了风电机组和储能之间调频功率的最优分配。
上述研究一方面只单独考虑储能辅助风电场跟踪发电计划或参与调频，工作模式较为单一；另一方面只从技术角度制定相应控制策略，而未在电力市场环境下[23-25]从经济最优角度制定储能出力。
现阶段储能建设和维护成本高昂，单一工作模式已不能保证风储电站收支平衡，因此探索储能新的运行方式、在保证电网频率安全的同时提高风储电站经济效益成为亟待解决的问题。文献[26]对储能系统参与辅助服务市场的经济性进行分析，结果表明储能从调频服务中获取的利润占总辅助服务利润的51%以上。文献[27]以系统总报价成本最小为目标，提出了储能参与日前能量市场和调频辅助服务市场协同优化调度模型。文献[28]提出给风电场配置储能，以风储联合体收益最大为目标，给出了储能减小风电场弃风并参与电网调频辅助服务的控制方法。文献[29]提出风储联合参与日前能量市场和调频辅助服务市场，实现风储联合竞标收益之和最大。但是文献[27-29]提出的考虑储能参与调频的风储运行模型均未计及电网频率安全性，忽略了当频率波动超出允许波动范围时对储能参与调频的要求。
综上所述，为加强风电可调度性和电网频率安全性，本文以日前调度为研究背景，提出利用储能辅助风电场跟踪调度计划同时提供调频服务的控制策略。首先构建了协调电网内部各发电资源发电量的日前调度计划形成过程，并利用区域电网调频模型计算调频极限，通过比较调频极限与等效负荷波动的大小来确定储能运行工况；其次提出辅助风电场跟踪日前调度计划和参与调频相结合的储能控制策略，并在电力市场背景下建立风储运行模型，用来获得储能最优出力；最后采用Matlab 进行算例仿真，分析所提方法和模型的有效性。
1 日前调度计划和电网调频极限分析
1.1 风电场日前调度出力计划的形成过程
考虑电网风电消纳能力限制和风速对风电场出力的影响，可利用调度中心制定日前调度出力计划（以下简称调度计划），协调电网内部各发电资源的发电量，如图1 所示。调度中心利用风电场预测出力、负荷预测出力、传统机组出力等数据，按式（1）制定风电场调度计划和传统机组调度计划，实现电网功率平衡。
式中，
分别为t 时刻风电场调度计划出力、传统机组调度计划出力、负荷预测出力。
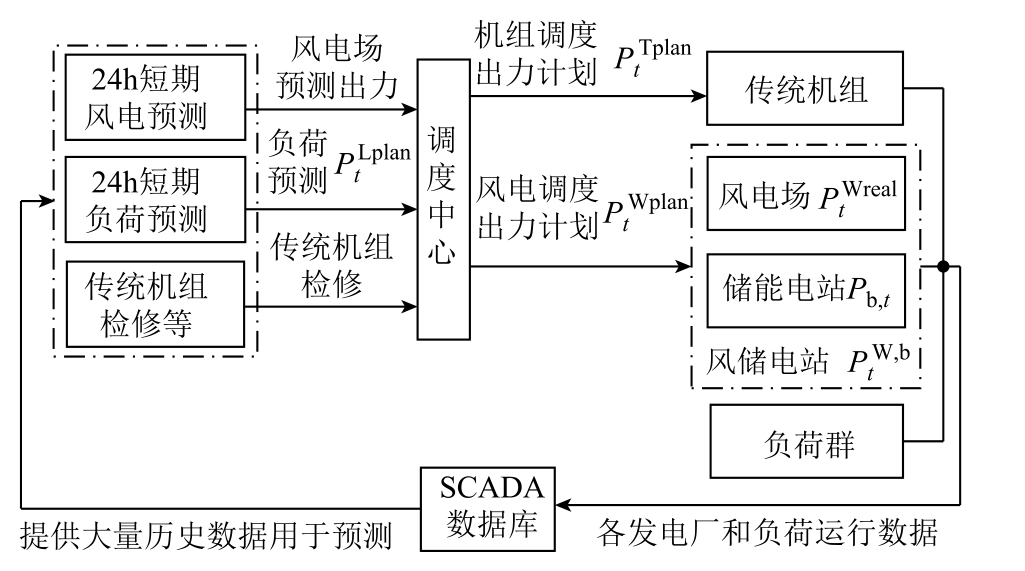
图1 调度计划形成示意图
Fig.1 Schematic diagram of the formation of the scheduling plan
图1 中，Pb,t 为储能在t 时刻的出力；PtWreal为风电场在t 时刻的实际出力，Pt W,b为风储电站在t 时刻的总出力。根据“清洁能源优先上网”原则[30-31]，调度中心可以通过减少传统机组发电量提高风电上网功率，故本文将风电场日前预测出力作为其调度出力计划，认为风电预测出力全被调度接纳[19]。
1.2 电网调频极限分析
由于风电出力的随机性会对电网频率产生不良影响，故将风电波动视为负的负荷波动，与常规负荷波动共同构成等效负荷波动，记为ΔPequL,t 。
引入调频极限来描述电网的极限调频能力，定义如下：在仅有传统电源参与调频的情况下，传统机组将电网频率维持在允许波动范围内所能承受的最大等效负荷波动（简称最大可承受等效负荷波动）称为电网调频极限，记为
在仅靠传统机组调频的情况下，当等效负荷波动超过调频极限时，传统机组的调频能力将不足以平衡等效负荷波动量，会产生调频功率缺额，导致频率偏差超过电网允许范围。由调频极限的定义可知，计算调频极限就是计算区域电网最大可承受等效负荷波动，下面具体介绍计算方法。区域电网调频模型如图2 所示。
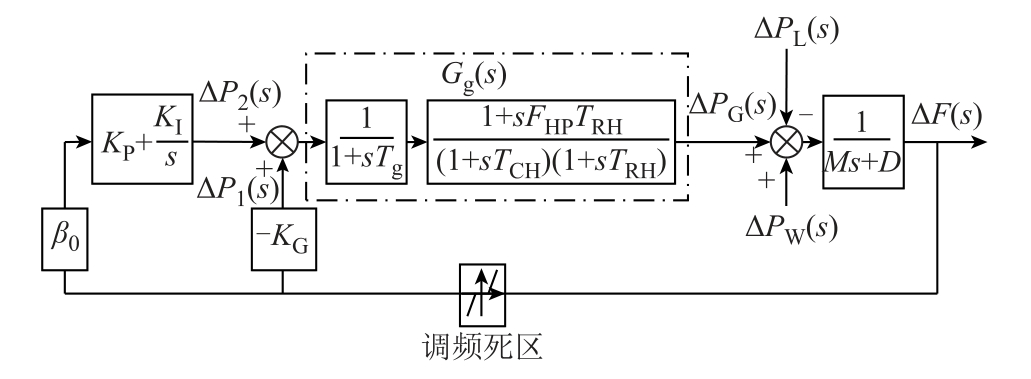
图2 区域电网调频模型
Fig.2 Regional grid frequency modulation model
图2 中，M 为电网惯性时间常数，D 为负荷阻尼系数，ΔPL ( s)为负荷波动，ΔPG ( s)为机组调频出力，ΔP1 ( s)为一次调频出力，ΔP2 ( s)为二次调频出力，ΔPW ( s)为风电波动，ΔF ( s)为电网频率偏差，KG 为机组单位调节功率，Tg 为火电机组调速器时间常数，FHP 为汽轮机再热器增益；TRH 为再热器时间常数；TCH 为汽轮机时间常数，Gg(s)为机组传递函数， β0为电力系统偏差系数，KP、KI 分别为控制器比例、积分系数，s 为拉普拉斯算子。
电网频率偏差大小取决于等效负荷和传统机组的有功功率平衡程度，有功功率不平衡量与频率偏差的关系为
式中，ΔPe quL( s)为等效负荷波动；ΔPG ( s)为
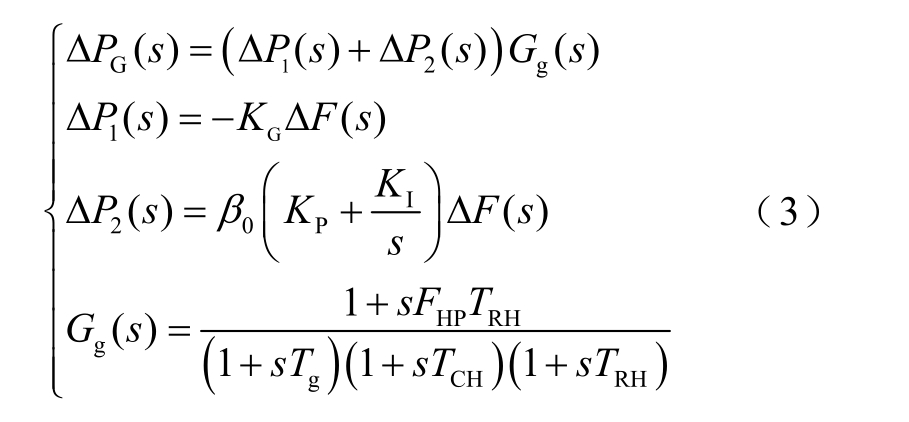
将式（3）代入式（2），整理得调频模型的传递函数H(s)为
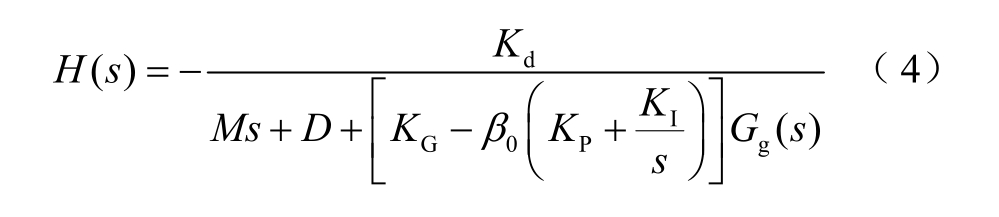
式中，Kd 为传统机组调频死区对频率的影响系数。
等效负荷波动与频率偏差、传递函数的关系为
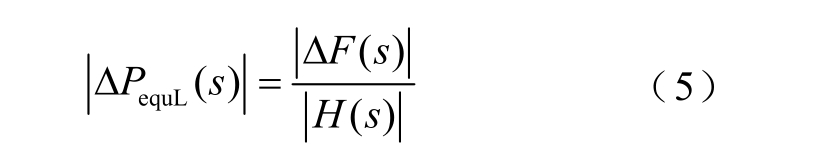
当电网允许的频率波动范围为
时，电网可承受的等效负荷波动
为
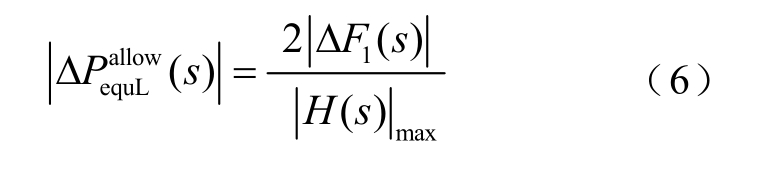
因此当电网所允许的频率波动达到最大范围
时，最大可承受等效负荷波动
为
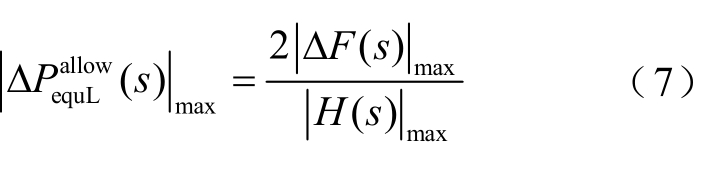
由传递函数 H ( s) 可得出区域电网幅频特性[32]，
求得，从而可由式（7）计算得到电网最大可承受等效负荷波动标幺值
（即调频极限）。
将标幺值换算为有名值，区域电网的调频极限为
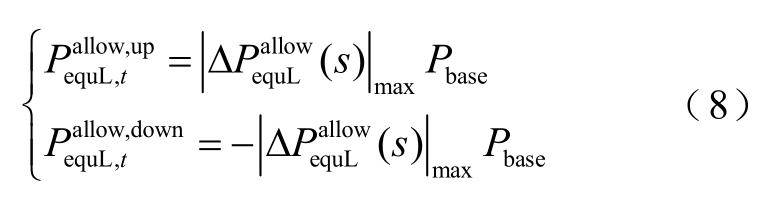
式中，Pbase 为基准功率；
为调频极限上限；
为调频极限下限。
2 储能最优控制策略
2.1 储能控制策略框架
根据1.1 节可以认为：同一时间，只要传统机组、风电场响应调度计划，负荷跟随预测出力，电网内部有功功率就能保持平衡，频率波动不会越限。但由于风电预测技术及风电本身特性的制约，风电场很难精确响应调度计划，会引发上网功率受限、考核费用高、电网频率不稳定等问题。
针对上述问题，从提高风电可调度性和电网频率稳定性的角度出发，本文提出风储电站中储能辅助风电场跟踪调度计划并提供调频辅助服务的控制策略，如图3 所示。
图3 控制策略框图
Fig.3 Block diagram of the control strategy
1）首先，按1.1 节形成风电场调度计划，按1.2节计算电网调频极限，并判断等效负荷波动是否超过电网调频极限。
2）由判断结果选择储能的工作模式，制定储能控制策略：
（1）当等效负荷波动不超过调频极限时，传统机组调频能力充足，最大频率波动不会超过允许范围，储能以跟踪调度计划为主要目标，通过充、放电调整风电场实际出力与调度计划的偏差，使其精确响应调度计划；同时由于储能辅助风电场跟踪调度计划时可能还有一部分功率并未投入使用，将这部分剩余功率用于向负荷或不具备调频能力的新能源电厂提供调频服务，获得调频收益。
（2）当等效负荷波动超过调频极限时，传统机组调频能力不足，最大频率波动将会超过允许范围，储能以保证电网频率安全为主要目标，强制储能参与调频，补充传统机组的调频功率缺额。
3）为了获得所提控制策略下储能用于跟踪调度计划和参与调频的最优出力，由步骤2）中风电场调度计划形成风储电站联合出力约束（简称风储出力约束），由电网调频极限形成频率安全约束，以风储电站利润最大为目标函数，建立基于风储出力约束和频率安全约束的风储运行模型，通过求解模型得到储能最优出力。
结合图1 和所提策略，储能出力、风储电站联网功率和风储电站总出力表达式如下。
、
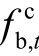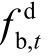分别为储能充、放电的0-1 变量，二者关系为
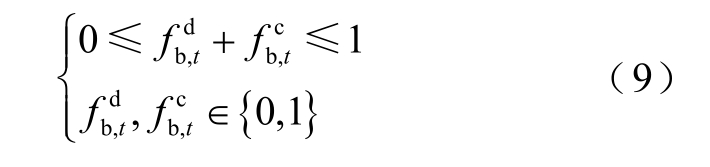
式（9）规定在同一时间，储能只能工作在充电状态或放电状态。
储能在t 时刻的出力Pb,t 为
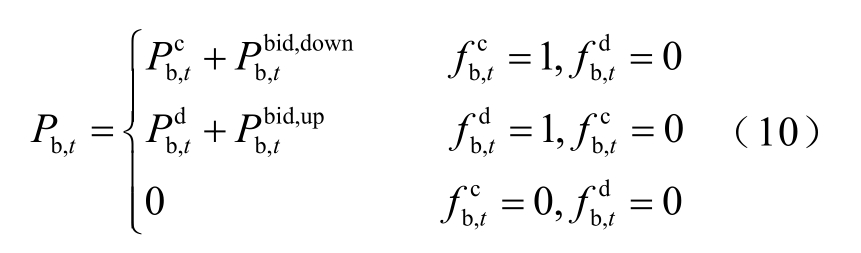
式中，
分别为储能在t 时刻的充电功率、放电功率、向下调频功率、向上调频功率。
t 时刻风储电站的实际联网功率
为
t 时刻风储电站实际联网和参与调频的总功率
为
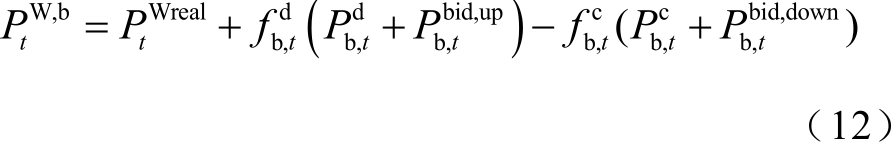
式（9）～式（12）中的
通过求解2.2 节风储运行模型获得。
2.2 风储联合运行模型
最优的储能充放电功率和调频功率是使风储电站利润最大的关键，而建立考虑2.1 节所提策略的风储运行模型是获得储能最优出力的基础。
2.2.1 目标函数
风储联合运行的目标是使风储电站的利润Cprofit 最大，目标函数包括两部分：风储电站运行成本及其收入。表示为
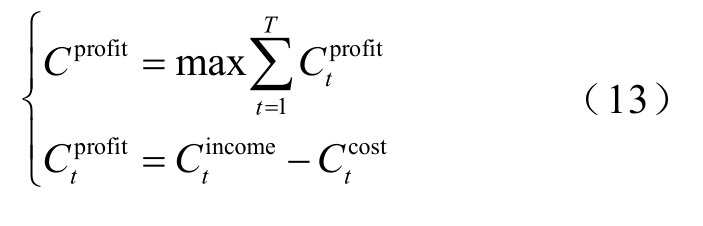
式中，
分别为t 时刻风储电站的利润、收入、运行成本；T 为总结算次数，取96。
1）风储电站运行成本
风储电站的运行成本主要由储能初始投资折旧费
储能运行成本
充放电过程中的能量损失
、风储电站出力偏离调度计划惩罚
构成，表达式为
（1）储能初始投资折旧
式中，ccap 为储能的单位容量成本[25]，取1 600 元/(kW·h)；Erate 为风电场配置的储能额定容量；r 为折现率，取8%；Tlife 为储能寿命周期，取10 年。
（2）储能寿命折损成本
储能在实际运行时，充放电会对其寿命有所影响，长时间运行还会导致更换成本，现将储能寿命衰减及其导致的更换成本简化为每个结算周期上的储能寿命折损成本，包括辅助风电场跟踪调度计划时的寿命折损
和储能提供调频辅助服务时的寿命折损
即
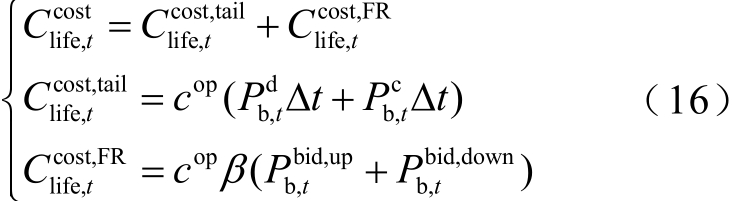
式中，cop 为折损费用系数，表示储能充放一个单位电量所产生的寿命折损费用，取100 元/(MW·h)； tΔ为一个结算周期；β 为调频电量系数，表示储能每提供1MW 的调频功率在实际运行时会充（放）β MW·h 的能量，单位为MW·h/MW，取0.13[29]。
（3）储能充放电过程中的能量损失成本
储能辅助风电场跟踪计划出力和参与调频时，充放电会导致相应的电能损耗，即
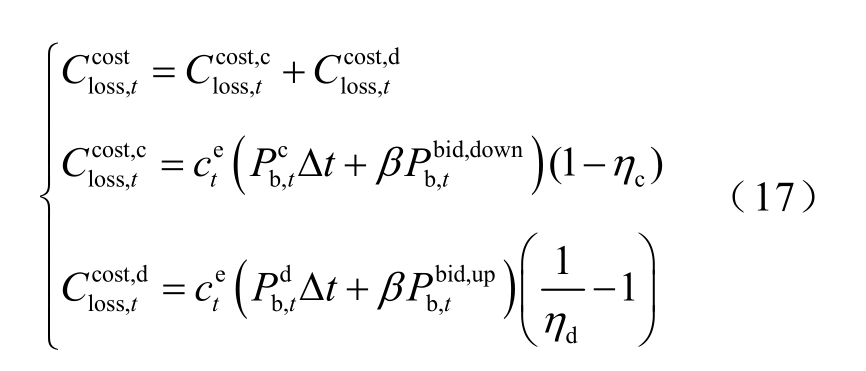
式中，
分别为充、放电能量损耗；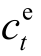
为风储电站上网电价，取520 元/(MW·h)； cη 、 dη 分别为充、放电效率，取95%。
（4）风储电站出力偏离惩罚
风电场出力偏离调度计划除了会引发调频费用，还会产生调峰、备用等一系列辅助服务费用，甚至危及电网频率安全，因此必须对偏离功率进行惩罚，且惩罚力度应较大，这样才能近似表示风储电站偏离调度计划对电网的不良影响，该费用每半个小时结算一次。
风储电站出力偏离惩罚
为
式中， cdev为单位功率缺额惩罚电价，取上网电价的两倍，即1 040 元/MW。
2）风储电站收入
风储电站的收入包括能量收入
和调频辅助服务收入
表达式为
（1）能量收入
风储电站的联网电量会获得能量收入，即
（2）调频辅助服务收入
在PJM 电力市场环境下[23]，储能给电网提供调频服务会获得调频辅助服务收入，包括调频容量收入和调频里程收入，即
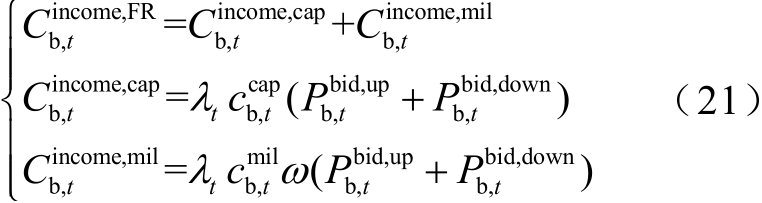
式中
分别为储能调频容量收入和调频里程收入； λ t为t 时刻的调频性能指标；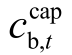
为调频容量价格，取100 元/MW；
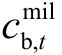为调频里程价格，取15 元/MW；ω 为平均里程，取2.75[28]。
为了便于分析，现假设：①任意一个调度周期内，储能调频功率将被调度优先考虑并全部接纳[28]，具体解释见附录；②储能能快速响应AGC(automatic generation control)调频指令。在PJM 电力市场中，调频性能指标 tλ 与精确度分数、相关性分数、延迟分数有关。基于假设②，可忽略相关性分数和延迟分数对 tλ 的影响，而精确度分数与储能在该时刻能否提供足够的调频功率有关，故 tλ 可简化为与储能电池能量状态（State of Energy, SOE）[33-34]有关的分段函数，表示为
式中， tλ 为t 时刻的调频性能指标； λmax 为调频性能指标最大值，取1； λmin 为调频性能指标最小值，取0.6；SOEt 为储能在t 时刻的剩余电量与满充时总电量的比值；SOElow 为SOE 理想区间下限，取0.2；SOEhigh 为SOE 理想区间上限，取0.8。调频性能指标与SOEt 的关系见附录。
2.2.2 约束条件
按储能主要目标不同，将风储联合运行模型的约束条件分为两种：以跟踪调度计划为主要目标时的约束和以保证电网频率安全为主要目标时的约束。
1）储能以跟踪调度计划为主要目标时的约束
（1）储能运行约束
储能系统在实际运行时，会受到电量约束和功率约束。
电量约束：由于储能系统建设成本昂贵，过度充放电会严重损害其寿命，因此在储能电量过低或过高时，应让其退出工作，联合运行模型的电量约束为
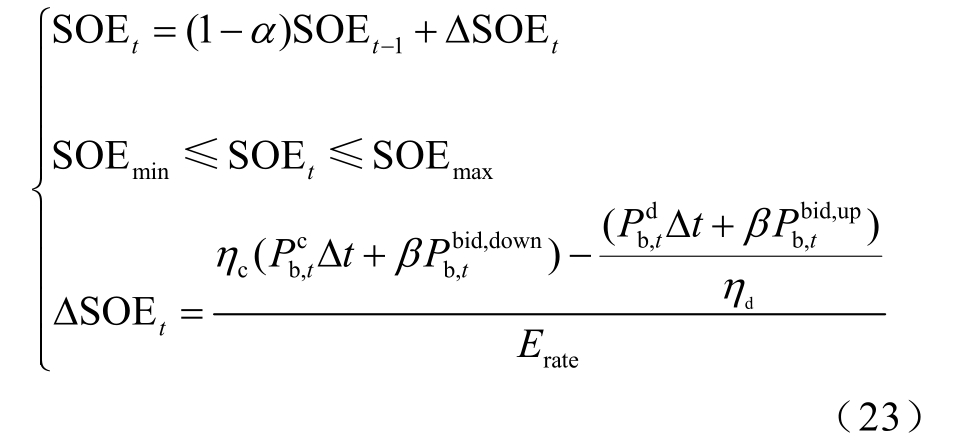
式中，SOE min 、SOE max 分别为储能SOE 的最小值和最大值，取0.1 和0.9；SOEt−1为t-1 时刻的储能剩余电量百分比；ΔSOEt 为t 时刻储能SOE 的变化量；α 为储能自放电率，取0。
功率约束包括储能辅助风电场跟踪调度计划时的功率约束和储能跟踪调度计划、并将剩余功率用于调频的输出功率约束。
储能辅助风电场跟踪调度计划时的功率约束为
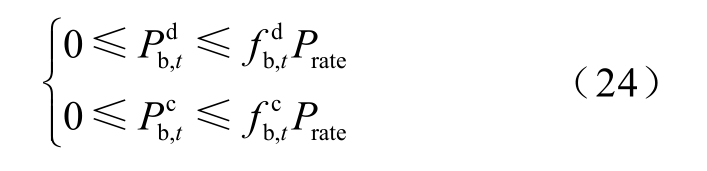
式中，Prate 为储能额定功率。
电池储能的充电过程不是一直不变的，需要经历恒流阶段和恒压阶段。在恒压阶段，储能SOE 对其充电功率有一定的影响[35-36]，二者之间的关系如附图3 所示。附图3 中，SOEset 为电池由恒流充电模式转变为恒压充电模式时的SOE 值，取0.8。
由附图3 可知，如果只用额定功率对储能充电功率进行限制，则将高估储能电池的充电能力，导致充电阶段无法充入预期的电量，降低了模型精确性。因此需要对储能的充电功率约束进一步精确化为
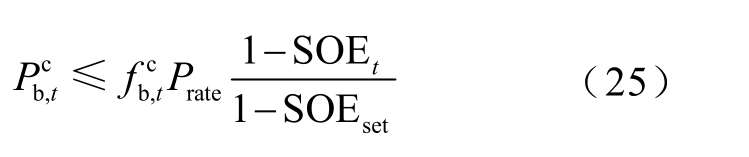
储能跟踪调度计划，并将剩余功率用于调频的输出功率约束为
式（26）规定储能的向上/向下调频功率不能超过其额定功率；储能跟踪计划出力与调频功率的总和不能超过其额定功率。
（2）风储电站联合出力约束
风电输出功率取决于实时风速，现有预测技术难免会有误差，因此设置调度计划误差带，一方面可以松弛风储电站出力约束，另一方面可以降低储能动作深度。误差带公式为
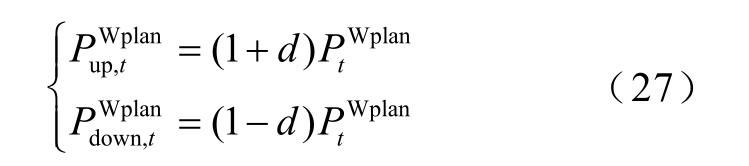
式中，d 为允许偏差，取3%[20]；
为调度计划上误差带；
为调度计划下误差带。
当等效负荷波动不超过调频极限时，储能以跟踪调度计划为主要目标，风储电站的联网功率
应在调度计划的误差带范围以内，由此形成风储出力约束，即
2）储能以电网频率安全为主要目标时的约束
储能以电网频率安全为主要目标时的约束有储能运行约束和频率安全约束。
储能运行约束：储能以保证电网频率安全为主要目标时的运行约束同样包含电量约束式（23）和功率约束式（24）～式（26）。
频率安全约束：由1.2 节分析可知，当等效负荷波动超过调频极限时，仅靠传统机组无法将频率维持在允许波动范围内，此时应强制储能提供调频功率。针对不同的负荷波动，将储能频率安全约束分为两种情况：
（1）当等效负荷波动超过电网调频极限上限，即
时，储能必须给超出
的等效负荷功率（记为ΔPequL1,t ）提供向上调频服务，补充传统机组调频缺额，如图4 所示，充放电标志为
图4 频率安全约束下储能出力示意图
Fig.4 Schematic diagram of energy storage output power under the frequency safety constraints
储能频率安全约束为
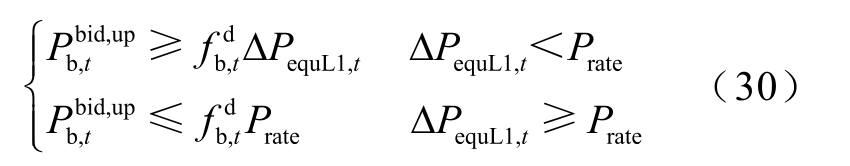
式中，
（2）同理，当等效负荷波动低于调频极限下限，即
时，储能必须给低于
的等效负荷功率（记为ΔPequL2,t）提供向下调频服务（见图4）。充放电标志为
储能的频率安全约束为
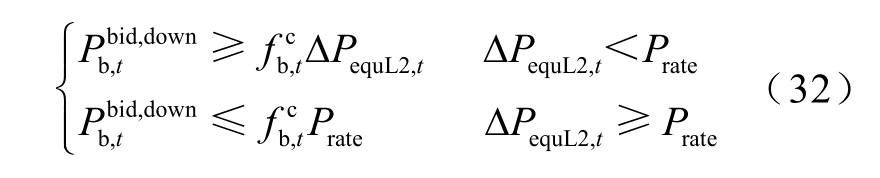
式中，
综上，风储运行模型按等效负荷波动可分为以下三种情况：
（1） 当等效负荷波动超过调频极限上限时，电网频率不安全，储能以维持电网频率安全为主要目标，频率安全约束为式（29）和式（30），适当放弃跟踪调度计划的能力，约束式（28）不予考虑。因此风储电站运行模型为式（9）、式（13）～式（21）、式（23）～式（26）、式（29）～式（30）。
（2）当等效负荷波动低于调频极限下限时，电网频率不安全，储能以维持电网频率安全为主要目标，频率安全约束为式（31）和式（32），适当放弃跟踪调度计划的能力，约束式（28）不予考虑。因此风储电站运行模型为式（9）、式（13）～式（21）、式（23）～式（26）、式（31）和式（32）。
（3）当等效负荷波动不超过调频极限时，传统机组调频能力充足，故频率安全约束不予考虑，储能以跟踪调度计划为主要目标，风储电站出力必须满足约束式（28）。风储电站运行模型为式（9）、式（13）～式（21）、式（23）～式（26）、式（28）。
2.2 节所提风储运行模型为混合整数非线性规划（Mixed-Integer Nonlinear Programming, MINLP）模型，可采用YALMIP 工具箱求解。储能最优充放电功率的计算流程如图5 所示。
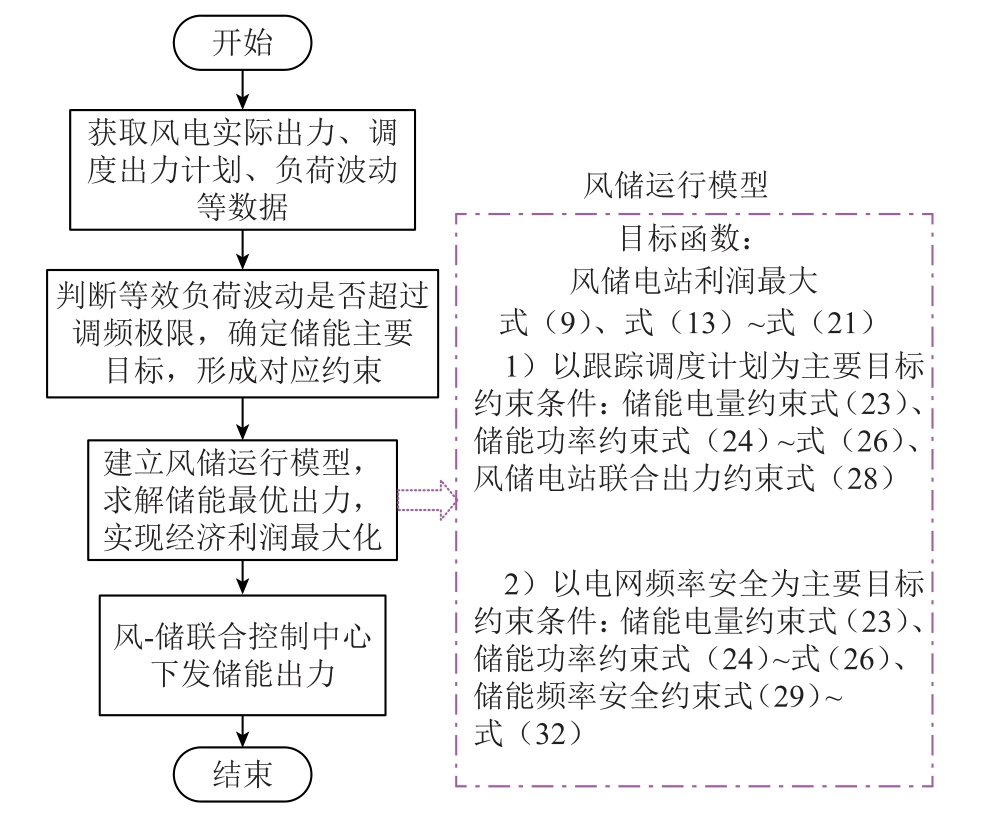
图5 储能最优出力计算流程
Fig.5 Calculation process of optimal output power of energy storage
2.3 评价指标
根据储能辅助风电场跟踪调度计划和参与调频的两种工况，提出以下评价指标。
跟踪调度计划评价指标Pindex 为
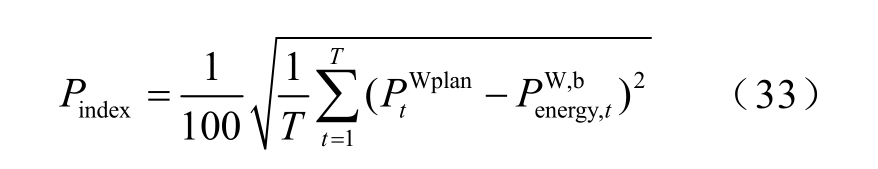
式（33）表示风储电站实际联网功率与调度计划之间的偏差方均根，Pindex 越小，说明风储电站跟踪调度计划的能力越好。
频率波动评价指标为
式中，Δfmax 为最大频率波动量。findex 越小，说明频率波动越小。
3 算例分析
为验证所提控制策略的有效性和经济性，采用如下算例系统：区域总装机容量为1 000MW，其中风电装机100MW（占10%），磷酸铁锂电池储能系统装机容量为30MW/120MW·h。在Matlab 中仿真第2 节的储能运行策略及模型。
3.1 电网调频极限验证和等效负荷波动分析
图2 中的区域调频模型参数[18]见附表1，通过多次仿真，比较传递函数与实际模型的频率波动曲线，取Kd=1.15。由调频模型传递函数可画出区域电网幅频特性曲线如图6a 所示。设定电网允许的频率波动范围为[49.7Hz，50.3Hz]，即
由图6a 可知传递函数的最大幅值
根据式（7）和式（8）计算可得区域电网调频极限标幺值为±0.075(pu)，有名值为±75MW。
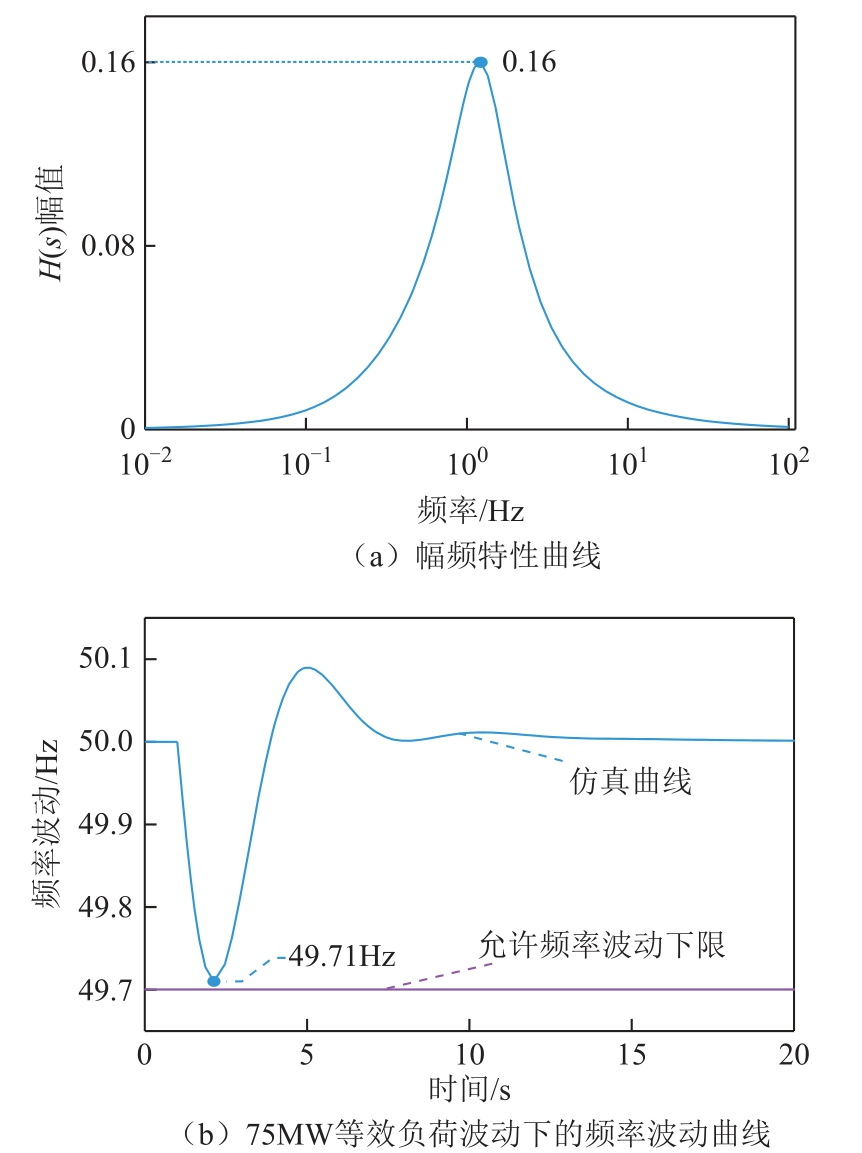
图6 幅频特性曲线与频率波动曲线
Fig.6 The amplitude-frequency characteristic curve and the frequency fluctuation curve
对区域电网受到75MW 等效负荷扰动的情况进行仿真，频率波动如图6b 所示，频率在2.1s 时下降至最低值49.71Hz，与设定的频率波动允许范围[49.7Hz，50.3Hz]下限仅差0.01Hz，若增大等效负荷波动，电网频率随时会跌出49.7Hz。故可以用75MW作为该电网的调频极限。
选取我国某地区一天的风电、负荷数据进行分析，区域等效负荷波动如图7 所示。图中采样时间步长为15 min，一天共96 个采样点。
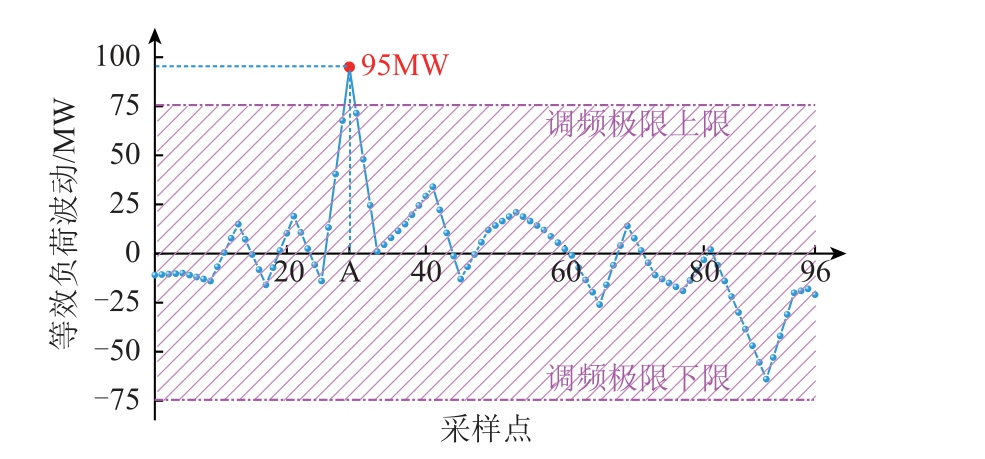
图7 等效负荷波动曲线
Fig.7 Equivalent load fluctuation curve
由图7 可见，区域等效负荷波动最大值出现在A 点处，达到95MW，此时如果电网中仅有传统机组参与调频，那么频率将会遭受威胁。
3.2 控制策略效果分析
为体现本文策略在控制储能辅助风电场跟踪调度计划和提高电网频率稳定性中的作用，分别讨论三种场景中的风储电站运行及电网频率波动情况。场景1：风电场未配置储能系统；场景2：风储联合跟踪调度计划但无频率安全约束；场景3：风储联合跟踪调度计划且有频率安全约束。现以日前调度为例，分析时间步长为15min 时的储能出力。
3.2.1 技术性分析
三种场景下风储电站出力和储能出力分别如图8 和图9 所示，图10 对比了场景2 和场景3 中的储能SOE 状态。
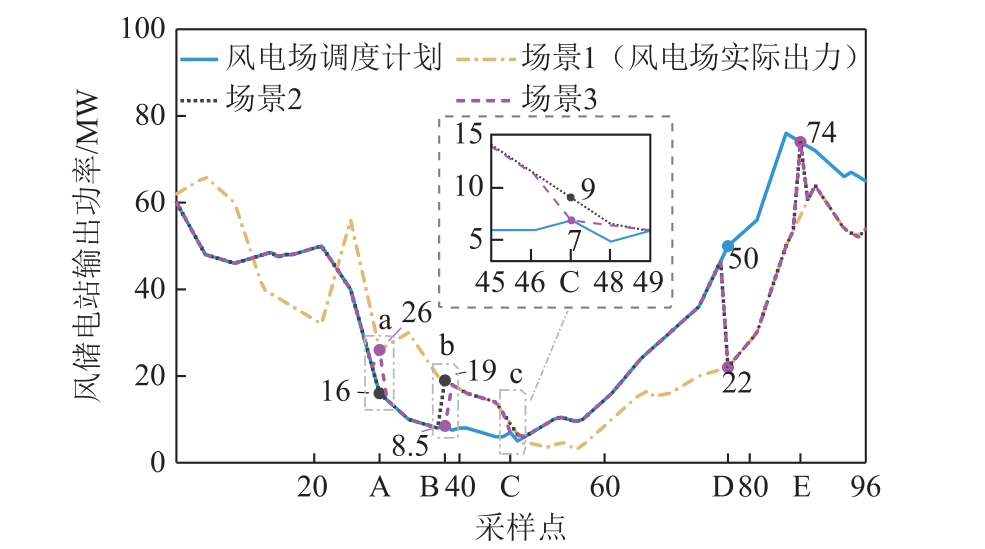
图8 风储电站出力曲线
Fig.8 The output power of wind-energy storage station
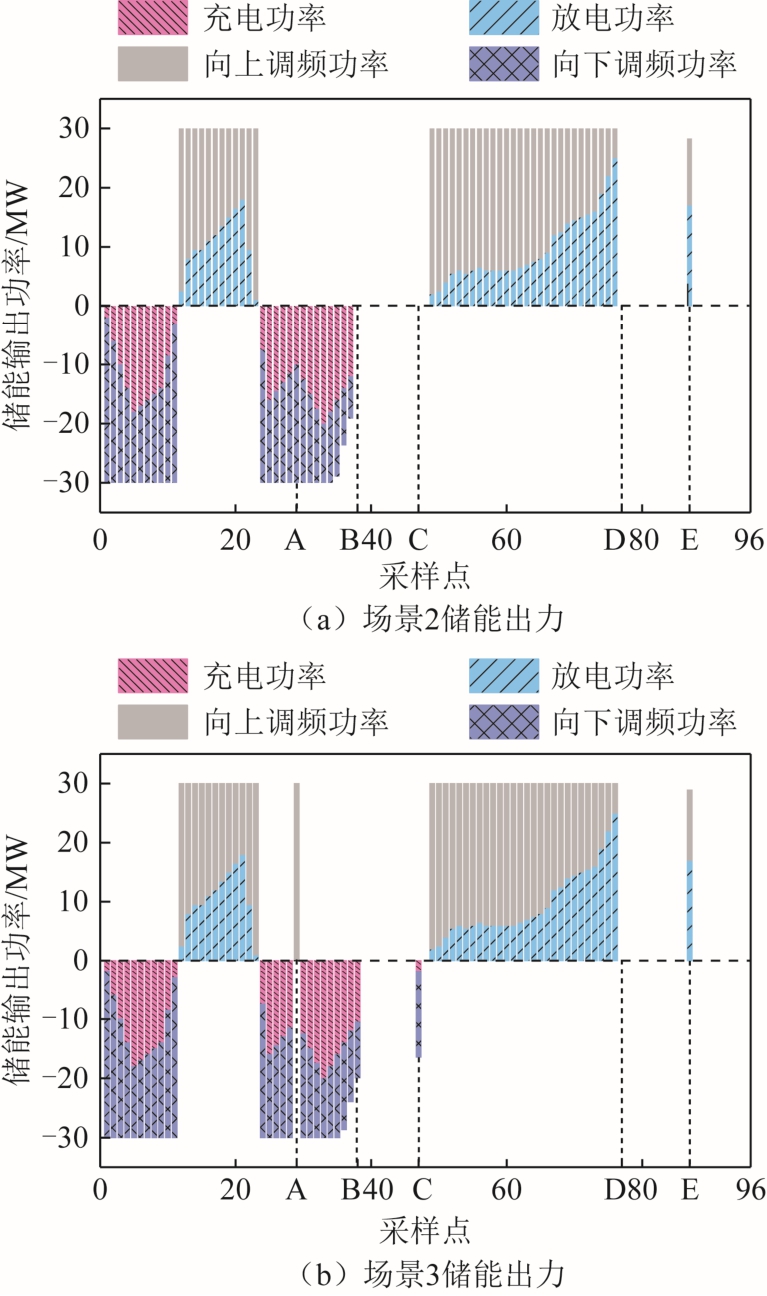
图9 储能最优出力
Fig.9 The optimal output power of energy storage
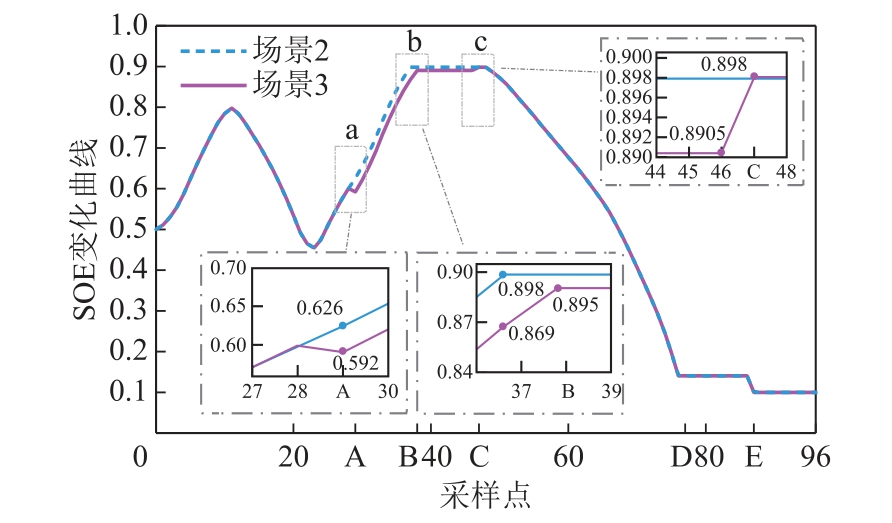
图10 SOE 变化曲线
Fig.10 The changing curve of SOE
由图8 可知，由于场景1 中未给风电场配置储能，所以风储电站出力等于风电场实际出力。而场景2 和场景3 的风储电站除了在A、B-C、D 之后的时段内偏离了调度计划外，其他时间均能响应调度计划。同时由图9 可知，在储能辅助风电场跟踪调度计划时，剩余功率被用于调频，这样能充分发挥储能的工作空间，B 点附近储能总输出功率有所降低是因为这些时段SOE 高于0.8，储能充电功率和向下调频功率受到SOE 限制有所下降。
三种场景的跟踪调度计划指标和频率指标计算结果见表1。结合图8 可知，场景1 跟踪调度计划的能力最差，场景3 的最好。场景3 的Pindex 比场景2 的低0.106%，比场景1 的低32.833%，因此本策略可以利用储能提高风电场跟踪调度计划的能力，具体分析如下。
表1 两种指标对比结果
Tab.1 Comparison result of two index
指标 场景1 场景2 场景3 Pindex 0.139 8 0.094 0 0.093 9 findex 0.37 0.37 0.24
在A 处，等效负荷扰动超过调频极限。场景2中未考虑频率安全约束，储能一直以辅助跟踪调度计划为主要目标，由图 9a 可知，此时储能充电10MW，使得风储电站能响应调度计划。场景3 的频率安全约束使得储能以保证电网频率安全为主要目标，强制储能参与调频，弥补传统机组的调频功率缺额，由图9b 可知，储能给超出调频极限的等效负荷波动提供了30MW 向上调频功率，放弃了跟踪调度计划的能力。
在B 处，等效负荷扰动并未超过调频极限，场景2 和场景3 中储能均以辅助风电场跟踪调度计划为主要目标。场景2 由于储能在A 处跟踪了调度计划，导致在B 处储能SOE 接近上限（如图10 区域b），故场景2 储能不动作。场景3 由于在A 处强制储能参与调频，SOE 有所下降（如图10 区域a），由图9b 可知此时储能进行充电，故场景3 能跟踪调度计划。
在C 处，等效负荷扰动没有超过调频极限，场景2 和场景3 均以辅助风电场跟踪调度计划为主要目标。但场景2 中储能SOE 在（C-1）处接近上限（如图10 区域c），所以场景2 储能不动作。场景3中在（C-1）处SOE 尚未达到上限，因此场景3 储能充电，如图9b 所示。上述B、C 两个时段内场景3储能动作是导致场景3Pindex 低于场景2 的主要原因。
在D 处，等效负荷扰动并未超过调频极限，场景2 和场景3 均以辅助风电场跟踪调度计划为主要目标。由图8 可知，此时风电场调度计划与实际出力偏差达到28MW，而场景2 和场景3 储能SOE 状态较低，一旦动作便会导致SOE 跌出SOE 下限，故两种情况储能均不动作。
在E 处，等效负荷扰动并未超过调频极限。场景2 和场景3 均以辅助风电场跟踪调度计划为主要目标。此阶段风电场调度计划与实际出力之间的差距较小，故两种场景中的储能均放电（见图9），从而使得风储电站出力跟踪调度计划。
为验证本策略在减小频率波动上的有效性，对该区域三种场景下受到95MW 等效负荷扰动进行仿真，频率波动曲线如图11 所示。
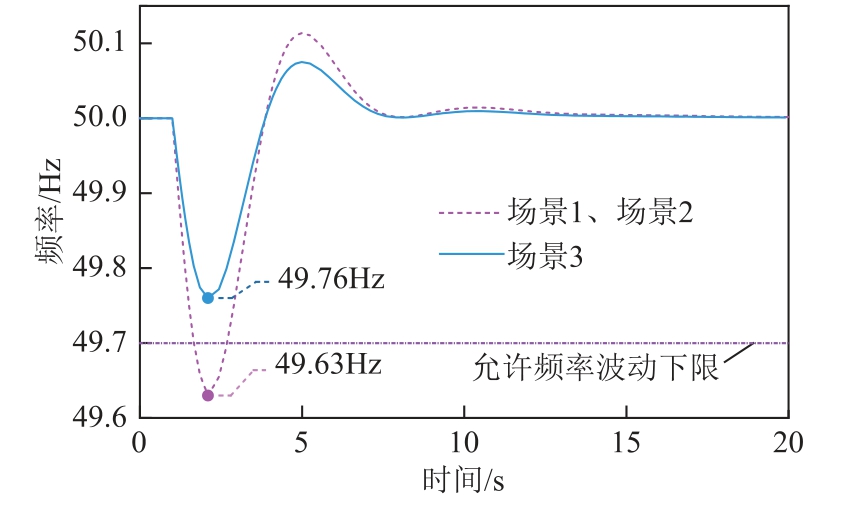
图11 95MW 等效负荷波动下的频率变化曲线
Fig.11 The change of frequency under 95MW equivalent load fluctuation
由图11 可知，虽然场景2 中储能在A 处给本区域电网提供了20MW 向下调频功率，但是与调频需求相反，只能通过联络线外送至合适的区域，对本区域电网的频率没有帮助，因此场景2 的频率波动与场景1 相同，最低频率低至49.63Hz。而由图9b 可知，场景3 储能提供了30MW 向上调频功率，在储能参与调频后，最低频率为49.76Hz，满足频率要求。
结合表1 和图11 可知，场景1 和场景2 的findex相同，场景3 的findex 比场景1 和场景2 减小35.1%，说明考虑频率安全约束后的区域电网频率最安全。
综上，所提策略不仅能提高风电场跟踪调度计划的能力，还能提高电网频率安全性。
3.2.2 经济性分析
表2 给出了场景2和场景3 的减少弃风量和储能调频功率。
表2 两种场景下减少弃风量和调频功率对比
Tab.2 The comparison of the amount of wind curtailment and frequency modulation power in case 2 and case 3
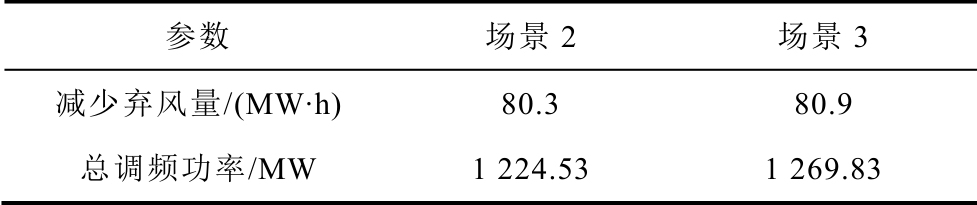
参数 场景2 场景3减少弃风量/(MW·h) 80.3 80.9总调频功率/MW 1 224.53 1 269.83
由表2 可以看出：场景3 的减少弃风量和累计调频功率均高于场景2。因为场景3 在A 处强制储能参与调频，SOE 有所下降，从而可以在B 点和C点附近吸收更多的过剩风电或提供更多的调频功率。
表3、表4、表5 分别给出了场景2 和场景3 的风储电站总成本、总收入、总利润。
由表5 可知，场景2 中储能始终以跟踪调度计划为主要目标，一天总利润为124 647 元。场景3中，储能在电网频率安全时以跟踪调度计划为主要目标，在电网频率不安全时以保证电网频率安全为主要目标，一天总利润为188 677 元，较场景2 提高33.9%。因为场景3 中储能的调频功率远远高于场景2（见表2），使得表4 中场景3 的调频收入增加，从而导致场景3 中风储电站利润大于场景2。
综上所述，本文提出的利用储能辅助风电场跟踪调度计划并参与调频的风储运行方式具有良好的经济效益。
表3 风储电站运行成本对比
Tab.3 The operating cost comparison of wind-energy storage station in case 2 and case 3
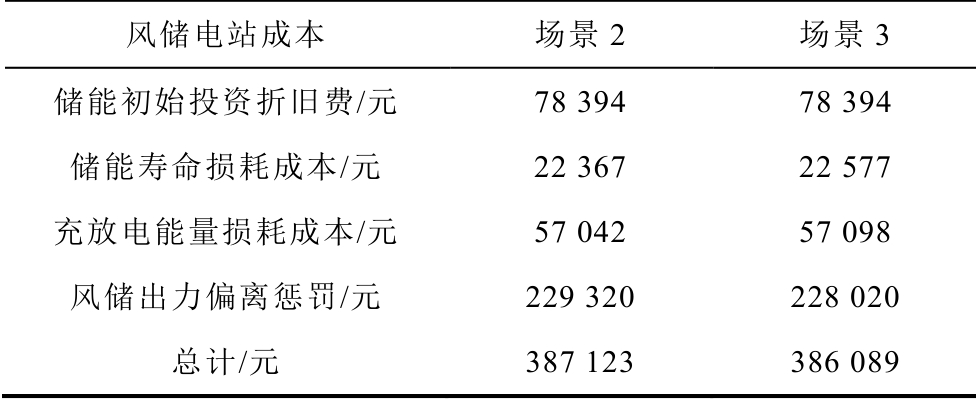
风储电站成本 场景2 场景3储能初始投资折旧费/元 78 394 78 394储能寿命损耗成本/元 22 367 22 577充放电能量损耗成本/元 57 042 57 098风储出力偏离惩罚/元 229 320 228 020总计/元 387 123 386 089
表4 风储电站收入对比
Tab.4 The income comparison of wind-energy storage station in case 2 and case 3
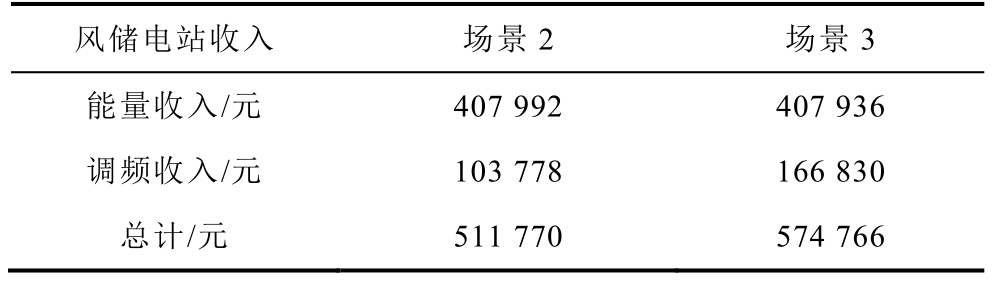
风储电站收入 场景2 场景3能量收入/元 407 992 407 936调频收入/元 103 778 166 830总计/元 511 770 574 766
表5 风储电站利润对比
Tab.5 The profit comparison of wind-energy storage station in case 2 and case 3
场景2 场景3风储电站利润/元 124 647 188 677
4 结论
在电力市场环境中，为了提高风电场跟踪调度计划能力和电网频率稳定性，最大化风储电站利润，提出了基于风电场调度计划和电网调频极限的储能系统优化运行策略，结论如下：
1）所提策略及模型在储能SOE 状态正常时能够提高风电场跟踪调度计划的能力，使跟踪调度计划指标较无储能时减少32.833%。
2）由电网调频极限形成的频率安全约束虽然在等效负荷波动超出调频极限时会导致风电场跟踪调度计划的能力下降，但却能强制储能提供调频功率，使得最大频率波动量较不考虑频率安全约束时减少35.1%，有效维护电网频率安全。
3）在计及初始投资折旧、储能运行损耗、出力偏离惩罚等几类运行成本和能量、调频等收入的情况下，本策略能使风储电站一天利润达到188 677元，说明在电力市场环境下将储能同时用于辅助风电场跟踪调度计划和参与调频具有良好的经济效益。
各区域电网内的调频资源和调频需求不可能完全平衡，如何跨区域协调调度各个区域电网中的调频资源，实现全网调频成本最低还有待进一步研究。
附 录
1. 储能调频功率被调度优先考虑全部接纳假设
以两区域互联系统为例，两区域互联系统如附图 1所示。图中，区域1 包含风储电站（W1+E1）、传统电厂（G1）、负荷（L1），调频电源包括风储电站和G1；区域2 包含风电场（W2）、传统电厂（G2）、负荷（L2），调频电源仅为G2，W2 不具备调频能力，是调频功率的需求方。
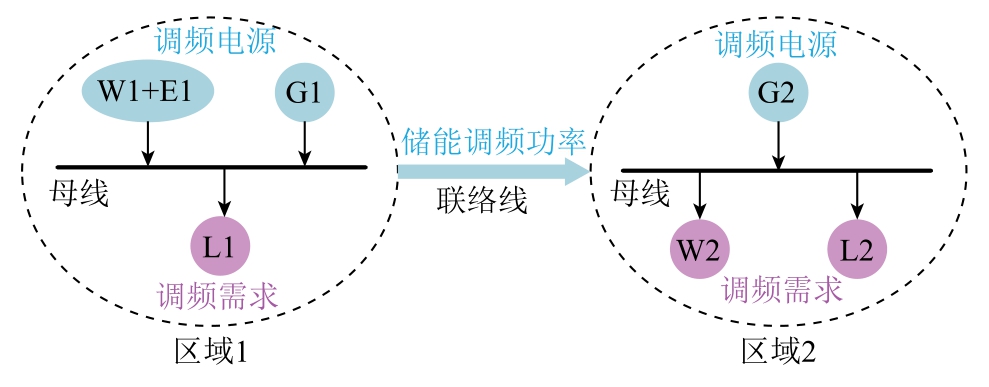
附图1 两区域互联示意图
App.Fig.1 Schematic diagram of interconnection of two regions
储能是电网中的优质调频资源，基于“快速调频资源优先调用”原则，在任意时段储能调频功率的调用优先级将高于调频能力不如储能的传统机组（G1/G2）；另外，若W2 和L2 的综合波动较大，G2 的调频能力很可能会出现不足，导致区域2 频率不稳定，考虑储能系统E1 在一个调频周期内可能出现调频能力过剩的情况，可将这部分富余的调频功率通过联络线外送至区域2，为新能源电站W2 或负荷L2 提供必要的辅助服务。
因此做出如下假设：任意一个调度周期内，储能调频功率能被调度优先考虑并全部接纳。
2. 调频性能指标与SOEt 的关系
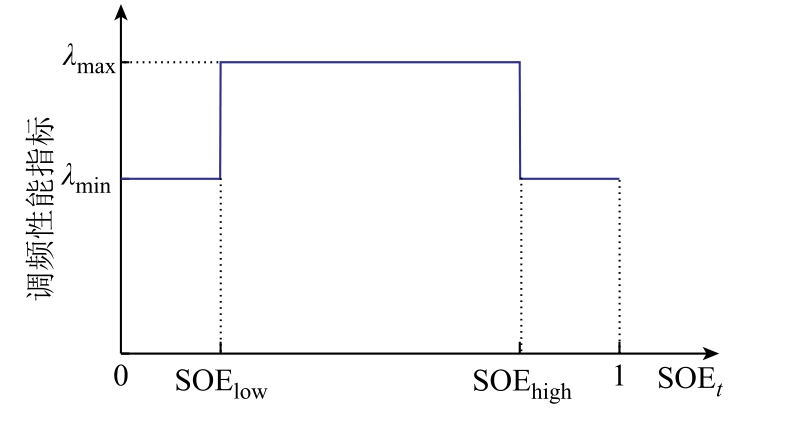
附图2 调频性能指标与SOE 的关系图
App.Fig.2 The relationship between frequency modulation performance index and SOE of energy storage
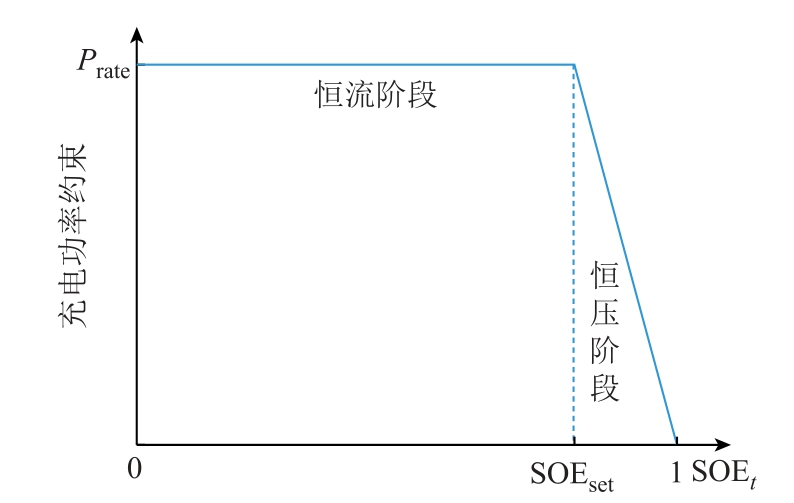
附图3 充电功率与SOE 的关系图
App.Fig.3 The relationship between the charging power and SOE of energy storage
附表1 调频模型参数
App.Tab.1 Parameters of the frequency modulation model
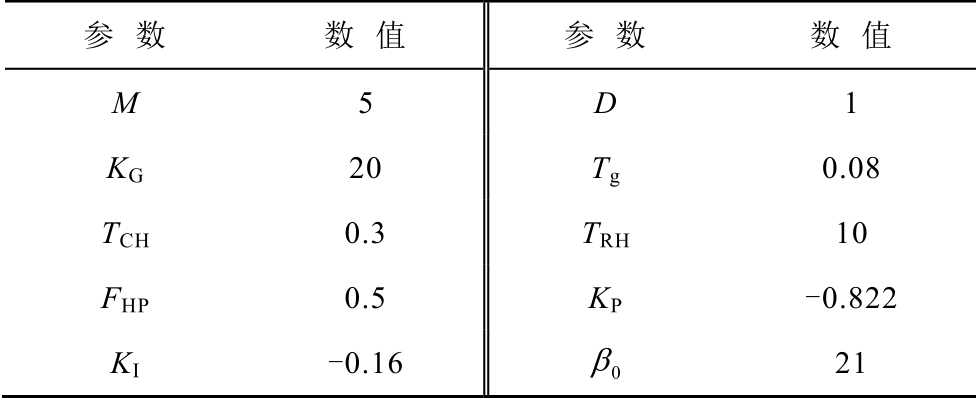
参 数 数 值 参 数 数 值M 5 D 1 KG 20 Tg 0.08 TCH 0.3 TRH 10 FHP 0.5 KP -0.822 KI -0.16 0β 21
[1] 国家能源局. 2019 年风电并网运行情况[EB/OL].[2020-02-28].http://www.nea.gov.cn/2020-02/28/c_138827910.htm.
National Energy Administration. Grid connected operation of wind power in 2019[EB/OL]. [2020-02-28].http://www.nea.gov.cn/2020-02/28/c_138827910.htm
[2] 内蒙古自治区能源局. 2019 年全区各盟市电力增速排行[EB/OL]. [2020-02-26]. http://nyj.nmg.gov.cn/index.php?v=show&cid=59&id=763.
Nei Monggol Autonomous Region Energy Administration. Power growth rate of all cities in the region in 2019[EB/OL]. [2020-02-26]. http://nyj.nmg.gov.cn/index .php?v=show&cid=59&id=763
[3] Zhang G, Ela E, Wang Q. Market scheduling and pricing for primary and secondary frequency reserve[J]. IEEE Transactions on Power Systems,2018, 34(4): 2914-2924.
[4] 严干贵, 赵伟哲, 张礼珏. 变速变桨距风电机组减载调频综合控制策略研究[J]. 东北电力大学学报,2018, 38(5): 1-8.
Yan Gangui, Zhao Weizhe, Zhang Lijue. Research on integrated control of deloading frequency regulation for variable speed and variable pitch angle wind turbines[J]. Journal of Northeast Electric Power University, 2018, 38(5):1-8.
[5] 方勇杰. 英国“8•9”停电事故对频率稳定控制技术的启示[J]. 电力系统自动化, 2019, 43(24): 1-5.
Fang Yongjie. Reflections on frequency stability control technology based on the blackout event of 9 August 2019 in UK[J]. Automation of Electric Power Systems, 2019, 43(24): 1-5.
[6] 李军徽, 冯喜超, 严干贵, 等. 高风电渗透率下的电力系统调频研究综述[J]. 电力系统保护与控制,2018, 46(2): 163-170.
Li Junhui, Feng Xichao, Yan Gangui, et al. Survey on frequency regulation technology in high wind penetration power system[J]. Power System Protection and Control, 2018, 46(2): 163-170.
[7] John E T B, David T Y. Emissions impacts of future battery storage deployment on regional power systems[J]. Applied Energy, 2020, 264: 114678.
[8] 李军徽, 张嘉辉, 穆钢, 等. 储能辅助火电机组深度调峰的分层优化调度[J]. 电网技术, 2019, 43(11):3961-3970.
Li Junhui, Zhang Jiahui, Mu Gang, et al. Hierarchical optimization scheduling of deep peak shaving for energy-storage auxiliary thermal power generating units[J]. Power System Technology, 2019, 43(11):3961-3970.
[9] 陈薇, 侯杨成, 张里, 等. 计及损耗的钒电池储能系统功率优化分配策略[J]. 电工技术学报, 2020,35(19): 4038-4047.
Chen Wei, Hou Yangcheng, Zhang Li, et al. Power optimization allocation strategy for vanadium battery energy storage system considering loss[J].Transactions of China Electrotechnical Society, 2020,35(19): 4038-4047.
[10] 郭伟, 赵洪山. 基于改进分布式一致性算法的电池储能阵列分组控制策略[J]. 电工技术学报, 2019,34(23): 4991-5000.
Guo Wei, Zhao Hongshan. Grouping control strategy of battery energy storage array system based on an improved distributed consensus algorithm[J].Transactions of China Electrotechnical Society, 2019,34(23): 4991-5000.
[11] 李建林, 牛萌, 王上行, 等. 江苏电网侧百兆瓦级电池储能电站运行与控制分析[J]. 电力系统自动化, 2020, 44(2): 28-35.
Li Jianlin, Niu Meng, Wang Shangxing, et al.Operation and control analysis of 100 MW class battery energy storage station on grid side in Jiangsu power grid of China[J]. Automation of Electric Power Systems, 2020, 44(2): 28-35.
[12] 中国风电新闻网. 湖北省能源局关于开展2020 年平价风电和平价光伏发电项目竞争配置工作的通知[EB/OL].[2020-06-09].http://www.chinawindnews.com/13774.html.
[13] 国家标准GB 38755—2019《电力系统安全稳定导则》[S]. 2020.
[14] 张峰, 张鹏, 梁军. 考虑风电功率不确定性的风电场出力计划上报策略[J]. 电力自动化设备, 2019,39(11): 34-40.
Zhang Feng, Zhang Peng, Liang Jun. Wind farm generation schedule strategy considering wind power uncertainty[J]. Electric Power Automation Equipment,2019, 39(11): 34-40.
[15] 李滨, 粟祎敏, 莫新梅, 等. 跟踪风电计划偏差的风储系统联合控制策略[J]. 电网技术, 2019, 43(6):2102-2108.
Li Bin, Su Yimin, Mo Xinmei, et al. Control strategy of hybrid wind-ES power system for tracking wind power planning deviation[J]. Power System Technology, 2019, 43(6): 2102-2108.
[16] 李欣然, 崔曦文, 黄际元, 等. 电池储能电源参与电网一次调频的自适应控制策略[J]. 电工技术学报, 2019, 34(18): 3897-3908.
LI Xinran, Cui Xiwen, Huang Jiyuan, et al. The selfadaption control strategy of energy storage batteries participating in the primary frequency regulation[J].Transactions of China Electrotechnical Society, 2019,34(18): 3897-3908.
[17] 李军徽, 侯涛, 穆钢, 等. 基于权重因子和荷电状态恢复的储能系统参与一次调频策略[J].电力系统自动化, 2020, 44(19): 63-72.
Li Junhui, Hou Tao, Mu Gang, et al. Primary frequency regulation strategy with energy storage system based on weight factors and state of charge recovery[J]. Automation of Electric Power Systems,2020, 44(19):63-72.
[18] 李若, 李欣然, 谭庄熙, 等. 考虑储能电池参与二次调频的综合控制策略[J]. 电力系统自动化, 2018,42(8): 74-82.
Li Ruo, Li Xinran, Tan Zhuangxi, et al. Integrated control strategy considering energy storage battery participating in secondary frequency regulation[J].Automation of Electric Power Systems, 2018, 42(8):74-82.
[19] 闫鹤鸣, 李相俊, 麻秀范, 等. 基于超短期风电预测功率的储能系统跟踪风电计划出力控制方法[J].电网技术, 2015, 39(2): 432-439.
Yan Heming, Li Xiangjun, Ma Xiufan, et al. Wind power output schedule tracking control method of energy storage system based on ultra-short term wind power prediction[J]. Power System Technology, 2015,39(2): 432-439.
[20] 马智慧, 李欣然, 谭庄熙, 等. 考虑储能调频死区的一次调频控制方法[J]. 电工技术学报, 2019,34(10): 2102-2115.
MA Zhihui, Li Xinran, Tan Zhuangxi, et al. Integrated control of primary frequency regulation considering dead band of energy storage[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2102-2115.
[21] Tan Zhuangxi, Li Xinran, He Li, et al. Primary frequency control with BESS considering adaptive SoC recovery[J]. International Journal of Electrical Power & Energy Systems, 2019, DOI: 10.1016/j.ijepes.2019.105588.
[22] 虞临波, 寇鹏, 冯玉涛, 等. 风储联合发电系统参与频率响应的模型预测控制策略[J]. 电力系统自动化, 2019, 43(12): 36-43.
Yu Linbo, Kou Peng, Feng Yutao, et al. Model predictive control strategy for combined wind-storage system to participate in frequency response[J].Automation of Electric Power Systems, 2019, 43(12):36-43.
[23] 陈达鹏, 荆朝霞. 美国调频辅助服务市场的调频补偿机制分析[J]. 电力系统自动化, 2017, 41(18): 1-9.
Chen Dapeng, Jing Zhaoxia. Analysis of frequency modulation compensation mechanism in frequency modulation ancillary service market of the united states[J]. Automation of Electric Power Systems, 2017,41(18): 1-9.
[24] 姜欣, 郑雪媛, 胡国宝, 等. 市场机制下面向电网的储能系统优化配置[J]. 电工技术学报, 2019,34(21): 4601-4610.
Jiang Xin, Zheng Xueyuan, Hu Guobao, et al.Optimization of battery energy storage system locating and sizing for the grid under the market mechanism[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4601-4610.
[25] 陈浩, 贾燕冰, 郑晋, 等. 规模化储能调频辅助服务市场机制及调度策略研究[J]. 电网技术, 2019,43(10): 3606-3617.
Chen Hao, Jia Yanbing, Zheng Jin, et al. Research on market mechanism and scheduling strategy of frequency regulation auxiliary service of large-scale energy storage[J]. Power System Technology, 2019,43(10): 3606-3617.
[26] 马恒瑞, 王波, 高文忠, 等. 区域综合能源系统中储能设备参与辅助服务的运行优化[J]. 电力系统自动化, 2019, 43(8): 34-40.
Ma Hengrui, Wang Bo, Gao Wenzhong, et al.Operation optimization of energy storage equipment participating in auxiliary service in regional integrated energy system[J]. Automation of Electric Power Systems, 2019, 43(8): 34-40.
[27] 谢敏, 韦薇, 李建钊, 等. 储能电站参与能量-调频市场联合调度模式研究[J]. 电力建设, 2019, 40(2):20-28.
Xie Min, Wei Wei, Li Jianzhao, et al. Research on combined dispatching mode of energy storage in energy market and regulation market[J]. Electric Power Construction, 2019, 40(2): 20-28.
[28] 胡泽春, 夏睿, 吴林林, 等. 考虑储能参与调频的风储联合运行优化策略[J]. 电网技术, 2016, 40(08):2251-2257.
Hu Zechun, Xia Rui, Wu Linlin, et al. Joint operation optimization of wind-storage union with energy storage participating frequency regulation[J].Power System Technology, 2016, 40(8): 2251-2257.
[29] 王杰, 方日升, 温步瀛. 风储联合系统参与能量市场和调频辅助服务市场协同优化[J]. 电器与能效管理技术, 2019(20): 51-57, 63.
Wang Jie, Fang Risheng, Wen Buying. Collaborative optimization in energy and frequency regulation markets for wind farm with energy storage[J].Electrical & Energy Management Technology, 2019(20):51-57,63.
[30] 文云峰, 杨伟峰, 汪荣华, 等. 构建100%可再生能源电力系统述评与展望[J]. 中国电机工程学报,2020, 40(6): 1843-1856.
Wen Yunfeng, Yang Weifeng, Wang Ronghua, et al.Review and prospect of toward 100% renewable energy power systems[J]. Proceedings of the CSEE,2020, 40(6): 1843-1856.
[31] Jacobson M Z, Delucchi M A, Bazouin G, et al. A 100% wind, water, sunlight (WWS) all-sector energy plan for Washington State[J]. Renewable Energy,2016, 86: 75-88.
[32] 李欣然, 邓涛, 黄际元, 等. 储能电池参与电网快速调频的自适应控制策略[J]. 高电压技术, 2017,43(7): 2362-2369.
Li Xinran, Deng Tao, Huang Jiyuan, et al. Battery energy storage systems self-adaptation control strategy in fast frequency regulation[J]. High Voltage Engineering, 2017, 43(7): 2362-2369.
[33] 李建林, 牛萌, 周喜超, 等. 能源互联网中微能源系统储能容量规划及投资效益分析[J]. 电工技术学报, 2020, 35(4): 874-884.
Li Jianlin, Niu Meng, Zhou Xichao, et al. Energy storage capacity planning and investment benefit analysis of micro-energy system in energy interconnection[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 874-884.
[34] 孙丙香, 李旸熙, 龚敏明, 等. 参与AGC 辅助服务的锂离子电池储能系统经济性研究[J]. 电工技术学报, 2020, 35(19): 4048-4061.
Sun Bingxiang, Li Yangxi, Gong Minming, et al.Study on the economy of energy storage system with lithium-ion battery participating in AGC auxiliary service[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4048-4061.
[35] Pandžić, H. Bobanac V. An accurate charging model of battery energy storage[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1416-1426.
[36] Vagropoulos S I, Bakirtzis A G. Optimal bidding strategy for electric vehicle aggregators in electricity markets[J]. IEEE Transactions on Power Systems,2013, 28(4): 4031-4041.