0 引言
风电机组精确、高效、实时的风速预测不仅可以提高风电并网的友好性,还能为风电机组的控制性能提升提供可靠的数据支撑。随着风电场的大规模建设和现场运维经验的不断增加,提高风电机组的控制性能和风能利用率已经成为风电研究的热点。研究表明,提前分钟级准确获取风电机组的风速预测值,可提高6%~10%风电机组的风能捕获率,降低风机16%~25%的疲劳载荷,延长风机桨叶的使用寿命[1-3],对风电场的经济安全运行具有重要的意义。
国内外学者对风速预测开展了大量的研究工作,并取得了一系列的成果。目前,风速预测的主要方法有持续预测法[4-5]、时间序列法[6-7]、神经网络预测法[8-10]、数值天气预报预测法[11-12]和空间相关性预测法[13-16]。其中,持续预测法原理简单,容易实现。持续预测法是将最近时刻的风速观测值作为下一时刻的风速预测值,在风速短期预测中,该方法的预测精度较高,在风速预测领域已经得到了广泛的应用。持续预测法的不足是要求风速前后数据具有很强的相似度,受季节变化、气压、地形、温度等因素影响较大[4]。时间序列法利用大量的历史数据进行训练,通过模型识别、参数估计和模型检验确定一个能够描述风速时序的模型,最后根据当前观测值进行风速预测,但时间序列法精准预测的前提是历史数据序列和外部环境因素不会发生突变,其适用性和强壮性有待加强[7]。神经网络预测法是模拟人脑神经元结构,通过大量数据学习、分类、识别、进化确定神经元节点和隐性非线性映射的模型,具有自学习和自适应的能力,广泛应用于风速短期预测,但难以确定科学的网络结构,易陷入局部最小点,预测结果不稳定,精度难以满足要求。数值天气预测主要利用风速、风向等气象预测信息,结合预测点的空间位置、地形特征推算出下一时刻的风速值,该方法计算量大,且依赖大量的天气预测数据,预测精度较差。空间相关性法利用风能在空间位置上存在的风速相关性,选择相关性较高的测风塔数据进行短期/超短期的风速预测,结合人工智能算法模型,空间相关性预测法表现出了良好的预测精度和可靠的预测性能,已经受到了专家学者们的普遍关注[13-20]。
上述风速预测的方法各有特点,在面向并网调度的中长期风速预测研究方面取得了丰硕的成果,短期/超短期的风速预测也广泛应用于电力系统的可靠性评估和潮流计算等领域。文献分析可知,当前的风速预测主要面向风电场场域的风功率预测和风电安全并网研究领域,面向风电机组控制性能提升方面,风速的超短时/实时预测研究鲜有开展。相关研究指出,提前10min 准确获取风速风向预测值,有利于风电机组保持最大风功率跟踪和强湍流效应预测,对提高风能捕获量,降低风机的极限载荷具有重要意义[21]。
风能在风电机组之间传播,上、下风位的机组间相互影响,充分考虑各机组的地理分布,利用风电机组间广泛存在的风速空间相关性,在风电场既有的拓扑结构和通信网络的基础上,实现风机之间的信息交互,将每台风电机组上独立风速/风向传感器组成感知阵列,可形成风电场风速/风向感知机联网。通过上风位关联机组的风速信息向下风位机组的传递共享,理论上可获得min 级的风速实时预测值[17]。基于机联网“关联-共享”的风速预测模式,为风电机组风速实时预测提供了新的思路[18],也为风电机组的前馈控制和风能高效利用打开广阔的想象空间,具有显著的经济效益和工程应用价值,值得关注与研究。
鉴于此,本文提出了基于机联网-空间相关性权重的风电机组风速预测框架,构建了一种实时预测模型及流程,基于卡尔曼滤波算法,对提出方法的可行性及有效性进行了验证。
1 基于机联网-空间相关性权重的风速预测框架
1.1 可行性分析
由于大气压差的存在,在特定的地理环境和复杂的大气运动作用下,风能在不同风电机组间传播时,其风速和风向都会有很强的时空联系,相邻机组的风速值往往存在广泛的相关性。并且风速越大,上下游之间的风速相关性越显著,空间相关性风速预测的效果越好,能可靠地降低大风时期的风速预测误差[20];另外,季风气候也是直接影响风电机组风速相关性的主要因素之一,我国的千万kW 级风电基地均处于季风区或蒙古高压之下,冬季风和夏季风的持续时间往往在7 个月以上,相比于欧美(季风现象不明显,北美不存在扩展的季风现象)利用空间相关性进行风速预测具有客观明显的优势[21-22]。综合我国风电基地分布位置和风速相关性预测的优势,本文基于风电机组间的风速相关性,利用风电场历史运行数据和当前风速观测值,重点开展风速实时预测研究。
查阅文献可知,风电场内风能传播受到季风气候的影响,其主导风向在一段时间内往往变化不大,处于同风带下空间位置相邻的风电机组间存在很强的风速空间相关性。理论上,当其风速相关系数达到一定的阈值范围,相邻风电机组间的风速大小相近,可以将上风位风机作为关联种子机组,利用其风速历史运行数据和当前观测值来预测下风位目标机组的下一时刻风速值。然而,风电机组间的风速相关性具有时变性和差异性,不同季节、不同时段、不同风速风向下存在较大差异,表现出季节性变化,在主导风向和中高风速区相关性高且稳定的特点[23]。利用单台风速关联的风电机组进行空间相关性风速实时预测,其预测误差会受关联种子机组选择的影响,若种子机组与目标机组在一段时间内风速相关性变化较大,则会给风速实时预测值造成很大的误差,因此单台关联风机空间相关性预测模式下的预测精度抗干扰性和容错性较差。相关研究已表明:以待测风电机组为目标机组,选取周边几个测风塔风速历史观测值为基础数据,采用风速空间相关性来预测目标机组未来风速,可有效降低预测误差[24]。可见在主导风向下选择目标机组上风位的多台邻近风电机组作为关联种子机组,根据不同时间窗口下各机组与目标机组的风速相关性,动态调整种子关联机组,可大幅提升关联机组筛选的容错性,保证风速预测精度的可靠性与强壮性。
此外,相关研究表明风能除具有风速相关性外,还具有传播路径空间上的时延性。风在通过风电机组风轮后速度会下降,即存在“尾流效应”,需要经过一定的空间距离才能恢复。工程上为减少尾流效益带来的风能衰减,在主风向上,风电机组的空间地理距离典型值为8~10 倍的机组风轮直径,典型距离为500~800m 之间。统计表明实际风场90%以上时间风速小于12m/s,那么对于12m/s 以下的风,比如10m/s 的风,从上风位机组传到下风位机组时间Ti+1 将不小于50s(对应500m 的行距),在时间尺度上可很好地匹配与风电机组偏航、变桨和发电控制的响应时间。再者,在拓扑结构上安装于风电机组上的传感器形成了风速风向等风参数密集型分布式传感器阵列,可为风电机组间的信息交互共享提供天然平台;在通信上,全场域分布的光纤通信网络,保证了风电机组风参数获取共享的时效性。
综上所述,由于风电机组间的空间位置/地面表面粗糙度短时间内不会发生改变。短时间内,利用上、下游风机之间风速存在的关联性和时延性,由风速相关性较强的相邻上风位机组的风速观测值,获得下风位风机的实时预测风速值,实现min 级的风速预测是可行的。
1.2 预测框架
图1 是构建的基于机联网-空间相关性权重的风电机组实时风速预测架构。主要包括信息共享机联网搭建与数据处理、关联共享风电机组种子筛选、目标机组风速实时预测模型三部分。

图1 基于机联网-空间相关性权重风电机组风速预测架构
Fig.1 Framework of real-time wind speed prediction with multi-turbine information sharing
1.2.1 信息共享机联网搭建与数据处理
风电机组的运行数据获取是多机信息共享的风速实时预测及后续分析的基础,运行数据可分为历史数据和实时数据两部分。其中,历史数据是目标机组相关性分析的主要数据源,决定着关联风电机组种子的筛选。从风电场SCADA 系统采集各风电机组的风速、风向历史时序数据后,需要进行以下数据预处理:
1)风电数据清洗:风电机组的运行异常停机和数据异常会使得风电历史数据存在一定的脏数据,在统计风电机组风速相关性前需要进行风电数据的清洗整定。
2)关联种子机组区域划分:空间距离越近的风电机组,其风速相关性越强[24],根据此原则,以待预测的风电机组为目标机组,选择距离最近场域内的N 台风电机组作为备选种子机组。
3)风向区筛选:风电机组间的风速相关性是具有气象条件性的,在主导风向上其风速相关性表现出很强的稳定性[27],因此本文考虑风向变化的影响,筛选出主风向下的风电机组作为研究对象机组。
风速实时数据的时效性和可靠性是影响目标机组风速预测结果的另一重要因素。理论上,风电机组自身的风速、风向等传感器可实时监测风机的各项风参数数据,通过风电机组间广泛互联的光纤通信,就形成了分布式风参数传感网络,因此,在风电场的网络拓扑结构的基础上即可建立风电机组风速信息共享的机联网。利用风电机组间的信息共享机制,可实时获取每台机组的风速、风向、温度、湿度等风参数信息,上传至控制中心,通过数据筛选并输入风速实时预测模型,即可获取目标机组的风速预测值。
1.2.2 信息共享风电机组筛选
风电机组间的风速相关性强弱直接决定了基于风速空间相关性风速预测结果的精度,所以关联风电机组的种子优选是风电机组实时预测体系中的关键部分。针对风速实时感知预测,目标机组的关联种子机组一般应为两台以上,方能保证其风速预测值的可靠性与抗干扰性。关联风电机组的筛选可按如下步骤进行:
1)风速相关性时序分析:由于风速相关性具有很强的时变性,因此要考虑关联机组的风速相关性时序变化,根据实际运行历史数据,分析备选种子机组与目标机组的风速相关系数随时段的变化特征,为后续的关联机组种子动态筛选提供依据。
2)动态关联种子机组筛选:根据不同时段待选风电机组与目标机组的相关系数,设定一个关联机组的阈值,当备选机组的风速相关系数达到阈值范围即可优选为关联种子机组。依此原则,即可获得不同时段下的动态关联种子机组的优选结果。
1.2.3 风电机组风速预测模型
基于多机关联的风电机组风速预测实质上是多台关联种子机组的组合风速预测,在空间相关性风速预测的基础上,以单台关联风电机组进行风速空间相关性实时预测,然后再对不同关联种子机组进行动态权重分析,最后将每台关联种子机组的预测结果进行动态加权组合获得最后的目标机组风速实时预测值。预测模型核心内容是关联种子机组预测组合权重的确定,其步骤如下:
1)预测时间窗口进行时间分段:由于风速相关性存在时变性,不同时间段内,同一台风机与目标机组的风速相关性存在波动性,需根据季节和地理位置下风电机组风速相关性的分布特征,选择适当的时间周期进行相关性统计,作为关联种子筛选的依据。
2)关联种子机组组合预测权重计算:以种子机组与目标机组的风速相关系数为对象,首先剔除相关性较低的种子机组,然后进行风速相关系数的归一化,由相关系数大小确定各时段内的动态组合权重系数。
2 机联网-空间相关性权重风速预测模型
2.1 预测模型
由上文可知,机联网-空间相关性权重风速预测首先应该进行单台关联风电机组的风速空间预测,其预测方差可简述为
式中, vit 为利用第i 台关联种子机组得到的风速实时预测值;vi ,t1- 为第i 台关联种子机组的前一时刻风速观测值; τi为第i 台关联种子机组与目标机组间的时间延时。
风速预测输出不仅与关联机组的观测值有关,还应考虑关联风电机组与目标机组在空间上存在的时间延迟。由于时间延迟与空间距离 di 和风速 vi大小有关,风速在短时间内不会突变,故可用平均风速代替,时间延迟为
由于风速预测结果受风速相关性的时变性特征影响较大,在利用风速相关性进行风速预测时,需随时间变化统计风速相关性,以便进行种子机组的更新和动态权重系数计算。设定用于种子机组更新的风速相关性统计时间周期为T,目标机组风速预测的时间周期为TF,则第j 个预测周期下种子机组更新周期起止时刻的滚动过程如式(3)所示。
式中,ts0 为样本数据起始时刻;tsj 为第j 个预测时刻的风速相关性统计开始时刻;tej 为第j 个预测时刻的风速相关性统计周期结束时刻。
由于风速预测结果受风速相关性的时变性特征影响较大,在利用风速相关性进行风速预测时,需随时间变化统计风速相关性,以便进行种子机组的更新和动态权重系数计算。考虑到风速预测的实时性,不宜频繁更换种子机组。设定用于种子机组更新的风速相关性统计时间周期为T,目标机组风速预测的时间周期为TF,则第j 个预测周期下种子机组更新周期起止时刻的滚动过程如图2 所示。
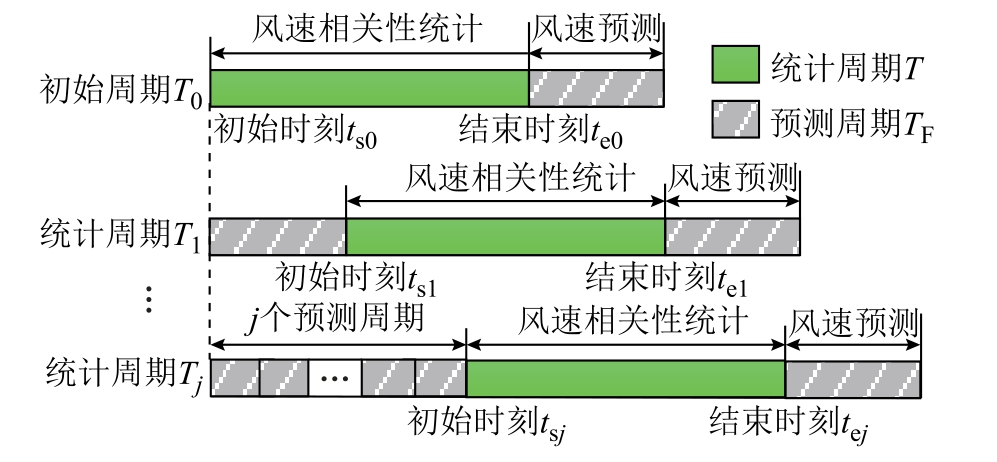
图2 关联机组更新周期示意图
Fig.2 Renewal period diagram of associated wind turbines
由图2 可知风速相关性统计周期T 保持不变,在第j 个更新周期内,风速相关性分析周期的初始时刻tsj 应在上一更新周期初始时刻的基础上推迟一个风速预测周期TF;其结束时刻 tej 与之同理。种子机组更新周期的开始时刻 tsj 和结束时刻 tej 计算如式(3)。
在关联种子的更新周期内,描述种子机组与目标机组的风速相关性,常用的有皮尔逊相关系数和Copula 函数。Copula 函数能较好地刻画变量之间多维度的非线性相关性,但计算过程较为复杂。本文主要为了验证机联网-空间相关性权重风速预测模型的有效性与可行性,故采用应用广泛,计算较简单的皮尔逊相关系数,其计算公式和组合权重因子分别为
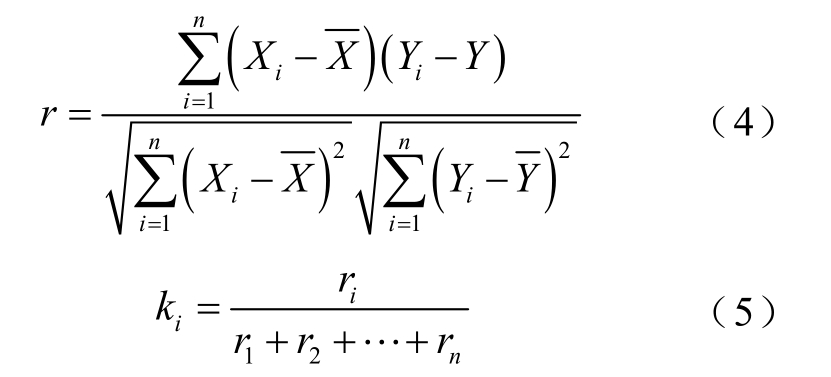
式中,ri为关联机组i 与目标机组的风速相关系数;k i为关联机组i 的组合权重因子。风速相关系数 ri越高,权重因子 k i就越大,关联种子机组i 在目标机组的风速预测结果中占的比例也就越大。
综上,风电机组的多机关联预测模型可表示为
式中,Vt 为目标机组的实时风速预测输出值。
2.2 预测流程
基于机联网-空间相关性权重的风电机组风速预测流程如图3 所示,主要包括风速风向时序采集预处理、关联风电机组种子筛选、多机关联预测模型搭建与风速预测输出等步骤。
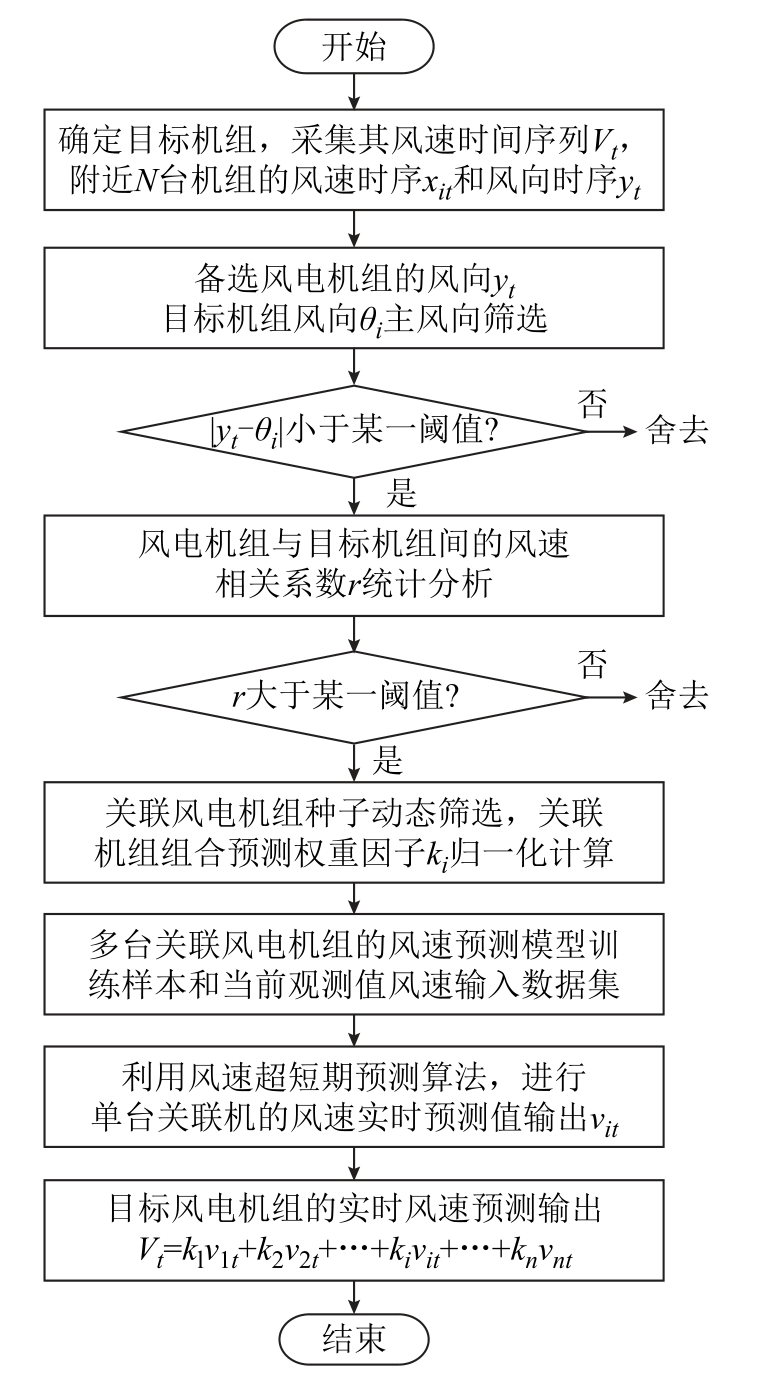
图3 机联网-空间相关性权重风电机组风速预测流程
Fig.3 Real-time wind speed forecasting process with multi-turbine information sharing
3 算例分析
本节以张北某风电场实际数据为样本,基于卡尔曼滤波算法实现前述建立的风速预测模型,并将其与持续预测法、传统空间预测方法预测结果进行对比,以验证所提方法的可行性与有效性。
3.1 卡尔曼滤波算法
卡尔曼滤波算法是一种有效的以最小方均误差来估计系统状态的计算方法,即通过将前一时刻预报误差反馈到原来的预报方程中,及时修正预报方程系数,以提高下一时刻的预报精度。在风速实时预测中,通过风速预测值的实时修正可以不断接近实际风速值,提高实时风速预测的精度。在卡尔曼滤波算法中,描述系统的数学模型是状态方程和量测方程,即
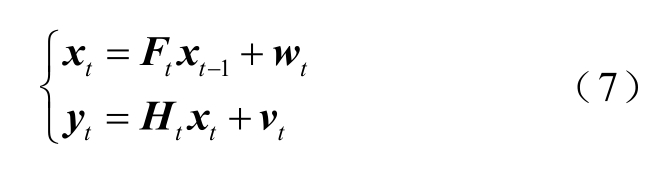
式中, xt为未知过程在t 时刻的状态向量; ty 为t 时刻的观测向量; Ft 和Ht 分别为系统矩阵及观测矩阵,且必须在滤波器应用之前确定; wt和 vt 分别为系统噪声和量测噪声,均假定为高斯白噪声且相互独立,与其相对应的协方差矩阵分别为Wt 和 Vt 。
3.2 案例分析数据及风电机组选择
案例数据来源于张北某风电场风电机组 2016年3 月份的实际运行数据,该样本数据的采样间隔为15min。以其中2016 年3 月1 日至2016 年3 月25 日的实际运行数据作为预测模型学习的训练集,利用2016 年3 月26 日至2016 年3 月30 日数据进行目标机组的风速预测及误差分析。
所选风电场地处华北平原与内蒙古高原连接带,地势平坦,冬季季风现象明显,风机为SE8215-L3/1 500kW 型风电机组,切入风速和切出风速分别为3m/s、20m/s,期间风电场主风向为东南方向。该风电场风电机组空间布局如图4 所示。

图4 风电场风机分布拓扑
Fig.4 Wind turbine distribution diagram
综合空间距离及沿风向布置关系,理论上若选择24 号机组为目标机组,21 号、22 号、23 号风电机组理论上均可作为种子机组。基于历史运行数据的相关性统计计算结果表明[23],上游21 号、22 号、23 号风电机组与24 号目标机组的风速相关性分别为0.676 5、0.905 67、0.868 59,参照风速相关性的判断准则,22 号、23 号两台风电机组属于高度相关机组,这两台机组可作为目标机组24 号风速关联种子机组。
3.3 不同风速预测方法预测结果对比分析
3.3.1 持续预测法预测结果
持续预测法是一种原理简单、容易实现、经济实用的预测方法。为了评估信息共享关联预测法对于小时间尺度的风速预测效果,本文选择24 号风电机组作为目标机组开展了持续法风速预测案例分析,预测结果如图5 所示。

图5 持续预测法风速预测
Fig.5 Wind speed forecasting based on continuous method
由图5 可知,基于持续预测法的风速预测结果整体精度较高,预测结果能较好地追踪风速变化。但是,在某些风速突变的样本点处,风速预测的误差较大。可见持续预测法对于风速前后数据相似度的依赖性较高,对于风速高频信号的预测,需改进并完善持续预测模型,以进一步提高风速预测精度。
3.3.2 传统空间相关性法预测结果
空间相关性法因其良好的预测精度与可靠性,已成为风电场风速预测领域的主流方法[15-20]。为了对比验证信息共享关联预测方法在相关性风速预测方面的优点,本文基于卡尔曼滤波算法利用传统空间相关性风速预测模型开展了传统空间相关性法风速预测算例分析。分别以22 号、23 号机组作为24号目标机组的关联预测机组,24 号机组风速实时预测值的预测结果如图6 所示。

图6 传统空间相关性风速预测结果
Fig.6 Single-turbine wind speed prediction based on spatial correlation
由图6 可知,24 号风电机组的实时风速预测精度和稳定性会因关联种子的不同而产生较大的差异性。以100h 的预测窗口为例,如图6a 中在前20h内的预测值与实际值误差很小,计算其平均绝对百分比误差为12.87%,但在后40h 时间段内其误差达到了30.34%;分析图6b 可知,在预测时间窗口内,以23 号风电机组为关联种子机组,目标机组的风速预测误差范围为8.23%~40.23%。统计22 号和23 号风电机组在预测时间窗口内的风速相关性发现,其风速相关系数具有强的时变性,导致预测误差的波动性比较大,可见,传统空间相关性风速预测模式下,风速预测的精度受关联种子机组及其与目标机组的风速相关性的影响较大。
3.3.3 机联网-空间相关性权重风速预测法预测结果
基于卡尔曼滤波算法的机联网-空间相关性权重的风电机组风速预测流程,选择多台风速相关性较强的关联风电机组,采用“多机共享关联+动态权重”模式对目标机组开展实时风速预测分析。设定种子机组更新时间周期T=10h,风速预测时间周期TF=10h,则关联种子机组的风速相关性的时变性统计和共享关联机组的动态权重计算结果见表1。
表1 关联风电机组的风速相关系数及动态权重
Tab.1 Wind speed correlation coefficient and dynamic weight of wind turbines

统计时段/h关联机组风速相关系数 动态权重系数22 号机组 23 号机组 22 号机组 23 号机组0~10 0.796 9 0.918 6 0.464 5 0.535 5 10~20 0.659 3 0.499 5 0.569 0 0.431 0 20~30 0.842 1 0.253 6 1.000 0 0.000 0 30~40 0.920 8 0.897 3 0.506 5 0.493 5 40~50 0.758 4 0.493 1 0.606 0 0.394 0 50~60 0.696 2 0.504 8 0.579 7 0.420 3 60~70 0.761 5 0.719 4 0.514 2 0.485 8 70~80 0.795 7 0.727 1 0.522 5 0.477 5 80~90 0.687 9 0.601 0 0.533 7 0.466 3 90~100 0.785 0 0.838 1 0.483 6 0.516 4
由表1 可知,22 号与23 号风电机组虽与24 号风电机组存在很显著的风速相关性,但在不同时间窗口内,其风速相关性差异变化可能会比较大。比如20~30h 时间窗口内,23 号风电机组与目标机组的风速相关性很微弱,不适合作为目标机组风速预测的种子机组,其组合预测权重应设置为零。图7为利用22 号、23 号风电机组多机共享关联预测得到的24 号风电机组风速预测结果。

图7 多机信息共享的风速预测结果
Fig.7 Wind speed forecasting results with multi-turbine information sharing
由图7 可得,基于提出的风速预测模式得到的24 号目标风电机组的风速预测值与实际值吻合度好,预测精度高,且预测结果稳定性好。
3.3.4 预测误差分析
图8 为案例分析中传统空间相关性风速预测和本文提出的机联网-空间相关性权重风速预测的时序误差结果对比。

图8 风速预测结果误差分析
Fig.8 Error analysis of wind speed prediction results
由图8 可知,提出的风速预测方法时序预测误差普遍比传统空间相关性风速预测误差小,预测结果与实际值差别较大的情况也很少发生;在误差分布上,传统单机空间相关性风速预测和多机共享关联预测的误差分布大致呈Weibull 分布。传统空间相关性风速预测的误差主要分布在25%以内,提出的机联网-空间相关性权重风速预测的误差集中分布在15%以内,预测误差大于50%的鲜有分布。
表2 所示为案例分析中不同预测方法的方均根误差RMSE、平均绝对误差MAE 和平均绝对百分比误差MAPE 量化分析结果。相关研究成果表明,持续预测法风速超短期预测时精度可靠,空间相关性法在数小时(天)的风速预测上与持续预测法相比具有更好的表现[13,15]。
表2 风速预测误差指标对比
Tab.2 Comparison of wind speed prediction error
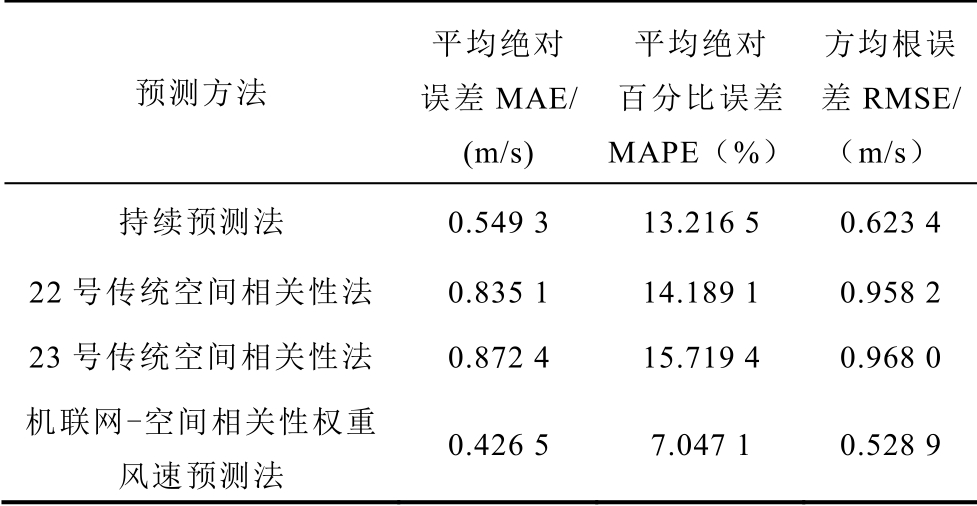
预测方法平均绝对误差MAE/(m/s)平均绝对百分比误差MAPE(%)方均根误差RMSE/(m/s)持续预测法 0.549 3 13.216 5 0.623 4 22 号传统空间相关性法 0.835 1 14.189 1 0.958 2 23 号传统空间相关性法 0.872 4 15.719 4 0.968 0机联网-空间相关性权重风速预测法0.426 5 7.047 1 0.528 9
由表2 可知,持续预测法平均百分比误差约为13%,传统空间相关性法预测百分比误差在15%左右,平均绝对误差在0.85m/s 左右;机联网-空间相关性权重风速预测法平均绝对误差和百分比误差分别为0.426 5m/s 和7%左右,预测精度与稳定性均有较明显的提升。
3.4 讨论与展望
1)持续预测法将最近一点的风速值作为下一时刻的风速预测值,其预测精度依赖前后风速数据的相似度,理论上风速观测值的采样时间越短,其风速预测值就越接近其实测值。但是,随着样本时间的增大,当前一时刻的风速观测值与后一时刻的风速值相似度不高时,利用持续法进行预测,就会带来较大的局部误差。如图5 中100~140、190~210 样本点时段内,风速序列并非平稳变化,持续法不能较好地处理风速突变的情况,造成了较大的局部预测误差,这也正是限制持续预测法不能进一步提高预测精度的原因。
2)传统的空间相关性风速预测方法的准确性依赖风电机组间的相关系数,风速相关性越强,预测精度越好[15]。研究已表明,风速相关性除了与空间位置有关,还受时序和气象的影响,具有时变性的特征[15,23]。图6 中80~105h 时序内正是因为风速相关系数的降低使得风速预测精度下降。
3)本文提出的机联网-空间相关性权重风速预测法,通过选择多台风速相关的风电机组作为关联种子,基于风速相关系数时序的变化计算动态权重因子,实现多种子机组间的风速信息共享与互补,有效降低了风速空间相关性的波动的影响,提高了风速预测精度和稳定性。
4)由于受样本数据的限制,案例分析中的数据样本采样时间为15min,限制了目标风电机组风速预测最小时间尺度为15min。理论上,基于信息共享的关联组合预测模型,根据所选样本数据的时间尺度,可以实现多尺度的风速预测。当采样周期为天,可进行中长期风速预测,有利于制定并网调度策略和风电场的规划设计;当采样周期为数小时,可实现风速短期预测,提高风电场的风能利用率;当风电场的运行数据存储采样周期达到数十秒或分钟级,即可进行风速实时预测,提高风电机组控制性能。缩短动态权重的更新时间间隔周期,有利于进一步提高目标机组的预测结果的精度,但会增加模型计算量,影响风电机组风速预测的计算效率。实际工程应用中,需综合考虑预测精度与时效性。
4 结论
本文提出的基于机联网-空间相关性权重风电机组风速实时预测模型及流程是可行有效的,具有预测精度高、容错性和稳健性好的特点。算例结果表明提出的机联网-空间相关性权重风速预测法可有效克服风速序列风速突变及风速空间相关性波动的影响,不仅适用于面向风机控制小时间尺度的风速预测,同样适用于面向并网风电功率预测中长时间尺度的风速预测,具有普适性。
[1] Bottasso C L, Pizzinelli P, Riboldi C E D, et al.LiDAR-enabled model predictive control of wind turbines with real-time capabilities[J]. Renewable Energy, 2014, 71(71): 442-452.
[2] Wang Na, Johnson K E, Wright A D. FX-RLS-based feed forward control for LIDAR-enabled wind turbine load mitigation[J]. IEEE Transactions on Control Systems Technology, 2012, 20(5): 1212-1222.
[3] Wang Na, Johnson K E, Wright A D. Comparison of strategies for enhancing energy capture and reducing loads using LIDAR and feed forward control[J]. IEEE Transactions on Control Systems Technology, 2013,21(4): 1129-1142.
[4] Mohammad A C, Sami F M, Trzynadlowski A M.Wind speed and wind direction forecasting using echo state network with nonlinear functions[J]. Renweable Energy, 2019,131: 879-889.
[5] Guo Yifei, Gao Houlei, Wu Qiuwei. A combined reliability model of VSC-HVDC connected offshore wind farms considering wind speed correlation[J].IEEE Transactions on Sustainable Energy, 2017, 8(4):1637-1646.
[6] 孙国强, 卫志农, 翟玮星. 基于 RVM 与 ARMA误差校正的短期风速预测[J]. 电工技术学报, 2012,27(8): 187-193.
Sun Guoqiang, Wei Zhinong, Zhai Weixing. Short term wind speed forecasting based on RVM and ARMA error correcting[J]. Transactions of China Electrotechnical Society, 2012, 27(8): 187-193.
[7] Erdem E, Shi J. ARMA based approaches for forecasting the tuple of wind speed and direction[J].Applied Energy, 2011, 88(4): 1405-1414.
[8] Ak R, Fink O, Zio E. Two machine learning approaches for short-term wind speed time-series prediction[J]. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(8): 1734-1747.
[9] 刘兴杰, 岑添云, 郑文书, 等. 基于模糊粗糙集与改进聚类的神经网络风速预测[J]. 中国电机工程学报, 2014, 34(19): 3162-3169.
Liu Xingjie, Cen Tianyun, Zheng Wenshu, et al.Neural network wind speed prediction based on fuzzy rough set and improved clustering[J]. Proceedings of the CSEE, 2014, 34(19): 3162-3169.
[10] Ak R, Vitelli V, Zio E. An interval-valued neural network approach for uncertainty quantification in short-term wind speed prediction[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(11): 2787-2800.
[11] Chen Niya, Qian Zheng, Nabney I T, et al. Wind power forecasts using Gaussian processes and numerical weather prediction[J]. IEEE Transactions on Power Systems, 2014, 29(2): 656-665.
[12] 彭小圣, 熊磊, 文劲宇, 等. 风电集群短期及超短期功率预测精度改进方法综述[J]. 中国电机工程学报, 2016, 36(23): 1-12.
Peng Xiaosheng, Xiong Lei, Wen Jinyu, et al. A summary of the state of the art for short-term and ultra-short-term wind power prediction of regions[J].Proceedings of the CSEE, 2016, 36(23): 6315-6326.
[13] 陈宁, 薛禹胜, 丁杰, 等. 利用空间相关性的超短期风速预测[J]. 电力系统自动化, 2017, 41(12): 124-130.
Chen Ning, Xue Yusheng, Ding Jie, et al. Ultra-short term wind prediction using spatial correlation[J].Automation of Electric Power Systems, 2017, 41(12):124-130.
[14] Damousis I G, Alexiadis M C, Theocharis J B, et al. A fuzzy model for wind speed prediction and power generation in wind parks using spatial correlation[J].IEEE Transactions on Energy Conversion, 2004, 19(2):352-361.
[15] 薛禹胜, 陈宁, 王树民, 等. 关于利用空间相关性预测风速的评述[J]. 电力系统自动化, 2017, 41(10):161-169.
Xue Yusheng, Chen Ning, Wang Shumin, et al.Review on wind speed prediction based on spatial correlation[J]. Automation of Electric Power Systems,2017, 41(10): 161-169.
[16] Li Pai, Guan Xiaohong, Wu Jiang, et al. Modeling dynamic spatial correlations of geographically distributed wind farms and constructing ellipsoidal uncertainty sets for optimization-based generation scheduling[J]. IEEE Transactions on Sustainable Energy, 2015, 6(4): 1594-1605.
[17] 韩兵, 周腊吾, 陈浩, 等. 大型风电机组激光雷达辅助模型预测控制方法[J]. 中国电机工程学报,2016, 36(18): 5062-5069.
Han Bing, Zhou Lawu, Chen Hao, et al. Approach to model predictive control of large wind turbine using light detection and ranging measurements[J].Proceedings of the CSEE,2016, 36(18): 5062-5069.
[18] Shen Xiaojun, Zhou Chongcheng, Li Guojie, et al.Overview of wind parameters sensing methods and framework of a novel MCSPV recombination sensing method for wind turbines[J]. Energies, 2018, 11(7):1747.
[19] Qin Zhilong, Li Wenyuan, Xiong Xiaofu. Generation system reliability evaluation incorporating correlations of wind speeds with different distributions[J]. IEEE Transactions on Power Systems,2013, 28(1): 551-558.
[20] 孙国强, 李逸驰, 向育鹏, 等. 计及风速时空相关性的含风电场电力系统动态随机最优潮流计算[J].中国电机工程学报, 2015, 35(17): 4308-4317.
Sun Guoqiang, Li Yichi, Xiang Yupeng, et al.Dynamic stochastic optimal power flow of wind integrated power system considering temporal and spatial correlation of wind speed[J]. Proceedings of the CSEE, 2015, 35(17): 4308-4317.
[21] 杨正瓴, 冯勇, 熊定方, 等. 基于季风特性改进风电功率预测的研究展望[J]. 智能电网, 2015, 3(1): 1-7.
Yang Zhengling, Feng Yong, Xiong Dingfang, et al.Research prospects of improvement in wind power forecasting based on characteristics of monsoons[J].Smart Grid, 2015, 3(1): 1-7.
[22] 修春波, 任晓, 李艳晴, 等. 基于卡尔曼滤波的风速序列短期预测方法[J]. 电工技术学报, 2014,29(2): 253-259.
Xiu Chunbo, Ren Xiao, Li Yanqing, et al. Short-term prediction method of wind speed series based on Kalman filtering fusion[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 255-259.
[23] 沈小军, 周冲成, 吕洪. 基于运行数据的风电机组间风速相关性统计分析[J]. 电工技术学报, 2017,32(16): 265-274.
Shen Xiaojun, Zhou Chongcheng, Lü Hong. Statistical analysis of wind speed correlation between wind turbines based on operational data[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 265-274.
[24] 杨正瓴, 刘阳, 张泽, 等. 采用最近历史观测值和PLSR 进行空间相关性超短期风速预测[J]. 电网技术, 2017, 41(6): 1815-1822.
Yang Zhengling, Liu Yang, Zhang Ze, et al. Ultrashort-term wind speed prediction with spatial correlation using recent historical observations and PLSR[J]. Power System Technology, 2017, 41(6):1815-1822.