0 引言
近年来随着化石能源储量日益下降及生态环境恶化趋势日益显著，太阳能由于属于安全环保、容易获取的新型可再生能源，正在发展成为世界新能源组成中的重要部分[1-6]。但由于光伏发电受制于材料物理性能限制，转换率较低，为了使光伏发电系统能够以较高效率利用太阳能，部分光伏发电技术研究者将研究重点转移至最大功率点跟踪（Maximum Power Point Tracking, MPPT）技术研究[7-8]。当光伏阵列的各组件所受光照度一样时，其P-U 曲线呈现单峰特性，传统MPPT 算法如扰动观测法[9]、电导增量法（Incremental Conductance, INC）[10]等可以较为准确地跟踪到最大功率点，然而实际应用中往往受安装环境及复杂气象因素影响，光伏阵列容易受到云雾、建筑物、积灰遮挡，导致其功率输出曲线呈现多峰特性，此时传统MPPT 控制方法往往会陷入局部寻优，无法准确跟踪到全局最大功率点（Global Maximum Power Point, GMPP），使得光伏阵列输出功率大幅降低，导致功率损耗[11-13]。
为了解决局部遮阴情况下传统 MPPT 控制方法无法搜索到GMPP 问题，国内外许多学者展开了大量的相关研究。文献[14]提出一种光伏阵列可重构优化配置方法，该方法根据光照在光伏阵列分布情况，采用矩阵式开关动态调整光伏阵列连接方式，减小由遮挡引起的功率损耗，虽然在一定程度上解决了功率失配问题，但由于其需要增加配置大量开关器件，导致系统硬件成本增加。文献[15-16]针对粒子群优化算法具有参数少、收敛速度较快优点，将其应用到光伏MPPT 控制中，取得了较为理想的控制效果。文献[17]针对粒子群算法在MPPT 控制中由于参数设置无法较为准确地跟踪到GMPP 问题，提出将粒子群与电导增量法相结合的复合控制算法，仿真结果表明该复合算法可以有效提高跟踪精度。文献[18]针对细菌觅食算法的寻优机制导致收敛精度与速度存在不足的问题，将全局学习方向与步长自适应调整策略引入到传统的细菌觅食算法中，同时利用两步法MPPT 控制策略将其应用到光伏MPPT 控制中，仿真结果表明所提方法能够在动态环境条件下高效地跟踪到GMPP，且鲁棒性较好。
鲸鱼优化算法（Whale Optimization Algorithm,WOA）是S. Mirjalili 等通过长期跟踪观察座头鲸捕食的行为方式，研究总结设计出的一种新型优化算法，与其他优化算法对比，该算法不仅原理简单易懂，所需手动调节设置的参数少，而且在算法运算速度方面也具备一定的优势，在炼钢终点预测[19]、短期风电预测[20]、车间调度[21]等诸多领域都取得了不错的应用效果。但WOA 与其他优化算法同样在收敛精度与跳出局部最优方面存在一定不足。本文首先在WOA 基础上引入对数权重因子与随机差分变异策略，增强了算法在全局搜索与局部开发协调性能及跳出局部最优能力；然后利用改进鲸鱼优化算法（Improved WOA, IWOA）与支持向量机回归相结合建立了光伏阵列最大功率点电压预测模型，并将其与电导增量法相结合应用到光伏MPPT 控制；最后利用Matlab/Simulink 搭建仿真模型，仿真结果表明本文所建立的光伏阵列最大功率点电压预测模型具有较高的预测精度，在光伏MPPT 控制应用中也取得了较为理想的效果，无论在局部遮阴或光照突变情况下都能快速准确搜索到GMPP。
1 局部遮阴下光伏阵列多峰特性分析
光伏电池的等效电路如图1 所示，图中， ID 为暗电流。
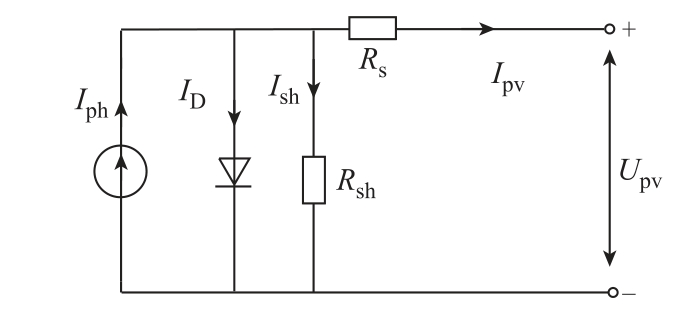
图1 光伏电池的等效电路
Fig.1 Equivalent circuit of photovoltaic cell
由电子学理论分析可推得其输出电流的数学方程表达式为
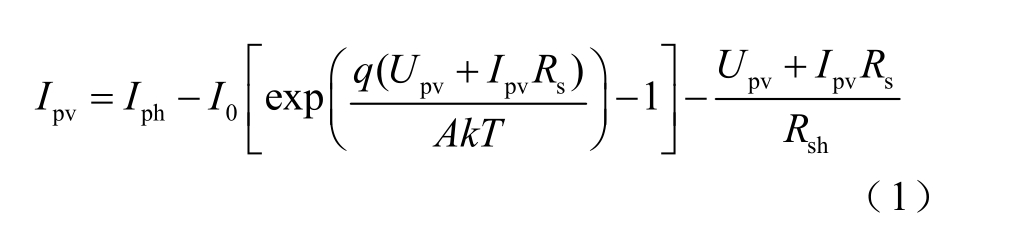
式中，Upv 和 Ipv 分别为单体光伏电池输出电压与输出电流； Iph 为光生电流；q 为电子电荷； I0 为反向饱和电流； Rsh 和 sR 分别为等效并联电阻与串联电阻；k 为玻耳兹曼常数，k=1.35×10-23J/K； A 为PN 结特性因子；T 为光伏电池的温度。
由于式（1）中A、 Rs、 Rsh 、 I0 参数的值与温度和光照强度等外部条件有关，而光照强度和温度会因环境而异，因此很难准确地测量到，工程上为方便分析其输出特性简化了其数学模型，提出简化参数关系为
式中，Im 为最大功率点输出电流；Isc 为短路电流；Um 为最大功率点输出电压；Uoc 为开路电压。
考虑到单体光伏电池最大输出电压也仅有微弱的0.6V 左右，无法直接应用到日常供电，工程应用中通常按照输出特性要求以一定的串并联方式将一定数量的单体光伏电池封装成光伏组件，再根据实际工程应用对电压电流的要求将一定数量的光伏阵列串并联起来组成光伏阵列。光伏组件处于局部遮阴情况下，部分单体电池将成为电路中的负载消耗能量，并导致光伏组件局部温度过高，形成“热斑效应”。为了防止“热斑效应”对光伏组件造成不可逆的损坏，通常会在光伏组件正极输出端与负极输出极间并联一个二极管。另外，为了防止各并联支路间的电流倒流，通常需要在并联电路间配置防逆二级管。因此光伏阵列的典型构造如图2所示。
图2 光伏阵列结构
Fig.2 Structure diagram of photovoltaic array
本文在Simulink 平台上建立了3×2 的光伏阵列仿真模型，利用该仿真模型对光伏阵列处于局部遮阴情况下的输出特性进行研究分析。将该光伏阵列的6 块光伏组件按照图2 所示进行编号，各光伏组件的具体参数：U oc 均为36.9V、 Isc 均为9A、最大输出电流 Im 均为8.34A、最大输出电压Um 均为30V。设置两种遮阴情况，其中，遮阴1：光伏组件温度25℃，PV1 与PV4 所受光照强度为600W/m2,PV2与PV5 所受光照强度为800W/m2,PV3 与PV6 所受光照强度为1 000W/m2；遮阴2：光伏组件温度25℃，PV1 与PV4 所受光照强度为800W/m2，PV2 与PV5所受光照强度为400W/m2,PV3 与PV6 所受光照强度为400W/m2。
图3 为两种局部遮阴情况下光伏阵列输出特性仿真曲线。
图3 局部遮阴下光伏阵列输出特性仿真曲线
Fig.3 Simulation curve of output characteristics of photovoltaic array under partial shading
由图3 分析可知，当光伏阵列受光不均匀时，其输出曲线将出现多个极值点，当光伏阵列处于遮阴情况1 时，其P-U 曲线具有三个极值点，I-U 曲线呈三阶梯形状；而当光伏阵列处于遮阴情况2 时，其P-U 曲线具有两个极值点，I-U 曲线呈双阶梯形状。综上可得，当光伏阵列处于不同遮挡情况，其功率输出曲线的峰值数量也有所差异，传统的MPPT 算法由于其搜索机制，将陷入局部寻优状态，无法准确跟踪到GMPP，因此研究适用于局部遮阴的光伏MPPT 控制算法就显得格外重要。
2 鲸鱼优化算法改进研究与性能验证
2.1 鲸鱼优化算法
WOA 是由S. Mirjalili 等[22]通过长期跟踪观察座头鲸捕食的行为方式，研究总结设计出的一种新型优化算法。座头鲸的螺旋气泡网捕食策略包括包围目标猎物、螺旋泡泡网攻击、搜索目标猎物三个环节，如图4 所示。
图4 座头鲸螺旋气泡网觅食策略
Fig.4 Foraging strategy of spiral bubble net by humpback whale
2.1.1 包围目标猎物
座头鲸在狩猎中可以通过识别目标猎物位置调整自身位置将其包围。在包围过程中，以当前距离目标猎物最近的个体座头鲸位置为当前最优解位置，其他座头鲸个体动态更新它们的位置向最优座头鲸位置靠近，包围目标猎物。该行数学模型为
式中， D 为最优个体位置与当前个体位置的距离；X∗( t)为当前最优解的位置向量； X ( t)为当前解的位置向量；t 为当前迭代；A 和C 为参数向量，其具体数学表达式分别为
式中， 1r 与 2r 为值在[0,1]中的随机向量；a 为迭代搜索中从2 线性减小到0 的参数，其数学表达式为
式中，tmax 为最大迭代次数。
2.1.2 螺旋泡泡网攻击
座头鲸的螺旋泡泡网攻击方式是按照收缩包围与螺旋前进对自身位置进行更新逐渐靠近猎物并发动攻击，螺旋式位置更新表示为
式中，l 为[0,1]之间的随机数；b 为常数参数。
2.1.3 搜索目标猎物
座头鲸除了利用螺旋泡泡网搜索目标猎物外，还会根据个体间彼此的位置进行随机游走寻找猎物。当随机控制参数
会迫使个体鲸鱼远离最优鲸鱼个体，根据随机选中的个体鲸鱼位置进行位置更新，执行全局探索；当
时，选择最优鲸鱼个体位置更新各鲸鱼个体位置，执行局部搜索，根据p 值，在螺旋运动和圆环包围猎物运动之间进行切换。数学模型为
式中，Xrand 为座头鲸群体中被随机选中的个体的位置向量。
2.2 改进鲸鱼优化算法
2.2.1 基于余弦变化的非线性控制因子
WOA 算法虽然原理简单易懂，所需手动调节设置的参数少，而且在算法运算速度方面也具备一定的优势，但从WOA 算法原理可知，其寻优与其他算法一样需要平衡局部开发与全局搜索能力，即通过参数A 的大小进行协调。而从式（5）又能够看出控制参数A 值的变化是取决于a 参数的变化，a 值越小表示算法局部开发能力越强，a 值越大表示算法在全局搜索方面的能力越强。a 为迭代搜索中从2 线性减小到0 的参数，而在实际复杂函数寻优中，控制因子a 以线性规律减小是无法满足的，易导致算法难以跳出局部最优，寻优效果欠佳。针对该不足，本文引入了余弦非线性控制因子，其具体表达式为
从式（11）可以看出，在前期迭过程中，a 值从2 开始以较为缓慢的速度减小，有利于进行充分的全局搜索，而后期迭代过程中，a 值的减小速度明显加快，有利于局部搜索，加快收敛速度。
2.2.2 自适应权重因子w 对数变化
文献[23]研究指出，当权重因子较大时，其搜索范围较大，有利于全局搜索；而当其值较小时，可在较小范围内执行高精度搜索。为了增强鲸鱼优化算法的寻优能力，本文引入具有对数变化规律的自适应权重因子，利用其对算法位置进行更新。权重位置调整数学模型为
式中，p 为[0,1]之间的随机数；p∗取值为0.5；自适应权重因子w(t)的数学公式为
由式（13）可知，在前期迭代过程中w 值较大，表示参与位置调整的步长值较大，算法全局探索能力较强，而到了迭代后期，w 值越来越小并接近零，算法局部搜索能力越来越强。
2.2.3 随机差分变异
根据基本鲸鱼优化算法原理可知，在寻优过程中当前个体会根据最优个体位置与自身距离进行位置更新，也就是说其他非当前最优个体将逐渐往最优个体位置逼近。很明显，这种更新方式存在一定弊端，也就是当当前最优个体的位置并不是全局最优时，随着迭代次数的增加，种群中的所有个体将被错误引导聚集在局部最优区域附近，使得群体多样性降低，导致算法早熟收敛，寻优精度低。针对该问题，本文吸取了差分进化算法中差分变异策略的优点，将随机差分变异策略融合到基本鲸鱼算法中去，即将群体中被随机选中的个体和当前最优个体分别与当前个体进行随机式差分生成新的个体，增加群体个体的多样性，防止算法由于早熟收敛陷入局部最优。
随机差分变异式为
式中， X ′为被随机选中个体的位置向量；u 为[0,1]之间的随机数。
2.3 IWOA 算法性能验证
为了对比改进的鲸鱼算法与普通鲸鱼算法的寻优效果，本文对国际上经常使用的七个通用基准测试函数进行测试，通用基准测试函数具体信息见表1。为了使性能测试对比具备公平性，统一将种群总个体数设置为30 个，最大迭代次数为500 次。测试对比结果见表2。
表1 七个通用基准测试函数
Tab.1 Seven general benchmark functions
函数表达式 搜索范围 最优值n f xx( )=∑ [-100,100] 0 2 1 i i=1 f xxi n{}2( ) max,1=ii ≤ ≤ [-100,100] 0 n n f xxx 3( )=∑+ ∏ [-10,10] 0 i i i=1 i=1 n f xx 4( )(0.5 )=∑+ [-100,100] 0[]2 i i=1 n f xix 5( )random 0,1=∑+ [-1.28,1.28] 0 4 i [ )i=1 n f xxx 6( )sin()= ∑− [-500,500] -418.982 9n i i i=1 n 2 f xxx 7∑( )(10cos(2π ) 10)=−+i i i=1[-5.12,5.12]0
从表2 可以清楚地观察到，IWOA 算法在单峰值测试函数寻优中能够以更快的速度搜索逼近理论最优值；同时，IWOA 算法在多峰值测试函数寻优中也具备一定的优势，与WOA 算法相比，其能够更快地跳出局部最优，寻优精度更高。
表2 WOA 与IWOA 函数测试对比结果
Tab.2 Comparison results of WOA and IWOA function tests
函数 WOA 最佳寻优值 IWOA 最佳寻优值f 1.118×10-75 4.582×10-91 1 f 24.155 2.662×10-7 2 f 7.840×10-53 8.139×10-77 3 f 0 0 4 f 5.411×10-127 1.674×10-167 5 f -8 831 -12 341 6 f 0 0 7
为了更加直观地体现出IWOA 算法在通用基准测试函数寻优中的优越性，本文给出IWOA 算法与WOA 算法在测试函数 f2 、 f3 、 f6 、 f7 寻优仿真对比，如图5 所示。
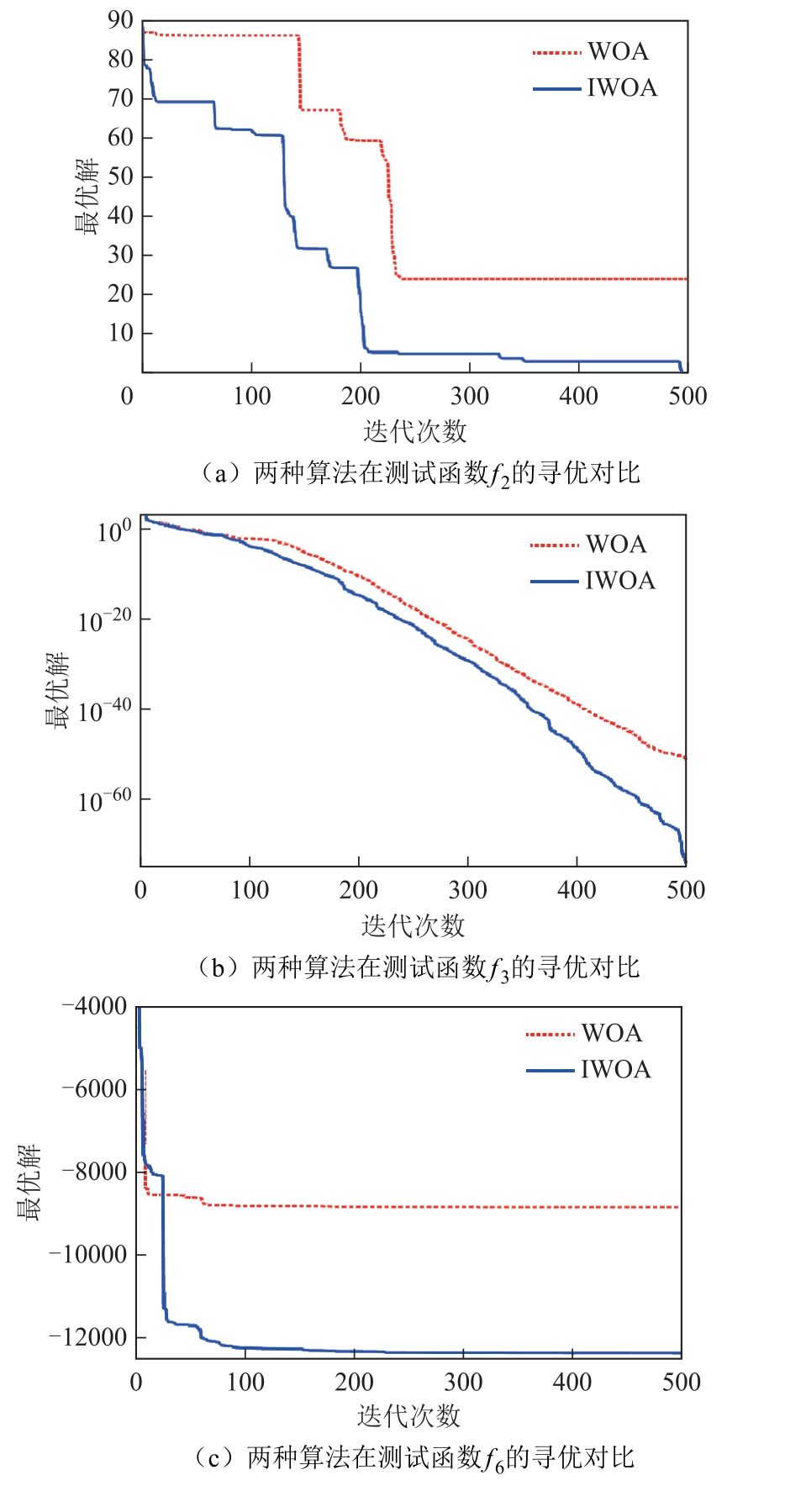
图5 两种算法在测试函数的寻优对比图
Fig.5 Comparison diagram of optimization between two algorithms in test function
为了进一步验证IWOA 算法对比其他优化算法在通用基准测试函数寻优中同样具备一定的优越性，本文采用 IWOA 算法与遗传算法（Genetic Algorithm, GA）、自适应遗传算法（Adaptive Genetic Algorithm, AGA）、粒子群算法（Particle Swarm Optimization, PSO）、自适应权重粒子群算法（Adaptive Particle Swarm Optimization, APSO）、基本鲸鱼算法对表1 的七个测试函数进行测试对比。统一将函数维度设置为30，群体个数为30，最大迭代次数为500 次，且为了避免偶然因素对测试结果的影响，每个测试函数独立运行20 次。计算每个算法20 次寻优的平均精度与标准差并记录，对比结果见表3。从表3 可以清楚地看出IWOA 算法相较于其他五种算法具备更好的寻优性能。
表3 GA、AGA、PSO、APSO、WOA 与IWOA 函数测试对比结果
Tab.3 Comparison results of GA, AGA,PSO, APSO,WOA and IWOA in function tests
GA AGA PSO函数平均值 标准差 平均值 标准差 平均值 标准差f 4.114×103 2.292×103 3.448×103 2.041×103 1 f 43.45 7.388 38.40 8.464 2 f 16.05 4.497 13.41 3.485 3 f 4.114×103 2.292×103 3.448×103 2.041×103 4 f 3.015 2.569 1.574 1.577 5 f -5.733×103 5.361×102 -5.683×103 6.555×102 6 f 78.58 12.04 74.90 12.60 7 APSO WOA函数平均值 标准差 平均值 标准差4.345 6.007 20.54 4.705 16.18 11.40 4.345 6.001 0.268 4 0.826-6.864×103 9.131×102 72.54 18.81 IWOA平均值 标准差f 1.461×10-6 2.488×10-6 3.294×10-73 1.444×10-72 7.649×10-90 3.420×10-89 1 f 5.212 2.995 51.84 30.50 4.668×10-11 1.471×10-10 2 f 13.58 10.27 2.072×10-50 8.723×10-50 2.008×10-62 5.783×10-62 3 f 1.461×10-6 2.488×10-6 1.541×10-34 6.890×10-34 0 0 4 f 2.416 7.785 3.221×10-114 1.423×10-113 5.429×10-141 2.428×10-140 5 f -7.866×103 6.849×102 -9.231×103 1.238×103 -1.018×104 1.131×103 6 f 1.008×102 18.52 5.684×10-15 2.542×10-14 0 0 7
3 基于IWOA-SVR 最大功率点电压预测模型建立与仿真对比分析
3.1 预测模型建立
支持向量机（Support Vector Machines, SVM）是由V. N. Vapnik 等提出的一种可用于回归预测以及解决各种分类问题的机器学习方法，其具体数学原理与公式推导参见文献[24]。支持向量回归（Support Vector Regression, SVR）算法具备优异的全局优化性能，在维数较高且具备复杂非线性特点的小数量样本回归预测应用中展现出了较好的泛化能力[25-26]，因此本文利用SVR 算法对光伏阵列最大输出功率点电压进行回归预测。根据光伏阵列输出特性分析可知，影响光伏阵列最大功率点电压值的因素主要有光照强度E、光伏组件温度T 和各光伏组件遮挡度S ，因本文研究的是3×2 的光伏阵列，所以将E、T 、 1S 、 S2 、 S3 设置为预测模型的输入变量，将MPP 对应的电压值设置为预测模型的输出变量，即
为了保证能够选择到较优的SVR 参数，需要一定数量的数据用于预测模型的训练及预测性能的验证，本文通过搭建3×2 光伏阵列仿真模型，根据气象条件人工仿真模拟出400 组数据，随机从中选取340 组数据作为训练样本，测试样本则取剩余60 组数据，利用其进行预测模型性能验证。
由于SVR 回归预测模型的性能在很大程度上受惩罚参数c 和核函数参数g 的影响，因此在模型建立中对c、g 进行最优选择是相当重要的。本文利用改进的鲸鱼算法对SVR 回归预测模型的参数c、 g 进行最优选择。IWOA-SVR 建模流程如图6所示。
图6 IWOA-SVR 建模流程
Fig.6 IWOA-SVR modeling flow chart
3.2 预测模型性能分析
为了验证所提IWOA-SVR 预测模型的优越性，本文将其与遗传算法进行参数最优选择的支持向量机回归预测模型（GA-SVR）、粒子群算法进行参数最优选择的支持向量机回归预测模型（PSO-SVR）进行对比。此外，为了进一步体现所提预测模型相较于其他预测算法建立的预测模型在预测准确度也具备一定优势，将其与BP 神经网络建立的预测模型、Elman 神经网络建立的预测模型进行对比。其中GA 参数设置： 1p =0.9，p 2 =0.01；PSO 参数设置：1c =1.5，c 2 =1.5；三种算法的种群个体总数均设置为40，最大迭代次数为200；选取径向基函数为支持向量机回归模型的内核。各预测模型在测试样本预测的预测误差指标见表4，GA-SVR、PSO-SVR、IWOA-SVR 预测效果对比如图7a 所示，IWOA-SVR、BP 神经网络、Elman 神经网络预测效果对比如图7b所示。
表4 不同预测模型的预测误差指标
Tab.4 Prediction error index of different prediction models
预测模型 RMSE MAE MAPE IWOA-SVR 3.033 9 2.311 8 0.030 7 PSO-SVR 3.618 1 2.740 4 0.036 7 Elman 5.014 1 3.075 9 0.042 0 GA-SVR 5.004 1 3.294 4 0.043 9 BP 7.621 7 5.483 0.069 1
结合表 4 与图 7 可知，本文所提出的基于IWOA-SVR 预测模型在预测性能上有了一定提升，相较于其他优化算法进行参数寻优的SVR 预测模型具有更高的预测精度。从表4 可以得到，IWOASVR 预测模型在RMSE、MAE、MAPE 三个预测误差指标上分别比GA-SVR 预测模型降低了1.970 2、0.9 8 2 6与0.0 1 3 2；在与P S O-S V R预测模型预测对比中，三个预测误差指标也分别降低了0.5 8 4 2、0.4 2 8 6与0.0 0 6；此外，在与其他预测算法建立的预测模型对比中，I W O A-S V R预测模型也具备更高的预测精度，R M S E、M A E、M A P E三个预测误差指标比B P神经网络预测模型分别降低了4.5 8 7 8、3.1 7 1 2与0.0 3 8 4；与E l m a n神经网络预测模型预测对比，R M S E、M A E、M A P E三个预测误差指标也分别降低了1.9 8 2、0.7 6 4 1与0.0 1 1 3。综上可知，基于I W O A-S V R光伏阵列最大功率点电压预测模型相较于其他预测模型具有更高的预测精度，能较为准确地预测到光伏阵列最大功率点电压。另外本文所提出的I W O A-S V R预测方法在计算复杂度也有一定的优势，三种同类型预测方法均采用M a t l a b编程实现，在同一台计算机上完成训练与预测所耗费的时间分别为：I W O A-S V R预测方法耗费2 3.8 1 4 7 s，其中训练所耗费时间为2 3.7 4 1 7 s，预测所用时间为0.0 0 7 3 s；G A-S V R预测方法耗时3 1.1 7 2 6 s；P S O-S V R预测方法耗时2 7.3 6 8 8 s。由此可见，I W O A-S V R预测模型训练时间最短，充分体现了计算复杂度低带来的优势，并且具备优异的实时性能。
图7 不同预测模型预测结果对比
Fig.7 Comparison of different forecasting models
4 基于IWOA-SVR 光伏多峰MPPT 算法研究与仿真分析
4.1 基于IWOA-SVR 与INC 结合的光伏多峰MPPT 算法
将IWOA-SVR 光伏阵列最大功率点电压预测模型与小步长电导增量法相结合应用到光伏MPPT控制中，其实质是非线性预测控制问题。该复合MPPT 控制算法的基本思路：首先采集环境参数与光伏阵列输出电压和电流数据，并计算每块光伏组件的遮阴度，将光照强度、每块光伏组件的温度及遮阴度进行归一化后作为IWOA-SVR 预测模型的输入变量，由IWOA-SVR 预测模型预测出最大功率点电压值，再利用一定的算法得到PWM 控制信号，将光伏阵列实际工作点调节到最大功率点，最后利用小步长INC 进行局部寻优，进一步提高跟踪精度。其中，为了防止IWOA-SVR 预测模型实时预测控制导致输出功率波动较大，本文对IWOA-SVR 预测设置了启动条件，即当光伏阵列所处环境条件变化较小时，由小步长INC 进行最大功率点跟踪，而当所处环境条件变化较大时，重新启动IWOA-SVR 预测并重复之前步骤，实现全局最大功率点追踪。重启条件数学公式如式（16）所示，该复合MPPT 控制算法流程如图8 所示。
式中，P′为当前采样时刻光伏阵列输出功率值；P为上一采样时刻光伏阵列输出功率值；ΔPset 为光伏阵列输出功率允许的最大变化量。
图8 复合MPPT 控制算法流程
Fig.8 Composite MPPT control algorithm flow chart
4.2 仿真对比分析
为了验证所提出的基于IWOA-SVR 与小步长INC 相结合的复合MPPT 控制算法的有效性，本文借助Matlab/Simulink 仿真软件搭建了复合MPPT 控制系统仿真模型如图9 所示。该仿真系统模型主要由六块光伏组件通过串并联组成的3×2 光伏阵列模块、基于IWOA-SVR 与小步长INC 相结合的复合MPPT 控制模块、Boost 变换模块及PWM 驱动模块。利用光伏阵列仿真模型仿真，可得当光阵列处于情况1：光照强度
S3=0.4、T = 21℃时，光伏阵列P-U 输出特性曲线有三个峰值点，其中第1 个峰值点的功率值大小为158W，对应电压为26.7V；第2 个峰值点功率值为235.2W，对应电压为57.3V；第3 个峰值点（即最大功率点）功率值为302.2W,对应最大功率点电压为87.1V。当处于情况2：光照强度E=300W/m2，S1=0.4、 S2=0.3、 S3=0.3、T =22.4℃时，光伏阵列P-U 输出特性曲线有两个峰值点，其中第1 个峰值点的功率值大小为186.6W，对应电压为54.2V；第2 个峰值点（即最大功率点）功率值为260.2W，对应电压为83.8V。将仿真前0.05s,光伏阵列所处情况设置为情况1，后0.05s 设置为情况2，分别采用基于IWOA-SVR 与小步长INC 相结合的复合MPPT控制算法与传统INC 进行仿真对比。两种算法的仿真结果如图10 所示。
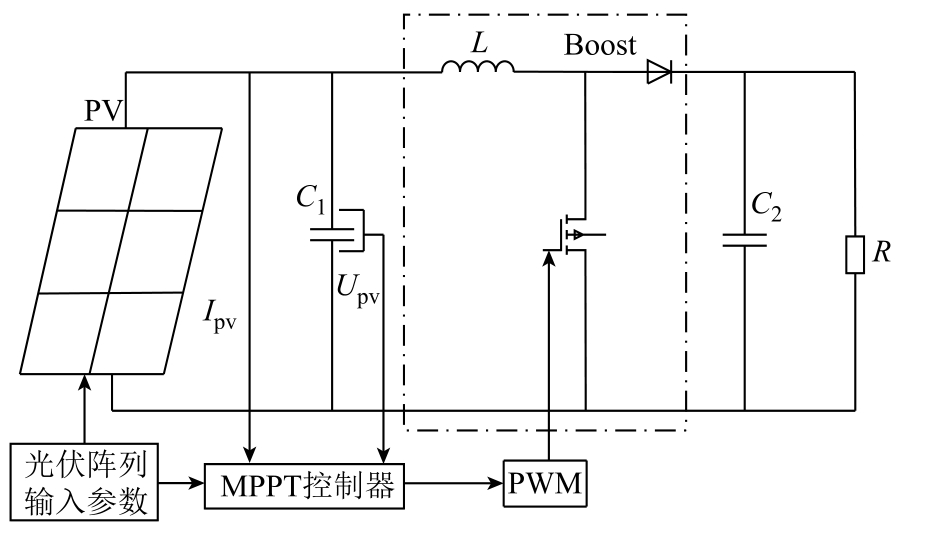
图9 MPPT 控制系统仿真模型
Fig.9 Simulation model of MPPT control system
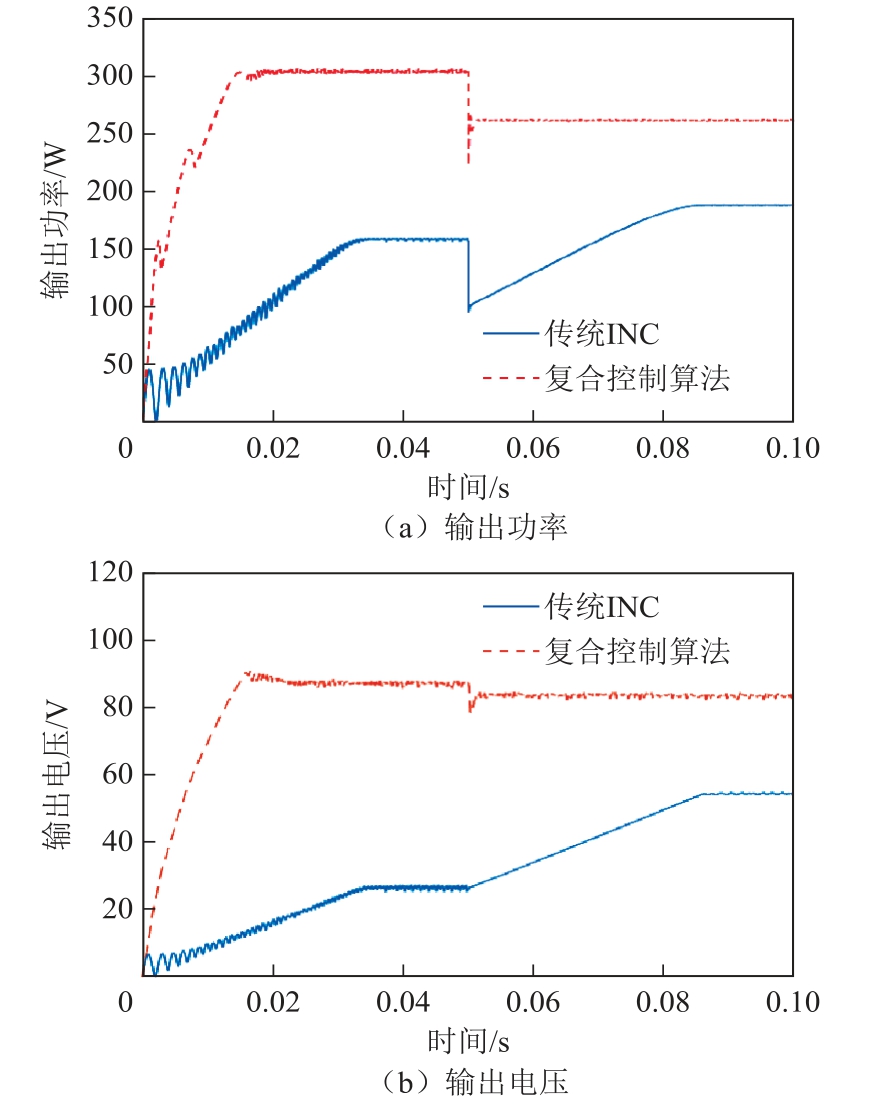
图10 两种算法的仿真结果对比
Fig.10 Comparison of simulation results
从图10 可知，在光伏阵列所处环境为情况1 时，传统INC 未能找到全局最大功率，只找到了第一个极值点，陷入了局部最优，系统经过0.033s 到达稳态，其输出功率为157W，输出电压约为27V，输出功率误差率达到了48.1%。当光伏阵列所处环境由情况1 突变为情况2 时，传统INC 依旧无法追踪到全局最大功率点，只找到了第一个极值点，系统经过0.036s 稳定追踪到第一个局部最优点，其输出功率为186.5W，输出电压为54V，输出功率误差率达到了28.3%。而本文提出的复合MPPT 控制算法在光伏阵列所处环境突变前，其跟踪效果很好，可以准确地跟踪到全局最大功率点，耗时0.015s 系统到达稳态，其输出功率为300.8W，输出电压为86.8V，输出功率误差率仅为0.46%。光伏阵列所处环境突变后，复合控制算法只耗时了0.001 25s 就重新追踪到全局最大功率点，系统达到稳定状态时，其输出功率为259.6W，输出电压为83.1V，输出功率误差率仅为0.31%。综上，本文提出的复合控制算法在光伏多峰MPPT 控制中能够准确快速地追踪到全局最大功率点，相较于传统INC 在跟踪速度与精度上有了大幅的提升。
5 结论
光伏阵列处在部分遮挡情况下，其P-U 特性曲线具有多个极值点，使得传统的MPPT 算法极易因误判而只能找到局部MPP，大幅降低了输出功率。为了更高效地利用太阳能，本文提出了一种基于改进鲸鱼算法优化SVR 与INC 相结合的复合MPPT控制算法。利用改进鲸鱼算法优异的寻优性能对SVR 预测模型的c、g 参数进行寻优，提高了SVR预测模型的预测准确度。将IWOA-SVR 预测模型与INC 相结合应用到光伏多峰MPPT 控制中，可快速准确地追踪到GMPP,有效规避陷入局部寻优现象，大幅提高了光伏发电系统的功率输出与降低跟踪时间。仿真结果表明：
1）改进的鲸鱼算法相较于普通鲸鱼算法具有更强的全局搜索与局部开发协调性能。
2）IWOA-SVR 预测模型相对于其他预测模型具有更高的预测精度。
3）IWOA-SVR 与INC 相结合的复合控制算法在光伏多峰MPPT 应用中具备优异的动态与稳态性能。
[1] Mohammadreza A, Kazem P. A novel reconfiguration procedure to extract maximum power from partiallyshaded photovoltaic arrays[J]. Solar Energy, 2018,173: 110-119.
[2] 李涛, 胡维昊, 李坚, 等. 基于深度强化学习算法的光伏-抽蓄互补系统智能调度[J]. 电工技术学报,2020, 35(13): 2757-2768.
Li Tao, Hu Weihao, Li Jian, et al. Intelligent economic dispatch for PV-PHS integrated system: a deep reinforcement learning-based approach[J]. Transactions of China Electrotechnical Society, 2020,35(13): 2757-2768.
[3] 赖昌伟, 黎静华, 陈博, 等. 光伏发电出力预测技术研究综述[J]. 电工技术学报, 2019, 34(6): 1201-1217.
Lai Changwei, Li Jinghua, Chen Bo, et al. Review of photovoltaic power output prediction technology[J].Transactions of China Electrotechnical Society, 2019,34(6): 1201-1217.
[4] 徐可寒, 张哲, 刘慧媛, 等. 光伏电源故障特性研究及影响因素分析[J]. 电工技术学报, 2020, 35(2):359-371.
Xu Kehan, Zhang Zhe, Liu Huiyuan, et al. Study on fault characteristics and its related impact factors of photovoltaic generator[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 359-371.
[5] 杨慧彪, 贾祺, 项丽, 等. 双级式光伏发电虚拟惯量控制策略[J]. 电力系统自动化, 2019, 43(10): 87-102.
Yang Huibiao, Jia Qi, Xiang Li, et al. Virtual inertia control strategies for double-stage photovoltaic power generation[J]. Automation of Electric Power Systems,2019, 43(10): 87-102.
[6] 郑庆杰, 陈为. 基于耦合电感的光伏逆变器漏电流抑制研究[J]. 电机与控制学报, 2020, 24(6): 43-54.
Zheng Qingjie, Chen Wei. Study on PV inverter ground leakage current reduction technology based on the coupling inductor[J]. Electric Machines and Control, 2020, 24(6): 43-54.
[7] 聂晓华, 赖家俊. 局部阴影下光伏阵列全局最大功率点跟踪控制方法综述[J]. 电网技术, 2014, 38(12):3279-3285.
Nie Xiaohua, Lai Jiajun. A survey on tracking and control approaches for global maximum power point of photovoltaic arrays in partially shaded environment[J].Power System Technology, 2014, 38(12): 3279-3285.
[8] 张明锐, 陈喆旸, 韦莉. 免疫萤火虫算法在光伏阵列最大功率点跟踪中的应用[J]. 电工技术学报,2020, 35(7): 1553-1562.
Zhang Mingrui, Chen Zheyang, Wei Li. Application of immune firefly algorithms in photovoltaic array maximum power point tracking[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1553-1562.
[9] Mohanty S, Subudhi B, Ray P K. A grey wolf- assisted perturb & observe MPPT algorithm for a PV system[J].IEEE Transactions on Energy Conversion, 2017, 32(1):340-347.
[10] Tey K S, Mekhilef S. Modified incremental conductance MPPT algorithm to mitigate inaccurate responses under fast-changing solar irradiation level[J]. Solar Energy, 2014, 101(1): 333-342.
[11] Bosco J, Mabel C. A novel cross diagonal view configuration of a PV system under partial shading conditions[J]. Solar Energy, 2017, 158: 760-773.
[12] Bana S, Saini R P. Experimental investigation on power output of different photovoltaic array configurations under uniform and partial shading scenarios[J]. Energy, 2017, 127: 438-453.
[13] Daliento S, Dinapoli F, Guerriero P, et al. A modified bypass circuit for improved hot spot reliability of solar panels subject to partial shading[J]. Solar Energy,2016, 134: 211-218.
[14] 夏永洪, 李梦茹, 曾繁鹏, 等. 基于TCT 结构及开关控制的光伏阵列重构[J]. 太阳能学报, 2018,39(10): 2797-2802.
Xia Yonghong, Li Mengru, Zeng Fanpeng, et al.Reconstruction of PV arrays based on TCT strcuture and switch control[J]. Acta Energiae Solaris Sinica,2018, 39(10): 2797-2802.
[15] Dileep G, Singh S N. An improved particle swarm optimization based maximum power point tracking algorithm for PV system operating under partial shading conditions[J]. Solar Energy, 2017, 158: 1006-1015.
[16] 朱艳伟, 石新春, 但扬清, 等. 粒子群优化算法在光伏阵列多峰最大功率点跟踪中的应用[J]. 中国电机工程学报, 2012, 32(4): 42-48, 20.
Zhu Yanwei, Shi Xinchun, Dan Yangqing, et al.Application of PSO algorithm in global MPPT for PV array[J]. Proceedings of the CSEE, 2012, 32(4): 42-48,20.
[17] 杨海柱, 岳刚伟, 康乐. 基于粒子群优化算法和电导增量法的多峰值MPPT 控制[J]. 电源学报, 2019,17(6): 128-136.
Yang Haizhu, Yue Gangwei, Kang Le. Multi-peak MPPT control based on PSO and INC algorithms[J].Journal of Power Supply, 2019, 17(6): 128-136.
[18] 商立群, 朱伟伟. 基于全局学习自适应细菌觅食算法的光伏系统全局最大功率点跟踪方法[J]. 电工技术学报, 2019, 34(12): 2606-2614.
Shang Liqun, Zhu Weiwei. Photovoltaic system global maximum power point tracking method based on the global learning adaptive bacteria foraging algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2606-2614.
[19] 郑威迪, 李志刚, 贾涵中, 等. 基于改进型鲸鱼优化算法和最小二乘支持向量机的炼钢终点预测模型研究[J]. 电子学报, 2019, 47(3): 700-706.
Zheng Weidi, Li Zhigang, Jia Hanzhong, et al.Research on prediction model of steelmaking end point based on LWOA and LSSVM[J]. Acta Electronica Sinica, 2019, 47(3): 700-706.
[20] 岳晓宇, 彭显刚, 林俐. 鲸鱼优化支持向量机的短期风电功率预测[J]. 电力系统及其自动化学报,2020, 32(2): 146-150.
Yue Xiaoyu, Peng Xiangang, Lin Li. Short-term wind power forecasting based on whales optimization algorithm and support vector machine[J]. Proceedings of the CSU-EPSA, 2020, 32(2): 146-150.
[21] 闫旭, 叶春明, 姚远远. 量子鲸鱼优化算法求解作业车间调度问题[J]. 计算机应用研究, 2019, 36(4):975-979.
Yan Xu, Ye Chunming, Yao Yuanyuan. Solving jobshop scheduling problem by quantum whale optimization algorithm[J]. Application Research of Computers, 2019, 36(4): 975-979.
[22] Mirjalili S, Lewis A. The whale optimization algorithm[J]. Advances in Engineering Software,2016, 95: 51-67.
[23] 张顶学, 关治洪, 刘新芝. 一种动态改变惯性权重的自适应粒子群算法[J]. 控制与决策, 2008, 23(11):1253-1257.
Zhang Dingxue, Guan Zhihong, Liu Xinzhi. Adaptive particle swarm optimization algorithm with dynamically changing inertia weight[J]. Control and Decision, 2008, 23 (11): 1253-1257.
[24] 邓乃扬, 田英杰. 支持向量机: 理论•算法与拓展[M]. 北京: 科学出版社, 2009.
[25] 鲍颜红, 冯长有, 任先成, 等. 基于支持向量机的在线暂态稳定故障筛选[J]. 电力系统自动化, 2019,43(22): 52-58.
Bao Yanhong, Feng Changyou, Ren Xiancheng, et al.Online transient stability fault screening based on support vector machine[J]. Automation of Electric Power Systems, 2019, 43(22): 52-58.
[26] 刘杰, 裴杰, 田明, 等. 基于支持向量机的电流互感器非线性校正方法研究[J]. 电机与控制学报,2020, 24(10): 130-138.
Liu Jie, Pei Jie, Tian Ming, et al. Research on nonlinear correction method of current transformer based on support vector machine[J]. Electric Machines and Control, 2020, 24(10): 130-138.