0 引言
为促进清洁太阳能资源利用，我国相继出台了一系列鼓励分布式光伏发展的政策[1-2]。据国家能源局对光伏发电并网统计可知，从 2016 年底到2020 年上半年，我国分布式光伏发电累计安装容量占比从13%达到31%，分布式光伏发电装机容量逐年上升迅猛[3-4]。分布式光伏发电集群由于其稳定、高效、灵活、友好并网特性，将逐渐成为电力生产和光伏能源消纳的新模式[5]，其整体效率也越来越受重视。
通常情况下，分布式光伏发电中，光伏组串与逆变器固定连接[6]。在早晚及阴雨天等低光照情况下逆变器处于轻载条件下运行[7]。然而，逆变器在轻载时工作效率很低。光伏逆变器转换效率受其输入功率影响，特别是当逆变器输入功率在额定功率20%以下时，随着输入功率下降，逆变器转换效率也会明显降低[8]。低光照下，组串逆变器大规模并网能量损失严重，直接降低了企业效益。
采取适当的措施，如改变光伏系统直流拓扑结构、添加开关设备等可以提高光伏系统效率[9-10]。一些文献研究了光伏组件在光伏阵列中的重构配置。文献[11]提出的重新配置方法将光伏（Photovoltaic,PV）板分为两部分，一部分光伏组件固定，另一部分光伏组件作为可重构部分。文献[12]和文献[13]分别采用动态和静态技术对光伏阵列重新配置，以均衡光伏阵列各串中的电流。上述文献均是对光伏组件串并联重构，在满足光伏串电压相同的前提下，提高光伏串的总电流。但是，大多数情况下，光伏组件都接受均匀的光照，改变光伏阵列中组件的连接状态难以提高光伏阵列输出功率，低光照条件下光伏系统效率仍然很低。
文献[14]综述了大量的逆变器拓扑结构，并根据系统的具体要求，选择逆变器拓扑结构提高性能。尽管在低功率运行条件下，特定拓扑及软开关可以改善逆变器的转换效率[15-18]，但由于半导体的固定损耗，逆变器在轻载时的效率仍然非常低。微型逆变器可实现每个模块的最佳运行，提高系统效率，但这种逆变器装置由于复杂的拓扑、低转换效率和额定功率限制，主要用于小型光伏发电系统[19-20]。
文献[9-10]综述了光伏系统结构，其中提到了团队概念，即多个逆变器以团队合作的方式运行。在低太阳辐射下，光伏阵列的所有串并联到一个逆变器，而其他逆变器断开。在增加辐射的情况下，光伏阵列被分成若干子阵列，这些子阵列连接到不同的独立工作的串联逆变器上。这种方式能够提高光伏发电性能。文献[20]提出具有共享直流母线和交流母线的连接方法。针对不同的负载条件调整多台逆变器的负载分配，使并联逆变器逐一从待机到满载运行，以减少功率损耗。这种控制策略比较简单，提升效率有限。文献[21]提出提高欧洲加权效率的策略，逐一使逆变器以满负荷的h%运转并具有最大效率的优先级。最后每个并网逆变器将从满负载的h%逐一移至满负载模式。文献[22]研究了逆变器的多种拓扑及调制策略解决高频循环电流问题，并推荐了具有低漏电流（例如H5 拓扑）的单相无变压器全桥逆变器。文献[20-22]的连接方法需要并联逆变器具有不同的控制参数以及一些特定的拓扑结构，抗干扰能力差，实际工程中的操作受限很大。文献[23-24]根据检测系统输入或输出功率，采用固定阈值方法改变不同逆变器工作台数提高光伏系统整体效率，灵活性较差。文献[25-26]中光伏阵列串联和并联一同使用，使光伏阵列与逆变器进行全网络匹配连接，以系统功率输出最大为目标控制切换装置。但该方法中光伏板直流侧任意串联会出现过电压现象，但文中未考虑电池板串并联保护。文献[27]利用直流可变拓扑结构，通过多目标的方式提高系统性能，但忽略了短时间内天气的波动性，可能会引起开关频繁动作和短时间的功率越限等问题。
考虑天气波动性的光伏系统运行情况，本文提出一种时间尺度下提高光伏发电转换效率的直流开关动态重构策略。基于光伏直流并联开关拓扑结构对多台逆变器运行台数进行控制。考虑光伏系统效率和开关动作次数等运行指标，控制逆变器运行台数，使性能指标最优。利用控制决策防止开关频繁切换和逆变器功率越限。基于最小二乘回归算法预测天气短时间变化范围，确定光伏系统允许的开关重构方案；基于投票理论方法对比历史时间内开关连接方案，得出最佳运行方案。通过本策略与常规连接方式和不考虑控制决策的连接方式对比，验证本文策略的可行性。
1 光伏群控系统直流拓扑结构
光伏串与逆变器固定连接的方式是比较常规的光伏系统结构，不能满足本文策略的需要。而本文基于文献[24]结构使光伏串与逆变器灵活连接，有效控制多台逆变器起停状态，提高系统运行性能。
1.1 光伏群控系统结构
常规分布式光伏发电系统主要由光伏电池板串和并网逆变器组成。常规情况下，光伏串固定接入逆变器，若干台逆变器并联接入电网并网运行[6]。为便于光伏串的相关表述，本文将常规连接方式进行简化处理，将正常配置1 台逆变器所需的光伏串统一定义为1 串光伏串。本文利用控制器使X 串光伏串与Y 台并网逆变器灵活连接构成光伏群控系统，光伏系统拓扑示意图如图1 所示。光伏串和并网逆变器分别通过直流电缆插头接入开关控制箱，其中控制箱放于逆变器侧连接光伏串与逆变器。控制箱中的数字信号处理器（Digital Signal Processing, DSP）和逆变器以通信接口连接，用来传输光伏串的电压和电流信息。DSP 根据设定的系统参数和实时数据做出不同时刻的控制决策，每过一段时间，发送一次逆变器起停状态及线路开关连接状态控制指令，使群控系统运行性能最优。
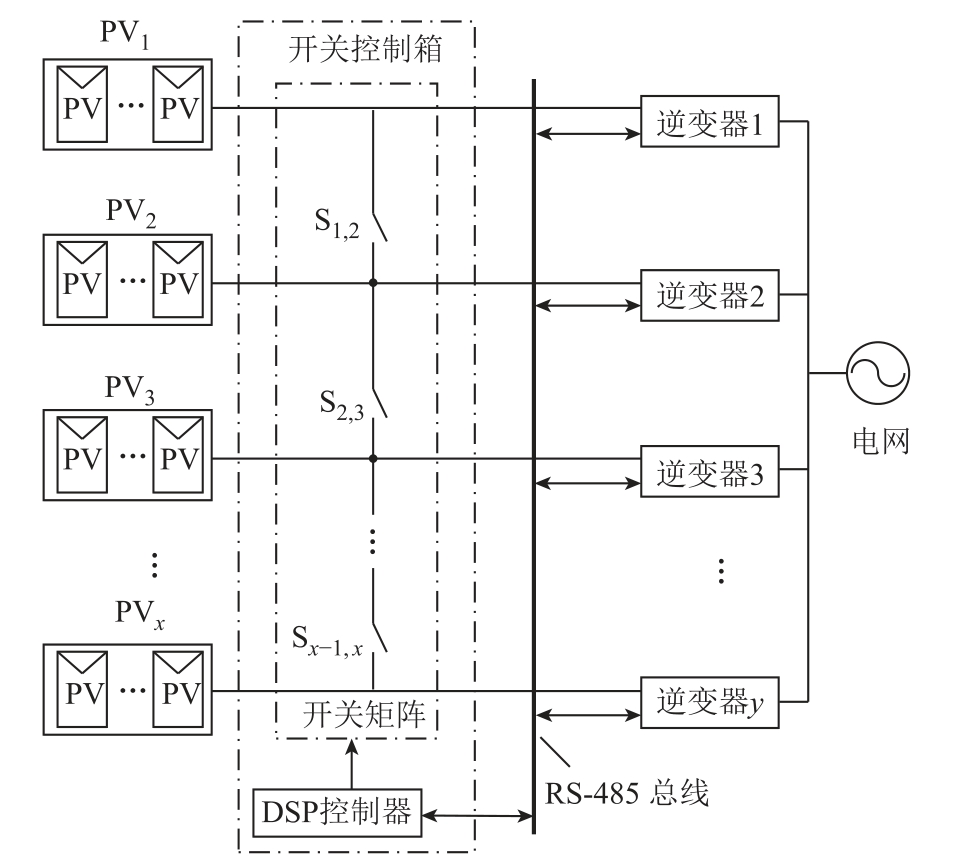
图1 光伏群控系统拓扑示意图
Fig.1 Topology of the PV group control system
1.2 群控系统功能
群控系统主要由光伏串、开关控制箱和逆变器组成，通过控制光伏串与逆变器连接并控制逆变器的起停，可以实现多光伏串与多逆变器的灵活组合，满足不同光照下系统运行要求。在低光照条件下，跨桥开关控制N 串光伏串并联到1 台逆变器并网发电，其他逆变器处于停机状态；随着光照增强，多串光伏串间重构并逐步起动更多逆变器并网发电；当光照足够强时，回归到常规连接方式，这时逆变器全部起动。同理，光照从最强到最弱的过程，跨桥开关控制光伏串连接逆变器数量从y 台逐渐变为1 台。
群控系统增加了光伏系统冗余性和可扩展性，且逆变器并联技术较为成熟[28-31]，在实际工程中易于实现。在目前大型分布式光伏电站若干台逆变器集中并联汇到一个并网点，再由多个并网点汇到一处集中升压连到大电网中。因此，可根据需要考虑由若干个小型群控系统组成光伏电站整个系统。开关控制箱具有即插即用功能，而光伏串和逆变器的电缆插头可直接和开关控制箱相连，操作简单。
2 运行效益指标函数
本节中研究了光伏系统的输出功率效益和开关动作成本，并建立了运行效益指标函数。
2.1 逆变器输出功率效益
首先从逆变器中获得所测电压和电流数据，然后计算各串光伏串电流和电压大小，再计算开关重构之后逆变器的输入功率，最后求出该段时间内逆变器输出功率效益。
将光伏串按1,2,…, X 的顺序编号排序，并将这些光伏串分为m 组，每组与1 台逆变器相连。其中第j 组中光伏串的数量记为 kj ，而未与光伏串连接的逆变器则待机运行。一般情况下，光伏组串配置相同，其输出特性基本一致。从逆变器获取输入电压和电流，即可确定该组中第z 串光伏串的电压和电流为
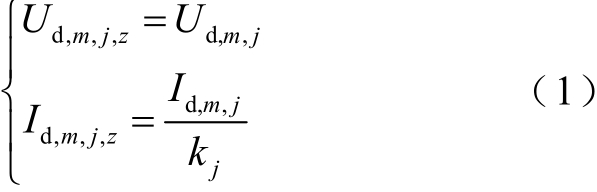
式中，U d, m ,j和 Id, m ,j分别为开关重构前第j 组逆变器的输入电压和电流；kj 为第 j 组光伏串数量；j=1,2,… , m。
将各组光伏串按原编号顺序进行排序，光伏串总个数X 与每组中光伏串数量关系为
再计算开关拟重构后第i 组逆变器输入电流、输入电压为
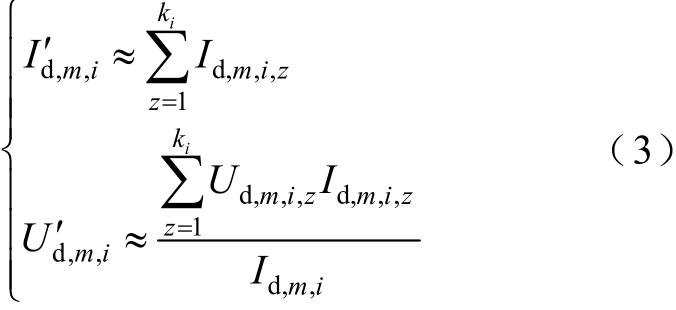
定义 ηi ( p)为开关拟重构后第i 组逆变器在输入功率p 处对应的转换效率，利用逆变器输入功率与转换效率求出群控系统输出总功率为
两次控制指令发出的时间间隔主要由主观因素决定，其设置时间不易过长。令每次发出的控制指令为一个切换点，则用当前切换点的数据近似作为切换间隔期间内平均数据，构建群控系统输出功率收益指标为
式中，CG 为光伏上网电价或售电电价；Tsw_interval 为控制系统连续两个控制指令的时间间隔。
2.2 开关动作成本
光伏串和逆变器不同数量之间连接，其连接方式多种多样。在不同连接方式之间切换时，群控系统中开关带电切换会对降低电气寿命，因此本文考虑降低开关动作次数来降低系统成本损耗。开关矩阵每次动作均需要对比上一次连接状态，确定开关动作数量。开关矩阵每次动作成本损耗为
式中，ksw 为需要动作的开关数量；Csw 为开关市场价格；Ksel 为开关电气寿命。
光伏系统本次控制指令时间点到下一次的运行效益指标为
3 群控系统切换策略
本节分析了光伏系统切换后逆变器可能会出现功率越限的情况，对光伏系统切换的连接方式作出限制。另外，频繁变化的天气可能会导致开关频繁切换。因此，对开关频繁切换的情况作出了系统控制决策。最后，提供了系统连接的最终方案。
3.1 考虑防功率越限的连接方案分析
系统切换时，逆变器输入量应满足其承受范围。另外，为防止出现光伏组串与被遮挡光伏组串并联导致失配损失严重的特殊问题，光伏串并联时电压差应满足一个约束范围。由式（3）可知，对于第i组逆变器所连接的光伏串来说，任意光伏串a 和b，
和
应满足
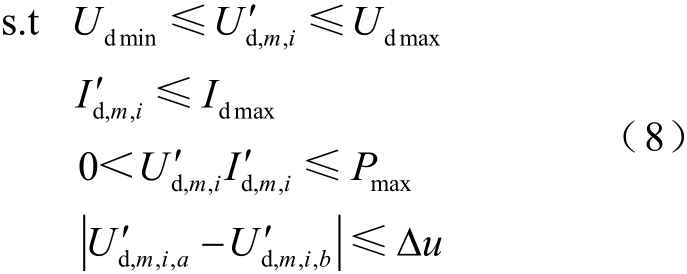
式中，Ud min 和Udmax分别为最大功率点跟踪最小和最大工作电压； Id max为逆变器规定的最大输入电流；Pm ax为逆变器规定的最大输入功率阈值； Δu 为光伏串电压差阈值。
光伏发电具有波动性和随机性等特点，在开关切换间隔期间，逆变器输入量可能会超过本身允许值。因此，本文有必要根据已有运行数据预测各逆变器输入功率变化趋势，给出其变化范围以增强系统可靠性。
本文利用最小二乘法回归方法分析切换前Tsw_before 时刻功率数据，预测本次切换到下一次切换时间段Tsw_interval 功率数据。线性回归预测相比非线性回归计算简便；对于可用参数较少的情况，光伏波动预测误差相对较小。因此，本文采用最小二乘法对光伏功率进行线性回归分析。利用拟合函数预测开关切换后Tsw_interval 时间内功率变化情况，使系统在切换空档期不出现功率越限情况。最后根据功率数据波动大小和历史经验确定预测数据可变范围。值得注意的是，由于线性回归的单调性，仅需计算初始和末端预测时间的数据即可初步获得光伏串预测的功率范围。
最小二乘法原理是根据最小化误差的二次方和来寻找数据最佳匹配函数。因此，一元线性最小二乘样本回归模型为
式中，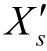
为数据样本第s 个自变量；
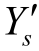为数据样本中对应
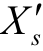的因变量；e s 为第s 个数据计算误差； 0β和 1β 分别为回归系数和偏移系数；x'和y'分别为拟合函数的自变量和因变量。
一般利用二次方损失函数Q 最小计算式（9）中的系数，即
可利用函数Q 对β 0和β1求偏导等于0 来确定系数大小，即
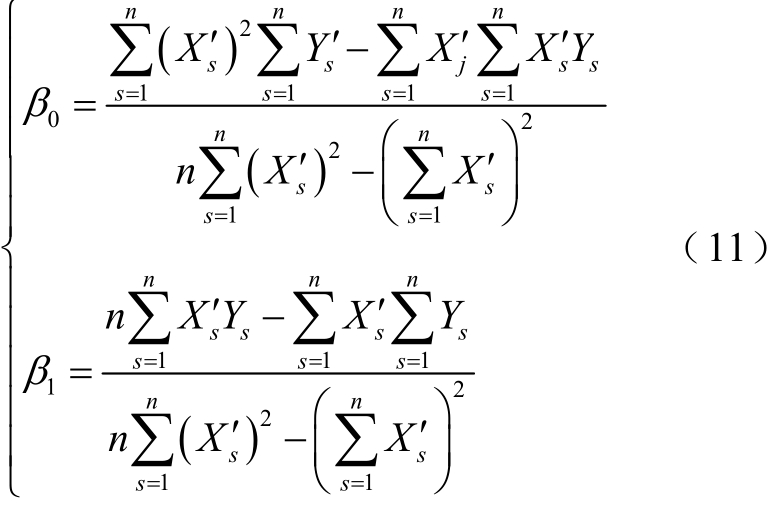
根据最小二乘法对功率数据进行 1 次曲线拟合，并利用其变化趋势对切换间隔期间功率作出简单预测。利用逆变器所连接的光伏串数量ki 及光伏功率波动情况计算得到切换时刻功率约束为
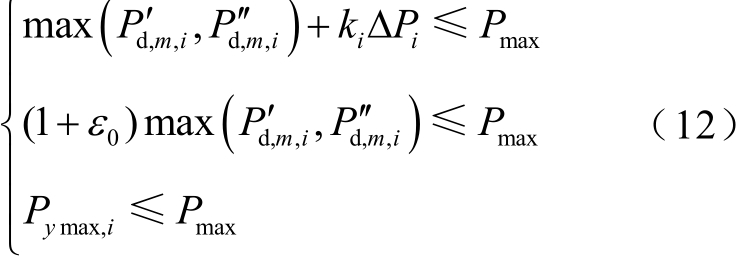
式中， Pd′, m, i 和 Pd′,′ m, i 分别为切换点前Tsw_interval 时刻m台逆变器工作时第i 组逆变器输入功率的线性拟合值和切换点后Tsw_interval 时刻第i 组逆变器输入功率的预测值；Pymax,i 为切换点前Tsw_ before 时间第i 组逆变器输入功率数据最大拟合值；ΔPi为第i 组中光伏串功率样本数据Yp,i 与功率拟合函数yp,i 最大差值，
ε 0为拟合函数功率波动系数。
3.2 群控系统控制决策
本策略对系统切换前Tsw_before 这段时间内的各光伏串输出功率平均值进行三次曲线拟合。对拟合曲线进行采样，采样时间间隔和数据的实时采集时间间隔相同。利用拟合采样值替代数据采集值进行数据计算。
控制器控制跨桥开关及逆变器起停可用0-1 矩阵算法处理。逆变器y 的起停状态用符号Sy,y 表示，PVx 与逆变器y 之间的跨桥开关连接状态用Sx,y 表示，其中x＜y。以三串光伏串与三台逆变器组成的发电单元为例，将Sy,y 和Sx,y 组成上三角矩阵用0-1矩阵表示为
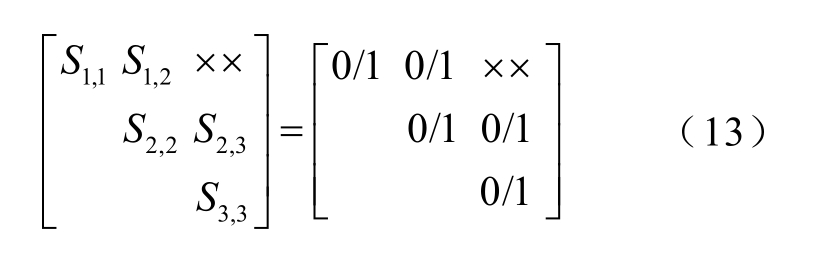
式中，0/1 代表连接或起停状态；0 表示开关断开或逆变器停运；1 表示开关连接或逆变器运行；“××”表示没有该连接。
由式（13）可知，通过两次切换时0 和1 异或关系可方便求解式（6）中开关动作数量。另外，由图1 开关拓扑可知，式（13）中0 和1 并非是完全重构组合。一般情况下，光伏发电单元内光伏组串数与逆变器台数较少，其组合方式数量很小，其数量尤其涉及一种整数无序分拆问题。考虑同品牌的光伏板和逆变器，以三串光伏串与三台逆变器配置的光伏群控系统为例，去除重复和不可连接的方式，组合方式有三种。本文策略主要是对离散数据进行计算，并在有限的开关组合方式中寻找最佳的连接方式，所涉及的数据量较小，采用穷举法求解即可快速准确求出各种连接方案的目标函数结果。将各种函数结果按大小进行排序可得到不同连接方式的优先选择顺序。
系统切换控制决策步骤如下：
1）切换系统程序初始化，光伏系统保持为常规连接。光伏系统获取光伏系统参数和逆变器历史输入、输出功率。
2）切换系统获取实时数据。
3）系统对实时数据进行初步判断，检测n 次数据采集内得到的功率数据是否有两次数据超过阈值Pmax。若超过则进行紧急操作处理，将该数值代入到式（7）中计算当前数据点最优连接方式；否则进行下一步操作。
4）切换系统间隔Tsw_interval 发送一次切换指令，期间系统保持上一次连接状态。在每个切换点处，切换点前Tsw_before 时间段数据通过1 次线性曲线和3 次曲线被拟合。通过式（14）判断功率数据变化曲线是否处于近似均匀变化状态。
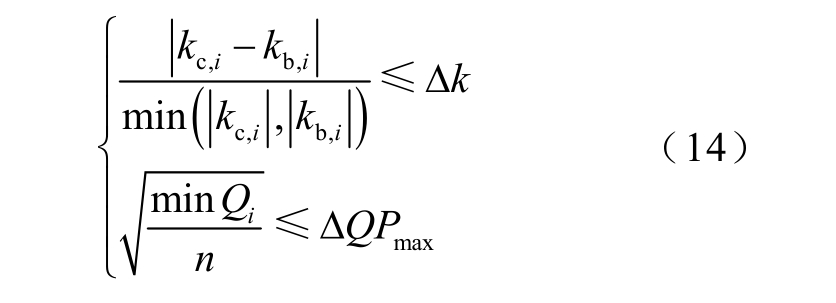
式中，kc,i 为线性拟合曲线当前切换点斜率；kb,i 为前一个切换点线性拟合曲线斜率；Qi 为线性拟合曲线平方损失函数；Δk 为斜率变化阈值，参考具有稳定天气变化下光伏功率曲线变化的范围选取，其中天气数据可从气象局或相关网站下载并处理，下同；ΔQ 为拟合函数平均误差阈值系数，参考略有波动天气下平均误差系数选取。
若满足式（14），曲线近似均匀变化，则将线性拟合曲线末端时刻的拟合值代入式（7）中进行计算。将不同连接方式下的函数大小排序，通过式（12）分析此次切换系统可靠性。获取最优连接方式，切换系统连接状态。
若不满足式（14）或Tsw_before 时间段内连接方式出现循环变换的情况，则执行防频繁切换连接方法。这种情况下的控制决策类似于一种投票理论的方式，具体为：选取拟合曲线的最大值、最小值、中位数等三种典型数值所在时刻的数据代入式（7）、式（8）、式（12）中计算，分别得出三个时刻的最优连接方式。将Tsw_before 时间段内拟合数据点代入上述几种连接方式对应的目标函数中进行计算，确定该连接限制下各数据点最佳连接方式。最后选出时间段内连接方式占比最多的方式作为开关频繁动作条件下最终连接方案。
5）系统进行切换判断后，继续获取实时数据。系统控制流程如图2 所示。
图2 系统控制流程
Fig.2 System control flow chart
一般情况下，Tsw_before＞Tsw_interval，为了使系统在设备初始化后尽快做出决策，在初始阶段需要对历史数据时间序列长度Tsw_before 进行调整，如式（15）所示。另外，在系统运行时，若触发紧急处理操作，则系统会因避免频繁操作而在下一次控制指令时刻暂停一次对数据处理。
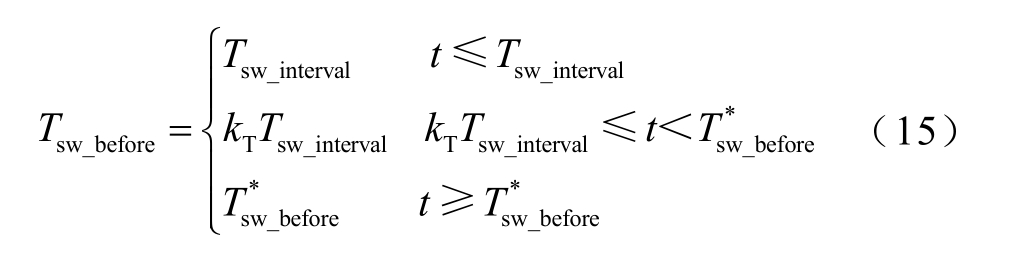
式中，t 为系统运行时间；
为系统稳定运行一段时间后数据分析的时间；kT 为满足式（15）的最大整数。
4 实验分析
本算例对多串光伏串和多台逆变器搭建的光伏群控系统分析系统整体效率。系统群控示意图如图3 所示，系统各种参数见表1。单串光伏串与单台逆变器配置容量均为5kW，初始状态每组光伏串数量ki 为1。
图3 实验平台
Fig.3 Experimental platform
4.1 算例
多台光伏串模拟器发出恒定的输出功率。在不同功率下，测量逆变器的输出功率，其中直流电压设置为400V。
表1 系统参数
Tab.1 System parameters
参 数 数 值开关价格Csw/元 120电气寿命Ksel/次 3×10×5上网电价或售电电价CG/[元/(kW·h)] 0.7光伏串电压差阈值Δu/V 20历史数据统计时间*T/min 15开关切换Tsw_interval/min 5最大功率点最小工作电压Udmin/V 200最大功率点最大工作电压Udmax/V 440逆变器最大承受电流Idmax/A 20逆变器最大输入阈值Pmax/W 5 050斜率变化阈值Δk 1拟合函数平均误差阈值系数ΔQ 0.01波动系数 0ε 0.05 sw_before
本节对比分析了不同配置场景下群控系统转换效率提升效果。光伏串数量和逆变器台数均为3、4或5 时，光伏模拟器额定功率从0.05 到1 变化，不同容量配置的群控系统在不同功率下逆变器总转换效率对比如图4 所示，其中横坐标为以群控系统容量配置为基准的逆变器总输入功率水平。从图4 中可以看出，在光伏串数量x=3, 4, 5 条件下和低于系统25%输入功率水平下，相比常规连接方式，逆变器总体效率均有提升。欧洲效率[21]是欧洲联合研究中心基于欧洲光照条件，赋予不同负载条件下逆变器转换效率权重，用来估算逆变器的总体效率。由于在国际上欧洲效率具有很大的参考价值，且在光伏逆变器产品手册中几乎都标有欧洲效率，因此本节用欧洲效率权重系数估算策略对逆变器总体效率提升效果。根据图4 显示的结果，在光伏串数量分别为x=3, 4, 5 条件下，欧洲效率分别提升了0.4%、0.44%和0.45%。通过分析多个场景下提升效果可知，随着群控系统中光伏组串数量增多，系统转换效率提升效果逐渐减弱。另外，考虑群控系统配置的光伏串数量增多导致计算量增大和提升效果减弱的问题，以及考虑实际工程中场地布局的问题，为了减小系统复杂程度，配置3～5 串光伏串的光伏群控系统较为合适。
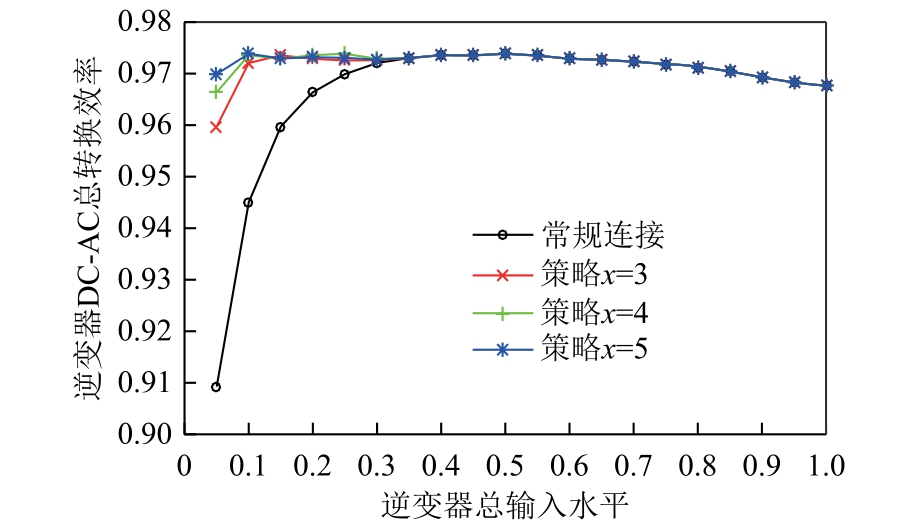
图4 逆变器DC-AC 总转换效率对比
Fig.4 comparison diagram of DC-AC conversion efficiency of the inverter
4.2 实验场景分析
建立三个光伏阵列和三台逆变器的群控系统平台进行1h 实验运行，对防功率越限功能进行分析。从DKASC 网站获取上午1h 光伏辐照度真实数据。将数据导入到光伏阵列模拟器中模拟光伏阵列功率变化趋势。设置逆变器超过最大输出功率5kW 断开与电网连接。
其他文献仅考虑目标函数忽略了天气变化的影响，对比了常规连接、仅考虑目标函数和本策略三种方案运行曲线如图5 和图6 所示。通过本策略方案运行曲线与前两种方案曲线对比来说明控制决策的有效性。
图5 系统1h 低功率运行曲线
Fig.5 Low-power operation curves of the system for 1h
4.2.1 防功率越限策略
图5 中，PAC/PN 表示群控系统中逆变器总输出与总额定功率的比值。从图5a 中可以看出光伏波动随机性很大，突然陡峭使得仅考虑目标函数情况下容易出现功率越限情况。在20～30min 和40～50min期间，由于光伏产生波动，系统超过设定的逆变器最大输出，使得逆变器不能正常工作。图5b 中本策略有效避免了因功率突然增加引起的功率越限情况，提高了系统可靠性。以上结果说明，考虑系统波动情况下防止系统功率越限的策略是有必要和可行的，也进一步得出了群控系统在低功率水平运行下转换效率有了很好的改善。
4.2.2 防止群控系统开关频繁动作策略
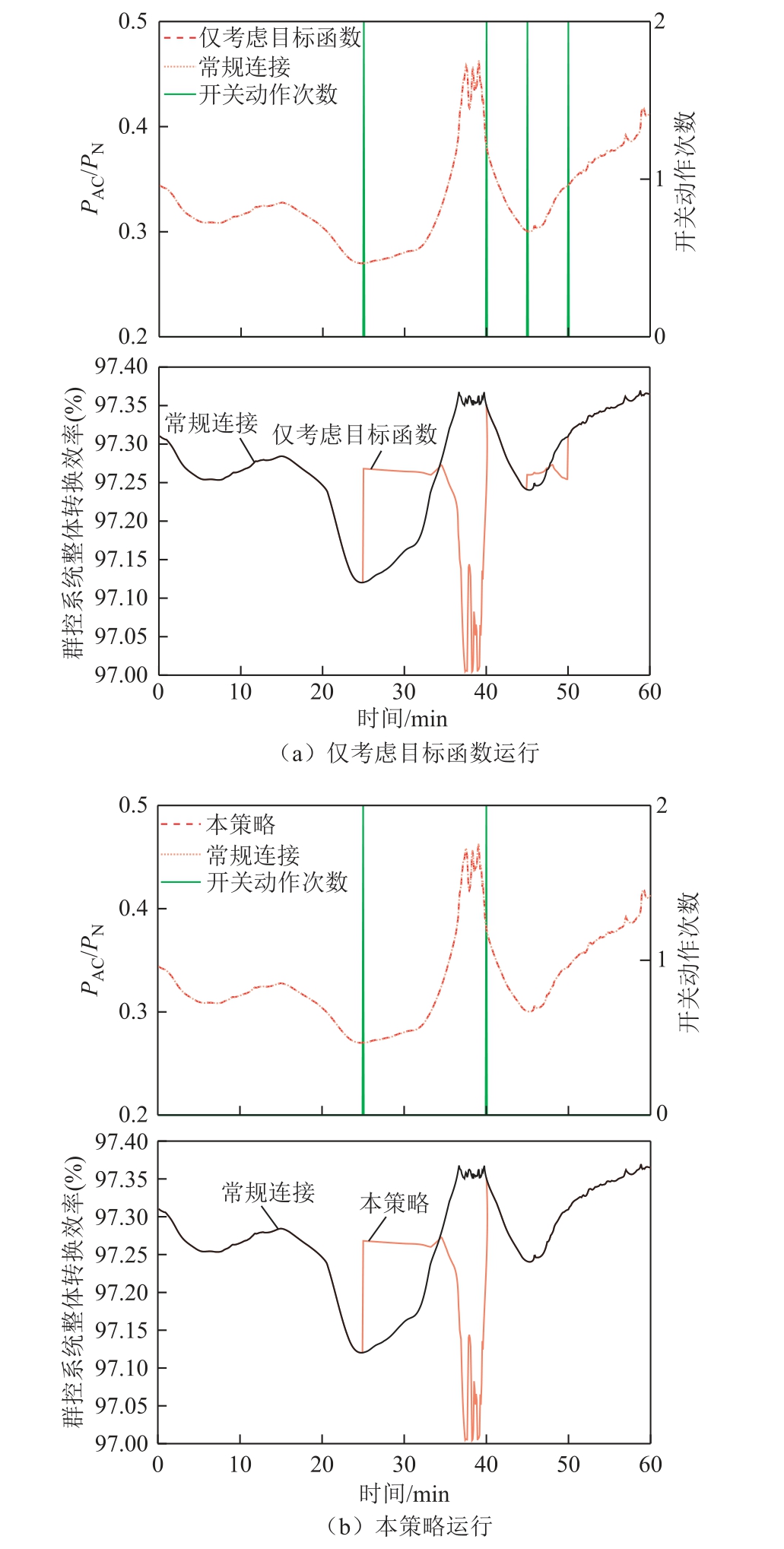
图6 系统1h 功率波动情况下运行曲线
Fig.6 Operating curves of the system under 1h power fluctuations
图6a 为仅考虑目标函数条件下，群控系统中的开关出现频繁动作情况。群控系统在20～50min 期间，系统切换后转换效率提升不大，甚至可能略有下降。但是，图6b 中采用控制策略之后群控系统减少了开关次数。从图6 中可以看出，频繁切换带来的效果并不一定好，可能还会对系统稳定性造成影响。根据以上分析，本文防止开关频繁切换的策略是可行且有效的。
5 结论
本文利用一种直流开关拓扑结构，对其连接方式及群控系统转换效率进行了分析，利用运行效益指标和控制决策，提出一种提升组串逆变器并行效率的直流侧开关重构策略。得出如下结论，可为光伏电站设计人员提供参考。
1）本文策略基于一种开关控制箱、多光伏串及逆变器组成群控系统。本文策略可以提高光伏逆变器总体效率，尤其在低光照下改善效果明显。
2）群控系统中，考虑群控系统配置的光伏串数量增多，导致计算量增大和提升效果减弱的问题以及考虑实际工程中场地布局的问题，为了减小系统复杂程度，群控系统中拥有较小数量的PV 串和逆变器较为合适。考虑光伏电站规模大小及逆变器位置等因素，建立若干个小型群控系统较为合适。
3）开关切换后，系统短时间内可能会超过系统要求的限值。对开关切换后短时间内的功率变化进行预测，防止逆变器功率越限是可行和有效的。
4）复杂多变的天气可能导致系统在切换的临界位置频繁变化，这种情况下开关切换带来的系统提升效果并不显著。频繁切换还可能给系统安全带来隐患，因此考虑防止频繁切换是有必要的。基于投票理论的方法选取历史时间内最适应的连接方式可以避免系统频繁切换。
[1] Li Hanfang, Lin Hongyu, Tan Qingkun, et al. Research on the policy route of China’s distributed photovoltaic power generation[J]. Energy Reports, 2020, 6: 254-263.
[2] Zhang Minhui, Zhang Qin. Grid parity analysis of distributed photovoltaic power generation in China[J].Energy, 2020, 206: 118165.
[3] 肖华锋, 王晓标, 张兴, 等. 非隔离光伏并网逆变技术的现状与展望[J]. 中国电机工程学报, 2020,40(4): 1038-1054.
Xiao Huafeng, Wang Xiaobiao, Zhang Xing, et al.State-of-the-art and future trend of transformerless photovoltaic grid-connected inverters[J]. Proceedings of the CSEE, 2020, 40(4): 1038-1054.
[4] 王文静, 王斯成. 我国分布式光伏发电的现状与展望[J]. 中国科学院院刊, 2016, 31(2): 165-172.
Wang Wenjing, Wang Sicheng. Status and prospect of Chinese distributed photovoltaic power generation system[J]. Bulletin of Chinese Academy of Sciences,2016, 31(2): 165-172.
[5] 盛万兴, 吴鸣, 季宇, 等. 分布式可再生能源发电集群并网消纳关键技术及工程实践[J]. 中国电机工程学报, 2019, 39(8): 2175-2186.
Sheng Wanxing, Wu Ming, Ji Yu, et al. Key techniques and engineering practice of distributed renewable generation clusters integration[J].Proceedings of the CSEE, 2019, 39(8): 2175-2186.
[6] 王震, 鲁宗相, 段晓波, 等. 分布式光伏发电系统的可靠性模型及指标体系[J]. 电力系统自动化,2011, 35(15): 18-24.
Wang Zhen, Lu Zongxiang, Duan Xiaobo, et al.Reliability model and indices of distributed photovoltaic power system[J]. Automation of Electric Power Systems, 2011, 35(15): 18-24.
[7] Du Yang, Lu D C, James G, et al. Modeling and analysis of current harmonic distortion from grid connected PV inverters under different operating conditions[J]. Solar Energy, 2013, 94: 182-194.
[8] Rampinelli G A, Krenzinger A, Romero F C.Mathematical models for efficiency of inverters used in grid connected photovoltaic systems[J]. Renewable and Sustainable Energy Reviews, 2014, 34: 578-587.
[9] Calais M, Myrzik J, Spooner T, et al. Inverters for single-phase grid connected photovoltaic systems-an overview[C]//2002 IEEE 33rd Annual IEEE Power Electronics Specialists Conference, Proceedings (Cat.No. 02CH37289), IEEE, Cairns, Qld., Australia, 2002,4: 1995-2000.
[10] Jana J, Saha H, Bhattacharya K D. A review of inverter topologies for single-phase grid-connected photovoltaic systems[J]. Renewable and Sustainable Energy Reviews, 2017, 72: 1256-1270.
[11] Mahmoud Y, Elsaadany E F. Enhanced reconfiguration method for reducing mismatch losses in PV systems[J]. IEEE Journal of Photovoltaics, 2017,7(6): 1746-1754.
[12] Ngoc T N, Sanseverino E R, Quang N N, et al. A hierarchical architecture for increasing efficiency of large photovoltaic plants under non-homogeneous solar irradiation[J]. Solar Energy, 2019, 188: 1306-1319.
[13] Krishna G S, Moger T. Enhancement of maximum power output through reconfiguration techniques under non-uniform irradiance conditions[J]. Energy,2019, 187: 115917.
[14] Dogga R, Pathak M K. Recent trends in solar PV inverter topologies[J]. Solar Energy, 2019, 183: 57-73.
[15] 韩富强, 王议锋, 陈梦颖, 等. 多模式切换运行的拓扑变换型多谐振软开关直流变换器及参数设计方法[J]. 电工技术学报, 2019, 34(22): 4728-4738.
Han Fuqiang, Wang Yifeng, Chen Mengying, et al. A topology-morphing multi-resonant soft-switching DC-DC converter with parameter design method for multi-mode operation[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4728-4738.
[16] 肖华锋. 非隔离型光伏并网逆变器软开关技术[J].中国电机工程学报, 2019, 39(3): 812-821.
Xiao Huafeng. Soft-switching techniques for transformerless photovoltaic grid-connected inverters[J].Proceedings of the CSEE, 2019, 39(3): 812-821.
[17] 王议锋, 陈博, 吕雯, 等. 拓扑变换型LLC-C 谐振软开关直流变换器[J]. 电工技术学报, 2019, 34(18):3810-3820.
Wang Yifeng, Chen Bo, Lü Wen, et al. A topology morphing LLC-C resonant soft-switching DC-DC converter[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3810-3820.
[18] 李永东, 徐杰彦, 杨涵棣, 等. 多电平变换器拓扑结构综述及展望[J]. 电机与控制学报, 2020, 24(9):1-12.
Li Yongdong, Xu Jieyan, Yang Handi, et al. Overview and prospect of multilevel converter topology[J].Electric Machines and Control, 2020, 24(9): 1-12.
[19] Hasan R, Mekhilef S, Seyedmahmoudian M, et al.Grid-connected isolated PV microinverters: a review[J]. Renewable & Sustainable Energy Reviews,2017, 67: 1065-1080.
[20] Zhang Li, Sun Kai, Xing Yan, et al. A modular gridconnected photovoltaic generation system based on DC bus[J]. IEEE Transactions on Power Electronics,2011, 26(2): 523-531.
[21] Zhang Li, Sun Kai, Hu Haibing, et al. A system-level control strategy of photovoltaic grid-tied generation systems for European efficiency enhancement[J].IEEE Transactions on Power Electronics, 2014, 29(7):3445-3453.
[22] Zhang Li, Sun Kai, Xing Yan, et al. Parallel operation of modular single-phase transformerless grid-tied PV inverters with common DC bus and AC bus[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(4): 858-869.
[23] Spertino F, Corona F, Di Leo P. Limits of advisability for master–slave configuration of DC-AC converters in photovoltaic systems[J]. IEEE Journal of Photovoltaics, 2012, 2(4): 547-554.
[24] 韩郁, 方廷, 张岚. 多逆变器光伏并网发电系统的群控策略和实现方法[J]. 可再生能源, 2009, 27(6):74-77.
Han Yu, Fang Ting, Zhang Lan. Group control strategy and realization methods for multi-inverter grid-connected PV systems[J]. Renewable Energy Resources, 2009, 27(6): 74-77.
[25] 胡克用, 胥芳, 艾青林, 等. 多逆变器光伏发电网络群控策略及实现方法[J]. 南京大学学报(自然科学), 2016, 52(2): 398-408.
Hu Keyong, Xu Fang, Ai Qinglin, et al. Group control strategy and realization method of multi-inverter for photovoltaic power generation network[J]. Journal of Nanjing University (Natural Sciences), 2016, 52(2):398-408.
[26] Hu Keyong, Li Wenjuan, Wang Lidong, et al.Topology and control strategy of power optimisation for photovoltaic arrays and inverters during partial shading[J]. IET Generation Transmission &Distribution, 2018, 12(1): 62-71.
[27] 薛世伟, 贾清泉, 苏亚超, 等. 组串式光伏发电系统直流侧可变拓扑及多目标控制策略[J]. 中国电机工程学报, 2019, 39(7): 1968-1975.
Xue Shiwei, Jia Qingquan, Su Yachao, et al. Variable DC side topology and multi-objective control strategy in group-string PV generation system[J]. Proceedings of the CSEE, 2019, 39(7): 1968-1975.
[28] 张磊, 王晓声, 孙凯, 等. 多模块并联逆变器系统中网侧电抗对谐振特性的影响分析[J]. 电工技术学报, 2017, 32(13): 109-117.
Zhang Lei, Wang Xiaosheng, Sun Kai, et al. Analysis of grid-side reactance's impact on resonance characteristic of multi-module parallel inverter system[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 109-117.
[29] 曹文远, 韩民晓, 谢文强, 等. 交直流配电网逆变器并联控制技术研究现状分析[J]. 电工技术学报,2019, 34(20): 4226-4241.
Cao Wenyuan, Han Minxiao, Xie Wenqiang, et al.Analysis on research status of parallel inverters control technologies for AC/DC distribution network[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4226-4241.
[30] 谢志为, 陈燕东, 伍文华, 等. 弱电网下多逆变器并网系统的全局高频振荡抑制方法[J]. 电工技术学报, 2020, 35(4): 885-895.
Xie Zhiwei, Chen Yandong, Wu Wenhua, et al. A global high-frequency oscillation suppression method for multi-inverter grid-connected system in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 885-895.
[31] 万晓凤, 詹子录, 丁小华, 等. 基于虚拟同步发电机的多逆变器并联改进控制策略[J]. 电机与控制学报, 2020, 24(2): 118-127.
Wan Xiaofeng, Zhan Zilu, Ding Xiaohua, et al.Improved control strategy of multi-inverter parallel based on virtual synchronous generator[J]. Electric Machines and Control, 2020, 24(2): 118-127.