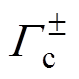表示正负极导线表面，
表示地面，
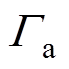表示长方形人工边界。摘要 迭代通量线方法是一种被广泛应用于求解高压直流输电线路下离子流问题的方法，在每根流线上需要求解一个多变量的最小二乘优化问题。该文从迭代通量线方法出发，结合递推格式将每根流线上问题简化为单变量优化问题，从而使得通量线方法的计算规模被大大减小。实验表明，该文所提方法能够有效提高求解效率和在不同初值下的鲁棒性。该文提出的低阶迭代通量线方法能够有效应用于具有复杂几何结构的离子流模型。
关键词：离子流 合成电场 高压直流输电线路 迭代通量线法
电晕放电是一种极不均匀场中的自持放电现象，当局部电场超过起晕电场时，电极附近空气将发生电离，形成电晕。对电晕放电现象进行建模时，考虑到光电子的运动速度远大于正负离子，因此将全空间分解为环绕电极的一层电离区以及电离区以外的传导区分别建模。将电离区内复杂的复合、吸附、电离等物理过程的模型称为电晕流体模型；在此基础上将电离层完全忽略，仅考虑传导区内正负离子在电场作用下作定向移动的简化模型称为离子流模型[1]。离子流模型在高压直流输电线路的电磁环境仿真中得到广泛应用[2-6]。
离子流模型对应的数学表达式为泊松方程-连续性方程耦合系统，其中连续性方程描述了空间离子流分布，而泊松方程描述了空间电荷与导线产生的合成电场分布。整个计算区域内外边界上电位分布以及Kapzov假设为泊松方程-连续性方程耦合系统提供了必要的定解条件。
通量线方法是一种被广泛用于求解合成电场和空间离子流分布的方法，该方法最开始被用于求解经Deutsch假设简化后的一维问题。在此基础上，提出一种消除Deustch假设的迭代通量线方法，该方法通过迭代修正通量线方向，逐步移除Deustch假设带来的影响[7-8]。通量线方法可以分为两类：①M. P. Sarma等提出的积分方程方法[9-10]；②乔骥等提出的有限差分方法[11-12]。本文从基于有限差分的迭代通量线方法出发，将待求解的常微分方程组离散为差分方程组，利用非线性最小二乘优化算法搜索满足边界条件并使得差分方程组残差最小的解。这种方法具有较好的普适性，同时适用于单极性和双极性模型。由于待优化变量个数正比于差分节点数，随着差值节点增多，相应的计算时长将显著增加；同时多变量优化问题对初值敏感，求解过程中容易失稳。本文从基于有限差分的通量线方法出发，结合递推格式，将多变量优化问题简化成单变量优化问题，从而提升原方法的效率和鲁棒性。
典型的双极性高压直流输电线路离子流计算模型示意图如图1所示，图中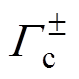，表示正负极导线表面，表示地面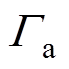，表示长方形人工边界。
高压直流输电线路下的离子流模型基于如下三个基本假设[13]：
（1）电离层对传导区的影响忽略不计。
（2）离子的扩散效应忽略不记。
（3）离子迁移率恒为一个常数。
传导区内空间电荷分布和电场分布对应的数学模型[14]为
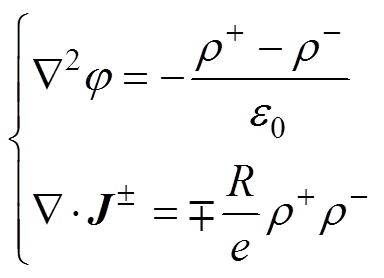（1）
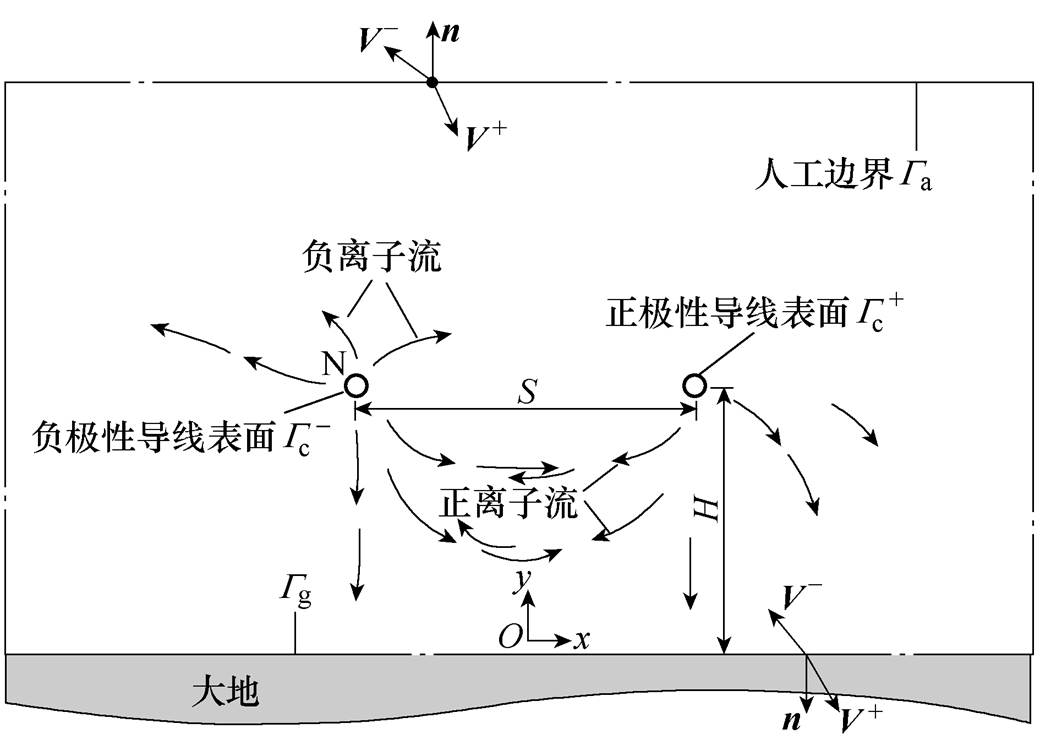
图1 离子流计算模型示意图
Fig.1 Calculation model of the ion flow problem
式中，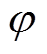
、
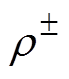为待求的空间电位与正负电荷分布；
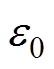为真空介电常数；R、e分别为正负离子的复合系数及电子电量；
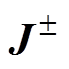为正负离子流，具体定义为
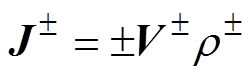（2）式中，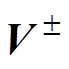
为正负电荷在电场强度E作用下定向运动速度，即
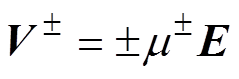（3）
式中，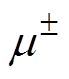
为正负离子迁移率，本文统一取为1.5× 10-4m2/(V·s)。基于速度场式（3），可以将外边界分解为正负电荷的流入、流出边界[15]，即
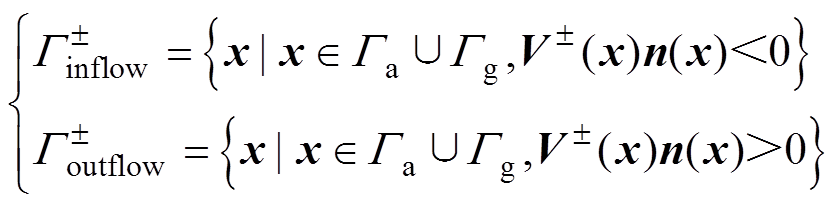（4）式中，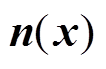
为边界x处的外法向量。式（1）中泊松方程，边界条件为
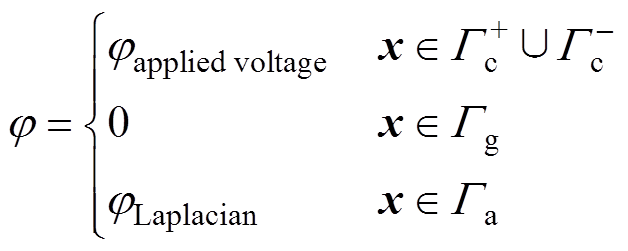（5）
即导线表面电位为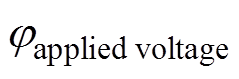
，地面电位为0V，而人工边界的电位等于拉普拉斯场对应的电位。式（1）中的连续性方程，需要提供流入边界的信息作为定解条件，有
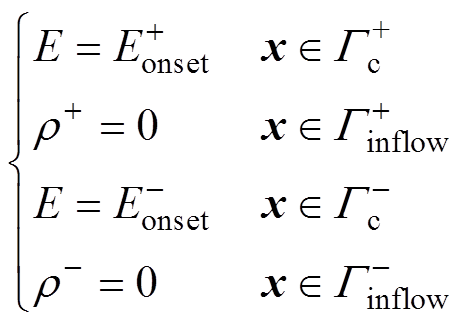（6）式中，正负极导线表面作为产生空间电荷的源，由Kapzov假设给出电场强度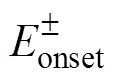
作为边界条件；而在外边界处没有电荷生成。综上，偏微分方程组式（1）和边界条件式（5）、式（6）组成了离子流模型对应的边值问题。
Deutsch假设认为空间电场强度和标称电场具有相同的方向，即
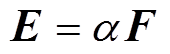（7）式中，F为标称电场矢量。标称场满足Poisson方程为
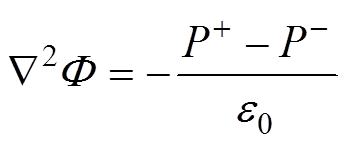（8）
式中，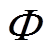
为标称电位；
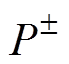为标称正负电荷密度。式（7）中标量场
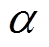为E和F幅值之比。在迭代通量线方法中，往往选择上一步得到的计算结果作为标称场。由标称电场下通量线
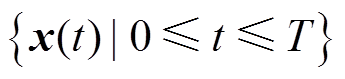定义为
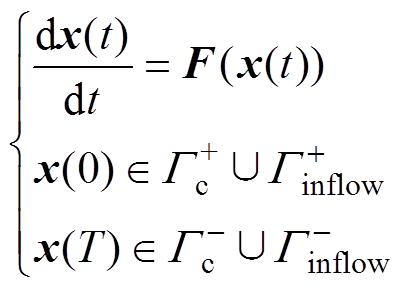（9）结合Deutsch假设可将二维或三维离子流问题转化为定义在通量线上的一维问题，原偏微分方程组式（1）被简化为关于沿线标称电位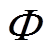的常微分方程组[11]，即
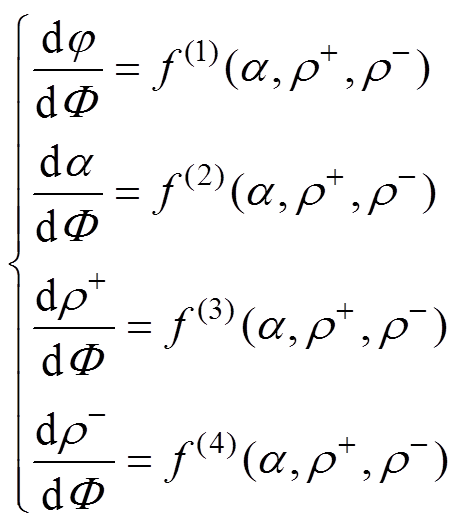（10）
式中，函数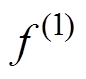
、
、
、
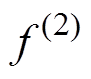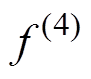定义分别为
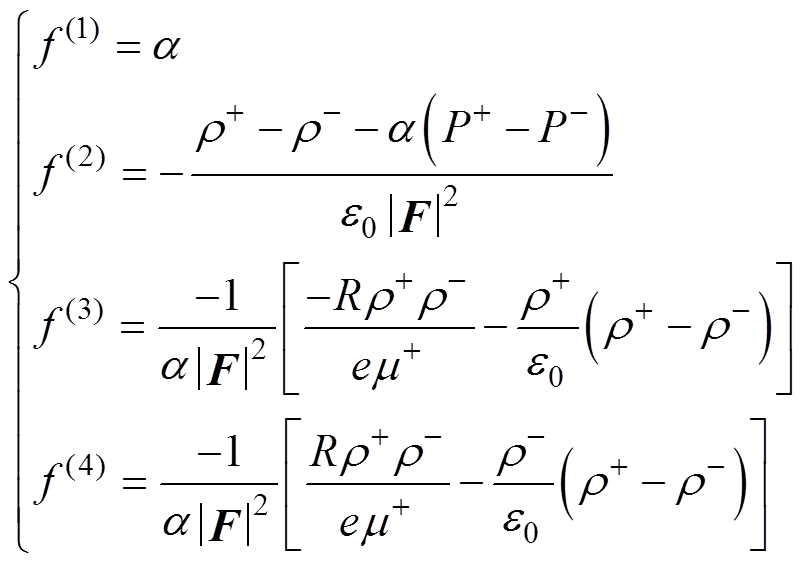（11）根据通量线起点和终点的位置，需要施加不同的边界条件，具体如下：
（1）起始于正极性导线，终止于负极性导线的通量线上边界条件式（5）、式（6）简化为
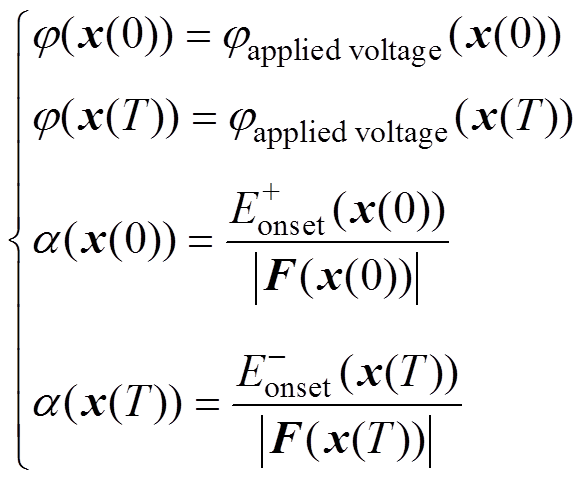（12）（2）起始于正极性导线，终止于地面的通量线上边界条件式（5）、式（6）简化为
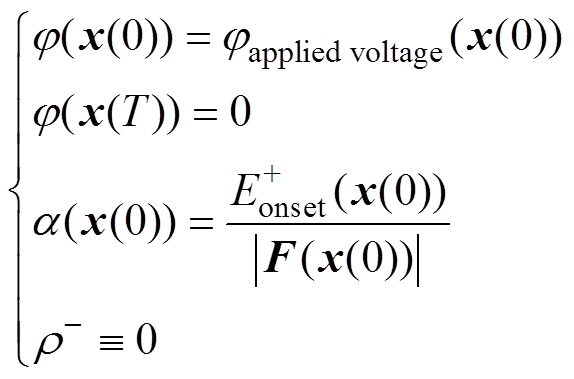（13）
（3）起始于地面，终止于负极性导线的通量线上边界条件式（5）、式（6）简化为
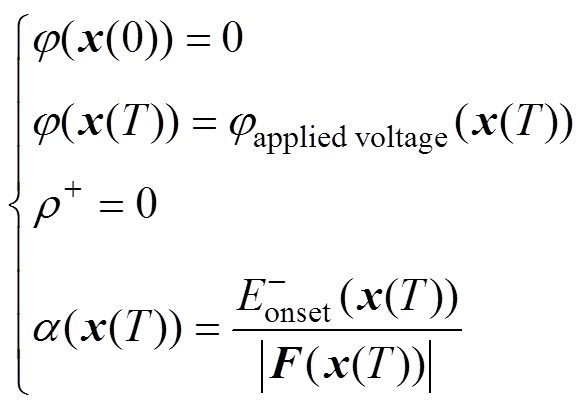（14）从上述边界条件可以看到，在起点或终点位于地面的通量线上，只需要考虑一种极性的空间电荷，称这样的模型为单极性模型；在起点和终点同时位于正负极导线表面的通量线上，则需要考虑两种极性的空间电荷，这样的模型被称为双极性模型。接下来将分别介绍如何处理这两类问题的方法。
单极性模型指的是仅考虑一种极性空间电荷的离子流模型。以常微分方程式（10）和边界条件式（13）构成的边值问题为例，此时沿线负离子分布为零，待求变量为、、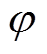
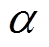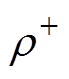。在流线上选取N个差值节点，即
（15）采用Crank-Nicolson差分格式将方程式（10）离散为代数方程组为
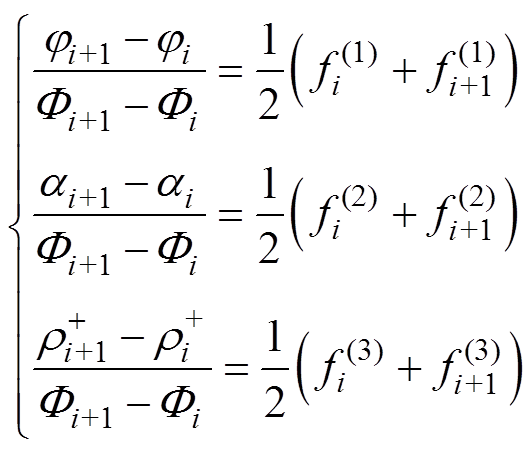（16）
2.2.1 传统迭代通量线方法
文献[7]中提出的迭代通量线方法处理单极性模型的具体步骤如下。
根据差分方程组式（16）可定义长度为3(N-1)的残差序列为
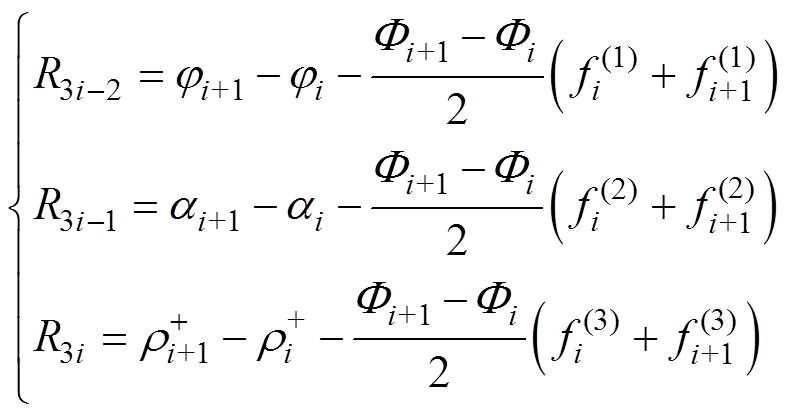（17）边界条件式（13）也改写成残差形式为
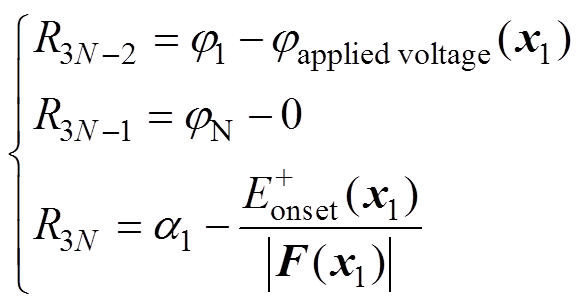（18）
文献[7]提出的通量线方法求解的问题规模为3N：寻找合适的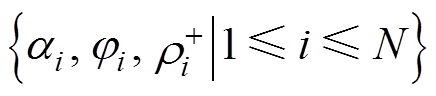
使得由式（17）、式（18）定义的3N个残差取得最小值。即原边值问题转化成自由度为3N的最小二乘优化问题[11]。
2.2.2 低阶通量线方法
将差分方程式（16）改写为递推格式为
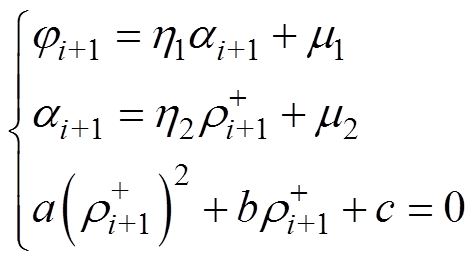（19）其中，各个系数的具体表达式如下
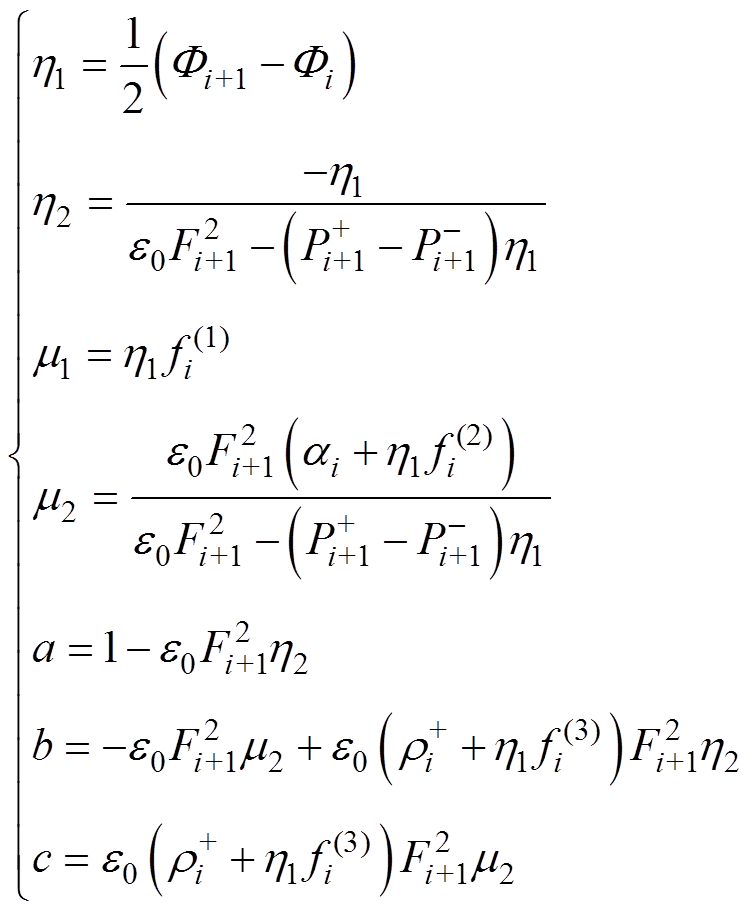（20）
式中，Fi为标称电场矢量F在第i个节点处的幅值。
注意到对于当前只包含正电荷的通量线，空间电荷从上游单元流入下游单元，因此当上游节点信息
、
、
已知时，根据递推关系式（19），可确定下游节点信息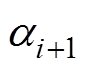
、
、
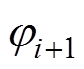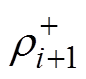。边界条件式（13）已经给出了位于流入边界的
、
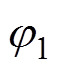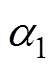，只要给定流入边界正电荷密度
，即可通过式（19）逐节点递推出沿线各节点的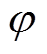、、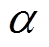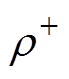，最终得到流出边界处的电位值
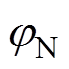，将这一函数关系简记为
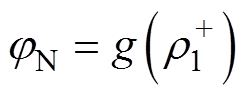（21）如果给定的流入边界正电荷密度合适，那么流出边界处的电位应当满足边界条件式（13），为地电位。原边值问题的求解转化为单变量的最小二乘优化问题：寻找流入边界正电荷密度，使得残差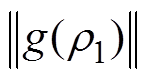
取最小值。
双极性模型指的是同时存在正极性和负极性空间电荷的离子流模型。采用Crank-Nicolson差分格式将常微分方程组式（10）离散为代数方程组，有
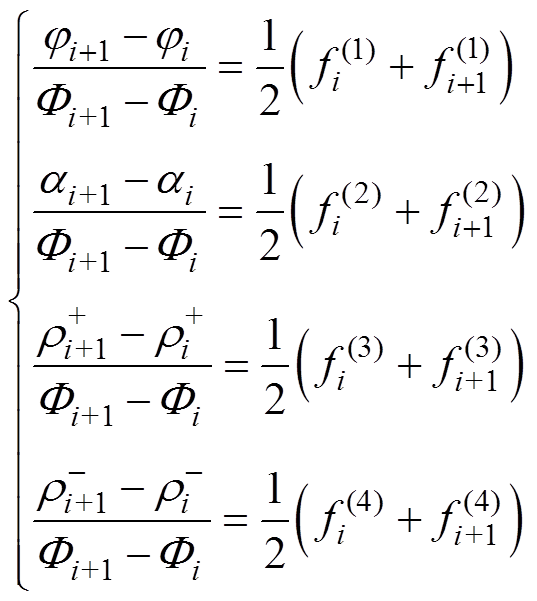（22）2.3.1 传统迭代通量线方法
文献[7]中提出的迭代通量线方法处理双极性模型的方式和单极性类似：差分方程组式（22）对应着4N-4项残差，边界条件式（12）对应着另外4项残差。在流线上的边值问题被转化为4N个变量的最小二乘优化问题[11]。
2.3.2 低阶通量线方法
双极性模型与单极性模型的不同在于流线上同时出现正负电荷，同时还需要考虑正负电荷相互复合。本文结合不动点迭代，在求解过程中将这两种电荷完全解耦：迭代过程中，每一步固定一种极性电荷，将原问题简化为单极性问题处理。具体流程如下：
（1）第k+1步，将第k步得到的计算结果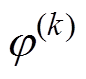
、
、
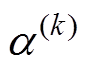及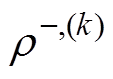
作为标称场。固定沿线正极性电荷分布，即
，求解负极性问题为
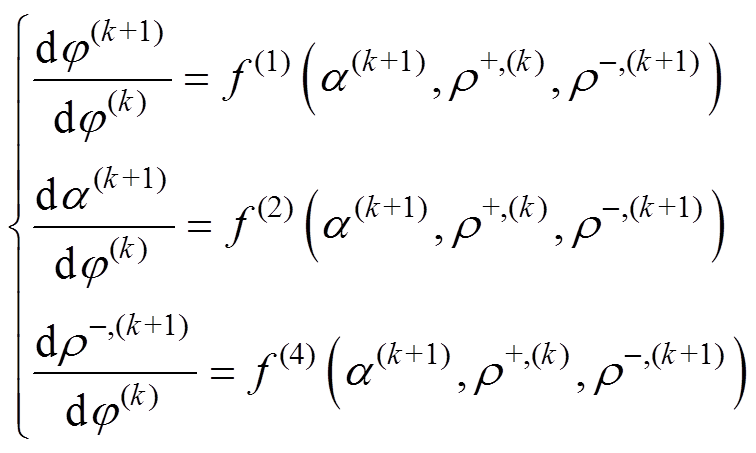（23）（2）第k+2步，将第k+1步得到的计算结果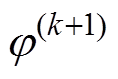
、
、
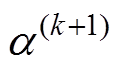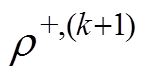及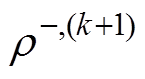
作为标称场。固定沿线负极性电荷分布，即
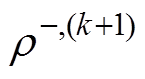=，求解正极性问题为
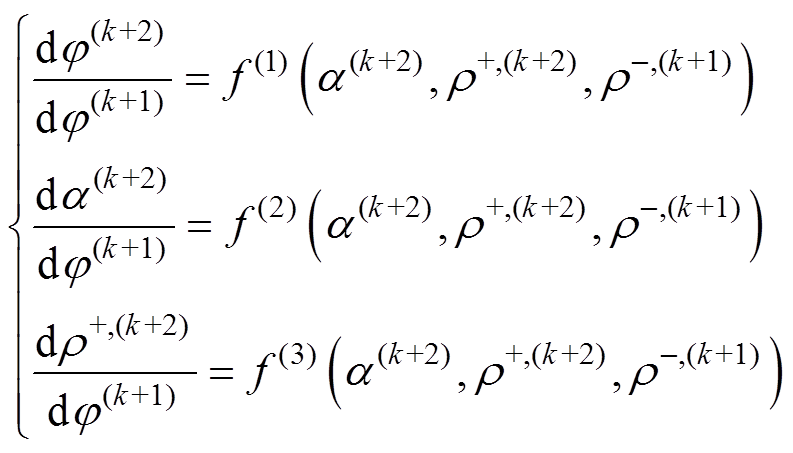（24）
重复上述两个步骤，直到最终计算结果收敛。
改进后迭代通量线方法的基本计算流程如图2所示。
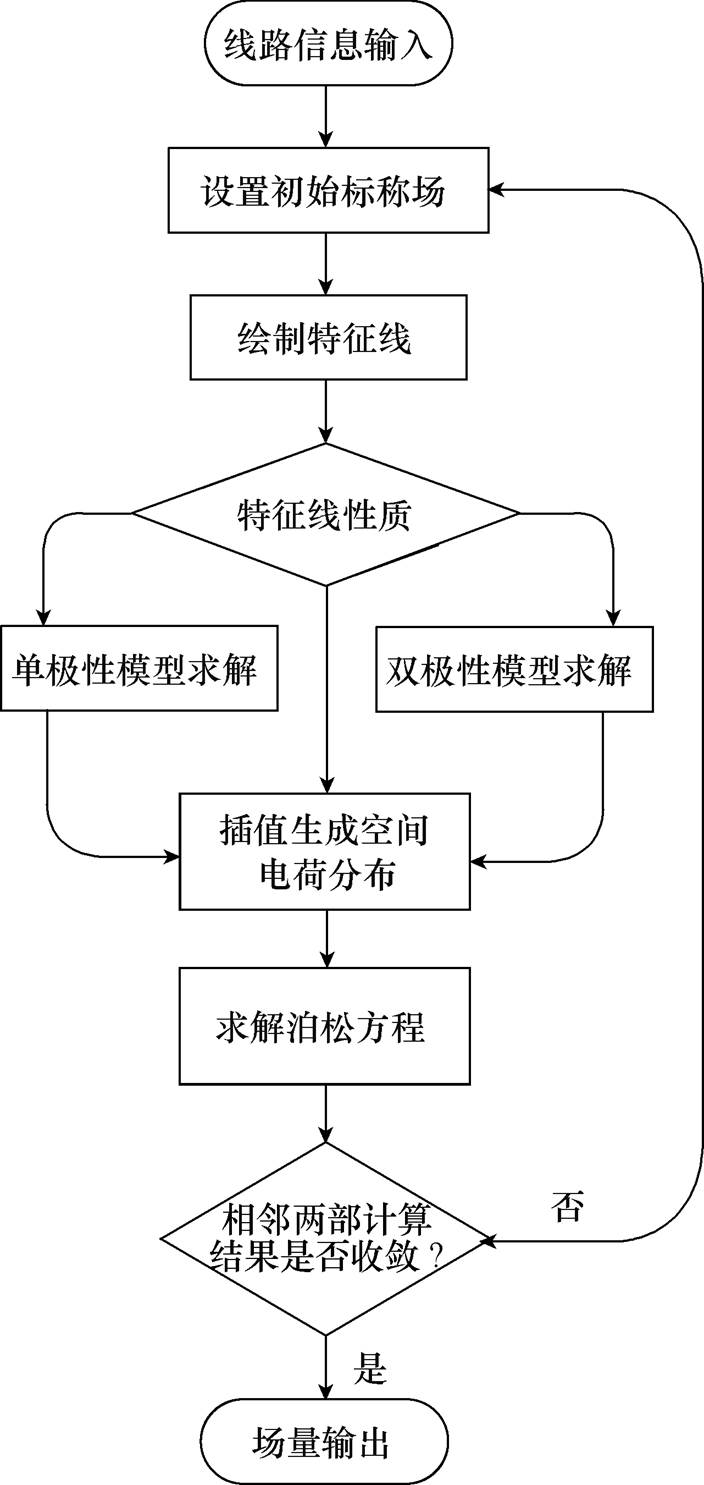
图2 迭代通量线方法计算流程
Fig.2 Flow diagram for the iterative flux tracing method
和文献[7]提出的传统迭代通量线方法相比，本文方法主要改进“单极性模型求解”和“双极性模型求解”这两个环节。文献[7]中方法在处理单根通量线上的边值问题时，同时求解全部差值节点上的未知量：单极性模型对应3N个未知量的最小二乘优化问题，双极性模型对应4N个未知量的最小二乘优化问题。随着差分节点数增加，计算时间会显著增长；同时作为多目标优化问题，对初值敏感，为使迭代稳定快速收敛，传统的迭代通量线方法需要估计沿线电荷密度，并以此作为迭代初值[16]。相较而言，本文方法利用递推公式使未知量简化为流入边界处的电荷密度：这样单极性模型被转化为一个单变量的优化问题；双极性模型则被转化为一个双变量优化问题。本文方法有效地减小了优化问题规模，未知数个数从3N～4N减小为1；同时算法的鲁棒性也得到显著提升，在不同的初值选取下都可以取得较好的收敛效果。
在图3所示的±300kV高压直流输电线路模型中分别选取两条通量线：一条起始于正极导线，终止于负极导线；另一条起始于正极导线，终止于地面。这两条通量线分别对应双极性模型和仅考虑正极性空间电荷的单极性模型。
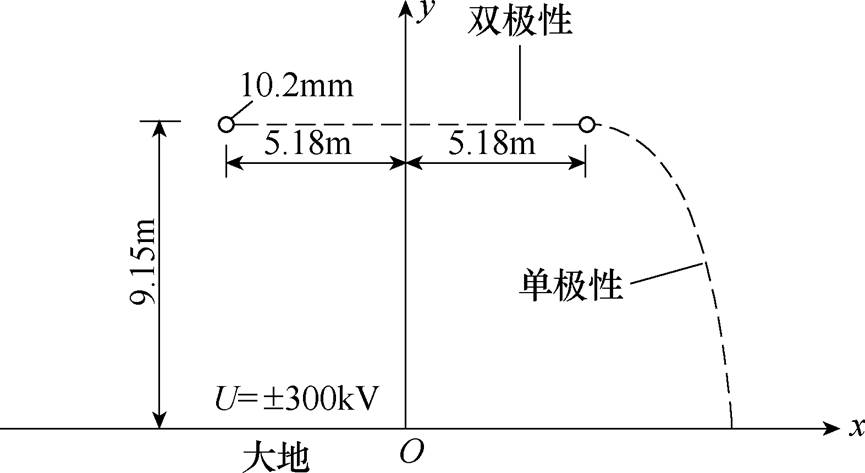
图3 ±300kV高压直流输电线路结构
Fig.3 Configuration of ±300kV HVDC transmission line
图4中比较了在单极性模型中，低阶通量线方法和文献[7]中迭代通量线方法的计算时间。可以看出，随着沿线差分点数增加，文献[7]方法耗时近似呈二次方量级增长，而低阶方法的耗时则呈线性增长。另外，对于低阶方法，在区间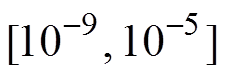
中任意选取迭代，对计算时间的影响较小，在300个差分节点情况下，也仅需要0.25s即可完成计算，而文献[7]方法则需要16s。
表1中比较了在不同差分点数下两种方法得到的正极性导线表面的电荷密度。可以看到，在单极性模型中，不同差分点数下文献[7]方法和本文提出的方法得到的结果完全相同。
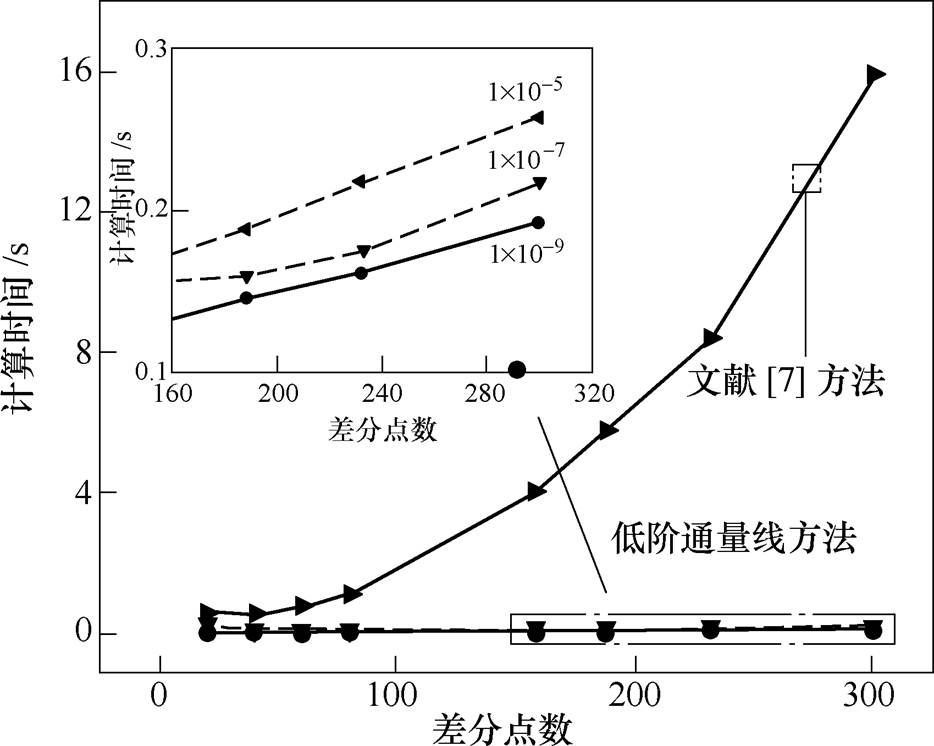
图4 单极性模型下文献[7]方法和低阶通量线方法计算时间对比
Fig.4 Comparison of the computational time between the existing method of Ref.[7] and the proposed low-order flux tracing method under the unipolar model
表1 单极性模型下文献[7]方法和低阶通量线方法正极性导线表面电荷密度对比
Tab.1 Comparison of the ion density on the conductor surface between the existing method of Ref.[7] and the proposed low-order flux tracing method under the unipolar model
差分点数流入边界正电荷密度/(nC/m2) 本文方法文献[7]方法 4030.05130.051 8030.97030.970 16031.13431.168 30031.18831.188
图5展示了两种方法在双极性模型中的计算结果。可以看到，随着差分点数的增长，本文提出方法的计算时长近似呈线性增加，在300个离散点时，在区间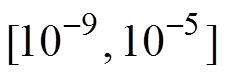
中选取迭代初值，对应计算总耗时不超过4s，而文献[7]方法则需要25s。
表2中分别对比了不同方法得到的双极性模型中正极性导线表面的正电荷密度和负极性导线表面的负电荷密度。由于引入了不动点迭代，在沿线的差分点数为40时，两种方法得到的电荷密度存在3%的相对误差，然而随着点数增加，电荷密度趋于稳定，两种方法获得的结果差别越来越小，点数为160时，相对误差小于0.5%，即本文提出的低阶方法具有和文献[7]方法相同的精度。
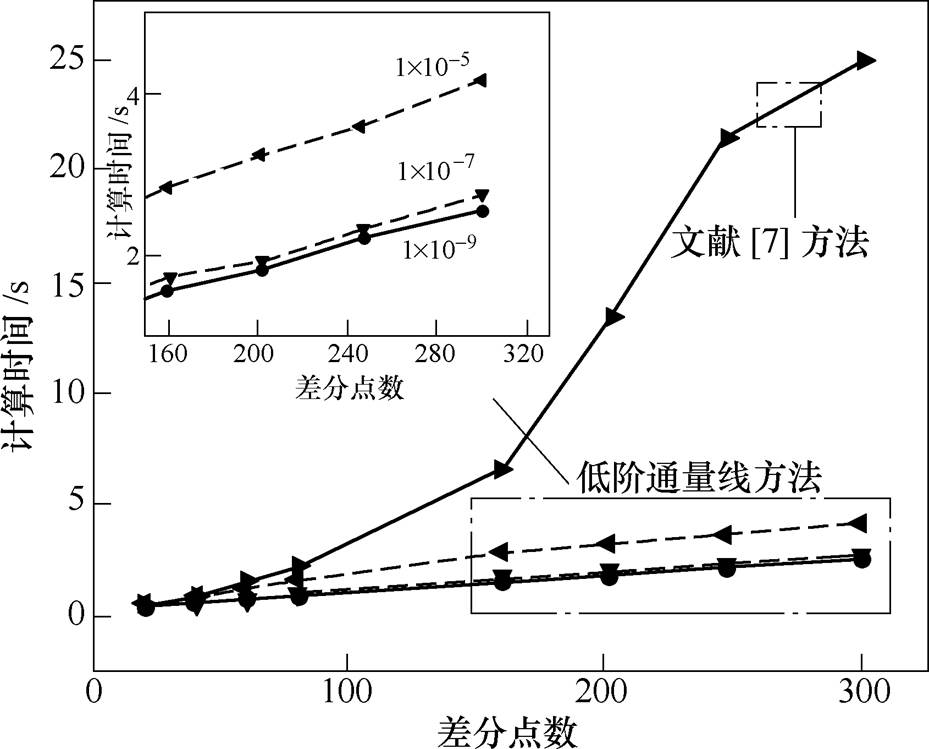
图5 双极性模型下文献[7]方法和低阶通量线方法计算时间对比
Fig.5 Comparison of the computational time between the existing method of Ref.[7] and the proposed low-order flux tracing method under the bipolar model
表2 双极性模型下文献[7]方法和低阶通量线方法导线表面正负电荷密度对比
Tab.2 Comparison of the positive and negative ion density on the conductor surface between the existing method of Ref.[7] and the proposed low-order flux tracing method under the bipolar model
差分点数正流入边界正电荷密度/ (nC/m2)负流入边界负电荷密度/ (nC/m2) 本文方法文献[7]方法本文方法文献[7]方法 40363.497372.368378.509386.495 80372.147375.014386.285389.364 160374.140375.890388.492390.596 300374.410375.990388.777390.741
本节在几何结构更复杂的±800kV六分裂高压直流输电线路模型中对比了低阶通量线方法和传统通量线方法，线路几何参数参见文献[17]。每根子导线表面等间距绘制16根流线，每根流线上差分点数为300。外循环迭代两次后计算结果趋于稳定，文献[7]方法耗时4 200s，而本文提出的低阶方法耗时620s，仅为传统方法的14.76%。
图6和图7分别比较了两种方法得到的地面上场量和实际测量结果[17]。可以看到，文献[7]方法和低阶方法得到的地面上电场强度和离子流密度完全相同，且和测量结果吻合性良好，即验证本文方法在具有复杂几何结构模型下的正确性。
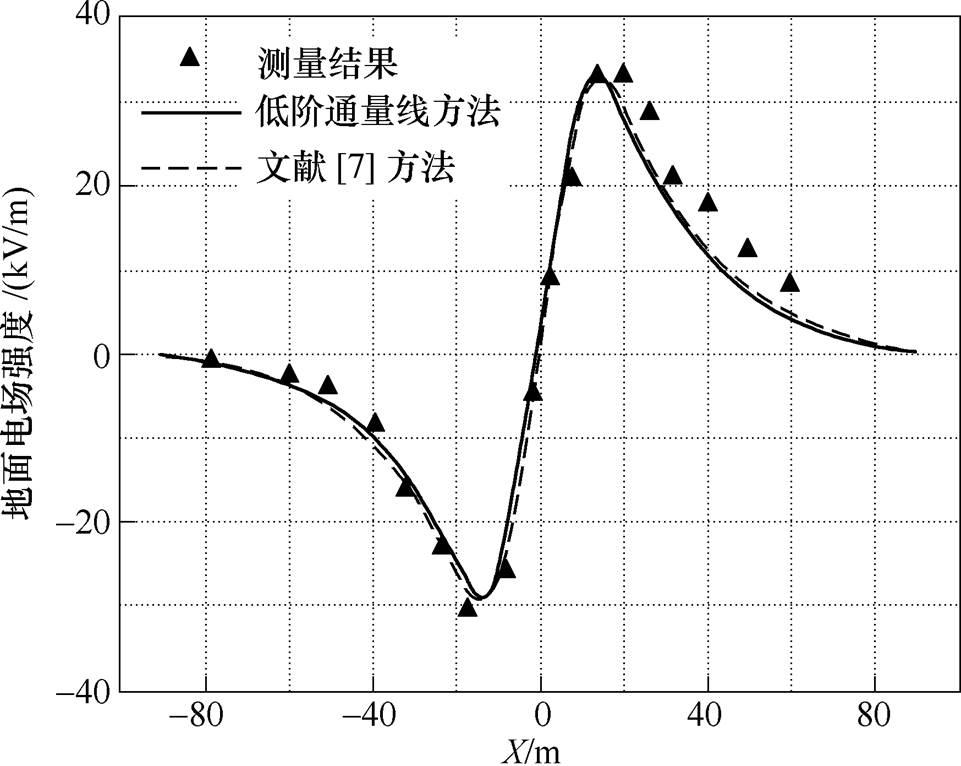
图6 ±800kV高压直流输电线路地面电场强度对比
Fig.6 Comparison of the electric field intensity on the ground level with different methods
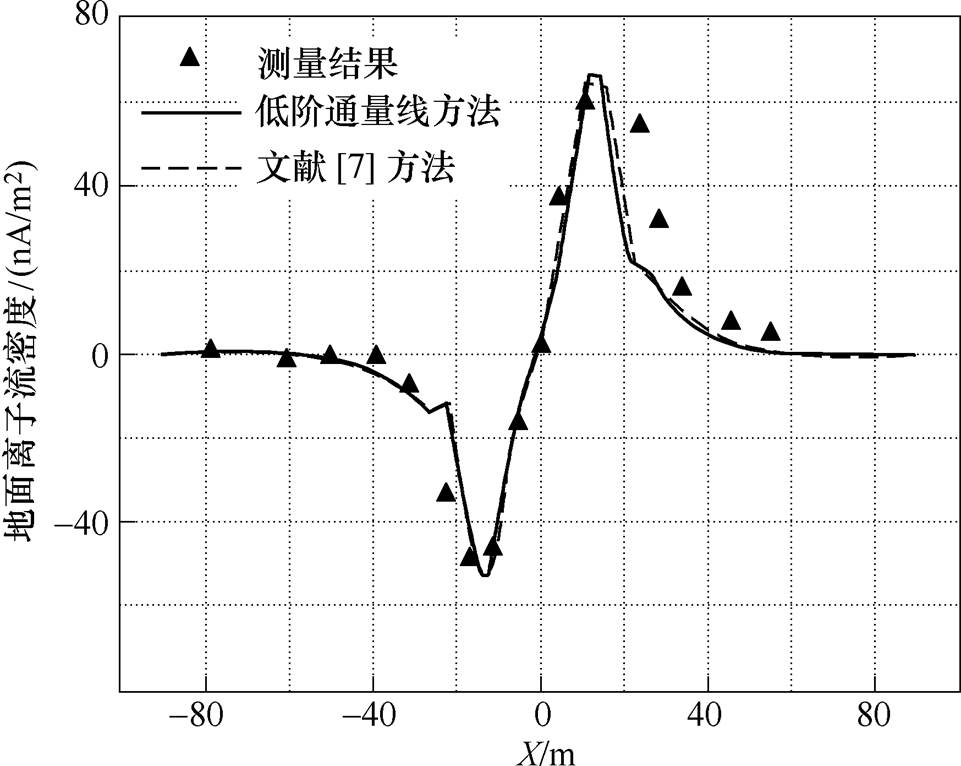
图7 ±800kV高压直流输电线路地面离子流密度对比
Fig.7 Comparison of the ion current density on the ground level with different methods
本文提出一种基于递推格式的低阶通量线方法用于计算高压直流输电线路空间离子流场及合成电场，将传统方法中涉及3N～4N个未知数的优化问题简化为单变量优化问题，显著减小问题规模，进而提高计算效率，同时使得问题对初值的鲁棒性大大提升。本文方法使得低阶通量线方法在具有复杂几何结构的模型中的应用成为可能。
参考文献
[1] 郑跃胜. 高压直流导线的电晕场特性研究[D]. 北京: 清华大学, 2012.
[2] Sarma M P, Janischewskyj W. DC corona on smooth conductors in air: steady state analysis of the ioni- zationlayer[J]. Proceedings of IEEE, 1969, 116(1): 161-166.
[3] 乔骥, 葛小宁, 邹军. 采用通量线-有限元混合方法求解有风条件下直流输电线路离子流场[J]. 电工技术学报, 2019, 34(5): 910-916.
Qiao Ji, Ge Xiaoning, Zou Jun. A flux tracing-finite element hybrid method for calculating ion-flow field of HVDC overhead lines in presence of wind[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 910-916.
[4] 杨帆, 代锋, 罗汉武, 等. 雾霾天气下的直流输电线路离子流场分布特性及其影响因素[J]. 电工技术学报, 2016, 31(12): 49-57.
Yang Fan, Dai Feng, Luo Hanwu, et al. The distribution characteristics and factor influence of the ionized field of DC transmission lines under haze weather[J]. Transactions of China Electrotechnical Society, 2016, 31(12): 49-57.
[5] 乔骥, 邹军, 袁建生, 等. 有屏蔽线时特高压直流输电线路地面电场与离子流场计算与分析[J]. 电网技术, 2017, 41(7): 2386-2392.
Qiao Ji, Zou Jun, Yuan Jiansheng, et al. Calculation of ground level electric field and ion flow of HVDC transmission line with shield wires[J]. Power System Technology, 2017, 41(7): 2386-2392.
[6] 乔骥, 路遥, 刘增训, 等. 横向风对特高压交直流混合线路地面电场与离子流场分布特性的影响[J]. 电网技术, 2018, 42(4): 1234-1240.
Qiao Ji, Lu Yao, Liu Zengxun, et al. Influence of transverse wind on ground-level electric field and ion flow field profiles of hybrid HVAC/HVDC trans- mission lines[J]. Power System Technology, 2018, 42(4): 1234-1240.
[7] 乔骥, 徐志威, 邹军, 等. 一种消除Deutch假设的高精度迭代特征线方法求解高压直流输电线路离子流场[J]. 电工技术学报, 2018, 33(19): 4419- 4425.
Qiao Ji, Xu Zhiwei, Zou Jun, et al. A high-accuracy iterative method of characteristics without deutsch assumption for calculating ion-flow field of HVDC overhead lines[J]. Transactions of China Electro- technical Society, 2018, 33(19): 4419-4425.
[8] Qiao Ji, Zhang Pengfei, Zhang Jiangong, et al. An iterative flux tracing method without deutsch assumption for ion-flow field of AC/DC hybrid transmission lines[J]. IEEE Transaction on Magnetics, 2018, 54(3): 1-4.
[9] Sarma M P, Janischewskyj W. Analysis of corona losses on DC transmission lines: I-unipolar lines[J]. IEEE Transactions on Power Apparatus and Systems. 1969, 88(5): 718-731.
[10] Sarma M P, Janischewskyj W. Analysis of corona losses on DC transmission lines: II-bipolar lines[J]. IEEE Transactions on Power Apparatus and Systems. 1969, 88(10): 1476-1491.
[11] 乔骥, 邹军, 袁建生, 等. 采用有限差分求解高压直流输电线路空间离子流场的新方法[J]. 电工技术学报, 2015, 20(6): 85-91.
Qiao Ji, Zou Jun, Yuan Jiansheng, et al. A new finite difference based approach for calculating ion flow field of HVDC transmission lines[J]. Transactions of China Electrotechnical Society, 2015, 20(6): 85-91.
[12] Qiao Ji, Zou Jun, Li Benliang. Calculation of the ionized field and the corona losses of high voltage direct current transmission lines using a finite difference based flux tracing method[J]. IET Generation, Transmission and Distribution, 2015, 9(4): 348-357.
[13] Francesco L, Vitantonio A. Filamentary ion flow: theory and experiments[M]. Hoboken: IEEE Press- Wiley, 2014.
[14] 崔翔, 周象贤, 卢铁兵. 高压直流输电线路离子流场计算方法研究进展[J]. 中国电机工程学报, 2012, 32(36): 130-141.
Cui Xiang, Zhou Xiangxian, Lu Tiebing. Recent progress in the calculation methods of ion flow field of HVDC transmission lines[J]. Proceedings of the CSEE, 2012, 32(36): 130-141.
[15] Qiao Ji, Zou Jun, Zhang Jiangong, et al. Ion flow field calculation of HVDC overhead lines using a high-order stabilization technique based on petrov- galerkin method[J]. IET Generation, Transmission and Distribution, 2018, 12(5): 1183-1189.
[16] 乔骥. 交直流并行线路离子流与混合电场计算方法及应用研究[D]. 北京: 清华大学, 2018
[17] Yin Han, Zhang Bo, He Jinliang, et al. Time domain finite volume method for ion-flow field analysis of bipolar high voltage direct current transmission lines[J]. IET Generation, Transmission and Distri- bution, 2012, 6(8): 785-791.
An Efficient and Robust Low-Order Iterative Flux Tracing Method for Calculating Ion Flow Field of HVDC Transmission Lines
Abstract The flux tracing method is widely applied to solve the ion-flow field problem of the HVDC transmission line model, which transforms the original boundary value problem into the least square problem along the flux line. In this paper, an improved flux tracing method is proposed. The multi-objective optimization problem in the original method has been simplified to a single-objective optimization problem by applying the recursion scheme. Numerical experiments show that the proposed method has significantly improved the efficient and stability, which can be effectively applied to ion-flow models with complex geometry structures.
keywords：Ion-flow field, total electric field, HVDC transmission lines, iterative flux tracing method
中图分类号：TM15
DOI: 10.19595/j.cnki.1000-6753.tces.200081
国家自然科学基金（52077111）和电网环境保护国家重点实验室开放基金（GYW51201901089）资助项目。
收稿日期 2020-01-20
改稿日期 2020-05-05
张建功 男，1975年生，高级工程师，主要研究方向为电力系统电磁兼容和电磁环境。E-mail: zhangjiangong@epri.sgcc.com.cn
邹 军 男，1971年生，教授，博士生导师，主要研究方向为电磁场理论及应用。E-mail: zoujun@tsinghua.edu.cn（通信作者）
（编辑 陈 诚）