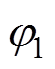和
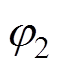分别为1号和2号逆变器的输出电压相位，如图1所示。1号和2号逆变器的线路阻抗为摘要 在直流微电网的传统下垂控制中，电路参数及线路阻抗的不一致造成DC-DC变换器下垂特性均存在差异，降低了变换器的均流精度。下垂控制还会造成一定程度的直流母线电压跌落。为了提高直流微电网的控制性能，模拟交流微电网的频率下垂控制机理，提出一种基于虚拟频率的多DC-DC变换器下垂控制方法。在控制器中构造了频率与输出电流成比例的虚拟交流量，利用低带宽通信共享各变换器的虚拟频率并求出平均值。该平均频率及虚拟交流量进一步用于产生虚拟无功功率以调整变换器的电压设定点，协调各变换器输出电流的大小。在不造成母线电压跌落的前提下，提高了多变换器间的负载电流分配精度。利用小信号模型分析虚拟频率下垂控制的闭环稳定性。最后，通过仿真和基于Starsim和dSPACE快速原型样机的实验，验证了该方法的有效性。
关键词：直流微电网 虚拟频率 下垂控制 并联均流 DC-DC变换器
随着全球能源短缺和环境问题的日益凸显，微电网作为一种高效利用可再生能源的技术受到广泛关注[1-2]。相较于交流微电网，直流微电网可以减少能量变换环节，同时提高系统的效率和可靠性，降低控制复杂程度[3]，已在船舶电力系统、航天系统、数据中心等独立供电系统得到初步应用[4-6]。直流微电网是一个多源多负荷系统，如何实现多变换器的并联均流是国内外研究的热点。
直流微电网系统中，由于各变换器的电感、电容及采样电路不可避免地存在差异，变换器的参数无法做到完全一致。变换器参数还会随时间和温度等外界因素变化。此外，各变换器之间存在一定距离，线路阻抗也存在差异。如果将多个变换器直接并联，很难保证各变换器均匀分担负载电流，造成诸多可靠性及稳定性问题。首先，输出电流大的变换器承受更大的电压、电流和温度应力，增加损坏机率，降低使用寿命；其次，在大负载情况下，必然导致输出电流最大的变换器率先达到最大电流限制，引起模式切换混乱或系统连锁保护动作，导致系统不能正常运行。多变换器的并联均流控制问题实质上是研究多变换器情况下功率的合理分配及母线电压的稳定性问题[7-24]。目前，直流微电网的变换器并联均流控制大致分为主从控制和对等控制。主从控制[7-8]是通过主控单元对全网信息进行处理，再将操作指令统一发送给每个从单元，从而实现多变换器的负载分配。主从控制方法简单、易实现，但控制性能依赖各单元间的高速通信，不利于系统的稳定运行和扩容，一旦发生通信问题，整个系统很可能会陷入瘫痪。主从控制还存在过度依赖单个主控单元的问题，降低了系统的可靠性。在对等控制策略[9-10]中，每个发电单元都有自己独立的本地控制器，每个发电单元可以根据本地控制器独立稳定运行。这种控制方式无需依赖设备间的通信，只需要本地信息就能实现自我管理和控制，增强了系统的可靠性和模块化，其中，应用最广泛的就是下垂控制。下垂控制的实质是利用变换器的输出电流作为反馈信号来增加变换器的等效输出阻抗，实现并联变换器间的均流。采用下垂控制的直流微电网系统具备更高的可靠性和即插即用性能，更加便于系统的扩容[11-12]。在下垂控制中，引入的虚拟阻抗越大，变换器内阻及线路阻抗对均流的影响越小，但同时母线电压偏差会越大，因此下垂控制中母线电压调节和电流分配精度之间存在矛盾[13-14]。文献[13]提出了一种阻性虚拟阻抗加补偿虚拟阻抗的改进下垂控制策略，阻性虚拟阻抗实现直流微电网稳态时的功率分配，补偿虚拟阻抗提升动态性能。文献[15]在虚拟阻抗的基础上提出了变下垂系数的优化方法，根据变换器内阻及线路阻抗的不同，设置不同的下垂系数以优化各电源间的电流分配。然而上述方法均没有解决母线电压跌落问题。
分层协调控制策略[16-17]根据时间尺度将微电网控制分为三个层面：设备级控制、二次控制和能量优化管理。底层设备级控制主要实现单个变换器的输出电压和电流控制，实现多变换器间均流控制；二次控制主要补偿下垂控制造成的母线电压跌落，多模式切换及提高电能质量；能量优化管理负责整个微电网能量管理与最优运行。二次控制是在下垂控制的基础上减小母线电压偏差和提高电流分配精度。从本质上来看，二次控制是传统下垂控制的改进方案。目前已有的二次控制可以分为两类，即集中式二次控制[16]和分布式二次控制[18-19]。文献[16]提出的集中二次控制设置了独立的母线电压控制器，通过测量微电网的直流母线电压及PI计算，平移变换器的下垂曲线，补偿下垂控制带来的母线电压跌落。集中二次控制的可靠性过度依赖母线电压调节器和母线电压传感器，容易产生单点故障。分布式二次控制利用通信获取其他变换器的电压和电流信息，由本地的控制器进行二次调节，可以避免集中式二次控制中存在的单点故障问题。文献[19]中各变换器间利用通信共享各变换器的电压和电流，从而可利用平均电压和电流平移变换器下垂曲线，达到既可以恢复母线电压又提高均流精度的目的。该方法需要同时得到并联变换器的平均输出电压和电流信息，变换器间通信交互的信息较多。文献[20-22]提出了多智能体一致性均流算法，每个发电单元利用稀疏通信仅与相邻单元共享输出电压和电流，经过一定次数迭代后，获得全局的平均电压和电流，对各变换器进行二次调节，恢复母线电压并提高均流均流精度，该方法虽然简化了通信网络连接，但依然需要同时共享电压和电流信息。文献[23-24]提出了基于频率注入的多变换器并联均流控制算法，根据注入交流信号的无功功率调节各变换器的输出电压，有效解决了线路阻抗差异造成的功率分配问题。虽然该方法实现了无通信情况下的均流控制，然而注入交流信号后输出电压纹波变大，降低了电能质量。
为解决DC-DC变换器并联时负荷电流分配不均及下垂控制引起母线电压跌落的问题，本文提出一种基于虚拟频率的直流微电网下垂控制策略。在变换器中构造出频率与输出电流大小成比例的虚拟交流量，并通过低带宽通信共享的方式求得虚拟交流量的平均频率，该频率作为协调各变换器输出电流大小的全局变量。由于直流微电网中DC-DC变换器的输出电流受控于输出电压的大小，虚拟频率下垂控制通过虚拟交流量的无功功率作为中间变量来调节输出电压，间接地实现变换器间电流的精确分配。该策略在仅需通信共享虚拟频率单一变量的情况下，既实现了变换器的精确均流，又不会造成母线电压跌落。最后利用小信号模型分析了虚拟频率下垂控制的稳定性，并通过仿真和实验证明了该方法的有效性。
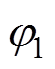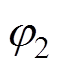在交流微电网中，并联逆变器间的功率分配通常由有功-频率下垂及无功-电压下垂控制来实现。在双逆变器并联模型中，可以将逆变器等效为电压源，E1和E2分别为1号逆变器和2号逆变器的输出电压幅值，UL为母线电压，和分别为1号和2号逆变器的输出电压相位，如图1所示。1号和2号逆变器的线路阻抗为
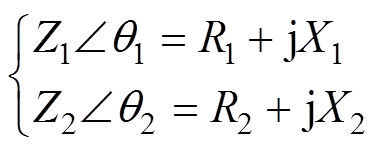（1）式中，R1和R2为线路电阻；X1和X2为线路电抗；q1和q2为阻抗角。
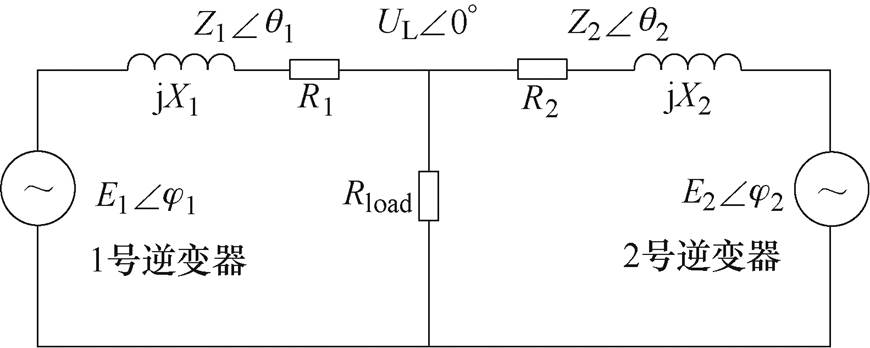
图1 并联逆变器的等效模型
Fig.1 The equivalent model of paralleled inverters
当把母线电压作为参考电压时，逆变器的输出功率为
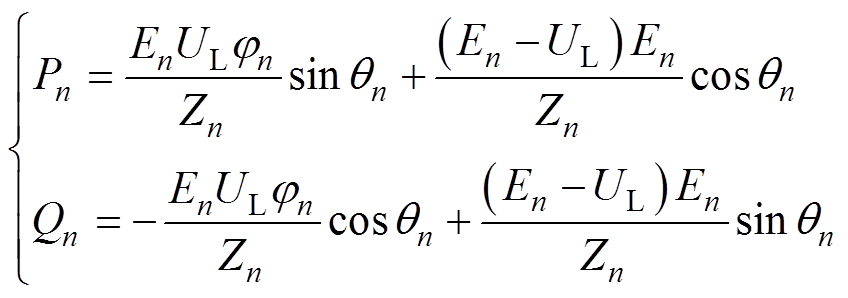n=1, 2（2）式中，Pn和Qn为第n个逆变器的有功功率和无功功率；En为第n个微源的交流压幅值；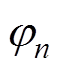
为第n个微源的交流压相位；Zn为第n个微源的线路阻抗；
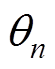为第n个微源的线路阻抗角。
下垂控制原理中有功功率与频率、无功功率与输出电压幅值的关系与大电网中同步机组一次调频曲线具有相似性，可利用下垂控制对微源的输出功率进行控制，交流系统下垂控制如图2所示。下垂控制表达式为
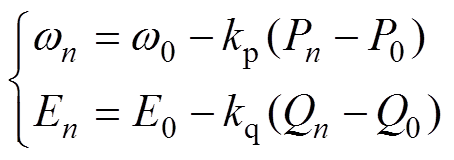（3）式中，wn为第n个逆变器输出电压的角频率；P0和Q0分别为逆变器的额定有功功率和无功功率；kp为有功功率下垂系数；kq为无功功率下垂系数。
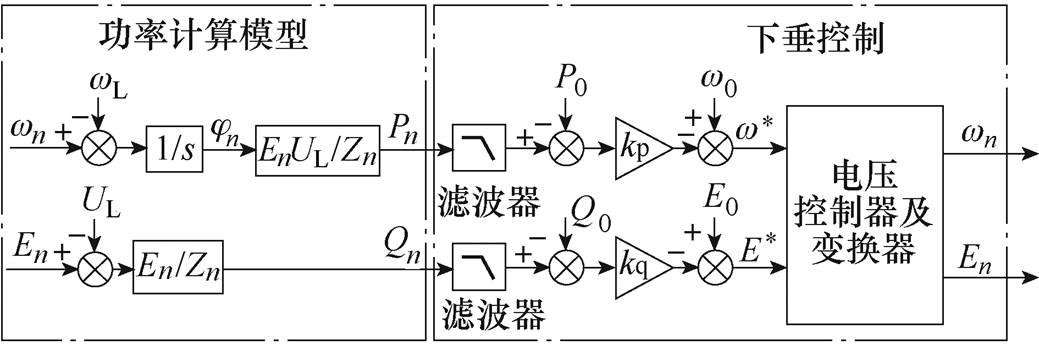
图2 交流系统下垂控制
Fig.2 Droop control in AC power system
由于微电网中各逆变器的频率是相同的，因此频率可以作为全局变量来协调各变换器的有功功率，并保持各变换器的有功功率相等。
直流微电网中要使各变换器能够均分负荷电流，实质上就是要协调控制各变换器的直流输出电压。传统控制方法通常采用电压-电流下垂，通过改变各变换器的下垂系数或平移下垂曲线实现功率的均分。在交流下垂系统中，存在一个能够全局可控的变量（频率），通过控制各逆变器频率能够高精度地均分有功功率。然而在直流系统中由于线路阻抗及变换器内阻的存在，各变换器输出直流电压不尽相同，系统中缺少一个全局可控的变量，因此直流微电网的传统下垂控制方法在实现负载电流均分和母线电压调节的效果上较差。在此基础上，本文提出一种基于虚拟频率的直流微电网多源并联均流控制方法，利用电流-虚拟频率下垂及虚拟无功-电压下垂，实现负荷电流的精确分配，基于虚拟频率的下垂控制框图如图3所示。每个变换器的控制部分由虚拟无功计算单元和下垂控制两部分组成。下垂控制中的电压控制器用于实现变换器输出电压的无差调节；电流-虚拟频率下垂控制环节和虚拟无功-电压下垂控制环节则通过低带宽通信虚拟一个低频低幅值的虚拟交流电压信号，利用虚拟的无功功率调节各变换器输出的直流电压，进而实现负荷电流的精确分配。
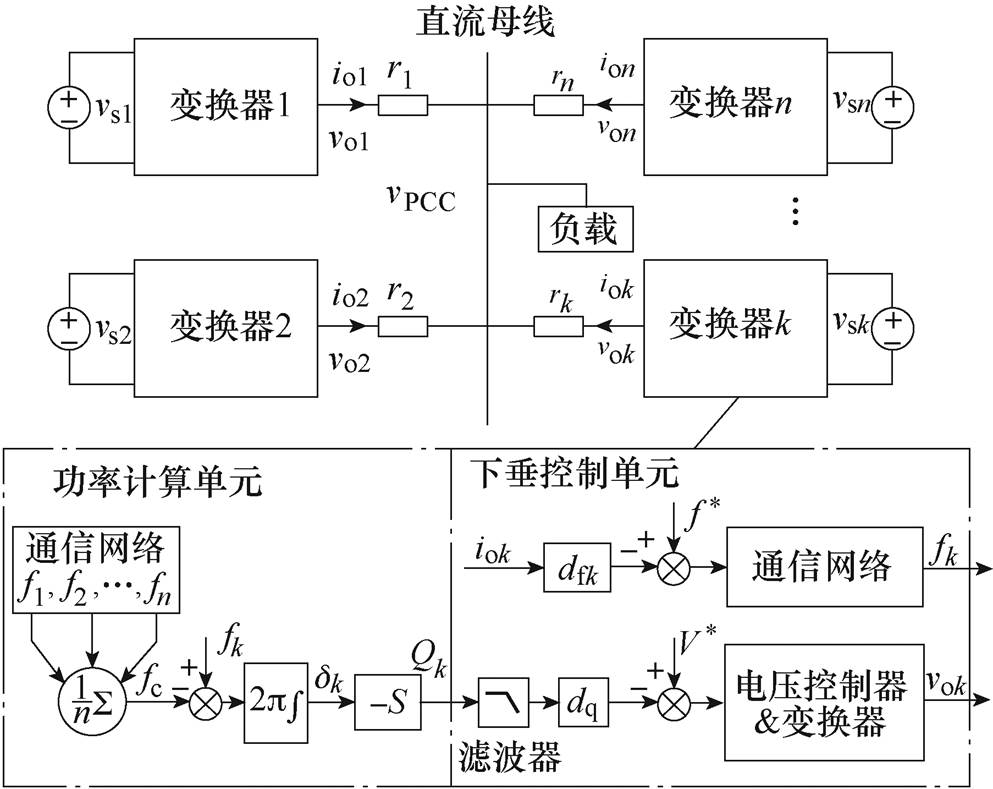
图3 基于虚拟频率的下垂控制框图
Fig.3 Droop control based on virtual frequency
变换器k的控制算法如图3所示，图中，虚拟交流电压的频率与变换器的输出直流电流成正比，虚拟频率要小于通信速度。因此，可利用输出电流构造出具有下垂特性的虚拟频率，有
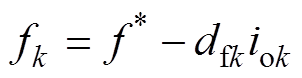（4）式中，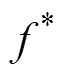
为虚拟频率的额定值（50Hz）；iok为变换器k的电流；dfk为变换器k的电流-频率下垂系数，满足
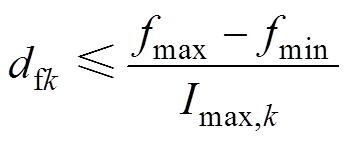（5）
式中，fmax和fmin分别为虚拟频率的最大和最小频率；Imax,k为变换器k的最大输出电流。
交流微电网中，频率为全局变量，各处频率均保持一致。直流微电网中，在未采取任何均流策略的情况下，DC-DC变换器输出电流难以保持一致，根据式（4）每个变换器的虚拟频率fk不能保持一致，该频率无法作为调节各变换器电流的全局统一变量。因此，利用低带宽通信共享各变换器的虚拟频率，求得所有变换器虚拟频率的平均值，作为调节变换器电流的公共虚拟频率，有
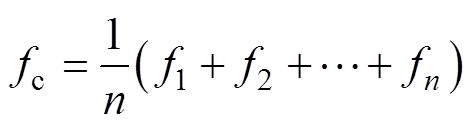（6）在稳态条件下，若各变换器虚拟频率均等于公共虚拟频率，则可保证变换器的输出电流与额定电流成比例共享，有
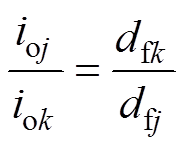（7）
式中，j和k为变换器j和变换器k。
直流微电网中DC-DC变换器的输出电流由输出电压、母线电压和线路电阻共同决定的，有
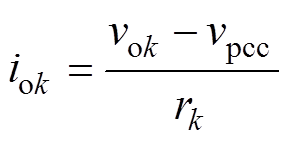（8）式中，vok为变换器k的输出电压；vpcc为母线电压；rk为变换器k的线路阻抗。
由于虚拟频率无法调节变换器输出电压，因此虚拟频率不能直接调节变换器的输出电流大小。要使变换器达到均流的效果，需要构造与虚拟频率相关的中间变量来调节输出电压，间接地实现均流控制。图2的交流微电网中，输出电压可通过无功功率进行调节，因此可在直流微电网中构造虚拟的无功功率实现电压调节。
由于直流微电网中，线路电抗的影响远小于电阻，因此，在计算虚拟无功功率时，假设线路阻抗为纯阻性，则根据式（2）构造出第k个DC-DC变换器的虚拟无功功率为
（9）式中，Sv为虚拟视在功率，该参数作为控制增益的一部分可适当调整；dk为虚拟相位，即
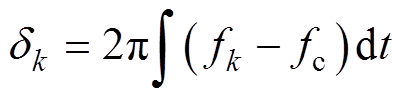（10）
利用变换器产生的虚拟无功来调整输出电压，有
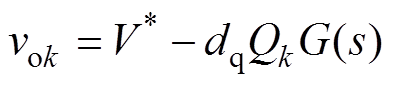（11）其中
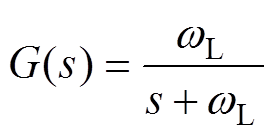
式中，dq为虚拟无功功率-电压下垂系数；V*为电压参考值；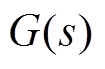
为低通滤波器，用来调节系统的相位裕度，满足稳定性要求。
引入虚拟无功补偿后，均流调节过程如图4所示。当变换器输出电流不等时，虚拟频率下垂导致变换器间产生频率和相位差；进而产生虚拟无功功率，利用无功功率补偿来改变输出电压；最终形成负反馈，实现负荷电流的均分。
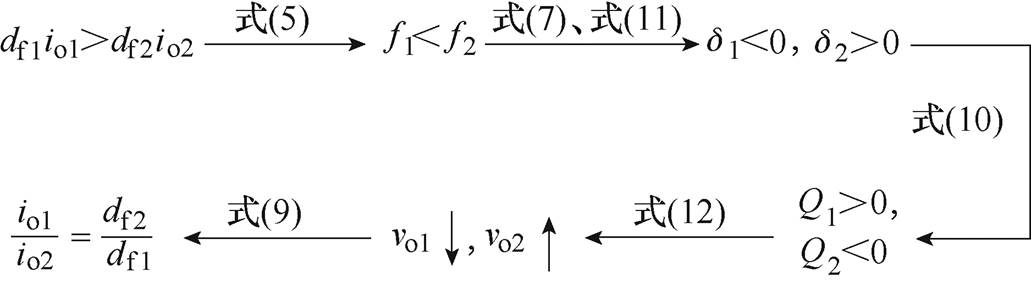
图4 无功电压反馈控制过程
Fig.4 Reactive power-voltage feedback control process diagram
直流微电网中，母线电压由各DC-DC变换器的输出电压、输出电流和线路电阻共同决定，有
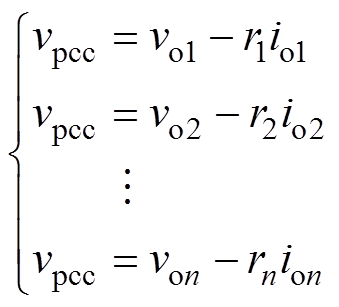（12）式（12）同时可以表示为
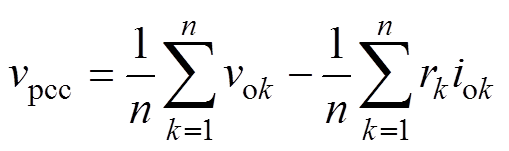（13）
在未采用任何均流策略前，由于电压闭环的作用，每个DC-DC变换器的输出电压均为无差调节。变换器的输出电压为
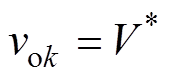（14）联立（13）和式（14）可以进一步得出母线电压为
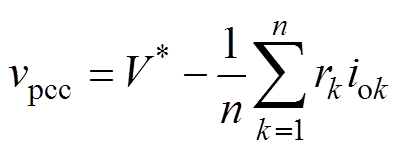（15）
由式（15）可以看出，不采用任何均流控制策略的情况下，母线电压跌落为线路阻抗压降的平均值。
经过虚拟无功补偿后，母线电压变为
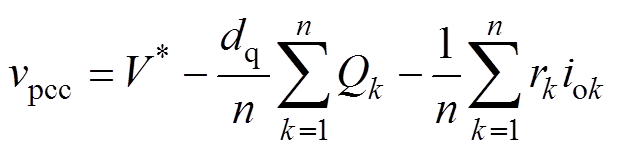（16）联立式（9）和式（10）可以得出，各变换器的虚拟无功之和为
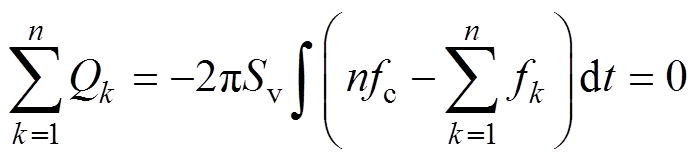（17）
从式（11）可以看出，虚拟无功补偿改变了单个变换器的输出电压，但根据式（15）～式（17）虚拟无功补偿不会引起母线电压跌落。
均流控制策略的稳定性是保证直流微电网稳定运行的关键。小信号分析是验证所提控制策略稳定性的有效方法。将式（9）～式（11）等效变换到复频域，得到
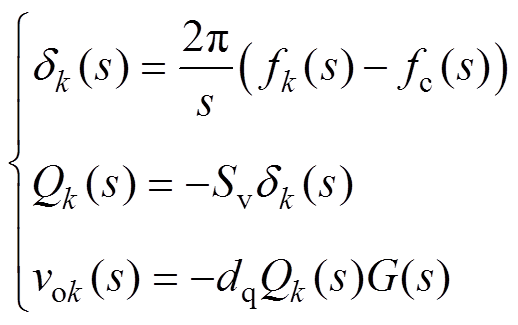（18）联立式（12）和式（18），得到虚拟频率控制的开环传递函数为
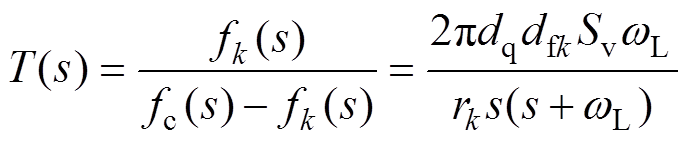（19）
该系统为典型I型系统，可以保证虚拟频率fk无静差地跟踪公共虚拟频率fc，保证稳态时虚拟频率全局一致，进而保证变换器输出电流严格按比例ioj:iok=dfk:dfj分配。
由式（19）得到如图5a所示的虚拟频率闭环控制框图，虚拟频率的闭环传递函数为
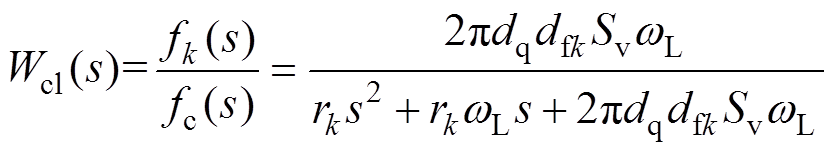（20）
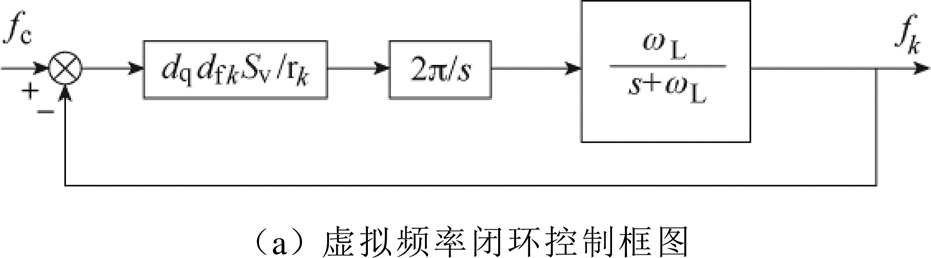
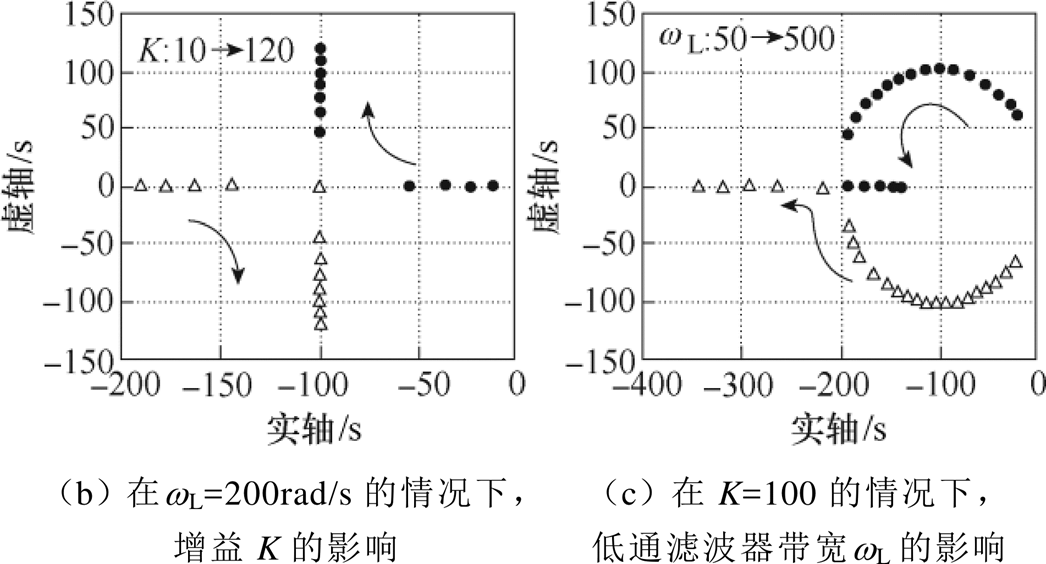
图5 控制控图及闭环根轨迹图
Fig.5 Control diagram and closed-loop root track diagram
为了验证所提策略的动态性能和稳定性，图5分别给出了虚拟频率闭环极点随K=2pdfkdqSv/rk和wL变化的根轨迹图。
增加增益K和wL将闭环极极点往左移动，远离s平面的虚轴，增加了系统的阻尼。当直流微电网结构不变时，变换器的线路阻抗保持恒定，因此，可以通过调整参数wL、dfk和dq来优化系统性能。变换器及控制器的参数见表1。例如，针对表1所示系统，选择I-f下垂系数dfk=0.25，Q-V下垂系数dq=1.3，低通滤波器截止频率wL=200rad/s，可得到阻尼比为0.7的理想系统。
表1 变换器及控制器的参数
Tab.1 The parameters of converters and controller
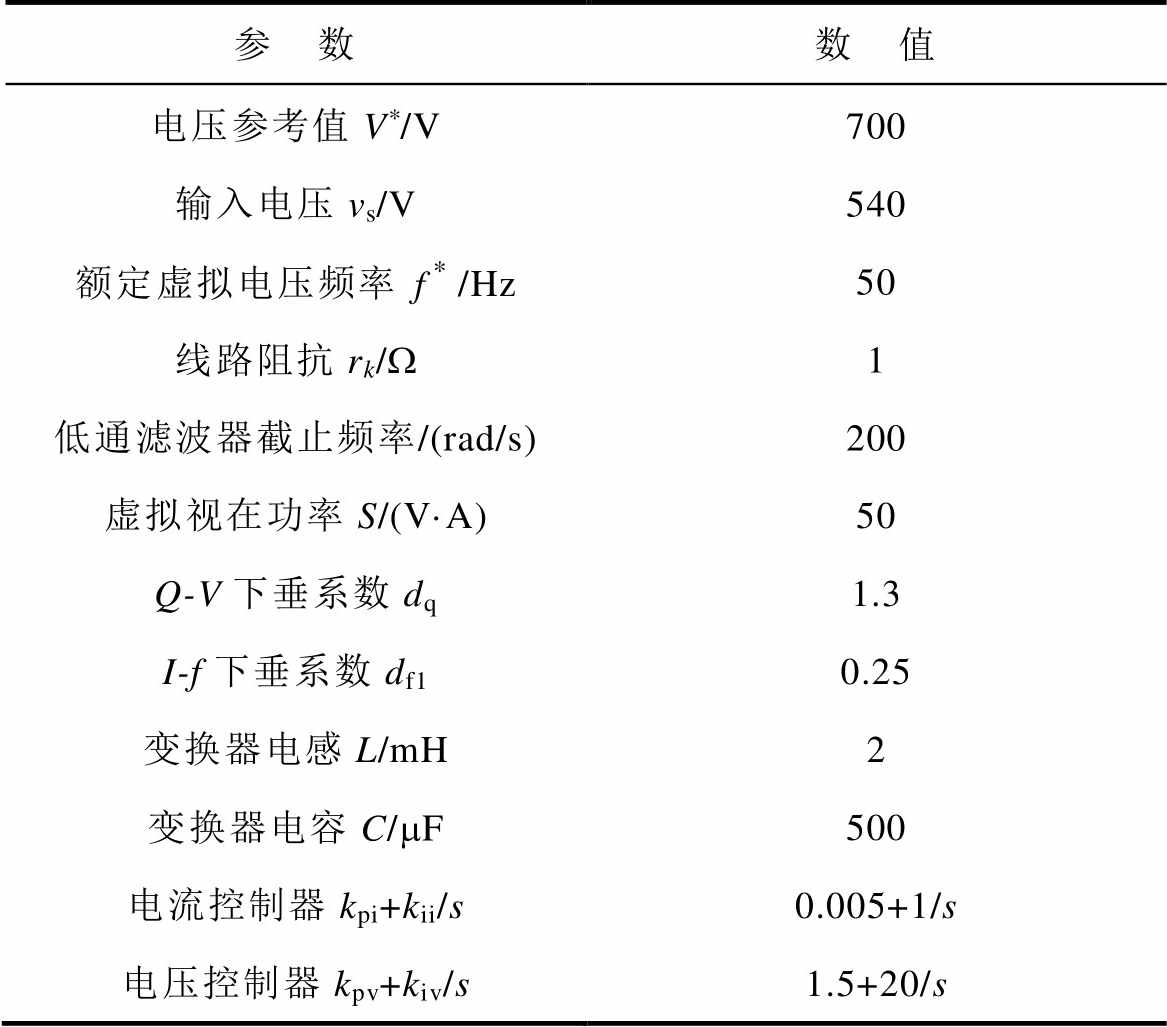
参 数数 值 电压参考值V*/V700 输入电压vs/V540 额定虚拟电压频率/Hz50 线路阻抗rk/W1 低通滤波器截止频率/(rad/s)200 虚拟视在功率S/(V·A)50 Q-V下垂系数dq1.3 I-f下垂系数df10.25 变换器电感L/mH2 变换器电容C/mF500 电流控制器kpi+kii/s0.005+1/s 电压控制器kpv+kiv/s1.5+20/s
为了验证所提控制策略在不同工况下的暂态特性和稳态特性，分析了两种情况：①两台容量相等的DC-DC变换器并联时，均流的稳态及动态特性；②两台容量不等的DC-DC变换器并联时，均流的稳态及动态特性。DC-DC变换器的拓扑采用Boost升压电路，变换器及控制器的仿真参数见表2。
表2 变换器及控制器的仿真参数
Tab.2 Simulated parameters of converters and controller
参 数数 值 仿真1仿真2 电压参考值V*/V700700 输入电压vs/V540540 额定虚拟电压频率/Hz5050 线路阻抗r1/W44 线路阻抗r2/W22 低通滤波器截止频率/(rad/s)200200 虚拟视在功率S/(V·A)5050 Q-V下垂系数dq1.31.3 I-f下垂系数df10.250.25 I-f下垂系数df20.250.5 变换器电感L/mH22 变换器电容C/mF500500 电流控制器kpi+kii/s0.005+1/s0.005+1/s 电压控制器kpv+kiv/s1.5+20/s1.5+20/s
本实验分析了两台相同容量DC-DC变换器并联均流的情况。初始负载功率为9.8kW；0～0.1s为软起动过程，保证变换器起动过程平稳过渡；在t =1s时，负荷突变为14.7kW，仿真结果如图6所示。图6a为变换器的输出电压及母线电压，可以看出，变换器并联起动过程超调量较小；母线电压跌落为线路电阻压降均值，例如，负载突变后，线路电阻r1=2W 的电压降为20V，线路电阻r2=4W 的电压降为40V，此时母线电压为670V，存在30V的电压偏差。图6b为变换器的输出电流及负载电流，在软起动过程中仅经过80ms的调整，两台DC-DC变换器的电流就达到一致，稳态时实现了精准的均分；负载突变时，动态调整时间也仅为60ms，直接的验证了该方法的有效性。同时，通过图6c中变换器的虚拟频率与公共虚拟频率的比较，也可以看出，在所提控制策略的作用下两台变换器的虚拟频率均迅速收敛到公共虚拟频率，间接地验证了均流策略的有效性。
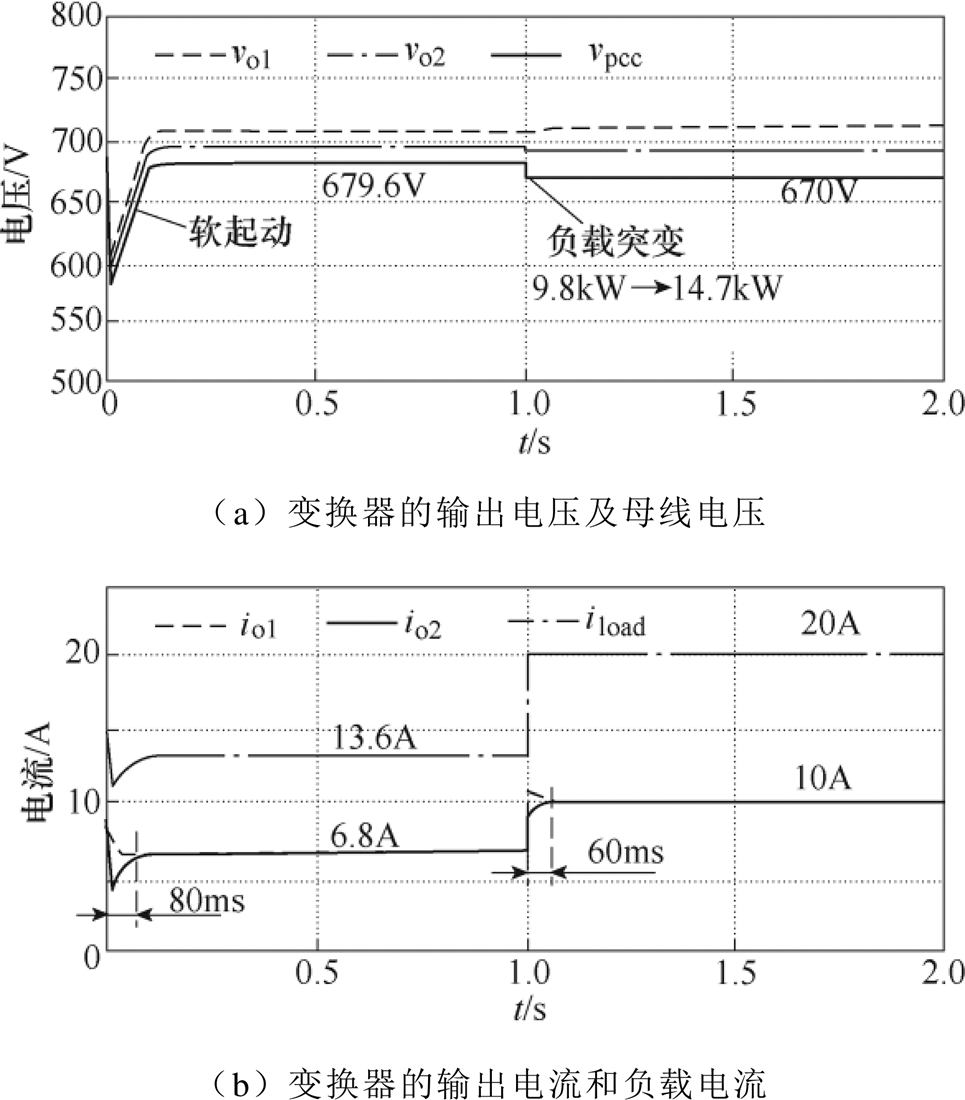
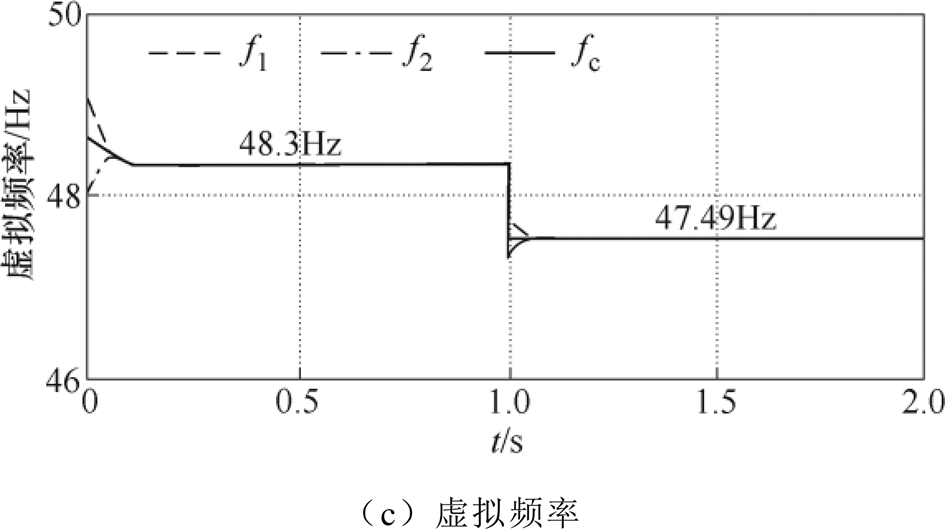
图6 两台相同容量变换器并联的仿真结果
Fig.6 Simulation results of two paralleled converters with equal power rating
本实验在1号DC-DC变换器容量为2号DC-DC变换器两倍的情况下，验证所提控制策略的有效性。初始负载功率为9.8kW；0～0.1s为软起动过程，保证变换器起动过程平稳过渡；在t =1s时，负荷突变为14.7kW，仿真结果如图7所示。通过对比图6a和图7a，发现在相同负载和线路阻抗的情况下，两者的母线电压不同，产生该现象的原因主要是变换器功率分配比例不同造成线路压降产生变化。图7a中同样是负载突变后，线路阻抗r1=2W 的电压降为13.34V，线路阻抗r2=4W 的电压降为53.32V，此时母线电压为666.7V，电压偏差变为33.3V，该情况下电压偏差同样为线路电路压降均值。图7b为变换器的输出电流及负载电流，在软起动过程中仅同样经过80ms的调整，两台DC-DC变换器的电流按2:1的比例精确分配；负载突变时，动态调整时间也仅为60ms，直接的验证了方法的有效性。对比图6c和图7c可以看出，不同容量的变换器在动态均流过程中虚拟频率的超调较大，稳态时两台变换器的虚拟频率依然收敛到公共虚拟频率。
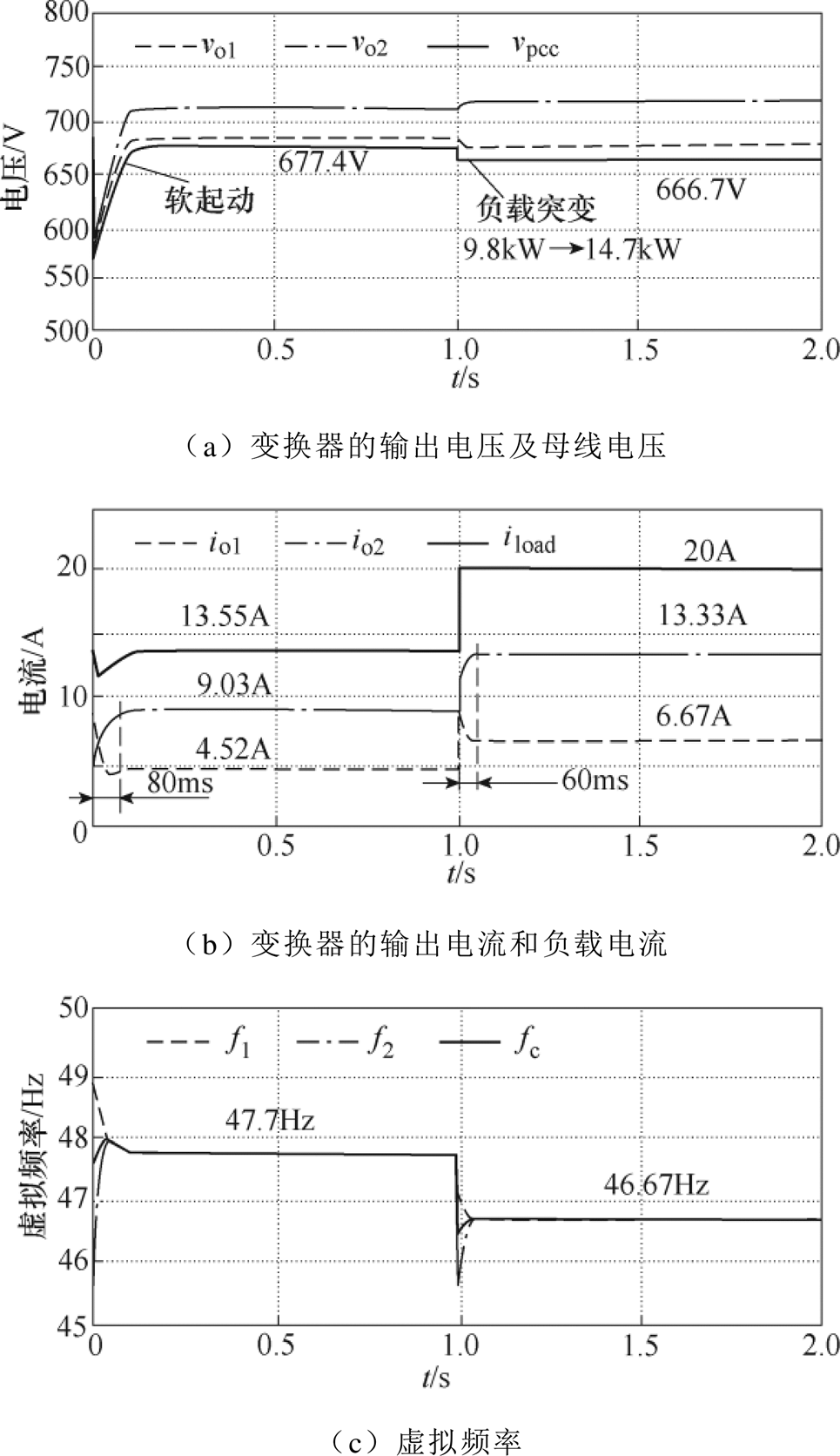
图7 两台不同容量变换器并联的仿真结果
Fig.7 Simulation results of two paralleled converters with unequal power rating
为了验证所提虚拟频率下垂控制策略的有效性，搭建了如图8所示的直流微电网半实物仿真平台。包括Starsim、dSPACE、两台采用Boost拓扑的DC-DC变换器、蓄电池组及电子负载等设备。由于该验证平台电压等级较低，该平台电路及所提控制策略参数见表3。与仿真相对应，半实物实验同样分别验证了所提策略对相同容量和不同容量DC-DC变换器的均流效果。
图8 实验硬件
Fig.8 Photograph of the experiment setup
表3 变换器及控制器的实验参数
Tab.3 Experimental parameters of converters and controller
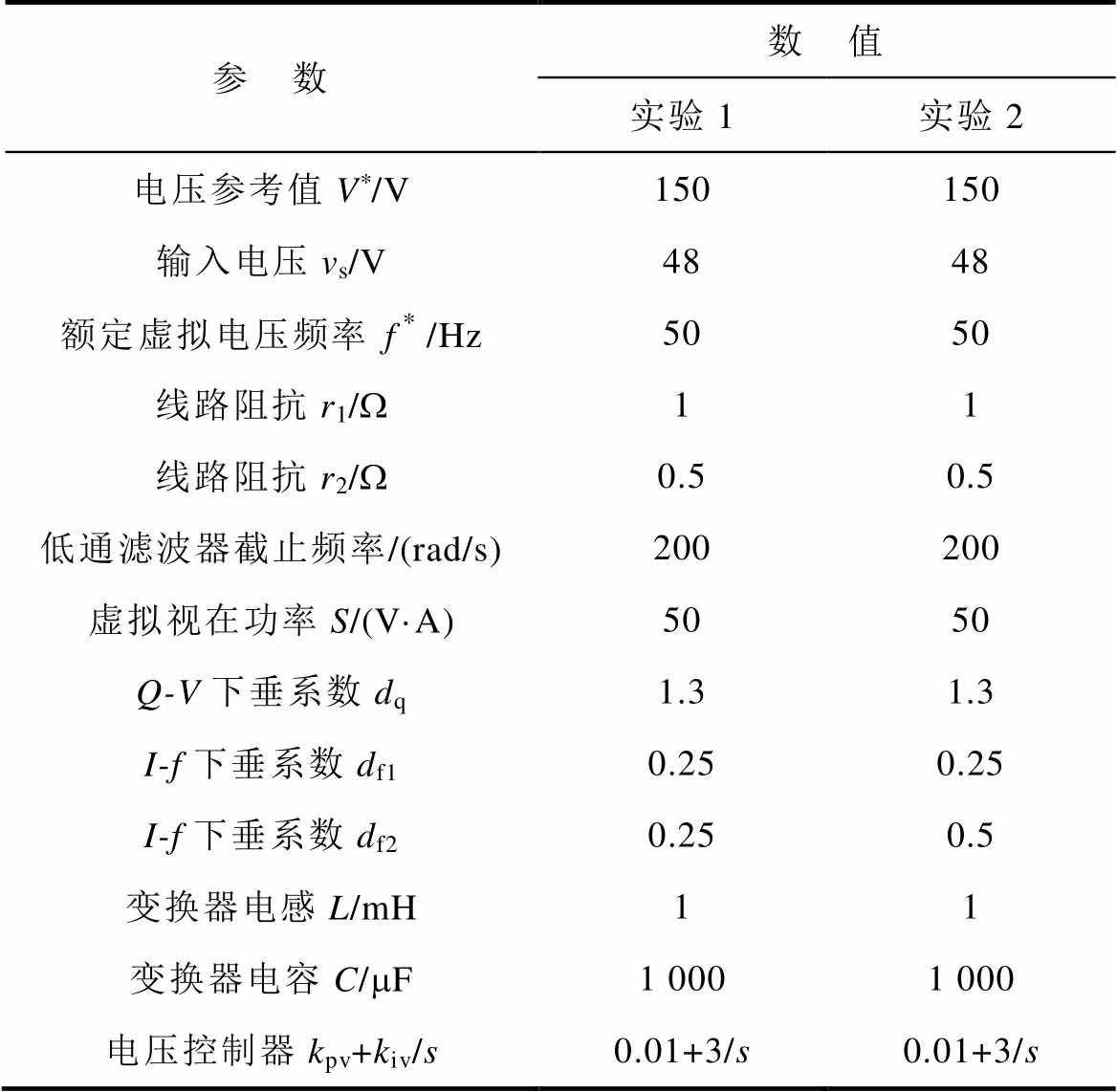
参 数数 值 实验1实验2 电压参考值V*/V150150 输入电压vs/V4848 额定虚拟电压频率/Hz5050 线路阻抗r1/W11 线路阻抗r2/W0.50.5 低通滤波器截止频率/(rad/s)200200 虚拟视在功率S/(V·A)5050 Q-V下垂系数dq1.31.3 I-f下垂系数df10.250.25 I-f下垂系数df20.250.5 变换器电感L/mH11 变换器电容C/mF1 0001 000 电压控制器kpv+kiv/s0.01+3/s0.01+3/s
本实验分析了两台相同容量DC-DC变换器并联均流的情况，如图9所示。图9a为所提控制策略起动前后的DC-DC变换器输出电压和电流。在不采用均流策略前，DC-DC变换器输出电压在闭环的作用下稳定在150V，1号变换器和2号变换器的输出电流按线路电阻的反比r2:r1=1:0.5分配。
图9 两台相同容量变换器并联的实验结果
Fig.9 Experimental results of two paralleled converters with equal power ratings
起动基于虚拟频率的下垂控制均流策略后，1号变换器输出电压变为150.25V，升高0.25V；2号变换器的输出电压变为149.75V，降低0.25V。输出电压的变化使得两台变换器电流比由2:1经过120ms迅速趋于1:1。图9b为负载突变对虚拟频率下垂控制策略的影响的波形，当负载由500W减小为300W时，1号和2号变换器电流经过80ms由1.67A降为1.0A。突变前后两台变换器均保持较高均流精度，暂态过程中两台变换器电流偏差较小。以上实验均验证了所提均流策略的有效性。
本实验分析了两台不同容量DC-DC变换器并联均流的情况，如图10所示。图10a为所提控制策略起动前后的DC-DC变换器输出电压和电流。在不采用均流策略前，1号变换器和2号变换器的输出电流按线路电阻的反比r2:r1=2:1分配；起动基于虚拟频率的下垂控制均流策略后，1号变换器和2号变换器的输出电流迅速调整为按期望的变换器容量比1:2分配。均流策略起动前后的鲜明对比，直接验证了所提控制策略的有效性。起动基于虚拟频率的下垂控制均流策略后，1号变换器输出电压升高0.5V，2号变换器的输出电压降低0.5V。与图9a相比，负载相同的情况下电压不同比例的输出电压变化更大，这一现象与仿真实验2的分析相吻合。图10b为负载突变对虚拟频率下垂控制策略的影响的波形，当负载由300W增大为500W时，1号变换器电流由1.33A变为2.2A，2号变换器电流由0.67A变为1.1A。负载突变前后两台变换器的电流均保持1:2的比例精确分配。不同容量的DC-DC变换器在虚拟频率下垂控制起动过程的动态调节时间为200ms，负载突变的动态调节时间为100ms，均大于同容量DC-DC变换器并联的动态调节时间。该实验也反映出，变换器容量会影响到虚拟下垂控制策略的均流速度。
图10 两台不同容量变换器并联的实验结果
Fig.10 Experimental results of two paralleled converters with unequal power ratings
本文提出了一种基于虚拟频率下垂控制的直流微电网多变换器均流方法。实验表明，在变换器容量相同及不相同的情况下，所提均流策略均可按变换器容量精确分配电流大小，同时不引起母线电压跌落。基于虚拟频率的下垂控制还在起动和负载突变的动态过程中表现出良好的调节性能。该均流策略的运算过程均在本地实现，仅需通过低带宽通信发送虚拟频率给其他变换器的控制系统，从而实现了微电网的分布式控制。
参考文献
[1] 谢文强, 韩民晓, 严稳利, 等. 考虑恒功率负荷特性的直流微电网分级稳定控制策略[J]. 电工技术学报, 2019, 34(16): 3430-3443.
Xie Wenqiang, Han Minxiao, Yan Wenli, et al. Hierarchical stability control strategy of DC micro- grid considering constant power load performance[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3430-3443.
[2] Zhang Qinjin, Liu Yancheng, Zhao Youtao, et al. A multi-mode operation control strategy for flexible microgrid based on sliding-mode direct voltage and hierarchical controls[J]. ISA Transactions, 2016, 61: 188-198.
[3] 朱晓荣, 李铮, 孟凡奇. 基于不同网架结构的直流微电网稳定性分析[J]. 电工技术学报, 2021, 36(1): 166-178.
Zhu Xiaorong, Li Zheng, Meng Fanqi. Stability analysis of DC microgrid based on different grid structures[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 166-178.
[4] Zahedi B, Norum L E. Modeling and simulation of all-electric ships with low-voltage DC hybrid power systems[J]. IEEE Transactions on Power Electronics, 2013, 28(10): 4525-4537.
[5] Gao Fei, Costabeber A, Asher G, et al. Control design and voltage stability analysis of a droop-controlled electrical power system for more electric aircraft[J]. IEEE Transactions on Industrial Electronics, 2017, 64(12): 9271-9280.
[6] Pavan Kumar Y V, Ravikumar B. A simple modular multilevel inverter topology for the power quality improvement in renewable energy based green building microgrids[J]. Electric Power Systems Research, 2016, 140: 147-161.
[7] Jiang Wei, Fahimi B. Active current sharing and sourcemanagement in fuel cell-battery hybrid power system[J]. IEEE Transactions on Industrial Electro- nics, 2010, 57(2): 752-761.
[8] 张项安, 张新昌, 唐云龙, 等. 微电网孤岛运行的自适应主从控制技术研究[J]. 电力系统保护与控制, 2014, 42(2): 81-86.
Zhang Xiang’an, Zhang Xinchang, Tang Yunlong, et al. Research on adaptive master-slave control of the islanded micro-grid[J]. Power System Protection and Control, 2014, 42(2): 81-86.
[9] Tah A, Das D. An enhanced droop control method for accurate load sharing and voltage improvement of isolated and interconnected DC microgrids[J]. IEEE Transactions on Sustainable Energy, 2016, 7(3): 1194-1204.
[10] Liu Sheng, Su Peng, Zhang Lanyong. A virtual negative inductor stabilizing strategy for DC micro- grid with constant power loads[J]. IEEE Access, 2018, 6: 59728-59741.
[11] Dragičević T, Guerrero J M, Vasquez J C, et al. Supervisory control of an adaptive-droop regulated dcmicrogrid with battery management capability[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 695-706.
[12] Wang Panbao, Lu Xiaonan, Yang Xu, et al. An improved distributed secondary control method for DC microgrids with enhanced dynamic current sharing performance[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6658-6673.
[13] 支娜, 张辉, 肖曦. 提高直流微电网动态特性的改进下垂控制策略研究[J]. 电工技术学报, 2016, 31(3): 31-39.
Zhi Na, Zhang Hui, Xiao Xi. Research on the improved droop control strategy for improving the dynamic characteristics of DC microgrid[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(3): 31-39.
[14] 刘琛, 赵晋斌, 王闪闪, 等. 基于单脉冲注入的直流微电网线路阻抗检测[J]. 电工技术学报, 2018, 33(11): 2584-2591.
Liu Chen, Zhao Jinbin, Wang Shanshan, et al. A line impedance identification based on single pulse injection in DC microgrid[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2584-2591.
[15] 刘子文, 苗世洪, 范志华, 等. 基于自适应下垂特性的孤立直流微电网功率精确分配与电压无偏差控制策略[J]. 电工技术学报, 2019, 34(4): 163-174.
Liu Ziwen, Miao Shihong, Fan Zhihua, et al. Accurate power allocation and zero steady-state error voltage control of the islanding DC microgird based on adaptive droop characteristics[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 163- 174.
[16] 王琛, 孟建辉, 王毅, 等. 含多种分布式电源的直流微电网硬件在环仿真系统设计与实现[J]. 电力系统保护与控制, 2018, 46(9): 146-154.
Wang Chen, Meng Jianhui, Wang Yi, et al. Design and implementation of hardware in-the-loop simu- lation system for DC microgrid with multiple DG units[J]. Power System Protection and Control, 2018, 46(9): 146-154.
[17] 郭伟, 赵洪山. 基于事件触发机制的直流微电网多混合储能系统分层协调控制方法[J]. 电工技术学报, 2020, 35(5): 1140-1151.
Guo Wei, Zhao Hongshan. Coordinated control method of multiple hybrid energy storage system in DC microgrid based on event-triggered mechanism[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1140-1151.
[18] Shafiee Q, Stefanovi C, Dragičević T, et al. Robust- networked control scheme for distributed secondary- control of islanded microgrids[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5363-5374.
[19] Lu Xiaonan, Guerrero J M, Sun Kai, et al. An improved droopcontrol method for DC microgrids based on lowbandwidth communication with DC bus voltagerestoration and enhanced current sharing accuracy[J]. IEEE Transactions on Power Electronics, 2014, 29(4): 1800-1812.
[20] 吕振宇, 吴在军, 窦晓波, 等. 基于离散一致性的孤立直流微网自适应下垂控制[J]. 中国电机工程学报, 2015, 35(17): 4397-4407.
Lü Zhenyu, Wu Zaijun, Dou Xiaobo, et al. An adaptive droop control for the islanded DC microgrid based on discrete consensus algorithm[J]. Pro- ceedings of the CSEE, 2015, 35(17): 4397-4407.
[21] 顾伟, 曹戈, 薛帅, 等. 基于有限时间一致性的直流微电网分布式协同控制方法[J]. 电力系统自动化, 2016, 40(24): 49-55, 84.
Gu Wei, Cao Ge, Xue Shuai, et al. Finite-time consensus based distributed cooperative control for DC microgrids[J]. Automation of Electric Power Systems, 2016, 40(24): 49-55, 84.
[22] Morstyn T, Savkin A, Hredzak B, et al. Multi-agent sliding mode control for state of charge balancing between battery energy storage systems distributed in a DC microgrid[J]. IEEE Transactions on Smart Grid, 2017, 9(5): 4735-4743.
[23] Peyghami S, Mokhtari H, Blaabjerg F. Decentralized load sharing in a low-voltage direct current microgrid with an adaptive droop approach based on a superi- mposed frequency[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(3): 1205-1215.
[24] Peyghami S, Davari P, Mokhtari H, et al. Synchronverter- enabled DC power sharing approach for LVDC microgrids[J]. IEEE Transactions on Power Electro- nics, 2017, 32(10): 8089-8099.
A Virtual Current-Frequency Droop Control in DC Microgrid
Abstract In DC microgrid, the inconsistency of DC-DC converter parameters and line impedance reduces the current sharing accuracy of droop control. Meanwhile, droop control inevitably causes DC bus voltage drop. To improve the current sharing performance among DC-DC converters, a droop control method based on virtual frequency is proposed by simulating the frequency droop control mechanism in AC microgrid. In the controller, a virtual AC variable whose frequency is proportional to the output current is constructed. The virtual frequency of each converter is shared by low bandwidth communication and the average value is calculated. The average frequency and virtual AC variable are further used to generate virtual reactive power to adjust the voltage setting point of the converter and coordinate the output current of each converter. On the premise of not causing bus voltage drop, the accuracy of load current distribution among converters is improved and the communication pressure is reduced. The stability of virtual frequency droop control is analyzed using small signal model. Finally, simulation and experiment based on Starsim and dSPACE verify the validity of the method.
keywords：DC microgrid, virtual frequency, droop control, current sharing, DC-DC converter
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.191275
国家自然科学基金项目（51979021，51709028）、中央高校基本科研业务费专项资金项目（3132019317）、辽宁省计划项目（2019JH8/10100045）和“双一流”建设专项（BSCXXM009）资助。
收稿日期 2019-09-28
改稿日期 2020-11-05
刘彦呈 男，1963年生，博士，教授，博士生导师，研究方向为交流电机控制、电力电子变换器、船舶电力推进技术、可再生能源发电和微电网。E-mail: liuyc3@163.com
庄绪州 男，1989年生，博士研究生，研究方向为船舶直流微电网、船舶综合电力系统、电力电子变换器。E-mail: zhuangxuzhou@163.com（通信作者）
（编辑 崔文静）