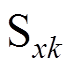 (
(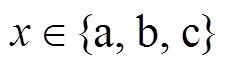 ,
,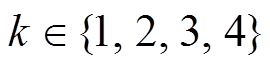 ),每相根据开关器件切换输出P、O、N三种状态,共计
),每相根据开关器件切换输出P、O、N三种状态,共计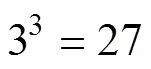 种开关状态,T型三电平逆变器的空间电压矢量如图2所示[21-24]。以A相为例,当Sa1、Sa2闭合,Sa3、Sa4断开时,开关状态为P状态;当Sa2、Sa3闭合,Sa1、Sa4断开时,开关状态为O状态;当Sa3、Sa4闭合,Sa1、Sa2断开时,开关状态为N状态。
种开关状态,T型三电平逆变器的空间电压矢量如图2所示[21-24]。以A相为例,当Sa1、Sa2闭合,Sa3、Sa4断开时,开关状态为P状态;当Sa2、Sa3闭合,Sa1、Sa4断开时,开关状态为O状态;当Sa3、Sa4闭合,Sa1、Sa2断开时,开关状态为N状态。摘要 三电平变流器控制系统采用有限集模型预测控制(FCS-MPC),滚动优化需要遍历所有开关状态,针对其导致处理器运算量增加、处理时间长的问题,提出一种T型三电平并网逆变器优化计算量的FCS-MPC方法。通过构建基于电压预测的单目标代价函数,避免设计权重系数问题,减化单次寻优的步骤;根据直流母线电位分布选择冗余小矢量,实现中点电位平衡,使每个控制周期的预测次数减小至3次,提高寻优效率。有限控制集在预测过程中将所包含矢量的加权误差二次方最小作为依据划分,并利用矢量角补偿系统延迟,提高预测精度,使并网电流质量得到改善。搭建基于RT-Lab的功率硬件在环仿真系统和物理装置验证所提控制策略,实验结果验证了所提理论分析的正确性和控制策略的有效性。
关键词:有限集模型预测控制 T型三电平 中点电位平衡 快速寻优
随着数字信号处理技术的飞速发展,以有限集模型预测控制(Finite Control Set-Model Predictive Control, FCS-MPC)为代表的复杂控制方法被逐渐应用于并网逆变器系统中[1-5]。FCS-MPC无需调制单元,能够适应各种非线性系统的控制。其本质是一种枚举法,即对所有可能的开关状态进行评估,用于下一控制周期[6-9]。对于三电平变流器,其空间矢量包含27种状态,若在预测控制中逐一遍历寻优,需要进行大量计算,对处理器产生工作负担[10-12]。
在变流器模型预测控制方面,为实现控制系统的在线快速寻优,国内外学者一方面针对物理架构进行设计,主要是利用具备并行运算能力的FPGA实现调制器功能,即模型预测控制过程中,将电流控制部分与调制部分分别处理,从而实现了开关信号的快速识别和输出,为处理器分担计算量;但该方法仅优化了调制脉冲过程,无法解决预测控制算法本身存在的复杂计算问题[13-15]。另一方面,从优化数字系统角度出发,FCS-MPC存在权重系数难以设计的问题,因此可以构建电压或电流的单目标代价函数,但对三电平中点电位平衡方案设计提出了更高要求。文献[13]利用调制器分配矢量占空比实现了中点电位平衡。文献[14]通过比较直流母线上、下电容的幅值,使每个控制周期选取适合的冗余小矢量控制中点电位。文献[15]通过判断电流方向和母线电压分布,选取规定的开关状态控制中点电位。上述方法在单目标函数的基础上实现了中点电位控制,能够避免权重系数选取困难,并减少每次遍历的计算量,但未解决优化三电平遍历寻优的解决方案。针对MPC每个控制周期的运算步骤和有限控制集优化,文献[16]提出用电压代替电流作为目标变量的方法,能够直接与待选矢量进行比较,简化了代价函数单次优化的步骤,其实验结果表明,电压直接预测较电流直接预测能够提升到150%的寻优效率。文献[17]提出两电平的改进方法,通过循环比较选择扇区,使预测次数仅为1,但该方法仅适用于两电平变流器,当直流侧阶数增大后无法达到同样的效果。文献[18-20]根据三电平的空间矢量分布特性,通过划定扇区的方法确定有限控制集,比较传统FCS-MPC方法,三种方法的遍历寻优次数能够从每个控制周期的27次缩减至12、10、3次,大大节省了在线计算时间,但未研究扇区的具体划分细则,根据其划分的有限控制集寻优遍历时,逆变器输出性能低于传统方法。
为此,本文首先详细分析了FCS-MPC的控制机理和算法特点,在此基础上提出一种T型三电平并网逆变器的改进FCS-MPC方法。构建了基于电压预测的单目标代价函数,并利用冗余小矢量控制直流侧中点电位;采用有限控制集划分方法基于最小加权误差二次方原则,并利用矢量角计算下一时刻的电压向量补偿系统的延迟。最后搭建基于RT-Lab的功率硬件在环仿真平台及物理装置,实验结果表明,所提出控制策略能够优化计算时间,提高处理器工作效率,同时改善了并网电流质量。
图1为T型三电平逆变器结构,输出侧经RL滤波器接入电网,其中包含直流侧电容C1、C2和12个开关器件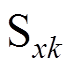 (
(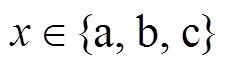 ,
,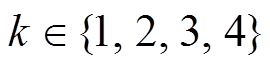 ),每相根据开关器件切换输出P、O、N三种状态,共计
),每相根据开关器件切换输出P、O、N三种状态,共计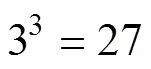 种开关状态,T型三电平逆变器的空间电压矢量如图2所示[21-24]。以A相为例,当Sa1、Sa2闭合,Sa3、Sa4断开时,开关状态为P状态;当Sa2、Sa3闭合,Sa1、Sa4断开时,开关状态为O状态;当Sa3、Sa4闭合,Sa1、Sa2断开时,开关状态为N状态。
种开关状态,T型三电平逆变器的空间电压矢量如图2所示[21-24]。以A相为例,当Sa1、Sa2闭合,Sa3、Sa4断开时,开关状态为P状态;当Sa2、Sa3闭合,Sa1、Sa4断开时,开关状态为O状态;当Sa3、Sa4闭合,Sa1、Sa2断开时,开关状态为N状态。
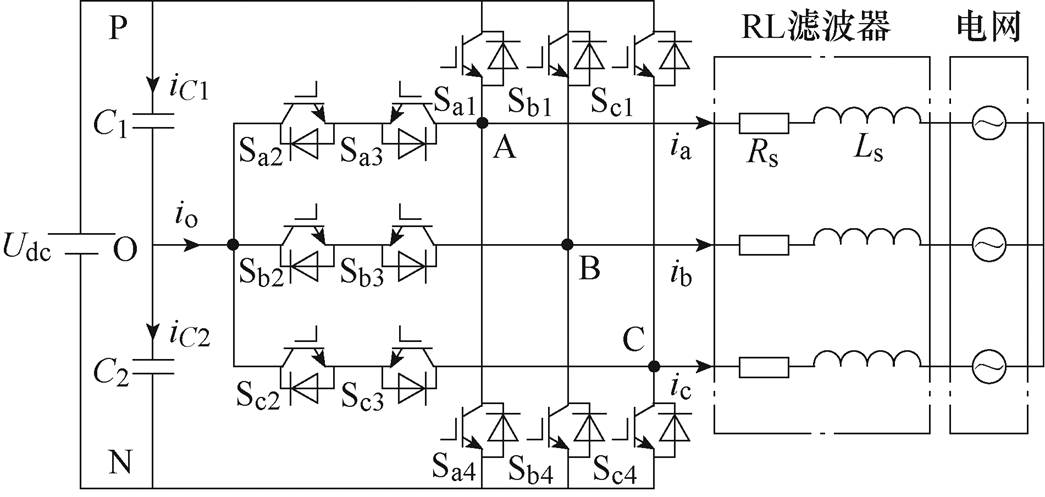
图1 T型三电平逆变器结构
Fig.1 Structure of T-type three-level inverter
对图1所示的T型三电平逆变器进行建模分析,网侧逆变器的动态模型可以表示为
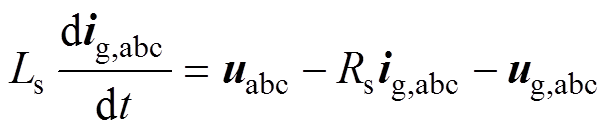 (1)
(1)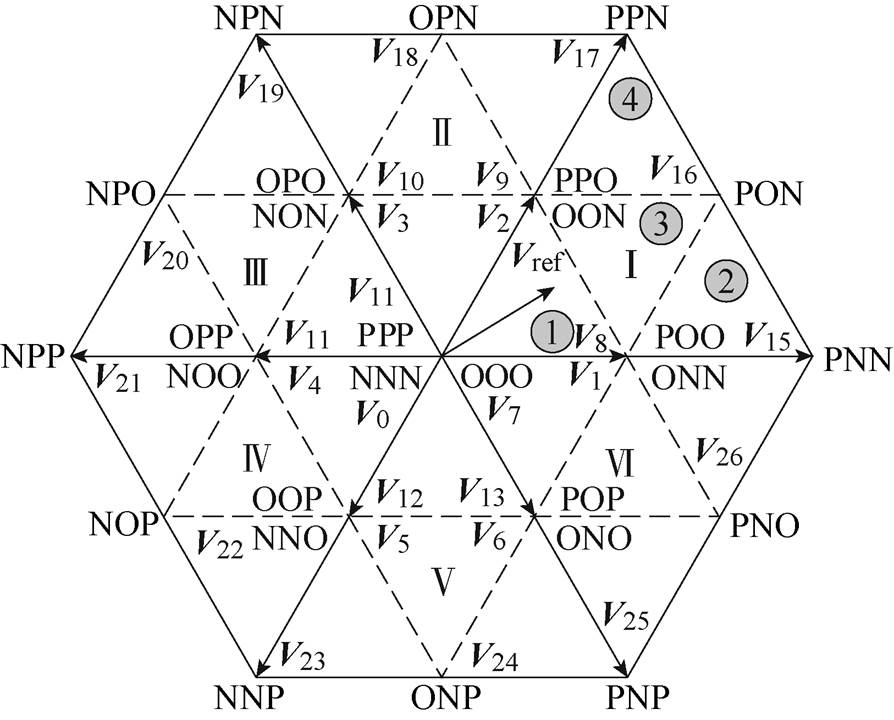
图2 T型三电平逆变器的空间电压矢量
Fig.2 Space voltage vector of T-type three-level inverter
式中,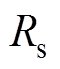 和
和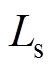 分别为寄生电阻和滤波电感;
分别为寄生电阻和滤波电感;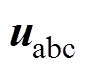 为逆变器输出的三相电压;
为逆变器输出的三相电压;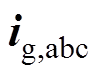 和
和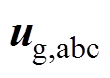 分别为并网电流和网侧交流电压。式(1)经过Clarke变换得到系统在
分别为并网电流和网侧交流电压。式(1)经过Clarke变换得到系统在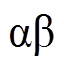 旋转坐标系下的简化模型为
旋转坐标系下的简化模型为
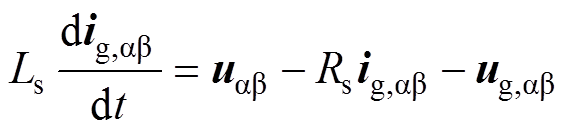 (2)
(2)由于模型预测控制器需要建立离散模型,因此采用前向欧拉法将式(2)中的电流变量离散化,即
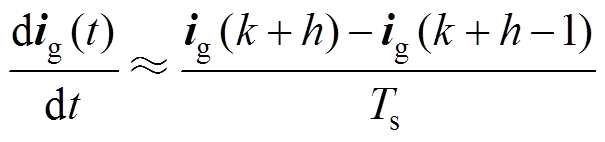 (3)
(3)
式中,Ts为采样时间;h为预测的周期次数,h=1时,为单步预测;h=2时,为两步预测。基于离散时间的并网电流表示为
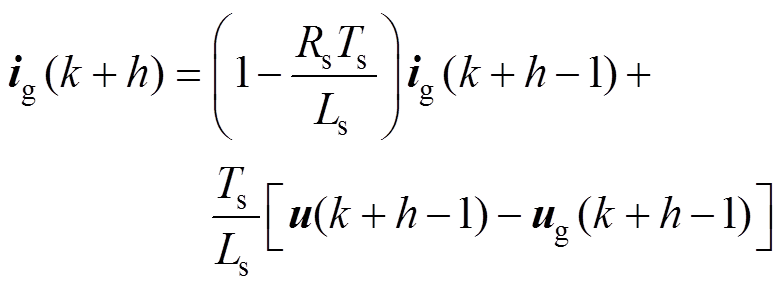 (4)
(4)同理,考虑直流侧电容的动态模型,电容电流的表达式为
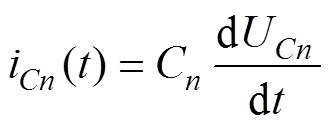 (5)
(5)
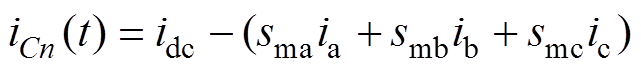 (6)
(6)式中,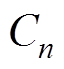 为上、下母线电容值,
为上、下母线电容值,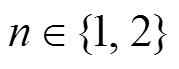 ;
;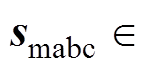
 表示三相开关状态。采用式(3)的方法进行离散化,得到基于离散时间的直流侧电容电压为
表示三相开关状态。采用式(3)的方法进行离散化,得到基于离散时间的直流侧电容电压为
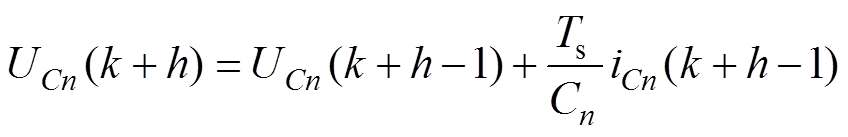 (7)
(7)FCS-MPC的代价函数在并网逆变器中通常选取电流、电压或功率作为主要约束变量,以电压约束变量为例,根据式(4),计算k时刻的网侧参考电压为
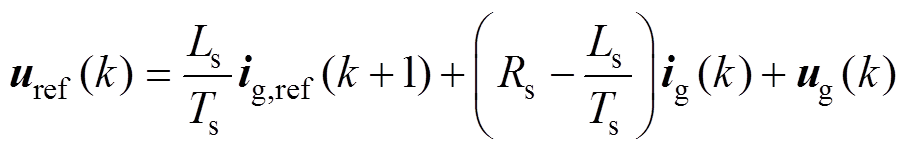 (8)
(8)式中,对于较短的采样时间,可近似认为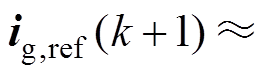
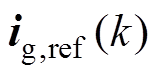 ,同时考虑直流母线中点平衡,增加附加项中点电位差,设代价函数为
,同时考虑直流母线中点平衡,增加附加项中点电位差,设代价函数为
 (9)
(9)
式中,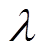 为权重系数,它的取值决定了所控制变量在全局优化中的优先级;
为权重系数,它的取值决定了所控制变量在全局优化中的优先级;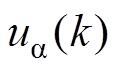 、
、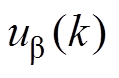 为有限控制集中各电压矢量在
为有限控制集中各电压矢量在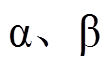 轴上的映射。考虑图2中的所有电压矢量,控制器需要在一个采样周期内遍历寻优27次,选取形成代价函数最小的电压矢量,输出开关数字信号。
轴上的映射。考虑图2中的所有电压矢量,控制器需要在一个采样周期内遍历寻优27次,选取形成代价函数最小的电压矢量,输出开关数字信号。
针对传统FCS-MPC方法存在的不足,从以下几个方面进行改进:①构建基于电压预测的单目标代价函数,并通过控制冗余小矢量平衡直流母线的快速寻优方法;②提升预测精度的有限控制集划分细则;③补偿系统延时的矢量角补偿策略。
传统算法中的权重系数整定需要反复实验,根据工况进行改变,并且在寻优过程中将增加计算量,本文利用冗余小矢量的工作特性,替代中点电位平衡函数。根据电压矢量的幅值大小,T型三电平逆变器的27个开关状态可以分为零矢量、小矢量、中矢量和大矢量。其中,每对冗余小矢量产生的输出线电压是相同的,但引起的中点电流极性相反,其导通路径示意图如图3所示。
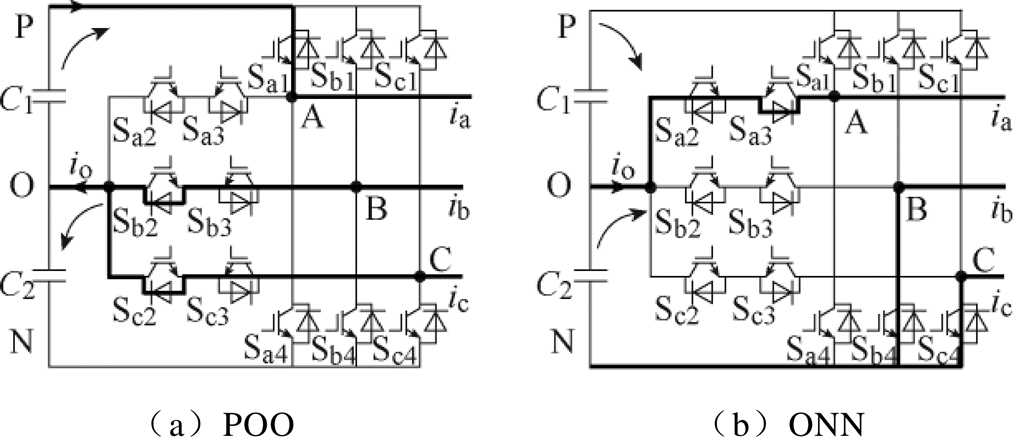
图3 小矢量作用过程
Fig.3 Effect process of small vector
设中点O流入逆变器方向为正,以POO/ONN为例,当P型小矢量作用时, 放电,流入中点O的电流为
放电,流入中点O的电流为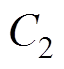 充电,此时,
充电,此时,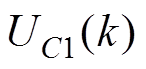 >
>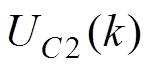 ;当N型小矢量作用时,
;当N型小矢量作用时,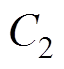 放电,电流从中点O流向逆变器,直流母线为
放电,电流从中点O流向逆变器,直流母线为 充电,此时,
充电,此时,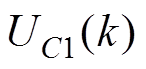 <
<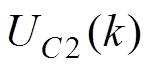 。这些冗余小矢量开关状态对于中点电流
。这些冗余小矢量开关状态对于中点电流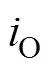 和直流母线电容电压的影响见表1,因此,选取不同的小矢量产生期望极性的中点电流能够平衡中点电位[25-27]。
和直流母线电容电压的影响见表1,因此,选取不同的小矢量产生期望极性的中点电流能够平衡中点电位[25-27]。
表1 小矢量开关状态及对应中点电流和电容充放电状态
Tab.1 Status of neutral-point current and capacitor charge and discharge with small vector switch state

开关状态直流母线电容状态 POOPPOOPOOPPOOPPOO放电充电 ONN充电放电 OON NON NOO NNO ONO
根据图2所示的空间电压矢量分布情况,可以分为Ⅰ~Ⅵ共计6个大扇区,每个大扇区分成4个小扇区,通过比较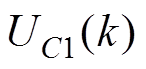 和
和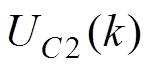 ,每个小扇区根据冗余小矢量的类型分为两种开关状态,各包含3个空间矢量。以第I扇区为例,有限控制集选取原则见表2。将上述的判断逻辑引入到传统方法的控制过程中,得到改进的T型三电平并网逆变器FCS- MPC框图如图4所示。
,每个小扇区根据冗余小矢量的类型分为两种开关状态,各包含3个空间矢量。以第I扇区为例,有限控制集选取原则见表2。将上述的判断逻辑引入到传统方法的控制过程中,得到改进的T型三电平并网逆变器FCS- MPC框图如图4所示。
表2 有限控制集选取原则
Tab.2 Principle of finite control set selection
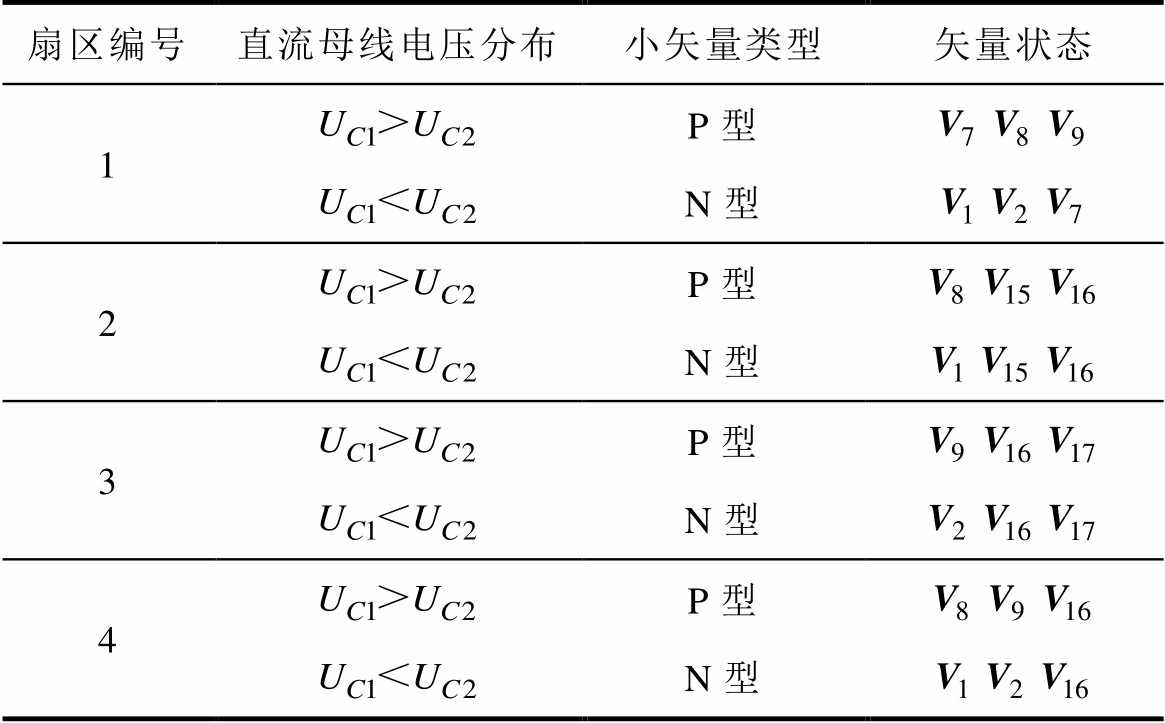
扇区编号直流母线电压分布小矢量类型矢量状态 1P型 N型 2P型 N型 3P型 N型 4P型 N型
图4中,有限集模型预测控制器的代价函数根据式(9)重新定义为

图4 改进T型三电平并网逆变器FCS-MPC框图
Fig.4 Diagram of FCS-MPC for improved T-type three-level grid-connected inverter
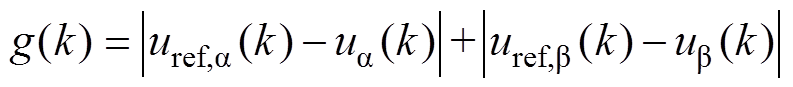 (10)
(10)式(10)将对所选控制集的开关状态进行比较,基于最小化原则选取最佳开关状态作用于下一采样时刻的代价函数。
电压矢量小扇区选取一般通过比较斜率判断,然而对于过调制范围,存在不能准确判断最近扇区的区域,使选取的三个矢量与参考矢量误差较大。为提升矢量选取的精度,本文提出了最小误差二次方判别法,首先根据图2所示的每个有效切换状态的电压矢量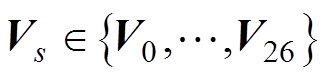 ,建立参考电压矢量
,建立参考电压矢量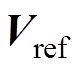 与
与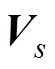 的预测误差二次方范数d为
的预测误差二次方范数d为
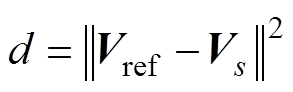 (11)
(11)则某一区域的加权误差二次方为
 (12)
(12)
式中,ea、eb 分别为电压矢量在a、b 轴上的误差。
由于零矢量的模长为0无需考虑,对于每个大扇区需要计算其余7个矢量的加权误差二次方,选择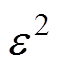 最小即为参考矢量所在扇区;同理对于每个小扇区,首先判断直流母线电容电压分布情况确定小矢量类型,然后计算4个小扇区的加权误差二次方,选择
最小即为参考矢量所在扇区;同理对于每个小扇区,首先判断直流母线电容电压分布情况确定小矢量类型,然后计算4个小扇区的加权误差二次方,选择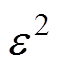 最小即为目标扇区。
最小即为目标扇区。
理想情况下,控制器能够在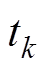 时刻同时完成A-D采样和代价函数计算,并实时控制逆变器开关动作,然而实际系统计算与控制时序如图5a所示,模型预测控制器需要经过计算时间后才能作用于实际系统,若实际系统未考虑补偿延时,这一问题可能会导致系统性能恶化。延时补偿原理如图5b所示,补偿方案通常基于式(4)进行多步预测,即在
时刻同时完成A-D采样和代价函数计算,并实时控制逆变器开关动作,然而实际系统计算与控制时序如图5a所示,模型预测控制器需要经过计算时间后才能作用于实际系统,若实际系统未考虑补偿延时,这一问题可能会导致系统性能恶化。延时补偿原理如图5b所示,补偿方案通常基于式(4)进行多步预测,即在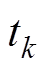 时刻计算
时刻计算 时刻的最优开关状态,然而该方法需要对参考量重新计算,会进一步延长计算时间。
时刻的最优开关状态,然而该方法需要对参考量重新计算,会进一步延长计算时间。
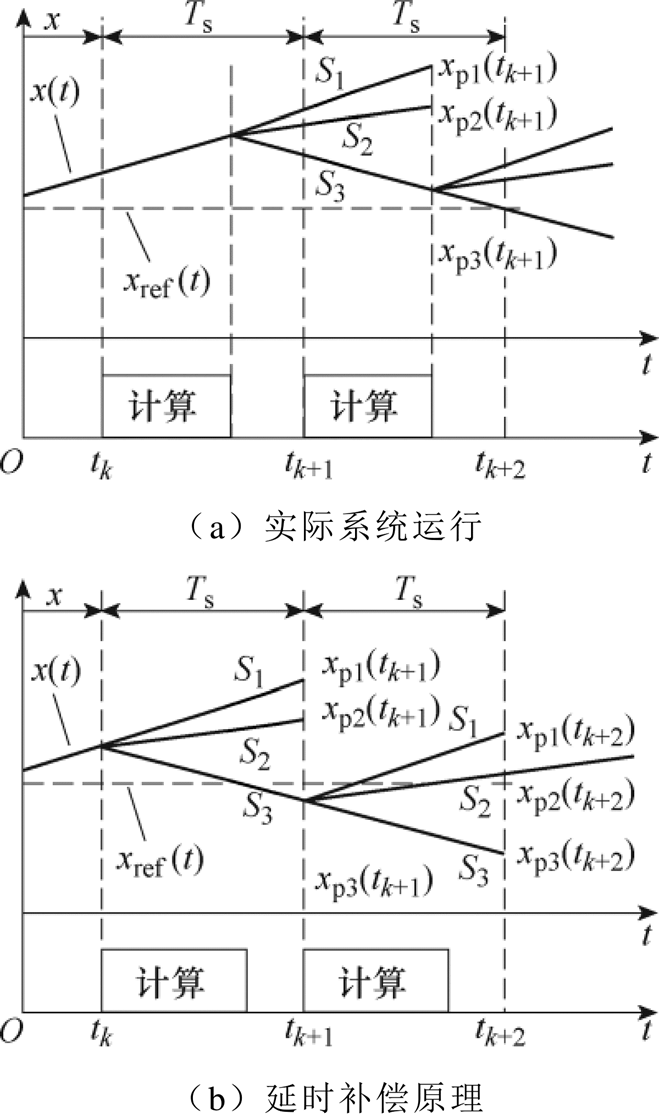
图5 FCS-MPC延时补偿原理
Fig.5 Principle of delay compensation for FCS-MPC
因此,考虑采用电压作为代价函数的约束变量,本文提出一种基于矢量角补偿电网电压的方法,令电压幅值为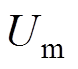 、矢量角为
、矢量角为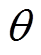 ,则
,则
 (13)
(13)当系统稳态运行时,假设tk+1时刻的参考电压矢量相位为
 (14)
(14)
式中,w 为矢量旋转角速度,代入式(13)得
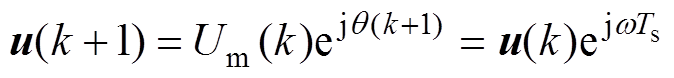 (15)
(15)因此,加入延时补偿的代价函数为
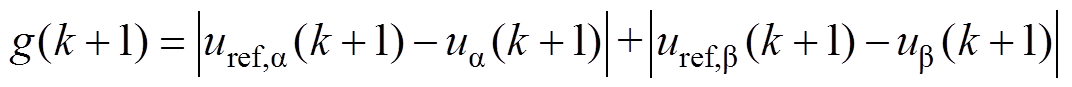 (16)
(16)
针对以上的控制算法,设计的FCS-MPC快速寻优方法流程如图6所示。
在模型预测过程中,预测精度会受到参数不确定性的影响,当建模错误或参数变化时,直接采用给定的系统模型选取最优矢量会改变控制器的性能。由于基于FCS-MPC的并网逆变器系统为非线性系统,目前尚未存在公认的鲁棒性分析方法。对此,本文对逆变器滤波电感参数进行了灵敏度分析,为模型预测控制器的参数设计提供了思路。
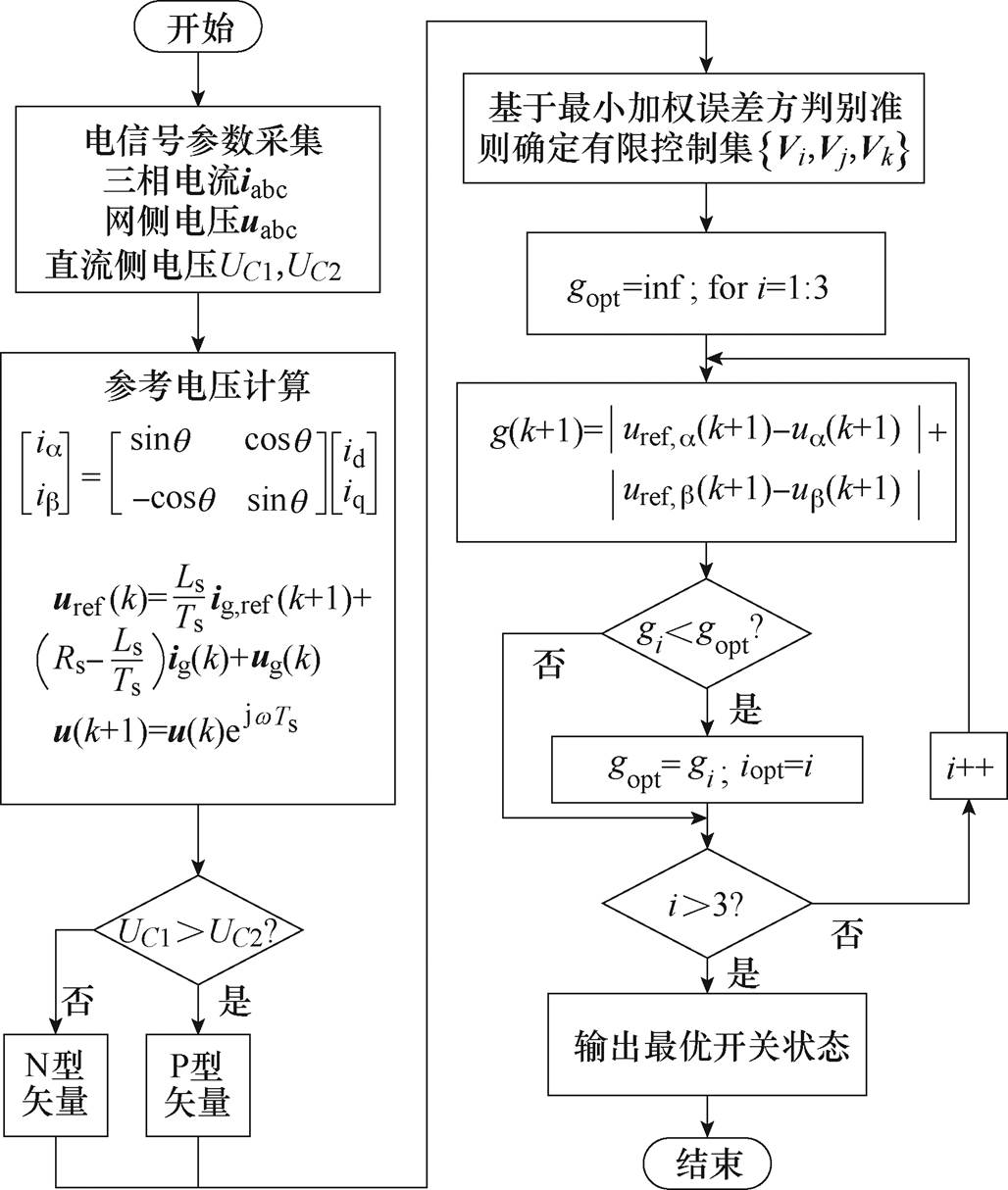
图6 FCS-MPC快速寻优方法流程
Fig.6 Logic block diagram of FCS-MPC fast optimization method
由于逆变器寄生电阻很小,本文忽略其变化的影响。假设模型电感参数为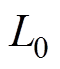 ,则考虑不确定变化参数
,则考虑不确定变化参数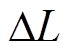 的实际电感参数为
的实际电感参数为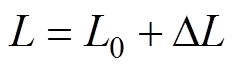 ,根据式(4),当模型电感参数变化时,修正的参数预测模型为
,根据式(4),当模型电感参数变化时,修正的参数预测模型为
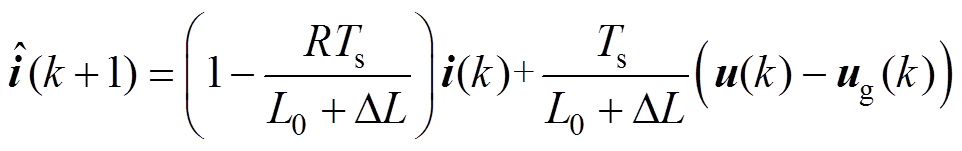 (17)
(17)则无误差模型与参数不确定模型预测的误差为
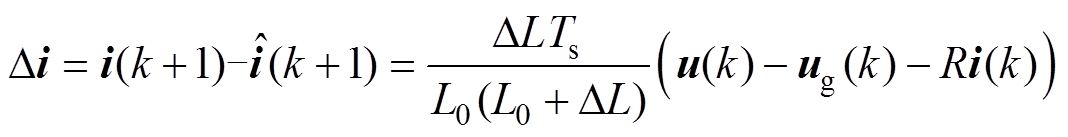 (18)
(18)
根据式(18),模型预测的计算误差取决于采样周期Ts、电感变化参数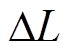 和参考电压与实际电网电压的误差。其中采样周期与误差成正比,因此通过减小FSC-MPC计算时间,缩短控制周期,能够提高预测精度;逆变器输出电压是根据电网电压对每个控制周期进行评估产生,因此其误差与参考电压在空间矢量中的位置和直流母线电压有关,不受电感参数的影响。由于预测算法是控制单个采样周期的,所以预测误差仅需考虑当前控制周期的状态,不会造成累计误差。
和参考电压与实际电网电压的误差。其中采样周期与误差成正比,因此通过减小FSC-MPC计算时间,缩短控制周期,能够提高预测精度;逆变器输出电压是根据电网电压对每个控制周期进行评估产生,因此其误差与参考电压在空间矢量中的位置和直流母线电压有关,不受电感参数的影响。由于预测算法是控制单个采样周期的,所以预测误差仅需考虑当前控制周期的状态,不会造成累计误差。
进一步分析参数变化的影响,设定工况采样频率10kHz,模型电感10mH,寄生电阻0.2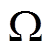 ,假设电压误差幅值固定10V并且与电流同相位,计算不同实际电感参数和电流大小情况下的误差
,假设电压误差幅值固定10V并且与电流同相位,计算不同实际电感参数和电流大小情况下的误差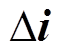 ,电感和电流参数变化对预测误差的影响如图7所示。
,电感和电流参数变化对预测误差的影响如图7所示。
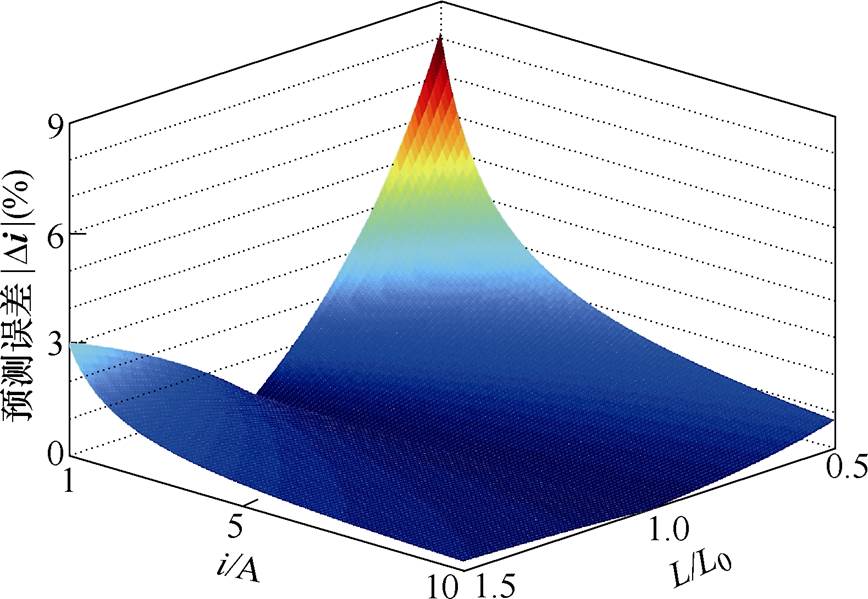
图7 电感和电流参数变化对预测误差的影响
Fig.7 The influence of inductance and current parameter changes on prediction errors
显然,当L/L0=1时,预测模型误差为0;当 L/L0<1时,预测误差随着比值的降低迅速增大;当L/L0>1时,预测误差随着比值的增大缓慢增加。这表明,预测误差与电感参数变化量呈非对称性,因此在设计模型预测控制器时建议模型电感参数值不要高于实际电感。此外,随着实际电流的增加,预测误差也相对降低,这是由式(18)中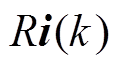 项导致,需要说明的是,若线路寄生电阻较大,实际电流变化导致的预测误差变化趋势将不同。
项导致,需要说明的是,若线路寄生电阻较大,实际电流变化导致的预测误差变化趋势将不同。
结合上述理论分析,搭建基于RT-Lab控制的T型三平并网逆变器功率硬件在环仿真平台,如 图8所示。其中,T型三电平的功率单元由3个F3L100R12W2H3_B11Z IGBT模块组成,RT-Lab控制器产生的驱动信号通过1EDI60H12AH芯片对其进行控制,电流和电压的反馈信号由LV25-P/SP2和LA55-P霍尔传感器实时采集,采集量通过I/O口输入RT-Lab OP5600实时仿真器(8核CPU,主频3.2GHz)进行运算控制。表3为实验系统参数。
4.1.1 逆变器输出性能分析
分析比较各类控制策略的逆变器输出性能,分别对传统FCS-MPC(A策略)、根据坐标轴斜线斜率判断有限控制集的快速FCS-MPC(B策略)和改进控制算法(C策略)进行实验。图9为三种算法的逆变器输出性能比较,给定的三相参考电流有效值为5A,图9a、图9b为A策略不同权重系数下的实验结果,图9c、图9d分别为B策略和C策略实验结果。图10为逆变器输出电流总谐波畸变率(Total Harmonic Distortion, THD)。

图8 T型三电平并网逆变器功率硬件在环仿真平台
Fig.8 Power hardware-in-the-loop platform of T-type three-level grid-connected inverter
表3 系统参数
Tab.3 Parameters of system

参 数数 值 直流侧电压/V240 网侧相电压(RMS)/V60 电网频率/Hz50 直流侧电容,/mF8 000 滤波电感/mH10 寄生电阻/W0.5 采样周期/ms100
可见,传统算法需要设计权重系数,其电流质量随着电流控制代价函数的权重占比增加而提升;改进FCS-MPC无需整定权重系数,通过判断最小误差二次方的方法获取有限控制集,能够大幅度提高电压矢量的识别精度,相比较仅根据坐标轴划分有限控制集的方法,电流的THD由原来的4.57%降低至3.41%,提升了并网电流质量。
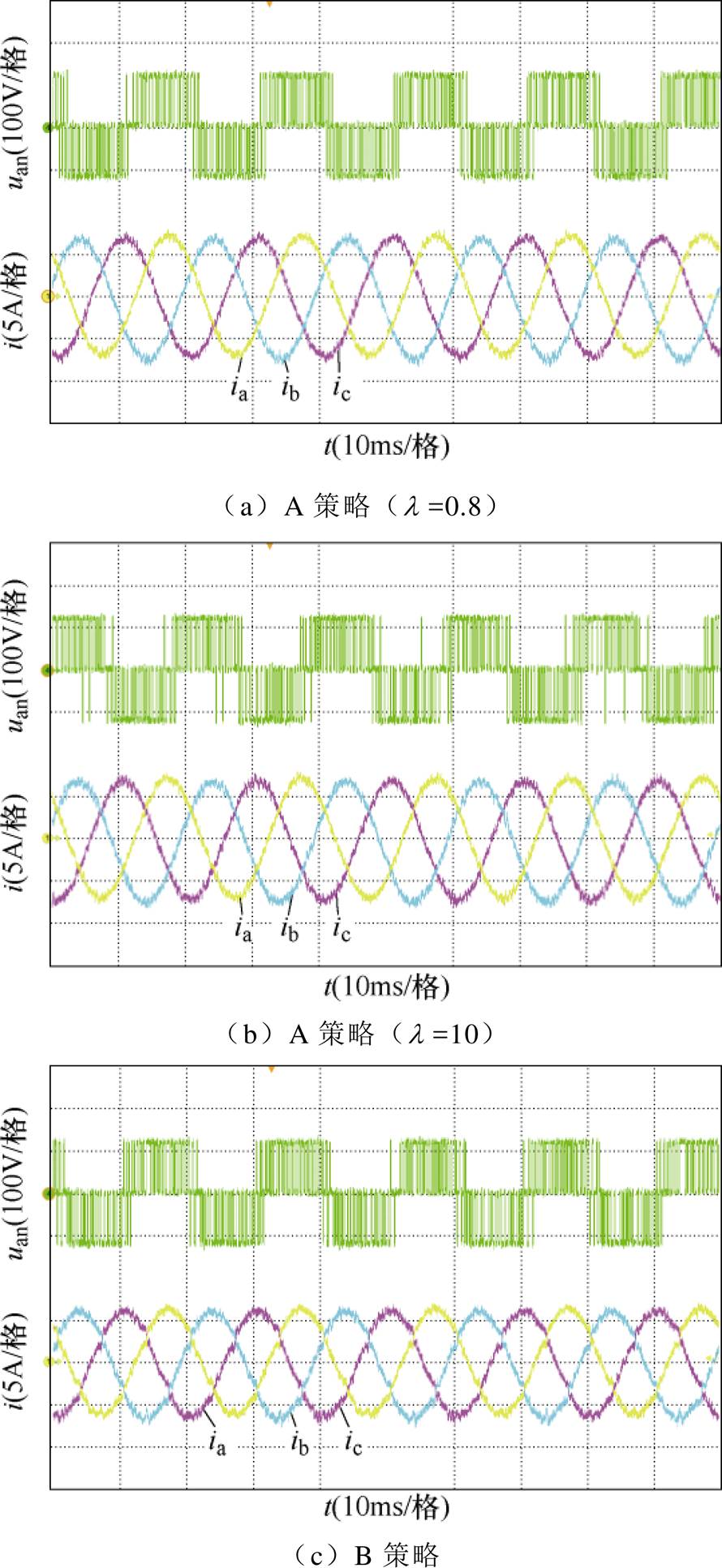
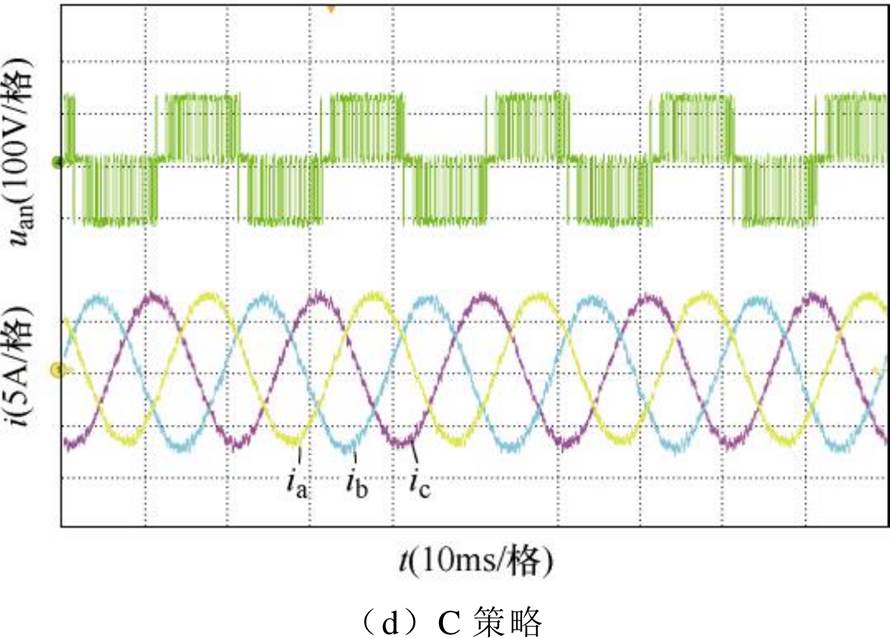
图9 各类控制策略的逆变器输出电流比较
Fig.9 Comparison of inverter output current of various control strategies
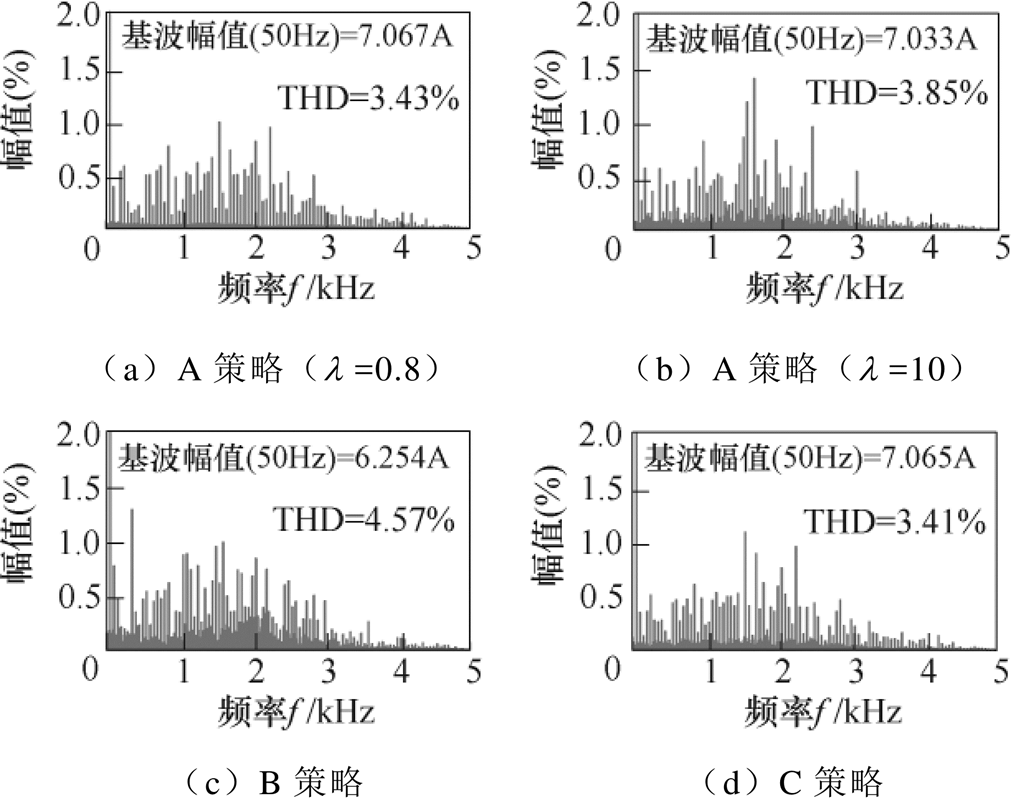
图10 逆变器输出电流THD
Fig.10 THD of inverter output current
4.1.2 动态响应性能分析
图11为电流突变实验,用来验证改进FCS-MPC的动态响应性能。图11a为电流衰减,三相指令电流的有效值由5A衰减至4A;图11b为电流跃升,电流由4A升高至5A。两种工况下,三相电流均能够有效地跟踪指令值,当指令电流变化时,实际电流能够在1ms内到达指令值并保证系统的稳定性,实验表明,改进FCS-MPC具备快速的动态响应能力。
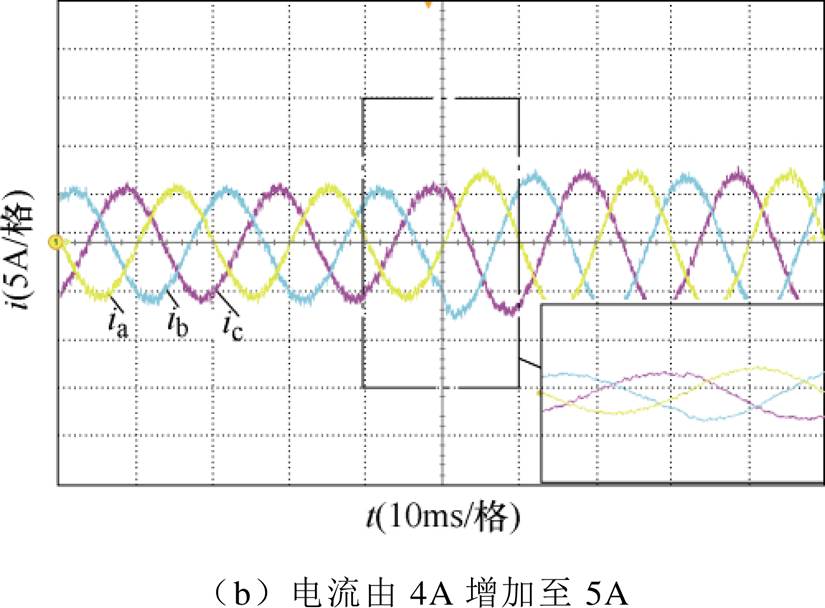
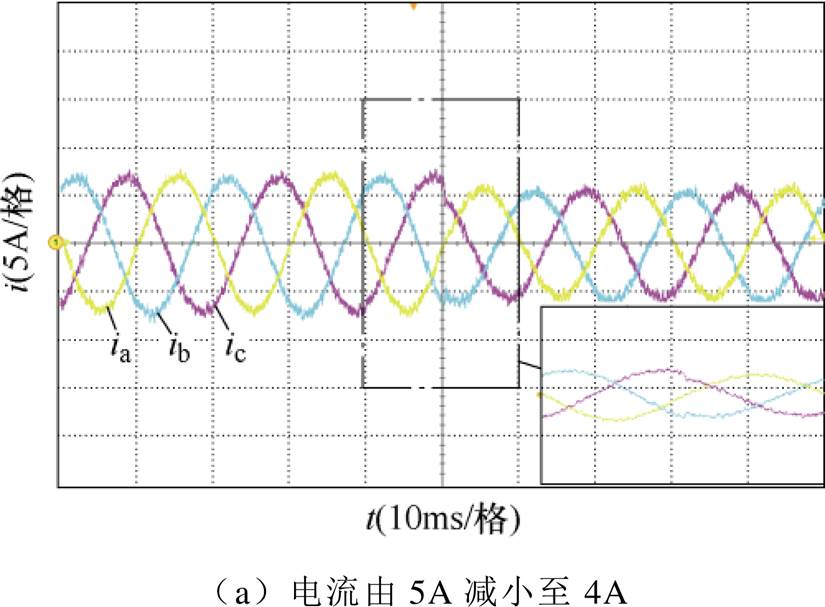
图11 电流突变实验
Fig.11 Experiment for current mutation
4.1.3 直流母线中点电位平衡能力分析
分析比对三种算法的直流母线中点电位平衡能力,直流侧中点电位及其电位差如图12所示。图12a、图12b分别为A策略在两种工况l =0.8和l =10时的实验结果,其平均电位差分别为5.34V、4.62V,表明传统算法的平衡能力取决于中点电位函数的权重占比;图12c、图12d分别为B、C策略的实验结果,平均电位差分别为8.65V、5.25V,表明,改进算法的有限控制集选取方法提升了冗余小矢量的判别精度,提高了中点电位控制能力。
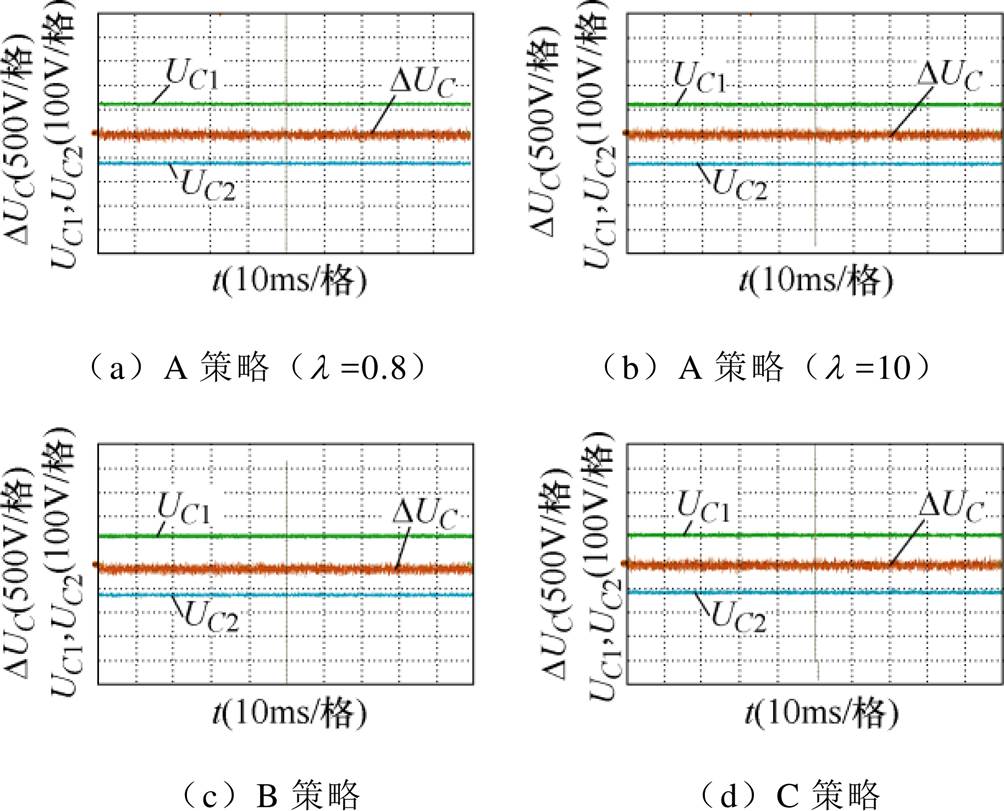
图12 直流侧中点电位及其电位差
Fig.12 Neutral-point potential and difference of DC
4.1.4 参数灵敏度分析
改进FCS-MPC在不同电感参数失配时的电流平均绝对误差如图13所示,模型电感参数设为L0= 10mH,实际电感参数分别为5mH、10mH和15mH。当指令电流较低时,三种工况下均具有较高的平均绝对误差,这是由FCS-MPC特性决定的,即式(18)中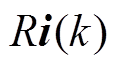 与参考电压差的误差较大引起的;当建模电感参数高于实际电感参数时,预测精度更低,所拟合的曲线符合第3节的理论分析结果。
与参考电压差的误差较大引起的;当建模电感参数高于实际电感参数时,预测精度更低,所拟合的曲线符合第3节的理论分析结果。
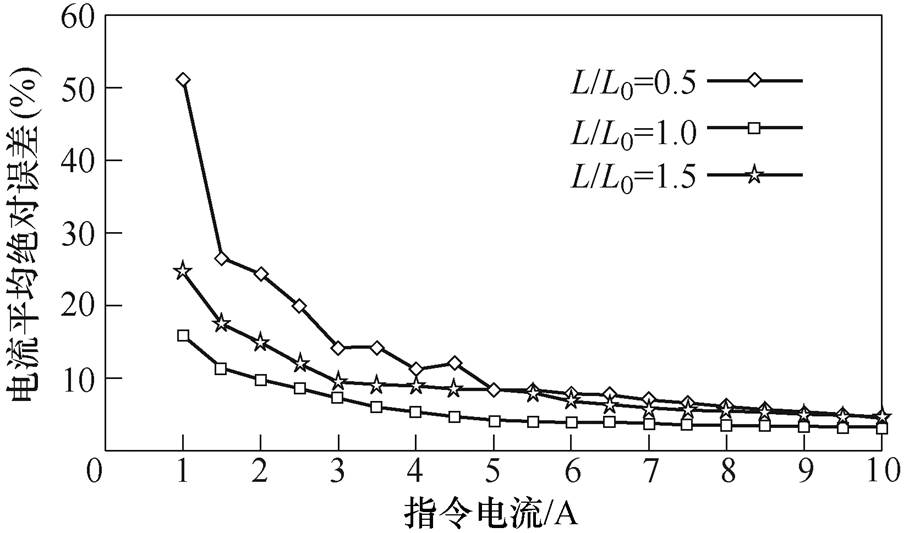
图13 不同电感参数失配时的电流平均绝对误差
Fig.13 Average absolute error of current under different inductance parameter mismatch
比较不同电感参数适配时的逆变器输出性能,根据3.2节的电流突变实验改变实际电感参数,不同电感参数失配环境下的电流波形如图14所示。与参数匹配的实验结果比较,电感参数变化对动态响应基本无影响,并且电感参数变化影响电流纹波的限制效果,当实际电感参数变大时,滤波效果更好,但由于预测精度降低,会对电压和电流的相位产生影响。
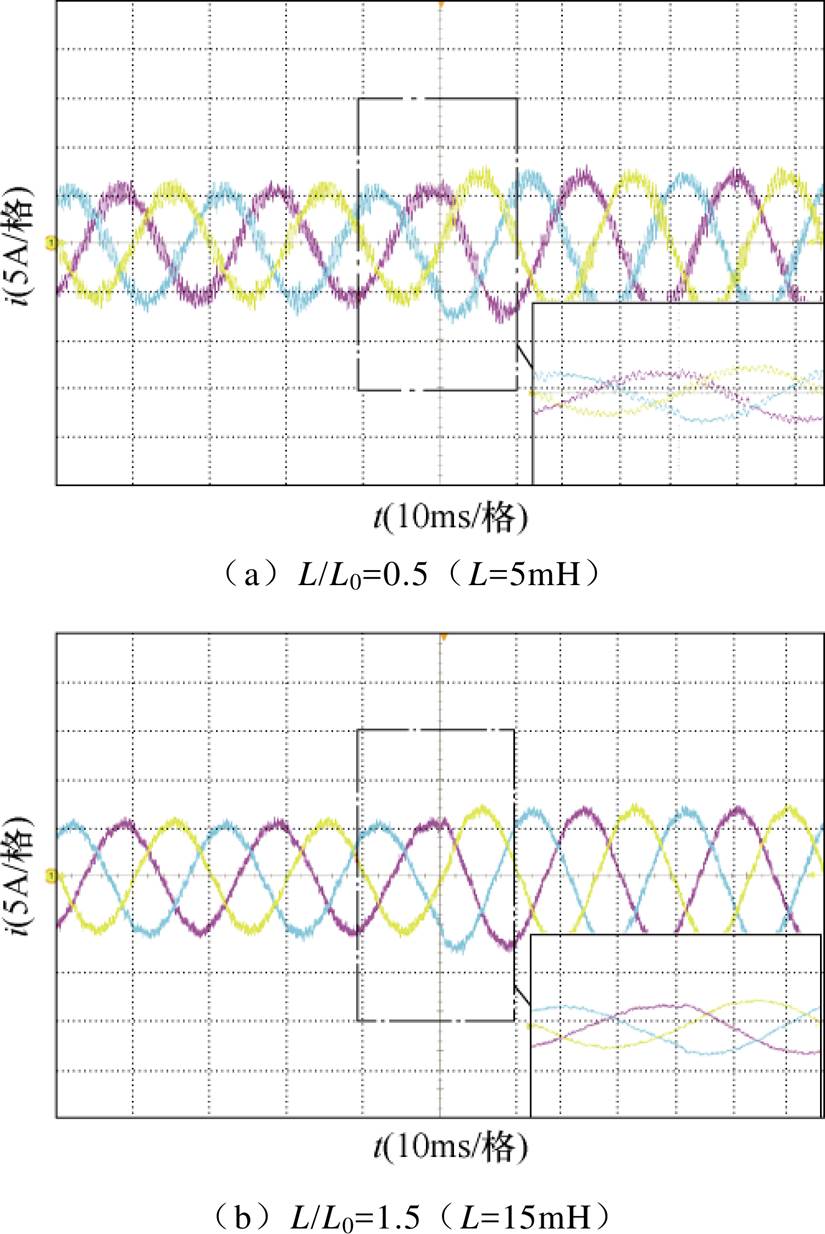
图14 不同电感参数失配环境下的电流波形
Fig.14 Current waveforms with different inductance parameters mismatch
4.1.5 计算效率分析
图15为三种策略的功率硬件在环仿真计算时间比较。模型预测控制器的计算时间由RT-Lab模型监控模块获取,其中,A策略平均计算时间为4.85ms(1.94~9.57ms),B策略的平均计算时间为2.09ms(1.10~5.55ms),C策略的平均计算时间为3.76ms(1.44~7.62ms)。对比A策略与C策略,改进控制算法的计算效率明显提升;对比B策略与C策略,改进控制算法由于引入扇区预测和延时补偿环节,占用了较多计算器资源,而根据经典扇区划分选取有限集能够快速地选择矢量。


图15 计算时间比较
Fig.15 Comparison of calculation time
综合实验分析,得到各类控制算法的性能见 表4。A策略的电流和中点电位控制能力主要由权重系数分配决定,由于每个周期需要预测所有电压矢量,其计算时间最长;B策略计算效率最高,有限控制集根据经典小扇区判断比较获取,但由于矢量圆存在未调制区域,将影响扇区判断,使得电流THD和中点电位差较大;C策略在B策略的基础上,改进了有限控制集选取方法,根据最小加权误差二次方准则,对每个大扇区所属的4个小扇区进行了寻优,优化了预测结果。
表4 三种控制策略比较
Tab.4 Comparison of three control strategies
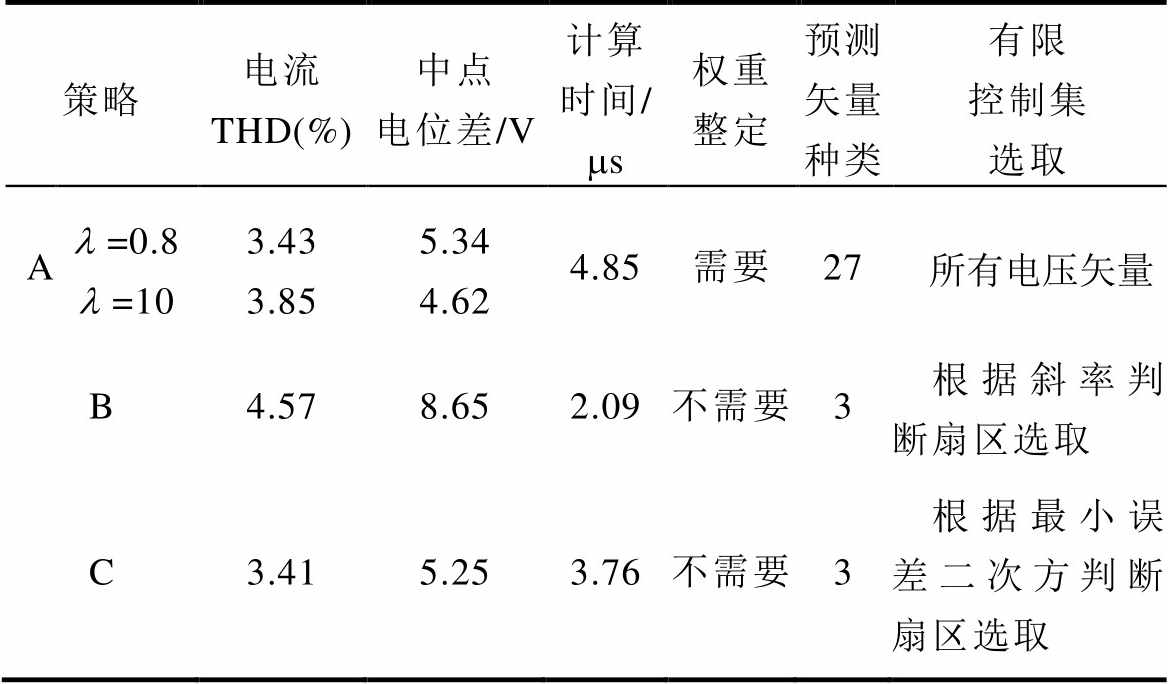
策略电流 THD(%)中点电位差/V计算时间/ms权重整定预测矢量种类有限控制集选取 Al=0.8l=103.433.855.34 4.624.85需要27所有电压矢量 B4.578.652.09不需要3根据斜率判断扇区选取 C3.415.253.76不需要3根据最小误差二次方判断扇区选取
三电平变流器主要采用DSP作为控制器,为了验证该方法在实际装置中的性能,设计了采用TMS320F28335作为主控制器的T型三电平物理样机,物理装置及测试环境如图16所示,系统参数与表3一致,DSP程序流程如图17所示。
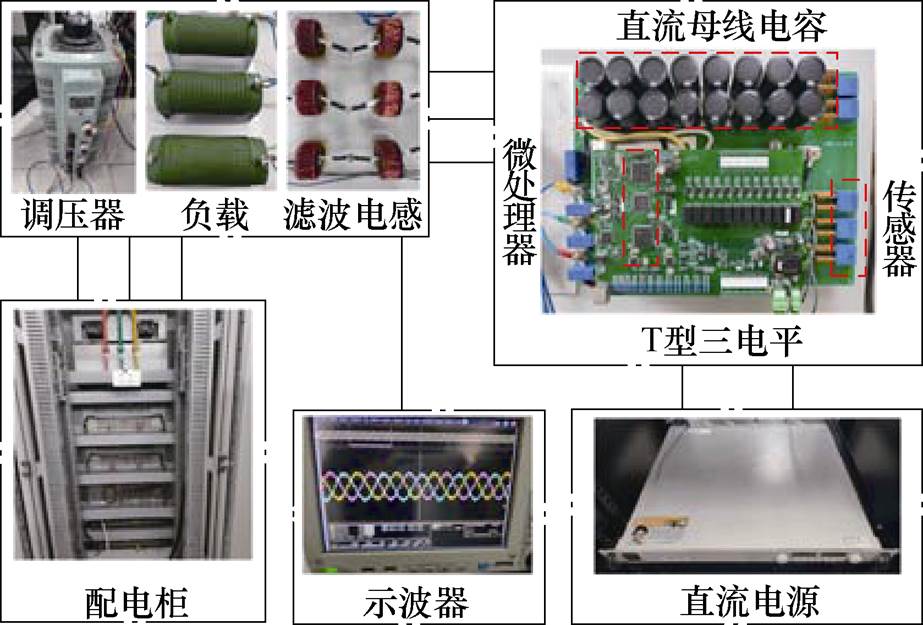
图16 T型三电平物理装置
Fig.16 Physical device T-type three-level
图17中,DSP程序包括主程序和每个动作周期中断子程序,主程序实现GPIO、PWM、ADC等系统资源初始化和程序流程控制;中断子程序在每个动作周期对数据采集和算法进行处理,通过预测控制生成12路PWM。
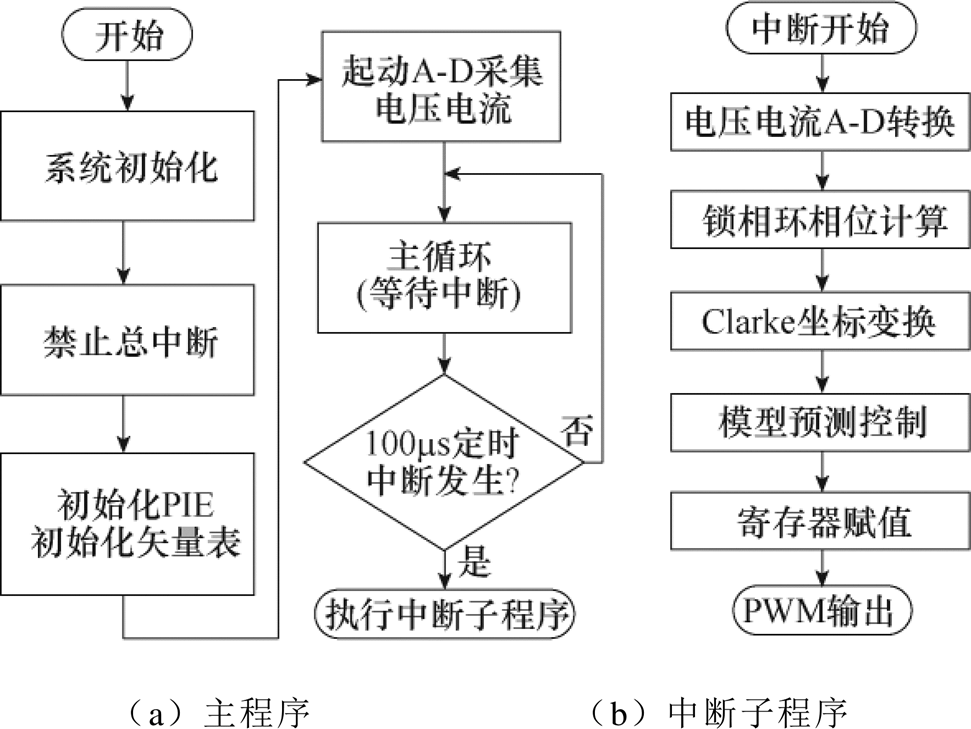
图17 DSP程序流程
Fig.17 Logic block diagram of DSP program
采用三种算法,物理装置的计算时间如图18所示,A、B、C策略的计算时间分别为61ms、28.7ms和38.2ms,相对于传统算法,本文提出的改进算法在计算效率上提升了78%。
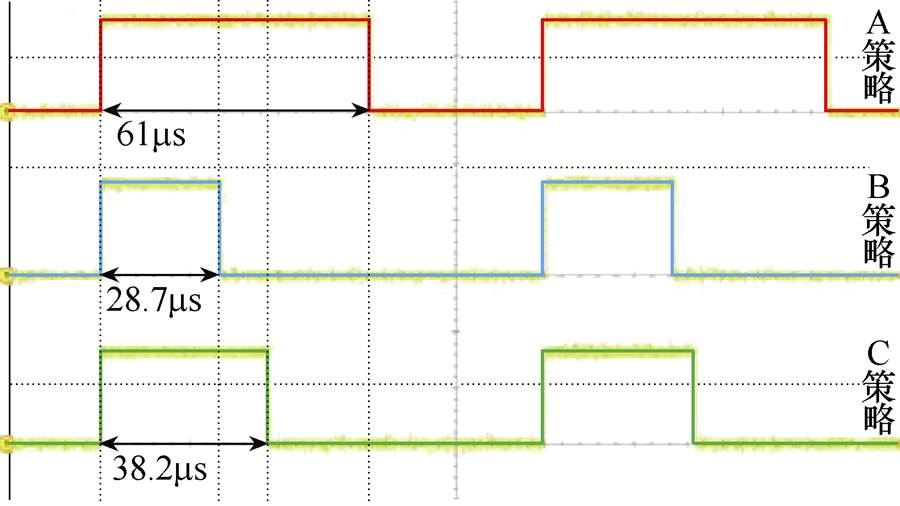
图18 逆变装置的计算时间
Fig.18 Calculation time of inverter device
基于改进算法的逆变装置稳态电流如图19所示,指令电流的有效值为5A,电流THD=3.66%,与功率硬件在环仿真结果比较,相同工况下的电流纹波较大,这是由于DSP的计算时间较长,在多步预测过程中,逆变器输出的实际电流与参考值会产生较大误差。基于改进算法的逆变装置电流的动态响应如图20所示,指令电流的有效值从4A突变至5A。可以看出,处理器的计算时间对改进算法的动态响应基本无影响,这是由于计算时间导致的延迟误差造成的,通过延迟补偿在采样点触发,电流能够有效跟踪参考值,保证动态性能不受计算效率约束。
图21为三电平A相IGBT的驱动信号。因为模型预测控制在每个采样周期仅输出一种电平,当前控制周期的电平能与上一周期一致时不需要进行状态切换,从而降低了IGBT的开关频率。根据实验结果,三电平FCS-MPC能够输出较高电能质量的波形,其开关频率集中在1/5~1/4的采样频率,有利于减小开关损耗。
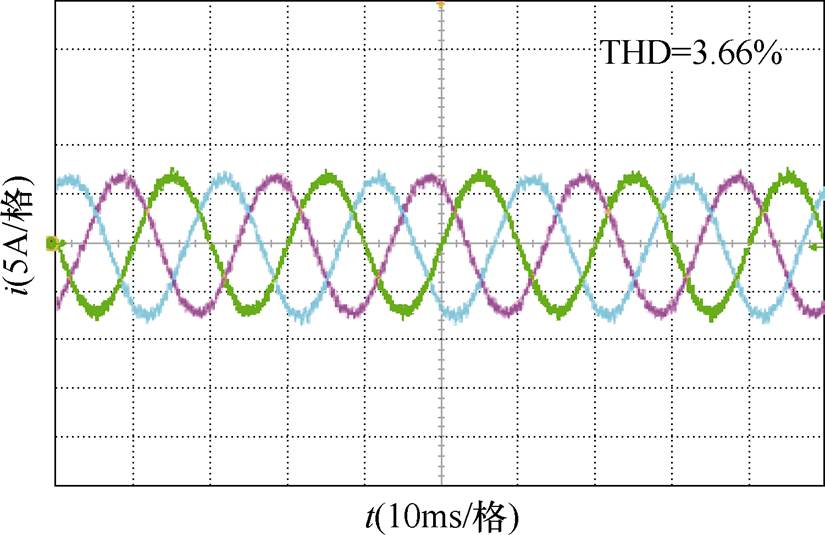
图19 基于改进算法的逆变装置稳态电流
Fig.19 Steady-state current of inverter device based on improved algorithm
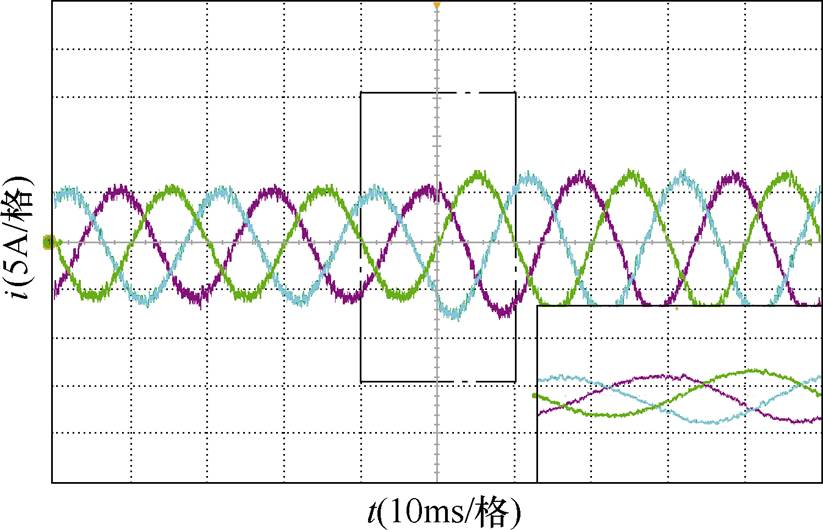
图20 基于改进算法的逆变装置电流的动态响应
Fig.20 Current dynamic response of inverter device based on improved algorithm

图21 A相IGBT驱动信号
Fig.21 IGBT drive signals of A-phase
本文主要研究了T型三电平并网逆变器的有限集模型预测控制方法。通过建模和原理分析,发现传统FCS-MPC方法存在寻优效率低、权重系数难于平衡设计的问题,对此提出了一种能够快速寻优的模型预测控制方法,利用冗余小矢量能够平衡中点电位的能力构建单一约束变量的代价函数,并且提出基于最小误差二次方原则的有限控制集划分细则和矢量角延迟补偿方法提升预测精度。最后搭建了基于RT-Lab的功率硬件在环仿真平台和物理样机进行验证,得到以下结论:
本文所提出的快速寻优方法对比传统方法,不受权重系数限制,实际工况下的计算效率提升了78%;对比根据经典扇区判断有限控制集的快速寻优方法,改进算法在计算效率方面存在劣势,但能够更好地控制中点电位和电流输出。功率硬件在环仿真与物理实验结果表明,FCS-MPC具有潜在的工程价值,随着数字处理器的发展,其性能将显著提高。本文方法的局限性在于:仅在传统有限集的基础上进行了细分,不能有效地提升预测精度,因此在相同采样周期内提升预测精度和电流质量将是下一步研究的重点。
参考文献
[1] Geyer T. 大功率变换器及工业传动模型预测控制[M]. 张永昌, 宋文祥, 徐伟, 译. 北京: 机械工业出版社, 2019.
[2] 杨勇, 谢门喜, 樊明迪, 等. T 型三电平单相逆变器有限开关状态模型预测控制方法[J]. 电机与控制学报, 2019, 23(3): 120-126.
Yang Yong, Xie Menxi, Fan Mingdi, et al. Finite switching state model predictive control for T-type three-level single-phase inverters[J]. Electric Machines and Control, 2019, 23(3): 120-126.
[3] 张晓, 谭力, 鲜嘉恒, 等. LCL并网逆变器预测电流控制算法[J]. 电工技术学报, 2019, 34(增刊1) : 189- 201.
Zhang Xiao, Tan Li, Xian Jiaheng, et al. Predictive current control algorithm for grid-connected inverter with LCL filter[J]. Transactions of China Electro- technical Society, 2019, 34(S1): 189-201.
[4] Shen Kun, Feng Jianghua, Zhang Jing. Finite control set model predictive control with feedback correction for power converters[J]. CES Transactions on Elec- trical Machines and Systems, 2018, 2(3): 312-319.
[5] Li Yu, Zhang Zhenbin, Li Kejun, et al. Predictive current control for voltage source inverters con- sidering dead-time effect[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(1): 35-42.
[6] Rodriguez J, Kazmierkowski M, Espinoza J, et al. State of the art of finite control set model predictive control in power electronics[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2): 1003-1016.
[7] 柳志飞, 杜贵平, 杜发达. 有限集模型预测控制在电力电子系统中的研究现状和发展趋势[J]. 电工技术学报, 2017, 32(22): 58-69.
Liu Zhifei, Du Guiping, Du Fada. Research status and development trend of finite control set model predi- ctive control in power electronics[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 58-69.
[8] 金涛, 沈学宇, 苏泰新, 等. 不平衡电网下并网逆变器的模型预测电流限幅灵活控制[J]. 电工技术学报, 2019, 34(11): 2342-2353.
Jin Tao, Shen Xueyu, Su Taixin, et al. Flexible model predictive control with peak current limitation for grid-connected inverter under unbalanced grid voltage[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2342-2353.
[9] 谢之光, 侯世英, 唐治德, 等. NPC三电平逆变器最优化虚拟电压矢量控制[J]. 电力系统自动化, 2017, 41(8): 95-102.
Xie Zhiguang, Hou Shiying, Tang Zhide, et al. Optimized virtual voltage vector control of NPC three-level inverter[J]. Automation of Electric Power Systems, 2017, 41(8): 95-102.
[10] Geyer T, Quevedo D E. Multistep finite control set model predictive control for power electronics[J]. IEEE Transactions on Power Electronics, 2015, 30(3): 1633-1644.
[11] Tarisciotti L, Zanchetta P, Watson A, et al. Modulated model predictive control for a three-phase active rectifier[J]. IEEE Transactions on Industry Appli- cations, 2015, 51(2): 1610-1620.
[12] Tarisciotti L, Formentini A, Gaeta A, et al. Model predictive control for shunt active filters with fixed switching frequency[J]. IEEE Transactions on Industry Applications, 2017, 53(1): 296-304.
[13] Donoso F, Mora A, Cárdenas R, et al. Finite-set model predictive control strategies for a 3L-NPC inverter operating with fixed switching frequency[J]. IEEE Transactions on Industrial Electronics, 2018, 65(5): 3954-3965.
[14] Yang Guoliang, Hao Shuai, Fu Chuntian, et al. Model predictive direct power control based on improved T-type grid-connected inverter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(1): 252-260.
[15] Bonala A K, Sandepudi S S, Muddineni V P. Selective finite-states model predictive control of grid interfaced 3L-NPC PV inverter for inherent capacitor voltage balancing[J]. IET Power Electronics, 2018, 11(13): 2072-2080.
[16] Barros J Dionísio, Silva J F A, Jesus Élvio G A. Fast-predictive optimal control of NPC multilevel converters[J]. IEEE Transactions on Industrial Elec- tronics, 2013, 60(2): 619-627.
[17] 张永昌, 杨海涛, 魏香龙. 基于快速矢量选择的永磁同步电机模型预测控制[J]. 电工技术学报, 2016, 31(6): 66-72.
Zhang Yongchang, Yang Haitao, Wei Xianglong. Model control of permanent magnet synchronous motors based on fast vector selection[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 66-72.
[18] 杨勇, 樊明迪, 谢门喜, 等. 三电平三相逆变器快速有限控制集模型预测控制方法[J]. 电机与控制学报, 2016, 20(8): 83-91.
Yang Yong, Fan Mingdi, Xie Menxi, et al. Fast finite control set model predictive control method for three-level three-phase inverters[J]. Electric Machines and Control, 2016, 20(8): 83-91.
[19] 王洋, 程志江, 李永东. 三电平并网变换器的模型预测控制[J]. 电力系统及其自动化学报, 2018, 30(10): 34-41.
Wang Yang, Cheng Zhijiang, Li Yongdong, et al. Model predictive control of three-level grid- connected converter[J]. Proceedings of the CSU- EPSA, 2018, 30(10): 34-41.
[20] Yang Yong, Wen Huiqing, Fan Mingdi, et al. A fast finite-switching-state model predictive control method without weighting factors for T-type three-level three- phase inverters[J]. IEEE Transactions on Industrial Informatics, 2019, 15(3): 1298-1310.
[21] 任碧莹, 孙向东, 余马晶, 等. T型三电平逆变器的并网电流D-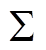 数字控制算法[J]. 电工技术学报, 2019, 34(8): 1708-1717.
数字控制算法[J]. 电工技术学报, 2019, 34(8): 1708-1717.
Ren Biying, Sun Xiangdong, Yu Majing, et al. D-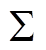 control algorithm of grid-connected current for a three-level T-type inverter[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1708-1717.
control algorithm of grid-connected current for a three-level T-type inverter[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1708-1717.
[22] 王建华, 骆芳芳, 季振东, 等. T型三电平变换器的通用PWM平均模型[J]. 中国电机工程学报, 2018, 38(2): 573-581.
Wang Jianhua, Luo Fangfang, Ji Zhendong, et al. A unified PWM averaged model for T-type three-level converter[J]. Proceedings of the CSEE, 2018, 38(2): 573-581.
[23] 李敏裕, 马晓军, 魏曙光, 等. T型逆变器中点电压全范围精确平衡研究[J]. 电工技术学报, 2018, 33(8): 1814-1825.
Li Minyu, Ma Xiaojun, Wei Shuguang, et al. Research on full range accurate balance of neutral point voltage for T-type inverter[J]. Transactions of China Electro- technical Society, 2018, 33(8): 1814-1825.
[24] 季宁一, 赵涛, 徐友, 等. T型三电平并网逆变器的设计与实现[J]. 电气技术, 2018, 19(8): 11-15.
Ji Ningyi, Zhao Tao, Xu You, et al. Design and implementation of T-type three-level grid-connected inverter[J]. Electrical Engineering, 2018, 19(8): 11-15.
[25] 冯腾, 康龙云, 胡毕华, 等. 基于无差拍控制的T型三电平逆变器中点电位平衡策略[J]. 电工技术学报, 2018, 33(8): 1827-1834.
Feng Teng, Kang Longyun, Hu Bihua, et al. A neutral point potential balancing strategy for three-level T-type inverter based on deadbeat control[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(8): 1827-1834.
[26] 陈鹏飞, 唐芬, 吴学智, 等. 三电平并网变流器中点电位自平衡特性分析及拓扑改进[J]. 电力系统自动化, 2019, 43(24): 171-180.
Chen Pengfei, Tang Fen, Wu Xuezhi, et al. Self- balancing characteristic analysis of neutral point potential and improved topology of three-level grid- connected converter[J]. Automation of Electric Power Systems, 2019, 43(24): 171-180.
[27] 李毅, 何英杰, 段文岩, 等. 一种三电平静止无功发生器滞环SVPWM电流控制方法研究[J]. 中国电机工程学报, 2017, 37(22): 6700-6707.
Li Yi, He Yingjie, Duan Wenyan, et al. A control strategy of neutral-point clamped three-level grid- connected inverter current hysteresis SVPWM[J]. Proceedings of the CSEE, 2017, 37(22): 6700-6707.
Finite Control Set Model Predictive Control Method with Fast Optimization Based on T-Type Three-Level Grid-Connected Inverter
Abstract Rolling optimization of Finite Control Set model predictive control (Finite Control Set-MPC, FCS-MPC) needs to traverse all the switch states in the three-level converter control system, which will cause the problems of increased processor calculation and long processing time. For this reason, this paper proposes a FCS-MPC method with optimized calculation amount of T-type three-level grid-connected inverter. By constructing a single objective cost function based on voltage prediction, the design of weighting factor is avoided and the steps of single optimization are reduced. For improving the efficiency of optimization, the redundant small vector is selected according to the DC bus potential distribution to balance the neutral-point potential and reduce the number of predictions per control cycle to 3 times. The finite control set is divided according to the minimum weighted error square of the included vectors in the prediction process, and the vector angle is used to compensate the system delay, thereby improving the prediction accuracy and the grid-connected current quality. A power hardware-in-the-loop simulation system based on RT-Lab and a physical device are established to verify the proposed control strategy. The results show that the proposed theoretical analysis is correct and the control strategy is effective.
keywords:Finite control set model predictive control, T-type three-level, balance of neutral-point potential, fast optimization
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.200083
国家自然科学基金资助项目(U2066208)。
收稿日期 2020-01-20
改稿日期 2020-09-24
辛业春 男,1982年生,博士,副教授,研究方向为柔性直流输电技术、输变电设备运行状态在线监测。E-mail: xinyechun@163.com
王延旭 男,1993年生,硕士研究生,研究方向为电力电子变流技术。E-mail: w_yanxu@163.com(通信作者)
(编辑 陈 诚)