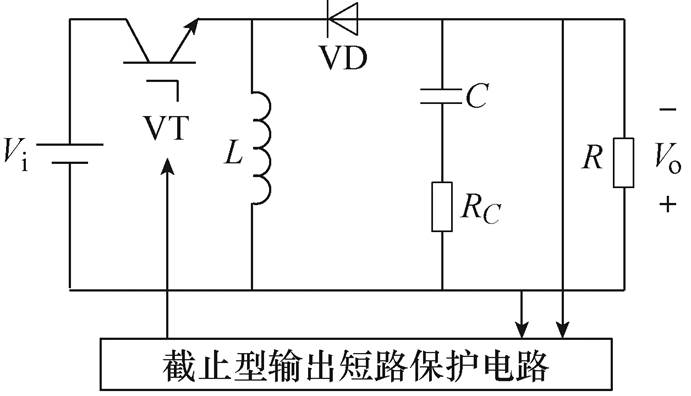
图1 输出本质安全型Buck-Boost变换器
Fig.1 Output intrinsically safe Buck-Boost converter
摘要 应用于煤矿、石化等危险环境的Buck-Boost变换器不仅要满足本质安全要求，同时还要满足电气性能指标如纹波电压的要求。现有本质安全开关变换器参数设计依据理想纹波电压表达式，但实际上受寄生参数如电容等效串联电阻（ESR）的影响，按照理想公式设计的电容无法满足纹波电压指标要求，通常要选择2～4倍的裕度，这样会增加变换器短路时爆炸风险。电容的ESR不仅会引起开关变换器纹波电压波形畸变，同时还对纹波电压的大小有重要影响，为了更好地指导本质安全Buck-Boost变换器的参数设计，该文分析电容ESR引起变换器纹波电压畸变的机理，建立考虑电容ESR的Buck-Boost变换器纹波电压精确数学模型及峰值电感电流模型，基于此模型提出在输入电压、负载电阻及电容ESR变化的动态范围内本质安全型Buck-Boost变换器的参数设计方法。实验结果表明，选择1.2倍裕度的电容即可满足Buck-Boost变换器纹波电压及输出本质安全要求，有效地提高了变换器的本质安全性能。
关键词：本质安全 Buck-Boost变换器 等效串联电阻（ESR） 输出纹波电压 参数设计
近年来，随着煤矿、石化等领域自动化和现代化程度的日益提高，本质安全电源在这些易燃、易爆环境中的监控、通信、仪表和自动控制系统中应用越来越广泛[1-4]。Buck-Boost变换器可以实现宽电压输入或宽电压输出，且具有体积小、效率高、质量轻等优点，因此在煤矿和石化等危险环境中具有广阔的应用前景，近年来得到了国内外学者的广泛关注[5-9]。
本质安全开关电源不仅要满足在最危险工况（如输出短路）时释放的能量不能引爆危险环境的气体等介质，同时还要满足电气性能指标如纹波电压的要求[6-7]。当前文献对输出本质安全型Buck- Boost变换器的分析和设计基于理想模型，未考虑某些重要寄生参数对电气性能及本质安全性能的影响[10-13]。文献[11]对理想Buck-Boost变换器的供能模式及纹波电压进行了研究，分别建立变换器工作在连续导电模式（Continuous Conduction Mode, CCM）和断续导电模式（Discontinuous Conduction Mode, DCM）时的纹波电压。文献[12]对理想Buck-Boost变换器在输入电压和负载电阻动态范围内输出本质安全的参数设计方法进行了研究。文献[13]在输入电压和负载电阻动态范围内对理想Buck-Boost变换器输出本质安全的最危险工况进行了深入研究，得出了最大短路火花放电能量的最危险工况。以上文献基于理想模型计算所获得的电容无法满足纹波电压的要求，通常会选择2～4倍的裕度。选择容量较大的电容会增加本质安全变换器发生短路故障时的爆炸风险[14-18]。
大量实验研究表明，电容的等效串联电阻（Equi- valent Series Resistance, ESR）对纹波电压等性能指标影响较大。具体表现为：ESR不仅会影响变换器电压增益、临界电感、电感峰值电流等，同时会导致纹波电压波形发生畸变。实验结果还发现，如果选择的电容ESR较大，即使选择2～4倍裕度也无法满足纹波电压指标要求。对普通Buck-Boost变换器而言，电容选择裕度较大可以更好地减小纹波电压；但是对本质安全型变换器而言，电容大小对输出短路释放能量有重要影响，在满足纹波电压要求前提下，减小电容容量对提高变换器的本质安全性能具有重要意义。因此，从提高输出本质安全变换器的电气性能指标及抑爆性能而言，合理选择电容的容量对本质安全变换器显得尤为关键和重要。而电容的合理选择则需要深入研究ESR对电感峰值电流及纹波电压等性能指标的影响情况。
通常电容的ESR随外界或开关电源本身工作温度发生变化时，ESR在一个动态范围内变化[19]，而ESR的变化则会引起变换器的纹波电压等性能指标发生变化。因此，本质安全型变换器的设计须考虑ESR动态变化对本质安全性能的影响，而传统本质安全变换器的设计仅考虑输入电压和负载电阻动态范围[20-22]。
本文讨论了滤波电容ESR对Buck-Boost变换器的稳态增益、临界电感以及峰值电流等参数的影响情况；分析了滤波电容ESR引起输出纹波电压畸变的机理，建立了纹波电压的精确数学模型；探讨了最危险工况即短路时释放的最大能量；提出了在输入电压、负载电阻和电容ESR的动态变化范围内输出本质安全型Buck-Boost变换器的参数设计方法；最后通过实验验证了理论分析的正确性。为危险环境中应用的本质安全型DC-DC变换器优化设计提供了理论参考。
输出本质安全型Buck-Boost变换器如图1所示。Vi为输入电压，VT为开关管，L为储能电感，VD为二极管，R为负载电阻，Vo为输出电压，滤波电容可等效为C和RC的串联，C为滤波电容，RC为输出滤波电容C的ESR。输出本质安全变换器通常需要引入截止型输出短路保护电路，在发生短路故障时，迅速切断输入端电源向后级流入的能量，从而提高输出本质安全性能[12]。
图1 输出本质安全型Buck-Boost变换器
Fig.1 Output intrinsically safe Buck-Boost converter
由于变换器通常满足：Vo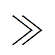
VPP，根据本质安全变换器的工作原理可知，发生短路时的放电能量W可表示为
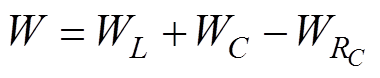（1）式中，WC为变换器短路时刻电容C释放的能量；WL为短路时刻电感L释放的能量；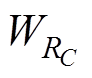
为短路期间RC所消耗的能量。由于RC短路期间要消耗能量，因此可以忽略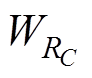，所以最大短路放电能量Wmax可近似为
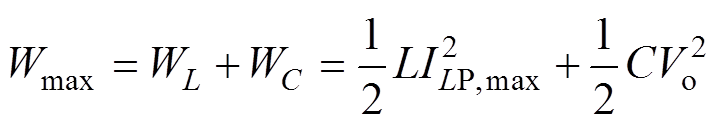（2）
式中，ILP,max为峰值电感电流在变换器输出电压、负载电阻和电容的ESR动态变化范围内的最大值。
Buck-Boost变换器可以等效为简单的纯容性电路进行输出本质安全判断，结合容性电路最小点燃电压曲线[23]，可知输出本质安全判断依据[20]为
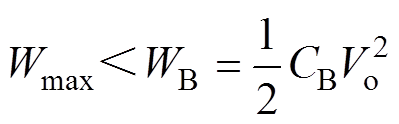（3）式中，WB为最小放电能量；CB为最小点燃电压V对应的电容，为了确保变换器输出满足本质安全要求，须满足V=KVo，K为安全系数（一般取1.5）[13]。若Wmax＜WB，则满足输出本质安全要求；若Wmax≥ WB，则不满足输出本质安全要求。
Buck-Boost变换器短路时刻电感释放的能量WL主要由峰值电感电流ILP,max所决定，但是变换器在实际运行时与工作模式有关。由文献[10]可知，工作模式分为CCM和DCM，CCM又可分为完全电感供能模式（Complete Inductor Supplying Mode, CISM）和不完全电感供能模式（Discomplete Inductor Supplying Mode, IISM）。由于每种工作模式对应不同的峰值电感电流ILP，而ILP又与变换器的本质安全性能相关，因此需讨论不同工作模式下的峰值电感电流。
Buck-Boost变换器工作在CCM时，开关管VT导通和关断时所对应的电路拓扑如图2所示。
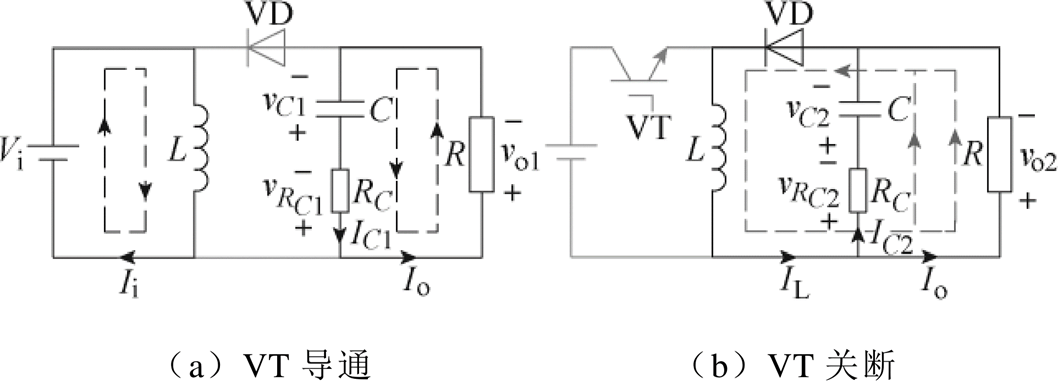
图2 Buck-Boost变换器工作模态
Fig.2 Buck-Boost converter working mode
当变换器工作在稳态时，由能量守恒可得
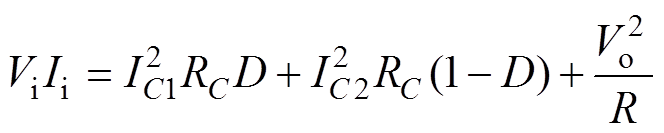（4）式中，Ii为输入电流；IC1为VT导通时电容C放电电流的平均值；IC2为VT关断时电容C充电电流的平均值；D为开关管VT的导通占空比。
分析图2可知，IC1和IC2分别为
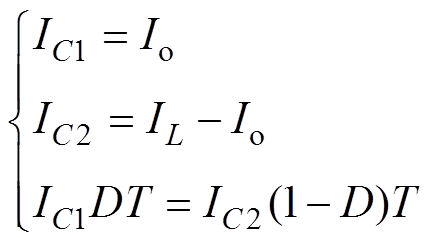（5）式中，Io为负载电流；IL为电感电流平均值。
联立式（4）、式（5）可得Vo与D之间关系为
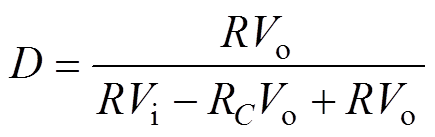（6）将式（6）分别对R、Vi和RC求偏导，可得
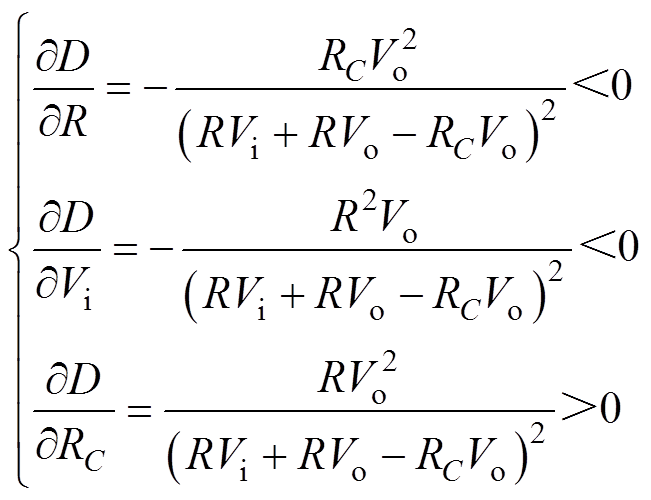（7）
由式（7）可知，Vo不变的情况下，随着R和Vi的增大，D将逐渐减小，而随着RC的增大，D将随之增大。
通过判断电感电流最小值ILV与负载电流Io之间的关系，便可确定变换器的工作模式，即当ILV＞Io时，变换器工作在CISM；当0＜ILV＜Io时，变换器工作在IISM；当ILV=0时，变换器工作在DCM；且电感电流的最大值ILP=IL+DiL/2，电感电流的最小值ILV=IL-DiL/2，不同工作模式时的电感电流如图3所示。图3中，RCISM、RIISM、RDCM分别为相应工作模式所对应的负载电阻，且满足RCISM＜RIISM＜RDCM。
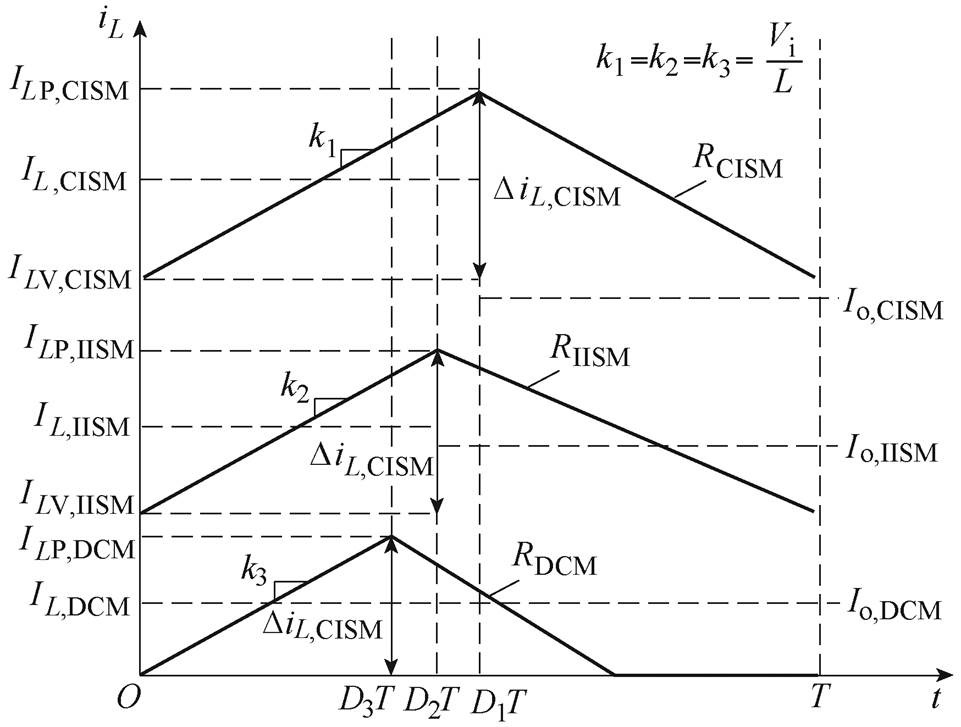
图3 不同工作模式时的电感电流
Fig.3 Inductance current in different working modes
联立式（5）、式（6）可得，IL以及VT导通期间电感电流的变化量DiL分别为
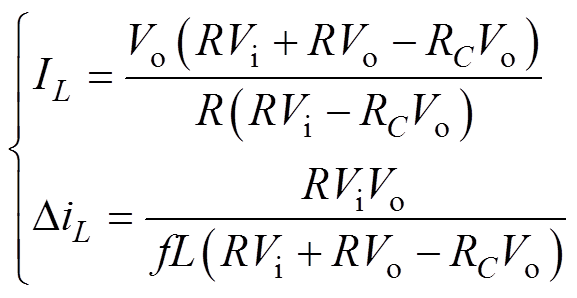（8）式中，f为功率开关管的工作频率。
将式（8）中的DiL对R求偏导，可得
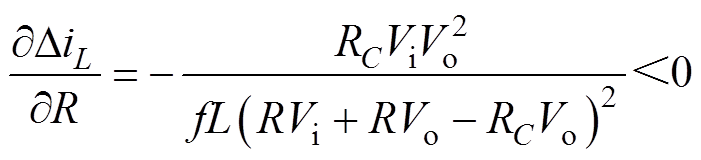（9）分析式（9）可知，当Vo及其他参数不变的情况下，随着R的增大，电感电流的变化量DiL将逐渐减小，即满足DiL,CISM＞DiL,IISM＞DiL,DCM。
将式（8）中的IL对R求偏导，可得
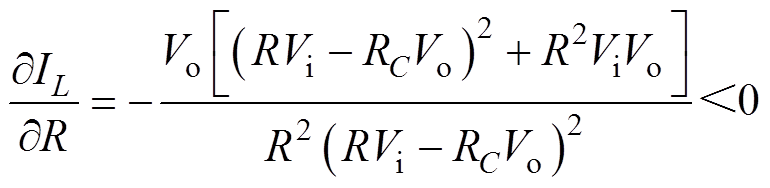（10）由式（10）可知，当Vo及其他参数不变的情况下，随着R的增大，IL将逐渐减小，即满足IL,CISM＞IL,IISM＞IL,DCM。综上所述，变换器工作在CISM时峰值电感电流最大，DCM时峰值电感电流最小。
变换器在实际运行时，除了负载电阻R以外，输入电压Vi和滤波电容C的ESR均会在一定范围内变化，即R取值范围为[Rmin, Rmax]、Vi取值范围为[Vi,min, Vi,max]、RC取值范围为[RC,min, RC,max]。由式（8）可知，这些参数变化均会影响峰值电感电流ILP的大小，下面进行具体分析。
将式（8）中的DiL和IL分别对Vi求偏导，可得
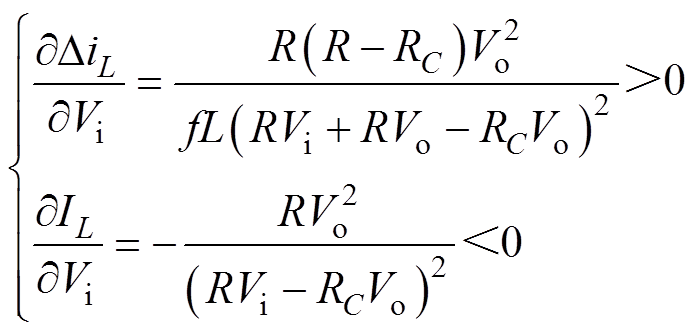（11）分析式（11）可知，当Vo及其他参数不变的情况下，随着Vi的增大，DiL将逐渐增大，而IL将逐渐减小，iL与R、RC、Vi之间的关系如图4所示。
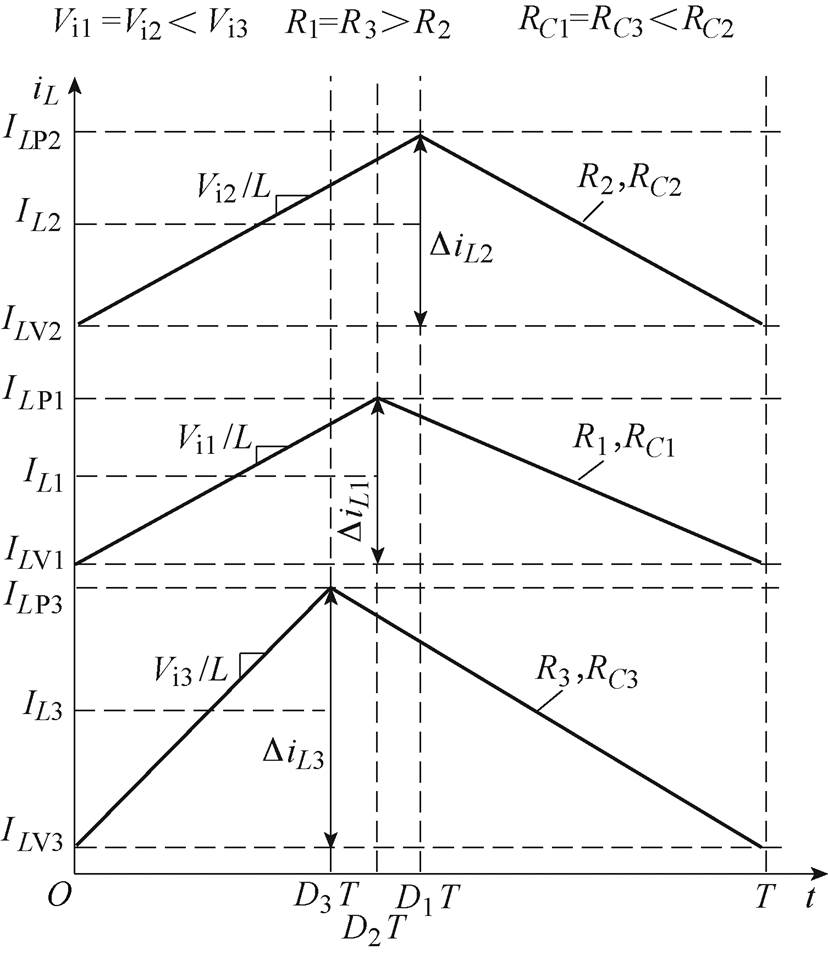
图4 iL与R、RC、Vi之间的关系
Fig.4 Relationship between iL and R、RC、Vi
由于ILV＞0，因此，IL＞DiL/2，即
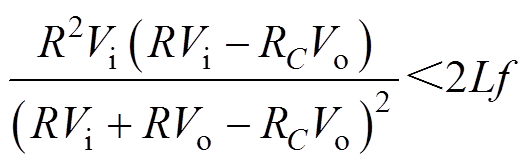（12）将式（12）代入式（11）可得
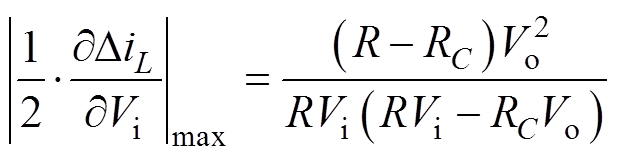（13）
联立式（11）和式（13）可得
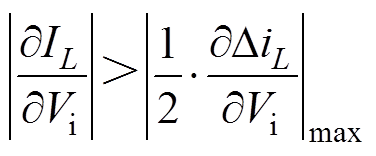（14）分析式（14）可知，随着Vi的增大，DiL/2的增长率小于IL的减小率，因此可知，随着Vi的增大，ILP将逐渐减小，并在Vi=Vi,min处取得极大值。
将式（8）中的DiL和IL分别对RC求偏导，可得
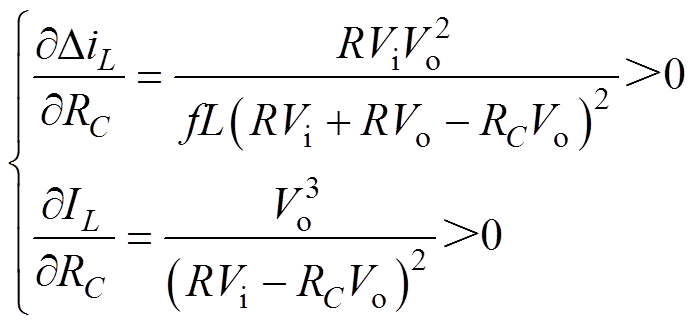（15）分析式（15）可知，当Vo及其他参数不变的情况下，随着RC的增大，DiL和IL均逐渐增大。因此，当RC=RC,max时，ILP取极大值。
综合以上分析可知，在R=Rmin、Vi=Vi,min、RC= RC,max时电感电流取得最大值，其最大值ILP,max为
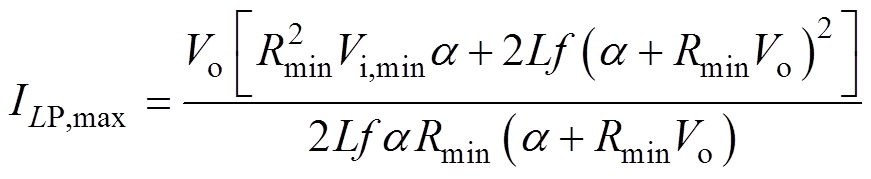（16）式中，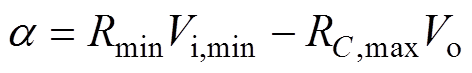
。
变换器短路时刻电容释放的能量WC主要由电容C的取值所决定，而C的取值与变换器输出纹波电压VPP大小密切相关。下面就对考虑滤波电容ESR的Buck-Boost变换器输出电压纹波进行建模分析。
变换器不同工作模式时的电感电流iL、电容电压vC、ESR两端电压
及输出电压vo波形如图5所示。图5中，VoV和VoP分别为变换器输出电压的最小值和最大值。由于不同工作模式纹波电压分析方法相同，为了节约篇幅，下面仅以变换器工作在CISM为例进行分析。工作在CISM时变换器在一个开关周期内分为四个阶段：
第一阶段（t0＜t＜t1
：该阶段对应电路拓扑如图2a所示，此时VT导通，电容C向负载R供能，列写KVL方程可得该时间段输出电压vo1(t)为
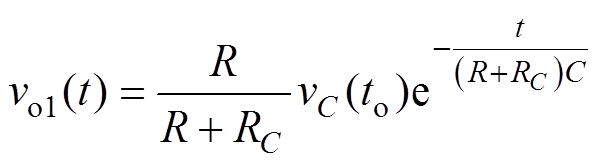（17）分析式（17）可知，随着时间t的增加，vo1(t)呈下降趋势，并在t1时刻达到极小值，如图5所示。
第二阶段（t=t1：在t0＜t＜t1时间段，输出电压为vo1(t)；在t1＜t＜t2时间段，输出电压为vo2(t)，由图2可知，vo1(t)和vo2(t)分别为
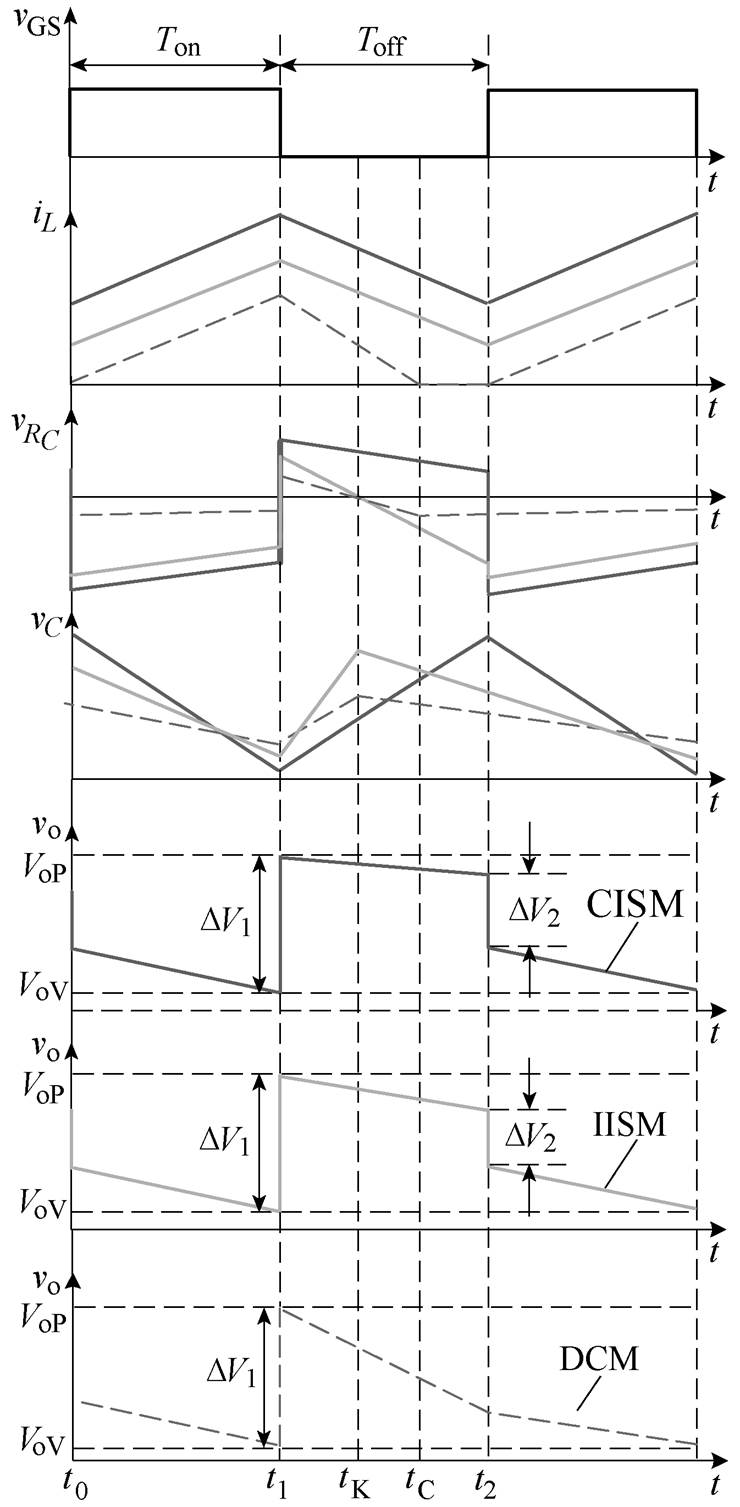
图5 变换器不同工作模式的输出纹波电压波形
Fig.5 Output ripple voltage waveforms of converter in different working modes
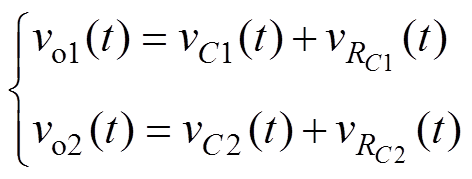（18）t1时刻，VT由导通变为关断，由图2可知，VT关断前和关断后RC两端的电压分别为
（19）
由于电容C两端电压不能发生突变，因此在t1时刻满足vC1(t1)=vC2(t1)。联立式（18）和式（19）可得，在t1时刻输出电压的变化量DV1为
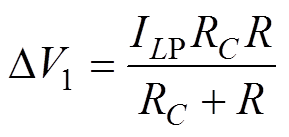（20）第三阶段（t1＜t＜t2：该阶段电路拓扑如图2b所示，VT关断，电感L开始向电容C充电，此时电容的充电电流iC(t)可表示为
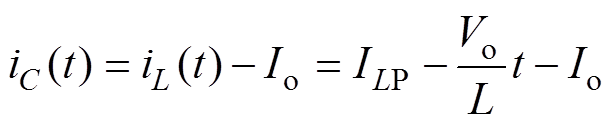（21）
在t1＜t＜t2期间，电容C两端电压变化量DvC(t)以及RC两端电压的变化量
分别为
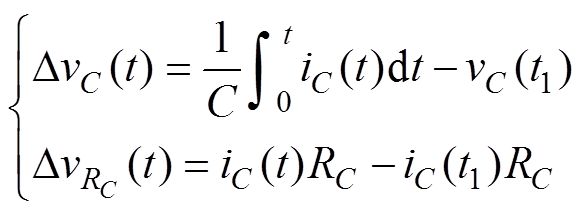（22）假设t1=0，vo2(t1)=0，联立式（8）、式（21）和式（22）可得，t1＜t＜t2期间输出电压的解析式v(t)为
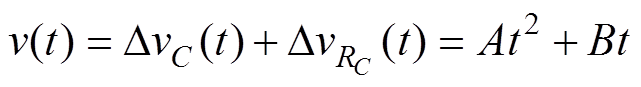（23）
其中
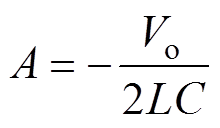
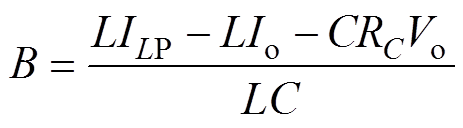
分析式（23）可知，a＜0；由于变换器参数的不同，因此在t1＜t＜t2期间，v(t)可能会出现三种不同波形，如图6所示。图6中，x1=0为v(t)的第一零点，x2=-b/a为v(t)的第二个零点，tm=-b/(2a)为v(t)的极值点，t2为VT关断周期所对应的时间，即t2= (1-D)T。
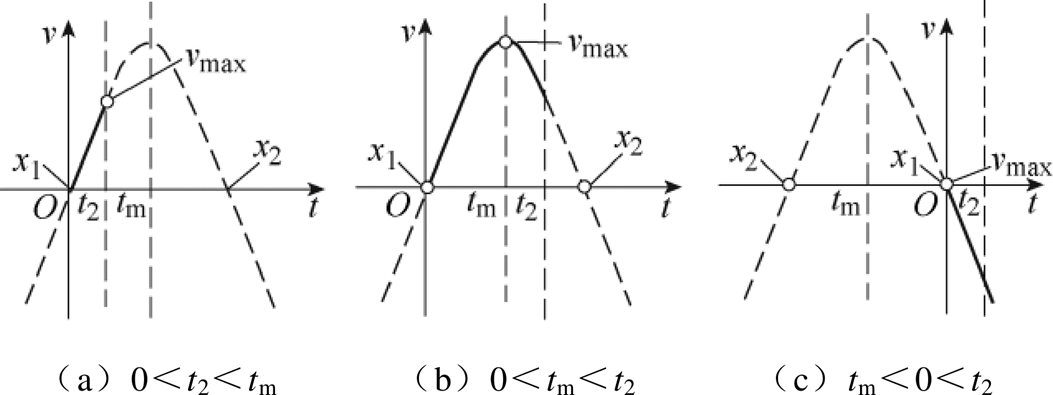
图6 t1～t2时间段输出纹波电压的形状
Fig.6 Output ripple voltage shape of t1-t2 time period
第四阶段（t=t2：t2时刻VT由关断变为导通，由图2可知，VT导通前和导通后RC两端的电压分别为
（24）同理，t2时刻满足vC1(t2)=vC2(t2)。联立式（18）和式（24），t2时刻输出电压的变化量DV2为
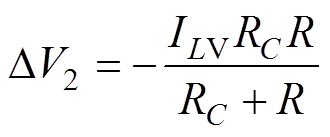（25）
t2时刻之后，VT导通，下一个开关周期重复开始。图5中，tK为iL≤Io的临界时间点，tC为iL=0的临界时间点。当t1≤t≤tK时，IISM和DCM与CISM工作在t1≤t≤t2期间的分析方法相同，不再赘述。通过Buck-Boost变换器的工作原理可知，IISM和DCM的iC均会在tK之后小于零，因此可知，输出电压呈下降趋势，并且由式（20）可知，DCM不会出现DV2。
综合分析可知，Buck-Boost变换器输出纹波电压具有两种类型，不同类型纹波电压的解析式见 表1。
一般情况下满足RRC ，因此类型一的输出纹波电压解析式化简可得
表1 不同类型纹波电压的解析式
Tab.1 Analytical expressions of different types of ripple voltage
纹波电压类型判别式纹波电压VPP解析式 类型一 类型二
（26）由第2.2节分析可知，该类型纹波电压的最大值将在R=Rmin、Vi=Vi,min、RC=RC,max时取得。
由表1可知，类型二的纹波电压解析式由DV1和v(t)两部分组成。通过式（23）可得曲线v(t)的极值点tm以及极值vm分别为
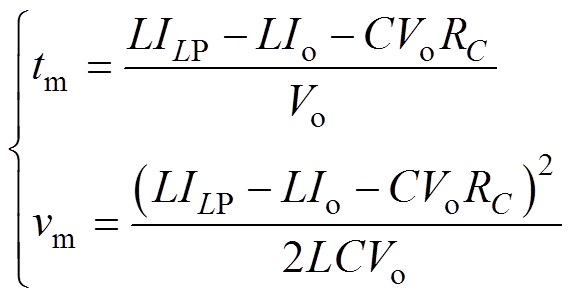（27）假设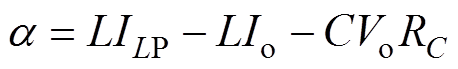
，将a 对R求偏导得
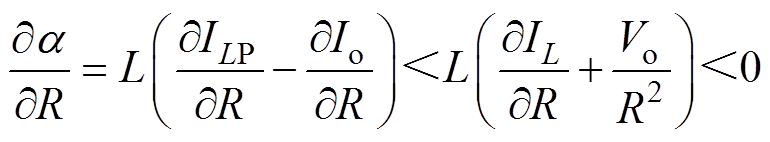（28）
由式（27）和式（28）可知，在t1～t2时间段内v(t)的极大值vm及对应的极值点tm随R的变化情况如图7所示。
由图7可知，类型二的纹波电压同样随着R的增大而减小，因此变换器工作于CISM时的纹波电压VPP最大，DCM时的VPP最小。同理可得，类型二的VPP随着Vi的增大而减小，随着RC的增大而增大，因此变换器VPP的最大值在R=Rmin、Vi=Vi,min、RC=RC,max时取得，具体分析和推导过程见附录。
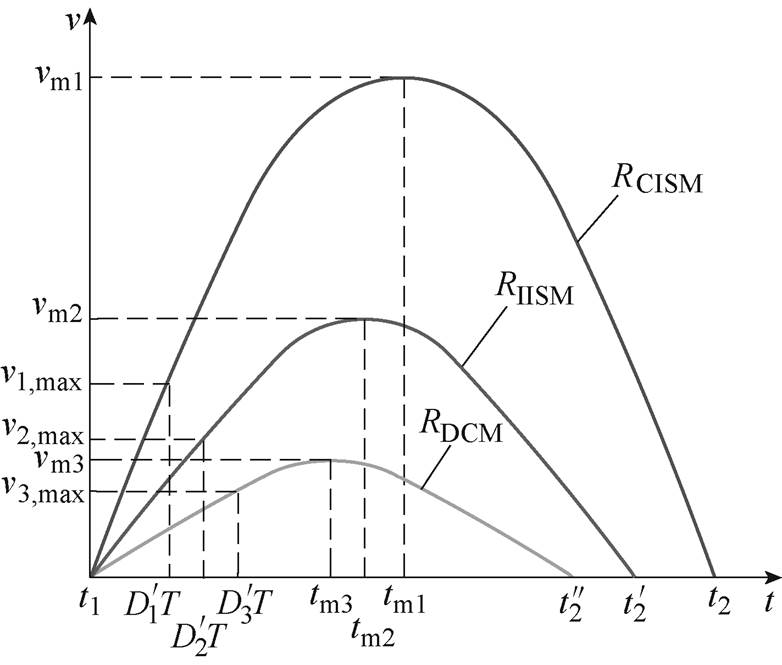
图7 t1～t2时间段内v(t)的极值情况
Fig.7 The extreme value of v(t) in t1-t2 period
由表1可知，通过判断tm是否大于零，可以将纹波电压的解析式分为两种类型；由式（27）可知，tm的大小与电容C有关，因此，令式（27）中tm=0，可得临界电容CK为
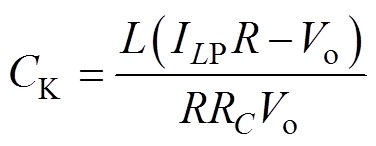（29）式中，CK为纹波电压类型一和类型二的临界电容，当变换器其他参数不变时，若电容选择满足C≥CK，则VPP如表1中类型一所示，此时纹波电压VPP与电容C的大小无关；若满足C＜CK，则VPP如表1中类型二所示。
将式（29）分别对Vi、R、RC求偏导可得
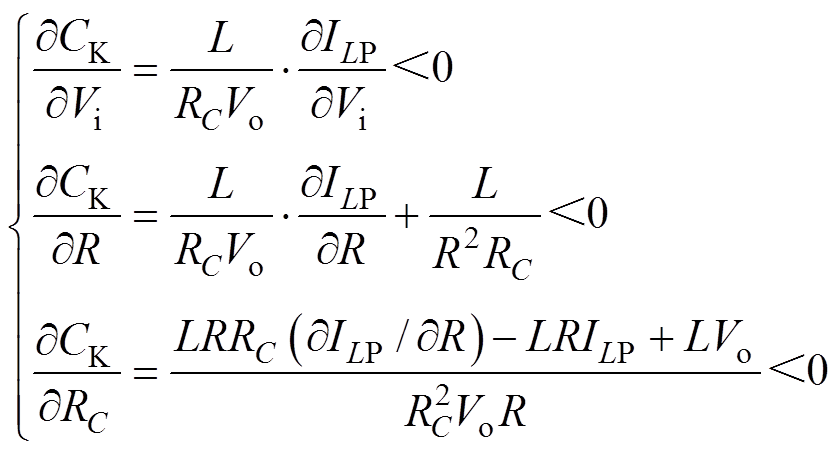（30）由式（30）可知，随着Vi、R、RC的增大，CK将逐渐减小，并在R=Rmin、Vi=Vi,min、RC=RC,min时取得最大值。
令电感电流ILV=0，分析式（8）可得变换器CCM和DCM的临界电感LC为
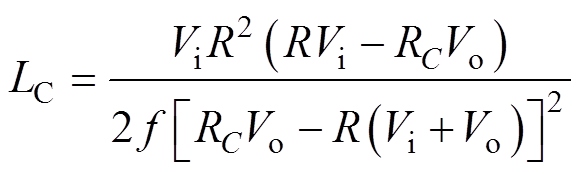（31）分析式（31）可知，当电感L＞LC时，变换器工作在CCM；当电感L＜LC时，变换器工作在DCM。
将式（31）分别对Vi、R和RC求偏导，可得
（32）由式（32）可知，LC随着Vi、R和RC的增大而增大，而电感的最小值Lmin通常由变换器工作模式决定，一般要求变换器输出电流大于某个值IA时工作于CCM[13]，联立式（31）和式（32）可得Lmin为
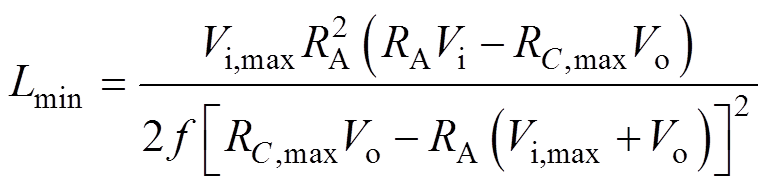（33）
式中，RA为IA所对应的负载电阻。
由表1可知，无论哪种类型的纹波电压解析式中均含有DV1，通过变换器的工作模式可确定电感的最小值Lmin，结合第3.2节的分析可知，将R=Rmin、Vi=Vi,min、RC=RC,max、L=Lmin代入式（20）便可求得DV1的最大值DV1,max。若DV1,max大于变换器所规定的纹波电压指标VPPB，则三种模式下的纹波电压均无法达到指标要求。因此电容C的设计需要根据DV1,max的具体大小进行选择。输出本质安全型Buck- Boost变换器的具体设计流程如图8所示。
1）给定变换器的工作参数，即确定输入电压范围[Vi,min, Vi,max]，负载范围[Rmin, Rmax]，输出电压Vo，工作频率f。通过式（16）和3.2节的分析可知，RC越大，变换器的峰值电感电流及输出纹波电压均会越大，因此需要规定RC的最大值RC,max。
2）由以上给定参数，确定变换器的电气性能指标（输出纹波电压指标VPPB，一般为Vo的2%左右）以及本质安全性能指标（最小放电能量WB）。
3）通过式（33）求得满足变换器工作模式要求的最小电感Lmin，进而求得DV1,max。
（1）若DV1,max≥VPPB。将式（26）对电感L求偏导得
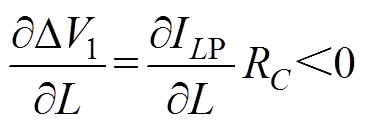（34）
图8 输出本质安全型Buck-Boost变换器设计流程
Fig.8 Design flow of output intrinsically on safe Buck-Boost converter
由式（34）可知，类型一的输出纹波电压随着电感L的增大而减小，因此令DV1,max=VPPB，求得满足输出纹波电压要求的最小电感Lmin1，即
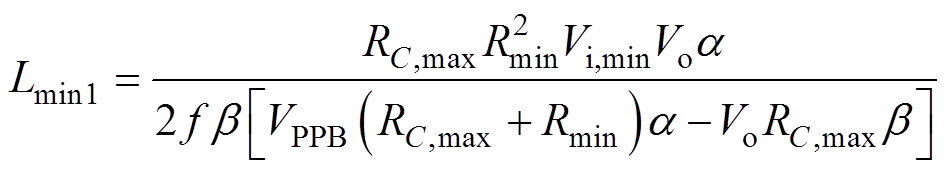（35）其中
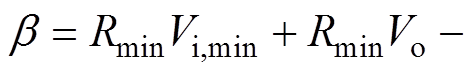
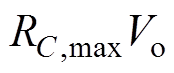
因此，此时DV1,max=VPPB，则只有类型一的输出纹波电压可以满足要求，联立式（16）、式（29）和式（30）可得此时所需要的最小电容Cmin1为
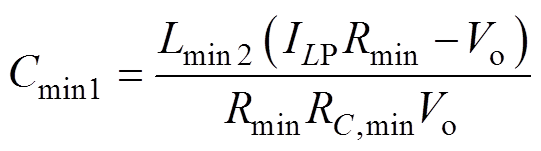（36）考虑到电路其余寄生参数的影响，实际中需选取一定裕度的电容，即C=1.2Cmin1。由式（2）可计算变换器短路时刻的最大短路放电能量Wmax。若Wmax＜WB，则满足输出本质安全要求；若Wmax≥ WB，则不符合本质安全要求，此时同样需要减小RC,max或提高开关频率f重新进行设计，直至满足要求。
（2）若DV1,max＜VPPB。当变换器工作于CCM时，式（23）可以简化为
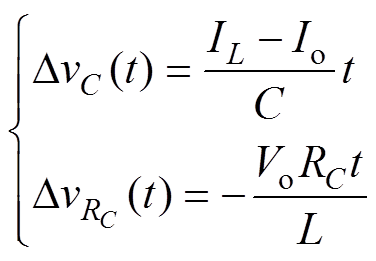（37）将式（37）分别对电容C求偏导，可得
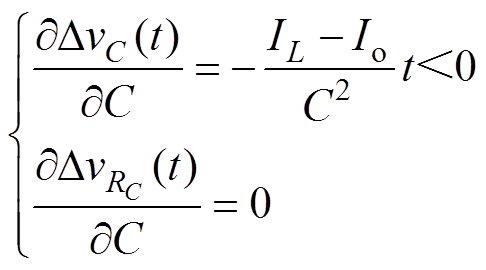（38）
分析式（38）可知，随着C的增大，v(t)的值将随之减小，又由于DV1的解析式中不包含电容C，因此类型二的输出纹波电压将随着电容C的增大而减小。
求解表1中类型二的纹波电压解析式，可得v(t2)和v(tm)分别为
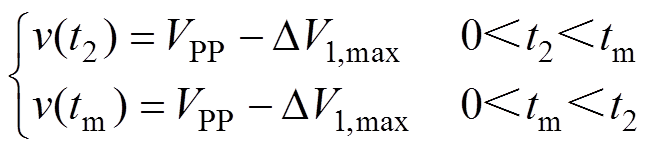（39）将R=Rmin、Vi=Vi,min、RC =RC,max代入式（39）便可求解得到此模式下所需要的最小电容Cmin= max{Cv(t2), Cv(tm)}，实际选取的电容C=1.2Cmin，并通过式（2）求得变换器短路时刻的最大短路放电能量Wmax。若Wmax＜WB，则满足输出本质安全要求；若Wmax≥WB，则不符合本质安全要求，此时同样需要减小RC,max或提高开关频率f重新进行设计，直至满足要求。
为了验证理论分析的正确性，搭建了一台应用于Ⅰ类环境（指煤矿井下电气设备）的Buck-Boost变换器。具体参数为：Vi=5～15V，R=50～200W，Vo=12V，f=40kHz，RC,max=180mW，VPPB=2%Vo= 240mV，要求其输出电流大于0.24A时工作在CCM，即RA=50W。根据以上给定数据对变换器进行参数设计，具体如下：
利用第4节给出的方法，根据容性电路的最小点燃电压曲线[23]，可得CB=90mF，并由式（3）可确定此时对应的最小点燃放电能量WB=6.48mJ；由式（33）可得Lmin=212mH，由给定参数可得DV1,max= 84.6mV＜VPPB，满足变换器所要求的输出纹波电压指标，由式（39）可求得Cmin=33mF，选择1.2倍裕度可得C=1.2Cmin=40mF，此时输出短路释放的最大能量Wmax=2.9mJ＜WB，满足输出本质安全判据，设计结束。下面进行实验验证。
（1）在设计的参数范围内取Vo=12V，f =40kHz，L=212mH，C=40mF，当负载电阻取50W、150W、200W时，对应的电感电流iL及纹波电压VPP波形如图9所示。
在输入电压为5V，输出电压为12V，取负载电阻范围50W、150W、200W 时，对应变换器的工作模式、电感电流峰值ILP,max、短路输出放电能量最大值Wmax及输出纹波电压VPP的理论分析和实验对比结果见表2。由图9和表2分析结果可知，随着负载阻值的增大，输出纹波电压的形状发生了变化，同时变换器输出纹波电压和电感最大峰值电流随着负载阻值的增大而减小，和理论分析一致；当R=50W，RC,max=180mW时，变换器工作在CISM，此时Wmax= 2.98mJ，VPP=216mV满足期望的指标要求；当R= 150W、200W 时，变换器分别工作在IISM和DCM，且实验结果与理论分析十分接近，验证了理论分析的正确性。
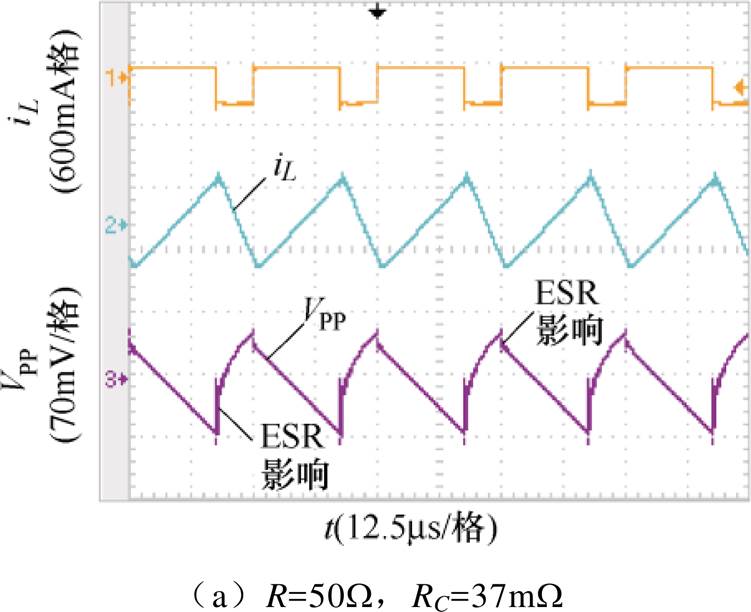
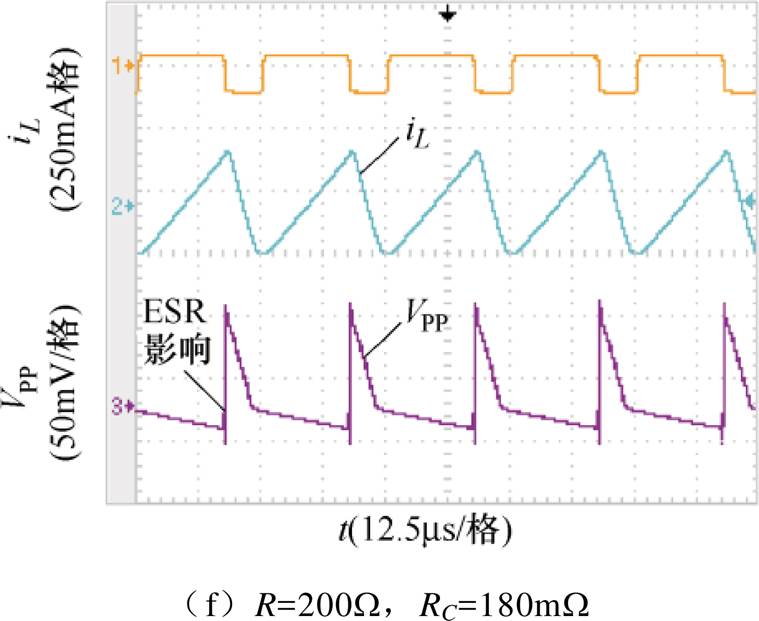
图9 不同负载时电感电流及输出纹波电压波形
Fig.9 Inductor current and output ripple voltage waveforms
表2 理论分析与实验对比结果
Tab.2 Short circuit discharge energy and ripple voltage and comparison results
R/WRC/ mW工作模式ILP,max/AWmax/mJVPP/mV 理论值实验值理论值实验值理论值实验值 5037CISM1.030.973.112.98106119 50180CISM1.030.963.112.98203216 15037IISM0.480.453.012.903951 150180IISM0.480.423.012.908390 20037DCM0.410.402.902.803148 200180DCM0.410.372.902.797486
（2）为了进一步说明本文所提设计方法的优越性，在上面给定的变换器参数基础上，得到了传统本质安全Buck-Boost变换器的设计方法与本文设计方法的对比结果，见表3。
分析表3可知，和文献[11]方法相比，本文提出方法有效地减小了电容容量和短路释放最大能量，从而提高了变换器本质安全性能。
表3 本质安全变换器设计方法对比
Tab.3 Comparison of intrinsically safe converter design methods
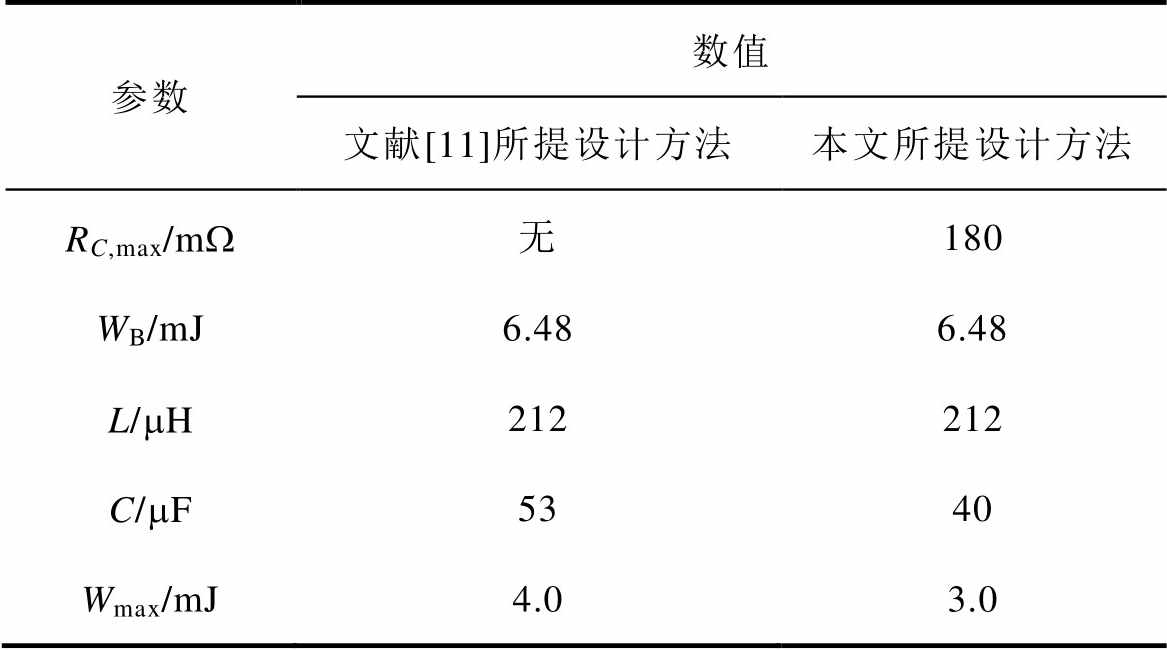
参数数值 文献[11]所提设计方法本文所提设计方法 RC,max/mW无180 WB/mJ6.486.48 L/mH212212 C/mF5340 Wmax/mJ4.03.0
（3）在设计的Buck-Boost变换器参数范围内选择L=212mH、C=40mF、RC=180mW、R=50～200W 时，输入电压分别选择5V、10V、15V时，变换器输出纹波电压随负载变化情况的实验测试结果如图10所示。输出短路放电最大能量随负载变化情况实验测试结果如图11所示。
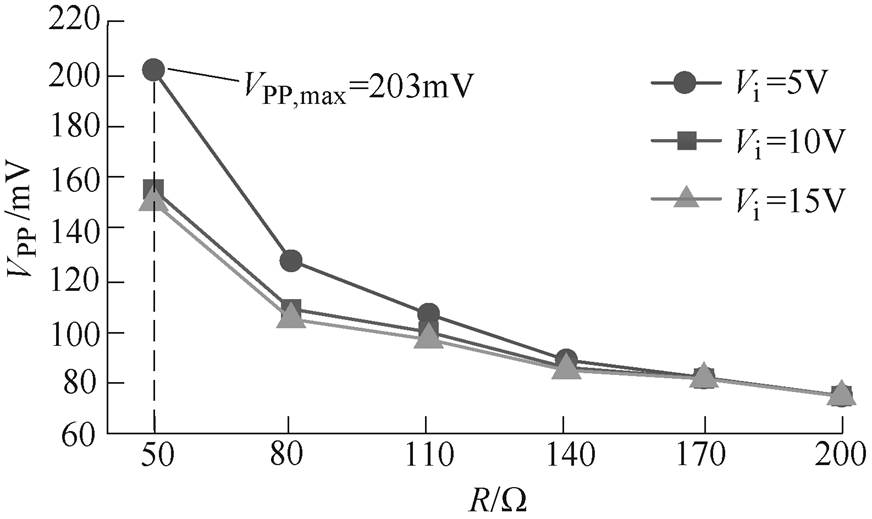
图10 纹波电压与负载及输入电压的关系
Fig.10 Ripple voltage vs input voltage and load
图11 输出短路放电能量与负载及输入电压的关系
Fig.10 Output short-circuit discharged energy vs load and input voltage
分析图10和图11可知，Buck-Boost变换器的输出纹波电压、输出短路放电能量均随着负载电阻及输入电压的增大而减小，且均在R=Rmin、Vi=Vi,min处取得最大值，实验测试结果与理论分析一致。同时分析图11可知，当R=50W、Vi=5V、RC=180mW时，变换器输出纹波电压为216mV，小于设定值240mV；输出短路最大放电能量Wmax=2.98mJ＜WB，由此可知，以上设计的参数满足输出本质安全Buck- Boost变换器的设计要求，验证了本文提出的本质安全参数设计方法的合理性。
1）电容的ESR是引起Buck-Boost变换器输出纹波电压波形畸变以及存在多种形状的主要原因。建立了考虑电容ESR的输出纹波电压及峰值电感电流的精确数学模型，且峰值电感电流及输出纹波电压均随着ESR的增大而增大。
2）本质安全Buck-Boost变换器的最大电感峰值电流、最大输出短路放电能量及最大输出纹波电压在R=Rmin、Vi=Vi,min、RC=RC,max处取得。
3）提出了一种在输入电压、负载电阻和电容ESR动态范围内本质安全Buck-Boost变换器参数设计方法，该方法可以减小滤波电容选择的裕度，从而有效地提高变换器的输出本质安全性能。
4）提出的考虑滤波电容ESR的输出纹波电压建模方法，以及输出本质安全开关Buck-Boost变换器参数的设计方法适用于其他DC-DC变换器。
V(t)与R、Vi之间的关系如附图1所示。当负载电阻增加DR时，为了维持Vo不变，占空比D会随之减小，即t增加Dt，附图1中，假设t＞tm，当负载R增加时，输出纹波电压随之减小；假设t≤tm，由式（23）可知，Dv1和Dv2分别为
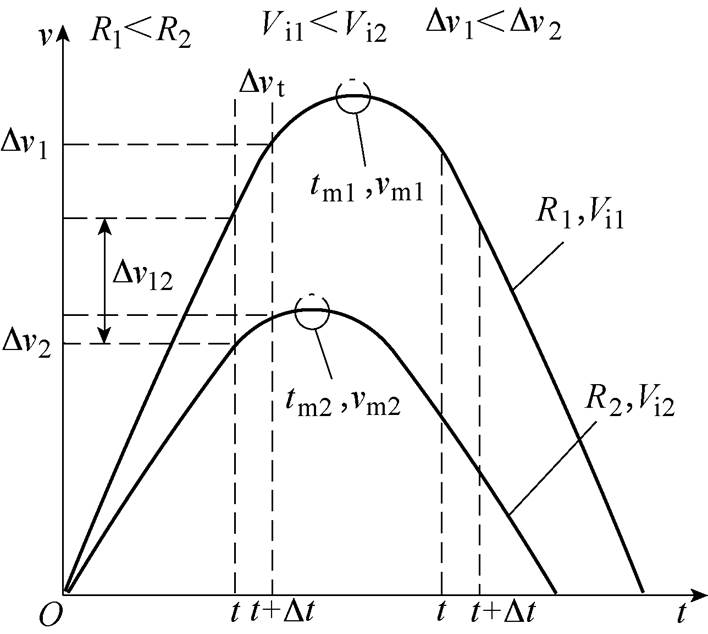
附图1 v(t)与R、Vi之间的关系
App. Fig.1 The relationship between v(t) and R、Vi
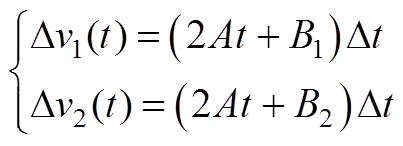（A1）由式（28）可知，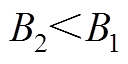
，则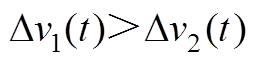
。将式（23）对时间t求偏导，可得Dv1为
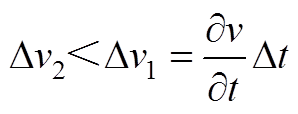（A2）
当R变化DR时，由式（7）可得Dt为
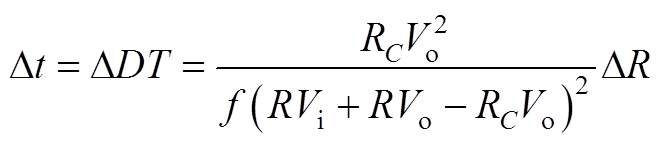（A3）联立式（A1）～式（A3）可得
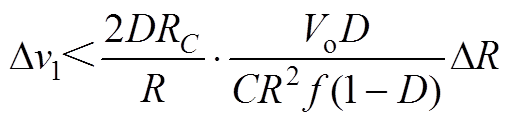（A4）
当负载R增加DR时，如附图1所示，输出纹波电压在t时刻会减小Dv12，将式（23）对R求偏导，可得Dv12为
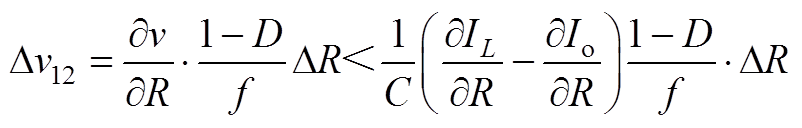（A5）继续分析式（A5），可得
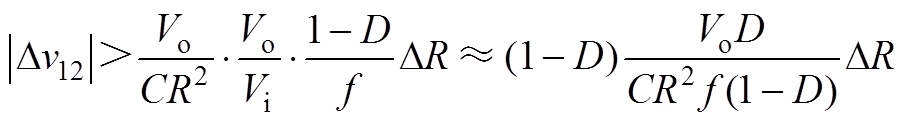（A6）
对比式（A4）和式（A6），可知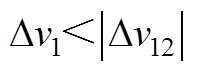
。从而可知，当负载R增加时，开关关断期间内的输出纹波电压将随之减小，DV1随着R的增大而减小。综上分析可得，变换器的输出纹波电压随着负载R的增大而减小，并在R=Rmin处取得极大值，即CCM时的纹波电压大于DCM的纹波电压。
当变换器工作于CCM时，式（23）可以简写为
（A7）将式（A7）对RC求偏导，可得
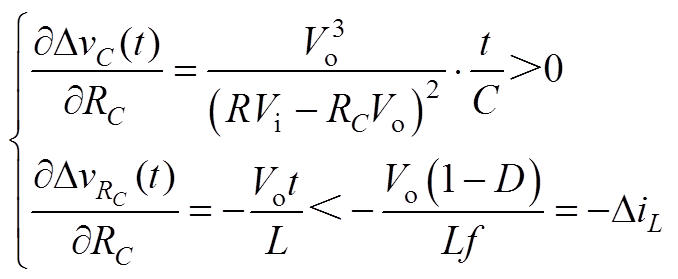（A8）
将DV1对RC求偏导，可得
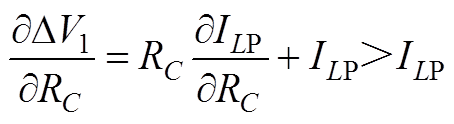（A9）对比式（A8）和式（A9）可知，随着RC的增加，DV1的增加量大于曲线v(t)的减小量，综上分析可知，输出纹波电压的极大值将在RC=RC,max处取得。
将a 对Vi求偏导，可得
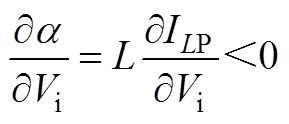（A10）由式（A10）可知，当输入电压增加DVi时，v(t)的tm以及vm均会减小。当Vi增加时，占空比会随之减小，因此输出纹波电压的变化趋势与增加DR时相同，如附图1所示。同理只需验证t≤tm时的纹波电压类型。
当Vi变化DVi时，由式（7）可得Dt为
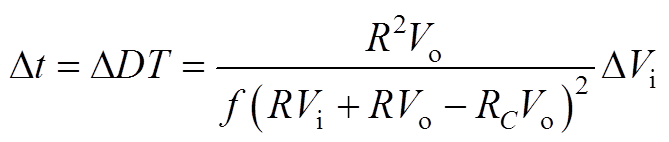（A11）联立式（A1）、式（A2）和式（A11）可得Dv1为
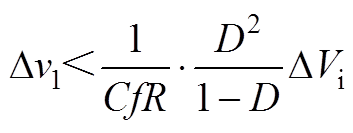（A12）
同理，将式（23）对Vi求偏导，可得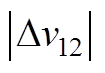
为
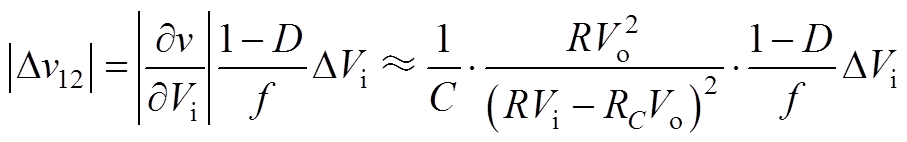（A13）分析式（A13）可得
（A14）
对比式（A12）和式（A14），可知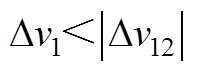。综上分析可得，变换器的输出纹波电压随着负载Vi的增大而减小，并在Vi=Vi,min处取得极大值。
参考文献
[1] Ripamonti, Giacomo, Saggini, et al. A novel inter- leaved tri-state Boost converter with lower ripple and improved dynamic response[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 28-32.
[2] Jonathan C, Jesus E, Pedro M, et al. A dual-edge pulsewidth modulator for fast dynamic response DC-DC converters[J]. IEEE Transactions on Industry Applications, 2019, 55(3): 2813-2822.
[3] Li Jing, Liu Jinjun. A novel Buck-Boost converter with low electric stress on components[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 2703-2713.
[4] Julio C, Jesus E, Jonathan C, et al. Quadratic Buck- Boost converter with positive output voltage and minimum ripple point design[J]. IET Power Elec- tronics, 2018, 11(7): 1306-1313.
[5] Vishwanatha S, Yogesh V H. Systematic circuit design and analysis of a non-ideal DC-DC pulse width modulation Boost converter[J]. IET Circuits Devices & Systems, 2018, 12(2): 144-156.
[6] Ren Lei, Gong Chunying, Zhao Yao. An online ESR estimation method for output capacitor of Boost converter[J]. IEEE Transactions on Power Electronics, 2019, 34(10): 10153-10165.
[7] 杨玉岗, 祁鳞, 吴建鸿. 三相交错并联磁集成Boost变换器的内部本质安全特性[J]. 电工技术学报, 2014, 29(4): 54-62.
Yang Yugang, Qi Lin, Wu Jianhong. Analysis of inner-intrinsic safety for three-phase interleaving magnetic integrated Boost converter[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 54-62.
[8] 程红, 李鹤群, 王聪. 准Z源Buck开关变换器输出短路火花发电模型研究[J]. 煤炭学报, 2012, 37(增刊2): 504-510.
Cheng Hong, Li Hequn, Wang Cong. Research on the output short circuit spark discharge mathematical model of quasi-Z-source Buck converter[J]. Journal of China Coal Society, 2012, 37(S2): 504-510.
[9] 于月森, 戚文艳, 伍小杰. 软火花电路的本质安全特性及优化分析[J]. 煤炭学报, 2014, 39(10): 2134- 2140.
Yu Yuesen, Qi Wenyan, Wu Xiaojie. Intrinsically safe characteristics and optimization analysis of soft-spark circuit[J]. Journal of China Coal Society, 2014, 39(10): 2134-2140.
[10] 刘树林, 刘健, 钟久明. Buck-Boost变换器的能量传输模式及输出纹波电压分析[J]. 电子学报, 2007, 35(8): 838-848.
Liu Shulin, Liu Jian, Zhong Jiuming, et al. Energy transmission modes and output ripple voltage of Buck-Boost converters[J]. ACTA Electronica Sinica, 2007, 35(8): 838-848.
[11] 刘树林, 刘健, 钟久明. 输出本质安全型Buck- Boost DC-DC变换器的分析与设计[J]. 中国电机工程学报, 2008, 28(3): 60-65.
Liu Shulin, Liu Jian, Zhong Jiuming. Analysis and design of output intrinsically safe Buck-Boost DC-DC converter [J]. Proceedings of the CSEE, 2008, 28(3): 60-65.
[12] 刘树林, 马一博, 文晓明, 等. 输出本安Buck- Boost变换器的最危险输出短路放电工况研究[J]. 电工技术学报, 2015, 30(14): 253-260.
Liu Shulin, Ma Yibo, Wen Xiaoming, et al. Study on the most dangerous output short circuit discharge conditions of output intrinsically safe Buck-Boost converter[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 253-260.
[13] 刘树林, 汪子为, 钟明航, 等. 基于Matlab的Boost变换器输出本安性能评价系统[J]. 煤炭学报, 2017, 42(增刊1): 282-287.
Liu Shulin, Wang Ziwei, Zhong Minghang, et al. Output intrinsic safety performance evaluation system of Boost converter based on Matlab[J]. Journal of China Coal Society, 2017, 42(S1): 282-287.
[14] 杨玉岗, 祁鳞, 李龙华. 交错并联磁集成Buck变换器本质安全性输出纹波电压的分析[J]. 电工技术学报, 2014, 29(6): 181-188.
Yang Yugang, Qi Lin, Li Longhua. Analysis of intrinsic safety output ripple voltage of interleaved parallel magnetically integrated Buck converter[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 181-188.
[15] 孟庆海, 王进己. 本质安全电感电路电弧放电时间双正态分布[J]. 电工技术学报, 2017, 32(2): 119- 124.
Meng Qinghai, Wang Jinji. Double normal distri- bution of arc discharge time in intrinsically safe inductive circuits[J]. Transactions of China Electro- technical Society, 2017, 32(2): 119-124.
[16] 赵永秀, 刘树林, 王瑶, 等. 安全火花试验电极热场致发射模型和温度效应的数值模拟研究[J]. 电工技术学报, 2019, 34(20): 4179-4187.
Zhao Yongxiu, Liu Shulin, Wang Yao, et al. Study on the model of thermal field emission and numerical simulation of temperature effect of safety spark test electrode[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4179-4187.
[17] 姚凯, 唐伟杰, 毕晓鹏, 等. Boost PFC变换器直流母线电容等效串联电阻和容值的一种在线监测方法[J]. 中国电机工程学报, 2017, 37(9): 2677-2686.
Yao Kai, Tang Weijie, Bi Xiaopeng, et al. An on-line monitoring method of DC bus capacitance equivalent series resistance and capacitance of Boost PFC converter[J]. Proceedings of the CSEE, 2017, 37(9): 2677-2686.
[18] 王立乔, 李占一, 刘乐, 等. 一种无电解电容单级Buck-Boost逆变器[J]. 电工技术学报, 2019, 34(20): 4295-4305.
Wang Liqiao, Li Zhanyi, Liu Le, et al. A single-stage Buck-Boost inverter with non-electrolytic capacitor[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4295-4305.
[19] 刘树林, 刘健. 开关变换器分析与设计[M]. 北京: 机械工业出版社, 2011.
[20] 刘树林, 刘健. 本质安全开关变换器[M]. 北京: 科学出版社, 2008.
[21] 皇金锋, 李林鸿, 董锋斌, 等. 考虑滤波电容ESR的Boost变换器输出纹波电压畸变机理及精确建模[J]. 中国电机工程学报, 2020, 40(16): 5326-5337.
Huang Jinfeng, Li Linhong, Dong Fengbin, et al. Distortion mechanism and accurate modeling of output ripple voltage of Boost converter on con- sidering filtering capacitor with ESR[J]. Proceedings of the CSEE, 2020, 40(16): 5326-5337.
[22] 皇金锋, 李林鸿, 谢锋, 等. 含有右半平面零点的开关DC-DC变换器暂态性能分析及频域法设计[J]. 电工技术学报, 2020, 35(10): 2170-2180.
Huang Jinfeng, Li Linhong, Xie Feng, et al. Transient performance analysis and frequency domain design of switched DC-DC converters with right half plane zero[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2170-2180.
[23] GB 3846.4 电工卷中国强制性国家标准汇编[S].北京: 中国标准出版社, 2003.
Analysis and Design of an Intrinsically Safe Buck-Boost Converter on Considering of the Filter Capacitor with Equivalent Series Resistance
Abstract The Buck-Boost converter used in coal mine, petrochemical and other dangerous environment should not only meet the requirements of intrinsic safety, but also meet the requirements of electrical performance indicators such as ripple voltage. The parameter design basis of the existing intrinsic safety switching converter is the ideal ripple voltage expression. However, due to the influence of parasitic parameters such as equivalent series resistance (ESR), the capacitor designed according to the ideal formula cannot meet the ripple voltage requirements, and a margin of 2～4 times is usually selected. This will increase the risk of explosion when the converter is short-circuited. Capacitor ESR not only causes the ripple voltage waveform distortion, but also has an important impact on the ripple voltage. In order to better guide the parameter design of intrinsically safe buck boost converter, the mechanism of ripple voltage distortion caused by capacitor ESR is analyzed, and the accurate mathematical model of ripple voltage and the peak inductance of Buck-Boost converter considering capacitor ESR are established. Then, the parameter design method of intrinsically safe Buck-Boost converter is proposed in the dynamic range of input voltage, load resistance and capacitance ESR. The experimental results show that the ripple voltage and output intrinsic safety requirements of Buck- Boost converter can be satisfied by selecting a capacitor with the margin of 1.2 times, which can effectively improve the intrinsic safety performance of the converter.
keywords：Intrinsically safe, Buck-Boost converter, equivalent series resistance (ESR), output ripple voltage, parameter design
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.200293
国家自然科学基金（51777167）和陕西理工大学人才启动（SLGQD1808）资助项目。
收稿日期 2020-03-24
改稿日期 2020-10-26
皇金锋 男，1978年生，博士，副教授，硕士生导师，研究方向为开关变换器的分析与设计。E-mail: jfhuang2000 @ 163.com（通信作者）
李林鸿 男，1992年生，硕士研究生，研究方向为开关变换器的分析与设计。E-mail: soarllh@163.com
（编辑 陈 诚）