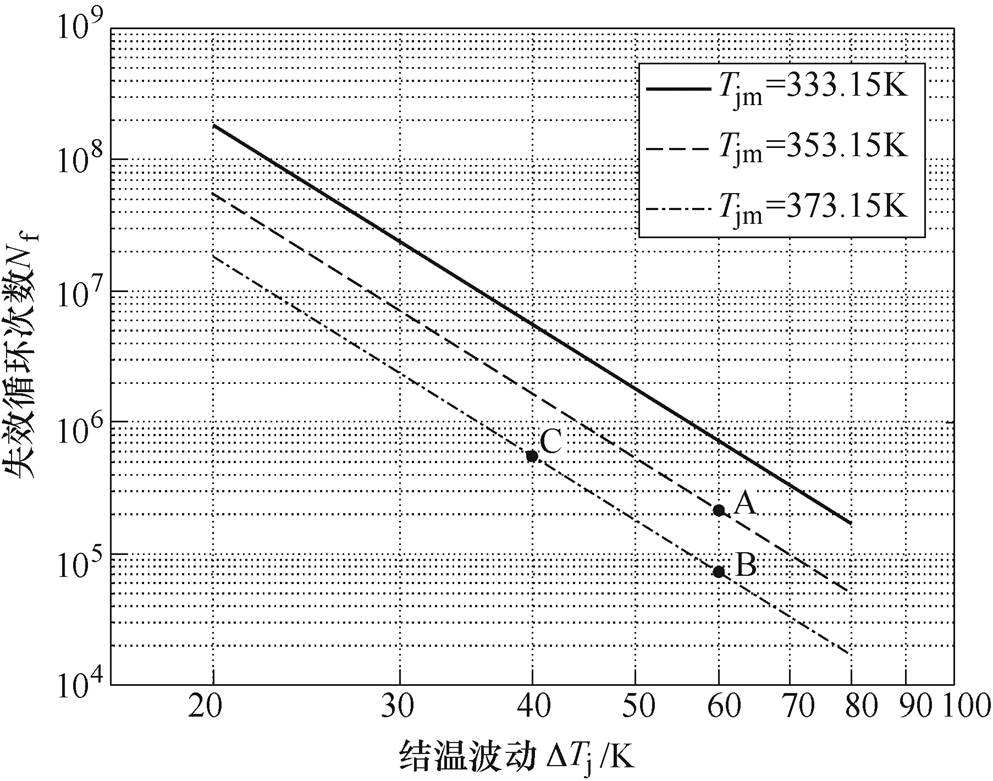
图1 IGBT可靠性与结温波动和平均结温的关系
Fig.1 IGBT reliability as a function of DTj and Tjm
摘要 绝缘栅双极型晶体管(IGBT)的热管理技术能降低其运行时的结温波动,提高器件的可靠性。针对IGBT外部热管理系统中的非线性成分,建立系统的仿射非线性模型。通过引入状态反馈线性化方法对其进行线性化,弥补目前IGBT热管理控制系统设计中缺乏精确数学模型的缺陷。基于线性二次型调节器(LQR)设计一种闭环控制方法,通过调节外部散热条件以平滑IGBT运行时由于负载波动导致的低频结温波动。基于Buck电路进行实验,实验证明,所提算法对负载电流在额定值的60%~100%范围内波动时,能够降低约60%的结温波动,提高IGBT约69倍的寿命。最后,基于小电流注入法在线测量结温,验证了基于模型计算结温的准确性。
关键词:IGBT外部热管理 非线性系统 状态反馈线性化 IGBT可靠性
电力电子系统主要用于功率处理和功率变换,其发展十分迅速,已被广泛应用于航天航空、工业自动化、交通运输和可再生能源发电等非平稳工况领域[1-3]。非平稳工况即变流器处理的功率会在一定范围内随机波动,这会导致功率半导体器件的结温随之波动,从而降低功率半导体器件的使用寿命[4-5]。据统计,功率半导体器件是变流装置中失效率最高的部件之一[6]。研究如何降低IGBT模块在非平稳工况下的结温波动,对提高变流器系统的可靠性具有重大意义。
针对IGBT模块的热管理方法可以分为内部热管理和外部热管理。内部热管理主要通过改变开关频率[7]、调节IGBT动态过程[8-9]和改变系统调制方式实现[10],其主要思路是改变IGBT模块的损耗以平滑由于负载功率波动导致的结温波动;外部热管理方法多用于补偿环境温度变化或控制平均结温,而针对平滑结温变化的研究相对较少[11]。Wang Xiang等基于调节风冷散热器风扇转速研究了可用于功率器件的外部热管理技术,实验达到了平滑温度波动的效果,但该文献仅对发热电阻[12]或直接对IGBT通以编程控制的电流来进行实验验证[13],并没有把所提算法应用在实际变流器中的功率器件上。J. N. Davidson等使用绝缘金属基板PCB作为单管功率器件的散热器,通过PID算法控制风速,进而调节PCB对环境的热阻,从而实现了IGBT单管的外部热管理[14],实现了平滑结温波动的目标,但是实验中使用的PID参数则是基于Ziegler- Nichols经验法进行设计,闭环设计缺乏理论和模型支撑。Li Cong等基于热电冷板(Thermoelectric Cooling, TEC)对实际逆变器进行了外部热管理相关的研究[15],建立了TEC的热网络模型,提出了一套泛用性较强的外部热管理方案,控制效果较好,但是文中并未对散热器进行研究。另外,基于散热器散热功率调节的IGBT热管理方法引入了较强的非线性成分,导致控制系统难以精确建模。基于观测器的方法能较好地预测IGBT瞬时结温,但是由于被控系统为非线性系统,观测器和控制器不一定具有分离特性[16],可能会给热管理控制器的设计带来困难。文献[17]基于模糊控制设计了热管理控制器,实现了抑制结温波动的目标,但和PID方法类似,其控制效果主要取决于设计人员的工程经验,缺乏理论支撑,对某些特定场合的设计难以推广使用。
本文针对现有IGBT模块外部热管理系统的闭环设计缺乏理论支撑的现状,首次将基于微分几何的精确线性化方法应用于IGBT外部热管理系统中。然后建立了系统的仿射非线性模型并将其线性化,提出了一个泛用性较强的外部热管理控制策略。最后在Buck电路中进行了实验验证,证明了所提方法的有效性。
IGBT模块热管理技术的主要思路为在器件处理的功率降低时,通过一些方法使其损耗上升(内部热管理)或是降低散热功率(外部热管理)以补偿结温的下降,从而降低器件的结温波动,但这样会不可避免地提高器件的平均结温。
焊接型IGBT因其工艺较为成熟,生产成本较低,在各种变流器中均有应用。其封装结构主要包括铝键合线、硅基芯片、焊料层、陶瓷基板和底板等。器件工作时,由于处理的功率和环境温度随时可能发生改变,使得IGBT结温产生波动,导致其封装结构受到反复的热应力冲击,模块封装性能逐渐退化甚至失效[18]。此外,由于各层材料的热膨胀系数均不同,器件的平均工作温度较高也会使得器件的退化失效。
图1为文献[19]给出的IGBT失效循环次数Nf与结温波动DTj和平均结温的关系。以图1中A、B、C三点为例,A点结温波动为60K,平均结温为353.15K,对应失效循环次数为2.14×105;保持结温波动不变,提高平均结温20K后如点B所示,失效循环次数降低为7.22×104;保持平均结温不变,降低结温波动20K后对应C点,失效循环次数提高为5.57×105,可见C点对应的结温应力下IGBT的寿命高于A点,即当器件结温波动减少量和平均结温增加量一样多时,器件的寿命会得到明显提升。IGBT寿命受结温波动影响更大,因此,在一定程度内牺牲平均结温以降低结温波动来提高IGBT的寿命是可行的。

图1 IGBT可靠性与结温波动和平均结温的关系
Fig.1 IGBT reliability as a function of DTj and Tjm
变流器设备的外部热管理控制系统框图如图2所示,变流器设备由变流器主电路和外部散热装置构成,控制部分包含主电路控制和外部热管理控制,其中主电路控制部分不是本文研究的内容,用虚线表示。图2中,外部热管理环节下的器件模型是指IGBT器件的输出特性和开关损耗特性;损耗模型是指器件的导通损耗和开关损耗模型;热网络模型则是指热路的一维等效模型。实验中,通过损耗模型和热网络模型能够对器件的结温进行估算,将结温的估算结果Tj作为反馈量,通过热管理算法调节散热器对环境的热阻RHS,从而实现对器件结温波动的控制。为了实现结温计算,需要测量IGBT的壳温Tc和电路的负载电流Ic等参数。
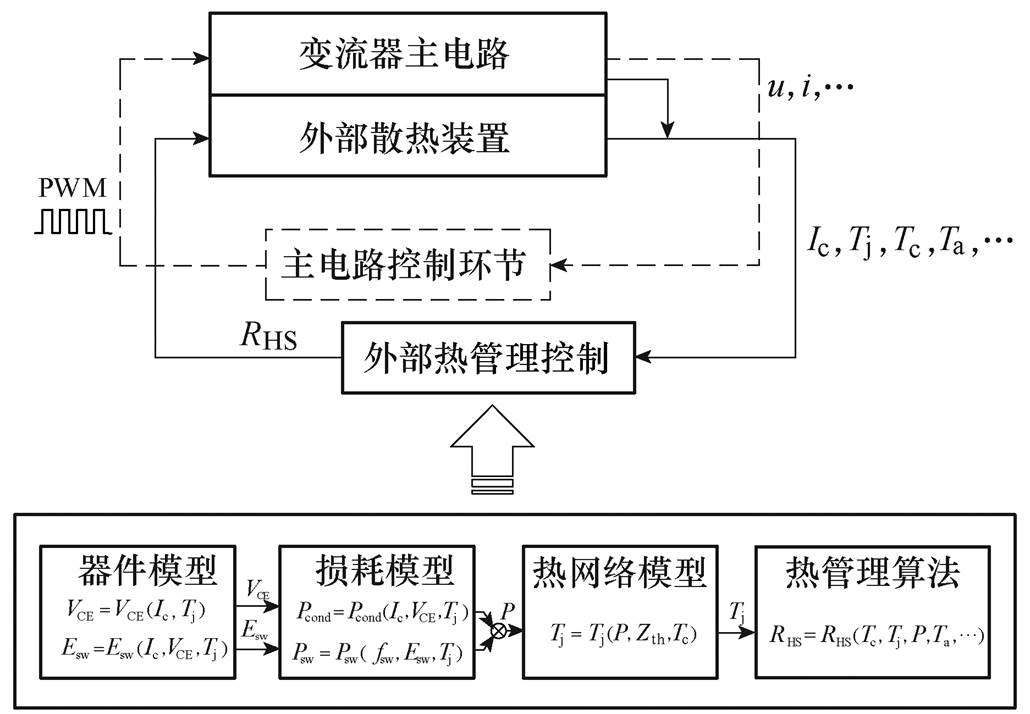
图2 控制系统框图
Fig.2 Control system block diagram
IGBT外部热管理方法的控制对象为器件结温,需要获取器件结温信息以进行反馈控制,通过损耗模型和热网络模型可以估算器件的结温。
IGBT模块损耗主要包括IGBT的导通损耗和开关损耗。根据器件的输出特性曲线,对结温进行线性插值,即可获得器件考虑结温时的导通损耗。IGBT导通损耗和电流的二阶关系式为
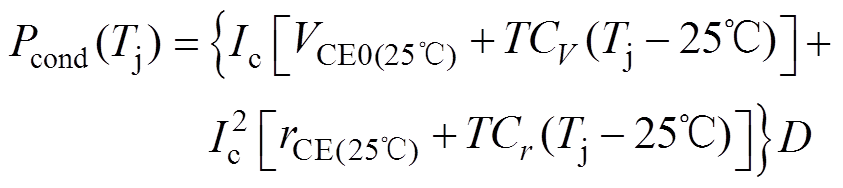 (1)
(1)式中,VCE、rCE分别为与结温有关的擎住电压和正向导通电阻[20];TCV、TCr为擎住电压和正向导通电阻的结温插值系数;D为占空比。同样对结温进行插值可得IGBT开关损耗,即
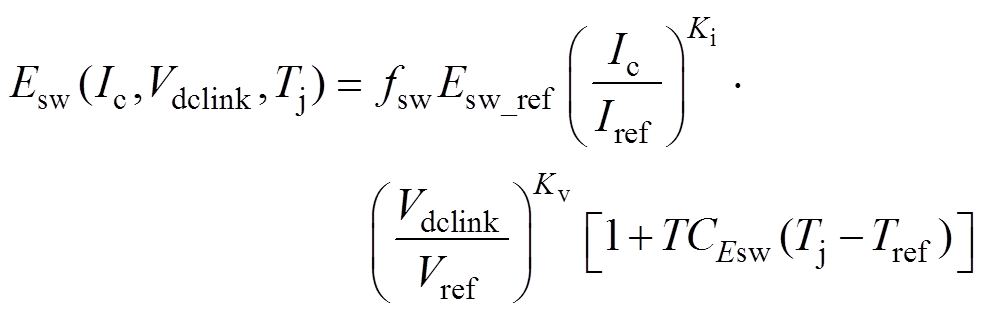 (2)
(2)
式中,Vdclink为实际母线电压;Ic为实际集电极电流;Esw_ref为器件手册给出的IGBT开关损耗参考值;Vref、Iref和Tref分别为开关损耗参考值对应的母线电压、集电极电流和结温外部条件;TCEsw为开关损耗的结温插值系数;Kv和Ki分别为开关损耗随电压和电流变化的系数[20]。
目前广泛采用基于电热比拟的一维等效RC热网络计算功率器件的结温[21]。RC热网络根据其拓扑结构的不同分为Foster网络和Cauer网络。因Cauer模型的每一个单元都具有一个公共地,所以更容易列写节点方程,本文中将使用Cauer模型进行相关研究。然而Cauer模型较复杂,求解结温需要耗费大量系统资源,因此将IGBT模块的多阶Cauer热网络模型简化为一阶Cauer RC单元进行后续的系统设计[22],包含散热器的IGBT模块Cauer热网络模型如图3所示。图3中,Rth_IGBT_i、Cth_IGBT_i (i=1, 2,…)分别为IGBT的多阶Cauer热网络热阻和热容参数,Rth_TIM为导热硅脂热阻(忽略导热硅脂热容),RHS、CHS分别为散热器对环境的热阻和热容,P为IGBT的损耗,Tj为IGBT结温,Tc为IGBT模块壳温,Ta为环境温度。RT、CT为简化的IGBT模块一阶Cauer热网络热阻和热容参数,可由器件手册中的降温曲线拟合得到。
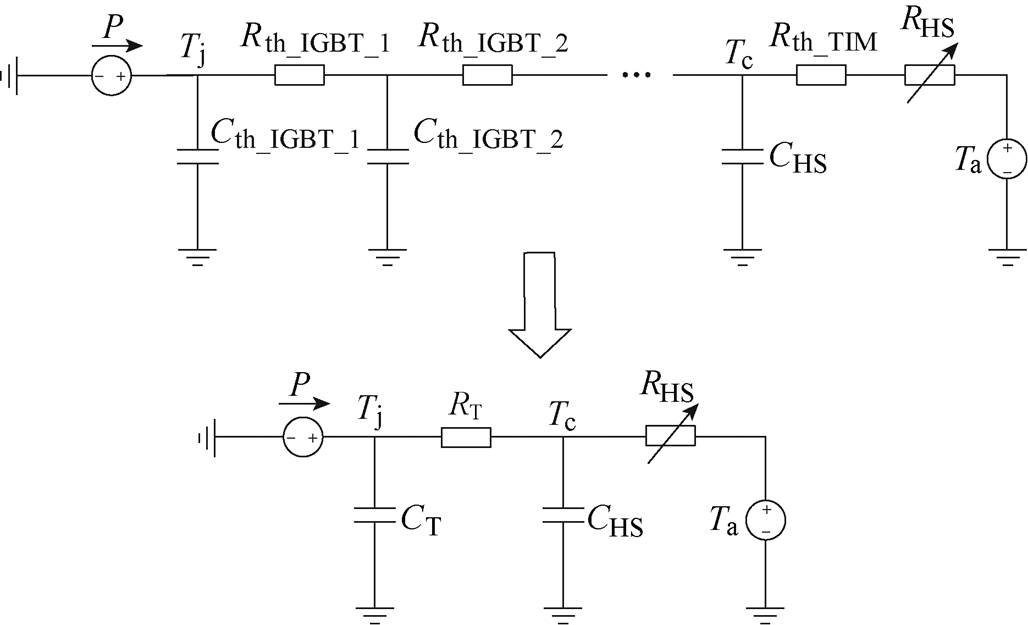
图3 包含散热器的IGBT模块Cauer热网络模型
Fig.3 Cauer thermal network of IGBT module and heatsink
本文中的IGBT结温估算也是在基于图3中简化的热网络模型上进行的。实验中使用热电偶对壳温进行采集,使用电流霍尔采集电流并通过损耗模型实时计算器件损耗,并通过采集的壳温和损耗实时计算结温。RC网络的全响应可以分解为零状态响应和零输入响应,与电路的RC响应计算方法一致。故结温表达式为
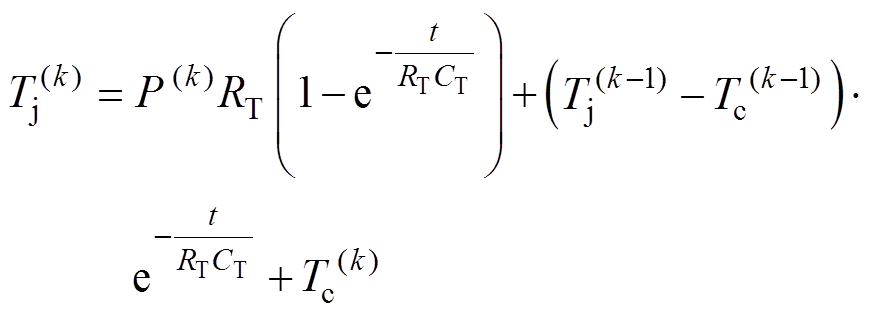 (3)
(3)式中,等式右面第一项为零状态响应,即RC热网络在功率脉冲P(k)作用下的响应;第二项为零输入响应,即RC热网络的初始结温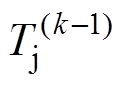 在温差
在温差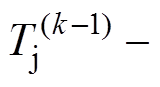
 作用下的响应。上标k表示离散化,将连续变化的功率和温度量以一定的时间周期离散为脉冲串以用于处理器计算。
作用下的响应。上标k表示离散化,将连续变化的功率和温度量以一定的时间周期离散为脉冲串以用于处理器计算。
对图3中简化的IGBT热网络模型,选取x= 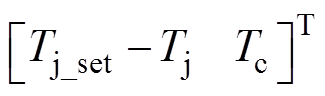 为状态变量,建立状态空间方程为
为状态变量,建立状态空间方程为
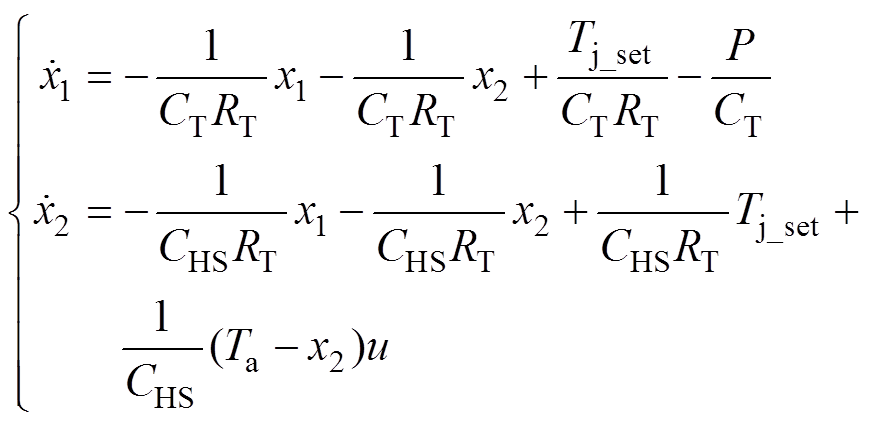 (4)
(4)式中,Tj_set为结温设定值;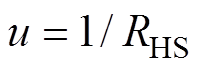 。选取系统输出y=x1。
。选取系统输出y=x1。
系统状态空间方程中存在输入量u和状态变量x2的乘积,且难以分离,为非线性系统,无法应用传统的线性系统控制器设计方法。观察发现,该系统符合仿射非线性模型的结构[16],可以基于状态反馈的方法,通过坐标变换将其线性化。
将该系统用仿射非线性模型表示为
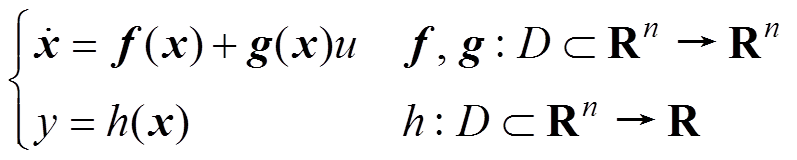 (5)
(5)其中
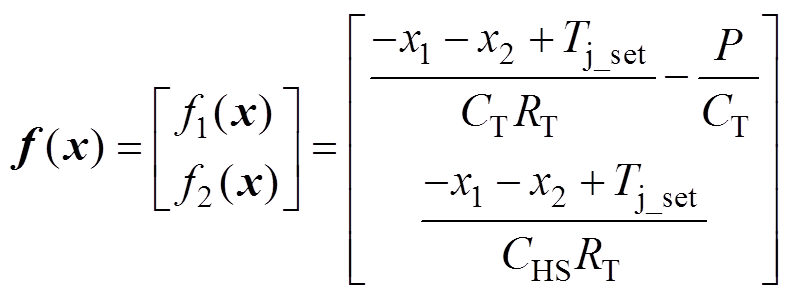
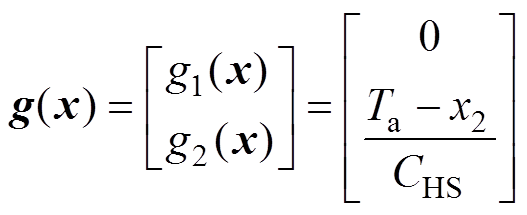
根据状态反馈线性化的条件[16],对式(5)所示的系统进行计算,证明系统能够进行状态反馈线性化。首先,计算矩阵
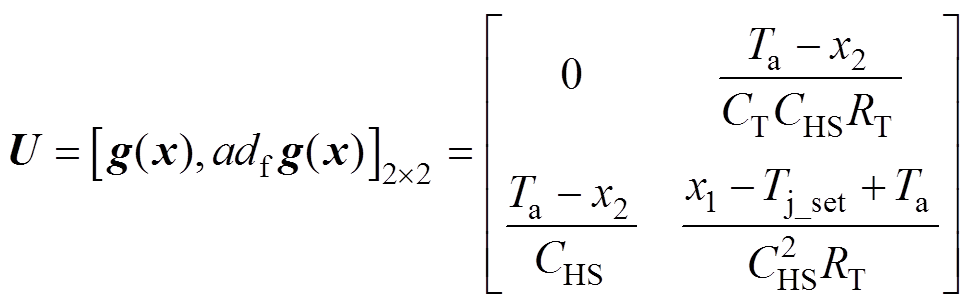 (6)
(6)式中,adfg(x)为f、g的Lie括号计算结果;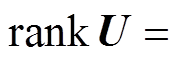
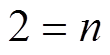 ,n为系统维数。
,n为系统维数。
再考察分布
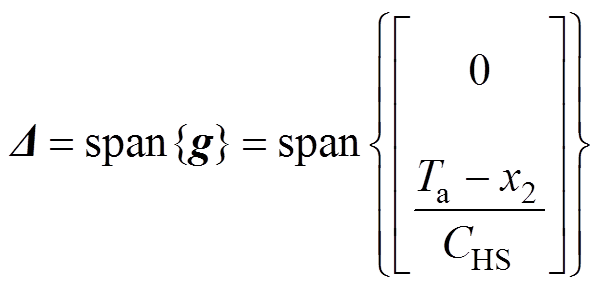 (7)
(7)因为n=2,所以分布span{g}在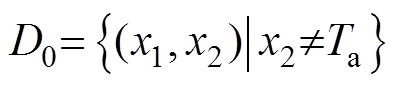
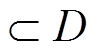 上是对合的[16],对于式(5)给出的仿射非线性系统是可以通过状态反馈进行精确线性化的。
上是对合的[16],对于式(5)给出的仿射非线性系统是可以通过状态反馈进行精确线性化的。
对式(6)描述的系统求解如Lie导数,有
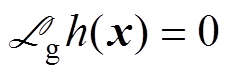 (8)
(8)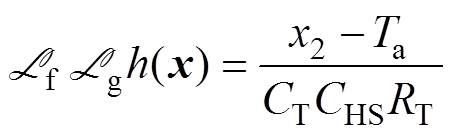 (9)
(9)
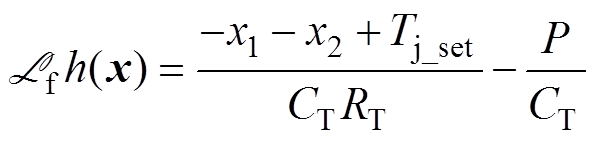 (10)
(10)
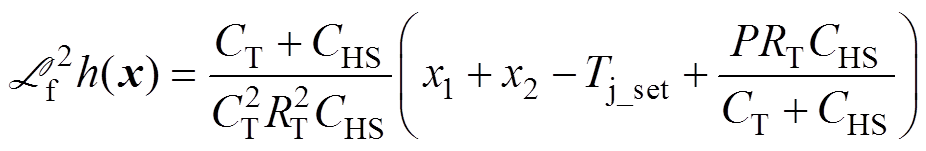 (11)
(11)由式(8)和式(10)知,该系统在D0时,有相对阶r=2=n[16]。因此只要找到了合适的坐标变换,系统能够完全线性化[16]。
选取坐标变换
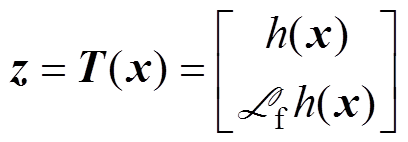 (12)
(12)代入式(5),得到线性化后的状态空间方程为
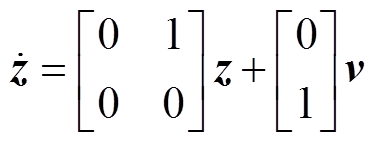 (13)
(13)
式中,z为线性化后的新系统的状态变量;v为新系统的输入,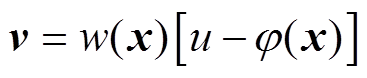 ,w(x)和j(x)分别为状态变量的函数,
,w(x)和j(x)分别为状态变量的函数,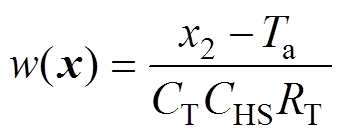 ,
,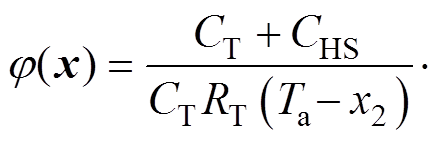
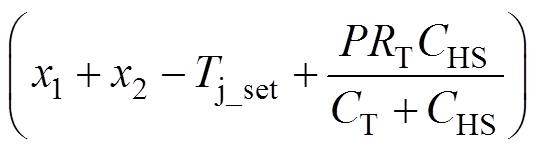 。
。
第2节利用状态反馈线性化的方法对IGBT热网络的节点温度系统进行了线性化的建模。下文将对结温闭环控制系统进行设计并基于Buck电路搭建实验平台。
IGBT外部热管理系统通过控制散热器热阻,使得IGBT结温稳定在设定值附近,减小结温波动。对于线性系统,线性二次型调节器(Linear Quadratic Regulator, LQR)的目标函数J具有特定的解析式,且目标函数的最优解易于形成闭环反馈控制律,在工程应用上较为广泛。其中,J为系统状态变量与设定值的差值和实现控制需要的广义能量的二次型函数。本文中,当闭环稳态实现最优设计时,状态变量与状态变量的期望值的差值应为0,即线性二次型调节器的目标函数J为最小值。
考察状态空间方程组式(13)中的状态变量z1、z2分别为
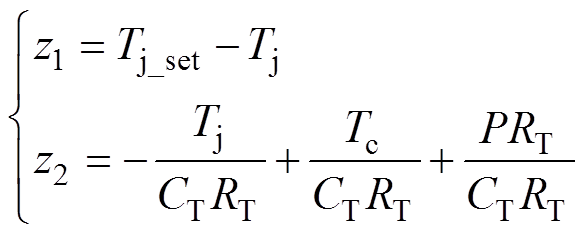 (14)
(14)设系统输入v为
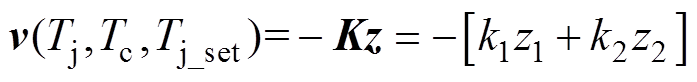 (15)
(15)
式中,K为状态反馈矩阵,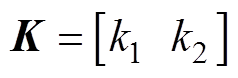 。
。
则散热器的热阻可表示为
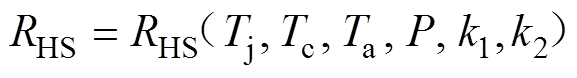 (16)
(16)由于选取了合适的原系统状态变量,则经过坐标变换后的系统状态变量z1、z2的闭环稳态理想值均为0,故可取最优控制性能指标为
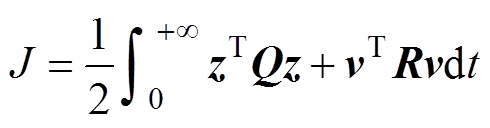 (17)
(17)
式中,Q和R为权重矩阵,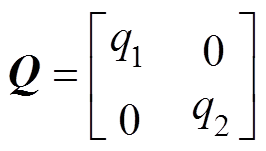 ,
,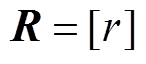 。
。
为了设计权重矩阵,引入无源性理论[23]:如果一个用能量函数H(t)描述的系统在没有输入的情况下,对任意时间t均满足H[x(t)]≤H[x(0)],则系统无源,且系统的能量将逐渐趋向最低点。
为了使得所设计的闭环系统能量函数无源,需要注入一种“无功力”[23]将系统变为无源系统。这个“无功力”在本文中可以理解为线性二次型调节器的评价函数J。为此可以用待定系数法求解权重矩阵Q。另外,需要使得系统能量最低点为所期望的点,即结温与期望值偏差为0,取系统能量函数为
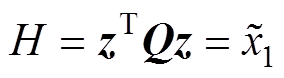 (18)
(18)则误差变量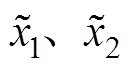 分别为
分别为
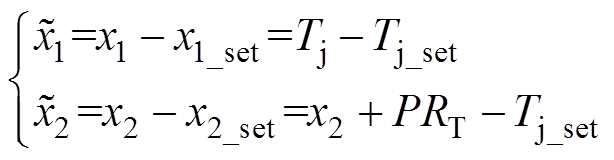 (19)
(19)
联立式(14)和式(19)可得
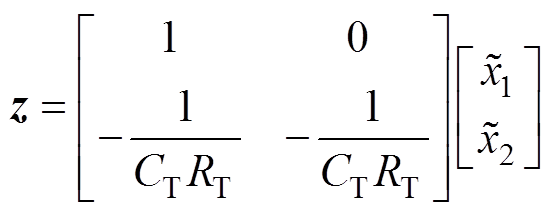 (20)
(20)将式(20)代入式(18),用待定系数法求解,解得q1=1,q2=0,再取r=0.01。在Matlab中求解Riccati代数方程[23],即可解得对应的状态反馈矩阵为K=[k1 k2]=[14.142 1 5.318 3]。
至此,在数学上推导了基于状态反馈精确线性化的方法,将原系统中的非线性成分消除,并基于线性二次型调节器和无源性理论对新系统进行闭环设计,得到了状态反馈矩阵K。
热管理闭环控制方法的应用如图4所示,主电路由于工况的随机性波动,从而引起IGBT损耗发生波动,导致结温波动。为了平滑结温波动,引入外部热管理方法。图中的结温闭环控制系统即为前文所述的反馈控制v=-Kz。通过对壳温和负载电流等参数进行实时测量得到状态变量z的取值,反馈控制基于模型估算结温,并根据结温的变化计算出系统输入v的值,从而计算出散热器对环境热阻应有的取值RHS,再通过调节风速控制实际的散热器热阻跟随计算值,最终实现平滑结温波动的目的。
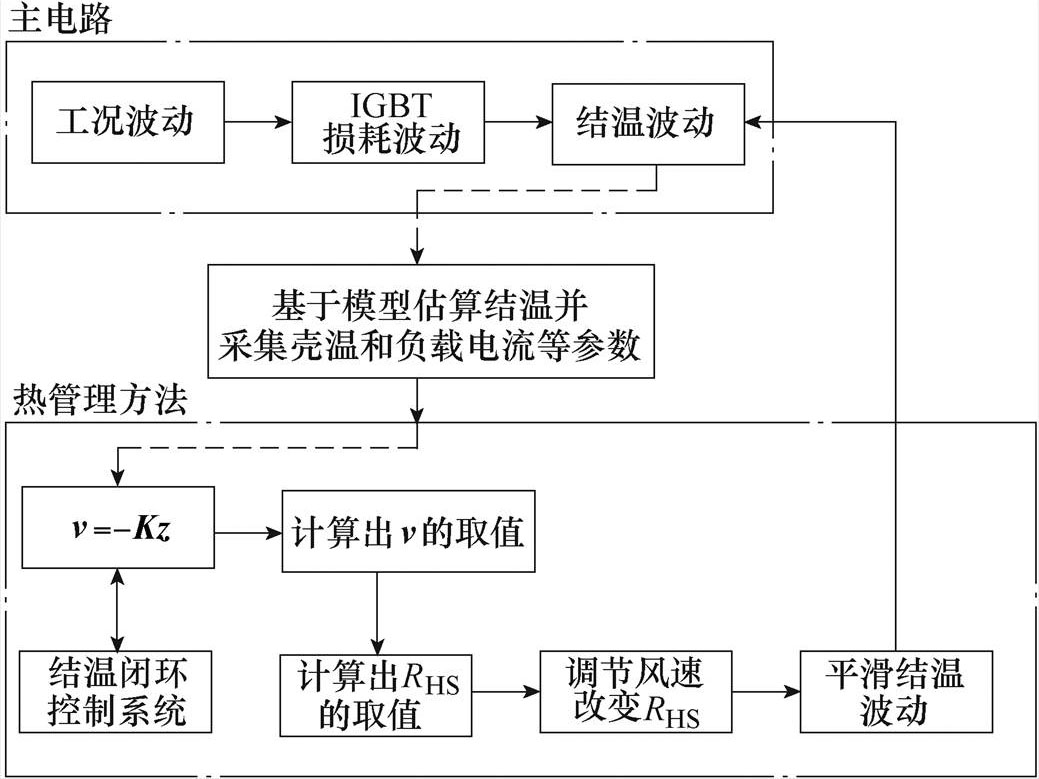
图4 热管理闭环控制方法的应用
Fig.4 Application of thermal management closed-loop control method
风冷散热器是通过调节风扇的占空比来调节其热阻的,故还需要通过离线标定确定散热器对环境的热阻值RHS与风扇占空比Dfan的关系。另外,由于RHS也受到热源功率大小的影响,在标定时将热源功率作为参量。
风冷散热器风机转速为系统的输入量,通过控制风机转速可以调节散热器对环境的热阻RHS,从而实现对IGBT结温的控制。设计Buck电路负载电流波动范围为额定值的60%~100%,经PLECS仿真分析,IGBT模块总损耗波动范围约为20~45W。
散热器对环境的热阻RHS与PWM调速风扇的占空比Dfan的关系由标定实验测得,测试时将IGBT与散热器安装在一起,对IGBT施加固定的直流加热电流,加热至热稳态后,测量散热器表面温度Tx(忽略IGBT模块与散热器之间的接触热阻,即认为Tc=Tx)、环境温度Ta和IGBT模块的总损耗Ploss以计算RHS,如式(21)所示。改变加热电流大小,以Ploss为参量,得到了RHS与占空比Dfan的关系RHS=f(Dfan),如图5所示。
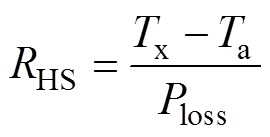 (21)
(21)IGBT外部热管理实验中,根据控制算法得到散热器热阻的目标值和基于模型计算出的IGBT模块损耗,利用图5的散热器离线标定值,以查表的形式确定此时散热器风扇占空比应取的大小。不同损耗对应不同的散热器热阻曲线,实验中根据计算的损耗选择标定的曲线中损耗最接近的一条。
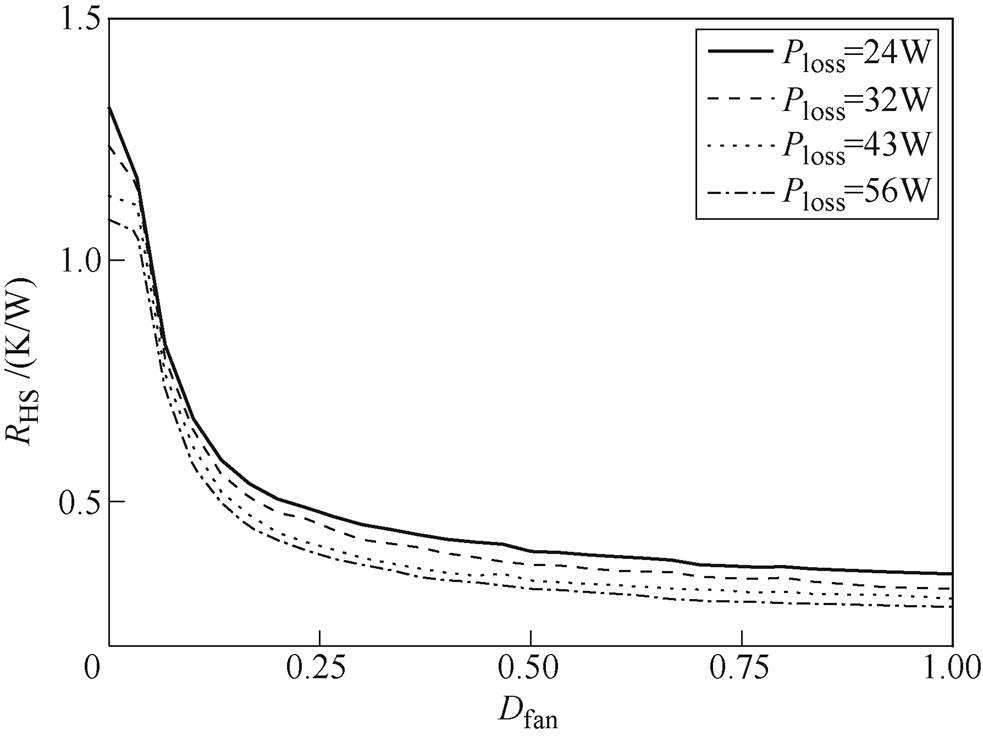
图5 RHS与风扇调速占空比的关系
Fig.5 RHS vs. Dfan speed regulation duty cycle
热管理实验平台由Buck电路作为主电路,电路参数见表1。输入电源为Chroma公司的62150- 450H,通过调节电子负载的参数实现负载电流的变化,电子负载的型号为Chroma公司的63804。基于Labview的上位机程序负责与电子负载和DSP进行通信,完成对电子负载的控制和电流、温度等数据的保存和实时显示。图6为热管理实验平台。
表1 实验平台参数
Tab.1 Experimental platform parameters
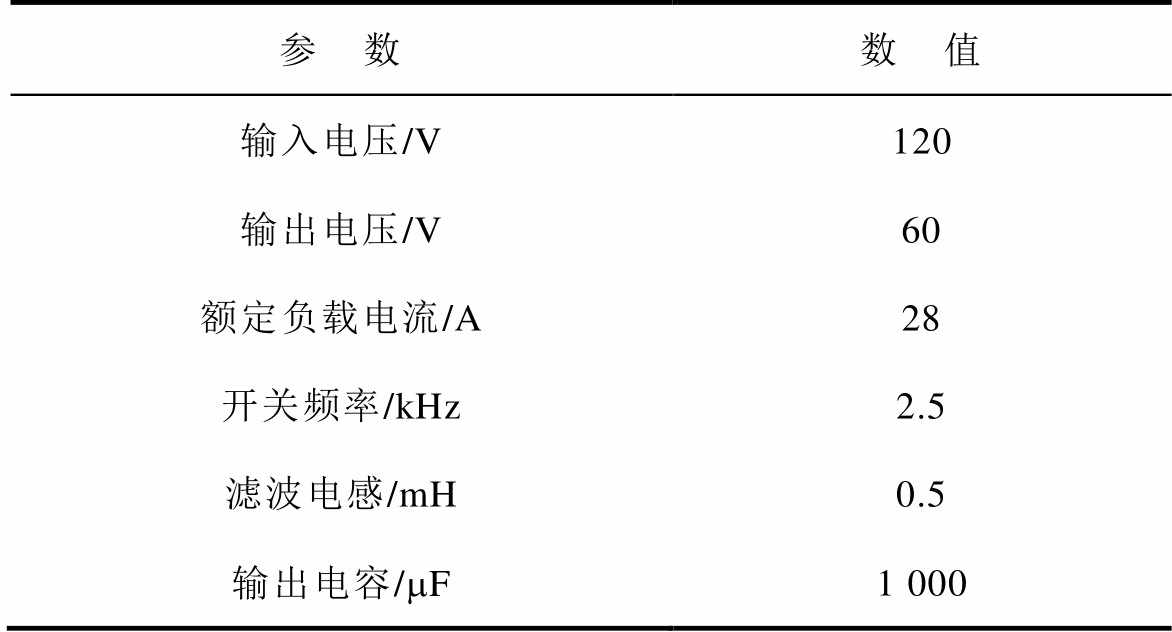
参 数数 值 输入电压/V120 输出电压/V60 额定负载电流/A28 开关频率/kHz2.5 滤波电感/mH0.5 输出电容/mF1 000

图6 热管理实验平台
Fig.6 Thermal management experimental platform
为验证所提结温计算模型的准确性和热管理方法的有效性,在搭建的平台中进行了实验。
通过调节负载电阻大小以调节负载电流,负载电流发生变化时,IGBT模块损耗也相应变化,使得器件结温发生一定程度的波动。当Buck电路负载电流在60%~100%范围内变动时,实验对比了采用所提热管理算法前后对结温波动的抑制效果。有无热管理控制算法的结温波动对比如图7所示。对比图7中的两条结温曲线发现,使用热管理算法后,器件结温波动降低,而平均结温升高。为了判定所提算法能够提高IGBT可靠性,本文基于IGBT的Coffin-Manson-Arrhenius解析寿命模型、Miner线性累积损伤模型和雨流计数法[24],分别计算了该工况下IGBT寿命差异。图8和图9分别为对采用热管理算法和散热器满额运行两种工况下的结温曲线进行雨流计数的结果。统计和计算结果显示,应用热管理算法之前,IGBT寿命为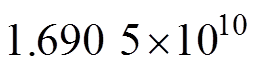 次循环,结温波动最大值为9.5℃;应用热管理算法后,IGBT寿命为
次循环,结温波动最大值为9.5℃;应用热管理算法后,IGBT寿命为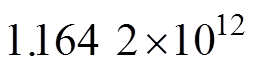 次循环,提高了约69倍,结温波动最大值约为3.8℃。
次循环,提高了约69倍,结温波动最大值约为3.8℃。
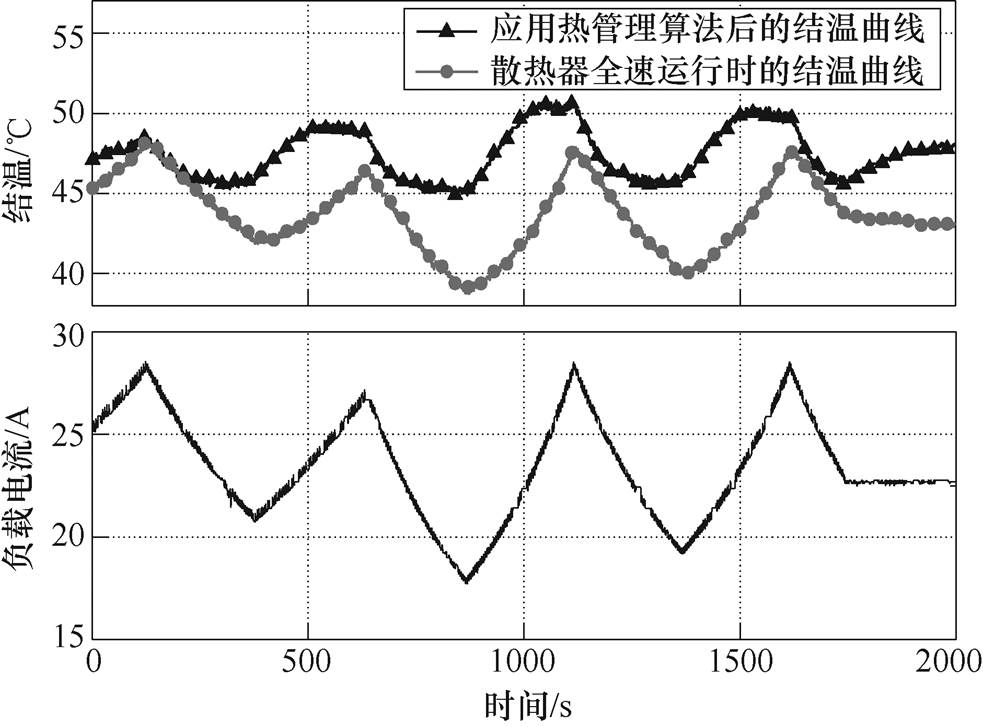
图7 有无热管理控制算法的结温波动对比
Fig.7 Junction temperature profile with and without the thermal regulation
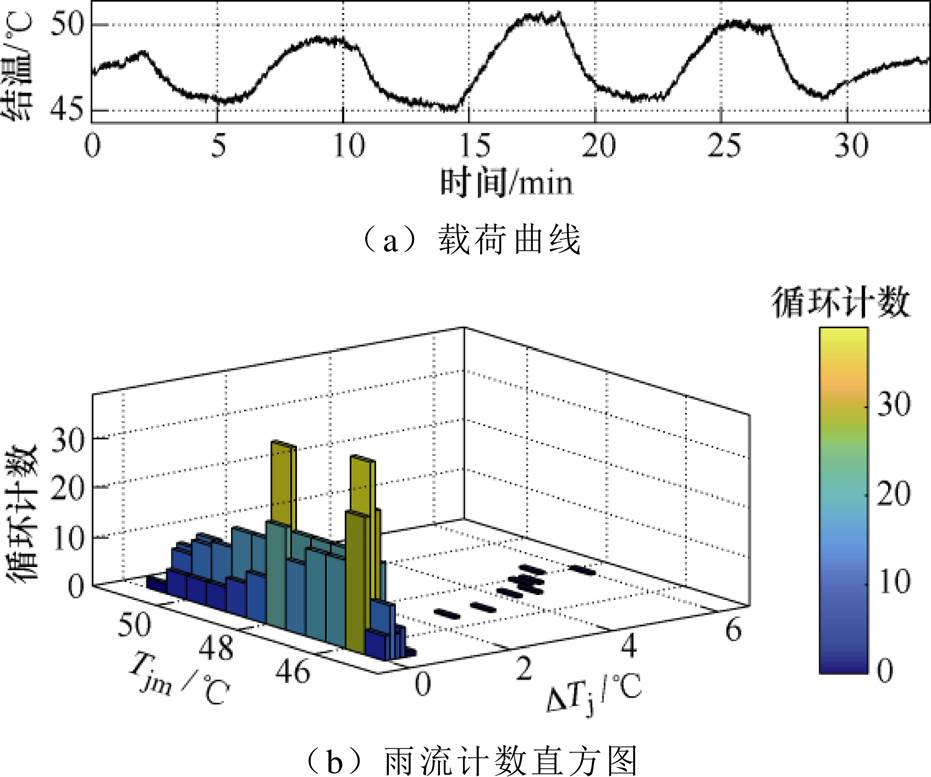
图8 使用热管理算法后的结温波动雨流计数结果
Fig.8 Rainflow counting result of junction temperature fluctuation with thermal regulation
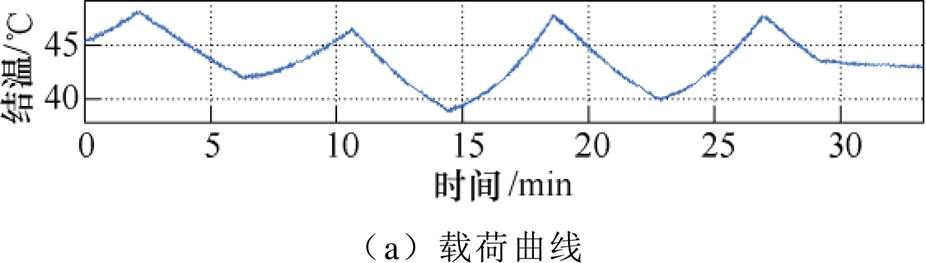
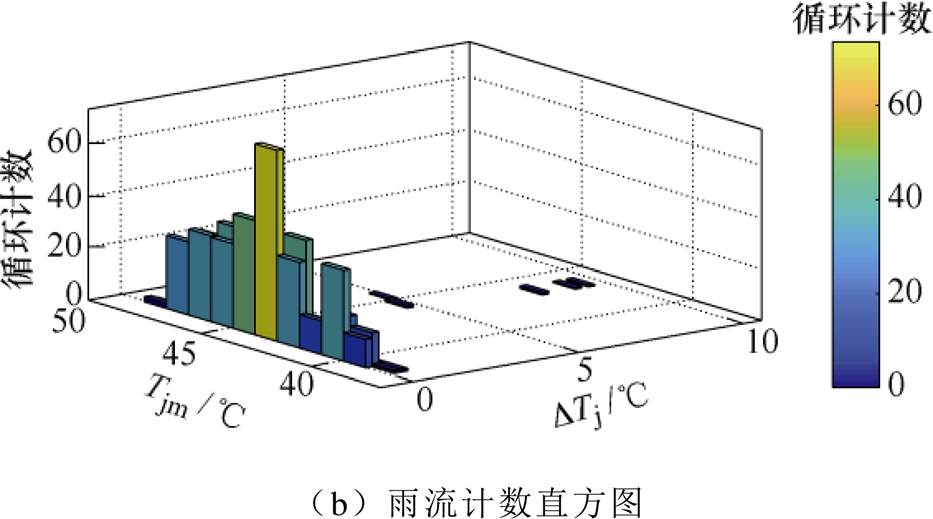
图9 未使用热管理算法后的结温波动雨流计数结果
Fig.9 Rainflow counting result of junction temperature fluctuation without thermal regulation
上述实验结温为模型计算所得,为验证模型的准确性和热管理算法的有效性,本文基于小电流注入法[25-27]对实验电路中DUT的结温进行了结温在线测量,并将测量结果和模型计算的结果进行对比。主电路拓扑结构如图10所示,其中,DUT为热管理对象,VT为额外新增的一个IGBT。
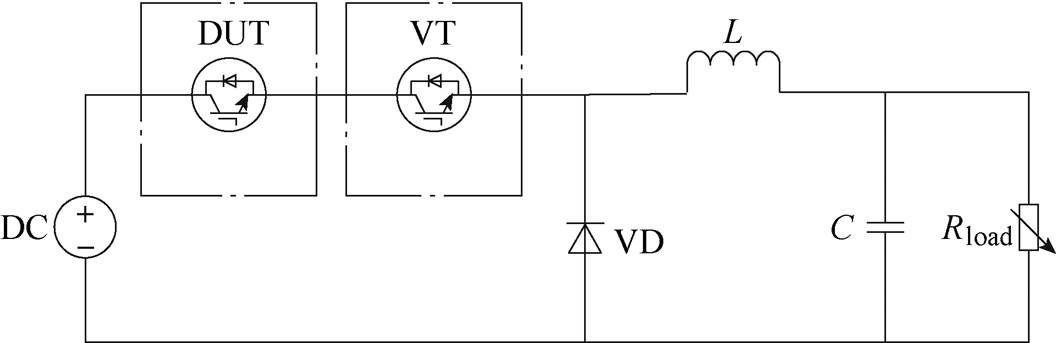
图10 主电路拓扑结构
Fig.10 Main circuit topology
为了使小电流注入法能够在线应用,需要在DUT正常关断的时间内,重新打开DUT并注入小电流,相应的IGBT的驱动时序如图11所示,其中VT的驱动信号为A信号,DUT的驱动信号为B信号。VT按Buck电路的控制正常开断,DUT在正常开断的基础上叠加一个额外的测量时序:即在DUT和VT正常关断后,将DUT重新打开以注入50mA小电流,经100ms的测量延时后,读取小电流下DUT的饱和压降,从而得到此时DUT的结温信息。与此同时,测量此时电路的负载电流大小,基于上一个测量周期测得的壳温数据得到基于模型计算的结温(假设测量延时内,壳温没有发生变化),并完成一组数据对比。在测量过程中,母线电压由VT阻断,不会影响原电路的功能。测量完成后,在VT开通前,将DUT关闭,以此循环。
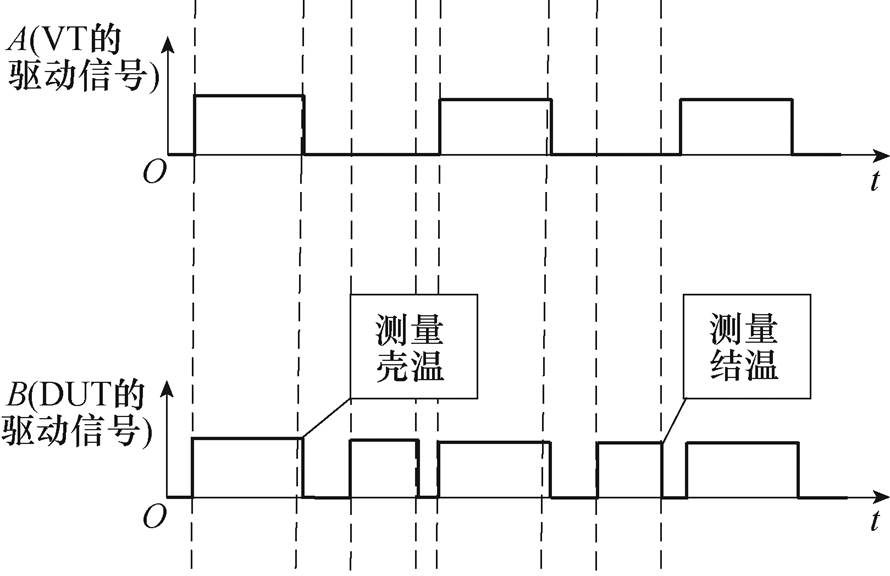
图11 IGBT的驱动时序
Fig.11 IGBT gate drive timing
基于上述时序,对模型计算的结温进行了验证,结果如图12、图13所示。图12为热管理时模型计算和实测结温的对比,图13为无热管理时模型计算和实测结温的对比。对比结果发现,两种情况下由模型计算的结温和实测结温相差较小,且变化趋势一致,可见模型较为准确,且使用模型预测结温的方法在IGBT热管理应用中具有较好的可行性。
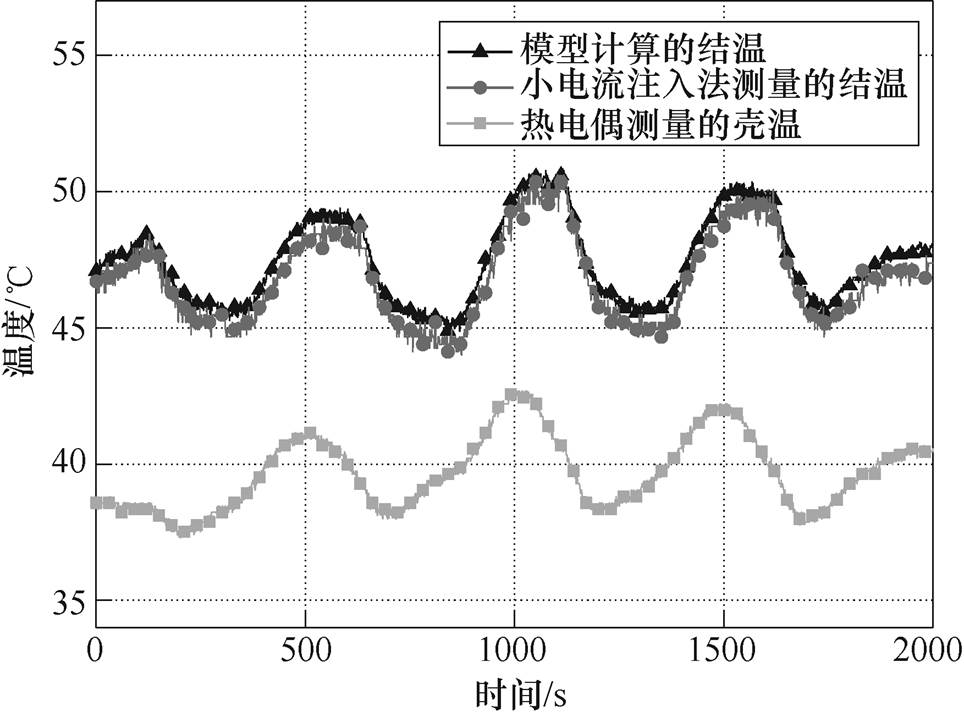
图12 热管理时模型计算和实测结温的对比
Fig.12 Comparison between model calculation and measured junction temperature with thermal regulation
IGBT模块的热管理技术能够平滑器件工作时的结温波动,提高变流器的可靠性。本文提出了一种IGBT外部热管理系统的建模方法,弥补了目前该研究领域中缺乏精确数学模型的现状,使得热管理控制系统设计具有了一定的理论支撑。该建模方法的泛用性较强,只需更改损耗计算模型,即可应用于各种需要进行热管理的变流器设备。本文主要研究内容和结论如下:
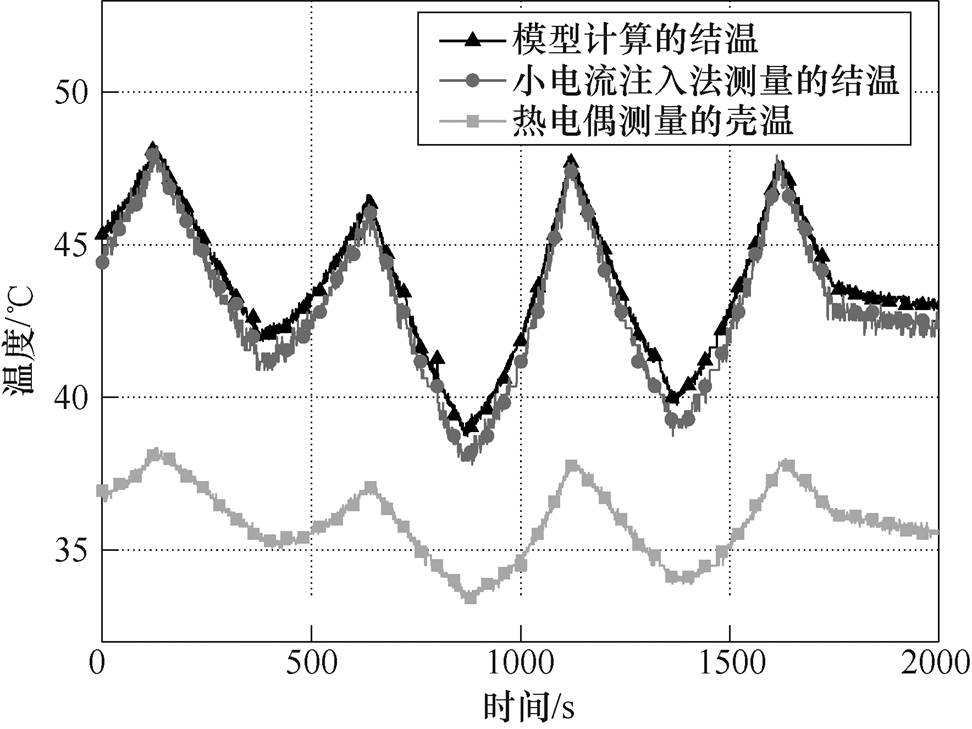
图13 无热管理时模型计算和实测结温的对比
Fig.13 Comparison between model calculation and measured junction temperature without thermal regulation
1)建立了IGBT模块和散热器的热网络模型并列写了状态空间方程,发现其中含有非线性成分,在热管理控制系统的设计中,难以应用常规的线性系统设计方法。
2)为了消除非线性成分对控制系统设计带来的困难,本文首次将状态反馈线性化的数学方法引入热管理系统建模中,推导出非线性坐标变化矩阵和状态反馈控制律,将模型中的非线性成分消去,实现了原系统的线性化,并基于无源性理论,设计了热管理闭环控制策略。
3)将所提建模和设计方法应用在Buck电路中。实验证明了所提方法的可行性,负载电流在额定值的60%~100%范围内变化时,该方法有效地降低了由于负载变化导致的低频结温波动,提高了IGBT约69倍的寿命。
参考文献
[1] Blaabjerg F, Liserre M, Ma Ke. Power electronics converters for wind turbine systems[J]. IEEE Transa- ctions on Industry Applications, 2012, 48(2): 708- 719.
[2] 王学梅, 张波, 吴海平. 基于失效物理的功率器件疲劳失效机理[J]. 电工技术学报, 2019, 34(4): 717-727.
Wang Xuemei, Zhang Bo, Wu Haiping. A review of fatigue mechanism of power devices based on physics-of-failure[J]. Transactions of China Electro- technical Society, 2019, 34(4): 717-727.
[3] Yang Yongheng, Sangwongwanich A, Blaabjerg F. Design for reliability of power electronics for grid- connected photovoltaic systems[J]. CPSS Transa- ctions on Power Electronics and Applications, 2016, 1(1): 92-103.
[4] 刘向向, 李志刚, 姚芳. 不同工作模式下的IGBT模块瞬态热特性退化分析[J]. 电工技术学报, 2019, 34(增刊2): 509-517.
Liu Xiangxiang, Li Zhigang, Yao Fang. Analysis of transient thermal degradation of IGBT modules under different operating modes[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 509-517.
[5] Wang Bo, Cai Jie, Du Xiong, et al. Review of power semiconductor device reliability for power con- verters[J]. CPSS Transactions on Power Electronics and Applications, 2017, 2(2): 101-117.
[6] Yang Shaoyong, Bryant A, Mawby P, et al. An industry-based survey of reliability in power elec- tronic converters[J]. IEEE Transactions on Industry Applications, 2011, 47(3): 1441-1451.
[7] Wu Junke, Zhou Luowei, Sun Pengju, et al. Smooth control of insulated gate bipolar transistors junction temperature in a small-scale wind power converter[J]. IET Power Electronics, 2016, 9(3): 393-400.
[8] 周雒维, 张益, 王博. 一种基于调节缓冲电容的IGBT热管理方法[J]. 电机与控制学报, 2019, 23(4): 28-36.
Zhou Luowei, Zhang Yi, Wang Bo. IGBT thermal management method based on snubber capacitor[J]. Electric Machines and Control, 2019, 23(4): 28-36.
[9] 吴军科, 周雒维, 王博, 等. 基于开关轨迹动态调整的变流器内部热管理[J]. 电源学报, 2016, 14(6): 46-52.
Wu Junke, Zhou Luowei, Wang Bo, et al. Internal thermal management of power converter based on switching trace adjustment[J]. Journal of Power Supply, 2016, 14(6): 46-52.
[10] Weckert M, Roth-Stielow J. Lifetime as a control variable in power electronic systems[C]//Emobility- Electrical Power Train, Leipzig, 2010: 1-6.
[11] 周雒维, 王博, 张益, 等. 非平稳工况下功率半导体器件结温管理技术综述[J]. 中国电机工程学报, 2018, 38(8): 2394-2407, 2549.
Zhou Luowei, Wang Bo, Zhang Yi, et al. Review on junction temperature management of power Semi- conductor devices under power fluctuation con- dition[J]. Proceedings of the CSEE, 2018, 38(8): 2394-2407, 2549.
[12] Wang Xiang, Castellazzi A, Zanchetta P. Observer based temperature control for reduced thermal cycling in power electronic cooling[J]. Applied Thermal Engineering, 2014, 64(1-2): 10-18.
[13] Wang Xiang, Wang Yun, Castellazzi A. Reduced active and passive thermal cycling degradation by dynamic active cooling of power modules[C]//IEEE 27th International Symposium on Power Semi- conductor Devices & IC's (ISPSD), Hong Kong, 2015: 309-312.
[14] Davidson J N, Stone D A, Foster M P. Real-time temperature monitoring and control for power electronic systems under variable active cooling by characterisation of device thermal transfer impe- dance[C]//7th IET International Conference on Power Electronics, Manchester, 2014: 1-6.
[15] Li Cong, Jiao Da, Jia Jizhou, et al. Thermoelectric cooling for power electronics circuits: modeling and active temperature control[J]. IEEE Transactions on Industry Applications, 2014, 50(6): 3995-4005.
[16] 姜长生, 吴庆宪, 费树岷. 现代非线性系统鲁棒控制基础[M]. 哈尔滨: 哈尔滨工业大学出版社, 2012.
[17] Murdock D A, Torres J E, Ramos T, et al. Active thermal control of power electronic modules[J]. IEEE Transactions on Industry Applications, 2006, 42(2): 552-558.
[18] Ciappa M. Selected failure mechanisms of modern power modules[J]. Microelectronics & Reliability, 2002, 42(4-5): 653-667.
[19] Scheuermann U, Hecht U. Power cycling lifetime of advanced power modules for different temperature swings[C]//8th PCIM Nuremberg, 2002: 59-64.
[20] 王希平, 李志刚, 姚芳. 模块化多电平换流阀IGBT器件功率损耗计算与结温探测[J]. 电工技术学报, 2019, 34(8): 1636-1646.
Wang Xiping, Li Zhigang, Yao Fang, et al. Power loss calculation and junction temperature detection of IGBT devices for modular multilevel valve[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(8): 1636-1646.
[21] Azoui T, Tounsi P, Pasquet G, et al. Dynamic compact thermal model for electrothermal modeling and design optimization of automotive power devices[C]// Thermal Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Micro- systems (EuroSimE), Linz, 2011: 1-6.
[22] Ma Ke, Liserre M, Blaabjerg F, et al. Thermal loading and lifetime estimation for power device considering mission profiles in wind power converter[J]. IEEE Transactions on Power Electronics, 2015, 30(2): 590-602.
[23] 帅定新, 谢运祥, 杨金明, 等. 基于状态反馈精确线性化单相全桥逆变器的最优控制[J]. 电工技术学报, 2009, 24(11): 120-126.
Shuai Dingxin, Xie Yunxiang, Yang Jinming, et al. Optimal control of single-phase full-bridge inverters by state feedback linearization[J]. Transactions of China Electrotechnical Society, 2009, 24(11): 120-126.
[24] 姚芳, 胡洋, 李铮, 等. 基于结温监测的风电IGBT热安全性和寿命耗损研究[J]. 电工技术学报, 2018, 33(9): 2024-2033.
Yao Fang, Hu Yang, Li Zheng, et al. Study on thermal safety and lifetime consumption of IGBT in wind power converters based on junction temperature monitoring[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 2024-2033.
[25] Bęczkowski S, Ghimre P, de Vega A R, et al. Online vce measurement method for wear-out monitoring of high power IGBT modules[C]//15th European Confer- ence on Power Electronics and Applications (EPE), Lille, 2013: 1-7.
[26] 王莉娜, 邓洁, 杨军一, 等. Si和SiC功率器件结温提取技术现状及展望[J]. 电工技术学报, 2019, 34(4): 703-716.
Wang Lina, Deng Jie, Yang Junyi, et al. Junction temperature extraction methods for Si and SiC power devices-a review and possible alternatives[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(4): 703-716.
[27] 任磊, 沈茜, 龚春英. 电力电子电路中功率晶体管结温在线测量技术研究现状[J]. 电工技术学报, 2018, 33(8): 1750-1761.
Ren Lei, Shen Qian, Gong Chunying. Overview of current junction temperature online measurement techniques of power transistors in power electronic converters[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1750-1761.
External Thermal Management of IGBT Based on State Feedback Linearization
Abstract Thermal management technology for insulated gate bipolar transistor (IGBT) can reduce junction temperature fluctuations during operation and improve the reliability of devices. In view of the nonlinear characteristics of the IGBT external thermal management system, an affine non-linear model of the system was established. The state feedback linearization method was introduced to linearize the system, which makes up for the current lack of accurate mathematical models in the design of IGBT thermal management control systems. Based on a linear quadratic regulator (LQR), a closed-loop control method was designed to smooth the low-frequency junction temperature fluctuations caused by load fluctuations during IGBT operation by adjusting external cooling conditions. The experimental verification based on the Buck circuit shows that the proposed algorithm can reduce the junction temperature fluctuation by about 60% and increase the life of the IGBT by about 69 times when the load current fluctuates within the range of 60%~100% of the rated value. Finally, the junction temperature was measured online based on the small current injection method, which verified the accuracy of the junction temperature calculation by the proposed model.
keywords:IGBT external thermal management, nonlinear system, state feedback linearization, IGBT reliability
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.200019
国家自然科学基金资助项目(51577020)。
收稿日期 2020-01-07
改稿日期 2020-05-29
孙 林 男,1994年生,硕士研究生,研究方向为功率半导体可靠性。E-mail: sunlin201f@qq.com
孙鹏菊 女,1982年生,教授,博士生导师,研究方向为并网逆变器稳定性分析、功率半导体可靠性等。E-mail: spengju.cqu.edu.cn(通信作者)
(编辑 陈 诚)