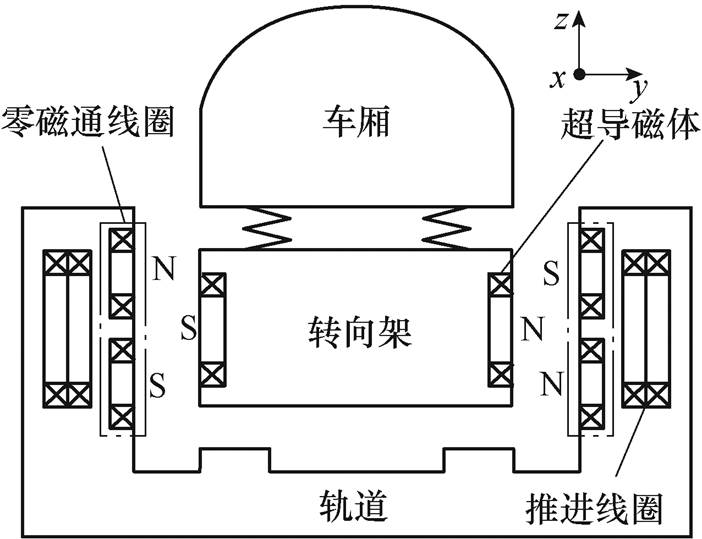
图1 超导电动悬浮列车结构示意图
Fig.1 Structure of superconducting EDS train
摘要 该文提出一种等效模拟零磁通式电动悬浮的系统，阐述系统的工作原理和结构组成，并结合有限元仿真与实验测试对系统的电磁力特性进行分析。建立系统的三维有限元模型，研究了线圈运动速度、磁体垂向与横向偏移、线圈极距对系统性能的影响规律。研制样机并进行实验测试，测试了不同工况下悬浮力的变化情况，并与仿真结果进行对比分析，证明了有限元模型的准确性与可靠性。另外，实验样机实现了磁体的起浮，为零磁通式电动悬浮在轨道交通的应用与设计提供了理论依据。
关键词：零磁通式电动悬浮 等效模拟 有限元分析 电磁力特性
目前一般认为传统轮轨列车的最高营运速度约为350km/h[1]，轮轨黏着力及弓网关系等因素限制其速度进一步提升，为达到更高效的运输要求，非接触运行的磁浮列车受到越来越多的关注。2019年9月，国家印发《交通强国建设纲要》提出研发“时速600km级的高速磁悬浮系统”。磁悬浮列车已成为未来高速轨道交通发展的一种趋势。
根据悬浮原理的不同，磁悬浮技术目前可大致分为常导电磁悬浮（Electromagnetic Suspension, EMS）和超导电动悬浮（Electrodynamic Suspension, EDS）[2-4]。电磁悬浮是依靠车载常导电磁铁与铁磁轨道相互吸引而实现列车悬浮，虽然德国将该技术开发得较为成熟，但其闭环控制系统复杂，且悬浮气隙较小（8～10mm），随着列车速度的提高，控制难度相应提高，且直线电机电枢绕组的电阻较大，在列车高速大推力运行时，铜耗和铁耗均较大，导致电机绕组发热严重，运行效率低[1]；而超导电动悬浮技术是利用车载超导磁体与地面轨道线圈之间感应耦合而产生的排斥性悬浮力使列车悬浮，虽然该种悬浮方式在静止或低速下无法实现悬浮，但在高速下具有高浮阻比、悬浮间隙大（约100mm）、自稳定等优势[5]。因此，就未来轨道交通发展需要的高速运行工况而言，超导电动悬浮技术更具优势。
电动磁悬浮列车由美国的J. R. Powell和G. T. Danby于1966年提出[6]。随后，世界多国纷纷投入到这种新颖悬浮方式的研究中[7-20]。而日本自电动磁悬浮列车概念提出至今，一直坚持对超导电动悬浮技术进行研究。日本铁科院不仅建立了电动磁悬浮列车电磁力解析计算模型，还在此基础上，结合动力学方程，引入阻尼线圈对列车振动进行优化设计，研究表明，半主动控制的阻尼线圈在减小供电量的同时，可有效抑制电动磁悬浮列车的振动[13]。在工业应用上，日本不断对电动磁悬浮列车进行更新换代，至今已研发了ML、MLU、MLX系列及基于MLX的L0车型。2015年，日本研发的L0系列电动磁悬浮列车达到了603km/h的地面轨道交通最高速度，引起了媒体和国际铁路行业的高度关注。另外，列车最高设计速度为500km/h的日本磁悬浮中央新干线（东京至名古屋区间，共286km）预计于2027年开通运营[14-15]。
而中国对电动磁悬浮列车的研究目前只处于起步阶段。万尚军等基于场-路相结合的分析方法，通过等效电路矩阵微分方程对地面线圈感应电流进行求解，采用虚位移法得到列车不同工况下的电磁力，对比分析了有无横向交叉连接结构的悬浮与导向性能。结果表明，横向交叉连接能有效地提高列车的悬浮与导向刚度，增强系统的稳定性[16]。王志涛等基于动态电路理论，结合谐波近似与毕奥萨伐尔定律推导了超导磁体与地面线圈之间的时变互感计算公式，基于动态电路理论建立了电动磁悬浮列车的场-路-运动耦合模型，采用能量法对列车的电磁力进行计算，并利用日本山梨实验线数据对计算模型进行验证[19]。陈殷等针对现有单边导体板式电动悬浮浮阻比小的缺点，提出了一种由导体板与双边Halbach永磁阵列构成的悬浮系统，建立并求解了空间矢量磁位方程，结合计算得到涡流分布与空间磁场，推导电磁力的二维数学表达式，并通过有限元仿真对解析模型进行验证[20]。由此可知，国内对电动悬浮列车的研究尚停留于理论阶段，实验论证较少，这难以实现电动磁悬浮列车在国内的应用化与运营化。而对电动磁悬浮列车进行实验研究，最直接、最理想的方式是建立全尺寸或缩比实验线对列车工况进行模拟，但由于电动磁悬浮列车需要一定的速度才能起浮，其实验线存在占用空间大、建设时间长、投资成本高等问题。因此，本文提出一种等效模拟零磁通式电动悬浮系统，可在室内完成对电动悬浮列车的等效模拟实验，建立三维有限元仿真模型，对系统的电磁力及其特性进行计算分析，并研制实验样机，通过实验测试来验证仿真模型的准确性。本文的研究成果将为电动悬浮实验研究提供参考，同时为电动悬浮的应用与设计提供理论 依据。
日本山梨实验线超导电动悬浮列车结构示意图[1]如图1所示。零磁通线圈与推进线圈沿x轴在轨道上均匀铺设，而超导磁体则放置于列车下部的转向架中。列车沿x轴方向运行时，车载磁体产生的移动磁场会切割零磁通线圈，而零磁通线圈独特的交叉连接结构使线圈上下两回路感应出方向相反的电流，如图2所示。
图1 超导电动悬浮列车结构示意图
Fig.1 Structure of superconducting EDS train
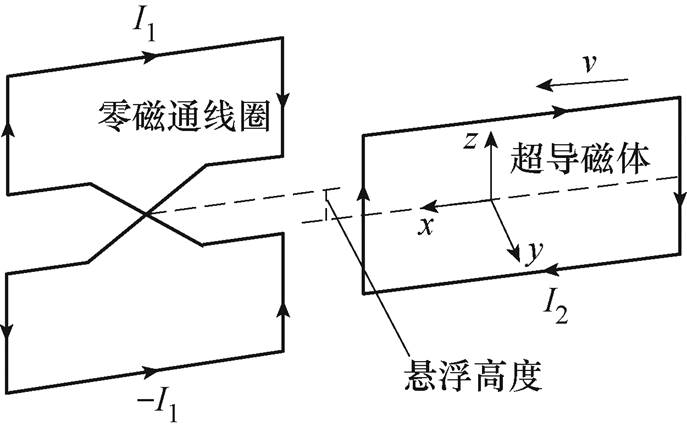
图2 零磁通线圈与超导磁体结构
Fig.2 Structure of null-flux coil and superconducting magnet
下回路线圈对车载磁体产生向上的排斥力，上回路线圈对车载磁体产生向上的吸引力，该悬浮力会随着列车速度增加而提高。列车静止或低速运行时，需依靠车载辅助轮进行支撑，而当列车达到一定速度时，悬浮力大于车载重力，列车可实现悬浮。
由此可知，电动悬浮系统主要由车载磁体、零磁通线圈组成，而车载磁体与零磁通线圈之间的相对运动是产生悬浮力的关键。本文建立了一种室内等效模拟装置，将零磁通线圈分为两组分别放置于磁体两侧的对称位置，每组零磁通线圈沿圆周方向均匀排布，电动悬浮等效方法如图3所示。保持磁体静止的同时使两侧零磁通线圈反向同步旋转，即可将实际电动磁悬浮列车车载磁体的直线运动等效为零磁通线圈的旋转运动。
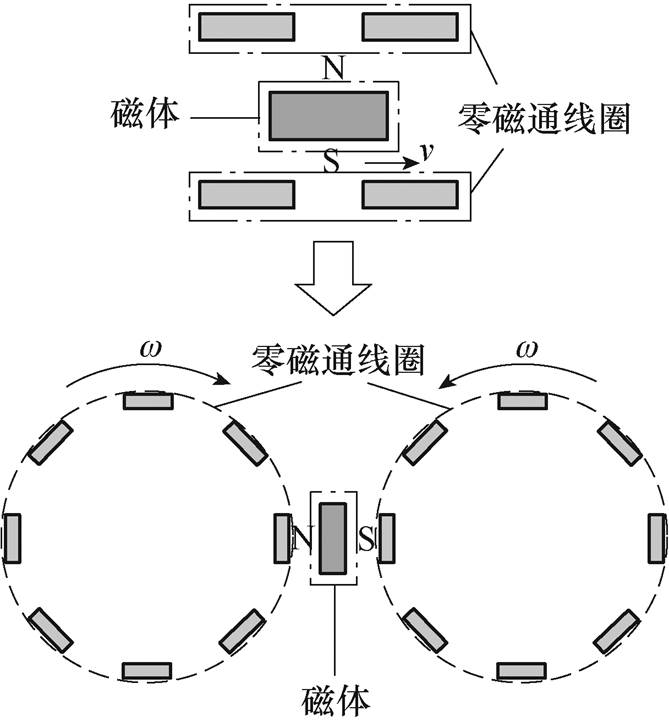
图3 电动悬浮等效方法
Fig.3 Equivalent method of EDS
本文采用永磁体替换了作为场源的超导磁体，将永磁体安装于与力传感器连接的夹具中，零磁通线圈安装于永磁体两侧的圆筒中，通过步进电机驱动两侧圆筒反向同步旋转，即可实现对电动悬浮系统的等效模拟，系统运行中永磁体与零磁通线圈之间的电磁力可由力传感器测得，图4为电动悬浮等效模拟系统结构。
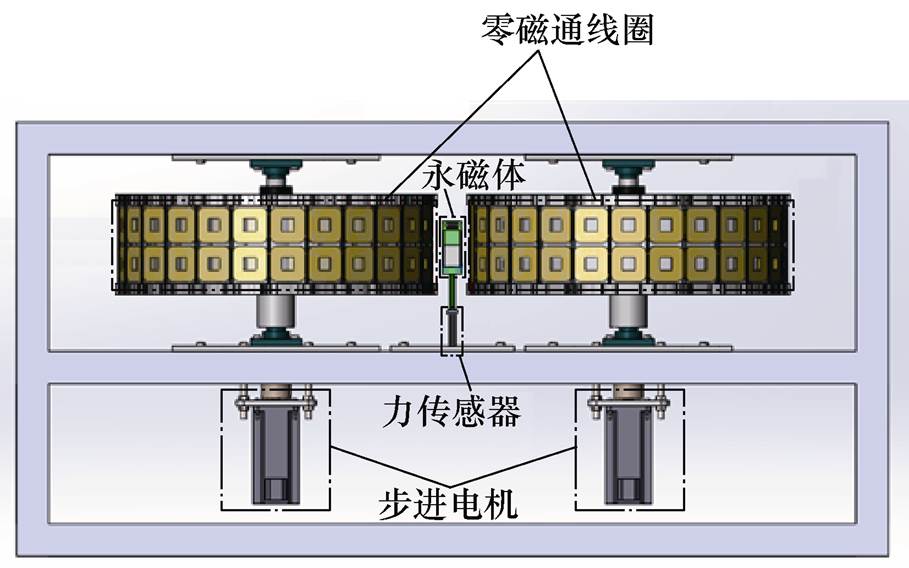
图4 电动悬浮等效模拟系统结构
Fig.4 Structure of EDS equivalent simulation system
为探究电动悬浮等效模拟系统的电磁力特性，本文建立了如图5所示的三维有限元模型，该模型主要由永磁体、零磁通线圈以及外部的空气域组成。由于模型中两侧零磁通线圈左右对称分布、距离较远，其相互影响可忽略不计，因此该模型只建立了单侧的零磁通线圈做等效计算。单侧零磁通线圈与永磁体之间电磁力的两倍即为电动悬浮等效模拟系统的总电磁力。表1给出了电动悬浮等效模拟系统的具体尺寸参数。
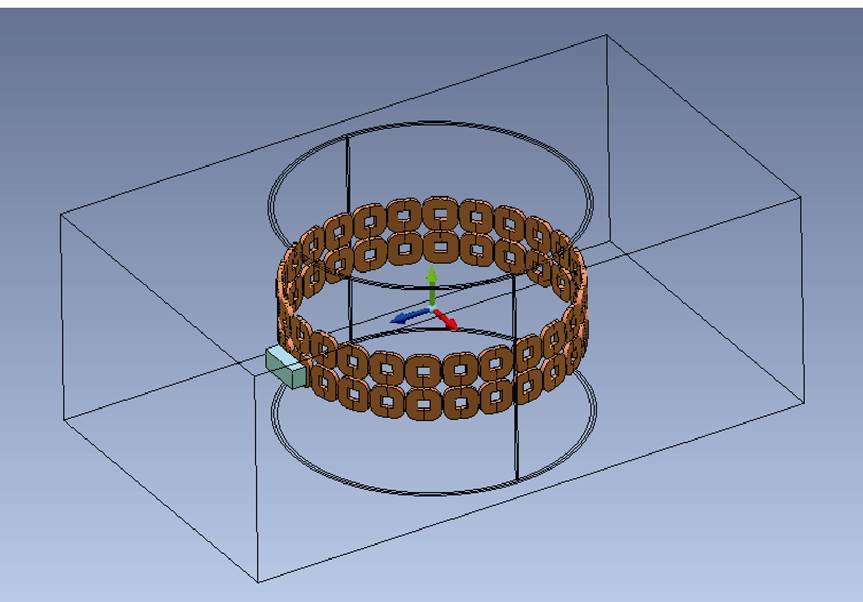
图5 电动悬浮等效模拟系统三维有限元模型
Fig.5 3-D finite element model of the EDS equivalent simulation system
模型建立完成后，再通过材料设置、电路搭建、网格剖分、边界设置、瞬态求解及后处理分析，即可计算永磁体在不同线圈转速、悬浮高度、横向偏移等状态下的电磁力。
表1 电动悬浮等效模拟系统尺寸参数
Tab.1 Specifications of the EDS equivalent simulation system
参 数数 值 永磁体长度/mm95 永磁体宽度/mm30 永磁体高度/mm40 永磁体牌号N52 零磁通线圈长度/mm138 零磁通线圈宽度/mm66 零磁通线圈厚度/mm9 零磁通线圈铜线线径/mm0.25 零磁通线圈匝数2 448 零磁通线圈旋转半径/mm285.5
由于电动悬浮是依靠地面线圈感应电流与车载磁体磁场作用而产生悬浮力，因此产生悬浮力的同
时必然会产生阻碍车体向前运动的磁阻力。由安培定律可知，悬浮线圈中的竖直边上的感应电流是产生磁阻力的主要因素。而零磁通线圈的特殊结构，使上下两侧回路竖直边上的感应电流反向，从而令上下两侧回路磁阻力反向，最终使总磁阻力较小，这是零磁通式电动悬浮系统具有高浮阻比的原因。
图6为悬浮高度20mm，无横向偏移，悬浮力及磁阻力随线圈转速的变化曲线。由图可知，当线圈转速为零时，由于永磁体与零磁通线圈之间无相对运动，零磁通线圈中没有感应电流，此时永磁体不受电磁力。悬浮力随着线圈转速增加而增加，当线圈转速约为4 000r/min时，悬浮力达到24N，之后随着线圈转速的增加，悬浮力增加缓慢，趋于饱和。基于电磁感应定律和洛伦兹定律，由式（1）可知，线圈转速的增加使其磁通变化率增大，进而提升感应电动势
，而随着转速进一步加快，感应电流角频率
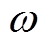的增加使线圈感抗增大，最终使线圈阻抗
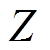上升，感应电流
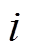增加缓慢，趋于稳定；而由式（2）可知，零磁通线圈稳定的感应电流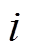及磁体在线圈处产生的磁感应强度
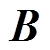会使悬浮力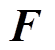
达到饱和状态。
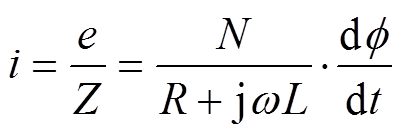（1）
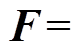
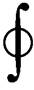
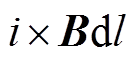（2）
式中，N、L、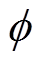
分别为零磁通线圈的匝数、电感及磁通。
就磁阻力而言，它会随着转速的增加先达到一个峰值，之后便会逐渐减小，这是由于磁阻力反映的是系统欧姆损耗，速度达到一定值后，线圈感应电流和电阻都保持恒定，即欧姆损耗功率不变，从而使磁阻力随着速度的提升而下降。由此可知，浮阻比随线圈转速的增大而增大，因此电动悬浮系统在高速工况下具有很高的浮阻比，这也是电动悬浮在高速领域应用的一个关键优势。
图6 不同转速时的电磁力变化曲线
Fig.6 Characteristic curves of electromagnetic forces with the change of rotational speed
电动悬浮系统的另一个优势在于其无需复杂控制系统的自稳定性，当磁体与地面线圈中相对位置发生偏移时，磁体所受电磁力也会发生相应变化从而使磁体恢复到原始位置。本节将基于有限元模型，对电动悬浮等效模拟系统的自稳定性进行分析。
图7描述了线圈转速为4 400r/min，无横向偏移，悬浮力及磁阻力随悬浮高度的变化曲线。当悬浮高度为零时，由于零磁通线圈中上下两侧回路中磁通相等，使两侧回路感应电动势抵消，此时无电磁力产生；随着悬浮高度的增加，悬浮力呈现出先增后减的趋势，即在一定悬浮高度变化范围内，电动悬浮系统存在自稳定性，但若磁体的悬浮高度越过这一范围，电动悬浮系统稳定性就会下降；而磁阻力随着悬浮高度的增加一直提升。
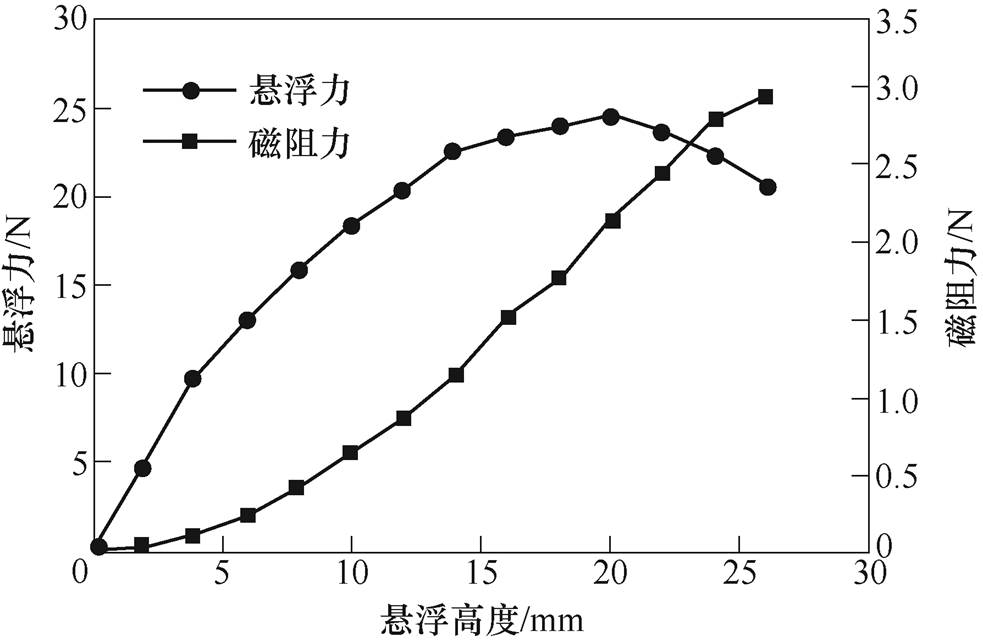
图7 不同悬浮高度时的电磁力变化曲线
Fig.7 Characteristic curves of electromagnetic forces with the change of levitation height
图8描述了线圈转速为4 400r/min，悬浮高度20mm，悬浮力、导向力、磁阻力随横向偏移的变化曲线。当横向偏移为零时，磁体所受两侧零磁通线圈的排斥力等大反向，体现为导向力为零；随着横向偏移的增加，导向力逐渐增大，充分体现了电动悬浮系统的横向自稳定性。由图8可知，随着横向偏移的增加，悬浮力和磁阻力也在不断增大。
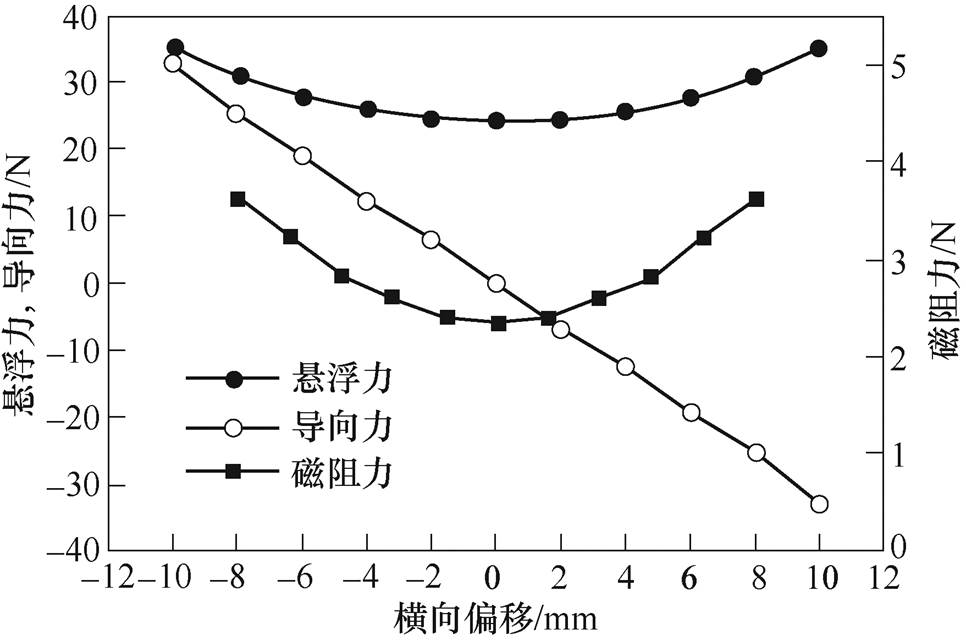
图8 不同横向偏移时的电磁力变化曲线
Fig.8 Characteristic curves of electromagnetic forces with the change of transverse displacement
因此，在设计电动悬浮系统时，应合理设计悬浮高度和横向偏移的变化区间，在满足悬浮载荷要求的前提下，需要保证系统的稳定性，且尽量降低系统磁阻力以提高运行效率。
图9描述了线圈转速4 400r/min，悬浮高度20mm，无横向偏移，不同线圈极距下的悬浮力随时间变化曲线。可以看出，悬浮力随时间周期性波动变化，其变化周期为
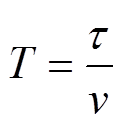（3）式中，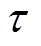
为线圈极距；
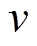为线圈运动速度。随着线圈极距的增加，悬浮力变化越来越慢，虽然悬浮力波峰值基本保持不变，但其波谷值逐渐减小，即悬浮力变化幅值逐渐增大，且总悬浮力呈下降趋势。
所以，在具有足够安装尺寸的条件下，减小线圈极距可提升电动悬浮系统的悬浮力及其稳定性。
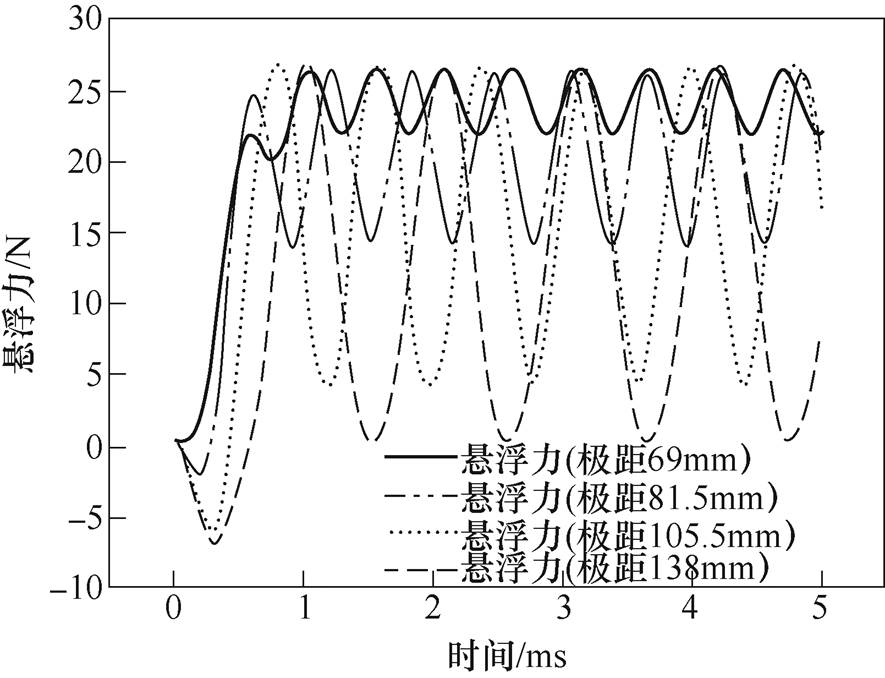
图9 不同线圈极距下的悬浮力随时间变化曲线
Fig.9 Time-dependent curves of levitation force with the change of coil pitch
为了对有限元模型的有效性和可靠性进行验证，根据表1参数研制了电动悬浮等效模拟系统样机，对悬浮力进行了测试，并实现了永磁体的悬浮。
图10为研制的电动悬浮等效模拟系统，系统整机主要由永磁体、零磁通线圈、磁体夹具、线圈安装圆筒、步进电机、力传感器、工业铝型材框架等组成。通过该系统可对不同工况下的电磁力进行模拟和测试。
图10 电动悬浮等效模拟系统
Fig.10 EDS equivalent simulation system
图11展示了在永磁体悬浮高度分别为11mm、16mm、21mm，永磁体与零磁通线圈之间的气隙分别为10mm、15mm的条件下，悬浮力随线圈转速变化的仿真与实验对比曲线。由图可知，随着线圈转速的增加，悬浮力逐渐增大，这与2.2节中的仿真分析一致；而气隙的减小会导致零磁通线圈处的磁场增加，从而使悬浮力提升。由仿真计算曲线和实验测试曲线对比可知，在转速较低时，仿真计算值和实验测试值吻合较好；但在高转速的情况下，实验测试值均大于仿真计算值，这是由于随着转速增加线圈所受离心力加大，旋转圆筒变形使线圈与磁体之间的气隙更小，从而导致悬浮力的实测值大于仿真值；测试结果验证了计算模型的准确性。
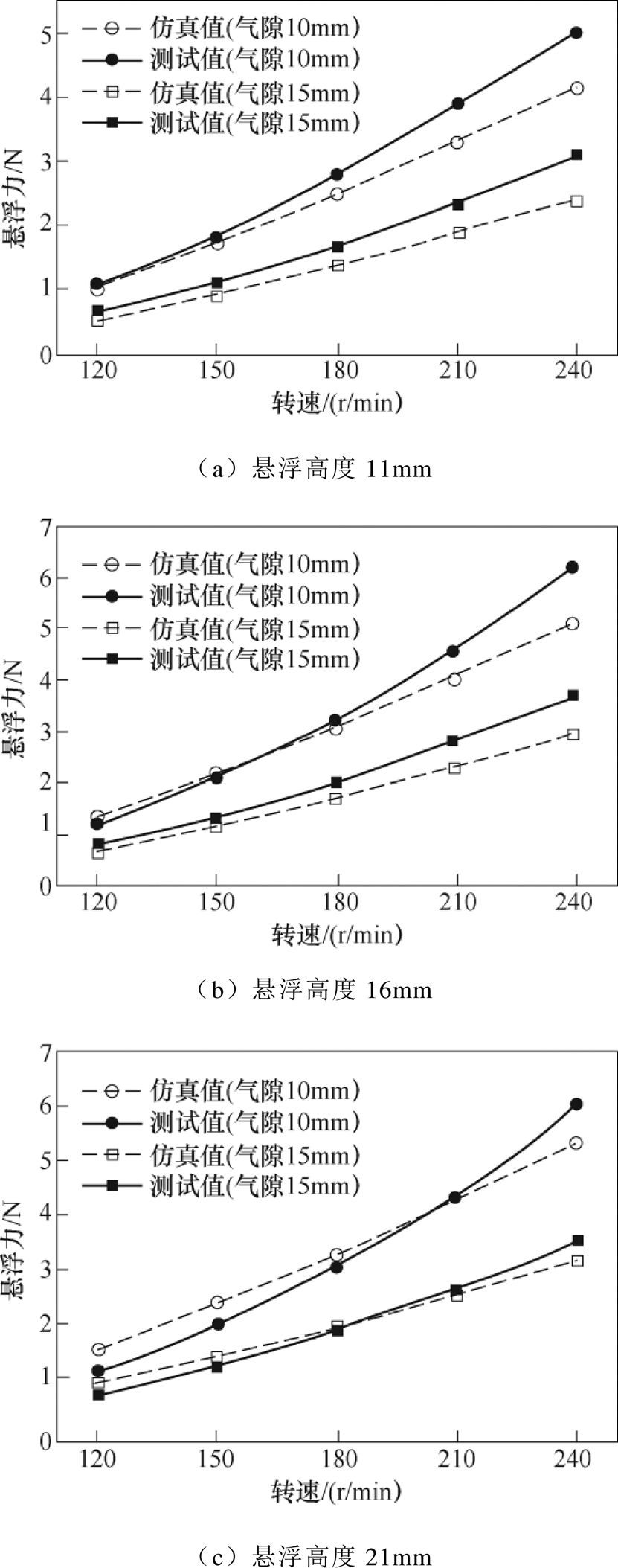
图11 悬浮力的实验测试与仿真计算对比
Fig.11 Comparison of levitation force between the measurement and the simulation
当永磁体起浮高度为20mm，永磁体与零磁通线圈气隙为15mm，线圈转速为390r/min时，可实现永磁体的悬浮，如图12所示。
图12 永磁体悬浮
Fig.12 Levitation of the permanent magnet
由上述仿真及实验结果可知，该实验样机的悬浮力还远不能满足实际应用中电动磁悬浮列车承载力的需求，但基于上述设计，实验样机的悬浮力已能够平衡永磁体的自重，实现永磁体的悬浮，再现了零磁通电动磁悬浮的物理原理。同时，实验与仿真结果吻合较好，证实了有限元计算模型的准确性。基于该有限元计算模型，通过变化零磁通线圈的几何尺寸，将永磁体替换为磁场更强的超导磁体，可以实现对实际应用的超导电动磁悬浮列车的性能模拟。
本文提出了一种零磁通式电动悬浮等效模拟系统，将车载磁体的直线运动等效为零磁通线圈的旋转运动，可在室内完成电动悬浮系统的模拟，结合有限元仿真与实验测试对系统的电磁力特性进行研究分析。建立三维有限元仿真模型，分析了悬浮力、导向力、磁阻力随线圈转速、悬浮高度、横向偏移、线圈极距的变化规律。研制样机并搭建实验平台，通过对悬浮力的测试与对比分析，验证了有限元模型的准确性。研究结果表明，零磁通电动悬浮系统在高速领域具有高的浮阻比，在一定偏移范围内具有较好的稳定性，线圈极距的减小可有效地提高悬浮力并减小其波动幅值。最终，通过该等效模拟系统实现了永磁体的悬浮。
参考文献
[1] 魏庆朝, 孔永健. 磁悬浮铁路系统与技术[M]. 北京:中国科学技术出版社, 2003.
[2] 程建峰, 苏晓峰. 磁悬浮列车的发展及应用[J]. 铁道车辆, 2003, 41(11): 14-17.
Cheng Jianfeng, Su Xiaofeng. Development and application of magnetic levitation trains[J]. Rolling Stock, 2003, 41(11): 14-17.
[3] 王家素, 王素玉. 超导技术应用[M]. 成都: 成都科技大学出版社, 1995.
[4] Lee H W, Kim K C, Lee J. Review of Maglev train technologies[J]. IEEE Transactions on Magnetics, 2006, 42(7): 1917-1925.
[5] 温旭辉, 徐善纲. 电动式磁悬浮系统分析综述[J]. 电工电能新技术, 1995, 14(3): 7-11.
Wen Xuhui, Xu Shangang. Analysis of electro- dynamic levitation systems[J]. Advanced Technology of Electrical Engineering and Energy, 1995, 14(3): 7-11.
[6] Powell J R, Danby G T. High speed transport by magnetically suspended trains[C]//ASME Winter Annual Meeting, New York, 1966: 66-WA/RR-5.
[7] Guderjahn C A, Wipf S L, Fink H J, et al. Magnetic suspension and guidance for high speed rockets by superconducting magnets[J]. Journal of Applied Physics, 1969, 40(5): 2133-2140.
[8] Davis L C, Borcherts R H. Superconducting paddle wheels, screws, and other propulsion units for high- speed ground transportation[J]. Journal of Applied Physics, 1973, 44(7): 3294-3299.
[9] Kyotani Y. Recent progress by JNR on Maglev[J]. IEEE Transactions on Magnetics, 1988, 24(2): 804- 807.
[10] Nakashima H. The superconducting magnet for the Maglev transport system[J]. IEEE Transactions on Magnetics, 1994, 30(4): 1572-1578.
[11] Rote D M, Cai Yigang. Review of dynamic stability of repulsive-force Maglev suspension systems[J]. IEEE Transactions on Magnetics, 2002, 38(2): 1383- 1390.
[12] 秦伟, 范瑜, 徐洪泽, 等. 高温超导运动磁场电磁Halbach初级结构直线感应磁悬浮电机[J]. 电工技术学报, 2018, 33(23): 5427-5434.
Qin Wei, Fan Yu, Xu Hongze, et al. A linear induction Maglev motor with HTS traveling magnetic electromagnetic Halbach array[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5427- 5434.
[13] Ohashi S, Ueshima T. Control method of the semi- active damper coil system in the superconducting magnetically levitated bogie against vertical and pitching oscillation[J]. IEEE Transactions on Magnetics, 2012, 48(11): 4542-4545.
[14] Ono M, Koga S, Ohtsuki H. Japan’s superconducting Maglev train[J]. IEEE Instrumentation and Measure- ment Magazine, 2002, 5(1): 9-15.
[15] Kim M, Jeong J H, Lim J, et al. Design and control of levitation and guidance systems for a semi-high-speed Maglev train[J]. Journal of Electrical Engineering and Technology, 2017, 12(1): 117-125.
[16] 万尚军, 钱金根, 倪光正, 等. 电动悬浮型磁悬浮列车悬浮与导向技术剖析[J]. 中国电机工程学报, 2000, 20(9): 22-25, 31.
Wan Shangjun, Qian Jingen, Ni Guangzheng, et al. Study of the levitation and guidance technology for electrodynamic suspension Maglev vehicle[J]. Pro- ceedings of the CSEE, 2000, 20(9): 22-25, 31.
[17] 李春生, 杜玉梅, 夏平畴, 等. 直线型Halbach磁体和导体板构成的电动式磁悬浮系统的分析及实验[J]. 电工技术学报, 2009, 24(1): 18-22.
Li Chunsheng, Du Yumei, Xia Pingchou, et al. Analysis and experimental testing of EDS Maglev with linear Halbach and conducting sheet[J]. Transa- ctions of China Electrotechnical Society, 2009, 24(1): 18-22.
[18] 朱熙, 范瑜, 李硕, 等. 旋转磁场电动式磁悬浮装置的状态方程与悬浮力控制[J]. 电工技术学报, 2011, 26(12): 1-6.
Zhu Xi, Fan Yu, Li Shuo, et al. State equations and lift force control of rotating field electrodynamic levitation device[J]. Transactions of China Electro- technical Society, 2011, 26(12): 1-6.
[19] 王志涛, 蔡尧, 龚天勇, 等. 基于场-路-运动耦合模型的超导电动悬浮列车特性研究[J]. 中国电机工程学报, 2019, 39(4): 1162-1171.
Wang Zhitao, Cai Yao, Gong Tianyong, et al. Characteristic studies of the superconducting electro- dynamic suspension train with a field-circuit-motion coupled model[J]. Proceedings of the CSEE, 2019, 39(4): 1162-1171.
[20] 陈殷, 张昆仑. 板式双边永磁电动悬浮电磁力计算[J]. 电工技术学报, 2016, 31(24): 150-156.
Chen Yin, Zhang Kunlun. Calculation of electro- magnetic force of plate type null double side permanent magnet electrodynamic suspension[J]. Transactions of China Electrotechnical Society, 2016, 31(24): 150-156.
Characteristic Analysis and Experiment of the Equivalent Simulation System for Null-Flux Electrodynamic Suspension
Abstract An equivalent null-flux electrodynamic suspension (EDS) simulation system was proposed, and its working principle and structure were described. The electromagnetic force characteristics of the system were analyzed by finite element simulation and experiment. A 3-D finite element model of the system was established, and then the effects of the coil velocity, the vertical and transverse displacement of the magnet, and the coil pitch on system performance were analyzed. A laboratory prototype was developed and tested. The variation of levitation force under different working conditions was tested. Comparisons between simulation and experiment have verified the accuracy and reliability of the finite element model. In addition, the laboratory prototype can realize the levitation of the magnet, which can provide theoretical support for the application and design of the null-flux EDS in rail transit．
keywords：Null-flux electrodynamic suspension, equivalent simulation, finite element analysis, electromagnetic force characteristics
中图分类号：U237
DOI: 10.19595/j.cnki.1000-6753.tces.200056
国家自然科学基金项目（52072318, 51722706）和四川省科技厅项目（2020ZYD010）资助。
收稿日期 2020-01-09
改稿日期 2020-03-03
王一宇 男，1996年生，硕士研究生，研究方向为磁悬浮理论及应用。E-mail: wangyiyu_swjtu@163.com
马光同 男，1982年生，研究员，博士生导师，研究方向为磁悬浮理论及应用。E-mail: gtma@swjtu.edu.cn（通信作者）
（编辑 崔文静）