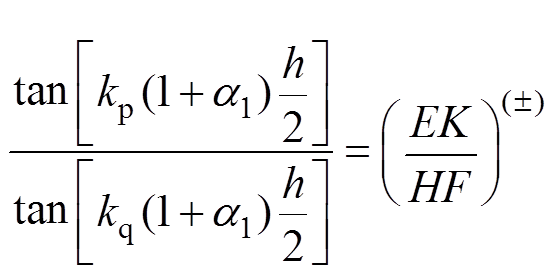 (1)
(1)摘要 鉴于兰姆波(Lamb波)在传播过程中衰减较慢,利用超声Lamb波对金属薄板的应力检测已成为国内外研究的热点。为了更深入了解Lamb波的传播特性与金属薄板应力之间的关系,该文根据Lamb波在各向同性板的频散计算公式,给出单向载荷不同应力下铝板的频散曲线,并数值分析了Lamb波基本模态和一阶模态与应力场在同方向上的传播变化。根据频散方程的计算结果,Lamb波A1模态在速度变化方面比使用其他模态要敏感;且越接近截止频率的一阶模态速度变化越明显。为了验证仿真结果,实验施加单向应力载荷作用于1mm厚的6061铝板,考虑到压电探头激发多模态特性,该文利用电磁超声换能器激发单模态Lamb波,对比基本模态与一阶模态相速度变化率,A1模态的波速变化明显,实验结果与仿真数据相符。因此,该文提出的单向应力加载下超声Lamb波传播特性的研究可为后续金属薄板应力检测提供重要依据。
关键词:Lamb波 电磁超声 应力加载 传播特性
板状构件尤其是厚度3mm以下的薄板,无论在航天工业、国防工业、汽车工业中都有广泛的应用。在实际的工程应用中,机械的振动、结构体的变形引起的外应力对薄板的影响较大[1]。超声兰姆(Lamb)波常应用于金属薄板高效无损检测技术 中[2],与体波相比,导波中的Lamb波具有传播距离长、效率高、灵敏度强、衰减小等优点[3]。因此,研究应力加载下金属薄板中Lamb波的传播特性,分析不同模态的信号特征,可以为薄板应力检测提供可靠的理论基础。
文献[4-5]中提出Lamb波对结构性质、温度和应力的变化非常敏感。上海大学张林文研究了各向同性板和多层复合板(常见板结构材料)中的Lamb波频散特性[6]。尽管如此,针对金属薄板的应力研究,关于Lamb波频散特性的表征问题以及相关声弹性理论的提出还很少。N. Gandhi等提供了一种较为全面的声弹性公式来分析初始各向同性板中双轴载荷的影响[7]。M. Munawwar等分析了在弹性非线性理论[8],并基于R. W. Ogden提出的不变公式的理论[9],研究了均匀应力对Lamb波传播的影响,但缺乏实验证明。Shi Feng等针对初始各向同性材料提出一种通过测量相速度变化来估计均匀双轴载荷的方法,但实验验证仅限于应用单向载荷[10]。Pei Ning等分析了施加应力对高阶Lamb波模态的影响关系,利用压电探头调节角度激励Lamb波的不同模态进行实验验证[11]。B. Ghodrati等利用耦合应力理论绘制了高频积下的相速度与群速度的频散曲线,研究了Lamb波在高频下的微观结构效应[12]。结果表明,在一定的范围下,预应力大小对基本模态和一阶模态的相位和群速度有显著影响。Ren Weiping等采用基于磁致伸缩的电磁超声换能器(Electromagnetic Acoustic Transducer, EMAT)在4mm厚钢板上产生S0 Lamb波,并利用EMAT探测到的S0 Lamb波信号的峰值对应力进行评估[13]。大多文献研究集中在载荷对压电超声探头激发的Lamb波基本模态的影响,缺少应力与电磁超声Lamb波基本模态和高阶模态的数值关系,没有直观反映应力对Lamb波传播特性的影响规律;且传统的压电探头依赖耦合剂,对耦合要求较高,受环境因素影响较大,所产生的Lamb波具有模态复杂、指向性较差的缺点,因而增加回波信号分析难度[14];较之压电超声换能器,EMAT为非接触型超声换能器,通过电磁耦合的方式在试件内部激发出超声波,具有低耦合、对检测表面要求低以及成本低的优点。更重要的是,电磁超声能高效、快捷地激发出特定频率的单一模态超声波[15],抑制其余模态的干扰,有利于研究应力加载对特定模态波的影响特性,增加模态的辨识度,方便后期数据处理。因此本文对此进行研究,为深入了解电磁超声Lamb波传播过程的应力响应特性奠定基础。
考虑到压电探头在薄板中激发出的超声导波具有多模态特性,研究采用电磁超声换能器激发超声Lamb波。本文的主要工作是研究应力加载下电磁超声Lamb波各模态的传播特性。基于应力与Lamb波同方向传播时的频散方程,对铝板中Lamb波在不同模态下应力与速度的变化进行数值计算,同时考虑声弹性效应,分析外加应力载荷、频厚积等参数对Lamb波传播特性的影响并总结规律,最后进行实验验证。
本研究采用文献[16-17]提出的理论分析,通过考虑声弹性效应和各向同性金属薄板中在单向载荷作用下Lamb波各向异性理论,得到波速与应力同方向情况下的Lamb波声弹性的频散方程为
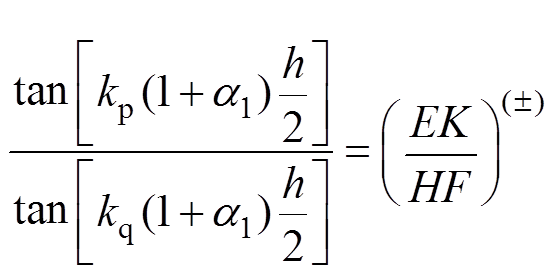 (1)
(1)式中,正号为对称模态;负号为反对称模态。kp、kq为Lamb波波数kx的变量函数;a1为施加单向应力下由泊松效应引起的位移变量系数;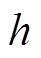 为板材厚度;E、H为波数kx和kp的变量函数;K、F为波数kx和kq的变量函数。
为板材厚度;E、H为波数kx和kp的变量函数;K、F为波数kx和kq的变量函数。
基于式(1),将各向同性板铝板作为典型材料,参数见表1,可以求解分析得到单向应力作用下铝板的Lamb波频散曲线。表1中,l、m 为拉梅常数,l、m、n为三阶弹性常数的默纳汉表示。
表1 6061-T6铝的材料参数
Tab.1 Material properties of 6061-T6 aluminum

参 数数 值 l/GPa54.308 m/GPa27.174 l/GPa-281.5 m/GPa-339.0 n/GPa-416.0 材料密度r/(kg/m3) 2 704 纵波声速vl/(m/s) 6 303 横波声速vt/(m/s)3 102
在铝板上沿Lamb波传播方向施加单向100MPa应力与零应力时,如图1所示绘制这两种情况下的模态频散曲线,实线为零应力时的频散曲线,虚线为施加100MPa应力的频散曲线;通过对比可知,应力与Lamb波传播方向相同时,不同应力所获得的频散曲线不同,因此应力改变了Lamb波的相速度。
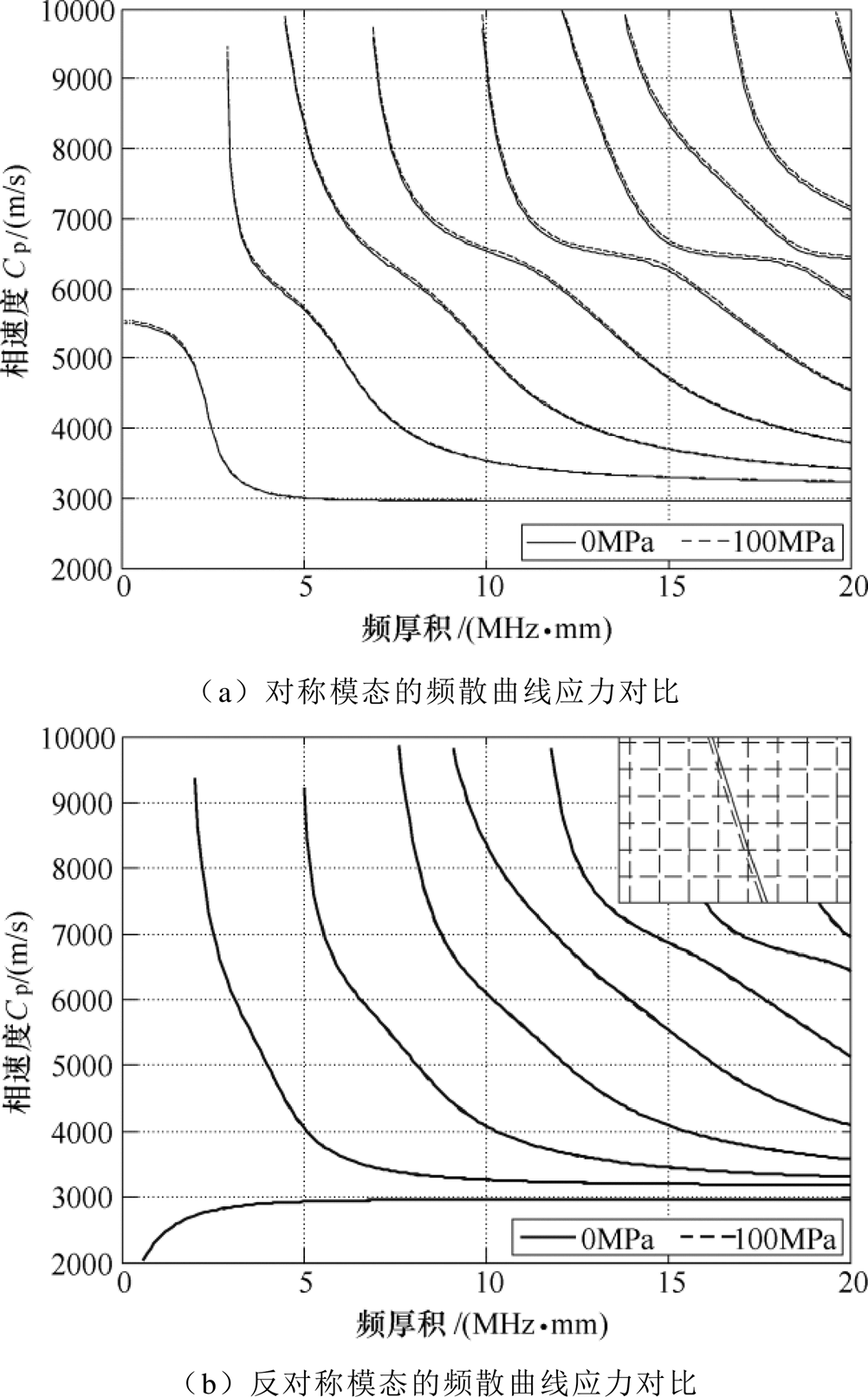
图1 在铝板上沿同方向施加100MPa应力传播的 Lamb波与无施加应力的频散曲线对比
Fig.1 Comparison of the dispersion curves of the Lamb wave propagating in the direction of 100MPa stress and without stress along a single axis on an aluminum plate
由于铝板中Lamb波的多模态特性,以及应力变化对各模态波速的影响相对较小,从图1中无法直接提取应力与波速变化量之间的对应关系,因此有必要设定新的参数来表征应力对波速的影响。本文采用波速相对变化率C来描述这一对应关系,有
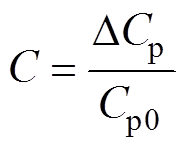 (2)
(2)其中
DCp=Cp- Cp0
式中,Cp为施加应力相速度;Cp0为零应力时的相速度;DCp为相速度的变化量。
基于Lamb波的频散方程式(1),分别计算了不同拉伸应力作用下Lamb波S0、A0、S1、A1这四种模态相速度的频散特性,如图2所示。因压应力与拉伸应力的趋势相反,为了清楚起见,这里没有显示压应力的结果。
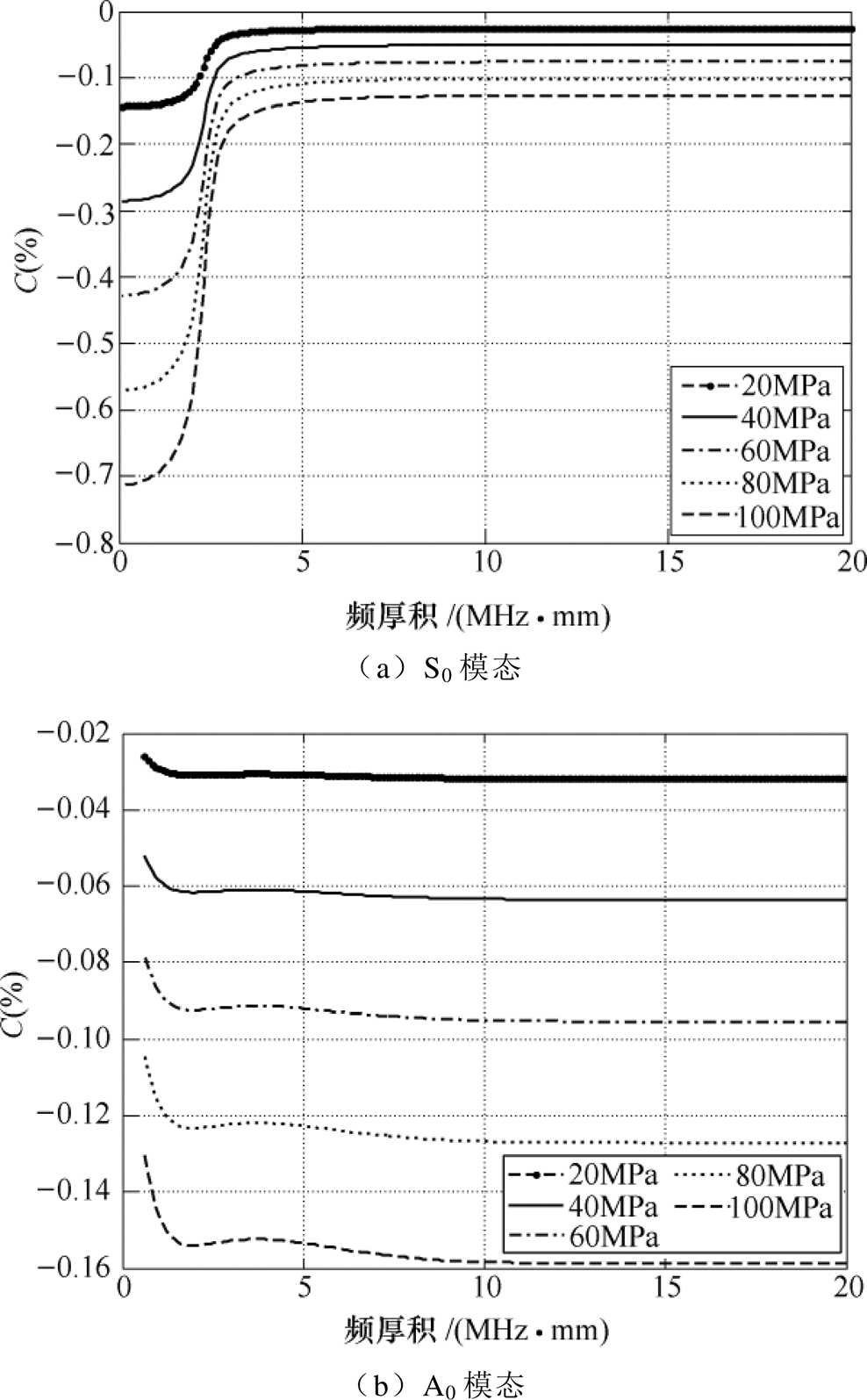

图2 沿轴向应力方向传播的相速度与频厚积的变化
Fig.2 Change in phase velocity with frequency-thickness for modes propagating along the direction of uniaxial applied stress
图2a给出了基本对称模态(S0)相对于零应力状态的相速度相对变化率,其与施加的载荷大小有关。从图中可以看出,在考虑施加拉应力作用下,参数C皆为负,表明拉伸应力导致S0模态的相速度减小。当施加应力为某一定值时,在频厚积为0~3MHz·mm范围内,随着频厚积的增加,相速度相对变化率逐渐减小;而在较高的频厚积(3~20MHz·mm)区域下,相速度相对变化率基本趋于恒定值;在频厚积不变的条件下,对铝板施加的拉应力越大,相速度相对变化率越大,相速度的变化也就越大,这种趋势在低频厚积(0~3MHz·mm)区域更为明显。
图2b所示的基本反对称模态(A0)的结果与S0不同。对于同一应力下,在低频厚积(0.6~2MHz·mm)区域时,频厚积增大,参数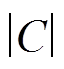 变大,则随着频厚积增加,相速度之差随之增加,而在较高频厚积(2~20MHz·mm)区域时,随着频厚积增参数
变大,则随着频厚积增加,相速度之差随之增加,而在较高频厚积(2~20MHz·mm)区域时,随着频厚积增参数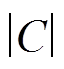 趋于稳定。不同应力下,随着应力增加,相速度相对变化率也随之增加,且整个频厚积(0~20MHz·mm)区域变化明显,但参数
趋于稳定。不同应力下,随着应力增加,相速度相对变化率也随之增加,且整个频厚积(0~20MHz·mm)区域变化明显,但参数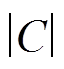 较小,最大应力加载30MPa时,速度相对变化率为0.16%,还不及S0模态变化的一半。
较小,最大应力加载30MPa时,速度相对变化率为0.16%,还不及S0模态变化的一半。
一阶对称Lamb波S1模态的相速度相对变化率如图2c所示。在低频厚积(0~8MHz·mm)下,当激励频率接近高阶模态的截止频率时,参数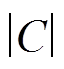 最大,相速度的变化都远高于S0模态。在较高频厚积(8~20MHz·mm)下,一阶模态与基本模态具有相似的特性:相速度的相对变化率趋于恒定值;最大变化量小于1.2%。
最大,相速度的变化都远高于S0模态。在较高频厚积(8~20MHz·mm)下,一阶模态与基本模态具有相似的特性:相速度的相对变化率趋于恒定值;最大变化量小于1.2%。
A1模态如图2d所示,与S1趋势基本相同,随着应力的增加,参数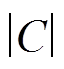 是逐渐变大的,因此应力改变了相速度,且最大变化量超过1.7%,相比其他模态,A1模态截止频率的相速度随着金属薄板应力变化其变化量最大;在同一应力下,低频厚积(0~5MHz·mm)时,随着频厚积的增加,参数
是逐渐变大的,因此应力改变了相速度,且最大变化量超过1.7%,相比其他模态,A1模态截止频率的相速度随着金属薄板应力变化其变化量最大;在同一应力下,低频厚积(0~5MHz·mm)时,随着频厚积的增加,参数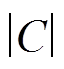 逐渐变小,则在接近截止频率时的A1模态速度相对变化量最大;而在较高频厚积(5~20MHz·mm)区域时,参数
逐渐变小,则在接近截止频率时的A1模态速度相对变化量最大;而在较高频厚积(5~20MHz·mm)区域时,参数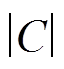 趋于稳定,速度相对变化率较小。
趋于稳定,速度相对变化率较小。
以往利用声弹性效应进行应力检测的工作研究主要集中在体波[18]和基本对称S0模态,这是由于体波容易激发、穿透深度强而Lamb波具有频散性和多模态特性,激发基本模态时模态少且S0模态速度相对快、测量准确。而根据以上数值分析结果表明,采用接近截止频率的A1波模态的相速度对应力场的敏感性较高,传播特性变化明显。
为验证四种模态(A0、A1、S0、S1)的传播特性,利用Lamb波进行铝板实验时,尽可能选择低的频厚积来避免Lamb波频散性、多模态带来的影响,由图2分析可知,S0、A0模态在低频厚积时可取最大速度变化率,而S1、A1这两种模态在接近截止频率时速度变化率最大,综上考虑,取对应的频厚积值,基本模态S0模态取1MHz、A0模态取2MHz,一阶模态取接近截止频率:S1模态取3MHz、A1模态取2.2MHz。
为了验证频散方程求解出的频散曲线与应力加载有关,并分析超声Lamb波的S0、A0、S1、A1这四种模态在铝板中的传播特性,本文设计了如图3所示的单向应力加载下Lamb波传播特性实验平台。
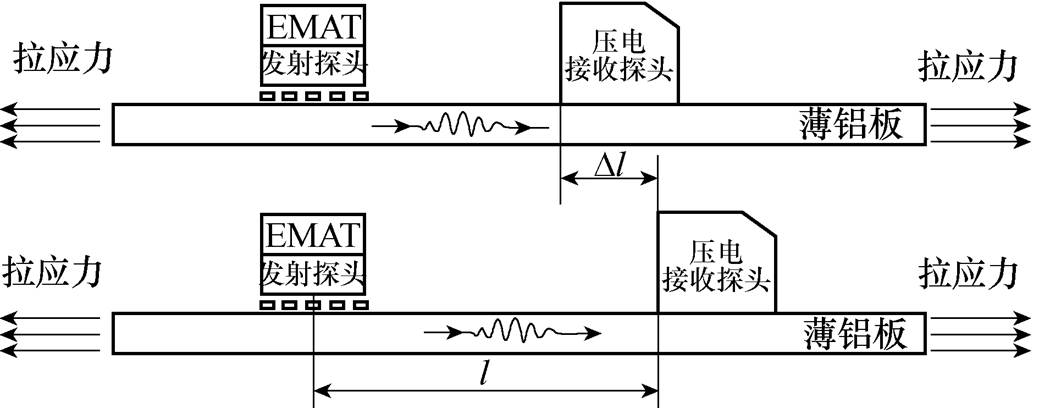
图3 单向应力加载下Lamb波传播特性实验平台
Fig.3 Schematic diagram of the experimental platform for Lamb wave propagation characteristics under unidirectional stress
EMAT激发电磁超声Lamb波结构如图4所示,电磁超声换能器主要基于洛伦兹力和磁致伸缩力两种机理。铝板为非铁磁性材料,电磁超声换能机理以洛伦兹力为主。其中,永磁铁提供偏置磁场,而通电线圈流过高频交流电,并会在线圈下方的铝板内部产生涡流,导体材料内呈现趋肤效应,导致涡流密度随材料深度呈指数衰减。被测试件趋肤层内感应涡流在偏置磁场作用下受到洛伦兹力,而交变的洛伦兹力会促使铝板材料内部结构发生高频振动,从而在铝板内部激发出超声波。超声波包括横波和纵波,Lamb波由横、纵波相互耦合,形成了这种传播状态受弹性介质端面边界限制的超声波[19]。

图4 EMAT激发电磁超声Lamb波结构
Fig.4 Schematic diagram of EMAT excited electromagnetic ultrasonic Lamb wave structure
由于曲折线圈在铝板中激发出的Lamb波与被测铝板的厚度和激励电流的频率有关,根据所测量铝板厚度选择合适的频厚积下,指定模态所对应的相速度大小,如设计A1模态的线圈时,铝板厚度为1mm,选择2.2MHz的频率作为激发频率,由图1找到对应的频厚积下的相速度,则Lamb波A1模态在此频厚积下的波长为l=Cp/f,单匝下线间距为d= l/2[20]。
为增强Lamb波幅值大小,抑制其他模态,采用双层三分裂多匝的线圈结构来激发Lamb波。激发探头的水平磁场采用两块钕铁硼永磁体产生,每块永磁体尺寸为45mm×25mm×10mm,剩磁0.84T。实验中选取波包群速度与频散曲线群速度相比,验证指定模态的正确性。EMAT较压电超声换能器没有耦合剂以及试件表面预处理的限制,有利于实验结果的后续处理。
试样为1mm厚的6061-T6型号铝板,主体长400mm、宽60mm,Lamb波由固定的EMAT激发,移动的压电探头接收;根据传播特性实验平台示意图搭建了一个实物实验装置平台如图5所示,图中,①是激发EMAT;②是接收压电探头,连接到前置放大器,获得10dB的增益,并使用③数字示波器测量信号,以0.25MHz的采样率进行数字化,并保存以提供后续的信号处理;④是Ritec RAM-5000,用于激发EMAT;⑤是万能试验机,可提供超过100MPa的负载,为了实验数值准确,根据试样的横截面积,施加应力在0~30MPa区间内。

图5 单向应力加载下Lamb波传播特性实验平台装置实物
Fig.5 The physical map of the experimental platform device of Lamb wave propagation characteristics under unidirectional stress loading
不同单向应力加载下,频厚积为2.2MHz·mm时,A1模态的接收信号如图6所示,波包明显,在这种情况下,可以通过速度识别接收信号中A1模态的波包。
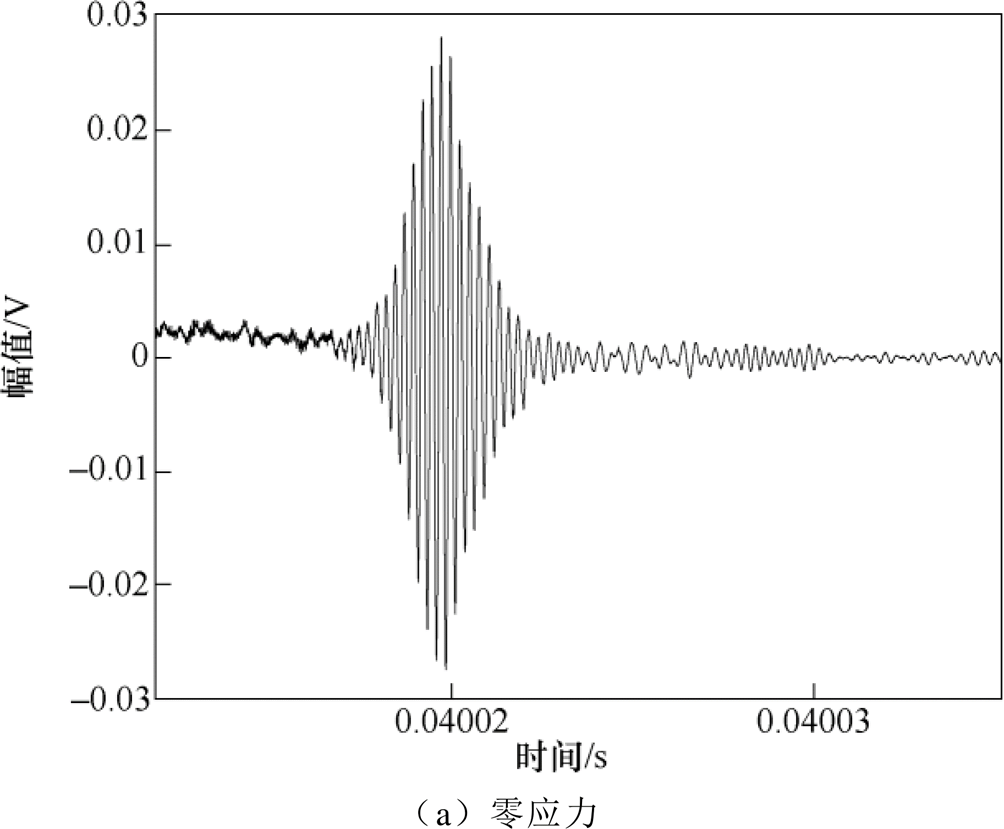
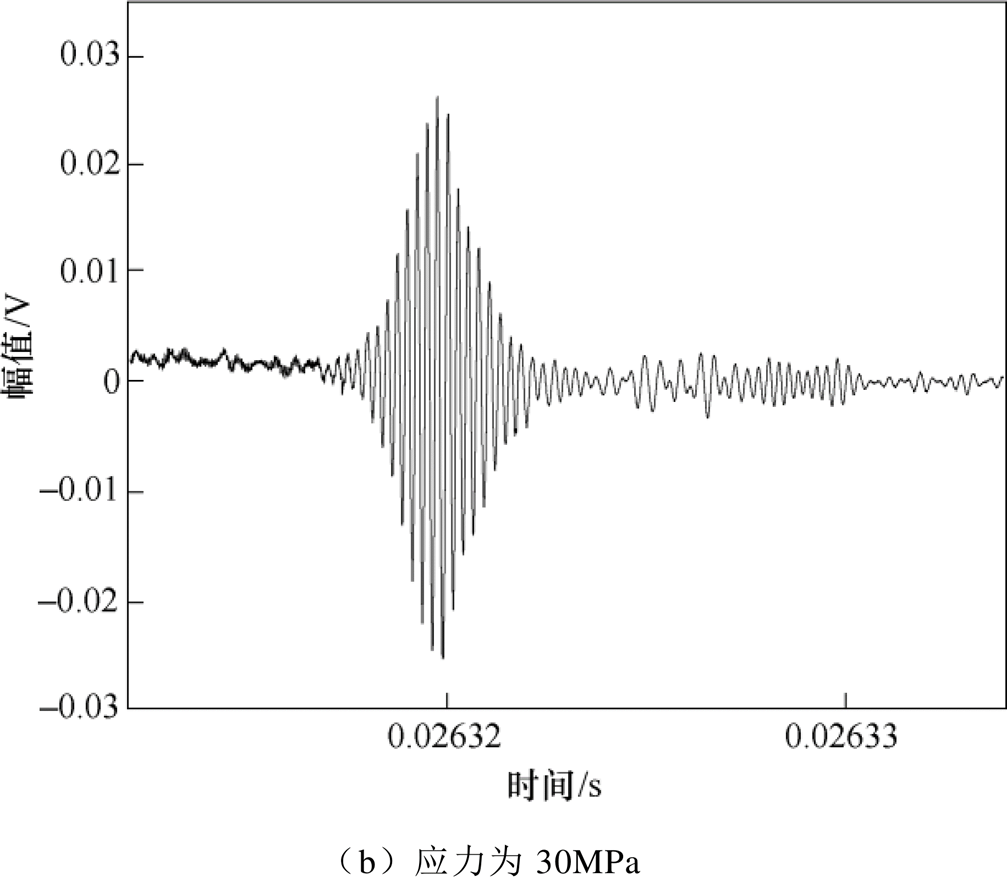
图6 不同单向应力加载下,频厚积为2.2MHz·mm时,A1模态的接收信号
Fig.6 Received signal of A1 mode when the frequency-thickness product is 2.2MHz·mm under unidirectional different stresses
设发射与接收探头的距离为l,Dl为接收探头的移动距离,改变Dl,接收相位为
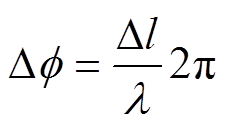 (3)
(3)当Dl等于l 的整数倍时,则
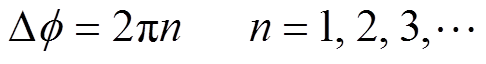 (4)
(4)
可知
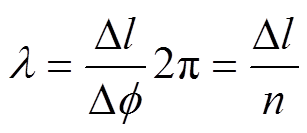 (5)
(5)求出波长根据
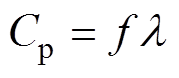 (6)
(6)
多次移动两个探头多次改变Dl,经Dl和n线性拟合求出l。图7分别为0MPa和30MPa应力作用下,多次实验结果线性拟合,0MPa时Dl-n斜率也就是波长为3.662 4mm,则相速度为8 057.28m/s;30MPa时,Dl-n斜率也就是波长为3.604 8mm,则相速度为7 930.56m/s。
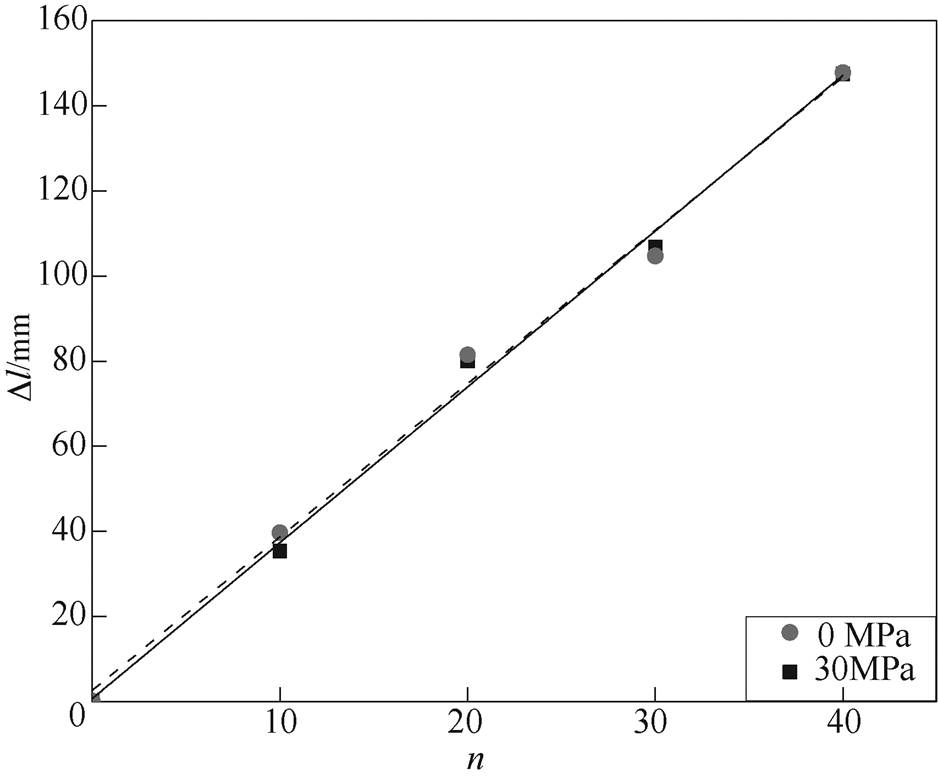
图7 频厚积为2.2MHz·mm时,0MPa与30MPa应力作用下A1模态的Dl-n实验数据
Fig.7 Dl-n experimental datas of A1 mode under the stress of 0MPa and 30MPa when the frequency thickness product is 2.2MHz·mm
频厚积为2.2MHz·mm时A1模态的速度变化如图8所示,实验结果中,实际测量的相速度与仿真结果均呈下降趋势;实验中,随着施加应力的不断增大,应力加载下薄铝板形变以及万能试验机实验施加应力值不能维持恒定不变,因而实验结果测量存在误差。
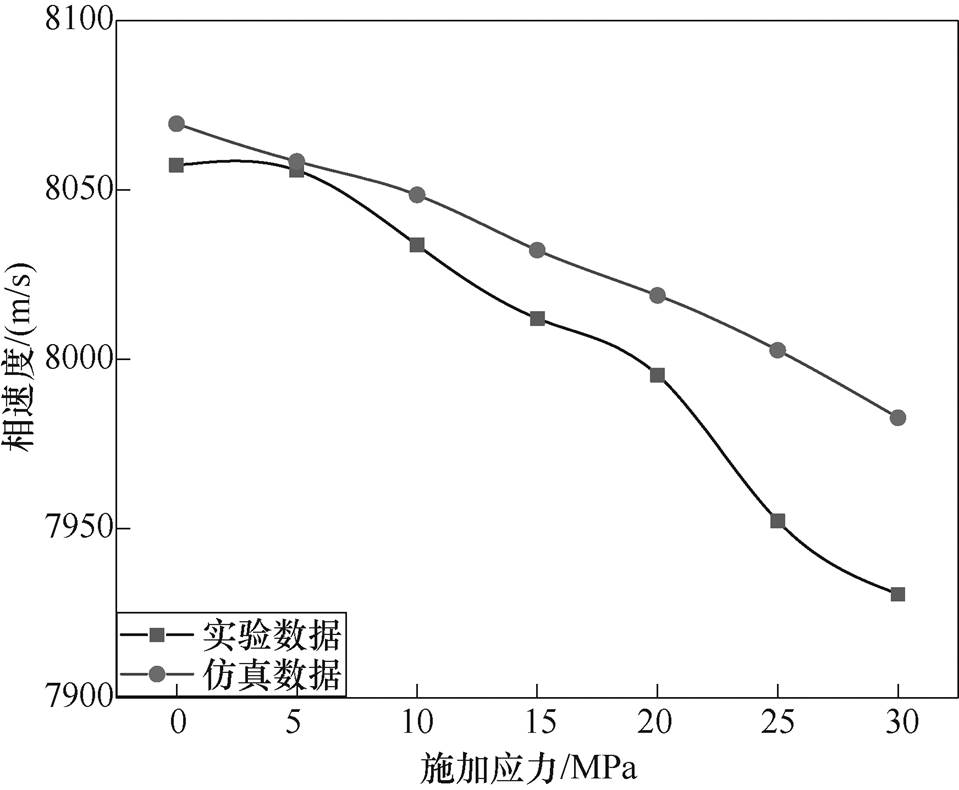
图8 频厚积为2.2MHz·mm时A1模态的仿真结果与实验结果速度变化对比
Fig.8 Comparison of A1 modal simulation results and experimental results with a frequency thickness product of 2.2MHz·mm
通过对各个模态的表征,研究施加单向应力负载对Lamb波传播速度的影响,对于这四种模态,随应力的速度变化如图9所示,随着应力的增加,各个模态的速度相对减小,在小于5MPa应力时,速度本身的变化不明显,而大于5MPa时,A1模态的速度变化较其他各模态变化明显增大,实验结果与仿真结果相符,A1模态具有较强的敏感性,因此用A1模态测量单向应力具有较好的前景。
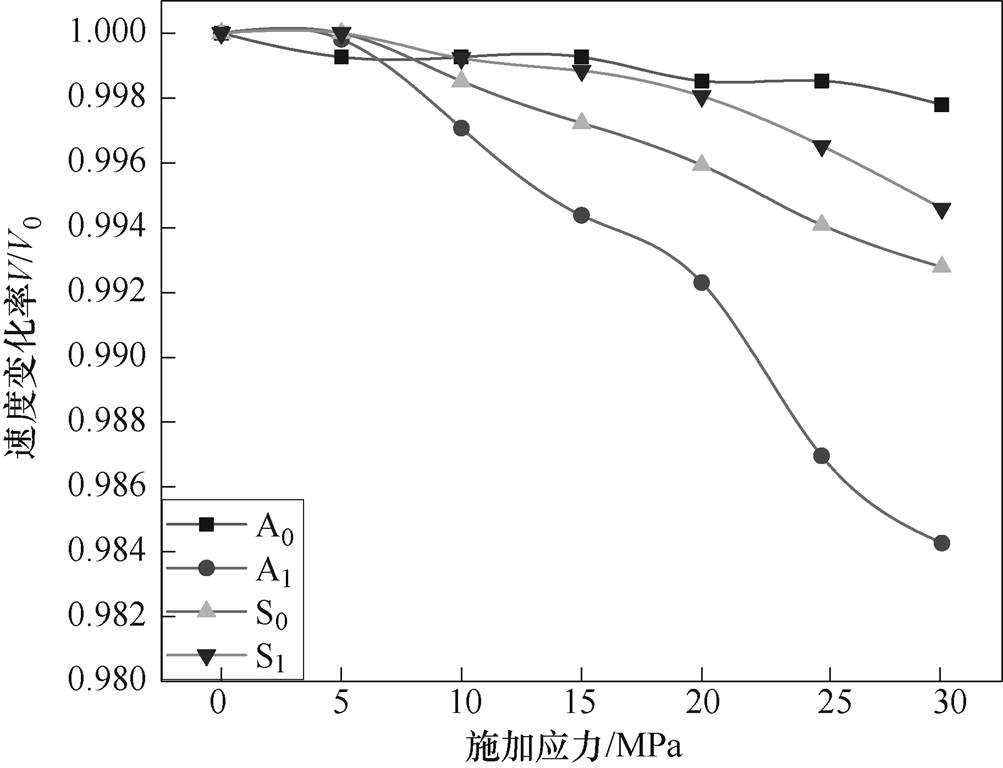
图9 四种模态随应力的速度变化
Fig.9 The four modes change with the speed of the stress
图10为A1模态下频厚积从2.2MHz·mm到4.0MHz·mm改变时速度随单向应力加载下的变化,对速度进行归一化处理,由图可知,同一频厚积下,相速度随单向应力的增加而变小;同一应力下,随着频厚积的增加,速度变化率减小,频厚积为2.2MHz·mm时速度变化较为明显,比其他频厚积敏感,符合仿真结果,不难看出,在接近截止频率时速度随单向应力变化最大。
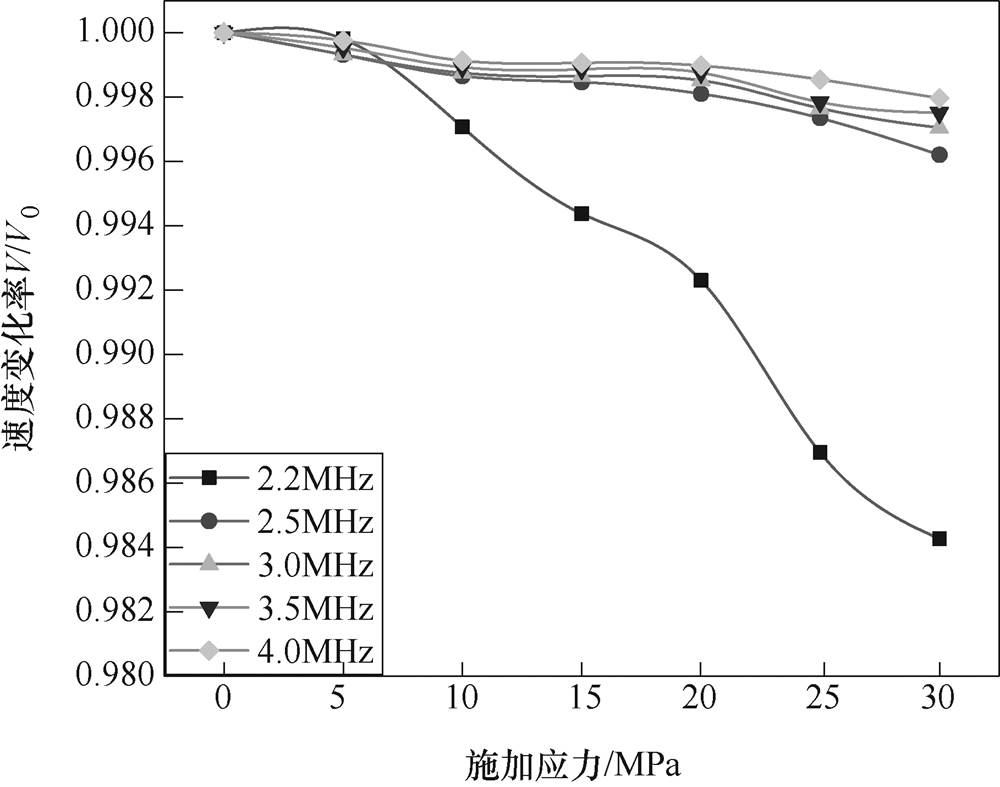
图10 A1模态从2.2MHz·mm到4.0MHz·mm频厚积下速度随单向应力加载下的变化
Fig.10 A1 mode changes with unidirectional stress at 2.2MHz·mm to 4.0MHz·mm frequency product
针对金属薄板单向载荷检测问题,本文主要研究了Lamb波各个模态的声弹性响应特性,具体工作如下:
1)本文基于单向应力作用的Lamb波频散方程,对Lamb波的频散特性进行数值分析,对比四种模态Lamb波的相速度随应力的变化规律,其中,A1模态相速度对薄板中应力变化响应最为灵敏。
2)通过电磁超声换能器激发单模态Lamb波,搭建铝板超声Lamb波实验平台,实验结果表明,在Lamb波与应力同方向的传播过程中各模态相速度随所加载应力的变化而变化,验证了超声Lamb波在应力作用下的声弹性效应。对于截止频率附近的高阶模态,它的声弹性响应特性大于基本模态。通过对比四种Lamb波模态在单向应力加载条件下的相速度变化规律,得出A1模态的相速度变化对应力的敏感程度明显高于其他模态的结论。
3)本文数值分析了单向加载下不同应力作用下Lamb波频散特性曲线,使用EMAT激发单模态Lamb波,使实验结果更加具有准确性。将电磁超声Lamb波特定模态灵敏的声弹性响应特性与Lamb波长距离传播的优异能力相结合,可以为大尺寸板状结构的应力测量提供新的思路。
参考文献
[1] 蔡智超, 刘素贞, 张闯, 等. 涡流式电磁声发射检测声波响应特性[J]. 电工技术学报, 2016, 31(24): 134-140.
Cai Zhichao, Liu Suzhen, Zhang Chuang, et al. Acoustic response characteristics of acoustic emission induced by eddy current exciting[J]. Transactions of China Electrotechnical Society, 2016, 31(24): 134- 140.
[2] Ponschab M, Kiefer D A, Rupitsch S J. Simulation- based characterization of mechanical parameters and thickness of homogeneous plates using guided waves[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2019, 66(12): 1898-1905.
[3] 李德志. 基于Lamb波的铝合金板材结构状态监测研究[D]. 济南: 山东大学, 2019.
[4] Veidt M, Ching-Tai Ng. Influence of stacking sequence on scattering characteristics of the fundamental anti- symmetric Lamb wave at through holes in composite laminates[J]. The Journal of the Acoustical Society of America, 2011, 129(3): 1280-1287.
[5] Ching-Tai Ng, Veidt M. Scattering characteristics of Lamb waves from debondings at structural features in composite laminates[J]. The Journal of the Acoustical Society of America, 2012, 132(1): 115-123.
[6] 张林文. 板结构材料中超声兰姆波信号传播特性的理论与实验研究[D]. 上海: 上海大学, 2017.
[7] Gandhi N, Michaels J E, Lee S J. Acoustoelastic Lamb wave propagation in biaxially stressed plates[J]. The Journal of the Acoustical Society of America, 2012, 132(3): 1284-1295.
[8] Munawwar M, Andrei K, Ching-Tai Ng. Effect of uniaxial stress on the propagation of higher-order Lamb wave modes[J]. International Journal of Non-Linear Mechanics, 2016, 86(1): 104-111.
[9] Ogden R W. Non-linear elastic deformations[M]. Chichester: Ellis Horwood, 1984.
[10] Shi Feng, Michaels J E, Lee S J. In situ estimation of applied biaxial loads with Lamb waves[J]. The Journal of the Acoustical Society of America, 2013, 133(2): 677-687.
[11] Pei Ning, Bond L J. Higher order acoustoelastic Lamb wave propagation in stressed plates[J]. The Journal of the Acoustical Society of America, 2016, 140(5): 3834-3843.
[12] Ghodrati B, Yaghootian A, Ghanbar Z A, et al. Lamb wave extraction of dispersion curves in micro/ nano-plates using couple stress theories[J]. Waves in Random and Complex Media, 2017, 28(1): 15-34.
[13] Ren Weiping, Xu Ke, Dixon S. A study of stress dependent magnetostriction on steel plate by analysis of an electromagnetically generated S0 Lamb wave[J]. Journal of Nondestructive Evaluation, 2019, 38(4): 1-10.
[14] 刘素贞, 董硕, 张闯, 等. 电磁超声加载方式对Lamb波模态的影响[J]. 电工技术学报, 2018, 33(19): 4426-4433.
Liu Suzhen, Dong Shuo, Zhang Chuang, et al. The influence of electromagnetic acoustic transducer loading way on the mode of Lamb[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4426-4433.
[15] 康磊. 用于铝板检测的电磁超声换能器优化设计技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2011.
[16] 王军, 王寅观. 金属薄板中Lamb波波速与静应力关系的理论研究[J]. 声学学报, 2006, 31(6): 527-531.
Wang Jun, Wang Yinguan. Research of relationship between Lamb wave velocity and static stress of metal plate[J]. Acta Acustica, 2006, 31(6): 527-531.
[17] Pei Ning, Bond L J. Comparison of acoustoelastic Lamb wave propagation in stressed plates for different measurement orientations[J]. The Journal of the Acoustical Society of America, 2017, 142(4): 327-331.
[18] Moll J, Kathol J, Fritzen C P. Open guided waves: online platform for ultrasonic guided wave measure- ments[J]. Structural Health Monitoring-An Inter- national Journal, 2019, 18(5): 1903-1914.
[19] 刘素贞, 张严伟, 张闯, 等. 基于电磁超声双换能器的单模态Lamb波激励方法研究[J]. 电工技术学报, 2018, 33(1): 140-147.
Liu Suzhen, Zhang Yanwei, Zhang Chuang, et al. Research on excitation method of single-mode Lamb wave based on electromagnetic acoustic double transducer[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 140-147.
[20] 张闯, 魏琦, 刘素贞, 等. 小尺寸试件检测用单向单模态电磁超声换能器设计[J]. 电工技术学报, 2019, 34(17): 3563-3571.
Zhang Chuang, Wei Qi, Liu Suzhen, et al. Design of unidirectional single-mode electromagnetic acoustic transducer for small size specimen detection[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3563-3571.
Wave Velocity Response Characteristics of Electromagnetic Ultrasonic Lamb Wave of Aluminum Plate under Unidirectional Load
Abstract In view of the fact that Lamb waves decay slowly during propagation, the use of ultrasonic Lamb waves for stress detection of thin metal plates has become a hot research method at home and abroad. In order to understand the relationship between the propagation characteristics of Lamb waves and the stress of thin metal plates, this paper gives the dispersion curve of aluminum plate under different stresses of unidirectional load according to the calculation formula of Lamb wave dispersion in isotropic plate. The propagation of the basic mode and first-order mode of Lamb wave and stress field in the same direction are analyzed. According to the calculation results of the dispersion equation, the Lamb wave A1 mode is more sensitive to speed changes than other modes, and the first-order modal speed closer to the cutoff frequency changes more obviously. The experiment of unidirectional stress load applying to a 6061-aluminum plate with a thickness of 1mm is carried out. Considering the multi-modal characteristics of piezoelectric probe excitation, the electromagnetic ultrasonic transducer is used to excite single-mode Lamb wave. Compared with the phase velocity change rates of the basic mode and the first-order mode, the wave velocity of the A1 mode changes obviously, and the experimental results are consistent with the simulation data, which can provide an important basis for the subsequent stress detection of thin metal plates.
keywords:Lamb wave, electromagnetic ultrasound, stress loading, propagation characteristics
中图分类号:TM47
DOI: 10.19595/j.cnki.1000-6753.tces.200054
国家自然科学基金项目(51777052,51977058)、河北省自然科学基金项目(E2017202055)、河北省高校重点项目(ZD2018214)和天津市北辰区科技创新专项(KJCX-XTCX-2019-12)资助。
收稿日期 2020-01-10
改稿日期 2020-04-24
张 闯 男,1982年生,博士,教授,研究方向为电工装备无损检测与评估。E-mail: czhang@hebut.edu.cn(通信作者)
李雪霏 女,1994年生,硕士,研究方向为超声应力检测技术及相关理论。E-mail: 291960305@qq.com
(编辑 崔文静)