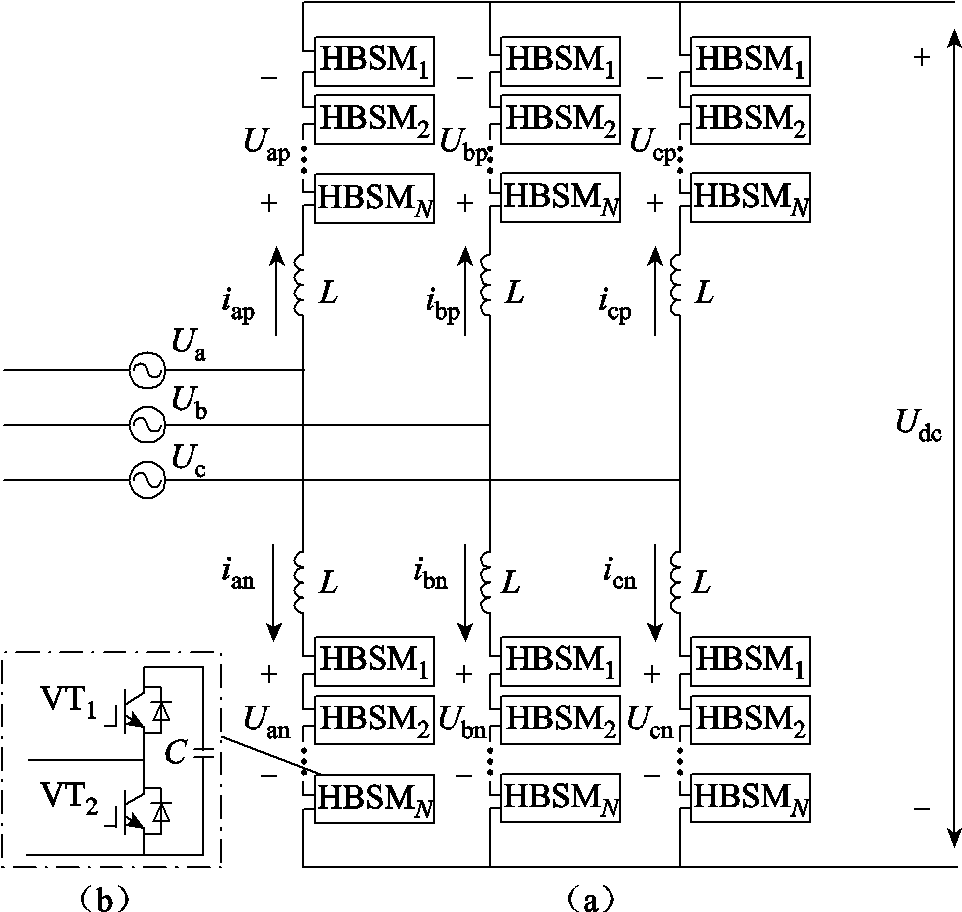
图1 模块化多电平换流器拓扑与半桥子模块结构
Fig.1 Modular multilevel converter topology and half-bridge submodule structure
摘要 模块化多电平换流器（MMC）发生直流故障后，换流站会出现明显的过电流，对MMC的可靠性产生严重影响。而故障暂态电流的精确计算是实现对暂态过电流有效评估的最直接的手段。为了精确计算MMC故障过电流，提出一种同时考虑交流系统与电容放电影响的故障电流精确计算方法，对桥臂等效模型进行了建模与分析，指出了桥臂电压对时间的微分应由电容项与子模块投入函数项组成。基于桥臂等效模型，建立了MMC直流故障下的状态方程，计算得出了MMC直流故障电流的数值解，对可能出现的最大过电流与最小过电流进行评估，并将此结果与电磁暂态仿真模型（EMT）中的仿真结果进行对比验证，证明了该方法的准确性。最后，将该计算方法与两种传统的故障电流计算分析方法进行了比较，指出了传统故障电流计算方法的不足之处，并进一步验证了该方法的有效性。该文提出的计算和分析方法可以为MMC关键部件的选型提供一定的参考，并为直流故障保护方案的设计提供依据。
关键词：模块化多电平换流器 直流故障 故障电流计算 过电流分析
模块化多电平变流器（Modular Multilevel Converter, MMC）由于具有电压、容量等级易于拓展、谐波含量低、开关频率和运行损耗小等优点，成为目前高压大容量柔性直流输电（Voltage Sourced Converter based High Voltage Direct Current, VSC-HVDC）换流站的主流选择，备受学术界和工业界的关注[1-3]。目前已投运的柔性直流输电工程大多采用半桥式子模块（Half Bridge Sub-Module, HBSM）结构，该结构拓扑简单，经济性良好，但不具备直流阻断能力[4-5]。
直流故障是柔性直流输电系统较严重的故障类型之一[6]。直流故障发生后，电网中各端换流站均向短路点注入故障电流，其直流线路的故障电流是各换流站故障电流分量的叠加，包含换流站数量越多，故障点电流的上升速率与幅值越大[7]。
近年来国内外对于直流故障的研究，大多集中于保护与故障清除方面[8-10]。在实际工程中，考虑到换流器检测、通信、控制的延时，从故障发生到换流器闭锁，通常有几毫秒的延迟时间。该时段内，迅速增大的故障电流可能会对换流器中IGBT等关键部件造成永久性损坏。因此该时段内故障暂态电流的精确计算对MMC关键部件的选型以及故障保护方案的设计至关重要。
在故障发生后至换流器闭锁之前，故障电流分为子模块电容放电电流和交流系统注入电流两部分，其中电容放电电流为主要部分[11]。对于该时段内故障电流计算，国内外已有部分文献进行了研究[11-19]，但对该问题的研究还不够深入。
在对于子模块电容放电电流的研究中，文献[11]提出子模块电容放电模型，采用一种RLC二阶等效电路计算子模块电容放电电流，但其简单地将单相上、下桥臂等效为一个电容值为2C/N（C为子模块电容值，N为单相上下桥臂投入的子模块总和）的电容，过于理想化。文献[12-13]指出了等效放电电容应介于C/N~2C/N之间。文献[13]通过描点逼近的方式得出了等效放电电容值取1.4C/N时最接近实际电容放电电流。文献[14]基于子模块电容电压均衡的假设，提出等效电容的具体计算公式，并指出调制比和短路时刻是影响等效放电电容取值的因素，但其仅采用等效电容模型来描述桥臂电压与电流的关系，并未充分考虑到子模块投入与切出对桥臂电压的影响。
而对于交流注入电流的研究，文献[11]简单认为交流注入电流为三相稳态短路电流，未考虑暂态过程的影响。文献[15]则认为在故障发生后较短时间内，交流注入电流大小与正常工作时相等，为正常运行时阀侧交流相电流。文献[16]同时考虑子模块放电电流与交流注入电流，提出一种基于状态方程的数值解法，但在计算过程中仍将各桥臂等效为一个电容模型，不能反映子模块投切对桥臂电压的影响。文献[17]采用仿真的方法求解交流注入电流大小，指出交流注入电流极小，与子模块电容放电电流相比，可忽略不计，但其仿真中所设定的换流器闭锁延迟时间较短，不能反映实际工程中闭锁延迟时间相对较长的情况，无法实现对暂态故障过程的精确解析。文献[18-19]采用将交流电流注入分量与子模块电容放电分量分别计算并叠加的方法，准确计算直流侧的故障电流。该方法本质上是采用交直流功率守恒的方法，通过计算交流侧功率输入来间接计算交流系统注入的直流侧故障电流，未考虑桥臂与交流系统相互影响的动态数学模型，因此仅能对直流侧故障电流进行计算，而无法实现对桥臂故障电流的计算。
本文在以上方法的基础上，将子模块电容放电和交流电流注入两个方面的暂态特性进行有机的结合，提出了一种MMC直流故障过电流的精确计算方法，可同时计算桥臂故障电流与直流侧故障电流。结合状态方程数值解法，计算得到直流故障下故障电流的数值解，探究故障时可能出现的最大和最小故障过电流，并将此结果与电磁暂态仿真结果进行对比验证，证明该方法的精确性。最后，将该方法与以上两种传统计算方法进行全面的比较，进一步验证了本文所提出方法的有效性。
现在工程常用的MMC系统主电路拓扑结构如图1a所示。换流器由三个相单元组成，每相包含上、下桥臂，每个桥臂包含桥臂电感L和N个半桥子模块。图1a中，Uj（j=a,b,c）为MMC交流阀侧相电压；Ujp、Ujn分别为j相上、下桥臂电压；ijp、ijn分别为j相上、下桥臂电流；各物理量方向如图1a所标注。
图1 模块化多电平换流器拓扑与半桥子模块结构
Fig.1 Modular multilevel converter topology and half-bridge submodule structure
图1b为MMC子模块示意图，子模块由上下两个IGBT及其反并联二极管组成的开关管VT1、VT2以及子模块电容C组成。通过控制开关管VT1和VT2，使模块处于投入或切除状态。同一时刻，每一相上、下桥臂总投入的模块数为N，从而保持直流母线电压为Udc；通过最近电平调制策略控制每一相上、下桥臂投入的子模块数量，并采用排序均压的策略保证各桥臂子模块电容电压均衡。
MMC发生直流故障后，换流器直流侧双极经小电阻短路。故障电流主要分为子模块电容放电电流和交流系统注入电流两部分，其中电容放电电流为主要部分[11]。对于投入的子模块，由于子模块电容会对子模块下部反并联二极管有反向电压阻断的作用，因此不论是电容放电电流还是交流注入电流，均从子模块上部开关管VT1及子模块电容流过。而对于切出的子模块，电容放电电流和交流注入电流均从下开关管VT2流过，故障电流路径如图2所示。故障发生后，桥臂电流会极快地上升。为了保证子模块功率器件不受损坏，需要在检测到直流故障后迅速采取闭锁IGBT、起动直流断路器及交流断路器[20-22]等操作。但实际工程中，从故障发生到换流器闭锁通常有几毫秒的延迟时间。在该时间内迅速上升的故障电流可能会对子模块功率器件造成永久的破坏。因此，对该时段内故障电流的计算至关重要。本文仅对换流器闭锁前几毫秒时间内的故障电流暂态过程进行分析。
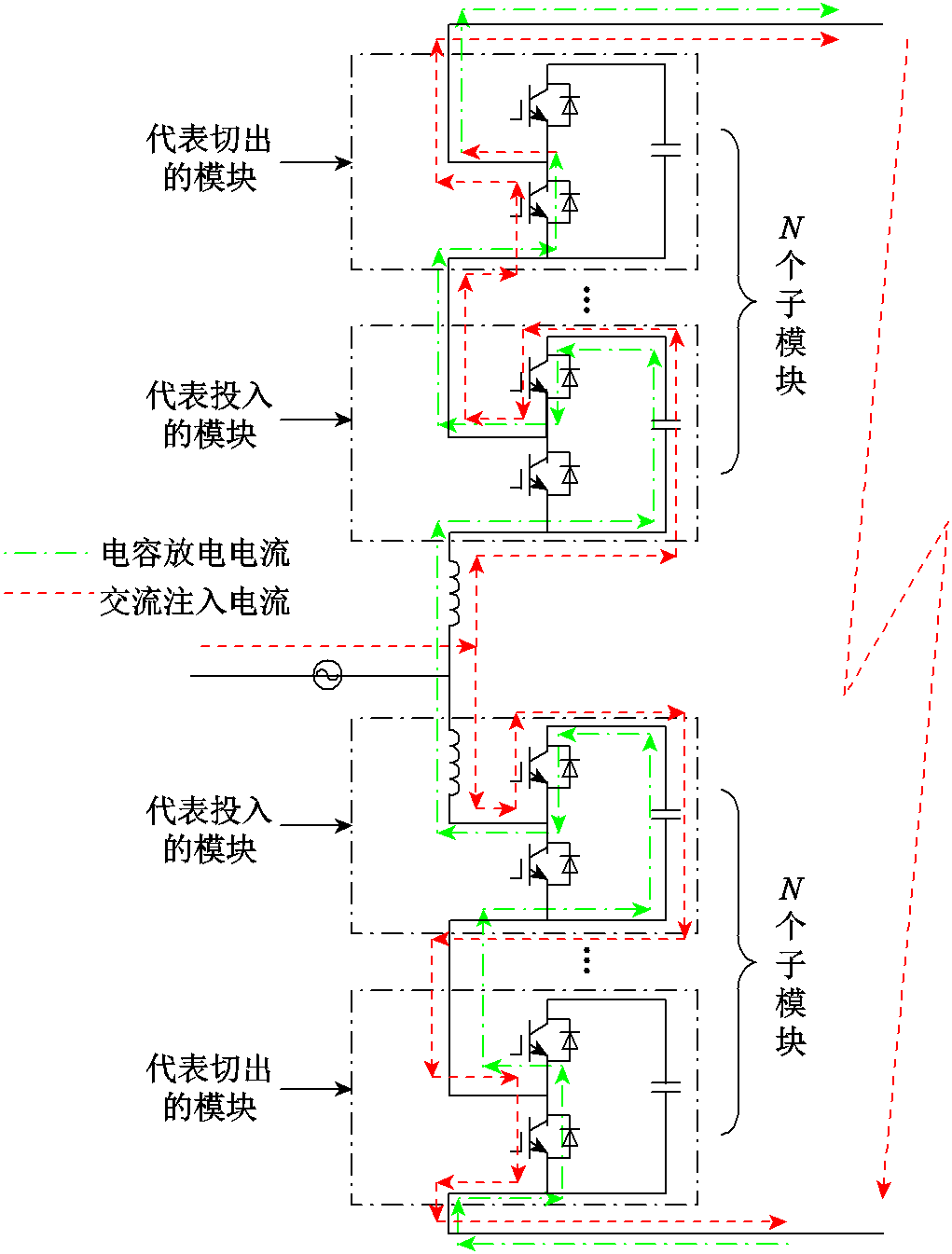
图2 直流故障发生后故障电流路径
Fig.2 Fault current path after DC fault
以A相上桥臂为例，对桥臂电压电流满足的数学关系进行推导，设通过上桥臂的电流与电压分别为iap(t)与Uap(t)，其正方向如图1a所示，子模块电容为C，桥臂子模块总个数为ns（含热备用子模块），换流器直流侧电压为Udc，当前时刻A相上桥臂投入的模块数为nap(t)。
当采用最近电平调制策略[23]时，nap(t)可表示为
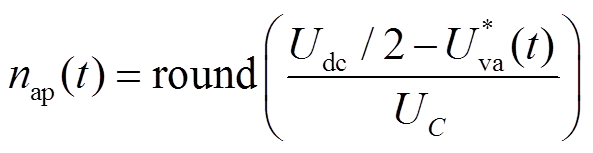（1）式中，round为取整函数；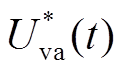
为换流器交流侧A相调制波；
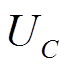为MMC子模块电容电压。
直流故障发生后，换流器在几个毫秒内即闭锁，由于时间过短，可以近似假设该时段内：①子模块电容电压下降有限；②IGBT能够正常开断，尚未失效。
假设桥臂均压策略良好，各子模块电容电压都近似保持均衡，则桥臂电压可表示为
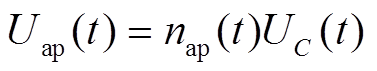（2）将式（2）对时间求导，得到
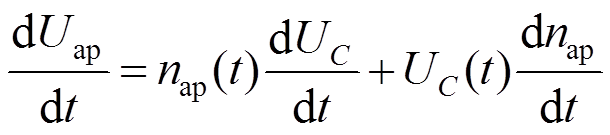（3）将式（2）代入式（3），消去等式右端第二项的UC(t)，可得
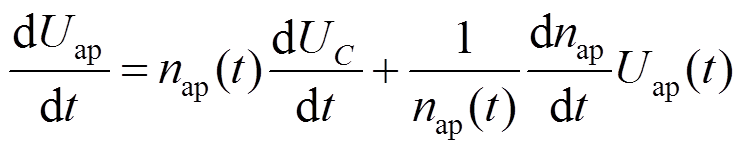（4）当桥臂内各子模块电容电压近似均衡时，子模块电容电压与桥臂电流关系可表示为[24]
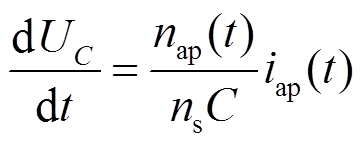（5）将式（5）代入式（4），得出
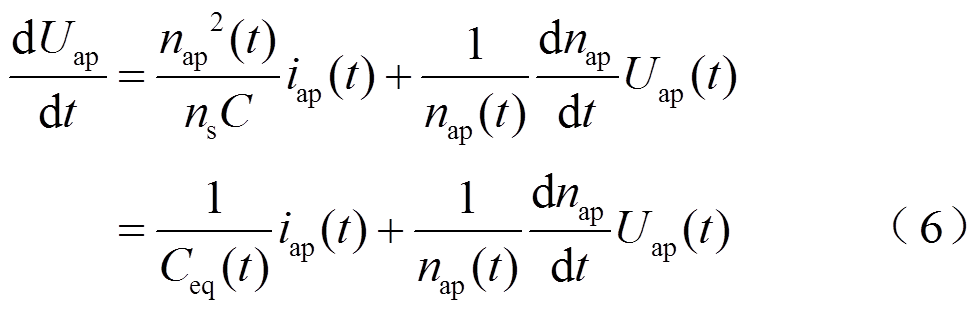
式中，Ceq(t)=nsC/nap2(t)。
式（6）即为均压条件下桥臂电压电流数学模型，其等号右边第一项为电容项，物理意义为均压策略下桥臂中子模块串联对外的等效电容[14]；第二项为子模块投入函数项，表示实时投入的子模块数量变化引起的桥臂电压变化。桥臂电压随时间的变化应由电容项与子模块投入函数项共同决定。
由于换流器闭锁前的时段内故障电流求解涉及高阶变系数微分方程[16]，难以得到解析解。因此，本文采用构建状态方程的方法计算故障电流暂态数值解。
MMC换流器发生直流故障时等效电路如图3所示。其中，Ua、Ub、Uc分别为交流系统三相电压；Ls和Rs分别为交流系统与变压器阻抗总和；L与R分别为桥臂电感与杂散电阻；Ldc与Rdc分别为包含换流器直流出口至短路点的线路参数和短路点电阻的总和；UN与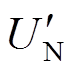
分别为直流侧两极对O点的电位；Ujk和ijk (j=a,b,c; k=p,n)分别为三相上下桥臂电压与桥臂电流。各物理量正方向如图3所标注。
由图3可以得出，对于A相上桥臂，满足
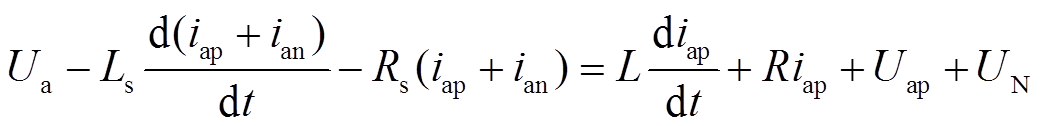（7）
图3 MMC直流故障等效电路
Fig.3 Equivalent circuit of MMC DC fault
同理，可列写B相与C相上桥臂关系式。将三相上桥臂关系式相加，并考虑到
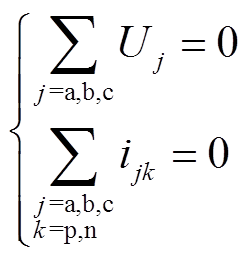（8）可得UN为
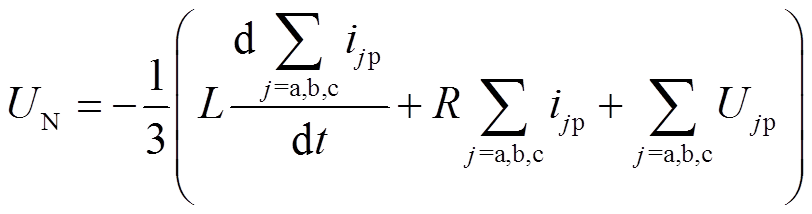（9）将式（9）代入式（7）可得
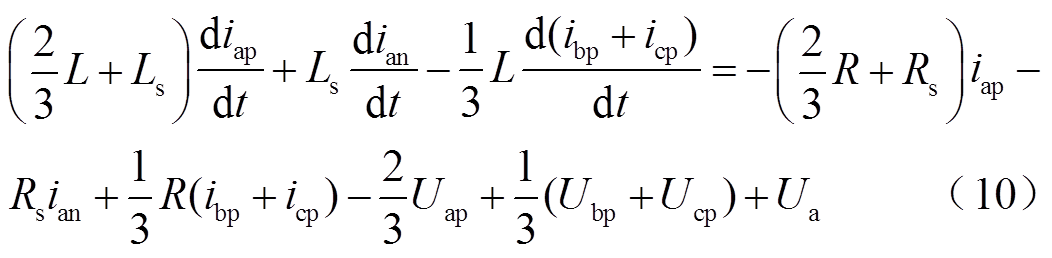
对于A相上、下桥臂与直流短路点形成的回路，由KVL可得
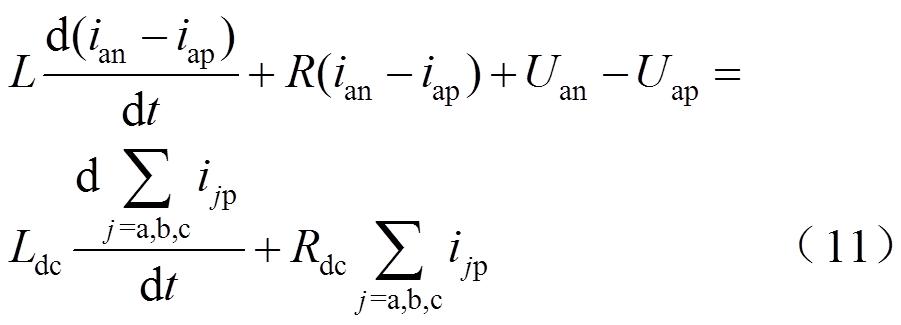
同理，按式（10）与式（11）的形式，对B相和C相的关系进行列写。结合2.1节所推导的桥臂电压电流数学模型，可以得到直流故障下以ijk和Ujk为状态变量的状态方程为
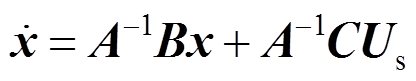（12）式中，x=[iap ian ibp ibn icp icn Uap Uan Ubp Ubn Ucp Ucn]T；Us=[Ua Ub Uc]T；A、B、C矩阵表达式见附录。
以直流故障时刻为零时刻，MMC换流站正常工作（t≤0）时，交流系统A相的相电压Ua与相电流ia分别为
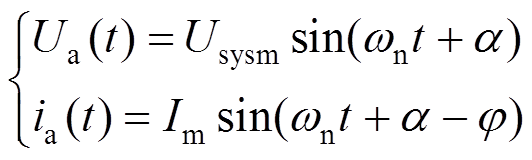（13）式中，ωn为工频角频率；α为故障时刻交流系统A相电压相角；φ为功率因数角；Usysm与Im分别为交流系统相电压与相电流的幅值。
以A相上桥臂为例，桥臂电流可表示为
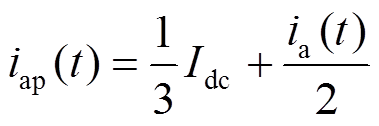（14）式中，Idc为换流器直流侧输出电流。
因此，故障零时刻，桥臂电压与电流可表示为
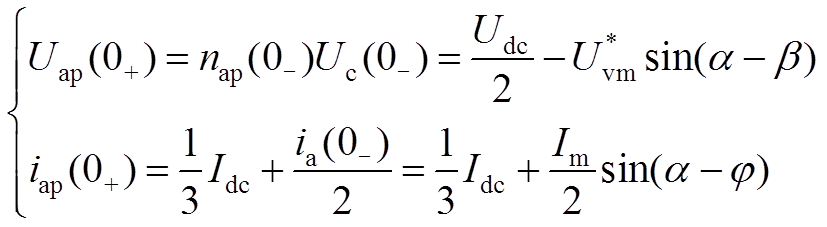（15）式中，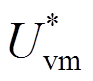
为换流器稳态运行时调制波幅值；β为稳态运行时交流系统相电压与换流器调制波的相位差。
同理，可得其余各桥臂电压电流初始值。
由式（15）可得，桥臂电压和电流的初始值与故障时刻交流系统相电压相角α有关。因此，故障时刻交流系统相电压相角α将会同时影响故障电流初始值与故障电流发展趋势，对故障电流有显著影响。
在换流器闭锁前的暂态过程中，控制系统仍按正常运行时控制策略对换流器进行控制。本文按照经典内外环控制策略[23]列写控制系统递推计算式[18]，从而对控制系统发出的调制波进行计算。
考虑换流器采用定直流电压控制与定无功功率控制时，外环控制瞬时表达式为
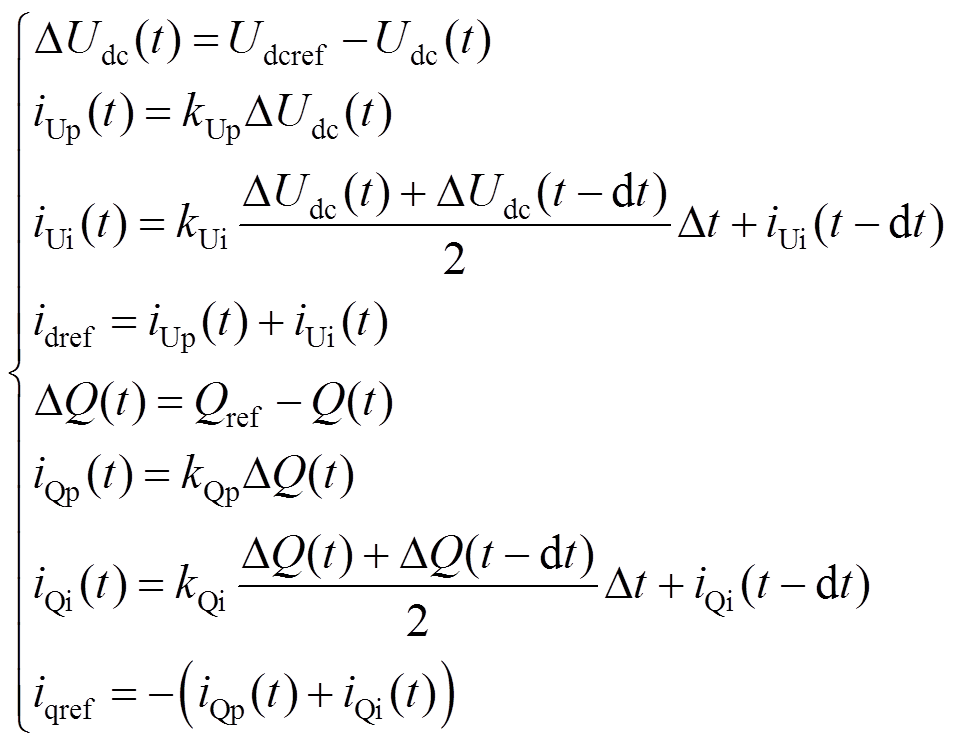（16）若换流器采取定有功功率控制时，则式（16）中前四个式子可表示为
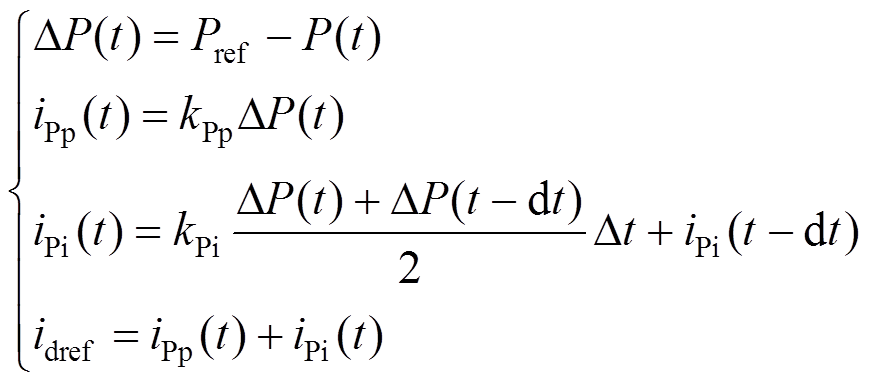（17）在外环控制器输出环节，还需加入限幅处理。
内环控制器瞬时表达式为
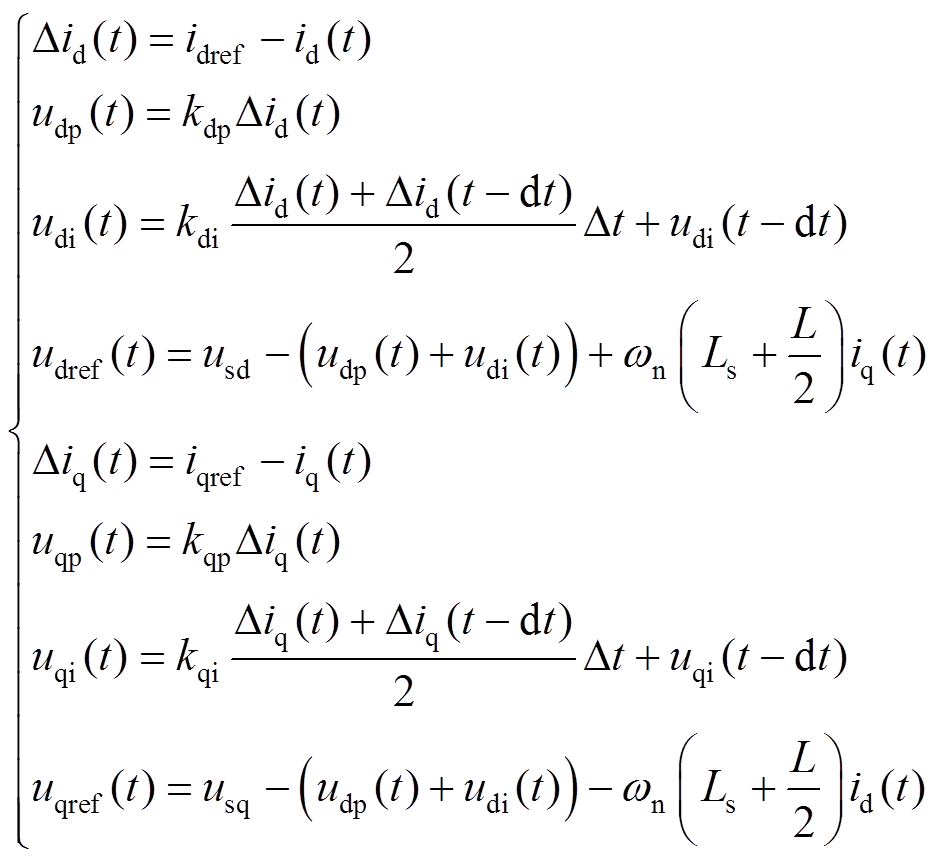（18）式中，Udcref为直流电压参考值；Qref为换流器输入无功功率参考值；Pref为换流器输入有功功率参考值；Udc(t)、Q(t)、P(t)分别为换流器瞬时直流电压、瞬时无功功率和瞬时有功功率；kUp、kUi、kQp、kQi、kPp、kPi分别为定直流电压、定无功功率以及定有功功率外环控制的比例和积分系数；id(t)、iq(t)分别为交流侧电流的d、q轴分量（以交流电流以流入换流器为正方向）；usd、usq分别为交流系统相电压的d、q轴分量；kdp、kdi、kqp、kqi分别为内环控制器d、q轴的比例和积分系数。
将内环控制器输出值udref(t)、uqref(t)进行dq-abc变换即可得到换流器调制波瞬时值。结合式（1），即可对桥臂投入子模块数量进行计算。
将2.3节中桥臂电压电流初始值及交流系统三相电压代入状态方程（12），并将控制系统递推式（16）~式（18）与投入子模块计算式（1）的计算结果代入式（12）中的B矩阵，即可进行状态方程递推计算，求解任意时刻故障电流的数值解。
由2.3节分析可知，故障时刻交流系统相电压相角α对故障电流初始值以及变化趋势有显著影响。本节在电磁暂态（Electromagnetic Transient, EMT）仿真模型中搭建MMC仿真模型，对第2节所述故障电流计算方法进行验证，并探究相角α对故障电流的影响规律。采用单端MMC模型，假定故障发生于换流器直流侧出口处，换流器在4ms内闭锁，系统参数见表1。
表1 MMC换流站系统参数
Tab.1 MMC system parameters
参数数值 系统容量/(MV·A)500 交流电网电压/kV230 变压器容量/(MV·A)530 变压器电压比230:166.57 变压器漏抗(%)15 直流电压/kV320 运行功率P, Q(pu)1.0, 0 子模块总数(含热备用)216 子模块额定电压/V1 600 桥臂电感值/mH60 子模块电容值/mF10 直流电抗器/mH50 直流侧短路电阻/Ω5
图4给出了采用状态方程计算得到的不同故障相角α下，A相上桥臂电流峰值iapmax与直流侧故障电流峰值idcmax的变化。从图4可观察得到，对于桥臂电流，故障相角α对其有着显著影响。在α=0°附近，A相上桥臂故障电流峰值到达最大值4 439A，该值即为故障发生至换流器闭锁时间内A相上桥臂故障电流可能出现的最大峰值；而在α=210°附近，A相上桥臂电流峰值到达最小值1 767A，该值即为A相上桥臂故障电流可能出现的最小峰值。
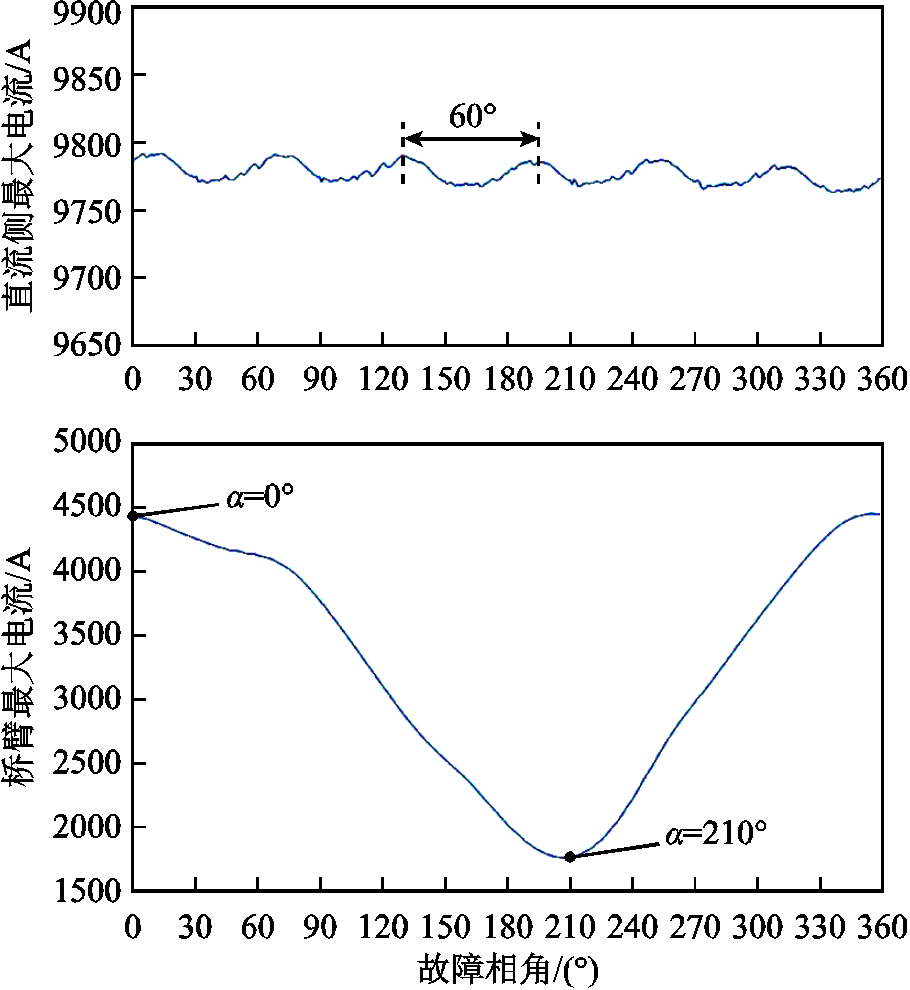
图4 A相上桥臂故障电流与直流侧故障电流与相角α的关系
Fig.4 Relationship between α and fault current of A phase upper arm and DC side
对于直流侧电流，则总体呈现出以60°为周期的波动变化，这主要是因为换流器三相等效电容放电状态呈周期性[14]。可以注意到其峰值随相角的变化很小，最大峰值与最小峰值相差不到30A，仅占直流故障电流的0.3%，可以忽略不计。因此，直流侧故障电流受故障时刻的影响较小，可以认为不同故障时刻直流侧故障电流特性近似相同。
图5给出了A相上桥臂故障电流在最大值与最小值对应相角下的计算值与仿真值，以及α=0°时直流侧故障电流随时间变化的计算值与仿真值。可以看出，状态方程计算值与EMT仿真结果高度吻合。由图5a桥臂电流随时间变化图可知，当α=0°时，桥臂故障电流在t=4ms时到达最大值4 447A，计算结果为4 439A，计算误差仅为0.20%；而当α=210°时，桥臂故障电流最大值为1 770A，计算结果为1 767A，计算误差仅为0.17%。由图5b可知，当α=0°时，直流侧故障电流随时间不断增大，直流故障电流在t=4ms时到达9 771A，计算结果为9 785A，计算误差仅为0.14%。
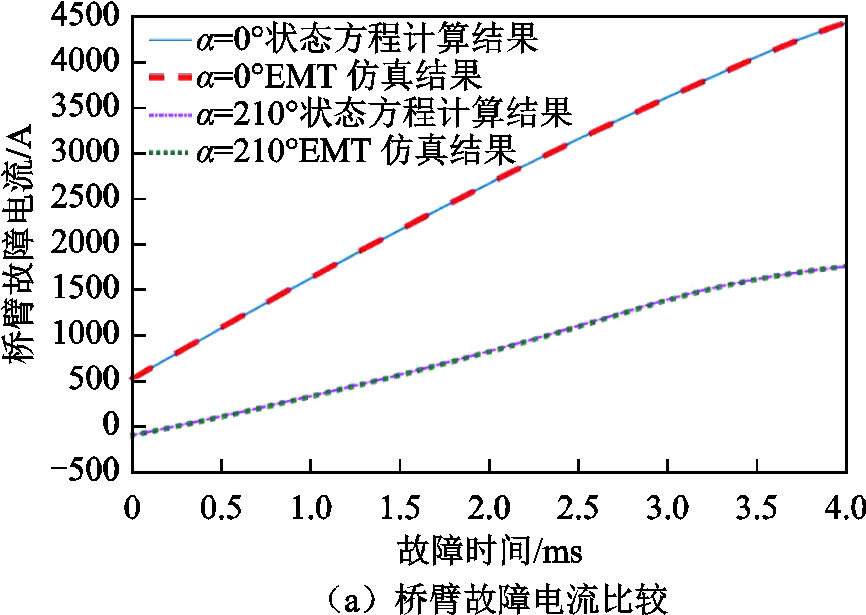
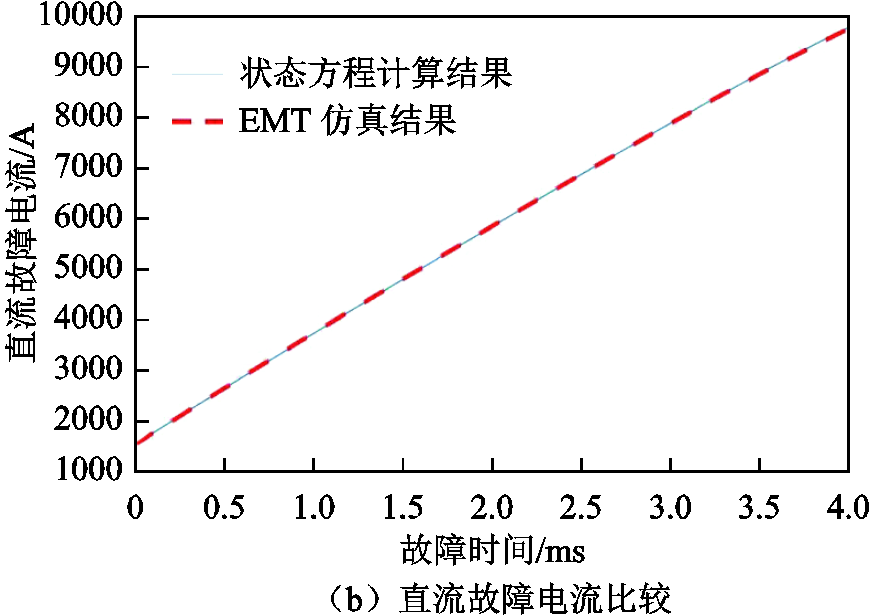
图5 A相上桥臂与直流侧故障电流随故障时间变化图
Fig.5 Fault current variation curve of upper arm and DC side of phase A with fault time
表2给出了不同相角α下的A相上桥臂电流与直流侧电流在t=4ms时的计算误差。可以看出，在不同相角下，桥臂电流平均误差最大仅为0.59%，直流侧电流平均误差最大仅为0.22%。状态方程计算值与仿真结果在不同相角α下均能较好的拟合，证明了本文所提出的故障电流计算方法有效。
表2 不同相角下的故障电流计算误差
Tab.2 The calculation error of current under different phase angles
故障相角α/(°)桥臂电流iap(%)直流侧电流idc(%) 00.200.14 900.120.22 1800.590.14 2700.390.22
在实际工程中，直流故障可能发生在直流电网任意一点，在线路较长时，线路可等效为RL模型[19]。图6a给出了线路单位阻感参数一定的条件下，换流器最大故障电流随故障点与换流器距离的变化关系，其中线路单位参数为Rline=0.014Ω/km，Lline= 0.82mH/km。可以看出随着故障点与换流站距离的增大，线路总阻感上升，换流器桥臂故障电流和直流侧故障电流的最大值均出现了显著的下降。而图6b则给出了故障点与换流器距离一定的条件下，换流器直流侧最大故障电流随线路单位参数的变化关系，其中故障点距换流器直流侧出口处40km。可以看出，线路单位长度电阻与电感越大，线路总阻感越大，最大故障电流将会随着线路总阻感的增大而降低。当故障发生在换流器直流侧出口处时，线路总阻感最小，故障电流最大，故障最为严重。
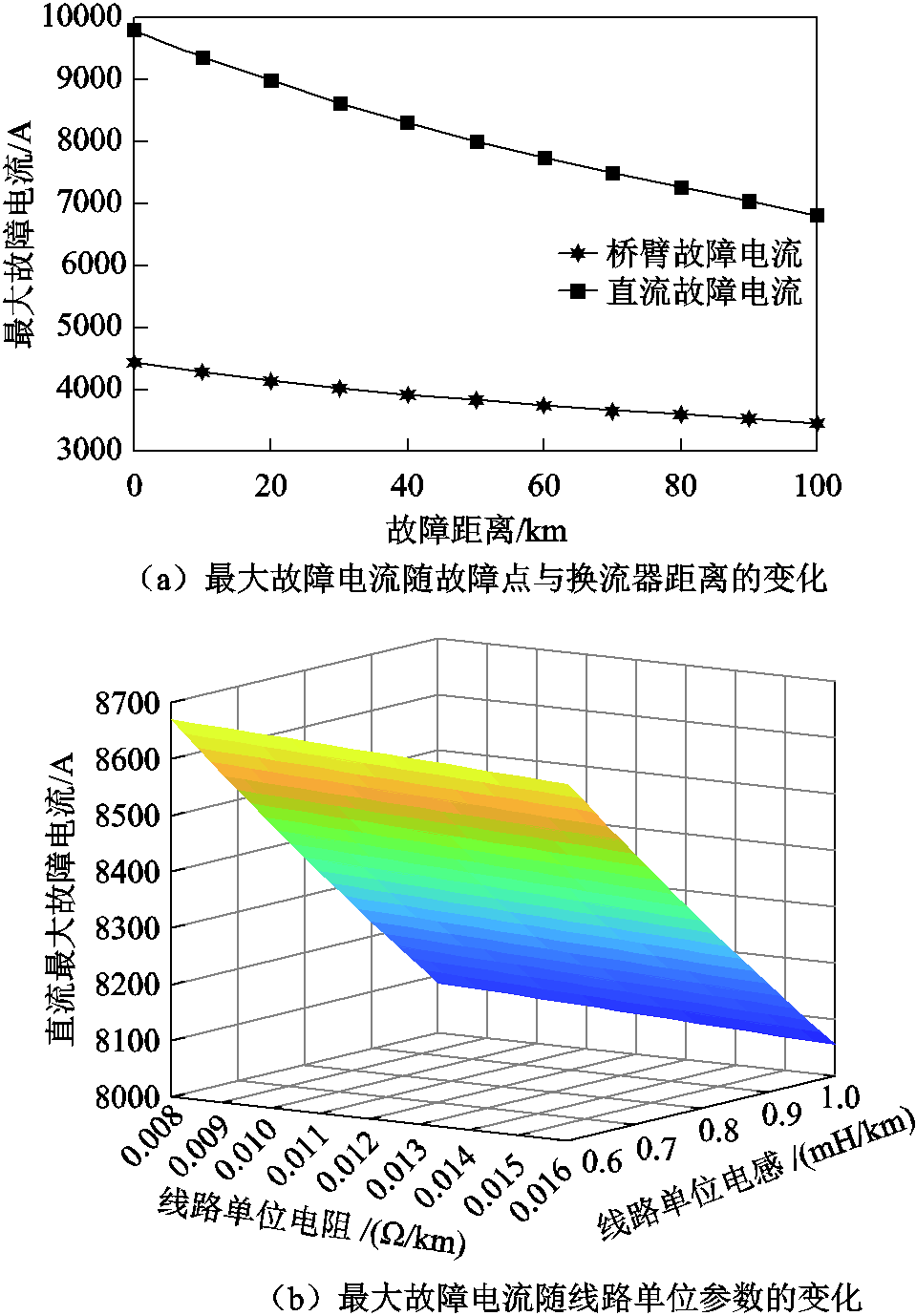
图6 换流器最大故障电流随故障点距离与线路单位参数的变化关系
Fig.6 Fault current maximum value with fault distance and line unit parameters change
为了进一步分析交流注入与子模块投入函数的影响，将本文所提出的故障电流计算方法与两种典型的传统故障电流计算方法进行了分析和比较。这两种方法为：①忽略交流系统注入电流的影响，仅考虑子模块电容放电的RLC等效电路计算方法[14]；②考虑了交流注入，但忽略子模块投入函数项，仅将桥臂等效为一个电容的计算方法[16]。计算选用表1中的系统参数。
图7给出了故障时刻相角α=0°的条件下，采用本文所提方法的A相上桥臂电流iap状态方程计算算值、仅考虑子模块电容放电时基于RLC等效电路得到的ia-C计算值以及EMT得出的桥臂故障电流iap的仿真值。由图7可以得出，在闭锁前的时段内，桥臂电流最大可达到4 447A。故障发生后，随时间增长，ia-C与iap差值迅速增大，交流系统注入电流急剧增加。在4ms时，ia-C与仿真结果差值可达1 034A，此时ia-C的计算误差为26.49%；而采用本文提出的计算方法得到的iap则始终与仿真结果高度吻合，4ms时计算误差仅为0.20%。
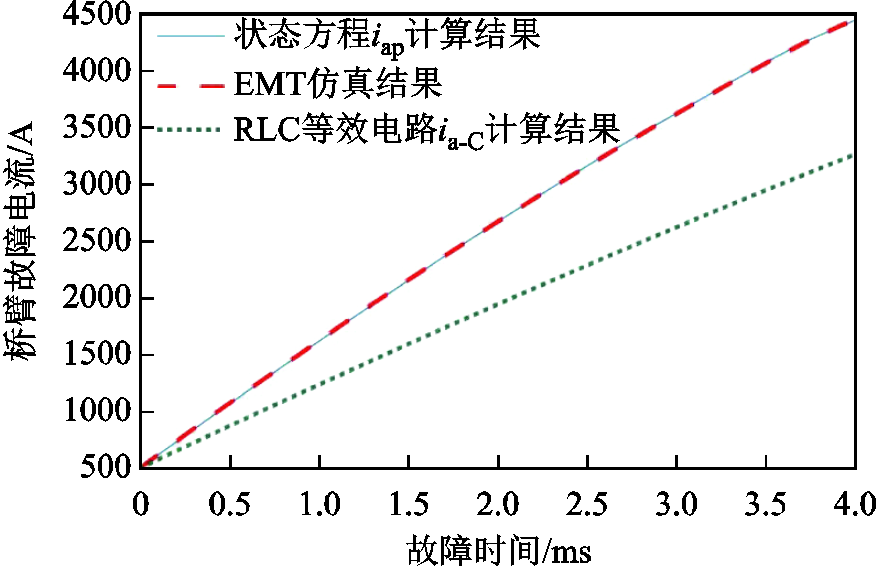
图7 α=0°时iap与ia-C计算结果
Fig.7 Calculation results of iap and ia-C when α=0°
图8则给出了故障时刻相角α=0°的条件下，采用本文所提方法的直流侧故障电流idc计算值、仅考虑子模块电容放电时基于RLC等效电路得到的idc-C计算值、直流侧故障电流idc的仿真值。由图8可知，故障发生后1.5ms内，idc-C与仿真值几乎一致，相差很小，这与文献[17]的结论一致。而随着时间增长，idc-C将显著低于仿真值。4ms时，直流侧故障电流可达到9 771A，而此时idc-C仅为8 783A，仅考虑电容放电时计算误差为10.11%，而采用本文提出的计算方法得到的idc计算值在4ms时误差仅为0.14%，与仿真结果高度吻合。
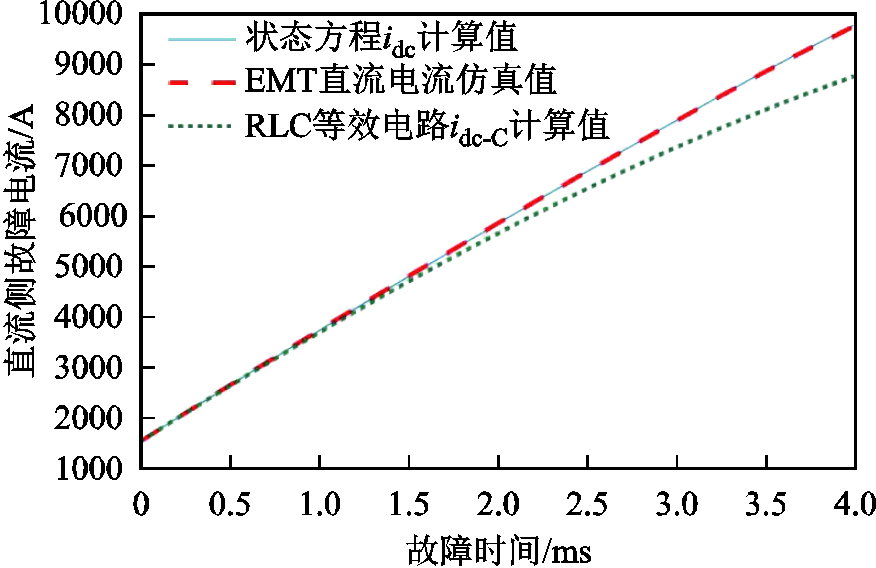
图8 α=0°时idc与idc-C计算结果
Fig.8 Calculation results of idc and idc-C when α=0°
因此，对于实际工程中换流器闭锁延迟时间相对较长的情况，仅考虑电容放电的故障电流计算结果将较实际故障电流明显偏低，不能准确描述故障暂态过程。为了精确计算故障电流，应同时考虑子模块电容放电电流与交流注入电流两个部分。
由式（6）可知，桥臂电压对时间的微分项由电容项与子模块投入函数项组成。其中，电容项表示桥臂子模块串联对外的等效电容，而投入函数项则表示子模块的投切对桥臂电压的影响。当忽略投入函数项，仅保留电容项时，桥臂可等效为一个电容模型。为了探究投入模块函数项的影响，此处按照文献[16]的计算方法，求解得到将桥臂等效为一个电容模型时的故障电流，并将此结果与本文所提出的同时考虑电容项和投入函数项的计算方法的结果相对比。图9给出了相角α=0°的条件下，A相上桥臂电流在上述两种方法下的计算结果与仿真值。而图10则给出了α=0°的条件下，直流侧故障电流在两种方法下的计算结果与仿真值。
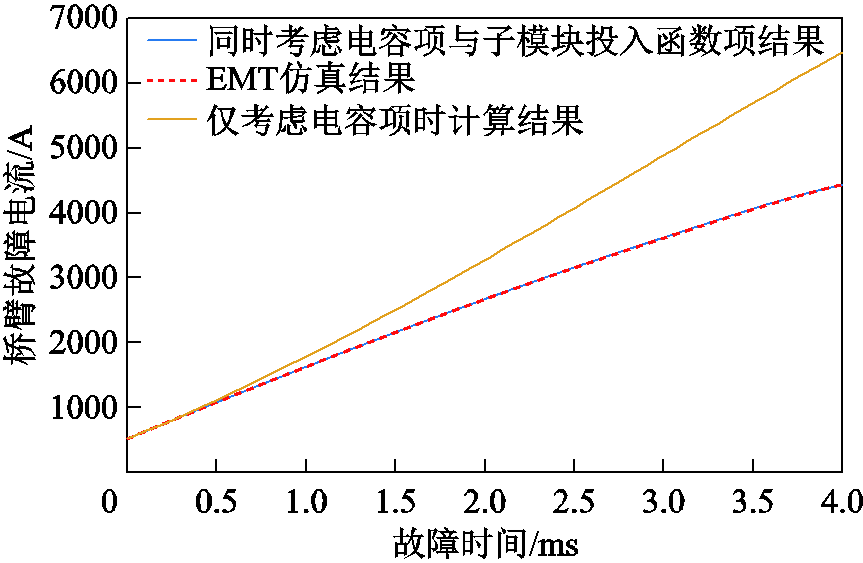
图9 α=0°时两种方法下的桥臂电流计算结果及仿真值
Fig.9 Calculation results and simulation values of arm current under two methods when α=0°
由图9可得，对于桥臂电流，仅考虑电容项时的故障电流计算结果将较仿真值显著偏大，并且随时间的增长，偏差值还将继续增大，4ms时，偏差值可达2 040A，计算误差为45.87%。由图10可知，对于直流侧电流，在2ms以前，仅考虑电容项时的故障电流计算结果与仿真结果非常接近。而在故障发生2ms后，仅考虑电容项的电流计算结果与仿真结果相比则逐渐偏低。4ms时，偏差值达到了531A，计算误差为5.43%。对比图8可知，由于考虑了交流电流注入，该方法与仅考虑电容放电的计算方法相比，计算的误差已有所降低但仍旧较大。
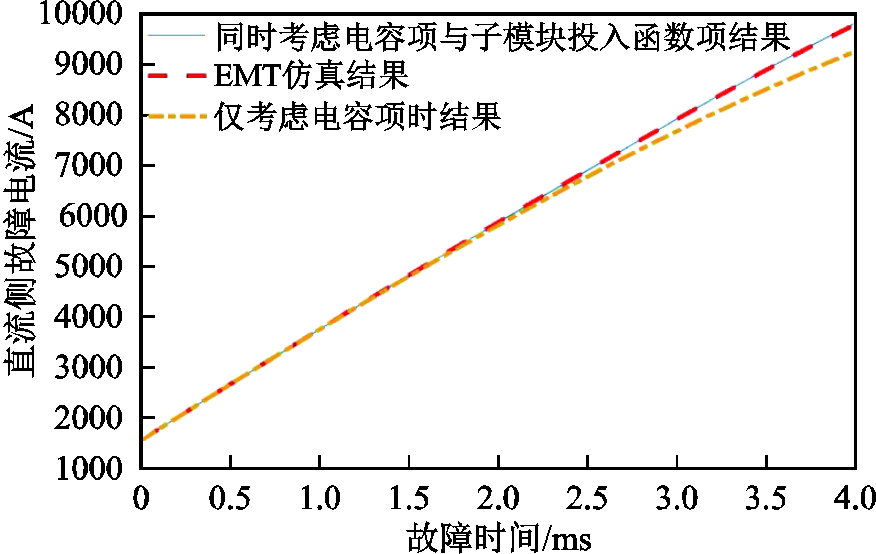
图10 α=0°时两种方法下的直流电流计算结果及仿真值
Fig.10 Calculation results and simulation values of arm current under two methods when α=0°
由上述仿真比较结果可知，投入函数项将对故障电流计算有显著影响，不可忽略，桥臂对时间的微分应同时包含电容项与投入模块函数项两部分。
本文在对桥臂等效模型分析的基础上，提出一种精确的直流故障电流的计算方法，采用状态方程数值解法求解故障电流，并将此结果与EMT仿真结果进行对比，得出以下结论：
1）桥臂电压对时间的微分项由电容项与子模块投入函数项组成。其中，电容项表示均压策略下桥臂子模块对外的串联等效电容；而子模块投入函数项则表示实时投入的子模块数量变化引起的桥臂电压变化。
2）故障时刻换流器交流系统相电压相角对桥臂故障电流初始值及其发展有显著影响。桥臂电流峰值将随相角的改变而变化，在特定的相角下有最大值。而对于直流侧故障电流，故障时刻相角的影响很小、可忽略不计，不同故障时刻直流侧故障电流特性近似相同。
3）在换流器闭锁延迟时间相对较长的情况下，交流系统注入电流与子模块投入函数项对故障电流的计算有显著影响，不可忽略。故障电流的计算应同时考虑交流系统注入电流与子模块投入函数项两个因素。
4）基于本文提出的故障电流计算方法，可大幅提高暂态故障电流计算的精确度。该方法可为MMC关键部件的选型提供一定的参考，并为直流短路故障保护方案的设计提供一定的依据。
状态方程式（12）各子矩阵表达式分别为
参考文献
[1]彭浩, 邓焰, 王莹, 等. 模块化多电平变换器模型及稳态特性研究[J]. 电工技术学报, 2015, 30(12): 120-127. Peng Hao, Deng Yan, Wang Ying, et al. Research about the model and steady-state performance for modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 120-127.
[2]苏见燊, 郭敬东, 金涛. 柔性直流电网中直流故障特性分析及线路故障重启策略[J]. 电工技术学报, 2019, 34(增刊1): 352-359. Su Jianshen, Guo Jingdong, Jin Tao. DC fault characteristics and line fault recovery strategy in flexible DC power network[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 352-359.
[3]许建中, 王乐, 武董一, 等. 采用子模块相关性坐标变换解耦的混合模块化多电平换流器可靠性建模[J]. 电工技术学报, 2019, 34(18): 3821-3830. Xu Jianzhong, Wang Le, Wu Dongyi, et al. Reliability modeling of hybrid modular multilevel converter using coordinate transformation based on decoupled sub-module correlations[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3821-3830.
[4]郝瑞祥, 杨晓峰, 薛尧, 等. 一种具有直流故障限流能力的模块化多电平换流器[J]. 电工技术学报, 2017, 32(6): 172-180. Hao Ruixiang, Yang Xiaofeng, Xue Yao, et al. A novel modular multilevel converter with DC fault current limiting capability[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 172-180.
[5]罗永捷, 蒲羿, 宋勇辉, 等. 混合型模块化多电平换流器启动冲击电流特性分析及控制策略[J]. 电工技术学报, 2020, 35(增刊1): 49-59. Luo Yongjie, Pu Yi, Song yonghui, et al. The inrush current characteristics and control strategies of hybrid modular multilevel converter systems during start-up processes[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 49-59.
[6]张国驹, 祁新春, 陈瑶, 等. 模块化多电平换流器直流双极短路特性分析[J]. 电力系统自动化, 2016, 40(12): 151-157. Zhang Guoju, Qi Xinchun, Chen Yao, et al. Characteristic analysis of modular multilevel converter under DC pole-to-pole short-circuit fault[J]. Automation of Electric Power Systems, 2016, 40(12): 151-157.
[7]孙吉波, 王宇, 刘崇茹, 等. 基于MMC的多端直流电网双极短路故障电流计算[J]. 电力自动化设备, 2018, 38(11): 72-78. Sun Jibo, Wang Yu, Liu Chongru, et al. Pole-to-pole short circuit current calculation of multi-terminal DC grid based on MMC[J]. Electric Power Automation Equipment, 2018, 38(11): 72-78.
[8]尹太元, 王跃, 段国朝, 等. 基于零直流电压控制的混合型MMC-HVDC直流短路故障穿越策略[J]. 电工技术学报, 2019, 34(增刊1): 343-351. Yin Taiyuan, Wang Yue, Duan Guozhao, et al. Zero DC voltage control based DC fault ride-through strategy for hybrid modular multilevel converter in HVDC[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 343-351.
[9]Nguyen T H, Khalifa H A H, El Moursi M. Alternating submodule configuration based MMCs with carrier-phase-shift modulation in HVDC systems for DC fault ride-through capability[J]. IEEE Transactions on Industrial Informatics, 2019, 15(9): 5214-5224.
[10]周光阳, 李妍, 何大瑞, 等. 含限流器的多端柔直系统故障保护策略[J]. 电工技术学报, 2020, 35(7): 1432-1443. Zhou Guangyang, Li Yan, He Darui, er al. Protection scheme for VSC-MTDC system with fault current limiter[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1432-1443.
[11]王姗姗, 周孝信, 汤广福, 等. 模块化多电平换流器HVDC直流双极短路子模块过电流分析[J]. 中国电机工程学报, 2011, 31(1): 1-7. Wang Shanshan, Zhou Xiaoxin, Tang Guangfu, et al. Analysis of submodule overcurrent caused by DC pole-to-pole fault in modular multilevel converter HVDC system[J]. Proceedings of the CSEE, 2011, 31(1): 1-7.
[12]Wang Weihua, Zhu Jin, Li Wei, et al. Analysis and hardware-in-the-loop simulation of a pole-to-pole DC fault in MMC-based HVDC systems[C]//13th Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference (COBEP/ SPEC), Fortaleza, 2015: 1-5.
[13]Jiang Bin, Gong Yanfeng, Cao Jun, et al. Fault current analysis of MMC based HVDC system under DC pole-to-pole fault condition[C]//International Conference on Renewable Power Generation (RPG 2015), Beijing, 2015: 1-5.
[14]段国朝, 王跃, 尹太元, 等. 模块化多电平变流器直流短路故障电流计算[J]. 电网技术, 2018, 42(7): 2145-2152. Duan Guozhao, Wang Yue, Yin Taiyuan, et al. DC short circuit current calculation for modular multilevel converter[J]. Power System Technology, 2018, 42(7): 2145-2152.
[15]马焕, 姚为正, 吴金龙, 等. 含桥臂阻尼的MMC-HVDC直流双极短路故障机理分析[J]. 电网技术, 2017, 41(7): 2099-2106. Ma Huan, Yao Weizheng, Wu Jinlong, et al. Analysis of DC pole-to-pole short circuit fault behavior in MMC-HVDC transmission systems with bridge arm damper[J]. Power System Technology, 2017, 41(7): 2099-2106.
[16]Li Bin, He Jiawei, Tian Jie, et al. DC fault analysis for modular multilevel converter-based system[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(2): 275-282.
[17]Leterme W, Beerten J, Hertem D V. Equivalent circuit for half-bridge MMC DC fault current contribution[C]//IEEE International Energy Conference, Leuven, 2016: 1-6.
[18]王威儒, 贺之渊, 李国庆, 等. 含交流影响的MMC-HVDC直流故障电流递推计算方法[J]. 中国电机工程学报, 2019, 39(增刊1): 313-320. Wang Weiru, He Zhiyuan, Li Guoqing, et al. Recursive calculation method of MMC-HVDC DC fault current with AC effect[J]. Proceedings of the CSEE, 2019, 39(S1): 313-320．
[19]Langwasser M, De Carne G, Liserre M, et al. Fault current estimation in multi-terminal HVDC grids considering MMC control[J]. IEEE Transactions on Power Systems, 2019, 34(3): 2179-2189.
[20]徐政, 刘高任, 张哲任. 柔性直流输电网的故障保护原理研究[J]. 高电压技术, 2017, 43(1): 1-8. Xu Zheng, Liu Gaoren, Zhang Zheren. Research on fault protection principle of DC grids[J]. High Voltage Engineering, 2017, 43(1): 1-8.
[21]李斌, 何佳伟, 李晔, 等. 多端柔性直流系统直流故障保护方案[J]. 中国电机工程学报, 2016, 36(17): 4627-4637. Li Bin, He Jiawei, Li Ye, et al. DC fault protection strategy for the flexible multi-terminal DC system[J]. Proceedings of the CSEE, 2016, 36(17): 4627-4637.
[22]Wang M, Beerten J, Van Hertem D. Frequency domain based DC fault analysis for bipolar HVDC grids[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(4): 548-559.
[23]徐政. 柔性直流输电系统[M]. 北京: 机械工业出版社, 2012.
[24]Ahmed N, Angquist L, Norrga S, et al. A computationally efficient continuous model for the modular multilevel converter[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2014, 2(4): 1139-1148.
The Accurate Calculation and Analysis of Overcurrent under Modular Multilevel Converter DC Fault
Abstract The modular multilevel converter (MMC) is vulnerable to DC fault. Significant overcurrent will occur on the converter after the fault, which has a serious impact on the reliability of MMC. The accurate calculation of fault transient current is crucial to evaluate the overcurrent. This paper presents an precise method to calculate MMC fault overcurrent. The proposed calculation method considers both the influence of grid voltage and DC capacitor discharging. The equivalent model of MMC is established and analyzed, it can be concluded that the differential of arm voltage to time should be composed of capacitance term and submodule switch function term. Based on the method, the numerical solution of the fault current under the DC fault was calculated. Maximum and minimum possible overcurrent was derived. The precision of calculation method was verified by the electromagnetic transient (EMT) simulation results. Finally, the proposed approach was further compared with the two conventional calculation methods. It is verified that the proposed approach has significantly higher accuracy than the conventional methods. The proposed approaches provide a numerical evaluation tool for the design of MMC and DC fault protection.
keywords：Modular multilevel converter, DC fault, fault current calculation, overcurrent analysis
中图分类号：TM71
DOI:10.19595/j.cnki.1000-6753.tces.L90188
国家重点研发计划（2018YFB0905800）和国家自然科学基金（51877206, 51721005）资助项目。
收稿日期 2020-06-30
改稿日期 2020-10-10
蔡 洋 男，1995年生，硕士研究生，研究方向为电力电子与电力传动。E-mail：caiyang1234@mail.iee.ac.cn
郭文勇 男，1979年生，研究员，博士生导师，研究方向为储能技术、风力发电和电力电子技术。E-mail：wyguo@mail.iee.ac.cn（通信作者）
（编辑 赫蕾）