图1 LCC-MMC串联型混合直流输电系统拓扑
Fig.1 Topology of LCC-MMC series hybrid HVDC transmission system
摘要 该文建立了整流侧为电网换相换流器(LCC)、逆变侧为LCC和模块化多电平换流器(MMC)串联的LCC-MMC串联型混合直流输电系统的小信号模型。首先,推导LCC的交直流侧等效电路和考虑内部动态特性的MMC的交直流侧等效电路;然后,基于等效电路构建系统整流侧模型和逆变侧模型,并对直流输电线路和控制系统进行建模,通过组合各个部分模型得到全系统模型;最后,通过线性化全系统模型得到全系统小信号模型。通过对比基于PSCAD/EMTDC搭建的电磁暂态模型验证小信号模型的准确性;基于小信号模型,分析MMC定直流电压控制参数、逆变侧LCC定直流电压控制参数、锁相环(PLL)参数和交流联络线参数对系统小信号稳定性的影响。该文所提出的LCC-MMC串联型混合直流输电系统的小信号模型可用于系统的小信号稳定性分析,从而为系统设计和参数选择提供有价值的参考。
关键词:电网换相换流器 模块化多电平换流器 串联型 混合直流输电 小信号建模
我国能源基地和负荷中心在空间上逆向分布的特点产生了能源资源大范围优化配置的迫切需求。由于具备远距离大容量输电的优势,直流输电技术在能源资源优化配置过程中发挥了重要作用[1]。其中,基于电网换相换流器的高压直流输电(Line Commutated Converter Based High Voltage Direct Current, LCC-HVDC)具有容量大、损耗小、技术成熟和成本较低等优点,但也具有占地面积大、不能向无源系统供电、逆变侧容易发生换相失败等缺点[2];基于模块化多电平换流器的高压直流输电(Modular Multilevel Converter Based High Voltage Direct Current, MMC-HVDC)的优缺点与LCC-HVDC恰好相反,具有占地面积小、能够向无源系统供电和没有换相失败问题等优点,并且有容量小、损耗大、技术不够成熟和成本较高等缺点[3]。因此,结合二者的技术优势,混合直流输电技术得到了快速发展[4-7]。
早期的混合直流输电系统多为单一送端、单一受端,并于两端分别采用不同类型换流器的系统,即LCC-MMC并联型混合直流输电系统[8-9]。近年来,学者们陆续提出了于同一端采用不同类型换流器串联的混合直流输电系统,即LCC-MMC串联型混合直流输电系统。例如,文献[10]提出了一种由电网换相换流器(Line Commutated Converter, LCC)和电压源换流器(Voltage Source Converter, VSC)串联而成的混合型换流器,具备自换相能力,适用于大规模风电直接经直流输电进行远距离外送。文献[11]提出了一种LCC-MMC串联混合型直流输电系统,具备交直流故障穿越能力,适用于远距离大容量架空线路。文献[12]提出了一种混合型级联直流输电系统,充分利用LCC和VSC特点以及特高压输电线路和直流电缆的优点,适用于跨区域、大容量、多落点直流输电。文献[13]提出了一种级联换流阀拓扑,同时具备特高压直流馈入和受端电网异步互联能力,适用于大容量可再生能源远距离输送,并能较好地解决大容量直流多馈入问题。LCC-MMC串联型混合直流输电系统不仅在学术研究方面备受关注,在工程应用方面同样发展迅速。我国目前规划建设的白鹤滩—江苏±800kV特高压直流输电工程,送端拟采用LCC,受端拟采用LCC与多个并联MMC串联,是LCC-MMC串联型混合直流输电系统应用于工程实践的典型案例。
LCC-MMC串联型混合直流输电系统具有如下优势:①当发生直流故障时,LCC可以阻断MMC对故障点的放电通路,因而无需配备价值高昂的直流断路器;②当发生交流故障时,MMC可以在一定程度上维持交流母线电压,从而降低LCC发生换相失败的概率;③即使LCC发生了换相失败,MMC依然能够传输一定的功率,有利于受端交流系统维持稳定。
在LCC-MMC串联型混合直流输电系统中,LCC和MMC在直流侧相互串联,在交流侧相互并联,二者之间具有紧密的电气耦合关系,在某些情况下可能导致系统小信号不稳定。基于系统小信号模型的小信号稳定性分析可以揭示系统的小信号不稳定现象,同时还可以为系统设计和参数选择提供重要参考,因此LCC-MMC串联型混合直流输电系统的小信号建模具有十分重要的意义。
已有许多学者对LCC-HVDC和MMC-HVDC的小信号建模和小信号稳定性分析进行了研究。文献[14-15]基于LCC的准稳态特性,建立LCC的小信号模型。文献[16]研究了多馈入LCC-HVDC之间的交互影响。文献[17]借助开关函数模型描述LCC交直流侧电压电流变换关系。文献[18]提出MMC在旋转坐标系下的统一建模方法。文献[19]考虑MMC的内部动态特性,建立了详细的MMC小信号模型。文献[20]提出基于MMC的直流电网的小信号模型的通用建模方法。文献[21]基于平均值模型,建立了MMC的小信号模型。
关于LCC-MMC并联型混合直流输电系统的小信号建模和小信号稳定性分析,文献[22]建立了送端为LCC、受端为MMC的LCC-MMC并联型混合直流输电系统的小信号模型,并利用特征值分析法分析了交流系统强度对于系统小信号稳定性的影响。文献[23]在文献[22]的基础上,进一步研究控制系统参数、MMC子模块电容和桥臂电感对于系统小信号稳定性的影响。文献[24]建立LCC-MMC并联型混合三端直流输电系统的小信号模型,对系统振荡模态进行辨识,并分析了控制系统参数和交流系统强度对系统小信号稳定性的影响。但是对于LCC-MMC串联型混合直流输电系统的小信号建模和小信号稳定性分析,目前尚未有文献报道。
本文建立了整流侧为LCC、逆变侧为LCC和MMC串联的LCC-MMC串联型混合直流输电系统的小信号模型。首先推导LCC的交直流侧等效电路和考虑内部动态特性的MMC的交直流侧等效电路,并基于等效电路构建系统整流侧和逆变侧模型,然后对直流输电线路和控制系统进行建模,通过组合各个部分模型获得全系统模型,最后通过线性化获得全系统小信号模型。与基于PSCAD/EMTDC搭建的电磁暂态模型进行对比,验证小信号模型的准确性并基于小信号模型分析MMC定直流电压控制参数等对系统小信号稳定性的影响。
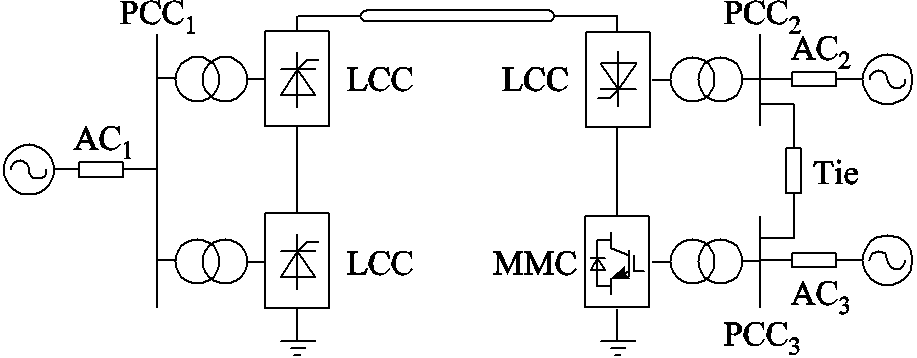
LCC-MMC串联型混合直流输电系统拓扑如图1所示。图1中,AC1为整流侧交流系统,AC2和AC3为逆变侧交流系统,AC2和AC3之间通过交流联络线Tie进行连接。整流站由两个12脉动LCC换流器串联构成,逆变站由一个12脉动LCC换流器和一个MMC换流器串联构成,逆变站LCC和MMC分别馈入AC2和AC3。交流系统通过公共耦合点(Point of Common Coupling, PCC)与换流站进行连接,PCC1~PCC3依次为AC1~AC3与换流站的连接点。

图1 LCC-MMC串联型混合直流输电系统拓扑
Fig.1 Topology of LCC-MMC series hybrid HVDC transmission system
图1所示LCC-MMC串联型混合直流输电系统的等效电路如图2所示,其中交流部分为一相等效电路,并省略了表示相别的下标。
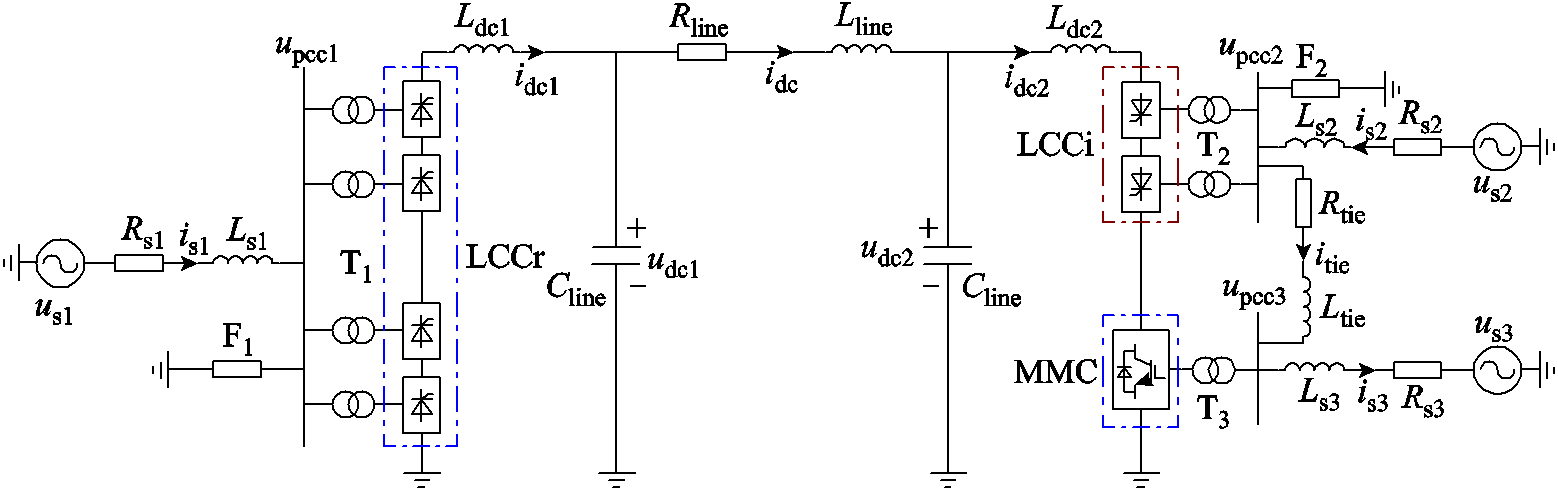
图2 LCC-MMC串联型混合直流输电系统等效电路
Fig.2 Equivalent circuit of LCC-MMC series hybrid HVDC transmission system
图2中,交流系统采用戴维南等效电路进行表示,us1(us2、us3)为AC1(AC2、AC3)的等值内电动势,Rs1(Rs2、Rs3)和Ls1(Ls2、Ls3)分别为AC1(AC2、AC3)的等值内电阻和等值内电感,is1(is2、is3)为流过Ls1(Ls2、Ls3)的电流。upcc1(upcc2、upcc3)为PCC1(PCC2、PCC3)的电压。Rtie和Ltie分别为Tie的线路电阻和线路电感,itie为流过Ltie的电流。LCCr为整流侧双12脉动LCC换流器,LCCi为逆变侧12脉动LCC换流器,F1和F2分别为LCCr和LCCi所需的滤波器和无功补偿装置,有关F1和F2的等效电路,参见附录。T1和T2分别为LCCr和LCCi的换流变压器,T3为MMC的连接变压器。Ldc1和Ldc2分别为整流侧和逆变侧平波电抗器的电感,idc1和idc2为流过它们的电流。直流输电线路采用p型等效电路进行表示,Rline、Lline和Cline分别为线路串联电阻、线路串联电感和线路并联电容,idc为流过Lline的电流,udc1和udc2为线路两端的电压。
为了建立图2所示的LCC-MMC串联型混合直流输电系统的小信号模型,本节将推导LCC的交直流侧等效电路和考虑内部动态特性的MMC的交直流侧等效电路。
为了便于推导和表示,系统的交流部分基于旋转坐标系进行建模。关于旋转坐标系的选取,有两种选择:一种是基于交流系统等值内电动势相角的旋转坐标系,称之为公共xy旋转坐标系(以下简称xy坐标系);另一种是基于锁相环(Phase-Locked Loop, PLL)输出相角的旋转坐标系,称之为本地dq旋转坐标系(以下简称dq坐标系)。由于不同的PLL输出的是各自锁定的PCC电压的相角,而在系统运行过程中,不同的PCC电压的相角是不一致的(不同的交流系统等值内电动势相角一致),因此基于不同的PLL输出相角的dq坐标系也是不一致的。为了便于统一,系统的交流部分基于xy坐标系进行建模。
由于MMC所采用的矢量控制策略基于dq坐标系,因此MMC的控制系统仍然基于dq坐标系进行建模。关于两种坐标系的相互转换参见附录。
LCC整流器示意图如图3所示。图中,ucrj(j=a,b,c,下同)为换相电压,ivrj为LCC整流器的交流电流,udcr和idcr分别为LCC整流器的直流电压和直流电流,VT1~VT6为晶闸管,Lcr为换相电感。
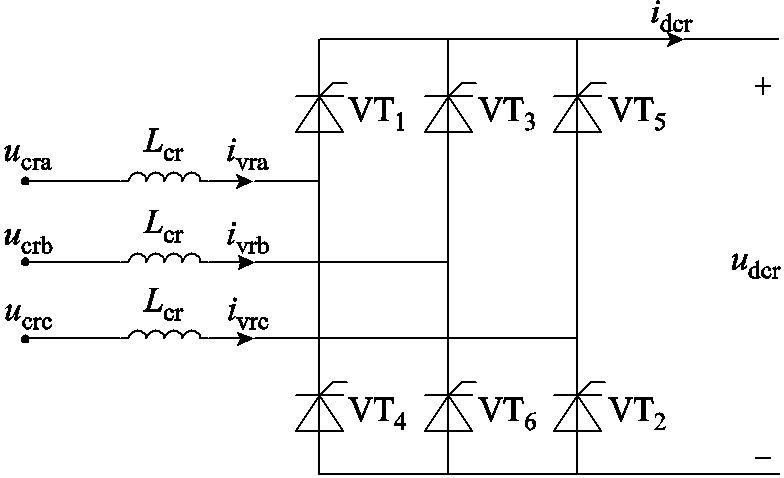
图3 LCC整流器示意图
Fig.3 Schematic diagram of LCC rectifier
设ucrj和ivrj在xy坐标系下的x轴分量和y轴分量分别为ucrx、ucry和ivrx、ivry,根据文献[25]可知,LCC整流器的输入、输出关系为
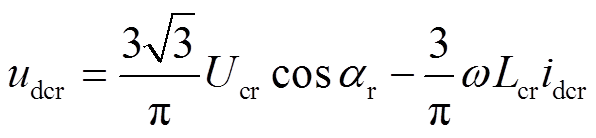 (1)
(1)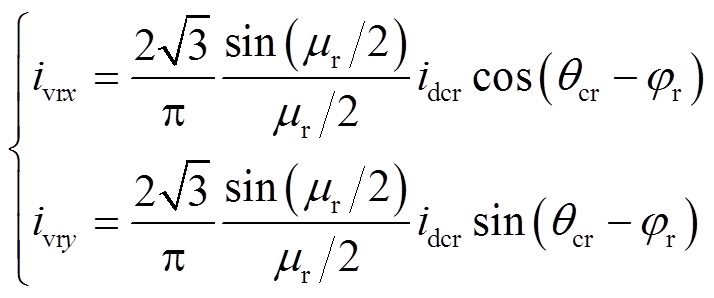 (2)
(2)式中,Ucr和qcr分别为ucrj的幅值和相角,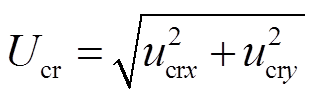 ,qcr=arctan(ucry/ucrx);ar、mr和jr分别为LCC整流器的滞后触发延迟角、换相重叠角和功率因数角。
,qcr=arctan(ucry/ucrx);ar、mr和jr分别为LCC整流器的滞后触发延迟角、换相重叠角和功率因数角。
根据式(1)和式(2)所描述的LCC整流器输入、输出关系,可得LCC整流器的交直流侧等效电路(交流侧等效电路为一相等效电路并省略了代表相别的下标)如图4所示。由图4可知,LCC整流器从交流侧看入等效为一个电流源,从直流侧看入等效为一个电压源。
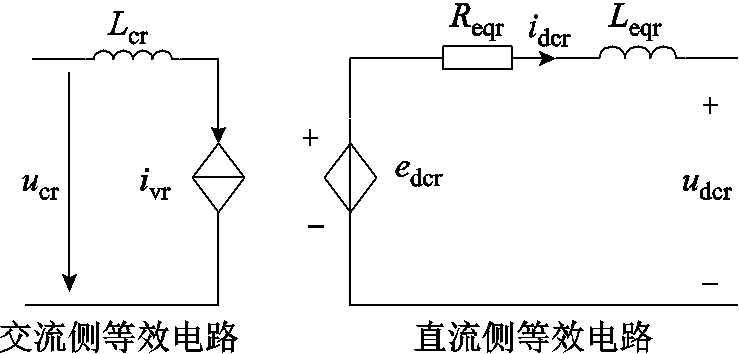
图4 LCC整流器交直流侧等效电路
Fig.4 Equivalent circuit of AC side and DC side of LCC rectifier
图4中,edcr、Reqr和Leqr分别为LCC整流器直流侧等值电动势、等值电阻和等值电感(从直流侧看入的换相电感的平均值[16]),edcr=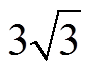 /pUcrcosar,Reqr=3/pwLcr,Leqr=[2-3mr/(2p)]Lcr。
/pUcrcosar,Reqr=3/pwLcr,Leqr=[2-3mr/(2p)]Lcr。
类似地,可以得到LCC逆变器的交直流侧等效电路(交流侧等效电路为一相等效电路并省略了代表相别的下标)如图5所示。相关变量的含义与表达式与LCC整流器类似,不再赘述。
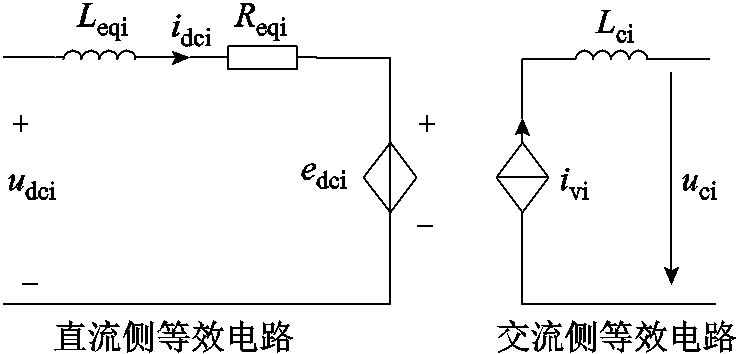
图5 LCC逆变器交直流侧等效电路
Fig.5 Equivalent circuit of AC side and DC side of LCC inverter
MMC示意图如图6所示。图中,uvj和ivj分别为MMC的交流电压和交流电流,udc和idc分别为MMC的直流电压和直流电流,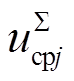 和
和 分别为MMC上桥臂和下桥臂的子模块电容电压之和,upj和unj分别为MMC上桥臂和下桥臂的桥臂电压,ipj和inj分别为MMC上桥臂和下桥臂的桥臂电流,mpj和mnj分别为MMC上桥臂和下桥臂的调制信号,Rarm和Larm分别为MMC的桥臂电阻和桥臂电感。
分别为MMC上桥臂和下桥臂的子模块电容电压之和,upj和unj分别为MMC上桥臂和下桥臂的桥臂电压,ipj和inj分别为MMC上桥臂和下桥臂的桥臂电流,mpj和mnj分别为MMC上桥臂和下桥臂的调制信号,Rarm和Larm分别为MMC的桥臂电阻和桥臂电感。
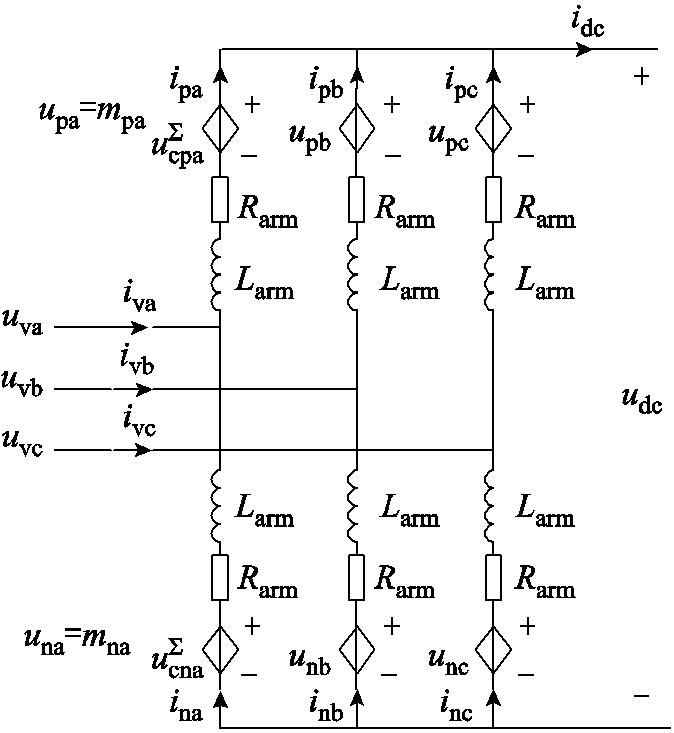
图6 MMC示意图
Fig.6 Schematic diagram of MMC
文献[18]在xy坐标系下建立了MMC的10阶动态模型,MMC的10个状态变量为[ivx, ivy, idc, 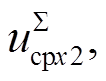
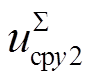 ,
, 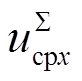 ,
, 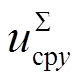 ,
, 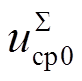 , icirx2, iciry2]T。其中,ivx和ivy分别为ivj在xy坐标系下的分量,代表MMC交流侧外特性。idc代表MMC直流侧外特性。
, icirx2, iciry2]T。其中,ivx和ivy分别为ivj在xy坐标系下的分量,代表MMC交流侧外特性。idc代表MMC直流侧外特性。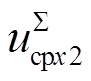 和
和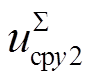 分别为
分别为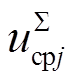 的二倍频分量在x2y2坐标系(旋转角频率为二倍基频)下的分量,
的二倍频分量在x2y2坐标系(旋转角频率为二倍基频)下的分量,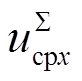 和
和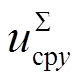 分别为
分别为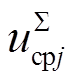 的基频分量在xy坐标系下的分量,
的基频分量在xy坐标系下的分量,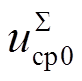 为
为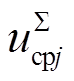 的直流分量,icirx2和iciry2分别为桥臂二倍频环流icirj在x2y2坐标系下的分量,以上变量代表MMC内部动态特性。
的直流分量,icirx2和iciry2分别为桥臂二倍频环流icirj在x2y2坐标系下的分量,以上变量代表MMC内部动态特性。
根据文献[18],可得ivx、ivy和idc的微分方程为
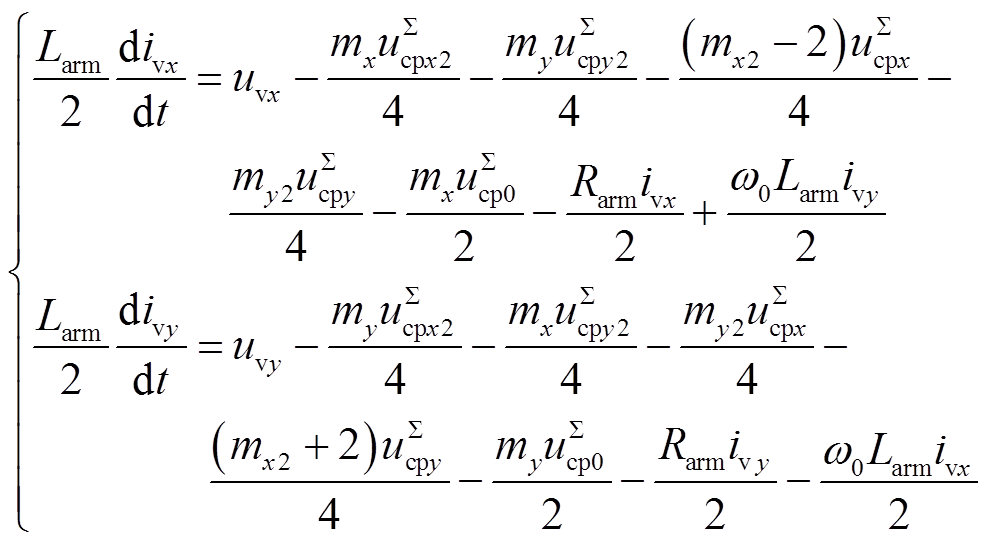 (3)
(3)
式中,mx2、my2和mx、my分别为调制信号m的二倍频分量和基频分量在x2y2和xy坐标系下的分量。
根据式(3)和式(4),可得MMC的交直流侧等效电路(交流侧等效电路为一相等效电路,并省略了代表相别的下标)如图7所示。由图7可知,MMC交直流侧均等值为一个电压源。
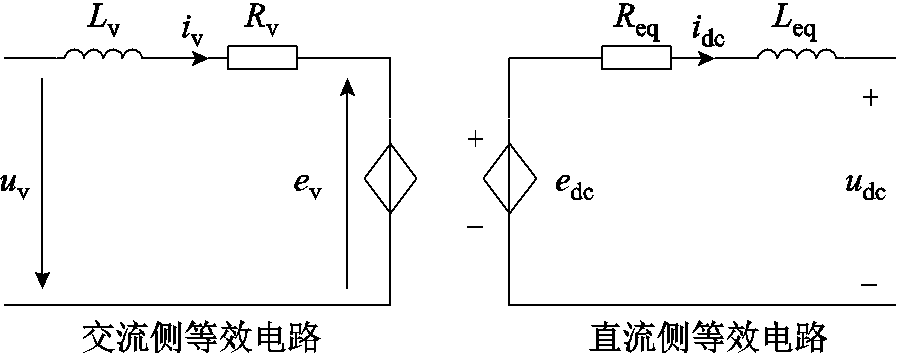
图7 MMC交直流侧等效电路
Fig.7 Equivalent circuit of AC side and DC side of MMC
图7中,ev为交流侧等值电动势,Rv和Lv分别为交流侧等值电阻和等值电感,Rv=Rarm/2,Lv=Larm/2。edc为直流侧等值电动势,Req和Leq分别为直流侧等值电阻和等值电感,Req=2Rarm/3,Leq=2Larm/3。ev和edc的表达式分别为
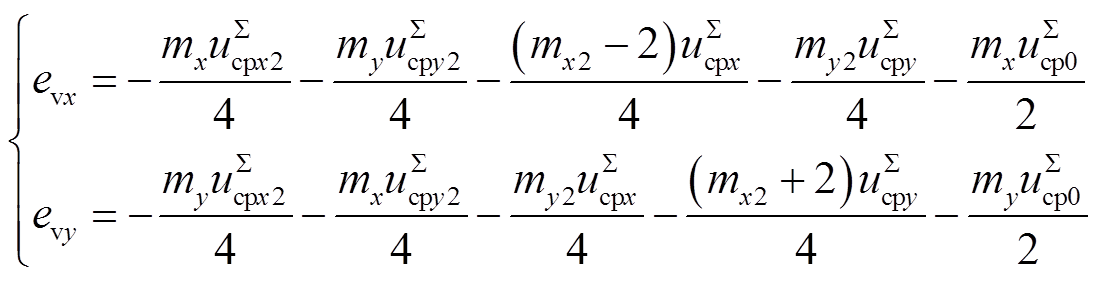 (5)
(5)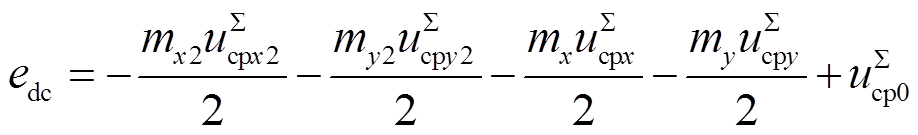 (6)
(6)由式(5)和式(6)可知,MMC内部状态变量虽然并不直接与外部发生交互,但是可以通过影响ev和edc来间接影响MMC的外特性。有关MMC内部状态变量的微分方程参见附录。
第2节推导了LCC的交直流侧等效电路和考虑内部动态特性的MMC的交直流侧等效电路。本节将基于等效电路推导系统整流侧动态模型和逆变侧动态模型,再结合直流输电线路动态模型和控制系统动态模型得到全系统动态模型,最后通过线性化全系统动态模型得到全系统小信号模型。
在图2所示的系统等效电路中,将LCCr用其交直流侧等效电路替代,可以得到系统整流侧等效电路,如图8所示。图8中,Us1Ð0°为AC1等值内电动势的幅值和相角,kT1为T1的电压比,RT1和LT1分别为T1折算到阀侧的漏电阻和漏电感,if1为流入F1的电流。
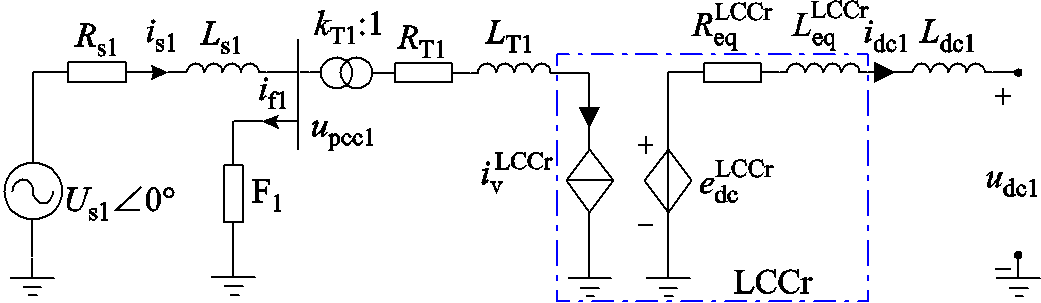
图8 系统整流侧等效电路
Fig.8 Equivalent circuit of rectifier side of system
下面将根据图8,推导系统整流侧动态模型。
由图8可知,is1的微分方程为
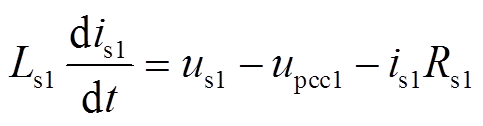 (7)
(7)将式(7)变换到xy坐标系下,得到
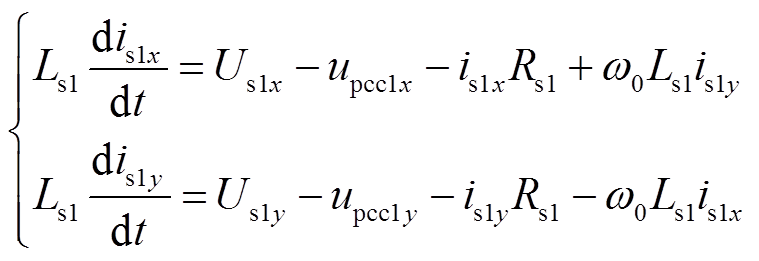 (8)
(8)式中,w0为交流系统额定角频率;is1x和is1y分别为is1在xy坐标系下的x轴分量和y轴分量,其余变量类似,不再赘述。特别地,由于xy坐标系基于交流系统等值内电动势相角,所以恒有Us1x=Us1,Us1y=0。
同样由图8可知,idc1的微分方程为
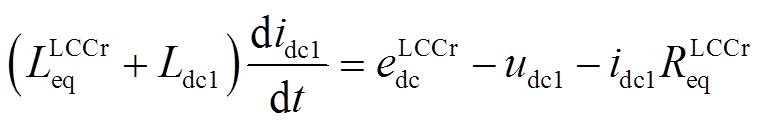 (9)
(9)upcc1的微分方程包含在F1的动态模型中,有关F1的动态模型参见附录。
3.2.1 直流部分动态模型
在图2所示的系统等效电路中,将LCCi和MMC分别用其直流侧等效电路替代,可以得到系统逆变侧等效电路的直流部分,如图9所示。
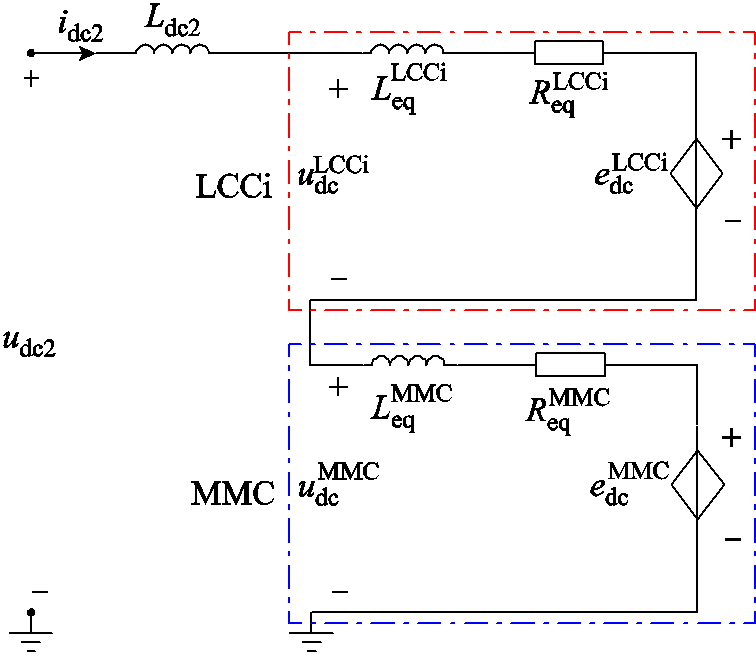
图9 系统逆变侧等效电路直流部分
Fig.9 DC part of equivalent circuit of inverter side of system
下面将根据图9推导系统逆变侧直流部分的动态模型。
由图9可知,idc2的微分方程为
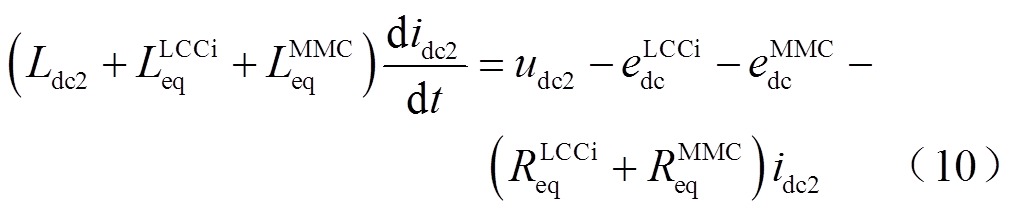
由式(10)可知,因为LCCi和MMC串联连接,idc2同时流经LCCi和MMC,所以idc2受到LCCi和MMC的共同影响。
由于LCCi和MMC均采用定直流电压控制,因此还需推导LCCi和MMC的直流端口电压的计算公式。
LCCi的直流端口电压的计算公式为
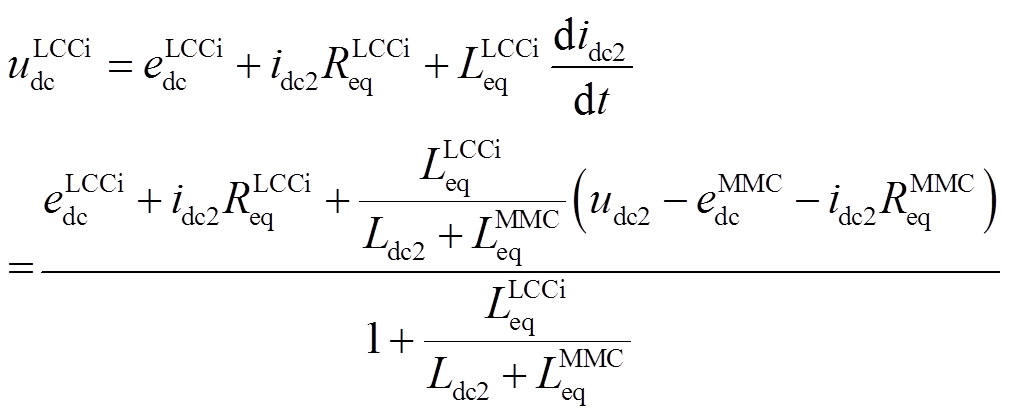 (11)
(11)MMC的直流端口电压的计算公式为
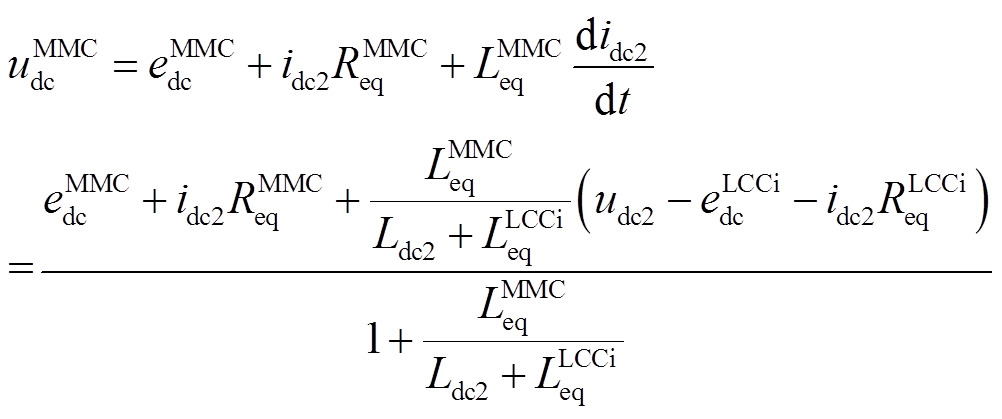 (12)
(12)由式(11)和式(12)可知,因为LCCi和MMC串联连接,所以在LCCi的直流端口电压和MMC的直流端口电压之间存在交互影响。
3.2.2 交流部分动态模型
在图2所示的系统等效电路中,将LCCi和MMC分别用其交流侧等效电路替代,可以得到系统逆变侧等效电路的交流部分,如图10所示。图10 中,Us2Ð0°和Us3Ð0°分别为AC2和AC3等值内电动势的幅值、相角。kT2和kT3分别为T2和T3的电压比,RT2、LT2和RT3、LT3分别为T2和T3折算到阀侧的漏电阻、漏电感。if2为流入F2的电流。
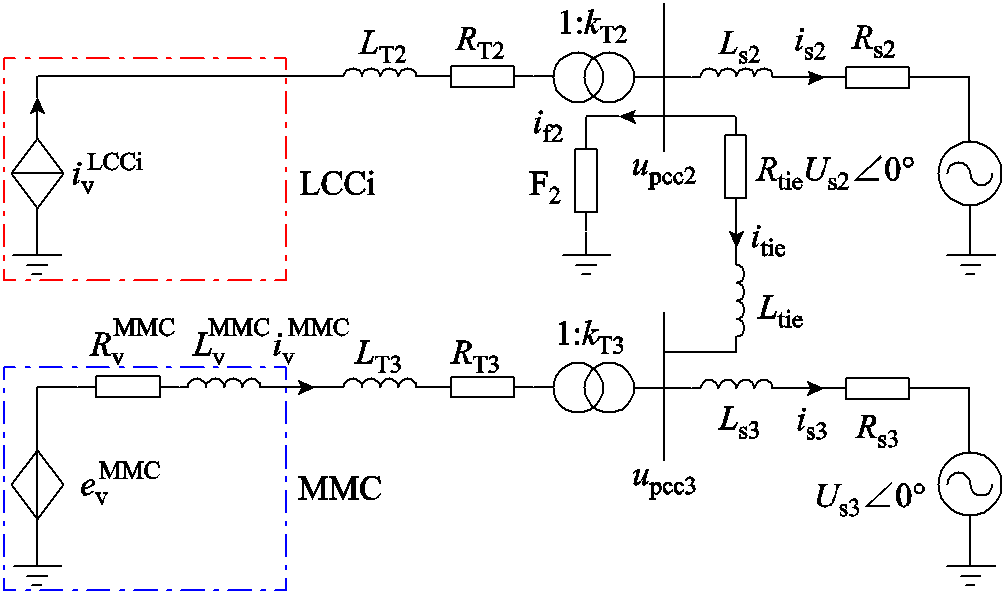
图10 系统逆变侧等效电路交流部分
Fig.10 AC part of equivalent circuit of inverter side of system
下面将根据图10,推导系统逆变侧等效电路交流部分的动态模型。
由图10可知,is2的微分方程为
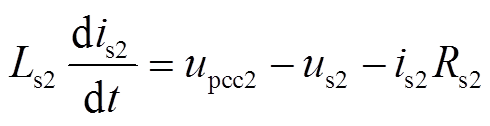 (13)
(13)将式(13)变换到xy坐标系下,得到
 (14)
(14)式中,is2x和is2y分别为is2在xy坐标系下的x轴分量和y轴分量,其余变量类似,不再赘述。
根据PCC3处的KCL约束可得
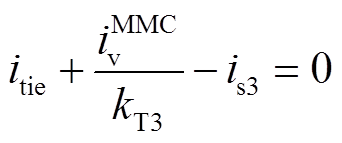 (15)
(15)根据式(15)可知,itie、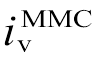 和is3三者之中只有两个独立的状态变量,将itie和
和is3三者之中只有两个独立的状态变量,将itie和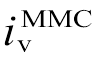 选为状态变量。由图9可知,itie的微分方程为
选为状态变量。由图9可知,itie的微分方程为
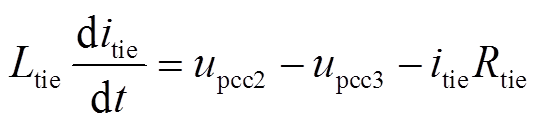 (16)
(16)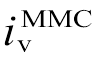 的微分方程为
的微分方程为
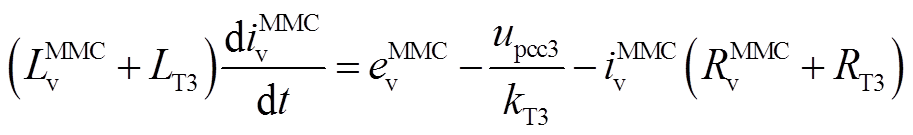 (17)
(17)将式(16)和式(17)分别变换到xy坐标系下,得到
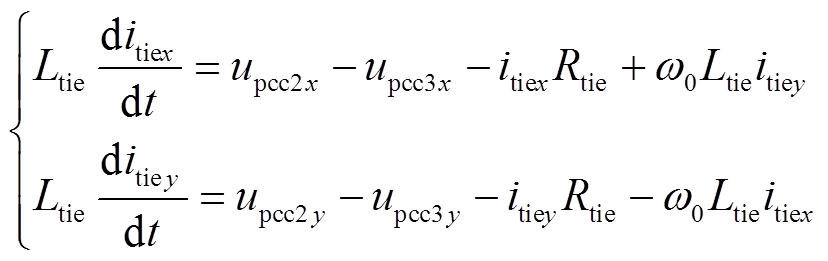 (18)
(18)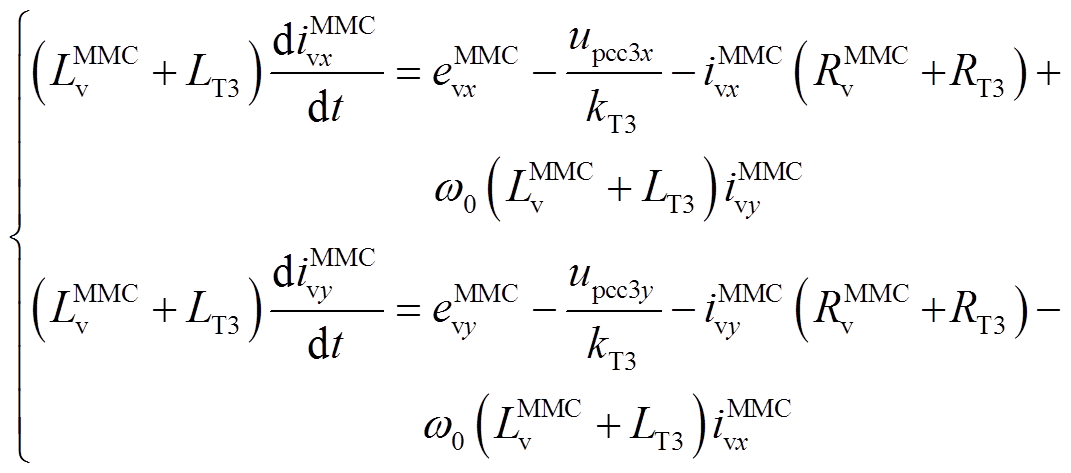 (19)
(19)式中,itiex、itiey和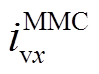 、
、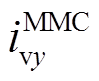 分别为itie和
分别为itie和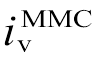 在xy坐标系下的x轴分量、y轴分量。
在xy坐标系下的x轴分量、y轴分量。
upcc2的微分方程包含在F2的动态模型中,有关F2的动态模型参见附录。
upcc3作为重要的中间变量,其计算公式为
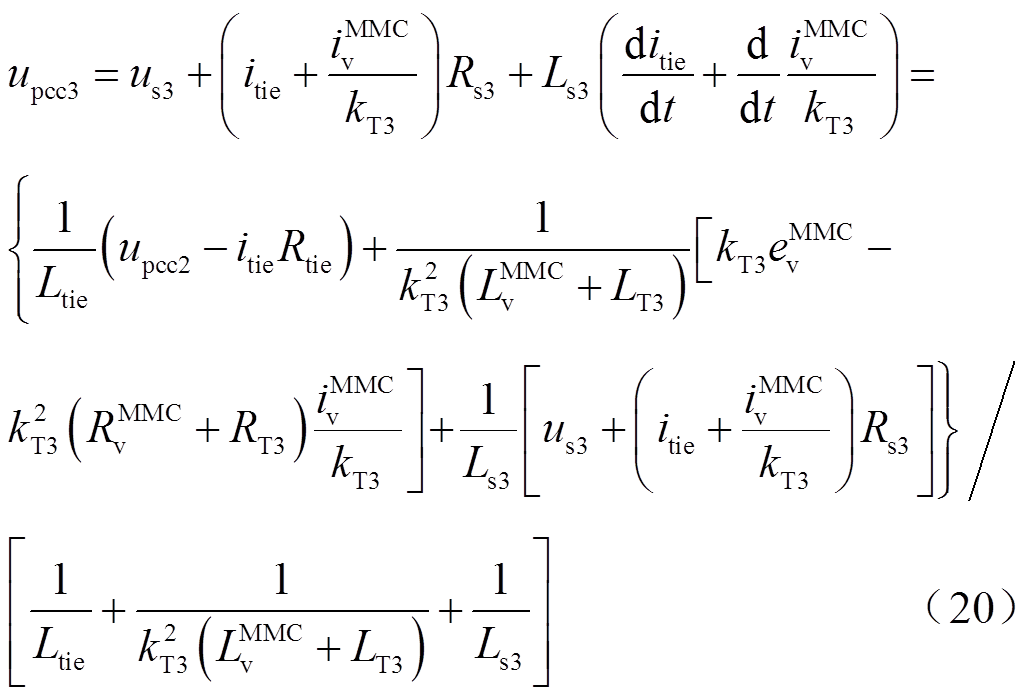
upcc3在xy坐标系下的x轴分量和y轴分量可以由式(20)得到,不再赘述。
由图2所示的系统等效电路可以直接写出直流输电线路的动态模型,即
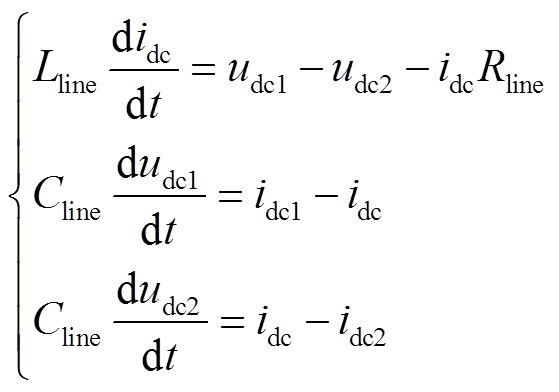 (21)
(21)3.4.1 PLL动态模型
PCC1~PCC3处均有一个PLL来锁定各自的电压相角,记为PLL1~PLL3。由于PLL1~PLL3的结构完全相同,故省略下标,统一使用PLL进行表示。PLL的结构如图11所示。图11中,qpcc和qpll分别为PCC电压相角和PLL输出相角,d为二者的差值。qpcc=arctan (upccy/upccx),d=qpcc-qpll。

图11 PLL示意图
Fig.11 Schematic diagram of PLL
由图11可得
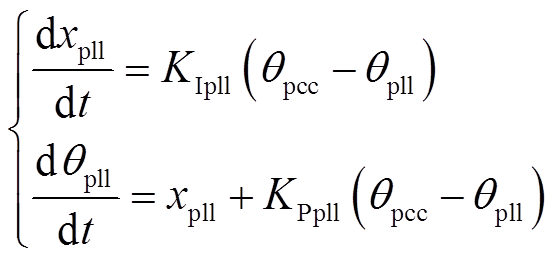 (22)
(22)式中,KPpll和KIpll分别为PI环节的比例系数和积分系数;xpll为PI环节的状态变量。
3.4.2 LCCr控制系统动态模型
LCCr控制系统的结构如图12所示,为定直流电流控制,Idcref为直流电流的参考值。图12中,idc1m为经过标幺、滤波(滤波环节为一阶惯性环节,下文中不经特别说明,滤波环节均为一阶惯性环节,不再赘述)之后的idc1,arord和ar分别为LCCr的触发延迟角的指令值和实际值,ar=arord+d1。
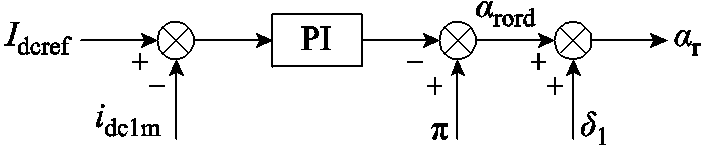
图12 LCCr控制系统示意图
Fig.12 Schematic diagram of controller of LCCr
idc1m的微分方程为
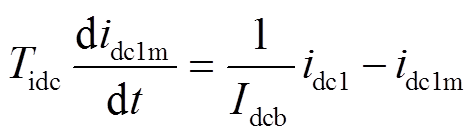 (23)
(23)式中,Idcb为直流电流的基准值;Tidc为一阶惯性环节的时间常数。
由图12可得
 (24)
(24)式中,KPLCCr和KILCCr分别为PI环节的比例系数和积分系数;xLCCr为PI环节的状态变量。
3.4.3 LCCi控制系统动态模型
LCCi控制系统的结构如图13所示,为定直流电压控制, 为LCCi直流电压的参考值。图13中,
为LCCi直流电压的参考值。图13中,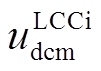 为经过标幺、滤波之后的
为经过标幺、滤波之后的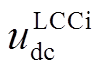 ,biord和bi分别为LCCi的超前触发延迟角的指令值和实际值,bi=biord-d2。
,biord和bi分别为LCCi的超前触发延迟角的指令值和实际值,bi=biord-d2。
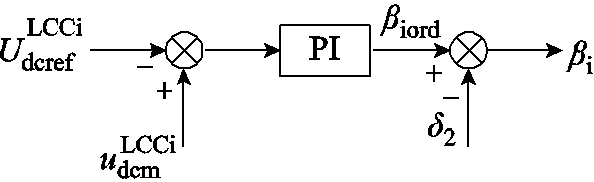
图13 LCCi控制系统示意图
Fig.13 Schematic diagram of controller of LCCi
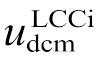 的微分方程为
的微分方程为
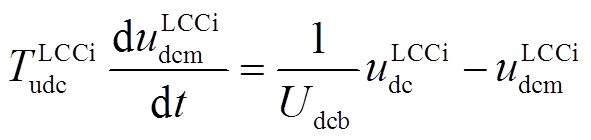 (25)
(25)
式中,Udcb为直流电压的基准值;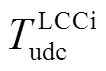 为一阶惯性环节的时间常数。
为一阶惯性环节的时间常数。
由图13可得
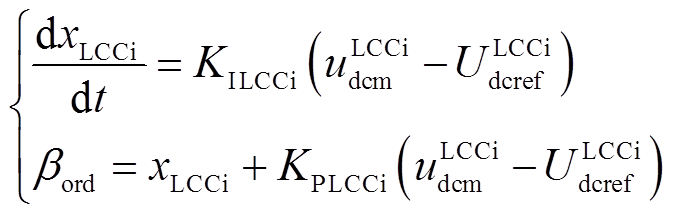 (26)
(26)式中,KPLCCi和KILCCi分别为PI环节的比例系数和积分系数;xLCCi为PI环节的状态变量。
3.4.4 MMC控制系统动态模型
MMC控制系统的示意图如图14所示。由图14可知,MMC控制系统基于dq坐标系,而由上文可知,MMC主电路基于xy坐标系,因此MMC主电路和控制系统之间的交互需要经过坐标系转换,有关坐标系转换方程参见附录。图14a为矢量控制,d轴外环和q轴外环分别控制直流电压和无功功率,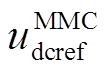 为MMC直流电压的参考值,Qref为无功功率的参考值,idref和iqref为内环参考值,Lpu为连接电感的标幺值。图14b为环流抑制控制,Icirdref和Icirqref为环流的参考值。图14a中的
为MMC直流电压的参考值,Qref为无功功率的参考值,idref和iqref为内环参考值,Lpu为连接电感的标幺值。图14b为环流抑制控制,Icirdref和Icirqref为环流的参考值。图14a中的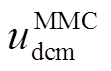 、Qm、idm、iqm、upcc3dm和upcc3qm以及图14b中的icirdm和icirqm均为相关变量经过标幺、滤波之后的值。
、Qm、idm、iqm、upcc3dm和upcc3qm以及图14b中的icirdm和icirqm均为相关变量经过标幺、滤波之后的值。
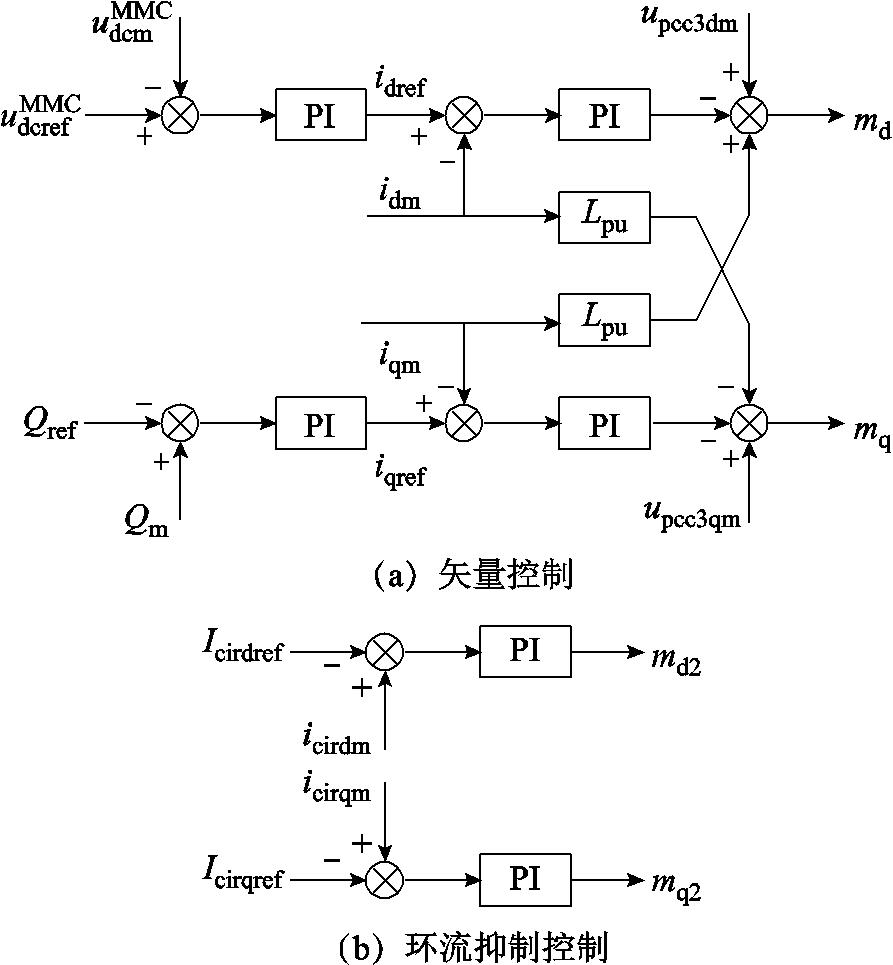
图14 MMC控制系统示意图
Fig.14 Schematic diagram of controller of MMC
由图14a可得
 (27)
(27)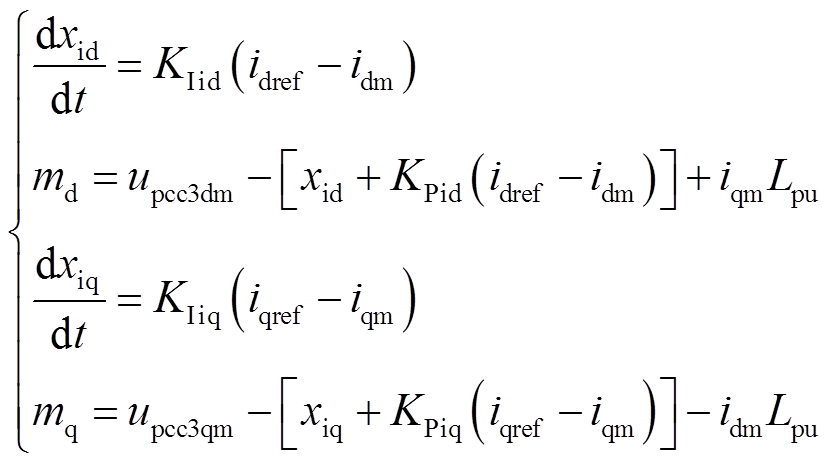 (28)
(28)由图14b可得
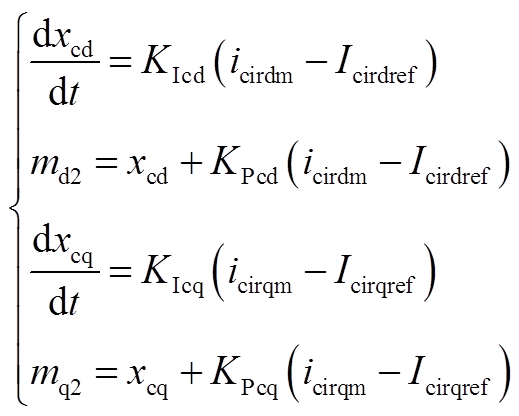 (29)
(29)式中,KPod、KIod和KPoq和KIoq分别为矢量控制d轴外环和q轴外环的比例系数、积分系数;KPid、KIid和KPiq、KIiq分别为矢量控制d轴内环和q轴内环的比例系数、积分系数;KPcd、KIcd和KPcq、KIcq分别为环流抑制控制d轴和q轴的比例系数、积分系数;xod、xoq、xid、xiq、xcd和xcq为相应PI环节的状态变量。
将上述系统整流侧动态模型、逆变侧动态模型、直流输电线路动态模型和控制系统动态模型组合起来即可得到全系统动态模型,其一般形式可以表示为
 (30)
(30)式中,x和u分别为系统的状态向量和输入向量,x为72´1的列向量,u=[Idcref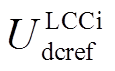
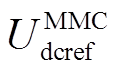 ]T。
]T。
将式(30)线性化即可得到全系统小信号模型为
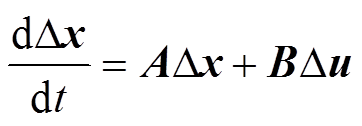 (31)
(31)式中,A、B分别为系统的状态矩阵和输入矩阵。
第3节中推导得到图2所示的LCC-MMC串联型混合直流输电系统的小信号模型,为了验证其准确性,根据图2在PSCAD/EMTDC平台上搭建了对应的电磁暂态模型,通过对比电磁暂态模型的仿真结果与小信号模型的计算结果,验证小信号模型的准确性。系统参数见表1。
为了验证小信号模型的准确性,设计了两种验
表1 系统参数
Tab.1 System parameters

类别参数数值 交流系统AC1额定容量/(MV·A)1 600 额定电压/kV500 短路比8.66 电抗/电阻8 AC2(AC3)额定容量/(MV·A)800 额定电压/kV500 短路比8.66 电抗/电阻8 变压器T1额定容量/(MV·A)478.2129 电压比500:169.0738 漏电抗(pu)0.18 T2额定容量/(MV·A)466.2576 电压比500:164.8469 漏电抗(pu)0.18 T3额定容量/(MV·A)800 电压比500:204.75 漏电抗(pu)0.1 换流器LCCr额定直流电压/kV800 额定直流电流/kA2 LCCi额定直流电压/kV390 额定直流电流/kA2 MMC额定直流电压/kV390 额定直流电流/kA2 桥臂子模块数量200 子模块电容/mF14000 桥臂电阻/W0.5 桥臂电感/H0.0334 平波电抗器Ldc1/H0.3 Ldc2/H0.3 交流联络线长度/km100 单位电阻/(W/km)0.028 单位电感/(H/km)0.000 86 直流输电线路Rline/W10 Lline/H1.62 Cline/mF13
证工况:
1)工况1:t=0s时系统处于稳定运行状态,t=0.5s时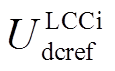 向下阶跃0.05(pu),系统响应如图15所示。图15中,实线EMT代表电磁暂态仿真结果,虚线SS代表小信号计算结果。
向下阶跃0.05(pu),系统响应如图15所示。图15中,实线EMT代表电磁暂态仿真结果,虚线SS代表小信号计算结果。
2)工况2:t=0s时系统处于稳定运行状态,t=0.5s时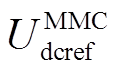 向下阶跃0.05(pu),系统响应如图16所示。
向下阶跃0.05(pu),系统响应如图16所示。

图15  阶跃时系统响应
阶跃时系统响应
Fig.15 Response of system with  stepping
stepping
由图15和图16可知,小信号模型的计算结果和电磁暂态模型的仿真结果基本一致,验证了小信号模型的准确性。
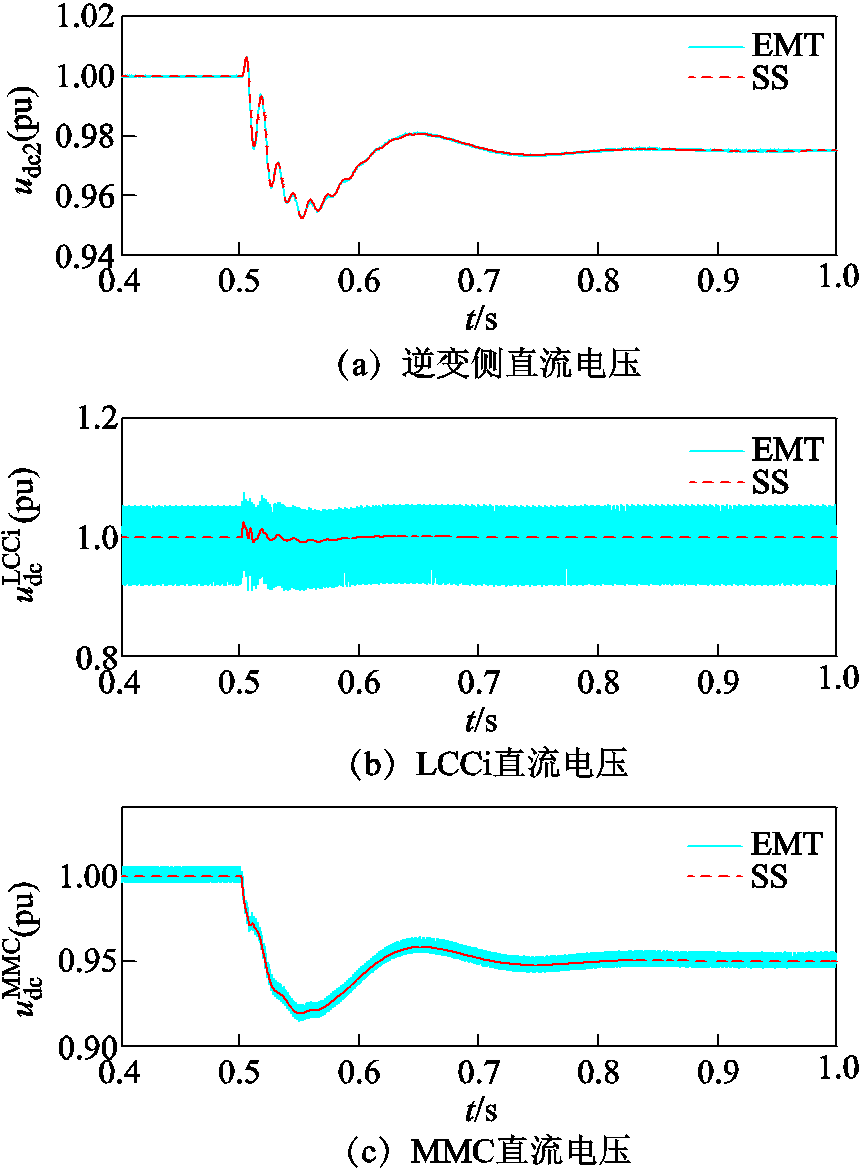

图16 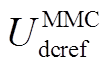 阶跃时系统响应
阶跃时系统响应
Fig.16 Response of system with 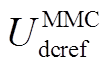 stepping
stepping
本节将基于第3节中推导的系统小信号模型分析MMC定直流电压控制参数、LCCi定直流电压控制参数、PLL参数和交流联络线参数对系统小信号稳定性的影响。
令比例系数KPod从10逐渐减小到0.1,间隔为0.1,系统根轨迹如图17所示。
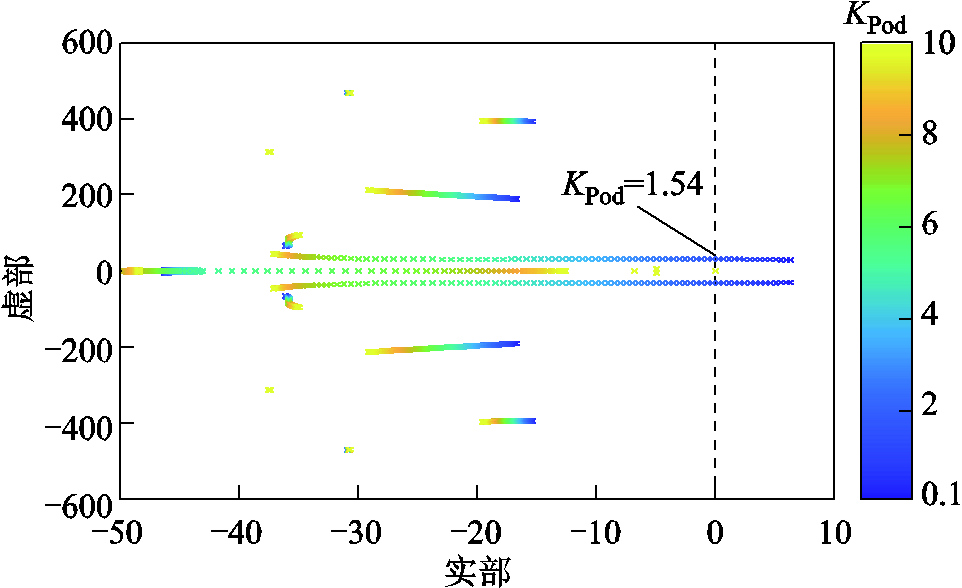
图17 KPod变化时系统根轨迹
Fig.17 Root loci of system with KPod varying
由图17可知,随着KPod逐渐减小,系统的主导极点逐渐向虚轴靠近,当KPod≤1.54时,系统出现右半平面极点,系统小信号失稳。当KPod=1.54时,系统振荡频率为4.97Hz。
为了验证上述分析结果的正确性,在PSCAD中,令KPod=1.54,t=0s时,系统处于平衡态,t=0.1s时,对系统施加小扰动(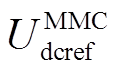 向下阶跃0.01(pu))相关波形如图18所示。
向下阶跃0.01(pu))相关波形如图18所示。
由图18可知,系统在受到小扰动后随即失稳,振荡频率为1/0.998´5Hz=5.01Hz,验证了上述分析结果的准确性。
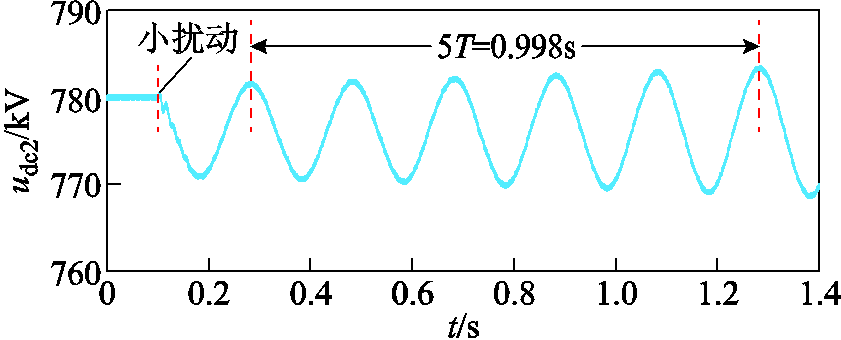
图18 系统小扰动失稳波形(KPod=1.54)
Fig.18 Unstable waveform of system under small disturbance(KPod=1.54)
令积分系数KIod从10逐渐增大到1 000,间隔为10,系统根轨迹如图19所示。

图19 KIod变化时系统根轨迹
Fig.19 Root loci of system with KIod varying
由图19可知,随着KIod逐渐增大,系统的主导极点逐渐向虚轴靠近,当KIod≥599时,系统出现右半平面极点,系统小信号失稳。当KIod=599时,系统振荡频率为12.10Hz。
为了验证上述分析结果的正确性,在PSCAD中,令KIod=599,t=0s时,系统处于平衡态,t=0.1s时,对系统施加小扰动(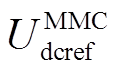 向下阶跃0.01(pu)),相关波形如图20所示。
向下阶跃0.01(pu)),相关波形如图20所示。

图20 系统小扰动失稳波形(KIod=0.99)
Fig.20 Unstable waveform of system under small disturbance(KIod=0.99)
由图20可知,系统在受到小扰动后随即失稳,振荡频率为1/0.414´5Hz=12.08Hz,验证了上述分析结果的准确性。
下面针对逆变侧仅为MMC的情形(系统参数与LCC和MMC串联情形中的MMC相同),分析MMC定直流电压控制参数对系统小信号稳定性的影响。首先令比例系数KPod从10逐渐减小到0.1,间隔为0.1,然后令积分系数KIod从10逐渐增大到1000,间隔为10,系统根轨迹分别如图21、图22所示。
由图21和图22可知,随着KPod的逐渐减小以及KIod的逐渐增大,逆变侧仅为MMC的情形与逆变侧为LCC和MMC串联的情形相比,系统的小信号稳定性的变化趋势相同,即系统的小信号稳定性逐渐减弱直至发生小信号失稳,但是在逆变侧为LCC和MMC串联的情形下,KPod和KIod具有更大的可行域。
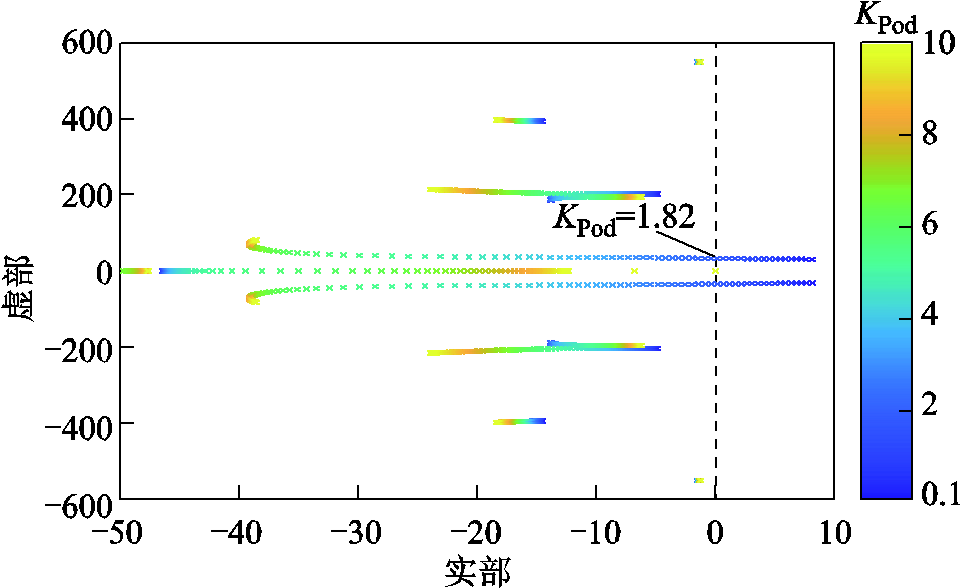
图21 KPod变化时系统根轨迹(逆变侧仅为MMC)
Fig.21 Root loci of system with KPod varying(only MMC on inverter-side)

图22 KIod变化时系统根轨迹(逆变侧仅为MMC)
Fig.22 Root loci of system with KIod varying (only MMC on inverter-side)
由3.2.1节可知,串联连接的LCC和MMC的直流端口电压之间存在交互影响,而MMC定直流电压控制以MMC的直流端口电压作为反馈输入,因而MMC的定直流电压控制受到LCC的影响。结合上面的分析结果,可知LCC和MMC串联连接可以扩大MMC定直流电压控制参数的可行域。
令比例系数KPLCCi从0.1逐渐增大到10,间隔为0.1,系统根轨迹如图23所示。
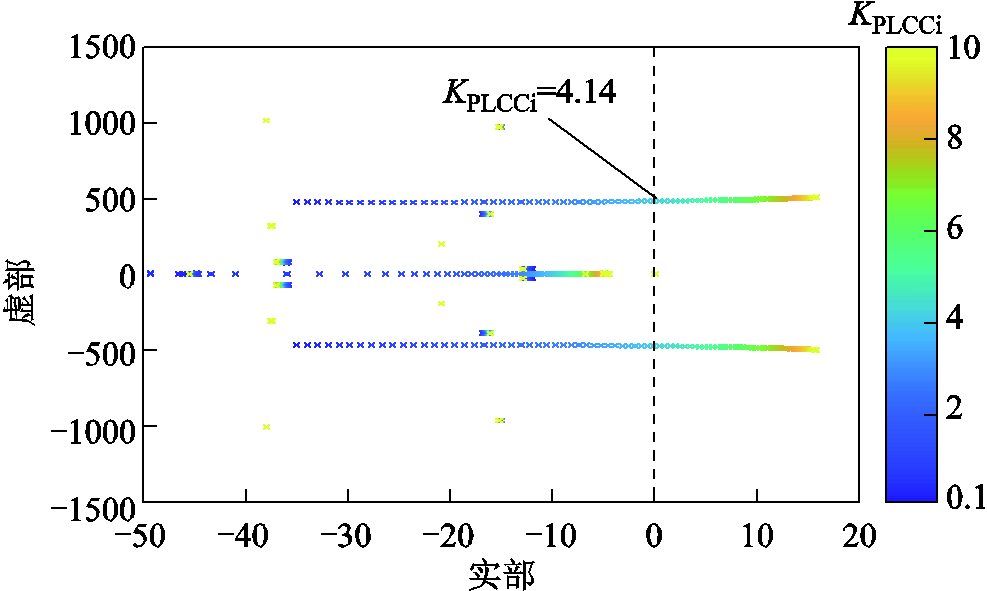
图23 KPLCCi变化时系统根轨迹
Fig.23 Root loci of system with KPLCCi varying
由图23可知,随着KPLCCi逐渐增大,系统的主导极点逐渐向右半平面移动。当KPLCCi≥4.14时,系统出现负阻尼,系统发生小信号失稳。
然后令积分系数KILCCi从10逐渐增大到1000,间隔为10,系统根轨迹如图24所示。
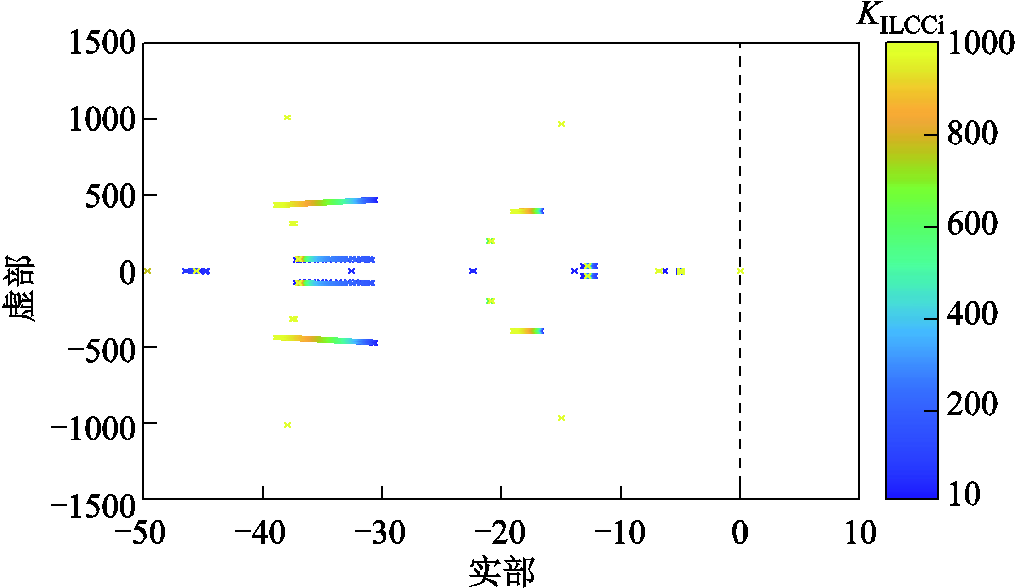
图24 KILCCi变化时系统根轨迹
Fig.24 Root loci of system with KILCCi varying
由图24可知,随着KILCCi逐渐增大,系统的所有极点始终保持在左半平面内,系统保持小信号稳定,并且随着KILCCi从10逐渐增大到1 000,系统的主要极点向远离虚轴的方向移动,系统的小信号稳定性增强。
首先分析LCCi的PLL参数变化对系统小信号稳定性的影响。令KPpll2从10变化至1000,间隔为10,在此过程中,令KIpll2=5KPpll2[17]。系统根轨迹如图25所示。
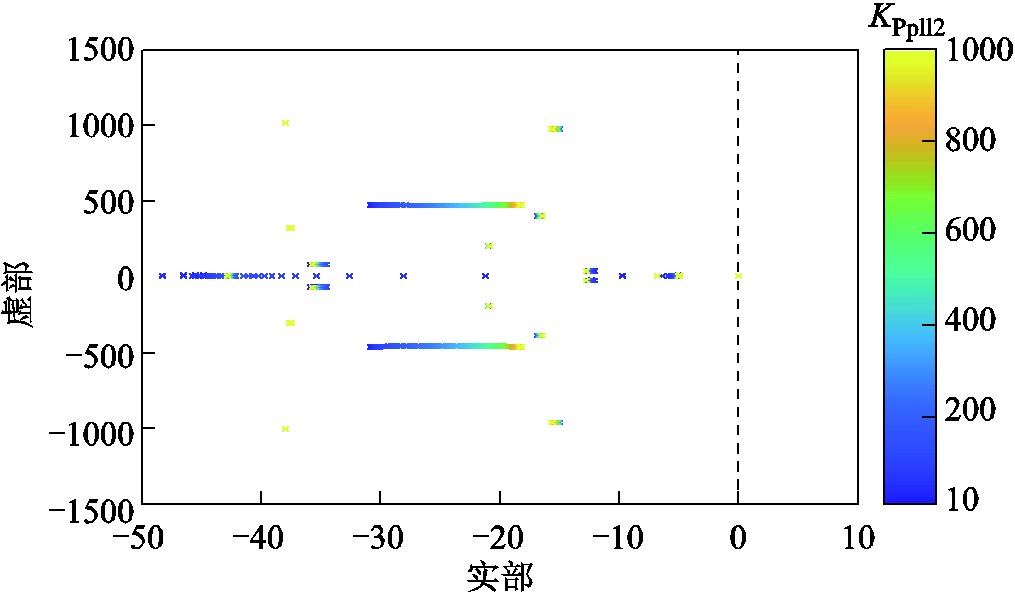
图25 KPpll2变化时系统根轨迹
Fig.25 Root loci of system with KPpll2 varying
由图25可知,随着KPpll2从10逐渐增大到1000,系统的所有极点始终保持在左半平面内,系统保持小信号稳定,并且随着KPpll2逐渐增大,系统主要极点向虚轴移动,系统的小信号稳定性有所减弱。
然后分析MMC的PLL参数变化对系统小信号稳定性的影响。令KPpll3从10变化至1 000,间隔为10,在此过程中,令KIpll3=5KPpll3。系统根轨迹如图26所示。
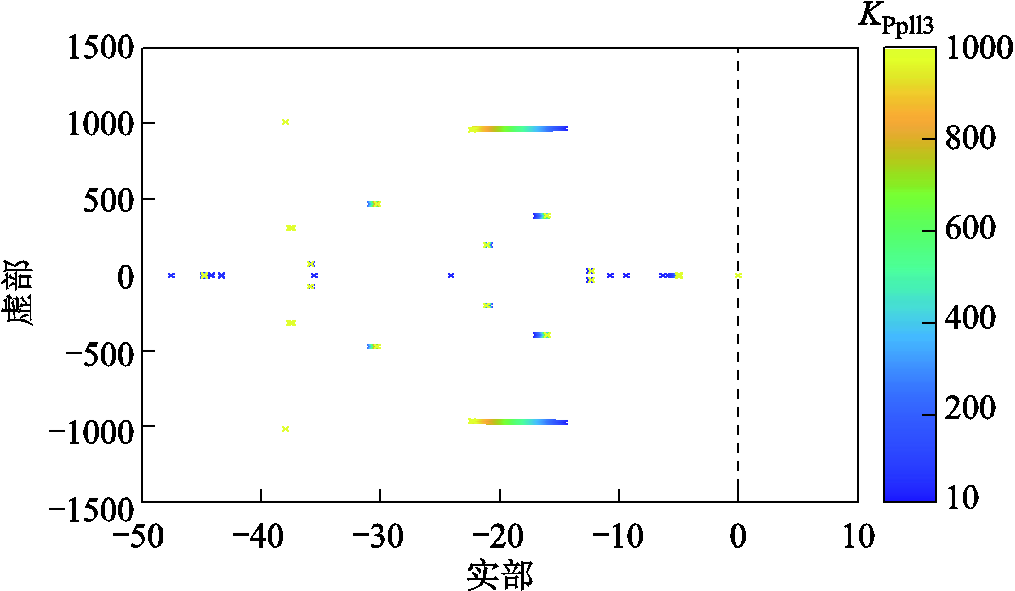
图26 KPpll3变化时系统根轨迹
Fig.26 Root loci of system with KPpll3 varying
由图26可知,随着KPpll3逐渐增大,系统的所有极点始终保持在左半平面内,系统保持小信号稳定,并且随着KPpll2从10逐渐增大至1 000,系统的主要极点远离虚轴,系统的小信号稳定性增强。
Tie参数Rtie和Ltie的值等于Tie的单位长度电阻和单位长度电感乘以Tie的长度,所以只需要改变Tie的长度即改变了Rtie和Ltie。下面分析Tie的长度变化对系统小信号稳定性的影响。
令Tie的长度从1km逐渐变化至20km,间隔为1km,系统的根轨迹如图27所示。
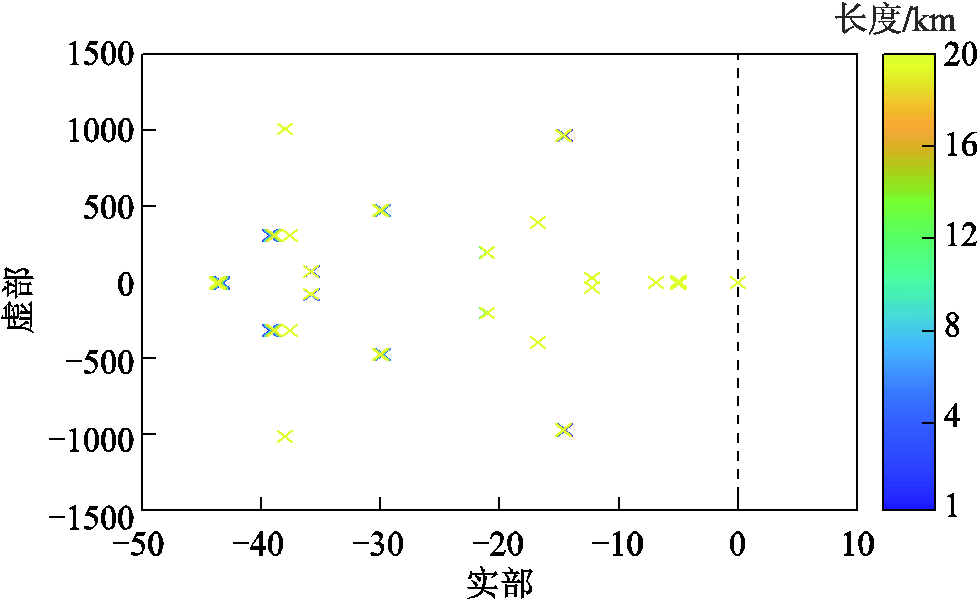
图27 Tie长度变化时系统根轨迹
Fig.27 Root loci of system with length of Tie varying
由图27可知,随着Tie的长度从1km逐渐增大至20km,系统的极点始终保持在左半平面内,即系统保持小信号稳定。并且,随着Tie的长度变化,系统的极点位置变化不大。
综上可知,Tie参数Rtie和Ltie对系统小信号稳定性的影响十分有限。一方面可能是由于受端交流系统较强;另一方面可能是由于受端交流系统AC2和AC3的结构、参数对称,交流联络线上流过的功率较小,AC2和AC3之间的电气耦合不够紧密。
本文建立了整流侧为LCC、逆变侧为LCC和MMC串联的LCC-MMC串联型混合直流输电系统的小信号模型。首先推导了LCC的交直流侧等效电路和考虑内部动态特性的MMC的交直流侧等效电路,并基于等效电路构建了系统整流侧和逆变侧的模型;然后对直流输电线路和控制系统进行了建模,通过组合各个部分模型获得全系统模型;最后通过线性化全系统模型获得全系统小信号模型。主要结论如下:
1)通过与基于PSCAD/EMTDC搭建的电磁暂态模型进行对比,验证了本文提出的小信号模型的准确性。
2)通过分析MMC定直流电压控制参数对系统小信号稳定性的影响,发现比例系数过小或者积分系数过大均会导致系统小信号失稳,同时LCC和MMC串联连接可以扩大MMC定直流电压控制参数的可行域。
3)通过分析逆变侧LCC定直流电压控制参数对系统小信号稳定性的影响,发现比例系数过大会导致系统小信号失稳,而适当增大积分系数可以增强系统的小信号稳定性。
4)通过分析PLL参数对系统小信号稳定性的影响,发现逆变侧LCC的PLL增益增大会减弱系统的小信号稳定性,而MMC的PLL增益增大会增强系统的小信号稳定性。
5)通过分析交流联络线参数对系统小信号稳定性的影响,发现交流联络线的参数变化对系统小信号稳定性的影响有限。
设xy坐标系与dq坐标系之间的夹角为q,则坐标系转换矩阵为
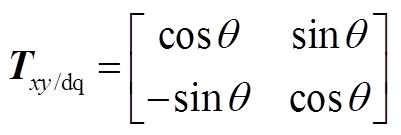 (A1)
(A1)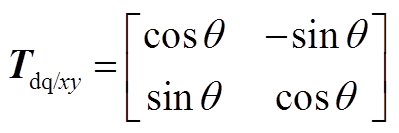 (A2)
(A2)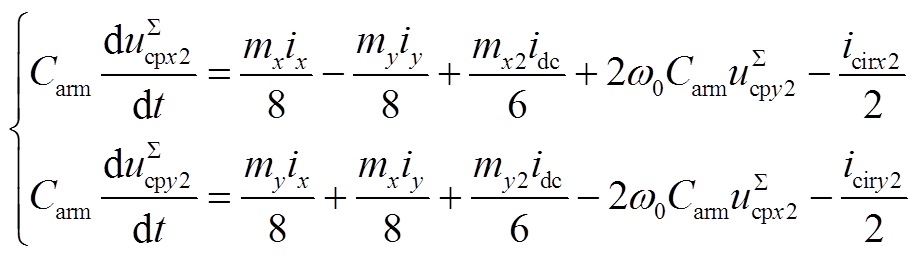 (A3)
(A3)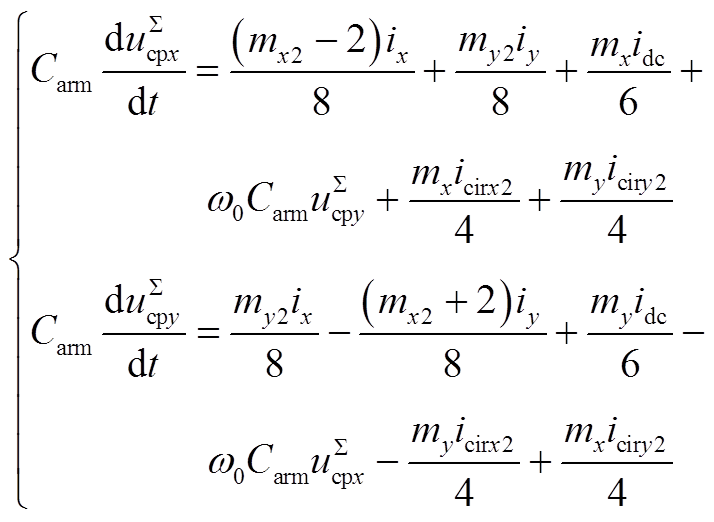 (A4)
(A4)
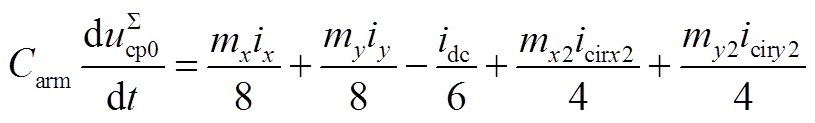 (A5)
(A5)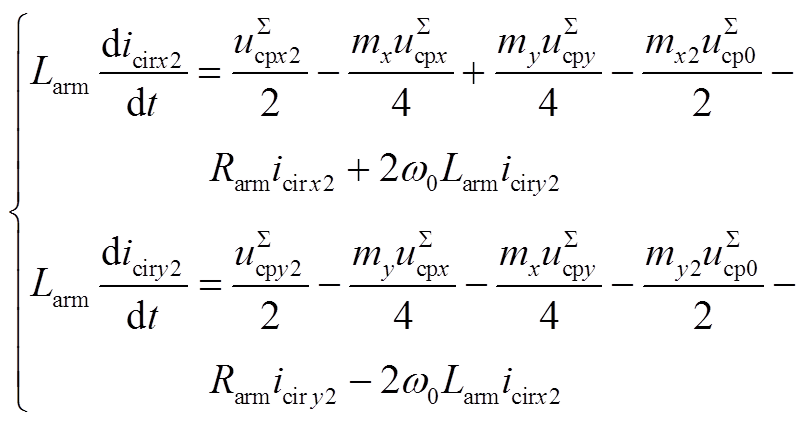 (A6)
(A6)式中,Carm=Csub/N,Csub为子模块电容,N为桥臂子模块数。
由于F1和F2的结构完全相同,故省略下标,统一使用F进行表示。F的等效电路如附图1所示。

附图1 F等效电路
App.Fig.1 Equivalent circuit of F
由附图1可得,F的动态模型为
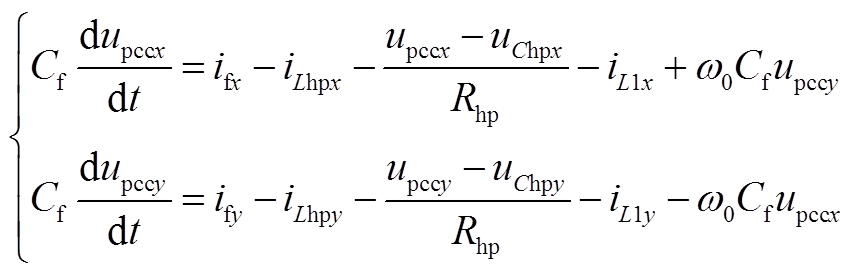 (A7)
(A7)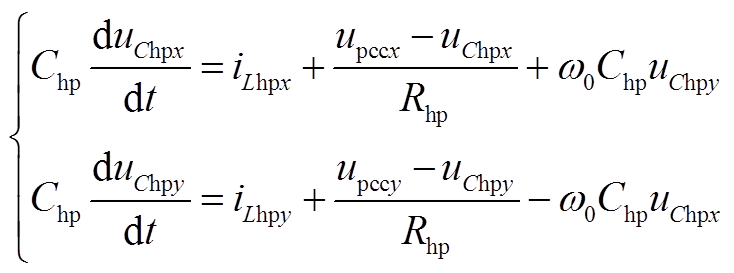 (A8)
(A8)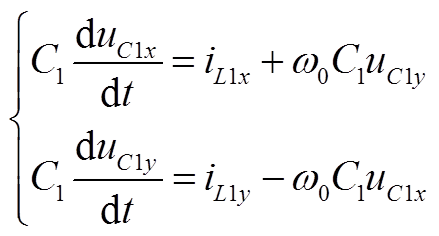 (A9)
(A9)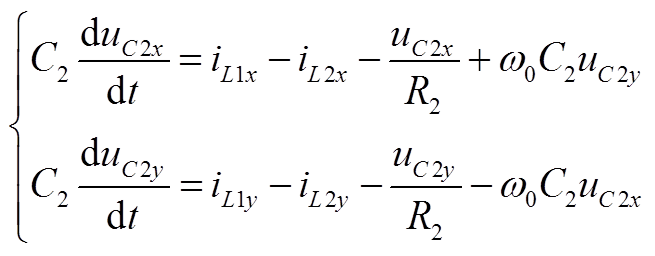 (A10)
(A10)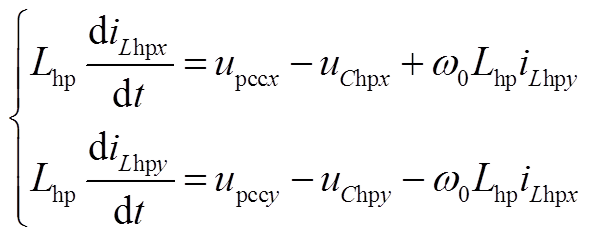 (A11)
(A11)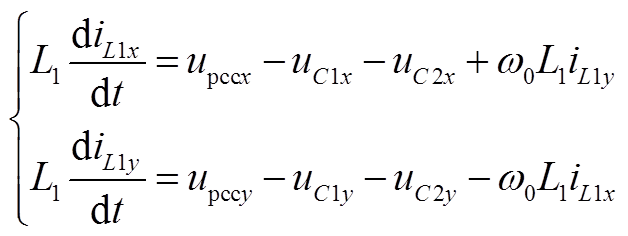 (A12)
(A12)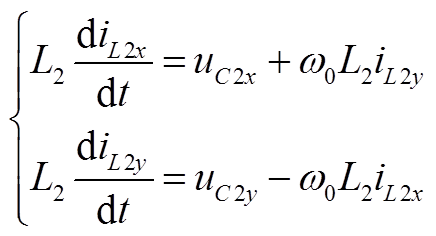 (A13)
(A13)参考文献
[1]汤广福, 庞辉, 贺之渊. 先进交直流输电技术在中国的发展与应用[J]. 中国电机工程学报, 2016, 36(7): 1760-1771. Tang Guangfu, Pang Hui, He Zhiyuan. R&D and application of advanced power transmission technology in China[J]. Proceedings of CSEE, 2016, 36(7): 1760-1771.
[2]赵畹君. 高压直流输电工程技术[M]. 北京: 中国电力出版社, 2010.
[3]徐政. 柔性直流输电系统[M]. 北京: 机械工业出版社, 2012.
[4]赵成勇. 混合直流输电[M]. 北京: 科学出版社, 2014.
[5]杨之翰, 李梦柏, 向往, 等. 基于无闭锁直流自耦变压器的LCC-HVDC与VSC-HVDC互联系统[J]. 电工技术学报, 2018, 33(增刊2): 499-510. Yang Zhihan, Li Mengbo, Xiang Wang, et al. Research on the interconnection system of VSC-HVDC and LCC-HVDC based on un-interrupted DC-DC autotransformer[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 499-510.
[6]郑安然, 郭春义, 殷子寒, 等. 提高弱交流系统下混合多端直流输电系统小干扰稳定性的控制参数优化调节方法[J]. 电工技术学报, 2020, 35(6): 1336-1345. Zheng Anran, Guo Chunyi, Yin Zihan, et al. Optimal adjustment method of control parameters for improving small-signal stability of hybrid multi-terminal HVDC system under weak AC condition[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1336-1345.
[7]王燕宁, 郭春义, 郑安然, 等. 极弱受端交流系统下LCC-MMC型混合直流输电系统的附加频率-电压阻尼控制[J]. 电工技术学报, 2020, 35(7): 1509-1520. Wang Yanning, Guo Chunyi, Zheng Anran, et al. Supplementary frequency-voltage damping control for LCC-MMC hybrid HVDC system connected to extremely weak receiving AC grid[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1509-1520.
[8]李广凯, 李庚银, 梁海峰, 等. 新型混合直流输电方式的研究[J]. 电网技术, 2006, 30(4): 82-86. Li Guangkai, Li Gengyin, Liang Haifeng, et al. Research on a novel hybrid HVDC system[J]. Power System Technology, 2006, 30(4): 82-86.
[9]唐庚, 徐政, 薛英林. LCC-MMC混合高压直流输电系统[J]. 电工技术学报, 2013, 28(10): 301-310. Tang Geng, Xu Zheng, Xue Yinglin. A LCC-MMC hybrid HVDC transmission system[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 301-310.
[10]林卫星, 文劲宇, 王少荣, 等. 一种适用于风电直接经直流大规模外送的换流器[J]. 中国电机工程学报, 2014, 34(13): 2022-2030. Lin Weixing, Wen Jinyu, Wang Shaorong, et al. A kind of converters suitable for large-scale integration of wind power directly through HVDC[J]. Proceedings of CSEE, 2014, 34(13): 2022-2030.
[11]徐政, 王世佳, 李宁璨, 等. 适用于远距离大容量架空线路的LCC-MMC串联混合型直流输电系统[J]. 电网技术, 2016, 40(1): 55-63. Xu Zheng, Wang Shijia, Li Ningcan, et al. A LCC and MMC series hybrid HVDC topology suitable for bulk power overhead line transmission[J]. Power System Technology, 2016, 40(1): 55-63.
[12]刘杉, 余军, 贺之渊, 等. 基于VSC与LCC混合的多点传输直流输电系统拓扑结构研究与特性分析[J]. 中国电机工程学报, 2018, 38(10): 2980-2988, 3148. Liu Shan, Yu Jun, He Zhiyuan, et al. Research on the topology and characteristic of multi-terminal HVDC based on VSC and LCC[J]. Proceedings of the CSEE, 2018, 38(10): 2980-2988, 3148.
[13]杨睿璋, 向往, 饶宏, 等. 一种适用于大容量功率馈入和异步电网互联的级联换流阀[J]. 中国电机工程学报, 2019, 39(17): 5182-5194, 5299. Yang Ruizhang, Xiang Wang, Rao Hong, et al. A cascaded converter dedicated for large capacity power infeed and asynchronous interconnection[J]. Proceedings of CSEE, 2019, 39(17): 5182-5194, 5299.
[14]Jovcic D, Pahalawaththa N, Zavahir M. Analytical modelling of HVDC-HVAC systems[J]. IEEE Transactions on Power Delivery, 1999, 14(2): 506-511.
[15]Jovcic D, Pahalawaththa N, Zavahir M. Small signal analysis of HVDC-HVAC interactions[J]. IEEE Transactions on Power Delivery, 1999, 14(2): 525-530.
[16]Karawita C, Annakkage U D. Multi-infeed HVDC interaction studies using small-signal stability assessment[J]. IEEE Transactions on Power Delivery, 2009, 24(2): 910-918.
[17]郭春义, 宁琳如, 王虹富, 等. 基于开关函数的LCC-HVDC换流站动态模型及小干扰稳定性[J]. 电网技术, 2017, 41(12): 3862-3870. Guo Chunyi, Ning Linru, Wang Hongfu, et al. Switching-function based dynamic model of LCC-HVDC station and small signal stability analysis[J]. Power System Technology, 2017, 41(12): 3862-3870.
[18]鲁晓军, 林卫星, 安婷, 等. MMC电气系统动态相量模型统一建模方法及运行特性分析[J]. 中国电机工程学报, 2016, 36(20): 5479-5491, 5724. Lu Xiaojun, Lin Weixing, An Ting, et al. A unified dynamic phasor modeling and operating characteristic analysis of electrical system of MMC[J]. Proceedings of the CSEE, 2016, 36(20): 5479-5491, 5724.
[19]李探, Aniruddha M Gole, 赵成勇. 考虑内部动态特性的模块化多电平换流器小信号模型[J]. 中国电机工程学报, 2016, 36(11): 2890-2899. Li Tan, Gole A M, Zhao Chengyong. Small-signal model of the modular multilevel converter considering the internal dynamics[J]. Proceedings of the CSEE, 2016, 36(11): 2890-2899.
[20]鲁晓军, 林卫星, 向往, 等. 基于模块化多电平换流器的直流电网小信号建模[J]. 中国电机工程学报, 2018, 38(4): 1143-1156, 1292. Lu Xiaojun, Lin Weixing, Xiang Wang, et al. Small signal modeling of MMC-based DC grid[J]. Proceedings of the CSEE, 2018, 38(4): 1143-1156, 1292.
[21]喻悦箫, 刘天琪, 王顺亮, 等. 基于平均值模型的双端MMC-HVDC系统小信号建模[J]. 中国电机工程学报, 2018, 38(10): 2999-3006, 3150. Yu Yuexiao, Liu Tianqi, Wang Shunliang, et al. Small signal modeling of two-terminal MMC-HVDC based on AVM model[J]. Proceedings of the CSEE, 2018, 38(10): 2999-3006, 3150.
[22]郭春义, 殷子寒, 王烨, 等. LCC-MMC型混合直流输电系统小干扰动态模型[J]. 中国电机工程学报, 2018, 38(16): 4705-4714, 4975. Guo Chunyi, Yin Zihan, Wang Ye, et al. Small-signal dynamic model of LCC-MMC hybrid HVDC system[J]. Proceedings of the CSEE, 2018, 38(16): 4705-4714, 4975.
[23]郭春义, 殷子寒, 王烨, 等. LCC-MMC型混合直流输电系统小干扰稳定性研究[J]. 中国电机工程学报, 2019, 39(4): 1040-1052. Guo Chunyi, Yin Zihan, Wang Ye, et al. Investigation on small-signal stability of hybrid LCC-MMC HVDC system[J]. Proceedings of the CSEE, 2019, 39(4): 1040-1052.
[24]Guo Chunyi, Zheng Anran, Yin Zihan, et al. Small-signal stability of hybrid multi-terminal HVDC system[J]. International Journal of Electrical Power & Energy Systems, 2019, 109: 434-443.
[25]Daryabak M, Filizadeh S, Jatskevich J, et al. Modeling of LCC-HVDC systems using dynamic phasors[J]. IEEE Transactions on Power Delivery, 2014, 29(4): 1989-1998.
Small-Signal Modelling of LCC-MMC Series Hybrid HVDC Transmission System
Abstract This paper establishes the small-signal model of LCC-MMC series hybrid HVDC transmission system, which rectifier side is LCC and which inverter side is series connect of LCC and MMC. Firstly, equivalent circuits of the AC and DC sides of LCC and equivalent circuits of the AC and DC sides of MMC considering internal dynamic characteristics are derived. Then, models of the rectifier and inverter sides of the system are constructed based on equivalent circuits. By combining each part of the above, consisting of the DC line and control system, the entire system's model is obtained. Finally, the small-signal model of the entire system is obtained by linearizing the entire system's model. The accuracy of the small-signal model is verified by comparing the electromagnetic transient model based on PSCAD/EMTDC. The influences of the constant DC voltage control parameters of MMC and LCC in the inverter-side, PLL parameters, and the tie line parameters on the small-signal stability of the system are analyzed based on the small-signal model. The small-signal model of LCC-MMC series hybrid DC transmission system proposed in this paper can be used for the system's small-signal stability analysis, thereby providing a valuable reference for system design and parameter selection.
keywords:Line commutated converter(LCC), modular multilevel converter(MMC), series connect, hybrid high voltage direct current, small-signal modelling
中图分类号:TM721.1
DOI:10.19595/j.cnki.1000-6753.tces.L90543
国家电网有限公司科技项目资助(5200-201958248A-0-0-00多落点级联混合直流输电系统关键技术研究)。
收稿日期 2020-07-20
改稿日期 2020-10-18
贺永杰 男,1995年生,硕士研究生,研究方向为直流输电技术。E-mail:yjhe1002@foxmail.com
向 往 男,1990年生,博士,研究方向为直流输电技术。E-mail:xiangwang1003@foxmail.com(通信作者)
(编辑 赫蕾)