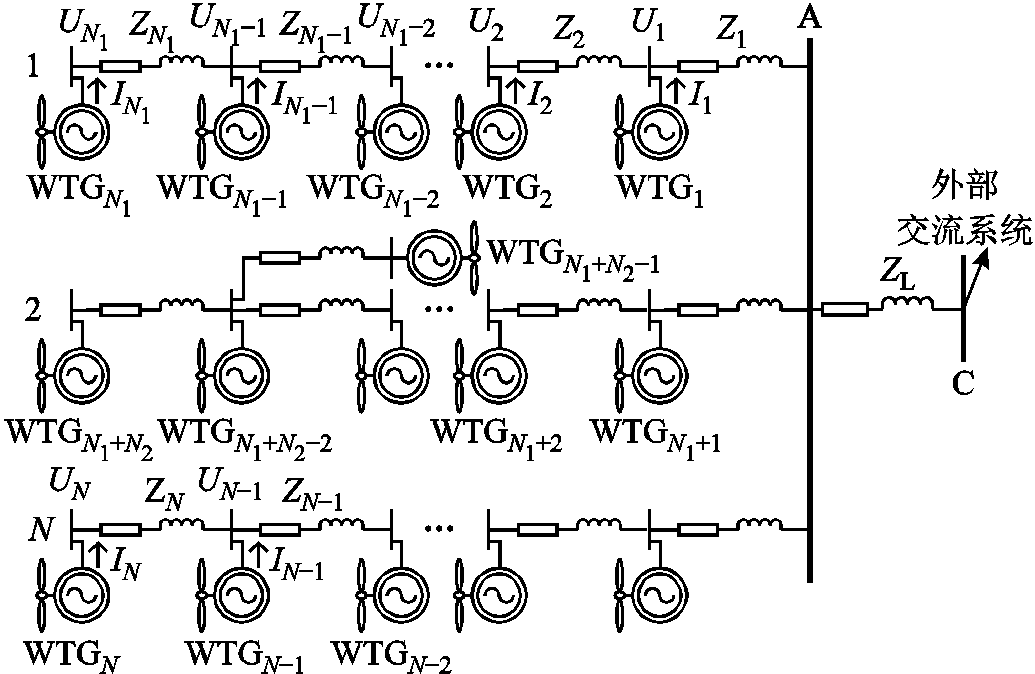
图1 并网风电场结构
Fig.1 Configuration of a grid-connected wind farm
摘要 考虑到在大型风电场规划阶段,如对所有方案采用全阶模型进行小干扰稳定性检验,会导致工作量大、效率低,不利于寻求最优方案,该文提出一种降阶模式计算方法。首先,建立风电场全阶线性化状态空间模型。然后,考虑风电场规划阶段,可对所选型号的风电机组(WTG)采用典型模型和参数,认为各WTG动态特性近似相同。通过对风电场线性化模型中的变量做等效变换,将N台WTG构成的风电场等效为N个相互独立的等效子系统。各等效子系统由一台并网WTG构成。根据等效子系统线性化状态空间模型的构建方式,提出一种用于风电场小干扰稳定性检验的降阶模式计算方法,可有效降低规划阶段风电场模式分析的计算量,且所得结果准确。最后,通过仿真算例,验证了所提方法的有效性。
关键词:风电场 线性化状态空间模型 小干扰稳定性检验 模式分析 等效子系统
随着风力发电技术的发展与广泛应用,大型风电场内可具有数百台风电机组(Wind Turbine Generator, WTG),WTG之间互联后产生的动态交互作用可能会对风电场小干扰稳定性产生显著影响[1-4]。因此,有必要在规划阶段,对风电场小干扰稳定性进行检验。而由于风电场规模的扩大,如果直接对所有WTG采用详细模型,所建立的风电场模型阶数高,求解计算量大、效率低[5-14]。因此,目前常采用风电场动态等效模型对风电场进行小干扰稳定性检验。建立风电场动态等效模型的常用方法可分为单机等效法和多机等效法两类。
单机等效法以一台等效WTG代表风电场内所有WTG,并将风电场内部的集电网络等效为一个外部阻抗[5-10,12-14]。集电网络等效常采用恒功率损耗法[12-14]。等效WTG容量为风电场额定容量,参数常采用容量加权平均法(Capacity Mean Value Method)或参数辨识法(Parameter Identification)确定。容量加权平均法以风电场内各WTG的额定容量与风电场额定容量的比值作为权重,计算所有WTG参数的加权平均值作为等效WTG的参数[12-14]。采用容量加权平均法建立风电场单机等效模型,计算量低;但是将等效模型用于风电场小干扰稳定性检验,所得结果的准确性仍有待证明[5,9]。
参数辨识法将等效WTG参数的计算转换为一个优化问题,目标函数为:相同工况或外部扰动下,等效WTG与风电场在输出功率等动态响应上的误差最小;待求量为等效WTG的参数[5-10]。由于参数辨识法涉及非线性优化问题的求解[5-10],一般需采用智能优化算法,如粒子群算法[6,8]、遗传算法[5,7],以及基于它们提出的改进算法[10]等。因此,参数辨识法在提高风电场单机等效模型准确度的同时,也增加了等效模型参数求解的计算量。而在风电场规划阶段,典型工况或外部扰动下,风电场输出功率等动态响应难以实测获取,需进行非线性仿真。在多种场景下对风电场动态响应进行仿真分析,并将仿真结果用于参数辨识,可在一定程度上提高等效模型的准确度,但也会导致工作量的增加。
多机等效法首先根据运行状态对WTG进行聚类,将风电场划分为几个由运行状态相似的WTG构成的风电机群[11-14],聚类分析常采用k均值聚类、c均值聚类和支持向量机等方法,聚类指标一般选用各WTG转子转速、端电压或输入风速等能够反映WTG运行状态的数据。然后,再对各风电机群作单机等效,等效方法常采用容量加权平均法[11-14],也有少量研究中采用参数辨识法[5]。由于考虑了各WTG运行状态的差异,多机等效法提高了等效准确度;但是对WTG进行聚类时,需要WTG的运行数据作为聚类指标。而在风电场规划阶段,若要获取这些数据,需进行非线性仿真。
综上所述,容量加权平均法用于风电场小干扰稳定性检验,所得结果的准确性仍有待进一步探讨。参数辨识法或多机等效法则需要风电场或WTG的实测或仿真数据的支持,才可建立风电场动态等效模型,用于风电场规划阶段进行小干扰稳定性检验也存在一定的局限性。
本文针对风电场规划中的小干扰稳定性检验,提出了一种降阶模式计算方法。首先对风电场内所有WTG采用详细模型,建立风电场全阶线性化模型。然后,考虑在风电场规划阶段,可对所选型号的WTG采用典型模型和参数;进而通过对风电场线性化模型中的变量作等效变换,将N台WTG构成的风电场等效为N个由一台WTG构成的等效子系统,并提出一种风电场降阶模式计算(Reduced- Order Modal Computation, ROMC)方法。最后,通过仿真算例,验证了所提方法的有效性。
图1为一N台WTG构成的风电场的示意图,ZL为风电外送通道的线路阻抗。此外,图1也可看作风电场内的一个风电机群,此时ZL为风电机群与风电场其余部分之间连接线路的阻抗。本文主要以风电场为例展开研究,所提方法也可用于将风电场内某一个风电机群看作一独立系统时,对该风电机群的小干扰稳定性检验。链式和干线式结构是风电场最常用的连接结构,本文将在这两种结构下对风电场小干扰稳定性问题展开研究。

图1 并网风电场结构
Fig.1 Configuration of a grid-connected wind farm
风电场内第k台WTG的线性化状态空间模型可表示为
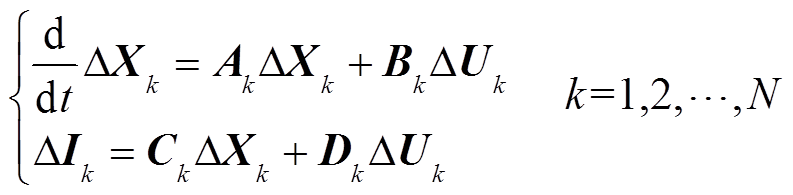 (1)
(1)其中
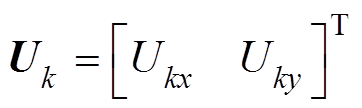
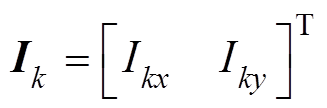
式中,D为变量或变量列向量的微小增量;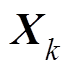 为第k台WTG的状态变量列向量;
为第k台WTG的状态变量列向量;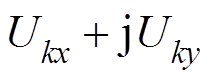 和
和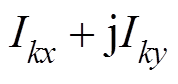 分别为交流电网公共x-y坐标系下第k台WTG的端电压和输出电流;
分别为交流电网公共x-y坐标系下第k台WTG的端电压和输出电流;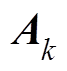 、
、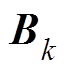 、
、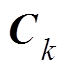 和
和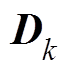 分别为第k台WTG的状态矩阵、控制矩阵、输出矩阵和反馈矩阵。为方便叙述,本文中用
分别为第k台WTG的状态矩阵、控制矩阵、输出矩阵和反馈矩阵。为方便叙述,本文中用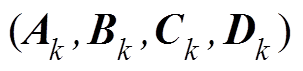 表示第k台WTG的线性化模型。
表示第k台WTG的线性化模型。
在风电场规划阶段,考虑外部系统容量远大于风电场容量,可将母线C看作无穷大母线[15],对风电场作为一独立系统的小干扰稳定性进行检验。由附录中的推导,可得风电场网络方程为
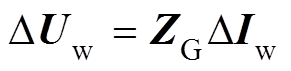 (2)
(2)式中,Iw为所有WTG输出电流构成的列向量,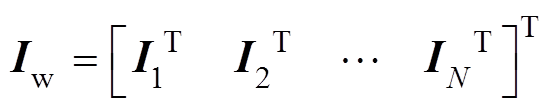 ;Uw为所有WTG端电压列向量,
;Uw为所有WTG端电压列向量,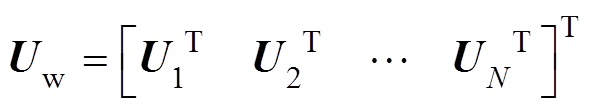 。
。
由式(1)可知
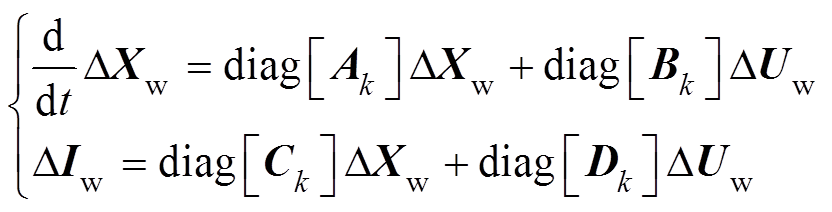 (3)
(3)式中,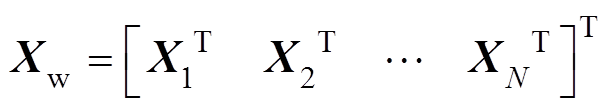 ;
;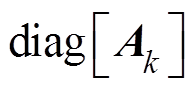 、
、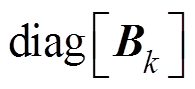 、
、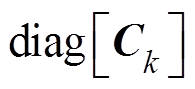 和
和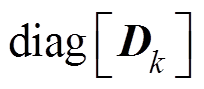 分别为对角线元素为
分别为对角线元素为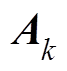 、
、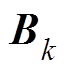 、
、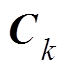 和
和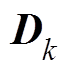 (
(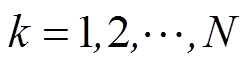 )的分块对角矩阵。
)的分块对角矩阵。
由式(2)和式(3)可得风电场线性化模型为
 (4)
(4)其中
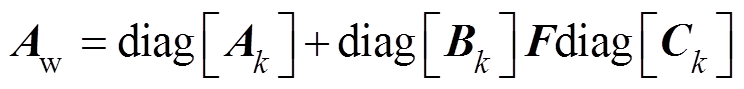
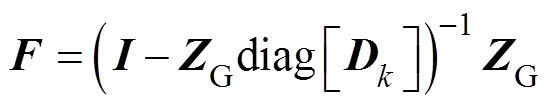
式中,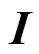 为
为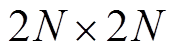 单位矩阵。式(4)所示为风电场全阶线性化状态空间模型。
单位矩阵。式(4)所示为风电场全阶线性化状态空间模型。
在风电场规划阶段,可对所选型号的WTG采用典型模型和参数,而且风电场内风速空间分布一般不会有太大差异,因此各WTG线性化模型相似,可假设各WTG的线性化模型相同,从而有
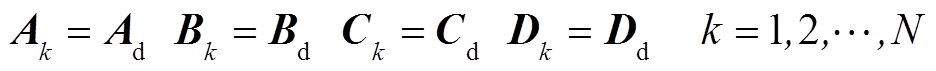 (5)
(5)文献[16]中采用了一种对风电场动态系统进行等效分解的思路,将N台WTG构成的风电场分解为N个相互独立且由一台WTG构成的等效子系统,进而研究了风电场动态等效方法及其理论依据;该方法对于研究如何降低风电场小干扰稳定性分析的计算量具有很好的参考意义。但是文献[16]中的推导是针对所有WTG经阻抗相同的线路并联接入汇流母线这一特殊结构下的风电场展开的,其中所提等效分解方法也仅适用于上述特定场景,无法用于对本文图1所示的这样一类更具一般性的风电场的等效分解。本文借鉴这一等效分解的思想,并结合模式分析理论中对矩阵进行模式分解的思路[17],推导了WTG非对称连接所构成风电场线性化模型的等效分解。具体推导过程如下。
2.1.1 风电场网络电抗矩阵的构建
由附录式(A3),忽略线路电阻,可得
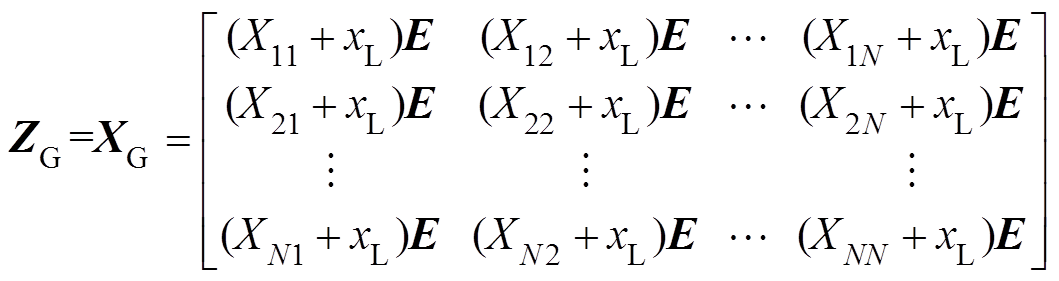 (6)
(6)式中,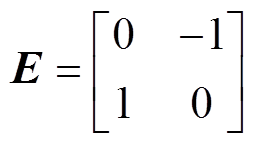 。矩阵
。矩阵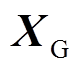 中的元素
中的元素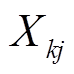 可根据如下原则确定:①
可根据如下原则确定:①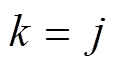 时,
时,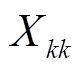 为连接WTGk到风电场汇流母线A的线路电抗之和;②
为连接WTGk到风电场汇流母线A的线路电抗之和;②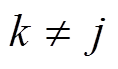 时,若WTGj与WTGk在同一支路上,
时,若WTGj与WTGk在同一支路上,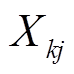 为连接WTGk与WTGj到风电场汇流母线A的线路的公共部分的电抗之和;③
为连接WTGk与WTGj到风电场汇流母线A的线路的公共部分的电抗之和;③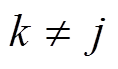 时,若WTGj与WTGk不在同一支路上,则
时,若WTGj与WTGk不在同一支路上,则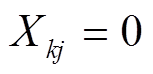 。
。
由式(6),可得到风电场网络电抗矩阵为
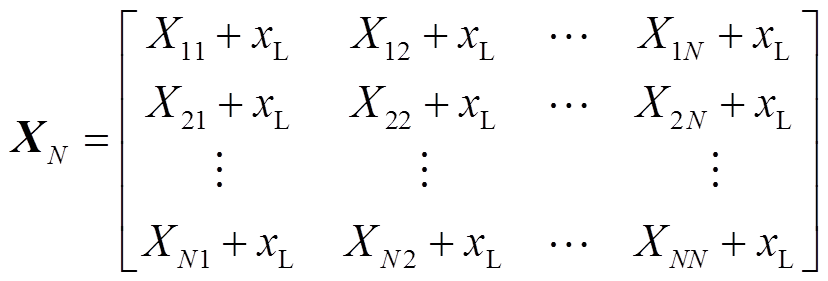 (7)
(7)2.1.2 风电场线性化模型等效分解
根据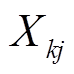 的形成原则,矩阵
的形成原则,矩阵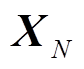 为一实对称矩阵。若其特征值为
为一实对称矩阵。若其特征值为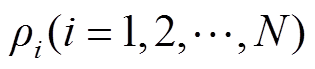 ,则存在矩阵
,则存在矩阵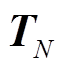 使得
使得
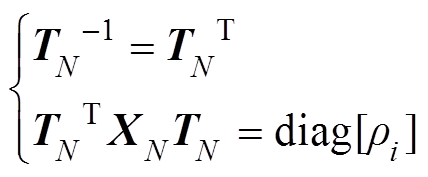 (8)
(8)式中,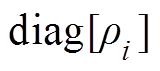 表示对角线元素为
表示对角线元素为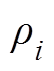 的对角矩阵。
的对角矩阵。
令
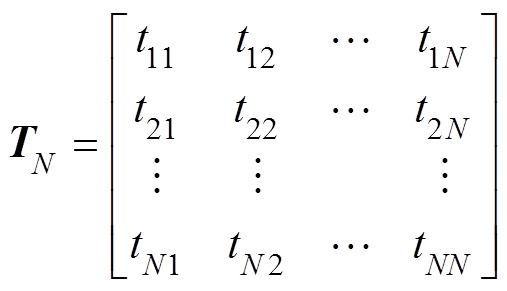
借鉴式(8)中对矩阵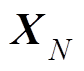 的模式分解,定义变换矩阵
的模式分解,定义变换矩阵
 (9)
(9)式中,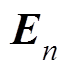 为
为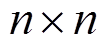 单位矩阵;
单位矩阵;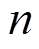 为WTG模型阶数;
为WTG模型阶数;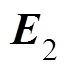 为
为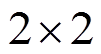 单位矩阵。
单位矩阵。
为对风电场线性化模型进行等效分解,首先对式(3)中的变量做变换
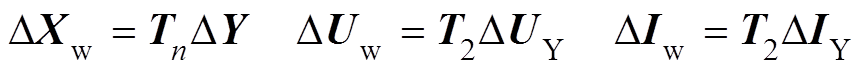 (10)
(10)然后,将式(10)与式(5)代入式(3)得
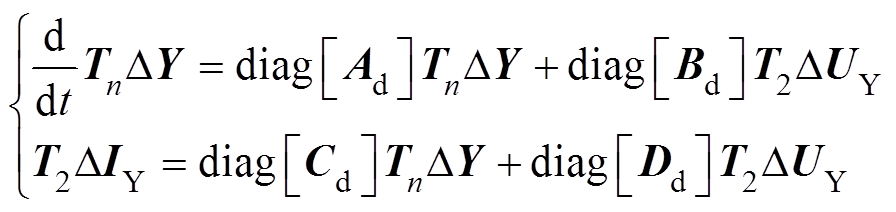 (11)
(11)由式(8)与式(9)可得
 (12)
(12)因此,对式(11)第1个方程左右两边同乘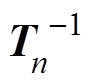 ,第2个方程左右两边同乘
,第2个方程左右两边同乘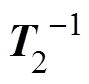 可得
可得
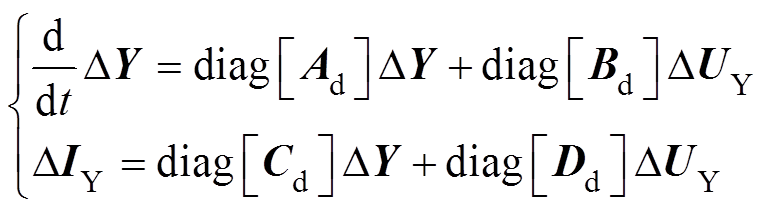 (13)
(13)最后,对于风电场网络方程,由式(8)的第2个方程
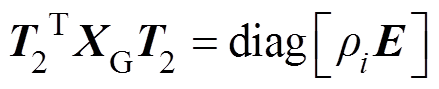 (14)
(14)因此,将式(6)与式(10)代入式(2),并在等式两边同乘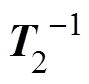 可得
可得
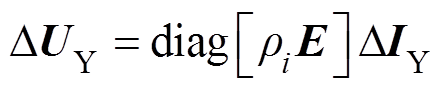 (15)
(15)由式(13)和式(15),经式(10)所示变量变换,原N台WTG构成的风电场的线性化模型可等效为如下N个相互独立的子系统,即
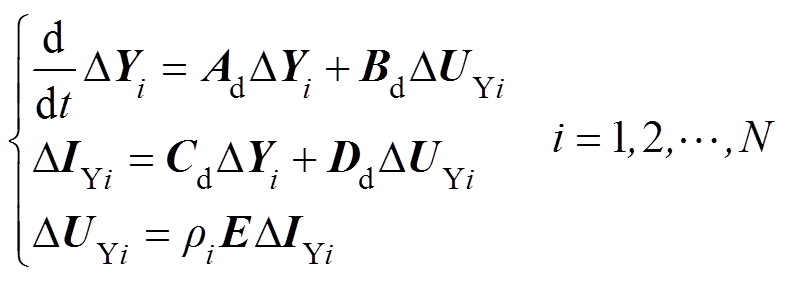 (16)
(16)其中,第i个等效子系统的线性化状态空间模型为
 (17)
(17)式中,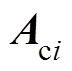 为第i个等效子系统的线性化状态空间矩阵,
为第i个等效子系统的线性化状态空间矩阵,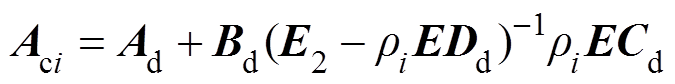 。
。
在2.1小节将式(4)所示风电场全阶模型等效为式(17)所示的N个等效子系统的推导过程中,作出了两点假设。假设1:风电场内各WTG的线性化模型相同;假设2:风电场连接线路电阻为0。对于上述两点假设作进一步分析与解释如下。
对于假设1:①一个风电场内一般采用同一型号的WTG,其初始参数设定相同。②风速差异会导致各WTG稳态功率输出具有一定差异,即各WTG的稳态运行点会有一定差异;但是在WTG型号相同的条件下,这一差异对WTG线性化模型影响不大,可认为各WTG的线性化模型“近似相同”。③一些规模较大的风电场可能由几个风电机群构成,各风电机群内WTG型号相同且风速空间分布差异不大,对此可依次将各个风电机群看作一独立系统,检验其小干扰稳定性;此时便是将图1所示系统看作风电场内的一个风电机群的情况;结合第1节的说明,风电场其余部分与外部交流系统总容量远大于该风电机群的容量,因此在规划阶段可认为母线C电压恒定,式(2)和式(4)分别为该风电机群的网络方程和全阶线性化模型。
对于假设2:①正常情况下,出厂时的参数设定可确保WTG作为一独立系统的稳定性,即矩阵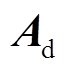 无位于复平面右半平面的特征值,本文中重点关注WTG并网运行时的稳定性;与交流系统间的弱连接或无功功率不足是并网风电场稳定性问题的常见诱因[18-20]。②弱连接一般是由风电外送通道线路电抗较大造成的,这一条件下风电场容易出现小干扰稳定性问题[18-19]。③线路电抗消耗无功功率过多,容易引发电压稳定问题,进而可能引发一系列稳定性问题[20-21]。④假设2关注线路电抗的影响,便是针对上述实际中较为常见的很大一类问题提出的。
无位于复平面右半平面的特征值,本文中重点关注WTG并网运行时的稳定性;与交流系统间的弱连接或无功功率不足是并网风电场稳定性问题的常见诱因[18-20]。②弱连接一般是由风电外送通道线路电抗较大造成的,这一条件下风电场容易出现小干扰稳定性问题[18-19]。③线路电抗消耗无功功率过多,容易引发电压稳定问题,进而可能引发一系列稳定性问题[20-21]。④假设2关注线路电抗的影响,便是针对上述实际中较为常见的很大一类问题提出的。
因此,可认为:①风电场内各WTG线性化模型近似相同;②连接线路电阻的影响可忽略。
由于各WTG线性化模型近似相同,在风电场规划阶段,可选择风电场内某一台WTG为代表,认为其他WTG线性化模型与代表WTG相同,从而得到式(5)中的矩阵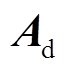 、
、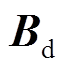 、
、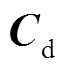 和
和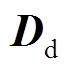 。忽略线路电阻,便可建立式(7)所示等效子系统模型。计算式(17)中矩阵
。忽略线路电阻,便可建立式(7)所示等效子系统模型。计算式(17)中矩阵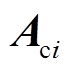 的特征值与计算式(4)中矩阵
的特征值与计算式(4)中矩阵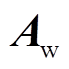 的特征值所得结果近似相同。通过对等效子系统进行模式分析,可检验风电场小干扰失稳风险。
的特征值所得结果近似相同。通过对等效子系统进行模式分析,可检验风电场小干扰失稳风险。
若一台WTG线性化模型的阶数为n,则矩阵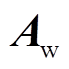 为一个
为一个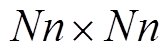 的方阵;通过计算矩阵
的方阵;通过计算矩阵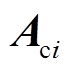 与
与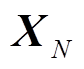 的特征值,可将一个
的特征值,可将一个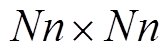 的方阵特征值的计算降阶为一个N阶方阵和N个n阶方阵特征值的计算。因此,本文所提方法为一降阶模式计算(Reduced-Order Modal Computation, ROMC)方法,可有效降低风电场小干扰稳定性检验的工作量。
的方阵特征值的计算降阶为一个N阶方阵和N个n阶方阵特征值的计算。因此,本文所提方法为一降阶模式计算(Reduced-Order Modal Computation, ROMC)方法,可有效降低风电场小干扰稳定性检验的工作量。
采用ROMC法检验风电场小干扰稳定性的步骤总结如下:
(1)根据风电场网络结构和参数,形成式(7)所示网络电抗矩阵,并计算其特征值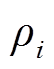 。
。
(2)选择风电场内某一台WTG为代表,按照其稳态运行点及WTG典型模型和参数,建立其线性化状态空间模型,得到矩阵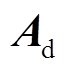 、
、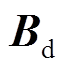 、
、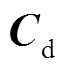 和
和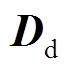 。
。
(3)依据式(17)形成矩阵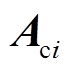 ,计算其特征值,由特征值计算结果,判断风电场小干扰稳定性。
,计算其特征值,由特征值计算结果,判断风电场小干扰稳定性。
由于在形成式(4)所示风电场全阶模型时考虑了线路电阻及WTG线性化模型的差异,而在形成式(17)所示等效子系统模型时忽略了上述两点;计算矩阵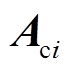 的特征值与计算矩阵
的特征值与计算矩阵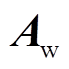 的特征值所得结果近似相同而非完全相同。但是其间微小的误差不影响对风电场小干扰失稳风险的判定。对于ROMC法在风电场规划阶段的具体应用,可作如下分析与讨论:
的特征值所得结果近似相同而非完全相同。但是其间微小的误差不影响对风电场小干扰失稳风险的判定。对于ROMC法在风电场规划阶段的具体应用,可作如下分析与讨论:
(1)ROMC法所得风电场模式计算结果与由全阶模型所得结果近似,因此,若风电场小干扰稳定性良好,则由ROMC法所得风电场主导模式应位于复平面左半平面且具有足够的稳定裕度;若风电场存在小干扰失稳风险,则由ROMC法所得风电场主导模式靠近虚轴或位于复平面右半平面。
(2)在风电场规划阶段,通常需要考虑多种设计方案,并从经济性、效益和稳定性等角度,对其进行综合对比和评价,以获得最优设计方案。为确保风电场实际运行中的小干扰稳定性,规划阶段应保证风电场主导模式均位于复平面左半平面,且具有一定的稳定裕度。对于各设计方案,如果均采用全阶模型作模式分析或非线性仿真分析,虽然结果准确,但也会造成小干扰稳定性检验工作量大、效率低。
(3)考虑上述分析与问题,可在风电场规划阶段引入ROMC法,一方面,可首先淘汰一部分明显具有小干扰稳定性问题或失稳风险的方案,不必对此类方案再作非线性仿真分析;另一方面,对于可初步确保小干扰稳定性的方案,也可根据ROMC法所得模式计算结果对其小干扰稳定性的优劣给出评价,并用于最优方案的选取。对于最优方案,可采用全阶模型和非线性仿真分析对其作进一步检验,以有效确保所选方案的小干扰稳定性。
综上所述,ROMC法用于风电场规划,可有效降低小干扰稳定性检验的工作量,也有助于尽可能地考虑更多方案,避免遗漏。对于大规模风电场,WTG数量大,可供考量的方案多,且风电场全阶模型阶数高,此时采用ROMC协助完成风电场小干扰稳定性检验工作,可有效提高工作效率,也有助于对比多种方案,获得最优解。
本节通过仿真算例验证ROMC法用于风电场小干扰稳定性检验的有效性。风电场采用DFIG风电场,DFIG模型见文献[22],参数见附录中附表1。仿真软件采用Matlab。
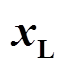 对风电场小干扰稳定性的影响分析
对风电场小干扰稳定性的影响分析本小节以图2所示的风电场为例,在 变化的过程中,采用ROMC法检验风电场小干扰稳定性,验证ROMC法的有效性。风电场由17台DFIG构成,各DFIG稳态有功输出均为0.1(pu),功率因数0.98;线路参数见附录中附表2。所有DFIG参数相同,稳态功率输出相同;但由于各DFIG间电气连接不对称,其端电压和输出电流稳态值略有差异。因此,各DFIG线性化模型“近似相同”。
变化的过程中,采用ROMC法检验风电场小干扰稳定性,验证ROMC法的有效性。风电场由17台DFIG构成,各DFIG稳态有功输出均为0.1(pu),功率因数0.98;线路参数见附录中附表2。所有DFIG参数相同,稳态功率输出相同;但由于各DFIG间电气连接不对称,其端电压和输出电流稳态值略有差异。因此,各DFIG线性化模型“近似相同”。
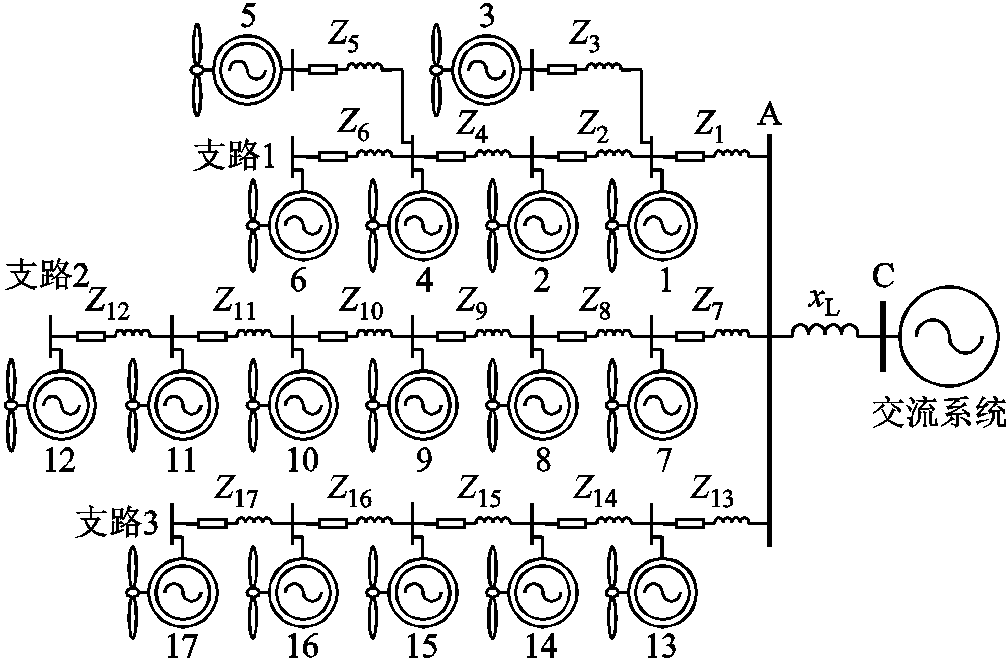
图2 算例风电场结构图(三支路)
Fig.2 Configuration of example wind farm (3 branches)
 依次取0.04、0.1、0.15和0.2,在这一过程中,采用ROMC法检验风电场小干扰稳定性。
依次取0.04、0.1、0.15和0.2,在这一过程中,采用ROMC法检验风电场小干扰稳定性。
首先,对于 的情况,形成式(7)所示风电场网络电抗矩阵
的情况,形成式(7)所示风电场网络电抗矩阵 ,计算
,计算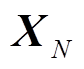 的特征值(
的特征值(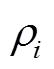 ,
,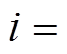
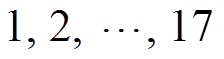 )所得结果见附录附表3。
)所得结果见附录附表3。
然后,以DFIG 6为代表,建立其线性化模型,并取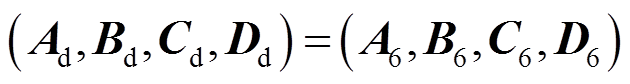 。
。
最后,根据式(17),形成等效子系统线性化状态空间矩阵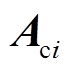 ,计算矩阵
,计算矩阵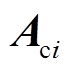 的特征值;根据参与因子,得到风电场各类振荡模式在复平面上的位置分别如图3a~图3d中“×”所示。其中,振荡模式1~4分别为:转子侧换流器(Rotor-Side Converter, RSC)d轴电流内环模式、RSC q轴电流内环模式、锁相环(Phase-Locked Loop, PLL)模式,以及网侧换流器(Grid-Side Converter, GSC)直流电压外环模式。对各类振荡模式参与度最高的风电场状态变量依次为:①RSC d轴电流内环积分控制器的输出和转子磁链;②RSC q轴电流内环积分控制器输出和转子磁链;③PLL输出电压相位和PLL积分控制器输出;④直流电容电压和GSC直流电压外环积分控制器输出。后文中将沿用这一对各类振荡模式的命名。
的特征值;根据参与因子,得到风电场各类振荡模式在复平面上的位置分别如图3a~图3d中“×”所示。其中,振荡模式1~4分别为:转子侧换流器(Rotor-Side Converter, RSC)d轴电流内环模式、RSC q轴电流内环模式、锁相环(Phase-Locked Loop, PLL)模式,以及网侧换流器(Grid-Side Converter, GSC)直流电压外环模式。对各类振荡模式参与度最高的风电场状态变量依次为:①RSC d轴电流内环积分控制器的输出和转子磁链;②RSC q轴电流内环积分控制器输出和转子磁链;③PLL输出电压相位和PLL积分控制器输出;④直流电容电压和GSC直流电压外环积分控制器输出。后文中将沿用这一对各类振荡模式的命名。
对于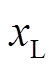 为0.1、0.15和0.2的情况,采用ROMC法计算风电场振荡模式,过程同上述对
为0.1、0.15和0.2的情况,采用ROMC法计算风电场振荡模式,过程同上述对 的情况的处理,得到风电场振荡模式1~4在复平面上的位置如图3a~图3d中“×”所示。
的情况的处理,得到风电场振荡模式1~4在复平面上的位置如图3a~图3d中“×”所示。
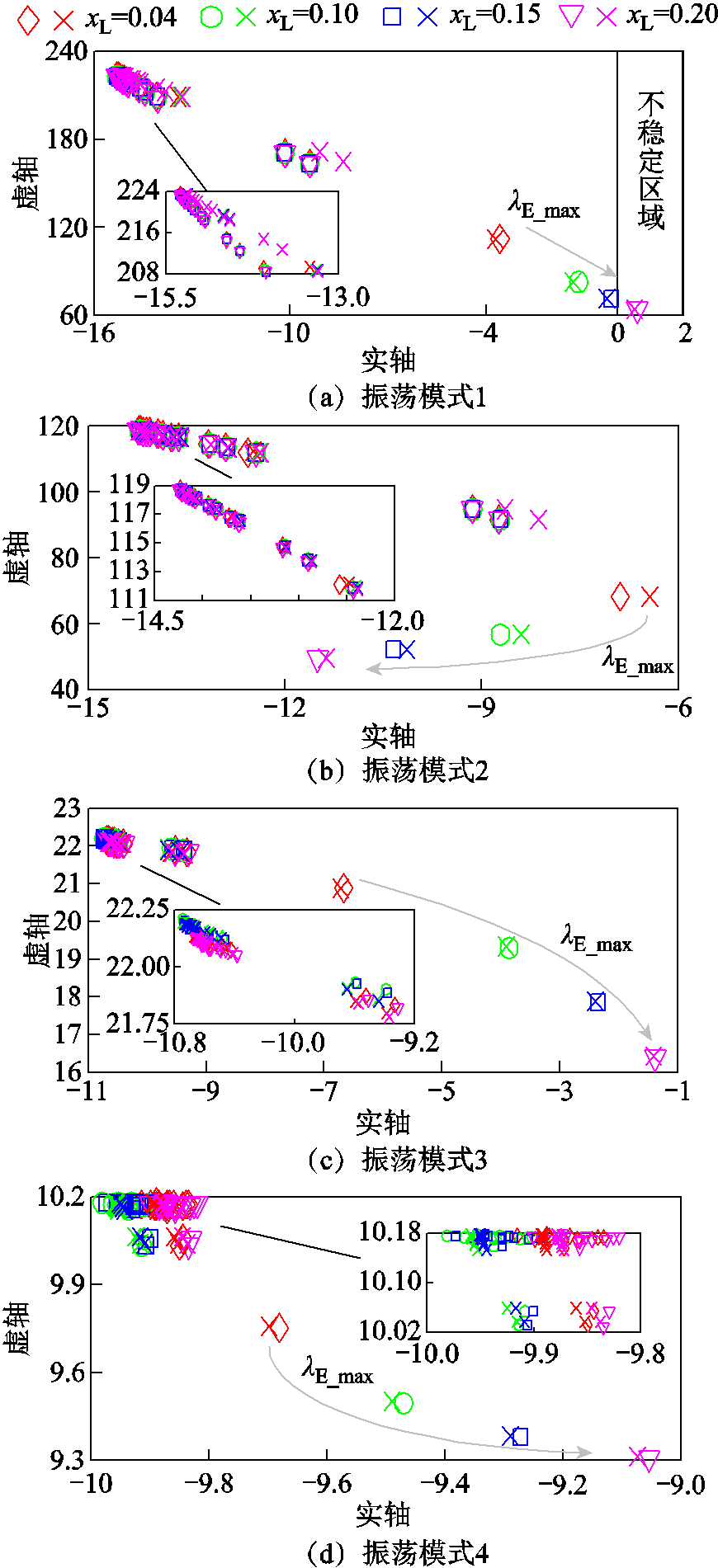
图3 风电场模式计算结果(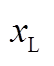 变化时)
变化时)
Fig.3 Modal computational results(when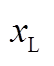 varies)
varies)
图3中,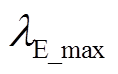 表示
表示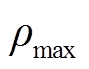 对应等效子系统的振荡模式,灰色箭头指示
对应等效子系统的振荡模式,灰色箭头指示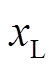 由0.04增大至0.20的过程中,
由0.04增大至0.20的过程中,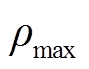 增大,
增大,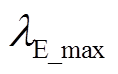 在复平面上的移动方向。
在复平面上的移动方向。
作为对比验证,分别在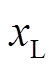 为0.04、0.10、0.15和0.20时,形成式(4)中风电场全阶线性化状态空间矩阵
为0.04、0.10、0.15和0.20时,形成式(4)中风电场全阶线性化状态空间矩阵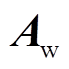 ;计算
;计算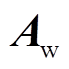 的特征值,得到风电场振荡模式在复平面上的分布情况如图3中菱形(◇)、空心圆(○)、方块(□)和三角(△)所示。为更加清晰地对比由ROMC法和全阶模型所得风电场振荡模式,对四类振荡模式,列出
的特征值,得到风电场振荡模式在复平面上的分布情况如图3中菱形(◇)、空心圆(○)、方块(□)和三角(△)所示。为更加清晰地对比由ROMC法和全阶模型所得风电场振荡模式,对四类振荡模式,列出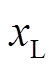 变化时
变化时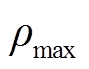 对应等效子系统的振荡模式计算结果见表1,包括振荡模式的数值、阻尼比和频率。
对应等效子系统的振荡模式计算结果见表1,包括振荡模式的数值、阻尼比和频率。
表1 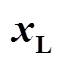 变化时部分振荡模式计算结果
变化时部分振荡模式计算结果
Tab.1 Part of the computational results when network configuration varied when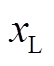 varies
varies

模式ROMC法全阶模型 振荡模式阻尼比频率振荡模式阻尼比频率 1-3.7+j111.953.3%17.8-3.6+j111.953.2%17.8 -1.4+j82.731.7%13.2-1.2+j82.831.5%13.2 -0.2+j71.010.3%11.3-0.1+j71.130.1%11.3 0.5+j63.80-0.8%10.20.6+j63.92-0.9%10.2 2-6.4+j68.399.4%10.9-6.7+j68.2510%10.9 -8.4+j56.8315%9.0-8.7+j56.7115%9.0 -10.1+j52.4719%8.4-10.3+j52.3419%8.3 -11.4+j49.5922%7.9-11.5+j49.4723%7.9 3-6.7+j20.9131%3.3-6.7+j20.9030%3.3 -3.9+j19.3420%3.1-3.86+j19.3120%3.1 -2.4+j17.8913%2.8-2.4+j17.8513%2.8 -1.4+j16.448.5%2.6-1.4+j16.408.4%2.6 4-9.7+j9.7671%1.6-9.7+j9.7571%1.6 -9.5+j9.5071%1.5-9.5+j9.5071%1.5 -9.3+j9.3970%1.5-9.3+j9.3870%1.5 -9.1+j9.3170%1.5-9.1+j9.3170%1.5
由图3及附表3和表1可得:
(1)采用ROMC法所得风电场振荡模式与由全阶模型所得结果在复平面上分布情况基本一致。验证了ROMC法用于风电场小干扰稳定性检验的有效性。
(2)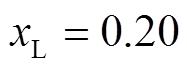 时,风电场有一RSC d轴电流内环模式位于复平面右半平面,风电场失去小干扰稳定性;ROMC法有效检验了风电场小干扰失稳风险。为对这一结论进行验证,现进行非线性仿真,仿真中扰动设置为由于局部风速变化,0.5s时,DFIG1、DFIG2、DFIG 3输入的机械功率提高10%,并于0.1s内均匀恢复,仿真结果如图4所示。由图4可知,
时,风电场有一RSC d轴电流内环模式位于复平面右半平面,风电场失去小干扰稳定性;ROMC法有效检验了风电场小干扰失稳风险。为对这一结论进行验证,现进行非线性仿真,仿真中扰动设置为由于局部风速变化,0.5s时,DFIG1、DFIG2、DFIG 3输入的机械功率提高10%,并于0.1s内均匀恢复,仿真结果如图4所示。由图4可知,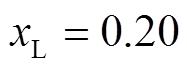 时,风电场失去小干扰稳定性,与由ROMC法所得分析结论一致。
时,风电场失去小干扰稳定性,与由ROMC法所得分析结论一致。
(3)随着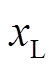 增大,
增大,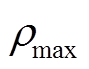 增大。对于振荡模式1、3、4,随着
增大。对于振荡模式1、3、4,随着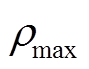 增大,
增大,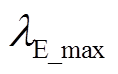 在复平面上向右移动,且阻尼比降低,风电场小干扰稳定性降低;对于振荡模式2,随着
在复平面上向右移动,且阻尼比降低,风电场小干扰稳定性降低;对于振荡模式2,随着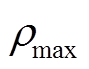 增大,
增大,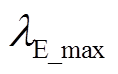 在复平面上向左移动,且阻尼比提高。
在复平面上向左移动,且阻尼比提高。
(4)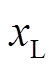 变化会影响风电场小干扰稳定性,在风电场规划阶段应注意对风电外送通道线路的选取;当风电场规划方案中风电外送通道线路型号或长度改变时,应注意对风电场小干扰稳定性进行检验。
变化会影响风电场小干扰稳定性,在风电场规划阶段应注意对风电外送通道线路的选取;当风电场规划方案中风电外送通道线路型号或长度改变时,应注意对风电场小干扰稳定性进行检验。
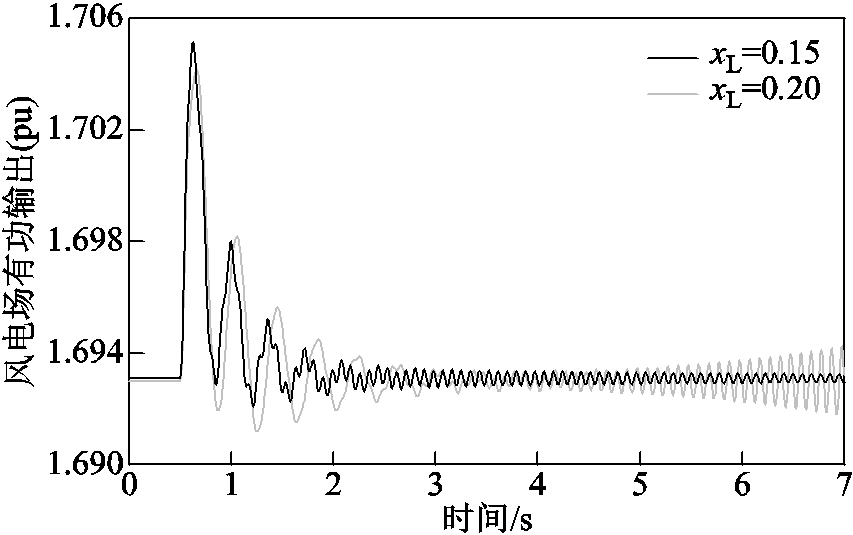
图4 非线性仿真结果(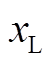 变化时)
变化时)
Fig.4 Non-linear simulation results(when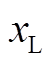 varies)
varies)
根据3.1小节的分析,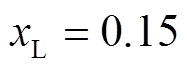 时,图2所示结构下风电场小干扰稳定。本小节中
时,图2所示结构下风电场小干扰稳定。本小节中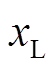 取0.15,分别在风电场采用图2所示3支路、图5a所示并联和图5b所示链式结构下,采用ROMC法检验其小干扰稳定性,验证ROMC法的有效性。DFIG运行与控制参数以及风电场内部线路参数同3.1小节。
取0.15,分别在风电场采用图2所示3支路、图5a所示并联和图5b所示链式结构下,采用ROMC法检验其小干扰稳定性,验证ROMC法的有效性。DFIG运行与控制参数以及风电场内部线路参数同3.1小节。
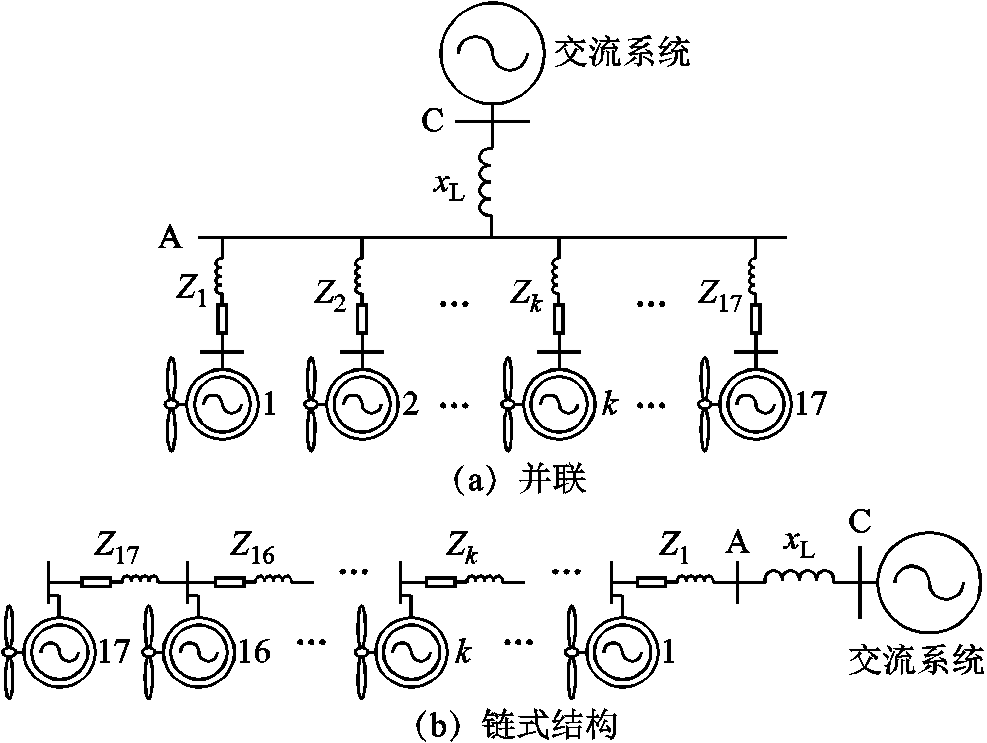
图5 其他结构下的算例风电场
Fig.5 Example wind farm in other configurations
首先,在风电场采用并联结构时,形成风电场网络电抗矩阵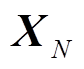 ,计算
,计算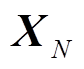 的特征值,所得结果见附表4。
的特征值,所得结果见附表4。
然后,以DFIG1为代表,建立其线性化模型,并取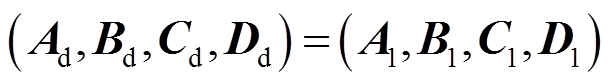 。
。
最后,按照式(17),形成等效子系统状态空间矩阵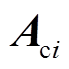 ;计算矩阵
;计算矩阵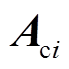 的特征值,得到风电场采用并联结构时,振荡模式1在复平面上的分布如图6a中“×”所示。
的特征值,得到风电场采用并联结构时,振荡模式1在复平面上的分布如图6a中“×”所示。
对于风电场采用三支路和链式结构的情况,采用ROMC法计算风电场振荡模式,过程同上述对并联情况的处理,得到振荡模式1在复平面上的分布分别如图6b和图6c中的“×”所示。
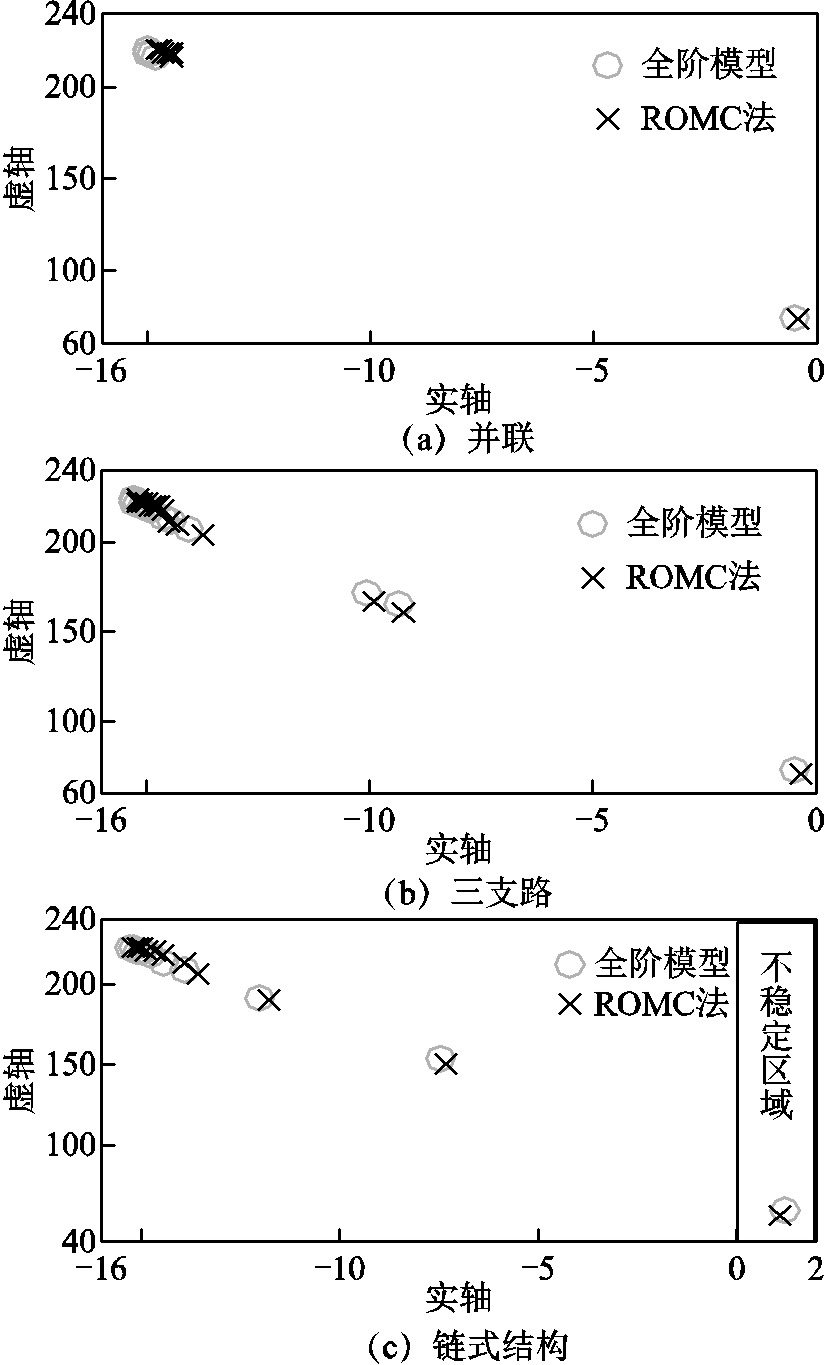
图6 风电场模式计算结果(不同结构)
Fig.6 Modal computational results (different configurations)
作为对比验证,依次对并联、三支路和链式结构下的风电场,建立式(4)所示风电场全阶线性化模型,计算矩阵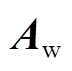 的特征值,得到振荡模式1在复平面上的分布情况分别如图6a、图6b和图6c中“○”所示。为更加清晰地对比由ROMC法和全阶模型所得风电场振荡模式,列出三种结构下,振荡模式1阻尼最差的三个数值结果见表2。由于空间限制,仅列出振荡模式1的计算结果,对于其他振荡模式,所得结果情况类似,但均位于复平面左半平面。
的特征值,得到振荡模式1在复平面上的分布情况分别如图6a、图6b和图6c中“○”所示。为更加清晰地对比由ROMC法和全阶模型所得风电场振荡模式,列出三种结构下,振荡模式1阻尼最差的三个数值结果见表2。由于空间限制,仅列出振荡模式1的计算结果,对于其他振荡模式,所得结果情况类似,但均位于复平面左半平面。
表2 部分振荡模式计算结果(不同结构)
Tab.2 Part of the computational results when network configuration varied(different configurations)
结构ROMC法全阶模型 振荡模式阻尼比频率振荡模式阻尼比频率 并联 (图6a)-0.44+j73.210.6%11.7-0.46+j73.220.6%11.7 -14.4+j217.236.6%34.6-14.8+j217.156.8%34.6 -14.5+j217.796.6%34.7-14.9+j217.706.8%34.6 三支路 (图6b)-0.1+j71.010.1%11.3-0.2+j71.130.3%11.3 -8.9+j163.875.2%26.1-9.4+j164.895.7%26.2 -9.8+j170.765.4%27.2-10.2+j171.685.9%27.3 链式 (图6c)0.9+j58.89-0.15%9.371.3+j59.62-0.2%9.49 -7.1+j149.564.7%23.80-7.5+j150.475.0%23.95 -11.1+j189.685.8%30.20-12.1+j190.226.3%30.28
由图6和表2可得如下分析结论:
(1)采用ROMC法所得风电场振荡模式与由全阶模型所得结果在复平面上的分布情况基本一致,验证了ROMC法的有效性。
(2)当风电场采用链式结构时,有一振荡模式位于复平面右半平面,ROMC法有效检验了风电场小干扰失稳风险。非线性仿真验证结果如图7所示。仿真中的扰动设置同3.1小节。
(3)在风电场规划阶段,应注意集电网络结构变化对风电场小干扰稳定性的影响,且应尽量避免采用链式结构将多台WTG接入汇流母线的连接方式。
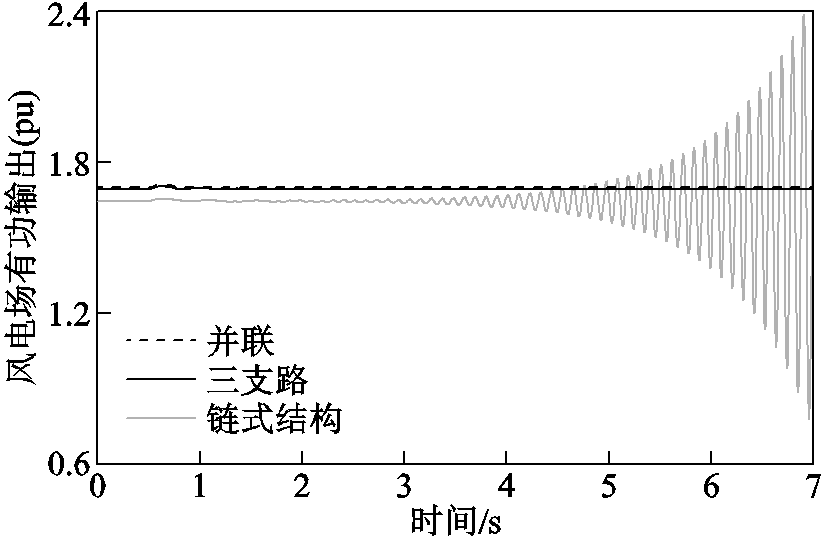
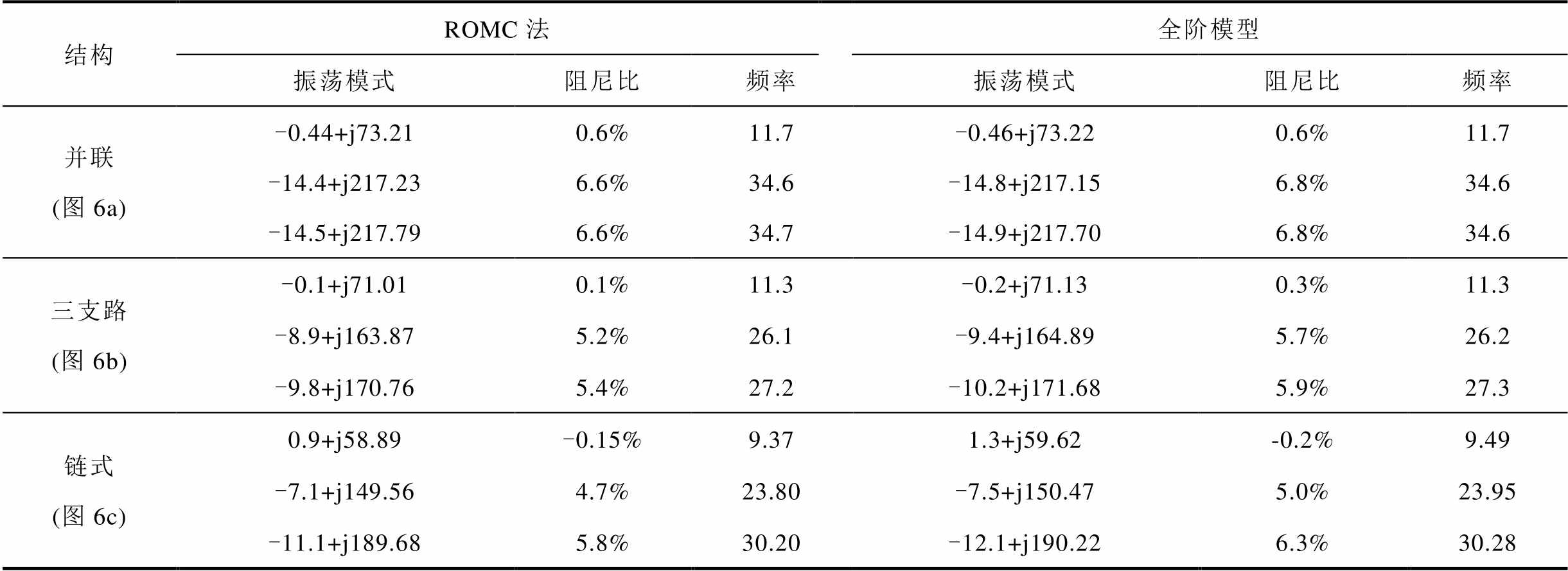
图7 非线性仿真结果(不同结构)
Fig.7 Non-linear simulation results(different configurations)
本小节以一个200台DFIG构成的风电场为例,验证ROMC法的有效性。风电场结构如图8所示,考虑图8a和图8b两种结构:图8a结构,风电场内25条支路,各支路上8台DFIG串联;图8b,风电场内8条支路,各支路上25台DFIG串联。为方便描述,相邻DFIG间,以及汇流母线A与相邻DFIG间的线路阻抗均为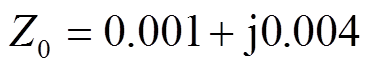 。DFIG参数见附表1。考虑风速空间分布差异造成的风电场内DFIG功率输出的差异,DFIG1稳态功率输出仍为0.1(pu),功率因数为0.98;其他DFIG功率输出在此基础上随机变化,且最大变化范围为±15%。此时,各DFIG稳态功率输出以及端电压和输出电流具有一定差异,但参数相同,因此,可认为各DFIG线性化模型近似相同。
。DFIG参数见附表1。考虑风速空间分布差异造成的风电场内DFIG功率输出的差异,DFIG1稳态功率输出仍为0.1(pu),功率因数为0.98;其他DFIG功率输出在此基础上随机变化,且最大变化范围为±15%。此时,各DFIG稳态功率输出以及端电压和输出电流具有一定差异,但参数相同,因此,可认为各DFIG线性化模型近似相同。
采用ROMC法检验风电场小干扰稳定性。
首先,形成图8a所示结构下风电场的网络电抗矩阵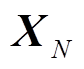 ,并计算
,并计算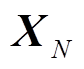 的特征值。
的特征值。
然后,以DFIG1为代表,建立其线性化模型,并取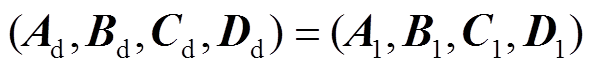 。
。
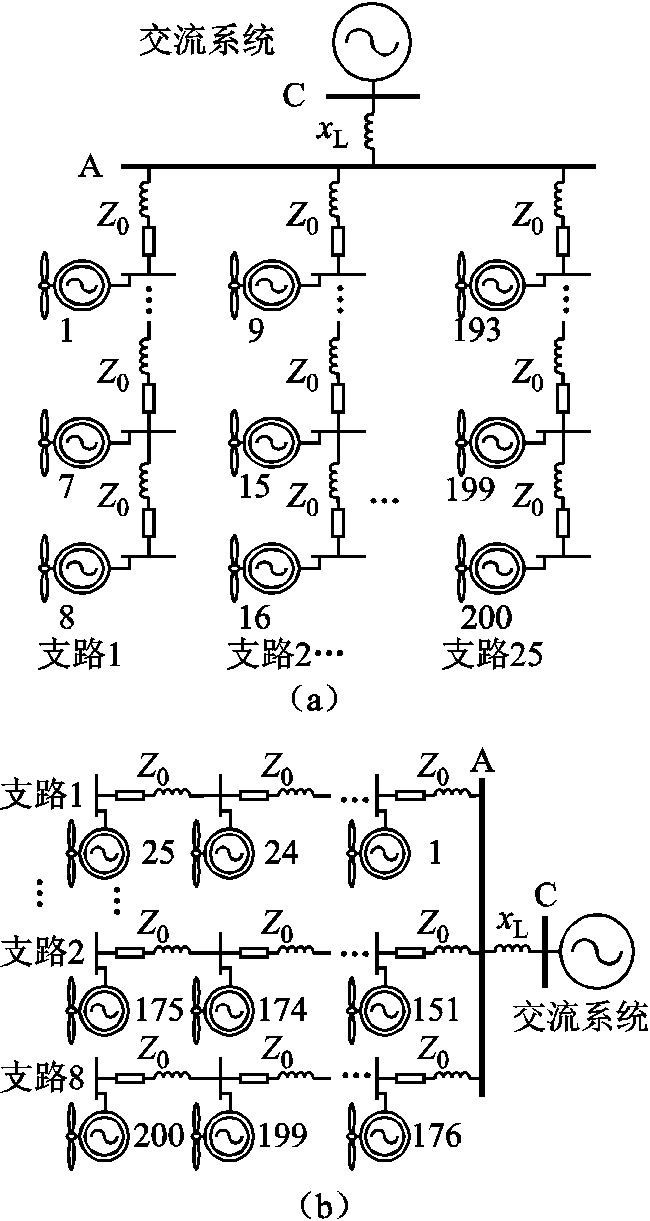
图8 大型算例风电场结构
Fig.8 Configuration of a large-scale example wind farm
最后,按照式(17),形成等效子系统状态空间矩阵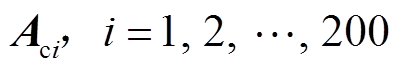 ;计算
;计算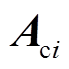 的特征值,得到采用图8a所示结构时,风电场振荡模式1在复平面上的分布如图9a中“×”所示。
的特征值,得到采用图8a所示结构时,风电场振荡模式1在复平面上的分布如图9a中“×”所示。
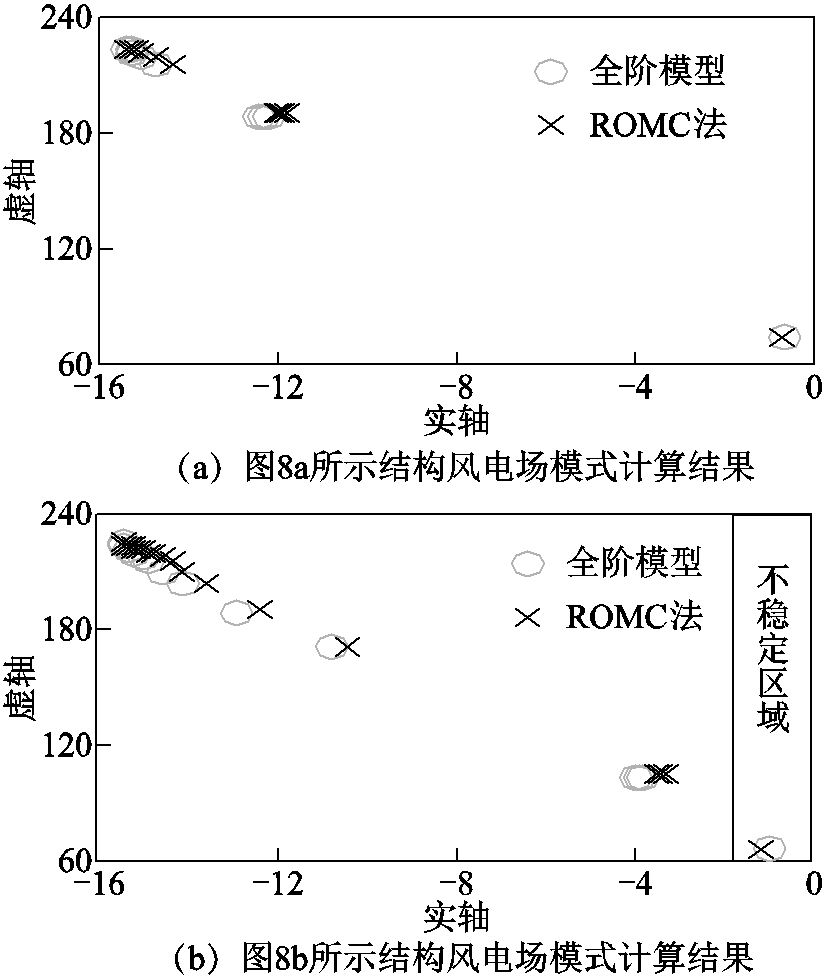
图9 模式计算结果(大型风电场)
Fig.9 Modal computation results (large-scale wind farm)
对于风电场采用图8b所示结构的情况,采用ROMC法计算风电场振荡模式,过程同上述对采用图8a所示结构的情况的处理,得到振荡模式1在复平面上的分布如图9b中“×”所示。
作为对比验证,分别对图8所示两种结构下的风电场,建立式(4)所示全阶线性化模型,计算矩阵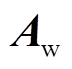 的特征值,得到振荡模式1在复平面上的分布情况分别如图9a和图9b中“○”所示。为更加清晰地对比由ROMC法和全阶模型所得风电场振荡模式,列出两种结构下,振荡模式1阻尼最差的三个数值结果见表3。对于其他振荡模式,所得结果情况类似,但均位于复平面左半平面。
的特征值,得到振荡模式1在复平面上的分布情况分别如图9a和图9b中“○”所示。为更加清晰地对比由ROMC法和全阶模型所得风电场振荡模式,列出两种结构下,振荡模式1阻尼最差的三个数值结果见表3。对于其他振荡模式,所得结果情况类似,但均位于复平面左半平面。
表3 部分振荡模式计算结果(大型风电场)
Tab.3 Part of the computational results when network configuration varied(large-scale wind farm)
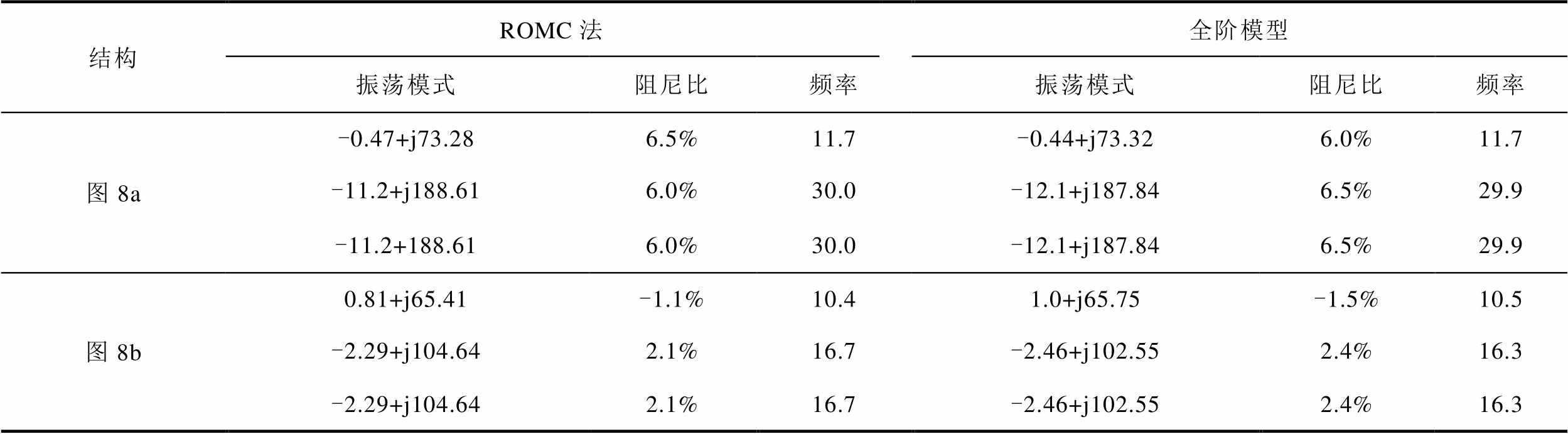
结构ROMC法全阶模型 振荡模式阻尼比频率振荡模式阻尼比频率 图8a-0.47+j73.286.5%11.7-0.44+j73.326.0%11.7 -11.2+j188.616.0%30.0-12.1+j187.846.5%29.9 -11.2+188.616.0%30.0-12.1+j187.846.5%29.9 图8b0.81+j65.41-1.1%10.41.0+j65.75-1.5%10.5 -2.29+j104.642.1%16.7-2.46+j102.552.4%16.3 -2.29+j104.642.1%16.7-2.46+j102.552.4%16.3
由图9可得如下结论:
(1)采用ROMC法所得风电场振荡模式与由全阶模型所得结果在复平面上的分布情况基本一致,验证了ROMC法的有效性。
(2)当风电场采用图8b所示结构时,有一振荡模式位于复平面右半平面。ROMC法有效检验了风电场小干扰失稳风险。非线性仿真验证结果如图10所示。仿真中的扰动设置同3.1小节。
(3)算例结果再次表明,集电网络结构变化会影响风电场小干扰稳定性,应尽量避免采用链式结构将多台WTG接入汇流母线的连接方式。
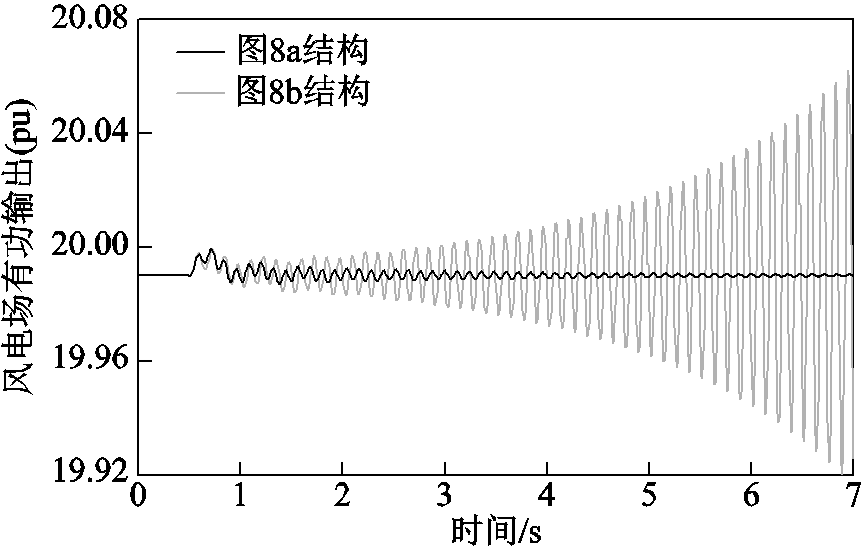
图10 非线性仿真结果(大型风电场)
Fig.10 Non-linear simulation results (large-scale wind farm)
本文提出了一种用于风电场小干扰稳定性检验的ROMC法。
1)根据风电场网络结构和参数,建立了风电场网络电抗矩阵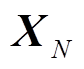 。在风电场规划阶段,对所有WTG采用典型模型与参数;通过变量等效变换,将N台WTG构成的风电场的线性化模型,等效为N个相互独立的等效子系统。等效子系统线性化模型可根据一台WTG的线性化模型和矩阵
。在风电场规划阶段,对所有WTG采用典型模型与参数;通过变量等效变换,将N台WTG构成的风电场的线性化模型,等效为N个相互独立的等效子系统。等效子系统线性化模型可根据一台WTG的线性化模型和矩阵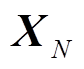 的特征值
的特征值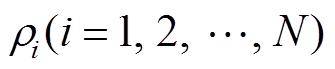 建立。
建立。
2)根据等效子系统线性化状态空间模型的构建方法,提出ROMC法。在规划阶段,用ROMC法检验风电场小干扰稳定性,所得结果准确,模式分析的计算量显著降低。
3)风电场网络结构和参数变化,会导致矩阵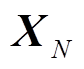 及其特征值
及其特征值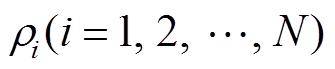 的变化,可能导致风电场小干扰稳定性降低甚至是失稳。
的变化,可能导致风电场小干扰稳定性降低甚至是失稳。
4)文中等效分解的推导是在风电场内各WTG线性化模型相似的条件下展开的,等效分解方法适用于由线性化模型相似的发电单元所构成的系统,如同型风电场或风电机群以及同型光伏电站,在规划阶段可认为其中设备的线性化模型相似,进而采用该方法对系统进行等效分解;对于发电单元线性化模型差异较大的系统,如多机电力系统,其中发电机容量和参数等差异较大,目前无法采用该方法分析系统动态特性。对于如何将等效分解的方法扩展至多机电力系统,则还有待进一步研究。
图1中,风电场内共M条支路,且第m (m=1,2,×××,M)条支路上有Nm台WTG接入。当各支路上WTG按照图1所示递减顺序编号时,第m条支路上WTG的编号范围为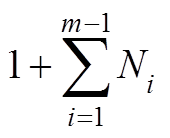 ~
~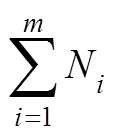 ,且第m条支路上WTGk的端电压为
,且第m条支路上WTGk的端电压为
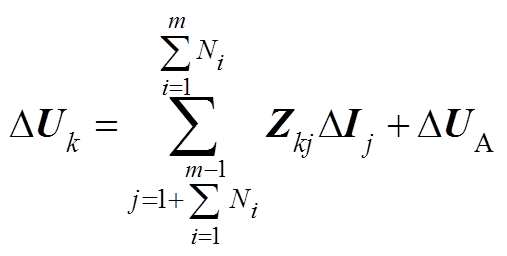 (A1)
(A1)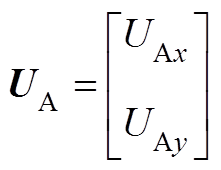
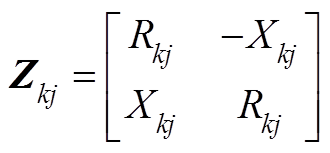
式中,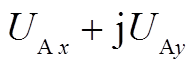 为交流电网公共xy坐标系下风电场汇流母线A的电压;
为交流电网公共xy坐标系下风电场汇流母线A的电压;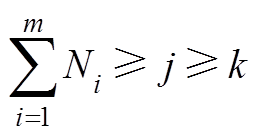 时,
时,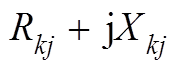 为连接WTGk到汇流母线A的线路阻抗之和;当
为连接WTGk到汇流母线A的线路阻抗之和;当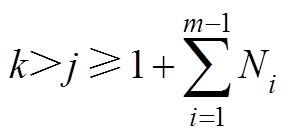 时,
时,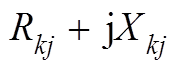 为连接WTGj到汇流母线A的线路阻抗之和。
为连接WTGj到汇流母线A的线路阻抗之和。
不考虑母线C电压波动,式(A1)中
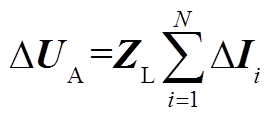 (A2)
(A2)其中
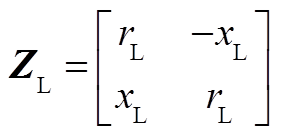
式中,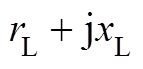 为连接母线A至母线C的线路阻抗。
为连接母线A至母线C的线路阻抗。
由式(A1)和式(A2)可得风电场网络方程为
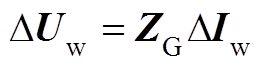 (A3)
(A3)式中
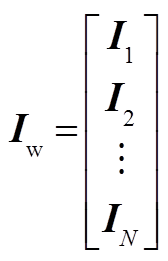
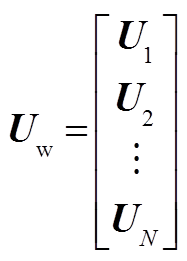
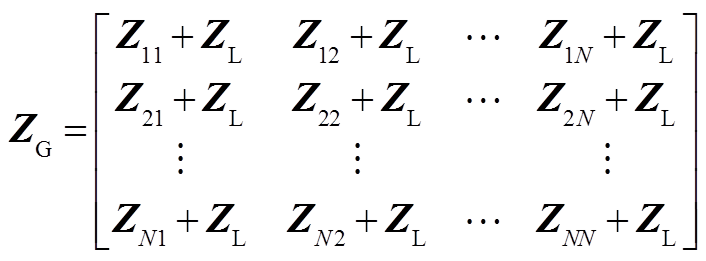
附表1 算例DFIG参数
App.Tab.1 Parameters of DFIG in study cases
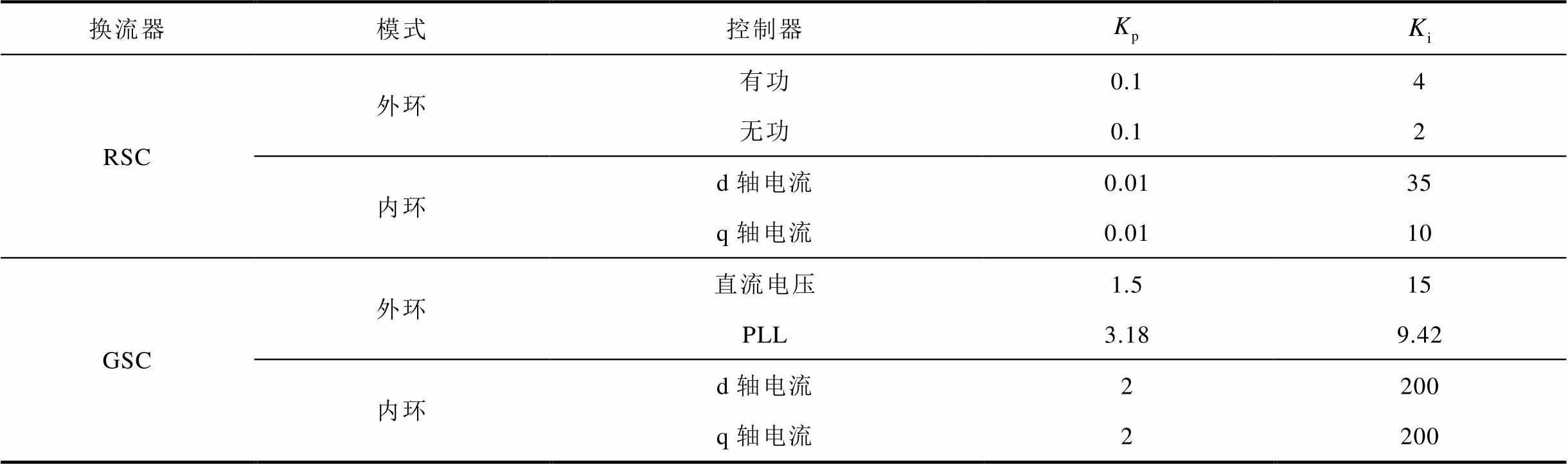
换流器模式控制器 RSC外环有功0.14 无功0.12 内环d轴电流0.0135 q轴电流0.0110 GSC外环直流电压1.515 PLL3.189.42 内环d轴电流2200 q轴电流2200
附表2 图2风电场内部线路参数
App.Tab.2 Parameters of lines inside the wind farm of Fig.2

iii 10.004+j0.01770.004+j0.018 7130.004+j0.017 20.004+j0.015 380.004+j0.015 3140.004+j0.017 30.004+j0.018 790.003+j0.013 6150.003+j0.013 6 40.005+j0.021 3100.003+j0.012 8160.004+j0.018 7 50.004+j0.017110.004+j0.019 6170.004+j0.018 7 60.004+j0.017120.004+j0.017
附表3 3.1小节风电场网络电抗矩阵特征值计算结果
App.Tab.3 Eigenvalues of network reactance matrixes in 3.1

0.040.003 8, 0.004, 0.004 3, 0.005 3, 0.005 5, 0.006 5, 0.00 72, 0.009 9, 0.012, 0.015, 0.017, 0.028, 0.035, 0.045, 0.212, 0.254, 0.90 0.10.003 8, 0.004, 0.004 3, 0.005 3, 0.005 5, 0.006 5, 0.007 2, 0.009 9, 0.012, 0.015, 0.017, 0.028, 0.035, 0.047, 0.0212, 0.254, 1.92 0.150.003 8, 0.004, 0.004 3, 0.005 3, 0.005 5, 0.006 5, 0.007 2, 0.009 9, 0.012, 0.015, 0.017, 0.028, 0.035, 0.047, 0.212, 0.255, 2.77 0.20.003 8, 0.004, 0.004 3, 0.005 3, 0.005 5, 0.006 5, 0.007 2, 0.009 9, 0.012, 0.015, 0.017, 0.028, 0.035, 0.048, 0.212, 0.255, 3.62
附表4 3.2小节风电场网络电抗矩阵特征值计算结果
App.Tab.4 Eigenvalues of network reactance matrixes in 3.2
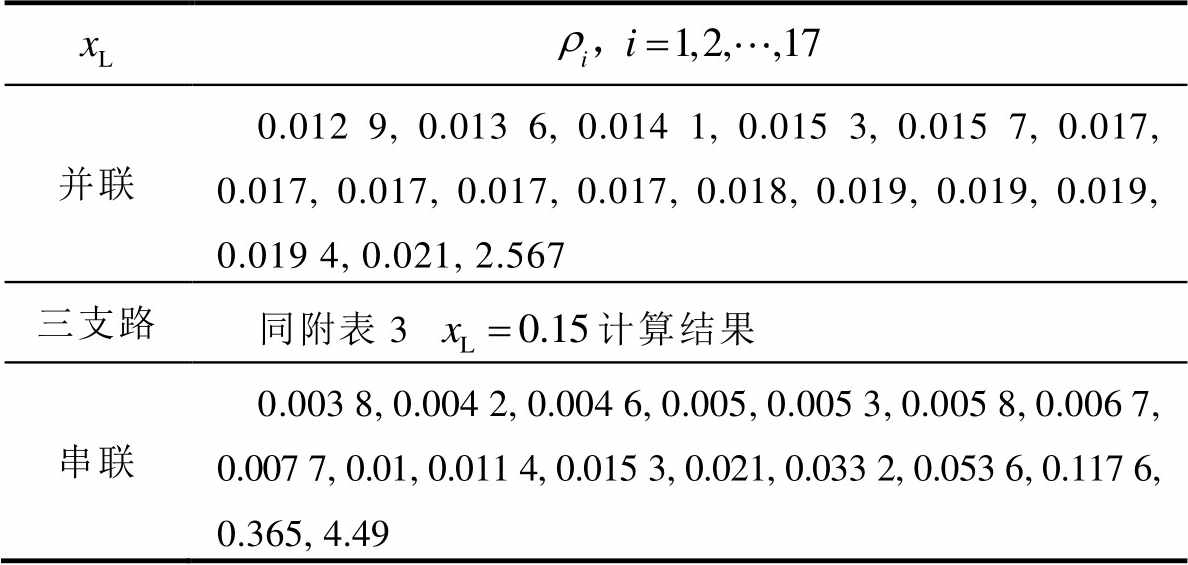
并联0.012 9, 0.013 6, 0.014 1, 0.015 3, 0.015 7, 0.017, 0.017, 0.017, 0.017, 0.017, 0.018, 0.019, 0.019, 0.019, 0.019 4, 0.021, 2.567 三支路同附表3 计算结果 串联0.003 8, 0.004 2, 0.004 6, 0.005, 0.005 3, 0.005 8, 0.006 7, 0.007 7, 0.01, 0.011 4, 0.015 3, 0.021, 0.033 2, 0.053 6, 0.117 6, 0.365, 4.49
参考文献
[1]王一凡, 赵成勇, 郭春义. 双馈风电场孤岛经模块化多电平换流器直流输电并网系统小信号稳定性分析与振荡抑制方法[J]. 电工技术学报, 2019, 34(10): 2116-2129. Wang Yifan, Zhao Chengyong, Guo Chunyi. Small- signal stability and oscillation suppression method for islanded doubly fed induction generator-based wind farm integrated by modular multilevel converter based HVDC system[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2116-2129.
[2]苏田宇, 杜文娟, 王海风. 多直驱永磁同步发电机并联风电场次同步阻尼控制器降阶设计方法[J]. 电工技术学报, 2019, 34(1): 116-127. Su Tianyu, Du Wenjuan, Wang Haifeng. A reduced order design method for sub-synchronous damping controller of multi-PMSGs parallel wind farm[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 116-127.
[3]周佩朋, 宋瑞华, 李光范, 等. 直驱风电机组次同步振荡阻尼控制方法及其适应性[J]. 电力系统自动化, 2019, 43(13): 177-188. Zhou Peipeng, Song Ruihua, Li Guangfan, et al. Damping control of subsynchronous oscillation for direct drive wind turbine generator and its adaptability[J]. Automation of Electric Power System, 2019, 43(13): 177-188.
[4]徐路遥, 兰洲, 陈飞, 等. 弱电网下无功控制对并网变流器稳定性影响分析[J]. 电力系统自动化, 2019, 43(15): 56-68. Xu Luyao, Lan Zhou, Chen Fei, et al. Analysis on impact of reactive power control on stability of grid-connected converter in weak grid[J]. Automation of Electric Power System, 2019, 43(15): 56-68.
[5]Wang Yinfeng, Lu Chao, Zhu Lipeng, et al. Comprehensive modeling and parameter identification of wind farms based on wide-area measurement systems[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(3): 383-393.
[6]El-Sharkawi M. Dynamic equivalent models for wind power plants[C]//2011 IEEE Power and Energy Society General Meeting, Detroit, 2011, DOI: 10.1109/PES.2011.6038934.
[7]Li H, Yang Chao, Zhao B, et al. Aggregated models and transient performances of a mixed wind farm with different wind turbine generator systems[J]. Electric Power Systems Research, 2012, 92: 1-10.
[8]张剑, 何怡刚. 基于轨迹灵敏度分析的永磁直驱风电场等值模型参数辨识[J]. 电工技术学报, 2020, 35(15): 3303-3313. Zhang Jian, He Yigang. Parameters identification of equivalent model of permanent magnet synchronous generator (PMSG) wind farm based on analysis of trajectory sensitivity[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3303-3313.
[9]Zhou Yuhao, Zhao Long, Lee W. Robustness analysis of dynamic equivalent model of DFIG wind farm for stability study[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 5682-5690.
[10]Erlich I, Shewarega F, Feltes C, et al. Determination of dynamic wind farm equivalents using heuristic optimization [C]// Power & Energy Society General Meeting, San Diego, CA, USA, 2012, DOI: 10.1109/ PESGM.2012.6345508.
[11]Zou Jianxiao, Peng Chao, Xu Hongbin, et al. A fuzzy clustering algorithm-based dynamic equivalent modelingmethod for wind farm with DFIG[J]. IEEE Transactions on Energy Conversion, 2015, 30(4): 1329-1337.
[12]吴红斌, 何叶, 赵波, 等. 基于改进K-means聚类算法的风电场动态等值[J]. 太阳能学报, 2018, 39(11): 3232-3238. Wu Hongbin, He Ye, Zhao Bo, et al. Research on dynamic equivalent of wind farm based on improved K-means clustering algorithm[J]. Acta Energiae Solaris Sinica, 2018, 39(11): 3232-3238.
[13]蔡文超, 杨炳元. 基于RTDS风电场等值建模若干问题的解决方案[J]. 电气技术, 2017, 18(6): 13-18. Cai Wenchao, Yang Bingyuan. Solution of some problems inequivalent modeling of wind farm based on RTDS[J]. Electric Engineering, 2017, 18(6): 13-18.
[14]Ali M, Ilie I, Milanovic J, et al. Wind farm model aggregation using probabilistic clustering[J]. IEEE Transactions on Power Systems, 2013, 28(1): 309-316.
[15]Rogers G. Power System Oscillations[M]. New York: Springer Science + Business Media, 2000.
[16]Du Wenjuan, Dong Wenkai, Wang Haifeng, et al. Dynamic aggregation of same wind turbines generators in parallel connection for studying oscillation stability of a wind farm[J]. IEEE Tran- sactions on Power Systems, 2019, 34(6): 4694-4705.
[17]杜文娟, 王海风. 电力系统低频功率振荡模式分析理论与方法[M]. 北京: 科学出版社, 2017.
[18]邵冰冰, 赵书强, 高本锋, 等. 连接弱交流电网的VSC-HVDC失稳机理及判据研究[J]. 电工技术学报, 2019, 34(18): 3884-3896. Shao Bingbing, Zhao Shuqiang, Gao Benfeng, et al. Instability mechanism and criterion analysis of VSC- HVDC connected to the weak AC power grid[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3884-3896.
[19]杨苓, 陈艳东, 罗安, 等. 多机并联接入弱电网的改进型带阻滤波器高频振荡的抑制[J]. 电工技术学报, 2019, 34(10): 2079-2091. Yang Ling, Chen Yandong, Luo An, et al. Suppression method of high-frequency oscillation by improved notch filter for multi-parallel inverters connected to weak grid[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2079-2091.
[20]段贵钟, 秦文萍, 逯瑞鹏, 等. 考虑风电接入与负荷不确定性的静态电压稳定性分析[J]. 电力系统保护与控制, 2018, 46(12): 108-114. Duan Guizhong, Qin Wenping, Lu Ruipeng, et al. Static voltage stability analysis considering the wind power and uncertainty of load[J]. Power System Protection and Control, 2018, 46(12): 108-114.
[21]徐政. 交直流电力系统动态行为分析[M]. 北京: 机械工业出版社, 2004.
[22]Fan Lingling, Kavasseri R, Miao Zhixin. Modeling of DFIG-based wind farms for SSR analysis[J]. IEEE Transactions on Power Delivery, 2010, 25(4): 2073-2082.
Reduced-Order Modal Computation Method for Small-Signal Stability Examination of a Wind Farm
Abstract In the planning stage of a large-scale wind farm, if the small-signal stability of all the schemes is examined by using full-order model, the large workload and low working efficiency will affect the solving of the optimal scheme, thus in this paper, a reduced-order modal computation method was proposed. The full-order linearized state-space model was established at first. Secondly, it was considered that in the planning stage of a wind farm, typical model and parameters of the type of wind turbine generator (WTG) selected could be used and the dynamics of the WTGs were similar. Thus a wind farm comprised of N WTGs could be equivalently decoupled into N independent subsystems through equivalent transformation on the variables of the linearized model. Each subsystem was comprised of a single grid-connected WTG. According to the state-space model of the equivalent subsystems, a reduced-order modal computation (ROMC) method was proposed, which could be used to exam the small-signal stability of a wind farm in planning stage accurately with computational burden obviously reduced. Finally, the effectiveness of the method proposed was validated through study cases.
keywords:Wind farm, linearized state-space model, small-signal stability examination, modal analysis, equivalent subsystem
中图分类号:TM712
DOI:10.19595/j.cnki.1000-6753.tces.200158
国家电网公司科技项目资助(5100-202036013A-0-0-00)。
收稿日期 2020-02-19
改稿日期 2020-04-09
董文凯 男,1992年生,博士研究生,研究方向为风电场动态等值与小干扰稳定性。E-mail:596167281@qq.com
杜文娟 女,1979年生,博士,教授,研究方向为电力系统稳定性分析与控制。E-mail:ddwenjuan@qq.com(通信作者)
(编辑 郭丽军)